二次函数基础练习题集大全(含答案解析)

合集下载

(完整版)求二次函数的解析式--专题练习题-含答案

求二次函数的解析式专题练习题姓名：班级：1．如图，在平面直角坐标系xOy 中，正方形OABC 的边长为2，点A ，C 分别在y 轴的负半轴和x 轴的正半轴上，抛物线y ＝ax 2＋bx ＋c 经过点A ，B 和D(4，－)，求抛物线的解析式．232．如图，二次函数y ＝ax 2＋bx ＋c 的图象与x 轴交于A ，B 两点，其中点A(－1，0)，点C(0，5)，D(1，8)都在抛物线上，M 为抛物线的顶点．(1)求抛物线的函数解析式；(2)求直线CM 的解析式；(3)求△MCB 的面积．3．已知一个二次函数，当x ＝1时，y 有最大值8，其图象的形状、开口方向与抛物线y ＝－2x 2相同，则这个二次函数的解析式是( )A ．y ＝－2x 2－x ＋3B ．y ＝－2x 2＋4C ．y ＝－2x 2＋4x ＋8D ．y ＝－2x 2＋4x ＋64．已知某二次函数的最大值为2，图象的顶点在直线y ＝x ＋1上，并且图象经过点(2，1)，求二次函数的解析式． 5．已知二次函数y ＝ax 2＋bx ＋c 的x 与y 的部分对应值如下表：x … －4 －3 －2 －10 …y …－5 0 3 4 3 …(1)求此二次函数的解析式；(2)画出此函数图象；(3)结合函数图象，当－4＜x≤1时，写出y的取值范围．6．已知一个二次函数的图象经过点A(－1，0)，B(3，0)和C(0，－3)三点；(1)求此二次函数的解析式；(2)对于实数m，点M(m，－5)是否在这个二次函数的图象上？说明理由．7．已知抛物线在x轴上截得的线段长是4，对称轴是x＝－1，且过点(－2，－6)，求该抛物线的解析式．8．已知y＝x2＋bx＋c的图象向右平移2个单位长度，再向下平移3个单位长度，得到的图象对应的函数解析式为y＝x2－2x－3.(1)b＝____，c＝____；(2)求原函数图象的顶点坐标；(3)求两个图象顶点之间的距离．9．如图，已知抛物线y＝－x2＋bx＋c的对称轴为直线x＝1，且与x轴的一个交点为(3，0)，那么它对应的函数解析式．10．如图，抛物线与x 轴交于A ，B 两点，与y 轴交于C 点，点A 的坐标为(2，0)，点C 的坐标为(0，3)，它的对称轴是直线x ＝－.12(1)求抛物线的解析式；(2)M 是线段AB 上的任意一点，当△MBC 为等腰三角形时，求M 点的坐标．答案:1. 解：y ＝x 2－x －216132. 解：(1)y ＝－x 2＋4x ＋5(2)y ＝－x 2＋4x ＋5＝－(x －2)2＋9，则M 点坐标为(2，9)，可求直线MC 的解析式为y ＝2x ＋5(3)把y ＝0代入y ＝2x ＋5得2x ＋5＝0，解得x ＝－，则E 点坐标为(－，0)，5252把y ＝0代入y ＝－x 2＋4x ＋5得－x 2＋4x ＋5＝0，解得x 1＝－1，x 2＝5，则B 点坐标为(5，0)，所以S △MCB ＝S △MBE －S △CBE ＝××9－××5＝1512152121523. D4. 解：∵函数的最大值是2，则此函数顶点的纵坐标是2，又顶点在y ＝x ＋1上，那么顶点的横坐标是1，设此函数的解析式是y ＝a(x －1)2＋2，再把(2，1)代入函数中可得a(2－1)2＋2＝1，解得a ＝－1，故函数解析式是y ＝－(x －1)2＋2，即y ＝－x 2＋2x ＋15. 解：(1)由表知，抛物线的顶点坐标为(－1，4)，设y ＝a(x ＋1)2＋4，把(0，3)代入得a(0＋1)2＋4＝3，解得a ＝－1，∴抛物线的解析式为y ＝－(x ＋1)2＋4，即y ＝－x 2－2x ＋3　(2)图象略(3)－5＜y≤46. 解：(1)设二次函数的解析式为y ＝a(x ＋1)(x －3)，由于抛物线的图象经过C(0，－3)，则有－3＝a(0＋1)(0－3)，解得a ＝1，∴二次函数的解析式为y ＝(x ＋1)(x －3)，即y ＝x 2－2x －3(2)由(1)可知y ＝x 2－2x －3＝(x －1)2－4，则y 的最小值为－4＞－5，因此无论m 取何值，点M 都不在这个二次函数的图象上7. 解：∵抛物线的对称轴为x ＝－1，在x 轴上截得的线段长为4，∴抛物线与x 轴的交点坐标为(－3，0)，(1，0)，设抛物线解析式为y ＝a(x ＋3)(x －1)，把(－2，－6)代入得a ·(－2＋3)·(－2－1)＝－6，解得a ＝2，所以抛物线解析式为y ＝2(x ＋3)(x －1)，即y ＝2x 2＋4x －68. (1) 2 0(2)(－1，－1)　(3)＝22＋32139. y ＝－x 2＋2x ＋310. 解：(1)y ＝－x 2－x ＋31212(2)由y ＝0得－(x ＋)2＋＝0，解得x 1＝2，x 2＝－3，1212258∴B(－3，0)．①当CM ＝BM 时，∵BO＝CO ＝3，即△BOC 是等腰直角三角形，∴当M 点在原点O 时，△MBC 是等腰三角形，∴M 点坐标为(0，0)；②当BC＝BM时，在Rt△BOC中，BO＝CO＝3，由勾股定理得OC2＋OB2222BC＝3，∴BM＝3，∴M点坐标(3－3，0)．2综上所述，M点坐标为(3－3，0)或(0，0)。

二次函数基础题(含答案)

姓名____＿_ 日期_____＿指导教师____＿__练习一二次函数1、t(秒）的数据如下表：时间t （秒）１ 2 3 4 … 距离s （米）2８1832…写出用t 表示s 的函数关系式. 2、下列函数：① 23y x ;② 21yx x x ;③ 224y x x x ;④ 21yx x ;⑤ 1y x x ,其中是二次函数的是，其中a,b ，c３、当m 时，函数2235y m x x （m 为常数）是关于x 的二次函数4、当____m 时，函数2221m m y mm x是关于x 的二次函数5、当____m时,函数2564mm ymx +3x 是关于x 的二次函数6、若点 A ( 2, m ）在函数 12-=x y 的图像上，则 A 点的坐标是＿＿＿＿.7、在圆的面积公式 S=πｒ2 中,s 与ｒ的关系是（ )A 、一次函数关系B 、正比例函数关系C 、反比例函数关系Ｄ、二次函数关系８、正方形铁片边长为15ｃm,在四个角上各剪去一个边长为x （cm ）的小正方形，用余下的部分做成一个无盖的盒子. (1)求盒子的表面积Ｓ(ｃｍ2）与小正方形边长x （c ｍ）之间的函数关系式; （２)当小正方形边长为3cm 时,求盒子的表面积．9、如图，矩形的长是４c ｍ,宽是 3cm,如果将长和宽都增加 x c ｍ，那么面积增加 y ｃｍ２， ① 求ｙ与 x 之间的函数关系式． ② 求当边长增加多少时,面积增加８cm 2．1０、已知二次函数),0(2≠+=a c ax y 当x ＝１时，y ＝ -1;当x=2时,y=2，求该函数解析式．11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料，建造猪舍三间,如图,它们的平面图是一排大小相等的长方形．（1）如果设猪舍的宽AB 为ｘ米,则猪舍的总面积Ｓ（米2）与ｘ有怎样的函数关系?（2）请你帮富根老伯计算一下，如果猪舍的总面积为3２米2，应该如何安排猪舍的长B Ｃ和宽A Ｂ的长度？旧墙的长度是否会对猪舍的长度有影响？怎样影响？练习二函数2ax y =的图象与性质１、填空:(１）抛物线221x y =的对称轴是 (或 ),顶点坐标是 ,当x 时，y 随x 的增大而增大，当x 时,ｙ随x 的增大而减小,当x ＝时，该函数有最值是；（2）抛物线221x y -=的对称轴是（或），顶点坐标是 ,当x 时,y 随x 的增大而增大，当x 时，y 随x 的增大而减小,当x ＝时，该函数有最值是；2、对于函数22x y =下列说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大,y 的值也增大；③y 随ｘ的增大而减小；④图象关于y 轴对称.其中正确的是 . 3、抛物线 y ＝-ｘ2 不具有的性质是（）A 、开口向下ﻩB 、对称轴是 y 轴C 、与 y 轴不相交Ｄ、最高点是原点4、苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足Ｓ＝12ｇt 2(ｇ=9.８),则ｓ与 t 的函数图像大致是( )A B C D５、函数2ax y =与b ax y +-=的图象可能是（）A.B. C. D.6、已知函数24mm y mx 的图象是开口向下的抛物线,求m 的值.7、二次函数12-=m mx y 在其图象对称轴的左侧,y 随x 的增大而增大，求ｍ的值.８、二次函数223x y -=，当x 1>x ２>0时，求ｙ１与y 2的大小关系.9、已知函数()422-++=m mx m y 是关于x 的二次函数,求:（1）满足条件的ｍ的值;（2） m 为何值时,抛物线有最低点？求出这个最低点,这时x 为何值时，y 随x 的增大而增大；（3） m 为何值时,抛物线有最大值？最大值是多少？当ｘ为何值时，y 随x 的增大而减小?1０、如果抛物线2y ax 与直线1y x 交于点,2b ，求这条抛物线所对应的二次函数的关系式．s t O st O stOs t O练习三函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时， y 随x 的增大而增大, 当x 时， y 随ｘ的增大而减小． 2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标、．3、任给一些不同的实数k ，得到不同的抛物线k x y +=2,当ｋ取0,1±时，关于这些抛物线有以下判断:①开口方向都相同；②对称轴都相同;③形状相同；④都有最底点.其中判断正确的是 .４、将抛物线122-=x y 向上平移４个单位后，所得的抛物线是，当x= 时，该抛物线有最（填大或小)值,是．５、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称，则m=＿＿＿___＿_；６、二次函数c ax y +=2()0≠a 中,若当ｘ取x １、x 2(x 1≠ｘ2）时，函数值相等,则当x 取x １＋ｘ2时,函数值等于 .练习四函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ,顶点坐标是 ,当x 时,ｙ随ｘ的增大而减小, 函数有最值 .2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标. (1)右移2个单位;(2）左移32个单位;（3)先左移1个单位,再右移4个单位.３、请你写出函数()21+=x y 和12+=x y 具有的共同性质（至少2个).4、二次函数()2h x a y -=的图象如图:已知21=a ，OA=O Ｃ，试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为Ａ，与y 轴交点为B,求A 、B 两点坐标及⊿ＡＯＢ的面积.6、二次函数2)4(-=x a y ，当自变量x 由0增加到2时,函数值增加6.(1)求出此函数关系式.(2）说明函数值y 随x 值的变化情况.７、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上,求k 的值.练习五 ()k h x a y +-=2的图象与性质１、请写出一个二次函数以(2, 3）为顶点，且开口向上.__＿＿_＿＿＿＿__＿. 2、二次函数 y=(x －１)２+２,当 x ＝__＿＿时,y 有最小值.3、函数 y ＝12(x-1)2+3，当 x ＿＿_＿时，函数值 y 随 x 的增大而增大.４、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向平移3个单位，再向平移2个单位得到．5、已知抛物线的顶点坐标为2,1，且抛物线过点3,0,则抛物线的关系式是6、如图所示，抛物线顶点坐标是P （１，3）,则函数ｙ随自变量x 的增大而减小的ｘ的取值范围是( )A 、ｘ＞3 Ｂ、ｘ＜3 C 、x>１ D 、x<１ 7、已知函数()9232+--=x y .（1）确定下列抛物线的开口方向、对称轴和顶点坐标；（2）当x= 时，抛物线有最值，是 .（3）当x 时,ｙ随x 的增大而增大;当x 时，y 随x 的增大而减小．（4）求出该抛物线与ｘ轴的交点坐标及两交点间距离; （5）求出该抛物线与y 轴的交点坐标;（6）该函数图象可由23x y -=的图象经过怎样的平移得到的?8、已知函数()412-+=x y .（1）指出函数图象的开口方向、对称轴和顶点坐标；（2）若图象与x 轴的交点为Ａ、B 和与y 轴的交点C ，求△ＡBC 的面积; （3）指出该函数的最值和增减性;（4）若将该抛物线先向右平移２个单位，在向上平移4个单位，求得到的抛物线的解析式; （5）该抛物线经过怎样的平移能经过原点.（6）画出该函数图象，并根据图象回答:当x 取何值时,函数值大于0；当ｘ取何值时,函数值小于０.练习六 c bx ax y ++=2的图象和性质1、抛物线942++=x x y的对称轴是 .２、抛物线251222+-=x x y 的开口方向是，顶点坐标是 .3、试写出一个开口方向向上,对称轴为直线x=－2，且与y 轴的交点坐标为(0,3)的抛物线的解析式 . ４、将ｙ＝x 2-2x+3 化成 y=a (x －ｈ）2+k 的形式,则 y ＝_＿__．５、把二次函数215322yx x的图象向上平移3个单位,再向右平移4个单位,则两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为__＿_＿____; 7、函数x x y +-=22有最____值,最值为_＿_____；8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位,再沿y 轴向上平移3个单位，得到的图象的函数解析式为122+-=x x y ，则ｂ与c 分别等于（ )Ａ、6,4 B 、－8，１４ C 、-６,6 D 、－８,-1４ 9、二次函数122--=x x y 的图象在x 轴上截得的线段长为( ） A 、22 Ｂ、23 C 、32 D 、3310、通过配方，写出下列函数的开口方向、对称轴和顶点坐标：（1)12212+-=x x y ; (2）2832-+-=x x y ; （３）4412-+-=x x y 1１、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位，再向上平移3个单位，问所得的抛物线有没有最大值,若有，求出该最大值；若没有，说明理由.12、求二次函数62+--=x x y 的图象与x 轴和ｙ轴的交点坐标13、已知一次函数的图象过抛物线223y x x 的顶点和坐标原点1）求一次函数的关系式; 2）判断点2,5是否在这个一次函数的图象上14、某商场以每台2５00元进口一批彩电．如每台售价定为２７００元,可卖出400台，以每10０元为一个价格单位，若将每台提高一个单位价格，则会少卖出5０台,那么每台定价为多少元即可获得最大利润?最大利润是多少元？练习七 c bx ax y ++=2的性质 1、函数2yx px q 的图象是以3,2为顶点的一条抛物线,这个二次函数的表达式为２、二次函数2224y mx x mm 的图象经过原点，则此抛物线的顶点坐标是３、如果抛物线2yax bxc 与y 轴交于点A (0,2),它的对称轴是1x ,那么ac b4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点,与y 轴交于点Ｃ,且线段AB 的长为1，△ABC 的面积为1,则b 的值为＿_____.５、已知二次函数c bx ax y ++=2的图象如图所示，则a ＿__0,ｂ__＿0，c___0,ac b 42-＿__＿0；6、二次函数c bx ax y ++=2的图象如图,则直线bc ax y += 的图象不经过第象限.7、已知二次函数2yax bx c （0≠a ）的图象如图所示,则下列结论:１）,a b 同号;2）当1x和3x 时,函数值相同;3）40a b ；4)当2y 时,x 的值只能为0；其中正确的是８、已知二次函数2224m mx x y +--=与反比例函数xm y 42+=的图象在第二象限内的一个交点的横坐标是－2,则ｍ＝９、二次函数2yx ax b 中，若0a b ,则它的图象必经过点( )A 1,1B 1,1C 1,1 D1,110、函数b ax y +=与c bx ax y ++=2的图象如图所示,则下列选项中正确的是（ )A 、0,0>>c abB 、0,0><c ab Ｃ、0,0<>c ab Ｄ、0,0<<c ab1１、已知函数c bx ax y ++=2的图象如图所示，则函数b ax y +=的图象是（）１２、二次函数c bx ax y ++=2的图象如图，那么ａbc 、2a+b 、a ＋b ＋ｃ、a-b+c 这四个代数式中,值为正数的有( ） A.4个Ｂ.3个 C.２个 D ．1个13、抛物线的图角如图，则下列结论: ①＞0；②；③＞;④＜1.其中正确的结论是（）.(A ）①② (B)②③ （C)②④ (D ）③④１4、二次函数2y ax bx c 的最大值是3a ，且它的图象经过1,2,1,6两点,求a 、b 、c15、试求抛物线2y ax bx c 与x 轴两个交点间的距离（240b ac )练习八二次函数解析式1、抛物线y=ａx ２+bx+ｃ经过A(-1,0）, B(３,0), Ｃ(0，１）三点，则a ＝ , b= , c=2、把抛物线y ＝x ２+2x-３向左平移3个单位,然后向下平移2个单位，则所得的抛物线的解析式为 . 3、二次函数有最小值为1,当0x时，1y ，它的图象的对称轴为1x ，则函数的关系式为 4、根据条件求二次函数的解析式 (1）抛物线过(-１,-6）、（1,-２)和（2,3）三点（2)抛物线的顶点坐标为(-1，-1)，且与y 轴交点的纵坐标为-3 (3）抛物线过（-1,0）,(3,0）,（１，-5）三点;（4）抛物线在ｘ轴上截得的线段长为4，且顶点坐标是（３，－2)；5、已知二次函数的图象经过1,1、2,1两点,且与x 轴仅有一个交点，求二次函数的解析式6、抛物线y=a ｘ2＋bx ＋c 过点(０，-1)与点（3,2）,顶点在直线y ＝3x-３上,a<0,求此二次函数的解析式.7、已知二次函数的图象与x 轴交于A(-2，0）、B(３,0)两点，且函数有最大值是２. （1）求二次函数的图象的解析式；（2）设次二次函数的顶点为P ，求△ABP 的面积.８、以x 为自变量的函数)34()12(22-+-++-=m m x m x y 中，m 为不小于零的整数，它的图象与x 轴交于点A 和B ，点A 在原点左边,点B 在原点右边．（１)求这个二次函数的解析式;(2）一次函数y ＝kx ＋b 的图象经过点A ，与这个二次函数的图象交于点C ，且ABC S ∆=１0,求这个一次函数的解析式.姓名＿_____ 日期_____＿＿指导教师__＿＿＿_＿练习九二次函数与方程和不等式１、已知二次函数772--=x kx y 与x 轴有交点,则k 的取值范围是 .２、关于x 的一元二次方程02=--n x x 没有实数根，则抛物线n x x y --=2的顶点在第_＿__＿象限；3、抛物线222++-=kx x y 与x 轴交点的个数为( ) A 、０ B 、1 C 、２ D 、以上都不对4、二次函数c bx ax y ++=2对于x 的任何值都恒为负值的条件是( )A 、0,0>∆>aB 、0,0<∆>aC 、0,0>∆<a Ｄ、0,0<∆<a 5、12++=kx x y 与k x x y --=2的图象相交,若有一个交点在x 轴上,则k 为( ) A 、0 B 、-１ C 、２ D 、416、若方程02=++c bx ax 的两个根是－３和1,那么二次函数c bx ax y ++=2的图象的对称轴是直线( )Ａ、x ＝－3 B 、x ＝-2 C 、x ＝-１ D 、x ＝1 7、已知二次函数2y x px q 的图象与x 轴只有一个公共点，坐标为1,0，求,p q 的值8、画出二次函数322--=x x y 的图象，并利用图象求方程0322=--x x 的解，说明ｘ在什么范围时0322≤--x x .9、如图：（1）求该抛物线的解析式；（2）根据图象回答：当x 为何范围时,该函数值大于0.1０、二次函数c bx ax y ++=2的图象过Ａ(－3,０),Ｂ(１，0）,Ｃ(0,3),点D 在函数图象上,点C 、D 是二次函数图象上的一对对称点，一次函数图象过点B 、D,求（１)一次函数和二次函数的解析式,(2）写出使一次函数值大于二次函数值的x 的取值范围.1１、已知抛物线22yx mx m ．（1)求证此抛物线与x 轴有两个不同的交点；（2)若m 是整数,抛物线22yx mx m 与x 轴交于整数点,求m 的值;（3)在(２）的条件下，设抛物线顶点为A,抛物线与x 轴的两个交点中右侧交点为B ．若M 为坐标轴上一点，且MA=MB ，求点Ｍ的坐标．练习十二次函数解决实际问题 1、某农场种植一种蔬菜,销售员张平根据往年的销售情况，对今年种蔬菜的销售价格进行了预测，预测情况如图,图中的抛物线表示这种蔬菜销售价与月份之间的关系.观察图像,你能得到关于这种蔬菜销售情况的哪些信息?（至少写出四条)2、某企业投资１00万元引进一条农产品生产线，预计投产后每年可创收3３万元,设生产线投产后，从第一年到第ｘ年维修、保养费累计．．为 y （万元),且 y=ax ２＋bx ，若第一年的维修、保养费为２万元，第二年的为 4 万元.求：y 的解析式.3、校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度 y (m) 与水平距离 x (m) 之间的函数关系式为ｙ＝-112x 2+23ｘ＋53,求小明这次试掷的成绩及铅球的出手时的高度．4、用 6m 长的铝合金型材做一个形状如图所示的矩形窗框，应做成长、宽各为多少时，才能使做成的窗框的透光面积最大?最大透光面积是多少？3.5 0.5 0 2 7 月份千克销售价(元)5、商场销售一批衬衫，每天可售出2０件,每件盈利４0元,为了扩大销售,减少库存，决定采取适当的降价措施,经调查发现,如果一件衬衫每降价 1 元，每天可多售出2 件.①设每件降价x 元,每天盈利ｙ元,列出ｙ与x 之间的函数关系式；②若商场每天要盈利1200 元,每件应降价多少元？③每件降价多少元时,商场每天的盈利达到最大？盈利最大是多少元？6、有一个抛物线形的拱形桥洞，桥洞离水面的最大高度为4m，跨度为１0ｍ，如图所示，把它的图形放在直角坐标系中.①求这条抛物线所对应的函数关系式.②如图,在对称轴右边1m 处，桥洞离水面的高是多少?7、有一座抛物线形拱桥，正常水位时桥下水面宽度为2０m,拱顶距离水面4ｍ.（１)在如图所示的直角坐标系中，求出该抛物线的解析式.(2）在正常水位的基础上,当水位上升h（ｍ)时,桥下水面的宽度为d（m),试求出用d表示h的函数关系式;(3）设正常水位时桥下的水深为２m,为保证过往船只顺利航行，桥下水面的宽度不得小于１8m,求水深超过多少米时就会影响过往船只在桥下顺利航行？8、某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示，为保证安全，要求行驶车辆顶部（设为平顶）与隧道顶部在竖直方向上高度之差至少要有0.５ｍ,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米？(精确到0.1ｍ)．ﻬ参考答案1:1、22ts=;2、⑤,-1,1,0;3、≠２，3，1;6、(2,3）;7、D；8、),2150(2254S2<<+-=xx1８9;9、xxy72+=,1;１０、22-=xy；1１、,244S2xx+-=当a<８时，无解,168<≤a时，AB＝４,ＢＣ=8，当16≥a时,AB=4,BC=8或ＡB＝2，BC=1６.参考答案２:1、（１）x=0,y轴,(0,0），>0，，＜0,０，小，0; （2)ｘ=０,ｙ轴，（０，０),<，>, 0,大,0;2、④;3、C;4、Ａ；5、Ｂ；6、-2；７、3-;８、021<<yy;9、（1）２或-3,(2）m＝2、y=0、x>0,(３）m=-３，y＝０,x＞0；10、292xy=参考答案3:1、下,x=0,(0，-3)，<0,>0；2、2312-=xy,1312+=xy，（0,-2），（０，１);3、①②③;4、322+=xy，0，小，3;5、1;6、c．参考答案4：1、(3,０),>3,大,y＝０;2、2)2(3-=xy,2)32(3-=xy,2)3(3-=xy;3、略；4、2)2(21-=xy;5、（3,0），（0,2７)，40．5；6、2)4(21--=xy，当x<4时,y随x的增大而增大，当ｘ>4时，y随x的增大而减小;7、-8，-2,4. 参考答案５:1、略；2、1；3、>1；4、左、下；5、342-+-=xxy；6、C；7、(１）下，x=2,（2,9),（２）2、大、9,（３)<2、>2,(4)( 32-,0)、( 32+,0）、32,（５)（０，-3）；（6）向右平移2个单位,再向上平移9个单位；8、(1)上、x=-1、(－1，－4)；(2）（－3，0）、(1，０)、(０,－3）、6,(3)-４,当x>-1 时,y随ｘ的增大而增大;当x<-１时，ｙ随x的增大而减小，（４)2)1(-=xy；（5)向右平移1个单位，再向上平移4个单位或向上平移3个单位或向左平移1个单位;（６）ｘ>1或x<-３、-3<x<1参考答案６:1、x=－2;2、上、（３,7）；3、略；4、2)1(2+-x ；５、5)1(212+--=x y ;6、(－2，0）（8,0);７、大、81;8、C ；9、Ａ；10、(1)1)2(212--=x y 、上、x=２、(2，－1),（2)310)34(32+--=x y、下、34=x 、(310,34）,(３）3)2(412---=x y 、下、x ＝2、（2,－3）；11、有、ｙ=6;1２、(2，0）（-3，0）（0,６);13、y=-2ｘ、否;１4、定价为3000元时，可获最大利润125００0元参考答案7：１、1162+-=x x y ；2、（-4,-4）;3、1;4、-3；5、>、＜、＞、＞;6、二；7、②③;8、-7；9、C;１0、D;11、Ｂ；12、C ；１3、B;1４、4422++-=x x y ；15、aac b 42-参考答案8：1、31-、32、1;２、1082++=x x y ；3、1422+-=x x y ；４、（1)522-+=x x y 、(2）3422---=x x y 、（3）41525452--=x x y 、（4)253212+-=x x y ;5、9194942+-=x x y ；6、142-+-=x x y ;7、（1)25482582582++-=x x y 、5;8、322++-=x x y 、y=－x-1或ｙ＝5ｘ＋５参考答案９：1、47-≥k 且0≠k ；2、一；3、C ；4、Ｄ;5、C;6、C;7、2,1;8、31,3,121≤≤-=-=x x x ；9、(1)x x y 22-=、x<0或x>２;１0、ｙ＝-x+1,322+--=x x y ，x ＜-2或ｘ>1;11、(1）略,(2）ｍ=2,(3)（１,0）或（0,１)参考答案10：１、①2月份每千克3.５元 ②7月份每千克0．5克 ③7月份的售价最低 ④2～7月份售价下跌;2、y ＝x ２＋x ；３、成绩1０米，出手高度35米;4、23)1(232+--=x S ,当x ＝１时，透光面积最大为23m 2；５、（1)y ＝（40－x) (２0＋２ｘ)=－2x 2＋60ｘ+800,(2）1200＝－2ｘ２+60x+８0０,x １＝20，x 2＝10 ∵要扩大销售 ∴x 取２0元,（3）ｙ＝-２（x 2－３0x)＋80０＝－2 (x-15)2＋12５0 ∴当每件降价1５元时，盈利最大为1250元；6、（１）设y ＝a (x-5)2+4，0=a (-5）2＋4,ａ=-254，∴y=－254 （x-5）2+４,（２)当x=6时,y ＝－254+4=3.4（m ）；７、（1)2251x y -=,（2）h d -=410，（３）当水深超过 2.７６ｍ时；8、)64(6412≤≤-+-=x x y ,x =3,m y 75.3496=-=,m 2.325.35.075.3≈=-,货车限高为3.2m.。

二次函数基础题(含答案)

初中数学二次函数基础复习一、二次函数的定义1. 抛物线m m x x y -++=2242经过坐标原点，则m 的值为 .2. 抛物线c bx x y ++=2的顶点坐标为（1，3），则b ＝，c ＝ .3.抛物线y ＝x 2＋3x 的顶点在 ( )A.第一象限B.第二象限C.第三象限D.第四象限 4.若直线y ＝ax ＋b 不经过二、四象限，则抛物线y ＝ax 2＋bx ＋c ( )A.开口向上，对称轴是y 轴B.开口向下，对称轴是y 轴C.开口向下，对称轴平行于y 轴D.开口向上，对称轴平行于y 轴5. 已知抛物线y ＝x 2＋(m －1)x －14的顶点的横坐标是2，则m 的值是 6. 抛物线322-+=x x y 的对称轴是 7. 若二次函数332-+=mx x y 的对称轴是直线x ＝1，则m ＝ . 8. 当n ＝________，m ＝______时，函数y ＝(m ＋n)nx ＋(m －n)x 的图象是抛物线，且其顶点在原点，此抛物线的开口________.9. 已知二次函数3222++-=a ax x y ，当a 时，该函数y 的最小值为０？10. 已知二次函数m x x y +-=62的最小值为１，那么m ＝11. (易错题)已知二次函数1)1(2-+-+=m x m mx y 有最小值为０，则m ＝ 12. 已知二次函数342-+-=m x x y 的最小值为3，则m ＝ 13. 已知二次函数253212++-=x x y 的图象上有三点)(),,(),,(332211y x C y x B y x A ，且3213x x x <<<，则321,,y y y 的大小关系为14. 抛物线223x y -=向左平移３个单位，再向下平移４个单位，所得到的抛物线的关系式为。

15. 将抛物线c bx ax y ++=2向上平移1个单位，再向右平移1个单位，得到1422--=x x y则a ＝，b ＝，c ＝ .16. 将抛物线y ＝ax 2向右平移2个单位，再向上平移3个单位，移动后的抛物线经过点(3，－1)，那么移动后的抛物线的关系式为____ _.17. 抛物线372++=x x y 与直线92+=x y 的交点坐标为。

初中数学二次函数综合复习基础题(含答案)

初中数学二次函数综合复习基础题一、单选题(共13道，每道8分)1.若二次函数的图象经过原点，则a的值必为（）A.1或2B.0C.1D.2答案：D试题难度：三颗星知识点：二次函数表达式2.在同一坐标系中，作，，的图象，它们的共同特点是()A.抛物线的开口方向向上B.都是关于x轴对称的抛物线，且y随x的增大而增大C.都是关于y轴对称的抛物线，且y随x的增大而减小D.都是关于y轴对称的抛物线，有公共的顶点答案：D试题难度：三颗星知识点：二次函数图象特征3.对于反比例函数，当x＞0时，y随x的增大而增大，则二次函数的大致图象是（）A. B.C. D.答案：C试题难度：三颗星知识点：二次函数图象初步判定4.抛物线可以由抛物线平移得到，则下列平移过程正确的是（）A.先向左平移2个单位，再向上平移3个单位B.先向左平移2个单位，再向下平移3个单位C.先向右平移2个单位，再向下平移3个单位D.先向右平移2个单位，再向上平移3个单位答案：B试题难度：三颗星知识点：二次函数图像平移5.已知二次函数，当x=-1时有最大值，把x=-5，-2，1时对应函数值分别记为y1，y2，y3，则y1，y2，y3的大小关系是（）A.y1＜y2＜y3B.y1＞y2＞y3C.y2＞y1＞y3D.y2＞y3＞y1答案：D试题难度：三颗星知识点：二次函数图像增减性、对称轴固定6.若二次函数，当时，y随x的增大而减小，则m的取值范围是（）A. B.C. D.答案：C试题难度：三颗星知识点：二次函数图像增减性、对称轴固定7.（2011四川雅安）已知二次函数的图象如图，其对称轴为直线x=-1，给出下列结果：①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0.则正确的结论是（）A.①②③④B.②④⑤C.②③④D.①④⑤答案：D试题难度：三颗星知识点：二次函数数形结合8.二次函数的图象经过点A（0，-3），B（2，-3），C（-1，0）．则此二次函数的表达式为（）A. B.C. D.答案：A试题难度：三颗星知识点：二次函数一般式9.有一条抛物线，三位学生分别说出了它的一些性质：甲说：对称轴是直线x=2；乙说：与x轴的两个交点距离为6；丙说：抛物线与x轴的交点和其顶点围成的三角形面积等于9，请选出一个满足上述全部条件的一条抛物线的解析式：（）A. B.C. D.答案：B试题难度：三颗星知识点：二次函数顶点式10.二次函数图象过A、C、B三点，点A的坐标为（-1，0），点B的坐标为（4，0），点C在y轴正半轴上，且AB=OC．求二次函数的解析式（）A. B.C. D.答案：A试题难度：三颗星知识点：二次函数交点式11.若直线与二次函数的图象交于A、B两点，求以A、B及原点O为顶点的三角形的面积（）．A. B.C. D.无法计算答案：C试题难度：三颗星知识点：二次函数初步综合12.设一元二次方程的两根分别为，，且，则，满足（）A. B.C. D.且答案：D试题难度：三颗星知识点：二次函数图象与方程、不等式13.设一元二次方程的两根分别为，，且，则二次函数的函数值y>m时自变量x的取值范围是（）A. B.C. D.答案：B试题难度：三颗星知识点：二次函数图象与方程、不等式。

二次函数基础测试题含答案

3．已知抛物线，其顶点为，与轴交于点，将抛物线绕原点旋转得到抛物线，点的对应点分别为，若四边形为矩形，则的值为（）
A． B． C． D．
【答案】D
【解析】
【分析】
先求出A(2，c-4)，B(0，c)，，结合矩形的性质，列出关于c的方程，即可求解．
【详解】
∵抛物线，其顶点为，与轴交于点，
【详解】
∵抛物线与x轴的一个交点在点（3，0）和（4，0）之间，而抛物线的对称轴为直线x=1，
∴抛物线与x轴的另一个交点在点（-2，0）和（-1，0）之间．
∴当x=-1时，y＞0，
即a-b+c＞0，所以①正确；
∵抛物线的对称轴为直线x=- =1，即b=-2a，
∴3a+b=3a-2a=a，所以②错误；
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论：①足球距离地面的最大高度为20m；②足球飞行路线的对称轴是直线；③足球被踢出9s时落地；④足球被踢出1.5s时，距离地面的高度是11m.其中正确结论的个数是（）
A．1B．2C．3D．4
【答案】B
【解析】
【分析】
【详解】
解：由题意，抛物线的解析式为y=ax（x﹣9），把（1，8）代入可得a=﹣1，
∵a*（a+1）＝a（a+1）﹣a+（a+1）＝a2+a+1＝（a+ ）2+ ＞0，
∴在实数范围内，无论a取何值，代数式a*（a+1）的值总为正数，故选项C正确；

二次函数基础练习题大全(含答案)

二次函数基础练习题练习一二次函数1、一个小球由静止开始在一个斜坡上向下滚动，通过仪器观察得到小球滚动的距离s （米）与时间t时间t （秒） 1 2 3 4 … 距离s （米） 281832…写出用t 表示s 的函数关系式： 2、下列函数：① 23y x ；② 21y x x x ；③ 224y x x x ；④ 21y x x ；⑤ 1yx x ，其中是二次函数的是，其中a，b，c3、当m 时，函数2235y mx x（m 为常数）是关于x 的二次函数4、当____m 时，函数2221mm y m m x 是关于x 的二次函数 5、当____m时，函数2564mm ymx +3x 是关于x 的二次函数6、若点 A ( 2, m ) 在函数 12-=x y 的图像上，则 A 点的坐标是＿＿＿＿.7、在圆的面积公式 S ＝πr 2 中，s 与 r 的关系是（）A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系8、正方形铁片边长为15cm ，在四个角上各剪去一个边长为x （cm ）的小正方形，用余下的部分做成一个无盖的盒子．(1)求盒子的表面积S （cm 2）与小正方形边长x （cm ）之间的函数关系式； (2)当小正方形边长为3cm 时，求盒子的表面积．9、如图，矩形的长是 4cm ，宽是 3cm ，如果将长和宽都增加 x cm ，那么面积增加 ycm 2， ① 求 y 与 x 之间的函数关系式. ② 求当边长增加多少时，面积增加 8cm 2.10、已知二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2，求该函数解析式.11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料，建造猪舍三间，如图，它们的平面图是一排大小相等的长方形.（1）如果设猪舍的宽AB 为x 米，则猪舍的总面积S （米2）与x 有怎样的函数关系？（2）请你帮富根老伯计算一下，如果猪舍的总面积为32米2，应该如何安排猪舍的长BC 和宽AB 的长度？旧墙的长度是否会对猪舍的长度有影响？怎样影响？练习二函数2ax y =的图像与性质1、填空：（1）抛物线221x y =的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；（2）抛物线221x y -=的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是； 2、对于函数22x y =下列说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图像关于y 轴对称.其中正确的是 . 3、抛物线 y ＝－x 2 不具有的性质是（）A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点4、苹果熟了，从树上落下所经过的路程 s 与下落时间 t 满足 S ＝12gt 2（g ＝9.8），则 s 与 t 的函数图像大致是（）A B C D5、函数2ax y =与b ax y +-=的图像可能是（）A ．B ．C ．D ．6、已知函数24mm ymx 的图像是开口向下的抛物线，求m 的值.7、二次函数12-=m mx y 在其图像对称轴的左侧，y 随x 的增大而增大，求m 的值.8、二次函数223x y -=，当x 1＞x 2＞0时，求y 1与y 2的大小关系. 9、已知函数()422-++=m mx m y 是关于x 的二次函数，求：（1）满足条件的m 的值；（2） m 为何值时，抛物线有最低点？求出这个最低点，这时x 为何值时，y 随x 的增大而增大；（3） m 为何值时，抛物线有最大值？最大值是多少？当x 为何值时，y 随x 的增大而减小？ 10、如果抛物线2yax 与直线1y x 交于点,2b ，求这条抛物线所对应的二次函数的关系式.s t OstOst O st O1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小. 2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标、 . 3、任给一些不同的实数k ，得到不同的抛物线k x y +=2，当k 取0，1±时，关于这些抛物线有以下判断：①开口方向都相同；②对称轴都相同；③形状相同；④都有最底点.其中判断正确的是 . 4、将抛物线122-=x y 向上平移4个单位后，所得的抛物线是，当x= 时，该抛物线有最（填大或小）值，是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称，则m ＝________；6、二次函数c ax y +=2()0≠a 中，若当x 取x 1、x 2（x 1≠x 2）时，函数值相等，则当x 取x 1+x 2时，函数值等于 .练习四函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ，顶点坐标是 ,当x 时,y 随x 的增大而减小，函数有最值 .2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标. （1）右移2个单位；（2）左移32个单位；（3）先左移1个单位，再右移4个单位. 3、请你写出函数()21+=x y 和12+=x y 具有的共同性质（至少2个）.4、二次函数()2h x a y -=的图象如图：已知21=a ，OA=OC ，试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ，与y 轴交点为B ，求A 、B 两点坐标及⊿AOB 的面积. 6、二次函数2)4(-=x a y ，当自变量x 由0增加到2时，函数值增加6.（1）求出此函数关系式.（2）说明函数值y 随x 值的变化情况.7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上，求k 的值.1、请写出一个二次函数以（2, 3）为顶点，且开口向上.＿＿＿＿＿＿＿＿＿＿＿＿.2、二次函数 y ＝(x －1)2＋2，当 x ＝＿＿＿＿时，y 有最小值.3、函数 y ＝12(x －1)2＋3，当 x ＿＿＿＿时，函数值 y 随 x 的增大而增大.4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向平移3个单位，再向平移2个单位得到.5、已知抛物线的顶点坐标为2,1，且抛物线过点3,0，则抛物线的关系式是6、如图所示，抛物线顶点坐标是P （1，3），则函数y 随自变量x 的增大而减小的x 的取值范围是（）A 、x>3B 、x<3C 、x>1D 、x<1 7、已知函数()9232+--=x y .（1）确定下列抛物线的开口方向、对称轴和顶点坐标；（2）当x= 时，抛物线有最值，是 .（3）当x 时，y 随x 的增大而增大；当x 时，y 随x 的增大而减小. （4）求出该抛物线与x 轴的交点坐标及两交点间距离；（5）求出该抛物线与y 轴的交点坐标；（6）该函数图象可由23x y -=的图象经过怎样的平移得到的？8、已知函数()412-+=x y .（1）指出函数图象的开口方向、对称轴和顶点坐标；（2）若图象与x 轴的交点为A 、B 和与y 轴的交点C ，求△ABC 的面积；（3）指出该函数的最值和增减性；（4）若将该抛物线先向右平移2个单位，在向上平移4个单位，求得到的抛物线的解析式；（5）该抛物线经过怎样的平移能经过原点.（6）画出该函数图象，并根据图象回答：当x 取何值时，函数值大于0；当x 取何值时，函数值小于0.1、抛物线942++=x x y 的对称轴是 .2、抛物线251222+-=x x y 的开口方向是，顶点坐标是 .3、试写出一个开口方向向上，对称轴为直线x=-2，且与y 轴的交点坐标为（0，3）的抛物线的解析式 .4、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，则 y ＝＿＿＿＿.5、把二次函数215322yx x的图象向上平移3个单位，再向右平移4个单位，则两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为_________； 7、函数x x y +-=22有最____值，最值为_______；8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位，再沿y 轴向上平移3个单位，得到的图象的函数解析式为122+-=x x y ，则b 与c 分别等于（） A 、6，4 B 、－8，14 C 、－6，6 D 、－8，－149、二次函数122--=x x y 的图象在x 轴上截得的线段长为（） A 、22 B 、23 C 、32 D 、3310、通过配方，写出下列函数的开口方向、对称轴和顶点坐标：（1）12212+-=x x y ；（2）2832-+-=x x y ；（3）4412-+-=x x y 11、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位，再向上平移3个单位，问所得的抛物线有没有最大值，若有，求出该最大值；若没有，说明理由. 12、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标 13、已知一次函数的图象过抛物线223y x x 的顶点和坐标原点1）求一次函数的关系式； 2）判断点2,5是否在这个一次函数的图象上14、某商场以每台2500元进口一批彩电.如每台售价定为2700元，可卖出400台，以每100元为一个价格单位，若将每台提高一个单位价格，则会少卖出50台，那么每台定价为多少元即可获得最大利润？最大利润是多少元？练习七 c bx ax y ++=2的性质1、函数2yx px q 的图象是以3,2为顶点的一条抛物线，这个二次函数的表达式为 2、二次函数2224y mx x mm 的图象经过原点，则此抛物线的顶点坐标是3、如果抛物线2yax bxc 与y 轴交于点A (0,2)，它的对称轴是1x ，那么ac b4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点，与y 轴交于点C ，且线段AB 的长为1，△ABC 的面积为1，则b 的值为______.5、已知二次函数c bx ax y ++=2的图象如图所示，则a___0，b___0，c___0，ac b 42-____0；6、二次函数c bx ax y ++=2的图象如图，则直线bc ax y +=的图象不经过第象限. 7、已知二次函数2yax bx c （0≠a ）的图象如图所示，则下列结论：1）,a b 同号；2）当1x 和3x 时，函数值相同；3）40a b ；4）当2y 时，x 的值只能为0；其中正确的是（第5题）（第6题）（第7题）（第10题） 8、已知二次函数2224m mx x y +--=与反比例函数xm y 42+=的图象在第二象限内的一个交点的横坐标是-2，则m= 9、二次函数2yx ax b 中，若0a b ，则它的图象必经过点（）A 1,1B 1,1C 1,1 D1,110、函数b ax y +=与c bx ax y ++=2的图象如上图所示，则下列选项中正确的是（） A 、0,0>>c ab B 、0,0><c ab C 、0,0<>c ab D 、0,0<<c ab 11、已知函数c bx ax y ++=2的图象如图所示，则函数b ax y +=的图象是（）12、二次函数c bx ax y ++=2的图象如图，那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中，值为正数的有（） A ．4个 B ．3个 C ．2个 D ．1个 13、抛物线的图角如图，则下列结论： ①＞0；②；③＞；④＜1.其中正确的结论是（）.（A ）①② （B ）②③ （C ）②④ （D ）③④14、二次函数2yax bx c 的最大值是3a ，且它的图象经过1,2，1,6两点，求a 、b 、c 的值。

二次函数基础分类练习题(含答案)

二次函数基础分类练习题练习一二次函数下列函数：①y =()21y x x x =-+；③ ()224y x x x =+-；④ 21y x x =+； ⑤ ()1y x x =-，其中是二次函数的是，其中a = ，b = ，c =3、当m 时，函数()2235y m x x =-+-（m 为常数）是关于x 的二次函数4、当____m =时，函数()2221m m y m m x --=+是关于x 的二次函数5、当____m =时，函数()2564m m y m x-+=-+3x 是关于x 的二次函数6、若点 A ( 2, m ) 在函数 12-=x y 的图像上，则 A 点的坐标是＿＿＿＿. 10、已知二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2，求该函数解析式.练习二函数2ax y =的图象与性质1、填空：（1）抛物线221x y =的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；（2）抛物线221x y -=的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；2、对于函数22x y =下列说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图象关于y 轴对称.其中正确的是 .3、抛物线 y ＝－x 2 不具有的性质是（）A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点5、函数2ax y =与b ax y +-=的图象可能是（）A．B．C．D ．练习三函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小. 2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标、 .3、任给一些不同的实数k ，得到不同的抛物线k x y +=2，当k 取0，1±时，关于这些抛物线有以下判断：①开口方向都相同；②对称轴都相同；③形状相同；④都有最底点.其中判断正确的是 .4、将抛物线122-=x y 向上平移4个单位后，所得的抛物线是，当x= 时，该抛物线有最（填大或小）值，是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称，则m ＝________；6、二次函数c ax y +=2()0≠a 中，若当x 取x 1、x 2（x 1≠x 2）时，函数值相等，则当x 取x 1+x 2时，函数值等于 .练习四函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ，顶点坐标是 ,当x 时,y 随x 的增大而减小，函数有最值 .练习五 ()k h x a y +-=2的图象与性质1、请写出一个二次函数以（2, 3）为顶点，且开口向上.＿＿＿＿＿＿＿＿＿＿＿＿.2、二次函数 y ＝(x －1)2＋2，当 x ＝＿＿＿＿时，y 有最小值.3、函数 y ＝12(x －1)2＋3，当 x ＿＿＿＿时，函数值 y 随 x 的增大而增大.7、已知函数()9232+--=x y .（1）确定下列抛物线的开口方向、对称轴和顶点坐标；（2）当x= 时，抛物线有最值，是 .（3）当x 时，y 随x 的增大而增大；当x 时，y 随x 的增大而减小.练习六 c bx ax y ++=2的图象和性质1、抛物线942++=x x y 的对称轴是 .2、抛物线251222+-=x x y 的开口方向是，顶点坐标是 .3、试写出一个开口方向向上，对称轴为直线x=-2，且与y 轴的交点坐标为（0，3）的抛物线的解析式 .4、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，则 y ＝＿＿＿＿.5、把二次函数215322y x x =---的图象向上平移3个单位，再向右平移4个单位，则两次平移后的函数图象的关系式是 6、抛物线1662--=x x y 与x 轴交点的坐标为_________； 7、函数x x y +-=22有最____值，最值为_______；练习七 c bx ax y ++=2的性质1、函数2y x px q =++的图象是以()3,2为顶点的一条抛物线，这个二次函数的表达式为2、二次函数2224y mx x m m =++-的图象经过原点，则此抛物线的顶点坐标是3、如果抛物线2y ax bx c =++与y 轴交于点A (0,2)，它的对称轴是1x =-，那么acb= 4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点，与y 轴交于点C ，且线段AB 的长为1，△ABC 的面积为1，则b 的值为______.5、已知二次函数c bx ax y ++=2的图象如图所示，则a___0，b___0，c___0，ac b 42-____0；6、二次函数c bx ax y ++=2的图象如图，则直线bc ax y +=的图象不经过第象限.10、函数b ax y +=与c bx ax y ++=2的图象如图所示，则下列选项中正确的是（）A 、0,0>>c abB 、0,0><c abC 、0,0<>c abD 、0,0<<c ab11、已知函数c bx ax y ++=2的图象如图所示，则函数b ax y +=的图象是（）练习八二次函数解析式1、抛物线y=ax 2+bx+c 经过A(-1,0), B(3,0), C(0,1)三点，则a= , b= , c=2、把抛物线y=x 2+2x-3向左平移3个单位，然后向下平移2个单位，则所得的抛物线的解析式为 .1、二次函数有最小值为1-，当0x =时，1y =，它的图象的对称轴为1x =，则函数的关系式为练习九二次函数与方程和不等式1、已知二次函数772--=x kx y 与x 轴有交点，则k 的取值范围是.2、关于x 的一元二次方程02=--n x x 没有实数根，则抛物线n x x y --=2的顶点在第_____象限；3、抛物线222++-=kx x y 与x 轴交点的个数为（）A 、0B 、1C 、2D 、以上都不对4、二次函数c bx ax y ++=2对于x 的任何值都恒为负值的条件是（）A 、0,0>∆>aB 、0,0<∆>aC 、0,0>∆<aD 、0,0<∆<a5、12++=kx x y 与k x x y --=2的图象相交，若有一个交点在x 轴上，则k 为（）A 、0B 、-1C 、2D 、41 6、若方程02=++c bx ax 的两个根是－3和1，那么二次函数c bx ax y ++=2的图象的对称轴是直线（）A 、x ＝－3B 、x ＝－2C 、x ＝－1D 、x ＝1。

二次函数练习题(含答案)

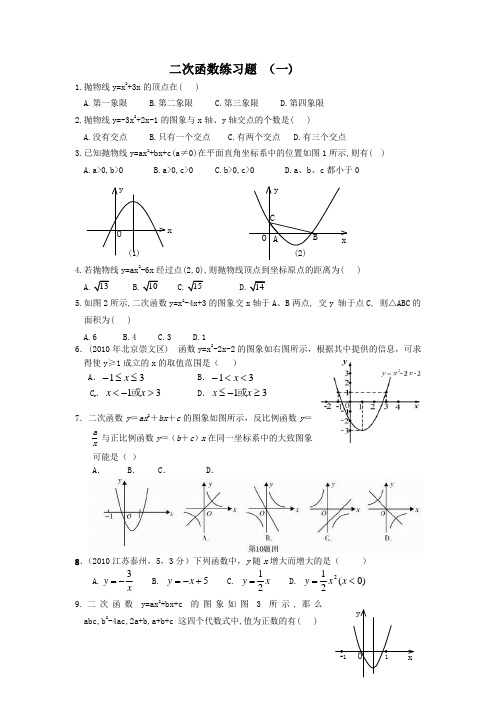
二次函数练习题（一)1.抛物线y=x 2+3x 的顶点在( )A.第一象限B.第二象限C.第三象限D.第四象限 2.抛物线y=-3x 2+2x-1的图象与x 轴、y 轴交点的个数是( ) A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点3.已知抛物线y=ax 2+bx+c(a≠0)在平面直角坐标系中的位置如图1所示,则有( ) A.a>0,b>0 B.a>0,c>0 C.b>0,c>0 D.a 、b 、c 都小于0(1) (2) 4.若抛物线y=ax 2-6x 经过点(2,0),则抛物线顶点到坐标原点的距离为( )5.如图2所示,二次函数y=x 2-4x+3的图象交x 轴于A 、B 两点, 交y 轴于点C, 则△ABC 的面积为( )A.6B.4C.3D.16．(2010年北京崇文区) 函数y=x 2-2x-2的图象如右图所示，根据其中提供的信息，可求得使y ≥1成立的x 的取值范围是（）A ．31≤≤-xB ．31<<-xC ．31>-<x x 或D ．31≥-≤x x 或7．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，反比例函数y ＝ax与正比例函数y ＝（b ＋c ）x 在同一坐标系中的大致图象可能是（）A ．B ．C ．D ．8．（2010江苏泰州，5，3分）下列函数中，y 随x 增大而增大的是（）A.x y 3-= B. 5+-=x y C. 12y x = D. )0(212<=x x y 9.二次函数y=ax 2+bx+c 的图象如图3所示,那么abc,b 2-4ac,2a+b,a+b+c 这四个代数式中,值为正数的有( )xy OxBACy OA.4个B.3个C.2个D.1个10.如图所示,当b<0时,函数y=ax+b 与y=ax 2+bx+c 在同一坐标系内的图象可能是( )11.二次函数y=2x 2- 4x+ 3 通过配方化为顶点式为y= _________, 其对称轴是______,顶点坐标为_______,抛物线开口________,当x_______时,y 随x 的增大而增大;当x____时,y 随x 的增大而减小;当x=______时,y 最值=________.12.已知抛物线y=ax 2+bx+c(a≠0)图象的顶点为P(-2,3),且过A(-3,0), 则抛物线的关系式为___________.13.若二次函数y=ax 2+bx+c 的图象经过点(0,-1),(5,-1), 则它的对称轴方程是________. 14.在同一坐标系内,抛物线y=ax 2与直线y=2x+b 相交于A 、B 两点,若点A 的坐标是(2,4),则点B 的坐标是_________.15.将抛物线y=ax 2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为__________.16.若抛物线y=ax 2+bx+c 经过(0,1)和(2,-3)两点,且开口向下,对称轴在y 轴左侧,则a 的取值范围是_________.17．已知抛物线y =ax 2+bx +c 的对称轴为x =2，且经过点(1，4)和点(5，0)，则该抛物线的解析式为_______________．18．函数y =2x 2 – 4x – 1写成y = a (x –h)2 +k 的形式是________，抛物线y =2x 2– 4x – 1的顶点坐标是_______，对称轴是__________．19．已知函数①y =x 2+1，②y =-2x 2+x ．函数____(填序号)有最小值，当x =____时，该函数的最小值是_______20．当m=_________时，函数y = (m 2－4))3(42-+--m x m mx + 3是二次函数，其解析式是__________________，图象的对称轴是_______________，顶点是________，当x =______时， y 有最____值_______．21．已知二次函数的图象开口向下，且与y 轴的正半轴相交．请你写出一个满足条件的二次函数的解析式：___________22．抛物线c bx ax y ++=2如右图所示，则它关于y析式是__________．23、（2010年宁波市）如图，已知二次函数bx x y +-=221的图象经过A （2，0）、B （0，－6）两点。

二次函数基础题(含答案)

二次函数基础练习练习一二次函数1、一个小球由静止开始在一个斜坡上向下滚动，通过仪器观察得到小球滚动的距离s （米）与时间t 时间t （秒） 1 2 3 4 … 距离s （米）281832…写出用t 表示s 的函数关系式. 2、下列函数：① 23y x ；② 21yx x x ；③ 224y x x x ；④ 21yx x ；⑤ 1y x x ，其中是二次函数的是，其中a，b ，c3、当m 时，函数2235y m x x （m 为常数）是关于x 的二次函数4、当____m 时，函数2221m m y m m x 是关于x 的二次函数5、当____m时，函数2564m m ymx+3x 是关于x 的二次函数6、若点 A ( 2, m ) 在函数 12-=x y 的图像上，则 A 点的坐标是＿＿＿＿.7、在圆的面积公式 S ＝πr 2 中，s 与 r 的关系是（）A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系 8、正方形铁片边长为15cm ，在四个角上各剪去一个边长为x （cm ）的小正方形，用余下的部分做成一个无盖的盒子．(1)求盒子的表面积S （cm 2）与小正方形边长x （cm ）之间的函数关系式；(2)当小正方形边长为3cm 时，求盒子的表面积．9、如图，矩形的长是 4cm ，宽是 3cm ，如果将长和宽都增加 x cm ，那么面积增加 ycm 2， ① 求 y 与 x 之间的函数关系式. ② 求当边长增加多少时，面积增加 8cm 2.10、已知二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2，求该函数解析式. 11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料，建造猪舍三间，如图，它们的平面图是一排大小相等的长方形.（1）如果设猪舍的宽AB 为x 米，则猪舍的总面积S （米2）与x有怎样的函数关系？（2）请你帮富根老伯计算一下，如果猪舍的总面积为32米2，应该如何安排猪舍的长BC 和宽AB 的长度？旧墙的长度是否会对猪舍的长度有影响？怎样影响？参考答案1：1、22t s =；2、⑤，-1，1，0；3、≠2，3，1；6、（2，3）；7、D ；8、),2150(2254S 2<<+-=x x 189；9、x x y 72+=，1；10、22-=x y ；11、,244S 2x x +-=当a<8时，无解，168<≤a 时，AB=4,BC=8，当16≥a 时，AB=4,BC=8或AB=2,BC=16.练习二函数2ax y =的图象与性质1、填空：（1）抛物线221x y =的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；（2）抛物线221x y -=的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；2、对于函数22x y =下列说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图象关于y 轴对称.其中正确的是 .3、抛物线 y ＝－x 2 不具有的性质是（）A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点4、苹果熟了，从树上落下所经过的路程 s 与下落时间 t 满足 S ＝12gt 2（g ＝9.8），则 s 与 t 的函数图像大致是（）A B C D5、函数2ax y =与b ax y +-=的图象可能是（）A ．B ．C ．D ．6、已知函数24mm ymx 的图象是开口向下的抛物线，求m 的值.7、二次函数12-=mmx y 在其图象对称轴的左侧，y 随x 的增大而增大，求m 的值.st O st O stOs t O8、二次函数223x y -=，当x 1＞x 2＞0时，求y 1与y 2的大小关系. 9、已知函数()422-++=m mx m y 是关于x 的二次函数，求：（1）满足条件的m 的值；（2） m 为何值时，抛物线有最低点？求出这个最低点，这时x 为何值时，y 随x 的增大而增大；（3） m 为何值时，抛物线有最大值？最大值是多少？当x 为何值时，y 随x 的增大而减小？ 10、如果抛物线2yax 与直线1y x 交于点,2b ，求这条抛物线所对应的二次函数的关系式.参考答案2：1、(1)x=0,y 轴，（0，0），>0，，<0，0，小，0; (2)x=0,y 轴，（0，0），<，>， 0，大，0;2、④；3、C ；4、A ；5、B ；6、-2；7、3-；8、021<<y y ；9、（1）2或-3，（2）m=2、y=0、x>0，（3）m=-3，y=0，x>0；10、292x y =练习三函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小.2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标、 . 3、任给一些不同的实数k ，得到不同的抛物线k x y +=2，当k 取0，1±时，关于这些抛物线有以下判断：①开口方向都相同；②对称轴都相同；③形状相同；④都有最底点.其中判断正确的是 .4、将抛物线122-=x y 向上平移4个单位后，所得的抛物线是，当x= 时，该抛物线有最（填大或小）值，是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称，则m ＝________；6、二次函数c ax y +=2()0≠a 中，若当x 取x 1、x 2（x 1≠x 2）时，函数值相等，则当x 取x 1+x 2时，函数值等于 .参考答案3：1、下，x=0，（0，-3），<0，>0；2、2312-=x y ，1312+=x y ，（0，-2），（0，1）；3、①②③；4、322+=x y ，0，小，3；5、1；6、c.练习四函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ，顶点坐标是 ,当x 时,y 随x 的增大而减小，函数有最值 .2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标. （1）右移2个单位；（2）左移32个单位；（3）先左移1个单位，再右移4个单位. 3、请你写出函数()21+=x y 和12+=x y 具有的共同性质（至少2个）. 4、二次函数()2h x a y -=的图象如图：已知21=a ，OA=OC ，试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ，与y 轴交点为B ，求A 、B 两点坐标及⊿AOB 的面积.6、二次函数2)4(-=x a y ，当自变量x 由0增加到2时，函数值增加6.（1）求出此函数关系式.（2）说明函数值y 随x 值的变化情况.7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上，求k 的值.参考答案4：1、（3，0），>3，大，y=0;2、2)2(3-=x y ，2)32(3-=x y ，2)3(3-=x y ;3、略；4、2)2(21-=x y ；5、（3，0），（0，27），40.5；6、2)4(21--=x y ，当x<4时，y 随x 的增大而增大，当x>4时，y 随x 的增大而减小；7、-8，-2，4.练习五 ()k h x a y +-=2的图象与性质1、请写出一个二次函数以（2, 3）为顶点，且开口向上.＿＿＿＿＿＿＿＿＿＿＿＿.2、二次函数 y ＝(x －1)2＋2，当 x ＝＿＿＿＿时，y 有最小值.3、函数 y ＝12(x －1)2＋3，当 x ＿＿＿＿时，函数值 y 随 x 的增大而增大.4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向平移3个单位，再向平移2个单位得到.5、已知抛物线的顶点坐标为2,1，且抛物线过点3,0，则抛物线的关系式是6、如图所示，抛物线顶点坐标是P （1，3），则函数y 随自变量x 的增大而减小的x 的取值范围是（）A 、x>3B 、x<3C 、x>1D 、x<1 7、已知函数()9232+--=x y .（1）确定下列抛物线的开口方向、对称轴和顶点坐标；（2）当x= 时，抛物线有最值，是 .（3）当x 时，y 随x 的增大而增大；当x 时，y 随x 的增大而减小. （4）求出该抛物线与x 轴的交点坐标及两交点间距离；（5）求出该抛物线与y 轴的交点坐标；（6）该函数图象可由23x y -=的图象经过怎样的平移得到的？ 8、已知函数()412-+=x y .（1）指出函数图象的开口方向、对称轴和顶点坐标；（2）若图象与x 轴的交点为A 、B 和与y 轴的交点C ，求△ABC 的面积；（3）指出该函数的最值和增减性；（4）若将该抛物线先向右平移2个单位，在向上平移4个单位，求得到的抛物线的解析式；（5）该抛物线经过怎样的平移能经过原点.（6）画出该函数图象，并根据图象回答：当x 取何值时，函数值大于0；当x 取何值时，函数值小于0.参考答案5：1、略；2、1；3、>1；4、左、下；5、342-+-=x x y ；6、C ；7、（1）下，x=2，（2，9），（2）2、大、9，（3）<2、>2,(4)( 32-,0)、( 32+,0)、 32，（5）（0，-3）；（6）向右平移2个单位，再向上平移9个单位；8、（1）上、x=-1、（-1，-4）；（2）（-3，0）、（1，0）、（0，-3）、6，（3）-4，当x>-1 时，y 随x 的增大而增大；当x<-1 时，y 随x 的增大而减小,(4) 2)1(-=x y ；（5）向右平移1个单位，再向上平移4个单位或向上平移3个单位或向左平移1个单位；（6）x>1或x<-3、-3<x<1练习六 c bx ax y ++=2的图象和性质1、抛物线942++=x x y 的对称轴是 .2、抛物线251222+-=x x y 的开口方向是，顶点坐标是 .3、试写出一个开口方向向上，对称轴为直线x=-2，且与y 轴的交点坐标为（0，3）的抛物线的解析式 .4、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，则 y ＝＿＿＿＿.5、把二次函数215322yx x的图象向上平移3个单位，再向右平移4个单位，则两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为_________；7、函数x x y +-=22有最____值，最值为_______；8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位，再沿y 轴向上平移3个单位，得到的图象的函数解析式为122+-=x x y ，则b 与c 分别等于（） A 、6，4 B 、－8，14 C 、－6，6 D 、－8，－149、二次函数122--=x x y 的图象在x 轴上截得的线段长为（） A 、22 B 、23 C 、32 D 、3310、通过配方，写出下列函数的开口方向、对称轴和顶点坐标：（1）12212+-=x x y ；（2）2832-+-=x x y ；（3）4412-+-=x x y 11、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位，再向上平移3个单位，问所得的抛物线有没有最大值，若有，求出该最大值；若没有，说明理由.12、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标 13、已知一次函数的图象过抛物线223y x x 的顶点和坐标原点1）求一次函数的关系式； 2）判断点2,5是否在这个一次函数的图象上14、某商场以每台2500元进口一批彩电.如每台售价定为2700元，可卖出400台，以每100元为一个价格单位，若将每台提高一个单位价格，则会少卖出50台，那么每台定价为多少元即可获得最大利润？最大利润是多少元？参考答案6：1、x=-2；2、上、（3，7）；3、略；4、2)1(2+-x ；5、5)1(212+--=x y ；6、（-2，0）（8，0）；7、大、81；8、C ；9、A ；10、（1）1)2(212--=x y 、上、x=2、（2，-1），（2）310)34(32+--=x y、下、34=x 、（310,34），（3）3)2(412---=x y 、下、x=2、（2，-3）；11、有、y=6；12、（2，0）（-3，0）（0，6）；13、y=-2x 、否；14、定价为3000元时，可获最大利润125000元练习七 c bx ax y ++=2的性质1、函数2yx px q 的图象是以3,2为顶点的一条抛物线，这个二次函数的表达式为 2、二次函数2224y mx x mm 的图象经过原点，则此抛物线的顶点坐标是3、如果抛物线2yax bxc 与y 轴交于点A (0,2)，它的对称轴是1x，那么ac b4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点，与y 轴交于点C ，且线段AB 的长为1，△ABC 的面积为1，则b 的值为______. 5、已知二次函数c bx ax y ++=2的图象如图所示，则a___0，b___0，c___0，ac b 42-____0；6、二次函数c bx ax y ++=2的图象如图，则直线bc ax y += 的图象不经过第象限.7、已知二次函数2y ax bx c （0≠a ）的图象如图所示，则下列结论：1）,a b 同号；2）当1x和3x 时，函数值相同；3）40ab ；4）当2y 时，x 的值只能为0；其中正确的是8、已知二次函数2224m mx x y +--=与反比例函数xm y 42+=的图象在第二象限内的一个交点的横坐标是-2，则m= 9、二次函数2yx ax b 中，若0a b ，则它的图象必经过点（）A 1,1B 1,1C 1,1D 1,110、函数b ax y +=与c bx ax y ++=2的图象如图所示，则下列选项中正确的是（）A 、0,0>>c abB 、0,0><c abC 、0,0<>c abD 、0,0<<c ab11、已知函数c bx ax y ++=2的图象如图所示，则函数b ax y +=的图象是（）12、二次函数c bx ax y ++=2的图象如图，那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中，值为正数的有（） A ．4个 B ．3个 C ．2个 D ．1个13、抛物线的图角如图，则下列结论： ①＞0；②；③＞；④＜1.其中正确的结论是（）.（A ）①② （B ）②③ （C ）②④ （D ）③④14、二次函数2yax bx c 的最大值是3a ，且它的图象经过1,2，1,6两点，求a 、b 、c15、试求抛物线2yax bx c 与x 轴两个交点间的距离（240b ac ）参考答案7：1、1162+-=x x y ；2、（-4，-4）；3、1；4、-3；5、>、<、>、>；6、二；7、②③；8、-7；9、C ；10、D ；11、B ；12、C ；13、B ；14、4422++-=x x y ；15、aac b 42-练习八二次函数解析式1、抛物线y=ax 2+bx+c 经过A(-1,0), B(3,0), C(0,1)三点，则a= , b= , c=2、把抛物线y=x 2+2x-3向左平移3个单位，然后向下平移2个单位，则所得的抛物线的解析式为 .3、二次函数有最小值为1，当0x 时，1y ，它的图象的对称轴为1x ，则函数的关系式为4、根据条件求二次函数的解析式（1）抛物线过（-1，-6）、（1，-2）和（2，3）三点（2）抛物线的顶点坐标为（-1，-1），且与y 轴交点的纵坐标为-3 （3）抛物线过（－1，0），（3，0），（1，－5）三点；（4）抛物线在x 轴上截得的线段长为4，且顶点坐标是（3，－2）；5、已知二次函数的图象经过1,1、2,1两点，且与x 轴仅有一个交点，求二次函数的解析式6、抛物线y=ax 2+bx+c 过点(0,-1)与点(3,2)，顶点在直线y=3x-3上，a<0,求此二次函数的解析式.7、已知二次函数的图象与x 轴交于A （-2，0）、B （3，0）两点，且函数有最大值是2. （1）求二次函数的图象的解析式；（2）设次二次函数的顶点为P ，求△ABP 的面积.8、以x 为自变量的函数)34()12(22-+-++-=m m x m x y 中，m 为不小于零的整数，它的图象与x 轴交于点A 和B ，点A 在原点左边，点B 在原点右边.(1)求这个二次函数的解析式；(2)一次函数y=kx+b 的图象经过点A ，与这个二次函数的图象交于点C ，且ABC S ∆=10,求这个一次函数的解析式.参考答案8：1、31-、32、1；2、1082++=x x y ；3、1422+-=x x y ；4、（1）522-+=x x y 、（2）3422---=x x y 、（3）41525452--=x x y 、（4）253212+-=x x y ；5、9194942+-=x x y ；6、142-+-=x x y ；7、（1）25482582582++-=x x y 、5；8、322++-=x x y 、y=-x-1或y=5x+5练习九二次函数与方程和不等式1、已知二次函数772--=x kx y 与x 轴有交点，则k 的取值范围是 .2、关于x 的一元二次方程02=--n x x 没有实数根，则抛物线n x x y --=2的顶点在第_____象限；3、抛物线222++-=kx x y 与x 轴交点的个数为（） A 、0 B 、1 C 、2 D 、以上都不对4、二次函数c bx ax y ++=2对于x 的任何值都恒为负值的条件是（） A 、0,0>∆>a B 、0,0<∆>a C 、0,0>∆<a D 、0,0<∆<a5、12++=kx x y 与k x x y --=2的图象相交，若有一个交点在x 轴上，则k 为（） A 、0 B 、-1 C 、2 D 、41 6、若方程02=++c bx ax 的两个根是－3和1，那么二次函数c bx ax y ++=2的图象的对称轴是直线（）A 、x ＝－3B 、x ＝－2C 、x ＝－1D 、x ＝1 7、已知二次函数2yx px q 的图象与x 轴只有一个公共点，坐标为1,0，求,p q 的值8、画出二次函数322--=x x y 的图象，并利用图象求方程0322=--x x 的解，说明x 在什么范围时0322≤--x x .9、如图：（1）求该抛物线的解析式；（2）根据图象回答：当x 为何范围时，该函数值大于0.10、二次函数c bx ax y ++=2的图象过A(-3,0),B(1,0),C(0,3),点D 在函数图象上，点C 、D 是二次函数图象上的一对对称点，一次函数图象过点B 、D ，求（1）一次函数和二次函数的解析式，（2）写出使一次函数值大于二次函数值的x 的取值范围.11、已知抛物线22yx mx m .（1）求证此抛物线与x 轴有两个不同的交点；（2）若m 是整数，抛物线22yx mx m 与x 轴交于整数点，求m 的值；（3）在（2）的条件下，设抛物线顶点为A ，抛物线与x 轴的两个交点中右侧交点为B. 若M 为坐标轴上一点，且MA=MB ，求点M 的坐标.参考答案9：1、47-≥k 且0≠k ；2、一；3、C ；4、D ；5、C ；6、C ；7、2，1；8、31,3,121≤≤-=-=x x x ；9、（1）x x y 22-=、x<0或x>2；10、y=-x+1，322+--=x x y ,x<-2或x>1;11、（1）略,(2)m=2,(3)(1，0)或（0，1）练习十二次函数解决实际问题1、某农场种植一种蔬菜，销售员张平根据往年的销售情况，对今年种蔬菜的销售价格进行了预测，预测情况如图，图中的抛物线表示这种蔬菜销售价与月份之间的关系.观察图像，你能得到关于这种蔬菜销售情况的哪些信息？（至少写出四条）2、某企业投资100万元引进一条农产品生产线，预计投产后每年可创收33万元，设生产线投产后，从第一年到第 x 年维修、保养费累计．．为 y （万元），且 y ＝ax 2＋bx ，若第一年的维修、保养费为 2 万元，第二年的为 4 万元.求：y 的解析式.3、校运会上，小明参加铅球比赛，若某次试掷，铅球飞行的高度 y (m) 与水平距离 x (m) 之间的函数关系式为 y ＝－112x 2＋23x ＋53，求小明这次试掷的成绩及铅球的出手时的高度. 4、用 6m 长的铝合金型材做一个形状如图所示的矩形窗框，应做成长、宽各为多少时，才能使做成的窗框的透光面积最大？最大透光面积是多少？5、商场销售一批衬衫，每天可售出 20 件，每件盈利 40 元，为了扩大销售，减少库存，决定采取适当的降价措施，经调查发现，如果一件衬衫每降价 1 元，每天可多售出 2件.① 设每件降价 x 元，每天盈利 y 元，列出 y 与 x 之间的函数关系式；② 若商场每天要盈利 1200 元，每件应降价多少元？③ 每件降价多少元时，商场每天的盈利达到最大？盈利最大是多少元？6、有一个抛物线形的拱形桥洞，桥洞离水面的最大高度为 4m ，跨度为 10m ，如图所示，把它的图形放在直角坐标系中.①求这条抛物线所对应的函数关系式.②如图，在对称轴右边 1m 处，桥洞离水面的高是多少？7、有一座抛物线形拱桥，正常水位时桥下水面宽度为20m ，拱顶距离水面4m.（1）在如图所示的直角坐标系中，求出该抛物线的解析式.（2）在正常水位的基础上，当水位上升h(m)时，桥下水面的宽度为d(m)，试求出用d 表示h 的函数关系式；3.50.50 2 7 月份千克销售价(元)（3）设正常水位时桥下的水深为2m ，为保证过往船只顺利航行，桥下水面的宽度不得小于18m ，求水深超过多少米时就会影响过往船只在桥下顺利航行？8、某一隧道内设双行线公路，其截面由一长方形和一抛物线构成，如图所示，为保证安全，要求行驶车辆顶部（设为平顶）与隧道顶部在竖直方向上高度之差至少要有0.5m ，若行车道总宽度AB 为6m ，请计算车辆经过隧道时的限制高度是多少米？（精确到0.1m ）.参考答案10：1、①2月份每千克3.5元 ②7月份每千克0.5克 ③7月份的售价最低 ④2～7月份售价下跌；2、y ＝x 2＋x ；3、成绩10米，出手高度35米；4、23)1(232+--=x S ，当x ＝1时，透光面积最大为23m 2；5、（1）y ＝(40－x) (20＋2x)＝－2x 2＋60x ＋800，（2）1200＝－2x 2＋60x ＋800，x 1＝20，x 2＝10 ∵要扩大销售 ∴x 取20元，（3）y ＝－2 (x 2－30x)＋800＝－2 (x －15)2＋1250 ∴当每件降价15元时，盈利最大为1250元；6、（1）设y ＝a (x －5)2＋4，0＝a (－5)2＋4，a ＝－254，∴y ＝－254 (x －5)2＋4，（2）当x ＝6时，y ＝－254＋4＝3.4(m)；7、（1）2251x y -=，（2）h d -=410，（3）当水深超过2.76m 时；8、)64(6412≤≤-+-=x x y ，x =3，m y 75.3496=-=，m 2.325.35.075.3≈=-，货车限高为3.2m.。

(完整版)二次函数基础练习题(含答案)

二次函数一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察得到小球滚动的距离s（米）与时间t（秒）的数据如下表：写出用t表示s 的函数关系式：1、下列函数：① 23y x；② 21y x x x；③ 224y x x x；④21y xx；⑤ 1y x x,其中是二次函数的是，其中a，b，c3、当m时，函数2235y m x x（m为常数）是关于x的二次函数4、当____m时，函数2221m my m m x是关于x的二次函数5、当____m时，函数2564m my m x+3x是关于x的二次函数6、若点 A ( 2, m）在函数12-=xy的图像上，则 A 点的坐标是＿＿＿＿.7、在圆的面积公式 S＝πr2中，s 与 r 的关系是( ）A、一次函数关系B、正比例函数关系C、反比例函数关系D、二次函数关系8、正方形铁片边长为15cm，在四个角上各剪去一个边长为x（cm)的小正方形，用余下的部分做成一个无盖的盒子．（1)求盒子的表面积S（cm2)与小正方形边长x(cm）之间的函数关系式；（2)当小正方形边长为3cm时，求盒子的表面积．9、如图，矩形的长是 4cm ，宽是 3cm ，如果将长和宽都增加 x cm,那么面积增加 ycm 2， ① 求y 与 x 之间的函数关系式。

② 求当边长增加多少时,面积增加 8cm 2。

10、已知二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2,求该函数解析式。

11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料，建造猪舍三间,如图，它们的平面图是一排大小相等的长方形。

（1）如果设猪舍的宽AB 为x 米，则猪舍的总面积S （米2）与x 有怎样的函数关系？（2）请你帮富根老伯计算一下,如果猪舍的总面积为32米2，应该如何安排猪舍的长BC 和宽AB 的长度？旧墙的长度是否会对猪舍的长度有影响？怎样影响？练习二函数2ax y =的图象与性质1、填空：(1）抛物线221x y =的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大,当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；(2）抛物线221x y -=的对称轴是（或 )，顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时,该函数有最值是；2、对于函数22x y =下列说法：①当x 取任何实数时,y 的值总是正的;②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图象关于y 轴对称.其中正确的是。

二次函数专项复习经典试题集锦(含答案)

二次函数专项复习经典试题集锦（含答案）一、选择题：1. 抛物线3)2(2+-=x y 的对称轴是（） A. 直线3-=xB. 直线3=xC. 直线2-=xD. 直线2=x2. 二次函数c bx ax y ++=2的图象如右图，则点),(acb M 在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 已知二次函数c bx ax y ++=2，且0<a ，0>+-c b a ，则一定有（） A. 042>-ac bB. 042=-ac bC. 042<-ac bD. ac b 42-≤04. 把抛物线c bx x y ++=2向右平移3个单位，再向下平移2个单位，所得图象的解析式是532+-=x x y ，则有（） A. 3=b ，7=c B. 9-=b ，15-=c C. 3=b ，3=cD. 9-=b ，21=c5. 下面所示各图是在同一直角坐标系内，二次函数c x c a ax y +++=)(2与一次函数c ax y +=的大致图象，有且只有一个是正确的，正确的是（）D6. 抛物线322+-=x x y 的对称轴是直线（） A. 2-=xB. 2=xC. 1-=xD. 1=x7. 二次函数2)1(2+-=x y 的最小值是（） A. 2-B. 2C. 1-D. 18. 二次函数c bx ax y ++=2的图象如图所示，若c b a M ++=24c b a N +-=，b a P -=4，则（） A. 0>M ，0>N ，0>P B. 0<M ，0>N ，0>P C. 0>M ，0<N ，0>P D. 0<M ，0>N ，0<P 二、填空题：9. 将二次函数322+-=x x y 配方成k h x y +-=2)(的形式，则y =______________________. 10. 已知抛物线c bx ax y ++=2与x 轴有两个交点，那么一元二次方程02=++c bx ax 的根的情况是______________________.11. 已知抛物线c x ax y ++=2与x 轴交点的横坐标为1-，则c a +=_________. 12. 请你写出函数2)1(+=x y 与12+=x y 具有的一个共同性质：_______________.13. 已知二次函数的图象开口向上，且与y 轴的正半轴相交，请你写出一个满足条件的二次函数的解析式：_____________________. 14. 如图，抛物线的对称轴是1=x ，与x 轴交于A 、B 两点，若B 点坐标是)0,3(，则A点的坐标是三、解答题：1. 已知函数12-+=bx x y 的图象经过点（3，2）.（1）求这个函数的解析式；（2）当0>x 时，求使y ≥2的x 的取值范围.2、如右图，抛物线n x x y ++-=52经过点)0,1(A ，与y 轴交于点B .（1）求抛物线的解析式；（2）P 是y 轴正半轴上一点，且△PAB 是以AB 为腰的等腰三角形，试求点P 的坐标.3．如图，抛物线y 1=﹣x 2+2向右平移1个单位得到抛物线y 2，回答下列问题：（1）抛物线y 2的顶点坐标；（2）阴影部分的面积S= ；（3）若再将抛物线y 2绕原点O 旋转180°得到抛物线y 3，求抛物线y 3的解析式．4．（1999•烟台）如图，已知抛物线y=ax 2+bx+交x 轴正半轴于A ，B 两点，交y 轴于点C ，且∠CBO=60°，∠CAO=45°，求抛物线的解析式和直线BC 的解析式．O xy1-1 BA5．如图，抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．（1）求此抛物线的解析式；（2）点P为抛物线上的一个动点，求使S△APC：S△ACD=5：4的点P的坐标．6．如图，抛物线y=a（x+1）2的顶点为A，与y轴的负半轴交于点B，且OB=OA．（1）求抛物线的解析式；（2）若点C（﹣3，b）在该抛物线上，求S△ABC的值．7．如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标及c的值；（2）设抛物线与y 轴交于点B ，与x 轴交于点C 、D （C 点在D 点的左侧），试判断△ABD 的形状．8、某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到赢利的过程，下面的二次函数图象（部分）刻画了该公司年初以来累积利润s （万元）与销售时间t （月）之间的关系（即前t 个月的利润总和s 与t 之间的关系）. （1）由已知图象上的三点坐标，求累积利润s （万元）与销售时间t （月）之间的函数关系式；（2）求截止到几月累积利润可达到30万元；（3）求第8个月公司所获利润是多少万元？参考答案一、选择题：题号 1 2 3 4 5 6 7 8 9 答案DDAADDDBD二、填空题： 1. 2)1(2+-=x y2. 有两个不相等的实数根3. 14. （1）图象都是抛物线；（2）开口向上；（3）都有最低点（或最小值）5.358512+-=x x y 或358512-+-=x x y 或178712+-=x x y 或178712-+-=x x y 6. 122++-=x x y 等（只须0<a ，0>c ） 7. )0,32(-8. 3=x ，51<<x ，1，4 三、解答题：1. 解：（1）∵函数12-+=bx x y 的图象经过点（3，2），∴2139=-+b . 解得2-=b . ∴函数解析式为122--=x x y .（2）当3=x 时，2=y . 根据图象知当x ≥3时，y ≥2.∴当0>x 时，使y ≥2的x 的取值范围是x ≥3.2. 解：（1）由题意得051=++-n . ∴4-=n . ∴抛物线的解析式为452-+-=x x y .（2）∵点A 的坐标为（1，0），点B 的坐标为)4,0(-. ∴OA =1，OB =4.在Rt △OAB 中，1722=+=OB OA AB ，且点P 在y 轴正半轴上.①当PB =PA 时，17=PB . ∴417-=-=OB PB OP . 此时点P 的坐标为)417,0(-.②当PA =AB 时，OP =OB =4 此时点P 的坐标为（0，4）.3. 解：（1）设s 与t 的函数关系式为c bt at s ++=2，由题意得⎪⎩⎪⎨⎧=++-=++-=++；5.2525,224,5.1c b a c b a c b a 或⎪⎩⎪⎨⎧=-=++-=++.0,224,5.1c c b a c b a 解得⎪⎪⎩⎪⎪⎨⎧=-==.0,2,21c b a ∴t t s 2212-=.（2）把s =30代入t t s 2212-=，得.221302t t -= 解得101=t ，62-=t （舍去）答：截止到10月末公司累积利润可达到30万元. （3）把7=t 代入，得.5.10727212=⨯-⨯=s把8=t 代入，得.16828212=⨯-⨯=s 5.55.1016=-. 答：第8个月获利润5.5万元.4. 解：（1）由于顶点在y 轴上，所以设这部分抛物线为图象的函数的解析式为1092+=ax y . 因为点)0,25(-A 或)0,25(B 在抛物线上，所以109)25(·02+-=a ，得12518-=a . 因此所求函数解析式为109125182+-=x y （25-≤x ≤25）.（2）因为点D 、E 的纵坐标为209，所以10912518209+-=，得245±=x .所以点D 的坐标为)209,245(-，点E 的坐标为)209,245(. 所以225)245(245=--=DE . 因此卢浦大桥拱内实际桥长为385227501.01100225≈=⨯⨯（米）. 5. 解：（1）∵AB =3，21x x <，∴312=-x x . 由根与系数的关系有121=+x x .∴11-=x ，22=x . ∴OA =1，OB =2，2·21-==amx x . ∵1tan tan =∠=∠ABC BAC ，∴1==OBOCOA OC . ∴OC =2. ∴2-=m ,1=a .∴此二次函数的解析式为22--=x x y .（2）在第一象限，抛物线上存在一点P ，使S △PAC =6. 解法一：过点P 作直线MN ∥AC ，交x 轴于点M ，交y 轴于N ，连结PA 、PC 、MC 、NA . ∵MN ∥AC ，∴S △MAC =S △NAC = S △PAC =6.由（1）有OA =1，OC =2. ∴6121221=⨯⨯=⨯⨯CN AM . ∴AM =6，CN =12. ∴M （5，0），N （0，10）.∴直线MN 的解析式为102+-=x y .由⎩⎨⎧--=+-=,2,1022x x y x y 得⎩⎨⎧==；4311y x ⎩⎨⎧=-=18,422y x （舍去） ∴在第一象限，抛物线上存在点)4,3(P ，使S △PAC =6. 解法二：设AP 与y 轴交于点),0(m D （m >0） ∴直线AP 的解析式为m mx y +=.⎩⎨⎧+=--=.,22m mx y x x y ∴02)1(2=--+-m x m x . ∴1+=+m x x P A ，∴2+=m x P . 又S △PAC = S △ADC + S △PDC =P x CD AO CD ·21·21+=)(21P x AO CD +. ∴6)21)(2(21=+++m m ，0652=-+m m ∴6=m （舍去）或1=m .∴在第一象限，抛物线上存在点)4,3(P ，使S △PAC =6.提高题1. 解：（1）∵抛物线c bx x y ++=2与x 轴只有一个交点，∴方程02=++c bx x 有两个相等的实数根，即042=-c b . ①又点A 的坐标为（2，0），∴024=++c b . ② 由①②得4-=b ，4=a .（2）由（1）得抛物线的解析式为442+-=x x y . 当0=x 时，4=y . ∴点B 的坐标为（0，4）. 在Rt △OAB 中，OA =2，OB =4，得5222=+=OB OA AB .∴△OAB 的周长为5265241+=++.2. 解：（1）76)34()10710710(1022++-=--⨯++-⨯=x x x x x S .当3)1(26=-⨯-=x 时，16)1(467)1(42=-⨯-⨯-⨯=最大S . ∴当广告费是3万元时，公司获得的最大年利润是16万元.（2）用于投资的资金是13316=-万元.经分析，有两种投资方式符合要求，一种是取A 、B 、E 各一股，投入资金为13625=++（万元），收益为0.55+0.4+0.9=1.85（万元）>1.6（万元）；另一种是取B 、D 、E 各一股，投入资金为2+4+6=12（万元）<13（万元），收益为0.4+0.5+0.9=1.8（万元）>1.6（万元）.3. 解：（1）设抛物线的解析式为2ax y =，桥拱最高点到水面CD 的距离为h 米，则),5(h D -，)3,10(--h B .∴⎩⎨⎧--=-=.3100,25h a h a 解得⎪⎩⎪⎨⎧=-=.1,251h a∴抛物线的解析式为2251x y -=.（2）水位由CD 处涨到点O 的时间为1÷0.25=4（小时），货车按原来速度行驶的路程为40×1+40×4=200<280， ∴货车按原来速度行驶不能安全通过此桥. 设货车的速度提高到x 千米/时，当2801404=⨯+x 时，60=x .∴要使货车安全通过此桥，货车的速度应超过60千米/时. 4. 解：（1）未出租的设备为10270-x 套，所有未出租设备的支出为)5402(-x 元. （2）54065101)5402()1027040(2++-=----=x x x x x y .∴540651012++-=x x y .（说明：此处不要写出x 的取值范围）（3）当月租金为300元时，租赁公司的月收益为11040元，此时出租的设备为37套；当月租金为350元时，租赁公司的月收益为11040元，此时出租的设备为32套.因为出租37套和32套设备获得同样的收益，如果考虑减少设备的磨损，应选择出租32套；如果考虑市场占有率，应选择出租37套.（4）5.11102)325(1015406510122+--=++-=x x x y . ∴当325=x 时，y 有最大值11102.5. 但是，当月租金为325元时，租出设备套数为34.5，而34.5不是整数，故租出设备应为34套或35套. 即当月租金为为330元（租出34套）或月租金为320元（租出35套）时，租赁公司的月收益最大，最大月收益均为11100元.16．如图，抛物线y 1=﹣x 2+2向右平移1个单位得到抛物线y 2，回答下列问题：（1）抛物线y 2的顶点坐标（1，2）；（2）阴影部分的面积S= 2 ；（3）若再将抛物线y 2绕原点O 旋转180°得到抛物线y 3，求抛物线y 3的解析式．考点：二次函数图象与几何变换．分析：直接应用二次函数的知识解决问题．解答：解：（1）读图找到最高点的坐标即可．故抛物线y 2的顶点坐标为（1，2）；（2分）（2）把阴影部分进行平移，可得到阴影部分的面积即为图中两个方格的面积=1×2=2；（6分）（3）由题意可得：抛物线y 3的顶点与抛物线y 2的顶点关于原点O 成中心对称．所以抛物线y3的顶点坐标为（﹣1，﹣2），于是可设抛物线y3的解析式为：y=a（x+1）2﹣2．由对称性得a=1，所以y3=（x+1）2﹣2．（10分）20．（1999•烟台）如图，已知抛物线y=ax2+bx+交x轴正半轴于A，B两点，交y轴于点C，且∠CBO=60°，∠CAO=45°，求抛物线的解析式和直线BC的解析式．考点：待定系数法求二次函数解析式；待定系数法求一次函数解析式．分析：根据抛物线的解析式，易求得C点的坐标，即可得到OC的长；可分别在Rt△OBC和Rt△OAC中，通过解直角三角形求出OB、OA的长，即可得到A、B的坐标，进而可运用待定系数法求得抛物线和直线的解析式．解答：解：由题意得C（0，）在Rt△COB中，∵∠CBO=60°，∴OB=OC•cot60°=1∴B点的坐标是（1，0）；（1分）在Rt△COA中，∵∠CAO=45°，∴OA=OC=∴A点坐标（，0）由抛物线过A、B两点，得解得∴抛物线解析式为y=x2﹣（）x+（4分）设直线BC的解析式为y=mx+n，得n=，m=﹣∴直线BC解析式为y=﹣x+．（6分）23．如图，抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．（1）求此抛物线的解析式；（2）点P为抛物线上的一个动点，求使S△APC：S△ACD=5：4的点P的坐标．考点：二次函数综合题．专题：压轴题；动点型．分析：（1）先根据直线y=x﹣3求出A、B两点的坐标，然后将它们代入抛物线中即可求出待定系数的值．（2）根据（1）中抛物线的解析式可求出C，D两点的坐标，由于△APC和△ACD同底，因此面积比等于高的比，即P点纵坐标的绝对值：D点纵坐标的绝对值=5：4．据此可求出P点的纵坐标，然后将其代入抛物线的解析式中，即可求出P点的坐标．解答：解：（1）直线y=x﹣3与坐标轴的交点A（3，0），B（0，﹣3）．则，解得，∴此抛物线的解析式y=x2﹣2x﹣3．（2）抛物线的顶点D（1，﹣4），与x轴的另一个交点C（﹣1，0）．设P（a，a2﹣2a﹣3），则（×4×|a2﹣2a﹣3|）：（×4×4）=5：4．化简得|a2﹣2a﹣3|=5．当a2﹣2a﹣3=5，得a=4或a=﹣2．∴P（4，5）或P（﹣2，5），当a2﹣2a﹣3＜0时，即a2﹣2a+2=0，此方程无解．综上所述，满足条件的点的坐标为（4，5）或（﹣2，5）．27．如图，抛物线y=a（x+1）2的顶点为A，与y轴的负半轴交于点B，且OB=OA．（1）求抛物线的解析式；（2）若点C（﹣3，b）在该抛物线上，求S△ABC的值．考点：待定系数法求二次函数解析式；二次函数图象上点的坐标特征．专题：计算题．分析：（1）由抛物线解析式确定出顶点A坐标，根据OA=OB确定出B坐标，将B坐标代入解析式求出a的值，即可确定出解析式；（2）将C坐标代入抛物线解析式求出b的值，确定出C坐标，过C作CD垂直于x轴，三角形ABC面积=梯形OBCD面积﹣三角形ACD面积﹣三角形AOB面积，求出即可．解答：解：（1）由投影仪得：A（﹣1，0），B（0，﹣1），将x=0，y=﹣1代入抛物线解析式得：a=﹣1，则抛物线解析式为y=﹣（x+1）2=﹣x2﹣2x﹣1；（2）过C作CD⊥x轴，将C（﹣3，b）代入抛物线解析式得：b=﹣4，即C（﹣3，﹣4），则S△ABC=S梯形OBCD﹣S△ACD﹣S△AOB=×3×（4+1）﹣×4×2﹣×1×1=3．点评：此题考查了待定系数法求二次函数解析式，熟练掌握待定系数法是解本题的关键．28．如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标及c的值；（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状．考点：二次函数综合题．分析：（1）先根据抛物线的解析式得出其对称轴，由此得到顶点A的横坐标，然后代入直线l的解析式中求出点A的坐标，再将点A的坐标代入抛物线的解析式y=x2﹣2x+c中，运用待定系数法即可求出c的值；（2）先由抛物线的解析式得到点B的坐标，再求出AB、AD、BD三边的长，然后根据勾股定理的逆定理即可确定△ABD是直角三角形．解答：解：（1）∵y=x2﹣2x+c，∴顶点A的横坐标为x=﹣=1，又∵顶点A在直线y=x﹣5上，∴当x=1时，y=1﹣5=﹣4，∴点A的坐标为（1，﹣4）．将A（1，﹣4）代入y=x2﹣2x+c，得﹣4=12﹣2×1+c，解得c=﹣3．故抛物线顶点A的坐标为（1，﹣4），c的值为﹣3；（2）△ABD是直角三角形．理由如下：∵抛物线y=x2﹣2x﹣3与y轴交于点B，∴B（0，﹣3）．当y=0时，x2﹣2x﹣3=0，解得x1=﹣1，x2=3，∴C（﹣1，0），D（3，0）．∵BD2=OB2+OD2=18，AB2=（4﹣3）2+12=2，AD2=（3﹣1）2+42=20，∴BD2+AB2=AD2，∴∠ABD=90°，即△ABD是直角三角形．。