海淀区初二数学全等三角形经典编辑50题证明
中考数学全等三角形证明经典50题(含答案)+经典因式分解练习题100道
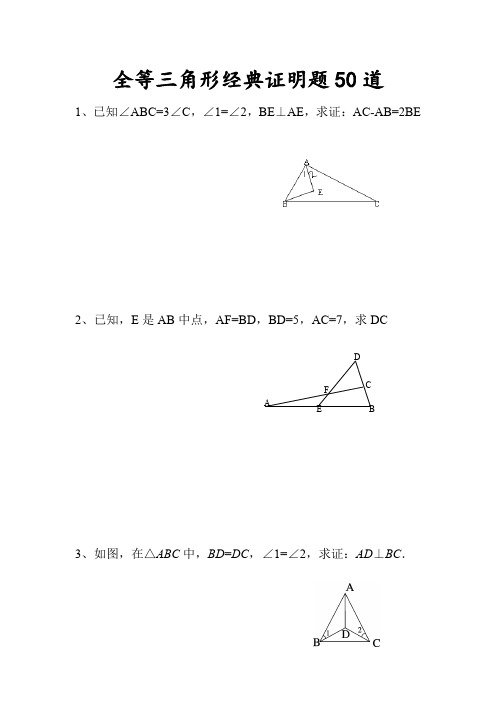
全等三角形经典证明题50道1、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE2、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC3、如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .FAEDC B4.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA5.(5分)如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.PCEDBA6.(6分)如图①,E、F分别为线段AC上的两个动点,且DE ⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.7.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):8.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .OEDCB AFE D CB A25、如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
证明:∵DF=CE , ∵DF-EF=CE-EF , 即DE=CF ,在∵AED 和∵BFC 中,∵ AD=BC , ∵D=∵C ,DE=CF ∵∵AED ∵∵BFC (SAS )26、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
最新-八年级全等三角形证明经典50题 精品

八年级全等三角形证明经典50题篇一:海淀区初二数学全等三角形经典50题证明海淀名校全等三角形证明经典50题(含答案)1已知:=4,=2,是中点,是整数,求?解析:延长到,使=,则三角形全等于三角形即==2在三角形中,-2已知:是中点,∠=90°,求证:?123已知:=,∠=∠,∠=∠,是中点,求证:∠1=∠2证明:连接和。
??因为=,=,∠=∠。
??所以三角形全等于三角形(边角边)。
??所以=,∠=∠。
????连接。
??在三角形中,=。
??所以∠=∠。
??又因为∠=∠。
??所以∠=∠。
??所以=。
????在三角形和三角形中,??=,=,??∠=∠+∠=∠+∠=∠。
??所以三角形和三角形全等。
??所以∠=∠(∠1=∠2)。
??4已知:∠1=∠2,=,,求证:=证明:??过点,作,交延长线于??则∠=∠,∠=∠2??又∵=??∴⊿≌⊿()??∴=??∵??∴∠=∠1??∵∠1=∠2??∴∠=∠??∴=??∴=5已知:平分∠,=+,求证:∠=2∠证明:??在上截取=,连接??∵平分∠??∴∠=∠??又∵=,=??∴⊿≌⊿()??∴∠=∠,=??∵=+??=+??∴=??∴∠=∠??∵∠=∠+∠=2∠??∴∠=2∠6已知:平分∠,⊥,∠+∠=180°,求证:=+证明:??在上取,使=,连接??因为⊥??所以∠=∠=90°??因为=,=,??所以△≌△??所以∠=∠??因为∠+∠=180°,∠+∠=180°??所以∠=∠??因为平分∠??所以∠=∠??又因为=??所以△≌△()??所以=??所以=+=+????12如图,四边形中,∥,、分别平分∠、∠,且点在上。
求证:=+。
证明在上截取=,连接??∠=∠,=,则⊿≌Δ(),∠=∠;??平行于,则∠+∠=180°;??又∠+∠=180°,则∠=∠;??又∠=∠,=,故⊿≌Δ(),=??所以,=+=+13。
八年级全等三角形证明经典50题含答案

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
八年级数学《全等三角形》证明经典40题

八年级数学《全等三角形》证明经典40题班级 姓名1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACAD BCB ACDF21 E5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
8.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C9.已知:AB=CD ,∠A=∠D ,求证:∠B=∠CCD B DC B A FEA10. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB11.已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC13.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .14. 如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBAPD A C B F A EDCB15.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .16.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B17.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .18、如图:DF=CE ,AD=BC ,∠D=∠C 。
全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DCAD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGBACDF21 E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=28. 已知:D 是AB 中点,∠ACB=90°,求证:1CD AB9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
八年级全等三角形证明经典50题(供参考)

全等三角形证明经典50题1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CADBCBA CDF2 1 ECA6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD8. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2A CDEF 21 ADBCDAB10.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC11.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C12.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
13.已知:AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证:∠F=∠CBACDF21ECDBDCBAFEA14.已知:AB=CD,∠A=∠D,求证:∠B=∠C15.P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB16.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:AC-AB=2BE17.已知,E是AB中点,AF=BD,BD=5,AC=7,求DC18.(5分)如图,在△ABC中,BD=DC,∠1=∠2,求证:AD⊥BC.19.(5分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBAAB CDP DACBFAEDCB20.(5分)如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.21.(6分)如图,△ABC中,AD是∠CAB的平分线,且AB=AC+CD,求证:∠C=2∠B22.(6分)如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.23.(7分)已知:如图,DC∥AB,且DC=AE,E为AB的中点,(1)求证:△AED≌△EBC.(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C 点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.PEDCBAOEDCBAFEADCBA25、(10分)如图:DF=CE ,AD=BC ,∠D=∠C 。
八年级全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
中考数学全等三角形证明经典50题(含答案)+经典因式分解练习题100道

全等三角形经典证明题50道1、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE2、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC3、如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .FAEDC B4.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA5.(5分)如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.PCEDBA6.(6分)如图①,E、F分别为线段AC上的两个动点,且DE ⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.7.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):8.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .OEDCB AFE D CB A25、如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
证明:∵DF=CE , ∵DF-EF=CE-EF , 即DE=CF ,在∵AED 和∵BFC 中,∵ AD=BC , ∵D=∵C ,DE=CF ∵∵AED ∵∵BFC (SAS )26、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
全等三角形证明经典50题(含答案)
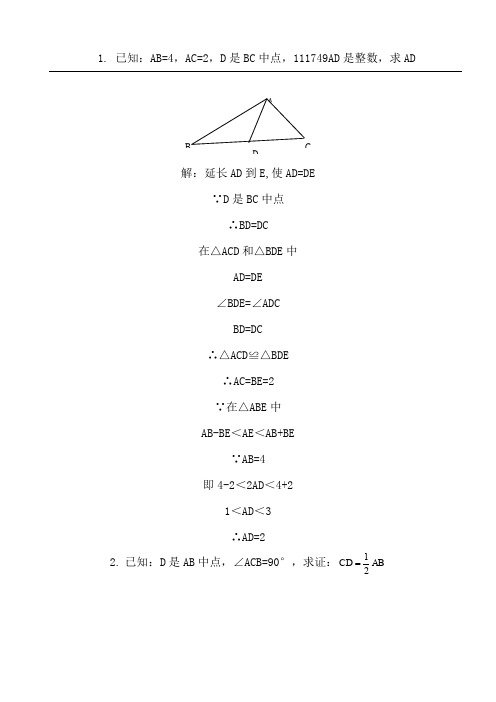
1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD ABA DB C延长CD 与P ,使D 为CP 中点。
连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB 3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24.5. 证明:连接BF 和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF 全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴∠EBF=∠BEF 。
C D FB C∵∠ABC=∠AED 。
∴∠ABE=∠AEB 。
∴AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF 和三角形AEF 全等。
∴∠BAF=∠EAF(∠1=∠2)。
6. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CG∠CGD =∠EFD又,EF ∥AB∴,∠EFD =∠1∠1=∠2∴∠CGD =∠2∴△AGC 为等腰三角形,AC =CG又EF =CG∴EF =AC7. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CB ACDF2 1EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD(SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C8.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE9.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 10. 已知:D 是AB 中点,∠ACB=90°,求证:1CD ABADB C在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 11.已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
初中专项训练全等三角形证明经典50题(含答案)
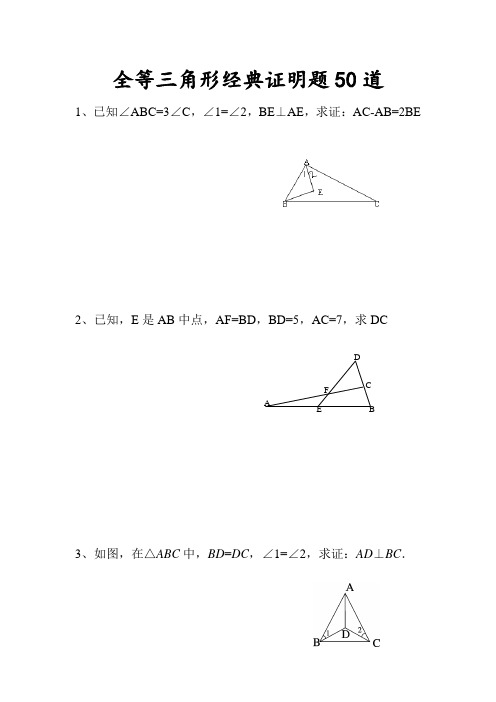
全等三角形经典证明题50道1、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE2、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC3、如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .FAEDC B4.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA5.(5分)如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.PCEDBA6.(6分)如图①,E、F分别为线段AC上的两个动点,且DE ⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC 于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.7.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):8.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .OEDCB AFE D CB A25、如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
FEDCBA证明:∵DF=CE , ∴DF-EF=CE-EF , 即DE=CF ,在△AED 和△BFC 中,∵ AD=BC , ∠D=∠C ,DE=CF ∴△AED ≌△BFC (SAS )26、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
全等三角形证明经典50题(含答案),推荐文档
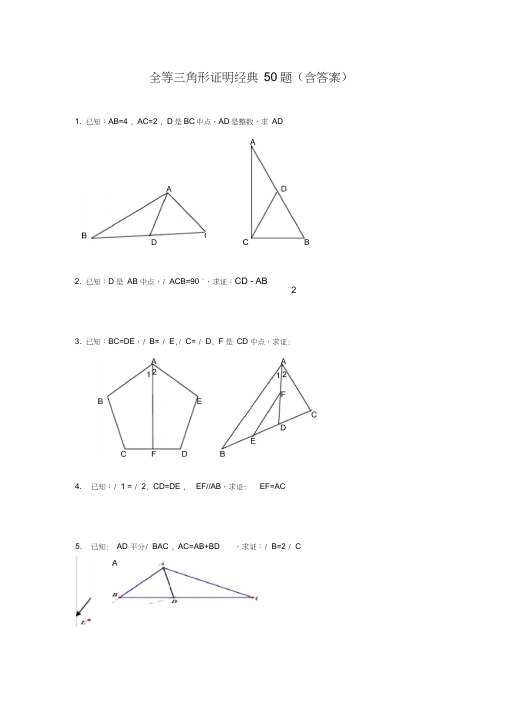
全等三角形证明经典50题(含答案)1. 已知:AB=4 , AC=2 , D是BC中点,AD是整数,求AD2. 已知:D 是AB 中点,/ ACB=90 °,求证:CD - AB2 3. 已知:BC=DE,/ B= / E,/ C= / D, F 是CD 中点,求证:4.5.已知:/ 1 = / 2, CD=DE ,已知:EF//AB,求证:EF=AC,求证:/ B=2 / C AD 平分/ BAC , AC=AB+BD6. 已知:AC 平分/ BAD , CE丄AB,/ B+ / D=180 °,求证:AE=AD+BE12. 如图,四边形ABCD中,AB上。
求证:BC=AB+DC。
13. 已知:AB//ED,/ EAB= / BDE , AF=CD ,14. P是/ BAC平分线AD上一点,AC>AB,求证:15. 已知/ ABC=3 / C,Z 1 = / 2, BE 丄AE,求证:D// DC , BE、CE 分别平分/ ABC、/ BCD,且点E在ADEF=BC,求证:/ F=Z CPC-PB<AC-ABAC-AB=2BE16. 已知,E 是 AB 中点,AF=BD , BD=5 , AC=7,求 DC21. 如图,△ ABC 中,AD 是/ CAB 的平分线,且 AB=AC+CD ,求证:/ C=2/ B22. (6分)如图①,E 、F 分别为线段 AC 上的两个动点,且 DE 丄AC 于E , BF 丄AC 于F , 若AB=CD , AF=CE , BD 交 AC 于点 M .(1) 求证:MB = MD , ME=MF(2) 当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立 请给予证明;若不成立请说明理由.18. 如图,在△ ABC 中,BD=DC ,/ 1 = / 2,求证:AD 丄BC .19. 如图,0M 平分/ POQ , MA 丄 OP,MB 丄 OQ ,求证:/ OAB= / OBA / PAB 的平分线与/ CBA 的平分线相交于 E , CE 的连线交 AP 于 D .求证:AD+BC=AB . N .23. 已知:如图,DC// AB,且DC=AE, E为AB的中点,(1)求证:△ AED◎△ EBC .(2)观看图前,在不添辅助线的情况下,除△E BC夕卜,请再写出两个与△ AED的面积相等的三角形.(直接写出结果,不要求证明):24. (7分)如图,△ ABC中,/ BAC=90度,AB=AC, BD是/ ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.25、如图:DF=CE AD=BC / D=Z G 求证:△ AED^A BFG26、(10 分)如图:AE、BC交于点M F 点在AM±, BE// CF, BE=CF求证:AM>^ ABC的中线。
初二数学-全等三角形证明经典50题
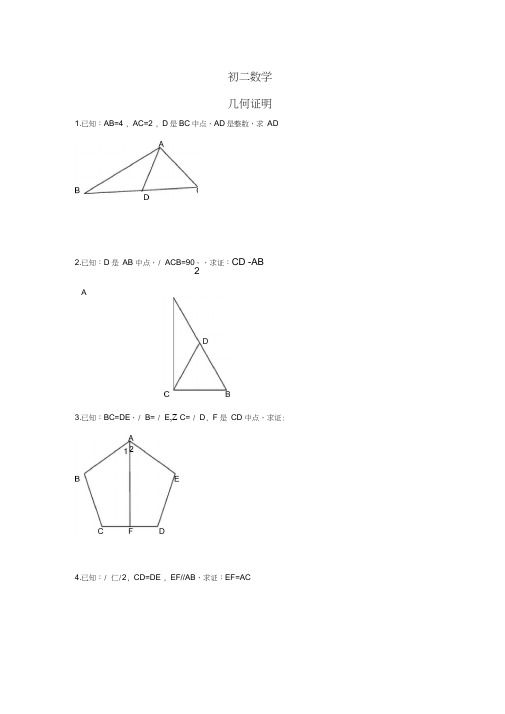
初二数学几何证明1.已知:AB=4 , AC=2 , D是BC中点,AD是整数,求AD2.已知:D 是AB 中点,/ ACB=90。
,求证:CD -AB2A3.已知:BC=DE,/ B= / E,Z C= / D, F 是CD 中点,求证:4.已知:/ 仁/2, CD=DE , EF//AB,求证:EF=AC已知:AD 平分/ BAC , AC=AB+BD ,求证:/ B=2 / C7.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 ADD5. AE=AD+BE,求证: O6.8.已知:D 是AB 中点,/ ACB=90 °,求证:CD 1 AB29.已知:BC=DE,/ B= / E,/ C= / D, F 是CD 中点,求证:12.已知:AC 平分/ BAD , CE丄AB , / B+ / D=180 °,求证:AE=AD+BECD=DE , EF//AB,求证:EF=AC10.已知:/ 1 = / 2,c12.如图,四边形ABCD中,AB // DC, BE、CE分别平分/ ABC、/ BCD,且点E在AD 上。
求证:BC=AB+DC。
D14.已知:AB=CD,/ A= / D,求证:/ B= / CB15. P 是/ BAC 平分线 AD 上一点,AC>AB ,求证:PC-PB<AC-AB17.已知,E 是 AB 中点,AF=BD , BD=5 , AC=7,求 DC18. ( 5 分)如图,在△ ABC 中,BD=DC ,/ 仁/2,求证:AD 丄 BC .19. ( 5分)如图,0M 平分/ POQ , MA 丄OP,MB 丄OQ , A 、B 为垂足,AB 交0M 于点N . 求证:/ OAB= /OBA16.已知/ ABC=3 / C ,Z 1 = / 2, BE 丄 AE ,求证:AC-AB=2BE20. ( 5分)如图,已知 AD // BC ,/ PAB 的平分线与/ CBA 的平分线相交于 E , CE 的连线 交 AP 于D .求证:AD+BC=AB .(6分)如图,△ ABC 中,AD 是/ CAB 的平分线,且 AB=AC+CD ,求证:/ C=2/ B22. (6分)如图①,E 、F 分别为线段 AC 上的两个动点,且 DE 丄AC 于E , BF 丄AC 于F , 若AB=CD , AF=CE , BD 交 AC 于点 M .(1) 求证:MB = MD , ME=MF(2) 当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立 请给予证明;若不成立请说明理由.23. ( 7分)已知:如图, DC // AB ,且DC =AE , E 为AB 的中点,(1)求证:△ AEDEBC.21.(2)观看图前,在不添辅助线的情况下,除△EBC夕卜,请再写出两个与△ AED的面积相等的三角形.(直接写出结果,不要求证明):24. (7分)如图,△ ABC中,/ BAC=90度,AB=AC, BD是/ ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F .求证:BD=2CE.25、(10分)如图: DF=CE AD=BC/ D=Z G 求证:△26、(10分)如图:AE、BC交于点M F点在AM上,求证:AM>^ ABC的中线。
全等三角形证明经典50的题目(含答案详解)

1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE ∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=22.已知:D是AB中点,∠ACB=90°,求证:12 CD AB延长CD与P,使D为CP中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB3.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2) 4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC过C作CG∥EF交AD的延长线于点G CG∥EF,可得,∠EFD=CGDDE=DC ∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF=CG ∠CGD=∠EFD 又,EF∥AB∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG 又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CADBCBACDF21E精彩文档证明:延长AB取点E,使AE=AC,连接DE ∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE 证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
(完整word版)八年级全等三角形证明经典50题(含答案).doc

1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求ADA 解:延长AD 至IJE,使AD=DE・・・D 是BC 中点BD=DC在厶ACD 和厶BDE 中AD=DEZBDE= ZADC BD=DCAA ACD A BDE•*. AC=BE=2・・•在△ ABE 中AB-BE < AE<AB+BE・・・AB=4即 4・2 <2AD < 4+21 < AD < 3・・・AD=2延长CD 与P,使D 为CP 中点。
连接VDP=DC,DA=DBA AC BP 为平行四边形又 Z ACB=90・・・平行四边形ACBP 为矩形AAB=CP=1/2AB 2.已知:D 是AB 中点,Z ACB=90 0,求证:CD [AB 2AAP,BP3.已知:BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点,求证:Z 1= Z2证明:连接BF和EF・・・ BC=ED,CF=DF, Z BCF= Z EDF・・・三角形BCF全等于三角形EDF(边角边)・・・ BF=EF, ZCBF=Z DEF连接BE在三角形BEF中,BF=EF/. Z EBF=Z BEFo・・・ Z ABC= Z AED o・・・ Z ABE= Z AEBo/. AB=AE o在三角形ABF和三角形AEF屮AB=AE,BF=EF,ZABF= Z ABE+ Z EBF= ZAEB+ Z BEF= Z AEF・・・三角形ABF和三角形AEF全等。
・・・ Z BAF= Z EAF(Z 1= Z 2)o4. 己知:Z 1= Z 2 , CD=DE , EF//AB ,求证:EF=AC过C作CG〃EF交AD的延长线于点GCG// EF,可得,Z EFD= CGDDE= DCZFDE= Z GDC (对顶角)AA EFD^A CGDEF= CGZCGD = Z EFD又,EF// AB・・・,Z EFD= Z 1Z1= Z 2・・・Z CGD= Z 2・・・△ AGC为等腰三角形,AC= CG又EF=CG・・・EF= AC5.已知:AD 平分Z BAC, AC=AB+BD ,求证:Z B=2 Z C证明:延长AB取点E,使AE=AC,连接DEVAD 平分Z BACAZ EAD=Z CAD・・・AE=AC, AD = ADA A AED^A ACD ( SAS)AZ E=Z CVAC = AB+BD・・・AE= AB+BD・・・AE= AB+BEABD = BE・・・Z BDE=Z EVZ ABC=Z E+ Z BDEAZ ABC = 2 ZEAZ ABC = 2 ZC6.己知:AC 平分Z BAD , CE丄AB , Z B+ Z D=180 ° ,求证:AE=AD+BE・・・CE丄AB ・・・Z CEB=Z CEF= 90° ・・・EB=EF, CE = CE, AACEB^ACEF ・・・Z B=Z CFEVZ B+Z D= 180 ° , ZCFE+Z CFA= 180 0AZ D = Z CFAVAC 平分Z BAD・・・Z DAC = Z FACVAC = AC・・・△ ADC 竺△ AFC ( SAS)/.AD = AF ・・・AE= AF+ FE= AD + BE解:延长AD至IJE,使AD=DE・・・D是BC中点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DC7.已知:AB=4 , AC=2 , D是BC屮点, AD是整数,求ADA 证明:在AE上取F,使EF= EB,连接CFAAACD^ABDE•*. AC=BE=2・・•在△ ABE中AB-BE < AE<AB+BE・・・AB=4即4・2 < 2AD < 4+21 < AD < 3・・・AD=218.已知:D 是AB 中点,Z ACB=90 0,求证:CD -AB2解:延长AD到E,使AD=DE・・・D是BC屮点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DCAA ACD A BDE•*. AC=BE=2•・•在A ABE中9.已知:BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点,求证:Z 1= Z2A证明:连接BF和EF。
八年级全等三角形证明经典50题含答案

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
八年级全等三角形证明经典50题含答案

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
八年级全等三角形证明经典50题含答案

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
八年级全等三角形证明经典50题-精品.pdf

求证: DE=DF .
A
E F
B
D
C
37.已知:如图 , AC BC 于 C , DE AC 于 E , AD AB 于 A , BC =AE .若 AB = 5 ,求 AD 的长?
A
D E
B
C
7
38.如图: AB=AC , ME ⊥ AB , MF ⊥ AC ,垂足分别为 E、 F,ME=MF 。求证: MB=MC
A
E
F
B
M
C
39. 如 图 , 给 出 五 个 等 量 关 系 : ① AD BC ② AC BD ③ CE DE ④ D C
⑤ DAB CBA .请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出
一种情况),并加以证明.
已知:
求证:
D
C
E
证明:
A
B
40.在△ ABC 中, ACB 90 , AC BC ,直线 MN 经过点 C ,且 AD MN 于 D , BE MN 于 E .(1) 当直线 MN 绕点 C 旋转到图 1 的位置时,求证: ① ADC ≌ CEB ;② DE AD BE ; (2) 当直线 MN 绕点 C 旋转到图 2 的位置时,( 1)中的结论还成立吗?若成立,请给出证明;若不成立,
F
D
2
10. 已知:∠ 1=∠ 2, CD=DE , EF//AB ,求证: EF=AC
A 12
F
C D E B
11. 已知: AD 平分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ C A
C
B
D
12. 已知: AC 平分∠ BAD , CE⊥ AB ,∠ B+ ∠D=180 °,求证: AE=AD+BE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀名校全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD?解析:延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2ADBC证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BECDB AB ACD F2 1 E证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
证明:在BC 上截取BF=BA,连接EF.∠ABE=∠FBE,BE=BE,则⊿ABE ≌ΔFBE(SAS),∠EFB=∠A;AB 平行于CD,则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠DCE,CE=CE,故⊿FCE ≌ΔDCE(AAS),FC=CD.所以,BC=BF+FC=AB+CD.13.已知:AB//ED ,∠EAB=∠BDE ,AF=C D ,EF=BC ,求证:∠F=∠C证明:AB//ED,AE//BD 推出AE=BD, 又有AF=CD,EF=BC所以三角形AEF 全等于三角形DCB , 所以:∠C=∠FDCB A F E14. 已知:AB=CD ,∠A=∠D ,求证:∠B=∠C证明:设线段AB,CD 所在的直线交于E ,(当AD<BC时,E 点是射线BA,CD 的交点,当AD>BC 时,E 点是射线AB,DC 的交点)。
则:△AED 是等腰三角形。
所以:AE=DE 而AB=CD 所以:BE=CE (等量加等量,或等量减等量)所以:△BEC 是等腰三角形所以:角B=角C.15. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB证明:作B 关于AD 的对称点B‘,因为AD 是角BAC 的平分线,B'在线段AC 上(在AC 中间,因为AB 较短)因为PC<PB’+B‘C,PC -PB’<B‘C,而B'C=AC-AB'=AC-AB,所以PC-PB<AC-AB16. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE证明:∠BAC=180-(∠ABC+∠C=180-4∠C ∠1=∠BAC/2=90-2∠C ∠ABE=90-∠1=2∠C 延长BE 交AC 于F因为,∠1 =∠2,BE ⊥AE 所以,△ABF 是等腰三角形AB=AF,BF=2BE ∠FBC=∠ABC-∠ABE=3∠C-2∠C=∠CBF=CFAC-AB=AC-AF=CF=BF=2BE17. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DCA B C D P D ACB FAE DC B证明:作AG ∥BD 交DE 延长线于G AGE 全等BDEAG=BD=5AGF ∽CDF AF=AG=5所以DC=CF=2 18.(5分)如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .证明:延长AD 至H 交BC 于H;BD=DC; 所以:∠DBC=∠角DCB;∠1=∠2;∠DBC+∠1=∠角DCB+∠2;∠ABC=∠ACB; 所以:AB=AC;三角形ABD 全等于三角形ACD;∠BAD=∠CAD;AD 是等腰三角形的顶角平分线所以:AD 垂直BC19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA证明:因为AOM 与MOB 都为直角三角形、共用OM ,且∠MOA=∠MOB 所以MA=MB 所以∠MAB=∠MBA 因为∠OAM=∠OBM=90度所以∠OAB=90-∠MAB ∠OBA=90-∠MBA 所以∠OAB=∠OBA20.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP于D .求证:AD +BC =AB .证明:做BE 的延长线,与AP 相交于F 点,∵PA//BC ∴∠PAB+∠CBA=180°,又∵,AE ,BE 均为∠PAB 和∠CBA 的角平分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB 为直角三角形在三角形ABF 中,AE ⊥BF ,且AE 为∠FAB 的角平分线 ∴三角形FAB 为等腰三角形,AB=AF,BE=EF 在三角形DEF 与三角形BEC 中,∠EBC=∠DFE,且BE=EF ,∠DEF=∠CEB ,∴三角形DEF与三角形BEC 为全等三角形,∴DF=BC ∴AB=AF=AD+DF=AD+BCPEDC BA21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B证明:在AB 上找点E ,使AE=AC ∵AE=AC ,∠EAD=∠CAD ,AD=AD ∴△ADE ≌△ADC 。
DE=CD ,∠AED=∠C ∵AB=AC+CD ,∴DE=CD=AB-AC=AB-AE=BE ∠B=∠EDB ∠C=∠B+∠ED B=2∠BDCB A22.如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.分析:通过证明两个直角三角形全等,即Rt△DEC≌Rt△BFA以及垂线的性质得出四边形BEDF是平行四边形.再根据平行四边形的性质得出结论.解答:解:(1)连接BE,DF.∵DE⊥AC于E,BF⊥AC于F,,∴∠DEC=∠BFA=90°,DE∥BF,在Rt△DEC和Rt△BFA中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA,∴DE=BF.∴四边形BEDF是平行四边形.∴MB=MD,ME=MF;(2)连接BE,DF.∵DE⊥AC于E,BF⊥AC于F,,∴∠DEC=∠BFA=90°,DE∥BF,在Rt△DEC和Rt△BFA中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA,∴DE=BF.∴四边形BEDF是平行四边形.∴MB=MD,ME=MF.23.已知:如图,DC∥AB,且DC=AE,E为AB的中点,(1)求证:△AED≌△EBC.(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):证明:(1)DC∥AE,且DC=AE,所以四边形AECD是平行四边形。
于是知AD=EC,且∠EAD=∠BEC。
由AE=BE,所以△AED≌△EBC。
(2)△AEC、△ACD、△ECD都面积相等。
24.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.OEDCBA求证:BD =2CE . 证明:延长BA 、CE ,两线相交于点F ∵BE ⊥CE ∴∠BEF=∠BEC=90° 在△BEF 和△BEC 中 ∠FBE=∠CBE, BE=BE, ∠BEF=∠BEC ∴△BEF ≌△BEC(ASA) ∴EF=EC ∴CF=2CE ∵∠ABD+∠ADB=90°,∠ACF+∠CDE=90° 又∵∠ADB=∠CDE ∴∠ABD=∠ACF 在△ABD 和△ACF 中 ∠ABD=∠ACF, AB=AC, ∠BAD=∠CAF=90° ∴△ABD ≌△ACF(ASA) ∴BD=CF ∴BD=2CE25、如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
26、如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
证明:∵BE‖CF ∴∠E=∠CFM ,∠EBM=∠FCM ∵BE=CF ∴△BEM ≌△CFM∴BM=CM ∴AM 是△ABC 的中线.27、如图:在△ABC 中,BA=BC ,D 是AC 的中点。
求证:BD ⊥AC 。
