备战中考物理杠杆平衡条件的应用问题(大题培优 易错 难题)
2020-2021备战中考物理杠杆平衡条件的应用问题(大题培优 易错 难题)附答案

一、初中物理杠杆平衡条件的应用问题 1.如图所示为建筑工地上常用的吊装工具,物体M为重5000N的配重,杠杆AB的支点为O,已知OA∶OB=1∶2,滑轮下面挂有建筑材料P,每个滑轮重100N,工人体重为700N,杠杆与绳的自重、滑轮组摩擦均不计,当工人用300N的力竖直向下以1m/s的速度
匀速拉动绳子时( )
A.工人对地面的压力为400N B.建筑材料P重为600N C.建筑材料P上升的速度为3m/s D.物体M对地而的压力为4400N 【答案】A 【解析】 【分析】 【详解】 A.当工人用300N的力竖直向下拉绳子时,绳子对工人会施加竖直向上的拉力,其大小也
为300N,此时人受竖直向下的重力G、竖直向上的拉力F、竖直向上的支持力F支,由力的平衡条件知道 F+F支=G 即 F支=G-F=700N-300N=400N 由于地面对人的支持力和人对地面的压力是一对相互作用力,大小相等,所以,工人对地面的压力 F压=F支=400N 故A正确;
B.由图知道,绳子的有效段数是n=2,且滑轮组摩擦均不计,由12FGG物动知道,
建筑材料P的重力 G=2F-G动 =2×300N-100N=500N 故B错误; C.因为物重由2段绳子承担,所以,建筑材料P上升的速度
11=1m/s=0.5m/s22vv绳
故C错误; D.以定滑轮为研究对象,定滑轮受向下的重力、3段绳子向下的拉力、杆对定滑轮向上的
拉力,由力的平衡条件知道 FA ′=3F+G定 =3×300N+100N=1000N 杠杆对定滑轮的拉力和定滑轮对杠杆的拉力是一对相互作用力,大小相等,即 FA=F′A =1000N 由杠杆的平衡条件知道 FA ×OA=FB ×OB 又因为OA:OB=1:2,所以
AB
1000=5N00N2FOAOAFOBOA
由于物体间力的作用是相互的,所以,杠杆对物体M的拉力等于物体M对杠杆的拉力,即 FB′=FB =500N 物体M受竖直向下的重力、竖直向上的支持力、竖直向上的拉力,则物体M受到的支持力为 FM支持 =GM -FB′=5000N-500N=4500N 因为物体间力的作用是相互的,所以物体M对地面的压力 FM压=FM支持=4500N 故D错误。 故选A。
备战中考物理知识点过关培优 易错 难题训练∶杠杆平衡条件的应用问题及详细答案

一、初中物理杠杆平衡条件的应用问题1.身高相同的兄弟二人用一根重力不计的均匀扁担抬起一个900N 的重物.已知扁担长为1.8m ,重物悬挂点与哥哥的肩之间的距离OA=0.8m ,如图所示.则A .以哥哥的肩A 为支点,可计算出弟弟承担的压力为400NB .以O 为支点,可计算出兄弟二人承担的压力之比为4:9C .以O 为支点,可计算出兄弟二人承担的压力之比为9:5D .以弟弟的肩B 为支点,可计算出哥哥承担的压力为600N【答案】A【解析】【分析】【详解】A .设哥哥承担的压力为F A ,弟弟承担的压力为FB ,以哥哥的肩A 为支点,由杠杆平衡条件可得:B F AB G OA ⨯=⨯,9000.84001.8B G OA N m F N AB m⨯⨯===, A 选项正确; BC .因为支点是固定点,杠杆能绕支点转动,图中的O 不符合支点的特点,B 、C 选项错误,不符合题意.D .以弟弟的肩B 为支点,由杠杆平衡条件可得:A F AB G OB ⨯=⨯,900N 1.0m =500N 1.8mA G OB F AB ⨯⨯==, D 选项错误,不符合题意;2.AC 硬棒质量忽略不计,在棒的B 、C 两点施加力F 1、F 2,F 2的方向沿OO'线,棒在图所示位置处于静止状态,则( )A .F 1<F 2B .F 1=221s F s C .F 1力臂等于s 1D .F 2方向沿OO '线向上【答案】D【解析】【详解】AC .由图知,F 2的方向沿OO ′线,其力臂最长,为s 2;而F 1的方向竖直向下,所以其力臂L 1是从A 点到F 1的垂线段,小于s 1,更小于s 2, 由F 1L 1=F 2L 2知,L 1<s 2,所以F 1一定大于F 2,故AC 不符合题意;B .由F 1L 1=F 2L 2知,F 1L 1=F 2s 2,即2211F s F L故B 不符合题意; D .已知F 1的方向是竖直向下的,为保持杠杆平衡,F 2的方向应该沿OO′向上,故D 符合题意。
2020-2021备战中考物理杠杆平衡条件的应用问题(大题培优 易错 难题)附答案解析
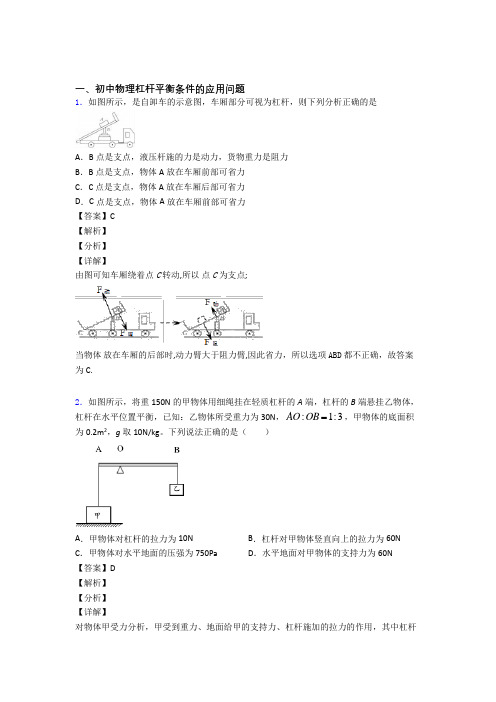
一、初中物理杠杆平衡条件的应用问题1.如图所示,是自卸车的示意图,车厢部分可视为杠杆,则下列分析正确的是A.B点是支点,液压杆施的力是动力,货物重力是阻力B.B点是支点,物体A放在车厢前部可省力C.C点是支点,物体A放在车厢后部可省力D.C点是支点,物体A放在车厢前部可省力【答案】C【解析】【分析】【详解】由图可知车厢绕着点C转动,所以点C为支点;当物体放在车厢的后部时,动力臂大于阻力臂,因此省力,所以选项ABD都不正确,故答案为 C.2.如图所示,将重150N的甲物体用细绳挂在轻质杠杆的A端,杠杆的B端悬挂乙物体,AO OB ,甲物体的底面积杠杆在水平位置平衡,已知:乙物体所受重力为30N,:1:3为0.2m2,g取10N/kg。
下列说法正确的是()A.甲物体对杠杆的拉力为10N B.杠杆对甲物体竖直向上的拉力为60N C.甲物体对水平地面的压强为750Pa D.水平地面对甲物体的支持力为60N【答案】D【解析】【分析】【详解】对物体甲受力分析,甲受到重力、地面给甲的支持力、杠杆施加的拉力的作用,其中杠杆施加的拉力与甲对杠杆的拉力为一对相互作用力,地面给甲的支持力和甲给地面的压力为一对相互作用力。
AB.根据杠杆平衡条件可知杠杆A端受到物体的拉力与OA的乘积等于乙给B端的拉力与OB的乘积相等,则有A330N90N1G OBFOA==⨯=乙即甲对杠杆的拉力为90N,杠杆施加的拉力与甲对杠杆的拉力为一对相互作用力,故AB项错误;CD.甲给地面的压力等于地面给甲的支持力为A150N90N60NF FG F==-=-=甲压支则甲物体对水平地面的压强260N300Pa0.2mFpS===压甲甲故C项错误,D项正确。
故选D。
3.如图所示为等刻度轻质杠杆,A处挂4牛的物体,若使杠杆在水平位置平衡,则在B处施加的力()A.可能为0.5牛B.一定为2牛C.一定为3牛D.可能是4牛【答案】D【解析】【分析】【详解】设杠杆每小格的长度为L,若在B点用垂直OB竖直向下的力使杠杆在水平位置平衡,此时所用的力最小,根据杠杆平衡条件1122Fl F l=可得min42F LG L⋅=⋅则有min24N22N44G LFL⋅⨯===若在B点斜拉使杠杆在水平位置平衡,由杠杆平衡条件1122Fl F l=可知2211F lFl=则此时杠杆左边的阻力与阻力臂的乘积不变,动力臂减小,故动力将增大,故若使杠杆在水平位置平衡,在B 点施加的力2N F ≥故选D 。
备战中考物理培优 易错 难题(含解析)之杠杆平衡条件的应用问题含答案解析

一、初中物理杠杆平衡条件的应用问题1.在我国古代书籍《墨经》中,对杠杆有精辟论述,并有许多巧妙的应用.如下图所示是在井上汲水的桔槔,下列对其在使用中正确的解释是A.桔槔是等臂杠杆,不省力也不费力B.向井内放送水桶时,人用的力气一定小于水桶的重力,所以省力C.桔槔是不等臂杠杆,动力臂小于阻力臂,是费力杠杆D.往上提水时,人用的力气一定小于桶与水的总重,所以省力【答案】D【解析】【分析】杠杆的分类:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂;要使杠杆平衡,作用在杠杆上的两个力(用力点、支点和阻力点)的大小跟它们的力臂成反比。
【详解】AC.由图可见,桔槔是不等臂杠杆,动力臂大于阻力臂,是省力杠杆,故AC错误;B.向井内放送水桶时,人用的力通过杠杆原理,与石头的重力相关,一般比木桶的重力要大,故B错误;D.往上提水时,因为有石头帮忙,人的力气比水和桶的总重力小,故D正确。
故选D。
【点睛】此题主要考查了对简单机械的认识,要掌握杠杆的要素。
2.如图所示,将重150N的甲物体用细绳挂在轻质杠杆的A端,杠杆的B端悬挂乙物体,AO OB ,甲物体的底面积杠杆在水平位置平衡,已知:乙物体所受重力为30N,:1:3为0.2m2,g取10N/kg。
下列说法正确的是()A.甲物体对杠杆的拉力为10N B.杠杆对甲物体竖直向上的拉力为60NC .甲物体对水平地面的压强为750PaD .水平地面对甲物体的支持力为60N【答案】D【解析】【分析】【详解】 对物体甲受力分析,甲受到重力、地面给甲的支持力、杠杆施加的拉力的作用,其中杠杆施加的拉力与甲对杠杆的拉力为一对相互作用力,地面给甲的支持力和甲给地面的压力为一对相互作用力。
AB .根据杠杆平衡条件可知杠杆A 端受到物体的拉力与OA 的乘积等于乙给B 端的拉力与OB 的乘积相等,则有A 330N 90N 1G OB F OA ==⨯=乙 即甲对杠杆的拉力为90N ,杠杆施加的拉力与甲对杠杆的拉力为一对相互作用力,故AB 项错误;CD .甲给地面的压力等于地面给甲的支持力为A 150N 90N 60N F F G F ==-=-=甲压支则甲物体对水平地面的压强260N 300Pa 0.2m F p S ===压甲甲 故C 项错误,D 项正确。
备战中考物理杠杆平衡(大题培优 易错 难题)含答案

一、初中物理杠杆平衡条件的应用问题 1.如图所示为建筑工地上常用的吊装工具,物体M是重5000N的配重,杠杆AB的支点为O,已知长度OA∶OB=1∶2,滑轮下面挂有建筑材料P,每个滑轮重100N,工人体重为
700N,杠杆与绳的自重、滑轮组摩擦均不计。当工人用300N的力竖直向下以1m/s的速度
匀速拉动绳子时( )
A.建筑材料P上升的速度为3m/s B.物体M对地面的压力为5000N C.工人对地面的压力为400N D.建筑材料P的重力为600N 【答案】C 【解析】 【分析】 【详解】 A.物重由2段绳子承担,建筑材料P上升的速度
v=12v绳=12×1m/s=0.5m/s 故A错误; B.定滑轮受向下的重力、3段绳子向下的拉力、杠杆对定滑轮向上的拉力,由力的平衡条
件可得 F A′=3F+G定=3×300N+100N=1000N 杠杆对定滑轮的拉力和定滑轮对杠杆的拉力是一对相互作用力,大小相等,即 FA= F A′=1000N 根据杠杆的平衡条件FA×OA=FB×OB,且OA:OB=1:2,所以
FB=FA×OAOB =1000N×2OAOA=500N 因为物体间力的作用是相互的,所以杠杆对物体M的拉力等于物体M对杠杆的拉力,即 F B′=FB=500N 物体M受竖直向下的重力、竖直向上的支持力、竖直向上的拉力,则物体M受到的支持力为 FM支持=GM− F B′=5000N−500N=4500N 因为物体间力的作用是相互的,所以物体M对地面的压力 FM压=FM支持=4500N 故B错误; C.当工人用300N的力竖直向下拉绳子时,因力的作用是相互的,则绳子对工人会施加竖
直向上的拉力,其大小也为300N,此时人受竖直向下的重力G、竖直向上的拉力F、竖直向上的支持力F支,由力的平衡条件可得F+F支=G,则 F支=G−F=700N−300N=400N 因为地面对人的支持力和人对地面的压力是一对相互作用力,大小相等,所以工人对地面的压力 F压=F支=400N 故C正确;
2020-2021备战中考物理 杠杆平衡条件的应用问题 培优 易错 难题练习(含答案)含答案

一、初中物理杠杆平衡条件的应用问题1.如图所示,杠杆在水平位置平衡.下列操作仍能让杠杆在水平位置保持平衡的是()A.两侧钩码同时向外移一格B.两侧钩码同时向内移一格C.在两侧钩码下方,同时加挂一个相同的钩码D.左侧增加一个钩码,右侧钩码向外移一格【答案】D【解析】【分析】【详解】设一个钩码的重力为G,横梁上一个格的长度为l,原来杠杆处于平衡状态,则有2332⨯=⨯G l G lA.两侧钩码同时向外移一格,左边为⨯=G l Gl248右边为⨯=339G l GlGl Gl<89杠杆右端下沉,故A项不符合题意;B.两侧钩码同时向内移一格,左边为⨯=G l Gl224右边为313⨯=G l Gl<34Gl Gl杠杆左端下沉,故B项不符合题意;C.同时加挂一个相同的钩码,左边为⨯=G l Gl339右边为⨯=G l Gl428<Gl Gl89杠杆左端下沉,故C项不符合题意;D.左侧增加一个钩码,右侧钩码向外移一格,左边为⨯=G l Gl339右边为⨯=G l Gl339=Gl Gl99杠杆平衡,故D项符合题意。
故选D。
2.如图所示,杠杆挂上钩码后刚好平衡,每个钩码的质量相同,在下列情况中,杠杆还能平衡的是A.左右钩码各向支点移一格B.左右各减少一个钩码C.左右各减少一半钩码D.左右各增加两个钩码【答案】C【解析】设杠杆的分度值为 L,一个钩码的重为G.原来4G×2L=2G×4L;左、右钩码各向支点移动一格,左边=4G×L=4GL,右边=2G×3L=6GL,左边<右边,杠杆向右端下沉,A不符合题意;左右各减少一个钩码,左边=3G×2L=6GL,右边=G×4L=4GL,左边>右边,杠杆向左下沉,B 不符合题意;左、右钩码各减少一半法码,左边=2G×2L=4GL,右边=G×4L=4GL,左边=右边,杠杆平衡;C符合题意;左右各增加两个钩码,左边=6G×2L=12GL,右边=4G×4L=16GL,左边<右边,杠杆右边下沉,D不符合题意,故选C.3.如图所示,作用在A点的各个力中,不可能使杠杆平衡的力是A.F3和F4B.F1和F3C.F2和F4D.F1和F2【答案】A【解析】【详解】因为力F3的作用线所在的直线过支点O,所以力F3的力臂为0,又因为0乘以任何数都为0,所以力F3不能使杠杆平衡;力F4使杠杆转动方向与重物使杠杆的转动方向相同,所以力F4不能使杠杆平衡;力F1和F2使杠杆转动方向与重物使杠杆转动方向相反,所以力F1和F2可以使杠杆平衡;故选A。
