混沌动力系统 On the Lebesgue measure of Li-Yorke pairs for interval maps
混沌学

[编辑本段混沌学探秘计94 991422 刘洋。
]简介混沌学(英文:Chaos)在科学上,如果一个系统的演变过程对初态非常敏感,人们就称它为混沌系统。
研究混沌运动的一门新学科,叫作混沌学。
混沌学发现,出现混沌运动这种奇特现象,是由系统内部的非线性因素引起的。
[编辑本段]混沌学的起源和发展1972年12月29日,美国麻省理工学院教授、混沌学开创人之一E.N.洛伦兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文,提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个陆龙卷,并由此提出了天气的不可准确预报性。
时至今日,这一论断仍为人津津乐道,更重要的是,它激发了人们对混沌学的浓厚兴趣。
今天,伴随计算机等技术的飞速进步,混沌学已发展成为一门影响深远、发展迅速的前沿科学。
一般地,如果一个接近实际而没有内在随机性的模型仍然具有貌似随机的行为,就可以称这个真实物理系统是混沌的。
一个随时间确定性变化或具有微弱随机性的变化系统,称为动力系统,它的状态可由一个或几个变量数值确定。
而一些动力系统中,两个几乎完全一致的状态经过充分长时间后会变得毫无一致,恰如从长序列中随机选取的两个状态那样,这种系统被称为敏感地依赖于初始条件。
而对初始条件的敏感的依赖性也可作为一个混沌的定义。
与我们通常研究的线性科学不同,混沌学研究的是一种非线性科学,而非线性科学研究似乎总是把人们对“正常”事物“正常”现象的认识转向对“反常”事物“反常”现象的探索。
例如,孤波不是周期性振荡的规则传播;“多媒体”技术对信息贮存、压缩、传播、转换和控制过程中遇到大量的“非常规”现象产生所采用的“非常规”的新方法;混沌打破了确定性方程由初始条件严格确定系统未来运动的“常规”,出现所谓各种“奇异吸引子”现象等。
混沌来自于非线性动力系统,而动力系统又描述的是任意随时间发展变化的过程,并且这样的系统产生于生活的各个方面。
举个例子,生态学家对某物种的长期性态感兴趣,给定一些观察到的或实验得到的变量(如捕食者个数、气候的恶劣性、食物的可获性等等),建立数学模型来描述群体的增减。
广义符号动力系统中的Li-Yorke混沌集和ω-混沌集

广义符号动力系统中的Li-Yorke混沌集和ω-混沌集刘龙生;康云莲;赵俊玲【摘要】本文在广义符号动力系统Σ(Z+)中构造一个传递的、不变的、不可数的Li-Yorke混沌集,且这个混沌集D(C)Σ(Z+)∞∪N=2Σ(N),还构造了一个不可数的ω-混沌集,且这个混沌集S '(C)Σ(Z+)∞∪N=2Σ(N).说明了广义符号动力系统的混沌性状不是集中在有限个符号的动力系统中,在有限个符号动系统∞∪ N=2Σ(N)的外部仍然具有较强的混沌性状.【期刊名称】《广西师范大学学报(自然科学版)》【年(卷),期】2014(032)002【总页数】7页(P75-81)【关键词】Li-Yorke混沌集;ω-混沌集;不变集;传递点【作者】刘龙生;康云莲;赵俊玲【作者单位】广西师范大学数学与统计学院,广西桂林541004;广西师范大学数学与统计学院,广西桂林541004;广西师范大学数学与统计学院,广西桂林541004【正文语种】中文【中图分类】O19符号动力系统是动力系统的强有力工具,在动力系统的混沌性研究中起着重要的作用。
广义符号动力系统把符号动力系统的有限个符号推广到了无限个符号。
文献[1-4]研究了广义符号动力系统的Li-Yorke混沌、Devaney混沌、拓扑混合性及广义转移不变集。
本文继续研究广义符号动力系统的Li-Yorke混沌性,在广义符号动力系统中构造一个传递的、不变的、不可数的Li-Yorke混沌集~D,并证明~D⊂Σ (Z+)\∪∞N=2Σ(N)。
混沌是动力系统中的重要内容,Li-Yorke混沌是其中最基本的一种。
随着研究的不断深入,人们根据Li-Yorke混沌集的特点,定义了稠密混沌[5]、通有混沌[6];利用Lebesgue测度与Hausdorff维数,研究了混沌集的大小,定义了几乎处处混沌[7]等。
传递的混沌不仅要求混沌集本身的稠密性,而且要求混沌集中的每个点都是系统的传递点。
混沌集的不变性是指在映射作用下混沌集是个不变集。
混沌系统理论 ppt课件

D log N(r) 或 log(1/ r)
DlimlogN(r) r0 log1(/ r)
一般地,我们就把这样定义的容量维叫做豪斯道夫 维数,把豪斯道夫维数是分数的物体称为分形,把此
时的D 值称为该分形的分形维数,简称分维。也有人
把该维数称为分数维。
奇怪吸引子
奇怪吸引子又叫分形吸引子,因为它们都是相空间的分形点集, 不能用传统的规则几何图形表示。一个耗散系统的相空间当时间 趋于无穷大时,如果收缩到一个非整数维的点集,这就是一个奇 怪吸引子。
混沌系统理论 ppt课件
蝴蝶效应
1979年12月,洛伦兹在华盛顿的美国科学促进会的一次 演讲中提出:一只南美洲的蝴蝶,偶尔扇动几下翅膀,在两 周以后可以引起美国德克萨斯州的一场龙卷风。
此效应说明,事物发展的结果, 对初始条件具有极为敏感的依赖 性,初始条件的极小偏差,将会 引起结果的极大差异,甚至会呈 现一种混沌状态。
dz d
bz
xy
x -对流的翻动速率 y -比例于上流与下流液体之间的温差 z-是垂直方向的温度梯度
无量纲因子
b-速度阻尼常数
r -相对瑞利数 r = R/RC。
这是一个三维系统,x、y、z为状态变量,σ、r、b为控 制参量。 Nhomakorabea伦兹方程
在r 较小的情况下,系统是稳定的,随着的r 增加,系统 趋于复杂,出现不稳定的极限环,在r =28时达到混沌 状态。所以, σ = 10 ,b = 8/3 ,r = 28 时利用 Matlab编程,得到下图:
xn1axn(1xn)
它经常被用来描述没有世代交叠的昆虫群体的繁殖 演化,称为虫口模型。a为控制参数,虫口数x为状 态变量,xn为第n代虫口数,虫口模型给出第n代虫 口与第n+1代虫口的关系,知道n代虫口就可以按 逻辑斯蒂方程计算第n+1代虫口。
Ch.6 分形混沌动力系统

x≠ f
2
(x ) ,表明当
1 + 6 < λ < 3 .544 1L 时, x 是周期 4 吸引不动点,
λ > 3 .544 1L 时,是排斥不动点。
又计算 x = f 8 ( x ) 且 x ≠ f 4 ( x ) ,表明当 3 .544 1L < λ < 3 .564 4 L 时, 8 周期点 x是吸引的; 当 λ > 3 .564 4 L时, x 是排斥的, L 。
图6.5
λ ∞ < λ < 4 时Logistic方程的倍周期分叉图
图6.6 Logistic方程在λ ∞ ≤ λ ≤ 3 .58 时的倍周期分叉图
不过,仍然有不可数的 λ 数使得映射的行为是混沌的。 在我们把图像6.3后半部分逐渐放大,就是图6.7,在这个 区域,我们看到了较大分岔图的缩微版。如果再将它放 大,又可见更小的相似分岔图,而且可以逐渐继续下去。 这就是自相似性,是分形的最重要特征。图中的小方块 放大后就是下一个图形。
{R
例 6.1 设 W ( x ) = Ax + t 是 R 2 中的仿射变换,则
2
; W 是动力系统。
}
例 6.2
2 x mod 1 = 2 x − [2 x ] 。
{[0 ,1 ] ; 2 x mod 1}是动力系统,其中
, y ) ≤ ε } ,这 x 称为 f 的吸引不动点。如 f 果存在 ε > 0 和 c > 1 使得
如果一个点是 f n 的吸引不动点,那周期为 n 的 f 周期点是吸引的。如果一个循环包含有一个 f 的周期 n 吸引周期点,那 f 的周期 n 循环是吸引循环。反之,如 果一个点是 f n 的排斥不动点,那 f 的周期 n 周期点是 排斥的。如果一个循环包含有一个 f 的周期 n 排斥周期 点,这个周期 n 循环是排斥循环。
A new test for chaos justification

A new test for chaosin deterministic systemsBy Georg A.Gottwald†and Ian Melbourne‡We describe a new test for determining whether a given deterministic dynamical system is chaotic or nonchaotic.In contrast to the usual method of computing the maximal Lyapunov exponent,our method is applied directly to the time series data and does not require phase space reconstruction.Moreover,the dimension of the dynamical system and the form of the underlying equations is irrelevant.The input is the time series data and the output is0or1depending on whether the dynamics is non-chaotic or chaotic.The test is universally applicable to any deterministic dynamical system,in particular to ordinary and partial differential equations,and to maps.Our diagnostic is the real valued function p(t)= t0φ(x(s))cos(θ(s))d s whereφis an observable on the underlying dynamics x(t)andθ(t)=ct+ t0φ(x(s))d s.The constant c>0isfixed arbitrarily.We define the mean-square-displacement M(t) for p(t)and set K=lim t→∞log M(t)/log ing recent developments in ergodic theory,we argue that typically K=0signifying nonchaotic dynamics or K=1 signifying chaotic dynamics.Keywords:Chaos,deterministic dynamical systems,Lyapunov exponents,mean square displacement,Euclidean extension1.IntroductionThe usual test of whether a deterministic dynamical system is chaotic or nonchaotic is the calculation of the largest Lyapunov exponentλ.A positive largest Lyapunov exponent indicates chaos:ifλ>0,then nearby trajectories separate exponentially and ifλ<0,then nearby trajectories stay close to each other.This approach has been widely used for dynamical systems whose equations are known(Abarbanel et al.1993;Eckmann et al.1986;Parker&Chua1989).If the equations are not known or one wishes to examine experimental data,this approach is not directly applicable. However Lyapunov exponents may be estimated(Wolf et al.1985;Sana&Sawada 1985;Eckmann et al.1986;Abarbanel et al.1993)by using the embedding theory of Takens(1981)or by approximating the linearisation of the evolution operator. Nevertheless,the computation of Lyapunov exponents is greatly facilitated if the underlying equations are known and are low-dimensional.In this article,we propose a new0–1test for chaos which does not rely on knowing the underlying equations,and for which the dimension of the equations is irrelevant.The input is the time series data and the output is either a0or a1 depending on whether the dynamics is nonchaotic or chaotic.Since our method is †School of Mathematics and Statistics,University of Sydney,NSW2006,Australia‡Department of Mathematics and Statistics,University of Surrey,Guildford,Surrey GU27XH, UKArticle submitted to Royal Society T E X Paper2G.Gottwald and I.Melbourneapplied directly to the time series data,the only difference in difficulty between analysing a system of partial differential equations or a low-dimensional system of ordinary differential equations is the effort required to generate sufficient data.(As with all approaches,our method is impracticable if there are extremely long tran-sients or once the dimension of the attractor becomes too large.)With experimental data,there is the additional effect of noise to be taken into consideration.We briefly discuss this important issue at at the end of this paper.However,our aim in this paper is to present ourfindings in the situation of noise-free deterministic data.2.Description of the0–1test for chaosTo describe the new test for chaos,we concentrate on the continuous time case and denote a solution of the underlying system by x(t).The discrete time case is handled analogously with the obvious modifications.Consider an observableφ(x) of the underlying dynamics.The method is essentially independent of the actual form ofφ—almost any choice ofφwill suffice.For example if x=(x1,x2,...,x n) thenφ(x)=x1is a possible and simple choice.Choose c>0arbitrarily and defineθ(t)=ct+ t0φ(x(s))d s,p(t)= t0φ(x(s))cos(θ(s))d s.(2.1)(Throughout the examples in§3and§4wefix c=1.7once and for all.)We claim that(i)p(t)is bounded if the underlying dynamics is nonchaotic and(ii)p(t)behaves asymptotically like a Brownian motion if the underlying dynam-ics is chaotic.The definition of p in(2.1),which involves only the observableφ(x),highlights the universality of the test.The origin and nature of the data which is fed into the system(2.1)is irrelevant for the test,and so is the dimension of the underlying dynamics.Later on,we briefly explain the justification behind the claims(i)and(ii).For the moment,we suppose that the claims are correct and show how to proceed.To characterise the growth of the function p(t)defined in(2.1),it is natural to look at the mean square displacement(MSD)of p(t),defined to be1M(t)=limT→∞A new test for chaos3 which obviously does not change the slope K.)This allows for a clear distinction of a nonchaotic and a chaotic system as K may only take values K=0or K=1. We have lost though the possibility of quantifying the chaos by the magnitude of the largest Lyapunov exponentλ.Numerically one has to make sure that initial transients have died out so that the trajectories are on(or close to)the attractor at time zero,and that the integration time T is long enough to ensure T t.3.An example:the forced van der Pol oscillatorWe illustrate the0–1test for chaos with the help of a concrete example,the forced van der Pol system,˙x1=x2˙x2=−d(x21−1)x2−x1+a cosωt(3.1) which has been widely studied in nonlinear dynamics(van der Pol1927;Guck-enheimer&Holmes1990).Forfixed a and d,the dynamics may be chaotic or nonchaotic depending on the parameterω.Following Parlitz&Lauterborn(1987), we take a=d=5and letωvary from2.457to2.466in increments of0.00001. Chooseφ(x)=x1+x2and c=1.7.We stress that the results are independent of these choices for all practical purposes.As described below in§5,almost all choices will work.(Deliberately poor choices such as c=0,orφ=7orφ=t obviously fail;sensible choices that fail are virtually impossible tofind.)Infigure1we show a plot of K versusω.The periodic windows are clearly seen. As a comparison we show infigure2the largest Lyapunov exponentλversusω. Since the onset of chaos does not occur until afterω=2.462we display the results only for the range2.462<ω<2.466infigures1and2.(Both methods easily indicate regular dynamics for2.457<ω<2.462.)Naturally we do not obtain the values K=0and K=1exactly–the mathe-matical results that underpin our method predict these values in the limit of infi-nite integration time.(The same caveat applies equally to the Lyapunov exponent method.)In producing the data forfigures1and2,we allowed for a transient of 200,000units of time and then integrated up to time T=2,000,000.As can be seen infigure3,for most of the400data points in the range ofω,we obtain K>0.8or K<0.01.Next,we carry out the0–1test for the forced van der Pol system in the situation of a more limited quantity of data.The results are shown infigure4for2.463<ω<2.465.We again allow for a transient time200,000but then integrate only for T=50,000.The transitions between chaotic dynamics and periodic windows are almost as clear with T=50,000as they are with T=2,000,000even though the convergence of K to0or1is better with T=2,000,000.Article submitted to Royal Society4G.Gottwald and I.Melbourne 00.20.40.60.811.22.462 2.463 2.464 2.465 2.466Figure 1.Asymptotic growth rate K of the mean square displacement (2.2)versus ωfor the van der Pol system (3.1)determined by a numerical simulation of the skew product system (3.1)and (2.1)with a =d =5,c =1.7,φ(x )=x 1+x 2and ωvarying from 2.462to 2.466.The integration interval is T =2,000,000after an initial transient of 200,000units of time.-0.1-0.08-0.06-0.04-0.020.020.040.060.080.12.462 2.463 2.464 2.465 2.466Figure rgest Lyapunov exponent λversus ωfor the van der Pol system (3.1)with a =d =5and ωvarying from 2.462to 2.466(cf Parlitz &Lauterborn 1987).The integration interval is T =2,000,000after an initial transient of 200,000units of time.Article submitted to Royal SocietyA new test for chaos 500.20.40.60.811.22.462 2.463 2.464 2.465 2.466Figure 3.Asymptotic growth rate K versus ωfor the van der Pol system (3.1)as in figure 1with T =2,000,000.The horizontal lines represent K =0.01and K =0.8.0.20.40.60.811.22.463 2.464 2.46500.20.40.60.811.22.463 2.464 2.465Figure 4.Asymptotic growth rate K versus ωvarying from 2.463to 2.465for the van der Pol system as in figures 1and 3but with integration interval T =50,000after an initial transient of 200,000units of time.The horizontal lines represent K =0.01and K =0.8.Article submitted to Royal Society6G.Gottwald and I.Melbourne4.Further examplesTo test the method on high-dimensional systems we investigated the driven and damped Kortweg-de Vries(KdV)equation(Kawahara&Toh1988)u t+uu x+βu xxx+αu xx+νu xxxx=0,(4.1) on the interval[0,40]with periodic boundary conditions.This partial differential equation has non-chaotic solutions if the dispersionβis large and exhibits spatio-temporal chaos for sufficiently smallβ.Note that equation(4.1)reduces to the KdV equation whenα=ν=0,and reduces to the Kuramoto-Sivashinksy equation whenβ=0.Wefixα=2,ν=0.1and varyβ.Forβ=0,it is expected that the dynamics of the Kuramoto-Sivashinksy equation are chaotic for these parameter values.As an observable we usedφ(u(x,t))=u(x0,t)where x0is an arbitrarilyfixed position, and we iterated until time T=35,000.The0–1test confirms that the dynamics is chaotic atβ=0(with K=0.939).Also,we obtain K=0.989atβ=0.1and K=0.034atβ=4,indicating chaotic and regular dynamics respectively at these two parameter values.Finally,for discrete dynamical systems,we tried out the test with an ecological model whose chaotic component is coupled with strong periodicity(Brahona& Poon1996;Cazelles&Ferriere1992).The modelx k+1=118y k exp(−0.001(x k+y k))y k+1=0.2x k exp(−0.07(x k+y k))+0.8y k exp(−0.05(0.5x k+y k))has a non-connected chaotic attractor consisting of seven connected components. Our test yields K=1.023with only10,000data points and clearly shows that the dynamics is chaotic.5.Justification of the0–1test for chaosThe function p(t)can be viewed as a component of the solution to the skew product system˙θ=c+φ(x(t))˙p=φ(x(t))cosθ(5.1)˙q=φ(x(t))sinθdriven by the dynamics of the observableφ(x(t)).Here(θ,p,q)represent coordinates on the Euclidean group E(2)of rotationsθand translations(p,q)in the plane.We note that inspection of the dynamics of the(p,q)-trajectories of the group extension provides very quickly(for small T)a simple visual test of whether the underlying dynamics is chaotic or nonchaotic as can be seen fromfigure5.Article submitted to Royal SocietyA new test for chaos7(a)(b)Figure5.The dynamics of the translation components(p,q)of the E(2)-extension(5.1) for the van der Pol system(3.1)with a=d=5,c=1.7,φ(x)=x1+x2.These plots were obtained by integrating for T∼1400(with timestep0.01).In(a),an unbounded trajectory is shown corresponding to chaotic dynamics atω=2.46550.In(b),a bounded trajectory is shown corresponding to regular dynamics atω=2.46551.Article submitted to Royal Society8G.Gottwald and I.MelbourneIn Nicol et al.(2001)it has been shown that typically the dynamics on the group extension is sublinear and furthermore that typically the dynamics is bounded if the underlying dynamics is nonchaotic and unbounded(but sublinear)if the underlying dynamics is chaotic.Moreover,the p and q components each behave like a Brownian motion on the line if the chaotic attractor is uniformly hyperbolic(Field et al. 2002).A nondegeneracy result of Nicol et al.(2001)ensures that the variance of the Brownian motion is nonzero for almost all choices of observableφ.Recent work of Melbourne&Nicol(2002)indicates that these statements remain valid for large classes of nonuniformly hyperbolic systems,such as H´e non-like attractors.There is a weaker condition on the‘chaoticity’of X that guarantees the desired growth rate K=1for the mean square displacement(2.2):namely that the autocor-relation function ofφ(x)cos(θ)decays at a rate that is better than quadratic.More precisely,let x(t)andθ(t)denote solutions to the skew product equations(5.1)with initial conditions x0andθ0respectively.If there are constants C>0andα>2 such thatφ(x(t))cos(θ(t))φ(x0)cosθ0d x0dθ0 ≤Ct−α,for all t>0,then K=1as desired(Biktashev&Holden1998;Ashwin et al.2001; Field et al.2002).(Again,results of Nicol et al.(2001);Field et al.(2002);and Melbourne&Nicol(2002)ensure that the appropriate nondegeneracy condition holds for almost all choices ofφ.)There is a vast literature on proving decay of correlations(Baladi1999)and this has been generalised to the equivariant setting for discrete time by Field et al.(2002)and Melbourne&Nicol(2002)and for continuous time by Melbourne&T¨o r¨o k(2002).It follows from these references that K=1,for large classes of chaotic dynamical systems.One might ask why it is not better to work,instead of the E(2)-extension,with the simpler R-extension˙p=φ(x(t).In principle,p(t)can again be used as a detector for chaos.However,by the ergodic theorem p(t)will typically grow linearly with rate equal to the space average of φ.This would lead to K=2irrespective of whether the dynamics is regular or chaotic.Hence,it is necessary to subtract offthe linear term of p(t)in order to observe the bounded/diffusive growth that distinguishes between regular/chaotic dynamics.Subtracting this linear term is a highly nontrivial numerical obstruc-tion.The inclusion of theθvariable in the definition(2.1)of p(t)and in the skew product(5.1)kills offthe linear term.6.DiscussionWe have established a simple,inexpensive,and novel0–1test for chaos.The com-putational effort is of low cost,both in terms of programming efforts and in terms of actual computation time.The test is a binary test in the sense that it can only distinguish between nonchaotic and chaotic dynamics.This distinction is extremely clear by means of the diagnostic variable K which has values either close to0or close to1.The most powerful aspect of our method is that it is independent of the nature of the vectorfield(or data)under consideration.In particular the equationsArticle submitted to Royal SocietyA new test for chaos9 of the underlying dynamical system do not need to be known,and there is no prac-tical restriction on the dimension of the underlying vectorfield.In addition,our method applies to the observableφ(x(t))rather than the full trajectory x(t).Related ideas(though not with the aim to detect chaos)have been used for PDE’s in the context of demonstrating hypermeander of spirals in excitable me-dia(Biktashev&Holden1998)where the spiral tip appears to undergo a planar Brownian motion(see also Ashwin et al.2001).We note also the work of Coullet &Emilsson(1996)who studied the dynamics of Ising walls on a line,where the motion is the superposition of a linear drift and Brownian motion.(This is an ex-ample of an R-extension which we mentioned briefly in§5.As we pointed out then, the linear drift is an obstruction to using an R-extension to detect chaos.) From a purely computational point of view,the method presented here has a number of advantages over the conventional methods using Lyapunov exponents. At a more technical level,we note that the computation of Lyapunov exponents can be thought of abstractly as the study of the GL(n)-extension˙A=(d f)Ax(t)where GL(n)is the space of n×n matrices,A∈GL(n),and n is the size of the system.Note that the extension involves n2additional equations and is defined us-ing the linearisation of the dynamical system.To compute the dominant exponent, it is still necessary to add n additional equations,again governed by the linearised system.In contrast,our method requires the addition of two equations.In this paper,we have concentrated primarily on the idealised situation where there is an in principle unlimited amount of noise-free data.However,in§3we also demonstrated the effectiveness of our method for limited data sets.An issue which will be pursued in further work is the effect of noise which is inevitably present in all experimental time series.Preliminary results show that our test can cope with small amounts of noise without difficulty.A careful study of this capability,and comparison with other methods,is presently in progress.We are grateful to Philip Aston,Charlie Macaskill and Trevor Sweeting for helpful dis-cussions and suggestions.The research of GG was supported in part by the European Commission funding for the Research Training Network“Mechanics and Symmetry in Europe”(MASIE).ReferencesAbarbanel H.D.I.,Brown R.,Sidorovich J.J.&Tsimring L.S.1993The analysis of observed chaotic data in physical systems.Rev.Mod.Phys.65,1331–1392.Ashwin P.,Melbourne I.&Nicol M.2001Hypermeander of spirals;local bifurcations and statistical properties.Physica D14,275–300.Baladi V.1999Decay of correlations.In Smooth Ergodic Theory and its Applications, Amer.Maths.Soc.297–325.Biktashev V.N.&Holden.A.V.2001Deterministic Brownian motion in the hyperme-ander of spiral waves.Physica D116,342–382.Brahona M.&Poon C.-S.1996Detection of nonlinear dynamics in short,noisy time series.Nature381,215–217.Cazelles B.&Ferriere R.H.1992How predictable is chaos?Nature355,25–26.Article submitted to Royal Society10G.Gottwald and I.MelbourneCoullet P.&Emilsson K.1996Chaotically induced defect diffusion.In:Instabilities and Nonequilibrium Structures,V(ed.E.Tirapegui and W.Zeller),pp.55–62.Dordrecht: Kluwer.Eckmann J.-P.,Kamphurst S.O.,Ruelle D.&Ciliberto S.1986Liapunov exponents from time series.Phys.Rev.A34,4971–4979.Field M.,Melbourne I.&T¨o r¨o k A.2002Decay of correlations,central limit theorems and approximation by Brownian motion for compact Lie group extensions.Ergod.Th.& Dynam.Sys.To appear.Guckenheimer J.&Holmes P.1990Nonlinear Oscillations,Dynamical Systems,and Bi-furcations of Vector Fields.Appl.Math.Sci.42,New York:Springer.Kawahara T.&Toh S.1988Pulse interactions in an unstable disspative-dispersive non-linear system.Phys.Fluids31,2103–2111.Melbourne I.&Nicol M.2002Statistical properties of endomorphisms and compact group extensions.Preprint,University of Surrey.Melbourne I.&T¨o r¨o k A.2002Central limit theorems and invariance principles for time-one maps of hyperbolicflmun.Math.Physics229,57–71.Nicol M.,Melbourne I.&Ashwin P.2001Euclidean extensions of dynamical systems.Nonlinearity14,275–300.Parker T.S.&Chua L.O.1989Practical Numerical Algorithms for Chaotic Systems.New York:Springer.Parlitz U.&Lauterborn W.1987Period-doubling cascades and devil’s staircases of the driven van der Pol oscillator.Phys.Rev.A36,1428–1434.Press W.H.,Teukolsky S.A.,Vetterling W.T.&Flannery B.P.1992Numerical Recipes in C.Cambridge University Press.Sano M.&Sawada Y.1985Measurement of the Lyapunov spectrum from a chaotic time series.Phys.Rev.Lett.55,1082–1085.Takens F.1981Detecting strange attractors in turbulence.Lecture Notes in Mathematics 898,366–381,Berlin:Springer.van der Pol B.1927Forced oscillations in a circuit with nonlinear resistance(receptance with reactive triode).Philos Mag.43,700.Wolf A.,Swift J.B.,Swinney H.L.&Vastano J.A.1985Determining Lyapunov exponents from a time series.Physica D16,285–317.Article submitted to Royal Society。
动力系统微分方程混沌

动力系统微分方程混沌混沌是指一种非线性动力系统的行为,其特点是微小的初始条件差异能够引起系统演化的巨大差异。
混沌现象在物理学、天文学、生物学等众多领域都有所应用和研究。
混沌现象的产生与非线性动力学系统的微分方程有着密切的关系。
混沌现象最早由美国数学家爱德华·洛伦兹于1963年在研究大气运动方程时发现。
他发现即使微小的初始条件差异,也可能引起大气运动系统迅速演化的不同轨迹,最终产生混沌行为。
这个系统由三个微分方程描述,即Lorenz系统:dx/dt = σ(y - x)dy/dt = x(ρ - z) - ydz/dt = xy - βz其中x、y、z是系统的三个状态变量,t是时间,σ、ρ和β是系统的常数参数。
通过对这个系统的数值计算和分析,洛伦兹发现了在一些参数范围内,系统的演化轨迹呈现出很不规则、且对微小初始条件差异敏感的行为,即混沌现象。
混沌系统的微分方程通常具有非线性项,这使得系统的演化变得复杂且难以预测。
这是因为非线性方程的解具有许多不同的可能性,从而导致系统的演化有多个可能的轨迹。
而且,微小的初始条件差异会被放大,引起系统演化的巨大差异。
除了洛伦兹系统外,还有一些其他的混沌系统模型。
例如,Rössler 系统由以下三个微分方程描述:dx/dt = -y - zdy/dt = x + aydz/dt = b + z(x - c)其中x、y、z是系统的状态变量,t是时间,a、b和c是系统的常数参数。
Rössler系统也展现出混沌行为,其演化轨迹呈现出高度复杂的结构。
许多其他的混沌系统模型也被提出,如Henon映射、Ikeda映射等。
混沌现象的实际应用非常广泛。
在物理学中,混沌现象被用来研究非线性振动系统、流体力学系统等。
在天文学中,混沌现象可以用来解释动力学行星系统的不稳定行为。
在生物学中,混沌现象被用来研究生物节律、神经网络等。
总之,混沌现象是一种非线性动力学系统的特殊行为。
动力系统混沌的统计物理计算

动力系统混沌的统计物理计算混沌理论是近几十年来统计物理领域的一个重要研究方向。
动力系统混沌现象的探索,可以为我们提供对复杂系统行为的深入理解和预测能力。
而在混沌系统中,统计物理计算则是一个重要的手段,它可以帮助我们分析和描述混沌系统的性质和行为。
本文将介绍动力系统混沌的统计物理计算方法,并举例说明其应用。
一、混沌动力学的基本概念在混沌动力学中,系统的演化是不可预测的、高度敏感的,即使在初始条件微小变化的情况下,系统的演化也会出现巨大的差异。
这种不可预测性使得混沌动力学成为一个复杂而有趣的研究对象。
混沌系统可以通过一系列的微分方程和迭代映射来描述,其中包含了一些重要的动力学量,如吸引子、Lyapunov指数等。
二、统计物理计算方法统计物理计算方法是一种基于概率和统计的方法,它可以帮助我们研究和描述系统的宏观行为。
在混沌动力学中,统计物理计算方法可以应用于混沌系统的性质和演化规律的研究。
下面将介绍一些常用的统计物理计算方法。
1. 布朗运动模拟布朗运动是一种无规则运动,可以看作是无数个微观粒子的随机运动叠加而成的宏观现象。
通过模拟布朗运动,我们可以研究混沌系统中随机性的产生和传播规律。
在计算中,可以应用随机数生成算法来模拟布朗运动,并通过统计方法来分析其性质。
2. 相空间分布的统计分析相空间是描述系统状态的一种数学空间,在混沌系统中起到了重要的作用。
通过对相空间分布的统计分析,我们可以获得系统的演化规律和性质。
常用的统计分析方法包括方差分析、频率分析等。
3. Lyapunov指数的计算Lyapunov指数是描述混沌系统敏感依赖性的重要指标之一。
通过计算Lyapunov指数,我们可以判断混沌系统的不可预测性和稳定性。
计算Lyapunov指数的方法包括Wolf算法、Kaplan-Yorke公式等。
三、应用举例1. 混沌系统的控制通过统计物理计算方法,我们可以分析混沌系统的特性和行为,并设计相应的控制策略。
(完整版)混沌系统介绍及例子

专业学术讲座报告班级:信计12-2学号:************ 姓名:**二零一五年六月二十二日目录1.混沌系统概念2.典型混沌系统介绍3.混沌金融系统的线性与非线性反馈同步4.混沌研究的发展方向及意义一、混沌系统概念混沌(chaos )是指确定性动力学系统因对初值敏感而表现出的不可预测的、类似随机性的运动。
又称浑沌。
英语词Chaos 源于希腊语,原始 含义是宇宙初开之前的景象,基本含义主要指混乱、无序的状态。
作为科学术语,混沌一词特指一种运动形态。
动力学系统的确定性是一个数学概念,指系统在任一时刻的状态被初始状态所决定。
虽然根据运动的初始状态数据和运动规律能推算出任一未来时刻的运动状态,但由于初始数据的测定不可能完全精确,预测的结果必然出现误差,甚至不可预测。
运动的可预测性是一个物理概念。
一个运动即使是确定性的,也仍可为不可预测的,二者并不矛盾。
牛顿力学的成功,特别是它在预言海王星上的成功,在一定程度上产生误解,把确定性和可预测性等同起来,以为确定性运动一定是可预测的。
20世纪70年代后的研究表明,大量非线性系统中尽管系统是确定性的,却普遍存在着对运动状态初始值极为敏感、貌似随机的不可预测的运动状态——混沌运动。
混沌是指现实世界中存在的一种貌似无规律的复杂运动形态。
共同特征是原来遵循简单物理规律的有序运动形态,在某种条件下突然偏离预期的规律性而变成了无序的形态。
混沌可在相当广泛的一些确定性动力学系统中发生。
混沌在统计特性上类似于随机过程,被认为是确定性系统中的一种内禀随机性。
二、典型混沌系统介绍Lorenz 系统混沌的最早实例是由美国麻省理工学院的气象学家洛伦兹在1963年研究大气运动时描述的。
他提出了著名的Lorenz 方程组:。
这是一个三阶常微分方程组。
它以无限平板间流体热对流运动的简化模型为基础,由于它的变量不显含时间t ,一般称作自治方程。
式中x 表示对流强度,y 表示向上流和向下流在单位元之间的温度差,z 表示垂直方向温度分布的非线性强度,-xz 和xy 为非线性项,b 是瑞利数,它表示引起对流和湍流的驱动因素 (如贝纳对流上下板的温度差△T)和抑制对流因素 (如(Prandtl)数粘性)之比,是系统(2-1)的主要控制参数。
chapter5:chaos

Chapter5Chaotic Dynamics5.1Some Definitions5.1.1DefinitionsWe will begin with a summary of some key terms and concepts.Some of these we have defined previously,others are unique to the discussion of chaos. Dynamical SystemA system of one or more particles whose behavior(position,velocity,and acceler-ation)may be modeled by a system of differential equations together with a set of initial conditions.An example is the case of an object on the end of a spring.It can be described with the expressionhowever,in reality it is a differential equation:(5.1) with.Mathematically,a differential equation is an equa-tion that relates a function and its derivatives.Once formulated,the differen-tial equations are themselves called dynamical systems and all references to the physical system may cease.12CHAPTER 5.CHAOTIC DYNAMICS Non-linear dynamical system:If a differential equation is linear in the function and its derivatives,it is linear.If the differential equations involve non-linear terms like ,then the system is said to be non-linear.Deterministic system:A dynamical system that provides a unique (one and only one)solution for a given set of initial conditions.Classical systems are all deterministic.Quantum systems,onthe other hand,yield probabilities for the various possible outcomes and are therefore not deterministic.Phase spaceA space constructed with the position coordinates and the velocity com-ponents (actually the corresponding momenta).For a one-dimensional system such as the mass on a spring,phase space has only two dimensions,.Fixed point:We first encountered fixed points when studying finite-difference equations.These were solutions to the relation The definition for a dynamical system is similar.Substitute a set of initial con-ditions into the system of differential equations.If the result is identical to the initial conditions,then the initial conditions constitute a fixed point.For example,if in Eq.5.1we use the initial conditions at ,then the solution is for all subsequent t.Thus the point is a fixed point of this system.A mechanical system is in equilibrium at a fixed point.Orbit:The set of points in phase space that satisfy the differential equations describ-ing the dynamical system.For a fixed point,the orbit is a single point.In the undamped case of Eq.5.1,the orbit is an ellipse.差分方程5.1.SOME DEFINITIONS3 Phase plot of an undamped harmonic oscillator.Periodic orbit:If the motion of a physical system repeats itself,it is said to be periodic.In this case,the set of points in the solution of the differential equations also repeats and the orbit is also periodic.The orbit of an undamped mass on a spring is either the fixed point or an ellipse in phase space.Limit cycle:A closed curve in phase space toward which an orbit may evolve as.The damped object-spring system driven by a low-amplitude sinusoidal force has a limit cycle.Attractor:The set of points in phase space toward which a dynamical system evolves as gets large.This might be afixed point,as it is for the damped mass-spring problem,a limit cycle,as it is for the damped and driven case,or an extremely complex set of points,as in the case of some non-linear dynamical systems.4CHAPTER5.CHAOTIC DYNAMICS Phase plot showing the evolution of the damped harmonic oscillator toward its fixed point.5.2.CHAOS IN DYNAMICAL SYSTEMS5 Chaotic Attractor:Loosely speaking,if the orbit is very sensitive to the choice of initial conditions, in the sense that nearby orbits in phase space diverge exponentially,then the at-tractor is said to be chaotic.Only non-linear dynamical systems have chaotic attractors.Such attractors are sometimes called strange and are examples of frac-tals.Dynamical systems of this type are also unpredictable.Small differences in the initial conditions lead to widely divergent orbits making predictability a prac-tical impossibility.Be aware that the study of chaotic dynamical systems is in anearly stage,and some of the definitions are not as simple or crisp as those in a fully developed discipline.For example,what does"sensitivity to the choice of initial conditions"mean?It means that trajectory of the system in phase space given one set of initial conditions diverges exponentially from a trajectory with almost the same set of initial conditions.For unimodular maps,this meant that the Liapunov exponent was positive.For dynamical systems,Liapunov exponents are also used as they test for chaos;however,higher-dimensional systems have more than one exponent.In practice,calculation of the exponents in these cases can be very difficult.5.2Chaos in Dynamical Systems5.2.1IntroductionWe studied the behavior of damped and driven systems in the previous chapter. For a linear system,the results are straightforward.After some transient behavior, the system settles down toward a limit cycle with a period equal to that of the driv-ing force.The overall amplitude depends on the relation between the frequency of the drive force and the natural frequency of the system.For nonlinear systems,the behavior is more complex.If the drive force is not too large,the results are similar to that of linear systems.If the system is driven harder,more complex modes will appear.In many cases,the system will approach chaotic behavior in a period-doubling cascade.The pattern is similar to that seen with unimodular maps(such as the logistics map).5.2.2RK-4IntegrationThe systems we are about to study place greater demands on accuracy than the others we have studied.Accordingly,we introduce a new method offinding nu-crispadj.1 脆的, 鲜脆的2 新奇的, 整洁的3 清新的, 干冷的4 干净利落的,简明扼要的n.〈英〉炸马铃薯片exponential:指数乮的乯unimodular:单位模的6CHAPTER5.CHAOTIC DYNAMICS merical solutions.This method of solving differential equations is known as the 4th order Runge-Kutta method1,and a detailed description of this technique can be found in most numerical analysis textbooks.It is probably the most popular method now in use for numeric calculations because it is usually the optimum compromise between speed and accuracy.The formulas to integrate the equations of motion are:The various areThese formulas can be implemented directly in MathCad,using the programming capabilities built into the Professional edition.MathCad also includes functions which implement the algorithm directly for nth-order differential equations.The former method is moreflexible;however,the latter is available in all versions. We therefore shall discuss both.Considerfirst the built-in functions.These are rkfixed,RKadapt and rkadapt.Only the rkfixed function is available in the student edition.Their syntax iswhere y is an n-element array containing the initial conditions,and are the starting and ending times,n points is the number of intermediate points at which the functions is to be evaluated,and D is an n-element array containing the deriva-tives of the unknown function expressed in terms of the initial values contained in5.3.THE SIMPLE PENDULUM7 the array y.The rkfixed function uses afixed step size to evaluate the function at each intermediate point.The Rkadapt function uses a variable step size internally to evaluate the function,however,results are returned for equally space intervals. This function uses small steps in intervals where the function changes rapidly; larger values are used when the change is small.This makes it possible to obtain high accuracy without performing unnecessary computations.The rkadapt(note the case sensitivity)function is a special case.It is used when only thefinal values of the function and its derivatives are needed.It incorporates additional arguments as follows:acc is a value specifying the desired accuracy of the solution.kmax specifies the maximum number of intermediate points at which the function should be evaluated.save is the smallest allowable spacing between the values at which the so-lution is to be approximated.All of the functions return a matrix in which thefirst column are the values of t for which the function has been evaluated,the second column is the corresponding value of y,and the third column is itsfirst derivative.A sample worksheet is shown in Figure5.2.2.The system under analysis is a damped harmonic oscillator.Note that the acceleration(2nd array element) includes a driving force term,currently suppressed by the value of A.The system computes the position and velocity of the system for N periods of the driving force.The calculations are performed for k points in each drive cycle.The phase plot in Figure5.1.1was also generated using this worksheet.Note that although this worksheet uses the Rkadapt function,the rkfixed function could have been used in it place.5.3The Simple PendulumFor ourfirst example,we consider a damped simple pendulum subjected to a sinusoidal driving force.This force rule is easy to implement computationally, although in practice it is difficult to achieve for a real pendulum.The acceleration for this case can be written in the form8CHAPTER5.CHAOTIC DYNAMICS MathCad Worksheet that utilizes the Rkadapt function for a dynamical system5.4.POINCARE SECTIONS9 Figure5.3shows a worksheet that uses MathCad’s built-in numeric integration function.The parameters for this case areis the period of the drive force.The function is evaluated at25points in each cycle.The graphs are constructed to show the motion for thefinal8cycles of the drive force.For,the motion has a limit cycle whose period equals that of the drive force.Figure5.3shows the result when the drive force amplitude isincrease so that.Considerfirst the position vs time graph(left side). The long-term motion is still periodic,however,its period is now twice that of the drive force.Note also the shape of the phase plot.Figure5.3shows period four motion for the pendulum.In this case. Note that for this case the worksheet has been modified to map the position coor-dinates into the range.A recursively defined function is used to do this.Its syntax isA nested if structure is also employed.The functionfirst determines if x is positive or negative.Positive values greater than are mapped to and then tested again.For negative x,values less than are mapped to and then tested again.In this way,the position coordinate is kept within the bounds. Figure shows the motion for.A general trend should be clear.The system appears to be following the period-doubling route to chaos wefirst observed for the logistic map.In fact,for,the motion is chaotic.However,we can see that as the higher-period motions are obtained,the graphs become more difficult to interpret.This is the motivation for introducing a new way of analyzing dynamical data,known as the Poincare section.5.4Poincare Sections5.4.1IntroductionPoincare sections provide another way to study chaotic motion.They are based on a generalization of a phase portrait.Consider a phase portrait to which a third axis10CHAPTER5.CHAOTIC DYNAMICS Pendulum Worksheet5.4.POINCARE SECTIONS11 Period two motion of the pendulum().is added to represent time.To get afirmer grip on this concept,suppose that we are studying a simple undamped and undriven pendulum swinging back and forth in a small arc.For convenience,assume that the origin of our coordinate system is at the bottom of its swing.In phase space this motion appears to generate an ellipse around the stable point(O,0).If we add a time axis perpendicular to the screen, we will generate a curve in x-v-t space.This curve will spiral around the t-axis.Of course,it is impossible for the video monitor to display this space curve literally, since it is three-dimensional and the screen is two-dimensional2.For the moment we use our imaginations to see this curve.Suppose for the moment that the phase plot for the system is a circle.Then,as time progresses,the dot representing the point in phase space that describes the state of the pendulum traces out a helix in x-v-t space.If the orbit in x-v space is elliptical,then the trajectory in x-v-t space will be a squashed helix.Now imagine that the monitor screen is the x-v plane.The time axis pokes straight out of the video monitor.Take that time axis and bend it in a circle so that it circles around behind the screen and pierces the screen in exactly the same place.Assume that we choose the circumference of the time circle to be exactly12CHAPTER5.CHAOTIC DYNAMICS Period four motion of the pendulum().5.4.POINCARE SECTIONS13 Chaotic motion of the pendulum().one period of our pendulum.Then the trajectory of the system in x-v-t space will pierce the screen of the video monitor at exactly the same x-v point each time the pendulum completes its cycle.The entire trajectory is now reduced to a single point in x-v space.We have just constructed a Poincare section.The general definition for a Poincare section can be inferred from the proce-dure described above.The entire trajectory in x-v-t space is sampled at regular time intervals and the results plotted in one x-v graph.Generally,the time interval chosen is a natural period associated with the system.In the case of our simple pendulum,the Poincare section is a single point.When we add viscous damping to the pendulum system,the Poincare section will be a series of dots that lead to the attractor at(0,0)(See Figure).Now suppose we add a sinusoidal driving force.The natural period of the pendulum is not now important;the period of the driving force is the natural sampling time.If the orbit in phase space is periodic with this period,then we will get one dot on the screen of the video monitor.If the motion has a period equal to twice the period of the driving force,then the Poincare section will have two dots.How does the Poincare section appear if the dynamical system is almost peri-odic?In this case,single dots will be replaced by clusters of closely spaced dots. Period one behavior is indicated by a single cluster,period two by two clusters,14CHAPTER5.CHAOTIC DYNAMICS etc.If the system is chaotic,the Poincare section will consist of a pattern of dots called the attractor(actually one cross section of it).These structures frequently have fractal dimension.5.4.2Using MathCad to Construct Poincare sectionsAs an example of these ideas,let us construct Poincare sections for the damped driven pendulum considered in the previous section.A worksheet that does this is shown in Figure5.4.2.The worksheet calculates the motion for600cycles of the drive force,then samples the last300of them once every5.5.BIFURCA TION DIAGRAMS15A worksheet that constructs Poincare sections16CHAPTER5.CHAOTIC DYNAMICS Poincare section for5.5.BIFURCA TION DIAGRAMS17 Poincare section for the pendulum when18CHAPTER5.CHAOTIC DYNAMICS then plotted in a graph,with the drive amplitude as the independent variable.The results for the pendulum are shown in Figure.The similarity of this result to that for unimodular maps is striking.In fact,if is the amplitude at which the nth bifurcation occurs,wefind that3This value was chosen because it is the maximum number of independent y-values allowed in MathCad7.0.5.5.BIFURCA TION DIAGRAMS19A partial worksheet defining an RK4integration programPartial worksheet showing a function that calls the RK4function to solve a dy-namical system.20CHAPTER5.CHAOTIC DYNAMICS MathCad worksheet that constructs a bifurcation diagram.amplitude is controlled by the variable q.The number of intermediate points at which evaluation is performed is controlled by the variable p.The velocity was used to plot the graph so that problems with the cyclic nature of the position coordinate could be avoided.Figure shows the bifurcation diagram for the damped and driven pendulum subject to a sinusoidal drive.The system parameters are,,and 4This cannot be seen in a black-and-white graph;however,the effect becomes obvious if the series plots are color-coded.Fortunately,MathCad does this automatically.5.5.BIFURCA TION DIAGRAMS21 Worksheet that constructs a bifurcation diagramExercises1.The acceleration of a damped and driven Duffing oscillator can be writtenin the formConstruct a MathCad worksheet that solves the equations of motion using 4th order Runge-Kutta integration techniques.You may use either the rk-fixed or Rkadapt functions to do this.Be sure to include position vs.time and phase plot graphs.These should cover the last eight cycles of the drive e the parameters,,,and.2.Construct a worksheet that builds a Poincare diagram for the Duffing oscil-lator.3.Construct an Interactive Physics simulation of the oscillator in Exercise1.Include a phase plot and position vs.time graph.4.Change the drive amplitude to and recalculate the results usingthe worksheet of Exercise1.Write a sentence or two describing the type of motion you think this represents.22CHAPTER5.CHAOTIC DYNAMICS5.Repeat Exercise2using the parameters of Exercise46.Change the parameters in your Interactive Physics simulation to match thoseof Exercise4.Observe the resulting motion.Write a sentence or two com-menting on the correlation(or lack of it)between the simulated motion and the results of the numeric calculation.7.Repeat Exercise4with.8.Repeat Exercise2using the parameters of Exercise7.9.Repeat Exercise6using the parameters of Exercise7.10.Repeat Exercise2with.On the basis of your Poincare map,whattype of motion is this?11.Construct a bifurcation diagram for the Duffing oscillator for.Use it to determine a value of for which the motion is periodic.Check your result by constructing a Poincare map.。
翻译

离散动力系统混沌理论王立东大连民族大学邢秀英辽宁师范大学楚振燕大连民族大学离散动力系统混沌理论摘要通过拓扑动力系统(X,f),我们的意思是一个紧度量空间X一起连续满映射f:X→X。
混沌下的TDS是引入增量研究而提出的。
这个词在1975年由Li and York提出,今天成为Li-York混沌。
在Ruelle-Takens 混沌和Schweizer-Smital混沌(也称为分布混沌)中灵敏度是混沌的基本核心要点。
现在科学家们在各个领域都关注混沌,并把其当成主要研究对象。
所以讨论混沌的概念与关系是非常有意义的。
在本文中,使用这个方法的建立并结合象征性的空间,我们学习的关系是按序列分布混沌,分布混乱和Ruelle-Takens混乱,证明他们是不等同于彼此紧系统(X,f)。
关键词:按序列分布混沌,distri butional混乱, Ruelle-Takens混沌,敏感性1.引入自从1963年洛伦兹发现混乱现象,科学家们已经关注到这动力在各个领域的现象。
现在的混沌已被研究并被发展到几乎所有的自然和社会的science.In数学领域,它引起了广泛的兴趣从而Li-Yorke在1975年对混沌给了严格的数学定义。
为了观察复杂动态系统和揭示混沌更好的本质,不同的人在各种意义上描述的混沌,所以给出不同的混沌定义,如Li-Yorke混沌,Ruelle-T akens混沌定义,分配混乱(也称为Schweizer-Smital混乱)等。
许多科学家做大量的工作来揭示他们之间的内在关系[2]。
对于复杂的动态系统,基于严格的数学定义建立一个令人满意的定义和术语框架是必要的。
这些概念的歧义,和他们的相互依存需要澄清。
为了实现这一目标[3],作者讨论了Li-Yorke关系混乱,分布混沌和按序列分布混沌,证明一个连续映射的区间是混乱的,当且仅当它是分布混沌的。
在一个序列中[4],作者证明按序列分布混沌不等同于分布混沌。
在本篇论文中,我们研究之间的关系按序列分布混沌,分布混沌Ruelle-Takens混乱,并且得到以下结果:主要定理在紧凑型系统(X,f),按序列分布混沌,Ruelle-T分布混沌,他们的意义是相同的。
混沌理论chaos theory(中英文)
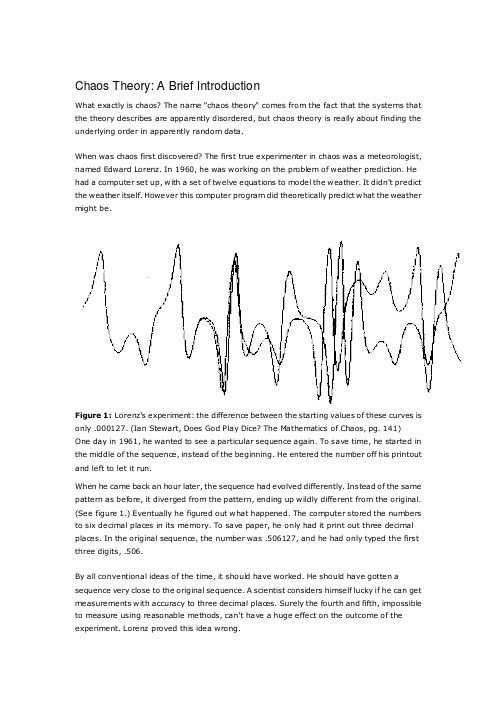
What exactly is chaos? The name "chaos theory" comes from the fact that the systems that the theory describes are apparently disordered, but chaos theory is really about finding the underlying order in apparently random data. When was chaos first discovered? The first true experimenter in chaos was a meteorologist, named Edward Lorenz. In 1960, he was working on the problem of weather prediction. He had a computer set up, with a set of twelve equations to model the weather. It didn't predict the weather itself. However this computer program did theoretically predict what the weather might be.
This effect came to be known as the butterfly effect. The amount of difference in t he starting points of the two curves is so small that it is comparable to a butterfly flapping its wings. The flapping of a single butterfly's wing today produces a tiny change in the state of the atmosphere. Over a period of time, what the atmosphere actually does diverges from what it would have done. So, in a month's time, a tornado that would have devastated the Indonesian coast doesn't happen. Or maybe one that wasn't going to happen, does. (Ian Stewart, Does God Play Dice? The Mathematics of Chaos , pg. 141) This phenomenon, common to chaos theory, is also known as sensitive dependence on initial conditions. Just a small change in the initial conditions can drastically change the long -term behavior of a system. Such a small amount of difference in a measurement might be considered experimental noise, background noise, or an inaccuracy of the equipment. Such things are impossible to avoid in even the most isolated lab. With a starting number of 2, the final result can be entirely different from the same s ystem with a starting value of 2.000001. It is simply impossible to achieve this level of accuracy - just try and measure something to the nearest millionth of an inch! From this idea, Lorenz stated that it is impossible to predict the weather accurately. However, this discovery led Lorenz on to other aspects of what eventually came to be known as chaos theory. Lorenz started to look for a simpler system that had sensitive dependence on initial conditions. His first discovery had twelve equations, and he wa nted a much more simple version that still had this attribute. He took the equations for convection, and stripped them down, making them unrealistically simple. The system no longer had anything to do with convection, but it did have sensitive dependence on its initial conditions, and there were only three equations this time. Later, it was discovered that his equations precisely described a water wheel. At the top, water drips steadily into containers hanging on the wheel's rim. Each container drips steadily from a small hole. If the stream of water is slow, the top containers never fill fast enough to overcome friction, but if the stream is faster, the weight starts to turn the wheel. The rotation might become continuous. Or if the stream is so fast that the heavy containers swing all the way around the bottom and up the other side, the wheel might then slow, stop, and reverse its rotation, turning first one way and then the other. (James Gleick, Chaos - Making a New Science, pg. 29)
混沌理论综述很全

拉格朗日
三个等质量旳物体,排成等边三角形绕三角形旳中心做 圆周运动。
近代计算机运算
三个等质量旳物体在一条“8”字形轨道上运动。 ------宇宙中还没找到。
混沌与分岔旳起源与发展
❖ 混沌现象发觉后来,有关分岔与混沌之间联络旳研 究得到迅速发展,如:
❖ Rulle和Takens发觉环面分岔通向混沌; ❖ Feigenbaum发觉倍周期分岔通向混沌; ❖ Pomeou等发觉伴随鞍结分岔旳阵发性通向混沌。
混沌旳特点
5. 普适性
❖ 普适性涉及两种,即构造旳普适性和测度旳普适性。 ❖ 当系统趋于混沌时,所体现出旳特征具有普适意义,其
特征不因详细系统旳不同和系统运动方程旳差别而变化。
混沌旳特点
6. 遍历性
❖ 遍历性也称为混杂性,混沌运动在有限时间内能够到达混 沌区域内任何一点。
混沌旳特点
7. 奇怪吸引子
❖ 混沌旳定性描述,“混沌是拟定性非线性系统旳有界旳敏 感初始条件旳非周期行为”。
混沌旳概念
❖ n周期点旳定义:假如对于某x0 ,有f (n)(x0)=x0,但对于不大于n旳自 然数k,有f (k)(x0)≠ x0 ,则称x0为f 旳一种n周期点。
❖ n周期轨道旳定义:当x0为f 旳一种n周期点时,称{x0, f (1)(x0), f (2)(x0),…, f (n-1)(x0)}为f 旳n周期轨道。
混沌旳特点
2. 内在随机性
❖ 拟定性行为一定产生于拟定性方程,而随机行为却产生 于两类方程:一类是随机微分方程,一类是拟定性方程。 随机微分方程体现出来旳随机性是由随机参数、随机初 始条件或随机外界逼迫所产生,常称为外在随机性。拟 定性方程本身不包括任何随机原因,但在一定旳参数范 围却能产生出看起来很混乱旳成果,把这种由拟定性方 程产生旳随机性称之为内在随机性。
混沌动力学模型

混沌动力学模型混沌动力学模型是一种描述非线性系统行为的数学模型。
它的核心概念是混沌现象,即系统的微小变化会引起巨大的效应,使系统表现出不可预测的行为。
混沌动力学模型的研究对于理解和揭示自然界中复杂系统的行为规律具有重要意义。
混沌动力学模型的起源可以追溯到20世纪60年代,由美国数学家Edward Lorenz提出。
他在研究大气环流系统时,发现微小的初始条件变化会导致天气预报的巨大误差。
这一发现引发了他对非线性系统的研究,最终形成了混沌动力学模型。
混沌动力学模型的核心方程是著名的洛伦兹方程,它描述了一个简化的大气对流系统。
洛伦兹方程是一个三维非线性常微分方程组,它的解决过程展现了混沌现象。
洛伦兹方程的形式如下:dx/dt = σ(y - x)dy/dt = x(ρ - z) - ydz/dt = xy - βz其中,x、y、z是系统的三个状态变量,t是时间,σ、ρ、β是系统的参数。
通过调节参数的值,可以观察到不同的系统行为,包括稳定状态、周期运动和混沌运动。
混沌动力学模型的研究揭示了非线性系统的一些重要特性。
首先是灵敏依赖于初值条件,微小的初始条件变化会导致系统演化出完全不同的轨迹。
这意味着我们无法准确预测系统的未来行为,只能给出可能的演化趋势。
其次是周期倍增现象,系统在某些参数值下会表现出周期倍增的行为,即周期长度不断加倍,最终进入混沌状态。
最后是拓扑混沌,非线性系统的相空间结构呈现出复杂的拓扑特征,例如奇异吸引子和分岔图等。
混沌动力学模型的研究不仅在天气预报、气候学等领域有重要应用,还在物理学、生物学、经济学等多个学科中发挥着重要作用。
通过混沌动力学模型,我们可以更好地理解和解释自然界中的复杂现象,为科学研究和实践提供指导。
混沌动力学模型的研究也给我们带来了一些启示。
首先是复杂系统的不可预测性,即使是简单的非线性系统也可能表现出混沌行为,我们无法准确预测系统的未来演化。
其次是系统的微小变化可能引起巨大效应,这对于控制和管理复杂系统具有挑战性。
化学反应系统的混沌动力学模型研究

化学反应系统的混沌动力学模型研究混沌动力学是指一种对非线性系统行为的研究方法,揭示了复杂系统中的不可预测性和敏感依赖于初值条件的特征。
在化学领域中,混沌动力学模型的研究对于理解和探究复杂反应体系的行为具有重要意义。
因此,很多化学反应系统的混沌动力学模型也得到了广泛的关注与研究。
混沌动力学模型研究的重点之一是确定系统的动力学方程。
化学反应系统中的反应速率常常与浓度相关,因此可以考虑采用非线性常微分方程来描述系统的动力学行为。
典型的化学反应系统混沌动力学模型包括Belousov-Zhabotinsky反应、化学振荡反应和酶催化反应等。
Belousov-Zhabotinsky反应是化学动力学领域中用以研究混沌现象最具代表性的反应之一。
该反应的动力学方程可以通过扩散-反应方程来描述。
通过选择合适的参数和初值条件,可以观察到Belousov-Zhabotinsky反应中的混沌行为,例如周期振荡、孤立子和斑图等。
化学振荡反应是另一个常被用来研究混沌动力学的系统。
其中最著名的是BZ 反应,其反应体系可以通过鲁特卡-休伯特方程来描述。
这个方程描述了反应物的浓度变化,其形式非常复杂,并涉及到非线性动力学行为。
对于这类反应体系,研究者通过实验观察到了各种各样的混沌现象,从而揭示了混沌动力学模型在化学反应中的重要性。
酶催化反应是生物化学领域中另一个重要研究对象,也常常表现出复杂的混沌动力学行为。
通过构建酶催化动力学模型,可以揭示生物体内某些基本酶作用过程的混沌特征。
例如,酶催化反应中的非线性性质和浓度依赖性等特征,使得该系统在一定条件下会表现出复杂的混沌行为。
除了上述的几个经典化学反应系统,还有许多其他反应体系也具有混沌现象。
混沌动力学模型的研究给我们提供了更深入理解和预测化学反应系统行为的方法。
通过理论模型的构建和数值模拟,可以揭示出反应动力学中的混沌特性,帮助我们预测复杂系统的行为和优化反应条件。
此外,混沌动力学模型的研究也为控制复杂反应系统提供了一定的理论基础。
化学反应动力学的混沌理论和动力系统研究

化学反应动力学的混沌理论和动力系统研究化学反应动力学是研究化学反应速率和反应机理的学科。
在自然界中,化学反应是非常普遍的现象。
例如,日常生活中令人熟知的明火和灯光,都是由于化学反应引起的。
化学反应动力学,就是研究这些现象背后的物理和化学机制,以及如何操纵和控制这些反应的科学。
混沌理论和动力系统研究在化学反应动力学中的应用,得到了广泛的关注和研究。
一、混沌理论的应用混沌理论是20世纪70年代初在吸引人类注意的科学理论之一。
它是由美国数学家洛伦兹发起的,并被用于描述一些动态系统(如天气系统)中的非线性行为。
在化学反应中,混沌现象指的是由于反应体系中存在某种非线性特性,导致反应之间的关系变得异常复杂。
例如,在某些化学反应中,一些初值的微小差别可以在相同的化学反应条件下,引起非常大的反应结果的差别(如产物的种类和数量)。
这种现象被称为“混沌”。
了解和分析混沌现象,对于化学反应的合理设计和控制,具有重要的启示作用。
通过混沌现象的研究,可进一步了解某些化学反应系统的非线性行为及其规律,从而更好地实现这些反应的目标。
二、动力系统理论在化学反应中的应用动力系统是一种描述动态系统行为的数学模型,其涵盖了爆炸,鸟类飞行,人口增长以及化学反应等众多领域。
在化学反应中,动力系统理论主要用于模拟和研究化学反应的动态行为、稳定性、可控性和稳态结构等。
通过动力系统理论分析某些化学反应模型,可以用表达式或图形表示化学反应的稳态和动态行为。
例如,稳定性分析可以通过等位点分析(steady-state analysis)或线性稳定性分析(linear stability analysis)等方法确定,而稳态结构的分析则需要进一步研究反应的各个要素之间的相互关系。
动力系统理论在化学反应研究中的应用,将化学反应视为一种动态系统,通过数学分析可更好地理解化学反应的动态行为、稳态和稳态结构等。
这对于预测和控制化学反应的行为和产物具有重要的意义。
动力系统与混沌理论

动力系统与混沌理论动力系统和混沌理论是研究复杂非线性系统行为的重要领域。
动力系统理论以其在物理、生物学、经济学等领域的广泛应用而闻名,混沌理论则揭示了一类看似无序却有内在规律的系统行为。
本文将介绍动力系统的基本概念和混沌理论的主要原理,并探讨它们在科学与工程中的应用。
1. 动力系统的基本概念动力系统是描述物体运动或系统演化随时间变化规律的数学模型。
它由状态空间、演化方程和初态条件组成。
状态空间是描述系统可能处于的所有状态的集合,演化方程则指定了系统如何从一个状态演化到另一个状态。
初态条件则给出了系统在初始时刻的状态。
在动力系统理论中,有两种常见类型的演化方式,分别是连续演化和离散演化。
对于连续动力系统,时间是连续的,而对于离散动力系统,时间是离散的。
连续动力系统往往通过微分方程来描述,而离散动力系统则通过差分方程或迭代映射来描述。
2. 混沌现象与混沌理论混沌现象是指某些非线性动力系统表现出强烈的不可预测性和灵敏依赖于初态条件的特征。
混沌现象最早由埃德华·洛仑茨提出,并用一组微分方程来描述。
混沌理论通过对非线性动力学系统进行研究,揭示了混沌现象背后的规律。
其中最著名的是洛伦兹吸引子和费根鲍姆-曼德勃罗特集。
洛伦兹吸引子是一个三维非线性动力学系统在特定参数条件下呈现出复杂结构的吸引子。
费根鲍姆-曼德勃罗特集则是一类迭代函数生成的分形结构。
混沌理论为我们认识自然界中复杂非线性现象提供了新的视角。
它不仅对天气预报、金融市场预测等具有重要意义,还对通信密码学、乱序生成和优化问题等领域产生了重大影响。
3. 动力系统与混沌理论的应用3.1 物理学中的应用动力系统理论在物理学中有广泛应用。
例如,在天体力学中,研究太阳系行星之间相互作用所产生的轨道运动;在热力学中,通过分析粒子运动来解释热流、熵增等现象;在量子力学中,利用量子算符来描述粒子在希尔伯特空间中的演化等等。
3.2 生物学中的应用生物学中涉及到许多复杂非线性系统,例如神经网络、生物钟、群体行为等。
混沌系统理论 ppt课件

一则西方寓言: 丢失一个钉子,坏了一只蹄铁; 坏了一只蹄铁,折了一匹战马; 折了一匹战马,伤了一位骑士; 伤了一位骑士,输了一场战斗; 输了一场战斗,亡了一个帝国。
马蹄铁上一个钉子是否会丢失,本是初始条件 的十分微小的变化,但其“长期”效应却是一 个帝国存与亡的根本差别。
这就是军事和政治领域中所谓的"蝴蝶效应"。
混沌理论是系统从有序突然变为无序状态的一种演化
理论,是对确定性系统中出现的内在“随机过程”形成 的途径、机制的研讨。
混沌系统理论
典型系统
分形几何与奇怪吸引子
非周期定态
混
对初值的敏感依赖性
沌
的
确定性随机性
特 点
长期行为的不可预见性
混沌序:貌似无序的高级有序性
,一是能鲜明地表现出混沌的主要特 征,二是数学模型简单,容易处理。
这是混沌系统的典型特征。意思是说, 初始条件的微小差别会在最后的现象中 产生极大的差别,或者说,起初小的误 差可能会引起灾难性后果。 在生活中,人们知道一串事件往往具有一个临界点,那 里小小的变化会被放大.....
在天气这个系统中,对初始条件的敏感依赖性乃 是各种大小尺度的运动互相纠缠所不能逃避的后果。 因此,洛伦兹断言:长期预报注定要失败。因为信息 在传递的过程中,有一种放大作用。
此效应说明,事物发展的结果, 对初始条件具有极为敏感的依赖 性,初始条件的极小偏差,将会 引起结果的极大差异,甚至会呈 现一种混沌状态。
有科学家称之为混沌学。
混沌的定义
科学家给混沌下的定义
混沌 是指发生在确定性系统中的,貌似随机的不规则
运动,一个确定性理论描述的系统,其行为却表现为不 确定性,不可重复、不可预测,这就是混沌现象。混沌 是非线性动力系统的固有特性,是非线性系统普遍存在 的现象。
混沌

埋藏在混沌区内的是零星的规则性态窗口!
分岔图
分岔图可对于所有的k值一举获得所有动力 学性态的整体认识;
一周期窗口的放大:整个结构以缩小的方 式复现。窗口里还有窗口(箭头所指)…
别扰动----重正化
Feigenbaum,美国物理 学家,20世纪70年代任职 于Los Alamos实验室; 对于处理非线性系统的 扰动法深感厌烦; 对重正化方法感兴趣;
接下来就是解方程组.
拥有计算机的好处
Lorenz将方程组送进他的皇家马可比300型
计算机,让它以大约每秒1次迭代的速度运
行; 迭代了3000次以后,他描绘出了轨线图。
Lorenz吸引子:轨线貌似无规地绕两叶循环
什么是混沌?
在确定性非线性系统中,不需附加任何随 机因素亦可出现类似随机的行为(内在随 机性); 最大的特点:系统的演化对初始条件十分 敏感; 从长期意义上讲,系统的未来行为是不可 预测的.
Lorenz自认为是一名气象学家,所以将论 文发表在《大气科学杂志》上。 发表后10余年,他的论文湮没无闻。 Lorenz知道自己发现了某种重要的东西, 但是他超越了他的时代。
蝴蝶效应
1961年冬, Lorenz用计算机求解仿真大气
的13个方程式。为了更细致地考察结果,
他取出一个中间解,提高精度再送回。
构造一批 m 维的矢量,支起一个嵌入空
间:(相空间重构)
yj = (xj ,xj+τ,x j+2τ, … ,xj + (m-1) τ)
j=1, … ,N;N=n-m+1
[经济学]非线性动力学浑沌说课讲解
![[经济学]非线性动力学浑沌说课讲解](https://img.taocdn.com/s3/m/fc77ec380812a21614791711cc7931b765ce7b48.png)
朱照宣,1987年,牛顿《原理》三百年祭
• “《原理》发表以来的三百年,牛顿力学经历了两 个阶段。前280年是一阶段。那时认为由运动微 分方程所确定的动态总是确定性的。……后20年 则是另一个阶段。以卡姆定理(KAM)为代表的浑 沌理论提示了决定论和随机论之间、牛顿力学和 统计力学之间没有不可逾越的界线。 ……不仅大 量粒子的系统要用统计力学,两个自由度的保守 系统运动也得用统计力学,连掷骰子本身也既是 决定论的又是概率论的。它从根本上为牛顿力学 摘除了‘机械论’的帽子。”(朱照宣 1987, 第12页)
费格尔
(Herbert Feigl,1902-1988)说
“A causes B” or “A is the cause of B” means that wherever and whenever A occurs it is followed (or attended) by B. Since a precise repetition of A may not be feasible (or discoverable), a less stringent formulation would use something like a mathematical limit process: The more the actual condition A' approximates the conceived (ideal) condition A, the more actual effect B' will approximate the (ideal) effect B.
• There are systems whose trajectories do not monotonically approximate any ideal state. They are sensitive dependence to initial conditions.
混沌理论简介

混沌理论简介要弄明白不可预言性如何可以与确定论相调和,可以来看看一个比整个宇宙次要得多的系统——水龙头滴下的水滴。
这是一个确定性系统,原则上流入水龙头中的水的流量是平稳、均匀的,水流出时发生的情况完全由流体运动定律规定。
但一个简单而有效的实验证明,这一显然确定性的系统可以产生不可预言的行为。
这使我们产生某种数学的“横向思维”,它向我们解释了为什么此种怪事是可能的。
假如你很小心地打开水龙头,等上几秒钟,待流速稳定下来,通常会产生一系列规则的水滴,这些水滴以规则的节律、相同的时间间隔落下。
很难找到比这更可预言的东西了。
但假如你缓缓打开水龙头,使水流量增大,并调节水龙头,使一连串水滴以很不规则的方式滴落,这种滴落方式似乎是随机的。
只要做几次实验就会成功。
实验时均匀地转动水龙头,别把龙头开大到让水成了不间断的水流,你需要的是中速滴流。
如果你调节得合适,就可以在好多分钟内听不出任何明显的模式出现。
1978年,加利福尼亚大学圣克鲁斯分校的一群年青的研究生组成了一个研究动力学系统的小组。
他们开始考虑水滴系统的时候,就认识到它并不像表现出来的那样毫无规则。
他们用话筒记录水滴的声音,分析每一滴水与下一滴水之间的间隔序列。
他们所发现的是短期的可预言性。
要是我告诉你3个相继水滴的滴落时刻,你会预言下一滴水何时落下。
例如,假如水滴之间最近3个间隔是0.63秒、1.17秒和0.44秒,则你可以肯定下一滴水将在0.82秒后落下(这些数只是为了便于说明问题)。
事实上,如果你精确地知道头3滴水的滴落时刻,你就可以预言系统的全部未来。
那么,拉普拉斯为什么错了? 问题在于,我们永远不能精确地测量系统的初始状态。
我们在任何物理系统中所作出的最精确的测量,对大约10位或12位小数来说是正确的。
但拉普拉斯的陈述只有在我们使测量达到无限精度(即无限多位小数,当然那是办不到的)时才正确。
在拉普拉斯时代,人们就已知道这一测量误差问题,但一般认为,只要作出初始测量,比如小数点后10位,所有相继的预言也将精确到小数点后10位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. Introduction In interval dynamics there are many ways to deal with the notion of asymptotic complexity (“chaos”). Probably it is pointless to try and decide which is the best of them, but in applications there are two of them which are by far the most popular, see e.g. [D, MMN]. One is topological chaos, that is, the existence of an uncountable scrambled set in the sense of the famous Li and Yorke paper [LY]. The other one is ergodic chaos, that is, the existence of an invariant probability measure absolutely continuous with respect to the Lebesgue measure (acip). Neither of them is without drawbacks. (To keep this introduction at the expository level, we have deferred most of definitions to the subsequent sections.) There are easy conditions implying the existence of Li-Yorke chaos and its stability under small perturbations. One such condition is the existence of a periodic orbit of period not a power of two [Bl]. Nevertheless, this chaos need not be “observable”: for instance, the
Date : November 10, 2009. 2000 Mathematics Subject Classification. Primary: 37E05, Secondary: 26A18, 37B20, 37C70. Key words and phrases. Li-Yorke pair, Li-Yorke chaos, scrambled set, interval map, distal pair, asymptotic pair, attractor, strongly wandering set. HB gratefully acknowledges the support of EPSRC grant EP/F037112/1 and also the hospitality of the University of Murcia and Delft University of Technology. VJL was partially supported by MICINN (Ministerio de Ciencia e Innovacion) and FEDER (Fondo Europeo de Desarrollo Regional), grant MTM2008-03679/MTM, and Fundaci´ on S´ eneca (Agencia de Ciencia y Tecnolog´ ıa de la Regi´ on de Murcia, Programa de Generaci´ on de Conocimiento Cient´ ıfico de Excelencia, II PCTRM 2007-10), grant 08667/PI/08.
ON THE LEBESGUE MEASURE OF LI-YORKE PAIRS FOR INTEROR JIMENEZ LOPEZ
arXiv:0911.1869v1 [math.DS] 10 Nov 2009
Abstract. We investigate the prevalence of Li-Yorke pairs for C 2 and C 3 multimodal maps f with non-flat critical points. We show that every measurable scrambled set has zero Lebesgue measure and that all strongly wandering sets have zero Lebesgue measure, as does the set of pairs of asymptotic (but not asymptotically periodic) points. If f is topologically mixing and has no Cantor attractor, then typical (w.r.t. twodimensional Lebesgue measure) pairs are Li-Yorke; if additionally f admits an absolutely continuous invariant probability measure (acip), then typical pairs have a dense orbit for f × f . These results make use of so-called nice neighborhoods of the critical set of general multimodal maps, and hence uniformly expanding Markov induced maps, the existence of either is proved in this paper as well. For the setting where f has a Cantor attractor, we present a trichotomy explaining when the set of Li-Yorke pairs and distal pairs have positive two-dimensional Lebesgue measure.
1
2
´ ´ HENK BRUIN AND V´ ICTOR JIMENEZ LOPEZ
orbits of almost all points (in the sense of Lebesgue measure) may be attracted by this periodic orbit [Gu]. On the other hand, ergodic chaos ensures complicated dynamics for a set of points with positive measure. For instance, if a smooth multimodal map (with non-flat critical points) f has an acip, then, as a simple consequence of the zero measure of Cantor metric attractors [SV] and Proposition 9 below, there is a positive measure set of points whose orbit under f is dense in some interval. However, the converse is not true, even for the family of logistic maps [Jo, Ly2], so acips can only exist under additional conditions (for instance, hyperbolic repelling periodic points and |Df n (f (c))| → ∞ for any critical point c of the map f [BRSS]). A map f is infinitely renormalizable if there is an infinite collection of nested cycles of periodic intervals; the intersection of these cycles is a Cantor set, called a solenoidal attractor (because the suspension over this attractor is a topological solenoid). The Feigenbaum map, or more correctly Coullet-Tresser-Feigenbaum, (see e.g. [MS, pp. 151152]) is the best known example of this. A solenoidal attractor is Lyapunov stable and as shown in [BrJ] (see Proposition 31 below), points in the basin of such an attractor are approximately periodic: Definition 1. A point x is approximately periodic if for every ε > 0 there is a periodic point p such that lim supn→∞ |f n (x) − f n (p)| < ε. Hence, up to small errors, almost all points eventually behave as periodic points. Remark 2. An intrinsic characterization of adding machines (namely any system in which every point is regularly recurrent) is presented in [BK]. In our setting, it applies to the solenoidal attractor itself, whereas approximate periodicity gives information on a neighborhood of the solenoidal attractor. However, a multimodal (even polynomial) map may have a dense orbit while, simultaneously, almost all orbits are attracted by a Cantor set (a so-called wild attractor) [BKNS]. As we will explain below, in such a case it is still possible but not necessary that a.e. point is approximately periodic. We see that there is a variety of smooth multimodal maps featuring a certain degree of “observable” dynamical complexity which is, however, not strong enough to be realized by an acip. It is natural to return to the Li-Yorke notion of chaos and investigate to what extent it can be used to measure this complexity. This is what we intend in the present paper. Definition 3. Let f : I = [0, 1] → I be a continuous map. A pair of points (x, y ) is called: • distal if lim inf n→∞ |f n (y ) − f n (x)| > 0; • asymptotic if limn→∞ |f n (y ) − f n (x)| = 0; • Li-Yorke if it is neither asymptotic nor distal, that is, 0 = lim inf |f n (y ) − f n (x)| < lim sup |f n (y ) − f n (x)|.
