钢结构课后部分习题
钢结构基本原理课后习题答案
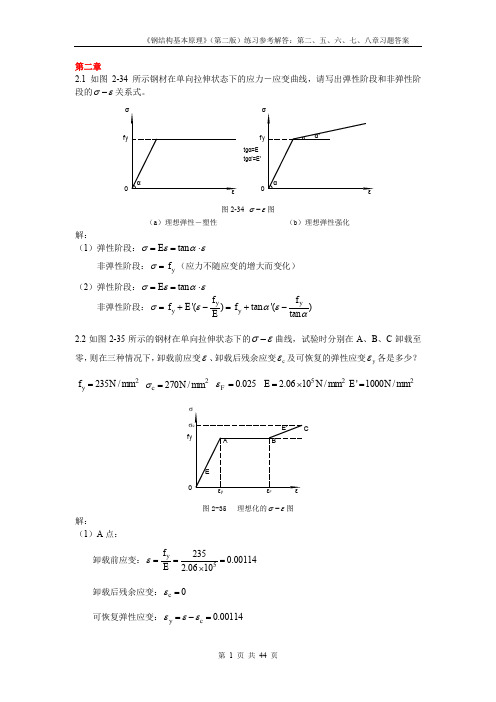
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构 武汉理工大学出版社 课后习题答案

钢结构课后习题答案(仅供参考)第三章 钢结构的连接3.1 试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B ,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/wf f N mm = 123α=213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=,,min 5.2f h mm ≥==, 8f h mm = 内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h m m = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。
223332480.720.76160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060260262481=⨯=<=⨯+=',取260mm 。
钢结构戴国欣主编课后习题答案

第三章 钢结构的连接3。
1 试设计双角钢与节点板的角焊缝连接(图3。
80)。
钢材为Q235B,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/w f f N mm = 123α=213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=, ,min min 1.5 1.512 5.2f h t mm ≥==, 8f h mm =内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑ 3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h mm = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf f N l mm h f ≥==⋅⨯⨯⨯∑,则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。
钢结构基本原理(沈祖炎)课后习题答案完全版
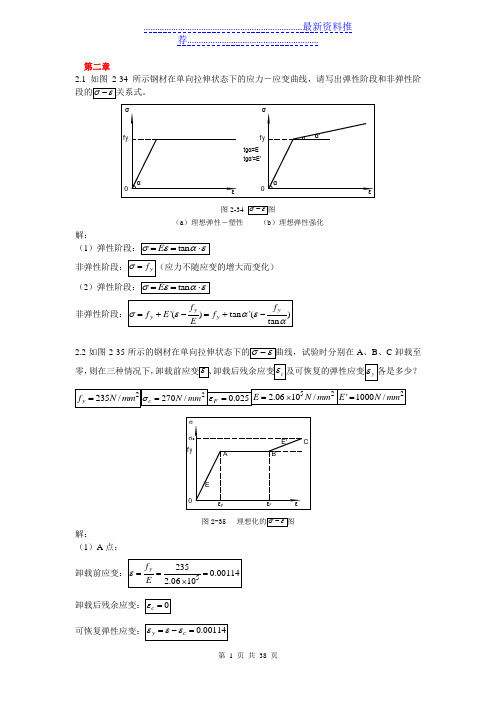
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶图(a)理想弹性-塑性(b )理想弹性强化解:(1(22.2如图2-35A 、B、C 卸载至零,则在三种情况下,图2-35解:(1)A 点:(2)B点:(3)C点:2.3作用时间之间的关系。
点、极限强度提高,而塑性韧性降低(时效现象)也会更高而更短。
钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。
一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低。
2.4试述导致钢材发生脆性破坏的各种原因。
答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,可能会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。
2.5 解释下列名词:(1)延性破坏延性破坏,也叫塑性破坏,破坏前有明显变形,并有较长持续时间,应力超过屈服点fy、并达到抗拉极限强度fu的破坏。
(2)损伤累积破坏指随时间增长,由荷载与温度变化,化学和环境作用以及灾害因素等使结构或构件产生损伤并不断积累而导致的破坏。
(3)脆性破坏脆性破坏,也叫脆性断裂,指破坏前无明显变形、无预兆,而平均应力较小(一般小于屈服点fy )的破坏。
(4)疲劳破坏指钢材在连续反复荷载作用下,应力水平低于极限强度,甚至低于屈服点的突然破坏。
(5)应力腐蚀破坏应力腐蚀破坏,也叫延迟断裂,在腐蚀性介质中,裂纹尖端应力低于正常脆性断裂应力临界值的情况下所造成的破坏。
(6)疲劳寿命指结构或构件中在一定恢复荷载作用下所能承受的应力循环次数。
钢结构的连接(课后习题)

第 2 章 钢结构的连接一、选择题1 直角角焊缝的强度计算公式 w c f l h N =t ≤ w f f 中,he 是角焊缝的——。
(A)厚度 (B)有效厚度 (C)名义厚度 (D)焊脚尺寸2 对于直接承受动力荷载的结构,计算正面直角焊缝时——。
(A)要考虑正面角焊缝强度的提高 (B)要考虑焊缝刚度影响。
(C)与侧面角焊缝的计算式相同 (D)取 f b =1.22 3 等肢角钢与钢板相连接时,肢背焊缝的内力分配系数为——。
(A)0.7 (B)0.75 (C)0.65 (D)0.354 直角角焊缝的有效厚度 c h ——。
(A)0.7 f h (B)4mm (C)1.2 f h (D)1.5 fh 5 在动荷载作用下,侧焊缝的计算长度不宜大于——·(A)60 f h (B)40 f h (C)80 f h (D)120 fh 6 角钢和钢板间用侧焊搭接连接,当角钢肢背与肢尖焊缝的焊脚尺寸和焊缝的长度都等同 时,————。
(A)角钢肢背的侧焊缝与角钢肢尖的侧焊缝受力相等(B)角钢肢尖侧焊缝受力大于角钢肢背的侧焊缝(C)角钢肢背的侧焊缝受力大于角钢肢尖的侧焊缝(D)由于角钢肢背和肢尖的侧焊缝受力不相等,因而连接受有弯矩的作用7 不需要验算对接焊缝强度的条件是斜焊缝的轴线和外力 N 之间的夹角满足——。
(A) q tan £1.5 (B) q tan >l,5 (C)q ≥70º (D) q <70º8 产生焊接残余应力的主要因素之一是——·(A)钢材的塑性太低 (B)钢材的弹性模量太高(C)焊接时热量分布不均 (D)焊缝的厚度太小9 钢结构连接中所使用的焊条应与被连接构件的强度相匹配,通常在被连接构件选用 Q345 时,焊条选用——。
(A)E55 (B)E50 (C)E43 (D)前三种均可10 焊缝连接计算方法分为两类,它们是——。
(A)手工焊缝和自动焊缝 (B)仰焊缝和俯焊缝(C)对接焊缝和角焊缝 (D)连续焊缝和断续焊缝11 焊接结构的疲劳强度的大小与——关系不大。
钢结构设计课后习题答案

1.1、屋盖结构主要组成部分是哪些?它们的作用是什么?A、屋架:支撑于柱或托架,承受屋面板或檩条传来的荷载;b、天窗:屋架跨度较大时,为了采光和通风的需要;C、支撑系统:用于增强屋架的侧向刚度,传递水平荷载和保证屋盖体系的整体稳定。
1.2、屋盖结构中有哪些支撑系统?支撑的作用是什么?(1)a、上弦横向水平支撑b、下弦横向水平支撑c、上弦纵向水平支撑d、下弦纵向水平支撑e、垂直支撑f、系杆(2)a、保证结构的空间整体性b、为弦杆提供适当的侧向支撑点c、承担并传递水平荷载d、保证结构安装时的稳定与方1.3、如何区分刚性系杆和柔性系杆?哪些位置需要设置刚性系杆?答:(1)刚性系杆:能承受压力,柔性系杆:只能承受拉力(2)上弦平面内檩条和大型屋面板可起到刚性系杆作用,因而可在屋架的屋脊和支座节点处设置系杆,当屋架横向支撑设置在第二柱间时所有系杆均为刚性系杆。
1.4实腹式和格构式檩条各适用于哪种情况?其优缺点是什么?答:(1)实腹式檩条常用于跨度为3~6m的情况,构造简单,制造及安装方便(2)桁架式檩条用于跨度较大(>6m)的情况,分为三种形式:A、平面桁架式檩条,受力明确,用料省,但侧向刚度较差,必须设置拉条;B、T形桁架式檩条,整体性差,应沿跨度全长设置钢箍;C、空间桁架式檩条,刚度好,承载力大,不必设置拉条,安装方便,但是构造复杂,适用跨度和荷载较大的情况1.5为什么檩条要布置拉条?答:为了给檩条提供侧向支撑,减小檩条沿屋面坡度方向的跨度,除了侧向刚度较大的空间桁架式和T形桁架式檩条外,在实腹式檩条和平面桁架式檩条之间设置拉条。
1.6三角形、梯形、平行弦桁架各适用于哪些屋盖体系?答:(1)三角形屋架:屋面坡度较大的有檩屋盖结构或中小跨度的轻型屋面结构(2)梯形屋架:用于屋面坡度较小的屋盖结构、工业厂房屋盖结构最常用形式(3)矩形屋架:用于托架或支撑体系中(4)曲拱屋架:用于有特殊要求的房屋中1.7屋架的腹杆有哪些体系?各有什么特征?答:(1)三角形腹杆:单斜杆式,长杆受拉,短杆受压,经济;人字式,腹杆数少,节点少,构造简单;芬克式,腹杆受力合理,可分开运输。
钢结构基本原理课后习题答案

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
(完整word版)钢结构基础第三章课后习题答案
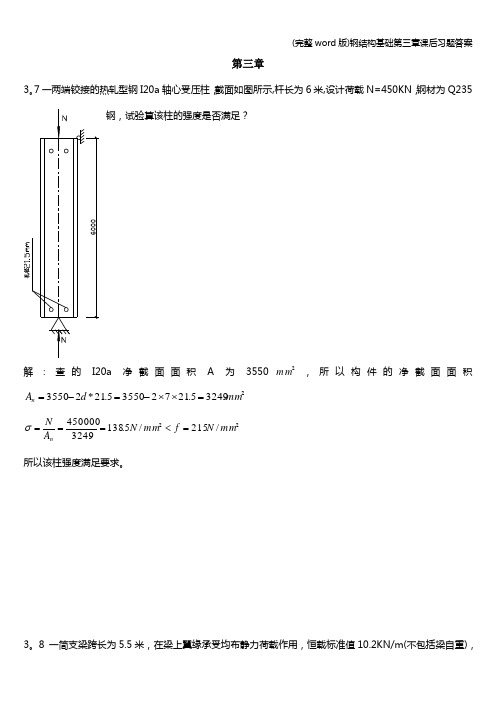
第三章3。
7一两端铰接的热轧型钢I20a 轴心受压柱,截面如图所示,杆长为6米,设计荷载N=450KN ,钢材为Q235钢,试验算该柱的强度是否满足?解:查的I20a 净截面面积A 为35502m m ,所以构件的净截面面积232495.217235505.21*23550mm d A n =⨯⨯-=-=22/215/5.1383249450000mm N f mm N A N n =<===σ 所以该柱强度满足要求。
3。
8 一简支梁跨长为5.5米,在梁上翼缘承受均布静力荷载作用,恒载标准值10.2KN/m(不包括梁自重),活荷载标准值25KN/m ,假定梁的受压翼缘有可靠的侧向支撑,钢材为Q235,梁的容许挠度为l/250,试选择最经济的工字型及H 型钢梁截面,并进行比较。
解:如上图示,为钢梁的受力图荷载设计值m KN q /24.47254.12.102.1=⨯+⨯= 跨中最大弯矩KNm ql M 63.1785.524.47818122=⨯⨯==f w M x x ≤=γσmax 所以3561091.7)21505.1/(1063.178mm fM w x x ⨯=⨯⨯=≥γ 查型钢表选择I36a ,质量为59.9kg/m,Wx 为8750003m m ,所以钢梁自重引起的恒载标注值m KN /58702.010008.99.59=÷⨯=,可见对强度影响很小,验算挠度即可:荷载标准值m KN q k /79.35252.1058702.0=++=挠度mm EI l q x k 13.1310576.11006.2384105.579.3553845851244=⨯⨯⨯⨯⨯⨯⨯==ω<[l/250]=22mm I36a 满足挠度要求。
查型钢表选择HN400x200x8x13,质量为66kg/m ,Wx 为11900003m m钢梁自重引起的恒载标注值m KN /6468.010008.966=÷⨯=,可见对强度影响很小,验算挠度即可:荷载标准值m KN q k /85.35252.106468.0=++=挠度mm EI l q x k 7.810237001006.2384105.585.3553845451244=⨯⨯⨯⨯⨯⨯⨯==ω<[l/250]=22mmHN400x200x8x13满足挠度要求。
钢结构基本原理课后习题答案

钢结构基本原理课后习题答案【篇一:钢结构基本原理(沈祖炎)课后习题答案完全版】2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的???关系式。
00图2-34 ???图(a)理想弹性-塑性(b)理想弹性强化解:(1)弹性阶段:??e??tan???非弹性阶段:??fy(应力不随应变的增大而变化)(2)弹性阶段:??e??tan???非弹性阶段:??fy?e(??fye)?fy?tan?(??fytan?)2.2如图2-35所示的钢材在单向拉伸状态下的???曲线,试验时分别在a、b、c卸载至零,则在三种情况下,卸载前应变?、卸载后残余应变?c及可恢复的弹性应变?y各是多少?fy?235n/mm2 ?c?270n/mm2 ?f?0.025e?2.06?105n/mm2e?1000n/mm20f图2-35 理想化的???图解:(1)a点:卸载前应变:??fye?235卸载后残余应变:?c?0 可恢复弹性应变:?y????c?0.00114卸载前应变:???f?0.025 卸载后残余应变:?c???fye?0.02386 可恢复弹性应变:?y????c?0.00114(3)c点:卸载前应变:???f??c?fye?0.025?0.035?0.06 ?卸载后残余应变:?c???c?0.05869 e可恢复弹性应变:?y????c?0.001312.3试述钢材在单轴反复应力作用下,钢材的?作用时间之间的关系。
??曲线、钢材疲劳强度与反复应力大小和答:钢材???曲线与反复应力大小和作用时间关系:当构件反复力??fy时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材???曲线基本无变化;当??fy时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材???曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理课后习题答案完全版
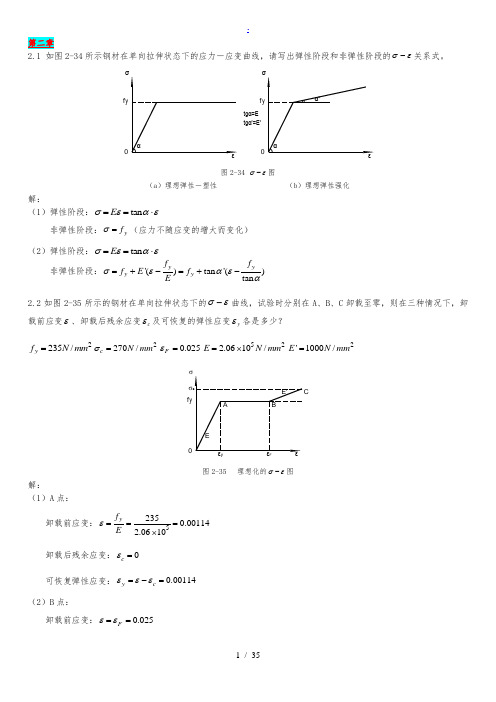
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan y yy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm =2270/c N mm σ=0.025F ε=522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解:(1)A 点: 卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构_武汉理工大学出版社_课后习题答案

(2)焊缝截面参数计算:取 h f 10mm
焊缝截面的形心: y1
150 7 3.5 2 69 7 (7 12 3.5) 2 193 7 ( 150 7 2 69 7 2 193 7
193 7 12 7) 2 75.5mm
3.2 试求图 3.81 所示连接的最大设计荷载。 钢材为 Q235B, 焊条为 E43 型, 手工焊, 角焊缝焊脚尺寸 h f 8mm ,
e1 30cm 。
焊脚尺寸: h f 8mm
205 2 2 45.6mm 焊缝截面的形心: x0 511.2 5.6 2 205 5.6 5.6 则 e2 205 45.6 162.2mm 2 205 5.6
2 max 3 2 1.1 ft w
(0.892 F ) 2 3 (0.417 F ) 2 1.148 F 1.1 ft w 1.1185 203.5( N / mm2 )
F 177.3KN
3.5 焊接工字形梁在腹板上设一道拼接的对接焊缝 (图 3.83) , 拼接处作用有弯矩 M 1122kN .m , 剪力 V=374KN, 钢材为 Q235B 钢,焊条用 E43 型,半自动焊,三级检验标准,试验算该焊缝的强度。
Ty
V 引起的应力: Vy
T rx 462.2 F 166.2 3.360 104 F IP 2.231108
V F 1.938 104 F h l 5158.72 ew
2
(4) (5.295 10 F ) [(
2
4
3.360 1.938 ) 104 F ]2 160 28.04 18.86 104 F 160 1.22
钢结构课后习题答案(DOC)

一、选择题1 钢材在低温下,强度 A 塑性 B ,冲击韧性 B。
(A) 提升 (B) 降落(C) 不变(D) 可能提升也可能降落2 钢材应力应变关系的理想弹塑性模型是—A—。
3 在构件发生断裂损坏前,有显然预兆的状况是 B 的典型特点。
(A) 脆性损坏(B) 塑性损坏(C) 强度损坏(D) 失稳损坏5 钢材的设计强度是依据—C—确立的。
(A) 比率极限(B) 弹性极限(C) 折服点(D) 极限强度6 结构工程中使用钢材的塑性指标,当前最主要用—D—表示。
(A) 流幅 (B) 冲击韧性(C) 可焊性 (D) 伸长率7钢材牌号 Q235, Q345,Q390是依据资料— A—命名的。
(A) 折服点(B)设计强度(C)标准强度(D)含碳量8钢材经历了应变硬化 ( 应变增强 ) 以后— A—。
(A) 强度提升(B)塑性提升(C)冷弯性能提升(D)可焊性提升9型钢中的 H 钢和工字钢对比,— B—。
(A)二者所用的钢材不一样(B) 前者的翼缘相对较宽(C) 前者的强度相对较高(D)二者的翼缘都有较大的斜度10钢材是理想的— C—。
(A) 弹性体(B)塑性体(C)弹塑性体(D)非弹性体11有两个资料分别为 Q235 和 Q345 钢的构件需焊接,采纳手工电弧焊,—B—采纳 E43焊条。
(A) 不得 (B) 能够(C) 不宜(D) 一定13 同类钢种的钢板,厚度越大,—A—。
(A) 强度越低(B) 塑性越好(C) 韧性越好(D) 内部结构缺点越少14 钢材的抗剪设计强度fv 与 f 相关,一般而言,fv =— A—。
(A)f / 3 (B) 3 f (C)f / 3 (D)3f16 钢材在复杂应力状态下的折服条件是由—D—等于单向拉伸时的折服点决定的。
(A) 最大主拉应力1 (B) 最大剪应力1 (C) 最大主压应力3 (D) 折算应力eq17 k是钢材的— A—指标。
(A) 韧性性能(B) 强度性能(C) 塑性性能(D) 冷加工性能18 大跨度结构应优先采纳钢结构,其主要原由是___D_ 。
钢结构基本原理课后习题答案(第二版)
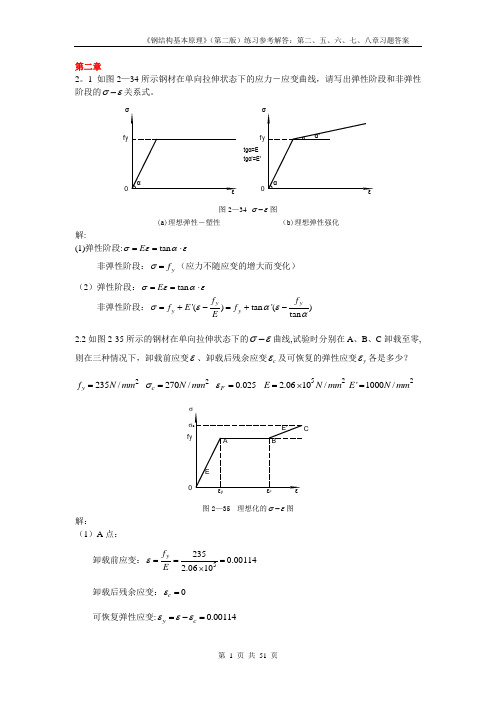
第二章2。
1 如图2—34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2—34 σε-图(a)理想弹性-塑性(b)理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2—35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2。
3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系.答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P 1073.3试设计如图所示双角钢和节点板间的角焊缝连接。
钢材Q235-B ,焊条E43型,手工焊,轴心拉力设计值N=500kN (静力荷载)。
①采用侧焊缝;②采用三面围焊。
解:角焊缝的强度设计值2160/wf f N mm =,焊缝内力分配系数为120.70,0.30K K ==。
焊角尺寸:max min min max (1~2)8(1~2)7~61.5 1.510 4.74f f h t mm mm mm h t mm=-=-==== 取6f h mm =①采用两边侧焊缝(转角处做绕角焊):110.7500350N K N kN =⋅=⨯=,220.3500150N K N kN =⋅=⨯=肢背计算长度:31135010260.420.720.76160w wf f N l mm h f ⨯===⨯⨯⨯⨯⨯⨯,取1270w l mm =; 肢尖计算长度:31215010111.6120.720.76160w w f f N l mm h f ⨯===⨯⨯⨯⨯⨯⨯,取2120w l mm =; ②采用三面围焊缝:正面角焊缝的长度等于相连角钢肢的宽度,即390w l b mm ==。
3320.720.7690 1.22160147.57w f w f f N h l f kN β=⨯⨯⋅⋅⋅=⨯⨯⨯⨯⨯=1132231147.570.750035073.79276.21221147.570.350015073.7976.2122N K N N kNN K N N kN=-=⨯-=-==-=⨯-=-= 311276.21106205.516211.5120.720.76160w f w f f N l h mm h f ⨯=+=+=+=⨯⨯⨯⨯⨯⨯,取1220w l mm =;32276.2110656.70662.7020.720.76160w f w f f N l h mm h f ⨯=+=+=+=⨯⨯⨯⨯⨯⨯,取270w l mm =。
P 1073.4有一托角钢,两边用角焊缝与柱相连,如图所示,钢材为Q345-A ,焊条E50型,手工焊,试确定焊缝厚度(焊缝有绕角,焊缝长度可不减2h f )。
已知:外力设计值N=400kN 。
解:角焊缝的强度设计值2200/wf f N mm =,20e mm =,400N kN =,4000.028M N e kN m =⋅=⨯=⋅。
弯矩产生的正应力:332226681010600/22200f e w e eM N mm h l h h σ⨯⨯⨯===⋅⨯竖向力产生的剪应力:32400101000/22200f e w e eN N mm h l h h τ⨯===⋅⨯ 应满足:2222260010001241868.851.22f w f f e e e f h h h στβ⎛⎫⎛⎫⎛⎫+=+=≤ ⎪ ⎪ ⎪⨯⎝⎭⎝⎭⎝⎭5.57e h mm ⇒≥7.950.7ef h h mm ⇒=≥ min max 1.5 1.518 6.36f h t mm === 综上所述取8f h mm =。
P 1073.6如图所示梁与柱的连接中,钢材为Q235-B ,弯矩设计值M=100kN.m ,剪力设计值V=600kN ,试完成下列设计和验算:(1)剪力V 由支托焊缝承受,焊条E43型,手工焊,求焊缝A 的高度h f ; (2)弯矩M 由普通螺栓承受,螺栓直径24mm ,验算螺栓是否满足要求。
解:(1)角焊缝的设计值2160/wf f N mm =,如图可知支托板采用三面围焊且有围角焊,焊缝计算长度可不减2f h 。
正面角焊缝承担:1 1.221603000.740992wf f e w f f N f h l h h β==⨯⨯⨯=; 侧面角焊缝承担:3216001040992wf f e w N N N h f h l =-=⨯-=33600104099216022500.760010 6.1996992f f f h h h mm⇒⨯-=⨯⨯⨯⨯⇒==取7f h mm =(2)普通C 级螺栓抗拉强度设计值2170/bt f N mm =,由题意知螺栓群受力为纯弯,因此中和轴位于最下排螺栓中心连线上,受拉最大的最外排螺栓所受拉力应为:331021122222410410010600106102(100200300500600)2(1492536)106104015010iN My y kN⨯⨯⨯⨯===⨯++++⨯++++⨯⨯==⨯∑受拉最大的最外排螺栓所受拉应力为:32212244401088.46/170/3.1424b t t N N mm f N mm d σπ⨯⨯===<=⨯ 满足。
P 1073.8如图所示螺栓连接采用Q235-B 级钢。
C 级螺栓直径d=20mm ,求此连接最大能承受的F max 值。
解:由附表1.4查得:22140/,305/bbv c f N mm f N mm ==。
因10604240151520300l mm d mm =⨯=<=⨯=,不用考虑承载力折减系数η。
单个螺栓受剪承载力设计值:223.1420214087.9244b bvv v d N n f kN π⨯==⨯⨯=(双剪) 单个螺栓承压承载力设计值:2020305122bb c cN dt fkN =⋅=⨯⨯=∑则: min 87.92bbv N N kN ==(由螺栓受剪承载力决定)此连接能承受的最大值:max min 1387.921142.96bF nN kN ==⨯=P 1725.3如习题5.3图所示,某焊接工字形等截面简支梁,跨度10m ,在跨中作用一静力集中荷载,该荷载由两部分组成,一部分为恒载,标准值为200kN ;另一部分为活载,标准值为300kN 。
荷载沿梁的跨度方向支撑长度为150mm 。
该梁在支座处设有支撑加劲肋。
若该梁采用Q235B 级钢制作,试验算该梁的强度、刚度是否满足要求。
解: 标准荷载:200300500k q kN =+=设计荷载: 1.2200 1.4300660q kN =⨯+⨯=梁跨中设计荷载最大弯矩:max 46601041650k /m M PL N ==⨯=荷 梁自重:g 0.30.020.008 1.27.859.8(0.0120.0096)76.930.021676.93 1.66/A kN mωγγ==⨯⨯+⨯⨯⨯=+⨯=⨯=0(2bt+t h )=(2)自重设计荷载: 1.2 1.66 1.992/q kN m =⨯=梁跨中自重设计荷载最大弯矩:22max 8 1.99210824.9k /m M qL N ==⨯=自 梁跨中最大弯矩:max max max 165024.91674.9k /m M M M N =+=+=荷自对x 轴惯性矩:23220x 0410.812012()2302(1202)122122115200446520561720t h I bt h t cm ω⨯⎡⎤⎡⎤=++=+⨯⨯⨯+⎢⎥⎢⎥⎣⎦⎣⎦=+=对x 轴截面模量:356172029060212022x x I W cm h ⨯===+⨯ 1、 正应力验算:622max 31674.910176.06/205/1.05906010x nx M N mm f N mm W σγ⨯===<=⨯⨯(2016t mm =>,2205/f N mm =) 满足。
2、 剪应力验算:660 1.99210339.962222y P gL V kN ⨯=+=+= 00064111111()12008120030020(120020)24224214400003660000 5.110x S h t h bt h t mm ω=⨯⨯⨯+⨯⨯+=⨯⨯⨯+⨯⨯⨯+=+=⨯ 3622max6339.9610 5.11038.6/125/5617.2108y xv x V S N mm f N mm I t τ⋅⨯⨯⨯===<=⋅⨯⨯ (816t mm =<,2125/v f N mm =)满足。
3、 局部压应力验算:梁在支座处设有支撑加劲肋,不用验算支座处局压。
52150520250Z y R l a h h mm =++=+⨯=1.0ψ=321.0660********/8250c Z Ff N mm t l ωψσ⋅⨯⨯===>=⋅⨯(816t mm ω=<,2215/f N mm =)不满足。
4、对梁腹板计算高度边缘处折算应力验算:621161674.910600178.90/5617.210x n M y N mm I σ⋅⨯⨯===⨯63130020610 3.6610S mm =⨯⨯=⨯36211633010 3.661026.9/5617.2108x V S N mm I t ωτ⋅⨯⨯⨯===⋅⨯⨯ 2330/c N mm σ=222222213178.90330178.90330326.932005.21108900590372170.8384039.04289.89 1.1215236.5/Z c c f N mm σσσσστβ=+-⋅+=+-⨯+⨯=+-+==>⋅=⨯= 不满足。
5、刚度验算:2max (200300)1011.6610125020.751270.7548k M kN m +⨯=+⨯⨯=+=⋅2266561270.7510101010.98251010 2.06105617.210400k x M l l mm mm E I ν⋅⨯⨯⨯===<=⋅⨯⨯⨯⨯ 满足。
P 1725.4如习题5.3中梁仅在支座处设有侧向支撑,该梁整体稳定能否满足要求。
若不能,采用何种措施?解:3364y 203002290101212bh I mm ⨯=⨯=⨯=⨯6901064.5521600yy I i mm A ⨯=== 110000154.9264.55y y l i λ=== 11100.020.5380.3 1.24l t b h ξ⨯===⨯ 由附表3.1查得:0.730.180.827b βξ=+=1222243202351()4.44320216124154.9222350.8271()00.44 1.15010.5060.6154.929060 4.4124235y b b b y x y t Ah W h f λϕβηλ⎡⎤⋅=⋅⋅⋅++⨯⎢⎥⎢⎥⎣⎦⎡⎤⨯⨯=⨯⨯⨯++⨯=⨯⨯=<⎢⎥⨯⎣⎦62m a x 31674.910184.870.506205103.73/906010b x M f N m m W σϕ⨯===>⋅=⨯=⨯ 不满足。
