钢结构基本原理课后习题答案
钢结构基本原理课后习题答案
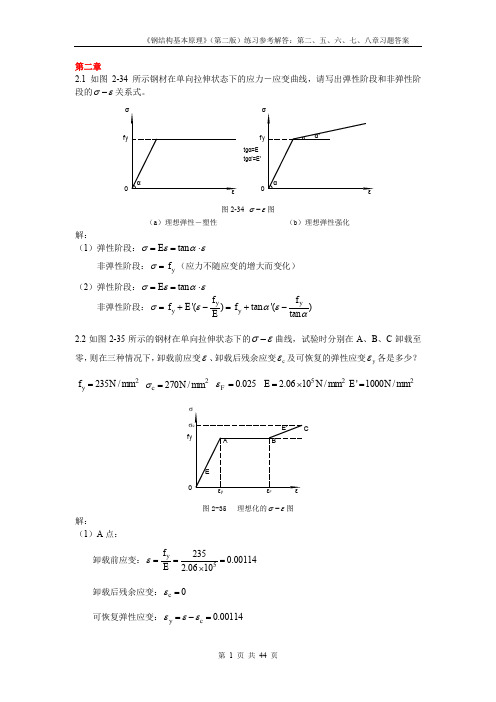
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理课后习题答案完全版

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理(沈祖炎)课后习题答案完全版

第二章2。
1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性时期和非弹性时期的关系式、图2-34 图(a)理想弹性-塑性ﻩﻩ (b)理想弹性强化解:(1)弹性时期:非弹性时期:(应力不随应变的增大而变化)(2)弹性时期:非弹性时期:2。
2如图2—35所示的钢材在单向拉伸状态下的曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变、卸载后残余应变及可恢复的弹性应变各是多少?图2—35ﻩ理想化的图解:(1)A 点:卸载前应变:卸载后残余应变:ﻩ可恢复弹性应变:(2)B 点:ﻩ卸载前应变:卸载后残余应变:ﻩ可恢复弹性应变:(3)C 点:ﻩ卸载前应变:卸载后残余应变:ﻩ可恢复弹性应变:2、3试述钢材在单轴反复应力作用下,钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材曲线与反复应力大小和作用时间关系:当构件反复力时,即材料处于弹性时期时,反复应力作用下钢材材性无变化,不存在残余变形,钢材曲线基本无变化;当时,即材料处于弹塑性时期,反复应力会引起残余变形,但若加载—卸载连续进行,钢材曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢材tgα'=E'f y0f y 0tgα=E曲线会相对更高而更短。
另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材曲线也会更高而更短。
钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。
一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低、2。
4试述导致钢材发生脆性破坏的各种原因。
答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,估计会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。
钢结构基本原理(沈祖炎)课后习题答案完全版
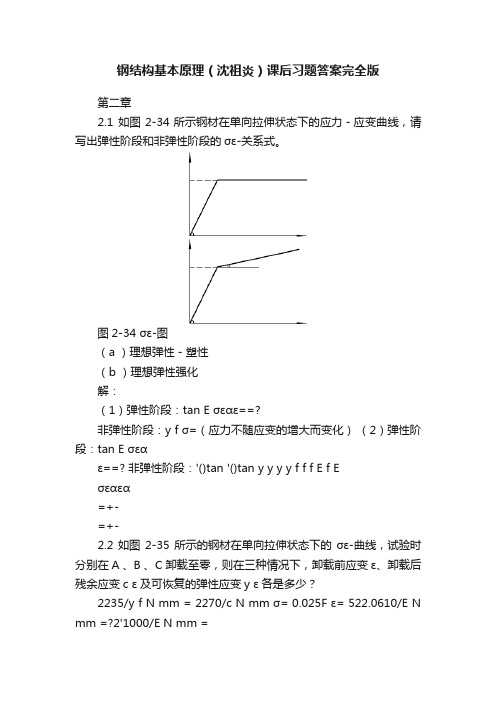
钢结构基本原理(沈祖炎)课后习题答案完全版第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==?非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==? 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =?2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===?卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=tgα'=E'f y 0f y 0tgα=E σf yCσF卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
(完整版)钢结构基本原理课后习题与答案完全版
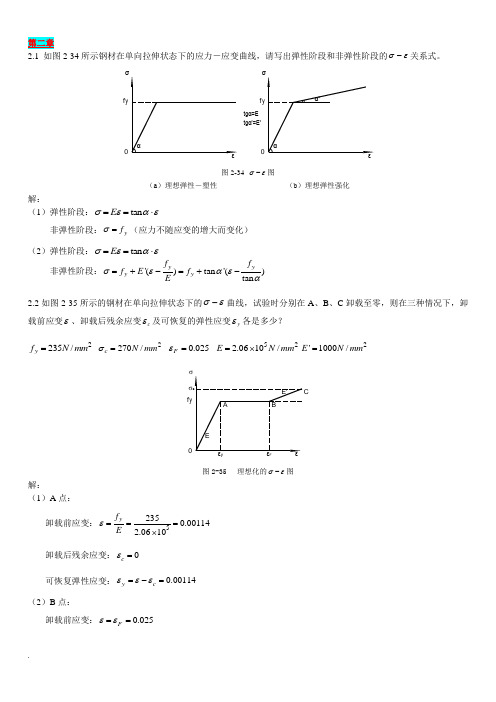
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理_沈祖炎_课后习题答案完全版
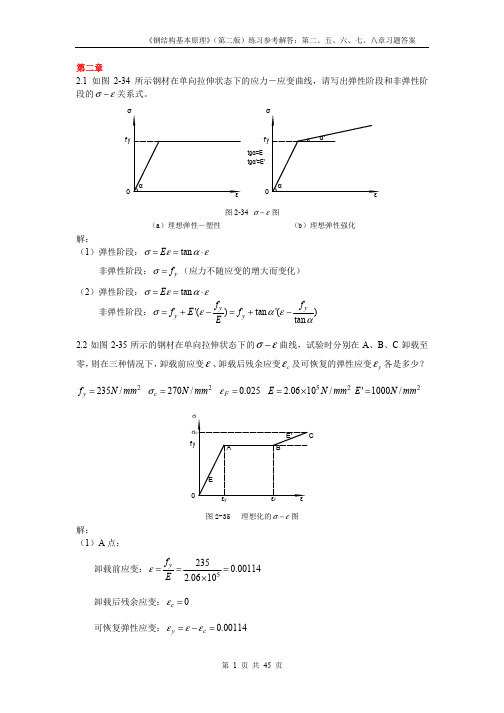
I xn =
1 1 × 240 × 1000 3 − × (240 − 8) × 960 3 = 2.8951 × 10 9 mm 4 12 12
W xn = W pn =
2.8951 × 10 9 = 5790208mm 3 500 1 × 8 × 960 2 + 240 × 20 × 980 = 6547200mm 3 4
f y = 235 N / mm 2 σ c = 270 N / mm 2 ε F = 0.025 E = 2.06 × 105 N / mm2 E ' = 1000 N / mm2
σ σc
fy A B E' C
E 0 εy εF ε
图 2-35
理想化的 σ − ε 图
解: (1)A 点: 卸载前应变: ε =
解: (1)弹性阶段: σ = Eε = tan α ⋅ ε 非弹性阶段: σ = f y (应力不随应变的增大而变化) (2)弹性阶段: σ = Eε = tan α ⋅ ε 非弹性阶段: σ = f y + E '(ε −
fy E
) = f y + tan α '(ε −
fy tan α
)
2.2 如图 2-35 所示的钢材在单向拉伸状态下的 σ − ε 曲线,试验时分别在 A、B、C 卸载至 零, 则在三种情况下, 卸载前应变 ε 、 卸载后残余应变 ε c 及可恢复的弹性应变 ε y 各是多少?
2 8
按式(4-13)
Mx N Mx 1500 × 10 3 + ≤ fd ⇒ + ≤ 215 ⇒ M x ≤ 742272.5 N ⋅ m An W xn 17280 5790208
钢结构基本原理(沈祖炎)课后习题答案完全版

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:tgα'=E'f y 0f y 0tgα=E σf yCσF(1)A 点: 卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点: 卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理课后习题答案

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
