c++蚁群算法最短路径代码
蚁群算法
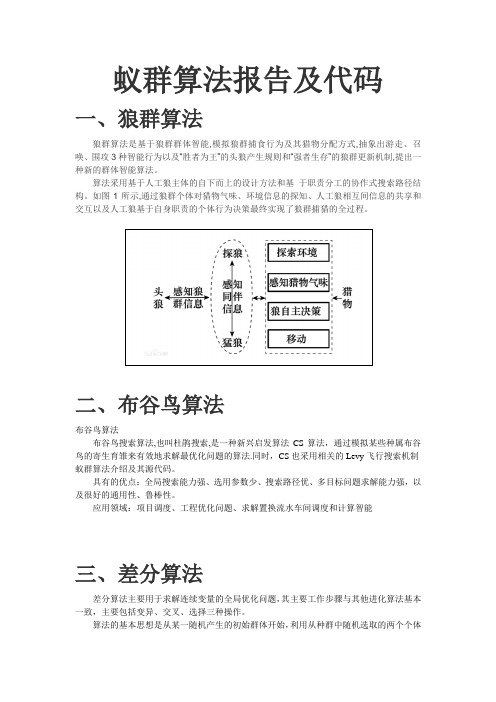
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。
算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。
如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。
二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法,通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时,CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。
具有的优点:全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强,以及很好的通用性、鲁棒性。
应用领域:项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题,其主要工作步骤与其他进化算法基本一致,主要包括变异、交叉、选择三种操作。
算法的基本思想是从某一随机产生的初始群体开始,利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源,将差向量加权后按照一定的规则与第三个个体求和而产生变异个体,该操作称为变异。
然后,变异个体与某个预先决定的目标个体进行参数混合,生成试验个体,这一过程称之为交叉。
如果试验个体的适应度值优于目标个体的适应度值,则在下一代中试验个体取代目标个体,否则目标个体仍保存下来,该操作称为选择。
在每一代的进化过程中,每一个体矢量作为目标个体一次,算法通过不断地迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程向全局最优解逼近。
四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。
从理论上分析,迭代过程中,在保留上一代最佳个体的前提下,遗传算法是全局收敛的。
五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法,是集群智能思想的一个具体应用,它的主要特点是不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。
蚁群算法最短路径求解

蚁群算法最短路径求解
蚁群算法是一种模拟蚂蚁寻找食物的行为,通过模拟蚂蚁在路径上的行为来寻找最短路径。
蚂蚁在寻找食物时,会释放一种化学物质,其他蚂蚁会跟随这种化学物质,最终找到食物。
这种化学物质被称为信息素,蚂蚁在路径上释放的信息素越多,其他蚂蚁就越容易跟随这条路径。
蚁群算法最短路径求解的过程可以分为以下几个步骤:
1. 初始化信息素:在开始求解之前,需要将所有路径上的信息素初始化为一个较小的值,通常为1/n(n为路径数量)。
2. 蚂蚁选择路径:每只蚂蚁在选择路径时,会根据信息素浓度和路径长度进行选择。
信息素浓度越高的路径,被选择的概率就越大。
同时,路径长度越短的路径,也被选择的概率就越大。
3. 更新信息素:当所有蚂蚁都选择完路径后,需要根据路径长度更新信息素。
路径长度越短的路径,信息素浓度就越高。
4. 重复执行:重复执行步骤2和步骤3,直到达到最大迭代次数或者找到最短路径为止。
5. 输出结果:输出最短路径和路径长度。
蚁群算法最短路径求解的优点是可以处理大规模的问题,同时也能够处理多目标问题。
但是,蚁群算法也存在一些缺点,例如容易陷入局部最优解、收敛速度较慢等问题。
因此,在实际应用中需要根据具体问题进行调整和优化。
蚁群算法路径优化matlab代码

蚁群算法路径优化matlab代码标题:蚁群算法路径优化 MATLAB 代码正文:蚁群算法是一种基于模拟蚂蚁搜索食物路径的优化算法,常用于求解复杂问题。
在路径优化问题中,蚂蚁需要从起点移动到终点,通过探索周围区域来寻找最短路径。
MATLAB 是一个常用的数值计算软件,可以用来实现蚁群算法的路径优化。
下面是一个基本的 MATLAB 代码示例,用于实现蚁群算法的路径优化:```matlab% 定义参数num_ants = 100; % 蚂蚁数量num_steps = 100; % 路径优化步数search_radius = 2; % 搜索半径max_iterations = 1000; % 最大迭代次数% 随机生成起点和终点的位置坐标start_pos = [randi(100), randi(100)];end_pos = [75, 75];% 初始化蚂蚁群体的位置和方向ants_pos = zeros(num_ants, 2);ants_dir = zeros(num_ants, 2);for i = 1:num_antsants_pos(i, :) = start_pos + randn(2) * search_radius; ants_dir(i, :) = randomvec(2);end% 初始化蚂蚁群体的速度ants_vel = zeros(num_ants, 2);for i = 1:num_antsants_vel(i, :) = -0.1 * ants_pos(i, :) + 0.5 *ants_dir(i, :);end% 初始时蚂蚁群体向终点移动for i = 1:num_antsans_pos = end_pos;ans_vel = ants_vel;for j = 1:num_steps% 更新位置和速度ans_pos(i) = ans_pos(i) + ans_vel(i);ants_vel(i, :) = ones(1, num_steps) * (-0.1 * ans_pos(i) + 0.5 * ans_dir(i, :));end% 更新方向ants_dir(i, :) = ans_dir(i, :) - ans_vel(i) * 3;end% 迭代优化路径max_iter = 0;for i = 1:max_iterations% 计算当前路径的最短距离dist = zeros(num_ants, 1);for j = 1:num_antsdist(j) = norm(ants_pos(j) - end_pos);end% 更新蚂蚁群体的位置和方向for j = 1:num_antsants_pos(j, :) = ants_pos(j, :) - 0.05 * dist(j) * ants_dir(j, :);ants_dir(j, :) = -ants_dir(j, :);end% 更新蚂蚁群体的速度for j = 1:num_antsants_vel(j, :) = ants_vel(j, :) - 0.001 * dist(j) * ants_dir(j, :);end% 检查是否达到最大迭代次数if i > max_iterationsbreak;endend% 输出最优路径[ans_pos, ans_vel] = ants_pos;path_dist = norm(ans_pos - end_pos);disp(["最优路径长度为:" num2str(path_dist)]);```拓展:上述代码仅仅是一个简单的示例,实际上要实现蚁群算法的路径优化,需要更加复杂的代码实现。
蚁群算法的Python代码及其效果演示(含注释)

蚁群算法的Python代码及其效果演示(含注释)以下为基本蚁群算法的Python代码(含注释)。
随时可以运行:from turtle import*from random import*from json import loadk=load(open("stats.json"))city_num,ant_num=30,30 #规定城市和蚂蚁总数x_data=k[0] #城市的x坐标之集合y_data=k[1] #城市的y坐标之集合best_length=float("inf")best_path=[]alpha=1beta=7rho=0.5potency_list=[1 for xx in range(city_num**2)]Q=1##城市的index从0开始#下面列表存储城市间距离def get_i_index(n):if n%city_num==0:return n//city_num-1else:return n//city_numdef get_j_index(n):if n%city_num==0:return city_num-1else:return n%city_num-1distance_list=[((x_data[get_i_index(z)]-x_data[get_j_index(z)])**2+(y_data[get_i_index(z)]-y_data[get_j_index(z)])**2)**0.5 for z in range(1,city_num**2+1)]class ant(object):def __init__(self,ant_index):self.ant_index=ant_indexself.cities=list(range(city_num))self.current_length=0self.current_city=randint(0,city_num-1)self.initial_city=self.current_cityself.cities.remove(self.current_city)self.path=[self.current_city]self.length=0#根据城市的index求出两城市间距离def get_distance(self,index_1,index_2):return distance_list[index_1*city_num+index_2]def get_potency(self,index_1,index_2):return potency_list[index_1*city_num+index_2]def get_prob_list(self):res=[self.get_potency(self.current_city,x)**alpha*(1/self.get_distance(self.current_city,x))**bet a for x in self.cities]sum_=sum(res)final_res=[y/sum_ for y in res]return final_res##轮盘赌选择城市def __choose_next_city(self):city_list=self.citiesprob_list=self.get_prob_list()tmp=random()sum_=0for city,prob in zip(city_list,prob_list):sum_+=probif sum_>=tmp:self.length+=self.get_distance(self.current_city,city)self.current_city=cityself.path.append(self.current_city)self.cities.remove(self.current_city)returndef running(self):global best_length,best_pathfor x in range(city_num-1):self.__choose_next_city()self.length+=self.get_distance(self.current_city,self.initial_city)self.path.append(self.initial_city)if self.length<best_length:best_length=self.lengthbest_path=self.pathreturn (self.path,self.length)def go():operation=[]for x in potency_list:x*=(1-rho)for x in range(ant_num):operation.append(ant(x).running())for x in operation:for y in range(city_num-1):potency_list[x[0][y]*city_num+x[0][y+1]]+=Q/x[1]#print(f"potency_list:{potency_list}")#print(f"best_path:{best_path}")#print(f"best_length:{best_length}")for yy in range(1000):go()print(f"best_length:{best_length}")pu()setpos(x_data[best_path[0]],y_data[best_path[0]])pd()for x in range(1,city_num+1):setpos(x_data[best_path[x]],y_data[best_path[x]]) 运行效果:。
蚁群算法matlab代码讲解

蚁群算法matlab代码讲解蚁群算法(Ant Colony Algorithm)是模拟蚁群觅食行为而提出的一种优化算法。
它以蚁群觅食的方式来解决优化问题,比如旅行商问题、图着色问题等。
该算法模拟了蚂蚁在寻找食物时的行为,通过信息素的正反馈和启发式搜索来实现问题的最优解。
在蚁群算法中,首先需要初始化一组蚂蚁和问题的解空间。
每只蚂蚁沿着路径移动,通过信息素和启发式规则来选择下一步的移动方向。
当蚂蚁到达目标位置后,会根据路径的长度来更新信息素。
下面是一个用MATLAB实现蚁群算法的示例代码:```matlab% 参数设置num_ants = 50; % 蚂蚁数量num_iterations = 100; % 迭代次数alpha = 1; % 信息素重要程度因子beta = 5; % 启发式因子rho = 0.1; % 信息素蒸发率Q = 1; % 信息素增加强度因子pheromone = ones(num_cities, num_cities); % 初始化信息素矩阵% 初始化蚂蚁位置和路径ants = zeros(num_ants, num_cities);for i = 1:num_antsants(i, 1) = randi([1, num_cities]);end% 迭代计算for iter = 1:num_iterations% 更新每只蚂蚁的路径for i = 1:num_antsfor j = 2:num_cities% 根据信息素和启发式规则选择下一步移动方向next_city = choose_next_city(pheromone, ants(i, j-1), beta);ants(i, j) = next_city;endend% 计算每只蚂蚁的路径长度path_lengths = zeros(num_ants, 1);for i = 1:num_antspath_lengths(i) = calculate_path_length(ants(i, :), distances);end% 更新信息素矩阵pheromone = (1 - rho) * pheromone;for i = 1:num_antsfor j = 2:num_citiespheromone(ants(i, j-1), ants(i, j)) = pheromone(ants(i, j-1), ants(i, j)) + Q / path_lengths(i); endendend```上述代码中的参数可以根据具体问题进行调整。
蚁群算法旅行商问题代码

蚁群算法旅行商问题代码蚁群算法(Ant Colony Optimization, ACO)是一种基于蚁群行为的优化算法,常用于解决组合优化问题,如旅行商问题(Travelling Salesman Problem, TSP)。
下面是一个简单的Python 实现,使用蚁群算法解决TSP问题:```pythonimport numpy as npclass AntColony:def __init__(self, distances, n_ants, n_best, n_iteration, decay, alpha=1, beta=2): """Args:distances (2D numpy.array): Square matrix of distances. Diagonal is assumed to be np.inf.n_ants (int): Number of ants running per iterationn_best (int): Number of best ants who deposit pheromonen_iteration (int): Number of iterationsdecay (float): Rate it which pheromone decays. The pheromone value is multiplied by decay, so 0.95 will lead to decay, 0.5 to much faster decay.alpha (int or float): exponenet on pheromone, higher alpha gives pheromone more weight. Default=1beta (int or float): exponent on distance, higher beta give distance more weight. Default=2"""self.distances = distancesself.pheromone = np.ones(self.distances.shape) / len(distances)self.all_inds = range(len(distances))self.all_paths = self.gen_all_paths()self.n_ants = n_antsself.n_best = n_bestself.n_iteration = n_iterationself.decay = decayself.alpha = alphaself.beta = betadef gen_all_paths(self):all_paths = []for i in self.all_inds:rest = set(self.all_inds)current = []rest.remove(i)for _ in range(len(self.distances)-1):to_visit = list(rest)probs = self.pheromone[i, to_visit]**self.alpha * ((1.0 / self.distances[i, to_visit])**self.beta)probs /= sum(probs)next_ind = np.random.choice(to_visit, p=probs)current.append((i, next_ind))i = next_indrest.remove(next_ind)all_paths.append(current)return all_pathsdef gen_path_dist(self, path):total_dist = 0for ant in path:total_dist += self.distances[ant]return total_distdef run(self):all_time_best_path = Noneall_time_best_dist = np.inffor i in range(self.n_iteration):all_paths = self.gen_all_paths()self.spread_pheronome(all_paths, self.n_best, self.distances)self.pheromone * self.decayif self.gen_path_dist(all_paths[0]) < all_time_best_dist:all_time_best_path = all_paths[0]all_time_best_dist = self.gen_path_dist(all_paths[0])self.global_best_path_ = all_time_best_pathself.global_best_dist_ = all_time_best_distreturn all_time_best_pathdef spread_pheronome(self, all_paths, n_best, dists):sorted_paths = sorted(all_paths, key=lambda x: self.gen_path_dist(x))for path in sorted_paths[:n_best]:for move in path:self.pheromone[move] += 1.0 / dists[move]# Example Usage:# Define distances between cities (replace this with your own data)distances = np.array([[np.inf, 2, 2, 5, 7],[2, np.inf, 4, 8, 2],[2, 4, np.inf, 1, 3],[5, 8, 1, np.inf, 2],[7, 2, 3, 2, np.inf]])# Create an AntColony instanceant_colony = AntColony(distances, n_ants=5, n_best=2, n_iteration=100, decay=0.95, alpha=1, beta=2)# Run the algorithmbest_path = ant_colony.run()print("Best Path:", best_path)print("Best Distance:", ant_colony.global_best_dist_)```这个示例中,`distances` 表示城市之间的距离矩阵。
最短路径——dijkstra算法代码(c语言)

最短路径——dijkstra算法代码(c语⾔)最短路径问题看了王道的视频,感觉云⾥雾⾥的,所以写这个博客来加深理解。
(希望能在12点以前写完)()⼀、总体思想1.初始化三个辅助数组s[],dist[],path[]s[]:这个数组⽤来标记结点的访问与否,如果该结点被访问,则为1,如果该结点还没有访问,则为0;dist[]:这个数组⽤来记录当前从v到各个顶点的最短路径长度,算法的核⼼思想就是通过不断修改这个表实现; path[]:这个数组⽤来存放最短路径;2.遍历图,修改上⾯的各项数组,每次只找最短路径,直到遍历结束⼆、代码实现1void dijkstra(Graph G, int v)2 {3int s[G.vexnum];4int dist[G.vexnum];5int path[G.vexnum];6for(int i = 0; i < G.vexnum; i++)7 {8 s[i] = 0;9 dist[i] = G.edge[v][i];10if(G.edge[v][i] == max || G.edge[v][i] == 0)11 {12 path[i] = -1;13 }14else15 {16 path[i] = v;17 }18 s[v] = 1;19 }2021for(int i = 0; i < G.vexnum; i++)22 {23int min = max;24int u;25for(int j = 0; j < G.vexnum; j++)26 {27if(s[j] != 1 && dist[j] < min)28 {29 min = dist[j];30 u = j;31 }32 }33 s[u] = 1;34for(int j = 0; j < G.vexnum; j++)35 {36if(s[j] != 1 && dist[j] > dist[u] + G.edge[u][j])37 {38 dist[j] = dist[u] + G.edge[u][j];39 path[j] = u;40 }41 }42 }43 }三、代码解释先⾃⼰定义⼀个⽆穷⼤的值max#define max infdijkstra算法传⼊的两个参为图Graph G;起点结点 int v;⾸先我们需要三个辅助数组1int s[G.vexnum];//记录结点时是否被访问过,访问过为1,没有访问过为02int dist[G.vexnum];//记录当前的从v结点开始到各个结点的最短路径长度3int path[G.vexnum];//记录最短路径,存放的是该结点的上⼀个为最短路径的前驱结点初始化三个数组1for(int i = 0; i < G.vexnum; i++)2 {3 s[i] = 0;//⽬前每个结点均未被访问过,设为04 dist[i] = G.edge[v][i];//dist[]数组记录每个从v结点开到其他i结点边的长度(权值)5if(G.edge[v][i] == max || G.edge[v][i] == 0)6 {7 path[i] = -1;8 }//如果v到i不存在路径或者i就是v结点时,将path[i]设为-1,意为⽬前v结点不存在路径到i9else10 {11 path[i] = v;12 }//反之,若v到i存在路径,则v就是i的前驱结点,将path[i] = v13 s[v] = 1;//从遍历起点v开始,即已经访问过顶点s[v]=114 }开始遍历数组并且每次修改辅助数组以记录⽬前的情况,直⾄遍历结束1for(int i = 0; i < G.vexnum; i++)2 {3int min = max;//声明⼀个min = max⽤来每次记录这次遍历找到的最短路径的长度(权值)4int u;//声明u来记录这次历找到的最短路径的结点5for(int j = 0; j < G.vexnum; j++)//开始遍历找⽬前的最短路径6 {7if(s[j] != 1 && dist[j] < min)8 {9 min = dist[j];10 u = j;11 }//找出v到结点j的最短路径,并且记录下最短路径的结点u = j12 }13 s[u] = 1;//找到结点u,即已访问过u,s[u] = 114for(int j = 0; j < G.vexnum; j++)//开始遍历修改辅助数组的值15 {16if(s[j] != 1 && dist[j] > dist[u] + G.edge[u][j])17 {18 dist[j] = dist[u] + G.edge[u][j];19 path[j] = u;20 }//如果v→j的路径⽐v →u→j长,那么修改dist[j]的值为 dist[u] + G.edge[u][j],并且修改j的前驱结点为path[j] = u21 }22 }遍历结束后,数组dist[]就是存放了起点v开始到各个顶点的最短路径长度最短路径包含的结点就在path数组中例如我们得到如下的path[]数组1 path[0] = -1;//0到⾃⼰⽆前驱结点2 path[1] = 0;//1的前驱为结点0,0⽆前驱结点,即最短路径为0 →13 path[2] = 1;//2的前驱结为点1,1的前驱结点0,0⽆前驱结点,即最短路径为0 →1 →24 path[3] = 0;//3的前驱为结点0,0⽆前驱结点,即最短路径为0 →35 path[4] = 2;//4的前驱结为点2,2的前驱结为点1,1的前驱结点0,0⽆前驱结点,即最短路径为0 →1 →2 →4 dijkstra对于存在负权值的图不适⽤,明天再更新Floyd算法叭。
蚁群算法MATLAB代码

蚁群算法MATLAB代码function [y,val]=QACSticload att48 att48;MAXIT=300; % 最大循环次数NC=48; % 城市个数tao=ones(48,48);% 初始时刻各边上的信息最为1rho=0.2; % 挥发系数alpha=1;beta=2;Q=100;mant=20; % 蚂蚁数量iter=0; % 记录迭代次数for i=1:NC % 计算各城市间的距离for j=1:NCdistance(i,j)=sqrt((att48(i,2)-att48(j,2))^2+(att48(i,3)-att48(j,3))^2);endendbestroute=zeros(1,48); % 用来记录最优路径routelength=inf; % 用来记录当前找到的最优路径长度% for i=1:mant % 确定各蚂蚁初始的位置% endfor ite=1:MAXITfor ka=1:mant %考查第K只蚂蚁deltatao=zeros(48,48); % 第K只蚂蚁移动前各边上的信息增量为零[routek,lengthk]=travel(distance,tao,alpha,beta);if lengthk<="">routelength=lengthk;bestroute=routek;endfor i=1:NC-1 % 第K只蚂蚁在路径上释放的信息量deltatao(routek(i),routek(i+1))=deltatao(routek(i),routek(i+1 ))+Q/lengthk;enddeltatao(routek(48),1)=deltatao(routek(48),1)+Q/lengthk;endfor i=1:NC-1for j=i+1:NCif deltatao(i,j)==0deltatao(i,j)=deltatao(j,i);endendendtao=(1-rho).*tao+deltatao;endy=bestroute;val=routelength;function [y,val]=travel(distance,tao,alpha,beta) % 某只蚂蚁找到的某条路径[m,n]=size(distance);p=fix(m*rand)+1;val=0; % 初始路径长度设为0tabuk=[p]; % 假设该蚂蚁都是从第p 个城市出发的for i=1:m-1np=tabuk(length(tabuk)); % 蚂蚁当前所在的城市号p_sum=0;for j=1:mif isin(j,tabuk)continue;elseada=1/distance(np,j);p_sum=p_sum+tao(np,j)^alpha*ada^beta;endendcp=zeros(1,m); % 转移概率for j=1:mif isin(j,tabuk)continue;elseada=1/distance(np,j);cp(j)=tao(np,j)^alpha*ada^beta/p_sum;endendNextCity=pchoice(cp);tabuk=[tabuk,NextCity];val=val+distance(np,NextCity);endy=tabuk;function y=isin(x,A) % 判断数x 是否在向量A 中,如在返回1 ,否则返回0 y=0;for i=1:length(A)if A(i)==xy=1;break;endendfunction y=pchoice(A)a=rand;tempA=zeros(1,length(A)+1); for i=1:length(A) tempA(i+1)=tempA(i)+A(i); endfor i=2:length(tempA)if a<=tempA(i)y=i-1;break;endend。
蚁群算法matlab代码

蚁群算法matlab代码蚁群算法,英文名为Ant Colony Algorithm,缩写为ACO,是一种启发式算法,是一种模拟蚂蚁寻找食物路径的算法。
在实际生活中,蚂蚁找到食物并返回巢穴后,将其找到食物的路径上的信息素留下,其他蚂蚁通过检测信息素来指导寻路,成为了一种集体智慧行为。
ACO也是通过模拟蚂蚁寻找食物路径的方式来寻找优化问题的最优解。
在ACO算法中,信息素是一个重要的概念,代表了走过某一路径的“好概率”,用这个“好概率”更新一些路径上的信息素,使得其他蚂蚁更可能选择经过这条路径,从而实现路径优化的目的。
在本文中,我们将讨论如何使用Matlab实现蚁群算法来优化问题。
1. 设定问题首先,我们要选取一个优化问题,并将其转换为需要在优化过程中进行选择的决策变量。
例如,我们想要优化旅行商问题(TSP)。
在TSP中,我们需要让旅行商以最短的距离经过所有城市,每个城市仅经过一次,最终回到出发的城市。
我们可以将每个城市编号,然后将TSP转化为一个最短路径选择的问题,即最短路径从编号为1的城市开始,经过所有城市,最终回到编号为1的城市。
2. 设定ACO参数在使用ACO优化问题时,需要设定一些参数,这些参数会影响算法的表现。
ACO算法需要设定的参数有:1.信息素含量:初始信息素的大小,即每个路径上的信息素浓度。
2.信息素挥发速度:信息素的随时间“减弱”程度。
3.信息素加成强度:蚂蚁经过路径后增加的信息素量。
4.启发式权重:用于计算启发式因子,即节点距离的贡献值。
5.蚂蚁数量:模拟蚂蚁数量,即同时寻找路径的蚂蚁个数。
6.迭代次数:模拟的迭代次数,即ACO算法运行的次数。
7.初始节点:ACO算法开始的节点。
3. 创建ACO优化函数我们可以使用Matlab来创建一个函数来实现ACO算法。
我们称其为“ACOoptimization.m”。
function best_path =ACOoptimization(city_location,iter_num,ant_num,init ial_path,alpha,beta,rho,update_flag) %ACO优化函数 %输入: %city_location: 城市坐标矩阵,格式为[x1,y1;x2,y2;...;xn,yn] %iter_num: 迭代次数 %ant_num: 蚂蚁数量 %initial_path: 起始路径,即初始解 %alpha,beta,rho: 超参数,用于调节蚂蚁选择路径的概率 %update_flag: 是否更新信息素的标志(1表示更新,0表示否) %输出: %best_path: 最优解,即最短路径%初始化信息素 pheromone = 0.01 *ones(length(city_location),length(city_location)); %初始化路径权重 path_weight =zeros(ant_num,1); %城市数量 n_cities =length(city_location);%主循环 for iter = 1:iter_num %一个迭代里所有蚂蚁都寻找一遍路径 for ant =1:ant_num %初始化蚂蚁位置current_city = initial_path; %标记是否经过了某个城市 visit_flag =zeros(1,n_cities);visit_flag(current_city) = 1; %用来存储当前路径 current_path = [current_city];%蚂蚁找东西 for i =1:n_cities-1 %计算路径概率p =calculate_probability(current_city,visit_flag,phero mone,city_location,alpha,beta); %蚂蚁选择路径 [next_city,next_index] = select_path(p);%路径更新current_path = [current_path;next_city];visit_flag(next_city) = 1;current_city = next_city;%更新路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end-1),:),city_location(current_path(end),:));end%加入回到起点的路径权重path_weight(ant) = path_weight(ant) +Euclidean_distance(city_location(current_path(end),:),city_location(current_path(1),:));%判断是否为最优解 ifant == 1 best_path = current_path; else if path_weight(ant) <path_weight(ant-1) best_path =current_path; end end%更新信息素 ifupdate_flag == 1 pheromone =update_pheromone(pheromone,path_weight,initial_path,current_path,rho); end end end end在函数中,我们首先定义了ACOalg函数的参数,包括城市坐标矩阵,迭代次数,蚂蚁数量,初始路径,超参数alpha,beta,rho,以及是否需要更新信息素。
蚁群算法python编程实现

蚁群算法python编程实现蚁群算法是一种基于群体智能的优化算法,在很多实际问题的求解中得到了广泛的应用。
本文将介绍如何使用Python语言实现蚁群算法,并提供一个简单的案例来说明其应用。
一、蚁群算法原理蚁群算法是一种模拟蚂蚁觅食行为的优化算法。
在蚂蚁觅食过程中,一只蚂蚁会释放一种信息素来引导其他蚂蚁找到食物,这种信息素会随着时间的推移逐渐消散。
而当一只蚂蚁找到食物时,它会释放更多的信息素,以加强路径的吸引力。
蚁群算法的基本流程如下:1. 初始化蚂蚁的位置和信息素的浓度。
2. 蚂蚁根据信息素和启发函数选择路径,更新信息素。
3. 重复第2步,直到满足停止条件。
4. 输出最优解。
二、蚁群算法python实现以下是一个简单的蚁群算法的Python实现:``` pythonimport random# 蚂蚁数量ants_num = 50# 迭代次数iter_num = 100# 信息素的初始浓度pheromone = 1.0# 信息素挥发系数evaporate = 0.5# 信息素增强系数enhance = 1.0# 启发函数中的信息素重要度alpha = 1.0# 启发函数中的路径长度重要度beta = 1.0# 城市距离矩阵distance_matrix = [[0, 10, 15, 20],[10, 0, 35, 25],[15, 35, 0, 30],[20, 25, 30, 0]]# 初始化信息素浓度矩阵pheromone_matrix = [[pheromone for j in range(4)] for i in range(4)]# 初始化蚂蚁位置ants = [[random.randint(0, 3)] for i in range(ants_num)] # 迭代过程for iter in range(iter_num):# 每只蚂蚁按照信息素和启发函数选择路径for i in range(ants_num):current_city = ants[i][-1]prob = [0 for j in range(4)]sum_prob = 0# 计算选择每个城市的概率for j in range(4):if j in ants[i]:prob[j] = 0else:prob[j] = (pheromone_matrix[current_city][j] ** alpha) * ((1.0 / distance_matrix[current_city][j]) ** beta)sum_prob += prob[j]# 选择下一个城市if sum_prob == 0:ants[i].append(random.randint(0, 3))else:r = random.uniform(0, sum_prob)s = 0for j in range(4):if j not in ants[i]:s += prob[j]if s > r:ants[i].append(j)break# 更新信息素for i in range(4):for j in range(4):if i != j:pheromone_matrix[i][j] *= evaporatefor k in range(ants_num):if j in ants[k] and i in ants[k]:pheromone_matrix[i][j] += enhance / distance_matrix[i][j] # 输出最优解best_ant = []best_distance = 0for i in range(ants_num):distance = 0for j in range(len(ants[i]) - 1):distance += distance_matrix[ants[i][j]][ants[i][j + 1]] if distance > best_distance:best_ant = ants[i][:]best_distance = distanceprint('Iteration {}: {} {}'.format(iter, best_ant,best_distance))```三、案例分析假设有4个城市需要进行旅行,它们之间的距离如下:```0 10 15 2010 0 35 2515 35 0 3020 25 30 0```运行以上Python代码,逐步输出结果如下:```Iteration 0: [0, 3, 1, 2, 0] 70Iteration 1: [0, 3, 1, 2, 0] 70Iteration 2: [0, 3, 1, 2, 0] 70...Iteration 98: [0, 3, 1, 2, 0] 70Iteration 99: [0, 3, 1, 2, 0] 70```可以看到,经过多次迭代后,蚂蚁选择的路径都是0-3-1-2-0,并且总路程为70。
蚁群算法及案例分析

群在选择下一条路径的时
候并不是完全盲目的,而是
按一定的算法规律有意识
地寻找最短路径
自然界蚁群不具有记忆的
能力,它们的选路凭借外
激素,或者道路的残留信
息来选择,更多地体现正
反馈的过程
人工蚁群和自然界蚁群的相似之处在于,两者优先选择的都
是含“外激素”浓度较大的路径; 两者的工作单元(蚂蚁)都
Eta=1./D;
%Eta为启发因子,这里设为距离的倒数
Tau=ones(n,n);
%Tau为信息素矩阵
Tabu=zeros(m,n);
%存储并记录路径的生成
NC=1;
%迭代计数器
R_best=zeros(NC_max,n); %各代最佳路线
L_best=inf.*ones(NC_max,1);%各代最佳路线的长度
for ii=2:N
R_best(NC,:)=Tabu(pos(1),:);
plot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)])
L_ave(NC)=mean(L);
hold on
NC=NC+1;
end
%第五步:更新信息素
Delta_Tau=zeros(n,n);
, 表示可根据由城市i到城市j的期望程度,可根据启发式算法具体确定,
一般为 。
= 0,算法演变成传统的随机贪婪算法最邻近城市被选中概率最大
= 0,蚂蚁完全只根据信息度浓度确定路径,算法将快速收敛,这样构出
的路径与实际目标有着较大的差距,实验表明在AS中设置α=1~2,β=2~5比较合
DrawRoute(C,Shortest_Route)
蚁群算法代码

#define MAXX 80
#define MAXY 23
#define MAX_FOOD 10000
#define TARGET_FOOD 200
#define MAX_SMELL 5000
#define SMELL_DROP_RATE 0.05
小小的蚂蚁总是能够找到食物,他们具有什么样的智能呢?设想,如果我们要为蚂蚁设计一个人工智能的程序,那么这个程序要多么复杂呢?首先,你要让蚂蚁能够避开障碍物,就必须根据适当的地形给它编进指令让他们能够巧妙的避开障碍物,其次,要让蚂蚁找到食物,就需要让他们遍历空间上的所有点;再次,如果要让蚂蚁找到最短的路径,那么需要计算所有可能的路径并且比较它们的大小,而且更重要的是,你要小心翼翼的编程,因为程序的错误也许会让你前功尽弃。这是多么不可思议的程序!太复杂了,恐怕没人能够完成这样繁琐冗余的程序。
为什么这么简单的程序会让蚂蚁干这样复杂的事情?答案是:简单规则的涌现。事实上,每只蚂蚁并不是像我们想象的需要知道整个世界的信息,他们其实只关心很小范围内的眼前信息,而且根据这些局部信息利用几条简单的规则进行决策,这样,在蚁群这个集体里,复杂性的行为就会凸现出来。这就是人工生命、复杂性科学解释的规律!
timeuse+=100;
oldsec = t.ti_sec;
}
timeuse+=t.ti_hund-oldhund;
oldhund = t.ti_hund;
if(tu>=60&&!CanFindFood)
{
gotoxy(1,MAXY+1);
printf(“Can not find food, maybe a block world.”);
蚁群算法求解函数最小值

蚁群算法求解函数最小值蚁群算法是一种群体智能算法,它模拟蚂蚁在寻找食物时留下信息、跟随信息和更新信息的行为。
其主要思想是让一群智能体(蚂蚁)在问题空间中随机游走,通过留下信息来指导其他蚂蚁的搜索,最终找到问题的最优解。
本文将介绍如何使用蚁群算法求解函数最小值问题。
1. 问题描述我们要求解函数f(x)的最小值,其中x是一个d维向量,f(x) = ∑(x_i^2),i=1,2,...,d。
因为所有维度上的值都是正的,所以函数的最小值为0。
但在搜索过程中,优化器需要在向量空间中寻找最小值。
2. 蚁群算法基本思想3. 蚁群算法具体实现1)初始化初始化迭代次数、蚁群大小、信息素浓度以及每只蚂蚁的位置和速度。
对于每个蚂蚁的初始位置和速度,可以使用随机值来生成。
同时,需要记录当前所有蚂蚁中最优的位置和最优的适应度值。
2)信息素选取蚂蚁在搜索过程中留下信息,用于指导其他蚂蚁的行动。
信息素的选择需要权衡两个因素,即蚂蚁个体的局部搜索策略和群体策略。
在局部策略方面,蚂蚁会在已经访问的路径上留下信息素,吸引其他蚂蚁走向已经访问过的区域。
在群体策略方面,信息素可以加速全局搜索,吸引更多的蚂蚁在全局范围内搜索。
3)更新信息素蚂蚁在搜索过程中留下信息,导致当前路径上信息素的浓度增加。
信息素的浓度会随着时间的推移而逐渐降低。
信息素的更新根据当前路径的质量,决定增加或者减少信息素的浓度。
4)更新速度和位置根据留下的信息素和当前位置,更新蚂蚁的速度和位置。
5)计算适应度根据当前位置计算适应度。
这里的适应度即函数的值。
6)更新最优值如果当前的适应度比已记录的最优适应度更优,则更新记录的最优适应度值和位置。
7)终止条件循环运行以上步骤,直到达到指定的迭代次数或满足特定的终止条件。
4. 代码实现示例以Python语言为例,下面给出了求解函数最小值的蚁群算法实现示例:```pythonimport numpy as npclass Ant(object):def __init__(self, dim, max_pos, min_pos):self.dim = dimself.max_pos = max_posself.min_pos = min_posself.pos = np.random.uniform(min_pos, max_pos, size=dim)self.velocity = np.random.uniform(min_pos, max_pos, size=dim)self.pbest = self.posself.pbest_fitness = float('inf')self.fitness = float('inf')def evaluate(self, f):self.fitness = f(self.pos)if self.fitness < self.pbest_fitness:self.pbest = self.posself.pbest_fitness = self.fitnessdef update_velocity(self, other_ant_pos, w, c1, c2, max_velocity):r1 = np.random.rand(self.dim)r2 = np.random.rand(self.dim)self.velocity = w * self.velocity + c1 * r1 * (self.pbest - self.pos) + c2 * r2 * (other_ant_pos - self.pos)self.velocity = np.clip(self.velocity, -max_velocity, max_velocity)def update_pos(self):self.pos = self.pos + self.velocityself.pos = np.clip(self.pos, self.min_pos, self.max_pos)class ACO(object):def __init__(self, f, dim=2, max_iter=100, n_ant=10, max_velocity=1, w=0.5, c1=1, c2=1, max_pos=10, min_pos=-10):self.f = fself.dim = dimself.max_iter = max_iterself.n_ant = n_antself.max_velocity = max_velocityself.w = wself.c1 = c1self.c2 = c2self.max_pos = max_posself.min_pos = min_posself.global_best_fitness = float('inf')self.global_best_pos = np.zeros(dim)self.ants = [Ant(dim, max_pos, min_pos) for i in range(n_ant)]self.init_random_ant()def init_random_ant(self):for ant in self.ants:ant.evaluate(self.f)if ant.fitness < self.global_best_fitness:self.global_best_fitness = ant.fitnessself.global_best_pos = ant.posdef search(self):for i in range(self.max_iter):for ant in self.ants:for other_ant in self.ants:if ant != other_ant:ant.update_velocity(other_ant.pos, self.w, self.c1, self.c2, self.max_velocity)ant.update_pos()ant.evaluate(self.f)if ant.fitness < self.global_best_fitness:self.global_best_fitness = ant.fitnessself.global_best_pos = ant.posdef run(self):self.search()print("best fitness: {:.6f}, best position:{}".format(self.global_best_fitness, self.global_best_pos))def f(x):return np.sum(x**2)aco = ACO(f)aco.run()```在这个实现中,我们用Ant表示每个蚂蚁,包含了位置、速度、适应度等信息。
蚁群算法最短路径matlab程序 - 副本

蚁群算法最短路径matlab程序 - 副本蚁群算法最短路径通用Matlab程序下面的程序是蚁群算法在最短路中的应用,稍加扩展即可应用于机器人路径规划function [ROUTES,PL,Tau]=ACASP(G,Tau,K,M,S,E,Alpha,Beta,Rho,Q) D=G2D(G);N=size(D,1);%N表示问题的规模(象素个数) MM=size(G,1);a=1;%小方格象素的边长Ex=a*(mod(E,MM)-0.5);%终止点横坐标if Ex==-0.5Ex=MM-0.5;endEy=a*(MM+0.5-ceil(E/MM)); Eta=zeros(1,N); for i=1:N if ix==-0.5 ix=MM-0.5;endiy=a*(MM+0.5-ceil(i/MM)); if i~=EEta(1,i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5;elseEta(1,i)=100;endendROUTES=cell(K,M);PL=zeros(K,M);%% -----------启动K轮蚂蚁觅食活动,每轮派出M只蚂蚁--------------------for k=1:Kdisp(k);for m=1:MW=S;Path=S;PLkm=0;TABUkm=ones(1,N);TABUkm(S)=0;DD=D;DW=DD(W,:);DW1=find(DW)for j=1:length(DW1)if TABUkm(DW1(j))==0 DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD); while W~=E&&Len_LJD>=1 PP=zeros(1,Len_LJD); for i=1:Len_LJDPP(i)=(Tau(W,LJD(i))^Alpha)*(Eta(LJD(i))^Beta);endPP=PP/(sum(PP)); Pcum=cumsum(PP);Select=find(Pcum>=rand);Path=[Path,to_visit]; PLkm=PLkm+DD(W,to_visit); W=to_visit;for kk=1:Nif TABUkm(kk)==0 DD(W,kk)=inf;DD(kk,W)=inf;endendTABUkm(W)=0;for j=1:length(DW1)if TABUkm(DW1(j))==0DW(j)=inf;endendLJD=find(DWLen_LJD=length(LJD);%可选节点的个数 end ROUTES{k,m}=Path; if Path(end)==EPL(k,m)=PLkm;elsePL(k,m)=inf;endendDelta_Tau=zeros(N,N);%更新量初始化for m=1:Mif PL(k,m) ROUT=ROUTES{k,m};TS=length(ROUT)-1;%跳数PL_km=PL(k,m);for s=1:TSx=ROUT(s);Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km;Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km;endendendTau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分,新增加一部分 end %% ---------------------------绘图-------------------------------- plotif=1;%是否绘图的控制参数if plotif==1%绘收敛曲线meanPL=zeros(1,K);minPL=zeros(1,K);for i=1:KPLK=PL(i,:);Nonzero=find(PLKPLKPLK=PLK(Nonzero);meanPL(i)=mean(PLKPLK);minPL(i)=min(PLKPLK);endfigure(1)plot(minPL);hold onplot(meanPL);grid ontitle('收敛曲线(平均路径长度和最小路径长度)'); xlabel('迭代次数');ylabel('路径长度');%绘爬行图figure(2)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]); hold onendendendhold onROUT=ROUTES{K,M};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)endplotif2=1;%绘各代蚂蚁爬行图if plotif2==1figure(3)axis([0,MM,0,MM])for i=1:MMfor j=1:MMif G(i,j)==1x1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); hold onelsex1=j-1;y1=MM-i;x2=j;y2=MM-i;x3=j;y3=MM-i+1;x4=j-1;y4=MM-i+1;fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);hold onendendendfor k=1:KPLK=PL(k,:);minPLK=min(PLK);pos=find(PLK==minPLK);m=pos(1);ROUT=ROUTES{k,m};LENROUT=length(ROUT);Rx=ROUT;Ry=ROUT;for ii=1:LENROUTRx(ii)=a*(mod(ROUT(ii),MM)-0.5);if Rx(ii)==-0.5Rx(ii)=MM-0.5;endRy(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));endplot(Rx,Ry)hold onendend将上述算法应用于机器人路径规划,优化效果如下图所示。
圆台上蚂蚁爬行最短路径问题

圆台上蚂蚁爬行最短路径问题
圆台上蚂蚁爬行最短路径问题的基本思想是,从一个点出发,经过多次爬行,最终到达另一个点,这一系列的爬行路径之中,路径总长度最短。
假设有一个圆台,有N个点,每个
点有一个指示物,每个指示物都有一个编码,它们之间存在多种不同的爬行方式,编码的大小也可以不同。
要解决这个问题,就要找到一条最短的爬行路径,经过N个点,按照指示物的
编码顺序,使得总长度最短。
圆台上蚂蚁爬行最短路径问题有多种解决方案,最常用的是蚁群算法(Ant Colony Optimization, ACO)。
蚁群算法是一
种模拟蚂蚁搜索食物的行为,将蚁群看作一个体系,利用群体智能,来解决复杂最优化问题。
在蚁群算法中,每只蚂蚁都会经过每个点,并在经过每个点时,根据路径的费用,进行一定的机制来增加其他蚂蚁的吸引力,从而使得搜索空间中的蚂蚁分布得更加均匀,更有效地搜索最优路径。
c语言最短路径搜寻算法

c语言最短路径搜寻算法
C 语言最短路径搜寻算法常用于在网图中寻找两点之间的最短路径,其中网图的最短路径分为单源最短路径和多源最短路径。
以下是两种常见的最短路径搜寻算法:- Dijkstra 算法:从一个起始点出发,到达一个终点,通过对路径权值的累加,找到最短路径。
- Floyd 算法:对于网中的任意两个顶点来说,之间的最短路径不外乎有两种情况。
一种是直接从一个顶点到另一个顶点的边的权值;另一种是先经过若干个顶点,最终达到另一个顶点,期间经过的边的权值和。
这两种算法都可以用 C 语言实现,你可以根据具体需求选择合适的算法。
若你想了解更多关于最短路径搜寻算法的内容,可以继续向我提问。
蚁群算法代码(求函数最值)

蚁群算法代码(求函数最值)function [F]=F(x1,x2) %⽬标函数F=-(x1.^2+2*x2.^*cos(3*pi*x1)*cos(4*pi*x2)+;Endfunction [maxx,maxy,maxvalue]=antcolony% 蚁群算法求函数最⼤值的程序ant=200; % 蚂蚁数量times=50; % 蚂蚁移动次数rou=; % 信息素挥发系数p0=; % 转移概率常数lower_1=-1; % 设置搜索范围upper_1=1; %lower_2=-1; %upper_2=1; %for i=1 : antX(i,1)=(lower_1+(upper_1-lower_1)*rand);%随机设置蚂蚁的初值位置X(i,2)=(lower_2+(upper_2-lower_2)*rand);tau(i)=F(X(i,1),X(i,2)); %第i只蚂蚁的信息量end %随机初始每只蚂蚁的位置step=; %⽹格划分单位f='-(x.^2+2*y.^*cos(3*pi*x)*cos(4*pi*y)+';[x,y]=meshgrid(lower_1:step:upper_1,lower_2:step:upper_2); z=eval(f); %eval函数,将字符串内的内容执⾏再赋给对象figure(1);mesh(x,y,z); %⽹格图hold on;plot3(X(:,1),X(:,2),tau,'k*') %蚂蚁初始位置hold on;text,,,'蚂蚁的初始分部位置')xlabel('x');ylabel('y');zlabel('f(x,y)');for t=1:times % 第t次移动lamda=1/t; %步长系数,随移动次数增⼤⽽减少[tau_best(t),bestindex]=max(tau); %第t次移动的最优值及其位置for i=1:ant %第i只蚂蚁p(t,i)=(tau(bestindex)-tau(i))/tau(bestindex); %最优值与第i只蚂蚁的值的差⽐% 计算状态转移概率endfor i=1:antif p(t,i)temp1=X(i,1)+(2*rand-1)*lamda; %移动距离temp2=X(i,2)+(2*rand-1)*lamda;else %全局搜索temp1=X(i,1)+(upper_1-lower_1)*;temp2=X(i,2)+(upper_2-lower_2)*;end %%%%%%%%%%%%%%%%%%%%%% 越界处理if temp1temp1=lower_1;endif temp1>upper_1temp1=upper_1;endif temp2temp2=lower_2;endif temp2>upper_2temp2=upper_2;end %%%%%%%%%%%%%%%%%%%%%%%if F(temp1,temp2)>F(X(i,1),X(i,2))% 判断蚂蚁是否移动X(i,1)=temp1;X(i,2)=temp2;endendfor i=1:anttau(i)=(1-rou)*tau(i)+F(X(i,1),X(i,2)); % 更新信息量end endfigure(2);mesh(x,y,z);hold on;x=X(:,1);y=X(:,2);plot3(x,y,eval(f),'k*')hold on;text,,,'蚂蚁的最终分布位置')xlabel('x');ylabel('y'),zlabel('f(x,y)');[max_value,max_index]=max(tau);maxx=X(max_index,1);maxy=X(max_index,2);maxvalue=F(X(max_index,1),X(max_index,2)); end function [F1]=F1(x) %⽬标函数F1=x.^2-2*x+1;End%蚁群算法求解⼀元函数F1=x^2-2*x+1 close clearclcant=10;times=40;rou=;p0=;lb=-2;ub=2;step=;x=lb::ub;for i=1:antX(i)=lb+(ub-lb)*rand;tau(i)=F1(X(i));endfigure(1);plot(x,F1(x));hold onplot(X,tau,'r*');for kk=1:10for t=1:timeslamda=1/t;%转移次数的倒数[tau_best(t),bestindex]=min(tau);for i=1:antp(t,i)=(tau(bestindex)-tau(i))/tau(bestindex);%转移概率(最优-蚂蚁i)/最优%此种概率选择易陷⼊局部最优解endfor i=1:antif p(t,i)temp=X(i)+(2*rand-1)*lamda;%蚂蚁移动elsetemp=X(i)+(ub-lb)*;endif temptemp=lb;endif temp>ubtemp=ub;endif F1(temp)X(i)=temp;endendfor i=1:anttau(i)=(1-rou)*tau(i)+F1(X(i));endendendfigure(2);plot(x,F1(x));hold onx=X(i);y=tau(i);plot(x,y,'g*');x1=X(length(X))y1=tau(length(tau))。
蚁群算法 最短路径python

蚁群算法最短路径python蚁群算法是一种模拟蚂蚁寻找食物的算法,可以用于求解最短路径问题。
下面是一个用Python实现的最短路径蚁群算法的示例程序:```pythonimport numpy as np# 定义城市距离矩阵distances = np.array([[0, 2, 3, 5],[2, 0, 4, 7],[3, 4, 0, 4],[5, 7, 4, 0]])# 初始化参数num_cities = 4 # 城市数量num_ants = 5 # 蚂蚁数量pheromone = 0.1 * np.ones((num_cities, num_cities)) # 信息素矩阵alpha = 1 # 信息素重要程度因子beta = 2 # 启发式因子Q = 1 # 常数因子decay = 0.1 # 信息素挥发因子max_iterations = 20 # 最大迭代次数# 主循环for i in range(max_iterations):# 初始化每只蚂蚁的位置和路径长度positions = np.zeros(num_ants, dtype=int)lengths = np.zeros(num_ants)for j in range(num_ants):positions[j] = np.random.randint(num_cities)# 逐个城市路径选择for k in range(num_cities - 1):for j in range(num_ants):# 计算每个城市的行走概率mask = np.ones(num_cities, dtype=bool)mask[positions[j]] = Falsepheromone_temp = np.power(pheromone[positions[j], mask], alpha) * \np.power(1.0 /distances[positions[j], mask], beta)prob = pheromone_temp / np.sum(pheromone_temp)# 轮盘赌选择下一个城市next_city = np.random.choice(num_cities - 1,p=prob) + \(1 if np.sum(mask[:positions[j]]) < positions[j] else 0)positions[j] = next_citylengths[j] += distances[positions[j-1],positions[j]]# 更新信息素delta_pheromone = np.zeros((num_cities, num_cities))for j in range(num_ants):for k in range(num_cities - 1):delta_pheromone[positions[j], positions[j+1]] += Q / lengths[j]pheromone = (1 - decay) * pheromone + delta_pheromone# 输出最短路径best_path_length = np.min(lengths)best_path = positions[np.argmin(lengths)]print(f"Iteration {i}: best path length{best_path_length}, best path {best_path}")```上述程序定义了一个$4\times 4$的城市距离矩阵(即城市之间的直线距离),包含4个城市。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
//calculate the changes of trial information
int i;
int j;
for(i=0;i<iAntCount;i++)
{
for (j=0;ants[i].tabu[j]!=iCityCount-1&&rValue[j]!=-1;j++)
tabu[m_iCityCount]=city;
m_iCityCount++;
AllowedCity[city]=0;
}
void ant::Clear()
{
m_dLength=0;
int i;
for(i=1;i<iCityCount;i++)
{
AllowedCity[i]=1;
project();
};
project::project()
{
//initial map,read map infomation from file . et.
initmap();
m_dLength=10e9;
ifstream in("poger.tsp");
struct city
{
for(j=0;j<iAntCount;j++)
{
int t=0;
while(iCityCount-1!=(rValue[j]=ants[j].move())&&rValue[j]!=-1&&t<20)
t++;
}
for(j=0;j<iAntCount;j++)
sel+=prob[i];
}
else
prob[i]=0;
}
double mRate=rnd(0,sel);
double mSelect=0;
for ( i=0;i<iCityCount;i++)
{
if(Map.distance[curCity][i]&&(AllowedCity[i]==1))
const int iItCount=20;//最大跌代次数
const double Q=100;
const double alpha=1;
const double beta=5;
const double rou=0.5;
int besttour[iCityCount];//最路径列表
mSelect+=prob[i] ;
if (mSelect>=mRate) {j=i;break;}
}
if (j==10000)
{
temp=-1;
for (i=0;i<iCityCount;i++)
{
if(Map.distance[curCity][i]&&(AllowedCity[i]==1))
prob[i]=0;
}
m_iCityCount=0; 源自addcity(0); }
void ant::UpdateResult()
{
// Update the length of tour
int i;
for(i=0;tabu[i]!=iCityCount-1;i++)
m_dLength+=Map.distance[tabu[i]][tabu[i+1]];
if (temp) {
temp=pow((1.0/Map.distance[curCity][i]),beta)*pow((Map.m_dTrial[curCity][i]),alpha);
j=i;
}
}
}
return j;
}
ant::ant()
{
m_dLength=m_dShortest=0;
{
int num;
int x;
int y;
}cc;
int i,j;
for(i=0;i<iCityCount;i++)
for(j=0;j<iCityCount;j++)
Map.distance[i][j]=0;
for (int k=0;k<eMax;k++)
{
{
if(rValue[j]!=-1)
ants[j].UpdateResult ();
}
//find out the best solution of the step and put it into temp
int t=0;
temp=ants[0].m_dLength;
while (ants[0].tabu[t]!=iCityCount-1&&t<iCityCount-1)
};
int ant::ChooseNextCity()
{
//Update the probability of path selection
//select a path from tabu[m_iCityCount-1] to next
int i;
int j=10000;
double temp=0;
int curCity=tabu[m_iCityCount-1];
for (i=0;i<iCityCount;i++)
if(Map.distance[curCity][i]&&(AllowedCity[i]==1))
{
temp+=pow((1.0/Map.distance[curCity][i]),beta)*pow((Map.m_dTrial[curCity][i]),alpha);
}
int
ant::move()
{
//the ant move to next town and add town ID to tabu.
int j;
j=ChooseNextCity();
}
}
void project::GetAnt()
{
//randomly put ant into map
int i=0;
srand((unsigned)time(NULL)+rand());
for (i=0;i<iAntCount;i++)
{
ants[i].addcity(0); //初始均从源节点出发
}
}
for (i=0;i<iCityCount;i++)
for (j=0;j<iCityCount;j++)
{
Map.m_dTrial[i][j]=(rou*Map.m_dTrial[i][j]+Map.m_dDeltTrial[i][j]); //rou有修改
Map.m_dDeltTrial[i][j]=0;
}
}
void project::initmap()
{
int i;
int j;
for(i=0;i<iCityCount;i++)
for (j=0;j<iCityCount;j++)
{
Map.m_dTrial[i][j]=1;
Map.m_dDeltTrial[i][j]=0;
};
GInfo Map;
class ant
{
private:
int ChooseNextCity();//选择城市
double prob[iCityCount];//选择城市的概率
int m_iCityCount; //城市数目
int AllowedCity[iCityCount];//没有走过的城市
#include<stdio.h>
#include<time.h>
const int maxInfinite=26767;
const int eMax=49;
const int iAntCount=20;//蚂蚁数量
const int iCityCount=20;//城市数量
break;
}
}
class project
{
public:
int rValue[iAntCount];
void UpdateTrial();
double m_dLength;
void initmap();
ant ants[iAntCount];
void GetAnt();
void StartSearch();
in>>cc.x>>cc.y>>cc.num;
Map.distance[cc.x-1][cc.y-1]=cc.num;
