3-2洛必达法则
第二节 洛必达法则3-2

第三章 第二节
10
二、用洛必达法则(间 接地)解 0 、 、0 、1 、 型未定式
0 0
关键:将这些类型未定式化为洛必达法则直接可解决的 类型 : 0 ), ( ). ( 0
1. 0 型
步骤: 例题
0
代数代换:其中之一取 倒数
求 lim x ln x
化简
e
1 连 续 1 x 0 2(1 x ) e 2
. f (0) f ( x)在x 0处连续
第三章 第二节 17
例题 试确定常数A,B,C的值,使得 e x 1 Bx Cx 2 1 Ax x3 , 其中 x3 是当 x 0时比x 高阶的无穷小。
x e lim
x
x
0
8
第三章 第二节
注意:洛必达法则是求未定式极限的一种有效方法, 但应与其它求极限方法结合使用。为便于求导,应先 化简。常用的化简方法有:等价变量代换、恒等变形 、有非零极限的因子分离出去、...。
x sin x 5) lim 3 tgx x 0
e e 6) lim x 0 x arctgx
3
第三章 第二节
18
三、小结
洛必达法则
型
取倒数、通分
0 ,1 , 型
0 0
指数代换
0 型 0 型
uv e v ln u
0 型
其中之一取倒数
洛必达法则只是函数未定式极限存在的充分条件; 对数列未定式不能直接地应用洛必达法则.
第三章 第二节 19
归纳起来,通常求未定型的步骤如下:
1 x lim x 1 ln x x 1
洛必达法则总结归纳

洛必达法则总结归纳
洛必达法则是经济学中一个重要的概念,用于描述市场中不同价格水平下的产品销售量。
它的核心思想是:产品价格与销售量之间存在着相互作用关系,当价格上升时,销售量将会下降;反之,当价格下降时,销售量则会上升。
总结归纳洛必达法则,我们可以得出以下几个关键点:
1. 市场需求的弹性:洛必达法则认为市场需求对价格的反应是弹性的,即当价格变动时,市场需求的反应程度与价格变动幅度成正比。
当价格变化较小时,市场需求的变化也会比较小;反之,当价格变化较大时,市场需求的变化也会比较大。
2. 价格与销售量的相互作用:洛必达法则认为,价格与销售量之间存在着相互作用关系。
当价格上升时,销售量将会下降;反之,当价格下降时,销售量则会上升。
因此,企业需要在制定产品价格时考虑到价格与销售量之间的平衡。
3. 最大化利润的实现:洛必达法则认为,企业应该通过制定合适的价格来最大化其利润。
当价格过高时,销售量会下降,从而减少利润;反之,当价格过低时,虽然销售量会增加,但是利润也会下降。
因此,企业需要通过市场调研等手段来确定商品的最佳价格,以实现最大化利润的目标。
4. 市场竞争的影响:洛必达法则还强调了市场竞争对于产品价格与销售量之间关系的影响。
在竞争激烈的市场中,企业需要通过制定更合适的价格来保持其竞争力,从而在市场中取得更大的份额。
总之,洛必达法则对于企业制定产品价格以及实现最大利润具有很重要的指导意义,企业应该通过市场调研、竞争分析等手段来确定最佳的价格水平。
3-2洛必达法则

a bx cos ax lim 1. b x 0 ax cos bx
例6.求
解: 原式 lim
1 x n 1
型
x
nx
1 0 lim x n x n
21
xn 型 例7. 求 lim x (n 0 , 0) . x e 解: (1) n 为正整数的情形. n x n1 n(n 1) x n2 lim 原式 lim x x e x 2 e x n! lim n x 0 x e 例6、例7说明:当 x 对数函数 ln x, 时,
20
ln sin ax lim .(a>0,b>0) 型 例5 求x 0 ln sin bx a cosax ln sin ax si nax a lim sin bx cos ax li lim 解 x 0 ln sin bx x m b cosbx b x 0 sin ax cos bx 0 si nbx
4.应用法则时,为使极限计算简单,应尽量使用无穷 小 的等价代换、重要极限及其它求极限的方法.
5.x a,x 时的未定式
型也有相应的法则.
19
定理 2.
2) f ( x) 与F ( x) 在 (a)内可导, f ( x) 存在 (或为∞) 3) lim xa F ( x ) f ( x) f ( x) lim lim (洛必达法则) xa F ( x ) xa F ( x ) 说明: 定理中 x a 换为 x a , x a , x , x , x 之一, 条件 2) 作相应的修改 , 定理仍然成立.
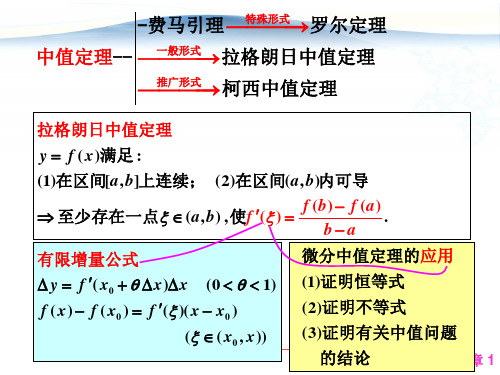
拉格朗日中值公式
说明:Lagrange中值定理是柯西中值定理的特殊情况.
复变函数3.2 洛必达
柯西中值定理
推广形式
拉格朗日中值定理 y f ( x )满足 : (1)在区间[a , b]上连续; (2)在区间( a , b)内可导 至少存在一点 (a , b) , 使f ( )
从而
f ( x) f ( x) lim lim xa F ( x ) xa F ( x )
3.2 洛必达法则·第3章 12
f ( x) 2) lim 0 的情形. 取常数 k 0 , x a F ( x )
f ( x) lim k x a F ( x )
f ( x) k F ( x) lim F ( x) x a
3.2 洛必达法则·第3章 16
xn 例6. 求 lim x (n 0 , 0) . x e (2) n 不为正整数的情形.
存在正整数 k , 使当 x > 1 时,
x k x n x k 1
从而 由(1)
x n x k 1 xk x x x e e e xk x k 1 lim x lim x 0 x e x e n x lim x 0 x e
6 cos 6 x 3. lim x 2 cos 2 x
2
3.2 洛必达法则·第3章 20
tan x . 例 求 lim x tan 3 x
2
( )
解 直接应用法则比较麻烦,先变形,再用法则
tan x sin x cos3x lim lim cos x x tan3 x x sin3 x
tan x x 0 求 lim 2 . ( ) 0 x 0 x tan x
3-2 洛必达法则

注意: 注意:
f ′(x) 0 (1) 如 ) 果 仍 属 型 且 f ′(x), F′(x) 满 , 足 F′(x) 0 定 的 件 可 继 使 洛 达 则 即 理 条 , 以 续 用 必 法 ,
f (x) f ′(x) f ′′(x) lim . = lim = lim =L x→ F(x) a x→ F (x) a x→ F ′(x) a ′ ′
×
3、运算过程中有非零极限因子(积的形式)可先算出极限。 、运算过程中有非零极限因子(积的形式)可先算出极限。
例:求 lim xe 2 x + xe x − 2e 2 x + 2e x (e − 1)
x 3
x→0
(代数和的形式不可以) 代数和的形式不可以)
xe x + x − 2e x + 2 xe x + e x + 1 − 2e x x 解:原式 = lim e . = lim 3 x →0 x →0 x 3x 2
ln sin ax ∞ lim , ( ) x→0 ln sin bx → ∞
定理1 设 (1 lim f (x) = 0, limF(x) = 0; 定理 )
x→ a x→ a
0 ( ) 0
(2) 在a点 某 心 域 , f ′(x)及 的 去 邻 内 F′(x) 都 在 F′(x) ≠ 0 存 且 ;
tanx − x . 求lim 2 x→ x tanx 0
0 ( ) 0
tanx− x x− sec2 x−1 x− 解: 原 = lim 式 = lim 3 2 x→ 0 x→ 0 x 3x
tan x 1 tan2 x 1 = lim 2 = lim 2 = . 3 x→ 3x 0 3 x→0 x
3-2第二节洛必达L’Hospital法则

系
高
等 数 学
.例如 当x→∞时,
x sin x 是, x cos x
型不定式
电 子 教
显然有.
lim x sin x 1 x x cos x
案
但是如果用洛必达法则,则得不出结果
lim x sin x lim (x sin x) lim 1 cos x lim (1 cos x)
子
教 案
在区间[a,x]或[x,a]上应用柯西中值定理
f (x) f (a) f ( ) , ( [a, x]) g(x) g(a) g ( )
武
x a, a
汉
科
技 学 院
lim f (x) lim f ( ) lim f (x) A
数 理
xa g(x) x g ( ) xa g (x)
ln cos x
exp[lim x0
x2
]
武 汉
exp[lim tgx ] exp[ 1 1]
x0 2 x
2
科
技 学
e1/ 2 1
院 数
e
理 系
(tgx) sec2 x
高
等 数
(3) lim (1 1 ) x lim e x ln(11/ x)
x0
院
数
理
系
高 等 数
例1 求下列极限
(1 x)a 1
(1) lim
;
学
x0
x
1
(2) lim n(e n 1) n
电 子
解: (1)是0/0型的,用洛必达法则,得到
教 案
lim (1 x)a 1 lim a(1 x)a1 a(1 0)a1 a
高等数学课件3-2洛必达法则

添加标题
洛必达法则的应用:洛必达法则在解决一些复杂的极限问题时非常有用,例如求解函数极限、求导数 等。
添加标题
洛必达法则的局限性:洛必达法则只适用于函数f(x)和g(x)在区间[a,b]上可导,且g'(x)≠0的情况。 如果g'(x)=0,那么洛必达法则不适用。
洛必达法则的推导技巧
洛必达法则是 微积分中一个 重要的法则, 用于解决极限
洛必达法则的逆推:洛必达法则的逆推形式包括洛必达法则的推广、洛必达法则的逆推、 洛必达法则的逆推等。
洛必达法则的扩展应用
洛必达法则在微 积分中的应用
洛必达法则在极 限计算中的应用
洛必达法则在函 数求导中的应用
洛必达法则在函 数求积中的应用
洛必达法则与其他数学方法的结合
洛必达法则与微 积分的结合:洛 必达法则是微积 分中的一个重要 定理,它可以用 来求解极限、导 数等问题。
洛必达法则的变种:洛必达法则的变种形式包括洛必达法则的推广、洛必达法则的逆推、 洛必达法则的逆推等。
洛必达法则的推广:洛必达法则的推广形式包括洛必达法则的推广、洛必达法则的逆推、 洛必达法则的逆推等。
洛必达法则的逆推:洛必达法则的逆推形式包括洛必达法则的推广、洛必达法则的逆推、 洛必达法则的逆推等。
YOUR LOGO
20XX.XX.XX
高等数学课件3-2洛必达法则
,
汇报人:
目 录
01 单 击 添 加 目 录 项 标 题
02 洛 必 达 法 则 的 背 景 和 定 义
03 洛 必 达 法 则 的 推 导 过 程
04 洛 必 达 法 则 的 应 用 实 例
05 洛 必 达 法 则 的 注 意 事 项 和 限 制
数论洛必达法则

数论洛必达法则-概述说明以及解释1.引言1.1 概述概述:数论洛必达法则是数学中一个重要的定理,它在解决极限计算问题中扮演着重要的角色。
洛必达法则主要用于解决形式为\frac{0}{0}或\frac{\infty}{\infty}的不定式极限问题。
这个法则的提出和应用,极大地简化了求解极限的复杂程度,成为数学分析中的重要工具。
在本文中,我们将对洛必达法则进行详细的介绍,包括其概念、应用和意义。
我们将深入探讨这一定理在数论领域中的重要性,以及它在数学研究和实际问题中的应用。
同时,我们也会对洛必达法则的局限性进行探讨,以及未来在这一领域中的发展展望。
通过本文的阐述,读者将更加深入地理解数论洛必达法则,并对数学研究中的极限问题有更深入的认识。
1.2 文章结构文章结构部分的内容:本文将分为引言、正文和结论三部分进行阐述。
引言部分将从概述、文章结构和目的三方面介绍数论洛必达法则的重要性和意义。
正文部分将详细介绍洛必达法则的概念、应用和意义,包括其在数论领域的具体运用和影响。
结论部分将对洛必达法则进行总结,并讨论其局限性和未来的发展方向,以展望洛必达法则在数论研究中的潜力。
每个部分将以清晰的逻辑顺序和详细的论证来展现洛必达法则在数论领域的重要性和价值。
1.3 目的本文旨在深入探讨数论中的洛必达法则,并分析其概念、应用和意义。
通过对洛必达法则进行系统性的介绍和解读,旨在帮助读者更好地理解这一重要的数学原理,并且探讨洛必达法则在数论领域中的具体运用。
同时,本文也将对洛必达法则的局限性进行深入分析,并展望未来在数论研究中的潜在应用。
通过本文的阐述,读者将能够更全面地了解洛必达法则在数论领域中的重要性和意义,以及未来可能的发展方向。
2.正文2.1 洛必达法则的概念洛必达法则是数学中的一个重要概念,通常用于解决极限计算中的不定式形式。
它最初由意大利数学家洛必达(L'Hôpital)在17世纪提出,并在微积分学中得到广泛应用。
高数习题答案3-2

习题3-21. 用洛必达法则求下列极限:(1)xx x )1ln(lim 0+→;(2)xe e x x x sin lim 0-→-; (3)ax a x a x --→sin sin lim ;(4)x x x 5tan 3sin lim π→;(5)22)2(sin ln lim x x x -→ππ;(6)n n mm a x ax a x --→lim ;(7)x x x 2tan ln 7tan ln lim 0+→;(8)xx x 3tan tan lim 2π→;(9)xarc x x cot )11ln(lim++∞→; (10)xx x x cos sec )1ln(lim 20-+→;(11)x x x 2cot lim 0→;(12)2120lim x x e x →;(13))1112(lim 21---→x x x ;(14)x x x a )1(lim +∞→;(15)x x x sin 0lim +→;(16)x x xtan 0)1(lim +→.解 (1)111lim 111lim )1ln(lim 000=+=+=+→→→x x xx x x x .(2)2cos lim sin lim 00=+=--→-→xe e x e e x x x x x x . (3)a x ax a x a x a x cos 1cos lim sin sin lim ==--→→.(4)535sec 53cos3lim 5tan 3sin lim 2-==→→x x x x x x ππ. (5)812csc lim 41)2()2(2cot lim )2(sin ln lim 22222-=---=-⋅-=-→→→x x x x x x x x πππππ. (6)n m n m n m a x n n m m a x a n m namx nx mx a x a x -----→→===--1111lim lim . (7)22sec 2tan 177sec 7tan 1lim 2tan ln 7tan ln lim 2200⋅⋅⋅⋅=+→+→x xx x x x x x177s e c 22s e c l i m 277t a n 2t a n l i m 272200=⋅⋅==+→+→x x x x x x . (8)x x x x x x x x x 2222222cos 3cos lim 3133sec sec lim 3tan tan lim πππ→→→=⋅= )s i n (c o s 23)3s i n (3c o s 2lim 312x x x x x -⋅-=→πxx x c o s 3c o s l i m2π→-= 3s i n3s i n 3l i m2=---=→x x x π.(9)22221lim 11)1(111lim cot arc )11ln(limxx x xx x x x x x x ++=+--⋅+=++∞→+∞→+∞→ 122lim 212lim ==+=+∞→+∞→x x x x .(10)x x xx x x x x x x x 22022020cos 1lim cos 1)1ln(cos lim cos sec )1ln(lim -=-+=-+→→→1s i n lim )sin (cos 22lim00==--=→→xx x x x x x .(注: cos x ⋅ln(1+x 2)~x 2) (11)2122sec 1lim 2tan lim2cot lim 2000=⋅==→→→x x x x x x x x . (12)+∞====+∞→+∞→→→1lim lim 1lim lim 21012022t t t t x x x x e t e x e e x(注: 当x →0时, +∞→=21xt . (13)2121lim 11lim 1112lim 12121-=-=--=⎪⎭⎫ ⎝⎛---→→→x x x x x x x x . (14)因为)1ln(lim )1(lim x ax x x x exa +∞→∞→=+, 而 221)(11lim 1)1ln(lim)1(ln(lim xx a x ax x a x a x x x x --⋅+=+=+∞→∞→∞→ a a a x ax x x ==+=∞→∞→1lim lim ,所以 a x ax x x x e e xa ==++∞→∞→)1l n (l i m )1(l i m. .(15)因为x x x x x e x ln sin 0sin 0lim lim +→+→=,而 x x x x x x x x x x c o tc s c 1lim csc ln lim ln sin lim 000⋅-==+→+→+→c o s s i n l i m 20=-=+→xx x x ,所以 1lim lim 0ln sin 0sin 0===+→+→e e x x x x x x .(16)因为x x x x e xln tan tan 0)1(lim -+→=,而 xx x x x x x x x 2000c s c 1limcot ln lim ln tan lim -==+→+→+→ 0s i n l i m 20=-=+→xx x , 所以 1l i m )1(l i m 0ln tan 0tan 0===-+→+→e e x x x x x x .2. 验证极限x x x x sin lim +∞→存在, 但不能用洛必达法则得出.解 1)s i n 1(l i m s i n l i m =+=+∞→∞→x x x x x x x , 极限x x x x sin lim +∞→是存在的. 但)cos 1(lim 1cos 1lim )()sin (limx x x x x x x x +=+=''+∞→∞→∞→不存在, 不能用洛必达法则. 3. 验证极限xx x x sin 1sin lim20→存在, 但不能用洛必达法则得出. 解 0011sin sin lim sin 1sin lim020=⋅=⋅=→→xx x x x x x x x , 极限x x x x sin 1sin lim 20→是存在的. 但xx x x x x x x x cos 1cos 1sin 2lim )(sin )1sin (lim020-=''→→不存在, 不能用洛必达法则. 4. 讨论函数⎪⎪⎩⎪⎪⎨⎧≤>+=-0])1([)(2111x e x e x x f x x 在点x =0处的连续性.解 21)0(-=e f ,)0(lim)(lim 21210f e e x f x x ===---→-→,因为]1)1l n (1[101100lim])1([lim )(lim -+-→-→+→=+=x x x x x x x x e ex x f ,而 200)1l n (l i m]1)1l n (1[1l i m x xx x x x x x -+=-++→+→ 21)1(21lim 2111lim 00-=+-=-+=+→+→x x x x x ,所以]1)1l n (1[101100lim])1([lim )(lim -+-→-→+→=+=x xx x x x x x e ex x f )0(21f e ==-.因此f (x )在点x =0处连续.习题 2-21. 推导余切函数及余割函数的导数公式: (cot x )'=-csc 2x ; (csc x )'=-csc x cot x .解 x x x x x x x x 2sin cos cos sin sin )sin cos ()(cot ⋅-⋅-='=' x xx x x 22222c s cs i n 1s i n c o s s i n -=-=+-=. x x xx x x c o t c s c s i n c o s )s i n 1()(c s c 2⋅-=-='='.2. 求下列函数的导数:(1)1227445+-+=x x x y ; (2) y =5x 3-2x +3e x ; (3) y =2tan x +sec x -1; (4) y =sin x ⋅cos x ; (5) y =x 2ln x ; (6) y =3e x cos x ; (7)xx y ln =;(8)3ln 2+=xey x ;(9) y =x 2ln x cos x ;(10)tt s cos 1sin 1++=;解 (1))12274()12274(14545'+-+='+-+='---x x x xx x y 2562562282022820x x x x x x +--=+--=---. (2) y '=(5x 3-2x +3e x )'=15x 2-2x ln2+3e x .(3) y '=(2tan x +sec x -1)'=2sec 2x +sec x ⋅tan x =sec x (2sec x +tan x ). (4) y '=(sin x ⋅cos x )'=(sin x )'⋅cos x +sin x ⋅(cos x )' =cos x ⋅cos x +sin x ⋅(-sin x )=cos 2x . (5) y '=(x 2ln x )'=2x ⋅ln x +x 2⋅x1=x (2ln x +1) .(6) y '=(3e x cos x )'=3e x ⋅cos x +3e x ⋅(-sin x )=3e x (cos x -sin x ).(7)22ln1ln 1)ln (x x x xx x x x y -=-⋅='='. (8)3422)2(2)3ln (x x e x x e x e x e y x x x x -=⋅-⋅='+='. (9) y '=(x 2ln x cos x )'=2x ⋅ln x cos x +x 2⋅x1⋅cos x +x 2 ln x ⋅(-sin x )2x ln x cos x +x cos x -x 2 ln x sin x . (10)22)cos 1(cos sin 1)cos 1()sin )(sin 1()cos 1(cos )cos 1sin 1(t tt t t t t t t t s +++=+-+-+='++='.3. 求下列函数在给定点处的导数: (1) y =sin x -cos x , 求6π='x y 和4π='x y .(2)θθθρcos 21sin +=,求4πθθρ=d d .(3)553)(2x x x f +-=, 求f '(0)和f '(2) . 解 (1)y '=cos x +sin x , 21321236s i n 6c o s 6+=+=+='=πππx y ,222224s i n 4c o s 4=+=+='=πππx y . (2)θθθθθθθθρcos sin 21sin 21cos sin +=-+=d d ,)21(4222422214c o s 44s i n 214πππππθρπθ+=⋅+⋅=+==d d . (3)x x x f 52)5(3)(2+-=', 253)0(='f , 1517)2(='f . 4. 以初速v 0竖直上抛的物体, 其上升高度s 与时间t 的关系是2021gt t v s -=.求:(1)该物体的速度v (t ); (2)该物体达到最高点的时刻. 解 (1)v (t )=s '(t )=v 0-gt . (2)令v (t )=0, 即v 0-gt =0, 得gv t 0=, 这就是物体达到最高点的时刻. 5. 求曲线y =2sin x +x 2上横坐标为x =0的点处的切线方程和法线方程. 解 因为y '=2cos x +2x , y '|x =0=2, 又当x =0时, y =0, 所以所求的切线方程为 y =2x ,所求的法线方程为x y 21-=, 即x +2y =0.6. 求下列函数的导数: (1) y =(2x +5)4 (2) y =cos(4-3x ); (3)23x e y -=; (4) y =ln(1+x 2); (5) y =sin 2x ; (6)22x a y -=; (7) y =tan(x 2);(8) y =arctan(e x ); (9) y =(arcsin x )2; (10) y =lncos x .解 (1) y '=4(2x +5)4-1⋅(2x +5)'=4(2x +5)3⋅2=8(2x +5)3. (2) y '=-sin(4-3x )⋅(4-3x )'=-sin(4-3x )⋅(-3)=3sin(4-3x ). (3)22233236)6()3(x x x xe x e x e y ----=-⋅='-⋅='. (4)222212211)1(11x x x x x x y +=⋅+='+⋅+='.(5) y '=2sin x ⋅(sin x )'=2sin x ⋅cos x =sin 2x . (6))()(21])[(22121222122'-⋅-='-='-x a x a x a y222122)2()(21xa x x x a --=-⋅-=-.(7) y '=sec 2(x 2)⋅(x 2)'=2x sec 2(x 2). (8)xx x x e e e e y 221)()(11+='⋅+='.(9) y '21arcsin 2)(arcsin arcsin 2x x x x -='⋅=.(10)x x x x x y tan )sin (cos 1)(cos cos 1-=-='⋅='.7. 求下列函数的导数: (1) y =arcsin(1-2x ); (2)211xy -=; (3)x e y x3cos 2-=;(4)xy 1arccos =;(5)xx y ln 1ln 1+-=;(6)x x y 2sin =;(7)x y arcsin =; (8))ln(22x a x y ++=; (9) y =ln(sec x +tan x ); (10) y =ln(csc x -cot x ). 解 (1)2221)21(12)21()21(11xx x x x y --=---='-⋅--='. (2))1()1(21])1[(21212212'-⋅--='-='---x x x y222321)1()2()1(21xx x x x --=-⋅--=-.(3))3)(3sin (3cos )2()3(cos 3cos )(2222'-+'-='+'='----x x e x x e x e x e y xxx x )3s i n 63(c o s 213s i n 33c o s 21222x x e x e x e xxx +-=--=---. (4)1||)1()1(11)1()1(1122222-=---='--='x x x x x x x y . (5)22)ln 1(2)ln 1(1)ln 1()ln 1(1x x x x x x x y +-=+--+-='. (6)222sin 2cos 212sin 22cos x x x x x x x x y -=⋅-⋅⋅='. (7)2222121)(11)()(11x x x x x x y -=⋅-='⋅-='. (8)])(211[1)(12222222222'+++⋅++='++⋅++='x a x a x a x x a x x a x y2222221)]2(211[1xa x x a x a x +=++⋅++=. (9) x xx x x x x x x x y sec tan sec sec tan sec )tan (sec tan sec 12=++='+⋅+='. (10) x xx x x x x x x x y csc cot csc csc cot csc )cot (csc cot csc 12=-+-='-⋅-='.8. 求下列函数的导数: (1)2)2(arcsin x y =;(2)2tan ln x y =;(3)x y 2ln 1+=; (4)xe y arctan=;(5)y =sin n x cos nx ; (6)11arctan -+=x x y ;(7)x x y arccos arcsin =;(8) y =ln[ln(ln x )] ;(9)xx xx y -++--+1111;(10)xxy +-=11arcsin .解 (1)'⋅=')2(arcsin )2(arcsin 2x x y)2()2(11)2(a r c s i n22'⋅-⋅=x x x 21)2(11)2(a r c s i n 22⋅-⋅=x x .242a r c s i n2x x -= (2))2(2sec 2tan 1)2(tan 2tan 12'⋅⋅='⋅='x x x x x yx x x c s c 212s e c 2t a n 12=⋅⋅=. (3))ln 1(ln 121ln 1222'+⋅+=+='x xx y )(l n ln 2ln 1212'⋅⋅+=x x xx x x 1ln 2ln 1212⋅⋅+=x x x 2ln 1ln +=.(4))(arctan arctan'⋅='x e y x)()(112arctan'⋅+⋅=x x e x)1(221)(11a r c t a n2a r c t a nx x e x x ex x +=⋅+⋅=.(5) y '=n sin n -1x ⋅(sin x )'⋅cos nx +sin n x ⋅(-sin nx )⋅(nx )' =n sin n -1x ⋅cos x ⋅cos nx +sin n x ⋅(-sin nx )⋅n=n sin n -1x ⋅(cos x ⋅cos nx -sin x ⋅sin nx )= n sin n -1x cos(n +1)x . (6)222211)1()1()1()11(11)11()11(11x x x x x x x x x x y +-=-+--⋅-++='-+⋅-++='. (7)222)(arccos arcsin 11arccos 11x x x x x y -+-='22)(a r c c o s a r c s i n a r c c o s 11x x x x +⋅-=22)(a r c c o s12x x -=π.(8))(ln ln 1)ln(ln 1])[ln(ln )ln(ln 1'⋅⋅='⋅='x x x x x y)l n (l n ln 11ln 1)ln(ln 1x x x x x x ⋅=⋅⋅=.(9)2)11()121121)(11()11)(121121(x x x x x x x x xx y -++--+--+--++-++=' 22111xx -+-=. (10)2)1()1()1(1111)11(1111x x x xx x x x x y +--+-⋅+--='+-⋅+--=' )1(2)1(1x x x -+-=.9. 设函数f (x )和g (x )可导, 且f 2(x )+g 2(x )≠0, 试求函数)()(22x g x f y +=的导数. 解 ])()([)()(212222'+⋅+='x g x f x g x f y )]()(2)()(2[)()(2122x g x g x f x f x g x f '+'⋅+=)()()()()()(22x g x f x g x g x f x f +'+'=.10. 设f (x )可导, 求下列函数y 的导数dxdy : (1) y =f (x 2);(2) y =f (sin 2x )+f (cos 2x ).解 (1) y '=f '(x 2)⋅(x 2)'= f '(x 2)⋅2x =2x ⋅f '(x 2).(2) y '=f '(sin 2x )⋅(sin 2x )'+f '(cos 2x )⋅(cos 2x )'= f '(sin 2x )⋅2sin x ⋅cos x +f '(cos 2x )⋅2cos x ⋅(-sin x ) =sin 2x [f '(sin 2x )- f '(cos 2x )]. 11. 求下列函数的导数: (1) y =ch(sh x ); (2) y =sh x ⋅e ch x ; (3) y =th(ln x ); (4) y =sh 3x +ch 2x ; (5) y =th(1-x 2); (6) y =arch(x 2+1); (7) y =arch(e 2x ); (8) y =arctan(th x );(9)xx y 2ch 21ch ln +=; (10))11(ch 2+-=x x y解 (1) y '=sh(sh x )⋅(sh x )'=sh(sh x )⋅ch x . (2) y '=ch x ⋅e ch x +sh x ⋅e ch x ⋅sh x =e ch x (ch x +sh 2x ) .(3))(ln ch 1)(ln )(ln ch 122x x x x y ⋅='⋅='. (4) y '=3sh 2x ⋅ch x +2ch x ⋅sh x =sh x ⋅ch x ⋅(3sh x +2) .(5))1(ch 2)1()1(ch 122222x x x x y --=-⋅-='.(6)222)1()1(112422++='+⋅++='x x x x x y . (7)12)(1)(142222-='⋅-='x xx x e e e e y . (8)xxx x x x x y 222222ch 1ch sh 11ch 1th 11)th ()th (11⋅+=⋅+='⋅+=' xx x 222sh 211sh ch 1+=+=.(9))ch (ch 21)ch (ch 124'⋅-'⋅='x xx x yx x xx x sh ch 2ch 21ch sh 4⋅⋅-=x x x x x x x x 323ch sh ch sh ch sh ch sh -⋅=-= x xxx x x 33332th ch sh ch )1ch (sh ==-⋅=. (10)'+-⋅+-⋅+-='+-⋅+-=')11()11(sh )11(ch 2])11(ch [)11(ch 2x x x x x x x x x x y)112(sh )1(2)1()1()1()112(sh 22+-⋅+=+--+⋅+-⋅=x x x x x x x x . 12. 求下列函数的导数: (1) y =e -x (x 2-2x +3); (2) y =sin 2x ⋅sin(x 2); (3)2)2(arctan x y =;(4)n x x y ln =;(5)t t t t ee e e y --+-=; (6)x y 1cos ln =;(7)x ey 1sin 2-=;(8)x x y +=;(9) 242arcsin x x x y -+=;(10)212arcsin t t y +=.解 (1) y '=-e -x (x 2-2x +3)+e -x (2x -2) =e -x (-x 2+4x -5).(2) y '=2sin x ⋅cos x ⋅sin(x 2)+sin 2x ⋅cos(x 2)⋅2x =sin2x ⋅sin(x 2)+2x ⋅sin 2x ⋅cos(x 2).(3)2arctan 44214112arctan 222x x x x y +=⋅+⋅='.(4)121ln 1ln 1+--=⋅-⋅='n n n n x x n x nx x x x y . (5)2222)1(4)())(())((+=+---++='-----tt t t t t t t t t t t e e e e e e e e e e e e y . (6)x x x x x x x y 1tan 1)1()1sin (1sec )1(cos 1sec 22=-⋅-⋅='⋅='. (7))1(1cos )1sin 2()1sin (21sin 21sin 22x xx exe y x x -⋅⋅-⋅='-⋅='--x e x x1s i n 222s i n 1-⋅⋅=. (8))211(21)(21x xx x x x x y +⋅+='+⋅+='xx x x +⋅+=412.(9)2arcsin )2(421214112arcsin 22x x x x x x y =-⋅-+⋅-⋅+='.(10)22222222)1()2(2)1(2)12(11)12()12(11t t t t tt t t t t y +⋅-+⋅⋅+-='+⋅+-=' )1(|1|)1(2)1()1(2)1(1222222222t t t t t t t +--=+-⋅-+=.总习题一1. 在“充分”、“必要”和“充分必要”三者中选择一个正确的填入下列空格内:(1)数列{x n }有界是数列{x n }收敛的________条件. 数列{x n }收敛是数列{x n }有界的________的条件.(2)f (x )在x 0的某一去心邻域内有界是)(lim 0x f x x →存在的________条件. )(lim 0x f x x →存在是f (x )在x 0的某一去心邻域内有界的________条件.(3) f (x )在x 0的某一去心邻域内无界是∞=→)(l i m 0x f x x 的________条件.∞=→)(lim 0x f x x 是f (x )在x 0的某一去心邻域内无界的________条件.(4)f (x )当x →x 0时的右极限f (x 0+)及左极限f (x 0-)都存在且相等是)(lim 0x f x x →存在的________条件.解 (1) 必要, 充分. (2) 必要, 充分. (3) 必要, 充分. (4) 充分必要.2. 选择以下题中给出的四个结论中一个正确的结论: 设f (x )=2x +3x -2, 则当x →0时, 有( ).(A )f (x )与x 是等价无穷小; (B )f (x )与x 同阶但非等价无穷小; (C )f (x )是比x 高阶的无穷小; (D )f (x )是比x 低阶的无穷小.解 因为x x xx x f x x x x x x x x 13lim 12lim 232lim )(lim0000-+-=-+=→→→→ 3ln 2ln )1ln(lim 3ln )1ln(lim 2ln 00+=+++=→→u u t t u t (令2x -1=t , 3x -1=u ) .所以f (x )与x 同阶但非等价无穷小, 故应选B .3. 设f (x )的定义域是[0, 1], 求下列函数的定义域: (1) f (e x ); (2) f (ln x ); (3) f (arctan x ); (4) f (cos x ).解 (1)由0≤e x ≤1得x ≤0, 即函数f (e x )的定义域为(-∞, 0]. (2) 由0≤ ln x ≤1得1≤x ≤e , 即函数f (ln x )的定义域为[1, e ].(3) 由0≤ arctan x ≤1得0≤x ≤tan 1, 即函数f (arctan x )的定义域为[0, tan 1]. (4) 由0≤ cos x ≤1得2222ππππ+≤≤-n x n (n =0, ±1, ±2, ⋅ ⋅ ⋅),即函数f (cos x )的定义域为[2,22ππππ+-n n ], (n =0, ±1, ±2, ⋅ ⋅ ⋅).4. 设⎩⎨⎧>≤=0 0 0)(x x x x f , ⎩⎨⎧>-≤=0 00)(2x x x x g , 求f [f (x )], g [g (x )], f [g (x )], g [f (x )].解 因为f (x )≥0, 所以f [f (x )]=f (x )⎩⎨⎧>≤=0 0 0x x x ;因为g (x )≤0, 所以g [g (x )]=0; 因为g (x )≤0, 所以f [g (x )]=0;因为f (x )≥0, 所以g [f (x )]=-f 2(x )⎩⎨⎧>-≤=0 002x x x .5. 利用y =sin x 的图形作出下列函数的图形:(1)y =|sin x |; (2)y =sin|x |; (3)2sin 2x y =.6. 把半径为R 的一圆形铁片, 自中心处剪去中心角为α的一扇形后围成一无底圆锥. 试将这圆锥的体积表为α的函数.解 设围成的圆锥的底半径为r , 高为h , 依题意有R (2π-α)=2πr , παπ2)2(-=R r ,παπαπαπ244)2(2222222-=--=-=R R R r R h . 圆锥的体积为παπαπαππ244)2(312222-⋅-⋅=RR V 22234)2(24a R -⋅-=πααππ(0<α<2π). 7. 根据函数极限的定义证明536lim 23=---→x x x x . 证明 对于任意给定的ε>0, 要使ε<----|536|2x x x , 只需|x -3|<ε, 取δ=ε, 当0<|x -3|<δ时, 就有|x -3|<ε, 即ε<----|536|2x x x , 所以536lim 23=---→x x x x .8. 求下列极限:(1)221)1(1lim -+-→x x x x ; (2))1(lim 2x x x x -++∞→;(3)1)1232(lim +∞→++x x x x ;(4)30sin tan lim x x x x -→; (5)x x x x x c b a 10)3(lim ++→(a >0, b >0, c >0); (6)x x x tan 2)(sin lim π→.解 (1)因为01)1(lim 221=+--→x x x x , 所以∞=-+-→221)1(1lim x x x x . (2))1()1)(1(lim )1(lim 2222x x x x x x x x x x x x ++++-+=-++∞→+∞→211111lim 1lim22=++=++=+∞→+∞→x x x x x x .(3)2121211)1221(lim )1221(lim )1232(lim ++∞→+∞→+∞→++=++=++x x x x x x x x x x 21212)1221()1221(l i m++++=+∞→x x x x e x x x x x =++⋅++=∞→+∞→21212)1221(lim )1221(lim . (4)x x x x x x x x x x x x x cos )cos 1(sin lim )1cos 1(sin lim sin tan lim 303030-=-=-→→→ 21)2(2lim cos 2sin 2sin lim320320=⋅=⋅=→→x x x x x x x x x (提示: 用等价无穷小换).(5)x c b a c b a xx x x xx xx x x x x x x x cb ac ba 3333010)331(lim )3(lim -++⋅-++→→-+++=++,因为e c b a x x x c b a xx x x =-+++-++→330)331(l i m , )111(lim 3133lim 00x c x b x a x c b a xx x x x x x x -+-+-=-++→→])1l n (1lim ln )1ln(1lim ln )1ln(1lim [ln 31000v c u b t a v u t +++++=→→→3ln )ln ln (ln 31abc c b a =++=, 所以 3ln 103)3(lim abc e c b a abc x x x x x ==++→. 提示: 求极限过程中作了变换a x -1=t , b x -1=u , c x -1=v . (6)xx x x xx x x tan )1(sin 1sin 12tan 2)]1(sin1[lim )(sin lim -⋅-→→-+=ππ, 因为e x xx =-+-→1s i n 12)]1(sin1[lim π,x x x x x x x c o s )1(s i n s i n l i mt a n )1(s i n l i m 22-=-→→ππ 01s i n c o s s i n lim )1(sin cos )1(sin sin lim 222=+-=+-=→→x x x x x x x x x ππ, 所以 1)(s i n lim 0tan 2==→e xx x π. 9. 设⎪⎩⎪⎨⎧≤+>=01sin )(2x x a x xx x f , 要使f (x )在(-∞, +∞)内连续, 应怎样选择数a ? 解 要使函数连续, 必须使函数在x =0处连续. 因为f (0)=a , a x a x f x x =+=--→→)(lim )(lim 200, 01sinlim )(lim 00==++→→xx x f x x , 所以当a =0时, f (x )在x =0处连续. 因此选取a =0时, f (x )在(-∞, +∞)内连续.。
3-2洛必达法则

0 0
关键:将其它类型未定式化为洛必达法则可解决 的类型 ( 0 ), ( ) .
0
1. 0 型
例5 解
求 lim x
x 2
e .
x
( 0 )
e
x
原式 lim
e
x
lim
x
2x
x
.
2
2. 型
例6 解
求 lim (
x 0
x 1 x
2
x
Hale Waihona Puke i mx ,无法继续.
正确解法 li m
1 x
2
x
1
1.
例11 解
求 lim
x cos x x
x
.
原式 lim
1 sin x 1
lim ( 1 sin x ).
x
x
洛必达法则失效。
原式 lim ( 1
sec x cos x
lim
x 0
解: 原式 =
ln[(1 x ) x ] sec x cos x ln (1 x x ) sec x cos x
2 4
2 2
2
lim
x 0
lim
x x
2
4
x 0 sec x
cos x
lim
x 0
2x 4x
3
sec x tan x
f ( x ) 与 F ( x ) 都趋于零或都趋于无穷大,那末 极限 lim f ( x) F ( x) 0 0 或 型未定式.
ln sin ax ln sin bx , (
洛必达法则(高考题)

洛必达法则(高考题)洛必达法则洛必达法则是微积分中的重要概念之一。
它用于求解未定式的极限,主要包括三个法则。
法则1:若函数f(x)和g(x)满足一定条件,那么它们的极限相等。
法则2:若函数f(x)和g(x)满足一定条件,且在正负无穷处极限存在,那么它们的极限相等。
法则3:若函数f(x)和g(x)满足一定条件,且在某一点的去心邻域内极限存在,那么它们的极限相等。
在使用洛必达法则求解极限时,需要注意以下几点:1.检查是否满足前提条件,否则结果可能不正确。
2.可以连续多次使用洛必达法则,直到求出极限为止。
3.若不满足前提条件,不能使用洛必达法则,需要从其他途径求解。
XXX在高考中也经常出现,例如以下题目:1.设函数f(x) = e^(-1-x-ax)/(x^2),求f(x)的单调区间和a的取值范围。
解:根据洛必达法则,当a = 1时,f(x) = e^(-1-x),f'(x) = e^(-1)。
当x∈(-∞,0)时,f'(x)。
0.因此,f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增。
又因为f(x)≥1/x^2,所以当x≥1时,f(x)≥1/e。
因此,a的取值范围为a≤1/2.经过格式修正和改写,文章变得更加清晰易懂。
首先,将文章中的数学符号进行修改,使其符合规范。
然后,删除掉明显有问题的段落,比如第一段中的“于是当x时,f(x).”这句话没有明确的意义。
最后,对每段话进行小幅度的改写,使其更加清晰易懂。
具体修改如下:首先,对于函数 $f(x)$,当 $f'(x) \geq 0$($x \geq 0$)时,有 $f(0) = 2$。
因此,当 $x \geq 0$ 时,$f(x) \geq 2$。
由不等式 $e。
1+x$($x \neq 0$)可得 $e^x - x。
1 -x$($x \neq 0$)。
因此,当 $a。
1$ 时,有:2f'(x) < e^x - 1 + 2a(e^{-x} - 1) = e^{-x}(e^x - 1)(e^x - 2a)$$因此,当 $x \in (0.\ln(2a))$ 时,$f'(x) < 0$,而 $f(0) = 2$,因此当 $x \in (0.\ln(2a))$ 时,$f(x) < 2$。
大学课程《高等数学》PPT课件:3-2 洛必达法则

型未定式
定理 2.
2) f (x)与F (x) 在U (a)内可导,
3) lim f (x) 存在 (或为∞) xa F (x) lim f (x) lim f (x) xa F (x) xa F (x)
(洛必达法则)
证: 仅就极限 lim f (x) 存在的情形加以证明 . xa F (x)
lim f (x) k lim f (x) k F (x) xa F (x) xa F (x)
lim f (x) k F (x) k 0 , 可用 1) 中结论 xa F (x)
lim
xa
f
(x) k F (x) F (x)
lim
xa
f F
( (
x) x)
k
lim f (x) lim f (x) xa F (x) xa F (x)
f (x) 2 F (x)
lim
xa
F (x) f (x)
1 lim f (x) lim F (x) xa F (x) xa f (x)
从而
lim f (x) lim f (x) xa F (x) xa F (x)
目录 上页 下页 返回 结束
lim f (x) 0 的情形. 取常数 k 0 , xa F (x)
即 lim f (x) lim f (x) .
F (x)
F (x)
例如,
极限不存在
1
目录 上页 下页 返回 结束
解决方法:
通分
转化
例8. 求 解: 原式=
0
00
0 取倒数
取对数
0
转化
转化
1
0
0 型
目录 上页 下页 返回 结束
洛必达法则的一些应用

洛必达法则的一些应用洛必达法则(Lotka-Volterra equations),也称为捕食-食饵模型,是对生态系统中捕食者和食饵之间相互作用关系的数学描述。
它由阿尔弗雷德·洛特卡(Alfred J. Lotka)和瓦尔特·福尔泰拉(Vito Volterra)于1920年代提出,成为生态学的重要理论基础之一、洛必达法则主要用于揭示生态系统中捕食者和食饵之间相互依赖和相互制约的关系,对生物多样性和生态平衡研究有着重要意义。
dx/dt = αx - βxydy/dt = δxy - γy其中,x表示食饵的种群数量,y表示捕食者的种群数量,t表示时间。
α、β、δ和γ分别表示捕食者对食饵的增长率、食饵被捕食的速率、捕食者的死亡率和食饵的自然增长率。
这个模型假设捕食者和食饵之间不存在其他相互作用。
1.解释捕食者-食饵动态:洛必达法则可以用来解释捕食者和食饵之间的种群动态变化。
当食饵的数量增多时,捕食者的数量也会相应增多;而当捕食者的数量增多时,食饵的数量会减少。
这种反馈机制使得捕食者和食饵之间能够达到一种相对平衡的状态。
2.研究生物多样性:洛必达法则可以用来研究生态系统中不同物种之间的相互作用和竞争关系。
通过观察捕食者和食饵的数量变化,可以了解不同物种对资源的利用和竞争情况,从而揭示生态系统的物种组成和多样性。
3.预测和控制生态系统变化:洛必达法则可以通过数学模拟来预测生态系统的变化趋势。
通过改变模型中的参数值,可以模拟不同环境条件下捕食者和食饵之间的相互作用,进而预测生态系统的稳定性和可持续性。
4.生物害虫防治:洛必达法则在农业害虫防治中有重要应用。
通过研究害虫与天敌(捕食者)之间的相互关系,可以选择合适的天敌进行生物防治,控制害虫数量从而减少农药使用。
5.环境保护和生态恢复:洛必达法则可以用来评估生态系统遭受破坏后的恢复能力。
通过研究捕食者和食饵之间的动态变化,可以了解恢复过程中物种之间的相互关系和依赖程度,从而指导生态恢复工作。
洛必达法则3个使用条件

洛必达法则3个使用条件洛必达法则是一种经典的管理理论,由马克·洛必达(Maxim Lopata)提出。
它认为,组织应该利用三种实用的原则:有效的沟通、及时的决策和及时的行动,来提高其绩效。
洛必达法则的三个使用条件是:1.有效的沟通:洛必达法则强调,组织必须建立有效的沟通,以正确传递信息并促进有效的决策和行动。
有效的沟通可以帮助管理者和员工正确地理解任务,明确其要求,从而实现有效的决策和行动。
组织应该使用口头和书面的沟通手段,以确保信息的及时传达。
2.及时的决策:洛必达法则认为,组织应该做出及时准确的决策,以确保它们能够有效实施及时的行动。
管理者应该采取必要的措施,收集和分析信息,以便做出正确的决策。
如果组织没有及时做出决策,就可能会出现决策失误,从而导致组织绩效的下降。
3.及时的行动:洛必达法则认为,组织必须采取及时的行动来实现其目标。
管理者应当采取必要的措施,以确保实施计划和调整行动方案,以实现最终目标。
及时的行动有助于组织更快地实现其目标,而延迟行动则会导致组织绩效的下降。
洛必达法则的三个使用条件是有效的沟通、及时的决策和及时的行动,它们可以帮助组织更有效地实现其目标,提高其绩效。
有效的沟通可以保证信息的及时传达,从而帮助管理者和员工正确理解任务,明确其要求。
及时的决策可以确保组织能够有效地实施行动,而延迟决策则会导致组织绩效的下降。
及时的行动也是重要的,可以确保组织更快地实现其目标,而延迟行动则会导致组织绩效的下降。
洛必达法则是一种经典的管理理论,可以帮助组织更有效地实现其目标,提高其绩效。
它提出了三个使用条件:有效的沟通、及时的决策和及时的行动,以确保组织能够有效地实现其目标。
组织应当加强沟通,做出及时准确的决策,采取及时的行动,以提高其绩效。
洛必达法则

f ( x) f '( ) 即•• g ( x) g '( )
( 在x与a之间)
下页
由于当x→a时,ξ→a,对上式两边取极限得
f ( x) f ( ) lim lim x a g ( x) x a g ( ) f ( x) f ( x) 即•• lim lim x a g ( x) x a g ( x )
注:每次使用罗必达法则之前,必须分析所求极限 是否满足法则条件,若不满足,应停止使用,改用 其他方法。
下页
“零比零”型未定式的定值法 x sin x lim 例 2 例 3 求 3 x 0 x x sin x lim1 cos x lim sin x 1 解 lim 解 x 0 x 0 3x 2 x 0 6 x 6 x3 例 例 43 求 lim 2
2
x e sin x 1 e sin x 1 lim lim 2 2 x 0 x 0 (sin x) x
2
x
e cos x e x sin x 1 lim lim x 0 x 0 2x 2 2
x
e x 1 sin x 例11 求极限 lim x x 0 (e 1)sin x
f (sin x) 1 f (sin x) 1 lim lim x 0 x 0 f ( x) 1 ln f ( x)
f (sin x) f (0) x lim x 0 sin x 0 f ( x) f (0)
所以不能用洛必达法则 但其极限是存在的 lim x sin x lim (1 sin x ) 1 x x x x
例14
e cos x lim 求 x 0 x sin x
洛必达法则例题

习题3−21. 用洛必达法则求下列极限:(1)xx x )1ln(lim 0+→; (2)xe e xx x sin lim 0−→−; (3)ax a x a x −−→sin sin lim ; (4)xx x 5tan 3sin lim π→; (5)22)2(sin ln lim x xx −→ππ; (6)n n mm a x ax a x −−→lim ;(7)x x x 2tan ln 7tan ln lim 0+→; (8)xx x 3tan tan lim2π→; (9)xarc x x cot )11ln(lim ++∞→; (10)xx x x cos sec )1ln(lim 20−+→; (11)x x x 2cot lim 0→; (12)2120lim x x e x →; (13)−−−→1112lim 21x x x ; (14)x x xa )1(lim +∞→; (15)x x x sin 0lim +→; (16)x x xtan 0)1(lim +→.解 (1)111lim 111lim )1ln(lim 000=+=+=+→→→xx x x x x x . (2)2cos lim sin lim 00=+=−−→−→xe e x e e xx x x x x . (3)a x ax a x a x a x cos 1cos lim sin sin lim ==−−→→. (4)535sec 53cos 3lim 5tan 3sin lim 2−==→→x x x x x x ππ. (5)812csc lim 41)2()2(2cot lim )2(sin ln lim 22222−=−−−=−⋅−=−→→→x x x x x x x x πππππ. (6)n m n m n m a x n n mm a x a nm na mx nx mx a x a x −−−−−→→===−−1111lim lim . (7)177sec 22sec lim 277tan 2tan lim 2722sec 2tan 177sec 7tan 1lim 2tan ln 7tan ln lim 22002200=⋅⋅==⋅⋅⋅⋅=+→+→+→+→x x x x x xx x x x x x x x . (8))sin (cos 23)3sin (3cos 2lim 31cos 3cos lim 3133sec sec lim 3tan tan lim 22222222x x x x x x x x x x x x x x −⋅−==⋅=→→→→ππππ 3sin 3sin 3lim cos 3cos lim22=−−−=−=→→x x x x x x ππ. (9)122lim 212lim 1lim 11)1(111lim cot arc )11ln(lim 2222==+=++=+−⋅+=++∞→+∞→+∞→+∞→+∞→x x x x x x x x x x x x x x x . (10)x x xx x x x x x x x 22022020cos 1lim cos 1)1ln(cos lim cos sec )1ln(lim −=−+=−+→→→(注: cos x ⋅ln(1+x 2)~x 2) 1sin lim )sin (cos 22lim 00==−−=→→xx x x x x x . (11)2122sec 1lim 2tan lim 2cot lim 2000=⋅==→→→x x x x x x x x . (12)+∞====+∞→+∞→→→1lim lim 1lim lim 21012022t t t t x x xx e t e x e e x (注: 当x →0时, +∞→=21xt ).(13)2121lim 11lim 1112lim 12121−=−=−−= −−−→→→x x x x x x x x . (14)因为)1ln(lim )1(lim x ax x x x e x a +∞→∞→=+, 而 a a a x ax xx ax a x x a x a x x x x x x ==+=−−⋅+=+=+∞→∞→∞→∞→∞→1lim lim 1)(11lim 1)1ln(lim )1(ln(lim 22, 所以 a x a x x x x e e x a ==++∞→∞→)1ln(lim )1(lim . .(15)因为x x x x x e x ln sin 0sin 0lim lim +→+→=, 而 0cos sin lim cot csc 1lim csc ln lim ln sin lim 20000=−=⋅−==+→+→+→+→xx x x x x x x x x x x x x , 所以 1lim lim 0ln sin 0sin 0===+→+→e e x x x x x x . (16)因为x x x x e xln tan tan 0)1(lim −+→=, 而 0sin lim csc 1lim cot ln lim ln tan lim 202000=−=−==+→+→+→+→xx x x x x x x x x x x , 所以 1lim )1(lim 0ln tan 0tan 0===−+→+→e e x x x x x x . 2. 验证极限x x x x sin lim+∞→存在, 但不能用洛必达法则得出. 解 1)sin 1(lim sin lim =+=+∞→∞→x x x x x x x , 极限xx x x sin lim +∞→是存在的. 但)cos 1(lim 1cos 1lim )()sin (lim x x x x x x x x +=+=′′+∞→∞→∞→不存在, 不能用洛必达法则. 3. 验证极限xx x x sin 1sin lim 20→存在, 但不能用洛必达法则得出.解 0011sin sin lim sin 1sinlim 020=⋅=⋅=→→x x x x x x x x x , 极限x x x x sin 1sin lim 20→是存在的. 但xx x x x x x x x cos 1cos 1sin 2lim )(sin )1sin (lim 020−=′′→→不存在, 不能用洛必达法则. 4. 讨论函数≤>+=−0 0 ])1([)(2111x e x ex x f x x 在点x =0处的连续性. 解 21)0(−=e f , )0(lim )(lim 212100f e e x f x x ===−−−→−→,因为 ]1)1ln(1[101100lim ])1([lim )(lim −+−→−→+→=+=x x x x x x x x e e x x f ,而 21)1(21lim 2111lim )1ln(lim ]1)1ln(1[1lim 00200−=+−=−+=−+=−++→+→+→+→x x x x x x x x x x x x x , 所以 )0(lim ])1([lim )(lim 21]1)1ln(1[101100f e e ex x f x x x x x x x x ===+=−−+−→−→+→. 因此f (x )在点x =0处连续.。
洛必达法则在导数中的应用

洛必达法则在导数中的应用山东省平度第一中学 王尊甫一、洛必达法则简介:法则1 若函数f(x) 和g(x)满足下列条件:(1) ()lim 0x af x →= 及()lim 0x ag x →=;(2)在点a 的去心邻域内,f(x) 与g(x) 可导且g '(x)≠0; (3)()()limx af x lg x →'=', 那么 ()()lim x a f x g x →=()()lim x a f x l g x →'='。
法则2 若函数f(x) 和g(x)满足下列条件:(1)()lim 0x f x →∞= 及()lim 0x g x →∞=;(2)0A ∃>,f(x) 和g(x)在(),A -∞与(),A +∞上可导,且g '(x)≠0;(3)()()lim x f x l g x →∞'=',那么 ()()limx f x g x →∞=()()limx f x l g x →∞'='。
法则3 若函数f(x) 和g(x)满足下列条件:(1) ()lim x af x →=∞及()lim x ag x →=∞; (2)在点a 的去心邻域内,f(x) 与g(x) 可导且g '(x)≠0; (3)()()limx af x lg x →'=', 那么 ()()lim x a f x g x →=()()lim x a f x l g x →'='。
利用洛必达法则求未定式的极限是微分学中的重点之一,在解题中应注意: ○1将上面公式中的x→a,x→∞换成x→+∞,x→-∞,x a+→,x a-→洛必达法则也成立。
○2洛必达法则可处理00,∞∞,0⋅∞,1∞,0∞,00,∞-∞型。
○3在着手求极限以前,首先要检查是否满足00,∞∞,0⋅∞,1∞,0∞,00,∞-∞型定式,否则滥用洛必达法则会出错。
洛必达法则的计算机应用

洛必达法则的计算机应用洛必达法则是微积分中常见的一种计算极限的方法,应用广泛。
在计算机领域中,洛必达法则同样有其独特的应用价值。
本文将讨论洛必达法则在计算机应用中的具体案例和实现方式。
一、探究洛必达法则洛必达法则最初是由法国著名数学家洛必达在17世纪发现并总结而来的,它是一种计算极限的方法。
在微积分学中,极限是对函数在某一点处的取值情况进行研究的重要方法之一。
而洛必达法则则是其中最常见的一种计算方法。
洛必达法则指出,函数$f(x)$在$x=a$处的极限,只有当$\lim_{x\to a}\frac{f(x)-f(a)}{x-a}$存在或为无穷时,$\lim_{x\toa}f(x)$才存在。
也就是说,如果$f(x)$在$x=a$处的极限存在,那么$\lim_{x\to a}\frac{f(x)-f(a)}{x-a}$必定存在,反之亦然。
二、洛必达法则的应用在计算机科学领域中,洛必达法则同样有着广泛的应用。
下面将介绍几种洛必达法则的实际应用场景。
1.计算机视觉计算机视觉是计算机科学领域的一个重要分支,主要研究如何让计算机看懂图片、视频等视觉信息。
在计算机视觉中,洛必达法则主要用来计算图像的梯度,从而进行边缘检测等操作。
在图像处理中,每个像素点都有一个灰度值,可以将其看作是一个函数$f(x)$。
洛必达法则可以帮助我们计算出函数在每个像素点处的梯度值,从而得到图像中每个像素点的边缘信息。
2.机器学习机器学习是计算机科学中的另一个重要分支,主要研究如何通过算法让计算机自己学习和优化。
在机器学习中,洛必达法则同样有着广泛的应用。
例如,在神经网络中,我们通常使用反向传播算法来训练模型。
而反向传播算法中,洛必达法则可以帮助我们计算出每个神经元的梯度,从而进行参数更新,提升模型的精度和泛化能力。
3.物理仿真物理仿真是另一个领域,包括电子游戏、动画制作、工程模拟等方面都有广泛的应用。
在物理仿真的过程中,我们需要通过计算机来模拟物体的运动轨迹、碰撞反应等物理规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机动
目录
上页
下页
返回
结束
例13
ln(1 + x + x 2 ) + ln(1 − x + x 2 ) 0 lim ( ) x →0 sec x − cos x 0
2 2 2
ln[(1 + x ) − x ] 解: 原式 = lim x →0 sec x − cos x ln (1 + x 2 + x 4 ) x2 + x4 = lim = lim 2 x → 0 sec x − cos x x → 0 1 − cos x cos x
1 ln ln 1 x ∞ lim+ ln y = lim+ x ln ln = lim+ ( ) 1 x →0 x →0 x x →0 ∞ ( 0⋅∞ ) x 1 令t= ln ln t ∞ 1 x ( ) = lim =0 ===== tlim → +∞ t → +∞ t ln t t ∞
x →0
x cos x − sin x = lim x →0 2 x3
(sin x ~ x , x → 0)
cos x + x ( − sin x ) − cos x = lim x →0 6x2 − x sin x − sin x = lim = lim 2 x →0 x →0 6x 6x 1 =− 6
f ( x ) f ( x ) − f (a ) f ′(ξ ) = = F ( x ) F ( x ) − F (a ) F ′(ξ )
Q 当 x → a时 ,ξ → a ,
(ξ 在 x 与 a 之间 )
∴
f ( x) f ′(ξ ) f ′(ξ ) f ′( x ) = lim lim = lim = lim x →a F ( x ) x → a F ′(ξ ) ξ → a F ′(ξ ) x → a F ′( x )
首先要确定所求 极限是否 为 ★ 使用洛必达法则时 , sin x 未定式 , 否则不能用洛必达法则 . 例: lim π x x→
∞ ★ 当x → a , x → ∞时的未定式 , 也有相应的洛必达法则 。 ∞
机动 目录 上页 下页 返回 结束
2
π
例1 求 lim 2
x → +∞
− arctan x 1 x .
x →0
2 1+ ln x
lim+ y = lim+ e
x →0
ln y
=e
x → 0+
lim ln y
= e2
机动 目录 上页 下页 返回 结束
例8
sin x lim( ) x →0 x
1 x2
( 1∞ )
1 sin x sin x 解 设 y=( ) , ln y = 2 ln x x x 1 sin x ln sin x − ln x lim ln y = lim 2 ln = lim x →0 x →0 x x →0 x x2
lim+ y = lim+ e
x →0
ln y
= e x→0
lim ln y
+
= e0 = 1
机动
目录
上页
下页
返回
结束
例10 解:
x → +∞
lim ( x + ln x − x ) ( ∞ − ∞ )
原式 = xlim → +∞
1 x
∞ ln x ( ) x + ln x + x ∞
1 = lim x → +∞ x +1 x + 2 x + ln x 2
∞
⎧0 ⋅ ln 0 ⎪ 取对数 ⎯⎯⎯→ ⎨∞ ⋅ ln 1 ⇒ 0 ⋅ ∞ . ⎪0 ⋅ ln ∞ ⎩
机动
目录
上页
下页
返回
结束
例7
x →0
lim+ (sin x )
2 1+ ln x
( 00 )
2 ln sin x ln y = 解 设 y = (sin x ) 1 + ln x ∞ 2 ln sin x ( ) lim+ ln y = lim+ x →0 x → 0 1 + ln x ∞ 2 x cos x = lim+ =2 x →0 sin x
tan x − x 求 lim 2 . x → 0 x tan x sec2 x − 1 tan x − x = lim 原式 = lim 3 x →0 x →0 3 x2 x tan 2 x 1 = lim = . 2 x→ 0 3 x 3
机动
目录
上页
下页
返回
结束
f ′( x ) (2)若 lim 不存在 ( ≠ ∞ )时 , F ′( x ) f ( x) f ′( x ) = lim ′ . lim F ( x) F ( x)
x 2 (1 + x 2 ) cos x = lim x →0 sin 2 x
=1
第三节 目录
上页
下页
返回
结束
说明: 洛必达法则只能用于函数极限的未定式, 对于数列极限的未定式,要先化成函数极 限,再用洛必达法则。
机动
目录
上页
下页
返回
结束
例14: 求 lim tan n (π + 2 ) n→ ∞ 4 n
π 2 2 解: 设 y = tan ( + ) , ln y = x ln tan( + ) , 4 x 4 x
机动
目录
上页
下页
返回
结束
f ′( x ) 0 仍属 型,且 f ′( x ), F ′( x ) 满足定理 的 ★ 如果 F ′( x ) 0 条件,可以继续 使用洛必达法则,即
f ( x) f ′( x ) f ′′( x ) lim = L. = lim = lim x→a F ( x ) x → a F ′( x ) x → a F ′′( x ) f ( x) f ′( x ) = lim . ★ 当x → ∞时 , 该法则仍然成立 。即 lim x →∞ F ( x ) x → ∞ F ′( x )
(
0 ) 0
1 − 2 解 原式 = lim 1 + x x → +∞ 1 − 2 x
x2 = 1. = lim 2 x → +∞ 1 + x
机动
目录
上页
下页
返回
结束
xn 求 lim λx . 其中n为正整数, λ > 0 ( ∞ ) 例2 x → +∞ e ∞
解
n! nx n−1 = L = lim n λx = 0 原式 = lim λx x → +∞ λ e x → +∞ λ e
(∞−∞)
1 解: 令 t = , 则 x 1 + 2t − 2 1 + t + 1 原式 = lim t → 0+ t2
= lim +
t →0
0 ( ) 0
(1 + 2 t )
−1 2
− (1 + t ) 2t
1 2
−1 2
− (1 + 2t ) + (1 + t ) = lim t → 0+ 2
0 ∞ 常把这种极限称为 或 型未定式 . 0 ∞
tan x 0 ,( ) 例如, lim x→ 0 x 0
ln sin ax ∞ lim ,( ) x→ 0 ln sin bx ∞
机动 目录 上页 下页 返回 结束
定理:设 (1) 当 x → a时 , 函数 f ( x ) 及 F ( x ) 都趋于零; ( 2) 在 a 点的某去心邻域内 f ′( x ) 及 F ′( x ) 都存在 且 F ′( x ) ≠ 0; f ′( x ) ( 3) lim 存在 (或为无穷大 ); x → a F ′( x ) f ( x) f ′( x ) = lim 那么 lim . x →a F ( x ) x → a F ′( x ) 定义 这种在一定条件下通过分子分母分别求导再 求极限来确定未定式的值的方法称为洛必达法则.
从例 4、例 5 知,当 x → +∞ 时,下列无穷大 量 ln x , xα (α > 0), a x ( a > 1)的阶数依次增高。
机动
目录
上页
下页
返回
结束
注意: (1)洛必达法则是求未定式的一种有效方法, 但与其它求极限方法(如两个重要极限,等价 无穷小代换等)结合使用,效果更好. 例4 解
α
( 0⋅∞ )
ln x ∞ lim x ln x = lim −α ( ) 解 x → +0 x → +0 x ∞ 1 1 x = lim = lim =0 −α −α −1 x → +0 − αx x → +0 − αx
例6 解
1 1 求 lim( − ). x → 0 sin x x
(∞−∞)
−3 2
−3 2
1 =− 4
机动
目录
上页
下页
返回
结束
1 例12 lim[ x ln(1 + ) − x ]; x →∞ x 1 2 解: lim [ x ln(1 + ) − x ] x →∞ x
2
(∞−∞) 1 (令 t = ) x
ln(1 + t ) − t 0 1 1 ( ) = lim [ 2 ln(1 + t ) − ] = lim 2 0 t →0 t →0 t t t 1 −1 −t 1 = lim 1 + t = lim =− t →0 t → 0 2 t (1 + t ) 2t 2
