(人教版)八年级数学平行四边形综合检测题1
2020年人教版初中数学八年级下册第18章《平行四边形》单元综合测试题含答案

平行四边形一.选择题(共10小题)1.如图,A、B两地被池塘隔开,小康通过下列方法测出了A、B间的距离:先在AB外选一他点C,然后测出AC,BC的中点M、N,并测量出MN的长为18m,由此他就知道了A、B间的距离.下列有关他这次探究活动的结论中,错误的是()A.AB=36m B.MN∥AB C.MN=CB D.CM=AC2.平行四边形两邻角的平分线相交所成的角的大小是()A.90°B.60°C.45°D.30°3.下列不能判定一个四边形是平行四边形的是()A.两组对边分别平行的四边形是平行四边形B.两组对边分别相等的四边形是平行四边形C.一组对边平行另一组对边相等的四边形是平行四边形D.对角线互相平分的四边形是平行四边形4.下列说法正确的有()①对角线互相平分的四边形是平行四边形;②平行四边形的对角互补;③平行线间的线段相等;④两个全等的三角形可以拼成一个平行四边形;⑤平行四边形的四内角之比可以是2:3:2:3.A.1个B.2个C.3个D.4个5.直角三角形中,两直角边分别是12和5,则斜边上的中线长是()A.34 B.26 C.8.5 D.6.56.如图,在菱形ABCD中,∠BAD=120°,点A坐标是(﹣2,0),则点B坐标为()A.(0,2)B.(0,)C.(0,1)D.(0,2)7.下列说法中,错误的是()A.平行四边形的对角线互相平分B.对角线互相垂直的四边形是菱形C.菱形的对角线互相垂直D.对角线互相平分的四边形是平行四边形8.如图,在△ABC中,∠BAC=90°,AB=8,AC=6,M为BC上的一动点,ME⊥AB于E,MF⊥AC于F,N为EF的中点,则MN的最小值为()A.4.8 B.2.4 C.2.5 D.2.69.如图,两把完全一样的直尺叠放在一起,重合的部分构成一个四边形,这个四边形一定是()A.矩形B.菱形C.正方形D.无法判断10.把一张长方形纸片ABCD按如图方式折一下,就一定可以裁出()纸片ABEF.A.平行四边形B.菱形C.矩形D.正方形二.填空题(共8小题)11.如图,在平行四边形ABCD中,∠BCD和∠ABC的平分线分别交AD于E、F两点,AB=6,BC=10,则EF的长度是.12.如图,四边形ABCD的对角线交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC =∠ADC中选出两个可使四边形ABCD是平行四边形,则你选的两个条件是.(填写一组序号即可)13.如图,将两条宽度都是为2的纸条重叠在一起,使∠ABC=45°,则四边形ABCD的面积为.14.如图,矩形ABCD中,AB=20cm,BC=4cm,点P从A开始沿折线A﹣B﹣C﹣D以4cm/s的速度运动,点Q从C开始沿CD边以1cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s),当t=时,四边形APQD 也为矩形.15.如图,在平行四边形ABCD中,AB=8,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=3,则AE的边长为.16.在▱ABCD中,AE平分∠BAD交边BC于E,DF⊥AE,交边BC于F,若AD=10,EF=4,则AB=.17.矩形ABCD与CEFG,如图放置,点B、C、E共线,点C、D、G共线,连接AF,取AF的中点H,连接GH,若BC=EF=4,CD=CE=2,则GH=.18.如图,正方形OABC在直角坐标系中,点B(﹣2,2),点D为BC的中点,点E在线段OC上运动,射线ED交AB延长线于点F,设E(0,t),当△AEF是以AE为腰的等腰三角形时,点E的坐标是.三.解答题(共7小题)19.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE 的长.20.在▱ABCD中,点E在CD边上,点F在AB边上,连接AE、CF、DF、BE,∠DAE=∠BCF.(1)如图1,求证:四边形DFBE是平行四边形;(2)如图2,设AE交DF于点G,BE交CF于点H,连接GH,若E是CD边的中点,在不添加任何辅助线的情况下,请直接写出图中以GH为边或对角线的所有平行四边形.21.已知:如图,在矩形ABCD中,点M、N在边AD上,且AM=DN,求证:BN=CM.22.如图,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证:AM=EF.23.已知,如图,∠ABC=∠ADC=90°,点E、F分别是AC、BD的中点,AC=10,BD=6.(1)求证:EF⊥BD;(2)求EF的长.24.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB 的平行线与DE的延长线交于点F,连接BF,AE.(1)求证:四边形BDCF为菱形;(2)若四边形BDCF的面积为24,tan∠EAC=,求CF的长.25.如图,在平行四边形ABCD中,过点D作DE⊥BC交BC于点E,且DE=AD,F为DC上一点,且AD=FD,连接AF与DE交于点G.(1)若∠C=60°,AB=2,求GF的长;(2)过点A作AH⊥AD,且AH=CE,求证:AB=DG+AH.第《18章平行四边形》单元测试题参考答案与试题解析一.选择题(共10小题)1.【分析】根据三角形的中位线定理即可判断;【解答】解:∵CM=MA,CNB,∴MN∥AB,MN=AB,∵MN=18m,∴AB=36m,故A、B、D正确,故选:C.【点评】本题考查的是三角形的中位线定理在实际生活中的运用,锻炼了学生利用几何知识解答实际问题的能力.2.【分析】根据平行四边形的性质得到∠DAB+∠ABC=180°,由角平分线可得∠BAO+∠ABO=90°,根据三角形的内角和定理得∠AOB=90°,即可得到所选选项.【解答】解:▱ABCD的∠DAB的平分线和∠ABC的平分线交于O,∴∠DAB+∠ABC=180°,∠DAO=∠BAO=∠DAB,∠ABO=∠CBO=∠ABC,∴∠BAO+∠ABO=90°,∴∠AOB=180°﹣90°=90°.故选:A.【点评】本题主要考查了平行四边形的性质,角平分线的定义,三角形的内角和定理等知识点,能综合利用性质进行证明是解此题的关键.3.【分析】根据平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形,即可选出答案.【解答】解:根据平行四边形的判定定理,A、B、D均符合是平行四边形的条件,C则不能判定是平行四边形.故选:C.【点评】此题主要考查学生对平行四边形的判定的掌握情况.对于判定定理:“一组对边平行且相等的四边形是平行四边形.”应用时要注意必须是“一组”,而“一组对边平行且另一组对边相等”的四边形不一定是平行四边形.4.【分析】根据平行四边形的判定定理以及性质定理即可判断.【解答】解:①正确;②平行四边形的对角相等,命题错误;③平行线间的平行线段相等,命题错误;④正确;⑤正确.故选:C.【点评】本题考查了平行四边形的判定定理以及性质定理,正确理解定理的内容是关键.5.【分析】利用勾股定理列式求出斜边,再根据直角三角形斜边上的中线等于斜边的一半解答.【解答】解:由勾股定理得,斜边==13,所以,斜边上的中线长=×13=6.5.故选:D.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理,熟记性质是解题的关键.6.【分析】根据菱形的性质可得∠OAB=∠BAD=60°,∠AOB=90°,解直角△AOB,求出OB,即可得到点B坐标.【解答】解:∵在菱形ABCD中,∠BAD=120°,点A坐标是(﹣2,0),∴∠OAB=∠BAD=60°,∠AOB=90°,在直角△AOB中,∵OA=2,∴OB=OA•tan∠OAB=2×=2,∴点B坐标为(0,2).故选:D.【点评】本题考查了菱形的性质,掌握菱形的两条对角线互相垂直,并且每一条对角线平分一组对角是解题的关键.也考查了锐角三角函数定义,坐标与图形性质.7.【分析】根据平行四边形和菱形的性质对各个选项进行分析从而得到最后答案.【解答】解:根据平行四边形和菱形的性质得到ACD均正确,而B不正确,因为对角线互相垂直的四边形也可能是梯形.故选:B.【点评】主要考查了平行四边形和特殊平行四边形的特性,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.菱形的特性是:四边相等,对角线互相垂直平分.8.【分析】过点A作AM⊥BC于点M′,根据勾股定理求出BC的长,再由三角形的面积公式求出AM′的长.根据题意得出四边形AEMF是矩形,故可得出AM=EF,MN=AM,当MN最小时,AM最短,此时M与M′重合,据此可得出结论.【解答】解:过点A作AM⊥BC于点M′,∵在△ABC中,∠BAC=90°,AB=8,AC=6,∴BC==10,∴AM′==.∵ME⊥AB于E,MF⊥AC于F,∴四边形AEMF是矩形,∴AM=EF,MN=AM,∴当MN最小时,AM最短,此时点M与M′重合,∴MN=AM′==2.4.故选:B.【点评】本题考查了矩形的性质的运用,勾股定理的运用,三角形的面积公式的运用,垂线段最短的性质的运用,解答时求出AM的最小值是关键.9.【分析】由条件可知AB∥CD,AD∥BC,再再证明AB=BC即可解决问题.【解答】解:过点D作DE⊥AB于E,DF⊥BC于F.∵两张长方形纸条的宽度相等,∴DE=DF.又∵平行四边形ABCD的面积=AB•DE=BC•DF,∴AB=BC,∴平行四边形ABCD为菱形.故选:B.【点评】本题考查了菱形的判定,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.10.【分析】根据折叠定理得:所得的四边形有三个直角,且一组邻边相等,所以可以裁出正方形纸片.【解答】解:由已知,根据折叠原理,对折后可得:∠FAB=∠B=∠AFE=90°,AB=AF,∴四边形ABEF是正方形,故选:D.【点评】此题考查了正方形的判定和折叠的性质,关键是由折叠原理得到四边形有三个直角,且一组邻边相等.二.填空题(共8小题)11.【分析】根据平行四边形的性质可知∠DEC=∠ECB,又因为CE平分∠BCD,所以∠DCE=∠ECB,则∠DEC=∠DCE,则DE=DC,同理可证AF=AB,那么EF就可表示为AF+ED﹣BC=2AB﹣BC,继而可得出答案.【解答】解:∵平行四边形ABCD,∴∠DEC=∠ECB,又CE平分∠BCD,∴∠DCE=∠ECB,∴∠DEC=∠DCE,∴DE=DC,同理可证:AF=AB,∴2AB﹣BC=AF+ED﹣BC=EF=2.故答案为2.【点评】本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题,难度不大,关键是解题技巧的掌握.12.【分析】根据AD∥BC可得∠DAO=∠OCB,∠ADO=∠CBO,再证明△AOD≌△COB可得BO=DO,然后再根据对角线互相平分的四边形是平行四边形可得答案.【解答】解:可选条件①③,∵AD∥BC,∴∠DAO=∠OCB,∠ADO=∠CBO,在△AOD和△COB中,,∴△AOD≌△COB(AAS),∴DO=BO,∴四边形ABCD是平行四边形.故答案为:①③.【点评】此题主要考查了平行四边形的判定,关键是掌握对角线互相平分的四边形是平行四边形.13.【分析】根据折叠的性质易知,重合部分为菱形,然后根据菱形的面积公式计算即可.【解答】解:如图,过点A作AE⊥BC于点E,AF⊥CD于点F.则AE=AF=2.∵纸条的对边平行,即AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∵两张纸条的宽度都是2,∴S四边形ABCD=BC×2=CD×2,∴BC=CD,∴平行四边形ABCD是菱形,即四边形ABCD是菱形.∴四边形ABCD的面积为2×2×=4.故答案是:4.【点评】本题主要考查菱形的性质和特殊角的三角函数值,通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.14.【分析】四边形APQD为矩形,也就是AP=DQ,分别用含t的代数式表示,解即可.【解答】解:根据题意,当AP=DQ时,四边形APQD为矩形.此时,4t=20﹣t,解得t=4(s).故答案是:4.【点评】本题考查了矩形的判定与性质.此题利用了矩形的对边相等的性质进行解题的.15.【分析】由平行四边形的性质和角平分线证出AD=DF,由F为DC中点,AB=CD,求出AD与DF 的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由AAS证明ADF≌△ECF全等,得出AF=EF,即可求出AE的长.【解答】解:∵AE为∠DAB的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=4,在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,∵平行四边形ABCD中,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=2×2=4,故答案为:4【点评】此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形全等是解本题的关键.16.【分析】根据平行线的性质得到∠ADF=∠DFC,根据角平分线的定义得到∠BAE=∠DAE,推出AB=BE,根据已知条件推出∠ADF=∠ADC,得到∠DFC=∠CDF,推出CF=CD,于是得到结论.【解答】解:①如图1,在▱ABCD中,∵BC=AD=10,BC∥AD,CD=AB,CD∥AB,∴∠DAE=∠AEB,∠ADF=∠DFC,∵AE平分∠BAD交BC于点E,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE,∵DF⊥AE,∴∠DAE+∠ADF=90°,∵∠BAD+∠ADC=180°,∴∠ADF=∠ADC,∴∠ADF=∠CDF,∵∠ADF=∠DFC,∴∠DFC=∠CDF,∴CF=CD,∴AB=BE=CF=CD∵EF=4,∴BC=BE+CF﹣EF=2AB﹣EF=2AB﹣4=10,∴AB=7;②如图2,在▱ABCD中,∵BC=AD=10,BC∥AD,CD=AB,CD∥AB,∴∠DAE=∠AEB,∠ADF=∠DFC,∵AE平分∠BAD交BC于点E,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE,∵DF⊥AE,∴∠DAE+∠ADF=90°,∵∠BAD+∠ADC=180°,∴∠ADF=∠ADC,∴∠ADF=∠CDF,∵∠ADF=∠DFC,∴∠DFC=∠CDF,∴CF=CD,∴AB=BE=CF=CD∵EF=4,∴BC=BE++EF+CF=2AB+EF=2AB+4=10,∴AB=3;综上所述:AB的长为7或3.故答案为:7或3.【点评】本题考查了等腰三角形的判定和性质,平行线的性质,平行四边形的性质,解答本题的关键是判断出AB=BE=CF=CD.17.【分析】延长GH交AD于点P,先证△APH≌△FGH得AP=GF=2,GH=PH=PG,再利用勾股定理求得PG=2,从而得出答案.【解答】解:如图,延长GH交AD于点P,∵四边形ABCD和四边形CEFG都是矩形,∴∠ADC=∠ADG=∠CGF=90°,AD=BC=4、GF=CE=2,∴AD∥GF,∴∠GFH=∠PAH,又∵H是AF的中点,∴AH=FH,在△APH和△FGH中,∵,∴△APH≌△FGH(ASA),∴AP=GF=2,PH=HG=PG,∵PD=AD﹣AP=2,GD=GC﹣CD=4﹣2=2∴GP==2∴GH=GP=故答案为:【点评】本题主要考查矩形的性质,解题的关键是掌握全等三角形的判定与性质、矩形的性质、勾股定理等知识点.18.【分析】由ASA证明△DBF≌△DCE,得出BF=CE=2﹣t,得出AF=AB+BF=4﹣t,即可得出点F的坐标;分两种情况:①当AE=AF时,根据勾股定理得出AE2=OA2+OE2,得出方程22+t2=(4﹣t)2,解方程即可求出t的值;②当AE=EF时,点E在AF的垂直平分线上,得出OE=AF,即t=(4﹣t),解方程即可求出t的值,从而求解.【解答】解:(1)∵四边形OABC是正方形,∴OA=AB=BC=OC=2,∠AOC=∠ABC=∠BCO=90°,∴∠FBD=90°,∵D是BC的中点,∴BD=CD,在△DBF和△DCE中,,∴△DBF≌△DCE(ASA),∴BF=CE=2﹣t,∴AF=AB+BF=4﹣t,∴D的坐标为(﹣2,4﹣t),当△AEF是以AE为腰的等腰三角形时,分两种情况:①当AE=AF时,∵AE2=OA2+OE2,∴22+t2=(4﹣t)2,解得:t=1.5;②当AE=EF时,点E在AF的垂直平分线上,∴OE=AF,即t=(4﹣t),解得:t=.综上所述:当△AEF是以AE为腰的等腰三角形时,点E的坐标是(0,1.5)或(0,).故答案为:(0,1.5)或(0,).【点评】考查了正方形的性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质等知识;本题综合性强,有一定难度,需要进行分类讨论才能得出结果.三.解答题(共7小题)19.【分析】延长BD与AC相交于点F,根据等腰三角形的性质可得BD=DF,再利用三角形的中位线平行于第三边并且等于第三边的一半可得DE=CF,然后求解即可.【解答】解:如图,延长BD与AC相交于点F,∵AD平分∠BAC,BD⊥AD,∴∠DAB=∠DAF,AD=AD,∠ADB=∠ADF,∴△ADB≌△ADF,∴AF=AB,BD=DF,∵AB=6,AC=10,∴CF=AC﹣AF=AC﹣AB=10﹣6=4,∵E为BC中点,∴DE是△BCF的中位线,∴DE=CF=×4=2.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的判定与性质,作辅助线构造出以DE为中位线的三角形是解题的关键.20.【分析】(1)由平行四边形的性质得出AB∥CD,∠ADE=∠CBF,AD=BC,由ASA证明△ADE≌△CBF,得出DE=BF,即可得出四边形DFBE是平行四边形;(2)由中点的定义得出DE=CE,由平行四边形的判定方法即可得出平行四边形.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∠ADE=∠CBF,AD=BC,在△ADE和△CBF中,,∴△ADE≌△CBF(ASA),∴DE=BF,又∵DE∥BF,∴四边形DFBE是平行四边形;(2)解:∵E是CD的中点,∴DE=CE,∴以GH为边的平行四边形有平行四边形GHFA、平行四边形GHBF、平行四边形GHED、平行四边形GHCE;以GH为对角线的平行四边形有GFHE.【点评】本题考查了平行四边形的性质与判定、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等得出DE=BF是解决问题(1)的关键.21.【分析】由矩形的性质可得出BA=CD、∠A=∠D,由AM=DN可得出AN=DM,进而即可证出△ABN≌△DCM(SAS),根据全等三角形的性质可证出BN=CM.【解答】证明:∵四边形ABCD为矩形,∴BA=CD,∠A=∠D.∵AM=DN,∴AN=DM.在△ABN和△DCM中,,∴△ABN≌△DCM(SAS),∴BN=CM.【点评】本题考查了矩形的性质以及全等三角形的判定与性质,利用全等三角形的判定定理SAS 证出△ABN≌△DCM是解题的关键.22.【分析】延长EM交AD于点P,延长FM交AB于点Q,根据正方形的性质可得出:四边形PMFD、BEMQ为正方形,四边形AQMP、MECF为矩形,进而可得出AQ=FM,QM=ME,结合∠AQM=∠FME=90°即可证出△AQM≌△FME(SAS),再利用全等三角形的性质可证出AM=EF.【解答】证明:延长EM交AD于点P,延长FM交AB于点Q,如图所示.∵四边形ABCD为正方形,点M为对角线BD上一点,∴四边形PMFD、BEMQ为正方形,四边形AQMP、MECF为矩形,∴AQ=PM=FM,QM=ME.在△AQM和△FME中,,∴△AQM≌△FME(SAS),∴AM=EF.【点评】本题考查了全等三角形的判定与性质、正方形的性质以及矩形的性质,利用全等三角形的判定定值SAS证出△AQM≌△FME是解题的关键.23.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半,可求BE=DE,根据等腰三角形的性质,可得结论;(2)根据题意可得BE=5,BF=3,根据勾股定理可求EF的长【解答】证明:(1)连接BE,DE∵∠ABC=∠ADC=90°,点E是AC的中点,∴BE=AC,DE=AC∴BE=DE∵点F是BD的中点,BE=DE∴EF⊥BD(2)∵BE=AC∴BE=5∵点F是BD的中点∴BF=DF=3在Rt△BEF中,EF===4【点评】本题考查了直角三角形斜边上的中线等于斜边的一半,等腰三角形的性质,勾股定理,熟练掌握直角三角形斜边上的中线等于斜边的一半是本题的关键.24.【分析】(1)求出四边形ADFC是平行四边形,推出CF=AD=BD,根据平行四边形的判定得出四边形BDCF是平行四边形,求CD=BD,根据菱形的判定得出即可;(2)设CE=2x,AC=3x,求出BC=4x,DF=AC=3x,根据菱形的面积公式求出x,求出EF和CE,根据勾股定理求出CF即可.【解答】(1)证明:DE⊥BC,∠ACB=90°,∴∠BED=∠ACB,∴DF∥AC,∵CF∥AB,∴四边形ADFC是平行四边形,∴AD=CF,∵D为AB的中点,∴AD=BD,∴BD=CF,∵BD∥CF,∴四边形BDCF是平行四边形,∵∠ACB=90°,D为AB的中点,∴DC=BD,∴四边形BDCF是菱形;(2)解:∵tan∠EAC==,∴设CE=2x,AC=3x,∵四边形BDCF是菱形,∴BE=CE=2x,∴BC=4x,∵四边形ADFC是平行四边形,∴DF=AC=3x,∵四边形BDCF的面积为24,∴=24,解得:x=2(负数舍去),∴CE=4,DF=6,∴DE=EF=×6=3,∵DE⊥BC,∴∠CEF=90°,∴由勾股定理得:CF===5.【点评】本题考查了勾股定理,平行四边形的判定和性质,菱形的判定,直角三角形的性质的应用,能熟记菱形的性质和判定定理是解此题的关键.25.【分析】(1)过G作GH⊥CD于H,根据三角形的内角和得到∠CDE=60°,根据平行四边形的性质得到AD∥BC,AB=CD=2,得到∠ADC=120°,解直角三角形即可得到结论;(2)根据全等三角形的性质得到∠ADH=∠EDC,∠H=∠C,DH=DC,根据平行四边形的性质得到AB=CD,AB∥CD,推出∠DFA=∠C,在DH上截取HM=AH,得到∠HAM=∠HMA,求得∠DAM =∠H,根据全等三角形的性质即可得到结论..【解答】解:(1)如图1,过G作GH⊥CD于H,∵DE⊥BC,∴∠DEC=90°,∵∠C=60°,∴∠CDE=60°,∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD=2,∴∠ADC=120°,∵AD=DF,∴∠DAF=∠DFA=30°,∴∠GDF=∠DFG,∴DG=GF,∵CD=2,∴DF=,∴HF=DF=,∴GF=1;(2)∵AH⊥AD,DE⊥BC,∴∠DAH=∠DEC=90°,在△ADE与△DEC中,,∴△ADE≌△DEC(SAS),∴∠ADH=∠EDC,∠H=∠C,DH=DC,∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠DAB=∠C,∠DFA=∠BAF,∵AD=DF,∴∠DAF=∠DFA,∴∠DFA=∠C,如图2,在DH上截取HM=AH,∴∠HAM=∠HMA,∴∠H=180°﹣2∠HAM,∵∠MAD=90°﹣∠HAM,∴∠DAM=∠H,∴∠MAD=∠GFD,在△ADM与△FDG中,,∴△ADM≌△FDG(ASA),∴DM=DG,∵AB=CD=DH=HM+DM,∴AB=AH+DG.【点评】本题考查了平行四边形的性质,全等三角形的判定和性质,直角三角形的性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.。
人教版八年级数学下册 平行四边形 测试卷 含答案

人教版八年级数学下册平行四边形测试卷一、选择题1.菱形具有而矩形不具有的性质是()A.对角线互相平分 B.四条边都相等C.对角相等D.邻角互补2.关于四边形ABCD:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等;以上四个条件中可以判定四边形ABCD 是平行四边形的有()A.1个 B.2个 C.3个 D.4个3.能判定一个四边形是菱形的条件是()A.对角线相等且互相垂直B.对角线相等且互相平分C.对角线互相垂直 D.对角线互相垂直平分4.正方形、菱形、矩形都具有的性质是()A.对角线相等B.对角线互相平分C.对角线互相垂直 D.对角线平分一组对角5.若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是()A.菱形B.对角线相互垂直的四边形C.正方形D.对角线相等的四边形6.下列说法中,不正确的是()A.有三个角是直角的四边形是矩形B.对角线相等的四边形是矩形C.对角线互相垂直的矩形是正方形D.对角线互相垂直的平行四边形是菱形7.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为()A.36°B.18°C.27°D.9°二、填空题8.平行四边形ABCD中,∠A=50°,AB=30cm,则∠B=,DC=cm.9.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD=cm.10.菱形的两条对角线分别是6cm,8cm,则菱形的边长为cm,面积为cm2.11.如图,△ABC中,EF是它的中位线,M、N分别是EB、CF的中点,若BC=8cm,那么EF=cm,MN=cm.12.若矩形的对角线长为8cm,两条对角线的一个交角为60°,则该矩形的边长为cm和cm.13.在▱ABCD中,若添加一个条件,则四边形ABCD是矩形;若添加一个条件,则四边形ABCD是菱形.14.如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=8cm,∠B=60°,则AB =cm.三、解答题15.如图,在平行四边形ABCD中,E、F是AC上的两点,且AE=CF.求证:DE=BF.16.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:(1)两条对角线的长度;(2)菱形的面积.17.如图所示,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠1=∠2,OB=6(1)求∠BOC的度数;(2)求△DOC的周长.18.如图:已知在△ABC中,AB=AC,D为BC上任意一点,DE∥AC交AB于E,DF∥AB交AC于F,求证:DE+DF=AC.19.如图,在菱形ABCD中,E为AD中点,EF⊥AC交CB的延长线于F.求证:AB与EF互相平分.参考答案1.菱形具有而矩形不具有的性质是()A.对角线互相平分 B.四条边都相等C.对角相等D.邻角互补【考点】矩形的性质;菱形的性质.【专题】选择题.【分析】与平行四边形相比,菱形的四条边相等、对角线互相垂直;矩形四个角是直角,对角线相等.【解答】解:A、对角线互相平分是平行四边形的基本性质,两者都具有,故A 不选;B、菱形四条边相等而矩形四条边不一定相等,只有矩形为正方形时才相等,故B符合题意;C、平行四边形对角都相等,故C不选;D、平行四边形邻角互补,故D不选.故选B.【点评】考查菱形和矩形的基本性质.2.关于四边形ABCD:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等;以上四个条件中可以判定四边形ABCD 是平行四边形的有()A.1个 B.2个 C.3个 D.4个【考点】平行四边形的判定.【专题】选择题.【分析】平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.按照平行四边形的判定方法进行判断即可.【解答】解:①符合平行四边形的定义,故①正确;②两组对边分别相等,符合平行四边形的判定条件,故②正确;③由一组对边平行且相等,符合平行四边形的判定条件,故③正确;④对角线互相平分的四边形是平行四边形,故④错误;所以正确的结论有三个:①②③,故选C.【点评】本题考查了平行四边形的判定,熟练掌握平行四边形的定义和判定方法是解答此类题目的关键.3.能判定一个四边形是菱形的条件是()A.对角线相等且互相垂直B.对角线相等且互相平分C.对角线互相垂直D.对角线互相垂直平分【考点】菱形的判定.【专题】选择题.【分析】根据菱形的判定方法:对角线互相垂直平分来判断即可.【解答】解:菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.只有D能判定为是菱形,故选D.【点评】本题考查菱形对角线互相垂直平分的判定.4.正方形、菱形、矩形都具有的性质是()A.对角线相等B.对角线互相平分C.对角线互相垂直 D.对角线平分一组对角【考点】正方形的性质;菱形的性质;矩形的性质.【专题】选择题.【分析】根据正方形、菱形、矩形对角线的性质,分析求解即可求得答案.【解答】解:∵正方形的对角线互相平分,互相垂直,相等且平分一组对角,菱形的对角线互相平分,互相垂直且平分一组对角,矩形的对角线互相平分且相等,∴正方形、菱形、矩形都具有的性质是:对角线互相平分.故选B.【点评】此题考查了正方形、菱形、矩形的性质.此题比较简单,注意熟记正方形、菱形、矩形对角线的性质是解此题的关键.5.若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是()A.菱形B.对角线相互垂直的四边形C.正方形 D.对角线相等的四边形【考点】矩形的判定;三角形中位线定理.【专题】选择题.【分析】此题要根据矩形的性质和三角形中位线定理求解;首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.【解答】解:已知:如图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形ABCD是对角线垂直的四边形.证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;∵四边形EFGH是矩形,即EF⊥FG,∴AC⊥BD;故选B.【点评】本题主要利用了矩形的性质和三角形中位线定理来求解.6.下列说法中,不正确的是()A.有三个角是直角的四边形是矩形B.对角线相等的四边形是矩形C.对角线互相垂直的矩形是正方形D.对角线互相垂直的平行四边形是菱形【考点】矩形的判定;菱形的判定;正方形的判定.【专题】选择题.【分析】根据各四边形的性质对各个选项进行分析从而得出最后答案.【解答】解:A、正确,有三个角是直角的四边形是矩形是矩形的判定定理;B、错误,对角线相等的四边形不一定是矩形,对角线相等的平行四边形才是矩形;C、正确,对角线互相垂直的矩形是正方形;D、正确,对角线互相垂直的平行四边形是菱形.故选B.【点评】考查了对四边形性质与判定的综合运用,特殊四边形之间的相互关系是考查重点.7.如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为()A.36°B.18°C.27°D.9°【考点】矩形的性质;三角形内角和定理.【专题】选择题.【分析】本题首先根据∠ADE:∠EDC=3:2可推出∠ADE以及∠EDC的度数,然后求出△ODC各角的度数便可求出∠BDE.【解答】解:已知∠ADE:∠EDC=3:2⇒∠ADE=54°,∠EDC=36°,又因为DE⊥AC,所以∠DCE=90°﹣36°=54°,根据矩形的性质可得∠DOC=180°﹣2×54°=72°所以∠BDE=180°﹣∠DOC﹣∠DEO=18°故选B.【点评】本题考查的是三角形内角和定理以及矩形的性质,难度一般.8.平行四边形ABCD中,∠A=50°,AB=30cm,则∠B=,DC=cm.【考点】平行四边形的性质.【专题】填空题.【分析】根据平行四边形的性质:平行四边形的对边相等且平行,即可求得.【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,DC=AB=30cm,∴∠A+∠B=180°,∵∠A=50°,∴∠B=130°.故答案为130°,30.【点评】此题考查了平行四边形的性质:平行四边形的对边相等且平行.解题时注意数形结合思想的应用.9.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD=cm.【考点】平行四边形的性质.【专题】填空题.【分析】根据平行四边形的性质可知,平行四边形的对角线互相平分,由于△BOC 的周长比△AOB的周长大2cm,则BC比AB长7cm,所以根据周长的值可以求出AB,进而求出CD的长.【解答】解:如图∵平行四边形的周长为20cm,∴AB+BC=10cm;又△BOC的周长比△AOB的周长大2cm,∴BC﹣AB=2cm,解得:AB=4cm,BC=6cm.∵AB=CD,∴CD=4cm故答案为:4.【点评】此题主要考查平行四边的性质:平行四边形的两组对边分别相等且平行四边形的对角线互相平分.10.菱形的两条对角线分别是6cm,8cm,则菱形的边长为cm,面积为cm2.【考点】菱形的性质.【专题】填空题.【分析】根据菱形的性质利用勾股定理可求得菱形的边长,根据面积公式可求得菱形的面积.【解答】解:菱形的两条对角线分别是6cm,8cm,得到两条对角线相交所构成的直角三角形的两直角边是×6=3cm和×8=4cm,那么它的斜边即菱形的边长=5cm,面积为6×8×=24cm2.故答案为5,24.【点评】本题考查的是菱形的性质以及其面积的计算方法的运用.11.如图,△ABC中,EF是它的中位线,M、N分别是EB、CF的中点,若BC=8cm,那么EF=cm,MN=cm.【考点】三角形中位线定理;梯形中位线定理.【专题】填空题.【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出EF的长,再利用梯形的中位线等于两底和的一半求出MN的长度.【解答】解:∵EF是△ABC的中位线,BC=8cm,∴EF=BC=×8=4cm,∵M、N分别是EB、CF的中点,∴MN=(EF+BC)=(4+8)=6cm.故答案为4,6.【点评】本题主要利用三角形的中位线定理和梯形的中位线定理求解,熟练掌握定理是解题的关键.12.若矩形的对角线长为8cm,两条对角线的一个交角为60°,则该矩形的边长为cm和cm.【考点】矩形的性质.【专题】填空题.【分析】根据矩形的性质得出∠ABC=90°,AB=DC,AD=BC,AC=BD,AC=2AO=2CO,BD=2BO=2DO,求出AO=BO=4cm,得出△AOB是等边三角形,推出AB=AO=4cm,在Rt△ABC中,由勾股定理求出BC即可.【解答】解:∵四边形ABCD是矩形,∴∠ABC=90°,AB=DC,AD=BC,AC=BD,AC=2AO=2CO,BD=2BO=2DO,∵AC=BD=8cm,∴AO=BO=4cm,∵∠AOB=60°,∴△AOB是等边三角形,∴AB=AO=4cm,在Rt△ABC中,由勾股定理得:BC===4,即矩形的边长是4cm,4cm,4cm,4cm,故答案为:4;4.【点评】本题考查了矩形性质,等边三角形的性质和判定,勾股定理的应用,注意:矩形的对角线互相平分且相等.13.在▱ABCD中,若添加一个条件,则四边形ABCD是矩形;若添加一个条件,则四边形ABCD是菱形.【考点】矩形的判定;平行四边形的性质;菱形的判定.【专题】填空题.【分析】根据矩形是对角线相等的平行四边形,菱形是邻边相等的平行四边形可得.【解答】解:在▱ABCD中,若添加一个条件AC=BD,则四边形ABCD是矩形;若添加一个条件AB=BC,则四边形ABCD是菱形.故答案为:AC=BD;AB=BC.【点评】本题主要考查的是矩形和菱形的判定定理.但需要注意的是本题的知识点是关于平行四边形、矩形、菱形之间的关系.14.如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=8cm,∠B=60°,则AB= cm.【考点】平行四边形的判定.【专题】填空题.【分析】过A作AE∥DC,可得到平行四边形AECD,从而可求得BE的长,由已知可得到△ABE是等边三角形,此时再求AB就不难求得了.【解答】解:等腰梯形ABCD中,AD∥BC,作AE∥DC,则四边形AECD是平行四边形,因而AB=AE,CE=AD,再由∠B=60°得到△ABE是等边三角形,AE=2cm,AB=2cm.【点评】此题考查平行四边形的判定及梯形中常见的辅助线的作法.15.如图,在平行四边形ABCD中,E、F是AC上的两点,且AE=CF.求证:DE=BF.【考点】平行四边形的性质;全等三角形的判定与性质.【专题】解答题.【分析】由平行四边形的性质得AD=CB,∠DAE=∠BCF,再由已知条件,可得△ADE≌△CBF,进而得出结论.【解答】证明:在平行四边形ABCD中,则AD=CB,∠DAE=∠BCF,又AE=CF,∴△ADE≌△CBF(SAS),∴DE=BF.【点评】本题主要考查平行四边形的性质及全等三角形的判定问题,应熟练掌握.16.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:(1)两条对角线的长度;(2)菱形的面积.【考点】菱形的性质.【专题】解答题.【分析】(1)由在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm,可求得△ABO是含30°角的直角三角形,AB=2cm,继而求得AC与BD的长;(2)由菱形的面积等于其对角线积的一半,即可求得答案.【解答】解:(1)∵四边形ABCD是菱形,∴AB=BC,AC⊥BD,AD∥BC,∴∠ABC+∠BAD=180°,∵∠ABC与∠BAD的度数比为1:2,∴∠ABC=×180°=60°,∴∠ABO=∠ABC=30°,∵菱形ABCD的周长是8cm.∴AB=2cm,∴OA=AB=1cm,∴OB==,∴AC=2OA=2cm,BD=2OB=2cm;(2)S菱形ABCD=AC•BD=×2×2=2(cm2).【点评】此题考查了菱形的性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.17.如图所示,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠1=∠2,OB=6(1)求∠BOC的度数;(2)求△DOC的周长.【考点】矩形的性质.【专题】解答题.【分析】(1)AE⊥BD,∠1+∠ABD=∠ADB+∠ABD,得出∠ACB=∠ADB=∠2=∠1=30°,可知△AOB为等边三角形,继而求出∠BOC的度数;(2)由(1)知,△DOC≌△AOB,OD=OC=CD=OB,继而求出△DOC的周长.【解答】解:(1)∵四边形ABCD为矩形,AE⊥BD,∴∠1+∠ABD=∠ADB+∠ABD=∠2+∠ABD=90°,∴∠ACB=∠ADB=∠2=∠1=30°,又AO=BO,∴△AOB为等边三角形,∴∠BOC=120°;(2)由(1)知,△DOC≌△AOB,∴△DOC为等边三角形,∴OD=OC=CD=OB=6,∴△DOC的周长=3×6=18.【点评】本题考查矩形的性质,难度适中,解题关键是根据矩形的性质求出∠1=∠2=∠ACB=30°.18.如图:已知在△ABC中,AB=AC,D为BC上任意一点,DE∥AC交AB于E,DF∥AB交AC于F,求证:DE+DF=AC.【考点】平行四边形的判定与性质;等腰三角形的性质.【专题】解答题.【分析】由题意可得四边形AEDF是平行四边形,得DE=AF再由等腰三角形的性质及平行线可得DF=CF,进而可求出其结论.【解答】证明:∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∴DE=AF,又AB=AC,∴∠B=∠C,∵DF∥AB,∴∠CDF=∠B,∴∠CDF=∠C,∴DF=CF,∴AC=AF+FC=DE+DF.【点评】本题主要考查平行四边形的判定及性质以及等腰三角形的性质问题,能够熟练求解.19.如图,在菱形ABCD中,E为AD中点,EF⊥AC交CB的延长线于F.求证:AB与EF互相平分.【考点】菱形的性质;平行四边形的判定与性质.【专题】解答题.【分析】由菱形的性质可证AC⊥BD,又已知EF⊥AC,所以AG=BG,GE=BD,AD∥BC,可证四边形EDBF为平行四边形,可证GE=GF,即证结论.【解答】证明:连接BD,AF,BE,在菱形ABCD中,AC⊥BD∵EF⊥AC,∴EF∥BD,又ED∥FB,∴四边形EDBF是平行四边形,DE=BF,∵E为AD的中点,∴AE=ED,∴AE=BF,又AE∥BF,∴四边形AEBF为平行四边形,即AB与EF互相平分.【点评】本题是简单的推理证明题,主要考查菱形的性质,同时综合利用平行四边形的判定方法及中位线的性质.。
【精选】人教版八年级下册数学第十八章《平行四边形》测试卷(含答案)

【精选】人教版八年级下册数学第十八章《平行四边形》测试卷(含答案)一、选择题(每题3分,共30分)1.已知在▱ABCD中,∠B+∠D=200°,则∠B的度数为( ) A.100° B.160° C.80° D.60°2.【2022·广东】如图,在△ABC中,BC=4,点D,E分别为AB,AC的中点,则DE=( )A.14B.12C.1 D.2(第2题) (第4题) (第5题) (第8题) 3.【2022·河北】依据所标数据,下列一定为平行四边形的是( )4.【教材P44例2改编】【2021·恩施州】如图,在▱ABCD中,AB=13,AD=5,AC ⊥BC,则▱ABCD的面积为( )A.30 B.60 C.65 D.65 25.【教材P53例1改编】如图,在矩形ABCD中,对角线AC,BD交于点O,∠AOB =60°,AB=5,则BD的长为( )A.20 B.15 C.10 D.56.【2021·河南】关于菱形的性质,以下说法不正确...的是( )A.四条边相等 B.对角线相等C.对角线互相垂直 D.是轴对称图形7.下列命题中,是真命题的为( )A.一组对边平行,另一组对边相等的四边形是平行四边形B.对角线互相垂直的四边形是菱形C.对角线相等的四边形是矩形D.一组邻边相等的矩形是正方形8.如图,已知在菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )A.16 3 B.16 C.8 3 D.89.【2022·青岛】如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则OE的长度为( )A.62B. 6 C.2 2 D.2 3(第9题) (第10题) (第11题) (第13题)10.【教材P68复习题T13拓展】【2022·恩施州】如图,在四边形ABCD中,∠A=∠B=90°,AD=10 cm,BC=8 cm,点P从点D出发,以1 cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )A.当t=4时,四边形ABMP为矩形B.当t=5时,四边形CDPM为平行四边形C.当CD=PM时,t=4D.当CD=PM时,t=4或6二、填空题(每题3分,共24分)11.如图,在▱ABCD中,AB=5,AC=8,BD=12,则△COD的周长是________.12.在Rt△ABC中,∠C=90°,AC=5,BC=12,则斜边上的中线CD=________. 13.【2021·益阳】如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC =BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是________(限填序号).14.如图,平行四边形ABCD的三个顶点的坐标分别为A(1,1),B(4,1),D(2,3),要把顶点A平移到顶点C的位置,则其平移方式可以是:先向右平移________个单位长度,再向上平移________个单位长度.(第14题) (第15题) (第16题) (第17题) 15.【2022·哈尔滨】如图,菱形ABCD的对角线AC,BD相交于点O.点E在OB 上,连接AE,点F为CD的中点,连接OF.若AE=BE,OE=3,OA=4,则线段OF的长为________.16.如图,在矩形ABCD中,E是BC边上一点,AE=AD,DF⊥AE于点F,连接DE,AE=5,BE=4,则DF=________.17.【2022·苏州】如图,在平行四边形ABCD中,AB⊥AC, AB=3, AC=4,分别以A,C为圆心,大于12AC的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF.则四边形AECF的周长为________.18.以正方形ABCD的边AD为边作等边三角形ADE,则∠BEC的度数是____________.三、解答题(19,20题每题8分,21,22题每题12分,其余每题13分,共66分)19.【2022·桂林】如图,在▱ABCD中,点E和点F是对角线BD上的两点,且BF =DE.(1)求证:BE=DF;(2)求证:△ABE≌△CDF.20.【2021·郴州】如图,四边形ABCD中,AB=DC,将对角线AC向两端分别延长至点E,F,使AE=CF, 连接BE,DF.若BE=DF,证明:四边形ABCD是平行四边形.21.【教材P55练习T2改编】【2021·长沙】如图,▱ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.(1)求证:▱ABCD是矩形;(2)求AD的长.22.【2021·十堰】如图,已知△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.(1)求证:四边形AECF是菱形;(2)若CF=2,∠FAC=30°,∠B=45°,求AB的长.23.如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.(1)求证:AE=BF;(2)若正方形的边长是5,BE=2,求AF的长.24.【2022·北京八中模拟】在▱ABCD中,AB≠AD,对角线AC,BD交于点O,AC =10,BD=16.点M,N在对角线BD上,点M从点B出发以每秒1个单位长度的速度向点D运动,到达点D时停止运动,同时点N从点D出发,运动至点B后立即返回,点M停止运动的同时,点N也停止运动,设运动时间为t 秒(t>0).。
人教版八年级下册数学 第18章 平行四边形 综合题经典必练

人教版八年级下册数学第18章平行四边形综合题经典必练1.如图,在▱ABCD中,对角线AC,BD相交于点O,过点O作MN⊥BD,分别交AD,BC于点M,N.(1)求证:OM=ON;(2)求证:四边形BNDM是菱形.2.如图,菱形ABCD中,∠B=60°,点E,F分别在AB,AD上,且BE=AF.(1)求证:△ECF为等边三角形;(2)连接AC,若AC将四边形AECF的面积分为1:2两部分,当AB=6时,求△BEC的面积.3.如图,在△ABC中,AB=13,AC=23,点D在AC上,若BD=CD=10,AE平分∠BAC.(1)求AE的长;(2)若F是BC中点,求线段EF的长.4.如图,▱ABCD的对角线AC、BD交于点O,M,N分别是AB、AD的中点.(1)求证:四边形AMON是平行四边形;(2)若AC=6,BD=4,∠AOB=90°,求四边形AMON的周长.5.如图,四边形ABCD是平行四边形,E、F分别是AB、CD的中点.(1)证明:四边形DEBF是平行四边形;(2)要使四边形DEBF是菱形,BD和AD需满足什么位置关系?请说明理由.6.如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A 运动,设点P运动的时间为t秒.(t>0)(1)当t=3时,BP=;(2)当t=时,点P运动到∠B的角平分线上;(3)请用含t的代数式表示△ABP的面积S;(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.7.如图所示,在▱ABCD中,AE⊥BD于点E,CF⊥BD于点F,延长AE至点G,使EG=AE,连接CG.(1)求证:△ABE≌△CDF;(2)求证:四边形EGCF是矩形.8.如图所示,平行四边形ABCD,对角线BD平分∠ABC;(1)求证:四边形ABCD为菱形;(2)已知AE⊥BC于E,若CE=2BE=4,求BD.9.如图,四边形ABCD是平行四边形,E、F分别为边AB、CD的中点,连接DE、DB、BF.(1)求证:∠DEB=∠BFD;(2)若∠ADB=90°,证明:四边形BFDE是菱形.10.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使得CF=BE,连接DF,(1)求证:四边形AEFD是矩形;(2)连接OE,若AB=13,OE=,求AE的长.11.如图,P为正方形ABCD的对角线上任一点,PE⊥AB于E,PF⊥BC于F.(1)判断DP与EF的关系,并证明;(2)若正方形ABCD的边长为6,∠ADP:∠PDC=1:3.求PE的长.12.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.(1)证明:四边形ADCE为菱形;(2)若∠B=60°,BC=6,求菱形ADCE的高.13.如图1,点E为正方形ABCD的边CD上一点,DF⊥AE于点F,交AC于点M,交BC于点G,在CD上取一点G′,使CG′=CG,连接MG′.(1)求证:∠AED=∠CG′M;(2)如图2,连接BD交AE于点N,交AC于点O,连接MN,MG′交AE于点H.①试判断MN与CD的位置关系,并说明理由;②若AB=12,DG′=G′E,求AH的长.14.如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,BF与CE相交于点H.(1)求证:四边形EHFG是平行四边形;(2)①若四边形EHFG是菱形,则平行四边形ABCD必须满足条件;②若四边形EHFG是矩形,则平行四边形ABCD必须满足条件.。
人教版八年级数学下册第十八章《平行四边形》综合测试卷(含答案)

人教版八年级数学下册第十八章《平行四边形》综合测试卷一、单选题(共30分)1.如图,在四边形ABCD 中,AB ∥CD ,要使四边形ABCD 是平行四边形,下列可添加的条件不正确的是( )A .AD =BCB .AB =CDC .AD ∥BC D .∥A =∥C 2.如图,在∥ABCD 中,连接AC ,∥ABC =∥CAD =45°,AB =2,则BC 的长是( )A 2B .2C .2D .43.如图,在长方形ABCD 中无重叠放入面积分别为216cm 和212cm 的两张正方形纸片,则图中空白部分的面积为( )2cmA .1683-B .1283-+C .843-D .423- 4.如图,已知平行四边形ABCD 的对角线AC ,BD 交于点O ,且AC =8,BD =10,则边AB 的长可以是( )A .1B .8C .10D .125.在平面直角坐标系中,A ,B ,C 三点的坐标分别为(0,0),(0,4),(1,1),以这三点为平行四边形的三个顶点,则第四个顶点不可能在( )A .第一象限B .第二象限C .第三象限D .第四象限 6.如图,矩形ABCD 和矩形CEFG ,AB =1,BC =CG =2,CE =4,点P 在边GF 上,点Q 在边CE 上,且PF =CQ ,连结AC 和PQ ,M ,N 分别是AC ,PQ 的中点,则MN 的长为( )A .3B .6C 37D 17 7.如图,菱形ABCD 对角线AC ,BD 交于点O ,15ACB ∠=︒,过点C 作CE AD ⊥交AD 的延长线于点E .若菱形ABCD 的面积为4,则菱形的边长为( )A .22B .2C .2D .48.如图,在ABC 中,90A ∠=,D 是AB 的中点,过点D 作BC 的平行线,交AC 于点E ,作BC 的垂线交BC 于点F ,若AB CE =,且DFE △的面积为1,则BC 的长为( )A .25B .5C .5D .10 9.如图,在矩形ABCD 内有一点F ,FB 与FC 分别平分∥ABC 和∥BCD ,点E 为矩形ABCD 外一点,连接BE ,CE .现添加下列条件:∥EB ∥CF ,CE ∥BF ;∥BE =CE ,BE =BF ;∥BE ∥CF ,CE ∥BE ;∥BE =CE ,CE ∥BF ,其中能判定四边形BECF 是正方形的共有( )A .1个B .2个C .3个D .4个 10.在平面直角坐标系中,长方形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点,若E 为x 轴上的一个动点,当∥CDE 的周长最小时,求点E 的坐标( )A .(一3,0)B .(3,0)C .(0,0)D .(1,0)二、填空题(共24分)11.在菱形ABCD 中,∥BAD =72°,点F 是对角线AC 上(不与点A ,C 重合)一动点,当ADF 是等腰三角形时,则∥AFD 的度数为_____.12.如图,在ABC 中,点M 为BC 的中点,AD 平分,BAC ∠且BD AD ⊥于点D ,延长BD 交AC 于点,N 若12,18AB AC ==,则MD =_______________________.13.如图,在Rt ∥ABC 中,∥ABC =90º,D 、E 、F 分别为AB 、BC 、CA 的中点,若BF =6,则DE =_____.14.平行四边形ABCD 的周长为60cm ,对角线AC 、BD 相交于点O ,∥AOB 的周长比∥BOC 的周长为8cm ,则AB 的长为_____cm .15.如图,在平行四边形ABCD 中,BF 平分∥ABC ,交AD 于点F ,CE 平分∥BCD ,交AD 于点E ,AB =8,BC =12,则EF 的长为__________.16.如图在Rt △ABC 中,∥ACB =90°,AC =4,BC =3,D 为斜边AB 上一点,以CD 、CB 为边作平行四边形CDEB ,当AD =_____,平行四边形CDEB 为菱形.17.如图,在平行四边形ABCD 中,AB =10,AD =6,AC ∥BC .则BD =_____.18.如图所示,在ΔABC 中,点D 是BC 的中点,点E ,F 分别在线段AD 及其延长线上,且DE =DF ,给出下列条件:∥BE ∥EC ;∥BF∥EC ;∥AB =AC∥从中选择一个条件使四边形BECF 是菱形,你认为这个条件是____(只填写序号).三、解答题(共66分)19.如图,在ABCD 中,对角线AC 与BD 相交于点O ,点,E F 分别为,OB OD 的中点,连接,AE CF .求证:AE CF .20.如图,∥ABCD 的对角线AC 、BD 交于点O ,E 、F 是对角线AC 上两点,AE =CF .求证:四边形DEBF 是平行四边形.21.如图,将∥ABCD 的边AB 延长至点E ,使BE=AB ,连接DE 、EC 、BD 、DE 交BC 于点O .(1)求证:∥ABD∥∥BEC ;(2)若∥BOD=2∥A ,求证:四边形BECD 是矩形.22.如图,在ABC ∆中,AD 是高,E F 、分别是AB AC 、的中点.(1)EF 与AD 有怎样的位置关系?证明你的结论;(2)若6,4BC AD ==,求四边形AEDF 的面积.23.如图,等边AEF ∆的顶点E ,F 在矩形ABCD 的边BC ,CD 上,且45CEF ∠=. 求证:矩形ABCD 是正方形.24.如图,在正方形ABCD 中,点E 、F 分别在边BC 和CD 上,且BE CF =,连接AE 、BF ,其相交于点G ,将BCF △沿BF 翻折得到BC F '△,延长FC '交BA 延长线于点H .(1)求证:AE BF =;(2)若3AB =,2EC BE =,求BH 的长.25.如图,在▱ABCD 中,AE∥BC ,AF∥CD ,垂足分别为E ,F ,且BE=DF (1)求证:▱ABCD 是菱形;(2)若AB=5,AC=6,求▱ABCD 的面积.26.如图,在矩形ABCD 中,AB =15,E 是BC 上的一点,将∥ABE 沿着AE 折叠,点B 刚好落在CD 边上点G 处;点F 在DG 上,将∥ADF 沿着AF 折叠,点D 刚好落在AG 上点H 处,且CE =45BE , (1)求AD 的长;(2)求FG 的长27.如图,BD是∥ABC的角平分线,过点作DE//BC交AB于点E,DF//AB交BC于点F.(1)求证:四边形BEDF是菱形;(2)若∥ABC=60°,∥ACB=45°,CD=6,求菱形BEDF的边长.28.(1)如图1,正方形ABCD中,E为边CD上一点,连接AE,过点A作AF∥AE 交CB的延长线于F,猜想AE与AF的数量关系,并说明理由;(2)如图2,在(1)的条件下,连接AC,过点A作AM∥AC交CB的延长线于M,观察并猜想CE与MF的数量关系,并说明理由;(3)解决问题:王师傅有一块如图所示的板材余料,其中∥A=∥C=90°,AB=AD.王师傅想切一刀后把它拼成正方形.请你帮王师傅在图3中画出剪拼的示意图.参考答案:1.A2.C3.B4.B5.C6.C7.A8.A9.D10.D11.108°或72°12.313.614.1915.416.7517.1318.∥22.(1)EF 垂直平分AD ;(2)6AEDF S 四边形. 24.5.25.S 平行四边形ABCD =24 26.(1)AD = 9;(2)FG =7.5 27.(2)628.(1)AE=AF (2)CE=MF ,。
(典型题)初中数学八年级数学下册第六单元《平行四边形》检测题(有答案解析)(1)

一、选择题1.一个多边形的内角和等于它的外角和的3倍,则它是( )边形.A .六B .七C .八D .九 2.如果一个多边形的内角和为1260︒,那么从这个多边形的一个顶点可以作( )条对角线.A .4B .5C .6D .73.已知如图:为估计池塘的宽度BC ,在池塘的一侧取一点A ,再分别取AB 、AC 的中点D 、E ,测得DE 的长度为20米,则池塘的宽BC 的长为( )A .30米B .60米C .40米D .25米 4.下面关于平行四边形的说法中,不正确的是( )A .对角线互相平分的四边形是平行四边形B .有一组对边平行,一组对角相等的四边形是平行四边形C .有一组对边相等,一组对角相等的四边形是平行四边形D .有两组对角相等的四边形是平行四边形5.如图,将四边形ABCD 去掉一个60°的角得到一个五边形BCDEF ,则∠1与∠2的和为( )A .60°B .108°C .120°D .240°6.如图,在周长为20厘米的平行四边形ABCD 中,AB ADAC BD ≠,,相交于点O ,OE BD ⊥交AD 于点E ,则ABE △的周长为( )A .10厘米B .12厘米C .14厘米D .16厘米 7.在ABCD 中,6AB =,4=AD ,则ABCD 的周长为( ) A .10B .20C .24D .12 8.一个多边形每个外角都等于30°,则这个多边形是几边形( )A .9B .10C .11D .129.如图,在ABCD 中,点,E F 分别在边BC AD ,上.若从下列条件中只选择一个添加到图中的条件中:①//AE CF ;②AE CF =;③BE DF =;④BAE DCF ∠=∠.那么不能使四边形AECF 是平行四边形的条件相应序号是( )A .①B .②C .③D .④10.如图,在四边形ABCD 中,90,32,7A AB AD ︒∠===,点,M N 分别为线段,BC AB 上的动点(含端点,但点M 不与点B 重合),点,E F 分别为,DM MN 的中点,则EF 长度的最大值为( )A .7B .2.5C .5D .3.511.下列命题的逆命题是真命题的是( )A .菱形的一条对角线平分一组对角B .在△ABC 中,若AC 2+BC 2=AB 2,则△ABC 是直角三角形C .若a >0,则2a =aD .平行四边形的对角线互相平分12.正多边形的一个外角的度数为72°,则这个正多边形的边数为( )A .4B .5C .6D .7二、填空题13.从一个多边形的一个顶点出发,一共可作9条对角线,则这个多边形的内角和是_________度.14.如图,在四边形ABCD 中,点P 是对角线BD 的中点,点E 、F 分别是AB 、CD 的中点,AD BC =,30PEF ∠=︒,则EPF ∠的度数是______.15.如图,在ABCD 中,对角线AC 、BD 相交于点O ,且DB BC ⊥,垂足为B ,若10AC =,6BD =,则BC 的长等于_______.16.如图,已知矩形ABCD 中,6cm AB =,8cm BC =,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,则四边形EFGH 的周长等于_____cm .17.如图,平行四边形ABCD ,将四边形CDMN 沿线段MN 折叠,得到四边形QPMN ,已知68BNM ︒∠=,则AMP ∠=_______.18.如图,已知矩形ABCD ,P 、R 分别是BC 和DC 上的点,E 、F 分别是PA ,PR 的中点.如果DR=3,AD=4,则EF 的长为______.19.如图,已知,,,AB DC AD BC E F ==在DB 上两点,且BF DE =,若30ADB ∠AEB =110︒,∠=︒,则BCF ∠的度数为________.20.已知//,AD BC 要使四边形ABCD 为平行四边形,需要增加的条件是____.(填一个你认为正确的条件).三、解答题21.如图,在ABC 中,,AB AC =,D 为CA 延长线上一点,DE BC ⊥于点E ,交AB 于点F .(1)求证:ADF 是等腰三角形;(2)若5AF BF ==,2BE =,求线段DE 的长.22.已知:如图,在BEDF 中,点A 、C 在对角线EF 所在的直线上,且AE CF =.求证:四边形ABCD 是平行四边形.23.已知∠MAN ,按要求完成下列尺规作图(不写作法,保留作图痕迹):(1)如图①,B 、C 分别在射线AM 、AN 上,求作□A BDC ;(2)如图②,点O 是∠MAN 内一点,求作线段PQ ,使P 、Q 分别在射线AM 、AN 上,且点O 是PQ 的中点.24.如图,五边形ABCDE 的内角都相等,EF 平分∠AED .求证:EF ⊥BC .25.如图,四边形ABCD 中,BE ⊥AC 交AD 于点G ,DF ⊥AC 于点F ,已知AF=CE ,AB=CD .(1)求证:四边形ABCD 是平行四边形;(2)如果∠GBC=∠BCD ,AG=6,GE=2,求AB 的长.26.如图,平行四边形ABCD 中,分别过A 、C 两点作AE BD ⊥,CF BD ⊥,垂足分别为E 、F ,连接CE 、AF .(1)若4AB =,3EF =30ABD ∠=︒,求ABD △的面积;(2)求证:AF CE =.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据多边形的内角和等于它的外角和的3倍可列方程求得边数.【详解】解:设多边形的边数为n ,根据题意得:(n−2)×180°=360°×3.解得n =8.故选:C .【点睛】本题主要考查的是多边形的内角和与外角和,掌握多边形的内角和公式是解题的关键.2.C解析:C【分析】先利用n边形的内角和公式算出n,再利用n边形的每一个顶点有(n-3)条对角线计算即可.【详解】根据题意,得(n-2)×180=1260,解得n=9,∴从这个多边形的一个顶点可以作对角线的条数为:n-3=9-3=6.故选C.【点睛】本题考查了n边形的内角和和经过每一个顶点可作的对角线条数,熟记多边形内角和公式,计算经过每一个顶点的对角线条数计算公式是解题的关键.3.C解析:C【分析】根据三角形中位线定理可得DE=12BC,代入数据可得答案.【详解】解:∵线段AB,AC的中点为D,E,∴DE=12BC,∵DE=20米,∴BC=40米,故选:C.【点睛】此题主要考查了三角形中位线定理,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.4.C解析:C【分析】根据平行四边形的判定分别对各个选项进行判断即可.【详解】A、∵对角线互相平分的四边形是平行四边形,∴选项A不符合题意;B、∵有一组对边平行,一组对角相等的四边形是平行四边形,∴选项B 不符合题意;C 、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,∴选项C 符合题意;D 、∵有两组对角相等的四边形是平行四边形,∴选项D 不符合题意;故选:C .【点睛】本题考查了平行四边形的判定;熟练掌握平行四边形的判定方法是解题的关键. 5.D解析:D【分析】利用四边形的内角和得到∠B +∠C +∠D 的度数,进而让五边形的内角和减去∠B +∠C +∠D 的度数即为所求的度数.【详解】∵四边形的内角和为(4−2)×180°=360°,∴∠B +∠C +∠D =360°−60°=300°,∵五边形的内角和为(5−2)×180°=540°,∴∠1+∠2=540°−300°=240°,故选D .【点睛】本题考查多边形的内角和知识,求得∠B +∠C +∠D 的度数是解决本题的突破点. 6.A解析:A【分析】由平行四边形求出OB=OD ,再利用等腰三角形的三线合一求出BE=DE 由此即可求出ABE △的周长.【详解】∵四边形ABCD 是平行四边形,∴OB OD =.∵OE BD ⊥,∴BE DE =,∴ABE △的周长为20210AB AE BE AB AE DE AB AD ++=++=+=÷=(厘米),故选:A.【点睛】此题考查平行四边形的对角线互相平分、对边相等的性质,等腰三角形的三线合一的性质. 7.B解析:B【分析】根据平行四边形的性质得出ABCD 的周长为:2AB+2AD ,求解即可.【详解】解:∵四边形ABCD为平行四边形,∴AB=CD=6,AD=BC=4,∴ABCD的周长为:2AB+2AD=2(6+4)=20,故选B.【点睛】本题考查了平行四边形的性质,解题的关键是掌握平行四边形的性质.8.D解析:D【分析】根据正多边形的性质,边数等于360°除以每一个外角的度数计算即可.【详解】∵一个多边形的每个外角都等于30°,外角和为360°,∴n=360°÷30°=12,故选D.【点睛】本题主要考查了多边形外角和、利用外角求正多边形的边数的方法,解题的关键是掌握任意多边形的外角和都等于360度.第II卷(非选择题)请点击修改第II卷的文字说明9.B解析:B【分析】利用平行四边形的性质,依据平行四边形的判定方法,即可得出不能使四边形AECF是平行四边形的条件.【详解】解:①∵四边形ABCD平行四边形,∴AD//BC,∴AF//EC,∵AE∥CF,∴四边形AECF是平行四边形;②∵AE=CF不能得出四边形AECF是平行四边形,∴条件②符合题意;③∵四边形ABCD平行四边形,∴AD=BC,AD∥BC,又∵BE=DF,∴AF=EC .又∵AF ∥EC ,∴四边形AECF 是平行四边形.④∵四边形ABCD 是平行四边形,∴∠B=∠D ,∵∠BAE=∠DCF ,∴∠AEB=∠CFD .∵AD ∥BC ,∴∠AEB=∠EAD .∴∠CFD=∠EAD .∴AE ∥CF .∵AF ∥CE ,∴四边形AECF 是平行四边形.综上所述,不能使四边形AECF 是平行四边形的条件有1个.故选:B .【点睛】本题考查了平行四边形的性质定理和判定定理,以及平行线的判定定理;熟记平行四边形的判定方法是解决问题的关键.10.B解析:B【分析】连接BD 、ND ,由勾股定理得可得BD=5,由三角形中位线定理可得EF=12DN ,当DN 最长时,EF 长度的最大,即当点N 与点B 重合时,DN 最长,由此即可求得答案.【详解】连接BD 、ND ,由勾股定理得,()()2222732AD AB +=+ ∵点E 、F 分别为DM 、MN 的中点,∴EF=12DN , 当DN 最长时,EF 长度的最大,∴当点N 与点B 重合时,DN 最长,∴EF 长度的最大值为12BD=2.5,故选B.【点睛】本题考查了勾股定理,三角形中位线定理,正确分析、熟练掌握和灵活运用相关知识是解题的关键.11.D解析:D【分析】根据这些命题的逆命题,然后判断真假即可.【详解】解:A、菱形的一条对角线平分一组对角的逆命题是一条对角线平分一组对角的四边形是菱形,逆命题是假命题;B、在△ABC中,若AC2+BC2=AB2,则△ABC是直角三角形的逆命题是若△ABC是直角三角形,则AC2+BC2=AB2,逆命题是假命题;C、若a>02a a2a a,则a>0,逆命题是假命题;D、平行四边形的对角线互相平分的逆命题是对角线互相平分的四边形是平行四边形,逆命题是真命题;故选:D.【点睛】本题考查了命题与定理的知识,解题的关键是能够正确的写出这些命题的逆命题,比较简单.12.B解析:B【分析】正多边形的外角和是360°,且正多边形的每个外角相等,因而用360°除以外角的度数,就得到外角和中外角的个数,外角的个数就是多边形的边数.【详解】∵正多边形的外角和是360°,∴360÷72=5,那么它的边数是5.故选B.【点睛】本题考查了多边形的内角与外角.根据正多边形的外角和求多边形的边数是常用的一种方法,需要熟练掌握.二、填空题13.1800【分析】设多边形边数为n 根据n 边形从一个顶点出发可引出(n-3)条对角线可得n-3=9计算出n 的值再根据多边形内角和(n-2)•180°可得答案【详解】设多边形边数为n 由题意得:n-3=9n解析:1800【分析】设多边形边数为n ,根据n 边形从一个顶点出发可引出(n-3)条对角线可得n-3=9,计算出n 的值,再根据多边形内角和(n-2)•180°可得答案.【详解】设多边形边数为n ,由题意得:n-3=9,n=12,内角和:()1221801800-⨯︒=︒.故答案为:1800.【点睛】本题主要考查了多边形的对角线,以及多边形内角和,关键是掌握n 边形从一个顶点出发可引出(n-3)条对角线,多边形内角和公式(n-2)•180°.14.【分析】根据中位线定理推出PE=ADPF=BC 由此得到PE=PF 推出△PEF 是等腰三角形根据三角形的内角和定理求出答案【详解】∵点是对角线的中点点分别是的中点∴PE=ADPF=BC ∵∴PE=PF ∴△解析:120︒【分析】根据中位线定理推出PE=12AD ,PF=12BC ,由此得到PE=PF ,推出△PEF 是等腰三角形,根据三角形的内角和定理求出答案.【详解】∵点P 是对角线BD 的中点,点E 、F 分别是AB 、CD 的中点,∴PE=12AD ,PF=12BC , ∵AD BC =,∴PE=PF ,∴△PEF 是等腰三角形,∴∠PFE=30PEF ∠=︒,∴EPF ∠=1803030120︒︒︒︒--=,故答案为:120︒.【点睛】此题考查三角形的中位线定义及定理,等腰三角形的判定及性质,三角形的内角和定理,熟记三角形的中位线的定义及定理是解题的关键.15.4【分析】由平行四边形的性质得出AD=BCOC=AC=5OB=BD=3cm由勾股定理得出BC的长即可【详解】解:∵四边形ABCD是平行四边形AC=10BD =6∴AD=BCOC=AC=5OB=BD=3解析:4【分析】由平行四边形的性质得出AD=BC,OC=12AC=5,OB=12BD=3cm,由勾股定理得出BC的长即可.【详解】解:∵四边形ABCD是平行四边形,AC=10,BD=6,∴AD=BC,OC=12AC=5,OB=12BD=3,∵DB⊥BC,∴∠OBC=90°,∴BC=22OC OB=4,故答案为:4.【点睛】本题考查了平行四边形的性质、勾股定理;熟练掌握平行四边形的性质是解题的关键.16.20【分析】连接ACBD根据三角形的中位线求出HGGFEFEH的长再求出四边形EFGH的周长即可【详解】如图连接ACBD四边形ABCD是矩形AC=BD=8cmEFGH分别是ABBCCDDA的中点HG解析:20【分析】连接AC、BD,根据三角形的中位线求出HG,GF,EF,EH的长,再求出四边形EFGH的周长即可.【详解】如图,连接AC、BD,四边形ABCD是矩形,AC=BD=8cm,E、F、G、H分别是AB、BC、CD、DA的中点,HG =EF =12AC =4cm ,EH =FG =12BD =4cm , 四边形EFGH 的周长等于4+4+4+4=16cm.【点睛】本题考查了矩形的性质,三角形的中位线的应用,能求出四边形的各个边的长是解此题的关键,注意:矩形的对角线相等,三角形的中位线平行于第三边,并且等于第三边的一半. 17.【分析】根据平行四边形的性质得得根据折叠的性质得根据平角的性质即可求解【详解】∵四边形ABCD 是平行四边形∴∴∵将四边形CDMN 沿线段MN 折叠得到四边形QPMN ∴∴故答案为【点睛】本题考察了平行四边 解析:44︒【分析】根据平行四边形的性质得//AD BC ,得68NMD ︒∠=,根据折叠的性质得68PMN NMD ︒∠=∠=,根据平角的性质即可求解.【详解】∵四边形ABCD 是平行四边形∴//AD BC∴68NMD BNM ︒∠=∠=∵将四边形CDMN 沿线段MN 折叠,得到四边形QPMN∴68PMN NMD ︒∠=∠=∴18044AMP PMN NMD ︒∠=︒-∠-∠=故答案为44︒.【点睛】本题考察了平行四边形的性质,平行线的性质,和利用平角求解未知角的度数;其中两直线平行,同位角相等,内错角相等,同旁内角互补.18.5【解析】试题分析:根据勾股定理求AR ;再运用中位线定理求EF 试题 解析:5【解析】试题分析:根据勾股定理求AR ;再运用中位线定理求EF .试题∵四边形ABCD 是矩形,∴△ADR 是直角三角形∵DR=3,AD=4∴∵E 、F 分别是PA ,PR 的中点∴EF=12AR=12×5=2.5. 考点:1.三角形中位线定理;2.矩形的性质.19.80【分析】先证明四边形ABCD 是平行四边形再通过条件证明最后根据全等三角形的性质及三角形外角性质即可得出答案【详解】∵∴四边形ABCD 是平行四边形∴在△AED 和△CFB 中∴∴∵∴故答案是【点睛】本解析:80【分析】先证明四边形ABCD 是平行四边形,再通过条件证明△△AED CFB ≅,最后根据全等三角形的性质及三角形外角性质即可得出答案.【详解】∵,AB DC AD BC ==,∴四边形ABCD 是平行四边形,∴ADE CBF ∠=∠,在△AED 和△CFB 中,AD CB ADE CBF DE BF =⎧⎪∠=∠⎨⎪=⎩,∴()△△AED CFB SAS ≅,∴DAE BCF ∠=∠,∵30ADB ∠AEB =110︒,∠=︒,∴1103080BCF DAE AEB ADB ∠=∠=∠-∠=︒-︒=︒,故答案是80︒.【点睛】本题主要考查了平行四边形的性质,结合外角定理计算是解题的关键. 20.AD=BC(答案不唯一)【分析】在已知一组对边平行的基础上要判定是平行四边形则需要增加另一组对边平行或平行的这组对边相等或一组对角相等均可【详解】解:根据平行四边形的判定方法知需要增加的条件是AD=解析:AD=BC(答案不唯一)【分析】在已知一组对边平行的基础上,要判定是平行四边形,则需要增加另一组对边平行,或平行的这组对边相等,或一组对角相等均可.【详解】解:根据平行四边形的判定方法,知需要增加的条件是AD=BC 或AB ∥CD 或∠A=∠C 或∠B=∠D .故答案为:AD=BC (或AB ∥CD ).【点睛】此题考查了平行四边形的判定,为开放性试题,答案不唯一,要掌握平行四边形的判定方法.三、解答题21.(1)证明见解析;(2)321DE =.【分析】(1)根据等边对等角和直角三角形两锐角互余可得∠D=∠BFE ,再等量代换可得∠D=∠AFD ,根据等角对等边即可证明;(2)过A 作AH ⊥BC ,根据中位线定理可得EH=2,根据三线合一可得EC ,再根据勾股定理可求.【详解】解:(1)∵AB=AC ,∴∠B=∠C ,∵DE ⊥BC , ∴∠C+∠D=90°,∠B+∠BFE=90°,∴∠D=∠BFE ,又∵∠BFE=∠AFD ,∴∠D=∠AFD ,∴AD=AF ,即△ADF 为等腰三角形;(2)过A 作AH ⊥BC ,∵5AF BF ==,DE ⊥BC ,∴EF//AH ,∴EF 是△BAH 的中位线,∵BE=2,∴EH=2,∵AB=AC ,∴BC=4BE=8,EC=HC+HE=BH+EH=6,∵DA=AF=5,AC=AB=10,∴DC=AD+AC=15,∴22156321DE =-=.【点睛】本题考查中位线定理、勾股定理、等腰三角形的性质和判定等.(1)中注意等边对等角,以及等角对等边的使用;(2)中能正确作出辅助线是解题关键.22.见解析.如图,连接BD ,交AC 于点O .由平行四边形的对角线互相平分可得OD OB =,OE OF =,结合已知条件证得OA OC =,由对角线互相平分的四边形是平行四边形即可判定四边形ABCD 是平行四边形.【详解】如图,连接BD ,交AC 于点O .∵四边形BEDF 是平行四边形,∴OD OB =,OE OF =.又∵AE CF =,∴AE OE CF OF +=+,即OA OC =,∴四边形ABCD 是平行四边形.【点睛】本题考查了平行四边形的性质及判定,作出辅助线,证明OD OB =、OA OC =是解决问题的关键.23.(1)详见解析;(2)详见解析【分析】(1)分别以B 、C 点为圆心,以AC 、AB 为半径画弧.两弧相交于点D ,则四边形ABDC 满足条件;(2)连接AO ,延长AO 到G 使OG =AO ,再作∠PGA =∠OAN 交AM 于P ,连接PO 并延长交AN 于Q ,则PQ 满足条件.【详解】(1)如图①,四边形ABDC 即为所求;(2)如图②,线段PQ 即为所求.【点睛】本题考查了作图−复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行四边形的判定与性质.24.证明见详解根据多边形内角和度数可得每一个角的度数,然后再利用四边形DFBC 内角和计算出∠EFC 的度数即可证明.【详解】解:解:∵五边形ABCDE 的内角都相等,∴∠C=∠D=∠AED=180°×(5-2)÷5=108°, 又 EF 平分∠AED ∴°1542FED AED ∠=∠= ∴在四边形DFBC 中°=360-D-C-FED EFC ∠∠∠∠=90°∴EF ⊥BC【点睛】此题主要考查了多边形内角和,关键是掌握多边形内角和定理:(n-2)•180° (n≥3且n 为整数).25.(1)见解析 (2)9【分析】(1)先证明Rt △ABE ≌Rt △CDF ,得到AB ∥CD ,即可判定平行四边形;(2)证明AB=GB ,根据勾股定理构造方程,解方程即可求解.【详解】解:(1)∵AF=CE ,∴AF-EF=CE-EF ,∴AE=CF ,∵BE ⊥AC ,DF ⊥AC ,,∴∠AEB=∠CFD=90°,∵AB=CD ,∴Rt △ABE ≌Rt △CDF ,∴∠BAE=∠DCF ,∴AB ∥CD ,∵AB=CD ,∴四边形ABCD 是平行四边形;(2)∵四边形ABCD 是平行四边形,∴AD ∥BC ,∠DAB=∠BCD ,∴∠AGB=∠GBC ,∵∠GBC=∠BCD ,∴∠AGB=∠BAG ,∴AB=GB ,设AB=GB=x ,则BE=x-2,∵BG ⊥AC ,∴2222AB BE AG GE -=-,∴()2222262x x --=- , 解得x=9,∴AB=9.【点睛】本题考查了平行四边的判定与性质,勾股定理,等腰三角形判定等知识,综合性较强,熟知相关定理并根据已知条件合理选择定理是解题关键.26.(1);(2)证明见解析【分析】(1)由平行四边形的性质得AB=CD ,AB ∥CD ,由平行线的性质得∠ABE=∠CDF ,由AAS 证得△ABE ≌△CDF ,得BE=DF ,在Rt △ABE 中,由含30°角直角三角形的性质得122AE AB ==,再由勾股定理求出BE ,进而得到BD 的长,进而求出ABD △的面积; (2)由(1)得△ABE ≌△CDF ,则AE=CF ,易证AE ∥CF ,得出四边形AECF 是平行四边形,即可得出结论.【详解】解:(1)∵四边形ABCD 是平行四边形,∴AB=CD ,AB ∥CD ,∴∠ABE=∠CDF ,又∵AE ⊥BD ,CF ⊥BD ,∴∠AEB=∠CFD=90°,在△ABE 和△CDF 中:ABE CDF AEB CFD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△CDF (AAS ),∴BE=DF ,∵在Rt △ABE 中,∠ABD=30°, ∴122AE AB ==,由勾股定理得:BE ==, ∴2223353BDBE EF , ∴112535322ABD SAE BD , 故答案为:(2) 由(1)得:△ABE ≌△CDF ,∴AE=CF ,∵AE ⊥BD ,CF ⊥BD ,∴∠AEF=∠CFE=90°,∴AE ∥CF ,∴四边形AECF 是平行四边形,∴AF=CE .【点睛】本题考查了平行四边形的判定与性质、平行线的性质、全等三角形的判定与性质、含30°直角三角形的性质、勾股定理、三角形面积计算等知识;熟练掌握平行四边形的判定与性质是解题的关键.。
人教版八年级数学下册第十八章-平行四边形章节测评试题(含答案解析)

人教版八年级数学下册第十八章-平行四边形章节测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OA C的坐标为()A.,1)B.(1,1)C.(1D.,1)2、如图菱形ABCD,对角线AC,BD相交于点O,若BD=8,AC=6,则AB的长是()A.5 B.6 C.8 D.103、如图,已知P 是AOB ∠平分线上的一点,60AOB ︒∠=,PD OA ⊥,M 是OP 的中点,4cm DM =,如果C 是OB 上一个动点,则PC 的最小值为( )A .8cmB .5cmC .4cmD .2cm4、顺次连接矩形各边中点得到的四边形是( )A .平行四边形B .矩形C .菱形D .正方形5、如图所示,公路AC 、BC 互相垂直,点M 为公路AB 的中点,为测量湖泊两侧C 、M 两点间的距离,若测得AB 的长为6km ,则M 、C 两点间的距离为( )A .2.5kmB .4.5kmC .5kmD .3km6、如图,已知四边形ABCD 和四边形BCEF 均为平行四边形,∠D =60°,连接AF ,并延长交BE 于点P ,若AP ⊥BE ,AB =3,BC =2,AF =1,则BE 的长为( )A .5B .C .D .7、如图,在菱形ABCD中,AB=5,AC=8,过点B作BE⊥CD于点E,则BE的长为()A.125B.245C.6 D.4858、如图,在平面直角坐标系中,点A是x轴正半轴上的一个动点,点C是y轴正半轴上的点,BC AC⊥于点C.已知16AC=,6BC=.点B到原点的最大距离为()A.22 B.18 C.14 D.109、如图,已知在正方形ABCD中,10AB BC CD AD====厘米,90A B C D∠=∠=∠=∠=︒,点E在边AB 上,且4AE=厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上以a厘米/秒的速度由C点向D点运动,设运动时间为t秒.若存在a与t的值,使BPE与CQP全等时,则t的值为()A.2 B.2或1.5 C.2.5 D.2.5或210、已知三角形三边长分别为7cm,8cm,9cm,作三条中位线组成一个新的三角形,同样方法作下去,一共做了五个新的三角形,则这五个新三角形的周长之和为()A .46.5cmB .22.5cmC .23.25cmD .以上都不对第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,在直角三角形ABC 中,∠B =90°,点D 是AC 边上的一点,连接BD ,把△CBD 沿着BD 翻折,点C 落在AB 边上的点E 处,得到△EBD ,连接CE 交BD 于点F ,BG 为△EBD 的中线.若BC =4,△EBG 的面积为3,则CD 的长为____________2、如图,在▱ABCD 中,BC =3,CD =4,点E 是CD 边上的中点,将△BCE 沿BE 翻折得△BGE ,连接AE ,A 、G 、E 在同一直线上,则AG =______,点G 到AB 的距离为______.3、如图,在ABC 中,2AB AC ==,90BAC ∠=︒,M ,N 为BC 上的两个动点,且MN AM AN +的最小值是________.4、一个三角形三边长之比为4∶5∶6,三边中点连线组成的三角形的周长为30cm ,则原三角形最大边长为_________cm .5、如图,在长方形ABCD 中,9DC =.在DC 上找一点E ,沿直线AE 把AED 折叠,使D 点恰好落在BC上,设这一点为F,若ABF的面积是54,则FCE△的面积=______________.三、解答题(5小题,每小题10分,共计50分)1、如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.(1)在图1中,画一个三边长都是有理数的直角三角形;(2)在图2中,画一个以BC为斜边的直角三角形,使它们的三边长都是无理数且都不相等;(3)在图3中,画一个正方形,使它的面积是10.2、如图,在Rt△ABC中,∠ACB=90°.(1)作AB的垂直平分线l,交AB于点D,连接CD,分别作∠ADC,∠BDC的平分线,交AC,BC于点E,F(尺规作图,不写作法,保作图痕迹);(2)求证:四边形CEDF是矩形.3、如图:在Rt ABC中,90∠=,点O为AB的中点,点P为直线BC上的动点(不与点A︒ACB︒∠=,30∆,连接BQ.B,C重合),连接OC,OP,以OP为边在OC的上方作等边OPQ(1)OBC是________三角形;=;(2)如图1,当点P在边BC上时,运用(1)中的结论证明CP BQ(3)如图2,当点P在CB的延长线上时,(2)中的结论是否依然成立?若成立,请加以证明,若不成立,请说明理由.4、如图,在▱ABCD中,对角线AC,BD交于点O,E是BD延长线上一点,且△ACE是等边三角形.(1)求证:四边形ABCD是菱形;(2)若∠AED=2∠EAD,AB=a,求四边形ABCD的面积.5、已知:如图,30∠=︒,45B∠=︒,AD是BC上的高线,CE是AB边上的中线,DG CE于G.ACDAB=,求线段AC的长;(1)若6(2)求证:CG EG.---------参考答案-----------一、单选题1、B【解析】【分析】作CD⊥x轴,根据菱形的性质得到OC=OA Rt△OCD中,根据勾股定理求出OD的值,即可得到C点的坐标.【详解】:作CD⊥x轴于点D,则∠CDO=90°,∵四边形OABC是菱形,OA∴OC=OA又∵∠AOC=45°,∴∠OCD=90°-∠AOC=90°-45°=45°,∴∠DOC=∠OCD,∴CD=OD,在Rt△OCD中,OC CD2+OD2=OC2,∴2OD2=OC2=2,∴OD2=1,∴OD=CD=1(负值舍去),则点C的坐标为(1,1),故选:B.【点睛】此题考查了菱形的性质、等腰直角三角形的性质以及勾股定理,根据勾股定理和等腰直角三角形的性质求出OD=CD=1是解决问题的关键.2、A【解析】【分析】由菱形的性质可得OA=OC=3,OB=OD=4,AO⊥BO,由勾股定理求出AB.【详解】解:∵四边形ABCD是菱形,AC=6,BD=8,∴OA=OC=3,OB=OD=4,AO⊥BO,在Rt△AOB中,由勾股定理得:5AB=,故选:A.【点睛】本题考查了菱形的性质、勾股定理等知识;熟练掌握菱形对角线互相垂直且平分的性质是解题的关键.3、C【解析】【分析】根据题意由角平分线先得到OPD △是含有30角的直角三角形,结合直角三角形斜边上中线的性质进而得到OP ,DP 的值,再根据角平分线的性质以及垂线段最短等相关内容即可得到PC 的最小值.【详解】解:∵点P 是∠AOB 平分线上的一点,60AOB ∠=︒, ∴1302AOP AOB ∠=∠=︒,∵PD ⊥OA ,M 是OP 的中点,4cm DM =∴28cm OP DM ==, ∴14cm 2PD OP ==∵点C 是OB 上一个动点∴当PC OB ⊥时,PC 的值最小,∵OP 平分∠AOB ,PD ⊥OA ,PC OB ⊥∴PC 最小值4cm PD ==,故选C .【点睛】本题主要考查了角平分线的性质、含有30角的直角三角形的选择,直角三角形斜边上中线的性质、垂线段最短等相关内容,熟练掌握相关性质定理是解决本题的关键.4、C【解析】【分析】如图,矩形ABCD 中,利用三角形的中位线的性质证明111,,,,222EF BD EF BD GH BD GH BD FG AC ∥∥,再证明四边形ABCD 是平行四边形,再证明,EF FG 从而可得结论.【详解】解:如图,矩形ABCD 中,,AC BD ∴=,,,E F G H 分别为四边的中点,111,,,,222EF BD EF BD GH BD GH BD FG AC ∥∥, ,,EF GH EF GH ∥∴ 四边形ABCD 是平行四边形,11,,,22AC BD EF BD FG AC === ,EF FG ∴= ∴ 四边形EFGH 是菱形.故选C .【点睛】本题考查的是矩形的性质,菱形的判定,三角形的中位线的性质,熟练的运用三角形的中位线的性质解决中点四边形问题是解本题的关键.5、D【解析】【详解】根据直角三角形斜边上的中线性质得出CM =12AB ,即可求出CM .【解答】解:∵公路AC,BC互相垂直,∴∠ACB=90°,∵M为AB的中点,AB,∴CM=12∵AB=6km,∴CM=3km,即M,C两点间的距离为3km,故选:D.【点睛】本题考查了直角三角形的性质,解题关键是掌握直角三角形斜边上的中线的性质:直角三角形斜边上的中线等于斜边的一半.6、D【解析】【分析】过点D作DH⊥BC,交BC的延长线于点H,连接BD,DE,先证∠DHC=90º,再证四边形ADEF是平行四边形,最后利用勾股定理得出结果.【详解】过点D作DH⊥BC,交BC的延长线于点H,连接BD,DE,∵四边形ABCD是平行四边形,AB=3,∠ADC=60º,∴CD=AB=3,∠DCH=∠ABC=∠ADC=60º,∵DH⊥BC,∴∠DHC =90º,∴∠ADC +∠CDH =90°,∴∠CDH =30°,在Rt △DCH 中,CH =12CD =32,DH ,∴222223(2)192BD BH DH =+=++=, ∵四边形BCEF 是平行四边形,∴AD =BC =EF ,AD ∥EF ,∴四边形ADEF 是平行四边形,∴AF ∥DE ,AF =DE =1,∵AF ⊥BE ,∴DE ⊥BE ,∴22219118BE BD DE =-=-=, ∴BE =故选D .【点睛】本题考查了平行四边形的判定与性质,勾股定理,解题的关键是熟练运用这些性质解决问题.7、B【解析】【分析】根据菱形的性质求得BD 的长,进而根据菱形的面积等于12AC BD CD BE ⋅=⋅,即可求得BE 的长【详解】解:如图,设,AC BD 的交点为O ,四边形ABCD 是菱形AC BD ∴⊥,142AO CO AC ===,DO BO =,5CD AB == 在Rt AOB 中,5AB =,4AO =3BO ∴26BD BO ∴== 菱形的面积等于12AC BD CD BE ⋅=⋅1168242255AC BD BE CD ⋅⨯∴==⨯= 故选B【点睛】本题考查了菱形的性质,掌握菱形的性质,求得BD 的长是解题的关键.8、B【解析】【分析】首先取AC的中点E,连接BE,OE,OB,可求得OE与BE的长,然后由三角形三边关系,求得点B到原点的最大距离.【详解】解:取AC的中点E,连接BE,OE,OB,∵∠AOC=90°,AC=16,∴OE=CE12=AC=8,∵BC⊥AC,BC=6,∴BE=10,若点O,E,B不在一条直线上,则OB<OE+BE=18.若点O,E,B在一条直线上,则OB=OE+BE=18,∴当O,E,B三点在一条直线上时,OB取得最大值,最大值为18.故选:B【点睛】此题考查了直角三角形斜边上的中线的性质以及三角形三边关系.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.9、D【解析】【分析】根据题意分两种情况讨论若△BPE≌△CQP,则BP=CQ,BE=CP;若△BPE≌△CPQ,则BP=CP=5厘米,BE=CQ=6厘米进行求解即可.解:当2a =,即点Q 的运动速度与点P 的运动速度都是2厘米/秒,若△BPE ≌△CQP ,则BP =CQ ,BE =CP ,∵AB =BC =10厘米,AE =4厘米,∴BE =CP =6厘米,∴BP =10-6=4厘米,∴运动时间t =4÷2=2(秒);当2a ≠,即点Q 的运动速度与点P 的运动速度不相等,∴BP ≠CQ ,∵∠B =∠C =90°,∴要使△BPE 与△OQP 全等,只要BP =PC =5厘米,CQ =BE =6厘米,即可.∴点P ,Q 运动的时间t =252 2.5BP ÷=÷=(秒).综上t 的值为2.5或2.故选:D .【点睛】本题主要考查正方形的性质以及全等三角形的判定,解决问题的关键是掌握正方形的四条边都相等,四个角都是直角;两边及其夹角分别对应相等的两个三角形全等.同时要注意分类思想的运用.10、C【解析】【分析】如图所示,8cm AB =,9cm BC =,7cm AC =,DE ,DF ,EF 分别是三角形ABC 的中位线,GH ,GI ,HI 分别是△DEF 的中位线,则14.5cm 2DE BC ==,14cm 2EF AB ==,1 3.5cm 2DF AC ==,即可得到△DEF 的周长==12cm DE DF EF ++,由此即可求出其他四个新三角形的周长,最后求和即可.解:如图所示,8cm AB =,9cm BC =,7cm AC =,DE ,DF ,EF 分别是三角形ABC 的中位线,GH ,GI ,HI 分别是△DEF 的中位线, ∴14.5cm 2DE BC ==,14cm 2EF AB ==,1 3.5cm 2DF AC ==, ∴△DEF 的周长==12cm DE DF EF ++,同理可得:△GHI 的周长==6cm HI HG GI ++,∴第三次作中位线得到的三角形周长为3cm ,∴第四次作中位线得到的三角形周长为1.5cm∴第三次作中位线得到的三角形周长为0.75cm∴这五个新三角形的周长之和为1263 1.50.75=23.25cm ++++,故选C .【点睛】本题主要考查了三角形中位线定理,解题的关键在于能够熟练掌握三角形中位线定理.二、填空题1【解析】【分析】由折叠的性质可得,BD CE ⊥,4BE BC ==,12CF CE =,由勾股定理可得,CE =得,26BCD BDE BEG S S S ===△△△,求得CF 的长度,即可求解.【详解】解:由折叠的性质可得,BD CE ⊥,4BE BC ==,12CF CE =,BCD BDE △≌△ ∴BCE 为等腰直角三角形,F 为CE 的中点,BCD BDE SS = ∴12BF CF EF CE ===由勾股定理可得,CE∴12BF CF EF CE ====∵BG 为△EBD 的中线,△EBG 的面积为3∴26BCD BDE BEG S S S ===△△△162BCD S BD CF =⨯=△,解得BD =∴DF BD BF =-=由勾股定理得:CD =【点睛】此题考查了折叠的性质,勾股定理以及直角三角形的性质,解题的关键是灵活利用相关性质进行求解.2、【解析】【分析】根据折叠性质和平行四边形的性质可以证明△ABG≌△EAD,可得AG=DE=2,然后利用勾股定理可得求出AF的长,进而可得GF的值.【详解】解:如图,GF⊥AB于点F,∵点E是CD边上的中点,∴CE=DE=2,由折叠可知:∠BGE=∠C,BC=BG=3,CE=GE=2,在▱ABCD中,BC=AD=3,BC∥AD,∴∠D+∠C=180°,BG=AD,∵∠BGE+∠AGB=180°,∴∠AGB=∠D,∵AB∥CD,∴∠BAG=∠AED,在△ABG和△EAD中,AGB DBAG AED BG AD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABG≌△EAD(AAS),∴AG=DE=2,∴AB=AE=AG+GE=4,∵GF⊥AB于点F,∴∠AFG=∠BFG=90°,在Rt△AFG和△BFG中,根据勾股定理,得AG2-AF2=BG2-BF2,即22-AF2=32-(4-AF)2,解得AF=118,∴GF2=AG2-AF2=4-12164=13564,∴GF,故答案为2.【点睛】本题考查了折叠的性质、平行四边形的性质、勾股定理等知识,证明△ABG≌△EAD是解题的关键.3【解析】【分析】过点A作AD//BC,且AD=MN,连接MD,则四边形ADMN是平行四边形,作点A关于BC的对称点A′,连接AA′交BC于点O,连接A′M,三点D、M、A′共线时,AM AN最小为A′D的长,利用勾股定理求A′D的长度即可解决问题.【详解】解:过点A作AD//BC,且AD=MN,连接MD,则四边形ADMN 是平行四边形,∴MD =AN ,AD =MN ,作点A 关于BC 的对称点A ′,连接A A ′交BC 于点O ,连接A ′M , 则AM =A ′M ,∴AM +AN =A ′M +DM ,∴三点D 、M 、A ′共线时,A ′M +DM 最小为A ′D 的长, ∵AD //BC ,AO ⊥BC ,∴∠DA A '=90°,∵2AB AC ==,90BAC ∠=︒,,∴BC=BO=CO =AO ,∴AA '=在Rt△AD A '中,由勾股定理得:A 'D =∴AM AN +【点睛】本题主要考查了等腰三角形的性质,平行四边形的判定与性质,勾股定理等知识,构造平行四边形将AN转化为DM是解题的关键.4、24【解析】【分析】由三边长之比得到三角形的三条中位线之比,再由这三条中位线组成的三角形周长求出三中位线长,推出边长,再比大小判断即可.【详解】∵ 如图,H、I、J分别为BC,AC,AB的中点∴12HI AB=,12IJ BC=,12HJ AC=又∵30HI IJ HJ++=∴60AB BC AC++=∵AB:AC:BC=4:5:6,即BC边最长∴660=244+5+6BC=⨯故填24.【点睛】本题考查了三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.5、6【解析】【分析】根据三角形的面积求出BF,利用勾股定理列式求出AF,再根据翻折变换的性质可得AD=AF,然后求出CF,设DE=x,表示出EF、EC,然后在Rt△CEF中,利用勾股定理列方程求解和三角形的面积公式解答即可.【详解】解:∵四边形ABCD是矩形∴AB=CD=9,BC=AD∵12•AB•BF=54,∴BF=12.在Rt△ABF中,AB=9,BF=12,由勾股定理得,15AF=.∴BC=AD=AF=15,∴CF=BC-BF=15-12=3.设DE=x,则CE=9-x,EF=DE=x.则x2=(9-x)2+32,解得,x=5.∴DE=5.∴EC=DC-DE=9-5=4.∴△FCE的面积=1122CF CE⨯⨯=×4×3=6.【点睛】本题考查了翻折变换的性质,矩形的性质,三角形的面积,勾股定理,熟记各性质并利用勾股定理列出方程是解题的关键.三、解答题1、(1)见解析;(2)见解析;(3)见解析【分析】(1)如图,AB =4,BC =3,5AC =,利用勾股定理逆定理即可得到△ABC 是直角三角形;(2)如图,AB =AC =BC ==△ABC 是直角三角形;(3)如图,AB BC CD AD =====AC =222AC AB BC =+,∠ABC =90°,即可得到四边形ABCD 是正方形,10ABCD SAB BC =⋅=.【详解】解:(1)如图所示,AB =4,BC =3,5AC =,∴222AC AB BC =+,∴△ABC 是直角三角形;(2)如图所示,AB ==AC =BC =∴222AC AB BC =+,∴△ABC 是直角三角形;(3)如图所示,AB BC CD AD ==== AC =∴222AC AB BC =+,∴∠ABC =90°,∴四边形ABCD 是正方形,∴10ABCDS AB BC =⋅=.【点睛】 本题主要考查了有理数与无理数,正方形的判定,勾股定理和勾股定理的逆定理,熟知相关知识是解题的关键.2、(1)见解析(2)见解析【分析】(1)利用垂直平分线和角平分线的尺规作图法,进行作图即可.(2)利用直角三角形斜边中线性质,以及角平分线的性质直接证明CED ∠与EDF ∠都是90︒,最后加上90ACB ∠=︒,即可证明结论.【详解】(1)答案如下图所示:分别以A 、B 两点为圆心,以大于2AB 长为半径画弧,连接弧的交点的直线即为垂直平分线l ,其与AB 的交点为D ,以点D 为圆心,适当长为半径画弧,分别交DA 于点M ,交CD 于点N ,交BD 于点T ,然后分别以点M ,N 为圆心,大于2MN 为半径画弧,连接两弧交点与D 点的连线交AC 于点E ,同理分别以点T ,N 为圆心,大于2TN 为半径画弧,连接两弧交点与D 点的连线交BC 于点F . (2)证明:D 点是AB 与其垂直平分线l 的交点,D ∴点是AB 的中点,CD ∴是Rt △ABC 上的斜边的中线,2AB CD AD ∴==, DE 、DF 分别是∠ADC ,∠BDC 的角平分线,12CDE ADE ADC ∴∠=∠=∠,12CDF CDB ∠=∠,EDF CDE CDF ∠=∠+∠,11190222EDF ADC CDB ADB ∴∠=∠+∠=∠=︒ , CD AD CDE ADE DE DE =⎧⎪∠=∠⎨⎪=⎩, ()CDE ADE SAS ∴∆∆≌,1902CED AED AEC ∴∠=∠=∠=︒, 在四边形CEDF 中,90ACB CED EDF ∠=∠=∠=︒,∴四边形CEDF 是矩形.【点睛】本题主要是考查了尺规作图、直角三角形斜边中线性质以及矩形的判定,熟练利用直角三角形斜边中线性质,找到三角形全等的判定条件,并且选择合适的矩形判定条件,是解决本题的关键.3、(1)等边;(2)见解析;(3)成立,理由见解析【分析】(1)根据含30度角的直角三角形的性质,直角三角形斜边上的中线等于斜边的一半可证明12BC OC OB AB ===,即可证明△OBC 是等边三角形; (2)先证明COP BOQ ∠=∠,即可利用SAS 证明COP BOQ ≌,得到CP BQ =;(3)先证明COP BOQ ∠=∠,即可利用SAS 证明COP BOQ ≌,得到CP BQ =.【详解】(1)∵∠ACB =90°,∠A =30°,O 是AB 的中点, ∴12BC OC OB AB ===, ∴△OBC 是等边三角形,故答案为:等边;(2)由(1)可知,OB OC =,60BOC ∠=︒, OPQ 是等边三角形,OP OQ ∴=,60POQ ∠=︒,60COP BOP BOQ ∴∠=︒-∠=∠,即COP BOQ ∠=∠,在COP 和BOQ △中OC OB COP BOQ OP OQ =⎧⎪∠=∠⎨⎪=⎩, ()COP BOQ SAS ∴≌,CP BQ ∴=;(3)成立,CP BQ =证明:由(1)可知,OB OC =,60BOC ∠=︒, OPQ 是等边三角形,OP OQ ∴=,60POQ ∠=︒,60COP BOP BOQ ∴∠=︒+∠=∠,即COP BOQ ∠=∠,在COP 和BOQ △中OC OB COP BOQ OP OQ =⎧⎪∠=∠⎨⎪=⎩, ()COP BOQ SAS ∴≌,CP BQ ∴=.【点睛】本题主要考查了等边三角形的性质与判定,全等三角形的性质与判定,含30度角的直角三角形的性质,直角三角形斜边上的中线,熟练掌握等边三角形的性质与判定条件是解题的关键.4、(1)见解析;(2)正方形ABCD的面积为2a【分析】(1)由等边三角形的性质得EO⊥AC,即BD⊥AC,再根据对角线互相垂直的平行四边形是菱形,即可得出结论;(2)证明菱形ABCD是正方形,即可得出答案.【详解】(1)证明:∵四边形ABCD是平行四边形,∴AO=OC,∵△ACE是等边三角形,∴EO⊥AC(三线合一),即BD⊥AC,∴▱ABCD是菱形;(2)解:∵△ACE是等边三角形,∴∠EAC=60°由(1)知,EO⊥AC,AO=OC∴∠AEO=∠OEC=30°,△AOE是直角三角形,∵∠AED=2∠EAD,∴∠EAD=15°,∴∠DAO=∠EAO﹣∠EAD=45°,∵▱ABCD是菱形,∴∠BAD=2∠DAO=90°,∴菱形ABCD 是正方形,∴正方形ABCD 的面积=AB 2=a 2.【点睛】本题考查了菱形的判定与性质、正方形的判定与性质、平行四边形的性质、等边三角形的性质等知识,证明四边形ABCD 为菱形是解题的关键.5、(1)(2)见解析【分析】(1)根据30°角所对直角边等于斜边的一半,得到AD =3,根据等腰直角三角形,得到CD =AD =3,根据勾股定理,得到AC 的长即可;(2)根据斜边上的中线等于斜边的一半,得到DE =DC ,根据等腰三角形三线合一性质,证明即可.【详解】(1)AD BC ⊥90ADB ADC ∴∠=∠=︒30B ∠=︒,6AB =132AD AB ∴== 45ACD ∠=︒45CAD ∴∠=︒3AD CD ∴==AC ∴=(2)连接DE90ADB ∠=︒,AE BE =12ED AB ∴=, 12AD AB =,AD CD =, ED CD ∴=,GD EC ⊥,EG CG ∴=.【点睛】 本题考查了30°角的性质,等腰直角三角形的性质,斜边上中线的性质,等腰三角形三线合一性质,熟练掌握性质是解题的关键.。
人教版八年级下册数学第十八章 平行四边形含答案(综合考试)

人教版八年级下册数学第十八章平行四边形含答案一、单选题(共15题,共计45分)1、平行四边形的对角线长为x、y,一边长为11,则x、y的值可能是()A.8和14B.10和8C.10和32D.12和142、如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若=2,则的值为()A. B. C. D.3、下列命题中错误的是A.两组对边分别相等的四边形是平行四边形B.对角线相等的平行四边形是矩形C.一组邻边相等的平行四边形是菱形D.对角线相等且互相垂直的四边形是正方形4、如图,在矩形ABCD中,E为AD的中点,∠BED的角平分线交BC于F.若AB=6,BC=16,则FC的长度为()A.4B.5C.6D.85、如图,把一张长方形纸片沿对角线折叠,点的对应点为,与相交于点,则下列结论不一定成立的是()A. 是等腰三角形B.C. 平分D.折叠后的图形是轴对称图形6、如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是()A.AB∥DCB.AC=BDC.AC⊥BDD.AB=DC7、如图,在中,点E是边上的中点,G为线段上一动点,连接,交于点F,若,则的值为()A.3B.2C.D.8、如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )A. B.1 C. D.29、如图,在中,,,,则的面积为()A.30B.60C.65D.10、下列定理中没有逆定理的是()A.等腰三角形的两底角相等B.平行四边形的对角线互相平分C.角平分线上的点到角两边的距离相等D.全等三角形的对应角相等11、菱形ABCD的一条对角线的长为6,边AB的长是方程的一个根,则菱形ABCD的周长为( )A.16B.12C.12或16D.无法确定12、如图,正方形ABCD的边长为,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB的延长线于点F,则EF的长为()A.2B.4C.2D.413、在四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是()A.OA=OC,OB=ODB.AD∥BC,AB∥DCC.AB=DC,AD=BC D.AB∥DC,AD=BC14、如图,已知菱形 A,B,C,D 的顶点 A(0,﹣1),∠D A C =60°.若点 P从点 A出发,沿A→B→C→D→A…的方向,在菱形的边上以每秒 1 个单位长度的速度移动,则第 2020 秒时,点 P 的坐标为()A.(2,0)B.(,0)C.(﹣,0)D.(0,1 )15、如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠B=60°,BC=3,△ABE的周长为6,则等腰梯形的周长是()A.8B.10C.12D.16二、填空题(共10题,共计30分)16、如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF=,则点F与点C的最小距离为________.17、以下四个命题:①如果三角形一边的中点到其他两边距离相等,那么这个三角形一定是等腰三角形:②两条对角线互相垂直且相等的四边形是正方形:③一组数据2,4,6.4的方差是2;④△OAB与△OCD是以O为位似中心的位似图形,且位似比为1:4,已知∠OCD=90°,OC=CD.点A、C在第一象限.若点D坐标为(2, 0),则点A坐标为(,),其中正确命题有________ (填正确命题的序号即可)18、如图,矩形中,、交于点,、分别为、的中点.若,则的长为________.19、如图,正方形ABCD中,△ABC绕点A逆时针旋转到AB′C′,AB′,AC′分别交对角线BD于点EF,若AE=8,则EF•ED的值为________.20、如图,在平行四边形ABCD中,AD=2AB.F是AD的中点,作CE⊥AB, 垂足E 在线段AB上,连接EF、CF,则下列结论:(1)∠DCF+ ∠D=90°;(2)∠AEF+∠ECF=90°;(3) =2 ; (4)若∠B=80 ,则∠AEF=50°.其中一定成立的是________ (把所有正确结论的字号都填在横线上).21、如图的平面直角坐标系中,A点的坐标是(4,3)。
(典型题)初中数学八年级数学下册第六单元《平行四边形》检测题(含答案解析)(1)

一、选择题1.如图,在ABCD 中,3AB =,4=AD ,60ABC ∠=︒,过BC 的中点E 作EF AB ⊥,垂足为点F ,与DC 的延长线相交于点H ,则DEF 的面积是( )A .63+B .43C .23D .623+ 2.如果一个多边形的内角和为1260︒,那么从这个多边形的一个顶点可以作( )条对角线.A .4B .5C .6D .73.如图,在ABCD 中,4CD =,60B ︒∠=,:2:1BE EC =,依据尺规作图的痕迹,则ABCD 的面积为( )A .12B .122C .123D .125 4.正多边形的每个外角为60度,则多边形为( )边形. A .4B .6C .8D .10 5.如图,在▱ABCD 中,AB=2.6,BC=4,∠ABC 的平分线交CD 的延长线于点E ,则DE 的长为( )A .2.6B .1.4C .3D .2 6.一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )A .4B .5C .6D .77.如图,将四边形ABCD 去掉一个60°的角得到一个五边形BCDEF ,则∠1与∠2的和为( )A .60°B .108°C .120°D .240°8.如图,下面不能判定四边形ABCD 是平行四边形的是( )A .AB //CD,AB CD =B .,AB CD AD BC ==C .B DAB 180,AB CD ︒∠+∠==D .B D,BCA DAC ∠=∠∠=∠9.如图,平行四边形ABCD 的周长是56cm ,ABC ∆的周长是36m ,则AC 的长为( )A .6cmB .12cmC .4cmD .8cm 10.如图,在平行四边形ABCD 中,AE 平分∠BAD ,交CD 边于E ,AD =3,EC =2,则AB的长为( )A .1B .2C .3D .5 11.若一个正n 边形的每个内角为156°,则这个正n 边形的边数是( )A .13B .14C .15D .16 12.如图,在平行四边形ABCD 中,下列结论错误的是( )A .∠BDC =∠ABDB .∠DAB =∠DCBC .AD =BC D .AC ⊥BD二、填空题13.已知,如图,//,AB DC AF 平分,BAE DF ∠平分CDE ∠,且AFD ∠比∠E 的2倍多30°,则AED =∠_____度.14.如图,点C 在线段AB 上,等腰ADC 的顶角120ADC =∠︒,点M 是矩形CDEF 的对角线DF 的中点,连接MB ,若63AB =,6AC =,则MB 的最小值为为______.15.如图,已知正五边形ABCDE ,过点A 作CD 的平行线,交CB 的延长线于点F ,点P 在正五边形的边上运动,运动路径为A B C D →→→.当AFP 为等腰三角形时,则AFP 的顶角为______度.16.如图,在四边形ABCD 中,点P 是对角线BD 的中点,点E 、F 分别是AB 、CD 的中点,AD BC =,30PEF ∠=︒,则EPF ∠的度数是______.17.如图,己知ABCD 中,点M 是BC 的中点,线段AM 、BD 互相垂直,AM=3,BD=6,则该平行四 边形的面积为____.18.平行四边形ABCD 中,若2B A ∠=∠,则C ∠的度数为__________.19.如图,1角硬币边缘镌刻的是正九边形,则这个正九边形每个内角的度数是________.20.如图,已知矩形ABCD ,P 、R 分别是BC 和DC 上的点,E 、F 分别是PA ,PR 的中点.如果DR=3,AD=4,则EF 的长为______.三、解答题21.如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,延长BC 到点E ,使CE BC =,连接DE .(1)求证:四边形ACED 是平行四边形;(2)已知5AB =,6AC =,若12CD BE =,求BDE 的周长. 22.如图,点E 在ABCD 外,连接BE ,DE ,延长AC 交DE 于F ,F 为DE 的中点.(1)求证://AF BE ;(2)若2AD =,60ADC ∠=︒,90ACD ∠=︒,2AC CF =,求BE 的长.23.如图,在每个小正方形的边长均为1的方格纸中,其中端点,A B 均在小正方形的顶点上.(1)在图中画出平行四边形ABCD ,点C 和点D 均在小正方形的顶点上,且平行四边形ABCD 的面积为12;(2)在图中画出以AB 为腰的等腰直角ABE △,且点E 在小正方形的顶点上; (3)连接DE ,直接写出DE 的长.24.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少. 25.如图,已知△ABC 中,AB=3,AC=5,∠BAE =∠CAE ,BE ⊥AE 于点E ,BE 的延长线交AC 于点D ,F 是BC 的中点,求EF 的长.26.如图,将平行四边形ABCO 放置在平面直角坐标系xOy 中,O 为坐标原点,若点A 的坐标是()6,0,点C 的坐标是()1,4.(1)点B 的坐标为_______;(2)求直线AC 的表达式;(3)若点C 关于x 轴的对称点为点E ,设过点E 的直线y kx b =+,与四边形ABCO 有公共点,结合函数图象,求k 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据平行四边形的性质得到AB =CD =3,AD =BC =4,求出BE 、BF 、EF ,根据相似得出CH =1,EH△DFH 的面积,即可求出答案.【详解】解:∵四边形ABCD 是平行四边形,∴AD =BC =4,AB ∥CD ,AB =CD =3,∵E 为BC 中点,∴BE =CE =2,∵∠B =60°,EF ⊥AB ,∴∠FEB =30°,∴BF =1,由勾股定理得:EF,∵AB ∥CD ,∴∠B =∠ECH ,在△BFE 和△CHE 中,B ECH BE CE BEF CEH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△BFE ≌△CHE (ASA ),∴EF =EHCH =BF =1,∴DH=4,∵S △DHF =12DH •FH= ∴S △DEF =12S △DHF= 故选:C .【点睛】本题主要考查对平行四边形的性质,平行线的性质,勾股定理,含30度角的直角三角形,三角形的面积,三角形的内角和定理等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.2.C解析:C【分析】先利用n 边形的内角和公式算出n ,再利用n 边形的每一个顶点有(n-3)条对角线计算即可.【详解】根据题意,得(n-2)×180=1260,解得n=9,∴从这个多边形的一个顶点可以作对角线的条数为:n-3=9-3=6.故选C.【点睛】本题考查了n 边形的内角和和经过每一个顶点可作的对角线条数,熟记多边形内角和公式,计算经过每一个顶点的对角线条数计算公式是解题的关键.3.C解析:C【分析】由作图痕迹可得EF 为AB 的中垂线,结合60B ∠=︒判断出△ABE 为等边三角形,从而结合边长求出ABCD 在BC 边上的高为23BC 的长度,最终计算面积即可.【详解】设尺规作图所得直线与AB 交于F 点,根据题意可得EF 为AB 的中垂线,∴AE=BE ,又∵60B ∠=︒,∴△ABE 为等边三角形,边长AB=CD=4,∴BF=2,BE=4,2223EF BE BF =-=∴ABCD 在BC 边上的高为23,又∵:2:1BE EC =,BE=4,∴EC=2,BC=2+4=6,∴ABCD S =23×6=123,故选:C .【点睛】本题考查平行四边形的性质,中垂线的识别与性质,以及等边三角形的判定与性质,准确根据作图痕迹总结出等边三角形是解题关键.4.B解析:B【分析】利用多边形的外角和360除以外角60得到多边形的边数.【详解】多边形的边数为36060÷=6,故选:B .【点睛】此题考查多边形的外角和定理,正多边形的性质,利用外角和除以外角的度数求正多边形的边数是最简单的题型.5.B 解析:B【分析】由平行四边形ABCD 中,BE 平分∠ABC ,可证得△BCE 是等腰三角形,继而利用DE=CE-CD ,求得答案.【详解】解:四边形ABCD 是平行四边形,AB//CD ∴,CD AB 2.6==,E ABE ∠∠∴=.BE 平分ABC ∠,ABE CBE ∴∠=∠,CBE E ∠∠∴=,CE BC4∴==,∴=-=-=.DE CE CD4 2.6 1.4故选:B.【点睛】此题考查了平行四边形的性质,能证得△BCE是等腰三角形是解此题的关键.6.C解析:C【分析】⨯=︒,设这个多边形是n边形,内角和是多边形的外角和是360︒,则内角和是2360720()-⋅︒,这样就得到一个关于n的方程,从而求出边数n的值.n2180【详解】解:设这个多边形是n边形,根据题意,得()-⨯︒=⨯,n21802360=.解得:n6即这个多边形为六边形.故选:C.【点睛】本题考查了多边形的内角和与外角和,熟记内角和公式和外角和定理并列出方程是解题的关键,根据多边形的内角和定理,求边数的问题就可以转化为解方程的问题来解决. 7.D解析:D【分析】利用四边形的内角和得到∠B+∠C+∠D的度数,进而让五边形的内角和减去∠B+∠C+∠D的度数即为所求的度数.【详解】∵四边形的内角和为(4−2)×180°=360°,∴∠B+∠C+∠D=360°−60°=300°,∵五边形的内角和为(5−2)×180°=540°,∴∠1+∠2=540°−300°=240°,故选D.【点睛】本题考查多边形的内角和知识,求得∠B+∠C+∠D的度数是解决本题的突破点.8.C解析:C【分析】根据平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形判断即可.【详解】根据平行四边形的判定,A、B、D均符合是平行四边形的条件,C则不能判定是平行四边形.故选C.【点睛】此题主要考查了学生对平行四边形的判定的掌握情况.对于判定定理:“一组对边平行且相等的四边形是平行四边形.”应用时要注意必须是“一组”,而“一组对边平行且另一组对边相等”的四边形不一定是平行四边形.9.D解析:D【分析】的周长=AB+BC+AC,而AB+BC为平行四边形ABCD的周长的一半,代入数值求解ABC即可.【详解】因为四边形ABCD是平行四边形,∴AB=DC,AD=BC,∵▱ABCD的周长是56cm,∴AB+BC=28cm,∵△ABC的周长是36cm,∴AB+BC+AC=36cm,∴AC=36cm−28cm=8cm.故选D.【点睛】本题考查了平行四边形的性质,根据题意列出三角形周长的关系式,结合平行四边形周长的性质求解是本题的关键.10.D解析:D【分析】首先证明DA=DE,再根据平行四边形的性质即可解决问题.【详解】解:∵四边形ABCD是平行四边形,∴BA∥CD,AB=CD,∴∠DEA=∠EAB,∵AE平分∠DAB,∴∠DAE=∠EAB,∴∠DAE=∠DEA,∴DE=AD=3,∴CD=CE+DE=2+3=5,∴AB=5.故选:D.【点睛】本题考查平行四边形的性质,等腰三角形的判定和性质等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.11.C解析:C【解析】试题分析:由一个正多边形的每个内角都为156°,可求得其外角的度数,继而可求得此多边形的边数,则可求得答案.解:∵一个正多边形的每个内角都为156°,∴这个正多边形的每个外角都为:180°﹣156°=24°,∴这个多边形的边数为:360°÷24°=15,故选C.考点:多边形内角与外角.12.D解析:D【分析】根据平行四边形的性质进行判断即可.【详解】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠BDC=∠ABD,故选项A正确;∵四边形ABCD是平行四边形,∴∠DAB=∠DCB,故选项B正确;∵四边形ABCD是平行四边形,∴AD=BC,故选项C正确;由四边形ABCD是平行四边形,不一定得出AC⊥BD,故选D.【点睛】本题主要考查平行四边形的性质,掌握平行四边形的相关知识点是解答本题的关键.二、填空题13.60【分析】过F作FG∥AB即可得出AB∥GF∥CD再根据平行线的性质以及角平分线的定义即可得到∠AFD=∠3+∠4依据四边形内角和等于360°即可得出∠AED的度数【详解】解:如图所示过F作FG∥解析:60【分析】过F作FG∥AB,即可得出AB∥GF∥CD,再根据平行线的性质以及角平分线的定义,即可得到∠AFD=∠3+∠4,依据四边形内角和等于360°,即可得出∠AED 的度数.【详解】解:如图所示,过F 作FG ∥AB ,∵AB ∥DC ,∴AB ∥GF ∥CD ,∴∠1=∠DFG ,∠2=∠AFG ,∴∠AFD=∠1+∠2,∵AF 平分∠BAE ,DF 平分∠CDE ,∴∠1=∠3,∠2=∠4,设∠E=α,则∠AFD=2α+30°,∴∠AFD=∠3+∠4=2α+30°,∵四边形AEDF 中,∠E+∠3+∠4+∠AFD=360°,∴α+2(2α+30°)=360°,解得α=60°,故答案为:60.【点睛】本题主要考查了平行线的性质以及四边形内角和的综合应用,解决问题的关键是作辅助线构造内错角,运用四边形内角和进行计算求解.14.【分析】过D 作DG ⊥AC 于G 取FC 中点H 连结MHHB 由等腰的顶角可得DG 平分∠ADCAG=CG=可求∠GDC=60°∠DCG=30°在Rt △DGC 中由勾股定理DC2=DG2+GC2即4DG2=DG2 解析:93-【分析】过D 作DG ⊥AC 于G ,取FC 中点H ,连结MH ,HB 由等腰ADC 的顶角120ADC =∠︒,可得DG 平分∠ADC ,AG=CG=1AC=32,可求∠GDC=60°,∠DCG=30°,在Rt △DGC 中,由勾股定理DC 2=DG 2+GC 2,即4DG 2=DG 2+9,可求33由M ,H 为中点,可得MH=1DC=32MB MH+HB ,MH 为定值,HB 最小时,MB 最短,BH ⊥CF ,可求∠HCB=60°,CH=()11BC=63-6=33-322,由勾股定理22933CB CH -=-,BH 最小3+9-33=923-【详解】解:过D 作DG ⊥AC 于G ,取FC 中点H ,连结MH ,HB ,∵等腰ADC 的顶角120ADC =∠︒,∴DG 平分∠ADC ,AG=CG=1AC=32, ∴∠GDC=60°,∠DCG=90°-∠GDC=90°-60°=30°,∴CD=2DG ,在Rt △DGC 中,由勾股定理DC 2=DG 2+GC 2,即4DG 2=DG 2+9,∴DG=3,CD=23,∵M ,H 为中点,∴MH=1DC=32, 根据两点之间线段最短,则有MBMH+HB ,MH 为定值, ∴HB 最小时,MB 最短,∴BH ⊥CF ,∠HCB=180°-∠DCA-∠DCF=180°-30°-90°=60°,CH=()11BC=63-6=33-322, BH=()2233333933CB CH CH -==-=-,BH 最小=3+9-33=923-,故答案为:923-.【点睛】本题考查等腰三角形的性质,勾股定理,30°角直角三角形性质,三角形中位线,三角形三边关系,掌握等腰三角形的性质,勾股定理,30°角直角三角形性质,三角形中位线,三角形三边关系是解题关键.15.36或72或108【分析】根据题意可以分情况谈论:①当AP=AF ;②当PF=FA ;③当FA=PF ;分别求其顶角的度数;【详解】解:易知正五边形的内角为:;∴∠CBA=108°=∠BAE ∴∠ABF=1解析:36或72或108【分析】根据题意可以分情况谈论:①当AP=AF ;②当PF=FA ;③当FA=PF ;分别求其顶角的度数;【详解】 解:易知正五边形的内角为:540=1085︒︒ ; ∴∠CBA=108°=∠BAE ,∴∠ABF=180°-108°=72°, ∠BAF=180108362︒-︒=︒ , ∴∠BFA=180°-72°-36°=72°;∴AB=AF , 若P 在AB 边上,不可能有PF=FA ,①若PA=PF ,则∠PAF=∠PFA=36°,∴顶角为∠APF=180°-36°×2=108°;②若PA=AF ,则P 与B 重合,此时顶角为∠PAF=36°;若P 在BC 边上,连接AC ,易知AC=CF ,不存在PA=AF ;①若PF=FA ,此时顶角为∠ PFA=72°,②若PA=PF ,则P 与C 重合,顶角为36°;若P 在CD 上,不存在等腰三角形;综上:顶角为108°或36°或72°;故答案为:36或72或108;【点睛】本题考查了正多边形的内角和公式和三角形的内角和问题,要注意分类讨论的问题,不要遗漏.16.【分析】根据中位线定理推出PE=ADPF=BC 由此得到PE=PF 推出△PEF 是等腰三角形根据三角形的内角和定理求出答案【详解】∵点是对角线的中点点分别是的中点∴PE=ADPF=BC ∵∴PE=PF ∴△解析:120︒【分析】根据中位线定理推出PE=12AD ,PF=12BC ,由此得到PE=PF ,推出△PEF 是等腰三角形,根据三角形的内角和定理求出答案.【详解】∵点P 是对角线BD 的中点,点E 、F 分别是AB 、CD 的中点,∴PE=12AD ,PF=12BC ,∵AD BC =,∴PE=PF ,∴△PEF 是等腰三角形,∴∠PFE=30PEF ∠=︒,∴EPF ∠=1803030120︒︒︒︒--=,故答案为:120︒.【点睛】此题考查三角形的中位线定义及定理,等腰三角形的判定及性质,三角形的内角和定理,熟记三角形的中位线的定义及定理是解题的关键.17.12【分析】由题意连接MD 根据三角形同底同高可得再利用平行四边形的性质得出进而运用面积的比例进行分析计算即可求得平行四边形的面积【详解】解:由题意连接MD ∵点M 是BC 的中点∴∵四边形是平行四边形∴∵ 解析:12【分析】由题意连接MD,根据三角形同底同高可得DBM DCM S S =,再利用平行四边形的性质得出 ABD DBC S S =,进而运用面积的比例进行分析计算即可求得平行四边形的面积.【详解】解:由题意连接MD,∵点M 是BC 的中点,∴DBM DCM S S =,22DBC DCM DBM S S S ==,∵四边形ABCD 是平行四边形,∴ABD DBC S S =,∵线段AM 、BD 互相垂直,AM=3,BD=6,∴S 四边形ABMD =1136922AM BD =⨯⨯=, ∵S 四边形ABMD =223DCM ABD DBC DCM DCM DCM DCM DCM ABCD S S S S S S S S S -=+-=+-=, ∴933DCM S=÷=, ∴44312D ABC M D C S S ==⨯=.故答案为:12.【点睛】本题考查平行四边形的性质,熟练掌握三角形同底同高其面积相等以及平行四边形的对角线平分平行四边形的面积是解题的关键.18.60°【分析】先根据平行四边形的性质得出∠A+∠B=180°∠A=∠C 再由∠B=2∠A 可求出∠A 的度数进而可求出∠C 的度数【详解】解:如下图∵四边形ABCD 是平行四边形∴∠A+∠B=180°∠A=∠解析:60°【分析】先根据平行四边形的性质得出∠A+∠B=180°,∠A=∠C ,再由∠B=2∠A 可求出∠A 的度数,进而可求出∠C 的度数.【详解】解:如下图,∵四边形ABCD 是平行四边形,∴∠A+∠B=180°,∠A=∠C ,∵∠B=2∠A ,∴∠A+2∠A=180°,∴∠A=∠C=60°.故答案为:60°.【点睛】本题考查的是平行四边形的性质.熟知平行四边形的对角相等,邻角互补是解答此题的关键.19.140°【分析】先根据多边形内角和定理:求出该多边形的内角和再求出每一个内角的度数【详解】解:该正九边形内角和=180°×(9-2)=1260°则每个内角的度数=故答案为:140°【点睛】本题主要考解析:140°【分析】先根据多边形内角和定理:180(2)n ︒•-求出该多边形的内角和,再求出每一个内角的度数.【详解】解:该正九边形内角和=180°×(9-2)=1260°,则每个内角的度数=12601409︒=︒. 故答案为:140°.【点睛】本题主要考查了多边形的内角和定理:180°•(n-2),比较简单,解答本题的关键是直接根据内角和公式计算可得内角和.20.5【解析】试题分析:根据勾股定理求AR;再运用中位线定理求EF试题解析:5【解析】试题分析:根据勾股定理求AR;再运用中位线定理求EF.试题∵四边形ABCD是矩形,∴△ADR是直角三角形∵DR=3,AD=4∴∵E、F分别是PA,PR的中点∴EF=12AR=12×5=2.5.考点:1.三角形中位线定理;2.矩形的性质.三、解答题21.(1)见解析;(2)24【分析】(1)由平行四边形的性质得出AD∥BC,AD=BC,结合CE=BC,得到AD=CE,可证明四边形ACED是平行四边形;(2)根据四边形ACED是平行四边形得到DE=AC=6,再证明∠BDE=90°,得到BE=2CD=2AB=10,利用勾股定理求出BD,可得△BDE的周长.【详解】解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵CE=BC,∴AD=CE=BC,∵AD∥BC,∴AD∥CE,∴四边形ACED是平行四边形;(2)∵四边形ACED是平行四边形,∴DE=AC=6,∵CD=BC=CE=12BE,∴∠CBD=∠CDB,∠CDE=∠CED,∴∠BDE=∠CDB+∠CDE=11802⨯︒=90°,∴BE=2CD=2AB=10,∴BD,∴△BDE 的周长=BD +BE +DE =8+10+6=24.【点睛】本题考查了平行四边形的性质与判定、三角形周长的计算;熟练掌握平行四边形的性质,并能进行推理论证与计算是解决问题的关键.22.(1)见解析;(2)23【分析】(1)连接BD 交AC 于点O ,根据平行四边形的性质可以判定OF 为△DBE 的中位线,即可证明; (2)根据AD=2,∠ACD=90°,∠ADC=60°,可求出AC 的长,再根据中位线的性质即可求解;【详解】解:(1)连接BD 交AC 于点O ,∵四边形ABCD 是平行四边形,∴OB OD =,∵DF EF =,∴OF 为△DBE 的中位线∴//AF BE .(2)∵AD=2,∠ACD=90°,∠ADC=60°, ∴3AC =∵OF 是DBE 的中位线,∴2BE OF =.∴222BE OC CF AC CF =+=+.∵2AC CF =,∴223BE AC ==【点睛】本题考查了三角形中位线的性质以及平行四边形的性质,正确掌握知识点是解题的关键; 23.(1)见解析;(2)见解析;(3)5DE =【分析】(1)由平行四边形ABCD 的面积为12,把,A B 分别往右平移3个单位长度,对应点分别为,,D C 从而可得答案;(2)如图,取格点,P 满足90,APB ∠=︒ 把APB △绕点A 逆时针旋转90,︒ ,P B 的对应点分别为,,H E 则ABE △即为所求作的等腰直角三角形;(3)利用勾股定理直接计算即可得到答案.【详解】解:(1)如图,把,A B 分别往右平移3个单位长度,对应点分别为,,D C 则四边形ABCD 即为所求作的平行四边形.理由如下:由平移的性质可得://,,AB CD AB CD =∴ 四边形ABCD 是平行四边形,3412.ABCD S =⨯=(2)如图,取格点,P 满足90,APB ∠=︒ 把APB △绕点A 逆时针旋转90,︒ ,P B 的对应点分别为,,H E 则ABE △即为所求作的等腰直角三角形,理由如下:由旋转可得:,90,AB AE BAE PAH =∠=∠=︒ABE ∴是以AB 为腰的等腰直角三角形.(3)由勾股定理得:2212 5.DE =+【点睛】本题考查的是平行四边形的作图与判定,平移的性质,旋转的性质,等腰直角三角形的定义,勾股定理的应用,掌握以上知识是解题的关键.24.这个多边形的边数是9【分析】多边形的内角和比外角和的3倍多180°,而多边形的外角和是360°,则内角和是1260度.n 边形的内角和可以表示成(n−2)•180°,设这个多边形的边数是n ,就得到方程,从而求出边数.【详解】设这个多边形的边数为n ,根据题意,得(n−2)•180=360×3+180,解得:n =9.则这个多边形的边数是9.【点睛】此题考查了多边形内角与外角,此题要结合多边形的内角和公式寻求等量关系,构建方程即可求解.25.1【分析】由已知得到AEB AED ≌后,再根据三角形全等的性质和中位线的性质可以得到解答 .【详解】解:在AEB △和AED 中90BAE DAE AE AEAEB AED ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∵AEB AED △≌△∴BE ED =,AD AB =∵BF FC = ∴1111()()(53)12222EF CD AC AD AC AB ==-=-=-= 【点睛】 本题考查三角形的综合应用,灵活应用三角形全等的判定和性质以及中位线的性质是解题关键.26.(1)(7,4);(2)y =-42455x +;(3)k ≤-4或k ≥45. 【分析】(1)根据平行四边形的性质及A 点和C 的坐标求出点B 的坐标即可;(2)设直线AC 的表达式为:y=kx+b ,把点A 的坐标是(6,0),点C 的坐标是(1,4)代入,解方程组即可得到结论;(3)根据轴对称的性质得到E (1,-4),分别求得直线OE ,AE ,BE 的解析式,于是得到结论.【详解】解:(1)∵四边形ABCO 是平行四边形,O 为坐标原点,点A 的坐标是(6,0),点C 的坐标是(1,4),∴BC=OA=6,6+1=7,∴点B 的坐标是(7,4),故答案为:(7,4);(2)设直线AC 的表达式为:y =kx +b ,∵点A 的坐标是(6,0),点C 的坐标是(1,4),∴604k b k b +=⎧⎨+=⎩, 解得:45245k b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴直线AC 的表达式为:y =42455x -+;(3)∵点C关于x轴的对称点为点E,点C的坐标是(1,4),∴E(1,-4),把O(0,0)和E(1,-4)代入y=kx+b得y=-4x;把A(6,0)和E(1,-4)代入y=kx+b得y=424 55x-;把B(7,4)和E(1,-4)代入y=kx+b得y=416 33x-;∴k的取值范围为:k≤-4或k≥45【点睛】本题考查了一次函数的综合题,一次函数的图象上点的坐标特征,待定系数法求一次函数的解析式,一次函数的图象与系数的关系等,求得对应点的坐标是解题的关键.。
秦都区五中八年级数学下册第十八章平行四边形单元综合测试题1新版新人教版

第十八章平行四边形单元测试题第一卷选择题一、选择题〔每题3分,共24分〕1.在平行四边形ABCD中,∠B=60°,那么以下各式中,不能成立的是( 〕A.∠D=60° B.∠A=120° C.∠C+∠D=180° D.∠C+∠A=180°2.矩形,菱形,正方形都具有的性质是〔)A.对角线相等 B.对角线互相平分 C.对角线平分一组对角 D.对角线互相垂直3.如图,▱ABCD的周长是28cm,△A BC的周长是22cm,那么AC的长为( 〕A. 6cm B. 12cm C. 4cm D. 8cm第3题第4题第5题第7题4.如下图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是( 〕A.10<m<12 B.2<m<22 C。
1<m<11 D.5<m<65.如图,如果平行四边形ABCD的对角线AC和BD相交于点O,那么图中的全等三角形共有〔〕A. 1对B. 2对C. 3对D. 4对6.已知菱形的边长为6cm,一个内角为60°,那么菱形较短的对角线长是〔〕A. 6cm B.cm C. 3cm D.cm7.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,那么∠CDF为〔〕A.80°B.70°C.65°D.60°8.菱形的周长为20cm,两邻角的比为1:2,那么较长的对角线长为( 〕A. 4。
5cm B. 4cm C. 5cm D. 4cm9.矩形的四个内角平分线围成的四边形〔〕A.一定是正方形 B.是矩形 C.菱形 D.只能是平行四边形10.在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如下图的方式折叠,使点A与点D重合,折痕为EF,那么△DEF的周长为( 〕A. 9。
第18章 平行四边形 人教版数学八年级下册素养综合检测(含解析)

第十八章 素养综合检测(满分100分,限时60分钟)一、选择题(每小题3分,共30分)1.(2023广西玉林期末)在平行四边形ABCD 中,∠A ∶∠B ∶∠C ∶∠D 的值可以是( )A.1∶2∶3∶4B.1∶2∶2∶1C.2∶3∶2∶3D.1∶1∶2∶22.(2023广东广州市华侨外国语学校期末)如图,在四边形ABCD 中,对角线AC 和BD 相交于点O,下列条件不能判定四边形ABCD 是平行四边形的是 ( )A.AB ∥DC,AD ∥BCB.AB=DC,AD=BCC.AB ∥DC,AD=BCD.OA=OC,OB=OD3.(2022广东中考)如图,在△ABC 中,BC=4,点D,E 分别为AB,AC 的中点,则DE=( )A.14B.12C.1D.24.(2023湖南株洲中考)一技术人员用刻度尺(单位:cm)测量某三角形边的长度.如图所示,已知∠ACB=90°,点D 为边AB 的中点,点A 、B 对应的刻度分别为1、7,则CD=( )A.3.5 cmB.3 cmC.4.5 cmD.6 cm5.如图,菱形ABCD 的一边中点M 到对角线交点O 的距离为3 cm,则菱形ABCD 的周长为( )A.10 cmB.12 cmC.16 cmD.24 cm6.如图,在矩形ABCD 中,对角线AC 与BD 相交于点O,过点A 作AE ⊥BD,垂足为点E,若∠EAD=3∠BAE,则∠EAO 的度数是( )A.60°B.67.5°C.45°D.22.5°7.(2023浙江宁波期末)如图,根据平行四边形中所标注的角的度数和线段的长度,一定能判定其为菱形的是( )8.(2022山东聊城中考)要检验一个四边形的桌面是不是矩形,可行的测量方案是( )A.测量两条对角线是否相等B.度量两个角是不是90°C.测量两条对角线的交点到四个顶点的距离是否相等D.测量两组对边是否分别相等9.(2021江苏泰州中考)如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设∠CBE=α,则∠AFP=( )A.2αB.90°-αC.45°+αD.90°-1α210.【新考向·尺规作图】(2023山东日照一模)如图,在矩形ABCDAC长为半径画弧,两中,AB<BC,连接AC,分别以点A,C为圆心,大于12弧交于点M,N,直线MN分别交AD,BC,AC于点E,F,O,连接CE,AF.下列结论:①四边形AECF是菱形;②∠AFB=2∠ACB;③AC·EF= CF·CD;④若AF平分∠BAC,则CF=3AB.其中正确结论的个数是( )A.4B.3C.2D.1二、填空题(每小题3分,共24分)11.如图,在平行四边形ABCD中,∠DAB的平分线AE交CD于点E,若∠AED=40°,则∠B的度数是 .12.(2023湖南长沙二模)如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,DE平分∠ADC,BC=4,则DE的长是 .13.【新独家原创】如图1,有一个边长为2的正方形MNPQ,将其分割成8块(其中I、J、H、G分别为OM、ON、OP、OQ的中点),再将其组合成如图2所示的矩形ABCD,则这个矩形ABCD的对角线长为 .14.如图,在△ABC中,D,E,F分别是边AB,AC,BC的中点,四边形DECF 的周长为18,则AC+BC的长为 .15.(2021北京中考)如图,在矩形ABCD中,点E,F分别在BC,AD上,AF=EC,只需添加一个条件即可证明四边形AECF是菱形,这个条件可以是 (写出一个即可).16.(2021江苏连云港中考)如图,菱形ABCD的对角线AC、BD相交于点O,OE⊥AD,垂足为E,AC=8,BD=6,则OE的长为 .17.(2023广东珠海期中)如图,在△ABC中,∠BAC=90°,AB=12,AC=16, P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM 长的最小值为 .18.(2020山东枣庄中考)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .三、解答题(共46分)19.(2023山东枣庄期末)(8分)如图,四边形ABCD的两条对角线相交于点O,E是DC边上一点,连接EO并延长交AB于点F.若OA=OC,AB∥CD.(1)求证:四边形ABCD是平行四边形;(2)若DE=1,AC+BD=10,△AOB的周长为9,求AF的长.20.(2023四川内江中考)(8分)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.(1)求证:FA=BD;(2)连接BF,若AB=AC,求证:四边形ADBF是矩形.21.(2023上海宝山期末)(10分)如图,在矩形ABCD中,对角线AC、BD相交于点O,E为CD的中点,连接OE并延长至点F,使EF=EO,连接DF、CF.(1)求证:四边形DOCF是菱形;(2)已知AB=6,∠DOE=30°,求AC的长.22.(2020北京中考)(10分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF,连接OE.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.23.(10分)课本再现:(1)如图1,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F,求证:四边形CEDF是正方形;深入探究:(2)如图2,在△ABC中,∠ACB=60°,CD平分∠ACB,过点D作DE⊥BC 于点E,DF⊥AC于点F,点H是CD的中点,连接HE,FH,EF.①判断四边形DFHE的形状,并证明;②已知CD=42,求FE的长.答案全解全析1.C ∵四边形ABCD 是平行四边形,∴∠A=∠C,∠B=∠D,∴选项C 符合题意,故选C.2.C 根据两组对边分别平行的四边形是平行四边形知选项A 中条件可以判定四边形ABCD 是平行四边形;根据两组对边分别相等的四边形是平行四边形知选项B 中条件可以判定四边形ABCD 是平行四边形;根据一组对边平行,另一组对边相等无法判定四边形ABCD 是平行四边形,故选项C 中的条件不能判定四边形ABCD 是平行四边形;根据两组对角线互相平分的四边形是平行四边形知选项D 中的条件可以判定四边形ABCD 是平行四边形.故选C.3.D ∵点D,E 分别为AB,AC 的中点,∴DE 是△ABC 的中位线,∴DE=12BC=12×4=2,故选D.4.B 由题图可得,AB=7-1=6(cm),∵∠ACB=90°,点D 为线段AB 的中点,∴CD=12AB=3 cm,故选B.5.D ∵四边形ABCD 是菱形,∴AB=AD=CD=BC,AC ⊥BD,又∵点M 是AB 的中点,∴AB=2OM=6 cm,∴菱形ABCD 的周长=4×6=24(cm),故选D.6.C ∵四边形ABCD 是矩形,∴∠BAD=90°,OA=OB,∴∠BAE+∠EAD=90°,∵∠EAD=3∠BAE,∴∠BAE+3∠BAE=90°,∴∠BAE=22.5°,∵AE ⊥BD,∴∠ABE=90°-∠BAE=90°-22.5°=67.5°,∵OA=OB,∴∠OAB=∠ABE=67.5°,∴∠EAO=∠OAB-∠BAE=67.5°-22.5°=45°,故选C.7.C 选项A,由题图中标注的角的度数可知平行四边形的邻边不相等,不能判定为菱形,故选项A不符合题意;选项B,由题图中标注的线段的长度不能得到平行四边形的邻边相等,不能判定为菱形,故选项B不符合题意;选项C,∵62+82=102,∴对角线互相垂直,∴根据题图中标注的线段的长度能判定为菱形,故选项C符合题意;选项D,由题图中标注的角的度数可知平行四边形的对角线不互相垂直,不能判定为菱形,故选项D不符合题意.故选C.8.C A.测量两条对角线是否相等,不能判断是不是平行四边形,更不能判断是不是矩形,故选项A不符合题意;B.度量两个角是不是90°,不能判断是不是平行四边形,更不能判断是不是矩形,故选项B不符合题意;C.测量两条对角线的交点到四个顶点的距离是否相等,可以判断是不是矩形,故选项C符合题意;D.测量两组对边是否分别相等,可以判断是不是平行四边形,但不能判断是不是矩形,故选项D不符合题意.故选C.9.B ∵四边形PBEF为正方形,∴∠PBE=90°,PF=PB,∵∠CBE=α,∴∠PBC=90°-α,∵四边形APCD是正方形,∴∠APF=90°=∠CPB,AP=CP.在△APF和△CPB中,AP=CP,∠APF=∠CPB, PF=PB,∴△APF≌△CPB(SAS),∴∠AFP=∠PBC=90°-α.故选B.10.C 根据作图知EF垂直平分AC,∴AO=CO,∵AD∥BC,∴∠EAO=∠FCO,在△AOE和△COF中,∠EAO=∠FCO,AO=CO,∠AOE=∠COF=90°,∴△AOE≌△COF(ASA),∴OE=OF,∵OA=OC,AC⊥EF,∴四边形AECF是菱形,故结论①正确;∴AF=CF,∴∠FAC=∠FCA,∵∠AFB=∠FAO+∠ACB,∴∠AFB=2∠ACB,AC·EF,故结论③不正确;∵四边故结论②正确;S四边形AECF=CF·CD=12形AECF为菱形,∴∠FAC=∠EAC,∵AF平分×90°=30°,∴AF=2BF,∴AB=3∠BAC,∴∠BAF=∠FAC=∠CAD=13BF,∵CF=AF,∴CF=2BF=23AB,故结论④不正确.故选C.311.答案 100°解析 ∵四边形ABCD是平行四边形,∴DC∥AB,AD∥BC,∴∠EAB=∠DEA=40°,∠DAB+∠B=180°,∵AE平分∠DAB,∴∠DAB=2∠BAE=80°,∴∠B=180°-∠DAB=100°.12.答案 2AB,∵DE平分解析 ∵∠ACB=90°,点D是斜边AB的中点,∴AD=CD=12BC=2.∠ADC,∴AE=EC,∴ED是△ABC的中位线,∴DE=1213.答案 13AB,解析 如图,由题意知CE=EF=FB=12∵原正方形的边长AB=2,∴CB=3,∴矩形ABCD的对角线长为22+32 =13.14.答案 18解析 ∵D,E,F 分别是边AB,AC,BC 的中点,∴DE,DF 都是△ABC 的中位线,EC=12AC,FC=12BC,∴DF=12AC=EC,DE=12BC=FC,∵四边形DECF 的周长为18,∴DE+FC+DF+EC=18,∴2DE+2DF=18,∴AC+BC=18.15.答案 AE=AF(答案不唯一)解析 答案不唯一,如添加条件AE=AF,在矩形ABCD 中,AD ∥BC,即AF ∥CE,∵AF=EC,∴四边形AECF 是平行四边形,∵AE=AF,∴四边形AECF 是菱形.16.答案 125解析 ∵四边形ABCD 是菱形,∴AC ⊥BD,AO=CO,DO=BO.∵AC=8,BD=6,∴AO=4,DO=3,∴AD=AO 2+DO 2=42+32=5.又∵OE ⊥AD,∴AO·DO 2=AD·OE 2,∴4×32=5OE 2,解得OE=125.17.答案 4.8解析 连接AP,如图所示,∵∠BAC=90°,AB=12,AC=16,∴BC=122+162=20,∵PE ⊥AB,PF ⊥AC,∴四边形AFPE 是矩形,∴EF=AP,EF 与AP 互相平分,∵M 是EF 的中点,∴M 为AP 的中点,∴PM=12AP,当AP ⊥BC 时,AP 最短,同样PM 也最短,此时AP=AB·AC BC =9.6,∴PM=12AP=4.8,∴PM 长的最小值为4.8.18.答案 85解析 如图,连接BD 交AC 于点O,∵四边形ABCD 为正方形,AC=8,∴BD ⊥AC,OD=OB=OA=OC=4,∵AE=CF=2,∴OA-AE=OC-CF,即OE=OF=2,∴四边形BEDF 为平行四边形,∵BD ⊥EF,∴四边形BEDF 为菱形,∴DE=DF=BE=BF,由勾股定理得DE=OD 2+OE 2=42+22=25,∴四边形BEDF 的周长=4DE=4×25=85.19.解析 (1)证明:∵AB ∥CD,∴∠BAO=∠DCO,∵OA=OC,∠BOA=∠DOC,∴△BOA ≌△DOC(ASA),∴OB=OD,∵OA=OC,∴四边形ABCD 是平行四边形.(2)∵四边形ABCD 是平行四边形,∴OB=12BD,OA=12AC,∴OA+OB=12(AC+BD)=5,∵△AOB 的周长为9,∴AB=9-(OA+OB)=4,∵AB ∥CD,∴∠ABO=∠CDO,∵∠BOF=∠DOE,OB=OD,∴△DOE ≌△BOF,∴BF=DE=1,∴AF=AB-BF=3.20.证明 (1)∵AF ∥BC,∴∠AFE=∠DCE,∠FAE=∠CDE,∵E 为AD 的中点,∴AE=DE,∴△AEF ≌△DEC(AAS),∴AF=DC,∵D 为BC 的中点,∴BD=CD,∴AF=BD.(2)∵AF=BD,AF ∥BD,∴四边形ADBF 是平行四边形,∵AB=AC,D 为BC 的中点,∴AD ⊥BC,∴∠ADB=90°,∴四边形ADBF 是矩形.21.解析 (1)证明:∵E 是CD 的中点,∴CE=DE,在△ODE 和△FCE 中,DE =CE,∠DEO =∠CEF,EO =EF,∴△ODE ≌△FCE(SAS),∴OD=CF.同理可得OC=DF,∴四边形DOCF 是平行四边形,∵四边形ABCD 是矩形,∴OC=OD,∴四边形DOCF 是菱形.(2)∵四边形ABCD 是矩形,∴AO=CO,∠BCD=90°,CD=AB=6,AC=BD,∵E 为CD 的中点,∴OE 是△BCD 的中位线,∴OE ∥BC,∴∠CBD=∠DOE=30°,∴AC=BD=2CD=12.22.解析 (1)证明:∵四边形ABCD 是菱形,∴DO=BO.∵E 是AD 的中点,∴EO ∥AB.∵EF ∥OG,∴四边形OEFG 是平行四边形.∵EF ⊥AB,∴∠EFB=90°,∴四边形OEFG 是矩形.(2)∵四边形ABCD 是菱形,∴AC ⊥BD,AB=AD=10.在Rt △AOD 中,E 为AD 的中点,∴AE=12AD=5,OE=12AD=5.在Rt △AFE 中,EF=4,∴AF=AE 2-EF 2=52-42=3.∵四边形OEFG 是矩形,∴FG=EO=5,∴BG=AB-AF-FG=2.23.解析 (1)证明:∵CD 平分∠ACB,DE ⊥BC,DF ⊥AC,∴DE=DF,∠DFC=90°,∠DEC=90°,∵∠ACB=90°,∴四边形CEDF 是正方形.(2)①四边形DFHE 为菱形.证明:∵CD 平分∠ACB,∠ACB=60°,∴∠FCD=∠ECD=30°,∵DE ⊥BC,DF ⊥AC,∴DF=DE=12CD,∵点H 是CD 的中点,∴FH=12CD,HE=12CD,∴DF=DE=HF=HE,∴四边形DFHE 为菱形.②设DH 与EF 的交点为O.∵CD=42,点H 是CD 的中点,∴HD=22,∵四边形DFHE 为菱形,∴HO=12DH=2,∵HF=12CD=DH=22,∴FE=2OF=2HF 2-OH 2=2(22)2-(2)2=26.。
2020-2021学年人教版八年级数学下册 第18章 《平行四边形》 单元综合测试卷(含答案)

人教版八年级数学下册第18章平行四边形单元综合测试卷(时间90分钟,满分120分)一、选择题(共10小题,3*10=30)1.已知▱ABCD的周长为32,AB=4,则BC的长为()A.4 B.12 C.24 D.282.如图,由六个全等的正三角形拼成的图,图中平行四边形的个数是()A.4个B.6个C.8个D.10个3.下列四组条件中,不能判定四边形ABCD是平行四边形的是()A.AB=DC,AD=BCB.AB∥DC,AD∥BCC.AB∥DC,AD=BCD.AB∥DC,AB=DC4.下列命题中,真命题是()A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形5.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是() A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形6. 如图,把矩形纸条ABCD沿EF,GH同时折叠,B,C两点恰好都落在AD边的P点处,若∠FPH =90°,PF=16,PH=12,则矩形ABCD的边BC长为()A .40B .44C .48D .607.一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为( ) A .8 B .12 C .16 D .328.将一张矩形纸片对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )A .三角形B .矩形C .菱形D .梯形 9.平行四边形的对角线一定具有的性质是( ) A .相等 B .互相平分C .互相垂直D .互相垂直且相等10.矩形ABCD 与CEFG 如图放置,点B ,C ,E 共线,点C ,D ,G 共线,连接AF ,取AF 的中点H ,连接GH.若BC =EF =2,CD =CE =1,则GH =( )A .1B .23C .22D .52二.填空题(共8小题,3*8=24)11.如图,在▱ABCD 中,DE 平分∠ADC ,AD =6,BE =2,则▱ABCD 的周长是________.12. 如图,已知▱ABCD 的对角线AC ,BD 交于点O ,且AC =8,BD =10,AB =5,则△OCD 的周长为__ __.13.如图,在平面直角坐标系中,△ACE 是以菱形ABCD 的对角线AC 为边的等边三角形,AC =2,点C 与点E 关于x 轴对称,则点D 的坐标是__ __.14.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC∶∠EDA=1∶2,且AC=10,则EC的长度是________.15.如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是线段AO,BO的中点.若AC+BD=30 cm,△OAB的周长为23 cm,则EF的长为__________.16.如图,在△ABC中,AB=BC,AB=12 cm,F是AB上一点,过点F作FE∥BC交AC于点E,过点E作ED∥AB交BC于点D,则四边形BDEF的周长是__ _.17.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为_______.18.菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,3),动点P从点A出发,沿A→B→C→D→A→B→……的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2 020秒时,点P的坐标为________.三.解答题(7小题,共66分)19.(8分) 如图所示,在▱ABCD中,AC,BD交于点O,点E,F分别是OA,OC的中点,请判断线段BE,DF的大小关系,并证明你的结论.20.(8分) 平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.已知:如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.21.(8分) 如图,在▱ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE =CF.22.(10分) 如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD 交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.23.(10分) 如图,△ABC中,∠ACB=90°,D为AB的中点,四边形BCED为平行四边形,DE,AC相交于F.连接DC,AE.(1)试确定四边形ADCE的形状,并说明理由.(2)若AB=16,AC=12,求四边形ADCE的面积.(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.24.(10分) 如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB,AC上的一动点,且满足BP=AQ,D是BC的中点.(1)求证:△PDQ是等腰直角三角形;(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.25.(12分) 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.参考答案1-5BBCCD 6-10CCCBC 11.20 12. 14 13.(33,0) 14.2.5 15.4 cm 16. 24cm 17. 10 18.(0,3) 19. 解:BE =DF.理由如下:连接DE ,BF. ∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD. ∵E ,F 分别是OA ,OC 的中点,∴OE =OF. ∴四边形BFDE 是平行四边形.∴BE =DF. 20. 证明:连接AC ,如图,在△ABC 和△CDA 中,⎩⎪⎨⎪⎧AB =CD CB =AD AC =CA ,∴△ABC ≌△CDA(SSS),∴∠BAC =∠DCA ,∠ACB =∠CAD ,∴AB ∥CD ,BC ∥AD ,∴四边形ABCD 是平行四边形21. 证明:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,∴∠BAE =∠DCF.又BE ⊥AC ,DF ⊥AC ,∴∠AEB =∠CFD =90°. 在△ABE 与△CDF 中, ⎩⎪⎨⎪⎧∠AEB =∠CFD ,∠BAE =∠DCF ,AB =CD ,∴△ABE ≌△CDF(AAS),∴AE =CF22. 证明:∵AF ∥CD ,∴∠AFE =∠CDE ,在△AFE 和△CDE 中,⎩⎪⎨⎪⎧∠AFE =∠CDE ,∠AEF =∠CED ,AE =CE ,∴△AEF ≌△CED.AF =CD ,∵AF ∥CD ,∴四边形ADCF 是平行四边形.∴AE =12AC ,又AC =2AB ,AE =AB ,∠EAD =∠BAD ,AD =AD ,∴△AED ≌△ABD.∴∠AED =∠B =90°,即DF ⊥AC. ∴四边形ADCF 是菱形23.解:(1)四边形ADCE 是菱形.理由:∵四边形BCED 为平行四边形,∴CE ∥BD ,CE =BD ,BC ∥DE. ∵D 为AB 的中点,∴AD =BD. ∴CE =AD. 又∵CE ∥AD ,∴四边形ADCE 为平行四边形.∵BC ∥DF ,∴∠AFD =∠ACB =90°,即AC ⊥DE. ∴四边形ADCE 为菱形.(2)在Rt △ABC 中,∵AB =16,AC =12,∴BC =47. ∵BC =DE ,∴DE =47. ∴四边形ADCE 的面积=12AC·DE =247.(3)当AC =BC 时,四边形ADCE 为正方形.证明:∵AC =BC ,D 为AB 的中点,∴CD ⊥AB ,即∠ADC =90°. ∴四边形ADCE 为正方形.∠ADP +∠ADQ =90°,即∠PDQ =90°,∴△PDQ 为等腰直角三角形(2)当P 点运动到AB 的中点时,四边形APDQ 是正方形; 理由:∵P 为AB 的中点,AB =AC ,BP =AQ ,∴点Q 为AC 的中点,在Rt △ABD 和Rt △ACD 中,DP =AP =12AB ,QD =AQ =12AC , ∴DP=AP =QD =AQ ,∴四边形APDQ 为菱形,又∵∠A =90°,∴四边形APDQ 是正方形25.解:(1)证明:在△ABC 和△ADC 中,⎩⎪⎨⎪⎧AB =AD ,CB =CD ,AC =AC ,∴△ABC ≌△ADC(SSS), ∴∠BAC =∠DAC.在△ABF 和△ADF 中,⎩⎪⎨⎪⎧AB =AD ,∠BAF =∠DAF ,AF =AF ,∴△ABF ≌△ADF ,∴∠AFD =∠AFB. 又∵∠AFB =∠CFE ,∴∠AFD =∠CFE.(2)证明:∵AB ∥CD ,∴∠BAC =∠ACD. 又由(1)知∠BAC =∠DAC ,∴∠CAD =∠ACD ,∴AD =CD. 又∵AB =AD ,CB =CD ,∴AB =CB =CD =AD ,∴四边形ABCD 是菱形.(3)当BE ⊥CD 时,∠EFD =∠BCD. 理由:∵由(2)知四边形ABCD 是菱形,∴CB =CD ,∠BCF =∠DCF.又CF =CF ,∴△BCF ≌△DCF ,∴∠CBF =∠CDF. 又∵BE ⊥CD ,∴∠BEC =∠DEF =90°.∴∠BCD +∠CBF =90°,∠EFD +∠CDF =90°. 又∵∠CBF =∠CDF ,∴∠EFD =∠BCD.。
(常考题)人教版初中数学八年级数学下册第三单元《平行四边形》检测题(答案解析)(1)

一、选择题1.如图,三个正方形围成一个直角三角形,64、400分别为所在正方形的面积,则图中字母M 所代表的正方形面积可表示为( )A .40064-B .2240064-C .2240064-D .40064+ 2.已知正方形ABCD 中,对角线4AC =,这个正方形的面积是( )A .8B .16C .82D .162 3.已知点()0,0A ,()0,4B ,()3,4C t +,()3,D t .记()N t 为ABCD 内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则()N t 所有可能的值为( )A .6、7B .7、8C .6、7、8D .6、8、9 4.顺次连接矩形ABCD 各边的中点,所得四边形是( )A .平行四边形B .正方形C .矩形D .菱形 5.如图,在正方形 ABCD 内有一个四边形AECF ,AE EF ⊥, CF EF ⊥且8AE CF ==,12EF =,则图中阴影分的面积为( )A .100B .104C .152D .3046.在菱形ABCD 中,∠ABC=60゜,AC=4,则BD=( )A .3B .23C .33D .437.如图,点P 是矩形ABCD 的对角线上一点,过点P 作//EF BC ,分别交,AB CD 于,E F ,连接,PB PD ,若1,3AE PF ==,则图中阴影部分的面积为( )A .3B .6C .9D .12 8.如图,点E 为矩形ABCD 的边BC 上的点,DF AE ⊥于点F ,且DF AB =,下列结论不正确的是( )A .DE 平分AEC ∠B .ADE ∆为等腰三角形C .AF AB =D .AE BE EF =+ 9.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,过点D 作DH ⊥AB 于点H ,连接OH ,若OA =6,S 菱形ABCD =48,则OH 的长为( )A .4B .8C .13D .610.如图,将长方形ABCD 沿对角线BD 折叠,使点C 落在点C ′处,BC ′交AD 于E ,AD =8,AB =4,则重叠部分(即BDE )的面积为( )A .6B .7.5C .10D .2011.如图,在矩形ABCD 中,3AB =,4=AD ,ABC ∠的平分线BE 交AD 于点E .点F ,G 分别是BC ,BE 的中点,则FG 的长为( )A .2B .52C .10D .32 12.如图,将三角形纸片ABC 沿过,AB AC 边中点D 、E 的线段DE 折叠,点A 落在BC 边上的点F 处,下列结论中,一定正确的个数是( )①BDF 是等腰三角形 ②12DE BC = ③四边形ADFE 是菱形 ④2BDF FEC A ∠+∠=∠A .1B .2C .3D .4二、填空题13.如图,在Rt △ABC 中,∠ACB =90°,CD 是斜边AB 上的中线,E 、F 分别为DB 、BC 的中点,若AB =8,则EF =_____.14.如图,EF 过ABCD 对角线的交点O ,交AD 于E ,交BC 于F ,若ABCD 的周长为19, 2.5OE =,则四边形EFCD 的周长为_____.15.己知菱形ABCD 的边长是3,点E 在直线AD 上,DE =1,联结BE 与对角线AC 相交于点M ,则AM MC的值是______.16.如图,在四边形ABCD 中,AC a =,BD b =,且AC BD ⊥顺次连接四边形ABCD 各边的中点,得到四边形1111D C B A ,再顺次连接四边形1111D C B A 各边中点,得到四边形2222A B C D …如此进行下去,得到四边形n n n n A B C D ,下列结论正确的有__________.①四边形2222A B C D 是矩形;②四边形4444A B C D 是菱形;③四边形5555A B C D 的周长是4a b +.17.如图,在ABCD 中,AC 与BD 相交于点O ,(1)若18cm,24cm AC BD ==,则AO =_______,BO =_______.又若13AB =厘米,则COD △的周长为________.(2)若AOB 的周长为30cm ,12cm AB =,则对角线AC 与BD 的和是________. 18.如图,菱形ABCD 的对角线相交于点O ,AC =12,BD =16,点P 为边BC 上一点,且P 不与写B 、C 重合.过P 作PE ⊥AC 于E ,PF ⊥BD 于F ,连结EF ,则EF 的最小值等于__________.19.把一张矩形纸片ABCD 按如图方式折叠,使顶点B 和顶点D 重合,折痕为EF .若38CDF ∠=︒,则EFD ∠ 的度数是_________.20.如图所示,在ABCD 中,AC 与BD 相交于点O ,若DAC EAC ∠=∠,4AE =,3AO =,则AEC S ∆的面积为____.三、解答题21.如图所示,小明在测量旗杆AB 的高度时发现,国旗的升降绳自然下垂到地面时,还剩余0.3米,小明走到距离国旗底部6米的C 处,把绳子拉直,绳子末端恰好位于他的头顶D 处,假设小明的身高为1.5米,求旗杆AB 的高度是多少米?22.如图,BD 为ABC 的角平分线,E 为AB 上一点,BE BC =,连结DE . (1)求证:BDC BDE ≅△△;(2)若7AB =,2CD =,90︒∠=C ,求ABD △的面积.23.如图,点E 在ABCD 内部,//,//AF BE DF CE .(1)求证:BCE ADF ≅∆;(2)求证:AEDF 1S 2ABCD S =四边形24.我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.但人们可以通过折纸把一个角三等分,今天我们就通过折纸把一个直角三等分.操作如下:第一步:如图①,对折长方形纸片ABCD ,使AD 与BC 重合,沿EF 对折后,得到折痕EF ,把纸片展平;第二步:如图②,再一次折叠纸片,使点A 落在EF 上(标记为点O ),并使折痕经过点B ;第三步:如图③,再展开纸片,得到折痕BR ,同时连接BO RO 、.这时就可以得到BR BO 、把直角ABC 三等分.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程. 已知:如图④,线段EF 是长方形ABCD 对折后的折痕,BOR ∆是由BAR ∆沿BR 折叠后得到的三角形 ,求证:25.如图,四边形ABCD 是平行四边形,∠BAD 的角平分线AE 交CD 于点F ,交BC 的延长线于点E .(1)求证:BE =CD ;(2)若BF 恰好平分∠ABE ,连接AC 、DE ,求证:四边形ACED 是平行四边形.26.如图1,正方形ABCD ,E 为平面内一点,且90BEC ∠=︒,把BCE 绕点B 逆时针旋转90︒得BAG ,直线AG 和直线CE 交于点F .(1)证明:四边形BEFG 是正方形;(2)若135AGD ∠=︒,猜测CE 和CF 的数量关系,并说明理由;(3)如图2,连接DF ,若13AB =,17CF =,求DF 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】要求图中字母所代表的正方形的面积,根据面积=边长×边长=边长的平方,设M 的边长为a ,直角三角形斜边的长为c ,另一直角边为b ,则2400c =,264b =,已知斜边和一直角边的平方,由勾股定理即可求出2a ,即可得到答案.【详解】设M 的边长为a ,直角三角形斜边的长为c ,另一直角边为b ,则2400c =,264b =,如图所示,在该直角三角形中,由勾股定理得:22240064a c b =-=-,故选:A .【点睛】本题主要考查勾股定理的应用和正方形的面积公式,解题的关键在于熟练运用勾股定理求出正方形的边长的平方.2.A解析:A【分析】根据勾股定理,可得正方形的边长,进而可得正方形的面积.【详解】∵正方形ABCD中,对角线4AC ,∴AB2+BC2=AC2,∴2AB2=42,∴AB2=8.故选:A.【点睛】本题主要考查的是正方形的性质,勾股定理,熟练掌握勾股定理是解题的关键.3.C解析:C【分析】分别求出t=1,t=1.5,t=2,t=0时的整数点,根据答案即可求出答案.【详解】解:当t=0时,A(0,0),B(0,4),C(3,4),D(3,0),此时整数点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),共6个点;当t=1时,A(0,0),B(0,4),C(3,5),D(3,1),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),共8个点;当t=1.5时,A(0,0),B(0,4),C(3,5.5),D(3,1.5),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),共7个点;当t=2时,A(0,0),B(0,4),C(3,6),D(3,2),此时整数点有(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(2,5),共8个点;故选项A错误,选项B错误;选项D错误,选项C正确;故选:C.【点睛】本题考查了平行四边形的性质.主要考查学生的理解能力和归纳能力.4.D解析:D【分析】利用三角形中位线定理,矩形对角线的性质,菱形的判定判断即可.【详解】如图,设矩形ABCD各边的中点依次为E,F,G,H,∴EF,FG,GH,HE分别是△ABC,△BCD,△CDA,△DAB的中位线,∴EF=12AC,FG=12BD,GH=12AC,EH=12BD,∵四边形ABCD是矩形,∴AC=BD,∴EF=FG=GH=HE,∴四边形EFGH 是菱形,故选D.【点睛】本题在矩形背景考查了三角形中位线定理,菱形的判定,矩形的性质,熟练运用三角形中位线定理,矩形的性质,菱形的判定是解题的关键.5.B解析:B【分析】由题意可证四边形AECF 是平行四边形,可得AO =CO ,EO =FO =12EF =6,由勾股定理可求AO =10,可得AC =20,由阴影分的面积=S 正方形ABCD -S ▱AECF 可求解.【详解】解:连接AC ,∵AE ⊥EF ,CF ⊥EF ,∴AE ∥CF ,且AE =CF ,∴四边形AECF 是平行四边形,∴AO =CO ,EO =FO =12EF =6, ∴AO 22AE EO +10,∴AC =20, ∴阴影分的面积=S 正方形ABCD -S ▱AECF =20202⨯-8×12=104, 故选:B .【点睛】本题考查了正方形的性质以及勾股定理的应用.此题综合性较强,解题时要注意数形结合思想的应用.6.D解析:D【分析】根据菱形的性质可得到直角三角形,利用勾股定理计算即可;【详解】如图,AC 与BD 相较于点O ,∵四边形ABCD 是菱形,4AC =,∴AC BD ⊥,2AO =,又∵∠ABC=60゜,∴30ABO ∠=︒,∴24AB AO ==, ∴224223BO =-=,∴243BD BO ==;故选D .【点睛】本题主要考查了菱形的性质,结合勾股定理计算是解题的关键. 7.A解析:A【分析】先根据矩形的性质证得DFP PBE SS =,然后求解即可.【详解】解:作PM ⊥AD 于M ,交BC 于N ,∴四边形AEPM 、四边形DFPM 、四边形CFPN 和四边形BEPN 都是矩形, ∵ADC ABC S S =△△,AMP AEP SS =,PBE PBN S S =,PFD PDM S S =,PFC PCN S S =, ∴S 矩形DFPM =S 矩形BEPN ,∵PM=AE=1,PF=NC=3,∴131322DFP PBE S S ==⨯⨯=△△, ∴S 阴=33+=322, 故选:A .【点睛】 本题主要考查矩形的性质、三角形的面积等知识,证得DFP PBE S S =是解答本题的关键. 8.C解析:C【分析】根据矩形的性质及HL 定理证明Rt △DEF ≌Rt △DEC ,然后利用全等三角形的性质进行推理判断【详解】解:在矩形ABCD 中,∠C=90°,AB=CD∵DF AE ⊥于点F ,且DF AB =∴∠DFE=∠C=90°,DF=CD在Rt △DEF 和Rt △DEC 中DF DC DE DE=⎧⎨=⎩ ∴Rt △DEF ≌Rt △DEC∴∠FDE=∠CDE ,即DE 平分AEC ∠,故A 选项不符合题意;∵Rt △DEF ≌Rt △DEC∴∠FED=∠CED又∵矩形ABCD 中,AD ∥BC∴∠ADE=∠CED∴∠FED=∠ADE∴AD=AE ,即ADE ∆为等腰三角形,故B 选项不符合题意∵Rt △DEF ≌Rt △DEC∴EF=EC在矩形ABCD 中,AD=BC ,又∵AD=AE∴AE=AD=BC=BE+EC=BE+EF ,故D 选项不符合题意由于AB=CD=DF ,但在Rt △ADF 中,无法证得AF=DF ,故无法证得AB=AF ,故C 选项符合题意故选:C .【点睛】本题考查矩形的性质及三角形全等的判定和性质,掌握相关性质定理正确推理论证是解题关键. 9.A解析:A【分析】由菱形的性质得出OA =OC =6,OB =OD ,AC ⊥BD ,则AC =12,由直角三角形斜边上的中线性质得出OH =12AB ,再由菱形的面积求出BD =8,即可得出答案. 【详解】解:∵四边形ABCD 是菱形,∴OA =OC =6,OB =OD ,AC ⊥BD ,∴AC =12,∵DH ⊥AB ,∴∠BHD =90°,∴OH =12BD , ∵菱形ABCD 的面积=12×AC×BD =12×12×BD =48, ∴BD =8,∴OH =12BD =4; 故选:A .【点睛】本题考查了菱形的性质,直角三角形的性质,菱形的面积公式,关键是根据直角三角形斜边上的中线性质求得OH=12BD . 10.C解析:C【分析】由折叠结合矩形的性质先证明,BE DE =设,BE DE x == 则8,AE x =- 再利用勾股定理求解,x 从而可得BDE 的面积.【详解】 解: 长方形ABCD ,8,4,AD AB ==//,AD BC ∴,ADB CBD ∴∠=∠由对折可得:,CBD C BD '∠=∠,ADB C BD '∴∠=∠,BE DE ∴=设,BE DE x == 则8,AE x =-由222,BE AB AE =+ ()22248,x x ∴=+-1680,x ∴=5,x ∴=5,DE BE ∴== 115410.22BDE S DE AB ∴==⨯⨯= 故选:.C【点睛】本题考查的是矩形与折叠问题,勾股定理的应用,矩形的性质,掌握以上知识是解题的关键.11.C解析:C【分析】连接CE ,由矩形的性质和角平分线的性质可得AB=AE=3,可得ED=1,由勾股定理可求CE 的长,由三角形中位线定理可求FG 的长;【详解】连接CE ,如图所示:∵四边形ABCD 是矩形,∴∠BAD=∠ABC=∠D=90°,AB=CD=3,AD=BC=4,AD ∥BC ,∴∠CBE=∠AEB ,∵BE 平分∠ABC.∴∠ABE=∠CBE=45°,∴∠ABE=∠AEB=45°,∴AB=AE=3,∴ED=AD-AE=4-3=1,在Rt △CDE 中 22221310DE CD +=+∵点F 、G 分别为BC 、BE 的中点,∴FG 是△CBE 的中位线,FG=1210 故选:C【点睛】本题考查了矩形的性质,勾股定理,等腰直角三角形的判定与性质,三角形中位线的定理等知识;熟练掌握矩形的性质和三角形中位线定理,求出EC 的长度是解题的关键. 12.C解析:C【分析】根据菱形的判定和等腰三角形的判定,采用排除法,逐条分析判断.【详解】解:①∵DE ∥BC ,∴∠ADE =∠B ,∠EDF =∠BFD ,又∵△ADE ≌△FDE ,∴∠ADE =∠EDF ,AD =FD ,AE =CE ,∴∠B =∠BFD ,∴△BDF 是等腰三角形,故①正确;同理可证,△CEF 是等腰三角形,∴BD =FD =AD ,CE =FE =AE ,∴DE 是△ABC 的中位线,∴DE =12BC ,故②正确; ∵∠B =∠BFD ,∠C =∠CFE ,又∵∠A +∠B +∠C =180°,∠B +∠BFD +∠BDF =180°,∠C +∠CFE +∠CEF =180°, ∴∠BDF +∠FEC =2∠A ,故④正确.而无法证明四边形ADFE 是菱形,故③错误.所以一定正确的结论个数有3个,故选:C .【点睛】本题考查了菱形的判定,中位线定理,等腰三角形的判定和性质,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定.二、填空题13.2【分析】根据直角三角形的性质求出再根据三角形中位线定理计算即可【详解】解:在中是斜边上的中线分别为的中点是的中位线故答案为:2【点睛】本题考查的是直角三角形的性质三角形中位线定理掌握三角形的中位线 解析:2【分析】根据直角三角形的性质求出CD ,再根据三角形中位线定理计算即可.【详解】解:在Rt ABC ∆中,90ACB ∠=︒,CD 是斜边AB 上的中线,8AB =,118422CD AB ∴==⨯=, E 、F 分别为DB 、BC 的中点,EF ∴是BCD ∆的中位线,114222EF CD ∴==⨯=, 故答案为:2.【点睛】本题考查的是直角三角形的性质、三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.14.145【分析】根据平行四边形的性质易证三角形全等进而易得AE=CF 故四边形的周长=AD+CD+EF 根据已知求解即可【详解】解:在平行四边形ABCD 中AD ∥BCAC 与BD 互相平分∴AO=OC ∠DAC=解析:14.5【分析】根据平行四边形的性质易证三角形全等,进而易得AE=CF ,故四边形EFCD 的周长=AD+CD+EF ,根据已知求解即可.【详解】解:在平行四边形ABCD 中,AD ∥BC ,AC 与BD 互相平分∴AO=OC ,∠DAC=∠ACB ,∠AOE=∠COF∴△AOE ≌△COF∴AE=CF ,OF=OE=2.5∴四边形EFCD 的周长=CF+DE+CD+EF=AE+DE+CD+EF=AD+CD+EF =19 2.52+×2 =14.5. 故答案为:14.5.【点睛】本题考查了平行四边形的性质以及三角形全等的证明,将所求线段转化为已知线段是解题的关键.15.或【分析】首先根据题意作图注意分为E 在线段AD 上与E 在AD 的延长线上然后由菱形的性质可得AD ∥BC 则可证得△MAE ∽△MCB 根据相似三角形的对应边成比例即可求得答案【详解】解:∵菱形ABCD 的边长是 解析:23或43【分析】 首先根据题意作图,注意分为E 在线段AD 上与E 在AD 的延长线上,然后由菱形的性质可得AD ∥BC ,则可证得△MAE ∽△MCB ,根据相似三角形的对应边成比例即可求得答案.【详解】解:∵菱形ABCD 的边长是3,∴AD=BC=3,AD ∥BC ,如图①:当E 在线段AD 上时,∴AE=AD -DE=3-1=2,∴△MAE ∽△MCB , ∴23MA AE MC BC ==; 如图②,当E 在AD 的延长线上时,∴AE=AD+DE=3+1=4,∴△MAE ∽△MCB ,∴43MA AE MC BC ==. ∴MA MC的值是23或43. 故答案为23或43.【点睛】此题考查了菱形的性质,相似三角形的判定与性质等知识.解题的关键是注意此题分为E 在线段AD 上与E 在AD 的延长线上两种情况,小心不要漏解.16.②③【分析】利用三角形的中位线的性质证明四边形是矩形四边形是菱形四边形是矩形四边形是菱形从而可得到规律序号n 是奇数时四边形是矩形当序号n 是偶数时四边形是菱形再探究n 是奇数时四边形的周长即可解决问题【 解析:②③【分析】利用三角形的中位线的性质证明四边形1111D C B A 是矩形,四边形2222A B C D 是菱形,四边形3333A B C D 是矩形,四边形4444A B C D 是菱形,从而可得到规律,序号n 是奇数时四边形是矩形,当序号n 是偶数时四边形是菱形,再探究n 是奇数时四边形的周长即可解决问题.【详解】解: 1111,,,A B C D 分别是,,,AB BC CD DA 的中点,1111111111//,,//,,22A B AC A B AC C D AC C D AC ∴== 11//,A D BD11111111//,,A B C D A B C D ∴=∴ 四边形1111D C B A 是平行四边形,,AC BD ⊥ 11//,A B AC 11//,A D BD1111,A B A D ∴⊥∴ 四边形1111D C B A 是矩形,1111,AC B D ∴=如图,2222,,,A B C D 分别是11111111,,,A B B C C D D A 的中点,∴ 2211221111,,22A B AC A D B D == 四边形2222A B C D 是平行四边形, 2222,A B A D ∴=∴ 四边形2222A B C D 是菱形,故①不符合题意,2222,A C B D ∴⊥同理可得:四边形3333A B C D 是矩形,四边形4444A B C D 是菱形,故②符合题意,······总结规律:四边形n n n n A B C D , 当序号n 是奇数时四边形是矩形,当序号n 是偶数时四边形是菱形,111111111111,,2222A B C D AC a A D B C BD b ====== ∴ 四边形1111D C B A 的周长为,a b + 如图, 四边形1111D C B A 是矩形,四边形2222A B C D 是菱形,2222,,,A B C D 分别是11111111,,,A B B C C D D A 的中点,222222112211,,,A C B D A C A D B D A B ∴⊥==由中位线的性质同理可得:33332233332211111111,,22242224A DBC BD a a D C A B A C b b ===⨯====⨯= 所以四边形3333A B C D 的周长为()1,2a b + 由规律可得:四边形5555A B C D 是矩形, 同理可得:四边形5555A B C D 的周长是()11.224a b a b +⨯+=故③符合题意. 故答案为②③.【点睛】本题考查三角形的中位线的性质,中点四边形,菱形的判定与性质,矩形的判定与性质,解题的关键是学会从特殊到一般,探究规律,利用规律解决问题.17.9cm12cm34cm36cm 【分析】(1)根据平行四边形对角线互相平分对边相等可得结果;(2)根据△AOB 的周长和AB 的长度得到AO+BO 从而得到AC+BD 【详解】解:(1)在平行四边形ABCD 中解析:9cm 12cm 34cm 36cm【分析】(1)根据平行四边形对角线互相平分,对边相等可得结果;(2)根据△AOB 的周长和AB 的长度,得到AO+BO ,从而得到AC+BD .【详解】解:(1)在平行四边形ABCD 中,∵AC=18cm ,BD=24cm ,∴AO=12AC=9cm=CO ,BO=12BD=12cm=DO , ∵AB=13cm ,∴CD=13cm ,∴COD △的周长为CO+DO+CD=9+12+13=34cm ,故答案为:9cm ,12cm ,34cm ;(2)∵△AOB 的周长为30cm ,∴AB+AO+BO=30cm ,∵AB=12cm ,∴AO+BO=30-12=18cm ,∴AC+BD=2AO+2BO=36cm .【点睛】此题考查了平行四边形的性质:平行四边形的对角线互相平分,平行四边形的对边相等. 18.48【分析】连接由菱形的性质解得再根据勾股定理解得继而证明四边形为矩形得到根据垂线段最短解得当时有最小值最后根据三角形面积公式解题即可【详解】连接四边形是菱形四边形为矩形当时有最小值此时的最小值为故 解析:4.8【分析】连接OP ,由菱形的性质解得118,622BO BD OC AC ====,再根据勾股定理解得10BC =,继而证明四边形OEPF 为矩形,得到FE OP =,根据垂线段最短解得当OP BC ⊥时,OP 有最小值,最后根据三角形面积公式解题即可.【详解】连接OP ,四边形ABCD 是菱形,12,16AC BD ==,AC BD ∴⊥118,622BO BD OC AC ==== 22643610BC OB OC ∴=+=+=,,PE AC PF BD AC BD ⊥⊥⊥∴四边形OEPF 为矩形,FE OP ∴=当OP BC ⊥时,OP 有最小值,此时1122OBC S OB OC BC OP =⋅=⋅ 68 4.810OP ⨯∴== EF ∴的最小值为4.8,故答案为:4.8.【点睛】本题考查菱形的性质、矩形的判定与性质、勾股定理、垂线段最短等知识,是重要考点,难度较易,掌握相关知识是解题关键.19.64°【分析】先根据矩形的性质求出∠CFD 的度数继而求出∠BFD 的度数根据图形折叠的性质得出∠EFD=∠BFE=∠BFD 即可得出结论【详解】解:∵ABCD 是矩形∴∠DCF=90°∵∠CDF=38°∴解析:64°【分析】先根据矩形的性质求出∠CFD 的度数,继而求出∠BFD 的度数,根据图形折叠的性质得出∠EFD=∠BFE=12∠BFD ,即可得出结论. 【详解】解:∵ABCD 是矩形,∴∠DCF=90°,∵∠CDF=38°,∴∠CFD=52°,∴∠BFD=180°-52°=128°,∵四边形EFDA 1由四边形EFBA 翻折而成,∴∠EFD=∠BFE=12∠BFD=12×128°=64°. 故答案为:64°.【点睛】本题考查的是矩形折叠问题,掌握轴对称的性质是关键.20.【分析】先证明△AEC 是等腰三角形再证OE ⊥AC 然后用勾股定理求出OE 即可求【详解】解:如图1连接OE ∵四边形ABCD 是平行四边形∴OA=OC=3AD ∥BC ∴∠DAC=∠ACB 又∵∴∠ACB=∠EA解析:37【分析】先证明△AEC 是等腰三角形,再证OE ⊥AC ,然后用勾股定理求出OE ,即可求AEC S ∆.【详解】解:如图1,连接OE ,∵四边形ABCD 是平行四边形,∴OA=OC=3,AD ∥BC ,∴∠DAC=∠ACB ,又∵DAC EAC ∠=∠,∴∠ACB=∠EAC ,∴AE=EC=4,∴△AEC 是等腰三角形,∴OE ⊥AC ,在Rt △AOE 中,由勾股定理得,AO 2+OE 2=AE 2,∴32+OE 2=42,∴∴162AEC s =⨯=故答案是:【点睛】本题综合考查了平行四边形的性质,等腰三角形的判定与性质和勾股定理等相关知识,证明△AEC 是等腰三角形是解本题的关键.三、解答题21.旗杆AB 的高度为10.6米【分析】过点D 作DE AB ⊥,垂足为E ,可证四边形BCDE 为长方形,可知 1.5BE CD ==米,设旗杆高度为x 米,则绳子长度为(0.3)AD x =+米,( 1.5)AE x =-米,在Rt ADE △中,由勾股定理,得222AE DE AD +=,222( 1.5)6(0.3)x x -+=+,解方程即可.【详解】解:过点D 作DE AB ⊥,垂足为E ,∵AB ⊥BC ,CD ⊥BC∴∠EBC=∠BCD=∠BED=90°,∴四边形BCDE 为长方形,∴ 1.5BE CD ==米,设旗杆高度为x 米,则绳子长度为(0.3)AD x =+米,( 1.5)AE AB BE x =-=-米, 在Rt ADE △中,由勾股定理,得222AE DE AD +=,∴222( 1.5)6(0.3)x x -+=+,整理得223 2.25360.60.09x x x x -++=++,即3.638.16x =,解得10.6x =.答:旗杆AB 的高度为10.6米.【点睛】本题考查勾股定理,矩形的判定与性质,一元一次方程的解法,掌握勾股定理,矩形的判定与性质,一元一次方程的解法,利用勾股定理结合旗杆与绳长的关系构造方程是解题关键.22.(1)证明见解析;(2)7【分析】(1)根据角平分线的性质可得DBC DBE ∠=∠,再根据已知条件BE BC =,BD BD =,即可证明;(2)根据(1)中结果,得2DE CD ==,90DEB C ∠=∠=︒,即可求得ABD △的面积.【详解】(1)∵BD 平分ABC ∠,∴DBC DBE ∠=∠,∴在BDC 和BDE 中,BD BD =,DBC DBE ∠=∠,BE BC =,∴BDC ≌BDE ;(2)∵BDC ≌BDE ,∴2DE CD ==,90DEB C ∠=∠=︒, ∴1172722ABD S AB DE =⋅=⨯⨯=△. 【点睛】本题考查了角平分线的性质、全等三角形的证明和性质、三角形面积等知识,解题的关键是熟练掌握运用以上知识点.23.(1)见解析;(2)见解析【分析】(1)先证明CBE DAF ∠=∠,BCE ADF ∠=∠,然后利用ASA 证明:△BCE ≌△ADF ; (2)根据点E 在ABCD 内部,可知:S △BEC +S △AED =12S ▱ABCD ,可得结论. 【详解】解:()1四边形ABCD 是平行四边形,,//AD BC AD BC =,180,ABC BAD ∴∠+∠=//,AF BE180,EAB BAF ∴∠+∠=︒,CBE DAF ∴∠=∠同理得,BCE ADF ∠=∠()BCE ADF ASA ∴∆≅∆()2点E 在ABCD 内部, ∴12BEC AED ABCD S S S ∆∆+=,由()1知: ,BCE ADF ∆≅∆BCE ADF S S ∆∆∴= ∴AEDF 1S 2ADF AED BEC AED ABCD S S S S S ∆∆∆∆=+=+=四边形.【点睛】此题主要考查了平行四边形的性质以及全等三角形的判定与性质,熟练利用三角形和平行四边形边的关系得出面积关系是解题关键.24.点O 在折痕EF 上,BR BO 、把ABC ∠三等分,见解析【分析】如图④,线段EF 是长方形ABCD 对折后的折痕,BOR ∆是BAR ∆沿BR 折叠后得到的三角形,点O 在折痕EF 上;连接AO , 根据折叠的性质可得△AOB 为等边三角形,然后结合矩形的性质即可求证所求问题.【详解】解:已知:如图④,线段EF 是长方形ABCD 对折后的折痕,BOR ∆是BAR ∆沿BR 折叠后得到的三角形,点O 在折痕EF 上.求证:BR BO 、把ABC ∠三等分证明:连接AO线段EF 是长方形ABCD 对折后的折痕 ∴EF 垂直平分AB 又点O 在对称轴EF 上AO BO ∴=BOR ∆是BAR ∆沿BR 折叠后得到的三角形,12BO AB ∴=∠=∠AO BO AB ∴==ABO ∴∆是等边三角形60ABO ︒∴∠=又12ABO ∠+∠=∠1230︒∴∠=∠= 又90ABC ︒∠= 330ABC ABO ︒∴∠=∠-∠=123∴∠=∠=∠BR BO ∴、把ABC ∠三等分.【点睛】本题主要考查矩形的性质及等边三角形的性质和判定,还考查了学生的观察力和动手能力,动手操作一下,问题更容易解决.25.(1)见解析;(2)见解析【分析】(1)根据平行四边形的性质得到AB =CD ,∠DAE =∠AEB ,利用AE 平分∠BAD ,推出∠BAE =∠AEB ,得到BE=AB ,即可得到结论;(2)根据BE =AB ,BF 平分∠ABE ,得到AF =EF ,证明△ADF ≌△ECF ,推出DF =CF ,即可得到结论.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB =CD ,∴∠DAE =∠AEB ,∵AE 平分∠BAD ,∴∠BAE =∠DAE ,∴∠BAE =∠AEB ,∴BE =AB ,∴BE=CD ;(2)∵BE =AB ,BF 平分∠ABE ,∴AF =EF ,在△ADF 和△ECF 中,DAE AEB AF EFAFD EFC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ADF ≌△ECF ,∴DF =CF ,又∵AF =EF ,∴四边形ACED 是平行四边形.【点睛】此题考查平行四边形的判定及性质,全等三角形的判定及性质,等腰三角形三线合一的性质,熟记各知识点并应用解决问题是解题的关键.26.(1)见解析;(2)CE=CF ,理由见解析;(3)52或122【分析】(1)根据正方形的判定定理进行证明即可;(2)证明Rt ADH ≌Rt BAG 得DH AG =,AH=BG ,再证明△DHG 是等腰直角三角形,可得DH=BH=AG ,最后由BEFG 是正方形可得结论;(3)分点F 在AB 右侧和左侧两种情况求解即可.【详解】解:(1)证明:90BEC =︒∠,把BCE 绕点B 逆时针旋转90︒得BAG , BE BG ∴=,90EBG ∠=︒,90BGA ∠=︒,则90BGF ∠=︒,90BEC EBG BGF ∴∠=∠=∠=︒,∴四边形BEFG 是正方形;(2)CE CF =,理由如下:过D 点作DH AF ⊥,垂足为H ,如图,四边形ABCD 是正方形,90BAD ∴∠=︒,AB AD =,90BGA ∠=︒,90DAH BAG ∴∠+∠=︒,90BAG ABG ∠+∠=︒,DAH ABG ∴∠=∠,在Rt ADH 和Rt BAG 中,90,DAH ABG BGA AHD AD AB ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩Rt ADH ∴≌()Rt BAG AAS ,DH AG ∴=,∵∠DGH =180°-∠AGD =45°∴在Rt △DHG 中,∠GDH =45°∴DH =GH =AG ∴1122AG GH AH BG === 又AG CE =,EF BG =,2EF CE ∴=,CE CF ∴=;(3)①点F 在AB 右侧时,如图,过D 作DK ⊥AG ,交其延长线于K .设正方形BEFG 的边长为x ,则BE x =,17CE x =-,在Rt BEC △中,13BC =,根据勾股定理可得,222BE CE BC +=,即222(17)13x x +-=,解得112x =,25(x =不符合条件,舍去),即12BG BE ==,17125AG CE ==-=,∵四边形BEFG 是正方形,∴∠BAD =90°.∵DK ⊥AG ,∴∠K =90°.∵∠BAG +∠KAD =180°—∠BAD =90°∠ADK +∠KAD =90°∴∠BAG =∠ADK在Rt △ABG 和Rt △DAK 中,90G K AB ADBAG ADK ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩所以Rt △ADK ≌Rt BAG ,则AK =BG =12,DK =AG =5,∵AF +FK =AK =BG=GF=AG +AF∴FK =AG =5在R t △DFK 中,根据勾股定理可得,DF =2252DK FK +=②点F 在AB 左侧时,如图,过D 作DK ⊥AG ,交其延长线于K .方法同①,可得FK =AG =12,在R t △DFK 中,根据勾股定理可得,DF 22122DK FK +=综上所述,DF 的长为522【点睛】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,正方形的性质,勾股定理,熟练掌握相关性质和定理是解本题的关键.。
人教版八年级下册第18章《平行四边形》章末质量检测题 (附答案解析)

人教版八年级下册第18章《平行四边形》章末质量检测题(满分100分时间80分钟)一.选择题(共10小题,满分30分)1.矩形不一定具有的性质是()A.对角线互相平分B.对角线互相垂直C.对角线相等D.是轴对称图形2.直角三角形两条直角边长分别是6和8,则斜边上的中线长为()A.3B.4C.5D.63.下列说法不正确的是()A.四边都相等的四边形是平行四边形B.两组对角分别相等的四边形是平行四边形C.对角线互相垂直的四边形是平行四边形D.两组对边分别平行的四边形是平行四边形4.如图,菱形ABCD中,∠D=130°,则∠1=()A.30°B.25°C.20°D.15°5.如图,矩形ABCD的对角线交于点O.若∠BAO=55°,则∠AOD等于()A.110°B.115°C.120°D.125°6.如图,点O是矩形ABCD的对角线AC的中点,点M是AD的中点.若AB=3,BC=4,则四边形ABOM的周长是()A.7B.8C.9D.107.如图,▱ABCD中,下列说法一定正确的是()A.AC=BD B.AC⊥BD C.AO=CO D.AB=BC8.如图,在正方形ABCD的外侧作等边△ADE,则∠AEB的度数为()A.10°B.12.5°C.15°D.20°9.如图,矩形ABCD中,BC>AB,对角线AC、BD交于O点,且AC=10,过B点作BE⊥AC于E点,若BE=4,则AD的长等于()A.8B.10C.3D.410.如图,在菱形ABCD中,点E为对角线AC上一点,且CE=CD,连接DE,若AB=5,AC=8,则=()A.B.C.D.二.填空题(共6小题,满分18分)11.平行四边形ABCD中,∠A比∠B小20°,那么∠C=.12.如图,在△ABC中,点D、E分別是AB,AC的中点,若BC=6,则DE=.13.菱形的两条对角线长分别为2cm和2cm,则该菱形的面积为cm2.14.如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于.15.在平面直角坐标系中,O为坐标系原点,A(﹣3,0)、B(﹣5,2)、C在坐标平面内,若以O、A、B、C为顶点的四边形是平行四边形,则点C坐标为.16.如图,在正方形ABCD中,AB=1,点E、F分别在边BC和CD上,AE=AF,∠EAF=60°,则CF的长是.三.解答题(共7小题,满分52分)17.如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若F A=FC.求证:四边形ADCE是平行四边形;18.如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE.求证:四边形BECD是矩形.19.如图,在平行四边形ABCD中,O是AB的中点,连接DO并延长交CB的延长线于点E,连接AE、DB.(1)求证:△AOD≌△BOE;(2)若DC=DE,判断四边形AEBD的形状,并说明理由.20.如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于点D,交AF于点B,交AC于点O.连接AD、BC.(1)求证:四边形ABCD是菱形;(2)若E为AB的中点,DE⊥AB,求∠BDC的度数;(3)在(2)的条件下,若AB=2,求矩形AFCG的面积.21.已知,四边形ABCD是菱形,∠B=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.(1)如图1,当点E是线段CB上任意一点时(点E不与B,C重合),求证:BE=CF;(2)如图2,当点E在线段CB的延长线上,连接AC,在不添加任何辅助线的情况下,直接写出图2中三对相等的线段(菱形ABCD相等的边除外).22.如图,在平面直角坐标系中,AB∥OC,A(0,12),B(a,c),C(b,0),并且a,b满足b=++16.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P、Q分别从点A、O同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒)(1)求B、C两点的坐标;(2)当t为何值时,四边形PQCB是平行四边形?并求出此时P、Q两点的坐标;(3)当t为何值时,△PQC是以PQ为腰的等腰三角形?并求出P、Q两点的坐标.23.如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,(1)当∠ADE=15°时,求∠DGC的度数;(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;(3)如图2,当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论.参考答案一.选择题(共10小题,满分30分)1.解:∵矩形的对角线线段,四个角是直角,对角线互相平分,∴选项A、C、D正确,选:B.2.解:∵直角三角形两条直角边长分别是6和8,∴斜边==10,∴斜边上的中线长=×10=5.选:C.3.解:A、四边都相等是四边形是菱形,也是平行四边形;该选项不合题意;B、两组对角分别相等的四边形是平行四边形,该选项不合题意;C、对角线互相垂直的四边形不是平行四边形,该选项符合题意;D、两组对边分别平行的四边形是平行四边形,该选项不合题意;选:C.4.解:∵四边形ABCD是菱形,∴DC∥AB,∠DAC=∠1,∵∠D=130°,∴∠DAB=180°﹣130°=50°,∴∠1=∠DAB=25°.选:B.5.解:∵四边形ABCD是矩形,∴OA=OB.∴∠BAO=∠ABO=55°.∴∠AOD=∠BAO+∠ABO=55°+55°=110°.选:A.6.解:∵O是矩形ABCD的对角线AC的中点,M是AD的中点,∴OM=CD=AB=1.5,∵AB=3,AD=4,∴AC==5,∵O是矩形ABCD的对角线AC的中点,∴BO=AC=2.5,∴四边形ABOM的周长为AB+AM+BO+OM=3+2+2.5+1.5=9,选:C.7.解:在▱ABCD中,可得:AO=OC,选:C.8.解:∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,又∵△ADE是正三角形,∴AE=AD,∠DAE=60°,∴△ABE是等腰三角形,∠BAE=90°+60°=150°,∴∠ABE=∠AEB=15°.选:C.9.解:∵四边形ABCD是矩形,∴∠BAD=90°,设AD=BC=a,AB=DC=b,∵AC=10,BE⊥AC,BE=4,∴a2+b2=102,又∵S矩形ABCD=2S△ABC∴ab=2××10×4=40,∵BC>AB,解得:a=4,b=2,即AD=4,选:D.10.解:连接BD交AC于点O,∵AB=CD=AD=5,∴CD=CE=5,∵AC=8,∴AE=3,OC=4,OE=1,在Rt△CDO中,由勾股定理可知:DO=3,在Rt△DOE中,由勾股定理可知:DE=,∴=,选:B.二.填空题(共6小题,满分18分)11.解:∵四边形ABCD为平行四边形,∴,解得:,∴∠C=∠A=80°.答案为:80°.12.解:∵点D、E分別是AB,AC的中点,∴DE=BC=×6=3,答案为:3.13.解:∵菱形的面积=对角线积的一半∴菱形的面积=×2×2=2cm2,答案为:214.解:∵四边形ABCD为平行四边形,∴AE∥BC,AD=BC,AB=CD,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE,∴AE+DE=AD=BC=6,∴AE+2=6,∴AE=4,∴AB=CD=4,∴▱ABCD的周长=4+4+6+6=20,答案为:20.15.解:如图所示:∵A(﹣3,0),∴OA=3,①当四边形OACB是平行四边形时,BC=OA=3,∵B(﹣5,2),∴C(﹣2,2),②当四边形OABC′是平行四边形时,BC'=OA=3,∵B(﹣5,2),∴C(﹣8,2);③当四边形OBAC′'是平行四边形时,∵A(﹣3,0),B(﹣5,2),∴C(2,﹣2),答案为:(﹣2,2)或(﹣8,2)或(2,﹣2).16.解:∵四边形ABCD是正方形,∴∠B=∠D=∠BAD=90°,AB=BC=CD=AD=1,在Rt△ABE和Rt△ADF中,,∴Rt△ABE≌Rt△ADF(HL),∴∠BAE=∠DAF,∵∠EAF=60°,∴∠BAE+∠DAF=30°,∴∠DAF=15°,在AD上取一点G,使∠GF A=∠DAF=15°,如图所示,∴AG=FG,∠DGF=30°,∴DF=FG=AG,DG=DF,设DF=x,则DG=x,AG=FG=2x,∵AG+DG=AD,∴2x+x=1,解得:x=2﹣,∴DF=2﹣,∴CF=CD﹣DF=1﹣(2﹣)=﹣1;答案为.三.解答题(共7小题,满分52分)17.证明:∵CE∥AB,∴∠BAC=∠ECA,在△DAF和△ECF中,∴△DAF≌△ECF(ASA),∴CE=AD,∴四边形ADCE是平行四边形;18.证明:∵AB=BC,BD平分∠ABC,∴BD⊥AC,AD=CD.∵四边形ABED是平行四边形,∴BE∥AD,BE=AD,∴BE=CD,∴四边形BECD是平行四边形.∵BD⊥AC,∴∠BDC=90°,∴▱BECD是矩形.19.证明:(1)∵四边形ABCD是平行四边形,∴AD∥CE.∴∠ADO=∠BEO.∵O是BC中点,∴AO=BO.又∠AOD=∠BOE.∴△AOD≌△BOE(AAS);(2)四边形AEBD是矩形,理由如下:∵△AOD≌△BOE,∴DO=EO.又AO=BO,∴四边形AEBD是平行四边形.∵DC=DE=AB,∴四边形AEBD是矩形.20.(1)证明:∵BD垂直平分AC,∴OA=OC,AD=CD,AB=BC,∵四边形AFCG是矩形,∴CG∥AF,∴∠CDO=∠ABO,∠DCO=∠BAO,且OA=OC ∴△COD≌△AOB(AAS),∴CD=AB,∴AB=BC=CD=DA,∴四边形ABCD是菱形.(2)∵E为AB中点,DE⊥AB,∴DE垂直平分AB,∴AD=DB,∵AD=AB,∴△ADB为等边三角形,∴∠DBA=60°,∵CD∥AB,∴∠BDC=∠DBA=60°.(3)∵∠BDC=60°,CB=CD,∴△CDB是等边三角形,∴BC=CD=BD=AB=2,∠DCB=60°∵CD∥AB∴∠DCB=∠CBF=60°,且∠F=90°,BC=2∴BF=1,CF=∴矩形AFCG的面积=AF×CF=3×=321.(1)证明:∵四边形ABCD是菱形,∠B=60°,∴AB=BC=CD=AD,∠B=∠D=60°,∴△ABC,△ADC是等边三角形,∴∠BAC=∠DAC=60°,∵∠BAC=∠EAF=60°,∴∠BAE=∠CAF,在△BAE和△CAF中,,∴△BAE≌△CAF(ASA),∴BE=CF.(2)解:AE=AF,BE=CF,CE=DF.由(1)知△ABC,△ADC是等边三角形,∴∠BAC=∠DAC=∠ACD=60°,∵∠BAC=∠EAF=60°,∠ABE=∠ACF,∴∠BAE=∠CAF,∵AB=AC,∴△BAE≌△CAF(ASA),∴AE=AF,BE=CF,∴BE+BC=CF+CD,即CE=DF.22.解:(1)∵b=++16,∴a=21,b=16,B(21,12)C(16,0);(2)由题意得:AP=2t,QO=t,则:PB=21﹣2t,QC=16﹣t,∵当PB=QC时,四边形PQCB是平行四边形,∴21﹣2t=16﹣t,解得:t=5,∴P(10,12)Q(5,0);(3)当PQ=CQ时,过Q作QN⊥AB,由题意得:122+t2=(16﹣t)2,解得:t=,P(7,12),Q(,0),当PQ=PC时,过P作PM⊥x轴,由题意得:QM=t,CM=16﹣2t,则t=16﹣2t,解得:t=,2t=,P(,12),Q(,0).23.解:(1)∵∠ADE=15°,∴∠FDE=15°,∠CDF=60°.∵DC=AD=DF,∴∠CFD=60°.又∠CFD=∠DGC+∠FDE=15°+∠DGC,∴∠DGC=45°;(2)不变,理由如下:∵△ADE与△FDE关于DE对称,∴∠AGD=∠DGF.设∠ADE=x,可得∠FDE=x,∠CDF=90°﹣2x,∵DC=AD=DF,∴∠CFD=45°+x.又∠CFD=∠DGC+∠FDE=x+∠DGC,∴∠DGC=45°;(3)四边形AGFM是正方形;理由:∵∠DAE=∠DFE=90°,点M为DE的中点,∴AM=FM=DM=DE,∴∠ADM=∠DAM,∠MDF=∠DFM,∴∠AME=∠FMF=2∠ADM=2∠MDF=45°,∴∠AMF=90°,∵∠MGF=45°,∴FM=FG,在△ADG与△FDG中,,∴△ADG≌△FDG(SAS),∴AG=FG,∴AM=MF=FG=AG,∵∠AMF=90°,∴四边形AGFM是正方形.。
人教版八年级数学下册 第18章 《平行四边形》 单元测试卷(包含答案)

人教版八年级数学下册第18章平行四边形单元综合测试卷(时间90分钟,满分120分)一、选择题(共10小题,3*10=30)1.在□ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则□ABCD的周长是() A.22 B.20 C.22或20 D.182. 如图,由六个全等的正三角形拼成的图,图中平行四边形的个数是()A.4个B.6个C.8个D.10个3.如图,在▱ABCD中,AE平分∠BAD,若CE=3 cm,AB=4 cm,则▱ABCD的周长是() A.20 cm B.21 cmC.22 cm D.23 cm4.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是()A.AB=BE B.DE⊥DCC.∠ADB=90° D.CE⊥DE5.如图,在▱ABCD中,∠ABC的平分线交AD于点E,∠BED=150°,则∠A的大小为( ) A.150° B.130° C.120° D.100°6.如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.其中会随点P的移动而变化的是()A.②③B.②⑤C.①③④D.④⑤7. 如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()A.15°或30°B.30°或45°C.45°或60°D.30°或60°8.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()A.1 B. 2 C.4-2 2 D.32-49.如图,是边长分别为4和8的正方形ABCD、正方形CEFG并排放在一起,连接BD并延长交EG 于点T,交FG于点P,则GT的长为()A.2 2 B.2 C. 2 D.110. 如图,在▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连接EF,BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( )A.1个B.2个C.3个D.4个二.填空题(共8小题,3*8=24)11.如图,在□ABCD中,对角线AC与BD交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折,若点B的落点记为B′,则DB′的长为______ .12.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为________.13. 已知平行四边形的三个顶点坐标分别为(-1,0)(0,2)(2,0),则在第四象限的第四个顶点的坐标为___________。
【精品】人教版八年级数学下册 第十八章 平行四边形 复习检测题(含答案)【3套】试题

人教版八年级数学下册第十八章平行四边形复习检测题(含答案)一、选择题。
1.下列命题中,错误的是()A.平行四边形的对角线互相平分B.菱形的对角线互相垂直平分C.矩形的对角线相等且互相垂直平分D.角平分线上的点到角两边的距离相等2.在▱ABCD中,已知AB=(x+1)cm,BC=(x-2)cm,CD=4 cm,则▱ABCD的周长为()A.5 cm B.10 cm C.14 cm D.28 cm3.直角三角形中,两直角边分别是12和5,则斜边上的中线长是()A.34 B.26 C.8.5 D.6.54.如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为()A.1 B.2 C. 3 D.1+ 35.正方形的一条对角线长为4,则这个正方形面积是()A.8 B.4 2 C.8 2 D.166.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为()A.13 B.14 C.15 D.167.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH等于()A.245B.125C .5D .48.如图,把矩形纸片ABCD 沿对角线BD 折叠,设重叠部分为△EBD ,则下列说法错误的是( )A .AB =CD B .∠BAE =∠DCEC .EB =ED D .∠ABE 一定等于30°9.如图,在矩形ABCD 中,E ,F 分别是AD ,BC 中点,连接AF ,BE ,CE ,DF 分别交于点M ,N ,四边形EMFN 是( )A .正方形B .菱形C .矩形D .无法确定10.将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD ,转动这个四边形,使它形状改变,当∠B =90°时,如图1,测得AC =2,当∠B =60°时,如图2,AC =( ) A. 2 B .2 C. 6 D .2 2二、填空题11.如图,在菱形ABCD 中,AC ,BD 相交于点O ,若∠BCO =55°,则∠ADO =____________.12.如图,在▱ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为____________.13.如图,矩形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E,AD =8,AB=4,则DE的长为____________.14.如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是____________.(写出一个即可)15.如图,正方形ABCO的顶点C,A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是____________.16.如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是____________.三、解答题(共52分)17.(10分)如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.(1)请写出图中两对全等的三角形;(2)求证:四边形BCEF是平行四边形.18.(10分)如图,AC是▱ABCD的对角线,∠BAC=∠DAC.(1)求证:AB=BC;(2)若AB=2,AC=23,求▱ABCD的面积.19.(10分)如图,已知,在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.(1)求证:四边形ADBE是矩形;(2)求矩形ADBE的面积.20.(10分)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?21.(12分)已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时,如图1,易证:AB=CG+CE.(1)当点E在线段BC的延长线上时(如图2),猜想AB,CG,CE之间的关系并证明;(2)当点E在线段CB的延长线上时(如图3),直接写出AB,CG,CE之间的关系.参考答案一、选择题1.C2.B3.D4.A5.A6.A7.A8.D9.B 10.A 二、填空题。
人教版八年级数学下册第十八章:平行四边综合复习训练
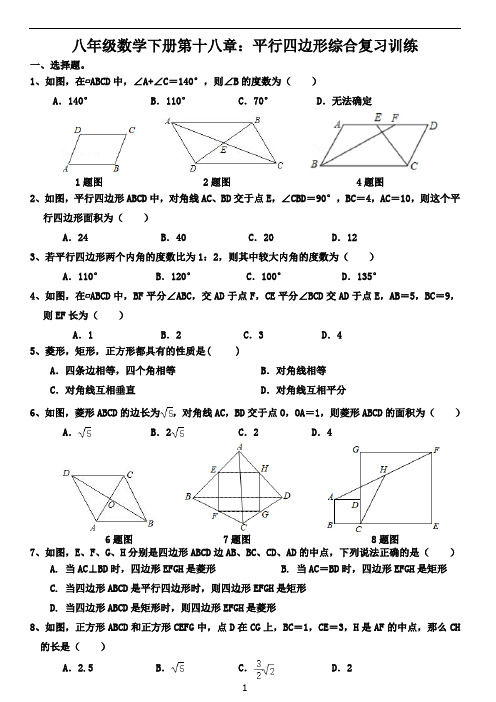
八年级数学下册第十八章:平行四边形综合复习训练一、选择题。
1、如图,在▱ABCD中,∠A+∠C=140°,则∠B的度数为()A.140° B.110° C.70° D.无法确定1题图 2题图 4题图2、如图,平行四边形ABCD中,对角线AC、BD交于点E,∠CBD=90°,BC=4,AC=10,则这个平行四边形面积为()A.24 B.40 C.20 D.123、若平行四边形两个内角的度数比为1:2,则其中较大内角的度数为()A.110° B.120° C.100° D.135°4、如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD交AD于点E,AB=5,BC=9,则EF长为()A.1 B.2 C.3 D.45、菱形,矩形,正方形都具有的性质是( )A.四条边相等,四个角相等 B.对角线相等C.对角线互相垂直 D.对角线互相平分6、如图,菱形ABCD的边长为,对角线AC,BD交于点O,OA=1,则菱形ABCD的面积为()A. B.2 C.2 D.46题图 7题图 8题图7、如图,E、F、G、H分别是四边形ABCD边AB、BC、CD、AD的中点,下列说法正确的是()A. 当AC⊥BD时,四边形EFGH是菱形B. 当AC=BD时,四边形EFGH是矩形C. 当四边形ABCD是平行四边形时,则四边形EFGH是矩形D. 当四边形ABCD是矩形时,则四边形EFGH是菱形8、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH9题图 10题图9、如图,已知正方形ABCD的边长为12,BE=EC,将正方形的边CD沿DE折叠到DF,延长EF交AB于G,连接DG.现有如下3个结论:①AG+EC=GE;②∠GDE=45°;③五边形DAGEC的周长是44,其中正确的个数为()A.0 B.1 C.2 D.310、如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④4FH=BD;其中正确结论的是()A.①②③ B.①②④ C.①③④D.②③④二、填空题。
人教版八年级下册数学第十八章《平行四边形》检测卷及答案解析

八年级下册数学第十八章《平行四边形》检测卷时间:90分钟满分:120分一、选择题(每小题4分,共40分)1.已知平行四边形一边长为10,一条对角线长为6,则它的另一条对角线α的取值范围为()A.4<α<16B.14<α<26C.12<α<20D.以上答案都不正确2.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是()A.45°B.35°C.22.5°D.15.5°3.将矩形纸片ABCD按如图的方式折叠,使点B与点D都与对角线AC的中点O重合,得到菱形AECF,若AB=3,则BC的长为()A.1B.2C2D34.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是()A.∠ABC=90°B.AC=BD C.OA=OB D.OA=AD5.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD 四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是()A.选①②B.选②③C.选①③D.选②④6.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若BD、AC的和为18cm,CD:DA=2∶3,△AOB的周长为13cm,那么BC的长是()A.y x=B.1902y x=-+C.2180y x=-+D.90y x=-+9.如图所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是()A.15米B.20米C.25米D.30米第6题第7题A.6cm B.9cm C.3cm D.12cm7.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE 交△ABC的外角∠ACM的平分线于点F,则线段DF的长为()A.7B.8C.9D.108.如图,在△ABC中,AE⊥BC于点E,BD⊥AC于点D;点F是AB的中点,连结DF,EF,设DFE x∠=°,ACB y∠=°,则()10.如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是()A.2B.3C.4D.5二、填空题(每小题4分,共20分)11.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是_________cm.12.如图,在□ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S□AEPH=_________.第12题第13题13.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是____________.14.如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为_________.第14题第15题15.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是__________.三、解答题(16-20小题,每小题8分;21-22小题,每小题10分)16.如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.(1)求证:AE=DE;(2)若∠C=65°,求∠BDE的度数.17.如图,在矩形ABCD中,以点B为圆心、BC长为半径画弧,交AD边于点E,连接BE,过C点作CF⊥BE,垂足为F.猜想线段BF与图中现有的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,并加以证明.结论:BF=______.证明:18.如图,在□ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=12BC,求证:四边形OCFE是平行四边形.19.如图,在□ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.(1)求证:四边形OBFE是平行四边形;(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.20.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.21.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB 的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.22.我们规定:横、纵坐标相等的点叫做“完美点”.(1)若点A(x,y)是“完美点”,且满足x+y=4,求点A的坐标;(2)如图1,在平面直角坐标系中,四边形OABC是正方形,点A坐标为(0,4),连接OB,E点从O向B运动,速度为2个单位/秒,到B点时运动停止,设运动时间为t.①不管t为何值,E点总是“完美点”;②如图2,连接AE,过E点作PQ⊥x轴分别交AB、OC于P、Q两点,过点E作EF⊥AE交x轴于点F,问:当E点运动时,四边形AFQP的面积是否发生变化?若不改变,求出面积的值;若改变,请说明理由.八年级下册数学第十八章《平行四边形》检测卷参考答案一、选择题(每小题4分,共40分)1.B2.C3.D4.D5.B6.A7.B8.B9.C10.C二、填空题(每小题4分,共20分)11;12.4;13.AD=BC;14.1;15.18.三、解答题(16-20小题,每小题8分;21-22小题,每小题10分)16.【分析】(1)由等腰三角形的性质可得∠C=∠A,由平行线的性质可得∠C=∠ADE,从而∠A=∠ADE;(2)先由三角形内角和求出∠ABC=50°,再由三线合一的性质可求出∠EBD=∠DBC=12∠ABC=25°,然后根据平行线的性质求解即可.【解析】(1)证明:∵DE∥BC,∴∠C=∠ADE,∵AB=BC,∴∠C=∠A,∴∠A=∠ADE,∴AE=DE.(2)∵△ABC中,AB=BC,∠C=65°,∴∠ABC=180°-65°-65°=50°,∵AB=BC,D为AC中点,∴∠EBD=∠DBC=12∠ABC=25°,∵DE∥BC,∴∠BDE=∠DBC=25°.17.【分析】猜想:BF=AE.根据已知及矩形的性质利用AAS判定△BFC≌△EAB,从而得到BF=AE.【解析】猜想:BF=AE.证明:∵四边形ABCD是矩形,∴∠A=90°.∵CF⊥BE,∴∠A=∠BFC=90°,∠AEB=∠FBC.∵BC=BE(同一半径),∴△BFC≌△EAB,∴BF=AE.18.【分析】利用三角形中位线定理判定OE∥BC,且OE=12BC.结合已知条件CF=12BC,则OE∥CF,由“有一组对边平行且相等的四边形为平行四边形”证得结论.【解析】∵四边形ABCD是平行四边形,∴点O是BD的中点.又∵点E是边CD的中点,∴OE是△BCD的中位线,∴OE∥BC,且OE=12 BC.又∵CF=12BC,∴OE=CF.又∵点F在BC的延长线上,∴OE∥CF,∴四边形OCFE是平行四边形.19.【分析】(1)首先证明OE是△ABC的中位线,推出OE∥BC,由EF∥OB,即可得出四边形OBFE是平行四边形;(2)当AD⊥BD时,四边形OBFE是矩形.只要证明∠EOB=90°即可解决问题.【解析】(1)∵四边形ABCD是平行四边形,∴点O是AC的中点,又∵点E是边AB的中点,∴OE是△ABC的中位线,∴OE∥BC,又∵点F在CB的延长线上,∴OE∥BF,∵EF∥BD,即EF∥OB,∴FC ⊥BD ,∴∠OBF =90°,∴四边形OBFE 是矩形.20.【分析】(1)先根据等腰三角形的三线合一可得BAD CAD ∠=∠,再根据角平分线的定义可得MAE CAE ∠=∠,从而可得90DAE ∠=°,然后根据垂直的定义可得90ADC AEC ∠=∠=°,最后根据矩形的判定即可得证;(2)先根据等腰直角三角形的性质可得45ACB B ∠=∠=°,再根据直角三角形的性质可得45CAD ACD ∠=∠=°,然后根据等腰三角形的定义可得CD =AD ,最后根据正方形的判定即可得.【解析】(1)∵在△ABC 中,AB =AC ,AD ⊥BC ,∴12BAD CAD BAC ∠=∠=∠(等腰三角形的三线合一),∵AN 是△ABC 外角∠CAM 的平分线,∴12MAE CAE CAM ∠=∠=∠,∴11118090222DAE CAD CAE BAC CAM ∠=∠+∠=∠+=⨯︒=∠︒,又∵AD BC ⊥,CE AN ⊥,∴90ADC AEC ∠=∠=︒,∴四边形ADCE 为矩形.(2)当△ABC 满足90BAC ∠=︒时,四边形ADCE 是一个正方形.证明如下:∵AB AC =,90BAC ∠=︒,∴45ACB B ∠=∠=︒,∵AD BC ⊥,∴45CAD ACD ∠=∠=︒,∴CD AD =,∵四边形ADCE 为矩形,∴矩形ADCE 是正方形,故当90BAC ∠=︒时,四边形ADCE 是一个正方形.21.【分析】(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案.(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF 的长,即可根据直角三角形斜边上的中线性质得出CO 的长.(3)根据平行四边形的判定以及矩形的判定得出即可.【解析】(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠2=∠5,∠4=∠6.∵MN∥BC,∴∠1=∠5,∠3=∠6.∴∠1=∠2,∠3=∠4.∴EO=CO,FO=CO.∴OE=OF.(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°.∵CE=12,CF=5,∴EF=13=.∴OC=12EF=6.5.(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:当O为AC的中点时,AO=CO,∵EO=FO,∴四边形AECF是平行四边形.∵∠ECF=90°,∴平行四边形AECF是矩形.22.【分析】(1)根据“完美点”定义可求点A坐标;(2)①由题意可求直线OB的解析式y=x,点E在直线OB上移动,则可证结论;②根据题意可证△EFQ≌△APE,可求PE=FQ,则可求四边形AFQP的面积.【详解】(1)∵点A(x,y)是“完美点”,∴x=y,∵x+y=4,∴x=2,y=2,∴A点坐标(2,2).(2)①∵四边形OABC是正方形,点A坐标为(0,4),∴AO=AB=BC=4,∴B(4,4).设直线OB 的解析式y =kx 过B 点,∴4=4k ,k =1.∴直线OB 解析式y =x ,设点E 坐标(x ,y ),∵点E 在直线OB 上移动,∴x =y ,∴不管t 为何值,E 点总是“完美点”.②∵E 点总是“完美点”,∴EQ =OQ .∵∠BAO =∠AOC =90°,PQ ⊥x 轴,∴四边形AOQP 是矩形,∴AP =OQ ,AO =PQ =4,∴AP =EQ .∵AE ⊥EF ,∴∠AEP +∠FEQ =90°,∠EAP +∠AEP =90°,∴∠FEQ =∠EAP .∵AP =EQ ,∠FEQ =∠EAP ,∠APE =∠EQF =90°,∴△APE ≌△EFQ ,∴PE =FQ .∵S 四边形AFQP =()2AP FQ AO =2(PE +EQ )=2×PQ =8,∴当E 点运动时,四边形AFQP 的面积不变,面积为8.。
(必考题)初中数学八年级数学下册第六单元《平行四边形》检测题(有答案解析)(1)
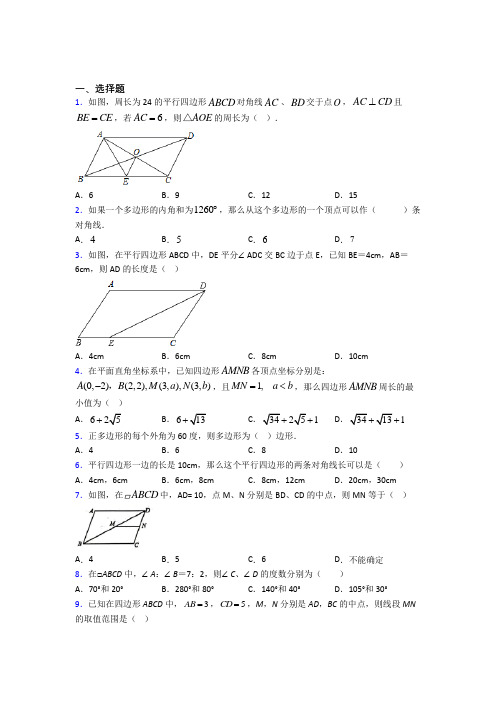
一、选择题1.如图,周长为24的平行四边形ABCD 对角线AC 、BD 交于点O ,AC CD ⊥且BE CE =,若6AC =,则AOE △的周长为( ).A .6B .9C .12D .152.如果一个多边形的内角和为1260︒,那么从这个多边形的一个顶点可以作( )条对角线. A .4B .5C .6D .73.如图,在平行四边形ABCD 中,DE 平分∠ADC 交BC 边于点E ,已知BE =4cm ,AB =6cm ,则AD 的长度是( )A .4cmB .6cmC .8cmD .10cm4.在平面直角坐标系中,已知四边形AMNB 各顶点坐标分别是:(0,2)(2,2),(3,),(3,)A B M a N b -,,且1,MN a b =<,那么四边形AMNB 周长的最小值为( ) A .625+ B .613+ C .34251++ D .34131++ 5.正多边形的每个外角为60度,则多边形为( )边形.A .4B .6C .8D .10 6.平行四边形一边的长是10cm ,那么这个平行四边形的两条对角线长可以是( ) A .4cm ,6cmB .6cm ,8cmC .8cm ,12cmD .20cm ,30cm7.如图,在ABCD 中,AD= 10,点M 、N 分别是BD 、CD 的中点,则MN 等于( )A .4B .5C .6D .不能确定 8.在□ABCD 中,∠A :∠B =7:2,则∠C 、∠D 的度数分别为( )A .70°和20°B .280°和80°C .140°和40°D .105°和 30°9.已知在四边形ABCD 中,3AB =,5CD =,M ,N 分别是AD ,BC 的中点,则线段MN的取值范围是( )A .14MN <<B .14MN <≤C .28MN <<D .28MN <≤10.如图,平行四边形ABCD 的对角线AC 与BD 相交于点O ,AB AC ⊥,若6AB =,8AC =,则BD 的长是( )A .10B .213C .413D .1211.如图,在周长为12cm 的▱ABCD 中,AB <AD ,AC 、BD 相交于点O ,OE ⊥BD 交AD 于E ,则△ABE 的周长为( )A .4cmB .5cmC .6cmD .7cm12.如图,在□ABCD 中,AB =4,BC =6,AC 的垂直平分线交AD 于点E ,则△CDE 的周长是( )A .7B .10C .11D .12二、填空题13.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图BD 是平行四边形ABCD 的对角线,点E 在BD 上,DC =DE =AE ,∠1=25°,则∠C 的大小是_____.14.一个正多边形的内角和为720︒,则这个多边形的外角的度数为______. 15.如图,在OABC 中,对角线,AC BD 相交于点,O AE BD ⊥于点,E CF BD ⊥于点,F 连接,AF CE ,给出下列结论:;AF CE OE OF ==①②;DE BF =③;④图中共有八对全等三角形.其中正确结论的序号是______.16.如图,已知点(3,2)A -,过点A 作AD x ⊥轴于点D ,点B 是x 轴正半轴上一个动点,连接AB ,以AB 为斜边,在AB 的上方构造等腰Rt ACB △,连接DC .在B 点运动的过程中,DC 与DB 的数量关系是____.17.有一个正五边形和一个正方形边长相等,如图放置,则∠1=______.18.如图,在ABCD 中,对角线AC 、BD 相交于点O ,且DB BC ⊥,垂足为B ,若10AC =,6BD =,则BC 的长等于_______.19.如图,平行四边形ABCD 中,AB=8cm ,AD=12cm ,点P 在AD 边上以每秒1cm 的速度从点A 向点D 运动,点Q 在BC 边上,以每秒4cm 的速度从点C 出发,在CB 间往返运动,两个点同时出发,当点P 到达点D 时停止(同时点Q 也停止),在运动以后,以P 、D、Q、B四点组成平行四边形的次数有______次.∠交边CD于,E BF平分B交边CD于,F若20.在ABCD中,AE平分A==则边AB的长为________________________.AD EF4,1,三、解答题21.如图,在平行四边形ABCD中,E为AD边上一点,BE平分∠ABC,连接CE,已知DE =6,CE=8,AE=10.(1)求AB的长;(2)求平行四边形ABCD的面积;22.已知:如图,在直角梯形ABCD中,∠B=90o,AD∥BC,AD=24cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/秒的速度运动,动点Q从C点开始沿CB边向B以3cm/秒的速度运动,P、Q分别从A、C同时出发,当点Q到端点B时,点P也随之停止运动,设运动时间为t秒.求:(1) t分别为何值时,四边形PQCD是平行四边形?(2)当 t=7秒时,判断四边形PQCD的形状.23.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标;(3)在平面内有一动点P,使得以P、A、B、C为顶点的四边形是平行四边形,满足条件的点P的个数为_______.24.如图1,在平面直角坐标系中,直线AB 与 x 轴、y 轴相交于A(6,0)、B(0,2)两点,动点C 在线段OA 上(不 与 )O 、A 重合 ),将线段CB 绕着点C 顺时针旋转 90° 得到CD ,当点D 恰好落在直线AB 时,过 点D 作DE ⊥x 轴于点E .(1)求证:BOC CED ∆≅∆;(2)求经过A 、B 两点的一次函数表达式,如图2,将BCD ∆沿x 轴正方向平移得B C D '''∆,当直线B′C′经过点D 时,求点D 的坐标、B C D '''∆的面积;(3)若点P 在y 轴上,点Q 在直线AB 上,是否存在以C 、D 、P 、Q 为顶点的四边形是平行四边形?若存在,通过画图说明理由,并指出点Q 的个数.25.已知,在四边形ABCD 中,160A C ︒∠+∠=,BE ,DF 分别为四边形ABCD 的外角CBN ∠,MDC ∠的平分线.(1)如图1,若//BE DF ,求C ∠的度数;(2)如图2,若BE ,DF 交于点G ,且//BE AD ,//DF AB ,求C ∠的度数. 26.如图,E F 、是平行四边形ABCD 的对角线AC 上的两点,且AE CF =.(1)证明:四边形BFDE是平行四边形;(2)延长BF交CD于G,若AE EF FC==,证明:点G是CD的中点.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】依据平行四边形ABCD的周长为24,即可得到AB+BC=12,再根据AO=12AC,OE=12AB,AE=12BC,即可得到△AOE的周长.【详解】解:∵平行四边形ABCD的周长为24,∴AB+BC=12,∵平行四边形ABCD对角线AC、BD交于点O,且BE=CE,∴AO=12AC=3,OE=12AB,∵AC⊥CD,且BE=CE,∴Rt△ABC中,AE=12BC,∴△AOE的周长=AO+AE+OE=3+12(BC+AB)=3+12×12=9,故选:B.【点睛】本题考查了平行四边形的性质、三角形的中位线定理等知识,解题的关键是灵活运用所学知识解决问题.2.C解析:C【分析】先利用n边形的内角和公式算出n,再利用n边形的每一个顶点有(n-3)条对角线计算即可.【详解】根据题意,得(n-2)×180=1260, 解得n=9,∴从这个多边形的一个顶点可以作对角线的条数为: n-3 =9-3 =6. 故选C. 【点睛】本题考查了n 边形的内角和和经过每一个顶点可作的对角线条数,熟记多边形内角和公式,计算经过每一个顶点的对角线条数计算公式是解题的关键.3.D解析:D 【分析】由已知平行四边形ABCD ,DE 平分∠ADC 可推出△DCE 为等腰三角形,所以得CE=CD=AB=6,那么AD=BC=BE+CE ,从而求出AD . 【详解】解:已知平行四边形ABCD ,DE 平分∠ADC , ∴AD ∥BC ,CD=AB=6cm ,∠EDC=∠ADE ,AD=BC , ∴∠DEC=∠ADE , ∴∠DEC=∠CDE , ∴CE=CD=6cm , ∴BC=BE+CE=4+6=10cm , ∴AD=BC=10cm , 故选:D . 【点睛】此题考查的知识点是平行四边形的性质及角平分线的性质,关键是由平行四边形的性质及角平分线的性质得等腰三角形通过等量代换求出AD .4.A解析:A 【分析】如图,把()02A -,向上平移一个单位得:()101A -,,作1A 关于直线3x =的对称点()261A -,, 连接2A B ,交直线3x =于N , 连接1A N ,则此时四边形AMNB 的周长最短,再利用勾股定理可得:AB ==25A B ==,利用AMNB C 四边形2AB MN A B =++从而可得答案.【详解】解:如图,把()02A -,向上平移一个单位得:()101A -,,作1A 关于直线3x =的对称点()261A -,, 连接2A B ,交直线3x =于N , 连接1A N ,122A N BN A N BN A B ∴+=+=, 由111//MN AA MN AA ==,, ∴ 四边形1AMNA 是平行四边形,12,A N AM A N ∴==所以此时:四边形AMNB 的周长最短,()()()2022261A B A --,,,,,,()()22022225AB ∴=-+--=,()()22262125A B =-+--=,2AMNB C AM AB BN MN A N BN AB MN =+++=+++四边形2AB MN A B =++ 251525 6.=++=+故选:.A 【点睛】本题考查的是图形与坐标,勾股定理的应用,轴对称的性质,平行四边形的判定与性质,掌握以上知识是解题的关键.5.B解析:B 【分析】利用多边形的外角和360除以外角60得到多边形的边数. 【详解】多边形的边数为36060÷=6, 故选:B . 【点睛】此题考查多边形的外角和定理,正多边形的性质,利用外角和除以外角的度数求正多边形的边数是最简单的题型.6.D解析:D【分析】平行四边形的这条边和两条对角线的一半构成三角形,应该满足第三边大于两边之差小于两边之和才能构成三角形.【详解】A. ∵2+3<10,不能够成三角形,故此选项错误;B. 4+3<10,不能够成三角形,故此选项错误;C. 4+6=10,不能够成三角形,故此选项错误;D. 10+10>15,能构成三角形,故此选项正确.故选D.7.B解析:B【分析】利用平行四边形的性质和三角形的中位线定理即可解决问题.【详解】∵四边形ABCD是平行四边形,∴BC=AD=10,∵点M、N分别是BD,CD的中点,∴MN=1BC=5,2故选:B.【点睛】本题考查了平行四边形的性质、三角形的中位线定理等知识,解题的关键是熟练掌握基本知识.8.C解析:C【分析】由平行四边形的性质可得∠A=∠C,∠B=∠D,∠A+∠B=180°,又有∠A:∠B=7:2,可求得∠A=140°,∠B=40°,即可得出结果.【详解】∵四边形ABCD是平行四边形,∴∠A=∠C,∠B=∠D,AD∥BC,∴∠A+∠B=180°又∵∠A:∠B=7:2∴∠A=140°,∠B=40°,∴∠C=140°,∠D=40°;故选C.【点睛】此题主要考查了平行四边形的性质;熟记平行四边形的两组对角分别相等,邻角互补是解题的关键.9.B解析:B 【分析】利用中位线定理作出辅助线,利用三边关系可得MN 的取值范围. 【详解】连接BD ,过M 作MG ∥AB ,连接NG . ∵M 是边AD 的中点,AB=3,MG ∥AB , ∴MG 是△ABD 的中位线,BG=GD ,1322MG AB ==; ∵N 是BC 的中点,BG=GD ,CD=5, ∴NG 是△BCD 的中位线,1522NG CD ==, 在△MNG 中,由三角形三边关系可知NG-MG <MN <MG+NG ,即53532222MN -<<+, ∴14MN <<,当MN=MG+NG ,即MN=4时,四边形ABCD 是梯形, 故线段MN 长的取值范围是1<MN≤4. 故选B . 【点睛】解答此题的关键是根据题意作出辅助线,利用三角形中位线定理及三角形三边关系解答.10.C解析:C 【分析】由平行四边形的性质得出OB=OD ,OA=OC=12AC=4,由AC ⊥AB ,根据勾股定理求出OB ,即可得出BD 的长. 【详解】解:∵四边形ABCD 是平行四边形, ∴OB=OD ,OA=OC=12AC=4, ∵AB ⊥AC ,∴由勾股定理得:==∴故选:C.【点睛】本题考查了平行四边形的性质、勾股定理;熟练掌握平行四边形的性质,由勾股定理求出OB是解题的关键.11.C解析:C【分析】根据平行四边形的性质得出OB=OD,进而利用线段垂直平分线得出BE=ED,进而解答即可.【详解】解:∵四边形ABCD是平行四边形,∴OB=OD,∵OE⊥BD,∴OE是线段BD的垂直平分线,∴BE=ED,∵△ABE的周长=AB+AE+BE=AB+AE+ED=AB+AD=6cm.故选:C.【点睛】此题考查平行四边形的性质,解题关键是根据平行四边形的性质得出OB=OD,再结合线段垂直平分线的定义解答.12.B解析:B【分析】由平行四边形的性质得出DC=AB=4,AD=BC=6,由线段垂直平分线的性质得出AE=CE,得出△CDE的周长=AD+DC,即可得出结果.【详解】∵四边形ABCD是平行四边形,∴DC=AB=4,AD=BC=6,∵AC的垂直平分线交AD于点E,∴AE=CE,∴△CDE的周长=DE+CE+DC=DE+AE+DC=AD+DC=6+4=10;故选:B.【点睛】本题考查了平行四边形的性质、线段垂直平分线的性质、三角形周长的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.二、填空题13.105°【分析】由已知根据等腰三角形的性质可以求出∠BAE的大小从而得到∠BAD的大小再根据平行四边形对角相等的性质可以得到答案【详解】解:∵DE=AE∠1=25°∴∠ADE=∠1=25°∴∠AEB解析:105°.【分析】由已知,根据等腰三角形的性质,可以求出∠BAE的大小,从而得到∠BAD的大小,再根据平行四边形对角相等的性质可以得到答案.【详解】解:∵DE=AE,∠1=25°,∴∠ADE=∠1=25°,∴∠AEB=∠1+∠ADE=50°,又∵平行四边形ABCD中,AB=CD,∴AB=AE,∴∠ABE=∠AEB=50°,∴∠BAE=80°,∠BAD=80°+25°=105°,又∵∠BAD=∠C,∴∠C=105°,故答案为:105°.【点睛】本题考查平行四边形的应用,熟练掌握平行四边形的性质、等腰三角形的性质、三角形的内外角性质是解题关键.14.60°【分析】首先设这个正多边形的边数为n根据多边形的内角和公式可得180(n-2)=720继而可求得答案【详解】解:设这个正多边形的边数为n∵一个正多边形的内角和为720°∴180(n-2)=72解析:60°【分析】首先设这个正多边形的边数为n,根据多边形的内角和公式可得180(n-2)=720,继而可求得答案.【详解】解:设这个正多边形的边数为n,∵一个正多边形的内角和为720°,∴180(n-2)=720,解得:n=6,∴这个正多边形的每一个外角是:360°÷6=60°.故答案为:60°.【点睛】本题考查了多边形的内角和与外角和的知识.此题难度不大,注意掌握方程思想的应用,注意熟记公式是关键.15.①②③【分析】根据平行四边形的性质全等三角形的判定和性质及中心对称的性质进行判断即可【详解】解:在中于点于点四边形是平行四边形故①②正确即故③正确∵和是中心对称图形点是对称中心易证∴共10对全等三角解析:①②③【分析】根据平行四边形的性质,全等三角形的判定和性质及中心对称的性质进行判断即可.【详解】解:在OABC 中,,,AB CD AD BC ==BD DB =,()ABD CDB SSS ∴≌,ABD CDB S ∴△△=S ,AE BD ⊥于点E ,CF BD ⊥于点F ,1122BD AE BD CF ∴=,//AE CF AE CF ∴=,∴四边形AECF 是平行四边形,,AF CE OE OF ∴== ,故①②正确,OB OD =,OD OE OB OF ∴+=+,即DE BF =,故③正确,∵,,OA OC OB OD OE OF ===,ABCD ∴和AECF 是中心对称图形,点O 是对称中心,易证,,,ADC CBA ABD CDB AOB COD AOD COB △≌△△≌△△≌△△≌△ , ,,,AEF CFE AFC CEA AOF COE COF AOE △≌△△≌△△≌△△≌△,,,,ABE CDF AFD CEB ABF CDE AED CFB △≌△△≌△△≌△△≌△,∴共10对全等三角形,故④错误;故答案为:①②③【点睛】本题是平行四边形的综合题,考查了平行四边形的判定和性质,全等三角形的判定和性质,中心对称的性质等知识,正确理解中心对称的性质是解本题的关键.16.【分析】以点C 为旋转中心将△CAD 逆时针旋转90°得△CBD′可得∠CAD=∠CBD′BD′=AD=2CD=CD′由等腰可得∠ADB+∠ACB=180º由四边形内角和∠CAD+∠CBD=360º-(2BD =+【分析】以点C 为旋转中心,将△CAD 逆时针旋转90°得△CBD′,可得∠CAD=∠CBD′,BD′=AD=2,CD=CD′,由AD x ⊥,等腰Rt ACB △,可得∠ADB+∠ACB=180º,由四边形内角和∠CAD+∠CBD=360º-(∠ADB+∠ACB )=180º,推出D 、B 、D′三点共线,在Rt △DCD′中,由勾股定理DD′=22CD +C =2CD 'D ,由DD′=BD+BD′=BD+2即可得出结论.【详解】解:以点C 为旋转中心,将△CAD 逆时针旋转90°得△CBD′,∴∠CAD=∠CBD′,BD′=AD=2,CD=CD′,∴AD x ⊥,等腰Rt ACB △,∴∠ADB+∠ACB=180º,∴∠CAD+∠CBD=360º-(∠ADB+∠ACB )=180º,∴∠CBD′+∠CBD=180º,∴D 、B 、D′三点共线,∵∠DCD′=90º,在Rt △DCD′中,∴DD′=22CD +C =2CD 'D ,∴DD′=BD+BD′=BD+2,∴2CD=BD+2,故答案为:2CD=BD+2.【点睛】本题考查等腰直角三角形的性质,图形的旋转,三点共线,勾股定理的应用等知识,掌握本题考查等腰直角三角形的性质,图形的旋转性质,三点共线证明方法,勾股定理的应用是解题关键.17.18°【解析】根据多边形的内角和公式可求得正五边形的内角∠BAE=108°所以∠1=∠BAE-∠BAG=108°-90°=18°解析:18°【解析】根据多边形的内角和公式可求得正五边形的内角∠BAE =108°,所以∠1=∠BAE -∠BAG =108°-90°=18°.18.4【分析】由平行四边形的性质得出AD =BCOC =AC =5OB =BD =3cm 由勾股定理得出BC 的长即可【详解】解:∵四边形ABCD 是平行四边形AC =10BD=6∴AD=BCOC=AC=5OB=BD=3 解析:4【分析】由平行四边形的性质得出AD=BC,OC=12AC=5,OB=12BD=3cm,由勾股定理得出BC的长即可.【详解】解:∵四边形ABCD是平行四边形,AC=10,BD=6,∴AD=BC,OC=12AC=5,OB=12BD=3,∵DB⊥BC,∴∠OBC=90°,∴BC=4,故答案为:4.【点睛】本题考查了平行四边形的性质、勾股定理;熟练掌握平行四边形的性质是解题的关键.19.3【解析】∵四边形ABCD是平行四边形∴BC=AD=12AD∥BC∵四边形PDQB 是平行四边形∴PD=BQ∵P的速度是1cm/秒∴两点运动的时间为12÷1=12s∴Q 运动的路程为12×4=48cm∴解析:3【解析】∵四边形ABCD是平行四边形,∴BC=AD=12,AD∥BC,∵四边形PDQB是平行四边形,∴PD=BQ,∵P的速度是1cm/秒,∴两点运动的时间为12÷1=12s,∴Q运动的路程为12×4=48cm,∴在BC上运动的次数为48÷12=4次.第一次PD=QB时,12−t=12−4t,解得t=0,不合题意,舍去;第二次PD=QB时,Q从B到C的过程中,12−t=4t−12,解得t=4.8;第三次PD=QB时,Q运动一个来回后从C到B,12−t=36−4t,解得t=8;第四次PD=QB时,Q在BC上运动3次后从B到C,12−t=4t−36,解得t=9.6.∴在运动以后,以P、D. Q、B四点组成平行四边形的次数有3次,故答案为3.点睛:本题考查了平行四边形的判定.注意能求出符合条件的所有情况是解此题的关键,注意掌握分类讨论思想的应用.20.或【分析】如图:根据题意可以作出两种不同的图形所以答案有两种情况因为在中平分交于点平分交于点所以;则求得的周长【详解】解:如图图①图②四边形是平行四边形平分平分由图①得:由图②得:为7或9故答案为: 解析:7或9【分析】如图:根据题意可以作出两种不同的图形,所以答案有两种情况.因为在ABCD 中,4=AD ,AE 平分DAB ∠交CD 于点E ,BF 平分ABC ∠交CD 于点F ,所以4DE AD CF BC ====;则求得ABCD 的周长.【详解】解:如图,图①图②四边形ABCD 是平行四边形,//AB CD ∴,4BC AD ==,AB CD =,EAB AED ∴∠=∠,ABF BFC ∠=∠,AE ∵平分DAB ∠,BF 平分ABC ∠,DAE BAE ∴∠=∠,CBF ABF ∠=∠,AED DAE ∴∠=∠,BFC CBF ∠=∠,AD DE ∴=,BC FC =,4DE CF AD ∴===,由图①得:4417CD DE CF EF =+-=+-=,7AB CD ∴==,由图②得:4419CD DE CF EF =++=++=,9AB ∴=,AB ∴为7或9.故答案为:7或9.【点睛】此题考查了平行四边形的性质:平行四边形的对边平行且相等.还考查了等腰三角形的判定与性质.注意如果有平行线与角平分线,一般会存在等腰三角形.解题时还要注意数形结合思想的应用.三、解答题21.(1)10;(2)128.【分析】(1)由平行四边形的性质及角平分线的定义可得出AB=AE,进而再利用题中数据即可求解结论;(2)易证△CED为直角三角形,则CE⊥AD,基础CE为平行四边形的高,利用平行四边形的面积公式计算即可.【详解】解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEB=∠CBE,∵BE平分∠ABC,∴∠ABE=∠AEB,∴AB=AE=10;(2)∵四边形ABCD是平行四边形.∴CD=AB=10,在△CED中,CD=10,DE=6,CE=8,∴ED2+CE2=CD2,∴∠CED=90°.∴CE⊥AD,∴平行四边形ABCD的面积=AD•CE=(10+6)×8=128.【点睛】本题考查了平行四边形的性质、平行四边形的面积公式运用及角平分线的性质等问题,解题的关键是熟练掌握有关性质.22.(1)t=6秒,四边形PQCD平行四边形;(2)t=7秒,四边形PQCD是等腰梯形.【分析】(1)当四边形PQCD是平行四边形时,必须有PD=CQ,而PD、CQ均可用含有t的式子表示出来,列方程解答即可.(2)当PQ=CD,PD≠QC时,四边形PQCD为等腰梯形.过P,D分别作PE⊥BC,DF⊥BC 后,可求出CF=2,所以当等腰梯形成立时,CQ=PD+4,然后列方程解答即可.【详解】解:(1)∵AD∥BC,∴当QC=PD时,四边形PQCD是平行四边形.此时有3t=24-t,解得t=6.∴当t=6s时,四边形PQCD是平行四边形.(2)当t=7秒时,四边形PQCD是等腰梯形分别过点P、D作PE⊥BC于E, DF⊥BC于F则四边形PEFD和四边形ABFD均为矩形当t=7时PA=7,PD=EF=24-7=17,CQ=21,∵AD=BF=24,∴CF=26-24=2,∴QE=QC-CF-EF=2由此可证△QPE≌△CDF;即,PQ=DC又AD∥BC,∴当t=7秒时,四边形PQCD是等腰梯形【点睛】本题主要考查了平行四边形、等腰梯形的判定,以及一元一次方程在几何图形中的应用,解题关键是利用数形结合思想找出等量关系解方程.23.(1)见解析;(2)画图见解析;B2(4,2-),C2(1,3-);(3)3【分析】(1)分别作出A、B、C的对应点A1、B1、C1即可;(2)分别作出B,C的对应点B2、C2即可;(3)分别作出P的位置即可.【详解】解:(1)如图:(2)如图,可以得到B2(4,2-),C2(1,3-);(3)如图,满足条件的P 点有3个.【点睛】本题考查的是图形的变换以及平行四边形的存在性,注意掌握旋转和平移作图的知识点和正确认识平行四边形即可.24.(1)见解析;(2)D (3,1),B C D '''∆的面积为52;(3)存在,满足条件点Q 存在三个点,如图所示见解析.【分析】(1)根据同角的余角相等得到BCO CDE ∠=∠,通过AAS 即可得到结论;(2)通过待定系数法求出直线 AB 的一次函数式,设 OC= ED =m ,从而得到点D 的坐标,进而即可求出B C D '''∆的面积;(3)分别以CD 为平行四边形的边和对角线,画出图形,即可得到结论.【详解】(1)证明:如图 1 中, 90BOC BCD CED ︒∠=∠=∠=90OCB DCE ︒∴∠+∠=,90DCE CDE ︒∠+∠=BCO CDE ∴∠=∠BC CD =BOC CED ∴∆≅∆(2)设直线 AB 的一次函数式为:y kx b =+∵直线 AB 与 x 轴, y 轴交于 A(6,0) , B(0,2)两点,∴062k b b =+⎧⎨=⎩,解得:132k b ⎧=-⎪⎨⎪=⎩∴可求得直线 AB 的一次函数式为:123y x =-+ BOC CED ∆≅∆∵BO=CE=2,设 OC= ED =m ,则 D( m+2,m ),把D(m+2,m) 代入得到123y x =-+,得m=1, ∴D(3,1)∴等腰直角 △BCD 腰长:5CB CD ==, ∵B C D '''∆与△BCD 的全等,∴B C D '''∆的面积=△BCD 的面积=52;(3)满足条件点 Q 存在三个点,如图所示【点睛】本题主要考查一次函数的图象和性质、三角形全等的判定和性质定理以及平行四边形的性质,熟练掌握全等三角形的判定和性质定理以及平行四边形的性质,以及分类讨论思想是解题的关键.25.(1)80C ∠=︒;(2)120C ∠=︒.【分析】(1)如图1,过点C 作CH ∥DF ,根据四边形的内角和为360°,求出∠MDC+∠CBN=160°,利用角平分线的定义可得:∠FDC+∠CBE=80°,最后根据平行线的性质可得结论;(2)如图2,连接GC 并延长,同理得:∠MDC+∠CBN=160°,∠FDC+∠CBE=80°,求出∠DGB=40°,可得结论.【详解】(1)如图1,过点C 作CH ∥DF ,∵BE∥DF,∴BE∥DF∥CH,∴∠FDC=∠DCH,∠BCH=∠EBC,∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,∴∠FDC=12∠CDM,∠EBC=12∠CBN,∵∠A+∠BCD=160°,∴∠ADC+∠ABC=360°-160°=200°,∴∠MDC+∠CBN=160°,∴∠FDC+∠CBE=80°,∴∠DCB=80°;(2)如图2,连接GC并延长,同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,∵BE∥AD,DF∥AB,∴∠A=∠MDF=∠DGB=∠NBG=40°,∵∠A+∠BCD=160°,∴∠BCD=160°-40°=120°.【点睛】本题考查了平行线的性质及其判定,多边形的内角和公式,三角形外角的性质,角平分线的定义,利用多边形的内角和公式和平行线的性质是解题关键.26.(1)证明过程见解析;(2)证明过程见解析;【分析】(1)由题意连接BD交AC于点O,由平行四边形的性质得AO=CO,BO=DO,证出EO=FO,即可得出四边形BFDE为平行四边形;(2)根据题意由平行四边形的性质得DE∥BF,即DE∥FG,证出FG是△CDE的中位线,得CG=DG即可.【详解】解:(1)连接BD交AC于点O,∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,又∵AE=CF,∴EO=FO,∴四边形BFDE为平行四边形;(2)由(1)知,四边形BFDE为平行四边形,∴DE//BF,即DE//FG,而AE=EF=FC,所以F为EC的中点,∴FG是△CDE的中位线,∴CG=DG,即G为CD的中点.【点睛】本题考查平行四边形的判定与性质以及三角形中位线定理等知识;熟练掌握平行四边形的判定与性质是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形综合检测题一、选择题(每题3分,共30分)1,一块均匀的不等边三角形的铁板,它的重心在( )A.三角形的三条角平分线的交点B.三角形的三条高线的交点C.三角形的三条中线的交点D.三角形的三条边的垂直平分线的交点2,如图1,如果□ABCD 的对角线AC 、BD 相交于点O ,那么图中的全等三角形共有( )A.1对B.2对C.3对D.4对3,平行四边形的一边长是10cm ,那么这个平行四边形的两条对角线的长可以是( )A.4cm 和6cmB.6cm 和8cmC.8cm 和10cmD.10cm 和12cm4,在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( )A.AC =BD ,AB =CD ,AB ∥CDB.AD //BC ,∠A =∠CC.AO =BO =CO =DO ,AC ⊥BDD.AO =CO ,BO =DO ,AB =BC5,如图2,过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线,分别相交于E 、F 、G 、H 四点,则四边形EFGH 为( )A.平行四边形 B 、矩形 C 、菱形 D. 正方形6,如图3,大正方形中有2个小正方形,如果它们的面积分别是S 1、S 2,那么S 1、S 2的大小关系是( )A.S 1 > S 2B.S 1 = S 2C.S 1<S 2D.S 1、S 2 的大小关系不确定7,矩形一个角的平分线分矩形一边为1cm 和3cm 两部分,则这个矩形的面积为( )A.3cm 2B. 4cm 2C. 12cm 2D. 4cm 2或12cm 28,如图4,菱形花坛 ABCD 的边长为 6m ,∠B =60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )B.20mC.22mD.24m9,如图5,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,则折痕EF 的长是( )A B . C D .图6 图4 F EDC B A 图5 图3 AD C B HE FG 图2B D 图110,如图6,是由两个正方形组成的长方形花坛ABCD ,小明从顶点A 沿着花坛间小路直到走到长边中点O ,再从中点O 走到正方形OCDF 的中心O 1,再从中心O 1走到正方形O 1GFH 的中心O 2,又从中心O 2走到正方形O 2IHJ 的中心O 3,再从中心O 3走2走到正方形O 3KJP 的中心O 4,一共走了31 2 m ,则长方形花坛ABCD 的周长是( )A.36 mB.48 mC.96 mD.60 m二、填空题(每题3分,共30分)11,如图7, 若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于___.12,如图8,过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的大小关系是S 1 S 2(填“>”或“<”或“=”).13,如图9,四边形ABCD 是正方形,P 在CD 上,△ADP 旋转后能够与△ABP ′重合,若AB =3,DP =1,则PP ′=___.14,已知菱形有一个锐角为60°,一条对角线长为6cm ,则其面积为___cm 2. 15,如图10,在梯形ABCD 中,已知AB ∥CD ,点E 为BC 的中点, 设△DEA 的面积为S 1,梯形ABCD 的面积为S 2,则S 1与S 2的关系为___.16,如图11,四边形ABCD 的两条对角线AC 、BD 互相垂直,A 1B 1C 1D 1四边形ABCD 的中点四边形.如果AC =8,BD =10,那么四边形A 1B 1C 1D 1的面积为___.17,如图12,□ABCD 中,点E 在边AD 上,以BE 为折痕,将△ABE 向上翻折,点A 正好落在CD 上的点F ,若△FDE 的周长为8,△FCB 的周长为22,则FC 的长为___.18,将一张长方形的纸对折,如图13所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n 次,可以得到 条折痕.…… 第一次对折 第二次对折 第三次对折图13图11A 1B 1C 1D 1 D A B C B 图12 D BA 图7 图9 图8N M Q D C B 图10 E D C B A三、解答题(共40分)19,如图1,4,等腰梯形ABCD 中,AD ∥BC ,∠DBC =45°,翻折梯形ABCD ,使点B 重合于D ,折痕分别交边AB 、BC 于点F 、E ,若AD =2,BC =8.求BE 的长.20,在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD 分割成四个部分,使含有一组对顶角的两个图形全等;(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有___组;(2)请在图15的三个平行四边形中画出满足小强分割方法的直线;(3)由上述实验操作过程,你发现所画的饿两条直线有什么规律?21,如图16,已知四边形ABCD 是平行四边形,∠BCD 的平分线CF 交边AB 于F ,∠ADC 的平分线DG 交边AB 于G .(1)线段AF 与GB 相等吗?(2)请你在已知条件的基础上再添加一个条件,使得△EFG 为等腰直角三角形,并说明理由.22,如图17,已知□ABCD 中,E 为AD 的中点,CE 的延长线交BA 的延长线于点E .(1)试说明线段CD 与F A 相等的理由;(2)若使∠F =∠BCF ,□ABCD 的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).23,(08上海市)如图,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形.(1)求证:四边形ABCD 是菱形;(2)若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.A B C D A B C D D CB A 图15 A BCDEF 图17图16B E 图18 F E DC B A 图1424,已知:如图19,四边形ABCD 是菱形,E 是BD 延长线上一点,F 是DB 延长线上一点,且DE =BF .请你以F 为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).(1)连结____________;(2)猜想:______=______;(3)证明:25,如图20,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC 上一点,连结EB ,过点A 作AM ⊥BE ,垂足为M ,AM 交BD 于点F .(1)试说明OE =OF ;(2)如图21,若点E 在AC 的延长线上,AM ⊥BE 于点M ,交DB 的延长线于点F ,其它条件不变,则结论“OE =OF ”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.EB AO C 图19 D A B F 图20 图21平行四边形综合检测题参考答案:一、1,C ;2,D ;3,D ;4,C ;5,C ;6,A ;7,D ;8,B ;9,D ;10,C .二、11,30°;12,=;13,14,15,1212S S =;16,20;17,7;18,15、2n -1.三、21,由题意得△BEF ≌△DFE,∴DE=BE,∵在△BDE 中,DE=BE,∠DBE=45°,∴∠BD E=∠DBE=45°,∴∠DEB=90°,∴DE ⊥BC.∴EC=12(BC-AD)= 12(8-2)=3.∴BE=5;22,(1)无数;(2)只要两条直线都过对角线的交点即可;(3)这两条直线过平行四边形的对称中心(或对角线的交点);23,:(1) 四边形ABCD 是平行四边形,AO CO ∴=.又ACE △是等边三角形,EO AC ∴⊥,即DB AC ⊥.∴平行四边形ABCD 是菱形;(2)ACE △是等边三角形,60AEC ∴∠=. EO AC ⊥ ,1302AEO AEC ∴∠=∠= . 2AED EAD ∠=∠ ,15EAD ∴∠= .45ADO EAD AED ∴∠=∠+∠= . 四边形ABCD 是菱形,290ADC ADO ∴∠=∠= .∴四边形ABCD 是正方形.24,(1)说明△CED ≌△CEA 即可,(2)BC =2AB ,理由略;25,(1)四边形ABCD 是矩形.连结OE .∵四边形ABCD 是平行四边形,∴DO =OB ,∵四边形DEBF 是菱形,∴DE =BE ,∴EO ⊥BD ,∴∠DOE = 90°,即∠DAE = 90°,又四边形ABCD 是平行四边形,∴四边形ABCD 是矩形.(2)解:∵四边形DEBF 是菱形,∴∠FDB =∠EDB ,又由题意知∠EDB =∠EDA ,由(1)知四边形ABCD 是矩形,∴∠ADF =90°即∠FDB +∠EDB +∠ADE =90°,则∠ADB = 60°,∴在Rt △ADB 中,有AD ∶AB =1:3,即3=BCAB ;26,(1)连结AF ;(2)猜想AF =AE ;(3)连结AC ,交BD 于O ,因为四边形ABCD 是菱形,所以AC ⊥BD 于O ,DO =BO ,因为DE =BF ,所以EO =BO 所以AC 垂直平分EF ,所以AF =AE ;27,(1)因为四边形ABCD 是正方形,所以∠BOE =∠AOF =90°,OB =OA ,又因为AM ⊥BE ,所以∠MEA +∠MAE =90°=∠AFO +∠MAE ,所以∠MEA =∠AFO ,所以Rt △BOE 可以看成是绕点O 旋转90°后与Rt △AOF 重合,所以OE =OF ;(2)OE =OF 成立.证明:因为四边形ABCD 是正方形,所以∠BOE =∠AOF =90°,OB =OA 又因为AM ⊥BE ,所以∠F +∠MBF =90°=∠B +∠OBE ,又因为∠MBF =∠OBE ,所以∠F =∠E ,所以Rt △BOE 可以看成是由Rt △AOF 绕点O 旋转90°以后得到的,所以OE =OF ;。
