[首发]四川省广安、眉山、内江、遂宁2018届高三第三次诊断性考试数学(理)试题(扫描版)
四川省广安、眉山、内江、遂宁2018届高三第三次诊断性

第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题。
从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What is the man doing?A. Listening to music.B. Trying to go to sleep.C. Taking care of the baby.2. What did the woman see?A. A horse.B. A house.C. An aircraft.3. Where could the speakers most likely be?A. At home.B. At an airport.C. At a ticket office.4. What’s the p robable relationship between the two speakers?A. Patient and doctor.B. Boss and secretary.C. Husband and wife.5. Who is probably the woman?A. A hotel clerk.B. A police officer.C. The man’s wife.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. What is the man doing?A. Smoking.B. Seeing a doctor.C. Doing scientific research.7. What does the woman ask the man to do?A. Give up his present job.B. Be more determined.C. Do more exercise.听第7段材料,回答第8至10题。
四川省广安、眉山、内江、遂宁2018届高三三诊理科综合试卷含答案

8.0 7.0 6.0 5.0 4.0 3.o 2,0 ⒈0
A。 :1B核 比劳He核 更稳 定
B。 台He核 的结合 能约 为 7MeV C。 两个寻H核 结合 成台He核 时释放 能量
D。 质 量 较 大 的核 一 定 比质 量 较 小 的核 的 比结 合 能 大
物 的年 代 ,r一 和 Y3+具 有 相 同 的 电子 层 结 构 ,Z原 子 的 最 外 层 电 子 数 是 其 电 子 层 数 的 2
倍 。下列相关说 法错误 的是
A。 简单 氢化物 的稳定性 :W<X
B。 单核 阴离子还原 性 :Z>X
C。 电解 Y的 熔 融氯化 物可制备 Y单 质 D。 WZ2分 子 中只存 在共 价键
B。 寒 冷 环 境 中体 温恒 定 是 因为机体 产 热 量 等 于散 热 量
C。 人 体 骨骼 肌 细胞 中产 热 量 最 多 的部 位 是 细胞 质 基 质
D。 下 丘 脑 是 体 温调 节 中枢但 不 能直 接 感 受 体 温 的变 化
4.植 物体 内有 多 种 激 素 对 各 种 生 命 活 动 进 行 调 节 。下 列 关 于 植 物 激 素 调 节 的叙 述 ,错 误
第 I卷 (共 126分 )
-、 选择题 ∶本题 共 13小 题 ,每 小题 6分 ,共 78分 。在 每小题 给 出的 四个选 项 中 ,只 有一项是
符合题 目要 求的。 1.下 列关 于高等动物细胞 有 丝分裂过程 的叙述 ,正 确 的是
A。 间期 结束 时染 色体 数 和 DNA分 子数 都加倍
的是
A。 生 长 素不 直 接参 与 细胞 代 谢 只能 给 细胞 传 达促 进 生 长 的信 息
2018届高考第三次诊断性考试数学试题(理)及答案

2018年普通高等学校招生全国统一考试**5月调研测试卷 理科数学第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}()|,,2A x x a B =≤=-∞,若A B ⊆,则实数a 的取值范围是( ) A .2a ≥ B .2a > C .2a ≤ D .2a <2. 已知i 为虚数单位,复数z 满足21iz z =+,则z =( ) A .2155i -- B .2155i + C .2i + D .2i - 3.设命题:,2ln 2x p x Q x ∃∈-<,则p ⌝为( )A .,2ln 2x x Q x ∃∈-≥B .,2ln 2x x Q x ∀∈-<C .,2ln 2x x Q x ∀∈-≥D .,2ln 2x x Q x ∀∈-= 4. 已知随机变量()22,XN σ,若()()1121P X a P X a ≤-+≤+=,则实数a =( )A . 0B .1 C. 2 D .45.山城农业科学研究所将5种不同型号的种子分别试种在5块并成一排的试验田里,其中,A B 两型号的种子要求试种在相邻的两块试验田里,且均不能试种在两端的试验田里,则不同的试种方法数为 ( ) A .12 B . 24 C. 36 D .486. 已知抛物线24y x =的焦点为F ,以F 为圆心的圆与抛物线交于M N 、两点,与抛物线的准线交于P Q 、两点,若四边形MNPQ 为矩形,则矩形MNPQ 的面积是( )A...37. 已知实数,x y 满足不等式组20x y x a x y +-≤⎧⎪≥⎨⎪≤⎩,且2z x y =-的最大值是最小值的2倍,则a =( ) A .34 B .56 C. 65 D .438. 《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.根据该问题设计程序框图如下,若输入103,97a b ==,则输出n 的值是( )A . 8B . 9 C. 12 D .169.一个正三棱柱的三视图如图所示,若该三棱柱的外接球的表面积为32π,则侧视图中的x 的值为 ( )A . 6B . 4 C. 3 D .210. 已知圆O 的方程为221x y +=,过第一象限内的点(),P a b 作圆O 的两条切线,PA PB ,切点分别为,A B ,若8PO PA =,则a b +的最大值为( )A .3B ..611. 已知双曲线()2222:10,0x y C a b a b -=>>的左右焦点分别为12,F F ,以2OF 为直径的圆M 与双曲线C 相交于,A B 两点,其中O 为坐标原点,若1AF 与圆M 相切,则双曲线C 的离心率为( )A B D12. 已知函数()32413327f x x x x =+++,等差数列{}n a 满足:()()()129911f a f a f a +++=,则下列可以作为{}n a 的通项公式的是( ) A .173n - B .2333n - C. 452n- D .49n - 第Ⅱ卷二、填空题:本大题共4小题,每小题5分,满分20分,将答案填在答题纸上 13.函数()22cos sin cos 1f x x x x =+-的最大值是 .14.已知0a >,且102a x ⎛ ⎝的展开式中常数项为5,则a = .15.在如图所示的矩形ABCD 中,点E P 、分别在边AB BC 、上,以PE 为折痕将PEB ∆翻折为PEB '∆,点B '恰好落在边AD 上,若1sin ,23EPB AB ∠==,则折痕PE = .16.已知点I 为ABC ∆的内心,2,3,4AC BC AB ===,若A I x A B y A C =+,则x y += .三、解答题 :本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 在ABC ∆中,A 为锐角,且()224sin 5cos sin cos 2422A A A A ππ⎛⎫⎫--=+ ⎪⎪⎝⎭⎭.(1)求A ;(2)若1,AC ABC =∆BC 边上的高.18. 从某校高三年级中随机抽取100名学生,对其高校招生体检表中的视图情况进行统计,得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在0.30.5的概率为110. (1)求,a b 的值;(2)若某大学A 专业的报考要求之一是视力在0.9以上,则对这100人中能报考A 专业的学生采用按视力分层抽样的方法抽取8人,调查他们对A 专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学A 专业的调查,记抽到的学生中视力在1.1 1.3的人数为ξ,求ξ的分布列及数学期望.19.如图,三棱柱111ABCA B C 中,011111,,60AC B A AB AA BAA ⊥=∠=. (1)求证:ABC ∆为等腰三角形;(2)若平面BAC ⊥平面11ABB A ,且AB CB =,求二面角11A CC B --的正弦值.20. 已知椭圆()2222:10x y C a b a b +=>>的离心率为2,且右焦点与抛物线2y =的焦点重合.(1)求椭圆的C 的方程;(2)设点P 为圆22:2x y Γ+=上任意一点,过P 作圆Γ的切线与椭圆C 交于,A B 两点,证明:以AB 为直径的圆经过定点,并求出该定点的坐标. 21.已知函数()()1ln f x x a x a R x=+-∈. (1)若直线1y x =+与曲线()y f x =相切,求a 的值; (2)若关于x 的不等式()2f x e≥恒成立,求a 的取值范围. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22. 选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos sin 1ρθρθ+=,曲线C 的极坐标方程为2sin8cos ρθθ=.(1)求直线l 与曲线C 的直角坐标方程;(2)设点()0,1M ,直线l 与曲线C 交于不同的两点,P Q ,求MP MQ +的值. 23.选修4-5:不等式选讲 已知函数()2f x x a x =-+.(1)当3a =时,求不等式()3f x ≥的解集;(2)若关于x 的不等式()0f x ≤的解集为{}|2x x ≤-,求实数a 的值.试卷答案一、选择题1-6: DACCBA 7-12: BBCBCA 二、填空题13 15. 278 16. 23三、解答题17.解:(1))1sin 4sin 1sin sin 223A AA A A π+=+⇒=⇒=;(2)1sin 42S bc A c ==⇒=,由余弦定理有:2222cos 13a b c bc A a =+-=⇒=由面积公式有:1213S ah h =⇒=. 18.解:(1)0.20.10.50100b b a ⨯=⇒=⇒=; (2)ξ的可能取值为0,1,2,3,概率为:()()321553338810300,15656C C C P P C C ξξ======, ()()12353333881512,35656C C C P P C C ξξ======,所以其分布列如下:则()568E ξ==. 19.解:(1)设AB 中点为D ,连接1,CD DA ,又设2AB =,则11,12AD AA ==, 又因为11cos 2BAA ∠=,所以1AB DA⊥, 又因为11111,CA A B CA DA⊥,所以11A B ⊥面1CDA ,所以11A B CD ⊥,又因为CD 为中线,所以ABC ∆为等腰三角形;(2)设以AB 中点D 为原点,分别以1,,DA DA DC 为,,x y z 轴建立空间直角坐标系,设2AB =,则()()(()(110,0,0,,,1,0,0,D A C B C --,故()()(110,3,3,1,3,0,1,0,CA CC CB =-=-=-,设面11ACC 的法向量()1111,,n x y z =,则有()1111103,1,10n x =⇒=-=⎪⎩,同理得:面1BCC的法向量()23,1,1n =-,设所求二面角为θ,则12123cos 5n n n n θ==,故4sin 5θ=.20.解:(1)由题意有:221263c e x y a c ⎧==⎪⇒+=⎨⎪=⎩;(2)由对称性,猜测该定点为()0,0O ,设该切线方程为y kx b =+,则有2222d b k ==⇒=+,联立方程有:()22222214260163y kx b k x kbx b x y =+⎧⎪⇒+++-=⎨+=⎪⎩,()()()222212121212211366021OA OB x x y y k x x kb x x b b k k =+=++++=--=+,所以OA OB ⊥,即原点以在AB 为直径的圆上.21.解:(1)()20220111111a x ax f x x a x x x a x --'=--==⇒=-⇒-=, 则有:()00000001ln 1ln 10f x x a x x x x x =+-=+⇒-+=, 令()()1ln 1101h x x x h x x x'=-+⇒=-=⇒=, 则()h x 在()0,1上单调递增,在()1,+∞上单调递减, 又因为()10h =,所以011x a =⇒=-; (2)令()12ln l x x a x x e=+--,则原命题等价于()0l x ≥恒成立, 又()221x ax l x x --'=,设2000110,x ax a x x --==-, 则()l x 在()00,x 上单减,在()0,x +∞上单增, 故只需()()00000001120,ln l x l x x x x x x e⎛⎫≥=+--- ⎪⎝⎭, 令()()21121ln 1ln m x x x x m x x x x e x ⎛⎫⎛⎫'=+---⇒=-+ ⎪ ⎪⎝⎭⎝⎭,所以()m x 在()0,1上单调递增,在()1,+∞上单调递减,又()10m m e e ⎛⎫==⎪⎝⎭,∴01,x e e ⎡⎤∈⎢⎥⎣⎦,即11,a e e e e ⎡⎤∈--⎢⎥⎣⎦. 22.解:(1)22cos sin 11,sin 8cos 8x y y x ρθρθρθθ+=⇒+==⇒=;(2)考虑直线方程1x y +=,则其参数方程为1x y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数),代入曲线方程有:2211810222t ⎛⎫-=⨯⇒-+= ⎪ ⎪⎝⎭,则有12MP MQ t t +=+=23.解:(1)()33,3323,3x x f x x x x x -≥⎧=-+=⎨+<⎩结合函数图像有:[)0,x ∈+∞;(2)由题意知()202f a -=⇒=或6a =-, 经检验,两种情况均符合题意,所以2a =或6a =-.。
四川省遂宁市2018届高三三诊考试理科综合试题

遂宁市高中2018届三诊考试理科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
全卷满分300分,考试时间150分钟。
注意事项:1.答题前,考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。
并检查条形码粘贴是否正确。
2.选择题使用2B铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
可能用到的相对原子质量:H-1 C-12 O-16 Fe-56 B-11 Ba-137 S-32 Ca-40 Cu-64 As-75第Ⅰ卷(选择题,共126分)一、选择题(本题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项符合题目要求)1.下列有关生物膜的叙述正确的是A.生物膜不参与生命系统边界构建B.生物膜都具有选择透过性和流动性C.小分子物质都通过跨膜方式穿过生物膜D.细胞膜内表面有糖类和蛋白质结合形成的糖被2.艾滋病是威胁人类健康的重要疾病之一,12月1日为世界艾滋病日,宣传预防艾滋病刻不容缓。
下列与艾滋病病原体有关的叙述,正确的是A.它用灭菌的牛肉膏蛋白胨培养基培养B.它由衣壳、核酸等组成,属原核生物C.它主要攻击T细胞,导致人体免疫功能障碍D.它通过血液、体液、握手、蚊虫叮咬等传播3.下图为某二倍体植物的一个造孢细胞通过分裂形成精子的过程,其中①~④表示细胞分裂,X、Y、Z表示分裂过程中产生的细胞。
据此分析,下列叙述正确的是A.过程③的细胞分裂前期有同源染色体但无联会配对现象B.细胞Z与过程④产生的精子中所含遗传信息不可能相同C.过程①处在中期和过程④处在后期的细胞染色体数不同D.该植物形成精子时需要减数分裂和有丝分裂的共同参与4.小麦干种子用蒸馏水浸泡,其萌发初期,代谢加强、干重增加。
相关叙述正确的是A.自由水含量增加,淀粉水解,干重增加B.吸收N、P等元素,为种子萌发做准备C.光合速率大于呼吸速率导致其干重增加D.脱落酸含量增加,诱导淀粉酶基因表达5.水杨酸是植物体内一种重要的内源激素,能诱导植物体内产生某些与抗病有关的蛋白质,提高抗病能力。
2018届四川省遂宁市高中三诊考试试卷与答案

{正文}2018届四川省遂宁市高中三诊考试英语试题本试卷分第Ⅰ卷(选择题,共100分)和第Ⅱ卷(非选择题,共50分)两部分。
总分150分,考试时间120分钟。
第Ⅰ卷第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.How will the speakers go back to London?A.By air. B.By train. C.By car.2.When will the speakers meet?A.On Monday. B.On Tuesday. C.On Wednesday. 3.What will the man do tonight?A.Attend a meeting. B.Go to a club. C.Stay at home. 4.How will the weather be this weekend?A.Snowy. B.Sunny. C.Stormy.5.What is wrong with the man?A.His feet hurt.B.His shoes don't fit him.C.He missed a long walk yesterday.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听下面一段材料,回答第6至7题。
6.What is wrong with the jacket?A.It is large in size.B.Its sleeves are short.C.It has a little dirt on it.7.What does the man offer to do?A.Reduce the price.B.Check the jacket.C.Find another jacket.听下面一段材料,回答第8至9题。
四川省2018届高三三诊理数试题

四川省2018届高三三诊理数试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,,若,则实数的取值范围是( )A. (0,4]B.C.D.【答案】C【解析】错误!未找到引用源。
,若错误!未找到引用源。
,则错误!未找到引用源。
,故选C.2. 欧拉公式 (为虚数单位)是瑞士数学家欧拉发明的,将指数的定义域扩大到复数集,建立了三角函数和指数函数的联系,被誉为“数学中的天桥”.根据欧拉公式可知, 错误!未找到引用源。
表示的复数的模为( )A. B. 1 C. D.【答案】B3. 已知某几何体的三视图如图所示,则该几何体的体积是( )A. 100B. 82C. 96D. 112【答案】A【解析】如图,几何体是长方体截去如图红色截面的三棱锥,所以几何体的体积是错误!未找到引用源。
,故选A.4. 已知函数(,,为常数,,, )的部分图像如图所示,则下列结论正确的是( )A. 函数的最小正周期为B. 直线是函数图象的一条对称轴C. 函数在区间上单调递增D. 将函数的图象向左平移个单位,得到函数的图象,则【答案】D错误!未找到引用源。
不是函数的对称轴,当错误!未找到引用源。
时,错误!未找到引用源。
,是先减后增,不是函数的单调递增区间,函数向左平移错误!未找到引用源。
个单位后得到函数错误!未找到引用源。
,所以D正确,故选D.5. 对于四面体,有以下命题:①若,则,,与底面所成的角相等;②若,,则点在底面内的射影是的内心;③四面体的四个面中最多有四个直角三角形;④若四面体的6条棱长都为1,则它的内切球的表面积为.其中正确的命题是( )A. ①③B. ③④C. ①②③D. ①③④【答案】D③正确,如图,错误!未找到引用源。
平面错误!未找到引用源。
,错误!未找到引用源。
,其中有4个直角三角形;④正确,正四面体的内切球的半径为错误!未找到引用源。
2018届四川省绵阳市高三第三次诊断性考试理科数学试题及答案

本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
第I 卷1至2页,第II 卷3至4页。
满分150分。
考试时间120分钟。
注意事项:1. 答题前,考生务必将自己的姓名、考号用0.5毫米的黑色签字笔填写在答题卡上,并将条形码粘贴在答题卡的指定位置。
2. 选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米的黑色签字笔书写在答题卡的对应框内,超出答题区域书写的答案无线;在草稿纸、试题卷上答题无效。
3. 考试结束后,将答题卡收回。
1. 已知集合{}1==x x M ,{}x x x N ==2,则=⋃N MA.{}1B.{}1,1-C.{}1,0D.{}1,0,1- 2. 复数25-i 的共轭复数是 A.i +-2 B.i +2 C.i --2 D.i -23. 执行如右图所示的程序框图,如输入2=x ,则输出的值为A.9B.9log 8C.5D.5log 84. 已知向量)1,3(-=a ,)2,1(-=b ,)1,2(=c .若),(R y x yc xb a ∈+=,则=+y x A.2 B.1 C.0 D.215. 已知命题a x R x p >sin ,:∈∃,若p ⌝是真命题,则实数a 的取值范围为A.1<aB.1≤aC.1=aD.1≥a6. 已知]2,2[-∈a ,则函数12)(2++=ax x x f 有零点的概率为 A.21 B.31 C.41D.517. 若抛物线x y C 4:21=的焦点F 恰好是双曲线)0,0(1:2222>>b a by a x C =-的右焦点,且1C 与2C 交点的连线过点F ,则双曲线2C 的离心率为A.12+B.122-C.223+D.226+ 8. 已知函数)0(sin )(>w wx x f =的一段图像如图所示,△ABC 的顶点A 与坐标原点O 重合,B 是)(x f 的图像上一个最低点,C 在x 轴上,若内角C B A ,,所对边长为c b a ,,,且△ABC 的面积S 满足22212a c b S -+=,将)(x f 右移一个单位得到)(x g ,则)(x g的表达式为 A.)2cos()(x x g π=B.)2cos()(x x g π-=C.)212sin()(+=x x gD.)212sin()(-=x x g9. 为了了解小学生的作业负担,三名调研员对某校三年级1至5名进行学情调查,已知这5个班在同一层楼并按班号排列。
2018届四川省遂宁市高中三诊考试试卷与答案

{正文}2018届四川省遂宁市高中三诊考试理科综合试题物理部分二、选择题(本题共8小题,每小题6分。
在每小题给出的四个选项中,第14-18题只有一项符合题目要求,第19-21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
)14.对核反应的下列说法正确的是A .核反应方程1441717281N He O H +→+是属于α衰变 B .发生核反应23411120H H He n +→+需要吸收能量 C .核反应2351891441920365603U n Kr Ba n +→++是属于裂变D .发生β衰变实质是质子向中子转变15.如图所示,圆弧形槽固定在地面上,COD 为水平直径,在光滑的半球形绝缘内壁有质量分别为m A 、m B 两带同种电荷的小球,各自带电量为q A 、q B ,A 、B 两小球与球心O 点连线与竖直方向分别成37°、53°夹角,处于静止状态,则A .质量关系一定满足m A > m BB .电荷量关系一定满足q A > q BC .现用外力将小球B 缓慢移动到球心O 点正下方,A 、B 系统电势能将减小D .突然向下撤去半球形凹槽,小球A 、B 将作曲线运动,且A 、B 系统电势能可能增大16.如图乙所示,在图中理想变压器的原、副线圈上有A 、B 、C 、D 四只相同的小灯泡,在原线圈加有如图甲所示的电压,原、副线圈匝数比为2∶1,开关闭合时A 小灯泡的功率为P (设整个过程四只小灯泡均未超过额定功率),则A .加在原线圈的电压随时间变化规律为220sin100()u t V π=B .变压器的输出功率为73PC .A 、B 、C 、D 四灯总功率为73PD .若断开开关S ,则B 、C 两小灯泡变暗17.如图所示,底边BC 长为2a 的等腰直角三角形区域ABC (∠A 为直角)内有垂直纸面向里的匀强磁场,磁感应强度大小为B ,在磁场边界顶点A 有一粒子源,源源不断地向磁场发射各种方向(均平行于纸面)且速度大小不同的带正电的粒子,已知粒子的比荷为k ,则下列关于粒子在磁场中运动的说法正确的是A .粒子不可能从C 点射出B .粒子最长运动时间为kB πC .沿AB 方向入射的粒子运动时间最长D .粒子最大的运动半径为a )12(-18.如图甲所示,相距为L 的金属导轨MN 、PQ 倾斜放置,与水平方向夹角为α,在NQ 上接一阻值为R 的电阻,装置处于与MN 、PQ 所在平面垂直的匀强磁场中。
四川省南充市2018届高三第三次诊断考试数学(理)试题 含答案

秘密 启封并使用完毕前ʌ考试时间:2018年4月24日下午15ʒ00~17ʒ00ɔ四川高三联合诊断考试数学试题(理科)㊀㊀本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)㊂第Ⅰ卷1至2页,第Ⅱ卷3至4页,共4页,满分150分,考试时间120分钟㊂考生作答时,须将答案答在答题卡上,在本试卷㊁草稿纸上答题无效,考试结束后,只将答题卡交回㊂第Ⅰ卷㊀选择题(共60分)注意事项:㊀㊀必须使用2B铅笔在答题卡上将所选答案对应的标题涂黑㊂㊀㊀第Ⅰ卷共12小题㊂一㊁选择题:本大题共12小题,每小题5分,共60分㊂在每小题给出的四个选项中,只有一项是符合题目要求的㊂1.已知集合A={x|x-1ɤ0},B={x|x2-4xɤ0},则AɘB=A.{x|xɤ4}㊀㊀㊀㊀B.{x|0ɤxɤ4}㊀㊀㊀㊀C.{x|0ɤxɤ1}㊀㊀㊀㊀D.{x|1ɤxɤ4}2.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=3+i,则z1z2=A.10B.-10C.-9+iD.-9-i3.已知cos(α+π4)=23,则sin(π4-α)的值等于A.23B.-23C.53D.ʃ534.如图,正方形ABCD中,点E,F分别是DC,BC的中点,那么EFң=A.12ABң+12ADңB.-12ABң-12ADңC.-12ABң+12ADңD.12ABң-12ADң5.为了从甲㊁乙两人中选一人参加数学竞赛,老师将二人最近的6次数学测试的分数进行统计,甲㊁乙两人的得分情况如茎叶图所示,若甲㊁乙两人的平均成绩分别是x甲,x乙,则下列说法正确的是A.x甲>x乙,乙比甲成绩稳定,应选乙参加比赛B.x甲>x乙,甲比乙成绩稳定,应选甲参加比赛C.x甲<x乙,甲比乙成绩稳定,应选甲参加比赛D.x甲<x乙,乙比甲成绩稳定,应选乙参加比赛6.执行如图所示的程序框图,输出的S值为A.3B.-6C.10D.-157.直线l过点(-4,0)且与圆(x+1)2+(y-2)2=25交于A,B两点,如果|AB|=8,那么直线l的方程为A.5x+12y+20=0B.5x-12y+20=0或x+4=0C.5x-12y+20=0D.5x+12y+20=0或x+4=08.已知函数f(x)在定义域(0,+ɕ)上是单调函数,若对于任意xɪ(0,+ɕ),都有f(f(x)-1x)=2,则f(15)的值是A.5B.6C.7D.89.已知长方体ABCD-A1B1C1D1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OAʅ平面BDE,则球O的表面积是A.8πB.16πC.20πD.32π10.在әABC中,角A,B,C所对的边分别为a,b,c,且cos2B+12sin2B=1,0<B<π2,若|BCң+ABң| =3,则16b ac的最小值为A.163(2-2)B.163(2+2)C.16(2-2)D.16(2+2)11.已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左㊁右焦点分别为F1㊁F2,过F2作平行于C的渐近线的直线交C于点P,若PF1ʅPF2,则C的渐近线方程为A.y=ʃx B.y=ʃ2x C.y=ʃ2x D.y=ʃ5x 12.已知定义在R上的偶函数f(x)在[0,+ɕ)上单调递减,若不等式f(-ax+ln x+1)+f(ax-ln x-1)ȡ2f(1)对任意xɪ[1,3]恒成立,则实数a的取值范是A.[1e,2+ln33]B.[1e,e]C.[1e,+ɕ) D.[2,e]第Ⅱ卷(共90分)二㊁填空题:本大题共4小题,每小题5分,共20分㊂13.(x -1)7的展开式中x 2的系数为.14.若实数x ,y 满足2x -y ȡ0,y ȡx ,y ȡ-x +b{且z =2x +y 的最小值为3,则b =.15.在әABC 中,AB =2,AC =3,BC 边上的中线AD =2,则әABC 的面积为.16.已知单位向量i ң,j ң,k ң两两的夹角均为θ(0<θ<π,且θʂπ2),若空间向量a ң=x i ң+y j ң+zk ң(x ,y ,z ɪR ),则有序实数组(x ,y ,z )称为向量a ң在 仿射 坐标系O -xyz (O 为坐标原点)下的仿射 坐标,记作a ң=(x ,y ,z )θ,有下列命题:①已知a ң=(1,3,-2)θ,b ң=(4,0,2)θ,则a ң㊃b ң=0;②已知a ң=(x ,y ,0)π3,b ң=(0,0,z )π3,其中x ,y ,z 均为正数,则当且仅当x =y 时,向量a ң,b ң的夹角取得最小值;③已知a ң=(x 1,y 1,z 1)θ,b ң=(x 2,y 2,z 2)θ,则a ң+b ң=(x 1+x 2,y 1+y 2,z 1+z 2)θ;④已知OA ң=(1,0,0)π3,OB ң=(0,1,0)π3,OC ң=(0,0,1)π3,则三棱锥O -ABC 的表面积S =2.其中真命题为(写出所有真命题的序号).三㊁解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤㊂17.(本题满分12分)已知{a n }是等比数列,a 1=2,且a 1,a 3+1,a 4成等差数列.(Ⅰ)求数列{a n }的通项公式;(Ⅱ)若b n =log 2a n ,求数列{b n }前n 项的和.18.(本题满分12分)某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为k ,当k ȡ85时,产品为一级品;当75ɤk <85时,产品为二级品,当70ɤk <75时,产品为三级品,现用两种新配方(分别称为A 配方和B 配方)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面的试验结果:(以下均视频率为概率)A 配方的频数分配表指标值分组[75,80)[80,85)[85,90)[90,95)频数10304020B 配方的频数分配表指标值分组[70,75)[75,80)[80,85)[85,90)[90,95)频数510154030(Ⅰ)若从B 配方产品中有放回地随机抽取3件,记 抽出的B 配方产品中至少1件二级品 为事件C ,求事件C 发生的概率P (C );(Ⅱ)若两种新产品的利润率y 与质量指标k 满足如下关系:y =t ,kȡ85,5t 2,75ɤk <85,t 2,70ɤk <75,{其中17<t <16,从长期来看,投资哪种配方的产品平均利润率较大?19.(本题满分12分)如图,四边形ABCD中,ABʅAD,ADʊBC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EFʊAB,现将四边形ABCD沿EF折起,使平面ABEFʅ平面EFDC.(Ⅰ)若BE=1,在折叠后的线段AD上是否存在一点P,且APң=λPDң,使得CPʊ平面ABEF?若存在,求出λ的值;若不存在,说明理由;(Ⅱ)当三棱锥A-CDF的体积最大时,求二面角E-AC-F的余弦值.20.(本题满分12分)已知椭圆C的中心在原点,离心率等于12,它的一个长轴端点恰好是抛物线y2=16x的焦点,(Ⅰ)求椭圆C的方程;(Ⅱ)已知P(2,3),Q(2,-3)是椭圆上的两点,A,B是椭圆上位于直线PQ两侧的动点.①若直线AB的斜率为12,求四边形APBQ面积的最大值.②当A,B运动时,满足øAPQ=øBPQ,试问直线AB的斜率是否为定值?请说明理由.21.(本题满分12分)已知函数f(x)=4x3-3x2cosθ+316cosθ,其中xɪR,θ为参数,且0ɤθ<2π.(Ⅰ)当cosθ=0时,判断函数f(x)是否有极值.(Ⅱ)要使函数f(x)的极小值大于零,求参数θ的取值范围.(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.㊀㊀请考生在22㊁23题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号22.(本题满分10分)选修4-4:坐标系与参数方程已知曲线C的极坐标方程是ρ-4sinθ=0,以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l过点M(1,0),倾斜角为34π.(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;(Ⅱ)设直线l与曲线C交于A,B两点,求|MA|+|MB|的值.23.(本题满分10分)选修4-5:不等式选讲已知函数f(x)=|x-2|.(Ⅰ)解不等式f(x)+f(x+1)ȡ5;(Ⅱ)若|a|>1,且f(ab)>|a|㊃f(b a),证明:|b|>2.四川高三联合诊断考试数学试题(理科)参考答案一㊁选择题:1.C㊀2.B㊀3.A㊀4.D㊀5.D㊀6.C㊀7.D㊀8.B㊀9.B㊀10.A㊀11.C㊀12.A 二㊁填空题13.-21㊀㊀14.94㊀㊀15.3154㊀㊀16.②③三㊁解答题17.解:(Ⅰ)设数列{a n}公比为q,则a3=a1㊃q2=2q2,a4=a1㊃q3=2q3,因为a1,a3+1,a4成等差数列,所以,a1+a4=2(a3+1)即2+2q2=2(2q2+1),整理得q2(q-2)=0,因为qʂ0,所以q=2,所以,a n=2ˑ2n-1=2n(nɪN∗). 6分(Ⅱ)因为b n=log2a n=log22n=n,所以S n=b1+b2+ +b n=1+2+ +n=n(n+1)2(nɪN∗) 12分18.解:(Ⅰ)由题意知,从B配方产品中随机抽取一次抽中二级品的概率为14,则没有抽中二级品的概率为34, 3分所以,P(C)=1-(34)3=3764. 5分(Ⅱ)A配方立品的利润分布列为y t5t2p0.60.4所以E(y)A=0.6t+2t2 8分B配方产品的利润分布列为y t5t2t2p0.70.250.05所以E(y)B=0.7t+1.3t2, 11分因为17<t<16,所以E(y)A-E(y)B=710t(t-17)>0所以投资A配方产品的平均利润率较大. 12分19.(Ⅰ)在折叠后的图中过C作CGʅFD,交FD于G,过G作GPʅFD交AD于P,连结PC,在四边形ABCD中,EFʊAB,ABʅAD,所以EFʅAD. 1分折起后AFʅEF,DFʅEF,又平面ABEFʅ平面EFDC,平面ABEFɘ平面EFDC=EF,所以FDʅ平面ABEF. 3分又AF⊂平面ABEF,所以FDʅAF,所以CG ʊEF ,PG ʊAF ,AP PD =FG GD =32,因为CG ɘPG =G ,EF ɘAF =F ,所以平面CPG ʊ平面ABEF ,因为CP ⊂平面CPG ,所以CP ʊ平面ABEF.所以在AD 存在一点P ,且AP ң=32PD ң,使CP ʊ平面ABEF.5分(Ⅱ)设BE =x ,所以AF =x (0<x ɤ4),FD =6-x ,故V A -CDF =13ˑ12ˑ2ˑ(6-x )ˑx =13(-x 2+6x )=13[9-(x -3)2]所以当x =3时,V A -CDE 取是最大值. 7分由(Ⅰ)可以F 为原点,以FE ,FD ,FA 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则A (0,0,3),D (0,3,0),C (2,1,0),E (2,0,0),所以AE ң=(2,0,-3),AC ң=(2,1,-3),FA ң=(0,0,3),FC ң=(2,1,0),设平面ACE 的法向量n 1ң=(x 1,y 1,z 1),则n 1ң㊃AC ң=0,n 1ң㊃AE ң=0,{即2x 1+y 1-3z 1=0,2x 1-3z 1=0,{令x 1=3,则y 1=0,z 1=2,则n 1ң=(3,0,2),9分设平面ACF 的法向量n 2ң=(x 2,y 2,z 2),则n 2ң㊃FA ң=0,n 2ң㊃FC ң=0,{即3z 2=02x 2+y 2=0,{令x 2=1,则y 2=-2,z 2=0,则n 2ң=(1,-2,0)11分所以cos<n 1ң,n 2ң>=n 1ң㊃n 2ң|n 1ң||n 2ң|=313ˑ5=36565.所以二面角E -AC -F 的余弦值为36565. 12分20.解:(Ⅰ)因为抛物线方程y 2=16x ,所以抛物线焦点为(4,0) 2分所以a =4㊀又a 2=b 2+c 2,e =c a =12所以a 2=16,b 2=12.所以椭圆C 的方程为x 216+y 212=1. 4分(Ⅱ)①设A (x 1,y 1),B (x 2,y 2),设直线AB 的方程为y =12x +t联立y =12x +tx 216+y 212=1ìîí㊀消y ,得x 2+tx +t 2-12=0ә=t 2-4(t 2-12)>0㊀又A ,B 在直线PQ 两侧的动点,所以-4<t <2. 6分所以x 1+x 2=-t ,x 1x 2=t 2-12.又P (2,3),Q (2,-3)所以S 四边形APBQ =12ˑ6ˑ|x 1-x 2|=3(x 1+x 2)2-4x 1x 2=348-3t 2㊀(-4<t <2)当t =0时,四边形APBQ 面积取得最大值为123.8分②当øAPQ =øBPQ 时,AP ,BP 斜率之和为O.设直线PA 的斜率为k ,则直线BP 的斜率为-k.设PA 的方程为y -3=k (x -2),联立y -3=k (x -2),3x 2+4y 2=48.{消y 得,(3+4k 2)x 2+8(3k -2k 2)x +4(4k 2+9-12k )-48=0,所以2+x 1=8k (2k -3)3+4k 2,同理2+x 2=8k (2k +3)3+4k 2. 10分所以x 1+x 2=16k 2-123+4k 2x 1-x 2=-48k3+4k 2所以k AB =y 2-y 1x 2-x 1=k (x 1+x 2)-4k x 1-x 2=12.所以AB 的斜率为定值1212分21.解:(Ⅰ)当cos θ=0时,f (x )=4x 3,x ɪR ,所以f ᶄ(x )=12x 2ȡ0,所以f (x )无极值. 2分(Ⅱ)因为f ᶄ(x )=12x 2-6x cos θ,设f ᶄ(x )=0,得x 1=0,x 2=cos θ2.由(Ⅰ),只需分下面两情况讨论:①当cos θ>0时当x ɪ(-ɕ,0)时,f ᶄ(x )>0,f (x )单调递增;当x ɪ(0,cos θ2)时,f ᶄ(x )<0,f (x )单调递减;当x ɪ(cos θ2,+ɕ)时,f ᶄ(x )>0,f (x )单调递增.所以当x =cos θ2时,f (x )取得极小值,极小值f (cos θ2)=-14cos 3θ+316cos θ, 4分要使f (cos θ2)>0㊀则有-14cos 3θ+316cos θ>0,所以0<cos θ<32,因为0ɤθ<2π,故π6<θ<π2或3π2<θ<11π6; 5分②当cos θ<0时,当x ɪ(-ɕ,cos θ2)时,f ᶄ(x )>0,f (x )单调递增;当x ɪ(cos θ2,0)时,f ᶄ(x )<0,f (x )单调递减;当x ɪ(0,+ɕ)时,f ᶄ(x )>0,f (x )单调递增;所以当x =0时,f (x )取得极小值. 6分极小值f (0)=316cos θ,若f (0)>0,则cos θ>0,矛盾.所以当cos θ<0时,f (x )的极小值不会大于零.综上所述,要使函数f (x )在R 内的极小值大于零,参数θ的取值范围是:(π6,π2)ɣ(3π2,11π6). 8分(Ⅲ)由(Ⅱ)知,函数f (x )在区间(-ɕ,0)与(cos θ2,+ɕ)内都是增函数,由题设,函数f (x )在(2a -1,a )内是增函数,则2a -1<aa ɤ0{或2a -1<a2a -1ȡcos θ2{10分由(Ⅱ)参数θɪ(π6,π2)ɣ(3π2,11π6)时0<cos θ<32要使2a -1ȡcos θ2恒成立,必有2a -1ȡ34㊀即a ȡ4+38㊀且a <1综上:a ɤ0或4+38ɤa <1.所以a 的取值范围是(-ɕ,0]ɣ[4+38,1). 12分22.解:(Ⅰ)因为ρ=4sin θ,所以ρ2=4ρsin θ所以x 2+y 2=4y ,即曲线C 的直角坐标方程为:x 2+(y -2)2=4直线l 的参数方程为x =1+t cos 3π4㊀(t 为参数)y =t sin3π4ìîí即x =1-22t ㊀(t 为参数)y =22tìîí 5分(Ⅱ)设点A ,B 对应的参数分别为t 1,t 2,将直线l 的参数方程代入曲线C 的直角坐标方程得(1-22t )2+(22t -2)2=4整理,得t 2-32t +1=0,所以t 1+t 2=32,t 1㊃t 2=1.{因为t 1>0,t 2>0,所以|MA |+|MB |=|t 1|+|t 2|=t 1+t 2=32. 10分23.(Ⅰ)解:|x -2|+|x -1|ȡ5.当x >2时,(x -2)+(x -1)ȡ5,x ȡ4;当1ɤx ɤ2时,(2-x )+(x -1)ȡ5,1ȡ5,无解;当x <2时,(2-x )+(1-x )ȡ5,x ɤ-1.综上,不等式的解集为:{x |x ȡ4或x ɤ-1}. 5分(Ⅱ)证明:f (ab )>|a |㊃f (b a)⇔|ab -2|>|a |㊃|ba -2|⇔|ab -2|>|b -2a |⇔(ab -2)2>(b -2a )2⇔a 2b 2+4-b 2-4a 2>0⇔(a 2-1)(b 2-4)>0.因为|a |>1,所以a 2-1>0,所以b 2-4>0,|b |>2. 10分。
2018届四川省广安市高三第三次诊断考试理科数学试题 及答案

2018届第三次诊断考试 数学试题(理工类)注意事项:1.本试卷满分150分,考试时间120分钟。
2.本试卷分为试题卷(1—4页)和答题卡两部分。
试题卷上不答题,请将第Ⅰ卷选择题和第Ⅱ卷非选择题的答案答在答题卡上的相应位置。
考试结束,只交答题卡。
3.可能用到的公式:球的表面积S =4πR 2,体积V =34πR 3,其中R 为球的半径. 柱体的体积V =Sh ,锥体的体积V =31Sh ,其中S 为底面积,h 为高. 数据x 1,x 2,…,x n 的平均数∑==n i i x n x 11,方差212)(1x x n s n i i -=∑=.第Ⅰ卷 (选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设复数z 满足z ·(i -1)=2i (其中i 为虚数单位),则z 等于 (A)1-i (B)1+i (C)-1+i (D)-1-i 2.设集合}032{2<--=x x x M ,}1log {2<=x x N ,则N M 等于(A)}31{<<-x x (B)}21{<<-x x (C)}10{<<x x (D)}20{<<x x3.设α为平面,a 、b 为两条不同的直线,则下列叙述正确的是 (A)若a ∥α,b ∥α,则a ∥b (B)若a ⊥α,a ∥b ,则b ⊥α; (C)若a ⊥α,a ⊥b ,则b ∥α (D)若a ∥α,a ⊥b ,则b ⊥α. 4.抛物线y =ax 2的准线方程为y =1,则实数a 之值为 (A)4 (B)41(C)41- (D)-45.已知向量a =(1,-1),b =(2,x ),若(a + b )∥(a - 2b ),则实数x 的值为(A)-2 (B)0 (C)1 (D)26.设等比数列{a n }的前n 项积n n a a a a P ⋅⋅⋅⋅= 321,若P 12=32P 7,则a 10等于(A)16 (B)8 (C)4 (D)27.已知f (x )是定义在R 上的奇函数,且当x <0时,f (x )=3x ,则f (log 94)的值为(A)-2 (B)21- (C)21 (D)2 8.关于函数f (x )=sin x (sinx-cosx)的叙述正确的是 (A)f (x )的最小正周期为2π (B)f (x )在]83,8[ππ-内单调递增(C)f (x )的图像关于)0,8(π-对称(D)f (x )的图像关于8π=x 对称9.如图,一个几何体的三视图(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为 (A)π (B)2π (C)3π (D)4π10.已知实数a ,b 满足b b a -++=-7632,则不等式)2(121->--a a a 成立的概率为(A)41 (B)31 (C)32 (D)43 第Ⅱ卷 (非选择题 共100分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题第9小题图区域内作答。
四川省内江市2018届高三第三次模拟考试数学(理)试题
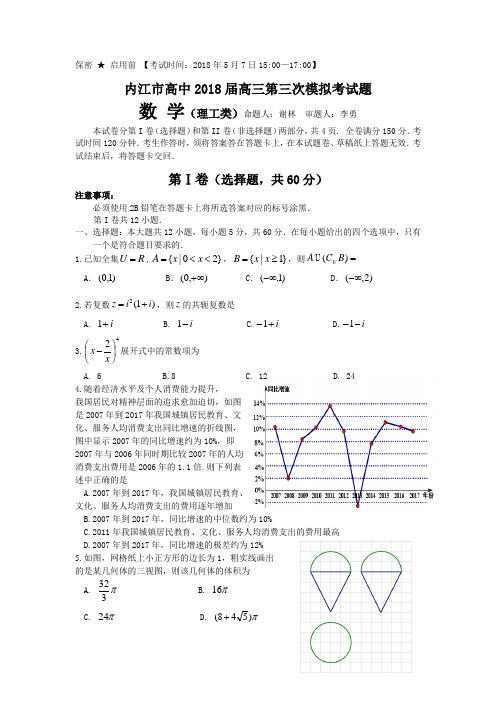
保密 ★ 启用前 【考试时间:2018年5月7日15:00—17:00】内江市高中2018届高三第三次模拟考试题数 学(理工类)命题人:谢林 审题人:李勇本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共4页. 全卷满分150分.考试时间120分钟.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.考试结束后,将答题卡交回.第Ⅰ卷(选择题,共60分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 第I 卷共12小题.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的. 1.已知全集R U =,}20|{<<=x x A ,}1|{≥=x x B ,则=)(B C A U U A .)1,0( B .),0(+∞ C .)1,(-∞ D .)2,(-∞ 2.若复数)1(2i i z +=,则z 的共轭复数是A. i +1B. i -1C.i +-1D.i --13.42⎪⎭⎫ ⎝⎛-x x 展开式中的常数项为A. 6B.8C. 12D. 244.随着经济水平及个人消费能力提升, 我国居民对精神层面的追求愈加迫切,如图 是2007年到2017年我国城镇居民教育、文 化、服务人均消费支出同比增速的折线图, 图中显示2007年的同比增速约为10%,即 2007年与2006年同时期比较2007年的人均 消费支出费用是2006年的1.1倍.则下列表 述中正确的是A.2007年到2017年,我国城镇居民教育、 文化、服务人均消费支出的费用逐年增加B.2007年到2017年,同比增速的中位数约为10%C.2011年我国城镇居民教育、文化、服务人均消费支出的费用最高D.2007年到2017年,同比增速的极差约为12%5.如图,网格纸上小正方形的边长为1,粗实线画出 的是某几何体的三视图,则该几何体的体积为 A.π332B. π16C. π24D. π)548(+6.已知双曲线:C )0,0(12222>>=-b a by a x 的一条渐近线与直线013=+-y x 平行,则双曲线C 的离心率为A.2B. 3C.332 D.257.我国南宋时期数学家秦九韶在他的著作《数书九章》中提出了计算多项式0111...)(a x a x a x a x f n n n n ++++=--的值的秦九韶算法,即将)(x f 的值改写成如下形式:0121)...))(...(()(a x a x a x a x a x f n n n +++++=--,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多 项式的值,这种算法至今仍是比较先进的算法.将秦九韶算法 用程序框图表示如右,则在空白处的执行框内填入的内容是 A. k a v x v )(+= B. k a vx v += C. v a x v k )(+= D. v x a v k +=8.在ABC ∆中,030=A ,2=AC ,且ABC ∆的面积为3,则=BCA. 2B.3C.2D. 1 9.7人乘坐2辆汽车,每辆汽车最多坐4人,则不同的乘车方法有A. 35种B.50种C.60种D. 70种 10.如图,正方体1111D C B A ABCD -的棱长为2,E 是棱AB 的中点,F 是侧面D D AA 11内一点,若//EF 平面D D BB 11,则EF 长度的最大值为 A. 6 B. 5 C. 2 D. 311.已知函数11sin )(--=x x x f π,则A. )(x f 在)3,1(上单调递增B. )(x f 在)3,1(上单调递减C.)(x f y =的图象关于点)0,1(对称D. )(x f y =的图象关于直线1=x 对称 12.某游乐园的摩天轮半径为40m ,圆心O 距地面的高度为43m ,摩天轮作匀速转动,每24分钟转一圈. 摩天轮在转动的过程中,游客从摩天轮距地面最低点处登上吊舱,若忽略吊舱的高度,小明在小强登上吊舱4分钟后登上吊舱,则小明登上吊舱t 分钟后(240≤≤t ),小强和小明距地面的高度之差为 A. )612cos(40ππ+tB. )612sin(40ππ+tC. )312cos(40ππ+t D. )312sin(40ππ+t 第Ⅱ卷(非选择题 共90分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.答在试题卷、草稿纸上无效.第II 卷共11小题. 二、填空题:本大题共4小题,每小题5分,共20分.13.已知b a ,的夹角为0902=== . 14.将函数)62sin()(π+=x x f 的图象向右移动6π个单位得到函数)(x g y =的图象,则=)6(πg . 15.设P 是椭圆14922=+y x 第一象限弧上任意一点,过P 作x 轴的平行线与y 轴和直线x y 32-=分别交于点N M ,,过P 作y 轴的平行线与x 轴和直线x y 32-=分别交于点Q R ,,设O 为坐标原点,则OMN ∆和ORQ ∆的面积之和为 .16.已知直线m y =与直线42-=x y ,曲线x e y x+=2分别交点B A ,,则线段AB 长度的最小值是 .三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(理科)(本小题满分12分)已知}{n a 是公比为2的等比数列,数列}{n b 满足:41=b ,62=b ,112++=+n n n n n b a b a .(Ⅰ)求1a 及数列}{n b 的通项公式;(Ⅱ)设n nn b c ⨯-+=2)1(1,求数列}{n c 的前n 2项和.18.(本小题满分12分)有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程a x b y ˆˆˆ+=(b ˆ精确到0.1),若某天的气温为15o C ,预测这天热奶茶的销售杯数;(Ⅱ)从表中的5天中任取一天,若已知所选取该天的热奶茶销售杯数大于120,求所选取该天热奶茶销售杯数大于130的概率.参考数据:125027191242222=+++,6602942710419130121324=⨯+⨯+⨯+⨯.参考公式:2121ˆ∑-∑-===ni i ni i i xn x yx n y x b,x b y aˆˆ-=19.(本小题满分12分)如图,四棱锥中P ABCD -,底面ABCD 为直角梯形,//AD BC ,90ADC ∠=︒,平面PAD ⊥底面ABCD ,PA PD =,2AD BC =.(Ⅰ)判断平面PBC 与平面PCD 是否垂直,并给出证明;(Ⅱ)若2PA =,1BC =,CD ,求二面角A PB C --的余弦值.20.(本小题满分12分)设O 为坐标原点,0>>b a ,椭圆1:22221=+b y a x E ,椭圆144:22222=+by a x E ,P 是椭圆2E 上一点.(Ⅰ)若直线OP 与椭圆1E 的一个交点为Q ,求OQOP ;(Ⅱ)已知点)2,0(B 在椭圆1E 上,椭圆1E 的离心率为22,过点P 的直线l 交于椭圆1E 于B A ,两点,且2=,求直线l 的方程.21.(本小题满分12分)已知函数⎪⎩⎪⎨⎧≥--<+-=0,10,)(23x ax e x x x x f x.(Ⅰ)若关于x 的方程3)()(2-+=-+x e x f x f x 在区间),0(+∞上有解,求a 的取值范围; (Ⅱ)若存在实数]2,0[,∈n m ,且1≥-n m ,使得)()(n f m f =,求证:e e a e -≤≤-21.请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.(本题满分10分)[选修4-4:极坐标与参数方程]在直角坐标系xOy 中,直线l 过点)2,1(-P ,倾斜角为4π. 以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θρcos 4=,直线l 与曲线C 交于BA ,两点.(Ⅰ)求直线l 的参数方程(设参数为t )和曲线C 的普通方程; (Ⅱ)求PBPA 11+的值.23.(本题满分10分)[选修4-5:不等式选讲] 设函数()1f x x m x m=++-. (Ⅰ)当1=m 时,求4)(≤x f 的解集; (Ⅱ)证明:2)(≥x f .内江市高中2018届高三第三次模拟考试题数学(理工类)参考答案及评分参考一.选择题(每小题5分,共12题,共60分)1.D2.C3.D4.B5.A6.C7.B8.A9.D 10.A 11.C 12.B 二.填空题(每小题5分,共4小题,共20分) 13.22 14.2115.3 16.22ln 5+三.解答题(共6小题,共70分) 17.解:(Ⅰ)由题,有22112b a b a =+ ∵}{n a 是公比为2的等比数列 ∴122a a = 又∵41=b ,62=b∴122411=+a a ,得21=a ...................................................3分 ∴n n n a a 2211=⨯=-,1122++==n n n a a ........................................4分 ∴11222++=+n n n n n b b ,即21=-+n n b b ∴}{n b 是首项为4,公差为2的等差数列∴22)1(21+=-+=n n b b n ..................................................6分 (Ⅱ)当n 为奇数时,0=n c ..................................................7分 当n 为偶数时,n n b c =∴n n b b b c c c 242221......+++=+++...........................................9分 由(Ⅰ)知,n n n b b b n 42)24(...106...2242+=++++=+++∴n n c c c n 42 (2)221+=+++................................................12分注:若对(Ⅱ)加难度,可设n nn b c ⨯-+=2)1(3. 18. 解:(Ⅰ)由表格中数据可得,4.12=x ,122=y ............................2分∴0.24.12621250122626602ˆ2121-≈⨯-⨯-=∑-∑-===ni i ni i i xn x yx n y x b..................................5分∴8.1464.120.2122ˆˆ=⨯+=-=x b y a∴热奶茶销售杯数关于气温的线性回归方程为8.1460.2ˆ+-=x y...................6分 ∴当气温为15oC 时,由回归方程可以预测热奶茶的销售杯数为1178.1168.146150.2ˆ≈=+⨯-=y(杯) ........................................8分 (Ⅱ)设A 表示事件“所选取该天的热奶茶销售杯数大于120”,B 表示事件“所选取该天的热奶茶销售杯数大于130”,则“已知所选取该天的热奶茶销售杯数大于120时,销售杯数大于130”应为事件A B |..................................................10分 ∵53)(=A P ,52)(=AB P ∴32)()()|(==A P AB P A B P∴已知所选取该天的热奶茶销售杯数大于120时,销售杯数大于130的概率为32.....12分 19.解:(Ⅰ)平面PBC 与平面PCD 不垂直. 证明如下:.........................1分 假设平面PBC ⊥平面PCD 过点B 作PC BQ ⊥于Q∵平面PBC ⊥平面PCD ,平面 PBC 平面PC PCD = ∴⊥BQ 平面PCD ∴CD BQ ⊥在直角梯形ABCD 中,由90ADC ∠=︒,//AD BC 知CD BC ⊥ 又∵B BC BQ =∴ ⊥CD 平面PBC ,故CD P C ⊥ ..........................................3分∵ 平面PAD ⊥底面ABCD ,平面PAD 底面ABCD AD =,AD CD ⊥∴ CD ⊥平面PAD ∴ CD ⊥PD在PCD ∆中,不可能有两个直角,所以假设不成立...............................5分 (Ⅱ)设AD 的中点为O ,连接PO ,OB ∵PA PD = ∴AD PO ⊥∵ 平面PAD ⊥底面ABCD ,平面PAD 底面ABCD AD =∴PO ⊥底面ABCD∵在直角梯形ABCD 中,90ADC ∠=︒,2AD BC = ∴OB AD ⊥以OA 、OB 、OP 所在直线分别为x 、y 、z 轴建立如图所示空间直角坐标系O xyz - ........................................................................... 7分 ∵2PA =,1BC =,CD =∴(1,0,0)A,B,(1C -,P ...........................8分∴(1AP =-,(1AB =-,(0,BP =,(1,0,0)BC =- 设平面PAB 的法向量为1(,,)n x y z =由1100n AP x n AB x ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩, 取1(3,1,1)n =同理可得平面PBC 的法向量2(0,1,1)n =.................10分∴121212cos ,5||||5n n n n n n ⋅<>===⋅. 由图形可知,所求二面角为钝角 ∴二面角A PB C --的余弦值5-.........................................12分 (第(Ⅰ)问也可以由向量法说明两平面不垂直)20.解:(Ⅰ)当直线OP 的斜率不存在时,Q P ,的坐标分别为),0(),2,0(b b ,2=OQOP...........................................................................2分 当直线OP 的斜率存在时,设直线kx y OP =:由⎪⎩⎪⎨⎧=+=12222b y ax kx y 得Q 点的坐标为),(222222b k a kab b k a ab ++或),(222222b k a kab b k a ab +-+-,故22221bk a ab k OQ ++=........................................................4分由⎪⎩⎪⎨⎧=+=1442222b y ax kx y 得P 点的坐标为)2,2(222222b k a kab b k a ab ++或)2,2(222222b k a kab b k a ab +-+-,故222212bk a ab k OP ++=∴2=OQOP .................................................................6分(Ⅱ)∵点)2,0(B 为椭圆1E 上一点 ∴2=b又∵椭圆1E 的离心率为22∴椭圆82:221=+y x E ,故椭圆322:222=+y x E ..............................7分 ∵AB AP 2=∴B 为AP 的中点...........................................................8分 当直线l 的斜率不存在时,B 不是AP 的中点,故不成立..........................9分 当直线l 的斜率不存在时,设直线2:+=kx y l ,),(),,(2211y x B y x A 由⎩⎨⎧=++=82222y x kx y 得08)21(22=++kx x k解得0,218221=+-=x k k x ,故2,21422221=+-=y kk y ∴)2142,218(222k k k k A +-+- ,故)21122,218(222k k k k P +++..............................11分 将P 点坐标代入椭圆322:222=+y x E 得32)21122(2)218(22222=++++kk k k∴0342024=-+k k ,解得1030±=k ∴直线l 的方程为21030+±=x y ............................................12分 21.解:(Ⅰ)∵当0>x 时,231)()(x x ax e x f x f x ++--=-+..................1分 ∴当0>x 时,方程3)()(2-+=-+x e x f x f x 可化为a xx =+22∴方程3)()(2-+=-+x e x f x f x 在区间),0(+∞上有解等价于方程a x x =+22在区间),0(+∞上有解....................................2分 设)0(2)(2>+=x x x x g ,则222)(xx x g -='当10<<x 时,0)(<'x g ,故)(x g 单调递减 当1≥x 时,0)(≥'x g ,故)(x g 单调递增∴)(x g 在),0(+∞上有最小值3)1(=g .........................................3分 又∵当+∞→x 时,+∞→)(x g ∴要使方程a xx =+22在),0(+∞有解,当且仅当3≥a ∴满足题意的a 的取值范围为),3[+∞..........................................4分(Ⅱ)a e x f x-=')(①当1≤a 时,0)(≥'x f 对任意0≥x 成立,故)(x f 在),0[+∞上单调递增∴当1≤a 时,不存在]2,0[,∈n m ,且1≥-n m ,使得)()(n f m f =...............5分 当1>a 时,令0)(≥'x f ,得a x ln ≥∴)(x f 在)ln ,0[a 上单调递减,在),(ln +∞a 上单调递增 ∵存在]2,0[,∈n m ,且1≥-n m ,使得)()(n f m f =∴2ln 0<<a ,即21e a <<..................................................6分当)0()2(f f =时,即212-=e a 时,满足题意...................................7分当)0()2(f f >且21e a <<时,即2112-<<e a 时 存在]2,0[,∈n m ,且1≥-n m ,使得)()(n f m f = 等价于2112-<<e a 且)0()1(f f ≤ ∴2112-<≤-e a e ..........................................................9分 当)0()2(f f <且21e a <<时,即2221e a e <<-时 存在]2,0[,∈n m ,且1≥-n m ,使得)()(n f m f = 等价于2221e a e <<-且)2()1(f f ≤ ∴e e a e -≤<-2221.......................................................11分 ∴综上所述,e e a e -≤≤-21...............................................12分22.解:(Ⅰ)∵直线l 过点)2,1(-P ,倾斜角为4π ∴直线l 以t 为参数的参数方程为⎪⎪⎩⎪⎪⎨⎧+-=+=t y t x 222221(t 为参数)......................3分∵曲线C 的极坐标方程为θρcos 4=∴曲线C 的普通方程为4)2(22=+-y x ........................................5分 (Ⅱ)将直线l 的参数方程代入曲线C 的普通方程,得01232=+-t t .............6分 设B A ,两点对应的参数为21,t t∵点P 在曲线C 的左下方 ∴21,t PB t PA ==..........................................................8分∴231111212121=+=+=+t t t t t t PB PA ........................................10分 23.解:(Ⅰ)当1=m 时,11)(-++=x x x f当1>x 时,x x f 2)(=由4)(≤x f ,解得21≤<x ...................................................2分 当11≤≤-x 时,2)(=x f ,满足4)(≤x f .....................................3分 当1-<x 时,x x f 2)(-=由4)(≤x f ,解得12-<≤-x综上所述,当1=m 时,4)(≤x f 的解集为]2,2[-................................5分 (Ⅱ)证明:mx m x x f 1)(-++= m x m x 1+-+≥ mm 1+=..................................................8分 mm 1+= 212=⋅≥m m ...........................................10分。
【精选高中试题】四川省遂宁市高三三诊考试数学(理)试题Word版含答案

遂宁市高中2018届三诊考试数学(理科)试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
总分150分。
考试时间120分钟。
第Ⅰ卷(选择题,满分60分)注意事项:1.答题前,考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。
并检查条形码粘贴是否正确。
2.选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3.考试结束后,将答题卡收回。
一、选择题(本大题共12小题,每小题5分,共60分。
) 1.已知集合{}3,2aM =,{},N a b =,若{}2MN =,则MN =A .{}0,2,3B .{}1,2,3C .{}0,1,2D .{}0,1,32.复数241iz i+=+(i 为虚数单位)在复平面内对应点的坐标是 A .()3,1- B .()1,3-C .()3,1D .()2,4 3.设,a b R ∈,则“()20a b a -<”是“a b <”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.在一圆柱中挖去一圆锥所得的机械部件的三视图如图所示,则此机械部件的表面积为A .π)27(-B .π)27(+C .π)26(+D .π)37(-5.已知函数2tan)sin 1(cos )(2xx x x f -+=,那么下面说法正确的是 A .函数)(x f 在]4,4[ππ-上是增函数,且最小正周期为π B .函数)(x f 在]4,4[ππ-上是减函数,且最小正周期为π C .函数)(x f 在]4,4[ππ-上是减函数,且最小正周期为π2 D .函数)(x f 在]4,4[ππ-上是增函数,且最小正周期为π2 6.若223x y x y ≤⎧⎪≤⎨⎪+≥⎩,则目标函数2x y z x +=的取值范围是A .[]2,5B .[]1,5C .1,22⎡⎤⎢⎥⎣⎦D .[]2,67. 如图,在ABC ∆中,AD AB ⊥,3BC BD =,1AD =,则AC AD ⋅=A.C8.程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S 为 A .120 B .84 C .56 D .289.已知P 是双曲线2213x y -=上任意一点,过点P 分别作双曲线的两条渐近线的垂线,垂足分别为A 、B ,则PA PB ⋅的值是 A .38-B .316C .D .不能确定10.已知5台机器中有2台存在故障,现需要通过逐台检测直至区分出2台故障机器为止.若检测一台机器的费用为2000元,则所需检测费的均值为 A .6400元 B .6800元 C .7000元 D .7200元11.已知A ,B ,C ,D 四点均在以点1O 为球心的球面上 ,且AB AC AD ===BC BD ==8CD =.若球2O 在球1O 内且与平面BCD 相切,则球2O 表面积的最大值为A .πB .4πC .16πD .64π12.设函数()f x 是定义在(,0)-∞上的可导函数,其导函数为'()f x ,且有22()'()f x xf x x +>,则不等式2(2018)(2018)x f x ++4(2)0f -->的解集为 A .(2020,0)- B .(,2020)-∞- C .(2016,0)- D .(,2016)-∞-第Ⅱ卷(非选择题,满分90分)注意事项:1.请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答,不能答在此试卷上。
四川省广安、眉山、内江、遂宁2018届高三第三次诊断性考试理科综合试题Word版含答案

广安、眉山、内江、遂宁2018届高三第三次诊断性考试理科综合试题一、选择题1.下列关于高等动物细胞有丝分裂过程的叙述,正确的是A.间期结束时染色体数和DNA分子数都加倍B.前期两组中心粒和姐妹染色单体都发生分离C.中期每条染色体的着丝点都排在一个平面上D.末期细胞板向内凹陷将细胞缢裂成两个部分2.实验人员利用特殊颜色反应对某未知样品的成分进行鉴定,所用试剂和实验结果(实验操作正确规范)如下表所示。
根据实验结果推测,该样品是A.葡萄糖溶液B.油水混合物C.可溶性淀粉溶液D.鸡蛋清稀释液3.体温恒定对于人体正常的生命活动至关重要。
下列与人体体温调节有关的叙述,正确的是A.炎热环境中机体增加排尿量是促进散热的重要途径B.寒冷环境中体温恒定是因为机体产热量等于散热量C.人体骨骼肌细胞中产热量最多的部位是细胞质基质D.下丘脑是体温调节中枢但不能直接感受体温的变化4.植物体内有多种激素对各种生命活动进行调节。
下列关于植物激素调节的叙述,错误的是A.生长素不直接参与细胞代谢只能给细胞传达促进生长的信息B.秋天落叶中脱落酸的合成量增加既受基因调控也受环境影响C.单侧光能影响生长素的横向运输但不影响生长素的极性运输D.生长素和乙烯对植物侧芽细胞的伸长都起着一定的调节作用5.科研人员通过人工授粉实现白菜(2n=20)和紫甘蓝(2n=18)的种间杂交,将获得的幼胚经离体培养得到幼苗甲,再用秋水仙素处理甲的顶芽获得幼苗乙。
下列叙述正确的是A.将幼苗甲培育成幼苗乙的遗传学原理是基因重组B.杂交得到幼苗甲表明白菜和紫甘蓝之间没有生殖隔离C.幼苗甲体细胞中染色体数目发生改变属于不遗传的变异D.幼苗乙长大成熟后细胞减数分裂中可以形成19个四分体6.人体生物钟与下丘脑SCN细胞中PER蛋白浓度呈周期性变化有关,与PER蛋白浓度变化有关的生理过程如图所示。
下列叙述正确的是A.由per基因两条模板链转录成的mRNA碱基排列顺序不同B.图中②过程的mRNA在核糖体上移动的方向是从右向左的C.SCN细胞通过③过程调节PER蛋白浓度的机制是反馈调节D.下丘脑能够调控生物节律是因为SCN 细胞中含有per 基因7、化学与生产生活密切相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PA,PB,PO的 斜 率 分 另 刂 为尼 1,尼 2,尼 3,
¨ ¨ ¨ ¨ ¨ ¨ ¨ … … … … ¨ ¨ ・¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ … … … … … ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨
秘 密 ★ 启 用前 【 考 试 时 间 :2018年 5月 17日 15:00~17:00】
2015级 高 三 毕业班 第 三次诊断性考试 数
:
毒 工 理 缸 类
)
(考 试 时 间 :120分 钟
试卷 满分 :150分
)
注意 事项 1.答 卷前 ,考 生 务 必 将 自己的 姓 名 、 准考 证 号填 写 在 答题 卡 上 。 2。 回 答选 择 题 时 ,选 出每 小题 答案后 ,用 铅 笔把 答题 卡 上 对应题 目的 答 案标 号 涂 黑 。如 需 改 动 ,用 橡 皮擦 干 净 后 ,再 选 涂 其 它答 案 标 号 。 回 答 非 选 择 题 时 ,将 答 案 写在 答 题 卡 上 。 口 写在 本试 卷 上 无效 。
D。
5O
9.已 知数列 〈 c″ )的 前 ″ = 曰 项 和为 S″ ,且 满足 n,a+S″ =1(彳 ∈Nx),则 数列 〈 〉 ″ 的通项公 式 Ω 刀
夕 八
A。
B。 C。 D。
⒊ll
z’
1O。
如 图是某几何体 的平 面展 开 图 ,其 中 四边 形 ABCD为 正 方 形 ,E,F 分别 为 PA,PD的 中点 。 在此几何 体 中 ,以 下结论 一 定 成立 的是
B.F(1)“ <F(2)<(F(O)
D。
F(2)(F(0)(F(1)
8.5名 同学分别参 加学校 甲 、 乙、 丙 3个 社 团的一 次 活动 ,若 其 中 至少 两名 同学 到 甲社 团 ,乙 、 丙社 团 每个社 团至少 一 人参加 ,则 不 同的参 加方 案种数 为
A。
14o
B。
12O
C。
80
教 考联盟 ・ 数学 (理 工 类 )试 题 第 1页 (共 4页 )
5.如 图是 某 校 阅卷 成 绩 评 定 程 序 ,Jl,J2,奶 为 某 次 考 试 三 个 评 阅 人 对 同 一 道 试 题 的 独 立 评 分 ,夕 为 该 题 的 最 终 得 分 ,若 臼 =7,
开始
J2=10,Js=8,贝 刂夕=
A。 9
B。 C。 D。
≤a 1ˉ 川
8.5
8
6.已 知点 C(Ω
)⑴ 为抛物线 y=4J上 一点 ,以 C为 圆心且 与抛物线准线相切的圆截直线 J=3所 得的弦长为 8,则 圆 C的
,8)(乙
A。
B。 C。
7,5
3ˉ 1|(阮 ˉ2
标准方程为
(J-3)2+(y-2≮02=16 (J-2)2+(丿 -2)2=17
C。 嘉
⒐ 卉
尸
直线 BE∥ PF 直 线 EF∥ 平 面 PBC 平 面 BCE⊥ 平 面 PAD
直线
PB与 DC所 成 角 为 60°
规 曲线 嘭 一 羞
⒒ 已知 点 则
A・
AJ捌
=× α >⒐ 。
⑴ 的左 、 右顶点 冻
,记Biblioteka P在 第 橡限 内 ,且
P在 双 曲线 C上 。 若 双 曲线 C的 离 心 率 为 镖
⒛ 14年 ⒛ 15年 ⒛ 16年 ⒛ 17年 ¨Ⅱ…ˉ 鼽跚 活跃用户数 活跃用户数增速 一十 一 营销费用增速
下列选项 中 ,说 法 与实 际情 况最相 符 的是
A。
B。 C。 D。
逐 年 比较 ,各 年 的活跃 用户数 与 营销 费用增 速均在增 加 逐季 度 比较 ,各 季度 的活跃 用 户增 速 与活跃 用 户数呈线性关 系 2015年 一 ⒛ 16年 该 电商平 台活跃用 户数增 速仍增 大 ⒛ 17年 该 电商平 台活跃 用户数逐 季度增 加
(J-9)2+(丿 一 ω 2=100
`=JL:至
=
一 ⒐ ← )2+cD,沔 /=器 锆
7.已 知 函数 r(J)=Asin(ω
J+甲 )(A,ω 均 为 正 的常 数 ,甲 |(号
)的 最 小
正周期 为 π ,当
J=詈
时 ,函 数 r(J)取 得 最 大 值 ,则 下 列 结 论 正 确 的是
A.F(0)(“ 1)(只 2) C.F(1)<r(O)(只 2)
B=
—2,3〉 〈
B。
扛轧冫
B。
2,3〉 〈
C。
C。
3,5) 〈
第 三象 限
D。
D。
(3,6)
2.在 复平 面 内 ,复 数
A。
应 的点 在 寸 第二象 限
“ “ 是 Ω ⊥ D” 的
B。 D。
第一象 限 充分 而不必要 条件 充 分必要条件
第 四象 限
=(^,-2),D=(1+^,1),则 3.已 知 向量 ¢
3.考 试 结 束 后 ,将 本试 卷和答题 卡 一 并 交回 。 -、 选择题 :本 题 共 12小 题 ,每 小题
5分 ,共 60分 。在 每小题 给 出的 四个选项 中 ,只 有 -项 是
若
符合题 目要求 的。
1.设
A。
集 合
A=",3,5〉
,B=〈 JJ2+PPz J+6=O)。
A∩ B=(3),则
A。 C。
^=1”
必要 而不充分 条件 既不充 分 也不 必要 条件
4.某 电商 平 台统 计 了 2O14年 -2O17年 间 的每个 季 度 的市 场 营销 费用 增 速 、 活跃 用 户 数 (单 位 :千 万 )及 其增 速 ,并 制成 如下统计 图表
35I・
:
¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ … … … … … … ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ … ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ ¨ … … … … … … … … … 40r¨ ¨
=¨
160% 140% 120% 100%
……¨ ………… ……… … J 15I… ¨¨
¨ 10卜 ¨ ∵ 。 t∵ 二
5
… 犄
80% 60% 40% 20%
o
1季 度 2季 度 3季 度 4季 度 1季 度 2季 度 3季 度 4季 度 l季 度 2季 度 3季 度 4季 度1季 度 2季 度 3季 度 4季 度
