2016八年级下期中数学试题
2016年湖北省八年级(下)期中数学试卷解析

2016-2017学年湖北省八年级(下)期中数学试卷一、精心选择,一锤定音!(本题10小题,每小题3分,共30分,每小题只有一个选项是正确的)1.计算的结果是()A.﹣3 B.3 C.﹣9 D.92.式子在实数范围内有意义,则x的取值范围是()A.x<1 B.x≥1 C.x≤﹣1 D.x>13.下列各组数能成为直角三角形三边的是()A.32、42、52 B.、、C.、2、D.、、14.下列各式中,属于最简二次根式的是()A.B.C.D.5.等腰三角形的底边长为6,底边上的中线长为4,它的腰长为()A.7 B. 6 C. 5 D. 46.已知△ABC的各边长度分别为3cm、4cm、5cm,则连接各边中点的三角形周长为()A.2cm B.7cm C.5cm D.6cm7.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为()A.30° B.60° C.90° D.120°8.如图,在菱形ABCD中,AB=3,∠ABC=60°,则对角线AC=()A.12 B.9 C. 6 D. 39.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是()A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤1310.如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…A n分别是正方形的中心,则这n个正方形重叠部分的面积之和是()A.n B.n﹣1 C.()n﹣1 D.n二、耐心填空,准确无误(每题3分,共计18分)11.计算﹣=.12.如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件,使ABCD成为菱形(只需添加一个即可)13.如图,已知OA=OB,那么数轴上点A所表示的数是.14.已知y=+﹣3,则2xy的值为.15.直角三角形的两边长为5和7,则第三边长为.16.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为.三、用心做一做,显显你的能力(本大题共8小题,共72分)17.(+)﹣2﹣.18.先化简,再求值:.19.如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8.(1)作图:用尺规作AB的垂直平分线,交BC于D,交AB于H.(保留作图痕迹)(2)在满足(1)的情况下,求BD的长.20.如图,在所给方格纸中,每个小正方形边长都是1,标号为①,②,③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图甲、图乙中的指定图形分割成三个三角形,使它们与标号为①,②,③的三个三角形分别对应全等.(1)图甲中的格点正方形ABCD;(2)图乙中的格点平行四边形ABCD.注:分割线画成实线.21.阅读下列材料,并解决相应问题:阅读:分母有理化就是把分母中的根号化去.例如:===+应用:用上述类似的方法化简下列各式:(1)(2)++…+.22.在海洋上有一近似于四边形的岛屿,其平面图如图,小明据此构造出该岛的一个数学模型(如图四边形ABCD)来求岛屿的面积,其中∠B=∠D=90°,AB=BC=15千米,CD=3千米,请求出四边形ABCD的面积.(结果保留根号)23.已知矩形ABCD中,M、N分别是AD、BC的中点,E、F分别是线段BM、CM的中点.(1)求证:△ABM≌DCM;(2)判断四边形MENF是(只写结论,不需证明);(3)在(1)(2)的前提下,当等于多少时,四边形MENF是正方形,并给予证明.24.已知:如图(1)四边形ABCD和四边形GCEF为正方形,B、C、E在同一直线.(1)试判断BG、DE的位置关系,请直接写出结论:;(2)若正方形GCEF绕C点顺时针旋转到图(2)的位置,(1)的结论是否仍成立?若成立,给予证明,若不成立?请说明理由.(3)在图(2)中,若正方形ABCD的边长为6,正方形CEFG边长为3,连结BE,DG求BE2+DG2的值.2016-2017学年湖北省八年级(下)期中数学试卷参考答案与试题解析一、精心选择,一锤定音!(本题10小题,每小题3分,共30分,每小题只有一个选项是正确的)1.计算的结果是()A.﹣3 B.3 C.﹣9 D.9考点:二次根式的性质与化简.专题:计算题.分析:原式利用二次根式的化简公式计算即可得到结果.解答:解:原式=|﹣3|=3.故选:B.点评:此题考查了二次根式的性质与化简,熟练掌握二次根式的化简公式是解本题的关键.2.式子在实数范围内有意义,则x的取值范围是()A.x<1 B.x≥1 C.x≤﹣1 D.x>1考点:二次根式有意义的条件.分析:根据二次根式的性质,被开方数大于等于0,解不等式即可.解答:解:根据题意得:x﹣1≥0,即x≥1时,二次根式有意义.故选:B.点评:主要考查了二次根式的意义和性质.概念:式子(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.3.下列各组数能成为直角三角形三边的是()A.32、42、52 B.、、C.、2、D.、、1考点:勾股定理的逆定理.分析:分别计算每一组中,较小两数的平方和,看是否等于最大数的平方,若等于就是直角三角形,否则就不是直角三角形.解答:解:A、因为(32)2+(42)2≠(52)2,所以不能构成直角三角形,此选项错误;B、因为()2+()2≠()2,所以不能构成直角三角形,此选项错误;C、因为()2+22≠()2,所以不能构成直角三角形,此选项错误;D、因为()2+()2=12,能构成直角三角形,此选项正确.故选D.点评:本题主要考查了勾股定理的逆定理,已知三条线段的长,判断是否能构成直角三角形的三边,判断的方法是:计算两个较小的数的平方和是否等于最大数的平方即可判断.4.下列各式中,属于最简二次根式的是()A.B.C.D.考点:最简二次根式.分析:判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.解答:解:A、被开方数含开的尽的因数,故A错误;B、被开方数含分母,故B错误;C、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故C正确;D、被开方数含开的尽的因数,故D错误;故选:C.点评:本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.5.等腰三角形的底边长为6,底边上的中线长为4,它的腰长为()A.7 B. 6 C. 5 D. 4考点:勾股定理;等腰三角形的性质.专题:压轴题.分析:根据等腰三角形的性质可知BC上的中线AD同时是BC上的高线,根据勾股定理求出AB的长即可.解答:解:∵等腰三角形ABC中,AB=AC,AD是BC上的中线,∴BD=CD=BC=3,AD同时是BC上的高线,∴AB==5,故选C.点评:本题考查勾股定理及等腰三角形的性质.解题关键是得出中线AD是BC上的高线,难度适中.6.已知△ABC的各边长度分别为3cm、4cm、5cm,则连接各边中点的三角形周长为()A.2cm B.7cm C.5cm D.6cm考点:三角形中位线定理.分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得中点三角形的周长等于原三角形的周长的一半求解即可.解答:解:∵△ABC的周长=3+4+5=12cm,∴连接各边中点的三角形周长=×12=6cm.故选D.点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,熟记定理并判断出中点三角形的周长等于原三角形的周长的一半是解题的关键.7.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为()A.30° B.60° C.90° D.120°考点:矩形的性质.专题:几何图形问题.分析:根据矩形的对角线互相平分且相等可得OB=OC,再根据等边对等角可得∠OBC=∠ACB,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.解答:解:∵矩形ABCD的对角线AC,BD相交于点O,∴OB=OC,∴∠OBC=∠ACB=30°,∴∠AOB=∠OBC+∠ACB=30°+30°=60°.故选:B.点评:本题考查了矩形的性质,等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.8.如图,在菱形ABCD中,AB=3,∠ABC=60°,则对角线AC=()A.12 B.9 C. 6 D. 3考点:菱形的性质;等边三角形的判定与性质.分析:根据菱形的性质及已知可得△ABC为等边三角形,从而得到AC=AB.解答:解:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC为等边三角形,∴AC=AB=3.故选D.点评:本题考查了菱形的性质和等边三角形的判定,难度一般,解答本题的关键是掌握菱形四边相等的性质.9.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是()A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13考点:勾股定理的应用.专题:压轴题.分析:最短距离就是饮料罐的高度,最大距离可根据勾股定理解答.解答:解:a的最小长度显然是圆柱的高12,最大长度根据勾股定理,得:=13.即a的取值范围是12≤a≤13.故选:A.点评:主要是运用勾股定理求得a的最大值,此题比较常见,难度不大.10.如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…A n分别是正方形的中心,则这n个正方形重叠部分的面积之和是()A.n B.n﹣1 C.()n﹣1 D.n考点:正方形的性质;全等三角形的判定与性质.专题:规律型.分析:根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为(n﹣1)个阴影部分的和.解答:解:由题意可得一个阴影部分面积等于正方形面积的,即是×4=1,5个这样的正方形重叠部分的面积和为:1×4,n个这样的正方形重叠部分的面积和为:1×(n﹣1)=n﹣1.故选:B.点评:此题考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分的面积和的计算方法,难点是求得一个阴影部分的面积.二、耐心填空,准确无误(每题3分,共计18分)11.计算﹣=.考点:二次根式的加减法.分析:先进行二次根式的化简,然后合并.解答:解:原式=3﹣=.故答案为:.点评:本题考查了二次根式的加减法,解答本题的关键是掌握二次根式的化简以及同类二次根式的合并.12.如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件OA=OC,使ABCD成为菱形(只需添加一个即可)考点:菱形的判定.专题:开放型.分析:可以添加条件OA=OC,根据对角线互相垂直平分的四边形是菱形可判定出结论.解答:解:OA=OC,∵OB=OD,OA=OC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴平行四边形ABCD是菱形,故答案为:OA=OC.点评:此题主要考查了菱形的判定,关键是掌握菱形的判定定理.13.如图,已知OA=OB,那么数轴上点A所表示的数是﹣.考点:勾股定理;实数与数轴.分析:首先根据勾股定理得:OB=.即OA=.又点A在数轴的负半轴上,则点A对应的数是﹣.解答:解:由图可知,OC=2,作BC⊥OC,垂足为C,取BC=1,故OB=OA===,∵A在x的负半轴上,∴数轴上点A所表示的数是﹣.故答案为:﹣.点评:熟练运用勾股定理,同时注意根据点的位置以确定数的符号.14.已知y=+﹣3,则2xy的值为﹣15.考点:二次根式有意义的条件.分析:根据非负数的性质列式求出x的值,再求出y的值,然后代入代数式进行计算即可得解.解答:解:根据题意得,2x﹣5≥0且5﹣2x≥0,解得x≥且x≤,所以,x=,y=﹣3,所以,2xy=2××(﹣3)=﹣15.故答案为:﹣15.点评:本题考查的知识点为:二次根式的被开方数是非负数.15.直角三角形的两边长为5和7,则第三边长为2或.考点:勾股定理.专题:分类讨论.分析:分7为斜边与7为直角边两种情况考虑,分别利用勾股定理即可求出第三边.解答:解:若7为斜边,根据勾股定理得:第三边为=2;若7为直角边,根据勾股定理得:第三边为=,故答案为:2或点评:此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.16.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为6.考点:轴对称-最短路线问题;正方形的性质.专题:计算题.分析:连接BD,DE,根据正方形的性质可知点B与点D关于直线AC对称,故DE的长即为BQ+QE的最小值,进而可得出结论.解答:解:连接BD,DE,∵四边形ABCD是正方形,∴点B与点D关于直线AC对称,∴DE的长即为BQ+QE的最小值,∵DE=BQ+QE===5,∴△BEQ周长的最小值=DE+BE=5+1=6.故答案为:6.点评:本题考查的是轴对称﹣最短路线问题,熟知轴对称的性质是解答此题的关键.三、用心做一做,显显你的能力(本大题共8小题,共72分)17.(+)﹣2﹣.考点:二次根式的加减法.分析:先把二次根式为最简二次根式,再计算即可.解答:解:原式=2+﹣﹣=.点评:本题考查了二次根式的加减运算,把二次根式化为最简二次根式是解题的关键.18.先化简,再求值:.考点:二次根式的化简求值;分式的化简求值.分析:此题要对代数式先通分,最简公分母是xy(x+y),再相减,能够熟练运用因式分解的方法进行约分.代值的时候,熟练合并同类二次根式.解答:解:原式=﹣===.当时,=.点评:此题综合考查了二次根式的混合运算和二次根式的加减运算.19.如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8.(1)作图:用尺规作AB的垂直平分线,交BC于D,交AB于H.(保留作图痕迹)(2)在满足(1)的情况下,求BD的长.考点:作图—基本作图;线段垂直平分线的性质.分析:(1)垂直平分线的作法为:将圆规的圆心分别处于线段的两端,各做一个圆弧(半径大于线段长的一半),并让其相交,将其交点相连即为该线段垂直平分线;(2)首先利用勾股定理求得斜边的长,从而求得BH的长,然后利用△BHD∽△BCA求得BD的长即可.解答:解:(1)如图:(2)∵∠C=90°,AC=6,BC=8,∴AB==10,∵HD垂直平分AB,∴AH=BH=5,∵△BHD∽△BCA,∴,即:,解得:BD=.点评:本题考查了尺规作图的知识,要牢记:将圆规的圆心分别处于线段的两端,各做一个圆弧(半径大于线段长的一半),并让其相交,将其交点相连即为该线段垂直平分线;20.如图,在所给方格纸中,每个小正方形边长都是1,标号为①,②,③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图甲、图乙中的指定图形分割成三个三角形,使它们与标号为①,②,③的三个三角形分别对应全等.(1)图甲中的格点正方形ABCD;(2)图乙中的格点平行四边形ABCD.注:分割线画成实线.考点:作图—应用与设计作图.专题:作图题.分析:(1)利用三角形的形状以及各边长进而拼出正方形即可;(2)利用三角形的形状以及各边长进而拼出平行四边形即可.解答:解:(1)如图甲所示:(2)如图乙所示:点评:此题主要考查了应用设计与作图,利用网格结合三角形各边长得出符合题意的图形是解题关键.21.阅读下列材料,并解决相应问题:阅读:分母有理化就是把分母中的根号化去.例如:===+应用:用上述类似的方法化简下列各式:(1)(2)++…+.考点:分母有理化.专题:阅读型.分析:(1)根据分式的性质,分子分母都乘以分母两个数的和,可得答案;(2)根据分式的性质,分子分母都乘以分母两个数的和,可得实数的运算,根据实数的运算,可得答案.解答:解:(1)原式===+;(2)原式=++…+=﹣1+﹣+…+﹣=﹣1.点评:本题考查了分母有理化,利用分式的性质:分子分母都乘以分母分母两个数的和或差得出平方差是解题关键.22.在海洋上有一近似于四边形的岛屿,其平面图如图,小明据此构造出该岛的一个数学模型(如图四边形ABCD)来求岛屿的面积,其中∠B=∠D=90°,AB=BC=15千米,CD=3千米,请求出四边形ABCD的面积.(结果保留根号)考点:勾股定理的应用.分析:连接AC,根据AB=BC=15千米,∠B=90°得到∠BAC=∠ACB=45° AC=15,再根据∠D=90°利用勾股定理求得AD的长后即可求面积;解答:解:连接AC∵AB=BC=15千米,∠B=90°∴∠BAC=∠ACB=45° AC=15千米,又∵∠D=90°,∴AD==12(千米)∴面积=S△ABC+S△ADC=112.5+18(平方千米).点评:本题考查了解直角三角形的应用,与实际问题相结合提高了同学们解题的兴趣,解题的关键是从实际问题中整理出直角三角形并求解.23.已知矩形ABCD中,M、N分别是AD、BC的中点,E、F分别是线段BM、CM的中点.(1)求证:△ABM≌DCM;(2)判断四边形MENF是菱形(只写结论,不需证明);(3)在(1)(2)的前提下,当等于多少时,四边形MENF是正方形,并给予证明.考点:矩形的性质;全等三角形的判定与性质;菱形的判定;正方形的性质.分析:(1)由矩形的性质得出AB=DC,∠A=∠D,再由M是AD的中点,根据SAS即可证明△ABM≌△DCM;(2)先由(1)得出BM=CM,再由已知条件证出ME=MF,EN、FN是△BCM的中位线,即可证出EN=FN=ME=MF,得出四边形MENF是菱形;(3)先证出∠AMB=45°,同理得出∠DMC=45°,证出∠BMC=90°,即可得出结论.解答:(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,AB=DC,∵M是AD的中点,∴AM=DM,在△ABM和△DCM中,,∴△ABM≌△DCM(SAS);(2)解:四边形MEBF是菱形;理由如下:由(1)得:△ABM≌△DCM,∴BM=CM,∵E、F分别是线段BM、CM的中点,∴ME=BE=BM,MF=CF=CM,∴ME=MF,又∵N是BC的中点,∴EN、FN是△BCM的中位线,∴EN=CM,FN=BM,∴EN=FN=ME=MF,∴四边形MENF是菱形;(3)解:当=2时,四边形MENF是正方形;证明如下:当=2时,AB=AM,∴△ABM是等腰直角三角形,∴∠AMB=45°,同理:∠DMC=45°,∴∠BMC=90°,∴四边形MENF是正方形.点评:本题考查了矩形的性质、全等三角形的判定与性质、菱形的判定、正方形的判定;熟练掌握矩形的性质以及菱形、正方形的判定方法,证明三角形全等是解决问题的关键.24.已知:如图(1)四边形ABCD和四边形GCEF为正方形,B、C、E在同一直线.(1)试判断BG、DE的位置关系,请直接写出结论:BG⊥DE;(2)若正方形GCEF绕C点顺时针旋转到图(2)的位置,(1)的结论是否仍成立?若成立,给予证明,若不成立?请说明理由.(3)在图(2)中,若正方形ABCD的边长为6,正方形CEFG边长为3,连结BE,DG 求BE2+DG2的值.考点:四边形综合题.分析:(1)根据已知,利用SAS判定△BCG≌△DCE,全等三角形的对应角相等,所以∠CBG=∠CDE,∠BGC=∠DEC,因为∠CBG+∠BGC=90°,所以∠BHE=90°,得出结论;(2)四边形ABCD是正方形推出△BCG≌△DCE.全等三角形的对应角相等,所以∠CBG=∠CDE,等量代换得出∠DOH=90°,推出BG⊥DE;(3)利用勾股定理得出BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2,进而得出答案即可.解答:(1)解:延长BG与DE交于点H,∵四边形ABCD、四边形CEFG都是正方形,∴BC=CD,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,∵在△BCG与△DCE中,,∴△BCG≌△DCE(SAS),∴∠CBG=∠CDE,∠BGC=∠DEC,∵∠CBG+∠BGC=90°,∴∠CBG+∠DEC=90°,∴∠BHE=90°,∴BG⊥DE,故答案为:BG⊥DE.(2)仍成立.证明:∵四边形ABCD、四边形CEFG都是正方形∴BC=CD,CG=CE,∠BCD=∠ECG=90°,∴∠BCG=∠DCE,∵在△BCG与△DCE中,,∴△BCG≌△DCE(SAS),∴∠CBG=∠CDE,又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,∴∠CDE+∠DHO=90°,∴∠DOH=90°,∴BG⊥DE.(3)∵BG⊥DE,∴BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2,又∵AB=6,CE=3,∴BD=6,GE=3,∴BD2+GE=+=90,∴BE2+DG2=90.点评:此题主要考查了全等三角形的判定与性质和勾股定理的应用,熟练利用全等三角形的性质是解此题关键.。
2016-2017学年度第二学期期中检测八年级数学试题(含答案)

2016-2017学年度第二学期期中检测八年级数学试题(全卷共120分,考试时间90分钟)一.选择题(本大题有8个小题,每小题3分,共24分,将正确选项填写在表格中相应位置)1.下列图形中,是中心对称图形的是(▲)A B C D2.下列调查中,适宜采用普查方式的是(▲)A.调查市场上某品牌老酸奶的质量情况B.调查某品牌圆珠笔芯的使用寿命C.调查乘坐飞机的旅客是否携带了危禁物品D.调查我市市民对《徐州夜新闻》的认可情况3.下列调查的样本选取方式,最具有代表性的是(▲)A.在青少年中调查年度最受欢迎的男歌手B.了解班上学生的睡眠时间.调查班上学号为双号的学生的睡眠时间C.为了了解你所在学校的学生每天的上网时间,向八年级的同学进行调查D.对某市的出租司机进行体检,以此反映该市市民的健康状况4.下列事件中,属于确定事件的是(▲)A.掷一枚硬币,着地时反面向上B.买一张福利彩票中奖了C.投掷3枚骰子,面朝上的三个数字之和为18D.五边形的内角和为540度5.如图,E、F、G、H分别是□ABCD各边的中点,按不同方式连接分别得到图○1、○2中两个不同的阴影部分甲、乙,关于甲、乙两个阴影部分,下列叙述正确的是( ▲ )A .甲和乙都是平行四边形B .甲和乙都不是平行四边形C .甲是平行四边形,乙不是平行四边形D .甲不是平行四边形,乙是平 行四边形6. 如图,在菱形ABCD 中,AC =6,BD =8,则菱形的周长是( ▲ )A .24B .48C .40D .207. 若依次连接四边形ABCD 各边的中点所得四边形是矩形,则四边形ABCD 一定是( ▲ )A .矩形B .菱形C .对角线互相垂直的四边形D .对角线相等的四边形 8. 如图,在□ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB 于E ,在线段AB 上,连接EF 、CF .则下列结论:○1∠BCD =2∠DCF ;○2∠ECF =∠CEF ;○3S △BEC =2S △CEF ;○4∠DFE =3∠AEF ,其中一定正确的是( ▲ )A .○1○2○4B .○1○2○4C .○1○2○3○4D .○2○3○4图(1)图(2)GF E HCDGF E HCDABBA 第5题图CDAB第6题图EFCDBA 第8题图二. 填空题(本大题有8个小题,每小题3分,共24分)9. 如图是某校参加各兴趣小组的学生人数分布扇形统计图,其中“演艺”兴趣小组一项所对应的角度是 ▲ °.10. 一只不透明的袋子里装有1个白球,3个黄球,6个红球,这些球除了颜色外都相同,将球搅匀,从中任意摸出1个球,有下列事件:○1该球是红球,○2该球是黄球,○3该球是白球.它们发生的概率分别记为P 1,P 2,P 3.则P 1,P 2,P 3的大小关系 ▲ .11. 在一个不透明的袋子里,装有若干个小球.这些小球只有颜色上的区别.已知其中只有两个红球.每次摸球前都将袋子里的球搅匀.随机摸出一个小球,记下颜色并将球放回袋子里.通过大量重复试验后,发现摸出红球的频率稳定在0.2,那么据此估计,袋子里的球的总数大约是 ▲ 个. 12. 在□ABCD 的周长是32cm ,AB =5cm ,那么AD = ▲ cm .13. 如图,在□ABCD 中,∠ABC 的平分线交AD 于点E ,AB =4,BC =6,则DE = ▲ . 14. 如图,在□ABCD 中,AD =6,点E 、F 分别是BD 、CD 的中点,则EF = ▲ . 15. 如图,G 为正方形ABCD 的边AD 上的一个动点,AE ⊥BG ,CF ⊥BG ,垂足分别为点E ,F ,已知AD =4,则AE 2+CF 2= ▲ .第9题图第13题图EABCD第14题图EF DABC第15题图FE CDABG16. 如图,在Rt △ABC 中,∠ACB =90,AC =3,BC =4,分别以AB 、AC 、BC 为边在AB 同侧作正方形ABEF ,ACPQ ,BDMC ,记四块阴影部分的面积分别为S 1、S 2、S 3、S 4,则1234S S S S +++= ▲ .三. 解答题(本大题共8小题,共72分)17. (本题8分)某自行车公司调查阳光中学学生对其产品的了解情况,随机抽取部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A 、B 、C 、D .根据调查结果绘制了如下尚不完整的统计图.根据所给数据,解答下列问题: (1)本次问卷共随机调查了名学生,扇形统计图中m = . (2)请根据数据信息补全条形统计图.(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?18. (本题8分)为了了解某中学初三年级650名学生升学考试的数学成绩,从中随机抽取了50名学生的数学成绩进行分析,并求得样本的平均成绩是93.5分.下面是根据抽取的学生数学成绩制作的统计表:分组频数累计频数 频率问卷情况条形统计图6168类型人数DCBA2468101214161820第16题图4321S S S S LMDMPQE F CAB60.5~70.5 正3 a70.5~80.5 正正6 0.1280.5~90.5 正正9 0.1890.5~100.5 正正正正17 0.34100.5~110.5 正正b 0.2110.5~120.5正5 0.1 合计501根据题中给出的条件回答下列问题: (1)表中的数据a = ,b = ;(2)在这次抽样调查中,样本是 ;(3)在这次升学考试中,该校初三年级数学成绩在90.5~100.5范围内的人数约为 人.19. (本题8分)在如图所示的网格纸中,建立了平面直角坐标系xOy ,点P (1,2),点A (2,5),B (-2,5),C (-2,3).(1) 以点P 为对称中心,画出△A ′B ′C ′,使△A ′B ′C ′与△ABC 关于点P对称,并写出下列点的坐标:B ′ ,C ′ ; yB A(2) 多边形ABCA ′B ′C ′的面积是 .20. (本题8分)如图,在□ABCD 中, AE ⊥BD ,CF ⊥BD ,垂足分别为E 、F .求证:(1)AE =CF ;(2)四边形AECF 是平行四边形. 证明:21. (本题8分)如图,已知矩形ABCD 中,E 是AD 上的一点,F 是AB 上的一点,EF ⊥EC ,且EF =EC ,DE =4cm ,矩形ABCD 的周长为32cm ,求AE 的长.解:22. (本题10分)如图,在平面直角坐标系xOy 中,点A (3,4),B (5,0),C (0,第20题图FEDABCBCA EDF 第22题图-2).在第一象限找一点D ,使四边形AOBD 成为平行四边形, (1) 点D 的坐标是 ;(2) 连接OD ,线段OD 、AB 的关系是 ;(3) 若点P 在线段OD 上,且使PC +PB 最小,求点P 的坐标. 解:23. (本题10分)将两张完全相同的矩形纸片ABCD 、FBED 按如图方式放置,BD 为重合的对角线.重叠部分为四边形DHBG ,(1) 试判断四边形DHBG 为何种特殊的四边形,并说明理由; (2) 若AB =8,AD =4,求四边形DHBG 的面积. 解:(1) (2)xyO AB CEGHFCDAB第23题图24. (本题12分)如图,正方形ABCO 的边OA 、OC 分别在x 、y 轴上,点B 坐标为(6,6),将正方形ABCO 绕点C 逆时针旋转角度a (0°<a <90°),得到正方形CDEF ,ED 交线段AB 于点G ,ED 的延长线交线段OA 于点H ,连CH 、CG . (1)求证:△CBG ≌△CDG ;(2)求∠HCG 的度数;并判断线段HG 、OH 、BG 之间的数量关系,说明理由;(3)连结BD 、DA 、AE 、EB 得到四边形AEBD ,在旋转过程中,四边形AEBD 能否为矩形?如果能,请求出点H 的坐标;如果不能,请说明理由. (1) 证明:(2)解:(3)解:x yOGHFEDACB第24题图2016-2017学年度第二学期第一次质量抽测八年级数学试题答案四.选择题(本大题有8个小题,每小题3分,共24分)题号 1 2 3 4 5 6 7 8答案 A C B D A D C B五.填空题(本大题有8个小题,每小题3分,共24分)9.108.10.P1>P2>P3.11.10.12.11.13.2.14.3.15.16.16.18.六.解答题(本大题共10小题,共72分)17.答案:(1)50,m=32;……4分(2)图略;……6分(3)1000(16%40%)100056%560⨯+=⨯=.答约有560人.……8分18.答案:(1)a=0.06,b=10;……4分(2)50名学生的数学成绩;……6分(3)221.……8分19.解:(1)B′(4,-1),C′(4,1),图, (4)分(其中图2分)(2)28.……8分xyB'C'CA'OB AP20. (本题8分)证明:(1)因为四边形ABCD 是平行四边形,所以AD =BC ,…1分因为AD ∥BC ,所以∠ADE =∠CBF ,……2分 因为AE ⊥BD ,CF ⊥BD ,所以∠AED =∠CFB =90°,…3分所以△ADE ≌△CBF ,……4分 所以AE =CF .……5分(2)因为AE ⊥BD ,CF ⊥BD ,所以∠AEF =∠CFE =90°,…6分 所以AE ∥CF ,……7分由(1)得AE =CF ,所以四边形AECF 是平行四边形.……8分 21. 解:因为EF ⊥EC ,所以∠CEF =90°,………………1分 所以∠AEF +∠DEC =90°,………………2分因为四边形ABCD 是矩形,所以∠A =∠D =90°,………………3分 所以∠AFE +∠AEF =90°,所以∠AFE =∠DEC ,………………4分又EF =EC ,所以△AEF ≌△DCE ,………………5分 所以AE =DC ,………………6分因为2(AD +DC )=32,所以2(AE +DE +AE )=32,………………7分 因为DE =4cm ,所以AE =6cm .………………8分第20题图FEDABC22. 解答:(1)(8,4),图.…………2分 (2)OD 与AB 互相垂直平分.图…………4分(3)连接AC 交OD 于点P ,点P 即是所求点.…………5分(有图也可以)设经过点O 、D 的函数表达式为1y k x =,则有方程148k =,所以112k =,所以直线OD 的函数表达式为12y x =.………………6分设过点C 、A 的一次函数表达式为2y k x b =+,则有方程组22,3 4.b k b =-⎧⎨+=⎩解得22,2.b k =-⎧⎨=⎩所以过点C 、A 的一次函数表达式为22y x =-,………………8分解方程组1,22 2.y y x ⎧=⎪⎨⎪=-⎩得4,32.3x y ⎧=⎪⎪⎨⎪=⎪⎩,所以点P (43,23).………………10分xyEPO ADBCEGCD23. (本题10分)解:(1)四边形DHBG 是菱形.………………1分 理由如下:因为四边形ABCD 、FBED 是完全相同的矩形, 所以∠A =∠E =90°,AD =ED , …………2分 所以DA ⊥AB ,DE ⊥BE ,所以∠ABD =∠EBD ,………………3分 因为AB ∥CD ,DF ∥BE ,所以四边形DHBG 是平行四边形,∠HDB =∠EBD ,………………5分 所以∠HDB =∠ABD , 所以DH =BH , 所以□DHBG 是菱形.………………6分 (2)由(1),设DH =BH =x ,则AH =8-x ,在Rt △ADH 中,222AD AH DH +=,即得2224(8)x x +-=, 解得5x =,即BH =5,………………9分所以菱形DHBG 的面积为5420HB AD ??. (10)分24. (本题12分) 解:(1)证明:∵正方形ABCO 绕点C 旋转得到正方形yGFECBCDEF ,∴CD =CB ,∠CDG =∠CBG =90°.………2分在Rt △CDG 和Rt △CBG 中,CD =CB ,CG =CG ,∴△CDG ≌△CBG (HL ).………………3分(2)解:∵△CDG ≌△CBG ,∴∠DCG =∠BCG 12DCB =∠,DG =BG .……………4分在Rt △CHO 和Rt △CHD 中,CH =CH ,CO =CD ,∴△CHO ≌△CHD (HL ).……………5分∴∠OCH =∠DCH 12OCD =∠,OH =DH ,…6分∴∠HCG =∠HCD +∠GCD 11145222OCD DCB OCB =∠+∠=∠=︒,…7分HG =HD +DG =HO +BG .………………8分(3)解:四边形AEBD 可为矩形. 如图,连接BD 、DA 、AE 、EB ,因为四边形AEBD 若为矩形,则四边形AEBD 为平行四边形,且AB =ED ,则有AB 、ED 互相平分,即G 为AB 中点的时候.因为DG =BG ,所以此时同时满足DG =AG =EG =BG ,即平行四边形AEBD 对角线相等,则其为矩形.所以当G 点为AB 中点时,四边形AEBD 为矩形.………………10分 ∵四边形DAEB 为矩形,∴AG =EG =BG =DG . ∵AB =6,∴AG =BG =3.………………11分 设H 点的坐标为(x ,0),则HO =x , ∵OH =DH ,BG =DG ,∴HD =x ,DG =3.在Rt △HGA 中,∵HG =x +3,GA =3,HA =6-x ,∴(x +3)2=32+(6-x )2,∴x =2. ∴H 点的坐标为(2,0).………………12分。
2016年第二学期八年级期中考试数学试题及答案1

2015学年第二学期八年级期中考试数学试题班别: 姓名: 座号: 分数:一、 填空题:(每小题4分,共48分)1、下列二次根式是最简二次根式的是 ( )。
A 、21B 、4C 、3D 、82、25)(-等于( )。
A 、-5B 、5C 、25D 、-253、已知三组数据:①2,3,4; ②3,4,5 ;③1,3,2。
分别以每组数据中的三个数据为三角形的三边长,构成直角三角形的有 ( )。
A 、①② B 、②③ C 、①③ D 、①②③4、在Rt △ABC 中,∠C =90°,a =12,b =16,则c 的长为 ( )。
A 、26 B 、18 C 、20 D 、215、菱形和矩形一定都具有的性质是 ( )。
A 、对角线相等 B 、对角线互相平分 C 、对角线互相平分且相等 D 、对角线互相垂直6、下列计算错误的是 ( )。
A 、14772⨯=B 、60302÷=C 、9258a a a +=D 、3223-= 7、已知四边形ABCD 是平行四边形,则下列各图中∠1与∠2一定不相等的是 ( )。
8.已知菱形的边长和一条对角线的长均为4cm ,则菱形的面积为( ) A.16cm 2B.223cmC.423cmD.823cm9、下列二次根式中能与2合并的二次根式的是( )。
A 、12B 、23C 、32D 、1810、在矩形ABCD 中,AB=3,BC=4,则点A 到对角线BD 的距离为 ( )。
A 、513 B 、5 C 、 2.5 D 、51211、若75n 是整数,则正整数n 的最小值是( )。
A 、2B 、3C 、4D 、512、已知a 、b 、c 是三角形的三边长,如果满足(a -6)2+8-b +10-c =0,则三角形的形状是( )A 、底与边不相等的等腰三角形B 、等边三角形C 、钝角三角形D 、直角三角形 二、填空题:(每小题4分,共32分)。
13、已知x x -=-3)32(,则x 的取值范围是: 。
2016-2016学年八年级数学下学期期中试卷 北师大版

2014年下学期八年级数学期中测试卷一、 选择题(本大题共11个小题,每小题3分,共33分) 在每小题给出的四个选项中,只有一项是正确的,请把正确选项的字母填在每题后的括号内。
1.下列因式分解错误的是( )A.x 2-y 2=(x +y)(x -y)B.x 2-6x +9=(x -3)2C.x 2+xy=x(x +y)D.x 2+y 2=(x +y)2 2.把x 2-y 2+2y -1分解因式结果正确的是( ) A .(x +y +1)(x -y -1) B .(x +y -1)(x -y -1) C .(x +y -1)(x -y +1) D .(x -y +1)(x +y +1) 3.下列从左到右的变形是因式分解的是( )A 、( a+3)(a -3)=a 2 –9B 、x 2+x -5=x(x+5)-5C 、x 2+1=x(x +x1.) D 、x 2+4x+4=(x+2)24.下列多项式中不能用平方差公式分解的是( )A .a 2-b 2B .-x 2-y 2C .49x 2- y 2z 2D .16m 4n 2-25p 25.如果32-a 是多项式942-+ma a 的一个因式,则m 的值是( ) A .0 B .6 C .12 D .-126、一元一次不等式组 的解集在数轴上表示正确的是 ( )A 、B 、C 、D 、7.无论x,y 为何值,x 2+y 2__4x+12y+41的值都是( )A .非负数B .正数C .零D .负数8.已知a 、b 、c 为ABC ∆的三边,且满足442222b a c b c a -=-,则ABC ∆是 ( ) A.等边三角形 B.直角三角形C.等腰三角形D.等腰三角形或直角三角形 9.不等式2(x-2)≤x-2的非负整数解的个数为( ) A . 1 B . 2 C . 3 D.410.若x 2-kxy + 9y 2是一个完全平方式,则k 等于 ( )A 3B ±3C 6D ±6 11、下列各式能用公式法分解的是( )。
【人教版】2015-2016年八年级下期中数学试卷及答案解析

【解答】 解:矩形的性质有: ① 矩形的对边相等且平行, ② 矩形的对角相等, 且都是直角,
③ 矩形的对角线互相平分、相等; 平行四边形的性质有: ① 平行四边形的对边分别相等且平行,
② 平行四边形的对角分别相
等, ③ 平行四边形的对角线互相平分;
∴矩形具有而平行四边形不一定具有的性质是对角线相等,
【点评】本题考查了矩形的性质及菱形的判定.注意掌握菱形的判定方法有三种:
① 定义:
一组邻边相等的平行四边形是菱形; ② 四边相等; ③ 对角线互相垂直平分的四边形是菱形.
9.矩形具有而一般的平行四边形不一定具有的特征(
)
A .对角相等 B.对角线相等
C.对角线互相平分 D .对边相等 【分析】举出矩形和平行四边形的所有性质, 找出矩形具有而平行四边形不具有的性质即可.
八年级(下)期中数学试卷(解析版)
参考答案与试题解析
一、选择题(每小题只有 1 个正确答案,每小题 3 分,共 30 分)
1.下列的式子一定是二次根式的是(
)
A.
B . C.
D.
【分析】根据二次根式的被开方数是非负数对每个选项做判断即可.
【解答】解: A 、当 x=0 时,﹣ x﹣ 2< 0,
无意义,故本选项错误;
为负数,则无实数根).
2.下列二次根式中属于最简二次根式的是(
)
A.
B.
C. D.
【分析】 B、 D 选项的被开方数中含有未开尽方的因数或因式; 母;因此这三个选项都不是最简二次根式. 【解答】解:因为: B、 =4 ;
C 选项的被开方数中含有分
C、 =
;
D、
=2
;
所以这三项都不是最简二次根式.故选 A .
2016---2017学年度下期期中考试八年级
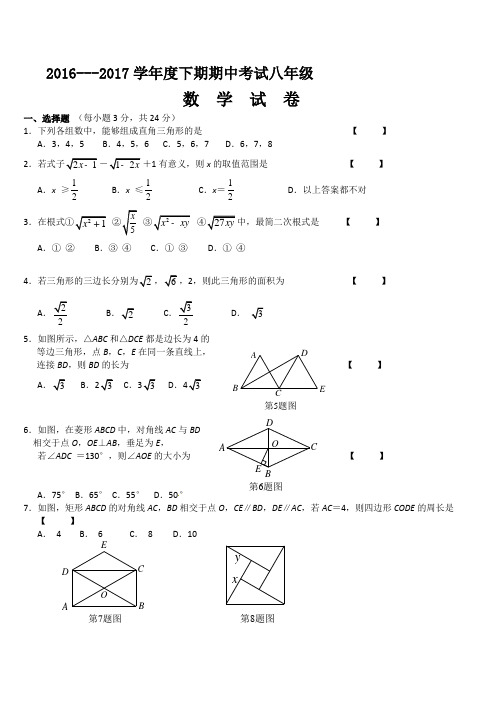
2016---2017学年度下期期中考试八年级数 学 试 卷一、选择题 (每小题3分,共24分)1.下列各组数中,能够组成直角三角形的是 【 】 A .3,4,5 B .4,5,6 C .5,6,7 D .6,7,8 2-1有意义,则x 的取值范围是 【 】 A .x ≥12 B .x ≤12 C .x =12D .以上答案都不对3【 】 A .① ② B .③ ④ C .① ③ D .① ④42,则此三角形的面积为 【 】 A.2BC.2 D .5.如图所示,△ABC 和△DCE 都是边长为4的等边三角形,点B ,C ,E 在同一条直线上, 连接BD ,则BD 的长为【 】 A B . C . D .6.如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,OE ⊥AB ,垂足为E , 若∠ADC =130°,则∠AOE 的大小为 【 】A .75°B .65°C .55°D .50°7.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,CE ∥BD ,DE ∥AC ,若AC =4,则四边形CODE 的周长是 【 】A . 4B . 6C . 8D .10第5题图ABD E第6题图O E AB C D第7题图ABC OE D y x第8题图8.如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x ,y 表示直角三角形的两条直角边(x > y ),请观察图案,指出下列关系式不正确...的是 【 】A .2249x y +=B .2x y -=C .2449xy +=D .13x y +=二、填空题( 每小题3分,共21分) 9.若x ,y 为实数,且∣x +2∣+3y -=0,则(x +y )2017的值为.10 .11. 实数a ,b 在数轴上的对应点如图所示,则∣a -b = .12.若x =27+x 2+(2x = .13.如图,在平面直角坐标系中,若菱形ABCD 的顶点A ,B 的坐标分别为(-3,0), (2,0),点D 在y 轴上,则点C 的坐标是 .14.如图所示,直线a 经过正方形ABCD 的顶点A ,分别过顶点D ,B 作DE ⊥a 于点E ,BF ⊥a 于点F ,若DE =4,BF =3,则EF = .15.如图,R t △ABC 中,∠B =90°,AB =3,BC =4,将△ABC 折叠,使点B 恰好落在斜边AC 上,与点B '重合,AE 为折痕,则E B '= .三、解答题:(本大题共8个小题,满分75分) 16.(每小题4分 共8分)计算:(101)2++; (2)a 532.第11题图0baB 'A BC E aA B C D E F第13题图第14题图第15题图17.(8分)x 的取值范围是什么?18.(9分)如图,每个小正方形的边长都是1, (1)求四边形ABCD 的周长和面积(2)∠BCD 是直角吗?19.(9分)如图所示,在□ABCD 中,点E ,F 分别在边BC 和AD 上,且CE =AF ,(1)求证:△ABE ≌ △CDF ;(2)求证:四边形AECF 是平行四边形.第18题图AB第19题图ABCDE F20.(10分) 如图所示,在菱形ABCD 中,点E ,F 分别是边BC ,AD 的中点,(1)求证:△ABE ≌ △CDF ;(2)若∠B =60°,AB =4,求线段AE 的长.21.(10分)如图所示,在矩形ABCD 中,对角线AC ,BD 相交于点O ,E 是CD 的中点,连接OE ,过点C 作CF∥BD 交线段OE 的延长线于点F ,连接DF .求证: (1)OD =CF ; (2)四边形ODFC 是菱形.22.(10分)如图所示,矩形ABCD 的对角线相交于点O ,OF ⊥AD 于点F ,OF =2cm ,AE ⊥BD 于点E ,且BE ﹕BD =1﹕4,求AC 的长.第20题图AB C DFE第21题图A B C D F E OA B OED F C 第22题图23.(11分)在平面内,正方形ABCD 与正方形CEFH 如图放置,连接DE ,BH ,两线交于M ,求证:(1)BH =DE ;(2)BH ⊥DE .HM A BF EC D 第23题图2016-2017学年度八年级(下)期中数学参考答案16.(1)1(4分) (2)7a 4分) 17.a =5; ……………………3分 5≤x ≤10 ……………………8分18.(1……………………3分面积14.5 ……………………6分(2)是……………………7分,证明:略.……………………9分 19.(1)略 5分 (2)略 9分20.(1)略 5分 (2)证出AE 是高 8分,AE = 10分 21.证明:(1)∵CF ∥BD ∴∠DOE =∠CFE ,∵E 是CD 的中点,∴CE =DE在△ODE 和△FCE 中,DOE CFE CE DE DEO CEFì??ïïï=íïï??ïïî,∴△ODE ≌△FCE (ASA )∴OD =CF .……………………6分(2)由(1)知OD =CF ,∵CF ∥BD ,∴四边形ODFC 是平行四边形在矩形ABCD 中,OC =OD ,∴四边形ODFC 是菱形.……………………10分22.解法一:∵四边形ABCD 为矩形,∴∠BAD =90°,OB =OD ,AC =BD ,又∵OF ⊥AD ,∴OF ∥AB ,又∵OB =OD ,∴ AB =2OF =4cm ,∵BE ︰BD =1︰4,∴BE ︰ED =1︰3 ……………………3分 设BE =x ,ED =3 x ,则BD =4 x ,∵AE ⊥BD 于点E∴22222AE AB BE AD ED =-=-,∴16-x 2=AD 2-9x 2………………6分 又∵AD 2=BD 2-AB 2=16 x 2-16 ,∴16-x 2=16 x 2-16-9x 2,8 x 2=32∴x 2=4,∴x =2 ……………………9分 ∴BD =2×4 =8(cm ),∴AC =8 cm . ……………………10分解法二:在矩形ABCD 中,BO =OD =12BD ,∵BE ︰BD =1︰4,∴BE ︰BO =1︰2, 即E 是BO 的中点 ……………………3分 又AE ⊥BO ,∴AB =A O ,由矩形的对角线互相平分且相等,∴AO =BO ……………………5分 ∴△ABO 是正三角形,∴∠BAO=60°,∴∠OAD=90°-60°=30°……………………8分在Rt△AOF中,AO=2OF=4,∴AC=2AO=8 ……………………10分23.(1)提示:证明:△BCH≌△DCE(SAS)……………………6分(2)由(1)知△BCH≌△DCE∴∠CBH=∠EDC设BH,CD交于点N,则∠BNC=∠DNH∴∠CBH+∠BNC=∠EDC+∠DNH=90°∴∠DMN=180°-90°=90°∴BH⊥DE.……………………11分。
福建省莆田2015-2016学年八年级(下)期中数学试卷(含解析)

2015-2016学年福建省莆田八年级(下)期中数学试卷一、选择题1.下列式子中,属于最简二次根式的是()A.B.C.D.2.下面各组数是三角形的三边的长,则能构成直角三角形的是()A.2,2,3 B.60,80,100 C.4,5,6 D.5,6,73.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是()A.12米B.13米C.14米D.15米4.使代数式有意义的x的取值范围是()A.x<3 B.x>3 C.x≤3D.x≥35.如图,在▱ABCD中,AD=6,AB=4,DE平分∠ADC交BC于点E,则BE的长是()A.2 B.3 C.4 D.56.如图,在矩形ABCD中,对角线AC=8cm,∠AOD=120°,则AB的长为()A.cm B.2cm C.cm D.4cm7.如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.118.如图,一只蚂蚁从长、宽都是4,高是6的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是()A.9 B.10 C.D.二、填空题9.在△ABC中,BC=6,E、F分别是AB、AC的中点,则EF=.10.菱形的两条对角线分别是6cm和8cm,则这个菱形的面积是cm2.11.比较大小:.(填“>”、“=”、“<”).12.化简=.13.写出“两组对边分别相等的四边形是平行四边形”的逆命题.14.+|b﹣4|=0,则=.15.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD=cm.16.如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第6个菱形的边长为.三、解答题(共9题,86分)17.计算(1)﹣(﹣)(2)+a﹣4+.18.先化简,再求值:÷(x+1﹣),其中x=﹣2.19.如图,▱ABCD的对角线ACBD有相交于点O,且E、F、G、H分别是OA、OB、OC、OD、的中点.求证:四边形EFGH是平行四边形.20.如图,▱ABCD,E、F分别在AD、BC上,且EF∥A B.求证:EF=C D.21.如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.22.如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.(1)求∠2、∠3的度数;(2)求长方形纸片ABCD的面积S.23.如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.(1)求证:四边形BDEF是菱形;(2)若AB=12cm,求菱形BDEF的周长.24.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥B C.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.25.某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①⇒②⇒③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC 的交点.(1)该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由.(2)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.(3)将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之间所满足的数量关系.(不需要证明)2015-2016学年福建省莆田八年级(下)期中数学试卷参考答案与试题解析一、选择题1.下列式子中,属于最简二次根式的是()A.B.C. D.【考点】最简二次根式.【专题】计算题.【分析】判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式的定义进行,或直观地观察被开方数的每一个因数(或因式)的指数都小于根指数2,且被开方数中不含有分母,被开方数是多项式时要先因式分解后再观察.【解答】解:A、=3,故A错误;B、是最简二次根式,故B正确;C、=2,不是最简二次根式,故C错误;D、=,不是最简二次根式,故D错误;故选:B.【点评】本题考查了最简二次根式的定义.在判断最简二次根式的过程中要注意:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.2.下面各组数是三角形的三边的长,则能构成直角三角形的是()A.2,2,3 B.60,80,100 C.4,5,6 D.5,6,7【考点】勾股数.【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.【解答】解:A、22+22≠32,故不能构成直角三角形;B、602+802=1002,故能构成直角三角形;C、42+52≠62,故不能构成直角三角形;D、52+62≠72,故不能构成直角三角形.故选B.【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.3.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是()A.12米B.13米C.14米D.15米【考点】勾股定理的应用.【专题】应用题.【分析】根据梯子、地面、墙正好构成直角三角形,再根据勾股定理解答即可.【解答】解:如图所示,AB=13米,BC=5米,根据勾股定理AC===12米.故选A.【点评】此题是勾股定理在实际生活中的运用,比较简单.4.使代数式有意义的x的取值范围是()A.x<3 B.x>3 C.x≤3D.x≥3【考点】二次根式有意义的条件.【分析】二次根式有意义时,被开方数为非负数,列不等式求解即可.【解答】解:根据题意得:3﹣x≥0,解得x≤3.故选C.【点评】本题考查的知识点为:二次根式的被开方数是非负数.5.如图,在▱ABCD中,AD=6,AB=4,DE平分∠ADC交BC于点E,则BE的长是()A.2 B.3 C.4 D.5【考点】平行四边形的性质.【分析】由四边形ABCD是平行四边形,可得BC=AD=6,CD=AB=4,AD∥BC,得∠ADE=∠DEC,又由DE 平分∠ADC,可得∠CDE=∠DEC,根据等角对等边,可得EC=CD=4,所以求得BE=BC﹣EC=2.【解答】解:∵四边形ABCD是平行四边形,∴BC=AD=6,CD=AB=4,AD∥BC,∴∠ADE=∠DEC,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠CDE=∠DEC,∴EC=CD=4,∴BE=BC﹣EC=2.故选:A.【点评】此题考查了平行四边形的性质、角平分线的定义与等腰三角形的判定定理.注意当有平行线和角平分线出现时,会出现等腰三角形.6.如图,在矩形ABCD中,对角线AC=8cm,∠AOD=120°,则AB的长为()A.cm B.2cm C.cm D.4cm【考点】矩形的性质.【分析】根据矩形的对角线相等且互相平分可得AO=BO=AC,再根据邻角互补求出∠AOB的度数,然后得到△AOB是等边三角形,再根据等边三角形的性质即可得解.【解答】解:在矩形ABCD中,AO=BO=AC=4cm,∵∠AOD=120°,∴∠AOB=180°﹣120°=60°,∴△AOB是等边三角形,∴AB=AO=4cm.故选D.【点评】本题考查了矩形的性质,等边三角形的判定与性质,判定出△AOB是等边三角形是解题的关键.7.如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.11【考点】平行四边形的性质;勾股定理.【分析】利用平行四边形的性质和勾股定理易求BO的长,进而可求出BD的长.【解答】解:∵▱ABCD的对角线AC与BD相交于点O,∴BO=DO,AO=CO,∵AB⊥AC,AB=4,AC=6,∴BO==5,∴BD=2BO=10,故选:C.【点评】本题考查了平行四边形的性质以及勾股定理的运用,是中考常见题型,比较简单.8.如图,一只蚂蚁从长、宽都是4,高是6的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是()A.9 B.10 C. D.【考点】平面展开﹣最短路径问题.【专题】数形结合.【分析】将长方体展开,得到两种不同的方案,利用勾股定理分别求出AB的长,最短者即为所求.【解答】解:如图(1),AB==;如图(2),AB===10.故选B.【点评】此题考查了立体图形的侧面展开图,利用勾股定理求出斜边的长是解题的关键,而两点之间线段最短是解题的依据.二、填空题9.在△ABC中,BC=6,E、F分别是AB、AC的中点,则EF=3.【考点】三角形中位线定理.【分析】根据三角形的中位线等于第三边的一半进行计算即可.【解答】解:∵E、F分别是AB、AC的中点,∴EF是△ABC的中位线,∴EF=BC=×6=3,故答案为:3.【点评】此题考查了三角形的中位线定理的数量关系,熟练掌握定理是解题的关键.10.菱形的两条对角线分别是6cm和8cm,则这个菱形的面积是24cm2.【考点】菱形的性质.【分析】直接利用菱形面积等于对角线乘积的一半进而得出答案.【解答】解:∵菱形的两条对角线分别是6cm和8cm,∴这个菱形的面积是:×6×8=24(cm2).故答案为:24.【点评】此题主要考查了菱形的性质,正确记忆菱形面积求法是解题关键.11.比较大小:<.(填“>”、“=”、“<”).【考点】实数大小比较.【分析】本题需先把进行整理,再与进行比较,即可得出结果.【解答】解:∵=∴∴故答案为:<.【点评】本题主要考查了实数大小关系,在解题时要化成同一形式是解题的关键.12.化简=.【考点】分母有理化.【分析】把分子分母同时乘以(﹣1)即可.【解答】解:原式==.故答案为:.【点评】本题考查的是分母有理化,分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.13.写出“两组对边分别相等的四边形是平行四边形”的逆命题“平行四边形是两组对边分别相等的四边形”.【考点】命题与定理.【专题】推理填空题.【分析】把一个命题的条件和结论互换就得到它的逆命题.【解答】解:“两组对边分别相等的四边形是平行四边形”的逆命题是:“平行四边形是两组对边分别相等的四边形”.故答案为:“平行四边形是两组对边分别相等的四边形”.【点评】此题主要考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.14.+|b﹣4|=0,则=2.【考点】非负数的性质:算术平方根;非负数的性质:绝对值.【分析】根据非负数的性质列出算式求出a、b的值,根据算术平方根的概念解答即可.【解答】解:由题意得,a﹣1=0,b﹣4=0,解得,a=1,b=4,则=2,故答案为:2.【点评】本题考查的是非负数的性质和算术平方根的概念,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.15.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD=4cm.【考点】平行四边形的性质.【分析】根据平行四边形的性质可知,平行四边形的对角线互相平分,由于△BOC的周长比△AOB的周长大2cm,则BC比AB长7cm,所以根据周长的值可以求出AB,进而求出CD的长.【解答】解:∵平行四边形的周长为20cm,∴AB+BC=10cm;又△BOC的周长比△AOB的周长大2cm,∴BC﹣AB=2cm,解得:AB=4cm,BC=6cm.∵AB=CD,∴CD=4cm故答案为:4.【点评】此题主要考查平行四边的性质:平行四边形的两组对边分别相等且平行四边形的对角线互相平分.16.如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第6个菱形的边长为18.【考点】菱形的性质.【专题】规律型.【分析】根据已知和菱形的性质可分别求得AC,AC1,AC2的长,从而可发现规律,根据规律不难求得第6个菱形的边长.【解答】解:连接DB,∵四边形ABCD是菱形,∴AD=A B.AC⊥DB,∵∠DAB=60°,∴△ADB是等边三角形,∴DB=AD=2,∴BM=1,∴AM==,∴AC=2AM=2,同理可得AC1=AC=6,AC2=AC1=6,AC3=AC2=18,AC4=AC3=18.故答案为:18.【点评】本题考查了菱形的性质,勾股定理,等边三角形的性质和判定的应用,解此题的关键是能根据求出的结果得出规律.三、解答题(共9题,86分)17.(2016春•莆田校级期中)计算(1)﹣(﹣)(2)+a﹣4+.【考点】二次根式的加减法.【分析】(1)首先化简二次根式,进而合并同类二次根式进而得出答案;(2)首先化简二次根式,进而合并同类二次根式进而得出答案.【解答】解:(1)﹣(﹣)=2﹣(3﹣×4)=2﹣=;(2)+a﹣4+=2a+a﹣2+=(3a﹣1).【点评】此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.18.先化简,再求值:÷(x+1﹣),其中x=﹣2.【考点】分式的化简求值.【分析】将原式括号中各项通分并利用同分母分式的减法法则计算,整理后再利用平方差公式分解因式,然后利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分得到最简结果,即可得到原式的值.【解答】解:÷(x+1﹣)=÷[﹣]=÷=×=当x=﹣2时,原式==.【点评】此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找出公因式,约分时,分式的分子分母出现多项式,应将多项式分解因式后再约分.19.如图,▱ABCD的对角线ACBD有相交于点O,且E、F、G、H分别是OA、OB、OC、OD、的中点.求证:四边形EFGH是平行四边形.【考点】平行四边形的判定与性质.【专题】证明题.【分析】由平行四边形的性质得出OA=OC,OB=OD,再由中点的定义得出OE=OG,OF=OH,即可证出四边形EFGH是平行四边形.【解答】证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵E、F、G、H分别是OA、OB、OC、OD、的中点,∴OE=OA,OG=OC,OF=OB,OH=OD,∴OE=OG,OF=OH,∴四边形EFGH是平行四边形.【点评】本题考查了平行四边形的判定与性质;熟记平行四边形的对角线互相平分,对角线互相平分的四边形是平行四边形是解决问题的关键.20.如图,▱ABCD,E、F分别在AD、BC上,且EF∥A B.求证:EF=C D.【考点】平行四边形的性质.【专题】证明题.【分析】根据平行四边形的性质可得AB=CD,AD∥BC,再判定四边形ABFE是平行四边形,进而可得AB=EF,再利用等量代换可得EF=C D.【解答】证明:∵四边形ABCD是平行四边形,∴AB=CD,AD∥BC,∴AE∥FB,∵EF∥AB,∴四边形ABFE是平行四边形,∴AB=EF,∴EF=C D.【点评】此题主要考查了平行四边形的判定和性质,关键是掌握平行四边形对边相等,两组对边分别平行的四边形是平行四边形.21.如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.【考点】勾股定理的逆定理;勾股定理.【分析】连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出△ACD是直角三角形,分别求出△ABC 和△ACD的面积,即可得出答案.【解答】解:连结AC,在△ABC中,∵∠B=90°,AB=3,BC=4,∴AC==5,S△ABC=AB•BC=×3×4=6,在△ACD中,∵AD=13,AC=5,CD=12,∴CD2+AC2=AD2,∴△ACD是直角三角形,∴S△ACD=AC•CD=×5×12=30.∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36.【点评】本题考查了勾股定理,勾股定理的逆定理的应用,解此题的关键是能求出△ABC和△CAD的面积,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.22.如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.(1)求∠2、∠3的度数;(2)求长方形纸片ABCD的面积S.【考点】翻折变换(折叠问题);矩形的性质.【专题】几何综合题.【分析】(1)根据AD∥BC,∠1与∠2是内错角,因而就可以求得∠2,根据图形的折叠的定义,可以得到∠4=∠2,进而可以求得∠3的度数;(2)已知AE=1,在Rt△ABE中,根据三角函数就可以求出AB、BE的长,BE=DE,则可以求出AD的长,就可以得到矩形的面积.【解答】解:(1)∵AD∥BC,∴∠2=∠1=60°;又∵∠4=∠2=60°,∴∠3=180°﹣60°﹣60°=60°.(2)在直角△ABE中,由(1)知∠3=60°,∴∠5=90°﹣60°=30°;∴BE=2AE=2,∴AB==;∴AD=AE+DE=AE+BE=1+2=3,∴长方形纸片ABCD的面积S为:AB•AD=×3=3.【点评】此题考查了矩形的性质,折叠的性质以及直角三角形的性质.此题难度不大,解题的关键是注意数形结合思想的应用.23.如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.(1)求证:四边形BDEF是菱形;(2)若AB=12cm,求菱形BDEF的周长.【考点】菱形的判定;三角形中位线定理.【专题】计算题;证明题;压轴题.【分析】(1)可根据菱形的定义“一组邻边相等的平行四边形是菱形”,先证明四边形BFED是平行四边形,然后再证明四边形的邻边相等即可.(2)F是AB的中点,有了AB的长也就求出了菱形的边长BF的长,那么菱形BDEF的周长也就能求出了.【解答】(1)证明:∵D、E、F分别是BC、AC、AB的中点,∴DE∥AB,EF∥BC,∴四边形BDEF是平行四边形,又∵DE=AB,EF=BC,且AB=BC,∴DE=EF,∴四边形BDEF是菱形;(2)解:∵AB=12cm,F为AB中点,∴BF=6cm,∴菱形BDEF的周长为6×4=24cm.【点评】本题的关键是判断四边形BDEF是菱形.菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.24.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥B C.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.【考点】矩形的判定;平行线的性质;等腰三角形的判定与性质;直角三角形斜边上的中线.【专题】压轴题.【分析】(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案;(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长;(3)根据平行四边形的判定以及矩形的判定得出即可.【解答】(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠2=∠5,∠4=∠6,∵MN∥BC,∴∠1=∠5,∠3=∠6,∴∠1=∠2,∠3=∠4,∴EO=CO,FO=CO,∴OE=OF;(2)解:∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°,∵CE=12,CF=5,∴EF==13,∴OC=EF=6.5;(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.证明:当O为AC的中点时,AO=CO,∵EO=FO,∴四边形AECF是平行四边形,∵∠ECF=90°,∴平行四边形AECF是矩形.【点评】此题主要考查了矩形的判定、平行四边形的判定和直角三角形的判定等知识,根据已知得出∠ECF=90°是解题关键.25.某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①⇒②⇒③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC 的交点.(1)该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由.(2)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.(3)将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之间所满足的数量关系.(不需要证明)【考点】旋转的性质;全等三角形的判定与性质;勾股定理;矩形的性质.【专题】计算题;操作型.【分析】(1)作辅助线,连接DN,在Rt△CDN中,根据勾股定理可得:ND2=NC2+CD2,再根据ON垂直平分BD,可得:BN=DN,从而可证:BN2=NC2+CD2;(2)作辅助线,延长MO交AB于点E,可证:△BEO≌△DMO,NE=NM,在Rt△BEN和Rt△MCN中,根据勾股定理和对应边相等,可证:CN2+CM2=DM2+BN2;(3)根据正方形的性质知:OA=OB,∠OAM=∠OBN,∠AOB=∠AOM+∠BOM=90°,∠MON为直角三角板的直角,可知:∠MON=∠BOM+∠BON=90°,可得:∠AOM=∠BON,从而可证:△AOM≌△BON,AM=BN,又AB=BC,可得:BM=CN,在Rt△ADM和△BCM中,根据勾股定理:DM2=AM2+AD2=BN2+AD2,MC2=MB2+BC2=CN2+BC2,故可得:CM2﹣CN2+DM2﹣BN2=2.【解答】解:(1)选择图①证明:连接DN.∵四边形ABCD是矩形,∴BO=DO,∠DCN=90°,∵ON⊥BD,∴NB=ND,∵∠DCN=90°,∴ND2=NC2+CD2,∴BN2=NC2+CD2.(2)CM2+CN2=DM2+BN2.理由如下:如图②,延长MO交AB于E,连接NE、NM.∵四边形ABCD是矩形,∴BO=DO,∠ABC=∠DCB=90°,∵AB∥CD,∴∠ABO=∠CDO,∠BEO=∠DMO,∴△BEO≌△DMO,∴OE=OM,BE=DM,∵NO⊥EM,∴NE=NM,∵∠ABC=∠DCB=90°,∴NE2=BE2+BN2,NM2=CN2+CM2,∴CN2+CM2=BE2+BN2,即CN2+CM2=DM2+BN2.(3)CM2﹣CN2+DM2﹣BN2=2.【点评】本题考查了图形的旋转变化,在解题过程中要综合应用勾股定理、矩形、正方形的特殊性质及三角形全等的判定等知识.。
2016年最新人教版八年级下数学期中测验题及答案

(1)求证;OE=OF;
(2)若BC=,求AB的长。
六解答题:(每小题10分,共20分)
25.如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
∴OE=OF
19.(1)证明:∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∵在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,
∴∠ABE=∠EBD=∠ABD,∠CDF=∠CDB,
∴∠ABE=∠CDF,
19.在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
20.如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PMAD,PNCD,垂足分别为M、N。
(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
26.如图,在等边三角形ABC中,BC=6cm.射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)求证:DE=BF;
期中考试】___2015-2016年八年级下期中数学试卷含答案解析

期中考试】___2015-2016年八年级下期中数学试卷含答案解析2015-2016学年___八年级(下)期中数学试卷一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1.要使分式的值为 $-\frac{1}{2}$,则 $x$ 的值为()A。
$x=1$。
B。
$x=2$。
C。
$x=-1$。
D。
$x=-2$2.下列说法正确的是()A。
对角线互相垂直的四边形是菱形B。
对角线相等的四边形是矩形C。
三条边相等的四边形是菱形D。
三个角是直角的四边形是矩形3.运用分式的性质,下列计算正确的是()A。
$\frac{3}{4} \div \frac{6}{5} = \frac{5}{8}$。
B。
$\frac{2}{3} \div \frac{1}{4} = \frac{1}{6}$。
C。
$\frac{5}{6} \times \frac{1}{4} = \frac{5}{24}$。
D。
$\frac{2}{3} + \frac{3}{4} = \frac{17}{12}$。
4.一个凸五边形的内角和为()A。
$360^\circ$。
B。
$540^\circ$。
C。
$720^\circ$。
D。
$900^\circ$5.根据下列表格对应值,判断关于 $x$ 的方程$ax^2+bx+c=0$($a\neq 0$)的一个解 $x$ 的取值范围为()begin{array}{|c|c|}hlinex & ax^2+bx+c \\hline1.1 & -0.59 \\hline1.2 & 0.84 \\hline1.3 &2.29 \\hline1.4 & 3.76 \\hlineend{array}A。
$-0.59<x<0.84$。
B。
$1.1<x<1.2$。
2016-2017学年八年级下学期数学期中考试试题及答案

2016-2017学年八年级下学期数学期中测试一、选择题〔每题3分,共30分〕1..若代数式0)21-+-x x x (有意义,则实数x 的取值范围是〔〕 A. x ≠ 1B.x ≥0C. x ≥0且x ≠1D.x ≥0且x ≠1,x ≠22.已知a <b,化简二次根式b a 3-的正确结果是〔〕A .ab a --B .ab a -C .ab aD .ab a -3、等边三角形的边长为2,则该三角形的面积为 〔 〕 A :43 B :3C :23 D :34.下列运算正确的是〔 〕A 、235=-B 、312914=C 、32321+=- D 、()52522-=-5.由线段a 、b 、c 组成的三角形不是直角三角形的是< >A 、a=7,b=24,c=25;B 、a=41,b=4,c=5;C 、a=54,b=1,c=34; D 、a=13,b=14,c=15; 5.若ABC ∆中,13,15AB cm AC cm ==,高AD=12,则BC 的长为〔 〕 A :14 B :4 C :14或4 D :以上都不对7.已知110a a+=,则1a a -的值为〔〕 A .22±B .8 C .6± D .68. 如图,过矩形ABCD 的四个顶点作对角线AC,BD 的平行线,分别相交于E,F,G,H 四点,则四边形EFGH 为A.平行四边形B.矩形C.菱形D.正方形9.如图,在矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,点D 落在点D ’处,则重叠部分△AFC的面积为〔〕.A .6B .8C .10D .1210. 如图,正方形ABCD 的边长为4,点E 在对角线BD 上,且△BAE=22.5 º,EF △AB ,垂足为F ,则EF 的长为〔〕 A .1 B .错误! C .4-2错误! D .3错误!-4二、填空题〔每题分3,共18分〕11.如果最简二次根式a +1与24-a 是同类二次根式,那么a =.12.如图由于台风的影响,一棵树在折断前〔不包括树根〕长度是m 16,树顶落在离树干底部A B C D F D’↑ ↓ ←m 8E DA Om 8处,则这棵树在离地面处折断.13.如图,▱ABCD 的对角线AC,BD 相交于点O,点E,F 分别是线段AO,BO 的中点.若AC+BD=24厘米,△OAB 的周长是18厘米,则EF=厘米.14..如图,每个小正方形的边长为1.在△ABC 中,点D 为AB 的中点,则线段CD 的长为;15.如图,在Rt ΔABC 中,∠ACB=90°,AC=4,BC=3,D 为斜边AB 上一点,以CD 、CB 为边作平行四边形CDEB,当AD=时,平行四边形CDEB 为菱形.16.如图,正方形ABCD 中,点E 在BC 上,且CE=14BC,点F 是CD 的中点,延长AF 与BC 的延长线交于点M.以下结论:①AB=CM ;②AE=AB+CE ;③S △AEF =ABCF S 31四边形;④∠AFE=90°,其中正确结论的个数有三.解答题〔共72分〕17.〔8分〕计算:<1> 〔2〕 18〔8分〕<1>先化简,再求值:1-12122a a a a +--,其中121+=a . <2>如图,实数a 、b 、c 在数轴上的位置,化简:错误!-︱a -b ︱+ 错误!.19.〔8分〕如图,Rt △ABC 中,∠C=90°,AD 平分∠CAB,DE ⊥AB 于E,若AC=6,BC=8,CD=3. 〔1〕求DE 的长;〔2〕求△ADB 的面积.20.〔8分〕如图,某校将一块△ABC 废地开辟为生物园,AB=100m,AC=80m,BC=60m.〔1〕若入口E 在边AB 上,且与A 、B 等距离,求从入口E 到出口C 的最短路线〔2〕若线段CD 是一条水渠,且D 点在边AB 上,已知水渠的造价为10元/米,则D 点在距A 点多远处时,水渠的造价最低?最低造价是多少?21.〔8分〕如图,△ABC 中,AB=AC,AD 是△ABC 的角平分线,点O 为AB 的中点,连接DO 并延长到点E,使OE=OD,连接AE,BE.<1>求证:四边形AEBD 是矩形.<2>当△ABC 满足什么条件时,矩形AEBD 是正方形,并说明理由.22.〔10分〕如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,MN 过点O 且与边AD 、BC 分别交于点M 和点N .〔1〕请你判断OM 与ON 的数量关系,并说明理由;〔2〕过点D 作DE ∥AC 交BC 的延长线于点E ,当AB =6,AC =8时,求△BDE 的周长.23.〔10分〕如图,已知平行四边形中,对角线交于点,是延长线上的点,且是等边三角形.〔1〕求证:四边形是菱形;〔2〕若求证:四边形是正方形. ABCD AC BD ,O E BD ACE △ABCD 2AED EAD ∠=∠ABCD )323125.0()4881(----)65()154(5333y x x y xy --÷•24.〔12分〕如图1,四边形ABCD 、DEFG 都是正方形,连接AE 、CG . 〔1〕求证:AE=CG ; 〔2〕观察图形,猜想AE 与CG 之间的位置关系,并证明你的猜想;〔3〕将正方形ABCD,绕点D 逆时针旋转一定的角度〔小于90度〕,如图2,请猜想AE 与CG 之间的关系,并证明你的猜想.2016-2017学年八年级下学期数学期中测试答案一、选择题〔每题3分,共36分〕1..若代数式0)21-+-x x x (有意义,则实数x 的取值范围是〔D 〕 A. x ≠ 1B.x ≥0C. x ≥0且x ≠1D.x ≥0且x ≠1,x ≠22.已知a <b,化简二次根式b a 3-的正确结果是〔A 〕A .ab a --B .ab a -C .ab aD .ab a -3、等边三角形的边长为2,则该三角形的面积为 〔B 〕 A :43 B :3C :23 D :34.下列运算正确的是〔 〕A 、235=-B 、312914=C 、32321+=- D 、()52522-=-5.由线段a 、b 、c 组成的三角形不是直角三角形的是< D >A 、a=7,b=24,c=25;B 、a=41,b=4,c=5;C 、a=54,b=1,c=34; D 、a=13,b=14,c=15; 5.若ABC ∆中,13,15AB cm AC cm ==,高AD=12,则BC 的长为〔C 〕 A :14 B :4 C :14或4 D :以上都不对7.已知110a a +=,则1a a -的值为〔C 〕 A .22±B .8 C .6± D .68. 如图,过矩形ABCD 的四个顶点作对角线AC,BD 的平行线,分别相交于E,F,G,H 四点,则四边形EFGH 为 < C >A.平行四边形B.矩形C.菱形D.正方形11.如图,在矩形ABCD 中,9.AB =8,BC =4,将矩形沿AC 折叠,点D 落在点D ’处,则重叠部分△AFC 的面积为〔C 〕.A .6B .8C .10D .12 10. 如图,正方形ABCD 的边长为4,点E 在对角线BD 上,且△BAE =22.5 º,EF △AB ,垂足为F ,则EF 的长为〔C 〕 A .1 B .错误!A B C D F D’↑ ↓ ← m 8E D C B A C .4-2错误! D .3错误!-4二、填空题〔每题分3,共18分〕11.如果最简二次根式a +1与24-a 是同类二次根式,那么a =1.12.如图由于台风的影响,一棵树在折断前〔不包括树根〕长度是m 16,树顶落在离树干底部m 8处,则这棵树在离地面6处折断.13.如图,▱ABCD 的对角线AC,BD 相交于点O,点E,F 分别是线段AO,BO 的中点.若AC+BD=24厘米,△OAB 的周长是18厘米,则EF=3厘米.14..如图,每个小正方形的边长为1,在△ABC 中,点D 为AB 的中点,则线段CD 的长为√262; 15.如图,在Rt ΔABC 中,∠ACB=90°,AC=4,BC=3,D 为斜边AB 上一点,以CD 、CB 为边作平行四边形CDEB,当AD=75时,平行四边形CDEB 为菱形. 16.如图,正方形ABCD 中,点E 在BC 上,且CE=14BC,点F 是CD 的中点,延长AF 与BC 的延长线交于点M.以下结论:①AB=CM ;②AE=AB+CE ;③S △AEF =ABCF S 31四边形;④∠AFE=90°, 其中正确结论的个数有①②④三.解答题〔共72分〕17.〔8分〕计算:<1> <2>18、〔8分〕<1>先化简,再求值:1-12122a a a a +--,其中121+=a . <2>如图,实数a 、b 、c 在数轴上的位置,化简:错误!-︱a -b ︱+ 错误!.19.〔8分〕如图,Rt △ABC 中,∠C=90°,AD 平分∠CAB,DE ⊥AB 于E,若AC=6,BC=8,CD=3. 〔1〕求DE 的长;〔2〕求△ADB 的面积.20.〔8分〕如图,某校将一块△ABC 废地开辟为生物园,AB=100m,AC=80m,BC=60m.〔1〕若入口E 在边AB 上,且与A 、B 等距离,求从入口E 到出口C 的最短路线〔2〕若线段CD 是一条水渠,且D 点在边AB 上,已知水渠的造价为10元/米,则D 点在距A 点多远处时,水渠的造价最低?最低造价是多少?解:〔1〕在△ABC 中,因为AC=80,BC=60,AB =100,所以所以∠C=90°,即△ABC 为直角三角形,)323125.0()4881(----故入口E到出口C的最短线路就是Rt△ABC斜边的中线CE,又因为CE=AB=50,所以入口E到出口C的最短距离为50m;〔2〕CD为Rt△ABC斜边上的高时,CD最短,此时水渠造价最低,因为CD×AB-AC×BC,所以CD=48m,在Rt△ACD中,,即,解得AD=64m,所以点D距点A64m时,水渠的造价最低,最低造价为48×10=480元21.〔8分〕如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.<1>求证:四边形AEBD是矩形.<2>当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.〔1〕证明:∵点O为AB的中点, OE=OD,∴四边形AEBD是平行四边形,∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴平行四边形AEBD是矩形;〔2〕当∠BAC=90°时,理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,∴AD=BD=CD,∵由〔1〕得四边形AEBD是矩形,∴矩形AEBD是正方形.22.〔10分〕如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.〔1〕请你判断OM与ON的数量关系,并说明理由;〔2〕过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.解:〔1〕∵四边形ABCD是菱形,∴AD∥BC,AO=OC∴OM=ON.〔2〕∵四边形ABCD是菱形,∴AC⊥BD,AD=BC=AB=6,∴BO==2,∴,∵DE∥AC,AD∥CE,∴四边形ACED是平行四边形,∴DE=AC=6,∴△BDE的周长是:BD+DE+BE=BD+AC+〔BC+CE〕=4+8+〔6+6〕=20即△BDE的周长是20.E C D B A O 23.〔10分〕如图,已知平行四边形中,对角线交于点,是延长线上的点,且是等边三角形.〔1〕求证:四边形是菱形;〔2〕若求证:四边形是正方形. 证明:〔1〕∵四边形ABCD 是平行四边形, ∴AO=CO.又∵△ACE 是等边三角形,∴EO⊥AC,即AC⊥BD,∴四边形ABCD 是菱形 〔2〕∵四边形ABCD 是平行四边形,∴AO=CO.又∵△ACE 是等边三角形,∴EO 平分∠AEC〔三线合一〕,∴∠AED=1/2∠AEC=1/2×60°=30°,又∵∠AED=2∠EAD∴∠EAD=15°,∴∠ADO=∠DAE+∠DEA=15°+30°=45°∵四边形ABCD 是菱形,∴∠ADC=2∠ADO=90°,∴平行四边形ABCD 是正方形. 24.〔12分〕如图1,四边形ABCD 、DEFG 都是正方形,连接AE 、CG .〔1〕求证:AE=CG ;〔2〕观察图形,猜想AE 与CG 之间的位置关系,并证明你的猜想;〔3〕将正方形ABCD,绕点D 逆时针旋转一定的角度〔小于90度〕,如图2,请猜想AE 与CG 之间的关系,并证明你的猜想.〔1〕证明:由题意得AD=CD,ED=GD,∠ADE=∠GDC=90°∴根据SAS 可证△EAD ≌△GCD,∴AE=CG ;〔2〕猜想:AE ⊥CG ;延长EA 交CG 于H,由〔1〕得∠CGD+∠GAH=∠CGD+∠EAD=∠CGD+∠GCD=90°∴AE ⊥CG ;〔3〕猜想:AE=CG ;AE ⊥CG .由题意得CD=AD,GD=ED,∠ADE=90+∠GDA=∠CDG ∴△EAD ≌△GCD ∴AE=CG,∠CGD=∠AED ∵∠AED+∠EOD=90°,∴∠CGD+∠EOD=90°,∵∠EOD=∠GOH,∴∠CGO+∠GOH=∠CGO+∠EOD=∠AED+∠EOD=90°,∴AE ⊥CG . ∴∠EAN=∠MAN .∵在△MAN 和△EAN 中,AE=AM ∠MAN=∠EAN AN=AN∴△MAN ≌△EAN 〔SAS 〕,∴EN=MN,即DN-DE=MN,∴DN-BM=MN.ABCD AC BD ,O E BD ACE △ABCD 2AED EAD ∠=∠ABCD。
2015-2016学年八年级(下)期中数学试卷含答案解析

2015-2016学年八年级(下)期中数学试卷一、选择题(本题共10小题,每小题3分,共30分)1.使式子有意义,则x的取值范围是()A.x>5 B.x≠5 C.x≥5 D.x≤52.下列二次根式中,属于最简二次根式的是()A.B.C.D.3.下列运算正确的是()A.()2=4 B. =﹣4 C. =×D.﹣=4.如图,直角三角形的三边长分为a、b、c,下列各式正确的是()A.a2+b2=c2B.b2+c2=a2C.c2+a2=b2D.以上都不对5.一个直角三角形的两边长分别为4cm、3cm,则第三条边长为()A.5cm B.4cm C. cm D.5cm 或cm6.下列各组数中不能作为直角三角形的三边长的是()A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,157.如图,在▱ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于()A.1cm B.2cm C.3cm D.4cm8.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等 D.邻角互补9.两条对角线互相垂直平分且相等的四边形是()A.矩形 B.菱形 C.正方形D.都有可能10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为()A.6 B.8 C.10 D.12二、填空题(本题共10小题,每小题4分,共40分)11.如图,△ABC中,D、E分别是AB、AC边的中点,且DE=7cm,则BC= cm.12.写出命题“对顶角相等”的逆命题.13.比较大小:.(填“>、<、或=”)14.如果+(b﹣7)2=0,则的值为.15.如图,有两棵树,一棵高10m,另一棵高4m,两树相距8m.一只小鸟从一棵树的树尖飞到另一棵树的树尖,那么这只小鸟至少要飞行m.16.如图,一只蚂蚁从长为7cm、宽为5cm,高是9cm的长方体纸箱的A点沿纸箱爬到B点,那么它所走的最短路线的长是cm.17.若矩形的对角线长为8cm,两条对角线的一个交角为60°,则该矩形的面积为cm2.18.菱形的两条对角线长分别为6和8,则这个菱形的周长为.19.若两对角线长分别为4cm和6cm的菱形的面积与一个正方形的面积相等,那么该正方形的边长为cm.20.如图,在矩形ABCD中,AD=4,AB=3,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是.三.解答题(共50分)21.计算:(1)(﹣)2﹣+(2)(3﹣)﹣(+)22.已知a=3+,b=3﹣,分别求下列代数式的值:(1)a2﹣b2(2)a2﹣2ab+b2.23.如图,在四边形ABCD中,∠A=90°,AD=3,AB=4,BC=12,CD=13,试判断△BCD的形状,并说明理由.24.如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.25.如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.26.如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求AC、OA以及平行四边形ABCD的面积.27.已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.(1)求证:△ABM≌△DCM;(2)判断四边形MENF是什么特殊四边形,并证明你的结论;(3)当AD:AB= 时,四边形MENF是正方形(只写结论,不需证明).2015-2016学年八年级(下)期中数学试卷参考答案与试题解析一、选择题(本题共10小题,每小题3分,共30分)1.使式子有意义,则x的取值范围是()A.x>5 B.x≠5 C.x≥5 D.x≤5【考点】二次根式有意义的条件.【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.【解答】解:∵式子有意义,∴x﹣5≥0,解得x≥5.故选C.【点评】本题考查的是二次根式有意义的条件,熟知二次根式中的被开方数是非负数是解答此题的关键.2.下列二次根式中,属于最简二次根式的是()A.B.C.D.【考点】最简二次根式.【分析】根据最简二次根式的条件进行判断即可.【解答】解: =,被开方数含分母,不是最简二次根式;=,被开方数含分母,不是最简二次根式;=2,被开方数中含能开得尽方的因数,不是最简二次根式;是最简二次根式,故选:D.【点评】本题考查的是最简二次根式的概念,最简二次根式的条件:(1)被开方数的因数是整数或字母,因式是整式;(2)被开方数中不含有可化为平方数或平方式的因数或因式.3.下列运算正确的是()A.()2=4 B. =﹣4 C. =×D.﹣=【考点】二次根式的混合运算.【分析】分别利用二次根式的性质以及结合二次根式混合运算法则化简求出答案.【解答】解:A、()2=4,正确;B、=4,故此选项错误;C、=×,故此选项错误;D、﹣无法计算,故此选项错误;故选:A.【点评】此题主要考查了二次根式的混合运算以及二次根式的化简,正确掌握二次根式的性质是解题关键.4.如图,直角三角形的三边长分为a、b、c,下列各式正确的是()A.a2+b2=c2B.b2+c2=a2C.c2+a2=b2D.以上都不对【考点】勾股定理.【分析】由勾股定理即可得出结论,注意a是斜边长.【解答】解:∵∠A=90°,∴由勾股定理得:b2+c2=a2.故选:B.【点评】本题考查了勾股定理;熟记勾股定理是解决问题的关键.5.一个直角三角形的两边长分别为4cm、3cm,则第三条边长为()A.5cm B.4cm C. cm D.5cm 或cm【考点】勾股定理.【分析】题中没有指明哪个是直角边哪个是斜边,故应该分情况进行分析.【解答】解:(1)当两边均为直角边时,由勾股定理得,第三边为5cm;(2)当4为斜边时,由勾股定理得,第三边为cm;故直角三角形的第三边应该为5cm或cm.故选:D.【点评】此题主要考查学生对勾股定理的运用,注意分情况进行分析.6.下列各组数中不能作为直角三角形的三边长的是()A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15【考点】勾股定理的逆定理.【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.【解答】解:A、1.52+22≠32,不符合勾股定理的逆定理,故正确;B、72+242=252,符合勾股定理的逆定理,故错误;C、62+82=102,符合勾股定理的逆定理,故错误;D、92+122=152,符合勾股定理的逆定理,故错误.故选A.【点评】本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.7.如图,在▱ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于()A.1cm B.2cm C.3cm D.4cm【考点】平行四边形的性质.【专题】几何图形问题.【分析】根据平行四边形的性质和角平分线的性质可以推导出等角,进而得到等腰三角形,推得AB=BE,所以根据AD、AB的值,求出EC的值.【解答】解:∵AD∥BC,∴∠DAE=∠BEA∵AE平分∠BAD∴∠BAE=∠DAE∴∠BAE=∠BEA∴BE=AB=3∵BC=AD=5∴EC=BC﹣BE=5﹣3=2故选:B.【点评】本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.8.菱形具有而矩形不具有的性质是()A.对角线互相平分B.四条边都相等C.对角相等 D.邻角互补【考点】矩形的性质;菱形的性质.【专题】证明题.【分析】与平行四边形相比,菱形的四条边相等、对角线互相垂直;矩形四个角是直角,对角线相等.【解答】解:A、对角线互相平分是平行四边形的基本性质,两者都具有,故A不选;B、菱形四条边相等而矩形四条边不一定相等,只有矩形为正方形时才相等,故B符合题意;C、平行四边形对角都相等,故C不选;D、平行四边形邻角互补,故D不选.故选:B.【点评】考查菱形和矩形的基本性质.9.两条对角线互相垂直平分且相等的四边形是()A.矩形 B.菱形 C.正方形D.都有可能【考点】多边形.【分析】如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是正方形,理由为:利用对角线互相平分的四边形为平行四边形得到ABCD为平行四边形,再利用对角线互相垂直的平行四边形为菱形,再利用对角线相等的菱形为正方形即可得证.【解答】解:如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是正方形,已知:四边形ABCD,AC⊥BD,OA=OC,OB=OD,AC=BD,求证:四边形ABCD为正方形,证明:∵OA=OC,OB=OD,∴四边形ABCD为平行四边形,∵AC⊥BD,∴平行四边形ABCD为菱形,∵AC=BD,∴四边形ABCD为正方形.故选C.【点评】此题考查了正方形的判定,以及角平分线定理,熟练掌握正方形的判定方法是解本题的关键.10.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC 的面积为()A.6 B.8 C.10 D.12【考点】翻折变换(折叠问题).【分析】因为BC为AF边上的高,要求△AFC的面积,求得AF即可,求证△AFD′≌△CFB,得BF=D′F,设D′F=x,则在Rt△AFD′中,根据勾股定理求x,于是得到AF=AB﹣BF,即可得到结果.【解答】解:易证△AFD′≌△CFB,∴D′F=BF,设D′F=x,则AF=8﹣x,在Rt△AFD′中,(8﹣x)2=x2+42,解之得:x=3,∴AF=AB﹣FB=8﹣3=5,∴S△AFC=•AF•BC=10.故选C.【点评】本题考查了翻折变换﹣折叠问题,勾股定理的正确运用,本题中设D′F=x,根据直角三角形AFD′中运用勾股定理求x是解题的关键.二、填空题(本题共10小题,每小题4分,共40分)11.如图,△ABC中,D、E分别是AB、AC边的中点,且DE=7cm,则BC= 14 cm.【考点】三角形中位线定理.【分析】根据三角形中位线定理得出BC=2DE,代入求出即可.【解答】解:∵D、E分别是AB、AC边的中点,且DE=7cm,∴BC=2DE=14cm,故答案为:14.【点评】本题考查了三角形中位线定理的应用,能熟记三角形的中位线定理的内容是解此题的关键,注意:三角形的中位线平行于第三边,并且等于第三边的一半.12.写出命题“对顶角相等”的逆命题如果两个角相等,那么这两个角是对顶角.【考点】命题与定理.【分析】根据逆命题的定义可以写出命题“对顶角相等”的逆命题,本题得以解决.【解答】解:命题“对顶角相等”的逆命题是如果两个角相等,那么这两个角是对顶角,故答案为:如果两个角相等,那么这两个角是对顶角.【点评】本题考查命题与定理,解题的关键是明确逆命题的定义,可以写出一个命题的逆命题.13.比较大小:<.(填“>、<、或=”)【考点】实数大小比较.【分析】先把两个实数平方,然后根据实数的大小比较方法即可求解.【解答】解:∵()2=12,(3)2=18,而12<18,∴2<3.故答案为:<.【点评】此题主要考查了实数的大小的比较,比较两个实数的大小,可以采用作差法、取近似值法、比较n次方的方法等.14.如果+(b﹣7)2=0,则的值为 3 .【考点】非负数的性质:算术平方根;非负数的性质:偶次方.【分析】首先利用偶次方的性质以及二次根式的性质进而得出a,b的值,进而求出答案.【解答】解:∵ +(b﹣7)2=0,∴a=2,b=7,则==3.故答案为:3.【点评】此题主要考查了非负数的性质,正确得出a,b的值是解题关键.15.如图,有两棵树,一棵高10m,另一棵高4m,两树相距8m.一只小鸟从一棵树的树尖飞到另一棵树的树尖,那么这只小鸟至少要飞行10 m.【考点】勾股定理的应用.【专题】应用题.【分析】根据“两点之间线段最短”可知:小鸟沿着两棵树的树尖进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.【解答】解:两棵树的高度差为6m,间距为8m,根据勾股定理可得:小鸟至少飞行的距离==10m.【点评】本题主要是将现实问题建立数学模型,运用数学知识进行求解.16.如图,一只蚂蚁从长为7cm、宽为5cm,高是9cm的长方体纸箱的A点沿纸箱爬到B点,那么它所走的最短路线的长是15 cm.【考点】平面展开﹣最短路径问题.【专题】推理填空题.【分析】根据题意,可以画出长方体的展开图,根据两点之间线段最短和勾股定理,可以解答本题.【解答】解:如右图所示,点A到B的最短路径是: cm,故答案为:15.【点评】本题考查平面展开﹣最短路径问题,解题的关键是明确两点之间线段最短,能画出图形的平面展开图.17.若矩形的对角线长为8cm,两条对角线的一个交角为60°,则该矩形的面积为cm2.【考点】矩形的性质.【专题】计算题.【分析】根据矩形的性质,画出图形求解.【解答】解:∵ABCD为矩形∴OA=OC=OB=OD∵一个角是60°∴BC=OB=cm∴根据勾股定理==∴面积=BC•CD=4×=cm2.故答案为.【点评】本题考查的知识点有:矩形的性质、勾股定理.18.菱形的两条对角线长分别为6和8,则这个菱形的周长为20 .【考点】菱形的性质;勾股定理.【分析】根据菱形的对角线互相垂直平分的性质,利用对角线的一半,根据勾股定理求出菱形的边长,再根据菱形的四条边相等求出周长即可.【解答】解:如图所示,根据题意得AO=×8=4,BO=×6=3,∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD,∴△AOB是直角三角形,∴AB===5,∴此菱形的周长为:5×4=20.故答案为:20.【点评】本题主要考查了菱形的性质,利用勾股定理求出菱形的边长是解题的关键,同学们也要熟练掌握菱形的性质:①菱形的四条边都相等;②菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.19.若两对角线长分别为4cm和6cm的菱形的面积与一个正方形的面积相等,那么该正方形的边长为2cm.【考点】正方形的性质;菱形的性质.【分析】已知对角线的长度,根据菱形的面积计算公式即可计算菱形的面积,进一步开方求得正方形的边长即可.【解答】解:根据对角线的长可以求得菱形的面积,根据S=ab=×4×6=12cm2,∵菱形的面积与正方形的面积相等,∴正方形的边长是=2cm.故答案为:2.【点评】本题考查了菱形的面积和正方形的面积计算的方法,本题中根据菱形对角线求得菱形的面积是解题的关键.20.如图,在矩形ABCD中,AD=4,AB=3,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是 6 .【考点】矩形的性质.【分析】用矩形的面积减去△ADQ和△BCP的面积求解即可.【解答】解:∵四边形ABCD为矩形,∴AD=BC=4.S阴影=S矩形ABCD﹣S△BPC﹣S△ADQ=AB•CB﹣BC•MB AD•AM=4×3﹣4×BM﹣×4×AM=12﹣2MB﹣2AM=12﹣2(MB+AM)=12﹣2×3=6.故答案为:6.【点评】本题主要考查的是矩形的性质、三角形的面积公式,将阴影部分的面积转化为S矩形ABCD﹣S△﹣S△ADQ求解是解题的关键.BPC三.解答题(共50分)21.计算:(1)(﹣)2﹣+(2)(3﹣)﹣(+)【考点】二次根式的混合运算.【专题】计算题.【分析】(1)先化简二次根式,再合并同类项即可解答本题;(2)根据去括号的法则去掉括号,然后合并同类项即可解答本题.【解答】解:(1)(﹣)2﹣+=3﹣2+3=4;(2)(3﹣)﹣(+)==.【点评】本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.22.已知a=3+,b=3﹣,分别求下列代数式的值:(1)a2﹣b2(2)a2﹣2ab+b2.【考点】二次根式的化简求值.【分析】(1)利用平方差公式分解因式后再代入计算;(2)利用完全平方差公式分解因式后再代入计算.【解答】解:当a=3+,b=3﹣时,(1)a2﹣b2,=(a+b)(a﹣b),=(3+3﹣)(3+﹣3+),=6×2,=12;(2)a2﹣2ab+b2,=(a﹣b)2,=(3﹣3+)2,=(2)2,=8.【点评】本题是运用简便方法进行二次根式的化简求值,熟练掌握平方差公式和完全平方公式是解题的关键.23.如图,在四边形ABCD中,∠A=90°,AD=3,AB=4,BC=12,CD=13,试判断△BCD的形状,并说明理由.【考点】勾股定理的逆定理;勾股定理.【分析】先根据勾股定理计算BD的长,再利用勾股定理的逆定理证明∠DBC=90°,所以:△BCD是直角三角形.【解答】解:△BCD是直角三角形,理由是:在△ABD中,∠A=90°,∴BD2=AD2+AB2=32+42=25,在△BCD中,BD2+BC2=52+122=169,CD2=132=169,∴BD2+BC2=CD2,∴∠DBC=90°∴△BCD是直角三角形.【点评】本题考查了勾股定理及其逆定理,熟练掌握定理的内容是关键,注意各自的条件和结论.24.如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.【考点】翻折变换(折叠问题).【专题】计算题.【分析】根据矩形的性质得DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则FC=4,设EC=x,则DE=EF=8﹣x,在Rt△EFC 中,根据勾股定理得x2+42=(8﹣x)2,然后解方程即可.【解答】解:∵四边形ABCD为矩形,∴DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,∵折叠矩形的一边AD,使点D落在BC边的点F处∴AF=AD=10,DE=EF,在Rt△ABF中,BF===6,∴FC=BC﹣BF=4,设EC=x,则DE=8﹣x,EF=8﹣x,在Rt△EFC中,∵EC2+FC2=EF2,∴x2+42=(8﹣x)2,解得x=3,∴EC的长为3cm.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理.25.如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.【考点】平行四边形的判定与性质;全等三角形的性质.【专题】证明题;压轴题.【分析】首先连接BD,交AC于点O,由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,即可求得OA=OC,OB=OD,又由AE=CF,可得OE=OF,然后根据对角线互相相平分的四边形是平行四边形.【解答】证明:连接BD,交AC于点O,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵AE=CF,∴OA﹣AE=OC﹣CF,即OE=OF,∴四边形DEBF是平行四边形.【点评】此题考查了平行四边形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.26.如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求AC、OA以及平行四边形ABCD的面积.【考点】平行四边形的性质.【分析】由四边形ABCD是平行四边形,可求得BC=AD=8,又由AC⊥BC,利用勾股定理即可求得AC 的长,然后由平行四边形的对角线互相平分,求得OA的长,继而求得平行四边形ABCD的面积.【解答】解:∵四边形ABCD是平行四边形,∴BC=AD=8,∵AB=10,AC⊥BC,∴AC==6,∴OA=AC=3,∴S平行四边形ABCD=BC•AC=8×6=48.【点评】此题考查了平行四边形的性质以及勾股定理.注意平行四边形的对边相等,对角线互相平分.27.已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.(1)求证:△ABM≌△DCM;(2)判断四边形MENF是什么特殊四边形,并证明你的结论;(3)当AD:AB= 2:1 时,四边形MENF是正方形(只写结论,不需证明).【考点】矩形的性质;全等三角形的判定与性质;菱形的判定;正方形的判定.【分析】(1)根据矩形的性质可得AB=CD,∠A=∠D=90°,再根据M是AD的中点,可得AM=DM,然后再利用SAS证明△ABM≌△DCM;(2)四边形MENF是菱形.首先根据中位线的性质可证明NE∥MF,NE=MF,可得四边形MENF是平行四边形,再根据△ABM≌△DCM可得BM=CM进而得ME=MF,从而得到四边形MENF是菱形;(3)当AD:AB=2:1时,四边形MENF是正方形,证明∠EMF=90°根据有一个角为直角的菱形是正方形得到结论.【解答】(1)证明:∵四边形ABCD是矩形,∴AB=CD,∠A=∠D=90°,又∵M是AD的中点,∴AM=DM.在△ABM和△DCM中,,∴△ABM≌△DCM(SAS).(2)解:四边形MENF是菱形.证明如下:∵E,F,N分别是BM,CM,CB的中点,∴NE∥MF,NE=MF.∴四边形MENF是平行四边形.由(1),得BM=CM,∴ME=MF.∴四边形MENF是菱形.(3)解:当AD:AB=2:1时,四边形MENF是正方形.理由:∵M为AD中点,∴AD=2AM.∵AD:AB=2:1,∴AM=AB.∵∠A=90,∴∠ABM=∠AMB=45°.同理∠DMC=45°,∴∠EMF=180°﹣45°﹣45°=90°.∵四边形MENF是菱形,∴菱形MENF是正方形.故答案为:2:1.【点评】此题主要考查了矩形的性质,以及菱形的判定和正方形的判定,关键是掌握菱形和正方形的判定方法.。
2016年初二数学下学期期中试题及答案(共7套)

2016年初二数学下学期期中试题及答案(共
7套)
初一数学下学期期中试卷及答案
※初二数学期中考试模拟试卷
※初二数学期中测试试卷
※初二数学期中考试复习题(鲁教版)
※初二数学期中备考模拟试题
※初二年级数学期中考试模拟试题
※初二数学下册期中模拟试题
※初二年级数学下册期中复习试题
反复的做题及练习不仅仅是为了让大家熟知题型,更是为了让大家了解自己知识的缺漏,从而找到正确的复习方向,初一数学下学期期中试卷及答案希望大家能用到实处,想要了解更多试题可点击八年级数学期中试卷获悉,预祝大家在期末考中都能取得理想的成绩。
***友情链接***
八年级期中复习为大家提供了初二年级所有的复习计划及复习重点,大家可参照这些复习计划进行合理的复习
规划~。
2016学年第二学期八年级期中数学试卷.doc

2016学年第二学期八年级期中数学试卷 姓名:一、选择题:(本题有10小题,每题3分,共30分) 1.下列运算正确的是( )A.2(3=- B.3= C.2(3= D3=-2.=,则( )A .3m ≥B .5m ≤C .35m ≤≤D .m 为一切实数 3.一元二次方程(2)2x x x -=-的根是( )A .1-B .0C .1和2D .1-和2 4.数据4、2、6的中位数和方差分别是( )A .2和83B .4和4C .4和83D .4和435.下列图形中,既是轴对称图形又是中心对称图形的有( )A .1个B .2个C .3个D .4个 6.当0x ≤时,化简1x - )A .12x -B .21x -C .1-D .1 7.已知关于x 的方程221(3)04x m x m --+=有两个不相等的实数根,m 的最大整数值为( )A .2B .1-C .0D .18.某同学参加了5科考试,平均成绩是68分,他想在下一科考试后使6科考试的平均成绩为70分,那么他第6科考试要得的分数应为( )A .72分B .74分C .78分D .80分 9.如图,在ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,若AE=4,AF=6,ABCD 的周长为40,则ABCD 的面积为( ) A .48 B .24 C .36 D .4010.有下列三个命题:①五边形的内角中至少有两个钝角;②十二边形共有54条对角线;③平行四边形的对角线互相平分;④6422+-x x 的值随x 的变化而变化,因此这个代数式没有最小值.其中正确命题的个数是( )A .1B .2C . 3D .4二、填空题:(本题有10小题,每题3分,共30分) 11=第9题图12.若一个多边形内角和等于1260°,则该多边形边数是13.一件商品原价100元,经过两次连续降价,现价81元,则平均每次降价的百分率是 14.设231022014m m m m +-=-+=,则15.一元二次方程2(1)210k x x ---=有两个实数根,则实数k 的取值范围是 16.某学习小组5位同学参加初中毕业生实验操作考试(满分20分)的平均成绩是16分,其中三位男生的方差为6(分2),两位女生的成绩分别为17分和15分。
2016—2017年八年级下册 数学期中试卷及答案解析

2016—2017年八年级第二学期数学期中试卷班别________姓名________分数_________一.选择题(每题3分,共30分)1.若式子在实数范围内有意义,则a的取值范围是()A.a>3 B.a≥3 C.a<3 D.a≤32.下列属于最简二次根式的是()A.B.C.D.3.下列计算正确的是()A.=2 B.3+=3C.+=D.+=34.如图所示,在Rt△ABC中,AB=8,AC=6,∠CAB=90°,AD⊥BC,那么AD的长为()A.1 B.2 C.3 D.4.85.下列语句正确的是()A.对角线互相垂直的四边形是菱形B.矩形的对角线相等C.有两边及一角对应相等的两个三角形全等D.平行四边形是轴对称图形6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为()A.cm B.4 cmC.cm D.3 cm7.如图,在平行四边形ABCD中,对角线AC⊥BD,且AC=8,CB=6,DH⊥AB于H,则AH等于()C.D.A.B.A.4 B.3 C.D.29.如图,在□ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于()A.2 B.3C.4 D.510.如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于()A.18 B.16 C.15 D.14二.填空题(每小题3分,共24分)11.=,(﹣)2=,=12.已知a=﹣,b=+,求a2+b2的值为.13.如图1 ,P(3,4)是直角坐标系中一点,则P到原点的距离是.图1 图2 图314.如图2,在□ABCD中,对角线AC与BD相交于点O,请添加一个条件,使□ABCD成为菱形(写出符合题意的一个条件即可)15.如图3,△ABC中,AC=15,AB=13,BC=14,则BC边上的高AD=.16.已知,在菱形ABCD中,AC=8,BD=6,则菱形的周长是.17.一个菱形的周长为52cm,一条对角线长为10cm,则其面积为cm2.18.如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=.三.解答题(共44分)19.化简与计算:(每小题5分,共10分)(1)2﹣6+3(2)×+3×220.(8分)如图,在△ABC中,∠ACB=90°,CD⊥AB于D(1)若AB=5cm,BC=3cm,求CD的长;(2)若BD=2,AD=4,求CD的长.21.(8分)如图,四边形ABCD是平行四边形,点E在BC上,点F在AD上,BE=DF,求证:AE=CF.22.(8分)如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC 是矩形.23.(10分)如图,□ABCD中,AC与BD相交于点O,∠ABD=2∠DBC,AE⊥BD于点E.(1)若∠ADB=25°,求∠BAE的度数;(2)求证:AB=2OE.2016—2017年八年级下册数学期中试卷参考答案与试题解析一.选择题(共10小题)1.(2017•无锡一模)若式子在实数范围内有意义,则a的取值范围是()A.a>3 B.a≥3 C.a<3 D.a≤3【分析】根据被开方数大于等于0列式计算即可得解.【解答】解:由题意得,a﹣3≥0,解得a≥3.故选B.【点评】本题考查的知识点为:二次根式的被开方数是非负数.2.(2016秋•新华区期末)下列属于最简二次根式的是()A.B. C. D.【分析】检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.【解答】解:A、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故A正确;B、被开方数含能开得尽方的因数或因式,故B错误;C、被开方数含能开得尽方的因数或因式,故C错误;D、被开方数含分母,故D错误;故选:A.【点评】本题考查最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式3.(2017•平顶山一模)下列计算正确的是()A.=2 B.3+=3C.+=D.+=3【分析】根据二次根式的加减法进行计算即可.【解答】解:A、=2,故A错误;B、3+不能合并,故B错误;C、+不能合并,故C错误;D、+=3+,故D正确,【点评】本题考查了二次根式的加减,掌握二次根式加减法的法则是解题的关键.4.(2017春•孝南区校级月考)如图所示,在Rt△ABC中,AB=8,AC=6,∠CAB=90°,AD⊥BC,那么AD的长为()A.1 B.2 C.3 D.4.8=AC•AB=BC•AD,【分析】先根据AB=8,AC=6,∠CAB=90°,利用勾股定理可求BC,再根据S△ABC可求AD.【解答】解:如右图所示,在Rt△ABC中,AB=8,AC=6,∠CAB=90°,∴BC===10,又∵S=AC•AB=BC•AD,△ABC∴6×8=10AD,∴AD=4.8.故选D.【点评】本题考查了勾股定理.注意直角三角形面积的两种求法,等于两直角边乘积的一半,也等于斜边乘以斜边上高的积的一半.5.(2017•启东市一模)下列语句正确的是()【分析】由菱形的判定、矩形的性质、全等三角形的判定、平行四边形的性质分别进行判断,即可得出结论.【解答】解:A、对角线互相垂直的四边形是菱形,不正确;B、矩形的对角线相等,正确;C、有两边及一角对应相等的两个三角形全等,不正确;D、平行四边形是轴对称图形,不正确;故选:B.【点评】本题考查了菱形的判定、矩形的性质、全等三角形的判定、平行四边形的性质;熟练掌握有关判定定理和性质定理是解决问题的关键.6.(2017春•武昌区校级月考)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为()【分析】先求出S A、S B、S C的值,再根据勾股定理的几何意义求出D的面积,从而求出正方形D 的边长.【解答】解:∵S A=6×6=36cm2,S B=5×5=25cm2,S C=5×5=25cm2,又∵S A+S B+S C+S D=10×10,∴36+25+25+S D=100,∴S D=14,∴正方形D的边长为cm.故选:A.【点评】本题考查了勾股定理,熟悉勾股定理的几何意义是解题的关键.7.(2017•东光县一模)如图,在平行四边形ABCD中,对角线AC⊥BD,且AC=8,CB=6,DH⊥AB 于H,则AH等于()A.B.C.D.【分析】先祝你四边形ABCD是菱形,根据菱形的面积等于对角线积的一半,可求得菱形的面积,又由菱形的对角线互相平分且垂直,可根据勾股定理得AB的长,根据菱形的面积的求解方法:底乘以高或对角线积的一半,即可得菱形的高.【解答】解:∵平行四边形ABCD中,对角线AC⊥BD,∴四边形ABCD是菱形,∴AC⊥BD,OA=OC=AC=4,OB=OD=3,∴AB=5cm,=AC•BD=AB•DH,∴S菱形ABCD∴DH==,故选A.【点评】此题考查了平行四边形的性质、菱形的判定与性质:菱形的对角线互相平分且垂直;菱形的面积的求解方法:底乘以高或对角线积的一半.8.(2017•新野县一模)如图,在平行四边形ABCD中,AD=7,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为()A.4 B.3 C.D.2【分析】利用平行四边形的性质以及角平分线的性质得出∠DEC=∠DCE,进而得出DE=DC=AB求出即可.【解答】解:∵在▱ABCD中,CE平分∠BCD交AD于点E,∴∠DEC=∠ECB,∠DCE=∠BCE,AB=DC,∴∠DEC=∠DCE,∴DE=DC=AB,∵AD=7,AE=4,∴DE=DC=AB=3.故选:B.【点评】此题主要考查了平行四边形的性质以及角平分线的性质,得出DE=DC=AB是解题关键.9.(2017•黔东南州模拟)如图,在▱ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于()A.2 B.3 C.4 D.5【分析】由四边形ABCD是平行四边形,根据平行四边形的对边相等,可得BC=AD=8,又由点E、F分别是BD、CD的中点,利用三角形中位线的性质,即可求得答案.【解答】解:∵四边形ABCD是平行四边形,∴BC=AD=8,∵点E、F分别是BD、CD的中点,∴EF=BC=×8=4.故选C.【点评】此题考查了平行四边形的性质与三角形中位线的性质.此题比较简单,注意掌握数形结合思想的应用.10.(2016•五指山校级模拟)如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于()A.18 B.16 C.15 D.14【分析】根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOD中,根据勾股定理可以求得AB的长,进而△ABD的周长.【解答】解:菱形对角线互相垂直平分,∴BO=OD=3,AO=OC=4,∴AB=5,∴△ABD的周长等于5+5+6=16,故选B.【点评】本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.二.填空题(共8小题)11.(2017秋•海宁市校级月考)=2,(﹣)2=3,=4.【分析】根据二次根式的乘除法法则和二次根式的性质计算即可.【解答】解:==2,(﹣)2=3,=4,故答案为:2;3;4.【点评】本题考查的是二次根式的乘除法,掌握二次根式的乘除法法则是解题的关键.12.(2017春•上虞区校级月考)已知a=﹣,b=+,求a2+b2的值为10.【分析】把已知条件代入求值.【解答】解:原式=(﹣)2+(+)2=5﹣2+5+2=10.故本题答案为:10.【点评】此题直接代入即可,也可先求出a+b、ab的值,原式=(a+b)2﹣2ab,再整体代入.13.(2017春•上虞区校级月考)如图P(3,4)是直角坐标系中一点,则P到原点的距离是5.【分析】根据两点间的距离公式便可解答.【解答】解:∵P点坐标为(3,4),∴OP==5.【点评】本题考查的是点在平面直角坐标系中坐标的几何意义及两点间的距离公式.14.(2016春•潮南区期末)如图,在▱ABCD中,对角线AC与BD相交于点O,请添加一个条件AB=AD,使▱ABCD成为菱形(写出符合题意的一个条件即可)【分析】根据邻边相等的平行四边形是菱形可得添加条件AB=AD.【解答】解:添加AB=AD,∵四边形ABCD是平行四边形,AB=AD,∴▱ABCD成为菱形.故答案为:AB=AD.【点评】此题主要考查了菱形的判定,关键是掌握一组邻边相等的平行四边形是菱形.15.(2017春•启东市校级月考)△ABC中,AC=15,AB=13,BC=14,则BC边上的高AD=12.【分析】AD为高,那么题中有两个直角三角形.AD在这两个直角三角形中,设BD为未知数,可利用勾股定理都表示出AD长.求得BD长,再根据勾股定理求得AD长.【解答】解:设BD=x,则CD=14﹣x,在Rt△ABD中,AD2+x2=132,在Rt△ADC中,AD2=152﹣(14﹣x)2,则有132﹣x2=152﹣(14﹣x)2,132﹣x2=152﹣196+28x﹣x2,解得x=5,在Rt△ABD中,AD==12.故答案为:12.【点评】本题考查了勾股定理,解决本题的关键在于利用两个直角三角形的公共边找到突破点.主要利用了勾股定理进行解答.16.(2017•大连模拟)已知,在菱形ABCD中,AC=8,BD=6,则菱形的周长是20.【分析】根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOB中根据勾股定理,可以求得AB的长,即可得出菱形ABCD的周长.【解答】解:如图所示,∵在菱形ABCD中,AC=8,BD=6,∴∠AOB=90°,AO=4,BO=3,∴Rt△AOB中,AB=5,∴菱形ABCD的周长=5×4=20.故答案为:20.【点评】本题考查了菱形各边长相等的性质,以及勾股定理在直角三角形中的运用,根据勾股定理计算出菱形的边长是解题的关键.17.(2017•长春一模)一个菱形的周长为52cm,一条对角线长为10cm,则其面积为120cm2.【分析】先由菱形ABCD的周长求出边长,再根据菱形的性质求出OA,然后由勾股定理求出OB,即可得出BD,再根据菱形的面积等于对角线乘积的一半计算即可.【解答】解:如图所示:∵四边形ABCD是菱形,∴AB=BC=CD=DA,AC⊥BD,OA=AC=5,OB=BD,∵菱形ABCD的周长为52cm,∴AB=13cm,在Rt△AOB中,根据勾股定理得:OB===12cm,∴BD=2OB=24cm,∴菱形ABCD的面积=×10×24=120cm2,故答案为120.【点评】本题考查了菱形的性质以及勾股定理的运用;熟练掌握菱形的性质和运用勾股定理计算是解决问题的关键.18.(2016•盐城)如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF=.【分析】延长CD,过点F作FM⊥CD于点M,连接GB、BD,作FH⊥AE交于点H,由菱形的性质和已知条件得出∠MFD=30°,设MD=x,则DF=2x,FM=x,得出MG=x+1,由勾股定理得出(x+1)2+(x)2=(2﹣2x)2,解方程得出DF=0.6,AF=1.4,求出AH=AF=0.7,FH=,证明△DCB是等边三角形,得出BG⊥CD,由勾股定理求出BG=,设BE=y,则GE=2﹣y,由勾股定理得出()2+y2=(2﹣y)2,解方程求出y=0.25,得出AE、EH,再由勾股定理求出EF即可.【解答】解:延长CD,过点F作FM⊥CD于点M,连接GB、BD,作FH⊥AE交于点H,如图所示:∵∠A=60°,四边形ABCD是菱形,∴∠MDF=60°,∴∠MFD=30°,设MD=x,则DF=2x,FM=x,∵DG=1,∴MG=x+1,∴(x+1)2+(x)2=(2﹣2x)2,解得:x=0.3,∴DF=0.6,AF=1.4,∴AH=AF=0.7,FH=AF•sin∠A=1.4×=,∵CD=BC,∠C=60°,∴△DCB是等边三角形,∵G是CD的中点,∴BG⊥CD,∵BC=2,GC=1,∴BG=,设BE=y,则GE=2﹣y,∴()2+y2=(2﹣y)2,解得:y=0.25,∴AE=1.75,∴EH=AE﹣AH=1.75﹣0.7=1.05,∴EF===.故答案为:.【点评】本题考查了菱形的性质、翻折变换的性质、勾股定理、等边三角形的判定与性质等知识;本题综合性强,难度较大,运用勾股定理得出方程是解决问题的关键.三.解答题(共5小题)19.(2017春•黄陂区月考)计算:(1)×+3×2(2)2﹣6+3.【分析】(1)二次根式乘法法则即可化简求值(2)将各二次根式化为最简二次根式,然后合并同类二次根式.【解答】解:(1)原式=7+30=37(2)原式=4﹣2+12=14【点评】本题考查二次根式的运算法则,解题的关键是熟练运用二次根式的运算法则,本题属于基础题型.20.(2017春•武昌区校级月考)如图,在△ABC中,∠ACB=90°,CD⊥AB于D(1)若AB=5cm,BC=3cm,求CD的长;(2)若BD=2,AD=4,求CD的长.【分析】(1)首先根据勾股定理求得直角三角形的另一直角边,再根据直角三角形的面积公式求得斜边上的高CD;(2)利用等角的余角相等得到∠B=∠ACD,则利用有两组角对应相等的两三角形相似可判断△ADC ∽△CDB;利用相似比得到=,然后利用比例性质求CD.【解答】解:(1)在直角三角形ABC中,AC===4(cm),根据直角三角形的面积公式,得CD===(cm)故CD的长为cm;(2)∵CD⊥AB于D,∴∠CDA=∠CDB=90°,∴∠BCD+∠B=90°∵∠ACB=90°,即∠BCD+∠ACD=90°,∴∠B=∠ACD,∴△ADC∽△CDB,∴=,即=,∴CD=2.【点评】本题考查了勾股定理,相似三角形的判定与性质,要熟练运用勾股定理以及直角三角形的面积公式,直角三角形斜边上的高等于两条直角边的乘积除以斜边.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用;再运用相似三角形的性质时主要利用相似比进行几何计算.21.(2017•邵阳县一模)如图,四边形ABCD是平行四边形,点E在BC上,点F在AD上,BE=DF,求证:AE=CF.【分析】根据平行四边形性质得出AD∥BC,且AD=BC,推出AF∥EC,AF=EC,根据平行四边形的判定推出四边形AECF是平行四边形,即可得出结论.【解答】证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形,∴AE=CF.【点评】本题考查了平行四边形的性质和判定的应用,注意:平行四边形的对边平行且相等,有一组对边平行且相等的四边形是平行四边形.22.(2016春•历下区期末)如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.【分析】根据平行四边形的判定推出四边形OBEC是平行四边形,根据菱形性质求出∠AOB=90°,根据矩形的判定推出即可.【解答】证明:∵BE∥AC,CE∥DB,∴四边形OBEC是平行四边形,又∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOB=90°,∴平行四边形OBEC是矩形.【点评】本题考查了菱形性质,平行四边形的判定,矩形的判定的应用,主要考查学生的推理能力.23.(2013•沙坪坝区模拟)如图,▱ABCD中,AC与BD相交于点O,∠ABD=2∠DBC,AE⊥BD于点E.(1)若∠ADB=25°,求∠BAE的度数;(2)求证:AB=2OE.【分析】(1)根据平行四边形的对边平行可得AD∥BC,再根据两直线平行,内错角相等可得∠DBC=∠ADB,然后求出∠ABD,再根据直角三角形两锐角互余列式计算即可求出∠BAE;(2)取AB的中点F,连接EF、OF,根据直角三角形斜边上的中线等于斜边的一半可得EF=BF=AB,根据等边对等角可得∠ABD=∠BEF,根据三角形的中位线平行于第三边并且等于第三边的一半可得OF∥BC,根据两直线平行,内错角相等可得∠DBC=∠EOF,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠EFO=∠EOF,再根据等角对等边可得EF=OE,从而得证.【解答】(1)解:在▱ABCD中,AD∥BC,∴∠DBC=∠ADB,∵∠ABD=2∠DBC,∠ADB=25°,∴∠ABD=2×25°=50°,∵AE⊥BD,∴∠BAE=90°﹣∠ABD=90°﹣50°=40°;(2)证明:如图,取AB的中点F,连接EF、OF,∵AE⊥BD,∴EF=BF=AB,∴∠ABD=∠BEF,∵AO=CO,∴OF是△ABC的中位线,∴OF∥BC,∴∠DBC=∠EOF,根据三角形的外角性质,∠BEF=∠EFO+∠EOF,又∵∠ABD=2∠DBC,∴∠EFO=∠EOF,∴EF=OE,∴OE=AB,∴AB=2OE.【点评】本题考查了平行四边形的对边平行,对角线互相平分的性质,直角三角形斜边上的中线等于斜边的一半,三角形的中位线平行于第三边并且等于第三边的一半,三角形的一个外角等于与它不相邻的两个内角的和的性质,作辅助线是解题的关键.。
2015—2016学年度第二学期八年级数学期中考试试题

2015-2016学年度第二学期八年级期中考试数 学 试 题(分值:120分 考试时间:120分钟)一、选择题(每小题3分,共36分),,A .6B .C .9D .4. □ABCD 中,∠A:∠B =1:2,则∠C 的度数为( ).A .30°B .45°C .60°D .120°5. 下列说法中正确的是( )A .两条对角线相等的四边形是矩形B .两条对角线互相垂直的四边形是菱形C .两条对角线互相垂直且相等的四边形是正方形D .两条对角线互相平分的四边形是平行四边形6 如图,菱形ABCD 中,E 、F 分别是AB 、AC 的中点,若EF =3,则菱形ABCD 的周长是( ) A .12 B .16 C .20 D .247、 如图,正方形ABCD 中,以对角线AC 为一边作 菱形AEFC ,则∠FAB 等于( ) A .22.5° B .45° C .30° D .135°8、 如图,在□ABCD 中,已知AD =5cm ,AB =3cm ,AE 平分∠BAD 交BC 边于点E ,则EC 等于A.1cmB.2cmC.3cmD.4cm7题 8题 9题9、如图,在矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,点D 落在点D’处,则重叠部分△AFC 的面积为( ).A .6B .8C .10D .12 10 能判定四边形ABCD 为平行四边形的条件是( )A 、AB ∥CD ,AD=BC; B 、∠A=∠B ,∠C=∠D;C 、AB ∥CD ,∠C=∠A; D 、AB=AD ,CB=CD6题A B C D F D’11 等腰三角形的一腰长为13,底边长为10,则它的面积为( )A.65B.60C.120D.13012.先化简再求值:当a=9时,求221a a a +-+的值,甲乙两人的解答如下:甲的解答为:原式1)1()1(2=-+=-+=a a a a ;乙的解答为:原式1712)1()1(2=-=-+=-+=a a a a a .在两人的解法中( )A .甲正确B .乙正确C .都不正确D .无法确定。
合肥市第五十中学2015-2016学年度八年级第二学期期中检测数学试卷

八年级数学试卷 第 1 页 共 4 页学校 班级 姓名 考号密封 线 内 不 得 答 题合肥市第五十中学2015-2016学年度八年级第二学期期中检测数 学 试 卷题 号 一 二 三 总 分 得 分得分 评卷人 一、选择题(本大题共10小题,每小题3分,共计30分.请将你认为正确的答案的代号填入下面的答题框中)1.下列二次根式中属于最简二次根式的是( )A .44+aB .48C .14D .ba 2.下列方程中属于一元二次方程的是( )A .()1122+=+x xB .3212=+xx C .02=++c bx axD .2322-=+x x x3.满足下列条件的△ABC ,不是直角三角形的是( )A .222b ac -= B .25:24:7::=c b a C .∠A=∠B+∠CD .∠A :∠B :∠C=5:12:134.用配方法解关于x 的方程0322=--x x ,配方后可得( )A .()412=-xB .()412=+x C .()1612=-x D .()1612=+x5.若01442=-+++x y y ,则()2016y x +等于( ) A .-1B .1C .2016D .-20166.如图,△ABC 的顶点A 、B 、C 在边长为1的正方形网格的格点上,BD 是△ABC 的AC 边上的高,则BD 的长为( )A .532 B .543 C .554 D .5537.若方程x 2-6x+7-m=0没有实数根,则m 的最大整数解是( )A .-1B .-2C .-3D .0题号 1 2 3 4 5 6 7 8 9 10 答案第6题图八年级数学试卷 第 2 页 共 4 页第14题图8.关于x 的方程()()002≠=++m k h m k h x m 均为常数,、、的解是2,321=-=x x .则方程0)3-(2=++k h x m 的解是( )A .1,621-=-=x xB .5,021==x xC .5,321=-=x xD .2,621=-=x x9.在坐标平面内有一点)3,2(-A ,O 为原点,在x 轴上找一点B ,使以O ,A ,B 为顶点的三角形为等腰三角形,则满足要求的B 点有几个( )A .1个B .2个C .3个D .4个10.图①所示的正方体木块棱长为6cm ,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A 爬行到顶点B 的最短距离为 cm .( )A .626+B .36C .6323+D .18得分 评卷人 二、填空题(本大题共5小题,每小题3分,共计15分)11.计算:=⨯-928 .12.如果一元二次方程043)222=-++-m x x m (有一个根为0,则m= . 13.对于任何实数,我们规定符号dc ba 的意义是bc ad d cb a -=,例如22345)2(5342-=⨯-⨯-=-,若当0442=+-x x 时,则32121--+x x xx = .14.如图,已知:AM ⊥MN ,BN ⊥MN ,垂足分别为M ,N ,点C 是MN 上使AC+BC 的值最小的点.若AM=3,BN=5,MN=15,则AC+BC= .15.已知两个关于x 的一元二次方程M :02=++c bx ax ,N :20cx bx a ++=,其中c a ≠,以下列四个结论中,正确的是 .①如果方程M 有两个不相等的实数根,那么方程N 也有两个不相等的实数根; ②如果方程M 有两根符号相同,那么方程N 的两根符号也相同; ③如果方程M 和方程N 有一个相同的根,那么这个根必是1x =;第10题图八年级数学试卷 第 3 页 共 4 页④如果5是方程M 的一个根,那么51是方程N 的一个根. 得分 评卷人 三、(本大题共7小题,共计55分)16.(6分)计算:()36123320160--+-17.(6分)解方程:04)2(3)2(2=----x x18.(8分)观察下列等式,探究其中的规律: ①2112111=-+,②121214131=-+,③301316151=-+, ④561418171=-+,…… (1)按以上规律写出第⑧个等式: (2)猜想并写出第n 个等式: (3)请证明猜想的正确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
乐红中学2016年八年级下数学期中学业水平考试
数学试卷
(全卷共三个大题,23个小题,共8页;满分120分,考试时间120分钟)
姓名:.得分.
一、单项选择题(本题满分32分,每小题4分)
1.的算术平方根是()
A.4 B.±4 C.2 D.±2
2.菱形具有而矩形不具有的性质是()
A.对角线互相平分B.四条边都相等
C.对角相等D.邻角互补
3.三角形的三边长分别为6,8,10,它的面积为()
A.30 B.40 C.24 D.48
4.若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是(
A.平行四边形B.矩形C.菱形D.正方形
5.若二次根式有意义,则x的取值范围是()
A.B.C.D.
6.下面条件中,能判定四边形是平行四边形的条件是()
A.一组对角相等B.对角线互相平分
C.一组对边相等D.对角线互相垂直
7.下列根式中属最简二次根式的()
A.B.C.D.
8.适合下列条件的△ABC中,直角三角形的个数为()
①a=,b=,c=②a=b,∠A=45°;③∠A=32°,∠B=58°;④a=7,b=24,c=25 ⑤a=2,b=2,c=4
A.2个B.3个C.4个D.5个
二、填空题(本题满分18分,每小题3分)
9.计算:+=.
10.平行四边形ABCD中,∠A=50°,AB=30cm,则∠B=,DC=
11.若,则ab=.
12.已知平行四边形ABCD的对角线AC,BD相交于点O,AB=5,AO=4,BO=3,则此四边形的周长是.
13.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,求该河流的宽度为m.
14.点E是正方形ABCD的边BC延长线上的一点,且CE=AC,若AE交CD于点F,则∠AFC= _______°
三、解答题(本题共9小题,满分70分)
15.(6分)计算:
16.(6分)已知:如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:DE=BF.
17.(6分)如图,有一只小鸟从小树顶飞到大树顶上,请问它飞行的最短路程是多少米(先画出示意图,然后再求解).
18.(7分)如图,在△ABC中,AD是∠BAC的平分线,DE∥AC交AB于E,DF∥AB 交AC于F,求证:四边形AEDF是菱形.
19.(6分)如图,某小同学在M 处用高1米(DM =1米)的测角仪测得旗杆AB 的顶端B 的仰角为30°,再向旗杆方向前进10米到F 处,又测得旗杆顶端B 的仰角为60°,请求出旗杆AB 的高度(结果保留根号).
20.(8分)如图,已知平行四边形ABCD ,DE 是ADC ∠的角平分线,交BC 于点E . (1)求证:CD CE =;(2)若BE CE =,80B ∠=︒,求DAE ∠的度数.
E
D C
B
A
21.(9分)问题背景:在△ABC中,AB、BC、AC 三边的长分别为、、,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你用上述方法计算△ABC的面积;
(2)画△DEF,DE、EF、DF三边的长分别为、、;
①判断三角形的形状,说明理由;
②求这个三角形的面积.
22.(10分)阅读材料:黑白双雄,纵横江湖;双剑合璧,天下无敌.这是武侠小说中常见的描述,其意是指两人合在一起,取长补短,威力无比.在二次根式中也有这种相辅相成的式
子,如:,的积不含根号,我们就说这两个式子互为
有理化因式,其中一个是另一个的有理化因式.于是二次根式可以这样解:
像这样通过分子、分母同乘一个式子把分母的根号化去或把根号中的分母化去,叫做分母有理化.类似地我们也可以将某个二次根式进行分子有理化(请同学们类比分母有理化的方法学习,留点悬念).
解决问题:
(1)的有理化因式是;
(2)计算;
(3)试比较的大小.
23.(12分)正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P 作PF⊥CD于点F。
如图1,当点P与点O重合时,显然有DF=CF.
⑴如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E。
①求证:DF =EF ;
②写出线段PC 、PA 、CE 之间的一个等量关系,并证明你的结论;
⑵若点P 在线段OC 上(不与点O 、C 重合),PE ⊥PB 且PE 交直线CD 于点E 。
请完成图3并判断⑴中的结论①、②是否分别成立?若不成立,写出相应的结论(所写结论均不必证明)
图1
图2
图3。
