勾股定理题型分类练习
勾股定理的几种类型归类练习

勾股定理的几种类型归类练习一.选择题(共23小题)1.如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,已知CE=3,CD=4,则AD长为()A.7B.8C.4D.42.如图,在△ABC中,∠C=90°,AD是△ABC的角平分线,若CD=3,则点D到AB 边的距离为()A.1B.C.2D.33.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=9,AB=15,则CE的长为()A.4B.C.D.54.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将△ACD沿直线AD 折叠,使点C落在斜边AB上的点E处,则CD的长为()cm.A.B.C.3D.5.如图,在矩形ABCD中,AB=10,BC=6.点E是边BC上一点,沿AE翻折△ABE,点B恰好落在CD边上点F处,则CE的长是()A.B.C.D.36.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为()A.3B.4C.5D.67.如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=5厘米,EF=12厘米,则边HF的长是()A.12厘米B.13厘米C.14厘米D.15厘米8.如图所示,把矩形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若∠FPH的度数恰好为90°,PF=4,PH=3,则矩形ABCD的边BC的长为()A.10B.11C.12D.159.把一张矩形纸片ABCD按如图所示的方式进行折叠,使点B恰好与点D重合,折痕为EF,其中AB=3,BC=3.则△DEF的面积是()A.6B.6C.3D.410.如图,将边长为8cm正方形纸片ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则线段CN的长是()A.6cm B.5cm C.4cm D.3cm11.如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=4cm,BC=8cm,则△BEF的面积为()A.12cm2B.10cm2C.8.6cm2D.8cm212.如图,将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若AB=6,则BC 的长为()A.2B.2C.4D.213.如图,将边长为8cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是()A.3cm B.4cm C.5cm D.6cm14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,小正方形的面积为5,则大正方形的面积为()A.12B.13C.14D.1515.我国是最早了解勾股定理的国家之一,根据《周髀算经》的记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”.三国时代的蒋铭祖对《蒋铭祖算经》勾股定理作出了详细注释,并给出了另外一种证明.下面四幅图中,不能证明勾股定理的是()A.B.C.D.16.如图,正方形内的数字代表所在正方形的面积,则A所在的正方形的面积为()A.B.28C.128D.10017.如图,图中所有的三角形都是直角三角形,所有的四边形都是正方形,其中A,B,C,D四个小正方形的面积之和等于12,则最大的正方形的边长为()A.2B.C.3D.418.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=6,BC=4,将四个直角三角形中边长为4的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是()A.56B.24C.64D.3219.如图,阴影部分是两个正方形,图中还有一个直角三角形和一个空白的正方形,阴影部分的面积为25cm2,直角三角形①中较长的直角边长12cm,则直角三角形①的面积是()A.16cm2B.25cm2C.30cm2D.169cm220.如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=5,BE=12,则EF的长是()A.7B.8C.7D.721.如图,一根大树被台风刮断,若树离地面3米处折断,树顶端落在离树底部4米处,则树折断之前有()A.5米B.7米C.8米D.10米22.如图,一棵大树在离地面9米高的B处断裂,树顶A落在离树底BC的12米处,则大树断裂之前的高度为()A.9米B.15米C.21米D.24米23.一旗杆在其的B处折断,量得AC=5米,则旗杆原来的高度为()A.米B.2米C.10米D.米二.填空题(共22小题)24.△ABC中,AB=AC=5,BC=8,BD为AC边的高线,则BD的长为.25.如图,在△ABC中,∠C=90°,DE⊥AB于D,交AC于点E,若BC=BD,AC=6cm,BC=8cm,AB=10cm,则△ADE的周长是.26.如图所示,在△ABC中,∠C=90°,DE⊥AB于点D,交AC于点E.若BC=BD,AC=4cm,BC=3cm,AB=5cm,则△ADE的周长是.27.如图,在△ABC中,∠ACB=90°,AC=9,BC=12,点D在边AB上,AD=AC,AE ⊥CD,垂足为F,与BC交于点E,则BE的长是.28.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为20cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为25cm,则该圆柱底面周长为.29.如图,在矩形ABCD中,点M为矩形AD的中点,连接CM,沿着CM折叠,点D的对应点D',N为BC上一点,且BN<CN,沿MN折叠,恰好AM与D'M重合,此时点A 的对应点为点D',若AB=6,BN=3.5,则A′到CM的距离为.30.如图,在矩形ABCD中,AB=6,BC=18,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为.31.如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C恰好落在AB边上的F处,则CE的长为.32.如图,在△ABC中,∠C=90°,AB的垂直平分线交AB、AC于点D、E,若AC=8,BD=5,则CE的长度是.33.如图所示,矩形纸片ABCD中,AB=4cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则AF的长为.34.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形EFGH拼成的大正方形ABCD.若AE=5,AB=13,则中间小正方形EFGH的面积是.35.将四个全等的直角三角形分别拼成正方形(如图1,2),边长分别为6和2.若以一个直角三角形的两条直角边为边向外作正方形(如图3),其面积分别为S1,S2.则S1﹣S2=.36.如图,在△ABC中,∠C=90°,AC=5,BC=12.以AB为一边在△ABC的同侧作正方形ABDE,则图中阴影部分的面积为.37.用三张正方形纸片,按如图所示的方式构成图案,已知围成阴影部分的三角形是直角三角形,S1=9,S3=25,则正方形S2的面积为.38.图1是一个勾股定理演示教具的正面示意图,当它倒过来时,大正方形中的全部墨水恰能注满两个小正方形.王老师有一个内长为11寸,内宽为9寸的木质盒子(如图2).现要自制一个这样的教具(由三个正方形和一个直角三角形组成),使得教具恰好摆入这个盒子中,以便保护和携带(如图3所示,A,B,C,D,E五点均紧贴盒子边缘,教具的厚度等于木盒的内高).此时盒子的空间利用率为.39.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E 的边长为7cm,则图中五个正方形A、B、C、D、E的面积和为cm2.40.如图,一旗杆离地面6m处折断,旗杆顶部落在离旗杆底部8m处,旗杆折断之前的高度是m.41.我国古代的数学名著《九章算术》中有这样一个题目“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?”译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵索沿地面退行,在离木柱根部8尺处时,绳索用尽,问绳索AC的长为尺.42.如图所示,一棵大树折断后倒在地上,请按图中所标的数据,计算大树没折断前的高度的结果是.43.有一棵9米高的大树,树下有一个1米高的小孩,如果大树在距地面4米处折断(未完全折断),则小孩至少离开大树米之外才是安全的.44.《九章算术》中有一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高一丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,则折断处离地面的高度为尺.45.如图,一棵大树在一次强台风中于离地面3m处折断倒下,树干顶部在根部4米处,这棵大树在折断前的高度为m.三.解答题(共13小题)46.如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以1cm/s的速度运动,设运动时间为t(s).(1)当△ABP为直角三角时,求t的值;(2)当△ABP为等腰三角形时,求t的值.47.如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=12,BD=5.(1)求证:△BDC是直角三角形;(2)求AC的长.48.如图,在△ABC中,AB=AC,AD⊥BC于点D,点E在AC边上,且∠CBE=45°,BE分别交AC,AD于点E、F.(1)如图1,若AB=13,BC=10,求AF的长;(2)如图2,若AF=BC,求证:BF2+EF2=AE2.49.如图,在△ABC中,AB=AC=13,F是BC中点,AF=12,D是AB中点,DE⊥AC 于点E.(1)求BF的长;(2)直接写出DE的长.50.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使点C落在斜边AB上的点E处,试求CD的长.51.如图,在三角形纸片ABC中,AB=15cm,AC=9cm,BC=12cm,现将边AC沿过点A 的直线折叠,使它落在AB边上.若折痕交BC于点D,点C落在点E处,你能求出BD 的长吗?请写出求解过程.52.如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.53.如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A出发沿AB方向以1cm/s的速度向终点B运动,点Q从点B出发沿BC方向以6cm/s的速度向终点C 运动,P,Q两点同时出发,设点P的运动时间为t秒.(1)求BC的长;(2)当t=2时,求P,Q两点之间的距离;(3)当AP=CQ时,求t的值?54.如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.(1)求BF与FC的长.(2)求EC的长.55.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是:大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式c2=,化简便得结论a2+b2=c2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题(1)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.56.如图,一棵竖直生长的竹子高为8米,一阵强风将竹子从C处吹折,竹子的顶端A刚好触地,且与竹子底端的距离AB是4米.求竹子折断处与根部的距离CB.57.《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地四尺,引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有4尺.牵着绳索(绳索头与地面接触)退行,在距木根部8尺处时绳索用尽,问绳索长是多少?根据题意求出绳索长.58.《九章算术》是我国古代最重要的数学著作之一其中记载了这样一个问题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?”译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺.牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽.问绳索长是多少尺?。
勾股定理(知识点+题型分类练习)

ABCabc弦股勾勾股定理(知识点)【知识要点】1. 勾股定理的概念:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方。
常用关系式由三角形面积公式可得:AB·CD=AC·BC2. 勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形,其中c为斜边。
3. 勾股数:①满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25;8,15,17等③用含字母的代数式表示n组勾股数:221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)4.判断直角三角形:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
(3)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
(4)如果三角形的三边长a 、b 、c 满足a 2+b 2=c 2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)用勾股定理逆定理判断三角形是否为直角三角形的一般步骤是: (1)确定最大边(不妨设为c );(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形;若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)5.直角三角形的性质(1)直角三角形的两个锐角互余。
可表示如下:∠C=90°⇒∠A+∠B=90°B(2)在直角三角形中,30°角所对的直角边等于斜边的一半。
勾股定理19个经典题型

勾股定理是数学中的一个重要定理,它指出在任何一个直角三角形中,两条直角边的平方和等于斜边的平方。
这一定理不仅在几何学中有着广泛的应用,而且在物理学、工程学等众多领域都有重要意义。
以下是一些勾股定理的经典题型,这些题型可以帮助学生更好地理解和掌握勾股定理的应用:1. **证明题**:给出一个三角形,证明其中一条边是斜边,另外两边是直角边。
2. **计算题**:给定一个直角三角形的两条直角边的长度,求斜边的长度。
3. **反问题计算题**:给定一个直角三角形的斜边和一条直角边的长度,求另一条直角边的长度。
4. **应用题**:一个房间的长是10米,宽是8米,求房间对角线的长度。
5. **构造题**:用尺子和圆规,仅使用勾股定理,构造一个特定面积的正方形。
6. **比例题**:如果一个直角三角形的两个锐角分别是30度和60度,求三边的长度比。
7. **相似题**:两个直角三角形相似,已知一个三角形的两个直角边分别是3米和4米,求另一个三角形的斜边长度。
8. **代数题**:设直角三角形的两条直角边为a和b,斜边为c根据勾股定理列出方程,并解方程。
9. **逆定理题**:判断一个三角形的三边长是否满足勾股定理的逆定理,即如果三边长满足a²+b²=c²,那么这个三角形是直角三角形。
10. **综合题**:在一个复杂的几何问题中,综合运用勾股定理和其他几何知识解决问题。
11. **平面几何题**:在平面直角坐标系中,给定两点A和B,求线AB的中点到A或B的距离。
12. **空间几何题**:在空间直角坐标系中,给定一个四面体的三个顶点,求第四个顶点的位置。
13. **历史题**:关于勾股定理的历史,提出和证明这一定理的人物是谁?14. **文化题**:在不同的文化中,勾股定理是如何被认知和应用的?15. **实际应用题**:在建筑设计中,如何使用勾股定理来计算结构的稳定性?16. **转换题**:将一个直角三角形的直角边从厘米转换为米。
勾股定理题型(很全面)

典型例题:一、利用勾股定理解决实际问题例题:水中芦苇梯子滑动1、有一个传感器控制的灯,安装在门上方,离地高4.5米的墙上,任何东西只要移至5米以内,灯就自动打开,一个身高1.5米的学生,要走到离门多远的地方灯刚好打开?2、如图,公路MN和公路PQ在P点处交汇,点A处有一所中学,AP=160米,点A 到公路MN 的距离为80米,假使拖拉机行驶时,周围100米以内会受到噪音影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响,请说明理由;如果受到影响,已知拖拉机的速度是18千米/小时,那么学校受到影响的时间为多少?3、如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我反走私A艇发现正东方向有一走私艇C以每小时6.4海里的速度偷偷向我领海开来,便立即通知正在MN在线巡逻的我国反走私艇B密切注意,反走私A艇通知反走私艇B时,A和C两艇的距离是20海里,A、B两艇的距离是12海里,反走私艇B测得距离C是16海里,若走私艇C的速度不变,最早会在什么时间进入我国领海?二、与勾股定理有关的图形问题1.已知△ABC是边长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的斜边长是.2.如图,直线l经过正方形ABCD的顶点B,点A、C到直线l的距离分别是1、2,则正方形的边长是____ _____.3.在直线上依次摆着七个正方形(如图),已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4=______ ___.4.如图,△ABC中,∠C=90°,(1)以直角三角形的三边为边向形外作等边三角形(如图①),探究S1+S2与S3的关系;(2)以直角三角形的三边为斜边向形外作等腰直角三角形(如图②),探究S1+S2与S3的关系;(3)以直角三角形的三边为直径向形外作半圆(如图③),探究S1+S2与S3的关系.图①图②图③5.如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a1,a2,a3,…,an,根据上述规律,则第n个正方形的边长an=___ _____记正方形AB-CD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,……,S n(n为正整数),那么S n=____ ____.6、如图,Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为.ABCDEFG1FE DAB CA B C D EG F F 三、关于翻折问题1、如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠,使AD 落在对角线BD 上,得折痕DG ,若AB = 2,BC = 1,求AG.2、如图,把矩形纸片ABCD 沿对角线AC 折叠,点B 落在点E 处,EC 与AD 相交于点F. (1)求证:△FAC 是等腰三角形;(2)若AB=4,BC=6,求△FAC 的周长和面积.3、如图,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上F 点处,已知cm CE 6=,cm AB 16=,求BF 的长.4、如图,一张矩形纸片ABCD 的长AD=9㎝,宽AB=3㎝。
勾股定理(易错必刷30题6种题型专项训练)(原卷版)

第1章勾股定理(易错必刷30题6种题型专项训练)一.勾股定理(共12小题)1.(2022春•潮安区校级月考)如图,以直角三角形一边向外作正方形,其中两个正方形的面积为100和64,则正方形A的面积为.2.(2021秋•莱西市期中)如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为.3.(2023春•荔城区期末)若一直角三角形两直角边长分别为6和8,则斜边长为.4.(2023春•中宁县期末)如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.(1)求AB的长;(2)求△ABC的面积;(3)求CD的长.5.(2022春•大荔县期末)如图,∠AOB=90°,点C在OA边上,OA=36cm,OB=12cm,点P从点A出发,沿着AO方向匀速运动,点Q同时从点B出发,以相同的速度沿BC方向匀速运动,P、Q两点恰好在C点相遇,求BC的长度?6.(2021•中原区开学)在△ABC中,AB=13cm,AC=20cm,高AD=12cm,则BC的长为cm.7.(2022•鄂尔多斯)如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE =,则AB的长是.8.(2023春•宣城月考)如图,等腰△ABC的底边长为16cm,腰长为10cm,D是BC上一动点,当DA与腰垂直时,则AD=cm.9.(2023春•南宁月考)如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.过点D作DE⊥AP于点E.在点P的运动过程中,当t为时,能使DE=CD?10.(2023春•抚顺月考)如图,在△ABC中,AB=AC,BC=20,D是AB上一点,且CD=16,BD=12.(1)求证:CD⊥AB;(2)求AC的长.11.(2022秋•秦淮区期末)如图,在△ABC中,∠BAC=90°,AD平分∠BAC,AB=4,AC=3,则BD的长是.12.(2022秋•平湖市期末)已知直角三角形的一直角边长为17,另两边的长为自然数,则满足条件的所有三角形的面积之和为.二.勾股定理的证明(共2小题)13.(2022春•连城县校级月考)观察“赵爽弦图”(如图),若图中四个全等的直角三角形的两直角边分别为a,b,a>b,根据图中图形面积之间的关系及勾股定理,可直接得到等式()A.a(a﹣b)=a2﹣ab B.(a+b)(a﹣b)=a2﹣b2C.(a﹣b)2=a2﹣2ab+b2D.(a+b)2=a2+2ab+b214.(2020秋•永嘉县校级期末)如图,四个全等的直角三角形围成正方形ABCD和正方形EFGH,即赵爽弦图.连接AC,分别交EF、GH于点M,N,连接FN.已知AH=3DH,且S正方形ABCD=21,则图中阴影部分的面积之和为()A.B.C.D.三.勾股定理的逆定理(共10小题)15.(2023春•滑县月考)下列四组线段中,能组成直角三角形的是()A.3,4,5B.2,3,4C.6,8,11D.7,23,2516.(2020秋•平山区校级月考)满足下列条件的△ABC,不是直角三角形的是()A.b2=c2﹣a2B.a:b:c=5:12:13C.∠C=∠A﹣∠B D.∠A:∠B:∠C=3:4:517.(2022秋•高陵区月考)如图,在4×4的正方形网格中(每个小正方形边长均为1),点A,B,C在格点上,连接AB,AC,BC,则△ABC的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定18.(2022秋•南城县校级月考)以下列三条线段为边能够组成直角三角形的有()个.(1)3,4,5(2)6.5,2.5,3(3)2.6,2.4,2(4)5,6,7A.1B.2C.3D.419.(2022秋•萍乡月考)下列满足条件的三角形中,不是直角三角形的是()A.在△ABC中,a=m2+n2,b=m2﹣n2,c=2mn,且m>n>0B.三边长的平方之比为1:2:3C.三内角的度数之比为3:4:5D.三边长分别为a,b,c,c=1+n2,b=n2﹣1,a=2n(n>1)20.(2022秋•南海区校级月考)已知a、b、c是△ABC的三边长,且满足关系(a2﹣c2+b2)2+|a﹣b|=0,则△ABC的形状为.21.(2022秋•高陵区月考)已知△ABC的三边a,b,c满足(a﹣9)2+(b﹣12)2+|c﹣15|=0,试判断△ABC的形状.22.(2022秋•浑南区月考)如图所示,已知△ABC中,CD⊥AB于D,AC=2,BC=1.5,DB=0.9.(1)求CD的长;(2)判断△ABC的形状,并说明理由.23.(2022秋•西湖区校级期中)如图,在△ABC中,CD⊥AB,AB=5,BC=,CD=2.(1)求DB的长;(2)求证:AC⊥BC.24.(2022秋•和平区校级期末)如图,有一张四边形纸片ABCD,AB⊥BC,经测得AB=3dm,BC=4dm,CD=2dm,AD=dm,求这张纸片的面积S.四.勾股数(共2小题)25.(2022秋•浑南区月考)下列各组数中,是勾股数的一组是()A.6,7,8B.5,12,13C.0.6,0.8,1D.2,4,526.(2022春•郾城区期末)如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为()A.47B.62C.79D.98五.勾股定理的应用(共1小题)27.(2021秋•牡丹区期末)在一棵树的5米高B处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A 处(离树10米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高米.六.平面展开-最短路径问题(共3小题)28.(2022秋•中原区校级月考)如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是()cm.A.25B.20C.24D.1029.(2022秋•铁岭月考)如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是.30.(2022秋•钦南区校级月考)如图,长方体的高为9dm,底面是边长为6dm的正方形.一只蚂蚁从顶点A开始爬向顶点B,那么它爬行的最短路程为()A.10dm B.12dm C.15dm D.20dm。
《勾股定理》主要题型

《勾股定理》主要题型题型一:直接考查勾股定理,已知两边求第三边例::如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?解:∵∠ACD=90°AD=13, CD=12∴AC2 =AD2-CD2=132-122=25∴AC=5又∵∠ABC=90°且BC=3 ∴由勾股定理可得AB2=AC2-BC2=52-32=16∴AB= 4例、一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?类型二:勾股定理的构造应用例、如图,已知:,,于P.求证:.解:连结BM,根据勾股定理,在中,.而在中,则根据勾股定理有.∴又∵(已知),∴.在中,根据勾股定理有,∴.题型三:在数轴上表示无理数例、在数轴上作出表示10的点.解:根据在数轴上表示无理数的方法,需先把10视为直角三角形斜边的长,再确定出两直角边的长度后即可在数轴上作出.解:以10为斜边的直角三角形的两直角边可以是3和1,所以需在数轴上找出两段分别长为3和1的线段,如图所示,然后即可确定斜边长,再用圆规在数轴上作出长为10的线段即可.题型四:利用勾股定理测量长度例、如图(8),水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.解:如图2,根据勾股定理,AC2+CD2=AD2,设水深AC= x米,那么AD=AB=AC+CB=x+0.5x2+1.52=( x+0.5)2解之得x=2.故水深为2米.题型五:利用勾股定理求线段的长1、如图4,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.解:根据题意得Rt△ADE≌Rt△AEF ∴∠AFE=90°, AF=10cm, EF=DE设CE=xcm,则DE=EF=CD-CE=8-x在Rt△ABF中由勾股定理得: AB2+BF2=AF2,即82+BF2=102,∴BF=6cm∴CF=BC-BF=10-6=4(cm)在Rt△ECF中由勾股定理可得: EF2=CE2+CF2,即(8-x) 2=x2+42∴64-16x+x2=2+16 ∴x=3(cm),即CE=3 cm例、如图,已知AB=13,BC=14,AC=15,AD⊥BC于D,求AD.解:∵BC=14,且BC=BD+DC,设BD=x,则DC=14﹣x,则在直角△ABD中,AB2=AD2+BD2,即132=AD2+x2,在直角△ACD中,AC2=AD2+CD2,即152=AD2+(14﹣x)2,整理计算得x=5,∴AD==12,类型六:数学思想方法(一)转化的思想方法例、如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.求线段EF的长。
勾股定理题型大全

1.已知等腰三角形的周长为24,腰长为x ,则x 的取值范围是 ································ ( ). A )x >12 (B )x <6 (C )6<x <12 (D )0<x <122.如图,等边三角形ABC 中,AD 是BC 上的高,取AC 的中点E , 连结DE ,则图中与DE 相等的线段有 ····························· ( ). (A )1条 (B )2条 (C )3条 (D )4条3.如图:∠EAF=15°,AB=BC=CD=DE=EF ,则∠DEF 等于( )。
A 、90° B 、 75° C 、70° D 、60°4..如图所示,要在河边修建一个水泵站,分别向张村、李庄送水,那么水泵站应修在河边什么地方,可使所用水管最短?画图并说明理由。
5、(10分)①如图:A 、B 是两个蓄水池,都在河流a 的 同侧,为了方便灌溉作物,要在河边建一个抽水站, 将河水送到A 、B 两地,问该站建在河边什么地方,•②如图:某地有两所大学和两条相交叉的公路,(点M ,N 表示大学,AO ,BO 表示公路).现计划修建 一座物资仓库,希望仓库到两所大学的距离相等,到 两条公路的距离也相等。
第十七章 勾股定理题实际应用型归纳专题训练

第十七章勾股定理题实际应用型归纳专题训练题型一:梯子滑落问题1.如图,一根长25m的梯子,斜靠在一竖直的墙上,这时梯子的底端距墙底端7m.如果梯子的顶端下滑4m,那么梯子的底端将向右滑动()A.15m B.9m C.7m D.8m2.一架长5m的梯子斜靠在墙上,梯子底端到墙的距离为3m.若梯子顶端下滑1m,那么梯子底端在水平方向上滑动了()A.1m B.小于1m C.大于1m D.无法确定AO=,若梯子的顶端沿墙下滑1m,这时梯子的底端也向右3.如图,一个梯子斜靠在一竖直的墙AO上,测得4m滑1m,则梯子AB的长度为________.4.如图所示,一个梯子AB长2.5米,顶端A靠墙AC上,这时梯子下端B与墙角C距离为0.7米,梯子滑动后停在DE的位置上,测得BD长为1.3米,则梯子顶端A下滑了_____米.5.如图,将长为2.5米长的梯子AB斜靠在墙上,BE的长度为0.7米.(1)求梯子上端到墙底端E的距离;AC=米)则梯脚B往外移多少米?(2)如果梯子顶端A沿墙下滑0.4米,(即0.46.如图,某火车站内部墙面MN 上有破损处(看作点A ),现维修师傅需借助梯子DE 完成维修工作.梯子的长度为5m ,将其斜靠在这面墙上,测得梯子底部E 离墙角N 处3m ,维修师傅爬到梯子顶部使用仪器测量,此时梯子顶部D 距离墙面破损处1m .(1)该火车站墙面破损处A 距离地面有多高?(2)如果维修师傅要使梯子顶部到地面的距离为4.8m .那么梯子底部需要向墙角方向移动多少米?题型二:树木折断问题7.如图,《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈=十尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,则折断处离地面的高度为()A .3尺B .3.2尺C .3.6尺D .4尺8.《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈10=尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?设折断处离地面的高度为x 尺,则可列方程为()A .()22310x x -=-B .()22310x x +=-C .()222310x x +=-D .()222310x x -=-9.《九章算术》中有“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意:有一根竹子原来高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?如图,设折断处距离地面a 尺,根据题意,则可列方程:__________.10.强大的台风使得一根旗杆在离地面3m处折断倒下,旗杆顶部落在离旗杆底部4m处,则旗杆折断之前的高度是_______.11.如图,在距张大爷家房屋17米处有一棵大树.在一次强风中,这颗大树从距地面8米处折断倒下,量得倒下部分AC的长是17米.请你通过计算,判断这棵大树倒下时是否会砸到张大爷的房子.12.如图,一木杆长13m,在离地面的点B处折断,木杆顶端C落在离木杆底端A的12m处.求木杆折断处离地面有多高?题型三:旗杆高度问题13.同学们想利用升旗的绳子、卷尺,测算学校旗杆的高度.爱动脑的小华设计了这样一个方案:如图,将升旗的绳子拉直刚好触底,此时测得绳子末端C到旗杆AB的底端B的距离为1米,然后将绳子末端拉直到距离旗杆5米的点E处,此时测得绳子末端E距离地面的高度DE为1米.请你根据小华的测量方案和测量数据,求出学校旗杆的高度.14.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B 离地面0.6m,荡秋千到AB的位置时,下端B 距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.15.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,请你求出旗杆的高度(滑轮上方的部分忽略不计).题型四:小鸟飞行距离16.如图,有两棵树,一棵树高AC是10米,另一棵树高BD是4米,两树相距8米(即CD=8米),一只小鸟从一棵树的树梢A点处飞到另一棵树的树梢B点处,则小鸟至少要飞行多少米?17.如图,某自动感应门的正上方A处装着一个感应器,离地的高度AB为2.7米,当人体进入感应器的感应范围内BC 米),感应门时,感应门就会自动打开.一个身高1.5米的学生CD正对门,缓慢走到离门1.6米的地方时( 1.6自动打开,AD为多少米?18.如图,有两根直杆隔河相对,杆CD高30m,杆AB高20m,两杆相距BC为50m,两杆顶各有一只鱼鹰,它们同时看到两杆之间的河面上E处浮起一条小鱼,以同样的速度同时飞下来夺鱼,两只鱼鹰同时到达,叼住小鱼.两杆底部距鱼的距离BE,CE各是多少?题型五:最短路径问题19.如图,有一个圆柱形仓库,它的高为10m,地面直径为8m,在该仓库下地面A处有一只蚂蚁,它想吃相对一侧外面中点B处的食物,蚂蚁爬行的速度是0.4m/min,那么蚂蚁吃到食物至少需要爬行( 取3)()A.32.5min B.minC.30min D.25.2min220.如图,圆柱形容器的高17cm,底面周长是24cm,在外侧底面S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm点F处有一苍蝇,急于捕获苍蝇充饥的蜘蛛所走的最短路线长度是()D.24cmA.20cm B.C21.如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯的长至少要_______米22.如图,在高为6米,坡面长度AB为10米的楼梯表面铺上地毯,则至少需要地毯______米.23.如图,长方体的长为15,宽为10,高为20,点B离点C的距离是5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?题型六:是否受台风影响问题24.如图,A城气象台测得台风中心在A城正西方向240km的O处,以每小时30km的速度向南偏东60 的OB方向移动,距台风中心150km的范围内是受台风影响的区域.(1)A城是否受到这次台风的影响?(2)求A城受台风影响的时间有多长?25.台风是一种自然灾害,它以台风中心为圆心在周围数十千米的范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A 的正南方向220km 的B 处有一台风中心,该台风中心现在正以15km/h 的速度沿北偏东30︒方向移动,若在距离台风中心130km 范围内都要受到影响.(结果精确到0.01) 2.236≈≈≈)(1)该城市是否会受到这次台风的影响?说明理由.(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?题型七:航海问题24.如图,甲货船以16海里/时的速度从港口A 出发向东北方向航行,乙货船以12海里/时的速度同时从港口A 出发向东南方向航行,离开港口2小时后两船之间的距离是()A .40海里B .32海里C .24海里D .20海里25.一艘渔船从港口A 沿北偏东60°方向航行60海里到达C 处时突然发生故障,位于港口A 正东方向的B 处的救援艇接到信号后,立即沿北偏东45°方向以40海里/小时的速度前去救援,救援艇到达C 处所用的时间为()A .32小时B .23小时C D26.在一次海上救援中,两艘专业救助船A、B同时收到某事故渔船P的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距60海里.(1)求收到求救讯息时事故渔船P与救助船B之间的距离(结果保留根号);(2)求救助船A、B分别以20海里/小时,15海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.27.如图,甲乙两船从港口A同时出发,甲船以16海里/时的速度向南偏东40︒航行,乙船向北偏东50︒航行,2小时后,甲船到达B岛,乙船到达C岛,若CB两岛相距40海里,∠的度数;(2)求乙船的航速是多少?(1)直接写出CAB题型八:水杯中筷子问题28.如图所示,将一根24cm 的筷子,置于底面直径为15cm ,高8cm 的圆柱形水杯中,设筷子露在杯子外面的长度cm h ,则h 的取值范围是()A .17cmh ≤B .8cm h ≥C .15cm 16cm h ≤≤D .7cm 16cm h ≤≤29.如图是一圆柱玻璃杯,从内部测得底面半径为6cm ,高为16cm ,现有一根长为25cm 的吸管任意放入杯中,则吸管露在杯口外的长度最少是()A .6cmB .5cmC .9cmD .(25cm -30.如图是一个圆柱形饮料罐,底面半径是3,高是4,上底面中心有一个小圆孔,则一条长10的直吸管露在罐外部分a 的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是()A .56a ≤≤B .36a ≤≤C .23a ≤≤D .12a ≤≤题型九:汽车超速问题31.如图,一辆小汽车在一条限速70km/h 的街路上沿直道行驶,某一时刻刚好行驶到路面车速检测仪A 的正前方60m 处的C 点,过了5s 后,测得小汽车所在的B 点与车速检测仪A 之间的距离为100m .(1)求B ,C 间的距离.(2)这辆小汽车超速了吗?请说明理由.32.超速行驶是引发交通事故的主要原因.上周末,小威等三位同学在幸福大道段,尝试用自己所学的知识检测车速,观测点设在到公路l 的距离为100m 的P 处.这时,一辆红旗轿车由西向东匀速驶来,测得此车从A 处行驶到B 处所用的时间为3s ,并测得60APO ∠=︒,45BPO ∠=︒,(1)求AP 的长?(2)试判断此车是否超过了80km /h 1.732≈)题型十:河宽问题33.如图,在一条绷紧的绳索一端系着一艘小船,河岸上一男孩拽着绳子另一端向右走,绳端从点C 移动到点E ,同时小船从点A 移动到点B ,且绳长始终保持不变,回答下列问题:(1)根据题意,可知AC ________BC CE +(填“>”“<”“=”);(2)若5CF =米,12AF =米,4AB =米,求男孩需向右移动的距离CE (结果保留根号).34.如图,某人从点A 划船横渡一条河,由于水流的影响,实际上岸地点C 离欲到达点B 有45m ,已知他在水中实际划了75m ,求该河流的宽度AB .。
勾股定理知识点与题型总结大全
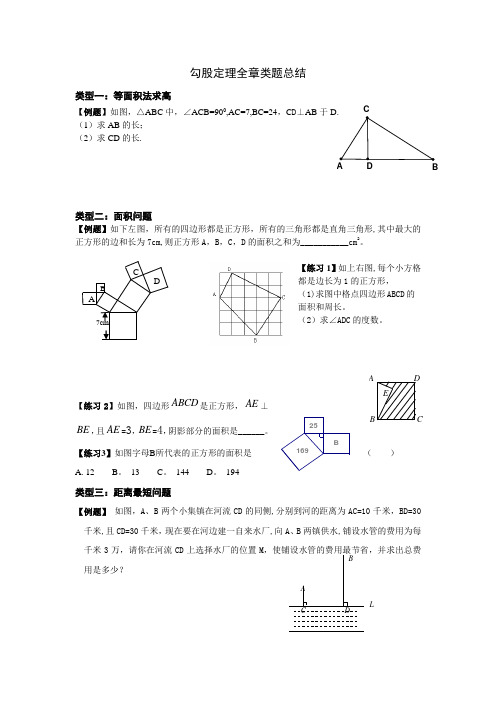
CA BD 勾股定理全章类题总结类型一:等面积法求高【例题】如图,△ABC 中,∠ACB=900,AC=7,BC=24,C D ⊥AB 于D. (1)求AB 的长; (2)求CD 的长.类型二:面积问题【例题】如下左图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A ,B ,C ,D 的面积之和为___________cm 2。
【练习1】如上右图,每个小方格都是边长为1的正方形, (1)求图中格点四边形ABCD 的面积和周长。
(2)求∠ADC 的度数。
【练习2】如图,四边形ABCD 是正方形,AE ⊥BE ,且AE =3,BE =4,阴影部分的面积是______。
【练习3】如图字母B 所代表的正方形的面积是( )A. 12 B 。
13 C 。
144 D 。
194类型三:距离最短问题【例题】 如图,A 、B 两个小集镇在河流CD 的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A 、B 两镇供水,铺设水管的费用为每千米3万,请你在河流CD 上选择水厂的位置M ,使铺设水管的费用最节省,并求出总费用是多少?ABCD7cmBD EB16925A BCDL【练习1】如图,一圆柱体的底面周长为20cm ,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A 出发,沿着圆柱的侧面爬行到点C ,试求出爬行的最短路程.【练习2】如图,一个牧童在小河的南4km 的A 处牧马,而他正位于他的小屋B的西8km 北7km 处,他想把他的马牵到小河边去饮水,然后回家。
他要完成这件事情所走的最短路程是多少?类型四:判断三角形的形状【例题】如果ΔABC 的三边分别为a 、b 、c ,且满足a 2+b 2+c 2+50=6a+8b+10c ,判断ΔABC 的形状.【练习1】已知△ABC 的三边分别为m 2-n 2,2mn ,m 2+n 2(m,n 为正整数,且m >n),判断△ABC 是否为直角三角形。
勾股定理培优---典型题型

典型题型题型一:利用勾股定理解决实际问题例1、如图,公路MN和公路PQ在P点处交汇,点A处有一所中学,AP=160米,点A到公路MN的距离为80米,假使拖拉机行驶时,周围100米以内会受到噪音影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响,请说明理由;如果受到影响,已知拖拉机的速度是18千米/小时,那么学校受到影响的时间为多少?题型二、与勾股定理有关的图形问题例2.如图,直线l经过正方形ABCD的顶点B,点A、C到直线l的距离分别是1、2,则正方形的边长是____ _____.题型三、关于翻折问题例3、如图,把矩形纸片ABCD沿对角线AC折叠,点B落在点E处,EC与AD相交于点F.若AB=4,BC=6,求△FAC的周长和面积.例4、如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知=,求BF的长.AB16cmCE6=,cm题型四、关于最短性问题例5、如图1,长方体的长为12cm,宽为6cm,高为5cm,一只蚂蚁沿侧面从A点向B 点爬行,问:爬到B点时,蚂蚁爬过的最短路程是多少?例6、如图壁虎在一座底面半径为2米,高为4米的油罐的下底边沿A处,它发现在自己的正上方油罐上边缘的B处有一只害虫,便决定捕捉这只害虫,为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿一条螺旋路线,从背后对害虫进行突然袭击.请问壁虎至少要爬行多少路程才能捕到害虫?题型五、关于勾股定理判定三角形形状例7、已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。
题型六、关于旋转中的勾股定理的运用:例8、如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△AC P′重合,若AP=3,求PP′的长。
勾股定理及常见题型分类

勾股定理及常见题型分类一、知识要点:1.勾股定理是指直角三角形斜边的平方等于两直角边平方和。
2.勾股定理的证明方法包括几何证明和代数证明,其中几何证明使用勾股树。
3.勾股定理的逆定理是指若一个三角形的三边满足勾股定理,则该三角形是直角三角形。
4.勾股定理常见题型包括勾股定理的应用、勾股定理的证明和勾股定理的逆定理。
二、典型题题型一:“勾股树”及其拓展类型求面积1.如图所示,正方形A、B、C、D构成了一棵勾股树,求最大正方形E的面积。
2.如图所示,直线l上有三个正方形a、b、c,已知a、c 的边长分别为6和8,求b的面积。
3.如图所示,以Rt△ABC的三边为直径分别向外作三个半圆,探索三个半圆的面积之间的关系。
4.如图所示,分别以直角三角形的三边向外作三个正三角形,其面积分别是S1、S2、S3,则它们之间的关系是S1+S2=S3.5.如图所示,依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是4、5、6、7.题型二:勾股定理与图形问题1.如图所示,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,依此类推,第n个等腰直角三角形的斜边长是n+1.2.如图所示,求该四边形的面积。
3.如图所示,已知在△ABC中,∠A=45°,AC=2,AB=3+1,则边BC的长为3.4.如图所示,某公司的大门为长方形ABCD,上部为以AD为直径的半圆,已知AB=2.3m,BC=2m,卡车高2.5m,宽1.6m,判断卡车是否能通过公司的大门,并说明理由。
5.如图所示,已知AD=8m,CD=6m,∠D=90°,AB=26m,BC=24m,求这块地的面积。
题型三:已知两边求第三边1.在直角三角形中,若两直角边的长分别为1cm、2cm,则斜边长为√5cm。
2.已知直角三角形的两边长为3cm、2cm,则另一条边长的平方是5cm²。
(完整word版)最新人教版第十七章勾股定理整理练习题及详细解析答案

题型一:直接考查勾股定理 例1。
在ABC ∆中,90C ∠=︒.(1)知6AC =,8BC =.求AB 的长.(2)已知17AB =,15AC =,求BC 的长。
题型二:应用勾股定理建立方程例2。
⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD =__________ ⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为___________ ⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为_______________例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长21EDCBA例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积题型三:实际问题中应用勾股定理例5。
如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mABCD E题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6。
已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为直角三角形。
① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c =例7。
三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状?题型五:勾股定理与勾股定理的逆定理综合应用例8。
已知ABC ∆中,13AB =cm ,10BC =cm ,BC 边上的中线12AD =cm ,求证:AB AC =【例1】、分析:直接应用勾股定理222a b c +=解:⑴10AB⑵8BC【例2】分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解解:⑴4AC =, 2.4AC BCCD AB⋅==3k ,4k ∴222(3)(4)15k k +=,3k ∴=,⑵ 两直角边的长分别为54S =⑶ 两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1302S ab ∴==2cm【例3】分析:此题将勾股定理与全等三角形的知识结合起来 解:作DE AB ⊥于E , 12∠=∠,90C ∠=︒ ∴ 1.5DE CD == 在BDE ∆中90,2BED BE ∠=︒= Rt ACD Rt AED ∆≅∆ AC AE ∴=在Rt ABC ∆中,90C ∠=︒222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=【例4】答案:6【例5】分析:根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m在Rt ADE ∆中,由勾股定理得10AD 【例6】答案:10m【例7】解:①22221.52 6.25a b +=+=,222.5 6.25c == ∴ABC ∆是直角三角形且90C ∠=︒②22139b c +=,22516a =,222bc a +≠ABC ∴∆不是直角三角形 【例8】解:此三角形是直角三角形理由:222()264a b a b ab +=+-=,且264c =222a b c ∴+= 所以此三角形是直角三角形【例9】证明:AD 为中线,5BD DC ∴==cm在ABD ∆中,22169AD BD +=,2169AB =222AD BD AB ∴+=,90ADB ∴∠=︒,222169AC AD DC ∴=+=,13AC =cm ,AB AC ∴=勾股定理练习题(家教课后练习)DCBADBA C1。
初中勾股定理练习题精选全文完整版

可编辑修改精选全文完整版第一章《勾股定理》练习题一、选择题(8×3′=24′) 1、在Rt △ABC 中,∠C=90°,三边长分别为a 、b 、c ,则下列结论中恒成立的是( ) A 、2ab<c 2 B 、2ab ≥c 2 C 、2ab>c 2 D 、2ab ≤c 22、已知x 、y 为正数,且│x 2-4│+(y 2-3)2=0,如果以x 、y 的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( ) A 、5 B 、25 C 、7 D 、153、直角三角形的一直角边长为12,另外两边之长为自然数,则满足要求的直角三角形共有( ) A 、4个 B 、5个 C 、6个 D 、8个4、下列命题①如果a 、b 、c 为一组勾股数,那么4a 、4b 、4c 仍是勾股数;②如果直角三角形的两边是3、4,那么斜边必是5;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a 、b 、c ,(a>b=c ),那么a 2∶b 2∶c 2=2∶1∶1。
其中正确的是( ) A 、①② B 、①③ C 、①④ D 、②④5、若△ABC 的三边a 、b 、c 满足a 2+b 2+c 2+338=10a+24b+26c ,则此△为( ) A 、锐角三角形 B 、钝角三角形 C 、直角三角形 D 、不能确定6、已知等腰三角形的腰长为10,一腰上的高为6,则以底边为边长的正方形的面积为( ) A 、40 B 、80 C 、40或360 D 、80或3607、如图,在Rt △ABC 中,∠C=90°,D 为AC 上一点,且DA=DB=5,又△DAB 的面积为10,那么DC 的长是( ) A 、4 B 、3 C 、5 D 、4.58、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。
现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,则CD 等于( ) A 、2㎝ B 、3㎝ C 、4㎝ D 、5㎝ 二、填空题(12×3′=36′)9、在△ABC 中,点D 为BC 的中点,BD=3,AD=4,AB=5,则AC=___________。
八年级勾股定理题型训练

以下是一些常见的八年级勾股定理题型,供您参考:
1. 在△ABC中,AB = 5,BC = 13,AC = 12,求tanC的值.
2. 已知$a = \sqrt{3} + 1$,$b = \sqrt{3} - 1$,求$a^{2} + b^{2} - c^{2}$的值.
3. 在$\bigtriangleup ABC$中,若$AB = 15$,$BC = 20$,$AC = 25$,则$\bigtriangleup ABC$是____三角形.
4. 已知在△ABC中,∠A=30°,∠B=60°,AC=3cm,则AB的长为_______.
5. 在△ABC中,∠C = 90°,AC = 3,BC = 4,将△ABC绕边AC 所在直线旋转一周得到圆锥,则该圆锥的侧面积是_______.
6. 在△ABC中,∠C = 90°,AC = 3,BC = 4,将△ABC绕边AC 所在直线旋转一周得到圆锥,则该圆锥的侧面积是_______.
7. 在直角三角形中,如果一个锐角是另一个锐角的2倍,那么,这两个锐角分别是_______度和_______度.
8. 在△ABC中,∠C = 90°,AB = 2AC,则sinB + cosB = _______.
9. 在直角三角形中,如果一个锐角是另一个锐角的2倍,那么这个三角形中三个内角的度数分别是_______、______、______.10. 在△ABC中,∠C = 90°,AC = 4,BC = 3,将△ABC绕边AC 所在直线旋转一周得到圆锥,则该圆锥的侧面积是_______.。
勾股定理题型分类(经典)

勾股定理全章复习类型一:已知两边求第三边例1:⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长变式练习:已知两条线段的长分别为15和8,当第三条线段取整数_____时,这三条线段能围成一个直角三角形.类型二:判断三角形形状例1:下列线段不能组成直角三角形的是( ).A. B. C. D. 2、若三角形的三边长为a ,b ,c ,且满足等式(a +b)2-c 2=2ab ,则此三角形是______三角形.变式练习1:判断由线段组成的三角形是不是直角三角形.(1)=7,=24,=25;(2)=,=1,=;(3),,();2、若边长为a 的正方形的面积等于长为b +c ,宽为b -c 的长方形的面积,则以a ,b ,c 为三边长的三角形是______三角形.3、已知△ABC 的三边为a ,b ,c ,且a +b =7,ab =12,c =5,试判定△ABC 的形状.类型三:勾股树及变形例1:如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A ,B ,C ,D 的面积之和为___________cm 2。
6,8,10a b c ===3,2,1===c b a 43,1,45===c b a 6,3,2===c b a a b c ,,a b c a 43b c 3422a m n =-22b m n =+2c mn =0m n >> A B C D7cm15题 变式练习:如图,正方形ABCD 的边长为2,其面积标记为S 1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S 2……按照此规律继续下去,则S 2018的值为( )A .(22)2015 B .(22)2016 C .(12)2015 D .(12)2016 类型四:勾股定理证明的应用例1:如图1,分别以直角△ABC 的三边AB ,BC ,CA 为直径向外作半圆.设直线AB 左边阴影部分的面积为S 1,右边阴影部分的面积和为S 2,则( )A S 1=S 2B S 1<S 2C S 1>S 2D 无法确定变式练习:如图,Rt△ABC 中,AC =5,BC =12,分别以它的三边为直径向上作三个半圆,则阴影部分面积为 .类型五:数轴表示数例题1:在数轴上表示√17变式练习:如图,数轴上有两个直角三角形Rt △ABO 、Rt △CDO ,OA 、OC 是斜边,且OB=1,AB=1,CD=1,OD=2,分别以O 为圆心,OA 、OC 为半径画弧交x 轴于E 、F ,则E 、F 分别对应的数是 。
第3章 勾股定理(压轴必刷30题5种题型专项训练)(原卷版)

第3章勾股定理(压轴必刷30题5种题型专项训练)一.勾股定理(共15小题)1.(2022秋•东台市期中)如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,动点P从点C出发,以每秒2cm的速度按C→A的路径运动,设运动时间为t秒.(1)出发2秒时,△ABP的面积为cm2;(2)当t为何值时,BP恰好平分∠ABC?2.(2022秋•建邺区校级期中)如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE 于点F,点G为AF的中点,∠ACD=2∠ACB.(1)说明DC=DG;(2)若DG=7,EC=4,求DE的长.3.(2022秋•天宁区校级期中)如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=6cm,动点P从点B 出发沿射线BC以2cm/s的速度移动,设运动的时间为t秒.(1)求BC边的长;(2)当△ABP为直角三角形时,求t的值;(3)当△ABP为等腰三角形时,求t的值.4.(2022春•张湾区期中)如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A 方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)出发2秒后,求PQ的长;(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.5.(2022秋•嵊州市期中)如图,△ABC中,BA=BC,CO⊥AB于点O,AO=4,BO=6.(1)求BC,AC的长;(2)若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.②设DE交直线BC于点F,连结OF,若S△OBF:S△OCF=1:4,则BD的长为(直接写出所有结果).6.(2022春•金乡县期中)在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.7.(2022秋•顺德区校级期中)如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.(1)问:∠ADC是否为直角?并说明理由;(2)求四边形ABCD的面积.8.(2023•从江县校级开学)定义:如图所示,点M,N把线段AB分割成AM,MN,NB,若以AM,MN,NB为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.(1)已知M,N把线段分割成AM,MN,NB,若AM=2,MN=4,BN2=12,则点M,N是线段AB的勾股分割点吗?请说明理由.(2)已知M,N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.9.(2022秋•闵行区期中)阅读材料:在直角三角形中,斜边和两条直角边满足定理:两条直角边的平方和,等于斜边的平方.因此如果已知两条边的长,根据定理就能求出第三边的长.例如:在Rt△ABC中,已知∠C=90°,AC=3,BC=4,由定理得AC2+BC2=AB2,代入数据计算求得AB=5.请结合上述材料和已学几何知识解答以下问题:已知:如图,∠C=90°,AB∥CD,AB=5,CD=11,AC=8,点E是BD的中点,那么AE的长为.10.(2022秋•江阴市期中)如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连接AP.(1)当t=3秒时,求AP的长度(结果保留根号);(2)当△ABP为等腰三角形时,求t的值;(3)过点D作DE⊥AP于点E.在点P的运动过程中,当t为何值时,能使DE=CD?11.(2022春•江源区期中)如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)当t=2秒时,求PQ的长;(2)求出发时间为几秒时,△PQB是等腰三角形?(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.12.(2022秋•上城区校级期中)已知△ACB为直角三角形,∠ACB=90°,作CD⊥AB.AF平分∠CAB,点M、N分别为AC、EF的中点,且AC=6,BC=8.(1)求证:CE=CF;(2)求证:MN∥AB;(3)请你连接DN,并求线段DN的长.13.(2022秋•江干区校级期中)如图,△ABC中,BA=BC,CO⊥AB于点O,AO=6,BO=9.(1)求BC,AC的长;(2)若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.②设直线DE交直线BC于点F连结OF,CD,若S△OBF:S△OCF=1:4,则CD的长为(直接写出结果).14.(2022秋•上城区校级期中)如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,(1)求证:△BCE≌△DCF;(2)若AB=21,AD=9,BC=CD=10,求AC的长.15.(2023•福田区校级开学)如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t.(1)AB=cm,AB边上的高为cm;(2)点D在运动过程中,当△BCD为等腰三角形时,求t的值.二.勾股定理的证明(共2小题)16.(2022秋•天宁区校级期中)操作与探究(1)图1是由有20个边长为1的正方形组成的,把它按图1的分割方法分割成5部分后可拼接成一个大正方形(内部的粗实线表示分割线),请你在图2的网格中画出拼接成的大正方形.(2)如果(1)中分割成的直角三角形两直角边分别为a,b,斜边为c.请你利用图2中拼成的大正方形证明勾股定理.(3)应用:测量旗杆的高度校园内有一旗杆,小希想知道旗杆的高度,经观察发现从顶端垂下一根拉绳,于是他测出了下列数据:①测得拉绳垂到地面后,多出的长度为0.5米;②他在距离旗杆4米的地方拉直绳子,拉绳的下端恰好距离地面0.5米.请你根据所测得的数据设计可行性方案,解决这一问题.(画出示意图并计算出这根旗杆的高度)17.(2022秋•南关区校级期末)【教材呈现】如图是华师版八年级上册124页的部分内容.勾股定理的“无字证明”在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”,【证明定理】如图,它由2个全等的直角三角形与一个小直角梯形组成,恰好拼成一个大直角梯形,也能证明勾股定理,请你写出证明过程.三.勾股定理的逆定理(共4小题)18.(2022秋•榕城区期中)如图,已知∠ADC =90°,AD =8,CD =6,AB =26,BC =24.(1)证明:△ABC 是直角三角形.(2)请求图中阴影部分的面积.19.(2022秋•冷水滩区期中)如图,在边长为1的小正方形组成的网格中,四边形ABCD 的顶点都在格点上.(1)求四边形ABCD的周长;(2)连接AC,试判断△ACD的形状,并说明理由.20.(2022秋•太仓市期末)如图,△ABC中,AD⊥BC,垂足为D,BD=1,AD=2,CD=4.(1)求证:∠BAC=90°;(2)点P为BC上一点,连接AP,若△ABP为等腰三角形,求BP的长.21.(2022秋•天宁区校级期中)如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2,试判断△ABC 的形状,并说明理由.四.勾股数(共1小题)22.(2022秋•蒲江县校级期中)若直角三角形的三边的长都是正整数,则三边的长为“勾股数”.构造勾股数,就是要寻找3个正整数,使它们满足“其中两个数的平方和(或平方差)等于第三个数的平方”,即满足以下关系:(ㅤㅤ)2+(ㅤㅤ)2=(ㅤㅤ)2;①或(ㅤㅤ)2﹣(ㅤㅤ)2=(ㅤㅤ)2;②要满足以上①、②的关系,可以从乘法公式入手,我们知道:(x+y)2﹣(x﹣y)2=4xy.③如果等式③的右边也能写成“(ㅤㅤ)2”的形式,那么它就符合②的关系.因此,只要设x=m2,y=n2,③式就可化成:(m2+n2)2﹣(m2﹣n2)2=(2mn)2.于是,当m,n为任意正整数,且m>n时,“m2+n2,m2﹣n2和2mn”就是勾股数,根据勾股数的这种关系式,就可以找出勾股数.(1)当m=2,n=1时,该组勾股数是;(2)若一组勾股数中最大的数与最小的数的和为72,且m﹣n=1,求m,n的值;(3)若一组勾股数中最大的数是2p2+6p+5(p是任意正整数),则另外两个数分别为,(分别用含p的代数式表示).五.勾股定理的应用(共8小题)23.(2022春•广州期中)如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B′离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.24.(2022春•平山县期中)在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)25.(2022秋•南岸区校级期中)如图1,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道,现有一辆卡车装满家具后,高为4米,宽为2.8米,(1)请问这辆送家具的卡车能通过这个通道吗?为什么?(2)如图2,若通道正中间有一个0.4米宽的隔离带,问一辆宽1.4米高3.9米的车能通过这个通道吗?为什么?26.(2022秋•济南期中)如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?27.(2023秋•碑林区校级月考)今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.(1)海港C受台风影响吗?为什么?(2)若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?28.(2022秋•内江期末)如图是盼盼家新装修的房子,其中三个房间甲、乙、丙,他将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作MA,如果梯子的底端P不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作NB.(1)当盼盼在甲房间时,梯子靠在对面墙上,顶端刚好落在对面墙角B处,若MA=1.6米,AP=1.2米,则甲房间的宽度AB=米.(2)当他在乙房间时,测得MA=2.4米,MP=2.5米,且∠MPN=90°,求乙房间的宽AB;(3)当他在丙房间时,测得MA=2.8米,且∠MP A=75°,∠NPB=45°.①求∠MPN的度数;②求丙房间的宽AB.29.(2022秋•汉台区校级期中)如图所示,有两根直杆隔河相对,一杆高30m,另一杆高20m,两杆相距50m.现两杆上各有一只鱼鹰,他们同时看到两杆之间的河面上E处浮起一条小鱼于是以同样的速度同时飞下来夺鱼结果两只鱼鹰同时到达,叼住小鱼.问,两杆底部距鱼的距离各是多少?30.(2022秋•邗江区期中)某单位有一块四边形的空地,∠B=90°,量得各边的长度如图(单位:米).现计划在空地内种草,若每平方米草地造价30元,这块地全部种草的费用是多少元?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类型一:勾股定理的直接用法
1、在Rt△ABC中,∠C=90°
(1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.
变式:在Rt△ABC中,∠C=90°,两直角边之比为3:5,c=217,求a,b
类型二:勾股定理的构造应用
2、如图,已知:在中,,,. 求:BC的长.
3已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的面积。
变式1:已知三角形三边长分别为13、20、21,求该三角形的面积
类型三:勾股定理的实际应用
(一)用勾股定理求两点之间的距离问题
4、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。
5、如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m。
假设拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?请说明理由,如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?
6.有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线长,已知门宽4尺,求竹竿高与门高。
(如图,水池中离岸边D点1.5米的C 处,直立长着一根芦苇,出水部分BC 的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.)
(二)用勾股定理求最短问题
6.如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.
变式:如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周
长为10cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁
正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的
最短路径是
A.13cm B.261cm C.61cm D.234cm
类型四:利用勾股定理作长为的线段
7、作长为、、的线段。
变式:如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段.请在图中画
A B
C D
8cm
出△ABC ,5,5,20===AC BC AB 并求出△ABC 的面积.
类型五:勾股定理勾股定理逆定理
8、四边形ABCD 中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD 的面积。
类型五:勾股定理证明图形的应用
1.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积
2. 如图所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8,正方形A 的面积是10,B 的面积是11,C 的面积是13,则D 的面积为_______.
在直线l 上依次摆放着三个正方形(如图所示).已知斜放置的正方形的面积是1,正放置的两个正方形的面积依次是s1,s2.则s1,s2,1之间的关系( )
A . s1+s2=1
B . s1+s2>1
C . s1+s2<1
D . 无法确定
B A C
如图,正方形ABCD 的边长为2,其面积标记为S 1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S 2,…按照此规律继续下去,则S 2015的值为( ) A . ()2012 B . ()2013
C . ()2012
D .
()2013
如图是“赵爽弦图”,△ABH 、△BCG 、△CDF 和△DAE 是四个全等的直角三角形,四边形ABCD 和EFGH 都是正方形,如
果AB =10,EF =2,那么AH 等于
类型六:关于翻折问题
1、如图,矩形纸片ABCD 的边AB=10cm ,BC=6cm ,E 为BC 上一点,将矩形纸片沿AE 折叠,点B 恰好落在CD 边上的点G 处,求BE 的长. .
2.如图,矩形纸片ABCD 中,点E 是AD 的中点,且AE =1,BE 的垂直平分线MN 恰好过点C ,则矩形的一边AB 的长度为( )
A .1
B .2
C .3
D .2
G H
F
E
D
C
A B
3.如图所示,将矩形ABCD 沿AC 折叠,使点B 落在B’处,B’C 与AD 边交于点E ,且BC=8,CE= 4
25
,求AB 的长.
变式:把一张矩形纸片(矩形ABCD )按如图方式折叠,使顶点B 和点D 重合,折痕为EF .若AB = 3 cm ,BC = 5 cm ,
求重叠部分△DEF 的面积.
类型七:勾股定理与坐标系 1.求出线段AB 的长度;
AB=_________; 2. 已知,形?若存在,请直接写出D
拓展:如图1,在⊿ABC 中,直角三角形,如图2和图3E
B'
D
C
A
A B
C F
E
′
D (B ’) A ’
O x y A
B
(0,2)(-4,0)。
