南京市联合体2016-2017学年七年级上期末学情检测卷含答案
2016-2017学年江苏省南京市七年级上学期数学期末试卷带答案

2016-2017学年江苏省南京市七年级(上)期末数学试卷一、选择题(本大题共8小题,每小题2分,共16分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡的相应位置上)1.(2分)3的相反数是()A.﹣ B.C.﹣3 D.32.(2分)我国2016年第一季度GDP总值经初步核算大约为159000亿元,数据159000用科学记数法表示为()A.1.59×104B.1.59×105C.1.59×104D.15.9×1043.(2分)下列计算正确的是()A.7a﹣3a=4 B.3a+2b=5ab C.3ab﹣2ba=ab D.3a+2a=5a24.(2分)单项式﹣a2b3的系数和次数分别是()A.﹣,2 B.,3 C.﹣,5 D.,65.(2分)如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是()A.2 B.2.5 C.4.5 D.76.(2分)下列四个平面图形中,不能折叠成无盖的长方体盒子的是()A.B.C.D.7.(2分)在“有理数的加法与减法运算”的学习过程中,我们做过如下数学实验.“把笔尖放在数轴的原点处,先向左移动3个单位长度,再向右移动1个单位长度,这时笔尖的位置表示什么数?”用算式表示以上过程和结果的是()A.(﹣3)﹣(+1)=﹣4 B.(﹣3)+(+1)=﹣2 C.(+3)+(﹣1)=+2 D.(+3)+(+1)=+48.(2分)已知有理数a,b所对应的点在数轴上的位置如图所示,则有()A.﹣a<0<b B.﹣b<a<0 C.a<0<﹣b D.0<b<﹣a二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡的相应位置上)9.(2分)甲、乙两地的海拔高度分别为20m和﹣10m,则甲地比乙地高m.10.(2分)在﹣4,0.5,0,π,,1.3•这些数中,无理数是.11.(2分)54°36′=度.12.(2分)方程2x+a=3x+2的解是x=1,则a=.13.(2分)写出一个主视图、左视图、俯视图都相同的几何体:.14.(2分)如图,OA⊥OC,∠BOC=50°,若OD平分∠AOC,则∠BOD=°.15.(2分)若单项式xy m与2x n﹣1y3是同类项,则m+n=.16.(2分)若代数式2a2﹣4b﹣1的值为3,则a2﹣2b的值是.17.(2分)如图,点A、O、B在同一条直线上,∠COB=25°,若从点O引出一条射线OD,使OD⊥OC,则∠AOD的度数为.18.(2分)按数字排列规律:,﹣,,﹣,…,写出第10个数为(n 为正整数).三、计算与求解(本大题共4小题,共23分)19.(8分)计算:(1)5﹣(﹣3)+|﹣2|;(2)(﹣+)×(﹣6)2.20.(5分)解方程:3+5x=2(x﹣3).21.(5分)先化简再求值:3(a2+2b)﹣(2a2﹣b),其中a=﹣2,b=1.22.(5分)一个长方形的周长为28cm,将此长方形的长减少2cm,宽增加4cm,就可成为一个正方形,那么原长方形的长和宽分别是多少?四、观察与比较(本大题共2小题,共12分)23.(6分)判断下列解答过程是否正确,如有错误,请正确解答.﹣=1解:3(y+1)﹣y﹣1=13y+3﹣y﹣1=13y﹣y=﹣1y=﹣.24.(6分)如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.(1)求∠DOB的度数;(2)OF是∠AOD的角平分线吗?为什么?五、操作与解释(本大题共2小题,共12分)25.(6分)如图是由大小相同的小立方块搭成的几何体,请在如图方格纸中画出该几何体的三视图.26.(6分)如图,点P是∠AOB的边OB上的一点.(1)过点M画OA的平行线MN;(2)过点P画OB的垂线,交OA于点C;(3)点C到直线OB的距离是线段的长度.六、问题与解决(本题8分)27.(8分)一快递员骑摩托车需要在规定的时间内把快递送到某地,若每小时行驶60km,就早到12分钟;若每小时行驶50km,就要迟到6分钟.(1)若设路程为xkm,请解答下列问题:以每小时60km的速度到达目的地所需的时间为,以每小时50km到达目的地所需的时间为;(用含有x的代数式表示)(2)列出方程,并求出快递员所要骑行的路程.七、探究与思考(本题9分)28.(9分)随着出行方式的多样化,某地区三类打车方式的收费标准如下:(如:乘坐8千米,耗时12分钟,出租车的收费为:12+2.4×(8﹣3)=24(元);滴滴打车的收费为:8×1.5+12×0.5=18(元);神州打车的收费为:8×2+12×0.6=23.2(元))解决问题:(假设打车的平均车速为30千米/小时)(1)小明乘车从新街口去南京南站,全程10千米,如果小明使用滴滴打车,需要支付的打车费用为;(2)小红乘车从南京博物院去南京青奥公园,用滴滴打车比乘坐出租车节省了3元.求南京博物院到南京青奥公园的路程;(3)神州打车为了和滴滴打车竞争客户,分别推出了优惠方式,滴滴打车对于乘车路程在5千米以上(含5千米)的客户每次收费立减9元;神舟打车车费5折优惠.对采用哪一种打车方式更合算提出你的建议.2016-2017学年江苏省南京市七年级(上)期末数学试卷参考答案与试题解析一、选择题(本大题共8小题,每小题2分,共16分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡的相应位置上)1.(2分)3的相反数是()A.﹣ B.C.﹣3 D.3【解答】解:3的相反数是﹣3.故选:C.2.(2分)我国2016年第一季度GDP总值经初步核算大约为159000亿元,数据159000用科学记数法表示为()A.1.59×104B.1.59×105C.1.59×104D.15.9×104【解答】解:159000=1.59×105,故选:B.3.(2分)下列计算正确的是()A.7a﹣3a=4 B.3a+2b=5ab C.3ab﹣2ba=ab D.3a+2a=5a2【解答】解:(A)原式=4a,故A错误;(B)3a与2b不是同类项,故B错误;(D)原式=5a,故D错误;故选:C.4.(2分)单项式﹣a2b3的系数和次数分别是()A.﹣,2 B.,3 C.﹣,5 D.,6【解答】解:单项式﹣a2b3的系数和次数分别是﹣,5,故选:C.5.(2分)如图,已知线段AB=9,BC=5,点D为线段AC的中点,则线段AD的长度是()A.2 B.2.5 C.4.5 D.7【解答】解:∵AB=9,BC=5,∴AC=AB+BC=14,∵D为线段AC的中点,∴AD=AC=7,故选:D.6.(2分)下列四个平面图形中,不能折叠成无盖的长方体盒子的是()A.B.C.D.【解答】解:D的两个侧面在同一边,无法折叠成无盖的长方体盒子,故选:D.7.(2分)在“有理数的加法与减法运算”的学习过程中,我们做过如下数学实验.“把笔尖放在数轴的原点处,先向左移动3个单位长度,再向右移动1个单位长度,这时笔尖的位置表示什么数?”用算式表示以上过程和结果的是()A.(﹣3)﹣(+1)=﹣4 B.(﹣3)+(+1)=﹣2 C.(+3)+(﹣1)=+2 D.(+3)+(+1)=+4【解答】解:∵把笔尖放在数轴的原点处,先向左移动3个单位长度,再向右移动1个单位长度,∴根据向左为负,向右为正得出(﹣3)+(+1)=﹣2,∴此时笔尖的位置所表示的数是﹣2.故选:B.8.(2分)已知有理数a,b所对应的点在数轴上的位置如图所示,则有()A.﹣a<0<b B.﹣b<a<0 C.a<0<﹣b D.0<b<﹣a【解答】解:∵a在原点的左侧,b在原点的右侧,∴a<0,b>0,∵a到原点的距离小于b到原点的距离,∴﹣b<a<0.故选:B.二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡的相应位置上)9.(2分)甲、乙两地的海拔高度分别为20m和﹣10m,则甲地比乙地高30 m.【解答】解:20﹣(﹣10)=20+10=30.故答案为:30.10.(2分)在﹣4,0.5,0,π,,1.3•这些数中,无理数是π.【解答】解:﹣4,0.5,0,,1.3都是有理数,π是无理数.故答案为:π.11.(2分)54°36′=54.6度.【解答】解:54°36′=54°+36÷60=54.6°,故答案为:54.6.12.(2分)方程2x+a=3x+2的解是x=1,则a=3.【解答】解:把x=1代入方程得:2+a=3+2,解得:a=3.故答案是:3.13.(2分)写出一个主视图、左视图、俯视图都相同的几何体:球或正方体.【解答】解:球的三视图都为圆;正方体的三视图为正方形;所以应填球或正方体.14.(2分)如图,OA⊥OC,∠BOC=50°,若OD平分∠AOC,则∠BOD=95°.【解答】解:∵∠AOC=90°,∵OD平分∠AOC,∴∠COD=∠AOC=×90°=45°.∵∠BOC=50°∴∠BOD=∠COD+∠BOC=45°+50°=95°.故答案为9515.(2分)若单项式xy m与2x n﹣1y3是同类项,则m+n=5.【解答】解:由题意可知:1=n﹣1,m=3,∴n=2,m=3∴m+n=5,故答案为:516.(2分)若代数式2a2﹣4b﹣1的值为3,则a2﹣2b的值是2.【解答】解:∵2a2﹣4b﹣1=3,∴2(a2﹣2b)=4,∴a2﹣2b=2故答案为:217.(2分)如图,点A、O、B在同一条直线上,∠COB=25°,若从点O引出一条射线OD,使OD⊥OC,则∠AOD的度数为65°或115°.【解答】解:如图1,∵OD⊥OC,∴∠DOC=90°,∵∠COB=25°,∴∠AOD=180°﹣90°﹣25°=65°,如图2,∵OD⊥OC,∴∠DOC=90°,∵∠COB=25°,∴∠BOD=90°﹣25°=65°,∴∠AOD=180°﹣65°=115°.故答案为:65°或115°.18.(2分)按数字排列规律:,﹣,,﹣,…,写出第10个数为﹣(n为正整数).【解答】解:∵第1个数是:=,第2个数是:﹣=﹣,第3个数是:=,第4个数是:﹣=﹣,…,∴第10个数是:﹣=﹣.故答案为﹣.三、计算与求解(本大题共4小题,共23分)19.(8分)计算:(1)5﹣(﹣3)+|﹣2|;(2)(﹣+)×(﹣6)2.【解答】解:(1)原式=5+3+2=10;(2)原式=(﹣+)×36=18﹣24+27=21.20.(5分)解方程:3+5x=2(x﹣3).【解答】解:去括号得:3+5x=2x﹣6,移项得:5x﹣2x=﹣6﹣3,合并得:3x=﹣9,解得:x=﹣3.21.(5分)先化简再求值:3(a2+2b)﹣(2a2﹣b),其中a=﹣2,b=1.【解答】解:3(a2+2b)﹣(2a2﹣b)=3a2+6b﹣2a2+b=a2+7b当a=﹣2,b=1时,原式=(﹣2)2+7×1=4+7=1122.(5分)一个长方形的周长为28cm,将此长方形的长减少2cm,宽增加4cm,就可成为一个正方形,那么原长方形的长和宽分别是多少?【解答】解:设长方形的长是xcm,则宽为(14﹣x)cm,根据题意得:x﹣2=(14﹣x)+4,解得:x=10,14﹣x=14﹣10=4.答:长方形的长为10cm,宽为4cm.四、观察与比较(本大题共2小题,共12分)23.(6分)判断下列解答过程是否正确,如有错误,请正确解答.﹣=1解:3(y+1)﹣y﹣1=13y+3﹣y﹣1=13y﹣y=﹣1y=﹣.【解答】解:有错误,正确如下:﹣=1,3(y+1)﹣(y﹣1)=63y+3﹣y+1=63y﹣y=6﹣42y=2y=1.24.(6分)如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.(1)求∠DOB的度数;(2)OF是∠AOD的角平分线吗?为什么?【解答】解:(1)∵OE平分∠AOC,∴∠AOC=2∠AOE=64°,∵∠DOB与∠AOC是对顶角,∴∠DOB=∠AOC=64°;(2)∵OE⊥OF,∴∠EOF=90°,∴∠AOF=∠EOF﹣∠AOE=58°,∵∠AOD=180°﹣∠AOC=116°,∴∠AOD=2∠AOF,∴OF是∠AOD的角平分线.五、操作与解释(本大题共2小题,共12分)25.(6分)如图是由大小相同的小立方块搭成的几何体,请在如图方格纸中画出该几何体的三视图.【解答】解:该几何体的三视图如图所示:26.(6分)如图,点P是∠AOB的边OB上的一点.(1)过点M画OA的平行线MN;(2)过点P画OB的垂线,交OA于点C;(3)点C到直线OB的距离是线段CP的长度.【解答】解:(1)OA的平行线MN如图所示.(2)OB的垂线PC如图所示.(3)点C到直线OB的距离是线段CP 的长度.故答案为CP.六、问题与解决(本题8分)27.(8分)一快递员骑摩托车需要在规定的时间内把快递送到某地,若每小时行驶60km,就早到12分钟;若每小时行驶50km,就要迟到6分钟.(1)若设路程为xkm,请解答下列问题:以每小时60km的速度到达目的地所需的时间为,以每小时50km到达目的地所需的时间为;(用含有x的代数式表示)(2)列出方程,并求出快递员所要骑行的路程.【解答】解:(1)设路程为xkm,以每小时60km的速度到达目的地所需的时间为;以每小时50km的速度到达目的地所需的时间为.故答案为:;.(2)根据题意得:+=﹣,解得:x=90.答:快递员需要骑行90km.七、探究与思考(本题9分)28.(9分)随着出行方式的多样化,某地区三类打车方式的收费标准如下:(如:乘坐8千米,耗时12分钟,出租车的收费为:12+2.4×(8﹣3)=24(元);滴滴打车的收费为:8×1.5+12×0.5=18(元);神州打车的收费为:8×2+12×0.6=23.2(元))解决问题:(假设打车的平均车速为30千米/小时)(1)小明乘车从新街口去南京南站,全程10千米,如果小明使用滴滴打车,需要支付的打车费用为25;(2)小红乘车从南京博物院去南京青奥公园,用滴滴打车比乘坐出租车节省了3元.求南京博物院到南京青奥公园的路程;(3)神州打车为了和滴滴打车竞争客户,分别推出了优惠方式,滴滴打车对于乘车路程在5千米以上(含5千米)的客户每次收费立减9元;神舟打车车费5折优惠.对采用哪一种打车方式更合算提出你的建议.【解答】解:(1)10×1.5+×60×0.5=25(元).故答案为:25.(2)设南京博物院到南京青奥公园的路程为xkm,当0<x≤3时,有1.5x+×60×0.5+3=12,解得:x=3.6(不合题意,舍去);当x>3时,有1.5x+×60×0.5+3=12+2.4(x﹣3),解得:x=18.答:南京博物院到南京青奥公园的路程为18km.(3)当乘车路程为n千米(n≥5)时,滴滴打车的费用为1.5n+×60×0.5﹣9=2.5n﹣9,神舟打车的费用为(2n+×60×0.6)×=1.6n.当2.5n﹣9<1.6n时,n<10;当2.5n﹣9=1.6n时,n=10;当2.5n﹣9>1.6n时,n>10.答:当乘车路程大于等于5公里小于10公里时,滴滴打车更合算;当乘车路程等于10公里时,两种打车方式费用相同;当乘车路程大于10公里时,神州打车更合算.附赠:数学考试技巧一、心理准备细心+认真=成功!1、知己知彼,百战百胜。
精品解析:江苏省南京师范大学附属中学2016-2017学年七年级上学期期末考试数学试题(解析版)
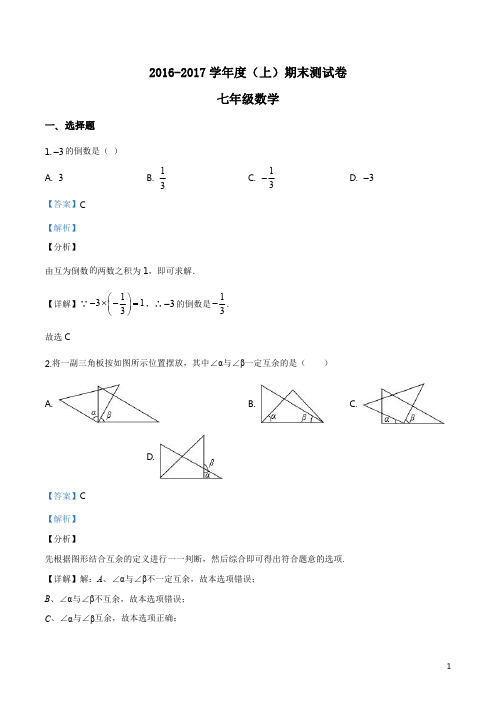
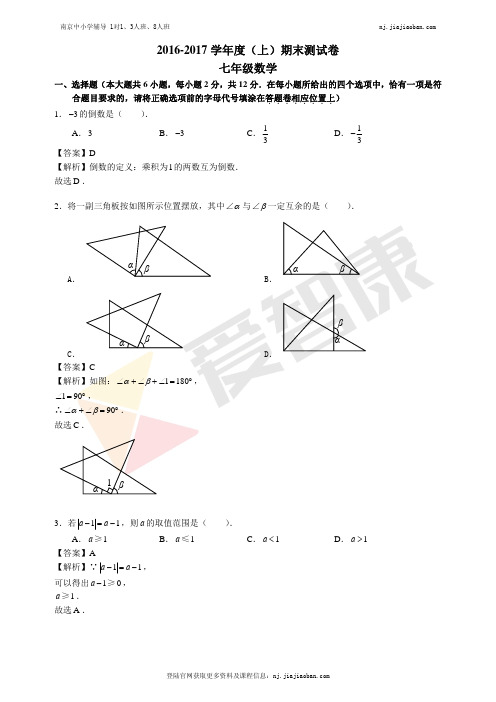
2016-2017学年度(上)期末测试卷七年级数学一、选择题1.3-的倒数是()A.3B.13 C.13- D.3-【答案】C【解析】【分析】由互为倒数的两数之积为1,即可求解.【详解】∵1313⎛⎫-⨯-=⎪⎝⎭,∴3-的倒数是13-.故选C2.将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是()A. B. C.D.【答案】C【解析】【分析】先根据图形结合互余的定义进行一一判断,然后综合即可得出符合题意的选项.【详解】解:A、∠α与∠β不一定互余,故本选项错误;B、∠α与∠β不互余,故本选项错误;C、∠α与∠β互余,故本选项正确;D、∠α与∠β不互余,∠α和∠β互补,故本选项错误;故选:C.【点睛】本题考查的知识点是对顶角、余角和补角.解题关键是熟记“互余的两个角的和等于90°”.3.若|a﹣1|=a﹣1,则a的取值范围是()A.a≥1B.a≤1C.a<1D.a>1【答案】A【解析】试题分析:由绝对值性质可得:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.因为|a﹣1|=a﹣1,所以a﹣1≥0,所以a≥1.选A.考点:绝对值的性质.【此处有视频,请去附件查看】4.如图是一个正方体的平面展开图,把展开图折叠成正方体后,“祝”字一面对面的字是()A.新B.年C.快D.乐【答案】D【解析】试题分析:正方体的平面展开图的特征:相对面展开后间隔一个正方形.由图可得“祝”字对面的字是“快”,故选:D.点睛:本题属于基础应用题,只需学生熟练掌握正方体的平面展开图的特征,即可完成.5.下列说法不正确的是()A.过任意一点可作已知直线的一条平行线B.在同一平面内两条不相交的直线是平行线C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直D.直线外一点与直线上各点连接的所有线段中,垂线段最短【答案】A【解析】试题分析:平面内,过直线外一点有且只有一条直线与已知直线平行,故A不正确;在同一平面内两条不相交的直线是平行线,这是平行线的概念,故B正确;在同一平面内,过直线外一点只能画一条直线与已知直线垂直,故C正确;直线外一点与直线上各点连接的所有线段中,垂线段最短,故D正确;故选:A.6.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需()根火柴.A.156B.157C.158D.159【答案】B【解析】根据第1个图案需7根火柴,7=1×(1+3)+3,第2个图案需13根火柴,13=2×(2+3)+3,第3个图案需21根火柴,21=3×(3+3)+3,得出规律第n个图案需n(n+3)+3根火柴,再把11代入即可求出答案.解:根据题意可知:第1个图案需7根火柴,7=1×(1+3)+3,第2个图案需13根火柴,13=2×(2+3)+3,第3个图案需21根火柴,21=3×(3+3)+3,…,第n个图案需n(n+3)+3根火柴,则第11个图案需:11×(11+3)+3=157(根);故选B.“点睛”此题主要考查图形的变化类,关键是根据题目中给出的图形,通过观察思考,归纳总结出规律,再利用规律解决问题,难度一般偏大,属于难题.【此处有视频,请去附件查看】二、填空题7.温度由1℃下降10℃后是________℃.【答案】-9【解析】试题分析:根据温度的关系,利用有理数的加减可得1-10=-9.故答案为:9.8.大家翘首以盼的南京地铁4号线将于2017年春节前开通,它从龙江站到仙林湖站线路长度33.8千米.则数据33.8用科学记数法表示为___________.【答案】3.38×10【解析】试题分析:由科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.因此33.8=3.38×10.9.若23m n +=-,则842m n --的值是________.【答案】14【解析】试题分析:根据整体思想,先提公因式,整体代入即可得8-4m-2n=8-2(2m+n)=8-2×(-3)=14.10.如果一个角是2015'︒,那么这个角的余角是___________︒.【答案】69.75【解析】试题分析:根据互余两角的和为90°,可求解余角为90°-20°15′=69°45′=69.75°.故答案为:60.7511.某商品的进价为每件100元,按标价打八折售出后每件可获利20元,则该商品的标价为每件____元.【答案】150【解析】设该商品的标价为每件x元,由题意得:80%x﹣100=20,解得:x=150,故答案为150.12.如图是一个数值运算的程序,若输出y的值为5,则输入的值为_______.【答案】±4【解析】试题分析:根据运算程序,可知运算的关系式为(x2-1)÷3,代入可得(x2-1)÷3=5,解方程可得x=±4.13.小明想度量图中点C到三角形ABC的边AB的距离,在老师的指导下小明完成了画图,那么____就是点C到直线AB的距离.【答案】线段CD的长度【解析】试题分析:根据点到直线的距离为点到直线的垂线段的长度,可知CD的长度为点C到AB的距离.故答案为:CD的长度互补的角是14.如图,直线AB与CD相交于O,OE与AB、OF与CD分别相交成直角.图中与COE________.【答案】EOD ∠和BOF∠【解析】试题分析:根据对顶角相等可知∠AOC=∠B OD,∠DOF=90°,可根据和为180°的两角互为补角,可知∠COE 的补角为∠EOD 何∠BOF.15.如图,已知数轴上点A 、B 、C 所表示的数分别为a 、b 、c ,点C 是线段AB 的中点,且2AB =,如果原点O 的位置在线段AC 上,那么2a b c +-=________.【答案】0【解析】试题分析:由题意及数轴上点的位置得:(a+b)÷2=c,即a+b=2c,则2a b c +-==0.故答案为0点睛:此题考查了有理数的混合运算,数轴,以及绝对值,熟练掌握运算法则是解本题的关键.16.线段1AB =,1C 是AB 的中点,2C 是1C B 的中点,3C 是2C B 的中点,4C 是3C B 的中点,依此类推……,线段2015AC 的长为____.【答案】2015112⎛⎫- ⎪⎝⎭【解析】试题分析:根据中点的意义,可知:1 C B =12AB,2C B =121 C B =12×12AB,……由此可知其规律为:n C B =1()2n 1n C B -,因此可知12015C B =20151(2AB,因此可求得2015AC =2015112⎛⎫- ⎪⎝⎭.故答案为:2015112⎛⎫- ⎪⎝⎭.三、解答题17.计算:(1)()()322453⎡⎤-÷⨯--⎣⎦;(2)()157242612⎛⎫+-⨯- ⎪⎝⎭【答案】(1)8(2)18-【解析】试题分析:根据有理数的混合运算,先算乘方,再算乘除,最后算加减,如果有括号先算括号里面的,然后结合乘方运算求解即可.试题解析:(1)()()322453⎡⎤-÷⨯--⎣⎦=-8÷4×[5-9]=-2×(-4)=8(2)()157242612⎛⎫+-⨯- ⎪⎝⎭=157(24)(24)(24)2612⨯-+⨯---=-12-20+14=-1818.解方程:(1)()432x x -=-;(2)223146x x +--=【答案】(1)1x =(2)0x =【解析】试题分析:根据一元一次方程的解法,去分母,去括号,移项,合并同类项,系数化为1,解方程即可.试题解析:(1)4-x=3(2-x)4-x=6-3x-x+3x=6-42x=2x=1(2)223146x x +--=3(x+2)-2(2x-3)=123x+6-4x+6=123x+4x=12-6-67x=0x=019.化简求值:()()2222274523a b a b ab a b ab +-+--,其中1a =-,2b =.【答案】228a b ab +,-30【解析】试题分析:根据去括号法则和合并同类项法则化简,然后代入求值即可.试题解析:原式228a b ab =+其中1a =-,2b =,代入得:原式()()2212812=-⨯+⨯-⨯=30-20.如图,是由若干个完全相同的小正方体组成的一个几何体.(1)请画出这个几何体的三视图;(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.【答案】(1)作图见解析(2)2【解析】试题分析:(1)根据题目中图形可知:主视图共3列,从左到右,第一列有3个小正方形,第二列有2个小正方形,第三列有1个小正方形,左视图共2列,从左到右,第一列有3个小正方形,第二列有1个小正方形,俯视图共2列,从左到右,第一列有2个小正方形,第二列有1个小正方形,第三列有1个小正方形.(2)可在第二层第一列第一行加一个,第三层第一列加一个,共2个.试题解析:(1)如图;(2)可在第二层第一列第一行加一个,第三层第一列加一个,共2个.考点:几何体的三视图.∠=∠,在射线AE上取一点D,使21.如图,利用直尺和圆规,在三角形ABC的边AC上方作EAC ACBAD BC=,连接CD.观察并回答所画的四边形是什么特殊的四边形?(尺规作图要求保留作图痕迹,不写作法)【答案】作图见解析【解析】试题分析:根据基本作图-做一个角等于一只角,结合题意画图,然后判断即可.试题解析:如下图所画的四边形为:平行四边形22.如图,90AOB ∠=︒,在AOB ∠的内部有一条射线OC .(1)画射线.OD OC ⊥(2)写出此时AOD ∠与BOC ∠的数量关系,并说明理由.【答案】(1)作图见解析(2)(1)AOD BOC ∠=∠或180AOD BOC ∠+∠=︒【解析】试题分析:(1)根据基本作图—做已知直线的垂线即可;(2)通过图形判断即可.试题解析:(1)画图,如下图(2)AOD BOC ∠=∠或180AOD BOC ∠+∠=︒23.已知关于m 的方程12(m -16)=-5的解也是关于x 的方程2(x -3)-n =3的解.(1)求m 、n 的值;(2)已知线段AB =m ,在射线AB 上取一点P ,恰好使AP PB =n ,点Q 为线段PB 的中点,求AQ 的长.【答案】(1)m =6,n =3;(2)AQ =214或152【解析】【分析】(1)先利用解一元一次方程的方法解出12(m -16)=-5中m 的值;因为两个方程同解,代入()233x n --=解出n 的值即可.(2)因为点P 的位置不能确定,故应分点P 在线段AB 上时,先根据比值求出AP ,PB 的长度,再根据中点定义求出PQ 的长度,相加即可求出AQ 的长度;当点P 在线段AB 的延长线上时,根据比值求出BP 的长度,再根据中点定义求出BQ 的长度,相加即可求出AQ 的长度.【详解】解:()()111652m -=-,1610m -=-,6m =,关于m 的方程()12651m -=-的解也是关于x 的方程()233x n --=的解.x m ∴=,将6m =,代入方程()233x n --=得:()2633n --=,解得:3n =,故63m n ==,;()2由()1知:63AP AB PB==,,①当点P 在线段AB 上时,如图所示:63AP AB PB == ,,9322AP BP ∴==,, 点Q 为PB 的中点,1324PQ BQ BP ∴===,9321244AQ AP PQ ∴=+=+=;②当点P 在线段AB 的延长线上时,如图所示:63AP AB PB== ,,3PB ∴=,点Q 为PB 的中点,32PQ BQ ∴==,315622AQ AB BQ ∴=+=+=.故214AQ =或152.24.图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示);使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm ,第2节套管长46cm ,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为x cm.(1)请直接写出第5节套管的长度;(2)当这根鱼竿完全拉伸时,其长度为311cm ,求x 的值.【答案】(1)34cm;(2)每相邻两节套管间重叠的长度为1cm.【解析】试题分析:(1)根据“第n 节套管的长度=第1节套管的长度﹣4×(n ﹣1)”,代入数据即可得出结论;(2)同(1)的方法求出第10节套管重叠的长度,设每相邻两节套管间的长度为xcm ,根据“鱼竿长度=每节套管长度相加﹣(10﹣1)×相邻两节套管间的长度”,得出关于x 的一元一次方程,解方程即可得出结论.试题解析:(1)第5节套管的长度为:50﹣4×(5﹣1)=34(cm ).(2)第10节套管的长度为:50﹣4×(10﹣1)=14(cm ),设每相邻两节套管间重叠的长度为xcm ,根据题意得:(50+46+42+…+14)﹣9x=311,即:320﹣9x=311,解得:x=1.答:每相邻两节套管间重叠的长度为1cm .考点:一元一次方程的应用.25.如图(1),点O 为线段AB 上一点,过点D 作射线OC ,使:1:2AOC BOC ∠∠=,将一直角三角板的直角顶点放在点O 处,一边OM 在射线OB 上,另一边ON 在线段AB 的下方.(1)将图(1)中的直角三角板绕点O 按逆时针方向旋转,使ON 落在射线OB 上(如图(2)),则三角板旋转的角度为____度;(2)继续将图2中的直角三角板绕点O 按逆时针方向旋转,使ON 在AOC ∠的内部(如图3).试求AOM ∠与NOC ∠度数的差;(3)若图1中的直角三角板绕点O 按逆时针方向旋转一周,在此过程中:①当直角边OM 所在直线恰好垂直于OC 时,AOM ∠的度数是________;②设直角三角板绕点O 按每秒15︒的速度旋转,当直角边ON 所在直线恰好平分AOC ∠时,求三角板绕点O 旋转时间t 的值.【答案】(1)90︒(2)30AOM NOC ∠-∠=︒(3)①150AOM ∠=︒或30°②4t =或()16s 【解析】试题分析:(1)根据旋转的性质可知,旋转角是∠MON.(2)如图3,利用角平分线的定义,结合已知条件,求得∠AOC=60°,然后根据直角的性质、图中角与角间的数量关系推出结论;(3)①根据旋转的定义,画图,然后根据周角和已知角求解;②根据速度和角平分线的性质,分逆时针和顺时针计算即可.试题解析:(1)90︒(2)30AOM NOC ∠-∠=︒(3)①150AOM ∠=︒或30︒②4t =或()16s 26.数轴上有A 、B 、C 三点,分别表示有理数26-、10-、20,动点P 从A 出发,以每秒1个单位的速度向右移动,当P 点运动到C 点时运动停止,设点P 移动时间为t 秒.(1)用含t 的代数式表示P 点对应的数:_________;(2)当P 点运动到B 点时,点Q 从A 点出发,以每秒2个单位的速度向C 点运动,Q 点到达C 点后,再立即以同样的速度返回A 点.①用含t 的代数式表示Q 点在由A 到C 过程中对应的数:_________;②当t =______时,动点P 、Q 到达同一位置(即相遇);③当3PQ =时,求t 的值.【答案】(1)26t -+;(2)①258t -;②32或1243;③3t =,29,35,1213,1273.【解析】【分析】(1)根据题意可得P 点对应的数;(2)①P 因为点从A 运动到B 点所花的时间为16秒,Q 点从A 运动到C 点所花的时间为23秒所以Q 点在由A 到C 过程中对应的数()26216258t t -+-=-为;②分为返回前相遇和返回后相遇两种情况:返回前相遇,P 的路程等于Q 的路程等于Q 的路程减去16;而返回后相遇,则是二者走的总路程是Q 到C 的路程的2倍,分别列式子求解.【详解】(1)P 点所对应的数为:26t-+(2)①258t -②P 点从A 运动到B 点所花的时间为16秒,Q 点从A 运动到C 点所花的时间为23秒当1639t ≤≤时,P :26t -+,Q :()26216258t t -+-=-26258t t -+=-,解之得32t =当3946t ≤≤时,P :26t -+,Q :()20239982t t--=-26982t t -+=-,解之得1243t =③3t =,29,35,1213,1273【点睛】考核知识点:一元一次方程应用.理解定义,列出方程是关键.。
学校16—17学年上学期七年级期末考试数学试题(扫描版)(附答案)

2016---2017学年度第一学期期末考试七年级数学试题参考答案一、选择题(每小题3分,共30分)1、B2、D3、B4、C5、A6、C7、D8、C9、C 10、B二、填空题(每小题4分,共24分)11、-8℃ 12、m=-2 n= 2 13、-2 14、-415、两点确定一条直线 16、(6n+2)三、解答题(共66分)17、解:(1) 原式=()2483917⎛⎫+-⨯-÷- ⎪⎝⎭…………2分 =()748399⎛⎫+-⨯-⨯- ⎪⎝⎭…………3分 =4247-+ …………4分 =13- …………5分(2) 原式=()15718369⎛⎫-+⨯- ⎪⎝⎭…………2分 =()()()157181818369⨯--⨯-+⨯- …………3分 =61514-+- …………4分 =5- …………5分18、解:(1) 222(52)2(3)xy x xy y y xy +-+--=2225226xy x xy y y xy +-+-+ …………2分=22x xy + …………3分 当12,2x y =-=时,原式=()()2122222-+⨯-⨯= …………4分 (2) 22(54)(542)x x x x -+++-+=2254542x x x x -+++-+…………5分=2(21)(45)(54)x x -+++-…………6分=291x x ++…………7分当2x =-时, 原式=2(2)9(2)113-+⨯-+=-…………8分19、(1)3(5)4(1)9x x x --+=+解: 315449x x x ---=+ …………2分349154x x x --=++ …………4分228x -= …………5分14x =- …………6分(2) 5415323412y y y +---=+ 解:()()()454312453y y y +--=+- …………2分 2016332453y y y +-+=+- …………3分2035243163y y y --=--- …………4分122y = …………5分16y = …………6分 20、解:(1)()20x - 360x -甲队整治河道天数 甲队整治河道总长度 …………4分(2)解:设甲队整治河道用时x 天,则乙队整治河道用时()20x -天. ()241620360x x +-= …………6分解方程,得 5x = …………8分 24120x = ()1620240x -= 答:甲队整治河道120米,乙队整治河道240米. …………10分 或 设甲队整治河道x 米,则乙队整治河道()360x -360202416x x -+= …………6分 解方程,得 120x = …………8分 360240x -=答:甲队整治河道120米,乙队整治河道240米. …………10分21、解:因为AD=7,BD=5所以AB=12 …………2分因为 点C 为线段AB 的中点所以 AC=6 …………4分 所以 CD=AD-AC=1 …………6分22、解:(1)因为OD 是∠AOC 的平分线,所以 ∠COD =21∠AOC.因为OE 是∠BOC 的平分线,所以∠COE =21∠BOC. …………2分所以∠DOE=∠COD+∠COE=21(∠AOC +∠BOC )=21∠AOB=90°.…………4分(2) 因为∠COD =65° OD 是∠AOC 的平分线所以 ∠AOD=∠COD=65° …………6分 因为∠DOE =90°所以 ∠AOE=∠AOD+∠DOE=155° …………8分23、解:(1)40000.93600⨯=(元)40000.83003500⨯+=(元)36003500100-=(元)答:小张购买优惠卡后再购物合算,能省100元. …………4分(2)设顾客购买x元的商品时,买卡与不买卡花钱相等.=+…………6分0.90.8300x x解方程,得x=3000答:顾客购买3000元的商品时,买卡与不买卡花钱相等. …………8分(3)设这台冰箱的进价为y元.+=?…………10分y y0.2540000.8y=解方程,得2560答:这台冰箱的进价为2560元. …………12分。
2016~2017学年度第一学期期末联合体七年级试卷
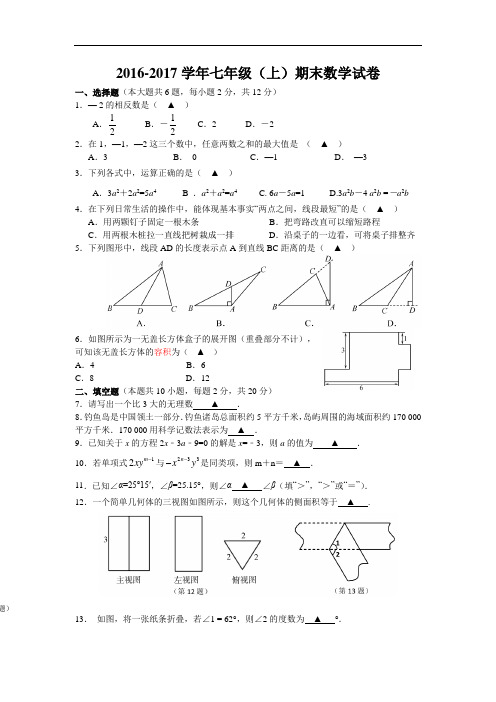
2016-2017学年七年级(上)期末数学试卷一、选择题(本大题共6题,每小题2分,共12分)1.— 2的相反数是( ▲ )A .12 B .-12 C .2 D .-22.在1,—1,—2这三个数中,任意两数之和的最大值是 ( ▲ )A .3B . 0C .—1D . —33.下列各式中,运算正确的是( ▲ )A .3a 2+2a 2=5a 4B .a 2+a 2=a 4 C. 6a -5a =1 D.3a 2b -4 a 2b =-a 2b4.在下列日常生活的操作中,能体现基本事实“两点之间,线段最短”的是( ▲ )A .用两颗钉子固定一根木条B .把弯路改直可以缩短路程C .用两根木桩拉一直线把树栽成一排D .沿桌子的一边看,可将桌子排整齐5.下列图形中,线段AD 的长度表示点A 到直线BC 距离的是( ▲ )6.如图所示为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为( ▲ )A .4B .6C .8D .12二、填空题(本题共10小题,每题2分,共20分)7.请写出一个比3大的无理数 ▲ .8.钓鱼岛是中国领土一部分.钓鱼诸岛总面积约5平方千米,岛屿周围的海域面积约170 000平方千米.170 000用科学记数法表示为 ▲ .9.已知关于x 的方程2x ﹣3a ﹣9=0的解是x =﹣3,则a 的值为 ▲ .10.若单项式12m xy -与233n x y --是同类项,则m +n = ▲ .11.已知∠α=25°15′,∠β=25.15°,则∠α ▲ ∠β(填“>”,“>”或“=”).12.一个简单几何体的三视图如图所示,则这个几何体的侧面积等于 ▲ .13. 如图,将一张纸条折叠,若∠1 = 62°,则∠2的度数为 ▲ °. 题)14.数轴上有A 、B 、C 三点,A 、B 两点所表示的数如图所示,若BC =2,则AC 的中点所表示的数是 ▲ .15.已知关于x 的一元一次方程1322016x x b +=+的解为x =2,那么关于y 的一元一次方程1(1)32(1)2016y y b ++=++的解y = ▲ . 16.如图都是由同样大小的黑棋子按一定规律摆出的图案,第①个图案有4个黑棋子,第②个图案有9个黑棋子,第③个图案有14个黑棋子,….依次规律,第n 个图案有499个黑棋子,则n = ▲ .三. 解答题(本大题共9题,共68分)17.(9分)计算:(1)(4)(3)6+---+-;(2)4211(10.5)2(3)3⎡⎤---⨯⨯--⎣⎦.18.(9分)解方程:(1)2(x +1)=1-(x +3);(2)5731164x x--+=.19.(6分)化简后再求值:()()2224232y x x y x ---+,其中1 2-==y x .20.(6分)(1)在方格纸上过点P 作线段AB 的平行线;(2)在方格纸上以AB 为边画一个正方形;(3)填空:若图中小方格的面积为1,则(2)中所作正方形的面积= ▲ .21.(6分)从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件.(1)这个零件的表面积是▲ ;(2)请按要求在边长为1网格图里画出这个零件的视图.22.(7分)如图,用总长为6米的铝合金条制作“日”字形窗框,已知窗的高比宽多0.5米,求窗户的透光面积.23.(7分)如图,直线AB 、CD 相交于点O ,OE ⊥CD ,OF 平分∠BOD .(1)图中除直角外,请写出一对相等的角: ▲ (写出符合的一对即可)(2)如果∠AOE =26°,求∠BOD 和∠COF 的度数.(所求的角均小于平角)24.(8分)一辆汽车A 地驶往B 地,前14路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为50 km/h ,在高速公路上行驶的速度为90 km/h ,汽车从A 地到B 地一共行驶了4 h .请根据以上信息,就该汽车行驶“时间”或“路程”提出一个问题,并用一元一次方程解决这个问题.问题: ▲ ?解答:25.(10分)【探索新知】如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.(1)一个角的平分线▲这个角的“巧分线”;(填“是”或“不是”)(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ▲;(用含α的代数式表示出所有可能的结果)【深入研究】如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.(3)当t为何值时,射线..是∠QPN的“巧分线”;..PM(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.请直接写出当射线PQ是∠MPN的“巧分线”时t的值.。
2016~2017学年度第一学期期末秦淮区七年级试卷

2016—2017学年度第一学期第二阶段学业质量监测试卷七年级数学(满分:100分 考试时间:100分钟)注意:1.选择题答案请用2B 铅笔填涂在答题卡...相应位置....上. 2.非选择题答案必须用0.5毫米黑色墨水签字笔写在答题卷上的指定位置,在其他位置答题一律无效.一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置.......上) 1.下列四个算式中,有一个算式与其他三个算式的计算结果不同,该算式是A .(-1)2B .-(-1)C .-12D .|-1|2.南京地铁4号线计划于2017年1月通车运营,地铁4号线一期工程全长为33800米,将33800用科学记数法表示为 A .33.8×103B .3.38×104C .33.8×104D .3.38×1053.下列各组单项式中,同类项一组的是A .3x 3y 与3xy 3B .2ab 2与-3a 2bC .a 2与b 2D .-2xy 与3yx 4.如图,有一个直径为1个单位长度的圆片,把圆片上的点A 放在原点,并把圆片沿数轴向右滚动1周,点A 到达点A ′ 的位置,则点A ′ 表示的数是 A .-πB .-π2C .π2D .π5.如图,将一张长方形纸片ABCD 沿EF 折叠,点D 、C 分别落在D ′、C ′的位置处,若 ∠1=56°,则∠DEF 的度数是A .56°B .62°C .68°D .124°6.将一副三角尺按如图方式进行摆放,∠1与∠2不一定...互补的是 (第4题)(第5题)1ABCDE FC ′D ′7.已知线段AB 、CD ,点M 在线段AB 上,结合图形,下列说法不正确...的是 A .过点M 画线段CD 的垂线,交CD 于点E B .过点M 画线段AB 的垂线,交CD 于点E C .延长线段AB 、CD ,相交于点F D .反向延长线段BA 、DC ,相交于点F8.一个长方形的长和宽分别为3 cm 和2 cm ,依次以这个长方形的长和宽所在的直线为旋转轴,把长方形旋转1周形成圆柱体甲和圆柱体乙,两个圆柱体的体积分别记作V甲、V 乙,侧面积分别记作S 甲、 S 乙,则下列说法正确的是 A .V 甲<V 乙,S 甲=S 乙 B .V 甲>V 乙,S 甲=S 乙 C .V 甲=V 乙,S 甲=S 乙 D .V 甲>V 乙,S 甲<S 乙二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卷相应位置.......上) 9.单项式-2x 2y 53的次数是 ▲ .10.比较大小:-3.13 ▲ -3.12.(填“<”、“=”或“>”)11.已知关于x 的一元一次方程x +2m =-1的解是x =1,则m 的值是 ▲ . 12.“两个数和的平方等于这两个数积的两倍加上这两个数的平方和”,在学过用字母表示数后,请借助符号描述这句话: ▲ . 13.若2a -b =2,则6+4b -8a = ▲ .14.如图,直线 a 、b 相交于点O ,将量角器的中心与点O 重合,发现表示60°的点在直线a 上,表示135°的点在直线b 上,则∠1= ▲ °.(第8题)A BM DF E (第7题)A1212B 12C 12 DO a 30° 60° 90°120°150° 0°180°b15.如图,将一刻度尺放在数轴上(数轴的单位长度是1 cm ),刻度尺上表示“0 cm ”、“8 cm ”的点分别对应数轴上的-2和x ,那么x 的值为 ▲ .16.如图,A 、B 是河l 两侧的两个村庄,现要在河l 上修建一个抽水站,使它到A 、B 两村庄的距离之和最小.数学老师说:连接AB ,则线段AB 与l 的交点C 即为抽水站的位置.其理由是: ▲ .17.互联网“微商”经营已经成为大众创业新途径.某微信平台上某件商品标价200元,按标价的九折销售,仍可获利20%.这件商品的进价是多少元?若设这件商品的进价为x 元,根据题意可列方程 ▲ .18.如图,在∠AOB 的内部有3条射线OC 、OD 、OE ,若∠AOC =50°,∠BOE =1n∠BOC ,∠BOD =1n∠AOB ,则∠DOE = ▲ °(用含n 的代数式表示).三、解答题(本大题共9小题,共64分.请在答题卷...指定区域内.....作答,解答时应写出文字说明、说理过程或演算步骤) 19.(8分)计算:(1) 48÷[(-2)3-(-4)]; (2)-23÷49×( 23 )2+(-1)4.20.(6分)先化简,再求值:x 2+(2xy -3y 2)-2(x 2+xy -2y 2),其中x =1,y =2.(第18题)AOC D EB(第16题)21.(8分)解方程:(1)5(x-1)-2(1-x)=3+2x;(2)x+12-1=2-3x2.22.(6分)观察下面的立体图形,把主视图、左视图、俯视图画出来.23.(6分)如图,直线AB、CD相交于点O,∠AOE=∠COF=90°.(1)∠DOE的余角是▲ (填写所有符合要求的角);(2)若∠DOE=70°,求∠BOF的度数.24.(6分)第十八届“飞向北京——飞向太空”全国青少年航空航天模型教育竞赛江苏预赛在南京举行.某校航模小组参赛选手中男生占该校参赛人数的一半,后来又增加2名男生,那么男生人数就占该校参赛人数的23.该校原有参赛男生多少人?(第22题)OFADE(第23题)B25.(7分)如图,已知∠α.(1)用直尺和圆规作∠AOB ,使∠AOB =∠α(保留作图的痕迹,不写作法); (2)用量角器画∠AOB 的平分线OC ;(3)在OC 上任取一点M (点M 不与点C 重合),过点M 分别画直线MP ⊥OA ,垂足为P ,画直线MN ‖OA ,交射线OB 于点N ,则点M 到射线OA 的距离是线段 ▲ 的长度,MN 与MP 的位置关系是 ▲ .26.(7分)如图,C 是线段AB 上一点,AB =16 cm ,BC =6 cm .(1)AC = ▲ cm ;(2)动点P 、Q 分别从A 、B 同时出发,点P 以2 cm/s 的速度沿AB 向右运动,终点为B ;点Q 以1 cm/s 的速度沿BA 向左运动,终点为A .当一个点到达终点时,另一个点也随之停止运动.求运动多少秒时,C 、P 、Q 三点中,有一点恰好是以另两点为端点的线段的中点?27.(10分)以下是两张不同类型火车的车票(“D ××××次”表示动车,“G ××××次”表示高铁):(第26题)(第25题) α(1)根据车票中的信息填空:该列动车和高铁是▲向而行(填“相”或“同”).(2)已知该列动车和高铁的平均速度分别为200km/h、300km/h,两列火车的长度不计.①经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到1h,求A、B两地之间的距离;②在①中测算的数据基础上,已知A、B两地途中依次设有5个站点P1、P2、P3、P4、P5,且AP1=P1P2=P2P3=P3P4=P4P5=P5B,动车每个站点都停靠,高铁只停靠P2、P4两个站点,两列火车在每个停靠站点都停留5min.求该列高铁追上动车的时刻...。
江苏省南京市四城区2016-2017学年度第一学期期末联考七年级语文试卷

第一学期期末联考七年级语文试卷
注意事项: 1.本试卷 6 页,共 100 分。考试时间 120 分钟。 2.答案一律用黑色墨水笔写在答题卷上,不能写在本试卷上。
一( 27 分)
1. 用诗文原句填空,其中第( 3)题还需填写作者..。( 11 分)
( 1)子曰: “知之者不如好之者,
▲
。”
(《 <论语 >十二章》 )
他不住帐篷,而是住在一座结实的石头房子里。看得出,他是一点一点地把一座破
旧的房子修整成现在的样子的。房顶很严实,一滴雨水也不漏。风吹在瓦上,发出海浪
拍打沙滩的声音。房间里收拾得很整齐,餐具洗得干干净净,地板上没有一点儿灰尘,
猎枪也上过了油。炉子上,还煮着一锅热腾腾的汤。看得出,他的刚刚刮过胡子。他的
怎样的无私,我就从心底里,对这位没有受过什么教育的普通农民,感到无限的敬佩。 他做到了只.有.上.帝.才.能.做.到.的.事. 。
12. “只有上帝才能做到的事”是指牧羊人做的什么事?请简要概括。(
3 分)
▲
13.按照括号中的要求回答问题。 ( 4 分)
( 1)狂风呼啸着穿过破房子的缝隙,像一只饥饿的野兽发出吼叫。
孩子们的笑声又开始在热闹的乡村聚会上飘荡。一直住在这里的老一辈人,已经被舒适
的新生活改变了。加上新来的居民,一万多口人的幸福生活,都源于这位叫艾力泽﹒布
菲的老人。
每当我想到这位种树的老人,他靠一个人的体力与毅力,把这片荒漠变成了绿洲,
我就觉得,人的力量是多么伟大啊!可是,想到要做成这样一件事,需要怎样的毅力,
▲
二( 43 分)
(一)阅读下面的文言文,完成 7~ 11 题。( 13 分)
杞人忧天 《列子》
2016~2017学年度第一学期期末新优质联盟七年级试卷

2016-2017学年度第一学期第二阶段学业质量监测试卷七年级数学注意事项:本试卷共6页.全卷满分100分.考试时间为100分钟.考生答题全部答在答题纸上,答在本试卷上无效.一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答题纸相应位置上) 1.3的绝对值是( ▲ )A .–3B .3C .13D .﹣132.下列计算正确的是( ▲ )A. 3a+4b =7abB. 7a -3a = 4C. 3a+2a =5a 2D. 3a 2b -4a 2b =﹣a 2b3.左图中的图形绕虚线旋转一周可得到的几何体是( ▲ )4. 如图,将正方体的平面展开图重新折成正方体后, “京”字对面的字是( ▲ )A .美B .丽C .我D .爱5.如果∠α的补角为150°,那么∠α的余角是( ▲ )A .30°B .150°C .120° D. 60°6.下列说法:①两点之间的所有连线中,线段最短 ②对顶角相等 ③过一点有且只有一条直线与已知直线平行 ④长方体是四棱柱,其中正确的有( ▲ )A . 1个B . 2个C . 3个D . 4个A BD 我爱 美 丽南 京(第4题)二、填空题(本题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题纸相应位置上) 7.2的相反数是 ▲ .8.据统计,截止2016年11月,南京市投放公共自行车累计达52000辆,为方便群众,缓解城市交通拥堵,倡导绿色交通,促进节能减排发挥了积极作用.将52000用科学9. 请任意写出一个无理数: ▲ .10.单项式–2 x y 2的系数是 ▲ ,次数是 ▲ .11.若关于x 的方程 2(x -1) + a =0的解是x =3,则a 的值为 ▲ .12.若单项式a m b 3与–3ab n 是同类项,则m + n = ▲ .13.如图,两个图形分别是某个几何体的主视图和俯视图,则该几何体可能是 ▲ .14. 如图,用火柴棒搭“小鱼”,则搭10条“小鱼”需用 ▲ 根火柴棒,搭n 条“小鱼” 所需火柴棒的根数为 ▲ (填写化简后的结果).15. 若x 2-2x -1=0,则代数式x 2-2x+1的值为 ▲ .16. 如图,点A 在数轴上对应的数为2,若点B 也在数轴上,且线段AB 的长为3,则 点B 在数轴上对应的数为 ▲ .(第14题)(第16题)主视图(第13题)三、解答题(本大题共10小题,共68分.请在答题纸指定区域内作答,解答时应写全过程)17.计算:(每题4分,共8分)(1) ﹣4 + 2-1; (2)(-6)2×(﹣12 -14 +16 +12 ) .18.(本题满分5分)先化简,再求值: 2a 2+3a +4(1-a ),其中a =﹣1.19.(本题满分9分)解方程:(1)(4分)1-3(x -2) = 4 ; (2)(5分)2x +13 -5x -16=1 .20.(本题满分6分)(1)由大小相同的小立方块搭成的几何体如左图,请在右图的方格中画出该几何体的俯 视图和左视图.(2)若现在你手头还有一些相同的小立方块,如果保持俯视图...和左视图...不变, 则在左图中最多可以再添加 ▲ 个小立方块.(第20题)如图,C 是线段AB 的中点.(1)若点D 在CB 上,且DB =2cm ,AD =8cm ,求线段CD 的长度;(2)若将(1)中的“点D 在CB 上”改为“点D 在CB 的延长线上”,其它条件不变,请 画出相应的示意图,并求出此时线段CD 的长度.22.(本题满分6分)某学生寄了2封信和一些明信片,一共用了5.6元. 已知每封信的邮费为1.2元,每 张明信片的邮费为0.8元.他寄了多少张明信片?23.(本题满分6分)如图,点P 在∠AOB 内.(1)过点P 画直线PC ∥OA ,交OB 于点C ; (2)过点C 画OA 的垂线,垂足为H ;(3)因为直线外一点和直线上各点连接的所有线段中, ▲ ,所以两条线段CH 、OC 的大小关系是: ▲ (用“<”号连接).ABC D(第21题)(第23题)如图,直线AB 、CD 相交于点O ,OE 平分∠BOD ,OF ⊥CD ,∠BOE =36°,求∠AOF 的度数.25.(本题满分7分)为了加强公民的节水意识,某市将要采用价格调控手段达到节水目的,设计了如下的 调控方案.(1)甲户居民五月份用水12吨,则水费为 ▲ 元.(2)乙户居民八月份缴纳水费40元,则该户居民八月份用水多少吨?(列方程解答)ABCDEF O(第24题)如图,射线OB 、OC 均从OA 开始,同时绕点O 逆时针旋转,OB 旋转的速度为每 秒6°,OC 旋转的速度为每秒2°. 当OB 与OC 重合时,OB 与OC 同时停止旋转.设旋 转的时间为t 秒.(1)当t =10,∠BOC = ▲ °. (2)当t 为何值时,射线OB ⊥OC ?(3)试探索:在射线OB 与OC 旋转的过程中,是否存在某个时刻,使得射线OB ,OC 与OA 中的某一条射线是另两条射线所成角的角平分线?若存在,请求出所有满足 题意的t 值,若不存在,请说明理由.ABCO(第26题)2016-2017学年度第一学期第二阶段学业质量监测试卷七年级数学参考答案及评分标准一、选择题(每小题2分,共12分)二、填空题(每小题2分,共20分)7. ﹣2 8. 5.2×104 9. 不唯一,如:π 10. ﹣2、3 11. ﹣412. 4 13.圆锥 14. 62,6n +2 15. 2 16. ﹣1或5三、解答题(本大题共10小题,共68分.请在答题纸指定区域内作答,解答时应写全过程)17.(8分)(1)解:原式=﹣2-1 …………………………………………………………… 2分 =﹣3 ………………………………………………………………… 4分 (2)解:原式=36×(-14+16) …………………………………… 1分 =36×(-14)+36×16……………………………………………… 2分=-9+6 ……………………………………………………………… 3分 =-3 ……………………………………………………………… 4分18.(5分)解:原式=2a 2+3a+4-4a …………………………………………………………… 2分 =2a2-a+4 …………………………………………………………… 3分 当 a =﹣1时,原式= 2×(﹣1)2-(﹣1)+4 …………………………………4分=2+1+4=7 …………………………………5分19.(9分)(1)解:1-3 x+6=4 ……………………………………………………………1分-3x=4-1-6 …………………………………………………………2分-3x=-3…………………………………………………………………3分x=1 ………………………………………………………………4分(2)解:2(2x+1)-(5x-1)=6 ………………………………………………1分4x+2-5x+1=6…………………………………………2分4x-5x=6-2-1……………………………………………3分-x=3………………………………………………4分x=-3………………………………………………5分20.(6分)(1).........2 分 (4)分俯视图左视图(2)2 (6)分21.(7分)解:(1)因为AD=8 cm,DB=2 cm,所以AB=AD+ DB=10 cm,………………1分又因为点C是线段AB的中点,所以CB=5 cm,……………………………2分所以CD=CB-DB= 3 cm;………………………………………………3分(2)画图正确…………………………………………………………………………4分因为AD=8 cm,DB=2 cm,所以AB=AD-DB=6 cm,…………5分又因为点C是线段AB的中点,所以CB= 3 cm,…………………………………6分所以CD=CB+DB=5 cm. ………………………………7分22.(6分)解:设他寄了x张明信片,根据题意得:…………………………………………1分1.2×2+0.8x=5.6 ………………………………………………………4分解得x=4 ……………………………………………………………5分答:他寄了4张明信片. ………………………………………………6分23.(6分) (1)画平行线正确,并标出了点C ………………………2分(2)画垂线正确,并标出了垂足H………………………4分(3)垂线段最短……………………………………………5分CH<OC ……………………………………………6分24.(6分)解:∵OE平分∠BOD,∴∠BOD=2∠BOE=72°. ………………………………………………2分∵∠AOC与∠BOD是对顶角,∴∠AOC=∠BOD=72°. ………………………………4分∵OF ⊥CD ,∴∠COF =90°. …………………………………………… 5分 ∴∠AOF =∠COF -∠AOC =90°-72°=18°. ……………… 6分(其它解法酌情给分)25. (7分)(1)31 …………… 2分(2)该户居民八月份用水x 吨,根据题意得: ………………………………… 3分 2.5×10+3(x -10)=40 ……………………………………………… 5分 解得 x =15 …………………………………………………………… 6分答:该户居民八月份用水15吨. ………………………………………… 7分 26.(8分) 解:(1)40° ……………………………………………………………………… 2分(2)①如图1,射线OB 与OC 多旋转了90°,则 6t -2t =90t =22.5 …………………………………………………… 4分②如图2,射线OB 与OC 多旋转了270°,则 6t -2t =270t =67.5 答:当t =22.5 或67.5时,射线OB ⊥OC . …………………………… 6分(3)因为当OB 与OC 重合时,OB 与OC 同时停止旋转.所以当OB 与OC 重合时,6t -2t =360t =90①如图3,OC 平分∠AOB ,则∠AOB =2∠AOC ,可得方程6t =2×2tA B C O 图1 AC BO 图2解得 t =0 (舍去)②如图4,OA 平分∠BOC ,则∠AOC =∠AOB , 可得方程2t =360-6t解得 t =45③如图5,OB 平分∠AOC ,则∠AOC =2∠AOB ,可得方程2t =2(6t -360)解得 t =72答:因为45<90,72<90所以存在某个时刻,使得射线OB ,OC 与OA 中的某一条射线是另两条射线所成角的角平分线,t =45或72. …………………………… 8分A C BO 图5 A BC O 图3 A C BO 图4。
2016~2017学年度第一学期期末联合体七年级答案

参考答案与评分标准二、填空题(本题共10小题,每题2分,共20分)7. 答案不唯一,如等π 8.1.7×105 9.—5; 10.6 11. >;12.18 13. 56; 14. 2或4 15.1 16.100三. 解答题(本大题共9题,共68分)17.(1)原式=-4+3+6 ……………3分(每个1分)=5 ……………4分(2)原式=-1-0.5×13×(2-9) ……………3分(每个1分) =16…………… 5分 18. (1)去括号得:2x +2=1-x -3 ……………2分移项合并得:3x =-4 …………… 3分解得:x =43- …………… 4分 (2))13(312)75(2-=+-x x …………………2分39121410-=+-x x …………………3分12143910-+-=-x x ……………4分1-=x ……………………5分19.原式=—x +6y 2-4x -8x+4y 2 …………………2分=—11x +10y 2 ……………4分当1 2-==y x 时原式=2110211)(-⨯+⨯- =-12……………………6分 20. (1)画图正确 ……………2分(2)画图正确 …………… 4分(3)20 ……………6分21. (1)24 ……………2分(2)……………6分22. 设窗的宽是x 米,则高为(x +0.5)米,由题意得:3x +2(x +0.5)=6, ……………3分解得:x =1. ……………5分则x +0.5=1.5.1×1.5=1.5答:窗户的透光面积1.5平方米. ……………7分23.(1)如∠DOF=∠BOF ; ……………2分(2)∵OE ⊥CD ,∴∠COE=90°,∴∠AOC=∠COE ﹣∠AOE=90°﹣26°=64°,∵∠AOC=∠BOD ,∴∠BOD=64°, ……………5分又∵OF 平分∠BOD ,∴∠DOF=∠BOD=×64°=32°,∴∠COF=180°﹣∠DOF=180°﹣32°=148°.……………8分24.解:参考问题1:汽车在普通公路上的行驶时间是多少h ?……………2分设汽车在普通公路上的行驶时间是x h .根据题意,得……………3分)4(90503x x -=⨯ ……………………………………………5分解得5.1=x ……………………………………7分答:汽车在普通公路上的行驶时间是1.5h .参考问题2:汽车在普通公路上的行驶路程是多少 km ?设汽车在普通公路上的行驶路程是x km .490350=+x x ,解得75=x , 答:略. (其它问题参照给分,如汽车在高速公路上的行驶时间是2.5h ,在高速公路上的行驶路程是225km ,总路程是300km )25.解:(1)是; ………………………………………………………1分(2)α31,α21,α32;(写出1个或两个给1分,写出三个给2分) ……………3分 (3)如图①,当∠MPN =2∠QPM 时,60)6010(2=-t ,解得9=t ;如图②,当∠QPN =2∠QPM 或2∠MPN 时,60210⨯=t ,解得12=t ;如图③,当∠QPM =2∠MPN 时,6026010⨯=-t .解得18=t ;所以,当t 的值为9,12,18时,射线PM 是∠QPN 的“巧分线”.…………………6分(4)4.2=t ,4=t ,6=t ………………………………………………………………………10分(提示:∠QPN=t 10,∠QPM=t t 10605-+建立三个方程)。
江苏省南京市联合体2016-2017学年度第一学期期末考试七年级语文试卷

南京市联合体2016-2017学年度第一学期期末考试七年级语文试卷注意事项:1.本试卷6页,共100分。
考试时间120分钟。
一(28分)1.用诗文原句填空,其中(4)(5)两题还需填写相关诗句的出处或作者。
(12分)(1)学而时习之,▲?(《〈论语〉十二章》)(2)晴空一鹤排云上,▲。
(刘禹锡《秋词》)(3)▲,山入潼关不解平。
(谭嗣同《潼关》)(4)▲,江春入旧年。
(王湾《▲》(出处))(5)▲,定然有美丽的街市。
(▲《天上的街市》)(6)白昼有一条神秘的航线,▲……(吴望尧《太阳船》)(7)古诗中的“雨”往往寄寓着诗人的独特情感。
如李商隐《夜雨寄北》中的“君问归期未有期,▲”,以雨衬托诗人的孤独凄凉;陆游《十一月四日风雨大作》中的“▲,铁马冰河入梦来”,则借风雨抒写作者的忧国之情。
(8)诸葛亮《诫子书》中常被人用作“志当存高远”的座右铭的句子是:▲,▲。
2. 下列加点字注音全部正确..的一项是(▲)(2分)A. 禀.告bǐng 雏.形chú 干涸.hé思想堕.落duòB. 狭隘.yì 尴.尬gān 匀称.chèn g 孪.生兄弟luánC. 惩.戒chěng 梦寐.mèi 绰.号chuò莽莽榛.榛zhēnD. 庇.护bì 蜷.伏quǎn 鄙.视bǐ随声附和.hé3.下列各项中分析不正确...的一项是(▲)(2分)不幸的是,我的太太在管教雁鹅上面花的心血,大半都被我的父亲........毁掉。
这位老先生.特别喜欢..公鹅勇敢..的骑士风度,他几乎每天都要把它们请到书房旁边、..雁鹅,尤其倾心四周..都用玻璃围起来的走廊上吃茶,无论怎么对他解说都没用。
而且那时他的视力已经很差了,一定要等到他的脚上踩满了鹅粪,他才会悟到这些客人做的好事。
(节选自劳伦兹《所罗门王的指环》)A. 这段话运用了拟人的修辞手法。
【树人】2016-2017学年第一学期初一数学期末试卷及答案
∵ 2m n 3 , ∴原式 8 2 (3)
14 . 10.如果一个角是 2015 ,那么这个角的余角是__________.
【答案】 6945 【解析】余角为: 90 2015
8960 2015 6945 .
AOC BOC 90 ,
∴ BOC AOD1 . ②∵ AOD1 BOC ,
AOD1 AOD2 180 ,
∴ AOD2 BOC 180 .
B D
登陆官网获取更多资料及课程信息:
南京中小学辅导 1对1、3人班、8人班
E C A 1 O 2 D B
F
15.如图,已知数轴上点 A 、 B 、 C 所表示的数分别为 a 、b 、 c ,点 C 是线段 AB 的中点,且 AB 2 ,
11 .某商品的进价为每件 100 元,按标价打八折售出后每件可获利 20 元,则该商品的标价每件 __________元.
【答案】 150 【解析】∵每件可获利 20 元,进价为 100 元, ∴售价为 120 元, 设标价为 x 元, ∴ x 80% 120 ,
x 150 .
12.如图是一个数值运算的程序,若输出 y 的值为 5 ,则输入的值为__________.
A
C O B
【答案】 ( 1 )如图所示射线 OD1 和射线 OD2 即为所求. ( 2 ) BOC AOD1 或 AOD2 BOC 180 【解析】 ( 1 )如图所示 射线 OD1 和射线 OD2 即为所求.
D1
A C O B
D2
( 2 )①∵ D1OC 90 , AOB 90 , ∴ AOD1 AOC 90 ,
江苏省南京市2016-2017学年七年级上学期期末模拟数学试卷

江苏省南京市2016-2017学年七年级上学期期末模拟数学试卷(满分:100分 考试时间:100分钟)一、选择题(本大题共8小题,每小题2分,共16分.) 1.-3的绝对值是 A .-13B .±3C .3D .-32.计算2–(–3) 4的结果是 ( )A . 20B .–10C . 14D . –203.下图表示某地区早晨、中午和午夜的温度(单位:℃).则下列说法正确的是A .午夜与早晨的温差是11℃B .中午与午夜的温差是0℃C .中午与早晨的温差是11℃D .中午与早晨的温差是3℃4.下列运算中,正确的是 A .-a 2b +2a 2b =a 2b B .2a -a =2C .3a 2+2a 2=5a 4D .2a +b =2ab5.已知代数式x +2y 的值是3,则代数式1-2x -4y 的值是 A .-2B .-5C . -8D .-116.下列图形中,线段PQ 的长表示点P 到直线MN 的距离是7.下左图能折叠成的长方体是8.甲、乙两城市间的铁路经过技术改造后,列车在两城市间的运行速度从100 km/h 提高到120 km/h ,运行时间缩短了2 h .若用方程描述其中数量之间的相等关系,设甲、乙两城市间的路程为x km ,则可得方程早晨 午夜 中午-7 -4 4 0 M Q N PA . MQP NC .MQP ND .M QP NB . A . B .C .D .(第7题)A .120x -100x =2B .100x -120x =2C .x 120-x100=2 D .x 100-x120=2二、填空题(本大题共10小题,每小题2分,共20分.)9. 在-4,0.5,0,π,-227,1.3 这些数中,是无理数的是 .10.若∠α=35°30',则∠α的补角的度数为 °.11.如图,将边长为a 的大正方形分割为9个相等的小正方形,则阴影部分的面积 是 (用含有a 的代数式表示,结果需化简).12.把两块三角板按图示那样拼在一起,则∠ABC = °.13.课本上有这样两个问题:如图,从甲地到乙地有3条路,走哪条路较近?从甲地到乙地能否修一条最短的路?这些问题与线段的一个基本事实相关,这个基本事实 是 .14.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.那么需要多少张餐桌拼在一起可坐90人用餐? 若设需要这样的餐桌x 张,可列方程15.有一个含a 的代数式,当a =2的时候,该代数式的值为–8,则此代数式可以为 . 16.如图, AO ⊥CO ,DO ⊥BO .若∠DOC =30º,则∠AOB 的度数为º.(第13题)(第11题)C(第12题) (第16题图)AOBDC17.如图,某长方体的表面展开图的面积为430,其中BC =5,EF =10,则AB = .18.如图,某点从数轴上的A 点出发,第1次向右移动1个单位长度至B 点,第2次从B 点向左移动2个单位长度至C 点,第3次从C 点向右移动3个单位长度至D 点,第4次从D 点向左移动4个单位长度至E 点,…,依此类推,经过 次移动后该点到原点的距离为2015个单位长度.三、计算与求解题(本大题共3小题,19题6分,20题8分,21题5分,共19分) 19.计算:(1)12+(-5)-6; (2)1-3×(-2)2÷16.20.解方程:(1)6x -7=5-5x ; (2)x -12+1=2x -23.21.先化简,再求值:7a 2b +(-4a 2b +5ab 2)-(2a 2b -3ab 2),其中a =-1,b =2.(第18题图) (第17题图)四、画图题(本大题共2小题,每小题6分,共12分) 22.画出如图所示物体的主视图、左视图、俯视图.23.三角形ABC 在方格纸中的位置如图所示.(1)将三角形ABC 向左平移5格后得到的三角形A'B'C',画出三角形A'B'C',其中点A 的对应点是A',点B 的对应点是B',点C 的对应点是C'; (2)过点C 画直线AB 的平行线l ;(3)直线l 与直线A'B'的位置关系是 .五、解答题(本大题共4小题,共33分)24.(6分)如图,直线AB 、CD 相交于点O ,OE 平分∠BOD ,∠BOE =36°.求∠AOC 的度数.(第24题)ABCDOEA BC(第23题)(第22题)正面25.(8分)一个长方形的场地,长是宽的2.5倍.现根据需要将这个长方形的场地进行扩建,若把它的长和宽各加长20m后,则它的长是宽的2倍.求扩建前长方形场地的长和宽.(请列方程解答)26.(9分)在同一平面内,如果以点、直线作为研究对象,那么点和直线的位置关系有两种——点在直线上、点在直线外,根据公共点个数的情况,不重合的两条直线的位置关系也有两种——相交(有一个公共点)、平行(没有公共点).下面我们改变对象进行研究(说明:下面的研究都是在同一平面内进行).(1)研究“射线和直线的位置关系”.已知射线AB和直线l,如果以“点A和直线l的位置关系”以及“射线AB和直线l的公共点个数的情况”作为标准,可以分为下面的四类(请把表格补充完整):(2)研究“线段和直线的位置关系”.已知线段AB和直线l,如果以“线段的端点A、B和直线l的位置关系”以及“线段AB和直线l的公共点的个数的情况”作为标准分类,你认为线段AB和直线l 有几种位置关系?请画出每一种位置关系的示意图.27.(10分)实际情境某中学七年级学生步行到郊外旅行.一班的学生组成前队,步行速度为4km/h,二班的学生组成后队,速度为6km/h.前队出发1h后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h.初步探索(1)联络员从他出发到第一次追上前队共用时h;逐步深入(2)联络员从他出发到第二次追上前队共用时多少?换个角度(3)当后队追上前队时,联络员共骑行了千米.思维发散(4)请你围绕联络员行进的时间..再提出一个与上面不同的问题并解答...或路程七年级数学参考答案及评分标准一、选择题(本大题共8小题,每小题2分,共16分)1.C 2.C 3.C 4.A 5.B 6.A 7.D 8.D 二、填空题(本大题共10小题,每小题2分,共20分)9.π 10.144.5 11.79a 2 12.120 13.两点之间线段最短 14.4x +2=90 15. 答案不唯一,如–4a 16.150 ° 17.11 18.4029或4030 三、计算与求解题(本大题共3小题,19题6分,20题8分,21题5分,共19分) 19.(本题6分)(1)解:原式=12-11 ····································································································· 2分 =1. ········································································································· 3分 (2)解:原式=1-3×4×6 ····························································································· 2分=-71. ····································································································· 3分20.(本题8分)(1)解:移项,得 6x +5x =5+7. ················································································ 2分 合并同类项,得 11x =12. ·············································································· 3分系数化为1,得 x =1211. ················································································· 4分(2)解法一:去分母,得3(x -1)+6=2(2x -2) ···························································· 1分 去括号,得3x -3+6=4x -4 ····································································· 2分 移项,合并同类项,得-x =-7 ································································ 3分 系数化为1,得x =7. ················································································ 4分解法二:去分母,得3(x -1)+6=2(2x -2) ···························································· 1分该方程可化为-(x -1)=-6 ······································································· 3分 解这个方程,得x =7. ··············································································· 4分21.(本题5分)解:原式=7a 2b -4a 2b +5ab 2-2a 2b +3ab 2 ······································································ 1分 =(7a 2b -4a 2b -2a 2b )+(5ab 2+3ab 2) ······························································· 2分 =a 2b +8ab 2. ······································································································ 3分 当a =-1,b =2时,a 2b +8ab 2=(-1)2×2+8×(-1)×22=-30. ················· 5分四、画图题(本大题共2小题,每小题6分,共12分) 22.(本题6分)解:················································································· 6分23.(本题6分)解:(1)图正确. ··············································································································· 2分 (2)图正确. ··············································································································· 4分 (3)互相平行. ··········································································································· 6分五、解答题(本大题共4小题,共33分) 24.(本题6分)解:因为OE 平分∠BOD ,∠BOE =36°,所以∠BOD =2∠BOE =72°. ······················································································ 3分 所以∠AOC =∠BOD =72°. ························································································ 6分25.(本题8分)解:设扩建前长方形场地的宽是x m ,则扩建前长方形场地的长是2.5x m . ············· 1分 根据题意,得 2.5x +20=2(x +20). ···································································· 4分 解这个方程,得x =40. ·························································································· 6分 2.5x =100. ················································································································ 7分 答:扩建前长方形场地的长是100 m ,宽是40 m . ·············································· 8分26.(本题9分)解:(1)第二幅图对位置关系的描述为:点A 在直线l 外,射线AB 和直线l 有1个公主视图左视图俯视图共点. ··················································································································· 1分第四幅示意图应为:···································································· 2分对其位置关系的描述为:点A 在直线l 上,射线AB 和直线l 有1个公共点.···································································· 3分(2)线段AB 和直线l 有5种位置关系. ················································································ 4分···································································· 9分(说明:图形正确但没有对位置关系的描述不扣分.)27.(本题10分)解:(1)12. ······················································································································· 2分 (2)方法一设联络员从追上前队开始到第一次与后队相遇共用x h .根据题意,得12x +6x =6-6×0.5.解这个方程,得x =16. ··················································································· 3分 设联络员第一次与后队相遇后再用时y h 第二次追上前队.ll ABl线段的端点A 、B 都在直线l 外,线段AB 与直线l 没有公共点线段的端点A 、B 都在直线l 外,线段AB 与直线l 有一个公共点线段的端点A 、B 都在直线l 上,线段AB 与直线l 有无数个公共点l线段的端点A 在直线l 上,线段AB 与直线l 有一个公共点 l线段的端点B 在直线l 上,线段AB 与直线l 有一个公共点根据题意,得4y =12y -12×16-4×16.解这个方程,得y =13. ··················································································· 4分 12+16+13=1.答:联络员从他出发到第二次追上前队共用1h .······································· 5分方法二设联络员从出发到第一次与后队相遇共用x h .根据题意,得12x +6x =2×12×0.5.解这个方程,得x =23. ··················································································· 3分 设联络员追上第一次前队后再用时y h 第二次追上前队. 根据题意,得4y =12y -2×12×(23-12).解这个方程,得y =12. ··················································································· 4分 12+12=1.答:联络员从他出发到第二次追上前队共用1h .······································· 5分(3)24. ····················································································································· 7分 (4)按照要求提出问题. ························································································· 8分 解决问题. ······································································································· 10分。
江苏省南京市联合体(栖霞、雨花、浦口等区)度七年级数学上学期期末考试试题(含解析) 苏科版

江苏省南京市联合体(栖霞、雨花、浦口等区)2015-2016学年度七年级数学上学期期末考试试题一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.计算|﹣3|的结果是()A.3 B. C.﹣3 D.2.一种面粉的质量标识为“50±0.25千克”,则下列面粉中合格的是()A.50.30千克B.49.51千克C.49.80千克D.50.70千克3.下列各题中合并同类项,结果正确的是()A.2a2+3a2=5a2B.2a2+3a2=6a2C.4xy﹣3xy=1 D.2x3+3x3=5x64.下列现象:(1)用两个钉子就可以把木条固定在墙上.(2)从A地到B地架设电线,总是尽可能沿着线段AB架设.(3)植树时,只要确定两棵树的位置,就能确定同一行树所在的直线.(4)把弯曲的公路改直,就能缩短路程.其中能用“两点确定一条直线”来解释的现象有()A.(1)(2) B.(1)(3) C.(2)(4) D.(3)(4)5.关于x的方程﹣ax=b(a≠0)的解是()A.x=B.x=﹣C.x=﹣D.x=6.点C在线段AB上,不能判定点C是线段中点的是()A.AC=BC B.AB=2AC C.AC+BC=AB D.AC=AB7.观察下图,请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来()A.B.C.D.8.数轴上三个点表示的数分别为p、r、s.若p﹣r=5,s﹣p=2,则s﹣r等于()A.3 B.﹣3 C.7 D.﹣7二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)9.﹣的倒数是,相反数是.10.六棱柱有面.11.马拉松(Marathon)国际上非常普及的长跑比赛项目,全程距离26英里385码,折合为42195米,用科学记数法表示42195为.12.已知∠α=34°,则∠α的补角为°.13.请列举一个单项式,使它满足系数为2,次数为3,含有字母a、b,单项式可以为.14.已知x<﹣1,则x、x2、x3的大小关系是.15.如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=63°,则∠AOD=.16.某商店在进价的基础上提高50元作零售价销售,商店又以8折(即售价的80%)的价格开展促销活动,这时一件商品所获利润为20元,则该商品进价为元.17.如图,下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么黄色的对面是.18.计算(++)﹣2×(﹣﹣﹣)﹣3×(++﹣)的结果是.三、解答题(本大题共9小题,共64分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.计算:(1)﹣11﹣(﹣3)×6;(2)[(﹣2)2﹣3 2]÷.20.先化简,再求值:2(x2﹣xy)﹣(3x2﹣6xy),其中x=,y=﹣1.21.解方程:(1)4(x﹣1)﹣3(2x+1)=7;(2)﹣1=.22.如图,已知AB=7,BC=3,点D为线段AC的中点,求线段DB的长度.23.如图是由一些棱长都为1cm的小正方体组合成的简单几何体.(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加块小正方体.24.把一些图书分给某班学生阅读,如果每人分3本则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?25.扬子江药业集团生产的某种药品的长方体包装盒的侧面展开图如图所示.根据图中数据,如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.26.几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.【回忆】如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.【探索】(1)如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.(2)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O 的位置,并说明理由.27.(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC=.(用含α与β的代数式表示)江苏省南京市联合体(栖霞、雨花、浦口等区)2015~2016学年度七年级上学期期末数学试卷参考答案与试题解析一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)1.计算|﹣3|的结果是()A.3 B. C.﹣3 D.【考点】绝对值.【分析】根据绝对值的性质进行计算.【解答】解:|﹣3|=3.故选A.【点评】本题考查了绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.2.一种面粉的质量标识为“50±0.25千克”,则下列面粉中合格的是()A.50.30千克B.49.51千克C.49.80千克D.50.70千克【考点】正数和负数.【分析】首先审清题意,明确“正”和“负”所表示的意义求出合格产品的范围,再求解即可.【解答】解:50﹣0.25=49.75,50+0.25=50.25,所以,面粉质量合格的范围是49.75~50.25,只有49.80千克在此范围内.故选C.【点评】本题考查了正数和负数,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.3.下列各题中合并同类项,结果正确的是()A.2a2+3a2=5a2B.2a2+3a2=6a2C.4xy﹣3xy=1 D.2x3+3x3=5x6【考点】合并同类项.【分析】所含字母相同且相同字母的指数也相同的项是同类项,同类项与字母的顺序无关.合并同类项的法则:系数相加减,字母与字母的指数不变.【解答】解:A、正确;B、2a2+3a2=5a2;C、4xy﹣3xy=xy;D、2x3+3x3=5x3.故选A.【点评】注意同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同.还要注意不是同类项的不能合并.4.下列现象:(1)用两个钉子就可以把木条固定在墙上.(2)从A地到B地架设电线,总是尽可能沿着线段AB架设.(3)植树时,只要确定两棵树的位置,就能确定同一行树所在的直线.(4)把弯曲的公路改直,就能缩短路程.其中能用“两点确定一条直线”来解释的现象有()A.(1)(2) B.(1)(3) C.(2)(4) D.(3)(4)【考点】直线的性质:两点确定一条直线.【分析】直接利用直线的性质以及两点确定一条直线的性质分析得出答案.【解答】解:(1)用两个钉子就可以把木条固定在墙上,根据是两点确定一条直线;(2)从A地到B地架设电线,总是尽可能沿着线段AB架设,根据是两点之间线段最短;(3)植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,根据是两点确定一条直线;(4)把弯曲的公路改直,就能缩短路程,根据是两点之间线段最短.故选:B.【点评】此题主要考查了线段以及直线的性质,正确把握相关性质是解题关键.5.关于x的方程﹣ax=b(a≠0)的解是()A.x=B.x=﹣C.x=﹣D.x=【考点】解一元一次方程.【专题】计算题;一次方程(组)及应用.【分析】方程系数化为1,即可求出解.【解答】解:方程﹣ax=b(a≠0),解得:x=﹣,故选B.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.6.点C在线段AB上,不能判定点C是线段中点的是()A.AC=BC B.AB=2AC C.AC+BC=AB D.AC=AB【考点】两点间的距离.【分析】根据线段中点的定义,结合选项一一分析,排除答案.显然A、B、D都可以确定点C是线段AB中点.【解答】解:A、AC=BC,则点C是线段AB中点;B、AB=2AC,则点C是线段AB中点;C、AC+BC=AB,则C可以是线段AB上任意一点;D、AC=AB,则点C是线段AB中点.故选:C.【点评】本题考查了两点间的距离,利用线段中点性质转化线段之间的倍分关系是解题的关键.7.观察下图,请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来()A.B.C.D.【考点】点、线、面、体.【分析】根据面动成体的原理以及空间想象力即可解.【解答】解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.故选D.【点评】考查学生立体图形的空间想象能力及分析问题,解决问题的能力.8.数轴上三个点表示的数分别为p、r、s.若p﹣r=5,s﹣p=2,则s﹣r等于()A.3 B.﹣3 C.7 D.﹣7【考点】数轴.【分析】利用已知将两式相加进而求出答案.【解答】解:∵p﹣r=5,s﹣p=2,∴p﹣r+s﹣p=5+2则s﹣r=7.故答案为:7.【点评】此题主要考查了代数式求值,正确利用已知条件相加求出是解题关键.二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)9.﹣的倒数是﹣2 ,相反数是.【考点】倒数;相反数.【分析】根据倒数,相反数的概念可知.【解答】解:﹣的倒数是﹣2,相反数是.【点评】主要考查相反数,倒数的概念及性质.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数;相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0.10.六棱柱有8 面.【考点】认识立体图形.【分析】根据六棱柱的概念和定义即解.【解答】解:六棱柱上下两个底面,侧面是6个长方形,所以共有8个面.故答案为:8.【点评】此题主要考查了认识立体图形,解决本题的关键是掌握六棱柱的构造特点.11.马拉松(Marathon)国际上非常普及的长跑比赛项目,全程距离26英里385码,折合为42195米,用科学记数法表示42195为 4.2195×104.【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将42195用科学记数法表示为4.2195×104.故答案为:4.2195×104.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.已知∠α=34°,则∠α的补角为146 °.【考点】余角和补角.【分析】直接利用互补两角的定义得出答案.【解答】解:∵∠α=34°,∴∠α的补角为:146°.故答案为:146.【点评】此题主要考查了互补两角的定义,正确把握定义是解题关键.13.请列举一个单项式,使它满足系数为2,次数为3,含有字母a、b,单项式可以为2a2b .【考点】单项式.【专题】开放型.【分析】要根据单项式系数和次数的定义来写,单项式中数字因数叫做单项式的系数,所有字母指数的和是单项式的次数.【解答】解:根据单项式系数和次数的定义,一个含有字母a、b且系数为﹣2,次数为3的单项式可以写为:2a2b.故答案为:2a2b.【点评】此题主要考查了单项式,要注意所写的单项式一定要符合单项式系数和次数的定义.14.已知x<﹣1,则x、x2、x3的大小关系是x3<x<x2.【考点】有理数大小比较.【专题】推理填空题;实数.【分析】首先判断出x<﹣1时,x<0,x2>0,x3<0;然后应用作差法,判断出x<﹣1时,x3<x,即可推得x、x2、x3的大小关系.【解答】解:∵x<﹣1时,x<0,x2>0,x3<0,∴x<x2,x3<x2,∵x<﹣1时,x2>1,∴x2﹣1>0,∴x3﹣x=x(x2﹣1)<0,∴x3<x,∴x3<x<x2.故答案为:x3<x<x2.【点评】(1)此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.(2)解答此题的关键是应用作差法,判断出x3、x的大小关系.15.如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=63°,则∠AOD=117°.【考点】余角和补角.【分析】利用互余的定义得出∠AOC的度数,进而求出∠AOD的度数.【解答】解:∵将一副三角板的直角顶点重合,∴∠AOB=∠COD=90°,∵∠BOC=63°,∴∠AOC=27°,∴∠AOD=117°.故答案为:117°.【点评】此题主要考查了互余两角的定义,正确掌握互余两角的定义是解题关键.16.某商店在进价的基础上提高50元作零售价销售,商店又以8折(即售价的80%)的价格开展促销活动,这时一件商品所获利润为20元,则该商品进价为100 元.【考点】一元一次方程的应用.【分析】设该商品进价为x元,则售价为(x+50)×80%,进一步利用售价﹣进价=利润列出方程解答即可.【解答】解:设该商品进价为x元,由题意得(x+50)×80%﹣x=20解得:x=100答:该商品进价为100元.故答案为:100.【点评】此题考查一元一次方程的实际运用,掌握销售问题中基本数量关系是解决问题的关键.17.如图,下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么黄色的对面是绿色.【考点】专题:正方体相对两个面上的文字.【分析】由图可得与黄色相邻的颜色分别为红、蓝、白、黑,即可得出与黄色相对的颜色.【解答】解:由图可得与黄色相邻的颜色分别为红、蓝、白、黑,故与黄色相对的颜色是绿色.故答案为:绿色.【点评】本题考查灵活运用正方体的相对面解答问题,立意新颖,是一道不错的题.18.计算(++)﹣2×(﹣﹣﹣)﹣3×(++﹣)的结果是﹣.【考点】有理数的混合运算.【专题】计算题;实数.【分析】原式利用乘法分配律计算,即可得到结果.【解答】解:原式=++﹣1+++﹣﹣﹣+=+(+﹣)+(+﹣)+(﹣1++﹣)=﹣+=﹣,故答案为:﹣【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.三、解答题(本大题共9小题,共64分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.计算:(1)﹣11﹣(﹣3)×6;(2)[(﹣2)2﹣3 2]÷.【考点】有理数的混合运算.【专题】计算题;实数.【分析】(1)原式先计算乘法运算,再计算加减运算即可得到结果;(2)原式先计算乘方运算,再计算乘除运算,最后计算加减运算即可得到结果.【解答】解:(1)原式=﹣11﹣(﹣18)=﹣11+18=7;(2)原式=(4﹣9)×=﹣5×=﹣6.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.20.先化简,再求值:2(x2﹣xy)﹣(3x2﹣6xy),其中x=,y=﹣1.【考点】整式的加减—化简求值.【专题】计算题;整式.【分析】原式去括号合并得到最简结果,将x与y的值代入计算即可求出值.【解答】解:原式=2x2﹣2xy﹣3x2+6xy=﹣x2+4xy,当x=,y=﹣1时,原式=﹣x2+4xy=﹣.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.21.解方程:(1)4(x﹣1)﹣3(2x+1)=7;(2)﹣1=.【考点】解一元一次方程.【专题】计算题;一次方程(组)及应用.【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)去括号得:4x﹣4﹣6x﹣3=7,移项合并得:﹣2x=14,解得:x=﹣7;(2)去分母得:3x+3﹣6=4﹣2x,移项合并得:5x=7,解得:x=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.22.如图,已知AB=7,BC=3,点D为线段AC的中点,求线段DB的长度.【考点】两点间的距离.【分析】根据线段的和差,可得AC的长,根据线段中点的性质,可得AD的长,再根据线段的和差,可得答案.【解答】解:由线段的和差,得AC=AB+BC=7+3=10.由D为线段AC的中点,得AD=AC=×10=5.由线段的和差,得DB=AB﹣AD=7﹣5=2,线段DB的长度为2.【点评】本题考查了两点间的距离,利用线段中点的性质得出AD长是解题关键.23.如图是由一些棱长都为1cm的小正方体组合成的简单几何体.(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加 6 块小正方体.【考点】作图-三视图;由三视图判断几何体.【分析】(1)左视图有2列,每列小正方数形数目分别为3,1,俯视图有4列,每列小正方形数目分别为2,1,1,1.据此可画出图形.(2)持俯视图和左视图不变,可以在第1列后面一排添加2个,第3列添加2个,第4列添加2个,最多添加6个小正方体.【解答】解:(1)如图所示:;(2)保持俯视图和左视图不变,最多可以再添加6块小正方体,故答案为:6.【点评】此题主要考查了作三视图,在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.24.把一些图书分给某班学生阅读,如果每人分3本则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?【考点】一元一次方程的应用.【分析】可设有x名学生,根据总本数相等和每人分3本,剩余20本,每人分4本,缺25本可列出方程,求解即可.【解答】解:设有x名学生,根据书的总量相等可得:3x+20=4x﹣25,解得:x=45.答:这个班有45名学生.【点评】本题考查了一元一次方程的应用,根据该班人数表示出图书数量得出等式方程是解题关键.25.扬子江药业集团生产的某种药品的长方体包装盒的侧面展开图如图所示.根据图中数据,如果长方体盒子的长比宽多4cm,求这种药品包装盒的体积.【考点】一元一次方程的应用.【分析】由图可知:设宽为xcm,则长为(x+4)cm,高为(18﹣x),根据长、宽、高的和为37列出方程,进一步利用长方体的体积计算方法解答即可.【解答】解:设宽为xcm,则长为(x+4)cm,高为(18﹣x),由题意得:2(x+4)+x+(18﹣x)=37解得:x=8…则x+4=12,(18﹣x)=58×5×12=480(cm3)答:这种药品包装盒的体积为480cm3.【点评】此题考查一元一次方程的实际运用,长方体的体积计算公式,看清图意,找出长、宽、高之间的关系是解决问题的关键.26.几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.【回忆】如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.【探索】(1)如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.(2)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O 的位置,并说明理由.【考点】作图—应用与设计作图.【分析】【回忆】根据两点之间线段最短即可确定;【探索】(1)根据垂线段最短即可解答;(2)根据两点之间线段最短即可解答.【解答】解:【回忆】如图所示:理由:两点之间线段最短;【探索】(1)如图所示:理由:点到直线的距离垂线段最短;(2)如图所示:理由:两点之间线段最短(到OA、OC最短在AC上;到OB、OD最短在BD上).【点评】本题考查了应用、作图设计,正确理解两点之间,线段最短是解决本题的关键.27.(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC=.(用含α与β的代数式表示)【考点】角的计算;角平分线的定义.【分析】(1)根据垂直的定义得到∠AOC=∠BOC=90°,根据角平分线的定义即可得到结论;(2)根据角平分线的定义得到∠EOD=∠AOD=×(80+β)=40+β,∠COF=∠BOC=×(80+β)=40+β,根据角的和差即可得到结论;(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE=(α+β),即可得到结论.【解答】解:(1)∵CO⊥AB,∴∠AOC=∠BOC=90°,∵OE平分∠AOC,∴∠EOC=∠AOC=×90°=45°,∵OF平分∠BOC,∴∠COF=∠BOC=×90°=45°,∠EOF=∠EOC+∠COF=45°+45°=90°;(2)∵OE平分∠AOD,∴∠EOD=∠AOD=×(80+β)=40+β,∵OF平分∠BOC,∴∠COF=∠BOC=×(80+β)=40+β,∠COE=∠EOD﹣∠COD=40+β﹣β=40﹣β;∠EOF=∠COE+∠COF=40﹣β+40+β=80°;(3)如图2,∵∠AOC=∠BOD=α,∠COD=β,∴∠AOD=α+β,∵OE平分∠AOD,∴∠DOE=(α+β),∴∠COE=∠DOE﹣∠COD==,如图3,∵∠AOC=∠BOD=α,∠COD=β,∴∠AOD=α+β,∵OE平分∠AOD,∴∠DOE=(α﹣β),∴∠COE=∠DOE+∠COD=.综上所述:,故答案为:.【点评】本题考查了角平分线的定义,角的计算,解题的关键是找出题中的等量关系列方程求解.。
2016—2017学年度南京联合体新初一上英语期末试题答卷含参考答案

2016—2017学年度第一学期期末学情检测卷七年级英语2017.01考试时间:100分钟满分:100分(将答案按序号填在答卷纸上............)选择题共50分1.WhatdoesSandyhaveforlunch?A. B. C.2.WhichisNancy’sfavouritefestival?A. B. C.3.WhatdoesthegirlbuyforJack?A. B. C.4.WhatdoesMillielikedoingafterclass?A. B. C.5.Wherewilltheygo?听对话,回答问题。
听下面的对话,每段对话后有几个小题,请根据你所听到的内容,从题中所给B、C三个选项中选出最佳选项。
听每段对话前,你将有时间阅读各个小题,5秒钟;听完后,你仍有秒钟的时间答题。
每段对话听两遍。
6.WhatcolourisPeter’smask?sbrown. B.It syellow. C.It sblack.B.Twiceaweek.C.Never.8.Wherearethespeakerstalking?A.Onabus.B.Inarestaurant.C.Inahospital.9.Howmanystudentsdon’thavethebooks?A.Forty.B.Twenty-five.C.Fifteen.10.Whatdoesthemanthinkoftheskirt?A.Itiscolourfulandnice.B.Itmatchestheblouseverywell.C.Itistoocolourfulanddoesnotgowellwiththeblouse.C)听短文,回答问题。
听下面的短文,短文后有几个小题,请根据你所听到的内容,从题中所给的A、B、C三个选项中选出最佳选项。
听短文前,你将有时间阅读各个小题,每小题5秒钟;听完后,你仍有5秒钟的时间答题。
2016~2017学年度第一学期期末秦淮区七年级答案

2016—2017学年度第一学期第二阶段学业质量监测试卷七年级数学参考答案及评分标准说明:本评分标准每题给出了一种或几种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.一、选择题(每小题2分,共16分)二、填空题(每小题2分,共20分)9.7 10.< 11.-1 12.答案不唯一,如:(a +b )2=2ab +a 2+b 2 13.-2 14.75 15.6 (说明:如果学生写6 cm 不给分) 16.两点之间线段最短 17. (1+20%)x =200×0.9 18.50n三、解答题(共64分) 19.(8分)解:(1)原式=48÷[-8+4] ························································································ 2分=48÷(-4) ····························································································· 3分 =-12. ································································································· 4分(2)原式=-8÷49×49+1 ························································································· 6分=-8+1 ································································································· 7分 =-7. ·································································································· 8分20.(6分)解: 原式=x 2+2xy -3y 2-2x 2-2xy +4y 2 ········································································· 2分=-x 2+y 2. ································································································· 4分 当x =1,y =2时,原式=-12+22=-1+4=3. ················································································· 6分21.(8分)解:(1)5x -5-2+2x =3+2x . ···················································································· 2分5x +2x -2x =3+5+2.5x =10. ······································································································· 3分 x =2. ·········································································································· 4分 (2) x +1-2=2-3x . ··························································································· 5分x +3x =2+2-1. ··························································································· 6分 4x =3.········································································································· 7分 x =34. ·········································································································· 8分22.(6分)解:如图所示. ·········································································································· 6分 (说明:每个视图画对得2分.)23.(6分)解:(1)∠AOC 、∠BOD 、∠EOF . ············································································· 3分(2)因为∠AOE =90°,所以∠BOE =180°-∠AOE =90°.因为∠DOE =70°,所以∠BOD =∠BOE -∠DOE =20°. ································································ 4分 因为∠COF =90°,所以∠DOF =180°-∠COF =90°.所以∠BOF =∠BOD +∠DOF =110°. ······························································ 6分 24.(6分)解: 设该校原有参赛男生x 人. ·················································································· 1分根据题意,得 x +2=23(2x +2). ············································································ 4分解这个方程,得 x =2. ······················································································· 5分 答:该校原有参赛男生2人. ··············································································· 6分25.(7分)解:(1)画图正确. ···································································································· 2分 (2)画图正确. ····································································································· 3分 (3)画图正确. ····································································································· 5分MP ,互相垂直. ·······························································································7分 26.(7分)解:(1)10; ············································································································· 1分αACMPONB俯视图主视图 左视图(2)设运动t 秒后,C 、P 、Q 三点中,有一点恰好是以另两点为端点的线段的中点.①若C 是PQ 的中点,则10-2t =6-t .解得t =4. ···································································································· 3分 ②若P 是CQ 的中点,则2t -10=12(6-t ).解得t =265. ·································································································· 5分③若Q 是CP 的中点,则2t -10=2(6-t ). 解得t =112.综上,运动4、265或112秒后,C 、P 、Q 三点中,有一点恰好是以另两点为端点的线段的中点. ············································································································ 7分27.(10分)解:(1)同. ············································································································· 2分(2)设A 、B 两地之间的距离为x km . ··································································· 3分根据题意,得x 200-x300=7-6+1. ··································································· 4分 解这个方程,得 x =1200. ··············································································· 5分 答:A 、B 两地之间的距离为1200 km . ······························································ 6分 (3)根据题意,可列出动车、高铁进出各站点的时刻表:因为高铁途经P 1站的时刻:7∶40,高铁途经P 3站的时刻:9∶05, 所以在从P 2站点开往P 3站点的途中,高铁追上动车. 设该列高铁出发y h 追上动车.根据题意,得 300(y -560)=200(y +1-1060). ························································ 8分解这个方程,得 y =2312. ················································································· 9分2312小时=1小时55分 答:该列高铁追上动车的时刻是8时55分. ····················································· 10分。
最新南京2017七年级上学期期末试卷(联合体)

2017/2018学年度第一学期期末测试试卷七年级数学(满分:100分 考试时间:100分钟)注意:1.选择题答案请用2B 铅笔填涂在答题卡...相应位置....上. 2.非选择题答案必须用0.5毫米黑色墨水签字笔写在答题卷上的指定位置,在其他位置答题一律无效.一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号涂在答题..卡.相应位置上.....) 1.-3的倒数为A. -3B. 3C. 13D. -132.一种面粉的质量标识为“50±0.25千克”,则下列面粉中合格的是 A. 50.30千克 B. 49.51千克C. 49.80千克D. 50.70千克3.计算-6÷12×2-18÷(-6)的结果是A .-21B .-3C .4D .74下列各题中合并同类项,结果正确的是A. 2a 2+3a 2=5a 2B. 2a 2+3a 2=6a 2C. 4xy -3xy =1D. 2x 3+3x 3=5x 65.某种商品的进价为18元,标价为x 元,由于该商品积压,商店准备按标价的8折销售,可保证利润率达到20%,则标价为A .26元B .27元C .28元D .29元 6. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有6条棱.该模型的形状对应的立体图形可能是A .三棱柱B .四棱柱C .三棱锥D .四棱锥7. 用一副直角三角板,不能画出的角是A. 15°B.75°C. 165°D. 145°8.球赛入场券有10元、15元、20元三种票价,老师用480元买了40张入场券,其中票价为10元的比票价为20元的多的张数是A .12B .16C .20D .24二、填空题(本大题共8小题,每小题2分,共16分.不需写出解答过程,请把答案直接填写在答题..卷.相应位置....上) 9.计算:||-3= ▲ ;-(-3)= ▲ .10.2016年南京实现GDP 约10 500亿元,成为全国第11个经济总量超过万亿的城市.用科学记数法表示10 500是 ▲ .11.已知点A 、B 在数轴上对应的数分别为-7和4,点C 是线段AB 的中点,则点C 表示的数为 ▲ .12.已知x =-1是方程2ax -5=a -3的解,则a = ▲ . 13.已知a -2b =3,则7-3a +6b = ▲ .14.下列三个日常现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上,老师测量某个同学的跳远成绩.其中,可以用“两点之间,线段最短”来解释的现象是 ▲ (填序号).15.如图是正方体的展开图,则原正方体相对两个面上的数字之和最大的值是 ▲ .16.如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC =65°,则∠AOD =▲ °.17.已知∠2是∠1的余角、∠3是∠1的补角,则∠3比∠2大 ▲ °.18.如图,把一张长方形纸条ABCD 沿EF 折叠,若∠BFC ′比∠BFE 多6°,则∠EFC = ▲ °.AEDCFGB D 'C '(第18题)(第15题)(第16题)AOBCD三、解答题(本大题共10小题,共64分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤) 19.计算(每题4分,共8分)(1)331⨯-+⎪⎭⎫ ⎝⎛-⨯316;(2)])2(6[21)1(32--⨯÷-.20.解方程(每题4分,共12分) (1)3(x -1)-4(2x +1)=7;(2)x -12-1=2+x 3;(3)⎩⎪⎨⎪⎧x +3y =-1,3x -2y =8.21.(4分)先化简,再求值:12 x -2 ⎝⎛⎭⎫x -13 y 2+⎝⎛⎭⎫-32 x +13 y 2,其中x =-2,y =23 .22.(5分)如图,读句画图,并回答问题 (1)画钝角△ABC 的高CD ;根据 ▲ ,因此CD ▲ AC ;(填>、<、=、≤、≥)(2)以△ABC 的边CB 上的点P 为顶点,用直尺与圆规画∠BPE =∠C ,∠BPE 的边PE 交线段AB 与点E .PE 与AC 的位置关系是 ▲ .(第22题)23.(5分)如图是由一些棱长都为1cm 的小正方体组合成的简单几何体. (1)请在下面方格纸中分别画出它的三视图;(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加 块小正方体.24.(6分)(1)列举两个实数,满足这两个数的和为正数,积为负数。
2016-2017学年度七年级(上)期末数学试卷含答案解析

2016-2017学年度七年级(上)期末数学试卷一、选择题1.如果水位升高7m时水位变化记作+7m,那么水位下降4m时水位变化记作()A.﹣3m B.3m C.﹣4m D.10m2.在2016年11月3日举行的第九届中国四部投资说明会上,现场签约116个项目,投资金额达130 944 000 000元,将130 944 000 000用科学记数法表示为()A.1.30944×1012B.1.30944×1011C.1.30944×1010D.1.30944×109 3.下列调查中,最适宜用普查方式的是()A.对一批节能灯使用寿命的调查B.对我国初中学生视力状况的调查C.对最强大脑节目收视率的调查D.对量子科卫星上某种零部件的调查4.若﹣4x m+2y4与2x3y n﹣1为同类项,则m﹣n()A.﹣4 B.﹣3 C.﹣2 D.﹣25.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是()A.B.C.D.6.已知x=3是关于x的方程5(x﹣1)﹣3a=﹣2的解,则a的值是()A.﹣4 B.4 C.6 D.﹣67.如图,点C在线段AB上,点D是AC的中点,如果CB=CD,AB=10.5cm,那么BC的长为()A.A2.5cm B.3cm C.4.5cm D.6cm8.如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么x﹣2y+z的值是()A.1 B.4 C.7 D.99.某种商品因换季准备打折出售,如果按照原定价的七五折出售,每件将赔10元,而按原定价的九折出售,每件将赚38元,则这种商品的原定价是()A.200元B.240元C.320元D.360元10.下列图形都是由同样大小的⊙按一定规律所组成的,其中第1个图形中一共有5个⊙,第2个图形中一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第1001个图形中基本图形的个数为()A.2998 B.3001 C.3002 D.3005二、填空题(共4小题,每小题3分,共12分)11.计算:18°36′=°.12.九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是.13.现定义新运算“※”,对任意有理数a、b,规定a※b=ab+a﹣b,例如:1※2=1×2+1﹣2=1,则计算3※(﹣5)=.14.如图是一个运算程序,若输入x的值为8,输出的结果是m,若输入x的值为3,输出的结果是n,则m﹣2n=.三、解答题(共78分)15.(5分)计算:75×(﹣)2﹣24÷(﹣2)3+4×(﹣2)16.(5分)解方程:=1+.17.(5分)如图,已知线段a、b,求作线段AB,使AB=2a+b.18.(5分)先化简,再求值:2(3xy2﹣2x2y)﹣3(2xy2﹣x2y)+4(xy2﹣2x2y),其中x=﹣2,y=﹣1.19.(7分)一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.20.(7分)如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.21.(7分)如图所示,已知数轴上两点A、B对应的数分别为﹣2、4,点P为数轴上一动点.(1)写出点A对应的数的倒数和绝对值;(2)若点P到点A,点B的距离相等,求点P在数轴上对应的数;(3)将点B向左移动7个单位长度,再向右移动2个单位长度,得到点C,在数轴上画出点C,并写出点C表示的是数.22.(7分)某企业已收购毛竹90吨,根据市场信息,如果对毛竹进行粗加工,每天可加工8吨,每吨可获利60元;如果进行精加工,每天可加工0.5吨,每吨可获利1200元.由于条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)内将这批毛竹全部销售,现将部分毛竹精加工,其余毛竹粗加工,并且恰好用30天完成.(1)求精加工和粗加工的天数;(2)该企业总共获得的利润是多少元?23.(8分)某市对市民看展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A:绿化造林B:汽车限行C:拆除燃煤小锅炉D:使用清洁能源.调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:(1)这次被调查的市民共有多少人?(2)请你将统计图1补充完整;(3)求图2中D项目对应的扇形的圆心角的度数.24.(10分)某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,巡逻了一段时间停留在A处,规定以岗亭为原点,向北方向为正,这段时间行驶记录如下(单位:千米):+10,﹣9,+7,﹣15,+6,﹣14,+4,﹣2(1)A在岗亭哪个方向?距岗亭多远?(2)若摩托车行驶1千米耗油0.12升,且最后返回岗亭,摩托车共耗油多少升?25.(12分)为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现,甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球,乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)求每套队服和每个足球的价格是多少?(2)若城区四校联合购买100套队服和a(a>10)个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)在(2)的条件下,若a=60,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?2016-2017学年度七年级(上)期末数学试卷参考答案与试题解析一、选择题1.如果水位升高7m时水位变化记作+7m,那么水位下降4m时水位变化记作()A.﹣3m B.3m C.﹣4m D.10m【考点】正数和负数.【分析】水位升高7m记作﹢7m,升高和下降是互为相反意义的量,所以水位下降几m就记作负几m.【解答】解:上升和下降是互为相反意义的量,若上升记作正,那么下降就记作负.水位升高7m时水位变化记作+7m,那么水位下降4m时水位变化记作﹣4m.故选C.【点评】本题考查了正负数在生活中的应用.理解互为相反意义的量是关键.2.在2016年11月3日举行的第九届中国四部投资说明会上,现场签约116个项目,投资金额达130 944 000 000元,将130 944 000 000用科学记数法表示为()A.1.30944×1012B.1.30944×1011C.1.30944×1010D.1.30944×109【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n 是负数.【解答】解:将130 944 000 000用科学记数法表示为:1.30944×1011.故选B.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.下列调查中,最适宜用普查方式的是()A.对一批节能灯使用寿命的调查B.对我国初中学生视力状况的调查C.对最强大脑节目收视率的调查D.对量子科卫星上某种零部件的调查【考点】全面调查与抽样调查.【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.【解答】解:A、对一批节能灯使用寿命的调查,调查具有破坏性,适合抽样调查,故A错误;B、对我国初中学生视力状况的调查,调查范围广适合抽样调查,故B错误;C、对最强大脑节目收视率的调查,调查范围广适合抽样调查,故C错误;D、对量子科卫星上某种零部件的调查,要求精确度高的调查,适合普查,故D 正确;故选:D.【点评】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.4.若﹣4x m+2y4与2x3y n﹣1为同类项,则m﹣n()A.﹣4 B.﹣3 C.﹣2 D.﹣2【考点】同类项.【分析】根据同类项:所含字母相同,并且相同字母的指数也相同,可得关于m 和n的方程,解出可得出m和n的值,代入可得出代数式的值.【解答】解:∵﹣4x m+2y4与2x3y n﹣1是同类项,∴m+2=3,n﹣1=4,解得:m=1,n=5,∴m ﹣n=﹣4.故选A .【点评】此题考查了同类项的知识,属于基础题,解答本题的关键是掌握同类项:所含字母相同,并且相同字母的指数也相同,难度一般.5.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是( )A .B .C .D .【考点】点、线、面、体.【分析】如图本题是一个平面图形围绕一条边为中心对称轴旋转一周根据面动成体的原理即可解.【解答】解:由长方形绕着它的一边所在直线旋转一周可得到圆柱体,如图立体图形是两个圆柱的组合体,则需要两个一边对齐的长方形,绕对齐边所在直线旋转一周即可得到, 故选:A .【点评】本题考查面动成体,需注意可把较复杂的体分解来进行分析.6.已知x=3是关于x 的方程5(x ﹣1)﹣3a=﹣2的解,则a 的值是( ) A .﹣4 B .4 C .6 D .﹣6【考点】一元一次方程的解.【分析】把x=3代入方程得出关于a 的方程,求出方程的解即可.【解答】解:把x=3代入方程5(x ﹣1)﹣3a=﹣2得:10﹣3a=﹣2,解得:a=4,故选B .【点评】本题考查了一元一次方程的解,解一元一次方程等知识点,能得出关于a的一元一次方程是解此题的关键.7.如图,点C在线段AB上,点D是AC的中点,如果CB=CD,AB=10.5cm,那么BC的长为()A.A2.5cm B.3cm C.4.5cm D.6cm【考点】两点间的距离.【分析】根据线段中点的性质,可得DA与CD的关系,根据线段的和差,可得关于BC的方程,根据解方程,可得答案.【解答】解:由CB=CD,得CD=BC.由D是AC的中点,得AD=CD=BC.由线段的和差,得AD+CD+BC=AB,即BC+BC+BC=10.5.解得BC=4.5cm,故选:C.【点评】本题考查了两点间的距离,利用线段的和差得出关于BC的方程是解题关键.8.如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么x﹣2y+z的值是()A.1 B.4 C.7 D.9【考点】专题:正方体相对两个面上的文字;相反数.【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点确定出相对面,再求出x、y、z的值,然后代入代数式计算即可得解.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“x”与“﹣8”是相对面,“y”与“﹣2”是相对面,“z”与“3”是相对面,∵相对面上所标的两个数互为相反数,∴x=8,y=2,z=﹣3,∴x﹣2y+z=8﹣2×2﹣3=1.故选:A.【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.9.某种商品因换季准备打折出售,如果按照原定价的七五折出售,每件将赔10元,而按原定价的九折出售,每件将赚38元,则这种商品的原定价是()A.200元B.240元C.320元D.360元【考点】一元一次方程的应用.【分析】如果设这种商品的原价是x元,本题中唯一不变的是商品的成本,根据利润=售价﹣成本,即可列出方程求解.【解答】解:设这种商品的原价是x元,根据题意得:75%x+10=90%x﹣38,解得x=320.故选C.【点评】本题考查了一元一次方程的应用.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.10.下列图形都是由同样大小的⊙按一定规律所组成的,其中第1个图形中一共有5个⊙,第2个图形中一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第1001个图形中基本图形的个数为()A.2998 B.3001 C.3002 D.3005【考点】规律型:图形的变化类.【分析】将原图形中基本图形划分为中间部分和两边部分,中间基本图形个数等于序数,两边基本图形的个数和等于序数加1的两倍,据此规律可得答案.【解答】解:∵第①个图形中基本图形的个数5=1+2×2,第②个图形中基本图形的个数8=2+2×3,第③个图形中基本图形的个数11=3+2×4,第④个图形中基本图形的个数14=4+2×5,…∴第n个图形中基本图形的个数为n+2(n+1)=3n+2当n=1001时,3n+2=3×1001+2=3005,故选:D.【点评】本题考查了图形的变化类,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,解决本题的关键在于将原图形划分得出基本图形的数字规律.二、填空题(共4小题,每小题3分,共12分)11.计算:18°36′=18.6°.【考点】度分秒的换算.【分析】根据小单位华大单位除以进率,可得答案.【解答】解:18°36′=18°+(36÷60)°=18.6°,故答案为:18.6.【点评】本题考查了度分秒的换算,利用小单位华大单位除以进率是解题关键.12.九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是92%.【考点】频数(率)分布直方图.【分析】利用合格的人数即50﹣4=46人,除以总人数即可求得.【解答】解:该班此次成绩达到合格的同学占全班人数的百分比是×100%=92%.故答案是:92%.【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.13.现定义新运算“※”,对任意有理数a、b,规定a※b=ab+a﹣b,例如:1※2=1×2+1﹣2=1,则计算3※(﹣5)=﹣7.【考点】有理数的混合运算.【分析】根据※的含义,以及有理数的混合运算的运算方法,求出3※(﹣5)的值是多少即可.【解答】解:3※(﹣5)=3×(﹣5)+3﹣(﹣5)=﹣15+3+5=﹣7故答案为:﹣7.【点评】此题主要考查了定义新运算,以及有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.14.如图是一个运算程序,若输入x的值为8,输出的结果是m,若输入x的值为3,输出的结果是n,则m﹣2n=16.【考点】代数式求值.【分析】先求出m、n的值,再代入求出即可.【解答】解:∵x=8是偶数,∴代入﹣x+6得:m=﹣x+6=﹣×8+6=2,∵x=3是奇数,∴代入﹣4x+5得:n=﹣4x+5=﹣7,∴m﹣2n=2﹣2×(﹣7)=16,故答案为:16.【点评】本题考查了求代数式的值,能根据程序求出m、n的值是解此题的关键.三、解答题(共78分)15.计算:75×(﹣)2﹣24÷(﹣2)3+4×(﹣2)【考点】有理数的混合运算.【分析】根据有理数的混合运算的运算方法,求出算式的值是多少即可.【解答】解:75×(﹣)2﹣24÷(﹣2)3+4×(﹣2)=3﹣24÷(﹣8)+4×(﹣2)=3+3﹣8=﹣2【点评】此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.16.解方程:=1+.【考点】解一元一次方程.【分析】方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:去分母得:3x+6=12+8x+4,移项合并得:﹣5x=10,解得:x=﹣2.【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.17.如图,已知线段a、b,求作线段AB,使AB=2a+b.【考点】作图—复杂作图.【分析】在射线AM上延长截取AC=CD=a,DB=b,则线段AB满足条件.【解答】解:如图,线段AB为所作.【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.18.先化简,再求值:2(3xy2﹣2x2y)﹣3(2xy2﹣x2y)+4(xy2﹣2x2y),其中x=﹣2,y=﹣1.【考点】整式的加减—化简求值.【分析】原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.【解答】解:原式=6xy2﹣4x2y﹣6xy2+3x2y+4xy2﹣8x2y=4xy2﹣9x2y,当x=﹣2,y=﹣1时,原式=﹣8+36=28.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.19.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.【考点】作图-三视图;由三视图判断几何体.【分析】主视图有3列,每列小正方形数目分别为3,4,2,左视图有2列,每列小正方数形数目分别为4,2,据此可画出图形.【解答】解:如图所示:.【点评】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.20.如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.【考点】角平分线的定义.【分析】先根据角平分线,求得∠BOE的度数,再根据角的和差关系,求得∠BOF 的度数,最后根据角平分线,求得∠BOC、∠AOC的度数.【解答】解:∵∠AOB=90°,OE平分∠AOB∴∠BOE=45°又∵∠EOF=60°∴∠FOB=60°﹣45°=15°∵OF平分∠BOC∴∠COB=2×15°=30°∴∠AOC=∠BOC+∠AOB=30°+90°=120°【点评】本题主要考查了角平分线的定义,根据角的和差关系进行计算是解题的关键.注意:也可以根据∠AOC的度数是∠EOF度数的2倍进行求解.21.如图所示,已知数轴上两点A、B对应的数分别为﹣2、4,点P为数轴上一动点.(1)写出点A对应的数的倒数和绝对值;(2)若点P到点A,点B的距离相等,求点P在数轴上对应的数;(3)将点B向左移动7个单位长度,再向右移动2个单位长度,得到点C,在数轴上画出点C,并写出点C表示的是数.【考点】数轴;绝对值;倒数.【分析】(1)根据倒数的定义和绝对值的性质可得点A对应的数的倒数和绝对值;(2)根据中点坐标公式可得点P在数轴上对应的数;(3)根据将点B向左移动7个单位长度,再向右移动2个单位长度,得到点C,可以得到点C表示的数,从而可以在数轴上表示出点C,并得到点C表示的数.【解答】解:(1)点A对应的数的倒数是﹣,点A对应的数的绝对值是2;(2)(﹣2+4)÷2=2÷2=1.故点P在数轴上对应的数是1;(3)如图所示:点C表示的数是﹣1.【点评】本题考查数轴、倒数、绝对值,解题的关键是明确数轴的含义,利用数形结合的思想解答问题.22.某企业已收购毛竹90吨,根据市场信息,如果对毛竹进行粗加工,每天可加工8吨,每吨可获利60元;如果进行精加工,每天可加工0.5吨,每吨可获利1200元.由于条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)内将这批毛竹全部销售,现将部分毛竹精加工,其余毛竹粗加工,并且恰好用30天完成.(1)求精加工和粗加工的天数;(2)该企业总共获得的利润是多少元?【考点】一元一次方程的应用.【分析】(1)设粗加工的天数为x天,则精加工的天数为(30﹣x)天,根据总质量=粗加工质量+精加工质量即可得出关于x的一元一次方程,解之即可得出结论;(2)根据总利润=粗加工的利润+精加工的利润代入数据即可得出结论.【解答】解:(1)设粗加工的天数为x天,则精加工的天数为(30﹣x)天,根据题意得:8x+0.5(30﹣x)=90,解得:x=10,30﹣x=20.答:粗加工的天数为10天,精加工的天数为20天.(2)10×8×60+20×0.5×1200=16800(元).答:该企业总共获得的利润是16800元.【点评】本题考查了一元一次方程的应用,根据数量关系列出一元一次方程(或列式计算)是解题的关键.23.某市对市民看展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A:绿化造林B:汽车限行C:拆除燃煤小锅炉D:使用清洁能源.调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:(1)这次被调查的市民共有多少人?(2)请你将统计图1补充完整;(3)求图2中D项目对应的扇形的圆心角的度数.【考点】条形统计图;扇形统计图.【分析】(1)根据A组有20人,所占的百分比是10%,据此即可求得总人数;(2)用(1)中求得的总人数减去其它三种的人数可得认同拆除燃煤小锅炉的人数,再补充统计图1即可;(3)用D项目对应的人数除以总人数,再乘以360度即可得对应的扇形的圆心角.【解答】解:(1)20÷10%=200(人).答:这次被调查的市民总人数是200人;(2)C组的人数是:200﹣20﹣80﹣40=60(人),统计图1补充如下:;(3)×360°=72°.答:图2中D项目对应的扇形的圆心角的度数是72°.【点评】本题主要考查了条形统计图的应用和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.24.(10分)(2016秋•榆林期末)某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,巡逻了一段时间停留在A处,规定以岗亭为原点,向北方向为正,这段时间行驶记录如下(单位:千米):+10,﹣9,+7,﹣15,+6,﹣14,+4,﹣2(1)A在岗亭哪个方向?距岗亭多远?(2)若摩托车行驶1千米耗油0.12升,且最后返回岗亭,摩托车共耗油多少升?【考点】正数和负数.【分析】(1)将各数相加,得数若为负,则A在岗亭南方,若为正,则A在岗亭北方;(2)将各数的绝对值相加,求得摩托车共行驶的路程,即可解答.【解答】解:(1)+10﹣9+7﹣15+6﹣14+4﹣2=10+7+6+4﹣9﹣15﹣14﹣2=﹣13(千米),答:A在岗亭南方,距离岗亭13千米处.(2))|+10|+|﹣9|+|+7|+|﹣15|+|+6|+|﹣14|+|+4|+|﹣2|=10+9+7+15+6+14+4+2+13=80(千米),0.12×80=9.6(升),答:摩托车共耗油9.6升.【点评】本题主要考查正数和负数的应用,解决此类问题时,要特别注意第(2)小题,无论向南行驶还是向北行驶,都是要耗油的.25.(12分)(2016秋•榆林期末)为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现,甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球,乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)求每套队服和每个足球的价格是多少?(2)若城区四校联合购买100套队服和a(a>10)个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)在(2)的条件下,若a=60,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?【考点】一元一次方程的应用;列代数式.【分析】(1)设每个足球的定价是x元,则每套队服是(x+50)元,根据两套队服与三个足球的费用相等列出方程,解方程即可;(2)根据甲、乙两商场的优惠方案即可求解;(3)把a=60代入(2)中所列的代数式,分别求得在两个商场购买所需要的费用,然后通过比较得到结论:在乙商场购买比较合算.【解答】解:(1)设每个足球的定价是x元,则每套队服是(x+50)元,根据题意得2(x+50)=3x,解得x=100,x+50=150.答:每套队服150元,每个足球100元;(2)到甲商场购买所花的费用为:150×100+100(a﹣)=100a+14000(元),到乙商场购买所花的费用为:150×100+0.8×100•a=80a+15000(元);(3)在乙商场购买比较合算,理由如下:将a=60代入,得100a+14000=100×60+14000=20000(元).80a+15000=80×60+15000=19800(元),因为20000>19800,所以在乙商场购买比较合算.【点评】本题考查了一元一次方程的应用解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.。
【金陵汇文】2016-2017学年第一学期初一数学期末试卷及答案

1 2
m
,
∴
DOE
AOD
AOE
1 2
(m
n)
1 2
m
n 2
,
选B.
D.
m
2
n
登陆官网获取更多资料及课程信息:
南京中小学辅导 1对1、3人班、8人班
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分.请把答案直接填写在答.题.卡.相.应.位.置.上) 7. 2 的相反数是__________. 【答案】 2 【解析】 2 的相反数是 2 .
(1
)
x
1
2
x
1
.
( 2 ) 22(x 1) 1 6 0 .
【答案】(1) x 1
(2) x 0
登陆官网获取更多资料及课程信息:
南京中小学辅导 1对1、3人班、8人班
【解析】( 1 )
x
1 2
x
1
,
解: 2x (1 x) 2 ,
2
1 2
1 6
1 7
1 8
3
1 6
1 7
1 8
1 9
的结果是__________.
( 3 )甲、乙两家商店都经营一种商品,一开始标价相同.甲先涨价 20% ,发现销量不好,接着降价 20%
出售;乙先降价 20% ,后来又涨价 20% .设最后的实际售价分别是 a甲 和 a乙 ,则
3.在某月的日历上用矩形圈到 a 、 b 、 c 、 d 四个数(如图),如果 d 18 ,那么 a b c ( ).
联合体2017七上期末答案

2017-2018第一学期七年级期末学情调研试卷(时间:100分钟 满分:100分)一、 选择题(每题2分,共16分)9.3,3 10.1.05×104 11.﹣1.5 12.﹣23 13.﹣214.② 15.1 16.115 17.90 18.122三、 解答题(共64分)19. (8分)(1)原式=-1+(﹣2) 2分=-3 4分(2)原式=1×2×(6+8) 3分=28 4分20.(12分)(1)解3x -3-8x -4=7 2分 ﹣5 x =15 3分x =﹣3 4分(2)解3x -3-6=4+2x 2分x =13 4分(3)解 得y =﹣1 2分得x =2 3分所以⎩⎪⎨⎪⎧x =2,y =﹣1 4分21.(4分)先化简,再求值:12 x -2 ⎝⎛⎭⎫x -13 y 2+⎝⎛⎭⎫-32 x +13 y 2,其中x =-2,y =23 .解 原式=12 x -2 x +23 y 2 -32 x +13 y 2 2分=-3 x +y 2 3分当x =-2,y =23 时,原式=6+(23 )=589 4分22.(5分)(1) 1分点与直线上所有点的连线,垂线段最短; 2分< 3分(2)作图正确 4分AC ∥PE 5分23. (5分)(1) 作图正确,每个1分; 3分(2) 3 5分24.(6分)(1)﹣3、5; 1分 一个正数、一个负数,并且正数的绝对值大于负数的绝对值; 3分(2)﹣5、3、4; 4分两个正数、一个负数,并且两个正数的绝对值之和大于负数的绝对值; 6分25. (6分)(1)6; 2分(2)求出CD =6 3分求出AC =7 4分(3)若点E 在CA 的延长线上,求出BE =14 5分若点E 在AC 线段上,求出BE =6 6分26.(6分)解(1)甲:16×3+2.5×32=128(元)乙:2.5×48=120(元)128—120=8(元)答:乙班比甲班少付8元。
2016-2017学年江苏省南京九中七年级(上)期末数学试卷

2016-2017学年江苏省南京(nán jīnɡ)九中七年级(上)期末数学试卷一、选择题(本大题共8小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答题纸相应(xiāngyīng)位置上)1.(2分)相反数是()A.﹣B.2 C.﹣2 D.2.(2分)全面贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进(tuījìn)燃煤电厂脱硫改造15000 000千瓦是《政府工作报告》中确定的重点任务之一.将数据15 000 000用科学记数法表示为()A.15×106B.1.5×107C.1.5×108D.0.15×1083.(2分)在﹣(﹣8),(﹣1)2007,﹣32,﹣|﹣1|,﹣|0|,﹣,中,负有理数共有(ɡònɡ yǒu)()A.4个B.3个C.2个D.1个4.(2分)元旦节期间,百货商场为了促销(cù xiāo),每件夹克按成本价提高50%后标价,后因季节关系按标价的8折出售,每件以60元卖出,这批夹克每件的成本价是()A.150元B.50元C.120元D.100元5.(2分)如图,已知线段AB=10cm,点N在AB上,NB=2cm,M是AB中点,那么线段MN的长为()A.5cm B.4cm C.3cm D.2cm6.(2分)如图OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD的度数是()度.A.40 B.60 C.20 D.307.(2分)用边长为1的正方形做了一套七巧板,拼成如图所示的一座桥,则桥中阴影(yīnyǐng)部分的面积为原正方形面积的()A.B.C.D.不能确定(quèdìng)8.(2分)如图所示,∠BAC=90°,AD⊥BC,则下列结论(jiélùn)中,正确的个数为()①AB⊥AC;②AD与AC互相(hù xiāng)垂直;③点C到AB的垂线(chuí xiàn)段是线段AB;④点A到BC的距离是线段AD的长度;⑤线段AB的长度是点B到AC的距离;⑥AD+BD>AB.A.2个B.3个C.4个D.5个二、填空题(本题共10小题,每小题2分,共20分,不需写出解答过程,请把答案直接填写在答题纸相应位置上)9.(2分)﹣的系数是,次数是.10.(2分)已知单项式3a m b2与﹣a4b n﹣1的和是单项式,那么m=,n=.11.(2分)比较大小:30.15°30°15′(用>、=、<填空)12.(2分)若∠α=50°26′,则∠α的余角为.13.(2分)已知x=1是方程2ax﹣5=a+3的解,则a=.14.(2分)若x﹣3y=﹣4,那么3+2x﹣6y的值是.15.(2分)某校在14:20开展“大课间”活动,这一时刻(shíkè)钟面上分针与时针所夹的角等于度.16.(2分)已知线段AB=24cm,直线(zhíxiàn)AB上有一点C,且BC=6cm,M是线段AC的中点,则AM=cm.17.(2分)把14个棱长为1的正方体,在地面上堆叠成如图所示的立体,然后(ránhòu)将露出的表面部分涂成红色,那么红色部分的面积为.18.(2分)根据所给出的三视图写出这个(zhè ge)几何体的名称,并计算(jì suàn)出它的体积是.三、解答题(本大题共9小题,共64分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(8分)计算:(1)(+﹣)÷(﹣)(2)﹣11﹣×[4﹣(﹣2)3.20.(5分)先化简,再求值.5(3a2b﹣ab2﹣1)﹣(ab2+3a2b﹣5),其中a=,b=.21.(8分)解下列方程(1)4﹣x=3(2﹣x).(2)2﹣=x﹣.22.(6分)已知:∠A、∠B互为补角,且∠B=3∠A.求∠A与∠B的度数.23.(7分)在课间活动中,小英、小丽和小华在操场上画出A,B两个区域,一起(yīqǐ)玩投包游戏,沙包落在A区域所得分值与落在B区域所得分值不同,当每人各投沙包四次时,其落点和四次总分如图所示.(1)沙包落在A区域和B区域所得(suǒ dé)分值分别是多少?(2)求出小华的四次总分.24.(8分)画图(huà tú)题:(1)在如图所示的方格纸中,经过(jīngguò)线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.(2)判断(pànduàn)EF、GH的位置关系是.(3)连接AC和BC,则三角形ABC的面积是.25.(6分)小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:(1)小明总共剪开了条棱.(2)现在(xiànzài)小明想将剪断的②重新(chóngxīn)粘贴到①上去,而且经过折叠以后,仍然可以(kěyǐ)还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助(bāngzhù)小明在①上补全.(3)小明说:他所剪的所有棱中,最长的一条(yī tiáo)棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.26.(6分)观察下列各图:(1)第1个图中有1个三角形,第2个图中有3个三角形,第3个图中有6个三角形,第4个图中有个三角形,…,根据这个规律可知第n个图中有个三角形(用含正整数n的式子表示);(2)问在上述图形中是否存在这样的一个图形,该图形中共有25个三角形?若存在,请画出图形;若不存在请通过具体计算说明理由;(3)在下图中,点B是线段AC的中点,D为AC延长线上的一个动点,记△PDA的面积为S1,△PDB的面积为S2,△PDC的面积为S3.试探索S1、S2、S3之间的数量关系,并说明理由.27.(10分)如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.(1)若BC:AC=4:7,求点C到原点的距离;(2)如图2,在(1)的条件下,动点P、Q两点同时(tóngshí)从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;(3)如图3,在(1)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段(xiànduàn)PT的中点,点N为线段OR的中点.请问PT﹣MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.2016-2017学年江苏省南京(nán jīnɡ)九中七年级(上)期末数学试卷参考答案与试题(shìtí)解析一、选择题(本大题共8小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合(fúhé)题目要求的,请将正确选项的序号填涂在答题纸相应位置上)1.(2分)相反数是()A.﹣B.2 C.﹣2 D.【分析(fēnxī)】一个数的相反数就是(jiùshì)在这个数前面添上“﹣”号.的相反数是﹣.【解答】解:的相反数是﹣,故选:A.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号.一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2.(2分)全面贯彻落实“大气十条”,抓好大气污染防治,是今年环保工作的重中之重.其中推进燃煤电厂脱硫改造15000 000千瓦是《政府工作报告》中确定的重点任务之一.将数据15 000 000用科学记数法表示为()A.15×106B.1.5×107C.1.5×108D.0.15×108【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将15 000 000用科学记数法表示为:1.5×107.故选:B.【点评(diǎn pínɡ)】此题考查(kǎochá)科学记数法的表示方法.科学记数法的表示形式为a×10n的形式(xíngshì),其中1≤|a|<10,n为整数(zhěngshù),表示时关键要正确确定a的值以及n的值.3.(2分)在﹣(﹣8),(﹣1)2007,﹣32,﹣|﹣1|,﹣|0|,﹣,中,负有理数共有(ɡònɡ yǒu)()A.4个B.3个C.2个D.1个【分析】根据相反数的定义、乘方的运算法则、绝对值的性质等逐一判断可得.【解答】解:在﹣(﹣8),(﹣1)2007,﹣32,﹣|﹣1|,﹣|0|,﹣,中,负有理数有:(﹣1)2007,﹣32,﹣|﹣1|,﹣这4个,故选:A.【点评】本题主要考查有理数的乘方,解题的关键是熟练掌握相反数的定义、乘方的运算法则、绝对值的性质等知识点.4.(2分)元旦节期间,百货商场为了促销,每件夹克按成本价提高50%后标价,后因季节关系按标价的8折出售,每件以60元卖出,这批夹克每件的成本价是()A.150元B.50元C.120元D.100元【分析】设这批夹克每件的成本价是x元,然后按照成本价×(1+50%)×0.8=60列出方程,解方程就可以成本价.【解答】解:设这批夹克每件的成本价是x元,依题意得:(1+50%)×0.8x=60,解得:x=50.答:这批夹克每件的成本价是50元.故选:B.【点评】此类题目贴近生活,有利于培养学生应用数学解决生活中实际问题的能力.解题时要明确打折,标价等概念.5.(2分)如图,已知线段(xiànduàn)AB=10cm,点N在AB上,NB=2cm,M 是AB中点,那么线段MN的长为()A.5cm B.4cm C.3cm D.2cm【分析(fēnxī)】根据M是AB中点(zhōnɡ diǎn),先求出BM的长度,则MN=BM﹣BN.【解答(jiědá)】解:∵AB=10cm,M是AB中点(zhōnɡ diǎn),∴BM=AB=5cm,又∵NB=2cm,∴MN=BM﹣BN=5﹣2=3cm.故选:C.【点评】本题考查了线段的长短比较,根据点M是AB中点先求出BM的长度是解本题的关键.6.(2分)如图OA⊥OB,∠BOC=30°,OD平分∠AOC,则∠BOD的度数是()度.A.40 B.60 C.20 D.30【分析】因为OD平分∠AOC,可以先求∠AOC,再求∠COD,利用角的和差关系求∠BOD的度数.【解答】解:∵OA⊥OB,∠BOC=30°,∴∠AOC=∠AOB+∠BOC=120°,∵OD平分∠AOC,∴∠AOD=∠AOC÷2=60°,∴∠BOD=∠AOB﹣∠AOD=30°.故选:D.【点评】此题主要考查了垂线和角平分线的定义在解题中的应用.7.(2分)用边长为1的正方形做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分(bù fen)的面积为原正方形面积的()A.B.C.D.不能确定(quèdìng)【分析(fēnxī)】读图分析阴影部分与整体(zhěngtǐ)的位置关系;易得阴影部分的面积即为△ABC的面积(miàn jī),是原正方形的面积的一半.【解答】解:读图可得,阴影部分的面积为原正方形的面积的一半,则阴影部分的面积为1×1÷2=;是原正方形的面积的一半;故选A.【点评】此题主要考查正方形对角线相互垂直平分相等的性质,读图也很关键.8.(2分)如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的个数为()①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD的长度;⑤线段AB的长度是点B到AC的距离;⑥AD+BD>AB.A.2个B.3个C.4个D.5个【分析】根据点到直线的距离,垂直的定义,三角形三边的关系,可得答案.【解答】解:由∠BAC=90°,AD⊥BC,得AB⊥AC,故①正确;AD与AC不垂直,故②错误;点C到AB的垂线段是线段AC的长,故③错误;点A到BC的距离(jùlí)是线段AD的长度,故④正确(zhèngquè);线段(xiànduàn)AB的长度是点B到AC的距离,故⑤正确(zhèngquè);AD+BD>AB,故⑥正确(zhèngquè);故选:C.【点评】本题考查了点到直线的距离,利用点到直线的距离,垂直的定义,三角形三边的关系是解题关键.二、填空题(本题共10小题,每小题2分,共20分,不需写出解答过程,请把答案直接填写在答题纸相应位置上)9.(2分)﹣的系数是,次数是3.【分析】单项式的系数是指单项式中的数字因数,次数是指所有字母的指数和.【解答】解:根据单项式系数和次数的定义可知,﹣的系数是,次数是3.【点评】解答此题的关键是理解单项式的概念,比较简单.注意π属于数字因数.10.(2分)已知单项式3a m b2与﹣a4b n﹣1的和是单项式,那么m=4,n= 3.【分析】本题是对同类项定义的考查,同类项的定义是所含有的字母相同,并且相同字母的指数也相同的项叫同类项,只有同类项才可以合并的.由同类项的定义可求得m和n的值.【解答】解:由同类项定义可知:m=4,n﹣1=2,解得m=4,n=3,故答案为:4;3.【点评(diǎn pínɡ)】本题考查了同类项的定义,只有同类项才可以进行相加减,而判断同类项要一看所含有的字母是否相同(xiānɡ tónɡ),二看相同字母的指数是否相同,难度适中.11.(2分)比较(bǐjiào)大小:30.15°<30°15′(用>、=、<填空(tiánkòng))【分析(fēnxī)】先进行度、分、秒的转化运算,注意以60为进制,然后对比即可得出答案.【解答】解:∵30.15°=30°9′,∴30°9′<30°15′.故答案为:<.【点评】本题主要考查了度、分、秒的转化运算,注意以60为进制,比较简单.12.(2分)若∠α=50°26′,则∠α的余角为39°34′.【分析】直接利用互为余角的定义得出答案.【解答】解:∵∠α=50°26′,∴∠α的余角为:90°﹣50°26′=89°60′﹣50°26′=39°34′.故答案为:39°34′.【点评】此题主要考查了互为余角的定义以及度分秒转换,正确把握定义是解题关键.13.(2分)已知x=1是方程2ax﹣5=a+3的解,则a=8.【分析】根据题意将x=1代入方程即可求出a的值.【解答】解:将x=1代入方程得:2a﹣5=a+3,解得:a=8.故答案为:8.【点评】此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.14.(2分)若x﹣3y=﹣4,那么(nà me)3+2x﹣6y的值是﹣5.【分析(fēnxī)】将x﹣3y=﹣4代入原式=3+2(x﹣3y),计算(jì suàn)可得.【解答(jiědá)】解:当x﹣3y=﹣4时,原式=3+2(x﹣3y)=3+2×(﹣4)=3﹣8=﹣5,故答案(dá àn)为:﹣5.【点评】本题主要考查代数式的求值,解题的关键是熟练掌握整体代入思想的运用.15.(2分)某校在14:20开展“大课间”活动,这一时刻钟面上分针与时针所夹的角等于50°度.【分析】根据时针与分针相距的份数乘以每份的度数,可得答案.【解答】解:14:20这一时刻钟面上分针与时针相距2份,14:20这一时刻钟面上分针与时针所夹的角30°×2﹣×20°=50°,故答案为:50.【点评】本题考查了钟面角,确定时针与分针相距的分数是解题关键.16.(2分)已知线段AB=24cm,直线AB上有一点C,且BC=6cm,M是线段AC的中点,则AM=15或9cm.【分析】应考虑到A、B、C三点之间的位置关系的多种可能,即点C在线段AB的延长线上或点C在线段AB上.【解答】解:①当点C在线段AB的延长线上时,此时AC=AB+BC=30cm,∵M是线段AC的中点,则AM=AC=15cm;②当点C在线段AB上时,AC=AB﹣BC=18cm,∵M是线段AC的中点,则AM=AC=9cm.故答案为:15或9【点评(diǎn pínɡ)】本题主要(zhǔyào)考查两点间的距离的知识点,利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.17.(2分)把14个棱长为1的正方体,在地面(dìmiàn)上堆叠成如图所示的立体,然后将露出的表面部分涂成红色,那么红色部分的面积为33.【分析(fēnxī)】此题可根据表面积的计算(jì suàn)分层计算得出红色部分的面积再相加.【解答】解:根据题意得:第一层露出的表面积为:1×1×6﹣1×1=5,第二层露出的表面积为:1×1×6×4﹣1×1×13=11,第三层露出的表面积为:1×1×6×9﹣1×1×37=17,所以红色部分的面积为:5+11+17=33,故答案为:33.【点评】此题考查的知识点是几何体的表面积,关键是在计算表面积时减去不露的或重叠的面积.18.(2分)根据所给出的三视图写出这个几何体的名称三棱柱,并计算出它的体积是60.【分析】根据三视图的形状,初步判断可得该几何体是一个三棱柱.根据三棱柱的体积计算即可.【解答(jiědá)】解:根据三视图的形状,初步判断可得该几何体是一个三棱柱(léngzhù);三棱柱的体积为:,故答案(dá àn)为:三棱柱;60.【点评(diǎn pínɡ)】本题给出直三棱柱的三视图,要求我们还原它的形状并求它的体积(tǐjī),着重考查了三视图的理解和柱体体积公式等知识,考查了空间想象能力,属于中档题三、解答题(本大题共9小题,共64分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)19.(8分)计算:(1)(+﹣)÷(﹣)(2)﹣11﹣×[4﹣(﹣2)3.【分析】(1)原式利用除法法则变形,计算即可求出值;(2)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可求出值.【解答】解:(1)原式=(+﹣)×(﹣36)=﹣18﹣30+3=﹣45;(2)原式=﹣1﹣×12=﹣1﹣4=﹣5.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.20.(5分)先化简,再求值.5(3a2b﹣ab2﹣1)﹣(ab2+3a2b﹣5),其中a=,b=.【分析】首先去括号,然后合并同类项,化简后再把a、b的值代入求解即可.【解答】解:原式=15a2b﹣5ab2﹣5﹣ab2﹣3a2b+5,=12a2b﹣6ab2,当a=,b=时,原式=12××﹣6××=1﹣=.【点评(diǎn pínɡ)】此题主要考查(kǎochá)了整式的化简求值,关键是掌握给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.21.(8分)解下列(xiàliè)方程(1)4﹣x=3(2﹣x).(2)2﹣=x﹣.【分析(fēnxī)】(1)根据一元一次方程的解法,去括号,移项(yí xiànɡ),合并同类项,系数化为1即可;(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.【解答】解:(1)去括号得,4﹣x=6﹣3x,移项得,﹣x+3x=6﹣4,合并同类项得,2x=2,系数化为1得,x=1;(2)去分母得,12﹣(x+5)=6x﹣2(x﹣1),去括号得,12﹣x﹣5=6x﹣2x+2,移项得,﹣x﹣6x+2x=2﹣12+5,合并同类项得,﹣5x=﹣5,系数化为1得,x=1.【点评】本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.22.(6分)已知:∠A、∠B互为补角,且∠B=3∠A.求∠A与∠B的度数.【分析】先设出∠A与∠B,再根据补角的和等于180°列式求解即可.【解答】解:设∠A=x,则∠B=3x根据题意得,x+3x=180°,解得:x=45°,∴∠A=45°,∠B=3×45°=135°,故∠A和∠B的度数(dù shu)分别为:∠A=45°,∠B=135°.【点评(diǎn pínɡ)】本题主要考查了邻补角的和等于180°的性质,根据比例的设未知数的方法是解题的关键,此设法(shèfǎ)比较简便且不容易出错.23.(7分)在课间活动中,小英、小丽和小华在操场上画出A,B两个区域,一起(yīqǐ)玩投包游戏,沙包落在A区域所得分值与落在B区域所得分值不同,当每人各投沙包四次时,其落点和四次总分如图所示.(1)沙包落在A区域(qūyù)和B区域所得分值分别是多少?(2)求出小华的四次总分.【分析】(1)设沙包落在A区域得分为x,则落在B区域得分为(33﹣3x),根据小丽得分列出方程2x+2(33﹣3x)=30,解方程求出x的值即可;(2)小华的总分=沙包落在A区域得分×1+沙包落在B区域得分×3,依此计算即可求解.【解答】解:(1)设沙包落在A区域得分为x,则落在B区域得分为(33﹣3x),由题意可列方程2x+2(33﹣3x)=30,解得x=9,33﹣3x=33﹣27=6.故沙包落在A区域得分为9分,落在B区域得分为6分.(2)小华四次总分为:9×1+6×3=9+18=27(分).故小华四次总分为(fēn wéi)27分.【点评(diǎn pínɡ)】此题主要(zhǔyào)考查了一元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.24.(8分)画图(huà tú)题:(1)在如图所示的方格纸中,经过(jīngguò)线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.(2)判断EF、GH的位置关系是垂直.(3)连接AC和BC,则三角形ABC的面积是10.【分析】(1)过点C作5×1的矩形的对角线所在的直线,可得AB的垂线和平行线;(2)易得EF与GH的位置关系是:垂直;(3)根据三角形的面积公式解答.【解答】解:(1)如图(2)EF与GH的位置(wèi zhi)关系是:垂直;(3)设小方格(fānɡ ɡé)的边长是1,则AB=2,CH=2,=×2×2=10.∴S△ABC【点评(diǎn pínɡ)】此题灵活考查了过直线外一点作它的平行线、垂线,以及学生(xué sheng)的观察、总结能力.25.(6分)小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个(yī ɡè)长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:(1)小明总共剪开了8条棱.(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.【分析】(1)根据平面图形得出剪开棱的条数,(2)根据长方体的展开图的情况可知有两种情况,(3)设最短的棱长高为acm,则长与宽相等为5acm,根据棱长的和是880cm,列出方程可求出长宽高,即可求出长方体纸盒的体积.【解答】解(1)小明共剪了8条棱,故答案为:8.(2)如图,四种情况.(3)∵长方体纸盒的底面是一个(yī ɡè)正方形,∴设最短的棱长高为acm,则长与宽相等(xiāngděng)为5acm,∵长方体纸盒所有(suǒyǒu)棱长的和是880cm,∴4(a+5a+5a)=880,解得a=20cm,∴这个(zhè ge)长方体纸盒的体积为:20×100×100=200000立方厘米.【点评(diǎn pínɡ)】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.26.(6分)观察下列各图:(1)第1个图中有1个三角形,第2个图中有3个三角形,第3个图中有6个三角形,第4个图中有10个三角形,…,根据这个规律(guīlǜ)可知第n个图中有个三角形(用含正整数n的式子(shì zi)表示);(2)问在上述图形中是否存在这样的一个图形,该图形中共有25个三角形?若存在,请画出图形;若不存在请通过(tōngguò)具体计算说明理由;(3)在下图中,点B是线段(xiànduàn)AC的中点,D为AC延长线上的一个动点,记△PDA的面积(miàn jī)为S1,△PDB的面积为S2,△PDC的面积为S3.试探索S1、S2、S3之间的数量关系,并说明理由.【分析】(1)第一个图中三角形的个数为1;第二个图中三角形的个数为3=1+2;第三个图中三角形的个数为6=1+2+3;…第n个图中三角形的个数为1+2+3+…+n=;当n=10时,可计算出第10个图中三角形的个数.(2)令=25,看n是否有正整数解即可.(3)由于B是AC中点,则△PAB和△PBC等底同高,故S△PBA=S△PBC,由此可得出S1+S3=2S2.【解答】解:(1)10;;(2)不存在(法一)当n=6时,三角形的个数为;当n=7时,三角形的个数为;所以不存在n使三角形的个数为25.(法二)由=25,得n(n+1)=50,而不存在两个连续整数的乘积为50,所以(suǒyǐ)不存在n使三角形的个数为25.(3)S1+S3=2S2.∵点B是线段(xiànduàn)AC的中点,∴AB=BC,∴S△PAB =S△PBC,∴S1+S3=2S2.【点评(diǎn pínɡ)】本题考查的是规律性问题以及三角形面积的求法;解答规律型问题时,通常是根据简单(jiǎndān)的例子找出一般化规律,然后根据规律去求特定的值.27.(10分)如图1,已知数轴上有三点(sān diǎn)A、B、C,AB=60,点A对应的数是40.(1)若BC:AC=4:7,求点C到原点的距离;(2)如图2,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;(3)如图3,在(1)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问PT﹣MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.【分析】(1)根据AB=60,BC:AC=4:7,得出BC=80,利用点A对应的数是40,即可得出点C对应的数;(2)假设点R速度为x单位长度/秒,根据点P、Q之间的距离与点Q、R的距离相等,得出等式方程求出即可;(3)分别表示出PR,MN的值,进而求出PT﹣MN的值.【解答(jiědá)】解:(1)如图1,∵AB=60,BC:AC=4:7,∴=,解得:BC=80,∵AB=60,点A对应(duìyìng)的数是40,∴B点对应(duìyìng)的数字为:﹣20,∴点C到原点的距离(jùlí)为:80﹣(﹣20)=100;(2)如图2,设R的速度(sùdù)为每秒x个单位,则R对应的数为40﹣5x,P对应的数为﹣100+15x,Q对应的数为10x+15,PQ=5x﹣115或115﹣5xQR=15x﹣25∵PQ=QR∴5x﹣115=15x﹣25或115﹣5x=15x﹣25解得:x=﹣9(不合题意,故舍去)或x=7∴动点Q的速度是9个单位长度/秒.(3)如图3,设运动时间为t秒P对应的数为﹣100﹣5t,T对应的数为﹣t,R对应的数为40+2t,PT=100+4t,M对应的数为﹣50﹣3t,N对应的数为20+t,MN=70+4t∴PT﹣MN=30,∴PT﹣MN的值不会发生变化,是30.【点评(diǎn pínɡ)】此题考查了一元一次方程的应用,根据已知得出各线段之间的等量关系是解题关键(guānjiàn),此题阅读量较大应细心分析.内容总结(1),根据这个规律可知第n个图中有个三角形(用含正整数n 的式子表示)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016—2017学年度第一学期期末学情检测卷七年级英语2017.01考试时间:100分钟满分:100分(将答案按序号填在答卷纸上............)选择题共50分一、听力(共15小题,每小题1分,满分15分)A) 听对话,选图片。
听下面5段对话,从题中所给的A、B、C三幅图片中选出最佳选项。
听每段对话前,你将有5秒钟的时间阅读题目;听完后,你仍有5秒钟的时间答题。
每段对话听两遍。
1. What does Sandy have for lunch?A. B. C.2. Which is Nancy’s favourite festival?A. B. C.3. What does the girl buy for Jack?A. B. C.4. What does Millie like doing after class?A. B. C.5. Where will they go?A. B. C.B) 听对话,回答问题。
听下面的对话,每段对话后有几个小题,请根据你所听到的内容,从题中所给的A、B、C 三个选项中选出最佳选项。
听每段对话前,你将有时间阅读各个小题,每小题5秒钟;听完后,你仍有5秒钟的时间答题。
每段对话听两遍。
6. What colour is Peter’s mask?A. It’s brown.B. It’s yellow.C. It’s black.7. How often does David exercise?A. Once a week.B. Twice a week.C. Never.8. Where are the speakers talking?A. On a bus.B. In a restaurant.C. In a hospital.9. How many students don’t have the books?A. Forty.B. Twenty-five.C. Fifteen.10. What does the man think of the skirt?A. It is colourful and nice.B. It matches the blouse very well.C. It is too colourful and does not go well with the blouse.C)听短文,回答问题。
听下面的短文,短文后有几个小题,请根据你所听到的内容,从题中所给的A、B、C三个选项中选出最佳选项。
听短文前,你将有时间阅读各个小题,每小题5秒钟;听完后,你仍有5秒钟的时间答题。
短文听两遍。
11. Where does Henry come from?A. America.B. England.C. China.12. Who’s Zhang Hua?A. Henry’s brother.B. Henry’s uncle.C. Henry’s friend.13. When does Henry visit Zhang Hua?A. At the weekend.B. During the holiday.C. On New Year’s Eve.14. Who teaches Henry to make dumplings?A. Zhang Hua.B. His brother.C. Mrs Zhang.15. What do the two boys NOT do on New Year’s Eve?A. They go boating in the park.B. They enjoy an interesting film.C. They watch lion dances and fireworks.二、单项填空(共15小题,每小题1分,满分15分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
16. Simon looks smart purple.A. onB. ofC. withD. in17. Jackie Chan is a Kungfu superstar. He is among the people all over the world.A. modernB. beautifulC. interestingD. popular18. —Is the man on the left your English teacher?—No, he teaches Biology. His classes are fun.A. weB. ourC. usD. ours19. —do you do at Halloween?—We play games and have lots of fun.A. HowB. WhereC. WhatD. When20.—This pair of shoes looks nice. Can I , madam?A. try them onB. try it onC. try on itD. try on them21. —Can you help me when the train leaves?—Sure, Mr Green.A. look forB. look outC. look atD. find out22. —What’s your , Jimmy?—I like dancing to music.A. workB. nameC. hobbyD. age23. —The price of a HUAWEI Mate 9 Pro will be more than 4000 yuan.—Yes, good things always much.A. payB. spendC. takeD. cost24. —Where’s Lucy?—She volleyball with her friends.A. practises playingB. is practising playingC. practisng playingD. is practisng to play25. How many syllables(音节) does the word “lovely” have?A. One.B. Two.C. Three.D. Four.26. Trainers are for a long walk.A. matchingB. matchC. fitD. fitting27. —Mike, let’s go to the zoo now.—OK. Just a . Let me change my shoes.A. secondB. minuteC. hourD. day28. —How about the comic books? It’s $65.—I can’t take it. The price is too for us students.A. highB. cheapC. expensiveD. much29. —Good afternoon! ?—I’d like some basketball cards.A. Can you help meB. What can I do for youC. How are youD. What can I help you30. —Dad, I’m going for Jim’s birthday party. I’ll be back before 10:00.—A. Be careful.B. Come home early.C. Have fun.D. Really?三、完形填空(共10小题,每小题1分,满分10分)阅读下面短文,从短文后所给各题的四个选项(A、B、C、D)中,选出可以填入空白处的最佳选项。
Food is important. Everyone needs to 31 well if he or she wants to have a strong body. Our minds also need a kind of food. This kind of food is 32 . We begin to get knowledge even when we are young. Small children are 33 in everything around them. They learn 34while they are watching and listening. When they are getting older, they begin to 35 science books, storybooks and anything else they like. When they find something new, they have to ask questions and 36 to find out the answers.What is the best 37 to get knowledge? If we learn 38 ourselves, we will get the most knowledge. If we are 39 getting answers from others and don’t ask why, we will never learn more and understand 40 . So we should believe in the saying that is never too old to learn.31. A. sleep B. read C. drink D. eat32. A. sport B. exercise C. knowledge D. meat33. A. interested B. interesting C. weak D. good34. A. everything B. something C. nothing D. anything35. A. lend B. write C. learn D. read36. A. try B. have C. think D. wait37. A. place B. school C. way D. road38. A. on B. with C. to D. by39. A. seldom B. always C. never D. sometimes40. A. harder B. much C. well D. better四、阅读理解(共10小题, 每小题1分,满分10分)阅读下列材料,从每题所给的四个选项(A、B、C、D)中,选出最佳选项。
