长安一中2017~2018学年度第一学期期末考试
2017-2018学年陕西省西安市长安区第一中学高二上学期期末考试英语试题(Word版)+听力

长安一中2017—2018学年度第一学期期末考试高二英语试题命题人:朱晓峰审题人:雷亚勤注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2. 答题前,考生务必将自己的姓名、班级填写在本试卷相应的位置。
3. 全部答案在答题卡上完成,答在本试卷上无效。
4. 满分150分;考试时间120分钟。
第Ⅰ卷(选择题共90分)第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A, B, C, 三个选项中选出最佳选项,并标在试卷相应的位置。
听完每段对话后,你都有10秒的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What does the man think of the book?A. Humorous.B. Scientific.C. Popular.2. Where does the dialogue probably take place?A. In a book store.B. In a classroom.C. In a library.3.Where is the woman‘s brother now?A. At home.B. In the office.C. In hospital.4.When will the man arrive at the airport?A. At 6:00.B. At 7:00.C. At 8:00.5. What size does the woman want?A. Size 6.B. Size 8.C. Size 10.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
陕西省西安市长安区第一中学2017-2018学年高一上学期期末-英语考试试题带答案

陕西省西安市长安区第一中学2017-2018学年高一上学期期末考试英语试题第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Why doesn’t the woman like to have red wine?A. Because she doesn’t like its taste.B. Because she prefers beer.C. Because she is afraid of getting drunk.2. What is the man going to buy?A. Food.B. DrinksC. Flowers.3. What are the two speakers doing?A. Looking for some suitcases.B. Booking tickets for a journey.C. Checking the woman’s baggage.4. Why would the woman rather stay at the hotel?A. It costs less money.B. It saves much labor.C. It feels more comfortable.5. What are the two speakers talking about?A. A painting.B. A country scene.C. A kind of drink.第二节(共15小题;每小题1.5分,共22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
陕西省西安市长安区第一中学2017-2018学年高一上学期期末考试英语试题+Word版含答案

长安一中2017~2018学年度第一学期期末考试高一英语试题命题人:陈格锋审题人:周凯俨第I卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Why doesn’t the woman like to have red wine?A.Bec ause she doesn’t like its taste.B.Because she prefers beer.C.Because she is afraid of getting drunk.2. What is the man going to buy?A.Food.B.DrinksC.Flowers.3. What are the two speakers doing?A.Looking for some suitcases.B.Booking tickets for a journey.C.Checking the woman’s baggage.4. Why would the woman rather stay at the hotel?A.It costs less money.B.It saves much labor.C.It feels more comfortable.5. What are the two speakers talking about?A.A painting.B.A country scene.C.A kind of drink.第二节(共15小题;每小题1.5分,共22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
【数学】陕西省西安市长安区第一中学2017-2018学年高二上学期期末考试(理)(word版附答案)

参考答案一.选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是满足题目要求的.二.填空题:(本大题共4小题,每小题5分,共20分.请把答案填写在答题纸的相应横线上.)13. 60. 14. 315. (,1)(0,1)-∞- 16.32三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.(注意:在试题卷上作答无效)17. (本小题满分10分)解析:对p :∵直线与圆相交,∴d =|1-m |2<1. ∴-2+1<m <2+1.对q :方程mx 2-x +m -4=0有一正根和一负根,∴令f (x )=mx 2-x +m -4,∴⎩⎪⎨⎪⎧ m >0,f (0)<0或⎩⎪⎨⎪⎧m <0,f (0)>0解得0<m <4. 又∵¬p 为真,∴p 假. 又∵p 或q 为真,∴q 为真.由数轴可得2+1≤m <4. 故m 的取值范围是2+1≤m <4.18.(本小题满分12分)解 (1)f ′(x )=a x -2bx ,∵函数f (x )在x =1处与直线y =-12相切, ∴⎩⎪⎨⎪⎧ f ′(1)=a -2b =0,f (1)=-b =-12, 解得⎩⎪⎨⎪⎧ a =1,b =12. (2)由(1)知,f (x )=ln x -12x 2, f ′(x )=1x -x =1-x 2x, 当1e ≤x ≤e 时,令f ′(x )>0,得1e≤x <1, 令f ′(x )<0,得1<x ≤e , ∴f (x )在[1e,1)上是增加的, 在(1,e]上是减少的, ∴f (x )max =f (1)=-12. 19. (本小题满分12分)解 (1)直线AB 的方程是y =22(x -p 2),与y 2=2px 联立,从而有4x 2-5px +p 2=0.所以x 1+x 2=5p 4,由抛物线定义得 |AB |=x 1+x 2+p =5p 4+p =9, 所以p =4,从而抛物线方程为y 2=8x .(2)由于p =4,则4x 2-5px +p 2=0,即x 2-5x +4=0,从而x 1=1,x 2=4,于是y 1=-22,y 2=42,从而B (4,42).设C (x 3,y 3),则OC →=(x 3,y 3)=(1,-22)+λ(4,42)=(4λ+1,42λ-22).又y 23=8x 3,即[22(2λ-1)]2=8(4λ+1),整理得(2λ-1)2=4λ+1,解得λ=0或λ=2.20. (本小题满分12分)解析:(1)由已知90BAP CDP ∠=∠=︒,得AB ⊥AP ,CD ⊥PD .由于AB ∥CD ,故AB ⊥PD ,从而AB ⊥平面P AD .又AB ⊂平面P AB ,所以平面P AB ⊥平面P AD.由(1)及已知可得(2A ,(0,0,)2P,(2B,(2C -.所以(22PC =--,CB =,(22PA =- ,(0,1,0)AB = . 设(,,)x y z =n 是平面PCB 的法向量,则00PC CB ⎧⋅=⎪⎨⋅=⎪⎩ n n,即0220x y z ⎧-+-=⎪⎨=,(0,2)=-n .设(,,)x y z =m 是平面PAB 的法向量,则00PA AB ⎧⋅=⎪⎨⋅=⎪⎩ m m,即0220x z y -=⎪⎨⎪=⎩, 可取(1,0,1)=m .则cos ,||||3⋅==-<>n m n m n m ,所以二面角A PB C --的余弦值为3-. 21.(本小题满分12分)解:(1)折痕为PP ′的垂直平分线,则|MP |=|MP ′|,由题意知圆E 的半径为2,∴|ME |+|MP |=|ME |+|MP ′|=2>|EP |,∴E 的轨迹是以E 、P 为焦点的椭圆,且a =,c =1,∴b 2=a 2﹣c 2=1, ∴M 的轨迹C 的方程为=1. (2)l 与以EP 为直径的圆x 2+y 2=1相切,则O 到l 即直线AB 的距离:=1,即m 2=k 2+1, 由,消去y ,得(1+2k 2)x 2+4kmx +2m 2﹣2=0,∵直线l 与椭圆交于两个不同点,∴△=16k 2m 2﹣8(1+2k 2)(m 2﹣1)=8k 2>0,k 2>0,设A (x 1,y 1),B (x 2,y 2),则,,y 1y 2=(kx 1+m )(kx 2+m )=k 2x 1x 2+km (x 1+x 2)+m 2=, 又=x 1x 2+y 1y 2=,∴,∴,==, 设μ=k 4+k 2,则,∴=,,∵S △AOB 关于μ在[,2]单调递增, ∴,∴△AOB 的面积的取值范围是[,].22. (本小题满分12分)(Ⅰ))(x f 的定义域为),0(+∞;3232/)1)(2(22)(x x ax x x x a a x f --=+--=. 当0≤a , )1,0(∈x 时,0)(/>x f ,)(x f 单调递增; /(1,),()0x f x ∈+∞<时,)(x f 单调递减.当0>a 时,/3(1)()(a x f x x x x -=. (1)20<<a ,12>a, 当)1,0(∈x 或x ∈),2(+∞a 时,0)(/>x f ,)(x f 单调递增; 当x ∈)2,1(a时,0)(/<x f ,)(x f 单调递减; (2)2=a 时,12=a,在x ∈),0(+∞内,0)(/≥x f ,)(x f 单调递增; (3)2>a 时,120<<a , 当)2,0(ax ∈或x ∈),1(+∞时,0)(/>x f ,)(x f 单调递增; 当x ∈)1,2(a 时,0)(/<x f ,)(x f 单调递减. 综上所述,当0≤a 时,函数)(x f 在)1,0(内单调递增,在),1(+∞内单调递减;当20<<a 时,)(x f 在)1,0(内单调递增,在)2,1(a 内单调递减,在),2(+∞a内单调递增;当2=a 时,)(x f 在),0(+∞内单调递增;当2>a ,)(x f 在)2,0(a 内单调递增,在)1,2(a内单调递减,在),1(+∞内单调递增. (Ⅱ)由(Ⅰ)知,1=a 时,/22321122()()ln (1)x f x f x x x x x x x --=-+---+ 23312ln 1x x x x x=-++--,]2,1[∈x , 令1213)(,ln )(32--+=-=xx x x h x x x g ,]2,1[∈x . 则)()()()(/x h x g x f x f +=-, 由01)(/≥-=xx x g 可得1)1()(=≥g x g ,当且仅当1=x 时取得等号. 又24326'()x x h x x--+=, 设623)(2+--=x x x ϕ,则)(x ϕ在x ∈]2,1[单调递减,因为10)2(,1)1(-==ϕϕ, 所以在]2,1[上存在0x 使得),1(0x x ∈ 时,)2,(,0)(0x x x ∈>ϕ时,0)(<x ϕ, 所以函数()h x 在),1(0x 上单调递增;在)2,(0x 上单调递减, 由于21)2(,1)1(==h h ,因此21)2()(=≥h x h ,当且仅当2=x 取得等号, 所以23)2()1()()(/=+>-h g x f x f , 即23)()(/+>x f x f 对于任意的]2,1[∈x 恒成立。
2017-2018学年陕西省西安市长安区第一中学高一数学上期末考试试题

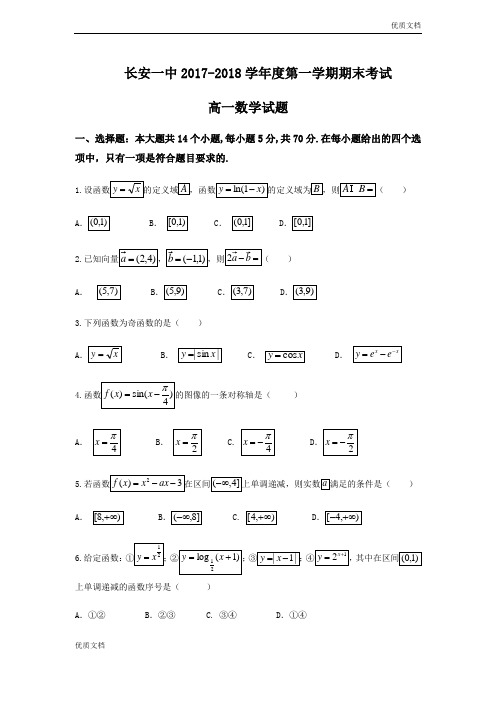
长安一中2017-2018学年度第一学期期末考试高一数学试题、选择题:本大题共14个小题,每小题5分,共70分.在每小题给出的四个选项中,只有一项是符合题目要求的1.设函数丫的定义域A,函数y =l n(1 -x)的定义域为B,则A B=( )A . (0,1)B . [0,1)C . (0,1] D.[0,1]2.已知向量a =(2,4), b=(-1,1), 则2a - b =( )A . (5,7)B . (5,9)C . (3,7)D. (3,9)3•下列函数为奇函数的是( )X x A. y 二x B. y =|sinx| C. y 二cosx D. y = e -e314•函数f(x)二sin(x-[)的图像的一条对称轴是( )JI JI JI JIA. X = —B. xC. X = -一D. X =- —4 2 4 225. 若函数f(x) =x -ax -3在区间(-::,4]上单调递减,则实数a满足的条件是( ) A . [8, ::) B .(-心,8] C. [4,二) D .[-4,::)1x 16. 给定函数:①y = x2;② log 1 (x 1):③y x -1| ; @讨=2,其中在区间(0,1)2上单调递减的函数序号是( )A .①②B .②③ C.③④ D .①④7. 函数f(x) =log2X • x-4的零点所在的区间是( )1A . (一,1)B . (1,2) C. (2,3) D . (3,4)28. 设a=log36 , b=log510, c=log714,则( )A . a b c B. b c a C. a c b D . c b a29. 函数f (x)二Asin( ^ ) b (A 0^ 0,| :K )的一部分图像如图所示,则2。
陕西省西安市长安区第一中学高二上学期期末考试数学(

陕西省西安市长安一中2017~2018学年度第一学期期末考试高二数学试题(理科)一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是满足题目要求的.)1. 设复数满足,则= ( )A. B. C. D. 2【答案】C【解析】复数满足=故选2. 已知命题“存在x0∈R,使+(a-1)x0+≤0”是假命题,则实数a的取值范围是( )A. (-∞,-1)B. (-1,3)C. (-3,+∞)D. (-3,1)【答案】B【解析】试题分析:原命题是假命题,所以其否定是真命题考点:全称命题特称命题及二次函数性质3. 在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120 km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )A. 30辆B. 1700辆C. 170辆D. 300辆【答案】B【解析】由频率分布直方图得:在这段时间内以正常速度通过该处的汽车的频率为估计辆车中在这段时间内以正常速度通过该处的汽车约有(辆)故选4. 用数学归纳法证明1+2+3+…+n2=,则当n=k+1时左端应在n=k的基础上加上( )A. k2+1B. (k+1)2C. D. (k2+1)+(k2+2)+(k2+3)+…+(k+1)2【答案】D【解析】试题分析:当n=k时,等式左端=,当n=k+1时,等式左端=,增加了2k+1项.故选D.考点:数学归纳法.5. 已知正四面体ABCD的棱长为a,点E,F分别是BC,AD的中点,则的值为( )A. a2B. a2C. a2D. a2【答案】C【解析】根据正四面体的的棱长为,画出图形如下:故选6. 直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为( ).A. 4B.C. 2D.【答案】A【解析】先根据题意画出图形:得到积分上限为,积分下限为曲线与直线在第一象限内围成的封闭图形的面积为而故曲边梯形的面积为故选7. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩。
陕西省西安市长安区第一中学2017-2018学年高二上学期期末考试语文试题(解析版)

长安一中2017——2018学年度第一学期期末考试高二语文试题现代文阅读(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成小题。
有人说到“经”,便有意无意地把它等同于“经典”,而提起“中国经典”,就转换成“儒家经典”,这种观念有些偏狭。
中国经典绝不是儒家一家经典可以独占的,也应包括其他经典,就像中国传统是“复数的”传统一样。
首先,中国经典应当包括佛教经典,也应当包括道教经典。
要知道,“三教合一”实在是东方的中国与西方的欧洲在文化领域中最不同的地方之一,也是古代中国政治世界的一大特色。
即使是古代中国的皇帝,不仅知道“王霸道杂之”,也知道要“儒家治世,佛教治心,道教治身”,绝不只用一种武器。
因此,回顾中国文化传统时,仅仅关注儒家的思想和经典,恐怕是过于狭窄了。
即便是儒家,也包含了相当复杂的内容,有偏重“道德自觉”的孟子和偏重“礼法治世”的荀子,有重视宇宙天地秩序的早期儒家和重视心性理气的新儒家。
应当说,在古代中国,关注政治秩序和社会伦理的儒家,关注超越世界和精神救赎的佛教,关注生命永恒和幸福健康的道教,分别承担着传统中国的不同责任,共同构成中国复数的文化。
其次,中国经典不必限于圣贤、宗教和学派的思想著作,它是否可以包括得更广泛些?比如历史著作《史记》《资治通鉴》,比如文字学著作《说文解字》,甚至唐诗、宋词、元曲里面的那些名著佳篇。
经典并非天然就是经典,它们都经历了从普通著述变成神圣经典的过程,这在学术史上叫“经典化”。
没有哪部著作是事先照着经典的尺寸和样式量身定做的,只是因为它写得好,被引用得多,被人觉得充满真理,又被反复解释,有的还被“钦定”为必读书,于是,就在历史中渐渐成了被尊崇、被仰视的经典。
因此,如今我们重新阅读经典,又需要把它放回产生它的时代里面,重新去理解。
经典的价值和意义,也是层层积累的,对那些经典里传达的思想、原则甚至知识,未必需要亦步亦趋“照办不走样”,倒是要审时度势“活学活用”,要进行“创造性的转化”。
陕西省西安市长安区第一中学2017-2018学年高二上学期期末考试数学(文)试题(解析)

陕西省西安市长安一中2017~2018学年度第一学期期末考试高二数学试题(文科)一、选择题(本大题共14小题,每小题5分,共70分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.命题“若α=4π,则tanα=1”的逆否命题是( ) A. 若α≠4π,则tanα≠1 B. 若α=4π,则tanα≠1 C. 若tanα≠1,则α≠4π D. 若tanα≠1,则α=4π 【答案】C 【解析】因为“若p ,则q ”的逆否命题为“若p ⌝,则q ⌝”,所以 “若α=4π,则tanα=1”的逆否命题是 “若tanα≠1,则α≠4π”. 【点评】本题考查了“若p ,则q”形式的命题的逆命题、否命题与逆否命题,考查分析问题的能力. 2.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( ) A. 抽签法 B. 系统抽样法C. 分层抽样法D. 随机数法【答案】C 【解析】按照各种抽样方法的适用范围可知,应使用分层抽样.选C考点:本题考查几种抽样方法的概念、适用范围的判断,考查应用数学方法解决实际问题的能力.3.双曲线2214x y -=的顶点到其渐近线的距离等于( )A. 2B. 1C.D.【答案】D 【解析】不妨取双曲线的顶点2,0(),双曲线的一条渐近线12y x =,由点到直线的距离公式得5d ==,故选D.4.设()ln f x x x =,若0()2f x '=,则0x =( ) A. 2e B. eC.1ln 22D. 2ln 2【答案】B 【解析】()()00ln 1,ln 12f x x f x x ''=+=+=,解得0x e =,故选B.5.为评估一种农作物的种植效果,选了n 块地作试验田.这n 块地的亩产量(单位:kg )分别为x 1,x 2,…,x n ,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 A. x 1,x 2,…,x n 的平均数 B. x 1,x 2,…,x n 的标准差 C. x 1,x 2,…,x n 的最大值 D. x 1,x 2,…,x n 的中位数【答案】B 【解析】评估这种农作物亩产量稳定程度的指标是标准差或方差,故选B.点睛:众数:一组数据出现次数最多的数叫众数,众数反映一组数据的多数水平; 中位数:一组数据中间的数(起到分水岭的作用),中位数反映一组数据的中间水平; 平均数:反映一组数据的平均水平;方差:反映一组数据偏离平均数的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定. 标准差是方差的算术平方根,意义在于反映一组数据的离散程度.6.下图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件)若这两组数据的中位数相等,且平均值也相等,则x 和y 的值分别为A. 5,5B. 3,5C. 3,7D. 5,7 【答案】B【解析】【分析】利用茎叶图、中位数、平均数的性质直接求解.【详解】由茎叶图得:∵甲、乙两组各5名工人某日的产量数据(单位:件)若这两组数据的中位数相等,∴65=60+y,解得y=5,∵平均值也相等,∴5662657074596167657855x+++++++++=,解得x=3.故选B.【点睛】本题考查实数值的求法,考查茎叶图、中位数、平均数的性质等基础知识,考查运算求解能力,是基础题.7.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是()A. 月接待游客量逐月增加B. 年接待游客量逐年增加C. 各年的月接待游客量高峰期大致在7,8月D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 【答案】A 【解析】 【分析】观察折线图可知月接待游客量每年7,8月份明显高于12月份,且折线图呈现增长趋势,高峰都出现在7、8月份,1月至6月的月接待游客量相对于7月至12月波动性更小.【详解】对于选项A ,由图易知月接待游客量每年7,8月份明显高于12月份,故A 错; 对于选项B ,观察折线图的变化趋势可知年接待游客量逐年增加,故B 正确; 对于选项C ,D ,由图可知显然正确.故选A.【点睛】本题考查折线图,考查考生的识图能力,属于基础题. 8.根据如下样本数据 x 345678y 4.02.50.5-0.52.0-3.0-可得到的回归方程为y bx a ∧=+,则( ) A. 0,0a b >< B. 0,0a b >>C. 0,0a b <<D. 0,0a b <>【答案】A 【解析】试题分析:依据样本数据描点连线可知图像为递减且在轴上的截距大于0,所以.考点:1.散点图;2.线性回归方程;9.“1a =”是“22cos sin y ax ax =-的最小正周期为π”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A 【解析】当1a =时,22cos sin =cos 2y ax ax x =-,所以周期为2==2T ππ,当22cos sin =cos2ax y ax ax =-的最小正周期为π时,2aππ= ,所以1a =±,因此“1a =”是“22cos sin y ax ax =-的最小正周期为π”的充分不必要条件.故选A.10.如图是函数()y f x =的导函数()y f x '=的图像,则下列判断正确的是( )A. 在区间()2,1-上,()f x 是增函数B. 在区间()1,3上,()f x 是减函数C. 在区间()4,5上,()f x 是增函数D. 2x =时,()f x 取到极小值 【答案】C 【解析】根据导函数的图象可知,当在区间()4,5上时,()0f x '> ,所以()f x 是增函数,故选C. 11.已知命题p :∃x ∈R ,x 2-x +1≥0.命题q :若a 2<b 2,则a <b ,下列命题为真命题的是( ) A. p q ∧ B. p q ¬∧C. p q ∧¬D. p q ∧¬¬【答案】B 【解析】【分析】先判定命题,p q 的真假,再结合复合命题的判定方法进行判定. 【详解】命题p :∃x=0∈R ,使x 2-x+1≥0成立. 故命题p 为真命题;当a=1,b=-2时,a 2<b 2成立,但a <b 不成立,故命题q 为假命题, 故命题p ∧q ,¬p ∧q ,¬p ∧¬q 均为假命题;命题p ∧¬q 为真命题, 故选B . 【点睛】本题以命题的真假判断与应用为载体,考查了复合命题,特称命题,不等式与不等关系,难度中档.12.【陕西省西安市长安区第一中学上学期期末考】已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,点A 在双曲线的渐近线上,OAF △是边长为2的等边三角形(O 为原点),则双曲线的方程为( )A. 221412x y -=B. 221124x y -=C. 2213x y -=D. 2213y x -=【答案】D 【解析】由题意结合双曲线的渐近线方程可得:2222tan 603c c a bba⎧⎪=⎪=+⎨⎪⎪==⎩,解得:221,3a b ==, 双曲线方程为:2213y x -=.本题选择D 选项.【考点】 双曲线的标准方程【名师点睛】利用待定系数法求圆锥曲线方程是高考常见题型,求双曲线方程最基础的方法就是依据题目的条件列出关于,,a b c 的方程,解方程组求出,a b ,另外求双曲线方程要注意巧设双曲线(1)双曲线过两点可设为221(0)mx ny mn -=>,(2)与22221x y a b-=共渐近线的双曲线可设为2222(0)x y a b λλ-=≠,(3)等轴双曲线可设为22(0)x y λλ-=≠等,均为待定系数法求标准方程.13.已知某运动员每次射击击中目标的概率为80%.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率.先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281根据以上数据估计该射击运动员射击4次至少击中3次的概率为( ) A. 0.852 B. 0.8192C. 0.8D. 0.75【答案】D 【解析】 【分析】因为射击4次至多击中2次对应的随机数组为7140,1417,0371,6011,7610,共5组,即可求得答案. 【详解】射击4次至多击中2次对应的随机数组为7140,1417,0371,6011,7610,共5组,∴ 射击4次至少击中3次的概率约为510.7520-=, 故选:D.【点睛】本题考查了根据随机模拟的方法估计概率,解题关键是掌握随机模拟的方法估计概率的方法,考查了分析能力,属于基础题.14.若函数()f x 满足()()2(x f x f x xe e ='-为自然对数底数),(0)1,f =其中()f x '为()f x 的导函数,则当0x >时,()()f x f x '的取值范围是( ) A. ](,2-∞ B. (]0,2C. ](1,2D. ](2,3【答案】C 【解析】 由题意,构造函数()xf x y e =,则()=2xf x x e'(),所以2()x f x x b e=+,2()()x f x x b e =+,(0)1,1f b =∴=,因此22()(1),()(1)xxf x x e f x x e '=+=+,2()21()1f x xf x x =++',当0x >时,221121xx <+≤+,当且仅当1x =时,等号成立,故选C. 二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在答题纸相应的位置).15.记函数()f x =的定义域为D ,在区间[]4,5-上随机取一个数x ,则x D ∈的概率是________. 【答案】59【解析】由260x x +-≥,即260x x --≤,得23x -≤≤,根据几何概型的概率计算公式得x D ∈的概率是()()325549--=--,故答案为59. 16.若函数3211()232f x x x ax =-++ 在2,3⎡⎫+∞⎪⎢⎣⎭上存在单调增区间,则实数a 的取值范围是_______. 【答案】1(,)9-+∞ 【解析】【详解】试题分析:2211()2224f x x x a x a ⎛⎫=-++=--++ ⎪⎝⎭'.当23x ⎡⎫∈+∞⎪⎢⎣⎭,时,()f x '的最大值为 22239f a ⎛⎫=+ ⎪⎝⎭',令2209a +>,解得19a >-,所以a 的取值范围是1,9⎛⎫-+∞ ⎪⎝⎭.考点:利用导数判断函数的单调性.17.设F 为抛物线2:=3C y x 的焦点,过F 且倾斜角为30的直线交C 于A ,B 两点,则AB =________.【答案】12 【解析】由2=3y x 知焦点3(0)4F ,,所以设直线AB 方程为3)34y x =-,联立抛物线与直线方程,消元得:21616890x x -+=,设1122(,),(,)A x y B x y ,则12212x x +=,根据抛物线定义知12213||=x 1222AB x p ++=+=.故填:12. 18.已知点P 在曲线41xy e =+上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是__________. 【答案】3,4ππ⎡⎫⎪⎢⎣⎭.【解析】∵4e 1x y =+,∴224e 4e 41(e 1)e 2e 1e 2e x x x x x x xy ---===+++++'. ∵e x >0,∴1e 2e xx +≥,当且仅当1e e xx=,即x =0时等号成立. ∴y ′∈[−1,0),∴tanα∈[−1,0).又α∈[0,π),∴α∈3π,π4⎡⎫⎪⎢⎣⎭.三、解答题(本大题共5小题,每小题12分,共60分.解答应写出文字说明,证明过程或演算步骤.)19.某旅游爱好者计划从3个亚洲国家A 1,A 2,A 3和3个欧洲国家B 1,B 2,B 3中选择2个国家去旅游. (1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A 1,但不包括B 1的概率. 【答案】(1)15P = ;(2)29P = 【解析】试题分析:利用列举法把试验所含的基本事件一一列举出来,然后再求出事件A 中的基本事件数,利用公式P (A )=求出事件A 的概率.试题解析:(Ⅰ)由题意知,从6个国家中任选两个国家,其一切可能的结果组成的基本事件有:{}{}{}{}{}{}{}{}{}{}{}{}121323111213212223313233,,,,,,,,,,,,,,,,,,,,,,,,A A A A A A AB A B A B A B A B A B A B A B A B {}{}{}121323,,,,,B B B B B B ,共15个.所选两个国家都是亚洲国家的事件所包含的基本事件有:{}{}{}121323,,,,,A A A A A A ,共3个,则所求事件的概率为:31155P ==. (Ⅱ)从亚洲国家和欧洲国家中各任选一个,其一切可能的结果组成的基本事件有:{}{}{}{}{}{}{}{}111213212223313233,,{,},,,,,,,,,,,,,,A B A B A B A B A B A B A B A B A B ,共9个,包含1A 但不包括1B 的事件所包含的基本事件有:{}{}1213,,,A B A B ,共2个, 所以所求事件的概率为:29P =. 【考点】古典概型【名师点睛】(1)对于事件A 的概率的计算,关键是要分清基本事件总数n 与事件A 包含的基本事件数m.因此必须解决以下三个方面的问题:第一,本试验是否是等可能的;第二,本试验的基本事件数有多少个;第三,事件A 是什么,它包含的基本事件有多少个.(2)如果基本事件的个数比较少,可用列举法把古典概型试验所包含的基本事件一一列举出来,然后再求出事件A 中的基本事件数,利用公式P (A )=求出事件A 的概率,这是一个形象、直观的好方法,但列举时必须按照某一顺序做到不重不漏.20.设函数f (x )=a ln x -bx 2(x >0),若函数f (x )在x =1处与直线y =-相切.(1)求实数a ,b 的值; (2)求函数f(x)在上的最大值.【答案】(1)112a b =⎧⎪⎨=⎪⎩.(2)f (x )max =12-.【解析】 【分析】(1)对f (x )进行求导()'fx , 欲求出切线方程,只需求出其斜率即可,故先利用导数求出在1x =处的导数值,再结合导数的几何意义即可求出切线的斜率,列出关于a ,b 的方程求解即可;(2)研究闭区间上的最值问题,先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值.【详解】(1)f ′(x )=-2bx ,∵函数f (x )在x =1处与直线y =-相切,∴'(1)211(1)2f a b f b =-=⎧⎪⎨=-=-⎪⎩解得(2)由(1)知,f (x )=ln x -x 2,f ′(x )=-x =,当≤x ≤e 时,令f ′(x )>0,得≤x <1, 令f ′(x )<0,得1<x ≤e,∴f (x )在[,1)上是增加的,在(1,e]上是减少的, ∴f (x )max =f (1)=-点睛:本题主要考查函数单调性的应用,利用导数研究曲线上某点的切线方程,导数在最大值、最小值问题中的应用,不等式的解法等基础知识,考查运算求解能力,化归与转化思想.21.某某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: [20,30),[30,40),[80,90]⋯ ,并整理得到如下频率分布直方图:(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例. 【答案】(1)0.4. (2)20人.(3) 3:2. 【解析】【详解】分析:(1)根据频率分布直方图可知,即可求解样本中分数不小于70的频率,进而得到 分数小于70的概率;(2)根据题意,根据样本中分数不小于50的频率为0.9,求得分数在区间[40,50)内的人数为5人,进而求得总体中分数在区间[40,50)内的人数;(3)由题意可知,样本中分数不小于70的学生人数为60人,求得样本中分数不小于70的男生人数,即可求解.详解:(1)根据频率分布直方图可知,样本中分数不小于70的频率为 (0.02+0.04)×10=0.6 ,样本中分数小于70的频率为1-0.6=0.4.∴从总体的400名学生中随机抽取一人其分数小于70的概率估计为0.4 (2)根据题意,样本中分数不小于50的频率为()0.010.020.040.02100.9+++⨯=,分数在区间[)40,50内的人数为1001000.955-⨯-=.所以总体中分数在区间[)40,50内的人数估计为540020100⨯=. (3)由题意可知,样本中分数不小于70的学生人数为()0.020.041010060+⨯⨯=,所以样本中分数不小于70的男生人数为160302⨯= 所以样本中的男生人数为30260⨯=,女生人数为1006040-=,男生和女生人数的比例为60:403:2= 点睛:本题主要考查了用样本估计总体和频率分布直方图的应用,其中对于用样本估计总体主要注意以下两个方面:1、用样本估计总体是统计的基本思想,而利用频率分布表和频率分布直方图来估计总体则是用样本的频率分布去估计总体分布的两种主要方法;2、频率分布表中的频数之和等于样本容量,各组中的频率之和等于1;在频率分布直方图中,各小长方形的面积表示相应各组的频率,所以,所有小长方形的面积的和等于1.22.设椭圆2221(3)3x y a a +=>的右焦点为F ,右顶点为A ,已知113||||||e OF OA FA +=,其中O 为原点,e 为椭圆的离心率.(1)求椭圆的方程;(2)设过点A 的直线l 与椭圆交于点B (B 不在x 轴上),垂直于l 的直线与l 交于点M ,与y 轴交于点H ,若BF HF ⊥,且MOA MAO ∠≤∠,求直线的l 斜率的取值范围.【答案】(1) 椭圆方程为22143x y +=;(2) 直线l 的斜率的取值范围为66(,][,)-∞-+∞.【解析】试题分析:(Ⅰ)求椭圆标准方程,只需确a 的值,由113e OF OA FA +=,得113()cc a a a c +=-,再利用222a c b -=,可解得a 的值;(Ⅱ)先化简条件:MOA MAO ∠=∠⇔MA MO =,即M 再OA 的中垂线上,1M x =,再利用直线与椭圆位置关系,联立方程组求;利用两直线方程组求H ,最后根据,列等量关系即可求出直线斜率的取值范围.试题解析:(Ⅰ)解:设(c,0)F ,由113e OF OA FA +=,即113()cc a a a c +=-,可得2223a c c -=,又2223a c b -==,所以21c =,因此24a =,所以椭圆的方程为22143x y +=.(Ⅱ)解:设直线的斜率为(),则直线的方程为.设,由方程组,消去,整理得.解得,或,由题意得,从而.由(Ⅰ)知,,设,有FH (1,)H y =-,2229412(,)4343k k BF k k -=++.由,得0BF HF ⋅=,所以222124904343Hky k k k -+=++,解得.因此直线的方程为.设,由方程组消去,解得.在MAO 中,,即,化简得,即,解得或.所以,直线的斜率的取值范围为.【考点】椭圆的标准方程和几何性质,直线方程【名师点睛】在利用代数法解决最值与范围问题时常从以下五个方面考虑: (1)利用判别式来构造不等关系,从而确定参数的取值范围;(2)利用已知参数的范围,求新参数的范围,解这类问题的核心是在两个参数之间建立等量关系; (3)利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围; (4)利用基本不等式求出参数取值范围; (5)利用函数的值域的求法,确定参数的取值范围.23.已知函数()ln f x x x =,()()23g x x ax a =-+-∈R .(1)若对任意()0,x ∈+∞,恒有不等式()()12f x g x ≥,求a 的取值范围; (2)证明:对任意()0,x ∈+∞,有12ln e e x x x>-. 【答案】(1)(],4-∞;(2)见解析 【解析】【详解】(1)当0x >时,()()()2113ln 32ln 22f x g x x x ax a x x x≥⇔≥-+-⇔≤++. 令()()32ln 0h x x x x x=++>. 则()min a h x ≤. 由()()()231x x h x x +'-=,知函数()h x 在区间()0,1上单调递减,在区间()1,+∞上单调递增.所以,()()min 14h x h ==. 故a 的取值范围是(],4-∞. (2)要证12ln e e x x x >-,只要证()2ln e ex x f x x x =>-. 由()ln 1f x x ='+,知()f x 在区间10,e ⎛⎫ ⎪⎝⎭上单调递减,在区间1,e⎛⎫+∞ ⎪⎝⎭上单调递增. 于是,当0x >时,()11e e f x f ⎛⎫≥=- ⎪⎝⎭. ①令()()20e e x x x x ϕ=->. 则()1ex xx ϕ='-.所以,()()11ex ϕϕ≤=-. ②显然,不等式①、②中的等号不能同时成立. 故当0x >时,()()f x x ϕ>,即12ln e e x x x>-。
陕西省长安一中2017-2018学年高一上学期期末考试语文试题(扫描版)

长安一中2017---2018学年度第一学期期末考试高一语文参考答案及评分标准一.论述类文本阅读(9分)1.C“‘十翼’表现出一种变化观”理解错误。
原文说“十翼”对《周易》义理的阐述,突出地表现出一种变化观。
2.C“就能科学地预测历史的发展变化”理解有误。
原文说“尽管有时占筮者在推断中也会结合对历史和现实的了解,但这类占筮法总体上笼罩在唯心主义、神秘主义的气氛之中,并非科学的方法”。
3.B“但各项内容很可能不一致,甚至还会出现两项之间矛盾对立的现象”有误。
原文说“然而,在每次占筮时,并不会八项内容都讲,因为甲项与乙项的结论很可能不一致,甚至是对立的”,可见“不一致”的不是“各项内容”,而是甲项与乙项的结论。
二、实用类文本阅读(12分)4.D“直接表现其高尚气节”错误,引用名人对传主的评价应该是“侧面”表现其高尚气节。
5.CE(A.“机械刻板的一面”不当,应该是“严格自律的一面”。
B.由原文第4段可知,增加人文色彩的是清华园里的“荷塘月色”和“自清”亭。
D.可能是“豁达”,也可能是出于无奈,但没有“乐观”。
)6.答案“生不逢时”是指他身处在战事混乱、政治动荡、物价飞涨、生活困难的不幸时代。
朱自清处境困窘但毫不妥协,这更能体现他人格的完美。
(1分)他身处困境,虽然生活清贫,但写作时仍然注重质量,每天最多写500字,这更能显出他的认真严谨。
②他身处动荡乱世,但不愿同流合污,改名“自清”以自励,取字“佩弦”以自警,这更能显出他的洁身自好。
③物价飞涨,生活艰难,但为揭露国民党政府的阴谋,抗议美国政府的侮辱,他第一个在声明上签字,这更能显出他的无畏和勇气。
④奄奄一息,生命垂危,但他仍嘱咐妻子拒绝美援,这更表现出他的坚定的君子气节。
(每点1分)解析根据原文“他的清贫一部分原因是写得太慢”,朱自清在清贫时没有忘却写作质量;根据原文“朱自华改名‘自清’,以勉励自己在困境中保持清白,不同流合污”,朱自清在困境中仍然保持清白;根据原文“朱自清第一个在声明上签了字”,朱自清生活困难,仍然拥有勇气揭穿阴谋;根据原文“我……已拒绝美援,不要去买配售的美国面粉……”,朱自清在弥留之际仍然保持气节。
陕西省西安市长安区第一中学2017-2018学年高一上学期期末考试物理试题含答案

长安一中2017~2018学年度第一学期期末考试高一物理试题命题人:张小周审题人:李蒙第I卷(选择题共60分)一、选择题(本题包括15小题.每小题4分,共60分。
其中1-11为单项选择12—15为多项选择,多项选择题全部选对的得4分,选对但不全得2分,有选错或不答的得0分)1.在物理学的重大发现中科学家们创造出了许多物理学方法,如理想实验法、控制变量法、极限思想法、建立物理模型法、类比法和科学假说法等等。
以下关于所用物理学研究方法的叙述正确的是: A.在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法,以及在力的合成过程中用一个力代替几个力,这里都采用了微元法B.根据速度定义式xvt∆=∆,当非常非常小时,就可以用xt∆∆表示物体在t时刻的瞬时速度,这是应用了极限思想方法C.玻璃瓶内装满水,用穿有透明细管的橡皮泥封口。
手捏玻璃瓶,细管内液面高度变化,说明玻璃瓶发生形变,该实验采用转换思想D.在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了等效替代的思想.2。
下列关于加速度的说法,正确的是:A.物体的速度越大,加速度也就越大B.物体的速度为零,加速度也一定为零C.物体的加速度大小等于速度的变化量与时间的比值D.物体加速度的方向和速度的方向总是一致3。
关于牛顿第一定律的说法中,正确的是:A。
由牛顿第一定律可知,物体在任何情况下始终处于静止状态和匀速直线运动状态B。
牛顿第一定律只是反映惯性大小的,因此也叫惯性定律C.牛顿第一定律反映了物体不受外力作用时的运动规律,因此,物体在不受力时才有惯性D.牛顿第一定律既揭示了物体保持原有运动状态的原因,又揭示了运动状态改变的原因4。
如图所示是A、B两运动物体的位移图象,下述说法中正确的是:A.A、B两物体开始时相距100 m,运动方向相同B.B物体做匀速直线运动,速度大小为20 m/s C.A、B两物体运动8 s时,在距A的出发点60 m处相遇D.A物体在运动中停了6 s5.这是同学们在课堂中接触过的一个实验,做直线运动的钢球,在钢球运动路线旁边放一块磁铁.由此判断物体做曲线运动的条件为:A.有初速度B.合力为零C.有合力且初速不为零D.合力方向与速度方向不在同一直线上6。
陕西省西安市长安区第一中学2017-2018学年高二上学期期末考试数学(文)试题 Word版含解析

陕西省西安市长安一中2017~2018学年度第一学期期末考试高二数学试题(文科)一、选择题(本大题共14小题,每小题5分,共70分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 命题“若,则”的否命题是( )A. 若,则B. 若,则C. 若,则D. 若,则.【答案】A【解析】因为否命题是将原命题的条件和结论同时否定,所以命题“若,则”的否命题是若,则,故选.2. 某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )A. 抽签法B. 系统抽样法C. 分层抽样法D. 随机数法【答案】C【解析】按照各种抽样方法的适用范围可知,应使用分层抽样.选C考点:本题考查几种抽样方法的概念、适用范围的判断,考查应用数学方法解决实际问题的能力.3. 双曲线的顶点到其渐近线的距离等于()A. 2B. 1C.D.【答案】D【解析】不妨取双曲线的顶点,双曲线的一条渐近线,由点到直线的距离公式得,故选D.4. 设,若,则等于( )A. B. C. D.【答案】B【解析】试题分析:,则,.故选B.考点:导数的运算.5. 为评估一种农作物的种植效果,选了块地作试验田.这块地的亩产量(单位:)分别为,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )A. 的平均数B. 的标准差C. 的最大值D. 的中位数【答案】B【解析】根据平均数,最大值,中位数,标准差的含义知,只有标准差是衡量一组数据稳定性的数字特征,故选B.6. 如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则和的值分别为( )A. 3,5B. 5,5C. 3,7D. 5,7【答案】A【解析】由茎叶图可知甲组的中位数为∵两组数的中位数相同∴乙组的中位数也为∴∵两组数据的平均值相等∴∴故选A7. 某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A. 月接待游客逐月增加B. 年接待游客量逐年增加C. 各年的月接待游客量高峰期大致在7,8月D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳【答案】A【解析】由已知中2014年1月至2016年12月期间月接待游客量(单位:万人)的数据可得:月接待游客量逐月有增有减,故A错误;年接待游客量逐年增加,故B错误;各年的月接待游客量高峰期大致在7,8月,故C正确;各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D错误;本题选择C选项.8. 根据如下样本数据:得到的回归方程为,则()A., B. , C. , D. ,【答案】C【解析】样本平均数,故选C.9. “”是“的最小正周期为”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】当时,,所以周期为,当的最小正周期为时,,所以,因此“”是“的最小正周期为”的充分不必要条件.故选A.10. 如图是函数的导函数的图像,则下面判断正确的是( )A. 在区间上是增加的B. 在区间上是减少的C. 在区间上是增加的D. 当时,取到极小值【答案】C【解析】根据导函数的图象可知,当在区间上时,,所以是增函数,故选C.11. 已知命题;命题若,则.下列命题为真命题的是( )A. B. C. D.【答案】B【解析】因为是真命题,命题若,则是假命题,所以是真命题,从而是真命题,故选B.12. 已知双曲线的左焦点为,点在双曲线的渐近线上,是边长为2的等边三角形(为原点),则双曲线的方程为()A. B. C. D.【答案】D【解析】由题意结合双曲线的渐近线方程可得:,解得:,双曲线方程为:.本题选择D选项.【考点】双曲线的标准方程【名师点睛】利用待定系数法求圆锥曲线方程是高考常见题型,求双曲线方程最基础的方法就是依据题目的条件列出关于的方程,解方程组求出,另外求双曲线方程要注意巧设双曲线(1)双曲线过两点可设为,(2)与共渐近线的双曲线可设为,(3)等轴双曲线可设为等,均为待定系数法求标准方程.13. 现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算机给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 46980371 6233 2616 8045 6011 3661 9597 7424 7610 4281根据以上数据统计该运动员射击4次至少击中3次的概率为( )A. 0.852B. 0.8192C. 0.8D. 0.75【答案】D【解析】试题分析:由题意知,在20组随机数中表示种射击4次至少击中3次的有多少组,可以通过列举得到共多少组随机数,根据概率公式,得到结果.解:由题意知模拟射击4次的结果,经随机模拟产生了如下20组随机数,在20组随机数中表示射击4次至少击中3次的有:7527 0293 9857 0347 4373 8636 9647 46986233 2616 8045 3661 9597 7424 4281,共15组随机数,∴所求概率为0.75.故选:D.考点:模拟方法估计概率.14. 若函数满足为自然对数底数),其中为的导函数,则当时,的取值范围是()A. B. C. D.【答案】C【解析】由题意,构造函数,则,所以,,,因此,,当时,,当且仅当时,等号成立,故选C.二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在答题纸相应的位置).15. 记函数的定义域为.在区间上随机取一个数,则的概率是______.【答案】【解析】由,即,得,根据几何概型的概率计算公式得的概率是.点睛:(1)当试验的结果构成的区域为长度、面积或体积等时,应考虑使用几何概型求解.(2)利用几何概型求概率时,关键是试验的全部结果构成的区域和事件发生的区域的寻找,有时需要设出变量,在坐标系中表示所需要的区域.(3)几何概型有两个特点:①无限性,②等可能性.基本事件可以抽象为点,尽管这些点是无限的,但它们所占据的区域都是有限的,因此可用“比例解法”求解几何概型的概率.16. 若函数在上存在递增区间,则的取值范围是________.【答案】【解析】试题分析:.当时,的最大值为,令,解得,所以a的取值范围是.考点:利用导数判断函数的单调性.17. 设为抛物线的焦点,过且倾斜角为的直线交于,两点,则________.【答案】12【解析】由知焦点,所以设直线AB方程为,联立抛物线与直线方程,消元得:,设,则,根据抛物线定义知.故填:.KS5U...KS5U...KS5U...KS5U...KS5U...KS5U...18. 已知点在曲线上,为曲线在点处的切线的倾斜角,则的取值范围是________.【答案】【解析】试题分析:∵,∴,∴,当且仅当x=0时,等号成立,根据正切函数图象可知考点:本题考查了导数的几何意义及正切函数不等式的解法点评:熟练掌握导数的几何意义是解决此类问题的关键,属基础题三、解答题(本大题共5小题,每小题12分,共60分.解答应写出文字说明,证明过程或演算步骤.)19. 某旅游爱好者计划从3个亚洲国家和3个欧洲国家中选择2个国家去旅游.(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括但不包括的概率.【答案】(1);(2)【解析】试题分析:(1)从这6个国家中任选2个,基本事件总数共15个,这2个国家都是亚洲国家的事件包含的基本事件共3个,由此求出其概率;(2)从亚洲国家和欧洲国家中各任选1个,利用列举法求出包括但不包括的概率.试题解析:(1)由题意得,从6个国家中人员两个国家,其一切可能的结果组成基本事件有:,,,,,,,共15个.所选两个国家都是亚洲的事件包含的基本事件有:,,,共3个,所以所求事件的概率为.(2)从亚洲国家和欧洲国家中任选一个,其一切可能的结果组成的基本事件有:,,共9个,包含但不包含的事件所包含的基本事件有共2个.所以所求事件的概率为.20. 设函数,若函数在处与直线相切.(Ⅰ)求实数的值;(Ⅱ)求函数在上的最大值.【答案】(1);(2).【解析】试题分析:通过对求导,利用函数在处与直线相切,通过联立方程组,计算即可得到结论;通过可知,,通过讨论在上的正负可知函数单调性,进而得到结论。
英语-陕西省西安市长安区第一中学2017-2018学年高一上学期期末考试试题

陕西省西安市长安区第一中学2017-2018学年高一上学期期末考试英语试题第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Why doesn’t the woman like to have red wine?A. Because she doesn’t like its taste.B. Because she prefers beer.C. Because she is afraid of getting drunk.2. What is the man going to buy?A. Food.B. DrinksC. Flowers.3. What are the two speakers doing?A. Looking for some suitcases.B. Booking tickets for a journey.C. Checking the woman’s baggage.4. Why would the woman rather stay at the hotel?A. It costs less money.B. It saves much labor.C. It feels more comfortable.5. What are the two speakers talking about?A. A painting.B. A country scene.C. A kind of drink.第二节(共15小题;每小题1.5分,共22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
2018届长安一中2017~2018学年度第一学期期末考试Word版 含答案)

长安一中2017~2018学年度第一学期期末考试高二化学试题(理科)(考试时间100分钟,满分100分)注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题纸上。
2.考生作答时,请将答案涂写在答题纸上,在本试卷上答题无效。
按照题号在各题的答题区域内作答,答题区域错误或超出答题区域书写的答案无效。
3.答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.保持答题纸纸面清洁、不破损、不折叠。
考试结束后,将本试卷自行保存,答题纸交回。
可能用到的相对原子质量:H 1 C 12 O 16 Fe 56第Ⅰ卷一、选择题:本题共21个小题,每小题2分,共42分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列化学方程式书写错误的是()A .NaHCO 3水解的离子方程式:3HCO -+ H 2O 23CO -+H 3O + B .NH 4Cl 水解的化学方程式:NH 4Cl+H 2O NH 3·H 2O+HClC .Al(OH)3的两性电离方程式:H ++AlO 2−+H 2OAl(OH)3Al 3++3OH − D .NaHSO 3的电离方程式:NaHSO 3Na ++3HSO -2.Mg-AgCl 电池是一种以海水为电解质溶液的水激活电池。
下列叙述错误的是()A .负极反应式为Mg - 2e -Mg 2+ B .正极反应式为Ag + + e - AgC .电池放电时Cl -由正极向负极迁移D .负极会发生副反应Mg + 2H 2OMg(OH)2 + H 2↑3.下列叙述正确的是()A .石油、沼气、天然气、植物油都属于可再生能源B .应用盖斯定律,可计算某些难以直接测量的反应的焓变C .水蒸气变为液态水时放出的能量就是该变化的反应热D .同温同压下,H 2(g)+Cl 2(g) 2HCl(g)在光照和点燃条件下的ΔH 不同 4.在一定条件下,使NO 和O 2在一密闭容器中进行反应,下列说法不正确的是()A .反应开始时,正反应速率最大,逆反应速率为零B.随着反应的进行,正反应速率逐渐减小,最后为零C.随着反应的进行,逆反应速率逐渐增大,最后不变D.随着反应的进行,正反应速率逐渐减小,最后不变5.在密闭容器中发生反应:C(s)+CO 2(g)2CO(g),下列说法不正确的是()A.增大CO2浓度可以加快反应速率B.升高温度可以加快反应速率C.容器体积不变时,向其中充入N2,反应速率不变D.增加碳的质量可以加快反应速率6.下列关于反应热和热化学方程式的描述中正确的是()A.HCl和NaOH反应的中和热ΔH=-57.3 kJ·mol-1,则H2SO4和Ca(OH)2反应的反应热ΔH=2×(-57.3) kJ·mol-1B.CO(g)的燃烧热是283.0 kJ·mol-1,则反应2CO2(g)2CO(g)+O2(g)的ΔH=+2×283.0 kJ·mol-1C.氢气的燃烧热为285.5 kJ·mol-1,则分解水的热化学方程式为2H2O(l)2H2(g)+O2(g) ΔH=+285.5 kJ·mol-1D.1 mol甲烷完全燃烧生成气态水和二氧化碳时所放出的热量是甲烷的燃烧热7.合成气(CO和H2)是目前化工常用的原料,下面是用甲烷制备合成气的两种方法:①CH4(g)+H2O(g)CO(g)+3H2(g) ΔH1=+216 kJ·mol-1;②2CH4(g)+O2(g)2CO(g)+4H2(g) ΔH2=-72 kJ·mol-1。
长安一中2017~2018学年度第一学期期末考试word版 含答案

长安一中2017~2018学年度第一学期期末考试高二化学试题(文科)注意事项:1. 考试时间100分钟,总分100分;2. 可能用到的相对原子质量:H-1 O-16 S-32 Fe-56第I卷(选择题共48分)一、选择题(共24小题,均为单选,每小题2分,共计48分)1.北京和张家口市联合申办2022年冬奥会,目前北京市政府正在全力改善空气质量。
以下不在空气质量报告范围内的是()A. O2B. NOC. NO2D. SO22. 化学与生活密切相关。
下列生活中常见物质的俗名与化学式相对应的是()A.小苏打—Na2CO3B. 明矾—KAl(SO4)2C. 消石灰—Ca(OH)2D. 甲醛—CH3OH3.糖类是维持人体生命活动所必需的营养物质,下列有关糖类的说法正确的是()①糖类物质都具有甜味②由C、H、O三种元素组成的有机物属于糖类③糖类也称碳水化合物,它们的化学组成都可以表示为C n(H2O)m④葡萄糖是单糖,因为其结构简单,且分子中官能团个数少⑤单糖不能水解成更简单的糖⑥蔗糖的相对分子质量是葡萄糖的2倍⑦葡萄糖兼具有醛类和多元醇的一些性质⑧淀粉和纤维素的分子式都为(C6H10O5)n,二者互为同分异构体A.②④B. ④⑤C. ⑤⑦D. ⑦⑧4.化学在日常生活中有着重要的应用。
下列说法不正确的是()A.做红烧鱼时,常加入一些食醋和酒会更香,是因为生成了少量的酯B.明矾是常用的混凝剂,可用于污水的杀菌和消毒C.物流运输中可以用浸泡过KMnO4溶液的纸张保鲜水果D.热水瓶胆中的水垢可以用食醋除去5. 医疗上葡萄糖被大量用于给病人输液的原因是()A.葡萄糖有甜味,能溶于水B.葡萄糖由C、H、O三种元素组成C.葡萄糖在人体内能直接进行新陈代谢D.相同质量葡萄糖被氧化所释放的能量比油脂多6.现有淀粉和鸡蛋清两种溶液,用下列试剂或方法不能区别它们的是()A.碘水B. 浓硝酸C. 加热D. 激光笔照射7.下列关于蛋白质的叙述中不正确的是()A.人工合成具有生命活力的蛋白质—结晶牛胰岛素是我国科学家在1965年首次合成的B.在蛋白质溶液中加入饱和硫酸铵溶液,蛋白质析出,加水,不溶解C.重金属盐类能使蛋白质凝结,所以误食重金属盐类能使人中毒D.浓硝酸溅在皮肤上能使皮肤变黄,这是由于浓硝酸和蛋白质发生了颜色反应8.油脂是人体重要的能源物质,下列关于油脂的叙述正确的是()A.油脂的主要成分是高级脂肪酸B.油脂属于天然有机高分子化合物C.煎炸食物的花生油比牛油的熔点高D.油脂可以在碱性条件下水解,用于制取肥皂9.在潮湿的空气中,钢铁很快发生电化学腐蚀,在此过程中一定不存在的电极反应是()A. 2H+ + 2e- = H2↑B. Fe - 3e- = Fe3+C. Fe - 2e- = Fe2+D. O2 + 2H2O + 4e- = 4OH-10.化学与科学、技术、社会、环境密切相关。
2017-2018学年陕西省西安市长安区第一中学高一上学期期末考试英语试题

2017-2018学年陕西省西安市长安区第一中学高一上学期期末考试英语试题第I卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Why doesn’t the woman like to have red wine?A.Because she doesn’t like its taste.B.Because she prefers beer.C.Because she is afraid of getting drunk.2. What is the man going to buy?A.Food.B.DrinksC.Flowers.3. What are the two speakers doing?A.Looking for some suitcases.B.Booking tickets for a journey.C.Checking the woman’s baggage.4. Why would the woman rather stay at the hotel?A.It costs less money.B.It saves much labor.C.It feels more comfortable.5. What are the two speakers talking about?A.A painting.B.A country scene.C.A kind of drink.第二节(共15小题;每小题1.5分,共22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
2017-2018学年陕西省西安市长安一中高一(上)期末数学试卷(解析版)

2017-2018学年陕西省西安市长安一中高一(上)期末数学试卷一、选择题(本大题共14小题,共70.0分)1.设函数的定义域A,函数y=ln(1-x)的定义域为B,则A∩B=()A. B. C. D.2.已知向量=(2,4),=(-1,1),则2-=()A. B. C. D.3.下列函数为奇函数的是()A. B. C. D.4.函数f(x)=sin(x-)的图象的一条对称轴是()A. B. C. D.5.若函数f(x)=x2-ax-3在区间(-∞,4]上单调递减,则实数a满足的条件是()A. B. C. D.6.给定函数①,②,③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是()A. ①②B. ②③C. ③④D. ①④7.函数f(x)=log2x+x-4的零点所在的区间是()A. B. C. D.8.设a=log36,b=log510,c=log714,则()A. B. C. D.9.函数f(x)=A sin(ωx+φ)+b(A>0,ω>0,|φ|<)的一部分图象如图所示,则()A. B.C. D.10.已知△ABC是边长为1的等边三角形,点D、E分别是边AB、BC的中点,连接DE并延长到点F,使得DE=2EF,则•的值为()A. B. C. D.11.函数y=-sin2x-3cos x+3的最小值是()A. 2B. 0C.D. 612. 已知f (x )=的值域为R ,那么a 的取值范围是( )A.B.C.D.13. 设α∈(0,),β∈(0,),且tanα=,则( )A.B.C.D.14. 已知函数f (x )=2sin (2x +)+2cos 2(x +)-1,把函数f (x )的图象向右平移个单位,得到函数g (x )的图象,若x 1,x 2是g (x )-m =0在[0,]内的两根,则sin (x 1+x 2)的值为( )A.B.C.D.二、填空题(本大题共6小题,共30.0分)15. 已知向量 =(-2,3), =(3,m ),且 ,则m =______. 16. 已知向量 , 满足| |=1,| |=2, 与 的夹角为60°,则| - |=______.17. 已知角α的终边过点P (4,-3),则2sinα+cosα的值为______.18. 奇函数f (x )的定义域为[-2,2],若f (x )在[0,2]上单调递减,且f (1+m )+f (m )<0,则实数m 的取值范围是______.19. 由于德国著名数学家狄利克雷对数论、数学分析和物理学的突出贡献,人们将函数是有理数是无理数命名为狄利克雷函数,已知函数f (x )=x -D (x ),下列说法中:①函数f (x )的定义域和值域都是R ; ②函数f (x )是奇函数;③函数f (x )是周期函数; ④函数f (x )在区间[2,3]上是单调函数. 正确结论是______.20. 已知函数,关于x 的方程 ∈ 有四个不同的实数解 则 的取值范围为______. 三、解答题(本大题共4小题,共50.0分) 21. 计算下列各式的值:(1)(2)(3).22. 如图所示,A ,B 分别是单位圆与x 轴、y 轴正半轴的交点,点P 在单位圆上,∠AOP =θ(0<θ<π),C 点坐标为(-2,0),平行四边形OAQP的面积为S.(1)求•+S的最大值;(2)若CB∥OP,求sin(2θ-)的值.23.已知向量=(m,cos2x),=(sin2x,1),函数f(x)=•,且y=f(x)的图象过点(,).(1)求m的值;(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.24.设f(x)=log()为奇函数,a为常数.(1)求a的值;(2)证明:f(x)在(1,+∞)内单调递增;(3)若对于[3,4]上的每一个x的值,不等式f(x)>()x+m恒成立,求实数m 的取值范围.答案和解析1.【答案】B【解析】解:数的定义域A={x|x≥0},函数y=ln(1-x)的定义域为B={x|1-x>0}={x|x<1},则A∩B={x|0≤x<1}=[0,1).故选:B.求得函数的定义域A,B,再由交集的定义,即可得到所求集合.本题考查函数的定义域的求法,考查集合的交集的定义和运算,属于基础题.2.【答案】A【解析】解:由=(2,4),=(-1,1),得:2-=2(2,4)-(-1,1)=(4,8)-(-1,1)=(5,7).故选:A.直接利用平面向量的数乘及坐标减法运算得答案.本题考查平面向量的数乘及坐标减法运算,是基础的计算题.3.【答案】D【解析】解:A.函数的定义域为[0,+∞),定义域关于原点不对称,故A为非奇非偶函数.B.f(-x)=|sin(-x)|=|sinx|=f(x),则f(x)为偶函数.C.y=cosx为偶函数.D.f(-x)=e-x-e x=-(e x-e-x)=-f(x),则f(x)为奇函数,故选:D.根据函数奇偶性的定义进行判断即可.本题主要考查函数奇偶性的判断,根据函数奇偶性定义是解决本题的关键.4.【答案】C【解析】解:由题意,令x-=kπ+,k∈z得x=kπ+,k∈z是函数f(x)=sin(x-)的图象对称轴方程令k=-1,得x=-故选:C.将内层函数x-看做整体,利用正弦函数的对称轴方程,即可解得函数f(x)的对称轴方程,对照选项即可得结果本题主要考查了正弦函数的图象和性质,三角复合函数对称轴的求法,整体代入的思想方法,属基础题5.【答案】A【解析】解:∵f(x)=x2-ax-3在区间(-∞,4]上递减,对称轴为x=,∴≥4,故a≥8,故选:A.根据函数f(x)=x2-ax-3在区间(-∞,4]上单调递减,则根据函数的图象知:对称轴必在x=4的右边,即≥4,解出即可.本题考查了二次函数的性质,属于基础题.6.【答案】B【解析】解:①是幂函数,其在(0,+∞)上即第一象限内为增函数,故此项不符合要求;②中的函数是由函数向左平移1个单位长度得到的,因为原函数在(0,+∞)内为减函数,故此项符合要求;③中的函数图象是由函数y=x-1的图象保留x轴上方,下方图象翻折到x轴上方而得到的,故由其图象可知该项符合要求;④中的函数图象为指数函数,因其底数大于1,故其在R上单调递增,不合题意.故选:B.本题所给的四个函数分别是幂函数型,对数函数型,指数函数型,含绝对值函数型,在解答时需要熟悉这些函数类型的图象和性质;①为增函数,②为定义域上的减函数,③y=|x-1|有两个单调区间,一增区间一个减区间,④y=2x+1为增函数.本题考查了函数的单调性,要注意每类函数中决定单调性的元素所满足的条件.7.【答案】C【解析】解:∵连续函数f(x)=log2x+x-4在(0,+∞)上单调递增∵f(2)=-1<0,f(3)=log23-1>0∴f(x)=log2x+x-4的零点所在的区间为(2,3)故选:C.连续函数f(x)=log2x+x-4在(0,+∞)上单调递增且f(2)=-1<0,f(3)=log23-1>0,根据函数的零点的判定定理可求本题主要考查了函数零点定义及判定的应用,属于基础试题8.【答案】D【解析】解:因为a=log36=1+log32,b=log510=1+log52,c=log714=1+log72,因为y=log2x是增函数,所以log27>log25>log23,∵,,所以log32>log52>log72,所以a>b>c,故选:D.利用log a(xy)=log a x+log a y(x、y>0),化简a,b,c然后比较log32,log52,log72大小即可.本题主要考查不等式与不等关系,对数函数的单调性的应用,不等式的基本性质的应用,属于基础题.9.【答案】D【解析】解:根据函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,|φ|<)的一部分图象,可得2A=4,A=2,b=A=2再根据==-,求得ω=2,再根据五点法作图可得2•+φ=π,∴φ=,f(x)=2sin(2x+)+2,故选:D.由函数的图象的顶点坐标求出A和b,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A和b,由周期求出ω,由五点法作图求出φ的值,属于基础题.10.【答案】C【解析】解:如图,∵D、E分别是边AB、BC的中点,且DE=2EF,∴•========.故选:C.由题意画出图形,把、都用表示,然后代入数量积公式得答案.本题考查平面向量的数量积运算,考查向量加减法的三角形法则,是中档题.11.【答案】B【解析】解:y=-sin2x-3cosx+3=cos2x-1-3cosx+3=(cosx-)2-,∵-1≤cosx≤1,令cosx=t,则-1≤t≤1,f(t)=(t-)2-,在[-1,1]上单调减,∴f(t)min=f(1)=0故选B.利用同角三角函数关系,把函数转换成关于cosx的函数,利用换元法,根据cosx的范围求得函数的最小值.本题主要考查了三角函数的性质,二次函数的性质.解题过程采用了换元法,把三角函数问题转换为二次函数的问题.12.【答案】C【解析】解:当x≥1时,f(x)=lnx,其值域为[0,+∞),那么当x<1时,f(x)=(1-2a)x+3a的值域包括(-∞,0),∴1-2a>0,且f(1)=(1-2a)+3a≥0,解得:,且a≥-1.故选:C.分段求解函数的值域,根据值域为R,即可求解.本题考查对数函数的单调性,分段函数的值域问题,较容易.13.【答案】C【解析】解:由tanα=,得:,即sinαcosβ=cosαsinβ+cosα,sin(α-β)=cosα=sin(),∵α∈(0,),β∈(0,),∴当时,sin(α-β)=sin()=cosα成立.故选:C.化切为弦,整理后得到sin(α-β)=cosα,由该等式左右两边角的关系可排除选项A,B,然后验证C满足等式sin(α-β)=cosα,则答案可求.本题考查三角函数的化简求值,训练了利用排除法及验证法求解选择题,是基础题.14.【答案】A【解析】利用三角函数公式将f(x)化简,根据平移变换规律求解g(x)解析式,根据x1,x2是g(x)-m=0在[0,]内的两根,即g(x1)=m,g(x2)=m,求解即可.本题主要考查三角函数的图象和性质,灵活利用辅助角公式是解决本题的关键.考查了函数y=Asin(ωx+φ)的图象变换规律,属于难题.解:函数f(x)=2sin(2x+)+2cos2(x+)-1,化简可得f(x)=2sin(2x+)+cos(2x+)=sin(2x++φ).其中sinφ=.cosφ=.图象向右平移个单位得到g(x)=sin[2x-)++φ]=sin(2x+φ).∵g(x)的周期T=,∵x1,x2是g(x)-m=0在[0,]内的两根,当x1=0时,可得g(x1)=sinφ,当x2=时,可得g(x2)=-sinφ,互为相反,∴x2=x1+.即g(x1)=m,g(x2)=m,可得:sin(2x1+φ)=sin(2x1+π+φ)=-sin(2x1+φ)令2x1+φ=0可得:x1=φ.x2=+φ.那么:sin(x1+x2)=sin(φ)=cosφ=.故选:A.15.【答案】2【解析】解:∵向量=(-2,3),=(3,m),且,∴=-6+3m=0,解得m=2.故答案为:2.利用平面向量数量积坐标运算法则和向量垂直的性质求解.本题考查实数值的求法,是基础题,解题时要认真审题,注意平面向量数量积坐标运算法则和向量垂直的性质的合理运用.16.【答案】【解析】解:如图,由余弦定理得:||===故答案为:.根据题意和根据向量的减法几何意义画出图形,再由余弦定理求出||的长度.本题考查的知识点有向量的夹角、向量的模长公式、向量三角形法则和余弦定理等,注意根据向量的减法几何意义画出图形,结合图形解答.17.【答案】-【解析】解:角α的终边过点P(4,-3),r=OP=5,利用三角函数的定义,求得sinα=-,cosα=,所以2sinα+cosα=-=.故答案为:.根据角α的终边过点P(4,-3),利用任意角的三角函数的定义,求出sinα,cosα的值,然后求出2sinα+cosα的值本题考查三角函数的定义,考查计算能力,掌握三角函数的定义,是本题顺利解答的前提.是基础题.18.【答案】,【解析】解:∵函数函数f(x)定义域在[-2,2]上的奇函数,则由f(1+m)+f(m)<0,可得f(1+m)<-f(m)=f(-m)又根据条件知函数f(x)在定义域上单调递减,∴-2≤-m<1+m≤2解可得,-<m≤1.故答案为:.由f(1+m)+f(m)<0,结合已知条件可得-2<3-2a<2-a<2,解不等式可求a的范围.本题主要考查了函数的奇偶性及函数的单调性在抽象函数中的应用,及不等式的求解,属于基础试题.19.【答案】①【解析】解:在①中,∵函数,命名为狄利克雷函数,函数f(x)=x-D(x),∴f(x)的定义域为有理数和无理数的并集,即f(x)的定义域为R,∴f(x)的值域为R,故①正确;在②中,f(-x)=-x-D(-x)=≠-f(x),故函数f(x)不是奇函数,故②错误;在③中,f(x)=x-D(x)=,不是周期函数,故③错误;在④中,当x∈[2,3]时,f(x)=x-D(x)=,不是单调函数,故④错误.故答案为:①.在①中,由狄利克雷函数的定义得函数f(x)=x-D(x)的定义域为R,从而f(x)的值域为R;在②中,f(-x)=-x-D(-x)=≠-f(x);在③中,f(x)=x-D(x)=,不是周期函数;在④中,当x∈[2,3]时,f(x)=x-D (x)=,不是单调函数.本题考查命题真假的判断,考查新定义、函数性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.20.【答案】(0,1)【解析】【分析】本题考查了数形结合的思想应用及学生的作图能力,同时考查了配方法的应用.作函数的图象,从而可得,推出的范围即可求解结果.【解答】解:作函数的图象如下,结合图象可知,,故,令得,或,令得,;故,故,故答案为(0,1).21.【答案】解:(1)原式=-10(+2)+1=+10-10-20+1=-.(2)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2=2lg 10+(lg 5+lg 2)2=2+(lg 10)2=2+1=3.(3)=.【解析】(1)利用指数幂的运算性质,化简所给的式子,可得结果.(2)利用对数的运算性质,化简所给的式子,可得结果.(3)由题意利用诱导公式,化简所给的式子,可得结果.本题主要考查指数幂的运算性质、对数的运算性质,诱导公式的应用,属于基础题.22.【答案】解:(1)由已知,得A(1,0),B(0,1).P(cos θ,sin θ),因为四边形OAQP是平行四边形,所以=+=(1+cosθ,sinθ).所以•=1+cosθ.(3分)又平行四边形OAQP的面积为S=|•|sin θ=sin θ,所以•+S=1+cosθ+sin θ=sin(θ+)+1.(5分)又0<θ<π,所以当θ=时,•+S的最大值为+1.(7分)(2)由题意,知=(2,1),=(cosθ,sinθ),因为CB∥OP,所以cosθ=2sinθ.又0<θ<π,cos2θ+sin2θ=1,解得sin θ=,cos θ=,所以sin2θ=2sin θcosθ=,cos 2θ=cos2θ-sin2θ=.所以sin(2θ-)=sin 2θcos-cos 2θsin=×-×=.(13分)【解析】(1)求出A(1,0),B(0,1).P(cos θ,sin θ),然后求解•,以及平行四边形OAQP的面积,通过两角和与差的三角函数,以及正弦函数的值域求解即可.(2)利用三角函数的定义,求出sin θ,cosθ,利用二倍角公式以及两角和与差的三角函数求解表达式的值.本题考查三角函数的定义,两角和与差的三角函数,三角函数的求值与化简.23.【答案】解:(1)∵已知,又∵f(x)过点,,∴,解得:.(2)由以上可得,,把f(x)的图象向左左移ϕ个单位后,得到.设g(x)的图象上符合题意的最高点为(x0,2),∵,解得x0=0,∴g(0)=2,解得,∴,∴-π+2kπ≤2x≤2kπ,k∈z,∈,∴f(x)的单调增区间为,,∈.【解析】(1)利用两个向量的数量积公式、两角和的正弦公式化简函数的解析式,再把点(,)代入,求得m的值.(2)根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的单调性,求得y=g(x)的单调递增区间.本题主要考查两个向量的数量积公式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于中档题.24.【答案】解:由题意,f(x)是奇函数,即f(-x)+f(x)=0,可得:log()+log()=log1.即,得:1-a2x2=-(x2-1)∴a2x2=x2,∴a=±1.检验:当a=1,不满足题意,∴a=-1,可得f(x)=log(),即:-log()=log(),f(x)为奇函数.(2)由(1)知f(x)=log(),设u=h(x)==1+,那么f(x)转化为g(u)=log u在(1,+∞)内是减函数,∴只需证明h(x)函数在(1,+∞)内单调递减即可;证明:设任意的x1,x2满足1<x1<x2,则h(x1)=,h(x2)=,那么:h(x1)-h(x2)=-()==∵1<x1<x2,∴x1-1>0,x2-1>0,x2-x1>0∴h(x1)-h(x2)>0,即h(x1)>h(x2).∴函数h(x)在(1,+∞)内单调递减即可;即f(x)在(1,+∞)内单调递增;(3)对于[3,4]上的每一个x的值,不等式f(x)>()x+m恒成立,只需f(x)min>+m即可.由(2)可知f(x)在(1,+∞)内单调递增;∴f(x)在[3,4]上单调递增;当x=3,f(x)取得最小值为-1,∵y=()x是减函数,∴当x=3,y取得最大值为,∴-1>,得:m<.故实数m的取值范围是(-∞,-).【解析】(1)根据f(x)是奇函数,即f(-x)+f(x)=0,即可求a的值;(2)利用复合函数的单调性只需证明内层函数在(1,+∞)内单调递减即可;(3)根据指数和对数函数单调性即可求解求解实数m的取值范围.本题考查了对数指数函数的单调性的运用和判断,复合函数的证明以及恒成立问题的转化思想.属于中档题.。
最新版陕西省西安市长安区高一上学期期末考试数学试题Word版含答案
长安一中2017-2018学年度第一学期期末考试高一数学试题一、选择题:本大题共14个小题,每小题5分,共70分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.)A..2.)A.3.下列函数为奇函数的是()A...4.)A..5.)A.6.给定函数:上单调递减的函数序号是()A.①② B.②③ C.③④ D.①④7.)A.8.)A..9.()A.10.1)A.11.)A.. 0 C. 2 D.612.()A.13.)A14.单位,的值为()A.二、填空题(每题5分,满分30分,将答案填在答题纸上)15.16.17.18.的取值范围是.19.由于德国著名数学家狄利克雷对数论、数学分析和物理学的突出贡献,人们将函数. 正确结论是.20.的取值范围为.三、解答题(本大题共4小题,共50分.解答应写出文字说明、证明过程或演算步骤.)21. 计算下列各式的值:(1(2(322.(1(2.23.(1(21.24..(1(2(3值范围.试卷答案一、选择题: 1-5.BADCA 6-10.BCADB 11-14. BCCA二、填空题:15. 2 16. 19.① 20.三、解答题:21.解:(1)-10(5+2)+1=49+105-105-20+1=-1679. (2)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2 =2lg 10+(lg 5+lg 2)2=2+(lg 10)2=2+1=3.(3)22. 解:(1(223.解:(1解得:(224.解:(1)为奇函数,所以恒成立,所以(2)由(1因为(3)由(2[3,4]长安一中2017~2018学年度第一学期期末考试高一数学参考答案一、选择题: 1-5.BADCA 6-10.BCADB 11-14. BCCA二、填空题:15. 2 16. 19.① 20.三、解答题:21.(12分)解:(1)10(5+2)+1=49+105-105-20+1=-1679.(2)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2=2lg 10+(lg 5+lg 2)2=2+(lg 10)2=2+1=3.(3)22. (12分)解:(1(223.(12分)解:(1解得:(224.(13分)解:(1)为奇函数,所以恒成立,所以(2)由(1因为(3)由(2[3,4]。
陕西省西安市长安区第一中学2017-2018学年高二上学期期末考试化学(理)试题含答案

长安一中2017~2018学年度第一学期期末考试高二化学试题(理科)命题人:杜凯王宁(考试时间100分钟,满分100分)注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题纸上。
2.考生作答时,请将答案涂写在答题纸上,在本试卷上答题无效。
按照题号在各题的答题区域内作答,答题区域错误或超出答题区域书写的答案无效.3.答案使用0。
5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
4.保持答题纸纸面清洁、不破损、不折叠。
考试结束后,将本试卷自行保存,答题纸交回。
可能用到的相对原子质量:H 1 C 12 O 16 Fe 56第Ⅰ卷一、选择题:本题共21个小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列化学方程式书写错误的是()A.NaHCO3水解的离子方程式:3HCO-+ H2O23CO-+H3O+B.NH4Cl水解的化学方程式:NH4Cl+H2O NH3·H2O+HCl C.Al(OH)3的两性电离方程式:H++AlO2−+H2O Al(OH)Al3++3OH−3D.NaHSO3的电离方程式:NaHSO3Na++3HSO2.Mg-AgCl电池是一种以海水为电解质溶液的水激活电池.下列叙述错误的是()A.负极反应式为Mg - 2e—Mg2+B.正极反应式为Ag+ + e-AgC.电池放电时Cl-由正极向负极迁移D.负极会发生副反应Mg + 2H2O Mg(OH)2 + H2↑3.下列叙述正确的是()A.石油、沼气、天然气、植物油都属于可再生能源B.应用盖斯定律,可计算某些难以直接测量的反应的焓变C.水蒸气变为液态水时放出的能量就是该变化的反应热D.同温同压下,H2(g)+Cl2(g)2HCl(g)在光照和点燃条件下的ΔH不同4.在一定条件下,使NO和O2在一密闭容器中进行反应,下列说法不正确的是()A.反应开始时,正反应速率最大,逆反应速率为零B.随着反应的进行,正反应速率逐渐减小,最后为零C.随着反应的进行,逆反应速率逐渐增大,最后不变D.随着反应的进行,正反应速率逐渐减小,最后不变5.在密闭容器中发生反应:C(s)+CO2(g)2CO(g),下列说法不正确的是()A.增大CO2浓度可以加快反应速率B.升高温度可以加快反应速率C.容器体积不变时,向其中充入N2,反应速率不变D.增加碳的质量可以加快反应速率6.下列关于反应热和热化学方程式的描述中正确的是()A.HCl和NaOH反应的中和热ΔH=-57.3 kJ·mol-1,则H2SO4和Ca(OH)2反应的反应热ΔH=2×(—57。
陕西省西安市长安区第一中学2017-2018学年高二上学期期末考试数学(理)试题(解析版)

陕西省西安市长安一中2017~2018学年度第一学期期末考试高二数学试题(理科)一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是满足题目要求的.)1.设复数z 满足(1+i)z =2i ,则|z |=( )A. 12B. 2C.D. 2【答案】C 【解析】 【分析】先求出z 的表达式,然后对其化简,求出复数的模即可.【详解】由题意,()()()2i 1i 2i 1i 1i 1i 1i z -===+++-,所以z =故选:C.【点睛】本题考查复数的四则运算,考查复数的模的计算,属于基础题. 2.已知命题“x R ∃∈,使212(1)02x a x +-+≤”是假命题,则实数a 的取值范围是( ) A. (,1)-∞- B. (1,3)- C. (3,)-+∞ D. (3,1)-【答案】B 【解析】 【分析】原命题等价于212(1)02x a x +-+>恒成立,故2()114202a ∆=--⨯⨯<即可,解出不等式即可. 【详解】因为命题“x R ∃∈,使212(1)02x a x +-+≤”是假命题,所以212(1)02x a x +-+>恒成立,所以2()114202a ∆=--⨯⨯<,解得13a -<<,故实数a 的取值范围是(1,3)-.故选B.【点睛】对于函数恒成立或者有解求参的问题,常用方法有:变量分离,参变分离,转化为函数最值问题;或者直接求函数最值,使得函数最值大于或者小于0;或者分离成两个函数,使得一个函数恒大于或小于另一个函数.而二次函数的恒成立问题,也可以采取以上方法,当二次不等式在R上大于或者小于0恒成立时,可以直接采用判别式法.3.在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120 km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )A. 30辆B. 1700辆C. 170辆D. 300辆【答案】B【解析】【分析】由频率分布直方图求出在这段时间内以正常速度通过该处的汽车的频率,由此能估2000辆车中,在这段时间内以正常速度通过该处的汽车约有多少辆.【详解】由频率分布直方图得:在这段时间内以正常速度通过该处的汽车的频率为()++⨯=,0.030.0350.02100.85∴估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有⨯=(辆),故选B.20000.851700【点睛】本题主要考查频率分布直方图的应用,属于中档题. 直方图的主要性质有:(1)直方图中各矩形的面积之和为1;(2)组距与直方图纵坐标的乘积为该组数据的频率;(3)每个矩形的中点横坐标与该矩形的纵坐标相乘后求和可得平均值;(4)直观图左右两边面积相等处横坐标表示中位数.4.用数学归纳法证明1+2+3+…+n 2=422n n +,则当n =k +1时左端应在n =k 的基础上加上() A. k 2+1B. (k +1)2C. ()()421412k k +++D. (k 2+1)+(k 2+2)+…+(k +1)2【答案】D 【解析】试题分析:当n=k时,等式左端=212k ++⋯+,当n=k+1时,等式左端=22222121231k k k k k ++⋯++++++++⋯++()()()(),增加了2k+1项.故选D . 考点:数学归纳法.5.已知空间四边形ABCD 的每条边和对角线的长都等于a ,点,E F 分别是,BC AD 的中点,则AE AF ⋅u u u r u u u r的值为( )A. 2aB.212a C.214a D.24a 【答案】C 【解析】 【分析】由题意可得11()22AB AC AE AF AD u u u r u u u u u u r u u r u u u ru r ⋅=+⋅,再利用两个向量的数量积的定义求得结果.【详解】解:11()22AB AC AE AF AD u u u r u u u u u u r u u r u u u ru r ⋅=+⋅1()4AB AD AC AD u u ur u u u r u u u r u u u r =⋅+⋅ ()22211cos60cos6044a a a ︒︒=+= 故选C【点睛】本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.6.直线4y x =与曲线3y x =在第一象限内围成的封闭图形的面积为( ).A. 4B. 42C. 2D. 22【答案】A 【解析】先根据题意画出图形:得到积分上限为2,积分下限为0曲线3y x =与直线4y x =在第一象限内围成的封闭图形的面积为()234x x dx -⎰而()23240214284404x x dx x x ⎛⎫-=-=-= ⎪⎝⎭⎰故曲边梯形的面积为4 故选A7.甲、乙、丙,丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有两位优秀,两位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩,根据以上信息,则( ) A. 乙、丁可以知道自己的成绩 B. 乙可以知道四人的成绩 C. 乙、丁可以知道对方的成绩 D. 丁可以知道四人的成绩【答案】A 【解析】 【分析】根据甲的所说的话,可知乙、丙的成绩中一位优秀、一位良好,再结合简单的合情推理逐一分析可得出结果.【详解】因为甲、乙、丙、丁四位同学中有两位优秀、两位良好,又甲看了乙、丙的成绩且还不知道自己的成立,即可推出乙、丙的成绩中一位优秀、一位良好, 又乙看了丙的成绩,则乙由丙的成绩可以推出自己的成绩,又甲、丁的成绩中一位优秀、一位良好,则丁由甲的成绩可以推出自己的成绩. 因此,乙、丁知道自己的成绩,故选A.【点睛】本题考查简单的合情推理,解题时要根据已知的情况逐一分析,必要时可采用分类讨论的思想进行推理,考查逻辑推理能力,属于中等题.8. 以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x ,y 的值分别为( )A. 2,5B. 5,5C. 5,8D. 8,8【答案】C 【解析】试题分析:由题意得5x =,116.8(915101824)85y y =+++++⇒=,选C. 考点:茎叶图9.已知条件p :x 2+2x -3>0;条件q :x >a ,且q ⌝的一个充分不必要条件是p ⌝,则a 的取值范围是( )A. [1,+∞)B. (-∞,1]C. (1,+∞)D. (-∞,-3]【答案】A 【解析】q ⌝的一个充分不必要条件是p ⌝,所以p 是q 的必要不充分条件,即{}{}{}2230|31x x a x x x x xx ≠⊂=-+-或,所以1a ≥故选A10.已知正四棱柱ABCD- A1B 1C 1D 1中 ,AB=2,CC 1=E 为CC 1的中点,则直线AC 1与平面BED 的距离为 A. 2 B.C.D. 1【答案】D 【解析】试题分析:因为线面平行,所求求线面距可以转化为求点到面的距离,选用等体积法.1//AC Q 平面BDE , 1AC ∴到平面BDE 的距离等于A 到平面BDE 的距离,由题计算得111112232323E ABD ABD V S CC -=⨯=⨯⨯⨯=,在BDE V 中,BE DE BD ====BD 边上的高2==,所以122BDE S =⨯=V 1133A BDE BDE V S h -==⨯V ,利用等体积法A BDE E ABD V V --=,得:13⨯=解得:1h = 考点:利用等体积法求距离11.已知双曲线C :22221x y a b-=(a >0,b >0)与直线0l y m ++=交于1122(,),(,),M x y N x y 其中11220,0,0,0,x y x y >>><,若0OM OQ +=u u u u v u u u v,且30MNQ ∠=o ,则双曲线C 的渐近线方程为( )A. 12y x =±B. y x =±C. 2y x =±D. y =【答案】B 【解析】()11M x y ,,()22N x y , 0OMOQ→+→=Q()Q x y ∴--,,MN K =3NQ K =-2121y y x x +∴=+联立方程22221x y a b y m⎧-=⎪⎨⎪=-⎩,解得212223x x b a +=-121212121223y y m m m x x x x x x +--∴===-+++223= 22a b =,1ba=± 则渐近线方程为y x =± 故选B点睛:本题考查了双曲线与直线的综合题目,依据条件给出Q 点坐标,利用角度转化为直线斜率问题,从而求出a b 、关系,计算出双曲线的渐近线方程,计算较大,需要转化,难度较大.12.设函数()(21)xf x e x ax a =--+,其中1a < ,若存在唯一的整数0x ,使得0()0f x <,则a 的取值范围是( )A. 3,12e ⎡⎫-⎪⎢⎣⎭B. 33,2e 4⎡⎫-⎪⎢⎣⎭C. 33,2e 4⎡⎫⎪⎢⎣⎭D. 3,12e ⎡⎫⎪⎢⎣⎭【答案】D 【解析】 【分析】 设()()21xg x ex =-,()1y a x =-,问题转化为存在唯一的整数0x使得满足()()01g x a x <-,求导可得出函数()y g x =的极值,数形结合可得()01a g ->=-且()312g a e-=-≥-,由此可得出实数a 的取值范围.【详解】设()()21xg x ex =-,()1y a x =-,由题意知,函数()y g x =在直线y ax a =-下方的图象中只有一个点的横坐标为整数,()()21x g x e x '=+,当21x <-时,()0g x '<;当12x >-时,()0g x '>.所以,函数()y g x =的最小值为12122g e -⎛⎫-=- ⎪⎝⎭.又()01g =-,()10g e =>.直线y ax a =-恒过定点()1,0且斜率为a , 故()01a g ->=-且()31g a a e -=-≥--,解得312a e≤<,故选D. 【点睛】本题考查导数与极值,涉及数形结合思想转化,属于中等题.二.填空题:(本大题共4小题,每小题5分,共20分.请把答案填写在答题纸的相应横线上.)13.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取_______名学生. 【答案】60 【解析】 【分析】采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查的. 【详解】∵该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6, ∴应从一年级本科生中抽取学生人数为:4300604556⨯=+++.故答案为60.14.做一个无盖的圆柱形水桶,若要使其体积是27π dm 3,且用料最省,则圆柱的底面半径为________ dm. 【答案】3 【解析】试题分析:设圆柱的高为h ,半径为r 则由圆柱的体积公式可得,πr 2h=27π,即,要使用料最省即求全面积的最小值,而S 全面积=πr 2+2πrh==(法一)令S=f (r ),结合导数可判断函数f (r )的单调性,进而可求函数取得最小值时的半径 (法二):S 全面积=πr 2+2πrh==,利用基本不等式可求用料最小时的r解:设圆柱的高为h ,半径为r则由圆柱的体积公式可得,πr 2h=27πS 全面积=πr 2+2πrh==(法一)令S=f (r ),(r >0)=令f′(r )≥0可得r≥3,令f′(r )<0可得0<r <3∴f (r )在(0,3)单调递减,在[3,+∞)单调递增,则f (r )在r=3时取得最小值 (法二):S 全面积=πr 2+2πrh====27π当且仅当即r=3时取等号当半径为3时,S 最小即用料最省 故答案为3点评:本题主要考查了圆柱的体积公式及表面积的最值的求解,解答应用试题的关键是要把实际问题转化为数学问题,根据已学知识进行解决.15.设函数()'f x 是奇函数()()f x a R ∈的导函数, ()10f -=,当0x >时, ()()'0xf x f x -<,则使不等式()0f x >成立的x 的取值范围是_____. 【答案】(,1)(0,1)-∞-U 【解析】试题分析:当0x >时,令()()2()()()0xf x f x f x g x g x x x-=⇒''=>,又(1)(1)(1)01f g f ==--=,所以当0x >时,由()01g x x >⇒>,满足()0f x >;因为()()f x g x x=为(,0)(0,)-∞⋃+∞偶函数,因此当0x <时,由()010g x x <⇒-<<,满足()0f x >;从而使得()0f x >成立的x 的取值范围是()()1,01,-⋃+∞考点:利用导数研究函数性质,利用导数解不等式16.在平面直角坐标系xOy 中,双曲线C 1:22221x y a b-=(a >0,b >0)的渐近线与抛物线C 2:x 2=2py (p >0)交于点O 、A 、B .若△OAB 的垂心为C 2的焦点,则C 1的离心率为________. 【答案】32【解析】双曲线1C :()2222100x y a b a b-=>>,的渐近线方程为b y x a =±与抛物线2C :22x py =联立, 可得0x =或2pbx a=±取2222pb pb A a a ⎛⎫ ⎪⎝⎭,,则22244AC b a k ab -= OAB Qn 垂心为2C 的焦点22414b a b ab a -⎛⎫∴⨯-=- ⎪⎝⎭2254a b ∴=()22254a c a ∴=- 32c e a ∴==综上所述,答案为32点睛:本题考查的是双曲线的方程与性质,抛物线的性质以及两直线垂直,意在考查学生生的逻辑推理能力和计算能力.首先要根据已知求出双曲线的渐近线方程与抛物线的焦点坐标,然后利用两直线垂直,即可建立关于a ,b 的方程,最后表示出c ,求得离心率.三、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知:p “直线0x y m +-=与圆22(1)1x y -+= 相交”;q :“方程240mx x m -+-=有一正根和一负根”.若p 或q 为真, 非p 为真,求实数m 的取值范围.【答案】214m +≤< 【解析】试题分析:先求出命题p ,q 的等价条件,然后利用若p q ∨为真,非p 为真,求实数m 的取值范围. 解析:对p :∵直线与圆相交,∴d =<1. ∴-+1<m <+1.对q :方程mx 2-x +m -4=0有一正根和一负根, ∴令f (x )=mx 2-x +m -4, ∴或解得0<m <4.又∵¬p 为真,∴p 假. 又∵p 或q 为真,∴q 为真. 由数轴可得+1≤m <4.故m 的取值范围是+1≤m <4.18.设函数f (x )=a ln x -bx 2(x >0),若函数f (x )在x =1处与直线y =-相切. (1)求实数a ,b 的值; (2)求函数f(x)在上的最大值.【答案】(1)112a b =⎧⎪⎨=⎪⎩.(2)f (x )max =12-. 【解析】 【分析】(1)对f (x )进行求导()'fx , 欲求出切线方程,只需求出其斜率即可,故先利用导数求出在1x =处的导数值,再结合导数的几何意义即可求出切线的斜率,列出关于a ,b 的方程求解即可;(2)研究闭区间上的最值问题,先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值.【详解】(1)f ′(x )=-2bx ,∵函数f (x )在x =1处与直线y =-相切,∴'(1)211(1)2f a b f b =-=⎧⎪⎨=-=-⎪⎩解得(2)由(1)知,f (x )=ln x -x 2,f ′(x )=-x =,当≤x ≤e 时,令f ′(x )>0,得≤x <1, 令f ′(x )<0,得1<x ≤e,∴f (x )在[,1)上是增加的,在(1,e]上是减少的, ∴f (x )max =f (1)=-点睛:本题主要考查函数单调性的应用,利用导数研究曲线上某点的切线方程,导数在最大值、最小值问题中的应用,不等式的解法等基础知识,考查运算求解能力,化归与转化思想.19.已知过抛物线()220y px p => 的焦点,斜率为22的直线交抛物线于()()()112212,,,A x y B x y x x <两点,且9AB = . (1)求抛物线的方程;(2)O 为坐标原点,C 为抛物线上一点,若OC OA OB λ=+u u u v u u u v u u u v,求λ的值.【答案】(1)y 2=8x .(2)λ=0,或λ=2. 【解析】【详解】试题分析:第一问求抛物线的焦点弦长问题可直接利用焦半径公式,先写出直线的方程,再与抛物线的方程联立方程组,设而不求,利用根与系数关系得出12x x +,然后利用焦半径公式得出焦点弦长公式12AB x x p =++,求出弦长,第二问根据联立方程组解出的A 、B 两点坐标,和向量的坐标关系表示出点C 的坐标,由于点C 在抛物线上满足抛物线方程,求出参数值. 试题解析:(1)直线AB 的方程是y =2(x-p 2),与y 2=2p x 联立,消去y 得8x 2-10p x +22p =0,由根与系数的关系得x 1+x 2=54p .由抛物线定义得|AB |=54p +p =9,故p=4 (2)由(1)得x 2-5x +4=0,得x 1=1,x 2=4,从而A (1,-22),B (4,42). 设OC u u u v=(x 3,y 3)=(1,-22)+λ(4,42)=(4λ+1,42λ-22), 又y =8x 3,即[22(2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1, 解得λ=0或λ=2.【点睛】求弦长问题,一般采用设而不求联立方程组,借助根与系数关系,利用弦长公式去求;但是遇到抛物线的焦点弦长问题时,可直接利用焦半径公式,使用焦点弦长公式12AB x x p =++,求出弦长.遇到与向量有关的问题,一般采用坐标法去解决,根据联立方程组解出的A 、B 两点坐标,和向量的坐标关系表示出点C 的坐标,由于点C 在抛物线上满足抛物线方程,求出参数值.20.如图,在四棱锥P−ABCD 中,AB//CD ,且90BAP CDP ∠=∠=o .(1)证明:平面P AB ⊥平面P AD ;(2)若P A =PD =AB =DC ,90APD ∠=o ,求二面角A −PB −C 的余弦值. 【答案】(1)见解析;(2)33-【解析】【详解】(1)由已知90BAP CDP ∠=∠=︒,得AB ⊥AP ,CD ⊥PD . 由于AB//CD ,故AB ⊥PD ,从而AB ⊥平面P AD . 又AB ⊂平面P AB ,所以平面P AB ⊥平面P AD . (2)在平面PAD 内作PF AD ⊥,垂足为F ,由(1)可知,AB ⊥平面PAD ,故AB PF ⊥,可得PF ⊥平面ABCD .以F 为坐标原点,FA u u u v的方向为x 轴正方向,AB u u u v 为单位长,建立如图所示的空间直角坐标系F xyz -.由(1)及已知可得22A ⎛⎫ ⎪ ⎪⎝⎭,20,0,2P ⎛⎫ ⎪ ⎪⎝⎭,2,1,02B ⎛⎫⎪ ⎪⎝⎭,22C ⎛⎫- ⎪ ⎪⎝⎭. 所以2222PC ⎛⎫=-- ⎪ ⎪⎝⎭u u u v ,)2,0,0CB =u u uv ,2222PA ⎛=- ⎝⎭u u u v ,()0,1,0AB =u u uv . 设(),,n x y z =r是平面PCB 的法向量,则0,0,n PC n CB ⎧⋅=⎨⋅=⎩u u uv r u u u v r 即220,2220,x y z x ⎧-+-=⎪⎨⎪=⎩ 可取(0,1,2n =--r.设(),,m x y z r=是平面PAB 的法向量,则0,0,m PA m AB ⎧⋅=⎨⋅=⎩u uu v r u u u v r 即220,0.x z y =⎪=⎩可取()1,0,1m =r. 则3cos ,3n m n m n m ⋅==-r rr rr r , 所以二面角A PB C --的余弦值为33-【名师点睛】高考对空间向量与立体几何考查主要体现在以下几个方面: ①求异面直线所成的角,关键是转化为两直线的方向向量的夹角;②求直线与平面所成角,关键是转化为直线的方向向量和平面的法向量的夹角;③求二面角,关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.21.一张坐标纸上涂着圆E :22(1)8x y ++=及点P (1,0),折叠此纸片,使P 与圆周上某点P '重合,每次折叠都会留下折痕,设折痕与直线EP '交于点M . (1)求M 的轨迹C 的方程;(2)直线:l y kx m =+与C 的两个不同交点为A ,B ,且l 与以EP 为直径的圆相切,若23,34OA OB ⎡⎤⋅∈⎢⎥⎣⎦u u u v u u u v ,求△ABO 的面积的取值范围.【答案】(1)2212x y +=;(2)62[,]43.【解析】试题分析:()1折痕为PP '的垂直平分线,则MP MP =',推导出E 的轨迹是以E ,P 为焦点的椭圆,且21a c ==,,由此能求出M 的轨迹C 的方程;()2l 与EP 为直径的圆22x 1y +=相切,从而221m k =+,由2212x y y kx m ⎧+=⎪⎨⎪=+⎩,得 ()222124220k xkmx m +++-=,由此利用根的判别式,韦达定理,向量的数量积,弦长公式,三角形面积公式,能求出AOB n 的面积的取值范围.解析:(1)折痕为PP ′的垂直平分线,则|MP |=|MP ′|,由题意知圆E 的半径为2,∴|ME |+|MP |=|ME |+|MP ′|=2>|EP |,∴E 的轨迹是以E 、P 为焦点的椭圆,且a =,c =1,∴b 2=a 2﹣c 2=1, ∴M 的轨迹C 的方程为2212xy +=.(2)l 与以EP 为直径的圆x 2+y 2=1相切, 则O 到l 即直线AB 的距离:=1,即m 2=k 2+1,由,消去y ,得(1+2k 2)x 2+4kmx +2m 2﹣2=0,∵直线l 与椭圆交于两个不同点,∴△=16k 2m 2﹣8(1+2k 2)(m 2﹣1)=8k 2>0,k 2>0,设A (x 1,y 1),B (x 2,y 2),则,,y 1y 2=(kx 1+m )(kx 2+m )=k 2x 1x 2+km (x 1+x 2)+m 2=,又=x 1x 2+y 1y 2=,∴,∴,==,设μ=k 4+k 2,则,∴=,,∵S △AOB 关于μ在[,2]单调递增, ∴,∴△AOB 的面积的取值范围是[,].22.已知()221()ln ,x f x a x x a R x -=-+∈. (Ⅰ)讨论()f x 的单调性;(Ⅱ)当1a =时,证明()3()'2f x f x +>对于任意的[]1,2x ∈成立. 【答案】(Ⅰ)见解析;(Ⅱ)见解析 【解析】试题分析:(Ⅰ)求()f x 的导函数,对a 进行分类讨论,求()f x 的单调性; (Ⅱ)要证()3()'2f x f x +>对于任意的[]1,2x ∈成立,即证3()'()2f x f x ->,根据单调性求解. 试题解析: (Ⅰ)的定义域为;223322(2)(1)'()a ax x f x a x x x x--=--+=. 当,时,'()0f x >,单调递增;(1,),'()0x f x ∈+∞<时,单调递减.当时,3(1)22'()()()a x f x x x x a a-=+-. (1),,当或x ∈时,'()0f x >,单调递增;当x ∈时,'()0f x <,单调递减;(2)时,,在x ∈内,'()0f x ≥,单调递增;(3)时,,当或x ∈时,'()0f x >,单调递增;当x ∈时,'()0f x <,单调递减.综上所述, 当时,函数在内单调递增,在内单调递减;当时,在内单调递增,在内单调递减,在内单调递增;当时,在内单调递增;当,在内单调递增,在内单调递减,在内单调递增.(Ⅱ)由(Ⅰ)知,时,22321122()'()ln (1)x f x f x x x x x x x --=-+---+23312ln 1x x x x x=-++--,,令,.则()'()()()f x f x g x h x -=+,由1'()0xg xx-=≥可得,当且仅当时取得等号.又24326 '()x xh xx--+=,设,则在x∈单调递减,因为,所以在上存在使得时,时,,所以函数()h x在上单调递增;在上单调递减,由于,因此,当且仅当取得等号,所以3 ()'()(1)(2)2 f x f x g h->+=,即3()'()2f x f x>+对于任意的恒成立.【考点】利用导函数判断函数的单调性,分类讨论思想.【名师点睛】本题主要考查导数的计算、应用导数研究函数的单调性、分类讨论思想.本题覆盖面广,对考生计算能力要求较高,是一道难题.解答本题,准确求导数是基础,恰当分类讨论是关键,易错点是分类讨论不全面、不彻底、不恰当,或因复杂式子变形能力差,而错误百出.本题能较好地考查考生的逻辑思维能力、基本计算能力、分类讨论思想等.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长安一中2017~2018学年度第一学期期末考试高二通用技术试题命题人:吕建群审题人:李永宁第一部分(选择题共50分)一、选择题(共16小题,每小题2分,计32分。
在每小题给出的四个选项中,只有一个..是符合题目要求的)1.近几年我国多地频繁出现PM2.5爆表现象,呼吸道感染患者剧增;自从2014年我国相继出台节能、减排、低碳等相关法律法规,环境保护问题备受国家和社会各界关注。
上述案例说明()A.利用技术只会破坏自然,人类不可能和自然成为朋友B.经济发展是社会进步的主要问题,环境是次要问题C.人类在利用技术时,不可忽视对环境可能造成的负面影响D.技术的发展给自然带来问题,故不能利用技术来改造自然2.下列事例体现技术具有解放人作用的是()A.英国细菌学家弗莱明发明了青霉素挽救了无数人的生命B.埃博拉疫苗的成功研制使接种者免遭该致命病毒的侵害C.某手机机身75%由可回收降解的植物性材质制造D.手机指纹识别系统使用户日常繁琐的解锁操作变得便捷图13.如图1所示,某新款智能眼镜通过内置的传感器监测眼球和眼皮活动,来判断用户的疲劳程度,并通过手机软件通知用户。
该产品设计主要体现了设计的()原则。
A.美观B.经济C.可持续发展D.创新4.新的传感器技术可以准确地监测到人们在运动时的各种数据。
将该技术应用到运动装备中,有助于运动员分析数据,调整动作,提升技能。
下列说法正确的是()A.传感器技术的发展为设计运动装备提供技术支持B.先进的传感器技术能帮助设计人员提升设计技能C.运动装备的生产技术成为传感器技术设计的平台D.传感器技术的发展对运动装备的设计不产生影响5.某校举办运动会,要求各班设计制作活动展板。
以下为设计制作过程的步骤:①制作、检测、评价和改进;②确定项目主题,制定设计目标;③提出解决问题的方案,权衡论证、决策;④详细的设计基本参数、功能、材料选取、人员安排等。
其正确的顺序是()A.③②①④B.②③④①C.③①②④D. ②①④③6.2015年9月20日我国新型运载火箭“长征六号”成功将20颗微小卫星送入太空,创造了中国航天一箭多星发射的新记录。
此前研究人员进行了大量技术试验,其中用计算机虚拟(仿真)现实中释放卫星过程的试验方法属于()A.优选试验法 B.模拟试验法C.强化试验法 D.虚拟试验法7.如图2所示的尺寸标注中错误的是 ( )A.10的标注 B.R15的标注C.20的标注 D.R16的标注图28.以下关于工艺的说法正确的是( )A.喷涂油漆工艺只是为了美观B.工艺就是工具的使用C.构件间的连接方法属于工艺D.零件装配不属于工艺9.下列关于自行车的设计,不属于...结构改变导致功能改变的是( ) A.改变颜色更加美观 B.采用折叠设计便于携带C.增加车筐方便置物D.采用避震结构减小颠簸10.为防止户外钢结构广告牌被大风刮倒和毁坏,广告牌结构设计应考虑的主要因素有①稳定性②安全性③美观性④强度⑤民俗⑥个性化需求( )A.②⑤⑥B.①②④C.①③④D.③⑤⑥11.西安永宁门俗称“南门”,是西安城中资格最老、沿用时间最长的一座。
从技术角度对其赏析,以下说法正确的是( )A.仿建的新箭楼使用轻型材料,重量更轻,内部空间更大B.南门不仅是西安亮丽的名片,更是西安不可复制的地标C.是集文物保护、历史街区、旅游景区、都市休闲、生态水系五大功能为一体的国际特色人文景区D.彰显了西安城市文化特质,更孕育了城市钟灵毓秀的气质,积淀了城市丰厚绵延的底蕴12.某配送中心要将货物由E 送往A 、B 、C 、D 四所超市,各处距离如图3所示(单位:km)。
下列最合理的派送路线为( )A .ECDABEB .EDABCEC .EDCBAED .EADCBE13.某款智能运动鞋集自动系带、GPS跟踪定位、自动调温、智能减震等功能于一身。
针对该智能运动鞋系统,下列说法不正确...的是( ) A .GPS 跟踪定位和智能减震是该系统的重要组成部分B .自动系带和自动调温是该系统的重要组成部分C .自动调温和智能减震两部分之间相互联系、相互作用D .该系统的整体功能,GPS 跟踪定位部分同样具有14.家庭装修初期,在设计厨房水电管线位置时,要提前规划好涮洗区、烹饪区、储物区、电器区等,这说明系统具有( )A .动态性B .相关性C .两面性D .环境适应性15.如图4所示的抽水马桶水箱水位控制系统中,属于检测装置的是( )A.进水阀B.支点C. 浮球D.出水阀16.功能模拟法就是以功能和行为的相似性为基础,用“模型”模拟“原型”的功能和行为的方法。
下列事例中,能体现功能模拟法的是( ) A .买西瓜时,通过“看瓜形、看瓜色、听瓜声、测弹性”判断西瓜的生熟B .中医通过“望、闻、问、切”来了解病人的病况,以此对病情作出判断C .家用扫地机器人能对地面环境进行侦测,将地面的垃圾清扫干净D .分析输入图像、声音或电信号后脑电波的反应,研究人脑内部结构二、多项选择题(共6小题,每小题3分,计18分。
在每小题给出的四个选项中,有两.个或两个以上......符合题目要求。
全选对的得3分,选对但不全的得1分,有错选的得0分) 17.某小区物业设计一款楼道夜间自动照明装置,在设计中需要考虑的因素是( ) 图3 图4A.传感器的类型B.照明装置的安全安装人员C.环境的干扰因素D.照明的延迟时间18.判断一个问题是否有价值,必须从以下哪些方面着手()A.所提出的问题是否遵循了基本的科学原理B.该问题是否尚未得到充分解决C.解决该问题投入与产出是否合理D.现有的技术条件能否解决这个问题19.下列产品中属于标准件的是()A.螺钉B.垫圈C.螺母D.锁20.如图5所示的脚手架,可以快速装卸,其中主要用于保持稳定性的措施是()A.脚手板采用网状结构B.支架间采用交叉斜拉杆C.四支支撑脚形成的支撑面要足够大D.支架带有登攀的梯子21.某地区为了提高土地利用率,实现增产增收,采用农业间作套种方式,使每亩的平均收入提高了近五成。
下列属于影响该套种系统优化的因素是()A.农作物田间管理B.套种的技术水平C.农作物亩产量D.病虫害的防治22.下列控制系统中,属于闭环控制系统的是()A.电冰箱的温度控制B.红绿灯定时控制系统C.带有红外热感应器马桶水箱的出水控制D.计算机的CPU上的风扇的转速控制第二部分(非选择题共50分)三、作图及填空题(共3个小题,计21分)23.(9分)如图所示为某对称机件的形体立体图。
请画出三视图,并标注出相关尺寸。
(支撑座均由厚度5mm的钢板制成)图524.(8分)广泛应用于医院、车站候车室等公共场所的直饮水机,具有自动加热、保温、净化水质等功能。
其工作原理为:当水温没有达到给定值,控制电路发出信号加热器开始工作,直饮水机进入工作状态;当温度与给定值相同时,加热器停止工作。
请回答下列问题:(1)从控制过程中有无人工干预的情形来分,该控制属于①控制;按有无反馈分,该控制系统属于②控制系统。
(4分)(2)该控制系统控制器是③,执行器是④,被控对象是⑤,输出量是⑥。
(4分)25.(4分)用3mm厚的钢板制作如图所示的T形紧固件,其加工环节主要有:①划线、②、③锯割、④钻孔,这四个环节的先后顺序为(只填写序号)。
完成这些工序必须用到的工具有:划针、角尺、样冲、铁锤、台虎钳、手锯、、防护眼镜、锉刀等。
该工件加工操作中不规范的是。
(只填写选项序号)A.起锯时,起锯角度约15°,当锯条深入工件2~3mm时才能够正常锯割B.冲眼时,样冲倾斜对准位置后扶正冲眼C.锉削时,锉刀要保持平稳而不上下摆动D.钻孔时,要带上手套才能用手触碰工件四、综合题(共两小题,计29分)26.(13分)某科技制作小组计划制作一把折叠椅,制作流程如下:A.准备材料和工具(1h);B.制作椅面(1h);C.制作折叠椅支撑架(1.5h);D.制作椅背(1h);E.组装(1.5h);F.调试(0.5h)。
请按要求完成下列各题:(1)画出合理的用时最短的流程方框图并算出时间。
(用各环节前的代码表示)(5分)(2)写出该流程优化的目的和意义。
(4分)(3)针对此优化,依据系统分析的原则进行系统分析。
(4分)27.(16分)近年来,长安一中图书管理有了新举措:在教学区设立图书角,摆放学习期刊、课外书籍、学生创新作品展示等。
请为该校设计一款教学区通用多功能展示架。
设计要求:①材料不限,成本低,易加工;②尺寸要求长宽高不超过1.5m×0.4m×1.8m;③能分类存放书籍和物品;④结构合理,稳固性好;⑤具有一定的装饰性和功能多样性。
请按要求完成下列各题:(1)用草图表达你的设计,写出必要的说明。
(6分)(2)针对你的设计,写出你是如何提高该作品稳固性的。
(4分)(3)根据你的设计,列举多功能展示架加工制作的工序(至少3项)和工具(至少3个) (6分)长安一中2017~2018学年度第一学期期末考试高二通用技术参考答案及评分标准第一部分(选择题 共50分)一、选择题(共16小题,每小题2分,计32分。
在每小题给出的四个选项中,只有一个..是符合题目要求的)二、多项选择题(共6小题,每小题3分,计18分。
在每小题给出的四个选项中,有两个..或两个以上符合题目要求。
全选对的得3分,选对但不全的得1分,有错选的得0分) 23.(9分)(共9分)(1)(3分)三视图象限正确且主视图、左视图、俯视图三个都正确得3分,每画错一个扣1分。
(2)(3分)三个视图高平齐、长对正、宽相等得3分,每错一项扣1分。
(3)(3分)尺寸标注中,尺寸数字、尺寸线、尺寸界线均须标注正确,6个尺寸每个0.5分。
24.(8分)(1)(共4分,每空2分)①自动 ②闭环(2)(共4分,每空1分)③控制电路 ④加热器 ⑤直饮水机 ⑥实际温度25.(4分)(每空1分)锉削 、 ①③②④ 、 台钻 、 D四、综合题(共两小题,计29分)26.(1)(5分)如图所示(环节内容填写正确,得1分;方框正确,得1分;箭头指向正确,每个1分;算出最短时间得2分)。
流程优化后最短时间是4.5h;流程优化后方框流程图为:(2流程优化的目的:提高工作效率,降低成本,降低劳动强度等(能答到流程优化目的中的两点即可得2分)。
流程优化的意义:指导我们正确做事,使生产、生活有序合理,提高效率,减少成本等(能答出流程优化意义中的两点即可得2分)。
(3)(4分)从系统分析的整体性原则来看,将折叠椅看成一个整体,将A、B、C、D、E、F的六个环节看成局部,优化时遵循局部服务于整体,节约时间,提高工作效率。
从系统分析的综合性原则来看,优化时要考虑该流程六个环节内在规律和机理,统筹兼顾,将串行工序改为并行工序,节约时间,提高效率。
