计算方法及其MATLAB实现第三章作业
最优化 马昌凤 第三章作业

最优化方法及其Matlab程序设计习题作业暨实验报告学院:数学与信息科学学院班级:12级信计一班姓名:李明学号:1201214049第三章 最速下降法和牛顿法一、上机问题与求解过程1、用最速下降法求212221216423),(x x x x x x f --+=的极小值。
解:仿照书上编写最速下降法程序如下:function [x,val,k]=grad(fun,gfun,x0) %功能:用最速下降法求解无约束化问题:min f(x) %输入:x0是初始点,fun,gfun 分别是目标函数和梯度 %输出:x,val 分别是近似嘴有点和最优值,k 是迭代次数 maxk=5000;rho=0.5;sigma=0.4;%一开始选择时选择的rho 和sibma 选择的数据不够合理,此处我参照书上的数据编写数据 k=0;epsilon=1e-5; while (k<maxk)g=feval(gfun,x0); %计算梯度 d=-g;%计算搜索方向if (norm(d)<epsilon),break ;end m=0;mk=0; while (m<20)%Armijo 搜索if (feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d) mk=m;break ;%直接利用Armijo 搜索公式,一开始的时候没有记住公式编写出现错误 end m=m+1; endx0=x0+rho^mk*d; k=k+1; end x=x0;val=feval(fun,x0) %求得每一个的函数值然后仿照书上建立两个目标函数和梯度的M 文件:function f=fun(x)f=3*x(1)^2+2*x(2)^2-4*x(1)-6*x(2); function g=gfun(x) g=[6*x(1)-4,4*x(2)-6]';选取初始点为']0,0[,调用函数程序,得出最小极值点为']500.1,6667.0[,极小值为8333.5-,在界面框中输入的程序如下:[x,val,k]=grad('fun','gfun',x0) val = -5.8333 x =0.6667 1.5000 val =-5.8333 k = 10从结果可以看出迭代次数为10次,如果选取不同的初值点则迭代次数不一样,但是极小值相同。
MATLAB计算方法3解线性方程组计算解法

直到(n-1) 原方程组化为
a11 x1 a12 x2 a1n xn a1,n1 a22 x2 a2 n xn a2 ,n1
ann xn an ,n1
(上三角方程组) (3.2) 以上为消元过程。
(n) 回代求解公式
a n ,n1 xn a nn n x k 1 [a k ,n1 a kj x j ] a kk j k 1 ( k n 1, n 2,...,1)
由矩阵乘法 (1) 1) l11 a11 l11
umj 1 ukj a kj ukj a kj l km umj
m 1
k 1
2 求L的第k列:用L的第i行 u的第k列
(i k 1, , n),即 ( l i 1 , , l ik , l kk , 0 0) ( u1k , u2 k , , ukk , 0 0)' a ik
( 2) 1)求u的第2行:用L的第2行 u的第j列 (j 2, , n) l 21 u1 j 1 u2 j a 2 j u2 j a 2 j l 21u1 j 2)求L的第2列:用L的第i行 u的第2列 (i 3,4, , n) l i 1 u12 l i 2 u22 a i 2 l i 2 (a i 2 l i 1 u12 ) / u22
m 1
l
k 1
im
umk l ik ukk a ik
k 1
l ik a ik l im umk ukk m 1
LU分解式: u1 j a1 j ( j 1,2, n) l i 1 a i 1 u11 ( i 2,3, , n) k 1 ukj a kj l km umj a kj m 1 ( j k , k 1, , n) k 1 l ik a ik l im umk ukk a ik m 1 ( i k 1, , n) ( k 2, 3, , n )
MATLAB应用第三章-符号计算

3. 1 数据类型 3.2 符号运算
数学运算中除了数值运算外,还有大量抽象运算(计算式中带有符号变 量、表达式的运算)。Matlab就是利用maple软件的符号运算功能来实 现这些符号运算的。 Maple : 通用的数学和工程软件,是世界上最值得信赖、最完整的数学 软件之一,被高等院校、研究机构和公司广泛应用,用户渗透超过97% 的世界主要高校和研究所,超过81%的世界财富五百强企业。 Maple提供世界上最强大的符号计算,无与伦比的数值计算,支持 用户界面开发和网络发布,内置丰富的数学求解库,覆盖几乎所有的数 学分支,所有的操作都是在一个所见即所得的交互式技术文档环境中完 成,完成计算的同时也生成了专业技术文件和演示报告。 Maple不仅仅提供编程工具,更重要的是提供数学知识。Maple是 教授、研究员、科学家、工程师、学生们必备的科学计算工具,从简单 的数字计算到高度复杂的非线性问题,Maple都可以帮助您快速、高效 地解决问题。用户通过Maple产品可以在单一的环境中完成多领域物理 系统建模和仿真、符号计算、数值计算、程序设计、技术文件、报告演 示、算法开发、外部程序连接等功能,满足各个层次用户的需要,从高 中学生到高级研究人员。
格 Eg 3-2 补充。 补充。 2)char函数创建:char(‘string1’,’string2’, …); Eg 3-3 各个字符串不须同大小, 各个字符串不须同大小,该函数自动补充空白 字符。 字符。 Eg 3-4
字符串与单元 1)cellstr将字符数组转换成单元数组。 2)char函数将单元数组转换成字符数组。 数组的转换 字符串的比较 1)strcmp(a,b):比较两个字符串所有字符是
Grand total is 33 elements using 462 bytes
matlab第三章课后部分答案

matlab第三章课后部分答案习题三3-2 从键盘输入一个三位整数,将它反向输出。
如输入639,输出为936程序如下:m=input('请输入一个三位整数:');m1=fix(m/100);%求m的百位整数m2=rem(fix(m/10),10);%求m的十位数字m3=rem(m,10);%求m的个位数字m=m3*100+m2*10+m1%反向输出m3-3 输入一个百分制成绩,要求输出成绩等级A,B,C,D,E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
程序如下:(1)if语句c=input('请输入成绩:');if c>=90&c<=100disp('A 成绩合理');elseif c>=80&c<=89disp('B 成绩合理');elseif c>=70&c<=79disp('C 成绩合理'); elseif c>=60&c<=69disp('D 成绩合理'); elseif c<60disp('E 成绩合理');elsedisp('成绩错误');end(2)switch语句c=input('请输入成绩:'); switch fix(c)case num2cell(90:100)disp('A 成绩合理'); case num2cell(80:89)disp('B 成绩合理'); case num2cell(70:79)disp('C 成绩合理'); case num2cell(60:69)disp('D 成绩合理'); case num2cell(0:59)disp('E 成绩合理');x=fix(rand(1,20)*89)+10;x1=fix(sum(x)/20);disp(['平均数是:',num2str(x1)])m=(rem(x,2)==0&x<x1);n=find(m);disp(['小于平均数的数是:',num2str(x(n))]); 3-6 输入20个数,求其中最大数和最小数。
数字信号处理Matlab练习第三章-080802084朱桂香

1.编写一个Matlab程序,用一个N点的复数离散傅里叶变换计算两个长度为N的实数序列的N点离散傅里叶变换,并将结果同直接使用两个N点离散傅里叶变换得到的结果进行比较。
n=0:11; %设定n的范围x1=cos(pi/6.*n); %给定序列x1[n]x2=(4/5).^n; %给定序列x2[n]w1=x1+1i*x2; %由序列x1[n]和x2[n]组成复数序列w1[n]w2=x1-1i*x2; %序列w1[n]的共轭序列w2[n]figure,subplot(2,1,1),stem(n,x1); %指定位置1,绘制序列x1[n]xlabel('n'); %设定序列x1[n]的横轴标注和纵轴标注ylabel('x1[n]');subplot(2,1,2),stem(n,x2); %指定位置2,绘制序列x2[n]xlabel('n'); %设定序列x2[n]的横轴标注和纵轴标注ylabel('x2[n]');figure,subplot(4,1,1),stem(abs(w1)); %指定位置1,绘制序列w1[n]幅度谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('magnitude');title('W1的幅度谱');subplot(4,1,2),stem(angle(w1)); %指定位置2,绘制序列w1[n]相位谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('phase');title('W1的相位谱');subplot(4,1,3),stem(abs(w2)); %指定位置3,绘制序列w2[n]幅度谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('magnitude');title('W2的幅度谱');subplot(4,1,4),stem(angle(w2)); %指定位置4,绘制序列w2[n]相位谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('phase');title('W2的相位谱');X1=fft(x1); %求序列x1[n]的离散傅里叶变换X1(k)X2=fft(x2); %求序列x2[n]的离散傅里叶变换X2(k)W1=fft(w1); %求序列w1[n]的离散傅里叶变换W1(k)W2=fft(w2); %求序列w2[n]的离散傅里叶变换W2(k)Y1=(1/2)*(W1+W2); %由W1(k)和W2(k)来求X1(k)Y2=(1/(2*1i))*(W1-W2); %由W1(k)和W2(k)来求X2(k)figure,subplot(2,1,1),stem(abs(X1)); %指定位置1,绘制|X1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X1(k)|');subplot(2,1,2),stem(abs(Y1)); %指定位置2,绘制|Y1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|Y1(k)|');figure,subplot(2,1,1),stem(abs(X2)); %指定位置1,绘制|X2(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X2(k)|');subplot(2,1,2),stem(abs(Y2)); %指定位置2,绘制|Y2(k)|xlabel('k'); %设定横轴标注和纵轴标注 ylabel('|Y2(k)|');结果图:nx 1[n]024681012nx 2[n ]图1 序列x1[n]和x2[n]02468101212nm a g n i t u d eW1的幅度谱24np h a s eW1的相位谱02468101212nm a g n i t u d eW2的幅度谱024681012-4-20np h a s e图2 w1和w2的幅度谱和相位谱图246k|X 1(k )|246k|Y 1(k )|图3 两种计算X1(k)的方法比较024681012246k|X 2(k )|024681012246k|Y 2(k )|图4 两种计算X2(k)的方法比较2.编写一个Matlab 程序,用两个N 点的复数离散傅里叶变换计算一个长度为2N 的实数序列的2N 点离散傅里叶变换,并将结果同直接使用一个2N 点离散傅里叶变换得到的结果进行比较。
matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境,已被广泛应用于不同领域。
Matlab的基本功能包括:数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。
Matlab第二章1.创建double的变量,并进行计算。
(1)a=87,b=190,计算a+b、a-b、a*b。
(2)创建uint8 类型的变量,数值与(1)中相同,进行相同的计算。
>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =>> c*dans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2,v=3,计算:(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u)ans =15.4189>> sqrt(u-3*v)/(u*v)ans =0 + 0.4410i4.计算如下表达式:(1)(2)>> (3-5*i)*(4+2*i)ans =22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。
matlab 教程 第三章Matlab 绘图与例题

机动 目录 上页 下页 返回 结束
二、三维网格图命令mesh
• mesh(X,Y,Z) 生成网格曲面,X,Y,Z是同维数的矩阵 • mesh(x,y,Z) x,y是向量,而Z是矩阵。等价于
机动 目录 上页 下页 返回 结束
三、三维表面图命令surf
• surf的调用格式与mesh相同,不同之处是surf绘的是曲面 而不是网格。
• 三维表面图可以用shading命令修饰其显式形式。
Matlab还提供了waterfall(x,y,z)及contour3(x,y,z)等命 令绘制三维图形。
3
2
在[0,4π]间的图形。
解:syms t
ezplot(‘2/3*exp(-t/2)*cos(3/2*t)’,[0,4*pi])
第二节 Matlab二维特殊图形
Matlab提供了许多其他的二维绘图指令, 大大扩充了Matlab的曲线作图指令,可以满足 用户的不同需要。
注 目录 上页 下页 返回 结束
axis equal 使坐标轴在三个方向上刻度增量相同
axis square 使坐标轴在三个方向上长度相同
axis
返回表示当前图形坐标轴的范围
机动 目录 上页 下页 返回 结束
第四节 Matlab空间曲面绘图
二元函数 z f (x, y) 的图形是三维空间曲面,函
数图形在了解二元函数的特性上帮助很大。
第3章 Matlab 绘图与例题
第一节
第3章
Matlab二维曲线绘图
一、基本绘图指令plot
第三章上机作业

第三章上机作业
一、上机要求
已知Hilbert矩阵H的元素为: =1/(i+j-1), 完成如下实验:
(1)编程计算H的行范数函数;
(2)编写计算H的行范数条件数函数(可以调用求逆函数,Mathematica为Inverse[H],Matlab为
inv(H), 其它语言自己去查找相应的逆矩阵程序使用);
(3)对n=1,2,…,20, 计算H的行范数条件数, 画出n同条件数的对数之间的关系图;
(4)令x=(1,1,…,1), 计算b=Hx, 对n=1,2,…,20, 求解=b,并计算x-的无穷范数和b-H.
(5)通过以上的数值实验, 你理解到了什么.
二、程序截图及结果
三、心得体会
通过实验对向量范数和矩阵范数有了更深的理解。
学习了通过编程实现对Hillbert矩阵行范数函数和行范数条件数的计算。
第三章作业参考答案

h( n) =
T − ( a + jb ) nT [e + e− ( a − jb ) nT ]u (n) 2
∞
H ( z ) = ∑ h( n) z − n =
n=0
T 1 1 [ ] + − aT − jbT −1 − aT jbT −1 2 1− e e z 1− e e z
模拟滤波器的幅频响应
1.4
1.2
1
0.8
0.6
0.4
0.2
0
0
0.5
1
1.5
2
2.5
3
3.5
3.6 一个采样数字处理低通滤波器,H(z)的截止频率 wc = 0.2π ,整个系统相当于一个模拟 低通滤波器,今采样频率 fs=1kHz,求等效于模拟低通的边界频率 fc。若采样频率 fs 分别改 变为 5kHz,200Hz,而 H(z)不变,问这时等效的模拟低通的边界频率又为多少? 解: fc =
T 1+ z −1 s= i 2 1− z −1
=
1 1+ z 1 + z −1 2 1 + z −1 3 1 + 2( ) 2( ) +( ) + 1 − z −1 1 − z −1 1 − z −1
−1
=
(1 − z −1 )3 6 + 2 z −2
(1 − z −1 )3 (1 − e − jω )3 幅频响应: H (e ) = | jω = 6 + 2 z −2 z =e 6 + 2e −2 jω
2 3
H a ( s) =
1 + 2( s / Ω c ) + 2 ( s / Ωc ) + ( s / Ωc )
MATLAB第三章

第三章微积分问题的计算机求解一、实验内容:题目1.试求出如下极限。
①limx→∞(3x +9x )1/ x,②lim x→∞[(x+2)x+2(x+3)x+3 ]/(x+5)2x+5【分析】:该题为单变量函数的极限。
极限问题可以用limit()函数直接求出。
要注意该函数的调用格式为:L=limit(fun,x,x0)(求极限),L=limit(fun,x,x0,’left’或’right’)(求极限)。
还需注意一开始要对函数的字符进行申明。
【解答】:(1)输入如下语句:>> syms x;f=(3^x+9^x)^(1/x);L=limit(f,x,inf)语句运行后显示如下:L =9(2)输入如下语句:>>syms x;f=(x+2)^(x+2)*(x+3)^(x+3)/(x+5)^(2*x+5);>> L=limit(f,x,inf)语句运行后显示如下:L =exp(-5)题目2.试求下面的双重极限。
①lim x→−1y→2 (x2y+xy3)/(x+y) 3,②limx→0 y→0 xy /√(xy+1)−1,③limx→0y→0 [1−cos(x2+y2)]/(x2+y2)e x2+y2。
【分析】:该题为多变量函数的极限问题。
他可以用嵌套使用limit()函数来解决。
在MATLAB上可以用L=limit(limit(f,x,x0),y,y0)或者L=limit(f,y,y0),x,x0)来解决。
其思想是所有的先关于X求导,再所有的关于y求导。
【解答】:(1)输入如下语句:>> syms x y>> f=(x^2*y+x*y^3)/(x+y)^3;>> L=limit(limit(f,x,-1),y,2)语句运行后显示如下:L =-6(2)输入如下语句:>> syms x yf=(x*y)/(sqrt(x*y+1)-1);L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =2(3)输入如下语句:>> syms x yf=(1-cos(x^2+y^2))/(sqrt(x^2+y^2)*exp(x^2+y^2));L=limit(limit(f,x,0),y,0)按ENTER键,语句运行后显示如下:L =题目3.求出下面函数的导数。
国家开放大学《Matlab语言及其应用》实验报告(第三章--绘制二维和三维图形)

——绘制二维和三维图形
姓名:学号:
实验名称
绘制二维和三维图形
实验目标
利用Matlab常见函数完成二维图形的绘制和图形的标注;实现三维曲线和曲面图形的绘制。
实验要求
熟悉Matlab基本绘图函数、图形处理函数,了解三维曲线和曲面图形的绘制方法。
实验步骤
1、用Matlab基本绘图函数绘制二维图形:根据已知数据,用plot函数画出正弦函数曲线,并进行相应标注。
enon
实验内容
1.二维曲线绘图
例:精细指令实例
2.三维曲线绘图
【例】三维曲线绘图基本指令演示一:plot3
t=(0:0.02:2)*pi;x=sin(t);y=cos(t);z=cos(2*t);
plot3(x,y,z,'b-',x,y,z, 'rd')三维曲线绘图(蓝实线和红菱形)
box on
legend('链','宝石')在右上角建立图例
subplot(121);
surf(x1,y1,z1);
subplot(122);
[x2,y2,z2]=sphere (30);
surf(x2,y2,z2);
clear;clf;
z=peaks;
subplot(1,2,1);mesh(z);% 透视
hidden off
subplot(1,2,2);mesh(z);%不透视
2、用三维曲线绘图基本指令plot 3绘制三维曲线图:t=0~2pi;x=sin(t);y=cos(t);z=cos(2*t);用plot3函数画出关于x,y,z的三维曲线图,并适当加标注。
matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境,已被广泛应用于不同领域。
Matlab的基本功能包括:数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。
Matlab第二章1.创建double的变量,并进行计算。
(1)a=87,b=190,计算a+b、a-b、a*b。
(2)创建uint8 类型的变量,数值与(1)中相同,进行相同的计算。
>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =ans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2,v=3,计算:(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u) ans =15.4189>> sqrt(u-3*v)/(u*v) ans =0 + 0.4410i 4.计算如下表达式:(1)(2)>> (3-5*i)*(4+2*i)22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。
Matlab第三章习题答案

Matlab第三章习题答案第三章3.5计算多项式乘法()()222254x x x x ++++>> a=[1 2 2];>> b=[1 5 4];>> c=conv(a,b)c =1 7 16 18 8poly2sym(c)ans =x^4 + 7*x^3 + 16*x^2 + 18*x + 83.6计算多项式的除法()()3231368/4x x x x ++++ >> a=[3 13 6 8];>> b=[1 4];>> [q r]=deconv(a,b)q =3 1 2r =0 0 0 0>> poly2sym(q)ans =3*x^2 + x + 23.8求多项式4324121459x x x x --++的微分和积分(1)微分:>> a=[4 -12 -14 5 9];>> b=polyder(a)b =16 -36 -28 5>> poly2sym(b)ans =16*x^3 - 36*x^2 - 28*x + 5(2)积分:polyint(a)ans =0.8000 -3.0000 -4.6667 2.5000 9.00000 >> poly2sym(ans)ans =(4*x^5)/5 - 3*x^4 - (14*x^3)/3 + (5*x^2)/2 + 9*x3.9求代数⽅程32349x x x +-+=0的解。
>> [x]=solve('x^3+3*x^2-4*x+9')x =- 7/(3*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 -1/108*108^(1/2)*4703^(1/2))^(1/3) - 17/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 - (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 - 1 7/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 + (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 – 1 3.10求线性⽅程组223430x xy y x x ?++=??-+=??的解 eqn1='x^2+x*y+y=3';>> eqn2='x^2-4*x+3=0';[x,y]=solve(eqn1,eqn2)x =13y =1-3/23.11求微分⽅程64dy y x dx=+的通解。
MATLAB计算方法与实现
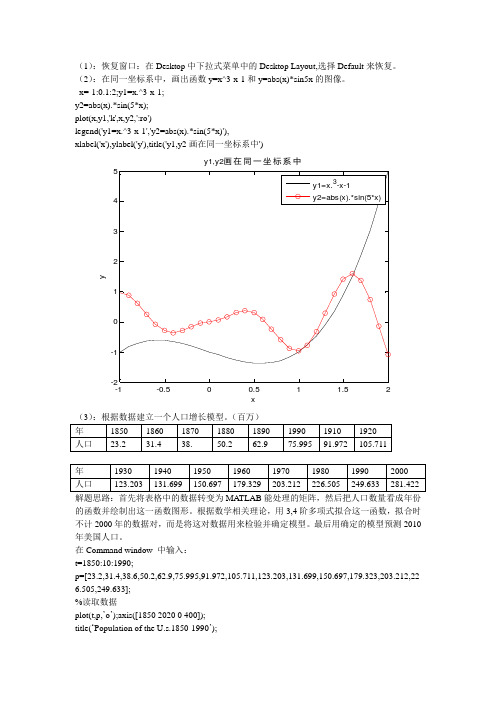
(1):恢复窗口:在Desktop 中下拉式菜单中的Desktop Layout,选择Default 来恢复。
(2):在同一坐标系中,画出函数y=x^3-x-1和y=abs(x)*sin5x 的图像。
x=-1:0.1:2;y1=x.^3-x-1; y2=abs(x).*sin(5*x); plot(x,y1,'k',x,y2,':ro')legend('y1=x.^3-x-1','y2=abs(x).*sin(5*x)'),xlabel('x'),ylabel('y'),title('y1,y2画在同一坐标系中')-1-0.500.51 1.52xyy1,y2画在同一坐标系中(3):根据数据建立一个人口增长模型。
(百万)的函数并绘制出这一函数图形。
根据数学相关理论,用3,4阶多项式拟合这一函数,拟合时不计2000年的数据对,而是将这对数据用来检验并确定模型。
最后用确定的模型预测2010年美国人口。
在Command window 中输入: t=1850:10:1990;p=[23.2,31.4,38.6,50.2,62.9,75.995,91.972,105.711,123.203,131.699,150.697,179.323,203.212,226.505,249.633]; %读取数据plot(t,p,’o ’);axis([1850 2020 0 400]); title(‘Population of the U.s.1850-1990’);ylabel(‘Millions ’);%绘制出数据的函数图形并加以修饰f1=polyfit(t,p,3);f2=polyfit(t,p,4);%对数据做3,4阶多项式拟合,结果分别为f1和f2 v=[polyval(f1,2000),polyval(f2,2000)];%计算当t=2000时多项式f1,f2的值 abs(v-251.422) %计算两个模型与2000年人口数的绝对误差。
现代数值计算方法(MATLAB版)第3章(1)

akk ,
(k )
(3.5)
福建师范大学
数计学院
8/15
k = 1, · · · , n − 1, mik = aik /akk , aij
(k +1) (k ) (k ) (k )
aik
(k +1) (k )
= 0, bi
(k +1)
= aij − mik akj ,
= bi − mik bk .
Back Close
(k )
(k )
(i = k + 1, · · · , n; j = k + 1, · · · , n.) 3
xn = bn /ann , k = n − 1, · · · , 1, xk =
(k ) bk n (k ) (k )
福建师范大学
(n)
(n)
−
j =k +1
akj xj
··· ··· ···
(1) a1n (2) a2n (2) a3n
(1) b1 (2) b2 (2) b3
福建师范大学
数计学院
6/15
··· ··· ··· ··· an2 an3 · · · ann bn
(2) (2) (2) (2)
Back Close
(2) aij
(1)
,
A(k) A(k) k
Dk = det Dk = 0
A11
(k −1)
A12
(k −1) (k )
(k −1) (k ) = a(1) 11 · · · ak −1,k −1 akk .
akk
akk = 0.
(k )
MATLAB第三章数值数组及其运算

行向量
如:array=[2, pi/2, sqrt(3), 3+5i]
x=[1,2,3,4,5都已知.如对 少量实验数据的处理可用此种方法.
4
(2) 冒号生成法: array=a: inc: b
<向量>
a---数组的第一个元素
inc---采样点之间的间隔, 即步长. 最后一个元素不一定等于b, 其大小为b’=a +inc*[(b-a)/inc]; 步长可以省略, 默认为 1; inc可以取正数或负数, 但要注意当取正时,要保证b>a, 数 组最后一个元素不超过b, 取负时b<a, 最后一个元素不小于b.
(2) 数值计算解法
delt=0.01; x=0:delt:4;
y=exp(-sin(x));
sx=delt*cumtrapz(y);
plot(x,y, 'r', 'LineWidth', 6); hold on;
plot(x, sx, '.b', 'MarkerSize', 15);
plot(x, ones(size(x)), 'k');
a inc>0 b
b inc>0 a
特点: 等差数列
方便对数据之间的间隔(步长)进行控制.但要注意三个数值之 间的关系,可能得到空数组.另外要注意生成的数组的元素的 个数.如x=a: (b-a)/n :b (b>a)得到n+1个元素的数组.
5
x=1:5x=[1,2,3,4,5]
y=5:-1:1y=[5, 4, 3, 2, 1]
2. 在命令窗中输入MyMatrix
11
3.5 二维数组的标识 (mxn, m>1, n>1)
MATLAB第三章和第四章作业

习题三1.选择题(1)已知a=4,b='4',下面说法错误的为C 。
A. 变量a比b占用的存储空间大B. 变量a和b可以进行加、减、乘、除运算C. 变量a和b的数据类型相同D. 变量b可以用eval命令执行(2)已知s='显示"hello"',则s的元素个数是B 。
A. 12B. 9C. 7D. 18(3)运行命令>>a=sym('pi','d')则对于变量a的描述D是正确的。
A. a是符号变量B. a显示为10位的数值C. a显示为32位的数值D. a不存在(4)对于符号表达式g=sym('sin(a*z)+cos(w*v)'),如果运行命令diff(g),则求导自变量是D。
A. aB. zC. wD. v(5)运行命令>>a=double(sym('sin(pi/2)')),则变量a是 C。
A. 符号变量B. 字符串'1'C. double型的数值1D. 出错(6)运行命令>>y=dsolve('x*D2y-3*Dy=x^2','t')求解微分方程,则D。
A. Dy是指dy/dxB. 得出的y是通解有一个常数符C1C. D2y是指d2y/dxD. 得出的y是通解有两个常数符C1和C2(7)有一个2行2列的元胞数组c,则c(2)是指C 。
A. 第1行第2列的元素内容B. 第2行第1列的元素内容C. 第1行第2列的元素D. 第2行第1列的元素(8)对于一个2行2列的元胞数组c,如果要删除第二列的元素,应该使用的命令是B 。
A.c{:,2}=[]B.c(:,2)=[]C.A、B两种方式均可D.A、B两种方式均不可(9)有一个3行10列的构架数组student,每个构架有name(姓名)、scores两个字段,其中scores是以1×5数组表示的五门课的成绩,那么要查看第4个学生的第2门课成绩,采用的命令中达不到要求的是。
数字信号处理及MATLAB实现第三章答案

3-11设是周期为N的周期序列,通过系统H(z)以后,求证序列为 证明:
在单位圆上对H(z)N等分采样,x(n)通过系统H(z)以后,输出频谱为
3-1求序列的DFS展开 解: 已知 ,则 3-2 (1) (2)
(3) (4) (5) (6) 解:(1) (2) (3) (4)
(5) 由,得 所以 (6) 因为,所以 3-3.答案略 3-4若,,,证明 证明: 3-5若,求证 证: 而
(为整数) 0 所以 于是 3-6令表示N点序列的N点DFT,试证明: (1)如果满足关系式,则。 (2)当N为偶数时,如果,则。 证: (1) N为偶数:N奇数: 而中间的一项应当满足:
因此必然有
这就是说,当N为奇数时,也有。 (b)当N为偶数:
当N为偶数时,为奇数,故;又由于故有 3-7 已知是N点有限长序列,。现将的每两点之间补进个零值点,得到 一个点的有限长序列
试求点DFT[]与的关系。 解:由 可得 而 所以是将(周期为N)延拓次形成的,即周期为。 3-8答案略 3-9设是一个2N点序列,具有如下性质
王能超-计算方法——算法设计及MATLAB实现课后代码

第一章插值方法1. 1 Lagrange 插值1.2逐步插值1. 3分段三次Hermite插值1.4分段三次样条插值第二章数值积分Simpson 公式■变步长梯形法Romberg加速算法三点Gauss公式第三章常微分方程徳差分方法改进的Euler方法四阶Runge-Kutta方法二阶Adams预报校正系统I改进的四阶Adams预报校正系统第四章方程求根二分法开方法Newton下山法快速弦截法第五章线性方程组的迭代法Jacobi迭代Gauss-Seidel 迭代超松弛迭代对称超松弛迭代第六章线性方程组的直接法追赶法■Cholesky 方法矩阵分解方法6. 4 Gauss列主元消去法第一章插值方法1. 1 Lagrange 插值计算Lagrange插值多项式在x=xO处的值. MATLAB文件:(文件名:)Sfunction [yO,N]= Lagrange eval(X,Y t xO)%X.Y是已知插值点坐标叙0是插值点%y0是Lagrange插值多项式在xO处的值%N是Lagrange插值函数的权系数m=length(X);N=zeros(m t1);y0=0;[for i=l:mN(i)=l;for j=l:mif J =1;N(i)=N(i)*(xO-X(j))/(X(i)-X(j));endendyO=yO+Y(i)*N(i);¥end用法》X=[-];Y=[-];》xO二;》[yO,N]= Lagrange_eval(X,Y,xO)1.2 逐步插值计算逐步插值多项式在x=xO处的值.MATLAB文件:(文件名:)function yO=Nevi1le eval(X,Y,xO)%X,Y是已知插值点坐标%x0是插值点%y0是Neville逐步插值多项式在xO处的值m=length(X);P=zeros(m,1);Pl二zeros(m.1);P=Y;for i=l:mPl 二P;k 二1;for j=i+l:mk=k+l;P(j)=Pl(j-l) + (Pl(j)-Pl(j-l))*(xO-X(k-l))/(X(j)-X(k-l));■endif abs(P(m)-P(m-1))<10 -6;yO二P (m);return;endendyO=P(m);用法》X=[…];Y=[…];》x0=;》y0= Nevi 1le eval(X.Y,xO)分段三次Hermite插值利用分段三次Hermite插值计算插值点处的函数近似值.MATLAB文件:(文件名:)function yO=Hermite interp(X,Y,DY,xO)%X,Y是已知插值点向量序列%DY是插值点处的导数值%x0插值点横坐标%y0为待求的分段三次Hermite插值多项式在xO处的值%N向量长度N=length(X);for i=l:Nif xO>=X(i)&& xO<=X(i+l)k=i: break:endendal=xO-X(k+l);a2=xO-X(k);a3= X(k)- X(k+1);y0= (al/a3)^2*(l-2*a2/a3)*Y(k) + (-a2/a3)*2*(1+2*a1/a3)*Y(k+1) +・・・(a1/a3)2*a2*DY(k) + (-a2/a3)2*a1*DY(k+1);用法》X=[-];Y=关于X的函数;DY=Y‘;》xO=插值横坐标;》yO==Hennite interp(X,Y,DY,xO)1.4分段三次样条插值计算在插值点处的函数值,并用来拟合曲线.MATLAB文件:(文件名:)function [yO,C]=Spline interp(X,Y,sO,sN,xO)%X,Y是已知插值坐标%sO,sN是两端点的一次导数值%x0是插值点%y0三次样条函数在xO处的值%C是分段三次样条函数的系数N=length(X);C二zeros (4.NT) ; h=zeros (1 ,N-1);mu=zeros (1 ■ NT) ;1 mt二zeros (1, NT);d=zeros(l ,N): %d表示右端函数值h=X(L2:N)-X(l,l:N-l);mu(l.N-l)=l; lmt (1,1)=1; mu(lJ:N-2)=h(l,l:N-2)/(h (l t l:N-2)+h(l,2:N-l)); lmt(l,2:N-l)=h(l r2:N-l)/(h(l t l:N-2)+h(l,2:N-l));d(l,l)=6*((Y(l,2)-Y(l,l))/h(l,l)-sO)/h(l,l); d(l t N)=6*(sN-(Y(hN)-Y(l t N-l))/h(l,N-l))/h(l t N-l);d(l t2:N-l)=6*((Y(l,3:N)-Y(l t2:N-l))/h(l,2:N-l)-(Y(l,2:N-l)-Y(l t l:N-2))/h(l,l:N-2))/(h(l J:N-2)+h(l,2:N-l));冬追赶法解三对角方程组bit=zeros(1,N-1);bit(l,l)=lmt(l,l)/2;for i=2:NTbit (l t i)=lmt (1, i)/(2-mu(1, i-l)*bit(l, i~l)):end y=zeros(l,N); y(l,l)=d(l,l)/2; for i=2:Ny(l, i) = (d(l, i)-mu(l, i-l)*y(l, i-l))/(2-mu(l, iT)*bit(l, iT)); endx=zeros(l,N);x(l.N)=y(l,N);for i=N-l:-l:1x(l, i)=y(l, i)-bit (1, i)*x(l, i+1);endv=zeros(l t N-l);v(lJ:N-l) = (Y(l,2:N)-Y(l J:N-l))/h(l ,1:N-1);C(4,:)=Y(1,1:N-1);&C(3,:)=v-h*(2*x(l J:N-l)+x(l,2:N))/6;C(2,:)=x(l,l:N-l)/2;C(l t:) = (x(l,2:N)-x(l J:N-l))/(6*h);if nargin<5yO 二0;elsefor j=l:N-1if x0>二X(l.j)& xO〈X(l.j+l)omg二xO-X(l.j);y0=((C(4,j)*omg+C(3■j))omg+C(2,j))*omg+C(1•j); endendend解:X=[,,,,];Y=[,,,,];sO二;sN=;[yO,C]=Spl ine intei'p(X t Y, sO, sN, xO);plot::, polyval (C(:・ 1) ,0:: / r-.);hold onplot::,polyval(C(:. 2) ,0::, 1 b J );plot::, polyval (C(:. 3) ,0:: / k* );plot::,polyval(C(:. 4)t0::);第二章数值积分Simpson 公式利用复化Simpson公式求被积函数f(x)在给定区间上的积分值. MATLAB文件:(文件名:) function S=FSimpson(f,a,b t N)%f表示被积函数句柄險i,b表示被积区间端点%N表示区间个数%S是用复化Simpson公式求得的积分值h=(b-a)/N;fa=feval(f,a):fb=feval(f,b);S二fa+fb;x=a;for i=l:Nx二x+h/2;fx=feval(f,x);S=S+4*fx;¥x=x+h/2;fx=feval(f t x);S=S+2*fx;endS=h*S/6;算例2:利用复化Simpson公式计算枳分S=「一竺・J()4 + ;r 解:后面都要用到的fl:function f=f1(x)f= x/(4+x"2);令f=@fl;a=0;b=l;运行S=FSimpson(f,a, b,N)这里的N值需要自己输入。
