选修4-4第1讲知能训练轻松闯关
人教版化学选修4:第一章第二节知能演练轻松闯关

一、单项选择题1.下列选项中说明乙醇作为燃料的优点的是( )①燃烧时发生氧化反应 ②充分燃烧的产物不污染环境 ③乙醇是一种可再生能源 ④燃烧时放出大量的热A .①②③B .①②④C .①③④D .②③④解析:选D 。
C 2H 6O 可以通过酿造方法制得,可知乙醇是一种可再生能源,乙醇完全燃烧的反应方程式为C 2H 6O +3O 2――→点燃2CO 2+3H 2O ,可知产物不引起污染,有机物燃烧时都发生氧化反应,这并不是乙醇作为燃料的优点。
2.下列有关能量转换的说法不.正确的是( ) A .煤燃烧是化学能转化为热能的过程B .化石燃料和植物燃料燃烧时放出的能量均来源于太阳能C .动物体内葡萄糖被氧化成CO 2是热能转变成化学能的过程D .植物通过光合作用将CO 2转化为葡萄糖是太阳能转变成化学能的过程 解析:选C 。
C 项葡萄糖被氧化成CO 2是化学能转化成热能。
3.已知下列热化学方程式: 12CH 4(g)+O 2(g)===12CO 2(g)+H 2O(l) ΔH =-445.15 kJ/molCH 4(g)+32O 2(g) ===CO(g)+2H 2O(l)ΔH =-607.3 kJ/molCH 4(g)+2O 2(g) ===CO 2(g)+2H 2O(l) ΔH =-890.3 kJ/molCH 4(g)+2O 2(g) ===CO 2(g)+2H 2O(g) ΔH =-802.3 kJ/mol 则CH 4的燃烧热为( ) A .445.15 kJ/molB .607.3 kJ/molC .890.3 kJ/molD .802.3 kJ/mol 解析:选C 。
CH 4燃烧热是指1 mol CH 4完全燃烧生成气态CO 2和液态水放出的热量。
A 错,因CH 4不为1 mol ,B 错,因燃烧产物不是CO 2,D 错,H 2O 不是液态。
4.下列热化学方程式叙述正确的是(ΔH 的绝对值均正确)( ) A .C 2H 5OH(l)+3O 2(g) ===2CO 2(g)+3H 2O(g) ΔH =-1367.0 kJ ·mol -1(燃烧热)B .NaOH(aq)+HCl(aq) ===NaCl(aq)+H 2O(l) ΔH =+57.3 kJ ·mol -1(中和热)C .S(s)+O 2(g) ===SO 2(g) ΔH =-296.8 kJ ·mol -1(反应热)D .2NO 2===O 2+2NOΔH =+116.2 kJ ·mol -1(反应热)解析:选C 。
教科版物理选修3-4:第1章1.3知能演练轻松闯关

1.单摆是为了研究振动而抽象出来的理想化模型,其理想化条件是()A.摆线质量不计B.摆线长度不伸缩C.摆球的直径比摆线长度短得多D.只要是单摆的运动就是一种简谐运动解析:选ABC.单摆由摆线和摆球组成,摆线只计长度不计质量,摆球只计质量不计大小,且摆线不伸缩,A、B、C正确.只有在摆角很小(θ<10°)的情况下,单摆的运动才是简谐运动.2.下列有关单摆运动过程中受力的说法中,正确的是()A.回复力是重力和摆线拉力的合力B.回复力是重力沿圆弧切线方向的一个分力C.单摆过平衡位置时合力为零D.回复力是摆线拉力的一个分力解析:选B.单摆经过平衡位置时,回复力等于零,但合力不为零,因摆球沿圆弧运动,在径线方向上有向心加速度,即存在向心力.3.如图所示为一单摆的振动图像,则()A.t1和t3时刻摆线的拉力等大B.t2和t3时刻摆球速度相等C.t3时刻摆球速度正在减小D.t4时刻摆线的拉力正在减小解析:选AD.由题图可知,t1和t3单摆振动的速度大小相等,故绳子拉力相等,A正确,B 错误;t3时刻质点正靠近平衡位置,速度正在增大,C错误;t4时刻正远离平衡位置,速度逐渐减小,绳子拉力减小,D正确.4.如图所示是单摆振动示意图,下列说法中正确的是()A.在平衡位置摆球的动能和势能均达到最大值B.在最大位移处势能最大,而动能最小C.在平衡位置绳子的拉力最大,摆球速度最大D.摆球由A→C运动时,动能变大,势能变小解析:选BCD.单摆的振动是简谐运动,机械能守恒,远离平衡位置运动,位移变大,势能变大,而动能减小;反之,向平衡位置运动时,动能变大而势能变小,故B、D正确,A错.小球在平衡位置只受重力和绳子拉力,在平衡位置C,拉力T=mg+m v2/r,由上述分析知,在平衡位置时动能最大,即v最大,故T也最大,所以C正确.一、选择题1.做一个单摆有下列器材可供选用,可以用来做成一个单摆的有()A.带小孔的实心木球B.带小孔的实心钢球C.长约1 m的细线D.长约10 cm的细线解析:选BC.制作单摆时应选用体积小、质量大的球和细、轻、弹性小的线.2.把实际的摆看作单摆的条件是()①细线的伸缩可以忽略②小球的质量可以忽略③细线的质量可以忽略④小球的直径比细线的长度小得多⑤小球的最大偏角足够小A.①②③④⑤B.①②③④C.①③④D.②③④⑤解析:选C.单摆的球应选择体积较小,质量较大的球;细线应选用较轻、弹性较小的线,且小球尺寸比细线要小得多.摆动时的摆角要小于5°,并非越小越好.应选C.3.(2012·安康高二检测)关于单摆,下列说法中正确的是()A.摆球受到的回复力方向总是指向平衡位置B.摆球受到的回复力是它的合力C.摆球经过平衡位置时,所受的合力为零D.摆角很小时,摆球受的合力的大小跟摆球对平衡位置的位移大小成正比解析:选A.根据回复力的定义选项A正确;单摆的回复力除指明在最高点外都不是摆球受力的合力,但不管在哪个位置均可认为是重力沿轨迹圆弧切线方向的分力,所以选项B错误;经过平衡位置时,回复力为零,但合力不为零,因悬线方向上要受向心力,选项C、D 错误.4.一个打磨得很精细的小凹镜,其凹面可视为接近平面.将镜面水平放置如图所示,一个小球从镜面边缘开始释放,小球在镜面上将会往复运动,以下说法中正确的是()A.小球的运动是简谐运动B.不能判断小球做简谐运动C.小球简谐运动的回复力是重力跟支持力的合力D.小球简谐运动的回复力是重力沿曲面切向的分力解析:选AD.由题意,很精细的小凹镜,其凹面可视为接近平面,故曲率半径远大于小镜的长度,小球在上面的运动是简谐运动,运动情况跟单摆相同.5.单摆做简谐运动时,下列说法正确的是()A.摆球质量越大、振幅越大,则单摆振动的能量越大B .单摆振动能量与摆球质量无关,与振幅有关C .摆球到达最高点时势能最大,摆线弹力最大D .摆球通过平衡位置时动能最大,摆线弹力最大解析:选AD.对于无阻尼单摆系统,机械能守恒,其数值等于最大位移处摆球的重力势能或平衡位置处摆球的动能。
人教版化学选修4:第一章第一节第1课时知能演练轻松闯关

一、单项选择题1.下列对化学反应的认识错误的是( ) A .会引起化学键的变化B .会产生新的物质C .必然引起物质状态的变化D .必然伴随着能量的变化解析:选C 。
化学变化的本质是旧化学键的断裂、新化学键的形成,化学变化中会产生新的物质并伴随能量变化,但物质状态不一定发生变化,如:N 2(g)+3H 2(g)高温、高压催化剂2NH 3(g)。
2.(2012·湖北孝感高二调研)下列物质间的反应,其能量变化符合右图的是( ) A .由铝和盐酸制氢气B .灼热的炭与二氧化碳反应C .Ba(OH)2·8H 2O 晶体和NH 4Cl 晶体混合D .碳酸钙的分解解析:选A 。
该图示为放热反应能量图。
A 为典型放热反应,B 、C 是吸热反应的典型代表;D 项碳酸钙分解时需高温持续加热,说明是吸热反应。
3.右图是一个一次性加热杯的示意图。
当水袋破裂时,水与固体碎块混合,杯内食物温度逐渐上升。
制造此加热杯可选用的固体碎块是( ) A .硝酸铵 B .生石灰C .氯化镁D .食盐解析:选B 。
当水袋破裂时,水与固体碎块混合,反应放热,使杯内食物温度逐渐上升。
选项中只有生石灰合适。
4.(2012·西安高二检测)下列反应既是氧化还原反应,又是吸热反应的是( ) A .镁片与稀硫酸的反应B.碘的升华C.灼热的炭与CO2的反应D.甲烷在氧气中的燃烧反应解析:选C。
A、D为放热反应,B为物理变化。
5.已知H2(g)+12O2(g)===H2O(g)ΔH=-242 kJ/mol,且氧气中1 mol O===O键完全断裂时吸收热量496 kJ,水蒸气中1 mol H—O键形成时放出热量463 kJ,则氢气中1 mol H—H键断裂时吸收热量为()A.920 kJ B.557 kJC.436 kJ D.188 kJ解析:选C。
E反应物键能-E生成物键能=ΔH。
故:E(H—H)+496 kJ×12-463 kJ×2=-242 kJ。
人教版化学选修4:第四章第四节知能演练轻松闯关

一、单项选择题1.下列有关金属腐蚀的说法中正确的是()A.金属腐蚀指不纯金属与接触到的电解质溶液进行化学反应而损耗的过程B.电化学腐蚀指在外加电流的作用下不纯金属发生化学反应而损耗的过程C.钢铁腐蚀最普遍的是吸氧腐蚀,负极吸收氧气,产物最终转化为铁锈D.金属的电化学腐蚀和化学腐蚀本质相同,但电化学腐蚀伴有电流产生解析:选D。
金属腐蚀的本质,主要是金属原子失电子被氧化,腐蚀的内因是金属的化学性质比较活泼,外因是金属与空气、水和其他腐蚀性的物质接触,腐蚀主要包括化学腐蚀和电化学腐蚀,所以A错误;电化学腐蚀指不纯金属发生化学反应而损耗的过程,不需要通过电流,所以B错误;钢铁腐蚀最普遍的是吸氧腐蚀,正极吸收氧气,而不是负极吸收氧气,所以C错误;只有选项D正确。
2.下列情况与电化学无关的是()A.轮船水线以下的船壳上装一定数量的锌块B.铝片不用特殊方法保存C.纯锌与稀H2SO4反应时,滴入少量CuSO4溶液后反应速率加快D.镀锌铁比镀锡铁更耐用解析:选B。
铝片与O2反应表面生成一层致密的氧化物薄膜,防止内部被腐蚀,与电化学无关。
3.某课外小组学生研究金属腐蚀的条件和速率,用金属丝将三根大小相同的铁钉分别固定在图示的三个装置中,再放在玻璃钟罩里保存相同的一段时间,下列对实验结束时现象的描述不.正确的是()A.装置Ⅰ左侧的液面一定会下降B.装置Ⅰ的左侧液面比装置Ⅱ的左侧液面低C.装置Ⅱ中的铁钉腐蚀最严重D.装置Ⅲ中的铁钉几乎没被腐蚀解析:选B。
Ⅱ中铁钉与铜丝相连,金属活动性相差较大,且用挥发性盐酸,因此装置Ⅱ中的铁钉腐蚀最严重,C选项正确。
Ⅰ中虽然也用了盐酸,但铁钉与铁丝相连,腐蚀不及Ⅱ,由于均发生了2H++2e-====H2↑,Ⅰ和Ⅱ均生成了气体,液面都会下降,装置Ⅱ的左侧液面比装置Ⅰ的左侧液面低,A选项正确,B选项错误;Ⅲ中虽然铁丝也与铜丝相连,但由于所装试剂为不挥发性硫酸,因此铁钉几乎没被腐蚀,D选项正确。
教科版物理选修3-4:第1章1.1知能演练轻松闯关

1.下列振动是简谐运动的有( )A .手拍乒乓球的运动B .弹簧的下端悬挂一个钢球,上端固定组成的振动系统C .摇摆的树枝D .从高处下落到光滑水泥地面上的小钢球的运动解析:选B.手拍乒乓球,球原来静止的位置为平衡位置,球向上和向下运动过程中受重力作用,不是简谐运动,A 错;B 为弹簧振子,为简谐运动,B 正确;C 中树枝摇摆,受树的弹力作用,但弹力的变化无规律,C 错;D 既不是机械振动,也不是简谐运动,D 错.2.(2012·西安高二检测) 一个质点做简谐运动,其振动图像如图所示,下列说法中正确的是( )A .振动周期为4 sB .振动频率为0.25 HzC .经过5 s 质点通过的路程为20 cmD .5 s 末质点的位移为零解析:选ABD.周期是完成一次全振动所用的时间,在图像上是两相邻同向极大值间的坐标差,所以周期是4 s .又频率f =1T ,所以f =0.25 Hz ,5 s 是54个周期,一个周期质点通过的路程为s =4A =20 cm ,所以经过5 s 质点通过的路程为25 cm.由题图可知5 s 末位置是0 cm ,所以5 s 末质点的位移为零.3.弹簧振子在AB 间做简谐振动,O 为平衡位置,AB 间距离是20 cm ,A 到B 运动时间是2 s ,如图所示,则( )A .从O →B →O 振子做了一次全振动B .振动周期为2 s ,振幅是10 cmC .从B 开始经过6 s ,振子通过的路程是60 cmD .从O 开始经过3 s ,振子处在平衡位置解析:选C.振子从O →B →O 只完成半个全振动,A 选项错误;从A →B 振子也只是半个全振动,半个全振动是2 s ,所以振动周期是4 s ,振幅是振动物体离开平衡位置的最大距离,振幅A =10 cm ,选项B 错误;t =6 s =32T ,所以振子经过的路程为4A +2A =6A =60 cm ,选项C 正确;从O 开始经过3 s, 振子处在极限位置A 或B ,D 选项错误.4.如图所示是某质点做简谐运动的振动图像,根据图像中的信息,回答下列问题:(1)质点在第2 s末的位移是多少?(2)质点振动过程中的最大位移为多少?(3)在前4 s内,质点经过的路程为多少?解析:(1)由x-t图像可以读出2 s末质点的位移为零.(2)质点的最大位移在前4 s发生在1 s末和3 s末,位移大小为10 cm.(3)前4 s质点正好完成一个往复的全振动.先朝正方向运动了距离为10 cm的一个来回,又在负方向上进行了一个10 cm距离的来回,故总路程为40 cm.答案:(1)0(2)10 cm(3)40 cm一、选择题1.关于简谐运动下列说法正确的是()A.简谐运动一定是水平方向的运动B.所有的振动都可以看做是简谐运动C.物体做简谐运动时一定可以得到正弦曲线形的轨迹线D.只要振动图像是正弦曲线,物体一定做简谐运动解析:选D.物体的简谐运动并不一定只在水平方向发生,各个方向都有可能发生,A错.简谐运动是最简单的振动,B错.做简谐运动的轨迹线并不是正弦曲线,C错.物体振动的图像是正弦曲线,一定是做简谐运动,D对.2.如图所示,弹簧振子以O为平衡位置,在B、C间振动,则()A.从B→O→C→O→B为一次全振动B.从O→B→O→C→B为一次全振动C.从C→O→B→O→C为一次全振动D.OB的大小不一定等于OC解析:选AC.O为平衡位置,B、C为两侧最远点,则从B起经O、C、O、B路程为振幅的4倍,即A说法对;若从O起始经B、O、C、B路程为振幅的5倍,超过一次全振动,即B说法错;若从C起经O、B、O、C路程为振幅的4倍,即C说法对;因弹簧振子的系统摩擦不考虑,所以振幅一定,D错.3.一个质点做简谐运动,当它每次经过同一位置时,一定相同的物理量是()A.速度B.加速度C.速率D.动能解析:选BCD.每次经过同一点x相同,弹力相同,动能相同,但v只是大小一定相同.4.如图所示,为某物体做简谐运动的图像,下列说法中正确的是()A .由P →Q 位移在增大B .由P →Q 速度在增大C .由M →N 位移是先减小后增大D .由M →N 位移始终减小解析:选AC.物体经过平衡位置向正方向运动,先后经过P 、Q 两点,故位移增大,速度减小;物体从正方向最大位移处向负方向运动,先后经过M 、N 两点,且N 点在平衡位置另一侧,故从M →N 位移先减小后增大.5.(2012·榆林高二检测)弹簧振子在AOB 之间做简谐运动,O 为平衡位置,测得A 、B 之间的距离为8 cm ,完成30次全振动所用时间为60 s ,则( )A .振子的振动周期是2 s ,振幅是8 cmB .振子的振动频率是2 HzC .振子完成一次全振动通过的路程是16 cmD .从振子通过O 点时开始计时,3 s 内通过的路程为24 cm解析:选CD.A 、B 之间距离为8 cm ,振幅是4 cm ,T =2 s ,f =0.5 Hz ,振子完成一次全振动通过的路程是4A ,即16 cm ,3 s 内运动1.5个周期,总路程为24 cm.6.(2012·徐州高二检测)如图所示,一个弹簧振子在A 、B 间做简谐运动,O 是平衡位置,把向右的方向选为正方向,以某时刻作为计时零点(t =0),经过1/4周期,振子具有正方向的最大加速度,那么如图所示的四个振动图像中能正确反映振动情况的图像是( )解析:选D.从计时起经14周期,振子具有正方向的最大加速度,即14周期末振子在负的最大位移处,说明开始计时时振子从平衡位置O 向负方向A 处运动,故选项D 正确.7.(2012·宁夏固原高二检测)一个做简谐运动的质点,其振幅是4 cm ,频率是2.5 Hz ,该质点从平衡位置经过2.5 s 后的位移大小和路程是( )A .4 cm ,24 cmB .4 cm ,100 cmC .0,24 cmD .0,100 cm解析:选B.因为简谐运动频率是2.5 Hz ,所以周期是0.4 s ,质点从平衡位置其经过2.5 s 是614个周期,因此位移大小是4 cm ,路程是4×4×⎝⎛⎭⎫6+14 cm =100 cm.8.一个质点做简谐运动的图像如图所示,下列结论正确的是( )A.质点的最大位移为4 cmB.质点完成一次全振动通过的路程为8 cmC.在10 s内质点通过的路程是20 cmD.质点在1 s末到4 s末的过程中通过的路程为6 cm解析:选BCD.由振动图像得质点的最大位移为2 cm,所以A项错误;从题图中可以得出,质点完成一次全振动通过的路程为2×4 cm=8 cm,所以B项正确;质点在10 s内通过的路程为2×10 cm=20 cm,所以C项正确;质点在1 s末到4 s末的过程中通过的路程为2×3 cm =6 cm,所以D项正确.9.如图所示,为某一弹簧振子的振动图像,下列说法正确的是()A.t1时刻,振子的位移为正,加速度为负B.t2时刻,振子的位移为负,速度为正C.t1与t2时刻,弹簧的长度相同D.t3时刻,振子的速度与t2时刻相同解析:选ACD.振动图像描述的是振子的位移随时间的变化规律.在横轴上方时,位移为正值,加速度为负值,而在横轴下方时,与在上方相反.在t1与t2时刻,振子的位移相同,说明振子一定在同一位置,所以弹簧长度相同.t2和t3时刻,振子位移大小相等、方向相反,位置关于平衡位置对称,速度大小相等,且都沿负方向,所以速度相同.10.(2012·开封高二检测)一弹簧振子沿x轴振动,振幅为4 cm,振子的平衡位置位于x轴上的O点.图上的a、b、c、d为四个不同的振动状态;黑点表示振子的位置,黑点上的箭头表示运动的方向.图像给出的①②③④四条振动图线,可用于表示振子的振动图像的是()A.若规定状态a时t=0,则图像为①B.若规定状态b时t=0,则图像为②C.若规定状态c时t=0,则图像为③D.若规定状态d时t=0,则图像为④解析:选AD.振子在状态a时t=0,此时的位移为3 cm,且向规定的正方向运动,故选项A 正确.振子在状态b时t=0,此时的位移为2 cm,且向规定的负方向运动,选项B不正确.振子在状态c时t=0,此时位移为-2 cm,且向规定的负方向运动,选项C不对.振子在状态d时t=0,此时位移为-4 cm,速度为零,故选项D正确.二、非选择题11.如甲图所示为一弹簧振子,如乙图所示为其振动图像,振子在AOB间做简谐运动,选向右为正方向.由图像可知振子的振动周期为________,振幅为________,t=0时质点在________点.t=0.2 s时质点在________点,速度方向与规定的正方向________(选填“相同”或“相反”).在图像的时间范围内质点具有正向最大加速度对应的时刻是________,质点具有正向最大速度对应的时刻是________.甲乙解析:从图像直接读出周期为0.8 s,振幅为10 cm.t=0时质点在正向最大位移处,即在B 点.t=0.2 s时,质点的位移为零,此时正以最大速度经O点向A点运动,速度方向与规定的正方向相反.具有正向最大加速度对应的时刻应为位移为负最大的时刻,即0.4 s.具有正向最大速度对应的时刻是过平衡位置且向B点运动的时刻,即0.6 s.答案:0.8 s10 cm B O相反0.4 s0.6 s12.物体做简谐运动,通过A点时的速度为v,经1 s后物体第一次以相同速度v通过B点,再经过1 s物体紧接着又通过B点,已知物体在2 s内所走过的总路程为12 cm.则该简谐运动的周期和振幅分别是多大?解析:物体通过A点和B点速度大小相等,A、B两点一定关于平衡位置O对称.依题意作出物体的振动轨迹草图如图甲所示,物体从A向右运动到B,即图甲中从1运动到2,时间为1 s,从2运动到3,又经过1 s,从1到3共经历了0.5T,即0.5T=2 s,T=4 s,2A=12 cm,A=6 cm.甲乙在乙图中,物体从A先向左运动,当物体第一次以相同的速度通过B点时,即图乙中从1运动到2时,时间为1 s,从2运动到3,又经过1 s,同样A、B两点关于O点对称,从图中可以看出从1到3共经历了1.5T,即1.5T=2 s,T=4/3 s,1.5×4A=12 cm,A=2 cm.答案:简谐运动的周期和振幅分别为T=4 s,A=6 cm或T=4/3 s,A=2 cm.。
选修4-4第一讲学案

2012—2013学年下学期高二文数学案第4周第一节平面直角坐标系学习目标:1.理解平面直角坐标系的定义,并会建立恰当的坐标系2.掌握坐标法解决几何问题的步骤并能灵活应用3.掌握平面直角坐标系中的伸缩变换公式并能灵活运用学习重点:理解平面直角坐标系中的伸缩变换学习难点:能够建立适当的坐标系解决数学问题学习过程:一、知识要点1.平面直角坐标系(1)平面直角坐标系的作用:使平面上的点与(有序实数对)、曲线与建立联系,从而实现的结合.(2)坐标法:根据集合对象的,选择适当的坐标系,建立它的,通过研究它的及与其他集合图形的。
(3)坐标法解决几何问题的“三部曲”:第一步:建立适当坐标系,用坐标和方程表示问题中涉及的元素,将几何问题转化为问题;第二步:通过代数运算解决代数问题;第三步:把代数运算结果翻译成结论.2.平面直角坐标系中的伸缩变换(1)平面直角坐标系中方程表示图形,那么平面图形的伸缩变换就可归纳为伸缩变换,这就是用研究变换.(2)设点(,)P x y是平面直角坐标系中的任意一点,在变换ϕ:的作用下,点(,)''',称ϕ为平面直角坐标系中P x yP x y对应到点(,)的,简称变换二、例题展示【探究一】运用坐标法解决问题例1、声响定位问题某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比其他两个观测点晚4s,已知各观测点到中心的距离都是1020m,试确定该巨响的位置。
(假定当时声音传播的速度为340m/s,各相关点均在同一平面上)解决此类应用题的关键:1、建立平面直角坐标系2、设点(点与坐标的对应)3、列式(方程与坐标的对应)4、化简5、说明建系时,根据几何特点选择适当的直角坐标系。
(1)如果图形有对称中心,可以选对称中心为坐标原点; (2)如果图形有对称轴,可以选择对称轴为坐标轴; (3)使图形上的特殊点尽可能多的在坐标轴上。
人教版化学选修4:第一章第一节第2课时知能演练轻松闯关

一、单项选择题1.(2012·岳阳高二测试)下列说法错误的是( )A .热化学方程式未注明温度和压强时,ΔH 表示标准状况下的数据B .热化学方程式各物质前的化学计量数不表示分子个数只表示物质的量C .同一化学反应,化学计量数不同,ΔH 不同,化学计量数相同而状态不同,ΔH 也不相同D .化学反应过程所吸收或放出的热量与参加反应的物质的物质的量成正比解析:选A 。
热化学方程式未注明温度和压强时,ΔH 指25 ℃,1.01×105 Pa 时测得的值(标准状况为0 ℃,1.01×105Pa)。
2.(2012·乌鲁木齐高二检测)为了测定酸碱反应的中和热,计算时至少需要的数据是( ) ①酸溶液的浓度和体积 ②碱溶液的浓度和体积 ③比热容 ④反应后溶液的质量 ⑤生成水的物质的量⑥反应前后温度变化 ⑦操作所需的时间A .①②③⑥B .①③④⑤C .③④⑤⑥D .全部 解析:选C 。
根据计算公式ΔH = -4.18×10-3·m (溶液)·(t 2-t 1)n (H 2O )kJ ·mol -1可知C 正确。
3.同温同压下,已知下列各反应为放热反应,下列各热化学方程式中ΔH 最小的是( )A .2A(l)+B(l)===2C(g) ΔH 1B .2A(g)+B(g) ===2C(g) ΔH 2C .2A(g)+B(g) ===2C(l) ΔH 3D .2A(l)+B(l) ===2C(l) ΔH 4解析:选C 。
等量的物质气态时的能量大于液态时的能量,由以上反应可知,C 选项中反应物2A(g)+B(g)的能量最高,生成物2C(l)的能量最低,该反应放热最多,ΔH 最小。
4.(2012·黄山高二调研)下列对H 2(g)+Cl 2(g) ===2HCl(g) ΔH =-184.6 kJ/mol 的叙述正确的是( )A .一分子H 2和Cl 2反应,放出热量184.6 kJB .1 mol H 2和Cl 2完全反应生成2 mol HCl 放出的热量为184.6 kJC .在25 ℃、101 kPa 时,1 mol 气态H 2和1 mol 气态Cl 2完全反应生成2 mol HCl 气体,放出的热量为184.6 kJD .在25 ℃、101 kPa 时,1 mol 气态H 2和1 mol 气态Cl 2完全反应生成2 mol HCl 气体,吸收的热量为184.6 kJ解析:选C 。
选修4-4--第1节

课 时 知 能 训 练
菜
单
新课标 ·数学(文)(广东专用)
【尝试解答】
自 主 落 实 · 固 基 础
(1)设点 A′(x′,y′),由伸缩变换 φ: x′=3x, 2
高 考 体 验 · 明 考 情
x′=3x 得 y 2y′=y y′= ,
-2 1 ∴x′= ×3=1,y′= =-1. 3 2 ∴点 A′的坐标为(1,-1). (2)设 P′(x′,y′)是直线 l′上任意一点.
菜
单
新课标 ·数学(文)(广东专用)
自 主 落 实 · 固 基 础
典 例 探 究 · 提 知 能
1.极坐标系的概念 (1)极坐标系:如图1所示, 在平面内取一个 定点 O,叫做极点, 自极点O引一条 射线 Ox,叫做极轴; 再选定一个长度单位,一个角度单位 (通常取弧度)及其正方向 (通常取 逆时针 方向), 这样就建立了一个极坐标系.
将(*)代入 2x+3y=0,得 x′+y′=0,
高 考 体 验 · 明 考 情
(*)
典 例 探 究 · 提 知 能
因此直线 2x+3y=0 变成直线 x′+y′=0.,
课 时 知 能 训 练
【答案】
x′+y′=0,
菜
单
新课标 ·数学(文)(广东专用)
自 主 落 实 · 固 基 础
(2012·惠州质检)在极坐标系(ρ,θ)(0≤θ<2π)中,曲线ρ=
自 主 落 实 · 固 基 础
(2011· 陕西高考)在直角坐标系 xOy 中,以原点为极点,x 轴的
x=3+cos θ 正半轴为极轴建立极坐标系, 设点 A, 分别在曲线 C1: B y=4+sin θ
(θ 为参数)和曲线 C2:ρ=1 上,则|AB|的最小值为________.
2014-2015学年高中数学(人教版选修4-4)配套课件第一讲 本讲小结

四、极坐标系与直角坐标系的有关问题 1.极径是距离,当然是正的,可为何又有“负极径”的概 念呢?“负极径”中的“负”的含义是什么?
名师剖析: 根据极径定义,极径是距离,当然是正 的. 极径是负的, 等于极角增加 π.负极径的负与数学中历 来的习惯相同,用来表示“反向”,比较来看,负极径比 正极径多了一个操作:将射线 OP“反向延长”.
(2)在直角坐标系内,一条曲线如果有方程,那么曲线 和它的方程是一一对应的 (解集完全相同且互相可以推导的 等价方程,只看作一个方程 ).可是在极坐标系内,虽然是 一个方程只能与一条曲线对应, 但一条曲线却可以与多个方 程对应,所以曲线和它的方程不是一一对应的.
(3)在直角坐标系内,曲线上每一点的坐标一定适合它的方 程,可是在极坐标系内,曲线上一点的所有坐标不一定都适合方
在空间的球坐标系中,方程 r=r0(r0 为正常数)表示球心 在原点,半径为 r0 的球面;方程 θ=θ0(0≤θ0<2π)表示过 z 轴 的半平面, 它与 Oxz 坐标面的夹角为 θ0; 方程 φ=φ0(0≤φ≤π) 表示顶点在原点, 半顶角为 φ0 的圆锥面, 它的中心轴是 z 轴, π π π φ0< 时它在上半空间,φ0> 时它在下半空间,φ0= 时它是 2 2 2 Oxy 平面,如下图所示:
下面给出点 M 的直角坐标与球坐标的变换公式. 由图可知 z=rcos φ,ρ=rsin φ, 而 x=ρcos θ=rsin φcos θ,y=ρsin θ=rsin φsin θ, 由此得坐标变换公式: x=rsin φcos θ, y=rsin φsin θ, z=rcos φ.
π π 程.例如给定曲线 ρ=θ,设点 P 的一极坐标为4,4,那么点 P
适合方程 ρ=θ,从而是曲线上的一个点,但点 P 的另一个极坐
苏教版高中化学选修四专题1第一单元第2课时知能演练轻松闯关

1.下列说法正确的是(双选)( )A .反应热是指反应过程中放出的热量B .热化学方程式的系数只能是整数C .在热化学方程式中无论是反应物还是生成物必须标明聚集状态D .所有的化学反应都伴随着能量变化解析:选CD 。
吸收或放出的热量都是反应热,A 错。
热化学方程式的系数也可以是分数,B 错。
C 、D 说法正确。
2.下列说法正确的是( )A .热化学方程式是指注明反应条件的化学方程式B .热化学方程式中各物质的化学计量数既表示物质的量,也表示分子的个数C .由C(石墨)―→C(金刚石) ΔH =+1.9 kJ·mol -1可知,金刚石比石墨稳定D .等量的硫蒸气和硫固体分别完全燃烧,前者放出的热量多解析:选D 。
热化学方程式是表示参加反应物质的量和反应热的关系的化学方程式,因此A 错;热化学方程式中各物质的化学计量数只表示物质的量,不表示分子的个数,B 项错;由C(石墨)―→C(金刚石) ΔH =+1.9 kJ·mol -1可知,金刚石能量高,不稳定,C 项错;因为硫固体变为硫蒸气要吸热,所以等量的硫蒸气和硫固体分别完全燃烧,前者放出的热量多是正确的。
3.热化学方程式C(s)+H 2O(g)===CO(g)+H 2(g) ΔH =+131.3 kJ·mol -1表示( )A .碳和水反应吸收131.3 kJ 能量B .1 mol 碳和1 mol 水反应生成1 mol 一氧化碳和1 mol 氢气并吸收131.3 kJ 热量C .1 mol 固态碳和1 mol 水蒸气反应生成1 mol 一氧化碳气体和1 mol 氢气并吸收131.3 kJ 热量D .1个固态碳原子和1分子水蒸气反应吸热131.3 kJ解析:选C 。
依据反应热的概念,表示按照热化学方程式计量数的物质的量反应时吸收或放出的热量,单位是kJ·mol -1,该热化学方程式表示1 mol 固态碳和1 mol 水蒸气反应生成1 mol一氧化碳气体和1 mol 氢气,吸收131.3 kJ 的热量,特别要指明水的状态。
人教版化学选修4:第三章第三节第1课时知能演练轻松闯关

一、单项选择题1.在盐类发生水解的过程中,下列说法正确的是()A.盐的水解不属于离子反应B.溶液的pH一定发生改变C.水的电离程度逐渐增大D.没有中和反应发生解析:选C。
本题考查的是盐类水解的实质。
盐的水解属于离子反应,选项A不正确;像CH3COONH4这样的弱酸弱碱盐,CH3COO-和NH+4的水解程度一样大,水解后溶液仍然呈中性,溶液的pH不发生改变,选项B也不正确;盐类发生水解,实质是促进水的电离,选项C正确;盐类水解反应的逆过程是中和反应,因此有中和反应发生。
故正确答案为C。
2.(2012·大连高二测试)下列反应既不是水解反应,又不是氧化还原反应的是()+H2O NH3·H2O+H+A.NH+O H2S+OH-B.HS-+H+H2O HBr+HBrOC.BrS+H2O H3O++HS-D.H解析:选D。
A项为NH+4的水解反应;B项是HS-的水解反应;C项是Br2与水的反应,属于氧化还原反应;D项为H2S的电离。
3.现有等浓度的下列溶液:①醋酸,②硫酸氢钠,③醋酸钠,④碳酸,⑤碳酸钠,⑥硫酸钠。
按溶液pH由小到大排列正确的是()A.④①②⑤⑥③B.⑥①②④③⑤C.②①④⑥③⑤D.①④②③⑥⑤解析:选C。
同等浓度的酸,越易电离的酸性越强,pH越小,同等浓度的强碱弱酸盐,酸越弱,对应的盐的水溶液碱性越强,pH越大。
4.下列操作中,能使水的电离平衡向右移动,而且所得溶液显酸性的是()A.在水中加入少量氯化钠,并加热到100 ℃B.在水中滴入稀硫酸C.在水中加入小苏打D.在水中加入氯化铝固体解析:选D。
A项溶液显中性;B项,加入稀H2SO4抑制水的电离;C项加入NaHCO3,HCO-3水解溶液显碱性;D项AlCl3中的Al3+水解,促进H2O的电离,且溶液显酸性。
5.有四种物质的量浓度相同且由+1价阳离子A+、B+和-1价阴离子X-、Y-组成的盐溶液。
据测定,常温下AX溶液和BY溶液的pH都为7,A Y溶液的pH>7,BX溶液的pH<7。
人教版化学选修4:第四章第一节知能演练轻松闯关

一、单项选择题1.对于原电池的电极名称,叙述错误的是()A.发生氧化反应的一极为负极B.正极为电子流入的一极C.比较不活泼的金属为负极D.电流流出的一极为正极解析:选C。
在原电池中,较活泼的金属为负极,失电子,发生氧化反应,故A正确,C 错误;电子流入(或电流流出)的一极为正极,B、D正确。
2.下列说法正确的是()A.原电池是把电能转化为化学能的装置B.原电池中电子流出的一极是正极,发生氧化反应C.原电池的两极发生的反应均为氧化还原反应D.形成原电池后,原电池中的阳离子向正极移动解析:选D。
原电池是把化学能转化为电能的装置,电子流出的一极是负极,负极发生氧化反应,电解质溶液中的阴离子向负极移动;电子流进的一极是正极,正极发生还原反应,电解质溶液中的阳离子向正极移动。
3.下列装置可以组成原电池的是()解析:选A。
B项中乙醇不是电解质溶液;C项装置不构成闭合回路;D项两极材料活泼性相同。
4.100 mL浓度为2 mol/L的盐酸跟过量的锌片反应,为加快反应速率,又不影响生成氢气的量,可采用的方法是()A.加入适量的6 mol/L的盐酸B.加入数滴氯化铜溶液C.加入适量蒸馏水D.加入适量的氯化钠溶液解析:选B。
增大氢离子浓度能加快反应速率,但由于是跟过量的锌片反应,所以再加入适量的6 mol/L的盐酸会增加生成氢气的量,故A错误;加入数滴氯化铜溶液,锌置换出铜以后,就会构成原电池,从而加快反应速率,故B正确;加入适量蒸馏水或加入适量的氯化钠溶液都会减小氢离子浓度,从而减慢了反应速率。
5.(2012·珠海高二检测)X、Y两根金属棒插入Z溶液中构成下图的装置,实验中电流表指针发生偏转,同时X棒变粗,Y棒变细,则X、Y、Z可能是下列中的()解析:选D X为正极,Y为负极,且电解质溶液中要有离子能够在X极析出,还要使Y极溶解。
6.将铁片和银片用导线连接置于同一稀盐酸溶液中,并经过一段时间后,下列叙述中正确的是()A.负极有Cl2逸出,正极有H2逸出B.负极附近Cl-的浓度减小C.正极附近Cl-的浓度逐渐增大D.溶液中Cl-的浓度基本不变解析:选D。
人教A版选修4-4:第一讲-坐标系-章末归纳提升
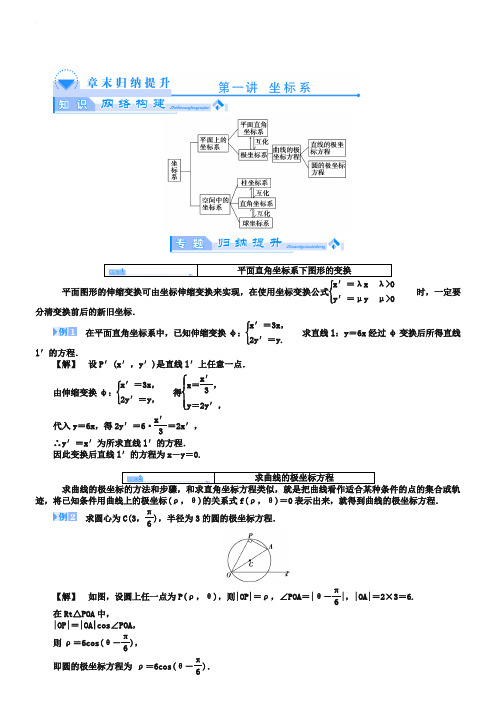
平面图形的伸缩变换可由坐标伸缩变换来实现,在使用坐标变换公式⎩⎪⎨⎪⎧x′=λλy′=μμ时,一定要分清变换前后的新旧坐标.在平面直角坐标系中,已知伸缩变换φ:⎩⎪⎨⎪⎧x′=3x ,2y′=y.求直线l :y =6x 经过φ变换后所得直线l′的方程.【解】 设P′(x′,y′)是直线l′上任意一点.由伸缩变换φ:⎩⎪⎨⎪⎧x′=3x ,2y′=y ,得⎩⎪⎨⎪⎧x =x′3,y =2y′,代入y =6x ,得2y′=6·x′3=2x′,∴y′=x′为所求直线l′的方程. 因此变换后直线l′的方程为x -y =0.迹,将已知条件用曲线上的极坐标(ρ,θ)的关系式f(ρ,θ)=0表示出来,就得到曲线的极坐标方程.求圆心为C(3,π6),半径为3的圆的极坐标方程.【解】 如图,设圆上任一点为P(ρ,θ),则|OP|=ρ,∠POA =|θ-π6|,|OA|=2×3=6.在Rt △POA 中,|OP|=|OA|cos ∠POA ,则ρ=6cos(θ-π6),即圆的极坐标方程为 ρ=6cos(θ-π6).已知定点A(a,0),动点P 对极点O 和点A 的张角∠OPA =π3.在OP 的延长线上取点Q ,使|PQ|=|PA|.当P 在极轴上方运动时,求点Q 的轨迹的极坐标方程.【解】 设Q ,P 的坐标分别是(ρ,θ),(ρ1,θ1),则θ=θ1.在△POA 中,ρ1=a sinπ3·sin(2π3-θ),|PA|=asin θsinπ3.又|OQ|=|OP|+|PA|,∴ρ=2acos(π3-θ).可以有极坐标方程,也可以有直角坐标方程.为了研究问题的方便,有时需要把在一种坐标系中的方程化为在另一种坐标系中的方程.它们之间的互化关系为:x =ρcos θ,y =ρsinθ;ρ2=x 2+y 2,tan θ=y x(x≠0).⊙O 1和⊙O 2的极坐标方程分别为ρ=4cos θ,ρ=-4sin θ. (1)把⊙O 1和⊙O 2的极坐标方程化为直角坐标方程; (2)求经过⊙O 1,⊙O 2交点的直线的直角坐标方程.【解】 以极点为原点,极轴为x 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位. (1)由ρ=4cos θ,得ρ2=4ρcos θ,所以x 2+y 2=4x.即x 2+y 2-4x =0为⊙O 1的直角坐标方程,同理x 2+y 2+4y =0为⊙O 2的直角坐标方程.(2)由⎩⎪⎨⎪⎧ x 2+y 2-4x =0,x 2+y 2+4y =0,解得⎩⎪⎨⎪⎧ x 1=0,y 1=0,⎩⎪⎨⎪⎧x 2=2,y 2=-2.即⊙O 1,⊙O 2交于点(0,0)和(2,-2),故过交点的直线的直角坐标方程为y =-x.为特殊.如本章中直角坐标与极坐标,直角坐标方程与极坐标方程,都是这种思想的体现.当ρ≥0,0≤θ<2π时,极坐标方程与直角坐标方程的相互转化就是等价转化.已知极坐标方程C 1:ρ=10,C 2:ρsin(θ-π3)=6,(1)化C 1、C 2的极坐标方程为直角坐标方程,并分别判断曲线形状; (2)求C 1、C 2交点间的距离.【解】 (1)由C 1:ρ=10,得ρ2=100,∴x 2+y 2=100,所以C 1为圆心在(0,0),半径等于10的圆.由C 2:ρsin(θ-π3)=6,得ρ(12sin θ-32cos θ)=6.∴y -3x =12,即3x -y +12=0. 所以C 2表示直线.(2)由于圆心(0,0)到直线3x -y +12=0的距离为d =1232+-2=6<r =10, 所以直线l 被圆截得的弦长|C 1C 2|=2r 2-d 2=2102-62=16.综合检测(一)第一讲 坐标系(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.将曲线y =sin 2x 按照伸缩变换⎩⎪⎨⎪⎧x′=2xy′=3y 后得到的曲线方程为( )A .y =3sin xB .y =3sin 2xC .y =3sin 12xD .y =13sin 2x【解析】 由伸缩变换,得x =x′2,y =y′3.代入y =sin 2x ,有y′3=sin x′,即y′=3sin x′.∴变换后的曲线方程为y =3sin x. 【答案】 A2.有相距1 400 m 的A 、B 两个观察站,在A 站听到爆炸声的时间比在B 站听到时间早4 s .已知当时声音速度为340 m/s ,则爆炸点所在的曲线为( )A .双曲线B .直线C .椭圆D .抛物线【解析】 设爆炸点为P ,则|PB|-|PA|=4×340<1 400 m,∴P 点在以A 、B 为焦点的双曲线上. 【答案】 A3.在极坐标系中,点(ρ,θ)与(-ρ,π-θ)的位置关系为( ) A .关于极轴所在直线对称 B .关于极点对称 C .重合D .关于直线θ=π2(ρ∈R)对称【解析】 取ρ=1,θ=π4,可知关于极轴所在直线对称.【答案】 A4.在极坐标系中,点A(2,π6)与B(2,-π6)之间的距离为( )A .1B .2C .3D .4【解析】 由A(2,π6)与B(2,-π6),知∠AOB =π3,∴△AOB 为等边三角形.因此|AB|=2. 【答案】 B5.(2018·新乡质检)极坐标方程4ρ·sin 2θ2=5表示的曲线是( )A .圆B .椭圆C .双曲线的一支D .抛物线【解析】 由4ρ·sin 2θ2=4ρ·1-cos θ2=2ρ-2ρcos θ=5,得方程为2x 2+y 2-2x =5,化简得y2=5x +254.∴该方程表示抛物线. 【答案】 D6.直线ρcos θ+2ρsin θ=1不经过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【解析】 由ρcos θ+2ρsin θ=1,得x +2y =1, ∴直线x +2y =1,不过第三象限.【答案】 C7.点M 的直角坐标为(3,1,-2),则它的球坐标为( )A .(22,3π4,π6)B .(22,π4,π6)C .(22,π4,π3)D .(22,3π4,π3)【解析】 设M 的球坐标为(r ,φ,θ),则⎩⎨⎧3=rsin φcos θ,1=rsin φsin θ,-2=rcos φ,解得⎩⎪⎨⎪⎧r =22,φ=3π4,θ=π6.【答案】 A8.极坐标系中,直线2ρsin(θ+π4)=2+2,与圆ρ=2sin θ的位置关系为( ) A .相离 B .相切C .相交D .以上都有可能 【解析】 直线2ρsin(θ+π4)=2+2与圆ρ=2sin θ的直角坐标方程分别为x +y =2+1,x 2+(y -1)2=1,圆心C(0,1)到直线x +y -(2+1)=0的距离为d =|1-2+2=1,又r =1,所以直线与圆相切.【答案】 B9.若点P 的柱坐标为(2,π6,3),则P 到直线Oy 的距离为( )A .1B .2 C. 3 D. 6【解析】 由于点P 的柱坐标为(ρ,θ,z)=(2,π6,3),故点P 在平面xOy 内的射影Q 到直线Oy 的距离为ρcos π6=3,可得P 到直线Oy 的距离为 6.【答案】 D10.圆ρ=4cos θ的圆心到直线tan θ=1的距离为( )A.22B. 2 C .2 D .2 2【解析】 圆ρ=4cos θ的圆心C(2,0), 如右图,|OC|=2, 在Rt △COD 中,∠ODC =π2,∠COD =π4,∴|CD|= 2.即圆ρ=4cos θ的圆心到直线tan θ=1的距离为 2. 【答案】 B11.设正弦曲线C 按伸缩变换⎩⎪⎨⎪⎧x′=12x y′=3y后得到曲线方程为y =sin x ,则正弦曲线C 的周期为( )A.π2B .πC .2πD .4π 【解析】 由伸缩变换知3y =sin 12x ,∴y =13sin 12x.∴T =2π12=4π.【答案】 D12.极坐标方程ρ=2sin(θ+π4)的图形是()【解析】 法一 圆ρ=2sin(θ+π4)是把圆ρ=2sin θ绕极点按顺时针方向旋转π4而得,圆心的极坐标为(1,π4),故选C.法二 圆ρ=2sin(θ+π4)的直角坐标方程为(x -22)2+(y -22)2=1,圆心为(22,22),半径为1,故选C.【答案】 C二、填空题(本大题共4小题,每小题5分,共20分,请把正确答案填在题中横线上)13.极坐标系中,ρ≥0,过点(1,0)倾斜角为π2的射线的极坐标方程为________.【解析】 设(ρ,θ)是射线上任意一点,则ρcos θ=1,且0≤θ<π2.【答案】 ρcos θ=1,0≤θ<π214.(2018·天津高考)已知圆的极坐标方程为ρ=4cos θ,圆心为C ,点P 的极坐标为(4,π3),则|CP|=________.【解析】 由ρ=4cos θ可得x 2+y 2=4x ,即(x -2)2+y 2=4,因此圆心C 的直角坐标为(2,0).又点P 的直角坐标为(2,23),因此|CP|=2 3.【答案】 2 315.(2018·湖南高考)在极坐标系中,曲线C 1:ρ(2cos θ+sin θ)=1与曲线C 2:ρ=a(a>0)的一个交点在极轴上,则a =________.【解析】 ρ(2cos θ+sin θ)=1,即2ρcos θ+ρsin θ=1对应的普通方程为2x +y -1=0,ρ=a(a>0)对应的普通方程为x 2+y 2=a 2.在2x +y -1=0中,令y =0,得x =22.将(22,0)代入x 2+y 2=a2得a =22.【答案】2216.(2018·陕西高考)直线2ρcos θ=1与圆ρ=2cos θ相交的弦长为________.【解析】 直线2ρcos θ=1可化为2x =1,即x =12,圆ρ=2cos θ两边同乘ρ得ρ2=2ρcos θ,化为直角坐标方程是x 2+y 2=2x ,即(x -1)2+y 2=1,其圆心为(1,0),半径为1,∴弦长为2×12-122= 3.【答案】 3三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)在同一平面直角坐标系中,经过伸缩变换⎩⎪⎨⎪⎧x′=2xy′=2y 后,曲线C 变为曲线(x′-5)2+(y′+6)2=1,求曲线C 的方程,并判断其形状.【解】 将⎩⎪⎨⎪⎧x′=2x y′=2y 代入(x′-5)2+(y′+6)2=1,得(2x -5)2+(2y +6)2=1,即(x -52)2+(y +3)2=14,故曲线C 是以(52,-3)为圆心,半径为12的圆.18.(本小题满分12分)(2018·洛阳模拟)已知直线的极坐标方程ρsin(θ+π4)=22,求极点到直线的距离.【解】 ∵ρsin(θ+π4)=22,∴ρsin θ+ρcos θ=1, 即直角坐标方程为x +y =1. 又极点的直角坐标为(0,0),∴极点到直线的距离d =|0+0-1|2=22.19.(本小题满分12分)(1)在极坐标系中,求以点(1,1)为圆心,半径为1的圆C 的方程; (2)将上述圆C 绕极点逆时针旋转π2得到圆D ,求圆D 的方程.【解】 (1)设M(ρ,θ)为圆上任意一点,如图,圆C 过极点O ,∠COM =θ-1, 作CK ⊥OM 于K ,则ρ=|OM|=2|OK|=2cos(θ-1), ∴圆C 的极坐标方程为ρ=2cos(θ-1).(2)将圆C :ρ=2cos(θ-1)按逆时针方向旋转π2得到圆D :ρ=2cos(θ-1-π2),即ρ=-2sin(1-θ).图120.(本小题满分12分)如图1,正方体OABC -D′A′B′C′中,|OA|=3,A′C′与B′D′相交于点P ,分别写出点C 、B′、P 的柱坐标.【解】 设点C 的柱坐标为(ρ1,θ,z 1),则ρ1=|OC|=3,θ1=∠COA =π2,z 1=0, ∴C 的柱坐标为(3,π2,0);设点B′的柱坐标为(ρ2,θ2,z 2),则ρ2=|OB|=|OA|2+|AB|2=32+32=32,θ2=∠BOA =π4,z 2=3,∴B′的柱坐标为(32,π4,3);如图,取OB 的中点E ,连接PE ,设点P 的柱坐标为(ρ3,θ3,z 3),则ρ3=|OE|=12|OB|=322,θ3=∠AOE =π4,z 3=3,点P 的柱坐标为(322,π4,3).21.(本小题满分12分)某一种大型商品,A 、B 两地都有出售,且价格相同,某地居民从两地之一购得商品后返回的费用是:每单位距离A 地的运费是B 地的运费的3倍,已知A 、B 两地的距离为10 km ,顾客选择A 或B 地购买这种商品的标准是:运费和价格的总费用较低,求A 、B 两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购贷地点?【解】 以A 、B 所在的直线为x 轴,AB 的中点O 为坐标原点,建立如图所示的平面直角坐标系. ∵|AB|=10,∴A(-5,0),B(5,0).设某地P 的坐标为(x ,y),且P 地居民选择A 地购买商品便宜,并设A 地的运费为3a 元/km ,则B 地的运费为a 元/km ,∵P 地居民购货总费用满足条件:价格+A 地运费≤价格+B 地运费,即有3a +2+y 2≤a -2+y 2, ∵a>0,∴3+2+y 2≤-2+y 2,两边平方,得9(x +5)2+9y 2≤(x-5)2+y 2,即(x +254)2+y 2≤(154)2,∴以点C(-254,0)为圆心,154为半径的圆是两地购货的分界线,圆C 内的居民从A 地购货,圆C 外的居民从B 地购货,圆C 上的居民可从A 、B 两地之一购货.22.(本小题满分12分)在极坐标系中,极点为O ,已知曲线C 1:ρ=2与曲线C 2:ρsin(θ-π4)=2交于不同的两点A ,B.(1)求|AB|的值;(2)求过点C(1,0)且与直线AB 平行的直线l 的极坐标方程.【解】 (1)法一 ∵ρ=2,∴x 2+y 2=4.又∵ρsin(θ-π4)=2,∴y =x +2.∴|AB|=2r 2-d 2=24-222=2 2. 法二 设A(ρ,θ1),B(ρ,θ2),θ1,θ2∈[0,2π),则sin(θ1-π4)=22,sin(θ2-π4)=22,∵θ1,θ2∈[0,2π),∴|θ1-θ2|=π2,即∠AOB =π2, 又|OA|=|OB|=2,∴|AB|=2 2.(2)法一 ∵曲线C 2的斜率为1,∴过点(1,0)且与曲线C 2平行的直线l 的直角坐标方程为y =x -1,∴直线l 的极坐标为ρsin θ=ρcos θ-1,即ρcos(θ+π4)=22.法二 设点P(ρ,θ)为直线l 上任一点,因为直线AB 与极轴成π4的角,则∠PCO =3π4或∠PCO =π4,当∠PCO =3π4时在△POC 中,|OP|=ρ,|OC|=1,∠POC =θ,∠PCO =3π4,∠OPC =π4-θ,由正弦定理可知:1π4-θ=ρsin π4,即ρsin(π4-θ)=22,即直线l 的极坐标方程为:ρsin(π4-θ)=22.同理,当∠PCO =π4极坐标方程也为ρsin(π4-θ)=22.当P 为点C 时显然满足ρsin(π4-θ)=22. 综上,所求直线l 的极坐标方程为ρsin(π4-θ)=22.。
(2021年整理)高中数学选修4-4知识点归纳

(完整版)高中数学选修4-4知识点归纳编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)高中数学选修4-4知识点归纳)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)高中数学选修4-4知识点归纳的全部内容。
(完整版)高中数学选修4-4知识点归纳编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望(完整版)高中数学选修4—4知识点归纳这篇文档能够给您的工作和学习带来便利.同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为〈(完整版)高中数学选修4—4知识点归纳〉这篇文档的全部内容.高中数学选修4—4知识点总结一、选考内容《坐标系与参数方程》高考考试大纲要求:1.坐标系:① 理解坐标系的作用.② 了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.③ 能在极坐标系中用极坐标表示点的位置,理解在极坐标系和平面直角坐标系中表示点的位置的区别,能进行极坐标和直角坐标的互化。
④ 能在极坐标系中给出简单图形(如过极点的直线、过极点或圆心在极点的圆)的方程。
通过比较这些图形在极坐标系和平面直角坐标系中的方程,理解用方程表示平面图形时选择适当坐标系的意义.2.参数方程:① 了解参数方程,了解参数的意义。
② 能选择适当的参数写出直线、圆和圆锥曲线的参数方程。
二、知识归纳总结:1.伸缩变换:设点),(y x P 是平面直角坐标系中的任意一点,在变换⎩⎨⎧>⋅='>⋅=').0(,y y 0),(x,x :μμλλϕ的作用下,点),(y x P 对应到点),(y x P ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换。
高考数学 第2课时 知能演练轻松闯关 新人教A版选修41(

2014年高考数学 第2课时 知能演练轻松闯关 新人教A 版选修4-1一、选择题1.(2012·高考北京卷)如图,∠ACB =90°,CD ⊥AB 于点D ,以BD 为直径的圆与BC 交于点E ,则( )A .CE ·CB =AD ·DB B .CE ·CB =AD ·ABC .AD ·AB =CD 2D .CE ·EB =CD 2解析:选A.在直角三角形ABC 中,根据直角三角形射影定理可得CD 2=AD ·DB ,再根据切割线定理可得CD 2=CE ·CB ,所以CE ·CB =AD ·DB .二、填空题2.如图,AB 是半圆O 的直径,C 是半圆O 上异于A ,B 的点,CD ⊥AB ,垂足为D ,已知AD =2,CB =43,则CD =________.解析:根据射影定理得CB 2=BD ×BA ,即(43)2=BD (BD +2),得BD =6.又CD 2=AD ×BD =12,所以CD =12=2 3.答案:2 33.(2012·高考天津卷)如图,已知AB 和AC 是圆的两条弦,过点B 作圆的切线与AC 的延长线相交于点D .过点C 作BD 的平行线与圆相交于点E ,与AB 相交于点F ,AF =3,FB=1,EF =32,则线段CD 的长为________.解析:由相交弦定理可得CF ·FE =AF ·FB ,得CF =2.又因为CF ∥DB ,所以CF DB =AF AB,得DB =83,且AD =4CD ,由切割线定理得DB 2=DC ·DA =4CD 2,得CD =43.答案:434.(2013·佛山模拟)如图,以AB =4为直径的圆与△ABC 的两边分别交于E ,F 两点,∠ACB =60°,则EF =________.解析:连接BF ,OE ,OF ,则BF ⊥AC ,∴∠CBF =30°,弦EF 所对的圆心角∠EOF =60°,故EF 等于圆的半径2.答案:25.(2012·高考广东卷)如图,圆O的半径为1,A、B、C是圆周上的三点,满足∠ABC=30°,过点A作圆O的切线与OC的延长线交于点P,则PA=________.解析:如图,连接OA.由∠ABC=30°,得∠AOC=60°,在直角三角形AOP中,OA=1,于是PA=OA tan 60°= 3.答案: 36.(2012·高考陕西卷)如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,则DF·DB=________.解析:由相交弦定理可知ED2=AE·EB=1×5=5.又易知△EBD与△FED相似,得DF·DB =ED2=5.答案:5三、解答题7.已知△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与点A,C重合),延长BD至E.(1)求证:AD的延长线平分∠CDE;(2)若∠BAC=30°,△ABC中BC上的高为2+3,求△ABC外接圆的面积.解:(1)证明:如图,设F 为AD 延长线上一点.∵A ,B ,C ,D 四点共圆, ∴∠CDF =∠ABC .又AB =AC ,∴∠ABC =∠ACB , 且∠ADB =∠ACB , ∴∠ADB =∠CDF ,对顶角∠EDF =∠ADB ,故∠EDF =∠CDF , 即AD 的延长线平分∠CDE .(2)设O 为外接圆圆心,连接AO 并延长交BC 于H , 则AH ⊥BC .连接OC ,由题意∠OAC =∠OCA =15°,∠ACB =75°, ∴∠OCH =60°.设圆半径为r ,则r +32r =2+3,得r =2,则外接圆的面积为4π. 8.(2013·泉州调研)如图,AB 是圆O 的直径,直线CE 和圆O 相切于点C ,AD ⊥CE 于点D ,若AD =1,∠ABC =30°,求圆O 的面积.解:∵CE 是⊙O 的切线,则∠ACD =∠ABC =30°.在Rt △ACD 中,AD AC=sin 30°,则AC =2. 又在Rt △ABC 中,∠ABC =30°,则AB =2AC =4.∴圆O 的面积S =⎝ ⎛⎭⎪⎫422π=4π.9.(2012·高考江苏卷)如图,AB 是圆O 的直径,D ,E 为圆O 上位于AB 异侧的两点,连接BD 并延长至点C ,使BD =DC ,连接AC ,AE ,DE .求证:∠E =∠C . 证明:连接OD ,因为BD =DC ,O 为AB 的中点,所以OD ∥AC ,于是∠ODB =∠C . 因为OB =OD ,所以∠ODB =∠B . 于是∠B =∠C .因为点A ,E ,B ,D 都在圆O 上,且D ,E 为圆O 上位于AB 异侧的两点,所以∠E 和∠B 为同弧所对的圆周角,故∠E =∠B .所以∠E =∠C . 10.如图所示,以直角三角形ABC 的直角边AC 为直径作⊙O ,交斜边AB 于点D ,E 为BC 边的中点,连接DE .请判断DE 是否为⊙O 的切线,并证明你的结论.解:DE 是⊙O 的切线.证明如下:如图,连接OD 、CD ,则OD =OC ,∴∠OCD =∠ODC .又AC 为⊙O 的直径,∴∠ADC =90°. ∴三角形CDB 为直角三角形.又E 为BC 的中点,∴DE =12BC =CE ,∴∠ECD =∠EDC .又∠OCD +∠ECD =90°,∴∠ODC +∠EDC =90°, 即∠ODE =90°,∴DE 为⊙O 的切线. 11.在△ABC 中,AB =AC ,过点A 的直线与其外接圆交于点P ,交BC 的延长线于点D ,连结CP .(1)求证:PC AC =PD BD;(2)若AC =3,求AP ·AD 的值.解:(1)证明:∵A 、B 、C 、P 四点共圆, ∴∠CPD =∠ABC . 又∵∠D =∠D ,∴△DPC ∽△DBA ,∴PC BA =PDBD ,又∵AB =AC ,∴PC AC =PDBD.(2)∵AB =AC ,∴∠ABC =∠ACB =∠CPD . ∵∠APC +∠CPD =180°, ∠ACB +∠ACD =180°. ∴∠APC =∠ACD .∴△APC ∽△ACD ,∴AP AC =AC AD. ∴AP ·AD =AC 2=9. 12.如图,已知C 点在圆O 直径BE 的延长线上,CA 切圆O 于A 点,∠ACB 的平分线分别交AE 、AB 于点F 、D .(1)求∠ADF 的度数;(2)若AB =AC ,求AC BC的值. 解:(1)∵AC 为圆O 的切线, ∴∠B =∠EAC .又CD 是∠ACB 的平分线,∴∠ACD =∠DCB , ∴∠B +∠DCB =∠EAC +∠ACD , 即∠ADF =∠AFD .又∵BE 为圆O 的直径,∴∠BAE =90°,∴∠ADF =12(180°-∠BAE )=45°.(2)∵∠B =∠EAC ,∠ACE =∠BCA ,∴△ACE ∽△BCA ,∴AC BC =AE BA. 又∵AB =AC ,∴∠B =∠ACB , ∴∠B =∠ACB =∠EAC ,由∠BAE =90°及三角形内角和定理知,∠B =30°. ∴在Rt △ABE 中, AC BC =AE BA =tan B =tan 30°=33. 13.如图,⊙O 的直径AB 的延长线与弦CD 的延长线相交于点P ,E 为⊙O 上一点,=,DE 交AB 于点F ,且AB =2BP =4.(1)求PF 的长度;(2)若圆F 与圆O 内切,直线PT 与圆F 切于点T ,求线段PT 的长度.解:(1)连接OC ,OD ,OE ,由同弧所对应的圆周角与圆心角之间的关系,结合题中条件弧长AE 等于弧长AC 可得∠CDE =∠AOC .又∠CDE =∠P +∠PFD ,∠AOC =∠P +∠OCP , 从而∠PFD =∠OCP ,故△PFD ∽△PCO ,∴PF PC =PD PO.由割线定理知,PC ·PD =PA ·PB =12,故PF =PC ·PD PO =124=3. (2)若圆F 与圆O 内切,设圆F 的半径为r , 因为OF =2-r =1,即r =1.所以OB 是圆F 的直径,且过P 点圆F 的切线为PT ,则PT 2=PB ·PO =2×4=8,即PT=2 2.14.(2012·高考课标全国卷)如图,D ,E 分别为△ABC 边AB ,AC 的中点,直线DE 交△ABC 的外接圆于F ,G 两点.若CF ∥AB ,证明:(1)CD =BC ;(2)△BCD ∽△GBD .证明:(1)因为D ,E 分别为AB ,AC 的中点, 所以DE ∥BC .又已知CF ∥AB ,故四边形BCFD 是平行四边形,所以CF =BD =AD .而CF ∥AD ,连接AF ,所以四边形ADCF 是平行四边形,故CD =AF .因为CF ∥AB ,所以BC =AF ,故CD =BC . (2)因为FG ∥BC ,故GB =CF .由(1)可知BD =CF ,所以GB =BD ,所以∠BGD =∠BDG .由BC =CD 知,∠CBD =∠CDB . 而∠DGB =∠EFC =∠DBC ,故△BCD ∽△GBD .。
选修4-4第1课时知能演练轻松闯关

一、选择题1.圆ρ=5cos θ-53sin θ的圆心坐标是( )A.⎝⎛⎭⎫-5,-4π3B.⎝⎛⎭⎫-5,π3C.⎝⎛⎭⎫5,π3D.⎝⎛⎭⎫-5,5π3 解析:选A.ρ2=5ρcos θ-53ρsin θ,x 2+y 2-5x +53y =0,⎝⎛⎭⎫x -522+⎝⎛⎭⎫y +5322=52,∴圆心的直角坐标为⎝⎛⎭⎫52,-523,注意圆心在第四象限,化为极坐标为⎝⎛⎭⎫5,5π3,注意ρ<0时点在极角终边的反向延长线上,∴与⎝⎛⎭⎫-5,-4π3表示同一个点. 2.(2013·湖南六校联考)已知直线l 的参数方程为⎩⎪⎨⎪⎧x =ty =t(t 为参数),圆C 的极坐标方程为ρ=2cos θ,则圆C 的圆心到直线l 的距离为( )A.12B.22C.14D.24解析:选B.将直线l 的参数方程化为普通方程得:x -y =0,将ρ=2cos θ的两边同乘以ρ得ρ2=2ρcos θ,即x 2+y 2=2x ,即(x -1)2+y 2=1,即圆心的坐标为(1,0),故圆心到直线x-y =0的距离d =112+(-1)2=22.二、填空题 3.(2012·高考陕西卷)直线2ρcos θ=1与圆ρ=2cos θ相交的弦长为________.解析:直线的方程为2x =1,圆的方程为x 2+y 2-2x =0,圆心为(1,0),半径r =1,圆心到直线的距离为d =|2-1|22+0=12,设所求的弦长为l ,则12=⎝⎛⎭⎫122+⎝⎛⎭⎫l 22,解得l = 3. 答案: 34.在极坐标系中,P ,Q 是曲线C :ρ=4sin θ上任意两点,则线段PQ 长度的最大值为________.解析:由曲线C :ρ=4sin θ得ρ2=4ρsin θ,x 2+y 2-4y =0,x 2+(y -2)2=4,即曲线C :ρ=4sin θ在直角坐标系下表示的是以点(0,2)为圆心、以2为半径的圆,易知该圆上的任意两点间的距离的最大值即是圆的直径长,因此线段PQ 长度的最大值是4.答案:4 5.(2012·高考湖南卷)在极坐标系中,曲线C 1:ρ(2cos θ+sin θ)=1与曲线C 2:ρ=a (a >0)的一个交点在极轴上,则a =________.解析:曲线C 1的直角坐标方程为2x +y =1,曲线C 2的直角坐标方程为x 2+y 2=a 2,C 1与x 轴的交点坐标为⎝⎛⎭⎫22,0,此点也在曲线C 2上,代入解得a =22.答案:226.(2013·贵阳调研)已知直线的极坐标方程为ρsin ⎝⎛⎭⎫θ+π4=22,则点A ⎝⎛⎭⎫2,7π4到这条直线的距离为________.解析:转化为直角坐标来解,直线方程化为x +y -1=0,点A 化为(2,-2),再用公式可求得点到直线的距离为22.答案:227.(2013·江西九校联考)在极坐标系中,曲线C 1:ρ=2cos θ,曲线C 2:θ=π4,若曲线C 1与C 2交于A 、B 两点,则线段AB =________.解析:曲线C 1与C 2均经过极点,因此极点是它们的一个公共点.由⎩⎪⎨⎪⎧ρ=2cos θ,θ=π4,得⎩⎪⎨⎪⎧ρ=2,θ=π4,即曲线C 1与C 2的另一个交点与极点的距离为2,因此AB = 2. 答案: 2 8.(2012·高考湖北卷)在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知射线θ=π4与曲线⎩⎪⎨⎪⎧x =t +1y =(t -1)2(t 为参数)相交于A ,B 两点,则线段AB 的中点的直角坐标为________.解析:记A (x 1,y 1),B (x 2,y 2),将θ=π4转化为直角坐标方程为y =x (x ≥0),曲线的直角坐标方程为y =(x -2)2,联立上述两个方程得x 2-5x +4=0,∴x 1+x 2=5,故线段AB 的中点坐标为⎝⎛⎭⎫52,52.答案:⎝⎛⎭⎫52,52 三、解答题9.设过原点O 的直线与圆(x -1)2+y 2=1的一个交点为P ,点M 为线段OP 的中点,当点P 在圆上移动一周时,求点M 轨迹的极坐标方程,并说明它是什么曲线.解:圆(x -1)2+y 2=1的极坐标方程为ρ=2cos θ⎝⎛⎫-π2≤θ≤π2,设点P 的极坐标为(ρ1,θ1),点M 的极坐标为(ρ,θ),∵点M 为线段OP 的中点,∴ρ1=2ρ,θ1=θ,将ρ1=2ρ,θ1=θ代入圆的极坐标方程, 得ρ=cos θ.∴点M 轨迹的极坐标方程为ρ=cos θ⎝⎛⎭⎫-π2≤θ≤π2,它表示原心在点⎝⎛⎭⎫12,0,半径为12的圆.10.在极坐标系下,已知圆O :ρ=cos θ+sin θ和直线l :ρsin(θ-π4)=22.(1)求圆O 和直线l 的直角坐标方程;(2)当θ∈(0,π)时,求直线l 与圆O 公共点的极坐标.解:(1)圆O :ρ=cos θ+sin θ,即ρ2=ρcos θ+ρsin θ,圆O 的直角坐标方程为:x 2+y 2=x +y ,即x 2+y 2-x -y =0,直线l :ρsin ⎝⎛⎭⎫θ-π4=22,即ρsin θ-ρcos θ=1, 则直线l 的直角坐标方程为y -x =1, 即x -y +1=0.(2)由⎩⎪⎨⎪⎧ x 2+y 2-x -y =0x -y +1=0,得⎩⎪⎨⎪⎧x =0y =1, 故直线l 与圆O 公共点的极坐标为⎝⎛⎭⎫1,π2.11.(2013·泉州质检)已知圆O 1和圆O 2的极坐标方程分别为ρ=2,ρ2-22ρcos ⎝⎛⎭⎫θ-π4=2.(1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程;(2)求经过两圆交点的直线的极坐标方程. 解:(1)由ρ=2知ρ2=4,所以x 2+y 2=4;因为ρ2-22ρcos ⎝⎛⎭⎫θ-π4=2, 所以ρ2-22ρ⎝⎛⎭⎫cos θcos π4+sin θsin π4=2, 所以x 2+y 2-2x -2y -2=0.(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为x +y =1. 化为极坐标方程为ρcos θ+ρsin θ=1,即ρsin ⎝⎛⎭⎫θ+π4=22. 12.在极坐标系中,如果A (2, π4),B (2,5π4)为等边三角形ABC 的两个顶点,求顶点C的极坐标(ρ≥0,0≤θ <2π).解:∵A (2,π4),∴ρ=2,θ=π4,∴x =ρcos θ=2cos π4=2,y =ρsin θ=2sin π4=2,即A 点的直角坐标为(2,2).同理可求B 点的直角坐标,x =2cos 54π=-2,y =2sin 54π=-2,即B (-2,-2).设C 点的直角坐标为(x ,y ),则⎩⎪⎨⎪⎧y x =-1,x 2+y 2=12,解之得⎩⎨⎧ x =6y =-6或⎩⎨⎧x =-6,y =6,即C 点的直角坐标为(6,-6)或(-6,6).当x =6,y =-6,即C 在第四象限时, ⎩⎪⎨⎪⎧ ρ2=x 2+y 2=12,tan θ=-1, ∴⎩⎪⎨⎪⎧ρ=23,θ=74π.当x =-6,y =6,即C 在第二象限时,⎩⎪⎨⎪⎧ρ2=x 2+y 2=12,tan θ=-1,∴⎩⎪⎨⎪⎧ρ=23,θ=34π,即点C 的极坐标是⎝⎛⎭⎫23,74π或⎝⎛⎭⎫23,34π. 13.(2012·高考课标全国卷)已知曲线C 1的参数方程是⎩⎪⎨⎪⎧x =2cos φy =3sin φ(φ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程是ρ=2.正方形ABCD的顶点都在C 2上,且A ,B ,C ,D 依逆时针次序排列,点A 的极坐标为⎝⎛⎭⎫2,π3. (1) 求点A ,B ,C ,D 的直角坐标;(2) 设P 为C 1上任意一点,求|P A | 2+|PB |2+|PC | 2+|PD |2的取值范围.解:(1)由已知可得A ⎝⎛⎭⎫2cos π3,2sin π3, B ⎝⎛⎭⎫2cos ⎝⎛⎭⎫π3+π2,2sin ⎝⎛⎭⎫π3+π2, C ⎝⎛⎭⎫2cos ⎝⎛⎭⎫π3+π,2sin ⎝⎛⎭⎫π3+π, D ⎝⎛⎭⎫2cos ⎝⎛⎭⎫π3+3π2,2sin ⎝⎛⎭⎫π3+3π2, 即A (1,3),B (-3,1),C (-1,-3),D (3,-1). (2)设P (2cos φ,3sin φ),令S =|P A |2+|PB |2+|PC |2+|PD |2,则S =16cos 2φ+36sin 2φ+16=32+20sin 2φ.因为0≤sin 2φ≤1,所以S 的取值范围是[32,52].。
湘教版高中数学选修学~知能演练轻松闯关

1.下列说法正确的是( )A .类比推理是由特殊到一般的推理B .演绎推理是由特殊到一般的推理C .归纳推理是由个别到一般的推理D .合情推理可以作为证明的步骤解析:选C.A 错:因为类比推理是特殊到特殊的推理;B 错:因为演绎推理是一般到特殊的推理;C 正确:因为归纳推理是由特殊到一般或部分到整体的推理;D 错:因为合情推理的结论不可靠,不能作为证明的步骤.2.(2012·奉节检测)“π是无限不循环小数,所以π是无理数”,以上推理的大前提是( )A .实数分为有理数和无理数B .π不是有理数C .无理数都是无限不循环小数D .有理数都是有限循环小数解析:选C.演绎推理的结论蕴涵于前提之中,本题由小前提及结论知选C.3.下面几种推理过程是演绎推理的是( )A .矩形对角线相等,正方形是矩形,所以,正方形的对角线相等B .我国地质学家李四光发现中国松辽平原和中亚西亚的地质结构类似,而中亚西亚有丰富的石油,由此,他推断松辽平原也蕴藏着丰富的石油C .由6=3+3,8=3+5,10=3+7,12=5+7,14=7+7,…,得出结论:一个偶数(大于4)可以写成两个素数的和D .由a 1=1,a n =n -1,求出S 1,S 2,S 3,猜想出数列的前n 项和S n 的表达式解析:选A.A 中“矩形的对角线相等”这是大前提,是真命题,该推理为三段论推理;B 中为类比推理;C 、D 都是归纳推理.4.(2012·大足调研)函数y =2x +5的图象是一条直线,用三段论表示为:大前提:______________________________________________________________________; 小前提:______________________________________________________________________; 结论:________________________________________________________________________. 解析:本题省略了大前提和小前提.答案:一次函数的图象是一条直线函数y =2x +5是一次函数函数y =2x +5的图象是一条直线一、选择题1.(2012·永川检测)下面几种推理过程是演绎推理的是( )A .两条直线平行,同旁内角互补,如果∠A 与∠B 是两条平行直线的同旁内角,则∠A +∠B =180°B .某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人数都超过50人C .由平面三角形的性质,推测空间四边形的性质D .在数列{a n }中,a 1=1,a n =12(a n -1+1a n -1)(n ≥2),由此归纳出{a n }的通项公式 解析:选A.大前提:两条直线平行,同旁内角互补.小前提:∠A 与∠B 是两条平行直线的同旁内角.结论:∠A +∠B =180°.2.推理过程“大前提:________,小前提:四边形ABCD 是矩形,结论:四边形ABCD 的对角线相等.”应补充的大前提是( )A .正方形的对角线相等B .矩形的对角线相等C .等腰梯形的对角线相等D .矩形的对边平行且相等解析:选B.由三段论的一般模式知应选B.3.“因为对数函数y =log a x 是增函数(大前提),而y =log 13x 是对数函数(小前提),所以y =log 13x是增函数(结论).”上面推理的错误是( )A .大前提错导致结论错B .小前提错导致结论错C .推理形式错导致结论错D .大前提和小前提都错导致结论错解析:选A.大前提是错误的,因为对数函数y =log a x (0<a <1)是减函数.4.(2012·大渡口质检)“所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数”,上述推理( )A .完全正确B .推理形式不正确C .错误,因为大小前提不一致D .错误,因为大前提错误解析:选A.大前提、小前提及推理形式都正确,所以推理也正确.5.对于任意的直线l 与平面α,在平面α内必有直线m ,使m 与l ( )A .平行B .相交C .垂直D .互为异面直线解析:选C.对于任意的直线l 与平面α,若l 在平面α内,则存在直线m ⊥l ;若l 不在平面α内,且l ⊥α,则平面α内任意一条直线都垂直于l ;若l 不在平面α内,且l 与α不垂直,则它的射影在平面α内为一条直线,在平面α内必有直线m 垂直于它的射影,则m 与l 垂直,综上所述,选C.6.设⊕是R 的一个运算,A 是R 的非空子集.若对于任意a ,b ∈A ,有a ⊕b ∈A ,则称A 对运算⊕封闭.那么下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )A .自然数集B .整数集C .有理数集D .无理数集解析:选C.A 错:因为自然数集对减法不封闭;B 错:因为整数集对除法不封闭;C 对:因为任意两个有理数的和、差、积、商都是有理数,故有理数集对加、减、乘、除法(除数不等于零)四则运算都封闭;D 错:因为无理数集对加、减、乘、除法都不封闭.二、填空题7.(2012·秀山检测)在求函数y =log 2x -2的定义域时,第一步推理中大前提是当a 有意义时,a ≥0;小前提是log 2x -2有意义;结论是________.解析:由大前提知log 2x -2≥0,解得x ≥4.答案:y =log 2x -2的定义域是[4,+∞)8.由“(a 2+a +1)x >3,得x >3a 2+a +1”的推理过程中,其大前提是________. 解析:∵a 2+a +1=(a +12)2+34>0. ∴(a 2+a +1)x >3⇒x >3a 2+a +1. 其前提依据为不等式的乘法法则:a >0,b >c ⇒ab >ac . 答案:a >0,b >c ⇒ab >ac9.已知a =5-12,函数f (x )=a x ,若实数m ,n 满足f (m )>f (n ),则m ,n 的大小关系为________.解析:∵a=5-12∈(0,1),∴函数f(x)=(5-12)x是减函数.故由f(m)>f(n)得m<n.答案:m<n三、解答题10.(2012·南开调研)规定C m x=x·(x-1)·…·(x-m+1)m×(m-1)×(m-2)×…×2×1,其中x∈R,m是正整数,求C5-15的值.解:规定C m x=x·(x-1)·…·(x-m+1)m×(m-1)×(m-2)×…×2×1,其中x∈R,m是正整数(大前提),C5-15中,-15∈R,5是正整数(小前提),∴C5-15=(-15)(-16)(-17)(-18)(-19)5×4×3×2×1=-11628(结论).11.已知{a n}是各项均为正数的等差数列.lg a1、lg a2、lg a4成等差数列,又b n=1a2n(n=1,2,…).证明:{b n}为等比数列.证明:∵lg a1、lg a2、lg a4成等差数列,∴2lg a2=lg a1+lg a4,即a22=a1a4.若{a n}的公差为d,则(a1+d)2=a1(a1+3d),a1d=d2,从而d(d-a1)=0.①若d=0,{a n}为常数列,相应{b n}也是常数列,{b n}是首项为正数,公比为1的等比数列.②若d=a1≠0,则a2n=a1+(2n-1)d=2n d,b n=1a2n=12n d.这时{b n}是首项b1=12d,公比为12的等比数列.综上,{b n}为等比数列.12.(创新题)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.求证:平面AEC⊥平面PDB.证明:∵四边形ABCD是正方形,∴AC⊥BD,∵PD⊥底面ABCD,∴PD⊥AC,∴AC⊥平面PDB,又∵AC⊂平面AEC,∴平面AEC⊥平面PDB.。
部编版高中数学高考数学选修4-4全套精品教案

中药饮片包装中的问题及管理措施摘要:中药饮片在我国传统医药中占据重要位置,是中医在治病防病中经常使用的一种中药形式。
近几年,随着人们对中医药重视程度的提高,中药饮片的销售量大幅增长,对减轻和消除患者病痛发挥了重要作用。
但目前我国中药饮片在包装方面还存在一定问题,需要进一步对中药饮片包装进行完善。
基于此,本文首先阐述了中药饮片包装存在的问题,然后提出了几条完善中药饮片包装的管理措施,希望能为提升我国中药饮片包装水平提供一些有益的参考和借鉴。
关键词:中药饮片;包装;管理措施中药饮片主要是指以中医药理论为指导,按照制剂、调剂和辨证施治的需要,经清洗、炮制、切割等多道工序处理后得到的中药材制成品。
中药饮片包装会在很大程度上影响中药的临床疗效,包装材料不适宜或包装标识不完整、不规范等会影响中药饮片的饮用质量,降低中药饮片的治疗效果[1]。
因此,研究和探讨完善中药饮片包装的管理措施具有非常重要的现实意义。
一、中药饮片包装中的问题1.包装材料和性质不相适应根据我国相关规定,生产中药饮片要选择与药品质量要求和药品性质相适应的容器和包装材料,严禁选择可能对中药饮片质量造成影响或与中药饮片性质不符的包装材料。
例如,对于一些不易发生虫蛀、霉变的中药饮片,可选用聚乙烯塑料薄膜作为内包装材料;对于那些容易发生虫蛀、霉变的中药饮片,则需选用高压尼龙聚乙烯复合薄膜作为内包装材料。
但通过对中药饮片进行检查发现,当前很多中药饮片未根据品种选择与之相适应的包装材料,甚至有些厂家不管中药饮片是否容易发生虫蛀或霉变,一律选用聚乙烯塑料薄膜作为内包装材料。
这样一来,就无法确保中药饮片在保质期内的质量。
2.标签不规范一是标签标注项目不全。
在检查中发现,部分来自GMP企业的中药饮片在品种资料中有批准文号,但在中药饮片的标签中却未标注批准文号;一些药店将用量较大的中药饮片随意拆零后自行填写标签,如麦冬、生地、杜仲、党参、薏米等,在拆零后的包装袋上仅标注中药饮片名称,而原标签上的其他内容则一律空缺,造成日后很难查找到中药饮片的生产厂家、生产批号等信息,不但容易造成中药饮片过期等问题,也难以就出现问题的中药饮片追溯厂家责任。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x=2cos φ, 4.(2016· 哈尔滨模拟)在平面直角坐标系中,曲线 C1 的参数方程为 (φ 为 y=sin φ 参数),以原点 O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线 C2 是圆心在极轴上且经 π π 过极点的圆,射线 θ= 与曲线 C2 交于点 D2, . 3 3 (1)求曲线 C1 的普通方程和曲线 C2 的直角坐标方程; π 1 (2)已知极坐标系中两点 A(ρ1,θ0),Bρ2,θ0+ ,若 A、B 都在曲线 C1 上,求 2+ 2 ρ1 1 2的值.
行胜于言
x′=2x, 1.在同一平面直角坐标系中,经过伸缩变换 后,曲线 C:x +y =36 变为 1 y ′= y 3
2 2
1
何种曲线,并求曲线的焦点坐标. 解:设圆 x2+y2=36 上任一点为 P(x,y),伸缩变换后对应的点的坐标为 P′(x′,y′), x=2x′, x′2 y′2 2 2 则 所以 4x′ +9y′ =36,即 + =1. 9 4 y=3y′, 2 2 x y 所以曲线 C 在伸缩变换后得椭圆 + =1, 9 4 其焦点坐标为(± 5,0). 2.(2015· 高考江苏卷)已知圆 C 的极坐标方程为 ρ2+ π 2 2ρsin(θ- )-4=0,求圆 C 的半径. 4 解:以极坐标系的极点为平面直角坐标系的原点 O,以极轴为 x 轴的正半轴,建立直角 坐标系 xOy. 2 2 圆 C 的极坐标方程为 ρ2+2 2ρ sin θ- cos θ-4=0, 2 2 2 化简,得 ρ +2ρsin θ-2ρcos θ-4=0. 则圆 C 的直角坐标方程为 x2+y2-2x+2y-4=0, 即(x-1)2+(y+1)2=6, 所以圆 C 的半径为 6. π 9π 3.(2016· 扬州质检)求经过极点 O(0,0),A6, ,B6 2, 三点的圆的极坐标方 2 4 程. 解:将点的极坐标化为直角坐标, 点 O,A,B 的直角坐标分别为(0,0),(0,6),(6,6), 故△OAB 是以 OB 为斜边的等腰直角三角形, 圆心为(3,3),半径为 3 2, 圆的直角坐标方程为(x-3)2+(y-3)2=18, 即 x2+y2-6x-6y=0, 将 x=ρcos θ,y=ρsin θ代入上述方程, 得 ρ2-6ρ(cos θ+sin θ)=0, π 即 ρ=6 2cosθ- . 4 4.圆 O1 和圆 O2 的极坐标方程分别为 ρ=4cos θ,ρ=-4sin θ. (1)把圆 O1 和圆 O2 的极坐标方程化为直角坐标方程; (2)求经过⊙O1,⊙O2 交点的直线的直角坐标方程. 解:(1)x=ρcos θ,y=ρsin θ, 由 ρ=4cos θ得 ρ2=4ρcos θ, 所以 x2+y2=4x, 即 x2+y2-4x=0 为⊙O1 的直角坐标方程. 同理,x2+y2+4y=0 为⊙O2 的直角坐标方程.
2 2
解:由 ρ=4sin θ,可得 x2+y2=4y, 即 x2+(y-2)2=4. 由 ρsin θ=a,可得 y=a. 设圆的圆心为 O′,y=a 与 x2+(y-2)2=4 的两交点 A,B 与 O 构成等边三角形,如图所 示. 由对称性知∠O′OB=30°,OD=a. 3 在 Rt△DOB 中,易求 DB= a, 3 3 所以 B 点的坐标为 a,a. 3 3 2 又因为 B 在 x2+y2-4y=0 上,所以 a +a2-4a=0, 3 4 2 即 a -4a=0,解得 a=0(舍去)或 a=3. 3 6.在直角坐标系 xOy 中,以 O 为极点,x 轴的正半轴为极轴建立极坐标系.曲线 C 的 π 极坐标方程为 ρcosθ- =1,M,N 分别为曲线 C 与 x 轴,y 轴的交点. 3 (1)写出曲线 C 的直角坐标方程,并求点 M,N 的极坐标; (2)设 MN 的中点为 P,求直线 OP 的极坐标方程. π 1 3 解:(1)由 ρcosθ- =1,得 ρ cos θ+ sin θ=1, 3 2 2 1 3 从而曲线 C 的直角坐标方程为 x+ y=1, 2 2 即 x+ 3y=2. θ=0 时,ρ=2,所以 M(2,0). π 2 3 2 3 π θ= 2 时,ρ= 3 ,所以 N . 3 ,2 2 3 (2)由(1)得点 M 的直角坐标为(2,0),点 N 的直角坐标为0, . 3 3 所以点 P 的直角坐标为1, , 3 2 3 π 则点 P 的极坐标为 , 3 ,6 π 所以直线 OP 的极坐标方程为 θ= ,ρ∈(-∞,+∞). 6
2
2பைடு நூலகம்
θ1= 3 ,
π
ρ =1, 1 解得 π θ1= 3 ,
设(ρ2,θ2)为点 Q 的极坐标, ρ2(sin θ2+ 3cos θ2)=5 3,
则有 π θ2= 3 ,
ρ =5, 2 解得 π θ2= 3 ,
由于 θ1=θ2,所以|PQ|=|ρ1-ρ2|=4, 所以线段 PQ 的长为 4. 3.(2016· 东北三校模拟)已知点 P 的直角坐标是(x,y).以平面直角坐标系的原点为极 坐标的极点,x 轴的正半轴为极轴,建立极坐标系.设点 P 的极坐标是(ρ,θ),点 Q 的极 坐标是(ρ,θ+θ0),其中 θ0 是常数.设点 Q 的直角坐标是(m,n). (1)用 x,y,θ0 表示 m,n; π (2)若 m,n 满足 mn=1,且 θ0= ,求点 P 的直角坐标(x,y)满足的方程. 4 x=ρcos θ, 解:(1)由题意知 y=ρsin θ, m = ρ cos ( θ + θ0), 且 n=ρsin(θ+θ0),
行胜于言
1.(2016· 唐山统一考试)已知圆 C:x +y =4,直线 l:x+y=2.以 O 为极点,x 轴的正 半轴为极轴,取相同的单位长度建立极坐标系. (1)将圆 C 和直线 l 的方程化为极坐标方程; (2)P 是 l 上的点,射线 OP 交圆 C 于点 R,又点 Q 在 OP 上且满足|OQ|· |OP|=|OR|2,当 点 P 在 l 上移动时,求点 Q 轨迹的极坐标方程. 解:(1)将 x=ρcos θ,y=ρsin θ代入圆 C 和直线 l 的直角坐标方程得其极坐标方程为 C:ρ=2,l:ρ(cos θ+sin θ)=2. (2)设 P,Q,R 的极坐标分别为(ρ1,θ),(ρ,θ),(ρ2,θ),则由|OQ|·|OP|=|OR|2, 得 ρρ1=ρ2 2. 2 又 ρ2=2,ρ1= , cos θ+sin θ 2ρ 所以 =4, cos θ+sin θ 故点 Q 轨迹的极坐标方程为 ρ=2(cos θ+sin θ)(ρ≠0). 2.(2016· 云南省师大附中适应性考试 )在直角坐标系 xOy 中,半圆 C 的参数方程为 x = 1 + cos φ , (φ 为参数,0≤φ≤π).以 O 为极点,x 轴的非负半轴为极轴建立极坐标 y=sin φ 系. (1)求 C 的极坐标方程; π (2)直线 l 的极坐标方程是 ρ(sin θ+ 3cos θ)=5 3,射线 OM:θ= 与半圆 C 的交 3 点为 O,P,与直线 l 的交点为 Q,求线段 PQ 的长. 解:(1)半圆 C 的普通方程为(x-1)2+y2=1(0≤y≤1), 又 x=ρcos θ,y=ρsin θ, π 所以半圆 C 的极坐标方程是 ρ=2cos θ,θ∈0, . 2 ρ = 2cos θ 1, 1 (2)设(ρ1,θ1)为点 P 的极坐标,则有
ρ2
x=2cos φ, 解:(1)因为 C1 的参数方程为 y=sin φ, x2 2 所以 C1 的普通方程为 +y =1. 4
π 由题意知曲线 C2 的极坐标方程为 ρ=2a· cos θ(a 为半径),将 D2, 代入,得 2= 3 1 2a× ,所以 a=2, 2 所以圆 C2 的圆心的直角坐标为(2,0),半径为 2, 所以 C2 的直角坐标方程为(x-2)2+y2=4. ρ2cos2θ 2 2 (2)曲线 C1 的极坐标方程为 +ρ sin θ=1, 4 4 即 ρ2= . 2 4sin θ+cos2θ 4 所以 ρ2 , 1= 4sin2θ0+cos2θ0 4 ρ2 2= π π 2 4sin θ0+ +cos2θ0+ 2 2 4 = 2 . sin θ0+4cos2θ0 2 2 2 2 1 1 4sin θ0+cos θ0 4cos θ0+sin θ0 5 所以 2+ 2= + = . 4 4 4 ρ1 ρ2
行胜于言 x +y -4x=0, (2)由 2 2 x +y +4y=0, x1=0, x2=2, 解得 或 y1=0 y2=-2. 即⊙O1,⊙O2 交于点(0,0)和(2,-2),过交点的直线的直角坐标方程为 y=-x. 5.(2014· 高考天津卷改编)在以 O 为极点的极坐标系中,圆ρ=4sin θ和直线 ρsin θ =a 相交于 A,B 两点.若△AOB 是等边三角形,求 a 的值.
行胜于言 m=ρcos θcos θ0-ρsin θsin θ0, 所以 n=ρsin θcos θ0+ρcos θsin θ0, m=xcos θ0-ysin θ0, 所以 n=xsin θ0+ycos θ0. 2 2 m= x- y, 2 2 (2)由(1)可知 又 mn=1, 2 2 n= x+ y, 2 2 2 2 2 2 所以 x- y x+ y=1. 2 2 2 2 x2 y2 整理得 - =1. 2 2 x2 y2 所以 - =1 即为所求方程. 2 2
