江苏省徐州市 2019最新RJ人教版 八年级数学 下册第二学期 期末考试教学质量检测监测调研 统联考真题模拟卷
2019年人教版八年级下册数学期末考试试卷及答案

第二学期期末质量监控试卷初二数学一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.在平面直角坐标系中,点(2,3)M -在A .第一象限B .第二象限C .第三象限D .第四象限 2.下列图形即是轴对称图形又是中心对称图形的是A .B .C .D .3.若一个多边形的内角和为540°,则这个多边形的边数为 A .4 B. 5 C. 6 D.74.如图,边长为1的方格纸中有一四边形ABCD (A ,B ,C ,D 四点均为格点),则该四边形的面积为A .4B .6C . 12D .24 5.用配方法解方程2470x x --=时,应变形为A .()2211x -= B .()2211x += C . ()2423x -= D .()2423x +=6.某市乘出租车需付车费y (元)与行车里程x (千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是A .1.5元B .2元C .2.12元D .2.4元 7.如图,在ABCD 中,AB=4,BC =7,∠ABC 的平分线交AD 于点E ,则DE 的长为 A .5B .4C .3D .28.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为 A .(1,3) B .(3,2) C .(0,3) D .(-3,3)9.已知:如图,折叠矩形ABCD ,使点B 落在对角线AC 上的点F 处,若BC=8,AB=6,则线段CE 的长度是A. 3B. 4C.5D.610.为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调CD BA查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是①每人乘坐地铁的月均花费最集中的区域在60—80元范围内; ②每人乘坐地铁的月均花费的平均数范围是40—60元范围内; ③每人乘坐地铁的月均花费的中位数在100—120元范围内; ④乘坐地铁的月均花费达到100元以上的人可以享受折扣. A.①④ B ③④ C ①③ D ①② 二、填空题(本题共18分,每小题3分) 11.一元二次方程022=-x x 的解为____________.12.请写出一个过一三象限且与y 轴交与点(0,1)的直线表达式 ____________。
2019新人教版八年级下册数学期末试卷及答案
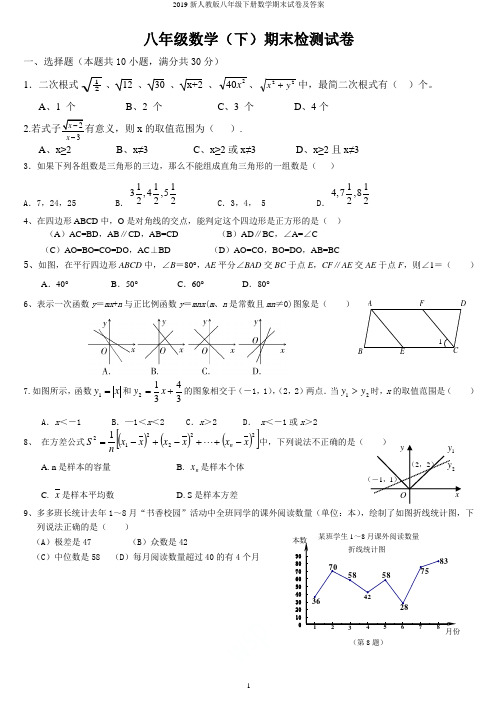
1FEDCBA(-1,1)1y (2,2)2yxyO10203040506070809012345678某班学生1~8月课外阅读数量折线统计图3670585842287583本数月份(第8题)12345678八年级数学(下)期末检测试卷一、选择题(本题共10小题,满分共30分) 1.二次根式21、12 、30 、x+2 、240x 、22y x +中,最简二次根式有( )个。
A 、1 个B 、2 个C 、3 个D 、4个 2.若式子2x -有意义,则x 的取值范围为( ).A 、x≥2B 、x≠3C 、x≥2或x≠3D 、x≥2且x≠33.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A .7,24,25B .1113,4,5222C .3,4, 5D .114,7,822 4、在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的是( )(A )AC=BD ,AB ∥CD ,AB=CD (B )AD ∥BC ,∠A=∠C (C )AO=BO=CO=DO ,AC ⊥BD (D )AO=CO ,BO=DO ,AB=BC5、如图,在平行四边形ABCD 中,∠B =80°,AE 平分∠BAD 交BC 于点E ,CF ∥AE 交AE 于点F ,则∠1=( )A .40°B .50°C .60°D .80°6、表示一次函数y =mx +n 与正比例函数y =mnx (m 、n 是常数且mn ≠0)图象是( )7.如图所示,函数x y =1和34312+=x y 的图象相交于(-1,1),(2,2)两点.当21y y >时,x 的取值范围是( )A .x <-1B .—1<x <2C .x >2D . x <-1或x >2 8、 在方差公式()()()[]2222121x x x x x x nS n -++-+-=中,下列说法不正确的是( )A. n 是样本的容量B. n x 是样本个体C. x 是样本平均数D. S 是样本方差9、多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( ) (A )极差是47(B )众数是42(C )中位数是58 (D )每月阅读数量超过40的有4个月ADOACB10、如图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为【 】A .54B .52C .53D .65二、填空题(本题共10小题,满分共30分)11.48-13-⎛⎫ ⎪ ⎪⎝⎭+)13(3--30-23-=12.边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1,S 2,则S 1+S 2的值为( )13. 平行四边形ABCD 的周长为20cm ,对角线AC 、BD 相交于点O ,若△BOC 的周长比△AOB 的周长大2cm ,则CD = cm 。
人教版2019年八年级下期末考试数学试卷及答案

第二学期期末统考 初 二 数 学一、选择题(共 24 分,每小题 3 分)下列各题均有四个选项,其中只有一个是符合题意的.1.函数 yx 2 A . x 2中自变量 x 的取值范围是B . x 2C . x 2D . x 22.五边形的内角和为A .180°B .360°C .540°D .720°3.在平面直角坐标系中,点 A (1,2)关于 x 轴对称的点的坐标是 A .(1,2) B .(1,-2) C .(-1,2) 4. 下列图形中,既是中心对称图形又是轴对称图形的是A .等边三角形B .平行四边形C .等腰梯形 5.已知 x 2 是一元二次方程 x 2+mx 8 0 的一个解,则 m 的值是D .(-1,-2) D .矩形 A . 2B . 2C .4D .2 或 46.某工厂由于管理水平提高,生产成本逐月下降. 原来每件产品的成本是 1600 元,两个月后,降至 900 元.如果产品成本的月平均降低率是 x ,那么根据题意所列方程正确的是A .1600(1x ) 900B . 900(1x ) 1600C .1600(1x )2900 D . 900(1x )216007. 10 名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm )如下表所示:甲队 乙队队员 1173 170队员 2 175 171队员 3 175 175队员 4 175 179队员 5 177 180设两队队员身高的平均数依次为 x , x ,身高的方差依次为 S2 甲, S2 乙,则下列关系中完全正确的是A . x x , S 2S 甲2乙B . x x , S 2S 甲2乙C . xx , S 甲乙2甲 S 2乙D . xx , S 甲乙2甲S 2乙8.如图,菱形 ABCD 中,AB =2,∠B =120°,点 M 是 AD 的中点,点 P 由点 A 出发,沿 A →B →C →D 作匀速运动,到达点 D 停止,则△APM 的面积 y 与点 P 经过的路程 x 之间的函数关系的图象大致是DMACyyyyP2 12 12 12 1BO1 2 3 4 5 6 x O 1 2 3 4 5 6 x O 1 2 3 4 5 6 x O1 2 3 4 5 6 xABCD甲 乙 甲 乙甲 乙二、填空题(共18分,每小题3分)A9.如图,在△ABC中,D,E分别是边AB,AC的中点,如果BC=8,那么DE=.D E10.某地未来7日最高气温走势如图所示,那么这组数据的极差为°C.B C周一周二周三周四周五周六周日A30℃32℃32℃29℃26℃25℃26℃BCD11.如图,在菱形ABCD中,AC,BD是对角线,如果∠BAC=70°,那么∠ADC等于.12.如果把代数式x2-2x+3化成(x h)2k的形式,其中h,k为常数,那么h+k 的值是.13.如图,在梯形ABCD中,AD∥BC,如果∠ABC=60º,BD平分∠ABC,且BD⊥DC,CD=4,那么梯形ABCD的周长是.14.如图,在平面直角坐标系中有一个边长为1的正方形OABC,边O A,A DOC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形ByCOBB C11,再以对角线O B1为边作第三个正方形O B B C122,……,照此规律作下去,则点B2的坐标为_________;点B2014的坐标为_________.B2B1三、解答题(共20分,每小题5分)C1C B 15.解方程:x24x 50.B3C2O A xC316.如图,将△ABC置于平面直角坐标系中,点A(-1,3),B(3,1),C(3,3).(1)请作出△ABC关于原点O的中心对称图形△A△’B’C’;(点A的对称点是点A’,点B的对称点是点B’,点C的对称点是点C’)(2)判断以A,B’,A’,B为顶点的四边形的形状,并直接写出这个四边形的周长.y4A 4321321OCB1234x 123417.已知一次函数y 12x 1的图象与x轴交于点A,与y轴交于点B.(1)求A,B两点的坐标;(2)过B点作直线B P与x轴交于点P,且△使A B P的面积为2,求点P的坐标.18.已知:如图,点E,F□是□ABCD中AB,DC边上的点,且AE=CF,联结DE,BF.求证:DE=BF.D F CA E B四、解答题(共24分,每小题6分)19.已知关于x的一元二次方程x22x 2k 40有两个不相等的实数根.(1)求k (2)若k 的取值范围;为正整数,且该方程的根都是整数,求k的值.20.为了解某校学生的身高情况,随机抽取该校若干名学生测量他们的身高,已知抽取的学生中,男生、女生的人数相同,利用所得数据绘制如下统计图表:身高分组表女生身高频数分布表男生身高频数分布直方图组别A B C D身高/cmx 155155x 160160x 165165x 170组别ABCDE频数81210c4频率a0.300.250.150.101412108642频数A B C D E身高/cmE x 170合计b 1.00请根据以上图表提供的信息,解答下列问题:(1)在女生身高频数分布表中:a=,b=,c=;(2)补全男生身高频数分布直方图;(3)已知该校共有女生400人,男生380人,请估计身高在165≤x<170之间的学生约有多少人.....21.为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?22.如图,矩形ABCD的对角线AC,BD交于点O,D E∥AC交BA的延长线于点E,点F在BC上,BF=BO,且AE=6,AD=8.(1)求BF的长;(2)求四边形OFCD的面积.EA DO五、解答题(共14分,每小题7分)BF C23.如图,在平面直角坐标系xOy中,直线l1与x轴交于点A(3,0),与y轴交于点B,且与直线l2:y43x的交点为C(a,4).(1)求直线l 的解析式;1(2)如果以点O,D,B,C 为顶点的四边形是平行四边形,直接写出点D的坐标;y4BCl2l1(3)将直线l1沿y轴向下平移3个单位长度得到直线l3,A3O x点P(m,n)为直线l2上一动点,过点P作x轴的垂线,分别与直线l,l13交于M,N.当点P在线段MN 上时,请直接写出m的取值范围...24.把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接写出结论;(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.A D A DFMNB EC E BMC图1N图2F初二数学试题答案及评分参考一、选择题(共24分,每小题3分)题号答案1D2C3B4D5A6C7B8B二、填空题(共18分,每小题3分)题号91011121314答案4740°320(-2,2)(21007,-21007)三、解答题(共20分,每小题5分)15.解方程:x24x 50.解:(x 5)(x 1)0,-------2分∴x 50或x 10.∴x 5,x 1.------- 5分1 216.解:(1)如右图:------- 3分4A321y4321OCB1234x(2)正方形;85.-------5分B‘1217.解:(1)令y=0,则x=-2;令x=0,则y=1;C ∴A 点坐标为(-2,0);B点坐标为(0,1).-------2分34A‘(2)∵△ABP的面积为2,∴12OB AP 2.-------3分又∵OB=1,∴AP=4.∴点P的坐标为(-6,0),(2,0).------- 5分18.证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.-------2分∵AE=CF,∴AB-AE=CD-CF,即EB=DF.-------3分D F C∴四边形DEBF是平行四边形.------- 4分∴DE=BF.-------5分A EB 其他证法相应给分.四、解答题(共24分,每小题6分)19.解:(1)∵方程x22x 2k 40有两个不相等的实数根,∴D=22- 4(2k-4)>0.-------2分∴k<52.-------3分(2)∵k为正整数,∴k=1,2.-------4分当k=1时,原方程为x2+2x-2=0,此方程无整数根,不合题意,舍去.-------5分当k=2时,原方程为x2+2x=0,解得,x=0,x=-212.符合题意.综上所述,k=2.-------6分20.解:(1)a=0.20,b=40,c=6,-------3分(2)如右图:-------4分141210频数(3)400创0.15+380840=60+76=136(人),864∴身高在165≤x<170之间的学生约有136人.-------6分2A B C D E身高/cm21.解:(1)当0#x180时,y=5x;-------1分当180<x?260时,y=5?180+7(x180),即y=7x-360;-------2分当x>260时,y=5创180+7(260-180)+9(x-260),即y=9x-880.’5x0x 180 ;综上所述, y7x 360 180 x 260 ;-------4 分9x 880x 260 .(2)当 x =200 时, y = 7 x - 360 = 7? 200 360 =1040(元).∴按“阶梯水价”收费,她家应缴水费 1040 元. -------6 分22.解: (1)∵四边形 ABCD 是矩形,∴∠BAD =90°,∴∠EAD =180°—∠BAD =90°. 在 △R t EAD 中,∵AE =6,AD =8,∴ DE =AE 2 + AD 2=10 .-------1 分E∵DE ∥AC ,AB ∥CD ,∴四边形 ACDE 是平行四边形. ∴AC =DE =10. -------2 分在 △R t ABC 中,∠ABC =90°,1∵OA =OC ,∴ BO = AC = 5 . -------3 分2AOD∵BF =BO ,∴BF =5. -------4 分(2)过点 O 作 OG ⊥BC 于点 G ,BGFC∵四边形 ABCD 是矩形, ∴∠BCD =90°,∴CD ⊥BC . ∴OG ∥CD .∵OB =OD ,∴BG =CG ,∴OG 是△BCD 的中位线. -------5 分 由(1)知,四边形 ACDE 是平行四边形,AE =6,∴CD =AE =6.∴OG = 1 2CD = 3 .∵AD =8,∴BC =AD =8.∴S D BCD 1 1 = 鬃BC CD = 24 , S = 鬃BF OG = 2 215 2.∴ S 四边形O FCD= S - S = D BCD D BOF 33 2. -------6 分其他证法相应给分. 五、解答题(共 14 分,每小题 7 分)23.解:(1)∵直线 l : y 2 4 3x 经过点 C (a ,4),∴ 4 3a = 4 ,∴ a = 3 .------- 1 分∴点 C (3,4).设直线 l 1的解析式为y kx b ,∵直线 l 1与 x 轴交于点 A ( 3 ,0),且经过点 C (3,4),∴ ,∴3k b 4.2 k ,3 b2.∴直线 l 1的解析式为y2 3x 2 .------- 2 分 (2)点 D 的坐标是(3,2),(3,6)或( - 3 , - 2 ).------- 5 分D BOF 3k b 0,(3)-32#x3.-------7分25.解:(1)MA=MN且MA⊥MN.(2)(1)中结论仍然成立.-------2分-------3分证明:联结DE,∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°.在△R t ADF中,∵M是DF的中点,∴MA=12DF =MD=MF.A D3∴∠1=∠3.∵N 是EF的中点,∴MN是△DEF的中位线.56∴1MN=DE2,MN∥DE.------- 4分E24B7MC∵△BEF为等腰直角三角形,∴BE=BF,∠EBF=90°.∵点E,F分别在正方形的边CB,AB的延长线上,N1∴AB+BF=CB+BE,即AF=CE.F ∴△ADF≌△CDE.------- 5分∴DF=DE,∠1=∠2.∴MA=MN,∠2=∠3.-------6分∵∠2+∠4=∠ABC=90°,∠4=∠5,∴∠3+∠5=90°,∴∠6=180°—(∠3+∠5)=90°.∴∠7=∠6=90°,MA⊥MN.-------7分其他证法相应给分.。
【强烈推荐】2019新人教版八年级下册数学期末试卷及答案

2019新人教版八年级下册数学期末试卷及答案(含答案)一、选择题(本题共10小题,满分共30分) 1.二次根式21、12 、30 、x+2 、240x 、22y x +中,最简二次根式有( )个。
A 、1 个B 、2 个C 、3 个D 、4个 2.x 的取值范围为( ).A 、x≥2B 、x≠3C 、x≥2或x≠3D 、x≥2且x≠33.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A .7,24,25B .1113,4,5222 C .3,4, 5 D .114,7,822 4、在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的是( )(A )AC=BD ,AB ∥CD ,AB=CD (B )AD ∥BC ,∠A=∠C (C )AO=BO=CO=DO ,AC ⊥BD (D )AO=CO ,BO=DO ,AB=BC5、如图,在平行四边形ABCD 中,∠B =80°,AE 平分∠BAD 交BC 于点E ,CF ∥AE 交AE 于点F ,则∠1=( )1FEDCBAA .40°B .50°C .60°D .80°6、表示一次函数y =mx +n 与正比例函数y =mnx (m 、n 是常数且mn ≠0)图象是()7.如图所示,函数x y =1和34312+=x y 的图象相交于(-1,1),(2,2)两点.当21y y >时,x 的取值范围是( )A .x <-1B .—1<x <2C .x >2D . x <-1或x >28、 在方差公式()()()[]2222121xx x x x x nS n -++-+-= 中,下列说法不正确的是( )A. n 是样本的容量B. n x 是样本个体C. x 是样本平均数D. S 是样本方差9、多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( ) (A )极差是47(B )众数是42(C )中位数是58(D )每月阅读数量超过40的有4个月10、如图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为【 】A .54B .52C .53D .65M PFE CBAA D O二、填空题(本题共10小题,满分共30分)11.48-1-⎝⎭+)13(3--30-23-=12.边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1,S 2,则S 1+S 2的值为( )13. 平行四边形ABCD 的周长为20cm ,对角线AC 、BD 相交于点O ,若△BOC 的周长比△AOB 的周长大2cm ,则CD = cm 。
新人教版2018-2019八年级下学期数学期末试卷及其答案

2018—2019学年度(下)学期期末教学质量检测八年级数学试卷参考答案考试时间:90分钟 试卷满分:100分一、选择题(每小题2分,共20分)1.D 2.B 3.A 4.B 5.C 6.C 7.B 8.D 9.C 10.A二、填空题(每小题2分,共16分)11.2x ≥-且1x ≠ 12.相等的角为对顶角 13.2cm 14.2516.12 17.x <-2 18.(2017,0) 三、解答题(19题8分,20题8分,共计16分)19. (1)解:-------------------------------------------------------------------------------------------4 (227a + 26=+. -------------------------------------------------2 当1a =时, 原式=1165652=+=+. ----------------------------4 20. 解:(1)如图1------------------------------------------------------------2(((5⎛-÷⨯ ⎝=-÷=-⨯=(2)如图2----------------------------------------------------------------4(3)如图3,连接AC ,由勾股定理得则AC 2=BC 2=10,AB 2=20---------------------------------------------------------5 ∴AC 2+BC 2=AB 2∴∠ACB=90°,-------------------------------------------------------------6 又AC=BC=,------------------------------------------------------------7 ∴∠ABC=∠BAC=45°.-------------------------------------------------------8四、解答题(21题8分,22题8分,共计16分)21.解:(1)补全条形统计图,如下图.------------------------------------------------------------------------4(2)86;92. ----------------------------------------------------------6(3)甲校:从平均分或从中位数上比较,甲校比乙校数学学业水平更好些乙校:从众数上比较,乙校比甲校数学学业水平更好些 ---------------822. (1)∵四边形ABCD 是矩形∴AD ∥BC ,----------------------1∴∠DEF =∠EFB (2)由折叠可知∠BEF =∠DEF (3)∴∠BEF =∠EFB.∴BE =BF (4)(2)∵四边形ABCD 是矩形∴∠A =90°由折叠知BE=ED,设BE=ED=x ,则AE=9-x----------------------------------------5 第22题图在Rt △ABE 中,由勾股定理得AE 2+AB 2=BE 2---------------------------------------6 ∴()22293x x -+=--------------------------------------------------------7 解得x=5∴BE=5---------------------------------------------------------------------8五、解答题(8分)23. 解:(1)由题意可得,8x +6y +5(20﹣x ﹣y )=120,---------------------------------------------------------------2 化简,得y =﹣3x+20,-------------------------------------------------------------------------------------3 即y 与x 的函数关系式为y =﹣3x+20;---------------------------------------------------4 (2)由题意可得,15×8x +14×6(﹣3x+20)+8×[120﹣8x ﹣6(﹣3x+20)]=1420,----------------6 解得,x =5,-------------------------------------------------------------------------------------7 ∴y =20﹣3×5=5,20﹣x ﹣y =10,答:加工甲、乙、丙三种型号配件的人数分别是5人、5人、10人.-------------8六、解答题(8分)24.解:(1)当40≤x ≤58时,设y 与x 的函数解析式为y =k 1x +b 1,由图象可得 第24题图,---------------------------------------------------------------------------1解得.-------------------------------------------------------------------------------2∴y=﹣2x+140.---------------------------------------------------------------------------------3当58<x≤71时,设y与x的函数解析式为y=k2x+b2,由图象得,------------------------------------------------------------------------------4解得,-----------------------------------------------------------------------------------5∴y=﹣x+82,------------------------------------------------------------------------------------6综上所述:y=;(2)设人数为a,当x=48时,y=﹣2×48+140=44,∴(48﹣40)×44=52+100a,------------------------------------------------------------7解得a=3;答:该店的员工有3人.----------------------------------------------------------------------------8七、解答题(8分) 25.(1)证明:延长EO 交AB 于H---------------------------------------------------------------------1 ∵四边形ABCD 为矩形∴CD ∥AB ,OD =OB-----------------------------------------------------------------------------2 ∴∠ODE =∠OBH ,∠OED =∠OHB ,-------------------------------------------------------3 ∴△ODE ≌△OBH (AAS )-------------------------------------------------------------------4 ∴DE =BH ,OE =OH------------------------------------------------------------------------------5 又OF ⊥OE∴EF=FH-------------------------------------------------------------------------------------------6 ∴BF -DE=BF -BH =FH=EF-----------------------------------------------------------------------7(2)八、解答题(8分)26.解:(1)令x=0,得y=4,∴B (0,4)令y=0,得x=4,∴A (4,0)-----------------------------------------------------------2 第25题图第26题图(2)设P (x ,y )y <0时,显然不成立①x <0,y >4时,∵△PBO 与△P AC 面积相等 ∴()1134()34222x y x ⨯⨯-=⨯⨯=-+-----------------------------------------------3解得x=-12,y=16∴P (-12,16)----------------------------------------------------------------------------------------4 ②当0≤x <4,0<y ≤4时∵△PBO 与△P AC 面积相等 ∴()113434222x y x ⨯⨯=⨯⨯=-+-----------------------------------------------------5 解得1216,77x y == ∴P 1216(,)77--------------------------------------------------------------------------------------------6 所以满足条件的点P 的坐标是(-12,16)或1216(,)77 (3)△PCO 周长的最小值是6---------------------------------------------------------------------8。
人教版2019年八年级下期末考试数学试卷含答案

一.选择题:(本题共32分,每小题4分)下列各题均有四个选项,其中只有一个是符合题意的,把“答B.C.D.13八年级数学试卷....题卡”上相应的字母处涂黑.1.下列图形中,是中心对称图形的是A. B. C. D.2.在平面直角坐标中,点P(-3,5)在()A.第一象限B.第二象限C.第三象限D.第四象限3.若一个多边形的内角和等于720°,则这个多边形的边数是A.8B.7C.6D.54.在一个不透明的盒子中放有2个黄色乒乓球和4个白色乒乓球,所有乒乓球除颜色外完全相同,从中随机摸出1个乒乓球,摸出白色乒乓球的概率为A.1212365.在函数y=1x-3中,自变量x的取值范围是()A.x≠3B.x≠0C.x>3D.x≠-36.正方形具有而矩形没有的性质是()A.对角线互相平分B.对边相等C.对角线相等D.每条对角线平分一组对角7.如图,函数y=a x-1的图象过点(1,2),则不等式a x-1>2的解集是A.x<1B.x>1C.x<2D.x>28.如图,矩形ABCD中,AB=1,AD=2,M是AD的中点,点P在矩形的边上,从点A出发沿A→B→C→D运动,到达点D运动终止.设△APM的面积为y,点P经过的路程为x,那么能正确表示y与x之间函数关系的图象是()D CPMA. B.A BC. D.二.填空题(本题共16分,每小题4分)9.如图,在□ABCD中,已知∠B=50°,那么∠C的度数是.A DB C10.已知一个菱形的两条对角线的长度分别为6和8,那么这个菱形的周长是.11.甲和乙一起练习射击,第一轮10枪打完后两人的成绩如图所示.通常新手的成绩不太稳定,那么根据图中的信息,估计甲和乙两人中的新手是;他们这10次射击成绩的方差的大小关系是s2甲s2“>”或“=”).乙(填“<”、12.如图所示,在平面直角坐标系中,已知点P的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…OPn(n为正整数).那么点P6的坐标是,点P2014的坐标是.三.解答题:(本题共30分)13.用指定的方法解下列方程:(每小题5分,本题共10分)x2+4x-1=0(用配方法)(2)2x2-8x+3=0(用公式法)(1)14.(本题5分)已知:如图,E、F□是ABCD对角线AC上两点,AF=CE.求证:BE∥DF.15.(本题5分)已知x2-5x=14,求代数式(x-1)(2x-1)-(x+1)2+1的值.16.(本题5分)如图,四边形ABCD中,E、F、G、H分别是AB、B D、C D、A C的中点.(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是.D G CHFA E B17.(本题5分)已知:关于错误!未找到引用源。
最新人教版数学八年级下册《期末考试卷》含答案

2019-2020学年度第二学期期末测试人教版八年级数学试题一、选择题(每小题3分,共30分)1.后面的式子中(1)13;(2)3-;(3)21x-+;(4)38;(5)213⎛⎫-⎪⎝⎭;(6)1(1)x x->;二次根式的个数有().A. 2个B. 3个C. 4个D. 5个2.对于二次根式29x+,以下说法不正确的是()A. 它是一个无理数B. 它是一个正数C. 它是最简二次根式D. 它有最小值为33.设55-的整数部分是a,小数部分是b,则-a b的值为().A. 15+ B. 15-+ C. 15-- D. 15-4.已知直角三角形两边的长为3和4,则此三角形的周长为()A. 12B. 7+7C. 12或7+7D. 以上都不对5.如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为()A.平行四边形B. 矩形C. 菱形D. 正方形6.已知平行四边形的一边长为10,则对角线的长度可能取下列数组中的().A. 4、8 B. 10、32 C. 8、10 D. 11、13 7.下列函数中,是一次函数的是().①2y x=-②2y x=-③22y x=-④2y=⑤21y x=-A. ①⑤ B. ①④⑤ C. ②③ D. ②④⑤8.若一个函数y kx b=+中,y随x的增大而增大,且0b<,则它的图象大致是()A. B. C. D.9.如图,在长方形ABCD 中,AB =2,BC =1,运点P 从点B 出发,沿路线B C D 作匀速运动,那么△ABP 的面积与点P 运动的路程之间的函数图象大致是( ).A. B. C. D. 10.如图:由火柴棒拼出的一列图形,第n 个图形是由(1)n +个等边三角形拼成的,通过观察,分析发现:第8个图形中平行四边形的个数( ).A. 16B. 18C. 20D. 22 二、填空题(每小题3分,共24分)11.当x ___________13x -12.为了解某篮球队队员身高,经调查结果如下:172cm 3人,173cm 2人,174cm 2人,175cm 3人,则该篮球队队员平均身高是__________cm .13.如图所示:分别以直角三角形ABC 三边为边向外作三个正方形,其面积分别用1S 、2S 、3S 表示,若125S =,39S =,则BC 的长为__________.14.如图,四边形ABCD 是正方形,点P 在CD 上,ADP △绕点A 顺时针旋转90︒后能够与ABP '△重合,若3AB =,1DP =,试求PP '的长是__________.15.将直线12y x =-向上平移一个单位长度得到的一次函数的解析式为_______________. 16.直线y kx b =+与x 轴、y 轴的交点分别为(1,0)-、(0,3)则这条直线的解析式为__________. 17.已知:一组数据a ,b ,c ,d ,e 的平均数是22,方差是13,那么另一组数据32a -,32b -,32c -,32d -,32e -的方差是__________.18.如图所示,平行四边形ABCD 中,点E 在边AD 上,以BE 为折痕,将ABE △向上翻折,点A 正好落在CD 上的F 处,若FDE V 的周长为8,FCB V 的周长为22,则FC 的长为__________.三、解答题(共46分)19.计算:112(348327)8-- 20.在一棵树的10米高处D 有两只猴子,其中一只猴子爬下树走到离树20米的池塘A ,另一只猴子爬到树顶C 后直接跃向池塘的A 处,如果两只猴子所经过距离相等,试问这棵树有多高.21.某中学形展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.(1)根据图示填写下表:班级平均数(分)中位数(分)众数(分)九(1)85九(2)85 100(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;(3)计算两班复赛成绩的方差.22.如图,在△ABC中,AB=AC,D是BC的中点,连接AD,在AD的延长线上取一点E,连接BE,CE.(1)求证:△ABE≌△ACE;(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.23.小聪和小明沿同一条路同时从学校出发到某超市购物,学校与超市的路程是4千米.小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达超市.图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:(1)小聪在超市购物的时间为分钟,小聪返回学校的速度为千米/分钟;(2)请你求出小明离开学校(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?的路程s(千米)与所经过的时间t(分钟)之间的函数关系式;答案与解析一、选择题(每小题3分,共30分)1.后面的式子中(1(2(3)(4(5;(61)x >;二次根式的个数有( ).A. 2个B. 3个C. 4个D. 5个 【答案】B【解析】【分析】0)a ≥的式子叫做二次根式可得答案.【详解】解:根据二次根式的定义:(1(3)(52中被开方数-3<0,不是二次根式,(4是立方根,不是二次根式,(61)x >中因1x >,故被开方数10x -<,不是二次根式;综上只有3个是二次根式;故选B.【点睛】此题主要考查了二次根式定义,关键是掌握被开方数是非负数.2. )A. 它是一个无理数B. 它是一个正数C. 它是最简二次根式D. 它有最小值为3 【答案】A【解析】分析】根据最简二次根式的定义:被开方数不含分母,被开方数不含开的尽的因数或因式,可得答案.3,当时x=0A 错误;故选A.【点睛】考查了最简二次根式,利用最简二次根式的性质是解题关键.3.设5-的整数部分是a ,小数部分是b ,则-a b 的值为( ).A. 1+B. 1-+C. 1-D. 1-【分析】只需首先对5估算出大小,从而求出其整数部分a,再进一步表示出其小数部分b,然后将其代入所求的代数式求值.【详解】解:∵4<5<9,∴2<5<3,-<-2.∴-3<5-<3.∴2<55∴a=2,-,∴b=5-5-2=35-+∴a-b=2-3+5= 15故选:B.【点睛】此题主要考查了估算无理数的大小,注意首先估算无理数的值,再根据不等式的性质进行计算.“夹逼法”是估算的一般方法,也是常用方法.4.已知直角三角形两边的长为3和4,则此三角形的周长为()A. 12B. 7+7C. 12或7+7D. 以上都不对【答案】C【解析】【详解】设Rt△ABC的第三边长为x,①当4为直角三角形的直角边时,x为斜边,由勾股定理得,x=22+=5,此时这个三角形的周长=3+4+5=12;②当4为直角三角形的斜边时,x为直角边,由勾股定34理得,x=22-=,此时这个三角形的周长=3+4+7=7+7.故选C4375.如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为()A. 平行四边形B. 矩形C. 菱形D. 正方形【分析】由题意易得四边形EFGH 是平行四边形,又因为矩形的对角线相等,可得EH=HG ,所以平行四边形EFGH 是菱形.【详解】∵HG ∥EF ∥AC ,EH ∥FG ∥BD ,HG=EF=AC ,EH=FG=BD ,∴四边形EFGH 是平行四边形,∵矩形的对角线相等,∴AC=BD ,∴EH=HG ,∴平行四边形EFGH 是菱形.故选C .【点睛】本题考查了矩形的性质及菱形的判定.注意掌握菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;②四边相等;③对角线互相垂直平分的四边形是菱形.熟练掌握矩形、菱形的性质是解题关键.6.已知平行四边形的一边长为10,则对角线的长度可能取下列数组中的( ).A. 4、8B. 10、32C. 8、10D. 11、13【答案】D【解析】【分析】 依题意画出图形,由四边形ABCD 是平行四边形,得OA=12AC ,OB=12BD ,又由AB=10,利用三角形的三边关系,即可求得答案.【详解】 解:∵四边形ABCD 是平行四边形,∴OA=12AC ,OB=12BD , ∵AB=10,对选项A ,∵AC=4,BD=8,∴OA=2,OB=4,∵OA+OB=6<10,∴不能组成三角形,故本选项错误;对选项B ,∵AC=10,BD=32,∴OA=5,OB=16,∵OA+AB=15<16,∴不能组成三角形,故本选项错误;对选项C ,∵AC=8,BD=10,∴OA=4,OB=5,∵OA+OB=9<10,∴不能组成三角形,故本选项错误;对选项D ,∵AC=11,BD=13,∴OA=5.5,OB=6.5,∵OA+OB=12>10,∴能组成三角形,故本选项正确.故选:D .【点睛】此题考查了平行四边形的性质以及三角形的三边关系.注意掌握数形结合思想的应用.特别注意实际判断中使用:满足两个较小边的和大于最大边,则可以构成三角形.7.下列函数中,是一次函数的是( ).①2y x =- ②2y x =-③22y x =- ④2y = ⑤21y x =- A. ①⑤B. ①④⑤C. ②③D. ②④⑤ 【答案】A【解析】【分析】根据一次函数的定义条件进行逐一分析即可.【详解】解:①y=-2x 是一次函数; ②2y x=-自变量x 在分母,故不是一次函数;③y=-2x 2自变量次数不为1,故不是一次函数;④y=2是常数,故不是一次函数;⑤y=2x-1是一次函数.所以一次函数是①⑤.故选:A .【点睛】本题主要考查了一次函数.解题的关键是掌握一次函数的定义,一次函数y=kx+b 的定义条件是:k 、b 为常数,k≠0,自变量次数为1.8.若一个函数y kx b =+中,y 随x 的增大而增大,且0b <,则它的图象大致是( ) A. B. C. D.【答案】B【解析】【分析】根据y 随x 的增大而增大,可以判断直线从左到右是上升的趋势,0b <说明一次函数与y 轴的交点在y 轴正半轴,综合可以得出一次函数的图像.【详解】根据y 随x 的增大而增大,可以判断直线从左到右是上升的趋势,0b <说明一次函数与y 轴的交点在y 轴正半轴,综合可以得出一次函数的图像为B故选B【点睛】本题主要考查了一次函数的图像,以及k 和b 对图像的影响,掌握一次函数的图像和性质是解题的关键.9.如图,在长方形ABCD 中,AB =2,BC =1,运点P 从点B 出发,沿路线B C D 作匀速运动,那么△ABP的面积与点P运动的路程之间的函数图象大致是().A. B. C. D.【答案】B【解析】【分析】首先判断出从点B到点C,△ABP的面积y与点P运动的路程x之间的函数关系是:y=x(0≤x≤1);然后判断出从点C到点D,△ABP的底AB的高一定,高都等于BC的长度,所以△ABP的面积一定,y与点P运动的路程x之间的函数关系是:y=1(1≤x≤3),进而判断出△ABP的面积y与点P运动的路程x之间的函数图象大致是哪一个即可.【详解】从点B到点C,△ABP的面积y与点P运动的路程x之间的函数关系是:y=x(0≤x≤1);因为从点C到点D,△ABP的面积一定:2×1÷2=1,所以y与点P运动的路程x之间的函数关系是:y=1(1≤x≤3),所以△ABP的面积y与点P运动的路程x之间的函数图象大致是:.故选B.【点睛】此题主要考查了动点问题的函数图象,考查了分类讨论思想的应用,解答此题的关键是分别判断出从点B到点C以及从点C到点D,△ABP的面积y与点P运动的路程x之间的函数关系.n 个等边三角形拼成的,通过观察,分析发现:10.如图:由火柴棒拼出的一列图形,第n个图形是由(1)第8个图形中平行四边形的个数().A. 16B. 18C. 20D. 22【答案】C【解析】【分析】根据图形易得:n=1时有1=12个平行四边形;n=2时有2=1×2个平行四边形;n=3时有4=22个平行四边形;n=4时有6=2×3个平行四边形;由此可知应分n 的奇偶,得出答案.【详解】解:∵n=1时有1=12个平行四边形;n=2时有2=1×2个平行四边形;n=3时有4=22个平行四边形;n=4时有6=2×3个平行四边形;…∴当为第2k-1(k 为正整数)个图形时,有k 2个平行四边形,当第2k (k 为正整数)个图形时,有k (k+1)个平行四边形,第8个图形中平行四边形的个数为即当k=4时代入得4×5=20个,故选C.【点睛】本题考查了图形的变化规律,通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.二、填空题(每小题3分,共24分)11.当x ___________【答案】≤13; 【解析】【分析】因为二次根式满足的条件是:含二次根号,被开方数大于或等于0,利用二次根式满足的条件进行求解.是二次根式,所以130x -≥, 所以13x ≤, 故答案为13≤. 【点睛】本题主要考查二次根式的定义,解决本题的关键是要熟练掌握二次根式的定义.12.为了解某篮球队队员身高,经调查结果如下:172cm 3人,173cm 2人,174cm 2人,175cm 3人,则该篮球队队员平均身高是__________cm .【答案】173.5.【解析】【分析】根据加权平均数的定义求解可得.【详解】解:(172×3+173×2+174×2+175×3)÷(3+2+2+3)=(516+346+348+525)÷10=1735÷10=173.5(cm )答:该篮球队队员平均身高是173.5cm .故答案为:173.5.【点睛】本题主要考查加权平均数,熟练掌握加权平均数的定义是解题的关键.13.如图所示:分别以直角三角形ABC 三边为边向外作三个正方形,其面积分别用1S 、2S 、3S 表示,若125S =,39S =,则BC 的长为__________.【答案】4.【解析】【分析】先设Rt △ABC 的三边分别为a 、b 、c ,再分别用a 、b 、c 表示S 1、S 2、S 3的值,由勾股定理即可得出S 2的值.【详解】解:设Rt △ABC 的三边分别为a 、b 、c ,∴S 1=a 2=25,S 2=b 2,S 3=c 2=9,∵△ABC 是直角三角形,∴c 2+b 2=a 2,即S 3+S 2=S 1,∴S 2=S 1-S 3=25-9=16,∴BC=4,故答案为:4.【点睛】本题考查的是勾股定理的应用及正方形的面积公式,熟知勾股定理是解答此题的关键. 14.如图,四边形ABCD 是正方形,点P 在CD 上,ADP △绕点A 顺时针旋转90︒后能够与ABP '△重合,若3AB =,1DP =,试求PP '的长是__________.【答案】5【解析】【分析】由正方形的性质得出AB=AD=3,∠ABC=∠D=∠BAD=90°,由勾股定理求出AP ,再由旋转的性质得出△ADP ≌△ABP′,得出10BAP′=∠DAP ,证出△PAP′是等腰直角三角形,得出2AP ,即可得出结果.【详解】解:∵四边形ABCD 是正方形,∴AB=AD=3,DP=1,∠ABC=∠D=∠BAD=90°,∴22223110AD DP ++==∵△ADP 旋转后能够与△ABP′重合,∴△ADP ≌△ABP′,∴10,∠BAP′=∠DAP ,∴∠PAP′=∠BAD=90°,∴△PAP′是等腰直角三角形,∴2AP=5 故答案为:5【点睛】本题考查了旋转的性质、勾股定理、全等三角形的性质、等腰直角三角形的性质;熟练掌握正方形和旋转的性质是解决问题的关键.15.将直线12y x =-向上平移一个单位长度得到的一次函数的解析式为_______________.【答案】112y x =-+ 【解析】 【详解】解:由平移的规律知,得到的一次函数的解析式为112y x =-+. 16.直线y kx b =+与x 轴、y 轴的交点分别为(1,0)-、(0,3)则这条直线的解析式为__________.【答案】y=3x+3.【解析】【分析】把(-1,0)、(0,3)代入y=kx+b 得到03k b b -+=⎧⎨=⎩,然后解方程组可. 【详解】解:根据题意得03k b b -+=⎧⎨=⎩, 解得33k b =⎧⎨=⎩, 所以直线的解析式为y=3x+3.故答案y=3x+3.【点睛】本题考查了待定系数法求一次函数的解析式:设一次函数的解析式为y=kx+b (k 、b 为常数,k≠0),然后把函数图象上两个点的坐标代入得到关于k 、b 的方程组,然后解方程组求出k 、b ,从而得到一次函数的解析式.17.已知:一组数据a ,b ,c ,d ,e 的平均数是22,方差是13,那么另一组数据32a -,32b -,32c -,32d -,32e -的方差是__________.【答案】117.【解析】【分析】根据平均数,方差的公式进行计算. 【详解】解:依题意,得X =1()5a b c d e ++++=22,∴a b c d e ++++=110,∴3a-2,3b-2,3c-2,3d-2,3e-2的平均数为'X =32323232321[]5a b c d e -+-+-+-+-()()()()()=15×(3×110-2×5)=64, ∵数据a ,b ,c ,d ,e 的方差13,S 2=15[(a-22)2+(b-22)2+(c-22)2+(d-22)2+(e-22)2]=13, ∴数据3a-2,3b-2,3c-2,3d-2,3e-2方差S′2=15[(3a-2-64)2+(3b-2-64)2+(3c-2-64)2+(3d-2-64)2+(3e-2-64)2] =15[(a-22)2+(b-22)2+(c-22)2+(d-22)2+(e-22)2]×9 =13×9=117.故答案为:117.【点睛】本题考查了平均数、方差的计算.关键是熟悉计算公式,会将所求式子变形,再整体代入. 18.如图所示,平行四边形ABCD 中,点E 在边AD 上,以BE 为折痕,将ABE △向上翻折,点A 正好落在CD 上的F 处,若FDE V 的周长为8,FCB V 的周长为22,则FC 的长为__________.【答案】7.【解析】【分析】依据△FDE 的周长为8,△FCB 的周长为22,即可得出DF+AD=8,FC+CB+AB=22,进而得到平行四边形ABCD 的周长=8+22=30,可得AB+BC=BF+BC=15,再根据△FCB 的周长=FC+CB+BF=22,即可得到CF=22-15=7.【详解】解:由折叠可得,EF=AE ,BF=AB .∵△FDE 的周长为8,△FCB 的周长为22,∴DF+AD=8,FC+CB+AB=22,∴平行四边形ABCD 的周长=8+22=30,∴AB+BC=BF+BC=15,又∵△FCB 的周长=FC+CB+BF=22,∴CF=22-15=7,故答案为:7.【点睛】本题考查了平行四边形的性质及图形的翻折问题,折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.三、解答题(共46分)19.计算:1212(3484327)8-- 【答案】3646-.【解析】【分析】首先开根号,然后再进行乘法运算,从而求解;【详解】解:原式=4(1239323)⨯--=14446108--= 3646-【点睛】此题考查学生的运算能力,注意根号的乘法,此题比较简单.20.在一棵树的10米高处D 有两只猴子,其中一只猴子爬下树走到离树20米的池塘A ,另一只猴子爬到树顶C 后直接跃向池塘的A 处,如果两只猴子所经过距离相等,试问这棵树有多高.【答案】树高为15m.【解析】【分析】设树高BC 为xm ,则可用x 分别表示出AC ,利用勾股定理可得到关于x 的方程,可求得x 的值.【详解】解:设树高BC xm ,则CD=x-10,则题意可知BD+AB=10+20=30,∴AC=30-CD=30-(x-10)=40-x ,∵△ABC 为直角三角形,∴AC 2=AB 2+BC 2,即(40-x )2=202+x 2,解得x=15,即树高为15m ,【点睛】本题主要考查勾股定理的应用,用树的高度表示出AC ,利用勾股定理得到方程是解题的关键. 21.某中学形展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.(1)根据图示填写下表: 班级平均数(分) 中位数(分) 众数(分) 九(1)85 九(2)85 100(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;(3)计算两班复赛成绩的方差.【答案】(1)九(1)的平均数为85,众数为85,九(2)班的中位数是80;(2)九(1)班成绩好些,分析见解析;(3)21S =70,22S =100【解析】【分析】(1)先根据条形统计图得出每个班5名选手的复赛成绩,然后平均数按照公式123451()x x x x x x n=++++ ,中位数和众数按照概念即可得出答案;(2)对比平均数和中位数,平均数和中位数大的成绩较好;(3)按照方差的计算公式222222123451]s x x x x x x x x x x n =-+-+-+-+-[()()()()()计算即可.【详解】解:(1)由图可知九(1)班5名选手的复赛成绩为:75、80、85、85、100,九(2)班5名选手的复赛成绩为:70、100、100、75、80,∴九(1)的平均数为(75+80+85+85+100)÷5=85, 九(1)的众数为85,把九(2)的成绩按从小到大的顺序排列为:70、75、80、100、100,∴九(2)班的中位数是80;(2)九(1)班成绩好些.因为两个班平均分相同,但九(1)班的中位数高,所以九(1)班成绩好些.(3)21S =22222(7585)(8085)(8585)(8585)(10085)5-+-+-+-+-=70 22S =22222(7085)(10085)(10085)(7585)(8085)5-+-+-+-+-=100【点睛】本题主要考查数据的统计与分析,掌握平均数,中位数,众数和方差是解题的关键.22.如图,在△ABC 中,AB=AC ,D 是BC 的中点,连接AD ,在AD 的延长线上取一点E ,连接BE ,CE .(1)求证:△ABE ≌△ACE ;(2)当AE 与AD 满足什么数量关系时,四边形ABEC 是菱形?并说明理由.【答案】(1)证明见解析(2)当AE=2AD (或AD=DE 或DE=12AE )时,四边形ABEC 是菱形 【解析】【详解】(1)证明:∵AB=AC点D 为BC 的中点∴∠BAE=∠CAE又∵AB=AC ,AE=AE∴△ABE ≌△ACE (SAS )(2)当AE=2AD (或AD=DE 或DE=12AE )时,四边形ABEC 是菱形 ∵AE=2AD ,∴AD=DE又点D 为BC 中点,∴BD=CD∴四边形ABEC 为平行四形∵AB=AC∴四边形ABEC 为菱形 23.小聪和小明沿同一条路同时从学校出发到某超市购物,学校与超市的路程是4千米.小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达超市.图中折线O ﹣A ﹣B ﹣C 和线段OD 分别表示两人离学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系,请根据图象回答下列问题:(1)小聪在超市购物的时间为 分钟,小聪返回学校的速度为 千米/分钟;(2)请你求出小明离开学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系式;(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?【答案】(1)15,415;(2)s =445t ;(3)3千米 【解析】【分析】(1)根据购物时间=离开时间﹣到达时间即可求出小聪在超市购物的时间;再根据速度=路程÷时间即可算出小聪返回学校的速度;(2)根据点的坐标利用待定系数法即可求出小明离开学校的路程s 与所经过的时间t 之间的函数关系式; (3)根据点的坐标利用待定系数法即可求出当30≤s ≤45时小聪离开学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系式,令两函数关系式相等即可得出关于t 的一元一次方程,解之即可求出t 值,再将其代入任意一函数解析式求出s 值即可.【详解】解:(1)30﹣15=15(分钟); 4÷(45﹣30)=415(千米/分钟). 故答案为:15;415. (2)设小明离开学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系式为s =mt +n , 将(0,0)、(45,4)代入s =mt +n 中,0454n m n =⎧⎨+=⎩,解得:4m 45n 0⎧=⎪⎨⎪=⎩, ∴s =445t . ∴小明离开学校的路程s 与所经过的时间t 之间的函数关系式为s =445t .(3)当30≤s ≤45时,设小聪离开学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系式为s =kt +b ,将(30,4)、(45,0)代入s =kt +b ,304450k b k b +=⎧⎨+=⎩,解得:4k 15b 12⎧=-⎪⎨⎪=⎩, ∴s =﹣415t +12. 令s =445t =﹣415t +12, 解得:t =1354, ∴s =445t =445×1354=3. 答:当小聪与小明迎面相遇时,他们离学校的路程是3千米.【点睛】本题考查了一次函数的应用以及待定系数法求一次函数解析式,解题的关键是:(1)根据数量关系列式计算;(2)根据点的坐标利用待定系数法求出函数关系式;(3)根据点的坐标利用待定系数法求出函数关系式.。
人教版2019学年八年级下数学期末试卷跟答案(共10套)

人教版2019学年八年级下数学期末试卷(一)一、选择题(每小题4分,共40分).1.下列各式中不属于分式的是()A.B.C.D.2.实验表明,人体内某种细胞的形状可近似地看作球,它的直径约为0.00000156米,则这个数用科学记数法表示为()A.0.156×10﹣5B.0.156×105C.1.56×10﹣6D.1.56×1063.在平面直角坐标系中,点P(3,4)关于y轴对称点的坐标为()A.(﹣3,4)B.(3,4)C.(3,﹣4)D.(﹣3,﹣4)4.函数中自变量x的取值范围是()A.x≠﹣1 B.x≠0 C.x=0 D.x≠15.在本学期数学期中考中,某小组8名同学的成绩如下:90、103、105、105、105、115、140、140,则这组数据的众数为()A.105 B.90 C.140 D.506.函数y=x﹣2的图象不经过()A.第一象限 B.第二象限 C.第三象限 D.第四象限7.如图,在▱ABCD中,AC与BD交于点O,下列说法正确的是()A.AC=BD B.AC⊥BD C.AO=CO D.AB=BC8.已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,则此菱形的面积为()A.48cm2B.24cm2C.18cm2D.12cm29.如图,矩形ABCD中,AC与BD交于点O,若∠AOB=60°,AB=5,则对角线AC的长为()A.5 B.7.5 C.10 D.1510.小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是()A.小亮骑自行车的平均速度是12km/hB.妈妈比小亮提前0.5小时到达姥姥家C.妈妈在距家12km处追上小亮D.9:30妈妈追上小亮二、填空题(每小题4分,共24分).11.计算:﹣=.12.将直线y=2x向下平移3个单位,得到的直线应为.13.已知反比例函数的图象经过点(2,3),则m=.14.如图,在▱ABCD中,∠B=70°,则∠D=°.15.甲、乙两人各进行10次射击比赛,平均成绩均为8环,方差分别是:S=3,S=1,则射击成绩较稳定的是(填“甲”或“乙”).16.如图1,在矩形ABCD中BC=5,动点P从点B出发,沿BC﹣CD﹣DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则DC=,y的最大值是.三、解答题(共86分).17.计算:(2﹣π)0﹣()﹣1+(﹣1)2016.18.解方程:.19.某校要在甲、乙两名学生中选拔一名参加市级歌唱比赛,对两人进行一次考核,两人的唱功、舞台形象、歌曲难度评分统计如下表所示,依次按三项得分的5﹕2﹕3确定最终成绩,”捐款活动.小明将捐款情况进行了统计,并绘制成如下的条形统计图(1)填空:该班同学捐款数额的众数是元,中位数是元;(2)该班平均每人捐款多少元?21.如图,在▱ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:四边形BFDE是平行四边形.22.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.求证:四边形OCED是菱形.23.如图,直线y1=k1x+b与反比例函数(x<0)的图象相交于点A、点B,其中点A的坐标为(﹣2,4),点B的坐标为(﹣4,m).(1)求出m,k1,k2,b的值;(2)请直接写出y1>y2时x的取值范围.24.某旅游风景区门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上超过10人的部分打b 折,设游客为x人,门票费用为y元,y与x之间的函数关系如图所示.(1)填空:a=,b=;(2)请求出:当x>10时,y与x之间的函数关系式;(3)导游小王带A旅游团到该景区旅游,付门票费用2720元(导游不需购买门票),求A 旅游团有多少人?25.如图,已知直线y=kx+b与坐标轴分别交于点A(0,8)、B(8,0),动点C从原点O 出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒.(1)直接写出直线的解析式:;(2)若E点的坐标为(﹣2,0),当△OCE的面积为5 时.①求t的值;②探索:在y轴上是否存在点P,使△PCD的面积等于△CED的面积?若存在,请求出P 点的坐标;若不存在,请说明理由.26.如图,正方形ABCD的边长为4,点P为对角线BD上一动点,点E在射线BC上.(1)填空:∠PBC=度.(2)若BE=t,连结PE、PC,则|PE+PC的最小值为,|PE﹣PC|的最大值是(用含t的代数式表示);(3)若点E 是直线AP与射线BC的交点,当△PCE为等腰三角形时,求∠PEC的度数.人教版2019学年八年级下数学期末试卷(二)一、选择题(每小题3分,共21分)每小题有四个答案,其中有且只有一个答案是正确的.请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答一律得0分.1.使分式有意义的x的取值范围为()A.x≠1 B.x≠﹣1 C.x≠0 D.x≠±12.点P(﹣1,4)关于x轴对称的点P′的坐标是()A.(﹣1,﹣4)B.(﹣1,4)C.(1,﹣4)D.(1,4)3.对角线相等且互相平分的四边形是()A.一般四边形B.平行四边形C.矩形D.菱形4.若点P(m﹣1,3)在第二象限,则m的取值范围是()A.m>1 B.m<1 C.m≥﹣1 D.m≤15.近视眼镜的度数s(度)是镜片焦距d(米)的反比例函数,其大致图象是()A.B.C.D.6.某工程队铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设x米,根据题意可列方程为()A.B.C.D.7.如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=,则折痕CE的长为()A.2 B.C.D.3二、填空题(每小题4分,共40分)在答题卡上相应题目的答题区域内作答.8.计算:=.9.已知函数y=﹣x+3,当x=时,函数值为0.10.某种流感病毒的直径是0.0000085cm,这个数据用科学记数法表示为cm.11.某中学生物兴趣小组调查了本地区几棵古树的生长年代,记录数据如下(单位:年):200,240,220,200,210.这组数据的中位数是.12.已知a+=3,则a2+的值是.13.将直线向下平移3个单位,得到直线.14.如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则AB为.15.点A(x1,y1),B(x2,y2)是反比例函数的图象上两点,若0<x1<x2,则y1、y2的大小关系是.16.已知样本x1,x2,x3,x4的平均数是,方差是S2,则样本x1+3,x2+3,x3+3,x4+3的平均数是;方差是.17.如图,在函数的图象上有点P1、P2、P3…、P n、P n,点P1的横+1坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P n、P n分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将+1图中阴影部分的面积从左至右依次记为S1、S2、S3…、S n,则S1=,S n=.(用含n的代数式表示)三、解答题(9小题,共89分)在答题卡上相应题目的答题区域内作答.18.计算:(π﹣2016)0+()﹣1﹣×|﹣3|.19.先化简,再求值:,其中x=﹣2.20.如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.21.某学校为选拔数学能力突出的学生参加中学生数学竞赛,组织了多次测试,其中甲乙两位同学成绩较为优秀,他们在六次赛前测试中的成绩(单位:分)如下表所示.如果根据这六次成绩选拔其中一人参加比赛,你认为哪一位比较合适?为什么?22.如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.(1)求∠ABD的度数;(2)求线段BE的长.23.黄商超市用2500元购进某种品牌苹果进行试销,由于销售状况良好,超市又调拨6000元资金购进该品牌苹果,但这次进货价比上次每千克少0.5元,购进苹果的数量是上次的3倍.(1)试销时该品牌苹果的进货价是每千克多少元?(2)如果超市按每千克4元的定价出售,当售出大部分后,余下600千克按五折出售完,那么超市在这两次苹果销售中共获利多少元?24.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN 交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.25.如图,已知反比例函数y=(k<0)的图象经过点,过点A作AB⊥x轴于点B,连结AO.(1)求k的值;=2S△AOC.求:(2)如图,若直线y=ax+b经过点A,与x轴相交于点C,且满足S△ABC①直线y=ax+b的表达式;②记直线y=ax+b与双曲线y=(k<0)的另一交点为D(n,﹣1),试求△AOD以及使得不等式ax+b>成立的x的取值范围.的面积S△AOD26.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E、F.(1)求:①点D的坐标;②经过点D,且与直线FC平行的直线的函数表达式;(2)直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请直接写出点M的坐标.人教版2019学年八年级下数学期末试卷(三)一、选择题:本大题共8小题,每小题4分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列各曲线中,不能表示y是x的函数的是()A. B.C. D.2.下列命题中,逆命题是真命题的是()A.直角三角形的两锐角互余B.对顶角相等C.若两直线垂直,则两直线有交点D.若x=1,则x2=13.函数y=中,自变量x的取值范围是()A.x≠0 B.x≥2 C.x>2且x≠0 D.x≥2且x≠04.2015年1月1日起,杭州市城区实行全新的阶梯水价,之前为了解某社区居民的用水情况,随机对该社区20户居民进行了调查,下表是这20户居民2014年8月份用水量的调查结果:那么关于这次用水量的调查和数据分析,下列说法错误的是()A.平均数是10(吨)B.众数是8(吨)C.中位数是10(吨)D.样本容量是20 5.如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为()A.x≥4 B.x<m C.x≥m D.x≤16.如图,E是正方形ABCD的边BC的延长线上一点,若CE=CA,AE交CD于F,则∠FAC的度数是()A.22.5° B.30°C.45°D.67.5°7.已知:|a|=3,=5,且|a+b|=a+b,则a﹣b的值为()A.2或8 B.2或﹣8 C.﹣2或8 D.﹣2或﹣88.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE= BC,成立的个数有()A.1个B.2个C.3个D.4个二、填空题:共6个小题,每小题3分,共18分.9.﹣﹣×+=.10.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于.11.直线y=﹣2x+m﹣3的图象经过x轴的正半轴,则m的取值范围为.12.如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是.13.若函数y=(a﹣3)x|a|﹣2+2a+1是一次函数,则a=.14.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是.三、解答题:共9个小题,满分70分.15.计算:(1);(2)()2﹣(3+)(3﹣).16.先化简,再求值:÷(2+),其中x=﹣1.17.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:乙校成绩统计表(1)在图①中,“80分”所在扇形的圆心角度数为;(2)请你将图②补充完整;(3)求乙校成绩的平均分;(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.18.如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.(1)根据图象,当x≥3时y为x的一次函数,请写出函数关系式;(2)某人乘坐13km,应付多少钱?(3)若某人付车费42元,出租车行驶了多少千米?19.如图,在平面直角坐标系中,已知点A(3,4),B(﹣3,0).(1)只用直尺(没有刻度)和圆规按下列要求作图.(要求:保留作图痕迹,不必写出作法)Ⅰ)AC⊥y轴,垂足为C;Ⅱ)连结AO,AB,设边AB,CO交点E.(2)在(1)作出图形后,直接判断△AOE与△BOE的面积大小关系.20.如图,在△ABC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB,若AB=20.求:△ABD的面积.21.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD 的中点,试说明四边形AECF是平行四边形.22.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.(1)求证:四边形BMDN是菱形;(2)若AB=4,AD=8,求MD的长.23.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.(1)求直线DE的函数关系式;(2)函数y=mx﹣2的图象经过点F且与x轴交于点H,求出点F的坐标和m值;(3)在(2)的条件下,求出四边形OHFG的面积.人教版2019学年八年级下数学期末试卷(四)一、精心选一选,慧眼识金.1.下列二次根式中是最简二次根式是()A.B.C. D.2.下列函数是一次函数的是()A.y=4x2﹣1 B.y=﹣C.y= D.y=3.已知▱ABCD中,∠B=4∠A,则∠D=()A.18°B.36°C.72°D.144°4.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是()A.3、4、5 B.6、8、10 C.、2、D.5、12、135.如图,在菱形ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=a,则菱形ABCD的周长为()A.16a B.12a C.8a D.4a6.学校组织领导、教师、学生、家长对教师的教学质量进行综合评分,满分为100分.张老师得分的情况如下:领导平均给分80分,教师平均给分82分,学生平均给分90分,家长评价给分84分,如果按照1:3:5:1的权进行计算,那么张老师的综合评分为()A.84分B.85分C.86分D.87分7.一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣3,0),B(0,2),当函数图象在第二象限时,自变量x的取值范围是()A.﹣3<x<0 B.x<0 C.﹣3<x<2 D.x>﹣38.如图,正方形ABCD的边长为2,动点P从C出发,在正方形的边上沿着C⇒B⇒A的方向运动(点P与A不重合).设P的运动路程为x,则下列图象中△ADP 的面积y关于x的函数关系()A.B.C.D.二、耐心填一填,一锤定音!(每小题2分,共16分)9.函数y=中自变量x的取值范围是.10.若x>1,化简=.11.一组数据101,98,99,100,102的平均数=100,方差S2=.12.如图,函数y=ax﹣1的图象过点(1,2),则不等式ax﹣1>2的解集是.13.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为.14.平行四边形ABCD的对角线AC、BD相交于点O,若AC+BD=24厘米,△OAB 的周长是18厘米,则AB=厘米.15.一个直角三角形的两边长为5cm,12cm,则这个直角三角形的第三边长为.16.如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为.三、认真算一算,又快又准!每题6分,共18分.17.计算:(﹣2)﹣.18.若a=,b=,求a2b+ab2的值.19.如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.四、细心想一想,用心做一做!每题8分,共32分.20.如图,矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E,若∠CAE=15°,求∠BOE的度数.21.八年级(1)班开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现.老师调查了全班50名学生在这次活动中做家务的时间,并将统计的时间(单位:时间)分成5组:A:0.5≤x<1,B:1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3;并制成两幅不完整的统计图(如图):请根据图中提供的信息,解答下列问题:(1)这次活动中学生做家务时间的中位数所在的组是;(2)补全频数分布直方图;(3)试估计全校3000名学生在家做家务的时间在1.5小时以上的有多少人?22.已知两条直线y1=k1x,y2=k2x﹣9交于点A(3,﹣6).(1)求k1,k2的值.(2)在平面直角坐标系中,画出两条直线的图象.(3)求这两条直线y轴围成的三角形的面积.23.如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO 上,且OE=OC.(1)求证:∠1=∠2;(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.五、你一定是生活中的智者!共10分.24.6月30日以来的强降雨造成某地洪灾.某市组织20辆汽车装运食品、药品和生活用品三种物质共100吨前往灾区.按计划20辆汽车都要装运,且每辆汽车只能装运同一种物质,且必须装满.根据下表提供的信息,解答下列问题.(1)设装运食品的车辆数为x,装运药品的车辆数为y,求y与x的函数关系式;(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么有几种车辆安排方案?请写出所用的方案.人教版2019学年八年级下数学期末试卷(五)一、选择题(每小题4分,共40分)1.化简分式,结果是()A.x﹣2 B.x+2 C.D.2.寨卡病毒是一种通过蚊虫进行传播的虫媒病毒,其直径约为0.0000021cm.将数据0.0000021用科学记数法表示为()A.2.1×10﹣7B.2.1×107C.2.1×10﹣6D.2.1×1063.下列图形中,不属于中心对称图形的是()A.等边三角形B.菱形C.矩形D.平行四边形4.如图,下列四组条件中.不能判定四边形ABCD是平行四边形的是()A.AB=DC,AD=BC B.AB∥DC,AD∥BC C.AB∥DC,AD=BCD.AB∥DC,AB=DC5.已知▱ABCD的周长为32,AB=4,则BC=()A.4 B.12 C.24 D.286.为筹备期末座谈会,班长对全班同学爱吃哪几种水果作了民意调查.根据调查数据决定最终买什么水果应参照的统计量是()A.众数B.中位数C.平均数D.方差7.为了解某小区中学生在暑期期间的学习情况,王老师随机调查了7位学生一天的学习时间,结果如下(单位:小时):3.5,3.5,5,6,4,7,6.5.这组数据的中位数是()A.6 B.6.5 C.4 D.58.如图,水以恒速(即单位时间内注入水的体积相同)注入如图的容器中,容器中水的高度h与时间t的函数关系图象可能为()A.B.C.D.9.已知函数y=2x﹣3的自变量x取值范围为1<x<5,则函数值的取值范围是()A.y<﹣2,y>2 B.y<﹣1,y>7 C.﹣2<y<2 D.﹣1<y<7 10.如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为()A.35°B.55°C.65°D.75°二、填空题(每题4分,共24分).11.若分式的值为0,则x的值等于.12.已知A(1,﹣2)与点B关于y轴对称.则点B的坐标是.13.甲、乙两人进行射击测试,每人射击10次.射击成绩的平均数都是8.5环,方差分别是:S甲2=3,S乙2=3.5.则射击成绩比较稳定的是(填“甲”或“乙“).14.在▱ABCD中,若∠B=50°,则∠C=°.15.在菱形ABCD 中,AC=3,BD=6,则菱形ABCD的面积为.16.已知函数y=2x+b经过点A(2,1),将其图象绕着A点旋转一定角度,使得旋转后的函数图象经过点B(﹣2,7).则①b=;②旋转后的直线解析式为.三、解答题(共86分).17.计算:.18.先化简,再求值:÷,其中x=﹣3.19.解分式方程:.20.如图,在平面直角坐标系中,已知一次函数y=﹣2x+6的图象与x轴交于点A,与y轴交于点B.试求出△OAB的面积.21.如图,在▱ABCD中,E,F分别在AD,BC上,且AE=CF,连结BE、DF.求证:BE=DF.22.某校八年级共有四个班,各班的人数如图1所示,人数比例如图2所示.(1)试求出该校八年级的学生总人数;(2)请补充条形统计表;(3)在一次数学考试中,1班、2班、3班、4班的平均成绩分别为92分、91分、90分、95分.试求出该校八年级学生在本次数学考试的平均分.23.如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.(1)求证:△OAE≌△OCF;(2)若OA=OD,猜想:四边形ABCD的形状,请证明你的结论.24.小聪、小明两兄弟一起从家里出发到泉港区图书馆查阅资料,已知他们家到区图书馆的路程是5千米.小聪骑自行车,小明步行,当小聪从原路回到家时,小明刚好到达区图书馆.图中折线O﹣A﹣B﹣C和线段OD分别表示两人离家的路程S(千米)与所经过的时间t (分钟)之间的函数关系,请根据图象回答下列问题:(1)填空:小聪在泉港区图书馆查阅资料的时间为分钟;(2)试求出小明离开家的路程S (千米)与所经过的时间t(分钟)之间的函数关系式;(3)探究:当小聪与小明迎面相遇时,他们离家的路程是多少千米?25.如图,在平面直角坐标系中,A(a,0)、B(0,b)是矩形OACB的两个顶点.定义:如果双曲线y=经过AC的中点D,那么双曲线y=为矩形OACB的中点双曲线.(1)若a=3,b=2,请判断y=是否为矩形OACB的中点曲线?并说明理由.(2)若y=是矩形OACB的中点双曲线,点E是矩形OACB与中点双曲线y=的另一个交点,连结OD、OE,四边形ODCE的面积S=4,试求出k的值.26.已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t.(1)求证:OE=OF.(2)在点E、F的运动过程中,连结AF.设线段AE、OE、OF、AF所形成的图形面积为S.探究:①S的大小是否会随着运动时间为t的变化而变化?若会变化,试求出S与t的函数关系式;若不会变化,请说明理由.②连结EF,当运动时间为t为何值时,△OEF的面积恰好等于的S.DE 图 1ACBD 图 2A C B人教版2019学年八年级下数学期末试卷(六)(全卷满分120分,考试时间120分钟)一、选择题:(每小题3分,共30分)1、H7N9禽流感病毒颗粒有多种形状,其中球形直径约为0.0000001 m .将0.0000001用科学记数法表示为( )A 、0.1×10-7B 、1×10-7C 、0.1×10-6D 、1×10-6 2、下列哪个点在函数3+-=x y 的图像上( ) A 、(-5,8) B 、(0.5,3) C 、(3,6) D 、(1,1)3、如果,那么等于( ) A 、3:2 B 、2:3 C 、2:5D 、3:54、某校男子篮球队12名队员的年龄如下:16、17、17、18、15、18、16、19、18、18、19、18,这些队员年龄的众数和中位数分别是 ( )A 、17、17B 、17、18C 、16、17D 、18、18 5、函数的图像经过点(1,-1),则函数的图像不经过第( )A 、一象限B 、二象限C 、三象限D 、四象限6、若分式2422---x x x 的值为零,则x 的值为( )A 、2和 、2 C 、-2 、47、如图1,在平行四边形ABCD 中,,CE 平分交AD 边于点E ,且,则AB 的长为( )、4 、3、、28、已知直线y =kx +b 经过一、二、四象限,则直线y =bx -k 的图象只能是( )32=ba ba a +xky =2-=kx y 2-B D 7=AD BCD ∠4=AE A B C 25D9、如图2,小明在作线段AB 的垂直平分线时,他是这样操作的:分别以点A 和点B 为圆心,以大于AB 的一半的长为半径画弧,两弧相交于点C 和点D ,则直线CD 就是所要作的线段AB 的垂直平分线。
人教版2019-2020学年度第二学期期末八年级数学试卷及答案

2019-2020学年度下学期期末八年级数学试卷一、选择题(共10小题, 每小题3分, 共30分)1. 二次根式2+x 在实数范围内有意义, 则x 的取值范围是( ) A. x≥-2 B.x≠0 C. x≠-2D. x >02.下图中分别给出了变量x 和y 之间的对应关系, 其中y 是x 的函数的是( )A B C D 3.下列各组数据中能作为直角三角形三边长的是() A .1、2、3B .1、2、3C .4、5、6D .3、4、54. 下列各式中,运算正确的是()A .2)2(2-=-B .1082=+C .482=⨯D .2222=+5. 甲、乙两班的学生人数相等,参加了同一次数学测试,两班的平均分都为83分,方差分别为45.22=甲s 和90.12=乙S ,那么成绩较为整齐的是()A 、甲班B 、乙班C 、两班一样整齐D 、无法确定6. 如图,已知△ABC 中,∠C=90°,AB 的垂直平分线交BC•于M ,交AB 于N ,若AC=6,MB=2MC ,则AB 为()A .26B .22C .32D .22-7. 矩形具有而菱形不一定具有的性质是()A .对角线相等B .四边相等C .对角线互相垂直D .对角线互相平分8. 第七届世界军人运动会将于2019年10月18日至27日在武汉举行。
光谷某中学开展了“助力军动会”志愿者招募活动,同学们踊跃报名参与竞选。
经选拔,最终每个班级都有同学光荣晋升为本次军运会志愿者。
下面的条形统计图描述了这些班级选拔出的志愿者人数的情况;下列说法错误的是()A.参加竞选的共有28个班级B.本次竞选共选拔出166名志愿者C.各班选拔出的志愿者人数的众数为4D.各班选拔出的志愿者人数的中位数为69.一次函数111b x k y +=和222b x k y +=中变量x 与y 的部分对应值如上表,下列结论: ①直线1y 、2y 与y 轴围成的三角形面积为100;②直线1y 、2y 互相垂直;③x >20时,1y >2y ;④方程0--2211=+b x k b x k 的解为x=25;其中正确的结论序号为()A.①③B. ①④C.①③④D.①②③④10.如图,正方形ABCD 的边长为2,点E 、F 分别为边AD 、BC 上的点,点G 、H 分别为边AB 、CD 上的点,线段GH 与EF 的夹角为45°,GH =3102.则EF =(). A .5B .3102 C .352 D .7二、填空题(共6小题, 每小题3分, 共18分)11. 化简-(-π)2=__________.12. 已知:在Rt △ABC 中,∠C=90°,∠A=30°,AC=2,则斜边AB 的长为_______. 13. 在直角坐标系中,若直线y =21x +3与直线y =-2x +a 相交于x 轴上,则直线y =-2x +a 不经过的象限是第_______象限.14. 如图:四边形ABCD 是菱形,∠ADC=100°,DH ⊥AB 交AC 于点F ,垂足为H ,则∠AFH 的度数为_________°.x… -10 0 20 … 1y … -5 5 25 … 2y …101525…班级个数 8 - 6 - 4 – 2 - 03 4 5 6 7 8 人数15. △ABC 中, AB =AC =5,S △ABC =7.5,则BC 的长为_______________.16. 定义:Min{a ,b}表示a 、b 中较小的数,一次函数y=kx+k -5的图像与函数y=Min{ -2x+11,2x-9}的图像有两个交点,则k 的取值范围是__________.三、解答题(共8题, 共72分) 17. (本题8分) 计算:(1)483316122+-(2)226324÷-)(18. (本题8分)已知直线l 1:y=kx+(k-3)与直线l 2:y=2x+b 交于点A (1,3),请求出这两条直线与x 轴所围成的三角形的面积。
2019人教版数学初二下册期末考试试题及答案

2019人教版数学初二下册期末考试一试题及答案八年级(下)期末考试数学试卷一、选择题(共10小题,每题3分,满分30分)1.若式子2存心义,则x的取值范围为()x3A.x≥2B.x≠3C.x≥2或x≠3D.x≥2且x≠32.以下各组数中,以a、b、c为边的三角形不是直角三角形的是()A.a=2,b=3,c=5B.,b=2,c=3C.a=6,b=8,c=10D.a=3,b=4,c=53.以下计算错误的选项是()A.3+22=5 2B.÷2=2C.2×3=D.2=4.设n为正整数,且n<<n+1,则n的值为()A.5 B.6 C.7 D.85.若一个等腰直角三角形的面积为8,则这个等腰三角形的直角边长为(A.22B.42C.4 D.82)6.如图,在平行四边形ABCD中,∠B=80°,AE均分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1=()A.40°B.50°C.60°D.80°7.小刚与小华本学期都参加5次数学考试(总分都为120分),数学老师想判断这两个同学的数学成绩谁更坚固,在做统计分析时,老师需要比较这两个人5次数学成绩的()A.方差B.均匀数C.众数D.中位数8.如图,已知四边形ABCD是平行四边形,以下结论中不正确的选项是()2019人教版数学初二下册期末考试一试题及答案A.当AB=BC时,平行四边形ABCD是菱形B.当AC⊥BD时,平行四边形A BCD是菱形C.当AC=BD时,平行四边形ABCD是正方形D.当∠ABC=90°时,平行四边形ABCD是矩形9.对于一次函数y=﹣2x+3,以下结论正确的选项是()A.图象过点(1,﹣1)B.图象经过一、二、三象限C.y随x的增大而增大D.当x>时,y<010.如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,抵达点D停止,则△APM的面积y与点P经过的行程x之间的函数关系的图象大概是()二、填空题(共6小题,每题4分,满分24分)11.比较大小:﹣2﹣3(填“<”或“=或”“>”)12.将正比率函数y=﹣2x的图象沿y轴向上平移5个单位,则平移后所得图象的分析式是.13.在平面直角坐标系中,A(﹣4,3),点O为坐标原点,则线段OA的长为.14.以以下图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=9,则EF的长为.2019人教版数学初二下册期末考试一试题及答案15.如,在△ABC中,∠ACB=90°,AC=6,AB=10,AB的垂直均分DE交AB于点D,交BC于点E,CE的等于.16.如,在平面直角坐系中有一个1的正方形OABC,OA,OC分在x、y上,假如以角OB作第二个正方形OBB1C1,再以角OB1作第三个正方形OB1B2C2,⋯,照此律作下去,点B6的坐.三、解答(共3小,分18分)17.(6分)算:+(2|.1)3|18.(6分)先化,再求:(1)?,此中a=1.(19.(6分)如,在平行四形ABCD中,已知AD>AB.(1)践与操作:作∠BAD的均分交BC于点E,在AD上截取AF=AB,接EF;(要求:尺作,保存作印迹,不写作法)(2)猜想并明:猜想四形ABEF的形状,并予明.四、答2019人教版数学初二下册期末考试一试题及答案20.(7分)已知:x=2+,y=2﹣.1)求代数式:x2+3xy+y2的值;2)若一个菱形的对角线的长分别是x和y,求这个菱形的面积?21.(7分)甲、乙两校参加区教育局举办的学生英语口语比赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了以下尚不圆满的统计图表.甲校成绩统计表分数7分8分9分10分人数1108(1)在如图中,“7分”所在扇形的圆心角等于°.(((((((((((2)请你将如图的统计图增补圆满.((((((((((3)经计算,乙校的均匀分是分,中位数是8分,请写出甲校的均匀分、中位数;并从均匀分和中位数的角度分析哪个学校成绩较好.(22.(7分)已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x ﹣4与x轴于D,与直线AB订交于点C.(1)求点C的坐标;(2)依据图象,写出对于x的不等式2x﹣4>kx+5的解集;(3)求△ADC的面积.2019人教版数学初二下册期末考试一试题及答案五、简答题23.(9分)某地为了激励居民节俭用水,决定推行两级收费制,即每个月用水量14吨时,不超出14吨(含14吨)时,每吨按政府补助优惠价收费;每个月超出超出部分每吨按市场调理价收费.小英家1月份用水20吨,交水费49元;2月份用水22吨,交水费56元.1)求每吨水的政府补助优惠价和市场调理价分别是多少?2)设每个月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;3)小英家3月份用水24吨,她家应交水费多少元?24.(9分)已知如图1,P为正方形ABCD的边BC上随意一点,BE⊥AP于点E,在AP 的延伸线上取点F,使EF=AE,连结BF,∠CBF的均分线交AF于点G.1)求证:BF=BC;2)求证:△BEG是等腰直角三角形;3)如图2,若正方形ABCD的边长为4,连结CG,当P点为BC的中点时,求CG的长.25.(9分)如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(﹣4,﹣4),点E是BC的中点,现将矩形折叠,折痕为EF,点F为折痕与y轴的交点,EF交x轴于G且使∠CEF=60°.(1)求证:△EFC≌△GFO;(2019人教版数学初二下册期末考试一试题及答案((2)求点D的坐标;(3)若点P(x,y)是线段EG上的一点,设△PAF的面积为s,求s与x的函数关系式并写出x的取值范围.一、选择题题号1答案D (每题2B3分,共3A30分)4C5C6B7A8C9D10B二、填空题(每题4分,共24分)11.>12.y=-2x+5..714.2.15.4.16.(8,-8).三、解答(每小6分,共18分)17.解:原式⋯⋯⋯⋯⋯4334-分3-13-243⋯⋯⋯⋯⋯6分18.解:原式2019人教版数学初二下册期末考试一试题及答案a 1 a 2 (a1)(a1) a 1a=31时 3-1原式=3+1-1 3- 3 =3⋯⋯⋯⋯⋯6分19.解:(1)如AE 就是所要求的角均分。
2019年八年级下册数学期末试卷及答案(新人教版)

初二下数学期末调研测试一、选择题(本题共10小题,满分共30分) 1.二次根式21、12 、30 、x+2 、240x 、22y x +中,最简二次根式有( )个。
A 、1 个B 、2 个C 、3 个D 、4个 2.若式子23x x --有意义,则x 的取值范围为( ).A 、x≥2B 、x≠3C 、x≥2或x≠3D 、x≥2且x≠33.如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A .7,24,25B .1113,4,5222C .3,4, 5D .114,7,822 4、在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的是( )(A )AC=BD ,AB ∥CD ,AB=CD (B )AD ∥BC ,∠A=∠C (C )AO=BO=CO=DO ,AC ⊥BD (D )AO=CO ,BO=DO ,AB=BC5、如下左图,在平行四边形ABCD 中,∠B =80°,AE 平分∠BAD 交BC 于点E ,CF ∥AE交AE 于点F ,则∠1=( )1FEDCBAA .40°B .50°C .60°D .80°6、表示一次函数y =mx +n 与正比例函数y =mnx (m 、n 是常数且mn ≠0)图象是( )7.如图所示,函数x y =1和34312+=x y 的图象相交于(-1,1),(2,2)两点.当21y y >时,x 的取值范围是( )A .x <-1B .—1<x <2C .x >2D . x <-1或x >2 8、 在方差公式()()()[]2222121x x x x x x nS n -++-+-=中,下列说法不正确的是(-1,1)1y (2,2)2yxyO(第7题)ADO( )A. n 是样本的容量B. n x 是样本个体C. x 是样本平均数D. S 是样本方差9、多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( ) (A )极差是47(B )众数是42(C )中位数是58(D )每月阅读数量超过40的有4个月10、如上右图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为【 】A .54 B .52C .53D .65二、填空题(本题共10小题,满分共30分)11.48-133-⎛⎫⎪ ⎪⎝⎭+)13(3--30 -23-= 12.边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1,S 2,则S 1+S 2的值为( )13. 平行四边形ABCD 的周长为20cm ,对角线AC 、BD 相交于点O ,若△BOC 的周长比△AOB 的周长大2cm ,则CD = cm 。
八年级数学第二学期期末试卷答案-最新学习文档

2019八年级数学第二学期期末试卷答案本文导航 1、首页2、八年级数学第二学期期末试卷答案-2:查字典数学网小编为大家整理了2019八年级数学第二学期期末试卷答案,希望对大家有帮助。
一、选择题(12小题,每题3分,共36分)1.能判定一个四边形是菱形的条件是( )(A)对角线相等且互相垂直 (B)对角线相等且互相平分(C)对角线互相垂直 (D)对角线互相垂直平分2.下列命题是假命题的是( )A.平行四边形的对边相等B.四条边都相等的四边形是菱形C.矩形的两条对角线互相垂直D.等腰梯形的两条对角线相等3.下列几组数据能作为直角三角形的三边长的是( )(A) 2,3,4 (B) 5,3,4 (C) 4,6,9 (D) 5,11,134.某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是( )A.众数是80B.中位数是75C.平均数是80D.极差是155.下列图形中,既是轴对称又是中心对称的图形是( )(A)正三角形 (B)平行四边形 (C)等腰梯形 (D)正方形6.在平面直角坐标系中,直线不经过( )(A)第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限7. 直角三角形两直角边边长分别为6cm和8cm,则连接这两条直角边中点的线段长为( )A.10cmB.3cmC.4cmD.5cm8.如图,平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别为(0,0),(5,0)、(2,3),则顶点C的坐标是( ).(A) (3,7) (B) (5,3) (C) (7,3) (D)(8,2)9.如图,将一张矩形纸片对折后再对折,然后沿着图中的虚线剪下,得到①、②两部分,将②展开后得到的平面图形是( )(A) 矩形 (B)平行四边形 (C)梯形 (D) 菱形10.如图,□ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为 ( )(A) 6cm (B) 12cm(C) 4cm (D) 8cm11.如图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是( )A.邻边不等的矩形B.等腰梯形C.有一角是锐角的菱形D.正方形12.如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )A、 B、C、 D、二、填空题(每题3分,共18分)13.若,那么 =_________14.若菱形的两条对角线长分别为6cm,8cm,则其周长为_________cm。
2019届人教版八年级下期末数学试题及答案

2019届数学人教版精品资料第二学期期末考试八年级数学试题(90分钟完成)一、选择题(每小题给出四个选项中只有一个是正确的,请把你认为正确的选项选出来,并将该选项的字母代号填入答题纸的相应表格中.)1x 的取值范围是 A.3x 2≥ B. 3x 2> C. 2x 3≥ D. 2x 3> 2.下列二次根式中,最简二次根式是3.下列命题的逆命题成立的是A .对顶角相等B .如果两个实数相等,那么它们的绝对值相等C .全等三角形的对应角相等D .两条直线平行,内错角相等4.如图,矩形ABCD 中,AB=3,AD=1,AB 在数轴上,若以点A 为圆心,对角线AC 的长为半径作弧交数轴的正半轴于M ,则点M 表示的实数为A . 2.5B .C.D.1 5.如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是A.平行四边形B. 菱形C.正方形D. 矩形6.在平面直角坐标系中,将正比例函数y=kx (k >0)的图象向上平移一个单位,那么平移后的图象不经过A.第一象限B. 第二象限C.第三象限D. 第四象限7.下列描述一次函数y=-2x+5图象性质错误的是A. y 随x 的增大而减小B. 直线经过第一、二、四象限C.直线从左到右是下降的D. 直线与x 轴交点坐标是(0,5)8.商场经理要了解哪种型号的洗衣机最畅销,在相关数据的统计量中,对商场经理来说最有意义的是A.平均数B.众数C.中位数D.方差9. 小华所在的九年级一班共有50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.65米,而小华的身高是1.66米,下列说法错误的是A .1.65米是该班学生身高的平均水平B .班上比小华高的学生人数不会超过25人C .这组身高数据的中位数不一定是1.65米D .这组身高数据的众数不一定是1.65米第4题图第10题图B D10.如图,已知ABCD 的面积为48,E 为AB 的中点,连接DE ,则△ODE 的面积为A.8B.6C.4D.3二、填空题:11.在一次学校的演讲比赛中,从演讲内容、演讲能力、演讲效果三个方面按照5:3:2计算选手的最终演讲成绩。
2019年人教版本初中八年级数学下册的期末试卷习题含答案

期末测试(时间:90分钟满分:120分)题号一二三总分合分人复分人得分一、选择题(每题3分,共30分)1.以下式子中,属于最简二次根式的是()A.12B.2C. D.7 32.?ABCD中,∠A=40°,则∠C=()A.40°B.50°C.130°D.140°3.以下计算错误的选项是()A.3+22=52 B.8÷2=2×3=6-2=24.(重庆中考)某校将举办一场“中国汉字听写大赛”,要求每班选举一名同学参加竞赛,为此,初三(1)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是96分,甲的成绩的方差是,乙的成绩的方差是,依照以上数据,以下说法正确的选项是()A.甲的成绩比乙的成绩牢固B.乙的成绩比甲的成绩牢固C.甲、乙两人的成绩相同牢固D.无法确定甲、乙的成绩谁更牢固5.以下各组数不能够作为直角三角形三边长的是(),4,5B.3,4,5 C.,,D.30,40,506.函数y=x-2的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限7.矩形、菱形、正方形都拥有的性质是()A.对角线相等B.对角线互相均分C.对角线互相垂直D.对角线均分对角8.2019年,某市发生了严重干旱,该市政府号召居民节约用水.为认识居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图.则关于这10户家庭的月用水量,以下说法错误的选项是()A.众数是6B.中位数是6C.平均数是6D.方差是49.(孝感中考)如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为()A.-1B.-5C.-4D.-310.(牡丹江中考)如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则以下结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是()A.1B.2C.3D.4二、填空题(每题4分,共24分)11.二次根式x-2有意义,则x的取值范围是.12.将正比率函数y=-2x的图象向上平移3个单位,则平移后所得图象的剖析式是.13.已知菱形的两条对角线长分别为1和4,则菱形的面积为____________.2x+y=b,x=-1,14.若已知方程组的解是则直线y=-2x+b与直线y=x-a的交点坐标是__________.x-y=a y=3.15.如图,在△MBN中,已知BM=6,BN=7,MN=10,点A,C,D分别是MB,NB,MN的中点,则四边形ABCD的周长是.16.如图,在矩形ABCD中,AC,BD订交于点O,AE均分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为____________.三、解答题(共66分)17.(8分)计算:3( 2-3)-24-|6-3|.18.(8分)如图,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,折痕为AE.若BC=10cm,AB=8cm,求EF的长.19.(8分)已知,一次函数y=kx+3的图象经过点A(1,4).求这个一次函数的剖析式;试判断点B(-1,5),C(0,3),D(2,1)可否在这个一次函数的图象上.20.(8分)如图,点D,C在BF上,AC∥DE,∠A=∠E,BD=CF.求证:AB=EF;连接AF,BE,猜想四边形ABEF的形状,并说明原由.21.(10分)某校要从小王和小李两名同学中优选一人参加全市知识竞赛,在近来的五次选拔测试中,他俩的成绩分别以下表:第1次第2次第3次第4次第5次小王60751009075小李70901008080依照上表解答以下问题:(1)完成下表:姓名平均成绩(分)中位数(分)众数(分)方差小王807575190小李在这五次测试中,成绩比较牢固的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?(3)历届竞赛表示,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加竞赛比较合适?说明你的原由.22.(12分)(潜江中考同的白杨树苗可供选择)为改进生态环境,防范水土流失,某村计划在汉江堤坡种植白杨树,其详尽销售方案以下:,现甲、乙两家林场有相甲林场购树苗数量不高出1000棵时高出1000棵的部分销售单价4元/棵元/棵乙林场购树苗数量不高出2000棵时高出2000棵的部分销售单价4元/棵元/棵设购买白杨树苗x棵,到两家林场购买所需花销分别为y甲(元),y乙(元).(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需花销为____________元,若都在乙林场购买所需花销为____________元;(2)分别求出y甲,y乙与x之间的函数关系式;若是你是该村的负责人,应入选择到哪家林场购买树苗合算,为什么?(1)23.(12分)以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和等边△ADE,连接EB,FD,交点为G.当四边形ABCD为正方形时(如图1),EB和FD的数量关系是EB=FD;当四边形ABCD为矩形时(如图2),EB和FD拥有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD可否发生变化?若是改变若是不变,请在图3中求出∠EGD的度数.,请说明原由;参照答案1.D2.A 3.A4.A)5.A6.B7.B8.D9.D10.C提示:①③④正确,②错误.11.x≥212.y=-2x+313.214.(-1,3)15.1316.75°17.原式=6-3-26-(3-6)=-6.18.由条件知AF=AD=BC=10cm,在Rt△ABF中,BF=AF2-AB2=102-82=6(cm),∴FC=BC-BF=106=4(cm).设EF=xcm,则DE=EF=x,CE=8-x,在Rt△CEF中,EF2=CE2+FC2,即x2=(8-x)2+42.解得x=5,即EF=5cm.19.(1)由题意,得k+3=4,解得k=1,∴该一次函数的剖析式是y=x+3.(2)由(1)知,一次函数的剖析式是y=x+3.当x=-1时,y=2,即点B(-1,5)不在该一次函数图象上;当x=0时,y=3,即点C(0,3)在该一次函数图象上;当x=2时,y=5,即点D(2,1)不在该一次函数图象上.20.(1)证明:∵AC∥DE,∴∠ACD=∠EDF.∵BD=CF,∴BD+DC=CF+DC,即BC=DF.又∵∠A=∠E,∴ABC≌△EFD(AAS).∴AB=EF.猜想:四边形ABEF为平行四边形,原由以下:由(1)知△ABC≌△EFD,∴∠B=∠F.∴AB∥EF.又∵AB=EF,∴四边形ABEF为平行四边形.21.(1)8480 801042(2)因为小王的方差是 190,小李的方差是104,而104<190,因此小李成绩较牢固.小王的优秀率为5×100%=40%,小李的优秀率为4×100%=80%.(3)5因为小李的成绩较小王牢固,且优秀率比小王的高,因此选小李参加竞赛比较合适.22.(1)59006000(2)y甲=4x(0≤x≤1000且x为整数),+200(x>1000且x为整数);y乙=4x(0≤x≤2000且x为整数),+800(x>2000且x为整数).(3)①当0≤x≤1000时,两家林场单价相同,因此到两林场购买所需要花销都相同;②当1000<x≤2000时,甲林场有优惠而乙林场无优惠,∴当1000<x≤2000时,到甲林场购买合算;③当x>2000时,y甲=+200,y乙=+800,y甲-y乙=+200-+800)=-600.(ⅰ)当y甲=y乙时,-600=0,解得x=3000.∴当x=3000时,到两林场购买所需要花销都相同;(ⅱ)当y甲<y乙时,-600<0,解得x<3000.∴当2000<x<000时,到甲林场购买合算;(ⅲ)当y甲>y乙时,-600>0,解得x>3000.∴当x>3000时,到乙林场购买合算.综上所述,当0≤x≤1000或x=3000时,到两林场购买所需要花销都相同;当1000<x<3000时,到甲林场购买合算;当x>3000时,到乙林场购买合算.23.(2)EB=FD.证明:∵△AFB 为等边三角形,∴AF=AB,∠FAB=60°.∵△ADE为等边三角形,∴AD=AE,∠EAD=60°.∴∴∠FAB+∠BAD=∠EAD+∠BAD,即∠FAD=∠BAE.∴△FAD≌△BAE.∴EB=FD.(3)∠EGD不发生变化.∵△ADE为等边三角形,∴∠AED=∠EDA=60°.∵△ABF,△AED均为等边三角形,AB=AF,∠FAB=60°,AE=AD,∠EAD=60°.∴∠FAD=∠BAE.∴△FAD≌△BAE.∴∠AEB=∠ADF.设∠AEB为x°,则∠ADF也为x°,于是有∠BED为(60-x)°,∠EDF为(60+x)°,∴∠EGD=180°-∠BED-∠EDF=180°-(60-x)°-(60+x)°=60°.。
2019学年人教版八年级下册期末考试数学试卷及答案

(人教版)精品数学教学资料八年级下学期期末考试数学试卷一、选择题(每小题3分,共42分)将唯一正确答案的代号字母填在下面的方格内1.(3分)若代数式在实数范围内有意义,则x的取值范围是()A.x≥2B.x>2C.x≠2D.2.(3分)(2013•莱芜)一组数据:10、5、15、5、20,则这组数据的平均数和中位数分别是()A.10,10B.10,C.11,D.11,103.(3分)下列函数(1)y=3πx;(2)y=8x﹣6;(3)y=;(4)y=﹣8x;(5)y=5x2﹣4x+1中,是一次函数的有()A.4个B.3个C.2个D.1个4.(3分)下列计算中,正确的是()A.B.C.D.5.(3分)如图,在▱ABCD中,延长CD至点E,延长AD至点F,连结EF,如果∠B=110°,那么∠E+∠F=()A.110°B.70°C.50°D.30°6.(3分)函数的自变量x的取值范围为()A.x≥2且x≠8B.x>2C.x≥2D.x≠87.(3分)下列命题中,真命题是()A.两条对角线垂直且相等的四边形是正方形B.两条对角线互相垂直的四边形是菱形C.两条对角线互相平分且相等的四边形是矩形D.同一底上两个角相等的四边形是等腰梯形8.(3分)若ab>0,mn<0,则一次函数的图象不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限9.(3分)如图,在梯形ABCD中,AB ∥DC,DE∥CB,若CD=4,△ADE周长为18,那么梯形ABCD的周长为()A.22B.26C.38D.3010.(3分)如图,菱形ABCD的周长为16,若∠BAD=60°,E是AB的中点,则点E的坐标为()A.(1,1)B.(,1)C.(1,)D.(,2)11.(3分)在下列各图象中,y不是x 函数的是()A.B.C.D.12.(3分)已知点(﹣6,y1),(8,y2)都在直线y=﹣x﹣6上,则y1,y2大小关系是()A.y>y2B.y1=y2C.y1<y2D.不能比较113.(3分)雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料米,B种布料米,可获利50元;做一套N型号的时装需用A种布料米,B种布料米,可获利润45元.当M型号的时装为多少套时,能使该厂所获利润最大()A.40B.44C.66D.8014.(3分)在某火车站托运物品时,不超过3kg的物品需付元,以后每增加1kg(不足1kg 按1kg计)需增加托运费元,则下列图象能表示出托运费y与物品重量x之间的函数关系式的是()A.B.C.D.二、填空题(共5小题,每小题3分,共15分)答案直接填在题中横线上15.(3分)如果,那么xy的值为_________ .16.(3分)一组数据0,﹣1,6,1,﹣1,这组数据的方差是_________ .17.(3分)(2008•广安)在平面直角坐标系中,将直线y=2x﹣1向上平移动4个单位长度后,所得直线的解析式为_________ .18.(3分)如图,在平面直角坐标系xOy中,直线与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交点交于点D,则点C的坐标为_________ ,点D的坐标为_________ .19.(3分)如图,在菱形ABCD中,AB=13cm,BC边上的高AH=5cm,那么对角线AC的长为_________ cm.三、解答题(共58分)20.(8分)计算(1)﹣÷(2×);(2).21.(6分)如图,在▱ABCD中,对角线AC,BD交于点O,点E,点F在BD上,且 BE=DF 连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.(1)求证:△AOE≌△COF;(2)若AC平分∠HAG,求证:四边形AGCH是菱形.22.某学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表:五项成绩素质考评得分(单位:分)班级行为规范学习成绩校运动会艺术获奖劳动卫生甲班10106107乙班108898丙班910969根据统计表中的信息解答下列问题:(1)请你补全五项成绩考评分析表中的数据:五项成绩考评比较分析表(单位:分)班级平均数众数中位数甲班10乙班8丙班9 9(2)参照表中的数据,你推荐哪个班为区级先进班集体?并说明理由;_________ (3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照按3:2:1:1:3的比确定,学生处的李老师根据这个平均成绩,绘制了一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,应推荐哪个班为市级先进班集体?23.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a 元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c 元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:设某户每月用水量x(立方米),应交水费y(元)月份用水量(m3)收费(元)9510927(1)求a,c的值;(2)当x≤6,x≥6时,分别写出y于x的函数关系式;(3)若该户11月份用水量为8立方米,求该户11月份水费是多少元?24.小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系.(1)小丽驾车的最高速度是_________ km/h;(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min时的速度;(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?25.(10分)(2013•赤峰)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.26.(12分)如图,已知点A(2,0)、B(﹣1,1),点P是直线y=﹣x+4上任意一点.(1)当点P在什么位置时,△PAB的周长最小?求出点P的坐标及周长的最小值;(2)在(1)的条件下,求出△PAB的面积.参考答案1-10、ADBDB ACBBB 11-14、CABA15、-616、17、y=2x+318、(﹣1,0);(0,)19、20、(1)(2)2+21、证明:(1)∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵BE=DF,∴OE=OF,在△AOE与△COF中,,∴△AOE≌△COF(SAS);(2)由(1)得△AOE≌△COF,∴∠OAE=∠OCF,∴AE∥CF,∵AH∥CG,∴四边形AGCH是平行四边形;∵AC平分∠HAG,∴∠HAC=∠GAC,∵AH∥CG,∴∠HAC=∠GCA,∴∠GAC=∠GCA,∴CG=AG;∴▱AGCH是菱形.22、解:(1)丙班的平均数为=(分);甲班成绩为6,7,10,10,10,中位数为10(分);乙班的众数为8分,填表如下:五项成绩考评比较分析表(单位:分)班级平均数众数中位数甲班1010乙班88丙班99(2)甲班,理由为:三个班的平均数相同,甲班的众数与中位数都高于乙班与丙班;故答案为:甲班;(3)根据题意得:丙班的平均分为9×+10×+9×+6×+9×=(分),补全条形统计图,如图所示:∵<<,∴依照这个成绩,应推荐丙班为市级先进班集体.23、解:(1)由题意5a=,解得a=;6a+(9﹣6)c=27,解得c=6.(2)依照题意,当x≤6时,y=;当x≥6时,y=6×+6×(x﹣6),y=9+6(x﹣6)=6x﹣27,(x>6)(3)将x=8代入y=6x﹣27(x>6)得y=6×8﹣27=21(元).24、解:(1)由图可知,第10min到20min之间的速度最高,为60km/h;(2)设y=kx+b(k≠0),∵函数图象经过点(20,60),(30,24),∴,解得,所以,y与x的关系式为y=﹣x+132,当x=22时,y=﹣×22+132=h;(3)行驶的总路程=×(12+0)×+×(12+60)×+60×+×(60+24)×+×(24+48)×+48×+×(48+0)×,=+3+10+7+3+8+2,=,∵汽车每行驶100km耗油10L,25、(1)证明:∵直角△ABC中,∠C=90°﹣∠A=30°.∴AB=AC=×60=30cm.∵CD=4t,AE=2t,又∵在直角△CDF中,∠C=30°,∴DF=CD=2t,∴DF=AE;解:(2)∵DF∥AB,DF=AE,∴四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,即当t=10时,▱AEFD是菱形;(3)当t=时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).理由如下:当∠EDF=90°时,DE∥BC.∴∠ADE=∠C=30°∴AD=2AE即60﹣4t=4t解得:t=∴t=时,∠EDF=90°.当∠DEF=90°时,DE⊥EF,∵四边形AEFD是平行四边形,∴AD∥EF,∴DE⊥AD,∴△ADE是直角三角形,∠ADE=90°,∵∠A=60°,∴∠DEA=30°,∴AD=AE,AD=AC﹣CD=60﹣4t,AE=DF=CD=2t,∴60﹣4t=t,解得t=12.综上所述,当t=时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°)∴小丽驾车从甲地到乙地共耗油:×=升.26、解:(1)作出点A关于直线y=﹣x+4的对称点C,连结BC交直线于点P,∴PA=PC,AD=CD,则PB+PA=PB+PC=BC,由直线y=﹣x+4得与x轴上的交点D为(4,0)、与y轴的交点为E为(0,4),∴OD=OE=4,则∠ODE=45°,则∠ADC=90°,∴AD=CD=2,∴点C的坐标是(4,2),设直线BC的解析式为y=kx+b,则有,解得:k=,b=,即直线BC的解析式为:y=x+.由方程组得:,即P的坐标是(,),由勾股定理得BC=、AB=,∴△PAB的周长是.(2)由直线BC的解析式y=x+得:点F的坐标是(﹣6,0),∴S△PAB=S△PAF﹣S△BAF=×AE×(﹣1)=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年江苏省徐州市第二学期期末考试
八年级数学试题
卷首语:亲爱的同学,快乐的一学期已经结束了,你的数学学习一定有很大 收获!来检测一下自己吧,请你认真审题,精心作答,细心检查。
相信你能取得好成绩!
(提醒:本卷共6页,满分为140分,考试时间为90分钟;答案全部涂、写在答题卡上,
写在本卷上无效.)、
一、选择题(每小题3分,共24分) 1.下列成语描述的事件为随机事件的是 A .守株待兔 B .缘木求鱼 C .水中捞月 D .水涨船高 2.下列图形中,是轴对称图形,但不是中心对称图形的是
3.下列调查方式较为合理的是
A.了解某班学生的身高,采用抽样的方式
B .调查某晶牌电脑的使用寿命,采用普查的方式 C.调查骆马湖的水质情况,采用抽样的方式
D.调查全国初中学生的业余爱好,采用普查的方式 4.下列分式中,与
x
y
3 相等的是 A ·2
2
3x y B .262x xy C .—x y 3--:-y ; D ·26x xy
5.下列运算正确的是 A.2+3=5
B .22—2=2
C ·)3()2(-⨯-=)2(-×)3(-
D .6÷3=3
6.为了解我市八年级学生的视力状况,从中随机抽取500名学生的视力状况进行分析,
此项调查的样本为 A .500 B .被抽取的500名学生 C .被抽取500名学生的视力状况 D .我市八年级学生的视力状况
7.若A(x l ,y 1)、B(x 2,y 2)都在函数y =
x
2018
的图像上,且x l <O <x 2,则 A .y 1<y 2 B .y 1=y 2 C .y 1>y 2 D ·y 1==- y 2 8.从一副扑克牌中任意抽取1张,下列事件: ①抽到“K ”;②抽到“黑桃”;③抽到“大王”;④抽到“黑色的”. 其中,发生可能性最大的事件是 A .① B .② C .③ D .④
八年级数学试题第1页(共6页)
二、填空题(每小题4分,共32分) 9.当m =________,分式
1
1
-+m m 的值为零. 10.若x -2有意义,则x 的取值范围是__________·
11.若□ABCD 的周长为20,且AC =5,则△ABC 的周长为__________· 12.若n 48是正整数,则n 可取到的最小正整数为_________·
13.如图,矩形ABCD 的对角线AC 、BD 相交于点O ,DE ∥AC ,CE ∥BD ,若BD =5,
则四边形DOCE 的周长为__________· 14.如图,若正比例函数y =﹣2x 与反比例函数y =
x
k
的图像相交于A (m ,2),B 两点. 则不等式﹣2x >
x
k
的解集为__________·
(第13题) (第14题) (第15题)
15.如图,△OAC 和+△BAD 都是等腰直角三角形,∠ACO =∠ADB =90°,反比例函数
y =
x
k
的图像经过点凡若OA2-AB2=12,则k =___________· 16.下图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
下面三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的 概率是0.616;
②随着实验次数的增加, “钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618; ③再次用计算机模拟实验,当投掷次数为1000时, “钉尖向上”的概率一定是0.620. 其中,不合理的是___________(填序号).
八年级数学试题第2页(共6页)
三、解答题(共84分) 17. (本题10分)计算:
(1)12—3
3
1
+∣3—2∣; (2)(3—2)2
—3×12.
18.(本题10分)
(1)计算: (m +2—
25-m )·m m --34
2; (2)解方程: 21-x =x
x
--21一3.
19.(本题9分)某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平
均每天的课外阅读时间/(单位:min),然后利用所得数据绘制成如下不完整的统计图 表.
课外阅读时间频数分布表 课外阅读时间频数分布直方图
(第19题)
根据图表中提供的信息,回答下列问题:
(1)a=__________,b=___________;
(2)将频数分布直方图补充完整;
(3)若该校共1 000名学生,估计有多少学生平均每天的课外阅读时间不少于50min?
八年级数学试题第3页(共6页)
20.(本题6分)如图,在方格纸中,,5~ABC为格点三角形.
(1)画出△ABC绕点C顺时针旋转后的格点△A1B1C,使得点P在△A1B1C的内部;
(2)在(1)的条件下,若∠ACB=n°,则∠A1CB=__________°(用含n的代数式表示).
(第20题)
21. (本题10分)在□ABCD中,BE⊥CD于点E,点F在AB 上,且AF=CE,连接DF.
(1)求证:四边形BEDF是矩形;
(2)连接CF,若CF平分∠BCD,且CE=3,BE=4,求矩形BEDF的面积.
(第21题)
22.(本题9分) “书香校园”活动中,某校同时购买了甲、乙两种图书,已知两种图书的购书款均为360元,甲种图书的单价比乙种图书低50%,甲种图书比乙种图书多4本. 甲、乙两种图书的单价分别为多少元?
八年级数学试题第4页(共6页)
23.(本题10分)一辆汽车通过某段公路时,行驶时间t(h)与行驶速度v(km/h)之间成反比例
函数关系,t =
v
k
,其图像为图中一段曲线,端点为A (35,1.2),B (m ,0.5). (1)求k 和m 的值
(2)若该路段限速60km /h ,则汽车通过该路段至少需要多少时间?
(第23题)
24. (本题10分)已知:如图,在正方形ABCD 中,点E 、F 、G 分别在AB 、AD 、CD 上,
AB =6,AE =2,DG >AE ,BF =EG ,BF 与EG 交于点P . (1)求证:BF ⊥EG;
(2)连接DP ,则DP 的最小值为___________·
(第24题)
八年级数学试题第5页(共6页)
25.(本题10分)探索函数y =x +(x >0)的图像和性质.
已知正比例函数y=x 与反比例函数y =x
1
在第一象限内的图像如图所示.若P 为函数 y =x+
x
1
(其中x >0)图像上任意一点,过P 作PC 垂直于x 轴且与已知函数的图像、 x 轴分别交于点A 、B 、C ,则PC =x +x
1
=AC +BC ,从而发现下述结论:
“点P 可以看作点A 沿竖直方向向上平移BC 个长度单位(PA =BC)而得到”.
(第25题)
(1)根据该结论,在图中作出函数y =x +x
1
>0)图像上的一些点,并画出该函数 的图像.
(2)观察图像,写出函数y =x +x
1
(x >0)两条件不同类型的性质.
八年级数学试题第6页(共6页)。
