最大流最小割

合集下载

第6讲最大流最小费用

第六讲最大流，最小费用
1. 网络、流、割 2. 最大流Ford-Fulkerson算法 3. 最大流最小费用问题 4. Busacker-Growan迭代算法
下回
停
一、网络、流、割
网络N就是规定了源和汇，并且每条边都赋予了非负整数权的赋权有向图D，其中此有向图D 称为网络N的基础有向图。定义：若
这里所介绍的求最大流最小费用的算法是迭代法，是由Busacker和Gowan在1961年提出的。主要步骤如下：
算法步骤：
【Busacker-Grown迭代法】
见word文档
第六讲习题
1. 求图中的最大流
17
23 56 43 13 18 23
28 14
23
2.求图中所示网络的最小费用最大流， (b,c)中b表示容量，c表示费用
定义：对于网络N=(V,A,C),称定义在弧集A上的函数f为网络N上的流；对于弧a,f(a)称为弧a上的流量，若a=(Vi,Vj),f(a)也可以记作f(Vi,Vj)或者fij; 对于顶点v,记f+(v)为点v流出的流量，f-(v)为点v 流入的流量。可行流：每个点的流量都小于等于容量，且流出的流量等于流入的流量，则称为可行流；最大流：可行流的最大值称为最大流。
1. D=(V,E)是一个有向图；
2. c是E上的正整数函数(容量函数)，c(e)代表边e 的容量；
3. 记X为发点集(源)，Y为收点集(汇)，V-X-Y称为中间点集。有向图D可记做(V,E,c,X,Y)
注意：根据网络的定义，对于任意一个有多个收、发点的网络，可通过简单的方法转换为只有一个发点和一个收点的网络。
定理： N中的流f是最大流当且仅当N不包含f可增路。最大流最小割定理：在任何网络中，最大流的值等于最小割的容量。

最小割定理

最小割定理最小割定理，也称最大流最小割定理，是数学界最经典的定理之一。

它可以用来证明在网络模型（Network Model）中的流量分配问题。

它能够很好的描述一个网络的分配，有助于解决许多流量路由领域的应用问题。

最小割定理的定义最小割定理指：设G=(V,E)为一个有向图，其中V为结点集，E 为边集，有向图中每条边e均有一个容量c(e)>0，对给定的源结点s 和汇结点t，它指出：对于给定的源点s和汇点t之间的所有有向路径中，最小割（Minimum Cut）的容量等于最大流（Maximum Flow）的容量。

这就是最小割定理的定义。

最小割定理的原理最小割定理的原理是建立在最大流的基础上的。

最大流的定义是指：给定一个图G=(V,E)，以及一个源结点s和汇结点t，最大流就（1）是从源结点s到汇结点t的最大流量F。

最小割定理有两个假设：在网络中，最大流和最小割之间存在着一种紧密的联系；（2）有一种算法可以在有限的时间内解决最大流的问题，并且解的有效性一定被保证。

事实上，最小割定理的证明是基于上述两个假设的。

首先，通过分析图的构造可以发现，对于任意的有向图G=(V,E)，其最大流最多只能达到最小割的容量，而这就是最小割定理的第一个假设。

其次，可以证明，有一种算法可以求出有限时间内的最大流，这也是最小割定理的第二个假设。

最小割定理的应用最小割定理在现实生活中有许多应用，举例来讲，在网络的路由选择过程中，最小割定理可以有效的帮助我们找出最有效的路径，从而提高网络的运行性能。

此外，最小割定理还可以用来优化网络资源分配问题，有助于我们更有效的使用网络资源。

最后，最小割定理还可以帮助我们分析众多复杂系统当中的关系，为有效的解决各种问题提供良好的理论基础。

结论最小割定理是一个重要的数学定理，可以说是数学界的一颗明珠。

它的重要性不言而喻，被广泛的应用在各种网络领域的应用中，帮助我们更有效的分配网络资源，提高网络的运行性能，以及分析各种复杂系统的关系等等。

MATLAB中的网络流与最大流最小割问题求解方法

MATLAB中的网络流与最大流最小割问题求解方法随着社会信息化的不断发展，网络已经成为了人们日常生活中不可或缺的一部分。

而网络的流量管理对于网络的高效运行至关重要。

在网络流领域中，最大流最小割问题是一种经典且重要的问题，它在图论和算法设计领域都具有广泛的应用。

在本文中，我们将介绍MATLAB中的网络流与最大流最小割问题求解方法。

一、网络流与最大流最小割问题简介网络流问题是指在网络中有一定容量限制的边上，如何使得网络中的流量达到最大的问题。

最大流最小割问题则是网络流问题的一个特殊情况，其中要求找到一个最小割，使得割后网络中的流量达到最大。

通常情况下，网络流问题常常以有向图的形式表示，每条边上都被赋予了一个容量，并存在一个源点和一个汇点。

二、MATLAB中的网络流包在MATLAB中，有许多优秀的网络流包可以用来求解网络流与最大流最小割问题。

其中，最为常用的是Network Flow Toolbox和Combinatorial Optimization Toolbox。

这两个包提供了一系列的函数和算法，可以帮助我们解决各种类型的网络流问题。

三、网络流与最大流最小割问题的建模与求解在使用MATLAB解决网络流与最大流最小割问题之前，首先我们需要进行问题的建模。

通常情况下，我们需要确定图的结构、边的容量和源点与汇点的位置。

在建模完成后，我们可以使用MATLAB中的网络流包提供的函数进行求解。

1. 使用Network Flow Toolbox求解网络流问题Network Flow Toolbox是MATLAB中一个常用的网络流包，它提供了一系列函数用于求解网络流与最大流最小割问题。

其中最常用的函数是maxflow函数，它可以用来计算网络中的最大流。

首先，我们需要使用网络流对象来表示图结构。

在建立网络流对象后，我们可以使用addnode函数向图中添加节点，使用addedge函数向图中添加边。

同时，我们可以使用setcaps函数来指定边的容量。

最大流最小割定理

做实验 2和3
1
1
2
2 5 t 9 3
最大净收益：(2+5+9) – ( 2+3+4 )= 16 – 最大流 9 = 7
实验仪器和实验的输出：构造图时要重新编号
6 s 3 2 4 3
仪器：1-3中b[i]=-1的点。
1
1
2
2 5 t 9 3
割边：如果存在弧<i,j>，满足：i∈S,b[i]>=0, j∈T,b[j]= -1, 那么弧<i,j>是一条割边
净收益=所有实验收入-相应实验方案割的容量
EjT
p C p p C
j k j j Ik T j 1 EjS Ik T m m j 1 EjS Ik T j 1
m
k
pj ( pj Ck ) pj cut ( S , T )
如做实验E2：需要仪器I2 和I3，与t组成集合T。 S与不做的实验E1和没用的仪器I1组成集合S。构成割：CUT(S,T) 净收益： E2:25-（6+7）=12 同理 : E1：10-（5+6）= -1 E1+E2：（10+25）-（5+6+7）=17
仪器 5 6 7 I3 I1 I2 实验
∞ ∞
∞ ∞
E1
10 t
S
E2
25
6 s 3 2 4 3
1
1
2
2 5 t 9 3
=(2+5+9)-9-(6+3)=(2+5+9)-(9+6+3)
做实验1：净收益：2-6=-4 =(2+5+9)-(5+9)-6=(2+5+9)-(5+9+6)

教程：最大流-最小割定理

割 1 2 3 4
正 6 5 5 5
逆 1 0 0 0
4
2
4
33
4
5
3
4
s1
6
21
1
3
4
2
5t
定理一：定理一：如果f是网络中的一个流，CUT（S,T）是任意一个割，如果f是网络中的一个流，CUT（S,T）是任意一个割，那的值等于正向割边的流量与负向割边的流量之差。么f的值等于正向割边的流量与负向割边的流量之差。
证明：设X和Y是网络中的两个顶点集合，用f（X,Y）表示从X 中的一个顶点指向Y的一个顶点的所有弧（弧尾在X中，弧头在Y中：X Y）的流量和. 只需证明：f=f(S,T)-f(T,S) 即可。
下列结论成立：下列结论成立：如果X∩Y= 那么：如果X∩Y= ∅ ，那么： f(X,(Y1∪Y2))=f(X,Y1)+f(X,Y2) f((X1∪X2),Y)=f(X1,Y)+f(X2,Y) 根据网络流的特点：根据网络流的特点：如果V既不是源点也不是汇点，那么：如果V既不是源点也不是汇点，那么： f({V},S∪T)f({V},S∪T)-f(S∪T,{V})=0; 任何一个点，流入的与流出的量相等。任何一个点，流入的与流出的量相等。如果V是源，那么：如果V是源，那么： f({V},S∪T)f({V},S∪T)-f(S∪T,{V})=f 对于S中的所有点V都有上述关系式，相加得到：对于S中的所有点V都有上述关系式，相加得到： f(S,S∪T)f(S,S∪T)-f(S∪T,S)=f
网络流之二
最大流最小割定理
一、割的有关概念和定量
1、割的定义：、割的定义：
CUT）是网络中顶点的一个划分，割（CUT）是网络中顶点的一个划分，它把网络中的所有顶点划分成两个顶点集合S 其中源点s∈S 汇点t∈T 记为CUT S,T）。 s∈S， t∈T。 CUT（两个顶点集合S和T，其中源点s∈S，汇点t∈T。记为CUT（S,T）。如右图：源点：s=1；汇点：t=5。如右图：源点：s=1；汇点：t=5。框外是容量，框内是流量框外是容量，

网络流应用练习题解析实际问题的网络流与最大流最小割定理

网络流应用练习题解析实际问题的网络流与最大流最小割定理网络流问题是图论中重要的研究领域之一，它在许多实际问题的建模和解决中起着重要作用。

其中，最大流最小割定理是网络流问题中的重要定理，它提供了求解最大流问题的有效方法。

本文将通过解析一些实际问题的网络流应用练习题，来深入探讨网络流与最大流最小割定理。

1. 垃圾分类问题假设有一个城市，有三个垃圾处理站A、B、C，以及六个垃圾源头节点S1、S2、S3、T1、T2、T3。

现在需要将这些垃圾源头节点分配到垃圾处理站，每个垃圾源头节点只能被分配到一个垃圾处理站，且每个垃圾处理站的容量是有限的。

我们的目标是使得分配到同一个垃圾处理站的垃圾源头节点之间的运输流量最小。

解决这个问题可以通过网络流建模。

首先，将每个垃圾源头节点S1、S2、S3连接到源点节点S，并设置边的容量为1，表示每个垃圾源头节点只能分配到一个垃圾处理站。

然后，将垃圾处理站A、B、C连接到汇点节点T，并设置边的容量为各垃圾处理站的容量限制。

通过最大流最小割定理，我们可以求解出最小的割，从而得到最小的运输流量，即分配到同一个垃圾处理站的垃圾源头节点之间的运输流量最小的方案。

2. 电网规划问题假设一个城市需要建设一张电网来满足居民和工业的用电需求。

城市中共有N个节点，其中有一个节点表示电厂，另一个节点表示消费者。

每个节点之间需要建设输电线路，每条线路都有一个最大输送电流的限制。

解决这个问题可以通过网络流建模。

首先，将电厂节点连接到源点节点S，并设置边的容量为电厂的最大发电能力。

然后，将消费者节点连接到汇点节点T，并设置边的容量为消费者的用电需求。

接下来，对于每对节点i和节点j之间需要建设的输电线路，将节点i连接到节点j，并设置边的容量为线路的最大输送电流限制。

通过最大流最小割定理，我们可以求解出最小的割，从而得到电网规划方案中的最大输送电流。

综上所述，网络流与最大流最小割定理在解决实际问题时具有广泛的应用。

最大流最小割

Min｛（）, , ｝=min｛6,9,8｝=6
给标号（6）：表明从第二个圈出来最近的一站是，总长度是6。
给（，）划成粗线。
划第三个圈。
表明：圈内的点已完成考察。
4）现已走出第三个圈，向奔。有四条路可走，最优路线在何方？即：
Min｛ ,（）, , ｝=min｛9,8,10,13｝=8
给标号（8）：表明从第三个圈出来后最近的一站是，总长度是8。
Min｛（）, ｝=｛4,6｝=4
给标号（4）：表明走出后走向的最短路目前看是，最优距离是4。
给（，）划成粗线。
划第二个圈。
现已完成第二个圈内的路已考察完毕，或者说，已走出包含，的第二个圈。
3）出了第二个圈，接着往下走，有三条路可走：（，），（，），（，）。那条路最近？记三条路长度为，，，即求：
3．最大匹配问题：
M表示G中所有的匹配集，即M=｛M|M为G的匹配集｝，|M|表示M的边数，若存在M0使任意的M∈M，|M0|≥|M|，则称M0是G的最大匹配。
即：
M0= ｛|M| | M G｝
注：G中最大匹配方案可能不唯一。
饱和点：M中任意边的端点称为（关于M的）饱和点，G中其他顶点称为非饱和点。
1）寻找可增广链：
a)先给标号（∆，+∞），其中∆意思是流入的结点，现没有，纯属一个符号。+∞表示的流出量。因它上面没有结点来控制它，故设为+∞.
b)接着检查与相邻接的点，，。已饱和，流量不可再增。再检查，可调整量为4-2=2，可提供量+∞，取调整量
= min｛4-2,+∞｝=2
给标号（+ ，2），其中+ 表示的所调整量2来自，且为正向流（向前流）。

最大流最小割算法概念

最大流最小割算法概念
最大流最小割算法是一种用于解决网络流问题的经典算法。

网络流问题可以用一个有向图来表示，其中每条边都有一个容量限制，该限制表示该边上能够通过的最大流量。

寻找最大流最小割即寻找从源节点到汇节点的最大流量以及割边的最小容量。

最大流最小割算法的核心思想是通过不断寻找增广路径来增加流量，直到无法找到增广路径为止。

增广路径是指从源节点到汇节点的一条路径，且该路径上的边的剩余容量均大于0。

当无法再找到增广路径时，找到的流即为最大流。

最小割是指将网络图分为两部分的一组割边，使得从源节点到汇节点的路径上的边的总容量最小。

最小割的容量等于最大流的容量。

因此，最大流和最小割问题是等价的。

最大流最小割算法的具体实现可以使用Ford-Fulkerson算法或者Edmonds-Karp算法等。

这些算法基于广度优先搜索或深度优先搜索来搜索增广路径，并通过调整流量来进行流的更新。

这些算法的时间复杂度通常为O(E * V^2)，其中E是边的数目，V是节点的数目。

网络流基础-最大流最小割定理

⽹络流基础-最⼤流最⼩割定理
最⼤流最⼩割定理，指⽹络流的最⼤流等于其最⼩割。

最⼤流指符合三个性质的前提下，从S到T能流过的最⼤流量。

最⼩割指符合割的定义，最⼩的割容量。

求最⼤流：
不断寻找增⼴路，计算能增加的最⼩流量，然后增加。

找到⼀条增光路，最多能流过2，则：
找到第⼆条路径：
最后还剩a-c-e⼀条，则可计算出最⼤流量为4。

但遇到以下情况，且第⼀条路径为a-b-c-d时，就不⾏了：
此时需要增加反向路径，即当减去增⼴路时，反向加上减去的流量，提供后悔的选择：
这样，当考虑a-c-b-d时，可以对冲掉b-c的流量。

证明：
定理⼀：对于任⼀割和任⼀流，流量等于正向割边流量减去反向割边流量。

即f = f c+ - f c-，其中c+代表正向割边流量。

推论：任⼀割容量必定⼤于等于任⼀流量，由于：C+ > f c+ > f c+ - f c- > f。

则如果存在某流量和某割，则此流量必定为最⼤流，此割必定为最⼩割。

当我们计算出最⼤流时，不妨思考下此时的残留⽹络：
此时残留⽹络不存在增⼴路，即不存在⼀条能从S到T的路径。

此时残留⽹络中，我们把S能到达的节点记为s'集，能到达T的节点记为t’集，则s'和t'构成割集。

在残留⽹络中，流量指容量为0的边（满流），⽽这些边⼜是割边，所以流量和等于割的容量和。

⽐如对于：
其⼀个残留⽹络为：
其中两条虚线边为满流的边，也是割边。

最大流最小割定理应用

最大流最小割定理应用嘿，朋友！想象一下这样一个场景，在一个繁忙的物流中心，货物像潮水一样涌来涌去。

工人们忙得不可开交，运输车辆来来往往，而负责调度的小李正抓耳挠腮。

这物流中心就好比一个复杂的网络，货物的运输路径就是其中的管道。

而最大流最小割定理，就在这看似混乱的场景中，发挥着神奇的作用。

小李看着眼前的货物堆积如山，心里那叫一个着急。

他不停地自言自语：“这可咋办呀？怎么才能让货物最快最有效地运输出去呢？” 一旁的老张走过来说：“小李啊，别愁啦，咱们得用用那个最大流最小割定理。

”小李一脸懵：“啥是最大流最小割定理？能救咱们这热锅上的蚂蚁？”老张笑了笑：“这你就不懂了吧！就好比水流，咱们要让水从一个地方流到另一个地方，得找到最大的流量和最小的阻碍，这最大流就是能通过的最多货物量，最小割就是那些关键的阻碍点。

”小李似懂非懂地点点头，开始跟着老张一起研究。

他们把物流中心的各个环节都仔细分析，找出那些容易造成堵塞的地方，就像找到了水流中的狭窄河道。

比如说，有个装卸区，每次只能处理有限的货物，这就是一个“瓶颈”。

还有运输路线中，有一段路经常堵车，这也是个大问题。

他们把这些问题一一梳理清楚，就好像在疏通一条条被堵住的水管。

“哎呀，原来如此！”小李恍然大悟，“这就像是给迷宫找到了出口！”老张也笑着说：“对呀，咱们只要解决了这些关键的阻碍，就能让货物像欢快的小溪一样顺畅流动啦！”经过一番努力，物流中心的效率大大提高，货物不再堆积，客户的满意度也直线上升。

你看，最大流最小割定理是不是很神奇？它可不只是在物流领域有用哦。

咱们生活中很多事情都能类比过来。

比如说，你每天安排学习时间，想要在有限的时间里学到最多的知识，这是不是也得找到那个“最大流”和“最小割”？再比如，城市的交通规划，要让车辆尽可能畅通无阻，不也得考虑这些道理吗？所以说啊，最大流最小割定理的应用简直无处不在，只要我们善于发现和运用，就能让很多复杂的问题变得简单清晰，让生活更加高效有序！。

网路的最大流和最小截

s (1,0)
(1,0) (3,0) t
(5,0) 3 (2,0) 5 (2,0)
• 福特-富克森定理：网路的最大流等于最小截集容量
1
6.4.3 确定网路最大流的标号法
• 从任一个初始可行流出发，如 0 流 • 基本算法：找一条从 s 到 t 点的增广链(augmenting path) • 若在当前可行流下找不到增广链，则已得到最大流 • 增广链中与 s 到 t 方向一致的弧称为前向弧，反之后向弧
上增广流；缺点是每次增广后要改变弧的费用，且出现负权值费用的弧 • 基于可行弧集的最大流算法：从 0 费用弧集开始应用最大流算法，然后根据计算信息提高费用的限界P，使可行弧集增大，再应用最大流算法，直至所有弧都进入可行弧集。这种算法是一种主-对偶规划的解法。使用这种方法的还有运输问题、匹配问题
5
最大流最小截集的标号法举例
(9,9)
(14,14) 1 s (15,10)
3
(6,5)
(16,15)
(3,1)
2 (12,10)
(13,12) 6 5
(6,3)
(5,5)
4
(4,4)
(7,5)
(22,22)
t
(19,11)
最小截集
(14,14)
1
(s+,) s (15,12)
(16,15)
(s+,3)(3,1)
10
广链；到第二步
3
最大流最小截的标号法步骤第二步：增广过程
1、对增广链中的前向弧，令 f=f+q(t)，q(t) 为节点 t 的标记值 2、对增广链中的后向弧，令 f=fq(t)
3、非增广链上的所有支路流量保持不变

异侧差最大值原理

异侧差最大值原理异侧差最大值原理也称作最小割定理，它是网络流理论当中的重要定理之一。

该原理指出，对于一个网络图中的任意源点和汇点，其最小割容量等于源点到汇点流量的最大值。

要理解异侧差最大值原理，首先需要了解最小割和最大流的概念。

最小割是指将图中的节点分成两个集合，使得每个集合中都至少包含一个端点，并且边的权值之和最小。

最大流是指在网络graph 中找到从源点s 到汇点t 的最大容量，即从s 到t 的最大流量。

换言之，最小割和最大流都是计算网络中某个容量的最大或最小值。

最小割和最大流的关系便是异侧差最大值原理的核心。

该原理的证明可以从以下两个方面进行考虑。

第一，我们可以证明任何流量为F 的路径必然被一个容量为F 的最小割截断。

因此，最大流一定小于等于最小割的容量。

这个证明思路就是利用反证法，假设存在一个F 流量的路径没有被最小割截断，则该路径的容量大于最小割，这与最小割是一个最小值的定义相矛盾。

第二，我们还可以证明存在一种最小割切断的方法与最大流相等。

这个证明思路是利用贪心算法的思想，在最小割中从源点开始不断向外扩展，直到遇到汇点为止。

此时，这个分割之所以是最小割，是因为再往外扩展无法更小，同时它也等于最大流量。

因此，综合上述两个证明，我们可以得到异侧差最大值原理的结论：网络图的任意两个节点的最小割容量等于这两个节点的最大流量。

换言之，任何一个网络可以通过割成两个子网络来计算最小割，而可以通过从源点及汇点之间流动的最大流量来计算两个子网络相互通信的最大容量。

总的来说，异侧差最大值原理在网络流理论和算法中是一个重要的基础定理，它帮助我们理解了网络最大容量和最小割之间的关系，并且提供了一种方法来计算复杂网络的最大容量。

在实际应用中，可以利用它来解决一系列问题，如最大带宽问题、最短路径问题、网络游戏中的网络连接问题等。

最大流-最小割问题

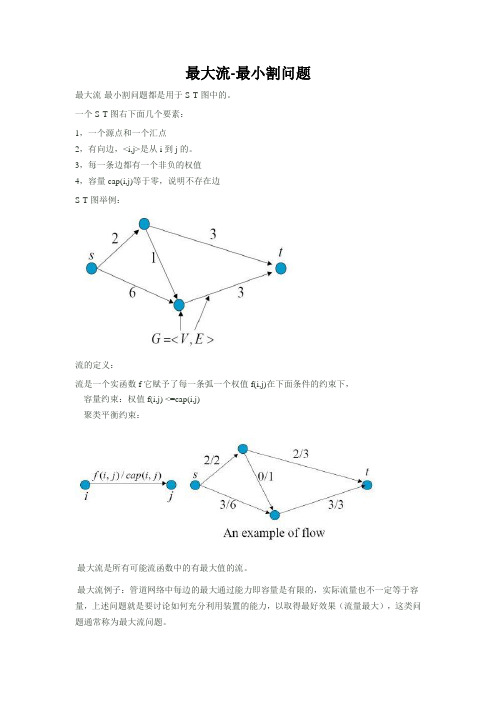
最大流-最小割问题
最大流-最小割问题都是用于S-T图中的。

一个S-T图右下面几个要素：
1，一个源点和一个汇点
2，有向边，<i,j>是从i到j的。

3，每一条边都有一个非负的权值
4，容量cap(i,j)等于零，说明不存在边
S-T图举例：
流的定义：
流是一个实函数f它赋予了每一条弧一个权值f(i,j)在下面条件的约束下，
---容量约束：权值f(i,j) <=cap(i,j)
---聚类平衡约束：
最大流是所有可能流函数中的有最大值的流。

最大流例子：管道网络中每边的最大通过能力即容量是有限的，实际流量也不一定等于容量，上述问题就是要讨论如何充分利用装置的能力，以取得最好效果（流量最大），这类问题通常称为最大流问题。

S-T割定义：
1，一个割是节点集合V的一个分割，分成了两个子集S和T. 2,当s属于S,v属于V时，这个割就是s-t切割
如图：
最小割的定义：
最小割是S-T切割中所有可能的S-T切割的能量最小的割。

最大流和最小割的关系：最大流<=最小割。

计算方法：。

最大流最小割定理

最⼤流最⼩割定理先来理解⼏个概念割在原先能够流通的⽹络中移除的边集，使得⽹络⽆法流通最⼩割所有的割中边权和最⼩的割即为最⼩割可以想象⼀下，Kido为了⾃给⾃⾜给⾃⼰建了超多供⽔管道（kido能进⾏光合作⽤），形成了⼀个⽹络，然后容量越⼤的管道防护设施越好，但是总有⼈想渴死Kido就想炸掉管道，但是贫乏的恐怖分⼦既想渴死kido⼜想节约成本，那么最节约成本的破坏管道的⽅案即为最⼩割最⼤流最⼩割定理在任何的⽹络中，最⼤流的值等于最⼩割的容量具体的证明分三部分1.任意⼀个流都⼩于等于任意⼀个割这个很好理解⾃来⽔公司随便给你家通点⽔，构成⼀个流恐怖分⼦随便砍⼏⼑砍出⼀个割由于容量限制，每⼀根的被砍的⽔管⼦流出的⽔流量都⼩于管⼦的容量每⼀根被砍的⽔管的⽔本来都要到你家的，现在流到外⾯加起来得到的流量还是等于原来的流管⼦的容量加起来就是割，所以流⼩于等于割由于上⾯的流和割都是任意构造的，所以任意⼀个流⼩于任意⼀个割2.构造出⼀个流等于⼀个割当达到最⼤流时，根据增⼴路定理残留⽹络中s到t已经没有通路了，否则还能继续增⼴我们把s能到的的点集设为S,不能到的点集为T构造出⼀个割集C[S,T],S到T的边必然满流否则就能继续增⼴这些满流边的流量和就是当前的流即最⼤流把这些满流边作为割，就构造出了⼀个和最⼤流相等的割相当于在残量⽹络中，源点能到达的结点的各个边的容量和为最⼤流所以如果我们要求⼀个最⼩割的边集，我们只要跑⼀编最⼤流，然后在残量⽹络中找正向边残量为0的边，那么这条边肯定在最⼩割⾥⾯，这样就可以得到⼀组最⼩割的边集3.最⼤流等于最⼩割设相等的流和割分别为Fm和Cm则因为任意⼀个流⼩于等于任意⼀个割任意F≤Fm=Cm≤任意C定理说明完成，证明如下：对于⼀个⽹络流图G=(V,E) G=(V,E)G=(V,E)，其中有源点s和汇点t，那么下⾯三个条件是等价的：1.流f是图G的最⼤流2.残留⽹络Gf不存在增⼴路3.对于G的某⼀个割(S,T)，此时f=C(S,T)⾸先证明1 => 2：我们利⽤反证法，假设流f是图G的最⼤流，但是残留⽹络中还存在有增⼴路p，其流量为fp。

最大流最小割定理

最大流最小割默认分类2010-06-20 15:39:10 阅读293 评论0 字号：大中小订阅最大流问题最大流问题是一类极为广泛的问题。

不仅在交通运输网络中有人流、车流、货物流、供水网络中有水流、金融系统中有现金流、通讯网络中信息流……等。

五十年代，Ford(福特)、Fulkerson(富克逊)建立的“网络流理论”，是网络应用的重要组成部分。

网络与流的概念对于有向图D=(V,A)，如果V中有一发点vs（亦称源还有一收点（亦称为汇）记为vt其余均为中间点，且对A中的每条弧均有权W(vi,vj)?0（简记为Wij，并称为弧容量），则称这样的赋权有向图D为容量网络，记为D=(V,A,W)。

通过D中弧(vi,vj)的物流量fij，称为弧(vi,vj)的流量。

所有弧上流量的集合f={fij}称为该网络D的一个流。

最大流最小截量定理：任一网络D中，最大流的流量=最小截集的截量。

最大流算法的邻接阵实现1. 最大流最小割定理介绍：把一个流网络的顶点集划分成两个集合S和T，使得源点s ∈S且汇点t ∈T，割(S,T)的容量C(S,T) =∑Cuv, 其中u∈S且v∈T。

从直观上看，截集(S,T)是从源点s到汇点t的必经之路，如果该路堵塞则流从s无法到达t。

于是我们可以得到下面的定理：最大流最小割定理：任意一个流网络的最大流量等于该网络的最小的割的容量。

这个定理的证明这里就不给出了，可以参考图论方面的资料。

2. 求最大流的Edmonds-Karp算法简介：若给定一个可行流F=(Fij)，我们把网络中使Fij=Cij的弧称为饱和弧，Fij<Cij的弧称为未饱和弧。

如果流网络中从i到j没有弧，我们添加一条从i到j且容量Cij=0的弧，这样整个流网络变成一个完全图。

如果从i到j有流量Fij，则从j到i的流量定义为Fji = -Fij 。

考虑一条从源点s出发到汇点t的路径p，如果对于每一段弧(i,j)属于p都有Fij < Cij，即每一条属于p的弧都是未饱和弧，则我们可以向这条路径上压入更多的流，使得其中的一条弧达到饱和。

运输网络最大流最小割定理

运输网络：最大流最小割定理定义设N = (V, E)是一个无环连通有向图。

则称N为一个网络或者运输网络，若N满足如下条件：a) 存在惟一的一个顶点a V，并且id (a)等于0。

顶点a称为源点。

b) 存在惟一的一个顶点z V，称为汇点，其中od (z)等于0。

c) 因为图N是带权图，所以存在从E到非负整数集合的一个函数，它赋给每条边e = (v ,w) E一个容量，记为c(e)= c(v, w)。

例定义如果N = (V, E)是一个运输网络，则从E到非负整数集合的函数f称为N的流(flow)，若a) 对于每条边e E，都有f (e) c(e)；并且b) 对于不同于源点a或者汇点z的每个v V，都有∑∈V w v w f),(=∑∈V w w v f),(。

（如果不存在边(v, w)，则f (v, w) = 0。

）例定义设f是一个运输网络N = (V, E)的一个流。

a) 称网络中的一条边e为饱和的，若f (e) = c(e)。

当f (e) < c(e)时，则称这条边为不饱和的。

b) 如果a是N的源点，则val(f) =∑∈V v v a f),(称为流的值(value of flow)。

c) 最大流具有最大可能值的流。

定义如果N = (V, E)是一个运输网络，并且C是N的相伴无向图的一个割集，则称C为一个割，若从这个网络中去掉C中边可以导致a和z的分离。

例割C1将网络中的顶点划分成两个集合：P = {a , b}和它的补集P= {d, g, h, z}，C1记作(P ,P )。

割的容量记作c (P ,P )，定义为定理设f 是网络N = (V , E )中的一个流。

如果C = (P ,P )是N 中任意一个割，则val(f )不能超过c (P ,P )。

推论1 如果f 是运输网络N = (V , E )中的一个流，则流出源点a 的流值等于流入汇点b 的流值。

推论2 设f 是运输网络N = (V , E )中的流，并且令(P ,P )表示一个割，其中val(f ) = c (P ,P )。

运筹学课件最大流与最小费用流

精选ppt
11
定义 9
设 l(P)
min l(e) ，其中 l(e)
eE ( P )
c(e)
f
(e)
f
(e)
e P ， e P
（1）若 l(P) 0 ，则称 P 链为 f 饱和链；
（2）若 l(P) 0 ，则称 P 链为 f 非饱和链。
定义 10 设 f 是一个流， P 是从源 s 到汇 t 的一条链，若 P 满足
（2）流出发点集 X 的净流量等于流入收点集Y 的净流量。
定义 4 设 f 是网络 N 的一个流，则 f 的流的价值 Val f 定义为
Val f ＝ f (e) f (e)
eN ( X )
eN (Y )
即流的价值是发点集的流出量，也是收点集的流入量。
精选ppt
7
注 3：任何一个多源多汇网络 N (V , E, c, X ,Y ) 都等价与一个单源单汇网络 N ' (V ', E', c', X ',Y ' ) 。在解决实际问题时，常把多源
则找到了一条增广路，沿该增广路对流 x 进行增广（增广的流量为 max f (t) ，增广路可以根据
得到），转 STEP1。
（3b）如果 t 没有标号（即 LIST= 且 maxf (t) 0 ），转 STEP1。
STEP4 从 LIST 中移走一个节点 i ；寻找从节点 i 出发的所有可能的增广弧：（4a）对非饱和前向弧 (i, j) ，若节点 j 没有标号（即 pred( j) 0 ），对 j 进行标号，即令
多汇网络转化为单源单汇网络。
（1）V ' V {s, t}， s,t 分别是 N ' 的发点与收点；（2） E' E {(s, x) | x X } {( y,t) | y Y}；（3）c' c(e), e E ；c' (s, x) , x X ，c' ( y,t) , y Y 。

834 最大流最小割定理

最大流最小割定理Max-flow Min-cut Theorem在网络 G =(V , E , s , t , c ) 中，任何一个满足 s ∈S ，t ∈T =V -S 的顶点 V 的划分 {S , T } 称作一个 s -t 割（s -t cut ），简称割（cut ）一个 s -t 割的容量（capacity ）定义为，记为 cap (S , T )如果图 G 的 s -t 割 (S , T ) 使得任意一个 G 的s -t 割 (S ’, T ’) 都有 cap ( S , T )≤cap (S ’, T ’)，则称 ( S , T ) 是图 G 的一个最小s -t 割，简称最小割（minimum cut ） (),,uv u S v Tu v E c ∈∈∈∑sabcdeft 15530151081596 1010101544sabcdeft 15530151081596 1010101544sabcdeft 15530151081596 1010101544一般而言，网络的最小 s -t 割不唯一sabt1111sab t1111sabt1111下面建立流与割之间的关系，首先引入一些符号的定义在网络 G =(V , E , s , t , c ) 中，假设 A , B 都是 V 的非空子集，定义，即从 A 穿出进入 B 的边的总流量，即从 A 穿出进入 B 的边的总容量()(),,,uvu A v Bu v Ef A B f ∈∈∈=∑()(),,,uvu A v Bu v Ec A B c ∈∈∈=∑T ’S ’T S 定理1假设 G =(V , E , s , t , c ) 是一个网络，令 f 是一个流，(S , T ) 是一个 s -t 割，则通过该割的流量等于由源 s 发出的流量。

即 f (S , T ) - f (T , S ) = | f | 。

特别地有 f (∙, t )=| f |证明（大意）对 |S | 进行归纳证明。

最大流最小割

第6讲最大流最小费用

最小割定理

MATLAB中的网络流与最大流最小割问题求解方法

最大流最小割定理

教程：最大流-最小割定理

网络流应用练习题解析实际问题的网络流与最大流最小割定理

最大流最小割

最大流最小割算法概念

网络流基础-最大流最小割定理

最大流最小割定理应用

网路的最大流和最小截

异侧差最大值原理

最大流-最小割问题

最大流最小割定理

最大流最小割定理

运输网络最大流最小割定理

运筹学课件 最大流与最小费用流

834 最大流最小割定理

运筹学课件最大流与最小费用流