【中国农大CAU考研 高数】2.10 函数作图
最新(考研高数)基本初等函数图像与性质
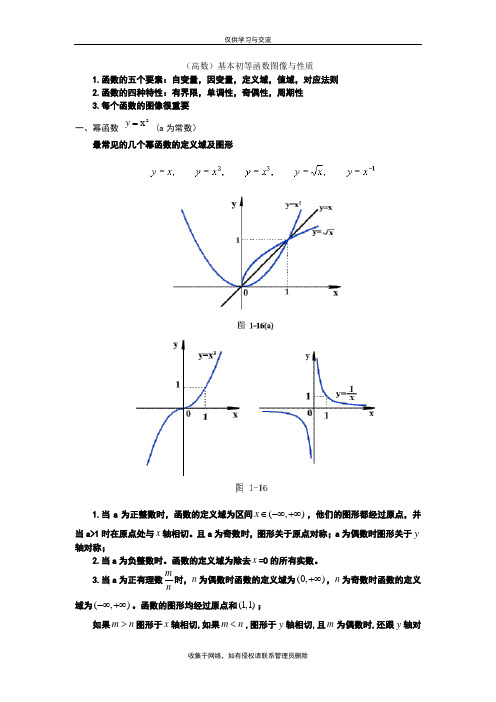
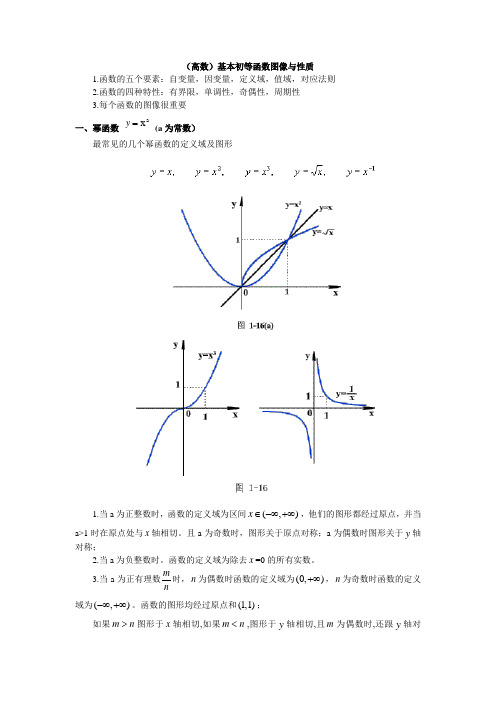
(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n均为奇数时,跟原点对称。
4.当a为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数。
二、指数函数xay=(a是常数且01a a>≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数xyalog=(a是常数且01a a>≠,),(0,)x∈+∞;四、三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数xy arctan=,),(+∞-∞∈x,)2,2(ππ-∈y,反余切函数xy cotarc=,),(+∞-∞∈x,),0(π∈y.Αα:阿尔法 Alpha Ββ:贝塔 BetaΓγ:伽玛 Gamma Δδ:德尔塔 DelteΕε:艾普西龙 Epsilon ζ :捷塔Zeta Ζη:依塔 Eta Θθ:西塔 Theta Ιι:艾欧塔 IotaΚκ:喀帕 Kappa ∧λ:拉姆达 LambdaΜμ:缪 Mu Νν:拗 NuΞξ:克西 Xi Οο:欧麦克轮 Omicron∏π:派 Pi Ρρ:柔 Rho∑σ:西格玛 Sigma Ττ:套 TauΥυ:宇普西龙 Upsilon Φφ:fai PhiΧχ:器 Chi Ψψ:普赛 PsiΩω:欧米伽 Omega七年级下册道德与法治第一次月考试卷班级姓名一.单选题(共18小题,每小题2分,共36分)1.欣赏漫画《宅童》,你最想对“宅童”说的是()①封闭自己,脱离现实世界,会使自己陷入孤立②这种把自己“宅”起来的做法,会使自己的人际关系萎缩③应该保持积极开放的态度,接触更多的人④在虚拟世界中获得成就感也能形成良好的性格,人生才更精彩。
考研高数基本初等函数图像与性质

(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1); 如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称。
4.当a 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x =0以外的一切实数。
二、指数函数x a y =(a 是常数且01a a >≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数x y a log =(a 是常数且01a a >≠,),(0,)x ∈+∞;四、三角函数正弦函数x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数反正弦函数x y arcsin =,]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数x y cot arc =,),(+∞-∞∈x ,),0(π∈y .Αα:阿尔法Alpha Ββ:贝塔BetaΓγ:伽玛Gamma Δδ:德尔塔DelteΕε:艾普西龙Epsilon ζ:捷塔Zeta Ζη:依塔Eta Θθ:西塔Theta Ιι:艾欧塔Iota Κκ:喀帕Kappa ∧λ:拉姆达Lambda Μμ:缪Mu Νν:拗NuΞξ:克西Xi Οο:欧麦克轮Omicron ∏π:派Pi Ρρ:柔Rho∑σ:西格玛Sigma Ττ:套TauΥυ:宇普西龙Upsilon Φφ:faiPhiΧχ:器Chi Ψψ:普赛PsiΩω:欧米伽Omega。
(完整)(考研高数)基本初等函数图像与性质
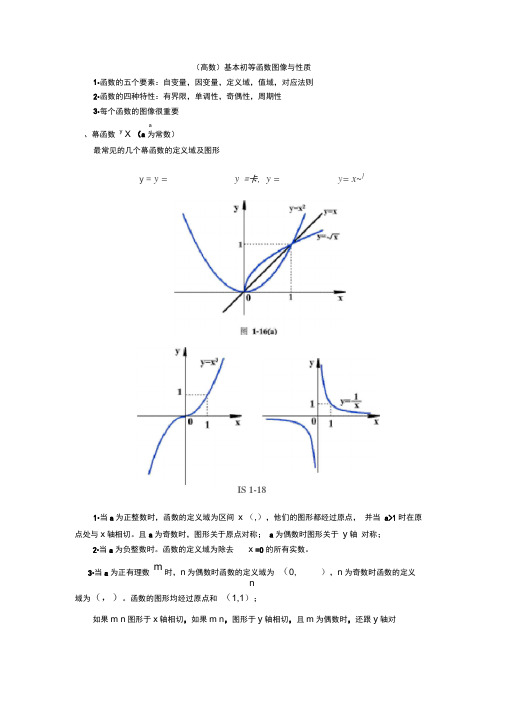
(高数)基本初等函数图像与性质1•函数的五个要素:自变量,因变量,定义域,值域,对应法则2•函数的四种特性:有界限,单调性,奇偶性,周期性3•每个函数的图像很重要a、幕函数y X (a为常数)最常见的几个幕函数的定义域及图形y = y = y=卡, y = y= x~]IS 1-181•当a为正整数时,函数的定义域为区间x (,),他们的图形都经过原点,并当a>1时在原点处与x轴相切。
且a为奇数时,图形关于原点对称;a为偶数时图形关于y轴对称;2•当a为负整数时。
函数的定义域为除去x =0的所有实数。
3•当a为正有理数m时,n为偶数时函数的定义域为(0, ),n为奇数时函数的定义n域为(,)。
函数的图形均经过原点和(1,1);如果m n图形于x轴相切,如果m n,图形于y轴相切,且m为偶数时,还跟y轴对称;m , n均为奇数时,跟原点对称。
4•当a为负有理数时,n为偶数时,函数的定义域为大于零的一切实数; 域为去除x=0以外的一切实数。
x / \、指数函数y a(a是常数且a 0, a 1),x(,)三、对数函数y loga x(a是常数且a 0, a 1),x (0,);图1-18n为奇数时,定义四、三角函数 正弦函数 y sinx , x ( , ) , y [ 1,1], 余弦函数y cosx , x ( , ) , y [ 11],五、反三角函数 y [——] 反正弦函数 y arcsinx , X [ 1,1] ,2’ 2 , 反余弦函数 y arccosx , x [ 1,1] , y [0,],k x k Z y 2 正切函数 k ky y 余切函数 x H b2U(n)tan x cotx 圈]-由闿 L-21BB 贝塔Beta AS 德尔塔 Delte Z :捷塔 Zeta Z n :依塔 Eta 11艾欧塔Iota A k 拉姆达 Lambda Nv 拗 Nu O o 欧麦克轮 Omicron Pp 柔 Rho T T 套 Tau ①申fai Phi 屮也普赛Psi 反正切函数y arctanx , X ( 反余切函数y arccotx , x ()y (o,) A a 阿尔法 Alpha r Y 伽玛 GammaE :艾普西龙 Epsilon OQ 西塔 Theta K K 喀帕 Kappa M& 缪 MuEE 克西Xi nn 派 Pi E cr 西格玛 SigmaYu 宇普西龙 Upsilon X x 器 ChiQw:欧米伽 Omega。
考研高等数学常用公式以及函数图像

正切 , , , 余切 , , ,
-----------------------------------(5)反三角函数----------------------------------
反正弦
,
,
反正切 , , 反余切 , ,
考研高等数学常用公式及函数图象
导数公式:
基本积分表:
三角函数的有理式积分:
一些初等函数: 两个重要极限:
三角函数公式:
·诱导公式:
函数
角A
sin
cos
tg
ctg
-α
-sinα
cosα
-tgα
-ctgα
90°-α
cosα
sinα
ctgα
tgα
90°+α
cosα
-sinα
-ctgα
-tgα
180°-α
sinα
( 是常数且 ), ;
-----------------------------------(3)对数函数----------------------------------
( 是常数且 ), ;
-----------------------------------(4) 三角函数----------------------------------
(*)式的通解
两个不相等实根
两个相等实根
一对共轭复根
二阶常系数非齐次线性微分方程
五类基本初等函数及图形
-----------------------------------(1)幂函数----------------------------------
, 是常数;
考研高数基本初等函数图像与性质

(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称。
4.当a 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x =0以外的一切实数。
二、指数函数 x a y =(a 是常数且01a a >≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数x y a log =(a 是常数且01a a >≠,),(0,)x ∈+∞; 四、三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数xy cotarc=,),(+∞-∞∈x,),0(π∈y.Αα:阿尔法Alpha Ββ:贝塔BetaΓγ:伽玛Gamma Δδ:德尔塔DelteΕε:艾普西龙Epsilon ζ :捷塔Zeta Ζη:依塔Eta Θθ:西塔Theta Ιι:艾欧塔IotaΚκ:喀帕Kappa ∧λ:拉姆达LambdaΜμ:缪Mu Νν:拗NuΞξ:克西Xi Οο:欧麦克轮Omicron∏π:派Pi Ρρ:柔Rho∑σ:西格玛Sigma Ττ:套TauΥυ:宇普西龙Upsilon Φφ:fai PhiΧχ:器Chi Ψψ:普赛PsiΩω:欧米伽Omega。
(整理)考研数学函数图像大全
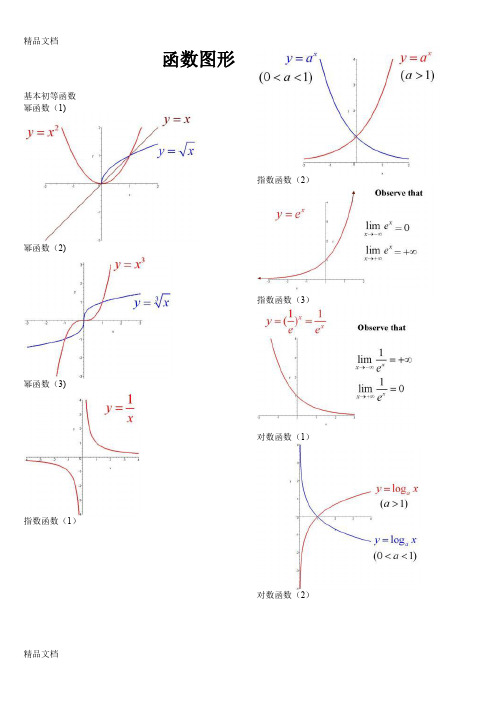
函数图形基本初等函数 幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)等价无穷小(x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1) 夹逼定理(2)数列的夹逼性(1) 数列的夹逼性(2)。
考研高数基本初等函数图像与性质

(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称。
4.当a 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x =0以外的一切实数。
二、指数函数 x a y =(a 是常数且01a a >≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数x y a log =(a 是常数且01a a >≠,),(0,)x ∈+∞; 四、三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y , 反余切函数x y cot arc =,),(+∞-∞∈x ,),0(π∈y . Αα:阿尔法 AlphaΒβ:贝塔 Beta Γγ:伽玛 GammaΔδ:德尔塔 Delte Εε:艾普西龙 Epsilonζ :捷塔 Zeta Ζ η:依塔 Eta Θθ:西塔 ThetaΙι:艾欧塔 Iota Κκ:喀帕 Kappa∧λ:拉姆达 Lambda Μμ:缪 MuΝν:拗 Nu Ξξ:克西 XiΟο:欧麦克轮 Omicron ∏π:派 PiΡρ:柔 Rho ∑σ:西格玛 SigmaΤτ:套 Tau Υυ:宇普西龙 UpsilonΦφ:fai Phi Χχ:器 ChiΨψ:普赛 Psi Ωω:欧米伽 Omega。
(考研高数)基本初等函数图像与性质
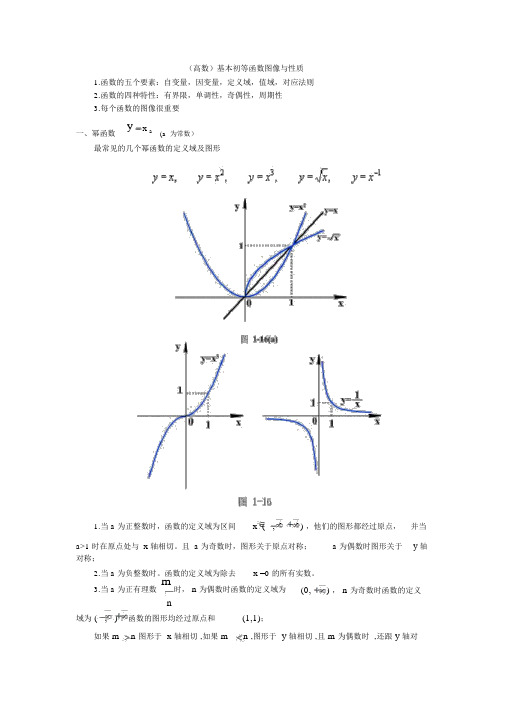
(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数yx a(a为常数)最常见的几个幂函数的定义域及图形1.当 a 为正整数时,函数的定义域为区间x ( , ) ,他们的图形都经过原点, 并当a>1 时在原点处与 x 轴相切。
且 a 为奇数时,图形关于原点对称; a 为偶数时图形关于y 轴对称;2.当 a 为负整数时。
函数的定义域为除去 x =0 的所有实数。
3.当 a 为正有理数m时, n 为偶数时函数的定义域为(0,) , n 为奇数时函数的定义n域为 ( , ) 。
函数的图形均经过原点和(1,1);如果 m n 图形于 x 轴相切 ,如果 m n ,图形于 y 轴相切 ,且 m 为偶数时 ,还跟 y 轴对称; m,n均为奇数时,跟原点对称。
4.当域为去除a 为负有理数时 , n为偶数时x =0以外的一切实数。
,函数的定义域为大于零的一切实数;n 为奇数时,定义二、指数函数y a x(a是常数且 a 0, a 1),x ( , )图形过( 0, 1)点, a>1 时,单调增加;0<a<1 时,单调减少。
今后用的较多。
三、对数函数y logax(a是常数且 a 0,a 1),x (0, );四、三角函数正弦函数 y sin x , x ( , ) , y [ 1,1] , 余弦函数ycos x , x(, ) , y [ 1,1] ,y tan x xkZ , y( , ) , 正切函数 ,2 , k余切函数ycot x, x k , k Z, y (, ) ;五、反三角函数y arcsin x , x[ 1,1] y [, ]反正弦函数 , 2 2 ,反余弦函数y arccosx , x[ 1,1] , y[ 0, ] ,y arctan x ,x (, )y (,)反正切函数,2 2 ,反余切函数y arc cot x ,x( , ) , y (0,) .Αα:阿尔法AlphaΓγ:伽玛Gamma Εε:艾普西龙Epsilon Θθ:西塔ThetaΚκ:喀帕KappaΜμ:缪 MuΞξ:克西Xi∏π:派Pi∑σ:西格玛SigmaΥυ:宇普西龙Upsilon Χχ:器 ChiΩω:欧米伽OmegaΒβ:贝塔 BetaΔδ:德尔塔Delteζ:捷塔ZetaΖη:依塔Eta Ιι:艾欧塔Iota∧λ:拉姆达LambdaΝν:拗N uΟο:欧麦克轮OmicronΡρ:柔RhoΤτ:套TauΦφ: fai PhiΨψ:普赛 Psi。
考研高等数学常用公式以及函数图像

考研高等数学常用公式及函数图象导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:函数 角A sincos tg ctg -α -sinα cosα -tgα -ctgα 90°-α cosα sinαctgαtgα 90°+α cosα -sinα -ctgα -tgα 180°-α si nα-cosα -tgα-ctgα 180°+α -sinα -cosα tgα ctgα 270°-α -cosα -sinα ctgα tgα 270°+α -cosα sinα -ctgα -tgα360°-α -sinα cosα -tgα -ctgα 360°+αsinαcosαtgαctgα·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
(考研高数)基本初等函数图像与性质
(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n 时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n均为奇数时,跟原点对称。
4.当a为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数。
二、指数函数xay=(a是常数且01a a>≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数xyalog=(a是常数且01a a>≠,),(0,)x∈+∞;四、三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y , 余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数 反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数xy arctan=,),(+∞-∞∈x,)2,2(ππ-∈y,反余切函数xy cotarc=,),(+∞-∞∈x,),0(π∈y.Αα:阿尔法Alpha Ββ:贝塔BetaΓγ:伽玛Gamma Δδ:德尔塔DelteΕε:艾普西龙Epsilon ζ :捷塔Zeta Ζη:依塔Eta Θθ:西塔Theta Ιι:艾欧塔IotaΚκ:喀帕Kappa ∧λ:拉姆达LambdaΜμ:缪Mu Νν:拗NuΞξ:克西Xi Οο:欧麦克轮Omicron∏π:派Pi Ρρ:柔Rho∑σ:西格玛Sigma Ττ:套TauΥυ:宇普西龙Upsilon Φφ:fai PhiΧχ:器Chi Ψψ:普赛PsiΩω:欧米伽Omega。
考研高等数学常用公式以及函数图像

考研高等数学常用公式及函数图象导数公式: 基本积分表:ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ三角函数的有理式积分:一些初等函数: 两个重要极限: 三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
(考研高数)基本初等函数图像与性质

(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数 a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n 时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称。
4.当a 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x =0以外的一切实数。
二、指数函数xay=(a是常数且01a a>≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数xyalog=(a是常数且01a a>≠,),(0,)x∈+∞;四、三角函数正弦函数xy sin=,),(+∞-∞∈x,]1,1[-∈y,余弦函数xy cos=,),(+∞-∞∈x,]1,1[-∈y,正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数 反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y , 反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数x y cot arc =,),(+∞-∞∈x ,),0(π∈y .Αα:阿尔法Alpha Ββ:贝塔BetaΓγ:伽玛Gamma Δδ:德尔塔DelteΕε:艾普西龙Epsilon ζ :捷塔Zeta Ζη:依塔Eta Θθ:西塔Theta Ιι:艾欧塔IotaΚκ:喀帕Kappa ∧λ:拉姆达LambdaΜμ:缪Mu Νν:拗NuΞξ:克西Xi Οο:欧麦克轮Omicron∏π:派Pi Ρρ:柔Rho∑σ:西格玛Sigma Ττ:套TauΥυ:宇普西龙Upsilon Φφ:fai PhiΧχ:器Chi Ψψ:普赛PsiΩω:欧米伽Omega。
【中国农大CAU考研数学】第三章

定义 设(X,Y)的分布函数为 F(x,y), 如果存在非负函数f(x,y)使 得对 x,y R
xy
F(x, y) P{X x,Y y} f (u,v)dudv
则称(X,Y)为连续型的二维随 机变量;称f(x,y)为(X,Y)的概 率密度(或简称联合概率密度)。
概率密度f(x,y)具有性质
P{x1≤X≤x2 , y1≤Y≤y2}
=F(x2,y2) -F(x2,y1)+F(x1,y1)
-F(x1,y2) (x1, y2)
(x2, y2)
Y
(x1, y1)
0
(x2, y1)
X
分布函数F(x,y)的基本性质 1°F(x,y)是变量x和y的不减函 数;
2°0≤F(x,y) ≤1, 且 对于任意的y, F(-∞ ,y)=0, 对于任意的x, F(x, -∞ )=0, F(-∞ , -∞ )=0, F(+∞ , +∞ )=1;
(1). 均匀分布: 定义 设D为闭区域面积为A,若随机变量 (X,Y) 的(联合)密度为:
1/ A
f (x, y)
0
(x, y) D 其它
则称:(X, Y)服从D上的均匀分布。
向平面上有界区域G上任投一质点,若质点落 在G内任一小区域B的概率仅与小区域的面积成 正比,而与B的形状及位置无关. 则质点的坐标 ( X,Y)在G上服从均匀分布.
飞机的重心在空中的状态 是由三个坐标、机头仰角、机 翼测角五个r.v 来确定的等等.
n个随机变量所构成的整体, 叫n维随机 向量或n维随机变量
§1 二维随机变量
设E是一个随机试验,其 样本空间为S,设X,Y是 定义在S上的随机变量,
由它们构成的一个向量 (X,Y)叫做二维随机向 量或二维随机变量。
考研高等数学常用公式以及函数图像

考研高等数学常用公式及函数图象导数公式:基本积分表:三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:函数 角A sin cos tg ctg -α -sin α cos α -tg α -ctg α 90°-α cos α sin α ctg α tgα 90°+αcos α-sin α -ctg α -tg α 180°-α sinα -cos α -tg α-ctg α180°+α -sinα -cos α tgα ctgα 270°-α -cosα -sin α ctg α tgα 270°+α -cosα sin α -ctg α -tg α 360°-α -sinα cos α -tg α-ctg α360°+α sinαcos αtgα ctgα·和差角公式: ·和差化积公式:2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβα-+-+=--+=+βαβαβαβαβαβαβαβαβαtg tg tg tg tg ⋅±=±=±±=±1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+=·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。
考研高数基本初等函数图像与性质

(高数)基本初等函数图像与性质1.函数的五个要素:自变量,因变量,定义域,值域,对应法则2.函数的四种特性:有界限,单调性,奇偶性,周期性3.每个函数的图像很重要一、幂函数a x =y (a 为常数)最常见的几个幂函数的定义域及图形1.当a 为正整数时,函数的定义域为区间(,)x ∈-∞+∞,他们的图形都经过原点,并当a>1时在原点处与x 轴相切。
且a 为奇数时,图形关于原点对称;a 为偶数时图形关于y 轴对称;2.当a 为负整数时。
函数的定义域为除去x =0的所有实数。
3.当a 为正有理数m n时,n 为偶数时函数的定义域为(0,)+∞,n 为奇数时函数的定义域为(,)-∞+∞。
函数的图形均经过原点和(1,1);如果m n >图形于x 轴相切,如果m n <,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称。
4.当a 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x =0以外的一切实数。
二、指数函数x a y =(a 是常数且01a a >≠,),),(+∞-∞∈x图形过(0,1)点,a>1时,单调增加;0<a<1时,单调减少。
今后用的较多。
三、对数函数x y a log =(a 是常数且01a a >≠,),(0,)x ∈+∞;四、三角函数正弦函数x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,正切函数x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;五、反三角函数反正弦函数x y arcsin =,]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数x y cot arc =,),(+∞-∞∈x ,),0(π∈y .Αα:阿尔法Alpha Ββ:贝塔BetaΓγ:伽玛Gamma Δδ:德尔塔DelteΕε:艾普西龙Epsilon ζ:捷塔Zeta Ζη:依塔Eta Θθ:西塔Theta Ιι:艾欧塔Iota Κκ:喀帕Kappa ∧λ:拉姆达Lambda Μμ:缪Mu Νν:拗NuΞξ:克西Xi Οο:欧麦克轮Omicron ∏π:派Pi Ρρ:柔Rho∑σ:西格玛Sigma Ττ:套TauΥυ:宇普西龙Upsilon Φφ:faiPhiΧχ:器Chi Ψψ:普赛PsiΩω:欧米伽Omega。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
斜渐近线求法:
lim f ( x) = a, lim[ f ( x) - ax] = b.
x x
x
那么 y = ax + b 就是曲线 y = f ( x) 的一条斜渐近线.
§2.10 函数作图
3. 水平渐近线
如果 lim f ( x) = b 或 lim f ( x) = b (b 为常数)
2x - 3
y
=
的性质并绘制函数图形.
( x - 2)2
解
(1) 函数的定义域为
x 2.
非奇非偶函数,且无对称性.
(2)
2x - 3
lim x2 ( x -
2)2
=
,
x = 2 为曲线的垂直渐近线.
2x - 3
lim
x
(
x
-
2)2
=
0
y = 0 为曲线的水平渐近线.
§2.10 函数作图
(3)
f
( x)
例2 求 y = x2 +的2渐x近+线e.x
解 分两种情形讨论.
lim f ( x) = lim
x x+
x+
lim f ( x) = lim
x x-
x-
x2 + 2x + ex
x
= +,
x2 + 2x + ex
x
= -1,
lim ( f ( x) + x) = lim ( x2 + 2x + e x + x)
f (x)
-8
9
-1
曲线 凸、降 拐 点 凹、降 极小值 凸、升
+
凹、降
(5) 令 x = 0, 得 y = - 3 ; 4
令 y = 0, 得 x = 3 .
y
2
再补充几点:
(-1, - 5), (3, 3), (5, 7 ).
9
9
(6) 描点作图.
O2
x
§2.10 函数作图
内容小结
1. 利用一阶导数、二阶导数的符号确定 函数的增减性、凹凸性、 拐点以及极值点.
=
-2( x (x -
- 1) 2)3 ,
f
( x)
=
4x - 2 ( x - 2)4
令 f ( x) = 0, 得 x = 1, 令 f ( x) = 0, 得 x = 1 .
(4) 列表讨论
2
x
(-, 1) 1 22
( 1 ,1) 2
1
(1, 2)
2 (2,+)
f ( x) - -
-0
+
-
f ( x) - 0 + + +
§2.10 函数作图
一、曲线的渐近线 二、函数作图
§2.10 函数作图
一、曲线的渐近线
1. 垂直渐近线
如果
lim f ( x ) = 或 lim f ( x ) =
x
x
+ 0
x
x
0
那么 x = x 就是 y = f ( x ) 的一条垂直渐近线
.
0
例如, y =
1
,
( x + 2)(x - 3)
一阶导数和二阶导数为零的全部实数根,并求出所有一阶导数不存在的点和 二阶导数不存在的点;依此划分定义区间;
§2.10 函数作图
(4) 按上述结果列表,确定函数的单调性、凹 凸性、极值和拐点;
(5) 求出曲线与坐标轴的交点,并求出曲线上 若干其它点;
(6) 描点作出函数图形.
§2.10 函数作图
例3 讨论函数
2. 综合运用函数的性态、较准确地作出函数的图形.
§2.10 函数作图
思考练习
选择题
曲线 y =
x|x|
的渐近线, 共有
( x - 1)( x - 2)
( A) 1条.
(B) 2条.
(C ) 3条. ( D) 4条.
§2.10 函数作图
思考练习
解答提示
选D. 包括2条垂直渐近线,2条水平渐近线.
lim
= ,
x-1 x + 1
x = -1 为曲线的垂直渐近线.
又 lim f ( x) = lim x2 + 5x + 1 = 1, x x x x( x + 1)
x2 + 5x -1
lim(
x
f
(
x)
-
x)
=
lim
x
x+1
- x = 4,
y = x + 4为曲线的斜渐近线.
§2.10 函数作图
x+
x-
那么 y = b 就是 y = f ( x) 的一条水平渐近线.
例如 y = arctan x,
lim arctan x =
x+
2
水平渐近线:
y = , 2
lim arctan x = -
x-
2
y = -. 2
§2.10 函数作图
例1
求 y = x2 +的5渐x近+线1.
x+1
解
x2 + 5xபைடு நூலகம்+1
本节内容结束
x-
x-
= lim
2x + ex
= -2.
x- x2 + 2 x + e x - x
y = - x - 2为曲线的斜渐近线.
§2.10 函数作图
二、曲线作图
函数作图的一般步骤: (1) 确定函数的定义域、值域,讨论函数的奇偶性、周期性;
(2) 求出曲线的渐近线; (3) 求出函数f (x)的一阶导数和二阶导数,求出使
1
1
lim
= lim
=
x-2 ( x + 2)( x - 3)
x3 ( x + 2)( x - 3)
垂直渐近线:
x = -2, x = 3.
§2.10 函数作图 2. 斜渐近线
如果 lim [ f ( x) - (ax + b)] = 0 x+ 或 lim [ f ( x) - (ax + b)] = 0 (a,b 为常数)(a 0) x-
