12_5磁场的能量 磁场能量密度
12.5磁场的能量 磁场能量密度

Wm = ∫ dWm = ∫ wmdV 体
V
V
(积分应遍及磁场存在的全空间。) 积分应遍及磁场存在的全空间。)
µo I 解: B = (R1< r < R2) 2πr 2 2 B µo I wm = = 2 2 2µo 8π r
Wm = ∫R wm2πrdr •1
1
I
R2 R1
I r
dr
1
R2
=∫
R2
1 2 计算。 也可用 Wm = LI 计算。 2
R1
µo I dr µo I 2 R2 ⋅ = ln 4π r 4π R1
回路电 阻所放 出的焦 耳热
3
12.4 磁场的能量
自感线圈磁能
第12章 电磁感应 12章
Wm
1 = LI 2
2r µ
2
l
R
ε
当电路中电流从 0 增加到稳定值 I0 时,电路附近 的空间逐渐建立起一定强度的磁场,磁场具有能量。 的空间逐渐建立起一定强度的磁场,磁场具有能量。 所以电源反抗自感电动势所做的功, 所以电源反抗自感电动势所做的功,就在建立磁场 电源反抗自感电动势所做的功 的过程中转化为磁场的能量。 的过程中转化为磁场的能量。 这个能量并未消耗,一旦条件许可就能释放出来, 这个能量并未消耗,一旦条件许可就能释放出来, 转变为其它形式的能量。 转变为其它形式的能量。 自感线圈也是一个储能元件,自感系数反映线圈储能的本领。 自感线圈也是一个储能元件,自感系数反映线圈储能的本领。 4
第五节 磁场的能量和能量密度

第五节磁场的能量和能量密度磁场的能量和能量密度(P631)1、目前在实验室里产生E=105伏/米的电场和B=104高斯的磁场是不难做到的。
今在边长为10厘米的立方体空间里产生上述两种均匀场,问所需的能量各为多少?解:2、利用高磁导率的铁磁体,在实验室产生B=5000高斯的磁场并不困难(1)求这磁场的能量密度ωm;(2)要想产生能量密度等于这个值的电场,问电场强度E的值应为多少?这在实验上容易作到吗?解:3、一导线弯成半径为R=5、0厘米的圆形,当其中载有I=100安的电流时,求圆心的磁场能量密度ωm。
解:4、一螺线管长300毫米,横截面积的直径为15毫米,有2500匝表面绝缘的导线均匀密绕而成,其中铁芯的磁导率μ=1000。
当它的导线中通有电流2安时,求管中心的磁能密度ωm。
解:5、一同轴线由很长的两个同轴的圆筒构成,内筒半径为1、0毫米,外筒半径为7、0毫米,有100安的电流从外筒流去,内筒流回,两筒的厚度可忽略。
两筒之间的介质无磁性(μ=1),求:(1)介质中的磁能密度ωm分布;(2)单位长度(1米)同轴线所储磁能Wm。
解:6、一根长直导线载有电流I,I均匀分布在它的横截面上。
证明:这导线内部单位长度的磁场能量为:μ0I2/16π。
解:7、一同轴线由很长的直导线和套在它外面的同轴圆筒构成,导线的半径为a,圆筒的内半径为b,外半径为c。
电流I由圆筒流去,由导线流回;在它们的横截面上,电流都是均匀分布的。
(1)求下列四处每米长度内所储磁能Wm的表达式:导线内,导线和圆筒之间,圆筒内,圆筒外;(2)当a=1、0毫米,b=4、0毫米,c=5、0毫米,I=10安时,每米长度的同轴线中储存磁能多少?解:8、试验算一下,用上述两种平均磁链法计算例题2的结果,都与磁能法一致。
解:。
静磁场与磁场能量计算

静磁场与磁场能量计算磁场是我们日常生活中常常遇到的物理现象之一。
它可以通过静磁场来描述,即指在不随时间变化的情况下,磁场的分布和性质。
磁场能量计算是研究静磁场中能量分布和变化的重要方法之一。
本文将探讨静磁场的基本概念以及磁场能量计算的方法。
首先,我们来了解一下静磁场的基本概念。
静磁场是指在不随时间变化的情况下,磁场的分布和性质。
它由磁场强度(B)和磁感应强度(H)来描述。
磁场强度是指单位面积上垂直于磁场方向的磁力线数目,而磁感应强度是指单位面积上垂直于磁场方向的磁通量。
磁场强度和磁感应强度之间的关系可以通过麦克斯韦方程组来描述,其中包括安培定律和高斯定律等。
在静磁场中,磁场能量是磁场具有的能量形式,它与磁场的分布和性质密切相关。
磁场能量的计算可以通过磁场能量密度和体积分布来实现。
磁场能量密度是指单位体积内的磁场能量,可以通过磁场强度和磁感应强度来计算。
具体而言,磁场能量密度可以表示为:W = (1/2) * B * H其中W表示磁场能量密度,B表示磁场强度,H表示磁感应强度。
磁场能量密度的计算可以通过对磁场强度和磁感应强度的积分来实现。
通过对整个空间内的磁场强度和磁感应强度进行积分,可以得到磁场的总能量。
除了磁场能量密度的计算,我们还可以通过磁场能量的体积分布来研究磁场的能量变化。
磁场能量的体积分布是指磁场能量在空间中的分布情况。
磁场能量的体积分布可以通过对磁场能量密度在空间中的积分来实现。
具体而言,磁场能量的体积分布可以表示为:W = ∫∫∫ (1/2) * B * H * dV其中W表示磁场能量,B表示磁场强度,H表示磁感应强度,dV表示体积元。
通过对整个空间内的磁场强度和磁感应强度进行积分,可以得到磁场的总能量。
磁场能量的计算对于研究磁场的性质和应用具有重要意义。
通过磁场能量的计算,我们可以了解磁场的能量分布和变化情况,进而研究磁场对物体的作用和相互作用。
例如,在电磁感应中,磁场能量的变化可以导致电场的产生和变化,从而产生感应电流和电动势。
反应磁场的性质的物理量

反应磁场的性质的物理量
磁场是一种物理量,它可以描述物体之间的相互作用。
它是一种由磁力线组成的力场,可以在空间中传播,并且可以影响物体的运动。
磁场的性质是由磁力线的方向和强度来决定的。
磁场的性质可以用一些物理量来描述,其中最重要的是磁通量密度。
磁通量密度是指磁力线在单位面积上的流量,它可以用牛顿/米2来表示。
磁通量密度可以用来表示磁场的强度,它可以用来描述磁场的方向和强度。
另一个重要的物理量是磁感应强度。
磁感应强度是指磁力线在单位长度上的流量,它可以用牛顿/米来表示。
磁感应强度可以用来表示磁场的方向,它可以用来描述磁场的方向和强度。
此外,还有一些其他的物理量可以用来描述磁场的性质,如磁场强度、磁场能量密度和磁场能量等。
磁场强度是指磁力线在单位体积上的流量,它可以用牛顿/米3来表示。
磁场能量密度是指磁力线在单位面积上的能量,它可以用牛顿/米2来表示。
磁场能量是指磁力线在单位体积上的能量,它可以用牛顿/米3来表示。
磁场的性质是由磁力线的方向和强度来决定的,它可以用一些物理量来描述,如磁通量密度、磁感应强度、磁场强度、磁场能量密度和磁场能量等。
这些物理量可以用来描述磁场的方向和强度,从而更好地理解磁场的性质。
磁场的性质对我们的日常生活有着重要的影响,它可以用来控制电机的运行,也可以用来控制电磁波的传播。
此外,磁场还可以用来检测物体的位置,从而实现定位功能。
因此,磁场的性质是非常重要的,它可以用一些物理量来描述,从而更好地理解磁场的性质。
12.5 磁场的能量Xiao(1)

体系的磁场能量密度: 1 2 1 2 1 2 1 wm ( B1 B2 ) B1 B2 2 B1 B2 2 2 2 2 体系的总磁场能量:
Wm wm dV
V
n1
n2
V
1 2 1 2 1 B1 dV B2 dV 2 B1 B2 dV V 2 V 2 2
2
体系的总磁场能量 1 2 1 2 1 Wm B1 dV B2 dV 2 B1 B2 dV V 2 V 2 V 2 1 1 2 2 L1I1 L2 I 2 MI1I 2 2 2 如果两线圈电流方向相反,两线圈的磁通量互相减弱, B1与B2方向相反,故 1 1 2 B1 B2V B1 B2V n1 n2 I1 I 2V MI1 I 2 2 体系的总磁场能量: 1 2 1 2 1 Wm B1 dV B2 dV 2 B1 B2 dV V 2 V 2 V 2 1 1 2 2 L1I1 L2 I 2 MI1I 2 2 2
互感磁能
两个耦合线圈的总磁能:
1 1 2 2 Wm L1 I10 L2 I 20 MI10 I 20 2 2
自感磁能 互感磁能
讨论: 如果两回路线圈电流方向相反,两线圈的磁通量互相减 弱,每个线圈中的自感电动势和互感电动势方向相反: dI1 dI 2 1 L1 M I1 R1 ( I1 0, I 2 0) 线圈1: dt dt dI 2 dI1 2 L2 M I 2 R2 线圈2: dt dt 重复前面推导,可得
2
当时间从零经过一段足够长的时间 T (弛豫时间) 后,两个线圈的电流分别由零逐渐增大到稳定值 I10和 I20,线圈中储存的能量达到饱和:
13-5磁场的能量 磁场能量密度解析
S
21
13-5
磁场的能量 磁场能量密度
麦克斯韦假设
麦 克 斯 韦 电 磁 场
方 程 的 积 分 形 式
dD (2)位移电流 jd dt q SD ds V dV B l E dl S t ds SB ds 0 D l H dl S ( jc t ) ds
1
13-5
磁场的能量 磁场能量密度
自感线圈磁能
1 2 Wm LI 2
I
L
L n2V ,
B nI
1 2 1 2 B 2 1 B2 Wm LI n V ( ) V 2 2 n 2
wmV
2
13-5
磁场的能量 磁场能量密度
磁场能量密度
B 1 1 2 wm H BH 2 2 2
13-5
磁场的能量 磁场能量密度
麦克斯韦(1831-1879)英国物理学家 经典电磁理论的奠基人 , 气体动理论创始人之一. 提 出了有旋场和位移电流的 概念 , 建立了经典电磁理 论 , 并预言了以光速传播的 电磁波的存在. 在气体动理 论方面 , 提出了气体分子按 速率分布的统计规律.
7
13-5
1 铁磁质 (非常数)
26
13-5
磁场的能量 磁场能量密度
例 有两个半径分别为 R 和 的“无限长”同 r 的 轴圆筒形导体,在它们之间充以相对磁导率为 磁介质.当两圆筒通有相反方向的电流 I 时,试 求 (1)磁介质中任意点 P 的磁感应强度的 大小;(2)圆柱体外面一点 Q 的 磁感强度. I 解 对称性分析
+ + + + + + + + +
12_5磁场的能量磁场能量密度解析

感电动势作功的过程中建立的。
12 – 5 磁场的能量 磁场能量密度
L2
先以磁通相助为例进行研究
能量是状态量,应与电流建立的过程无关。为此 分两步建立磁场。
I 1)线圈“2”开路,让线圈“1”中电流由0
10
2)维持线圈“1”中电流不变,让线圈“2”中电
L1 M L2
W 'm
1 2
L2
I
2 20
L1 I1
L2 M 21 I20
1 2
L1 I120
M21I10I20 (2)
与(1)式比较
Wm
1 2
L1 I120
1 2
L2
I
2 20
M12 I10 I20 (1)
W 'm Wm M12 M 21
12 – 5 磁场的能量 磁场能量密度 第十二章电磁感应 电磁场
WL1
1 2
LI120
WL 2
1 2
LI
2 20
W互 M12I10I20
互感线圈的总磁能:
Wm
1 2
L1 I120
1 2
L2
I
2 20
M12I10I20 (1)
建立电流的方式也可反过来:
21由))0维线持圈线“圈1”“开2路”中,电让流线不圈变“,2”让中线电圈流“1”中I 20
电
I10
流由0
12 – 5 磁场的能量 磁场能量密度 第十二章电磁感应 电磁场
1 2
L2
I
2 20
M12I10 I20…..
***
12 – 5 磁场的能量 磁场能量密度 第十二章电磁感应 电磁场
总而言之: 互感电路的磁场能量
§13-5磁场的能量磁场的能量密度
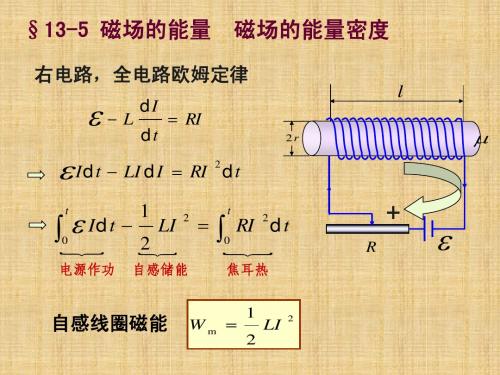
2
Wm = =
∫ ∫
V
wm d V
µ
⋅ ( 2π rdr ⋅ 1)
µI 2
2 2
8π r 2 R2 µ I =∫ ⋅ dr R1 4 π r R2 µI 2 = ln 4π R1
V
r dr
R2
1 W m = LI 2
2
R2 L= ln 2 π R1
µ
第§13-5节完 13-
Maxell方程组 §13-6 位移电流 Maxell方程组 13麦克斯韦( 麦克斯韦(1831-1879) ) 英国物理学家。 英国物理学家。经典 电磁理论的奠基人, 电磁理论的奠基人, 气体 动理论创始人之一。 动理论创始人之一。①提 出了有旋场、 出了有旋场、位移电流的 概念, 概念, 建立了经典电磁理 论;②预言了以光速传播 的电磁波的存在。 的电磁波的存在。 ③在 气体动理论方面, 气体动理论方面, 提出了 气体分子按速率分布的统 计规律。 计规律。
一 位移电流 全电流安培环路定理
稳恒磁场中,安培环路定理 稳恒磁场中,
∫ H ⋅ dl = ∑ I = ∫ j ⋅ ds
l s
以 L 为边做任意曲面 S1 和 S2
∫LH ⋅ dl = ∫S1 j ⋅ ds = I
S1
-
S2
+ + + +
∫ H ⋅ dl = ∫
L
S2
j ⋅ ds = 0
I
−σ dD +σ + - dt +
∫ D ⋅ ds = ∑ q dφ ∫ E ⋅ d l = − dt
S
l
m
∫ B ⋅ ds = 0 ∫ H ⋅ dl = I + I
电场和磁场的能量密度

电场和磁场的能量密度能量密度是指单位体积内所含能量的大小,对于电场和磁场而言,它们也具有能量密度的概念。
本文将探讨电场和磁场的能量密度,并对其计算方式进行详细介绍。
一、电场的能量密度电场的能量密度表示单位体积内电场能量的大小。
假设在真空中存在一个电场,其电场强度为E,而该电场所储存的能量密度为u。
根据物理定律,电场的能量密度可以通过以下公式进行计算:u = 0.5 * ε0 * E^2其中,ε0是真空介质的介电常数,约等于8.85x10^-12 C^2/(N·m^2)。
当然,在具体问题中,如果电场在某一区域内不均匀分布,就需要采用积分形式进行计算。
具体的计算方法请参考电场能量密度的积分公式。
二、磁场的能量密度磁场的能量密度表示单位体积内磁场能量的大小。
假设在真空中存在一个磁场,其磁场强度为B,而该磁场所储存的能量密度为u。
根据物理定律,磁场的能量密度可以通过以下公式进行计算:u =0.5 * B^2 /μ0其中,μ0是真空中的磁导率,约等于4πx10^-7 T·m/A。
同样地,在具体问题中,如果磁场在某一区域内不均匀分布,就需要采用积分形式进行计算。
具体的计算方法请参考磁场能量密度的积分公式。
综上所述,电场和磁场都具有能量密度这一概念。
通过计算电场和磁场的能量密度,我们可以更好地理解和描述它们的能量分布情况。
这也为我们深入研究电磁波传播、电磁辐射等现象提供了基础。
当然,实际应用中,我们还需要考虑电磁场的耦合问题,即电场和磁场相互作用的情况。
在这种情况下,我们需要综合考虑电场和磁场的能量密度,以及它们之间的相互关系,进一步分析和描述整个电磁场的特性。
总结起来,电场和磁场作为电磁学中的基本概念,它们都具有能量密度的概念。
通过计算能量密度,我们可以更好地理解电场和磁场的能量分布情况,并在实际应用中加以运用。
相信通过对电场和磁场能量密度的研究,我们可以更深入地了解电磁学的原理和应用。
12-(5)磁场的能量

I Rdt
2 0
t
3 磁场能量 在开关闭合和断开后,阻碍 原电路的电流变化的过程就是 对线圈冲放磁场能量的过程。 磁场 能量
R
A
1 2 Wm LI 2
BATTERY
电池
以长直密绕螺线管为例,B nI
R R
L
B
1 2 Wm LI 2 1 2 B 2 1 B2 n V ( ) V 2 n 2
16
三 感应电动势
1 起因:导体运动 - 磁通量变化
动生电动势
2 大小:
i
b
a
Ek dl
Ek v B
Ek v B
dΦm i dt
3 方向:标量
1 起因:磁场变化 - 磁通量变化
感生电动势
B ds 2 大小: L Ek dl t S
附加储存的能量
t di di1 W21 21 I 2dt M 21 I 2dt M 21 I 2 1 dt M 21 I10 I 20 0 0 0 dt dt 1 2 1 2 系统总能量 W W1 W2 W12 LI10 LI 20 M 21 I10 I 20 10 2 2
BATTERY
电池
5
磁场能量只能反映空间体积 V 内 的总能量,不能反映磁场的能量分 布情况。须引入描写磁场分布的物 理量---能量密度。 磁场能量 密度
l
1 B2 Wm V 2
n
Wm wm V 1 B2 1 1 2 H BH 2 2 2
S I
磁场的能量只与磁场和磁场分布的空间有关。
t
t
能量密度计算公式 打印

能量密度计算公式打印
能量密度计算公式。
能量密度是指单位体积或单位质量的物质所包含的能量。
在物
理学中,能量密度通常用来描述电磁场、引力场和其他物理场的能
量分布情况。
能量密度的计算公式取决于所研究的物质或场的性质。
对于电磁场的能量密度,其计算公式为:
\[ u = \frac{1}{2} \left( \varepsilon E^2 +
\frac{B^2}{\mu} \right) \]
其中,\( u \) 表示能量密度,\( \varepsilon \) 表示介电
常数,\( E \) 表示电场强度,\( B \) 表示磁感应强度,\( \mu \) 表示磁导率。
对于引力场的能量密度,其计算公式为:
\[ u = \frac{1}{2} \cdot \text{引力场强度}^2 \cdot
\text{引力场介质的密度} \]
这些公式提供了计算能量密度的方法,通过这些公式,我们可以了解不同物质或场的能量分布情况,从而更好地理解和研究物质的性质和行为。
磁场的能量磁场能量密度
(1)“麦克斯韦位移电流假设”
jd
D t
或者
Id
d D
dt
(2)麦克斯韦位移电流假设的实质是… … …
例1 流
有一圆形平行平板。电若容略器去,边缘效应。, 现求对(其1)R充两电极,3使板.0电间c路的m上位的移传电导流电;
(2)两极板间离开轴线的距离为的Ic点 dQ d处t 的2磁.感5A强度。
位移电流
Id
S
jd
ds
D ds
S t
t
D
ds
dΨ
D
S
dt
通过电场中某一截面的位移电流等于通过该截面电位移 通量对时间的变化率.
-
Id
+ +
-+
I - +
- +c
全电流
Is Ic Id
H dl
L
Is
Ic
d D
dt
1)全电流是连续的; 2)位移电流和传导电流一样激发磁场; 3)传导电流产生焦耳热,位移电流不产生焦耳热.
知
,求单位长度同轴电缆的磁能和自感. 设金属芯线内的磁场可略.
R1, R2 , I ,
解 由安培环路定律可求H
磁能
r R1 , H 0, B 0
R1
r
R2 ,
H
I
2r
,
B
I 2r
r R2 , H 0, B 0
则 R1 r R2 ,磁能密度
wm
1 2
BH
1 2
I
2r
2
wm
1 2
LH
dl
S1
j
ds
I
H dl
12_45磁场的能量解读

12-4 磁场能量
电磁场 麦克斯韦电磁场方程的积分形式 静电场和恒定磁场的基本方程: 静电场高斯定理 SD ds V dV q
静电场环流定理
磁场高斯定理
Hale Waihona Puke l E dl 0 B ds 0
S
安培环路定理 H dl I j ds
第十二章 电磁感应
12-4 磁场能量 一.磁场的能量
磁场能量密度
B2 1 1 2 wm H BH 2 2 2
则
已知
B2 wm 2
匀强磁场能 量 非匀强磁场 能量
Wm wmV
Wm wm dV
V V
B dV 2
2
12-4 磁场能量
麦克斯韦(1831-1879)英国物理学家 经典电磁理论的奠基人 , 气体动理论创始人之一. 提 出了有旋场和位移电流的 概念 , 建立了经典电磁理 论 , 并预言了以光速传播的 电磁波的存在. 在气体动理 论方面 , 提出了气体分子按 速率分布的统计规律.
l
S
12-4 磁场能量
(1)变化磁场激发有旋电场 Ek
麦 克 斯 韦 电 磁 场
麦克斯韦假设
dD (2)变化电场激发有旋磁场,位移电流密度 jd dt
方 程 的 积 分 形 式
q SD ds V dV B l E dl S t ds SB ds 0 D l H dl S ( jc t ) ds
电磁场能量密度分析

电磁场能量密度分析在我们生活的这个世界中,电磁场无处不在。
从手机通信到电力传输,从无线电波到X 射线,电磁场的应用涵盖了现代科技的诸多领域。
而要深入理解电磁场的性质和行为,其中一个重要的概念就是电磁场能量密度。
电磁场具有能量,这一事实是现代物理学的基本认识之一。
那么,什么是电磁场能量密度呢?简单来说,它是指单位体积内电磁场所具有的能量。
为了更清晰地理解电磁场能量密度,我们先来看看电场的能量。
当一个电荷在电场中移动时,电场会对电荷做功。
这意味着电场中存在着能量。
对于一个均匀电场 E,一个带有电荷量 q 的电荷在电场中移动距离 d,电场对电荷所做的功为 W = qEd。
而电场的能量可以通过对这个功进行积分来计算。
在一个平行板电容器中,电场强度 E 是均匀的。
假设电容器的两个极板面积为 S,间距为 d,极板间的电压为 U。
则电场强度 E = U / d,电容 C =εS / d(其中ε 是介电常数)。
电容器所储存的电能为 W =1/2 CU²=1/2 εS (U/d)² d =1/2 εE² Sd。
由于电容器的体积为 V = Sd,所以电场的能量密度为 w_e = 1/2 εE²。
接下来看看磁场的能量。
当电流通过一个线圈时,会产生磁场。
磁场也具有能量。
对于一个均匀磁场 B,一个面积为 S 的平面在磁场中转动,磁通量发生变化,从而产生感应电动势。
磁场对电流做功,这表明磁场中存在能量。
在一个充满均匀磁场 B 的空间中,假设一个长度为 l 的导体棒以速度 v 垂直于磁场运动,产生的感应电动势为 E = Blv,电流 I = E / R (R 是回路电阻)。
在时间 dt 内,外力克服安培力所做的功为 dw = I²R dt =(Blv)²/ R dt = B² l² v²/ R dt。
由于导体棒移动的距离为 dx = vdt,所以单位体积内磁场的能量为 w_m = 1/2 B²/μ(其中μ 是磁导率)。
高二物理竞赛课件:磁场的能量(共15张PPT)

磁场的能量
一、磁能的来源
LR
电流建立过程 磁场储存能量 稳态时:电源作功 = 焦耳热
当K1 电路接通
1K 2
I 增加:电源作功=反抗L作功+焦耳热
电源作功>焦耳热 有能量储存 K由12 电路断开
结论:电源 提供的能量 的一部分储 存在线圈的 磁场内。
I 减小:L作功=焦耳热
有能量放出
LI L
自感线圈也是一个储 能元件,自感系数反 映线圈储能的本领
磁场能量密度与电场能量密度公式的比较
dV
w
V 在有限区域内
磁场能量公式与电场能量公式具有完全对称的形式!
自感系数只与 装置的几何因 素和介质有关
例题2 有一同轴电缆,由半径为a和b的同轴长圆筒组 成,电流I 由内筒一端流入,经外筒的另一端流出,两
筒间充满磁导率为μ的均匀介质,求单位长度同轴电缆
的自感系数。
解:由安培环路定律可以证明
磁场只存在于两筒之间,距轴为r (a<r<b)处的磁感应强度为
ba
B I
1 2
LI 2
W 1 L I 2 1 n2V I 2 1 ( nI )2V B2 V
m2
2
2
2
磁场能量密度为: w Wm B2
m V 2
wm
B2
2
wm
1 2
BH
1 2
H2
HB
电场能量密度
磁场的能量为: Wm V wmdV
we
1 2
E2
V 是磁场分布的整个空间。
自感储能与电容储能比较
例题3 一长直螺线管,单位长度上的匝数为n,有一 半径为r的圆环放在螺线管内,环平面与管轴垂直,求 螺线管与圆环的互感系数。
§13-5磁场的能量磁场的能量密度

µ
1 1 I 则 R1 < r < R2 ,磁能密度 wm = BH = µ 2 2 2πr
2
1 I wm = µ 2 2πr
∂D jd = ∂t
或者
dψ D Id = dt
(2)麦克斯韦位移电流假设的实质是… … … 麦克斯韦位移电流假设的实质是
有一圆形平行平板电容器, 现对其充电, 例1 有一圆形平行平板电容器, R = 3.0cm。现对其充电, 使电路上的传导电流 I c = d Q d t = 2 . 5 A 。若略去边缘 效应, 两极板间的位移电流; 效应, 求(1)两极板间的位移电流; (2)两极板间离开轴线的距离为的点 r = 2 .0 cm 处 P 的磁感强度。 的磁感强度。
c= 1 = 1 8 .85 × 10 −12 ⋅ 4π × 10 − 7 = 2 .9994 实了他的预言。 1888年赫兹的实验证实了他的预言。麦克斯韦 年赫兹的实验证实了他的预言 理论奠定了经典动力学的基础, 理论奠定了经典动力学的基础,为无线电技术和现 代电子通讯技术发展开辟了广阔前景。 代电子通讯技术发展开辟了广阔前景。
135磁场的能量磁场的能量密度电磁场的平均能量密度磁场的能量密度磁场能量密度电磁场能量密度磁场能量密度公式磁场强度磁通密度磁场强度电流密度开关变压器磁场密度磁通密度和磁场强度
§13-5 磁场的能量 磁场的能量密度 13右电路, 右电路,全电路欧姆定律
ε
t
Idt − LI dI = RI 2 dt ε
5的磁场能量

5的磁场能量
磁场能量的大小与磁场强度(B)以及物体所处位置的磁感应强度(H)有着密切的关系。
在磁场中,物体所具有的磁场能量可以通过计
算得到。
对于给定的一个闭合回路,其单位长度的磁场能量(w)可以表示
为磁场强度(B)与磁感应强度(H)的乘积,即w=BH。
这一关系式表明,磁场能量的大小与磁场强度及磁感应强度间存在着线性关系。
在磁力线被称为磁感线的空间中,磁感应强度(H)与磁场强度(B)具有一定的关系,即B=μ0H,其中μ0为真空中的磁导率,具有一个常量值。
由此可知,磁场能量与磁场强度以及磁感应强度间的关
系可以写为w=μ0B²。
在磁场中,物体的磁场能量与其形状、大小以及材料的参数也有关。
对于一个长直导线所产生的磁场而言,其单位长度的磁场能量(w)可以通过计算得到,w=μ0I²/(2πr),其中μ0为真空中的磁导率,I
为电流强度,r为距离导线轴线的距离。
对于一个螺线管,其磁场能量的计算较为复杂,但同样可以得到
一个与磁场强度及磁感应强度相关的关系。
总的来说,磁场能量的计算与磁场强度(B)、磁感应强度(H)
以及物体的形状和参数等因素息息相关。
在具体的应用中,可以通过
对磁场的物理量进行合理的计算和分析,来得到磁场能量大小的准确
结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2 自感磁能 W 1 = LI10 L 2
ε M12 I1
εL2 I2
I10时要克 服自感电动势作 功,即自感电动 势作负功, 势作负功,变为
WL2 =
2
LI
2 20
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
2)维持线圈“1”中电流不变,让线圈“2”中电 )维持线圈“ 中电流不变 让线圈“ 中电 中电流不变, 流由0 I20 流由
W'm = W ∴M12 = M21 m
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
按照磁场的近距作用观点, 按照磁场的近距作用观点,磁 能也是定域在磁场中的。 能也是定域在磁场中的。 可以引入磁场能量密度的概念。 可以引入磁场能量密度的概念。 以载流长直螺线管为例: 以载流长直螺线管为例:
1 1 2 Wm = µH V体 = BHV体 2 2
W m 能量密度w 单位体积内的磁场能量): m 能量密度 m(单位体积内的磁场能量): w = 单位体积内的磁场能量 V体 2 Wm B 1 2 1 ∴wm = = µH = BH = V体 2 µ 2 2
12 – 5 磁场的能量 磁场能量密度
电源所 作的功 自感线圈磁能
电源克服自 电阻上的 感电动势所 热损耗 做的功
Wm
ห้องสมุดไป่ตู้
1 2 = LI 0 2
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
2、 考察在开关断开后的一 段时间内, 段时间内,电路中的电流衰 过程: 减过程: 由全电路欧姆定律
L
电池
R
ε L = IR →ε LI = I 2 R
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
三、互感磁能 L1 M L2 “1” “2”
初始状态: 初始状态: I1 = 0 I2 = 0 稳定状态: 稳定状态:
I1
I2 I1 = I10 I2 = I20
显然: 显然:互感电路中的磁能是克服自感电动势及 互感电动势作功的过程中建立的。 互感电动势作功的过程中建立的。
2
第十二章电磁感应 第十二章电磁感应 电磁场
B 1 1 2 ∴ wm = = µH = BH 2µ 2 2
可以证明它对磁场是普遍成立的。 可以证明它对磁场是普遍成立的。 对非均匀磁场
dW 1 m w = = B⋅ H m dV 2
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
L1 M L2 “1” “2”
能量是状态量,应与电流建立的过程无关。 能量是状态量,应与电流建立的过程无关。为此 分两步建立磁场。 分两步建立磁场。
1)线圈“2”开路,让线圈“1”中电流由0 线圈“2”开路,让线圈“1”中电流由 开路 I10 维持线圈“1”中电流不变 让线圈“2”中电 中电流不变, 2)维持线圈“1”中电流不变,让线圈“2”中电 流由0 流由0 I
r < R1 ,
H =0
µ µ
R2
I R1 < r < R2 , H = 2π r
r > R2 , H = 0
R1 < r < R2
则
1 1 I 2 2 ) wm = µH = µ ( 2 2π r 2
12 – 5 磁场的能量 磁场能量密度
Wm = ∫ wm dV = ∫
V
1 R1 < r < R2 wm = µ ( 2 2π r 2 µI
1 2 说明: 说明:载流线圈的磁场能量可以用公式 W自 = LI , 2
也可以用磁场能量密度公式对空间求积分计算。 也可以用磁场能量密度公式对空间求积分计算。在已 知自感系数的情况下,应用第一种公式计算较为简单。 知自感系数的情况下,应用第一种公式计算较为简单。
12 – 5 磁场的能量 磁场能量密度
V
第十二章电磁感应 第十二章电磁感应 电磁场 2 I 2 µI ) = 2 2
8π r
8π r
2 2
dV
单位长度壳层体积
d V = 2π r d r ⋅ 1 2 R2 µI µ I 2 R2 ln Wm = ∫ dr = R1 4 π r 4π R1
µ
r dr
R2
µ R2 1 2 ln Wm = LI L = 2 π R1 2
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
1 2 1 2 W 1 = LI10 WL2 = LI20 L 2 2 W = M12I10I20 互
互感线圈的总磁能: 互感线圈的总磁能:
1 1 2 2 Wm = L I10 + L I20 + M12I10I20 ⋯ 1) ( 1 2 2 2
1 2 1 2 W 1 = LI10 W 2 = LI20 L L 2 2
I10克服 εM12 作功: 作功:
dI2 I10dt A = ∫ − ε M12 I10dt = ∫ − M12 dt
= −M12I10 ∫
建立互感磁能
I20 0
dI2 = −M12I10I20
W = M12I10I20 互
第十二章电磁感应 第十二章电磁感应 电磁场
如图同轴电缆,中间充以磁介质 中间充以磁介质,芯线与圆筒上的 例 如图同轴电缆 中间充以磁介质 芯线与圆筒上的 电流大小相等、方向相反. 电流大小相等、方向相反 已知 R 1 , R 2 , I , µ , 求单位 长度同轴电缆的磁能和自感. 设金属芯线内的磁场可略. 长度同轴电缆的磁能和自感 设金属芯线内的磁场可略 解 由安培环路定律可求 H
ε
BATTER Y
两边同时对时间进行积分 0 dI 1 2 左边积分: 左边积分: LIdt = ∫ − L dt = ∫ − LIdI = LI0 ∫ε I0 dt 2 为自感线圈提供的能量 t 1 2 1 2 右边积分: 右边积分:I Rdt = LI0 为电路所消耗的焦耳热 自感线圈磁能 W m = LI 02 ∫0 2 2
建立电流的方式也可反过来: 建立电流的方式也可反过来: 1)线圈“1”开路,让线圈“2”中电流由 I20 )线圈“ 开路 让线圈“ 中电流由 开路, 中电流由0 2)维持线圈“2”中电流不变,让线圈“1”中电 中电流不变, )维持线圈“ 中电流不变 让线圈“ 中电 流由0 I10 流由
12 – 5 磁场的能量 磁场能量密度
ε L + ε = IR →ε LI + εI = I 2 R
dI → ε I − LI = I 2R dt
dI → εI = LI + I 2R dt
两边同时积分: 两边同时积分:
∫
∞
0
Iεdt = ∫
I0
0
∞ t 1 2 dI = LI + ∫ I 2 Rdt L Idt + ∫ IRIdt 0 0 2 dt
i
K E R
若电流衰减过程 L
εL
磁场能量→ R焦耳热
二、自感磁能 1、 考察在开关合上后的一
L
R
段时间内, 段时间内,电路中的电流滋 长过程: 长过程: 由全电路欧姆定律
ε
BATTER Y
电池
ε L + ε = IR
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
20
I1
I2
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
1)线圈“2”开路,让线圈“1”中电流由0 线圈“2”开路,让线圈“1”中电流由 开路
L1 M L2
I10
ε L1
I1由0
2)维持线圈“1”中电流不变,让线圈“2”中电 )维持线圈“ 中电流不变 让线圈“ 中电 中电流不变, 流由0 I20 要克服自感电动势 εL2作功, 作功, 流由 同时为维持I10不变,I10要克服 εM12作功 同时为维持 不变, 前者建立互感磁能 1
2
2µ
V体
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场 l
B = µH
上式还可以写成: 由 上式还可以写成:
µ
S n I
磁场的能量只与磁场和磁场分布的空间有关。 磁场的能量只与磁场和磁场分布的空间有关。 内的总能量, 磁场能量只能反映空间体积 V 内的总能量,不能 反映磁场的能量分布情况。 反映磁场的能量分布情况。须引入描写磁场分布的物 理量----能量密度。 理量 能量密度。 能量密度
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
一、一般讨论
K ε
R
对纯电阻电路
ε做功→ R,焦耳热
i
K E R
若加一线圈, 若加一线圈,如电流滋长过程
εL
L ε提供的能量
→ 焦耳热+ 磁场能量
12 – 5 磁场的能量 磁场能量密度
第十二章电磁感应 第十二章电磁感应 电磁场
由能量密度计算任意一个磁场的能量: 由能量密度计算任意一个磁场的能量: 1)先确定体积元内的磁场能量, )先确定体积元内的磁场能量,
dWm = wmdV体
2).再计算体积 ) 再计算体积 再计算体积V体内的磁场能量, 内的磁场能量, 内的磁场能量
Wm = ∫V dW = ∫V wmdV m 体
积分应遍及磁场 存在的全空间。 存在的全空间。
l
µ
S I
