建筑施工工程-静定梁受力分析
(工程力学)第11章静定结构受力分析

q
ql
l l 2l q
ql
ql ql
2 ql 2
q
ql 2
A
B
Q AB
Q BA
MA0 QBA1q1/l4
FY0 QAB5q/l4
4l
2l l l
1 ql
2
ql
1 ql 2
例: 作内力图 ql
q
ql
l l 2l
4l
2l l l
ql
q
1 ql
2
ql
内力计ql q算l 的关键在于: 正确区分ql 2 基本部分和ql 2 附
例:求跨中截面内力
q
A
FAx
C
l
F Ay
解: FAx 0,FAy ql/2(),
FBy ql/2()BFra bibliotekFx 0, NC 0
F By
Fy
0,Q C
0
Mc 0, MC ql2 / 8
(下侧受拉)
3.作内力图的基本方法 内力方程式:
M M ( x ) 弯矩方程式
例:作图示粱内力图
q A
Q Q ( x ) 剪力方程式 N N ( x ) 轴力方程式 B 解: FAx 0,FAy ql/2(),
NdN
微分关系: dQ(x) / dx q(x)
Q(x)
Q dQ
截面弯矩dx等于该截面一
dM(x) / dx Q(x) 侧的所有外力对该截面
的力矩之和
d 2M(x) / dx2 q(x)
1.无荷载分布段(q=0),Q图 Pl 为水平线,M图为斜直线. M图
自由端无外力偶
则无弯矩.
Q图
例: 作内力图
Q图 力偶
结构力学I-第三章 静定结构的受力分析(梁、刚架)

14:32
LOGO
梁的内力计算的回顾
FQ FN M0 Fx O FQ+ ΔFQ FN+ ΔFN M+ ΔM δ(x) x
直杆增量关系
增量关系
FN Fx FQ Fy M M 0
*另一种表述
M
Fy
y
dFN qx dx dFQ qy dx dM FQ dx
MA
FB=12 kN
ME m, 20KN
q
M D 18KN m,
M E 26KN m, 区段叠加法,
L M并可求出: 。 B 16KN m
MF
M F 18KN m,
F sE 3. 作弯矩图以及剪力图
L MG 6KN m,
Page 21
R MG 4KN m,
绘制: 1 由内力方程式画出图形; 2 利用微分关系画出图形。
直杆微分关系
dFN qx dx dFQ q y dx dM FQ m dx
FQ FN
qy FQ+ dFQ
m qx O FN+ dFN M+ dM x
M
y
dx
集中力怎么办?
Page 14
计算思路:从刚片出发、从结点出发;
平面几何不变体系的组成规律 三角形规律:二元体(两杆一铰)、两刚片、三刚片; 灵活运用 撤去二元体,几何不变—>大刚片,虚铰选择,三刚片选择
Page 1
LOGO
第二章 结构的几何构造分析
回顾
灵活应用:虚铰、刚片的选择、无穷远处虚铰特性;
无多不变
3 能否运用三刚片规则?
第四次课——第03章 静定结构受力分析(1)——静定梁

层次图
32 / 51
第三章 静定结构受力分析
第二节 多跨静定梁的计算
1. 多跨静定梁的组成 2. 构造特点
由若干单跨梁通过铰连接而成,并由若干支座与基 础连接而组成的静定梁,是桥梁和屋盖系统中常用 的一种结构形式。
3. 组成顺序
基本部分 附属部分
层次图
33 / 51
第三章 静定结构受力分析
1 / 51
第三章 静定结构受力分析
第一节 单跨静定梁的计算
1、截面法求截面内力 内力定义 轴力= 横截面上应力沿轴切线方向投影的代数和。 剪力= 横截面上应力沿轴法线方向投影的代数和。 弯矩= 横截面上应力对轴心力矩的代数和。 内力正负号规定
FN FN
FN FN
FQ
FQ
FQ FQ
第二节 多跨静定梁的计算
1. 2. 3. 4. 多跨静定梁的组成 构造特点 组成顺序 传力关系
• 力作用在基本部分上时,仅在自身上产生内力和弹性 变形,附属部分不受力,但可以有刚体位移 • 力作用在附属部分上时,可使自身和基本部分上均产 生内力和弹性变形 • 力的传力顺序与组成顺序相反。
34 / 51
第一节 单跨静定梁的计算
1、截面法求截面内力 2、内力与荷载之关系 • 积分关系
FP
q
MAB A FQAB
B
m
B
MBA
FQBA
B 端剪力等于A 端 剪力减去该段荷载 q 图的面积,再减 去集中力的和。 B 端弯矩等于A 端 弯矩加上该段剪力 图的面积,再加上 集中力偶的和。
10 / 51
FQBA FQAB q( x)dx FPi
15 17
最新多跨静定连续梁受力分析

Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=6
MA6=-(Pi*Ai+qAi2/2),(i=6)
第7跨内力分析:
Pi=RBi-1,i=7
RBi=qLi*[1-(Ai/Li)2]/2-Pi*(Ai/Li),i=7
第5跨内力分析:
Pi=RBi-1,i=5
RBi=qLi*[1-(Ai/Li)2]/2-Pi*(Ai/Li),i=5
Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=5
MA5=-(Pi*Ai+qAi2/2),(i=5)
第6跨内力分析:
Pi=RBi-1,i=6
Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=2
MA2=-(Pi*Ai+qAi2/2),(i=2)
第3跨内力分析:
Pi=RBi-1,i=3
RBi=qLi*[1-(Ai/Li)2]/2-Pi*(Ai/Li),i=3
Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=3
MA3=-(Pi*Ai+qAi2/2),(i=3)
第4跨内力分析:
Pi=RBi-1,i=4
RBi=qLi*[1-(Ai/Li)2]/2-Pi*(Ai/Li),i=4
Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=4
建筑力学静定刚架

力的平衡原理是指刚架在力的作用下,各部分所受的力矩和力系平衡,即没有 外力矩作用时,刚架不会发生转动或移动。这个原理是静定刚架受力分析的基 础,通过力的平衡原理可以推导出刚架的内力和变形。
力的分布与传递
总结词
力的分布与传递是静定刚架受力分析的重要内容,它涉及到力的分布规律和传递 路径。
详细描述
选择截面
根据刚架的承载能力和稳 定性要求,选择合适的截 面尺寸和形状,如矩形、 工字形等。
确定高度
根据刚架的跨度和承载能 力要求,确定合适的高度, 以保证刚架的稳定性和承 载能力。
刚架的材料选择
钢材
钢材具有较高的强度和刚度,适 用于承受较大载荷的刚架。
铝合金
铝合金具有轻便、耐腐蚀等优点, 适用于需要减轻结构重量的刚架。
在静定刚架中,力的分布与传递是相互关联的。力的分布规律是指力在刚架各部 分之间的分配情况,而力的传递路径则是指力从一端传递到另一端的路径。通过 分析力的分布与传递,可以确定刚架各部分的受力状态和内力分布。
刚架的弯矩与剪力
总结词
弯矩与剪力是静定刚架受力分析的关键因素,它们决定了刚架的变形和应力分布。
截面ห้องสมุดไป่ตู้寸等。
04
静定刚架的施工与安装
施工前的准备
场地勘察
对施工现场进行实地勘察,了解地形、地质、水 文等条件,以便制定合理的施工方案。
设计审查
仔细审查静定刚架的设计图纸,确保设计符合规 范要求,并明确各部位的结构特点和施工要求。
材料采购
根据设计要求和施工需要,采购合格的钢材、连 接件等材料,并确保材料质量符合标准。
稳定性好
由于静定刚架的各部分之间都是刚性连接,没有相对位移,因此 其稳定性较好,能够承受较大的外力作用。
结构力学 第3章静 定梁、平面刚架受力分析

q 与 q’间的转换关系:
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
(1)求支座反力:
解:
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核:
Y
qj 6
qj 6
ql 3
0
第3章
(2)AC段受力图:
(3)AD段受力图:
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
(1)在无荷区段q(x)=0,剪力图为水平直线,弯矩图为斜直线。
(2)在q(x)=常量段,剪力图为斜直线,弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
(3)集中力作用点两侧,剪力值有突变、弯矩图形成尖点;集中力偶作用点两 侧,弯矩值突变、剪力值无变化。
解:
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
(1)计算支座反力
静定结构的内力分析

静定结构的内力分析-建筑结构
一级注册建筑师
静定结构按其受力特性,可以分为静定梁、静定刚架、三铰拱、静定桁架和静定组合结构。
一、静定梁
1 .截面内力分量及正负号规定
平面杆件的任一截面上一般有三个内力分量:轴力N ,剪力Q 和弯矩M 。
内力的正负号一般规定为:
(1 )轴力以受拉为正;
(2 )剪力以绕隔离体顺时针方向为正;
( 3 )弯矩一般不规定正负号(对水平梁通常以使梁的下侧受拉为正)。
内力图一般以杆轴为基线绘制。
弯矩图规定画在杆件的受拉侧,无需标明正负号;剪力图和轴力图则可画在杆件的任一侧(对水平杆件通常将正的剪力和轴力绘于杆件上侧),但需标明正负号。
2 .截面法
截面法是结构内力分析的基本方法。
截面法计算结构内力的基本步骤为:
(1)将结构沿拟求内力的截面切开。
(2)取截面任一侧的部分为隔离体,作出隔离体的受力图;受力图中的力包括两部分:外荷载和截断约束处的约束力(截面内力或支座反力),未知截面内力一般假设为正号方向。
(3)利用静力平衡条件计算所求内力。
对于平面结构,一般情况下隔离体上的各力组成一平面任意力系,故有三个独立的平衡方程(投影方程或力矩方程):
或
特殊情况下,例如截取的是一个铰节点,则各丸组成一平面汇交力系,故有两个独立的投影平衡方程:
本篇文章来源于《中国注册建筑师考试网》。
《静定梁与静定刚架》课件

根据刚架的受力特点,合理分布材 料,使材料得到充分利用,降低成 本。
注意事项
注意梁的挠度和侧弯
根据载荷大小和分布,合理选择截面尺寸和材料,以控制梁的挠度和侧弯在允许 范围内。
考虑施工条件限制
在设计和施工过程中,应充分考虑施工条件限制,如施工空间、吊装能力等。
注意事项
• 注意载荷变化的影响:载荷的大小和分布可能会 发生变化,应在设计时充分考虑这些因素对梁的 影响。
静定刚架的应用实例
工业厂房
静定刚架在工业厂房中应用广泛,如厂房的柱、梁、支撑等 结构,能够承受较大的荷载,保证厂房的正常运行。
设备支撑
在大型设备或机械的支撑结构中,静定刚架也得到了广泛应 用,能够提供稳定可靠的支撑,确保设备的正常运行和使用 寿命。
静定梁与静定刚架的比较与选择
受力特点
静定梁和静定刚架在受力特点上有所不同。静定梁主要承受弯矩和剪力作用,而静定刚架 则主要承受轴力和弯矩作用。因此,在选择时需要根据实际需求和受力特点进行比较。
静定梁在受力时,其支座反力的 大小和方向可以通过截面的平衡
条件求出。
静定梁的内力计算
静定梁的内力计算可以通过截面的平衡条件进行,不需要引入未知数和求解方程组 。
静定梁的内力包括剪力和弯矩,可以通过截面的平衡条件求出剪力和弯矩的大小和 方向。
静定梁的内力计算可以通过手算或使用计算软件进行,手算需要掌握截面的平衡条 件和内力的计算方法。
BIG DATA EMPOWERS TO CREATE A NEW ERA
04
静定梁与静定刚架的应用实例
静定梁的应用实例
桥梁结构
静定梁广泛应用于桥梁设计中,如简 支梁桥、连续梁桥等,具有结构简单 、受力明确、施工方便等优点。
静定梁和刚架内力分析

(0<x<l ) (0≤x<l)
M
(-)
(c)
x
2.作剪力图和弯矩图:
由剪力方程可知,当 0 <x <l,时(即 AB 段上),剪力为 常数,因此剪力图为一条水平的直线;由弯矩方程可知,AB 梁段上沿着轴线方向弯矩呈线性变化,因此,弯矩图为一条斜 直线,只需求出两个端截面上
F A FQ x m m l
在列平衡方程求解内力时,需事先确定截面内力的方向, 而此时截面内力为未知力,因此,一般假定截面内力沿其正向 作用,则计算得到的正负号就是该截面内力的正负号。 另外,在利用截面法求解前,通常先确定支座反力,因支 座反力并无正负规定,在求支反力前可任意假设正方向。
若结果为正,则表示支反力实际方向与假设方向相同;
上所有外力对该截面形心的力矩的代数和。
其中外力对横截面形心之矩正负号选取规律为: (1)力——不论横截面左侧还是右侧,只要向上就取正,
反之取负;
(2)力偶——横截面左侧顺时针或右侧逆时针取正,反之 取负。 利用上述结论,可以不画分离体的受力图、不列平衡方 程,直接得出横截面的剪力和弯矩。这种方法称为直接法。 直接法将在以后求指定截面内力中被广泛使用。
2
求梁指定截面上的内力的方法: 剪力:梁任一横截面上的剪力在数值上等于该截面一侧梁段 上所有外力在平行于截面方向投影的代数和。 其中外力正负号选取规律为: 横截面左侧梁段上向上的外力取正,横截面右侧梁段上
向下的外力取正;反之取负。
简记为左上右下取正,反之取负。
弯矩:梁任一横截面上的弯矩在数值上等于该截面一侧梁段
若外力或外力偶矩使所考虑的梁段产生向下凸的变形(即 上部受压,下部受拉)时,等式右方取正号,反之,取负号。 此规律可简化记为“下凸弯矩正”或“左顺,右逆弯矩 正” ,相反为负。
3静定结构的受力分析-梁结构力学

1 结构力学多媒体课件◆几何特性:无多余约束的几何不变体系◆静力特征:仅由静力平衡条件可求全部反力和内力◆常见静定结构:梁、刚架、三铰拱、桁架和组合结构。
◆静定结构受力分析的内容:反力和内力的计算,内力图的绘制和受力性能分析。
◆静定结构受力分析的基本方法:选取脱离体,建立平衡方程。
◆注意静力分析(拆)与构造分析(搭)的联系◆学习中应注意的问题:多思考,勤动手。
本章是后面学习的基础,十分重要,要熟练掌握!容易产生的错误认识:“静定结构内力分析无非就是选取隔离体,建立平衡方程,以前早就学过了,没有新东西”一、反力的计算4kN1kN/mDCBA2m2m 4mCB A20kN/m 4m4m2m6mDCB A(1)上部结构与基础的联系为3个时,对整体利用3个平衡方程,就可求得反力。
(2)上部结构与基础的联系多于三个时,不仅要对 整体建立平衡方程,而且必须把结构打开, 取隔离体补充方程。
1、内力分量及正负规定轴力F N :截面上应力沿杆轴法线方向的合力。
以拉力为正,压力为负。
剪力F Q :截面上应力沿杆轴切线方向的合力。
以绕隔离体顺时针转为正,反之为负。
弯矩M :截面应力对截面中性轴的力矩。
不规定正负,但弯矩图画在受拉侧。
在水平杆中, 当弯矩使杆件下部纤维受拉时为正。
A 端B 端杆端内力 F Q ABF N ABM AB正 F N BA F Q BAM BA 正2、内力的计算方法K截面法:截开、代替、平衡。
内力的直接算式(截面内力代数和法)=截面一边所有外力沿截面法线方向投影的代数和。
轴力FN外力背离截面投影取正,反之取负。
剪力F=截面一边所有外力沿截面切线方向投影代数和。
Q外力绕截面形心顺时针转动,投影取正,反之取负。
弯矩M =截面一边所有外力对截面形心的外力矩之和。
外力矩和弯矩使杆同侧受拉时取正,反之取负。
2、内力的计算方法【例】如图所示简支梁,计算截面C 、D 1、D 2的内力。
2m 4m 2mA2kN/mCBD 1 D 210kN0.2m10kN3.75kN0.25kN3、绘制内力图的规定内力图是表示结构上各截面的内力各杆件轴线分布规律的图形, 作图规定:弯矩图一律绘在受拉纤维一侧,图上不注明正负号;剪力图和轴力图可绘在杆轴线的任一侧(对水平杆件通常把正号的剪力和轴力绘于上方),但必须注明正负号,且正负不能绘在同一侧。
结构力学静定梁的内力分析

(d)
M M M FQdx m 0
M m
(e)
以上两式,为荷载与内力的增量 关系。式(e)忽略了一阶微量。
增量关系的几 何意义
在集中力作用点(集中力垂直 与杆轴或有垂直于杆轴的分量) 两侧截面,剪力有突变,突变 值即为该集中力或垂直于杆轴 的分量;弯矩相同。
在集中力偶作用截面两侧,弯矩 有突变,突变值即为该集中力偶; 剪力相同。
a
M
0
M1
1 2
qa 2
FAy a
M
用文字写 明受拉侧
取截面1右侧为隔离体 计算可得同样结果
3.直接法求指定 截面的内力
由例3-1-1内力计算结果 分析,指定截面的内力可 用该截面一侧的外力直接 表示,即:
轴力 (FN)
截面一侧所有外力在指定 截面法线方向投影的代数 和,以与截面外法线方向 相反为正。
剪力 (FQ)
截面一侧所有外力在指定 截面切线方向投影的代数 和,左上、右下为正。
弯矩(M)
截面一侧所有外力对 指定截面形心力矩的 代数和。
例3-1-2 用直接法,求例 3-1-1图(a)所示伸臂梁截 面2上的内力。
M
(a)
解
支座反力计算同例3-1-1。内力 可由右图所示受力图直接计算:
M
F A x F A y
3a 2
FP
4 5
a
(↓)
(箭头标出 实际方向)
MA 0
FBy
3a
M
q 3a
3a 2
FP
4 5
4a
0
(↑) FBy
1 M 3a
q 3a
3a 2
FP
4 4a 5
箭头标出实 际方向
静定结构的受力分析

M A 0KN m
M B 17KN m
M C 26KN m
M E 30KN m
M
L F
23KN
m
M
R F
7KN
m
M G 0KN m
依次在M图上定出各控制点旳弯矩值,在AB、 BC、EF和FG各段以等直线连接。CE段有均 布荷载,须叠加上以CE为跨度旳简支梁在均 布荷载作用下旳弯矩图。经过计算D点旳弯矩 为36KN.m
❖ 选用隔离体
FNDB
A 5kN
FQDB MDB D2
D1
FQDA
5kN
MDA
B
FNDA
4kN
A FQDC 5kN
D3 FNDC MDC
5kN B
4kN
❖ 分别对隔离体应用平衡条件,可得内力如下:
FNDA FQDA
0 5kN
M DA 5kN m
左侧受拉
FNDB 4kN FQDB 5kN M DB 15kN m
B
43FP
A FP
4
FP.a
4
FP
4
FPa
弯矩图
F
E
剪力图
FE
-
FP
DC
Fpa
FP
2
2
+
C
D
Fpa
4
A B
BA
-
FP
4
内力计算旳关键在于: 正确区别基本部分和附
属部分. 熟练掌握单跨梁旳计算.
例:试求铰D旳位置,使正负弯矩峰值相等。
q
A
D
B
l-x
x
l
C l
❖ 先求得支座反力为 q(l x)
静定结构内力分析-1静定梁

解: RD = q(l − x) / 2(↑)
M B = qx 2 / 2 + q(l − x) x / 2
M B = 0.086ql 2
q(l − x) 2 / 8 = qx 2 / 2 + q(l − x) x / 2
q
0.086ql 2
x = 0.172l
0.086ql 2 l
x
q
0.086ql 2 l
第2章
静定结构受力分析
§2-1 静定梁受力分析
一.单跨梁 单跨梁
1.单跨梁支座反力 单跨梁支座反力
§2-1 静定梁受力分析
一.单跨梁 单跨梁
1.单跨梁支座反力 单跨梁支座反力 例.求图示梁支座反力 求图示梁支座反力 解:
∑F ∑F ∑m
X
= )
F Ax A MA
例: 作内力图
q A B l l C
q l 2 /2 M图 ql ql/2 FQ图
(1)无荷载分布段(q=0), FQ 图为水平线,M图为斜直线. (1)无荷载分布段 无荷载分布段( 图为水平线, 图为斜直线. (2)均布荷载段(q=常数), FQ 图为斜直线,M图为抛物线, (2)均布荷载段 常数), 均布荷载段( 图为斜直线, 图为抛物线, 且凸向与荷载指向相同. 且凸向与荷载指向相同. (3)集中力作用处, FQ 图有突变,且突变量等于力值; M (3)集中力作用处 集中力作用处, 图有突变,且突变量等于力值; 图有尖点,且指向与荷载相同. 图有尖点,且指向与荷载相同.
l/2
l
M
M
l
练习: 练习: 利用微分关系等作弯矩图
1 FPl 2
l
1 FPl 4
FP
l/2
静定结构受力分析

详细描述
剪切位移的大小与外力的大小和结构的抗剪 刚度有关。在静定结构中,剪切位移可以通 过测量结构上两点之间的相对位移来计算。
影响因素
影响剪切位移的因素包括外力的大小 、结构的剪切面面积、材料的剪切模 量和截面的剪切面面积等。
扭转变位移计算
扭转变位移是由于结构受到扭矩作用而产生的扭转变 形,导致结构在扭转变形方向上发生相对位移。
ቤተ መጻሕፍቲ ባይዱ
剪切内力计算
剪切内力
由于剪切力作用产生的内力。
剪切力的计算
根据外力的大小和方向,通过 力的平衡条件计算剪切力。
剪切变形的特点
剪切变形主要表现为相邻部分之 间的相对错动,其变形量与材料 的性质和剪切力的大小有关。
剪切承载能力的分析
根据材料的剪切强度指标,分 析结构的剪切承载能力,确保
结构的安全性。
扭转变形内力计算
弯曲位移计算
总结词
弯曲位移是由于结构受到垂直于轴线的力而产生的弯曲变 形,导致结构轴线发生弯曲。
公式
弯曲位移的公式通常为 Δ=F*L^2/(4*EI),其中 F 是外力 ,L 是跨度,E 是材料的弹性模量,I 是截面的惯性矩。
详细描述
弯曲位移通常通过测量结构上两点之间的直线距离变化来 计算。在静定结构中,弯曲位移的大小与外力的大小和结 构的抗弯刚度有关。
02
它涉及到结构力学、材料力学、 弹性力学等多个学科领域,是工 程设计和施工中的基础性工作。
静定结构的定义与特点
静定结构是指在没有外力作用下,能够 保持平衡状态的结构。
静定结构的特点包括:没有多余的约束 ,所有约束都是必要的;在受到外力作 用时,只产生与外力等值反向的位移; 在去掉约束后,不会产生多余的自由度
第三章静定结构受力分析

内力的概念和表示在平面杆件的任意截面上,将内力一般分为三个分量:轴力F N 、剪力F Q 和弯矩MM A轴力----截面上应力沿杆轴切线方向的合力。
轴力以拉力为正。
剪力----截面上应力沿杆轴法线方向的合力。
剪力以绕微段隔离体顺时针转者为正。
内力的概念和表示弯矩----截面上应力对截面形心的力矩。
在水平杆件中,当弯矩使杆件下部受拉时,弯矩为正。
作图时,轴力图和剪力图要注明正负号,弯矩图规定画在杆件受拉的一侧,不用注明正负号。
内力的计算方法梁的内力的计算方法主要采用截面法。
截面法可用“截开、代替、平衡”六个字来描述:1.截开----在所求内力的截面处截开,任取一部分作为隔离体;隔离体与其周围的约束要全部截断。
2.代替----用截面内力代替该截面的应力之和;用相应的约束力代替截断约束。
3.平衡----利用隔离体的平衡条件,确定该截面的内力。
内力的计算方法利用截面法可得出以下结论:1.轴力等于截面一边的所有外力沿杆轴切线方向的投影代数和;2.剪力等于截面一边所有外力沿杆轴法线方向的投影代数和;3.弯矩等于截面一边所有外力对截面形心力矩的代数和。
以上结论是解决静定结构内力的关键和规律,应熟练掌握和应用。
分段叠加法画弯矩图1.叠加原理:几个力对杆件的作用效果,等于每一个力单独作用效果的总和。
= +=+2.分段叠加原理:上述叠加法同样可用于绘制结构中任意直杆段的弯矩图。
例例:下图为一简支梁,AB段的弯矩可以用叠加法进行计算。
(1)(2)(3)(4)静定多跨连续梁的实例现实生活中,一些梁是由几根短梁用榫接相连而成,在力学中可以将榫接简化成铰约束,这样由几个单跨梁组成几何不变体系,称作为静定多跨连续梁。
下图为简化的静定多跨连续梁。
静定多跨梁的受力特点结构特点:图中AB依靠自身就能保持其几何不变性的部分称为基本部分,如图中AB;而必须依靠基本部分才能维持其几何不变性的部分称为附属部分,如图中CD。
受力特点:作用在基本部分的力不影响附属部分,作用在附属部分的力反过来影响基本部分。
梁的受力分析及静态试验1

第一章绪论LI引言随着现代社会的进展,经济的提高和科技的进步,我们我国的土木工程建设项目正处于新的高潮期,重大的工程结构,如超大跨桥梁、超高层建筑、大型场馆和大型水利工程等正在不断建成,桥梁工程的进展如今更是突飞猛进。
梁是由支座支撑的主要承受弯矩和剪力的构件。
在机械,建筑等工程中存在大量受弯曲的杆件,例如起重机大梁,火车轮轴等,主要承受的外力以横向力为主。
社会的飞速进展给人们带来了诸多的便利,同时,也使我们我国的建筑土木行业得到了空前的进展,在建筑结构中,不管从它的承载力还是构造等,梁的地位显得尤为重要,由于在建筑结构中,梁是最具有典型特征的元素,它以多种形态展现在人们面前,以线性受力体系为主要的特征。
1. 2国内外梁受力分析讨论的现状20世纪以来,世界各地也相继兴建了很多以斜拉桥、悬索桥为主的大跨桥粱结构。
斜拉桥的主跨也从当时的100米左右进展到了现在的上千米。
90年月到现在,仅我们我国建筑的主跨在400米以上的斜拉桥也已有几十座。
现在世界上跨度超过IOOO米的悬索桥则更是不计其数。
由于这些大跨桥梁不仅可以满意更大流量的交通要求,并且造型轻快美观。
一般都是作为城市交通运输的重要枢纽工程和标志性建筑,投资特别巨大,对国民经济持续、稳定的进展有着特别重要的作用,这些结构假如一旦发生损坏,就会造成特别重大的人员伤亡和经济损失,并且也会产生极坏的社会影响,桥梁损坏造成的严峻损失也将是难以估量的。
桥梁在长期运营过程中也不行避开的会受到环境和有害化学物质的侵蚀,并要承受车辆,风暴、地震、破坏、爆炸、疲惫等因素的作用,这些因素使桥梁的自身性能不断退化,从而导致结构的各部分在没有达到设计年限就发生不同程度的损伤和劣化。
其中,循环荷载作用下的疲惫损伤累积和有损结构在动力荷载作用下的裂纹失稳扩展是造成很多桥梁发生灾难性事故的主要缘由,据美国土木工程协会(ASCE)统计斟,80%〜90%钢结构的破坏与疲惫损伤有关。
第3章_静定结构的内力分析
静定结构受力分析
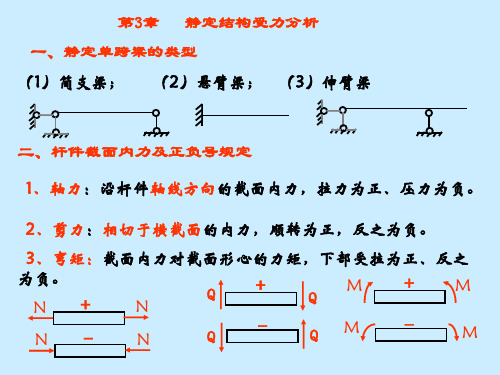
一、静定单跨梁的类型
(1)简支梁;
(2)悬臂梁; (3)伸臂梁
二、杆件截面内力及正负号规定 1、轴力:沿杆件轴线方向的截面内力,拉力为正、压力为负。 2、剪力:相切于横截面的内力,顺转为正,反之为负。
3、弯矩:截面内力对截面形心的力矩,下部受拉为正、反之 为负。 + + M M Q Q + N N - - M M Q Q - N N
C 60
B
叠加法绘制直杆弯矩图 一、简支梁弯矩图的叠加方法
MA
A
q L
MB
B
MA
MAB中 1 qL2 MB 8
若MA、MB在杆的两侧,怎么画?
MA MB q
A
MA
MAB中
B MB
+
A 1 qL2 8
B
MAB中= ( MA + MB)/2
MA A
P a b
MB B MA M Pab L MB
L
M怎么计算?
C A 3.75kN 2m
D
4m
B
2m 0.25kN
ND左 = -10kN
求截面C、D左、D右的内力。 解:1、求支座反力 2、C截面的内力 取C截面以左为对象:
QD左 = 3.75-2×2 =-0.25kN MD左 = 3.75×6-2×2×5
=2.5kNm
4、D右截面的内力 取D右截面以右为对象:
三、内力图的校核
除一般校核平衡条件和荷载、内力微分关系外,重点是校核 刚结点处的平衡条件,即∑X = 0 , ∑Y = 0,∑M = 0
例1:作图示刚架的弯矩图。 2kN/m C A B 5m 4m
16
4
C
B MCB = 0 MBC = 2×4×2 =16kNm(上拉) MBA = 2×4×2 = 16kNm(右拉) MAB =2×4×2 = 16kNm(右拉)
静定梁和刚架内力分析

平面桁架分类: 1. 平行弦桁架 2. 三角形桁架
3. 抛物线桁架
4. 梯形桁架
按几何组成分类 简单桁架 (simple truss)
联合桁架 (combined truss)
复杂桁架 (complicated truss)
按受力特点分类:
1. 梁式桁架
2. 拱式桁架
结点法(nodal analysis method)
FQ图(kN)
9
9
例:作图示多跨静定梁的内力图,并求出各支座反力。
1m
4m
4m
4m
1m
2.静定平面刚架(frame)
悬臂刚架
静 定 刚 架
A
D C
简支刚架
B
三铰刚架
D
E
刚架--具有刚结点的由 直杆组成的结构。
组合式刚架
静定刚架的内力图绘制方法: 一般先求反力,然后求杆段控制 截面弯矩,用叠加法逐个杆段 绘制。
40 D 30
80
FNDE FNED
E
30
FNDC
FNEB
FQ
FN 30 kN
40 kN
80 kN
例3、试作图示刚架的弯矩图 附属 部分
基本 部分
弯矩图如何?
对梁和刚架等受弯结构作内力图的顺序:
1.一般先求反力(不一定是全部反力)。 2.利用截面法求控制截面弯矩。以便将结构用 控制截面拆成为杆段(单元)。 3.在结构图上利用叠加法作每一杆件(单元) 的弯矩图,从而得到结构的弯矩图。
-8 kN
YDE CD 0.75 X DE CE 0.5
0
-33 34.8 19 -8
-33
-33 -8
-33 34.8 19
(整理)多跨静定连续梁受力分析

第8跨内力分析:
Pi=RBi-1,i=8
(四)安全预评价内容RBi=qLi*[1-(Ai/Li)2]/2-Pi*(Ai/Li),i=8
2.间接市场评估法Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=8
第4跨内力分析:
Pi=RBi-1,i=4
RBi=qLi*[1-(Ai/Li)2]/2-Pi*(Ai/Li),i=4
Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=4
MA4=-(Pi*Ai+qAi2/2),(i=4)
第5跨内力分析:
Pi=RBi-1,i=5
Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=6
MA6=-(Pi*Ai+qAi2/2),(i=6)
第7i/Li)2]/2-Pi*(Ai/Li),i=7
Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=7
MA2=-(Pi*Ai+qAi2/2),(i=2)
第3跨内力分析:
Pi=RBi-1,i=3
RBi=qLi*[1-(Ai/Li)2]/2-Pi*(Ai/Li),i=3
Mi=qLi2*[1-(Ai/Li)2]2/8-Pi*Ai*[1-(1+(Ai/Li))2/2+Ai/Li],i=3
MA3=-(Pi*Ai+qAi2/2),(i=3)
单跨静定梁、多跨静定梁受力分析

E 1m B 1m C 20
取AD为隔离体
20kN/m QD
A 1m D 10
MC ND
Σx=0 Σy=0
ND=0
10-20×1-QD=0 QD=-10kN
ΣMD=0
MD=10×1-
20×1×0.5=0kN·m
精选可编辑ppt
12
20kN/m
10kN·m
10kN
A 1m D 1m E 1m B 1m C
剪力方程 弯矩方程
22
20kN/m
A
C
x
1m
20
A
10 2.5
A
QC=20(1-x) B
0≤x≤1
MC=-10(1-x)2
x=0 B Q图(kN) x=1
Q=20 Q=0
B
M图 (kN·m)
精选可编辑ppt
x=0
x=0.5 x=1
M=-10
M=-2.5 M=0
23
20kN/m
A 1m
20
A
10 2.5
19
AC x 1m
20
A
20
A
20kN B
Q=20 M=-20×(1-x)
注意: 弯矩图不标正负, 标在受拉侧
B Q图(kN) Q=20
B
M图 (kN·m)
精选可编辑ppt
x=0 M=-20
x=1 M=0
20
A
1m
20
A
20
A
20kN B
受力特征
仅在杆件端部有集中 荷载,而AB间无荷载
内力图特征
1m
10kN·m BA
1m
10kN·m 2m
A 5
