股票投资组合分析——基于均值-方差模型
投资组合管理中的资产配置模型

投资组合管理中的资产配置模型资产配置是投资组合管理中的重要环节,旨在平衡投资者的风险和回报预期。
为了实现这个目标,投资者需要借助资产配置模型,将资金分配到不同的资产类别中。
本文将介绍几种常见的资产配置模型,包括马科维茨均值-方差模型、资本市场线模型和资产组合的最优分配模型。
1. 马科维茨均值-方差模型马科维茨均值-方差模型是资产配置中最经典的模型之一。
它通过考虑不同资产之间的相关性和预期收益率来计算资产的风险和预期收益。
该模型的核心思想是通过分散投资来降低风险,即在多个资产之间进行组合投资。
具体来说,该模型通过计算投资组合的期望收益率和方差,并构建有效边界,找到具有最佳收益风险比的投资组合。
2. 资本市场线模型资本市场线模型是基于资本资产定价模型(CAPM)的资产配置模型。
它认为投资组合的预期收益率应该与投资组合的贝塔值相关,贝塔值反映了投资组合相对于市场的风险敏感度。
该模型通过选择合适的贝塔值来实现投资组合的最优配置。
具体来说,投资者可以通过加权分配市场组合和无风险资产来确定最佳配置比例,以实现期望收益率与风险的平衡。
3. 资产组合的最优分配模型资产组合的最优分配模型是基于现代投资组合理论和均值-方差分析的模型。
它通过将资产配置问题转化为数学规划问题,以找到投资组合的最优分配比例。
具体来说,该模型考虑投资者的风险偏好和预期收益率,通过最小化投资组合的风险和最大化投资组合的预期收益率,找到最佳的资产配置比例。
综上所述,投资组合管理中的资产配置模型对于实现投资目标至关重要。
不同的模型可以根据投资者的需求和风险偏好进行选择和应用。
通过合理的资产配置,投资者可以在获取较高回报的同时有效控制投资风险,最大化投资组合的效益。
然而,投资决策需要基于充分的市场研究和分析,以及对资产配置模型的准确理解和应用。
均值—方差证券资产组合理论

均值—方差证券资产组合理论1. 简介均值—方差证券资产组合理论,也被称为马科维茨模型,是现代投资组合理论的基础。
该理论由美国经济学家哈里·马科维茨于1952年提出,并在1959年获得了诺贝尔经济学奖。
这一理论通过权衡资产组合的预期收益率和风险来寻找最佳的投资组合。
2. 理论原理均值—方差证券资产组合理论的核心原理在于风险与收益之间的平衡。
根据该理论,投资者可以通过有效的资产配置,实现在给定风险水平下最大化投资组合的预期收益率。
具体来说,均值—方差模型在计算资产组合时,考虑了以下两个重要指标:2.1 均值均值指的是资产组合的预期收益率。
通过对各个资产的历史数据进行分析和估计,可以计算出每个资产的预期收益率,并据此求得资产组合的整体预期收益率。
2.2 方差方差表示资产组合的风险程度。
在均值—方差模型中,方差用于衡量资产之间的波动性和相关性。
如果两个资产的收益变动具有较高的相关度,那么它们之间的方差较小;反之,如果两个资产的收益变动独立或者相关度较低,那么它们之间的方差较大。
3. 资产组合优化基于均值—方差证券资产组合理论,投资者可以通过优化资产组合来实现风险与收益之间的最佳平衡。
具体的资产组合优化包括以下几个步骤:3.1 数据准备在优化资产组合之前,首先需要收集并整理相关的数据。
这些数据包括各个资产的历史收益率、期望收益率以及方差。
通常,投资者可以通过金融数据提供商或者证券公司获取这些数据。
3.2 风险-收益曲线通过对各个资产的历史数据进行分析和计算,可以得到不同投资组合的风险和收益指标。
在优化资产组合之前,投资者可以绘制出风险-收益曲线,以便直观地了解不同投资组合之间的收益和风险的关系。
3.3 最优组合根据风险-收益曲线,可以找到在给定风险水平下具有最高预期收益率的投资组合。
这个投资组合被称为最优组合,也是均值—方差模型的核心输出。
3.4 边际效益在确定最优组合后,投资者可以通过计算边际效益来衡量每个资产对投资组合的贡献。
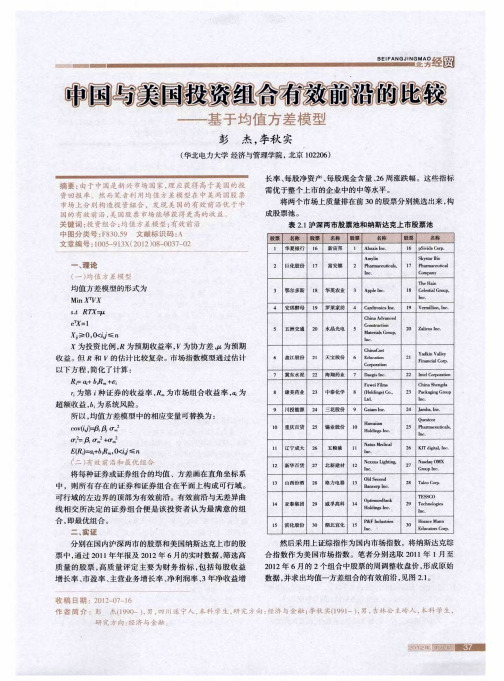
中国与美国投资组合有效前沿的比较——基于均值方差模型
参 考文献 :
【】 E wnJ Etn 现 代 投 资 组 合 理 论 与 投 资 分 析 [ . l d i . i ' o. MI 北
京 : 械 工 业 出版 社 ,0 8 机 20.
1 金 2 J
图 2 国内股票有效前沿 . 1
龙, 王正 . 通 m t b 精 a a 金融 计算f 】 京 : l M. 北 电子
滞 后 , 议多使 用表格 、 建 图纸 和简 明扼要 的语 言进 行 沟通 , 并 注意保存双方 对相关 问题 的意见和 承诺 。
另外 , 于采购环节 , 对 需要更 加注重技 术与质量 的稳 定
1 照项 目合 同及 采购总体 进度计划 的要求 编制工 厂 . 按 交 货计 划 , 协 助和 检查 货代 公 司运 输计 划 , 点 关注 大 并 重 型 设备及 其 附件及 出 口设 备 ,和 涉及安 全 的压力容 器 、 吊
不 符等情 况 , 需要 提前 制定必 要 的预防对 策 , 防患 于未然 。 作好 设计 与采购 的复查 , 量将问题解 决在境 内。 尽
( ) 他建议 五 其 .
是全新 的挑战 , 在不断 学习 、 真总结 提高 、 但 认 与合 作方 加
【] 何 小峰 , 5 黄 嵩. 资 银 行 学【 . 京 : 京 大 学 出版 投 M1 北 北
社 .0 2 20.
益率很 小时 , 收益率 的上 升带来 的方 差的上升很小 。 而当收 益率超过 2 % , . 时 曲线 很平缓 , 5 这说 明当要求收益率上升很
小 的单位时 , 方差上升也很大 。可认 为 2 % . 是投资临界点。 5 国 内股票市 场逊色于 国外股票市场 。因为在既定 的风 险水 平下 , 国外投 资收 益远高 于 国内投资 组合 。即使是 财 务 表现 极佳 的 3 家上 市公 司股票 也 比不 上在纳 斯达克 上 0
马柯维茨均值-方差模型

中通常以资产的历史收益率的协方差度量资产风险与相关性,这种计算方法存在预期误差,
即未来实际协方差矩阵与历史协方差矩阵间的存在偏差。
例 1.以华北制药、中国石化、上海机场三只股票,如何构使用马柯维茨模型构建投资 组合模型资产数据如下表:
表 三只股票的日回报率、风险数据及协方差矩阵
收益率均值(%)
收益率标准差(%)
Rp
E(rp )
和
2 p
分别是投资组合的期望回报率和回报率的方差。
函数语法:
[PortRisk, PortReturn] = portstats(ExpReturn, ExpCovariance, PortWts)
输入参数:
ExpReturn:资产预期收益率
ExpCovariance:资产的协方差矩阵
PortWts:资产权重 输出参数: PortRisk:资产组合风险(标准差) PortReturn:资产组合预期收益(期望)
例:在例 1 中,假设等权重配置华北制药、中国石化、上海机场,则资产组合的风险与
收益为多少 M 文件:
ExpReturn = [ ];
ExpCovariance = *
[
;
;
];
PortWts=1/3*ones(1,3);
[PortRisk, PortReturn] = portstats(ExpReturn, ExpCovariance,PortWts)
>>PortRisk =
PortReturn =
注释: ones(n,m)为生产元素都为 1 的 n×m 矩阵, ones(1,3)=[1,1,1].
>> PortRisk =
*
PortReturn = *
马克维茨均值-方差模型

马克维茨均值-方差模型马克维茨均值方差模型(Markowitz MeanVariance Model)是投资组合理论中的一种经典模型,旨在求解投资组合中各个资产的权重,以达到最优的风险收益平衡。
本文将一步一步回答与该模型相关的问题,并详细探讨其应用和局限性。
第一步:理解均值方差模型的基本概念马克维茨均值方差模型的核心思想是基于投资者根据期望收益和风险偏好,通过构建有效前沿,选择最优的投资组合。
其中,均值是指资产的期望收益,方差是指资产收益的波动程度。
该模型假设投资者的决策基于"均值方差效用函数",并将投资者的目标简化为寻找最大化投资收益或最小化投资风险的点。
第二步:计算资产预期收益率和协方差矩阵在马克维茨均值方差模型中,首先需要计算各个资产的预期收益率和协方差矩阵。
预期收益率可以通过历史数据或专业分析师的预测得出。
协方差矩阵则衡量不同资产之间的相关性和波动性,反映了资产收益的联动程度。
通过计算预期收益率和协方差矩阵,可以为后续的建模提供基础数据。
第三步:优化模型求解最优投资组合在构建投资组合时,需要设定投资者的目标和约束条件。
目标可以是最大化预期收益或最小化投资风险,约束条件可以包括资产权重的上下限、风险承受能力等。
利用数学优化方法,如线性规划或二次规划,可以求解出最优投资组合,即在给定约束条件下最大化预期收益或最小化投资风险。
第四步:有效前沿和资产配置通过改变投资组合中不同资产的权重,可以构建不同的投资组合。
根据马克维茨均值方差模型,我们可以绘制出一个被称为"有效前沿"的曲线,表示在给定风险水平下,能够达到的预期收益的最优组合。
有效前沿帮助投资者了解可行的投资组合,从中选择最佳的配置方案。
第五步:风险敞口和资产多样化马克维茨均值方差模型强调了通过资产多样化来降低投资风险。
投资者可以通过在投资组合中加入不同类型、不同行业、不同地域等各类资产,从而分散和平衡风险。
均值_方差模型在股市最优投资组合选择中的实证研究_孙曼曼

3)机械费的控制:尽理减少施工中所消耗的机械台班量,通过全 理施工组织、机械调配,提高机械设备的利用率和完好率,同时,加强 现场设备的维修、保养工作,降低大修、经常性修理等各项费用的开 支,避免不正当使用造成机械设备的闲置。 3.4 加强质量管理,控制返工率
下:
rit=
pit -pi(t-1) pi(t-1)
其 中 ,pit 是 第 i 支 股 票 在 第 t 天 的 收 盘 价 p; i(t-1)是 第 i 支 在 第 t-1
天的收盘价。
2.2 结果分析
2.2.1 运用 MATLAB 对数据进行建模,得到结果如下:
(1)当期望收益为 0.05 时,标准差为 0.14308,各 个 股 票 的 投 资 权
力、协调能力、工期控制能力的综合体现。 S
[责任编辑:杨扬]
(上接第 74 页)
【参考文献】 [1]哈 里·马 柯 维 茨 .2000.资 产 选 择 - 投 资 的 有 效 分 散 化 [M]. 刘 军 霞 , 张 一 弛 , 译 . 北 京:首都经济贸易大学出版社.
[2] 徐 成 贤 ,袁 晓 玲 ,薛 宏 刚 .优 化 金 融 学 [M].科 学 出 版 社 ,2003. [3]杨尚.基于 MATLAB 与 EXCEL 工 具 的 均 值-方 差 模 型[J].阴 山 学 刊,2007,21 (2):42-45.
【摘 要】本文从以人为本的角度,从三个方面对如何构建和谐企业文化,提高企业核心竟争力进行了探讨。 【关键词】企业文化;核心竟争力;协调发展
基于均值—方差模型的保险资金投资组合研究

=
利 用 ma l b t 可以 计 算 给 定 收 益 率情 况 a 下的最优投资 比例。
3数据的选取及计算
本 文 选 取2 0 到 2 0 年 三 年 各 类资 产 0 7 09 的 收 益 率 , 到 债 券 和 权 益 类 投 资 收 益 率 得 向量 为 ( . I 3 7 %)协 方 差 矩 阵 为 4 I %, . 7 , 00 480 l .0 0 3 3 0 0 3 7 4 5 0 . 9 9 8 01 0
f f
=W ' CW
我 们 用 向 量 W =( 1W , 3 表 示银 行 W, 2W ) 存 款 、 券 、 益 类 的 投 资 比 例 , 有 债 权 则 W >0 1 w <0 1。 据 保 险 资 金 的 投 资 1 ., 4 . 根
∑ = ' W R
0 9980 1 . 3 7 4 5 00 0 4 8 0 l 0 0 . 0 33 0 利 用 ma l b 求 解规 划功 能 I 得 到 投 t 的 a 2 ] , 资 比 例 :6 .5 w =3 %, = .5 , 91 %, ' 0 08 %
∑ = 1
W ≥oi ,, , i (=1 …,) 2 z
其中 为第 f 种资产所 占的权重 , ( =1 , 2 3 … , ) 表 资 产 的 收 益 率 , 向 量 , , n代 列 W =( w , , ), 0 , 2・ 歹 向量 R= ‘ , , 一 ( , … ) , 为 投 资 组 合 方 差 , 为 投 资 组 合 收 益
最小, n : . 0 x 0 mi 仃 =53 2 1~。 3 4结果分析
有 计 算 结 果 可 以 看 出 , 优 投 资 比 例 最 中 权 益 类 投 资 的 比 例 偏 小 , 和 我 国 目前 这 的 资本 市 场 有 关 , 国 目前投 资 渠 道 较 窄 , 我 权 益类投资主要集 中在股票市场 , 20 而 07 和 2 0 年 的 股 票 市 场 起 伏 很 大 , 剧 了权 08 加 益 类 投 资 的 风 险 。 此 , 保 险 公 司来 说 , 因 对 应 该低 风 险 , 另外 , 国 也 应 该 开 发 新 的 投 资 渠 道 , 我 从而 降低各类资金的投资风险 。
证券投资组合理论-马科维兹的均值一方差模型

2020/5/14
6
❖ 瑞典皇家科学院决定将1990年诺贝尔奖授予 纽约大学哈利.马科维茨(Harry Markowitz) 教授,为了表彰他在金融经济学理论中的先驱 工作—资产组合选择理论。
2020/5/14
7
主要贡献
❖ 发展了一个在不确定条件下严格陈述的可操作的 选择资产组合理论:均值方差方法 Mean-
下方差最小的投资组合,并导出投资者只在有效边
界上选择投资组合。根据马科维兹资产组合的概念,
欲使投资组合风险最小,除了多样化投资于不同的
股票之外,还应挑选相关系数较低的股票。因此,
马科维兹的“均值-方差组合模型”不只隐含将资
金分散投资于不同种类的股票,还隐含应将资金投
资于不同产业的股票。同时马科维兹均值-方差模
2020/5/14
8
❖ 投资组合理论的基本思想:投资组合是一个 风险与收益的tradeoff问题,此外投资组合通 过分散化的投资来对冲掉一部分风险。
——“nothing ventured, nothing gained”
——"for a given level of return to minimize the risk, and for a given level of risk level to maximize the return“
最后,通过求解二次规划,可以算出有 效投资组合的集合,计算结果指明各种 证券在投资者的资金中占多大份额,以 便实现投资组合的效性——即对给定的 风险使期望回报率最大化,或对于给定 的期望回报使风险最小化。
2020/5/14
13
一些需准备的概念
1.证券投资组合的选择
❖狭义的定义:是指如何构筑各种有价 证券的头寸(包括多头和空头)来最 好地符合投资者的收益和风险的权衡。
均值-方差模型理论及其在我国股票市场的应用

均值-方差模型理论及其在我国股票市场的应用一、引言均值-方差模型是现代投资组合理论的重要组成部分,它通过衡量资产的预期收益率和风险水平,援助投资者做出合理的资产配置决策。
本文将对均值-方差模型的理论基础及其在我国股票市场的应用进行探讨。
二、均值-方差模型的理论基础1.1 均值-方差模型的基本原理均值-方差模型是由美国经济学家马科维茨于1952年提出的一种金融投资组合选择方法。
其基本原理是通过计算资产的预期收益率和风险,以追求投资组合风险最小的预期收益率。
1.2 组合的风险与收益干系均值-方差模型假设资产的收益率听从正态分布,并通过方差衡量风险。
通过构建不同权重的资产组合,可以寻找到预期收益率最高,且方差最小的组合。
1.3 投资组合的有效边界均值-方差模型还引入了有效边界的观点。
有效边界是指在给定预期收益率水平下,最小化投资组合方差的全部可能投资组合的集合。
通过有效边界,投资者可以在风险和收益之间找到合适的平衡点。
三、均值-方差模型在我国股票市场的应用2.1 资产预期收益率的计算在我国股票市场,资产预期收益率可以通过对历史数据进行分析和对市场进步趋势的猜测来确定。
常用的方法包括股票收益率的历史平均值、市盈率、市净率等指标计算。
2.2 风险的器量均值-方差模型中,风险通过资产的方差来器量。
在我国股票市场,常用的风险器量方法有股票收益率的历史标准差、波动率等。
2.3 投资组合优化利用均值-方差模型,投资者可以计算不同权重下投资组合的预期收益和风险水平,并找到有效边界上的最优投资组合。
通过优化投资组合,投资者可以实现风险最小化与收益最大化的目标。
2.4 风险偏好和投资组合选择投资者的风险偏好对投资组合的选择有着重要影响。
依据投资者的风险承受能力和投资目标,可以选择不同风险水平下的投资组合,以达到最佳配置效果。
2.5 动态调整与重平衡在实际投资过程中,市场波动和投资者风险偏好的变化可能导致投资组合的变动。
投资组合分析方法

投资组合分析方法1. 均值方差模型(Mean-Variance Model):均值方差模型是由Harry Markowitz于20世纪50年代提出的,是一种基于风险和收益的投资组合优化模型。
该模型通过计算投资组合的预期收益率和方差,寻找投资组合最佳的风险收益平衡点。
它的核心思想是通过将不同标的的收益率与协方差考虑在内,寻找一组权重,使得投资组合的风险最小,同时达到期望的收益。
2. 黑-利曼投资组合理论(Black-Litterman Model):黑-利曼投资组合理论是由Fischer Black和Robert Litterman于20世纪90年代提出的一种投资组合分析方法。
该模型采用贝叶斯推断的方法,将投资者的个人观点与市场均衡进行结合,通过反推隐含的市场收益率,进而评估投资组合的配置权重。
该方法能够充分利用市场信息与投资者个人观点的结合,提高投资组合的配置效果。
3. 市场模型(Market Model):市场模型是一种基于资本资产定价模型(CAPM)的投资组合分析方法。
该模型通过对波动性的度量,评估投资组合在市场中的系统性风险与回报之间的关系。
市场模型主要利用回归分析方法,通过计算投资组合的贝塔系数,衡量投资组合相对于市场的敏感性。
投资者可以根据市场模型的结果,调整投资组合的权重,以实现风险与收益的平衡。
4. 下侧风险模型(Downside Risk Model):下侧风险模型是一种相对于标准差(波动性)更加关注投资组合负向波动性的风险分析方法。
该模型通过计算下侧风险指标(如下侧标准差、价值-at-Risk等),对投资组合的下行风险进行度量和评估。
下侧风险模型更加注重投资组合在市场下行时的表现,能够帮助投资者更好地管理投资组合的风险。
除了以上介绍的方法,还有一些其他的投资组合分析方法,如收益风险模型(Return-Risk Model)、马科维茨投资组合优化模型(Markowitz Portfolio Optimization Model)等。
股票投资组合分析——基于均值-方差模型

股票投资组合分析——基于均值-方差模型
周廷森
【期刊名称】《经济研究导刊》
【年(卷),期】2022()23
【摘要】中国资本市场30多年的发展,为企业及投资者提供了较为广阔的投融资
平台。
随着股票这一金融市场中的主要交易品种在投资者资产配置中的作用越发凸显,对普通投资者来说,如何合理构造证券投资组合获取超额收益成为一个重要议题。
利用2019年沪深300第四季度公司财务指标数据,首先对财务指标做聚类,再通过主成分分析对财务指标降维,从每个簇中选取评分较高的股票组成股票集合之后根
据马科维茨的均值方差模型计算各证券的资金分配比例,构建证券投资组合,最后通
过夏普比率和索提诺比率对该投资组合进行业绩评价。
结果显示,此组合的业绩较
为优秀。
【总页数】4页(P85-88)
【作者】周廷森
【作者单位】贵州大学经济学院
【正文语种】中文
【中图分类】F832
【相关文献】
1.基于原—对偶内点算法的股票投资组合分析——兼论Markowitz均值—方差模型的应用
2.基于均值-方差模型的投资组合分析
3.基于均值-方差模型的股票投资
组合构造分析4.均值方差投资组合分析模型5.可信性测度下基于均值–方差–VaR–偏度–正弦熵的模糊投资组合分析
因版权原因,仅展示原文概要,查看原文内容请购买。
均值—方差模型与均值—半方差模型的实证分析

均值—方差模型与均值—半方差模型的实证分析李晓;李红丽【摘要】在马科维茨均值—方差模型中,风险即是期望收益率的不确定性,并用资产组合收益率的方差定量地来刻画风险。
然而,投资者在实际投资活动中,只有当期望收益率低于其预想的收益水平时,才认为是风险,否则不认为是风险。
于是,就引出用半方差刻画风险的另一种风险度量方法。
文章通过选择适当的股票组合,对方差和半方差这两种不同的风险度量方法进行对比研究,结果表明,在风险水平相同情况下,均值—半方差模型可以使我们获得更高的期望收益率。
%In the Markowitz value-variance model,the risk for the expected rate of return to understand the uncertainty,so ground-breaking use of Markowitz portfolio yield variance(or standard deviation) to characterize quantitatively these types of uncertainty.Markowitz's portfolio theory and its model to become the beginning of modern finance.However,the actual investment of investors in its activities,often with a different understanding of risk,that is,only when the expected rate of return below the expected level of returns,the only risk that is otherwise the risk is not considered.Thus,the characterization leads to the risk of semi-variance with another method of risk measurement.This article by selecting the appropriate portfolio of shares,the other poor and semi-variance of these two different methods of risk measure comparative study,results showed that the risk level in the same circumstances,the mean-semi-variance model allows us to obtain higher expected rate of return.【期刊名称】《郑州航空工业管理学院学报》【年(卷),期】2011(029)006【总页数】5页(P135-139)【关键词】均值—方差模型;均值—半方差模型;实证分析;证券投资组合【作者】李晓;李红丽【作者单位】郑州大学商学院,河南郑州450001;郑州大学商学院,河南郑州450001【正文语种】中文【中图分类】F830.59一、引言任一资产和资产组合(无风险资产除外),由于其未来的收益存在一定的不确定性,因而存在风险。
基于均值-方差模型的保险资金投资组合研究

投资者在考虑每一次投资选择时 , 其依据是某一持仓 时间内的证券收益 的概率分布 ; 投资者是厌恶 风
险的 , 即在一定的风险水平上 , 投资者期望收益最大 ; 相对应 的是在一定的收益水平上 , 投资者希望风险最
收稿 日期 : 2 0 1 3 - 0 3 - 0 1 : 修 回日期 : 2 0 1 3 — 0 4 — 2 7 .
摘
要: 首先 介 绍 了马科 维 茨的均 值 一 方差模 型 , 然后 求 出 了 2 0 0 6 - 2 0 1 0年 期 间 的股 票收 益 率 、 证 券投
资基 金 收 益率 、 国债 收益 率 、 企 业债 收 益 率、 银行存款利率, 最后 根 据 保 监 会 对 保 险 公 司 资金 使 用 的要 求 建 立数 学模 型 求 出 了保 险公 司的最优投 资组合 为 6 5 . 6 8 %投 资于存 款 和 国债 , 2 9 . 2 %投 资 于企 业债 , 5 . 1 2 %投 资
于基 金 。
关键 词 : 均值 一 方 差模 型 ; 投 资组 合 ; 实证研 究
中图分 类号 : F 8 4 0 . 4 文献 标 志码 : A
从现代保险公司的经营业务 中可 以看 出, 承保业务是资金来 源的重要渠道 , 而投资业务则是 主要 的盈 利途径 。与商业银行注重资本充足率不 同, 保险业作为经 营风险 的行业 , 对偿付能力 的要求尤为严格 。保 险资金投资业务作为保险公司偿付能力的重要保障 , 不仅要有 良好 的赢利性也要 注重对风险的有效控制 。 保监会为了控制风险, 把保 险资金的投资渠道限制的很严格 , 使得当前我国保险业资金运用率 、 收益率都 比 较低。因此 , 如何在监管部门的要求下 , 合理 的运用保险资金 , 提高保险资金的利用率成为保险公 司能否在
投资组合优化模型及算法分析

投资组合优化模型及算法分析投资组合优化是投资者在面对多种投资选择时,通过合理配置资金,以达到最大化收益或最小化风险的目标。
在过去的几十年中,投资组合优化模型和算法得到了广泛的研究和应用。
本文将对投资组合优化模型及其相关算法进行分析。
一、投资组合优化模型1.1 均值-方差模型均值-方差模型是投资组合优化中最经典的模型之一。
该模型基于投资者对资产收益率的期望值和方差的假设,通过最小化方差来寻找最优投资组合。
该模型的优点是简单易懂,但也存在一些问题,如对收益率的假设过于简化,无法处理非正态分布的情况。
1.2 均值-半方差模型均值-半方差模型是对均值-方差模型的改进。
该模型将方差替换为半方差,即只考虑收益率小于预期收益率的风险。
相比于均值-方差模型,均值-半方差模型更加关注投资组合的下行风险,更适用于风险厌恶型投资者。
1.3 风险平价模型风险平价模型是基于风险平价原则构建的投资组合优化模型。
该模型将不同资产的风险权重设置为相等,以实现风险的均衡分配。
风险平价模型适用于投资者对不同资产风险敏感度相同的情况,但对于风险敏感度不同的情况,该模型可能无法提供最优解。
二、投资组合优化算法2.1 最优化算法最优化算法是投资组合优化中常用的算法之一。
最优化算法通过数学优化方法,如线性规划、二次规划等,寻找最优投资组合。
这些算法能够在较短的时间内找到最优解,但对于大规模的投资组合问题,计算复杂度较高。
2.2 蒙特卡洛模拟蒙特卡洛模拟是一种基于随机抽样的方法,通过生成大量样本来近似计算投资组合的风险和收益。
该方法能够处理非线性和非正态分布的情况,并且可以考虑到不同资产之间的相关性。
但蒙特卡洛模拟也存在一些问题,如计算时间较长和结果的随机性。
2.3 遗传算法遗传算法是一种模拟生物进化的优化算法。
该算法通过模拟自然选择、交叉和变异等过程,逐步优化投资组合。
遗传算法能够处理非线性和非凸优化问题,并且对于大规模投资组合问题具有较好的适应性。
证券投资组合的均值-方差分析

t he o pt i ma l i nv e s t me nt pr o po r t i o n a c c or d i ng t h e c a l c u l a t i o n o f t he RRR.
Ke y wo r d s :i n v e s t me n t s e c u r i t i e s ;me a n — v a r i a n c e a n a l y s i s ;M a r k o wi t z t h e o r y ;RRR( Re q u i r e d Ra t e o f Re t u r n ) .
PANG S u - j u a n , CHE a r t me n t o f F o u n d a t i o n ,F u j i a n C o mme r c i a l C o l l e g e ,F u z h o u 3 5 0 0 1 2 , Ch i n a ;
2 . De p a r t me n t o f Ma t h e ma t i c s ,Pu t i a n Un i v e r s i t y,Pu t i a n 3 5 1 1 0 0,Chi n a )
基于Markowitz理论的股票组合投资模型

Financial View金融视线 | MODERN BUSINESS 现代商业137基于Markowitz理论的股票组合投资模型李方圆郑州大学国际学院 河南郑州 450052摘要:本文基于Markowitz的均值-方差组合模型,在特定的期望收益下,以投资组合的风险最小化为目标建立了单目标优化模型。
然后通过选取沪深300指数股票的相关数据进行实证分析和灵敏度分析,检验了模型的合理性与实用性。
根据此模型进行投资,简化了投资策略,使得投资操作更加简便,适合于绝大多数投资者进行股票的买卖,并可确保在风险非常小的情况下,取得预期的投资收益。
关键词:均值-方差组合模型;单目标优化模型;灵敏度分析中图分类号:F224;F830.59 文献识别码:A 文章编号:1673-5889(2019)26-0137-02一、引言作为宏观经济的晴雨表,股票市场是中国经济发展的一个重要组成部分。
随着股票市场的逐步完善,越来越来的人参与到股票市场中,进行股票的买卖。
如今,中国的股票市场有3000多只股票,股票的涨跌变化也是受到多种因素的影响。
面对股市的纷繁复杂,想要取得一定的收益确实是一件比较困难的事情。
所以,进行股票的投资组合分析,对于提高人们参与的积极性以及股票市场 的完善将具有非常重要的现实意义。
美国经济学家Markowitz [1]在1952年首次提出投资组合理论(Portfolio Theory),该理论包含两个重要内容:均值-方差分析方法和投资组合有效边界模型。
投资组合理论用均值和方差来刻画收益和风险。
该理论的思想主要是在一定的风险下尽可能使得收益最大化,或者在一定的收益下尽可能使得风险最小化。
本文将在投资组合理论的基础上构建股票的投资组合模型,然后进行实证分析和灵敏度分析来验证模型的合理性。
二、问题陈述中国的股票市场尚不成熟,投机过度、政策驱动的负效应、功能不健全等问题容易导致股市的动荡,这不仅对众多投资者造成很大损失,也对国家的金融发展产生很多不利的影响。
两类风险模型下的均值—方差投资组合博弈问题的开题报告

两类风险模型下的均值—方差投资组合博弈问题的开题报告一、问题背景均值—方差投资组合博弈问题是指在多支股票中选择一定数量的股票,组成一个投资组合,使得该投资组合的预期收益最大,同时风险最小。
其中,风险通常用方差或标准差来表示。
该问题是金融学中的重要问题,对于个人和机构的资产管理具有重要的意义。
在现实中,投资组合的表现往往受多种因素影响,如市场环境、经济政策等,使得该问题更加复杂。
在实际中,人们对风险有着不同的理解。
有些投资者认为市场的波动是正常的,它反映了市场的活力,深度参与市场是收益的前提,因此,这类投资者认为,只要在收益预期范围内,就可以接受一定的风险。
而有些投资者则更为保守,他们更加关注投资组合的稳定性、资产流动性等风险因素,这类投资者更加倾向于减少风险。
在实际中,针对不同的风险偏好,可以采用不同的风险模型。
其中,最常见的是“均值—方差模型”和“风险价值模型”。
两类模型的本质差异在于对于风险的度量方法不同。
二、研究意义针对均值—方差投资组合博弈问题,在两种风险模型下进行研究,可以得出不同的投资策略。
这对于不同偏好的投资者,都能提供借鉴。
对于风险偏好较高的投资者,在均值—方差模型下,可以优化投资组合,将投资风险最小化。
而对于风险偏好较低的投资者,在风险价值模型下,可以将收益最大化的同时,将风险控制在可承受的范围内。
三、研究方法1.理论分析针对两种模型,分别进行理论分析。
在均值—方差模型中,通过求解投资组合的均值和方差,得到最小化方差的投资组合。
在风险价值模型中,通过求解风险价值函数,得到将风险控制在一定范围内的投资组合。
2.实证分析选取一定数量的股票,利用历史数据,对两种模型下的投资组合进行模拟。
通过计算组合收益、方差或风险价值,得到不同模型下的最优组合。
四、预期结果根据理论分析和实证分析,得到两种模型下的最优投资组合。
对于风险偏好较高的投资者,将提供投资组合的最小风险方案。
而对于风险偏好较低的投资者,将提供收益最大化的同时,控制风险的投资策略。
基于贝叶斯方法的均值-方差投资组合选择

基于贝叶斯方法的均值-方差投资组合选择
袁子甲;李仲飞
【期刊名称】《现代管理科学》
【年(卷),期】2009(000)005
【摘要】传统均值-方差模型应用于投资实践时将参数的估计值看作是其真实取值,从而忽略了估计风险对投资决策的影响.基于此,文章提出了基于贝叶斯方法的均值-方差模型,并介绍了最优投资组合的求解过程.贝叶斯分析框架的引入将有效克服传统均值-方差模型对参数取值的敏感性,使得模型的稳健性得到显著提高.
【总页数】2页(P20-21)
【作者】袁子甲;李仲飞
【作者单位】中山大学岭南学院;中山大学岭南学院
【正文语种】中文
【中图分类】F2
【相关文献】
1.基于加权可能性均值和方差的投资组合选择的一个注记 [J], 颜燕梅;王达布希拉图
2.基于ARMA模型与均值-方差模型的我国股市投资组合选择 [J], 凌俊;黄婧颖;谢湘生;杨超进;谭艳娴
3.基于投资者情绪的均值-方差投资组合选择研究 [J], 罗琰;刘晓星;
4.基于投资者情绪的均值-方差投资组合选择研究 [J], 罗琰;刘晓星
5.人民银行职业年金投资组合选择研究——基于马科维茨均值-方差模型 [J], 汪中冬
因版权原因,仅展示原文概要,查看原文内容请购买。
均值-方差分析方法和投资组合有效边界模型。

该理论包含两个重要内容:均值-方差分析方法和投资组合有效边界模型。
在发达的证券市场中,马科维茨投资组合理论早已在实践中被证明是行之有效的,并且被广泛应用于组合选择和资产配置。
但是,我国的证券理论界和实务界对于该理论是否适合于我国股票市场一直存有较大争议。
从狭义的角度来说,投资组合是规定了投资比例的一揽子有价证券,当然,单只证券也可以当作特殊的投资组合.本文讨论的投资组合限于由股票和无风险资产构成的投资组合。
人们进行投资,本质上是在不确定性的收益和风险中进行选择。
投资组合理论用均值—方差来刻画这两个关键因素。
所谓均值,是指投资组合的期望收益率,它是单只证券的期望收益率的加权平均,权重为相应的投资比例.当然,股票的收益包括分红派息和资本增值两部分.所谓方差,是指投资组合的收益率的方差。
我们把收益率的标准差称为波动率,它刻画了投资组合的风险。
人们在证券投资决策中应该怎样选择收益和风险的组合呢?这正是投资组合理论研究的中心问题。
投资组合理论研究“理性投资者”如何选择优化投资组合。
所谓理性投资者,是指这样的投资者:他们在给定期望风险水平下对期望收益进行最大化,或者在给定期望收益水平下对期望风险进行最小化。
因此把上述优化投资组合在以波动率为横坐标,收益率为纵坐标的二维平面中描绘出来,形成一条曲线。
这条曲线上有一个点,其波动率最低,称之为最小方差点(英文缩写是MVP)。
这条曲线在最小方差点以上的部分就是著名的(马考维茨)投资组合有效边界,对应的投资组合称为有效投资组合.投资组合有效边界一条单调递增的凹曲线. 如果投资范围中不包含无风险资产(无风险资产的波动率为零),曲线AMB是一条典型的有效边界.A点对应于投资范围中收益率最高的证券。
如果在投资范围中加入无风险资产,那么投资组合有效边界是曲线AMC。
C点表示无风险资产,线段CM是曲线AMB的切线,M是切点。
M点对应的投资组合被称为“市场组合"。
如果市场允许卖空,那么AMB是二次曲线;如果限制卖空,那么AMB 是分段二次曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
股票投资组合分析——基于均值-方差模型
股票投资组合分析——基于均值-方差模型
概述:
在金融领域,股票投资是一种常见的投资方式。
投资者希望通过合理配置不同股票的组合来降低投资风险并获得更高的收益。
基于均值-方差模型,本文将对股票投资组合进行分析,以帮
助投资者做出更明智的投资决策。
一、均值-方差模型简介
均值-方差模型是一种常见的金融模型,用于评估资产组合的
预期收益和风险。
该模型基于以下两个假设:
1. 假设收益率服从正态分布,即所有的资产收益率都可以用
均值和方差来衡量。
2. 假设投资者关注的是资产组合的整体风险和收益,而不是
单个资产的风险和收益。
二、构建股票投资组合
在构建股票投资组合之前,投资者首先需要选择合适的股票。
选择股票的关键是分析其基本面、行业前景和估值等因素,以确定是否具备投资潜力。
在选择股票后,投资者可以通过确定权重的方式将它们组合在一起。
三、计算投资组合的预期收益率和风险
通过均值-方差模型,可以计算投资组合的预期收益率和风险。
预期收益率可以通过计算加权平均值得出,其中权重为各个股票的权重。
预期风险可以通过计算投资组合的方差得出。
四、有效前沿和最优投资组合
有效前沿是指在给定风险水平下,能够获得最大预期收益的所有投资组合构成的边界。
在有效前沿上,每个投资组合的预期
收益率都是相同的,但风险不同。
最优投资组合则是在风险水平给定的情况下,能够获得最大预期收益的投资组合。
五、资本市场线和风险资产定价模型
资本市场线是连接无风险利率和最优投资组合的直线。
它描述了预期收益率与风险之间的关系。
在资本市场线上,每个投资组合的预期收益率都是最大的。
风险资产定价模型则是通过比较资产的预期收益率和风险,判断它们是否被正确定价。
六、买入和卖出策略
通过股票投资组合的分析,投资者可以根据自己的风险承受能力和投资目标制定买入和卖出策略。
根据预期收益率和风险,投资者可以决定是否进行调整或平衡投资组合。
七、风险管理和监控
风险管理和监控是投资组合管理的重要环节。
投资者应定期评估投资组合的风险水平,并根据市场情况进行调整。
同时,投资者还可以通过多样化投资组合来降低整体风险。
八、案例分析
本文通过一个案例进行分析。
假设投资者选择了苹果、微软和亚马逊这三只股票,以等权重方式构建投资组合。
通过计算预期收益率和风险,可以得出投资组合的预期收益和风险水平。
结论:
股票投资组合分析是投资者进行投资决策的重要工具。
基于均值-方差模型,可以分析投资组合的预期收益和风险,并选择
最优投资组合。
然而,投资者在进行股票投资时仍需注意行业前景、宏观经济环境等因素,以及合理的风险管理和监控策略,来实现长期稳健的投资回报
投资组合分析是投资者进行投资决策的重要工具,通过对不同资产的收益和风险进行评估,帮助投资者选择最优的投资组合,从而实现长期稳健的投资回报。
本文将通过一个案例来说明股票投资组合分析的过程。
首先,投资者需要选择投资组合中的资产。
在本案例中,投资者选择了苹果、微软和亚马逊这三只股票作为投资组合的资产。
选择资产的过程中,投资者需要考虑行业前景、公司财务状况、竞争力等因素。
苹果、微软和亚马逊作为知名科技公司,具有良好的财务状况和市场竞争力,因此被视为潜在的投资标的。
其次,投资者需要计算每个资产的预期收益率和风险。
预期收益率是指投资者预计可以从投资中获得的收益,而风险是指投资的不确定性和波动性。
在计算预期收益率时,投资者可以参考历史数据和分析师的预测。
风险可以通过计算资产的波动率来衡量,波动率越大,风险越高。
在本案例中,假设苹果的预期收益率为10%,微软的预期收益率为8%,亚马逊的预期收益率为12%。
苹果的波动率为15%,微软的波动率为12%,亚马逊的波动率为18%。
通过计算可以得出投资组合的预期收益率和风险水平。
然后,投资者需要根据自己的风险承受能力和投资目标制定买入和卖出策略。
根据预期收益率和风险,投资者可以决定是否进行调整或平衡投资组合。
对于风险偏好较高的投资者,他们可能更愿意选择高风险高回报的资产;而对于风险偏好较低的投资者,他们可能更愿意选择低风险低回报的资产。
在风险管理和监控方面,投资者应定期评估投资组合的风险水平,并根据市场情况进行调整。
同时,投资者还可以通过多样化投资组合来降低整体风险。
多样化投资可以通过投资不
同行业、不同地区、不同资产类别等方式来实现,从而分散投资风险。
最后,投资者需要不断监控投资组合的表现,并根据需要进行调整。
市场环境和投资标的的变化可能会导致投资组合的预期收益和风险发生变化,因此投资者需要及时调整投资组合以适应市场的变化。
总的来说,股票投资组合分析是一项复杂而重要的工作。
通过对资产的预期收益率和风险进行评估,投资者可以选择最优的投资组合,并制定买入和卖出策略。
同时,投资者还需要注意行业前景、宏观经济环境等因素,以及合理的风险管理和监控策略,来实现长期稳健的投资回报
综上所述,股票投资组合分析是一个复杂而重要的过程。
投资者需要考虑多个因素,包括资产的预期收益率和风险水平,个人的风险承受能力和投资目标,以及市场环境和投资标的的变化等。
通过评估资产的预期收益率和风险,投资者可以选择最优的投资组合,并制定相应的买入和卖出策略。
在进行股票投资组合分析时,预期收益率是一个关键的指标。
投资者可以通过分析历史数据、公司基本面、行业前景等来估计资产的未来收益。
在选择投资组合时,投资者应该寻找具有较高预期收益率的资产,以增加投资组合的整体收益。
然而,预期收益率只是投资决策的一部分,风险水平同样重要。
投资者应该考虑投资组合的整体风险水平,并根据自己的风险承受能力和投资目标来制定相应的投资策略。
对于风险偏好较高的投资者,他们可能更愿意选择高风险高回报的资产;而对于风险偏好较低的投资者,他们可能更愿意选择低风险低回报的资产。
在风险管理和监控方面,投资者应该定期评估投资组合的风险水平,并根据市场情况进行调整。
同时,投资者还可以通过多样化投资组合来降低整体风险。
多样化投资可以通过投资不同行业、不同地区、不同资产类别等方式来实现,从而分散投资风险。
最后,投资者需要不断监控投资组合的表现,并根据需要进行调整。
市场环境和投资标的的变化可能会导致投资组合的预期收益和风险发生变化,因此投资者需要及时调整投资组合以适应市场的变化。
综上所述,股票投资组合分析需要综合考虑多个因素,包括预期收益率、风险水平、个人风险偏好、市场环境等。
通过评估资产的预期收益率和风险,投资者可以选择最优的投资组合,并制定相应的买入和卖出策略。
同时,投资者还需要注意行业前景、宏观经济环境等因素,以及合理的风险管理和监控策略,来实现长期稳健的投资回报。
总的来说,股票投资组合分析是一项复杂而重要的工作,需要投资者不断学习和提升自己的投资能力,以取得更好的投资结果。
