第3章 土中应力计算
合集下载
土力学3.土中应力计算
h1
γ1 γ2 γ′3
γ1 h 1
h2
水位面
γ1 h 1 + γ 2 h 2
1.地下水位以上土层 地下水位以上土层 采用天然重度， 采用天然重度，地下 水位以下土层采用浮 重度 2.非均质土中自重应 非均质土中自重应 力沿深度呈折线分布
h3
γ1 h1 + γ 2h2 + γ′3h3
三、水平向自重应力
pmin=0
基底压力重分布
偏心荷载作用在 基底压力分布图 形的形心上
1 l F + G = pmax × 3 − e b 2 2
p max
2 (F + G ) = l 3 − e b 2
三、基底附加压力 基底附加压力：作用于地基表面， 基底附加压力：作用于地基表面，由于建造建筑物而
附加应力分布规律 距离地面越深， 距离地面越深，附加应力的分布范围越广 在集中力作用线上的附加应力最大， 在集中力作用线上的附加应力最大，向两侧逐渐减 小 同一竖向线上的附加应力随深度而变化 在集中力作用线上， →∞， 在集中力作用线上，当z＝0时，σz→∞，随着深 度增加， 度增加，σz逐渐减小 竖向集中力作用引起的附加应力向深部向四周无限 传播，在传播过程中，应力强度不断降低（ 传播，在传播过程中，应力强度不断降低（应力扩 散）
I o o
III IV II
σ z = (K c Ⅰ− K c Ⅱ − K c Ⅲ + K c Ⅳ ) p
垂直三角形分布荷载 dp布辛涅斯克解 积 分
σ σ
z1
= K t1 p = K t2 pt
z2
矩形基础角点 下的竖向附加 应力系数， 应力系数，均 为m,n的函数 , 的函数
γ1 γ2 γ′3
γ1 h 1
h2
水位面
γ1 h 1 + γ 2 h 2
1.地下水位以上土层 地下水位以上土层 采用天然重度， 采用天然重度，地下 水位以下土层采用浮 重度 2.非均质土中自重应 非均质土中自重应 力沿深度呈折线分布
h3
γ1 h1 + γ 2h2 + γ′3h3
三、水平向自重应力
pmin=0
基底压力重分布
偏心荷载作用在 基底压力分布图 形的形心上
1 l F + G = pmax × 3 − e b 2 2
p max
2 (F + G ) = l 3 − e b 2
三、基底附加压力 基底附加压力：作用于地基表面， 基底附加压力：作用于地基表面，由于建造建筑物而
附加应力分布规律 距离地面越深， 距离地面越深，附加应力的分布范围越广 在集中力作用线上的附加应力最大， 在集中力作用线上的附加应力最大，向两侧逐渐减 小 同一竖向线上的附加应力随深度而变化 在集中力作用线上， →∞， 在集中力作用线上，当z＝0时，σz→∞，随着深 度增加， 度增加，σz逐渐减小 竖向集中力作用引起的附加应力向深部向四周无限 传播，在传播过程中，应力强度不断降低（ 传播，在传播过程中，应力强度不断降低（应力扩 散）
I o o
III IV II
σ z = (K c Ⅰ− K c Ⅱ − K c Ⅲ + K c Ⅳ ) p
垂直三角形分布荷载 dp布辛涅斯克解 积 分
σ σ
z1
= K t1 p = K t2 pt
z2
矩形基础角点 下的竖向附加 应力系数， 应力系数，均 为m,n的函数 , 的函数
第三章 土体中的应力计算(1-3节)
4
3.均质、等向问题 理想弹性体是均质且各向同性的。天然
地基是各向异性的。但当土层性质变化 不大时，这样假定对竖直应力分布引起 的误差通常在容许范围之内。
5
二、地基中的几种应力状态
1．三维应力状态（空间应力状态）
局部荷载作用下，地基中的应力状态属 三维应力状态。每一点的应力可写成矩 阵形式
24
25
在空间将z相同的点连 接成曲面即形成应力泡。
当地基表面作用有几个集中力时，根据弹 性体应力叠加原理求出附加应力的总和
26
（二）水平集中力作用-西罗提解
z
3Ph
2
xz 2 R5
(3- 9)
27
28
二、矩形面积上各种分布荷载作用下的附 加应力计算
（一）矩形面积竖直均布荷载 1．角点下的应力
x
K
s x
p
τ
xz
K
s xz
p
(3- 25) (3- 26)
剪Kx应s和力K分xzs布分系别数为（水表平3向-5应）力，m分布x ,系n 数z和。
BB
55
P
56
57
（三）条形面积竖直三角形分布荷载 条形面积上竖直三角形分布荷载在地基
内引起的应力也可利用应力叠加原理， 通过积分求得。
zM ' (KsI KsII KsIII KsIV ) p
(3 -13a)
37
第二种情况：计算矩形面积外任一点M’ 下深度为z的附加应力(图3-17b)。设法使 M’点为几个小矩形的公共角点，然后将 其应力进行代数迭加。
zM ' (KsI KsII KsIII KsIV ) p
29
3.均质、等向问题 理想弹性体是均质且各向同性的。天然
地基是各向异性的。但当土层性质变化 不大时，这样假定对竖直应力分布引起 的误差通常在容许范围之内。
5
二、地基中的几种应力状态
1．三维应力状态（空间应力状态）
局部荷载作用下，地基中的应力状态属 三维应力状态。每一点的应力可写成矩 阵形式
24
25
在空间将z相同的点连 接成曲面即形成应力泡。
当地基表面作用有几个集中力时，根据弹 性体应力叠加原理求出附加应力的总和
26
（二）水平集中力作用-西罗提解
z
3Ph
2
xz 2 R5
(3- 9)
27
28
二、矩形面积上各种分布荷载作用下的附 加应力计算
（一）矩形面积竖直均布荷载 1．角点下的应力
x
K
s x
p
τ
xz
K
s xz
p
(3- 25) (3- 26)
剪Kx应s和力K分xzs布分系别数为（水表平3向-5应）力，m分布x ,系n 数z和。
BB
55
P
56
57
（三）条形面积竖直三角形分布荷载 条形面积上竖直三角形分布荷载在地基
内引起的应力也可利用应力叠加原理， 通过积分求得。
zM ' (KsI KsII KsIII KsIV ) p
(3 -13a)
37
第二种情况：计算矩形面积外任一点M’ 下深度为z的附加应力(图3-17b)。设法使 M’点为几个小矩形的公共角点，然后将 其应力进行代数迭加。
zM ' (KsI KsII KsIII KsIV ) p
29
第3章 土体中的应力计算
1. M(x、y、z)点的应力： ( 、 、 )点的应力：
3P z3 3P σz = ⋅ 5 = ⋅ cos3 θ 2π R 2π R2 3P z2 x 3Px τzx = ⋅ = ⋅ cos2 θ 2π R5 2π R3 3P z2 y 3Py τzy = ⋅ = ⋅ cos2 θ 2π R5 2π R3
mn 1 n2 ] * ⋅[ − 2π m2 + n2 (1+ n2 ) m2 + n2 +1
同理，可以求得最大荷载角点下任意深度z处 的竖直附加应力σz 为： σz = α tc' p0 = (α c- α tc) p0 （3-7）
3P z5 P 3 σz = = 5 z2 2π R 2π
5
其中 = x2 + y2 + z2 R
(3-3)
P =α P 2 2 z2 ( r z) +1 z 1
(3-4)
其中α = α (r/z)称为集中荷载作用下的应力分布系数 具体的α 值见教材p79表3.5.1
b
图3-11 矩形面积上作用 三角形分布时角 点下的附加应力
根据布希涅斯克解，dP在角点1下深度z处M点 引起的竖向附加应力dσz为：
3p0 xz3 dσ z = 2π b x2 + y2 + z 2
(
)
5
dxdy
2
将上式沿矩形面积积分后，可得出竖直三角形 荷载作用在矩形面上时，在零角点下任意深度 z处所引起的竖直附加应力σz为： σz = α tc p0 （3-6） 式中 α tc =
y z
x
图3-4
2. 与材料力学比较 与材料力学比较（用摩尔圆解决问题时）
土力学课件 第3章 土中应力分布及计算.
计算如图所示水下地基土中的自重应力分布
水面 a 8m
粗砂 r=19KN/m3 rsat=19.5KN/m3
黏土r=19.３KN/m3 4m rsat=19.４KN/m3 W=20%,WL=55%,WP=24%
b 76KPa 176KPa c 253.2KPa
解：水下的粗砂层受到 水的浮力作用， 其有效重度： r , rsat rw 19.5 10 9.5 KN / m 3 粘土层因为W WP , 所以I L 0, 故认为土层 不受到水的浮力作用， 土层面上还受到 上面的静水压力作用。 a点：Z 0， CZ 0 KPa； b点：Z 8m, 该点位于粗砂层中，
应力符号规定
法向应力以压为正，剪应力方向的符号规定则与材料力 学相反。材料力学中规定剪应力以顺时针方向为正，土力学 中则规定剪应力以逆时针方向为正。
压为正，拉为负，剪应力以逆时针为正
土中的自重应力计算
土中应力按其起因可分为自重应力和附加应力两种。
自重应力是土受到重力作用产生的应力，自重应力一般是自 土体形成之日起就产生于土中。
二.成层土自重应力计算 地基土通常为成层土。当地基为成层土体时，设各土层 的厚度为hi，重度为ri，则在深度z处土的自重应力计算公 式为：
cz i hi
i 1
n
z hi
i 1
n
n—从地面到深度z处的土层数； hi—第i层土的厚度，m。 成层土的自重应力沿深度呈折线分布，转折点位于r值 发生变化的土层界面上。
◇若0＜IL＜1，土处于塑性状态，土颗粒是否受到水的 浮力作用就较难肯定，在工程实践中一般均按土体受 到水浮力作用来考虑。
四．存在隔水层时土的自重应力计算
当地基中存在隔水层时，隔水层面以下土的自重应力应 考虑其上的静水压力作用。
第3章-土应力计算
z z1 z 2
2 均布荷载时， p0 2kN / m
2 三角形荷载时， p0max 98 2 96kN / m
35/74
A点附加应力计算表格
均布荷载时 p0=2.000kN/m2 Kz1 3 0.6 0.234 z1 (kN/m2) 0.468 三角荷载时
Z(m)
z
3/74
第三章 土中应力计算 3.1 土的自重压力
沿水平面均匀分布，且与z成正比，即随深度 按直线规律分布。
天然地面 σcz
cz
cz z
σcz= z
z
cy
cx
1 1
z
4/74
第三章 土中应力计算 3.1 土的自重压力
cz i hi
i 1
n
天然地面
2/74
第三章 土中应力计算 3.1 土的自重压力
研究目的：确定土体的初始应力状态。 研究方法：土体简化为连续体，应用连续体 力学(例如弹性力学)方法来研究土中应力的 分布。
假设天然土体是一个半无限体，地面以下土质 均匀，天然重度为 (kN/m3)，则在天然地面下任 意深度z(m)处的竖向自重应力 cz (kPa)可取作用于 该深度水平面上任一单位面积上土柱的重量 z l 计算 即： cz
p II I z M
III IV
o
III IV
o
II I
z K cⅠ KcⅡ Kc Ⅲ K cⅣ p
25/74
均布矩形荷载下任意点的应力计算
计算点在基底边缘 II I
o
o
z K cⅠ KcⅡ p
计算点在基底边缘外
o III I
土力学与地基基础——第3章 地基土中的应力计算
2021/1/5
57.0kPa
80.1kPa
103.1kPa 150.1kPa
n
cz1h12h2nhn ihi i1
194.1kPa
第三节 基底压力分布和计算
基底压力：建筑物荷载通过基础传递给地基的压力，也是地 基作用于基础底面的反力，因此又称为地基反力。为计算上部荷载 在地基土层中引起的附加应力，必须首先研究基础底面处接触面的 压力大小与分布情况。
l
l/2-e e>l/6
2021/1/5
偏心荷载作用线
应与基底压力的
b
合力作用线重合
FG1 2pma x32l eb
pmax
2F G
3 l eb
2
三、基底附加压力
• 基底附加压力：作用于地基表面，由于建造建筑物而新增加的压力 称为基底附加压力。
• 建筑物建造前，土中早已存在自重应力，天然土层在自重应力作用 下的变形早已结束，只有基底附加应力才能引起地基的附加应力和 变形
有集中力的，但它在土的应力计算中是一个基本公式，应用集中力的解 答，通过叠加原理或者数值积分的方法可以得到各种分布荷载作用时的 土中应力计算公式。
• 集中荷载作用下的附加应力 • 矩形分布荷载作用下的附加应力 • 条形分布荷载作用下的附加应力 • 圆形分布荷载作用下的附加应力
基本解 叠加原理
2021/1/5
砂性土： 应考虑浮力作用。 液性指数 IL >=1 流动状态，自由水，考虑浮力；
粘性土： 液性指数 IL <=0 固体状态，结合水，不考虑浮； 液性指数 0<IL <1塑性状态，难确定，按不利状态。
液性指数 IL <=0，认为是不透水层（坚硬粘土或岩层），对于不 透水层，由于不存在水的浮力，所以层面和层面以下的自重应力按 上覆土层的水土总重计算。
第三章.土中应力.ppt
弹性地基，绝对刚性基础 抗弯刚度EI=∞ → M≠0； 反证法: 假设基底压力与荷载分布相同， 则地基变形与柔性基础情况必然一致； 分布: 中间小, 两端无穷大。
§3 土体中的应力计算 §3.2 基底压力计算
二.基底压力分布
弹塑性地基，有限刚度基础
— 荷载较小 — 荷载较大
砂性土地基
— 接近弹性解 — 马鞍型 — 抛物线型 — 倒钟型
3P z3 3
1
P
z 2 R5 2 [1 (r / z)2 ]5/ 2 z2
ቤተ መጻሕፍቲ ባይዱ
3
2
1 [1 (r / z)2 ]5/2
3
2
1
[1 tg2 ]5/2
z
P z2
集中力作用下的 应力分布系数
r / z tg
§3 土体中的应力计算 §3.3 地基中附加应力的计算
§3 土体中的应力计算 §3.2 基底压力计算
建筑物设计
上部结构 基础 地基
上部结构的自重及各种荷 载都是通过基础传到地基 中的。
基础结构的外荷载 基底反力 基底压力 附加应力
地基沉降变形
基底压力计算
影响因素 计算方法 分布规律
基底压力：基础底面传递 给地基表面的压力，也称 基底接触压力。
暂不考虑上部结构的影 响，使问题得以简化； 用荷载代替上部结构。
六. 竖直线布荷载作用下的附加应力计算－弗拉曼解
--B氏解的应用
z
2pz3 (x2 z2 )2
x
2px2z (x2 z2 )2
M
xy
x
y yz
z
z
3Ph 2
§3 土体中的应力计算 §3.2 基底压力计算
二.基底压力分布
弹塑性地基，有限刚度基础
— 荷载较小 — 荷载较大
砂性土地基
— 接近弹性解 — 马鞍型 — 抛物线型 — 倒钟型
3P z3 3
1
P
z 2 R5 2 [1 (r / z)2 ]5/ 2 z2
ቤተ መጻሕፍቲ ባይዱ
3
2
1 [1 (r / z)2 ]5/2
3
2
1
[1 tg2 ]5/2
z
P z2
集中力作用下的 应力分布系数
r / z tg
§3 土体中的应力计算 §3.3 地基中附加应力的计算
§3 土体中的应力计算 §3.2 基底压力计算
建筑物设计
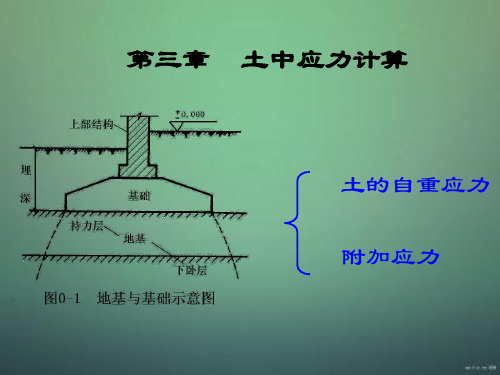
上部结构 基础 地基
上部结构的自重及各种荷 载都是通过基础传到地基 中的。
基础结构的外荷载 基底反力 基底压力 附加应力
地基沉降变形
基底压力计算
影响因素 计算方法 分布规律
基底压力：基础底面传递 给地基表面的压力，也称 基底接触压力。
暂不考虑上部结构的影 响，使问题得以简化； 用荷载代替上部结构。
六. 竖直线布荷载作用下的附加应力计算－弗拉曼解
--B氏解的应用
z
2pz3 (x2 z2 )2
x
2px2z (x2 z2 )2
M
xy
x
y yz
z
z
3Ph 2
第3章土中的应力计算汇总
第3章⼟中的应⼒计算汇总第三章地基中的应⼒计算§3-1 概述⼀、⼟体应⼒计算的⽬的：1、⽤于计算⼟体的变形，如建筑物的沉降；2、⽤于验算⼟体的稳定，如边坡的稳定性。
⼆、相关的概念1、⽀撑建筑物荷载的⼟层称为地基。
2、建筑物的下部通常要埋在地下⼀定的厚度，使之坐落在较好的地层上。
由天然⼟层直接⽀撑建筑物的称为天然地基3、软弱地基其承载⼒和变形不能满⾜设计要求，经加固后⽀撑建筑物的称为⼈⼯地基。
4、⽽与地基相接触的建筑物底部称为基础。
5、与建筑物基础底⾯直接接触的⼟层称为持⼒层。
6、将持⼒层下⾯的⼟层称为下卧层。
7、分类：（1）⼟体的应⼒按引起的原因分为⾃重应⼒和附加应⼒；⾃重应⼒——在未建造基础前，由⼟体⾃⾝的有效重量所产⽣的应⼒。
附加应⼒——由于建筑物荷载在地基内部引起的引⼒。
由外荷（静的或动的）引起的⼟中应⼒。
（2）按⼟体中⼟⾻架和⼟中孔隙（⽔、⽓）的应⼒承担作⽤原理或应⼒传递⽅式可分为有效应⼒和孔隙应（压）⼒。
有效应⼒——由⼟⾻架传递（或承担）的应⼒。
孔隙应⼒——由⼟中孔隙流体⽔和⽓体传递（或承担）的应⼒。
孔隙应⼒分为：静孔隙应⼒和超静孔隙应⼒。
对于饱和⼟体由于孔隙应⼒是通过⼟中孔隙⽔来传递的，因⽽它不会使⼟体产⽣变形，⼟体的强度也不会改变。
由于⼟层有其特殊的性质，作为地基的⼟层在上部荷载作⽤下将产⽣应⼒和变形。
从⽽给建筑物带来⼀系列⼯程问题，最主要的是地基的稳定问题和变形问题。
如果地基内部产⽣的应⼒在途的强度所允许的范围内时，⼟体是稳定的；反之，如果地基内部某⼀区域中的应⼒超过了⼟的强度，那么，哪⾥的⼟体将发⽣破坏，并可能会引起整个地基产⽣滑动⽽失去稳定，从⽽导致建筑物倾倒。
如果地基⼟的变形量超过了允许值，即使⼟体尚未破坏，也会造成建筑物毁坏或失去使⽤价值。
因此，为保证建筑物的安全和正常使⽤，设计时必须对地基进⾏强度和稳定性分析并计算基础的沉降量。
为此，就要研究在各种荷载作⽤下地基内部的应⼒分布规律。
第三章-土体中的应力计算
3P z 3 z 5 2 R
式中
P z K 2 z
为竖向集中力作用竖向附加应力系 数（查表）。
§3 土体中的应力计算
P z K 2 z
特点
§3.3 地基中附加应力的计算
一. 竖直集中力作用下的附加应力计算－布辛内斯克课题
3 1 K 2 [1 (r / z )2 ]5 / 2
3.P作用线上，r=0, K=3/(2π）,z=0, σz→∞，z→∞，σz=0 4.在某一水平面上z=const，r=0, K最大，r↑，K减小，σz减小 5.在某一圆柱面上r=const，z=0, σz=0，z↑，σz先增加后减小
6.σz 等值线－应力泡
P
P
球根 应力 球根
0.1P
0.05P
0.02P 0.01P
cy
假设土体为均匀连续介质，并为半无限空 间体，在距地表深度z处，土体的自重应力 为：
cz = z
自重产生的水平应力将在土压力计算部分 介绍。
若地基由多层土所组成
c 1h1 2 h2 ...... n hn h
i 1
n
i i
c 1h1 2 h2 ...... n hn h
七. 条形面积竖直均布荷载作用下的附加应力计算
任意点下的附加应力—F氏解的应用
p
z K s zp x K s xp xz K s xz p
y
B
x
z
x
z
M
x z s s Ks , K , K F ( B , x , z ) F ( , ) F( m , n ) z x xz B B
土力学及基础工程第三章-土中应力计算
2、垂直三角形分布荷载
dp布辛奈斯克解 积 分
z1 Kt1 p z2 Kt 2 pt
t f m, n
n z/b m l /b
矩形基础角点 下的竖向附加 应力系数，均 为m,n的函数
表(2-4)
3、圆形分布荷载
z r P0
均布圆形荷载 中心下的附加
• 在集中力作用线上的附加应力最大，向 两侧逐渐减小
• 同一竖向线上的附加应力随深度而变化
• 在集中力作用线上，当z＝0时，σz→∞， 随着深度增加,σz 逐渐减小
• 竖向集中力作用引起的附加应力向深部 向四周无限传播，在传播过程中，应力 强度不断降低（应力扩散）
二、矩形基础地基中的附加应力计算
矩形基础角点 下的竖向附加
第三章 土中应力计算
土的自重应力
附加应力
天然地面
z
cz z
cx cy K0 cz
cy
cz cx
五、例题分析
• 【例】一地基由多层土组成，地质剖面如下图所示，试 计算并绘制自重应力σcz沿深度的分布图。
57.0kPa
80.1kPa
103.1kPa 150.1kPa
n z/b m l /b
角点法计算地基附加应力Ⅰ
p
III IV
II o
I
III o II
IV
I
z
M
z KccⅠKcⅡ KccⅢ KccⅣ p
角点法计算地基附加应力Ⅱ
计算点在基底边缘
o
o II
z KccⅠKcⅡp
I
计算点在基底边缘外
o
III
oIV
z B (cI cII cIII cIV)P0 4.95KPa
第3章土体应力计算
3
σ v = σ cz + u0 = γ 1h1 + γ 2 h2 + γ ' h3 + γ w h3 = γ 1h1 + γ 2 h2 + γ 3 sat h3
σ h = σ ch + u0 = K 0σ cz + u0
3-2
地基中的自重应力
γ
γ′
均质地基
γ1 (γ < γ ) γ2
1 2
γ′ 2
d rd
p n = p m in − γ 0 d
p t = p m ax − p m in
3-4
地基中的附加应力计算
计算假定：地基土是各项同性的、均质的、线性变形体，而 计算假定：地基土是各项同性的 均质的 线性变形体， 各项同性 且在深度和水平方向上都是无限的 深度和水平方向上都是无限的。 且在深度和水平方向上都是无限的。 应力计算可分为空间问题和平面问题。 应力计算可分为空间问题和平面问题。 空间问题
y c x b b c b p1 pmax
pmax pmin
Fv M x M y = ± ± l ⋅ b Wx Wy
a
x a d
L
p2
y
p1 Fv Mx My = ∓ ± p2 l ⋅ b W底压力与基底附加应力
二、刚性基础下基底压力分布
（二）偏心荷载下的基底压力 3. 偏心荷载下条形基础的基底压力
'
3
3-2
地基中的自重应力
无侧向变形条件下，侧向应力： 无侧向变形条件下，侧向应力：
σ ch = σ cx = σ cy = K 0σ cz
K0——静止侧压力系数，它是土体在无侧向变形条件下侧 静止侧压力系数， 无侧向变形条件下 静止侧压力系数 它是土体在无侧向变形条件下侧 向（水平向）有效应力与竖向有效应力之比。 水平向）有效应力与竖向有效应力之比。 之比
σ v = σ cz + u0 = γ 1h1 + γ 2 h2 + γ ' h3 + γ w h3 = γ 1h1 + γ 2 h2 + γ 3 sat h3
σ h = σ ch + u0 = K 0σ cz + u0
3-2
地基中的自重应力
γ
γ′
均质地基
γ1 (γ < γ ) γ2
1 2
γ′ 2
d rd
p n = p m in − γ 0 d
p t = p m ax − p m in
3-4
地基中的附加应力计算
计算假定：地基土是各项同性的、均质的、线性变形体，而 计算假定：地基土是各项同性的 均质的 线性变形体， 各项同性 且在深度和水平方向上都是无限的 深度和水平方向上都是无限的。 且在深度和水平方向上都是无限的。 应力计算可分为空间问题和平面问题。 应力计算可分为空间问题和平面问题。 空间问题
y c x b b c b p1 pmax
pmax pmin
Fv M x M y = ± ± l ⋅ b Wx Wy
a
x a d
L
p2
y
p1 Fv Mx My = ∓ ± p2 l ⋅ b W底压力与基底附加应力
二、刚性基础下基底压力分布
（二）偏心荷载下的基底压力 3. 偏心荷载下条形基础的基底压力
'
3
3-2
地基中的自重应力
无侧向变形条件下，侧向应力： 无侧向变形条件下，侧向应力：
σ ch = σ cx = σ cy = K 0σ cz
K0——静止侧压力系数，它是土体在无侧向变形条件下侧 静止侧压力系数， 无侧向变形条件下 静止侧压力系数 它是土体在无侧向变形条件下侧 向（水平向）有效应力与竖向有效应力之比。 水平向）有效应力与竖向有效应力之比。 之比
3土中的应力计算
σcx＝K0 σcz = K0 γ z
第三章 土中应力计算 3.2 土的自重应力
二、成层土中自重应力
土中竖向和侧向的自重应力一般均指有效自重应力，计算时， 土中竖向和侧向的自重应力一般均指有效自重应力，计算时，对地下 有效自重应力 水位以下土层必须以有效重度 代替天然重度 为简便起见， 天然重度。 水位以下土层必须以有效重度γ ' 代替天然重度。为简便起见，常把竖 简称为自重应力， 表示。 向有效自重应力σcz简称为自重应力，并以符号σc表示。 若地基是由多层土所组成， 若地基是由多层土所组成，设各层的厚度为h1、h2、…hi、…hn，则地 基中第n层底面处的竖向土自重应力： 基中第n层底面处的竖向土自重应力：
σ（kPa） （ ）
σcz＝γ z
z
地基中的初始应力，即地基中任一点的自重应力 自重应力， 地基中的初始应力，即地基中任一点的自重应力，只需用竖向应力和 水平向应力表示。 水平向应力表示。天然地面下任意深度z处水平面上的竖向自重应力为
σcz＝γ z
竖直面上的水平向自重应力为 为静止侧压力系数。 K0 为静止侧压力系数。
土中应力计算 第三章 土中应力计算
3.1 概述
要保证建筑物的安全和正常使用必须控制其沉降量和 要保证建筑物的安全和正常使用必须控制其沉降量和不均匀沉降差值 沉降量 差异沉降量）不超过一定范围，对软粘土地基上的建筑物尤为重要。 （差异沉降量）不超过一定范围，对软粘土地基上的建筑物尤为重要。沉降 分析是土力学的基本课题之一。 分析是土力学的基本课题之一。 沉降量的大小主要取决于土体产生变形的原因 土体本身的性状两个方 土体产生变形的原因和 沉降量的大小主要取决于土体产生变形的原因和土体本身的性状两个方 面。 土体产生变形的原因主要是土体中应力状态的改变 应力状态的改变（ 土体产生变形的原因主要是土体中应力状态的改变（如地面荷载引起地 基中应力场的改变，在地基中产生附加应力）。 基中应力场的改变，在地基中产生附加应力）。 土体本身的性状主要指土的压缩性 土的压缩性（ 应力－应变关系）， ），是指土体在 土体本身的性状主要指土的压缩性（或应力－应变关系），是指土体在 附加应力作用下产生的效应。 附加应力作用下产生的效应。
第三章 土中应力的计算
z 2 z 2( aeoh) z 2(ebfo) q( t 1 t 2 )
（3）三角形荷载FEC（最大值为p－q）
作用范围3，4块，对M点引起的竖向应力σz3
z 3 z 3(ofcg) z 3( hogd ) ( p q)( t 3 t 4 )
第三章
土中应力的计算
3.1 概述
土中的应力—指土体在自重、构筑物荷载以及 其它因素（如水渗流、地震等）作用下，土体中 所产生的应力，包括自重应力和附加应力。
自重应力—土体受自重作用而产生的应力。
附加应力—土体受建筑物等外荷载作用而产生 的应力。
1、土中应力计算目的 为了对建筑物地基基础进行沉降（变形）、 承载力与稳定性分析，必须掌握建筑前后土中应 力的分布和变化情况。
2、偏心荷载作用时，基底压力按偏心受压公式计算：
Pmax
min
F G M F G 6e (1 ) A W A l
式中： F＋G、M－作用在基础底面中 心的竖直荷载及弯矩， M=(F＋G)e； e－荷载偏心距； W－基础底面的抵抗矩（抗弯截 面系数），对矩形基础 W＝bl2/6; b、l－基础底面的宽度与长度。
IL w wP 50 25 1.09 1 w L w P 48 25
故受浮力作用，其浮重度为：
'
( s w ) ( 26.8 9.81) 16.8 7.1 kN/m3 s (1 w ) 26.8 (1 0.50)
a 点：z = 0 m，σcz=γz=0; b 点：z = 2 m，σcz=γz=19 ×2=38 kPa c 点：z = 5 m , σcz =∑γihi=19 ×2+10 ×3=68 kPa， d 点：z = 9 m，σcz =∑γihi=19 ×2+10 ×3＋7.1 ×4＝96.4 kPa 土层中的自重应力cz分布，如图所示。
土力学与地基基础 土3-1
第三章 土中应力计算
土体的两个基本性质：
应力～应变关系：非线性 各向异性：成层等
假定： 把地基土视为均匀的各向同性的半无限空间线性
弹性体。 这种假定虽与土体的实际情况有出入，但因弹性
理论方法计算简单，且实践证明，当基底压力在 一定范围内时，用弹性理论的计算结果能满足实 际工程的要求。所以，可认为地基土符合半无限 体的假定而引用弹性理论公式。
第三章 土中应力计算
第三章 土中应力计算
问题1：为什么要了解土中应力？ 问题2：土体中都有哪些应力？ 问题3：这些应力怎么计算？
其分布规律如何？
这场官司谁打赢? 广州有一百货公司在西关上下九某街，在将原来二层 的职工宿舍拆建后拟建成八层的宿舍楼，邻近约1米 多有一栋移居国外老华侨的三层楼房。当百货公司的 职工宿舍楼建到四层的时候，老华侨的楼房先后出现 地面沉降，楼面倾斜，墙身开裂等现象。
附加应力： • 附加应力是由于基础等外部荷载所引起的应力。在
附加应力作用下，地基土将产生压缩变形，引起地 基沉降，由于建筑物荷载差异和地基土不均匀等原 因，基础各部分的沉降往往不均匀。当不均匀沉降 超过一定限度时，将导致建筑物的开裂、倾斜甚至 破坏。
两种应力产生的原因不同，因而分布规律和计算方法也不同。
市房地资源局一位负责人告诉记者，上海市自1921年明显出现地面沉降现象以来， 至1965年市区地面平均下降1.69米，最大年均沉降量达110毫米。作为我国最早认 识地面沉降危害的城市，上海于六十年代着手对地下水开采采取总量控制，实行 计划用水，以及采用将地表水(自来水)直接灌入地下含水层，使地下水位抬高， 从而达到恢复土层弹性控制地面沉降目的的人工回灌措施。自1965年实行人工回 灌至今，累计回灌地下的水量已达六亿立方米左右。通过采取控制地下水开采、 地下水人工回灌两项措施，本市地面沉降从历史最高的100毫米，到目前控制的 10毫米左右，1966年至2000年全市地面沉降累计为0.218米，控沉效果显著。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 土体中的应力计算 Stress in soil
土中应力(自重应力和附加应力 的计算方法 土中应力 自重应力和附加应力)的计算方法 自重应力和附加应力 有效应力原理的概念和应用
第三章 土体中的应力计算
第一讲
第三章 土体中的应力计算
§3.0 绪 论 Summary §3.1 地基中的应力状态 Stress State §3.2 土体的自重应力计算 Geostatic Stress §3.3 地基中的附加应力计算 Additional Stresses §3.4 基底压力计算 Foundation Pressure Contact Pressure §3.5 有效应力原理 Effective Stress Principle
绪 论
土的三大工程问题 土的三大工程问题 三大
土的渗流问题 土的变形问题 土的强度问题 地基中的应力状态 强 度 问 题 题 形 问
弹塑性模型 应力应变关系
σ1 −σ 3
(σ 1 − σ 3 ) y
刚塑性模 型
变
ε1
绪 论
土体中的应力计算
地基
土体的自重应力 外荷：基底压力 外荷： 地基中的附加应力 有效应力原理
§3.1 地基中的应力状态
一、一般应力状态－三维问题
σz
τzx
τxy
σx
6个独立 个独立 应力、 应力、应变分量
o x z
σ y τyz
σ x τxy τxz = τyx σ y τyz σij τzx τzy σ z
ε x γxy γxz εij = γyx ε y γyz γzx γzy ε z
σz
σ y τyz
§3.1 地基中的应力状态
二、平面应变状态－二维问题
应变条件
εy = 0;
γzx ≠ 0 γxy = γyz = 0;
应力条件
τ yx =τ xy = 0 τ yz =τ zy = 0 σy ν ε y = − (σx +σz ) = 0
σy = ν(σx + σz )
E E
独立变量
一般应力状态－ 一般应力状态－三维问题 平面应变状态－ 平面应变状态－二维问题 侧限应力状态－ 侧限应力状态－一维问题 基于上述的规定和假定，并将自重应力和附加应力 基于上述的规定和假定，并将 和 的计算归结为侧限应变、 的计算归结为侧限应变、平面应变或者一般应变等 不同的应力状态条件， 不同的应力状态条件，可采用弹性力学方法解决地 基中的应力计算问题。 基中的应力计算问题。
水平向： 水平向： σsx = σsy = K0σsz γ1
Z
水平向： H1 水平向： σ sx = σ sy = K0σ sz = K0 ∑γ i Hi
γ2 γ3
H2
H3
容重：地下水位以上用天然容重γ 容重：地下水位以上用天然容重γ
地下水位以下用浮容重γ′ 地下水位以下用浮容重γ′
思考题：水位骤降后， 思考题：水位骤降后，原水位到现水位之 间渗透性较小的饱和土层用什么容重？ 间渗透性较小的饱和土层用什么容重？
§3.1.3 土力学中应力符号的规定
正应力以压应力为正，剪应力以逆时针旋转 压应力为正 逆时针旋转为正 正应力以压应力为正，剪应力以逆时针旋转为正
§3.2 土体的自重应力计算
一、 水平地基中的自重应力
竖直向： 均质地基 竖直向： σsz = γz σ sz = W A = γzA A =γz
ν K0 = 1−ν 成层地基 竖直向： 竖直向： σsz = ∑γi Hi σsz = γ1H1 +γ 2H2 +γ3H3
§3.2 土体的自重应力计算
一、 水平地基中的自重应力
自重应力分布规律
σsz = γz σsz = ∑γi Hi
自重应力分布线的斜率是容重； 自重应力分布线的斜率是容重； 自重应力在等容重地基中随深度呈直线分布； 自重应力在等容重地基中随深度呈直线分布； 自重应力在成层地基中呈折线分布； 自重应力在成层地基中呈折线分布； 在土层分界面处和地下水位处发生转折。 在土层分界面处和地下水位处发生转折。
相间如何分担应力 基底压力在地基中引起的应力， 基底压力在地基中引起的应力， 所谓的“附加” 所谓的“附加”是指在原来自重 应力基础上增加的应力， 应力基础上增加的应力，建筑物 沉降的主要原因 建筑物修建以前， 建筑物修建以前，地基中由土体 本身的有效重量所产生的应力。 本身的有效重量所产生的应力。 修建后， 修建后，建筑物重量等外荷载引 起的基础底部对地基的作用力。 起的基础底部对地基的作用力。
γ
γ′
均质地基
成层地基
γ1 (γ
1
< γ2 )
γ2
γ′ 2
第三章 土体中的应力计算
§3.0 绪 论 Summary §3.1 地基中的应力状态 Stress State §3.2 土体的自重应力计算 Geostatic Stress §3.3 地基中的附加应力计算 Additional Stresses §3.4 基底压力计算 Foundation Pressure Contact Pressure §3.5 有效应力原理 Effective Stress Principle
ε1
§3.1 地基中的应力状态
§ 3.1.1 土的应力应变关系假定
土体－均质等向、 土体－均质等向、线弹性连续介质
碎散体 非线性 弹塑性 非均质 各向异性 连续介质 宏观平均 应力较小时，塑性区小 应力较小时， 距破坏较远 土层性质变化不大时
线弹性体
均质等向
应用材料力学和弹性力学方法进行分析
§3 Summary §3.1 地基中的应力状态 Stress State §3.2 土体的自重应力计算 Geostatic Stress §3.3 地基中的附加应力计算 Additional Stresses §3.4 基底压力计算 Foundation Pressure Contact Pressure §3.5 有效应力原理 Effective Stress Principle
§3.1 地基中的应力状态
§ 3.1.1 土的应力应变关系假定
土体－ 土体－线弹性体
σ1 − σ 3
刚塑性模 型
应力应变关系
线弹性 服从广义虎克定律 Generalized Hooke’s law
σ1 −σ 3
(σ 1 − σ 3 ) y
理想弹塑性模型
ε1
简化是否合理？ 简化是否合理？ Reasonable?
§3.2 土体的自重应力计算
自重应力：在修建建筑物以前， 自重应力：在修建建筑物以前，地基中由土体
本身的有效重量而产生的应力 本身的有效重量而产生的应力 有效重量
计算目的： 计算目的：确定土体的初始应力状态 水平地基中的自重应力 ∞ ∞ ∞ ∞ y z ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ o ∞ x
§3.2 土体的自重应力计算
三、侧限应力状态－一维问题
应变条件
εy = εx = 0;
γ xy = γ yz = γ zx = 0
应力条件
τxy = τyz = τzx = 0; σx = σy ;
ν σx = σy = σz = K0σz; 1− ν
独立变量
σz , εz = F(z)
σx ν εx = − σy + σz = 0; E E
§ 3.1.1 土的应力应变关系假定
土体－均质等向、 土体－均质等向、线弹性连续介质 弹性理论
理论——弹性力学解 → 求解“弹性”土体中的应力 弹性力学解 求解“弹性” 理论 方法——解析方法 解析方法 方法
∆P σ= ∆A
优点：简单， → 优点：简单，易于绘成图表等
σx ν εx = − σy + σz E E σy ν εy = − (σz + σx ) E E σ ν εz = z − σx + σy E E
三、侧限应力状态－一维问题
应变条件 εy = εx = 0;
γ xy = γ yz = γ zx = 0
o x y
A B
• 水平地基 → 半无限空间体； 半无限空间体 • 任何竖直面都是对称面； 任何竖直面都是对称面；
z
σsA = σsB
• 土质点或土单元不可能有侧向位移 → 侧限应变条件； 侧限应变条件 条件； • 半无限弹性地基内的自重应力只与 有关。 半无限弹性地基内的自重应力只与Z有关 有关。
一、 水平地基中的自重应力
计算假定： 计算假定：
水平地基 → 半无限空间体 → 半无限弹性体 侧限应变条件 → 一维问题
计算方法： 计算方法：
地下水位以上用天然容重 地下水位以下用浮容重
∞ ∞ ∞ ∞ y z
o ∞ ∞ ∞ ∞
∞ x
复习
§3.1 地基中的应力状态
§3.1.1 土的应力应变关系假定
土体－均质等向、 土体－均质等向、线弹性连续介质体
§3.1 地基中的应力状态
§3.1.3 土力学中应力符号的规定
符号规定 材料力学 正应力 剪应力 拉为正 顺时针为正 土力学 压为正 逆时针为正
土力学中以压 应力为主， 应力为主，规 压应力为正 定压应力为正
莫尔圆应力分析 符号规定
τzx
σz
+
o z
x σ τ x xz
-
τzx σx
σz +
-
τ zx σ z
σx, σz , τxz; εx, εz , γxz; = F(x, z)
ε x γxy γxz 0 0 ε γ εij = γyx 0y 0 yz γ γzx 0 zy ε z
σ x τxy τxz 0 0 σ 0 σij = τyx σ yy τyz τzx τzy σ z 0
土中应力(自重应力和附加应力 的计算方法 土中应力 自重应力和附加应力)的计算方法 自重应力和附加应力 有效应力原理的概念和应用
第三章 土体中的应力计算
第一讲
第三章 土体中的应力计算
§3.0 绪 论 Summary §3.1 地基中的应力状态 Stress State §3.2 土体的自重应力计算 Geostatic Stress §3.3 地基中的附加应力计算 Additional Stresses §3.4 基底压力计算 Foundation Pressure Contact Pressure §3.5 有效应力原理 Effective Stress Principle
绪 论
土的三大工程问题 土的三大工程问题 三大
土的渗流问题 土的变形问题 土的强度问题 地基中的应力状态 强 度 问 题 题 形 问
弹塑性模型 应力应变关系
σ1 −σ 3
(σ 1 − σ 3 ) y
刚塑性模 型
变
ε1
绪 论
土体中的应力计算
地基
土体的自重应力 外荷：基底压力 外荷： 地基中的附加应力 有效应力原理
§3.1 地基中的应力状态
一、一般应力状态－三维问题
σz
τzx
τxy
σx
6个独立 个独立 应力、 应力、应变分量
o x z
σ y τyz
σ x τxy τxz = τyx σ y τyz σij τzx τzy σ z
ε x γxy γxz εij = γyx ε y γyz γzx γzy ε z
σz
σ y τyz
§3.1 地基中的应力状态
二、平面应变状态－二维问题
应变条件
εy = 0;
γzx ≠ 0 γxy = γyz = 0;
应力条件
τ yx =τ xy = 0 τ yz =τ zy = 0 σy ν ε y = − (σx +σz ) = 0
σy = ν(σx + σz )
E E
独立变量
一般应力状态－ 一般应力状态－三维问题 平面应变状态－ 平面应变状态－二维问题 侧限应力状态－ 侧限应力状态－一维问题 基于上述的规定和假定，并将自重应力和附加应力 基于上述的规定和假定，并将 和 的计算归结为侧限应变、 的计算归结为侧限应变、平面应变或者一般应变等 不同的应力状态条件， 不同的应力状态条件，可采用弹性力学方法解决地 基中的应力计算问题。 基中的应力计算问题。
水平向： 水平向： σsx = σsy = K0σsz γ1
Z
水平向： H1 水平向： σ sx = σ sy = K0σ sz = K0 ∑γ i Hi
γ2 γ3
H2
H3
容重：地下水位以上用天然容重γ 容重：地下水位以上用天然容重γ
地下水位以下用浮容重γ′ 地下水位以下用浮容重γ′
思考题：水位骤降后， 思考题：水位骤降后，原水位到现水位之 间渗透性较小的饱和土层用什么容重？ 间渗透性较小的饱和土层用什么容重？
§3.1.3 土力学中应力符号的规定
正应力以压应力为正，剪应力以逆时针旋转 压应力为正 逆时针旋转为正 正应力以压应力为正，剪应力以逆时针旋转为正
§3.2 土体的自重应力计算
一、 水平地基中的自重应力
竖直向： 均质地基 竖直向： σsz = γz σ sz = W A = γzA A =γz
ν K0 = 1−ν 成层地基 竖直向： 竖直向： σsz = ∑γi Hi σsz = γ1H1 +γ 2H2 +γ3H3
§3.2 土体的自重应力计算
一、 水平地基中的自重应力
自重应力分布规律
σsz = γz σsz = ∑γi Hi
自重应力分布线的斜率是容重； 自重应力分布线的斜率是容重； 自重应力在等容重地基中随深度呈直线分布； 自重应力在等容重地基中随深度呈直线分布； 自重应力在成层地基中呈折线分布； 自重应力在成层地基中呈折线分布； 在土层分界面处和地下水位处发生转折。 在土层分界面处和地下水位处发生转折。
相间如何分担应力 基底压力在地基中引起的应力， 基底压力在地基中引起的应力， 所谓的“附加” 所谓的“附加”是指在原来自重 应力基础上增加的应力， 应力基础上增加的应力，建筑物 沉降的主要原因 建筑物修建以前， 建筑物修建以前，地基中由土体 本身的有效重量所产生的应力。 本身的有效重量所产生的应力。 修建后， 修建后，建筑物重量等外荷载引 起的基础底部对地基的作用力。 起的基础底部对地基的作用力。
γ
γ′
均质地基
成层地基
γ1 (γ
1
< γ2 )
γ2
γ′ 2
第三章 土体中的应力计算
§3.0 绪 论 Summary §3.1 地基中的应力状态 Stress State §3.2 土体的自重应力计算 Geostatic Stress §3.3 地基中的附加应力计算 Additional Stresses §3.4 基底压力计算 Foundation Pressure Contact Pressure §3.5 有效应力原理 Effective Stress Principle
ε1
§3.1 地基中的应力状态
§ 3.1.1 土的应力应变关系假定
土体－均质等向、 土体－均质等向、线弹性连续介质
碎散体 非线性 弹塑性 非均质 各向异性 连续介质 宏观平均 应力较小时，塑性区小 应力较小时， 距破坏较远 土层性质变化不大时
线弹性体
均质等向
应用材料力学和弹性力学方法进行分析
§3 Summary §3.1 地基中的应力状态 Stress State §3.2 土体的自重应力计算 Geostatic Stress §3.3 地基中的附加应力计算 Additional Stresses §3.4 基底压力计算 Foundation Pressure Contact Pressure §3.5 有效应力原理 Effective Stress Principle
§3.1 地基中的应力状态
§ 3.1.1 土的应力应变关系假定
土体－ 土体－线弹性体
σ1 − σ 3
刚塑性模 型
应力应变关系
线弹性 服从广义虎克定律 Generalized Hooke’s law
σ1 −σ 3
(σ 1 − σ 3 ) y
理想弹塑性模型
ε1
简化是否合理？ 简化是否合理？ Reasonable?
§3.2 土体的自重应力计算
自重应力：在修建建筑物以前， 自重应力：在修建建筑物以前，地基中由土体
本身的有效重量而产生的应力 本身的有效重量而产生的应力 有效重量
计算目的： 计算目的：确定土体的初始应力状态 水平地基中的自重应力 ∞ ∞ ∞ ∞ y z ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ o ∞ x
§3.2 土体的自重应力计算
三、侧限应力状态－一维问题
应变条件
εy = εx = 0;
γ xy = γ yz = γ zx = 0
应力条件
τxy = τyz = τzx = 0; σx = σy ;
ν σx = σy = σz = K0σz; 1− ν
独立变量
σz , εz = F(z)
σx ν εx = − σy + σz = 0; E E
§ 3.1.1 土的应力应变关系假定
土体－均质等向、 土体－均质等向、线弹性连续介质 弹性理论
理论——弹性力学解 → 求解“弹性”土体中的应力 弹性力学解 求解“弹性” 理论 方法——解析方法 解析方法 方法
∆P σ= ∆A
优点：简单， → 优点：简单，易于绘成图表等
σx ν εx = − σy + σz E E σy ν εy = − (σz + σx ) E E σ ν εz = z − σx + σy E E
三、侧限应力状态－一维问题
应变条件 εy = εx = 0;
γ xy = γ yz = γ zx = 0
o x y
A B
• 水平地基 → 半无限空间体； 半无限空间体 • 任何竖直面都是对称面； 任何竖直面都是对称面；
z
σsA = σsB
• 土质点或土单元不可能有侧向位移 → 侧限应变条件； 侧限应变条件 条件； • 半无限弹性地基内的自重应力只与 有关。 半无限弹性地基内的自重应力只与Z有关 有关。
一、 水平地基中的自重应力
计算假定： 计算假定：
水平地基 → 半无限空间体 → 半无限弹性体 侧限应变条件 → 一维问题
计算方法： 计算方法：
地下水位以上用天然容重 地下水位以下用浮容重
∞ ∞ ∞ ∞ y z
o ∞ ∞ ∞ ∞
∞ x
复习
§3.1 地基中的应力状态
§3.1.1 土的应力应变关系假定
土体－均质等向、 土体－均质等向、线弹性连续介质体
§3.1 地基中的应力状态
§3.1.3 土力学中应力符号的规定
符号规定 材料力学 正应力 剪应力 拉为正 顺时针为正 土力学 压为正 逆时针为正
土力学中以压 应力为主， 应力为主，规 压应力为正 定压应力为正
莫尔圆应力分析 符号规定
τzx
σz
+
o z
x σ τ x xz
-
τzx σx
σz +
-
τ zx σ z
σx, σz , τxz; εx, εz , γxz; = F(x, z)
ε x γxy γxz 0 0 ε γ εij = γyx 0y 0 yz γ γzx 0 zy ε z
σ x τxy τxz 0 0 σ 0 σij = τyx σ yy τyz τzx τzy σ z 0