1-2017清华大学自主招生暨领军计划试题解析
清华大学自主招生数学试题解析

• 1・2017年清华大学自主招生暨领军计划试题解析已知-•根绳子放在数轴的[0・斗」区阳丄二线密度二皿-护.求绳子的质屋- 解答加解答 件先冇cos 単十 i iin 4?5二(cos 警cos 夸一 sin 警sin 弩: 二 cos + isin再I ] i 归纳法,可得3 警+ Tn 警,1 E.世到 ttJ -' = 1,则 cw 1 — w -' TW " - C4J _':7W + ru _l —2 COS 〒 T tv ' + ⑴ 二 2cCrS 号.战/(tw )/(a/ )f( OJ ? )/(oi 1)/(w)/(w _1 )/(w 2 )/(«"*)(4?十 W 十 2)(^~2十 J 十 2)(^ 十 y + 2)(W _1 + 胪 + 2) (1 十洞十2^ + w -] + 1 + 2M + 2w a 十 2w l + 4)(1 十 4 2^ + OJ -2 + 1 + 2^ + 2^ + 2M _r + 4)(6 + Gcos^ + 4cos 警)(6 + g 警 + Seos 警)(6 + ficos y - 4tos yj(6 + 4cOH 弩- E 阮、(6 - 6孕y + isin ^,/(x) = x z 十龙+若则f (川)几』〉的值为+ i^cos ^sin 警 + sin 警cos 弩 5-75-l)(6 + ?5- 1、4• 1・《高校自主招生一数学》 贾广素工作室• 2 •=11.若 0「门 +flCOS (A :-l )= 0 有唯--解,则(A.厲的值唯• B. 口的值不唯一C 门的值不存在D.以上都不对解答选A.因为f (兀)=217 +acos (A :-l )关于x = l 对称,所以若f (x )^唯一零点,则零点只 能为1.将兀=1彳弋入,得到a = T,此时f (x ) =2|x_11 -cos (x-l ),^检验« = -1符合 题意"04已知皿1 *2 ,衍皿&€ {1、Z ,3,4:} ,口3皿4》为口I ■吐.心皿4中不同数字的种类哀如N (1J23) =3,N (122,1}二2,求所有的256个(血心gg )的排列所得 7V ("l 山2 ,如■心)的平均值为().解答选D-N 5\心、a 3心)为1的个数为4;N (心•如,為虫J 为2的个数为CS (CS+2Q ) = 84; N (尙0 心皿Q 为3的个数为二144*N (Q i *2 *麻3皿4 )为球的个数为A] — 24.117^从而 iijfR^^6(4xi + 84X2+114X3 + 24X1) = ^.在△/WC 中 *sinZ/l + sinz^/?sinz^C 的最大值为(解答选E市积化和差公式得sin^A + sin^Bsm^C=sin^A + y (cost^B - ZC) - cos(^B + 乙CM-sin^A - -^COB ^A + ~|~cos(Z 百—乙 C) 冬 sin^A - -^-cosZ^/4 + 令Y I s + (_ 4)- Z 卩)+ YA - 32175 64A- iB.1 +75D.无报大值4《高校自主招生一数学》贾广素工作室在= = + j时取等号*四人做一道选项为A.B,C.D的选择题•四牛同学的对话知厂赵:我选A.钱:我选B,GD当屮的-个一孙古我选C李古我选6四个人毎人只选了…个选项川1' R倂不相同'我中貝有一个人说谥•则说谎的人町能是诽1 解答孙或李.用列衣法•只中O代表选该选项.X代表没有选该选项一如赵说谎•则无人选A(见表1八弟盾一表1A B C D赵XX孙0O如钱说谎,则赵、钱均选A(见表2)-矛曲.表2A H C赵O践O如孙说谎.则可得如表3所示的情况:成7..O _______X• 3 *《高校自主招生一数学》贾广素工作室如李说谎.则川'得in* 4所示的悄况•成立.表4A B C D赵O钱X OO0X已知2・ lvC?C, I 2 + IV I = 1 H, I z2 + H'2 I 二4?则I ZW I (解答选注意到1 - | z + w | - - | (z w)21 = \ z2w2+ 2zw | , 从【对冇1 | z2 + | - 21 ziv | 与I $ 21 砂| 一]护+ \沪从而(最小值可以取测例如辽二捋7.⑷二上尹,最大值亦可以取到’例如辽二今+寺人⑷二-3 +丄)2 21往四面体PABC ABC为等边三角形,边长为乳“二乳珂?二4./V二乳贝W四而体P/W0的体积为().A. 3B. 2屈C. /1TD. /10解答选C件先PC2= PB Z+ BC\故PB±反\设P到底而的高足PH.则BC± UH ZABH =30°设PH = h.AH =a^H^b,CH = c”山余弦定理得+ A2= 32・护+护二学,+ h2 -5\07A.有最大值普B有最大值号C有最小值另 D.有最小值号* 5 *如图[所示,已知曲线+ / = l 以及直线i lt y =弄仏;y = _yx,曲线E 与八交于A,B 两点“与h 交于C-D 两点.在E 上任找一点P (不与A^.C-D 重合几直线AP.M 分 别与仏交于M,N两点,则(A,B. C, D. 解答选BC•设P 的坐标为(利小八则乎+冗二I •此吋PA 的方程为v 42ya - -7—匕-找)・Xo - V2円?的方程为+ ©)•分别与方程尸-专工联立,可得_ 72 y a + ~2X ^尤 M 二-; -------_号-列+屈09二 yri .对于函数=e i (jt-l)a (x-2),H 下选项正确的是( A.冇2个极大值 B冇2个扱小值 U 1是极大值点 解答BC, 求导数:/"(x) = e^ECx - l)2(x -2) -- I)C A -2) +=c T (x + /3)(x -^/3)(JT - 1).则f 〔C 右2个极小值门是极大值点.D. 1是极小值点(x - I}2]10在椭圆上存在2个不同的点Q,使得丨021,二丨OM I 丨(釈 在椭圆上存在4个不同的点Q,使得丨%]—|OM| |QV| 在椭圆上存在2亍不同的点0使得住椭圆上存在4个不同的点0使得△NfAsAQMO rfl 对称性,不奶设A RC D 的塑标分别为-罟- - 72图!0M\ \ 0N\ - 0M - ON -\OM\\ON\ = \ 0A\\可^\OQ\2= \o^\ \o^\’可选Wt A/.C2四点.若△MXIsAQTfO.则只能选耽刈•觸足A + 2y + 3z- 100的非负整数解的组数为(A 883B 884 C. 885).D 886Zy种数00—5C5110—484920-474830—4546h・・h・・33u1表5解的组数为51 + 49 + 4W + 46 + 45 + - + 4 + 3 + 1 + 0 =百甘 4.{(x t y,z) | x +2y + 3z^l,JC,y T z>0} ■求V的体积+这是-个玄角呗休•三条玄角边丘是1以寺.故休积为春一已知f(x)=c2x +e -ax.^ X^).均右只站孑厶求a的取值范围一解答rtl f (X) = c21 + c1- m符/CO) = 2,又f (JC ) =2c^J + c J- ◎该导歯数在[th +«■)上递増‘故贾求 f (0)=3-^>0,即a<3.州图2所小』为闘山II屈心• f E在岡.11运动JL满出/AM-艸+则-W)* 6 ** 7・的中点E 的轨迹为()-A.圆B.稱圆 U 双曲线的一支 D.线段解答选入 由E 为中点'得PE Z + QE& 二 BE 2 十 OE 2 BO-=厝.做动点到两疋点距离的平方和为足f (因此动点E 的轨迹为慎1 一15L_已知椭圜方程为为苴右准线上一点,过P 向椭圆作切蜒,切点分别为恻的左恆点対几则( 人解答选AU汁先汴.意到结论:在椭圆准线上作取一点•过该点作椭•圆的两条切线*那么两切点的连 线必过该准线村应的倩点(虚明略)-应用结论•可知/XF/W 的周氏九定值•且越AH 乖胃于横轴吋它的值忌小.此时JT] Xi 码,骷"百€ (1,2,3,4,5,6? T 且 JC],x z T x 3T x 4,嘉■站各不相同,则禰足心一5忌+ 10x a - 10氐+ 5x s -x a = 0的解的组数为參少?解答6.首先心-应是5的倍数点x 产1皿之或机=6t x fi = L 考虑方程-+ 10的—10盟」5心 一 5 或-5x-i + 10氏 一 W 鹤 + 5嘉二一 5* 即-x 2 - 2X 3 - 2x x + A :5 = I或—X2 + 2^3 — 2也 + Jts - — 1注意到肌-乱不足2的倍数•战由上面的方服有也-耳厂乳軌-心一 -1或若砧-应一 -1心-占二]・或者X 5 _ X? = -3、心-心=1或若也-也二】* -工4二-1故这个方程有M+3二6纽解.已知 A e { - KOJ ZV e (2,3,4,5,映射 f : A^B. li^ 足 x 十 f(x) +球J )为壷数.求f 的个数. 解答50.A. \AB\的扯小值为1 C. AFA13的周艮为定值B. \AB\的毘小值师 D. A MB 的面积为定值' 8 -注意到 X + /(JC ) +xf(x) = <x + l)(f(x) +1)-1. + 十 1)为偶数. 故若x 为偶数,则f (巧为奇数•即f(0)二3或和N - “的取值任意,由乘法原 理可得,答案为2x5a ^50.解答选匚一注总到公式fm 二故dH 错误.另一方血M ©/? *从而川门币二0-故F (丽}=- 最后•如 A 二 0•则 P(AB)>0.U 知实数厲』满足a 2+ a =3b 2 +2乩且 H 则C 解答a ACD若 a<b,则 / + a<h~ + b<2( b 2+ b)<3b~ + = 矛盾.另一方面■若3b 2 + 2b= a 2 + a^(2h)2 + 2b>3b 2 +2乩矛盾.最U 若 b^2a 侧 a 2a ~ 3b~ + 2b^3(2a¥ +4a^>a - + a * 矛盾. 故得选项为ACD1 + A :| 4 1 + A2 +I + X t0]7 ~卿( hA.显窍有】个乩小于1 B 虽务有2个在小于2 C. mHx {, --■, x 2 di?} ^2 (J17D. max { x } T , JC 2 AU \ ^2 016解答ABD.如有2个绪小于】・则上式左边大于占 + j ])•矛盾一 如有3个摘小于厶则匕式左边大于占+出+占■不质. 再注意到x t =^=-= ^01T = 2O16是一组解点匚不陇立. 如 max{jt! ,Xi»***tX aM7 }<2 Olfii 则―-—+ ―1— + ■■■ + -------- ! ----- > --------- 1 --- + -------- - ---- + ■■■ + ------ ! -----1 + 利 h1 + X 2O I 7 1 +2 0161 +2 0161 +2 016矛质.已知事件月—n<P<l?)<lt!WiJ(A . /n = i -re/?)C, H 丽=0B . p(^|A)= i-r(B)D. P(J\B)=QA. b<aB a<bC a<2b D. b<2a已知严■,总期均为大于o 的实数.a故答案选AB6 ' 8 -《高校自主招生一数学》 贾广素工作室入{和 + 几 + zd 是等比数列B.若存在 m .>1— y… - z m ,则 JCi = yi = Zi1 q 1U 若心二-才忌二才则= ( - 1)"亠尹D 以上均不正确解答选BC首先*当首项^i = ^i-zi= 0时・皿+几十為}不是等比数列.其次,若存在啣>l,s = % =昭,解方程组可得x…L -i = y^-i = z^-t =2x Mt 从而递推 可得Xi 二力=巧,一 1 弓 ’ 1出次*由Xi = 一忑心二亍得}■] + Zi - 2x2 + X] =2,则幷“*斗爲二3 •不,根据递推式用為=(-1)”十右.故答棗选BCA 3 n r., =0. 5 B. 3 H * r h =0,6 C. 3 M r fl = () 7 [>, 3 » < =0,8 解答选2假设不存在航’便得 仏=0 5.则山H =O^ioo =0. 85,必存亦「使得hVU •硏5.若k 是偶数•不妨设血二三⑴汀汕笆筈於3<*・不符令题意;若血是奇数"设氐二加T-l.f炭厂+,只能f 矛氐所以选项A 正确 4= 08同理可得选项D 正确. 如果此人第2、86次全部投中•排除B,C.一同学打球■记g 为投起次后的命中率,已知心—AsFL 版则一足有().。
清华2017领军试题及答案

2017清华领军试题与答案(2017清华领军)1.质量m 的小球从距轻质弹簧上端h 处自由下落,已知重力加速度为g,弹簧的劲度系数为k,小球在运动过程中的最大动能E max 为 C解:小球运动到重力和弹力相等的位置时速度最大(2017清华领军)2、一颗子弹以水平速度v0 穿透一块在光滑水平面上迎面滑来的木块后,二者运动方向均不变。
设子弹与木块间相互作用力恒定,木块最后速度为v,则 AC A.v0越大,v 越大 B.v0越小,v 越大C.子弹质量越大,v 越大 D.木块质量越小,v 越大解:子弹穿透木块过程中,子弹与木块间相互作用力恒定,两者都做匀减速运动,子弹的位移与木块的位移大小之和等于木块的厚度.若质量不变,则两者的加速度不变,当子弹的初速度v0越大时,子弹穿过木块的时间越短,且木块的位移越小,由于木块初速度和加速度不变,所以末速度v越大,如下图所示.故A正确,B错误.C、子弹的质量越大,由于作用力不变,则加速度越小,初速度v0一定,则子弹位移越大,木块位移越小,由于木块初速度和加速度不变,所以末速度v越大,如下图所示.故C正确.D、木块质量越小,其加速度越大,初速度不变,子弹穿过木块的时间变大,则木块末速度v变小,如下图所示.故D错误.(2017清华领军)3. 已知地球半径R e=6400km。
卫星在距赤道20000km 上空运行,求在赤道上的人能观察到此卫星的最长时间间隔为 CA.42100s B.38200s C.34700s D.20800s解:假设地球自转的方向如图顺时针,赤道上的人能看到卫星的范围由A顺时针到B)/(cos21RRAoBs-=∠卫星的角速度22GmMmRRω=得3GMRω=地球自转角速度224sπω=时间间隔9.89sAOBt hωω∠==-(2017清华领军)4.在粗糙地面上,某时刻乒乓球的运动状态如图所示,判断一段时间后乒乓球可能的运动状况 ABCA.静止 B.可能向右无滑动滚动C.可能向左无滑动滚动 D.只向右平动不转动解:和地面的接触点的速度是平动速度(向右)+转动速度(向右)地面的摩擦力使转动和平动均减速若转动初速度和平动初速度相等,则最后静止。
2017清华领军试题
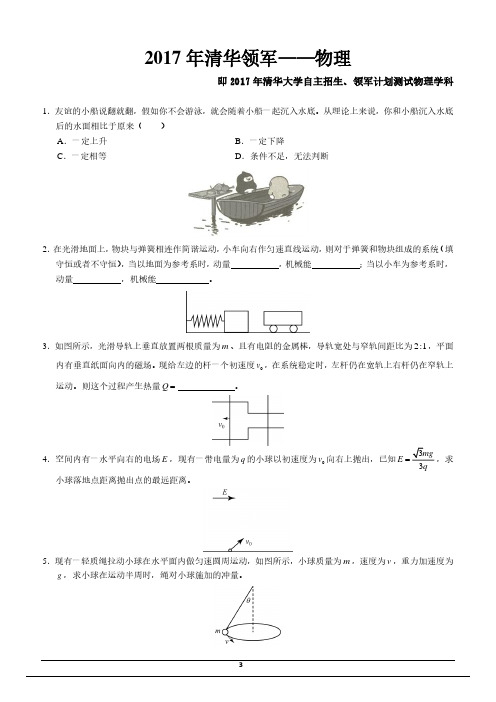
13.有一左端封闭、右端开口的均匀 U 形管,左管内有一段水银分割出两端长度相等的气柱,如图所示,现 向右管缓慢注入水银,设平衡后上段气体为 l1 ,下端气体长 l2 ,则 l1 与 l2 的关系为( A. l1 l2 C. l1 l2 B. l1 l2 D.无法确定,视注入水银的量 )
███████████████████
4
湖底, 7℃ ,则湖深约( A. 5m B. 10m C. 15m D. 20m
)
12.一用钉鞘锁定的导热活塞将导热气缸分成体积相等的左右两室, P 右 =5: 3 ,拔出钉鞘后活塞移动至稳 左:P 定状态,外界温度恒定,则( A.稳定后左右两室体积比为 5: 3 C.左室气体吸热 ) B.左室气体对右室气体做功 D.右室气体吸热
7 .在水平面内,金属棒 MN 一角速度 绕 O 点顺时针旋转,空间内有竖直向下的磁场,如图所示。已知
MO NO ,则下列说法正确的是(
A. M 点电势高于 N 点 C.若增大 ,则 MN 点电势差增大
) B. M 点电势低于 N 点 D.若增大 B ,则 MN 点电势差增大
8.在如图所示电路中,小灯泡规格为“ 6V , 3W ” , R3 4 ,电源内阻为 1 ,电压表、电流表均为理想电 表,闭合开关,调节滑动变阻器阻值,使电压表示数为 0 ,此时灯泡正常发光,电流表的示数为 1A ,则 电源电动势 E ,输出功率 P , R2 。
3mg ,求 3q
5.现有一轻质绳拉动小球在水平面内做匀速圆周运动,如图所示,小球质量为 m ,速度为 v ,重力加速度为
g ,求小球在运动半周时,绳对小球施加的冲量。
███████████████████
3
6.如图所示,有 a 、 b 两个物体, a 物体沿长 L 、倾角为 、动摩擦因数 0.5 的斜面滑下后,在长为 L 的 光滑水平面 BC 上运动; b 从 C 点上方高为 4.5L 处下落。二者同时释放,在 C 处相遇,则 sin = 。
()2017清华大学自主招生暨领军计划数学试题[精校版,带解析]历年自主招生考试数学试题大全,文档
![()2017清华大学自主招生暨领军计划数学试题[精校版,带解析]历年自主招生考试数学试题大全,文档](https://img.taocdn.com/s3/m/58b1bfe3844769eae109ed57.png)
. WORD格式.资料.2021年清华大学自主招生暨领军方案试题1.函数f(x)(x2a)e x有最小值,那么函数g(x)x22xa的零点个数为〔〕A.0B.1C.2D.取决于a的值【答案】C【解析】注意f/(x)e x g(x),答案C.2.ABC的三个内角A,B,C所对的边为a,b,c.以下条件中,能使得ABC的形状唯一确定的有〔〕A.a1,b2,cZB.A1500,asinA csinC2asinC bsinB C.cosAsinBcosC cos(B C)cosBsinC0,C600 D.a3,b1,A600【答案】AD.3.函数f(x) x21,g(x) lnx,以下说法中正确的有〔〕A.f(x),g(x)在点(1,0)处有公切线B.存在f(x)的某条切线与g(x)的某条切线平行C.f(x),g(x)有且只有一个交点D.f(x),g(x)有且只有两个交点专业.整理.WORD 格式.资料 .【答案】BD【解析】注意到y x1为函数g(x)在 (1,0)处的切线,如图,因此答案BD .4.过抛物线y 2 4x 的焦点F 作直线交抛物线于A,B 两点,M 为线段AB 的中点.以下说法中正确的有〔〕3一定相离A .以线段AB 为直径的圆与直线x2B .|AB|的最小值为 4C .|AB|的最小值为2D .以线段BM 为直径的圆与y 轴一定相切【答案】AB【解析】对于选项A ,点M 到准线x1的距离为1(|AF||BF|)1|AB|,于是以线段AB 为直径3 2212, 1的圆与直线x1一定相切,进而与直线x一定相离;对于选项B ,C ,设A(4a 2,4a),那么B( ),124aa于是 |AB| 4a22,最小值为4AB中点到准线的距离的 2倍去得到最小值;.也可将|AB|转化为4a 2对于选项D ,显然BD 中点的横坐标与1|BM|不一定相等,因此命题错误.2225.F 1,F 2是椭圆C:x 2y21(ab0)的左、右焦点,P 是椭圆C 上一点.以下说法中正确的有a b〔〕A .a 2b 时,满足 F 1PF 2 900的点P 有两个B .a2b 时,满足F 1PF 2900的点P 有四个C . PF 1F 2的周长小于4aa 2D . PF 1F 2的面积小于等于2专业.整理.WORD格式.资料.【答案】ABCD.【解析】对于选项A,B,椭圆中使得F1PF2最大的点P位于短轴的两个端点;对于选项C,F1PF2的周|PF1||PF2|sinF1PF21|PF1|2长为2a2c4a;选项D,F1PF2的面积为1|PF2|1a2.2222 6.甲、乙、丙、丁四个人参加比赛,有两花获奖.比赛结果揭晓之前,四个人作了如下猜测:甲:两名获奖者在乙、丙、丁中;乙:我没有获奖,丙获奖了;丙:甲、丁中有且只有一个获奖;丁:乙说得对.四个人中有且只有两个人的猜测是正确的,那么两个获奖者是〔〕A.甲B.乙C.丙D.丁【答案】BD【解析】乙和丁同时正确或者同时错误,分类即可,答案:BD.7.AB为圆O的一条弦〔非直径〕,OC AB于C,P为圆O上任意一点,直线PA与直线OC相交于点M,直线PB与直线OC相交于点N.以下说法正确的有〔〕A.O,M,B,P四点共圆B.A,M,B,N四点共圆C.A,O,P,N四点共圆D.以上三个说法均不对【答案】AC【解析】对于选项A,OBM OAM OPM即得;对于选项B,假设命题成立,那么MN为直径,必然有MAN为直角,不符合题意;对于选项C,MBN MOP MAN即得.答案:AC.8.sinA sinB sinC cosA cosB cosC是ABC为锐角三角形的〔〕A.充分非必要条件B.必要非充分条件C.充分必要条件D.既不充分也不必要条件【答案】B专业.整理.WORD格式.资料.【解析】必要性:由于sinB sinC sinB sin(B)sinB cosB1,2类似地,有sinC sinA1,sinB sinA1,于是sinA sinB sinC cosA cosBcosC.不充分性:当A,B C4时,不等式成立,但ABC不是锐角三角形.29.x,y,z为正整数,且x y z,那么方程1111的解的组数为〔〕x y z2A.8B.10C.11D.12【答案】B【解析】由于11113,故3x6.2x y z x假设x3,那么(y6)(z6)36,可得(y,z)(7,42),(8,24),(9,18),(10,15),(12,12);假设x4,那么(y4)(z4)16,可得(y,z)(5,20),(6,12),(8,8);假设x 5,那么3112,y20,y5,6,进而解得(x,y,z)(5,5,10);10y z y3假设x6,那么(y3)(z3)9,可得(y,z)(6,6)).答案:B.10.集合A{a1,a2, ,a n},任取1 i j k n,a i a j A,a j a k A,a k a i A这三个式子中至少有一个成立,那么n的最大值为〔〕A.6B.7C.8D.9【答案】B11.10,610,1210,那么以下各式中成立的有〔〕A.tan tan tan tan tan tan3B.tan tan tan tan tan tan3专业.整理.WORD格式.资料.C.tan tan tan3tan tan tanD.tan tan tan3tan tan tan【答案】BD【解析】令x tan,y tan,z tan,那么yx z y x z3,所以1xy1yz1zxyz3(1xy),z y3(1yz),x z3(1zx),以上三式相加,即有xyyzzx3.类似地,有113(11),113(11),113(11),以上三式相加,即有x y xy y z yz z x zx111x y z3.答案BD.xy yz zx xyz12.实数a,b,c满足a bc 1,那么4a14b14c1的最大值也最小值乘积属于区间〔〕A.(11,12)B.(12,13)C.(13,14)D.(14,15)【答案】B【解析】设函数f(x)4x1,那么其导函数f/(x)2,作出f(x)的图象,函数f(x)的图象在x14x13处的切线y221(x1)21,以及函数f(x)的图象过点(1,0)和(3,7)的割线73342y4x1,如图,于是可得4x14x1221(x1)21,左侧等号当x1或77777334x3右侧等号当x121,当a b1时取得;最小值为时取得;时取得.因此原式的最大值为c2337,当a b1,c3时取得,从而原式的最大值与最小值的乘积为73(144,169).答案B.42专业.整理. WORD 格式.资料 .13., ,z,yz1, x 2 y 221,那么以下结论正确的有〔 〕x y Rx zA .xyz 的最大值为B .xyz 的最大值为427C .z 的最大值为2D .z 的最小值为133【答案】ABD14.数列{a n }满足a 11,a 2 2,a n26a n1 a n (nN*),对任意正整数n ,以下说法中正确的有〔〕A .a n 2 1a n2a n 为定值B.a n1(mod9) 或a n 2(mod9)C .4a n1a n 7为完全平方数D.8a n1a n 7为完全平方数【答案】ACD【解析】因为a n22a n3a n1a n22(6an2a n 1)an1a n226a n2an1a n 2 1a n 2(an26a n 1)a n 2 1 a n 21a n2a n ,选项A 正确;由于a 311,故a n 2 1 a n2a n a n 2 1 (6a n1a n )a na n 2 16a n 1a n a n 27,又对任意正整数恒成立,所以4a n1a n 7(a n1a n )2,8a n1a n7(a n1a n )2,应选项C 、D 正确.计算前几个数可判断选项B 错误.说明:假设数列{a n }满足a n 2 pa n 1a n ,那么a n 21a n2a n 为定值.15.假设复数z 满足z11,那么z 可以取到的值有〔 〕zA .1B . 1C .51 D .512222【答案】CD专业.整理.WORD格式.资料.【解析】因为|z|1z11,故51|z|51,等号分别当z51i和z51i时|z|z2222取得.答案CD.16.从正2021边形的顶点中任取假设干个,顺次相连构成多边形,假设正多边形的个数为〔〕A.6552B.4536C.3528D.2021【答案】C【解析】从2021的约数中去掉1,2,其余的约数均可作为正多边形的边数.设从2021个顶点中选出k个构成正多边形,这样的正多边形有2021个,因此所求的正多边形的个数就是2021的所有约数之和减去2021 k和1008.考虑到202125327,因此所求正多边形的个数为(12481632)(139)(17)202110083528.答案C.17.椭圆x2y21(a b0)与直线l1:y1x,l2:y1x,过椭圆上一点P作l1,l2的平行线,a2b222a分别交l1,l2于M,N两点.假设|MN|为定值,那么〔〕bA.2B.3C.2D.5【答案】C【解析】设点P(x,y),可得111111,成心M(x0y0,x0y0),N(x0y0,x0y0)00224242|MN|1x024y02为定值,所以a2416,a2,答案:C.4b21b4说明:〔1〕假设将两条直线的方程改为ya1M,N,使得|MN| kx,那么;〔2〕两条相交直线上各取一点b k为定值,那么线段MN中点Q的轨迹为圆或椭圆.18.关于x,y的不定方程x21652y的正整数解的组数为〔〕A.0B.1C.2D.3【答案】B专业.整理.WORD格式.资料.19.因为实数的乘法满足交换律与结合律,所以假设干个实数相乘的时候,可以有不同的次序.例如,三个实数a,b,c相乘的时候,可以有(ab)c,(ba)c,c(ab),b(ca),等等不同的次序.记n个实数相乘时不同的次序有I n种,那么〔〕A.I22B.I312C.I496D.I5120【答案】B【解析】根据卡特兰数的定义,可得I n C n1A n n 1Cnn1n!n1.答案:AB.2n2(n1)!C2n1关于卡特兰数的相关知识见?卡特兰数——计数映射方法的伟大胜利?.20.甲乙丙丁4个人进行网球淘汰赛,规定首先甲乙一组、丙丁一组进行比赛,两组的胜者争夺冠军.4个人相互比赛的胜率如表所示:表中的每个数字表示其所在的选手击败其所在列的选手的概率,例如甲击败乙的概率是,乙击败丁的概率是.那么甲刻冠军的概率是.【答案】【解析】根据概率的乘法公式,所示概率为0.3(0.5 0.3 0.5 0.8).21.在正三棱锥P ABC中,ABC的边长为1.设点P到平面ABC的距离为x,异面直线AB,CP的距离为y.那么limy.x3【答案】2【解析】当x时,CP趋于与平面ABC垂直,所求极限为ABC中AB边上的高,为3.2专业.整理. WORD 格式.资料 .22.如图,正方体 ABCDA 1B 1C 1D 1的棱长为1,中心为O,BF1BC,A 1E 1A 1A ,那么四面体OEBF2 4的体积为 .1【答案】96【解析】如图,V OEBF V OEBF1V GEBF1V EGBF11V EBCC 1B 1 1 .2 22 16 962sin 2nx)dx23.(x )2n1(1.【答案】02)2n 1(1 sin 2nx)dxx2n1(1 sin 2nx)dx 0.【解析】根据题意,有 (x24.实数x,y 满足(x 2 y 2)3 4x 2y 2,那么x 2 y 2的最大值为.【答案】1【解析】根据题意,有(x 2y 2)34x 2y 2(x 2 y 2)2,于是x 2y 2 1,等号当x 2y 21 时取得,2因此所求最大值为 1.25.x,y,z 均为非负实数,满足(x 1)2 (t 1)2 (z 3)227 ,那么xy z 的最大值与最小值分别22 4为.【答案】22 32【解析】由柯西不等式可知,当且仅当(x,y,z)(1,1,0)时,xy z 取到最大值3.根据题意,有22专业.整理. WORD 格式.资料 .x 2 y 2 z 2 x2y3z 13 ,于是 13 (x yz)23(x yz)y,解得xy z223 .于是4 42x y z 的最小值当(x,yz)(0,0,223)时取得,为22 3.2226.假设O 为ABC 内一点,满足S AOB :S BOC :S COA4:3:2 ,设AOABAC ,那么.【答案】23【解析】根据奔驰定理,有2 4 299 .327.复数zcos2isin2,那么z 3z 2z 2 2.33z1 3【答案】2i2【解析】根据题意,有z3z 2z 221 z 2zcos5isin51 3i .z3 32228.z 为非零复数,z ,40的实部与虚部均为不小于1的正数,那么在复平面中,z 所对应的向量OP 的10 z端点P 运动所形成的图形的面积为.【答案】2001003 3003x y1,R),由于401,【解析】设zxyi(x,y 40z ,于是 10 1040y如图,弓形面积为z|z|2 40x1, 1,x 2y 2 x 2 y 21202(sin 6)100 100,四边形ABCD 的面积为21(10 3 10)101003100.2632专业.整理.WORD 格式.资料 .于是所示求面积为2(100100)(1003100)200 1003300.333,那么sin4xsin2xsinxsinx 29.假设tan4xcos4xcos2xcos2xcosx.3cos8xcos4x cosx【答案】3【解析】根据题意,有sin4x sin2xsinx sinxcos8xcos4xcos4xcos2x cos2xcosx cosx(tan8x tan4x) (tan4x tan2x) (tan2xtanx)tanxtan8x3.30.将16个数:4个1,4个2,4个3,4个4填入一个 4 4的数表中,要求每行、每列都恰好有两个偶数,共有种填法.【答案】44100031.设A 是集合{1,2,3, ,14}的子集,从A 中任取 3个元素,由小到大排列之后都不能构成等差数列,那么A中元素个数的最大值为 .【答案】8【解析】一方面,设A {a 1,a 2, ,a k },其中kN *,1 k 14.不妨假设a 1 a 2a k .假设k 9,由题意,a 3 a 1 3,a 5 a 37,且a 5a 3 a 3 a 1,故a 5a 17.同理a 9a 5 7.又因为a 9 a 5 a 5 a 1,所以a 9a 1 15,矛盾!故k8.另一方面,取 A {1,2,4,5,10,11,13,14},满足题意.综上所述, A 中元素个数的最大值为8.专业.整理。
清华大学自主招生试题含答案
一、 选择题1.设复数z=cos23π+isin 23π,则2111-1z z +-=() (A)0(B)1(C)12(D)322.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的()条件 (A)充分不必要(B)必要不充分(C)充要(D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则()(A)|OA|·|OB|≥2(B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点(D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1),且满足:①()f x >0,x ∈(-1,0);②()f x +()f y =()1x yf xy++,x 、y ∈(-1,1),则()f x 为(A)奇函数(B)偶函数(C)减函数(D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)?kx 有()(A)2个极大值点(B)3个极大值点(C)2个极小值点(D)3个极小值点 6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sin(B?A)?2sin2A=0,则有(??) (A)b=2a (B)△ABC 的周长为3(C)△ABC 的面积为33(D)△ABC 的外接圆半径为337.设函数2()(3)xf x x e =-,则()(A)()f x 有极小值,但无最小值(B)()f x 有极大值,但无最大值 (C)若方程()f x =b 恰有一个实根,则b>36e (D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则()(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ,12y y +=b(D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为() (A)1(B)2 (C)3(D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n ,总存在正整数m ,使得n S =m a ,则() (A ){n a }可能为等差数列(B ){n a }可能为等比数列(C ){n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ,总存在正整数m ,使得n a =m S 11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是()(A)甲(B)乙(C)丙(D)丁12.长方体ABCD?1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为(??)(A)13(B)23(C)2(D)313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ,其面积为S ,则()(A)若S=4,则k 的值唯一(B)若S=12,则k 的值有2个 (C)若D 为三角形,则0<k ≤23(D)若D 为五边形,则k>4 14.△ABC 的三边长是2,3,4,其外心为O ,则OA AB OB BC OC CA ⋅+⋅+⋅=() (A)0(B)?15 (C)?212(D)?29215.设随机事件A 与B 互相独立,且P(B)=0.5,P(A?B)=0.2,则()(A)P(A)=0.4(B)P(B?A)=0.3 (C)P(AB)=0.2(D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分,则这两部分的面积之比的() (A)最小值为34(B)最小值为45(C)最大值为43(D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形,则不同的选法有() (A)105种(B)225种(C)315种(D)420种18.已知存在实数r ,使得圆周222x y r +=上恰好有n 个整点,则n 可以等于() (A)4(B)6 (C)8(D)1219.设复数z 满足2|z|≤|z?1|,则() (A)|z|的最大值为1(B)|z|的最小值为13(C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数,a =(mcosα,msinα),b =(ncosβ,nsinβ),其中α,β∈[0,2π)α,β∈[0,2π).定义向量12a =(2α,2α),12b =(2β2β),记θ=α?β,则()(A)12a ·12a =a (B)1122ab ⋅=2θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足:1a =6,13n n n a a n++=,则() (A)?n ∈N?,n a <3(1)n +(B)?n ∈N?,n a ≠2015(C)?n ∈N?,n a 为完全平方数(D)?n ∈N?,n a 为完全立方数 22.在极坐标系中,下列方程表示的图形是椭圆的有()(A )ρ=1cos sin θθ+(B )ρ=12sin θ+(C )ρ=12cos θ-(D )ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+,则()(A )()f x ≤43(B)|()f x |≤5|x|(C)曲线y=()f x 存在对称轴(D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ,若△ABC 为锐角三角形,则()(A)sinA>cosB(B)tanA>cotB(C)222a b c +>(D)333a b c +>25.设函数()f x 的定义域是(?1,1),若(0)f =(0)f '=1,则存在实数δ∈(0,1),使得(?)(A)()f x >0,x ∈(?δ,δ)(B)()f x 在(?δ,δ)上单调递增 (C)()f x >1,x ∈(0,δ)(D)()f x >1,x ∈(?δ,0)26.在直角坐标系中,已知A(?1,0),B(1,0).若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n),总存在两个不同的点i P ,j P ,使得|sin ∠A i P B?sin ∠A j P B|≤13,则n 的最小值为(?) (A)3(B)4 (C)5(D)627.设非负实数x,y 满足2x+y=1,则的(??)(A)最小值为45(B)最小值为25(C)最大值为1(D)最大值为13+28.对于50个黑球和49个白球的任意排列(从左到右排成一行),则()(A)存在一个黑球,它右侧的白球和黑球一样多(B)存在一个白球,它右侧的白球和黑球一样多 (C)存在一个黑球,它右侧的白球比黑球少一个(D)存在一个白球,它右侧的白球比黑球少一个 29.从1,2,3,4,5中挑出三个不同数字组成五位数,其中有两个数字各用两次,例如12231,则能得到的不同的五位数有()(A)300个(B)450个(C)900个(D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0,则() (A)L 是轴对称图形(B)L 是中心对称图形 (C)L?{(x,y)∣22x y +≤1}(D)L?{(x,y)∣?12≤y ≤12} ##Answer##1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+-- =212sin 2sincos333i πππ-⋅-22cos()sin()33sin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]66i ππ-+-1sin )662i i ππ+-=1,选B2.【简解】()p q k l a a a a +-+=[(p+q)-(k+l)]d ,与公差d 的符号有关,选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅==2,正确;答案(B),|OA|+|OB|≥2≥2,正确;答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x -方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程,错误;答案(D),原点到直线AB :(111x x -)x-y+1=0的距离≤1,正确。
清华等17所高校自主招生笔试真题

清华等17所高校自主招生笔试真题清华等17所高校2017年自主招生笔试真题南开大学6月10日、11日,南开大学2017年自主招生考试顺利举行,533名考生参加了现场测试。
笔试题量很大,涵盖了语文、数学知识的学科能力测试,更多地考查学生的思辨能力和平时知识的积累。
1、“祝考生考得都会,蒙得都对”是一个什么命题并证明清华大学2017年6月10日,清华大学率先开始了自主选拔测试,2017年有近6000多人参加清华初试,2017年清华自主招生、领军计划、自强计划笔试采用同一套试卷进行测试。
清华大学初试采用笔试形式,考试科目为:数学与逻辑、理科综合(物化)、文科综合(文史),学生依据填报的专业类参加其中两个科目的考试。
初试结果将在报名系统内公布。
据悉,2017年清华笔试在全国44个城市设有61考点,相比去年增加25个考点,其中,每个城市还设有多个考点。
考试安排:初试时间:2017年6月10日上午9:00-12:00复试时间:2017年6月16日-18日,(具体测试时间以报名系统内公布为准)。
笔试题型:理科:数学30题,物理20题,化学18题,一共68题,180分钟合在一起考的。
文科:数学35题,语文12题,历史20题。
笔试试题文科综合(文史)类笔试试题:考题有明清时的自然经济瓦解、抗日战争、诗词等内容,不是考知识点记忆,主要考查阅读面、逻辑思维深度等,数学与逻辑难度较大。
化学试题成为新考查内容今年化学成为新考查内容。
刘震表示,新增化学试题注重对学科基础内容的考查、综合多模块内容、加强化学学科的应用性、创新试题的设问模式,充分体现化学学科的学术价值,考查了考生的基础知识、综合能力、科学素养和创新精神,关注环境问题,讨论产生酸雨的原因及危害、食品中的增塑剂与人体健康等社会焦点问题。
物理试题注重基本概念的准确理解和灵活运用。
通过采用单选和多选题随机编排的方式,来考查学生构建正确、合理的物理模型,综合运用物理知识分析、解决实际问题的能力,同时增加了能力考查的区分度。
清华大学自主招生暨领军计划试题

A. P (A) = 0.4
B. P (B − A) = 0.3
C. P (AB) = 0.2
解析 ABC.
根据题意,有如下联表:
) D. P (A + B) = 0.9
AA B 0.2 0.3
B 0.2 0.3
16. 过 △ABC 的重心作直线将 △ABC 分成两部分,则这两部分的面积之比的 (
6 ,于是原式最小值为 3 .
事实上,显然 x, y, z ∈ [0, 1] ,于是
5x + 4y + 3z ⩾ 4x2 + 4y2 + 3z = −z2 + z + 3 = z(1 − z) + 3 ⩾ 3,
等号当 x = y = 0 且 z = 1 时取得.
10. 设数列 {an} 的前 n 项和为 Sn.若对任意的正整数 n,总存在正整数 m,使得 Sn = am,则 ( ) A. {an} 可能为等差数列 B. {an} 可能为等比数列 C. {an} 的任意一项均可写成 {an} 的两项之差 D. 对任意正整数 n ,总存在正整数 m ,使得 an = Sm 解析 AC. 对于选项 A,取 an = n, n = 1, 2, · · · 即可; 对于选项 B,若 {an} 为等比数列,设其公比为 q ,显然 q ̸= ±1 .根据题意,对任何正整数 n ,均有
y
y = kx + m
O
x
y = f (x)
A. 2 个极大值点 解析 BC.
B. 3 个极大值点
C. 2 个极小值点
D. 3 个极小值点
相当于以直线 y = kx + m 为 x 轴观察函数 y = f (x) 的图象的极值点.
2017年清华大学领军计划物理-参考答案

2017年清华大学领军计划测试
物理学科
有一质量为m的小球从距离轻质弹簧上端h处自由下落,弹簧的劲度系数为k,试求小球在运动过程中的最大动能E kmax。
(已知重力加速度为g)
参考答案:E kmax=mgh+m2g2
2k
设有一卫星在距离赤道20000km上空自西向东运行,求赤道上的人能观察到此卫星的时间间隙,已知地球半径R e=6400km。
参考答案:9.9h
有一半径为2r的线圈,内部磁场的分布如图所示,且两部分磁场的磁感应强度均为B。
有一长为4r的金属杆横在中间,其电阻为R,金属杆的右半边线圈电阻为R,左半边线圈电阻为2R。
当两个磁场磁感应强度从B缓慢变化至0时,求通过右半边的电荷量q。
参考答案:4πr 2B
5R
2。
清华大学2017年领军计划试题

清华大学2017年自主招生与领军计划数学试题(1)设函数2()xx f x ee ax =+-,若对0,()2xf x ∀≥≥,则实数a 的取值范围是()(,3]A -∞ ()[3,)B +∞ ()(,2]C -∞ ()[2,)D +∞解答:问题等价于22x x e e ax +≥+在[0,)+∞上恒成立;记2()xx g x e e =+,()2h x ax =+,两函数均过(0,2),且(0)3g '=,可知(,3]a ∈-∞.答案A.(2)设,A B 为两个随机事件,且,0()1A B P A ⊂<<,则()()1()A P AB P B =- ()()1()B P AB P B =-()(|)()C P B A P B = ()(|)()D P B A P B =解答:(A )()1()1()P AB P AB P A =-=-,所以A 错;(B )()()1()1()P AB P A B P A B P B ==-=-,所以B 对;(C )()()(|)1()()P AB P A P B A P A P A ===,所以C 错; (D )()()()(|)1()1()P B A P B P A P B A P A P A --==--,所以D 错;答案B.(3)从0,1,2,,9中选出三个不同数字组成四位数(其中的一个数字用两次),如5242,这样的四位数共有()1692A 个 (B)3672个 (C)3708个 (D)3888个解答:十个数中先选出3个数,再从中选出一个作为用两次的,再选出两个位置放这个数,剩下两个数再排列一下,共有32104324320C C ⨯⨯⨯=个.下面考虑0被排在了首位的情况:1°0在后三位还出现了一次:则在剩下9个数中再选两个,于是有293!216C ⨯=个.2°0只出现在首位:则在剩下9个数中再选两个,其中一个重复两次,于是有2923216C ⨯⨯=个.于是符合题目要求的四位数共有43202162163888--=个. 答案D.(4)已知集合{1,0,1}M =-,{2,3,4,5,6}N =,设映射:f M N →满足:对任意的,()()x M x f x xf x ∈++是奇函数,这样的映射f 的个数()25A (B)45 (C)50 (D)100解答:设()()()g x x f x xf x =++则(1)1g -=-,(0)(0)g f =,(1)12(1)g f =+,(1),(1)g g -均为奇数,所以只需令(0)f 为奇数,所以共有52550⨯⨯=种选择. 答案C.(5)若关于x 的方程12cos(1)0x a x -+-=只有一个实数解,则实数a 的值()1A -等于 (B)1等于 (C)2等于 (D)不唯一解答:显然12x -与cos(1)a x -均关于1x =对称,若有1x =之外的解,则均成对出现,所以要只有一个解,则只能在1x =处,此时1a =- 当1a =-时,1x ≠时121x ->,1cos(1)1a x -≤-≤,确实只有1x =一个解.答案A.(6)设,a b 为非零向量,且2b a =,则b 与b a -夹角的最大值为(B )()12A π(B)6π(C)4π(D)3π 解答:因为2b a =,取OD b =,则平移向量a 的起点到点O ,则向量a 的终点在以O 为圆心,以2b 为半径的圆上,则b 与b a -夹角为COD ∠,根据几何意义可知,当CD 与圆O相切时,夹角最大,此时,OC CD ⊥,则1sin 2OC COD OD ∠==,则6COD π∠=. 所以0,6πα⎡⎤∈⎢⎥⎣⎦. 答案B.(7)已知三棱锥P ABC -的底面为边长为3的正三角形,且3,4,5,PA PB PC ===则P ABC -的体积为(C )()3A解答:因为3AB AC AP ===,过点A 向面PBC 作垂线PH ,因为斜边长相等,则射影相等,可知H 到顶点,,P B C 距离相等,因此H 为PBC 的外心,因为PBC 为直角三角形,所以H 为PC 的中点.AH ⊥平面PBC,则2AH ==,所以113432P ABC A PBC V V --==⋅⋅⋅=答案C.(8)设函数432()2(2)2(12)41f x x x m x m x m =-++-+++,若对任意的实数,()0,x f x ≥则实数m 的取值范围是(A )()[0,)A +∞ 1()[,)2B +∞ ()[0,1]C 1()[,1]2D解答::()4322()02221440f x x x x x m x x ≥⇔-+-++-+≥即()()()()()2224322442221211m x x x x x x m x x x-+≥--+-+⇔-≥--+则,题目等价于对任意的实数,x ()()()222211m x x x-≥--+恒成立,当2x =时,不等式显然成立,当2x ≠时,题目等价于对任意的实数,x ()()()222112x x m x -+≥--恒成立, 因为()()()2221102x x x -+-≤-,而且0能取到,所以()()()222112x x x -+--的最大值为0, 因此0m ≥. 答案A.(9)设正实数,,,x y z w 满足22020x y z w yz wx z y --+=⎧⎪-=⎨⎪≥⎩,则z y 的最小值为 D()62A + ()622B + ()632C + ()642D +解答:设z t z yt y =⇒=,则22(2)21x w y t y t wx t +=+⎧⎪=⎨⎪≥⎩,由均值不等式可得,22(2)22(2)8y t xw y t xw +≥⇔+≥, 又因为22y t wx =,所以222(2)16y t y t +≥,则2(2)16642,642t t t t +≥⇔≥+≤-,又因为1t ≥,所以642t ≥+, 答案D.(10)给定圆O 及圆内一点P ,设,A B 是圆O 的两个动点,满足90APB ︒∠=,则AB 的中点的轨迹为 (A)()A 一个圆 ()B 一个椭圆 ()C 一段双曲线 ()D 一段抛物线解答:如图,建立平面直角坐标系,不妨假设圆O 的方程为222,x y R +=()(),00P m m R ≤<,则OM AB ⊥,所以222AM OA OM =-,因为AM PM =,所以222PM OA OM =-, 设(),M x y ,则22222()x m y R x y -+=--化简得:2222m x y mx 22R +-+=,即2222x y 224m R m ⎛⎫-+=-⎪⎝⎭, 所以轨迹为一个圆. 答案A.(11)方程23100x y z ++=的非负整数解的个数是()883A ()884B ()885C ()886D 解答:令2x y t +=,先研究3100t z +=的解的个数,然后对于t 的每一个可能的取值0t ,分别研究02x y t +=的解的个数.将未知问题(三元)转化为已知问题(二元)去解决。
