2015冬A2-14-量子物理
量子物理基础知识点复习
Aeiml
(1)
其中
ml
2mr 2E 2
(2)
(1)式是 的有限连续函数。要使其满足在任一
给定 值时为单值,就需要 ( ) ( 2 )
e e 或
iml
iml ( 2 )
由此得 eiml 2 1
(3)
(3)式给出ml 必须是整数,即
ml 1,2,...
m me / 1 v2 / c2
v 3 c 2
h h 1 h
p mv 3 mec
(10)
四、不确定关系
1. 位置和动量的不确定关系:微观粒子在某个方向上 的坐标和动量不能同时准确地确定,其中一个不确定 量越小,另一个不确定量就越大。
xpx 2
yp y 2
(19)
根据能量和动量关系有 p 2mE k
处 Ek E,再由
E
2 2mr 2
ml2
,而此
圆周运动的粒子的角动量(此角动量矢量沿z轴方 向)为
L rp ml
即角动量也量子化了,而且等于 的整数倍。
(20)
七、原子中的电子
1. 四个量子数,取值范围,物理意义。
1) 主量子数 n 1,2,3,4, ,它决定原子系统的能量。 n 1,2,3,4, 分别代表 K,L,M,N 等壳层。
第12章 量子物理基础知识点复习
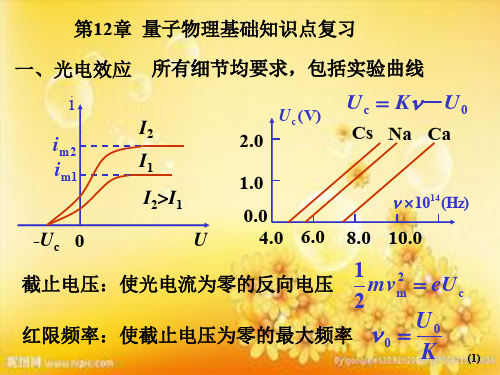
一、光电效应 所有细节均要求,包括实验曲线
i
im 2 im1
I2 I1
Uc(V) Uc K-U0
2.0
Cs Na Ca
1.0
I2>I1
1014(Hz)
0.0
-Uc 0
大学物理15 量子物理基础1

m
o
0.1A
(2) 若使其质量为m=0.1g的小球以与粒子相同的 速率运动,求其波长
若 m=0.1g 的小球速率 vm v
vm
v
q BR m
则 :m
h m vm
h m
1 v
h m
m q BR
h q BR
m m
6.64 10 27 0.1 10 3
6.641034
m
px x h
考虑到在两个一级极小值之外还有电子出现,
运动,则其波长为多少? (粒子质量为ma =6.64ⅹ10-27kg)(05.08…)
解:
(1)
求粒子德布罗意波长 h h
p m v
先求:m v ?
而:q vB
m
v2 R
m v q BR
h m v
h q BR
6.63 10 34 1.601019 0.025 0.083102
1.001011
( x,t ) 0 区别于经典波动
(
x,
t)
e i 2
0
(t x
)
自由粒子沿x方向运动时对应的单色平面波波函数
设运动的实物粒子的能量为E、动量为 p,与之相 关联的频率为 、波长为,将德布罗意关系式代入:
考虑到自由粒子沿三维方向的传播
式中的 、E 和 p 体现了微观粒子的波粒二象性
2、概率密度——波函数的统计解释 根据玻恩对德布罗意波的统计解释,物质波波
p mv h
德布罗意公式(或假设)
与实物粒子相联系的波称为德布罗意波(或物质波)
h h h
p mv m0v
1
v2 c2
如果v c,则 h
m0v
量子物理学的开创者和奠基人

量子物理学的开创者和奠基人一.量子物理学的开创者和奠基人普朗克和爱因斯坦并称为二十世纪最重要的两大物理学家。
他因发现能量量子化而对物理学的又一次飞跃做出了重要贡献,并在1918年荣获诺贝尔物理学奖1874年,普朗克进入慕尼黑大学攻读数学专业,后改读物理学专业。
1877年转入柏林大学,曾聆听亥姆霍兹和基尔霍夫教授的讲课,1879年获得博士学位。
1930年至1937年任德国威廉皇家学会的会长,该学会后为纪念普朗克而改名为马克斯·普朗克学会从博士论文开始,普朗克一直关注并研究热力学第二定律,发表诸多论文。
大约1894年起,开始研究黑体辐射问题,发现普朗克辐射定律,并在论证过程中提出能量子概念和常数h(后称为普朗克常数,也是国际单位制千克的标准定义[2] ),成为此后微观物理学中最基本的概念和极为重要的普适常量。
1900年12月14日,普朗克在德国物理学会上报告这一结果,成为量子论诞生和新物理学革命宣告开始的伟大时刻。
由于这一发现,普朗克获得了1918年诺贝尔物理学奖。
二.后世纪念以其命名的太空望远镜:世界最大远红外线望远镜成功升空2009年5月14日13时12分(格林尼治时间,北京时间为14日21时12分),欧洲阿丽亚娜5-ECA型火箭携带欧洲航天局两颗科学探测卫星“赫歇尔”和“普朗克”,从法属圭亚那库鲁航天中心发射升空。
据欧航局和欧洲阿丽亚娜空间公司电视直播报道,发射地当天天气晴好,火箭按照预定时间点火,随后搭载两个探测卫星腾空而起。
发射约30分钟后,“赫歇尔”和“普朗克”先后脱离火箭,开始自主飞行。
在确认探测卫星与火箭成功分离后,圭亚那航天控制中心响起了热烈的掌声,欧航局局长让-雅克多尔丹和阿丽亚娜空间公司行政总裁让—伊夫勒加尔起身拥抱,表示庆祝。
多尔丹在随后发表的讲话中说,随着“赫歇尔”和“普朗克”的发射,人类又向探索宇宙的起源迈进了一步。
从发射到卫星与火箭分离虽然只有30分钟,但却凝聚了参与这项计划的欧洲15国多年的心血和梦想。
大学基础物理学答案(习岗)第10章

129第十章 量子物理基础本章提要1. 光的量子性· 物体由于自身具有一定温度而以电磁波的形式向周围发射能量的现象称热辐射。
· 在任何温度下都能全部吸收照射到其表面上的各种波长的光(电磁波),的物体称为绝对黑体,简称黑体。
· 单位时间内从物体单位表面积发出的、波长在λ附近单位波长间隔内电磁波的能量称单色辐射本领(又称单色辐出度),用)(T M λ表示· 单位时间内物体单位表面积发出的包括所有波长在内的电磁波的辐射功率称为辐射出射度,用则M 表示,M 与)(T M λ的关系为0()d M M T λλ∞=⎰2. 维恩位移定律在不同的热力学温度T 下,单色辐射本领的实验曲线存在一个峰值波长λm , T 和λm 满足如下关系:λm T b =其中,b 是维恩常量。
该式称维恩位移定律。
3. 斯忒藩—玻尔兹曼定律· 黑体的辐射出射度M 与温度T 的关系为4T M σ=其中,σ为斯忒藩—玻尔兹曼常量。
该结果称斯忒藩—玻尔兹曼定律。
· 对于一般的物体4T M εσ=ε称发射率。
4. 黑体辐射· 能量子假说:黑体辐射不是连续地辐射能量,而是一份份地辐射能量,并且每一份能量与电磁波的频率ν成正比,满足条件E nhv =,其中n =1,2,3,…,等正整数,h 为普朗克常数。
这种能量分立的概念被称为能量量子化,130每一份最小的能量E hv =称为一个能量子。
· 普朗克黑体辐射公式(简称普朗克公式)为112)(/52-=kT hc e hc T M λλλπ其中,h 是普朗克常量。
由普朗克公式可以很好地解释黑体辐射现象。
· 光子假说:光是以光速运动的粒子流,这些粒子称为光量子,简称光子。
一个光子具有的能量为νh E =动量为 λh p =5. 粒子的波动性· 实物粒子也具有波粒二象性,它的能量E 、动量p 与和它相联系的波的频率ν、波长λ满足关系2E mc h ν==λh p m u ==这两个公式称为德布罗意公式或德布罗意假设。
量子力学简介

第五版
15-8 量子力学简介
(1) 经典的波与波函数
机械波 y(x,t) Acos2π(t x )
电磁波
E
(
x,t
)
E0
c
os2π(t
x
)
H
(
x,t)
H0
cos2π(t
x
)
经典波为实函数
y ( x,t )
Re[
i 2π(t x
Ae
)
]
第十五章 量子物理
1
物理学
第五版
15-8 量子力学简介
15-8 量子力学简介
讨论: 1 粒子能量量子化
Ep
能
量
En
n2
h2 8ma2
o ax
基态 能量
E1
h2 8ma 2
,
(n 1)
激发态能量
En
n2
h2 8ma 2
n2E1,
(n 2,3,)
一维无限深方势阱中粒子的能量是量子化的 .
第十五章 量子物理
21
物理学
第五版
15-8 量子力学简介
2 粒子在势阱中各处出现的概率密度不同
波函数
(x) 2 sin nπ x
aa
概率密度
(x) 2 2 sin2 ( nπ x)
aa
例如,当 n =1时, 粒子在 x = a /2处出 现的概率最大
第十五章 量子物理
22
物理学
第五版
15-8 量子力学简介
3 波函数为驻波形式,阱壁处为波节, 波腹的个数与量子数 n 相等
1926年建立了以薛定谔方 程为基础的波动力学,并建立 了量子力学的近似方法 .
河北省邢台市2023-2024学年高二上学期期末物理试题(含答案)
河北省邢台市2023-2024学年高二上学期期末物理试题姓名:__________ 班级:__________考号:__________1.量子力学是研究物质世界微观粒子运动规律的物理学分支,它为人类科技进步、科学发展作出了许多贡献,量子科技或将帮助人类实现如今难以企及的梦想。
下列关于量子理论的创立,说法正确的是()A.爱因斯坦首先提出了能量子假设B.普朗克首先认为微观粒子的能量是不连续的C.在对热辐射研究的过程中,很多学者由于“紫外灾难”而失去了生命D.黑体只从外界吸收电磁波,不向外界辐射电磁波2.随着生活水平的提高,电子秤已成为日常生活中不可或缺的一部分。
如图所示是用平行板电容器制成的厨房用电子秤及其电路简图。
称重时,把物体放到电子秤面板上,压力作用会导致平行板上层膜片电极下移,则下列说法正确的是()A.电容器的电容减小B.电容器的带电电荷量减少C.膜片下移过程中,电流表有b到a的电流D.电容器两极板的电压增大3.如图所示,三根长直通电导线中的电流大小相同,通过b、d导线的电流方向垂直纸面向里,通过c导线的电流方向垂直纸面向外,a点为b、d两点连线的中点,ac垂直bd,且ab=ad=ac,则c导线受到的安培力方向()A.由a指向c B.由c指向a C.由a指向b D.由a指向d4.在如图甲所示的电路中,电感线圈的直流电阻可忽略不计,闭合开关S后一段时间电路达到稳定状态。
t=0时刻断开开关S,LC振荡电路中产生电磁振荡,LC振荡电路随时间t变化的规律如图乙所示(其纵轴表示的物理量未标出)。
下列说法正确的是()A.图乙可以表示电感线圈中的电流随时间变化的图像B.图乙可以表示电容器所带电荷量随时间变化的图像C.t=T4时刻,磁场能最大D.将自感系数L和电容C同时增大为原来的2倍,电磁振荡的频率变为原来的145.如图甲所示,在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,线框产生的感应电动势随时间变化的图像如图乙所示,下列说法正确的是()A.t=5×10−3s时,线框平面与中性面重合B.t=1.5×10−2s时,通过线框的磁通量变化率为零C.线框与磁场方向的夹角为60°时,感应电动势的瞬时值为155.5VD.线框产生的交变电动势的有效值为311V6.回旋加速器的结构示意图如图所示,D1和D2是两个中空的、半径为R的半圆形金属盒,两盒之间留有窄缝,它们之间接一定频率的交流电。
关于量子力学-经典力学-相对论力学的统一性理论可行性研究(续2)--对量子物理研究发展提供一点线索

关于量子力学-经典力学-相对论力学的统一性理论可行性研究(续2)--对量子物理研究发展提供一点线索
周万连
【期刊名称】《通讯世界》
【年(卷),期】2015(000)010
【摘要】本文进一步对《关于量子力学-经典力学相对论力学的统一性力量可行性研究》一文作深入研究与拓展,论证了三合一波动方程的适用范围,提出了“质量”存在的新观点,说明了介子的由来及强、弱相互作用力的媒介性质,为量子物理的研究发展提供一点线索。
【总页数】2页(P196-197)
【作者】周万连
【作者单位】中国地震台网中心,北京100000
【正文语种】中文
【中图分类】O412
【相关文献】
1.关于量子力学-经典力学-相对论力学的统一性理论可行性研究(续2)--对量子
物理研究发展提供一点线索 [J], 周万连;
2.关于量子力学-经典力学-相对论力学的统一性理论可行性研究(续7)——牛顿万
有引力定律的量子化及经典力学的量子化初探 [J], 周万连;
3.关于量子力学-经典力学-相对论力学的统一性理论可行性研究续(18)
——新量子力学概要之补充(5) [J], 周万连
4.关于量子力学-经典力学-相对论力学的统一性理论可行性研究续19
——新量子力学概要之补充(6) [J], 周万连
5.关于量子力学-经典力学-相对论力学的统一性理论可行性研究(续)——对量子物理研究发展提供一点线索 [J], 周万连
因版权原因,仅展示原文概要,查看原文内容请购买。
量子力学课件(完整版)

Light beam
metal
electric current
11
能量量子化的假设
造成以上难题的原因是经典物理学认为 能量永远是连续的。
如果能量是量子化的,即原子吸收或发 射电磁波,只能以“量子”的方式进行, 那末上述问题都能得到很好的解释。
12
能量量子化概念对难题的解释
原子寿命 ①原子中的电子只能处于一系列分立的能级之中。
18
当 kT hc(高频区)
E(, T)
2hc2 5
e hc
kT
Wein公式
当 kT hc(低频区)
E(, T)
2c 4
kT
Rayleigh–Jeans公式
19
能量量子化概念对难题的解释
对光电效应的解释
如果电子处于分立能级且入射光的能 量也是量子化的,那么只有当光子的能 量(E =hυ)大于电子的能级差,即E =hυ > En-Em时,光电子才会产生。如 果入射光的强度足够强,但频率υ足够 小,光电子是无法产生的。
2 , k 2 / ,
得到 d 2 0,所以,t x(t)
dk 2 m
物质波包的观点夸大了波动性的一面,抹杀 了粒子性的一面,与实际不符。
45
(2)第二种解释:认为粒子的衍射行为是大 量粒子相互作用或疏密分布而产生的行为。 然而,电子衍射实验表明,就衍射效果 而言, 弱电子密度+长时间=强电子密度+短时间 由此表明,对实物粒子而言,波动性体 现在粒子在空间的位置是不确定的,它是以 一定的概率存在于空间的某个位置。
2
这面临着两个问题:
1、信号电磁波所覆盖的区域包括大量的 元件,每个元件的工作状态有随机性,但 器件的响应具有统计性;
大学物理教学 51.量子力学基础-2

1
称为归一化
V
的波函数
a) 波函数的归一化
Байду номын сангаас
若
ψ
2
dV
1,寻找一个系数k使得
k
ψ
2
dV
1,
V
V
这一过程称为波函数的归一化。
b) 波函数的归一化系数
2dV
2
CψdV1
V
V
C k 就称为归一化系数。 Cψ
,ψ所描述的粒子状态相同
5
例:讨论一维自由粒子在空间各点出现的概率。
xPx 2 h h / 2
t E 2
同一微观粒子,其坐标和动量不能同时被准确测定(波粒二象性)。
对y、z方向有类似的表达式。 不确定关系式一般用于估算。
2
●
波函数 自由粒子的波函数
(r,t)
0ei
2
h
( Et Pr)
● 波函数的物理意义 (统计解释)
(r,t)(r)e iEt
16
4. 定态 薛定谔方程的应用
[[22m22 ddx222V ((xr)]((xr))EE(x()r)
1)设求粒一子维处无在限势深阱、V方(x势)中阱中粒子的[2波m2函ddx数22VV( x()x)](x)E(x)
13
3. 定态薛定谔方程
i
(r,t
t
)[
2 2m
2
V
(r,t
)]
(r,t
)
设若粒粒子子的所波处函的数力为场:不随( 时r ,间t) 变化( r ,)则f( 薛t) 定谔方程可化简。
V
湖南省自然科学基金学科分类目录及代码

B0102 B010201 B010202 B010203 B010204
配位化学 固体配位化学 溶液配位化学 功能配合物化学
B0103 B010301 B010302 B010303
生物无机化学 金属蛋白(酶)化学 生物微量元素化学 细胞生物无机化学 生物矿化及生物界面化学
B0104 B010401 B010402 B010403 B010404
偏微分方程
A0108
几何、物理和力学中的偏微分方程 A010801 非线性椭圆和非线性抛物方程 混合型、退化型偏微分方程 A010802 A010803
非线性发展方程和无穷维动力系统 A010804
数学物理 规范场论与超弦理论 可积系统及其应用
A0109 A010901 A010902
概率论与随机分析 马氏过程与遍历论 随机分析与随机过程 随机微分方程 极限理论
A0110 A011001 A011002 A011003 A011004
数理统计 抽样调查与试验设计 时间序列与多元分析 数据分析与统计计算
A0111 A011101 A011102 A011103
2
运筹学 线性与非线性规划 组合最优化 随机最优化 可靠性理论
A0112 A011201 A011202 A011203 A011204
3
数值逼近与计算几何 谱方法及高精度数值方法 有限元和边界元方法 多重网格技术及区域分解 自适应方法 并行算法
A011706 A011707 A011708 A011709 A011710 A011711
A. 数理科学部 力学 力学中的基本问题和方法 理性力学与力学中的数学方法 物理力学 力学中的反问题
A05 A0501 A050101 A050102 A050103 A050104 A050105 A050106
第十五章 量子物理 习题解答

n=1: E1 = −13.6ev
n=2:
E2
=
E1 22
=
−3.4ev
≈
−5.44 ×10−19
J
n=4 n=3
n=3:
E3
=
E1 32
=
−1.51ev
≈
−2.416 ×10−19
J
n=4:
E4
=
E1 42
=
−0.85ev
≈
−1.36 ×10−19
J
n=2
跃迁谱线波长 λ = c = hc ,则虚线光谱的波长分别为 ν ∆E
ν1 −ν 0 = Ua1 = 2 ,整理后的答案 C。 ν 2 −ν 0 Ua2
15.4 光电效应和康普顿效应都包含有光子和电子的相互作用过程。对此,下面几种说法中 正确的是【D】
(A)两种效应中电子和光子组成的系统都服从动量守恒定律和能量守恒定律; (B)两种效应都相当于电子和光子的弹性碰撞过程; (C)两种效应都属于电子吸收光子的效应; (D)光电效应是吸收光子的过程,而康普顿效应则相当于光子和电子的弹性碰撞过程。 分析:光电效应与康普顿效应的物理本质是相同的,都是个别光子与个别电子的相互作用。 但二者有明显差别。其一,入射光的波长不同。入射光若为可见光或紫外光,表现为光电效应; 若入射光是 X 光,则表现为康普顿效应。其二,光子和电子相互作用的微观机制不同。在光电
=
3 2
kT
,
动量
p2
= ( mv )2
=
1 mv2 ⋅ 2m = 2
Ek
⋅ 2m ,德布罗意波长 λ
=
h p
=
h Ek ⋅ 2m
注意:动能 Ek = p2 2m 同样适用于非相对论性的微观粒子(低速运动)。
量子物理第3讲——薛定谔方程 定态薛定谔方程 一维无限深势阱 一维有限高势垒【VIP专享】

C2 l / 2, l 为整数,但奇偶性与n相反 . 11
所以
(x)
C1
cos(n
a
x
l ).
2
归一化:
a/2 | (x) |2
a/ 2
dx
1 2
aC12
1
C1 2 / a .
波函数: (x) 2 cos( n x l ) ,
a a2
几率密度: (x) 2 2 cos2 (n x l ) ,
微粒在体积元 dV内出现的概率为:
dW | (x, y, z,t) |2 dV
2
波函数的归一化条件:
(x, y, z,t) 2 dV 1
波函数的标准条件:单值、有限、连续。 坐标和动量的不确定度关系
x Px / 2
能量和时间的不确定度关系
E t / 2
3
六、薛定谔方程
1、薛定谔方程
来源:基本假定之一,不可证明,只可检验。
地位:低速运动微观粒子的基本规律,地位同牛顿 定律。
成功解释氢原子能级和电(磁)场中氢原子光谱线 的分裂, 分享1933年Nobel物理奖。
6
2、定态薛定谔方程
定态:粒子于力场中运动时,势能与时间无关, 总能量不随时间变化的状态。
定态波函数:用于描述处于定态的粒子的波函数。
量子物理第3讲 ——薛定谔方程 定态薛定谔方程
一维无限深势阱 一维有限高势垒
主要内容
六、薛定谔方程
1
德布罗意公式
v E mc2 , h h .
hh
P m
自由粒子物质波的波函数
(r ,
t
)
0e
i(
Et
Pr)
在某处发现一个微粒的概率正比于描述该微粒的 波函数振幅的平方。
量子物理 算符

2015-1-26
13
7
球坐标系中的角动量算符
2015-1-26
13
8
球坐标系中的角动量平方算符
2015-1-26
13
9
球坐标系中的动能算符
2015-1-26
13
10
逆算符、复共轭、标积和转置
如果通过方程 能够唯一地解出 则称G是A的逆算符。记作 逆算符满足如下关系: 如果A与B的逆存在,则乘积的逆: 把算符中所有量换成其复共 轭,构成该算符的复共轭。 对任意两个波函数,引入标积的概念: 如果算符G满足 则称G是A的转置算符。记作 可以将转置算符写成标积的形式:
2015-1-26 13 4
角动量与坐标和动量的对易关系
利用Levi-Civita符号可以将角动量的各分量统一写成: 重复指标表示对该 指标做遍历求和。 请按这个法则写出角动量的其他两个分量的表达式。 用这种表达方式可以得到与角动量有关的对易关系:
请写出全部对易关系的显明表达式。
2015-1-26 13 5
2015-1-26易关系。 请按上述方法证明:
基本对易关系
统一写成
利用这几个基本对易关系可以导出其他力学量之间的 对易关系。但需要在数学上充点电。 定义三阶反对称张量Levi-Civita符号: 任意一对指标每交换一次,要改变一个正负号。 如果有任何两个指标相同,则这个量等于零。 作为课外练习,请写出Levi-Civita符号的全部分量。
算符
算符
2015-1-26
13
1
线性算符
要直接利用坐标表象中的波函数计算其他力学量的平均 值,必须引入算符的概念。 在量子力学中,算符代表对波函数的一种运算。 满足以下运算规则的算符叫做线性算符:
2015 年第一届凝聚态物理会议

18:30-19:10 8:30-12:00
大会报告
地点
活动
清华大学大礼堂门厅 报到注册
清华大学大礼堂
薛其坤 院士(致辞)
清华大学大礼堂
于渌 院士(大会报告)
汤超 教授(大会报告)
清华观畴园(万人食堂) 午餐
分会报告
地点
分会主题
清华六教 A 区大厅 报到注册
17:55-18:07 18:07-18:32
of Michigan
简少恺 清华大学高 Correlated double-Weyl semimetals with Coulomb interactions: possible applications to
等研究院 HgCr2Se4 and SrSi2
2
会议日程:
日期
时间
7 月 14 日 15:00-17:00
地点 清华大学物理系大厅
活动 报到注册
17:00-20:00 西郊宾馆大厅
报到注册
日期 7 月 15 日
7 月 15 日
7 月 16 日
时间 8:00-11:00 9:00-9:15 9:15-11:45 12:00-13:00
大会报告
时间:2015 年 7 月 15 日上午 9:00-12:00 主持人:陈曦 教授,清华大学物理系
时间 9:00-9:05 9:05-9:15 9:15-10:15 10:15-10:45 10:45-11:45
报告人 向涛 院士 中国科学院物理研究所 薛其坤 院士 清华大学 于渌 院士 中国科学院物理研究所
学
休息
15:25-15:50 贾爽 北京大学 外尔半金属的输运性质
量子物理的基本概念.ppt

量子物理的基本概念
玻恩假设 物质波不代表实在物理量的波动,而是刻画粒子在空间概率分 布的概率波。
r,t 2 r ,t r ,t 概率密度
物理涵义: 代表 t 时刻 在 r 端点处单位体积中发现一个粒
子的概率
波函数 称为概率幅
一 经典理论的困难 按经典电磁理论,带电粒子受到入射电磁波的作用而发生受
迫振动,从而向各个方向辐射电磁波,散射束的频率应与入射束 频率相同,带电粒子仅起能量传递的作用.
可见,经典理论无法解释波长变长的散射线.
量子物理的基本概念
二 量子解释 1 物理模型
光子 0
y
电子
v0 0
x
y
光子
x
电子
一部分能量传给电子,散射光子能量减少,频率下降、波长
变大. (2)光子与原子中束缚很紧的电子发生碰撞,近似与整个
原子发生弹性碰撞时,能量不会显著减小,所以散射束中出现
与入射光波长相同的射线.
3 定量计算
y h e
能量守恒
hv0 m0c2 h mc 2
h
c
0
e0
c e
x
动量守恒
由 0 ccos第二项数量级约00243A,只有0也很 小时,才有明显的
3. 为什么还有 0的散射光存在? 光子与束缚较紧的电子的碰撞,应看作是和整个原子相碰。因
原子质量 >> 光子质量,在弹性碰撞中散射光子的能量(波长)
几乎不变。
量子物理的基本概念
4. 光具有波粒二象性 一般而言,光在传递过程中,波动性较为显著;光与
截止频率与材料有关与光强无关.
量子物理第3讲——薛定谔方程 定态薛定谔方程 一维无限深势阱 一维有限高势垒

3
六、薛定谔方程
1、薛定谔方程
自由粒子 的波函数
(r,
t)
i
0e
( EtPr )
,
可以看出:
E (r,t) i (r,t),
t
P
x
(r,
t
)
i
x
(r,
t
),
ቤተ መጻሕፍቲ ባይዱ
P
y
(r,
t
)
i
y
(r,
t
),
2 2m
2
V
(r)
(r,
t)
i
t
(r,
t)
分离变量法:设 (r,t) (r) f (t)
i
则:
f (t)
df (t) dt
1 (r)
2 2m
2
V
(r)
(r)
7
i f (t)
df (t) dt
1 (r )
电子,当 E 1eV , V 0 2eV ,
o
a 2 A时 , T 0.51;
o
a 5A时 , T 0.006
制作扫描隧穿显微镜 ( STM )
15
STM下硅表面结构重现 16
利用STM搬迁原子为电子造的“量子围栏” 17
例:质量为 m的粒子处于一维
对称势场
V (x)
0 , 0 x L;
V
(
x)
V0
,
x 0, x
量子力学的常数之谜

量子力学的常数之谜量子力学是描述微观粒子行为的理论,它提供了解释微观世界现象的关键框架。
在量子力学中,存在一些被称为常数的神秘数值,它们在理论中扮演着重要的角色。
这些常数包括普朗克常数、狄拉克常数和费米常数,它们如何产生以及其背后的物理意义一直是物理学家们探索的课题之一。
普朗克常数是量子力学中最重要的常数之一,通常用h表示。
它指示了微观世界中的能量量子化现象。
普朗克常数的大小为6.62607015×10^(-34)焦耳·秒。
普朗克常数的发现来自于黑体辐射的研究。
当研究者试图解释黑体辐射现象时,他们发现只有假设能量是量子化的,才能与实验结果相符。
通过将能量与频率之间的关系进行量子化,普朗克常数得以引入。
从此,量子理论得以建立,开启了量子力学的大门。
狄拉克常数,以符号ħ表示,是普朗克常数的一半,即ħ=h/2π。
狄拉克常数在量子力学中起着重要的角色,尤其在描述自旋和角动量时具有关键的作用。
它揭示了微观粒子的自旋性质以及与角动量相关的现象。
狄拉克常数的意义在于它连接了量子力学和相对论,为量子场论的发展奠定了基础。
费米常数,以符号F表示,是描述物质微观粒子的特性的常数。
费米常数定义了费米子的统计行为,它们服从费米-狄拉克统计,具有泡利不相容原理。
费米常数的数值为F=2.196×10^(-25)克。
费米常数的发现与研究电子的行为密切相关,帮助我们理解电子的排布和运动特性。
这些常数的出现并非巧合,它们是量子力学理论建立的基石,与微观粒子行为的量子性密切相关。
普朗克常数描述了能量的量子化,狄拉克常数联系了量子力学和相对论,而费米常数定义了费米子的统计行为。
这些常数的神秘性和重要性使得物理学家们对其产生了浓厚的兴趣。
尽管我们对这些常数的存在和数值有所了解,但我们仍然面临一个难题,那就是为什么这些常数的数值正是它们现在的样子?为什么它们的数值不同于其他任何数值?这些问题至今尚未得到满意的解答。
量子物理-薛定谔方程省公开课一等奖全国示范课微课金奖PPT课件
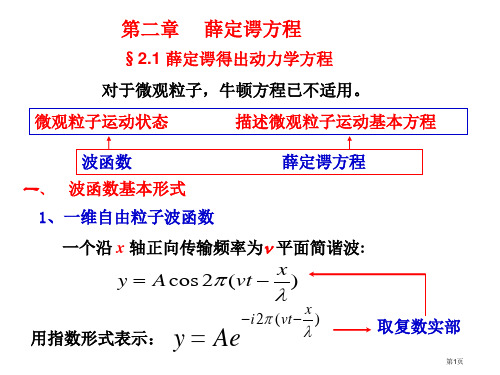
d 2 3
d x2
2m(
E
2
U
0
)
3
k '2 3
x a 2 (2)
k 2mE 2 (x) Asin(kx )
k ' 2m(U0 E) 设通解: 3 (x) Cek'x Dek'x
边界条件:
x D=0
U
xa/2
2
(
a 2
)
3
(
a 2
)
U0
(
d 2 (
dx
x)
)
x
a 2
(
d 3 (
§2.3 势垒穿透
1、一维半无限深方势阱
x a 2
U (x) 0 a 2 x a 2
U0 x a 2
2、势垒穿透;隧道效应
U
设三个区域波函数分别为
1, 2 , 3 在 x a 2 区域
1 0
U0
1
2
3
E
●
●
-a/2 o a/2 x
第21页
d 2 2
d x2
2mE
2
2
k 2 2
a 2 x a 2 (1)
第二章 薛定谔方程
§2.1 薛定谔得出动力学方程
对于微观粒子,牛顿方程已不适用。
微观粒子运动状态
描述微观粒子运动基本方程
波函数 一、 波函数基本形式
薛定谔方程
1、一维自由粒子波函数
一个沿 x 轴正向传输频率为 平面简谐波:
y A cos 2 (vt x )
i2 (vt x )
用指数形式表示: y Ae
dx
x)
)
x
a 2
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1D
2
根据波尔理论,氢原子中的电子在n=4的轨道上运动的动能与基态的轨道上运动的动能之比为
A、1/4;
B、1/8;
C、1/16;
D、1/32。
[ C ]
3
4
5
金属的光电效应的红限频率依赖于
A、入射光的频率;
B、入射光的强度;
C、金属的逸出功;
D、入射光的频率和金属的逸出功。
[ C ]
6
7 D
已知一单色光照射在钠表面上,测得光子的最大动能是1.2eV,而钠的红限波长是5400埃,那么入射光的波长是
逸出功W=hc/λ=6.63*10^-34*3*10^8/5400*10^-10=3.68*10^-19J 动能1/2*mv^2=1.2eV=1.2*1.6*10^-19=1.92*10^-19J 根据光电效应, hc/λ=1/2*mv^2+W=5.6*10^-19 解得λ=3552埃 8
用频率为ν1的单色光照射某种金属时,测得饱和电流为I 1,以频率为ν2的单色光照射该金属时,测得饱和电流为I 2,若I 1> I 2,则
A 、ν1 >ν2;
B 、ν1 <ν2;
C 、ν1 =ν2;
D 、ν1与ν2的关系还不能确定。
[ D ]
无法比较。
饱和光电流与光强有关,相同频率不同光强的光束,光强越大,饱和光电流也越大。
所以这两个频率没办法比较。
9
若α粒子(电量为2e )在磁感应强度为B 的均匀磁场中沿半径为R 的圆形轨道运动,则α粒子的德布罗意波长是:
A 、()/2h eR
B ; B 、()/h eRB ;
C 、()1/2eRBh ;
D 、()1/eRBh 。
[ A ]
10
11
12
13
14
处于n =4激发态的氢原子,它回到基态的过程中,所发出的光波波长最短为_____97______nm ,最长为___1857________nm 。
max
min
7max 77min
71
111
11=(
);=()
3414
144144
18.7510187577 1.0971016160.972310971515 1.09710R R m nm R m nm R λλλλ----→===⨯=⨯⨯→===⨯=⨯⨯
15
(一)能量最低原理:
在核外电子的排布中,通常状况下,电子总是尽先占有能量最低的原子轨道,只有当这些原子轨道占满后,电子才依次进入能量较高的原子轨道,这个规律叫能量最低原理。
(二)泡利不相容原理:
在同一个原子里,不能有两个或两个以上的粒子处于完全相同的状态,这个结论叫泡利不相容原理。
(三)洪特规则:
在同一亚层中的各个轨道上,电子的排布尽可能单独分占不同的轨道,而且自旋方向相同,这样排布整个原子能量最低。
16
在氢原子发射光谱的巴耳末线系中有一频率为6.15×1014 Hz的谱线,它是氢原子从能级E n= -0.84 eV跃迁到能级E k= -3.4 eV而发出的。
(普朗克常量h = 6.63×10-34 J·S ,基本电荷e = 1.6×10-19 C )
341419
6.6310 6.1510 2.551.610
h eV ν--⨯⨯⨯==⨯ 17
h h
p m λ=
=
v
c m p m ==
=
=
v
0 =λ∴==nm 00421.0.
18
试估计处于基态的氢原子被能量为 12.09 eV 的光子激发时,其电子的轨道半径增加多少倍?
答案:4倍、9倍
2
13.6
13.6-12.09=
,3n n = 最高跃迁到了第三能级,还有第二能级。
第二能级就为四倍,三能级就为九倍
19
20
处于基态的氢原子被外来单色光激发后发出的光仅有三条谱线,问此外来光的频率为多少?
(里德伯常量R =1.097×107 m -1)
解:由于发出的光线仅有三条谱线,按:
)1
1(~22n
k cR c -=⋅=ν
ν n =3,k =2 得一条谱线.
n =3,k =1 得一条谱线. n =2,k =1 得一条谱线.
可见氢原子吸收外来光子后,处于n =3的激发态.以上三条光谱线中,频率最大的一条是: )3
111(
22-=cR ν=2.92×1015 Hz 这也就是外来光的频率.
21
22
23 D
24
25
处于激发态的钠原子,发出波长为589nm 的光子的时间平均约为10-
8s 。
根据不确定度关系
式,光子能量不确定量的大小E ∆=_____________,发射波长的不确定度范围(即所谓谱线宽度)是______________。
3426
8
6.6310 6.631010h E t h E J t ---⨯∆∆≈→∆===⨯∆ 2192
(
) 1.1510hc
hc
E
E m hc
λλλλ
λ
-∆∆=∆=
∆→∆=
=⨯
26
2
E pc E mc ==
E h h p c c νλ=
== E h ν=
27
28
P339,L2,3.7CM 29
30 8
主量子数为n 的壳层,最多可容纳2n²个电子
主量子数为n 的壳层有n 个亚层,第k 个亚层有2k-1个轨道(1≤k≤n ),也就是n 个亚层共有1+3+5+7+...+(2n-1)=(1+2n-1)n/2 =n²个轨道,而每个轨道上至多可以容纳两个电子。
因此,n 个亚层最多可容纳2n²个电子。
所以主量子数为n 的壳层最多可容纳2n²个电子。
31
若要使电子的德布罗意波长为1Å,需要多大的加速电压?(普朗克常量
346.6310h J s -=⨯⋅,电荷191.6010e C -=⨯,电子质量319.1110e m kg -=⨯) 解:
首先由德布罗意关系:h
p λ
=
,
由动量的定义可以得:e p m v =,
根据动能定理可以得到:电场对电子所做的功转变为电子的动能
2
1
2
e U e m v v =
=
2
2
2342
223119102
2(6.6310) 1.5110()229.1110 1.6010(110)
e
e h m h Uem h U V m e λ
λλ----==⨯===⨯⨯⨯⨯⨯⨯⨯。
