2015自贡一诊四川省自贡市2015届高三第一次诊断性考试数学答案
四川省成都市2015届高三第一次诊断数学(文)试题及答案
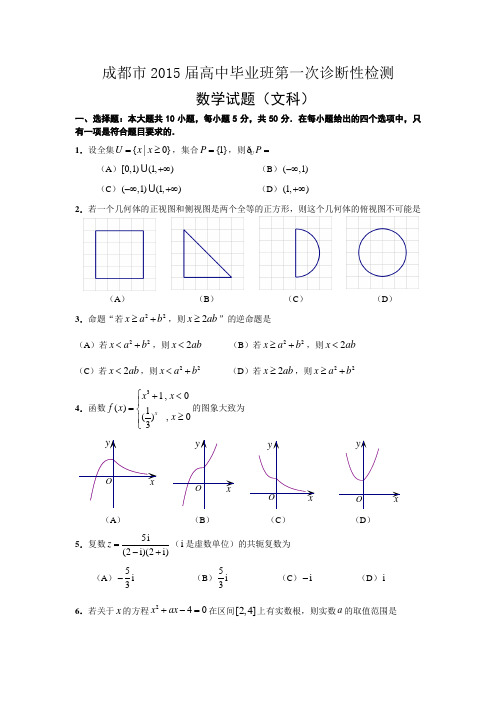
成都市2015届高中毕业班第一次诊断性检测数学试题(文科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{|0}=≥U x x,集合{1}=P,则UP=ð(A)[0,1)(1,)+∞(B)(,1)-∞(C)(,1)(1,)-∞+∞(D)(1,)+∞2.若一个几何体的正视图和侧视图是两个全等的正方形,则这个几何体的俯视图不可能是(A)(B)(C)(D)3.命题“若22≥+x a b,则2≥x ab”的逆命题是(A)若22<+x a b,则2<x ab(B)若22≥+x a b,则2<x ab(C)若2<x ab,则22<+x a b(D)若2≥x ab,则22≥+x a b4.函数31,0()1(),03xx xf xx⎧+<⎪=⎨≥⎪⎩的图象大致为(A)(B)(C)(D)5.复数5i(2i)(2i)=-+z(i是虚数单位)的共轭复数为(A)5i3-(B)5i3(C)i-(D)i6.若关于x的方程240+-=x ax在区间[2,4]上有实数根,则实数a的取值范围是消费支出/元(A )(3,)-+∞ (B )[3,0]- (C )(0,)+∞ (D )[0,3] 7.已知53cos()25+=πα,02-<<πα,则sin 2α的值是 (A )2425 (B )1225 (C )1225- (D )2425-8.已知抛物线:C 28y x =,过点(2,0)P 的直线与抛物线交于A ,B 两点,O 为坐标原点,则OA OB ⋅的值为(A )16- (B )12- (C )4 (D )0 9.已知m ,n 是两条不同直线,α,β是两个不同的平面,且n ⊂β,则下列叙述正确的是(A )若//m n ,m ⊂α,则//αβ (B )若//αβ,m ⊂α,则//m n (C )若//m n ,m α⊥,则αβ⊥ (D )若//αβ,m n ⊥,则m α⊥ 10.如图,已知正方体1111ABCD A B C D -棱长为4,点H 在棱1AA 上,且11HA =.点E ,F 分别为棱11B C ,1C C 的中点,P 是侧面11BCC B 内一动点,且满足⊥PE PF .则当点P 运动时, 2HP 的最小值是 (A)7(B)27-(C)51-(D)14-二、填空题:本大题共5小题,每小题5分,共25分. 11.已知100名学生某月饮料消费支出情况的频率分布直方图如右图所示.则这100名学生中,该月饮料消费支出超过150元的人数是________.12.若非零向量a ,b 满足a b a b +=-,则a ,b 的夹ABCD1A 1B 1C 1D HPEF角的大小为__________.13.在∆ABC 中,内角,,A B C 的对边分别为,,a b c ,若2=c a ,4=b ,1cos 4=B .则边c 的长度为__________.14.已知关于x 的不等式()(2)0---≤x a x a 的解集为A ,集合{|22}=-≤≤B x x .若“x A ∈”是“x B ∈”的充分不必要条件,则实数a 的取值范围是__________. 15.已知函数21()()2f x x a =+的图象在点n P (,())n f n (*n ∈N )处的切线n l 的斜率为n k ,直线n l 交x 轴,y 轴分别于点(,0)n n A x ,(0,)n n B y ,且11y =-.给出以下结论: ①1a =-;②记函数()=n g n x (*n ∈N ),则函数()g n 的单调性是先减后增,且最小值为1;③当*n ∈N 时,1ln(1)2n n n y k k++<+; ④当*n ∈N时,记数列的前n 项和为n S ,则1)n n S n -<. 其中,正确的结论有 (写出所有正确结论的序号)三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)口袋中装有除编号外其余完全相同的5个小球,编号依次为1,2,3,4,5.现从中同时取出两个球,分别记录下其编号为,m n . (Ⅰ)求“5+=m n ”的概率; (Ⅱ)求“5≥mn ”的概率.17.(本小题满分12分)如图,在多面体ECABD 中,EC ⊥平面ABC ,//DB EC ,ABC ∆为正三角形,F 为EA 的中点,2EC AC ==,1BD =.(Ⅰ)求证:DF //平面ABC ; (Ⅱ)求多面体ECABD 的体积. 18.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且122+=-n n S ;数列{}n b 满足11b =,12n n b b +=+.*n ∈N .(Ⅰ)求数列{}n a 和{}n b 的通项公式;(Ⅱ)记n n n c a b =,*n ∈N .求数列{}n c 的前n 项和n T .19.(本小题满分12分)某大型企业一天中不同时刻的用电量y (单位:万千瓦时)关于时间t (024t ≤≤,单位:小时)的函数()y f t =近似地满足()sin()(0,0,0)f t A t B A ωϕωϕπ=++>><<,下图是该企业一天中在0点至12点时间段用电量y 与时间t 的大致图象. (Ⅰ)根据图象,求A ,ω,ϕ,B 的值; (Ⅱ)若某日的供电量()g t (万千瓦时)与时间t (小时)近似满足函数关系式205.1)(+-=t t g (012t ≤≤).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1). 参考数据:20.(本小题满分13分)已知椭圆Γ:12222=+by a x (0>>b a )的右焦点为)0,22(,且过点.(Ⅰ)求椭圆Γ的标准方程;(Ⅱ)设直线:()l y x m m =+∈R 与椭圆Γ交于不同两点A 、B ,且AB =点0(,2)P x 满足=PA PB ,求0x 的值.21.(本小题满分14分) 已知函数()ln 2mf x x x=+,()2g x x m =-,其中m ∈R ,e 2.71828= 为自然对数的底数.(Ⅰ)当1m =时,求函数()f x 的极小值;(Ⅱ)对1[,1]e x ∀∈,是否存在1(,1)2m ∈,使得()()1>+f x g x 成立?若存在,求出m 的取值范围;若不存在,请说明理由;(Ⅲ)设()()()F x f x g x =,当1(,1)2m ∈时,若函数()F x 存在,,a b c 三个零点,且a b c <<,求证: 101ea b c <<<<<.数学(文科)参考答案及评分意见第Ⅰ卷(选择题,共50分)一、选择题:(本大题共10个小题,每小题5分,共50分)1.A ; 2.C ; 3.D ;4.A ;5.C ;6.B ;7.D ;8.B ;9.C ;10.B .第Ⅱ卷(非选择题,共100分)二、填空题:(本大题共5个小题,每小题5分,共25分)11.30 12.90︒ 13.4 14.[2,0]- 15.①②④ 三、解答题:(本大题共6个小题,共75分) 16.(本小题满分12分)解:同时取出两个球,得到的编号,m n 可能为: (1,2),(1,3),(1,4),(1,5) (2,3),(2,4),(2,5) (3,4),(3,5)(4,5)…………………………………………………………………………………6分(Ⅰ)记“5+=m n ”为事件A ,则 21()105==P A .……………………………………………………………………………3分(Ⅱ)记“5≥mn ”为事件B ,则 37()11010=-=P B .…………………………………………………………………… 3分 17.(本小题满分12分)(Ⅰ)证明:作AC 的中点O ,连结BO .在∆AEC 中,//=FO 12EC ,又据题意知,//=BD 12EC . ∴//=FO BD ,∴四边形FOBD 为平行四边形. ∴//DF OB ,又⊄DF 面ABC ,⊂OB 平面ABC .∴//DF 面ABC .………………………6分 (Ⅱ)据题意知,多面体ECABD 为四棱锥-A ECBD . 过点A 作⊥AH BC 于H .∵⊥EC 平面ABC ,⊂EC 平面ECBD , ∴平面⊥ECBD 平面ABC .又⊥AH BC ,⊂AH 平面ABC ,平面 ECBD 平面=ABC BC , ∴⊥AH 面ECBD .∴在四棱锥-A ECBD 中,底面为直角梯形ECBD,高=AH .∴1(21)232-+⨯=⨯=A ECBD V ∴多面体ECABD6分 18.(本小题满分12分) 解:(Ⅰ)∵122+=-n n S ① 当2≥n 时,122-=-n n S ② ①-②得,2=n n a (2≥n ).∵当2≥n 时,11222--==nn n n a a ,且12=a .∴数列{}n a 是以2为首项,公比为2的等比数列,∴数列{}n a 的通项公式为1222-=⋅=n n n a .………………………………………4分又由题意知,11b =,12n n b b +=+,即12+-=n n b b ∴数列{}n b 是首项为1,公差为2的等差数列,∴数列{}n b 的通项公式为1(1)221=+-⨯=-n b n n .……………………………2分(Ⅱ)由(Ⅰ)知,(21)2=-n n c n ……………………………………………………1分 ∴231123252(23)2(21)2-=⨯+⨯+⨯++-⋅+-⋅ n n n T n n 231121232(25)2(23)2(21)2-+=⨯+⨯++-⋅+-⋅+-⋅ n n n n T n n n ④由 -④得2311222222222(21)2-+-=+⨯+⨯++⋅+⋅--⋅ n n n n T n (1)分23112(12222)(21)2-+-=++++--⋅ n nn n T n∴12222(21)212+-⋅-=⨯--⋅-n n n T n (1)分∴111224222+++-=⋅--⋅+n n n n T n 即1(32)24+-=-⋅-n n T n ∴1(23)24+=-+n n T n∴数列{}n c 的前n 项和1(23)24+=-+n n T n ………………………………………3分19.(本小题满分12分) 解:(Ⅰ)由图知12T =,6πω=.………………………………………………………1分2125.15.22m i n m a x =-=-=y y A ,225.15.22min max =+=+=y y B .……………2分 ∴0.5sin()26y x πϕ=++.又函数0.5sin()26y x πϕ=++过点(0,2.5).代入,得22k πϕπ=+,又0ϕπ<<,∴2πϕ=.…………………………………2分综上,21=A ,6πω=,2πϕ=,21=B . ………………………………………1分即2)26sin(21)(++=ππt t f . (Ⅱ)令)()()(t g t f t h -=,设0)(0=t h ,则0t 为该企业的停产时间. 由0)11()11()11(<-=g f h ,0)12()12()12(>-=g f h ,则)12,11(0∈t . 又0)5.11()5.11()5.11(<-=g f h ,则)12,5.11(0∈t . 又0)75.11()75.11()75.11(>-=g f h ,则)75.11,5.11(0∈t .又0)625.11()625.11()625.11(<-=g f h ,则)75.11,625.11(0∈t .又0)6875.11()6875.11()6875.11(>-=g f h ,则)6875.11,625.11(0∈t .…4分……………………………………………1分 ∴应该在11.625时停产.……………………………………………………………1分 (也可直接由)625.11()625.11()625.11(<-=g f h ,0)6875.11()6875.11()6875.11(>-=g f h ,得出)6875.11,625.11(0∈t ;答案在11.625—11.6875之间都是正确的;若换算成时间应为11点37分到11点41分停产)20.(本小题满分13分)(Ⅰ)由已知得=a,又=c ∴2224=-=b a c .∴椭圆Γ的方程为141222=+y x .…………………………………………………4分 (Ⅱ)由⎪⎩⎪⎨⎧=++=,1412,22y x m x y 得01236422=-++m mx x ① ………………………1分∵直线l 与椭圆Γ交于不同两点A 、B ,∴△0)123(163622>--=m m , 得216<m .设),(11y x A ,),(22y x B ,则1x ,2x 是方程①的两根,则2321mx x -=+, 2123124-⋅=m x x .∴12=-==AB x又由AB =231294-+=m ,解之2m =±.……………………………3分 据题意知,点P 为线段AB 的中垂线与直线2=y 的交点. 设AB 的中点为),(00y x E ,则432210m x x x -=+=,400mm x y =+=, 当2m =时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x -=-+,即1y x =--. 令2=y ,得03x =-.…………………………………………………………………2分 当2m =-时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x +=--,即1y x =-+. 令2=y ,得01x =-.………………………………………………………………2分综上所述,0x 的值为3-或1-. 21.(本小题满分14分)解:(Ⅰ)1m =时,1()ln ,02=+>f x x x x. ∴221121()22-'=-=x f x x x x ……………………………………………………………………1分由()0'>f x ,解得12>x ;由()0'<f x ,解得102<<x ; ∴()f x 在1(0,)2上单调递减,1(,)2+∞上单调递增. (2)分∴=极小值)(x f 11()ln 11ln 222f =+=-.…………………………………………………… 2分(II )令1()()()1ln 21,,12⎡⎤=--=+-+-∈⎢⎥⎣⎦m h x f x g x x x m x x e ,其中1(,1)2m ∈由题意,()0h x >对1,1x e ⎡⎤∈⎢⎥⎣⎦恒成立,∵2221221()1,,122-+-⎡⎤'=--=∈⎢⎥⎣⎦m x x m h x x x x x e ∵1(,1)2m ∈,∴在二次函数222=-+-y x x m 中,480∆=-<m ,∴2220-+-<x x m 对∈x R 恒成立∴()0'<h x 对1,1x e ⎡⎤∈⎢⎥⎣⎦恒成立, ∴()h x 在1,1e ⎡⎤⎢⎥⎣⎦上单减. ∴min 5()(1)ln11212022==+-+-=->m h x h m m ,即45>m .故存在4(,1)5∈m 使()()f x g x >对1,1⎡⎤∀∈⎢⎥⎣⎦x e 恒成立.……………………………………4分(III )()(ln )(2),(0,)2mF x x x m x x=+-∈+∞,易知2x m =为函数()F x 的一个零点, ∵12>m ,∴21>m ,因此据题意知,函数()F x 的最大的零点1>c , 下面讨论()ln 2mf x x x=+的零点情况,∵2212()22m x m f x x x x -'=-=. 易知函数()f x 在(0,)2m上单调递减,在(,)2m +∞上单调递增.由题知()f x 必有两个零点,∴=极小值)(x f ()ln 1022=+<m mf ,解得20<<m e ,∴122<<m e ,即(,2)2∈eme .…………………………………………………………3分 ∴11(1)ln10,()ln 11102222=+=>=+=-<-=m m em emf f e e .…………………1分 又10101010101()ln 10100224---=+=->->m m f e e e e e .101()0,()0,(1)0f e f f e -∴><>.10101e a b c e -∴<<<<<<.101a b c e∴<<<<<,得证.……………………………………………………………1分。
四川省自贡市2015届高三第一次诊断政治试题及答案word2015、2

自贡市普高2015届第一次诊断性考试政治试题第I卷(选择题共48分)1、右图曲线反映的是一定时期某种商品需求、供给和价格的关系。
下列判断正确的是()①当P=P0时,该商品供给与需求平衡②当P>P0时,该商品会出现“货多不值钱”的现象③当P<P0时,该商品并不围绕价值上下波动④当Q=Q0时,该商品会出现“物以稀为贵”的现象A、①③B、①②C、②④D、③④2、中国商务部有关数据显示,2013年,已有22个国家和地区对中国发起94起贸易救济调查,同比增长22%。
中国已经连续20年成为遭遇贸易摩擦和反倾销调查最多的国家。
这表明()①中国出口产品竞争力降低②贸易全球化加剧国际贸易争端③优化出口结构,坚持以质取胜④中国企业必须提高权利意识和规则意识A、①③B、②③C、①④D、②④3、全国政协十二届一次会议以来,共收到提案5884件,经审查立案5403件。
提案是政协委员和参加政协的各党派、人民团体以及政协专门委员会,向政协全体会议或者常务委员会会议提出的、经提案委员会审查立案后,交承办单位办理的书面意见和建议。
政协提案()①是人民政协履行参政议政职能的一种重要方式②由政协委员向人大或者政府抽出,亲要求答复③有利于促进党和国家机关决策民主化、科学化④具有法律约束力,对承办单位起法律监督作用A、①②B、③④C、①③D、②④4、“贤路当广而不当狭,言路当开而不当塞”“大智兴邦,不过集众思”这样的古语启示政府要()①审慎行使权力,坚持民主决策②坚持民主执政,提高执法水平③密切联系群众,广泛集中民智④完善信息搜集和智力支持系统,人民直接决策A、①③B、③④C、②③D、①④5、2013年,李克强在泰国访问时,与泰国总理英拉签署了《中泰政府关于泰国铁路基础设施发展与泰国农产品交换的政府间合作项目的谅解备忘录》。
这一合作方式被媒体形象称为“高铁换大米”。
这一事件()A、反映了两国都是发展中国家,有着共同的国情B、体现了两国之间的根本利益是一致的C、体现了我国外交政策的宗旨D、反映了国际竞争日益激烈清单,顾名思义就是记载有关项目的明细单。
四川省自贡市高三数学第一次诊断性考试试卷 理(无答案)

自贡市普高2015届第一次诊断性考试数 学(理工类)本试题卷分第一部分(选择题)和第二部分(非选择题).第一部分1至3页,第二部分4至6页,共6页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.满分150分.考试时间120分钟.考试结束后,只交回答题卡,试题卷学生自己保留.第一部分(选择题 共50分)注意事项:1.选择题必须使用2B 铅笔将答案标号填涂在答题卡上对应题目标号的位置上. 2.本部分共10小题,每小题5分,共50分.一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}5M x x =<,}1log |{3>=x x N ,则=⋂N M (A )φ (B ){}05x x << (C ){}15x x << (D ){}35x x << 2. 在数列{a n }中,252,1a a ==,如果数列{}21n a +是等差数列,那么8a 等于(A )13(B )12(C )23(D )13. 设R b a ∈,,则“0>>b a ”是“ba 11<”的 (A )充分而不必要条件 (B )必要而不充分条件(C)充要条件(D)既不充分又不必要条件4.62xx⎛-⎪⎝⎭的二项展开式中2x的系数为(A)480 (B)192(C)-192 (D)-4805. 以下茎叶图记录了甲、乙两组各6名学生在一次英语听力测试中的成绩(单位:分)甲组乙组9 6 0 9x 2 1 5 y87 4 2 1 4若甲组数据的中位数为13.5,乙组数据的平均数为17.5,则x、y的值分别为(A)2,5 (B)5,5(C)5,8 (D)8,86. 如图所示是一个几何体的三视图,若该几何体的体积为12,则主视图中三角形的高x的值为(A)1 2(B)3 4(C)1(D)3 27. 若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为奇数,则不同的取法共有(A )60种 (B )63种 (C )65种 (D )66种 8. 为了得到函数sin(2)6y x π=-的图象,可以将函数cos 2y x =的图象(A )向左平移6π个单位 (B )向右平移6π个单位 (C )向左平移3π个单位 (D )向右平移3π个单位 9. 函数()f x 是R 上的偶函数,且对于任意x R ∈都有(1)()f x f x +=-,当[)0,1x ∈时,()f x x =.那么在区间[]3,4-上,函数()f x 的图像与函数1y x -=的图像的交点个数是(A )3 (B )5 (C )7 (D )910. 设正实数,,x y z 满足22340x xy y z -+-=,则当zxy取得最大值时,z y x 212-+的最大值为(A )0 (B )1 (C )49(D )3第二部分(非选择题 共100分)注意事项:1. 必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.答在试题卷上无效.2. 本部分共11小题,共100分.二、填空题:本大题共5小题,每小题5分,共25分. 11. 321i i-+(i 为虚数单位)的值为 . 12. 右图中所示的是一个算法的框图,已知31=a ,输出的7b =,则2a 的值是 .13. 某校高三年级为了解学生学习情况,在2000名学生中随机抽取200名,并统计这200名学生的某次模拟考试成绩,得到了样本的频率分布直方图(如图)。
2015届四川成都市高中毕业班第一次诊断性检测数学理(2014.12)word版

成都市2015届高中毕业班第一次诊断性检测数学试题(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{|0}=≥U x x,集合{1}=P,则UP=ð(A)[0,1)(1,)+∞(B)(,1)-∞(C)(,1)(1,)-∞+∞(D)(1,)+∞2.若一个几何体的正视图和侧视图是两个全等的正方形,则这个几何体的俯视图不可能是(A)(B)(C)(D)3.已知复数z43i=--(i是虚数单位),则下列说法正确的是(A)复数z的虚部为3i-(B)复数z的虚部为3(C)复数z的共轭复数为z43i=+(D)复数z的模为54.函数31,0()1(),03xx xf xx⎧+<⎪=⎨≥⎪⎩的图象大致为(A)(B)(C)(D)5.已知命题p:“若22≥+x a b,则2≥x ab”,则下列说法正确的是(A)命题p的逆命题是“若22<+x a b,则2<x ab”(B)命题p的逆命题是“若2<x ab,则22<+x a b”(C)命题p的否命题是“若22<+x a b,则2<x ab”(D)命题p的否命题是“若22x a b≥+,则2<x ab”6.若关于x的方程240+-=x ax在区间[2,4]上有实数根,则实数a的取值范围是G FEHPACBDA 1B 1C 1D 1(A )(3,)-+∞ (B )[3,0]- (C )(0,)+∞ (D )[0,3]7.已知F 是椭圆22221+=x y a b(0>>a b )的左焦点,A 为右顶点,P 是椭圆上一点,⊥PF x 轴.若14=PF AF ,则该椭圆的离心率是 (A )14(B )34 (C )12(D 8.已知m ,n 是两条不同直线,α,β是两个不同的平面,且//m α,n ⊂β,则下列叙述正确的是(A )若//αβ,则//m n (B )若//m n ,则//αβ(C )若n α⊥,则m β⊥ (D )若m β⊥,则αβ⊥9.若552sin =α,1010)sin(=-αβ,且],4[ππα∈,]23,[ππβ∈,则αβ+的值是 (A )74π (B )94π (C )54π或74π (D )54π或94π 10.如图,已知正方体1111ABCD A B C D -棱长为4,点H 在棱1AA 上,且11HA =.在侧面11BCC B 内作边长为1的正方形1EFGC ,P 是侧面11BCC B 内一动点,且点P 到平面11CDD C 距离等于线段PF 的长.则当点P 运动时, 2HP 的最小值是(A )21(B )22 (C )23 (D )25二、填空题:本大题共5小题,每小题5分,共25分.11.若非零向量a ,b 满足a b a b +=-,则a ,b 的夹角的大小为__________. 12.二项式261()x x-的展开式中含3x 的项的系数是__________.(用数字作答)13.在∆ABC 中,内角,,A B C 的对边分别为,,a b c ,若2=c a ,4=b ,1cos 4=B ,则∆ABC 的面积=S __________.14.已知定义在R 上的奇函数()f x ,当0x ≥时,3()log (1)=+f x x .若关于x 的不等式2[(2)](22)f x a a f ax x ++≤+的解集为A ,函数()f x 在[8,8]-上的值域为B ,若“x A ∈”是“x B ∈”的充分不必要条件,则实数a 的取值范围是__________.15.已知曲线C :22y x a =+在点nP (n (0,a n >∈N )处的切线n l 的斜率为n k ,直线n l 交x 轴,y 轴分别于点(,0)n n A x ,(0,)n n B y ,且00=x y .给出以下结论: ①1a =;②当*n ∈N 时,n y 的最小值为54; ③当*n ∈N时,n k <; ④当*n ∈N 时,记数列{}n k 的前n 项和为n S,则1)<n S .其中,正确的结论有 (写出所有正确结论的序号)三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球.(Ⅰ)求恰有一个黑球的概率;(Ⅱ)记取出红球的个数为随机变量X ,求X 的分布列和数学期望()E X .17.(本小题满分12分)如图,ABC ∆为正三角形,EC ⊥平面ABC ,//DB EC ,F 为EA 的中点,2EC AC ==,1BD =.(Ⅰ)求证:DF //平面ABC ;(Ⅱ)求平面DEA 与平面ABC 所成的锐二面角的余弦值.已知数列{}n a 的前n 项和为n S ,且22n n S a =-;数列{}n b 满足11b =,12n n b b +=+.*n ∈N .(Ⅰ)求数列{}n a ,{}n b 的通项公式;(Ⅱ)记n n n c a b =,*n ∈N .求数列{}n c 的前n 项和n T . 19.(本小题满分12分)某大型企业一天中不同时刻的用电量y (单位:万千瓦时)关于时间t (024t ≤≤,单位:小时)的函数()y f t =近似地满足()sin()(0,0,0)f t A t B A ωϕωϕπ=++>><<,下图是该企业一天中在0点至12点时间段用电量y 与时间t 的大致图象. (Ⅰ)根据图象,求A ,ω,ϕ,B 的值; (Ⅱ)若某日的供电量()g t (万千瓦时)与时间t (小时)近似满足函数关系式205.1)(+-=t t g (012t ≤≤).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1). 参考数据:已知椭圆Γ:12222=+by a x (0>>b a )的右焦点为)0,22(,且椭圆Γ上一点M 到其两焦点12,F F 的距离之和为(Ⅰ)求椭圆Γ的标准方程;(Ⅱ)设直线:(l y x m m =+∈R)与椭圆Γ交于不同两点A ,B ,且AB =点0(,2)P x 满足=PA PB ,求0x 的值. 21.(本小题满分14分)已知函数2()ln mx f x x =-,2()emx mx g x m =-,其中m ∈R 且0m ≠.e 2.71828=为自然对数的底数.(Ⅰ)当0m <时,求函数()f x 的单调区间和极小值;(Ⅱ)当0m >时,若函数()g x 存在,,a b c 三个零点,且a b c <<,试证明:10e a b c -<<<<<;(Ⅲ)是否存在负数m ,对1(1,)x ∀∈+∞,2(,0)x ∀∈-∞,都有12()()f x g x >成立?若存在,求出m 的取值范围;若不存在,请说明理由.数学(理科)参考答案及评分意见第Ⅰ卷(选择题,共50分)一、选择题:(本大题共10个小题,每小题5分,共50分)1.A ; 2.C ; 3.D ;4.A ;5.C ;6.B ;7.B ;8.D ;9.A ;10.B .第Ⅱ卷(非选择题,共100分)二、填空题:(本大题共5个小题,每小题5分,共25分)11.90︒ 12.20- 1314.[2,0]- 15.①③④ 三、解答题:(本大题共6个小题,共75分) 16.(本小题满分12分) 解:(Ⅰ)记“恰有一个黑球”为事件A ,则21243641()205⋅===C C P A C .………………………………………………………4分 (Ⅱ)X 的可能取值为0,1,2,则343641(0)205====C P X C …………………………………………………………2分122436123(1)205⋅====C C P X C …………………………………………………2分 1(2)()5===P X P A ………………………………………………………2分 ∴X 的分布列为∴X 的数学期望1310121555=⨯+⨯+⨯=EX .………………………………2分 17.(本小题满分12分)(Ⅰ)证明:作AC 的中点O ,连结BO .在∆AEC 中,//=FO 12EC ,又据题意知,//=BD 12EC .∴//=FO BD ,∴四边形FOBD 为平行四边形. ∴//DF OB ,又⊄DF 平面ABC ,⊂OB 平面ABC .∴//DF 平面ABC .……………………………………4分 (Ⅱ)∵//FO EC ,∴⊥FO 平面ABC .在正∆ABC 中,⊥BO AC ,∴,,OA OB OF 三线两两垂直.分别以,,OA OB OF 为,,z x y 轴,建系如图. 则(1,0,0)A ,(1,0,2)-E,D . ∴(2,0,2)=-AE,(1=-AD . 设平面ADE 的一个法向量为1(,,z)=x y n ,则110⎧⋅=⎪⎨⋅=⎪⎩AE AD n n,即2200-+=⎧⎪⎨-++=⎪⎩x z x z ,令1=x ,则1,0==z y .∴平面ADE 的一个法向量为1(1,0,1)=n . 又平面ABC 的一个法向量为2(0,0,1)=n .∴121212,2⋅>===cos <n n n n n n . ∴平面DEA 与平面ABC.…………………………8分 18.(本小题满分12分) 解:(Ⅰ)∵22n n S a =- ①当2≥n 时,1122--=-n n S a ②①-②得,122-=-n n n a a a ,即12-=n n a a (2≥n ). 又当1≥n 时,1122=-S a ,得12=a .∴数列{}n a 是以2为首项,公比为2的等比数列,∴数列{}n a 的通项公式为1222-=⋅=n n n a .……………………………………4分 又由题意知,11b =,12n n b b +=+,即12+-=n n b b ∴数列{}n b 是首项为1,公差为2的等差数列,∴数列{}n b 的通项公式为1(1)221=+-⨯=-n b n n .…………………………2分 (Ⅱ)(Ⅱ)由(Ⅰ)知,(21)2=-nn c n ……………………………………………1分 ∴231123252(23)2(21)2-=⨯+⨯+⨯++-⋅+-⋅n n n T n n ③231121232(25)2(23)2(21)2-+=⨯+⨯++-⋅+-⋅+-⋅n n n n T n n n ④由 -④得2311222222222(21)2-+-=+⨯+⨯++⋅+⋅--⋅n n n n T n ………………1分23112(12222)(21)2-+-=++++--⋅n n n n T n∴12222(21)212+-⋅-=⨯--⋅-n n n T n ………………………………………………1分∴111224222+++-=⋅--⋅+n n n n T n 即1(32)24+-=-⋅-n n T n ∴1(23)24+=-+n n T n∴数列{}n c 的前n 项和1(23)24+=-+n n T n ……………………………………3分 19.(本小题满分12分) 解:(Ⅰ)由图知12T =,6πω=.………………………………………………………1分2125.15.22m i n m a x =-=-=y y A ,225.15.22min max =+=+=y y B .……………2分 ∴0.5sin()26y x πϕ=++.又函数0.5sin()26y x πϕ=++过点(0,2.5).代入,得22k πϕπ=+,又0ϕπ<<,∴2πϕ=.…………………………………2分综上,21=A ,6πω=,2πϕ=,21=B . ………………………………………1分即2)26sin(21)(++=ππt t f . (Ⅱ)令)()()(t g t f t h -=,设0)(0=t h ,则0t 为该企业的停产时间. 由0)11()11()11(<-=g f h ,0)12()12()12(>-=g f h ,则)12,11(0∈t . 又0)5.11()5.11()5.11(<-=g f h ,则)12,5.11(0∈t . 又0)75.11()75.11()75.11(>-=g f h ,则)75.11,5.11(0∈t . 又0)625.11()625.11()625.11(<-=g f h ,则)75.11,625.11(0∈t .又0)6875.11()6875.11()6875.11(>-=g f h ,则)6875.11,625.11(0∈t .…4分……………………………………………1分 ∴应该在11.625时停产.……………………………………………………………1分(也可直接由)625.11()625.11()625.11(<-=g f h ,0)6875.11()6875.11()6875.11(>-=g f h ,得出)6875.11,625.11(0∈t ;答案在11.625—11.6875之间都是正确的;若换算成时间应为11点37分到11点41分停产) 20.(本小题满分13分)(Ⅰ)由已知2=a得=a=c ∴2224=-=b a c .∴椭圆Γ的方程为141222=+y x .…………………………………………………4分 (Ⅱ)由⎪⎩⎪⎨⎧=++=,1412,22y x m x y 得01236422=-++m mx x ① ………………………1分∵直线l 与椭圆Γ交于不同两点A 、B ,∴△0)123(163622>--=m m , 得216<m .设),(11y x A ,),(22y x B ,则1x ,2x 是方程①的两根,则2321mx x -=+, 2123124-⋅=m x x .∴12=-==AB x又由AB =231294-+=m ,解之2m =±.……………………………3分 据题意知,点P 为线段AB 的中垂线与直线2=y 的交点. 设AB 的中点为),(00y x E ,则432210m x x x -=+=,400mm x y =+=, ①当2m =时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x -=-+,即1y x =--. 令2=y ,得03x =-.…………………………………………………………………2分 ②当2m =-时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x +=--,即1y x =-+. 令2=y ,得01x =-.………………………………………………………………2分 综上所述,0x 的值为3-或1-. 21.(本小题满分14分)解:(Ⅰ)2222)(ln )ln 21()(ln ln 2)(ln 1ln 2)(x x mx x x x x m x x x x x mx f -⋅=-=⋅--='(0>x 且1≠x ).∴由0)(>'x f ,得21e x >;由0)(<'xf ,得210e x <<,且1≠x .……………………1分∴函数)(x f的单调递减区间是(0,1),(1,单调递增区间是),(+∞e .………………2分∴me e f x f 2)()(-==极小值.………………………………………………………………1分(Ⅱ)222(2)(),(0)mx mx mx mxmxe mx e m mx mx g x m e e--'=-=>. ∴()g x 在(,0)-∞上单调递增,2(0,)m上单调递减,2(,)m +∞上单调递增. ∵函数()g x 存在三个零点.∴20(0)02402()00>⎧>⎧⎪⎪⎪⇒⇒<<⎨⎨<⎪⎪-<⎩⎪⎩m g m e g m m m e . ∴02<<me …………………………………………………………………………………3分 由(1)(1)0-=-=-<mmg m me m e .∴22()(1)0=-=-<em em me e g e m m e e.……………………………………………………1分综上可知,()0,(0)0,(1)0<>-<g e g g ,结合函数()g x 单调性及a b c <<可得:(1,0),(0,),(,)a b e c e ∈-∈∈+∞.即10a b e c -<<<<<,得证.…………………………………………………………1分 (III )由题意,只需min max ()()>f x g x第 11 页 共 11 页 ∵2(12ln )()(ln )-'=mx x f x x 由0<m ,∴函数()f x 在12(1,)e 上单调递减,在12(,)e +∞上单调递增. ∴12min ()()2==-f x f e me .………………………………………………………………2分 ∵(2)()-'=mxmx mx g x e 由0<m ,∴函数()g x 在2(,)m -∞上单调递增,2(,0)m 上单调递减. ∴max 224()()==-g x g m m e m.……………………………………………………………2分 ∴242->-me m e m ,不等式两边同乘以负数m ,得22242-<-m e m e. ∴224(21)e m e +>,即224(21)m e e >+. 由0<m,解得(21)m e e <-+.综上所述,存在这样的负数(,(21)∈-∞-+m e e 满足题意.……………………………1分。
四川省自贡市高三化学第一次诊断试题扫描版

四川省自贡市2015届高三化学第一次诊断试题(扫描版)- 1 -- 2 -- 3 -- 4 -- 5 -届第一次诊断性考试理科综合(化学)自贡市高2015 参考答案及评分意见 分)卷(选择题共第I42- 6 -D C C B A B D分) 共58第II 卷(非选择题 .(每空2分,共16分)8 5︰1 三角锥形(1) C —N 键键能大C —N 键的键长短于C —C ,所以C (2)由于N 原子半径小于原子半径,所以 310 2262610N43()第四周期第IB 族 1S288/a 2S 或【 2PAr 3S 】 3P3d 3d A ----O +5 H +10 OH (4)5 Cl===7Cl +2 ClO +ClO 22314分)9.(每空2分,共1)①弱电解质 < ②AD (1-△+659.8 kJ ·mol(g) O(g) ===COH== (g) (2)CH +4 H(g)+2 H22426324ccK cc O) (O(NH) /(H )① == (N)·)·(32223d ③ ② > 14分).(每空2分,共10b ))过滤 (2Ⅰ.(1 干燥管中无水硫酸铜变蓝,澄清石灰水明显无变化(3)甲。
)B →D Ⅱ.(1 49n/9m ×100%或98n/18m 或(2)吸收空气中的CO 和水蒸汽; 49n/9m 2分,共分)1411.(每空2 )增大接触面积,加快浸出反应速率,提高浸出率(1+2+3+3+2不被氧化)使Fe ),保护还原为FeFe ,(同时生成Ti2( 高温 + 2CO (3)TiO+ 2C + 2Cl TiCl 4 2 2;或分馏)((4)蒸馏HClO↓+ 4·xH+ (2+n)HO===TiO TiCl(5)224 2加入大量水并加热,都能使水解反应向正反应方向进行,促进水解趋于完全。
--2+2O===Ti)(6TiO+4e2- 7 -。
2015年四川卷数学试题及答案(理)

2015年普通高等学校招生全国统一考试(四川)数学(理科)第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{|(1)(2)0}A x x x =+-<,集合{|13}B x x =<<,则AB( )A.{x|—1〈x<3} B 。
{x|-1〈x<1} C.{x |1<x<2} D 。
{x |2〈x<3}2.设i 是虚数单位,则复数32i i-=( ) A.—iB.-3iC 。
i.D 。
3i3.执行如图所示的程序框图,输出S 的值是( )A.32B.32 C.—12D 。
124.下列函数中,最小正周期为π且图象关于原点对称的函数是( )A 。
cos(2)2y x π=+B 。
sin(2)2y x π=+C. sin 2cos 2y x x =+ D 。
sin cos y x x =+5。
过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则AB =( )(A)433(B )23 (C )6 (D)43 6.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )(A )144个 (B )120个 (C)96个 (D )72个7. 设四边形ABCD 为平行四边形,6AB =,4AD =。
若点M ,N 满足3BM MC =,2DN NC =,则.AM NM =( )(A)20 (B)15 (C )9 (D )68.设a ,b 都是不等于1的正数,则“333a b >>”是“log 3log 3a b <"的(A )充要条件 (B )充分不必要条件 (C )必要不充分条件 (D)既不充分也不必要条件 9. 如果函数()()()()21281002f x m x n x m n =-+-+≥≥,在区间122⎡⎤⎢⎥⎣⎦,单调递减,则mn 的最大值为( ) (A )16(B )18(C )25(D )81210. 设直线l 与抛物线24y x =相交于A ,B 两点,与圆()()22250x y r r -+=>相切于点M ,且M为线段AB 的中点。
四川省绵阳市2015届高三第一次诊断试题 数学理 Word含答案

某某 ★ 启用前 【考试时间:2014年10月31日15:00—17:00】某某市高中2012级第一次诊断性考试数学(理工类)本试卷分第I 卷(选择题)和第II 卷(非选择题)。
第I 卷1至2页,第II 卷2至4页.共4页。
满分150分。
考试时间120分钟.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
考试结束后,将答题卡交回。
第Ⅰ卷(选择题,共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
第I 卷共10小题。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1. 已知集合A ={x ∈Z |x 2-1≤0},B ={x |x 2-x -2=0},则A ∩B =(A) ∅(B) {2}(C) {0}(D) {-1}2.下列说法中正确的是(A)命题“)0(∞+∈∀,x ,12>x ”的否定是“)0(0∞+∉∃,x ,02x ≤1” (B)命题“)0(∞+∈∀,x ,12>x ”的否定是“)0(0∞+∈∃,x ,02x ≤1” (C)命题“若b a >,则22b a >”的逆否命题是“若22b a <,则b a <” (D)命题“若b a >,则22b a >”的逆否命题是“若2a ≥2b ,则a ≥b ”3.设各项均不为0的数列{a n }满足n n a a 21=+(n ≥1),S n 是其前n 项和,若5422a a a =,则S 4=(A) 42(B)28 (C) 233+(D) 266+4.如图,正六边形ABCDEF 的边长为1,则DB AD ⋅=(A) -3 (B)3- (C) 3(D)35.已知53)4cos(=-x π,那么sin 2x =(A)2518 (B)2524±(C)257- (D)2576.已知x ,y 满足⎪⎩⎪⎨⎧≤--≥-+≥+-,,,0330101y x y x y x 则2x -y 的最大值为(A) 1 (B) 2(C) 3 (D) 4 7.已知x ∈[π-,π],则“x ∈]22[ππ,-”是“sin(sin x )<cos(cos x )成立”的(A)充要条件(B)必要不充分条件(C) 充分不必要条件(D) 既不充分也不必要条件8.)(x f 是定义在非零实数集上的函数,)(x f '为其导函数,且0>x 时,0)()(<-'x f x f x ,记5log )5(log 2.0)2.0(2)2(22222.02.0f c f b f a ===,,,则 (A)c b a <<(B)c a b << (C)b a c <<(D)a b c <<9.已知函数⎪⎩⎪⎨⎧>≠><-=0)10(log 01)2sin()(x a a x x x x f a ,,且,,π的图象上关于y 轴对称的点至少有3对,则实数a 的取值X 围是 (A) )330(,(B) )155(,(C))133(, (D))550(, 10.已知∈b a ,R ,且1+x e ≥b ax +对x ∈R 恒成立,则ab 的最大值是(A)321e (B)322e (C) 323e (D)3e第II 卷(非选择题共100分)注意事项:必须使用黑色墨迹签字笔在答题卡上题目所指的答题区域内作答。
自贡一中高2015级第一学期10月月考数学试题及参考答案

自贡一中高2015级第一学期10月月考数 学 试 题一、 选择题:(本大题共10小题,每小题5分,共50分, 每小题有且只有一项是符合题目要求的。
请把机读卡上对应正确答案的番号涂黑。
) 1. 如果{}|2A x x =>-,那么( )A .0A ⊆B .{}0A ∈C .A ∅∈D .{}0A ⊆2. 设全集{}1,2,3,4,5,6U =,{}2,4,5A =,{}3,4,5,6B =,则右图中阴影部分表示的集合为( )A .()U C AB B .()()U U C A C B C .()U A C B D. ()U A C B 3. 下列各组函数表示同一函数的是( )A .2()()f x g x == B .0()1,()f x g x x ==C .(0)(),()||(0)x x f x g t t x x ≥⎧==⎨-<⎩D .21()1,()1x f x x g x x -=+=-4. 函数2()f x =的定义域是( )A. 1[,1]3-B. 1(,1)3- C. 11(,)33- D. 1(,)3-∞- 5. 下列四个函数中,在(0,)+∞上为增函数的是( )A.()3f x x =-B. 2()3f x x x =-C. 3()2f x x =-+ D. ()||f x x =-6.设集合{}|22M x x =-≤≤,{}|02N y y =≤≤,给出下列四个图形,其中能表示以集合M 为定义域,N 为值域的函数关系的是( )7. 若函数221y x x =--在区间(,22]a -∞-上是减函数,则实数a 的取值范围是( )A .3(,]2-∞ B .3(,]2-∞- C .3[,)2+∞ D .3[,)2-+∞ 8. 已知函数()y f x =在R 上为单调函数,且(0)1f =,(1)0f =,则()0f x >的解集是( )A.(0,)+∞B. (0,1)C. (1,)+∞D.(,1)-∞9. 若函数1(0)()(2),(0)x x f x f x x +≥⎧=⎨+<⎩,则(3)f -的值为( )A .5B .-1C .1D .210. 设{}1,2,3,4I =, A 与B 是I 的子集, 若{}1,3A B = ,则称(,)A B 为一个“理想配集”.那么符合此条件的“理想配集”的个数是( ) (规定(,)A B 与(,)B A 是两个不同的“理想配集”)A. 16B. 9C. 8D. 4 二、填空题:(每小题5分,共25分,把答案填在.....第.II ..卷.题中横线上.....。
四川省自贡市普高高三第一次诊断性考试数学答案

自贡市普高2015届第一次诊断性考试数学参考答案及评分标准一、选择题(50分)理科DBACC CADAB 文科 BCACD CBDAB 二、填空题(25分)11. -1 12. 11 13. 1200(或写成1100对) 14. 1 15. ①②④ 三、解答题(75分)16.理科(Ⅰ)解 由已知111(1)31(2)3n nn n a n a s n +-⎧=≥⎪⎪⎨⎪=≥⎪⎩s 得.1n a +-111=)33n n n n a s s a --=(…………2分即1n a +=4(2)3n a n ≥…………3分∴数列{a n }是以a 2为首项,以43为公比的等比数列.又112111333s a a ===,…………5分∴214()33n n a -= (n ≥2).∴211)14()(2)33n n n a n -=⎧⎪=⎨≥⎪⎩(…………7分(Ⅱ)解:b n =43log (14n a+ )=[]14344log ()33n n -=…………9分.∴1b n b n +1=1n (1+n )=1n -11+n.…………10分∴T n =1b 1b 2+1b 2b 3+1b 3b 4+…+1b n b n +1=⎝⎛⎭⎫11-12+⎝⎛⎭⎫12-13+⎝⎛⎭⎫13-14+…+⎝⎛⎭⎫1n -11+n …………11分=1-11+n =n1+n.…………12分文科(Ⅰ)解 由已知1111(1)311(2)3n nn n a n a s n +-⎧=+≥⎪⎪⎨⎪=+≥⎪⎩s 得.1n a +-111=)33n n n n a s s a --=(…………3分即1n a +=4(2)3n a n ≥又11211411333s a a =+=+=143n n a a +∴=…………5分 ∴数列{a n }是1a 以为首项,以43为公比的等比数列.…………6分∴14=()3n n a - …………7分(Ⅱ)解:b n =43log 1n a+ =434log ()3n n = …………9分.∴1b n b n +1=1n (1+n )=1n -11+n.…………10分∴T n =1b 1b 2+1b 2b 3+1b 3b 4+…+1b n b n +1=⎝⎛⎭⎫11-12+⎝⎛⎭⎫12-13+⎝⎛⎭⎫13-14+…+⎝⎛⎭⎫1n -11+n …………11分=1-11+n =n1+n.…………12分17.理科(Ⅰ)设“甲、乙两人最后积分之和为20分”为事件,A “甲得0分、乙得20分”为事件B ,“甲得10分、乙得10分”为事件C ,“甲得20分、乙得0分”为事件D …….1分 又21339()(1)()(1)244128P B =--=,………….2分11333()(1)(1)224464P C =⋅-⋅⋅-=,………….3分21131()()(1)(1)22432P D =--=………….4分 ()P A =()P B +()P C +()P D =931191286432128++=;………….5分 (Ⅱ)ξ的取值可为:0,10,20,30,40,………….6分11(0)122P ξ==-=111(10)(1)224P ξ==-=2111(20)(1)=228P ξ==-,3111(30)(1)=2216P ξ==-(),411(40)=216P ξ==()所以ξ的分布列可为………….11分数学期望111117501020304024816168E ξ=⨯+⨯+⨯+⨯+⨯=(12分)y文科解:(Ⅰ)由题意可得:2540360180x y==,所以31,x y ==………………4分 (Ⅱ)记从高一年级抽取的3名同学为123,,a a a ,从高二年级抽取的2名同学为12,b b , 则从高一、高二抽取的5名同学中选2名同学作问卷调查的基本事件有:12131112232122313212(,),(,),(,),(,),(,),(,),(,),(,),(,),(,)a a a a a b a b a a a b a b a b a b b b共有10种,………………………………………………………………………………7分 设选中的这2人都来自高一年级的事件为X ,则X 包含的基本事件有1213111223(,),(,),(,),(,),(,)a a a a a b a b a a 共3种,……10分 因此,()310P X =………………………………………12分 18.理科(I )解法一:根据题设条件建立如图所示的以A 为原点的空间坐标系,有 )3,0,0()0,2,0()0,0,1(C D B …………2分设平面BCD 的法向量),,(z y x =,则⎩⎨⎧=+-=+-⇒⎪⎩⎪⎨⎧=⋅=⋅030200z x y x BC n BD n 可得 )2,3,6(=………….4分76==∴d ………….6分 解法二:等积法ABD C BCD A V V --= AC S d S ABD BCD ⋅=⋅∴∆∆3131计算得:,27,1==∆∆BCD ABD S S 76=∴d方法三:直接法AD AC AB AC ⊥⊥, ABD AC 平面⊥∴ BD AC ⊥∴所以ACF BD 平面⊥ BCD ACF 平面平面⊥∴作CF AH ⊥于H ,则有BCD AH 平面⊥计算得:76=⋅=CF AC AF AH(II )方法一:由(1)建立的空间直角坐标系, 设平面BDE 的法向量为),,(z y x =,则有⎩⎨⎧=+-=+-⇒⎪⎩⎪⎨⎧=⋅=⋅0200z y z x DE m 可得)2,1,2(=………….8分 z y又平面BCD 的法向量为)2,3,6(=n 2119||||,cos =⋅>=<n m n m ………….10分 所以,所求二面角的平面角的余弦值为2119.………….12分方法二:连结EF ,ACF BD 平面⊥ CF BD ,EF BD ⊥⊥∴是所求二面角的平面角CFE ∠∴计算得:557553==CF ,EF21192cos 222=⋅-+=∠CF EF CE CF EF CFE 所以,所求二面角的平面角的余弦值为2119.文科解: (Ⅰ)CMEN BD 平面// 且MN B BDD CMEN =⋂11平面平面BD MN //∴ 又DN BM //∴四边形BMND 是矩形………….2分又CMEN CN NE EM MC 平面与正方体的侧面相交于、、、 由正方体的性质得////CM NE CN ME 、 ∴四边形CMEN 平行四边形………….4分连接MN 和EC 交于P, 连接AC 和BD 交于O,连结PO ,则PO BM = 又PO 为ACE ∆的中位线所以2121===AE PO BM ………….6分(Ⅱ)根据正方体性质有:ABCD A A 平面⊥1 BD A A ⊥∴1 在底面正方形中,BD AC ⊥∴ 所以11A ACC BD 平面⊥………….9分 又BD MN //∴11MN ACC A ∴⊥平面 CMEN MN 平面⊂ 所以11A ACC CMEN 平面平面⊥………….12分19. 解:(Ⅰ)2()2sin cos 1)f x x x x =+-sin 222sin(2)3x x x π=+=+………………………………………………………2分()y f x ∴=的最小正周期为22T ππ== ………………………………………3分由3222232k x k πππππ+≤+≤+得:7,1212k x k k Z ππππ+≤≤+∈, ()y f x ∴=的单调递减区间是]7,1212k k k Z ππππ⎡++∈⎢⎣………6分(Ⅱ)∵()26A f π-=,∴2sin()33A ππ-+=sin A =………………7分 (文科)∵02A π<<,∴3A π=.由正弦定理得:sin sin sin b cB C A a++=,7b c +=,∴13b c += ……………………………………………………9分 由余弦定理2222cos a b c bc A =+-得:22()22cos a b c bc bc A =+--,即491693bc =-,∴40bc = ………………………………………………………11分∴11sin 4022ABC S bc A ∆==⨯=…………………………………………12分 (理科)∵0A π<<,∴233A ππ=或.由正弦定理得:sin sin sin b c B C A a ++=,7b c +=,∴13b c += ……………………………………………………9分 由余弦定理2222cos a b c bc A =+-得:22()22cos a b c bc bc A =+--, 即491692bc bc =-±,∴40bc = 或 120bc =………………………10分 当120bc =时由13b c +=此三角形无解。
四川省自贡市普高高三第一次诊断性考试生物答案

高2015届自贡一诊生物试题参考答案及评分标准
一、选择题
1.D
2. C
3. A
4. D
5. B
6.C
7.A
二、非选择题
8.(14分,每空1分)
(1)促甲状腺激素释放 [X]促甲状腺
(2)单向突触小泡(特异性)受体
(3)渗透压 [ Z ]抗利尿激素乳酸增加
(4)神经和体液作用时间较长(持久)
(5)吞噬抗原淋巴因子
9. (8分,每空1分)
(1)叶绿体、线粒体②③(2)类囊体膜内膜
(3)16 8 (4)36 适当升高二氧化碳浓度、适当增大光照强度、增大昼夜温差(答出其中一点给分)
10.(10分,每空1分)
(1)兼性厌氧 C
6H
12
O
6
→2C
2
H
5
OH +2CO
2
+ 能量(或C
6
H
12
O
6
→2C
2
H
5
OH +2CO
2
)
(2)18~25 红葡萄皮的色素进入发酵液半乳糖醛酸(3)选择培养皿 1000
低于一个菌落可由两个或多个细胞形成
11、(16分,除标明的分数外每空1分)
⑴①类比推理X
②灰毛 RR 2/3 (2分 )
③ RrX T Y(2分 ) RrX T X T或RrX T X t (2分)
⑵①限制性核酸内切酶(限制酶)、DNA连接酶 (2分)
② a.长尾雌鼠:短尾雌鼠:长尾雄鼠:短尾雄鼠=1:1:1:1 (2分 )
b.长尾雌鼠:短尾雌鼠:长尾雄鼠:短尾雄鼠=1:3:1:3 (2分 )。
四川省自贡市2015届高三化学第一次诊断试题(扫描版)

四川省自贡市2015届高三化学第一次诊断试题(扫描版)自贡市高2015届第一次诊断性考试理科综合(化学)参考答案及评分意见第I卷(选择题共42分)D C C B A B D第II卷(非选择题共58分)8.(每空2分,共16分)(1)5︰1 三角锥形(2)由于N原子半径小于C原子半径,所以C—N键的键长短于C—C,所以C—N键键能大(3)第四周期第IB 族 1S2 2S2 2P6 3S2 3P6 3d10 或【Ar】3d10 4288/a3N A (4) 5 Cl2+10 OH-===7Cl-+2 ClO-+ClO3-+5 H2O9.(每空2分,共14分)(1)①弱电解质<②AD(2)CH4(g)+2 H2O(g) ===CO2(g) +4 H2(g) △H== +659.8 kJ·mol-1(3)① K == c4(NH3)·c3(O2) /c2(N2)·c6(H2O)② >③ d10.(每空2分,共14分)Ⅰ.(1)过滤(2)b(3)甲。
干燥管中无水硫酸铜变蓝,澄清石灰水明显无变化Ⅱ.(1)B→D(2)吸收空气中的CO2和水蒸汽; 49n/9m或98n/18m或49n/9m×100% 11.(每空2分,共14分)(1)增大接触面积,加快浸出反应速率,提高浸出率(2)使Fe3+还原为Fe2+,(同时生成Ti3+),保护Fe2+不被氧化(3)TiO2 + 2C + 2Cl2高温TiCl4 + 2CO(4)蒸馏(或分馏);(5) TiCl4 + (2+n)H2O===TiO2·xH2O↓+ 4HCl加入大量水并加热,都能使水解反应向正反应方向进行,促进水解趋于完全。
(6)TiO2+4e-===Ti+2O2-。
【爆款】四川省成都市2015届高三第一次诊断试题-数学(理)Word版含答案.doc
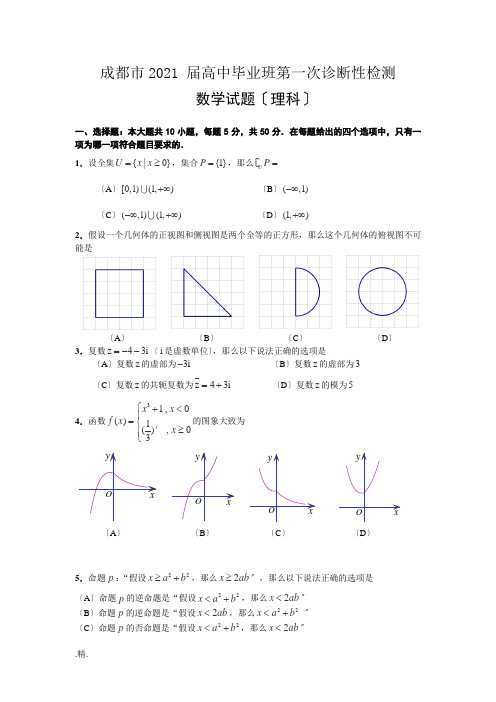
成都市2021 届高中毕业班第一次诊断性检测数学试题〔理科〕一、选择题:本大题共10小题,每题5分,共50分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1.设全集{|0}=≥U x x,集合{1}=P,那么UP =〔A〕[0,1)(1,)+∞〔B〕(,1)-∞〔C〕(,1)(1,)-∞+∞〔D〕(1,)+∞2.假设一个几何体的正视图和侧视图是两个全等的正方形,那么这个几何体的俯视图不可能是〔A〕〔B〕〔C〕〔D〕3.复数z43i=--〔i是虚数单位〕,那么以下说法正确的选项是〔A〕复数z的虚部为3i-〔B〕复数z的虚部为3〔C〕复数z的共轭复数为z43i=+〔D〕复数z的模为54.函数31,0()1(),03xx xf xx⎧+<⎪=⎨≥⎪⎩的图象大致为〔A〕〔B〕〔C〕〔D〕5.命题p:“假设22≥+x a b,那么2≥x ab〞,那么以下说法正确的选项是〔A〕命题p的逆命题是“假设22<+x a b,那么2<x ab〞〔B〕命题p的逆命题是“假设2<x ab,那么22<+x a b〞〔C〕命题p的否命题是“假设22<+x a b,那么2<x ab〞yxOxyOxyO xyOGFEHPACBDA 1B 1C 1D 1〔D 〕命题p 的否命题是“假设22x a b ≥+,那么2<x ab 〞6.假设关于x 的方程240+-=x ax 在区间[2,4]上有实数根,那么实数a 的取值范围是 〔A 〕(3,)-+∞ 〔B 〕[3,0]- 〔C 〕(0,)+∞ 〔D 〕[0,3]7.F 是椭圆22221+=x y a b〔0>>a b 〕的左焦点,A 为右顶点,P 是椭圆上一点,⊥PF x轴.假设14=PF AF ,那么该椭圆的离心率是 〔A 〕14〔B 〕34 〔C 〕12〔D8.m ,n 是两条不同直线,α,β是两个不同的平面,且//m α,n ⊂β,那么以下表达正确的选项是〔A 〕假设//αβ,那么//m n 〔B 〕假设//m n ,那么//αβ 〔C 〕假设n α⊥,那么m β⊥ 〔D 〕假设m β⊥,那么αβ⊥9.假设552sin =α,1010)sin(=-αβ,且],4[ππα∈,]23,[ππβ∈,那么αβ+的值是 〔A 〕74π 〔B 〕94π 〔C 〕54π或74π 〔D 〕54π或94π 10.如图,正方体1111ABCD A B C D -棱长为4,点H 在棱1AA 上,且11HA =.在侧面11BCC B 内作边长为1的正方形1EFGC ,P 是侧面11BCC B 内一动点,且点P 到平面11CDD C 距离等于线段PF 的长.那么当点P 运动时, 2HP 的最小值是〔A 〕21〔B 〕22 〔C 〕23 〔D 〕25二、填空题:本大题共5小题,每题5分,共25分.11.假设非零向量a ,b 满足a b a b +=-,那么a ,b 的夹角的大小为__________. 12.二项式261()x x-的展开式中含3x 的项的系数是__________.〔用数字作答〕 13.在∆ABC 中,内角,,A B C 的对边分别为,,a b c ,假设2=c a ,4=b ,1cos 4=B ,那么∆ABC 的面积=S __________.14.定义在R 上的奇函数()f x ,当0x ≥时,3()log (1)=+f x x .假设关于x 的不等式2[(2)](22)f x a a f ax x ++≤+的解集为A ,函数()f x 在[8,8]-上的值域为B ,假设“x A ∈〞是“x B ∈〞的充分不必要条件,那么实数a 的取值范围是__________.15.曲线C :22y x a =+在点n P (n 〔0,a n >∈N 〕处的切线n l 的斜率为n k ,直线n l 交x 轴,y 轴分别于点(,0)n n A x ,(0,)n n B y ,且00=x y .给出以下结论: ①1a =;②当*n ∈N 时,n y 的最小值为54; ③当*n ∈N 时,n k <④当*n ∈N时,记数列{}n k 的前n 项和为n S ,那么1)<-n S .其中,正确的结论有 〔写出所有正确结论的序号〕三、解答题:本大题共6小题,共75分.解容许写出文字说明、证明过程或演算步骤. 16.〔本小题总分值12分〕口袋中装有除颜色,编号不同外,其余完全一样的2个红球,4个黑球.现从中同时取出3个球.〔Ⅰ〕求恰有一个黑球的概率;〔Ⅱ〕记取出红球的个数为随机变量X ,求X 的分布列和数学期望()E X .17.〔本小题总分值12分〕如图,ABC ∆为正三角形,EC ⊥平面ABC ,//DB EC ,F 为EA 的中点,2EC AC ==,1BD =.〔Ⅰ〕求证:DF //平面ABC ;〔Ⅱ〕求平面DEA 与平面ABC 所成的锐二面角的余弦值. 18.〔本小题总分值12分〕数列{}n a 的前n 项和为n S ,且22n n S a =-;数列{}n b 满足11b =,12n n b b +=+.*n ∈N .〔Ⅰ〕求数列{}n a ,{}n b 的通项公式;〔Ⅱ〕记n n n c a b =,*n ∈N .求数列{}n c 的前n 项和n T . 19.〔本小题总分值12分〕某大型企业一天中不同时刻的用电量y 〔单位:万千瓦时〕关于时间t 〔024t ≤≤,单位:小时〕的函数()y f t =近似地满足()sin()(0,0,0)f t A t B A ωϕωϕπ=++>><<,以下图是该企业一天中在0点至12点时间段用电量y 与时间t 的大致图象. 〔Ⅰ〕根据图象,求A ,ω,ϕ,B 的值; 〔Ⅱ〕假设某日的供电量()g t 〔万千瓦时〕与时间t 〔小时〕近似满足函数关系式205.1)(+-=t t g 〔012t ≤≤〕.当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻〔准确度0.1〕. 参考数据:20.〔本小题总分值13分〕椭圆Γ:12222=+by a x 〔0>>b a 〕的右焦点为)0,22(,且椭圆Γ上一点M 到其两焦点12,F F 的距离之和为43〔Ⅰ〕求椭圆Γ的标准方程;〔Ⅱ〕设直线:(l y x m m =+∈R)与椭圆Γ交于不同两点A ,B ,且32AB =设点0(,2)P x 满足=PA PB ,求0x 的值. 21.〔本小题总分值14分〕函数2()ln mx f x x =-,2()emx mx g x m =-,其中m ∈R 且0m ≠.e 2.71828=为自然对数的底数.〔Ⅰ〕当0m <时,求函数()f x 的单调区间和极小值;〔Ⅱ〕当0m >时,假设函数()g x 存在,,a b c 三个零点,且a b c <<,试证明: 10e a b c -<<<<<;〔Ⅲ〕是否存在负数m ,对1(1,)x ∀∈+∞,2(,0)x ∀∈-∞,都有12()()f x g x >成立?假设存在,求出m 的取值范围;假设不存在,请说明理由.t 〔时〕10 11 12 11.5 11.25 11.75 11.625 11.6875 ()f t 〔万千瓦时〕 2.25 2.4332.5 2.48 2.462 2.496 2.490 2.493 ()g t 〔万千瓦时〕53.522.753.1252.3752.5632.469数学〔理科〕参考答案及评分意见第一卷〔选择题,共50分〕一、选择题:〔本大题共10个小题,每题5分,共50分〕1.A ; 2.C ; 3.D ;4.A ;5.C ;6.B ;7.B ;8.D ;9.A ;10.B .第二卷〔非选择题,共100分〕二、填空题:〔本大题共5个小题,每题5分,共25分〕11.90︒ 12.20- 1314.[2,0]- 15.①③④ 三、解答题:〔本大题共6个小题,共75分〕 16.〔本小题总分值12分〕 解:〔Ⅰ〕记“恰有一个黑球〞为事件A ,那么21243641()205⋅===C C P A C .……………………………………………………………4分〔Ⅱ〕X 的可能取值为0,1,2,那么343641(0)205====C P X C ……………………………………………………………2分122436123(1)205⋅====C C P X C ………………………………………………………2分1(2)()5===P X P A ………………………………………………………………2分∴X 的分布列为∴X 的数学期望1310121555=⨯+⨯+⨯=EX .…………………………………2分 17.〔本小题总分值12分〕〔Ⅰ〕证明:作AC 的中点O ,连结BO .在∆AEC 中,//=FO 12EC ,又据题意知,//=BD 12EC .∴//=FO BD ,∴四边形FOBD 为平行四边形. ∴//DF OB ,又⊄DF 平面ABC ,⊂OB 平面ABC .∴//DF 平面ABC .……………………………………4分 〔Ⅱ〕∵//FO EC ,∴⊥FO 平面ABC .在正∆ABC 中,⊥BO AC ,∴,,OA OB OF 三线两两垂直. 分别以,,OA OB OF 为,,z x y 轴,建系如图. 那么(1,0,0)A ,(1,0,2)-E ,D . ∴(2,0,2)=-AE ,(=-AD . 设平面ADE 的一个法向量为1(,,z)=x y n ,那么1100⎧⋅=⎪⎨⋅=⎪⎩AE AD n n ,即2200-+=⎧⎪⎨-+=⎪⎩x z x z ,令1=x ,那么1,0==z y .∴平面ADE 的一个法向量为1(1,0,1)=n . 又平面ABC 的一个法向量为2(0,0,1)=n . ∴121212,⋅>===cos <n n n n n n .∴平面DEA 与平面ABC .…………………………8分 18.〔本小题总分值12分〕 解:〔Ⅰ〕∵22n n S a =- ①当2≥n 时,1122--=-n n S a ②①-②得,122-=-n n n a a a ,即12-=n n a a 〔2≥n 〕. 又当1≥n 时,1122=-S a ,得12=a .∴数列{}n a 是以2为首项,公比为2的等比数列,∴数列{}n a 的通项公式为1222-=⋅=n n n a .………………………………………4分又由题意知,11b =,12n n b b +=+,即12+-=n n b b ∴数列{}n b 是首项为1,公差为2的等差数列,∴数列{}n b 的通项公式为1(1)221=+-⨯=-n b n n .……………………………2分〔Ⅱ〕〔Ⅱ〕由〔Ⅰ〕知,(21)2=-n n c n ………………………………………………1分∴231123252(23)2(21)2-=⨯+⨯+⨯++-⋅+-⋅n n n T n n231121232(25)2(23)2(21)2-+=⨯+⨯++-⋅+-⋅+-⋅n n n n T n n n ④由-④得2311222222222(21)2-+-=+⨯+⨯++⋅+⋅--⋅n n n n T n (1)分23112(12222)(21)2-+-=++++--⋅n n n n T n∴12222(21)212+-⋅-=⨯--⋅-n n n T n …………………………………………………1分∴111224222+++-=⋅--⋅+n n n n T n 即1(32)24+-=-⋅-n n T n ∴1(23)24+=-+n n T n∴数列{}n c 的前n 项和1(23)24+=-+n n T n ………………………………………3分19.〔本小题总分值12分〕 解:〔Ⅰ〕由图知12T =,6πω=.………………………………………………………1分2125.15.22minmax =-=-=y y A ,225.15.22min max =+=+=y y B .……………2分∴0.5sin()26y x πϕ=++.又函数0.5sin()26y x πϕ=++过点(0,2.5).代入,得22k πϕπ=+,又0ϕπ<<,∴2πϕ=.…………………………………2分综上,21=A ,6πω=,2πϕ=,21=B . ………………………………………1分 即2)26sin(21)(++=ππt t f . 〔Ⅱ〕令)()()(t g t f t h -=,设0)(0=t h ,那么0t 为该企业的停产时间. 由0)11()11()11(<-=g f h ,0)12()12()12(>-=g f h ,那么)12,11(0∈t . 又0)5.11()5.11()5.11(<-=g f h ,那么)12,5.11(0∈t . 又0)75.11()75.11()75.11(>-=g f h ,那么)75.11,5.11(0∈t . 又0)625.11()625.11()625.11(<-=g f h ,那么)75.11,625.11(0∈t .又0)6875.11()6875.11()6875.11(>-=g f h ,那么)6875.11,625.11(0∈t .…4分……………………………………………1分 ∴应该在11.625时停产.……………………………………………………………1分 〔也可直接由0)625.11()625.11()625.11(<-=g f h ,0)6875.11()6875.11()6875.11(>-=g f h ,得出)6875.11,625.11(0∈t ;答案在11.625—11.6875之间都是正确的;假设换算成时间应为11点37分到11点41分停产〕20.〔本小题总分值13分〕〔Ⅰ〕由2=a得=a,又=c ∴2224=-=b a c .∴椭圆Γ的方程为141222=+y x .…………………………………………………4分 〔Ⅱ〕由⎪⎩⎪⎨⎧=++=,1412,22y x m x y 得01236422=-++m mx x ① ………………………1分∵直线l 与椭圆Γ交于不同两点A 、B ,∴△0)123(163622>--=m m , 得216<m .设),(11y x A ,),(22y x B ,那么1x ,2x 是方程①的两根,那么2321mx x -=+, 2123124-⋅=m x x .∴2222129312(312)21244=+-=⨯--=⨯-+AB k x x m m m . 又由32AB =,得231294-+=m ,解之2m =±.……………………………3分 据题意知,点P 为线段AB 的中垂线与直线2=y 的交点. 设AB 的中点为),(00y x E ,那么432210m x x x -=+=,400mm x y =+=,当2m =时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x -=-+,即1y x =--. 令2=y ,得03x =-.…………………………………………………………………2分当2m =-时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x +=--,即1y x =-+. 令2=y ,得01x =-.………………………………………………………………2分 综上所述,0x 的值为3-或1-. 21.〔本小题总分值14分〕解:〔Ⅰ〕2222)(ln )ln 21()(ln ln 2)(ln 1ln 2)(x x mx x x x x m x x x x x mx f -⋅=-=⋅--='〔0>x 且1≠x 〕.∴由0)(>'x f ,得21e x >;由0)(<'xf ,得210e x <<,且1≠x .……………………1分∴函数)(x f 的单调递减区间是e),单调递增区间是),(+∞e .………………2分∴me e f x f 2)()(-==极小值.………………………………………………………………1分〔Ⅱ〕222(2)(),(0)mx mx mx mxmxe mx e m mx mx g x m e e--'=-=>. ∴()g x 在(,0)-∞上单调递增,2(0,)m 上单调递减,2(,)m+∞上单调递增.∵函数()g x 存在三个零点.∴20(0)02402()00>⎧>⎧⎪⎪⎪⇒⇒<<⎨⎨<⎪⎪-<⎩⎪⎩m g m e g m m m e .∴02<<me …………………………………………………………………………………3分 由(1)(1)0-=-=-<mmg m me m e .∴22()(1)0=-=-<em em me e g e m m e e.……………………………………………………1分综上可知,()0,(0)0,(1)0<>-<g e g g ,结合函数()g x 单调性及a b c <<可得:(1,0),(0,),(,)a b e c e ∈-∈∈+∞.即10a b e c -<<<<<,得证.…………………………………………………………1分 〔III 〕由题意,只需min max ()()>f x g x ∵2(12ln )()(ln )-'=mx x f x x 由0<m ,∴函数()f x 在12(1,)e 上单调递减,在12(,)e +∞上单调递增.∴12min ()()2==-f x f e me .………………………………………………………………2分 ∵(2)()-'=mxmx mx g x e由0<m ,∴函数()g x 在2(,)m -∞上单调递增,2(,0)m上单调递减. ∴max 224()()==-g x g m m e m .……………………………………………………………2分 ∴242->-me m e m ,不等式两边同乘以负数m ,得22242-<-m e m e.∴224(21)e m e+>,即224(21)m e e >+.由0<m,解得m <.综上所述,存在这样的负数(,∈-∞m 满足题意.……………………………1分.精.。
四川省自贡市普高高三第一次诊断性考试——语文语文
四川省自贡市普高2015届高三第一次诊断性考试语文试题参考答案一、(12分,每小题3分)1.B(A“犷”读ɡuǎnɡ,C“称”读chèn,D弄读nònɡ)2.A(B杆→竿,C暑→署,D废→费)3.A(不一而足,不止一种或一次,而是很多。
B舍近求远,舍弃近的寻找远的,比喻做事走弯路或方法不对头。
与句意不合。
C至此,到这个时候。
与句意不合。
D比翼,翅膀挨着翅膀飞。
与句意不合)4.B(A主宾搭配不当。
C前后矛盾,不合逻辑。
D宾语中心词残缺)二、(9分,每小题3分)5.B(“是我国古代钻井工艺成熟的标志”错,张冠李戴)6.D(“保障了内地人民的正常生活”错,不合文意)7.C(A“一整套完善的顿钻凿井技术”错,原文无此信息。
B“如果没有卓筒井采卤技术,就不会爆发海湾战争”假设不成立,原文只是一个比喻。
D“自贡是最早生产井盐的地方,也是井盐生产量最大,质量最好的地区”错,原文无此信息)三、(6分,每小题3分)8.C(干,冒犯。
)9.D(均为副词,竟然。
A分别为:连词,表目的;介词,因。
B分别为:代词,他;代词,他们的。
C分别为:动词,给;介词,跟,和)四、(31分)10.(8分)(1)(4分)又请求恢复连坐的法令制度,谨慎对待巡抚的选拔,表彰坚守节操的士人,加重对贪赃官吏的惩罚。
(一句1分。
各句关键词“复”“慎”“旌”“重”译错,该句不得分。
句意不正确,酌情扣分。
)(2)(4分)平时常常愤世嫉俗,想要凭借自己的力量来挽救,所以即使担任有名无实的官职,也多次提出建议。
(一句1分。
各句关键词“恒”“以身”“居”“数”译错,该句不得分。
句意不正确,酌情扣分。
)11.(5分)①积极问政,听取官员建议;②崇尚节俭;③打击官场不良风气,严惩贪官;④提拔正直有才的官员,表彰坚守节操的士人;⑤早建立国之本;⑥公平礼仪制度,不因人施政。
(一点1分。
答出5点即给满分)12.(4分)君子一言以为知/一言以为不知/言不可不慎也/夫子之不可及也/犹天之不可阶而升也/夫子之得邦家者/所谓立之斯立/道之斯行/绥之斯来/动之斯和(一处0.5分)13.(8分)(1)(4分)轻松愉悦的心境。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自贡市普高2015届第一次诊断性考试数学参考答案及评分标准一、选择题(50分)理科DBACC CADAB 文科 BCACD CBDAB 二、填空题(25分)11. -1 12. 11 13. 1200(或写成1100对) 14. 1 15. ①②④ 三、解答题(75分)16.理科(Ⅰ)解 由已知111(1)31(2)3n nn n a n a s n +-⎧=≥⎪⎪⎨⎪=≥⎪⎩s 得.1n a +-111=)33n n n n a s s a --=(…………2分即1n a +=4(2)3n a n ≥…………3分∴数列{a n }是以a 2为首项,以43为公比的等比数列.又112111333s a a ===,…………5分∴214()33n n a -= (n ≥2).∴211)14()(2)33n n n a n -=⎧⎪=⎨≥⎪⎩(…………7分(Ⅱ)解:b n =43log (14n a+ )=[]14344log ()33n n -=…………9分.∴1b n b n +1=1n (1+n )=1n -11+n.…………10分∴T n =1b 1b 2+1b 2b 3+1b 3b 4+…+1b n b n +1=⎝⎛⎭⎫11-12+⎝⎛⎭⎫12-13+⎝⎛⎭⎫13-14+…+⎝⎛⎭⎫1n -11+n …………11分=1-11+n =n1+n.…………12分文科(Ⅰ)解 由已知1111(1)311(2)3n nn n a n a s n +-⎧=+≥⎪⎪⎨⎪=+≥⎪⎩s 得.1n a +-111=)33n n n n a s s a --=(…………3分即1n a +=4(2)3n a n ≥又11211411333s a a =+=+=143n n aa +∴=…………5分 ∴数列{a n }是1a 以为首项,以43为公比的等比数列.…………6分∴14=()3n n a - …………7分(Ⅱ)解:b n =43log 1n a+ =434log ()3nn = …………9分.∴1b n b n +1=1n (1+n )=1n -11+n.…………10分∴T n =1b 1b 2+1b 2b 3+1b 3b 4+…+1b n b n +1=⎝⎛⎭⎫11-12+⎝⎛⎭⎫12-13+⎝⎛⎭⎫13-14+…+⎝⎛⎭⎫1n -11+n …………11分=1-11+n =n1+n.…………12分17.理科(Ⅰ)设“甲、乙两人最后积分之和为20分”为事件,A “甲得0分、乙得20分”为事件B ,“甲得10分、乙得10分”为事件C ,“甲得20分、乙得0分”为事件D …….1分 又21339()(1)()(1)244128P B =--=,………….2分 11333()(1)(1)224464P C =⋅-⋅⋅-=,………….3分 21131()()(1)(1)22432P D =--=………….4分()P A =()P B +()P C +()P D =931191286432128++=;………….5分 (Ⅱ)ξ的取值可为:0,10,20,30,40,………….6分11(0)122P ξ==-=111(10)(1)224P ξ==-=2111(20)(1)=228P ξ==-,3111(30)(1)=2216P ξ==-(), 411(40)=216P ξ==()所以ξ的分布列可为ξ10 203040P121418116116………….11分yAB C EDxzF 数学期望111117501020304024816168E ξ=⨯+⨯+⨯+⨯+⨯=(12分) 文科解:(Ⅰ)由题意可得:2540360180x y ==,所以31,x y ==………………4分 (Ⅱ)记从高一年级抽取的3名同学为123,,a a a ,从高二年级抽取的2名同学为12,b b , 则从高一、高二抽取的5名同学中选2名同学作问卷调查的基本事件有:12131112232122313212(,),(,),(,),(,),(,),(,),(,),(,),(,),(,)a a a a a b a b a a a b a b a b a b b b共有10种,………………………………………………………………………………7分 设选中的这2人都来自高一年级的事件为X ,则X 包含的基本事件有1213111223(,),(,),(,),(,),(,)a a a a a b a b a a 共3种,……10分 因此,()310P X =………………………………………12分18.理科(I )解法一:根据题设条件建立如图所示的以A 为原点的空间坐标系,有 )3,0,0()0,2,0()0,0,1(C D B …………2分设平面BCD 的法向量),,(z y x n =,则⎩⎨⎧=+-=+-⇒⎪⎩⎪⎨⎧=⋅=⋅030200z x y x BC n BD n 可得 )2,3,6(=n ………….4分76||||=⋅=∴n AB n d ………….6分 解法二:等积法ABD C BCD A V V --= AC S d S ABD BCD ⋅=⋅∴∆∆3131计算得:,27,1==∆∆BCD ABDS S 76=∴d方法三:直接法AD AC AB AC ⊥⊥, A B D AC 平面⊥∴ BD AC ⊥∴所以A C F BD 平面⊥ B C D A C F平面平面⊥∴作CF AH ⊥于H ,则有B C D AH 平面⊥计算得:76=⋅=CF AC AF AH(II )方法一:由(1)建立的空间直角坐标系, 设平面BDE 的法向量为),,(z y x m =,则有C D B FAE z xy⎩⎨⎧=+-=+-⇒⎪⎩⎪⎨⎧=⋅=⋅0200z y z x DE m BE m 可得)2,1,2(=m ………….8分又平面BCD 的法向量为)2,3,6(=n 2119||||,cos =⋅⋅>=<n m n m n m ………….10分 所以,所求二面角的平面角的余弦值为2119.………….12分方法二:连结EF ,ACF BD 平面⊥ CF BD ,EF BD ⊥⊥∴是所求二面角的平面角CFE ∠∴计算得:557553==CF ,EF21192cos 222=⋅-+=∠CF EF CE CF EF CFE 所以,所求二面角的平面角的余弦值为2119.文科解: (Ⅰ)CMEN BD 平面// 且MN B BDD CMEN =⋂11平面平面BD MN //∴ 又DN BM //∴四边形BMND 是矩形………….2分又CMEN CN NE EM MC 平面与正方体的侧面相交于、、、由正方体的性质得////CM NE CN ME 、∴四边形CMEN 平行四边形………….4分连接MN 和EC 交于P , 连接AC 和BD 交于O,连结PO ,则PO BM = 又PO 为ACE ∆的中位线 所以2121===AE PO BM ………….6分 (Ⅱ)根据正方体性质有:ABCD A A 平面⊥1 BD A A ⊥∴1 在底面正方形中,BD AC ⊥∴ 所以11A ACC BD 平面⊥………….9分 又BD MN //∴11MN ACC A ∴⊥平面 CMEN MN 平面⊂ 所以11A ACC CMEN 平面平面⊥………….12分 19. 解:(Ⅰ)2()2sin cos 3(2cos 1)f x x x x =+-sin 23cos 22sin(2)3x x x π=+=+………………………………………………………2分()y f x ∴=的最小正周期为22T ππ== ………………………………………3分由3222232k x k πππππ+≤+≤+得:7,1212k x k k Z ππππ+≤≤+∈, ()y f x ∴=的单调递减区间是]7,1212k k k Z ππππ⎡++∈⎢⎣………6分(Ⅱ)∵()326A f π-=,∴2sin()333A ππ-+=,∴3sin 2A = ………………7分 (文科)∵02A π<<,∴3A π=.由正弦定理得:sin sin sin b cB C A a++=, 即13331472b c +=⨯,∴13b c += ……………………………………………………9分 由余弦定理2222cos a b c bc A =+-得:22()22cos a b c bc bc A =+--,即491693bc =-,∴40bc = ………………………………………………………11分 ∴113sin 40103222ABC S bc A ∆==⨯⨯=…………………………………………12分 (理科)∵0A π<<,∴233A ππ=或.由正弦定理得:sin sin sin b cB C A a++=, 即13331472b c +=⨯,∴13b c += ……………………………………………………9分 由余弦定理2222cos a b c bc A =+-得:22()22cos a b c bc bc A =+--, 即491692bc bc =-±,∴40bc = 或 120bc =………………………10分 当120bc =时由13b c +=此三角形无解。
……………11分 ∴113sin 40103222ABC S bc A ∆==⨯⨯=…………………………………………12分 20. 解:(Ⅰ)设点C 的坐标为(x,y),∵→AC =→AD +→AB =(9,5), …………2分即(x 0-1,y-1)=(9,5)………….4分∴x 0=10,y=6,即点C (10,6)………….6分(Ⅱ)由P (x,y ),则:→BP =→AP -→AB =(x-7,y-1)∵M 为AB 的中点,∴M (4,1)……….7分如图由题知1//2MB CD 1123MP MP PC MC ∴=∴=∴→MC =3→MP …………8分 ∴→AC =→AM +→MC =2 1→AB +3→MP =21 (6,0) +3(x-4,y-1)=(3x-9,3y-3) ………….9分 又|→AB |=|→AD | ∴平行四边形ABCD 为菱形∴BD →⊥→AC ∴→BP ⊥→AC ………….10分即:(x-7)(3x-9)+(y-1)(3y-3)=0 ∴2x +2y -10x-2y+22=0 ………….11分 因为点P 不能在直线AB 上,所以y ≠1………….12分∴点P 满足的方程为:2x +2y -10x-2y+22=0 (y ≠1)………….13分21. (Ⅰ)当2a =时,2()2ln 2f x x x x =-+,2()22f x x x'=-+,切点坐标为(11),, 切线的斜率(1)2k f '==,则切线方程为12(1)y x -=-,即21y x =-. ····························· 2分 (Ⅱ)2()2ln g x x x m =-+,则22(1)(1)()2x x g x x xx-+-'=-=,∵1[e]e x ∈,,故()0g x '=时,1x =.当11ex <<时,()0g x '>;当1e x <<时,()0g x '<.故()g x 在1x =处取得极大值(1)1g m =-. ·············································································· 4分又211()2e e g m =--,2(e)2e g m =+-,2211(e)()4e 0e eg g -=-+<,则1(e)()e g g <,∴()g x 在1[e]e,上的最小值是(e)g . ······················································································· 6分()g x 在1[e]e ,上有两个零点的条件是2(1)10,11()20,eeg m g m =->⎧⎪⎨=--≤⎪⎩解得2112e m <≤+, ∴实数m 的取值范围是21(12]e+,. ··························································································· 8分 (Ⅲ)∵()f x 的图象与x 轴交于两个不同的点12(0)(0)A x B x ,,,, ∴方程22ln 0x x ax -+=的两个根为12x x ,,则211122222ln 0,2ln 0,x x ax x x ax ⎧-+=⎪⎨-+=⎪⎩两式相减得1212122(ln ln )()x x a x x x x -=+--……………………………………….9 分又2()2ln f x x x ax =-+,2()2f x x a x'=-+,则1212124()()2x x f x x a x x +'=-+++1212122(ln ln )4x x x x x x -=-+-.··················· 10分 (理科)12()02x x f +'<下证1212122(ln ln )40x x x x x x --<+-(*),即证明2111222()ln 0x x x x x x -+<+,12x t x =, ∵120x x <<,∴01t <<,即证明2(1)()ln 01t u t t t -=+<+在01t <<上恒成立. ·················· 12分∵22222(1)2(1)114(1)()(1)(1)(1)t t t u t t t t t t t -+---'=+=-=+++,又01t <<,∴()0u t '>,∴()u t 在(0,1)上是增函数,则()(1)0u t u <=,从而知2111222()ln 0x x x x x x -+<+,故(*)式<0,即12()02x x f +'<成立………….14分。
