人教版八年级数学上12.2第4课时“斜边、直角边”精选练习1
人教版八年级上册12.2第4课时利用“斜边、直角边”判定直角三角形全等同步练习

人教版八年级上册12.2第4课时利用“斜边、直角边”判定直角三角形全等同步练习第4课时利用“斜边、直角边”判定直角三角形全等一,选择题1.下列说法不正确的是( ).A.一个锐角和其对边对应相等的两个直角三角形全等B.两边及第三边上的高对应相等的两个锐角三角形全等C.两边及其中一边上的高对应相等的两个锐角三角形全等D.斜边对应相等的两个直角三角形全等2.在Rt △ABC 和Rt △A ′B ′C ′中,∠C =∠C ′=90°,∠A =∠B ′,AB =B ′A ,则下列结论中正确的是()A.AC =A ′C ′B.BC =B ′C ′C.AC =B ′C ′D.∠A =∠A ′3.下列结论错误的是( )A .全等三角形对应边上的高相等B .全等三角形对应边上的中线相等C .两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等D .两个直角三角形中,两个锐角相等,则这两个三角形全等4.两个直角三角形全等的条件是()A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.一条斜边和一直角边对应相等5.如图,已知那么添加下列一个条件后,仍无法判定的是()A .B .ABC ADC △≌△CB CD =BAC DAC =∠∠C .D .6.如图所示,△ABC 中,AB =AC ,AD ⊥BC 交D 点,E 、F 分别是DB 、DC 的中点,则图中全等三角形的对数是()A.1B.2C.3D.47.已知在△ABC 和△DEF 中,∠A=∠D=90°,则下列条件不能判定△ABC 和△DEF全等的是( ).A.AB=DE ,AC=DFB.AC=EF ,BC=DFC.AB=DE ,BC=EFD.∠C=∠F ,BC=EF8.如图,已知AB=AC ,AD=AE ,AF ⊥BC 于点F ,则图中全等三角形共有( ).A.1对B.2对C.3对D.4对二,填空题9.如图,DE ⊥AB ,DF ⊥AC , AE =AF ,请找出一对全等的三角形:.BCA DCA =∠∠90B D ==?∠10.如图,已知AC ⊥BD ,BC =CE ,AC =DC .试分析∠B +∠D = .11.如图,有一正方形窗架,盖房时为了稳定,在上面钉了两个等长的木条与分别是的中点,可证得,理由是,于是是的中点.12.如图,M 是BC 上一点,过点M 作MD ⊥AB 于点D ,且MC=MD.如果AC=8 cm,AB=10 cm,那么 BD= cm .13.如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等.已知∠ABC=32°,则∠DFE 的度数是 .GF GE E F ,,AD BC ,Rt AGE △≌G14.如图,AD⊥BE,垂足C是BE的中点,AB=DE,求证:AB∥DE.15.如图,在△ABC中,AD是它的角平分线,且BD=CD,DE,DF分别垂直于AB,AC,垂足为点E,F.求证:BE=CF.16.如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是点E,F,那么CE=DF吗?17(1)如图①,点A,E,F,C在一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC.若AB=CD,试证明BD平分EF;(2)若将图①变为图②,其余条件不变时,上述结论是否仍然成立?请说明理由.① ②参考答案1.D 根据三角形全等的条件去验证.选项D 中只有斜边对应相等,不符合直角三角形全等的条件.2.C 3.D 4.D 5.C 6.D 7.B8.D △ABD ≌△ACE ,△ADF ≌△AEF ,△ABF ≌△ACF ,△ABE ≌△ACD.9.10.90°11.,HL ,12.2 在Rt △AMC 和Rt △AMD 中,∴Rt △AMC ≌Rt △AMD.∴AC=AD=8 cm .又AB=10 cm, ∴BD=2 cm .13.58° 在Rt △ABC和Rt △DEF 中,∴Rt △ABC ≌Rt △DEF (HL).∴∠DFE=∠ACB=90°-32°=58°.14.证明∵C 是BE 的中点,∴BC=CE.∵AD ⊥BE ,∴∠ACB=∠DCE=90°.Rt Rt ADE ADF △≌△Rt Rt AGE BGF △≌△AB在Rt△ACB和Rt△DCE中,∴Rt△ACB≌Rt△DCE(HL).∴∠B=∠E.∴AB∥DE.15.证明在△AED和△AFD中,∴△AED≌△AFD.∴DE=DF.在Rt△BDE和Rt△CDF中,∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.16.解CE=DF.理由如下:在Rt△ABC与Rt△BAD中,∴Rt△ABC≌Rt△BAD(HL).∴AC=BD,∠CAB=∠DBA.在△ACE和△BDF中,∴△ACE≌△BDF(AAS).∴CE=DF.17.分析先证明两个直角三角形全等,再由全等三角形的对应边相等和对应角相等的性质,推出EG与FG所在的三角形全等.(1)证明∵DE⊥AC,BF⊥AC,∴∠DEC=∠BFA=90°.∵AE=CF,∴AE+EF=CF+EF,∴AF=CE.在Rt△ABF和Rt△CDE中,∴Rt△ABF≌Rt△CDE(HL).∴BF=DE.在△BFG和△DEG中,∴△BFG≌△DEG(AAS).∴FG=EG,即BD平分EF.(2)解结论仍然成立.理由如下:∵AE=CF,∴AF=CE.∵BF⊥AC,DE⊥AC,AB=CD,∴Rt△ABF≌Rt△CDE.∴BF=DE,易证△BFG≌△DEG.∴FG=EG,即结论仍然成立.。
人教版八年级数学上册12.2第4课时“斜边、直角边”

2.判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等
D
B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
3.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点
E ,AD、CE交于点H,已知EH=EB=3,AE=4, 则 CH的长为( A )
A.1 B.2 C.3
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.(重点)
(1)一个锐角和这个角的对边对应相等;
A (
)
E (
)
别为C、D,AD=BC.
C
AB=CD,
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.
我们知道,证明三角形全等不存
在SSA定理.
D
F
讲授新课
一 直角三角形全等的判定(“斜边、直角边”定理)
B
CB′
C′
2.两个直角三角形中,有一条直角边和一锐角对应相等,这两
个直角三角形全等吗?为什么?
3.两个直角三角形中,两直角边对应相等,这两个直角三角形 全等吗?为什么?
动脑想一想
B
如图,已知AC=DF,BC=EF,
证明: ∵ BD⊥AC,CE⊥AB,
∠B=∠E,△ABC≌△DEF吗? ∴∠BEC=∠BDC=90 °.
D
CE=BD, BC=CB .
B
C
∴ Rt△EBC≌Rt△DCB (HL).
变式训练1
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BD
平分EF.
AB=CD,
Rt△ABF≌Rt△CDE(HL).
B
AF=CE.
F
八年级数学上册-人教版八年级上册数学12.2第4课时“斜边、直角边”精选练习1

第 4 课时“斜边、直角边”一、选择题 :1.两个直角三角形全等的条件是 ( )A. 一锐角对应相等 ;B.两锐角对应相等;C. 一条边对应相等 ;D.两条边对应相等2.如图 , ∠ B=∠D=90°, BC=CD,∠ 1=30°,则∠ 2 的度数为 ( )A. 30 °B. 60°C. 30°和60°之间D.以上都不对3.假如两个直角三角形的两条直角边对应相等 , 那么两个直角三角形全等的依照是( )A. AASB.SASC.HLD.SSS4.已知在△ ABC和△ DEF中, ∠A=∠ D=90° , 则以下条件中不可以判断△ABC和△DEF全等的是 ( )A.AB=DE,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠F,BC=EF5.如图,AB∥EF∥ DC,∠ABC=90°,AB=DC,那么图中有全等三角形()A.5对;B.4对;C.3对;D.2对6.要判断两个直角三角形全等 , 以下说法正确的有 ( )①有两条直角边对应相等; ②有两个锐角对应相等; ③有斜边和一条直角边对应相等 ; ④有一条直角边和一个锐角相等 ; ⑤有斜边和一个锐角对应相等 ;⑥有两条边相等 .A.6 个B.5个C.4个D.3个A1A DEB D2B F CC第 2题图第5题图第7题图第8题图7.如图,已知AB AD,那么增添以下一个条件后,仍没法判断△ABC≌△ADC的是()A.CB CD B.∠BAC∠DAC C .∠BCA∠DCA D.∠B∠D908.如图,已知 AD是△ ABC的 BC边上的高,以下能使△ ABD≌△ ACD的条件是()A.AB=AC B.∠BAC=90°C.BD=AC D.∠ B=45°二、填空题 :9.有________和一条 ________对应相等的两个直角三角形全等 , 简写成“斜边直角边”或用字母表示为“ ___________”.10.判断两个直角三角形全等的方法有 ______________________________.11.如图,已知 AC⊥ BD于点 P, AP=CP,请增加一个条件,使△ ABP≌△ CDP(不可以增添协助线),你增添的条件是_________________________________12.如图,在 Rt △ ABC 和 Rt △ DCB 中, AB=DC,∠ A=∠ D=90°, AC 与 BD交于点 O,则有△ ________≌△ ________,其判定依据是 ________,还有△ ________≌△ ________,其判断依照是 ________.第 11题图第12题图第13题图13.如图,在△ ABC中,AD⊥ BC于 D, BE⊥ AC于 E,AD与 BE 订交于点 F,若 BF=AC,则∠ ABC=_______第14题图第15题图第16题图14. 如图,已知∠ 1=∠2=90°, AD=AE,那么图中有对全等三角形.15. 如图, Rt △ ABC中,∠ C=90°, AC=8, BC=4, PQ=AB,点 P 与点 Q 分别在 AC 和 AC 的垂线 AD 上移动,则当 AP=_______时,△ ABC≌ △ APQ.16.如图,在 Rt △ ABC中,∠ BAC=90°, AB=AC,分别过点 B, C 作过点 A的直线的垂线 BD, CE,若 BD=4cm, CE=3cm,则 DE=________cm .17.如图,有两个长度相同的滑梯(即 BC=EF),左边滑梯的高度 AC 与右侧滑梯水平方向的长度 DF 相等,则∠ ABC+∠ DFE=__________度18.如图,南京路与八一街垂直,西安路也与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,近来的路程为 __________m.第17题图第18题图三、解答题 :19.如图,AB AC , AD BC于点 D, AD AE, AB均分DAE 交 DE 于点 F ,请你写出图中三对全等三角形,并选用此中一对加以证明...20.在△ ABC中,AB=CB,∠ABC=90o,F 为 AB延伸线上一点 , 点 E 在 BC上, 且 AE=CF.(1)求证 : Rt △ ABE≌Rt △CBF;(2)若∠ CAE=30o, 求∠ ACF度数 .21.如图 AB=AC,CD⊥ AB于 D,BE⊥AC于 E, BE与 CD订交于点 O.(1)求证 AD=AE;(2)连结 OA,BC,试判断直线 OA, BC的关系并说明原因.22.已知如图 ,AB=AC,∠BAC=90°,AE 是过 A 点的一条直线 , 且 B、C 在 DE 的异侧,BD⊥AE于 D,CE⊥ AE于 E, 求证 :BD=DE+CE.ADCBE23.已知如图 , 在△ ABC中, 以 AB、AC为直角边 , 分别向外作等腰直角三角形 ABE、ACF,连结 EF,过点 A 作 AD⊥BC,垂足为 D,反向延伸 DA交 EF 于点 M.(1)用圆规比较 EM与 FM的大小 .(2)你能说明由 (1) 中所得结论的道理吗 ?FMEAB D C第 4 课时斜边、直角边(HL)一、选择题1.D2.B3.B4.B5.C6.C7.C8.A二、填空题9.斜边 , 直角边 ,HL 10. SSS、 ASA、AAS、SAS、 HL11.BP=DP 或 AB=CD或∠ A=∠ C 或∠ B=∠ D.12.ABC,DCB,HL,AOB,DOC,AAS. `13. 45 °14. 315. 4 或 8 16. 717. 90 °18. 500三、解答题19.解:( 1 )△ADB≌△ADC 、△ABD≌△ABE 、△AFD ≌△AFE 、△BFD ≌△ BFE 、△ ABE ≌△ ACD (写出此中的三对即可) .(2)以△ADB≌ ADC为例证明.证明:AD BC ,ADB ADC 90° .在 Rt △ ADB 和 Rt △ ADC 中,AB AC, AD AD ,Rt △ ADB ≌ Rt △ ADC .20. 解:( 1)∵∠ ABC=90°, ∴∠ CBF=∠ ABE=90°.在 Rt△ ABE和 Rt△CBF中,∵AE=CF, AB=BC,∴Rt△ABE≌Rt△CBF(HL)(2)∵AB=BC,∠ABC=90°,∴∠CAB=∠ACB=45° .∵∠ BAE=∠CAB-∠CAE=45°-30 ° =15°.由( 1)知 Rt △ABE≌ Rt△CBF,∴∠BCF=∠BAE=15° ,∴∠ ACF=∠ BCF+∠ACB=45°+15°=60° .21.( 1)证明:在△ ACD与△ ABE中,∵∠ A=∠A,∠ ADC=∠ AEB=90°, AB=AC,∴△ ACD≌△ ABE,∴AD=AE.(2)相互垂直,在 Rt△ADO与△ AEO中,∵OA=OA,AD=AE,∴△ ADO≌△ AEO,∴∠ DAO=∠ EAO,即 OA是∠ BAC的均分线,又∵ AB=AC,∴OA⊥BC.22.证明:∵ BD⊥AE于 D,CE⊥AE于E ∴∠ ADB=∠ AEC=90°∵∠ BAC=90°∴∠ ABD+∠ BAD=∠ CAE+∠BAD ∴∠ ABD=∠ CAE在△ ABD和△ CAE中ABD CAEADB CEAAB CA∴△ ABD≌△ CAE(AAS)∴BD=AE,AD=CE∵AE=AD+DE∴ BD=CE+DE23.解: (1)EM=FM(2)作 EH⊥AM,垂足为 H,FK⊥ AM,垂足为K 先说明 Rt△EHA≌Rt △ADB 得 EH=ADRt △FKA≌Rt△ ADC得 FK=AD 得 EH=FK在 Rt△ EHK与 Rt △FKM中 ,Rt △EHM≌Rt△FKM 得 EM=FM.。
人教版数学八年级上册12.2第4课时斜边、直角边优秀教学案例

(三)学生小组讨论
1.分组讨论:将学生分成小组,让他们在小组内进行讨论,共同探究斜边和直角边的关系,并解决一些实际问题。
2.分享与交流:让学生分享自己的小组讨论成果,促进学生之间的交流和思维碰撞。
(四)反思与评价
1.引导学生自我反思:让学生回顾自己的学习过程,思考自己在探究斜边和直角边关系时的优点和不足。
2.同伴评价:鼓励学生互相评价,互相学习,共同提高。
3.教师评价:教师对学生的学习过程和成果进行评价,给予肯定和鼓励,并提出改进建议。
四、教学内容与过程
(一)导入新课
1.利用多媒体展示一个实际问题:展示一个建筑物的高度需要测量,但是直接测量有困难,引导学生思考如何使用斜边和直角边的关系来解决问题。
3.培养学生运用数学知识解决实际问题的意识,提高学生对数学学科的实用性和价值的认识。
三、教学策略
(一)情景创设
1.以实际问题引入:通过展示一个实际问题,如测量一个物体的高度,引导学生思考如何使用斜边和直角边的关系来解决问题。
2.利用多媒体展示:利用多媒体课件展示斜边和直角边的实际应用场景,如建筑设计、物理实验等,让学生感受到数学与现实的联系。
在教学过程中,我将注重启发式教学,通过引导学生观察、思考和讨论,让学生主动发现斜边和直角边的关系,并能够运用这一关系解决实际问题。同时,我还会运用多媒体教学手段,为学生提供丰富的学习资源,激发学生的学习兴趣,提高学生的学习积极性。
希望通过本节课的教学,学生能够更好地理解斜边和直角边的关系,提高他们的数学思维能力和解决问题的能力。同时,我也将不断反思和总结教学过程,不断提高自己的教学水平,为学生提供更好的教学服务。
新人教版初中数学八年级上册精品教案12.2 第4课时 “斜边、直角边”1

第4课时 “斜边、直角边”1.理解并掌握三角形全等的判定方法——“斜边、直角边”.(重点)2.经历探究“斜边、直角边”判定方法的过程,能运用“斜边、直角边”判定方法解决有关问题.(难点)一、情境导入舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个办法吗?(2)如果他只带了一个卷尺,能完成这个任务吗?工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗?二、合作探究探究点一:应用“斜边、直角边”判定三角形全等如图,已知∠A =∠D =90°,E 、F 在线段BC 上,DE 与AF 交于点O ,且AB =CD ,BE =CF .求证:Rt △ABF ≌Rt △DCE .解析:由题意可得△ABF 与△DCE 都为直角三角形,由BE =CF 可得BF =CE ,然后运用“HL ”即可判定Rt △ABF 与Rt △DCE 全等.证明:∵BE =CF ,∴BE +EF =CF +EF ,即BF =CE .∵∠A =∠D =90°,∴△ABF 与△DCE都为直角三角形.在Rt △ABF 和Rt △DCE 中,∵⎩⎪⎨⎪⎧BF =CE ,AB =CD , ∴Rt △ABF ≌Rt △DCE (HL).方法总结:利用“HL ”判定三角形全等,首先要判定这两个三角形是直角三角形,然后找出对应的斜边和直角边相等即可.探究点二:“斜边、直角边”判定三角形全等的运用【类型一】 利用“HL ”判定线段相等如图,已知AD ,AF 分别是两个钝角△ABC 和△ABE 的高,如果AD =AF ,AC =AE .求证:BC =BE .解析:根据“HL ”证Rt △ADC ≌Rt △AFE ,得CD =EF ,再根据“HL ”证Rt △ABD ≌Rt △ABF ,得BD =BF ,最后证明BC =BE .证明:∵AD ,AF 分别是两个钝角△ABC 和△ABE 的高,且AD =AF ,AC =AE ,∴Rt △ADC ≌Rt △AFE (HL).∴CD =EF .∵AD =AF ,AB =AB ,∴Rt △ABD ≌Rt △ABF (HL).∴BD =BF .∴BD -CD =BF -EF .即BC =BE .方法总结:证明线段相等可通过证明三角形全等解决,作为“HL ”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.【类型二】 利用“HL ”判定角相等或线段平行如图,AB ⊥BC ,AD ⊥DC ,AB =AD ,求证:∠1=∠2.解析:要证角相等,可先证明全等.即证Rt △ABC ≌Rt △ADC ,进而得出角相等.证明:∵AB ⊥BC ,AD ⊥DC ,∴∠B =∠D =90°,∴△ABC 与△ACD 为直角三角形.在Rt△ABC 和Rt △ADC 中,∵⎩⎪⎨⎪⎧AB =AD ,AC =AC ,∴Rt △ABC ≌Rt △ADC (HL),∴∠1=∠2. 方法总结:证明角相等可通过证明三角形全等解决.【类型三】 利用“HL ”解决动点问题如图,有一直角三角形ABC ,∠C =90°,AC =10cm ,BC =5cm ,一条线段PQ =AB ,P 、Q 两点分别在AC 上和过A 点且垂直于AC 的射线AQ 上运动,问P 点运动到AC 上什么位置时△ABC 才能和△APQ 全等?解析:本题要分情况讨论:(1)Rt △APQ ≌Rt △CBA ,此时AP =BC =5cm ,可据此求出P 点的位置.(2)Rt △QAP ≌Rt △BCA ,此时AP =AC ,P 、C 重合.解:根据三角形全等的判定方法HL 可知:(1)当P 运动到AP =BC 时,∵∠C =∠QAP =90°.在Rt △ABC 与Rt △QPA 中,∵⎩⎪⎨⎪⎧AP =BC ,PQ =AB ,∴Rt △ABC ≌Rt △QPA (HL),∴AP =BC =5cm ;(2)当P 运动到与C 点重合时,AP =AC .在Rt △ABC 与Rt △QPA中,∵⎩⎪⎨⎪⎧AP =AC ,PQ =AB ,∴Rt △QAP≌Rt △BCA (HL),∴AP =AC =10cm ,∴当AP =5cm 或10cm 时,△ABC 才能和△APQ 全等.方法总结:判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.【类型四】 综合运用全等三角形的判定方法判定直角三角形全等如图,CD ⊥AB 于D 点,BE ⊥AC 于E 点,BE ,CD 交于O 点,且AO 平分∠BAC .求证:OB =OC .解析:已知BE ⊥AC ,CD ⊥AB 可推出∠ADC =∠BDC =∠AEB =∠CEB =90°,由AO 平分∠BAC 可知∠1=∠2,然后根据AAS 证得△AOD ≌△AOE ,根据ASA 证得△BOD ≌△COE ,即可证得OB =OC .证明:∵BE ⊥AC ,CD ⊥AB ,∴∠ADC =∠BDC =∠AEB =∠CEB =90°.∵AO 平分∠BAC ,∴∠1=∠2.在△AOD 和△AOE 中,∵⎩⎪⎨⎪⎧∠ADC =∠AEB ,∠1=∠2,OA =OA ,∴△AOD ≌△AOE (AAS).∴OD =OE .在△BOD 和△COE 中,∵⎩⎪⎨⎪⎧∠BDC =∠CEB ,OD =OE ,∠BOD =∠COE ,∴△BOD ≌△COE (ASA).∴OB =OC .方法总结:判定直角三角形全等的方法除“HL ”外,还有:SSS 、SAS 、ASA 、AAS.三、板书设计“斜边、直角边”1.斜边、直角边:斜边和一条直角边分别相等的两个直角三角形全等.简记为“斜边、直角边”或“HL ”.2.方法归纳:(1)证明两个直角三角形全等的常用方法是“HL ”,除此之外,还可以选用“SAS ”“ASA ”“AAS ”以及“SSS”.(2)寻找未知的等边或等角时,常考虑转移到其他三角形中,利用三角形全等来进行证明.本节课的教学主要通过分组讨论、操作探究以及合作交流等方式来进行.在探究直角三角形全等的判定方法——“斜边、直角边”时,要让学生进行合作交流.在寻找未知的等边或等角时,常考虑将其转移到其他三角形中,利用三角形全等来进行证明.此外,还要注重通过适量的练习巩固所学的新知识.。
人教版八年级上册数学全等三角形练习题及答案一
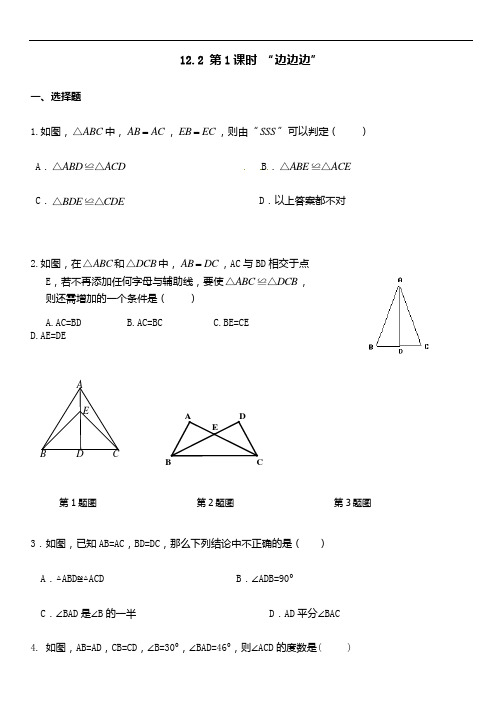
12.2 第1课时 “边边边”一、选择题1.如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可以判定( ) A .ABD ACD △≌△ B .ABE ACE △≌△ C .BDE CDE △≌△D .以上答案都不对2.如图,在ABC △和DCB △中,AB DC =,AC 与BD 相交于点E ,若不再添加任何字母与辅助线,要使ABC DCB △≌△,则还需增加的一个条件是( )A.AC=BDB.AC=BCC.BE=CED.AE=DE3.如图,已知AB=AC ,BD=DC ,那么下列结论中不正确的是( ) A .△ABD ≌△ACD B .∠ADB=90° C .∠BAD 是∠B 的一半D .AD 平分∠BAC4. 如图,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )EDCB AA EB D C第1题图第2题图第3题图A.120°B.125°C.127°D.104°第4题图第5题图5. 如图,线段AD与BC交于点O,且AC=BD,AD=BC,则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D6. 如图,AB=CD,BC=DA,E、F是AC上的两点,且AE=CF,DE=BF,,那么图中全等三角形共有()对A.4对 B.3对 C.2对 D.1对7. 如图,AB=CD,BC=AD,则下列结论不一定正确的是().A.AB∥DCB. ∠B=∠DC. ∠A=∠CD. AB=BC第7题图8. 如果△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x -1,若这两个三角形全等,则x 等于( )A .73B .3C .4D .5二、填空题9.(2011湖北十堰)工人师傅常用角尺平分一个任意角。
做法如下:如图,∠AOB 是一个任意角,在边OA ,OB 上分别取OM=ON ,移动角尺,使角尺 两边相同的刻度分别与M ,N 重合,过角尺顶点C 作射线OC 。
12.2 第4课时 直角三角形全等的判定(“HL”)练习题 人教版八年级数学上册

第4课时直角三角形全等的判定(“HL”)知识点 1 用“HL”判定直角三角形全等1.如图1,可直接用“HL”判定Rt△ABC和Rt△DEF全等的条件是 ()图1A.AC=DF,BC=EFB.∠A=∠D,AB=DEC.AC=DF,AB=DED.∠B=∠E,BC=EF2.如图2所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则直接得到Rt△PEA≌Rt△PFA的依据是 ()图2A.AASB.ASAC.HLD.SSS3.如图3,若要用“HL”证明Rt△ABC≌Rt△ABD,则需要添加的一个条件是.图34.如图4,BD,CE均是△ABC的高,且BE=CD.求证:△BEC≌△CDB.图4 知识点 2 直角三角形全等的灵活运用5.如图5,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,那么下列各组条件中,不能判定Rt△ABC≌Rt△A'B'C'的是 ()图5A.AB=A'B'=5,BC=B'C'=3B.AB=B'C'=5,∠A=∠B'=40°C.AC=A'C'=5,BC=B'C'=3D.AC=A'C'=5,∠A=∠A'=40°6.如图6,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足分别为D,E.若BD=4 cm,CE=3 cm,则DE= cm.图67.如图7,点E,F在BC上,AE⊥BC,DF⊥BC,AC=DB,BE=CF.求证:AC∥DB.图7 8.如图8所示,为了固定电线杆AD,将两根长均为10 m的钢丝一端同系在电线杆上的点A处,另一端固定在地面上的两个锚上,那么两个锚(B,C)离电线杆底部(D)的距离相等吗?为什么?图8【能力提升】9.如图9所示,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,则图中全等三角形共有 ()图9A.2对B.3对C.4对D.5对10.如图10,D为Rt△ABC中斜边BC上的一点,且BD=AB,过点D作BC的垂线,交AC于点E.若AE=12 cm,则DE的长为 cm.图1011.如图11,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从点A同时出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP= 时,△ABC与△APQ全等.图1112.如图12,已知在Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,点E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并证明.图1213.如图13①,AB=4 cm,AC⊥AB,BD⊥AB,AC=BD=3 cm.点P在线段AB上以1 cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等?判断此时线段PC和线段PQ的位置关系,请分别说明理由.(2)如图②,将图①中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t 的值;若不存在,请说明理由.图13第4课时 直角三角形全等的判定(“HL ”)1.C [解析] “HL ”是斜边、直角边分别相等,则必须有AB=DE ,故排除A,D 两个选项,而选项B 中另一个条件为∠A=∠D ,不是直角边对应相等,故排除选项B .故选C .2.C3.答案不唯一,如AC=AD 或BC=BD4.证明:∵BD ,CE 均是△ABC 的高,∴∠BEC=∠CDB=90°.在Rt △BEC 和Rt △CDB 中,{BC =CB,BE =CD,∴Rt △BEC ≌Rt △CDB (HL).5.B [解析] 在Rt △ABC 和Rt △A'B'C'中,∠C=∠C'=90°,选项A 符合直角三角形全等的判定方法“HL ”;选项B 不符合三角形全等的判定方法;选项C 符合三角形全等的判定方法“SAS ”;选项D 符合三角形全等的判定方法“ASA ”.6.7 [解析] ∵∠BAC=90°,∠ADB=∠AEC=90°,∴∠BAD+∠EAC=90°,∠BAD+∠DBA=90°. ∴∠EAC=∠DBA.又∵AB=AC ,∴△ABD ≌△CAE (AAS). ∴AD=CE ,BD=AE. ∴DE=AD+AE=CE+BD=7 cm .故答案为7. 7.证明:∵BE=CF ,∴BE+EF=CF+EF ,即BF=CE.∵AE ⊥BC ,DF ⊥BC , ∴∠AEC=∠DFB=90°.在Rt △AEC 和Rt △DFB 中,{AC =DB,CE =BF,∴Rt △AEC ≌Rt △DFB (HL). ∴∠ACE=∠DBF.∴AC ∥DB.8.解:相等.理由如下:∵AD ⊥BC ,∴∠ADB=∠ADC=90°.在Rt △ADB 和Rt △ADC 中,{AB =AC,AD =AD,∴Rt △ADB ≌Rt △ADC (HL). ∴BD=CD ,即两个锚(B ,C )离电线杆底部(D )的距离相等. 9.B [解析] ∵AB=AC ,BD=CD ,AD=AD ,∴△ABD ≌△ACD (SSS).∴∠B=∠C.又∵∠DEB=∠DFC=90°,BD=CD ,∴△BED ≌△CFD (AAS).∴DE=DF.在Rt △AED 和Rt △AFD 中,∵AD=AD ,DE=DF ,∴Rt △AED ≌Rt △AFD (HL).故图中共有3对全等三角形. 10. 12 [解析] 如图,连接BE. 在Rt △DBE 和Rt △ABE 中,{DB =AB(已知),BE =BE(公共边),∴Rt △DBE ≌Rt △ABE (HL).∴AE=DE.又AE=12 cm,∴DE=12 cm .11.5或10 [解析] ∵AX ⊥AC ,∴∠PAQ=90°.∴∠C=∠PAQ=90°.分两种情况:①当AP=BC=5时, 在Rt △ABC 和Rt △QPA 中,{AB =QP,BC =PA,∴Rt △ABC ≌Rt △QPA (HL);②当AP=CA=10时, 在Rt △ABC 和Rt △PQA 中,{AB =PQ,CA =AP,∴Rt △ABC ≌Rt △PQA (HL).综上所述,当点P 运动到AP=5或10时,△ABC 与△APQ 全等. 故答案为5或10. 12.解:BF ⊥AE. 证明:∵∠ACB=90°,∴∠ACE=∠BCD=90°.在Rt △BDC 和Rt △AEC 中,{CB =CA,BD =AE,∴Rt △BDC ≌Rt △AEC (HL). ∴∠CBD=∠CAE. ∵∠CAE+∠E=90°, ∴∠CBD+∠E=90°. ∴∠BFE=90°,即BF ⊥AE.13.解:(1)当t=1时,△ACP ≌△BPQ ,此时PC ⊥PQ. 理由:当t=1时,AP=BQ=1 cm,∴BP=AC=3 cm .在△ACP 和△BPQ 中,{AP =BQ,∠A =∠B =90°,AC =BP,∴△ACP ≌△BPQ (SAS). ∴∠ACP=∠BPQ.∴∠APC+∠BPQ=∠APC+∠ACP=90°. ∴∠CPQ=90°,即PC ⊥PQ.(2)存在.由题意得AP=t cm,BP=(4-t )cm,AC=3 cm,BQ=xt cm .分两种情况讨论: ①若△ACP ≌△BPQ , 则AC=BP ,AP=BQ ,即{3=4−t,t =xt,解得{t =1,x =1; ②若△ACP ≌△BQP , 则AC=BQ ,AP=BP , 即{3=xt,t =4−t,解得{t =2,x =32. 综上所述,当x=1,t=1或x=32,t=2时,△ACP 与△BPQ 全等.。
人教版八年级数学上册12.2第4课时“斜边、直角边”

文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
B
几何语言:
在Rt△ABC和Rt△ A′B′C′ 中,
A
C
AB=A′B′,
B′
BC=B′C′,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
A′
C′
判一判 判断满足下列条件的两个直角三角形是否全等,不
Rt△ABF≌Rt△CDE(HL).
C
BF=DE
∠BFG=∠DEG ∠BGF=∠DGE
Rt△GBF≌Rt△GDE(AAS).
FG=EG BD平分EF
ARDt△=A【ABFF,≌分Rt△析CD】E(H本L). 题要分情况讨论:(1)Rt△APQ≌Rt△CBA,此时AP=BC=5cm, ∴利R用t△可全AB等据C证≌R明此t△两Q求条PA线(出H段L相)P,等点,的这是位常见置的.思路(.2)Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
E ,AD、CE交于点H,已知EH=EB=3,AE=4, 则 CH的长为( A )
A.1 B.2 C.3
D.4
课堂小结
内容
斜边和一条直角边对应相 等的两个直角三角形全等.
“斜边、 直角边”
前 提 条
件
使用方 法
在直角三角形中
只须找除直角外的两个条件即 可(两个条件中至少有一个条 件是一对对应边相等)
如图,已知AC=DF,BC=EF, ∠B=∠E,△ABC≌△DEF吗?
我们知道,证明三角形全等不存 在SSA定理.
D
F
讲授新课
一 直角三角形全等的判定(“斜边、直角边”定理)
B A
人教版八年级上册数学斜边、直角边测试题

第4课时“斜边、直角边”一、选择题:1. 两个直角三角形全等的条件是( )A.一锐角对应相等;B.两锐角对应相等;C.一条边对应相等;D.两条边对应相等2. 如图,∠B=∠D=90°,BC=CD,∠1=30°,则∠2的度数为( )A. 30°B. 60°C. 30°和60°之间D. 以上都不对3. 如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的依据是( )A. AASB.SASC.HLD.SSS4. 已知在△ABC 和△DEF 中,∠A=∠D=90°,则下列条件中不能判定△ABC 和△DEF 全等的是( )A.AB=DE,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠F,BC=EF5. 如图,AB ∥EF ∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )A.5对;B.4对;C.3对;D.2对6. 要判定两个直角三角形全等,下列说法正确的有( )①有两条直角边对应相等; ②有两个锐角对应相等; ③有斜边和一条直角边对应相等; ④有一条直角边和一个锐角相等; ⑤有斜边和一个锐角对应相等; ⑥有两条边相等. A.6个 B.5个 C.4个 D.3个12A BCDB AEFCD第2题图 第5题图 第7题图 第8题图7. 如图,已知AB AD =,那么添加下列一个条件后,仍无法判定ABC ADC △≌△的是( )A .CB CD = B .BAC DAC =∠∠ C .BCA DCA =∠∠D .90B D ==︒∠∠8. 如图,已知AD 是△ABC 的BC 边上的高,下列能使△ABD ≌△ACD 的条件是( ) A . A B=AC B . ∠BAC=90° C . B D=AC D .∠B=45°二、填空题:9.有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.10.判定两个直角三角形全等的方法有______________________________.11.如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP(不能添加辅助线),你增加的条件是_________________________________12.如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.第11题图第12题图第13题图13.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=_______第14题图第15题图第16题图14.如图,已知∠1=∠2=90°,AD=AE,那么图中有对全等三角形.15.如图,Rt△ABC中,∠C=90°,AC=8,BC=4,PQ=AB,点P与点Q分别在AC和AC的垂线AD上移动,则当AP=_______时,△ABC≌△APQ.16.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=________cm .17.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=__________度18.如图,南京路与八一街垂直,西安路也与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程为__________m.第17题图第18题图三、解答题:19. 如图,,于点,,平分交于点,AB AC AD BC D AD AE AB DAE DE F=⊥=∠请你写出图中三对..全等三角形,并选取其中一对加以证明.20.在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证: Rt△ABE≌Rt△CBF;(2)若∠CAE=30º,求∠ACF度数.21. 如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.(1)求证AD=AE;(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.22. 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.BAE CD23. 已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.(1)用圆规比较EM与FM的大小.(2)你能说明由(1)中所得结论的道理吗?B AE MFC D第4课时 斜边、直角边(HL )一、选择题1.D2.B3.B4.B5.C6.C7.C8.A二、填空题9. 斜边,直角边,HL 10. SSS 、ASA 、AAS 、SAS 、HL11. BP=DP 或AB=CD 或∠A=∠C 或∠B=∠D .12.ABC,DCB,HL,AOB,DOC,AAS. `13. 45° 14. 315. 4或8 16. 7 17. 90° 18. 500三、解答题19.解:(1)ADB ADC △≌△、ABD ABE △≌△、AFD AFE △≌△、BFD BFE △≌△、ABE ACD △≌△(写出其中的三对即可). (2)以△ADB ≌ADC 为例证明.证明:,90AD BC ADB ADC ⊥∴∠=∠=°.在Rt ADB △和Rt ADC △中,,,AB AC AD AD ==∴ Rt ADB △≌Rt ADC △.20.解:(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°.在Rt△ABE和Rt△CBF中,∵AE=CF, AB=BC, ∴Rt△ABE≌Rt△CBF(HL)(2) ∵AB=BC, ∠ABC=90°, ∴∠CAB=∠ACB=45°.∵∠BAE=∠CAB-∠CAE=45°-30°=15°.由(1)知 Rt△ABE≌Rt△CBF,∴∠BCF=∠BAE=15°, ∴∠ACF=∠BCF+∠ACB=45°+15°=60°.21.(1)证明:在△ACD与△ABE中,∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,∴△ACD≌△ABE,∴AD=AE.(2)互相垂直,在Rt△ADO与△AEO中,∵OA=OA,AD=AE,∴△ADO≌△AEO,∴∠DAO=∠EAO,即OA是∠BAC的平分线,又∵AB=AC,∴OA⊥BC.22.证明:∵BD ⊥AE 于D,CE ⊥AE 于E∴∠ADB=∠AEC=90°∵∠BAC=90°∴∠ABD+∠BAD=∠CAE+∠BAD∴∠ABD=∠CAE在△ABD 和△CAE 中ABD CAE ADB CEAAB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△CAE(AAS)∴BD=AE,AD=CE∵AE=AD+DE∴BD=CE+DE23. 解:(1)EM=FM(2)作EH ⊥AM,垂足为H,FK ⊥AM,垂足为K先说明Rt △EHA ≌Rt △ADB 得EH=ADRt △FKA ≌Rt △ADC 得FK=AD 得EH=FK在Rt △EHK 与Rt △FKM 中,Rt △EHM ≌Rt △FKM得EM=FM.答题方法:试卷检查五法重视答案,要对结果负责不少同学都说,明明题目都会做,然而考试时却不是这里出错就是那里出错,总是拿不了高分。
人教版八年级数学上12.2第4课时“斜边、直角边”精选练习2.docx

初中数学试卷桑水出品第4课时 “斜边、直角边”一、选择题1.在Rt △ABC 和Rt △A ′B ′C ′中,∠C =∠C ′=90°,∠A =∠B ′,AB =B ′A ,则下列结论中正确的是( )A.AC =A ′C ′B.BC =B ′C ′C.AC =B ′C ′D.∠A =∠A ′2.下列结论错误的是( )A .全等三角形对应边上的高相等B .全等三角形对应边上的中线相等C .两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等D .两个直角三角形中,两个锐角相等,则这两个三角形全等 3.两个直角三角形全等的条件是( )A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.一条斜边和一直角边对应相等 4.如图,已知AB AD =,那么添加下列一个条件后, 仍无法判定ABC ADC △≌△的是( )A .CB CD = B .BAC DAC =∠∠ C .BCA DCA =∠∠D .90B D ==︒∠∠5.如图所示,△ABC 中,AB =AC ,AD ⊥BC 交D 点,E 、F 分别是DB 、DC 的中点,则图中全等三角形的对数是( )A.1B.2C.3D.4ABCD(第4题)二、填空题6. 如图,DE ⊥AB , DF ⊥AC , AE =AF ,请找出一对全等的三角形: . 7.如图,已知AC ⊥BD ,BC =CE ,AC =DC .试分析∠B +∠D = .8.如图,有一正方形窗架,盖房时为了稳定,在上面钉了两个等长的木条GF 与GE E F ,, 分别是AD BC ,的中点,可证得Rt AGE △≌ ,理由是 ,于是G 是 的中点.三、解答题9.如图,已知AD AF ,分别是两个钝角ABC △和ABE △的高,如果AD AF =,AC AE =. 求证:BC BE =.A D CBEA B CFEDG参考答案1.C 2.D 3.D 4.C 5.D6.Rt Rt ADE ADF △≌△ 7.90° 8.Rt Rt AGE BGF △≌△,HL ,AB9.根据“HL ”证Rt Rt ADC AFE △≌△,CD EF ∴=,再根据“HL ”证Rt Rt ABD ABF △≌△,BD BF ∴=,BD CD BF EF ∴-=-,即BC BE =.。
人教版八年级上册数学 12.2 第4课时 “斜边、直角边”学案1
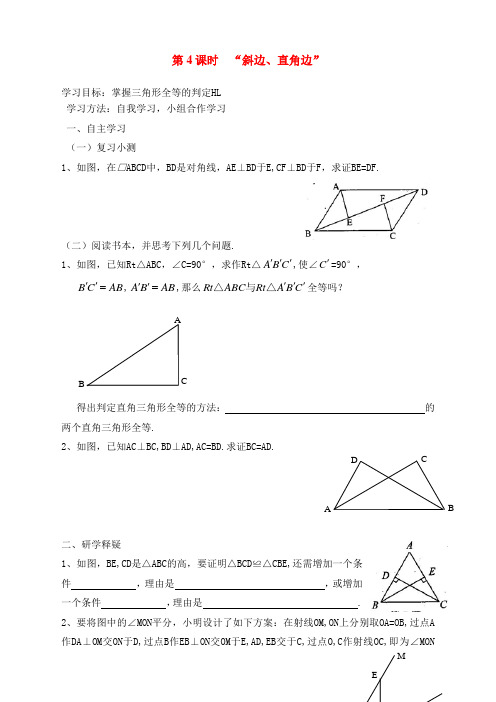
第4课时 “斜边、直角边”学习目标:掌握三角形全等的判定HL学习方法:自我学习,小组合作学习一、自主学习(一)复习小测1、如图,在□ABCD 中,BD 是对角线,AE⊥BD于E,CF⊥BD于F ,求证BE=DF.(二)阅读书本,并思考下列几个问题.1、如图,已知Rt △ABC ,∠C=90°,求作Rt △C B A ''',使∠C '=90°,AB C B ='',AB B A ='',那么C B A Rt ABC Rt '''△与△全等吗?得出判定直角三角形全等的方法: 的两个直角三角形全等.2、如图,已知AC ⊥BC,BD ⊥AD,AC=BD.求证BC=AD.二、研学释疑1、如图,BE,CD 是△ABC 的高,要证明△BCD ≌△CBE,还需增加一个条件 ,理由是 ,或增加一个条件 ,理由是 .2、要将图中的∠MON 平分,小明设计了如下方案:在射线OM,ON 上分别取OA=OB,过点A 作DA ⊥OM 交ON 于D,过点B 作EB ⊥ON 交OM 于E,AD,EB 交于C,过点的平分线,试说明这样做的理由.三、实践探究1、在C B A Rt ABC Rt '''△与△中,∠C=∠C '=90°,下列条件中能判定两三角形全等的有( )①C A AC ''=,∠A=∠A '; ②C A AC ''=,B A AB ''=;③C A AC ''=,C B BC ''= ; ④B A AB ''=,∠A=∠A '.A. 1个B. 2个C. 3个D. 4个2、如图,AD 是△ABC 的高,E 为AC 上一点,BE 交AD 于F ,且有BF=AC,FD=CD.求证:(1)△BFD ≌△ACD ;(2)BE ⊥AC.四、拓展延伸如图,在△ABC中,已知D 是BC 的中点,DE⊥AC,DF⊥AB ,垂足非别是E ,F ,DE=DF ,求证AB=AC.五、小结:。
586.八年级新人教版数学上册12.2 第4课时 “斜边、直角边”3(同步练习)

12.2三角形全等的判定(4)一、选择题1.在Rt △ABC 和Rt △A ′B ′C ′中,∠C =∠C ′=90°,∠A =∠B ′,AB =B ′A ,则下列结论中正确的是( ) A.AC =A ′C ′ B.BC =B ′C ′ C.AC =B ′C ′D.∠A =∠A ′2.下列结论错误的是( )A .全等三角形对应边上的高相等B .全等三角形对应边上的中线相等C .两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等D .两个直角三角形中,两个锐角相等,则这两个三角形全等 3.两个直角三角形全等的条件是( )A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.一条斜边和一直角边对应相等 4.如图,已知AB AD =,那么添加下列一个条件后, 仍无法判定ABC ADC △≌△的是( )A .CB CD = B .BAC DAC =∠∠ C .BCA DCA =∠∠D .90B D ==︒∠∠5.如图所示,△ABC 中,AB =AC ,AD ⊥BC 交D 点,E 、F 分别是DB 、DC 的中点,则图中全等三角形的对数是( )A.1B.2C.3D.4二、填空题6. 如图,DE ⊥AB , DF ⊥AC , AE =AF ,请找出一对全等的三角形: .ABCD(第4题)7.如图,已知AC ⊥BD ,BC =CE ,AC =DC .试分析∠B +∠D = .8.如图,有一正方形窗架,盖房时为了稳定,在上面钉了两个等长的木条GF 与GE E F ,,分别是AD BC ,的中点,可证得Rt AGE △≌ ,理由是 ,于是G 是 的中点. 三、解答题9.如图,已知AD AF ,分别是两个钝角ABC △和ABE △的高,如果AD AF =,AC AE =.求证:BC BE =. 参考答案1.C 2.D 3.D 4.C 5.D6.Rt Rt ADE ADF △≌△ 7.90° 8.Rt Rt AGE BGF △≌△,HL ,AB 9.根据“HL ”证Rt Rt ADC AFE △≌△,CD EF ∴=,再根据“HL ”证Rt Rt ABD ABF △≌△,BD BF ∴=,BD CD BF EF ∴-=-,即BC BE =.初中数学公式大全1 过两点有且只有一条直线2 两点之间线段最短A D CBEA B CFEDG3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12 两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180 °18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 平行四边形判定定理 1 两组对角分别相等的四边形是平行四边形21 平行四边形判定定理 2 两组对边分别相等的四边形是平行四边形22 平行四边形判定定理 3 对角线互相平分的四边形是平行四边形23 平行四边形判定定理 4 一组对边平行相等的四边形是平行四边形24 矩形性质定理 1 矩形的四个角都是直角25 矩形性质定理 2 矩形的对角线相等26 矩形判定定理 1 有三个角是直角的四边形是矩形27 矩形判定定理 2 对角线相等的平行四边形是矩形28 菱形性质定理 1 菱形的四条边都相等29 菱形性质定理 2 菱形的对角线互相垂直,并且每一条对角线平分一组对角30 菱形面积= 对角线乘积的一半,即S= (a×b )÷231 菱形判定定理1 四边都相等的四边形是菱形32 菱形判定定理2 对角线互相垂直的平行四边形是菱形33 正方形性质定理1 正方形的四个角都是直角,四条边都相等34 正方形性质定理 2 正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角35 定理1 关于中心对称的两个图形是全等的36 定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分37 逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称38 等腰梯形性质定理等腰梯形在同一底上的两个角相等。
部编人教版八年级数学上册第12章 全等三角形 12.2.4 利用斜边、直角边判定直角三角形全等【习题课件】

夯实基础·逐点练
(2)若∠ABC=35°,则∠CAO=___2_0_°___.
【点拨】在使用HL证明两直角三角形全等时,一定要 说 明 是 直 角 三 角 形 , 本 题 易 忽 视 指 出 △ ACB 和 △BDA为直角三角形,而直接用HL证明.
整合方法·提升练
10.如图,AD为△ABC的高,E为AC上一点,BE交AD于
A.4 cm
B.5 cm C.6 cm D.7 cm
夯实基础·逐点练
4.【2018•泰州】如图,∠A=∠D=90°,AC=DB,AC, DB相交于点O.求证:OB=OC.
证明:在Rt△ABC和Rt△DCB中, AC=BD, CB=BC,
∴Rt△ABC≌Rt△DCB(HL) , ∴∠OBC=∠OCB, ∴OB=OC.
探究培优·拓展练
(2)如图②,若AC=DC,在不添加任何辅助线的情况下, 请直接写出图②中四对全等的直角三角形.
解:△ACB≌△DCE; △EMC≌△BNC, △AON≌△DOM, △AOB≌△DOE.
探究培优·拓展练
13 . 如 图 , 已 知 AB = AE , ∠ B = ∠ E , BC = ED , AF⊥CD.求证:F是CD的中点.
夯实基础·逐点练
5.下列条件中,不能判定两个直角三角形全等的 是( B ) A.两条直角边对应相等 B.两个锐角对应相等 C.一个锐角和一条直角边对应相等 D.斜边和一条直角边对应相等
夯实基础·逐点练
6.如图所示,已知AB=AD,那么添加下列一个条件 后,仍无法判定△ABC≌△ADC的是( C ) A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学试卷
灿若寒星整理制作
第4课时 “斜边、直角边”
一、选择题:
1. 两个直角三角形全等的条件是( )
A.一锐角对应相等;
B.两锐角对应相等;
C.一条边对应相等;
D.两条边对应相等
2. 如图,∠B=∠D=90°,BC=CD ,∠1=30°,则∠2的度数为( ) A. 30° B. 60° C. 30°和60°之间 D. 以上都不对
3. 如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的 依据是( )
A. AAS
B.SAS
C.HL
D.SSS
4. 已知在△ABC 和△DEF 中,∠A=∠D=90°,则下列条件中不能判定△ABC 和 △DEF 全等的是( )
A.AB=DE,AC=DF
B.AC=EF,BC=DF
C.AB=DE,BC=EF
D.∠C=∠F,BC=EF
5. 如图,AB ∥EF ∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( ) A.5对; B.4对; C.3对; D.2对
6. 要判定两个直角三角形全等,下列说法正确的有( )
①有两条直角边对应相等; ②有两个锐角对应相等; ③有斜边和一条直角边对应相等; ④有一条直角边和一个锐角相等; ⑤有斜边和一个锐角对应相等; ⑥有两条边相等.
A.6个
B.5个
C.4个
D.3个
1
2A B
C
D
第2题图 第5题图 第7题图 第8题图
B
A
E
F
C
D
7. 如图,已知AB AD =,那么添加下列一个条件后,仍无法判定ABC ADC △≌△的是( )
A .C
B CD = B .BA
C DAC =∠∠ C .BCA DCA =∠∠
D .90B D ==︒∠∠
8. 如图,已知AD 是△ABC 的BC 边上的高,下列能使△ABD≌△ACD 的条件是( ) A . A B=AC B . ∠BAC=90° C . B D=AC D . ∠B=45°
二、填空题:
9.有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.
10.判定两个直角三角形全等的方法有______________________________.
11.如图,已知AC ⊥BD 于点P ,AP=CP ,请增加一个条件,使△ABP ≌△
CDP (不能添加辅助线),你增加的条件是_________________________________
12.如图,在Rt △ABC 和Rt △DCB 中,AB=DC ,∠A=∠D=90°,AC 与BD
交于点O ,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.
第11题图 第12题图 第13题图
13.如图,在△ABC 中,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点F ,若BF=AC ,则∠ABC=_______
第14题图 第15题图 第16题图
14.如图,已知∠1=∠2=90°,AD=AE ,那么图中有 对全等三角形.
15.如图,Rt△ABC中,∠C=90°,AC=8,BC=4,PQ=AB,点P与点Q分
别在AC和AC的垂线AD上移动,则当AP=_______时,△ABC≌△APQ.
16.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A
的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=________cm .
17.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与
右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=__________度
18.如图,南京路与八一街垂直,西安路也与八一街垂直,曙光路与环
城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程为__________m.
第17题图第18题图
三、解答题:
19. 如图,,
于点,,平分交于点,请AB AC AD BC D AD AE AB DAE DE F
=⊥=∠
你写出图中三对
..全等三角形,并选取其中一对加以证明.
20.在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证: Rt△ABE≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.
21. 如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
22. 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异
侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
B
A
E C
D
23. 已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、
ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
(1)用圆规比较EM与FM的大小.
(2)你能说明由(1)中所得结论的道理吗?
B A
E M
F
C D
第4课时 斜边、直角边(HL )
一、选择题
1.D
2.B
3.B
4.B
5.C
6.C
7.C
8.A
二、填空题
9. 斜边,直角边,HL 10. SSS 、ASA 、AAS 、SAS 、HL 11. BP=DP 或AB=CD 或∠A=∠C 或∠B=∠D . 12.ABC,DCB,HL,AOB,DOC,AAS. `13. 45° 14. 3 15. 4或8 16. 7 17. 90° 18. 500
三、解答题
19.解:(1)ADB ADC △≌△、ABD ABE △≌△、AFD AFE △≌△、
BFD BFE △≌△、 ABE ACD △≌△(写出其中的三对即可). (2)以△ADB ≌ADC 为例证明. 证明:
,90AD BC ADB ADC ⊥∴∠=∠=°.
在Rt ADB △和Rt ADC △中,
,,AB AC AD AD == ∴ Rt ADB △≌Rt ADC △.
20.解:(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°.
在Rt △ABE 和Rt △CBF 中,
∵AE=CF, AB=BC, ∴Rt △ABE ≌Rt △CBF(HL)
(2) ∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠ACB=45°. ∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知 Rt △ABE ≌Rt △CBF , ∴∠BCF=∠BAE=15°, ∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
21.(1)证明:在△ACD 与△ABE 中,
∵∠A=∠A ,∠ADC=∠AEB=90°,AB=AC , ∴△ACD ≌△ABE , ∴AD=AE .
(2)互相垂直,
在Rt △ADO 与△AEO 中, ∵OA=OA ,AD=AE , ∴△ADO ≌△AEO , ∴∠DAO=∠EAO , 即OA 是∠BAC 的平分线, 又∵AB=AC , ∴OA ⊥BC .
22.证明:∵BD ⊥AE 于D,CE ⊥AE 于E ∴∠ADB=∠AEC=90° ∵∠BAC=90°
∴∠ABD+∠BAD=∠CAE+∠BAD ∴∠ABD=∠CAE
在△ABD 和△CAE 中
ABD CAE ADB CEA AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩
∴△ABD ≌△CAE(AAS) ∴BD=AE,AD=CE ∵AE=AD+DE ∴BD=CE+DE
23. 解:(1)EM=FM
(2)作EH ⊥AM,垂足为H,FK ⊥AM,垂足为K 先说明Rt △EHA ≌Rt △ADB 得EH=AD Rt △FKA ≌Rt △ADC 得FK=AD 得EH=FK
在Rt △EHK 与Rt △FKM 中,Rt △EHM ≌Rt △FKM 得EM=FM.。
