江西省遂川中学、永丰中学10-11学年高二数学上学期12月月考 理【会员独享】
江西省遂川中学2019-2020学年高二上学期第一次月考数学(理)试卷

2021届高二上学期第一次月考理数选择题(每小题5分)1.已知直线310ax y --=与直线2()103a x y -++=垂直,则a 的值为( D )A .11,3-B .1,13C .1,13-- D .1,13-2、若(2,1)P -为圆22(1)25x y -+=的弦AB 的中点,则直线AB 的方程是( A )A .30x y --=B .230x y +-=C .10x y +-=D .250x y --=3、直线l 过点P(-1,2)且与以点M(-3,-2),N(4,0)为端点的线段恒相交,则l 的斜率取值范围是( D ) (A)[-,5] (B)[-,0)∪(0,2] (C)(-∞,-)∪[5,+∞) (D)(-∞,-]∪[2,+∞)4、已知圆C 的半径为2,圆心在x 轴正半轴上,直线3440x y ++=与圆C 相切,则圆C 的方程为( D )A .22230x y x +--=B .2240x y x ++=C .22230x y x ++-=D .22-40x y x +=5、设直线l 的方程为cos 30()x y R θθ++=∈,则直线l 的倾斜角α的取值范围是( C )A .[0,]πB .,42ππ⎡⎫⎪⎢⎣⎭C .3,44ππ⎡⎤⎢⎥⎣⎦D .πππ3π,,4224⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦6、两条平行线l 1,l 2分别过点P (-1,2),Q (2,-3),它们分别绕P ,Q 旋转,但始终保持平行,则l 1,l 2之间距离的取值范围是( D )A .(5,+∞)B .(0,5]C .(34,+∞)D .(0,34]7、设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤5,2x -y ≤4,-x +y ≤1,y ≥0,则目标函数z =3x +5y 的最大值为( )A .6B .19C .21D .458、将圆()()22:324C x y -+-=的周长分为2:1两部分,A .0或C D 9、一辆卡车宽1.6 m ,要经过一个半圆形隧道(半径为3.6 m),则这辆卡车的平顶车篷篷顶距地面高度不得超过(B )A .1.4 mB .3.5 mC .3.6 mD .2.0 m10、方程1-x 2=x +k 有惟一解,则实数k 的范围是( D )A .k =-2B .k ∈(-2,2)C .k ∈[-1,1)D .k =2或-1≤k <1 11、已知圆的方程为x 2+y 2-4x -6y +11=0,直线l :x +y -t =0,若圆上有且只有两个不同的点到直线l 的距离等于22,则参数t 的取值范围为( A )A .(2,4)∪(6,8)B .(2.4]∪[6,8)C .(2,4)D .(6,8)12、已知圆22:1C x y +=,点P 为直线142x y+=上一动点,过点P 向圆C 引两条切线,,,PA PB A B 为切点,则直线AB 经过定点( B )A .11,24⎛⎫⎪⎝⎭ B .11,42⎛⎫⎪⎝⎭ C.,04⎛⎫ ⎪ ⎪⎝⎭D.4⎛⎫ ⎪ ⎪⎝⎭ 一、填空题(每小题5分) 13、过点P (2,3)的直线l 与x 轴,y 轴的正半轴分别交于A ,B 两点,O 为坐标原点,则S △AOB 的最小值为__12______14、已知圆C 的圆心在x 轴的正半轴上,点M (0,5)在圆C 上,且圆心到直线2x -y =0的距离为455,则圆C 的方程为__(x -2)2+y 2=9 15、已知实数x ,y 满足⎩⎪⎨⎪⎧y ≥1,y ≤2x -1,x +y ≤m .如果目标函数z =x -y 的最小值为-1,则实数m =__5______.16、在平面直角坐标系xOy 中,直线1:20l kx y -+=与直线2:20l x ky +-=相交于点P ,则当实数k 变化时,点P 到直线40x y --=的距离的最大值为__二、解答题17.ABC △的顶点)1,3(-A ,AB 边上的中线所在的直线方程为059106=-+y x ,B ∠的平分线所在的直线方程为0104=+-y x ,求BC 边所在的直线方程. 设A 关于B ∠的平分线的对称点),(00'y x A ,则000031410022143x y y x +-⎧-+=⎪⎪⎨+⎪=-⎪-⎩,解得0017x y =⎧⎨=⎩,即)7,1('A ,设),104(a a B -,则AB 中点的坐标为⎪⎭⎫⎝⎛--21,274a a . 且满足059106=-+y x ,即47161059022a a --⋅+⋅-=,∴5=a .∴(1,0,5)B . ∵'A 也在直线BC 上, ∴BC 所在直线的方程为06592=-+y x .18已知圆C 经过点()2,1A -和直线10x y +-=相切,且圆心在直线2y x =-上.(1)求圆C 的方程;(2)若直线22y x =-与圆C 交于A ,B 两点,求弦AB 的长.【解析】(1)因为圆心在直线2y x =-上,设圆心为(),2C a a -,则圆C 的方程为()()()22220x a y a r r -++=>,,即弦AB 的长为 (1)若,过点作圆的切线,求该切线方程; (2)若为圆的任意一条直径,且(其中为坐标原点),求圆的半径. 解析:(1)若,圆:,圆心 ,半径为3. 若切线斜率不存在,圆心到直线的距离为3,∴直线为圆的一条切线; 若切线斜率存在,设切线方程为:,化简为:,则圆心到直线的距离,解得:. ∴切线方程为或;(2)圆的方程可化为,圆心 ,则,设圆的半径,∵为圆的任意一条直径,∴,且, 则,又∵,解得:,∴圆的半径为.20.某旅游景区的一家庭作坊计划每天制作高档、中档、低档3种旅游纪念品共50个,制作一个高档纪念品需要14分钟,利润为12元;制作一个中档纪念品需要12分钟,利润为11元;制作一个低档纪念品需要9分钟,利润为7元.若已知每天制作时间不超过11小时,则这个家庭作坊每天制作旅游纪念品的最大利润为多少元.解析:设每天制作高档纪念品x 个,中档纪念品y 个,则制作低档纪念品(50-x -y )个,每天的利润为z 元,z =12x +11y +7(50-x-y )=5x +4y +350,约束条件为⎩⎪⎨⎪⎧x ∈N *,y ∈N *,14x +12y +9(50-x -y )≤660,50-x -y ≥0,即⎩⎪⎨⎪⎧x ∈N *,y ∈N *,5x +3y ≤210,x +y ≤50,可行解为图中阴影部分中的整点.由⎩⎪⎨⎪⎧5x +3y =210,x +y =50,解得⎩⎪⎨⎪⎧x =30,y =20,即A (30,20).易知z =5x +4y +350在A (30,20)处取最大值,所以z max =5×30+4×20+350=580,即最大利润为580元.21.已知定点()0,4A -,点P 圆224x y +=上的动点.(1)求AP 的中点C 的轨迹方程; (2)若过定点1,12B ⎛⎫-- ⎪⎝⎭的直线l 与C 的轨迹交于,M N 两点,且MN =求直线l 的方程.【解析】(1)设()()00,,,C x y P x y ,由题意知:00220002424x x y y x y +=-=+⎧⎪⎪⎪⎨=⎪⎪⎪⎩,化简得()2221x y ++=,故C 的轨迹方程为()2221x y ++=。
江西省遂川中学高三第一次月考试卷(数学理).doc

江西省遂川中学高三第一次月考试卷(数学理)一、选择题(每小题5分,共60分)1、设全集为U ,A B ⋂=∅,则下列结论一定正确的是( )(A )()()U U C A C B ⋂=∅ (B )()()U U C A C B U ⋃=(C )B 是U C A 的真子集 (D )A 是U C B 的真子集2、命题“存在00,20x x R ∈≤”的否定是( ) (A )不存在00,20x x R ∈> (B )存在00,20x x R ∈≥(C )对任意的,20x x R ∈≤ (D )对任意的,20x x R ∈>3、函数y =的定义域为( )(A )()4,1--(B )()4,1-(C )()1,1-(D )(1,1]-4、“22a -≤≤”是“实系数一元二次方程210x ax ++=有虚根”的( )(A )必要不充分条件 (B )充分不必要条件(C )充要条件 (D )既不充分也不必要条件5、值域为{}2,5,10,其对应关系为21y x =+的函数个数为( ) (A )1 (B )8 (C )27 (D )396、设()f x 是定义在R 上单调递减的奇函数,若12230,0,x x x x +>+>310x x +>,则( )(A )123()()()0f x f x f x ++< (B )123()()()0f x f x f x ++>(C )123()()()0f x f x f x ++= (D )123()()()f x f x f x +>7、定义在R 上的函数()f x 满足2log (1),0()(1)(2),0x x f x f x f x x -≤⎧=⎨--->⎩,则(2010)f 的值为( ) (A )1- (B )0 (C )1 (D )28、用{}min ,,a b c 表示,,a b c 三个数中的最小值,设{}()()min 2,2,100x f x x x x =+-≥,则()f x 的最大值为( )(A )4 (B )5 (C )6 (D )79、下列图像中有一个是函数1)1(31)(223+-++=x a ax x x f )0,(≠∈a R a 的导数)(x f ' 的图像,则(1)f -等于( )(A )13 (B )13- (C )73 (D )53或13- 10、已知函数()f x 是定义在R 上的偶函数,且1(1)()f x f x +=,若()f x 在[]1,0-上是减函数,则()f x 在[]2,3上是( )(A )增函数 (B )减函数(C )先增后减函数(D )先减后增函数11、函数2()log 3sin(2)f x x x π=-零点的个数是( )(A )13 (B )14 (C )15 (D )1612、设函数()f x 的定义域为R ,若存在与x 无关的正常数M ,使()f x M x ≤对一切实数x 均成立,则称()f x 为“有界泛函”,给出以下函数:()21()f x x =;()2()2x f x =;()23()1x f x x x =++;()4()sin f x x x =。
江西省吉安市永丰中学2019-2020学年高二上学期期中考试数学(理)试题 Word版含答案【7套汇总】

永丰中学2019-2020学年第一学期高二期中考试数学(理科)试卷命题人:陈保进 时间:120分钟 满分:150分一、选择题(本大题共12题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.直线310x ++=的倾斜角是( ) A .1500B .600C .1200D .13502.已知命题01,:0200>--∈∃x x R x p ,则p ⌝为( )A .R x ∈∀,012≤--x xB .R x ∈∀,210x x -->C .0x R∃∈,20010x x --≤ D .0x R∃∈,1020>--x x3.下列说法中正确的是( )A .一个命题的逆命题为真,则它的逆否命题一定为真B .“a b >”与“a c b c +>+”不等价C .“220a b +=,则,a b 全为0”的逆否命题是“若,a b 全不为0, 则220a b +≠”D .一个命题的否命题为真,则它的逆命题一定为真4.如图,O A B ∆'''是水平放置的OAB ∆的直观图,3='A O ,4='B O ,则OAB ∆的周长为 ( )A. 10+B ..10 D .125.设m 、n 是两条不同的直线,α、β是两个不同的平面,下列命题正确的是( ) A .若m α⊂,n β⊂,且//αβ,则//m n B .若m α⊂,n ⊂α,且//m β,//n β,则//αβC .若m n ⊥,m α⊂,且n β⊂,则αβ⊥D .若m α⊥,n β⊥,且αβ⊥,则m n ⊥6.点B 是点(1,2,3)A 在坐标平面yoz 内的投影,则OB 等于( )ABC D 7.圆锥的母线长为4,侧面展开图为一个半圆,则该圆锥表面积为( ) A .10π B .12π C .16π D .18π8.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( )A .12+π B .32+π C.123+π D .323+π 9.由直线2y x =+上的点向圆22(4)(2)1x y -++=引切线,则切线长的最小值为( ) A .30BC .24D10.如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题: ①AF GC ⊥;②BD 与GC 成异面直线且夹角为600; ③//BD MN ;④BG 与平面ABCD 所成的角为450. 其中正确的个数是( ) A .1 B .2C .3D .411.已知三棱锥P ABC -的顶点都在球O 的球面上,若PA ⊥平面ABC ,AB BC ⊥,2PA =,4AB BC ==,则球O 的表面积为( )A .12πB .π16C .24πD .36π12.如图,在棱长为1的正方体1111ABCD A B C D -中,点,E F 分别是棱111,B B B C 的中点,点G 是棱1CC 的中点,则过线段AG 且平行于平面1A EF 的截面的面积为( ) A .1 B .98 C .89D .二、填空题(本大题共4小题,每小题5分,共20分)13.已知直线310ax y --=与直线2()103a x y -++=垂直,则a 的值为 .14.已知,x y 满足条件020x y x y x -≤⎧⎪+≤⎨⎪≥⎩,则2z x y =+的最大值为 .15.圆02222=+-++a y x y x 截直线02=++y x 所得弦的长度为4,则实数=a . 16.已知∠ACB=90o ,P 为平面ABC 外一点,PC=2,点P 到∠ACB 两边AC ,BC那么点P 到平面ABC 的距离为_________.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.) 17.(本小题10分)己知直线2x ﹣y ﹣1=0与直线x ﹣2y+1=0交于点P .(1)求过点P 且平行于直线3x+4y ﹣15=0的直线1l 的方程;(结果写成直线方程的一般式) (2)求过点P 并且在两坐标轴上截距相等的直线2l 的方程.(结果写成直线方程的一般式)18.(本小题12分)命题p :函数)0)(34lg(22>-+-=a a ax x y 有意义,命题q :实数x 满足023<--x x . (1)当1=a 时,若q p ∧是真命题,求实数x 的取值范围; (2)若q 是p 的充分不必要条件,求实数a 的取值范围.19.(本小题12分)如图,在三棱锥P ABC -中,PA AB ⊥,PA BC ⊥,AB BC ⊥,2PA AB BC ===,D 为线段AC 的中点,E 为线段PC 上一点.(1)求证:平面BDE ⊥平面PAC ;(2)当PA // 平面BDE 时,求三棱锥P BDE -的体积.20.(本小题12分)如图,长方体1111D C B A ABCD -的底面ABCD 是正方形,点E 在棱1AA 上,1EC BE ⊥. (1)证明:⊥BE 平面11C EB ;(2)若E A AE 1=,求二面角1C EC B --的余弦值.E21.(本小题12分)如图,平面PAD ⊥平面ABCD ,PA PD =,四边形ABCD 为平行四边形,4ABC π∠=,2AB AC ==,M 为线段AD 的中点,点N 满足2PN ND =. (1)求证:直线PB // 平面MNC ;(2)若3=PA ,求直线BP 与平面PCD 所成角的正弦值.22.(本小题12分)已知圆C 过点(1,4),(3,2)M N ,且圆心在直线430x y -=上. (1)求圆C 的方程;(2)平面上有两点(2,0),(2,0)A B -,点P 是圆C 上的动点,求22||||AP BP +的最小值; (3)若Q 是x 轴上的动点,,QR QS 分别切圆C 于,R S 两点,试问:直线RS 是否恒过定点?若是,求出定点坐标,若不是,说明理由.永丰中学2019-2020学年第一学期高二期中考试数学(理科)参考答案二、填空题 13. 311-或 14. 4 15. -4 16.2 三、解答题17、解:(1)联立⎩⎨⎧=+-=--012012y x y x ,解得⎩⎨⎧==11y x ,∴P (1,1).设直线l 1的方程为3x+4y+m=0,把P (1,1)代入可得:3+4+m=0,解得m=-7.∴直线l 1的方程为3x+4y ﹣7=0.(2)当直线l 2经过原点时,可得方程为:y=x .当直线l 2不过原点时,可设方程为:y+x=a ,把P (1,1)代入可得1+1=a ,可得a=2. ∴直线l 2的方程为x+y ﹣2=0.综上可得:直线l 2的方程为x+y ﹣2=0或x ﹣y=0. 18、解:(1),1=a P:0342>-+-x x ,31<<xq:32<<x若q p ∧为真,则p,q 同时为真,即32<<x .(2)P:03422>-+-a ax x ,0)3)((<--a x a x (a>0),则a x a 3<<,若q 是p 的充分不必要条件,即)(3,2是),(a a 3(a>0)的真子集. 所以21≤≤a .19、解:(1)证明:PA AB ⊥,PA BC ⊥, PA ∴⊥平面ABC又BD ⊂平面ABC PA BD ∴⊥2AB BC ==,D 为线段AC 的中点, BD AC ∴⊥ BD ∴⊥平面PAC BD ⊂平面BDE∴平面BDE ⊥平面PAC(2)//PA 平面BDE ,平面PAC 平面BDE ED =//ED PA ∴又D 为AC 中点,E ∴为PC 中点12443P BDE A BDE E ABD E ABC P ABCABC V V V V V S AP -----∆∴=====⨯⨯311222131=⨯⨯⨯⨯ 20.解:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BE EC ⊥,且1111C EC C B =⋂,所以BE ⊥平面11EB C .(2)由(1)知190BEB ∠=︒.由题设知Rt ABE △≌11Rt A B E △,所以45AEB ∠=︒,故AE AB =,12AA AB =.以D 为坐标原点,DA 的方向为x 轴正方向,||DA 为单位长,建立空间直角坐标系D –xyz ,则C (0,1,0),B (1,1,0),1C (0,1,2),E(1,0,1),(1,0,0)CB =,(1,1,1)CE =-,1(0,0,2)CC =. 设平面EBC 的法向量为n =(x ,y ,x ),则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x x y z =⎧⎨-+=⎩ 所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =(x ,y ,z ),则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩m m 即20,0.z x y z =⎧⎨-+=⎩ 所以可取m =(1,1,0). 于是1cos ,||||2⋅<>==-n m n m n m .由于所求二面角为钝角,所以二面角余弦值为21-.21、解:(1)证明:连接BD ,交MC 于点O ,连接NO在平行四边形ABCD 中,因为12MD BC =,所以12OD OB =, 又因为2PN ND =,即12ND PN =,所以ON PB ∕∕, 又因为ON ⊂平面MNC ,PB ⊄平面MNC , 所以直线PB ∕∕平面MNC .(2)证明:因为PA PD =,M 为线段AD 的中点,所以PM AD ⊥,又因为平面PAD ⊥平面ABCD ,且交线为AD ,PM ⊂平面PAD 所以PM ⊥平面ABCD在平行四边形ABCD 中,因为45ABC ∠=︒,2AB AC ==,所以AB AC ⊥以A 为原点,,AB AC 所在直线为x 轴,y 轴,平行PM 的直线为z 轴,建立空间直角坐标系,E由PA=3,AM=2,可得PM=1, 则,,P(-1,1,1)因为(2,0,0)DC =,),(1,1-1=DP 设(,,)x y z =n 为平面DCP 的一个法向量, 则⎩⎨⎧=+-=02z y x x ,取y=1,则)1,1,0(=n ,又(3,1,1)BP =-,记直线BP 与平面PCD 所成角为θ, 则11222112,cos sin =⨯=><=θ. 22.解:(1)由题意知,圆心C 在直线430x y -=上,设圆心为 又因为圆C 过点(1,4),(3,2)M N ,,解得3a =,所以圆心C 为(3,4),半径 所以圆C 方程为22(3)(4)4x y -+-=.(2)设(,)P x y ,则即22||||AP BP +的最小值为26.(3)设(,0)Q t ,则以CQ 为直径的圆圆心为则圆D 方程为 整理得22(3)430x y t x y t +-+-+=,直线RS 为圆C 与圆D 的相交弦2222(3)430(3)(4)4x y t x y t x y ⎧+-+-+=⎨-+-=⎩, 两式相减,可得得RS 直线方程(3)43210t x y t -++-=, 即(3)34210x t x y -++-=,令3034210x x y -=⎧⎨+-=⎩,解得33x y =⎧⎨=⎩,即直线RS 恒过定点()3,3.永丰中学2019-2020学年第一学期高二年级期中考试数学(文科)试卷时间:120分钟 总分:150分一、选择题(本大题共有12小题,每题5分,共60分) 1.关于下列几何体,说法正确的是( )A .图①是圆柱B .图②和图③是圆锥C .图④和图⑤是圆台D .图⑤是圆台 2.垂直于同一条直线的两条直线一定( ) A .平行 B .相交 C .异面 D .以上都有可能 3.下列命题错误的是( )A .命题“若022=+y x ,则0==y x ”的逆否命题为“若y x ,中至少有一个不为0则022≠+y x ”B .若命题01,:0200≤+-∈∃x x R x p ,则01,:2>+-∈∀⌝x x R x pC .ABC ∆中,B A sin sin >是B A >的充要条件D .若向量,a b 满足0<⋅b a,则a 与b 的夹角为钝角4.已知直线l 的斜率3k ≤l 的倾斜角的范围是( ) A .[0,]3πB .[,]32ππC .[0,](,)32πππD .[,]3ππ5.若点在圆的内部,则实数a 的取值范围是( )A .B .C .或D .6.已知直线l :01=++ny mx 平行于直线m :0534=++y x ,且l 在y 轴上的截距为13,则n m ,的值分别为( )A .4,3B .-4,3C .-4,-3D .4,-3 7.如图,在正方体1111ABCD A B C D -中,M , N 分别为棱111,C D CC 的中点,以下四个结论:①直线DM 与1CC 是相交直线;②直线AM 与NB 是平行直线;③直线BN 与1MB 是异面直线;④直线AM 与1DD 是异面直线.其中正确的个数为( ) A .1 B .2 C .3 D .48.如图,平行四边形O A B C ''''是水平放置的一个平面图形的直观图,其中''4O A =,''2O C =,30A O C ︒'''∠=则下列叙述正确的是( ) A .原图形是正方形 B .原图形是非正方形的菱形C .原图形的面积是D .原图形的面积是9.一只蚂蚁从正方体ABCD -A 1B 1C 1D 1的顶点A 出发,经正方体的表面,按最短路线爬行到顶点C 1的位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )A .①②B .③④C .①③D .②④10.下列各图是正方体和正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点不共面的图形是( )11.已知圆C :(x ﹣3)2+(y ﹣4)2=1和两点A (﹣m ,0),B (m ,0)(m >0),若圆C 上存在点P ,使得∠APB=90°,则m 的最大值为( ) A .7 B .6 C .5D .412.如图所示,在三棱台111ABC A B C -中,点D 在11A B 上,且1AA BD ∥,点M 是111A B C △内(含边界)的一个动点,且有平面BDM ∥平面1A C ,则动点M 的轨迹是( ) A .平面 B .直线 C .线段,但只含1个端点 D .圆二、填空题(本大题共有4小题,每题5分,共20分)13.若将一个圆锥侧面沿一条母线剪开,其展开图是半径为2 cm 的半圆,则该圆锥的高为________cm .14.已知)1,1(-P ,)2,2(Q ,若直线:l 1-=mx y 与射线PQ (P 为端点)有交点,则实数m 的取值范围是 .15.如图,已知正三棱柱的底面边长为2,高为5,一质点自A 点出发,沿着三棱柱的侧面绕行两周到达A 1点的最短路线的长为________.16.点M (x ,y )在函数y =13y x ++的取值范围是 .三、解答题(本大题共有6小题,其中第17题10分,其他题每题12分,共70分)17.(本小题10分)一条光线从点M(2,3)射出,遇x轴反射后经过N(-1,6),求入射光线所在直线方程。
江西省吉安市永丰中学2021-2022学年高二上学期第二次月考数学(理)试题

∵圆 可化为 ,
∴圆心为 ,半径为1,
又∵圆心 到直线 的距离 ,
∵ 的面积最小时,点C到直线 的距离最短,该最短距离即圆心到直线 的距离减去圆的半径,
故 面积的最小值为 .故选:D.
11.曲线 与直线 有两个不同的交点时实数 的范围是()
A. B. C. D.
A
A. B. C. D.
A
求出圆 的圆心坐标和半径,作出圆 关于直线 的对称圆 ,连结 ,则 与直线 的交点即为 点,此时 点为 与圆 的交点关于直线 对称的点, 为 与圆 的交点, 的最小值为 .
详解】
由圆 ,圆 ,
可知圆 圆心 ,半经为1,如图,
圆 圆心为 ,半经为2,
圆 关于直线 的对称圆为圆 ,
所以至少有两个面互相平行,故D正确.故选:D
2.不等式组 ,表示的平面区域是图中的()
A. B.
C. D.
C
画出直线 取下半部分,画出 取右下方,可得选项.
, 平面区域在直线 下方,排除选项A;
画出 ,取直线的右下方,排除B,D,故选:C
本题考查二元一次不等式组表示的平面区域,考查学生数形结合思想,属于基础题.
D.棱柱的所有面中,至少有两个面互相平行
D
根据棱柱的定义依次判断选项即可.
对选项A,由棱柱的定义知:长方体为棱柱,长方体的侧面是矩形,故A错误;
对选项B,当棱柱为直棱柱时,侧棱才为棱柱的高,故B错误;
对选项C,正六棱柱的相对侧面互相平行,故C错误;
对选项D,由棱柱的定义可知:棱柱的上下底面一定平行,
所以 ,化简得点 的轨迹方程为 .
求 的最小值,即求 的最小值,也即求原点 到直线 的距离,
江西省遂川中学、永丰中学高二数学上学期12月月考 理【会员独享】.doc

江西省遂川中学、永丰中学高二上学期12月月考(数学理)一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中, 只有一项是符合题目要求的) 1. 命题:“a 、b 都是偶数,则a+b 是偶数”的逆否命题是 ( ) A .a 、b 都不是偶数,则a+b 不是偶数 B.a 、b 不都是偶数,则a+b 不是偶数 C .a+b 不是偶数,则a 、b 都不是偶数 D.a+b 不是偶数,则a 、b 不都是偶数2.若点P (0,2)与点Q (-2,0)关于直线L 对称,则L 的方程是 ( ) A .x +y =0 B. x -y =0 C .x +y +1=0 D. x -y +1=03. 命题“065,2>-+∈x x Z x 有对任意的”的否定是 ( ) A .065,2≤-+∈x x Z x 有对任意的 B .065,2>-+∈x x Z x 使存在 C .065,2≤-+∈x x Z x 使存在 D . 65,2-+∈x x Z x 有对任意的<04.过点A (3,4)的圆22(2)(1)1x y -+-=的切线方程是 ( ) A .4x +3y =0 B .4x -3y =0C .4x -3y =0或x =3D .4x +3y =0或x =35.与圆A :060422=--+x y x 内切且与圆B :0422=++x y x 外切的动圆圆心的轨迹为( )A .圆B .线段C .椭圆D .双曲线6. 条件p :1>x 且1>y ,条件q :2>+y x 且1>xy ,则条件p 是条件q 的 ( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件7.下列四个正方体图形中,A B 、为正方体的两个顶点,M N P 、、分别为其所在棱的中点,能得出//AB 平面MNP 的图形的序号是 ( )A. ①、③B. ①、④C. ②、③D. ②、④8.P 、A 、B 、C 是球面上的四个点,PA 、PB 、PC 两两垂直,且1PA PB PC ===,则该球的表面积等于 ( ) A .2πB .3πC .4πD .12π9. 双曲线)0(122≠=-mn n y m x 的离心率为2,焦点与椭圆1251622=+y x 的焦点重合,则m 的值为( )A .427-B .49-C .427D .4910.已知点P 为抛物线22y x =上的动点,点P 在y 轴上的射影是M ,A 点坐标为7(,4)2,则||||PA P M +的最小值是 ( )A .112B .4C .92D .5二、填空题(本大题共5小题,每小题5分,满分25分) 11. 若命题“p 或q ”为真,“非p ”为真,则“非q ”为 命题。
遂川县第一高级中学2018-2019学年上学期高二数学12月月考试题含答案

遂川县第一高级中学2018-2019学年上学期高二数学12月月考试题含答案 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1. 如图,在四棱锥P ﹣ABCD 中,PA ⊥平面ABCD ,底面ABCD 是菱形,AB=2,∠BAD=60°.(Ⅰ)求证:BD ⊥平面PAC ;(Ⅱ)若PA=AB ,求PB 与AC 所成角的余弦值; (Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.【考点】直线与平面垂直的判定;点、线、面间的距离计算;用空间向量求直线间的夹角、距离.2. 某几何体的三视图如图所示,则它的表面积为( )A .B .C .D .3. 若当R x ∈时,函数||)(x a x f =(0>a 且1≠a )始终满足1)(≥x f ,则函数3||log xx y a =的图象大致是 ( )【命题意图】本题考查了利用函数的基本性质来判断图象,对识图能力及逻辑推理能力有较高要求,难度中等. 4. 直径为6的球的表面积和体积分别是( )A .144,144ππB .144,36ππC .36,144ππD .36,36ππ5. 函数y=的图象大致是( )A .B .C .D .6. 设a ,b ∈R ,i 为虚数单位,若2+a i 1+i =3+b i ,则a -b 为( )A .3B .2C .1D .07. ()()22f x a x a =-+ 在区间[]0,1上恒正,则的取值范围为( )A .0a >B .0a <<C .02a <<D .以上都不对8. 某校新校区建设在市二环路主干道旁,因安全需要,挖掘建设了一条人行地下通道,地下通道设计三视图中的主(正)视力(其中上部分曲线近似为抛物)和侧(左)视图如图(单位:m ),则该工程需挖掘的总土方数为( )A .560m 3B .540m 3C .520m 3D .500m 39. 已知集合{| lg 0}A x x =≤,1={|3}2B x x ≤≤,则A B =( ) A .(0,3] B .(1,2]C .(1,3]D .1[,1]2【命题意图】本题考查对数不等式解法和集合的运算等基础知识,意在考查基本运算能力.10.已知,,那么夹角的余弦值( )A .B .C .﹣2D .﹣11.已知函数f (x )=m (x ﹣)﹣2lnx (m ∈R ),g (x )=﹣,若至少存在一个x 0∈[1,e],使得f (x 0)<g (x 0)成立,则实数m 的范围是( )A .(﹣∞,]B .(﹣∞,)C .(﹣∞,0]D .(﹣∞,0)12.将函数y=cosx 的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位,所得函数图象的一条对称轴方程是( )A .x=πB .C .D .二、填空题13.已知()f x 是定义在R 上函数,()f x '是()f x 的导数,给出结论如下: ①若()()0f x f x '+>,且(0)1f =,则不等式()xf x e -<的解集为(0,)+∞;②若()()0f x f x '->,则(2015)(2014)f ef >; ③若()2()0xf x f x '+>,则1(2)4(2),n n f f n N +*<∈;④若()()0f x f x x'+>,且(0)f e =,则函数()xf x 有极小值0; ⑤若()()xe xf x f x x'+=,且(1)f e =,则函数()f x 在(0,)+∞上递增.其中所有正确结论的序号是 .14.已知[2,2]a ∈-,不等式2(4)420x a x a +-+->恒成立,则的取值范围为__________. 15.已知向量,满足42=,2||=,4)3()(=-⋅+,则与的夹角为 .【命题意图】本题考查向量的数量积、模及夹角知识,突出对向量的基础运算及化归能力的考查,属于容易题. 16.如图,△ABC 是直角三角形,∠ACB=90°,PA ⊥平面ABC ,此图形中有 个直角三角形.17.球O的球面上有四点S,A,B,C,其中O,A,B,C四点共面,△ABC是边长为2的正三角形,平面SAB⊥平面ABC,则棱锥S﹣ABC的体积的最大值为.18.某高中共有学生1000名,其中高一年级共有学生380人,高二年级男生有180人.如果在全校学生中抽取1名学生,抽到高二年级女生的概率为19.0,先采用分层抽样(按年级分层)在全校抽取100人,则应在高三年级中抽取的人数等于.三、解答题19.已知数列{a n}的前n项和为S n,且S n=a n﹣,数列{b n}中,b1=1,点P(b n,b n+1)在直线x﹣y+2=0上.(1)求数列{a n},{b n}的通项a n和b n;(2)设c n=a n•b n,求数列{c n}的前n项和T n.20.如图所示,在正方体ABCD﹣A1B1C1D1中,E、F分别是棱DD1、C1D1的中点.(Ⅰ)证明:平面ADC1B1⊥平面A1BE;(Ⅱ)证明:B1F∥平面A1BE;(Ⅲ)若正方体棱长为1,求四面体A1﹣B1BE的体积.21.如图,正方形ABCD 中,以D 为圆心、DA 为半径的圆弧与以BC 为直径的半圆O 交于点F ,连接CF 并延长交AB 于点E . (Ⅰ)求证:AE=EB ;(Ⅱ)若EF •FC=,求正方形ABCD 的面积.22.(本题12分)如图,D 是Rt BAC ∆斜边BC 上一点,AC =. (1)若22BD DC ==,求AD ; (2)若AB AD =,求角B .23.24.(本小题满分10分)选修4-5:不等式选讲.已知函数f(x)=|x+1|+2|x-a2|(a∈R).(1)若函数f(x)的最小值为3,求a的值;(2)在(1)的条件下,若直线y=m与函数y=f(x)的图象围成一个三角形,求m的范围,并求围成的三角形面积的最大值.24.某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B 产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式.(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润约为多少万元.(精确到1万元).遂川县第一高级中学2018-2019学年上学期高二数学12月月考试题含答案(参考答案)一、选择题1.【答案】【解析】解:(I)证明:因为四边形ABCD是菱形,所以AC⊥BD,又因为PA⊥平面ABCD,所以PA⊥BD,PA∩AC=A所以BD⊥平面PAC(II)设AC∩BD=O,因为∠BAD=60°,PA=AB=2,所以BO=1,AO=OC=,以O为坐标原点,分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系O﹣xyz,则P(0,﹣,2),A(0,﹣,0),B(1,0,0),C(0,,0)所以=(1,,﹣2),设PB与AC所成的角为θ,则cosθ=|(III)由(II)知,设,则设平面PBC的法向量=(x,y,z)则=0,所以令,平面PBC的法向量所以,同理平面PDC的法向量,因为平面PBC⊥平面PDC,所以=0,即﹣6+=0,解得t=,所以PA=.【点评】本小题主要考查空间线面关系的垂直关系的判断、异面直线所成的角、用空间向量的方法求解直线的夹角、距离等问题,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力2.【答案】A【解析】解:由三视图知几何体为半个圆锥,且圆锥的底面圆半径为1,高为2,∴母线长为,圆锥的表面积S=S底面+S 侧面=×π×12+×2×2+×π×=2+.故选A .【点评】本题考查了由三视图求几何体的表面积,解题的关键是判断几何体的形状及三视图的数据所对应的几何量.3. 【答案】C【解析】由||)(x a x f =始终满足1)(≥x f 可知1>a .由函数3||log xx y a =是奇函数,排除B ;当)1,0(∈x 时,0||log <x a ,此时0||log 3<=xx y a ,排除A ;当+∞→x 时,0→y ,排除D ,因此选C . 4. 【答案】D 【解析】考点:球的表面积和体积. 5. 【答案】C【解析】解:∵f (﹣x )==﹣f (x ),∴函数y=的图象关于原点对称,故排除B ,当x →+∞时,y →0,且为正值,故排除A 、D , 故选C .【点评】本题考查了函数的图象的判断,常利用排除法.6. 【答案】【解析】选A.由2+a i1+i=3+b i 得,2+a i =(1+i )(3+b i )=3-b +(3+b )i , ∵a ,b ∈R ,∴⎩⎪⎨⎪⎧2=3-b a =3+b,即a =4,b =1,∴a -b =3(或者由a =3+b 直接得出a -b =3),选A. 7. 【答案】C【解析】试题分析:由题意得,根据一次函数的单调性可知,函数()()22f x a x a =-+在区间[]0,1上恒正,则(0)0(1)0f f >⎧⎨>⎩,即2020a a a >⎧⎨-+>⎩,解得02a <<,故选C. 考点:函数的单调性的应用. 8. 【答案】A【解析】解:以顶部抛物线顶点为坐标原点,抛物线的对称轴为y 轴建立直角坐标系,易得抛物线过点(3,﹣1),其方程为y=﹣,那么正(主)视图上部分抛物线与矩形围成的部分面积S 1==2=4,下部分矩形面积S 2=24,故挖掘的总土方数为V=(S 1+S 2)h=28×20=560m 3.故选:A .【点评】本题是对抛物线方程在实际生活中应用的考查,考查学生的计算能力,属于中档题.9. 【答案】D【解析】由已知得{}=01A x x <?,故A B =1[,1]2,故选D .10.【答案】A【解析】解:∵,,∴=,||=,=﹣1×1+3×(﹣1)=﹣4,∴cos <>===﹣,故选:A .【点评】本题考查了向量的夹角公式,属于基础题.11.【答案】 B【解析】解:由题意,不等式f (x )<g (x )在[1,e]上有解,∴mx <2lnx ,即<在[1,e]上有解,令h (x )=,则h ′(x )=,∵1≤x ≤e ,∴h ′(x )≥0,∴h (x )max =h (e )=,∴<h (e )=, ∴m<.∴m 的取值范围是(﹣∞,). 故选:B .【点评】本题主要考查极值的概念、利用导数研究函数的单调性等基础知识,解题时要认真审题,注意导数性质的合理运用.12.【答案】B【解析】解:将函数y=cosx 的图象上各点的横坐标伸长到原来的2倍(纵坐标不变), 得到y=cos x,再向右平移个单位得到y=cos[(x )],由(x )=k π,得x =2k π,即+2k π,k ∈Z ,当k=0时,,即函数的一条对称轴为,故选:B【点评】本题主要考查三角函数的对称轴的求解,利用三角函数的图象关系求出函数的解析式是解决本题的关键.二、填空题13.【答案】②④⑤【解析】解析:构造函数()()xg x e f x =,()[()()]0xg x e f x f x ''=+>,()g x 在R 上递增,∴()xf x e-<()1x e f x ⇔<()(0)g x g ⇔<0x ⇔<,∴①错误;构造函数()()x f x g x e =,()()()0xf x f xg x e '-'=>,()g x 在R 上递增,∴(2015)(2014)g g >,∴(2015)(2014)f ef >∴②正确;构造函数2()()g x x f x =,2()2()()[2()()]g x xf x x f x x f x xf x '''=+=+,当0x >时,()0g x '>,∴1(2)(2)n n g g +>,∴1(2)4(2)n n f f +>,∴③错误;由()()0f x f x x '+>得()()0xf x f x x '+>,即()()0xf x x'>,∴函数()xf x 在(0,)+∞上递增,在(,0)-∞上递减,∴函数()xf x 的极小值为0(0)0f ⋅=,∴④正确;由()()x e xf x f x x '+=得2()()x e xf x f x x-'=,设()()xg x e xf x =-,则()()()xg x e f x xf x ''=--(1)x x x e e e x x x=-=-,当1x >时,()0g x '>,当01x <<时,()0g x '<,∴当0x >时,()(1)0g x g ≥=,即()0f x '≥,∴⑤正确.14.【答案】(,0)(4,)-∞+∞【解析】试题分析:把原不等式看成是关于的一次不等式,在2],[-2a ∈时恒成立,只要满足在2],[-2a ∈时直线在轴上方即可,设关于的函数44)2(24)4(x f(x )y 22+-+-=-+-+==x x a x a x a 对任意的2],[-2a ∈,当-2a =时,044)42(x )2(f(a)y 2>++--+=-==x f ,即086x )2(2>+-=-x f ,解得4x 2x ><或;当2a =时,044)42(x )2(y 2>-+-+==x f ,即02x )2(2>-=x f ,解得2x 0x ><或,∴的取值范围是{x|x 0x 4}<>或;故答案为:(,0)(4,)-∞+∞.考点:换主元法解决不等式恒成立问题.【方法点晴】本题考查了含有参数的一元二次不等式得解法,解题时应用更换主元的方法,使繁杂问题变得简洁,是易错题.把原不等式看成是关于的一次不等式,在2],[-2a ∈时恒成立,只要满足在2],[-2a ∈时直线在轴上方即可.关键是换主元需要满足两个条件,一是函数必须是关于这个量的一次函数,二是要有这个量的具体范围. 15.【答案】32π【解析】16.【答案】 4【解析】解:由PA ⊥平面ABC ,则△PAC ,△PAB 是直角三角形,又由已知△ABC 是直角三角形,∠ACB=90°所以BC ⊥AC ,从而易得BC ⊥平面PAC ,所以BC ⊥PC ,所以△PCB 也是直角三角形,所以图中共有四个直角三角形,即:△PAC ,△PAB ,△ABC ,△PCB .故答案为:4【点评】本题考查空间几何体的结构特征,空间中点线面的位置关系,线面垂直的判定定理和性质定理的熟练应用是解答本题的关键.17.【答案】.【解析】解:由题意画出几何体的图形如图由于面SAB⊥面ABC,所以点S在平面ABC上的射影H落在AB上,根据球体的对称性可知,当S在“最高点”,也就是说H为AB中点时,SH最大,棱锥S﹣ABC的体积最大.∵△ABC是边长为2的正三角形,所以球的半径r=OC=CH=.在RT△SHO中,OH=OC=OS∴∠HSO=30°,求得SH=OScos30°=1,∴体积V=Sh=××22×1=.故答案是.【点评】本题考查锥体体积计算,根据几何体的结构特征确定出S位置是关键.考查空间想象能力、计算能力.18.【答案】25【解析】考点:分层抽样方法.三、解答题19.【答案】【解析】解:(1)∵S n=a n﹣,∴当n≥2时,a n=S n﹣S n﹣1=a n﹣﹣,即a n=3a n﹣1,.∵a1=S1=﹣,∴a1=3.∴数列{a n}是等比数列,∴a n=3n.∵点P(b n,b n+1)在直线x﹣y+2=0上,∴b n+1﹣b n=2,即数列{b n}是等差数列,又b1=1,∴b n=2n﹣1.(2)∵c n=a n•b n=(2n﹣1)•3n,∵T n=1×3+3×32+5×33+…+(2n﹣3)3n﹣1+(2n﹣1)3n,∴3T n=1×32+3×33+5×34+…+(2n﹣3)3n+(2n﹣1)3n+1,两式相减得:﹣2T n=3+2×(32+33+34+…+3n)﹣(2n﹣1)3n+1,=﹣6﹣2(n﹣1)3n+1,∴T n=3+(n﹣1)3n+1.20.【答案】【解析】(Ⅰ)证明:∵ABCD﹣A1B1C1D1为正方体,∴B1C1⊥平面ABB1A1;∵A1B⊂平面ABB1A1,∴B1C1⊥A1B.又∵A1B⊥AB1,B1C1∩AB1=B1,∴A1B⊥平面ADC1B1,∵A1B⊂平面A1BE,∴平面ADC1B1⊥平面A1BE;(Ⅱ)证明:连接EF,EF∥,且EF=,设AB1∩A1B=O,则B1O∥C1D,且,∴EF∥B1O,且EF=B1O,∴四边形B1OEF为平行四边形.∴B1F∥OE.又∵B1F⊄平面A1BE,OE⊂平面A1BE,∴B1F∥平面A1BE,(Ⅲ)解:====.21.【答案】【解析】证明:(Ⅰ)∵以D 为圆心、DA 为半径的圆弧与以BC 为直径半圆交于点F , 且四边形ABCD 为正方形,∴EA 为圆D 的切线,且EB 是圆O 的切线,由切割线定理得EA 2=EF •EC ,故AE=EB .(Ⅱ)设正方形的边长为a ,连结BF , ∵BC 为圆O 的直径,∴BF ⊥EC ,在Rt △BCE 中,由射影定理得EF •FC=BF 2=,∴BF==,解得a=2,∴正方形ABCD 的面积为4.【点评】本题考查两线段相等的证明,考查正方形面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.22.【答案】(1)2=AD ;(2)3π=B .【解析】考点:正余弦定理的综合应用,二次方程,三角方程.【方法点晴】本题主要考查三角形中的解三角形问题,解题的关键是合理选择正、余弦定理..当有三边或两边及其夹角时适合选择余弦定理,当有一角及其对边时适合选择正弦定理求解,解此类题要特别注意,在没有明确的边角等量关系时,要研究三角形的已知条件,组建等量关系,再就是根据角的正弦值确定角时要结合边长关系进行取舍,这是学生们尤其要关注的地方. 23.【答案】【解析】解:(1)f (x )=|x +1|+2|x -a 2|=⎩⎪⎨⎪⎧-3x +2a 2-1,x ≤-1,-x +2a 2+1,-1<x <a 2,3x -2a 2+1,x ≥a 2,当x ≤-1时,f (x )≥f (-1)=2a 2+2, -1<x <a 2,f (a 2)<f (x )<f (-1), 即a 2+1<f (x )<2a 2+2, 当x ≥a 2,f (x )≥f (a 2)=a 2+1,所以当x =a 2时,f (x )min =a 2+1,由题意得a 2+1=3,∴a =±2. (2)当a =±2时,由(1)知f (x )= ⎩⎪⎨⎪⎧-3x +3,x ≤-1,-x +5,-1<x <2,3x -3,x ≥2,由y =f (x )与y =m 的图象知,当它们围成三角形时,m 的范围为(3,6],当m =6时,围成的三角形面积最大,此时面积为12×|3-(-1)|×|6-3|=6.24.【答案】【解析】解:(1)投资为x 万元,A 产品的利润为f (x )万元,B 产品的利润为g (x )万元, 由题设f (x )=k 1x ,g (x )=k2,(k 1,k 2≠0;x ≥0)由图知f (1)=,∴k 1= 又g (4)=,∴k 2= 从而f (x )=,g (x )=(x ≥0)(2)设A 产品投入x 万元,则B 产品投入10﹣x 万元,设企业的利润为y 万元 y=f (x )+g (10﹣x )=,(0≤x ≤10),令,∴(0≤t≤)当t=,y max ≈4,此时x=3.75∴当A 产品投入3.75万元,B 产品投入6.25万元时,企业获得最大利润约为4万元.【点评】本题考查利用待定系数法求函数的解析式、考查将实际问题的最值问题转化为函数的最值问题.解题的关键是换元,利用二次函数的求最值的方法求解.。
江西省部分高中学校2023-2024学年高二上学期10月联考数学试题

A.8
B.6
C.4
D.2
12.已知双曲线
C
:
x a
2 2
y2 b2
1a
0, b
0 的左、右焦点分别为 F1 c,0 , F2
c,0 ,P
是 C 右支上一点,下列结论正确的有( )
A.若 C 的离心率为 7 ,则过点 M 2,3 与 C 的渐近线相同的双曲线的方程是
2 y2 x2 1 32
江西省部分高中学校 2023-2024 学年高二上学期 10 月联考数 学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知直线 l1 的倾斜角为110 ,若直线 l2 与 l1 垂直,则 l2 的倾斜角为( )
A.10
则 C 的离心率为 3
三、填空题
13.若直线 l :ax by 8 0 是圆 x 22 y 4 2 1 的一条对称轴,则 a 2b =
.
14.法国数学家加斯帕尔·蒙日发现:过圆 E : x2 y2 a2 b2 a b 0 上任意一点作
双曲线
C
:
x2 a2
y2 b2
1 的两条切线,这两条切线互相垂直,我们通常把这个圆 E 称作双
B. 20
C. 70
D. 200
2.圆心为 1, 3 ,且经过坐标原点的圆的标准方程为( )
A. x 12 y 32 100
B. x 12 y 32 100
C. x 12 y 32 10
D. x 12 y 32 10
3.已知双曲线 C 的焦点与椭圆 E : y2 x2 1的上、下顶点相同,且经过 E 的焦点, 16 7
江西省吉安市遂川中学1617学年度高二上学期第一次月考

江西省吉安市遂川中学2016—2017学年度上学期第一次月考高二数学理试题一、选择题(每小题5分)1.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则这个几何体是A.三棱锥B.三棱柱C.四棱锥D.四棱柱2.下列命题中:(1)、平行于同一直线的两个平面平行;(2)、平行于同一平面的两个平面平行;(3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行.其中正确的个数有( )A.1B.2C.3D.43.体积为8的正方体的顶点都在同一球面上,则该球面的表面积为(A ) (B )(C ) (D )4.如果一个水平放置的图形的斜二测直观图是一个底角为,腰和上底均为的等腰梯形,那么原平面图形的面积是( )A .B .C .D .5.设是两条不同的直线,是两个不同的平面,则下列命题正确的是①ββαα//,,m m 则若⊥⊥ ②n m n m ⊥⊂⊥则若,,//,ββαα ③βαβα//,//,,则若n m n m ⊂⊂ ④若αββα⊥⊥⊥⊥m m n n 则,,, ①② ③④ ①③ ②④6.如图,E 、F 分别是三棱锥P-ABC 的棱AP 、BC 的中点,PC=10,AB=6,EF=7,则异面直线AB 与PC 所成的角为( )A. 90°B. 60°C. 45°D. 30°7.一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( )A.1:8 B.错误!未找到引用源。
C.1:6 D.错误!未找到引用源。
8.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于( )A、1:2B、1:3C、D、9.已知正四棱柱ABCD- A1B1C1D1中,AB=2,CC1= E为CC1的中点,则直线AC1与平面BED的距离为( )A 2BCD 110.若三棱锥的所有顶点都在球的球面上,⊥平面,,,,则球的表面积为()A.B.C.D.11.已知三棱锥的所有顶点都在球的球面上,是边长为的正三角形,为球的直径,且,则此棱锥的体积为()A. B. C. D.12.在封闭的直三棱柱内有一个体积为V的球,若,,,,则V的最大值是(A)4π (B)(C)6π(D)二、填空题(每小题5分)13.已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长___________.14.如图,正方体的棱长为1,分别为线段上的点,则三棱锥的体积为____________.15.已知三棱锥,若,,两两垂直,且,,则三棱锥的内切球半径为.16.如图,与是四面体中互相垂直的棱,,若,且+CDACBDAB,则四面体的体积的最大值是。
江西省遂川中学高二物理上学期第二次月考试题【会员独享】
江西省遂川中学2011-2012学年高二上学期第二次月考物理试卷第Ⅰ卷(选择题共40分)一、选择题(本题共10小题,每小题4分。
在每个小题给出的四个选项中,至少有一个选项是正确的,全部选对的得4分,选不全的得2分,有选错或不答的得0分)1. 下列物理量中哪些与检验电荷无关?()A.电场强度EB.电势UC.电势能εD.电场力F2.横截面的直径为d、长为l的导线,两端电压为U,当这三个量中一个改变时,对自由电子定向运动的平均速率的影响是()A.电压U加倍,自由电子定向运动的平均速率不变B.导线长度l加倍,自由电子定向运动的平均速率加倍C.导线横截面的直径加倍,自由电子定向运动的平均速率不变D.以上说法均不正确3.图在E为电源,R1、R2为电阻,K为电键.现用多用电表测量流过电阻R2的电流.将多用电表的选择开关调至直流电流挡(内阻很小)以后,正确的接法是()A.保持K闭合,将红表笔接在a处,黑表笔接在b处B.将K断开,将红表笔接在a处,黑表笔接在b处C.保持K闭合,将红表笔接在b处,黑表笔接在a处D.将K断开,将红表笔接在b处,黑表笔接在a处4.右表是某逻辑电路的真值表,该电路是()5. 如图所示,图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图不能作出判断的是()A.带电粒子所带电荷的符号B.带电粒子在a、b两点的受力方向C.带电粒于在a、b两点的速度何处较大D.带电粒子在a、b两点的电势能何处较大6.如图所示,A、B、C分别表示理想电流表或电压表,灯L1与L2的额定电压相同,灯L1的额定功率大于灯L2的额定功率,当电键S闭合时,L1、L2恰好能正常发光.若A、B、C的示数均不为零,则可判定()A.A、B、C均为电流表B.A、B、C均为电压表C.B为电压表,A、C为电流表D .B 为电流表,A 、C 为电压表7.在如图所示的电路中,观察三只小灯泡亮度的变化和两只电压表示数的变化情况.如果滑动变阻器的滑片P 由a 端滑至b 端的过ΔU 1的绝对值为ΔU 2,则下列说法正确的是( ) A.L 1、L 3变暗,L 2变亮 B.L 3变暗,L 1、L 2变亮 C. ΔU 1>ΔU 2D. ΔU 1<ΔU 2 8.某同学按如图电路进行实验,电压表内阻看作无限大,电流表内阻看作零。
江西省赣州市永丰中学高二数学理月考试卷含解析

江西省赣州市永丰中学高二数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 过抛物线的焦点作直线交抛物线于两点,如果,那么=( )A. 6B. 8C. 9D. 10参考答案:B【分析】根据抛物线的性质直接求解,即焦点弦长为.【详解】抛物线中,,∴,故选B.【点睛】是抛物线的焦点弦,,,抛物线的焦点弦长为,抛物线的焦点弦长为,抛物线的焦点弦长为,抛物线的焦点弦长为.2. 若圆的圆心到直线的距离为则()A.或B.或C.或D. 或参考答案:C3. 已知,,,…,若,(,均为正实数),则类比以上等式,可推测,的值,+=()A.35 B.40 C.41 D.42参考答案:C 4. 点位于()A.B.C.D.参考答案:C略5. 若M(x,y)满足,则M的轨迹()A.双曲线B.直线C.椭圆D.圆参考答案:C【考点】轨迹方程.【专题】计算题;转化思想;综合法;圆锥曲线的定义、性质与方程.【分析】由题意, =,可得(x,y)到(2,1)的距离与到直线2x+y﹣4=0的距离的比为,即可得出结论.【解答】解:,可化为=,∴(x,y)到(2,1)的距离与到直线2x+y﹣4=0的距离的比为,利用椭圆的定义,可得轨迹是椭圆.故选:C.【点评】本题考查曲线与方程,考查椭圆的定义,正确变形是关键.6. 函数的图象是( )A.B.C.D.参考答案:D【考点】函数的图象.【专题】数形结合.【分析】本题考查的知识点是分段函数图象的性质,及函数图象的作法,由绝对值的含义化简原函数式,再分段画出函数的图象即得.【解答】解:函数可化为:当x>0时,y=1+x;它的图象是一条过点(0,1)的射线;当x<0时,y=﹣1+x.它的图象是一条过点(0,﹣1)的射线;对照选项,故选D.【点评】本小题主要考查函数、函数的图象、绝对值的概念等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.7. 直线2x+ay+3=0的倾斜角为120°,则a的值是A.B.- C.2 D.-2参考答案:A8. 椭圆的中心在原点,左右焦点在轴上,分别是椭圆的上顶点和右顶点,是椭圆上一点,且轴,,则此椭圆的离心率等于()A. B.C. D.参考答案:D试题分析:如图所示,设椭圆的方程为,所以时,,所以,又,所以,所以,所以,,所以,故选D.考点:椭圆的几何性质.【方法点晴】本题主要考查了椭圆的几何性质,其中解答中涉及到椭圆的标准方程,直线的斜率公式,椭圆的几何性质等知识点的综合考查,本题的解答中根据椭圆的标准方程表示椭圆的交点及顶点坐标,再根据椭圆的方程,已知椭圆上的点的横坐标求出其纵坐标,根据两点坐标求直线的斜率,以及两平行直线的斜率的关系,即可求解离心率,属于基础题.9. 若实数x,y满足,则的最小值是( )A. 1B. 0C.D. 9参考答案:A10. 三张卡片的正反面上分别写有数字0与2,3与4,5与6,把这三张卡片拼在一起表示一个三位数,则三位数的个数为()A. 36 B.40 C.44 D.48参考答案:B略二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数f(x)是定义在R上的偶函数,若对于,都有,且当时,,则______.参考答案:【分析】根据条件关系得到当时,函数是周期为4的周期函数,利用函数的周期性和奇偶性进行转化求解即可.【详解】解:对于,都有,∴,即当时,函数是周期为4的周期函数,∵当时,,∴,,则.故答案为:0.【点睛】本题主要考查函数值的计算,根据条件求出函数的周期,以及利用函数的周期性和奇偶性进行转化是解决本题的关键.12. 直线过点(—4,0)且与圆交于两点,如果,那么直线的方程为参考答案:或略13. .参考答案:514. 若是正数,且满足,用表示中的最大者,则的最小值为___ _______参考答案:略15. 已知点,是椭圆的动点。
2024-2025学年江西省吉安市遂川中学高二(上)开学数学试卷(含答案)

2024-2025学年江西省吉安市遂川中学高二(上)开学数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.若α是第三象限角,且sin (α+β)⋅cosβ−sinβcos(α+β)=−513,则tan α2的值为( )A. −5B. 5C. −513D. 5132.从圆x 2−2x +y 2−2y +1=0外一点P(3,2)向这个圆作两条切线,则两切线夹角的余弦值为( )A. 12B. 35C.32D. 03.若将函数f(x)=2cosx(cosx +sinx)−1的图象向左平移π4个单位长度得到g(x)的图象,则g(x)图象的对称中心的坐标是( )A. (−3π8+kπ,0)(k ∈Z) B. (−π8+kπ,0)(k ∈Z)C. (−3π8+kπ2,0)(k ∈Z)D. (−π8+kπ2,0)(k ∈Z)4.已知椭圆C :x 22+y 2=1的右焦点为F ,右准线为l ,点A ∈l ,线段AF 交C 于点B ,若FA =3FB ,则|AF |=( )A.2B. 2C.3 D. 35.在四棱锥P−ABCD 中,E 为线段AD 上靠近A 的三等分点,F 为线段PC 上一点,当PA//平面EBF 时,PFPC=( )A. 3B. 4C. 13D. 146.如图,已知正方形ABCD 的边长为2,若动点P 在以AB 为直径的半圆上(正方形ABCD 内部,含边界),则PC ⋅PD 的取值范围为( )A. (0,4)B. [0,4]C. (0,2)D. [0,2]7.已知过抛物线C:y2=4x的焦点F的直线与C相交于A,B两点,y轴上一点P满足PA⊥PF,则OP⋅OB= ( )A. 1B. 2C. −1D. −28.在锐角△ABC中,角A,B,C的对边分别为a、b、c,S为△ABC的面积,a=4,且2S=a2−(b−c)2,则△ABC的周长的取值范围是( )A. (8,45+4]B. (12,25+2]C. (8,25+2]D. (12,45+4]二、多选题:本题共3小题,共18分。
高二数学上学期第一次月考试题 理 11

遂川中学2021-2021学年高二数学上学期第一次月考试题 理一、选择题〔每一小题5分〕1.点A 〔-3,1,-4〕,点A 关于x 轴的对称点的坐标为 ( ) A.〔-3,-1,4〕 B.〔-3,-1,-4〕 C.〔3,1,4〕 D.〔3,-1,-4〕310ax y --=与直线2()103a x y -++=垂直,那么a 的值是〔 〕A .11,3- B .1,13C .1,13--D .1,13-(2,1)P -为圆22(1)25x y -+=的弦AB 的中点,那么直线AB 的方程是〔 〕A .30x y --=B .230x y +-=C .10x y +-=D .250x y --=l 过点P(-1,2)且与以点M(-3,-2),N(4,0)为端点的线段恒相交,那么l 的斜率取值范围是( )A.[-,5]B.[-,0)∪(0,2]C.(-∞,-)∪[5,+∞)D.(-∞,-]∪[2,+∞)5.一辆卡车宽1.6 m ,要经过一个半圆形隧道(半径为3.6 m),那么这辆卡车的平顶车篷篷顶距地面高度不得超过( ) A .1.4 m B .3.5 mC .3.6 mD .2.0 mC 的半径为2,圆心在x 轴正半轴上,直线3440x y ++=与圆C 相切,那么圆C 的方程为〔 〕A .22230x y x +--=B .2240x y x ++=C .22230x y x ++-=D .22-40x y x +=l 1,l 2分别过点P (-1,2),Q (2,-3),它们分别绕P ,Q 旋转,但始终保持平行,那么l 1,l 2之间间隔 的取值范围是( )A .(5,+∞)B .(0,5]C .(34,+∞)D .(0,34]x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤5,2x -y ≤4,-x +y ≤1,y ≥0,那么目的函数z =3x +5y 的最大值为( )A .6B .19C .21D .45():00l mx ny m n n +--=≠将圆()()22:324C x y -+-=的周长分为2:1两局部,那么直线l的斜率为〔 〕 A .0或者B .0CDl 的方程为cos 30()x y R θθ++=∈,那么直线l 的倾斜角α的取值范围是〔 〕A .[0,]πB .,42ππ⎡⎫⎪⎢⎣⎭C .3,44ππ⎡⎤⎢⎥⎣⎦D .πππ3π,,4224⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦11、方程1-x 2=x +k 有唯一解,那么实数k 的范围是( )A .k =- 2B .k ∈(-2,2)C .k ∈[-1,1)D .k =2或者-1≤k <112、圆的方程为x 2+y 2-4x -6y +11=0,直线l :x +y -t =0,假设圆上有且只有两个不同的点到直线l 的间隔 等于22,那么参数t 的取值范围为( ) A .(2,4]∪[6,8) B .(2,4)∪(6,8) C .(2,4) D .(6,8) 二、填空题〔每一小题5分〕13.A(2,1,1),B 〔-2,2,3〕,在z 轴上有点P 到A 、B 两点的间隔 相等,那么P 点的坐标是_____P (2,3)的直线l 与x 轴,y 轴的正半轴分别交于A ,B 两点,O 为坐标原点,那么S △AOB 的最小值为________15.假设实数x ,y 满足不等式组⎩⎪⎨⎪⎧x +3y -3≥0,2x -y -3≤0,x -my +1≥0且x +y 的最大值为9,那么实数m =____16、在平面直角坐标系xOy 中,直线1:20l kx y -+=与直线2:20l x ky +-=相交于点P ,那么当实数k 变化时,点P 到直线40x y --=的间隔 的最大值为________. 三、解答题17.〔10分〕ABC △的顶点)1,3(-A ,AB 边上的中线所在的直线方程为059106=-+y x ,B ∠的平分线所在的直线方程为0104=+-y x ,求BC 边所在的直线方程.18.〔12分〕圆C 经过点()2,1A -和直线10x y +-=相切,且圆心在直线2y x =-上. 〔1〕求圆C 的方程;〔2〕假设直线22y x =-与圆C 交于A ,B 两点,求弦AB 的长.19.〔12分〕圆.〔1〕假设,过点作圆的切线,求该切线方程;〔2〕假设为圆的任意一条直径,且〔其中为坐标原点〕,求圆的半径.20.〔12分〕某旅游景区的一家庭作坊方案每天制作高档、中档、低档3种旅游纪念品一共50个,制作一个高档纪念品需要14分钟,利润为12元;制作一个中档纪念品需要12分钟,利润为11元;制作一个低档纪念品需要9分钟,利润为7元.假设每天制作时间是不超过11小时,那么这个家庭作坊每天制作旅游纪念品的最大利润为多少元.21.〔12分〕定点()0,4A -,点P 圆224x y +=上的动点.〔1〕求AP 的中点C 的轨迹方程;〔2〕假设过定点1,12B ⎛⎫-- ⎪⎝⎭的直线l 与C 的轨迹交于,M N 两点,且MN =线l 的方程.22.〔12分〕圆C :(x -3)2+(y -4)2=4,直线1l 过定点A (1,0).(1)假设1l 与圆相切,求1l 的方程;(2)假设1l 与圆相交于P ,Q 两点,线段PQ 的中点为M ,又1l 与2l :x +2y +2=0的交点为N ,判断AM ·AN 是否为定值,假设是,那么求出定值;假设不是,请说明理由.2021届高二上学期第一次月考理数选择题〔每一小题5分〕1.直线310ax y --=与直线2()103a x y -++=垂直,那么a 的值是〔 D 〕 A .11,3- B .1,13C .1,13--D .1,13-2、假设(2,1)P -为圆22(1)25x y -+=的弦AB 的中点,那么直线AB 的方程是〔 A 〕 A .30x y --= B .230x y +-= C .10x y +-=D .250x y --=3、直线l 过点P(-1,2)且与以点M(-3,-2),N(4,0)为端点的线段恒相交,那么l 的斜率取值范围是( D )(A)[-,5] (B)[-,0)∪(0,2] (C)(-∞,-)∪[5,+∞) (D)(-∞,-]∪[2,+∞)4、圆C 的半径为2,圆心在x 轴正半轴上,直线3440x y ++=与圆C 相切,那么圆C 的方程为〔 D 〕A .22230x y x +--=B .2240x y x ++=C .22230x y x ++-=D .22-40x y x += 5、设直线l 的方程为cos 30()x y R θθ++=∈,那么直线l 的倾斜角α的取值范围是〔 C 〕 A .[0,]π B .,42ππ⎡⎫⎪⎢⎣⎭ C .3,44ππ⎡⎤⎢⎥⎣⎦ D .πππ3π,,4224⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦6、两条平行线l 1,l 2分别过点P (-1,2),Q (2,-3),它们分别绕P ,Q 旋转,但始终保持平行,那么l 1,l 2之间间隔 的取值范围是( D ) A .(5,+∞) B .(0,5] C .(34,+∞)D .(0,34]7、设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤5,2x -y ≤4,-x +y ≤1,y ≥0,那么目的函数z =3x +5y 的最大值为( )A .6B .19C .21D .458、假设直线():00l mx ny m n n +--=≠将圆()()22:324C x y -+-=的周长分为2:1两局部,那么直线l 的斜率为〔 B 〕A .0或者B .0CD9、一辆卡车宽1.6 m ,要经过一个半圆形隧道(半径为3.6 m),那么这辆卡车的平顶车篷篷顶距地面高度不得超过( B )A .1.4 mB .3.5 mC .3.6 mD .2.0 m10、方程1-x 2=x +k 有惟一解,那么实数k 的范围是( D )A .k =- 2B .k ∈(-2,2)C .k ∈[-1,1)D .k =2或者-1≤k <1 11、圆的方程为x 2+y 2-4x -6y +11=0,直线l :x +y -t =0,假设圆上有且只有两个不同的点到直线l 的间隔 等于22,那么参数t 的取值范围为( A ) A .(2,4)∪(6,8) B .(2.4]∪[6,8) C .(2,4) D .(6,8)12、圆22:1C x y +=,点P 为直线142x y+=上一动点,过点P 向圆C 引两条切线,,,PA PB A B 为切点,那么直线AB 经过定点〔 B 〕A .11,24⎛⎫ ⎪⎝⎭B .11,42⎛⎫⎪⎝⎭ C.⎫⎪⎪⎝⎭D.⎛ ⎝⎭ 一、填空题〔每一小题5分〕13、过点P (2,3)的直线l 与x 轴,y 轴的正半轴分别交于A ,B 两点,O 为坐标原点,那么S △AOB 的最小值为__12______14、圆C 的圆心在x 轴的正半轴上,点M (0,5)在圆C 上,且圆心到直线2x -y =0的间隔 为455,那么圆C 的方程为__(x -2)2+y 2=915、实数x ,y 满足⎩⎪⎨⎪⎧y ≥1,y ≤2x -1,x +y ≤m .假如目的函数z =x -y 的最小值为-1,那么实数m =__5______.16、在平面直角坐标系xOy 中,直线1:20l kx y -+=与直线2:20l x ky +-=相交于点P ,那么当实数k 变化时,点P 到直线40x y --=的间隔的最大值为__ 二、解答题17.ABC △的顶点)1,3(-A ,AB 边上的中线所在的直线方程为059106=-+y x ,B ∠的平分线所在的直线方程为0104=+-y x ,求BC 边所在的直线方程. 设A 关于B ∠的平分线的对称点),(00'y x A ,那么000031410022143x y y x +-⎧-+=⎪⎪⎨+⎪=-⎪-⎩,解得0017x y =⎧⎨=⎩,即)7,1('A ,设),104(a a B -,那么AB 中点的坐标为⎪⎭⎫⎝⎛--21,274a a . 且满足059106=-+y x ,即47161059022a a --⋅+⋅-=,∴5=a .∴(1,0,5)B . ∵'A 也在直线BC 上, ∴BC 所在直线的方程为06592=-+y x . 18圆C 经过点()2,1A -和直线10x y +-=相切,且圆心在直线2y x =-上. 〔1〕求圆C 的方程;〔2〕假设直线22y x =-与圆C 交于A ,B 两点,求弦AB 的长.【解析】〔1〕因为圆心在直线2y x =-上,设圆心为(),2C a a -,那么圆C 的方程为()()()22220x a y a r r -++=>,又圆C 与10x y +-=相切,所以21122a a a r --+==,因为圆C 过点()2,1A -,所以()()()22212122a a a +-+-+=,解得1a =,所以圆C 的方程为()()22122x y -++=.〔2〕设AB 的中点为D ,圆心为C ,连CD ,AD ,222255CD +-==,2AC =,由平面几何知识知22230225AB AD AC CD ==-=,即弦AB 的长为2305. 19.圆.〔1〕假设,过点作圆的切线,求该切线方程;〔2〕假设为圆的任意一条直径,且〔其中为坐标原点〕,求圆的半径. 解析:〔1〕假设,圆:,圆心,半径为3.假设切线斜率不存在,圆心到直线的间隔 为3,∴直线为圆的一条切线;假设切线斜率存在,设切线方程为:,化简为:,那么圆心到直线的间隔 ,解得:. ∴切线方程为或者;〔2〕圆的方程可化为,圆心,那么,设圆的半径,∵为圆的任意一条直径,∴,且,那么,又∵,解得:,∴圆的半径为.20.某旅游景区的一家庭作坊方案每天制作高档、中档、低档3种旅游纪念品一共50个,制作一个高档纪念品需要14分钟,利润为12元;制作一个中档纪念品需要12分钟,利润为11元;制作一个低档纪念品需要9分钟,利润为7元.假设每天制作时间是不超过11小时,那么这个家庭作坊每天制作旅游纪念品的最大利润为多少元.解析:设每天制作高档纪念品x 个,中档纪念品y 个,那么制作低档纪念品(50-x -y )个,每天的利润为z 元,z =12x +11y +7(50-x -y )=5x +4y +350,约束条件为⎩⎪⎨⎪⎧x ∈N *,y ∈N *,14x +12y +9〔50-x -y 〕≤660,50-x -y ≥0,即⎩⎪⎨⎪⎧x ∈N *,y ∈N *,5x +3y ≤210,x +y ≤50,可行解为图中阴影局部中的整点.由⎩⎪⎨⎪⎧5x +3y =210,x +y =50,解得⎩⎪⎨⎪⎧x =30,y =20, 即A (30,20).易知z =5x +4y +350在A (30,20)处取最大值,所以z max =5×30+4×20+350=580,即最大利润为580元.21.定点()0,4A -,点P 圆224x y +=上的动点.〔1〕求AP 的中点C 的轨迹方程; 〔2〕假设过定点1,12B ⎛⎫-- ⎪⎝⎭的直线l 与C 的轨迹交于,M N两点,且MN =l 的方程.【解析】〔1〕设()()00,,,C x y P x y ,由题意知:00220002424x x y y x y +=-=+⎧⎪⎪⎪⎨=⎪⎪⎪⎩,化简得()2221x y ++=,故C 的轨迹方程为()2221x y ++=。
江西省吉安市遂川新江中学高二数学理月考试题含解析

江西省吉安市遂川新江中学高二数学理月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该集合体的俯视图为:()参考答案:C略2. 已知△ABC的内角A,B,C的对边分别为a,b,c,若csinC=acosB+bcosA,则△ABC的形状为()A.锐角三角形B.等边三角形C.直角三角形D.钝角三角形参考答案:C考点:正弦定理.专题:解三角形.分析:已知等式利用正弦定理化简,解答:解:已知等式csinC=acosB+bcosA,利用正弦定理化简得:sin2C=sinAcosB+sinBcosA=sin (A+B)=sinC,∵sinC≠0,∴sinC=1,∴C=90°,则△ABC为直角三角形,故选:C.点评:此题考查了正弦定理,以及两角和与差的正弦函数公式,熟练掌握正弦定理是解本题的关键.3. 如果命题“”为假命题,则()A.、均为假命题 B.、均为真命题C.、中至少有一个假命题 D.、中至少有一个真命题参考答案:D4. 一条走廊宽 2 m, 长 8 m, 用 6 种颜色的 1 1 m的整块地砖来铺设(每块地砖都是单色的, 每种颜色的地砖都足够多), 要求相邻的两块地砖颜色不同, 那么所有的不同拼色方法有A. 个B. 个C. 个D. 个参考答案:解析:铺第一列(两块地砖)有种方法;其次铺第二列.设第一列的两格铺了、两色(如图),那么,第二列的上格不能铺色.若铺色,则有种铺法;若不铺色,则有种方法. 于是第二列上共有种铺法. 同理,若前一列铺好,则其后一列都有种铺法.因此,共有种铺法.故选D.5. 椭圆的焦点为F1,F2,点P在椭圆上,若,则的面积为()A. B. C. D.参考答案:A6. 的值为()A.B.C.2+D.2﹣参考答案:B【考点】两角和与差的正切函数.【分析】由条件利用两角和的正弦公式,求得所给式子的值.【解答】解: ==tan(45°+15°)=tan60°=,故选:B.7. 对于a∈R,直线(x+y﹣1)﹣a(x+1)=0恒过定点P,则以P为圆心,为半径的圆的方程是()A.x2+y2+2x+4y=0 B.x2+y2+2x﹣4y=0C.x2+y2﹣2x+4y=0 D.x2+y2﹣2x﹣4y=0参考答案:B【考点】圆的一般方程;恒过定点的直线.【专题】计算题;直线与圆.【分析】联解直线x+y﹣1=0与x+1=0的方程,可得直线(x+y﹣1)﹣a(x+1)=0恒过定点P(﹣1,2).由圆的标准式方程,写出圆的方程再化成一般式方程,可得本题答案.【解答】解:联解,可得x=﹣1,y=2∴直线(x+y﹣1)﹣a(x+1)=0恒过定点P(﹣1,2)因此以P为圆心,为半径的圆的方程是(x+1)2+(y﹣2)2=5化成一般式可得x2+y2+2x﹣4y=0故选:B【点评】本题给出直线经过定点P,求以P为圆心且为半径的圆.着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识,属于基础题.8. 有8件产品,其中3件是次品,从中任取3件,若X表示取得次品的件数,则()A.B.C.D.参考答案:B根据题意,9. 命题是()A. B.C. D.参考答案:C10. 设直线与平面相交但不垂直,则下列说法中正确的是( )A.在平面内有且只有一条直线与直线垂直B.过直线有且只有一个平面与平面垂直C.与直线垂直的直线不可能与平面平行D.与直线平行的平面不可能与平面垂直参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 阅读如图所示的程序框图,运行相应的程序,若输入n的值为6,则输出S的值为.参考答案:147;12. 复数z=为虚数单位)的共轭复数是_________.参考答案:【分析】先由复数的除法运算化简,再根据共轭复数的概念,即可得出结果.【详解】因为,所以,其共轭复数为.故答案为13. △ABC中,a=2,∠A=30°,∠C=45°,则△ABC的面积S的值是.参考答案:+1考点:三角形的面积公式.专题:解三角形.分析:由正弦定理可得,求出c值,利用两角和正弦公式求出sinB的值,由S△ABC =acsinB 运算结果解答:解:B=180°﹣30°﹣45°=105°,由正弦定理可得,∴c=2.sinB=sin(60°+45°)==,则△ABC的面积S△ABC =acsinB=×2×2×=+1,故答案为:+1点评:本题考查两角和正弦公式,正弦定理的应用,求出sinB的值,是解题的关键.14. 函数的单调递增区间为_____________.参考答案:(0,1)函数有意义,则:,且:,由结合函数的定义域可得函数的单调递增区间为,故答案为.15. 一圆形纸片的半径为10cm,圆心为O,F为圆内一定点,OF=6cm,M为圆周上任意一点,把圆纸片折叠,使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD与OM交于P点(如图),以FO所在直线为x轴,线段FO的中垂线为y轴,建立直角坐标系,则点P的轨迹方程为.参考答案:以FO所在直线为x轴,线段FO的中垂线为y轴,建立直角坐标系。
江西省吉安市遂川中学2024-2025学年高二上学期开学考试数学试题

江西省吉安市遂川中学2024-2025学年高二上学期开学考试数学试题一、单选题1.若α是第三象限角,且()()5sin cos sin cos 13αβββαβ+-⋅+=-,则tan 2α的值为( ) A .5- B .5 C .513- D .5132.从圆222210x x y y -+-+=外一点()3,2P 向这个圆作两条切线,则两切线夹角的余弦值为( )A .12B .35CD .63.若将函数()()2cos cos sin 1f x x x x =+-的图象向左平移π4个单位长度得到()g x 的图象,则()g x 图象的对称中心的坐标是( )A .()3ππ,08k k ⎛⎫-+∈ ⎪⎝⎭Z B .()ππ,08k k ⎛⎫-+∈ ⎪⎝⎭Z C .()3ππ,082k k ⎛⎫-+∈ ⎪⎝⎭Z D .()ππ,082k k ⎛⎫-+∈ ⎪⎝⎭Z 4.已知椭圆C :2212x y +=的焦点F 1,0 ,直线l :2x =,点A l ∈,线段AF 交C 于点B ,若3FA FB =u u u r u u u r ,则AF u u u r 等于( )AB .2CD .35.在四棱锥P ABCD -中,底面ABCD 为平行四边形,E 为线段AD 上靠近A 的三等分点,F 为线段PC 上一点,当//PA 平面EBF 时,PF PC=( )A .3B .4C .13D .146.如图,已知正方形ABCD 的边长为2,若动点P 在以AB 为直径的半圆上(正方形ABCD内部,含边界),则PC PD ⋅u u u r u u u r 的取值范围为( )A . 0,4B . 0,4C . 0,2D . 0,2 7.已知过抛物线2:4C y x =的焦点F 的直线与C 相交于,A B 两点,y 轴上一点P 满足PA PF ⊥,则OP OB ⋅=u u u r u u u r ( )A .1B .2C .1-D .2- 8.在锐角ABC V 中,角,,A B C 的对边分别为,,,a b c S 为ABC V 的面积,4a =,且()222S a b c =--,则ABC V 的周长的取值范围是( )A .(4⎤⎦B .(2⎤⎦C .(2⎤⎦D .(4⎤⎦二、多选题9.已知直线l 10y -+=,则下列结论正确的是( )A .直线l 的一个法向量为)B .若直线m :10x +=,则l m ⊥C .点)到直线l 的距离是2D .过()与直线l 40y --=10.设点A ,12,F F 的坐标分别为()()()1,1,1,0,1,0--,动点(),P x y 满足:4=,则下列说法正确的有( )A .点P 的轨迹方程为22143x y += B .25PA PF +<C .存在4个点P ,使得1PAF V 的面积为32D .11PA PF +>11.ABC V 中,角,,A B C 所对的边为,,a b c 下列叙述正确的是( )A .若2220a b c +->,则ABC V 一定是锐角三角形B .若cos cos cos a b c A B C==,则ABC V 一定是等边三角形 C .若A B >,则cos cos A B <D .若2b a c ≥+,则π0,3B ⎛⎤∈ ⎥⎝⎦三、填空题12.已知4,3a b ==r r ,且()()23261a b a b -+=r r r r g ,则a r 与b r 夹角的余弦值为:.13.设向量),sin a x x =r ,()cos ,sin b x x =r ,π0,2x ⎡⎤∈⎢⎥⎣⎦. (1)若a b =r r ,则x 的值为;(2)设函数()f x a b =⋅r r ,则()f x 的最大值为.14.已知双曲线1C :()22210y x b b -=>与椭圆2C :(2221x y a a +=>有公共的焦点1F ,2F ,且1C 与2C 在第一象限的交点为M ,若12MF F △的面积为1,则a 的值为.四、解答题15.已知函数π()2cos 6f x x ωθ⎛⎫=-+ ⎪⎝⎭(0,0π)ωθ><<的最小正周期为π,且(0)0f =. (1)求函数()f x 的解析式并分别写出()f x 取最大值与最小值时相应x 的取值集合;(2)求函数π()6g x f x ⎛⎫=- ⎪⎝⎭,ππ,62x ⎡⎤∈-⎢⎥⎣⎦的单调递减区间.16.如图,在ABC V 中,已知2AB =,3AC =,60BAC ∠=o,N 是AC 的中点,23BM BC =u u u u r u u u r ,设AM 与BN 相交于点P .(1)求cos MPN ∠的值;(2)若CP xAB yAC =+u u u r u u u r u u u r ,求x y +的值.17.如图,在四棱锥,P ABCD PA -⊥底面,ABCD //AD BC ,,AB BC ⊥4,PA AD ==1,BC AB =(1)证明:平面PCD ⊥平面PAC ;(2)求AD 与平面PCD 所成角的正弦值.18.已知椭圆()2222:10x y C a b a b +=>>C 的左,右焦点与短轴两个端点构成的四边形面积为(1)求椭圆C 的方程;(2)若直线:10(0)l x my m --=≠与x 轴交于点T ,与椭圆C 交于,P Q 两点,过点P 作x 轴的垂线交椭圆C 交于另一点R ,求TQR △面积的最大值.19.在三棱锥P ABC -中,1PC BC ==,2AC =,AP =90ACB ∠=︒,PB 的中点为M ,点D 在线段AB 上,且满足DB DP =.(1)求证:PB CD⊥;(2)当平面PDC⊥平面ABC时,①求点P到平面ABC的距离;②若N为AB的中点,求平面PAC与平面MNC夹角的余弦值.。
遂川县二中2018-2019学年上学期高二数学12月月考试题含解析

遂川县二中2018-2019学年上学期高二数学12月月考试题含解析班级__________ 姓名__________ 分数__________一、选择题1. 从1,2,3,4,5中任取3个不同的数,则取出的3个数可作为三角形的三边边长的概率是( )A .B .C .D .2. 数列{a n }的通项公式为a n =﹣n+p ,数列{b n }的通项公式为b n =2n ﹣5,设c n =,若在数列{c n }中c 8>c n (n ∈N *,n ≠8),则实数p 的取值范围是( )A .(11,25)B .(12,16]C .(12,17)D .[16,17)3. 定义运算,例如.若已知,则=( )A .B .C .D .4. 已知函数f (x+1)=3x+2,则f (x )的解析式是( )A .3x ﹣1B .3x+1C .3x+2D .3x+4A .甲B .乙C .丙D .丁6. 已知抛物线C :y x 82=的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若2=,则=QF ( ) A .6B .3C .38D .34 第Ⅱ卷(非选择题,共100分)7. O 为坐标原点,F 为抛物线的焦点,P 是抛物线C 上一点,若|PF|=4,则△POF 的面积为( )A .1B .C .D .28. 如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位:cm ),则此几何体的表面积是( )A .8cm 2B . cm 2C .12 cm 2D .cm 29. 某三棱锥的三视图如图所示,该三棱锥的体积是( ) A . 2 B .4 C .34 D .38【命题意图】本题考查三视图的还原以及特殊几何体的体积度量,重点考查空间想象能力及对基本体积公式的运用,难度中等.10.一个几何体的三视图如图所示,则该几何体的体积是( )A .64B .72C .80D .112【命题意图】本题考查三视图与空间几何体的体积等基础知识,意在考查空间想象能力与运算求解能力.11.已知一组函数f n(x)=sin n x+cos n x,x∈[0,],n∈N*,则下列说法正确的个数是()①∀n∈N*,f n(x)≤恒成立②若f n(x)为常数函数,则n=2③f4(x)在[0,]上单调递减,在[,]上单调递增.A.0 B.1 C.2 D.312.函数f(x)是以2为周期的偶函数,且当x∈(0,1)时,f(x)=x+1,则函数f(x)在(1,2)上的解析式为()A.f(x)=3﹣x B.f(x)=x﹣3 C.f(x)=1﹣x D.f(x)=x+1二、填空题13.过原点的直线l与函数y=的图象交于B,C两点,A为抛物线x2=﹣8y的焦点,则|+|=.14.给出下列命题:①存在实数α,使②函数是偶函数③是函数的一条对称轴方程④若α、β是第一象限的角,且α<β,则sinα<sinβ其中正确命题的序号是.15.已知函数f (x )=x 2+x ﹣b+(a ,b 为正实数)只有一个零点,则+的最小值为 .16.在ABC ∆中,已知角C B A ,,的对边分别为c b a ,,,且B c C b a sin cos +=,则角B 为 . 17.函数y=1﹣(x ∈R )的最大值与最小值的和为 2 .18.二面角α﹣l ﹣β内一点P 到平面α,β和棱l 的距离之比为1::2,则这个二面角的平面角是 度.三、解答题19.设函数f (x )=lnx+,k ∈R .(Ⅰ)若曲线y=f (x )在点(e ,f (e ))处的切线与直线x ﹣2=0垂直,求k 值; (Ⅱ)若对任意x 1>x 2>0,f (x 1)﹣f (x 2)<x 1﹣x 2恒成立,求k 的取值范围;(Ⅲ)已知函数f (x )在x=e 处取得极小值,不等式f (x )<的解集为P ,若M={x|e ≤x ≤3},且M ∩P ≠∅,求实数m 的取值范围.20.如图,正方形ABCD 中,以D 为圆心、DA 为半径的圆弧与以BC 为直径的半圆O 交于点F ,连接CF 并延长交AB 于点E . (Ⅰ)求证:AE=EB ;(Ⅱ)若EF •FC=,求正方形ABCD 的面积.21.对于任意的n∈N*,记集合E n={1,2,3,…,n},P n=.若集合A满足下列条件:①A⊆P n;②∀x1,x2∈A,且x1≠x2,不存在k∈N*,使x1+x2=k2,则称A具有性质Ω.如当n=2时,E2={1,2},P2=.∀x1,x2∈P2,且x1≠x2,不存在k∈N*,使x1+x2=k2,所以P2具有性质Ω.(Ⅰ)写出集合P3,P5中的元素个数,并判断P3是否具有性质Ω.(Ⅱ)证明:不存在A,B具有性质Ω,且A∩B=∅,使E15=A∪B.(Ⅲ)若存在A,B具有性质Ω,且A∩B=∅,使P n=A∪B,求n的最大值.22.如图,在长方体ABCD﹣A1B1C1D1中,AB=2,AD=1,A1A=1,(1)求证:直线BC1∥平面D1AC;(2)求直线BC1到平面D1AC的距离.23.已知函数f(x)=|x﹣5|+|x﹣3|.(Ⅰ)求函数f(x)的最小值m;(Ⅱ)若正实数a,b足+=,求证:+≥m.24.在某大学自主招生考试中,所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩的数据统计如图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.(Ⅰ)求该考场考生中“阅读与表达”科目中成绩为A的人数;(Ⅱ)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生“数学与逻辑”科目的平均分;(Ⅲ)已知参加本考场测试的考生中,恰有两人的两科成绩均为A.在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率.遂川县二中2018-2019学年上学期高二数学12月月考试题含解析(参考答案)一、选择题1.【答案】A【解析】解:从1,2,3,4,5中任取3个不同的数的基本事件有(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5)共10个,取出的3个数可作为三角形的三边边长,根据两边之和大于第三边求得满足条件的基本事件有(2,3,4),(2,4,5),(3,4,5)共3个,故取出的3个数可作为三角形的三边边长的概率P=.故选:A.【点评】本题主要考查了古典概型的概率的求法,关键是不重不漏的列举出所有的基本事件.2.【答案】C【解析】解:当a n≤b n时,c n=a n,当a n>b n时,c n=b n,∴c n是a n,b n中的较小者,∵a n=﹣n+p,∴{a n}是递减数列,∵b n=2n﹣5,∴{b n}是递增数列,∵c8>c n(n≠8),∴c8是c n的最大者,则n=1,2,3,…7,8时,c n递增,n=8,9,10,…时,c n递减,∴n=1,2,3,…7时,2n﹣5<﹣n+p总成立,当n=7时,27﹣5<﹣7+p,∴p>11,n=9,10,11,…时,2n﹣5>﹣n+p总成立,当n=9时,29﹣5>﹣9+p,成立,∴p<25,而c8=a8或c8=b8,若a8≤b8,即23≥p﹣8,∴p≤16,则c8=a8=p﹣8,∴p﹣8>b7=27﹣5,∴p>12,故12<p≤16,若a8>b8,即p﹣8>28﹣5,∴p>16,∴c8=b8=23,那么c8>c9=a9,即8>p﹣9,∴p<17,故16<p<17,综上,12<p<17.故选:C .3. 【答案】D【解析】解:由新定义可得,====.故选:D .【点评】本题考查三角函数的化简求值,考查了两角和与差的三角函数,是基础题.4. 【答案】A【解析】∵f (x+1)=3x+2=3(x+1)﹣1 ∴f (x )=3x ﹣1 故答案是:A【点评】考察复合函数的转化,属于基础题.5. 【答案】C【解析】解:∵甲、乙、丙、丁四人的平均环数乙和丙均为8.8环,最大,甲、乙、丙、丁四人的射击环数的方差中丙最小, ∴丙的射击水平最高且成绩最稳定,∴从这四个人中选择一人参加该运动会射击项目比赛, 最佳人选是丙. 故选:C .【点评】本题考查运动会射击项目比赛的最佳人选的确定,是基础题,解题时要认真审题,注意从平均数和方差两个指标进行综合评价.6. 【答案】A解析:抛物线C :y x 82的焦点为F (0,2),准线为l :y=﹣2,设P (a ,﹣2),B (m ,),则=(﹣a ,4),=(m ,﹣2),∵,∴2m=﹣a ,4=﹣4,∴m 2=32,由抛物线的定义可得|QF|=+2=4+2=6.故选A .7. 【答案】C【解析】解:由抛物线方程得准线方程为:y=﹣1,焦点F (0,1),又P为C上一点,|PF|=4,可得y P=3,代入抛物线方程得:|x|=2,P∴S△POF=|0F|•|x P|=.故选:C.8.【答案】C【解析】解:由已知可得:该几何体是一个四棱锥,侧高和底面的棱长均为2,故此几何体的表面积S=2×2+4××2×2=12cm2,故选:C.【点评】本题考查的知识点是棱柱、棱锥、棱台的体积和表面积,空间几何体的三视图,根据已知判断几何体的形状是解答的关键.9.【答案】B10.【答案】C.【解析】11.【答案】D【解析】解:①∵x∈[0,],∴f(x)=sin n x+cos n x≤sinx+cosx=≤,因此正确;n②当n=1时,f1(x)=sinx+cosx,不是常数函数;当n=2时,f2(x)=sin2x+cos2x=1为常数函数,当n≠2时,令sin2x=t∈[0,1],则f n(x)=+=g(t),g′(t)=﹣=,当t∈时,g′(t)<0,函数g(t)单调递减;当t∈时,g′(t)>0,函数g(t)单调递增加,因此函数f n(x)不是常数函数,因此②正确.③f4(x)=sin4x+cos4x=(sin2x+cos2x)2﹣2sin2xcos2x=1﹣==+,当x∈[0,],4x∈[0,π],因此f4(x)在[0,]上单调递减,当x∈[,],4x∈[π,2π],因此f4(x)在[,]上单调递增,因此正确.综上可得:①②③都正确.故选:D.【点评】本题考查了三角函数的图象与性质、倍角公式、平方公式、两角和差的正弦公式,考查了推理能力与计算能力,属于中档题.12.【答案】A【解析】解:∵x∈(0,1)时,f(x)=x+1,f(x)是以2为周期的偶函数,∴x∈(1,2),(x﹣2)∈(﹣1,0),f(x)=f(x﹣2)=f(2﹣x)=2﹣x+1=3﹣x,故选A.二、填空题13.【答案】4.【解析】解:由题意可得点B和点C关于原点对称,∴|+|=2||,再根据A为抛物线x2=﹣8y的焦点,可得A(0,﹣2),∴2||=4,故答案为:4.【点评】本题主要考查抛物线的方程、简单性质,属于基础题,利用|+|=2||是解题的关键.14.【答案】②③.【解析】解:①∵sinαcosα=sin2α∈[,],∵>,∴存在实数α,使错误,故①错误,②函数=cosx是偶函数,故②正确,③当时,=cos(2×+)=cosπ=﹣1是函数的最小值,则是函数的一条对称轴方程,故③正确,④当α=,β=,满足α、β是第一象限的角,且α<β,但sinα=sinβ,即sinα<sinβ不成立,故④错误,故答案为:②③.【点评】本题主要考查命题的真假判断,涉及三角函数的图象和性质,考查学生的运算和推理能力.15.【答案】9+4.【解析】解:∵函数f(x)=x2+x﹣b+只有一个零点,∴△=a﹣4(﹣b+)=0,∴a+4b=1,∵a,b为正实数,∴+=(+)(a+4b)=9++≥9+2=9+4当且仅当=,即a=b时取等号,∴+的最小值为:9+4故答案为:9+4【点评】本题考查基本不等式,得出a+4b=1是解决问题的关键,属基础题.16.【答案】4【解析】考点:正弦定理.【方法点晴】本题考查正余弦定理,根据正弦定理,将所给的含有边和角的等式化为只含有角的等式,再利用180,消去多余的变量,从而解出B角.三角函数题目在高考中的难度逐渐增加,以考查三三角形的三角和是角函数的图象和性质,以及三角形中的正余弦定理为主,在2016年全国卷()中以选择题的压轴题出现.17.【答案】2【解析】解:设f(x)=﹣,则f(x)为奇函数,所以函数f(x)的最大值与最小值互为相反数,即f(x)的最大值与最小值之和为0.将函数f(x)向上平移一个单位得到函数y=1﹣的图象,所以此时函数y=1﹣(x∈R)的最大值与最小值的和为2.故答案为:2.【点评】本题考查了函数奇偶性的应用以及函数图象之间的关系,奇函数的最大值和最小值互为相反数是解决本题的关键.18.【答案】75度.【解析】解:点P可能在二面角α﹣l﹣β内部,也可能在外部,应区别处理.当点P在二面角α﹣l﹣β的内部时,如图,A、C、B、P四点共面,∠ACB为二面角的平面角,由题设条件,点P到α,β和棱l的距离之比为1::2可求∠ACP=30°,∠BCP=45°,∴∠ACB=75°.故答案为:75.【点评】本题考查与二面角有关的立体几何综合题,考查分类讨论的数学思想,正确找出二面角的平面角是关键.三、解答题19.【答案】【解析】解:(Ⅰ)由条件得f′(x)=﹣(x>0),∵曲线y=f(x)在点(e,f(e))处的切线与直线x﹣2=0垂直,∴此切线的斜率为0,即f′(e)=0,有﹣=0,得k=e;(Ⅱ)条件等价于对任意x1>x2>0,f(x1)﹣x1<f(x2)﹣x2恒成立…(*)设h(x)=f(x)﹣x=lnx+﹣x(x>0),∴(*)等价于h(x)在(0,+∞)上单调递减.由h′(x)=﹣﹣1≤00在(0,+∞)上恒成立,得k≥﹣x2+x=(﹣x﹣)2+(x>0)恒成立,∴k≥(对k=,h′(x)=0仅在x=时成立),故k的取值范围是[,+∞);(Ⅲ)由题可得k=e,因为M∩P≠∅,所以f(x)<在[e,3]上有解,即∃x∈[e,3],使f(x)<成立,即∃x∈[e,3],使m>xlnx+e成立,所以m>(xlnx+e)min,令g(x)=xlnx+e,g′(x)=1+lnx>0,所以g(x)在[e,3]上单调递增,g(x)min=g(e)=2e,所以m>2e.【点评】本题考查导数的运用:求切线的斜率和单调区间,主要考查函数的单调性的运用,考查不等式存在性和恒成立问题的解决方法,考查运算能力,属于中档题.20.【答案】【解析】证明:(Ⅰ)∵以D为圆心、DA为半径的圆弧与以BC为直径半圆交于点F,且四边形ABCD为正方形,∴EA为圆D的切线,且EB是圆O的切线,由切割线定理得EA2=EF•EC,故AE=EB.(Ⅱ)设正方形的边长为a,连结BF,∵BC为圆O的直径,∴BF⊥EC,在Rt△BCE中,由射影定理得EF•FC=BF2=,∴BF==,解得a=2,∴正方形ABCD的面积为4.【点评】本题考查两线段相等的证明,考查正方形面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.21.【答案】【解析】解:(Ⅰ)∵对于任意的n∈N*,记集合E n={1,2,3,…,n},P n=.∴集合P3,P5中的元素个数分别为9,23,∵集合A满足下列条件:①A⊆P n;②∀x1,x2∈A,且x1≠x2,不存在k∈N*,使x1+x2=k2,则称A具有性质Ω,∴P3不具有性质Ω.…..证明:(Ⅱ)假设存在A,B具有性质Ω,且A∩B=∅,使E15=A∪B.其中E15={1,2,3,…,15}.因为1∈E15,所以1∈A∪B,不妨设1∈A.因为1+3=22,所以3∉A,3∈B.同理6∈A,10∈B,15∈A.因为1+15=42,这与A具有性质Ω矛盾.所以假设不成立,即不存在A,B具有性质Ω,且A∩B=∅,使E15=A∪B.…..解:(Ⅲ)因为当n≥15时,E15⊆P n,由(Ⅱ)知,不存在A,B具有性质Ω,且A∩B=∅,使P n=A∪B.若n=14,当b=1时,,取A1={1,2,4,6,9,11,13},B1={3,5,7,8,10,12,14},则A1,B1具有性质Ω,且A1∩B1=∅,使E14=A1∪B1.当b=4时,集合中除整数外,其余的数组成集合为,令,,则A2,B2具有性质Ω,且A2∩B2=∅,使.当b=9时,集中除整数外,其余的数组成集合,令,.则A3,B3具有性质Ω,且A3∩B3=∅,使.集合中的数均为无理数,它与P14中的任何其他数之和都不是整数,因此,令A=A1∪A2∪A3∪C,B=B1∪B2∪B3,则A∩B=∅,且P14=A∪B.综上,所求n的最大值为14.…..【点评】本题考查集合性质的应用,考查实数值最大值的求法,综合性强,难度大,对数学思维要求高,解题时要认真审题,注意分类讨论思想的合理运用.22.【答案】【解析】解:(1)因为ABCD﹣A1B1C1D1为长方体,故AB∥C1D1,AB=C1D1,故ABC1D1为平行四边形,故BC1∥AD1,显然B不在平面D1AC上,故直线BC1平行于平面DA1C;(2)直线BC1到平面D1AC的距离即为点B到平面D1AC的距离(设为h)以△ABC为底面的三棱锥D1﹣ABC的体积V,可得而△AD1C中,,故所以以△AD1C为底面的三棱锥B﹣﹣AD1C的体积,即直线BC 1到平面D 1AC 的距离为.【点评】本题考查了线面平行的判定定理,考查线面的距离以及数形结合思想,是一道中档题.23.【答案】【解析】(Ⅰ)解:∵f (x )=|x ﹣5|+|x ﹣3|≥|x ﹣5+3﹣x|=2,…(2分) 当且仅当x ∈[3,5]时取最小值2,…(3分) ∴m=2.…(4分)(Ⅱ)证明:∵( +)[]≥()2=3,∴(+)×≥()2,∴+≥2.…(7分)【点评】本题主要考查绝对值不等式和均值不等式等基础知识,考查运算求解能力,考查化归与转化思想.24.【答案】【解析】解:(Ⅰ)因为“数学与逻辑”科目中成绩等级为B 的考生有10人, 所以该考场有10÷0.25=40人,所以该考场考生中“阅读与表达”科目中成绩等级为A 的人数为: 40×(1﹣0.375﹣0.375﹣0.15﹣0.025)=40×0.075=3人;(Ⅱ)该考场考生“数学与逻辑”科目的平均分为:×=2.9;(Ⅲ)因为两科考试中,共有6人得分等级为A ,又恰有两人的两科成绩等级均为A , 所以还有2人只有一个科目得分为A ,设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A 的同学,则在至少一科成绩等级为A 的考生中,随机抽取两人进行访谈,基本事件空间为:Ω={{甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁}},一共有6个基本事件.设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,则P(B)=.【点评】本小题主要考查统计与概率的相关知识,具体涉及到频率分布直方图、平均数及古典概型等内容.。
2024届江西省吉安市遂川县高二上数学期末学业水平测试试题含解析
2024届江西省吉安市遂川县高二上数学期末学业水平测试试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
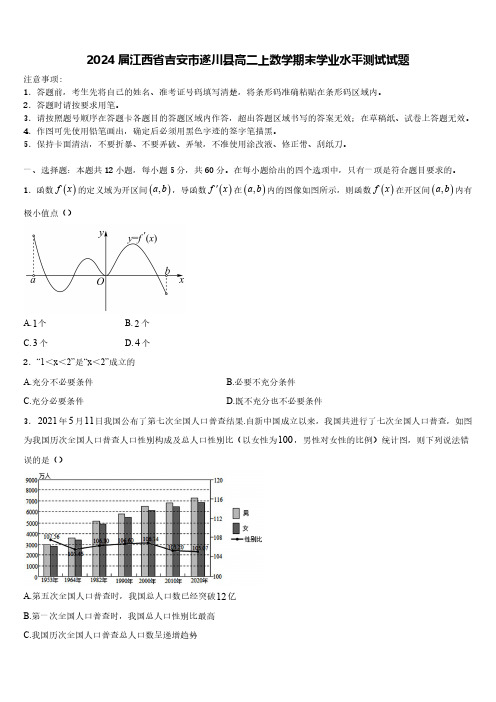
1.函数()f x 的定义域为开区间(),a b ,导函数()f x '在(),a b 内的图像如图所示,则函数()f x 在开区间(),a b 内有极小值点()A.1个B.2个C.3个D.4个2.“1<x <2”是“x <2”成立的A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3.2021年5月11日我国公布了第七次全国人口普查结果.自新中国成立以来,我国共进行了七次全国人口普查,如图为我国历次全国人口普查人口性别构成及总人口性别比(以女性为100,男性对女性的比例)统计图,则下列说法错误的是()A.第五次全国人口普查时,我国总人口数已经突破12亿B.第一次全国人口普查时,我国总人口性别比最高C.我国历次全国人口普查总人口数呈递增趋势D.我国历次全国人口普查总人口性别比呈递减趋势4.倾斜角为45°,在y 轴上的截距是2-的直线方程为()A.20x y -+= B.20x y --=C.20x --= D.20x ++=5.在四棱锥A BCD -中,,M N 分别为,AB CD 的中点,则()A.111222MN AD AC AB=+- B.111222MN AD AC AB=++C.111222MN AD AC AB=--+D.111222MN AD AC AB=-+6.已知点()2,0A -,()2,0B ,()4,3C ,动点P 满足PA PB ⊥,则PC 的取值范围为()A.[]2,5B.[]2,8C.[]3,7 D.[]4,67.在数列{}n a 中,150a =-,1n n a a n +=+,则46a =()A.985 B.1035C.2020D.20708.已知向量123,,e e e 是两两垂直的单位向量,且1231332,2a e e e b e e =+-=+ur u r u r u r r r r ,则a b ⋅= ()A.5B.1C.-1D.79.如果椭圆22110036x y +=上一点P 到焦点1F 的距离等于6,则线段1PF 的中点M 到坐标原点的距离等于()A.7B.10C.12D.1410.已知F 是抛物线28y x =的焦点,直线l 是抛物线的准线,则F 到直线l 的距离为()A.2 B.4C.6D.811.若直线:l y x m =+与圆()()22:114C x y -+-=只有一个公共点,则m 的值为()B.C.D.±12.在棱长为2的正方体1111ABCD A B C D -中,P 是棱1CC 上一动点,点O 是面AC 的中心,则AP AO ⋅的值为()A.4B.C.2D.不确定二、填空题:本题共4小题,每小题5分,共20分。
遂川县民族中学2018-2019学年上学期高二数学12月月考试题含解析

遂川县民族中学2018-2019学年上学期高二数学12月月考试题含解析班级__________ 姓名__________ 分数__________一、选择题1. (文科)要得到()2log 2g x x =的图象,只需将函数()2log f x x =的图象( )A .向左平移1个单位B .向右平移1个单位C .向上平移1个单位D .向下平移1个单位 2. 已知集合A={0,1,2},则集合B={x ﹣y|x ∈A ,y ∈A}的元素个数为( ) A .4B .5C .6D .93. 某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )A .20+2πB .20+3πC .24+3πD .24+3π4. 已知函数()cos()3f x x π=+,则要得到其导函数'()y f x =的图象,只需将函数()y f x =的图象( )A .向右平移2π个单位 B .向左平移2π个单位 C. 向右平移23π个单位 D .左平移23π个单位5. 已知函数f (x )=3cos (2x ﹣),则下列结论正确的是( )A .导函数为B .函数f (x )的图象关于直线对称C .函数f (x )在区间(﹣,)上是增函数D .函数f (x )的图象可由函数y=3co s2x 的图象向右平移个单位长度得到6. 在ABC ∆中,角A ,B ,C 的对边分别是,,,BH 为AC 边上的高,5BH =,若2015120aBC bCA cAB ++=,则H 到AB 边的距离为( )A .2B .3 C.1 D .47. ()()22f x a x a =-+ 在区间[]0,1上恒正,则的取值范围为( )A .0a >B .0a <<C .02a <<D .以上都不对8. 学校将5个参加知识竞赛的名额全部分配给高一年级的4个班级,其中甲班级至少分配2个名额,其它班级可以不分配或分配多个名额,则不同的分配方案共有( )A .20种B .24种C .26种D .30种9. 已知圆C 1:x 2+y 2=4和圆C 2:x 2+y 2+4x ﹣4y+4=0关于直线l 对称,则直线l 的方程为( ) A .x+y=0 B .x+y=2 C .x ﹣y=2 D .x ﹣y=﹣210.集合{}{}2|ln 0,|9A x x B x x =≥=<,则AB =( )A .()1,3B .[)1,3C .[]1,+∞D .[],3e 11.已知函数,,若,则( )A1 B2 C3 D-112.双曲线4x 2+ty 2﹣4t=0的虚轴长等于( )A .B .﹣2tC .D .4二、填空题13.利用计算机产生1到6之间取整数值的随机数a 和b ,在a+b 为偶数的条件下,|a ﹣b|>2发生的概率是 .14.若命题“∃x ∈R ,x 2﹣2x+m ≤0”是假命题,则m 的取值范围是 .15.设曲线y=x n+1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ,令a n =lgx n ,则a 1+a 2+…+a 99的值为 .16.在正方体ABCD ﹣A 1B 1C 1D 1中,异面直线A 1B 与AC 所成的角是 °.17.在△ABC 中,若a=9,b=10,c=12,则△ABC 的形状是 .18.曲线在点(3,3)处的切线与轴x 的交点的坐标为 .三、解答题19.【南师附中2017届高三模拟二】如下图扇形AOB 是一个观光区的平面示意图,其中AOB ∠为23π,半径OA 为1km ,为了便于游客观光休闲,拟在观光区内铺设一条从入口A 到出口B 的观光道路,道路由圆弧AC 、线段CD 及线段BD 组成.其中D 在线段OB 上,且//CD AO ,设AOC θ∠=.(1)用θ表示CD 的长度,并写出θ的取值范围; (2)当θ为何值时,观光道路最长?20.已知函数f (x )=x 2﹣ax+(a ﹣1)lnx (a >1). (Ⅰ) 讨论函数f (x )的单调性; (Ⅱ) 若a=2,数列{a n }满足a n+1=f (a n ). (1)若首项a 1=10,证明数列{a n }为递增数列;(2)若首项为正整数,且数列{a n }为递增数列,求首项a 1的最小值.21.(本小题满分13分) 已知函数32()31f x ax x =-+, (Ⅰ)讨论()f x 的单调性;(Ⅱ)证明:当2a <-时,()f x 有唯一的零点0x ,且01(0,)2x ∈.22.已知三次函数f(x)的导函数f′(x)=3x2﹣3ax,f(0)=b,a、b为实数.(1)若曲线y=f(x)在点(a+1,f(a+1))处切线的斜率为12,求a的值;(2)若f(x)在区间[﹣1,1]上的最小值、最大值分别为﹣2、1,且1<a<2,求函数f(x)的解析式.23.等差数列{a n} 中,a1=1,前n项和S n满足条件,(Ⅰ)求数列{a n} 的通项公式和S n;(Ⅱ)记b n=a n2n﹣1,求数列{b n}的前n项和T n.24.已知等差数列满足:=2,且,成等比数列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江西省遂川中学、永丰中学10-11学年高二上学期12月月考(数学理)一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中, 只有一项是符合题目要求的)1. 命题:“a 、b 都是偶数,则a+b 是偶数”的逆否命题是 ( ) A .a 、b 都不是偶数,则a+b 不是偶数 B.a 、b 不都是偶数,则a+b 不是偶数 C .a+b 不是偶数,则a 、b 都不是偶数 D.a+b 不是偶数,则a 、b 不都是偶数2.若点P (0,2)与点Q (-2,0)关于直线L 对称,则L 的方程是 ( ) A .x +y =0B. x -y =0C .x +y +1=0 D. x -y +1=03. 命题“065,2>-+∈x x Z x 有对任意的”的否定是 ( ) A .065,2≤-+∈x x Z x 有对任意的 B .065,2>-+∈x x Z x 使存在 C .065,2≤-+∈x x Z x 使存在 D .65,2-+∈x x Z x 有对任意的<0 4.过点A (3,4)的圆22(2)(1)1x y -+-=的切线方程是 ( ) A .4x +3y =0 B .4x -3y =0C .4x -3y =0或x =3D .4x +3y =0或x =35.与圆A :060422=--+x y x 内切且与圆B :0422=++x y x 外切的动圆圆心的轨迹为( ) A .圆 B .线段 C .椭圆 D .双曲线6. 条件p :1>x 且1>y ,条件q :2>+y x 且1>xy ,则条件p 是条件q 的 ( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件7.下列四个正方体图形中,A B 、为正方体的两个顶点,M N P 、、分别为其所在棱的中点,能得出//AB 平面MNP 的图形的序号是 ( )A. ①、③B. ①、④C. ②、③D. ②、④8.P 、A 、B 、C 是球面上的四个点,PA 、PB 、PC 两两垂直,且1PA PB PC ===,则该球的表面积等于 ( ) A .2πB .3πC .4πD .12π9. 双曲线)0(122≠=-mn n y m x 的离心率为2,焦点与椭圆1251622=+y x 的焦点重合,则m 的值为( )A .427-B .49-C .427D .4910.已知点P 为抛物线22y x =上的动点,点P 在y 轴上的射影是M ,A 点坐标为7(,4)2,则||||PA P M +的最小值是 ( )A .112B .4C .92D .5二、填空题(本大题共5小题,每小题5分,满分25分)11. 若命题“p 或q ”为真,“非p ”为真,则“非q ”为 命题。
12.一个几何体的三视图如图所示, 则它的体积为 .13.椭圆92x +162y =1的两焦点为F1、F2,点P 在椭圆上,且∠F1PF2 =3π, 则△PF1F2的面积为 .14.设O 为坐标原点,向量(1,2,3)OA =,(2,1,2)OB =,(1,1,2)OP =,点Q 在直线OP 上运动,则当QA QB ⋅取得最小值时,点Q 的坐标为___________.15.设αβγ、、为两两不重合的平面,l m n 、、为两两不重合的直线, 给出下列四个命题:①若//αγβγαβ⊥⊥,,则;②若//////m n m n ααββαβ⊂⊂,,,,则; ③若////l l αβαβ⊂,,则; ④若////.l m n l m n αββγγαγ===,,,,则其中正确的命题是。
三、解答题(本大题共6小题,16-19每题12分,20题13分,21题14分,共75分) 16.(本题满分12分) 已知直线1:80l mx y n ++=和2:210l x my +-=.(1)若点(0,1)Q 到直线2l的距离为1,求m 的值;(2)若1l 和2l 相交于点(,1)P m -,求m 、n 的值;(3)若12//l l ,且1l 过点(25,-1),求m 、n 的值。
17.(本题满分12分)已知圆C 的圆心与点(21)P -,关于直线1y x =+对称.直线34110x y +-=与圆C 相交于A B ,两点,且6AB =,求圆C 的方程.(12分)18.(本题满分12分)已知221122x y p k k +=+-:方程表示焦点在y 轴上的椭圆;:1(2)q y k x -=+直线与抛物线24y x =有两个公共点。
若“p 或q ”为真,“p 且q ”为假,求k 的取值范围。
19.(本题满分12分)如图,在四棱锥P ABCD -中,侧面PAD 是边长为2正三角形,且与底面ABCD 垂直,底面ABCD 是菱形,60BAD ∠=,N 是PB 中点,截面DAN 交PC 于M . (1)求证://MN 平面PAD ; (2)求点C 到平面ADMN 的距离.20. (本题满分13分) 已知棱长为2的正方体1111ABCD A B C D -中,,E F 分别是11,BC A D 的中点.试求:(1)求1A C与DE 所成的角的余弦值;(2)求AD 与平面1B EF所成的角的正弦值; (3)求二面角1B EF B--的大小的余弦值.AB CC1DAB1D E F21.(本题满分14分)已知((),,1(),0,(a a y b x a -⊥+==(1)点P (x ,y )的轨迹C 的方程;(2)若直线)0(3:≠+=m m x y l 与曲线C 交于A ,B 两点,D (0,-1)且有|AD|=|BD|,试求m 的值.参考答案一、选择题 DACCC ABBAC二、填空题 假 2333 (38,34,34) ③④三、解答题16.解:(11=,解得32m =-. (4分)(2)由题意得280,210.m n m m ⎧-+=⎨--=⎩解得1,7,m n =⎧⎨=⎩ (8分)(3)由8,221m m m n⎧=⎪⎪⎨⎪≠⎪⎩-得4,2m n =≠-或4,2m n =-≠ 又1l 过点(25,-1)得m =4,n =-2(舍去)或m =-4,n =18 (12分)17. 解析:圆心的坐标为(0,1)-, (5分)2222(411)3185r --=+=, (10分)所以圆的方程为22(1)18x y ++=. (12分)18.解:p 真:10220221k k k k +>⎧⎪->⎨⎪->+⎩113k ∴-<<(4分)q 真:221(2)4840014(1,0)(0,)02y k x ky y k k y x k ⎧-=+-++=⎪≠⎧⎨=∈-⎨⎪∆>⎩⎩ (8分) i) p q 真假 {0}k ∈ ;ii) p q 假真11[,)32k ∈ 故11{0}[,)32k ∈ (12分) 19.证明:(1)AD//BC ,PBC BC ⊂面∴//AD PBC 面。
又∵AD ⊂面ADMN ,ADMNPBC=MN 面面,∴//AD MN 。
而AD PAD ⊂面,∴MN //PAD 平面 (5分)(2)取AD 中点O ,连结BO ,BD 。
在PAB ∆中,∵,AP AD AB PN PB ===,∴ANPB ⊥在△ABD 中,∵AD=AB ,060BAD ∠=,∴三角形ABD 为等边三角形 ∴BO AD ⊥ 又PO AD ⊥,PO BO O =,∴AD POB ⊥面,∴AD PB ⊥ 又∵ADAN A =,∴ADMN PB ⊥面 (10分)PO=BO=3 PB=6 BN= 26∵BC ∥面ADMN, ∴C 到平面ADMN 的距离为26(12分)20.答:建立空间坐标系,D 为原点,1,,DA DC DD 所在的直线分别为,,x y z 轴,则有1111(2,0,0),(2,2,0),(0,2,0),(0,0,0),(2,0,2),(2,2,2),(0,2,2),(0,0,2)A B C D A B C D(1)1(1,2,0),(1,0,2),(2,2,2),(1,2,0)E F AC DE =--=115cos ,A C DE ∴<>=,故1A C 与DE 所成的角的余弦值是1515. (4分)(2)1(2,0,0),(0,2,2),(1,0,2)AD EF EB =-=-=,平面1B EF的一个法向量n1(2,1,1)=-,11||6sin ||||AD n AD n θ∙==⋅,故AD 与平面1B EF 所成的角的正弦值是36. (8分)(3)平面1B EF 的一个法向量n1(2,1,1)=-,平面BEF 的一个法向量n2(0,1,1)=,所以12cos ,3n n <>=,二面角1B EF B --的为锐角,所以二面角1B EFB --的余弦值为33(13分)21.解:(1)由已知223→→=b a即 2233y x +=,所以P 的轨迹方程为 1322=-y x (6分)(2)设 ),(),(2211y x B y x A ,,AB 中点E 坐标为),(00y x ⎪⎩⎪⎨⎧=-+=13322y x m x y ,消去y 得:033182622=+++m mx x由韦达定理得:262691390021my m x m x x -=-=-=+,,则 (10分) 则AB 垂直平分线方程为)269(3126mx m y +-=+,又点D (0,-1)在AB 的垂直平分线上,代入方程得213=m (13分)(注:也可由DE 的斜率为31269126,31-=-+--m m 得,解得)213=m 由)0(3:213≠+==m m x y l m 时直线与双曲线C 相交,符合题意, 所以213=m (若已计算△>0,得m2>26,则无需检验) (14分)学习资料 崩孞尛。
