江西省南昌市2015届高三第一轮复习训练数学(2)(函数1)

合集下载

江西省南昌市第三中学2015届高三上学期第二次月考数学(文)试题

1、命题“对任意x R ∈,都有20x ≥”的否定为（）A ．对任意x R ∈,使得20x <B ．不存在x R ∈,使得20x <C ．存在0x R ∈,使得200x ≥D ．存在0x R ∈,使得200x <2、已知集合{M x y =|=，{}2log (2)N x y x ==-，则()R C M N I （）A ．[1,2)B ．(,1)[2,)-∞+∞C ．[0,1]D ．(,0)[2,)-∞+∞3、若sin60333,log cos60,log tan 60a b c ︒==︒=︒,则（）A.a b c >>B.a c b >>C. c b a >>D.b a c >>4、某三棱锥的三视图如图2所示,则该三棱锥的体积是（）A ．16B ．13 C ．23D ．15、下面是关于公差0d >的等差数列{}n a 的四个命题:{}1:n p a 数列是递增数列；{}2:n p na 数列是递增数列； 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列；{}4:3n p a nd +数列是递增数列；其中的真命题为 ( )A ．12,p pB ．34,p pC ．23,p pD ．14,p p6、设函数()3sin(2)14f x x π=++,将()y f x =的图像向右平移(0)ϕϕ>个单位,使得到江西省南昌市第三中学2015届高三上学期第二次月考数学文试题的图像关于y 对称,则ϕ的最小值为（）A.8π B.38πC.4π D.34π7、设()f x 是定义在(,0)(0,)-∞+∞上的函数，如果对于任意给定的等比数列{}n a ，有(){}n a f 仍是等比数列，则称()f x 为“保等比数列函数”.现有定义在(,0)(0,)-∞+∞上的如下函数： ①2()f x x =； ②()2x f x =； ③()x x f =；④()ln f x x =，则其中是“保等比数列函数”的()f x 的序号为（）A ． ①②B ． ③④C ． ①③D ． ②④8、若a r 、b r 、c r 均为单位向量，且0a b =r rg ，则a b c +-r r r 的最小值为（）A1 B ．1 C1+ D9. 设实数x ，y 满足约束条件，12002y x y x ⎧≤⎪⎪≥⎨⎪≤≤⎪⎩且目标函数z=ax+by （a>0，b>0）的最大值为1，则12a b+的最小值为 ( ) A. 4 B. 8 C. 9 D. 610．如图，直角梯形ABCD 中，∠A ＝90°，∠B ＝45°，底边AB ＝5，高AD ＝3，点E 由B 沿折线BCD 向点D 移动，EM ⊥AB 于M ，EN ⊥AD 于N ，设BM ＝x ，矩形AMEN 的面积为y ，那么y 与x 的函数关系的图像大致是（）第Ⅱ卷非选择题（共100分）二、填空题: 把答案填写在答题卡相应的题号后的横线上（本大题共5小题,每小题5分,共25分） 11、如果()xf x e =，则()'0____.f=12、某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵树是前一天的2倍,则需要的最少天数n(n∈N +)等于_____________.13、点P （x ，y ）在直线20x y +-=上，则33xy+的最小值为 . 14、如果函数()()cos f x k x π=在[]0,1上至少取得最小值1008次，则正数k 的最小值是______________. 15. 定义“正对数”:0(01)ln ln (1)x x x x +<<⎧=⎨≥⎩，，,现有四个命题:①若0,0>>b a ,则a b a b++=ln )(ln ; ②若0,0>>b a ,则b a ab ++++=ln ln )(ln ③若0,0>>b a ,则b a ba+++-=ln ln )(ln④若0,0>>b a ,则2ln ln ln )(ln ++≤++++b a b a其中的真命题有____________ (写出所有真命题的序号)三、解答题:解答应写出文字说明、证明过程或演算步骤（本大题共6小题,共75分） 16、（本小题满分12分）记函数()f x =的定义域为A ，()()()lg 11g x x x =-+⎡⎤⎣⎦的定义域为B ，求集合A 、B 、A B I 。

高中数学一轮复习：第二章函数的概念与基本初等函数(必修1)课后跟踪训练12

课后跟踪训练(十二)基础巩固练一、选择题1．若函数f (x )在区间[－2,2]上的图象是连续不断的曲线，且f (x )在(－2,2)内有一个零点，则f (－2)·f (2)的值( )A ．大于0B ．小于0C ．等于0D ．不能确定[解析] 若函数f (x )在(－2,2)内有一个零点，且该零点是变号零点，则f (－2)·f (2)<0，否则， f (－2)·f (2)>0，故选D.[答案] D2．(2019·湖北襄阳四校联考)函数f (x )＝3x ＋x 3－2在区间(0,1)内的零点个数是( )A ．0B ．1C ．2D ．3[解析] 由题意知f (x )单调递增，且f (0)＝1＋0－2＝－1<0，f (1)＝3＋1－2＝2>0，即f (0)·f (1)<0且函数f (x )在(0,1)内连续不断，所以f (x )在区间(0,1)内有一个零点．故选B.[答案] B3．(2018·吉林省实验中学段考)若函数f (x )＝x 2－ax ＋1在区间⎝ ⎛⎭⎪⎫12，3上有零点，则实数a 的取值范围是( ) A ．(2，＋∞) B ．[2，＋∞) C.⎣⎢⎡⎭⎪⎫2，52D.⎣⎢⎡⎭⎪⎫2，103[解析] 解法一：当f ⎝ ⎛⎭⎪⎫12·f (3)<0时，函数在区间⎝ ⎛⎭⎪⎫12，3上有且仅有一个零点，即⎝ ⎛⎭⎪⎫54－a 2(10－3a )<0，解得52<a <103；当⎩⎪⎨⎪⎧12<a2<3，Δ＝a 2－4≥0，f ⎝ ⎛⎭⎪⎫12>0，f (3)>0时，函数在区间⎝ ⎛⎭⎪⎫12，3上有一个或两个零点，解得2≤a <52；当a ＝52时，函数的零点为12和2，符合题意；当a ＝103时，函数的零点为13或3，不符合题意．综上，a 的取值范围是⎣⎢⎡⎭⎪⎫2，103.故选D.解法二：令f (x )＝0，则a ＝x 2＋1x .令g (x )＝x 2＋1x ，而g ′(x )＝1－1x 2.当x ∈⎝ ⎛⎭⎪⎫12，1时，g ′(x )<0；当x ∈(1,3)时，g ′(x )>0，∴g (x )在⎝ ⎛⎭⎪⎫12，1上单调递减，在(1,3)上单调递增，∴g (x )的值域为⎣⎢⎡⎭⎪⎫2，103.∴a 的取值范围是⎣⎢⎡⎭⎪⎫2，103.故选D. [答案] D[解析] g (x )＝f (x )－m 有三个不同的零点等价于f (x )＝m 有三个不同的根，等价于函数y ＝f (x )与y ＝m 的图象有三个不同的公共点．在同一直角坐标系中画出函数y ＝f (x )，y ＝m 的图象(如图所示)，观察其交点个数，显然当－14<m <0时，两个函数图象有三个不同的公共点．故选C.[答案] C5.(2018·安徽安庆二模)定义在R 上的函数f (x )满足f (x )＝⎩⎪⎨⎪⎧x 2＋2，x ∈[0，1)，2－x 2，x ∈[－1，0)，且f (x ＋1)＝f (x －1)，若g (x )＝3－log 2x ，则函数F (x )＝f (x )－g (x )在(0，＋∞)内的零点个数为( )A ．3B ．2C ．1D ．0[解析] 由f (x ＋1)＝f (x －1)，知f (x )的周期是2，画出函数f (x )和g (x )的部分图象，如图所示，由图象可知f (x )与g (x )的图象有2个交点，故F (x )有2个零点．故选B.[答案] B 二、填空题6．函数f (x )＝ln(2x )－1的零点为________． [解析] 由ln(2x )－1＝0，得2x ＝e ，所以x ＝e2. 故f (x )＝ln(2x )－1的零点为e2. [答案] e27．(2019·四川绵阳模拟)函数f (x )＝2x－2x －a 的一个零点在区间(1,2)内，则实数a 的取值范围是________．[解析] 由题意，知函数f (x )在(1,2)上单调递增，又函数一个零点在区间(1,2)内，所以⎩⎨⎧f (1)<0，f (2)>0，即⎩⎨⎧－a <0，4－1－a >0，解得0<a <3，故填(0,3)．[答案] (0,3)8．(2019·山东济宁高三期末)设x 1，x 2是方程ln|x －2|＝m (m 为实常数)的两根，则x 1＋x 2的值为________．[解析] 方程ln|x －2|＝m 的根即函数y ＝ln|x －2|的图象与直线y ＝m 的交点的横坐标，因为函数y ＝ln|x －2|的图象关于x ＝2对称，且在x ＝2两侧单调，值域为R ，所以对任意的实数m ，函数y ＝ln|x －2|的图象与直线y ＝m 必有两交点，且两交点关于直线x ＝2对称，故x 1＋x 2＝4.[答案] 4 三、解答题9．(2019·烟台模拟)已知二次函数f (x )＝x 2＋(2a －1)x ＋1－2a ， (1)判断命题：“对于任意的a ∈R ，方程f (x )＝1必有实数根”的真假，并写出判断过程；(2)若y ＝f (x )在区间(－1,0)及⎝ ⎛⎭⎪⎫0，12内各有一个零点，求实数a 的取值范围．[解] (1)“对于任意的a ∈R ，方程f (x )＝1必有实数根”是真命题．依题意，f (x )＝1有实根，即x 2＋(2a －1)x －2a ＝0有实根，因为Δ＝(2a －1)2＋8a ＝(2a ＋1)2≥0对于任意的a ∈R 恒成立，即x 2＋(2a －1)x －2a ＝0必有实根，从而f (x )＝1必有实根．(2)依题意，要使y ＝f (x )在区间(－1,0)及⎝ ⎛⎭⎪⎫0，12内各有一个零点，只需⎩⎪⎨⎪⎧ f (－1)>0，f (0)<0，f ⎝ ⎛⎭⎪⎫12>0，即⎩⎪⎨⎪⎧3－4a >0，1－2a <0，34－a >0，解得12<a <34.故实数a 的取值范围为{a ⎪⎪⎪⎭⎬⎫12<a <34.10．(2019·贵州调研)设函数f (x )＝⎪⎪⎪⎪⎪⎪1－1x (x >0)．(1)作出函数f (x )的图象；(2)当0<a <b ，且f (a )＝f (b )时，求1a ＋1b 的值；(3)若方程f (x )＝m 有两个不相等的正根，求m 的取值范围． [解] (1)如图所示．(2)∵f (x )＝⎪⎪⎪⎪⎪⎪1－1x＝⎩⎪⎨⎪⎧1x －1，x ∈(0，1]，1－1x ，x ∈(1，＋∞)，故f (x )在(0,1]上是减函数，而在(1，＋∞)上是增函数．由0<a <b 且f (a )＝f (b )，得0<a <1<b ，且1a －1＝1－1b ，∴1a ＋1b ＝2. (3)由函数f (x )的图象可知，当0<m <1时，函数f (x )的图象与直线y ＝m 有两个不同的交点，即方程f (x )＝m 有两个不相等的正根．能力提升练11．(2019·云南昆明一模)设函数f (x )＝e x ＋x －2，g (x )＝ln x ＋x 2－3.若函数f (x )，g (x )的零点分别为a ，b ，则有( )A ．g (a )<0<f (b )B ．f (b )<0<g (a )C ．0<g (a )<f (b )D ．f (b )<g (a )<0[解析] 易知函数f (x )，g (x )在定义域上都是单调递增函数，且f (0)＝－1<0，f (1)＝e －1>0，g (1)＝－2<0，g (2)＝ln2＋1>0，所以a ，b 存在且唯一，且a ∈(0,1)，b ∈(1,2)，从而f (1)<f (b )<f (2)，g (0)<g (a )<g (1)，于是f (b )>0，g (a )<0，即g (a )<0<f (b )．[答案] A12．(2019·昆明市高三质检)已知函数f (x )＝⎩⎪⎨⎪⎧x 2－4x ＋a ，x <1，ln x ＋1，x ≥1，若方程f (x )＝2有两个解，则实数a 的取值范围是( )A ．(－∞，2)B ．(－∞，2]C ．(－∞，5)D ．(－∞，5][解析] 解法一：当x ≥1时，由ln x ＋1＝2，得x ＝e ，由方程f (x )＝2有两个解知，当x <1时，方程x 2－4x ＋a ＝2有唯一解．令g (x )＝x 2－4x ＋a －2＝(x －2)2＋a －6，则g (x )在(－∞，1)上单调递减，所以当x <1时，g (x )＝0有唯一解，则g (1)<0，得a <5，故选C.解法二：随着a 的变化引起y ＝f (x )(x <1)的图象上下平移，作出函数y ＝f (x )的大致图象，如图，由图象知，要使f (x )＝2有两个解．则a －3<2，得a <5，故选C.[答案] C13．(2019·河南名校联考)已知函数f (x )＝x 2－m cos x ＋m 2＋3m －8有唯一的零点，则实数m 的值为________．[解析] 由题意，函数f (x )为偶函数，在x ＝0处有定义且存在唯一零点，所以唯一零点为0，则02－m cos0＋m 2＋3m －8＝0，解得m ＝－4或m ＝2.将m ＝－4代入解析式，得f (x )＝x 2＋4cos x －4，分离得两个函数y ＝－x 2＋4，y ＝4cos x ，如图知f (x )存在3个零点，不符合题意，仅m ＝2时f (x )存在唯一零点．[答案] 214．已知函数f (x )＝－x 2＋2e x ＋m －1，g (x )＝x ＋e 2x (x >0)．(1)若y ＝g (x )－m 有零点，求m 的取值范围；(2)确定m 的取值范围，使得g (x )－f (x )＝0有两个相异实根．[解] (1)作出g (x )＝x ＋e 2x (x >0)的大致图象如图(1)．图(1)可知若使y ＝g (x )－m 有零点，则只需m ≥2e.(2)若g (x )－f (x )＝0有两个相异实根，即g (x )与f (x )的图象有两个不同的交点，作出g (x )＝x ＋e 2x (x >0)的大致图象如图(2)．图(2)∵f (x )＝－x 2＋2e x ＋m －1＝－(x －e)2＋m －1＋e 2. ∴其图象的对称轴为x ＝e ，开口向下，最大值为m －1＋e 2.故当m －1＋e 2>2e ，即m >－e 2＋2e ＋1时，g (x )与f (x )有两个交点，即g (x )－f (x )＝0有两个相异实根．∴m 的取值范围是(－e 2＋2e ＋1，＋∞)．拓展延伸练15．(2019·山西质量检测)已知f (x )＝⎩⎪⎨⎪⎧2x ＋1，x ≤0，|ln x |，x >0，则方程f [f (x )]＝3的根的个数是( )A ．3B ．4C ．5D ．6[答案] C16．已知函数f (x )＝⎩⎨⎧|log 2(x －1)|，1<x ≤3，12x 2－92x ＋10，x >3，若方程f (x )＝m 有四个不同的实根x 1，x 2，x 3，x 4，且满足x 1<x 2<x 3<x 4，则⎝ ⎛⎭⎪⎫m x 1＋m x 2(x 3＋x 4)的取值范围为________．[解析] 方程f (x )＝m 有四个不同的实数根x 1，x 2，x 3，x 4可转化为函数f (x )的图象与直线y ＝m 有四个不同的交点，且交点的横坐标分别为x 1，x 2，x 3，x 4，作出函数f (x )的大致图象如图所示，结合图象得0<m <1，且f (x 1)＝f (x 2)＝f (x 3)＝f (x 4)．由f (x 1)＝f (x 2)可得，|log 2(x 1－1)|＝|log 2(x 2－1)|，又1<x 1<2<x 2，所以log 2(x 1－1)＋log 2(x 2－1)＝0，得(x 1－1)(x 2－1)＝1，整理得x 1x 2＝x 1＋x 2，所以1x 1＋1x 2＝1. 由f (x 3)＝f (x 4)及二次函数图象的对称性，得x 3＋x 4＝9，所以⎝ ⎛⎭⎪⎫m x 1＋m x 2(x 3＋x 4)＝m ⎝ ⎛⎭⎪⎫1x 1＋1x 2(x 3＋x 4)＝9m ∈(0,9)．[答案](0,9)。

江西省南昌市2015届高三零模调研测试数学(文)试题(扫描版)

2014—2015学年度南昌市高三年级调研测试卷数学(文科)参考答案及评分标准又∵03B π<<，∴2333B πππ<+<， ∴当32B ππ+=，即6B π=时，ABC ∆的周长l取得最大值2+………………………12分18.解：（1）因为241n n S a =-，当1n =时，11112412S a a =-⇒=……………………2分又由11241241n n n n S a S a ++=-⎧⎨=-⎩，两式相减得： 11244n n n a a a ++=-即12n n a a +=，………………4分所以数列{}n a 是以首项为12，公比为2的等比数列，22n n a -= …………………………6分（2）*2,2N n a n n ∈=-，在12111...212n n n n b a b a b a n -+++=--中，令1,n =则111111121,, 1.222b a a b =--==∴= 因为1211211 (212)n n n n n b a b a b a b a n --++++=--， ()a ………8分所以11122221111...2,(2)22n n n n n b a b a b a b a n n -----++++=--≥，将上式两边同乘公比2得，12112...21,(2)n n n n b a b a b a n n --+++=--≥， ()b ………10分()a 减去()b 得，1,.(2)2n n n b a b n n =∴=≥，55b = …………………………………12分19. 解：（1）取PB 中点G ,连接,AG FG ，又F 分别为PC 的中点.GF ∴是PBC ∆的中位线，即1//2GF BC 又四边形ABCD 底面是平行四边形，E 分别为AB 的中点1//2AE BC ∴//GF AE ∴,即四边形AEFG 是平行四边形所以，//EF AG 又AG ⊂平面PAB 。

江西省南昌市2015届高三一模考试数学(理科)

2015 届南昌市第一次模拟考试数学试卷(理科) 参考答案
一、选择题 1 题目答案
理科一模
2 A
3 A
4 A
5 C
6 C
7 B
8 B
9 B
10 C
11 B
12 A
5
D
二、填空题 13.
3 4
14. 4
15. [
2 10 , ] 3 3
16 ( 1,0) (0,)
三、解答题 17. （Ⅰ）解：等差数列 {a n } ， a1 1 ， S 3 6 ， d 1 ，故 a n n ………3 分
A. 2 或
3
B. 2 或
A．2 个 9. 给出下列命题
B．3 个
C．4 个
D．5 个
5 2 3 4 5 ① 若 (1 x) a 0 a1 x a 2 x a3 x a 4 x a5 x ，则 | a1 | | a2 | | a3 | | a4 | | a5 | 32
12.设函数 f ( x ) ( x a ) 2 (ln x 2 2a) 2 , 其中 ( x 0, a R ) ,存在 x0 使得 f ( x0 ) 实数 a 值是 A.
4 成立，则 5
1 5
B.
2 5
C.
1 2
D. 1
第Ⅱ卷
本卷包括必考题和选考题两个部分。第（13）题—第（21）题为必考题，每个考生都必须作答。第（22）题—第（24）题为选考题，考生根据要求作答。二．填空题：本大题共四小题，每小题 5 分。 13. a, b.c, d 四封不同的信随机放入 A, B, C , D 4 个不同的信封里，每个信封至少有一封信。其中 a 没有放入 A 中的概率是 14. 直三棱柱 ABC A1 B1C1 中， BAC 90 0 ,矩形 BCC1 B1 的面积为 2 ,则直三棱柱

江西省南昌市2015届高三第一次模拟测试数学(文)试题(扫描版)

2014—2015学年度南昌市高三第一次模拟测试卷数学(文科)参考答案及评分标准一、选择题13. 2 14. [2,6] 15. π4 16. (1,0)-三、解答题17.解：（Ⅰ）等差数列}{n a ，11=a ，63=S ，1=∴d ，故n a n = ………3分⎪⎩⎪⎨⎧=⋅⋅⋅⋅=⋅⋅⋅⋅--)2(2)1(211321321 n n S n S n b b b b b b b b ，)2()1(÷得n a S S n n n n b 2221===--)2(≥n ， 222111===S b ,满足通项公式，故n n b 2= ………7分（Ⅱ）设n n a b >λ恒成立n n 2>⇒λ恒成立，设n n c c n c n n n n 2121+=⇒=+ 当2≥n 时，1<n c ，}{n c 单调递减， ………10分 21)(1max ==∴c c n ，故21>λ. ………12分18. 解：（Ⅰ）设“学生甲或学生乙被选中复查”为事件A,第三组人数为500.06515⨯⨯=，第四组人数为500.04510⨯⨯=，第五组人数为500.0255⨯⨯=， ………2分根据分层抽样知，第三组应抽取3人，第四组应抽取2人，第五组应抽取1人， ………4分所以2().5P A = ………6分（Ⅱ）记第三组选中的三人分别是123,,A A A ，第四组选中的二人分别为12,B B ，第五组选中的人为C ，从这六人中选出两人，有以下基本事件：121311121,,,,A A A A A B A B A C ，2321222313231212,,,,,,,,,A A A B A B A C A B A B A C B B B C B C ，共15个基本事件， ………9分符合一人在第三组一人在第四组的基本事件有1112,,A B A B 21223132,,,,A B A B A B A B ，共6个，所以所求概率62155P ==。

2015年江西省南昌市高考一模数学试卷(文科)【解析版】

2015年江西省南昌市高考数学一模试卷（文科）一、选择题:本大题共12小题，每小题5分，满分60分，在每小题给出的四个选项中，只有一项是符合题目要求的一项。

1．（5分）已知i为虚数单位，则复数z＝（﹣1﹣2i）i在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限2．（5分）若集合A＝{x|x（x﹣4）≤0}，B＝{x|log2（x2﹣x）＞1}，则A∩B＝（）A．（2，4]B．[2，4]C．（﹣∞，0）∪[0，4]D．（﹣∞，﹣1）∪[0，4]3．（5分）如图，在正方体ABCD﹣A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P﹣BCD的正视图与侧视图的面积之比为（）A．1：1B．2：1C．2：3D．3：24．（5分）已知过定点P（2，0）的直线l与曲线y＝相交于A，B两点，O为坐标原点，当S△AOB＝1时，直线l的倾斜角为（）A．150°B．135°C．120°D．不存在5．（5分）已知实数x，y满足，若目标函数z＝2x+y的最大值与最小值的差为2，则实数m的值为（）A．4B．3C．2D．﹣6．（5分）给出下列命题：①命题“∀x∈R，x2+x+1＞0”的否定是“∃x0∈R，x02+x0+1＜0”②设回归直线方程＝2﹣3x，当变量x增加一个单位时，平均增加3个单位③已知sin（θ﹣）＝，则cos（﹣2θ）＝．其中正确命题的个数为（）A．0B．1C．2D．37．（5分）在△ABC中，角A，B，C所对的边分别为a，b，c，c＝1，B＝45°，cos A＝，则b等于（）A．B．C．D．8．（5分）若双曲线C：﹣＝1的一条渐近线的倾斜角为，则双曲线C 的离心率为（）A．2或B．C．2或D．29．（5分）如图所示程序框图，其功能是输入x的值，输出相应的y值，若要使输入的x值与输出的y值相等，则这样的x值有（）A．1个B．2个C．3个D．4个10．（5分）如图：M（x M，y M），N（x N，y N）分别是函数f（x）＝A sin（ωx+φ）（A＞0，ω＞0）的图象与两条直线l1：y＝m，l2：y＝﹣m（A≥m≥0）的两个交点，记S＝|x N﹣x M|，则S（m）图象大致是（）A．B．C．D．11．（5分）设无穷数列{a n}，如果存在常数A，对于任意给定的正数ɛ（无论多小），总存在正整数N，使得n＞N时，恒有|a n﹣A|＜ɛ成立，就称数列{a n}的极限为A，则四个无穷数列：①{（﹣1）n×2}；②{n}；③{1++++…+}；④{}，其极限为2共有（）A．1个B．2个C．3个D．4个12．（5分）已知点P（x1，y1）是函数f（x）＝2x上一点，点Q（x2，y2）是函数g（x）＝2lnx上一点，若存在x1，x2使得|PQ|≤成立，则x1的值为（）A．B．C．D．1二、填空题：本大题共4小题，每小题5分。

江西省南昌二中2015届高三上第一次考试数学(理)试题及答案

南昌二中2015届高三上学期第一次考试数学（理）试题一、选择题：本大题共10个小题；每小题5分，共50分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．1. 若集合{}xy x A2==，集合{}x y x B ==,则=⋂B A ( )A ．()0,+∞B ．()+∞,1C ． [)+∞,0D ．()+∞∞-, 2．下列函数中，在其定义域内既是奇函数又是减函数的是 ( ) A ．R x x y ∈-=,3B ．R x x y ∈=,sinC ．R x xy ∈=-,31D ．R x x y ∈=,)21(3．已知正角α的终边上一点的坐标为（32cos,32sinππ），则角α的最小值为( ) A ．65π B ．32π C ．35π D ．611π4．命题“所有能被5整除的数都是偶数”的否定形式是( ) A ．所有不能被5整除的数都是偶数 B ．所有能被5整除的数都不是偶数 C ．存在一个不能被5整除的数都是偶数 D ．存在一个能被5整除的数不是偶数5．设函数1()7,02()0x x f x x ⎧-<⎪=≥，若()1f a <，则实数a 的取值范围是 ( )A ．(,3)-∞-B ．(1,)+∞C ．(3,1)-D ．(,3)(1,)-∞-+∞6．已知,135)4sin(-=+πx 则x 2sin 的值等于 ( ) A ．169120 B ．169119 C ．169120- D ．119169-8．已知函数xx y cos =关于原点对称，则函数111)2121(cos 2)(2----=x x x f 的对称中心的坐标为( )A ． )1,1(-B ． )1,1(C ．)1,1(-D ．)1,1(--9．定义在R 上的可导函数)(x f ，当),1(+∞∈x 时，0)1)(()()1(''>--⋅-x x f x f x 恒成立，若)2(f a =， )3(21f b =， )2(121f c -=，则c b a ,,的大小关系是( )A ．b a c <<B ．c b a <<C ．c a b <<D ．b c a <<10．设函数x x x f )41(log )(4-=，xx x g ⎪⎭⎫⎝⎛-=41log )(41的零点分别为21x x 、，则( )A ． 121=x xB ．1021<<x xC ．2121<<x xD ． 21x x 2≥二、填空题：本大题共5个小题；每小题5分，共25分．三、解答题：本大题共6个小题共75分．每题解答过程写在答题卡上．16.（12分）已知命题P ：函数)(x f 为),0(+∞上单调减函数,实数m 满足不等式)23()1(m f m f -<+.命题Q ：当]2,0[π∈x ，函数a x x m ++-=1sin 2sin 2。

江西省南昌市2015届高三第二次模拟考试数学理科试题有答案(扫描版)

2015 年高三测试卷数学(理科)参考答案及评分标准一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的．二、填空题：本大题共4小题，每小题5分．13．214．13π 15．1316．2212x y -= 三、解答题：解答应写出文字说明，证明过程或演算步骤．17．解：（Ⅰ）由点,C B 的坐标可以得到34AOC π∠=，23AOB π∠=，…………………2分所以cos cos()COB AOC AOB ∠=∠+∠1()2222=-⨯--4=-；……6分（Ⅱ）因为c =23AOB π∠=，所以3C π=，所以2sin sin a b A B ===，………8分所以22sin 2sin()3a b A A π+=+-2sin()6A π=+，2(0)3A π<<，……………………11分所以当3A π=时，a b +最大，最大值是12分18．解：（Ⅰ）该校运动会开幕日共有13种选择，其中运动会期间至少两天空气质量优良的选择有：1日，2日，3日，5日，9日，10日，12日，所以运动会期间至少两天空气质量优良的概率是2713P =．…………………………………6分（Ⅱ）随机变量ξ所有可能取值有：0,1,2,3；………………………………………………7分(0)P ξ==113，(1)P ξ==613，(2)P ξ==613，(3)P ξ==113，……………………9分所以随机变量ξ的分布列是：随机变量ξ的数学期望是1661012313131313E ξ=⨯+⨯+⨯+⨯=2113．……………………12分 19．（Ⅰ）证明：在梯形ABCD 中，因为2AD DC CB ===，4AB =，4212cos 22CBA -∠==，所以60,ABC ∠=︒由余弦定理求得AC=90ACB ∠=︒即BC⊥又因为平面AEFC ⊥平面ABCD ，所以BC ⊥平面所以BC AG ⊥，………………………………………3分在矩形AEFC 中，tan 1AE AGE EG ∠==，4AGE π∴∠=tan 1CF CGF GF ∠==，4CGF π∠=，所以2CGF AGE π∠+∠=，即AG CG ⊥，所以AG ⊥平面BCG ；……………………………………………………………………………6分（Ⅱ）FC AC ⊥，平面AEFC ⊥平面ABCD ，所以FC ⊥平面ABCD ，以点C 为原点，,,CA CB CF 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则)(0,0,0),(0,2,0),1,0)C A B D-,G ，…………………………8分平面BCG 的法向量(3,0,GA =，设平面GCD 的法向量(,,)n x y z =，则0n CG n CD ⎧⋅=⎪⎨⋅=⎪⎩，从而00x z y +=⎧⎪-=，令1x =则(1,3,1)n =-，…………………………………………………………………………10分所以cos ,n GA <>==，…………………………………………………11分而二面角D —GCB 为钝角，故所求二面角的余弦值为．………………………………………………………………12分 20．解：（Ⅰ）当l 垂直于OD 时||AB 最小，因为||OD =2r ==，…………………………………2分因为圆1C 222:(0)x y r r +=>的一条直径是椭圆2C 的长轴，所以2a =，又点D 在椭圆22222:1(0)x y C a b a b +=>>上，所以291414b b+=⇒=，所以圆1C 的方程为224x y +=，椭圆2C 的方程为22143x y +=；………………………5分（Ⅱ）椭圆2C 的右焦点F 的坐标是(1,0)，当直线m 垂直于x 轴时，||PQ = ||4MN =，四边形PMQN 的面积S =当直线m 垂直于y 轴时，||4PQ =，||3MN =，四边形PMQN 的面积6S =，…………6分……………………10分当直线m 不垂直于坐标轴时，设n 的方程为(1)y k x =-(0)k ≠，此时直线m 的方程为1(1)y x k=--，圆心O 到直线m的距离为：d =，所以||PQ ==，…………8分将直线n 的方程代入椭圆2C 的方程得到：()22224384120k x k x k +-+-=，||MN =所以：四边形PMQN 的面积1||||2S PQ MN =⋅===∈，综上：四边形PMQN的面积的取值范围是．…………………………………………12分21．解：（Ⅰ）21221'()22x ax f x x a x x-+=+-=(0)x >，记2()221g x x ax =-+………1分（一）当0a ≤时，因为0x >，所以()10g x >>，函数()f x 在(0,)+∞上单调递增；……2分（二）当0a <≤时，因为24(2)0a =-≤△，所以()0g x ≥，函数()f x 在(0,)+∞上单调递增；…………………………………………………………………………………………………3分（三）当a >0()0x g x >⎧⎨>，解得x∈，所以函数()f x 在区间上单调递减，在区间(0,),()2a a +∞上单调递增．…………………………5分（Ⅱ）由（1）知道当(1a ∈时，函数()f x 在区间(0,1]上单调递增，所以(0,1]x ∈时，函数()f x的最大值是(1)22f a =-，对任意的a ∈，都存在0(0,1]x ∈使得不等式20()ln()f x a m a a +>-成立，等价于对任意的(1a ∈，不等式222ln ()a a m a a -+>-都成立，……………………………………6分即对任意的(1a ∈，不等式2ln (2)20a ma m a +-++>都成立，记2()ln (2)2h a ama m a =+-++，则(1)0h =，1(21)(1)'()2(2)a ma h a ma m a a --=+-+=，因为(1a ∈，所以210a a->，当1m ≥时，对任意(1a ∈，10ma ->，所以'()0h a >，即()h a 在区间上单调递增，()(1)0h a h >=成立；…………………………………………………………………………9分当1m <时，存在0(1a ∈使得当0(1,)a a ∈时，10ma -<，'()0h a <，()h a 单调递减，从而()(1)0h a h <=，所以(1a ∈时，()0h a >不能恒成立．综上：实数m 的取值范围是[1,)+∞．……………………………………………………………12分 22．解：AF 是圆的切线，且18,15AF BC ==，∴由切割线定理得到2218(15)12AF FB FC FB FB FB =⋅⇒=⋅+⇒=，…………………3分 ,AB AD ABD ADB =∴∠=∠，则,//FAB ABD AF BD ∠=∠∴，…………………………………………………………………6分又//AD FC ，∴四边形ADBF 为平行四边形．12,,18AD FB ACF ADB F ACAF ==∠=∠=∠∴==，//,18AE ADAD FC AE BC∴=-，解得8AE =。

江西省2015届高三数学理一轮复习备考试题：函数

江西省2015届高三数学一轮复习备考试题函数一、选择题1、（2014年江西高考）函数)ln()(2x x x f -=的定义域为A.)1,0(B. ]1,0[C. ),1()0,(+∞-∞D. ),1[]0,(+∞-∞ 2、（2013年江西高考）函数ln(1-x)的定义域为A ．（0,1） B.[0,1) C.(0,1] D.[0,1]3、（2012年江西高考）若函数211()21x x f x x x⎧+≤⎪=⎨>⎪⎩，则f(f(10)=A.lg101B.bC.1D.0 4、（崇义中学2015届高三上学期第一次月考）已知324log 0.3log 3.4log 3.615,5,,5a b c ⎛⎫=== ⎪⎝⎭则( )．A ．a b c >>B ．b a c >>C ．a c b >>D ．c a b >>5、（红色六校2015届高三第一次联考）已知函数⎩⎨⎧>≤+=0,10,2)(x nx x kx x f ()k R ∈，若函数()y f x k =+有三个零点，则实数k 的取值范围是（）A ．2k ≤B ．10k -<<C ．21k -≤<-D ．2k ≤-6、（井冈山中学2015届高三第一次月考）在222,log ,xy y x y x===，这三个函数中，当7、（乐安一中2015届高三上学期开学考试）学科网在下列区间中，函数f(x)＝e x＋4x －3的零点所在的区间( ) A ．(－14，0) B ．(0，14) C ．(14，12) D ．(12，34) 8、（南昌二中2015届高三上学期第一次考）下列函数中，在其定义域内既是奇函数又是减函数的是 ( ) A ．R x x y ∈-=,3 B ．R x x y ∈=,sin C ．R x xy ∈=-,31D ．R x x y ∈=,)21(9、（南昌三中2015届高三上学期第一次月考）已知y ＝f(2x)的定义域为[－1，1]，则y＝f(log 2x)的定义域为( )A ．[－1，1]B ．[12，2] C ．[1，2] D ．[2，4]10、（南昌市八一中学2015届高三8月月考）已知a ＞b ，函数f （x ）=（x ﹣a ）（x ﹣b ）的图象如图所示，则函数g （x ）=log a （x+b ）的图象可能为（）)()1(x f x f -=+，且在[1,0]-上单调递增，设)3(f a =， )2(f b =，(2)c f =-，则c b a ,,大小关系是( ).A.c ba >> B.bc a >> C.a c b >> D.a b c >>12、（遂川中学2015届高三上学期第一次月考）下列四个图中，函数可能是( )13、（2014届江西省高三4月模拟）函数lg(2)y x =-的定义域为A. （－2，0）B. （0，2）C. （－2，2）D. [2,2)-14、（南昌三中2014届高三第七次考试）若函数121)(+=x x f ，则该函数在()+∞∞-,上是（）A ．单调递减无最小值B ．单调递减有最小值C ．单调递增无最大值D ．单调递增有最大值 15、（吉安一中2014届高三下学期第一次模拟）已知10a b c >>>>，对以下不等式①a b c c > ②11abc c > ③11abc c ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭④1111abc c ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭⑤11log log cc a b>，其中成立的是（） A. ①②⑤B. ②③④C. ②③⑤D. ③④⑤二、解答题1、（2013年江西高考）已知函数1()=(1-2-)2f x a x ，a 为常数且>0a . (1) 证明：函数()f x 的图像关于直线1=2x 对称； (2) 若0x 满足00(())=f f x x ，但00()f x x ≠，则称0x 为函数()f x 的二阶周期点，如果()f x 有两个二阶周期点12,,x x 试确定a 的取值范围；(3) 对于（2）中的12,x x 和a ，设x 3为函数f （f （x ））的最大值点，A （x 1，f （f （x 1））），B （x 2，f （f （x 2））），C （x 3，0），记△ABC 的面积为S （a ），讨论S （a ）的单调性. 2、（崇义中学2015届高三上学期第一次月考）定义在R 上的奇函数f(x)有最小正周期2，x ∈(0,1)时，()142+=x x x f(1)求f(x)在 []1,1-上的解析式；（4分）(2)讨论f(x)在（0,1）上的单调性。

2015届南昌市高三调研考试数学卷试题分析

2014届江西省南昌市高三调研考试数学卷试卷分析孙建民章建荣周启新郑永盛饶云松肖英文一、试卷的基本情况1．试卷形式考卷采用闭卷考试的形式。

试卷由选择、填空和解答三大部分组成，其中，选择题共12小题，共60分；填空题共4小题，共20分；解答题共7小题(期中22,23是2选1的选做题)，共70分；全卷满分150分，考试时间120分钟。

2. 命题意图：参照全国新课标1卷的命题特点，立足于考查学生在第一轮复习阶段的基础知识、基本技能、基本数学思想与方法,试题有一定的覆盖面、一定的基础性、一定的层次性，发挥试卷的调研诊断功能，同时也希望能肯定、鼓励高三离毕业班师生对数学学科的投入和热情。

加强对学生运算能力、思维能力、空间想象能力和分析问题解决问题的考查；加强考查学生用数学知识和思维方法分析解决现实生活的有关问题的应用能力。

试卷力求吻合高考的方向，有利于高三复习方向及复习节奏的稳定。

在试卷的形式上，分理科卷和文科卷，在试题的题型结构上与2014年全国新课标1卷基本保持一致。

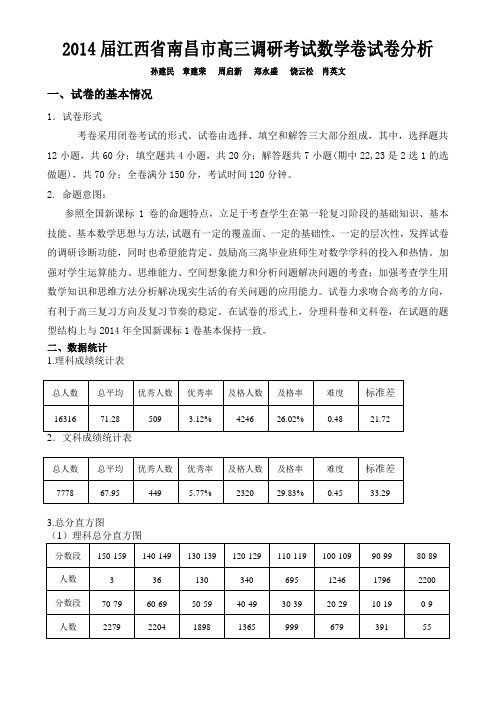
二、数据统计1.理科成绩统计表总人数总平均优秀人数优秀率及格人数及格率难度标准差1631671.28509 3.12%424626.02%0.4821.722．文科成绩统计表总人数总平均优秀人数优秀率及格人数及格率难度标准差777867.95449 5.77%232029.83%0.4533.293.总分直方图（1）理科总分直方图分数段150-159140-149130-139120-129110-119100-10990-9980-89人数336130340695124617962200分数段70-7960-6950-5940-4930-3920-2910-190-9人数227922041898136599967939155数学（理科）直方图5001000150020002500150140-149130-139120-129110-119100-10990-9980-8970-7960-6950-5940-4930-3920-2910-190-9系列1（2）文科总分直方图分数段 150-159 140-149 130-139 120-129 110-119 100-109 90-99 80-89 人数 3 37 104 239 462 644 816 754 分数段 70-79 60-69 50-59 40-49 30-39 20-29 10-19 0-9 人数677655577589624646507119数学（文科）直方图100200300400500600700800900150140-149130-139120-129110-119100-10990-9980-8970-7960-6950-5940-4930-3920-2910-190-9系列14..各题得分情况统计表（1）理科客观题数据分析8.26%76.74%8.56% 6.36%0%10%20%30%40%50%60%70%80%90%ABCD3.33% 3.16%14.62%78.74%0%10%20%30%40%50%60%70%80%90%ABCD第1题第2题3.33% 5.82%7.43%83.28%0%10%20%30%40%50%60%70%80%90%ABCD8.86%6.42%69.46%15.05%0%10%20%30%40%50%60%70%80%ABCD第3题第4题1.68%6.10%48.58%42.42%0%10%20%30%40%50%60%ABCD第5题第6题第7题第8题第9题第10题第11题第12题（2）理科主观题数据分析题号一二17 18 19 20 21 22 考试人数1631616316163161631616316163161631616316平均分40.32 7.31 7.77 3.09 3.79 3.11 2.06 3.91 优秀人数548235664417202085186971704优秀率33.60% 2.18%39.48% 4.41%12.78% 1.14%0.59%10.44%及格人数1015920398086151327712992402187及格率62.26%12.50%49.56%9.27%16.98% 1.83% 1.47%13.40%难度0.67 0.37 0.65 0.26 0.32 0.26 0.17 0.39 标准差10.63 3.96 3.43 3.00 3.38 2.25 1.63 2.34（3）文科客观题数据分析第1题第2题第3题第4题第5题第6题第7题第8题第9题第10题第11题第12题（4）文科主观题数据分析题号一二 16 17 18 19 20 21总人数 7453 7453 7453 7453 7453 7453 7453 7453 总平均 28.83 8.24 4.76 3.49 6.84 3.73 2.28 2.44 优秀人数 7 187 1271 434 3193 376 295 308 优秀率 0.09% 2.51% 17.05% 5.82% 42.84% 5.04% 3.96% 4.13% 及格人数 2100 1709 1926 584 3818 1306 527 475 及格率 26.12% 22.93% 25.84% 7.84% 51.23% 17.52% 7.07% 6.37% 难度 0.60 0.41 0.40 0.29 0.57 0.31 0.19 0.24 标准差 7.01 4.51 3.85 3.12 4.40 3.16 2.31 2.40二、典型错误分析17题：(1）失分多因把周期误为2π或2π，而算错ω的值；（2）用角A,B （或边a ，b ）列出周长表达式后，不推导,便由A ＝B （或a ＝b ）求得周长最值，被扣分；用余弦定理得到a2＋b2＋ab ＝3 ⇒a b≤1，再由a ＋b≥2ab 误推得a ＋b≤2而推得周长最值，被扣分； 18题：（理科）该题考查数列中n S 与n a 的关系，等差、等比数列的概念以及数列求和，重在考查基础知识和通性通法，基本会用n S 与n a 的关系式，转化到数列{}n a 的递推关系，从而证得第（1）问，但第（2）问做得很不理想，主要有下面三个方面错误：一是审题时将12.a a 误认为12a a ⨯；二是由1S 求得13a =或11a =-，但同学没发现1a 与5a 同号，没将1a 舍弃；三是弄懂了数列{}n a ，但在求n S 时，只考虑了5n …时268n S n n =-+，没考虑当14n剟时的情形。

2015高考数学(文)一轮复习题有答案解析阶段示范性金考卷二

阶段示范性金考卷二一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知i 2＝－1，则复数z ＝i3i －i 2014在复平面内对应的点位于( )A ．第一象限C ．第三象限解析：z ＝－i i ＋1＝－i (1－i )(1＋i )(1－i )－12)．答案：Dsin(π＋θ)＝3，则cos(π－2θ)＝( )B ．－1225 D.725cos θ＝35，cos(π－2θ)＝－cos2θ，由1＝2×(35)2－1＝－725，所以cos(π－2θ)＝－cos2θ＝725，故选D.答案：D3．已知向量a ＝(3，－1)，向量b ＝(sin α，cos α) ，若a ⊥b ，则sin 2α－2cos 2α的值为( )A.710B ．－1710C.1710 D ．－710解析：由a ⊥b 可得3sin α＝cos α，故tan α＝13；sin 2α－2cos 2α＝sin 2α－2cos 2αsin 2α＋cos 2α＝tan 2α－2tan 2α＋1＝－1710. 答案：B4．已知正三角形ABC 的边长为1，点P 是AB 边上的动点，点Q 是AC 边上的动点，且AP →＝λAB →，AQ →＝(1－λ)AC →，λ∈R ，则BQ →·CP →的最大值为( )B. －32 D. －38解析：BQ ·CP ＝(BA ＋AQ )·(CA ＋AP →) ＝[BA →＋(1－λ)AC →]·(CA →＋λAB →)＝[AB →·AC →－λAB 2→＋(λ－1)AC 2→＋λ(1－λ)AB →·AC →] ＝(λ－λ2＋1)×1×1×cos60°－λ＋λ－1＝12(－λ2＋λ)－12 ＝－12(λ－12)2－38(λ≤R )．当λ＝12时，则BQ →·CP →的最大值为－38.故选D 项．答案：D5．将函数y ＝sin2x 位，所得函数图象对应的解析式为(A ．y ＝sin(2x －π4)＋1 C ．y ＝2sin 2x解析：函数y ＝sin2x －π4)1个单位，所得函数图象(1－2sin 2x )＋1＝2sin 2x ，故选C.)(ω>0，－π2<φ<π2) 的图象关于直线x φ＝( )．－π3 B ．－π6 C.π6D.π3解析：π3－π12≥14×2πω，解得ω≥2，故当ω取最小值时，f (x )＝sin(2x ＋φ)，根据f (π12)＝0，得sin(π6＋φ)＝0，由于－π2<φ<π2，所以φ＝－π6.答案：B7．已知向量a ，b 满足a ·(a ＋b )＝3，且|a |＝2，|b |＝1，则向量a 与b 的夹角为( )A.π6B.π3C.2π3D.5π6解析：由a ·(a ＋b )＝3得，|a |21.cos 〈a ，b 〉＝a ·b |a |·|b |＝－12.故向量a 答案：C8．若函数f (x )＝sin(2x －π4)＋间为( )B ．[0，π2] D ．[－π2，0]x ＋3π4)＝sin(2x －π4)－cos(2x －π4)＝2sin(2cos x 的一个单调递减区间是[0，π]，，π2]．答案：B9．已知函数f (x )＝sin(ωx ＋φ)(x ∈R )(ω>0，|φ|<π2)的部分图象如图所示，如果x 1，x 2∈(－π6，π3)，且f (x 1)＝f (x 2)，则f (x 1＋x 2)＝( )A.12 C.32解析：由图象可知T ＝2[π3－(x ＋φ)，又f (x )过点(－π6，0)，|φ|<π2，．∵x 1，x 2∈(－π，π)，且f (x 1)＝f 212＝π6，且满足|3AM →－AB →－AC →|＝( )B.14C.13D.12解析：由|3AM →－AB →－AC →|＝0得→＋AC →)．如图，AB →＋AC →＝AD →，由于＝13AD →，所以S △ABM ＝13S △ABD ＝13S △ABC .＝35，则sin(2x ＋π6)的值为( ) B.1325 D.725x cos π6－cos x sin π6＝35，32sin x －12cos x ＝35，两边平方得12sin 2x ＋14－34sin2x ＝925，∴12·1－cos2x 2＋14－34sin2x ＝925，即sin2x ·32＋cos2x ·12＝725，∴sin(2x ＋π6)＝725.答案：D12．设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若3(a cos B＋b cos A )＝2c sin C ，a ＋b ＝4(a ，b 在变化)，且△ABC 的面积最大值为3，则此时△ABC 的形状是( ) A ．锐角三角形 B ．直角三角形 C ．等腰三角形D ．正三角形解析：由正弦定理得3(sin A cos B ＋cos A sin B )＝2sin 2C ，即3sin(A ＋B )＝3sin C ＝2sin 2C ，即sin C ＝3，积S ＝12ab sin C ＝34ab ≤34(a ＋b 2)2此时a ＝b ＝2，选择C.答案：C二、填空题(本大题共4在题中的横线上)，x＝(x,1)，其中x >0，若(a －2b )∥(2a ＋，2a ＋b ＝(16＋x ，x ＋1)，由题意得(8x 2＝16，又∵x >0，∴x ＝4.，OA →＝a －b ，OB →＝a ＋b ，若△OAB 是以O 为直角顶点的等腰直角三角形，则△OAB 的面积为________．解析：由题意得，|a |＝1，又△OAB 是以O 为直角顶点的等腰直角三角形，所以OA →⊥OB →，|OA →|＝|OB →|.由OA →⊥OB →得(a －b )·(a ＋b )＝|a |2－|b |2＝0，所以|a |＝|b |，由|OA →|＝|OB →|得|a －b |＝|a ＋b |，所以a ·b ＝0.所以|a ＋b |2＝|a |2＋|b |2＝2，所以|OB →|＝|OA →|＝2，故S △OAB ＝12×2×2＝1.答案：115．[2013·海淀区期末练习]函数f (x )＝A sin(2x ＋φ)(A >0，φ∈R )的部分图象如图所示，那么f (0)＝________.解析：由图可知，A ＝2，f (π)＝2， )＝1，＝－π6＋2k π(k ∈Z )， π)＝2×(－12)＝－1. |a |＝|b |＝|c |＝1，则a ·(b ＋c )＝________.解析：依题意得|3a |＝3，|4b |＝4，|5c |＝5，又3a ＋4b ＋5c ＝0，所以向量3a 、4b 、5c 首尾相接构成一个直角三角形，因此有a ·b ＝0，a ·(b ＋c )＝a ·b ＋a ·c ＝a ·c ＝|a |·|c |cos θ＝cos θ＝－35(其中θ为向量a 与c 的夹角)．答案：－35三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)[2014·河北高三质检]已知在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且a cos C ＋32c ＝b .(1)求角A ；(2)若a ＝1，且3c －2b ＝1解：(1)由a cos C ＋32c ＝b ，得∵sin B ＝sin(A ＋C )＝sin A cos C ＋∴32sin C ＝cos A sin C ，又sin Cb ＝a ，即3sin C －2sin B ＝sin A . ∴B ＋π6＝π3，即B ＝π6.18．(本小题满分12分)已知函数f (x )＝3sin x cos x ＋sin 2x －32，将函数f (x )的图象向左平移π6个单位长度后得函数g (x )的图象，设△ABC 的三个角A ，B ，C 的对边分别为a ，b ，c ；(1)若f (C )＝0，c ＝6,2sin A ＝sin B ，求a ，b 的值．(2)若g (B )＝0且m ＝(cos A ，cos B )，n ＝(1，sin A －cos A tan B )，求m ·n 的取值范围．解：(1)f (x )＝3sin x cos x ＋sin 2x －32＝32sin2x ＋12(1－cos2x )－32＝32sin2x －12cos2x －1＝sin(2x －π6)－1.f (C )＝sin(2C －π6)－1＝0∵2sin A ＝sin B 由余弦定理知：a 2＋b 2－2由①②解得：a ＝23，b ＝(2)由题意知g (x )＝sin(2x ＋π6)sin(2B ＋π6)＝1，∴B ＝π6，－33cos A )＝12cos A ＋32sin A ＝sin(A ＋π6)A ＋π6∈(π6，π)．＋π6)(0,1]．19．(本小题满分12分)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，已知(2a ＋b )cos C ＋c cos B ＝0.(1)求角C 的大小；(2)若c ＝4，求使△ABC 面积取得最大值时的a ，b 的值．解：(1)由已知及由正弦定理得(2sin A ＋sin B )cos C ＋sin C cos B ＝0，所以2sin A cos C ＋(sin B cos C ＋sin C cos B )＝0，所以sin(B ＋C )＋2sin A cos C ＝0，即sin A ＋2sin A cos C ＝0.因为0<A <π，sin A >0，所以cos C ＝－12，所以C ＝2π3.(2)因为△ABC 的面积为S ＝12ab sin C ＝34ab ，若使得S 取得最大值，只需要ab 取得最大值．由余弦定理可得，c 2＝a 2＋b 2－即16＝a 2＋b 2＋ab ≥3ab ，故ab故使得△ABC 20．(本小题满分12分)－12(的图象上两相邻对称轴间的距离为π4.的图象向右平移π8个单位，再将所得图象上各点的)，得到函数y ＝g (x )的图象，求g (cos 2ωx －12＝32sin2ωx ＋cos2ωx ＋12－12＝sin(2ωx ＋π6)，由题意知f (x )的最小正周期T ＝π2，T ＝2π2ω＝πω＝π2，ω＝2，所以f (x )＝sin(4x ＋π6)．由2k π＋π2≤4x ＋π6≤2k π＋3π2(k ∈Z )，得k π2＋π12≤x ≤k π2＋π3(k ∈Z )，所以函数f (x )的单调递减区间为[k π2＋π12，k π2＋π3](k ∈Z )．(2)将f (x )的图象向右平移π8个单位后，得到y ＝sin[4(x －π8)＋π6]＝sin(4x －π3)的图象，再将所得图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，得到y ＝sin(2x －π3)．因为0≤x ≤π2，所以－π3≤2x －π3≤当2x －π3＝－π3，即x ＝0时，g (当2x －π3＝π2，即x ＝5π12时，g (x )21．(本小题满分12分)[2014·长沙一模]风景秀美的凤凰湖畔有四棵高大的银杏树，记作A 、B 、P 、Q ，欲测量P 、Q 两棵树和A 、P 两棵树之间的距离，但湖岸部分地方围有铁丝网不能靠近，现可测得A 、B 两点间的距离为100 m ，如图，同时也能测量出∠P AB ＝75°，∠QAB ＝45°，∠PBA ＝60°，∠QBA ＝90°，则P 、Q 两棵树和A 、P 两棵树之间的距离各为多少？解：在△P AB 中，∠APB ＝180°－(75°＋60°)＝45°，由正弦定理得AP sin60°＝100sin45°，解得AP ＝50 6.在△QAB 中，∠ABQ ＝90°，∴AQ ＝100 2.又∠P AQ ＝75°－45°＝30°，由余弦定理得PQ 2＝AP 2＋AQ 2－2AP ·AQ ·cos ∠P AQ ＝(506)2＋(1002)2－2×506×1002×∴PQ ＝5000＝50 2.∴P 、Q 两棵树之间的距离为为50 6 m.22．(本小题满分12分)设角A 知向量m ＝(sin A ＋sin C ，sin B －sin m ⊥n . 2B 2)，求|s ＋t |的取值范围．C )＋(sin 2B －sin A sin B )＝0， a ，b ，c 为内角A ，B ，C ab ，＝12，∵0<C <π，∴C ＝π3.(2)∵s ＋t ＝(cos A,2cos 2B 2－1)＝(cos A ，cos B )，∴|s ＋t |2＝cos 2A ＋cos 2B＝cos 2A ＋cos 2(2π3－A )＝1＋cos2A 2＋1＋cos (4π3－2A )2＝14cos2A －34sin2A ＋1 ＝－12sin(2A －π6)＋1，∵0<A <2π3，∴－π6<2A －π6<7π6，∴－12<sin(2A －π6)≤1，∴12≤|s ＋t |2<54，∴22≤|s ＋t新课标第一网系列资料。

高考数学一轮总复习第2章函数的概念与基本初等函数(ⅰ)第9节函数模型及其应用跟踪检测文含解析

第二章函数的概念与基本初等函数(Ⅰ)第九节函数模型及其应用A 级·基础过关|固根基|1.一根蜡烛长20 cm ，点燃后每小时燃烧5 cm ，燃烧时剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为图中的( )解析：选B 由题意知h ＝20－5t(0≤t≤4)，图象应为B 项．2．某家具的标价为132元，若降价以九折出售(即优惠10%)，仍可获利10%(相对进货价)，则该家具的进货价是( )A ．118元B ．105元C ．106元D ．108元解析：选D 设进货价为a 元，由题意知132×(1－10%)－a ＝10%·a ，解得a ＝108.3．根据有关资料，围棋状态空间复杂度的上限M 约为3361，而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N最接近的是( )(参考数据：lg 3≈0.48) A ．1033B ．1053C ．1073D ．1093解析：选D M≈3361，N≈1080，M N ≈33611080，则lg M N ≈lg 33611080＝lg 3361－lg 1080＝361lg 3－80≈93.∴M N≈1093. 4．某汽车销售公司在A ，B 两地销售同一种品牌的汽车，在A 地的销售利润(单位：万元)为y 1＝4.1x－0.1x 2，在B 地的销售利润(单位：万元)为y 2＝2x ，其中x 为销售量(单位：辆)，若该公司在两地共销售16辆该种品牌的汽车，则能获得的最大利润是( )A ．10.5万元B ．11万元C ．43万元D ．43.025万元解析：选C 设公司在A 地销售该品牌的汽车x 辆，则在B 地销售该品牌的汽车(16－x)辆．所以利润y ＝4.1x －0.1x 2＋2(16－x)＝－0.1x 2＋2.1x ＋32＝－0.1⎝⎛⎭⎪⎫x －2122＋0.1×2124＋32.因为x∈[0，16]，且x∈N，所以当x ＝10或11时，总利润取得最大值43万元．5．设某公司原有员工100人从事产品A 的生产，平均每人每年创造产值t 万元(t 为正数)．公司决定从原有员工中分流x(0＜x ＜100，x∈N *)人去进行新开发的产品B 的生产．分流后，继续从事产品A 生产的员工平均每人每年创造产值在原有的基础上增长了1.2x%.若要保证产品A 的年产值不减少，则最多能分流的人数是( )A ．15B ．16C ．17D ．18解析：选B 由题意，分流前每年创造的产值为100t 万元，分流x 人后，每年创造的产值为(100－x)(1＋1.2x%)t 万元，则由⎩⎪⎨⎪⎧0＜x ＜100，x∈N *，（100－x ）（1＋1.2x%）t≥100t，解得0＜x≤503.因为x∈N *，所以x 的最大值为16.6．当生物死亡后，其体内原有的碳14的含量大约每经过5 730年衰减为原来的一半，这个时间称为“半衰期”．当死亡生物体内的碳14含量不足死亡前的千分之一时，用一般的放射性探测器就测不到了．若某死亡生物体内的碳14用该放射性探测器探测不到，则它经过的“半衰期”个数至少是( )A ．8B ．9C ．10D ．11解析：选C 设该死亡生物体内原来的碳14的含量为1，则经过n 个“半衰期”后的含量为⎝ ⎛⎭⎪⎫12n，由⎝ ⎛⎭⎪⎫12n＜11 000，得n≥10，所以，若某死亡生物体内的碳14用该放射性探测器探测不到，则它至少需要经过10个“半衰期”．7．(2019届北京东城模拟)小菲在学校选修课中了解到艾宾浩斯遗忘曲线，为了解自己记忆一组单词的情况，她记录了随后一个月的有关数据，绘制图象，拟合了记忆保持量f(x)与时间x(天)之间的函数关系f(x)＝⎩⎪⎨⎪⎧－720x ＋1，0<x≤1，15＋920x－12，1<x≤30.某同学根据小菲拟合后的信息得到以下结论： ①随着时间的增加，小菲的单词记忆保持量降低； ②9天后，小菲的单词记忆保持量低于40%； ③26天后，小菲的单词记忆保持量不足20%.其中正确结论的序号有________．(请写出所有正确结论的序号)解析：由函数解析式可知f(x)随着x 的增加而减少，故①正确；当1<x≤30时，f(x)＝15＋920x －12，则f(9)＝15＋920×9－12＝0.35，即9天后，小菲的单词记忆保持量低于40%，故②正确；f(26)＝15＋920×26－12>15，故③错误．答案：①②8.有一批材料可以建成200 m 长的围墙，如果用此材料在一边靠墙的地方围成一块矩形场地，中间用同样的材料隔成三个面积相等的矩形(如图所示)，则围成的矩形场地的最大面积为________ m 2.(围墙厚度不计)解析：设围成的矩形场地的长为x m ，则宽为200－x 4 m ，则S ＝x·200－x 4＝14(－x 2＋200x)＝－14(x －100)2＋2 500.∴当x ＝100时，S max ＝2 500 m 2. 答案：2 5009．已知投资x 万元经销甲商品所获得的利润为P ＝x 4；投资x 万元经销乙商品所获得的利润为Q ＝a2x(a ＞0)．若投资20万元同时经销这两种商品或只经销其中一种商品，使所获得的利润不少于5万元，则a的最小值为________．解析：设投资乙商品x 万元(0≤x≤20)，则投资甲商品(20－x)万元．则利润分别为Q ＝a 2x(a ＞0)，P ＝20－x4，由题意得P ＋Q≥5，0≤x≤20时恒成立，则化简得a x ≥x2，在0≤x≤20时恒成立．(1)x ＝0时，a 为一切实数； (2)0＜x≤20时，分离参数a≥x2，0＜x≤20时恒成立，所以a≥5，a 的最小值为 5. 答案： 510．已知某服装厂生产某种品牌的衣服，销售量q(x)(单位：百件)关于每件衣服的利润x(单位：元)的函数解析式为q(x)＝⎩⎪⎨⎪⎧1 260x ＋1，0＜x≤20，90－35x ，20＜x≤180，求该服装厂所获得的最大效益是多少元？解：设该服装厂所获效益为f(x)元，则f(x)＝100xq(x)＝⎩⎪⎨⎪⎧126 000x x ＋1，0＜x≤20，100x （90－35x ），20＜x≤180.当0＜x≤20时，f(x)＝126 000x x ＋1＝126 000－126 000x ＋1，f(x)在区间(0，20]上单调递增，所以当x ＝20时，f(x)有最大值120 000；当20＜x≤180时，f(x)＝9 000x －3005·x x ，则f′(x)＝9 000－4505·x ，令f′(x)＝0，所以x ＝80.当20＜x ＜80时，f′(x)＞0，f(x)单调递增；当80≤x≤180时，f′(x)≤0，f(x)为单调递减，所以当x ＝80时，f(x)有极大值，也是最大值240 000.由于120 000＜240 000.故该服装厂所获得的最大效益是240 000元. B 级·素养提升|练能力|11.将甲桶中的a L 水缓慢注入空桶乙中，t min 后甲桶中剩余的水量符合指数衰减曲线y ＝ae nt.假设过5 min 后甲桶和乙桶的水量相等，若再过m min 甲桶中的水只有a4L ，则m 的值为( )A ．5B ．8C ．9D ．10解析：选A ∵5 min 后甲桶和乙桶的水量相等，∴函数y ＝f(t)＝ae n t 满足f(5)＝ae 5n＝12a ，可得n ＝15ln 12，∴f(t )＝a·⎝ ⎛⎭⎪⎫12t 5，因此，当k min 后甲桶中的水只有a4 L 时，f(k)＝a·⎝ ⎛⎭⎪⎫12k 5＝14a ，即⎝ ⎛⎭⎪⎫12k 5＝14，∴k ＝10，由题可知m ＝k －5＝5.12．“好酒也怕巷子深”，许多著名品牌是通过广告宣传进入消费者视线的．已知某品牌商品靠广告销售的收入R 与广告费A 之间满足关系R ＝a A(a 为常数)，广告效应为D ＝a A －A.那么精明的商人为了取得最大广告效应，投入的广告费应为________．(用常数a 表示)解析：令t ＝A(t ≥0)，则A ＝t 2，所以D ＝at －t 2＝－t －12a 2＋14a 2，所以当t ＝12a ，即A ＝14a 2时，D取得最大值．答案：14a 213．(2019年北京卷)李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒．为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x 元．每笔订单顾客网上支付成功后，李明会得到支付款的80%.(1)当x ＝10时，顾客一次购买草莓和西瓜各1盒，需要支付________元；(2)在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x 的最大值为________．解析：(1)当x ＝10时，一次购买草莓和西瓜各1盒，共60＋80＝140(元)，由题可知顾客需支付140－10＝130(元)．(2)设每笔订单金额为m 元，当0≤m＜120时，顾客支付m 元，李明得到0.8m 元，0.8m ≥0.7m ，显然符合题意，此时x ＝0；当m≥120时，根据题意得(m －x)80%≥m ×70%，所以x≤m8，而m≥120，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x≤⎝ ⎛⎭⎪⎫m 8min ，而⎝ ⎛⎭⎪⎫m 8min＝15，所以x≤15.综上，当0≤x≤15时，符合题意，所以x 的最大值为15.答案：(1)130 (2)1514．十九大提出对农村要坚持精准扶贫，至2020年底全面脱贫．现有扶贫工作组到某山区贫困村实施脱贫工作，经摸底排查，该村现有贫困农户100家，他们均从事水果种植，2017年底该村平均每户年纯收入为1万元．扶贫工作组一方面请有关专家对水果进行品种改良，提高产量；另一方面，抽出部分农户从事水果包装、销售工作，其人数必须小于种植的人数．从2018年初开始，若该村抽出5x 户(x∈Z，1≤x≤9)从事水果包装、销售工作，经测算，剩下从事水果种植的农户的年纯收入每户平均比上一年提高x20，而从事包装、销售的农户的年纯收入每户平均为⎝ ⎛⎭⎪⎫3－14x 万元(参考数据：1.13＝1.331，1.153≈1.521，1.23＝1.728)．(1)至2020年底，为使从事水果种植的农户能实现脱贫(每户年均纯收入不低于1万6千元)，至少要抽出多少户从事包装、销售工作？(2)至2018年底，该村每户年均纯收入能否达到1.35万元？若能，请求出从事包装、销售的户数；若不能，请说明理由．解：(1)至2020年底，种植户平均收入＝（100－5x ）⎝ ⎛⎭⎪⎫1＋x 203100－5x≥1.6，即⎝ ⎛⎭⎪⎫1＋x 203≥1.6，即x≥20(31.6－1)．由题中所给数据，知1.15＜31.6＜1.2，所以3＜20(31.6－1)＜4. 所以x 的最小值为4，此时5x≥20，即至少要抽出20户从事包装、销售工作． (2)至2018年底，假设该村每户年均纯收入能达到1.35万元．每户的平均收入为5x ⎝ ⎛⎭⎪⎫3－14x ＋（100－5x ）⎝ ⎛⎭⎪⎫1＋x 20100≥1.35，化简得3x 2－30x ＋70≤0.因为x∈Z 且1≤x≤9，所以x∈{4，5，6}．所以当从事包装、销售的户数达到20至30户时，能达到，否则，不能．。

江西省南昌市2015高三第一次模拟测试数学理试卷

江西省南昌市2015高三第一次模拟测试数学理试卷一. 选择题（本大题共12小题，每小题5分，满分60分. 在每小题给出的四个选项中，只有一项是符合题目要求的. ） 1. 已知i 为虚数单位，则复数12iz i+=在复平面内对应的点位于（） A. 第一象限B. 第二象限C. 第三象限D. 第四象限2. 若集合{}1381x x A =≤≤，(){}22log 1x x x B =->，则A B =（） A. (]2,4 B. []2,4 C. ()[],00,4-∞D. ()[],10,4-∞-3. 如图，在正四棱柱1111CD C D AB -A B 中，点P 是面1111C D A B 内一点，则三棱锥CD P -B 的正视图与侧视图的面积之比为（） A. 1:1B. 2:1C. 2:3D. 3:24. 已知过定点()2,0P 的直线l与曲线y =A ，B 两点，O 为坐标原点，当∆AOB 的面积取到最大值时，直线l 的倾斜角为（）A. 150B. 135C. 120D. 不存在5. 已知实数x ，y 满足1040x y x y y m +-≥⎧⎪+-≤⎨⎪≥⎩，若目标函数2z x y =+的最大值与最小值的差为2，则实数m 的值为（） A. 4B. 3C. 2D. 12-6. 在C ∆AB 中，角A ，B ，C 所对的边分别是a ，b ，c ，若1c =，45B =，3cos 5A =，则b 等于（）A. 53B.107C. 57D.147. 以坐标原点为对称中心，两坐标轴为对称轴的双曲线C 的一条渐近线倾斜角为3π，则双曲线C 的离心率为（）A. 2B. 2或3C.3D. 28. 如图所示程序框图，其功能是输入x 的值，输出相应的y 值. 若要使输入的x 值与输出的y 值相等，则这样的x 值有（）A. 2个B. 3个C. 4个D. 5个9. 给出下列命题：①若()523450123451x a a x a x a x a x a x -=+++++，则1234532a a a a a ++++=②α，β，γ是三个不同的平面，则“γα⊥，γβ⊥”是“//αβ”的充分条件③已知1sin 63πθ⎛⎫-= ⎪⎝⎭，则7cos 239πθ⎛⎫-= ⎪⎝⎭其中正确命题的个数为（） A. 0B. 1C. 2D. 310. 如图，(),x yM M M ，(),x y N N N 分别是函数()()sin f x x ωϕ=A +（0A >，0ω>）的图象与两条直线1:l y m =，2:l y m =-（0m A ≥≥）的两个交点，记S x x N M =-，则()S m 图象大致是（）A.B.C.D.11. 设无穷数列{}n a ，如果存在常数A ，对于任意给定的正数ε（无论多小），总存在正整数N ，使得n >N 时，恒有n a ε-A <成立，就称数列{}n a 的极限为A . 则四个无穷数列：①(){}12n-⨯；②()()11111335572121n n ⎧⎫⎪⎪+++⋅⋅⋅+⎨⎬⨯⨯⨯-+⎪⎪⎩⎭；③231111112222n -⎧⎫++++⋅⋅⋅+⎨⎬⎩⎭；④{}231222322n n ⨯+⨯+⨯+⋅⋅⋅+⨯，其极限为2共有（） A. 4个B. 3个C. 2个D. 1个12. 设函数()()()222ln 2f x x a x a =-+-，其中0x >，R a ∈，存在0x 使得()045f x ≤成立，则实数a 的值为（） A. 15B. 25C. 12D. 1二. 填空题（本大题共4小题，每小题5分，共20分. ）13. a ，b ，c ，d 四封不同的信随机放入A ，B ，C ，D 4个不同的信封里，每个信封至少有一封信，其中a 没有放入A 中的概率是 .14. 已知直三棱柱111C C AB -A B 中，C 90∠BA =，侧面11CC B B 的面积为2，则直三棱柱111C C AB -A B 外接球表面积的最小值为 .15. 已知三角形C AB 中，C AB =A ，C 4B =，C 120∠BA =，3C BE =E ，若P 是C B 边上的动点，则AP⋅AE 的取值范围是 .16. 已知函数(),01lg ,0ax f x x x x ⎧≤⎪=-⎨⎪>⎩，若关于x 的方程()0f f x =⎡⎤⎣⎦有且只有一个实数解，则实数a 的取值范围为 .三. 解答题（本大题共6小题，共70分. 解答应写出文字说明. 证明过程或演算步骤. ）17. （本小题满分12分）已知等差数列{}n a 的前n 项和为n S ，11a =，36S =，正项数列{}n b 满足1232nSn bb b b ⋅⋅⋅=.()1求数列{}n a ，{}n b 的通项公式；()2若n n b a λ>对n *∈N 均成立，求实数λ的取值范围.18. （本小题满分12分）某市教育局为了了解高三学生体育达标情况，对全市高三学生进行了体能测试，经分析，全市学生体能测试成绩X 服从正态分布()280,σN （满分为100分），已知()750.3P X <=，()950.1P X ≥=，现从该市高三学生中随机抽取三位同学.()1求抽到的三位同学该次体能测试成绩在区间[)80,85，[)85,95，[]95,100各有一位同学的概率；()2记抽到的三位同学该次体能测试成绩在区间[]75,85的人数为ξ，求随机变量ξ的分布列和数学期望ξE .19. （本小题满分12分）如图，C A 是圆O 的直径，B . D是圆O 上两点，C 2C 2CD 2A =B ==，PA ⊥圆O 所在的平面，13BM =BP .()1求证：C //M 平面D PA ；()2若C M 与平面C PA 求AP 的值.20. （本小题满分12分）已知圆:E 221924x y ⎛⎫+-= ⎪⎝⎭经过椭圆C :22221x y a b+=（0a b >>）的左. 右焦点1F . 2F ，且与椭圆C 在第一象限的交点为A ，且1F ，E ，A 三点共线. 直线l 交椭圆C 于M ，N 两点，且λMN =OA （0λ≠）.()1求椭圆C 的方程；()2当三角形AMN 的面积取到最大值时，求直线l 的方程.21. （本小题满分12分）已知函数()()2ln 12xf x ax x =+-+（0a >）. ()1当12a =时，求()f x 的极值； ()2若1,12a ⎛⎫∈⎪⎝⎭，()f x 存在两个极值点1x ，2x ，试比较()()12f x f x +与()0f 的大小； ()3求证：()12!n n en ->（2n ≥，n ∈N ）.请考生在第22-24题中任选一题作答，如果多做，则按所做的第一题计分. 22. （本小题满分10分）选修4-1：几何证明选讲如图所示，PA 为圆O 的切线，A 为切点，PO 交圆O 于B ，C 两点，20PA =，10PB =，C ∠BA 的角平分线与C B 和圆O 分别交于点D 和E .()1求证：C C AB⋅P =PA⋅A ； ()2求D A ⋅AE 的值.23. （本小题满分10分）选修4-4：坐标系与参数方程以坐标原点为极点，以x 轴的非负半轴为极轴建立极坐标系，已知曲线C 的参数方程为x t y t⎧=⎪⎨=⎪⎩（t 为参数）. ()1曲线C 在点()1,1处的切线为l ，求l 的极坐标方程； ()2点A的极坐标为4π⎛⎫⎪⎝⎭，且当参数[]0,t π∈时，过点A 的直线m 与曲线C 有两个不同的交点，试求直线m 的斜率的取值范围.24. （本大题满分10分）选修4-5：不等式选讲已知函数()f x x x a =-（R a ∈）.()1若2a =，解关于x 的不等式()f x x <；()2若对任意的(]0,4x ∈都有()4f x <，求a 的取值范围.参考答案一. 选择题二. 填空题13. 34 14. π4 15. 210[,]33- 16. ),0()0,1(+∞- 三. 解答题17. （1）解：等差数列}{n a ，11=a ，63=S ，1=∴d ，故n a n =………3分⎪⎩⎪⎨⎧=⋅⋅⋅⋅=⋅⋅⋅⋅--)2(2)1(211321321 n n S n Sn b b b b b b b b ，)2()1(÷得na S S n n n nb 2221===--)2(≥n ， 222111===S b ,满足通项公式，故n n b 2=………7分（2）设n n a b >λ恒成立nn2>⇒λ恒成立，设n n c c n c n n n n 2121+=⇒=+ 当2≥n 时，1<n c ，}{n c 单调递减，………10分21)(1max ==∴c c n ，故21>λ. ………12分 18. 解：（1）(8085)1(75)0.2P X P X ≤<=-≤=，(8595)0.30.10.2P X ≤<=-=，所以所求概率330.20.20.10.024P A =⨯⨯⨯=；………6分（每个结果各2分）（2）(7585)12(75)0.4P X P X ≤≤=-<=，所以ξ服从二项分别(3,0.4)B ，3(0)0.60.216P ξ===，2(1)30.40.60.432P ξ==⨯⨯=，………8分 2(2)30.40.60.288P ξ==⨯⨯=，3(3)0.40.064P ξ===，………10分所以随机变量ξ的分布列是30.4 1.2E ξ=⨯=19. 解：（1）作AB ME ⊥于E ,连接CE ,ME ∴∥AP …①AC 是圆O 的直径，222===CD BC AC ，BC ABDC AD ⊥⊥∴,,030=∠=∠∴CAD BAC ,………2分 060=∠=∠DCA BCA ,3==AD AB=,3331==BA BE 33tan ==∠BC BE BCE , CAD ECA BCE ∠==∠=∠∴030EC ∴∥AD …②，………4分由①②，且E CE ME = ,∴平面MEC ∥平面PAD ,⊆CM 平面MEC ,⊄CM 平面PAD ∴CM ∥平面PAD ………6分（2）依题意，如图以A 为原点，直线AB ，AP 分别为x,z 轴建立空间坐标系，设a AP =)0,23,23(),,0,0(),0,1,3(),0,0,3(),0,0,0(D a P C B A 设面PAC 的法向量为),,(z y x =，设CM 与平面PAC 所成角为θ⎪⎩⎪⎨⎧=+=⋅==⋅030yx az 设3=x ，)0,3,3(-=∴n ，………8分+=+=)3,1,33(a --= 55123993122||||||sin 22=+=++⨯===∴a a n CM θ………10分 3=∴a ………12分20. （1）解：如图圆E 经过椭圆C 的左右焦点12,F F ,1,,F E A 三点共线,∴1F A 为圆E 的直径,212AF F F ∴⊥2219(0)24x +-=,2±=∴x ,2=∴c ………2分189||||||2212122=-=-=F F AF AF ,4||||221=+=AF AF a222a b c =+，解得2,a b ==4分∴椭圆C 的方程22142x y +=，………5分（2）点A的坐标(0)MN OA λλ=≠，………6分故设直线的方程为y x m =+22142y x m x y ⎧=+⎪⎪⎨⎪+=⎪⎩2220x m ∴++-=，设1122(,),(,)M x y N x y2221212,2,2480x x x x m m m ∴+==-∆=-+>，22m ∴-<<………8分21||||MN x x =-== 点A到直线的距离d =2214||||22AMNm m S MN d m ∆-+=⋅==≤=………10分当且仅当224m m -=，即m =，直线的方程为y x =………12分 21. 解：（1）22)211ln()(+-+=x x x x f ，定义域2020211->⇒⎪⎩⎪⎨⎧≠+>+x x x ， 22')2(2)2(421)(+-=+-+=x x x x x f ，)2,2(-∴递减，),2(+∞递增故12ln )2()(-==f x f 极小值，没有极大值. ………3分（2）22)1ln()(+-+=x x ax x f ，),1(+∞-∈ax ， 222')2)(1()1(4)2(41)(++--=+-+=x ax a ax x ax a x f ………4分 )1,21(∈a ，)41,0()1(∈-∴a a ，a a a a )1(21--<-∴ 0)1(42=--a ax ，aa a x )1(2-±=∴………5分 aa a aa a a a a a x f x f 2121421214])1(21ln[])1(21ln[)()(21+-----+-----+-+=+2212442()()ln[(12)]ln[(12)]22121a f x f x a a a a -+=-+=-+--- 设12-=a t ，当)1,21(∈a 时，)1,0(∈t ，22ln )()()(221-+==+∴tt t g x f x f 设当)1,0(∈t 时，22ln 2)(-+=tt t g ，0)1(222)(22'<-=-=tt t tt g ………7分 )(t g 在)1,0(∈t 上递减，0)1()(=>g t g ，即0)0()()(21=>+f x f x f 恒成立综上述)0()()(21f x f x f >+………8分（3）当)1,0(∈t 时，022ln 2)(>-+=tt t g 恒成立，即011ln >-+tt 恒成立设n t 1=),2(N n n ∈≥，即011ln >-+n n，n n ln 1>-∴ 1ln 2,2ln 3,3ln 4,,1ln n n ∴>>>->123(1)ln 2ln 3ln 4ln ln 234n n n ∴++++->++++=⨯⨯⨯⨯=()!ln n>-∴2)1(nn ()!ln n ∴),2(!2)1(N n n n e n n ∈≥>-………12分22. 解：（1）∵PA 为圆O 的切线,,PAB ACP ∴∠=∠又P ∠为公共角,PCA PAB ∆∆∽AB PC PA AC ⋅=⋅…………4分（2）∵PA 为圆O 的切线,BC 是过点O 的割线,2,PA PB PC ∴=⋅………6分40,30PC BC ∴==又∵022290,900CAB AC AB BC ∠=∴+==又由（1）知12AB PA AC AB AC PC ==∴==,连接EC ,则,CAE EAB ∠=∠ ADB ACE ∆∆∽，………8分ACAD AE AB =AD AE AB AC 360⋅=⋅==………10分23. 解：（1）,,x t y t ⎧=⎪⎨=⎪⎩222=+∴y x 点(1,1)C 在圆上，故切线方程为2=+y x ………2分2cos sin =+∴θρθρ，切线的极坐标方程：2)4sin(=+πθρ………5分（2）2)2(+-=x k y 与半圆)0(222≥=+y y x 相切时21|22|2=+-k k0142=+-∴k k 32-=∴k ，32+=k （舍去）………. 8分设点)0,2(-B 222202-=+-=AB K ,故直线m 的斜率的取值范围为]22,32(--. ………10分24. 解：（1）当2a =时，不等式()f x x <即|2|x x x -< 显然0x ≠，当0x >时，原不等式可化为：|2|1121x x -<⇒-<-<13x ⇒<<……2分当0x <时，原不等式可化为：|2|121x x ->⇒->或21x -<- 3x ⇒>或1x <∴0x <………4分综上得：当2a =时，原不等式的解集为{|130}x x x <<<或………5分（2）∵对任意(0,4]x ∈都有()4f x <即4()4x x a -<-<⇒(0,4]x ∀∈，44x a x x x -<<+恒成立………. 6分设4(),(0,4]g x x x x =-∈，4()p x x x =+，(0,4]x ∈,则对任意(0,4]x ∈， 44x a x x x-<<+恒成立⇔max min ()()g x a p x <<，(0,4]x ∈………7分 ∵24'()1,g x x =+当(0,4]x ∈时'()0g x >∴函数()g x 在(0,4]上单调递增，∴max ()(4)3g x g ==………8分又∵24'()1p x x =-＝2(2)(2)x x x -+，∴()p x 在(0,2]上递减,]4,2[上递增 ∴min ()(2)4p x p ==. ………9分故)4,3(∈a ………10分。

届高三数学一轮复习-函数的图像及其应用(共58张PPT)

考点贯通
抓高考命题的“形”与“神”
作函数的图象
[例 1] 作出下列函数的图象： (1)y＝12|x|； [解] 作出 y＝12x 的图象，保留 y＝12x 图象中 x≥0 的部分，加上 y＝12x 的图象中 x>0 部分关于 y 轴的对称部分，即得 y＝12|x|的图象，如图中实线部分．
(2)y＝|log2(x＋1)|； (3)y＝2xx－－11； [解] (2)将函数 y＝log2x 的图象向左平移 1 个单位，再将 x 轴下方的部分沿 x 轴翻折上去，即可得到函数 y＝|log2(x＋1)|的图象，如图． (3)因为 y＝2xx－－11＝2＋x－1 1，故函数图象可由 y＝1x的图象向右平移 1 个单位，再向上平移 2 个单位而得，如图．
(2)伸缩变换：
f(ωx) ． y＝f(x)―0―<AA>―<1―，1，―横横―坐坐―标―标不―不变―变，―，纵―纵―坐坐―标标―伸缩―长―短为―为原―原来―来的―的―AA倍―倍→ y＝ Af(x) ．
(3)对称变换： y＝f(x)―关―于―x―轴―对―称→y＝－f(x) ； y＝f(x)―关―于―y―轴―对―称→y＝ f(－x)； y＝f(x)―关―于―原――点―对―称→y＝－f(－x) ． (4)翻折变换： y＝f(x)―去将―掉―y轴y―轴右―左边―边的―图―图， ―象―保翻―留折―y到轴―左―右边―边―去图→y＝ f(|x|) ； y＝f(x)―将―x―轴―下―方保―的留―图x―轴象―上翻―方―折图―到―上―方―去→y＝ |f(x)| .
⊥AB交AB于E，当l从左至右移动(与线段
AB有公共点)时，把四边形ABCD分成两部分，设AE＝x，
左侧部分的面积为y，则y关于x的图象大致是

2014~2015学年度最新江西省2015届高考冲刺数学试题及答案

江西省高安中学高考冲刺数学试题一、选择题：(本大题共6小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．)1.已知全集U=R ，集合103x A x x ⎧-⎫=≤⎨⎬+⎩⎭，集合B x y x R ⎧⎫⎪⎪==∈⎨⎬⎪⎪⎩⎭，则()U A C B ⋂为（） A ． {}31x x -<≤- B ．{}31x x -≤<- C ．{}31x x -≤≤- D ．{}31x x -<<- 2. 已知函数)0(cos sin 3)(>+=ωωωx x x f 的图象与x 轴交点的横坐标构成一个公差为2π的等差数列，把函数)(x f 的图象沿x 轴向左平移6π个单位，得到函数)(x g 的图象.关于函数)(x g ，下列说法正确的是（）A. 在]2,4[ππ上是增函数B. 其图象关于直线4π-=x 对称C. 函数)(x g 是奇函数D. 当]32,6[ππ∈x 时，函数)(x g 的值域是]1,2[-3．给定区域:D 44420x y x y x y x +≥⎧⎪+≤⎪⎨+≥⎪⎪≥⎩，令点集000000{(,)|,,(,)T x y D x y x y =∈∈Z 是z x y =+在D 上取得最大值或最小值的点}，则T 中的点最多能确定三角形的个数为（）A ．15B ．25C ．28D ．324. 函数14)62sin(2-+=xx x y π的图象大致为（）5．已知四棱锥P －ABCD 的底面四边形ABCD 的对边互不平行，现用一平面α去截此四棱锥，且要使截面是平行四边形，则这样的平面α（）A 、有且只有一个B 、有四个C 、有无数个D 、不存在 6．定义在R 上的函数320f x ax bx cx a =++≠()()的单调增区间为11-(,)，若方程2320a f x bf x c ++=(())()恰有4个不同的实根，则实数a 的值为（）A ．12B ．12- C ．1 D. －1二、填空题：(本大题共4小题，每小题5分)7、已知O 为的外心，若3450OA OB OC +-=，则∠C ＝＿＿＿＿8、已知双曲线 22221(0,0)x y a b a b -=>>上一点C ，过双曲线中心的直线交双曲线于A 、B 两点，记直线AC 、BC 的斜率分别为12,k k ，当12121ln ln k k k k ++最小时，双曲线离心率为。

江西省高考数学一轮复习导数及其应用(含积分)备考试题

江西省2015届高三数学一轮复习备考试题导数及其应用（含积分）一、选择题1、（2014年江西高考）若12()2(),f x x f x dx =+⎰则1()f x dx =⎰A.1-B.13-C.13 D.12、（2013年江西高考）若22221231111,,,x S x dx S dx S e dx x ===⎰⎰⎰则123S S S 的大小关系为 A.123S S S << B.213S S S << C.231S S S << D.321S S S <<3、（乐安一中2015届高三上学期开学考试）定义在(0,)+∞上的单调递减函数()f x ，若()f x 的导函数存在且满足'()()f x x f x >，则下列不等式成立的是（） A ．3(2)2(3)f f < B ．3(4)4(3)f f < C ．2(3)3(4)f f < D ．(2)2(1)f f <4、（南昌二中2015届高三上学期第一次考）定义在R 上的可导函数)(x f ，当),1(+∞∈x 时，0)1)(()()1(''>--⋅-x x f x f x 恒成立，若)2(f a =， )3(21f b =， )2(121f c -=，则c b a ,,的大小关系是( )A ．b a c <<B ．c b a <<C ．c a b <<D ．b c a <<5、（南昌三中2015届高三上学期第一次月考）设()ln f x x x =，若0'()2f x =，则0x =（） A. 2e B. e C.ln 22D. ln 26、（南昌市八一中学2015届高三8月月考）已知函数f （x ）在R 上满足f （1+x ）=2f （1﹣x ）﹣x 2+3x+1，则曲线y=f （x ）在点（1，f （1））处的切线方程是学科网（） A ． x ﹣y ﹣2=0 B ． x ﹣y=0 C ． 3x+y ﹣2=0 D ． 3x ﹣y ﹣2=0 7、（南昌市新建二中2015届高三9月月考）设()f x 是定义在R 上的可导函数，且满足()()f x f x '>，对任意的正数a ，下面不等式恒成立的是( ).A.()(0)af a e f <B.()(0)af a e f > C.(0)()a f f a e <D ．(0)()af f a e> 8、（遂川中学2015届高三上学期第一次月考）由直线3x π=-，3x π=，0y =与曲线cos y x =所围成的封闭图形的面积为( )A .12B .1C .32D . 39、（南昌三中2014届高三第七次考试）已知二次函数2()1f x ax bx =++的导函数为'()f x ，且'(0)f ＞0，()f x 的图象与x 轴恰有一个交点，则'(1)(0)f f 的最小值为 ( ) A ．3 B ．32 C ．2 D ．5210、（吉安一中2014届高三下学期第一次模拟）设函数2()()f x g x x =+，曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+，则曲线()y f x =在点(1,(1))f 处切线的斜率为（）A. 4B. 14-C. 2D. 12-二、填空题1、（2014年江西高考）若曲线xy e -=上点P 处的切线平行于直线210x y ++=，则点P 的坐标是________.2、（2013年江西高考）设函数()f x 在(0,)+∞内可导，且()x x f e x e =+，则(1)xf =3、（2012年江西高考）计算定积分121(sin )x x dx -+=⎰___________。

江西省南昌市2015届高三第一次模拟测试理科数学试题

江西省南昌市2015届高三第一次模拟测试数学（理）一、选择题（本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1、已知i 为虚数单位，则复数12iz i+=在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2、若集合{}1381x x A =≤≤，(){}22log 1x x x B =->，则A B =（） A ．(]2,4 B ．[]2,4 C ．()[],00,4-∞ D ．()[],10,4-∞-3、如图，在正四棱柱1111CD C D AB -A B 中，点P 是面1111C D A B 内一点，则三棱锥CD P -B 的正视图与侧视图的面积之比为（）A ．1:1B ．2:1C ．2:3D ．3:24、已知过定点()2,0P 的直线l与曲线y =A ，B 两点，O 为坐标原点，当∆AOB 的面积取到最大值时，直线l 的倾斜角为（）A ．150B ．135C ．120D ．不存在5、已知实数x ，y 满足1040x y x y y m +-≥⎧⎪+-≤⎨⎪≥⎩，若目标函数2z x y =+的最大值与最小值的差为2，则实数m 的值为（）A ．4B ．3C ．2D ．12-6、在C ∆AB 中，角A ，B ，C 所对的边分别是a ，b ，c ，若1c =，45B =，3cos 5A =，则b 等于（）A ．53B ．107C ．57 D．147、以坐标原点为对称中心，两坐标轴为对称轴的双曲线C 的一条渐近线倾斜角为3π，则双曲线C 的离心率为（）A ．2B ．2CD ．2 8、如图所示程序框图，其功能是输入x 的值，输出相应的y 值．若要使输入的x 值与输出的y 值相等，则这样的x 值有（）A ．2个B ．3个C ．4个D ．5个 9、给出下列命题：①若()523450123451x a a x a x a x a x a x -=+++++，则1234532a a a a a ++++= ②α，β，γ是三个不同的平面，则“γα⊥，γβ⊥”是“//αβ”的充分条件③已知1sin 63πθ⎛⎫-= ⎪⎝⎭，则7cos 239πθ⎛⎫-= ⎪⎝⎭其中正确命题的个数为（）A ．0B ．1C ．2D ．310、如图，(),x y M M M ，(),x y N N N 分别是函数()()sin f x x ωϕ=A +（0A >，0ω>）的图象与两条直线1:l y m =，2:l y m =-（0m A ≥≥）的两个交点，记S x x N M =-，则()S m 图象大致是（）A ．B ．C ．D ．11、设无穷数列{}n a ，如果存在常数A ，对于任意给定的正数ε（无论多小），总存在正整数N ，使得n >N 时，恒有n a ε-A <成立，就称数列{}n a 的极限为A ．则四个无穷数列：①(){}12n-⨯；②()()11111335572121n n ⎧⎫⎪⎪+++⋅⋅⋅+⎨⎬⨯⨯⨯-+⎪⎪⎩⎭；③231111112222n -⎧⎫++++⋅⋅⋅+⎨⎬⎩⎭；④{}231222322nn ⨯+⨯+⨯+⋅⋅⋅+⨯，其极限为2共有（）A ．4个B ．3个C ．2个D ．1个 12、设函数()()()222ln 2f x x a x a =-+-，其中0x >，R a ∈，存在0x 使得()045f x ≤成立，则实数a 的值为（）A ．15B ．25C ．12D ．1 二、填空题（本大题共4小题，每小题5分，共20分．）13、a ，b ，c ，d 四封不同的信随机放入A ，B ，C ，D 4个不同的信封里，每个信封至少有一封信，其中a 没有放入A 中的概率是．14、已知直三棱柱111C C AB -A B 中，C 90∠BA =，侧面11CC B B 的面积为2，则直三棱柱111C C AB -A B 外接球表面积的最小值为．15、已知三角形C AB 中，C AB =A ，C 4B =，C 120∠BA =，3C BE =E ，若P 是C B 边上的动点，则AP⋅AE 的取值范围是．16、已知函数(),01lg ,0ax f x x x x ⎧≤⎪=-⎨⎪>⎩，若关于x 的方程()0f f x =⎡⎤⎣⎦有且只有一个实数解，则实数a 的取值范围为．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） 17、（本小题满分12分）已知等差数列{}n a 的前n 项和为n S ，11a =，36S =，正项数列{}n b 满足1232n S nbb b b ⋅⋅⋅=． ()1求数列{}a ，{}b 的通项公式；()2若n n b a λ>对n *∈N 均成立，求实数λ的取值范围．18、（本小题满分12分）某市教育局为了了解高三学生体育达标情况，对全市高三学生进行了体能测试，经分析，全市学生体能测试成绩X 服从正态分布()280,σN （满分为100分），已知()750.3P X <=，()950.1P X ≥=，现从该市高三学生中随机抽取三位同学．()1求抽到的三位同学该次体能测试成绩在区间[)80,85，[)85,95，[]95,100各有一位同学的概率；()2记抽到的三位同学该次体能测试成绩在区间[]75,85的人数为ξ，求随机变量ξ的分布列和数学期望ξE ． 19、（本小题满分12分）如图，C A 是圆O 的直径，B 、D 是圆O 上两点，C 2C 2CD 2A =B ==，PA ⊥圆O 所在的平面， 13BM =BP ．()1求证：C //M 平面D PA ；()2若C M 与平面C PA 所成角的正弦值为5时，求AP 的值．20、（本小题满分12分）已知圆:E 221924x y ⎛⎫+-= ⎪⎝⎭经过椭圆C :22221x y a b +=（0a b >>）的左、右焦点1F 、2F ，且与椭圆C 在第一象限的交点为A ，且1F ，E ，A 三点共线．直线l 交椭圆C 于M ，N 两点，且λMN =OA （0λ≠）． ()1求椭圆C 的方程；()2当三角形AMN 的面积取到最大值时，求直线l 的方程．21、（本小题满分12分）已知函数()()2ln 12xf x ax x =+-+（0a >）． ()1当12a =时，求()f x 的极值； ()2若1,12a ⎛⎫∈⎪⎝⎭，()f x 存在两个极值点1x ，2x ，试比较()()12f x f x +与()0f 的大小；()3求证：()12!n n en ->（2n ≥，n ∈N ）．请考生在第22-24题中任选一题作答，如果多做，则按所做的第一题计分． 22、（本小题满分10分）选修4-1：几何证明选讲如图所示，PA 为圆O 的切线，A 为切点，PO 交圆O 于B ，C 两点，20PA =，10PB =，C ∠BA 的角平分线与C B 和圆O 分别交于点D 和E ． ()1求证：C C AB⋅P =PA⋅A ；()2求D A ⋅AE 的值．23、（本小题满分10分）选修4-4：坐标系与参数方程以坐标原点为极点，以x 轴的非负半轴为极轴建立极坐标系，已知曲线C 的参数方程为x t y t⎧=⎪⎨=⎪⎩（t 为参数）．()1曲线C 在点()1,1处的切线为l ，求l 的极坐标方程；()2点A的极坐标为4π⎛⎫⎪⎝⎭，且当参数[]0,t π∈时，过点A 的直线m 与曲线C 有两个不同的交点，试求直线m 的斜率的取值范围． 24、（本大题满分10分）选修4-5：不等式选讲已知函数()f x x x a =-（R a ∈）．()1若2a =，解关于x 的不等式()f x x <；()2若对任意的(]0,4x ∈都有()4f x <，求a 的取值范围．江西省南昌市2015届高三第一次模拟测试数学（理）参考答案及评分标准二、填空题 13.34 14. π4 15. 210[,]33- 16),0()0,1(+∞- 三、解答题17. （Ⅰ）解：等差数列}{n a ，11=a ，63=S ，1=∴d ，故n a n = ………3分⎪⎩⎪⎨⎧=⋅⋅⋅⋅=⋅⋅⋅⋅--)2(2)1(211321321 n n S n Sn b b b b b b b b ，)2()1(÷得n aS S n n n n b 2221===--)2(≥n ， 222111===S b ,满足通项公式，故n n b 2= ………7分（Ⅱ）设n n a b >λ恒成立nn2>⇒λ恒成立，设n n c c n c n n n n2121+=⇒=+ 当2≥n 时，1<n c ，}{n c 单调递减， ………10分21)(1max ==∴c c n ，故21>λ. ………12分18. 解：（Ⅰ）(8085)1(75)0.2P X P X ≤<=-≤=，(8595)0.30.10.2P X ≤<=-=，所以所求概率330.20.20.10.024P A =⨯⨯⨯=； ………6分（每个结果各2分）（Ⅱ）(7585)12(75)0.4PX P X ≤≤=-<=，所以ξ服从二项分别(3,0.4)B ，3(0)0.60.216P ξ===，2(1)30.40.60.432P ξ==⨯⨯=，………8分 2(2)30.40.60.288P ξ==⨯⨯=，3(3)0.40.064P ξ===，………10分所以随机变量ξ的分布列是19. 解：（Ⅰ）作AB ME ⊥于E ,连接CE , ME ∴∥AP …① AC 是圆O 的直径，222===CD BC AC ，BC AB DC AD ⊥⊥∴,, 030=∠=∠∴CAD BAC , ………2分060=∠=∠DCA BCA ,3==AD AB=,3331==BA BE 33tan ==∠BC BE BCE , CAD ECA BCE ∠==∠=∠∴030EC ∴∥AD …②，………4分由①②，且E CE ME = ,∴CM ∥ 平面PAD ………6分（Ⅱ）依题意，如图以A 为原点，直线AB ，AP 分别为x,z 轴建立空间坐标系，设a AP =)0,23,23(),,0,0(),0,1,3(),0,0,3(),0,0,0(D a P C B A 设面PAC 的法向量为),,(z y x =，设CM 与平面PAC 所成角为θ ⎪⎩⎪⎨⎧=+=⋅==⋅030y x AC n az 设3=x，)0,3,3(-=∴， ………8分CB BM CB CM+=+= )3,1,33(a CM --=∴ 55123993122||||||sin 22=+=++⨯===∴a a n CM θ ………10分 3=∴a ………12分20．（Ⅰ）解：如图圆E 经过椭圆C 的左右焦点12,F F ,1,,F E A 三点共线, ∴1F A 为圆E 的直径,212AF F F ∴⊥2219(0)24x +-=, 2±=∴x ,2=∴c ………2分 189||||||2212122=-=-=F F AF AF , 4||||221=+=AF AF a222a b c =+，解得2,a b ==………4分∴椭圆C 的方程22142x y +=，………5分（Ⅱ）点A 的坐标 (0)MN OAλλ=≠，， ………6分故设直线的方程为y x m =+ 22142y x m x y ⎧=+⎪⎪⎨⎪+=⎪⎩ 2220x m ∴++-=，设1122(,),(,)M x y N x y 2221212,2,2480x x x xm m m ∴+==-∆=-+>，22m ∴-<< ………8分||||MN x x =-==点A到直线的距离d =2214||||22AMNm m S MN d m ∆-+=⋅==≤= ………10分当且仅当224m m -=，即m =，直线的方程为y x =………12分 21.解：（Ⅰ）22)211ln()(+-+=x x x x f ，定义域2020211->⇒⎪⎩⎪⎨⎧≠+>+x x x ， 22')2(2)2(421)(+-=+-+=x x x x x f ，)2,2(-∴递减，),2(+∞递增故12ln )2()(-==f x f 极小值，没有极大值. ………3分（Ⅱ）22)1ln()(+-+=x x ax x f ，),1(+∞-∈ax ， 222')2)(1()1(4)2(41)(++--=+-+=x ax a ax x ax a x f ………4分 )1,21(∈a ，)41,0()1(∈-∴a a ， a a a a )1(21--<-∴ 0)1(42=--a ax ， aa a x )1(2-±=∴ ………5分aa a aa a a a a a x f x f 2121421214])1(21ln[])1(21ln[)()(21+-----+-----+-+=+2212442()()ln[(12)]ln[(12)]22121a f x f x a a a a -+=-+=-+--- 设12-=a t ，当)1,21(∈a 时，)1,0(∈t ，22ln )()()(221-+==+∴tt t g x f x f 设当)1,0(∈t 时，22ln 2)(-+=t t t g ，0)1(222)(22'<-=-=t t t t t g ………7分 )(t g 在)1,0(∈t 上递减，0)1()(=>g t g ，即0)0()()(21=>+f x f x f 恒成立综上述)0()()(21f x f x f >+ ………8分（Ⅲ）当)1,0(∈t 时，022ln 2)(>-+=t t t g 恒成立，即011ln >-+tt 恒成立设n t 1=),2(N n n ∈≥，即011ln >-+n n ，n n ln 1>-∴1ln 2,2ln 3,3ln 4,,1ln n n ∴>>>->123(1)ln 2ln 3ln 4ln ln 234n n n ∴++++->++++=⨯⨯⨯⨯=()!ln n>-∴2)1(nn ()!ln n ∴),2(!2)1(N n n n en n ∈≥>- ………12分 22.解：（Ⅰ）∵ PA 为圆O 的切线, ,PAB ACP ∴∠=∠又P ∠为公共角,PCA PAB ∆∆∽ AB PC PA AC ⋅=⋅ …………4分（2）∵PA 为圆O 的切线,BC 是过点O 的割线, 2,PA PB PC ∴=⋅ ………6分40,30PC BC ∴== 又∵022290,900CAB AC AB BC ∠=∴+==又由（Ⅰ）知12AB PA AC AB AC PC ==∴==,连接EC ,则,CAE EAB ∠=∠ADB ACE ∆∆∽， ………8分ACADAE AB =AD AE AB AC 360⋅=⋅== ………10分23.解：（Ⅰ）,,x t y t ⎧=⎪⎨=⎪⎩222=+∴y x 点(1,1)C 在圆上，故切线方程为2=+y x ………2分2cos sin =+∴θρθρ，切线的极坐标方程：2)4sin(=+πθρ………5分（Ⅱ）2)2(+-=x k y 与半圆)0(222≥=+y y x 相切时21|22|2=+-kk0142=+-∴k k 32-=∴k ，32+=k （舍去）……….8分设点)0,2(-B 222202-=+-=AB K ,故直线m 的斜率的取值范围为]22,32(--. ………10分 24．解：（Ⅰ）当2a =时，不等式()f x x <即|2|x x x -<显然0x ≠，当0x >时，原不等式可化为： |2|1121x x -<⇒-<-<13x ⇒<< (2)分当0x <时，原不等式可化为：|2|121x x ->⇒->或21x -<-3x ⇒>或1x < ∴0x < (4)分综上得：当2a =时，原不等式的解集为{|130}x x x <<<或 ………5分（Ⅱ）∵对任意(0,4]x ∈都有()4f x < 即4()4x x a -<-<⇒(0,4]x ∀∈，44x a x x x-<<+恒成立 ……….6分设4(),(0,4]g x x x x =-∈，4()p x x x=+，(0,4]x ∈,则对任意(0,4]x ∈，44x a x x x-<<+恒成立⇔max min ()()g x a p x <<，(0,4]x ∈ ………7分∵24'()1,g x x=+当(0,4]x ∈时'()0g x > ∴函数()g x 在(0,4]上单调递增，第 11 页共 11 页又∵24'()1p x x =-＝2(2)(2)x x x-+，∴()p x 在(0,2]上递减,]4,2[上递增 ∴min ()(2)4p x p ==. ………9分故)4,3(∈a ………10分。

2015年江西省南昌市高考一模数学试卷(理科)【解析版】

第ห้องสมุดไป่ตู้1 页（共 24 页）
A．
B．
C．
D．
7．（5 分）以坐标原点为对称中心，两坐标轴为对称轴的双曲线 C 的一条渐近线的倾斜角为，则双曲线 C 的离心率为（）
A．2 或
B．2 或
C．
D．2
8．（5 分）如图所示程序框图，其功能是输入 x 的值，输出相应的 y 值，若要使输入的 x 值与输出的 y 值相等，则这样的 x 值有（）
其中正确命题的个数为（）
A．0
B．1
C．2
D．3
10．（5 分）如图：M（xM，yM），N（xN，yN）分别是函数 f（x）＝Asin（ωx+φ）（A＞0，ω＞0）的图象与两条直线 l1：y＝m，l2：y＝﹣m（A≥m≥0）的两个交点，记 S＝|xN﹣xM|，则 S（m）图象大致是（）
A．
B．
（1）求椭圆 C 的方程；（2）当三角形 AMN 的面积取得最大值时，求直线 l 的方程．
第 4 页（共 24 页）
21．（12 分）已知函数 f（x）＝ln（1+ax）﹣ （a＞0）．
（1）当 a＝时，求 f（x）的极值；
（2）若 a
，f（x）存在两个极值点 x1，x2，试比较 f（x1）+f（x2）与 f
17．（12 分）已知等差数列{an}的前 n 项和为 Sn，a1＝1，S3＝6，正项数列{bn}
第 3 页（共 24 页）
满足 b1•b2•b3…bn＝2 ．
（1）求数列{an}，{bn}的通项公式；（2）若 λbn＞an 对 n∈N*均成立，求实数 λ 的取值范围． 18．（12 分）某市教育局为了了解高三学生体育达标情况，对全市高三学生进行

江西省南昌市2014-2015学年高考数学第一轮复习函数训练题1

2014－2015学年度南昌市新课标高三第一轮复习训练题数学（二）（函数1）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知)(x f 是奇函数，)(x g 是偶函数，且4)1()1(,2)1()1(=-+=+-g f g f ，则)1(g 等于A ．4B ．3C ．2D ．1 2．函数)1ln(x x y -=的定义域为 A ．(0,1) B ．(0,1] C ．[0,1) D ．[0,1]3．若函数ax y =与xb y -=在),0(+∞上都是减函数，则bx ax y +=2在),0(+∞上 A ．单调递减 B ．单调递增 C ．先增后减 D ．先减后增4．下列函数中，在(1,1)-内有零点且单调递增的是 A ．2log (2)y x =+B ．21xy =-C ．212y x =-D ．3y x =- 5．若a b c <<，则函数()()()()()()()f x x a x b x b x c x a x c =--+--+--的两个零点分别位于区间A ．(,)a b ,(,)b cB ．(,)a -∞,(,)a bC ．(,)b c ,(,)c +∞D ．(,)a -∞,(,)c +∞ 6．定义在R 上的函数)(x f y =在),(a -∞上是增函数，且函数)(a x f y +=是偶函数，当a x a x ><21,，且a x a x -<-21时，有A ．)()(21x f x f >B ．)()(21x f x f ≥C ．)()(21x f x f <D ．)()(21x f x f ≤7．设函数)(2)(2R x x x g ∈-=，⎩⎨⎧≥-<++=)(,)(),(,4)()(x g x x x g x g x x x g x f ，则)(x f 的值域是A ．9[,0](1,)4-+∞B ．[0)+∞，C ．9[,)4-+∞D ．9[,0](2,)4-+∞8．已知函数)(x f 对任意R x ∈都有)3(2)()6(f x f x f =++，)1(-=x f y 的图像关于点)0,1(对称，且4)1(=f ，则=)2015(f A ．0 B ．4- C ．8- D ．16-9．函数()y f x =，x D ∈，若存在常数C ，对任意的1x D ∈，存在唯一的2x D ∈，使得12()()f x f x C =，则称函数()f x 在D 上的几何平均数为C .已知3()f x x =，[1,2]x ∈，则函数()f x 在[1,2]上的几何平均数为A.2 B ．2 C ．4D ．2210．在如图所示的锐角三角形空地中，欲建一个面积不小于2300m 的内接矩形花园(阴影部分)，则其边长x (单位：m )的取值范围是 A ．]20,15[ B ．]25,12[ C ．]30,10[ D ．]30,20[二、填空题：本大题共5小题；每小题5分，共25分，把答案填在题中的横线上.11．若)(x f 的定义域为R ,2)(>'x f 恒成立，2)1(=-f ,则42)(+>x x f 解集为． 12．已知函数()f x 是定义在(,0)(0,)-∞+∞上的奇函数，在(0,)+∞上单调递减，且0)3()21(>->f f ，则方程()0f x =的根的个数为 . 13．若存在正数x 使1)(2<-a x x成立，则a 的取值范围是 .14．若函数14)(2+=x xx f 在区间)12,(+m m 上是单调递增函数，则m 的取值范围是． 15．若函数)(x f y =的值域是]3,1[，则函数)3(21)(+-=x f x F 的值域是．三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或推演步骤.16．已知⎩⎨⎧<-≥-=-=.0,2,0,1)(,1)(2x x x x x g x x f（1）求)]2([g f 和)]2([f g 的值；（2）求)]([x g f 和)]([x f g 的表达式．17．已知函数)(x f y =的定义域为R ，且对任意R b a ∈,，都有)()()(b f a f b a f +=+．且当0>x 时，0)(<x f 恒成立，.3)3(-=f （1）证明：函数)(x f y =是R 上的减函数；（2）证明：函数)(x f y =是奇函数；（3）试求函数)(x f y =在),](,[*N n m n m ∈上的值域. .18．已知函数)(x f 的定义域为R ，且满足)()2(x f x f -=+．若f (x )为奇函数，且当10≤≤x 时，x x f 21)(=，求使21)(-=x f 在区间]2014,0[上的所有x 的个数．19．设()f x 是定义在R 上的奇函数，且对任意实数x ，恒有(2)()f x f x +=-．当[0,2]x ∈时，2()2f x x x =-. （1）求证：()f x 是周期函数；（2）当[2,4]x ∈时，求()f x 的解析式；（3）计算(0)(1)(2)(2014)f f f f ++++．20．（1）已知函数()y f x =的定义域为R ，且当R x ∈时，()()f m x f m x +=-恒成立，求证()y f x =的图象关于直线x m =对称；（2）若函数2log |1|y ax =-的图象的对称轴是2x =，求非零实数a 的值．21．已知函数x b b ax x f ⋅-+-=22242)(，).,()(1)(2R b a a x x g ∈---= （1）当0=b 时，若)(x f 在]2,(-∞上单调递减，求a 的取值范围；（2）求满足下列条件的所有整数对),(b a ：存在0x ，使得0()()f x f x 是的最大值，0()()g x g x 是的最小值.2014－2015学年度南昌市新课标高三第一轮复习训练题数学（二）参考答案11．(1)-+∞， 12．2 13．(1)-+∞， 14．(－1,0] 15．[51]--，三.解答题：本大题共6小题，共75分16．解：(1)由已知，g (2)＝1，f (2)＝3，∴f [g (2)]＝f (1)＝0，g [f (2)]＝g (3)＝2.(2)当x ≥0时，g (x )＝x －1，∴f [g (x )]＝(x －1)2－1＝x 2－2x ；当x ＜0时， g (x )＝2－x ，∴f [g (x )]＝(2－x )2－1＝x 2－4x ＋3；⎩⎨⎧<+-≥-=∴.0,34,0,2)]([22x x x x x x x g f 当x ≥1或1-≤x 时，f (x )≥0，∴g [f (x )]＝f (x )－1＝x 2－2；当11<<-x 时，0)(<x f ，.3)(2)]([2x x f x f g -=-=∴⎩⎨⎧<<---≤≥-=∴.11,3,11,2)]([22x x x x x x f g 或 17．（1）证明：设任意R x x ∈21,，且21x x <，f (x 2)＝f [x 1＋(x 2－x 1)]＝f (x 1)＋f (x 2－x 1)．∵x 2－x 1＞0，∴f (x 2－x 1)＜0.∴f (x 2)＝f (x 1)＋f (x 2－x 1)＜f (x 1)，故f (x )是R 上的减函数．（2）证明：∵f (a ＋b )＝f (a )＋f (b )恒成立， ∴可令a ＝－b ＝x ，则有f (x )＋f (－x )＝f (0)．又令a ＝b ＝0，则有f (0)＝f (0)＋f (0)，∴f (0)＝0.从而任意的R x ∈，f (x )＋f (－x )＝0，∴f (－x )＝－f (x )．)(x f y =∴是奇函数． (3)解：)(x f y = 是R 上的单调递减函数，)(x f y =∴在],[n m 上也是减函数，故f (x )在],[n m 上的最大值f (x )max ＝f (m )，最小值f (x )min ＝f (n )．)1()1()1()]1(1[)(nf n f f n f n f ==-+=-+= ，同理f (m )＝mf (1)．又f (3)＝3f (1)＝－3，.)(,)(,1)1(n n f m m f f -=-=∴-=∴ )(x f y =∴在],[n m 上的值域为].,[m n -- 18. 解：当0≤x ≤1时，1()2f x x =，设－1≤x ≤0，则0≤－x ≤1，∴11()()22f x x x -=-=- ∵f (x )是奇函数，∴f (－x )＝－f (x )．∴1()2f x x -=-，即1()2f x x =. ).11(21)(≤≤-=∴x x x f 又设1＜x ＜3，则－1＜x －2＜1. ∴f (x －2)＝12(x －2)．又)()]([]2)[()2()2(x f x f x f x f x f -=---==--=--=- ，).2(21)(-=-∴x x f )31)(2(21)(<<--=∴x x x f ．⎪⎩⎪⎨⎧<<--≤≤-=∴.31),2(21,11,21)(x x x x x f 由21)(-=x f ，解得1-=x .又∵f (x ＋2)＝－f (x )，∴f (x ＋4)＝－f (x ＋2)＝－[－f (x )]＝f (x )，)(x f ∴是以4为周期的周期函数．21)(-=∴x f 的所有)(14Z n n x ∈-=. 令2014140≤-≤n ，则4201541≤≤n ，又Z n ∈ ，).(5031Z n n ∈≤≤∴ ∴在]2014,0[上共有503个x 使.21)(-=x f19．解：（1）)()2(x f x f -=+ ，).()2()4(x f x f x f =+-=+∴ )(x f ∴是周期为4的周期函数．(2)当]0,2[-∈x 时，]2,0[∈-x ，由已知得.2)()(2)(22x x x x x f --=---=-又)(x f 是奇函数，.2)(,2)()(22x x x f x x x f x f +=∴--=-=-∴又当]4,2[∈x 时，]0,2[4-∈-x ，).4(2)4()4(2-+-=-∴x x x f 又)(x f 是周期为4的周期函数，∴f (x )＝f (x －4)＝(x －4)2＋2(x －4)＝x 2－6x ＋8. ∴当]4,2[∈x 时，.86)(2+-=x x x f(3)f (0)＝0，f (2)＝0，f (1)＝1，f (3)＝－1.又)(x f 是周期为4的周期函数， f (0)＋f (1)＋f (2)＋f (3)＝f (4)＋f (5)＋f (6)＋f (7) == f (2 009)＋f (2010)＋f (2011)＋f (2012)=0.又0)2()1()2014()2013(=+=+f f f f ，.0)2014()2()1()0(=++++∴f f f f 20．解：（1）设P (x 0，y 0)是y ＝f (x )图象上任意一点，则y 0＝f (x 0)．又P 点关于x ＝m 的对称点为P ′，则P ′的坐标为(2m －x 0，y 0)．又f (x ＋m )＝f (m －x )，得f (2m －x 0)＝f [m ＋(m －x 0)]＝f [m －(m －x 0)]＝f (x 0)＝y 0. 即P ′(2m －x 0，y 0)在y ＝f (x )的图象上．∴y ＝f (x )的图象关于直线x ＝m 对称．（2）对定义域内的任意x ，有f (2－x )＝f (2＋x )恒成立．∴|a (2－x )－1|＝|a (2＋x )－1|恒成立，即|－ax ＋(2a －1)|＝|ax ＋(2a －1)|恒成立．又0≠a ，012=-∴a ，.21=∴a 21．解: (1）当0b =时，()24f x ax x =-，若0a =，()4f x x =-，则()f x 在]2,(-∞上单调递减，符合题意；若0a ≠，要使()f x 在]2,(-∞上单调递减，必须满足0,42,2a a>⎧⎪⎨≥⎪⎩∴01a <≤．综上所述，a 的取值范围是]1,0[.(2）若0a =,()f x =-,则()f x 无最大值，故0a ≠，∴()f x 为二次函数，要使)(x f 有最大值，必须满足20,420,a b b <⎧⎨+-≥⎩即0a <且11b ≤+，此时，0x =()f x 有最大值．又()g x 取最小值时，0x a =，a =∈Z ，则2a ，∵0a <且11b ≤+，∴)20a a <≤∈Z ，得1a =-，此时1b =-或3b =．∴满足条件的整数对(),a b 是()()1,1,1,3---．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2014－2015学年度南昌市新课标高三第一轮复习训练题数学（二）（函数1）命题人：黄润华学校：江西师大附中审题人：刘倍倍学校：南昌二中一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知)(x f 是奇函数，)(x g 是偶函数，且4)1()1(,2)1()1(=-+=+-g f g f ，则)1(g 等于A ．4B ．3C ．2D ．12．函数)1ln(x x y -=的定义域为A ．(0,1)B ．(0,1]C ．[0,1)D ．[0,1]3．若函数ax y =与xby -=在),0(+∞上都是减函数，则bx ax y +=2在),0(+∞上 A ．单调递减 B ．单调递增 C ．先增后减 D ．先减后增4．下列函数中，在(1,1)-内有零点且单调递增的是A ．2log (2)y x =+B ．21x y =-C D ．3y x =- 5．若a b c <<，则函数()()()()()f x x a x b x a x c =--++--的两个零点分别位于区间A ．(,)a b ,(,)b cB ．(,)a -∞,(,)a bC ．(,)b c ,(,)c +∞D ．(,)a -∞,(,)c +∞ 6．定义在R 上的函数)(x f y =在),(a -∞上是增函数，且函数)(a x f y +=是偶函数，当a x a x ><21,，且a x a x -<-21时，有A ．)()(21x f x f >B ．)()(21x f x f ≥C ．)()(21x f x f <D ．)()(21x f x f ≤7．设函数)(2)(2R x x x g ∈-=，⎩⎨⎧≥-<++=)(,)(),(,4)()(x g x x x g x g x x x g x f ，则)(x f 的值域是A ．9[,0](1,)4-+∞B ．[0)+∞，C ．9[,)4-+∞D ．9[,0](2,)4-+∞8．已知函数)(x f 对任意R x ∈都有)3(2)()6(f x f x f =++，)1(-=x f y 的图像关于点)0,1(对称，且4)1(=f ，则=)2015(f A ．0 B ．4- C ．8- D ．16-9．函数()y f x =，x D ∈，若存在常数C ，对任意的1x D ∈，存在唯一的2x D ∈，使得C =，则称函数()f x 在D 上的几何平均数为C .已知3()f x x =，[1,2]x ∈，则函数()f x 在[1,2]上的几何平均数为A.2 B ．2C ．4D ．2210．在如图所示的锐角三角形空地中，欲建一个面积不小于2300m 的内接矩形花园(阴影部分)，则其边长x (单位：m )的取值范围是 A ．]20,15[ B ．]25,12[ C ．]30,10[ D ．]30,20[二、填空题：本大题共5小题；每小题5分，共25分，把答案填在题中的横线上.11．若)(x f 的定义域为R ,2)(>'x f 恒成立，2)1(=-f ,则42)(+>x x f 解集为．12．已知函数()f x 是定义在(,0)(0,)-∞+∞上的奇函数，在(0,)+∞上单调递减，且0)3()21(>->f f ，则方程()0f x =的根的个数为 . 13．若存在正数x 使1)(2<-a x x 成立，则a 的取值范围是 .14．若函数14)(2+=x xx f 在区间)12,(+m m 上是单调递增函数，则m 的取值范围是． 15．若函数)(x f y =的值域是]3,1[，则函数)3(21)(+-=x f x F 的值域是．三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或推演步骤.16．已知⎩⎨⎧<-≥-=-=.0,2,0,1)(,1)(2x x x x x g x x f（1）求)]2([g f 和)]2([f g 的值；（2）求)]([x g f 和)]([x f g 的表达式．17．已知函数)(x f y =的定义域为R ，且对任意R b a ∈,，都有)()()(b f a f b a f +=+．且当0>x 时，0)(<x f 恒成立，.3)3(-=f （1）证明：函数)(x f y =是R 上的减函数；（2）证明：函数)(x f y =是奇函数；（3）试求函数)(x f y =在),](,[*N n m n m ∈上的值域. .18．已知函数)(x f 的定义域为R ，且满足)()2(x f x f -=+．若f (x )为奇函数，且当10≤≤x 时，x x f 21)(=，求使21)(-=x f 在区间]2014,0[上的所有x 的个数．19．设()f x 是定义在R 上的奇函数，且对任意实数x ，恒有(2)()f x f x +=-．当[0,2]x ∈时，2()2f x x x =-. （1）求证：()f x 是周期函数；（2）当[2,4]x ∈时，求()f x 的解析式；（3）计算(0)(1)(2)(2014)f f f f ++++L ．20．（1）已知函数()y f x =的定义域为R ，且当R x ∈时，()()f m x f m x +=-恒成立，求证()y f x =的图象关于直线x m =对称；（2）若函数2log |1|y ax =-的图象的对称轴是2x =，求非零实数a 的值．21．已知函数x b b ax x f ⋅-+-=22242)(，).,()(1)(2R b a a x x g ∈---=（1）当0=b时，若)(x f 在]2,(-∞上单调递减，求a 的取值范围；（2）求满足下列条件的所有整数对),(b a ：存在0x ，使得0()()f x f x 是的最大值，0()()g x g x 是的最小值.2014－2015学年度南昌市新课标高三第一轮复习训练题数学（二）参考答案一．选择题：本大题共10小题，每小题5分，共50分11．(1)-+∞， 12．2 13．(1)-+∞， 14．(－1,0] 15．[51]--，三.解答题：本大题共6小题，共75分 16．解：(1)由已知，g (2)＝1，f (2)＝3，∴f [g (2)]＝f (1)＝0，g [f (2)]＝g (3)＝2.(2)当x ≥0时，g (x )＝x －1，∴f [g (x )]＝(x －1)2－1＝x 2－2x ；当x ＜0时， g (x )＝2－x ，∴f [g (x )]＝(2－x )2－1＝x 2－4x ＋3；⎩⎨⎧<+-≥-=∴.0,34,0,2)]([22x x x x x x x g f当x ≥1或1-≤x 时，f (x )≥0，∴g [f (x )]＝f (x )－1＝x 2－2；当11<<-x 时，0)(<x f ，.3)(2)]([2x x f x f g -=-=∴⎩⎨⎧<<---≤≥-=∴.11,3,11,2)]([22x x x x x x f g 或 17．（1）证明：设任意R x x ∈21,，且21x x <，f (x 2)＝f [x 1＋(x 2－x 1)]＝f (x 1)＋f (x 2－x 1)．∵x 2－x 1＞0，∴f (x 2－x 1)＜0.∴f (x 2)＝f (x 1)＋f (x 2－x 1)＜f (x 1)，故f (x )是R 上的减函数．（2）证明：∵f (a ＋b )＝f (a )＋f (b )恒成立， ∴可令a ＝－b ＝x ，则有f (x )＋f (－x )＝f (0)．又令a ＝b ＝0，则有f (0)＝f (0)＋f (0)，∴f (0)＝0.从而任意的R x ∈，f (x )＋f (－x )＝0，∴f (－x )＝－f (x )．)(x f y =∴是奇函数． (3)解：)(x f y = 是R 上的单调递减函数，)(x f y =∴在],[n m 上也是减函数，故f (x )在],[n m 上的最大值f (x )max ＝f (m )，最小值f (x )min ＝f (n )．)1()1()1()]1(1[)(nf n f f n f n f ==-+=-+= ，同理f (m )＝mf (1)．又f (3)＝3f (1)＝－3，.)(,)(,1)1(n n f m m f f -=-=∴-=∴ )(x f y =∴在],[n m 上的值域为].,[m n --18. 解：当0≤x ≤1时，1()2f x x =，设－1≤x ≤0，则0≤－x ≤1，∴11()()22f x x x -=-=-∵f (x )是奇函数，∴f (－x )＝－f (x )．∴1()2f x x -=-，即1()2f x x =.).11(21)(≤≤-=∴x x x f又设1＜x ＜3，则－1＜x －2＜1. ∴f (x －2)＝12(x －2)．又)()]([]2)[()2()2(x f x f x f x f x f -=---==--=--=- ，).2(21)(-=-∴x x f )31)(2(21)(<<--=∴x x x f ．⎪⎩⎪⎨⎧<<--≤≤-=∴.31),2(21,11,21)(x x x x x f由21)(-=x f ，解得1-=x .又∵f (x ＋2)＝－f (x )，∴f (x ＋4)＝－f (x ＋2)＝－[－f (x )]＝f (x )，)(x f ∴是以4为周期的周期函数．21)(-=∴x f 的所有)(14Z n n x ∈-=. 令2014140≤-≤n ，则4201541≤≤n ，又Z n ∈ ，).(5031Z n n ∈≤≤∴ ∴在]2014,0[上共有503个x 使.21)(-=x f19．解：（1）)()2(x f x f -=+ ，).()2()4(x f x f x f =+-=+∴ )(x f ∴是周期为4的周期函数．(2)当]0,2[-∈x 时，]2,0[∈-x ，由已知得.2)()(2)(22x x x x x f --=---=- 又)(x f 是奇函数，.2)(,2)()(22x x x f x x x f x f +=∴--=-=-∴ 又当]4,2[∈x 时，]0,2[4-∈-x ，).4(2)4()4(2-+-=-∴x x x f 又)(x f 是周期为4的周期函数，∴f (x )＝f (x －4)＝(x －4)2＋2(x －4)＝x 2－6x ＋8. ∴当]4,2[∈x 时，.86)(2+-=x x x f(3)f (0)＝0，f (2)＝0，f (1)＝1，f (3)＝－1.又)(x f 是周期为4的周期函数， f (0)＋f (1)＋f (2)＋f (3)＝f (4)＋f (5)＋f (6)＋f (7) == f (2 009)＋f (2010)＋f (2011)＋f (2012)=0. 又0)2()1()2014()2013(=+=+f f f f ，.0)2014()2()1()0(=++++∴f f f f 20．解：（1）设P (x 0，y 0)是y ＝f (x )图象上任意一点，则y 0＝f (x 0)．又P 点关于x ＝m 的对称点为P ′，则P ′的坐标为(2m －x 0，y 0)．又f (x ＋m )＝f (m －x )，得f (2m －x 0)＝f [m ＋(m －x 0)]＝f [m －(m －x 0)]＝f (x 0)＝y 0. 即P ′(2m －x 0，y 0)在y ＝f (x )的图象上．∴y ＝f (x )的图象关于直线x ＝m 对称．（2）对定义域内的任意x ，有f (2－x )＝f (2＋x )恒成立．∴|a (2－x )－1|＝|a (2＋x )－1|恒成立，即|－ax ＋(2a －1)|＝|ax ＋(2a －1)|恒成立．又0≠a ，012=-∴a ，.21=∴a 21．解: (1）当0b =时，()24f x ax x =-，若0a =，()4f x x =-，则()f x 在]2,(-∞上单调递减，符合题意；若0a ≠，要使()f x 在]2,(-∞上单调递减，必须满足0,42,2a a>⎧⎪⎨≥⎪⎩∴01a <≤．综上所述，a 的取值范围是]1,0[.(2）若0a =,()f x =-,则()f x 无最大值，故0a ≠，∴()f x 为二次函数，要使)(x f 有最大值，必须满足20,420,a b b <⎧⎨+-≥⎩即0a <且11b ≤，此时，0x ()f x 有最大值．又()g x 取最小值时，0x a =，a =∈Z，则2a =，∵0a<且11b≤，∴)20a a <≤∈Z ，得1a =-，此时1b =-或3b =．∴满足条件的整数对(),a b 是()()1,1,1,3---．。