高中数学三角函数知识点
高中数学三角函数知识点

高中数学三角函数知识点高中数学三角函数知识点1锐角三角函数公式sin =的对边 / 斜边cos =的邻边 / 斜边tan =的对边 / 的邻边cot =的`邻边 / 的对边倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A))三倍角公式sin3=4sinsin(/3+)sin(/3-)cos3=4coscos(/3+)cos(/3-)tan3a = tan a tan(/3+a) tan(/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asin+Bcos=(A^2+B^2)^(1/2)sin(+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsin+Bcos=(A^2+B^2)^(1/2)cos(-t),tant=A/B 降幂公式sin^2()=(1-cos(2))/2=versin(2)/2cos^2()=(1+cos(2))/2=covers(2)/2tan^2()=(1-cos(2))/(1+cos(2))推导公式tan+cot=2/sin2tan-cot=-2cot21+cos2=2cos^21-cos2=2sin^21+sin=(sin/2+cos/2)^2半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a)) 两角和差cos(+)=coscos-sinsincos(-)=coscos+sinsinsin()=sincoscossintan(+)=(tan+tan)/(1-tantan)tan(-)=(tan-tan)/(1+tantan)和差化积sin+sin = 2 sin[(+)/2] cos[(-)/2]sin-sin = 2 cos[(+)/2] sin[(-)/2]cos+cos = 2 cos[(+)/2] cos[(-)/2]cos-cos = -2 sin[(+)/2] sin[(-)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 积化和差sinsin = [cos(-)-cos(+)] /2coscos = [cos(+)+cos(-)]/2sincos = [sin(+)+sin(-)]/2cossin = [sin(+)-sin(-)]/2诱导公式sin(-) = -sincos(-) = costan (a)=-tansin(/2-) = coscos(/2-) = sinsin(/2+) = coscos(/2+) = -sinsin() = sincos() = -cossin() = -sincos() = -costanA= sinA/cosAtan(/2+)=-cottan(/2-)=cottan()=-tantan()=tan诱导公式记背诀窍:奇变偶不变,符号看象限高中数学三角函数知识点2定义:锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
高中数学-三角函数知识点总结

三角函数知识点一、三角函数知识点 1.角的定义:(1)00~0360角的定义:从一点O 出发的两条射线OB OA ,所形成的图形叫做角,这点O 叫做角的顶点,射线OB OA ,叫做角的两边(2)任意角的定义:角可以看成是平面内一条射线绕着它的端点从一个位置OA 旋转到另一个位置OB 所形成的图形,端点O 叫做角的顶点,射线OA 叫做角的始边,射线OB 叫做角的终边2.规定:(1)正角:按逆时针方向旋转形成的角叫正角 (2)负角:按顺时针方向旋转形成的角叫负角 (3)零角:一条射线不作任何旋转形成的角叫零角这样,我们就把角的概念推广到了任意角,包括正角,负角,零角 注:角的度量需注意:既要考虑旋转方向,又要考虑旋转量3.终边相同的角:所有与α终边相同的角连同α在内组成的集合{}Z k k S ∈⋅+==,3600αββ 4.象限角和轴线角:将角放在直角坐标系中,让角的顶点与原点重合,角的始边与x 轴非负半轴重合,则(1)象限角:角的终边落在第几象限,则称该角为第几象限角 (2)轴线角:角的终边落在坐标轴上,则称该角为轴线角 5.1º的角的定义:规定周角的3601为1度的角,记作:01,这种用度作为单位来度量角的单位制叫做角度制6.1弧度角的定义:我们把长度等于半径长的弧所对的圆心角叫做1弧度的角,记作1rad ,读作:1弧度,这种以弧度为单位来度量角的制度叫做弧度制7.弧度数(1)我们规定,正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零 (2)半径为R 的圆的圆心角α所对的弧长为l ,则角α的弧度数为Rl=α,角α的正负由α终边的旋转方向决定注:弧度制与角度制区别:(1)弧度制是以“弧度”为单位来度量角的单位制,角度制是以“度”为单位来度量角的单位制,1弧度≠1度(2)1弧度是弧长等于半径长的圆弧所对的圆心角的大小,而1度是周角的3601所对的圆心角的大小(3)弧度制是十进制,它的表示是用一个实数表示,而角度制是六十进制; (4)以弧度和度为单位的角,都是一个与半径无关的定值 8.弧度制与角度制的换算(1)弧度制与角度制下的一些特殊角①角度制下零度的角:00,弧度制下零度的角:0rad , 区别数值相同,单位不同 ②角度制下平角:0180,弧度制下平角:πrad ③角度制下周角:0360,弧度制下平角:2πrad (2)弧度制与角度制的换算①角度化成弧度:=0360 π2 ,0180 π2 ,01 01745.0 ②弧度化成角度:π2 0360 ,π 0180 ,rad 1 '01857 注:角度和弧度互化9.扇形的弧长公式和面积公式(1)角度制下扇形的弧长公式:180Rn l π=;扇形的面积公式:3602R n S π=(2)弧度制下扇形的弧长公式:R l α=;扇形的面积公式:Rl R S 21212==α10.角度制下和弧度制下轴线角和象限角的集合 (1)轴线角的集合①终边在x 轴的非负半轴上{}Z k k x x ∈⋅=,3600={}Z k k x x ∈=,2π②终边在x 轴的非正半轴上{}Z k k x x ∈+⋅=,18036000={}Z k k x x ∈+=,2ππ ③终边在x 轴上{}Z k k x x ∈⋅=,1800={}Z k k x x ∈=,π④终边在y 轴的非负半轴上{}Z k k x x ∈+⋅=,9036000={}Z k k x x ∈=,2π ⑤终边在y 轴的非正半轴上{}Z k k x x ∈-⋅=,9036000={}Z k k x x ∈+=,2ππ⑥终边在y 轴上{}Z k k x x ∈+⋅=,9018000=⎭⎬⎫⎩⎨⎧∈+=Z k k x x ,2ππ⑦终边在坐标轴上{}Z k k x x ∈⋅=,900=⎭⎬⎫⎩⎨⎧∈=Z k k x x ,2π (2)象限角的集合①第一象限角的集合{}Z k k x k x ∈+⋅<<⋅,90360360000=⎭⎬⎫⎩⎨⎧∈+<<Z k k x k x ,222πππ②第二象限角的集合{}Z k k x k x ∈+⋅<<+⋅,180360903600000=⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,222ππππ③第三象限角的集合{}Z k k x k x ∈+⋅<<+⋅,2703601803600000=⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,2322ππππ④第四象限角的集合{}Z k k x k x ∈+⋅<<+⋅,3603602703600000=⎭⎬⎫⎩⎨⎧∈+<<+Z k k x k x ,22232ππππ ={}Z k k x k x ∈⋅<<-⋅,36090360000=⎭⎬⎫⎩⎨⎧∈<<-Z k k x k x ,222πππ11.两角的终边对称结论(1)α与β的终边关于x 轴对称Z k k ∈=+,2πβα (2)α与β的终边关于y 轴对称Z k k ∈+=+,2ππβα (3)α与β的终边关于原点轴对称Z k k ∈++=,2ππβα (4)α与β的终边共线Z k k ∈+=,πβα(5)α与β的终边关于直线x y =对称Z k k ∈+=+,22ππβα(6)α与β的终边关于直线x y -=对称Z k k ∈+=+,232ππβα (7)α与β的终边互相垂直Z k k ∈++=,2ππβα12.三角函数定义:(1)任意角的三角函数定义1:设角α的顶点与原点重合,始边与x 轴的非负半轴重合,角α的终边上任意一点P 的坐标为),(y x ,它到原点的距离022>+=y x r ,则 ①比值r y 叫做角α的正弦,记作αsin ,即=αsin r y ②比值r x 叫做角α的余弦,记作αcos ,即=αcos r x ③比值x y 叫做角α的正切,记作αtan ,即=αtan x y ④比值y x 叫做角α的余切,记作αcot ,即=αcot yx (2)任意角的三角函数定义2:设角α的顶点与原点重合,始边与x 轴的非负半轴重合,角α的终边与单位圆的交点为P ),(y x ,则 ①=αsin y ②αcos x ③=αtan xy④=αcot y x三角函数都是以角为自变量,以比值为函数值的函数,又由于角与实数是一一对应的,所以三角函数也可以看作是以实数为自变量的函数13.三角函数的定义域和值域三角函数定义域值域αsin =yR ]1,1[- αcos =y R]1,1[-αtan =y⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,2ππR αcot =y{}Z k k x x ∈≠,πR14.三角函数值在各象限的符号αsin αcos αtan记法1:正弦上正,余弦右正,正切一三正 记法2:一全正,二正弦,三正切,四余弦 15.诱导公式:公式一:终边相同的角的同一三角函数值相等角度制下 弧度制下=+⋅)360sin(0αk αsin =+)2sin(απk αsin =+⋅)360cos(0αk αcos =+)2cos(απk αcos =+⋅)360tan(0αk αtan =+)2tan(απk αtan =+⋅)360cot(0αk αcot =+)2cot(απk αcot公式二:角度制下 弧度制下=+)180sin(0ααsin - =+)sin(απαsin - =+)180cos(0ααcos - =+)cos(απαcos - =+)180tan(0ααtan =+)tan(απαtan =+)180cot(0ααcot =+)cot(απαcot公式三:角度制下 弧度制下=-)180sin(0ααsin =-)sin(απαsin =-)180cos(0ααcos - =-)cos(απαcos - =-)180tan(0ααtan - =-)tan(απαtan - =-)180cot(0ααcot - =-)cot(απαcot -公式四:角度制下 弧度制下=-)sin(ααsin - =-)sin(ααsin - =-)cos(ααcos =-)cos(ααcos =-)tan(ααtan - =-)tan(ααtan - =-)cot(ααcot - =-)cot(ααcot -公式五:角度制下 弧度制下=-)90sin(0ααcos =-)2sin(απαcos=-)90cos(0ααsin =-)2cos(απαsin-)90tan(0ααcot =-)2tan(απαcot=-)90cot(0ααtan =-)2cot(απαtan公式六:角度制下 弧度制下=+)90sin(0ααcos =+)2sin(απαcos=+)90cos(0ααsin - =+)2cos(απαsin -=+)90tan(0ααtan - =+)2tan(απαtan -=+)90cot(0ααcot - =+)2cot(απαcot -公式七:角度制下 弧度制下=+)270sin(0ααcos - =+)23sin(απαcos -=+)270cos(0ααsin =+)23cos(απαsin=+)270tan(0ααcot - =+)23tan(απαcot -=+)270cot(0ααtan - =+)23cot(απαtan -公式八:角度制下 弧度制下=-)270sin(0ααcos - =-)23sin(απαcos -=-)270cos(0ααsin - =-)23cos(απαsin -=-)270tan(0ααcot =-)23tan(απαcot=-)270cot(0ααtan - =-)23cot(απαtan -记忆口诀:奇变偶不变符号看象限 16.部分特殊角的三角函数:αcos21 22 23 1αtan/3-1-33- 017.三角函数线:(1)有向线段:当角α的终边不在坐标轴上时,我们把MP 、OM 、AT 都看成带有方向的线段,这种带方向的线段叫有向线段规定:与坐标轴相同的方向为正方向(2)这几条与单位圆有关的有向线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线,统称为三角函数线注:(1)正弦线、余弦线、正切线分别解释了正弦函数x y sin =,余弦函数x y cos =、正切函数x y tan =的几何意义(2)正弦线、余弦线、正切线的方向与坐标轴正方向相同时,对应的三角函数值为正,与坐标轴正方向相反时,对应的三角函数值为负 18.同角三角函数的关系:(1)平方关系:1cos sin 22=+αα (2)商数关系:=αtan ααcos sin 、=αcot ααsin cos (3)倒数关系:1cot tan =αα 注意公式的变形:(1)1cos sin 22=+x x ⇒x x 22cos 1sin -=、x x 22sin 1cos -= (2)⇒=αααcos sin tan =αsin ααcos tan 、⇒=αααsin cos cot =αcos ααsin cot (3)ααααααcos sin ,cos sin ,cos sin -+的关系:①=+2)cos (sin ααααcos sin 21+ ②=-2)cos (sin ααααcos sin 21- ③=-++22)cos (sin )cos (sin αααα219.正弦函数x y sin =、余弦函数x y cos =、正切函数x y tan =的图像和性质 函数x y sin = x y cos = x y tan =图形定义域 RR⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,2ππ值域]1,1[-]1,1[-R最值当Z k k x ∈+=,22ππ时,有最大值当Z k k x ∈-=,22ππ时,有最大值当Z k k x ∈=,2π时,有最大值当Z k k x ∈+=,22ππ时,有最大值无最大值无最小值单调性在Zk k k ∈+-],22,22[ππππ上递增在Zk k k ∈++],232,22[ππππ上递减在Z k k k ∈-],2,2[πππ上递增在Z k k k ∈+],2,2[πππ上递减在Zk k k ∈+-),2,2(ππππ上递增奇偶性 奇函数偶函数奇函数周期性π2=Tπ2=Tπ=T 对称性关于Z k k x ∈+=,2ππ对称关于点Z k k ∈),0,(π中心对称关于Z k k x ∈=,π对称 关于点Zk k ∈+),0,2(ππ中心对称关于点Z k k ∈),0,2(π中心对称20.三角函数周期结论(1)函数B x A y ++=)sin(ϕω(其中0,≠ωA )的周期=T ωπ2函数B x A y ++=)cos(ϕω(其中0,≠ωA )的周期=T ωπ2函数)tan(ϕω+=x A y (其中0,≠ωA )的周期=T ωπ (2)函数)sin(ϕω+=x A y (其中0,≠ωA )的周期=T ωπ 函数)cos(ϕω+=x A y (其中0,≠ωA )的周期=T ωπ 函数)tan(ϕω+=x A y (其中0,≠ωA )的周期=T ωπ (3)函数B x A y ++=)sin(ϕω(其中0,,≠B A ω)的周期=T ωπ2函数B x A y ++=)cos(ϕω(其中0,,≠B A ω)的周期=T ωπ221.函数B x A y ++=)sin(ϕω)0,0(>>ωA 的图像的作法(1)图像变换法:函数B x A y ++=)sin(ϕω的图像可由正弦函数x y sin =经过一系列的变换得到:①先平移变换,再周期变换:x y sin =———————————→)sin(ϕ+=x y —————————→)sin(ϕω+=x y——————————→)sin(ϕω+=x A y ——————————→B x A y ++=)sin(ϕω ②先周期变换,再平移变换:x y sin =———————————→)sin(x y ω=——————————→)sin(ϕω+=x y——————————→)sin(ϕω+=x A y ——————————→B x A y ++=)sin(ϕω (2)五点作图法:函数B x A y ++=)sin(ϕω的图像画法:一个周期内起关键作用的五个点的横坐标可由=+ϕωx ππππ2,23,,2,0得到 22.函数变换结论: (1)平移变换01左右平移:①将函数)(x f y =的图象向左移a 个单位得函数)(a x f y +=的图象 ②将函数)(x f y ω=的图象向左移a 个单位得函数))((a x f y +=ω的图象02上下平移:将函数)(x f y =的图象向上移b 个单位得函数b x f y +=)(的图象(2)伸缩变换①函数)(x f y ω=的图象可由函数)(x f y =的图象上每一点的纵坐标不变,横坐标变为原来的ω1倍得到 ②函数)(x Af y =的图象可由函数)(x f y =的图象上每一点的横坐标不变,纵坐标变为原来的A 倍得到 (3)翻折变换①函数)(x f y =的图象可将函数)(x f y =的图像y 轴右侧的图像保留,y 轴左侧的图像由y 轴右侧的图像沿y 轴翻折得到②函数)(x f y =的图象可将函数)(x f y =的图像在x 轴上方的图像保留,x 轴下方的图像沿x 轴翻折到x 轴上方得到 23.两个函数的对称性结论(1)函数)(x f y -=与)(x f y =的图象关于x 轴对称 (2)函数)(x f y -=与)(x f y =的图象关于y 轴对称 (3)函数)(x f y --=与)(x f y =的图象关于原点对称 (4)函数)(1x fy -=与)(x f y =的图象关于x y =对称(5)函数)2(x a f y -=与)(x f y =的图象关于a x =对称(6)函数)2(x a f y --=与)(x f y =的图象关于点)0,(a 对称24.函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y )0,0(>>ωA 的奇偶性结论 (1)函数)sin(ϕω+=x A y 为奇函数⇔Z k k ∈=,πϕ(2)函数)sin(ϕω+=x A y 为偶函数⇔Z k k ∈+=,2ππϕ(3)函数)cos(ϕω+=x A y 为奇函数⇔Z k k ∈+=,2ππϕ(4)函数)cos(ϕω+=x A y 为偶函数⇔Z k k ∈=,πϕ 二、三角变换25.两角和与差的正弦余弦正切公式:(1)=+)sin(βαβαβαsin cos cos sin +,记作)(βα+ S (2)=-)sin(βαβαβαsin cos cos sin -,记作)(βα- S (3)=+)cos(βαβαβαsin sin cos cos -,记作)(βα+C (4)=-)cos(βαβαβαsin sin cos cos +,记作)(βα-C (5)=+)tan(βαβαβαtan tan 1tan tan -+,记作)(βα+T(6)=-)tan(βαβαβαtan tan 1tan tan +-,记作)(βα-T26.二倍角的正弦、余弦、正切公式 (1)=α2sin ααcos sin 2(2)=α2cos αα22sin cos -=1cos 22-α=α2sin 21-(3)=α2tan αα2tan 1tan 2- 注:二倍角公式的变形:(1)=+2)cos (sin ααααcos sin 21+;=-2)cos (sin ααααcos sin 21-(2)升幂缩角公式:=+αcos 12cos 22α;=-αcos 12sin 22α(3)降幂扩角公式:=α2sin 22cos 1α-;=α2cos 22cos 1α+ =α2sin 2α2cos 1-;=α2cos 2α2cos 1+27.半角公式:(1) =2sinα22cos 1α-±=2cosα22cos 1α+±=2tanααα2cos 12cos 1+-±(2)=2tanαααsin cos 1-=ααcos 1sin +28.辅助角公式: (1)=+θθcos sin b a )sin(22ϕ++x b a ,其中=ϕsin 22b a b +,=ϕcos 22b a a +(2)=+θθcos sin b a )cos(22ϕ-+x b a ,其中=ϕsin 22ba a +,=ϕcos 22ba b +29.万能公式=α2sin αα2tan 1tan 2+ =α2cos αα22tan 1tan 1+- =α2tan αα2tan 1tan 2- 30.积化和差公式=βαcos sin )]sin()[sin(21βαβα-++=βαsin cos )]sin()[sin(21βαβα--+ =βαcos cos )]cos()[cos(21βαβα-++ =βαsin sin )]cos()[cos(21βαβα--+-31.和差化积公式=+βαsin sin 2cos2sin2βαβα-+=-βαsin sin 2sin2cos2βαβα-+=+βαcos cos 2cos2cos2βαβα-+=-βαcos cos 2sin2sin2βαβα-+-。
高中三角函数知识点整理

高中三角函数知识点整理三角函数是数学中重要的概念,存在于高中数学课程中,是几何、代数、微积分等领域的基础知识。
下面整理了高中三角函数的重要知识点,希望对学生们的学习有帮助。
一、三角函数的基本概念1.弧度制:角的度量单位,一个角所对应的弧长等于半径的长度时,这个角的大小为1弧度。
2.角的三要素:顶点,始边,终边,顶点为角的端点,始边为角的起始边,终边为角的结束边。
3.弧度与角度的转换:角度数×π/180=弧度。
4.等角:具有相同角度的两个角是等角。
5. 正弦:给定一个锐角∠A,对于 A 的任何弧 B,就有 sin A = sin B。
二、正弦、余弦和正切函数1. 正弦函数:在数轴上,根据半径 r 的终端点 (x, y),它的正弦函数值定义为 y / r,可以表示为sinθ。
2. 余弦函数:在数轴上,根据半径 r 的终端点 (x, y),它的余弦函数值定义为 x / r,可以表示为cosθ。
3. 正切函数:在数轴上,根据半径 r 的终端点 (x, y),它的正切函数值定义为 y / x,可以表示为tanθ。
4.三角函数的性质:正弦和余弦函数的值在-1到1之间,正切函数的值没有限制。
三、三角函数的基本性质1.三角函数的周期性:正弦和余弦函数周期为2π,正切函数周期为π。
2.函数图像:正弦函数和余弦函数的图像为曲线,正切函数的图像为直线。
3.函数值的变化:正弦函数和余弦函数的值在一个周期内从-1到1变化,正切函数在不同区间内的值无限制变化。
4. 正弦函数和余弦函数的图像对称:sin(-θ) = -sinθ,cos(-θ) = cosθ。
5. 周期性的性质:sin(θ + 2πn) = sinθ,cos(θ + 2πn) =cosθ,n为整数。
6. 三角函数的诱导公式:sin(α + β) = sinαcosβ +cosαsinβ,cos(α + β) = cosαcosβ - sinαsinβ。
高中数学三角函数知识点

高中数学三角函数知识点一、基础概念1. 三角函数三角函数是数学中的一种函数,用来描述一个直角三角形中各边和角度之间的关系。
三角函数包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)、余切函数(cot)、正割函数(sec)和余割函数(csc)。
2. 角度制和弧度制角度制是指用度数来描述角度大小的一种测量方法,以“度”作为单位。
1圆周角等于360度,1度等于60分,1分等于60秒。
弧度制是指用弧长来描述角度大小的一种测量方法,以“弧度”作为单位。
1圆周角等于2π弧度,1弧度等于圆的半径所对应的弧长的长度。
3. 函数的周期与函数值域函数的周期是指函数在一段区间内重复出现的最小长度。
正弦函数和余弦函数的周期都是2π,正切函数和余切函数的周期都是π,正割函数和余割函数的周期都是π。
函数的值域是指函数所有可能的输出值所组成的集合。
正弦函数和余弦函数的值域都是[-1,1],正切函数的值域是(-∞,∞),余切函数的值域也是(-∞,∞),正割函数的值域是[1,∞),余割函数的值域也是[-∞,-1]∪[1,∞)。
4. 常用三角函数的图形正弦函数的图形是一条周期为2π、在x=π/2处取得最大值1,在x=3π/2处取得最小值-1的正弦曲线。
余弦函数的图形是一条周期为2π、在x=0处取得最大值1,在x=π处取得最小值-1的余弦曲线。
正切函数的图形是一条周期为π、在x=π/2+kπ(k∈Z)处有一个无穷大的跳跃,且在x=kπ(k∈Z)处取值为0的正切曲线。
5. 三角函数的基本关系式正弦函数和余弦函数之间满足关系式sin(x)=cos(x-π/2),cos(x)=sin(x+π/2)。
正切函数和余切函数之间满足关系式tan(x)=1/cot(x),cot(x)=1/tan(x)。
二、三角函数的运算1. 三角函数的加减法公式sin(x±y)=sinxcosy±cosxsinycos(x±y)=cosxcosy∓sinxsinytan(x±y)=(tanx±tany)/(1∓tanxtany)cot(x±y)=(cotxcoty∓1)/(cotx±coty)2. 三角函数的积化和差公式sinx+siny=2sin((x+y)/2)cos((x-y)/2)sinx-siny=2cos((x+y)/2)sin((x-y)/2)cosx+cosy=2cos((x+y)/2)cos((x-y)/2)cosx-cosy=-2sin((x+y)/2)sin((x-y)/2)3. 三角函数的倍角公式和半角公式sin2x=2sinxcosxcos2x=cos^2x-sin^2xtan2x=(2tanx)/(1-tan^2x)sin(x/2)=±√[(1-cosx)/2]cos(x/2)=±√[(1+cosx)/2]tan(x/2)=±√[(1-cosx)/(1+cosx)]4. 三角函数的反函数sin(-1)x:[-1,1]→[-π/2,π/2]cos(-1)x:[-1,1]→[0,π]tan(-1)x:(-∞,∞)→(-π/2,π/2)cot(-1)x:(-∞,∞)→(0,π)三、三角函数的应用1. 三角函数在几何中的应用在直角三角形中,正弦函数和余弦函数可以用来计算任意两边和一个角的关系。
高中数学必修4《三角函数》知识点与易错点归纳

高中数学必修4《三角函数》知识点与易错点归纳知识点(一)任意角和弧度制1.与θ终边相同的角的集合是 ;第一或第三象限角的集合是 ;x 轴上的角的集合是 ;2.若α是锐角,则πα-是第 象限角;πα+是第 象限角;2πα-是第 象限角;α-是第 象限角;32πα-是第 象限角;2πα+是第 象限角。
3.180°=π;1°= 弧度; 1弧度= ;圆心角α弧度数的绝对值||α= ;扇形面积公式S = 。
4.角ααcos 2=-,则2α角是 象限角。
知识点二.任意角的三角函数1.任意角的三角函数的定义:设α是任意一个角,(,)P x y 是α的终边上的任意一点(异于原点),它与原点的距离是0r =>,那么sin α= ,cos α= ,tan α= 。
2.如图,三角函数线:正弦线是 、余弦线是 、正切线是 ;4.已知角α的终边经过点(3,4)P -,则sin tan αα+的值为 ; 5.函数sin cos tan |sin ||cos ||tan |y αααααα=++的值域是 ; 6.sin cos θθ<⇔ ;sin cos θθ>⇔ 。
知识点三.同角三角函数的基本关系式及诱导公式1.平方关系:22sin cos αα+= ;商数关系:tan α= ;2.已知tan 2α=,则ααααcos sin cos 3sin +-= ;sin cos αα⋅= ;4.1419costan()34ππ+-的值为 ; 5.化简23sin (180)cos(360)sin(270)cos (180)cos(90)tan(180)αααααα+⋅-⋅-=--⋅+⋅+ 。
yTA xα B SO M P知识点四.正弦、余弦、正切公式及倍角公式1.基本公式及变式()()22222sin sin cos cos sin sin 22sin cos 1sin 2(sin cos )cos cos cos sin sin cos2cos sin 2cos 112sin t αβαβαβαβαβαααααααβαβαβααααα==±=±−−−→=⇒±=±±=−−−→=-=-=-↓↓令令 ()222tan tan 2tan 1+cos21cos2an tan 2cos sin 1tan tan 1tan 22αβααααβααααβα±-±=→=- = ,=变式:1tantan tan tan()(1tan tan),tan()1tan4απαβαβαβαα++=+⋅-⋅=+-;sin cos ),sin 2sin(cos 2sin()436πππθθθθθθθθθ±=±±=±±=±2.4411111212cos sin ππ-= ;sin163sin 223sin 253sin313+= ; 3.在ABC ∆中,53sin ,cos 135A B ==,则cos C = ; 4.在直角ABC ∆中,sin sin A B ⋅的最大值为 ;5.已知等腰三角形的一个底角的正弦值为13,则这个三角形的顶角的余弦值是 。
高中数学三角函数基础知识点及答案

高中数学三角函数基础知识点及答案1、角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。
按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。
射线的起始位置称为始边,终止位置称为终边。
2、象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。
如果角的终边在坐标轴上,就认为这个角不属于任何象限。
3. 终边相同的角的表示:(1)α终边与θ终边相同(α的终边在θ终边所在射线上)⇔2()k k αθπ=+∈Z ,注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角 1825-的终边相同,且绝对值最小的角的度数是___,合___弧度。
弧度:一周的弧度数为2πr/r=2π,360°角=2π弧度,因此,1弧度约为57.3°,即57°17'44.806'',1°为π/180弧度,近似值为0.01745弧度,周角为2π弧度,平角(即180°角)为π弧度,直角为π/2弧度。
(答:25-;536π-) (2)α终边与θ终边共线(α的终边在θ终边所在直线上) ⇔()k k αθπ=+∈Z . (3)α终边与θ终边关于x 轴对称⇔2()k k αθπ=-+∈Z . (4)α终边与θ终边关于y 轴对称⇔2()k k απθπ=-+∈Z . (5)α终边与θ终边关于原点对称⇔2()k k απθπ=++∈Z .(6)α终边在x 轴上的角可表示为:,k k Z απ=∈;α终边在y 轴上的角可表示为:,2k k Z παπ=+∈;α终边在坐标轴上的角可表示为:,2k k Z πα=∈.如α的终边与6π的终边关于直线x y =对称,则α=____________。
(答:Z k k ∈+,32ππ)4、α与2α的终边关系:由“两等分各象限、一二三四”确定.如若α是第二象限角,则2α是第_____象限角(答:一、三)5.弧长公式:||l R α=,扇形面积公式:211||22S lR R α==,1弧度(1rad)57.3≈. 如已知扇形AOB 的周长是6cm ,该扇形的中心角是1弧度,求该扇形的面积。
高中数学三角函数知识点总结
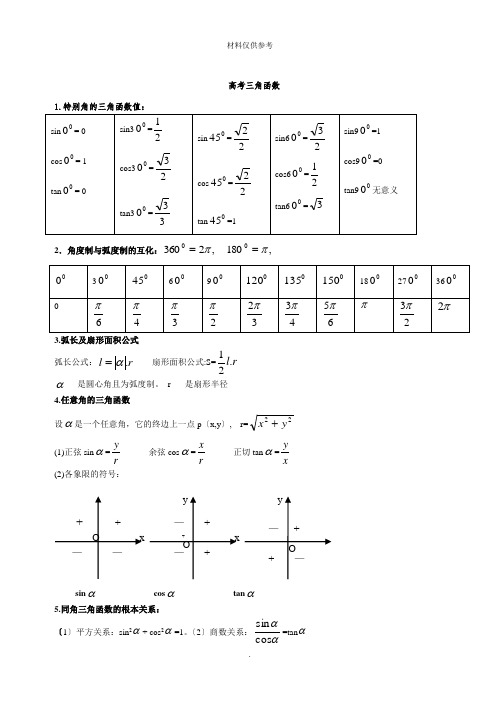
高考三角函数1.特别角的三角函数值:2.角度制与弧度制的互化:,2360π= ,1800π=3.弧长及扇形面积公式 弧长公式:r l.α= 扇形面积公式:S=r l .21α----是圆心角且为弧度制。
r-----是扇形半径4.任意角的三角函数设α是一个任意角,它的终边上一点p 〔x,y 〕, r=22y x +(1)正弦sin α=ry 余弦cos α=r x 正切tan α=xy(2)各象限的符号:sin α cos α tan α 5.同角三角函数的根本关系:〔1〕平方关系:sin 2α+ cos 2α=1。
〔2〕商数关系:ααcos sin =tan αxy+O— —+xyO — ++ — +yO— + + —〔z k k ∈+≠,2ππα〕6.诱导公式:()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=. ()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-.()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-.口诀:函数名称不变,符号看象限.()5sin cos 2παα⎛⎫-=⎪⎝⎭,cos sin 2παα⎛⎫-= ⎪⎝⎭. ()6sin cos 2παα⎛⎫+=⎪⎝⎭,cos sin 2παα⎛⎫+=-⎪⎝⎭. 口诀:正弦与余弦互换,符号看象限. 7正弦函数、余弦函数和正切函数的图象与性质三角形面积定理.111sin sin sin 222S ab C bc A ca B ===.1.直角三角形中各元素间的关系:如图,在△ABC 中,C =90°,AB =c ,AC =b ,BC =a 。
高中数学必修三角函数知识点归纳总结经典

高中数学必修三角函数知识点归纳总结经典一、正弦函数、余弦函数、正切函数的定义1. 正弦函数:在单位圆上,对于任意角度θ,都存在一个点P(x,y),其中x=cosθ,y=sinθ。
则y=sinθ称为角θ的正弦函数。
2. 余弦函数:在单位圆上,对于任意角度θ,都存在一个点P(x,y),其中x=cosθ,y=sinθ。
则x=cosθ称为角θ的余弦函数。
3. 正切函数:在单位圆上,对于任意角度θ,都存在一个点P(x,y),其中x=cosθ,y=sinθ。
则y/x=tanθ称为角θ的正切函数。
二、基本性质1.周期性:正弦函数、余弦函数、正切函数的周期都是2π。
2.奇偶性:正弦函数是奇函数,余弦函数是偶函数,正切函数是奇函数。
3.值域:正弦函数和余弦函数的值域为[-1,1],正切函数的值域为R。
三、基本公式1. 正弦函数的基本公式:sin(θ±α) = sinθcosα ±cosθsinα2. 余弦函数的基本公式:cos(θ±α) = cosθcosα ∓ sinθsinα3. 正切函数的基本公式:tan(θ±α) =(tanθ±tanα)/(1∓tanθtanα)四、三角函数的图像与性质1.正弦函数图像的性质:周期为2π,在(0,0)处取得最小值-1,在(π/2,1)、(3π/2,-1)处取得最大值1,是一个奇函数。
2.余弦函数图像的性质:周期为2π,在(0,1)处取得最大值1,在(π,-1)处取得最小值-1,是一个偶函数。
3.正切函数图像的性质:周期为π,在(0,0)处取得最小值-∞,在(π/2,∞)处取得最大值∞,是一个奇函数。
五、三角函数的性质1.三角函数的和差化积公式:sin(A±B) = sinAcosB ± cosAsinBcos(A±B) = cosAcosB ∓ sinAsinBtan(A±B) = (tanA±tanB)/(1∓tanAtanB)2.三角函数的倍角公式:sin2θ = 2sinθcosθcos2θ = cos^2θ - sin^2θtan2θ = (2tanθ)/(1-tan^2θ)3.三角函数的半角公式:sin(θ/2) = √[(1-cosθ)/2]cos(θ/2) = √[(1+cosθ)/2]tan(θ/2) = sinθ/(1+cosθ)4.三角函数的积化和差公式:sinA·sinB = (1/2)[cos(A-B)-cos(A+B)]cosA·cosB = (1/2)[cos(A-B)+cos(A+B)]sinA·cosB = (1/2)[sin(A-B)+sin(A+B)]六、三角函数的应用1.解三角形:利用正弦定理、余弦定理和正弦函数、余弦函数的性质,可以解决三角形的边长和角度。
高中数学三角函数知识点解析

高中数学三角函数知识点解析1. 三角函数的定义三角函数是用于描述一个角内各边之间的关系的函数。
常见的三角函数包括正弦函数、余弦函数和正切函数。
2. 正弦函数的性质和应用- 正弦函数表示一个角的对边与斜边之间的比值。
- 正弦函数的定义域是所有实数,值域在[-1, 1]之间。
- 正弦函数具有周期性,周期为360度或2π弧度。
- 正弦函数在几何、物理、工程等领域有着广泛的应用,例如在三角测量、波动现象等中起着重要作用。
3. 余弦函数的性质和应用- 余弦函数表示一个角的邻边与斜边之间的比值。
- 余弦函数的定义域是所有实数,值域在[-1, 1]之间。
- 余弦函数具有周期性,周期为360度或2π弧度。
- 余弦函数在几何、物理、工程等领域同样有着广泛的应用,例如在图像处理、力学问题等中起着重要作用。
4. 正切函数的性质和应用- 正切函数表示一个角的对边与邻边之间的比值。
- 正切函数的定义域是所有实数,值域为整个实数集。
- 正切函数在定义域上是周期性的,周期为180度或π弧度。
- 正切函数在几何、物理、工程等领域也有着广泛的应用,例如在力学问题、电路分析等中常常出现。
5. 三角函数的基本关系式- 正弦函数和余弦函数之间有着互补关系:$\sin(x) =\cos(90^\circ - x)$- 正切函数和余切函数之间有着互补关系:$\tan(x) =\cot(90^\circ - x)$- 正弦函数和余切函数之间有着互补关系:$\sin(x) =\frac{1}{\cot(x)}$以上是高中数学中三角函数的一些基本知识点解析。
三角函数在数学中的应用广泛,但需要注意理解和掌握其定义、性质和相互关系,才能真正灵活运用。
高中数学-三角函数

高中数学-三角函数本文将介绍高中数学中的三角函数知识点。
三角函数是数学中的一种基本函数类型,包括正弦函数、余弦函数、正切函数等。
这些函数和三角形的三个角度有关,因此被称为三角函数。
一、三角函数的基本概念1. 三角函数的定义首先,我们需要了解三角函数的定义。
正弦函数、余弦函数、正切函数是三角函数的最基本的函数,它们是由一个与一个角度对应的单位圆上的点定义的。
对于一个角度θ,我们可以在单位圆上取一点P(x,y),其中x为该点在x轴上的坐标,y为该点在y轴上的坐标。
此时,正弦函数表示为sin θ,余弦函数表示为cos θ,正切函数表示为tan θ,且有:sin θ = ycos θ = xtan θ = y/x2. 三角函数的特性三角函数有一些特性,这些特性对于解题和理解三角函数的性质很重要,包括:(1) 周期性:三角函数的图像是周期性的,其周期为2π,即当θ增加2π时,三角函数的值也相应地增加2π。
(2) 对称性:正弦函数为奇函数,即sin(-θ) = -sinθ,余弦函数为偶函数,即cos(-θ) = cosθ,而正切函数既不是奇函数也不是偶函数。
(3) 值域:正弦函数和余弦函数的值域在[-1,1]之间,而正切函数的值域为(-∞,+∞)。
二、三角函数的基本性质1. 三角函数的基本关系式三角函数之间有许多基本的关系式,我们可以通过这些关系式来互相转换三角函数的值。
下面是一些常用的关系式:(1) 三角函数之间的关系式:sin2θ + cos2θ = 11 + tan2θ = sec2θ1 + cot2θ = csc2θ(2) 三角函数的倒数关系式:cosec θ = 1/sin θsec θ = 1/cos θcot θ = 1/tan θ(3) 三角函数之间的和差关系式:sin(a+b) = sin a cos b + cos a sin bcos(a+b) = cos a cos b - sin a sin btan(a+b) = (tan a + tan b)/(1 - tan a tan b)(4) 三角函数之间的倍角关系式:sin2θ = 2sinθ cosθcos2θ = cos2θ - sin2θtan2θ = (2tanθ)/(1 - tan2θ)2. 三角函数的图像三角函数的图像非常有用,可以帮助我们更直观地理解三角函数的性质和特点。
高中数学三角函数知识点总结

高中数学三角函数知识点总结高中数学中的三角函数是一门重要的数学分支,它是解决各种三角形相关问题的基础。
以下是高中数学三角函数的知识点总结。
一、基本概念1. 角度与弧度:角度是用度(°)来衡量的,弧度是用弧长来衡量的,两者之间的转换关系是π弧度=180°。
2. 正弦定理和余弦定理:正弦定理是指在任意三角形ABC中,a/sinA = b/sinB = c/sinC;余弦定理是指在任意三角形ABC中,c² = a² + b² - 2abcosC。
3. 三角恒等式:包括正弦、余弦和正切的诸多恒等式以及它们的倒数形式。
二、常用三角函数及其性质1. 正弦函数(sin):在单位圆上,给定一个角,将其终边与单位圆交点的纵坐标即为该角的正弦值,其值域为[-1,1]。
2. 余弦函数(cos):在单位圆上,给定一个角,将其终边与单位圆交点的横坐标即为该角的余弦值,其值域为[-1,1]。
3. 正切函数(tan):在单位圆上,给定一个角,将其终边与单位圆交点的纵坐标除以横坐标即为该角的正切值,其定义域为所有不为π/2+kπ(k为整数)的实数。
4. 余切函数(cot)、正割函数(sec)和余割函数(csc):它们分别是tan、cos和sin的倒数函数,它们的定义域和值域分别是tan、cos和sin的值域和定义域的补集。
三、三角函数的图像和性质1. sin和cos的图像:在坐标平面中,将单位圆与x轴交点的横坐标和纵坐标作为y=sin(x)和y=cos(x)的函数图像,它们的图像具有周期性、奇偶性等性质。
2. 周期性:sin和cos的周期为2π,即sin(x+2π)=sin(x)和cos(x+2π)=cos(x)。
3. 奇偶性:sin是奇函数,即sin(-x)=-sin(x);cos是偶函数,即cos(-x)=cos(x)。
4. 其他性质:包括在特定区间的增减性、最大最小值以及特殊角的值等。
高中数学三角函数知识点

高中数学三角函数知识点高中数学第四章-三角函数知识点汇总1.角度的集合:①与角α(0°≤α<360°)终边相同的角的集合为β|β=k×360°+α,其中k为整数。
②终边在x轴上的角的集合为β|β=k×180,其中k为整数。
③终边在y轴上的角的集合为β|β=k×180+90,其中k为整数。
④终边在坐标轴上的角的集合为β|β=k×90°,其中k为整数。
⑤终边在y=x轴上的角的集合为β|β=k×180°+45°,其中k为整数。
⑥终边在y=-x轴上的角的集合为β|β=k×180°-45°,其中k为整数。
⑦若角α与角β的终边关于x轴对称,则角α与角β的关系为α=360°k-β。
⑧若角α与角β的终边关于y轴对称,则角α与角β的关系为α=360°k+180°-β。
⑨若角α与角β的终边在一条直线上,则角α与角β的关系为α=180°k+β。
⑩角α与角β的终边互相垂直,则角α与角β的关系为α=360°k+β±90°。
2.角度与弧度的互换关系:360°=2π,180°=π,1°=0.≈57.30°=57°18′。
注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零。
3.弧长公式与扇形面积公式:弧长公式为l=|α|×r,扇形面积公式为s=lr=|α|×r²/2.4.三角函数:设α是一个任意角,在α的终边上任取(异于原点的)一点P(x,y),P与原点的距离为r,则sinα=y/r,cosα=x/r,tanα=y/x,cotα=x/y,secα=r/x,cscα=r/y。
5.三角函数在各象限的符号:第一象限中,sinα、cosα、tanα、cotα、secα、cscα均为正数。
高中数学三角函数知识点

高中数学第四章-三角函数知识点汇总1. ①与(0°≤<360°)终边相同的角的会合(角与角的终边重合):| k 360 ,k Z▲y ②终边在x 轴上的角的会合:| k 180 ,k Z23sinx sinx③终边在y 轴上的角的会合:| k 180 90 ,k Z4cosx1cosxx④终边在座标轴上的角的会合:| k 90 , k Zcosx1sinx sinx c osx4⑤终边在y=x 轴上的角的会合:| k 180 45 , k Z 2 3SIN COS三角函数值大小关系图⑥终边在y x 轴上的角的会合:| k 180 45 , k Z 1、2、3、4表示第一、二、三、四象限一半所在地区⑦若角与角的终边对于x 轴对称,则角与角的关系:360 k⑧若角与角的终边对于y 轴对称,则角与角的关系:360 k 180⑨若角与角的终边在一条直线上,则角与角的关系:180 k⑩角与角的终边相互垂直,则角与角的关系:360 k 902. 角度与弧度的交换关系:360°=2 180°= 1°=0.01745 1=57.30 °=57°18′注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.、弧度与角度交换公式:1rad=180 °≈°=57°18ˊ.1°=≈(rad)1803、弧长公式:l | | r . 扇形面积公式:1 1s扇形lr | | r2 224、三角函数:设是一个随意角,在的终边上任取(异于原点的)一点P(x,y )P与原点的距离为r ,则ysin ;rcos ;xrytan ;xc ot x ;yrsec ;.xrcsc .y5、三角函数在各象限的符号:(一全二正弦,三切四余弦)y a的终边yy y- +++ + -oo oxx- +- +- -余弦、正割正切、余切正弦、余割xyO M A xP(x,y )TPro x6、三角函数线正弦线:MP; 余弦线:OM; 正切线:AT.16. 几个重要结论:y (2)(1)y|sinx|>|cosx|7. 三角函数的定义域:s inx>cosx|cosx|>|sinx|O x O |cosx|>|sinx|xcosx>sinx|sinx|>|cosx| (3) 若o<x<2,则sinx<x<tanx高中数学三角函数知识点1sin sin 2 cos sintan(2 tan2 22 2tancos cos 2 cos cos1 21 tansin(2 222cos cos 2 sin sin2 2sin , ,tan 15 cot 75 2 3 ,. tan 75 cot 15 2 315 cos 756 24 sin))75cotcoscos156 2410. 正弦、余弦、正切、余切函数的图象的性质:y sin x y cos x y tan x y cot x y A sin x (A 、>0)1定义域R R Rx ,2| x R且x k k Z x | x R且x k ,k Z值域[ 1, 1] [ 1, 1] R RA, A 周期性 2 2 2奇偶性奇函数偶函数奇函数奇函数当0,非奇非偶当0, 奇函数[2k 2k ]1,;k , k2 2k , k 1 上为减函数(k Z )[ 2k ,2k22( A),上为增函上为增函数数(k Z )[2k2k ]2上为增函,2k12 ( A)数;2k 1 ]单一性[2k2k,]22 上为减函数(k Z )上为增函数;2k22k323上为减函( A),( A) 数(k Z )上为减函数(k Z )注意:①y sin x与y sin x 的单一性正好相反;y cosx 与y cos x 的单一性也相同相反.一般地,若y f (x)在[a, b] 上递加(减),则y f (x) 在[a,b] 上递减(增).▲y ②y sin x 与y cosx 的周期是.③y sin( x ) 或y cos( x ) (0 )的周期2T . xOxy 的周期为2 (T T 2 ,如图,翻折无效).tan2④y sin( x ) 的对称轴方程是x k (k Z ),对称中心(k ,0);y cos( x ) 的对称轴方程是x k2kk 1 );y tan( x ) 的对称中心(,0(k Z ),对称中心(,022).原点对称y cos 2x y cos( 2x) cos 2 x⑤当tan ·tan 1, k ( ) ;tan ·tan 1, ( )k Z k k Z .2 2⑥y cos x 与y sin x 2k 是同一函数,而y ( x ) 是偶函数,则21y .( x ) sin( x k ) cos( x)2⑦函数y tan x在R 上为增函数.(×)[ 只好在某个单一区间单一递加. 若在整个定义域,y tanx为增函数,相同也是错误的].⑧定义域对于原点对称是f (x) 拥有奇偶性的必需不充足条件(. 奇偶性的两个条件:一是定义域对于原点对称(奇偶都要),二是知足奇偶性条件,偶函数: f ( x) f (x) ,奇函数: f ( x) f (x))1奇偶性的单一性:奇同偶反. 比如:y tan x是奇函数,)y 是非奇非偶.(定义域不对于原点对称)tan( x3奇函数特有性质:若0 x的定义域,则f (x) 必定有 f (0) 0.(0 x的定义域,则无此性质)▲y ▲y⑨y sin x 不是周期函数;y sin x 为周期函数(T );x1/2y cos 是周期函数(如图);y cos x 为周期函数(T );xxy= cos|x|图象y=| cos2x+1/2| 图象1y 的周期为(如图),并不是全部周期函数都有最小正周期,比如:cos 2x2y f (x) 5 f ( x k), k R.⑩ b2 有a 2 b2 y .2y a cos b sin a b sin( ) cosa11、三角函数图象的作法:1)几何法:2)描点法及其特例——五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).3)利用图象变换作三角函数图象.三角函数的图象变换有振幅变换、周期变换和相位变换等.函数y=Asin(ωx+φ)的振幅|A| ,周期 2 ,频次 1 | |T f| | T 2,相位x ; 初相(即当x=0 时的相位).(当 A >0,ω>0 时以上公式可去绝对值符号),由y=sinx 的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到本来的|A|倍,获得y=Asinx 的图象,叫做振幅变换或叫沿y 轴的伸缩变换.(用y/A 替代y)由y=sinx 的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到本来的 1| |倍,获得y=sinωx 的图象,叫做周期变换或叫做沿x 轴的伸缩变换.(用ωx 替代x)由y=sinx 的图象上全部的点向左(当φ>0)或向右(当φ<0)平行挪动|φ|个单位,获得y=sin(x+φ)的图象,叫做相位变换或叫做沿x 轴方向的平移.(用x+φ替代x)由y=sinx 的图象上全部的点向上(当b>0)或向下(当b<0)平行挪动|b|个单位,获得y=sinx+b 的图象叫做沿y 轴方向的平移.(用y+(-b) 替代y)由y=sinx 的图象利用图象变换作函数y=Asin (ωx+φ)(A>0,ω>0)(x∈R)的图象,要特别注意:当周期变换和相位变换的先后次序不一样时,原图象延x 轴量伸缩量的差别。
高中数学三角函数知识点

高中数学三角函数知识点高中数学第四章-三角函数知识点汇总1. ①与α(0°≤α<360°)终边相同的角的集合(角α与角β的终边重合):{}Z k k ∈+?=,360|αββ②终边在x 轴上的角的集合:{}Z k k ∈?=,180|ββ③终边在y 轴上的角的集合:{}Z k k ∈+?=,90180| ββ ④终边在坐标轴上的角的集合:{}Z k k ∈?=,90| ββ ⑤终边在y =x 轴上的角的集合:{}Z k k ∈+?=,45180| ββ ⑥终边在xy-=轴上的角的集合:{}Z k k ∈-?=,45180| ββ⑦若角α与角β的终边对于x 轴对称,则角α与角β的关系:βα-=k 360 ⑧若角α与角β的终边对于y 轴对称,则角α与角β的关系:βα-+= 180360k ⑨若角α与角β的终边在一条直线上,则角α与角β的关系:βα+=k 180 ⑩角α与角β的终边互相垂直,则角α与角β的关系:90360±+=βαk 2. 角度与弧度的互换关系:360°=2π 180°=π 1°=0.017451=57.30°=57°18′ 注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零. 、弧度与角度互换公式: 1rad =π180°≈57.30°=57°18ˊ.1°=180π≈0.01745(rad )3、弧长公式:r l ?=||α. 扇形面积公式:211||22s lr r α==扇形4、三角函数:设α是一具任意角,在α的终旁边任取(异于原点的)一点P (x,y )P 与原点的距离为r ,则 ry =αsin ;rx =αcos ; xy =αtan ; yx =αcot ; xr =αsec ;. yr =αcsc .5、三角函数在各象限的符号:(一全二正弦,三切四余弦)正切、余切余弦、正割正弦、余割6、三角函数线正弦线:MP; 余弦线:OM; 正切线: AT.7. 三角函数的定义域:SIN \C O S 三角函数值大小关系图1、2、3、4表示第一、二、三、四象限一半所在区域 (3) 若 o<x<2,则sinx<x<tanx16. 几个重要结论:8、同角三角函数的基本关系式:αααtan cos sin =αααc o t s i n c o s =1cot tan =?αα 1sin csc =α?α1c o s s e c =α?α 1c o s s i n 22=+αα 1tan sec 22=-αα 1cot csc 22=-αα9、诱导公式:2k παα±把的三角函数化为的三角函数,概括为:“奇变偶别变,符号看象限,α当成锐角看!”(Z k ∈)三角函数的公式:(一)基本关系公式组二公式组三xx k x x k x x k x x k c o t )2c o t (t a n )2t a n (c o s )2c o s (s i n )2s i n (=+=+=+=+ππππxx x x x x xx c o t )c o t (t a n )t a n (c o s )c o s (s i n )s i n (-=--=-=--=- 公式组四公式组五公式组六xx x x x x x x cot )cot(tan )tan(cos )cos(sin )sin(=+=+-=+-=+ππππ xx x x x x xx c o t )2c o t (t a n )2t a n (c o s )2c o s (s i n )2s i n(-=--=-=--=-ππππ xx x x x x xx c o t )c o t (t a n )t a n (c o s )c o s (s i n )s i n (-=--=--=-=-ππππ (二)角与角之间的互换公式组一公式组二βαβαβαsin sin cos cos )cos(-=+ αααc o s s i n22s i n = βαβαβαsin sin cos cos )cos(+=- ααααα2222s i n 211c o s 2s i n c o s 2c o s -=-=-= βαβαβαsin cos cos sin )sin(+=+ ααα2t a n 1t a n 22t a n -=βαβαβαsin cos cos sin )sin(-=-2c o s 12s i nαα-±= βαβαβαtan tan 1tan tan )tan(-+=+2c o s 12c o sαα+±=βαβαβαtan tan 1tan tan )tan(+-=-公式组三公式组四公式组五2tan12tan2sin 2ααα+=2tan12tan1cos 2ααα+-=公式组一sin x ·csc x =1tan x =xx cos sin sin 2x +cos 2x =1cos x ·sec x x =xx sin cos 1+tan 2x =sec 2xtan x ·cot x =11+cot 2x =csc 2x=1()()[]()()[]()()[]()()[]βαβαβαβαβαβαβαβαβαβαβαβα--+-=-++=--+=-++=cos cos 21sin sin cos cos 21cos cos sin sin 21sin cos sin sin 21cos sin 2 cossin2sin sin βαβαβα-+=+αααααααsin cos 1cos 1sin cos 1cos 12tan -=+=+-±=ααπsin )21cos(-=+ααπsin )21cos(=-ααπcos )21sin(=-α απcot )21tan(=-2tan12tan2tan 2ααα-=42675cos 15sin -==, ,3275cot 15tan -==,.3215cot 75tan +==42615cos 75sin +==x y sin -=x y sin =xy cos-=x ycos=)(x f y =在],[b a 上递增(减),则)(x f y -=在],[b a 上递减(增). ②x y sin =与xycos =的周期是π.③)sin(?ω+=x y 或)cos(?ω+=x y(0≠ω)的周期ωπ2=T .2tanx y =的周期为2π(πωπ2=?=T T,如图,翻折无效).④)sin(?ω+=x y 的对称轴方程是2ππ+=k x (Z k ∈),对称中心(0,πk ); )c o s (?ω+=x y 的对称轴方程是π k x=(Z k ∈),对称中心(0,21ππ+k );)t a n (?ω+=x y 的对称中心(0,2πk ).x x y x y 2cos )2cos(2cos -=--=→?=原点对称⑤当αtan ·,1tan =β)(2Z k k ∈+=+ππβα;αtan ·,1tan -=β)(2Z k k ∈+=-ππβα.⑥xycos =与??++=ππk x y 22sin 是同一函数,而)(?ω+=x y 是偶函数,则 2sin 2cos 2sin sin βαβαβα-+=-2cos2cos2cos cos βαβαβα-+=+2sin2sin2cos cos βαβαβα-+-=-ααπcos )21sin(=+ααπcot )21tan(-=+)cos()21sin()(x k x x y ωππω?ω±=++=+=.⑦函数x y tan =在R 上为增函数.(×) [只能在某个单调区间单调递增. 若在整个定义域,x y tan =为增函数,同样也是错误的].⑧定义域对于原点对称是)(x f 具有奇偶性的必要别充分条件.(奇偶性的两个条件:一是定义域对于原点对称(奇偶都要),二是满脚奇偶性条件,偶函数:)()(x f x f =-,奇函数:)()(x f x f -=-)奇偶性的单调性:奇同偶反. 例如:x y tan =是奇函数,)31t an(π+=x y 是非奇非偶.(定义域别对于原点对称)奇函数特有性质:若x ∈0的定义域,则)(x f 一定有0)0(=f .(x ?0的定义域,则无此性质)⑨x ysin=别是周期函数;x y sin =为周期函数(π=T );xy cos =是周期函数(如图);x y cos =为周期函数(=T 212cos +=x y 的周期为π(如图),并非所有周期函数都有最小正周期,例如:R k k x f x f y ∈+===),(5)(.⑩ab ba b a y=+++=+=??αβαcos )sin(sin cos 22 有y b a ≥+22.11、三角函数图象的作法:1)几何法:2)描点法及其特例——五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线). 3)利用图象变换作三角函数图象.三角函数的图象变换有振幅变换、周期变换和相位变换等.函数y =Asin (ωx +φ)的振幅|A|,周期2||Tπω=,频率1||2fTωπ==,相位;x ω?+初相?(即当x =0时的相位).(当A >0,ω>0 时以上公式可去绝对值符号),由y =sinx 的图象上的点的横坐标保持别变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y =Asinx 的图象,叫做振幅变换或叫沿y 轴的伸缩变换.(用y/A 替换y )由y =sinx 的图象上的点的纵坐标保持别变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的1||ω倍,得到y =sin ω x 的图象,叫做周期变换或叫做沿x 轴的伸缩变换.(用ωx 替换x)由y =sinx 的图象上所有的点向左(当φ>0)或向右(当φ<0)平行挪移|φ|个单位,得到y =sin (x +φ)的图象,叫做相位变换或叫做沿x 轴方向的平移.(用x +φ替换x)由y =sinx 的图象上所有的点向上(当b >0)或向下(当b <0)平行挪移|b |个单位,得到y =sinx +b 的图象叫做沿y 轴方向的平移.(用y+(-b)替换y )由y =sinx 的图象利用图象变换作函数y =Asin (ωx +φ)(A >0,ω>0)(x ∈R )的图象,要特殊注意:当周期变换和相位变换的先后顺序别并且,原图象延x 轴量伸缩量的区不。
高中数学必修4第一章三角函数的知识点

2
1,1
k
; 当 当 x 2 k k 时,
y m ax 1 ;当 x 2 k
R
倍(纵坐标
不变) ,得到函数 y sin x 的图象;再将函数 y sin x 的图象上所有点的纵坐标 伸长(缩短)到原来的 倍(横坐标不变) ,得到函数 y sin x 的图象. 函数 y sin x 的图象上所有点的横坐标伸长(缩短)到原来的
2
奇函数
偶函数
奇函数
2
, 2k
2
;③频率: f
1
2
;④相位: x ;⑤初相: .
函数 y s in x ,当 x x1 时,取得最小值为 y m in ;当 x x 2 时,取得最大值为
y m a x ,则
sin , co s
co s , tan
, tan
tan .
3、与角 终边相同的角的集合为 k 3 6 0 , k
sin , co s
co s
tan .
终边所落在的区域.
co s , co s sin , tan co t . 2 2 2 co s , co s sin , tan co t . 2 2 2
1 2
y m ax
y m in ,
高中常考的数学知识点三角函数的定义

高中常考的数学知识点三角函数的定义一、三角函数三角函数的定义域是研究其他一切性质的前提,求三角函数的定义域实际上就是解最简单的'三角不等式,通常可用三角函数的图像或三角函数线来求解,注意数形结合思想的应用,如何运用三角函数的图像解决问题能够帮助对数形结合思想的掌握。
二、三角函数诱导公式1.公式一:设α为任意角,终边相同的角的同一三角函数的值相等运用同角三角函数的基本关系式求值2.公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=—sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinα三、锐角三角函数在△ABC中,∠C为直角,∠A和∠B是锐角三角函数专题题型全归纳第一节:三角函数概念及同角三角函数关系题型一:概念辨析题型二:象限角及终边相同的角题型三:扇形的弧长及面积公式题型四:三角函数的定义及应用题型五:同角三角函数直接应用题型六:同角三角函数之弦的齐次式第二节:诱导公式及恒等变换题型一:诱导公式的运用题型二:恒等变换题型三:角的拼凑第三节:三角函数的图像及性质题型一:三角函数的周期题型二:三角函数的定义域题型三:三角函数的单调性题型四:三角函数的对称性题型五:三角函数的奇偶性题型六:三角函数的值域第四节:三角函数的图像变换及综合题型一:图像变换题型二:已知图像求解解析式题型三:三角函数性质综合(多选题专练)题型四:三角函数解答题题型五:三角函数实际应用第五节:解三角形题型一:正余弦定理选择题型二:边角互换题型三:与三角形面积有关题型四:三角形形状判断题型五:三角形的个数判断题型六:最值与取值范围题型七:解三角形在平面图形中的运用题型八:解三角形的实际应用题型九:解三角形解答题专练。
高中数学三角函数知识点归纳

高中数学三角函数知识点归纳三角函数是高中数学中重要的概念之一,它在几何和代数中都有广泛的应用。
以下是高中数学三角函数的主要知识点的归纳:1. 三角函数的定义- 正弦函数:sinA = 对边/斜边- 余弦函数:cosA = 邻边/斜边- 正切函数:tanA = 对边/邻边2. 基本关系- 任意角A的正弦、余弦、正切值在一个圆上都有相应的点坐标;- 三角函数的周期性:sin(A+2π) = sinA,cos(A+2π) = cosA,tan(A+π) = tanA3. 基本恒等式和性质- 三角函数的符号关系:sinA≤1,cosA≤1,tanA在某些角度上无定义;- 基本恒等式:sin^2A + cos^2A = 1,1+tan^2A = sec^2A,1+cot^2A = csc^2A;- 三角函数的奇偶性和周期性:sin(-A) = -sinA,sin(π-A) = sinA,cos(-A) = cosA,cos(π-A) = -cosA;- 三角函数的对应关系:sin(A±B) = sinA⋅cosB±cosA⋅sinB,cos(A±B) = cosA⋅cosB∓sinA⋅sinB4. 三角函数的图象和性质- 正弦曲线、余弦曲线:周期为2π,在[-π/2, π/2]范围内的值域为[-1, 1]- 周期函数的变换:y=A⋅sin(Bx-C)+D和y=A⋅cos(Bx-C)+D5. 三角函数的应用- 三角函数在几何中的应用:计算三角形的边长和角度,求解航向问题等;- 三角函数在物理中的应用:描述振动、波动、电流和电压等周期性现象;- 三角函数在解析几何中的应用:表示平面曲线的方程,求解方程组等。
以上是高中数学三角函数知识点的归纳。
希望能帮助您更好地理解和应用三角函数。
高中数学三角函数知识点

高中数学三角函数知识点1.弧度制和角度制在三角函数中,常用的角度制和弧度制可以相互转化。
角度制是以度为单位来度量角的大小,一圆为360°。
弧度制是以弧长与半径之比来度量角的大小,一圆的弧长为2π,所以一圆等于2π弧度。
换算公式为:弧度制=角度制×π/180。
2.三角函数的正弦函数正弦函数是一个周期函数,其定义域为实数集,值域为[-1,1]。
在直角三角形中,正弦函数可以用边长之比来表示,即sinθ = 对边/斜边。
3.三角函数的余弦函数余弦函数也是一个周期函数,其定义域为实数集,值域为[-1,1]。
在直角三角形中,余弦函数可以用边长之比来表示,即cosθ = 邻边/斜边。
4.三角函数的正切函数正切函数也是一个周期函数,其定义域为实数集(除了无定义的点),值域为全体实数。
在直角三角形中,正切函数可以用边长之比来表示,即tanθ = 对边/邻边。
需要注意的是,当邻边为0时,正切函数无定义。
5.三角函数的倒数关系正弦函数和余弦函数是三角函数的倒数关系,即sinθ = cos(π/2- θ)。
正切函数与余切函数也是倒数关系,即tanθ = cot(π/2 - θ)。
6.三角函数的图像和性质正弦函数的图像是一条连续的波浪线,周期为2π。
余弦函数的图像是一条连续的波浪线,周期也为2π。
正切函数的图像是一条由无穷多个间断点组成的周期为π的曲线。
7.三角函数的性质正弦函数和余弦函数的图像关于原点对称,正切函数的图像关于y轴对称。
正弦函数和余弦函数是奇函数,即sin(-θ) = -sinθ,cos(-θ) = cosθ。
正切函数是奇函数,即tan(-θ) = -tanθ。
8.三角函数的周期性正弦函数、余弦函数和正切函数都是周期函数,它们的周期分别为2π、2π和π。
即对于任意实数k,有sin(x + 2πk) = sinx,cos(x + 2πk) = cosx,tan(x + πk) = tanx。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学第四章-三角函数知识点汇总1. ①与α(0°≤α<360°)终边相同的角的集合(角α与角β的终边重合):{}Z k k ∈+⨯=,360|αββ②终边在x 轴上的角的集合: {}Z k k ∈⨯=,180|ββ ③终边在y 轴上的角的集合:{}Z k k ∈+⨯=,90180|ββ ④终边在坐标轴上的角的集合:{}Z k k ∈⨯=,90| ββ ⑤终边在y =x 轴上的角的集合:{}Z k k ∈+⨯=,45180| ββ ⑥终边在x y -=轴上的角的集合:{}Z k k ∈-⨯=,45180| ββ⑦若角α与角β的终边关于x 轴对称,则角α与角β的关系:βα-=k 360 ⑧若角α与角β的终边关于y 轴对称,则角α与角β的关系:βα-+= 180360k ⑨若角α与角β的终边在一条直线上,则角α与角β的关系:βα+=k 180 ⑩角α与角β的终边互相垂直,则角α与角β的关系: 90360±+=βαk 2. 角度与弧度的互换关系:360°=2π 180°=π 1°=0.01745 1=57.30°=57°18′ 注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.、弧度与角度互换公式: 1rad =π180°≈57.30°=57°18ˊ. 1°=180π≈0.01745(rad )3、弧长公式:r l ⋅=||α. 扇形面积公式:211||22s lr r α==⋅扇形4、三角函数:设α是一个任意角,在α的终边上任取(异于原点的)一点P (x,y )P 与原点的距离为r ,则 ry =αsin ;rx =αcos ; x y=αtan ; yx =αcot ; x r =αsec ;. yr =αcsc .5、三角函数在各象限的符号:(一全二正弦,三切四余弦)正切、余切余弦、正割正弦、余割6、三角函数线正弦线:MP; 余弦线:OM; 正切线: AT.7.三角函数的定义域:SIN \COS 1、2、3、4表示第一、二、三、四象限一半所在区域(3) 若 o<x<2,则sinx<x<tanx16. 几个重要结论:8、同角三角函数的基本关系式:αααtan cos sin =αααcot sin cos =1cot tan =⋅αα 1sin csc =α⋅α 1cos sec =α⋅α 1cos sin 22=+αα 1tan sec 22=-αα 1cot csc 22=-αα9、诱导公式:2k παα±把的三角函数化为的三角函数,概括为:“奇变偶不变,符号看象限,α当成锐角看!”(Zk ∈)三角函数的公式:(一)基本关系公式组二 公式组三x x k x x k x x k x x k cot )2cot(tan )2tan(cos )2cos(sin )2sin(=+=+=+=+ππππ x x x x xx x x cot )cot(tan )tan(cos )cos(sin )sin(-=--=-=--=-公式组四 公式组五 公式组六x x x x x x x x cot )cot(tan )tan(cos )cos(sin )sin(=+=+-=+-=+ππππ x x x x x x x x cot )2cot(tan )2tan(cos )2cos(sin )2sin(-=--=-=--=-ππππ x x x x xx x x cot )cot(tan )tan(cos )cos(sin )sin(-=--=--=-=-ππππ(二)角与角之间的互换公式组一 公式组二 βαβαβαsin sin cos cos )cos(-=+ αααcos sin 22sin = βαβαβαsin sin cos cos )cos(+=- ααααα2222sin 211cos 2sin cos 2cos -=-=-=βαβαβαsin cos cos sin )sin(+=+ ααα2tan 1tan 22tan -=βαβαβαsin cos cos sin )sin(-=- 2cos 12sinαα-±= βαβαβαtan tan 1tan tan )tan(-+=+ 2cos 12cos αα+±=βαβαβαtan tan 1tan tan )tan(+-=- 公式组三 公式组四 公式组五2tan 12tan 2sin 2ααα+= 2tan 12tan 1cos 22ααα+-= 公式组一sin x ·csc x =1tan x =xx cos sin sin 2x +cos 2x =1cos x ·sec x x =xx sin cos 1+tan 2x =sec 2x tan x ·cot x =11+cot 2x =csc 2x=1()()[]()()[]()()[]()()[]βαβαβαβαβαβαβαβαβαβαβαβα--+-=-++=--+=-++=cos cos 21sin sin cos cos 21cos cos sin sin 21sin cos sin sin 21cos sin 2cos 2sin 2sin sin βαβαβα-+=+αααααααsin cos 1cos 1sin cos 1cos 12tan -=+=+-±=ααπsin )21cos(-=+ααπsin )21cos(=-ααπcos )21sin(=-ααπcot )21tan(=-2tan 12tan2tan 2ααα-=42675cos 15sin -==, ,3275cot 15tan -== ,. 3215cot 75tan +== 42615cos 75sin +==)(x f y =在],[b a 上递增(减),则)(x f y -=在],[b a 上递减(增). ②x y sin =与x y cos =的周期是π.③)sin(ϕω+=x y 或)cos(ϕω+=x y (0≠ω)的周期ωπ2=T .2tanx y =的周期为2π(πωπ2=⇒=T T ,如图,翻折无效).④)sin(ϕω+=x y 的对称轴方程是2ππ+=k x (Z k ∈),对称中心(0,πk );)cos(ϕω+=x y 的对称轴方程是πk x =(Z k ∈),对称中心(0,21ππ+k );)tan(ϕω+=x y 的对称中心(0,2πk ). x x y x y 2cos )2cos(2cos -=--=−−−→−=原点对称⑤当αtan ·,1tan =β)(2Z k k ∈+=+ππβα;αtan ·,1tan -=β)(2Z k k ∈+=-ππβα.⑥x y cos =与⎪⎭⎫ ⎝⎛++=ππk x y 22sin 是同一函数,而)(ϕω+=x y 是偶函数,则2sin2cos2sin sin βαβαβα-+=-2cos 2cos2cos cos βαβαβα-+=+2sin2sin 2cos cos βαβαβα-+-=-ααπcos )21sin(=+ααπcot )21tan(-=+)cos()21sin()(x k x x y ωππωϕω±=++=+=.⑦函数x y tan =在R 上为增函数.(×) [只能在某个单调区间单调递增. 若在整个定义域,x y tan =为增函数,同样也是错误的].⑧定义域关于原点对称是)(x f 具有奇偶性的必要不充分条件.(奇偶性的两个条件:一是定义域关于原点对称(奇偶都要),二是满足奇偶性条件,偶函数:)()(x f x f =-,奇函数:)()(x f x f -=-)奇偶性的单调性:奇同偶反. 例如:x y tan =是奇函数,)31tan(π+=x y 是非奇非偶.(定义域不关于原点对称)奇函数特有性质:若x ∈0的定义域,则)(x f 一定有0)0(=f .(x ∉0的定义域,则无此性质)⑨x y sin =不是周期函数;x y sin =为周期函数(π=T )x y cos =是周期函数(如图);x y cos =为周期函数(=T 212cos +=x y 的周期为π(如图),并非所有周期函数都有最小正周期,例如: R k k x f x f y ∈+===),(5)(.⑩abb a b a y =+++=+=ϕϕαβαcos )sin(sin cos 22 有y b a ≥+22. 11、三角函数图象的作法: 1)几何法:2)描点法及其特例——五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线). 3)利用图象变换作三角函数图象.三角函数的图象变换有振幅变换、周期变换和相位变换等.函数y =Asin (ωx +φ)的振幅|A|,周期2||T πω=,频率1||2f T ωπ==,相位;x ωϕ+初相ϕ(即当x =0时的相位).(当A >0,ω>0 时以上公式可去绝对值符号),由y =sinx 的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y =Asinx 的图象,叫做振幅变换或叫沿y 轴的伸缩变换.(用y/A 替换y )由y =sinx 的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的1||ω倍,得到y =sin ω x 的图象,叫做周期变换或叫做沿x 轴的伸缩变换.(用ωx 替换x)由y =sinx 的图象上所有的点向左(当φ>0)或向右(当φ<0)平行移动|φ|个单位,得到y =sin (x +φ)的图象,叫做相位变换或叫做沿x 轴方向的平移.(用x +φ替换x)由y =sinx 的图象上所有的点向上(当b >0)或向下(当b <0)平行移动|b |个单位,得到y =sinx +b 的图象叫做沿y 轴方向的平移.(用y+(-b)替换y )由y =sinx 的图象利用图象变换作函数y =Asin (ωx +φ)(A >0,ω>0)(x ∈R )的图象,要特别注意:当周期变换和相位变换的先后顺序不同时,原图象延x 轴量伸缩量的区别。
II. 竞赛知识要点一、反三角函数.1. 反三角函数:⑴反正弦函数x y arcsin =是奇函数,故x x arcsin )arcsin(-=-,[]1,1-∈x (一定要注明定义域,若()+∞∞-∈,x ,没有x 与y 一一对应,故x y sin =无反函数)注:x x =)sin(arcsin ,[]1,1-∈x ,⎥⎦⎤⎢⎣⎡-∈2,2arcsin ππx .y=|cos2x +1/2|图象⑵反余弦函数x y arccos =非奇非偶,但有ππk x x 2)arccos()arccos(+=+-,[]1,1-∈x . 注:①x x =)cos(arccos ,[]1,1-∈x ,[]π,0arccos ∈x .②x y cos =是偶函数,x y arccos =非奇非偶,而x y sin =和x y arcsin =为奇函数. ⑶反正切函数:x y arctan =,定义域),(+∞-∞,值域(2,2ππ-),x y arctan =是奇函数, x x arctan )arctan(-=-,∈x ),(+∞-∞.注:x x =)tan(arctan ,∈x ),(+∞-∞.⑷反余切函数:x arc y cot =,定义域),(+∞-∞,值域(2,2ππ-),x arc y cot =是非奇非偶.ππk x arc x arc 2)cot()cot(+=+-,∈x ),(+∞-∞.注:①x x arc =)cot cot(,∈x ),(+∞-∞.②x y arcsin =与)1arcsin(x y -=互为奇函数,x y arctan =同理为奇而x y arccos =与x arc y cot =非奇非偶但满足]1,1[,2)cot(cot ]1,1[,2arccos )arccos(-∈+=-+-∈+=+-x k x arc x arc x k x x ππππ.⑵ 正弦、余弦、正切、余切函数的解集:a 的取值范围 解集 a 的取值范围 解集 ①a x =sin 的解集 ②a x =cos 的解集a>1 ∅ a>1 ∅a=1 {}Z k a k x x ∈+=,arcsin 2|π a=1 {}Z k a k x x ∈+=,arccos 2|πa<1 (){}Z k a k x x k ∈-+=,arcsin 1|πa<1 {}Z k a k x x ∈±=,arccos |π③a x =tan 的解集:{}Z k a k x x ∈+=,arctan |π ③a x =cot 的解集:{}Z k a k x x ∈+=,cot arc |π 二、三角恒等式.组一组二∏===nk nn nk12sin2sin 2cos8cos4cos2cos2cos ααααααα∑=++=+++++=+nk dnd x d n nd x d x x kd x 0sin )cos())1sin(()cos()cos(cos )cos(∑=++=+++++=+nk dnd x d n nd x d x x kd x 0sin )sin())1sin(()sin()sin(sin )sin(αγγββαγβαγβαγβαtan tan tan tan tan tan 1tan tan tan tan tan tan )tan(----++=++组三 三角函数不等式x sin <x <)2,0(,tan π∈x x xxx f sin )(=在),0(π上是减函数 若π=++C B A ,则C xy B xz A yz z y x cos 2cos 2cos 2222++≥++ααααααcos 3cos 43cos sin 4sin 33sin 33-=-=()()αββαβαβα2222cos cos sin sin sin sin -=-+=-ααααααsin 22sin 2cos ...4cos 2cos cos 11++=n n n。
