数字信号处理实验程序2.
数字信号处理实验参考程序

幼儿园防溺水宣传计划幼儿园安全宣传一、概述随着社会的发展和进步,人民生活水平不断提高,对幼儿教育的重视也日益增加。
幼儿园作为儿童成长发展的重要场所,其安全工作显得尤为重要。
溺水是儿童意外伤害中的一大杀手,因此我们应该加强对幼儿园防溺水的宣传工作,提高教职员工和家长的安全意识,有效预防溺水事故的发生。
二、宣传目标1. 提高园内教职员工对溺水危险的认识和防范意识;2. 提高家长对幼儿园溺水安全问题的重视,强化家庭教育;3. 增强幼儿对自我保护的意识和能力,懂得遵守安全规则。
三、宣传策略1. 制定相关政策和措施,设置明确的安全责任人,强化安全管理;2. 利用多种形式的媒体,如横幅、宣传画、安全标识等,进行宣传教育;3. 注重开展家长会、学习班等形式的公开宣传活动,使家长积极参与;4. 制作宣传材料,比如安全知识手册、安全教育视瓶等,定期进行宣传;5. 通过特色活动,如安全教育周、实地演练等形式,增强幼儿对安全问题的认识。
四、宣传内容1. 水域危险认知提醒家长和教职员工,加强对水域危险的认知,不让幼儿单独接近水域,及时发现危险并加强监护;2. 安全教育通过故事、图片等形式,向幼儿们普及溺水知识,教会他们正确的自救和呼救方式;3. 安全设施使用指导孩子如何正确使用安全设施,如救生圈、游泳圈等,增强自我保护能力;4. 灾害逃生组织模拟演练,让孩子们了解常见溺水灾害的逃生方法和注意事项。
五、宣传形式1. 安全知识手册制作具体的幼儿园防溺水的安全知识手册,向家长发放,让家长了解幼儿园的安全措施;2. 安全教育视瓶制作针对幼儿的安全教育视瓶,通过播放的形式让幼儿加深对安全知识的理解;3. 安全演练定期组织模拟演练,让孩子们亲身体验安全逃生的情景,增强安全意识和逃生能力;4. 公开宣传通过家长会、学习班等形式,公开宣传防溺水的重要性,引导家长和教职员工重视这一问题。
六、宣传效果评估1. 制定评估方案建立一套完整的宣传效果评估方案,包括对教职员工、家长及幼儿的问卷调查等,定期进行评估;2. 持续改进根据评估结果,及时发现宣传工作中的不足和问题,做出合理调整,持续改进宣传效果;3. 宣传效果展示定期向相关部门和家长公示宣传工作的效果,增强公众对幼儿园安全工作的信任和支持。
数字信号处理 实验报告 实验二 应用快速傅立叶变换对信号进行频谱分析

数字信号处理实验报告实验二应用快速傅立叶变换对信号进行频谱分析2011年12月7日一、实验目的1、通过本实验,进一步加深对DFT 算法原理合基本性质的理解,熟悉FFT 算法 原理和FFT 子程序的应用。
2、掌握应用FFT 对信号进行频谱分析的方法。
3、通过本实验进一步掌握频域采样定理。
4、了解应用FFT 进行信号频谱分析过程中可能出现的问题,以便在实际中正确应用FFT 。
二、实验原理与方法1、一个连续时间信号)(t x a 的频谱可以用它的傅立叶变换表示()()j t a a X j x t e dt +∞-Ω-∞Ω=⎰2、对信号进行理想采样,得到采样序列()()a x n x nT =3、以T 为采样周期,对)(n x 进行Z 变换()()n X z x n z +∞--∞=∑4、当ωj ez =时,得到序列傅立叶变换SFT()()j j n X e x n e ωω+∞--∞=∑5、ω为数字角频率sT F ωΩ=Ω=6、已经知道:12()[()]j a m X e X j T T Tωωπ+∞-∞=-∑ ( 2-6 )7、序列的频谱是原模拟信号的周期延拓,即可以通过分析序列的频谱,得到相应连续信号的频谱。
(信号为有限带宽,采样满足Nyquist 定理)8、无线长序列可以用有限长序列来逼近,对于有限长序列可以使用离散傅立叶变换(DFT )。
可以很好的反映序列的频域特性,且易于快速算法在计算机上实现。
当序列()x n 的长度为N 时,它的离散傅里叶变换为:1()[()]()N knN n X k DFT x n x n W-===∑ 其中2jNN W eπ-=,它的反变换定义为:101()[()]()N knN k x n IDFT X k X k W N --===∑比较Z 变换式 ( 2-3 ) 和DFT 式 ( 2-7 ),令kN z W -=则1()()[()]|kNN nkN N Z W X z x n W DFT x n ---====∑ 因此有()()|kNz W X k X z -==k N W -是Z 平面单位圆上幅角为2kNπω=的点,也即是将单位圆N 等分后的第k 点。
数字信号处理综合实验

数字信号处理综合实验一、实验目的本实验旨在通过数字信号处理技术的综合应用,加深对数字信号处理原理和方法的理解,提高学生的实际操作能力和问题解决能力。
二、实验原理数字信号处理是利用数字计算机对摹拟信号进行采样、量化和编码,然后进行数字运算和处理的技术。
本实验主要涉及以下几个方面的内容:1. 信号采集与预处理:通过摹拟信号采集电路将摹拟信号转换为数字信号,然后进行预处理,如滤波、降噪等。
2. 数字滤波器设计:设计和实现数字滤波器,包括FIR滤波器和IIR滤波器,可以对信号进行滤波处理,提取感兴趣的频率成份。
3. 时域和频域分析:对采集到的信号进行时域和频域分析,如时域波形显示、功率谱密度估计等,可以了解信号的时域和频域特性。
4. 信号重构与恢复:通过信号重构算法对采集到的信号进行恢复,如插值、外推等,可以还原信号的原始特征。
三、实验内容根据实验原理,本实验的具体内容包括以下几个部份:1. 信号采集与预处理a. 使用摹拟信号采集电路将摹拟信号转换为数字信号,并通过示波器显示采集到的信号波形。
b. 对采集到的信号进行预处理,如去除噪声、滤波等,确保信号质量。
2. 数字滤波器设计a. 设计并实现FIR滤波器,选择合适的滤波器类型和参数,对采集到的信号进行滤波处理。
b. 设计并实现IIR滤波器,选择合适的滤波器类型和参数,对采集到的信号进行滤波处理。
3. 时域和频域分析a. 对采集到的信号进行时域分析,绘制信号的时域波形图,并计算信号的均值、方差等统计指标。
b. 对采集到的信号进行频域分析,绘制信号的功率谱密度图,并计算信号的频域特性。
4. 信号重构与恢复a. 使用插值算法对采集到的信号进行重构,恢复信号的原始特征。
b. 使用外推算法对采集到的信号进行恢复,还原信号的原始特征。
四、实验步骤1. 搭建信号采集电路,将摹拟信号转换为数字信号,并通过示波器显示采集到的信号波形。
2. 对采集到的信号进行预处理,如去除噪声、滤波等,确保信号质量。
数字信号处理实验报告 (2)

实验一信号、系统及系统响应一、实验目的1、熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定的理解。
2、熟悉时域离散系统的时域特性。
3、利用卷积方法观察分析系统的时域特性。
4、掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。
二、实验原理采样的的过程既是连续信号离散化的过程。
采用单位冲击串进行采样,为使采样信号能不失真的还原为采样前的信号,根据奈奎斯特采样率,采样频率应该大于信号最高频率的2倍。
因为时域的采样既是对时域的离散化处理,时域离散频域会进行周期延拓,为了防止频域频谱混叠,必须满足奈奎斯特采样定律。
线性卷积的过程为:反褶,移位,相乘,相加。
设一个N1点的序列与一个N2的序列进行卷积则得到N1+N2-1点的序列。
时域卷积,对应频域的相乘。
序列的傅里叶变换即DTFT 。
具有的性质有: 线性,移位性,对偶性,等等。
三、实验内容及步骤1)分析采样序列的特性。
产生采样序列()a x n ,A 444.128=,a =,0Ω=。
a 、 取采样频率s f 1kHz =,即T 1ms =。
观察所采样()a x n 的幅频特性()j X e ω和)(t x a 的幅频特性()X j Ω在折叠频率处有无明显差别。
应当注意,实验中所得频谱是用序列的傅立叶变换公式求得的,所以在频率量度上存在关系:T ω=Ω。
b 、改变采样频率,s f 300Hz =,观察()j X eω的变化并做记录。
c 、 进一步降低采样频率,s f 200Hz =,观察频谱混叠是否明显存在,说明原因,并记录()j X e ω的幅频曲线。
上图是采用不同采样频率时所得到的序列及其对应的傅里叶变换,从图中可以看到,当采样频率比较低时,频谱会发生混叠,且频率越低,混叠现象越明显。
增大采样频率可以有效地防止混叠。
2) 离散信号、系统和系统响应分析。
a 、观察信号()b x n 和系统h ()b n 的时域和频域持性;利用线形卷积求信号()b x n 通过系统h ()b n 的响应y(n),比较所求响应y(n)和h ()b n 的时域及频域特性,注意它们之间有无差异,绘图说明,并用所学结论解释所得结果。
数字信号处理实验参考程序

实验一参考程序:1 产生10点的单位抽样序列δ(n);function unit_pulse(N)% unit_pulse.mN=10;x=zeros(1,N);x(1)=1;n=0:N-1;figure(1);stem(n,x);xlabel('单位抽样序列')axis([-1 20 0 1.1])2产生10点同时移位3位的单位抽样序列δ(n-3);function shift_unit_pulse(N,k)% shift_unit_pulse.mN=10;k=3;x=zeros(1,N);x(k+1)=1;n=0:N-1;figure(2);stem(n,x);xlabel('移位3位的单位抽样序列')axis([-1 10 0 1.1])function [x, n]=i shift_unit_pulse (n0,ns,nf)n=[0:9];x=[(n-3)==0]3产生任意序列f(n)=8δ(n)+7δ(n-1)+6δ(n-2) +5δ(n-3)+ 4δ(n-4)+7δ(n-5);function arbitrary_pulse(N)% arbitrary_pulse.mN=10x=zeros(1,N);x(1)=8;x(2)=7;x(3)=6;x(4)=5;x(5)=4;x(6)=7;n=0:N-1;figure(3);stem(n,x);xlabel('任意序列f(n)')axis([-1 10 0 9])4产生N=10点的单位阶跃序列function unit_step(N)% unit_step.mN=10;x=ones(1,N);n=0:N-1;figure(4);stem(n,x);xlabel('单位阶跃序列')axis([-1 15 0 1.1])5产生斜率为3,n0=4,点数为20点的斜坡序列g(n)=B(n-n0)function slope(N,k,B)% slope.mN=20;k=4;B=3;x=[zeros(1,k) ones(1,N-k)];for i=1:Nx(i)=B*x(i)*(i-k);endn=0:N-1;figure(5);stem(n,x);xlabel('斜坡序列')axis([-1 20 0 90])6产生幅度A=3,频率f=100,初始相位 =1.2,点数为32点的正弦序列。
“数字信号处理”实验报告二

实验报告课程名称:数字信号处理实验任课教师:杨鉴实验名称:离散时间系统的时域分析年级、专业:2015级通信工程学号:**********姓名:***日期:2017 年10 月9 日云南大学信息学院一、实验1.通过MATLAB仿真一些简单的离散时间系统,并研究他们的时域特性。
2.掌握卷积在MATLAB的算法并理解滤波的概念。
二、实验内容1. 假定另一个系统为y[n]=x[n]x[n-1],修改程序P2.3,计算这个系统的输出序列y1[n],y2[n]和y[n]。
比较y[n]和yt[n]。
这两个序列是否相等?该系统是线性系统吗?2. 考虑另一个系统:y[n]=nx[n]+x[n-1],修改程序P2.4,以仿真上面的系统并确定该系统是否为时不变系统。
3.修改程序P2.7,计算长度为15的序列h[n]和长度为10的序列x[n]的卷积,重做问题Q2.28。
h[n]和x[n]的样本值你自己给定。
4.修改程序P2.9,将输入序列改变成扫频正弦序列(长度为301、最低频率为0、最高频率为0.5)。
那个滤波器能更好的抑制输入信号x[n]的高频分量?三、主要算法与程序Q2.11:clf;n = 0:40;a = 2;b = -3;f1=0.1;f2=0.4;x11=[0 cos(2*pi*f1*n) 0];x12=[0 0 cos(2*pi*f1*n)];x21=[0 cos(2*pi*f2*n) 0];x22=[0 0 cos(2*pi*f2*n)];x = a*x11 + b*x21;y1 = x11.*x12;y2 = x21.*x22;xd = a*x12+b*x22;y = x.*xd;yt = a*y1 + b*y2;d = y - yt; % Compute the difference output d[n]% Plot the outputs and the difference signalsubplot(3,1,1)stem([0 n 0],y);ylabel('Amplitude');title('Output Due to Weighted Input: a \cdot x_{1}[n] + b \cdot x_{2}[n]');subplot(3,1,2)stem([0 n 0],yt);ylabel('Amplitude');title('Weighted Output: a \cdot y_{1}[n] + b \cdot y_{2}[n]'); subplot(3,1,3)stem([0 n 0],d);xlabel('Time index n');ylabel('Amplitude');title('Difference Signal');Q2.17:clf;n = 0:40; D = 10;a = 3.0;b = -2;x = a*cos(2*pi*0.1*n) + b*cos(2*pi*0.4*n);xd = [zeros(1,D) x];nd=0:length(xd)-1;y=(n.*x)+[0 x(1:40)];yd=(nd.*xd)+[0 xd(1:length(xd)-1)];d = y - yd(1+D:41+D);subplot(3,1,1)stem(n,y);ylabel('振幅');title('输出 y[n]'); grid;subplot(3,1,2)stem(n,yd(1:41));ylabel('振幅');title('由于延时输入 x[n-10]的输出'); grid;subplot(3,1,3)stem(n,d);xlabel('时间序号 n'); ylabel('振幅');title('差值信号');grid;Q2.29:clf;h = [3 2 1 -2 1 0 -4 0 3 1 5 4 0 3 5]; % impulse responsex = [1 -2 3 -4 3 2 1 5 6 1]; % input sequencey = conv(h,x);n = 0:23;subplot(2,1,1);stem(n,y);xlabel('时间序号n');ylabel('振幅');title('用卷积得到的输出'); grid;x1 = [x zeros(1,14)];y1 = filter(h,1,x1);subplot(2,1,2);stem(n,y1);xlabel('时间序号 n'); ylabel('振幅');title('由滤波生成的输出'); grid;Q2.35:f=w/2pi=(2a*n+b)/2pi=[0,0.5],所以b=0,a*n<=0.5*pi,当n=300时,a取pi/600。
数字信号处理实验(吴镇扬)答案-2
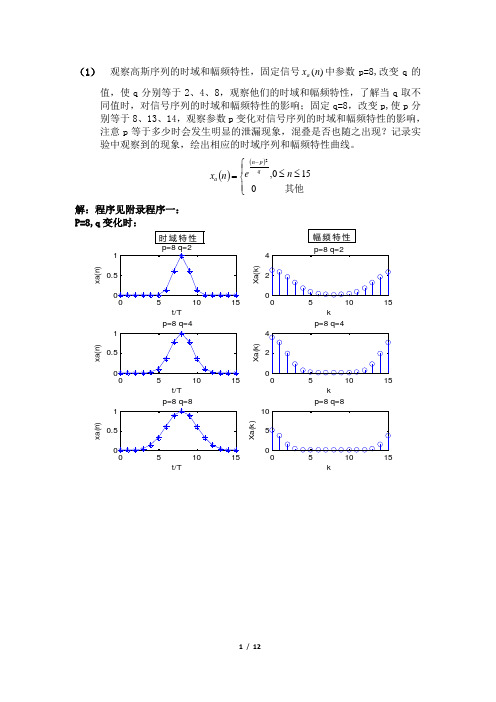
(1) 观察高斯序列的时域和幅频特性,固定信号)(n x a 中参数p=8,改变q 的值,使q 分别等于2、4、8,观察他们的时域和幅频特性,了解当q 取不同值时,对信号序列的时域和幅频特性的影响;固定q=8,改变p,使p 分别等于8、13、14,观察参数p 变化对信号序列的时域和幅频特性的影响,注意p 等于多少时会发生明显的泄漏现象,混叠是否也随之出现?记录实验中观察到的现象,绘出相应的时域序列和幅频特性曲线。
()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解:程序见附录程序一:P=8,q 变化时:t/T x a (n )k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )51015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析:由高斯序列表达式知n=p 为期对称轴; 当p 取固定值时,时域图都关于n=8对称截取长度为周期的整数倍,没有发生明显的泄漏现象;但存在混叠,当q 由2增加至8过程中,时域图形变化越来越平缓,中间包络越来越大,可能函数周期开始增加,频率降低,渐渐小于fs/2,混叠减弱;当q 值固定不变,p 变化时,时域对称中轴右移,截取的时域长度渐渐地不再是周期的整数倍,开始无法代表一个周期,泄漏现象也来越明显,因而图形越来越偏离真实值,p=14时的泄漏现象最为明显,混叠可能也随之出现;(2) 观察衰减正弦序列 的时域和幅频特性,a=0.1,f=0.0625,检查谱峰出现的位置是否正确,注意频谱的形状,绘出幅频特性曲线,改变f ,使f 分别等于0.4375和0.5625,观察这两种情况下,频谱的形状和谱峰出现的位置,有无混叠和泄漏现象?说明产生现象的原因。
【精品】数字信号处理实验报告

【精品】数字信号处理实验报告
1 实验目的
本次实验的目的是在MATLAB软件环境中运用数字信号处理理论,通过实验操作来检验用于数字信号处理的算法的正确性,以便明确数字信号处理理论在实际应用中的重要作用。
2 实验原理
数字信号处理实验的原理是使用MATLAB进行数字信号处理算法实验,首先,设置一些用于数字信号处理的参数,如传输函数、离散时间区间、采样频率、滤波器类型等;其次,按照信号处理的算法进行编程实现,搭建一个数字信号处理系统,在MATLAB下对信号进行处理,包括采样、滤波和量化等;最后,对处理后的信号进行数字分析,监测数字信号处理后的变化趋势,验证数字信号处理算法的正确性。
3 实验步骤
(1) 建立信号处理实验系统:选择一个常见的信号处理算法,运用MATLAB软件分别编写信号发生程序、信号采样程序、滤波程序和信号量化程序;
(2) 运行实验程序:实验同学可以自行设置参数,如传输函数、离散时间区间、采样频率、滤波器类型等,调整完毕后,点击“run”,运行实验程序;
(3) 观察实验结果:运行完毕后,可以观察MATLAB的图形结果,以此来分析信号处理算法的性能;
(4) 对结果进行分析:经过上述实验操作后,可以根据所得到的实验结果来判断信号处理算法的性能,如输出信号的噪声抑制能力、良好的时域和频域性能等,从而验证信号处理理论在实际应用中的价值。
4 总结。
数字信号处理实验二

实验二信号的分析与处理综合实验一、实验目的目的:综合运用数字信号处理的理论知识进行信号的采样,重构,频谱分析和滤波器的设计,通过理论推导得出相应结论,再利用Matlab作为编程工具进行计算机实现,从而加深对所学知识的理解,建立概念。
二、基本要求1.掌握数字信号处理的基本概念、基本理论和基本方法;2.学会MA TLAB的使用,掌握MA TLAB的程序设计方法;3.掌握用MA TLAB设计简单实验验证采样定理的方法;4.掌握在Windows环境下语音信号采集的方法;5.学会用MA TLAB对信号进行频谱分析;6.掌握MA TLAB设计FIR和IIR数字滤波器的方法;三、实验内容1.利用简单正弦信号设计实验验证采样定理:(1)Matlab产生离散信号的方法,作图的方法,以及基本运算操作(2)对连续正弦信号以不同的采样频率作采样(3)对采样前后信号进行傅立叶变换,并画频谱图(4)分析采样前后频谱的有变化,验证采样定理。
掌握画频谱图的方法,深刻理解采样频率,信号频率,采样点数,频率分辨率等概念2.真实语音信号的采样重构:录制一段自己的语音信号,并对录制的信号进行采样;画出采样前后语音信号的时域波形和频谱图;对降采样后的信号进行插值重构,滤波,恢复原信号。
(1)语音信号的采集(2)降采样的实现(改变了信号的采样率)(3)以不同采样率采样后,语音信号的频谱分析(4)采样前后声音的变化(5)对降采样后的信号进行插值重构,滤波,恢复原信号3.带噪声语音信号的频谱分析(1)设计一频率已知的噪声信号,与实验2中原始语音信号相加,构造带噪声信号(2)画出原始语音信号和加噪声后信号,以及它们的频谱图(3)利用频谱图分析噪声信号和原语音信号的不同特性4.对带噪声语音信号滤波去噪:给定滤波器性能指标,采样窗函数法或双线性变换设计滤波器,并画出滤波器的频率响应;然后用自己设计的滤波器对采样的语音信号进行滤波,画出滤波后信号的时域波形和频谱,并对滤波前后的信号进行对比,分析信号的变化;回放语音信号;(1)分析带噪声信号频谱,找出噪声所在的频率段(2)利用matlab中已有的滤波器滤波(3)根据语音信号特点,自己设计滤波器滤波(4)比较各种滤波器性能(至少四种),选择一种合适的滤波器将噪声信号滤除(5)回放语音信号,比较滤波前后声音的变化四、实验原理参考《数字信号处理》教材《数字信号处理的MATLAB实现》万永革编著五、主要实验仪器及材料微型计算机、Matlab。
DSP实验报告2-数字信号处理

23 系 2012 级 丛松宇 PB12210075
3. clear; n=1:8; for i=1:4 x(i)=i; end for i=5:8 x(i)=9-i; end close all; subplot(2,4,1); stem(x);grid on; title('8 点三角波序列'); subplot(2,4,2); stem(abs(fft(x,8)));grid on; n=1:16; for i=9:16 x(i)=0; end subplot(2,4,3); stem(x);grid on; title('16 点三角波序列'); subplot(2,4,4); stem(abs(fft(x,16)));grid on; n=1:8; for i=1:4 x(i)=5-i; end
23 系 2012 级 丛松宇 PB12210075
1.② n=0:15; q=8;p=8; x=exp(-1*(n-p).^2/q); close all; subplot(3,2,1); stem(x),grid on title('q=8,p=8 的时域特性'); subplot(3,2,2); stem(abs(fft(x))),grid on;title('频域特性'); q=8;p=13; x=exp(-1*(n-p).^2/q); subplot(3,2,3); stem(x),grid on title('q=8,p=13 的时域特性'); subplot(3,2,4); stem(abs(fft(x))),grid on;title('频域特性'); q=8;p=14; x=exp(-1*(n-p).^2/q); subplot(3,2,5); stem(x),grid on title('q=8,p=14 的时域特性'); subplot(3,2,6); stem(abs(fft(x))),grid on;title('频域特性');
数字信号处理实验三

数字信号处理实验三数字信号处理实验三是针对数字信号处理课程的一项实践性任务。
本实验旨在通过实际操作,加深对数字信号处理理论的理解,并培养学生的实验能力和问题解决能力。
在本实验中,我们将学习和实践以下内容:1. 实验目的本实验的目的是通过使用MATLAB软件进行数字信号处理,加深对数字信号处理基本概念和算法的理解,掌握数字信号的采样、量化、滤波等基本操作。
2. 实验器材在本实验中,我们将使用以下器材:- 个人计算机- MATLAB软件3. 实验步骤本实验的具体步骤如下:步骤一:信号生成首先,我们需要生成一个模拟信号,可以是正弦信号、方波信号或其他类型的信号。
在MATLAB中,我们可以使用相关函数生成这些信号。
生成信号的目的是为了后续的数字信号处理操作提供输入。
步骤二:信号采样在本步骤中,我们将对生成的模拟信号进行采样。
采样是指在一定的时间间隔内对信号进行离散化处理,得到离散时间上的信号序列。
在MATLAB中,我们可以使用采样函数对信号进行采样。
步骤三:信号量化在本步骤中,我们将对采样后的信号进行量化。
量化是指将连续的信号离散化为一组离散的幅值。
在MATLAB中,我们可以使用量化函数对信号进行量化。
步骤四:信号滤波在本步骤中,我们将对量化后的信号进行滤波。
滤波是指通过一系列滤波器对信号进行处理,以去除不需要的频率成分或噪声。
在MATLAB中,我们可以使用滤波函数对信号进行滤波。
步骤五:信号重构在本步骤中,我们将对滤波后的信号进行重构。
重构是指将离散化的信号恢复为连续的信号。
在MATLAB中,我们可以使用重构函数对信号进行重构。
步骤六:信号分析在本步骤中,我们将对重构后的信号进行分析。
分析是指对信号的频谱、功率等特性进行分析,以了解信号的特点和性能。
在MATLAB中,我们可以使用分析函数对信号进行分析。
4. 实验结果在完成以上步骤后,我们可以得到经过数字信号处理的结果。
这些结果可以是经过采样、量化、滤波和重构后的信号波形,也可以是信号的频谱、功率等特性。
数字信号处理实验报告

数字信号处理实验报告数字信号处理实验报告一、实验目的本实验旨在通过数字信号处理的方法,对给定的信号进行滤波、频域分析和采样率转换等操作,深入理解数字信号处理的基本原理和技术。
二、实验原理数字信号处理(DSP)是一种利用计算机、数字电路或其他数字设备对信号进行各种处理的技术。
其主要内容包括采样、量化、滤波、变换分析、重建等。
其中,滤波器是数字信号处理中最重要的元件之一,它可以用来提取信号的特征,抑制噪声,增强信号的清晰度。
频域分析是指将时域信号转化为频域信号,从而更好地理解信号的频率特性。
采样率转换则是在不同采样率之间对信号进行转换,以满足不同应用的需求。
三、实验步骤1.信号采集:首先,我们使用实验室的信号采集设备对给定的信号进行采集。
采集的信号包括噪声信号、含有正弦波和方波的混合信号等。
2.数据量化:采集到的信号需要进行量化处理,即将连续的模拟信号转化为离散的数字信号。
这一步通常通过ADC(模数转换器)实现。
3.滤波处理:将量化后的数字信号输入到数字滤波器中。
我们使用不同的滤波器,如低通、高通、带通等,对信号进行滤波处理,以观察不同滤波器对信号的影响。
4.频域分析:将经过滤波处理的信号进行FFT(快速傅里叶变换)处理,将时域信号转化为频域信号,从而可以对其频率特性进行分析。
5.采样率转换:在进行上述处理后,我们还需要对信号进行采样率转换。
我们使用了不同的采样率对信号进行转换,并观察采样率对信号处理结果的影响。
四、实验结果及分析1.滤波处理:经过不同类型滤波器处理后,我们发现低通滤波器可以有效抑制噪声,高通滤波器可以突出高频信号的特征,带通滤波器则可以提取特定频率范围的信号。
这表明不同类型的滤波器在处理不同类型的信号时具有不同的效果。
2.频域分析:通过FFT处理,我们将时域信号转化为频域信号。
在频域分析中,我们可以更清楚地看到信号的频率特性。
例如,对于噪声信号,我们可以看到其频率分布较为均匀;对于含有正弦波和方波的混合信号,我们可以看到其包含了不同频率的分量。
数字信号处理实验二时域采样和频域采样

数字信号处理实验二时域采样和频域采样数字信号处理是一门研究信号的数字化表示、处理和传输的学科。
在数字信号处理中,时域采样和频域采样是两种常用的信号分析方法。
下面我们将对这两种采样方法进行详细介绍和比较。
一、时域采样时域采样是数字信号处理中最基本的采样方法之一。
它通过对连续时间信号进行离散时间采样,将连续时间信号转换为离散时间信号。
时域采样的基本原理是,如果一个连续时间信号f(t)在采样时刻t=kT(k=0,1,2,)上的值f(kT)能够被准确地测量,则可以通过这些采样值重建出原始信号。
时域采样的优点是简单易行,适用于大多数信号的采样。
但是,时域采样也存在一些缺点。
首先,如果信号中含有高于采样率的频率成分,这些高频成分将会被混叠到低频部分,导致信号失真。
这种现象被称为混叠效应。
其次,时域采样需要大量的采样数据才能准确地重建出原始信号,这会占用大量的存储空间和计算资源。
二、频域采样频域采样是一种在频域上对信号进行采样的方法。
它通过对信号进行傅里叶变换,将信号转换到频域,然后对频域中的信号进行采样。
频域采样的基本原理是,如果一个离散时间信号f(n)的傅里叶变换在频域上有有限的带宽,那么频域上的信号可以被认为是无穷多个离散的冲激函数的线性组合。
通过对这些冲激函数的幅度和相位进行采样,可以得到频域采样值。
相比时域采样,频域采样具有一些优点。
首先,频域采样可以避免混叠效应,因为高频成分在频域中可以被准确地表示和处理。
其次,频域采样只需要采样信号的幅度和相位信息,而不必存储大量的采样数据,可以节省存储空间和计算资源。
此外,频域采样还可以用于对信号进行压缩和编码,以便于信号的传输和存储。
然而,频域采样也存在一些缺点。
首先,傅里叶变换需要将信号从时域转换到频域,这需要使用复杂的数学运算和计算。
其次,频域采样的结果通常需要经过逆傅里叶变换才能得到原始信号的离散时间表示,这同样需要复杂的数学运算和计算。
此外,频域采样的结果可能存在频率混叠和泄漏现象,这会影响到重建出的原始信号的质量。
数字信号处理实验二

实验二 快速傅里叶变换(FFT)及其应用一、思考题(1) 实验中的信号序列()c x n 和()d x n 在单位圆上的z 变换频谱()()c j j d X e X e ωω和会相同吗如果不同,说出哪一个低频分量更多一些,为什么答:设j Z r e ω=⨯ ()()n n G z g n z ∞-=-∞=⨯∑因为为单位圆,故r=1.因为()()j j n n G e g n eωω∞-=-∞=⨯∑,故3723456704()(8)23432j j n j n j j j j j j j c n n X e nen e e e e e e e e ωωωωωωωωωω---------===+-=++++++∑∑ 7235670()(4)43223j j n j j j j j j d n X e n ee e e e e e ωωωωωωωω-------==-=+++---∑比较可知频谱不相同,()c X n 的低频分量多。
(2) 对一个有限长序列进行DFT 等价于将该序列周期延拓后进行DFS 展开,因为DFS 也只是取其中一个周期来运算,所以FFT 在一定条件下也可以用以分析周期信号序列。
如果实正弦信号()sin(2),0.1x n fn f π== 用16点FFT 来做DFS 运算,得到的频谱是信号本身的真实谱吗为什么答:针对原来未经采样的连续时间信号来说,FFT 做出来的永远不会是信号本身的真实频谱,只能够是无限接近。
FFT 频谱泄露问题是一定会存在的,因为毕竟采样率再高,也不能完全达到原来的连续时间信号准确。
原题的采样率是1/10,就是将2*pi 分成10份,即每个正弦波周期进行10次采样,这样的采样率很低,而最后你只截取16个点来做分析,泄露一般会挺严重,看到的频谱,应该是一个上头尖,下面慢慢变宽的尖锥形,而纯正的正弦波的理想频谱应该是在某频点只有一个尖峰。
二.?实验原理:?(1)混叠:采样序列的频谱是被采样信号频谱的周期延拓,当采样频率不满足奈奎斯特采样定理的时候,就会发生混叠,使得刺痒后的序列信号的频谱不能真实的反映原采样信号的频谱。
数字信号处理实验程序2

2.1clcclose all;n=0:15;p=8;q=2;x=exp(-(n-p).^2/q);figure(1);subplot(3,1,1);stem(n,x);title('exp(-(n-p)^2/q),p=8,q=2');xk1=fft(x,16);q=4;x=exp(-(n-p).^2/q);subplot(3,1,2);xk2=fft(x,16);stem(n,x);title('exp(-(n-p)^2/q),p=8,q=4');q=8;x=exp(-(n-p).^2/q);xk3=fft(x,16);subplot(3,1,3);stem(n,x);title('exp(-(n-p)^2/q),p=8,q=8');%时域特性figure(2);subplot(3,1,1);stem(n,abs(xk1));title('exp(-(n-p)^2/q),p=8,q=2');subplot(3,1,2);stem(n,abs(xk2));title('exp(-(n-p)^2/q),p=8,q=4');subplot(3,1,3);stem(n,abs(xk3));title('exp(-(n-p)^2/q),p=8,q=8');%频域特性%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%p=8;q=8;figure(3);subplot(3,1,1);stem(n,x);title('exp(-(n-p)^2/q),p=8,q=8');xk1=fft(x,16);p=13;x=exp(-(n-p).^2/q);subplot(3,1,2); xk2=fft(x,16);stem(n,x);title('exp(-(n-p)^2/q),p=13,q=8');p=14;x=exp(-(n-p).^2/q);xk3=fft(x,16);subplot(3,1,3);stem(n,x);title('exp(-(n-p)^2/q),p=14,q=8');%时域特性figure(4);subplot(3,1,1);stem(n,abs(xk1));title('exp(-(n-p)^2/q),p=8,q=8');subplot(3,1,2);stem(n,abs(xk2));title('exp(-(n-p)^2/q),p=13,q=8');subplot(3,1,3);stem(n,abs(xk3));title('exp(-(n-p)^2/q),p=14,q=8');%频域特性2.2clcclose alln=0:15;f=0.0625;a=0.1;xb1=exp(-a*n).*sin(2*pi*f*n);xk1=fft(xb1,16);f=0.4375;xb2=exp(-a*n).*sin(2*pi*f*n);xk2=fft(xb2,16);f=0.5625;xb3=exp(-a*n).*sin(2*pi*f*n);xk3=fft(xb3,16);figure(1);subplot(3,1,1);stem(n,xb1);title('f=0.0625');subplot(3,1,2);stem(n,xb2);title('f=0.4375');subplot(3,1,3);stem(n,xb3);title('f=0.5625');figure(2);subplot(3,1,1);stem(n,abs(xk1));title('f=0.0625');subplot(3,1,2);stem(n,abs(xk2));title('f=0.4375');subplot(3,1,3);stem(n,abs(xk3));title('f=0.5625');2.3clcclose all;N=8;n=0:N-1;xc=0:7;xd=0:7;for m=0:7;if(0<=m & m<=3)xc(m+1)=m;xd(m+1)=4-m;elseif(4<=m & m<=7)xc(m+1)=8-m;xd(m+1)=m-4;endendfigure(1);subplot(2,1,1);stem(n,xc);title('三角波序列');subplot(2,1,2);stem(n,xd);title('反三角波序列');xck=fft(xc,N);xdk=fft(xd,N);figure(2);subplot(2,1,1);stem(n,abs(xck));title('三角波序列8点fft'); subplot(2,1,2);stem(n,abs(xdk));title('反三角波序列8点fft'); figure(3);xck1=fft(xc,32);xdk1=fft(xd,32);subplot(2,1,1); stem(0:4*N-1,abs(xck1));title('三角波序列32点fft');subplot(2,1,2);stem(0:4*N-1,abs(xdk1));title('反三角波序列32点fft');2.4clcclose allN=16;detaf=1/16;n=0:N-1;x=sin(2*pi*0.125*n)+cos(2*pi*(0.125+detaf) *n);xk=fft(x,N);figure(1);subplot(2,1,1);stem(n,abs(xk));title('N=16,Δf=1/16');detaf=1/64;x=sin(2*pi*0.125*n)+cos(2*pi*(0.125+detaf) *n);xk1=fft(x,N);subplot(2,1,2);stem(n,abs(xk1));title('N=16,Δf=1/64');N=128;detaf=1/16;n=0:N-1;x=sin(2*pi*0.125*n)+cos(2*pi*(0.125+detaf) *n);xk=fft(x,N);figure(2);subplot(2,1,1);stem(n,abs(xk));title('N=128,Δf=1/16');detaf=1/64;x=sin(2*pi*0.125*n)+cos(2*pi*(0.125+detaf) *n);xk1=fft(x,N);subplot(2,1,2);stem(n,abs(xk1));title('N=128,Δf=1/64');2.5clcclose allN=16;p=8;q=2;a=.1;f=.0625;n=0:N-1;xa=exp(-(n-p).^2/q);xb=exp(-a*n).*sin(2*pi*f*n);xak=fft(xa,N);xbk=fft(xb,N);f=ifft(xak.*xbk,N);figure(1);subplot(4,1,1);stem(0:N-1,xa);title('xa(n)=exp(-(n-p)^2/q)'); subplot(4,1,2);stem(0:N-1,xb);title('xb(n)=exp(-a*n)*sin(2*pi*f*n)'); subplot(4,1,3);stem(0:N-1,f);title('xa(n)⊙xb(n)');xak1=fft(xa,2*N);xbk1=fft(xb,2*N);h=ifft(xak1.*xbk1,2*N);subplot(4,1,4);stem(0:2*N-2,h(1:2*N-1));title('xa*xb');2.6clcclose allN=512;xe=rand(1,N)-0.5;for m=0:7;if(0<=m & m<=3)xc(m+1)=m;elseif(4<=m & m<=7)xc(m+1)=8-m;endendxck=fft(xc,71);f=0:518;fm=0:141;for m=1:8;xm=xe((m-1)*64+1:m*64);xmk=fft(xm,71);fm(1:71)=fm(72:142);fm(72:142)=ifft(xmk.*xck,71);if m==2f(1:7)=fm(1:7);endif m>1f((m-2)*64+8:(m-1)*64)=fm(8:64);f((m-1)*64+1:(m-1)*64+7)=fm(65:71)+fm(72 :78);endif m==8f((m-1)*64+8:m*64+7)=fm(79:142);endendstem(0:512+6,f);%%%%重叠相加法title('重叠相加法');for m=1:8xm1(8:71)=xe((m-1)*64+1:m*64);if m==1xm1(1:7)=0;else xm1(1:7)=xe((m-1)*64-6:(m-1)*64);endxmk1=fft(xm1,71);fm1=ifft(xmk1.*xck,71);f1((m-1)*64+1:m*64)=fm1(8:71);endxmk2=fft(xe(506:512),71);h=ifft(xmk2.*xck,71);f1(513:519)=h(8:14);figure(2)stem(0:518,f1);title('重叠保留法');fa=conv(xc,xe);detaf=f1-f;figure(3);stem(0:518,detaf);2.7clcclose allN=16;p=8;q=2;a=.1;n=0:N-1;f=0.0625;xa=exp(-(n-p).^2/q);xb=exp(-a*n).*sin(2*pi*f*n);xak=fft(xa,N*2);xbk=fft(xb,2*N);rm=real(ifft(conj(xak).*xbk));rm=[rm(N+2:2*N) rm(1:N)];m=(-N+1):N-1;stem(m,rm);title('线性相关');figure(2);xak1=fft(xa,N);xbk1=fft(xb,N);rm1=real(ifft(xak1.*xbk1,N));stem(n,rm1);3.1clearclose allwc=2*1000*tan(2*pi*300/(2*1000)); wt=2*1000*tan(2*pi*200/(2*1000)); [N,wn]=cheb1ord(wc,wt,0.8,20,'s'); [B,A]=cheby1(N,0.8,wn,'high','s'); [num,den]=bilinear(B,A,1000); [h,w]=freqz(num,den);f=w/pi*500;plot(f,20*log10(abs(h)));axis([0,500,-80,10]);grid;xlabel('频率/Hz');ylabel('幅度/dB');3.2clear;close all;wc=2*pi*200;wr=2*pi*300;[n1,wn1] = buttord(wc,wr,1,25,'s'); [B,A]=butter(n1,wn1,'low','s'); [num1,den1]=impinvar(B,A,1000); [h1,w]=freqz(num1,den1);wc=2*1000*tan(2*pi*200/(2*1000)); wr=2*1000*tan(2*pi*300/(2*1000)); [n,wn] = buttord(wc,wr,1,25,'s'); [B,A]=butter(n,wn,'low','s');[num2,den2]=bilinear(B,A,1000); [h2,w]=freqz(num2,den2);f=w/pi*500;plot(f,20*log10(abs(h1)),'-.',f,20*log10(abs(h2 )),'-');legend('脉冲响应不变法','双线性变换法'); axis([0,500,-80,10])grid;xlabel('频率/Hz');ylabel('幅度/dB');3.3clearclose allwc=2*8000*tan(2*pi*1200/(2*8000));wr=2*8000*tan(2*pi*2000/(2*8000));[n,wn]=buttord(wc,wr,0.5,40,'s');[B,A]=butter(n,wn,'low','s');[num,den]=bilinear(B,A,8000);[h1,w]=freqz(num,den);[n,wn]=cheb1ord(wc,wr,0.5,40,'s');[B,A]=cheby1(n,0.5,wn,'low','s');[num,den]=bilinear(B,A,8000);[h2,w]=freqz(num,den);[n,wn]=ellipord(wc,wr,0.5,40,'s');[B,A]=ellip(n,0.5,40,wn,'low','s');[num,den]=bilinear(B,A,8000);[h3,w]=freqz(num,den);f=w/pi*4000;plot(f,20*log10(abs(h1)),'-.',f,20*log10(abs(h2 )),'.-',f,20*log10(abs(h3)),'-');axis([0,4000,-100,10]);grid;xlabel('频率/Hz');ylabel('幅度/dB');legend('Butterworth','Chebyshev','Ellicptic') hold onx=1200;plot(x)3.4clearclose all;[n,wc]=buttord([2000 3000],[1500 6000],3,20,'s');[B,A]=butter(n,wc,'bandpass','s');[num,den]=bilinear(B,A,30000);[h1,w]=freqz(num,den);[num,den]=impinvar(B,A,30000);[h2,w]=freqz(num,den);f=w/pi*15000;plot(f,20*log10(abs(h1)),'-.',f,20*log10(abs(ab s(h2))));grid on;axis([0,3000,-100,0]);legend('脉冲响应不变法','双线性变换'); xlabel('频率/Hz');ylabel('幅度/dB');3.5clearclose allw1=2*10000*tan(2*pi*1000/(2*10000));w2=2*10000*tan(2*pi*2000/(2*10000));w3=2*10000*tan(2*pi*500/(2*10000));w4=2*10000*tan(2*pi*3000/(2*10000)); [n,wn]=cheb1ord([w3 w4],[w1 w2],3,18,'s') [B,A]=cheby1(n,3,wn,'stop','s');[num,den]=bilinear(B,A,10000);[h,w]=freqz(num,den);f=w/pi*5000;plot(f,20*log10(abs(h)));axis([0,5000,-100,0]);gridxlabel('频率/Hz');ylabel('幅度/dB');4.1%N=45,计算并画出矩形框、汉明窗、布莱克曼窗的归一化的幅度谱,并比较各自的主要特点%(1)矩形窗(Rectangle Window)调用格式:w=boxcar(n),根据长度n 产生一个矩形窗w。
数字信号处理实验

实验二 IIR、FIR数字滤波器设计
三、实验内容
1. 产生三频率叠加的信号。 2. 显示其频谱分布。 3. 设计一低通IIR滤波器,滤除最高频率信号。 4. 设计一低通FIR滤波器, 滤除两个高频信号。
实验二 I个频率分量,三个信号的频率分 别为100Hz,1400Hz,3000Hz,功率大小一样,绘制其时域 及频谱; ②设计一IIR滤波器,滤除1400Hz和3000Hz,IIR滤波器要求 幅度特性图在通带和阻带均为单调下降,阻带衰减大于40dB ,绘制滤波器及滤波后的时域及频谱; ③设计一FIR滤波器,滤除3000Hz的信号,FIR滤波器(任选 一个要求) i.带内波动小于1dB,带外衰减大于47dB
二、学时安排
2学时
实验一模拟信号采样与重构及频谱分析FFT
三、实验内容
1 给定一连续信号,如正弦、矩形等信号,采用 数字化方式进行近似表示,并描述其频谱,绘 制对应的时域及频谱图。
2 对该连续信号,按不同采样频率进行采样,绘 制对应的时域离散信号的时域及频域图,分析 不同采样率对频谱的影响。
3 对按不同采样率离散后的信号分别采用理想低 通或零阶保持器进行恢复,比较恢复效果。
ii. 过渡带小于4 /8
绘制FIR滤波器及滤波后的时域及频谱;
实验报告填写要求
1. 按照电子工程系实验报告格式要求进行填写;
2. 附上实验的MATLAB原程序;
实验结束时
实验设计完成后,请在场指导老师进行检查程 序及结果,得到老师允许后方可离开。 实验指导老师为:
数字信号处理实验
实验一模拟信号采样与重构及频谱分析FFT
一、实验目的
本实验重在使学生通过MATLAB的编程仿真及绘图,对模 拟信号按照采样定理的要求进行采样,图形表示,再对离散信 号进行无失真重构,对采样前后的信号进行频谱分析,使学生 能够利用计算机完成对信号的上述处理与变换功能,分析频谱 现象。
数字信号处理实验二时域采样和频域采样

实验二-时域采样和频域采样一、实验目的时域采样理论与频域采样理论是数字信号处理中的重要理论。
要求掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念,以及频率域采样定理及其对频域采样点数选择的指导作用。
二、实验原理及方法1、时域采样定理的要点:a)对模拟信号)(t x a 以间隔T 进行时域等间隔理想采样,形成的采样信号的频谱)(ˆΩj X 是原模拟信号频谱()aX j Ω以采样角频率s Ω(T s /2π=Ω)为周期进行周期延拓b)采样频率s Ω必须大于等于模拟信号最高频率的两倍以上,才能使采样信号的频谱不产生频谱混叠。
利用计算机计算上式并不方便,下面我们导出另外一个公式,以便用计算机上进行实验。
2、频域采样定理的要点:a)对信号x(n)的频谱函数X(ej ω)在[0,2π]上等间隔采样N 点 则N 点IDFT[()N X k ]得到的序列就是原序列x(n)以N 为周期进行周期延拓后的主值区序列。
三、实验内容及步骤1、时域采样理论的验证程序:clear;clcA=444.128;a=50*sqrt(2)*pi;w0=50*sqrt(2)*pi;Tp=50/1000;F1=1000;F2=300;F3=200;T1=1/F1;T2=1/F2;T3=1/F3;n1=0:Tp*F1-1;n2=0:Tp*F2-1;n3=0:Tp*F3-1;x1=A*exp(-a*n1*T1).*sin(w0*n1*T1);x2=A*exp(-a*n2*T2).*sin(w0*n2*T2);x3=A*exp(-a*n3*T3).*sin(w0*n3*T3);f1=fft(x1,length(n1));f2=fft(x2,length(n2)); %f3=fft(x3,length(n3)); %k1=0:length(f1)-1;fk1=k1/Tp; %k2=0:length(f2)-1;fk2=k2/Tp; % k3=0:length(f3)-1;fk3=k3/Tp; % subplot(3,2,1)stem(n1,x1,'.')title('(a)Fs=1000Hz');xlabel('n');ylabel('x1(n)');subplot(3,2,3)stem(n2,x2,'.')title('(b)Fs=300Hz');xlabel('n');ylabel('x2(n)');subplot(3,2,5)stem(n3,x3,'.')title('(c)Fs=200Hz');xlabel('n');ylabel('x3(n)');subplot(3,2,2)plot(fk1,abs(f1))title('(a) FT[xa(nT)],Fs=1000Hz'); xlabel('f(Hz)');ylabel('·ù¶È')subplot(3,2,4)plot(fk2,abs(f2))title('(b) FT[xa(nT)],Fs=300Hz'); xlabel('f(Hz)');ylabel('·ù¶È')subplot(3,2,6)plot(fk3,abs(f3))title('(c) FT[xa(nT)],Fs=200Hz'); xlabel('f(Hz)');ylabel('·ù¶È')结果分析:由图2.2可见,采样序列的频谱的确是以采样频率为周期对模拟信号频谱的周期延拓。
数字信号处理实验(吴镇扬)答案-2
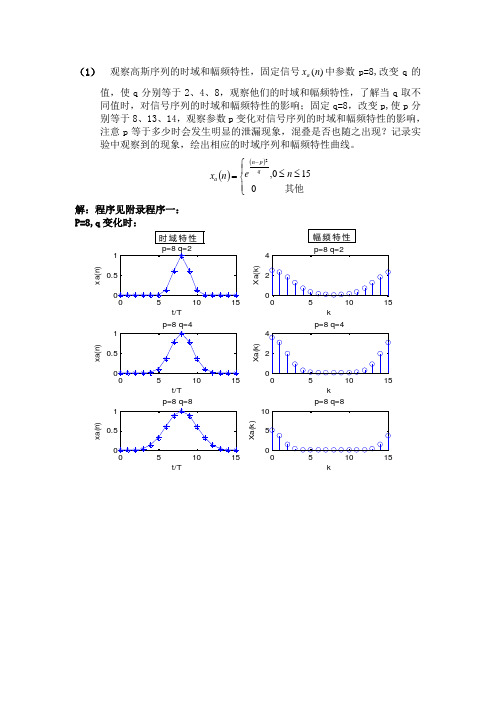
(1) 观察高斯序列的时域和幅频特性,固定信号)(n x a 中参数p=8,改变q 的值,使q 分别等于2、4、8,观察他们的时域和幅频特性,了解当q 取不同值时,对信号序列的时域和幅频特性的影响;固定q=8,改变p,使p 分别等于8、13、14,观察参数p 变化对信号序列的时域和幅频特性的影响,注意p 等于多少时会发生明显的泄漏现象,混叠是否也随之出现?记录实验中观察到的现象,绘出相应的时域序列和幅频特性曲线。
()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解:程序见附录程序一:P=8,q 变化时:t/T x a (n )p=8 q=2k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )p=13 q=851015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析:由高斯序列表达式知n=p 为期对称轴; 当p 取固定值时,时域图都关于n=8对称截取长度为周期的整数倍,没有发生明显的泄漏现象;但存在混叠,当q 由2增加至8过程中,时域图形变化越来越平缓,中间包络越来越大,可能函数周期开始增加,频率降低,渐渐小于fs/2,混叠减弱;当q 值固定不变,p 变化时,时域对称中轴右移,截取的时域长度渐渐地不再是周期的整数倍,开始无法代表一个周期,泄漏现象也来越明显,因而图形越来越偏离真实值,p=14时的泄漏现象最为明显,混叠可能也随之出现;(2) 观察衰减正弦序列 的时域和幅频特性,a=0.1,f=0.0625,检查谱峰出现的位置是否正确,注意频谱的形状,绘出幅频特性曲线,改变f ,使f 分别等于0.4375和0.5625,观察这两种情况下,频谱的形状和谱峰出现的位置,有无混叠和泄漏现象?说明产生现象的原因。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1clcclose all;n=0:15;p=8;q=2;x=exp(-(n-p.^2/q;figure(1;subplot(3,1,1;stem(n,x;title('exp(-(n-p^2/q,p=8,q=2'; xk1=fft(x,16;q=4;x=exp(-(n-p.^2/q;subplot(3,1,2;xk2=fft(x,16;stem(n,x;title('exp(-(n-p^2/q,p=8,q=4'; q=8;x=exp(-(n-p.^2/q;xk3=fft(x,16;subplot(3,1,3;stem(n,x;title('exp(-(n-p^2/q,p=8,q=8';%时域特性figure(2;subplot(3,1,1;stem(n,abs(xk1;title('exp(-(n-p^2/q,p=8,q=2';subplot(3,1,2;stem(n,abs(xk2;title('exp(-(n-p^2/q,p=8,q=4';subplot(3,1,3;stem(n,abs(xk3;title('exp(-(n-p^2/q,p=8,q=8';%频域特性%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%p=8;q=8;figure(3;subplot(3,1,1;stem(n,x;title('exp(-(n-p^2/q,p=8,q=8';xk1=fft(x,16;p=13;x=exp(-(n-p.^2/q;subplot(3,1,2; xk2=fft(x,16;stem(n,x;title('exp(-(n-p^2/q,p=13,q=8';p=14;x=exp(-(n-p.^2/q;xk3=fft(x,16;subplot(3,1,3;stem(n,x;title('exp(-(n-p^2/q,p=14,q=8';%时域特性figure(4; subplot(3,1,1;stem(n,abs(xk1;title('exp(-(n-p^2/q,p=8,q=8';subplot(3,1,2;stem(n,abs(xk2;title('exp(-(n-p^2/q,p=13,q=8';subplot(3,1,3;stem(n,abs(xk3;title('exp(-(n-p^2/q,p=14,q=8';%频域特性2.2 clcclose alln=0:15;f=0.0625;a=0.1;xb1=exp(-a*n.*sin(2*pi*f*n;xk1=fft(xb1,16;f=0.4375;xb2=exp(-a*n.*sin(2*pi*f*n;xk2=fft(xb2,16;f=0.5625;xb3=exp(-a*n.*sin(2*pi*f*n;xk3=fft(xb3,16;figure(1;subplot(3,1,1;stem(n,xb1;title('f=0.0625';subplot(3,1,2;stem(n,xb2; title('f=0.4375'; subplot(3,1,3; stem(n,xb3; title('f=0.5625'; figure(2; subplot(3,1,1; stem(n,abs(xk1; title('f=0.0625'; subplot(3,1,2; stem(n,abs(xk2; title('f=0.4375'; subplot(3,1,3; stem(n,abs(xk3; title('f=0.5625';2.3clcclose all;N=8;n=0:N-1;xc=0:7;xd=0:7;for m=0:7;if(0<=m & m<=3xc(m+1=m;xd(m+1=4-m;elseif(4<=m & m<=7 xc(m+1=8-m;xd(m+1=m-4;endendfigure(1;subplot(2,1,1;stem(n,xc;title('三角波序列'; subplot(2,1,2;stem(n,xd;title('反三角波序列';xck=fft(xc,N;xdk=fft(xd,N;figure(2;subplot(2,1,1;stem(n,abs(xck;title('三角波序列8点fft'; subplot(2,1,2; stem(n,abs(xdk;title('反三角波序列8点fft'; figure(3; xck1=fft(xc,32;xdk1=fft(xd,32;subplot(2,1,1; stem(0:4*N-1,abs(xck1; title('三角波序列32点fft';subplot(2,1,2;stem(0:4*N-1,abs(xdk1;title('反三角波序列32点fft';2.4clcclose allN=16;detaf=1/16;n=0:N-1;x=sin(2*pi*0.125*n+cos(2*pi*(0.125+detaf *n; xk=fft(x,N;figure(1;subplot(2,1,1;stem(n,abs(xk;title('N=16,Δf=1/16';detaf=1/64;x=sin(2*pi*0.125*n+cos(2*pi*(0.125+detaf *n; xk1=fft(x,N;subplot(2,1,2;stem(n,abs(xk1;title('N=16,Δf=1/64';N=128;detaf=1/16;n=0:N-1;x=sin(2*pi*0.125*n+cos(2*pi*(0.125+detaf *n; xk=fft(x,N;figure(2;subplot(2,1,1;stem(n,abs(xk;title('N=128,Δf=1/16';detaf=1/64;x=sin(2*pi*0.125*n+cos(2*pi*(0.125+detaf *n; xk1=fft(x,N;subplot(2,1,2;stem(n,abs(xk1;title('N=128,Δf=1/64';2.5clcclose allN=16;p=8;q=2;a=.1;f=.0625;n=0:N-1;xa=exp(-(n-p.^2/q;xb=exp(-a*n.*sin(2*pi*f*n;xak=fft(xa,N;xbk=fft(xb,N;f=ifft(xak.*xbk,N;figure(1;subplot(4,1,1;stem(0:N-1,xa;title('xa(n=exp(-(n-p^2/q'; subplot(4,1,2;stem(0:N-1,xb;title('xb(n=exp(-a*n*sin(2*pi*f*n'; subplot(4,1,3; stem(0:N-1,f;title('xa(n⊙xb(n';xak1=fft(xa,2*N;xbk1=fft(xb,2*N;h=ifft(xak1.*xbk1,2*N;subplot(4,1,4;stem(0:2*N-2,h(1:2*N-1;title('xa*xb';2.6clcclose allN=512;xe=rand(1,N-0.5;for m=0:7;if(0<=m & m<=3xc(m+1=m;elseif(4<=m & m<=7xc(m+1=8-m;endendxck=fft(xc,71;f=0:518;fm=0:141;for m=1:8;xm=xe((m-1*64+1:m*64; xmk=fft(xm,71;fm(1:71=fm(72:142;fm(72:142=ifft(xmk.*xck,71; if m==2f(1:7=fm(1:7;endif m>1f((m-2*64+8:(m-1*64=fm(8:64;f((m-1*64+1:(m-1*64+7=fm(65:71+fm(72 :78; endif m==8f((m-1*64+8:m*64+7=fm(79:142;endendstem(0:512+6,f;%%%%重叠相加法title('重叠相加法';for m=1:8xm1(8:71=xe((m-1*64+1:m*64;if m==1xm1(1:7=0;else xm1(1:7=xe((m-1*64-6:(m-1*64;endxmk1=fft(xm1,71;fm1=ifft(xmk1.*xck,71;f1((m-1*64+1:m*64=fm1(8:71; endxmk2=fft(xe(506:512,71;h=ifft(xmk2.*xck,71;f1(513:519=h(8:14;figure(2stem(0:518,f1;title('重叠保留法';fa=conv(xc,xe;detaf=f1-f;figure(3;stem(0:518,detaf;2.7clcclose allN=16;p=8;q=2;a=.1;n=0:N-1;f=0.0625;xa=exp(-(n-p.^2/q;xb=exp(-a*n.*sin(2*pi*f*n; xak=fft(xa,N*2;xbk=fft(xb,2*N;rm=real(ifft(conj(xak.*xbk; rm=[rm(N+2:2*N rm(1:N]; m=(-N+1:N-1;stem(m,rm;title('线性相关';figure(2;xak1=fft(xa,N;xbk1=fft(xb,N;rm1=real(ifft(xak1.*xbk1,N; stem(n,rm1;3.1clearclose allwc=2*1000*tan(2*pi*300/(2*1000; wt=2*1000*tan(2*pi*200/(2*1000;[N,wn]=cheb1ord(wc,wt,0.8,20,'s'; [B,A]=cheby1(N,0.8,wn,'high','s';[num,den]=bilinear(B,A,1000; [h,w]=freqz(num,den;f=w/pi*500;plot(f,20*log10(abs(h;axis([0,500,-80,10];grid;xlabel('频率/Hz';ylabel('幅度/dB';3.2clear;close all;wc=2*pi*200;wr=2*pi*300;[n1,wn1] = buttord(wc,wr,1,25,'s'; [B,A]=butter(n1,wn1,'low','s';[num1,den1]=impinvar(B,A,1000; [h1,w]=freqz(num1,den1;wc=2*1000*tan(2*pi*200/(2*1000; wr=2*1000*tan(2*pi*300/(2*1000; [n,wn] = buttord(wc,wr,1,25,'s'; [B,A]=butter(n,wn,'low','s';[num2,den2]=bilinear(B,A,1000; [h2,w]=freqz(num2,den2;f=w/pi*500;plot(f,20*log10(abs(h1,'-.',f,20*log10(abs(h2 ,'-';legend('脉冲响应不变法','双线性变换法'; axis([0,500,-80,10] grid;xlabel('频率/Hz';ylabel('幅度/dB';3.3clearclose allwc=2*8000*tan(2*pi*1200/(2*8000;wr=2*8000*tan(2*pi*2000/(2*8000;[n,wn]=buttord(wc,wr,0.5,40,'s';[B,A]=butter(n,wn,'low','s';[num,den]=bilinear(B,A,8000;[h1,w]=freqz(num,den;[n,wn]=cheb1ord(wc,wr,0.5,40,'s';[B,A]=cheby1(n,0.5,wn,'low','s';[num,den]=bilinear(B,A,8000;[h2,w]=freqz(num,den;[n,wn]=ellipord(wc,wr,0.5,40,'s';[B,A]=ellip(n,0.5,40,wn,'low','s';[num,den]=bilinear(B,A,8000;[h3,w]=freqz(num,den;f=w/pi*4000;plot(f,20*log10(abs(h1,'-.',f,20*log10(abs(h2 ,'.-',f,20*log10(abs(h3,'-'; axis([0,4000,-100,10];grid;xlabel('频率/Hz';ylabel('幅度/dB';legend('Butterworth','Chebyshev','Ellicptic' hold onx=1200;plot(x3.4clearclose all;[n,wc]=buttord([2000 3000],[1500 6000],3,20,'s';[B,A]=butter(n,wc,'bandpass','s';[num,den]=bilinear(B,A,30000;[h1,w]=freqz(num,den;[num,den]=impinvar(B,A,30000;[h2,w]=freqz(num,den;f=w/pi*15000;plot(f,20*log10(abs(h1,'-.',f,20*log10(abs(ab s(h2;grid on;axis([0,3000,-100,0];legend('脉冲响应不变法','双线性变换'; xlabel('频率/Hz';ylabel('幅度/dB';3.5clearclose allw1=2*10000*tan(2*pi*1000/(2*10000;w2=2*10000*tan(2*pi*2000/(2*10000;w3=2*10000*tan(2*pi*500/(2*10000;w4=2*10000*tan(2*pi*3000/(2*10000; [n,wn]=cheb1ord([w3 w4],[w1 w2],3,18,'s' [B,A]=cheby1(n,3,wn,'stop','s';[num,den]=bilinear(B,A,10000;[h,w]=freqz(num,den;f=w/pi*5000;plot(f,20*log10(abs(h;axis([0,5000,-100,0];gridxlabel('频率/Hz';ylabel('幅度/dB';4.1%N=45,计算并画出矩形框、汉明窗、布莱克曼窗的归一化的幅度谱,并比较各自的主要特点%(1矩形窗(Rectangle Window调用格式:w=boxcar(n,根据长度n 产生一个矩形窗w。
