(采用BP神经网络完成非线性函数的逼近)神经网络
BP网络的优缺点介绍1-1

BP神经网络的优缺点介绍人工神经网络(Artificial Neural Network)又称连接机模型,是在现代神经学、生物学、心理学等学科研究的基础上产生的,它反映了生物神经系统处理外界事物的基本过程,是在模拟人脑神经组织的基础上发展起来的计算系统,是由大量处理单元通过广泛互联而构成的网络体系,它具有生物神经系统的基本特征,在一定程度上反映了人脑功能的若干反映,是对生物系统的某种模拟,具有大规模并行、分布式处理、自组织、自学习等优点,被广泛应用于语音分析、图像识别、数字水印、计算机视觉等很多领域,取得了许多突出的成果。
最近由于人工神经网络的快速发展,它已经成为模式识别的强有力的工具。
神经网络的运用展开了新的领域,解决其它模式识别不能解决的问题,其分类功能特别适合于模式识别与分类的应用。
多层前向BP网络是目前应用最多的一种神经网络形式, 它具备神经网络的普遍优点,但它也不是非常完美的, 为了更好的理解应用神经网络进行问题求解, 这里对它的优缺点展开一些讨论。
首先BP神经网络具有以下优点:1) 非线性映射能力:BP神经网络实质上实现了一个从输入到输出的映射功能,数学理论证明三层的神经网络就能够以任意精度逼近任何非线性连续函数。
这使得其特别适合于求解内部机制复杂的问题,即BP神经网络具有较强的非线性映射能力。
2) 自学习和自适应能力:BP神经网络在训练时,能够通过学习自动提取输出、输出数据间的“合理规则”,并自适应的将学习内容记忆于网络的权值中。
即BP神经网络具有高度自学习和自适应的能力。
3) 泛化能力:所谓泛化能力是指在设计模式分类器时,即要考虑网络在保证对所需分类对象进行正确分类,还要关心网络在经过训练后,能否对未见过的模式或有噪声污染的模式,进行正确的分类。
也即BP神经网络具有将学习成果应用于新知识的能力。
4) 容错能力:BP神经网络在其局部的或者部分的神经元受到破坏后对全局的训练结果不会造成很大的影响,也就是说即使系统在受到局部损伤时还是可以正常工作的。
BP神经网络及深度学习研究-综述(最新整理)

BP神经网络及深度学习研究摘要:人工神经网络是一门交叉性学科,已广泛于医学、生物学、生理学、哲学、信息学、计算机科学、认知学等多学科交叉技术领域,并取得了重要成果。
BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
本文将主要介绍神经网络结构,重点研究BP神经网络原理、BP神经网络算法分析及改进和深度学习的研究。
关键词:BP神经网络、算法分析、应用1 引言人工神经网络(Artificial Neural Network,即ANN ),作为对人脑最简单的一种抽象和模拟,是人们模仿人的大脑神经系统信息处理功能的一个智能化系统,是20世纪80 年代以来人工智能领域兴起的研究热点。
人工神经网络以数学和物理方法以及信息处理的角度对人脑神经网络进行抽象,并建立某种简化模型,旨在模仿人脑结构及其功能的信息处理系统。
人工神经网络最有吸引力的特点就是它的学习能力。
因此从20世纪40年代人工神经网络萌芽开始,历经两个高潮期及一个反思期至1991年后进入再认识与应用研究期,涌现出无数的相关研究理论及成果,包括理论研究及应用研究。
最富有成果的研究工作是多层网络BP算法,Hopfield网络模型,自适应共振理论,自组织特征映射理论等。
因为其应用价值,该研究呈愈演愈烈的趋势,学者们在多领域中应用[1]人工神经网络模型对问题进行研究优化解决。
人工神经网络是由多个神经元连接构成,因此欲建立人工神经网络模型必先建立人工神经元模型,再根据神经元的连接方式及控制方式不同建立不同类型的人工神经网络模型。
现在分别介绍人工神经元模型及人工神经网络模型。
1.1 人工神经元模型仿生学在科技发展中起着重要作用,人工神经元模型的建立来源于生物神经元结构的仿生模拟,用来模拟人工神经网络[2]。
人们提出的神经元模型有很多,其中最早提出并且影响较大的是1943年心理学家McCulloch和数学家W. Pitts在分析总结神经元基本特性的基础上首先提出的MP模型。
神经网络在函数逼近中的应用

二 基于BP神经网络逼近函数 基于BP神经网络逼近函数
步骤1:假设频率参数k=1,绘制要逼近的非线性 步骤1:假设频率参数k=1,绘制要逼近的非线性 函数的曲线。函数的曲线如图1 函数的曲线。函数的曲线如图1所示 k=1; p=[p=[-1:.05:8]; t=1+sin(k*pi/4*p); plot( plot(p,t,'-'); '); title('要逼近的非线性函数'); title('要逼近的非线性函数'); xlabel('时间'); xlabel('时间'); ylabel('非线性函数'); ylabel('非线性函数');
图3 训练过程 从以上结果可以看出,网络训练速度很快,很 快就达到了要求的精度0.001。 快就达到了要求的精度0.001。
步骤4 步骤4: 网络测试 对于训练好的网络进行仿真: y2=sim(net,p); figure; plot(p,t,'plot(p,t,'-',p,y1,':',p,y2, '--') '--') title('训练后网络的输出结果'); title('训练后网络的输出结果'); xlabel('时间'); xlabel('时间'); ylabel('仿真输出'); ylabel('仿真输出'); 绘制网络输出曲线,并与原始非线性函数曲线以 及未训练网络的输出结果曲线相比较,比较出来 的结果如图4 的结果如图4所示。
BP网络在函数逼近中的应用 BP网络在函数逼近中的应用
BP神经网络实验报告

BP神经网络实验报告一、引言BP神经网络是一种常见的人工神经网络模型,其基本原理是通过将输入数据通过多层神经元进行加权计算并经过非线性激活函数的作用,输出结果达到预测或分类的目标。
本实验旨在探究BP神经网络的基本原理和应用,以及对其进行实验验证。
二、实验方法1.数据集准备本次实验选取了一个包含1000个样本的分类数据集,每个样本有12个特征。
将数据集进行标准化处理,以提高神经网络的收敛速度和精度。
2.神经网络的搭建3.参数的初始化对神经网络的权重和偏置进行初始化,常用的初始化方法有随机初始化和Xavier初始化。
本实验采用Xavier初始化方法。
4.前向传播将标准化后的数据输入到神经网络中,在神经网络的每一层进行加权计算和激活函数的作用,传递给下一层进行计算。
5.反向传播根据预测结果与实际结果的差异,通过计算损失函数对神经网络的权重和偏置进行调整。
使用梯度下降算法对参数进行优化,减小损失函数的值。
6.模型评估与验证将训练好的模型应用于测试集,计算准确率、精确率、召回率和F1-score等指标进行模型评估。
三、实验结果与分析将数据集按照7:3的比例划分为训练集和测试集,分别进行模型训练和验证。
经过10次训练迭代后,模型在测试集上的准确率稳定在90%以上,证明了BP神经网络在本实验中的有效性和鲁棒性。
通过调整隐藏层结点个数和迭代次数进行模型性能优化实验,可以发现隐藏层结点个数对模型性能的影响较大。
随着隐藏层结点个数的增加,模型在训练集上的拟合效果逐渐提升,但过多的结点数会导致模型的复杂度过高,容易出现过拟合现象。
因此,选择合适的隐藏层结点个数是模型性能优化的关键。
此外,迭代次数对模型性能也有影响。
随着迭代次数的增加,模型在训练集上的拟合效果逐渐提高,但过多的迭代次数也会导致模型过度拟合。
因此,需要选择合适的迭代次数,使模型在训练集上有好的拟合效果的同时,避免过度拟合。
四、实验总结本实验通过搭建BP神经网络模型,对分类数据集进行预测和分类。
人工神经网络原理、分类及应用

学 术 论 坛240科技资讯 SCIENCE & TECHNOLOGY INFORMATION神经网络是一门发展十分迅速的交叉学科,它是由大量的处理单元组成非线性的大规模自适应动力系统。
神经网络具有分布式存储、并行处理、高容错能力以及良好的自学习、自适应、联想等特点。
该模型对于拟合现实复杂世界有着重要的实用价值。
1 神经网络简介人工神经网络(Artificial Neural Network,ANN),亦称神经网络(Neural Network,NN),是一种应用类似于大脑神经突触连接结构进行信息处理的数学模型,它是在人类对自身大脑组织结合和思维机制的认识理解基础之上模拟出来的,它是根植于神经科学、数学、统计学、物理学、计算机科学以及工程科学的一门技术。
心理学家Mcculloch,数学家Pitts在20世纪40年代第一次提出了神经网络模型,从此开创了神经科学理论的研究时代,此后半个世纪神经网络技术蓬勃发展。
神经网络是一种计算模型,由大量的神经元个体节点和其间相互连接的加权值共同组成,每个节点都代表一种运算,称为激励函数(activation function)。
每两个相互连接的节点间都代表一个通过该连接信号加权值,称值为权重(weight),神经网络就是通过这种方式来模拟人类的记忆,网络的输出则取决于网络的结构、网络的连接方式、权重和激励函数。
而网络本身通常是对自然界或者人类社会某种算法或函数的逼近,也可能是一种逻辑策略的表达。
神经网络的构筑理念是受到生物的神经网络运作启发而产生的。
人工神经网络则是把对生物神经网络的认识与数学统计模型向结合,借助数学统计工具来实现。
另一方面在人工智能学的人工感知领域,我们通过数学统计学的方法,使神经网络能够具备类似于人的决定能力和简单的判断能力,这种方法是对传统逻辑学演算的进一步延伸。
2 神经网络模型及训练2.1生物神经元模型人脑是自然界所造就的高级动物,人的思维是由人脑来完成的,而思维则是人类智能的集中体现。
MATLAB神经网络(2)BP神经网络的非线性系统建模——非线性函数拟合

MATLAB神经⽹络(2)BP神经⽹络的⾮线性系统建模——⾮线性函数拟合2.1 案例背景在⼯程应⽤中经常会遇到⼀些复杂的⾮线性系统,这些系统状态⽅程复杂,难以⽤数学⽅法准确建模。
在这种情况下,可以建⽴BP神经⽹络表达这些⾮线性系统。
该⽅法把未知系统看成是⼀个⿊箱,⾸先⽤系统输⼊输出数据训练BP神经⽹络,使⽹络能够表达该未知函数,然后⽤训练好的BP神经⽹络预测系统输出。
本章拟合的⾮线性函数为y=x12+x22该函数的图形如下图所⽰。
t=-5:0.1:5;[x1,x2] =meshgrid(t);y=x1.^2+x2.^2;surfc(x1,x2,y);shading interpxlabel('x1');ylabel('x2');zlabel('y');title('⾮线性函数');2.2 模型建⽴神经⽹络结构:2-5-1从⾮线性函数中随机得到2000组输⼊输出数据,从中随机选择1900 组作为训练数据,⽤于⽹络训练,100组作为测试数据,⽤于测试⽹络的拟合性能。
2.3 MATLAB实现2.3.1 BP神经⽹络⼯具箱函数newffBP神经⽹络参数设置函数。
net=newff(P, T, S, TF, BTF, BLF, PF, IPF, OPF, DDF)P:输⼊数据矩阵;T:输出数据矩阵;S:隐含层节点数;TF:结点传递函数。
包括硬限幅传递函数hardlim、对称硬限幅传递函数hardlims、线性传递函数purelin、正切型传递函数tansig、对数型传递函数logsig;x=-5:0.1:5;subplot(2,6,[2,3]);y=hardlim(x);plot(x,y,'LineWidth',1.5);title('hardlim');subplot(2,6,[4,5]);y=hardlims(x);plot(x,y,'LineWidth',1.5);title('hardlims');subplot(2,6,[7,8]);y=purelin(x);plot(x,y,'LineWidth',1.5);title('purelin');subplot(2,6,[9,10]);y=tansig(x);plot(x,y,'LineWidth',1.5);title('tansig');subplot(2,6,[11,12]);y=logsig(x);plot(x,y,'LineWidth',1.5);title('logsig');BTF:训练函数。
BP神经网络的基本原理_一看就懂

BP神经网络的基本原理_一看就懂BP神经网络(Back Propagation Neural Network)是一种常用的人工神经网络模型,用于解决分类、回归和模式识别问题。
它的基本原理是通过反向传播算法来训练和调整网络中的权重和偏置,以使网络能够逐渐逼近目标输出。
1.前向传播:在训练之前,需要对网络进行初始化,包括随机初始化权重和偏置。
输入数据通过输入层传递到隐藏层,在隐藏层中进行线性加权和非线性激活运算,然后传递给输出层。
线性加权运算指的是将输入数据与对应的权重相乘,然后将结果进行求和。
非线性激活指的是对线性加权和的结果应用一个激活函数,常见的激活函数有sigmoid函数、ReLU函数等。
激活函数的作用是将线性运算的结果映射到一个非线性的范围内,增加模型的非线性表达能力。
2.计算损失:将网络输出的结果与真实值进行比较,计算损失函数。
常用的损失函数有均方误差(Mean Squared Error)和交叉熵(Cross Entropy)等,用于衡量模型的输出与真实值之间的差异程度。
3.反向传播:通过反向传播算法,将损失函数的梯度从输出层传播回隐藏层和输入层,以便调整网络的权重和偏置。
反向传播算法的核心思想是使用链式法则。
首先计算输出层的梯度,即损失函数对输出层输出的导数。
然后将该梯度传递回隐藏层,更新隐藏层的权重和偏置。
接着继续向输入层传播,直到更新输入层的权重和偏置。
在传播过程中,需要选择一个优化算法来更新网络参数,常用的优化算法有梯度下降(Gradient Descent)和随机梯度下降(Stochastic Gradient Descent)等。
4.权重和偏置更新:根据反向传播计算得到的梯度,使用优化算法更新网络中的权重和偏置,逐步减小损失函数的值。
权重的更新通常按照以下公式进行:新权重=旧权重-学习率×梯度其中,学习率是一个超参数,控制更新的步长大小。
梯度是损失函数对权重的导数,表示了损失函数关于权重的变化率。
神经网络原理及BP网络应用实例

神经网络原理及BP网络应用实例摘要:本文主要对神经网络原理进行系统地概述,再列举BP网络在曲线逼近中的应用。
神经网络是一门发展十分迅速的交叉学科,它是由大量的处理单元组成非线性的大规模自适应动力系统。
神经网络具有分布式存储、并行处理、高容错能力以及良好的自学习、自适应、联想等特点。
随着计算机的发展,目前已经提出了多种训练算法和网络模型,其中应用最广泛的是前馈型神经网络。
本文将介绍人工神经网络的基本概念、基本原理、BP神经网络、自适应竞争神经网络以及神经网络的应用改进方法。
关键字:神经网络;收敛速度;BP网络;改进方法The principle of neural network and the applicationexamples of BP networkAbstract:Neural network is a cross discipline which now developing very rapidly, it is the nonlinearity adaptive power system which made up by abundant of the processing units . The neural network has features such as distributed storage, parallel processing, high tolerance and good self-learning, adaptive, associate, etc. Currently various training algorithm and network model have been proposed , which the most widely used type is Feedforward neural network model. Feedforward neural network training type used in most of the method is back-propagation (BP) algorithm. This paper will introduces the basic concepts, basic principles, BP neural network, adaptive competitive neural network and the application of artificial neural network.Keywords:neural network,convergence speed,BP neural network,improving method1 神经网络概述1.1 生物神经元模型人脑是由大量的神经细胞组合而成的,它们之间相互连接。
神经网络的类型

概述本文主要介绍了当前常用的神经网络,这些神经网络主要有哪些用途,以及各种神经网络的优点和局限性。
1 BP神经网络BP (Back Propagation)神经网络是一种神经网络学习算法。
其由输入层、中间层、输出层组成的阶层型神经网络,中间层可扩展为多层。
相邻层之间各神经元进行全连接,而每层各神经元之间无连接,网络按有教师示教的方式进行学习,当一对学习模式提供给网络后,各神经元获得网络的输入响应产生连接权值(Weight)。
然后按减小希望输出与实际输出误差的方向,从输出层经各中间层逐层修正各连接权,回到输入层。
此过程反复交替进行,直至网络的全局误差趋向给定的极小值,即完成学习的过程。
初始权值阈值的确定:所以权值及阈值的初始值应选为均匀分布的小数经验值,约为(-2.4/F~2.4/F)之间,其中F 为所连单元的输入层节点数1.1 主要功能(1)函数逼近:用输入向量和相应的输出向量训练一个网络以逼近一个函数。
(2)模式识别:用一个待定的输出向量将它与输入向量联系起来。
(3)分类:把输入向量所定义的合适方式进行分类。
(4)数据压缩:减少输出向量维数以便传输或存储。
1.2 优点及其局限性BP神经网络最主要的优点是具有极强的非线性映射能力。
理论上,对于一个三层和三层以上的BP网络,只要隐层神经元数目足够多,该网络就能以任意精度逼近一个非线性函数。
其次,BP神经网络具有对外界刺激和输入信息进行联想记忆的能力。
这是因为它采用了分布并行的信息处理方式,对信息的提取必须采用联想的方式,才能将相关神经元全部调动起来。
BP 神经网络通过预先存储信息和学习机制进行自适应训练,可以从不完整的信息和噪声干扰中恢复原始的完整信息。
这种能力使其在图像复原、语言处理、模式识别等方面具有重要应用。
再次,BP 神经网络对外界输入样本有很强的识别与分类能力。
由于它具有强大的非线性处理能力,因此可以较好地进行非线性分类, 解决了神经网络发展史上的非线性分类难题。
强化学习算法中的非线性函数逼近方法详解(八)

强化学习算法中的非线性函数逼近方法详解强化学习是一种机器学习方法,旨在让智能体通过与环境的交互学习如何最大化累积奖励。
在强化学习中,智能体需要学习一个策略,以便在面对不同的环境状态时做出正确的决策。
一个重要的问题是如何表示和逼近值函数和策略函数,以便在复杂的环境中进行学习。
在本文中,我们将详细介绍强化学习算法中的非线性函数逼近方法。
1. 线性函数逼近在传统的强化学习算法中,值函数和策略函数通常使用线性函数逼近来表示。
线性函数逼近的优点是简单易于理解和实现,但其局限性也很明显。
例如,在面对复杂的状态空间时,线性函数逼近可能无法准确地表示值函数和策略函数,从而导致学习性能的下降。
2. 非线性函数逼近为了解决线性函数逼近的局限性,研究者们提出了多种非线性函数逼近方法。
其中最常用的方法之一是基于神经网络的函数逼近。
神经网络具有强大的拟合能力,可以学习复杂的非线性关系,因此被广泛应用于强化学习算法中。
3. 深度强化学习深度强化学习是将深度学习和强化学习相结合的一种方法。
在深度强化学习中,值函数和策略函数通常使用深度神经网络来进行非线性函数逼近。
深度神经网络具有多层隐藏层,能够学习更加复杂的特征表示,从而提高值函数和策略函数的逼近能力。
4. 非线性函数逼近的挑战虽然非线性函数逼近方法在强化学习中取得了很大的成功,但也面临着一些挑战。
首先,非线性函数逼近方法通常需要大量的数据来训练模型,这对于一些复杂的环境来说可能不够高效。
其次,非线性函数逼近方法的训练过程可能不够稳定,需要仔细的调参和技巧。
5. 改进方法为了克服非线性函数逼近方法的挑战,研究者们提出了多种改进方法。
例如,可以结合传统的强化学习算法和非线性函数逼近方法,提高算法的稳定性和效率。
另外,也可以通过引入更加复杂的模型结构和训练技巧来提高非线性函数逼近方法的性能。
总结强化学习算法中的非线性函数逼近方法是一个复杂而又重要的研究领域。
通过本文的介绍,读者可以对非线性函数逼近方法有一个更加全面的了解。
思维进化算法在BP神经网络拟合非线性函数中的应用研究

思维进化算法在BP神经网络拟合非线性函数中的应用研究刘俊【摘要】直接使用BP神经网络拟合非线性函数,具有预测精度差、收敛速度慢等缺点。
该文提出利用极强全局搜索能力的思维进化算法来优化BP神经网络。
首先根据BP神经网络拓扑结构构建思维进化算法模型,然后用思维进化算法得到的最优解作为BP神经网络的初始权值和阈值,最后利用MATLAB软件对多个非线性函数进行拟合仿真实验,比较思维进化算法优化BP神经网络和单纯使用BP神经网络的预测结果。
数据表明,优化后的BP神经网络具有更高的拟合精度和更短的网络训练时间。
%Owing to the poor accuracy,slow convergence speed and other shortcomings after the direct appli-cation of BP neural network in the fitting of nonlinear functions,this paper proposed that BP neural network can be optimized by mind evolutionary algorithm,which enjoys strong global search ability. Firstly,the mind evolu-tionary algorithm model is constructed based on neural network topology;then,it is used to get the optimal solu-tions,which is served as initial weights and the threshold value of BP neural network;lastly,the MATLAB soft-ware is used to simulate multiple nonlinear function fitting,comparing the different results between optimized BP neural network and simply application of the BP neural network. Statistics indicate that the optimized BP neural network enjoys higher accuracy and shorter training time.【期刊名称】《绵阳师范学院学报》【年(卷),期】2015(000)002【总页数】5页(P79-83)【关键词】思维进化算法;BP神经网络;函数拟合【作者】刘俊【作者单位】商洛学院电子信息与电气工程学院,陕西商洛 726000【正文语种】中文【中图分类】TP183在工程应用领域中,经常需要对大量采集的历史数据进行函数拟合.然而这些数据常常是复杂、多元的非线性关系,传统的最小二乘、多项式回归等拟合方法无法满足拟合精度要求.人工神经网络具有良好的非线性并行处理能力,强大的学习和泛化能力,为非线性函数拟合提供了有效途径.张宝堃等[1]利用非线性映射能力较强的BP 神经网络拟合了一组单输入单输出非线性函数,但该方法存在局部最优问题等缺点[2,3].徐富强等[4]采用遗传算法优化BP 神经网络的初始权值和阈值,并用于非线性函数拟合,该方法全局搜索能力较强,但误差依然较大.沈学利等[5]将粒子群优化算法应用于BP神经网络的参数训练,对非线性函数拟合有一定的效果,但存在精度较差,容易陷入局部最优等[6]缺点.本文提出了思维进化算法与BP 神经网络结合的算法,利用思维进化算法优化BP 神经网络的初始权值和阈值,通过多个非线性函数拟合实验验证了该算法的强拟合能力和有效性.1 思维进化算法1.1 思维进化算法概述思维进化算法(Mind Evolutionary Algorithm,简称MEA)由孙承意等[7]研究者于1998年提出,该算法是针对遗传算法的缺陷[8]而提出的一种新型进化算法,其思想来源于模仿人类思维进化过程.思维进化算法继承了遗传算法的“群体”和“进化”的思想,提出了新的操作算子——“趋同”和“异化”,这两种操作相互协调,其中任一操作改进都可以提高算法的整体搜索效率.由于思维进化算法具有良好的扩充性、移植性和极强的全局优化能力,已经成功应用于图像处理、自动控制、经济预测等领域[9-13]1.2 思维进化算法基本思想思维进化算法是一种通过趋同、异化等操作,不断迭代进行优化学习的方法,基本的进化过程如下:(1)群体生成.在解空间中随机生成P 个个体,所有个体组成一个群体.根据适应度函数计算出每个个体的得分.(2)子群体生成.得分最高的前M 个个体作为优胜个体,前第M+1 到第M+N 共N 个个体作为临时个体.以所选优胜个体和临时个体为中心,生成M 个优胜子群体和N 个临时子群体,每个子群体的个体数目为P/(N+M).(3)趋同操作.各子群体内部个体为成为胜者而进行局部竞争,此过程为趋同过程.若一个子群体不在产生新的胜者(即子群体成熟),则竞争结束,该子群体的得分就是子群体中最优个体的得分,并把得分张贴在全局公告板上.直到所有子群体全部成熟,趋同过程结束.(4)异化操作.成熟后的子群体之间为成为胜者而进行全局竞争,不断探索新的解空间,此过程为异化操作.从全局公告板上,比较优胜子群体和临时子群体的得分高低,完成子群体间的替换、废弃、个体释放的过程,最后得到全局最优个体及其得分.(5)迭代操作.异化结束后,被释放的个体重新被新的临时子群体补充,重复(3)-(4)过程,直到最优个体的得分不再提高或迭代结束,则认为运算收敛,输出最优个体.思维进化算法框图如图1 所示:图1 思维进化算法框图Fig.1 Block diagram of mind evolutionary algorithm 2 BP 神经网络BP(Back Propagation)神经网络一种误差反向传播的多层前馈神经网络,由Rumelhart 和McCelland 等学者在1986年提出.BP 神经网络由三层网络--输入层、隐含层和输出层组成,隐含层可以有一层或多层.输入信号经输入层逐层传输到各隐含层,最后传向输出层.隐含层和输出层根据相应神经元的权值和阈值完成数据计算工作.若输出结果不满足期望值,误差信号反向逐层传到各隐含层和输入层,利用梯度最速下降法,调整各神经元的权值和阈值.输入正向传播和误差反向传播反复迭代,直到输出误差最小或输出达到期望值,计算结束.利用BP 神经网络拟合非线性函数的一般过程如下:(1)构建BP 神经网络.根据需要拟合的非线性函数特征,确定隐含层层数,选择各层网络节点数目和隐含层、输出层传输函数等.(2)训练BP 神经网络.初始化连接权值和阈值,设定学习速率和训练目标;依次计算隐含层输出、输出层输出和输出误差;根据误差信号,依次更新各层神经元间的权值和阈值;反复迭代,直到输出误差最小或满足期望值,训练结束.(3)BP 神经网络预测.用训练好的BP 网络预测非线性函数输出,然后分析预测结果. BP 神经网络具有较强的非线性映射能力,拟合函数具有一定的效果,但拟合精度较低,且容易陷入局部极值点.为了提高精度,实现全局优化,本文采用思维进化算法来优化BP 神经网络,实现非线性函数的高精度拟合.3 MEA-BP 神经网络拟合非线性函数的算法实现思维进化算法在BP 神经网络拟合非线性函数的算法实现,首先根据拟合函数的输入输出参数确定BP 神经网络拓扑结构,进而得到思维进化算法个体的编码长度,并构建优化算法模型.然后,用思维进化算法对BP 神经网络的初始权值和阈值进行优化,选取训练数据的均方误差的倒数作为各个种群和个体的得分函数,经过不断趋同、异化、迭代,输出最优个体.最后解析最优个体,得到BP 神经网络的初始权值和阈值,再利用训练数据样本训练BP 神经网络,利用测试数据样本预测网络性能.优化算法实现流程图如图2 所示.图2 算法流程图Fig.2 Flow chart of mind evolutionary algorithm4 仿真实验为了验证思维进化算法优化BP 神经网络后的预测精度,选择非线性函数式(1)进行拟合.采用MATLAB 软件编程实现BP 神经网络拟合算法和思维进化算法优化BP 神经网络拟合算法,并对这两种算法的预测精度进行比较.拟合的非线性函数如下:4.1 参数设置拟合函数为两个输入,一个输出,设定BP 网络拓扑结构为2-10-1,即输入层、隐含层和输出层的节点数分别为2个、10 个和1 个.网络学习速率为0.1,训练次数1000 次,训练目标10-6.隐含层和输出层的传输函数都选择S 型正切函数‘tansig’;网络训练函数选择L-M 算法函数‘trainlm’;权值学习函数选择梯度下降动量学习函数‘learngdm’.思维进化算法种群大小设定为400,优胜子种群和临时子种群个数全部为5,子种群大小为40,个体编码长度为21,迭代次数20,适应度函数为均方误差的倒数.根据式(1)随机产生2000 组数据,任取1950 组用于训练网络,其余50 组用于预测网络.4.2 结果分析为了清晰观察网络优化后的预测结果,首先利用1950 组数据分别训练BP 神经网络和思维进化算法优化后的BP 神经网络,然后利用训练后的两个网络预测其余50 组数据,最后分析比较这两种算法的预测误差和误差百分比参数.预测误差及误差百分比如图3 和图4 所示.图3 BP 神经网络与MEA-BP 神经网络预测误差比较Fig.3 Prediction errors between BP neural network and MEA-BP neural network图4 BP 神经网络与MEA-BP 神经网络预测误差百分比Fig.4 Percentage of prediction errors between BP neural network and MEA-BP neural network 从图3 和图4 可以清楚看到,对于非线性函数,BP 神经网络具有一定的拟合能力,但预测精度仍然较差,但是,经过思维进化算法优化后的BP 神经网络预测误差明显减小,且误差相对稳定.其他预测参数比较如表1 所示.表1 BP 神经网络与MEA-BP 神经网络预测结果比较Tab.1 Prediction results of BP neural network and MEA-BP neural network从表1 可以看到,MEA-BP 神经网络预测误差远小于BP 神经网络的预测误差,且网络训练时间也较短,可见MEA-BP 神经网络具有更高的拟合性能.4.3 其他函数的拟合按照同样的参数设定和拟合方法,对其他非线性函数进行拟合实验,实验函数如式(2)、(3)和(4).通过网络训练和预测,得到两种算法的实验结果,如表2 所示.表2 实验结果比较Tab.2 Comparison of experimental consequences从表2 中可以看出,对非线性函数拟合,经过思维进化算法优化后的BP 神经网络的预测精度高于直接使用BP 神经网络,且网络训练时间相对较短,也可以看出优化后的BP 神经网络泛化性能得到进一步提高.5 结语本文采用全局搜索能力极强的思维进化算法对BP 神经网络进行优化.该算法的基本思想是在训练BP 神经网络前,利用思维进化算法对BP 神经网络的初始权值和阈值进行优化,以提高网络的准确性.从多个非线性函数拟合实验结果分析比较得到,思维进化算法优化BP 神经网络的性能明显优于BP神经网络,非线性函数拟合精度更高.本文研究方法在工程和实验的数据拟合方面具有重要意义,也为研究和改进神经网络提供了一种新的思路,为解决其他实际问题提供了新的手段.参考文献:[1]张宝堃,张宝一.基于BP 神经网络的非线性函数拟合[J].电脑知识与技术,2012,8(27):6579-6583.[2]Li Song,Liu Lijun,Huo Man.Prediction for short-term traffic flow based on modified PSO optimized BP neural network[J].Systems Engineering-Theory & Practice,2012,32(9):2045-2049.[3]Xu Yishan,Zeng Bi,Yin Xiuwen,et al.BP neural network and its applications based on improved PSO[J].Computer Engineering and Applications,2009,45(35):233-235.[4]徐富强,钱云,刘相国.GA-BP 神经网络的非线性函数拟合[J].微计算机信息,2012,28(7):148-150.[5]沈学利,张红岩,张纪锁.改进粒子群算法对BP 神经网络的优化[J].计算机系统应用,2012,19(2):57-61.[6]乔冰琴,常晓明.改进粒子群算法在BP 神经网络拟合非线性函数方面的应用[J].太原理工大学学报,2012,43(5):558-559.[7]Chengyi Sun.Mind-Evolution-Based Machine Learning:Frameworkand the Implementation of Optimization[A].In:Proceedings of IEEE International Conference on Intelligent Engineering Systems[C].1998,355-359.[8]谢刚.免疫思维进化算法及其工程应用[D].太原:太原理工大学,2006,27-28.[9]Sun Yan,Sun Yu,Sun Chengyi.Clustering and Reconstruction of Color images Using MEBML[A].In:Proceedings of International Conference on Neural Networks & Brain[C].Beijing,China,1998,361-365.[10]Cheng Mingqi.Gray image segmentation on MEBML frame [J].Intelligent Control and Automation,2000,1:135-137.[11]Chengyi Sun,Yan Sun,Yu Sun.Economic prediction system using double models[J].Systems,Man,and Cyberntics,2000,3:1978-1983. [12]韩晓霞,谢克明.基于思维进化算法的模糊自寻优控制[J].太原理工大学学报,2004,35(5):523-525.[13]Keming Xie,Changhua Mou,Gang Xie.The multi-parameter combination mind-evolutionary-based machine learning and its application[J].Systems,Man,and Cybernetics,2000,1:183-187.。
神经网络激活函数[BP神经网络实现函数逼近的应用分析]
![神经网络激活函数[BP神经网络实现函数逼近的应用分析]](https://img.taocdn.com/s3/m/6f4ac08759f5f61fb7360b4c2e3f5727a5e924b1.png)
神经网络激活函数[BP神经网络实现函数逼近的应用分析]神经网络激活函数是神经网络中非常重要的组成部分,它决定了神经网络的非线性特性,并且对于神经网络的求解效果和性能有着重要的影响。
本文将对神经网络激活函数进行详细的分析和探讨,并以BP神经网络实现函数逼近的应用为例进行具体分析。
1.神经网络激活函数的作用(1)引入非线性:神经网络通过激活函数引入非线性,使其具备处理非线性问题的能力,能够更好的逼近任意非线性函数。
(2)映射特征空间:激活函数可以将输入映射到另一个空间中,从而更好地刻画特征,提高神经网络的表达能力,并且可以保留原始数据的一些特性。
(3)增强模型的灵活性:不同的激活函数具有不同的形状和性质,选择合适的激活函数可以增加模型的灵活性,适应不同问题和数据的特点。
(4)解决梯度消失问题:神经网络中经常会遇到梯度消失的问题,通过使用合适的激活函数,可以有效地缓解梯度消失问题,提高神经网络的收敛速度。
2.常用的神经网络激活函数(1)Sigmoid函数:Sigmoid函数是一种常用的激活函数,它的输出值范围在(0,1)之间,具有平滑性,但是存在梯度消失问题。
(2)Tanh函数:Tanh函数是Sigmoid函数的对称形式,它的输出值范围在(-1,1)之间,相对于Sigmoid函数来说,均值为0,更符合中心化的要求。
(3)ReLU函数:ReLU函数在输入为负数时输出为0,在输入为正数时输出为其本身,ReLU函数简单快速,但是容易出现神经元死亡问题,即一些神经元永远不被激活。
(4)Leaky ReLU函数:Leaky ReLU函数是对ReLU函数的改进,当输入为负数时,输出为其本身乘以一个小的正数,可以解决神经元死亡问题。
(5)ELU函数:ELU函数在输入为负数时输出为一个负有指数衰减的值,可以在一定程度上缓解ReLU函数带来的神经元死亡问题,并且能够拟合更多的函数。
3.BP神经网络实现函数逼近的应用BP神经网络是一种常用的用于函数逼近的模型,它通过不断调整权重和偏置来实现对目标函数的拟合。
(完整word版)BP神经网络实验报告

BP 神经网络实验报告一、实验目的1、熟悉MATLAB中神经网络工具箱的使用方法;2、经过在MATLAB下面编程实现BP网络逼近标准正弦函数,来加深对BP网络的认识和认识,理解信号的正向流传和误差的反向传达过程。
二、实验原理由于传统的感知器和线性神经网络有自己无法战胜的弊端,它们都不能够解决线性不能分问题,因此在实质应用过程中碰到了限制。
而BP 网络却拥有优异的繁泛化能力、容错能力以及非线性照射能力。
因此成为应用最为广泛的一种神经网络。
BP 算法的根本思想是把学习过程分为两个阶段:第一阶段是信号的正向流传过程;输入信息经过输入层、隐层逐层办理并计算每个单元的实质输出值;第二阶段是误差的反向传达过程;假设在输入层未能获取希望的输出值,那么逐层递归的计算实质输出和希望输出的差值〔即误差〕,以便依照此差值调治权值。
这种过程不断迭代,最后使得信号误差到达赞同或规定的范围之内。
基于 BP 算法的多层前馈型网络模型的拓扑结构如上图所示。
BP 算法的数学描述:三层BP 前馈网络的数学模型如上图所示。
三层前馈网中,输入向量为: X ( x1 , x2 ,..., x i ,..., x n )T;隐层输入向量为:Y( y1 , y2 ,..., y j ,...y m ) T;输出层输出向量为: O (o1 , o2 ,..., o k ,...o l )T;希望输出向量为:d(d1 ,d 2 ,...d k ,...d l )T。
输入层到隐层之间的权值矩阵用 V 表示,V(v1 , v2 ,...v j ,...v m ) Y,其中列向量v j为隐层第 j 个神经元对应的权向量;隐层到输出层之间的权值矩阵用W 表示,W( w1 , w2 ,...w k ,...w l ) ,其中列向量 w k为输出层第k个神经元对应的权向量。
下面解析各层信号之间的数学关系。
对于输出层,有y j f (net j ), j1,2,..., mnet j v ij x i , j1,2,..., m对于隐层,有O k f (net k ), k1,2,...,lm net k wjkyi, k1,2,...,lj0以上两式中,转移函数 f(x) 均为单极性Sigmoid 函数:1f ( x)x1 ef(x) 拥有连续、可导的特点,且有 f ' (x) f ( x)[1 f ( x)]以上共同构成了三层前馈网了的数学模型。
BP神经网络

BP神经网络在函数逼近中的实现1.1 概述BP神经网络是目前人工神经网络模式中最具代表性,应用得最广泛的一种模型,具有自学习、自组织、自适应和很强的非线性映射能力,可以以任意精度逼近任意连续函数.近年来,为了解决BP网络收敛速度慢,训练时间长等不足,提出了许多改进算法.然而,在针对实际问题的BP网络建模过程中,选择多少层网络,每层多少个神经元节点,选择何种传递函数等,均无可行的理论指导,只能通过大量的实验计算获得.MATLAB中的神经网络工具箱(Neural NetworkToolbox,简称NNbox),为解决这一问题提供了便利的条件.神经网络工具箱功能十分完善,提供了各种MATLAB函数,包括神经网络的建立、训练和仿真等函数,以及各种改进训练算法函数,用户可以很方便地进行神经网络的设计和仿真,也可以在MATLAB源文件的基础上进行适当修改,形成自己的工具包以满足实际需要。
此项课题主要是针对MATLAB软件对BP神经网络的各种算法的编程,将神经网络算法应用于函数逼近和样本含量估计问题中,并分析比较相关参数对算法运行结果的影响。
人工神经网络(Artificial Neural Networks,NN)是由大量的、简单的处理单元(称为神经元)广泛地互相连接而形成的复杂网络系统,它反映了人脑功能的许多基本特征,是一个高度复杂的非线性动力学系统。
神经网络具有大规模并行、分布式存储和处理、自组织、自适应和自学习能力,特别适合处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题。
神经网络的发展与神经科学、数理科学、认知科学、计算机科学、人工智能、信息科学、控制论、机器人学、微电子学、心理学、微电子学、心理学、光计算、分子生物学等有关,是一门新兴的边缘交叉学科。
神经网络具有非线性自适应的信息处理能力,克服了传统人工智能方法对于直觉的缺陷,因而在神经专家系统、模式识别、智能控制、组合优化、预测等领域得到成功应用。
bp神经网络的基本原理

bp神经网络的基本原理
BP神经网络是一种常用的人工神经网络模型,用于解决分类和回归问题。
它的基本原理是通过反向传播算法来调整网络的权重和偏置,从而使网络能够学习和逼近输入输出之间的非线性关系。
BP神经网络由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据,隐藏层是网络中间的处理层,输出层给出最终的结果。
每个神经元都与前一层的神经元以及后一层的神经元相连接,每个连接都有一个权重值。
BP神经网络的学习过程首先需要给定一个训练数据集,并设置好网络的结构和参数。
然后,通过前向传播将输入数据从输入层传递到隐藏层和输出层,计算网络的输出结果。
接着,根据输出结果与实际输出之间的差异,使用误差函数来评估网络的性能。
在反向传播阶段,根据误差函数的值,利用链式法则计算每个连接的权重和偏置的梯度。
然后,根据梯度下降法更新连接的权重和偏置,使误差不断减小。
这个过程反复进行,直到网络输出的误差达到了可接受的范围或者训练次数达到了预设的最大值。
通过不断地调整权重和偏置,BP神经网络可以逐渐学习到输入输出之间的映射关系,从而在面对新的输入数据时能够给出合理的输出。
同时,BP神经网络还具有一定的容错性和鲁棒性,可以处理一些噪声和不完整的数据。
总的来说,BP神经网络的基本原理是通过反向传播算法来训练网络,将输入数据从输入层传递到输出层,并且根据实际输出与期望输出之间的差异来优化网络的权重和偏置,以达到学习和逼近输入输出之间关系的目的。
基于BP神经网络的PID控制系统设计

基于BP神经网络的PID控制系统设计摘要本文主要研究一个基于神经网络的自适应PID控制系统的设计方法,利用BP神经网络对被控对象进行在线辨识和控制。
基于BP神经网络学习算法设计出两个神经网络模型:一个利用神经网络(NNM)对非线性映射的逼近能力,对被控对象进行辨识,另一个构成具有PID结构的控制器(NNC)。
通过神经网络NNM的在线学习和修正,产生对被控对象输出的预测作用,然后由网络NNC实施控制作用,从而实现对辨识对象的PID控制。
在利用神经网络对系统进行辨识时,选用白噪声信号作为系统的输入信号,以提高系统的辨识精度;另外,为了得到神经网络控制器的初始化权值,本文在自整定过程中采用常规PID控制器整定方法之一的稳定边界法。
在设计过程中运用MATLAB语言工具箱进行编程,并通过SIMULINK动态仿真工具对一阶非线性对象进行了仿真。
仿真结果表明了利用神经网络对系统进行辨识的有效性,并用经辨识所得到的输出值取代系统的实际输出值,利用神经网络NNC对系统进行控制,获得了满意的控制效果。
关键词:神经网络,BP学习算法,自适应,参数优化,辨识1 综述PID调节器从问世至今已历经了半个多世纪,在这几十年中,人们为它的发展和推广做出了巨大的努力,使之成为工业过程控制中主要的和可靠的技术工具。
近几十年来,现代控制理论迅速发展,出现了许多先进的控制算法,但到目前为止,即使在微处理技术迅速发展的今天,过程控制中大部分控制规律都未能离开PID,这充分说明PID控制仍具有很强的生命力。
过程工业控制中实际应用最多的仍是常规的PID控制算法,这是因为PID控制具有结构简单、容易实现、控制效果好和鲁棒性强等特点,且PID算法原理简明,参数物理意义明确,理论分析体系完整,为广大控制工程师所熟悉。
但在生产现场往往由于参数整定不好而使PID控制器控制效果欠佳,整定的好坏不但会影响到控制质量,而且还会影响到控制器的性能。
PID控制中一个至关重要的问题,就是控制器三参数(比例系数、积分时间、微分时间)的整定。
BP神经网络
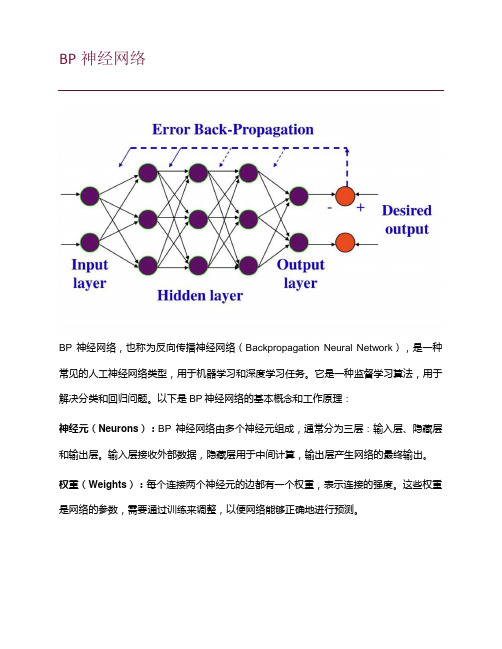
BP神经网络BP神经网络,也称为反向传播神经网络(Backpropagation Neural Network),是一种常见的人工神经网络类型,用于机器学习和深度学习任务。
它是一种监督学习算法,用于解决分类和回归问题。
以下是BP神经网络的基本概念和工作原理:神经元(Neurons):BP神经网络由多个神经元组成,通常分为三层:输入层、隐藏层和输出层。
输入层接收外部数据,隐藏层用于中间计算,输出层产生网络的最终输出。
权重(Weights):每个连接两个神经元的边都有一个权重,表示连接的强度。
这些权重是网络的参数,需要通过训练来调整,以便网络能够正确地进行预测。
激活函数(Activation Function):每个神经元都有一个激活函数,用于计算神经元的输出。
常见的激活函数包括Sigmoid、ReLU(Rectified Linear Unit)和tanh(双曲正切)等。
前向传播(Forward Propagation):在训练过程中,输入数据从输入层传递到输出层的过程称为前向传播。
数据经过一系列线性和非线性变换,最终产生网络的预测输出。
反向传播(Backpropagation):反向传播是BP神经网络的核心。
它用于计算网络预测的误差,并根据误差调整网络中的权重。
这个过程分为以下几个步骤:1.计算预测输出与实际标签之间的误差。
2.将误差反向传播回隐藏层和输入层,计算它们的误差贡献。
3.根据误差贡献来更新权重,通常使用梯度下降法或其变种来进行权重更新。
训练(Training):训练是通过多次迭代前向传播和反向传播来完成的过程。
目标是通过调整权重来减小网络的误差,使其能够正确地进行预测。
超参数(Hyperparameters):BP神经网络中有一些需要人工设置的参数,如学习率、隐藏层的数量和神经元数量等。
这些参数的选择对网络的性能和训练速度具有重要影响。
BP神经网络在各种应用中都得到了广泛的使用,包括图像分类、语音识别、自然语言处理等领域。
人工智能实验报告-BP神经网络算法的简单实现

⼈⼯智能实验报告-BP神经⽹络算法的简单实现⼈⼯神经⽹络是⼀种模仿⼈脑结构及其功能的信息处理系统,能提⾼⼈们对信息处理的智能化⽔平。
它是⼀门新兴的边缘和交叉学科,它在理论、模型、算法等⽅⾯⽐起以前有了较⼤的发展,但⾄今⽆根本性的突破,还有很多空⽩点需要努⼒探索和研究。
1⼈⼯神经⽹络研究背景神经⽹络的研究包括神经⽹络基本理论、⽹络学习算法、⽹络模型以及⽹络应⽤等⽅⾯。
其中⽐较热门的⼀个课题就是神经⽹络学习算法的研究。
近年来⼰研究出许多与神经⽹络模型相对应的神经⽹络学习算法,这些算法⼤致可以分为三类:有监督学习、⽆监督学习和增强学习。
在理论上和实际应⽤中都⽐较成熟的算法有以下三种:(1) 误差反向传播算法(Back Propagation,简称BP 算法);(2) 模拟退⽕算法;(3) 竞争学习算法。
⽬前为⽌,在训练多层前向神经⽹络的算法中,BP 算法是最有影响的算法之⼀。
但这种算法存在不少缺点,诸如收敛速度⽐较慢,或者只求得了局部极⼩点等等。
因此,近年来,国外许多专家对⽹络算法进⾏深⼊研究,提出了许多改进的⽅法。
主要有:(1) 增加动量法:在⽹络权值的调整公式中增加⼀动量项,该动量项对某⼀时刻的调整起阻尼作⽤。
它可以在误差曲⾯出现骤然起伏时,减⼩振荡的趋势,提⾼⽹络训练速度;(2) ⾃适应调节学习率:在训练中⾃适应地改变学习率,使其该⼤时增⼤,该⼩时减⼩。
使⽤动态学习率,从⽽加快算法的收敛速度;(3) 引⼊陡度因⼦:为了提⾼BP 算法的收敛速度,在权值调整进⼊误差曲⾯的平坦区时,引⼊陡度因⼦,设法压缩神经元的净输⼊,使权值调整脱离平坦区。
此外,很多国内的学者也做了不少有关⽹络算法改进⽅⾯的研究,并把改进的算法运⽤到实际中,取得了⼀定的成果:(1) 王晓敏等提出了⼀种基于改进的差分进化算法,利⽤差分进化算法的全局寻优能⼒,能够快速地得到BP 神经⽹络的权值,提⾼算法的速度;(2) 董国君等提出了⼀种基于随机退⽕机制的竞争层神经⽹络学习算法,该算法将竞争层神经⽹络的串⾏迭代模式改为随机优化模式,通过采⽤退⽕技术避免⽹络收敛到能量函数的局部极⼩点,从⽽得到全局最优值;(3) 赵青提出⼀种分层遗传算法与BP 算法相结合的前馈神经⽹络学习算法。
基于BP神经网络算法的函数逼近

基于BP神经网络算法的函数逼近神经网络是一种基于生物神经元工作原理构建的计算模型,可以通过学习和调整权重来逼近非线性函数。
其中,基于误差反向传播算法(BP)的神经网络是最常见和广泛应用的一种,其能够通过反向传播来调整网络的权重,从而实现对函数的近似。
BP神经网络的算法包括了前馈和反向传播两个过程。
前馈过程是指输入信号从输入层经过隐藏层传递到输出层的过程,反向传播过程是指将网络输出与实际值进行比较,并根据误差来调整网络权重的过程。
在函数逼近问题中,我们通常将训练集中的输入值作为网络的输入,将对应的目标值作为网络的输出。
然后通过反复调整网络的权重,使得网络的输出逼近目标值。
首先,我们需要设计一个合适的神经网络结构。
对于函数逼近问题,通常使用的是多层前馈神经网络,其中包括了输入层、隐藏层和输出层。
隐藏层的神经元个数和层数可以根据具体问题进行调整,一般情况下,通过试验和调整来确定最优结构。
然后,我们需要确定误差函数。
对于函数逼近问题,最常用的误差函数是均方误差(Mean Squared Error)。
均方误差是输出值与目标值之间差值的平方和的均值。
接下来,我们进行前馈过程,将输入值通过网络传递到输出层,并计算出网络的输出值。
然后,我们计算出网络的输出与目标值之间的误差,并根据误差来调整网络的权重。
反向传播的过程中,我们使用梯度下降法来最小化误差函数,不断地调整权重以优化网络的性能。
最后,我们通过不断训练网络来达到函数逼近的目标。
训练过程中,我们将训练集中的所有样本都输入到网络中,并根据误差调整网络的权重。
通过反复训练,网络逐渐优化,输出值逼近目标值。
需要注意的是,在进行函数逼近时,我们需要将训练集和测试集分开。
训练集用于训练网络,测试集用于评估网络的性能。
如果训练集和测试集中的样本有重叠,网络可能会出现过拟合现象,导致在测试集上的性能下降。
在神经网络的函数逼近中,还有一些注意事项。
首先是选择适当的激活函数,激活函数能够在网络中引入非线性,使网络能够逼近任意函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制系统仿真与模型处理设计报告
(采用BP神经网络完成非线性函数的逼近)
1、题目要求:
(1)确定一种神经网络、网络结构参数和学习算法。
(2)选择适当的训练样本和检验样本,给出选取方法。
(3)训练网络使学习目标误差函数达到0.01,写出学习结束后的网络各参数,并绘制学习之前、第100次学习和学习结束后各期望输出曲线、实际输出曲线。
绘制网络训练过程的目标误差函数曲线。
(4)验证网络的泛化能力,给出网络的泛化误差。
绘制网络检验样本的期望输出曲线和网络输出曲线。
(5)分别改变神经网络的中间节点个数、改变网络的层数、改变学习算法进行比较实验,讨论系统的逼近情况,给出你自己的结论和看法。
2、设计方案:
在MATLAB中建立M文件下输入如下命令:
x=[0:0.01:1];
y=2.2*power(x-0.25,2)+sin(5*pi*x);
plot(x,y)
xlabel('x');
ylabel('y');
title('非线性函数');
得到如下图形,即所给的非线性函数曲线图:
构造一个1-7-1的BP神经网络,第一层为输入层,节点个数为1;第二层为隐层,节点个数为7;变换函数选正切s型函数(tansig);第三层为输出层,节点个数为1,输出层神经元传递函数为purelin函数。
并且选Levenberg-Marquardt算法(trainlm)为BP网络的学习算法。
对于该初始网络,我们选用sim()函数观察网络输出。
继续在M函数中如下输入。
net=newff(minmax(x),[1,7,1],{'tansig','tansig','purelin'},'trainlm'); y1=sim(net,x);
figure;
plot(x,y,'b',x,y1,'r')
title('期望输出与实际输出比较');
xlabel('t');
则得到以下所示训练的BP网络期望输出与实际输出曲线比较:
应用函数train()对网络进行训练之前,需要预先设置训练参数。
将最大训练次数为100次,训练精度设置为0.01,学习速度为0.01。
net.trainParam.epochs=100;
net.trainParam.goal=0.001;
net.trainParam.lr=0.01;
net=train(net,x,y);
y2=sim(net,x);
plot(x,y,'-r',x,y2,'*g')
title('训练后的结果');
下图为网络训练过程,可以看到,当训练4次以后,就已达要求。
下图为训练后的结果曲线,“*”为学习过后的曲线,红线为期望输出,两条曲线已经很相近了。
这说明经过训练后,BP网络对非线性函数的逼近效果相当好。
接着检验网络的泛化能力,在M文件后,继续输入
err=y-y2;
plot(x,y2,'*g',x,err,'+c');
得到以下图形,由图可知,网络具有很好的泛化能力。
将神经网络的节点数为3时,相关图形如下。
从上面3个图中我们可以看出,当节点为3时,经过训练后,BP网络对非线性函数的逼近效果明显减弱,并且在经过100次训练后仍然达不到所要求的输出精度。
我由此推出,当层数一样多的时候,隐层神经元数目愈多,则BP网络逼近非线性函数的能力越强。
我把上述的层数分布:1-7-1改为1-3-5-1,得到以下的结果:
从三幅图中我们可以看到,在神经元数目一样的情况下,不同的层数对结果
是有明显影响的。
我将原训练函数trainlm改为traingd,得到以下输出结果。
从三幅图可以看出,将trainlm改为traingd之后,连所要求的精度都不能达到。
我由此推出,训练算法对非线性函数的逼近有一定影响,应当选择适合的训练算法。
3、总结:
通过这次作业,我总算对神经网络有了一定的了解,在实践中学习的确能加深对知识的理解和运用能力。
这次我特地没有用nntool工具箱,而是采用M文件编辑,也算对其有了初步的掌握,感觉M文件编写很灵活,分号的作用很明显,
和命令窗口相比也更容易修改参数。
