《三角形的外角》练习题
八年级初二上册数学人教版课时练《 三角形的外角》01(含答案)

《第十一章三角形 11.2.2三角形的外角》课时练一、选择题1.如图,在中,46C ∠=︒,将ABC 沿直线l 折叠,点C 落在点D 的位置,则12∠-∠的度数是( )A .23︒B .92︒C .46︒D .无法确定 2.如图,//AB CD ,165∠=︒,235∠=︒,则B 的度数是( )A .20︒B .25︒C .30D .35︒ 3.已知直线12//l l ,一块含30角的直角三角板如图所示放置,125∠=︒,则2∠=( )A .45︒B .50︒C .55︒D .60︒ 4.如图,直角三角形ABC 的顶点A 在直线m 上,分别度量:①①1,①2,①C ;①①2,①3,①B ;①①3,①4,①C ;①①1,①2,①3,可判断直线m 与直线n 是否平行的是( )A .①B .①C .①D .① 5.将一副三角板按如图所示摆放,直角三角尺AOB 的锐角顶点A 与另一三角尺ACD 的直角顶点重合在一起,(其中45OAB ∠=︒,60C ∠=°),直角边AD 与OB 交于点E ,若//AB CD ,则BED ∠的度数为( ).A .60︒B .65︒C .70︒D .75︒6.如图,将含30°角的直角三角板ABC 放在平行线α和b 上,①C =90°,①A =30°,若①1=20°,则①2的度数等于( )A .60°B .50°C .40°D .30°7.如图,直线//MN PQ ,点A 是MN 上一点,MAC ∠的角平分线交PQ 于点B ,若120∠=︒,2116∠=︒,则3∠的大小为( )A .136°B .148°C .146°D .138°8.如图,把ABC 纸片沿DE 折叠,点A 落在四边形BCED 的外部,1100∠=︒,244∠=︒,则A ∠的度数为( )A .32°B .30°C .28°D .26°9.如图,直线a①b ,直线AC 分别交a 、b 于点B 、C ,直线AD 交a 于点D .若①1=20°,①2=65°,则①3度数等于( )A .30°B .45°C .60°D .85°10.如图,四边形ABCD 是长方形,点F 是DA 长线上一点,G 是CF 上一点,并且ACG AGC ∠=∠,GAF F ∠=∠.若15ECB ∠=︒,则ACF ∠的度数是( )A .15︒B .20︒C .30D .45︒二、填空题 11.如图,若115EOC ∠=︒,则A B C D E F ∠+∠+∠+∠+∠+∠=____________.12.如图在直角三角形ABC 中,①ACB =90°,①A =50°,D 是AB 上的点,将①ACD 沿直线CD 翻折,使点A 恰好落在BC 上的点E 处,则①BDE =________.13.如图,直线a ①b ,一块含60°角的直角三角板ABC (①A =60°)按如图所示放置.若①1=50°,则①2的度数为__°.14.如图,AC BD ⊥于C ,E 是AB 上一点,CE CF ⊥,//,DF AB EH 平分,BEC DH ∠平分BDG ∠,则:H ∠与ACF ∠之间的数最关系为______.15.如图,在ABC 中,ABC C ∠=∠,100A ∠=︒,BD 平分ABC ∠交AC 于点D ,点E 是BC 上一个动点.若DEC 是直角三角形,则BDE ∠的度数是______.三、解答题16.小明在学习三角形的知识时,发现如下数学问题:已知线段AB ,CD 交于点E ,连结时AD ,BC .(1)如图①,若100D B ∠=∠=︒,DAB ∠的平分线与BCE ∠的平分线交于点G ,求G ∠的度数;(2)如图①,若90D B ∠=∠=︒,AM 平分DAB ∠,CF 平分BCN ∠,请判断CF 与AM 的位置关系,并说明理由.17.如图,在①ABC 中,D 是AB 上一点,E 是AC 上一点,BE ,CD 相交于点F . (1)若①A =62°,①ACD =36°,①ABE =20°,则①BFD 的度数为 °;(2)若①ADF+①AEF =180°,①FBC =①FCB ,试判断①A 与①FBC 之间的数量关系,并说明理由.18.如图,CD是①ABC的角平分线,DE①BC,交AC于点E.(1)若①A=45°,①BDC=70°,求①CED的度数;(2)若①A-①ACD=34°,①EDB=97°,求①A的度数.19.已知AM①BN,BD平分①ABN交AM于点D,E为射线BA上的点,设①ABD=α.(1)如图1,求①ADB的度数(用α表示);(2)如图2,若F为AD上的点,①EFD的平分线所在直线分别交BD、ED于点G、H,当HG//BE时,求①BEF的度数(用α表示).20.(问题背景)①MON=90°,点A、B分别在OM、ON上运动(不与点O重合).(问题思考)(1)如图①,AE、BE分别是①BAO和①ABO的平分线,随着点A、点B的运动,①AEB=.(2)如图①,若BC是①ABN的平分线,BC的反向延长线与①OAB的平分线交于点D.①若①BAO =70°,则①D = °.①随着点A 、B 的运动,①D 的大小会变吗?如果不会,求①D 的度数;如果会,请说明理由;(问题拓展)(3)在图①的基础上,如果①MON =a ,其余条件不变,随着点A 、B 的运动(如图①),①D = .(用含a 的代数式表示)21.已知ABC 中,AE 是ABC 的角平分线,72B ∠=︒,36C ∠=︒.(1)如图①,若AD BC ⊥于点D ,求DAE ∠的度数;(2)如图①,若P 为AE 上一个动点(P 不与A ,E 重合),且PF BC ⊥于点F 时,则EPF ∠=_____;(3)探究:如图①,ABC 中,已知B ,C ∠均为锐角,B C ∠>∠,AE 是ABC 的角平分线,若P 为线段AE 上一个动点(P 不与E 重合),且PF BC ⊥于点F 时,请写出EPF ∠与B ,C ∠的关系,并说明理由.22.(问题情境):如图AB //CD ,120PAB ∠=,140PCD ∠=,求APC ∠的度数. 小明的思路是:过P 作PE //AB ,通过平行线性质来求APC ∠.(1)按小明的思路,求APC ∠的度数;(2)(问题迁移):如图2,AB //CD ,点P 在射线OM 上运动,记①P AB =α,①PCD =β,当点P 在B 、D 两点之间运动时,问①APC 与α、β之间有何数量关系?请说明理由;(3)(问题应用):在(2)的条件下,如果点P 在B 、D 两点外侧运动时(点P 与点O 、B 、D 三点不重合),请直接写出①APC 与α、β之间的数量关系.23.(1)已知AB ①CD ,E 是AB 、CD 间一点,如图1,给它取名“M 型”;有结论:E A C ∠=∠+∠;如图2,给它取名“铅笔头型”,有结论:360A E C ∠+∠+∠=︒;①在图3 “M型”中,AF、CF分别平分①A、①C,则①F与①E的关系是;①在图4 “铅笔头型”中,延长EC到G,AF、CF分别平分①A、①DCG,则①F与①E的关系是;(2)若直线AB与直线CD不平行,连接EG,且EG同时平分①BEF和①FGD.①如图5,请探究①1、①2、①F之间的数量关系?并说明理由;①如图6,①1比①2的3倍多18°,①2是①F的23,求①F的度数.参考答案1.B 2.C 3.C 4.B 5.D 6.B 7.B 8.C 9.B 10.C11.230°12.10°13.11014.2①H +①ACF =180°15.30°或70°.16.(1)100°;(2)平行17.(1)62;(2)①A =2①FBC18.(1)130°;(2)55°19.(1)①ADB =α;(2)①BEF =2α20.(1)135°;(2)①45;①①D 的度数不随着点A 、B 的运动而发生变化;①D =45°;(3)12α. 21.(1)18DAE ∠=︒;(2)18°;(3)2B C EPF ∠-∠∠=. 1902∠=︒-∠F E 22.(1)100゜;(2)①APC =α+β;(3)当P 点在线段OB 上运动时,APC ∠=β-α;当P 点在射线DM 上运动时,APC ∠=α-β23.(1)①2E F ∠=∠;① ;(2)① ;①27F ∠=︒ ()1122F ∠=∠+∠。
(完整)三角形的外角(习题及答案)

三角形的外角(习题)➢ 例题示范例1:已知:如图,点E 是直线AB ,CD 外一点,连接DE 交AB 于点F ,∠D =∠B +∠E . 求证:AB ∥CD .D CEA B F①读题标注 ②梳理思路要证AB ∥CD ,需要考虑同位角、内错角、同旁内角.因为已知∠D =∠B +∠E ,而由外角定理得∠AFE =∠B +∠E ,故∠D =∠AFE ,所以AB ∥CD . ③过程书写 证明:如图,∵∠AFE 是△BEF 的一个外角(外角的定义)∴∠AFE =∠B+∠E (三角形的外角等于与它不相邻的两个内角的和)∵∠D =∠B +∠E (已知) ∴∠AFE =∠D (等量代换)∴AB ∥CD (同位角相等,两直线平行)➢ 巩固练习1. 如图,在△ABC 中,∠1是它的一个外角,∠1=115°,∠A =40°,∠D =35°,则∠2=________.21E F DCBA2. 已知:如图,在△ABC 中,∠BAC =50°,∠C =60°,AD ⊥BC ,BE 是∠ABC 的平分线,AD ,BE 交于点F ,则∠AFB 的度数为____________.DC EA BFF BAEC Dα第2题图 第3题图3. 将一副直角三角板按如图所示的方式叠放在一起,则图中∠α的度数为( )A .45°B .60°C .75°D .904. 如图,已知∠A =25°,∠EFB =95°,∠B =40°,则∠D 的度数为_____________.FEDCB AD CEAB第4题图 第5题图5. 如图,已知AD 是△ABC 的外角∠CAE 的平分线,∠B =30°,∠DAE =50°,则∠D =_______,∠ACB =_______.6. 如图,在△ABC 中,∠A =40°,∠ABC 的平分线BD 交AC 于点D ,∠BDC =70°,求∠C 的度数.解:如图,∵∠BDC 是△ABD 的一个外角 (_____________________) ∴∠BDC =∠A +∠ABD(_____________________)∵∠A =40°,∠BDC =70° (_____________________)∴∠ABD =_______-________=________—________ =________(_____________________)∵BD 平分∠ABC(_____________________)∴∠ABC =2∠ABD=_____×______=__________(_____________________)∴∠C =180°-∠A —∠ABC=180°-________-_______ =________(_____________________)第4题图DCAB7.已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于点F,∠A=60°,∠E=55°,求∠B的度数.8.已知:如图,在△ABC中,BD平分∠ABC,交AC于点D,DE∥BC交AB于点E,∠A=45°,∠BDC=60°,求∠AED的度数.➢思考小结1.在证明过程中:(1)要证平行,找_______角、_______角、_______角.(2)要求一个角的度数:①由平行,想_______相等、________相等、__________互补;②由直角考虑互余,由平角考虑_______,由对顶角考虑____________;③若把一个角看作三角形的内角,考虑_______________________________;④若把一个角看作三角形的外角,考虑__________________________________________.E DCBA2.阅读材料欧几里得公理体系几何学创建的初期,内容是繁杂和混乱的.人们进行几何推理时,总是拿自己掌握的一些“基本事实”作为大前提去进行推理,而每个人心中的“基本事实”不尽相同.这就导致很多内容无法沟通,也没有统一的标准.这时,有必要将几何的内容,用逻辑的“锁链”整理、穿连起来.第一个完成这件工作的是古希腊数学家欧几里得(Euclid).欧几里得知识渊博,数学造诣精湛,尤其擅长几何证明.当他意识到几何学有必要做出系统整理的时候,就开始着手编写自己的著作《原本》了.他的思路是这样的:首先给出一些最基本的定义,如“点是没有部分的”,“线是没有宽度的”等;接着他列出了5条公设和5条公理作为推理的基本事实,而之后所有的推理都必须建立在这5条公设和5条公理基础上来进行.5条公设是:(1)从任意点到任意点作直线是可能的.(2)把有限直线不断沿直线延长是可能的.(3)以任意点为中心和任意距离为半径作一圆是可能的.(4)所有直角彼此相等.(5)若一直线与两条直线相交,且若同侧所交两内角之和小于两直角,则两直线无限延长后必相交于该侧的另一点.5条公理是:(1)跟同一件东西相等的一些东西,它们彼此也是相等的.(2)等量加等量,总量仍相等.(3)等量减等量,余量仍相等.(4)彼此重合的东西是相等的.(5)整体大于部分.其中5条公设主要对作图进行了相应的规范,而5条公理则主要从代数推理上进行规定.欧几里得基于上述这些公设和公理,推导出了平面几何中几乎所有的结论,从而构成了一个完整的几何体系,我们称之为欧氏几何.而他的著作《原本》中关于平面几何的部分,被翻译成中文叫做《几何原本》,正是我们平面几何的原型.而欧几里得这种对几何知识进行系统化、理论化的总结方法就被称之为公理法,而《原本》正是公理化体系的最好阐释.【参考答案】➢巩固练习1.40°2.125°3.C4.20°5.20°,70°6.∵∠BDC是△ABD的一个外角(外角的定义)∴∠BDC=∠A+∠ABD(三角形的外角等于与它不相邻的两个内角的和)∵∠A=40°,∠BDC=70°(已知)∴∠ABD=∠BDC—∠A=70°-40°=30°(等式的性质)∵BD平分∠ABC(已知)∴∠C=180°-∠A-∠ABC=180°-40°-60°=80°(三角形的内角和等于180°)7.解:如图,∵EF∥BC(已知)∴∠ECD=∠E(两直线平行,内错角相等)∵∠E=55°(已知)∴∠ECD=55°(等量代换)∵CE是△ABC的一个外角平分线(已知)∴∠ACD=2∠ECD=2×55°=110°(角平分线的定义)∵∠ACD是△ABC的一个外角(外角的定义)∴∠ACD=∠A+∠B(三角形的外角等于与它不相邻的两个内角的和)∵∠A=60°(已知)∴∠B=∠ACD—∠A=110°—60°=50°(等式的性质)8.解:如图,∵∠BDC是△ABD的一个外角(外角的定义)∴∠BDC=∠ABD+∠A(三角形的外角等于与它不相邻的两个内角的和)∵∠A=45°,∠BDC=60°(已知)∴∠ABD=∠BDC—∠A=60°-45°=15°(等式的性质)∵BD平分∠ABC(已知)∴∠ABC=2∠ABD=2×15°=30°(角平分线的定义)∵DE∥BC(已知)∴∠AED=∠ABC(两直线平行,同位角相等)∴∠AED=30°(等量代换)➢思考小结1.(1)同位、内错、同旁内.(2)①同位角、内错角、同旁内角;②互补,对顶角相等;③三角形的内角和等于180°.④三角形的外角等于与它不相邻的两个内角的和.。
初一数学三角形的外角试题

初一数学三角形的外角试题1.已知,如图,点是中边上的一点,点是边延长线上一点,说明:.【答案】见解析【解析】本题主要考查的是三角形外角与内角的关系. 由于∠DCB是△DCE的一个外角,所以∠DCB>∠CDE;又因为∠ADB是△BCD的一个外角,所以∠ADB>∠DCB,故∠ADB>∠CDE.证明:∵∠DCB是△DCE的一个外角∴∠DCB>∠CDE∵∠ADB是△BCD的一个外角∴∠ADB>∠DCB∴∠ADB>∠CDE2.已知,如图,中,的平分线与的平分线交于点,若,求的度数.【答案】【解析】本题考查的是三角形内角和定理、三角形内角及外角平分线的性质. 根据三角形外角的性质和角平分线的性质表示出两角和的一半,用180°减去两角和的一半即可.∵∠ACE是△ABC的外角,∴∠ACE=∠A+∠ABC,∵BD是∠ABC的角平分线,∴∠DBC=∠ABC,∵CD是外角∠ACE的角平分线,∴∠DCE=∠ACD=∠ACE,∵∠D=∠DCE-∠DBC=∠ACE-∠ABC=(∠ACE-∠ABC)=∠A=×80°=40°.∴∠D的度数是40°.3.已知,如图,在中,是高和的交点,观察图形,试猜想和之间具有怎样的数量关系,并论证你的猜想.【答案】.证明见解析【解析】本题主要考查了三角形的外角性质和三角形内角和定理. 由于∠DOE是△AOE的外角,故∠DOE=∠OAE+∠AEO=∠OAE+90°=∠OAE+∠ADC,即∠C+∠DOE=∠OAE+∠ADC+∠C=180°解:∠C+∠DOE=180°.∵AD,BE是△ABC的高(已知),∴∠AEO=∠ADC=90°(高的意义),∵∠DOE是△AOE的外角(三角形外角的概念),∴∠DOE=∠OAE+∠AEO(三角形的一个外角等于不相邻的两个内角的和)=∠OAE+90°(∠AEO=90°)=∠OAE+∠ADC(∠ADC=90°)∴∠C+∠DOE=∠OAE+∠C+∠ADC=90°+90°=180°.另法:在四边形CEOD中,∠C+∠EOD+90°+90°=360°,则∠C+∠EOD=180°.4.如图所示,已知AB∥CD,∠A=55°,∠C=20°,则∠P= ;O【答案】35°【解析】本题主要考查的是平行线的性质及三角形内角与外角的关系.∵AB∥CD,∠A=55°∴∠AOC=∠A=55°∵∠C=20°∴∠P=∠AOC-∠C=55°-20°=35°5.如图所示,∠A +∠B+∠C+∠D+∠E= ;【答案】180°【解析】本题主要考查了三角形的外角和内角和定理因为∠1=∠B+∠D,∠2=∠C+∠E,所以∠A +∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°6.如图所示,已知AB∥CD,则()A.∠1=∠2+∠3 .B.∠1=2∠2+∠3C.∠1=2∠2-∠3D.∠1=180°-∠2-∠3【答案】A【解析】本题主要考查的是平行线的性质及三角形内角与外角的关系.因为AB∥CD,所以∠ABD=∠3,因此∠1=∠2+∠ABD=∠2+∠3;7.若一个三角形三个内角的度数之比为1∶2∶3,则与之相邻的三个外角的度数之比为()A.1∶2∶3B.3∶2∶1C.3∶4∶5D.5∶4∶3【答案】D【解析】本题主要考查了三角形内角和定理及内角与外角的关系. 先根据三角形的三个内角度数之比为1∶2∶3及三角形内角和定理求出三个内角的度数,再分别求出其对应的外角度数即可设三角形三个内角分别为,则,解得,所以三角形三个内角分别为30°,60°,90°,与之相邻的三个外角的度数分别为150°,120°,90°,故选D8.一个零件的形状如图所示,按规定∠A应等于90°,∠B和∠C应分别是32°和21°,检验工人量得∠BDC=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.【答案】不合格【解析】本题主要考查了三角形内角和定理. 连接AD,利用三角形内角与外角的关系求出此零件合格时∠BDC的度数与已知度数相比较即可.解:如图,连接AD并延长至E,则∠CDE=∠C+∠CAD,∠BDE=∠B+∠BAD,所以∠BDC=∠CDE+∠BDE=∠C+∠CAD+∠B+∠BAD=21°+32°+90°=143°≠148°,所以这个零件不合格.9.图中()是△ABC的外角.A.∠1B.∠2C.∠3D.∠4【答案】C【解析】本题考查的是三角形外角的定义根据三角形外角的定义解答.根据三角形外角的定义可知,∠3是此三角形的外角.故选C.10.如图,△ABC中,D是BC上一点,F是BA延长线上一点,连接DF交AC于E,且∠B=42°,∠C=59°,∠DEC=47°,求∠F的度数.【答案】【解析】本题考查的是三角形内角和定理、外角定理、对顶角相等由∠B=42°,∠C=59°,根据三角形的外角定理即可求得∠FAE,再根据对顶角相等求得∠AEF,最后根据三角形内角和定理即可求得∠F的度数.∠B=42°,∠C=59°,∠FAE=∠B+∠C=101°,∠DEC=47°,∠AEF=47°,∠∠FAE∠AEF。
三角形的外角(理由挖空)(一)(通用版)(含答案)

三角形的外角(理由挖空)(一)(通用版)试卷简介:利用三角形外角定理进行角的计算,并借助三角形外角定理训练学生有理有据的推理和证明,重点考查学生对每一步推理依据的掌握情况.一、单选题(共10道,每道10分)1.如图,直线∥,若∠1=150°,∠2=70°,则∠3的度数为( )A.70°B.80°C.65°D.60°答案:B解题思路:试题难度:三颗星知识点:三角形外角定理2.如图,已知∠A=35°,∠B=20°,∠C=25°,则∠BDC的度数为( )A.55°B.60°C.80°D.90°答案:C解题思路:试题难度:三颗星知识点:三角形外角定理3.已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于点F,∠A=50°,∠E=55°,则∠B的度数为()A.70°B.60°C.55°D.50°答案:B解题思路:试题难度:三颗星知识点:平行线的判定、性质4.一副三角板按如图所示叠放在一起,则图中α的度数为( )A.90°B.105°C.120°D.135°答案:B解题思路:试题难度:三颗星知识点:三角形外角定理5.如图,P为△ABC内任一点,延长CP交AB于点D,则下列结论一定正确的是( )A.∠1=∠2+∠3B.∠1=∠2+∠A+∠ACDC.∠2=∠A+∠ACDD.∠3=∠A+∠ACD答案:D解题思路:试题难度:三颗星知识点:三角形外角定理6.已知△ABC中,∠BAC=50°,∠ABC=60°,AD⊥BC,BE⊥AC,垂足分别分D,E,AD,BE相交于点H,则∠AHB的度数为( )A.90°B.100°C.110°D.120°答案:C解题思路:试题难度:三颗星知识点:三角形外角定理7.已知:如图,点D在CA的延长线上,点E在AB的延长线上,点F在BC的延长线上.求证:∠ACF+∠BAD+∠CBE=360°.证明:如图,∵∠ACF是△ABC的一个外角(外角的定义)∴∠ACF=∠1+∠2(_______________________)∵∠BAD是△ABC的一个外角(外角的定义)∴∠BAD=∠2+∠3(三角形的一个外角等于和它不相邻的两个内角的和)∵∠CBE是△ABC的一个外角(外角的定义)∴∠CBE=∠1+∠3(三角形的一个外角等于和它不相邻的两个内角的和)∵∠1+∠2+∠3=180°(_______________________)∴∠ACF+∠BAD+∠CBE=∠1+∠2+∠2+∠3+∠1+∠3=2(∠1+∠2+∠3)=360°(等式的性质)①同角或等角的余角相等;②同角或等角的补角相等;③三角形的内角和是180°;④三角形的一个外角等于和它不相邻的两个内角的和;⑤平角的定义.以上空缺处依次所填正确的是( )A.④⑤B.②③C.④③D.①⑤答案:C解题思路:试题难度:三颗星知识点:三角形外角定理8.已知:如图,AB∥CD,∠EBA=60°,∠D=50°,求∠E的度数.解:如图,∵AB∥CD(已知)∴∠EBA=∠EFC(两直线平行,同位角相等)∵∠EBA=60°(已知)∴∠EFC=60°(等量代换)∵∠EFC是△EDF的一个外角(外角的定义)∴∠EFC=∠D+∠E(_______________________)∵∠D=50°(已知)∴∠E=∠EFC-∠D=60°-50°=10°(_______________________)①三角形的内角和是180°;②同角或等角的补角相等;③三角形的一个外角等于和它不相邻的两个内角的和;④等式的性质;⑤等量代换.以上空缺处依次所填正确的是( )A.③④B.③⑤C.②④D.①⑤答案:A解题思路:试题难度:三颗星知识点:三角形外角定理9.已知:如图,在△ABC中,AD是∠BAC的角平分线,∠B=∠1,∠ADC=80°.求∠C的角度.解:如图,∵∠ADC是△ABD的一个外角(外角的定义)∴∠ADC=∠1+∠B(_______________________)∵∠B=∠1(已知)∴∠ADC=2∠1(等式的性质)∵∠ADC=80°(已知)∴∠1=∠ADC=40°(_______________________)∵AD是∠BAC的角平分线(已知)∴∠2=∠1=40°(角平分线的定义)∴∠C=180°-∠2-∠ADC=180°-40°-80°=60°(_______________________)①三角形的内角和是180°;②同角或等角的补角相等;③三角形的一个外角等于和它不相邻的两个内角的和;④等式的性质;⑤等量代换.以上空缺处依次所填正确的是( )A.②④①B.③④①C.③②①D.②⑤④答案:B解题思路:试题难度:三颗星知识点:三角形外角定理10.已知:如图,AB∥EF,∠E=∠CAE,∠DAB=65°.求∠ACF的度数.解:如图,∵AB∥EF(已知)∴∠DAB=∠E(_______________________)∵∠DAB=65°,(已知)∴∠E=65°(等量代换)∵∠E=∠CAE(已知)∴∠CAE=65°(_______________________)∵∠ACF是△ACE的一个外角(外角的定义)∴∠ACF=∠E+∠CAE=65°+65°=130°(_______________________)①两直线平行,同位角相等;②同位角相等,两直线平行;③等量代换;④等式的性质;⑤三角形的一个外角等于和它不相邻的两个内角的和;⑥三角形的内角和是180°.以上空缺处依次所填正确的是( )A.①③⑤B.①③⑥C.②③⑤D.②④⑥答案:A解题思路:试题难度:三颗星知识点:三角形外角定理第11页共11页。
三角形的外角性质

三角形的外角性质精选题35道一.选择题(共14小题)1.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=()A.35°B.95°C.85°D.75°2.如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是()A.γ=2α+βB.γ=α+2βC.γ=α+βD.γ=180°﹣α﹣β3.如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为()A.15°B.20°C.25°D.30°4.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于()A.30°B.40°C.60°D.70°5.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=()A.70°B.80°C.90°D.100°6.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是()A.45°B.60°C.75°D.85°7.如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是()A.110°B.120°C.130°D.140°8.如图所示,△ABC中,AB=AC,过AC上一点作DE⊥AC,EF⊥BC,若∠BDE=140°,则∠DEF=()A.55°B.60°C.65°D.70°9.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边对齐,则∠1的度数为()A.30°B.45°C.60°D.75°10.如图,在△ABC中,∠ABC=40°,∠ACD=76°,BE平分∠ABC,CE平分△ABC 的外角∠ACD,则∠E=()A.40°B.36°C.20°D.18°11.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD 等于()A.40°B.45°C.50°D.55°12.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是()A.15°B.30°C.45°D.60°13.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为()A.60°B.65°C.75°D.85°14.如图,在△AEC中,点D和点F分别是AC和AE上的两点,连接DF,交CE的延长线于点B,若∠A=25°,∠B=45°,∠C=36°,则∠DFE=()A.103°B.104°C.105°D.106°二.填空题(共15小题)15.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=°.16.将一副三角板如图叠放,则图中∠α的度数为.17.如图,∠A+∠B+∠C+∠D+∠E的度数为度.18.如图是一副三角板叠放的示意图,则∠α=.19.如图,在△ABC中,∠BAC=40°,∠ACB=60°,D为△ABC形外一点,DA平分∠BAC,且∠CBD=50°,求∠DCB=.20.如图,已知∠BDC=142°,∠B=34°,∠C=28°,则∠A=.21.如图,BE平分∠ABC,CE平分外角∠ACD,若∠A=42°,则∠E=°.22.将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=.23.如图,∠BCD=150°,则∠A+∠B+∠D的度数为.24.点O是△ABC内一点,∠A=85°,∠1=15°,∠2=40°,则∠BOC=.25.如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°﹣7°=83°.当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2,易知∠1=∠2.若A1A2⊥AO,光线又会沿A2→A1→A原路返回到点A,此时∠A=°.…若光线从A点出发后,经若干次反射能沿原路返回到点A,则锐角∠A的最小值=°.26.如图,∠ACD是△ABC的外角,若∠B=50°,∠ACD=120°,∠A=.27.如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C=度.28.一次数学活动课上.小聪将一副三角板按图中方式叠放,则∠α等于.29.如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=.三.解答题(共6小题)30.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE 交AC的延长线于点E.(1)求∠CBE的度数;(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.31.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+12∠A,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∠1=12∠ABC,∠2=12∠ACB∴∠1+∠2=12(∠ABC+∠ACB)又∵∠ABC+∠ACB=180°﹣∠A∴∠1+∠2=12(180°−∠A)=90°−12∠A∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°−12∠A)=90°+12∠A探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC 与∠A有怎样的关系?请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC 与∠A有怎样的关系?(只写结论,不需证明)结论:.32.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE 交AC的延长线于点E,点F为AC延长线上的一点,连接DF.(1)求∠CBE的度数;(2)若∠F=25°,求证:BE∥DF.33.如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC、∠BOA的度数.34.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.35.如图,△ABC中,∠ABC=∠C=70°,BD平分∠ABC,求∠ADB的度数.。
初中数学:三角形的外角检测题(含答案)

初中数学:三角形的外角检测题(含答案)总分100分时间40分钟一、选择题(每题5分)1、若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )A.直角三角形B.锐角三角形C.钝角三角形D.无法确定【答案】C【解析】试题分析:三角形的一个外角和与它相邻的内角互补,当外角小于与它相邻的内角时,所以这个内角是钝角.解:如下图所示,∠ACD<∠ACB,∵∠ACB+∠ACD=180°,∴∠ACB>90°.∴△ACB是钝角三角形.故应选C.考点:三角形的外角2、已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )A.90°B.110°C.100°D.120°【答案】C【解析】试题分析:根据三角形的三个外角的度数比为2:3:4,设三角形的三个外角是2x、3x、4x,根据三角形外角和是360°列方程求出x的值,求出每个外角的度数,根据外角的度数求出三角形的内角度数.解:设三角形的三个外角是2x、3x、4x,根据题意可得:x+3x+4x=360°,解得:x=40°,∴三角形最小的外角的度数是2x=80°,∴三角形最大的内角的度数是180°-80°=100°.考点:三角形外角的性质3、已知等腰三角形的一个外角是120°,则它是( )A.等腰直角三角形B.一般的等腰三角形C.等边三角形D.等腰钝角三角形【答案】C【解析】试题分析:根据三角形的一个外角是120°,求出三角形的一个内角是60°,根据有一个角是60°的等腰三角形是等边三角形判定结果.解:如下图所示,∵∠ACD=120°,∴∠ACB=60°,又∵△ABC是等腰三角形,∴△ABC是等边三角形.故应选C.考点:1.三角形外角的性质;2.等腰三角形的判定.二、填空题(每题8分)4、如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA 到E,连EF,则∠1,∠2,∠3的大小关系是______【答案】∠1>∠2>∠3【解析】试题分析:根据三角形外角大于与它不相邻的任何一个内角.解:∵∠1是△ABC的外角,∴∠1>∠2,∵∠2是△AEF的外角,∴∠2>∠3,∴∠1>∠2>∠3.考点:三角形外角的性质5、△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是______(填“锐角”、“直角”或“钝角”)。
三角形的外角练习题

三角形的外角练习题一、选择题1. 三角形的一个外角等于与它不相邻的两个内角的和,这个说法是:A. 正确B. 错误2. 一个三角形的外角和等于多少度?A. 360度B. 180度C. 90度D. 120度3. 如果一个三角形的两个内角分别是40度和60度,那么第三个内角的度数是:A. 40度B. 60度C. 80度D. 100度4. 一个三角形的外角等于它相邻内角的补角,这个说法是:A. 正确B. 错误5. 直角三角形的外角中,最大的外角是:A. 45度B. 90度C. 135度D. 180度二、填空题6. 如果三角形的一个内角是50度,那么它的一个外角是________度。
7. 一个三角形的三个内角之和是________度。
8. 如果一个三角形的外角是120度,那么它相邻的内角是________度。
9. 等边三角形的每个外角是________度。
10. 已知三角形的一个外角是70度,那么它相邻的内角是________度。
三、判断题11. 一个三角形的外角可以大于90度。
()12. 一个三角形的外角可以小于60度。
()13. 等腰三角形的两个底角的外角相等。
()14. 直角三角形的一个锐角的外角等于它的邻角。
()15. 一个三角形的外角和内角的和总是等于180度。
()四、计算题16. 已知三角形ABC中,角A是45度,角B是75度,求角C的度数以及角C的外角。
17. 如果一个三角形的内角之和为180度,且其中一个内角为70度,求另外两个内角的度数,并计算这两个内角的外角。
18. 在三角形DEF中,如果角D是90度,角E是30度,求角F的度数以及角F的外角。
19. 已知三角形GHI的三个内角分别为60度,60度,60度,求这个三角形的外角和。
20. 如果一个三角形的外角和为360度,且其中一个外角为80度,求相邻内角的度数。
五、简答题21. 解释为什么三角形的外角和总是等于360度。
22. 描述在已知三角形一个内角的情况下,如何计算它的外角。
三角形的外角(习题及答案)

度数.
ED
BC
3
思考小结
8.在证明过程中:
(1)要证平行,找_______角、_______角、_______角.
(2)要求一个角的度数:
①由平行,想_______相等、________相等、__________互补;
②由直角考虑互余,由平角考虑_______,由对顶角考虑
的度数为()
A.45°B.60°C.75°D.90
4.如图,已知∠A=25°,∠EFB=95°,∠B=40°,则∠D的度数为
_____________.
E
D
C
A
F
ACD
B
EB
第4题图第5题图
5.如图,已知AD是△ABC的外角∠CAE的平分线,∠B=30°,
∠DAE=50°,则∠D=_______,∠ACB=_______.
三角形的外角(习题)
例题示范
例1:已知:如图,点E是直线AB,CD外一点,连接DE交
AB于点F,∠D=∠B+∠E.
求证:AB∥CD.
E
E
AFBAFB
CDCD
①读题标注
②梳理思路
要证AB∥CD,需要考虑同位角、内错角、同旁内角.
因为已知∠D=∠B+∠E,而由外角定理得∠AFE=∠B+∠E,
故∠D=∠AFE,所以AB∥CD.
∠D=35°,则∠2=________.
D
C
2 E
1
ABF
1
2. 已知:如图,在△ABC中,∠BAC=50°,∠C=60°,AD⊥BC,
BE是∠ABC的平分线,AD,BE交于点F,则∠AFB的度数
三角形的外角练习题

D
三角形外角的性质:
A
性质1、三角形的一个外角等于
与它不相邻的两个内角的 B
C
和。 ∠B+∠C=∠CAD
性质2、三角形的一个外角大于任何
一个与它不相邻的内角。
∠CAD > ∠B, ∠CAD > ∠C
∠1+∠2 +∠3 = 360°
A 1
3 B
C 2
三角形的外角和等于360°
课堂反馈: 1、三角形的一个外角等于两个内角的和。( )
∵ ∠DEC是△ABE的一个外角 (外角的定义),
∴ ∠DEC>∠A(三角形的一个外角大于和它不相邻的 任何一个外角).
∴ ∠BDC>∠A (不等式的性质).
三角形的外角三个性质:
①三角形的一个外角与它相邻的内角互补。
② 三角形的一个外角等于与它不相邻 的两个内角的和。
③三角形的一个外角大于任何一个与它 不相邻的内角。
D
间的数量关系,因此需要添加
辅助线。那如何添加辅助线才
能建立这几个角之间的联系呢? A
B
1、已知:国旗上的正五角星形如图所示. 求:∠A+∠B+∠C+∠D+∠E的度数.
分析:设法利用外角把这五个角“凑” 到一个三角形中,运用三角形内角和性 质来求解.
A
B
H 2 1F
C
E D
Байду номын сангаас
解:∵∠1是△BDF的一个外角(外角的定义), ∴ ∠1=∠B+∠D(三角形的一个外 角等于和它不相邻的两个内角的和). 又∵ ∠2是△EHC的一个外角(外角的定义 ∴), ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的 两个内角的和).
三角形的外角专题(含答案)
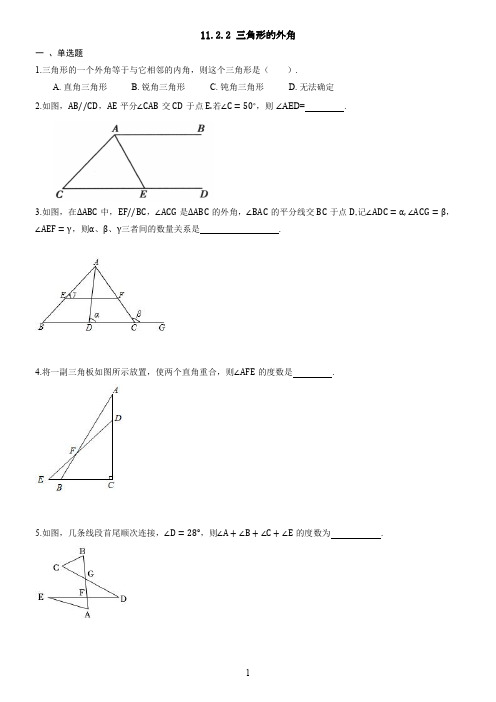
11.2.2三角形的外角一、单选题1.三角形的一个外角等于与它相邻的内角,则这个三角形是().A.直角三角形B.锐角三角形C.钝角三角形D.无法确定2.如图,AB//CD,AE平分∠CAB交CD于点E.若∠C=50∘,则∠AED=.3.如图,在ΔABC中,EF//BC,∠ACG是ΔABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则α、β、γ三者间的数量关系是.4.将一副三角板如图所示放置,使两个直角重合,则∠AFE的度数是.5.如图,几条线段首尾顺次连接,∠D=28°,则∠A+∠B+∠C+∠E的度数为.6.下列命题中,属于假命题的是( )A.三角形中至少有一个角大于60∘B.如果三条线段长分别为4cm,6cm,9cm,那么这三条线段能组成三角形C.三角形的外角等于与它不相邻的两个内角的和D.如果一个三角形是轴对称图形,那么这个三角形一定是等腰三角形7.在△ABC中,∠A=60∘,∠C=2∠B,则∠C的度数为.8.如图,在ΔABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为.9.一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形二、填空题10.如图,BE平分∠ABC,CE平分ΔABC外角∠ACD,若∠E=25°,则∠A度数为______.11.如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若∠A=30∘,则∠1+∠2的度数为__________. 12.如图所示的折线图形中,α+β的度数为__________. 13.如图,四边形纸片ABCD中,∠A=75∘,∠B=65∘,将纸片折叠,使点C,D分别落在AB边上的点C′,D′处,折痕为MN,则∠AMD'+∠BNC'的度数是__________. 三、解答题14.如图,在△ABC中,∠B=20°,∠ACB=110°,AE平分∠BAC,AD⊥BD于点D,求∠DAE的度数.15.如图,将ΔABC分别沿AB,AC翻折得到ΔABD和ΔAEC,线段BD与AE交于点F,连接BE. (1)如果∠ABC=16°,∠ACB=30°,求∠DAE的度数; (2)如果BD⊥CE,求∠CAB的度数.11.2.2三角形的外角1.【答案】A;【解析】略2.【答案】B;【解析】该题考查了平行线的性质、角平分线的定义、外角的性质,掌握好基本性质及定义的解答该题的关键. 根据平行线的性质得出∠CAB=180∘−∠C=130∘,根据角平分线的定义得出∠CAE=12∠CAB=65∘,根据∠AED是ΔACE的外角,得出∠AED=∠C+∠CAE=115∘,即可得出结果. 解:∵AB//CD,∴∠C+∠CAB=180∘, ∴∠CAB=180∘−∠C=130∘,∵AE平分∠CAB,∴∠CAE=12∠CAB=65∘,∵∠AED是ΔACE的外角,∴∠AED=∠C+∠CAE=115∘,故选B.3.【答案】B;【解析】解:∵EF//BC, ∴∠γ=∠B, 由三角形的外角性质得,∠α=∠B+∠BAD=∠γ+∠BAD, ∠β=∠α+∠CAD, ∵AD是∠BAC的平分线, ∴∠BAD=∠CAD, ∴∠α−∠β=∠γ−∠α, ∴∠β=2α−∠γ. 故选:B. 根据两直线平行,同位角相等可得∠γ=∠B,然后根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠α、∠β,再根据角平分线的定义可得∠BAD=∠CAD,然后整理即可得解. 此题主要考查了平行线的性质,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解答该题的关键.4.【答案】B;【解析】解:∵∠EDC=45°, ∴∠ADF=135°, ∵∠AFE是ΔADF的一个外角, ∴∠AFE=∠A+∠ADF=30°+135°=165°, 故选:B. 根据邻补角的概念求出∠ADF,再根据三角形的外角性质计算即可. 此题主要考查的是三角形的外角性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解答该题的关键.5.【答案】B;【解析】解:∵如图可知∠BGD=∠C+∠B,∠GFE=∠E+∠A, 又∵∠BGD=∠D+∠GFD, ∴∠B+∠C=∠D+∠GFD, 又∵∠GFE+∠GFD=180°, ∴∠E+∠A+∠B+∠C−∠D=180°, 又∵∠D=28°, ∴∠A+∠B+∠C+∠E=180°+28°=208°. 故选:B. 首先求出∠C+∠B=∠D+∠GFD,然后证明出∠A+∠B+∠C+∠E−∠D=180°,最后结合∠D=28°求出∠A+∠B+∠C+∠F的度数. 此题主要考查了三角形内角的外角,解答本题的关键是求出∠C+∠A+∠E+∠B−∠D=180°,此题难度不大.6.【答案】A;【解析】 该题考查命题与定理,解答该题的关键是熟练掌握三角形的三边关系、内角和定理、三角形外角的性质、等腰三角形的性质,属于中考常考题型. 根据三角形的三边关系、内角和定理、三角形外角的性质、等腰三角形的性质即可一一判断. 解:A、错误. B、正确.理由:4+6>9. C、正确.角形的外角等于与它不相邻的两个内角的和. D、正确.如果一个三角形是轴对称图形,那么这个三角形一定是等腰三角形.故选A.7.【答案】C;【解析】略8.【答案】A;【解析】解:∵∠ABC的平分线与∠ACE的平分线交于点D, ∴∠1=∠2,∠3=∠4, ∵∠ACE=∠A+∠ABC, 即∠1+∠2=∠3+∠4+∠A, ∴2∠1=2∠3+∠A, ∵∠1=∠3+∠D, ∴∠D=12∠A=12×30°=15°. 故选:A. 先根据角平分线的定义得到∠1=∠2,∠3=∠4,再根据三角形外角性质得∠1+∠2=∠3+∠4+∠A,∠1=∠3+∠D,则2∠1=2∠3+∠A,利用等式的性质得到∠D=12∠A,然后把∠A的度数代入计算即可. 该题考查了三角形内角和定理,关键是根据三角形内角和是180°和三角形外角性质进行分析.9.【答案】D;【解析】略10.【答案】50°;【解析】解:∵∠E=25°, ∴∠ECD−∠EBD=∠E=25°, ∵BE平分∠ABC, ∴∠EBD=12∠ABC, ∵CE平分∠ACD, ∴∠ECD=12∠ACD, ∴∠A=∠ACD−∠ABC=2×(∠EBD−∠ECD)=2×25°=50°, 故答案为:50°. 根据三角形的外角性质得到∠ECD−∠EBD=∠E=25°,根据角平分线的定义、三角形的外角性质计算,得到答案. 此题主要考查的是三角形的外角性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解答该题的关键.11.【答案】60∘;【解析】解:∠A′DA=180∘−∠1,∠A′EA=180∘−∠2,∠A′=∠A=30∘. ∵∠A′+∠A′DA+∠A+∠AEA′=360∘, ∵30∘+180∘−∠1+30∘+180∘−∠2=360∘,∴∠1+∠2=60°.12.【答案】85°;【解析】解:∠1=a+70∘,∠2=β+65∘,∵∠1+∠2+140∘=360∘. ∴a+70∘+β+65∘+140∘=360∘,∴α+β=85∘. 13.【答案】80∘;【解析】解:∵∠A+∠B+∠C+∠D=360°,∴∠C+∠D=220°,∠MD′B=∠D, ∠NC′A=∠C,∴∠MD′B+∠NC′A=220°,∵∠MD′B+∠NC′A+∠D′MN+∠C′NM=360°,∴∠D′MN+∠C′NM=140°,∵∠A+∠B+∠AMD′+∠D'MN+∠BNC'+∠C'NM=360°,∴140∘+140∘+∠AMD'+∠BNC'=360°, ∴∠AMD°+∠BNC'=80∘.14.【答案】解:在△ABC中,∠B=20°,∠ACB=110°, ∴∠BAC=180°-20°-110°=50°, ∵AE平分∠BAC, ∴∠BAE=12∠BAC=25°, ∴∠AEC=∠B+∠BAC=20°+25°=45°, ∵AD⊥BD于点D, ∴∠D=90°, ∴∠DAE=90°-∠AED=90°-45°=45°.;【解析】 先根据三角形内角和定理求出∠BAC的度数,由角平分线定义得出∠BAE的度数,再由三角形外角的性质求出∠AEC的度数,进而得出答案. 此题主要考查的是三角形内角和定理.熟悉定理与性质并准确识图,理清图中各角度之间隐含的关系是解决本题的关键.15.【答案】解:(1)∵△ABC沿AC、AB翻折得到△AEC和△ABD, ∴△AEC≌△ABC,△ABD≌△ABC. ∴∠2=∠1=30°,∠4=∠3=16°, ∠EAC=∠BAD=∠BAC=180°-30°-16°=134°, ∵∠DAC=360°-∠BAD-∠BAC, ∴∠DAC=360°-134°-134°=92°, ∴∠DAE=∠EAC-∠DAC=134°-92°=42°; (2)∵BD⊥CE, ∴∠5=90°, ∴∠DBC+∠ECB=90°. ∵∠1=∠2,∠3=∠4, ∴∠DBC+∠ECB=2∠3+2∠1=90°. ∴∠3+∠1=45°, 在△ABC中,∠CAB=180°-(∠3+∠1)=180°-45°=135°.;【解析】 (1)由折叠的性质可得∠2=∠1=30°,∠4=∠3=16°,由周角的性质和外角性质可求解; (2)由三角形内角和定理可求解. 该题考查了翻折变换,三角形的内角和定理,外角性质,灵活运用折叠的性质是本题的关键.。
三角形外角练习题

三角形外角练习题三角形是初中数学中常见的几何图形,可以通过多种方式进行分类和研究。
其中,三角形的内角和外角是一个重要的概念。
本文将介绍一些关于三角形外角的练习题,以帮助读者巩固对该概念的理解。
练习题一:已知三角形内角的度数,求外角的度数已知一个三角形的内角1为80度,内角2为100度,求内角1对应的外角的度数和内角2对应的外角的度数。
解答:要求内角1对应的外角的度数,我们可以利用一个性质来计算。
在三角形中,内角的补角加上相应外角的度数等于180度。
因此,内角1对应的外角的度数为180度减去80度,即100度。
同样地,内角2对应的外角的度数为180度减去100度,即80度。
练习题二:已知三角形内角的大小关系,推断外角的大小关系已知一个三角形的内角1小于内角2,内角2小于内角3。
根据这一信息,我们能得出什么关于三个外角的大小关系?解答:根据三角形内角的性质,内角的大小关系与相应外角的大小关系恰好相反。
所以,内角1小于内角2,内角2小于内角3,则外角1大于外角2,外角2大于外角3。
练习题三:利用三角形外角的性质求解问题已知一个三角形的两个外角的度数分别为70度和100度。
求第三个外角的度数,并判断该三角形的性质。
解答:根据三角形外角的性质,三个外角的度数之和为360度。
已知两个外角分别为70度和100度,那么第三个外角的度数为360度减去这两个已知角的度数之和,即360度减去70度再减去100度,即190度。
通过判断第三个外角的度数,我们可以进一步判断三角形的性质。
由于第三个外角的度数为190度,大于180度,并且两个已知角之和小于180度,因此可以判断该三角形为非直角三角形。
练习题四:判断三角形形状的问题已知一个三角形的两个外角的度数分别为45度和130度。
根据这两个外角的度数,判断该三角形的形状。
解答:根据三角形外角的性质,一个三角形的外角度数小于等于180度。
已知两个外角的度数分别为45度和130度,它们的和为175度,小于180度。
初二数学三角形外角练习题

初二数学三角形外角练习题三角形是初中数学中重要的几何概念之一,而三角形的外角则是对我们理解三角形性质和解题有着重要影响的概念。
本文将通过列举一些三角形外角的练习题,帮助初二学生加深对三角形外角的理解和应用。
练习题1:已知三角形ABC,点D为BC延长线上一点,且∠ACD = 151°,∠BAC = 65°,求∠ABC的度数。
解答:根据三角形外角与其对应内角的关系可知,∠ABC = ∠ACD -∠BAC = 151° - 65° = 86°。
练习题2:已知三角形DEF中,∠D = 90°,∠F = 72°,点G在EF上,且∠DGF = 52°,求∠EDG的度数。
解答:根据三角形外角与其对应内角的关系可知,∠EDG = ∠DGF + ∠F = 52° + 72° = 124°。
练习题3:已知三角形MNP中,∠M = 38°,∠P = 108°,点Q在MN上,且∠PNQ = 82°,求∠Q的度数。
解答:根据三角形外角与其对应内角的关系可知,∠Q = ∠PNQ + ∠P = 82° + 108° = 190°。
练习题4:已知三角形XYZ中,∠X = 45°,∠Z = 100°,点W在YZ上,且∠XWZ = 30°,求∠W的度数。
解答:根据三角形外角与其对应内角的关系可知,∠W = ∠XWZ + ∠Z = 30° + 100° = 130°。
练习题5:已知△ABC和△DEF为等边三角形,且它们的外角∠A和∠D相等,求∠A的度数。
解答:等边三角形的内角都为60°,因此∠A = 180° - 60° - 60° = 60°。
通过以上练习题的解答,我们可以进一步理解和应用三角形外角与其对应内角之间的关系。
人教版八年级数学上册习题:11.三角形的外角习题

三角形的外角(习题)例题示范例1:已知:如图,点E 是直线AB ,CD 外一点,连接DE 交AB 于点F ,∠D =∠B +∠E . 求证:AB ∥CD .D CEA B F①读题标注 ②梳理思路要证AB ∥CD ,需要考虑同位角、内错角、同旁内角.因为已知∠D =∠B +∠E ,而由外角定理得∠AFE =∠B +∠E ,故∠D =∠AFE ,所以AB ∥CD . ③过程书写 证明:如图,∵∠AFE 是△BEF 的一个外角(外角的定义)∴∠AFE =∠B+∠E (三角形的外角等于与它不相邻的两个内角的和)∵∠D =∠B +∠E (已知) ∴∠AFE =∠D (等量代换)∴AB ∥CD (同位角相等,两直线平行)巩固练习1. 如图,在△ABC 中,∠1是它的一个外角,∠1=115°,∠A =40°,∠D =35°,则∠2=________.21E F DCBA2. 已知:如图,在△ABC 中,∠BAC =50°,∠C =60°,AD ⊥BC ,BE 是∠ABC 的平分线,AD ,BE 交于点F ,则∠AFB 的度数为____________.DC EA BFF BAEC Dα第2题图 第3题图3. 将一副直角三角板按如图所示的方式叠放在一起,则图中∠α的度数为( )A .45°B .60°C .75°D .904. 如图,已知∠A =25°,∠EFB =95°,∠B =40°,则∠D 的度数为_____________.FEDCB AD CEAB第4题图 第5题图5. 如图,已知AD 是△ABC 的外角∠CAE 的平分线,∠B =30°,∠DAE =50°,则∠D =_______,∠ACB =_______.6. 如图,在△ABC 中,∠A =40°,∠ABC 的平分线BD 交AC 于点D ,∠BDC =70°,求∠C 的度数. 解:如图,∵∠BDC 是△ABD 的一个外角 (_____________________) ∴∠BDC =∠A +∠ABD(_____________________) ∵∠A =40°,∠BDC =70°(_____________________)∴∠ABD =_______-________=________-________ =________(_____________________) ∵BD 平分∠ABC(_____________________)∴∠ABC =2∠ABD=_____×______ =__________(_____________________)∴∠C =180°-∠A -∠ABC=180°-________-_______ =________(_____________________)第4题图D CABFEA7.已知:如图,CE是△ABC的一个外角平分线,且EF∥BC交AB于点F,∠A=60°,∠E=55°,求∠B的度数.8.已知:如图,在△ABC中,BD平分∠ABC,交AC于点D,DE∥BC交AB于点E,∠A=45°,∠BDC=60°,求∠AED的度数.思考小结1.在证明过程中:(1)要证平行,找_______角、_______角、_______角.(2)要求一个角的度数:①由平行,想_______相等、________相等、__________互补;②由直角考虑互余,由平角考虑_______,由对顶角考虑____________;③若把一个角看作三角形的内角,考虑_______________________________;④若把一个角看作三角形的外角,考虑__________________E DCBA________________________.2.阅读材料欧几里得公理体系几何学创建的初期,内容是繁杂和混乱的.人们进行几何推理时,总是拿自己掌握的一些“基本事实”作为大前提去进行推理,而每个人心中的“基本事实”不尽相同.这就导致很多内容无法沟通,也没有统一的标准.这时,有必要将几何的内容,用逻辑的“锁链”整理、穿连起来.第一个完成这件工作的是古希腊数学家欧几里得(Euclid).欧几里得知识渊博,数学造诣精湛,尤其擅长几何证明.当他意识到几何学有必要做出系统整理的时候,就开始着手编写自己的著作《原本》了.他的思路是这样的:首先给出一些最基本的定义,如“点是没有部分的”,“线是没有宽度的”等;接着他列出了5条公设和5条公理作为推理的基本事实,而之后所有的推理都必须建立在这5条公设和5条公理基础上来进行.5条公设是:(1)从任意点到任意点作直线是可能的.(2)把有限直线不断沿直线延长是可能的.(3)以任意点为中心和任意距离为半径作一圆是可能的.(4)所有直角彼此相等.(5)若一直线与两条直线相交,且若同侧所交两内角之和小于两直角,则两直线无限延长后必相交于该侧的另一点.5条公理是:(1)跟同一件东西相等的一些东西,它们彼此也是相等的.(2)等量加等量,总量仍相等.(3)等量减等量,余量仍相等.(4)彼此重合的东西是相等的.(5)整体大于部分.其中5条公设主要对作图进行了相应的规范,而5条公理则主要从代数推理上进行规定.欧几里得基于上述这些公设和公理,推导出了平面几何中几乎所有的结论,从而构成了一个完整的几何体系,我们称之为欧氏几何.而他的著作《原本》中关于平面几何的部分,被翻译成中文叫做《几何原本》,正是我们平面几何的原型.而欧几里得这种对几何知识进行系统化、理论化的总结方法就被称之为公理法,而《原本》正是公理化体系的最好阐释.【参考答案】巩固练习1.40°2.125°3.C4.20°5.20°,70°6.∵∠BDC是△ABD的一个外角(外角的定义)∴∠BDC=∠A+∠ABD(三角形的外角等于与它不相邻的两个内角的和)∵∠A=40°,∠BDC=70°(已知)∴∠ABD=∠BDC-∠A=70°-40°=30°(等式的性质)∵BD平分∠ABC(已知)∴∠ABC=2∠ABD=2×30°=60°(角平分线的定义)∴∠C=180°-∠A-∠ABC=180°-40°-60°=80°(三角形的内角和等于180°)7.解:如图,∵EF∥BC(已知)∴∠ECD=∠E(两直线平行,内错角相等)∵∠E=55°(已知)∴∠ECD=55°(等量代换)∵CE是△ABC的一个外角平分线(已知)∴∠ACD=2∠ECD=2×55°=110°(角平分线的定义)∵∠ACD是△ABC的一个外角(外角的定义)∴∠ACD=∠A+∠B(三角形的外角等于与它不相邻的两个内角的和)∵∠A=60°(已知)∴∠B=∠ACD-∠A=110°-60°=50°(等式的性质)8.解:如图,∵∠BDC是△ABD的一个外角(外角的定义)∴∠BDC=∠ABD+∠A(三角形的外角等于与它不相邻的两个内角的和)∵∠A=45°,∠BDC=60°(已知)∴∠ABD=∠BDC-∠A=60°-45°=15°(等式的性质)∵BD平分∠ABC(已知)∴∠ABC=2∠ABD=2×15°=30°(角平分线的定义)∵DE∥BC(已知)∴∠AED=∠ABC(两直线平行,同位角相等)∴∠AED=30°(等量代换)思考小结1.(1)同位、内错、同旁内.(2)①同位角、内错角、同旁内角;②互补,对顶角相等;③三角形的内角和等于180°.④三角形的外角等于与它不相邻的两个内角的和.。
(完整版)三角形的外角练习题及标准答案
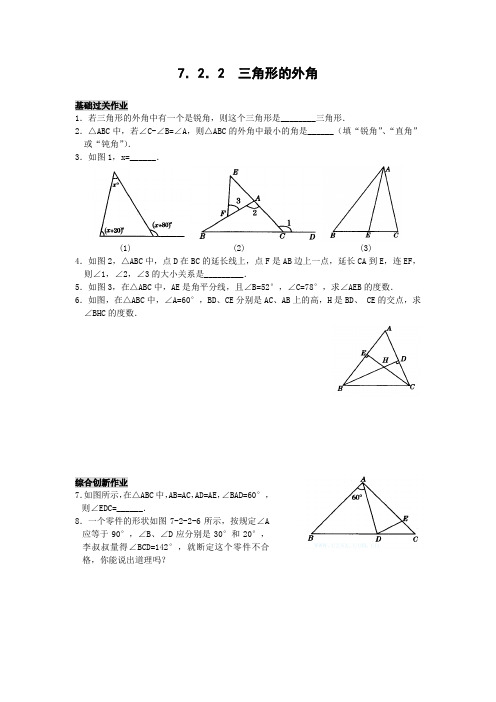
7.2.2 三角形的外角基础过关作业1.若三角形的外角中有一个是锐角,则这个三角形是________三角形.2.△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是______(填“锐角”、“直角”或“钝角”).3.如图1,x=______.(1) (2) (3)4.如图2,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连EF,则∠1,∠2,∠3的大小关系是_________.5.如图3,在△ABC中,AE是角平分线,且∠B=52°,∠C=78°,求∠AEB的度数.6.如图,在△ABC中,∠A=60°,BD、CE分别是AC、AB上的高,H是BD、•CE的交点,求∠BHC的度数.综合创新作业7.如图所示,在△ABC中,AB=AC,AD=AE,∠BAD=60°,则∠EDC=______.8.一个零件的形状如图7-2-2-6所示,按规定∠A应等于90°,∠B、∠D应分别是30°和20°,李叔叔量得∠BCD=142°,就断定这个零件不合格,你能说出道理吗?9.(1)如图7-2-2-7(1),求出∠A+∠B+∠C+∠D+∠E+∠F的度数;(2)如图7-2-2-7(2),求出∠A+∠B+∠C+∠D+∠E+∠F的度数.10.(易错题)三角形的三个外角中最多有_______个锐角.培优作业11.(探究题)(1)如图,BD、CD分别是△ABC的两个外角∠CBE、∠BCF•的平分线,试探索∠BDC与∠A之间的数量关系.(2)如图,BD为△ABC的角平分线,CD为△ABC的外角∠ACE的平分线,它们相交于点D,试探索∠BDC与∠A之间的数量关系.12.(趣味题)如图,在绿茵场上,足球队员带球进攻,总是向球门AB冲近,说明这是为什么?数学世界七桥问题18世纪在哥尼斯堡城的普莱格尔河上有七座桥,将河中的两个岛和河岸连接.如图所示.城中的居民经常沿河过桥散步,于是就提出一个问题:•能否一次不重复地把这七座桥走遍?可是,走来走去,这个愿望还是无法实现.该怎样走才好呢?•这就是著名的哥尼斯堡七桥问题.••好奇的人把这个问题拿给当时的大数学家欧拉(1707~1783).欧拉以深邃的洞察力很快证明了这样的走法不存在.你知道欧拉是根据什么道理证明的吗?答案:1.钝角2.直角点拨:∵∠C-∠B=∠A,∴∠C=∠A+∠B.又∵(∠A+∠B)+∠C=180°,∴∠C+∠C=180°,∴∠C=90°,∴△ABC的外角中最小的角是直角.3.60 点拨:由题意知x+80=x+(x+20).解得x=60.4.∠1>∠2>∠3点拨:∵∠1是∠2的外角,∠2是∠3的外角,∴∠1>∠2>∠3.5.解:∠BAC=180°-(∠B+∠C)=180°-(52°+78°)=50°.∵AE是∠BAC的平分线,∴∠BAE=∠CAE=12∠BAC=25°.∴∠AEB=∠CAE+∠C=25°+78°=103°.6.解:在△ACE中,∠ACE=90°-∠A=90°-60°=30°.而∠BHC是△HDC的外角,所以∠BHC=∠HDC+∠ACE=90°+30°=120°.7.30°点拨:设∠CAD=2a,由AB=AC知∠B=12(180°-60°-2a)=60°-•a,•∠ADB=180°-∠B-60°=60°+a,由AD=AE知,∠ADE=90°-a,所以∠EDC=180°-∠ADE-∠ADB=30°.8.解法1:如答图1,延长BC交AD于点E,则∠DEB=∠A+∠B=90°+30°=•120°,从而∠DCB=∠DEB+∠D=120°+20°=140°.若零件合格,∠DCB应等于140°.李叔叔量得∠BCD=142°,因此可以断定该零件不合格.(1) (2) (3)点拨:也可以延长DC与AB交于一点,方法与此相同.解法2:如答图2,连接AC并延长至E,则∠3=∠1+∠D,∠4=∠2+∠B,因此∠DCB=∠1+∠D+∠2+∠B=140°.以下同方法1.解法3:如答图3,过点C作EF∥AB,交AD于E,则∠DEC=90°,∠FCB=∠B=•30°,所以∠DCF=∠D+∠DEC=110°,从而∠DCB=∠DCF+∠FCB=140°.以下同方法1.说明:也可以过点C作AD的平行线.点拨:上述三种解法应用了三角形外角的性质:三角形的一个外角等于它不相邻的两个内角的和.9.解:(1)由图知∠A+∠F=∠OQA,∠B+∠C=∠QPC,∠D+∠E=∠EOP.而∠OQA、•∠QPC、∠EOP是△OPQ的三个外角.∴∠OQA+∠QPC+∠EOP=360°.∴∠A+∠B+∠C+∠D+∠E+∠F=∠OQA+∠QPC+∠EOP=360°.(2)360°点拨:方法同(1).10.1 点拨:本题易因混淆内角、外角的概念,而误填为3.11.解:(1)∠BDC=90°-12∠A.理由:∠ABC+∠ACB=180°-∠A.∠EBC+∠FCB=(180°-∠ABC)+(180°-∠ACB)=360°-(∠ABC+∠ACB)=180°+∠A.∵BD、CD分别为∠EBC、∠FCB的平分线,∴∠CBD=12∠EBC,∠BCD=12∠FCB.∴∠CBD+∠BCD=12(∠EBC+∠FCB)=12×(180°+∠A)=90°+12∠A.在△BDC中,∠BDC=180°-(∠CBD+∠BCD)=180°-(90°+12∠A)=90°-12∠A.(2)∠BDC=12∠A.理由:∵∠ACE是△ABC的外角,∴∠ACE=∠A+∠ABC,∵CD是∠ACE的平分线,BD是∠ABC的平分线,∴∠DCE=12∠ACE=12∠A+12∠ABC,∠DBC=12∠ABC.∵∠DCE是△BCD的外角,∴∠BDC=∠DCE-∠DBC=12∠A+12∠ABC-12∠ABC=12∠A.12.解:如图,设球员接球时位于点C,他尽力向球门冲近到D,此时不仅距离球门近,射门更有力,而且对球门AB的张角也扩大,球就更容易射中.理由说明如下:延长CD到E,则∠ADE>∠ACE,∠BDE>∠BCE,∴∠ADE+∠BDE>∠ACE+∠BCE,即∠ADB>∠ACB.点拨:解此题关键是将生活中的问题抽象为数学问题.数学世界答案:欧拉将七桥布局转化为图所示的简单图形,于是七桥问题就变成一个一笔画的问题.这个图形显然无法一笔画出,也就是说,•要想一次无重复地走遍这七座桥是办不到的.。
初中数学专题--三角形的外角-练习含答案

11。
2。
2三角形的外角基础知识一、选择题1.(20**•襄阳)如图,在△ABC 中,D 是BC 延长线上一点,∠B=40°,∠ACD=120°,则∠A 等于( )A .60°B .70°C .80°D .90°答案:C2.(20**•湘西州)如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD 的度数是( )A .15°B .25°C .30°D .10°答案:A3。
设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ 中 ( )A 。
有两个锐角、一个钝角B 。
有两个钝角、一个锐角C 。
至少有两个钝角 D.三个都可能是锐角答案:C4。
(20** 江苏省南通市) 如图,△ABC 中,∠C =70°,若沿图中虚线截去∠C ,则∠1+∠2等于 ( )A .360°B .250°C .180°D .140°答案:B5.已知△ABC,(1)如图1,若P 点是∠ABC 和∠ACB 的角平分线的交点,则∠P=90°+21∠A; (2)如图2,若P 点是∠ABC 和外角∠ACE 的角平分线的交点,则∠P=90°—∠A;A C B12(3)如图3,若P 点是外角∠CBF 和∠BCE 的角平分线的交点,则∠P=90°—21∠A . 上述说法正确的个数是( )A .0个B .1个C .2个D .3个答案:C6.(20**•漳州)将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是()A .45°B .60°C .75°D .90°答案:C7。
如图,∠BDC=98°,∠C=38°,∠B=23°,∠A 的度数是( )A .61°B .60°C .37°D .39°答案:C8。
三角形的外角练习题熟练计算三角形的外角大小

三角形的外角练习题熟练计算三角形的外角大小在学习三角形的几何性质中,计算三角形的外角大小是一个重要的内容。
下面通过练习题来熟练计算三角形的外角大小。
1.已知三角形ABC,AB=5cm,BC=7cm,CA=8cm。
求角A的外角大小。
解答:根据三角形的外角性质,外角等于两个非邻边的内角之和。
首先计算角A的两个非邻边的内角,即角B和角C。
根据余弦定理有:cos A = (b^2 + c^2 - a^2) / (2bc)代入已知数据:cos A = (7^2 + 8^2 - 5^2) / (2 * 7 * 8)= (49 + 64 - 25) / 112= 88 / 112= 0.7857由反余弦函数得:A = arccos(0.7857) ≈ 39.23°角A的外角大小等于角B和角C的和,即 180° - 39.23° = 140.77°。
因此,角A的外角大小约为 140.77°。
2.已知三角形DEF,DE=10cm,EF=12cm,FD=14cm。
求角D的外角大小。
解答:同样地,首先计算角D的两个非邻边的内角,即角E和角F。
根据余弦定理有:cos D = (e^2 + f^2 - d^2) / (2ef)代入已知数据:cos D = (12^2 + 14^2 - 10^2) / (2 * 12 * 14)= (144 + 196 - 100) / 336= 240 / 336= 0.7143由反余弦函数得:D = arccos(0.7143) ≈ 44.77°角D的外角大小等于角E和角F的和,即 180° - 44.77° = 135.23°。
因此,角D的外角大小约为 135.23°。
通过以上两道练习题,我们可以熟练计算三角形的外角大小。
在实际问题中,计算三角形的外角大小可以帮助我们判断三角形的形状、性质以及解决相关几何问题。
八年级数学上册三角形的外角精选练习题

八年级数学上册三角形的外角精选练习题一、选择题:1.CD‖AB,∠ 1 = 120 °, ∠ 2=80°,则∠ e是a.40°b.60°c.80°d.120°2.将三角形板的直角顶点放在正方形的一侧,∠ 1=30°,以及∠ 2=50°,则∠ 3是a.80b.]50c.30d.203.已知ab‖CD的程度,∠ EBA=45°,∠ e+∠ D是a.30°b.60°c.90°d.45°4.如果图中有四条不平行的直线L1、L2、L3和L4,则七个角将被切割。
关于这七个角的度关系,以下哪项是正确的a.∠2=∠4+∠7b.∠3=∠1+∠6c.∠1+∠4+∠6=180°d.∠2+∠3+∠5=360°5.一对三角形板有两个直角三角形。
如果它们叠在一起∠ α什么是a.165°b.120°c.150°d.135°6.直线ab‖CD,∠ a=70°,∠ C=40°,则∠ e等于a.30°b.40°c.60°d.70°7.以下四种形式:,∠ 1 = ∠ 2一定是真的a.b.c.d.8.企业规模关系∠ A.∠ 1.∠ 2是a.∠a>∠1>∠2b.∠2>∠1>∠ac.∠a>∠2>∠1d.∠2>∠a>∠1二、填空9.将一副常规的三角尺按如方式放置,则中∠aob的度数为________10.L‖m,等腰直角三角形ABC的直角顶点C在直线m上,如果∠ 那么β=20°∠ α是________11.若三角形的外角中有一个是锐角,则这个三角形是________三角形.12.在△ ABC,如果∠ C-∠ B=∠ a、外角中的最小角度△ 或“钝角”13.x=______.14.在△ 美国广播公司,∠ a=45°,∠ B=60°,然后是外角∠ ACD=度15.已知△abc是等边三角形,点b、c、d、e在同一直线上,且cg=cd,df=de,则∠e=_________ 度.16.放置一对直角三角形板,使30°角三角形板的一个直角侧与45°α=的三角形板的一个直角侧重合。
