八年级上册第3章 勾股定理培优题含答案
苏科版八年级上册第三章《勾股定理》单元专题培优训练卷【含答案】

苏科版八年级上册第三章《勾股定理》单元专题培优训练卷一.选择题1.下列各组数中,不是勾股数的一组是()A.3,4,5B.4,5,6C.6,8,10D.5,12,132.三个正方形的面积如图所示,则S的值为()A.3B.12C.9D.43.在△ABC中,∠A、∠B、∠C的对边分别记为a、b、c.下列条件中;不能说明△ABC 是直角三角形的是()A.∠A=∠B=∠C B.a2=b2+c2C.∠A+∠B=∠C D.a:b:c=3:4:54.如图,∠C=90o,AB=12,BC=3,CD=4,若∠ABD=90°,则AD的长为()A.8B.10C.13D.155.如图,一棵大树在暴风雨中被台风刮倒,在离地面3米处折断,测得树顶端距离树根4米,已知大树垂直地面,则大树高约多少米?()A.5米B.8米C.9米D.256.若a、b、c是△ABC三条边的长,且满足a2﹣2ab+b2+|a2+b2﹣c2|=0,则△ABC是()A.等腰三角形B.等腰直角三角形C.直角三角形D.锐角三角形7.将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露出在杯子外面长为hcm,则h的取值范围是()A.0≤h≤12B.12≤h≤13C.11≤h≤12D.12≤h≤24 8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列结论:①x2+y2=49;②x﹣y=2;③2xy+4=49;④x+y=7.其中正确的结论是()A.①②B.②④C.①②③D.①③二.填空题9.在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是.10.在△ABC中,若∠C=90°,∠A=46°,则∠B=°.11.在△ABC中,∠C=90°,若a=5,b=12,则c=.12.如图,是一个直角三角形以三边为边长向外作三个正方形,则字母A所代表的正方形的面积为.13.如图在Rt△ABC中,∠C=90°,CD⊥AB于D,若AC=12,BC=5,则CD =.14.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要m.15.我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐,问水深几何?”(注:丈,尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.设这个水池深x尺,则根据题意,可列方程为.16.“赵爽弦图”巧妙的利用面积关系证明了勾股定理.如图所示的“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,若AB=10,EF=2,则AH=.三.解答题17.某中学校园有一块四边形草坪ABCD(加图所示),测得∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m,求这块四边形草坪的面积.18.如图,在四边形ABCD中,已知∠B=90°,AB=3,BC=4,CD=12,AD=13,求证AC⊥CD.19.八(3)班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作:(1)测得BD的长度为25米;(2)根据手中剩余线的长度计算出风筝线BC的长为65米;(3)牵线放风筝的小明身高1.68米.求风筝的高度CE.20.三水九道谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A拉回点B的位置(如图).在离水面高度为8m的岸上点C,工作人员用绳子拉船移动,开始时绳子AC的长为17m,经过10秒后游船移动到点D的位置,此时BD=6m,问工作人员拉绳子的速度是多少?21.在甲村至乙村的公路旁有一块山地需要开发,现有一C处需要爆破,已知点C与公路上的停靠点A的距离为800米,与公路上另一停靠点B的距离为600米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径450米范围内不得进入,问在进行爆破时,公路AB段是否有危险需要暂时封锁?请通过计算进行说明.22.我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式,这种方法称之为“无字证明”,它比严谨的数学证明更为优雅与有条理.下面是用三块全等的直角三角形移、拼、补所形成的“无字证明”图形.(1)此图可以用来证明你学过的什么定理?请写出定理的内容;(2)已知直角三角形直角边长分别为a、b,斜边长为c,图1、图2的面积相等,请你根据此图证明(1)中的定理.参考答案一.选择题1.解:A、32+42=52,能构成直角三角形,是整数,故是勾股数,此选项错误;B、42+52≠62,不是勾股数,此选项正确;C、62+82=102,三边是整数,同时能构成直角三角形,故是勾股数,此选项错误;D、52+122=132,是正整数,故是勾股数,此选项错误.故选:B.2.解:如图,由题意可得:AB=4,AC=5,∵AC2=AB2+BC2,∴BC2=25﹣16=9,∴S=9,故选:C.3.解:A、∵∠A=∠B=∠C,∠A+∠B+∠C=180°,∴∠A=∠B=∠C=60°,∴△ABC不为直角三角形,故此选项符合题意;B、∵a2=b2+c2,∴△ABC为直角三角形,故此选项不合题意;C、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴∠C=90°,∴△ABC为直角三角形,故此选项不合题意;D、∵a:b:c=3:4:5,设a=3x,b=4x,c=5x,∵(3x)2+(4x)2=(5x)2,∴能构成直角三角形,故此选项不合题意;故选:A.4.解:在Rt△BCD中,∠C=90o,由勾股定理得:BD=,在Rt△ABD中,∠ABD=90°,由勾股定理得:AD=,故选:C.5.解:设大树高约有x米,由勾股定理得:(x﹣3)2=32+42,解得:x=8,答:大树高约8米.故选:B.6.解:∵a2﹣2ab+b2+|a2+b2﹣c2|=0,即(a﹣b)2+|a2+b2﹣c2|=0,∴(a﹣b)2=0,且|a2+b2﹣c2|=0,∴(a﹣b)2=0,且a2+b2=c2,∴a=b,且△ABC是直角三角形,∴△ABC是等腰直角三角形,故选:B.7.解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).当筷子与杯底及杯高构成直角三角形时h最小,如图所示:此时,AB===13(cm),故h=24﹣13=11(cm).故h的取值范围是:11cm≤h≤12cm.故选:C.8.解:由题意知,由①﹣②得2xy=45 ③,∴2xy+4=49,①+③得x2+2xy+y2=94,∴(x+y)2=94,∴x+y=.∴结论①②③正确,④错误.故选:C.二.填空题9.解:设相邻两个结点的距离为m,则此三角形三边的长分别为3m、4m、5m,∵(3m)2+(4m)2=(5m)2,∴以3m、4m、5m为边长的三角形是直角三角形.(如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形)故答案为:如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形.10.解:∵∠C=90°,∠A=46°,∴∠B=90°﹣46°=44°,故答案为:44.11.解:在△ABC中,∠C=90°,a=5,b=12,∴,故答案为:13.12.解:∵正方形PQED的面积等于225,∴即PQ2=225,∵正方形PRGF的面积为289,∴PR2=289,又△PQR为直角三角形,根据勾股定理得:PR2=PQ2+QR2,∴QR2=PR2﹣PQ2=289﹣225=64,则正方形QMNR的面积为64.故答案是:64.13.解:Rt△ABC中,∠C=90°,由勾股定理得:AB=,由S△ABC=得:∴5×12=13×CD,∴CD=.故答案为:.14.解:由勾股定理得:楼梯的水平宽度==12,∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,∴地毯的长度至少是12+5=17(米).故答案为:17.15.解:设水池里水的深度是x尺,由题意得,(x+1)2=x2+25,故答案为:(x+1)2=x2+25.16.解:∵AB=10,EF=2,∴大正方形的面积是100,小正方形的面积是4,∴四个直角三角形面积和为100﹣4=96,设AE为a,DE为b,即4×ab=96,∴2ab=96,a2+b2=100,∴(a+b)2=a2+b2+2ab=100+96=196,∴a+b=14,∵a﹣b=2,解得:a=8,b=6,∴AE=8,AH=DE=6,∴AH=8﹣2=6.故答案为:6.三.解答题17.解:连接AC,如图:∵∠B=90°,AB=24m,BC=7m,∴AC2=AB2+BC2=242+72=625,∴AC=25(m).又∵CD=15m,AD=20m,152+202=252,即AD2+DC2=AC2,∴△ACD是直角三角形,∴S四边形ABCD=S△ABC+S△ADC=•AB•BC+•AD•DC=×24×7+×20×15=234(m2).答:这块四边形草坪的面积是234m2.18.证明:∵∠B=90°,∴△ABC为直角三角形,又∵AB=3,BC=4,∴根据勾股定理得:AC==5,又∵CD=12,AD=13,∴AD2=132=169,CD2+AC2=122+52=144+25=169,∴CD2+AC2=AD2,∴△ACD为直角三角形,∠ACD=90°,即AC⊥CD.19.解:在Rt△CDB中,由勾股定理得,CD2=BC2﹣BD2=652﹣252=3600,所以,CD=±60(负值舍去),所以,CE=CD+DE=60+1.68=61.68(米),答:风筝的高度CE为61.68米.20.解:由题意得:∠B=90°,∵BC=8m,BD=6m,∴CD===10m,∵AC=17m,∴绳子移动了AC﹣DC=17﹣10=7(m),用时10秒,∴工作人员拉绳子的速度是7÷10=0.7米/秒.21.解:公路AB不需要暂时封锁.理由如下:如图,过C作CD⊥AB于D.∵CA⊥CB,∴∠ACB=90°,因为BC=800米,AC=600米,所以,根据勾股定理有AB==1000(米).因为S△ABC=AB•CD=BC•AC所以CD===480(米).由于400米<480米,故没有危险,因此AB段公路不需要暂时封锁.22.解:(1)勾股定理:直角三角形的两条直角边长分别为a、b,斜边长为c,那么a2+b2=c2;(2)图1的面积为:S1=,图2的面积为S2=,∵图1、图2的面积相等,∴=,∴a2+b2=c2.。
八年级上册第3章勾股定理培优题含答案
第 3 章勾股定理综合提优卷(时间: 60 分钟满分:100分)一、填空题(每题 3 分,共 30 分)1.如图,在一次狂风灾祸中,一棵大树在离地面 3 米处折断,树的顶端落在离树杆底 4 米处,那么这棵树折断以前的高度是 _______米.2.直角三角形一条直角边与斜边分别为 4 cm和 5 cm,则斜边上的高等于 _______cm.3.如图,在直角三角形 ABC中,∠ C= 90°, AC=12, BC=5,则以 AB为直径的半圆的面积为 _______.4.如图,在四边形ABCD中,∠ A= 90°,若 AB= 4 cm, AD=3 cm,CD= 12 cm,BC = 13 cm,则四边形 ABCD的面积是 _______.5.木匠师傅要做一个长方形桌面,做好后量得长为80 cm,宽为 60 cm,对角线为100 cm,则这个桌面 _______.(填“合格”或“不合格”)6.甲、乙两人同时从同一地址出发,甲往东走了8 km,乙往南走了 6 km,这时两人相距 _______km.7.如图,学校有一块长方形花铺,有很少量人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们只是少走了 _______步路(假定 2 步为 1 米),却踩伤了花草.8.如图,以 Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边 AB=a,则图中暗影部分的面积为 _______.9.如图,在 Rt△ABC中,∠ BCA= 90°,点 D 是 BC上一点, AD=BD,若 AB=8,BD =5,则 CD=_______.10.着手操作:在矩形纸片 ABCD 中, AB =3,BD = 5.以下图,折叠纸片使点 A 落在边 BC 上的 A' 处,折痕为 PQ .当点 A' 在边 BC 上挪动时,折痕的端点 P 、Q 也随之挪动.若限制点 P 、Q 分别在边 AB 、AD 上挪动,则点 A' 在边 BC 上可挪动的最大距离为 _______.二、选择题(每题 3 分,共 30 分)11.以下各组数中,能够组成勾股数的是 ( ) .A .13,16,19B .17,21, 23C .18,24,36D .12,35, 3712.以下命题中,是假命题的是 ( ) .A .在△ ABC 中,若∠B =∠C =∠ A ,则△ ABC 是直角三角形B .在△ ABC 中,若 a 2= (b +c) (b -c) ,则△ ABC 是直角三角形C .在△ ABC 中,若∠ A :∠ B :∠ C =3:4:5,则△ ABC 是直角三角形D .在△ ABC 中,若 a :b :c =5:4:3,则△ ABC 是直角三角形13.向来角三角形的三边分别为 2,3,x ,那么以 x 为边长的正方形的面积为 ( ). A .13 B .5C . 13 或 5D . 414.如图是一株漂亮的勾股树,此中全部的四边形都是正方形,全部的三角形都是直角三角形,若正方形 A 、 B 、 C 、 D的边长分别是 3,5,2,3,则最大的正方形 E 的面积是 ( ) .A .13B .26C .47D .9415.在 Rt △ABC 中,∠ C =90°, AC =3,BC =4,则点 C 到 AB 的距离是( ) .A . 12B . 4C . 3D . 95 25 4 416.已知向来角三角形的木板,三边的平方和为 1800 cm 2,则斜边长为 ( ) .A .30 cmB . 80 cmC .90 cmD .120 cm17.底面周长为 12,高为 8 的圆柱体上有一只小蚂蚁要从点 A 爬到点 B ,则蚂蚁爬 行的最短距离是 ( ) .A .10B .8C .5D .418.如,已知矩形ABCD沿着直 BD折叠,使点 C落在 C' , BC,交 AD于点 E,AD=8,AB=4, DE的 ( ) .A.3 B.4 C.5 D.619.如,四形 ABCD中,AC、BD是角,△ ABC是等三角形,∠ ADC=30°,AD=3,BD=5, CD的 ( ) .A.3 2 B. 4 C.2 5 D.20.如,正方体 ABCD-A1B1C1D1的棱 1,黑、白两个甲壳虫同从点 A 出,以同样的速度分沿棱向前爬行,黑甲壳虫爬行的路是AA1→A1D1→⋯⋯,白甲壳虫爬行的路是AB→BB1→⋯⋯,而且都按照以下:所爬行的第n+2 与第 n 条棱所在的直必是既不平行也不订交(此中n 是正整数).那么当黑、白两个甲壳虫各爬行完第2013 条棱分停止在所到的正方体点,它之的距离是( ).A.0B.1 C .2D. 3三、解答(共40 分)21.如,已知在△ ABC中, CD⊥ AB于 D,AC=20,BC= 15,DB=9.(1)求 DC的;(2)求 AB的.22.察以下各式,你有什么?32=4+ 5, 52=12+ 13,72= 24+25,92=40+ 41,⋯究竟是偶合,是有什么律涵此中呢?你合相关知行研究.若132= a+b, a,b 的可能是多少?23.如所示,一船以16 n mi1e /h 的速度从港口 A 出向北方向航行,另一轮船以 12 n mi1e/ h 的速度同时从港口出发向东南方向航行,那么走开港口 A2h 后,两船相距多远?24.如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是 a,b,斜边长为 c 和一个边长为 c 的正方形,请你将它们拼成一个能证明勾股定理的图形.(1)画出拼成的这个图形的表示图;(2)证明勾股定理.25.如图, A、 B 两个村庄在河 CD的同侧, A、B 两村到河的距离分别为 AC=1 km,BD=3 km, CD=3 km此刻河畔 CD上建一水厂向 A、B 两村输送自来水,铺设水管的花费为 20 000 元/千米,请你在河 CD边上选择水厂地点 O,使铺设水管的花费最省,并求出铺设水管的总花费?26.如图,公路 MN和公路 PQ在点 P 处交汇,且∠ QPN=30°,点 A 处有一所中学,AP=160 米,假定拖沓机行驶时,四周 100 米之内会遇到噪音的影响,那么拖沓机在公路 MN上沿 PN方向行驶时,学校能否回遇到噪声的影响?说明原因.假如受影响,已知拖沓机的速度为18 千米/时,那么学校受影响的时间为多少秒?参照答案1.8 2 .2.4 3 . 1694.36 cm285.合格 6 . 10 7 .8 8 .a2 29.1.4 10 . 211.D 12 .C 13 .C 14 . C 15 .A 16 .A 17 .A 18 . C 19 .B 20 . C 21.(1)12 (2)2522.a=84, b=8523.2h 后24.略25.作点 A 对于河 CD的对称点 A' ,连结 A'B 交河 CD于 O点,点 O就是水厂的地点,26.24 秒。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,在3×4的正方形网格图中,小正方形的边长为1,的顶点均在格点上,则下列关于的说法错误的是()A.是直角三角形B.C.面积为4D. 边上的高为2、如图,长方形ABCD中,AB=4,BC=3,将其沿直线MN折叠,使点C与点A重合,则CN的长为().A. B. C. D.3、如图,⊙O直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足M,OM:OD=3:5,则AB 的长是()A.2cmB.3cmC.4cmD.2 cm4、已知的两直角边分别是,,则的斜边上的高是()A. B. C. D.5、下列各组数中能作为直角三角形的三边长的是()A.1,2,3B.4,5,6C.6,8,10D.9,11,16、如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上一点,将△ABE沿AE 折叠,使点B落在点F处,连结CF,当△CEF为直角三角形时,BE的长是()A.4B.3C.4或8D.3或67、如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有()A.5个B.4个C.3个D.2个8、下列四组数据表示三角形的三边长,其中不能构成直角三角形的一组数据是( )A.1 cm, cm, 4cmB.5cm, 12cm, 13cm:C.3cm, 4cm,5cm: D.7cm, 24cm, 25 cm9、一个直角三角形中,两条直角边长为3和4,则它的斜边长为()A.2B.C.5D.2510、如图,O为圆锥的顶点,M为圆锥底面上一点,点P在OM上,一只蜗牛从点P出发,绕圆锥侧面沿最短路线爬行一圈回到点P,若沿OM将圆锥侧面剪开并展开,则所得的侧面展开图是()A. B. C. D.11、矩形ABCD中,E,F,M为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为()A.5B.C.6D.12、如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为()A.6B.8C.12D.1013、如图,已知平分,于,于,且.若,,,的长为()A.8B.8.5C.9D.714、如图,在平面直角坐标系中,的斜边OA在第一象限,并与x轴的正半轴夹角为30度,C为OA的中点,BC=1,则A点的坐标为()A. B. C. D.15、如图1,园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是()A.24米2B.36米2C.48米2D.72米2二、填空题(共10题,共计30分)16、已知矩形纸片的边,(如图),将它折叠后,点落在边的中点处,那么折痕的长为________.17、在平面直角坐标系中,点P(-, -1)到原点的距离是________ 。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图所示,在等边△ABC中,E是AC边的中点,AD是BC边上的中线,P是AD上的动点,若AD=5,则EP+CP的最小值为()A.2B.4C.5D.72、下列各组数中,不能作为直角三角形的三边长的是()A.1,,2B.7,12,15C.3,4,5D.5,12,133、点到原点的距离为()A.3B.4C.5D.以上都不对4、以下列各组数为边长,能组成直角三角形的是()A.2,3,4B.10,8,4C.7,25,24D.7,15,125、如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明准备从南京路与八一街的交叉口去书店,且按图中的街道行走,最近的路程为()A. B. C. D.6、如图,在△ABC中,∠C=90°,AB=5 ,BC=3,则tanB的值是()A. B. C. D.7、如图,AB,AC分别是⊙O的直径和弦,于点D,连接BD,BC,且,,则BD的长为()A. B.4 C. D.4.88、“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则中间小正方形与大正方形的面积差是()A.-9B.-36C.-27D.-349、在△ABC中,已知∠C=90°,BC=4,sinA= ,那么AC边的长是()A.6B.2C.3D.210、如图,数轴上点A所表示的实数是().A. B. C. D.211、如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,,直线交圆于E,,则圆的半径为()A.4B.3C.D.12、如图,圆柱的底面直径和高均为4,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是()A. B. C. D.13、如图,在中,,则 sinB 的值为()A. B. C. D.14、、、为三边,下列条件不能判断它是直角三角形的是()A. B. ,, C.D. ,,(为正整数)15、如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是3,则AB长为()A. B.1 C.2 D.3二、填空题(共10题,共计30分)16、AB是⊙O的直径,弦CD垂直平分半径OA,若CD长为6,则⊙O的半径长为________.17、如图:中,,平分交于,点在的延长线上,满足,若,,则线段的长为________.18、在△ABC中,AD为高线,若AB+BD=CD,AC=4 ,BD=3,则线段BC的长度为________.19、如图,已知OA=AB,数轴上点C表示的实数是________,点E表示的实数是________.20、如图,在Rt△ACB中,∠ACB=90°,BC=3,AC=4,在直线BC上找一点P,使得△ABP为以AB为腰的等腰三角形,则PC的长度为________.21、如图,在四边形ABCD中,∠A=90°,AB=3 ,AD=3,点M,N分别为线段BC,AB 上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为________.22、如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则点D到直线BC的距离为________.23、一个直角三角形的两边长为3和5,则第三边为________.24、平面直角坐标系中,已知点A(﹣1,﹣3)和点B(1,﹣2),则线段AB 的长为________25、如图,正方体的棱长为5,一只蚂蚁如果要沿着正方体的表面从点A爬到点B,需要爬行的最短距离是________.三、解答题(共5题,共计25分)26、在Rt△ABC中,∠ACB=90°,AC=3,tanB= ,求AB的值.27、如图,在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm.动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间t,使得△PBC为等腰三角形.28、四边形ABCD中,AB∥ DC , BC=b,AB=AC=AD=a,如图24-1-4-11,求BD 的长.图24-1-4-1129、如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,在ABC中,AC=BC,∠ACB=90°,过点C作CD⊥AB交∠CAB的平分线AE于点O,点P是AC延长线上一点,OP=OB,现有下列结论:①∠OCP=∠OEB;②∠POB=90°;③CP=OD;④SCOP =SCOE;⑤PC2+BC2=OP2+OB2.其中正确的有()A.1个B.2个C.3个D.4个2、如图,直线l为等腰梯形ABCD的对称轴,点P在直线l上,且PC+PB最小,则点P应位于()A.点P1处 B.点P2处 C.点P3处 D.点P4处3、要登上某建筑物,靠墙有一架梯子,底端离建筑物3m,顶端离地面4m,则梯子的长度为()A.2mB.3mC.4mD.5m4、已知直角三角形的两边长是方程x2﹣7x+12=0的两根,则第三边长为()A.7B.5C.D.5或5、如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a ∥b∥c.若a与b之间的距离是3,b与c之间的距离是5,则正方形ABCD的面积是()A.16B.30C.34D.646、设边长为3的正方形的对角线长为a,下列关于a的四种说法:① a是无理数;② a可以用数轴上的一个点来表示;③ 3<a<4;④ a是18的算术平方根.其中,所有符合题意说法的序号是A.①④B.②③C.①②④D.①③④7、a、b、c为△ABC三边,满足下列条件的三角形不是直角三角形的是()A.∠C=∠A-∠BB.a:b:c = 1 : :C.∠A∶∠B∶∠C=5∶4∶3D. ,8、直角三角形两直角边分别为5、12,则这个直角三角形斜边上的高为().A.6B.8.5C.D.9、三角形的三边长分别为6,8,10,它的最长边上的高为()A.6B.4.8C.2.4D.810、在边长为2的正方形ABCD中,P为AB上一动点,E为AD中点,PE交CD 延长线于Q,过E作EF⊥PQ交BC延长线于F,则下列结论:①△APE≅△DQE;②PQ=EF;③当P为AB中点时,CF= ;④若H为QC中点,当P从A移动到B 时,线段EH扫过的面积为.其中正确的是()A.①②B.①②④C.②③④D.①②③11、下列数组中,不是勾股数组的是 ( )A.8,12,15B.7,25,24C.5,12,13D.3k,4k,5k(k为正整数)12、已知一个直角三角形的两条边长分别是6和8,则第三边长是()A.10B.8C.2D.10或213、若直角三角形的两直角边长分别为5、12,则这个直角三角形的斜边长是()A.13B.C.169D.14、如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+ 的值最小时,线段PD的长是()A. B. C. D.15、如图,在四边形ABCD中,AB=BC=2 ,AD=2,∠B=∠D=90°,则CD 等于()A.2B.C.2D.二、填空题(共10题,共计30分)16、如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,AE=CD,若⊙O的半径为5,则弦CD的长为________.17、如图,半径为且坐标原点为圆心的圆交轴、轴于点、、、,过圆上的一动点(不与重合)作,且在右侧)⑴连结,当时,则点的横坐标是________.⑵连结,设线段的长为,则的取值范围是________.18、如图,在中,,.将绕点B 逆时针旋转60°,得到,则边的中点D与其对应点的距离是________.19、如图,将矩形纸片ABCD沿直线AF翻折,使点B恰好落在CD边的中点E 处,点F在BC边上,若CD=6,则AD=________.20、如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要________元钱.21、如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为________.22、如图,已知直线AB∥CD,AB与CD之间的距离为,∠BAC=60°,则AC=________.23、如图,已知图中每个小方格的边长为1,则点C到AB所在直线的距离等于________.24、如图,在由12个边长都为1且有一个锐角为60°的小菱形组成的网格中,点P是其中的一个顶点,以点P为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长________ .25、如图,AD是的中线,,把沿着直线AD对折,点C落在点E的位置,如果,那么线段BE的长度为________.三、解答题(共5题,共计25分)26、如图,在Rt△ABC中,∠C=90°,BC=8,tanB= ,点D在BC上,且BD=AD,求AC的长和cos∠ADC的值.27、如图(1),在∆ABC中,AB=BC=5,AC=6,∆ABC沿BC方向平移得到△ECD,连接AE、AC和BE相交于点O。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,将一根长25cm的细木棒放入长、宽、高分别为的长方体盒子中,则细木棒露在外面的最短长度是()cmA.20B.15C.10D.52、如果△ABC的三个顶点A,B,C所对的边分别为a,b,c,那么下列条件中,不能判断△ABC是直角三角形的是()A.∠A=25°,∠B=65°B.∠A:∠B:∠C=2:3:5C. a:b:c=::D. a=6,b=10,c=123、如图,A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )A.(2,0)B.(4,0)C.(-2 ,0)D.(3,0)4、如图,正方形ABCD中,点EF分别在BC、CD上,△AEF是等边三角形,连AC交EF于G,下列结论:①∠BAE=∠DAF=15°;②AG= GC;③BE+DF=EF;④S△CEF =2S△ABE,其中正确的个数为()A.1B.2C.3D.45、直角三角形的两直角边分别为5厘米、12厘米,则斜边上的高是()A.6厘米B.8厘米C. 厘米D. 厘米6、如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE。
将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF。
下列结论:①△ ABG ≌△AFG;②BG=GC;③AG∥CF;④S△FGC=。
其中正确结论的个数是()个A.1B.2C.3D.47、已知△ABC中,∠C=90°,若AC= ,BC=1,则sinA的值是()A. B. C. D.8、如图在矩形ABCD中,AB=2 ,BC=10,E、F分别在边BC,AD上,BE=DF将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE、△CHF,若AG分别平分∠EAD,则GH的长为( )A.3B.4C.5D.79、如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值是()A. B. C. D.10、下列命题中,不正确的是()A.n边形的内角和等于(n﹣2)•180°B.边长分别为3,4,5,的三角形是直角三角形C.垂直于弦的直径平分弦所对的两条弧D.圆的切线垂直于半径11、如图,在平面直角坐标系xOy中,直线y=﹣x+4与x轴、y轴分别交于点A、B,M是y轴上的点(不与点B重合),若将△ABM沿直线AM翻折,点B 恰好落在x轴正半轴上,则点M的坐标为()A.(0,﹣4 )B.(0,﹣5 )C.(0,﹣6 )D.(0,﹣7 )12、如图,△ABC中,∠C=90°,D是BC边上一点,∠ADC=3∠BAD,BD=8,DC=7,则AB的值为()A.15B.20C.2 +7D.2 +13、下列各组数中,可以组成直角三角形的是()A.1:2:3B.2,3,4C.3,4,5D.3 2, 4 2, 5 214、如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )A.8B.4C.2D.815、在Rt△ABC中,两直角边长分别为3和4,则斜边的长度是( )A.2B.C.5D. 或5二、填空题(共10题,共计30分)16、如图,已知菱形ABCD中,∠BAD=120°,对角线AC与BD相交于点O,且AC=,则对角线BD的长为________.17、在直角三角形中,有两条边长分别是8和6.则斜边上的中线长是________.18、如图,在边长为4的等边三角形ABC中,AD是BC边上的高,E,F是AD上的两点,则阴影部分的面积是________19、等腰三角形的腰长为1cm,底边长为cm,则它的底角的正切值为________.20、在Rt△ABC中,∠BAC=90°,且a+c=9,a-c=4,则b的值是________.21、如图,在Rt△ABC中,已知∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为________.22、白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的P点饮马,饮马后再到B点宿营,若A、B到水平直线L(L表示小河)的距离分别是2,1,AB 两点之间水平距离是4,则AP+PB最小值=________.23、如图,矩形ABCD中,AB=2 ,AD=6,P为边AD上一点,且AP=2,在对角线BD上寻找一点M,使AM+PM最小,则AM+PM的最小值为________.24、如图,一棵大树在离地面3m、5m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部6m处,则大树折断前的高度是________.25、小华和小红都从同一点O出发,小华向北走了9米到A点,小红向东走了12米到了B点,则AB为________ 米.三、解答题(共5题,共计25分)26、如图,方格纸上每个小正方形的面积为1.⑴在方格纸上,以线段AB为边画正方形ABCD,并计算所画正方形ABCD的面积.⑵请你在图上分别画出面积为5正方形A1B1C1D1和面积为10的正方形A 2B2C2D2,正方形的各个顶点都在方格纸的格点上.27、如图,已知在菱形ABCD中,∠ABC=60°,对角线AC=8,求菱形ABCD的周长和面积.28、已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积.29、我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积。
八年级初二数学 数学勾股定理的专项培优练习题(含答案

八年级初二数学 数学勾股定理的专项培优练习题(含答案一、选择题1.如图,点A 的坐标是(2)2,,若点P 在x 轴上,且APO △是等腰三角形,则点P 的坐标不可能是( )A .(2,0)B .(4,0)C .(-22,0)D .(3,0) 2.如图,在矩形纸片ABCD 中,AD =9,AB =3,将其折叠,使点D 与点B 重合,折痕为EF ,那么折痕EF 的长为( )A .3B .6C .10D .9 3.如图,在Rt ABC ∆中,90, 5 ,3ACB AB cm AC cm ︒∠=== ,动点P 从点B 出发,沿射线BC 以1 /cm s 的速度移动,设运动的时间为t 秒,当∆ABP 为等腰三角形时,t 的值不可能为( )A .5B .8C .254D .2584.已知三角形的三边长分别为a ,b ,c ,且a+b=10,ab=18,c=8,则该三角形的形状是( )A .等腰三角形B .直角三角形C .钝角三角形D .等腰直角三角形5.如图,AB =AC ,∠CAB =90°,∠ADC=45°,AD =1,CD =3,则BD 的长为( )A .3B .11C .23D .46.如图,P 为等边三角形ABC 内的一点,且P 到三个顶点A ,B ,C 的距离分别为3,4,5,则△ABC 的面积为( )A .2539+B .2539+C .18253+D .25318+ 7.三个正方形的面积如图,正方形A 的面积为( )A .6B .36C .64D .88.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知90A ∠=︒正方形ADOF 的边长是2,4BD =,则CF 的长为( )A .6B .2C .8D .109.如图,是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF 的长是( )A .14B .13C .143D .14210.如图,在Rt △ABC 中,∠A=90°,AB=6,AC=8,现将Rt △ABC 沿BD 进行翻折,使点A 刚好落在BC 上,则CD 的长为( )A .10B .5C .4D .3二、填空题11.如图,AB =12,AB ⊥BC 于点B , AB ⊥AD 于点A ,AD =5,BC =10,E 是CD 的中点,则AE 的长是____ ___.12.如图,在△ABC 中,OA =4,OB =3,C 点与A 点关于直线OB 对称,动点P 、Q 分别在线段AC 、AB 上(点P 不与点A 、C 重合),满足∠BPQ =∠BAO.当△PQB 为等腰三角形时,OP 的长度是_____.13.以直角三角形的三边为边向外作正方形P ,Q ,K ,若S P =4,S Q =9,则K S =___14.如图所示,“赵爽弦图”是由8个全等的直角三角形拼接而成的,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为123,,S S S ,已知12310S S S ++=,则2S 的值是____.15.已知x ,y 为一个直角三角形的两边的长,且(x ﹣6)2=9,y =3,则该三角形的第三边长为_____.16.如图,P 是等边三角形ABC 内的一点,且PA=3,PB=4,PC=5,以BC 为边在△ABC 外作△BQC ≌△BPA ,连接PQ ,则以下结论中正确有_____________ (填序号)①△BPQ 是等边三角形 ②△PCQ 是直角三角形 ③∠APB=150° ④∠APC=135°17.如图,Rt △ABC 中,∠C =90°,AB =5,BC =4,斜边AB 的垂直平分线DE 交边BC 于点D ,连接AD ,线段CD 的长为_________.18.在ABC 中,12AB AC ==,30A ∠=︒,点E 是AB 中点,点D 在AC 上,32DE =,将ADE 沿着DE 翻折,点A 的对应点是点F ,直线EF 与AC 交于点G ,那么DGF △的面积=__________.19.如图的实线部分是由Rt ABC ∆经过两次折叠得到的.首先将Rt ABC ∆沿高CH 折叠,使点B 落在斜边上的点B '处,再沿CM 折叠,使点A 落在CB '的延长线上的点A '处.若图中90ACB ∠=︒,15cm BC =,20cm AC =,则MB '的长为______.20.如图,在等腰△ABC 中,AB =AC ,底边BC 上的高AD =6cm ,腰AC 上的高BE =4m ,则△ABC 的面积为_____cm 2.三、解答题21.如图,在矩形ABCD 中,AB=8,BC=10,E 为CD 边上一点,将△ADE 沿AE 折叠,使点D 落在BC 边上的点F 处.(1)求BF 的长;(2)求CE 的长.22.定义:如图1,点M 、N 把线段AB 分割成AM 、MN 和BN ,若以AM 、MN 、BN 为边的三角形是一个直角三角形,则称点M 、N 是线段AB 的勾股分割点.(1)已知点M 、N 是线段AB 的勾股分割点,若2AM =,3MN =,求BN 的长; (2)如图2,在Rt ABC △中,AC BC =,点M 、N 在斜边AB 上,45MCN ∠=︒,求证:点M 、N 是线段AB 的勾股分割点(提示:把ACM 绕点C 逆时针旋转90︒);(3)在(2)的问题中,15ACM ∠=︒,1AM =,求BM 的长.23.已知ABC ∆中,如果过项点B 的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为ABC ∆的关于点B 的二分割线.例如:如图1,Rt ABC ∆中,90A ︒∠=,20C ︒∠=,若过顶点B 的一条直线BD 交AC 于点D ,若20DBC ︒∠=,显然直线BD 是ABC ∆的关于点B 的二分割线.(1)在图2的ABC ∆中,20C ︒∠=,110ABC ︒∠=.请在图2中画出ABC ∆关于点B 的二分割线,且DBC ∠角度是 ;(2)已知20C ︒∠=,在图3中画出不同于图1,图2的ABC ∆,所画ABC ∆同时满足:①C ∠为最小角;②存在关于点B 的二分割线.BAC ∠的度数是 ;(3)已知C α∠=,ABC ∆同时满足:①C ∠为最小角;②存在关于点B 的二分割线.请求出BAC ∠的度数(用α表示).24.如图,△ABC 中AC =BC ,点D ,E 在AB 边上,连接CD ,CE .(1)如图1,如果∠ACB =90°,把线段CD 逆时针旋转90°,得到线段CF ,连接BF , ①求证:△ACD ≌△BCF ;②若∠DCE =45°, 求证:DE 2=AD 2+BE 2;(2)如图2,如果∠ACB =60°,∠DCE =30°,用等式表示AD ,DE ,BE 三条线段的数量关系,说明理由.25.如图, ABD 为边长不变的等腰直角三角形,AB AD =,90BAD ∠=︒,在 ABD 外取一点 E ,以A 为直角顶点作等腰直角AEP △,其中 P 在ABD 内部,90EAP ∠=︒,2AE AP ==E 、P 、D 三点共线时,7BP =下列结论:①E 、P 、D 共线时,点B 到直线AE 5②E 、P 、D 共线时, 13ADP ABP S S ∆∆+==532ABD S ∆+③; ④作点 A 关于 BD 的对称点 C ,在 AEP 绕点 A 旋转的过程中,PC 的最小值为5+232-;⑤AEP △绕点A 旋转,当点E 落在AB 上,当点P 落在AD 上时,取BP 上一点N ,使得AN BN =,连接 ED ,则AN ED ⊥.其中正确结论的序号是___.26.我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:(1)叙述勾股定理(用文字及符号语言叙述);(2)证明勾股定理;(3)若大正方形的面积是13,小正方形的面积是1,求()2a b +的值.27.如图,在△ABC 中,∠C =90°,把△ABC 沿直线DE 折叠,使△ADE 与△BDE 重合.(1)若∠A =35°,则∠CBD 的度数为________;(2)若AC =8,BC =6,求AD 的长;(3)当AB =m(m>0),△ABC 的面积为m +1时,求△BCD 的周长.(用含m 的代数式表示)28.如图1,在平面直角坐标系中,直线AB 经过点C (a ,a ),且交x 轴于点A (m ,0),交y 轴于点B (0,n ),且m ,n 6m -n ﹣12)2=0.(1)求直线AB 的解析式及C 点坐标;(2)过点C 作CD ⊥AB 交x 轴于点D ,请在图1中画出图形,并求D 点的坐标;(3)如图2,点E (0,﹣2),点P 为射线AB 上一点,且∠CEP =45°,求点P 的坐标.29.如图1,点E 是正方形ABCD 边CD 上任意一点,以DE 为边作正方形DEFG ,连接BF ,点M 是线段BF 中点,射线EM 与BC 交于点H ,连接CM .(1)请直接写出CM 和EM 的数量关系和位置关系.(2)把图1中的正方形DEFG 绕点D 顺时针旋转45︒,此时点F 恰好落在线段CD 上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由.(3)把图1中的正方形DEFG 绕点D 顺时针旋转90︒,此时点E 、G 恰好分别落在线段AD 、CD 上,连接CE ,如图3,其他条件不变,若2DG =,6AB =,直接写出CM 的长度.30.在平面直角坐标系中,点A (0,4),B (m ,0)在坐标轴上,点C ,O 关于直线AB 对称,点D 在线段AB 上.(1)如图1,若m =8,求AB 的长;(2)如图2,若m =4,连接OD ,在y 轴上取一点E ,使OD =DE ,求证:CE =2DE ; (3)如图3,若m =43,在射线AO 上裁取AF ,使AF =BD ,当CD +CF 的值最小时,请在图中画出点D 的位置,并直接写出这个最小值.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【详解】解:(1)当点P在x轴正半轴上,①以OA为腰时,∵A的坐标是(2,2),∴∠AOP=45°,OA=22,∴P的坐标是(4,0)或(22,0);②以OA为底边时,∵点A的坐标是(2,2),∴当点P的坐标为:(2,0)时,OP=AP;(2)当点P在x轴负半轴上,③以OA为腰时,∵A的坐标是(2,2),∴OA= 22∴OA=AP=2∴P的坐标是(-220).故选D.2.C解析:C【分析】做点F 做FH AD ⊥交AD 于点H ,因此要求出EF 的长,只要求出EH 和HF 即可;由折叠的性质可得BE=DE=9-AE ,在Rt ABE △中应用勾股定理求得AE 和BE ,同理在Rt BC F 'Rt ABE △中应用勾股定理求得BF ,在Rt EFH 中应用勾股定理即可求得EF .【详解】过点F 做FH AD ⊥交AD 于点H .∵四边形EFC B '是四边形EFCD 沿EF 折叠所得,∴ED=BE ,CF=C F ',3BC CD '==∵ED=BE ,DE=AD-AE=9-AE∴BE=9-AE∵Rt ABE △,AB=3,BE=9-AE∴()22293AE AE -=+∴AE=4∴DE=5∴9C F BC BF BF '=-=-∴Rt BC F ',3BC '=,9C F BF '=-∴()22293BF BF -+=∴BF=5,EH=1∵Rt EFH ,HF=3,EH=1 ∴22223110EF EH HF =+=+故选:C .【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题. 3.C解析:C【分析】根据ABP △为等腰三角形,分三种情况进行讨论,分别求出BP 的长度,从而求出t 值即可.【详解】在Rt ABC 中,222225316BC AB AC =-=-=,4BC cm ∴=,①如图,当AB BP =时, 5 ,5BP cm t ==;②如图,当AB AP =时,∵AC BP ⊥,∴28 BP BC cm ==,8t =;③如图,当BP AP =时,设AP BP xcm ==,则4,3( )CP x cm AC cm =-=,∵在Rt ACP 中,222AP AC CP =+,∴()22234x x =+-, 解得:258x =, ∴258t =, 综上所述,当ABP △为等腰三角形时,5t =或8t =或258t =. 故选:C .【点睛】本题考查了勾股定理,等腰三角形的性质,注意分类讨论.4.B解析:B【解析】【分析】根据完全平方公式利用a+b=10,ab=18求出22a b +,即可得到三角形的形状.【详解】∵a+b=10,ab=18,∴22a b +=(a+b )2-2ab=100-36=64,∵,c=8,∴2c =64,∴22a b +=2c ,∴该三角形是直角三角形,故选:B.【点睛】此题考查勾股定理的逆定理,完全平方公式,能够利用完全平方公式由已知条件求出22a b +是解题的关键.5.B解析:B【分析】过点A 作AE ⊥AD 交CD 于E ,连接BE ,利用SAS 可证明△BAE ≌△CAD ,利用全等的性质证得∠BED=90°,最后根据勾股定理即可求出BD.【详解】解:如图,过点A 作AE ⊥AD 交CD 于E ,连接BE.∵∠DAE=90°,∠ADE=45°,∴∠ADE=∠AED=45°,∴AE=AD=1,∴在Rt △ADE 中,22112+=∵∠DAE=∠BAC=90°,∴∠DAE+∠EAC=∠BAC+∠EAC ,即∠CAD=∠BAE ,又∵AB=AC,∴△BAE ≌△CAD(SAS),∴CD=BE=3,∠AEB=∠ADC=45°,∴∠BED=90°,∴在Rt △BED 中,()22223211BE DE +=+=故选B.【点睛】本题考查了全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理等知识,作辅助线构造出全等三角形是解题的关键.6.A解析:A【解析】分析:将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,延长BP,作AF⊥BP于点F.AP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数,在直角△APF中利用三角函数求得AF和PF的长,则在直角△ABF中利用勾股定理求得AB的长,进而求得三角形ABC的面积.详解:∵△ABC为等边三角形,∴BA=BC,可将△BPC绕点B逆时针旋转60°得△BEA,连EP,且延长BP,作AF⊥BP于点F.如图,∴BE=BP=4,AE=PC=5,∠PBE=60°,∴△BPE为等边三角形,∴PE=PB=4,∠BPE=60°,在△AEP中,AE=5,AP=3,PE=4,∴AE2=PE2+PA2,∴△APE为直角三角形,且∠APE=90°,∴∠APB=90°+60°=150°.∴∠APF=30°,∴在直角△APF中,AF=12AP=32,PF=3AP=332.∴在直角△ABF中,AB2=BF2+AF2=(4+332)2+(32)2=25+123.则△ABC的面积是3•AB2=3•(25+12)253故选A.点睛:本题考查了等边三角形的判定与性质、勾股定理的逆定理以及旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.7.B解析:B【分析】根据直角三角形的勾股定理,得:两条直角边的平方等于斜边的平方.再根据正方形的面积公式,知:以两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积.【详解】解:A的面积等于100-64=36;故选:B.【点睛】本题主要考查勾股定理的证明:以两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积.8.A解析:A【分析】设CF=x,则AC=x+2,再由已知条件得到AB=6,BC=6+x,再由AB2+AC2=BC2得到62+(x+2)2=(x+4)2,解方程即可.【详解】设CF=x,则AC=x+2,∵正方形ADOF的边长是2,BD=4,△BDO≌△BEO,△CEO≌△CFO,∴BD=BE,CF=CE,AD=AF=2,∴AB=6,BC=6+x,∵∠A=90°,∴AB2+AC2=BC2,∴62+(x+2)2=(x+4)2,解得:x=6,即CF=6,故选:A.【点睛】考查正方形的性质、勾股定理,解题关键是设CF=x,则AC=x+2,利用勾股定理得到62+(x+2)2=(x+4)2.9.D解析:D【分析】24和10为两条直角边长时,求出小正方形的边长14,即可利用勾股定理得出EF的长.【详解】解:∵AE=10,BE=24,即24和10为两条直角边长时,小正方形的边长=24-10=14,∴EF=22+=.1414142故选D.【点睛】本题考查了勾股定理、正方形的性质;熟练掌握勾股定理是解决问题的关键.10.B解析:B【分析】根据“在Rt△ABC中”和“沿BD进行翻折”可知,本题考察勾股定理和翻折问题,根据勾股定理和翻折的性质,运用方程的方法进行求解.【详解】∵∠A=90°,AB=6,AC=8,∴BC=2286+=10,根据翻折的性质可得A′B=AB=6,A′D=AD,∴A′C=10-6=4.设CD=x,则A′D=8-x,根据勾股定理可得x2-(8-x)2=42,解得x=5,故CD=5.故答案为:B.【点睛】本题考察勾股定理和翻折问题,根据勾股定理把求线段的长的问题转化为方程问题是解决本题的关键.二、填空题11.5【详解】解:如图,延长AE交BC于点F,∵点E是CD的中点,∴DE=CE,,∵AB⊥BC,AB⊥AD,∴AD∥BC,∴∠ADE=∠BCE且DE=CE,∠AED=∠CEF,∴△AED≌△FEC(ASA),∴AD=FC=5,AE=EF,∴BF=BC-FC=5,∴在Rt △ABF 中,13AF ==,6.52AF AE == 故答案为:6.5.12.1或78【分析】 分为三种情况:①PQ BP =,②BQ QP =,③BQ BP =,由等腰三角形的性质和勾股定理可求解.【详解】解:分为3种情况:①当PB PQ =时,4=OA ,3OB =,∴5BC AB ===, C 点与A 点关于直线OB 对称,BAO BCO ∴∠=∠,BPQ BAO ∠=∠,BPQ BCO ∴∠=∠,APB APQ BPQ BCO CBP ∠=∠+∠=∠+∠,APQ CBP ∴∠=∠,在APQ 和CBP 中,BAO BCP APQ B PQ B P C P ∠=∠⎧⎪∠=∠⎨=⎪⎩, ()APQ CBP AAS ∴△≌△,∴5AP BC ==,1OP AP OA ∴=-=;②当BQ BP =时,BPQ BQP ∠=∠,BPQ BAO ∠=∠,BAO BQP ∴∠=∠,根据三角形外角性质得:BQP BAO ∠>∠,∴这种情况不存在;③当QB QP =时,QBP BPQ BAO ∠=∠=∠,PB PA ∴=,设OP x =,则4PB PA x ==-在Rt OBP △中,222PB OP OB =+,222(4)3x x ∴-=+, 解得:78x =; ∴当PQB △为等腰三角形时,1OP =或78; 【点睛】本题考查了勾股定理,等腰三角形的性质,全等三角形的性质和判定的应用,解题的关键是熟练掌握所学的性质进行解题,注意分类讨论.13.5或13【分析】根据已知可得题意中的图是一个勾股图,可得S P +S Q =S K 为从而易求S K .【详解】解:如下图所示,若A=S P =4.B=S Q =9,C=S K ,根据勾股定理,可得A+B=C ,∴C=13.若A=S P =4.C=S Q =9,B=S K ,根据勾股定理,可得A+B=C ,∴B=9-4=5.∴S K 为5或13.故答案为:5或13.【点睛】本题考查了勾股定理.此题所给的图中,以直角三角形两直角边为边所作的正方形的面积和等于以斜边为边所作的正方形的面积.14.103. 【分析】 根据八个直角三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形,得出CG=NG ,CF=DG=NF ,再根据()21S CG DG =+,22S GF =,()23S NG NF =-,12310S S S ++=,即可得出答案.【详解】∵八个直三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形∴CG=NG ,CF=DG=NF∴()2222122S CG DG CG DG CG DG GF CG DG =+=++=+ 22S GF =()22232S NG NF NG NF NG NF =-=+-∴2222212322310S S S GF CG DG GF NG NF NG NF GF ++=+⋅+++-⋅== ∴2103GF =故2103S = 故答案为103. 【点睛】 本题主要考查了勾股定理的应用,用到的知识点由勾股定理和正方形、全等三角形的性质.15.【解析】【详解】∵(x-6)2=9,∴x-6=±3,解得:x 1=9,x 2=3,∵x ,y 为一个直角三角形的两边的长,y=3,∴当x=3时,x 、y =;当x=9时,x 、y =;当x=9时,x 为斜边、y 为直角边,则第三边为263922=-.故答案为:【点睛】本题主要考查了勾股定理的应用,正确分类讨论是解决问题的关键,解题时注意一定不要漏解.16.①②③【解析】【详解】解:∵△ABC 是等边三角形,60ABC ∴∠=,∵△BQC ≌△BPA ,∴∠BPA =∠BQC ,BP =BQ =4,QC =PA =3,∠ABP =∠QBC ,60PBQ PBC CBQ PBC ABP ABC ∴∠=∠+∠=∠+∠=∠=,∴△BPQ 是等边三角形,①正确.∴PQ =BP =4,2222224325,525PQ QC PC +=+===,222PQ QC PC ∴+=,90PQC ∴∠=,即△PQC 是直角三角形,②正确.∵△BPQ 是等边三角形,60PBQ BQP ∴∠=∠=,∵△BQC ≌△BPA ,∴∠APB =∠B QC ,6090150BPA BQC ∴∠=∠=+=,③正确.36015060150APC QPC QPC ∴∠=---∠=-∠,90PQC PQ QC ∠=≠,,45QPC ∴∠≠,即135APC ∠≠,④错误.故答案为①②③.17.78. 【解析】∵∠C =90°,AB =5,BC =4,∴AC .∵AB 的垂直平分线DE 交边BC 于点D ,∴BD =AD .设CD =x ,则AD =BD =4-x ,在Rt △ACD 中,2223(4)x x +=- ,解得:78x =.故答案为:78.18.9或9【分析】通过计算E 到AC 的距离即EH 的长度为3,所以根据DE 的长度有两种情况:①当点D 在H 点上方时,②当点D 在H 点下方时,两种情况都是过点E 作EH AC ⊥交AC 于点E ,过点G 作GQ AB ⊥交AB 于点Q ,利用含30°的直角三角形的性质和勾股定理求出AH,DH 的长度,进而可求AD 的长度,然后利用角度之间的关系证明AG GE =,再利用等腰三角形的性质求出GQ 的长度,最后利用2DGF AED AEG SS S =-即可求解.【详解】①当点D 在H 点上方时,过点E 作EH AC ⊥交AC 于点E ,过点G 作GQ AB ⊥交AB 于点Q ,12AB = ,点E 是AB 中点,162AE AB ∴== . ∵EH AC ⊥,90AHE ∴∠=︒ .30,6A AE ∠=︒=,132EH AE ∴== , 22226333AH AE EH ∴=-=-=. 32DE =,2222(32)33DH DE EH ∴=-=-= , DH EH ∴=,333AD AH DH =-=, 45EDH ∴∠=︒,15AED EDH A ∴∠=∠-∠=︒ .由折叠的性质可知,15DEF AED ∠=∠=︒, 230AEG AED ∴∠=∠=︒ ,AEG A ∴∠=∠,AG GE ∴= . 又GQ AE ⊥ ,132AQ AE ∴== . 30A ∠=︒ ,12GQ AG ∴=. 222GQ AQ AG += , 即2223(2)GQ GQ +=, 3GQ ∴= .2DGF AED AEG S S S =- ,112(333)36363922DGF S ∴=⨯⨯-⨯-⨯⨯=-; ②当点D 在H 点下方时,过点E 作EH AC ⊥交AC 于点E ,过点G 作GQ AB ⊥交AB 于点Q ,12AB = ,点E 是AB 中点,162AE AB ∴== . ∵EH AC ⊥,90AHE ∴∠=︒.30,6A AE ∠=︒= ,132EH AE ∴== , 22226333AH AE EH ∴=-=-=.32DE =,2222(32)33DH DE EH ∴=-=-= ,DH EH ∴=,3AD AH DH =+=,45DEH ∴∠=︒ ,90105AED A DEH ∴∠=︒-∠+∠=︒ .由折叠的性质可知,105DEF AED ∠=∠=︒,218030AEG AED ∴∠=∠-︒=︒ ,AEG A ∴∠=∠,AG GE ∴= .又GQ AE ⊥ ,132AQ AE ∴== . 30A ∠=︒,12GQ AG ∴= . 222GQ AQ AG += , 即2223(2)GQ GQ +=,GQ ∴= .2DGF AED AEG S S S =- ,1123)36922DGF S ∴=⨯⨯⨯-⨯=,综上所述,DGF △的面积为9或9.故答案为:9或9.【点睛】本题主要考查折叠的性质,等腰三角形的判定及性质,等腰直角三角形的性质,勾股定理,含30°的直角三角形的性质,能够作出图形并分情况讨论是解题的关键. 19.3【分析】根据题意利用折叠后图形全等,并利用等量替换和等腰三角形的性质进行综合分析求解.【详解】解:由题意可知','ACM A CM BCH B CH ≅≅,∵15cm BC =,20cm AC =,∴'15,'20,BC B C cm AC A C cm ====''20155A B cm =-=,∵90ACB ∠=︒,∴'A M AB ⊥(等量替换),CH AB ⊥(三线合一),∴25,AB cm = 利用勾股定理假设MB '的长为m ,'257AM AM m ==-,则有222(257)5m m +-=,解得3m =,所以MB '的长为3.【点睛】本题考查几何的翻折问题,熟练掌握并综合利用等量替换和等腰三角形的性质以及勾股定理分析是解题的关键.20.【分析】 根据三角形等面积法求出32AC BC = ,在Rt△ACD 中根据勾股定理得出AC 2=14BC 2+36,依据这两个式子求出AC 、BC 的值.【详解】 ∵AD 是BC 边上的高,BE 是AC 边上的高, ∴12AC•BE=12BC•AD, ∵AD=6,BE =4, ∴AC BC =32, ∴22AC BC =94, ∵AB=AC ,AD⊥BC,∴BD=DC =12BC , ∵AC 2﹣CD 2=AD 2,∴AC 2=14BC 2+36, ∴221364BC BC +=94, 整理得,BC 2=3648⨯, 解得:BC=∴△ABC 的面积为12×cm 2故答案为:【点睛】本题考查了三角形的等面积法以及勾股定理的应用,找出AC 与BC 的数量关系是解答此题的关键.三、解答题21.(1)BF长为6;(2)CE长为3,详细过程见解析.【分析】(1)由矩形的性质及翻折可知,∠B=90°,AF=AD=10,且AB=8,在Rt△ABF中,可由勾股定理求出BF的长;(2)设CE=x,根据翻折可知,EF=DE=8-x,由(1)可知BF=6,则CF=4,在Rt△CEF中,可由勾股定理求出CE的长.【详解】解:(1)∵四边形ABCD为矩形,∴∠B=90°,且AD=BC=10,又∵AFE是由ADE沿AE翻折得到的,∴AF=AD=10,又∵AB=8,在Rt△ABF中,由勾股定理得:,故BF的长为6.(2)设CE=x ,∵四边形ABCD为矩形,∴CD=AB=8,∠C=90°,DE=CD-CE=8-x,又∵△AFE是由△ADE沿AE翻折得到的,∴FE=DE=8-x,由(1)知:BF=6,故CF=BC-BF=10-6=4,CF+CE=EF,在Rt△CEF中,由勾股定理得:222∴2224+x=(8-x),解得:x=3,故CE的长为3.【点睛】本题考查了折叠的性质:折叠是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,利用勾股定理求解是本题的关键.22.(12)见解析;(3)2【分析】(1)分两种分割法利用勾股定理即可解决问题;(2)如图,过点A作AD⊥AB,且AD=BN.只要证明△ADC≌△BNC,推出CD=CN,∠ACD=∠BCN,再证明△MDC≌△MNC,可得MD=MN,由此即可解决问题;(3)过点B作BP⊥AB,使得BP=AM=1,根据题意可得△CPB≌△CMA,△CMN≌△CPN,利用全等性质推出∠BNP=30°,从而得到NB和NP的长,即得BM.【详解】解:(1)当MN最长时,,当BN最长时,(2)证明:如图,过点A作AD⊥AB,且AD=BN,在△ADC和△BNC中,AD BN DAC B AC BC =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△BNC (SAS ),∴CD=CN ,∠ACD=∠BCN ,∵∠MCN=45°,∴∠DCA+∠ACM=∠ACM+∠BCN=45°,∴∠MCD=∠MCN ,在△MDC 和△MNC 中,CD CN MCD MCN CM CM =⎧⎪∠=∠⎨⎪=⎩,∴△MDC ≌△MNC (SAS ),∴MD=MN在Rt △MDA 中,AD 2+AM 2=DM 2,∴BN 2+AM 2=MN 2,∴点M ,N 是线段AB 的勾股分割点;(3)过点B 作BP ⊥AB ,使得BP=AM=1,根据(2)中过程可得:△CPB ≌△CMA ,△CMN ≌△CPN ,∴∠AMC=∠BPC=120°,AM=PB=1,∠CMN=∠CPN=∠A+∠ACM=45°+15°=60°,∴∠BPN=120°-60°=60°,∴∠BNP=30°,∴NP=2BP=2=MN ,∴BN=22213-=,∴BM=MN+BN=23+.【点睛】本题是三角形的综合问题,考查了全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.23.(1)作图见解析,20DBC ∠=︒;(2)作图见解析,35BAC ∠=︒;(3)∠A =45°或90°或90°-2α或1452α︒-,或α=45°时45°<∠BAC <90°.【分析】(1)根据二分割线的定义,只要把∠ABC 分成90°角和20°角即可;(2)可以画出∠A=35°的三角形;(3)设BD 为△ABC 的二分割线,分以下两种情况.第一种情况:△BDC 是等腰三角形,△ABD 是直角三角形;第二种情况:△BDC 是直角三角形,△ABD 是等腰三角形分别利用直角三角形的性质、等腰三角形的性质和三角形的内角和定理解答即可.【详解】解:(1)ABC ∆关于点B 的二分割线BD 如图4所示,20DBC ∠=︒;故答案为:20°;(2)如图所示:∠BAC=35°;(3)设BD 为△ABC 的二分割线,分以下两种情况.第一种情况:△BDC 是等腰三角形,△ABD 是直角三角形,易知∠C 和∠DBC 必为底角, ∴∠DBC =∠C =α.当∠A =90°时,△ABC 存在二分分割线;当∠ABD =90°时,△ABC 存在二分分割线,此时∠A =90°-2α;当∠ADB =90°时,△ABC 存在二分割线,此时α=45°且45°<∠A <90°;第二种情况:△BDC 是直角三角形,△ABD 是等腰三角形,当∠DBC =90°时,若BD =AD ,则△ABC 存在二分割线,此时1809014522A αα︒-︒-∠==︒-; 当∠BDC =90°时,若BD =AD ,则△ABC 存在二分割线,此时∠A =45°,综上,∠A=45°或90°或90°-2α或1452α︒-,或α=45°时,45°<∠BAC<90°.【点睛】本题考查的是二分割线的理解与作图,属于新定义题型,主要考查了等腰三角形的性质、直角三角形的性质和三角形的内角和定理等知识,正确理解二分割线的定义、熟练掌握等腰三角形和直角三角形的性质是解答的关键.24.(1)①详见解析;②详见解析;(2)DE2=EB2+AD2+EB·AD,证明详见解析【分析】(1)①根据旋转的性质可得CF=CD,∠DCF=90°,再根据已知条件即可证明△ACD≌△BCF;②连接EF,根据①中全等三角形的性质可得∠EBF=90°,再证明△DCE≌△FCE得到EF=DE 即可证明;(2)根据(1)中的思路作出辅助线,通过全等三角形的判定及性质得出相等的边,再由勾股定理得出AD,DE,BE之间的关系.【详解】解:(1)①证明:由旋转可得CF=CD,∠DCF=90°∵∠ACD=90°∴∠ACD=∠BCF又∵AC=BC∴△ACD≌△BCF②证明:连接EF,由①知△ACD≌△BCF∴∠CBF=∠CAD=∠CBA=45°,∠BCF=∠ACD,BF=AD∴∠EBF=90°∴EF2=BE2+BF2,∴EF2=BE2+AD2又∵∠ACB=∠DCF=90°,∠CDE=45°∴∠FCE=∠DCE=45°又∵CD=CF,CE=CE∴△DCE≌△FCE∴EF=DE∴DE2= AD2+BE2⑵DE2=EB2+AD2+EB·AD理由:如图2,将△ADC 绕点C 逆时针旋转60°,得到△CBF ,过点F 作FG ⊥AB ,交AB 的延长线于点G ,连接EF ,∴∠CBE=∠CAD ,∠BCF=∠ACD , BF=AD∵AC=BC ,∠ACB=60°∴∠CAB=∠CBA =60°∴∠ABE=120°,∠EBF=60°,∠BFG=30°∴BG=12BF ,FG=3BF ∵∠ACB=60°,∠DCE=30°,∴∠ACD+∠BCE=30°,∴∠ECF=∠FCB+∠BCE=30°∵CD=CF ,CE=CE∴△ECF ≌△ECD∴EF=ED在Rt △EFG 中,EF 2=FG 2+EG 2又∵EG=EB+BG∴EG=EB+12BF , ∴EF 2=(EB+12BF )2+(3BF )2 ∴DE 2= (EB+12AD )2+(3AD )2 ∴DE 2= EB 2+AD 2+EB ·AD【点睛】本题考查了全等三角形的性质与旋转模型,解题的关键是找出全等三角形,转换线段,并通过勾股定理的计算得出线段之间的关系.25.②③⑤【分析】①先证得ABE ADP ≅,利用邻补角和等腰直角三角形的性质求得90PEB ∠=︒,利用勾股定理求出BE ,即可求得点B 到直线AE 的距离;②根据①的结论,利用APD ABP ABE APB S S S S ∆∆∆+=+AEP BEP S S ∆∆=+即可求得结论; ③在Rt AHB 中,利用勾股定理求得2AB ,再利用三角形面积公式即可求得ABD S ∆;④当A P C 、、共线时,PC 最小,利用对称的性质,AB BC =的长,再求得AC 的长,即可求得结论;⑤先证得ABP ADE ≅,得到ABP ADE ∠=∠,根据条件得到ABP NAB ∠=∠,利用互余的关系即可证得结论.【详解】①∵ABD 与AEP 都是等腰直角三角形,∴90BAD ∠=︒,90EAP ∠=︒,AB AD =,AE AP =,45APE AEP ∠=∠=︒, ∴EAB PAD ∠=∠, ∴()ABE ADP SAS ≅,∴180********AEB APD APE ∠=∠=︒-∠=︒-︒=︒,∴1354590PEB AEB AEP ∠=∠-∠=︒-︒=︒,∴222PE BE PB +=,∵2AE AP ==,90EAP ∠=︒, ∴22PE AE ==,∴()22227BE +=, 解得:3BE =,作BH ⊥AE 交AE 的延长线于点H ,∵45AEP ∠=︒,90PEB ∠=︒, ∴180180904545HEB PEB AEP ∠=︒-∠-∠=︒-︒-︒=︒,∴26sin 453HB BE =︒==, ∴点B 到直线AE 6,故①错误; ②由①知:ABE ADP ≅,2EP =,3BE =∴APD ABP ABE APB S S S S ∆∆∆∆+=+AEP BEP S S ∆∆=+1122AE AP PE EB =⨯⨯+⨯⨯112223 22=⨯⨯+⨯⨯13=+,故②正确;③在Rt AHB中,由①知:6EH HB==,∴62AH AE EH=+=+,2222225662322AB AH BH⎛⎫⎛⎫=+=++=+⎪ ⎪⎪ ⎪⎭⎝⎭,21153222ABDS AB AD AB∆=⋅==+,故③正确;④因为AC是定值,所以当A P C、、共线时,PC最小,如图,连接BC,∵A C、关于BD的对称,∴523AB BC==+∴225231043AC BC==+=+∴minPC AC AP=-,10432=+⑤∵ABD与AEP都是等腰直角三角形,∴90BAD∠=︒,90EAP∠=︒,AB AD=,AE AP=,在ABP和ADE中,AB ADBAP DAEAP AE=⎧⎪∠=∠⎨⎪=⎩,∴()ABP ADE SAS≅,∴ABP ADE∠=∠,∵AN BN=,∴ABP NAB∠=∠,∴EAN ADE∠=∠,∵90EAN DAN∠+∠=︒,∴90ADE DAN ∠+∠=︒,∴AN DE ⊥,故⑤正确;综上,②③⑤正确,故答案为:②③⑤.【点睛】本题是三角形的综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理的应用,三角形的面积公式,综合性强,全等三角形的判定和性质的灵活运用是解题的关键.26.(1)见解析;(2)证明见解析;(3)25.【分析】(1)直接叙述勾股定理的内容,并用字母表明三边关系;(2)利用大正方形面积、小正方形面积和4个直角三角形的面积和之间的关系列式整理即可证明;(3)将原式利用完全平方公式展开,由勾股定理的内容可得出()2a b +为大正方形面积和4个直角三角形的面积和,根据已知条件即可求得.【详解】解:(1)勾股定理:直角三角形两直角边的平方和等于斜边的平方.在直角三角形中,两条直角边分别为 a 、b ,斜边为 c ,a 2+b 2= c 2.(2)∵ S 大正方形=c 2,S 小正方形=(b-a)2,4 S Rt △=4×12ab=2ab , ∴ c 2=2ab+(b-a)2=2ab+b 2-2ab+a 2=a 2+b 2,即 a 2+b 2= c 2.(3)∵ 4 S Rt △= S 大正方形- S 小正方形=13-1=12,∴ 2ab=12.∴ (a+b)2= a 2+b 2+2ab=c 2+2ab=13+12=25.【点睛】本题考查勾股定理的内容及勾股定理的几何验证,利用等面积法证明勾股定理及运用勾股定理是解答此题的关键.27.(1)∠CBD=20°;(2)AD=164;(3) △BCD 的周长为m+2 【分析】(1)根据折叠可得∠1=∠A=35°,根据三角形内角和定理可以计算出∠ABC=55°,进而得到∠CBD=20°;(2)根据折叠可得AD=DB,设CD=x,则AD=BD=8-x,再在Rt△CDB中利用勾股定理可得x2+62=(8-x)2,再解方程可得x的值,进而得到AD的长;(3)根据三角形ACB的面积可得11 2AC CB m=+,进而得到AC•BC=2m+2,再在Rt△CAB中,CA2+CB2=BA2,再把左边配成完全平方可得CA+CB的长,进而得到△BCD的周长.【详解】(1)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,∴∠1=∠A=35°,∵∠C=90°,∴∠ABC=180°-90°-35°=55°,∴∠2=55°-35°=20°,即∠CBD=20°;(2)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,∴AD=DB,设CD=x,则AD=BD=8-x,在Rt△CDB中,CD2+CB2=BD2,x2+62=(8-x)2,解得:x= 74,AD=8-74=164;(3)∵△ABC 的面积为m+1,∴12AC•BC=m+1,∴AC•BC=2m+2,∵在Rt△CAB中,CA2+CB2=BA2,∴CA2+CB2+2AC•BC=BA2+2AC•BC,∴(CA+BC)2=m2+4m+4=(m+2)2,∴CA+CB=m+2,∵AD=DB,∴CD+DB+BC=m+2.即△BCD的周长为m+2.【点睛】此题主要考查了图形的翻折变换,以及勾股定理,完全平方公式,关键是掌握勾股定理,以及折叠后哪些是对应角和对应线段.28.(1)y=-2x+12,点C坐标(4,4);(2)画图形见解析,点D坐标(-4,0);(3)点P的坐标(143-,643)【分析】(1)由已知的等式可求得m、n的值,于是可得直线AB的函数解析式,把点C的坐标代入可求得a的值,由此即得答案;(2)画出图象,由CD⊥AB知1AB CDk k=-可设出直线CD的解析式,再把点C代入可得CD的解析式,进一步可求D点坐标;(3)如图2,取点F(-2,8),易证明CE⊥CF且CE=CF,于是得∠PEC=45°,进一步求出直线EF的解析式,再与直线AB联立求两直线的交点坐标,即为点P.【详解】解:(1)∵6m-+(n﹣12)2=0,∴m=6,n=12,∴A(6,0),B(0,12),设直线AB解析式为y=kx+b,则有1260bk b=⎧⎨+=⎩,解得212kb=-⎧⎨=⎩,∴直线AB解析式为y=-2x+12,∵直线AB过点C(a,a),∴a=-2a+12,∴a=4,∴点C坐标(4,4).(2)过点C作CD⊥AB交x轴于点D,如图1所示,设直线CD解析式为y=12x+b′,把点C(4,4)代入得到b′=2,∴直线CD解析式为y=12x+2,∴点D坐标(-4,0).(3)如图2中,取点F (-2,8),作直线EF 交直线AB 于P ,图2∵直线EC 解析式为y =32x -2,直线CF 解析式为y =-23x +203, ∵32×(-23)=-1, ∴直线CE ⊥CF ,∵EC =13CF =13∴EC =CF ,∴△FCE 是等腰直角三角形,∴∠FEC =45°,∵直线FE 解析式为y =-5x -2,由21252y x y x =-+⎧⎨=--⎩解得143643x y ⎧=-⎪⎪⎨⎪=⎪⎩, ∴点P 的坐标为(1464,33-). 【点睛】本题是一次函数的综合题,综合考查了坐标系中两直线的垂直问题、两条直线的交点问题和求特殊角度下的直线解析式,并综合了勾股定理和等腰直角三角形的判定和性质,解题的关键是熟知坐标系中两直线垂直满足121k k =-,一次函数的交点与对应方程组的解的关系.其中,第(3)小题是本题的难点,寻找到点F (-2,8)是解题的突破口.29.(1),CM ME CM EM =⊥;(2)见解析;(3)25CM =【解析】【分析】(1)证明ΔFME ≌ΔAMH ,得到HM=EM ,根据等腰直角三角形的性质可得结论. (2)根据正方形的性质得到点A 、E 、C 在同一条直线上,利用直角三角形斜边上的中线等于斜边的一半可知. (3)如图3中,连接EC ,EM ,由(1)(2)可知,△CME 是等腰直角三角形,利用等腰直角三角形的性质解决问题即可.【详解】解:(1)结论:CM =ME ,CM ⊥EM .理由:∵AD ∥EF ,AD ∥BC ,∴BC ∥EF ,∴∠EFM =∠HBM ,在△FME 和△BMH 中,EFM MBH FM BMFME BMH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△FME ≌△BMH (ASA ),∴HM =EM ,EF =BH ,∵CD =BC ,∴CE =CH ,∵∠HCE =90°,HM =EM ,∴CM =ME ,CM ⊥EM .(2)如图2,连接BD ,∵四边形ABCD 和四边形EDGF 是正方形,∴45,45FDE CBD ︒︒∠=∠=∴点B E D 、、在同一条直线上,∵90,90BCF BEF ︒︒∠=∠=,M 为BF 的中点, ∴12CM BF =,12EM BF =,∴CM ME =, ∵45EFD ∠=︒,∴135EFC ∠=︒,∵CM FM ME ==,∴,MCF MFC MFE MEF ∠=∠∠=∠∴135MCF MEF ∠+∠=︒,∴36013513590CME ∠=︒-︒-︒=︒,∴CM ME ⊥.(3)如图3中,连接EC ,EM .由(1)(2)可知,△CME是等腰直角三角形,∵22=+=EC26210∴CM=EM=25【点睛】本题考查的是正方形的性质、全等三角形的判定定理和性质定理以及直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.30.(1)AB=45;(2)见解析;(3)CD+CF的最小值为47.【分析】(1)根据勾股定理可求AB的长;(2)过点D作DF⊥AO,根据等腰三角形的性质可得OF=EF,根据轴对称的性质等腰直角三角形的性质可得AF=DF,设OF=EF=x,AE=4﹣2x,根据勾股定理用参数x表示DE,CE的长,即可证CE=2DE;(3)过点B作BM⊥OB,在BM上截取BM=AO,过点C作CN⊥BM,交MB的延长线于点N,根据锐角三角函数可得∠ABO=30°,根据轴对称的性质可得AC=AO=4,BO=BC =43,∠ABO=∠ABC=30°,∠OAB=∠CAB=60°,根据“SAS”可证△ACF≌△BMD,可得CF=DM,则当点D在CM上时,CF+CD的值最小,根据直角三角形的性质可求CN,BN的长,根据勾股定理可求CM的长,即可得CF+CD的最小值.【详解】(1)∵点A(0,4),B(m,0),且m=8,∴AO=4,BO=8,在Rt△ABO中,AB=2245+=AO BO(2)如图,过点D作DF⊥AO,∵DE=DO,DF⊥AO,∴EF=FO,∵m=4,∴AO=BO=4,∴∠ABO=∠OAB=45°,。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,在⊙O中,AB是⊙O的直径,AB=12,点C、D是的三等分点,M 是AB上一动点,则CM+DM的最小值是()A.16B.12C.8D.62、如图,圆柱形容器中,高为1.2 m,底面周长为1m,在容器内壁离容器底部0.3 m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m 与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为()m(容器厚度忽略不计).A.1.8B.1.5C.1.2D.1.33、如图,在矩形ABCD中,O是对角线AC、BD的交点,点E,F分别是OD,OC 的中点.如果AC=10,BC=8,那么EF的长为()A.6B.5C.4D.34、在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积()A.4B.6C.16D.555、某直角三角形最长边为17,最短边长为8,则第三边长为()A.9B.15C.20D.256、如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()A.2B.8C.2D.27、如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为()A.10B.8C.D.68、如图,在正方形ABCD中,对角线AC,BD交于点0,过点0的直线分别交边AD,BC于点E,F,EF=6.则AE2+BF2的值为()A.9B.16C.18D.369、在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N.给出以下结论,= ,其中正确的个数有()①HO=OF ②0F2=ON·OB③HM=2MG ④S△HOMA.1B.2C.3D.410、下列各组数,可以作为直角三角形的三边长的是()A.8,12,20B.2,3,4C.8,10,6D.5,13,1511、如图,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB =6,△ABF的面积是24,则FC等于()A.1B.2C.3D.412、如图,矩形ABCD的对角线AC,BD相交于点O,AD=3,∠AOD=60°,则AB的长为()A.3B.2C.3D.613、如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()A. B. C. D.14、下列四组线段中,可以构成直角三角形的是A.2,3,4B.3,4,5C.4,5,6D.7,8,915、如图,▱ABCD的对角线AC,BD交于点O,AC⊥AB,AB=,BO=3,那么AC的长为()A.2B.C.3D.4二、填空题(共10题,共计30分)16、如图,在△ABC和△EDB中,∠C=∠EBD=90°,点E在AB上.若△ABC≌△EDB,AC=4,BC=3,则AE=________.17、阅读下面的材料勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.由图1可以得到(a+b)2=4×ab+c2,整理,得a2+2ab+b2=2ab+c2.所以a2+b2=c2.如果把图1中的四个全等的直角三角形摆成图2所示的正方形,请你参照上述证明勾股定理的方法,完成下面的填空:由图2可以得到________整理,得________所以________18、等腰三角形的腰长为5,一腰上的高为3,则这个等腰三角形底边的长为________ .19、如图,△ABC中,∠B=90°,AB=4, BC=3,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是________。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、下列四组线段中,不能作为直角三角形三条边的是()A.8,15,17B.1,2,C.7,23,25D.1.5,2,2.52、已知三角形两边的长分别是4和3,第三边的长是一元二次方程x2-8x+15=0的一个实数根,则该三角形的面积是()A.12或B.6C.6或2D.3、如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m.如果保持梯子底端的位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,那么小巷的宽度为( )A.0.7 mB.1.5 mC.2.2 mD.2.4 m4、直角三角形两条直角边长分别是5和12,则第三边上的中线长为()A.5B.6C.6.5D.125、下列各组数中,是勾股数的一组是()A.7,8,9B.8,15,17C.1,1,2D.2,3,46、△ABC中,AB=13,AC=15,高AD=12,则BC的长为()A.14B.4C.14或4D.以上都不对7、如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.∠ADC=30°,AD=3,BD=5,则CD的长为()A. B.4 C. D.4.58、已知直角三角形两边的长为3和4,则第三边的长为()A.5B.C.5或﹣1D.以上都不对9、如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是()A.16B.18C.19D.2110、如图, 三个正方形围成一个直角三角形,64、400分别为所在正方形的面积,则图中字母所代表的正方形面积是()A.336B.164096C.464D.15590411、如图,已知RtΔABC中,∠ACB=90°,AC= 4,BC=3,以AB边所在的直线为轴,将ΔABC旋转一周,则所得几何体的表面积是().A. πB.24πC. πD.12π12、在△ABC中,命题:①若∠B=∠C-∠A,则△ABC是直角三角形.②若a2=(b+c)(b-c),则△ABC是直角三角形.③若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形.④若a∶b∶c=5∶4∶3.则△ABC是直角三角形.其中假命题个数为( )A.1个B.2个C.3个D.4个13、如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为()A.3B.4C.5D.614、在Rt△ABC中,∠C=90°,,AC=8cm,则BC的长度为().A.3cmB.4cmC.5cmD.6cm15、如图,点A、B、C、D均在边长为1的正方形网格的格点上,则sin∠BAC 的值为()A. B.1 C. D.二、填空题(共10题,共计30分)16、在△ABC中,∠A=30°,AB=6,BC=2 .则AC的长为________.17、如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是________.18、在四边形中,且,,,,则________.19、如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则CD的长为________.20、如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG 的长=________.21、如图,是等腰直角三角形,,为边上一点,且,连结,过点C作于点E,交于点F.若,则的长为________.22、如图所示.△ABC为等腰直角三角形,∠ACB=90°,点M为AB边的中点,点N为射线AC上一点,连接BN,过点C作CD⊥BN于点D。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、下列各组线段中的三个长度:①9,12,15;②7,24,25;③32, 42,52;④3a,4a,5a(a>0);⑤m2﹣n2, 2mn,m2+n2(m,n为正整数,且m>n)其中可以构成直角三角形的有()A.5组B.4组C.3组D.2组2、如图,在⊙O中,半径为13,弦AB垂直于半径OC交OC于点D,AB=24,则CD的长为()A.5B.12C.8D.73、如图,在等边△ABC中.AB=2。
N为AB上一点,且AN=1,∠BAC的平分线交BC于点D.M是AD上的动点,连结BM、MN。
则BM+MN的最小值是( ) 。
A. B.2 C.1 D.34、有一个著名的希波g拉蒂月牙问题:如图1,以直角三角形的各边为直径分别向上作半圆,则直角三角形的面积可表示成两个月牙形的面积之和.现将三个半圆纸片沿直角三角形的各边向下翻折得到图2,把较小的两张半圆纸片的重叠部分面积记为S1,大半圆纸片未被覆盖部分的面积记为S2,则直角三角形的面积可表示成( )A.S1+S2B.S2-S1C.S2-2S1D.S1·S25、如图,平面直角坐标系中,A点坐标为,点在直线上运动,设的值为,则下面能够大致反映w与m的函数关系的图象是()A. B. C. D.6、如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是()A.2B.2C.4D.47、五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是()A. B. C. D.8、如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为( ).A. B. C. D.9、如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )A.10B.8C.6D.410、直角三角形两条直角边的和为7,面积为6,则斜边为().A. B.5 C. D.711、一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )A.9分米B.15分米C.5分米D.8分米12、如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC 于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有()①△ABC是等腰三角形;②BF=AC;③BH:BD:BC=1::;④GE2+CE2=BG2.A.1个B.2个C.3个D.4个13、如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?()A.10B.11C.12D.1314、如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是()A. B. C. D.15、如图所示:数轴上点A所表示的数为a,则a的值是()A. +1B.- +1C. -1D.二、填空题(共10题,共计30分)16、在中,,,,该三角形最长边上的高为________cm.17、如图,在△ABC中,∠C=90°,AC=6,BC=8,CD是斜边AB上的中线,G是△ABC的重心,GH⊥AB于H,则GH=________.18、如图,△ABC中,点O是重心,过点O的两条线段BE⊥AD.若BD=10,BO =8,则AO的长为________.19、如图,已知直线l:y= x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N 1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M8坐标为________.20、如图,已知,数轴上点A对应的数是________21、如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为________.22、如图所示,直线 y=x+2 与两坐标轴分别交于 A、B 两点,点 C 是 OB 的中点,D、E 分别是直线 AB、y 轴上的动点,则△CDE 周长的最小值是________.23、在△ABC中,AB=AC=41 cm,BC=80 am,AD为∠A的平分线,则S△=________ABC24、在Rt△ABC中,∠ACB= AC=4,BC=3,CD是AB边上的高.则CD的长为________25、如图,在Rt△ABC中,∠A=90°,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,若BE=2,则AC的长为________.三、解答题(共5题,共计25分)26、如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.求AB的长.27、小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示).28、如图,点A、D、B在同一直线上,BC=15,CD=12,AC=13,AD=5.求AB的长.29、写出如图格点△ABC各顶点的坐标,求出此三角形的周长.30、如图,四边形ABCD中,∠B=90°,AB=4,BC=3,CD=12,AD=13,求这个四边形ABCD的面积参考答案一、单选题(共15题,共计45分)1、B2、C3、A4、B5、A6、A7、C8、C9、B10、B11、D12、C13、C14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、30、。
八年级初二数学 数学勾股定理的专项培优练习题(含答案

一、选择题1.如图,在平行四边形ABCD 中,∠DBC=45°,DE ⊥BC 于E ,BF ⊥CD 于F ,DE ,BF 相交于H ,BF 与AD 的延长线相交于点G ,下面给出四个结论:①2BD BE =; ②∠A=∠BHE ;③AB=BH ; ④△BCF ≌△DCE , 其中正确的结论是( )A .①②③B .①②④C .②③④D .①②③④2.如图,在矩形纸片ABCD 中,AD =9,AB =3,将其折叠,使点D 与点B 重合,折痕为EF ,那么折痕EF 的长为( )A .3B .6C .10D .93.“勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在ABC 中,90ACB ∠=︒,分别以ABC 的三条边为边向外作正方形,连结EB ,CM ,DG ,CM 分别与AB ,BE 相交于点P ,Q .若30ABE ∠=︒,则DG QM的值为( )A 3B 5C .45D 314.如图,所有的四边形都是正方形,所有的三角形都是直角三角形。
若正方形A 、B 、C 、D 的边长是3、5、2、3,则最大正方形E 的面积是A .13B .225+C .47D .135.在△ABC 中,∠BCA=90∘,AC=6,BC=8,D 是AB 的中点,将△ACD 沿直线CD 折叠得到△ECD ,连接BE ,则线段BE 的长等于( )A .5B .75C .145D .3656.直角三角形的面积为 S ,斜边上的中线为 d ,则这个三角形周长为 ( ) A .22d S d ++B .2d S d --C .22d S d ++D .()22d S d ++7.下列结论中,矩形具有而菱形不一定具有的性质是( ) A .内角和为360° B .对角线互相平分 C .对角线相等D .对角线互相垂直 8.如图,在数轴上点A 所表示的数为a ,则a 的值为( )A .15-B .15C .5-D .15-+9.已知M 、N 是线段AB 上的两点,AM =MN =2,NB =1,以点A 为圆心,AN 长为半径画弧;再以点B 为圆心,BM 长为半径画弧,两弧交于点C ,连接AC ,BC ,则△ABC 一定是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形 10.在下列以线段a 、b 、c 的长为边,能构成直角三角形的是( )A .a =3,b =4,c =6B .a =5,b =6,c =7C .a =6,b =8,c =9D .a =7,b =24,c =25 二、填空题11.如图所示的网格是正方形网格,则ABC ACB ∠+∠=__________°(点A ,B ,C 是网格线交点).12.如图,ACB △和ECD 都是等腰直角三角形,CA CB =,CE CD =,ABC 的顶点A 在ECD 的斜边上.若3AE =,7AD =,则AC 的长为_________13.如图,△ABC 是一个边长为1的等边三角形,BB 1是△ABC 的高,B 1B 2是△ABB 1的高,B 2B 3是△AB 1B 2的高,……B n-1B n 是△AB n-2B n-1的高,则B 4B 5的长是________,猜想B n-1B n 的长是________.14.如图,四边形ABDC 中,∠ABD =120°,AB ⊥AC ,BD ⊥CD ,AB =4,CD =43,则该四边形的面积是______.15.如图所示,“赵爽弦图”是由8个全等的直角三角形拼接而成的,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为123,,S S S ,已知12310S S S ++=,则2S 的值是____.16.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,AD=4,AB=3,则CD=_________17.如图,P 是等边三角形ABC 内的一点,且PA=3,PB=4,PC=5,以BC 为边在△ABC 外作△BQC ≌△BPA ,连接PQ ,则以下结论中正确有_____________ (填序号)①△BPQ 是等边三角形 ②△PCQ 是直角三角形 ③∠APB=150° ④∠APC=135°18.如图所示,四边形ABCD 是长方形,把△ACD 沿AC 折叠到△ACD′,AD′与BC 交于点E ,若AD =4,DC =3,求BE 的长.19.如图,由两个直角三角形和三个正方形组成的图形,已知25AB = ,24AC = 其中阴影部分面积是_____________平方单位.20.在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB , 且 BD=3,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD 的长是____________.三、解答题21.在等边ABC 中,点D 是线段BC 的中点,120,EDF DE ∠=︒与线段AB 相交于点,E DF 与射线AC 相交于点F .()1如图1,若DF AC ⊥,垂足为,4,F AB =求BE 的长;()2如图2,将()1中的EDF ∠绕点D 顺时针旋转一定的角度,DF 仍与线段AC 相交于点F .求证:12BE CF AB +=.()3如图3,将()2中的EDF ∠继续绕点D 顺时针旋转一定的角度,使DF 与线段AC 的延长线交于点,F 作DN AC ⊥于点N ,若,DN FN =设,BE x CF y ==,写出y 关于x 的函数关系式.22.如图,在两个等腰直角ABC 和CDE △中,∠ACB = ∠DCE=90°.(1)观察猜想:如图1,点E 在BC 上,线段AE 与BD 的数量关系是 ,位置关系是 ;(2)探究证明:把CDE △绕直角顶点C 旋转到图2的位置,(1)中的结论还成立吗?说明理由;(3)拓展延伸:把CDE △绕点C 在平面内自由旋转,若AC = BC=10,DE=12,当A 、E 、D 三点在直线上时,请直接写出 AD 的长.23.如图,已知ABC ∆中,90B ∠=︒,8AB cm =,6BC cm =,P 、Q 是ABC ∆边上的两个动点,其中点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B C →方向运动,且速度为每秒2cm ,它们同时出发,设出发的时间为t 秒.(1)当2t =秒时,求PQ 的长;(2)求出发时间为几秒时,PQB ∆是等腰三角形?(3)若Q 沿B C A →→方向运动,则当点Q 在边CA 上运动时,求能使BCQ ∆成为等腰三角形的运动时间.24.如图1,在△ABC 中,AB =AC ,∠BAC =90°,D 为AC 边上一动点,且不与点A 点C 重合,连接BD 并延长,在BD 延长线上取一点E ,使AE =AB ,连接CE .(1)若∠AED =20°,则∠DEC = 度;(2)若∠AED =a ,试探索∠AED 与∠AEC 有怎样的数量关系?并证明你的猜想; (3)如图2,过点A 作AF ⊥BE 于点F ,AF 的延长线与EC 的延长线交于点H ,求证:EH 2+CH 2=2AE 2.25.如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB =∠ECD =90°,点D 在边AB 上,点E 在边AC 的左侧,连接AE .(1)求证:AE =BD ;(2)试探究线段AD 、BD 与CD 之间的数量关系;(3)过点C 作CF ⊥DE 交AB 于点F ,若BD :AF =1:2,CD 36,求线段AB 的长.26.如果一个三角形的两条边的和是第三边的两倍,则称这个三角形是“优三角形”,这两条边的比称为“优比”(若这两边不等,则优比为较大边与较小边的比),记为k . (1)命题:“等边三角形为优三角形,其优比为1”,是真命题还是假命题?(2)已知ABC 为优三角形,AB c =,AC b =,BC a =,①如图1,若90ACB ∠=︒,b a ≥,6b =,求a 的值.②如图2,若c b a ≥≥,求优比k 的取值范围.(3)已知ABC 是优三角形,且120ABC ∠=︒,4BC =,求ABC 的面积.27.在ABC ∆中,AB AC =,CD 是AB 边上的高,若10,45AB BC ==.(1)求CD 的长.(2)动点P 在边AB 上从点A 出发向点B 运动,速度为1个单位/秒;动点Q 在边AC 上从点A 出发向点C 运动,速度为v 个单位秒()v>1,设运动的时间为()0t t >,当点Q 到点C 时,两个点都停止运动.①若当2v =时,CP BQ =,求t 的值.②若在运动过程中存在某一时刻,使CP BQ =成立,求v 关于t 的函数表达式,并写出自变量t 的取值范围.28.在ABC ∆中,90ACB ∠=︒,6AC BC ==,点D 是AC 的中点,点E 是射线DC 上一点,DF DE ⊥于点D ,且DE DF =,连接CF ,作FH CF ⊥于点F ,交直线AB 于点H .(1)如图(1),当点E 在线段DC 上时,判断CF 和FH 的数量关系,并加以证明; (2)如图(2),当点E 在线段DC 的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当ABC △和CFH △面积相等时,点E 与点C 之间的距离;如果不成立,请说明理由.29.(已知:如图1,矩形OACB 的顶点A ,B 的坐标分别是(6,0)、(0,10),点D 是y 轴上一点且坐标为(0,2),点P 从点A 出发以每秒1个单位长度的速度沿线段AC ﹣CB 方向运动,到达点B 时运动停止.(1)设点P 运动时间为t ,△BPD 的面积为S ,求S 与t 之间的函数关系式;(2)当点P 运动到线段CB 上时(如图2),将矩形OACB 沿OP 折叠,顶点B 恰好落在边AC 上点B ′位置,求此时点P 坐标;(3)在点P 运动过程中,是否存在△BPD 为等腰三角形的情况?若存在,求出点P 坐标;若不存在,请说明理由.30.如图1,已知△ABC 是等边三角形,点D ,E 分别在边BC ,AC 上,且CD =AE ,AD 与BE 相交于点F .(1)求证:∠ABE =∠CAD ;(2)如图2,以AD 为边向左作等边△ADG ,连接BG .ⅰ)试判断四边形AGBE 的形状,并说明理由;ⅱ)若设BD =1,DC =k (0<k <1),求四边形AGBE 与△ABC 的周长比(用含k 的代数式表示).【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】先判断△DBE 是等腰直角三角形,根据勾股定理可推导得出BE ,故①正确;根据∠BHE 和∠C 都是∠HBE 的余角,可得∠BHE=∠C ,再由∠A=∠C ,可得②正确;证明△BEH ≌△DEC ,从而可得BH=CD ,再由AB=CD ,可得③正确;利用已知条件不能得到④,据此即可得到选项.【详解】解:∵∠DBC=45°,DE ⊥BC 于E ,∴在Rt △DBE 中,BE 2+DE 2=BD 2,BE=DE ,∴BE ,故①正确;∵DE ⊥BC ,BF ⊥DC ,∴∠BHE 和∠C 都是∠HBE 的余角,∴∠BHE=∠C ,又∵在▱ABCD 中,∠A=∠C ,∴∠A=∠BHE ,故②正确;在△BEH 和△DEC 中,BHE C HEB CED BE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△BEH ≌△DEC ,∴BH=CD ,∵四边形ABCD 为平行四边形,∴AB=CD ,∴AB=BH ,故③正确;利用已知条件不能得到△BCF ≌△DCE ,故④错误,故选A.【点睛】本题考查了平行四边形的性质、等腰直角三角形的判定与性质、勾股定理、全等三角形的判定与性质等,熟练掌握相关性质与定理是解题的关键.2.C解析:C【分析】做点F 做FH AD ⊥交AD 于点H ,因此要求出EF 的长,只要求出EH 和HF 即可;由折叠的性质可得BE=DE=9-AE ,在Rt ABE △中应用勾股定理求得AE 和BE ,同理在Rt BC F 'Rt ABE △中应用勾股定理求得BF ,在Rt EFH 中应用勾股定理即可求得EF .【详解】过点F 做FH AD ⊥交AD 于点H .∵四边形EFC B '是四边形EFCD 沿EF 折叠所得,∴ED=BE ,CF=C F ',3BC CD '==∵ED=BE ,DE=AD-AE=9-AE∴BE=9-AE∵Rt ABE △,AB=3,BE=9-AE∴()22293AE AE -=+∴AE=4∴DE=5∴9C F BC BF BF '=-=-∴Rt BC F ',3BC '=,9C F BF '=-∴()22293BF BF -+=∴BF=5,EH=1∵Rt EFH ,HF=3,EH=1 ∴22223110EF EH HF =+=+故选:C .【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题. 3.D解析:D【分析】先用已知条件利用SAS 的三角形全等的判定定理证出△EAB ≌△CAM ,之后利用全等三角形的性质定理分别可得30EBA CMA ==︒∠∠,60BPQ APM ==︒∠∠,12PQ PB =,然后设1AP =,继而可分别求出2PM =,312PQ =,所以32QM QP PM =+=;易证Rt △ACB ≌Rt △DCG (HL),从而得DG AB ==然后代入所求数据即可得DGQM的值.【详解】解:∵在△EAB 和△CAM 中 ,AE AC EAB CAM AB AM =⎧⎪=⎨⎪=⎩∠∠, ∴△EAB ≌△CAM (SAS ), ∴30EBA CMA ==︒∠∠, ∴60BPQ APM ==︒∠∠, ∴90BQP ∠=︒,12PQ PB =, 设1AP =,则AM =2PM =,1PB =,12PQ =,∴2QM QP PM =+=+=; ∵ 在Rt △ACB 和Rt △DCG 中,CG BCAC CD =⎧⎨=⎩, Rt △ACB ≌Rt △DCG (HL ),∴DG AB ==∴1DGGM==. 故选D . 【点睛】本题主要考查了勾股定理,三角形全等的判定定理和性质定理等知识.4.C解析:C 【分析】根据勾股定理即可得到正方形A 的面积加上B 的面积加上C 的面积和D 的面积是E 的面积.即可求解. 【详解】四个正方形的面积的和是正方形E 的面积:即222233=92549=47+5+2++++;故答案为C . 【点睛】理解正方形A ,B ,C ,D 的面积的和是E 的面积是解决本题的关键.5.C解析:C 【分析】根据勾股定理及直角三角形的中线、翻折得CD=DE=BD=5,CE=AC=6,作DH ⊥BE 于H ,EG ⊥CD 于G ,证明△DHE ≌△EGD ,利用勾股定理求出75EH DG ==,即可得到BE. 【详解】∵∠BCA=90∘,AC=6,BC=8, ∴22226810ABAC BC ,∵D 是AB 的中点, ∴AD=BD=CD=5,由翻折得:DE=AD=5,∠EDC=∠ADC ,CE=AC=6, ∴BD=DE ,作DH ⊥BE 于H ,EG ⊥CD 于G , ∴∠DHE=∠EGD=90︒,∠EDH=12∠BDE=12(180︒-2∠EDC )=90︒-∠EDC , ∴∠DEB= 90︒-∠EDH=90︒-(90︒-∠EDC)=∠EDC , ∵DE=DE , ∴△DHE ≌△EGD , ∴DH=EG ,EH=DG , 设DG=x ,则CG=5-x ,∵2EG =2222DE DG CE CG -=-, ∴222256(5)x x -=--, ∴75x =, ∴75EH DG ==, ∴BE=2EH=145, 故选:C.【点睛】此题考查翻折的性质,勾股定理,等腰三角形的性质,将求BE 转换为求其一半的长度的想法是关键,由此作垂线,证明△DHE ≌△EGD ,由此求出BE 的长度.6.D解析:D 【解析】 【分析】根据直角三角形的性质求出斜边长,根据勾股定理、完全平方公式计算即可。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、满足下列条件的三角形中,不是直角三角形的是()A.三内角之比为1:2:3B.三边长的平方之比为1:2:3C.三边长之比为3:4:5D.三内角之比为3:4:52、在由小正方形组成的网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是()A. M点B. N点C. P点D. Q点3、将下列长度的三根木棒首尾顺次连接,能构成直角三角形的是( )A.2、3、4B.4、5、6、C.6、7、8D.5、12、134、如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为()A. B. C. D.5、如图所示的“赵爽弦圈”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为n,较短直角边长为b.若nb=8,大正方形的面积为25,则小正方形的边长为( )A.9B.6C.4D.36、如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD =6,则BE的长是()A.4B.3C.2D.17、如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为()A.2B.2C.4D. 2+28、已知a,b为直角三角形的两边,+(b-4)2=0,则这个三角形第三边的长是()A.25B.5C.D.5或9、如图,矩形中,O为的中点,过点O作分别交于点若则的长为()A.2B.C.D.10、把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D =30°,斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D 1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为()A. B. C. D.411、如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用()A.3mB.5mC.7mD.9m12、如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,则AB的长度为()A.2 mB.4 mC.4 mD.6m13、我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示),如果大正方形的面积是49,小正方形的面积为4,直角三角形的两直角边长分别为a,b,那么下列结论:(1)a2+b2=49,(2)b﹣a=2,(3)ab= ,(4)a+b= 中,正确结论的个数有()A.4个B.3个C.2个D.1个14、若点在正比例函数的图象上,则点A到坐标原点的距离为( )A.7B.5C.4D.315、如图,在矩形ABCD中,AB=24,BC=12,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为()A.60B.80C.100D.90二、填空题(共10题,共计30分)16、如图,在中,,,,为边上(不与、重合的动点过点分别作于点,于点,则线段的最小值是________.17、如图,已知正方形ABCD的边长为4,点P在BC边上,且BP=1,Q为对角线AC上的一个动点,则△BPQ周长的最小值为________18、如图,在△ABC中,AC=BC,D为AB的中点,F为BC边上一点,连接CD、AF交干点E.若∠FAC=90°-3∠BAF,BF:AC=2:5,EF=2,则AB长为________.19、如图所示,以的三边向外作正方形,其面积分别为、、,若,,则________.20、如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,AD⊥BC于点D,则AD的长为________.21、如图为4×4的网格(每个小正方形的边长均为1),请画两个格点正方形(顶点在小正方形顶点处)要求:其中一个边长是有理数,另一个边长是大于3的无理数,并写出其边长,∴边长为________.∴边长为________.22、在半径为5cm的圆中,有一点P满足OP=3cm,则过点P的最短弦长为________cm.23、如右图所示,某警察在点A(−2,4)接到任务,前去阻截在点B(−10,0)的劫包摩托车,劫包摩托车从点B沿x轴向原点方向匀速行驶,警察立即拦下一辆摩托车前去阻截,若两辆摩托车行驶速度相等,则相遇时警察的坐标为________.24、在△ABC中,AB=2,AC= , ∠B=45°,则BC=________25、七巧板被誉为“东方魔板”.小明利用七巧板(如图1)中各板块的边长之间的关系拼成一个凸六边形,则该凸六边形(如图2)的周长是________.三、解答题(共5题,共计25分)26、在Rt△ABC中,∠ACB=90°,AC=3,tanB= ,求AB的值.27、如图,小巷左右两侧是竖着的墙,两墙相距2.2米。
八年级初二数学数学勾股定理的专项培优练习题(及答案

一、选择题1.△ABC 的三边分别为,,a b c ,下列条件能推出△ABC 是直角三角形的有( ) ①222a c b -=;②2()()0a b a b c -++=;③ ∠A =∠B -∠C; ④∠A ∶∠B ∶∠C =1∶2∶3 ;⑤111,,345a b c ===;⑥10,a = 24,b = 26c = A .2个 B .3个 C .4个 D .5个2.如图,四边形ABCD 中,AC ⊥BD 于O ,AB =3,BC =4,CD =5,则AD 的长为( )A .1B .32C .4D .233.已知等边三角形的边长为a ,则它边上的高、面积分别是( )A .2,24a a B .23,4a a C .233,a a D .233,4a a 4.已知:如图在△ABC ,△ADE 中,∠BAC=∠DAE=90°,AB=AC ,AD=AE ,点C ,D ,E 三点在同一条直线上,连接BD ,BE ,以下四个结论:①BD=CE ;②BD ⊥CE ;③∠ACE+∠DBC=45°;④BE 2=2(AD 2+AB 2),其中结论正确的个数是( )A .1B .2C .3D .45.如图,在△ABC 中,∠ACB =90°,AB 的中垂线交AC 于D ,P 是BD 的中点,若BC =4,AC =8,则S △PBC 为( )A .3B .3.3C .4D .4.56.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是一根竹子,原高一丈(一丈=10尺)一阵风将竹子折断,某竹梢恰好抵地,抵地处离竹子底部6尺远,则折断处离地面的高度是( )A .5.3尺B .6.8尺C .4.7尺D .3.2尺 7.下列各组线段能构成直角三角形的一组是( )A .30,40,60B .7,12,13C .6,8,10D .3,4,6 8.在Rt△ABC 中,∠C=90°,AC=3,BC=4,则点C 到AB 的距离是( )A .34B .35C .45D .125 9.如图,BD 为ABCD 的对角线,45,DBC DE BC ︒∠=⊥于点E ,BF ⊥DC 于点F ,DE 、BF 相交于点H ,直线BF 交线段AD 的延长线于点G ,下列结论:①12CE BE = ;②A BHE ∠=∠;③AB=BH;④BHD BDG ∠=∠;⑤222BH BG AG +=;其中正确的结论有( )A .①②③B .②③⑤C .①⑤D .③④10.有下列的判断: ①△ABC 中,如果a 2+b 2≠c 2,那么△ABC 不是直角三角形②△ABC 中,如果a 2-b 2=c 2,那么△ABC 是直角三角形③如果△ABC 是直角三角形,那么a 2+b 2=c 2以下说法正确的是( )A .①②B .②③C .①③D .②二、填空题11.如图,Rt ABC 中,90A ∠=︒,8AC =,6AB =,DE AC ⊥,13CD BC =,13CE AC =,P 是直线AC 上一点,把CDP 沿DP 所在的直线翻折后,点C 落在直线DE 上的点H 处,CP 的长是__________12.如图是由边长为1的小正方形组成的网格图,线段AB ,BC ,BD ,DE 的端点均在格点上,线段AB 和DE 交于点F ,则DF 的长度为_____.13.如图,30AOB ∠=︒,点,M N 分别在,OA OB 上,且6,8OM ON ==,点,P Q 分别在,OB OA 上运动,则PM PQ QN ++的最小值为______.14.已知x ,y 为一个直角三角形的两边的长,且(x ﹣6)2=9,y =3,则该三角形的第三边长为_____.15.如图,直线l 上有三个正方形a ,b ,c ,若a ,c 的边长分别为5和12,则b 的面积为_________________.16.如图,Rt△ABC 中,∠BCA =90°,AB =5,AC =2,D 为斜边AB 上一动点(不与点A ,B 重合),DE ⊥AC ,DF ⊥BC ,垂足分别为E 、F ,连接EF ,则EF 的最小值是_____.17.如图,把平面内一条数轴x 绕点O 逆时针旋转角θ(0°<θ<90°)得到另一条数轴y ,x 轴和y 轴构成一个平面斜坐标系.规定:已知点P 是平面斜坐标系中任意一点,过点P 作y 轴的平行线交x 轴于点A ,过点P 作x 轴的平行线交y 轴于点B ,若点A 在x 轴上对应的实数为a ,点B 在y 轴上对应的实数为b ,则称有序实数对(a ,b )为点P 的斜坐标.在平面斜坐标系中,若θ=45°,点P 的斜坐标为(1,2),点G 的斜坐标为(7,﹣2),连接PG ,则线段PG 的长度是_____.18.如图,由两个直角三角形和三个正方形组成的图形,已知25AB = ,24AC = 其中阴影部分面积是_____________平方单位.19.观察:①3、4、5,②5、12、13,③7、24、25,……,发现这些勾股数的“勾”都是奇数,且从3起就没断过.根据以上规律,请写出第8组勾股数:______.20.如图,直线423y x =+与x 轴、y 轴分别交于点B 和点A ,点C 是线段OA 上的一点,若将ABC ∆沿BC 折叠,点A 恰好落在x 轴上的'A 处,则点C 的坐标为______.三、解答题21.如图,,90,8,6,,ABC B AB cm BC cm P Q ︒∆∠===是边上的两点,点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 沿B C A →→运动,且速度为每秒2cm ,它们同时出发,设出发的时间为t 秒.(1)出发2秒后,求线段PQ 的长;(2)求点Q 在BC 上运动时,出发几秒后,PQB 是等腰三角形;(3)点Q 在边CA 上运动时,求能使BCQ ∆成为等腰三角形的运动时间.22.如图,已知ABC ∆中,90B ∠=︒,8AB cm =,6BC cm =,P 、Q 是ABC ∆边上的两个动点,其中点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B C →方向运动,且速度为每秒2cm ,它们同时出发,设出发的时间为t 秒.(1)当2t =秒时,求PQ 的长;(2)求出发时间为几秒时,PQB ∆是等腰三角形?(3)若Q 沿B C A →→方向运动,则当点Q 在边CA 上运动时,求能使BCQ ∆成为等腰三角形的运动时间.23.如图,在边长为2的等边三角形ABC 中,D 点在边BC 上运动(不与B ,C 重合),点E 在边AB 的延长线上,点F 在边AC 的延长线上,AD DE DF ==. (1)若30AED ∠=︒,则ADB =∠______.(2)求证:BED CDF △≌△.(3)试说明点D 在BC 边上从点B 至点C 的运动过程中,BED 的周长l 是否发生变化?若不变,请求出l 的值,若变,请求出l 的取值范围.24.如图,△ABC 中,∠ACB =90°,AB =5cm ,BC =3cm ,若点P 从点A 出发,以每秒2cm 的速度沿折线A ﹣C ﹣B ﹣A 运动,设运动时间为t 秒(t >0).(1)若点P 在AC 上,且满足PA =PB 时,求出此时t 的值;(2)若点P 恰好在∠BAC 的角平分线上,求t 的值;(3)在运动过程中,直接写出当t 为何值时,△BCP 为等腰三角形.25.如图, ABD 为边长不变的等腰直角三角形,AB AD =,90BAD ∠=︒,在 ABD 外取一点 E ,以A 为直角顶点作等腰直角AEP △,其中 P 在 ABD 内部,90EAP ∠=︒,2AE AP ==,当E 、P 、D 三点共线时,7BP =.下列结论:①E 、P 、D 共线时,点B 到直线AE 的距离为5;②E 、P 、D 共线时, 13ADP ABP S S ∆∆+=+;=532ABD S ∆+③; ④作点 A 关于 BD 的对称点 C ,在 AEP 绕点 A 旋转的过程中,PC 的最小值为5+232-;⑤AEP △绕点A 旋转,当点E 落在AB 上,当点P 落在AD 上时,取BP 上一点N ,使得AN BN =,连接 ED ,则AN ED ⊥.其中正确结论的序号是___.26.我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:(1)叙述勾股定理(用文字及符号语言叙述);(2)证明勾股定理;(3)若大正方形的面积是13,小正方形的面积是1,求()2a b +的值.27.如图,在△ABC 中,∠C =90°,把△ABC 沿直线DE 折叠,使△ADE 与△BDE 重合.(1)若∠A =35°,则∠CBD 的度数为________;(2)若AC =8,BC =6,求AD 的长;(3)当AB =m(m>0),△ABC 的面积为m +1时,求△BCD 的周长.(用含m 的代数式表示)28.如图1,在平面直角坐标系中,直线AB 经过点C (a ,a ),且交x 轴于点A (m ,0),交y 轴于点B (0,n ),且m ,n 满足6m -+(n ﹣12)2=0.(1)求直线AB 的解析式及C 点坐标;(2)过点C 作CD ⊥AB 交x 轴于点D ,请在图1中画出图形,并求D 点的坐标;(3)如图2,点E (0,﹣2),点P 为射线AB 上一点,且∠CEP =45°,求点P 的坐标.29.在ABC ∆中,90ACB ∠=︒,6AC BC ==,点D 是AC 的中点,点E 是射线DC 上一点,DF DE ⊥于点D ,且DE DF =,连接CF ,作FH CF ⊥于点F ,交直线AB 于点H .(1)如图(1),当点E 在线段DC 上时,判断CF 和FH 的数量关系,并加以证明; (2)如图(2),当点E 在线段DC 的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当ABC △和CFH △面积相等时,点E 与点C 之间的距离;如果不成立,请说明理由.30.已知n 组正整数:第一组:3,4,5;第二组:8,6,10;第三组:15,8,17;第四组:24,10,26;第五组:35,12,37;第六组:48,14,50;…(1)是否存在一组数,既符合上述规律,且其中一个数为71?若存在,请写出这组数;若不存在,请说明理由;(2)以任意一个大于2的偶数为一条直角边的长,是否一定可以画出一个直角三角形,使得该直角三角形的另两条边的长都是正整数?若可以,请说明理由;若不可以,请举出反例.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据勾股定理的逆定理,三角形的内角和定理,分别对每个选项进行判断,即可得到答案.【详解】解:∵222a c b -=,得222a b c =+,符合勾股定理逆定理,则①正确;∵2()()0a b a b c -++=,得到222a c b +=,符合勾股定理逆定理,则②正确; ∵∠A =∠B -∠C ,得∠B=∠A+∠C ,∵∠A+∠B+∠C=180°,∴∠B=90°,故③正确;∵∠A ∶∠B ∶∠C =1∶2∶3,∠A+∠B+∠C=180°, ∴318090123C ∠=︒⨯=︒++,故④正确; ∵222111()()()453+≠,则⑤不能构成直角三角形,故⑤错误;∵222102426+=,则⑥能构成直角三角形,故⑥正确;∴能构成直角三角形的有5个;故选择:D.【点睛】本题考查了勾股定理的逆定理,以及三角形的内角和定理,解题的关键是熟练掌握用勾股定理的逆定理和三角形内角和定理进行判断三角形是直角三角形.2.B解析:B【分析】设OA =a ,OB =b ,OC =c ,OD =d ,根据勾股定理求出a 2+b 2=AB 2=9,c 2+b 2=BC 2=16,c 2+d 2=CD 2=25,即可证得a 2+d 2=18,由此得到答案.【详解】设OA =a ,OB =b ,OC =c ,OD =d ,由勾股定理得,a 2+b 2=AB 2=9,c 2+b 2=BC 2=16,c 2+d 2=CD 2=25,则a 2+b 2+c 2+b 2+c 2+d 2=50,∴a 2+d 2+2(b 2+c 2)=50,∴a 2+d 2=50﹣16×2=18,∴AD =221832a d +==, 故选:B .【点睛】此题考查勾股定理的运用,根据题中的已知条件得到直角三角形,再利用勾股定理求出未知的边长,解题中注意直角边与斜边.3.C解析:C【分析】作出等边三角形一边上的高,利用直角三角形中,30°角所对的直角边等于斜边的一半,得出BD ,利用勾股定理即可求出AD ,再利用三角形面积公式即可解决问题.【详解】解:如图作AD ⊥BC 于点D .∵△ABC 为等边三角形,∴∠B =60°,∠B AD =30°∴1122BD AB a == 由勾股定理得,2222213()22AD AB BD a a a =-=-= ∴边长为a 的等边三角形的面积为12×a ×32a =34a 2, 故选:C .【点睛】本题考点涉及等边三角形的性质、含30°角的直角三角形、勾股定理以及三角形面积公式,熟练掌握相关性质定理是解题关键.4.C解析:C【解析】试题分析:①∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.∵在△BAD和△CAE中,AB=AC,∠BAD=∠CAE,AD=AE,∴△BAD≌△CAE(SAS).∴BD=CE.本结论正确.②∵△BAD≌△CAE,∴∠ABD=∠ACE.∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°.∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°.∴BD⊥CE.本结论正确.③∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°.∴∠ABD+∠DBC=45°.∵∠ABD=∠ACE,∴∠ACE+∠DBC=45°.本结论正确.④∵BD⊥CE,∴在Rt△BDE中,利用勾股定理得:BE2=BD2+DE2.∵△ADE为等腰直角三角形,∴AD,即DE2=2AD2.∴BE2=BD2+DE2=BD2+2AD2.而BD2≠2AB2,本结论错误.综上所述,正确的个数为3个.故选C.5.A解析:A【分析】根据线段垂直平分线的性质得到DA=DB,根据勾股定理求出BD,得到CD的长,根据三角形的面积公式计算,得到答案.【详解】解:∵点D在线段AB的垂直平分线上,∴DA=DB,在Rt△BCD中,BC2+CD2=BD2,即42+(8﹣BD)2=BD2,解得,BD=5,∴CD=8﹣5=3,∴△BCD的面积=12×CD×BC=12×3×4=6,∵P是BD的中点,∴S△PBC=12S△BCD=3,故选:A.【点睛】本题考查的是线段垂直平分线的性质、直角三角形的性质、勾股定理,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.6.D【分析】根据题意结合勾股定理得出折断处离地面的长度即可.【详解】解:设折断处离地面的高度OA 是x 尺,根据题意可得:x 2+62=(10-x )2,解得:x=3.2,答:折断处离地面的高度OA 是3.2尺.故选D .【点睛】此题主要考查了勾股定理的应用,根据题意正确应用勾股定理是解题关键.7.C解析:C【分析】根据勾股定理的逆定理解答即可.【详解】A 、∵222304060+≠,∴该选项的三条线段不能构成直角三角形;B 、∵22271213+≠,∴该选项的三条线段不能构成直角三角形;C 、∵2226810+=,∴该选项的三条线段能构成直角三角形;D 、∵222346+≠,∴该选项的三条线段不能构成直角三角形;故选:C .【点睛】此题考查勾股定理的逆定理,掌握勾股定理的逆定理的计算法则及正确计算是解题的关键.8.D解析:D【解析】在Rt △ABC 中 ∠C=90°,AC=3,BC=4,根据勾股定理求得AB=5,设点C 到AB 的距离为h ,即可得12h×AB=12AC×BC ,即12h×5=12×3×4,解得h=125,故选D. 9.B解析:B【分析】根据直角三角形的意义和性质可以得到解答.解:由题意,90BHE HBE C HBE A C ∠+∠=∠+∠=︒∠=∠,∴A BHE C ∠=∠=∠,②正确;∵∠DBC=45°,DE ⊥BC ,∴∠EDB=∠DBC=45°,∴BE=DE∴Rt BEH Rt DEC ≅,∴BH=CD=AB ,③正确;∵AB CD BF CD ⊥,,∴AB ⊥CD ,∴222AB BG AG +=即 222BH BG AG +=,⑤正确,∵没有依据支持①④成立,∴②③⑤正确故选B .【点睛】本题考查直角三角形的意义和性质,灵活应用有关知识求解是解题关键.10.D解析:D【分析】欲判断三角形是否为直角三角形,这里给出三边的长,需要验证两小边的平方和等于最长边的平方即可.【详解】①c 不一定是斜边,故错误;②正确;③若△ABC 是直角三角形,c 不是斜边,则a 2+b 2≠c 2,故错误,所以正确的只有②,故选D.【点睛】本题考查了勾股定理以及勾股定理的逆定理,熟练掌握勾股定理以及勾股定理的逆定理的内容是解题的关键.二、填空题11.53或203【分析】 根据折叠后点C 的对应点H 与AC 的位置关系分类讨论,分别画出对应的图形,利用勾股定理求出各边的长,再根据折叠的性质与勾股定理列出对应的方程即可求出结论.【详解】解:①当折叠后点C 的对应点H 在AC 的下方时,如下图所示∵Rt ABC 中,90A ∠=︒,8AC =,6AB =,根据勾股定理可得BC=2210AB AC += ∵13CD BC =,13CE AC =, ∴13CD BC ==103,13CE AC ==83 ∵DE AC ⊥根据勾股定理可得DE=222CD CE -=由折叠的性质可得:DH=CD=103,CP=PH ∴EH=DH -DE=43设CP=PH=x ,则EP=CE -CP=83-x 在Rt △PEH 中,EP 2+EH 2=PH 2即(83-x )2+(43)2=x 2 解得:x=53即此时CP=53; ②当折叠后点C 的对应点H 在AC 的上方时,如下图所示根据折叠的性质可得DH=CD=103,CP=PH ∴EH=DH +DE=163 设CP=PH=y ,则EP= CP -CE =y -83 在Rt △PEH 中,EP 2+EH 2=PH 2即(y -83)2+(163)2=y 2 解得:y=203即此时CP=203. 综上所述:CP=53或203. 故答案为:53或203. 【点睛】 此题考查的是勾股定理和折叠问题,掌握利用勾股定理解直角三角形、折叠的性质和分类讨论的数学思想是解决此题的关键.12.2【分析】连接AD 、CD ,由勾股定理得:22435AB DE ==+=,224225BD =+=,22125CD AD ==+=,得出AB =DE =BC ,222BD AD AB +=,由此可得△ABD 为直角三角形,同理可得△BCD 为直角三角用形,继而得出A 、D 、C 三点共线.再证明△ABC ≌△DEB ,得出∠BAC =∠EDB ,得出DF ⊥AB ,BD 平分∠ABC ,再由角平分线的性得出DF =DG =2即可的解.【详解】连接AD 、CD ,如图所示:由勾股定理可得,22435AB DE ==+=,224225BD =+=22125CD AD ==+,∵BE=BC=5,∴AB=DE =AB =BC ,222BD AD AB +=,∴△ABD 是直角三角形,∠ADB =90°,同理可得:△BCD 是直角三角形,∠BDC =90°,∴∠ADC =180°,∴点A 、D 、C 三点共线, ∴225AC AD BD ===,在△ABC 和△DEB 中,AB DE BC EB AC BD =⎧⎪⎨⎪=⎩=,∴△ABC ≌△DEB(SSS),∴∠BAC =∠EDB ,∵∠EDB+∠ADF =90°,∴∠BAD+∠ADF =90°,∴∠BFD =90°,∴DF ⊥AB ,∵AB=BC ,BD ⊥AC ,∴BD 平分∠ABC ,∵DG ⊥BC ,∴DF =DG =2.【点睛】本题考查全等三角形的性质与判定以及勾股定理的相关知识,解题的关键是熟练掌握勾股定理和过股定理的逆定理.13.10【分析】首先作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,连接M ′N ′,即为MP +PQ +QN 的最小值,易得△ONN ′为等边三角形,△OMM ′为等边三角形,∠N ′OM ′=90°,继而可以求得答案.【详解】作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,连接M ′N ′,即为MP +PQ +QN 的最小值.根据轴对称的定义可知:∠N ′OQ =∠M ′OB =30°,∠ONN ′=60°,OM ′=OM =6,ON ′=ON =8,∴△ONN ′为等边三角形,△OMM ′为等边三角形,∴∠N ′OM ′=90°.在Rt △M ′ON ′中,M ′N ′=22''OM ON +=10. 故答案为10.【点睛】本题考查了最短路径问题,根据轴对称的定义,找到相等的线段,得到直角三角形是解题的关键.14.106232【解析】【详解】∵(x-6)2=9,∴x-6=±3,解得:x 1=9,x 2=3,∵x ,y 为一个直角三角形的两边的长,y=3,∴当x=3时,x 、y 都为直角三角形的直角边,则斜边为223332+=;当x=9时,x 、y 都为直角三角形的直角边,则斜边为2293310+= ;当x=9时,x 为斜边、y 为直角边,则第三边为263922=-.故答案为:310,62或32. 【点睛】本题主要考查了勾股定理的应用,正确分类讨论是解决问题的关键,解题时注意一定不要漏解.15.169【解析】解:由于a 、b 、c 都是正方形,所以AC =CD ,∠ACD =90°;∵∠ACB +∠DCE =∠ACB +∠BAC =90°,即∠BAC =∠DCE ,∠ABC =∠CED =90°,AC =CD ,∴△ACB ≌△DCE ,∴AB =CE ,BC =DE ; 在Rt △ABC 中,由勾股定理得:AC 2=AB 2+BC 2=AB 2+DE 2,即S b =S a +S c =22512+=169. 故答案为:169.点睛:此题主要考查对全等三角形和勾股定理的综合运用,结合图形求解,对图形的理解能力要比较强.1625 【解析】试题分析:根据勾股定理可求出BC=1,然后根据∠BCA =90°,DE ⊥AC ,DF ⊥BC ,证得四边形CEDF 是矩形,连接CD ,则CD=EF ,当CD⊥AB 时,CD 最短,即25. 25 点睛:本题考查了勾股定理的运用,矩形的判定和性质以及垂线段最短的性质,同时也考查了学生综合运用性质进行推理和计算的能力.17.5【分析】如图,作PA ∥y 轴交X 轴于A ,PH ⊥x 轴于H .GM ∥y 轴交x 轴于M ,连接PG 交x 轴于N ,先证明△ANP ≌△MNG (AAS ),再根据勾股定理求出PN 的值,即可得到线段PG 的长度.【详解】如图,作PA ∥y 轴交X 轴于A ,PH ⊥x 轴于H .GM ∥y 轴交x 轴于M ,连接PG 交x 轴于N .∵P (1,2),G (7.﹣2),∴OA =1,PA =GM =2,OM =7,AM =6,∵PA ∥GM ,∴∠PAN =∠GMN ,∵∠ANP =∠MNG ,∴△ANP ≌△MNG (AAS ),∴AN =MN =3,PN =NG ,∵∠PAH =45°,∴PH =AH =2,∴HN =1, ∴2222215PN PH NH =+=+=∴PG =2PN =5.故答案为5【点睛】本题考查了全等三角形的综合问题,掌握全等三角形的性质以及判定定理、勾股定理是解题的关键.18.49【分析】先计算出BC 的长,再由勾股定理求出阴影部分的面积即可.【详解】∵∠ACB=90︒,25AB = ,24AC =,∴22222252449BC AB AC =-=-=,∴阴影部分的面积=249BC =,故答案为:49.【点睛】此题考查勾股定理,能利用根据直角三角形计算得到所需的边长,题中根据勾股定理的图形得到阴影部分面积等于BC 的平方是解题的关键.19.17,144,145【分析】由题意观察题干这些勾股数,根据所给的勾股数找出三个数之间的关系即可.【详解】解:因为这些勾股数的“勾”都是奇数,且从3起就没断过,所以从3、5、7…依次推出第8组的“勾”为17,继续观察可知弦-股=1,利用勾股定理假设股为m ,则弦为m+1,所以有22217(1)m m +=+,解得144m =,1145m +=,即第8组勾股数为17,144,145.故答案为17,144,145.【点睛】本题属规律性题目,考查的是勾股数之间的关系,根据题目中所给的勾股数及勾股定理进行分析即可.20.(0,34). 【分析】 由423y x =+求出点A 、B 的坐标,利用勾股定理求得AB 的长度,由此得到53122OA '=-=,设点C 的坐标为(0,m ),利用勾股定理解得m 的值即可得到答案. 【详解】 在423y x =+中,当x=0时,得y=2,∴A (0,2) 当y=0时,得4203x +=,∴32x =-,∴B(32-,0), 在Rt △AOB 中,∠AOB=90︒,OA=2,OB=32,∴52AB ===, ∴53122OA '=-=, 设点C 的坐标为(0,m )由翻折得ABC A BC '≌,∴2A C AC m '==-,在Rt A OC '中, 222A C OC A O ''=+,∴222(2)1m m -=+,解得m=34, ∴点C 的坐标为(0,34). 故答案为:(0,34). 【点睛】此题考查勾股定理,翻折的性质,题中由翻折得ABC A BC '≌是解题的关键,得到OC 与A’C 的数量关系,利用勾股定理求出点C 的坐标. 三、解答题21.(1)出发2秒后,线段PQ 的长为2)当点Q 在边BC 上运动时,出发83秒后,△PQB 是等腰三角形;(3)当t 为5.5秒或6秒或6.6秒时,△BCQ 为等腰三角形.【分析】(1)由题意可以求出出发2秒后,BQ 和PB 的长度,再由勾股定理可以求得PQ 的长度; (2)设所求时间为t ,则可由题意得到关于t 的方程,解方程可以得到解答; (3)点Q 在边CA 上运动时,ΔBCQ 为等腰三角形有三种情况存在,对每种情况进行讨论可以得到解答.【详解】(1)BQ=2×2=4cm ,BP =AB−AP=8−2×1=6cm ,∵∠B=90°,由勾股定理得:===∴出发2秒后,线段PQ 的长为(2)BQ=2t ,BP=8−t由题意得:2t=8−t解得:t=83∴当点Q 在边BC 上运动时,出发83秒后,△PQB 是等腰三角形;(3) ∵∠ABC=90°,BC=6,AB=8,∴=10.①当CQ=BQ 时(图1),则∠C=∠CBQ ,∵∠ABC=90°,∴∠CBQ+∠ABQ=90°,∠A+∠C=90°,∴∠A=∠ABQ ,∴BQ=AQ ,∴CQ=AQ=5,∴BC+CQ=11,∴t=11÷2=5.5秒;②当CQ=BC时(如图2),则BC+CQ=12∴t=12÷2=6秒③当BC=BQ时(如图3),过B点作BE⊥AC于点E,∴BE=6824105 AB BCAC⋅⨯==,所以CE=22BC BE-=185=3.6,故CQ=2CE=7.2,所以BC+CQ=13.2,∴t=13.2÷2=6.6秒.由上可知,当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.【点睛】本题考查三角形的动点问题,利用分类讨论思想和方程方法、综合力学的运动知识和三角形边角的有关知识求解是解题关键.22.(1)132)83;(3)5.5秒或6秒或6.6秒【分析】(1)根据点P 、Q 的运动速度求出AP ,再求出BP 和BQ ,用勾股定理求得PQ 即可; (2)由题意得出BQ BP =,即28t t =-,解方程即可;(3)当点Q 在边CA 上运动时,能使BCQ ∆成为等腰三角形的运动时间有三种情况: ①当CQ BQ =时(图1),则C CBQ ∠=∠,可证明A ABQ ∠=∠,则BQ AQ =,则CQ AQ =,从而求得t ;②当CQ BC =时(图2),则12BC CQ +=,易求得t ;③当BC BQ =时(图3),过B 点作BE AC ⊥于点E ,则求出BE ,CE ,即可得出t .【详解】(1)解:(1)224BQ cm =⨯=,8216BP AB AP cm =-=-⨯=,90B ∠=︒, 222246213()PQ BQ BP cm =+=+=; (2)解:根据题意得:BQ BP =,即28t t =-,解得:83t =; 即出发时间为83秒时,PQB ∆是等腰三角形;(3)解:分三种情况:①当CQ BQ =时,如图1所示:则C CBQ ∠=∠,90ABC ∠=︒,90CBQ ABQ ∴∠+∠=︒,90A C ∠+∠=︒,A ABQ ∴∠=∠BQ AQ ∴=,5CQ AQ ∴==,11BC CQ ∴+=,112 5.5t ∴=÷=秒.②当CQ BC =时,如图2所示:则12BC CQ +=1226t ∴=÷=秒.③当BC BQ =时,如图3所示:过B 点作BE AC ⊥于点E , 则68 4.8()10AB BC BE cm AC ⨯=== 22 3.6CE BC BE cm ∴=-=,27.2CQ CE cm ∴==,13.2BC CQ cm ∴+=,13.22 6.6t ∴=÷=秒.由上可知,当t 为5.5秒或6秒或6.6秒时,BCQ ∆为等腰三角形.【点睛】本题考查了勾股定理、三角形的面积以及等腰三角形的判定和性质;本题有一定难度,注意分类讨论思想的应用. 23.(1)90°;(2)证明见解析;(3)变化,234l +≤<.【分析】(1)由等边三角形的性质可得∠ABC=∠ACB=60°,由等腰三角形的性质可求DAE=∠DEA=30°,由三角形内角和定理可求解;(2)根据等腰三角形的性质,可证得∠CDF=∠DEA 和∠EDB=∠DFA ,由此可利用“ASA”证明全等;(3)根据全等三角形的性质可得l =2+AD ,根据AD 的取值范围即可得出l 的取值范围.【详解】解:(1)∵△ABC 是等边三角形,∴AB=AC=BC=2,∠ABC=∠ACB=60°,∵AD=DE∴∠DAE=∠DEA=30°,∴∠ADB=180°-∠BAD-∠ABD=90°,故答案为:90°;(2)∵AD=DE=DF ,∴∠DAE=∠DEA ,∠DAF=∠DFA ,∵∠DAE+∠DAF=∠BAC=60°,∴∠DEA+∠DFA=60°,∵∠ABC=∠DEA+∠EDB=60°,∴∠EDB=∠DFA ,∵∠ACB=∠DFA+∠CDF=60°,∴∠CDF=∠DEA ,在△BDE 和△CFD 中∵CDF DEA DE DF EDB DFA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BDE ≌△CFD (ASA )(3)∵△BDE ≌△CFD ,∴BE=CD ,∴l =BD+BE+DE=BD+CD+AD=BC+AD=2+AD ,当D 点在C 或B 点时,AD=AC=AB=2,此时B 、D 、E 三点在同一条直线上不构成三角形,2+AD=4;当D 点在BC 的中点时,∵AB=AC ,∴BD=112BC =,AD ==此时22l AD =+=综上可知24l +≤<.【点睛】本题考查全等三角形的性质和判定,勾股定理,等边三角形的性质,等腰三角形的性质,三角形内角和定理.(1)掌握等腰三角形等边对等角是解决此问的关键;(2)中注意角之间的转换;(3)中注意临界点是否可取.24.(1) 2516;(2)83t =或6;(3)当153,5,210t =或194时,△BCP 为等腰三角形. 【分析】(1)设存在点P ,使得PA PB =,此时2PA PB t ==,42PC t =-,根据勾股定理列方程即可得到结论;(2)当点P 在CAB ∠的平分线上时,如图1,过点P 作PE AB ⊥于点E ,此时72BP t =-,24PE PC t ==-,541BE =-=,根据勾股定理列方程即可得到结论; (3)在Rt ABC 中,根据勾股定理得到4AC cm =,根据题意得:2AP t =,当P 在AC上时,BCP 为等腰三角形,得到PC BC =,即423t -=,求得12t =,当P 在AB 上时,BCP 为等腰三角形,若CP PB =,点P 在BC 的垂直平分线上,如图2,过P 作PE BC ⊥于E ,求得194t =,若PB BC =,即2343t --=,解得5t =,PC BC =③,如图3,过C 作CF AB ⊥于F ,由射影定理得;2BC BF AB =⋅,列方程2234352t --=⨯,即可得到结论. 【详解】 解:在Rt ABC 中,5AB cm =,3BC cm =,4AC cm ∴=,(1)设存在点P ,使得PA PB =,此时2PA PB t ==,42PC t =-,在Rt PCB 中,222PC CB PB +=,即:222(42)3(2)t t -+=,解得:2516t =, ∴当2516t =时,PA PB =; (2)当点P 在BAC ∠的平分线上时,如图1,过点P 作PE AB ⊥于点E ,此时72BP t =-,24PE PC t ==-,541BE =-=,在Rt BEP 中,222PE BE BP +=,即:222(24)1(72)t t -+=-,解得:83t =, 当6t =时,点P 与A 重合,也符合条件,∴当83t =或6时,P 在ABC ∆的角平分线上; (3)根据题意得:2AP t =,当P 在AC 上时,BCP 为等腰三角形,PC BC ∴=,即423t -=,12t ∴=, 当P 在AB 上时,BCP 为等腰三角形,CP PB =①,点P 在BC 的垂直平分线上,如图2,过P 作PE BC ⊥于E ,1322BE BC ∴==, 12PB AB ∴=,即52342t --=,解得:194t =, PB BC =②,即2343t --=,解得:5t =,PC BC =③,如图3,过C 作CF AB ⊥于F ,12BF BP ∴=, 90ACB ∠=︒,由射影定理得;2BC BF AB =⋅,即2234352t --=⨯, 解得:5310t =, ∴当15319,5,2104t =或时,BCP 为等腰三角形. 【点睛】本题考查了等腰三角形的判定,三角形的面积,难度适中.利用分类讨论的思想是解(3)题的关键.25.②③⑤【分析】①先证得ABE ADP ≅,利用邻补角和等腰直角三角形的性质求得90PEB ∠=︒,利用勾股定理求出BE ,即可求得点B 到直线AE 的距离;②根据①的结论,利用APD ABP ABE APB S S S S ∆∆∆+=+AEP BEP S S ∆∆=+即可求得结论; ③在Rt AHB 中,利用勾股定理求得2AB ,再利用三角形面积公式即可求得ABD S ∆; ④当A P C 、、共线时,PC 最小,利用对称的性质,AB BC =的长,再求得AC 的长,即可求得结论;⑤先证得ABP ADE ≅,得到ABP ADE ∠=∠,根据条件得到ABP NAB ∠=∠,利用互余的关系即可证得结论.【详解】①∵ABD 与AEP 都是等腰直角三角形,∴90BAD ∠=︒,90EAP ∠=︒,AB AD =,AE AP =,45APE AEP ∠=∠=︒, ∴EAB PAD ∠=∠, ∴()ABE ADP SAS ≅,∴180********AEB APD APE ∠=∠=︒-∠=︒-︒=︒,∴1354590PEB AEB AEP ∠=∠-∠=︒-︒=︒,∴222PE BE PB +=,∵2AE AP ==,90EAP ∠=︒, ∴22PE AE ==, ∴()22227BE +=, 解得:3BE =,作BH ⊥AE 交AE 的延长线于点H ,∵45AEP ∠=︒,90PEB ∠=︒, ∴180180904545HEB PEB AEP ∠=︒-∠-∠=︒-︒-︒=︒,∴26sin 453HB BE =︒==, ∴点B 到直线AE 6,故①错误; ②由①知:ABE ADP ≅,2EP =,3BE =∴APD ABP ABE APB S S S S ∆∆∆∆+=+AEP BEP S S ∆∆=+ 1122AE AP PE EB =⨯⨯+⨯⨯11222322=⨯⨯+⨯⨯ 13=+,故②正确;③在Rt AHB 中,由①知:6EH HB ==, ∴622AH AE EH =+=+, 22222256623AB AH BH ⎛⎫⎛⎫=+=++=+ ⎪ ⎪ ⎪ ⎪⎭⎝⎭, 21153222ABD S AB AD AB ∆=⋅==+,故③正确; ④因为AC 是定值,所以当A P C 、、共线时,PC 最小,如图,连接BC ,∵A C 、关于 BD 的对称,∴523AB BC ==+∴225231043AC BC ==+=+∴ min PC AC AP =-,10432=+⑤∵ABD 与AEP 都是等腰直角三角形,∴90BAD ∠=︒,90EAP ∠=︒,AB AD =,AE AP =, 在ABP 和ADE 中,AB AD BAP DAE AP AE =⎧⎪∠=∠⎨⎪=⎩,∴()ABP ADE SAS ≅,∴ABP ADE ∠=∠,∵AN BN =,∴ABP NAB ∠=∠,∴EAN ADE ∠=∠,∵90EAN DAN ∠+∠=︒,∴90ADE DAN ∠+∠=︒,∴AN DE ⊥,故⑤正确;综上,②③⑤正确,故答案为:②③⑤.【点睛】本题是三角形的综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理的应用,三角形的面积公式,综合性强,全等三角形的判定和性质的灵活运用是解题的关键.26.(1)见解析;(2)证明见解析;(3)25.【分析】(1)直接叙述勾股定理的内容,并用字母表明三边关系;(2)利用大正方形面积、小正方形面积和4个直角三角形的面积和之间的关系列式整理即可证明;(3)将原式利用完全平方公式展开,由勾股定理的内容可得出()2a b +为大正方形面积和4个直角三角形的面积和,根据已知条件即可求得.【详解】解:(1)勾股定理:直角三角形两直角边的平方和等于斜边的平方.在直角三角形中,两条直角边分别为 a 、b ,斜边为 c ,a 2+b 2= c 2.(2)∵ S 大正方形=c 2,S 小正方形=(b-a)2,4 S Rt △=4×12ab=2ab , ∴ c 2=2ab+(b-a)2=2ab+b 2-2ab+a 2=a 2+b 2,即 a 2+b 2= c 2.(3)∵ 4 S Rt △= S 大正方形- S 小正方形=13-1=12,∴ 2ab=12.∴ (a+b)2= a 2+b 2+2ab=c 2+2ab=13+12=25.【点睛】本题考查勾股定理的内容及勾股定理的几何验证,利用等面积法证明勾股定理及运用勾股定理是解答此题的关键.27.(1)∠CBD=20°;(2)AD=164;(3) △BCD的周长为m+2【分析】(1)根据折叠可得∠1=∠A=35°,根据三角形内角和定理可以计算出∠ABC=55°,进而得到∠CBD=20°;(2)根据折叠可得AD=DB,设CD=x,则AD=BD=8-x,再在Rt△CDB中利用勾股定理可得x2+62=(8-x)2,再解方程可得x的值,进而得到AD的长;(3)根据三角形ACB的面积可得11 2AC CB m=+,进而得到AC•BC=2m+2,再在Rt△CAB中,CA2+CB2=BA2,再把左边配成完全平方可得CA+CB的长,进而得到△BCD的周长.【详解】(1)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,∴∠1=∠A=35°,∵∠C=90°,∴∠ABC=180°-90°-35°=55°,∴∠2=55°-35°=20°,即∠CBD=20°;(2)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,∴AD=DB,设CD=x,则AD=BD=8-x,在Rt△CDB中,CD2+CB2=BD2,x2+62=(8-x)2,解得:x= 74,AD=8-74=164;(3)∵△ABC 的面积为m+1,∴12AC•BC=m+1,∴AC•BC=2m+2,∵在Rt△CAB中,CA2+CB2=BA2,∴CA2+CB2+2AC•BC=BA2+2AC•BC,∴(CA+BC)2=m2+4m+4=(m+2)2,∴CA+CB=m+2,∵AD=DB,∴CD+DB+BC=m+2.即△BCD的周长为m+2.【点睛】此题主要考查了图形的翻折变换,以及勾股定理,完全平方公式,关键是掌握勾股定理,以及折叠后哪些是对应角和对应线段.28.(1)y=-2x+12,点C坐标(4,4);(2)画图形见解析,点D坐标(-4,0);(3)点P的坐标(143-,643)【分析】(1)由已知的等式可求得m、n的值,于是可得直线AB的函数解析式,把点C的坐标代入可求得a的值,由此即得答案;(2)画出图象,由CD⊥AB知1AB CDk k=-可设出直线CD的解析式,再把点C代入可得CD的解析式,进一步可求D点坐标;(3)如图2,取点F(-2,8),易证明CE⊥CF且CE=CF,于是得∠PEC=45°,进一步求出直线EF的解析式,再与直线AB联立求两直线的交点坐标,即为点P.【详解】解:(1)∵6m-+(n﹣12)2=0,∴m=6,n=12,∴A(6,0),B(0,12),设直线AB解析式为y=kx+b,则有1260bk b=⎧⎨+=⎩,解得212kb=-⎧⎨=⎩,∴直线AB解析式为y=-2x+12,∵直线AB过点C(a,a),∴a=-2a+12,∴a=4,∴点C坐标(4,4).(2)过点C作CD⊥AB交x轴于点D,如图1所示,设直线CD解析式为y=12x+b′,把点C(4,4)代入得到b′=2,∴直线CD解析式为y=12x+2,∴点D坐标(-4,0).(3)如图2中,取点F(-2,8),作直线EF交直线AB于P,图2∵直线EC解析式为y=32x-2,直线CF解析式为y=-23x+203,∵32×(-23)=-1,∴直线CE⊥CF,∵EC=13CF=13∴EC=CF,∴△FCE是等腰直角三角形,∴∠FEC=45°,∵直线FE解析式为y=-5x-2,由21252y xy x=-+⎧⎨=--⎩解得143643xy⎧=-⎪⎪⎨⎪=⎪⎩,∴点P的坐标为(1464,33 -).【点睛】本题是一次函数的综合题,综合考查了坐标系中两直线的垂直问题、两条直线的交点问题和求特殊角度下的直线解析式,并综合了勾股定理和等腰直角三角形的判定和性质,解题的关键是熟知坐标系中两直线垂直满足121k k=-,一次函数的交点与对应方程组的解的关系.其中,第(3)小题是本题的难点,寻找到点F(-2,8)是解题的突破口. 29.(1)CF FH=,证明见解析;(2)依然成立,点E与点C之间的距离为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章勾股定理综合提优卷
(时间:60分钟满分:100分)
一、填空题(每题3分,共30分)
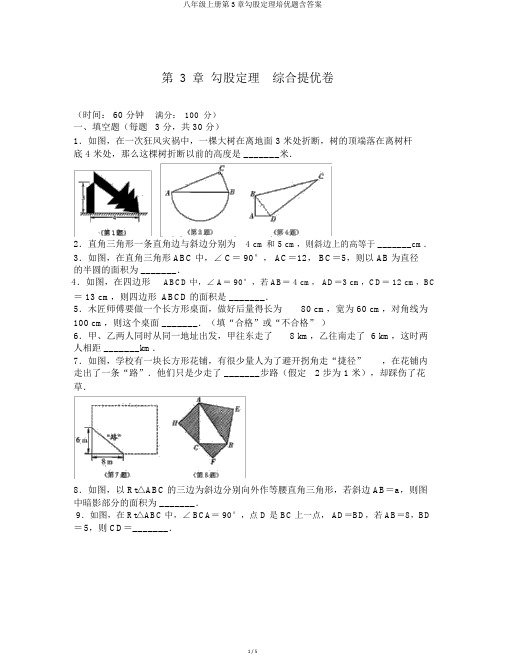
1.如图,在一次暴风灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底4米处,那么这棵树折断之前的高度是_______米.
2.直角三角形一条直角边与斜边分别为4 cm和5 cm,则斜边上的高等于_______cm.3.如图,在直角三角形ABC中,∠C=90°,AC=12,BC=5,则以AB为直径的半圆的面积为_______.
4.如图,在四边形ABCD中,∠A=90°,若AB=4 cm,AD=3 cm,CD=12 cm,BC =13 cm,则四边形ABCD的面积是_______.
5.木工师傅要做一个长方形桌面,做好后量得长为80 cm,宽为60 cm,对角线为100 cm,则这个桌面_______.(填“合格”或“不合格”)
6.甲、乙两人同时从同一地点出发,甲往东走了8 km,乙往南走了6 km,这时两人相距_______km.
7.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了_______步路(假设2步为1米),却踩伤了花草.
8.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=a,则图中阴影部分的面积为_______.
9.如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD =5,则CD=_______.
10.动手操作:在矩形纸片ABCD中,AB=3,BD=5.如图所示,折叠纸片使点A 落在边BC上的A'处,折痕为PQ.当点A'在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点A'在边BC上可移动的最大距离为_______.
二、选择题(每题3分,共30分)
11.下列各组数中,可以构成勾股数的是( ).
A.13,16,19 B.17,21,23
C.18,24,36 D.12,35,37
12.下列命题中,是假命题的是( ).
A.在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
B.在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C.在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC是直角三角形
D.在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
13.一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( ).A.13 B.5
C.13或5 D.4
14.如图是一株美丽的勾股树,其中所有的四边形都是正方
形,所有的三角形都是直角三角形,若正方形A、B、C、D
的边长分别是3,5,2,3,则最大的正方形E的面积
是( ).
A.13 B.26
C.47 D.94
15.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( ).
A.12
5
B.
4
25
C.
3
4
D.
9
4
16.已知一直角三角形的木板,三边的平方和为1800 cm2,则斜边长为( ).A.30 cm B.80 cm
C.90 cm D.120 cm
17.底面周长为12,高为8的圆柱体上有一只小蚂蚁要从点A爬到点B,则蚂蚁爬行的最短距离是( ).
A.10 B.8
C.5 D.4
18.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC,交AD于点E,AD=8,AB=4,则DE的长为( ).
A.3 B.4 C.5 D.6
19.如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则CD的长为( ).
A.32B.4 C.25D.4.5
20.如图,设正方体ABCD-A
1B
1
C
1
D
1
的棱长为1,黑、白两个甲壳虫同时从点A出发,
以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA
1→A
1
D
1
→……,白甲壳
虫爬行的路线是AB→BB
1
→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ).
A.0 B.1 C.2 D.3
三、解答题(共40分)
21.如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
(1)求DC的长;
(2)求AB的长.
22.观察下列各式,你有什么发现?
32=4+5,52=12+13,72=24+25,92=40+41,…
这到底是巧合,还是有什么规律蕴涵其中呢?请你结合有关知识进行研究.若132=a+b,则a,b的值可能是多少?
23.如图所示,一轮船以16 n mi1e/h的速度从港口A出发向东北方向航行,另
一轮船以12 n mi1e/h的速度同时从港口出发向东南方向航行,那么离开港口A2h 后,两船相距多远?
24.如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是a,b,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图;
(2)证明勾股定理.
25.如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1 km,BD=3 km,CD=3 km现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米,请你在河CD边上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用?
26.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160米,假设拖拉机行驶时,周围100米以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否回受到噪声的影响?说明理由.如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?
参考答案
1.8 2.2.4 3.169 8
4.36 cm2
5.合格 6. 10 7.8 8.
2 2 a
9.1.4 10.2
11.D 12.C 13.C 14.C 15.A 16.A 17.A 18.C 19.B 20.C 21.(1)12 (2)25
22.a=84,b=85
23.2h后
24.略
25.作点A关于河CD的对称点A',连接A'B交河CD于O点,点O就是水厂的位置,26.24秒。
