八年级下-平移和旋转培优训练题-含详细答案

合集下载

培优专题5 平移与旋转 (含解答)-

培优专题5 平移与旋转平移是几何变换中最常用的变换之一，用它可以将一些不在同一三角形中要证的两条线段或两角，进行“搬家”，把它们搬到同一个三角形（或平行四边形）中，再利用图形的性质与题设条件，找到解（或比）的途径．平移法能把分散的条件集中起来，收到事半功倍的效果．旋转也是几何变换中较常用的变换之一，在解决问题中主要应用在以下两个方面：一是在题设条件和结论间联系不易沟通或条件不易集中利用的情形下，通过旋转起到铺路架桥作用；二是图形错综复杂，但图形中的量与量之间的关系多，这时也可以看能否使用旋转的办法，移动部分图形，使题目中隐蔽着的关系明朗起来，从而找到解题途径．平移、旋转两种变换在使用中，一定要善于观察变换前后哪些量变了，哪些量没变．只有这样，我们才能充分发挥两种变换的功能，达到有效解决相关问题的目的．例1如图，在△ABC中，D、E是BC边上两点，BD=CE，试说明AB+AC>AD+AE．分析利用平移变换，•将图中已知条件转化为梯形的对角线之和大于两腰之和．解：把△ABD作平移，使BD与EC重合，分别过点E作AB的平行线，过点A作BC•的平行线，两线交于点F，连结CF．再连结EF交AC于O．则AB=EF，∠ABD=∠FEC．∵BD=CE，∴△ABD≌△FEC．∴AD=CF．在梯形AECF中，AO+OE>AE，FO+OC>CF，∴AO+OE+FO+OC>AE+CF．即AC+EF>AE+CF．∴AB+AC>AD+AE．练习11．如图，梯形ABCD中，AD∥BC，已知AD+BC=3，AC=3，BD=6，求此梯形的面积．2．如图，长方形花园ABCD中，AB=a，AD=b，花园中建有一条长方形道路LMPQ•及一条平行四边形道路RSTK，若LM=RS=c，求花园中可绿化部分的面积．3．如图，△ABC中，E、F分别为AB、AC边上的点，且BE=CF，试说明EF<BC．例2 如图，△ABC中，∠ACB=90°，M是AB的中点，∠PMQ=90°，请说明PQ2=•AP2+BQ2．分析本题中PQ、AP、BQ不在同一个三角形中，•如果将它们平移，•使PQ、BQ分别转化为PD、AD，将三线段转化在同一三角形中，巧妙运用直角三角形中的勾股定理求解．解：将BQ平移到AD，连结PD、MD．∵BQ∥AD，∴∠BAD=∠ABC．∵MA=MB，BQ=AD，∴△AMD≌△BMQ，∴∠AMD=∠BMQ．而∠AMQ+∠BMQ=180°，∴∠AMQ+∠AMD=180°．∴D、M、Q三点共线．∴∠PMD=∠PMQ=90°，MD=MQ．∴PQ=PD．∵∠PAD=∠BAC+∠BAD=∠BAC+∠ABC=90°．∴△PAD为直角三角形，PD2=AP2+AD2．∴PQ2=AP2+BQ2．1．如图，EFGH是正方形ABCD的内接四边形，∠BEG与∠CFH都是锐角，•已知EG=3，FH=4，四边形EFGH的面积为5，求正方形ABCD的面积．2．如图，△ABC中，∠B=90°，M、N分别是AB、BC上的点，AN、CM•交于点P，•若BC=AM，BM=CN，求∠APM的度数．3．如图，六边形ABCDEF中，AB∥DE，BC∥EF，CD∥AF，且AB-ED=CD-AF=EF-BC>0，请问，六边形ABCDEF的六个角是否都相等．例3如图，在正方形ABCD的边BC和CD上分别取点M和点K，并且∠BAM=∠MAK．求证：BM+KD=KA．分析把Rt△BAM绕点A顺时针旋转90°到△ADM′，使BM与DN拼成一条线段的KM′，只要证明KM′=KA即可．证明：把Rt△ABM绕点A旋转90°，则点B变为点D，M变为M′，则Rt•△BAM•≌Rt•△ADM′，∴∠M′=∠BMA∴DM′=BM．∵∠BAM=∠MAK，∴∠KAM′=∠MAD．∴∠KAM′=∠M′．∴AK=KM′．∴BM+KD=AM．1．如图，在正方形ABCD中，N是DC的中点，M是AD上异于D•的点，•且∠NMB=∠MBC，求AMAB的值．2．如图，P是等边△ABC内一点，∠APB、∠BPC、∠CPA的大小之比为5：6：7，•求以PA、PB、PC之比为边的三角形三内角之比（从小到大）．3．如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，AH⊥BC，且AH=1，•求四边形ABCD的面积．例4如图，在等腰三角形ABC中，∠CAB=90°，P是△ABC内一点，且PA=1，PB=3，PC=7，求∠APC 的度数．分析本题将△BAP绕点A旋转90°，得到△CAQ，构造直角三角形，利用勾股定理求解解：将△BAP绕点A旋转90°，使AB与AC重合，得△CAQ，则△CAQ≌△BAP．∴AQ=AP=1，CQ=BP=3，∠CAQ=∠PAB，∴∠PAQ=∠PAC+∠CAQ=∠PAC+∠PAB=90°Rt△AQP中，PQ2=AQ2+AP2=2，∴PQ=2，∴∠APQ=45°．在△CPQ中，PQ=2，CQ=3CP=7，CQ2=CP2+PQ2．∴△CPQ是直角三角形，∠CPQ=90°．∴∠APC=∠CPQ+∠APQ=135°．练习41．等边三角形内一点到三个顶点距离分别为3、4、5，则此等边三角形边长的平方为________．2．如图，P是正方形内的点，若PA=1，PB=2，PC=3，求∠APB的度数．3．如图，正方形ABCD的边长为1，AB、AD各有一点P、Q，若△APQ的周长为2，•求∠PCQ．例5 如图，在△ABC中，AB=3，AC=2，以BC为边的三角形BPC是等边三角形，求AP的最大、最小值．分析通过旋转把AP转移到有两条边确定的三角形中，利用三角形的性质求最值．解：把△ABP绕B点顺时针旋转60°得△DBC，则△ABP≌△DBC．∴DC=AP，BD=BA，∠DBA=60°．∴△ABD是等边三角形，AD=AB=3．在△ACD中，有DC<AD+AC=5，当C在DA的延长线上时才有DC=AD+AC=5，说明DC≤5，•即AP≤5．……①在△ACD中，有DC>AD-AC=1时，当C在DA线段上时才有DC=AD-AC=1，说明DC≥1，•即AP≥1．……②由①②得AP最大值为5，最小值为1．练习51．如图，正方形ABCD中，有一个内接三角形AEF，若∠EAF=45°，AB=8，EF=7，•求△EFC的面积．2．如图，在△ABC中，AB=5，AC=13，过BC上的中线AD=6，求BC的长．3．如图，已知△ABC中，AB=AC，D为三角形内一点，∠ADB>∠ADC．试证明：•CD>BD．答案:练习11．解：将BD 平移到CE 交AD 延长线于点E ，则四边形BDEC 为平行四边形∴DE=BC ，CE=BD ，S △BCD =S △CDE ∵△ABC 与△DBC 同底等高， ∴S △ABC = S △BCD = S △CDE∵S 梯形ABCD = S △ABC + S △ACD = S △CDE + S △ACD = S △ACE ．又AE=AD+DE=3=2236AC CE +=+，∴△ACE 为直角三角形，∠ACE=90°． ∴S 梯形ABCD = S △ACE =12·AC·CE=322．2．解：把长方形和平行四边形道路平移，在移动过程中道路面积不变，如图，则四块空白可组成长（b-c ），宽（a-c ）的空白长方形，其面积为（b-c ）（a-c ）=ab-bc-ac+c 2．3．解：将EF 平移为BG ，BF 平移为FG ，作∠CFG 的角平分线交BC 于D ，连结DG ，•则由平移知四边形BEFG 是平行四边形． ∴EF=BG ，BE=FG ． ∵BE=CF ，∴FG=CF ． ∵∠1=∠2，FD=FD ． ∴△FGD ≌△FCD （SAS ）． ∴DG=CD ．在△BGD 中， ∵BG<BD+DG ，∴EF<BC ．练习21．解：过E 、F 、G 、H 分别平移AD 、AB ，交点分别为P 、Q 、R 、T ，则四边形PQRT•为矩形．设正方形边长为a ，PQ=b ，PT=c ，由勾股定理得b= 223a -，c=224a -， ∵S △AEH =S △TEH ，S △BEF =S △PEF ， S △CFG =S △QFG ， S △DGH =S △RGH 则S 正方形ABCD +S 矩形PQRT =2S 四边形EFGH ∴a 2+b·c=10．即a 2+223a -·224a -=10．∴5a2=44，a2=445．∴S正方形ABCD=445．2．解：把MC平移，使点M至A点，过A作MC的平行线，过点C作AB的平行线，•两线交于点D，则MC=AD．∠APM=∠NPC=∠NAD……①∵BM=NC，CD=AM=BC，∠DCN=∠CBM=90°，∴△DCN≌△CBM．从而DN=MC，∴DN=DA……②∴∠CMB=∠DNC．∵∠BCM+∠DMB=90°，∴∠BCM+∠DNC=90°．即MC∥AD．∴ND⊥AD．……③由①，②，③得∠APM=45°．3．解：六个角都相等且都等于120°．将AB沿着BC平移到QC，CD沿着DE平移到ER，EF沿着FA平移到AP，∵AB∥ED，BC∥EF，CD∥AF，∴AB=QC，BC=AQ，CD=ER，DE=CR，EF=AP，FA=PE．∵AB-ED=CD-AF=EF-BC，∴QC-CR=ER-PE=AP-AQ．即PQ=PR=QR．∴∠1=∠2=∠3=60°．由平行线性质知：∠A=∠B=∠C=∠D=∠E=∠F=120°．练习31．解：将△BAM绕B点旋转90°，A点变为C点，M点变为P点，连结MP，则△BAM≌△BCP．∴∠BPC=∠BMA=∠CBM=∠NMB．∵BM=BP，∴∠NMP=∠NPM．∴MN=NP=NC+CP=NC+AM．设AB=1，AM=x，在Rt△MND中，则有12+x=221()(1)2x+-．∴x=13．即AMAB=13．2．解：将△ABP绕B点顺时针旋转60°得△BCP′，连结PP′，则△ABP≌△CBP′．∴AP=P′C，BP=BP′，∠APB=∠CP′B．∵∠PBP′=60°，∴△BPP′是等边三角形．∴PP′=BP，∠BPP′=60°=∠BP′P．∵∠APB：∠BPC：∠CAP=5：6：7，又∠APB+∠BPC+∠CPA=360°，∴∠APB=100°，∠BPC=120°，∠CPA=140°，∴∠1=120°-60°=60°，∠2=100°-60°=40°，∠PCP′=180°-60°-40°=80°．由PA=P′C，PP′=PB，∴△PP′C是由PA、PB、PC组成的三角形．∴三内角之比为2：3：4．3．解：将△ABH绕A点旋转90°得△ADP，则△ABH≌△ADP．∴∠APD=∠AHB=90°，AH=AP．∵∠BAD=∠BCD=90°，∠HAP=90°．∴四边形AHCP是正方形．∵AH=1，∴S正方形AHCP=1=S四边形AHCD+S△ADP．S四边形ABCD=S四边形AHCD+S△ABH．又∵S△AOP =S△ABH．∴S四边形ABCD=S正方形AHCP=1．练习41．解：如图，以A为中心将△ACP绕A顺时针旋转60°，则C与B重合，P与P′重合，连结AP′，BP′，PP′则AP′=AP，BP′=CP，∠PAP′=60°．∴△APP′是等边三角形，PP′=3．△BPP′中，BP=4，PP′=3，BP′=CP=5．由32+42=52．∴△BPP′为直角三角形，∠BPP′=90°．∴∠BPA=150°．过B作BE⊥AP，交AP延长线于E．∵∠EPB=180°-150°=30°，在Rt△BEP中，BP=4，BE=2，EP=23，Rt△ABE中，BE=2，AE=23+3，AB2=22+（23+3）2=25+123．2．解：将△ABP绕B点旋转90°，得△CBP′，连结PP′，则△ABP≌△CBP′．∴PB=BP′=2，AP=P′C=1，∠APB=∠CP′B．在Rt△PBP′中，BP=BP′=2，∴PP′=22，∠BP′P=45°．在△PP′C中，PC=3，P′C=1，PP′=22．有PC2=P′C2+P′P2，∴△PP′C是直角三角形，∠PP′C=90°．∴∠APB=∠CP′B=∠BP′P+∠PP′C=135°．3．解：将△CDQ绕C点旋转90°，得△CBM，则△CDO≌△CBM，∠QCM=90°．∵∠D=90°，∠CBA=90°，∴P、B、M在一条直线上．∵QA+AP+QP=2，DQ+AQ+AP+BP=2，∴QP=DQ+BP．∵BM=DQ，PM=PB+BM，∴QP=PM．又CP=CP，CQ=CM．∴△CQP≌△CMP．∴∠QCP=∠PCM．又∠QCP+∠PCM=∠QCM=900∴∠PCQ=45°．练习51．解：把△ADF绕A点旋转到△ABD′的位置．∵∠D和∠ABC均为直角，∴D′、B、E三点在一条直线上，∵∠EAF=45°，∴∠D′AE=45°．在△AD′E和△AEF中，AD′=AF，AE=AE，∠D′AE=∠EAF，∴△AD′E≌△AFE．∴S△D`EF =2S△AD`E =S ABEFD=S正方形ABCD-S△EFC．∴S△EFC =S正方形ABCD-S ABEFD=S正方形ABCD-2S△AD`E =82-2×12×8×7=8．2．解：将△ADC绕D点旋转180°得△BDE．∵BD=CD．- 11 - ∴C 与B 重合，设A 落到E 处，显然A 、D 、E 共线．在△ABE 中，BE=AC=13，AB=5，AE=2AD=12．则有132=122+52．∴△ABE 为直角三角形，∠BAE=90°．在Rt △ABD 中，AB=5，AD=6，则有BD=2256 =61．∴BC=2BD=261．3．证明：将△ABD 绕A 点旋转∠BAC 的度数，得△ACE ，连结DE ．由于AB=AC ． ∴B 与C 重合，则△ABD ≌△ACE ． ∵AD=AE ，∴∠1=∠2．∵∠AEC=∠ADB>∠ADC ．∴∠4>∠3，∴CE<DC ．∵BD=CE ，∴CD>BD ．。

(精练)北师大版八年级下册数学第三章图形的平移与旋转含答案

北师大版八年级下册数学第三章图形的平移与旋转含答案一、单选题(共15题，共计45分)1、下列图形中，既是中心对称图形又是轴对称图形的是（）A. B. C. D.2、下列图形中，是轴对称图形但不是中心对称图形的是（）A. B. C. D.3、下列图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.4、下列各网格中的图形是用其图形中的一部分平移得到的是（）A. B. C.D.5、下列图形中，是轴对称图形但不是中心对称图形的是（）A. B.C. D.6、下列交通标志图案中，是中心对称图形的是（）A. B. C. D.7、下列四个图形中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.8、下列图形是中心对称图形的是（）A. B. C. D..9、下列图形中可以由一个基础图形通过平移变换得到的是（）A. B. C. D.10、如图，将△ABC沿边BC向右平移2个单位长度得到△DEF，若AC的长为3个单位长度，则四边形ACFD的周长为（）A.6B.10C.8D.1211、如图，将正方形图案绕中心O旋转180°后，得到的图案是（）A. B. C. D.12、如图的方格纸中，左边图形到右边图形的变换是（）A.向右平移7格B.以AB的垂直平分线为对称轴作轴对称变换，再以AB 为对称轴作轴对称变换C.绕AB的中点旋转180°，再以AB为对称轴作轴对称D.以AB为对称轴作轴对称，再向右平移7格13、下列图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.14、下列图形中，既是轴对称图形又是中心对称图形的是（）A.正五边形B.正方形C.平行四边形D.正三角形15、将点 A( 2, -1) 向左平移 3 个单位长度，再向上平移 4 个单位长度得到点 B ，则点B 的坐标是（）A.(5, 3)B.( -1, 3)C.( -1, -5)D.(5, -5)二、填空题(共10题，共计30分)16、在直角坐标系中，△ABC的顶点坐标是A（﹣1，2）、B（﹣3，1）、C （0，﹣1）．（1）若将△ABC向右平移2个单位得到，画出△A′B′C′，A点的对应点A′的坐标是________ ．（2）若将△A′B′C′绕点C′按顺时针方向旋转90°后得到△A1B1C′，则A′点的对应点A1的坐标是________ ．（3）直接写出两次变换过程中线段BC扫过的面积之和为________ ．17、将一个自然数旋转180°后，可以发现一个有趣的现象，有的自然数旋转后还是自然数．例如，808，旋转180°后仍是808．又如169旋转180°后是691．而有的旋转180°后就不是自然数了，如37．试写一个五位数，使旋转180°后仍等于本身的五位数________．（数字不得完全相同）18、如图，在矩形ABCD中，AB＝5，BC＝3，将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF，点A落在矩形ABCD的边CD上，连结CE，CF，若∠CEF＝α，则tanα＝________．19、如图，已知面积为1的正方形ABCD的对角线相交于点O，过点O任作一条直线分别交AD，BC于E，F，则阴影部分的面积是________20、一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是________．21、如图所示，P是等边△ABC内一点，△BMC是由△BPA旋转所得，则∠PBM=________度．22、中，，，，将此三角形绕点旋转，当点落在直线上的点处时，点落在点处，此时点到直线的距离为________．23、如图，已知在矩形0ABC中，0A=3，OC=2，以边OA，OC所在的直线为轴建立平面直角坐标系xOy，反比例函数y= （x>0）的图象经过点B，点P(t，0）是x轴正半轴上的动点，将点B绕点P顺时针旋转90°，使点B恰好落在反比例y= （x>0）的图象上，则t的值是________。

北师大版八年级数学下册《图形的平移与旋转》单元测试卷及答案含有详细解析

北师大版八年级数学下册《图形的平移与旋转》单元测试卷一、选择题1、如图，将周长为8的△ABC 沿BC 方向平移1个单位得到△DEF ，则四边形ABFD 的周长为（） A ．6 B ．8C ．10 D ．122、下列四个图案中，不能由1号图形平移得到2号图形的是( )3、下列四个图形分别是四届国际数学家大会的会标，其中有( )个是中心对称图形。

A ．1B ．2C ．3D ．4 4、下列说法中，不正确的是( ) A ．图形平移是由移动的方向和距离所决定的 B ．图形旋转是由旋转中心和旋转角度所决定的C ．任意两条相等的线段都成中心对称D ．任意两点都成中心对称5、在平面直角坐标系中，若将三角形上各点的纵坐标都减去3，横坐标保持不变，则所得图形在原图形的基础上( )A ．向左平移了3个单位长度B ．向下平移了3个单位长度C ．向上平移了3个单位长度D ．向右平移了3个单位长度 6、如图，在64方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（）（第6题图）（第7题图）A ．格点MB ．格点NC ．格点PD ．格点Q7、如图，△ABC 经过平移后得到△DEF ，则下列说法中正确的有( )①AB ∥DE ，AB ＝DE ；②AD ∥BE ∥CF ，AD ＝BE ＝CF ；③AC ∥DF ，AC ＝DF ；④BC ∥EF ，BC ＝EF 。

A ．1 个B ．2个C ．3个D ．4个 8、如图所示,如果把△ABC 的顶点A 先向下平移3格,再向左平移1格到达A'点,连接A'B ,则线段A'B 与线段AC 的关系是 ( )A ．垂直B ．相等C ．平分D ．平分且垂直（第8题图）（第9题图）（第10题图）9、如图，△DEC 是由△ABC 经过了如下的几何变换而得到的：①以AC 所在直线为对称轴作轴对称，再以C 为旋转中心，顺时针旋转90°；②以C 为旋转中心，顺时针旋转90°得△A ′B ′C ′，再以A ′C ′所在直线为对称轴作轴对称；③将△ABC 向下向左各平移1个单位长度，再以AC 的中点为中心作中心对称，其中正确的变换有( ) A ．①② B ．①③ C ．②③ D ．①②③ 10、如图，将△ABC 绕点B 顺时针旋转60°得△DBE ，点C 的对应点E 恰好落在AB 的延长线上，连接AD.下列结论一定正确的是( )A. ∠ABD ＝∠EB. ∠CBE ＝∠CC. AD ∥BCD. AD ＝BC二、填空题11、用等腰直角三角板画∠AOB=45°，并将三角板沿OB 方向平移到如图所示的虚线处后绕点M 逆时针方向旋转22°，则三角板的斜边与射线OA 的夹角α为______度．12、在平面直角坐标系中，将点A(1，5)向右平移2个单位长度，可以得到对应点的坐标A ′_________；将点A(1，5)向下平移6个单位长度，可以得到对应点的坐标A ″________。

初二数学下册平移和旋转练习题

初二数学下册平移和旋转练习题平移和旋转是初中数学下册的重要内容之一，本文将为你提供一些
平移和旋转的练习题，以帮助你更好地理解和掌握这些概念。

练习题一：
1. 将点A(3, 4)向左平移4个单位，得到点B，求点B的坐标。

2. 当一个图形按照向右平移5个单位后，再向上平移3个单位，得
到新位置。

如果原来一个顶点的坐标是(2, -1)，求它的新坐标。

3. 将线段AB平移到线段CD，并保持长度不变。

若线段AB的长度为5个单位，C和D的坐标分别为(1, 3)和(5, 7)，求A和B的坐标。

练习题二：
1. 将点E(2, 5)绕点O(0, 0)逆时针旋转90°，求旋转后点的坐标。

2. 将点F(-1, 3)绕点O(2, -1)顺时针旋转180°，求旋转后点的坐标。

3. 将线段GH绕点O(0, 0)逆时针旋转60°，线段GH的长度为6个
单位，求旋转后线段的端点坐标。

练习题三：
1. 已知正方形ABCD的边长为10个单位，将其顺时针旋转90°得到新的正方形EFGH，求点E、F、G、H的坐标。

2. 已知长方形IJKL的宽为8个单位，高为5个单位，将其绕点O(0, 0)逆时针旋转45°得到新的长方形MNOP，求点M、N、O、P的坐标。

3. 将原点O(0, 0)绕点A(3, 4)逆时针旋转30°，求旋转后点的坐标。

以上是初二数学下册平移和旋转练习题的部分内容，通过这些练习可以帮助同学们巩固和提升对平移和旋转的理解和运用能力。

希望大家认真完成练习，加深对这些知识点的记忆和理解，从而提高数学水平。

八年级数学下册《第三章图形的平移与旋转》单元测试题含答案

第三章图形的平移与旋转第Ⅰ卷(选择题共30分)一、选择题(每小题3分，共30分)1．下列英文字母既是中心对称图形又是轴对称图形的是( )图12．如图2所示的各组图形中，由图形甲变成图形乙，既能用平移，又能用旋转的是( )图23．如图3，如果将△ABC的顶点A先向下平移3格，再向左平移1格到达A′点，连接A′B，那么线段A′B与线段AC的关系是( )图3A．互相垂直 B．相等C．互相平分 D．互相垂直且平分4．如图4，将△PQR先向右平移2个单位长度，再向下平移3个单位长度，则顶点P 平移后的坐标是( )图4A．(－2，－4) B．(－2，4) C．(2，－3) D．(－1，－3)5．已知A(－1，3)，B(2，－3)两点，现将线段AB平移至A1B1，如果A1(a，1)，B1(5，－b)，那么a b的值是( )A ．16B ．25C ．32D ．496．如图5所示，将边长为2的正方形ABCD 沿对角线AC 向右平移，使点A 移至线段AC 的中点A ′处，得到新正方形A ′B ′C ′D ′，则新正方形与原正方形重叠部分(图中阴影部分)的面积是( )图5A. 2B.12 C ．1 D.147．如图6所示，在△ABC 中，AB ＝4，BC ＝6，∠B ＝60°，将△ABC 沿射线BC 的方向平移，得到△A ′B ′C ′，再将△A ′B ′C ′绕点A ′逆时针旋转一定角度后，点B ′恰好与点C 重合，则平移的距离和旋转角的度数分别为( )图6A ．4，30°B ．2，60°C ．1，30°D ．3，60°8．如图7，在△ABC 中，∠CAB ＝75°，在同一平面内，将△ABC 绕点A 旋转到△AB ′C ′的位置，使得CC ′∥AB ，则∠BAB ′的度数为( )图7A ．30°B ．35°C ．40°D ．50°9．如图8，将△ABC 绕点C (0，1)旋转180°得到△A ′B ′C ，若点A 的坐标为(a ，b )，则点A ′的坐标是( )图8A ．(－a ，－b )B ．(－a ，－b －1)C ．(－a ，－b ＋1)D ．(－a ，－b ＋2) 10．如图9所示，在Rt △ABC 中，∠ACB ＝90°，∠B ＝30°，AC ＝1，且AC 在直线l 上，将△ABC 绕点A 顺时针旋转到位置①，可得到点P 1，此时AP 1＝2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2＝2＋3；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3＝3＋3……按此规律继续旋转，直到得到点P为止，则AP等于( )图9A．＋673 3 B．＋672 3 C．＋672 3 D．＋673 3第Ⅱ卷(非选择题共70分)二、填空题(每小题3分，共18分)11．有下列运动：①物体随传送带的移动；②踢足球时，足球的移动；③轻轨列车在笔直轨道上行驶；④从书的某一页翻到下一页时，这一页上的某个图形的移动．其中属于平移现象的有________．(将所有正确的序号都填上)12．如图10，把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC 于点D.若∠A′DC＝90°，则∠A＝________°.图1013.如图11，在平面直角坐标系中，点A的坐标为(－1，2)，点C的坐标为(－3，0)，先将点C绕点A逆时针旋转90°，再向下平移3个单位长度，此时点C的对应点的坐标为________．图1114．如图12，在等边三角形ABC中，AB＝10，D是BC的中点，将△ABD绕点A旋转后得到△ACE，则线段DE的长为________．图1215．如图13，在△ABC中，∠C＝90°，AC＝BC＝2，将△ABC绕点A顺时针旋转60°到△AB′C′的位置，连接C′B，则C′B的长为________．图1316．有两张完全重合的长方形纸片，小亮同学将其中一张绕点A顺时针旋转90°后得到长方形AMEF(如图14①)，连接BD，MF，此时他测得∠ADB＝30°.小红同学用剪刀将△BCD 与△MEF剪去，与小亮同学探究．他们将△ABD绕点A顺时针旋转得到△AB1D1，AD1交MF于点K(如图②)，设旋转角为β(0°＜β＜90°)，当△AFK为等腰三角形时，旋转角β的度数为________．图14三、解答题(共52分)17．(6分)青花瓷是我国民族艺术瑰宝之一，它以洁白细腻的胎体、晶莹透明的釉色、幽靓浓艳的纹饰、华美丰富的造型而闻名于世，它的清新雅丽、质朴率真最能代表中华民族含蓄而豪迈的民族风格，因而素有“国瓷”之誉．请欣赏下面这幅青花瓷图案，试用两种方法分析图案的形成过程．图1518．(6分)如图16，在△ABC和△ADE中，点E在BC边上，∠BAC＝∠DAE，∠B＝∠D，AB＝AD.(1)求证：△ABC≌△ADE；(2)如果∠AEC＝75°，将△ADE绕着点A逆时针旋转一定角度(小于90°)后与△ABC重合，求这个旋转角的大小．图1619．(6分)如图17，桌面内，直线l上摆放着两个大小相同的三角板，它们中较大锐角的度数为60°.将△ECD沿直线l向左平移到△E′C′D′的位置，使点E′落在AB上，P 为AC与E′D′的交点，试解决下列问题：(1)求∠CPD′的度数；(2)求证：AB⊥E′D′.图1720．(6分)如图18，△ABC是边长为3的等边三角形，将△ABC沿直线BC向右平移BC 的长度，得到△DCE，连接BD，交AC于点F.(1)猜想AC与BD的位置关系，并证明你的结论；(2)求线段BD的长．图1821．(6分)如图19，用等腰直角三角板画∠DOB＝45°，并将三角板沿OB方向平移到如图所示的△AMB处后，再将三角板绕点M逆时针旋转22°得到△EMC，EM与OD交于点D，求此时三角板的斜边与射线OD的夹角∠ODM的度数．图1922．(6分)如图20所示，在平面直角坐标系中，有一直角三角形ABC，且A(0，5)，B(－5，2)，C(0，2)，△AA1C1是由△ABC经过旋转变换得到的．图20(1)由△ABC旋转得到△AA1C1的旋转角的度数是多少？并写出旋转中心的坐标；(2)请你画出仍以(1)中的旋转中心为旋转中心，将△AA1C1按顺时针，△ABC按逆时针各旋转90°后得到的两个三角形，并写出△AA1C1按顺时针旋转90°后点A1的对应点A2的坐标；(3)利用变换前后所形成的图案证明勾股定理(设△ABC的两直角边长分别为a，b，斜边长为c)．23．(8分)如图21所示，△ABC，△ECD都是等边三角形．(1)试确定AE，BD之间的大小关系；(2)如果把△CDE绕点C按逆时针方向旋转到如图②所示的位置，那么(1)中的结论还成立吗？请说明理由．图2124．(8分)如图22，在正方形ABCD中，E为BC上任意一点，将△ABE旋转后得到△CBF.(1)指出旋转中心和旋转角的度数；(2)判断AE与CF的位置关系；(3)如果正方形的面积为18 cm2，△BCF的面积为4 cm2，那么四边形AECD的面积是多少？图221．D 2.C 3.D 4.A 5.C 6.B7．B 8．A 9．D 10.D11.①③12.55 13.(1，－3) 14.5 3 15.3－1 16.60°或15°17．解：(答案不唯一)方案一：以一个花瓣为基本图案，依次旋转45°，90°，135°，180°，225°，270°，315°可得到整个图案；方案二：以相邻两个花瓣为基本图案，依次旋转90°，180°，270°可得到整个图案．18．解：(1)证明：在△ABC和△ADE中，∵∠BAC＝∠DAE，AB＝AD，∠B＝∠D，∴△ABC≌△ADE.(2)∵△ABC≌△ADE，∴AC与AE是一组对应边，∴∠CAE为旋转角．∵AE＝AC，∠AEC＝75°，∴∠ACE＝∠AEC＝75°，∴∠CAE＝180°－75°－75°＝30°.即旋转角为30°.19．解：(1)由平移的性质知DE∥D′E′，∴∠CPD′＝∠CED＝60°.(2)证明：由平移的性质知CE∥C′E′，∠CED＝∠C′E′D′＝60°，∴∠BE′C′＝∠BAC＝30°，∴∠BE′D′＝90°，∴AB⊥E′D′.20．解：(1)AC⊥BD.证明如下：∵△DCE是由△ABC平移而得到的，∴△DCE≌△ABC，AC∥DE.又∵△ABC是等边三角形，∴BC＝CD＝CE＝DE，∠DCE＝∠CDE＝60°，∴∠DBC＝∠BDC＝30°，∴∠BDE＝90°，∴DE⊥BD.∵AC∥DE，∴AC⊥BD.(2)在Rt△BED中，∵BE＝6，DE＝3，∴BD＝BE2－DE2＝62－32＝3 3.21．解：∵三角板绕点M逆时针旋转了22°，∴∠BMC＝22°.∵∠DMC＝45°，∴∠OMD＝180°－45°－22°＝113°.又∵∠DOB＝45°，∴∠ODM＝180°－113°－45°＝22°，即此时三角板的斜边与射线OD的夹角∠ODM的度数是22°.22．解：(1)旋转角为90°，旋转中心的坐标为(－1，1)．(2)如图所示，点A1的对应点A2的坐标为(－2，－3)．(3)证明：设AC＝a，BC＝b，则正方形AA1A2B的面积为c2，正方形C1C2C3C的面积为(b －a)2，由图可得c2－(b－a)2＝4×12 ab，即c2－b2＋2ab－a2＝2ab，∴c2＝a2＋b2. 23．解：(1)在△ACE和△BCD中，∵AC＝BC，∠ACE＝∠BCD＝60°，CE＝CD，∴△ACE≌△BCD，∴AE＝BD.(2)成立．理由如下：∵∠ACB＝∠ECD＝60°，∴∠ACE＝∠BCD.在△ACE和△BCD中，∵AC＝BC，∠ACE＝∠BCD，CE＝CD，∴△ACE≌△BCD，∴AE＝BD.24．解：(1)旋转中心是点B，旋转角是90°.(2)如图，延长AE交CF于点M.∵△CBF是由△ABE旋转得到的，∴△CBF≌△ABE，∴∠FCB＝∠EAB.∵∠AEB＝∠CEM，∴∠BAE＋∠AEB＝∠FCB＋∠CEM.∵四边形ABCD是正方形，∴∠ABE＝90°，∴∠BAE＋∠AEB＝90°，∴∠FCB＋∠CEM＝90°，∴∠CME＝90°，∴AE⊥CF.(3)∵△CBF≌△ABE，△CBF的面积为4 cm2，∴△ABE的面积为4 cm2.∵正方形的面积为18 cm2，∴四边形AECD的面积为14 cm2.11/ 11。

(典型题)初中数学八年级数学下册第三单元《图形的平移与旋转》测试(含答案解析)(1)

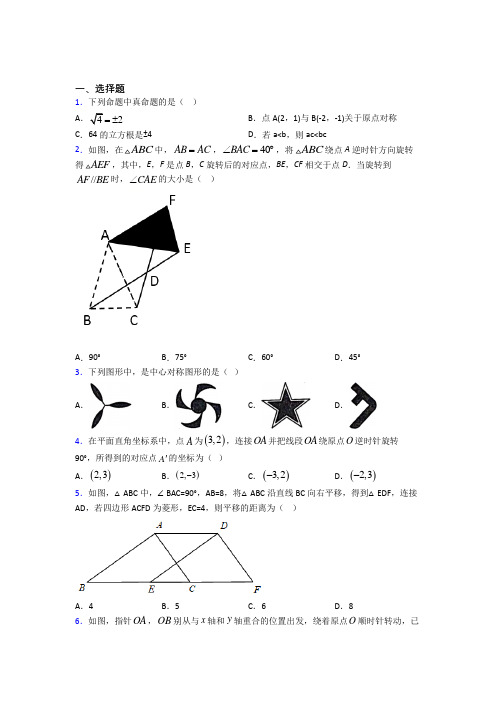
一、选择题1．下列命题中真命题的是（）A ．42=±B ．点A(2，1)与B(-2，-1)关于原点对称C ．64的立方根是±4D ．若a<b ，则ac<bc 2．如图，在ABC 中，AB AC =，40BAC ∠=︒，将ABC 绕点A 逆时针方向旋转得AEF ，其中，E ，F 是点B ，C 旋转后的对应点，BE ，CF 相交于点D ．当旋转到//AF BE 时，CAE ∠的大小是（）A ．90°B ．75°C ．60°D ．45°3．下列图形中，是中心对称图形的是（）A ．B ．C ．D ． 4．在平面直角坐标系中，点A 为()3,2，连接OA 并把线段OA 绕原点O 逆时针旋转90°，所得到的对应点A '的坐标为（）A ．()2,3B ．()2,3-C ．()3,2-D ．()2,3- 5．如图，△ABC 中，∠BAC=90°，AB=8，将△ABC 沿直线BC 向右平移，得到△EDF ，连接AD ，若四边形ACFD 为菱形，EC=4，则平移的距离为（）A ．4B ．5C ．6D ．86．如图，指针OA ，OB 别从与x 轴和y 轴重合的位置出发，绕着原点O 顺时针转动，已知OA每秒转动45°，OB的转动速度是OA的13，则第2020秒时，OA与OB之间夹角的度数为（）A．130°B．145°C．150°D．165°7．图1是正方体的平面展开图，六个面的点数分别为1、2、3、4、5、6，将点数朝外折叠成一枚正方体骰子，并放置于水平桌面上，如图2所示，若骰子初始位置为图2所示的状态，将骰子向右翻滚90 ，则完成1次翻转，此时骰子朝下一面的点数是2，那么按上述规则连续完成2次翻折后，骰子朝下一面的点数是3；则连续完成2020次翻折后，骰子朝下一面的点数是（）A．2 B．3 C．4 D．58．中国的传统建筑许多窗格图案蕴含着对称之美，现从中选取以下四种窗格图案，其中只是中心对称图形但不是轴对称图形的是（）A．B．C．D．9．在直角坐标系中，ABC 的顶点()1,5A -，()3,2B ，()0,1C ，将ABC 平移得到A B C '''，点A 、B 、C 分别对应A '、B '、C '，若点()1,4A '，则点'C 的坐标（） A ．()2,0- B ．()2,2- C ．()2,0 D ．()5,110．如图，点O 为平面直角坐标系的原点，点A 在x 轴上，OAB 是边长为4的等边三角形，以O 为旋转中心，将OAB 按顺时针方向旋转60°，得到OA B ''△，那么点A '的坐标为（）A ．(2,23)B ．(2,4)-C ．(2,22)-D ．(2,23)- 11．下列图形中，是中心对称图形，但不是轴对称图形的是（）A ．B ．C ．D ． 12．下列图形是物理学中的力学、电学等器件的平面示意图，从左至右分别代表小车、音叉、凹透镜和砝码，其中是中心对称图形的是（）A ．B ．C ．D ．二、填空题13．如图，把ABC 绕点A 顺时针旋转50°得到ADE ，点B 的对应点是D ，则直线BC 与DE 所夹的锐角是______．14．如图①，O 为直线AB 上一点，作射线OC ，使60BOC ∠=︒，将一个直角三角尺如图摆放，直角顶点在点O 处，一条直角边OP 在射线OA 上．将图①中的三角尺绕点O 以每秒10°的速度按逆时针方向旋转（如图②所示），在旋转一周的过程中，第t 秒时，OQ 所在直线恰好平分AOC ∠，则t 的值为_______．15．如图，ABC 是等边三角形．若将AC 绕点A 逆时针旋转角α后得到AC '，连接BC '和CC '，则BC C '∠的度数为________．16．如图①，O 为直线AB 上一点，作射线OC ，使120AOC ∠=︒，将一个直角三角尺如图摆放，直角顶点在点O 处，一条直角边OP 在射线OA 上，将图①中的三角尺绕点O 以每秒6︒的速度按顺时针方向旋转（如图②所示），在旋转一周的过程中第t 秒时OP 所在直线恰好平分BOC ∠，则t 的值为________．17．如图，在△ABC 中，AB ＝4，BC ＝6，∠B ＝60°，将△ABC 沿射线BC 的方向平移2个单位后，得到A B C '''，连接A C '，则A B C ''的周长为________．18．如图，ODC ∆是由OAB ∆绕点O 顺时针旋转40︒后得到的图形，若点D 恰好落在AB 上，且105AOC ∠=︒，则C ∠的度数是_______．19．如图，将△ABC 沿BC 方向平移到△DEF ，若A 、D 间的距离为1，CE ＝2，则BF ＝_____．20．在 ABC 内的任意一点 ()P a b ，经过平移后的对应点为 ()1P cd ，，已知 ()32A ，在经过此次平移后对应点 1A 的坐标为 ()51-，，则 c d a b +-- 的值为________________．三、解答题21．如图，ABC 中，90C ∠=︒．ABC 绕点B 逆时针旋转，旋转角为α，点C '为点C 的对应点．（1）请用尺规作图法画出旋转后的A BC ''△；（2）若90α=︒，3BC =，4AC =．求A A '的长．22．如图，ABC 是直角三角形，90C ∠=︒，将ABC 绕点B 逆时针旋转60︒至DEB ，点E 落在AB 上，DE 延长线交AC 所在直线于点F ．（1）求AFE ∠的度数；（2）求证：AF EF DE +=．23．如图，在平面直角坐标系中，ABC ∆的三个顶点的坐标分别是(1,4)A -，(3,2)B -，(0,2)C ．（1）将ABC ∆以点C 为旋转中心旋转180°，画出旋转后对应的11A B C ∆；（2）平移ABC ∆，若A 的对应点2A 的坐标为()3,2--，画出平移后的222A B C ∆；（3）若将222A B C ∆绕某一点旋转可以得到11A B C ∆，请直接写出旋转中心的坐标． 24．如图，在Rt ABC △中，90ACB ∠=︒，点D 、E 分别在AB ，AC 上，CE BC =，连接CD ，将线段CD 绕点C 按顺时针方向旋转90︒后得CF ，连接EF ．（1）补充完成图形；（2）若//EF CD ，求证：90BDC ∠=︒．25．如图，已知直线y ＝kx ＋2与直线y ＝3x 交于点A （1，m ），与y 轴交于点B ．（1）求k 和m 的值；（2）求△AOB 的周长；（3）设直线y ＝n 与直线y ＝kx ＋2，y ＝3x 及y 轴有三个不同的交点，且其中两点关于第三点对称，求出n 的值．26．如图，ABC 在平面直角坐标系中，顶点的坐标分别为()1,4A -，()4,5B -，(5,2)C -．（1）画出与ABC 关于原点中心对称的111A B C △；（2）将ABC 绕点1O 顺时针旋转90︒得到111A B C △，2AA 是点A 所经过的路径，则旋转中心1O 的坐标为________________．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】根据算术平方根、点关于原点对称、立方根以及不等式的性质进行判断即可．【详解】解：A 42=，故原选项是假命题，不符合题意；B . 点A (2，1)与B (-2，-1)关于原点对称,是真命题，故此选项是真命题，符合题意；C .64的立方根是4，故原选项是假命题，不符合题意；D .当c ≤0时ac ≥bc ，故原选项是假命题，不符合题意；故选B【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．2．C解析：C【分析】由旋转的性质可得∠EAF ＝∠BAC ＝40°，AB ＝AE ，由平行线的性质可求∠FAE ＝∠AEB ＝40°，由等腰三角形的性质和三角形内角和定理可求∠BAE 的度数，进而即可求解．【详解】解：∵将△ABC 绕点A 逆时针方向旋转得△AEF ，∴∠EAF ＝∠BAC ＝40°，AB ＝AE ，∵AF ∥BE ，∵AB ＝AE ，∴∠ABE ＝∠AEB ＝40°，∴∠BAE ＝180°−40°−40°＝100°，∴∠CAE ＝100°-40°=60°，故选：C ．【点睛】本题考查了旋转的性质，等腰三角形的性质，平行线的性质，求出∠AEB 的度数是本题的关键．3．B解析：B【分析】根据中心对称图形的概念对各选项分析判断即可得解．【详解】解：A 、不是中心对称图形，故本选项不符合题意；B 、是中心对称图形，故本选项符合题意；C 、不是中心对称图形，故本选项不符合题意；D 、不是中心对称图形，故本选项不符合题意．故选：B ．【点睛】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与原图重合．4．D解析：D【分析】如图：过点A 作AB x ⊥轴于点B ，过点'A 作D y A '⊥轴于点D ，可得'ABO ODA ∆∆≌，所以，3OD =，'2DA =，即可求解点'A 的坐标【详解】如图，过点A 作AB x ⊥轴于点B ，过点'A 作'A D x ⊥轴于点D ，∴∠ABO =∠A 'DO =90°，由题意得AO=A 'O ，∠AO A '=90°，∵90AOB AOD ∠+∠=︒，∴AOB A OD '∠=∠，∴'AOB A OD ∆∆≌，∴OB=OD =3,AB=A 'D =2，∵点A '在第二象限，∴点A '坐标为(2,3)-．故选：D ．【点睛】本题考查了坐标与图形变换—旋转，在平面直角坐标系中，求点的坐标，采用作x 轴或y 轴的垂线段，实现化斜为直，是一种常见方法．5．C解析：C【分析】根据平移的性质可得8,,AB DE AC DF BC EF ====，设AC DF CF AD x ====，求得BC=4x +，再由勾股定理理出方程求解即可．【详解】解：由平移的性质可得：8,,AB DE AC DF BC EF ====又∵四边形ACFD 是菱形∴设AC DF CF AD x ====又∵4EC =∴4BC EF CF CE x ==+=+又∵∠90BAC ︒=∴222AB AC BC +=∴2228(4)x x +=+解得，6x =即6AD DF CF AC ====故平移的距离为：6AD =故选：C ．【点睛】本题主要考查了平移的性质，熟练掌握平移的基本性质是解答此题的关键．6．C解析：C【分析】先求出线段OA 、OB 第2020秒时旋转的度数，再除以360°，即可确定最终状态时OA 、OB 的位置，再求其夹角度数即可．【详解】由题意可知OB的速度为每秒转动145153⨯︒=︒．则第2020秒时，线段OA旋转度数=2020×45°=90900°，线段OB旋转度数=2020×15°=30300°．90900°÷360°=252⋯⋯180°，30300°÷360°=84⋯⋯60°，此时OA、OB的位置如图所示，OA与OB之间的夹角度数=90°+60°=150°．故选：C．【点睛】本题考查线段的旋转，解题的关键是利用旋转周期确定最终状态时OA、OB所在位置．7．C解析：C【分析】先根据平面图形确定各对面的点数，根据翻转发现规律：每四次为一个循环，用2020除以4得到翻转完成2020次后的图形，即可得到答案．【详解】由平面图形可知：1与6是对面，2与5是对面，3与4是对面，这是一个正方体，完成1次翻转时骰子朝下一面的点数是2，完成5次翻转后朝下一面的点数还是2，故每四次为一个循环，∵20204505÷=，∴连续完成2020次翻折后，与图2的位置相同，骰子朝下一面的点数是4，故选：C．【点睛】此题考查图形类规律探究，正方体展开图，旋转的性质，正确理解旋转的规律并运用规律解决问题是解题的关键．8．A解析：A【分析】本题根据中心对称图形和轴对称图形的定义可直接得出结果．【详解】A 选项属于中心对称图形但不是轴对称图形，故正确；B 选项既属于中心对称图形也属于轴对称图形，故不正确；C 选项既属于中心对称图形也属于轴对称图形，故不正确；D 选项既属于中心对称图形也属于轴对称图形，故不正确．故选：A ．【点睛】本题考查了中心对称图形和轴对称图形的定义，属于基础题，熟练掌握中心对称图形和轴对称图形的定义是解题的关键．9．C解析：C【分析】根据点A 的平移规律，求出点'C 的坐标即可．【详解】∵()15A -，向右平移2个单位，向下平移1个单位得到()'14A ，， ∴()01C ，向右平移2个单位，向下平移1个单位得到()'20C ，，故选：C ．【点睛】此题考查点的坐标的平移规律：横坐标左减右加，纵坐标上加下减，熟记规律是解题的关键．10．D解析：D【分析】根据旋转得到A '与点B 重合，过点B 作BC AO ⊥于点C ，利用等边三角形的性质求出OC 和BC 的长，得到坐标．【详解】解：如图，AOB 绕着点O 顺时针旋转60︒得到OA B ''△，此时A '与点B 重合，过点B 作BC AO ⊥于点C ，∵△OAB 是边长为4的等边三角形，∴AB=BO ，BC AO ⊥，∴AC=OC=2，根据勾股定理，2216423=-=-=，BC BO OC∴()2,23A'-．故选：D．【点睛】本题考查图形的旋转和等边三角形的性质，解题的关键是掌握等边三角形的性质．11．B解析：B【分析】根据轴对称图形与中心对称图形的概念判断即可．【详解】A、不是中心对称图形，是轴对称图形，不符合题意；B、是中心对称图形，但不是轴对称图形，符合题意；C、既是中心对称图形，又是轴对称图形，不符合题意；D、不是中心对称图形，是轴对称图形，不符合题意；故选：B．【点睛】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后和原图形重合．12．C解析：C【分析】根据中心对称图形的定义，结合选项所给图形进行判断即可．【详解】解：A、不是中心对称图形，故本选项错误；B、不是中心对称图形，故本选项错误；C、是中心对称图形，故本选项正确；D、不是中心对称图形，故本选项错误；故选C．【点睛】此题主要考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与原图重合．二、填空题13．50°【分析】根据旋转的性质即可得到结论【详解】解：∵将△ABC 绕点A 顺时针旋转50°得到△ADE 点B 的对应点是点D ∴直线BC 与直线DE 所夹的锐角=旋转角=50°故答案为：50°【点睛】本题考查了旋解析：50°【分析】根据旋转的性质即可得到结论．【详解】解：∵将△ABC 绕点A 顺时针旋转50°得到△ADE ，点B 的对应点是点D ，∴直线BC 与直线DE 所夹的锐角=旋转角=50°，故答案为：50°．【点睛】本题考查了旋转的性质，熟记旋转变换时，对应线段的夹角与旋转角的关系是解题的关键．14．3或21【分析】过点O 作直线DE 平分∠AOC 根据及DE 平分∠AOC 求得∠AOE=∠BOD=当OQ 与OD 重合时所在直线恰好平分；当OQ 与OE 重合时所在直线恰好平分式求值即可【详解】过点O 作直线DE 平分解析：3或21【分析】过点O 作直线DE 平分∠AOC ，根据60BOC ∠=︒及DE 平分∠AOC ，求得∠AOE=∠BOD=60︒，当OQ 与OD 重合时，OQ 所在直线恰好平分AOC ∠，；当OQ 与OE 重合时，OQ 所在直线恰好平分AOC ∠，式求值即可．【详解】过点O 作直线DE 平分∠AOC ，如图，∵60BOC ∠=︒，∴120AOC ∠=︒∵DE 平分∠AOC ，∴∠AOE=∠BOD=60︒，当OQ 与OD 重合时，OQ 所在直线恰好平分AOC ∠，∴t=1809060310--=（秒）；当OQ 与OE 重合时，OQ 所在直线恰好平分AOC ∠， ∴36090602110t --==，故答案为：3或21．．【点睛】此题考查旋转角度计算，平分线的性质，有理数的混合运算，正确理解图形中旋转所得角度及OQ 所在的位置是解题的关键．15．30°【分析】由旋转的性质得出AC=AC ∠CAC=α由三角形的内角和定理求出∠ACC 的度数由等边三角形的性质得出AB=AC 由等腰三角形的性质求出∠ACB 的度数则可得出答案【详解】解：∵将AC 绕点A 逆解析：30°．【分析】由旋转的性质得出AC=AC'，∠CAC'=α，由三角形的内角和定理求出∠AC'C 的度数，由等边三角形的性质得出AB=AC'，由等腰三角形的性质求出∠AC'B 的度数，则可得出答案．【详解】解：∵将AC 绕点A 逆时针旋转角α后得到AC'，∴AC=AC'，∠CAC'=α，∴∠ACC'=∠AC'C=1809022︒-αα︒-， ∵△ABC 是等边三角形，∴AB=AC ，∠BAC=60°，∴AB=AC'， ∴∠AC'B=180606022αα-=︒-︒-︒， ∴∠BC'C=∠AC'C-∠AC'B=(90°−2α)−(60°−2α)=30°．故答案为：30°．【点睛】本题考查了等边三角形的性质，旋转的性质，等腰三角形的性质，三角形内角和定理，熟练掌握旋转的性质是解题的关键．16．25或55【分析】根据平角的定义得到∠BOC ＝60°根据角平分线定义列出方程可求解【详解】解：∵∠AOC ＝120°∴∠BOC ＝60°∵OP 所在直线恰好平分∠BOC ∴∠BOP ＝∠BOC ＝30°或∠BO解析：25或55【分析】根据平角的定义得到∠BOC ＝60°，根据角平分线定义列出方程可求解．【详解】解：∵∠AOC ＝120°，∴∠BOC ＝60°，∵OP 所在直线恰好平分∠BOC ，∴∠BOP ＝12∠BOC ＝30°，或∠BOP ＝180°-30°＝150°， ∴6t ＝180-30或6t ＝180+150，∴t ＝25或55，故答案为：25或55．【点睛】本题考查了一元一次方程的应用，考查了角平分线定义，平角的定义，列出正确的方程是本题的关键．17．12【分析】根据平移的性质得则可计算则可判断为等边三角形继而可求得的周长【详解】平移两个单位得到的又是等边三角形的周长为故答案为：12【点睛】本题考查了平移的性质：把一个图形整体沿某一直线方向移动会解析：12【分析】根据平移的性质得2BB '=，4A B AB ''==，=60A B C B ∠''∠=︒，则可计算624B C BC BB '=-'=-=，则4A B B C ''='=，可判断A B C ''△为等边三角形，继而可求得A B C ''△的周长．【详解】 ABC 平移两个单位得到的A B C '''，2BB ∴'=，AB A B =''，4AB =，6BC =，4A B AB ∴''==，624B C BC BB '=-'=-=，4A B B C ∴''='=，又60B ∠=︒，60A B C ∴∠''=︒，A B C ∴''是等边三角形，A B C ∴''的周长为4312⨯=．故答案为：12．【点睛】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同．新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．18．45°【分析】根据旋转的性质可得∠AOD=∠BOC=40°AO=DO 再求出∠BOD ∠ADO 然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算解即可求解【详解】解：∵是绕点O 顺时针旋转40°解析：45°【分析】根据旋转的性质可得∠AOD=∠BOC=40°，AO=DO ，再求出∠BOD ，∠ADO ，然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算解B ∠，即可求解．【详解】解：∵ODC ∆是OAB ∆绕点O 顺时针旋转40°后得到的图形，∴∠AOD=∠BOC=40°，AO=DO ，∵∠AOC=105°，∴∠BOD=105°-40°×2=25°，∠ADO=∠A=12（180°-∠AOD ）=12（180°-40°）=70°，由三角形的外角性质得，∠B=∠ADO-∠BOD=70°-25°=45°∴∠C=45°．故答案为：45°．【点睛】本题考查了旋转的性质，等腰三角形的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质并准确识图是解题的关键．19．4【分析】根据平移的性质由AD=1得到BE=1CF=1再根据BF=BE+EC+CF 计算即可得到答案；【详解】解：根据平移的性质由AD=1得：BE=1CF=1由∵BF=BE+EC+CF ∴BF=1+2+解析：4【分析】根据平移的性质，由AD=1得到BE=1，CF=1，再根据BF= BE+EC+CF ，计算即可得到答案；【详解】解：根据平移的性质，由AD=1得：BE=1，CF=1，由∵BF= BE+EC+CF ，∴BF= 1+2+1=4，故答案为：4；【点睛】本题主要考查了平移的性质，能根据AD=1得到BE=1，CF=1是解题的关键． 20．-1【分析】由A （32）在经过此次平移后对应点A1的坐标为（5-1）可得△ABC 的平移规律为：向右平移2个单位向下平移3个单位由此得到结论【详解】解：由A （32）在经过此次平移后对应点A1的坐标为（解析：-1【分析】由A （3，2）在经过此次平移后对应点A 1的坐标为（5，-1），可得△ABC 的平移规律为：向右平移2个单位，向下平移3个单位，由此得到结论．【详解】解：由A （3，2）在经过此次平移后对应点A 1的坐标为（5，-1）知c=a+2、d=b -3，即c -a=2、d -b=-3，则c+d -a -b=2-3=-1，故答案为：1-．【点睛】本题考查的是坐标与图形变化——平移，牢记平面直角坐标系内点的平移规律：上加下减、右加左减是解题的关键．三、解答题21．（1）作图见解析，（2）52．【分析】（1）作BA′=BA ，A′C′=AC 即可；（2）根据勾股定理求出AB ，由旋转可知，△AB A′是等腰直角三角形，根据勾股定理可求A A '．【详解】解：（1）旋转后的A BC ''△如图所示；（2）∵90C ∠=︒，3BC =，4AC =， ∴2222435AB AC BC +=+=，由旋转可知，∠ABA′=90°，AB=A′B=5，22225552AA AB A B ''=+=+=【点睛】本题考查了旋转作图和性质，勾股定理，解题关键是熟练运用旋转性质和勾股定理． 22．（1）60︒；（2）见解析【分析】（1）由旋转的性质可得：∠D=∠A ，∠DBE=∠ABC=60°，再根据三角形内角和定理可得AFE DBE ∠=∠；（2）连接BF ，根据旋转性质证Rt Rt ()BCF BEF HL △≌△,得EF CF =，故AF EF AF CF +=+．【详解】解：（1）∵ABC 是直角三角形，ABC 绕点B 逆时针旋转60︒至DEB ，∴∠D=∠A ，∠DBE=∠ABC=60°又∵∠BED=∠AEF∴60AFE DBE ∠=∠=︒．（2）连接BF ． BDE 由ABC 旋转而得，90DEB ∴∠=︒，DE AC =，BC BE =．在Rt BCF △和Rt BEF 中， BC BE BF BF =⎧⎨=⎩Rt Rt ()BCF BEF HL ∴△≌△，EF CF ∴=，AF EF AF CF AC DE ∴+=+==．【点睛】本题考核知识点：旋转性质．根据旋转性质得出对应角相等，对应边相等是关键． 23．（1）见解析；（2）见解析；（3）旋转中心为(1,1)--【分析】（1）根据网格结构找出点A 、B 绕点C 旋转180°后的对应点1A 、1B 的位置，然后顺次连接即可；（2）根据网格结构找出点A 、B 、C 平移后的位置，然后顺次连接即可；（3）根据旋转的性质，确定出旋转中心即可．【详解】解：（1）11A B C 如图所示；（2）222A B C ∆如图所示；（3）如图所示，旋转中心为(1,1)--．【点睛】本题考查了利用旋转变换作图，利用平移变换作图，熟练掌握网格结构以及旋转的性质，准确找出对应点的位置是解题的关键．24．（1）图形见解析；（2）证明见解析．【分析】（1）根据题意，利用旋转性质将图形补全，并按要求标清相应的字母即可；（2）由旋转的性质得到∠DCF 为直角，由EF 与CD 平行，得到∠F 为直角，利用SAS 得到△BDC 与△EFC 全等，利用全等三角形对应角相等即可得证．【详解】（1）解：所补图形如图所示：（2）证明：由旋转的性质得：DC FC =，90DCF ∠=︒，∴90DCE ECF ∠+∠=︒．90ACB ∠=︒，∴90BCD DCE ∠+∠=︒．BCD ECF ∴∠=∠．//EF DC ，180DCF F ∴∠+∠=︒．90F ∴∠=︒．在BCD ∆和ECF ∆中，BC EC BCD ECF DC FC =⎧⎪∠=∠⎨⎪=⎩，()BCD ECF SAS ∴∆≅∆．90BDC F ∴∠=∠=︒．【点睛】此题考查了旋转的性质，以及全等三角形的判定与性质，熟练掌握旋转的性质是解本题的关键．25．（1）m=3，k=1；（2）C △AOB 210；（3）n 的值为32或125或6．【分析】（1）由直线y ＝3x 交于点A （1，m ），可得m=3，A(1，3)，由直线y ＝kx ＋2与直线y ＝3x 交于点A （1，3），代入得3=k+2，解得k=1；（2）求出直线y ＝x ＋2与y 轴交于点B （0，2）利用勾股定理两点距离公式AB ，OA ，OB ，可求周长C △AOB 210（3）先求出直线y ＝n 与直线y ＝x ＋2，y ＝3x 及y 轴有三个不同的交点，E （n-2，n ）,D （3n ，n ），C （0，n ），其中两点关于第三点对称，共有三种情况，①E （n-2，n ）,D （3n ，n ），关于C （0，n ）对称；②E （n-2，n ）, C （0，n ），关于D （3n ，n ）对称；③D （3n ，n ），C （0，n ）,关于E （n-2，n ）对称,列出两点距离等式，即可求出n 的值．【详解】解：（1）直线y ＝3x 交于点A （1，m ），∴m=3，A(1，3)直线y ＝kx ＋2与直线y ＝3x 交于点A （1，3），∴3=k+2，∴k=1；（2）直线y ＝x ＋2与y 轴交于点B ．则x=0，y=2，B （0，2），，C △AOB ；（3）直线y ＝n 与直线y ＝x ＋2，y ＝3x 及y 轴有三个不同的交点，E （n-2，n ）,D （3n ，n ），C （0，n ），其中两点关于第三点对称，共有三种情况，①E （n-2，n ）,D （3n ，n ），关于C （0，n ）对称，则n-2+3n =0， 32n =， ②E （n-2，n ）, C （0，n ），关于D （3n ，n ）对称，则3n = 23n n --， 23n n --=3n ±， 23n n --=3n 或23n n --=3n -， n=6或n=2舍去，③D （3n ，n ），C （0，n ）,关于E （n-2，n ）对称,，则()2=23n n n ---， ()()2=23n n n ±---，2=23n n n --+或2=23n n n -+-+， 125n =或n=0(舍去)，综合以上三种情况n 的值为32或125或6．【点睛】本题考查待定系数法求点坐标与解析式，勾股定理两点距离公式，中心对称的性质，掌握待定系数法求点坐标与解析式，勾股定理两点距离公式，中心对称的性质，会利用分类思想解决中心对称是关键．26．（1）作图见解析；（2）()4,1-【分析】（1）找到点A 关于原点的对称点1A ，点B 关于原点的对称点1B ，点C 关于原点的对称点1C 即可得到111A B C △；（2）连接2AA 并作它的垂直平分线，再连接2CC 并作它的垂直平分线，交于点1O 即为所求．【详解】解：（1）如图所示：111A B C △即为所求，（2）如图，连接2AA 并作它的垂直平分线，再连接2CC 并作它的垂直平分线，交于点1O ，∴()14,1O -．【点睛】本题考查图形的中心对称和旋转，解题的关键是掌握中心对称图形的画法和确定旋转中心的方法．。

(完整版)平移与旋转练习题精选(有答案)

22 、如下图， E 是正方形 ABCD 中 CD 边上任一点，以点 A 为中心，把△ ADE 顺时针旋转 90°，在给出图
形中画出旋转后的图形，并完成下列填空．（ 1）因为点 A 是对称中心，所以它的对应点是 (
)；
（ 2 ）正方形 ABCD 中， AD=AB ，∠ DAB=90° ，所以旋转后点 D 与点 (
)重合．
23 、如图所示， E、 F 分别是△ ABC 的边 AB 、 AC 的两定点，在 BC 上求一点 M ，使△ MEF 的周长最短。
26、如图：若∠ AOD= ∠ BOC=60 °,A 、O、C 三点在同一条线上，△
求：（ 1）旋转中心，（ 2）旋转角度数，
（ 3）图中经过旋转后能重合的三角形共有几对？若
（ 3）∵∠ FDE=45° ，∠ ADC=9°0 ，∴∠ ADF+ ∠ EDC=9°0 -45°=45°，∵∠ GDF= ∠ GDA+ ∠ADF，∠ GDA= ∠EDC， ∴∠ GDF= ∠EDC+ ∠ADF=45° ．
26 、（ 1） .O 点 (2).60 度 (3).3 对，成立，因为角 AOD为 60 度，角 DOC为 120 度，向加 180 度，所以成立 (4).90 因为角 BOC=角 AOD=45度，所以应旋转 90 度 (5).120 度
二、填空题
11、 O 12 、C
∠ EOB 顺时针
AO=DO 90°
∠ AOD= ∠BOE ．
13 、由图可知， OB 、OD 是对应边，∠ BOD 是旋转角，所以，旋转角∠ BOD= ∠AOD- ∠AOB=127° -90 °=37 度
14 、解：∵ AD∥ BC，∠ EFB=65°，∴ DEF=65° ，又∵∠ DEF= ∠ D′ EF，∴∠ D′ EF=65°，∴∠ AED′ =50°

完整版北师大版八年级数学下册第三章图形的平移与旋转单元培优卷含答案

北师大版2019年八年级数学下册图形的平移与旋转单元培优卷—■、选择题1 •在如图五幅图案中，（2）、（3）、（4）、（5）中哪•幅图案可以通过平移图案（1）得到（）3.观察下列银行标志，从图案看既是轴对称图形又是中心对称图形的有（）A ・1个 B. 2个 C. 3个 D. 4个4. 如图，在10X6的网格中，每个小方格的边长都是1个单位，将AABC 平移到ADEF 的位置，）下闻正确的平移步骤是（・D •先向右平移5个单位，再向下平移2个单位5•如图，在AABC 中，ZCAB=90° ,将ZiABC 绕点A 顺时针旋转60。

得AADE,则ZEAB 的度数为A. 20°B. 25°C. 28°D. 30° 6.如图,在平面直角坐标系中，点B 、C 、E 、在y 轴上,RtAABC 经过变换得到RtAODE.若）则这种变换可以是（AC=2）, 1, 0的坐标为（C 点. A.A ABC 绕点C 顺时针旋转90° B. A ABC 绕点C 顺时针旋转90° C. A ABC 绕点C 逆时针旋转90° D. A ABC 绕点C 逆时针旋转90° ，再向下平移3，再向下平移1，再向下平移1，再向下平移37 •如图，在平面虎角坐标系A ABC 绕某•点F 旋转•定的角度得到AA' B‘ C' •根据图形变换前后的关系可得点P 的坐标为( )A. (2)B. (3)C. (4)D. (5) 2.民族图案是数学文化中的•块瑰宝.下列图案中，既不是中心对称图形也不是轴对称图形的是A •先向左平移5个单位, B.先向右平移5个单位, C •先向左平移5个单位, 再向下平移2个单位再向下平移2个单位再向上平移2个单位A. (0, 1) B・(1,・ 1) C. (0, - 1) D. (1,0)8.如图，在ZkABC中，ZCAB=65°,将Z\ABC在平而内绕点A旋转到AAB' C'的位置，使CC' 〃AB,则旋转角的度数为( )° 65. D° 50. C° 40. B° 35. A・9•如图，把直角梯形ABCD沿AD方向平移到梯形EFGH, HG=24m, MG=8m, MC=6m.则阴影部：. m )分地的面积是(.A. 168B. 128C. 98D. 15610•将两个斜边长相等的三角形纸片如图①放置，其中ZACB=ZCED=90° , ZA=45° , ZD=30°•把△DCE绕点C顺时针旋转15°得到ADCE,如图②，连接DB,则ZEDB的叫度数为()A. 10°B. 20°C. 7.5°D. 15°二、填空题.,，要在台阶上铺满地毯水平距离米1. 5,其高度AB=4米,BC = 5米如图11.,台阶的宽度为则地毯的面积为.12.如图，为了把AABC 平移得到AA' B‘ C'，可以先将AABC向右平移格，再向上平移格.13.如图，将周长为8的AABC沿BC方向向右平移1个单位得到ADEF,则四边形ABFD的周长为.14•如图，将AAOB绕点0逆时针旋转90°，得到AA' OB' •若点A的坐标为(a,b),则・_________ 的坐标为A点.15.逆时针旋PC=10・若将APAC绕点A,如图，P是正三角形ABC内的•点.且PA=6PB=8, °・，ZAPB= 转后,得到AMAB,则点P与点M之间的距离为的对应点的坐标为 .90 (3, 4)绕原点逆时针旋转。

(典型题)初中数学八年级数学下册第三单元《图形的平移与旋转》检测题(有答案解析)

一、选择题1．在平面直角坐标系中，将直线1:32=--l y x 沿坐标轴方向平移后，得到直线2l 与1l 关于坐标原点中心对称，则下列平移作法正确的是（） A ．将1l 向右平移4个单位长度 B ．将1l 向左平移6个单位长度 C ．将1l 向上平移6个单位长度D ．将1l 向上平移4个单位长度2．下列图形中，既是中心对称又是轴对称图形的是（）A ．B ．C ．D ．3．如图，将矩形ABCD 绕点C 顺针旋转90°到矩形A B C D ''''的位置，若4,2AB AD ==，则图中阴影部分的面积为（）A ．4233π-B ．4433π-C ．8233π-D ．8433π-4．如图，将△ABC 绕点C 顺时针旋转得到△DEC ，使点A 的对应点D 恰好落在边AB 上，点B 的对应点为E ，连接BE ，下列四个结论： ①AC ＝AD ；②AB ⊥EB ；③BC ＝EC ；④∠A ＝∠EBC ；其中一定正确的是（）A．①②B．②③C．③④D．②③④5．如图，指针OA，OB别从与x轴和y轴重合的位置出发，绕着原点O顺时针转动，已知OA每秒转动45°，OB的转动速度是OA的13，则第2020秒时，OA与OB之间夹角的度数为（）A．130°B．145°C．150°D．165°6．下列全国各地地铁标志图中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．7．中国的传统建筑许多窗格图案蕴含着对称之美，现从中选取以下四种窗格图案，其中只是中心对称图形但不是轴对称图形的是（）A ．B ．C ．D ．8．下列标志既是轴对称图形又是中心对称图形的是（） A ．B ．C ．D ．9．已知点A 的坐标为(2,1)--，点B 的坐标为(0,2)-，若将线段AB 平移至A B ''的位置，点A '的坐标为(3,2)-，则点B '的坐标为（） A ．(3,2)--B ．(0,1)C ．(1,1)-D ．(1,1)-10．如图所示图形中，既是轴对称图形，又是中心对称图形的是（） A ．B ．C ．D ．11．如图所示，在ABC ∆中，70CAB ∠=︒，将ABC ∆绕点A 旋转到AB C ''∆的位置，使得C A AB '⊥，则BAB '∠的度数为( )A ．10︒B ．20︒C ．30D ．50︒12．下列图形中，既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．二、填空题13．如图，点D 是等腰直角三角形 ABC 内一点，AB ＝AC ，若将△ABD 绕点A 逆时针旋转到△ACE 的位置，则∠AED 的度数为________________．14．如图，在平面直角坐标系中，将△ABC绕点A顺时针旋转到△AB1C1的位置，点B，O （分别落在点B1，C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，再将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去，…，若点A(3，0)，B(0，4)，AB=5，则点B2021的坐标为________．15．如图，ABC是等边三角形，点P是ABC内一点．APC△沿逆时针方向旋转后与AP B'△重合，最小旋转角等于__________︒．16．在平面直角坐标系xoy中，已知点A(2，3)，若将OA绕原点O逆时针旋转90°得到OA′，则点A′的坐标是____________．17．在一块边长为10米的正方形草坪上修了横竖各两条宽都为2米的长方形小路（图中阴影部分）将草坪分隔成如图所示的图案，则图中未被小路覆盖的草坪的总面积为__________平方米．18．如图，在平面直角坐标系中，三角形ABC经过平移后得到三角形A′B′C′，且平移前后三角形的顶点坐标都是整数．若点P（12，﹣15）为三角形ABC内部一点，且与三角形A′B′C′内部的点P′对应，则对应点P′的坐标是_____．19．如图，将△AOB 绕点O 按逆时针方向旋转50°后得到△COD ，如果∠AOB ＝15°，那么∠AOD 的度数为_____．20．如图∆DEF 是由∆ABC 绕着某点旋转得到的，则这点的坐标是__________.三、解答题21．如图1，点O 为直线AB 上一点，过O 点作射线OC ，使:1:2AOC BOC ∠∠=，将一直角三角板的直角顶点放在点O 处，一边OM 在射线OB 上，另一边ON 在直线AB 的下方．（1）将图1中的三角板绕点O 按逆时针方向旋转至图2的位置，使得ON 落在射线OB上，此时三角板旋转的角度为度；（2）继续将图2中的三角板绕点O 按逆时针方向旋转至图3的位置，使得ON 在AOC ∠的内部．试探究AOM ∠与NOC ∠之间的数量关系，并说明理由；（3）在上述直角三角板从图1逆时针旋转到图3的位置的过程中，若三角板绕点O 按10︒每秒的速度旋转，当直角三角板的直角边ON 所在直线恰好平分AOC ∠时，求此时三角板绕点O 的运动时间t 的值．22．如图，在正方形ABCD 中，请仅用无刻度直尺按下列要求作图（保留作图痕迹，不写作法）．（1）在图①中，将线段AB 绕点O 逆时针旋转一定角度，使点A 与点B 重合，点B 与点C 重合，作出点O 的位置．（2）在图②中，E 为AB 的中点，将ABD △绕点D 逆时针旋转某个角度，得到CFD △，使DA 与DC 重合，作出CFD △．23．如图，在平面直角坐标系中，已知ABC 的顶点的坐标分别是A （5-，2），B （2-，4），C （1-，1）．（1）在图中作出111A B C △，使111A B C △和ABC 关于x 轴对称；（2）画出将ABC 以点O 为旋转中心，顺时针旋转90︒对应的222A B C △；（3）直接写出点B 关于点C 对称点的坐标．24．ABC 在平面直角坐标系中的位置如图，点(0,4)A ，点(2,2)B ，点(1,1)C ．（1）将ABC 向左平移4个单位得到111A B C △（点A 、B 、C 的对应点分别为1A 、1B 、1C ），画出111A B C △．（2）222A B C △和111A B C △关于x 轴对称（点1A 、1B 、1C 的对称点分别为2A 、2B 、2C ），画出222A B C △．（3）在x 轴上画出一点P ，使1PA PA +的值最小，直接写出点P 的坐标为______． 25．如图，已知ABC 的三个顶点在小方格顶点上（小方格的边长为1个单位长度），按下列要求画出图形和回答问题：（1）在图中画出：ABC 绕点C 按顺时针方向旋转90︒后的图形111A B C △；（2）在图中画出：（1）中的111A B C △关于直线MN 的轴对称的图形222A B C △；（3）在（2）中的222A B C △可以用原ABC 通过怎样的一次运动得到的？请你完整地描述这次运动的过程．26．在建立平面直角坐标系的方格纸中，每个小方格都是边长为1的小正方形，ABC ∆的顶点均在格点上，点P 的坐标为(1,0)-，请按要求画图与作答(1)把ABC ∆绕点P 旋转180°得A B C '''∆． (2)把ABC ∆向右平移6个单位得A B C ''''''∆．(3) A B C '''∆与A B C ''''''∆是否成中心对称，若是，找出对称中心P '，并写出其坐标．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】先画出图象，求出直线1l 与坐标轴交点A 、B 坐标，根据中心对称的性质得到对应点D 、C 坐标，利用待定系数法求出直线2l 解析式，直线平移的规律即可求解．【详解】解：如图，把y=0代入32y x =--得到23x=-，把x=0代入32y x =--得到y=-2， ∴直线32y x =--与x 轴、y 轴的交点分别为A 2,03⎛⎫- ⎪⎝⎭、B （0,-2），∵直线2l 与1l 关于坐标原点中心对称， ∴点A 关于原点对称的点D 的坐标为2,03⎛⎫⎪⎝⎭，点B 关于原点对称的点C 的坐标为（0,2）设2l 的解析式为y kx b =+，则2032k b b ⎧+=⎪⎨⎪=⎩，解得32k b =-⎧⎨=⎩∴2l 的解析式为32y x =-+∴直线2l 可以看做直线1l 向上平移4个单位得到．故选：D 【点睛】本题考查了求一次函数与坐标轴的交点、待定系数法、一次函数的平移、中心对称的性质等知识，熟知一次函数的知识和中心对称的性质是解题关键．2．D解析：D【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：A 、是轴对称图形，不是中心对称图形； B 、是轴对称图形，不是中心对称图形； C 、是轴对称图形，不是中心对称图形． D 、是轴对称图形，也是中心对称图形；故选：D ．【点睛】本题考查中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，3．C解析：C 【分析】连接CE ，由矩形的性质可知90A B C A D C ''''∠=∠=︒，在Rt EB C '中，可证4,2CE CD AB CB BC AD ''======，结合余弦定义解得60ECB '∠=︒，继而由正弦定义解得23B E '=，最后根据阴影面积=扇形DCE 面积Rt EB C '-面积解题．【详解】解：连接CE ，矩形A B CD '''中，90A B C A D C ''''∠=∠=︒ 在Rt EB C '中，4,2CE CD AB CB BC AD ''====== 21cos 42B C ECB CE ''∠=== 60ECB '∴∠=︒ 3sin 60B E CE '∴︒==23B E '∴=22604160418=22323360236023S B C B E πππ⨯⨯''∴-⋅=-⨯⨯=-阴影，故选：C ．【点睛】本题考查旋转、特殊角的三角函数值、扇形面积等知识，是重要考点，难度较易，掌握相关知识是解题关键．4．C解析：C【分析】根据旋转的性质，得到对应边相等，旋转角相等，从而去判断命题的正确性．【详解】解：∵旋转，∴AC DC =，但是旋转角不一定是60︒，∴ACD △不一定是等边三角形，∴AC AD =不一定成立，即①不一定正确；∵旋转，∴BC EC =，故③正确；∵旋转，∴ACD BCE ∠=∠，∵等腰三角形ACD 和等腰三角形BCE 的顶角相等，∴它们的底角也相等，即A EBC ∠=∠，故④正确；∵90A ABC ∠+∠=︒不一定成立，∴90EBC ABC ∠+∠=︒不一定成立，∴AB EB ⊥不一定成立，即②不一定正确．故选：C ．【点睛】本题考查旋转的性质，解题的关键是掌握图形旋转的性质．5．C解析：C【分析】先求出线段OA 、OB 第2020秒时旋转的度数，再除以360°，即可确定最终状态时OA 、OB 的位置，再求其夹角度数即可．【详解】由题意可知OB 的速度为每秒转动145153⨯︒=︒．则第2020秒时，线段OA 旋转度数=2020×45°=90900°，线段OB 旋转度数=2020×15°=30300°．90900°÷360°=252⋯⋯180°，30300°÷360°=84⋯⋯60°，此时OA 、OB 的位置如图所示，OA 与OB 之间的夹角度数=90°+60°=150°．故选：C．【点睛】本题考查线段的旋转，解题的关键是利用旋转周期确定最终状态时OA、OB所在位置．6．D解析：D【分析】根据中心对称图形和轴对称图形的概念判断．【详解】解：A．既不是轴对称图形，也不是中心对称图形；B．既不是轴对称图形，也不是中心对称图形；C．既不是轴对称图形，也不是中心对称图形；D．既是轴对称图形又是中心对称图形；故选：D．【点睛】本题考查的是中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．7．A解析：A【分析】本题根据中心对称图形和轴对称图形的定义可直接得出结果．【详解】A选项属于中心对称图形但不是轴对称图形，故正确；B选项既属于中心对称图形也属于轴对称图形，故不正确；C选项既属于中心对称图形也属于轴对称图形，故不正确；D选项既属于中心对称图形也属于轴对称图形，故不正确．故选：A．【点睛】本题考查了中心对称图形和轴对称图形的定义，属于基础题，熟练掌握中心对称图形和轴对称图形的定义是解题的关键．8．A解析：A【分析】根据中心对称图形与轴对称图形的概念判断即可．【详解】解：A、既是轴对称图形，又是中心对称图形．故正确；B、是轴对称图形，不是中心对称图形．故错误；C、不是轴对称图形，是中心对称图形．故错误；D、不是轴对称图形，也不是中心对称图形．故错误．故选：A．【点睛】本题考查的是中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．9．C解析：C【分析】根据平移的性质，以及点A，B的坐标，可知点A的横坐标加上了1，纵坐标加上了1，所以平移方法是：先向左平移1个单位，再向上平移3个单位，根据点B的平移方法与A点相同，即可得到答案．【详解】∵A（-2，-1）平移后对应点A'的坐标为（-3，2），∴A点的平移方法是：先向左平移1个单位，再向上平移3个单位，∴B点的平移方法与A点的平移方法是相同的，∴B（0，-2）平移后B'的坐标是：（0-1，-2+3）即（-1，1）．故选：C．【点睛】本题考查了坐标与图形的变化-平移，解决问题的关键是运用平移中点的变化规律：横坐标右移加，左移减；纵坐标上移加，下移减．10．B解析：B【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：A、是轴对称图形，不是中心对称图形．故不符合题意；B、是轴对称图形，也是中心对称图形．故符合题意；C、不是轴对称图形，是中心对称图形．故不符合题意；D、不是轴对称图形，也不是中心对称图形．故不符合题意．故选：B．【点睛】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．11．B解析：B【分析】先求出∠C′AC的度数，然后根据旋转的性质即可求得答案.【详解】'⊥，∵C A AB∴∠C′AB=90°，∵∠CAB=70°，∴∠C′AC=∠C′AB-∠CAB=20°，∵∠BAB′与∠C′AC都是旋转角，∴∠BAB′=∠C′AC=20°，故选B.【点睛】本题考查了旋转的性质，求出∠C′AC的度数是解题的关键.12．B解析：B【分析】观察四个选项中的图形，根据轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合；找出既是轴对称图形又是中心对称图形的那个即可得出结论．【详解】A是中心对称图形；B既是轴对称图形又是中心对称图形；C是轴对称图形；D不是轴对称图形，是中心对称图形．故选：B．【点睛】此题考查中心对称图形以及轴对称图形，牢记轴对称及中心对称图形的特点是解题的关键．二、填空题13．45°【分析】如图由题意可以判断为等腰直角三角形即可解决问题【详解】解：由旋转变换的性质知：；为直角三角形∴∴为等腰直角三角形故答案为【点睛】该题考查了旋转变换的性质及其应用问题；应牢固掌握旋转变换解析：45°【分析】如图，由题意可以判断ADE 为等腰直角三角形，即可解决问题．【详解】解：由旋转变换的性质知：EAD CAB ∠=∠，AE AD =； ABC 为直角三角形，90CAB ∴∠=︒，∴90EAD ∠=︒，∴ADE 为等腰直角三角形，45AED ∴∠=︒，故答案为45︒．【点睛】该题考查了旋转变换的性质及其应用问题；应牢固掌握旋转变换的性质．14．（121280）【分析】首先根据已知求出三角形三边长度然后通过旋转发现BB2B4…每偶数之间的B 相差12个单位长度根据这个规律可以求得B2021的坐标【详解】解：∵AO=3BO=4∠AOB=90°∴解析：（12128，0）【分析】首先根据已知求出三角形三边长度，然后通过旋转发现，B 、B 2、B 4…每偶数之间的B 相差12个单位长度，根据这个规律可以求得B 2021的坐标．【详解】解：∵AO=3，BO=4，∠AOB=90°∴，∴OA+AB 1+B 1C 2=3+5+4=12，∴B 2的横坐标为：12，且B 2C 2=4，∴B 4的横坐标为：2×12=24，∵2021÷2=1010…1，∴点B 2021的横坐标为：1010×12+3+5=12128．2021÷3=673…2，∴点B 2021的纵坐标为0，∴B 2021（12128，0），故答案为：（12128，0）．【点睛】此题考查了点的坐标规律变换，通过图形旋转，找到所有B 点之间的关系是本题的关键．题目难易程度适中，可以考查学生观察、发现问题的能力．15．60【分析】根据等边三角形的性质求出∠BAC=确定两个旋转的图形中的对应点即可得到答案【详解】由旋转知旋转角为∠BAC ∵是等边三角形∴∠BAC=故答案为：60【点睛】此题考查旋转的性质等边三角形的性解析：60【分析】根据等边三角形的性质求出∠BAC=60︒，确定两个旋转的图形中的对应点即可得到答案．【详解】由旋转知旋转角为∠BAC ，∵ABC 是等边三角形，∴∠BAC=60︒，故答案为：60．【点睛】此题考查旋转的性质，等边三角形的性质，正确理解图形中的旋转关系是解题的关键． 16．【分析】先作出图形然后写出坐标即可【详解】解：如图：则A′的坐标是故答案是【点睛】本题主要考查了坐标与图形的旋转变换根据题意正确画出图形成为解答本题的关键解析：()3,2-【分析】先作出图形，然后写出坐标即可．【详解】解：如图：则A′的坐标是()3,2-．故答案是()3,2-．【点睛】本题主要考查了坐标与图形的旋转变换，根据题意正确画出图形成为解答本题的关键． 17．36【分析】把四条线路平移到两侧再表示出未被小路覆盖的草坪的边长即可算出面积【详解】解：如图所示：（10-4）×（10-4）=36（平方米）故答案为：36【点睛】此题主要考查了图形的平移关键是掌握平解析：36【分析】把四条线路平移到两侧，再表示出未被小路覆盖的草坪的边长即可算出面积．【详解】解：如图所示：（10-4）×（10-4）=36（平方米），故答案为：36．【点睛】此题主要考查了图形的平移，关键是掌握平移是指图形的平行移动，平移时图形中所有点移动的方向一致，并且移动的距离相18．（）【分析】依据对应点的坐标变化即可得到三角形ABC向左平移2个单位向上平移3个单位后得到三角形A′B′C′进而得出点P′的坐标【详解】解：由图可得C（20）C（03）∴三角形ABC向左平移2个单位解析：（32，145）【分析】依据对应点的坐标变化，即可得到三角形ABC向左平移2个单位，向上平移3个单位后得到三角形A′B′C′，进而得出点P′的坐标．【详解】解：由图可得，C（2，0），C'（0，3），∴三角形ABC向左平移2个单位，向上平移3个单位后得到三角形A′B′C′，又∵点P（12，﹣15）为三角形ABC内部一点，且与三角形A′B′C′内部的点P′对应，∴对应点P′的坐标为（12﹣2，﹣15＋3），即P'（32-，145），故答案为：（32-，145）．【点睛】此题主要考查了坐标与图形变化，关键是注意观察组成图形的关键点平移后的位置．解题时注意：横坐标，右移加，左移减；纵坐标，上移加，下移减．19．65°【分析】首先根据旋转变换的性质求出∠AOC的度数结合∠AOB＝15°即可解决问题【详解】解：由题意及旋转变换的性质得：∠AOC＝∠BOD＝50°∵∠AOB＝15°∴∠AOD＝50°+15°＝6解析：65°【分析】首先根据旋转变换的性质求出∠AOC 的度数，结合∠AOB ＝15°，即可解决问题．【详解】解：由题意及旋转变换的性质得：∠AOC ＝∠BOD ＝50°，∵∠AOB ＝15°，∴∠AOD ＝50°+15°＝65°，故答案为：65°．【点睛】本题主要考查了旋转变换的性质及其应用问题，熟练掌握旋转的性质是解题的关键． 20．（01）【解析】试题分析：根据旋转的性质对应点到旋转中心的距离相等可知只要连接两组对应点作出对应点所连线段的两条垂直平分线其交点即为旋转中心试题解析：（0，1）．【解析】试题分析：根据旋转的性质，对应点到旋转中心的距离相等，可知，只要连接两组对应点，作出对应点所连线段的两条垂直平分线，其交点即为旋转中心．试题如图，连接AD 、BE ，作线段AD 、BE 的垂直平分线，两线的交点即为旋转中心O′．其坐标是（0，1）．考点: 坐标与图形变化-旋转．三、解答题21．（1）90︒；（2）30AOM NOC ∠-∠=︒，理由见解析；（3）5秒或10秒【分析】（1）根据旋转的性质求出旋转角即可；（2）利用平角的定义，结合已知条件可得到60AOC ∠=︒，再根据直角的性质、图中角与角的数量求解即可；（3）需要分类讨论计算即可；【详解】（1）根据旋转的性质可知，旋转角为90MON ∠=︒，故答案是90︒；（2）如图，30AOM NOC ∠-∠=︒，理由如下：∵180AOC BOC ∠+∠=︒，:1:2AOC BOC ∠∠=，∴2180AOC AOC ∠+∠=︒，∴60AOC ∠=︒，∴60AON CON ∠+∠=︒，①∵90MON ∠=︒，∴90AOM AON ∠+∠=︒，②②-①得：30AOM NOC ∠-∠=︒；（3）当ON 平分AOC ∠时， ∴1302AON AOC ∠=∠=︒， ∴30103t =︒÷︒=秒；当OA 的反向延长线平分AOC ∠时， ∴旋转角度=30180210︒+︒=︒，∴2101021t =︒÷︒=秒；∴t 的值为5秒或10秒．【点睛】本题主要考查了旋转的应用，结合角平分线的定义准确计算是解题的关键．22．（1）如图所示，点O 即为所求．见解析；（2）如图所示，CFD △即为所求．见解析．【分析】（1）依题意做出两条对应点的中垂线的交点既是旋转中心，旋转中心刚好在正方形中心，由于尺子没刻度，则连接两条对角线交点既是点O 的位置．（2）依题意得旋转角度90o 为，由于尺子没有刻度，第一步连接AC,BD 交点O,再连接EO 并延长EO 交DC 为H ，则H 为DC 中点，第二步连接AH 并延长交BC 延长线与F,由△ADH ≌△FCH 即可得出CF=AD ，从而得到CFD △．【详解】（1）如图所示，点O 即为所求.（2）如图所示，CFD △即为所求.【点睛】本题主要考察了图形的旋转，全等三角形等知识点，准确记住旋转中心找法和全等三角形的判定方法是解题关键．0,2-23．（1）见解析；（2）见解析；（3）()【分析】（1）根据轴对称性质即可在图中作出△A1B1C1，使△A1B1C1和△ABC关于x轴对称；（2）根据旋转的性质即可画出将△ABC以点O为旋转中心，顺时针旋转90°对应的△A2B2C2；（3）根据B（-2，4），C（-1，1）．即可写出点B关于点C对称点的坐标．【详解】解：（1）如图，△A1B1C1即为所求；（2）如图，△A2B2C2即为所求；（3）点B关于点C对称点的坐标为（0，-2）．【点睛】本题考查了作图-旋转变换，作图-轴对称变换，解决本题的关键是掌握旋转和轴对称的性质．24．（1）见解析；（2）见解析；（3）见解析，P（-2，0）【分析】（1）利用点平移的坐标规律，分别写出点A、B、C的对应点A1、B1、C1的坐标，然后描点可得△A 1B 1C 1；（2）分别作出点1A 、1B 、1C 关于x 轴的对称点分别为2A 、2B 、2C ，然后顺次连接即可；（3）连接AA 2交x 轴于点P ，求出直线AA 2的解析式，令y=0即可求出点P 的坐标．【详解】解：（1）如图所示，（2）如图所示，（3）连接AA 2交x 轴于点P ，则点P 即为所求，根据题意得，A （0，4），A 2（-4，-4），设直线AA 2的解析式为y=kx+b ，将A （0，4），A 2（-4，-4）代入y=kx+b ，得444b k b =⎧⎨-+=-⎩ ，解得24k b =⎧⎨=⎩∴24y x =+令y=0，则2x+4=0，解得，x=-2，∴P （-2，0）【点睛】此题主要考查了平移作图和作轴对称图形，熟练掌握网格结构准确找出对应点的位置是解题的关键．25．（1）图见解析；（2）图见解析；（3）将ABC 沿着BC 翻折一次可得到222A B C △．【分析】（1）先根据旋转的定义画出点111,,A B C ，再顺次连接即可得；（2）先根据轴对称的定义画出点222,,A B C ，再顺次连接即可得；（3）先根据旋转和轴对称的性质可得1122A B B A A B ==，1122AC C C A A ==，BC 与22B C 重合，再根据翻折的定义即可得．【详解】（1）先根据旋转的定义画出点111,,A B C ，再顺次连接即可得111A B C △，如图所示：（2）先根据轴对称的定义画出点222,,A B C ，再顺次连接即可得222A B C △，如图所示：（3）由旋转和轴对称的性质得：1122A B B A A B ==，1122AC C C A A ==，BC 与22B C 重合，则将ABC 沿着BC 翻折一次即可得到222A B C △．【点睛】本题考查了画旋转图形、画轴对称图形、图形的翻折，熟练掌握图形的运动是解题关键． 26．（1）图见解析；（2）图见解析；（3）成中心对称，P '的坐标为（2,0）【分析】（1）根据网格结构找出点A 、B 、C 绕点P 旋转180°后的对应点A '，B '，C '位置，然后顺次连接即可；（2）根据网格结构找出点A 、B 、C 绕点P 旋转180°后的对应点A ''，B ''，C ''位置，然后顺次连接即可；（3）将对应点连线，观察图形即可求解．【详解】（1）如图：（2）如图：（3）如图，A B C '''∆与A B C ''''''∆成中心对称，对称中心P '的坐标为（2,0）．【点睛】此题考查旋转的性质，画旋转的图形，平移的规律，画平移的图形，确定对称中心，掌握中心对称的性质及平移的规律是解题的关键．。

八年级数学下册第三章《图形的平移与旋转》单元测试题-北师大版(含答案)

八年级数学下册第三章《图形的平移与旋转》单元测试题-北师大版（含答案）一、单选题（本大题共12小题，每小题3分，共36分)1．今年4月，被称为“猪儿虫”的璧山云巴正式运行．云巴在轨道上运行可以看作是（）A ．对称B ．旋转C ．平移D ．跳跃2．在平面直角坐标系中，点(4,)P m n -，(,2)Q m n -均在第一象限，将线段PQ 平移，使得平移后的点P 、Q 分别落在x 轴与y 轴上，则点P 平移后的对应点的坐标是（）A ．(4,0)-B ．(4,0)C ．(0,2)D ．(0,2)-3．如图，在Rt ABC △中，90ABC ∠=︒，2AB BC =ABC 绕点A 逆时针转60°得到AB C ''△，则BC '的长是（）A 31B ．232C ．32D ．234．如图，将ABC 绕点A 逆时针旋转40︒得到ADE ，AD 与BC 相交于点F ，若80E ∠=︒且AFC 是以线段FC 为底边的等腰三角形，则BAC ∠的度数为（）A ．55︒B ．60︒C ．65︒D ．70︒5．下列命题是真命题的是（）A ．一个角的补角一定大于这个角B ．平行于同一条直线的两条直线平行C ．等边三角形是中心对称图形D ．旋转改变图形的形状和大小6．如图，在△ABC 中，AB =AC ，若M 是BC 边上任意一点，将△ABM 绕点A 逆时针旋转得到△ACN ，点M 的对应点为点N ，连接MN ，则下列结论一定正确的是（）A ．AB AN = B ．AB NC ∥ C ．AMN ACN ∠=∠D ．MN AC ⊥7．如图，点A 的坐标为()0,2，点B 是x 轴正半轴上的一点，将线段AB 绕点A 按逆时针方向旋转60°得到线段AC ．若点C 的坐标为(),3m ，则m 的值为（）A 43B 221C 53D 421 8．以图（1）（以O 为圆心，半径为1的半圆）作为“基本图形”，分别经历如下变换，不能得到图（2）的是（）A ．绕着OB 的中点旋转180°即可 B ．先绕着点O 旋转180°，再向右平移1个单位C ．先以直线AB 为对称轴进行翻折，再向右平移1个单位D ．只要向右平移1个单位9．平面直角坐标系中，O 为坐标原点，点A 的坐标为()5,1-，将OA 绕原点按逆时针方向旋转90︒得OB ，则点B 的坐标为（）A ．()5,1-B ．()1,5--C ．()5,1--D ．()1,5-10．小明把一副三角板按如图所示叠放在一起，固定三角板ABC ，将另一块三角板DEF 绕公共顶点B 顺时针旋转（旋转角度不超过180°）．若两块三角板有一边平行，则三角板DEF 旋转的度数可能是（）A ．15°或45°B ．15°或45°或90°C ．45°或90°或135°D ．15°或45°或90°或135°11．如图，ABC 与A B C '''关于点O 成中心对称，则下列结论不成立的是（）A ．点A 与点A '是对称点B ．BO B O '=C ．AOB A OB ''∠=∠D ．ACB C A B '''∠=∠ 12．如图，已知△ABC 中，∠CAB ＝20°，∠ABC ＝30°，将△ABC 绕A 点逆时针旋转50°得到△AB ′C ′，以下结论：∠BC ＝B ′C ′，∠AC ∠C ′B ′，∠C ′B ′∠BB ′，∠∠ABB ′＝∠ACC ′，正确的有（）A ．∠∠∠B ．∠∠∠C ．∠∠∠D ．∠∠∠二、填空题（本大题共8小题，每小题3分，共24分)13．已知点A （﹣2，b ）与点B （a ，3）关于原点对称，则a ﹣b =______．14．如图．两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C 的方向平移到DEF 的位置，8,3==AB DP ，平移距离为6，则阴影部分的面积为____________．15．如图，边长为2的等边ABO 在平面直角坐标系的位置如图所示，点O 为坐标原点，点A 在x 轴上，以点O 为旋转中心，将ABO 按顺时针方向旋转120°，得到OA B ''△，则点A '的坐标为_____．16．如图，在ABC 中，∠C ＝90°，点D 、E 分别在AC 、BC 上，∠CDE ＝45°，ECD 绕点D 顺时针旋转x 度（45<x <180）到11E C D △，则1BEE ∠等于______度．（用含x 的代数式表示）17．如图，在宽为13米、长为24米的长方形地面上修筑同样宽的道路（图中阴影部分），道路的宽为2米，余下部分种植草坪. 则草坪的面积为__________.18．如图，在平面直角坐标系中，ABC 的顶点A ，B 的坐标分别是()0,2A ，()2,1B -．平移ABC 得到A B C '''，若点A 的对应点A '的坐标为()1,0-，则点B 的对应点B '的坐标是_____________．19．线段MN 是由线段EF 经过平移得到的，若点(1,3)-E 的对应点(4,7)M -，则点(3,2)F --的对应点N 的坐标是____________．20．如图，DEF ∆是由ABC ∆通过平移得到，且点,,,B E C F 在同一条直线上，如果14BF =，6EC =．那么这次平移的距离是_________．三、解答题（本大题共5小题，每小题8分，共40分)21．如图，已知图中A 点和B 点的坐标分别为()2,4-和()2,2-．(1)请在图1中画出坐标轴建立适当的直角坐标系；(2)写出点C 的坐标为______；(3)在y 轴上有点D ．满足20DBC S =△，则点D 的坐标为______；(4)已知第一象限内有两点()4,M m n -，(),3N m n -．平移线段MN 使点M 、N 分别落在两条坐标轴上．则点M 平移后的对应点的坐标是______．22．如图，点A 在射线OX 上，OA a =．如果OA 绕点O 按逆时针方向旋转(0360)<≤︒n n 到OA '，那么点A '的位置可以用(),︒a n 表示．(1)按上述表示方法，若3a =，37n =，则点A '的位置可以表示为______；(2)在（1）的条件下，已知点B 的位置用()3,74︒表示，连接A A '、A B '．求证：A A A B ''=．23．如图，()1,0A ，点B 在y 轴上，将三角形OAB 沿x 轴负方向平移，平移后的图形为三角形DEC ，点C 的坐标为()3,2-．(1)点B 的坐标为_______，点E 的坐标为______；(2)点P 从点O 出发，沿OB BC CD →→移动，若点P 的速度为每秒1个单位长度，运动时间为()0t t >秒． ∠用含t 的式子表示点P 的坐标；∠当t 为多少时，点P 的横坐标与纵坐标互为相反数；∠当三角形AEP 的面积为2时，直接．．写出此时t 的值．24．在平面直角坐标系中，A（－2，4），B（－3，－1），C（0，2）．将∠ABC平移至∠A1B1C1，点A对应点A1（3，3），点B对应点B1，点C对应点C1．(1)画出平移后的∠A1B1C1，并写出B1的坐标；(2)求∠ABC的面积；(3)若存在点D（m，n）使得∠BB1D和∠BB1C面积相等，其中m，n均为绝对值不超过5的整数，则点D的坐标为_________．25．在平面直角坐标系xOy中，对于点A，规定点A的α变换和β变换．α变换：将点A向左平移一个单位长度，再向上平移两个单位长度；β变换：将点A向右平移三个单位长度，再向下平移一个单位长度(1)若对点B进行α变换，得到点（1，1），则对点B进行β变换后得到的点的坐标为．=，求m的值．(2)若对点C（m，0）进行α变换得到点P，对点C（m，0）进行β变换得到点Q，OP OQ(3)点D为y轴的正半轴上的一个定点，对点D进行α变换后得到点E，点F为x轴上的一个动点，对点F进行β变+的最小值为，直接写出点D的坐标．换之后得到点G，若DG EF参考答案1．C2．A3．A4．B5．B6．C7．C8．D9．B10．D11．D12．B13．514．3915．（1316．452x ⎛⎫+ ⎪⎝⎭ 17．242平方米18．()1,3-19．（−6，2）20．421．(1)1(2)（3，2）(3)（0，﹣6）或（0，10）(4)（0，3）或（﹣4，0）22．(1)(3,37°)23．(1)（0，2），（2-，0）(2)∠当点P 在OB 上时，点P 的坐标为（0，t ）；点P 在BC 上时，点P 的坐标（2t -，2）；当点P 在CD 上时，点P 的坐标为（3-，7t -）；∠当t =4时，点P 的横坐标与纵坐标互为相反数；∠t 的值为43或17324．(1)B1的坐标（2，﹣2）(2)6(3)（﹣5，3）或（0，2）或（5，1）或（﹣1，﹣5）25．(1)（5，-2）(2)58m=-(3)（0，32）。

(好题)初中数学八年级数学下册第三单元《图形的平移与旋转》测试卷(含答案解析)

一、选择题1．在平面直角坐标系中，A （0，3），B （4，0），把△AOB 绕点O 旋转，使点A ，B 分别落在点A ′，B ′处，若A ′B ′∥x 轴，点B ′在第一象限，则点A 的对应点A ′的坐标为（） A ．（912,55-） B ．（129,55-） C ．（1612,55-） D ．（1216,55-） 2．将点(3,1)绕原点顺时针旋转90︒得到的点的坐标是（）A ．(3,1)--B ．(1,3)-C ．(3,1)-D ．(1,3)- 3．下面是几种病毒的形态模式图，这些图案中既不是轴对称图形也不是中心对称图形的是（）A ．B ．C ．D ．4．如图，将矩形ABCD 绕点C 顺针旋转90°到矩形A B C D ''''的位置，若4,2AB AD ==，则图中阴影部分的面积为（）A ．4233π- B ．4433π- C ．8233π- D ．8433π- 5．下列图形中，既是轴对称图形，又是中心对称图形的是（）A ．B ．C ．D ． 6．在平面直角坐标系xOy 中，ABC 与A B C '''关于原点O 成中心对称的是（） A ． B ．C．D．7．如图，点A，B的坐标分别为（1，1）、（3，2），将△ABC绕点A按逆时针方向旋转90°，得到△A'B'C'，则B'点的坐标为（）A．（﹣1，3）B．（－1，2）C．（0，2）D．（0，3）8．在奔驰、宝马、丰田、三菱等汽车标志图形中，为中心对称图形的是（）A．B．C．D．9．在线段，直角三角形，平行四边形，长方形，正五角星，正方形，等边三角形中，既是轴对称图形，又是中心对称图形的图形有（）A．3个B．4个C．5个D．6个10．如图，点D是等腰直角三角形ABC内一点，AB=AC，若将△ABD绕点A逆时针旋转到△ACE的位置，则∠AED的度数为（）A．25°B．30°C．40°D．45°11．如图，已知ABC 和A B C '''关于点O 成中心对称，则下列结论错误的是（）．A ．ABC ABC '''∠=∠B ．AOB A OB ''∠=∠C ．AB A B ''=D ．OA OB '= 12．如图，△ABC 沿线段BA 方向平移得到△DEF ，若AB ＝6，AE ＝2．则平移的距离为（）A ．2B ．4C ．6D ．8二、填空题13．如图，在Rt ABC 和Rt CDE △中，90ACB DCE ∠=∠=︒，30A ∠=︒，45E ∠=︒，B ，C ，E 三点共线，Rt ABC △ 不动，将Rt CDE △绕点C 逆时针旋转()0360a α︒<<︒，当DE //BC 时，α=____________．14．如图，在△ABC 中，∠BAC ＝105°，将△ABC 绕点A 逆时针旋转得到△AB ′C ′．若点B 恰好落在BC 边上，且AB ′＝CB ′，则∠C ′的度数为_____°．15．平面直角坐标系xOy 中，先作出点P (2,3)-关于y 轴的对称点，再将该对称点先向下平移1个单位，再向左平移2个单位得到点P 1，称为完成一次图形变换，再将点P 1进行同样的图形变换得到点P 2，以此类推，则点P 2020的坐标为___________．16．如图，在ABC ∆中，90,3,4ACB AC BC ∠=︒==，将ABC ∆绕点C 顺时针旋转90︒得到'''A B C ∆，若P 为AB 边上一动点，旋转后点P 的对应点为点P'，则线段'PP 长度的取值范围是________．17．如图，在平面直角坐标系xOy 中，点A （2，m ）绕坐标原点O 逆时针旋转90°后，恰好落在图中阴影区域（包括边界）内，则m 的取值范围是_____．18．点P （m +2，2m +1）向右平移1个单位长度后，正好落在y 轴上，则m ＝_____． 19．已知：如图，在AOB ∆中，9034AOB AO cm BO cm ︒∠===，，，将AOB ∆绕顶点O ，按顺时针方向旋转得到11A OB ∆，线段1OB 与边AB 相交于点D ，则线段1B D 最大值为=________cm20．已知等边△ABC 的边长为4，点P 是边BC 上的动点，将△ABP 绕点A 逆时针旋转60°得到△ACQ ，点D 是AC 边的中点，连接DQ ，则DQ 的最小值是_____．三、解答题21．已知：如图1，AOB 和COD 都是等边三角形．（1）求证：①AC ＝BD ；②∠APB ＝60°；（2）如图2，在AOB 和COD 中，OA ＝OB ，OC ＝OD ，∠AOB ＝∠COD ＝α，则AC 与BD 间的等量关系为，∠APB 的大小为22．如图1，已知ABC 中，1,90,AB BC ABC ==∠=︒把一块含30角的直角三角板DEF 的直角顶点D 放在AC 的中点上（直角三角板的短直角边为,DE 长直角边为DF ），将直角三角板DEE 绕D 点按逆时针方向旋转．（1）在图1中．DE 交AB 于,M DF 交BC 于N ．①求证：DM DN =；②在这一过程中，直角三角板DEF 与三角形ABC 的重叠部分为四边形,DMBN 请说明四边形DMBN 的面积是否发生变化？若发生变化，请说明如何变化的；若不发生变化，请求出其面积．（2）继续旋转至如图2的位置，延长AB 交DE 于,M 延长BC 交DF 于,N DM DN =是否仍然成立？（请写出结论，不用证明．）（3）继续旋转至如图3的位置，延长FD 交BC 于N ，延长ED 交AB 于,M DM DN =是否仍然成立？（请写出结论，不用证明．）23．如图，在平面直角坐标系中，已知ABC 的三个顶点坐标分別是()2,1A -，()1,2B -，()3,3C -（1）将ABC 向上平移4个单位长度得到111A B C △，请画出111A B C △；（2）请画出与ABC 关于y 轴对称的222A B C △；（3）请写出1A 、2A 的坐标．24．在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，ABC 的顶点均在格点上，点A 的坐标是(3,1)--．（1）将ABC 关于x 轴对称得到111A B C △，画出111A B C △，并写出点1B 的坐标；（2）把111A B C △平移，使点B 平移到2(3,4)B ，请作出111A B C △平移后的222A B C △，并写出2A 的坐标；（3）已知ABC 中有一点(,)D a b ，求222A B C △中的对应点2D 的坐标．25．如图，在正方形ABCD 中，点E 是AB 边上的一点（与A ，B 两点不重合），将BCE 绕着点C 旋转，使CB 与CD 重合，这时点E 落在点F 处，联结EF ．（1）按照题目要求画出图形；（2）若正方形边长为3，1BE =，求AEF 的面积；（3）若正方形边长为m ，BE n =，比较AEF 与CEF △的面积大小，并说明理由． 26．如图，已知ABC 的三个顶点在小方格顶点上（小方格的边长为1个单位长度），按下列要求画出图形和回答问题：（1）在图中画出：ABC 绕点C 按顺时针方向旋转90︒后的图形111A B C △；（2）在图中画出：（1）中的111A B C △关于直线MN 的轴对称的图形222A B C △；（3）在（2）中的222A B C △可以用原ABC 通过怎样的一次运动得到的？请你完整地描述这次运动的过程．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】设A′B′交y轴于T′，利用勾股定理可求出A′B′的长度，再利用三角形面积公式求出OT的长度，最后再利用勾股定理即可求出A′T′的长度，即可求出A′点坐标．【详解】解：如图，设A′B′交y轴于T′．∵A（0，3），B（4，0），∴OA＝3，OB＝4，∵∠A ′OB ′＝90°，OT'⊥A ′B ′，OA ＝OA ′＝3，OB ＝OB ′＝4，∴AB ＝A ′B ′＝22OA OB +=2234+=5，∵A OB S ''=12•OA ′•OB ′＝12•A ′B ′•OT ′， ∴OT ′＝125， ∴A ′T ′＝22OA OT '-＝221293()55-=， ∴A ′（-95，125）．故选：A ．【点睛】本题考查坐标与图形的变化-旋转，熟练利用勾股定理解直角三角形以及三角形的面积公式是解答本题的关键．2．B解析：B【分析】根据旋转的性质即可确定点坐标．【详解】解：点绕原点旋转90度的坐标变换规律：横、纵坐标互换位置，且纵坐标变为相反数，则点（3，1）绕原点O 顺时针旋转90°得到的点的坐标为（1，-3），如图，故选：B ．【点睛】本题考查了坐标与图形变化-旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°． 3．C解析：C【分析】根据轴对称图形和中心对称图形的定义进行判定即可；【详解】A 、是轴对称图形不是中心对称图形，故不符合题意；B 、是轴对称图形不是中心对称图形，故不符合题意；C 、既不是轴对称图形也不是中心对称图形，故符合题意；D 、既是轴对称图形又是中心对称图形，故不符合题意；故选：C ．【点睛】本题考查了轴对称图形和中心对称图形，正确理解轴对称图形和中心对称图形的定义是解题的关键；4．C解析：C【分析】连接CE ，由矩形的性质可知90A B C A D C ''''∠=∠=︒，在Rt EB C '中，可证4,2CE CD AB CB BC AD ''======，结合余弦定义解得60ECB '∠=︒，继而由正弦定义解得23B E '=，最后根据阴影面积=扇形DCE 面积Rt EB C '-面积解题．【详解】解：连接CE ，矩形A B CD '''中，90A B C A D C ''''∠=∠=︒在Rt EB C '中，4,2CE CD AB CB BC AD ''======21cos 42B C ECB CE ''∠=== 60ECB '∴∠=︒3sin 60B E CE '∴︒== 23B E '∴=22604160418=22323360236023S B C B E πππ⨯⨯''∴-⋅=-⨯⨯=-阴影，故选：C ．【点睛】本题考查旋转、特殊角的三角函数值、扇形面积等知识，是重要考点，难度较易，掌握相关知识是解题关键．5．A解析：A【分析】根据轴对称图形和中心对称图形的定义即可判断结论；【详解】A是轴对称图形也是中心对称图形，故本项正确；B不是轴对称图形，也不是中心对称图形，故本项错误；C是轴对称图形不是中心对称图形，故本项错误；D不是轴对称图形，是中心对称图形，故本项错误；故选：A．【点睛】本题考查轴对称图形，中心对称图形，熟记相关概念是解题的关键．6．D解析：D【分析】根据关于y轴对称的点的坐标特征对A进行判断；根据关于x轴对称的点的坐标特征对B 进行判断；根据关于原点对称的点的坐标特征对C、D进行判断．【详解】解：A、△ABC与△A'B'C'关于y轴对称，所以A选项不符合题意；B、△ABC与△A'B'C'关于x轴对称，所以B选项不符合题意；C、△ABC与△A'B'C'关于（-12，0）对称，所以C选项不符合题意；D、△ABC与△A'B'C'关于原点对称，所以D选项符合题意；【点睛】本题考查了中心对称：把一个图形绕着某个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点．中心对称的性质：关于中心对称的两个图形能够完全重合；关于中心对称的两个图形，对应点的连线都经过对称中心，并且被对称中心平分．7．D解析：D【分析】根据题意画出图形，然后结合直角坐标系即可得出B'的坐标．【详解】解：如图，根据图形可得：点B′坐标为（0，3），故选：D．【点睛】本题考查了旋转作图的知识及旋转后坐标的变化，解答本题的关键是根据题意所述的旋转三要素画出图形，然后结合直角坐标系解答．8．B解析：B【分析】据中心对称图形的概念，结合图形特征即可求解．【详解】A、不是中心对称图形，故此选项错误；B、是中心对称图形，故此选项正确；C、不是中心对称图形，故此选项错误；D、不是中心对称图形，故此选项成文；故选：B．【点睛】本题考查中心对称图形的概念：在同一平面内，如果把一个图形绕某一点旋转180度，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．9．A解析：A【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：线段，长方形，正方形是轴对称图形，也是中心对称图形，符合题意；正五角星，等边三角形是轴对称图形，不是中心对称图形，不符合题意；平行四边形不是轴对称图形，是中心对称图形，不符合题意；直角三角形既不是轴对称图形，也不是中心对称图形，不符合题意．共3个既是轴对称图形又是中心对称图形．故选：A．【点睛】考查了中心对称图形与轴对称图形的概念，判断轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；判断中心对称图形的关键是要寻找对称中心，旋转180度后与原图重合．10．D解析：D【分析】由题意可以判断△ADE 为等腰直角三角形，即可解决问题．【详解】解：如图，由旋转变换的性质知：∠EAD=∠CAB ，AE=AD ；∵△ABC 为直角三角形，∴∠CAB=90°，△ADE 为等腰直角三角形，∴∠AED=45°，故选：D ．【点睛】该题考查了旋转变换的性质及其应用问题；应牢固掌握旋转变换的性质．11．D解析：D【分析】根据三角形和中心对称的性质求解，即可得到答案．【详解】∵ABC 和A B C '''关于点O 成中心对称∴ABC A B C '''∠=∠AOB A OB ''∠=∠AB A B ''=OA OA '=OB OB '=∴OA OB '=错误，其他选项正确故选：D ．【点睛】本题考查了三角形和中心对称图形的知识；解题的关键是熟练掌握三角形和中心对称图形的性质，从而完成求解．12．B解析：B【分析】根据平移变换的性质解决问题即可.【详解】解：∵AB ＝6，AE ＝2，∴BE ＝AB ﹣AE ＝6﹣2＝4，∴平移的距离为4，故选：B.【点睛】此题考查平移的要素：距离，平移前后对应点所连的线段的长度即为平移的距离.二、填空题13．45º或225º【分析】根据旋转方向与旋转角的度数范围可得当DE ∥BC 时画出两种符合条件的图形分别利用平行线的性质与三角形内角得定理即可求得相应的旋转角的度数【详解】解：此题可分两种情况：如图1：∵解析：45º或225º【分析】根据旋转方向与旋转角的度数范围，可得当DE ∥BC 时，画出两种符合条件的图形，分别利用平行线的性质与三角形内角得定理即可求得相应的旋转角的度数．【详解】解：此题可分两种情况：如图1：∵90DCE ∠=︒，45E ∠=︒，∴45D ∠=︒．∵DE ∥BC ，∴45BCD D ∠=∠=︒．∵90ACB ∠=︒．∴45ACD ACB BCD ∠=∠-∠=︒．即旋转角α的度数为45º．如图2：∵DE ∥BC ，∴45BCE E ∠=∠=︒．∴225?ACD ACB BCE DCE ∠=∠+∠+∠=．即旋转角α的度数为225º．综上所述，旋转角α的度数为45º或225º．故答案为：45º或225º．【点睛】此题考查了旋转角的计算，掌握旋转角的定义并能运用平行线的性质正确求出旋转角的度数是解题的关键．14．25【分析】由旋转的性质可得∠C=∠CAB=AB 由等腰三角形的性质可得∠C=∠CAB ∠B=∠ABB 由三角形的外角性质和三角形内角和定理可求解【详解】解：∵AB=CB ∴∠C=∠CAB ∴∠ABB=∠C+解析：25【分析】由旋转的性质可得∠C=∠C'，AB=AB'，由等腰三角形的性质可得∠C=∠CAB'，∠B=∠AB'B ，由三角形的外角性质和三角形内角和定理可求解．【详解】解：∵AB'=CB'，∴∠C=∠CAB'，∴∠AB'B=∠C+∠CAB'=2∠C ，∵将△ABC 绕点A 按逆时针方向旋转得到△AB'C'，∴∠C=∠C'，AB=AB'，∴∠B=∠AB'B=2∠C ，∵∠B+∠C+∠CAB=180°，∴3∠C=180°-105°，∴∠C=25°，∴∠C'=∠C=25°，故答案为：25．【点睛】本题考查了旋转的性质，等腰三角形的性质，灵活运用这些的性质解决问题是本题的关键．15．【分析】按程序先作y 轴对称求出点坐标横坐标-2纵坐标-1完成一次图形变换求出P 变换后的坐标找出几次变换后规律奇次变换点的横坐标x=0偶次变换点的横坐标x=-2纵坐标变一次下移一个单位【详解】解：完成解析：(2,2017)--【分析】按程序先作y 轴对称，求出点坐标，横坐标-2，纵坐标-1，完成一次图形变换求出P 变换后的坐标，找出几次变换后规律奇次变换点的横坐标x=0，偶次变换点的横坐标x=-2，纵坐标变一次下移一个单位．【详解】解：完成1次图形变换，点P (2,3)-关于y 轴的对称点（2，3），横坐标2-2=0，纵坐标3-1=2，P 1（0，2），完成2次图形变换，点P 1 (0,2)关于y 轴的对称点（0，2），横坐标0-2=-2，纵坐标2-1=1，P 2（-2，1），完成3次图形变换，点P 2（-2，1）关于y 轴的对称点（2，1），横坐标3-3=0，纵坐标1-1=0，P 3（0，0），完成4次图形变换，点P 3（0，0）关于y 轴的对称点（0，0），横坐标0-2=-2，纵坐标0-1=-1，P 4（-2，-1），……,完成2020次图形变换，点P 2019（0，3-2019）关于y 轴的对称点（0，-2016），横坐标0-2=-2，纵坐标-2016-1=-2017，P 2020（-2，-2017）．故答案为：（-2，-2017）．【点睛】本题考查图形规律探索问题，掌握图形程序变换的轴对称性质和平移特征，关键是找到变换规律奇次变换点的横坐标x=0，偶次变换点的横坐标x=-2，纵坐标变一次下移一个单位．16．【分析】过点C 作CH ⊥AB 于H 利用勾股定理求出AB 结合直角三角形的面积即可求出CH 由旋转易得为等腰直角三角形从而得出求出CP 的取值范围即可求出结论【详解】解：过点C 作CH ⊥AB 于H ∵在中∴AB=∵=解析：5PP '≤≤【分析】过点C 作CH ⊥AB 于H ，利用勾股定理求出AB ，结合直角三角形的面积即可求出CH ，由旋转90︒易得PCP '△为等腰直角三角形，从而得出PP '=，求出CP 的取值范围即可求出结论．【详解】解：过点C 作CH ⊥AB 于H ，∵在ABC 中，90,3,4ACB AC BC ∠=︒==∴225AC BC +∵ABC S =12AC·BC=12AB·CH ∴12×3×4=12×5CH 解得CH=125由旋转90︒易得PCP '△为等腰直角三角形，所以2PP CP '=， ∵P 在线段AB 上移动，故当点P 与点B 重合时，CP 最大值等于CB 等于4；当点P 与点H 重合时，CP 最小值等于CH 等于125， ∴1222425CP ≤≤则122425PP '≤≤ 故答案为：122425PP '≤≤ 【点睛】此题考查的是勾股定理、旋转的性质、等腰直角三角形的性质，掌握勾股定理、旋转的性质、等腰直角三角形的性质是解题关键．17．﹣3≤m≤﹣25【分析】如图将阴影区域绕着点O 顺时针旋转90°与直线x ＝2交于CD 两点则点A （2m ）在线段CD 上结合点CD 的纵坐标即可求出m 的取值范围【详解】如图将阴影区域绕着点O 顺时针旋转90°与解析：﹣3≤m≤﹣2.5．【分析】如图，将阴影区域绕着点O 顺时针旋转90°，与直线x ＝2交于C ，D 两点，则点A （2，m ）在线段CD 上，结合点C,D 的纵坐标，即可求出m 的取值范围.【详解】如图，将阴影区域绕着点O 顺时针旋转90°，与直线x ＝2交于C ，D 两点，则点A （2，m ）在线段CD 上，又∵点D 的纵坐标为﹣2.5，点C 的纵坐标为﹣3，∴m 的取值范围是﹣3≤m ≤﹣2.5，故答案为﹣3≤m ≤﹣2.5．【点睛】考查旋转的性质，根据旋转的性质，画出图形是解题的关键.18．-3【详解】点P （m+22m+1）向右平移1个单位长度后正好落在y 轴上则故答案为：-3解析：-3【详解】点P （m+2，2m+1）向右平移1个单位长度后(3,21)m m ++ ，正好落在y 轴上，则30,3m m +==-故答案为：-319．【分析】根据已知条件由勾股定理可得AB=5当时OD 最小由等积法可得代入数据可得即可求出线段最大值【详解】在中∴AB=∵∴OD 最小时最大当时OD 最小即OD 为的高∴即解得：∴线段最大值为：=cm 故答案为解析：85【分析】根据已知条件由勾股定理可得AB=5，当1B O AB ⊥时，OD 最小，由等积法可得AO OB AB OD =，代入数据可得125OD =，即可求出线段1B D 最大值．【详解】在Rt AOB 中，34AO cm BO cm ==，，∴22345+=，∵11B D B O OD =-，14B O BO cm ==，∴OD 最小时，1B D 最大，当1B O AB ⊥时，OD 最小，即OD 为AOB 的高，∴AO OB AB OD =，即345OD ⨯=，解得：125OD =， ∴线段1B D 最大值为：1245-=85cm ，故答案为：85．【点睛】本题主要考查了勾股定理，线段的最值问题，根据图形分析线段取得最值的情况是解题的关键．20．【分析】根据旋转的性质即可得到∠BCQ ＝120°当DQ ⊥CQ 时DQ 的长最小再根据勾股定理即可得到DQ 的最小值【详解】解：如图由旋转可得∠ACQ ＝∠B ＝60°又∵∠ACB ＝60°∴∠BCQ ＝120°∵ 解析：3【分析】根据旋转的性质，即可得到∠BCQ ＝120°，当DQ ⊥CQ 时，DQ 的长最小，再根据勾股定理，即可得到DQ 的最小值．【详解】解：如图，由旋转可得∠ACQ ＝∠B ＝60°，又∵∠ACB ＝60°，∴∠BCQ ＝120°，∵点D 是AC 边的中点，∴CD ＝2，当DQ ⊥CQ 时，DQ 的长最小，此时，∠CDQ ＝30°，∴CQ ＝12CD ＝1， ∴DQ 22213-=，∴DQ 的最小值是3，故答案为3．【点睛】本题主要考查线段最小值问题，关键是利用旋转、等边三角形的性质及勾股定理求解．三、解答题21．（1）①见解析，②见解析；（2）AC ＝BD ，α【分析】（1）①根据△AOB 和△COD 都是等边三角形，求出∠AOC=∠BOD ，根据SAS 推出△AOC ≌△BOD ，根据全等三角形的性质得出AC=BD ；②由△AOC ≌△BOD ，可得∠CAO=∠DBO ，根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB ，推出∠APB=∠AOB 即可；（2）根据∠AOB=∠COD=α，求出∠AOC=∠BOD ，根据SAS 推出△AOC ≌△BOD ，根据全等三角形的性质得出AC=BD ，∠CAO=∠DBO ，根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB ，推出∠APB=∠AOB 即可．【详解】证明：（1）①∵△AOB 和△COD 都是等边三角形，∴OA=OB ，OC=OD ，∠AOB ＝∠COD ＝60°，∴∠AOC ＝∠BOD ，在△AOC 和△BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△BOD （SAS ），∴AC ＝BD ，∠CAO ＝∠DBO ，②设AC 与BO 交于E ，∵△AOC ≌△BOD ，∴∠CAO ＝∠DBO ，∵∠AEO=∠BEP ，∴∠CAO+∠AOB ＝∠DBO+∠APB ，∴∠APB ＝∠AOB ＝60°．（2）AC=BD ，∠APB=α，理由如下：∵∠AOB=∠COD=α，∴∠AOC=∠BOD ，在△AOC 和△BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△BOD ，∴AC=BD ，∠CAO=∠DBO ，设AC 与BO 交于E ，∵∠AEO=∠BEP ，∴∠CAO+∠AOB=∠DBO+∠APB ，∴∠APB=∠AOB=α，故答案为AC=BD ，α．【点睛】本题考查三角形旋转，三角形全等判定与性质，三角形内角和，掌握三角形旋转，三角形全等判定与性质，三角形内角和是解题关键．22．（1）①见解析；②不变，14；（2）成立；（3）成立【分析】（1）连接BD ，证明△DMB ≌△DNC ．根据已知，全等条件已具备两个，再证出∠MDB=∠NDC ，用ASA 证明全等，四边形DMBN 的面积不发生变化，因为它的面积始终等于△ABC 面积的一半；（2）成立．同样利用（1）中的证明方法可以证出△DMB ≌△DNC ；（3）结论仍然成立，方法同（1）．【详解】解：()1①如图，连接DB ，在Rt ABC ∆中，,,AB BC AD DC ==45,90,45A C BDC ABD CBD ∴∠=∠=︒∠=︒∠=∠=︒45,ABD C ∴∠=∠=︒,DB DC AD ∴==90,MDB BDN CDN BDN ∠+∠=∠+∠=,MDB NDC ∴∠=∠,BMD CND ∴∆≅∆DM DN ∴=；②四边形DMBN 的面积不发生变化；由①知，,BMD CND ∆≅∆BMD CND S S ∆∴∆=DBN DMB DBN DNC DMBN S S S S S ∆∆∆∆∴=+=+四边形 1111112224DBC ABC S S ∆∆===⨯⨯⨯= ()2DM = DN 仍然成立.理由如下:连接BD 由(1)知BD ⊥AC ，BD= CD ，∴∠ABD=∠ACB = 45°，∴∠ABD+∠MBD= 180°，∠ACB+∠NCD= 180°，∴∠MBD=∠NCD ，∵BD ⊥AC ，∴∠MDB +∠MDC = 90° ，又∠NDC +∠MDC = 90°，∴∠MDB=∠NDC ，在△MDB 和△NDC 中，∵∠MBD=∠NCD ，BD= CD ，∠MDB= ∠NDC.∴△MDB ≌△NDC (ASA)∴DM = DN ，()3DM = DN 成立，理由如下:连接BD ，由(1) 知BD ⊥AC ，BD= AD ，∴∠BAD=∠ABD = 45°，∴∠MBD=∠NCD= 45°，∵BD ⊥AC ，∴∠MDB +∠NDB = 90° ，又∠NDC +∠NDB = 90°，∴∠MDB=∠NDC ，在△MDB 和△NDC 中∵∠MBD=∠NCD ，BD= CD ，∠MDB= ∠NDC.∴△MDB ≌△NCD (ASA)，∴DM = DN ．【点睛】本题考查了利用ASA 求三角形全等，还运用了全等三角形的性质，等腰直角三角形的性质，及等腰三角形三线合一定理，勾股定理和面积公式的利用等知识.23．（1）见解析；（2）见解析；（3）1(2,3)A ，2(2,1)--A ．【分析】（1）根据平移的性质先作出三角形三个顶点，然后连线作图；（2）根据轴对称的性质，先做出三角形三个顶点关于x 轴的对称点，然后连线作图；（3）根据图形写出相应的点的坐标【详解】解：（1）如图所示：111A B C △，即为所求：（2）如图所示：222A B C △，即为所求：（3）1(2,3)A ，2(2,1)--A ．【点睛】本题考查平移及轴对称作图，认真审题，正确作出图形对应的顶点是解题关键． 24．（1）图见解析，点B 1的坐标为（-2，4）；（2）图见解析，A 2的坐标为（2，1）；（3）D 2的坐标为（a+5，-b ）．【分析】（1）分别作出点A 、B 、C 关于x 轴对称得到的对应点，再顺次连接可得；（2）根据B 1（-2，4）和2(3,4)B ，可得平移方式为向右平移5个单位，分别作出△A 1B 1C 1向右平移5个单位所得对应点，再顺次连接可得；（3）根据图形的变换方式即可得出D 点的变换方式，从而可得点2D 的坐标．【详解】解：（1）如图所示，△A 1B 1C 1即为所求，点B 1的坐标为（-2，4）；（2）如图所示，△A 2B 2C 2即为所求，A 2的坐标为（2，1）；（3）△A 2B 2C 2中的对应点D 2的坐标为（a+5，-b ）．【点睛】本题考查坐标与图形变换—轴对称和平移．理解点的变换和对应图形变换的关系是解题关键．25．（1）见解析；（2）4；（3）CEF AEF S S >△△，见解析【分析】（1）根据题意去旋转BCE ，画出图象；（2）由旋转的性质得1DF BE ==，求出AE 和AF 的长，即可求出AEF 的面积；（3）用（2）的方法表示出AEF 的面积，再用四边形AECF 的面积减去AEF 的面积得到CEF △的面积，比较它们的大小．【详解】（1）如图所示：（2）根据旋转的性质得1DF BE ==，∴312AE =-=，314AF =+=， ∴142AEF S AE AF ∆=⨯⨯=；（3）根据旋转的性质得DF BE n ==， 221111()()2222AEF AE AF m S n m n m n =⨯⨯=-+=-△， ∵CBE CDF S S =△△，∴AECF ABCD S S =四边形四边形， ∴2222211112222CEF AEF AECF S S S m m n m n ⎛⎫=-=⎪⎝--=+⎭四边形△△， ∵0n >， ∴222211112222m n m n +>-， ∴CEF AEF S S >△△．【点睛】本题考查旋转的性质，解题的关键是掌握图形旋转的性质，以及利用割补法求三角形面积的方法．26．（1）图见解析；（2）图见解析；（3）将ABC 沿着BC 翻折一次可得到222A B C △．【分析】（1）先根据旋转的定义画出点111,,A B C ，再顺次连接即可得；（2）先根据轴对称的定义画出点222,,A B C ，再顺次连接即可得；（3）先根据旋转和轴对称的性质可得1122A B B A A B ==，1122AC C C A A ==，BC 与22B C 重合，再根据翻折的定义即可得．【详解】（1）先根据旋转的定义画出点111,,A B C ，再顺次连接即可得111A B C △，如图所示：（2）先根据轴对称的定义画出点222,,A B C ，再顺次连接即可得222A B C △，如图所示：（3）由旋转和轴对称的性质得：1122A B B A A B ==，1122AC C C A A ==，BC 与22B C 重合，则将ABC 沿着BC 翻折一次即可得到222A B C △．【点睛】本题考查了画旋转图形、画轴对称图形、图形的翻折，熟练掌握图形的运动是解题关键．。

八年级下册《平移和旋转》培优提高题

北师大版八下平移和旋转一：知识点1．平移的定义与规律关键：平移不改变图形的形状和大小,也不会改变图形的方向．1平移的规律：经过平移,对应线段、对应角分别相等,•对应点所连的线段平行且相等或共线且相等．2简单作图平移的作图主要关注要点：1．方向,2．距离．整个平移的作图,就象把整个图案的每个特征点放在一套平行的轨道上滑动一样,每个特征点滑过的距离是一样的．2．旋转的定义与规律1定义：在平面内,将一个图形绕一个定点沿某个方向转动一个角度,•这样的图形运动称为旋转．关键：旋转不改变图形的大小和形状,但改变图形的方向．2旋转的规律经过旋转,图形上的每一点,都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等．3简单的旋转作图：旋转作图关键有两点：①旋转方向,②旋转角度．主要分四步：边、转、截、连．旋转就象把每个特征点与旋转中心用线连住的风筝,每个点转的角度是相同的,每个点与旋转中心的距离是不会改变的,即对应点与旋转中心距离相等．1．如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE 沿着AB边向右平移,当点D落在BC上时,平移的距离为A．3 B．4 C．5 D．61题 2题 3题2．如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是A．4 B．2C．4D．83．如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为cm2．A．B．C．D．4．在平面直角坐标系中,将点Am﹣1,n+2先向右平移3个单位,再向上平移2个单位,得到点A′,若点A′位于第二象限,则m、n的取值范围分别是A．m＜0,n＞0 B．m＜1,n＞﹣2 C．m＜0,n＜﹣2 D．m＜﹣2,m＞﹣45．下列生活现象中,属于平移的是A．足球在草地上滚动 B．拉开抽屉C．投影片的文字经投影转换到屏幕上 D．钟摆的摆动6．在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是A．64m2B．32m2C．128m2D．96m27．如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形An BnCnDnn＞2,若ABn的长度为2016,则n的值为6题 7题 8题A．400 B．401 C．402 D．4038．如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△AC P′重合,如果AP=4,那么P,P′两点间的距离为A．4 B．4C． 4 D．89题 10题 11题9．如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是 A．50°B．60°C．70°D．80°10．如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD．把△ABC绕着点D逆时针旋转m0＜m＜180度后,如果点B恰好落在初始Rt△ABC的边上,那么m为 A．70°B．70°或120°C．120°D．80°11．如图所示,已知△ACB△DFE与是两个全等的直角三角形,量得它们的斜边长为2cm,较小锐角为30°,将这两个三角形摆成如图1所示的形状,使点B．C．F．D 在同一条直线上,且点C与点F重合,将图1中的△ACB绕点C顺时针方向旋转到图2的位置,点E在AB边上,AC交DE于点G,则线段FG的长为A．2 B． C．D．212．如图△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,已知AP=3,则PP′的长度是A ．3B ．C ．D ．413、如图所示：正方形ABCD 中E 为BC 的中点,将面ABE 旋转后得到△CBF.1指出旋转中心及旋转角度．2判断AE 与CF 的位置关系．3如果正方形的面积为18cm 2,△BCF 的面积为4cm 2,问四边形AECD 的面积是多少 14、已知,如图△ABC 中,∠ACB=90°,AC=BC,P 是△ABC 内一点,且PA=3,PB=1,PC=2,求∠BPC; 15.如图,直角梯形ABCD 中,AD ∥BC,AB ⊥BC,AD = 2,将腰CD 以D 为中心逆时针旋转90°至DE,连接AE 、CE,ADE 的面积为3,求BC 的长．16.如图,有边长为1的等边△ABC 和顶角为120°的等腰△DBC,•以D 为顶点作∠MDN=60°角,两边分别交AB 、AC 于M 、N 的三角形,连结MN,1、求证MN=BM+CN ；2、试说明△AMN 的周长为2．3、若M,N 分别在AB,CA 的延长线上,则1中结论还成立吗如果不成立,MN,BM,CN 又满足什么关系17.操作：在△ABC 中,AC ＝BC ＝2,∠C ＝900,将一块等腰三角形板的直角顶点放在斜边AB 的中点P 处,将三角板绕点P 旋转,三角板的两直角边分别交射线AC 、CB 于D 、E 两点．图①、②、③是旋转三角板得到的图形中的3种情况．研究： 1三角板绕点P 旋转,观察线段PD 和PE 之间有什么数量关系并结合图②加以证明．2三角板绕点P 旋转,△PBE 能否为等腰三角形若能,指出所有情况即写出△PBE 为等腰三角形时CE 的长；若不能,请说明理由．18.如图1,已知∠DAC=90°,△ABC 是等边三角形,点P 为射线AD 上任意一点点P 与点A 不重合,连结CP,将线段CP 绕点C 顺时针旋转60°得到线段CQ,连结QB 并延长交直线AD 于点E ．1如图1,猜想∠QEP= °；2如图2,3,若当∠DAC 是锐角时,其它条件不变,猜想∠QEP 的度数,并证明P BA C北师大版八下平移和旋转参考答案一．选择题共12小题1．C；2．C；3．A；4．D；5．B；6．D；7．C；8．B；9．B；10．B；11．C；12．B；。

八年级下数学第11章图形的平移与旋转测试题及答案

八下数学第11章图形的平移与旋转测试题一、选择题（每小题3分，共36分）1、下列现象是数学中的平移的是（）A、冰化成水B、电梯由一楼升到二楼C、导弹击中目标后爆炸D、卫星绕地球运动2、下列运动是属于旋转的是（）A、滾动过程中篮球的滚动B、钟表的钟摆的摆动C、气球升空的运动D、一个图形沿某直线对折过程3、P是正AABC内的一点，将△PBC逆时针方向旋转到△P1BA，则ZPBP1的度数是（）A.45°B.60°C.90°D.120°4、下列说法正确的是（）A.若△ABC^△DEF，则△ABC可以看作是由ADEF平移得到的B.若ZA=ZB,则ZA可以看作是由ZB平移得到的C.若ZA经过平移后为ZA',则ZA=ZA'D.若线段a//b，则线段a可以看作由线段b平移得到的5、.下列图形中，是由（1）仅通过平移得到的是（）6、在如图所示的单位正方形网格中，△ABC经过平移后得到厶A1B1C1,已知在AC上一点P（2.42）平移后的对应点为P］，点P］绕点0逆时针旋转180°得到对应点P2,则P2点的坐标为（）A.（1.4，－1）B.（1.5，2）C.（1.6，1）D.（2.4，1）AP1BC旋转90。

得到△DCF，连结EF ，若ZBEC=6O o ,则ZEFD 的度数为（）A 、100 B 、150 C 、200D 、250 7题图8、如图，甲图案变成乙图案，既能用平移，又能用旋转的是OO甲乙9、下列图形中，绕某个点旋转180 ①正方形 A.5个10、如图，的度数为（A.60°XBC能与自身重合 ②长方形③等边三角形④线段B.2个C.3个D.4个将△ABC 绕点A 逆时针旋转一定角度，得到△ADE ，若ZCAE=65°,ZE=70°）. B.75°C.85°D.90°11、如图，两个边长相等的两个正方形ABCD 和OEFG ，若将正方形OEFG 绕点0按逆时针方向旋转150°，两个正方形的重叠部分四边形OMCN 的面积（A.不变B.先增大再减小C.先减小再增大） D.不断增大 7、如图，在正方形ABCD 中，E 为DC 边上的点，连结BE ，将△BCE 绕点C 顺时针方向乙，且AD 丄BC ，则ZBACAGB11题图F三、 21、.O12、如图，在直角坐标系中，点A 、B 的坐标分别为（1,4）和（3,0）,点C 是y 轴上的一个动点，且A 、B 、C 三点不在同一条直线上，当△ABC 的周长最小时,点C 的坐标是（）A.(0,0)B.(0,1)C.(0,2)D.(0,3)二、填空题（每小题3分，共24分）13、图形的平移、旋转、中心对称中，其相同的性质是14、经过平移，对应点所连的线段;经过旋转，对应点到旋转中心的距离 15、等边三角形绕着它的三边中线的交点旋转至少度，能够与本身重合．16、甲图向上平移2个单位得到乙图，乙图向左平移2个单位得到丙图，丙图向下平移2个单位得到丁那么丁图向平移个单位可以得到甲图．．19、如图，在等边厶ABC 中，AB=6,D 是BC 的中点，将△ABD 绕点A 旋转后得到△ACE ,那么线段DE 的长度为20、如图，把，QQ ”笑脸放在直角坐标系中，已知左眼A 的坐标是（-2,3），嘴唇C 点的坐标为（-1，1），贝U 将此叫Q ” 笑脸向右平移3个单位后，右眼B 的坐标是解答题（60分）（6分）经过平移，AABC 的边AB 移到了E .作出平移后的三角形.22、（6分）如图，四边形ABCD 的ZBAD=ZC=90,AB=AD,AE 丄BC 于E,BEA 旋转后能与DFA 重合.（1）旋转中心是哪一点? （2）旋转了多少度?3）若AE=5cm,求四边形AECF 的面积.23、（8分）如图,在平面直角坐标系xoy 中,A （1，），B （1，），①求出△ABC 的面积.② 作出△ABC 向下平移1个单位，再向左平移2个单位后ABC.19题图18、、如图，将矩形ABCD 绕点A 顺时针旋转到矩形''勺位置，旋转角为20题图(0〈<90)。