遗传算法合集
遗传算法——遗传算法

21
(5)机器人
例如,遗传算法已经在移动机器人路径规划、关节 机器人运动轨迹规划、机器人结构优化和行为协调等方 面得到研究和应用。
4
遗传算法的基本操作为:
(1)复制(Reproduction Operator)
复制是从一个旧种群中选择生命力强的个体位串产生 新种群的过程。具有高适应度的位串更有可能在下一代 中产生一个或多个子孙。
复制操作可以通过随机方法来实现。首先产生0~1之 间均匀分布的随机数,若某串的复制概率为40%,则当 产生的随机数在0.40~1.0之间时,该串被复制,否则被 淘汰。
出了“遗传算法”一词,并发表了遗传算法应用方面的第一 篇论文。他发展了复制、交叉、变异、显性、倒位等遗传算 子,在个体编码上使用了双倍体的编码方法。在遗传算法的 不同阶段采用了不同的概率,从而创立了自适应遗传算法的 概念。
16
(3)K.A.De Jong 1975年,De Jong博士在其博士论文中结合模式定理
2
(1)遗传:这是生物的普遍特征,亲代把生物信息交 给子代,子代总是和亲代具有相同或相似的性状。生 物有了这个特征,物种才能稳定存在。
(2)变异:亲代和子代之间以及子代的不同个体之间 的差异,称为变异。变异是随机发生的,变异的选择 和积累是生命多样性的根源。
(3)生存斗争和适者生存:具有适应性变异的个体被 保留下来,不具有适应性变异的个体被淘汰,通过一 代代的生存环境的选择作用,性状逐渐逐渐与祖先有 所不同,演变为新的物种。
对于一个需要进行优化的实际问题,一般可按下述 步骤构造遗传算法: 第一步:确定决策变量及各种约束条件,即确定出个体 的表现型X和问题的解空间; 第二步:建立优化模型,即确定出目标函数的类型及数 学描述形式或量化方法;
遗 传 算 法 详 解 ( 含 M A T L A B 代 码 )

GATBX遗传算法工具箱函数及实例讲解基本原理:遗传算法是一种典型的启发式算法,属于非数值算法范畴。
它是模拟达尔文的自然选择学说和自然界的生物进化过程的一种计算模型。
它是采用简单的编码技术来表示各种复杂的结构,并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。
遗传算法的操作对象是一群二进制串(称为染色体、个体),即种群,每一个染色体都对应问题的一个解。
从初始种群出发,采用基于适应度函数的选择策略在当前种群中选择个体,使用杂交和变异来产生下一代种群。
如此模仿生命的进化进行不断演化,直到满足期望的终止条件。
运算流程:Step 1:对遗传算法的运行参数进行赋值。
参数包括种群规模、变量个数、交叉概率、变异概率以及遗传运算的终止进化代数。
Step 2:建立区域描述器。
根据轨道交通与常规公交运营协调模型的求解变量的约束条件,设置变量的取值范围。
Step 3:在Step 2的变量取值范围内,随机产生初始群体,代入适应度函数计算其适应度值。
Step 4:执行比例选择算子进行选择操作。
Step 5:按交叉概率对交叉算子执行交叉操作。
Step 6:按变异概率执行离散变异操作。
Step 7:计算Step 6得到局部最优解中每个个体的适应值,并执行最优个体保存策略。
Step 8:判断是否满足遗传运算的终止进化代数,不满足则返回Step 4,满足则输出运算结果。
运用遗传算法工具箱:运用基于Matlab的遗传算法工具箱非常方便,遗传算法工具箱里包括了我们需要的各种函数库。
目前,基于Matlab的遗传算法工具箱也很多,比较流行的有英国设菲尔德大学开发的遗传算法工具箱GATBX、GAOT以及Math Works公司推出的GADS。
实际上,GADS就是大家所看到的Matlab中自带的工具箱。
我在网上看到有问为什么遗传算法函数不能调用的问题,其实,主要就是因为用的工具箱不同。
因为,有些人用的是GATBX带有的函数,但MATLAB自带的遗传算法工具箱是GADS,GADS当然没有GATBX里的函数,因此运行程序时会报错,当你用MATLAB来编写遗传算法代码时,要根据你所安装的工具箱来编写代码。
遗传算法总结

遗传算法总结遗传算法概念遗传算法是模仿⾃然界⽣物进化机制发展起来的随机全局搜索和优化⽅法,它借鉴了达尔⽂的进化论和孟德尔的遗传学说。
其本质是⼀种⾼效、并⾏、全局搜索的⽅法,它既能在搜索中⾃动获取和积累有关空间知识,并⾃适应地控制搜索过程以求得最优解遗传算法操作使⽤适者⽣存的原则,在潜在的解决⽅案种群中逐次产⽣⼀个近视最优⽅案。
在遗传算法的每⼀代中,根据个体在问题域中的适应度值和从⾃然遗传学中借鉴来的再造⽅法进⾏个体选择,产⽣⼀个新的近视解。
这个过程导致种群中个体的进化,得到的新个体⽐原个体更适应环境,就像⾃然界中的改造⼀样。
应⽤遗传算法在⼈⼯智能的众多领域具有⼴泛应⽤。
例如,机器学习、聚类、控制(如煤⽓管道控制)、规划(如⽣产任务规划)、设计(如通信⽹络设计、布局设计)、调度(如作业车间调度、机器调度、运输问题)、配置(机器配置、分配问题)、组合优化(如TSP、背包问题)、函数的最⼤值以及图像处理和信号处理等等。
遗传算法多⽤应与复杂函数的优化问题中。
原理遗传算法模拟了⾃然选择和遗传中发⽣的复制、交叉、和变异等现象,从任⼀初始种群出发,通过随机选择、交叉、变异操作,产⽣⼀群更适合环境的个体,使群体进⾏到搜索空间中越来越好的区域,这样⼀代⼀代地不断繁衍进化,最后收敛到⼀群最适合环境的个体求得问题的最优解。
算法流程1.编码:解空间中的解数据x,作为作为遗传算法的表现型形式。
从表现型到基本型的映射称为编码。
遗传算法在进⾏搜索之前先将解空间的解数据表⽰成遗传空间的基本型串结构数据,这些串结构数据的不同的组合就构成了不同的点。
2.初始种群的形成:随机产⽣N个初始串数据,每个串数据称为⼀个个体,N个串数据构成了⼀个群体。
遗传算法以这N个串结构作为初始点开始迭代。
设置进化代数计数器t 0;设置最⼤进⾏代数T;随机⽣成M个个体作为初始群体P(0)。
3.适应度检测:适应度就是借鉴⽣物个体对环境的适应程度,适应度函数就是对问题中的个体对象所设计的表征其优劣的⼀种测度。
遗传算法合集

遗传算法合集遗传算法简介遗传算法是一类模拟生物进化的智能优化算法,它是由于六十年代提出的。
目前,遗传算法已成为进化计算研究的一个重要分支。
与传统优化方法相比,遗传算法的优点是:·群体搜索·不需要目标函数的导数·概率转移准则遗传算法研究热点·收敛性证明·新型高效的遗传算子设计·遗传算法与局部优化算法的结合·遗传算法在各领域的应用研究·软计算与计算智能中的遗传算法遗传算法著作1.陈国良等,遗传算法及其应用,国防出版社in Natural and Artificial Systems, Ann Arbor: Univ. of Michigan Press, 1975Algorithms in Search, Optimization and Machine Learning. Reading, MA: Addison-Wesley, 1989 Handbook of Genetic Algorithms, Van Nostrand ReinholdGenetic Algorithms + Data Structures=Evolution Programs, Spinger Press,1996Algorithms & Engineering Design, 1997,Genetic Algorithms in Engineering and Computer Science,1995Introducion to Genetic Algorithms,1996,Genetic Algorithms and Simulated Annealing,1987,Genetic Algorithms and Robotics,1991,Genetic Programming,1992,Genetic Algorithms and Investiment Strategies,1994遗传算法站点Genetic Algorithms ArchiveAdaptive Systems LAB (GASLAB) GASLAB is hosted by the Computer Science Department of the University of Nevada-Reno.3.4. publications: (downloading website)Genetic Algorithms Laboratory Prof. David E. Goldberg, DirectorState University Genetic Algorithms Research and Applications Group (GARAGE) Bill Punch (,5) Erik Goodman (,5)下载2.用遗传算法进行路径规划下载3.最短路问题的简便算法下载4.带多重选择的最短路问题下载5.用原始-对偶算法求解过指定顶点的最短路下载6.给定限制期条件下最小风险路径的选取算法下载7.带有e约束的网络最短路算法下载8.无线网络中最短路径的标记与减少计算量的方法下载9.遗传算法用于从EM雷达数据提取地下古墓遗迹定位信下载息10.对FLOYD算法的两点注记下载11.应用单亲遗传算法进行树状管网优化布置下载。
遗传算法(GeneticAlgorithm)..

被选定的一组解 根据适应函数选择的一组解 以一定的方式由双亲产生后代的过程 编码的某些分量发生变化的过程
遗传算法的基本操作
➢选择(selection):
根据各个个体的适应值,按照一定的规则或方法,从 第t代群体P(t)中选择出一些优良的个体遗传到下一代 群体P(t+1)中。
等到达一定程度时,值0会从整个群体中那个位上消失,然而全局最 优解可能在染色体中那个位上为0。如果搜索范围缩小到实际包含全局 最优解的那部分搜索空间,在那个位上的值0就可能正好是到达全局最 优解所需要的。
2023/10/31
适应函数(Fitness Function)
➢ GA在搜索中不依靠外部信息,仅以适应函数为依据,利 用群体中每个染色体(个体)的适应值来进行搜索。以染 色体适应值的大小来确定该染色体被遗传到下一代群体 中的概率。染色体适应值越大,该染色体被遗传到下一 代的概率也越大;反之,染色体的适应值越小,该染色 体被遗传到下一代的概率也越小。因此适应函数的选取 至关重要,直接影响到GA的收敛速度以及能否找到最优 解。
2023/10/31
如何设计遗传算法
➢如何进行编码? ➢如何产生初始种群? ➢如何定义适应函数? ➢如何进行遗传操作(复制、交叉、变异)? ➢如何产生下一代种群? ➢如何定义停止准则?
2023/10/31
编码(Coding)
表现型空间
基因型空间 = {0,1}L
编码(Coding)
10010001
父代
111111111111
000000000000
交叉点位置
子代
2023/10/31
111100000000 000011111111
基本遗传算法【精品毕业设计】(完整版)

基本遗传算法【精品毕业设计】(完整版)遗传算法1、遗传算法⽣物学基础和基本理论达尔⽂⾃然选择学说认为,⽣物要⽣存下去,就必须进⾏⽣存⽃争。
⽣存⽃争包括种内⽃争、种间⽃争以及⽣物跟⽆机环境之间的⽃争三个⽅⾯。
在⽣存⽃争中,具有有利变异(mutation)的个体容易存活下来,并且有更多的机会将有利变异传给后代;具有不利变异的个体就容易被淘汰,产⽣后代的机会也少得多。
因此,凡是在⽣存⽃争中获胜的个体都是对环境适应性⽐较强的。
达尔⽂把这种在⽣存⽃争中适者⽣存,不适者淘汰的过程叫做⾃然选择。
达尔⽂的⾃然选择学说表明,遗传和变异是决定⽣物进化的内在因素。
遗传是指⽗代与⼦代之间,在性状上存在的相似现象。
变异是指⽗代与⼦代之间,以及⼦代的个体之间,在性状上或多或少地存在的差异现象。
在⽣物体内,遗传和变异的关系⼗分密切。
⼀个⽣物体的遗传性状往往会发⽣变异,⽽变异的性状有的可以遗传。
遗传能使⽣物的性状不断地传送给后代,因此保持了物种的特性,变异能够使⽣物的性状发⽣改变,从⽽适应新的环境⽽不断地向前发展。
⽣物的各项⽣命活动都有它的物质基础,⽣物的遗传与变异也是这样。
根据现代细胞学和遗传学的研究得知,遗传物质的主要载体是染⾊体(chromsome),染⾊体主要是由DNA(脱氧核糖核酸)和蛋⽩质组成,其中DNA⼜是最主要的遗传物质。
现代分⼦⽔平的遗传学的研究⼜进⼀步证明,基因(gene)是有遗传效应的⽚段,它储存着遗传信息,可以准确地复制,也能够发⽣突变,并可通过控制蛋⽩质的合成⽽控制⽣物的性状。
⽣物体⾃⾝通过对基因的复制(reproduction)和交叉(crossover),即基因分离、基因⾃由组合和基因连锁互换)的操作使其性状的遗传得到选择和控制。
同时,通过基因重组、基因变异和染⾊体在结构和数⽬上的变异产⽣丰富多采的变异现象。
需要指出的是,根据达尔⽂进化论,多种多样的⽣物之所以能够适应环境⽽得以⽣存进化,是和上述的遗传和变异⽣命现象分不开的。
(完整版)遗传算法简介及代码详解

遗传算法简述及代码详解声明:本文内容整理自网络,认为原作者同意转载,如有冒犯请联系我。
遗传算法基本内容遗传算法为群体优化算法,也就是从多个初始解开始进行优化,每个解称为一个染色体,各染色体之间通过竞争、合作、单独变异,不断进化。
遗传学与遗传算法中的基础术语比较染色体:又可以叫做基因型个体(individuals)群体/种群(population):一定数量的个体组成,及一定数量的染色体组成,群体中个体的数量叫做群体大小。
初始群体:若干染色体的集合,即解的规模,如30,50等,认为是随机选取的数据集合。
适应度(fitness):各个个体对环境的适应程度优化时先要将实际问题转换到遗传空间,就是把实际问题的解用染色体表示,称为编码,反过程为解码/译码,因为优化后要进行评价(此时得到的解是否较之前解优越),所以要返回问题空间,故要进行解码。
SGA采用二进制编码,染色体就是二进制位串,每一位可称为一个基因;如果直接生成二进制初始种群,则不必有编码过程,但要求解码时将染色体解码到问题可行域内。
遗传算法的准备工作:1) 数据转换操作,包括表现型到基因型的转换和基因型到表现型的转换。
前者是把求解空间中的参数转化成遗传空间中的染色体或者个体(encoding),后者是它的逆操作(decoding)2) 确定适应度计算函数,可以将个体值经过该函数转换为该个体的适应度,该适应度的高低要能充分反映该个体对于解得优秀程度。
非常重要的过程。
遗传算法基本过程为:1) 编码,创建初始群体2) 群体中个体适应度计算3) 评估适应度4) 根据适应度选择个体5) 被选择个体进行交叉繁殖6) 在繁殖的过程中引入变异机制7) 繁殖出新的群体,回到第二步实例一:(建议先看实例二)求 []30,0∈x 范围内的()210-=x y 的最小值1) 编码算法选择为"将x 转化为2进制的串",串的长度为5位(串的长度根据解的精度设 定,串长度越长解得精度越高)。
优化算法之遗传算法(GeneticAlgorithm,GA)

优化算法之遗传算法(GeneticAlgorithm,GA)⽬录概述遗传算法(Genetic Algorithm, GA) 起源于对⽣物系统所进⾏的计算机模拟研究。
它是模仿⾃然界⽣物进化机制发展起来的 随机全局搜索和优化⽅法,借鉴了达尔⽂的进化论和孟德尔的遗传学说。
其本质是⼀种⾼效、并⾏、全局搜索的⽅法,能在搜索过程中⾃动获取和积累有关搜索空间的知识,并⾃适应地控制搜索过程以求得最佳解。
相关术语基因型(genotype):性状染⾊体的内部表现;表现型(phenotype):染⾊体决定的性状的外部表现,或者说,根据基因型形成的个体的外部表现;个体(individual):指染⾊体带有特征的实体;种群(population):个体的集合,该集合内个体数称为种群的⼤⼩编码(coding):DNA中遗传信息在⼀个长链上按⼀定的模式排列。
遗传编码可看作从表现型到基因型的映射。
解码(decoding):基因型到表现型的映射。
交叉(crossover):两个染⾊体的某⼀相同位置处DNA被切断,前后两串分别交叉组合形成两个新的染⾊体。
也称基因重组或杂交;变异(mutation):复制时可能(很⼩的概率)产⽣某些复制差错,变异产⽣新的染⾊体,表现出新的性状。
进化(evolution):种群逐渐适应⽣存环境,品质不断得到改良。
⽣物的进化是以种群的形式进⾏的。
适应度(fitness):度量某个物种对于⽣存环境的适应程度。
选择(selection):以⼀定的概率从种群中选择若⼲个个体。
⼀般,选择过程是⼀种基于适应度的优胜劣汰的过程。
复制(reproduction):细胞分裂时,遗传物质DNA通过复制⽽转移到新产⽣的细胞中,新细胞就继承了旧细胞的基因。
遗传算法的实现过程遗传算法的实现过程实际上就像⾃然界的进化过程那样。
⾸先寻找⼀种对问题潜在解进⾏“数字化”编码的⽅案,(建⽴表现型和基因型的映射关系)。
然后⽤随机数初始化⼀个种群(那么第⼀批袋⿏就被随意地分散在⼭脉上),种群⾥⾯的个体就是这些数字化的编码。
常见的遗传算法

常见的遗传算法
常见的遗传算法有:
1. 标准遗传算法(SGA):是最早也是最基本的遗传算法,包括选择、交叉、变异和复制等基本操作。
2. 遗传编程(GP):将遗传算法应用于生成计算机程序的领域,通过遗传操作对程序进行优化和演化。
3. 约束处理遗传算法(CGA):在传统遗传算法的基础上,加入对问题约束条件的处理和优化,以确保产生的解满足特定的约束条件。
4. 多目标遗传算法(MOGA):解决多个目标决策问题的遗传算法,同时考虑多个目标函数的优化,并通过适应度分配方法来选择适应度较好的个体。
5. 免疫算法(IA):通过模拟免疫系统的工作原理,利用选择、变异等机制进行优化和搜索。
6. 遗传模拟退火算法(GASA):将模拟退火算法与遗传算法相结合,通过遗传操作和模拟退火操作进行全局搜索和局部优化。
7. 遗传神经网络(GNN):将遗传算法和神经网络相结合,通过遗传操作对神经网络结构和参数进行优化和演化。
8. 差分进化算法(DE):基于群体的随机搜索算法,通过选择、交叉和变异等操作对个体进行优化。
以上是一些常见的遗传算法,根据问题和需求的不同,可以选择适合的遗传算法进行优化和搜索。
遗传算法(GeneticAlgorithms)

遗传算法(GeneticAlgorithms)遗传算法前引:1、TSP问题1.1 TSP问题定义旅⾏商问题(Traveling Salesman Problem,TSP)称之为货担郎问题,TSP问题是⼀个经典组合优化的NP完全问题,组合优化问题是对存在组合排序或者搭配优化问题的⼀个概括,也是现实诸多领域相似问题的简化形式。
1.2 TSP问题解法传统精确算法:穷举法,动态规划近似处理算法:贪⼼算法,改良圈算法,双⽣成树算法智能算法:模拟退⽕,粒⼦群算法,蚁群算法,遗传算法等遗传算法:性质:全局优化的⾃适应概率算法2.1 遗传算法简介遗传算法的实质是通过群体搜索技术,根据适者⽣存的原则逐代进化,最终得到最优解或准最优解。
它必须做以下操作:初始群体的产⽣、求每⼀个体的适应度、根据适者⽣存的原则选择优良个体、被选出的优良个体两两配对,通过随机交叉其染⾊体的基因并随机变异某些染⾊体的基因⽣成下⼀代群体,按此⽅法使群体逐代进化,直到满⾜进化终⽌条件。
2.2 实现⽅法根据具体问题确定可⾏解域,确定⼀种编码⽅法,能⽤数值串或字符串表⽰可⾏解域的每⼀解。
对每⼀解应有⼀个度量好坏的依据,它⽤⼀函数表⽰,叫做适应度函数,⼀般由⽬标函数构成。
确定进化参数群体规模、交叉概率、变异概率、进化终⽌条件。
案例实操我⽅有⼀个基地,经度和纬度为(70,40)。
假设我⽅飞机的速度为1000km/h。
我⽅派⼀架飞机从基地出发,侦察完所有⽬标,再返回原来的基地。
在每⼀⽬标点的侦察时间不计,求该架飞机所花费的时间(假设我⽅飞机巡航时间可以充分长)。
已知100个⽬标的经度、纬度如下表所列:3.2 模型及算法求解的遗传算法的参数设定如下:种群⼤⼩M=50;最⼤代数G=100;交叉率pc=1,交叉概率为1能保证种群的充分进化;变异概率pm=0.1,⼀般⽽⾔,变异发⽣的可能性较⼩。
编码策略:初始种群:⽬标函数:交叉操作:变异操作:选择:算法图:代码实现:clc,clear, close allsj0=load('data12_1.txt');x=sj0(:,1:2:8); x=x(:);y=sj0(:,2:2:8); y=y(:);sj=[x y]; d1=[70,40];xy=[d1;sj;d1]; sj=xy*pi/180; %单位化成弧度d=zeros(102); %距离矩阵d的初始值for i=1:101for j=i+1:102d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*...cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));endendd=d+d'; w=50; g=100; %w为种群的个数,g为进化的代数for k=1:w %通过改良圈算法选取初始种群c=randperm(100); %产⽣1,...,100的⼀个全排列c1=[1,c+1,102]; %⽣成初始解for t=1:102 %该层循环是修改圈flag=0; %修改圈退出标志for m=1:100for n=m+2:101if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))<...d(c1(m),c1(m+1))+d(c1(n),c1(n+1))c1(m+1:n)=c1(n:-1:m+1); flag=1; %修改圈endendendif flag==0J(k,c1)=1:102; break %记录下较好的解并退出当前层循环endendendJ(:,1)=0; J=J/102; %把整数序列转换成[0,1]区间上实数即染⾊体编码for k=1:g %该层循环进⾏遗传算法的操作for k=1:g %该层循环进⾏遗传算法的操作A=J; %交配产⽣⼦代A的初始染⾊体c=randperm(w); %产⽣下⾯交叉操作的染⾊体对for i=1:2:wF=2+floor(100*rand(1)); %产⽣交叉操作的地址temp=A(c(i),[F:102]); %中间变量的保存值A(c(i),[F:102])=A(c(i+1),[F:102]); %交叉操作A(c(i+1),F:102)=temp;endby=[]; %为了防⽌下⾯产⽣空地址,这⾥先初始化while ~length(by)by=find(rand(1,w)<0.1); %产⽣变异操作的地址endB=A(by,:); %产⽣变异操作的初始染⾊体for j=1:length(by)bw=sort(2+floor(100*rand(1,3))); %产⽣变异操作的3个地址%交换位置B(j,:)=B(j,[1:bw(1)-1,bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]);endG=[J;A;B]; %⽗代和⼦代种群合在⼀起[SG,ind1]=sort(G,2); %把染⾊体翻译成1,...,102的序列ind1num=size(G,1); long=zeros(1,num); %路径长度的初始值for j=1:numfor i=1:101long(j)=long(j)+d(ind1(j,i),ind1(j,i+1)); %计算每条路径长度endend[slong,ind2]=sort(long); %对路径长度按照从⼩到⼤排序J=G(ind2(1:w),:); %精选前w个较短的路径对应的染⾊体endpath=ind1(ind2(1),:), flong=slong(1) %解的路径及路径长度xx=xy(path,1);yy=xy(path,2);plot(xx,yy,'-o') %画出路径以上整个代码中没有调⽤GA⼯具箱。
遗传算法课件PPT

*
五.GA的各种变形(15)
切点
实数编码的合法性修复 交叉 单切点交叉
*
五.GA的各种变形(16)
双切点交叉(与单切点交叉类似) 该方法最大的问题:如何在实际优化中保持可行性。
切点
切点
*
五.GA的各种变形(17)
X
Y
*
五.GA的各种变形(7)
顺序交叉( OX )Order Crossover:可看做是带有不同修复程序的部分映射交叉的变形。
OX步骤:
选切点X,Y;
交换中间部分;
从切点Y后第一个基因起列出原顺序,去掉已有基因;
从切点Y后第一个位置起,按顺序填入。
*
五.GA的各种变形(8)
OX例题:
列出基因:6 7 2 1 3 4 5 7 6 4 3 1 2 5
*
五.GA的各种变形(26)
加入的意义(同线性标定中ξ 的意义)
加入使最坏个体仍有繁殖的可能, 随 的增大而减小
的取值:
, , , 调节 和 ,从而来调节
*
五.GA的各种变形(27)
引入 的目的: 调节选择压力,即好坏个体选择概率的 差,使广域搜索范围宽保持种群的多样性,而 局域搜索细保持收敛性。如下图表示: 开始:希望选择压力小 后来:希望选择压力大
*
五.GA的各种变形(33)
顺序选择:
01
步骤:
02
从好到坏排序所有个体
03
定义最好个体的选择概率为 ,则第 个个体的选择概率为:
04
*
由于
五.GA的各种变形(34)
有限时要归一化,则有下面的公式:
最经典的遗传算法教程

遗传算法在应用中的一些基本问题
1)知识的编码 二进制和十进制的比较:二进制有更多图式和更大的搜索范 围;十进制更接近于实际操作。
精度
Q
U max U min 2l 1
Umax 和 Umin 分别为变量的最大和最小值。 l 是二进制的长度
2)适应度函数。 a) 适应度函数值必须非负。根据情况做适当的处理
经过选择,在t+1代,图式H的数量m(H,t+1)为:
f (hi )
m(H ,t 1) n
ps
(hi
)
n
i,hiPH n
i,hiPH
f (xi )
i1
m(H ,t) f (H )n / fi (n是种群中染色体的个数)
m(H ,t) f (H ) / fi / n
m(H ,t) f (H ) / f ,
A 0111000H1 Fra bibliotek1****0
H2 H3
***10 ** 0111000
图式
H 4 *******
图式的描述: ⑴ 定义长度(H)——H左右二端有定义位置之间的距离; ⑵ 图式的阶次(或固定长度)O(H)——H中非*位(有定义位) 的个数。
图式定理的推导 ①图式在选择过程中的增加.
举例:
⒈具有6个染色体的二进制编码、适应度值、Pc累计 值。
染色体的 适应度和所占的比例
用转轮方法进行选择
⒉10个染色体种群按比例的选择过程 染色体被选的概率
1 染色体编号
适应度
8
被选概率 0.1
适应度累计 8
2 3 4 5 6 7 8 9 10
2 17 7 2 12 11 7 3 7
0.02 0.22 0.09 0.02 0.16 0.14 0.09 0.03 0.09 10 27 34 36 48 59 66 69 76
(完整)基本遗传算法

基本遗传算法Holland创建的遗传算法是一种概率搜索算法,它利用某种编码技术作用于称为染色体的数串,其基本思想是模拟由这些串组成的个体进化过程.该算法通过有组织的、然而是随机的信息交换,重新组合那些适应性好的串.在每一代中,利用上一代串结构中适应性好的位和段来生成一个新的串的群体;作为额外增添,偶尔也要在串结构中尝试用新的位和段来替代原来的部分。
遗传算法是一类随机优化算法,它可以有效地利用已有的信息处理来搜索那些有希望改善解质量的串.类似于自然进化,遗传算法通过作用于染色体上的基因,寻找好的染色体来求解问题.与自然界相似,遗传算法对待求解问题本身一无所知,它所需要的仅是对算法所产生的每个染色体进行评价,并基于适应度值来改变染色体,使适应性好的染色体比适应性差的染色体有更多的繁殖机会.第一章遗传算法的运行过程遗传算法模拟了自然选择和遗传中发生的复制、交叉和变异等现象,从任一初始种群(Population)出发,通过随机选择、交叉和变异操作,产生一群更适应环境的个体,使群体进化到搜索空间中越来越好的区域,这样一代一代地不断繁衍进化,最后收敛到一群最适应环境的个体(Individual),求得问题的最优解。
一.完整的遗传算法运算流程完整的遗传算法运算流程可以用图1来描述。
由图1可以看出,使用上述三种遗传算子(选择算子、交叉算子和变异算子)的遗传算法的主要运算过程如下:(1)编码:解空间中的解数据x,作为遗传算法的表现形式。
从表现型到基因型的映射称为编码.遗传算法在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合就构成了不同的点。
(2)初始群体的生成:随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了一个群体。
遗传算法以这N个串结构作为初始点开始迭代。
设置进化代数计数器t←0;设置最大进化代数T;随机生成M个个体作为初始群体P(0)。
(3)适应度值评价检测:适应度函数表明个体或解的优劣性。
遗传算法总结

遗传算法总结简介遗传算法(Genetic Algorithm,简称GA)是一种基于生物进化过程中的遗传机制和自然选择原理的优化方法。
它模拟了自然界的进化过程,通过对问题空间中的个体进行选择、交叉和变异等操作,逐步搜索并优化解的过程。
遗传算法被广泛应用于解决各种优化、搜索和机器学习问题。
基本原理遗传算法的基本原理是通过模拟自然选择和遗传机制,寻找问题空间中的最优解。
其主要步骤包括初始化种群、选择操作、交叉操作、变异操作和确定终止条件等。
1.初始化种群:遗传算法的第一步是生成一个初始种群,其中每个个体代表一个可能的解。
个体的编码可以使用二进制、整数或实数等形式,具体根据问题的特点而定。
2.选择操作:选择操作通过根据适应度函数对种群中的个体进行评估和排序,选择较优的个体作为下一代种群的父代。
通常采用轮盘赌选择、竞争选择等方法来进行选择。
3.交叉操作:交叉操作模拟了生物遗传中的交配过程。
从父代个体中选择一对个体,通过交叉染色体的某个位置,生成下一代个体。
交叉操作可以通过单点交叉、多点交叉或均匀交叉等方式进行。
4.变异操作:变异操作引入了种群中的一定程度的随机性,通过改变个体的染色体或基因,以增加种群的多样性。
变异操作可以是位变异、部分反转、插入删除等方式进行。
5.确定终止条件:遗传算法会循环执行选择、交叉和变异操作,直到满足一定的终止条件。
常见的终止条件有达到最大迭代次数、找到最优解或达到计算时间限制等。
优点和局限性优点•遗传算法可以在大规模问题空间中进行全局搜索,不受问题的线性性和连续性限制。
它适用于解决多目标和多约束问题。
•遗传算法具有自适应性和学习能力,通过不断的进化和优胜劣汰过程,可以逐步收敛到最优解。
•遗传算法易于实现和理解,可以直观地表示问题和解决方案。
局限性•遗传算法需要选择合适的编码方式和适应度函数,以及调整交叉和变异的概率等参数。
这些参数的选择对算法的性能和结果有较大影响,需要经验和调整。
遗传算法解释及代码(一看就懂)

遗传算法解释及代码(一看就懂)遗传算法( GA , Genetic Algorithm ) ,也称进化算法。
遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。
因此在介绍遗传算法前有必要简单的介绍生物进化知识。
一.进化论知识作为遗传算法生物背景的介绍,下面内容了解即可:种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ) :一个遗传因子。
染色体 ( Chromosome ):包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。
适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
简单说来就是:繁殖过程,会发生基因交叉( Crossover ) ,基因突变( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。
那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。
二.遗传算法思想借鉴生物进化论,遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。
这样进化N代后就很有可能会进化出适应度函数值很高的个体。
举个例子,使用遗传算法解决“0-1背包问题”的思路:0-1背包的解可以编码为一串0-1字符串(0:不取,1:取);首先,随机产生M个0-1字符串,然后评价这些0-1字符串作为0-1背包问题的解的优劣;然后,随机选择一些字符串通过交叉、突变等操作产生下一代的M个字符串,而且较优的解被选中的概率要比较高。
这样经过G代的进化后就可能会产生出0-1背包问题的一个“近似最优解”。
编码:需要将问题的解编码成字符串的形式才能使用遗传算法。
遗传算法1..

遗传算法计算过程
遗传算法通常包含以下几个步骤。 • Step 1: 构造满足约束条件的染色体,将问题的 解使用有效且通用的编码方式转变成计算机能够 识别的字符串; • Step 2: 利用其他算法生产一组可行解,再随机 产生一定数量的初始种群; • Step 3: 定义或设计一个适应度函数,求出染色 体的适应度值。适应度是唯一能够衡量染色体优 劣的参数,最终的目的就是寻求适应度值最大的 染色体,则为满意解;
• 燃油消耗受众多因素的影响,为了便于实 际应用,假定油耗与行驶距离和载重有关, 是乘积关系。 • 配送中心标记为0,顾客点分别为1、2、 3· · · · · · 27,各点间距离已知,需求量已知。 • 车型有A、B、C三种,最大装载量已知。 • 各种车型的固定成本已知。 • 参数设置如下:种群规模P=30,交叉率 Pc=1.0,算法的终止条件为最大迭代次数 为 1000。
• Step 1:构造编码 将车辆的路径选择进行排列,形式如下 {1,2,3,4,5,······27} • Step 2: 产生可行解和初始种群 随机产生一组初始种群30个,种群中的 每一组解都对应其最优装载,每一个最优 装载都对应一个成本,其中成本最低的装载的生成,举例说明 假设其中一个路径选择是 {17, 10, 24, 25, 26, 21, 27, 19, 4, 16, 14, 18, 15, 6, 9, 7, 8, 11, 2, 1, 22, 20, 23, 3, 12, 13, 5} 需求量查表可知。 得到的成本最小的装载方式就是最优装载
变异过程是指按照已经求出的该序列的 最优装载的车辆数对序列进行划分,对每 辆车负责的区域内的线路节点利用贪心算 法进行重排,使之行驶路径最小,并求出 其成本。 交叉、变异结束之后对30组序列数据进 行比较,选择成本最小的一组保留,再将 30组序列继续进行复制、选择、交叉、变 异,得到一组最优值后与原保留最优值比 较,保留成本最小的那一组。 一直迭代1000次得到的成本最小值的那 一组序列就是最终结果。
遗传算法总结
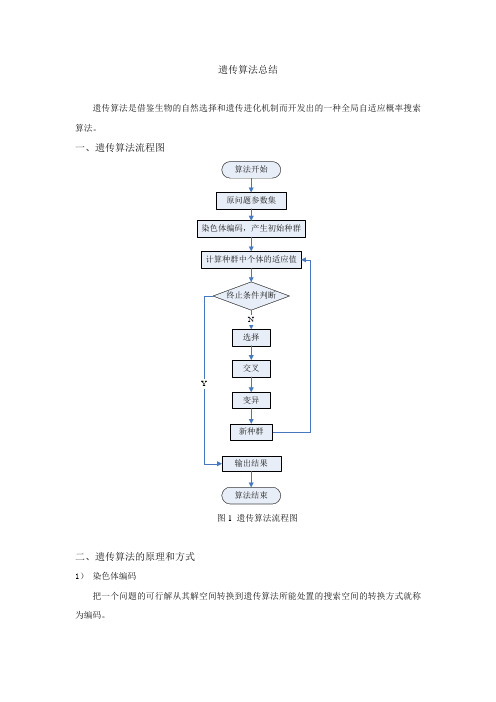
遗传算法总结遗传算法是借鉴生物的自然选择和遗传进化机制而开发出的一种全局自适应概率搜索算法。
一、遗传算法流程图图1 遗传算法流程图二、遗传算法的原理和方式1)染色体编码把一个问题的可行解从其解空间转换到遗传算法所能处置的搜索空间的转换方式就称为编码。
De Jong 曾提出了两条操作性较强的有效编码原那么:编码原那么一:应利用能易于产生与所求问题相关的且具有低阶、短概念长度模式的编码方案;编码原那么二:应利用能使问题取得自然表示或描述的具有最小编码字符集的编码方案。
编码方式要紧有以下几种:二进制编码方式、格雷码编码方式、浮点数编码方式、符号编码方式、参数级联编码方式、多参数交叉编码方式。
2) 适应值计算由解空间中某一点的目标函数值()f x 到搜索空间中对应个体的适应度函数值(())Fit f x 的转换方式大体上有一下三种:a . 直接以待解的目标函数值()f x 转化为适应度函数值(())Fit f x ,令() (())=() f x Fit f x f x ⎧⎨-⎩目标函数为最大化函数目标函数为最小化函数b . 关于最小值的问题,做以下转化max max () () (())0 C f x f x C Fit f x -<⎧=⎨⎩其他,其中max C 是()f x 的最大输入值。
c . 假设目标函数为最小值问题,1(()), 0, ()01()Fit f x c c f x c f x =≥+≥++ 假设目标函数为最大值问题,1(()), 0, ()01()Fit f x c c f x c f x =≥-≥+- 3) 选择、交叉、变异遗传算法利用选择算子来对群体中的个体进行优胜劣汰操作:依照每一个个体的适应度值大小选择。
适应度较高的个体被遗传到下一代群体中的概率较大;适应度较低的个体的被遗传到下一代群体中的概率较小。
其当选择的方式有:轮盘赌选择、随机竞争选择、最正确保留选择、无回放随机选择、确信式选择等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
遗传算法合集
遗传算法简介
遗传算法是一类模拟生物进化的智能优化算法,它是由J.H.Holland于六十年代提出的。
目前,遗传算法已成为进化计算研究的一个重要分支。
与传统优化方法相比,遗传算法的优点是:
·群体搜索
·不需要目标函数的导数
·概率转移准则
遗传算法研究热点
·收敛性证明
·新型高效的遗传算子设计
·遗传算法与局部优化算法的结合
·遗传算法在各领域的应用研究
·软计算与计算智能中的遗传算法
遗传算法著作
1.陈国良等,遗传算法及其应用,国防出版社
2.J.H.Holland,Adaptation in Natural and Artificial Systems, Ann Arbor: Univ. of
Michigan Press, 1975
3.D.E.Goldberg,Genetic Algorithms in Search, Optimization and Machine Learning.
Reading, MA: Addison-Wesley, 1989
4.L.D.Davis, Handbook of Genetic Algorithms, Van Nostrand Reinhold
5.Z.Michalewicz, Genetic Algorithms + Data Structures=Evolution Programs, Spinger
Press,1996
6.M.Gen,R.Cheng,Genetic Algorithms & Engineering Design, 1997
7.Wiely,Genetic Algorithms in Engineering and Computer Science,1995
8.M.Mitchell,An Introducion to Genetic Algorithms,1996
9.Davis,Genetic Algorithms and Simulated Annealing,1987
10.Davidor,Genetic Algorithms and Robotics,1991
11.Koza,Genetic Programming,1992
12.Bauer,Genetic Algorithms and Investiment Strategies,1994
遗传算法站点
1.The Genetic Algorithms Archive
/galist/
2.Genetic Adaptive Systems LAB (GASLAB)
GASLAB is hosted by the Computer Science Department of the University of Nevada-Reno.
/~sushil/papers/conference/conf.html
/
3.http://www.mat.sbg.ac.at/~uhl/GA.html
4./research/gag/
email:kdejong@
publications: (downloading website)
/research/gas/pubs.html
5.Illinois Genetic Algorithms Laboratory Prof. David E. Goldberg, Director ./illigal.home.html
6.Michigan State University
Genetic Algorithms Research and Applications Group (GARAGE)
Bill Punch (punch@,517-353-3541)
Erik Goodman (goodman@,517-355-6453)
/
7.ftp:///pub/EC/GA/
遗传算法应用的参考文章
1.用遗传算法求解最短路径问题下载
2.用遗传算法进行路径规划下载
3.最短路问题的简便算法下载
4.带多重选择的最短路问题下载
5.用原始-对偶算法求解过指定顶点的最短路下载
6.给定限制期条件下最小风险路径的选取算法下载
7.带有e约束的网络最短路算法下载
8.无线网络中最短路径的标记与减少计算量的方法下载
9.遗传算法用于从EM雷达数据提取地下古墓遗迹定位信
下载
息
10.对FLOYD算法的两点注记下载
11.应用单亲遗传算法进行树状管网优化布置下载。
