湖南省2011年普通高等学校对口招生考试数学试题
湖南省对口高考2011年数学模拟学训练试卷(2)5

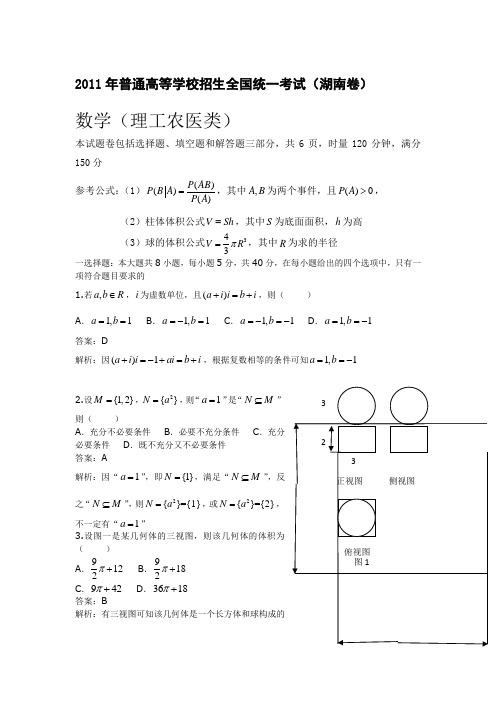
湖南省2011年普通高等学校对口招生考试数学模拟试卷(2)第Ⅰ卷(选择题,共40分)考生注意事项:请用2A 铅笔在答题卡上.....作答,在试题卷上答题无效.......... 一、选择题:本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.i 是虚数单位,=+ii 33A .12341-B .i 12341- C .i 6321+ D .i 6321- 2.若集合}21log |{21≥=x x A ,则=A C RA .⎪⎪⎭⎫ ⎝⎛+∞⋃-∞,22]0,( B .⎪⎪⎭⎫⎝⎛+∞,22 C .⎪⎪⎭⎫⎢⎣⎡+∞⋃-∞,22]0,( D .⎪⎪⎭⎫⎢⎣⎡+∞,22 3.设向量)21,21(),0,1(==b a ,则下列结论中正确的是A .||||b a =B .22=⋅b a C .b b a 与-垂直 D .b a //4.若)(x f 是R 上周期为5的奇函数,且满足,2)2(,1)1(==f f 则)4()3(f f -=A .-1B .1C .-2D .25.双曲线方程为1222=-y x ,则它的右焦点坐标为A .)0,22(B .)0,25(C .)0,26(D .)0,3(6.设0>abc ,二次函数c bx ax x f ++=2)(的图象可能是7.若=∈=+x x x x tan ),,0(,51cos sin 则πA .53-B .43C .2512-D .34-8.五项不同的工程由3个工程队承包,每队至少承包一项,则不同的承包方案A .420B .240C .150D .909.已知随机变量ξ~B (n, p ),且E (ξ)=1.6, D (ξ)=1.28,则n, p 分别是A .n=10, p=0.6B .n=8, p=0.2C .n=2, p=0.8D .n=8, p=0.410.下列四个命题: ① +∞→x limx1= 0; ② +→1lim x 1-x = 0; ③ 2lim -→x 222++x xx 不存在;④ 设f (x ) =⎪⎩⎪⎨⎧+≥)<(,(,01)0x x x x ,则0lim →x f (x ) = 0.其中不正确的是 A .①② B .②③ C . ③④ D . ①④第Ⅱ卷(非选择题 共80分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上.....作答,在试题卷上答题无效.......... 二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置.11.3|4||2|>-+-x x ”的解集为 . 12.若n xx x )1(3+的展开式中第七项为常数项,则n=___________13.设曲线ax y e =在点(0,1)处的切线与直线410x y +-=垂直,则a = .14.在正项等比数列}{n a 中,374a a =,则数列2{log }n a 的前9项之和为 .15.甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球,先从甲罐中随机取出一球放入乙罐,分别以A 1,A 2和A 3表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B 表示由乙罐取出的球是红球的事件,则下列结论中正确的是 (写出所有正确结论的编号). ①52)(1=B P ; ②115)|(1=A B P ;③事件B 与事件A 1相互独立; ④A 1,A 2,A 3是两两互斥的事件;⑤)(B P 的值不能确定,因为它与A 1,A 2,A 3中究竟哪一个发生有关.16.从总数为N 的一群学生中抽取一个容量为100的样本,若每个学生被抽取的概率为41,则N 的值为 .三、解答题(本大题共7小题,前5小题每题8分,其中第22、23小题为选做题且每题10分,共50分,解答写出必要的文字说明,注明过程及演算步骤) 17.已知关于x 的不等式:.113)1(<--+x x a(1)当1=a 时,求该不等式的解集; (2)当0>a 时,求该不等式的解集18.设ABC ∆是锐角三角形,c b a ,,分别是内角A ,B ,C 所对边长,并且.sin )3sin()3sin(sin 22B B B A +-+=ππ(Ⅰ)求角A 的值;(Ⅱ)若12,AB AC a ⋅==c b ,(其中c b <).19.已知等差数列{}n a 中,11a =,前10项和10100S =。
湖南省2011年普通高等学校对口招生考试

湖南省2011年普通高等学校对口招生考试机电类专业综合知识模拟试题(二)一、单选题(5分×20=100分)1、根据图1主、俯视图选择正确的左视图。
()2、要得到如图2所示的尺寸标注形式,选用的命令是()A、dimlinearB、dimalignedC、dimcontinueD、dimbaseline3、适用于两轴直径较小、同心度较高、工作平稳的场合、并在机床上应用广泛的联轴器是()A、套筒联轴器B、滑块联轴器C、万向联轴器D、弹性柱销联轴器4、在同一轴上不同轴段的键槽应布置在同一母线上,目的是()A、便于一次装夹后完成加工B、便于轴上零件的装拆C、便于轴上零件的轴向定位D、便于轴上零件的周向定位5、一铰链四杆机构,连架杆尺寸分别为a=400mm,C=500mm,连杆尺寸为b=600mm,机架尺寸为d=300mm。
该四杆机构为()A、曲柄摇杆机构B、双曲柄机构C、双摇杆机构D、导杆机构6、一对外啮合的标准直齿圆柱齿轮传动,已知其齿数分别为z1=30,z2=50,模数m=5,下列尺寸计算正确的是()A、d1=150mm,d a2=160mm,a=200mmB、d2=250mm,h=11.25mm,a=400mmC、P=5πmm,d a1=160mm,d f1=137.5mmD、h a=5mm,d a2=260mm,d f2=140mm7、有一双头丝杆传动,螺距为6 mm,要求螺母移动0.2 mm时,刻度盘转过一格。
此刻度盘(固定在丝杆端部)圆周应均匀刻线数为()A、30B、40C、60D、1008、下列措施中,不能提高轴疲劳强度的是()A、改进轴的结构,降低应力集中B、提高轴的表面质量C、改变轴上零件的布置,以减小轴上载荷D、通过热处理整体淬硬9、定轴轮系中,直接外啮合的主从动两轮之间若加入偶数个惰轮,会出现()A. 主从两轮转向相同B. 主从两轮转向相反C. 改变传动比大小D. 对中心距无影响10、有一双圆销外啮合槽轮机构,槽轮有六条槽,主动件转速为120r/min,当主动件转1转时,槽轮停歇时间为( )秒。
2011年全国高考文科数学试题及答案-湖南

2011年普通高等学校招生全国统一考试(湖南卷)文史类本试题包括选择题、填空题和解答题三部分,共6页.时量120分钟,满分150分. 参考公式(1)柱体体积公式V Sh =,其中S 为底面面积,h 为高. (2)球的体积公式343V R π=,其中R 为球的半径. 一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{1,2,3,4,5},{2,4},U U M N M C N === 则N =( ) A .{1,2,3} B .{1,3,5} C.{1,4,5} D.{2,3,4} 答案:B解析:画出韦恩图,可知N ={1,3,5}。
2.若,,a b R i ∈为虚数单位,且()a i i b i +=+,则A.1,1a b == B.1,1a b =-= C.1,1a b ==- D.1,1a b =-=- 答案:C解析:因()1a i i ai b i +=-+=+,根据复数相等的条件可知1,1a b ==-。
3."1""||1"x x >>是的A .充分不必要条件 B.必要不充分条件C .充分必要条件D .既不充分又不必要条件 答案:A解析:因"1""||1"x x >⇒>,反之"||1""11"x x x >⇒><-或,不一定有"1"x >。
4.设图1是某几何体的三视图,则该几何体的体积为 A .942π+ B.3618π+ C.9122π+ D.9182π+答案:D解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+()。
正视图 侧视图俯视图 图1由2222()110(40302030)7.8()()()()60506050n ad bc K K a b c d a c b d -⨯⨯-⨯==≈++++⨯⨯⨯算得,附表:参照附表,得到的正确结论是( )A . 有99%以上的把握认为“爱好该项运动与性别有关”B . 有99%以上的把握认为“爱好该项运动与性别无关”C . 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D . 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” 答案:A解析:由27.8 6.635K ≈>,而2( 6.635)0.010P K ≥=,故由独立性检验的意义可知选A.6.设双曲线2221(0)9x y a a -=>的渐近线方程为320,x y ±=则a 的值为( ) A .4 B .3 C .2 D .1答案:C解析:由双曲线方程可知渐近线方程为3y x a=±,故可知2a =。
2011年湖南省高考数学文科试题及答案

2011年普通高等学校招生全国统一考试(湖南卷)数学(文史类)本试题卷包括选择题、填空题、解答题三部分,共6页,时量120分钟,满分150分参考公式:(1)()(|)()P AB P B A P A =,其中,A B 为两个基本事件,且()0P A >. (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高. (3)球的体积公式343V R π=,其中R 为球的半径. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集{1,2,3,4,5},{2,4},U U M N M C N ===U I 则N =( )A .{1,2,3}B .{1,3,5}C .{1,4,5}D . {2,3,4} 2. 若,,a b R i ∈为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B . 1,1a b =-=C . 1,1a b ==-D . 1,1a b =-=-3. “1x >”是“||1x >”的( )A .充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件 4. 设图1是某几何体的三视图,则该几何体的体积为 ( )A .942π+B .3618π+C .9122π+ D .9182π+ 5. 通过询问110名性别不同的的大学生是否爱好某项运动,得到如下的列联表.由22()()()()()n ad bc K a b c d a c b d -=++++算得,22110(40302020)7.860506050K ⨯-⨯=≈⨯⨯⨯,附表如右下,参照附表,得到的正确结论( )A .有99%以上的把握认为“爱好该项运动与性别有关”B .有99%以上的把握认为“爱好该项运动与性别无关”C .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”6. 设双曲线2221(0)9x y a a -=>的渐近线方程为320x y =±,则a 的值为( ) A .4 B .3 C .2 D .1 7. 曲线sin 1sin cos 2x y x x =-+在点(,0)4M π处的切线的斜率为( )A .-12B . 12C . -22D . 228. 已知函数2()1,()4 3.xf x eg x x x =-=-+-若有()()f a g b =,则b 的取值范围为( )A .[2-2,2+2]B .(2-2,2+2)C . [1,3]D .(1,3)二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分.把答案填在答题卡中对应题号后的横线上.(一)选做题(请考生在第9、10两题中任选一题作答,如果全做,则按前一题记分)9. 在直角坐标系xOy 中,曲线1C的参数方程为2cos (x y ααα=⎧⎪⎨=⎪⎩为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为(cos s i n )10ρθθ-+=,则1C 与2C 的交点个数为 .10. 已知某试验范围为[10,90],若用分数法进行4次优选试验,则第二次试点可以是 (只写出其中一个也正确). (二)必做题(11~16题)11. 若执行如图2所示的框图,输入12341,2,4,8,x x x x ==== 则输出的数等于 .12. 已知()f x 为奇函数,()()9g x f x =+,(2)3g -=,则(2)f = .13. 设向量a ,b 满足|a|=25,b =(2,1),且a 与b 的方向相反,则a 的坐标为 .14. 设1m >,在约束条件,,1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数5z x y =+的大值为4,则m 的值为 。
湖南省近七年(2011-2017)对口高考数学试题分类

湖南省近七年(2011-2017)对口高考数学试题分类近七年湖南省普通高等学校对口招生考试的数学试题中,填空和选择题占据了很大比例。
以下是一些题目和解答:1.(2011.1)不等式(x-2)(x+1)≤0的解集是()A.(-1,2)B.(-∞,2) ∪ (2,+∞)C.[-1,2]D.(-∞,-1) ∪ [2,+∞]2.(2012.3)不等式2x-3>1的解集为()A.(1,2)B.(-∞,1) ∪ (2,+∞)C.(-∞,1)D.(2,+∞)3.(2013.7)不等式x^2-2x-3>0的解集为()A.(-3,1)B.(-∞,-3) ∪ (1,+∞)C.(-1,3)D.(-∞,-1) ∪ (3,+∞)4.(2014.7)若a<0,则关于x的不等式(x-3a)(x+2a)<0的解集为()A.{x|3a-2a} C.{x|-2a3a}5.(2015.8)不等式1-2x<3的解集为()A.{x|x-1} C.{x|-2<x<4} D.{x|-1<x<2}6.(2016.4)不等式2x+1>5的解集为()A.{x|x>2}B.{x|x2}7.(2016.13)若不等式x^2+x-c≤0的解集为{x-2≤x≤1},则c=5.8.(2017.7)不等式x-5x+6<0的解集为()A.{x|x3} C.{x|x3} D.{x|2<x<3}9.(2017.14)若关于x的不等式2x+b<3的解集为{x-3<x<5},则b=-1.1.(2011.2)方程x^2-px+q=0有解的充分必要条件是p^2-4q≥0.2.(2012.2)"x>3"是"x^2>9"的充分必要条件。
3.(2013.3)"x=2"是"(x-1)(x-2)=0"的充要条件。
2011年湖南省高考数学文科试题及答案

2011年普通高等学校招生全国统一考试(湖南卷)数学(文史类)本试题卷包括选择题、填空题、解答题三部分,共6页,时量120分钟,满分150分参考公式:(1)()(|)()P AB P B A P A =,其中,A B 为两个基本事件,且()0P A >. (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高. (3)球的体积公式343V R π=,其中R 为球的半径. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集{1,2,3,4,5},{2,4},U U M N M C N ===U I 则N =( )A .{1,2,3}B .{1,3,5}C .{1,4,5}D . {2,3,4} 2. 若,,a b R i ∈为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B . 1,1a b =-=C . 1,1a b ==-D . 1,1a b =-=-3. “1x >”是“||1x >”的( )A .充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件 4. 设图1是某几何体的三视图,则该几何体的体积为 ( )A .942π+B .3618π+C .9122π+ D .9182π+ 5. 通过询问110名性别不同的的大学生是否爱好某项运动,得到如下的列联表.由22()()()()()n ad bc K a b c d a c b d -=++++算得,22110(40302020)7.860506050K ⨯-⨯=≈⨯⨯⨯,附表如右下,参照附表,得到的正确结论( )A .有99%以上的把握认为“爱好该项运动与性别有关”B .有99%以上的把握认为“爱好该项运动与性别无关”C .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”6. 设双曲线2221(0)9x y a a -=>的渐近线方程为320x y =±,则a 的值为( ) A .4 B .3 C .2 D .1 7. 曲线sin 1sin cos 2x y x x =-+在点(,0)4M π处的切线的斜率为( )A .-12B . 12C . -22D . 228. 已知函数2()1,()4 3.x f x e g x x x =-=-+-若有()()f a g b =,则b 的取值范围为( )A .[2-2,2+2]B .(2-2,2+2)C . [1,3]D .(1,3)二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分.把答案填在答题卡中对应题号后的横线上.(一)选做题(请考生在第9、10两题中任选一题作答,如果全做,则按前一题记分)9. 在直角坐标系xOy 中,曲线1C的参数方程为2cos (x y ααα=⎧⎪⎨=⎪⎩为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为(cos sin )10ρθθ-+=,则1C 与2C 的交点个数为 .10. 已知某试验范围为[10,90],若用分数法进行4次优选试验,则第二次试点可以是 (只写出其中一个也正确). (二)必做题(11~16题)11. 若执行如图2所示的框图,输入12341,2,4,8,x x x x ==== 则输出的数等于 .12. 已知()f x 为奇函数,()()9g x f x =+,(2)3g -=,则(2)f = .13. 设向量a ,b 满足|a|=25,b =(2,1),且a 与b 的方向相反,则a 的坐标为 .14. 设1m >,在约束条件,,1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数5z x y =+的大值为4,则m 的值为 。
2011年湖南省对口高考数学模拟试卷

湖南省2008年普通高等学校对口招生考试数学模拟试卷班级 姓名 计分一、选择题(本题共10个小题,每小题5分,共50分)1、含有三个实数的集合可表示为{a,ab,1},也可表示为{a 2,a+b ,0},则a 2003 +b 2003的值为 -------( ) A .0 B .1 C .—1 D .1±2、下面四个结论:①偶函数的图象一定与y 轴相交;②奇函数的图象一定通过原点;③偶函数的图象关于y 轴对称;④既是奇函数、又是偶函数的函数一定是).(0)(R x x f ∈=其中正确的命题的个数是 -------( ) A .4个B .1个C .2个D .3个3、 设向量=⋅︒︒=︒︒=则),37cos ,53(cos ),67cos ,23(cos -------( )A .23B .21 C .-23 D .-21 4、在等差数列1,4,7,……中,5995是它的 -------( )A .第1999项B .第2005项C .第2003项D .第2001项5、某小学为了让同学们记住北京奥运会开幕的时间,让同学们做一个游戏,把20080808这个数中的8个数字进行任意排列,规定最高位不能是0,看谁得到的数字最多,则符合条件的数字最多有 -------( ) A 、35 B 、105 C 、140 D 、2806、函数y =cos2x 的图象,可由y=cos(2x -)3π的图象,经过下列哪种平移变换得到 -------( ) A .向左平移3π个单位 B .向右平移3π个单位C .向左平移6π个单位 D .向右平移6π个单位 7、.若一个圆的圆心在抛物线x y 42=的焦点处,且此圆与直线01=++y x 相切,则这个圆的方程是 -------( )A .01222=--+x y xB .01222=+++x y xC .01222=+-+y y xD .01222=+++y y x8、在平面α内的两条直线l 、m 都平行于平面β是平面βα//的-------( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .不充分也不必要条件9、已知x x x f cos sin )(1-=、记x f x f ()(12'=),…..,)()(1x f x f n n '=-),2,(*≥∈n N n 则: =++++)2(......)2()2()2(2008321ππππf f f f -------( )A 、1-B 、0C 、3-D 、310、)11(lim 22--+∞→x x x x 的值为 -------( )A .1B .21C .2D .不存在二.填空题(每小题5分,共40分)11、已知=+=--=+y x y x y x 则,sin 4,2cos 3θθ 12、函数xx y --=312log 2的定义域为 . 13、23210-=N n C C ,则=n15、已知等差数列{}n a 的前n 项和为n S ,且1012S =,2017,S =则30S 为 . 16、复数i z 62+=,则Z 的三角形式为:______________.17、已知1)1(+=x x x f .则=')(x f .18、如图所示,在四面体ABCD 中,E 、F 分别是AC 与BD 的中点,若CD = 2AB = 4,EF⊥BA,则EF与CD所成角为 .答题卡一、选择题:(本大题共10小题,每小题5分,共50分)11. 12. 13. 14.15. 16. 17. 18. 三.解答题(本大题共7小题,共60分,解答写出文字或演算步骤.)19、已知}0x=m-xP(10分)-xxxQ=<{|},-{2≥|6(1)若P⊆Q,求实数m的取值范围;(2)若ΦP,求实数m的取值范围.=⋂Q20、已知,cos ),(cos ,cos )a x x b x x == ,()221f x a b m =⋅+-(,x m R ∈), (1)求()f x 关于x 的表达式(可含m ),并求()f x 的最小正周期;(2)若0,3x π⎡⎤∈⎢⎥⎣⎦,且()f x 的最小值为5,求m 的值21、已知等差数列{}n a 满足11a =,22n n a a =,其前n 项和为n S . (Ⅰ)若55n S =,求n ;(Ⅱ)各项均为正数的等比数列{}n b 的前n 项和为n T ,若34b a =,37T a =,求n T .(1)设数列{}n a 公差为d ,由11a =,22n n a a =,得 ()()121211n d n d +-=+-⎡⎤⎣⎦即1d = ∴()11n a n n =+-=,()()1122n n n a a n n S ++==而 55n S =,即()1552n n +=,解得10n = (6)分(2)由3437b a T a =⎧⎨=⎩,得21211147b q b b q b q ⎧=⎪⎨++=⎪⎩ 解之得1923b q =⎧⎪⎨=-⎪⎩(舍),112b q =⎧⎨=⎩∴()()1111221112n n n n b q T q-⋅-===--- …12分22、一个透明的口袋内装有分别写着“08”、“奥运”且大小相同的球共7个,已知从摸出2个球都写着“奥运”的概率是71,甲、乙两个小朋友做游戏采用不放回的方式从口袋中轮流摸取一个球,甲先选,乙后选取,然后甲再取……,直到两个小朋友中有1个人取得“奥运”时游戏终止,每个球在每次被取到的机会均相同。
2011年普通高等学校招生全国统一考试高考数学教师精校版含详解湖南理

2011年湖南理一、选择题(共8小题;共40分)1. 若a,b∈R,i为虚数单位,且a+i i=b+i,则 A. a=1,b=1B. a=−1,b=1C. a=−1,b=−1D. a=1,b=−12. 设M=1,2,N=a2,则"a=1"是"N⊆M"的 A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件3. 如图是某几何体的三视图,则该几何体的体积为 .A. 92π+12 B. 92π+18 C. 9π+42 D. 36π+184. 通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好402060不爱好203050总计6050110由K2=n ad−bc2a+b c+d a+c b+d 算得K2=110×40×30−20×20260×50×60×50≈7.8附表:P K2≥k0.0500.0100.001k 3.841 6.63510.828参照附表,得到的正确结论是 A. 在犯错误的概率不超过0.1%的前提下,认为"爱好该项运动与性别有关"B. 在犯错误的概率不超过0.1%的前提下,认为"爱好该项运动与性别无关"C. 有99%以上的把握认为"爱好该项运动与性别有关"D. 有99%以上的把握认为"爱好该项运动与性别无关"5. 设双曲线x2a2−y29=1a>0的渐近线方程为3x±2y=0,则a的值为 A. 4B. 3C. 2D. 16. 由直线x=−π3,x=π3,y=0与曲线y=cos x所围成的封闭图形的面积为 A. 12B. 1 C. 32D. 37. 设m>1,在约束条件y≥x,y≤mx,x+y≤1下,目标函数z=x+my的最大值小于2,则m的取值范围为A. 1,1+2B. 1+2,+∞C. 1,3D. 3,+∞8. 设直线x=t与函数f x=x2,g x=ln x的图象分别交于点M,N,则当∣MN∣达到最小时t的值为A. 1B. 12C. 52D. 22二、填空题(共8小题;共40分)9. 在直角坐标系xOy中,曲线C1的参数方程为x=cosαy=1+sinα α为参数,在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为ρcosθ−sinθ+1=0,则C1与C2的交点个数为.10. 设x,y∈R,且xy≠0,则 x2+1y 1x+4y2的最小值为.11. 如图,A、E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为.12. 设S n是等差数列a n n∈N∗的前n项和,且a1=1,a4=7,则S5=.13. 若执行如图所示的框图,输入x1=1,x2=2,x3=3,x=2,则输出的数等于.14. 在边长为1的正三角形ABC 中,设BC =2BD ,CA =3CE ,则AD ⋅BE= .15. 如图所示,EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则(1)P A = ;(2)P B ∣A = .16. 对于n ∈N ∗,将n 表示为n =a 0×2k +a 1×2k−1+a 2×2k−2+⋯+a k−1×21+a k ×20.当i =0时,a i =1,当1≤i ≤k 时,a i 为0或1.记I n 为上述表示中a i 为0的个数(例如:1=1×20,4=1×22+0×21+0×20,则I 1 =0,I 4 =2),则I 12 = ;2I n 127n =1= .三、解答题(共6小题;共78分)17. 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足c sin A =a cos C .(1)求角C 的大小; (2)求 3sin A −cos B +π4 的最大值,并求取得最大值时角A ,B 的大小.18. 某商店试销某种商品20天,获得如下数据:日销售量 件 0123频数1595试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率.(1)求当天商品不进货的概率;(2)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望.19. 如图,在圆锥PO中,已知PO=⊙O的直径AB=2,C是AB的中点,D为AC的中点.(1)证明:平面POD⊥平面PAC;(2)求二面角B−PA−C的余弦值.20. 如图,长方体物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v v>0,雨速沿E移动方向的分速度为c c∈R.E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与∣v−c∣×S成正比,比例系数为110;(2)其它面的淋雨量之和,其值为12,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=32时.(1)写出y的表达式;(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度v,使总淋雨量y最少.21. 如图,椭圆C1:x2a2+y2b2=1a>b>0的离心率为32,x轴被曲线C2:y=x2−b截得的线段长等于C1的长半轴长.(1)求C1,C2的方程;(2)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交与点D,E.①证明:MD⊥ME;②记△MAB,△MDE的面积分别是S1,S2.问:是否存在直线l,使得S1S2=1732?请说明理由.22. 已知函数f x=x3,g x=x+x.(1)求函数 x=f x−g x的零点个数,并说明理由;(2)设数列a n n∈N∗满足a1=a a>0,f a n+1=g a n,证明:存在常数M,使得对于任意的n∈N∗,都有a n≤M.答案第一部分 1. D 【解析】因为 a +i i =−1+a i =b +i ,根据复数相等的条件可知a =1,b =−1. 2. A 【解析】因为" a =1 ",即N = 1 ,满足" N ⊆M ",反之" N ⊆M ",则N = a 2 = 1 ,或N = a 2 = 2 ,不一定有" a =1 ".3. B【解析】由三视图可知该几何体是一个长方体和球构成的组合体,其体积V =4π 3 3+3×3×2=9π+18.4. C 【解析】由题意K 2=7.8>6.635,有0.01=1%的机会错误,即有99%以上的把握认为“爱好这项运动与性别有关”.同时,在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关”;5. C【解析】由双曲线方程可知渐近线方程为y =±3ax ,故可知a =2. 6. D 【解析】由定积分知识可得S = cos x d x π3−π3=sin x ∣−π3π3=32− −32= 3.7. A【解析】根据约束条件画出可行域如图所示,将目标函数化为斜截式为y =−1mx +zm,平移x +my =0,结合图形可以看出当目标函数过y =mx 与x +y =1的交点B 时取到最大值.联立 y =mx ,x +y =1,得交点坐标为B 1m +1,m m +1 .将其代入目标函数得z max =1+m 2m +1.由题意可得1+m 2m +1<2,又m >1,所以1<m <1+8. D【解析】由题可得∣MN ∣=x 2−ln x x >0 ,不妨令 x =x 2−ln x ,则 ʹ x =2x −1x ,令ʹ x =0解得x = 22. 因为当x ∈ 0, 22时, ʹ x <0,当x ∈ 22,+∞ 时, ʹ x >0,所以当x = 22时,∣MN ∣达到最小,即t =22. 第二部分 9. 2 10. 9 【解析】x 2+1y 2 1x 2+4y 2 =1+1x 2y2+4x 2y 2+4≥5+2 4=9, 当且仅当x 2y 2=12时取等号. 11.2 33【解析】由题可知,∠AOB =∠AOE =60∘,OA =OB =OE =2,得△ABO 和△AEO 为正三角形,则AD = 3,AE =2. 由△AEF ∽△BDF ,得AF FD=AE BD=2.所以3−AF=2,解得AF =2 33.12. 25 13. 23 【解析】S = 1−2 2+ 2−2 2+ 3−2 2=2.14. −14【解析】依题意,AD=CD −CA =12CB −CA ,BE=CE −CB =13CA −CB . 所以AD ⋅BE = 12CB −CA ⋅ 13CA −CB =−12−13+76CB ⋅CA =−14. 15. 2π,14【解析】由几何概型概率计算公式可得:P A =S 正圆=2; 由条件概率的计算公式可得:P B ∣A =P AB=2π×142π=1.16. 2,1093【解析】将n 表示为n =a 0×2k +a 1×2k−1+a 2×2k−2+⋯+a k−1×21+a k ×20,实际上是将十进制的数转化为二进制的数.(1)因为12=1×23+1×22+0×21+0×20,所以I 12 =2. (2)当n =1时,二进制为1,则I 1 =0,2I 1 =20.即2I 1 =30. 当n =2时,二进制为10,则I 2 =1,2I 2 =21; 当n =3时,二进制为11,则I 3 =0,2I 3 =20;则 2I n3n =2=21+20=31. 当n =4时,二进制为100,则I 4 =2,2I 4 =22; 当n =5时,二进制为101,则I 5 =1,2I 5 =21; 当n =6时,二进制为110,则I 6 =1,2I 6 =21; 当n =7时,二进制为111,则I 7 =0,2I 7 =20.则 2I n7n =4=22+21+21+20=32. 类似地,有 2I n 15n =8=33, 2I n 31n =16=34, 2I n 63n =32=35, 2I n 127n =64=36. 于是 2I n 127n =1=30+31+32+33+34+35+36=1093. 第三部分17. (1)由正弦定理得sin C sin A =sin A cos C .因为0<A <π,所以sin A >0,从而sin C =cos C ,又cos C ≠0,所以tan C =1,则C =π4. (2)由(1)知B =3π4−A .于是3sin A −cos B +π4= 3sin A −cos π−A= 3sin A +cos A=2sin A +π6.因为0<A <3π4,所以π<A +π<11π, 从而当A +π6=π2,即A =π3时,2sin A +π6取最大值2.综上所述, 3sin A −cos B +π4 的最大值为2,此时A =π3,B =5π12.18. (1)记事件A 为当天不进货,事件B 为当天销售了0件,事件C 为当天销售了1件,则P A =P B +P C =1+5=3.(2)记事件D 为当天销售了2件,记事件E 为当天销售了3件. 第二天开始营业时该商品有3件包括第一天销售了0件、2件或3件. 由题意知,X 的可能取值为2,3.P X =2 =P C =520=14. P X =3 =P B +P D +P E =34.故X 的分布列为X 23P13 X 的数学期望为EX =2×14+3×34=114.19. (1)连接OC ,因为OA=OC,D为AC的中点,所以AC⊥OD.又PO⊥底面⊙O,AC⊂底面⊙O,所以AC⊥PO.因为OD,PO是平面POD内的两条相交直线,所以AC⊥平面POD.而AC⊂平面PAC,所以平面POD⊥平面PAC.(2)在平面POD中,过O作OH⊥PD于H,由(1)知,平面POD⊥平面PAC,所以OH⊥平面PAC,又PA⊂平面PAC,所以PA⊥OH.在平面PAO中,过O作OG⊥PA于G,连接HG,则有PA⊥平面OGH,从而PA⊥HG,所以∠OGH是二面角B−PA−C的平面角.在Rt△ODA中,OD=OA⋅sin45∘=2 2 ,在Rt△POD中,OH=PO2+OD2=2×222+2=10,在Rt△POA中,OG=PO⋅OA PO2+OA2=22+1=6 ,在Rt△OHG中sin∠OGH=OH=10563=15 5,所以cos∠OGH=10 5 ,故二面角B−PA−C的余弦值为105.20. (1)由题意知,E移动时单位时间内的淋雨量为320∣v−c∣+12,故y=100v320∣v−c∣+12=53∣v−c∣+10.(2)由(1)知,当0<v≤c时,y=53c−3v+10=53c+10v−15;当c<v≤10时,y=5v3v−3c+10=510−3c+15.故y=53c+10v−15,0<v≤c,510−3c+15,c<v≤10.①当0<c≤103时,y是关于v的减函数.故当v=10时,y min=20−3c2.②当103<c≤5时,在0,c上,y是关于v的减函数;在c,10上,y是关于v的增函数;故当v=c时,y min=50c.21. (1)由题意知e=c=3,从而a=2b,又2=a,解得a=2,b=1.故C1,C2的方程分别为x 24+y2=1,y=x2−1.(2)①由题意知,直线l的斜率存在,设为k,则直线l的方程为y=kx.由y=kx,y=x2−1.得x2−kx−1=0,设A x1,y1,B x2,y2,则x1,x2是上述方程的两个实根,于是x1+x2=k,x1x2=−1.又点M的坐标为0,−1,所以k MA⋅k MB=y1+1x1⋅y2+1x2=kx1+1kx2+1x1x2=k2x1x2+k x1+x2+112=−k2+k2+1=−1,故MA⊥MB,即MD⊥ME.②设直线MA的斜率为k1,则直线MA的方程为y=k1x−1,由y=k1x−1,y=x2−1.解得x=0,y=−1.或x=k1,y=k12−1.则点A的坐标为k1,k12−1.又直线MB的斜率为−1k1,同理可得点B的坐标为 −1k1,1k12−1.于是S1=1∣MA∣⋅∣MB∣=11+k12⋅∣k1∣⋅1+112⋅∣∣∣−11∣∣∣=1+k121.由y=k1x−1,x2+4y2−4=0.得1+4k12x2−8k1x=0,解得x=0,y=−1.或x=8k112, y=4k12−112.则点D的坐标为8k11+4k12,4k12−11+4k12.又直线ME的斜率为−1k1,同理可得点E的坐标为−8k14+k12,4−k124+k12.于是S2=1∣MD∣⋅∣ME∣=321+k12⋅∣k1∣1212,因此S1 2=14k12+412+17.由题意知1 644k12+4k12+17=1732,解得k12=4 或 k12=1 .又由点A,B的坐标可知k=k12−1k12k1+1k1=k1−11,所以k=±32.故满足条件的直线l存在,且有两条,其方程分别为y=32x和y=−32x.22. (1)由 x=x3−x−x知,x∈0,+∞,而 0=0,且1=−1<0,2=6−2>0,则x=0为 x的一个零点,且 x在1,2内有零点,因此 x至少有两个零点.x=x x2−1−x−12,记φx=x2−1−x−1,则φʹx=2x+12x−3.当x∈0,+∞时,φʹx>0,因此φx在0,+∞上单调递增,则φx在0,+∞内至多只有一个零点.因此 x在0,+∞内也至多只有一个零点,综上所述, x有且只有两个零点.(2)记 x的正零点为x0,即x03=x0+x0①当a<x0时,由a1=a,即a1<x0.而a23=a1+a1<x0+x0=x03,因此a2<x0.由此猜测:a n<x0.下面用数学归纳法证明:1)当n=1时,a1<x0显然成立;2)假设当n=k k≥1时,有a k<x0成立,则当n=k+1时,由a k+13=a k+a k<x0+x0=x03知,a k+1<x0,因此,当n=k+1时,a k+1<x0成立.故对任意的n∈N∗,a n<x0成立.②当a≥x0时,由(1)知, x在x0,+∞上单调递增.则 a≥ x0=0,即a3≥a+a.从而a23=a1+a1=a+a≤a3,即a2≤a,由此猜测:a n≤a.下面用数学归纳法证明:1)当n=1时,a1≤a显然成立;2)假设当n=k k≥1时,有a k≤a成立,则当n=k+1时,由a k+13=a k+a k≤a+a≤a3知,a k+1≤a,因此,当n=k+1时,a k+1≤a成立.故对任意的n∈N∗,a n≤a成立.综上所述,存在常数M=max x0,a,使得对于任意的n∈N∗,都有a n≤M.。
2011年高考湖南卷理科数学试题及答案2011年高考湖南卷理科数学试题及答案

正视图侧视图俯视图 图1 2011年普通高等学校招生全国统一考试 理科数学(湖南卷)参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+则 A .1a =,1b = B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==-2.设集合{}{}21,2,,M N a ==则 “1a =”是“N M ⊆”的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分又不必要条件3.设图1是某几何体的三视图,则该几何体的体积为 A .9122π+B .9182π+C .942π+D .3618π+4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:由()()()()()22n ad bc K a b c d a c b d -=++++算得,()22110403020207.860506050K ⨯⨯-⨯=≈⨯⨯⨯.2()P K k ≥0.050 0.010 0.001 k3.8416.635 10.828参照附表,得到的正确结论是A .再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别无关”5.设双曲线()222109x y a a -=>的渐近线方程为320x y ±=,则a 的值为A .4B .3C .2D .16.由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为A .12B .1C .32D .37.设m >1,在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z=x+my 的最大值小于2,则m 的取值范围为 A .(1,12+) B .(12+,+∞)C .(1,3 )D .(3,+∞)8.设直线x=t 与函数2()f x x = ()ln g x x = 的图像分别交于点M,N,则当MN 达到最小时t 的值为A .1B .12C .52 D .22一天下午化学教案天气很热化学教案一位年轻小伙子大汗淋漓二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡...中对应号后的横线上。
2011年普通高等学校招生全国统一考试高考数学教师精校版含详解湖南文

2011年湖南文一、选择题(共8小题;共40分)1. 设全集U=M∪N=1,2,3,4,5,M∩∁U N=2,4,则N= A. 1,2,3B. 1,3,5C. 1,4,5D. 2,3,42. 若a,b∈R,i为虚数单位,且a+i i=b+i,则 A. a=1,b=1B. a=−1,b=1C. a=−1,b=−1D. a=1,b=−13. “ x>1”是“ x >1”的 A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件4. 如图是某几何体的三视图,则该几何体的体积为 A. 9π+42B. 36π+18C. 92π+12 D. 92π+185. 通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好402060不爱好203050总计6050110由K2=n ad−bc2a+b c+d a+c b+d 算得K2=110×40×30−20×20260×50×60×50≈7.8附表:P K2≥k0.0500.0100.001k 3.841 6.63510.828参照附表,得到的正确结论是 A. 在犯错误的概率不超过0.1%的前提下,认为"爱好该项运动与性别有关"B. 在犯错误的概率不超过0.1%的前提下,认为"爱好该项运动与性别无关"C. 有99%以上的把握认为"爱好该项运动与性别有关"D. 有99%以上的把握认为"爱好该项运动与性别无关"6. 设双曲线x2a −y29=1a>0的渐近线方程为3x±2y=0,则a的值为 A. 4B. 3C. 2D. 17. 曲线y=sin xsin x+cos x −12在点Mπ4,0处的切线的斜率为 A. −12B. 12C. −22D. 228. 已知函数f x=e x−1,g x=−x2+4x−3,若有f a=g b,则b的取值范围为 A. 2−2,2+2B. 2−2,2+2C. 1,3D. 1,3二、填空题(共8小题;共40分)9. 在直角坐标系xOy中,曲线C1的参数方程为x=2cosαy=3sinα α为参数,在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为ρcosθ−sinθ+1=0,则C1与C2的交点个数为.10. 已知某试验范围为10,90,若用分数法进行4次优选试验,则第二次试点可以是.11. 若执行如图所示的框图,输入x1=1,x2=2,x3=4,x4=8,则输出的数等于.12. 已知f x为奇函数,g x=f x+9,g−2=3,则f2=.13. 设向量a,b满足a=2b=2,1,且a与b的方向相反,则a的坐标为.14. 设m>1,在约束条件y≥xy≤mxx+y≤1下,目标函数z=x+5y的最大值为4,则m的值为.15. 已知圆C:x2+y2=12,直线l:4x+3y=25.①圆C的圆心到直线l的距离为;②圆C上任意一点A到直线l的距离小于2的概率为.16. 给定k∈N∗,设函数f:N∗→N∗满足:对于任意大于k的正整数n,f n=n−k.(1)设k=1,则其中一个函数f在n=1处的函数值为;(2)设k=4,且当n≤4时,2≤f n≤3,则不同的函数f的个数为.三、解答题(共6小题;共78分)17. 在△ABC中,角A,B,C所对的边分别为a,b,c,且满足c sin A=a cos C.(1)求角C的大小;(2)求3sin A−cos B+π4的最大值,并求取得最大值时角A,B的大小.18. 某河流上的一座水力发电站,每年六月份的发电量Y(单位:万千瓦时)与该河上游在六月份的降雨量X(单位:毫米)有关,据统计,当X=70时,Y=460;X每增加10,Y增加5.已知近20年X的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.(1)完成如下的频率分布表:近20年六月份降雨量频率分布表降雨量70110140160200220频率120420220(2)假定今年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.19. 如图,在圆锥PO中,已知PO=⊙O的直径AB=2,点C在AB上,且∠CAB=30∘,D为AC的中点.(1)证明:AC⊥平面POD;(2)求直线OC和平面PAC所成角的正弦值.20. 某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少.从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.(1)求第n年初M的价值a n的表达式;(2)设A n=a1+a2+⋯+a nn,若A n大于80万元,则M继续使用,否则须在第n年初对M更新.证明:须在第9年初对M更新.21. 已知平面内一动点P到点F1,0的距离与点P到y轴的距离的差等于1.(1)求动点P的轨迹C的方程;(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l2与轨迹C相交于点D,E,求AD⋅EB的最小值.−a ln x a∈R.22. 设函数f x=x−1x(1)讨论函数f x的单调性.(2)若f x有两个极值点x1和x2,记过点A x1,f x1,B x2,f x2的直线斜率为k.问:是否存在a,使得k=2−a ?若存在,求出a的值;若不存在,请说明理由.答案第一部分1. B2. D 【解析】因为a+i i=−1+a i=b+i,根据复数相等的条件可知a=1,b=−1.3. A 【解析】因“ x>1” ⇒“ x >1”,反之“ x >1” ⇒“ x>1或x<−1”,不一定有“ x>1”.4. D 【解析】由三视图可知该几何体是一个长方体和球构成的组合体,其体积V=43π323+3×3 ×2=92π+18.5. C【解析】由题意K2=7.8>6.635,有0.01=1%的机会错误,即有99%以上的把握认为“爱好这项运动与性别有关”.同时,在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关”;6. C 【解析】由双曲线方程可知渐近线方程为y=±3ax,故可知a=2.7. B 【解析】yʹ=cos x sin x+cos x−sin x cos x−sin xsin x+cos x2=1sin x+cos x2,所以yʹx=π4=1sinπ+cosπ2=12.8. B 【解析】由题可知f x=e x−1>−1,g x=−x−22+1≤1.若有f a=g b,则−b2+4b−3>−1,解得2−2<b<2+2.第二部分9. 2【解析】曲线C1:x24+y23=1,曲线C2:x−y+1=0,联立方程消y得7x2+8x−8=0,易得Δ>0,故有2个交点.或者由直线C2上的点0,1在椭圆C1内部,所以直线与椭圆必有两个交点.10. 40或60【解析】由区间长度为80,可以将其等分8段,利用分数法选取试点:x1=10+5×90−10=60,x2=10+90−60=40.由对称性可知,第二次试点可以是40或60.11. 154【解析】输出的数等于x=x1+x2+x3+x44=154.12. 6g−2=f−2+9=3,则f−2=−6,又f x为奇函数,所以f2=−f−2=6.13. −4,−214. 3【解析】画出可行域,如图,可知z=x+5y在点A11+m ,m1+m处取最大值4,解得m=3.15. 5,16【解析】①由点到直线的距离公式可得d=42+32=5;②可求与直线4x+3y=25平行且距离为2,与圆相交的直线方程为4x+3y=15.由①可知圆心到直线的距离为5,所以圆心到直线4x+3y=15的距离为3,从而直线4x+3y=15与圆x2+y2=12相交所得的弦长为23,对应劣弧所对的圆心角为π3,故所求概率为P=π32π=16.16. m m∈N∗,16【解析】(1)由题可知f n∈N∗,而k=1时,n>1则f n=n−1∈N∗,故只须f1∈N∗,故f1=m,m∈N∗;(2)由题可知k=4,n>4,则f n=n−4∈N∗,而n≤4时,2≤f n≤3,即f n∈2,3,即n∈1,2,3,4,f n∈2,3,故不同的函数f的个数为24=16.17. (1)由正弦定理得sin C sin A=sin A cos C.因为0<A<π,所以sin A>0,从而sin C=cos C,又cos C≠0,所以tan C=1,则C=π4.(2)由(1)知B=3π4−A.于是3sin A−cos B+π=3sin A−cosπ−A=3sin A+cos A=2sin A+π6.因为0<A<3π4,所以π<A+π<11π,从而当A+π6=π2,即A=π3时,2sin A+π6取最大值2.综上所述,3sin A−cos B+π4的最大值为2,此时A=π3,B=5π12.18. (1)在所给数据中,降雨量为110毫米的有3个,为160毫米的有7个,为200毫米的有3个,故近20年六月份降雨量频率的分布表为:降雨量70110140160200220频率120320420720320220(2)P=P Y<490 或 Y>530=P X<130 或 X>210=120+320+220=3 10,故今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率为310.19. (1)因为OA=OC,D是AC的中点,所以AC⊥OD.又PO⊥底面⊙O,AC⊂底面⊙O,所以AC⊥PO.又因为OD,PO是平面POD内的两条相交直线,所以AC⊥平面POD.(2)由(1)知,AC⊥平面POD,又AC⊂平面PAC,所以平面POD⊥平面PAC,如图,在平面POD中,过O作OH⊥PD于H.则OH⊥平面PAC.连接CH,则CH是OC在平面PAC上的射影,所以∠OCH是直线OC和平面PAC所成的角.在Rt△POD中,OH=PO⋅OD PO2+OD2=2×122+4=2 3 ,在Rt△OHC中,sin∠OCH=OH=2.20. (1)当n≤6时,数列a n是首项为120,公差为−10的等差数列.a n=120−10n−1=130−10n;当n≥6时,数列a n是以a6为首项,公比为34的等比数列,又a6=70,所以a n=70×34n−6.因此,第n年初,M的价值a n的表达式为a n=130−10n,n≤6, 70×3n−6,n≥7.(2)设S n表示数列a n的前n项和,由等差及等比数列的求和公式得:当1≤n≤6时,S n=120n−5n n−1,A n=120−5n−1=125−5n;当n≥7时,S n=S6+a7+a8+⋯+a n=570+70×34×4×1−34n−6=780−210×3n−6,A n=780−210×34n−6 n.因为a n是递减数列,所以A n是递减数列,又A8=780−210×348−68=824764>80,A9=780−210×349−6=7679<80,所以须在第9年初对M更新.21. (1)设动点P的坐标为x,y,由题意有− x =1.化简得y2=2x+2 x ,当x≥0时,y2=4x;当x<0时,y=0.所以动点P的轨迹C的方程为:y2=4x x≥0 和 y=0x<0.(2)由题意知,直线l1的斜率存在且不为0,设为k,则l1的方程为y=k x−1.由y=k x−1,y2=4x,得k2x2−2k2+4x+k2=0.设A x1,y1,B x2,y2,则x1,x2是上述方程的两个实根,于是x1+x2=2+4k2,x1x2=1.因为l1⊥l2,所以l2的斜率为−1k.设D x3,y3,E x4,y4,则同理可得x3+x4=2+4k2,x3x4=1,所以AD⋅EB= AF+FD⋅ EF+FB=AF⋅EF+AF⋅FB+FD⋅EF+FD⋅FB=AF⋅FB+FD⋅EF=x1+1x2+1+x3+1x4+1=1+2+42+1+1+2+4k2+1=8+4 k2+1 k2≥8+4×2k2⋅1 2=16.当且仅当k2=1k,即k=±1时,AD⋅EB取最小值16.22. (1)f x的定义域为0,+∞,fʹx=1+1x2−ax=x2−ax+1x2.令g x=x2−ax+1,其判别式Δ=a2−4.①当a ≤2时,Δ≤0,fʹx≥0,故f x在0,+∞上单调递增.②当a<−2时,Δ>0,g x=0的两根都小于0,在0,+∞上,fʹx>0,故f x在0,+∞上单调递增.③当a>2时,Δ>0,g x=0的两根为x1=a− a2−42,x2=a+ a2−4,当0<x<x1时,fʹx>0;当x1<x<x2时,fʹx<0;当x>x2时,fʹx>0.故f x分别在0,x1,x2,+∞上单调递增,在x1,x2上单调递减.综上知,当a≤2时,f x在定义域0,+∞上单调递增;当a>2时,f x在区间0,a− a2−42与a+ a2−42,+∞ 上单调递增;在区间a− a2−42,a+ a2−42上单调递减.(2)由(1)知,a>2. x1,x2与(1)中相同.因为f x1−f x2=x1−x2+x1−x212−a ln x1−ln x2,所以普通高等学校招生全国统一考试高考数学教师精校版含详解完美版k=f x1−f x212=1+112−a⋅ln x1−ln x212.又由(1)知,x1x2=1.于是k=2−a⋅ln x1−ln x212.若存在a,使得k=2−a.则ln x1−ln x212=1,即ln x1−ln x2=x1−x2,亦即x2−1x2−2ln x2=0x2>1∗.再由(1)知,函数 t=t−1t−2ln t在0,+∞上单调递增,而x2>1,所以x2−12−2ln x2>1−1−2ln1=0,这与∗式矛盾.故不存在a,使得k=2−a.。
2011年湖南高考数学理科试卷(带详解)

2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的.1.若,a b ∈R ,i 为虚数单位,且(i)i i a b +=+,则 ( ) A .1,1a b == B .1,1a b =-= C .1,1a b =-=- D .1,1a b ==-【测量目标】复数的四则运算.【考查方式】利用复数相等的条件直接求值. 【难易程度】容易 【参考答案】D【试题解析】因(i)i 1i i a a b +=-+=+,根据复数相等的条件可知1,1a b ==-. 2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则 ( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分又不必要条件 【测量目标】集合间的关系,充分必要条件. 【考查方式】给出两个集合直接考查. 【难易程度】容易 【参考答案】A【试题解析】因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”.3.如图一是某几何体的三视图,则该几何体的体积为 ( )第3题图A .9π122+ B .9π182+ C .9π42+ D .36π18+【测量目标】由三视图求几何体的体积.【考查方式】给出三视图,通过判断直接求体积. 【难易程度】容易 【参考答案】B【试题解析】由三视图可知该几何体是一个长方体和球构成的组合体, 其体积3439π()332π+18322V =+⨯⨯=. 4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男 女 总计爱好40 20 60 不爱好20 30 50 总计60 50 110由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:2()P K k … 0.0500.010 0.001 k3.8416.63510.828参照附表,得到的正确结论是 ( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关” 【测量目标】独立性检验.【考查方式】给出统计图表直接考查. 【难易程度】容易 【参考答案】C【试题解析】由27.8 6.635,K ≈>而2( 6.635)0.010P K =…,故由独立性检验的意义可知选C.5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为 ( )A .4B .3C .2D .1【测量目标】双曲线的简单几何性质.【考查方式】由双曲线方程直接求出渐近线方程,再结合给出的渐近线方程比较求解. 【难易程度】容易 【参考答案】C【试题解析】:由双曲线方程可知渐近线方程为3y x a=±,故可知2a =. 6. 由直线ππ,,033x x y =-==与曲线cos y x =所围成的封闭图形的面积为( ) A .12 B .1 C.2D【测量目标】定积分的几何意义.【考查方式】直接给出曲线和直线方程求面积. 【难易程度】容易 【参考答案】D【试题解析】由定积分知识可得ππ33ππ33cosd sin |(22S x x --===-=⎰7. 设1m >,在约束条件1y xy mx x y ⎧⎪⎨⎪+⎩………下,目标函数z x my =+的最大值小于2,则m 的取值范围为 ( ) A.(1,1 B.(1)+∞ C .(1,3) D .(3,)+∞ 【测量目标】线性规划求最值.【考查方式】给出约束条件和目标函数的范围求目标函数y 轴系数的值. 【难易程度】容易 【参考答案】A【试题解析】可知z x my =+在点1(,)11m m m++取最大值,由 21211m m m+<++解得11m <<. 8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为 ( )A .1B .12C .2D .2【测量目标】利用导数判断单调性求最值.【考查方式】利用直线与曲线相交,求相交直线方程再运用导数性质求解. 【难易程度】容易 【参考答案】D【试题解析】由题2||ln MN x x =-,(0)x >不妨令2()ln h x x x =-,则1()2h x x x'=-,令()0h x '=解得2x =,因(0,)2x ∈时,()0h x '<,当()2x ∈+∞时,()0h x '>,所以当2x =时,||MN 达到最小,即2t =.二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上.一、选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题记分) 9.在直角坐标系xOy 中,曲线C 1的参数方程为cos ,1sin x y αα=⎧⎨=+⎩(α为参数)在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为()cos sin 10ρθθ-+=,则1C 与2C 的交点个数为 . 【测量目标】坐标系与参数方程.【考查方式】给出极坐标方程与参数方程,将其转化为普通方程后解不等式求解. 【难易程度】容易【参考答案】2【试题解析】曲线221:(1)1C x y +-=,2:10C x y -+=,由圆心到直线的距离01d ==<,故1C 与2C 的交点个数为2. 10.设,x y ∈R ,则222211()(4)x y y x++的最小值为 . 【测量目标】不等式选讲.【考查方式】给出两个乘式直接考查. 【难易程度】中等 【参考答案】9【试题解析】由柯西不等式可知2222211()(4)(12)9x y y x+++=…. 11.如图,,A E 是半圆周上的两个三等分点,直径4BC =,AD BC ⊥,垂足为D , BE 与AD 相交与点F ,则AF 的长为 .第11题图【测量目标】几何证明选讲.【考查方式】通过线段和圆的位置关系考查. 【难易程度】容易【参考答案】3【试题解析】由题可知,60AOB EOC ∠=∠=,2OA OB ==,得1OD BD ==,3DF =,又23AD BD CD ==,所以3AF AD DF =-=. 二、必做题(12~16题)12.设n S 是等差数列*{}()n a n ∈N 的前n 项和,且141,7a a ==,则5______S = 【测量目标】等差数列的前n 项和.【考查方式】给出等差数列某两项的值求出通项再求和. 【难易程度】容易 【参考答案】25【试题解析】由141,7a a ==可得11,2,21n a d a n ===-,所以5(19)5252S +⨯==. 13.若执行如图所示的框图,输入1231,2,3,2x x x x ====, 则输出的数等于 .第13 题图【测量目标】循环结构的程序框图. 【考查方式】直接给出程序框图考查. 【难易程度】中等 【参考答案】23【试题解析】由框图的算法功能可知,输出的数为三个数的方差,则222(12)(22)(32)233S -+-+-==. 14.在边长为1的正三角形ABC 中,设2,3BC BD CA CE == ,则________AD BE =.【测量目标】平面向量在平面几何中的运用. 【考查方式】给出向量间的关系求解. 【难易程度】容易 【参考答案】14-【试题解析】由题12AD CD CA CB CA =-=- ,13BE CE CB CA CB =-=-,所以111171()()232364AD BE CB CA CA CB CB CA =--=--+=-. 15.如图, EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则(1)=______P A ();(2)=______P B A (|)第15题图【测量目标】几何概型.【考查方式】利用两个图形面积的比值求解. 【难易程度】容易 【参考答案】(1)2π;(2)1=4PB A (|) 【试题解析】(1)由几何概型概率计算公式可得2==πS P A S 正圆(); (2)由条件概率的计算公式可得21×1π4===24πP AB P B A P A ()(|)().16.对于*n ∈N ,将n 表示为1210012122222k k k k k n a a a a a ---=⨯+⨯+⨯++⨯+⨯ ,当0i =时,1i a =,当1i k 剟时,i a 为0或1.记()I n 为上述表示中i a 为0的个数,(例如0112=⨯,2104120202=⨯+⨯+⨯:故(1)0,(4)2I I ==)则(1)(12)_____I = (2)127()12______I n n ==∑【测量目标】排列组合及其应用. 【考查方式】利用特定的条件求解. 【难易程度】较难 【参考答案】(1)2;(2)1093【试题解析】(1)因3211212+120202=⨯⨯+⨯+⨯,故(12)2I =;(2)在2进制的(2)k k …位数中,没有0的有1个,有1个0的有11C k -个,有2个0的有21C k -个,……有m 个0的有1C m k -个,……有1k -个0的有11C 1k k --=个.故对所有2进制为k 位数的数n ,在所求式中的()2I n 的和为:0112211111112C 2C 2C 23k k k k k k ------⨯++++=. 又712721=-恰为2进制的最大7位数,所以1277()1122231093I n k n k -===+=∑∑.三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)在ABC △中,角,,A B C 所对的边分别为,,a b c ,且满足sin cos c A a C =.(I )求角C 的大小;(II πcos()4A B -+的最大值,并求取得最大值时角,A B 的大小. 【测量目标】正弦定理,三角函数的最值. 【考查方式】给出边角之间的关系求解. 【难易程度】容易 【试题解析】(I )由正弦定理得sin sin sin cos .C A A C = 因为0π,A <<所以sin 0.A >πsin cos .cos 0,tan 1,4C C C C C =≠==从而又所以则.(步骤1) (II )由(I )知3π.4B A =-于是 πcos()cos(π)4A B A A -+=--πcos 2sin().6A A A =+=+3πππ11ππππ0,<+<,=,,46612623A A A A <<∴+= 从而当即时π2sin()6A +取最大值2.(步骤2)πcos()4A B -+的最大值为2,此时π5π,.312A B ==(步骤3) 18. 某商店试销某种商品20天,获得如下数据:当天营业结束后检查存货,若发现存货少于2件,则当天进货补充..至3件,否则不进货...,将频率视为概率.(Ⅰ)求当天商品不进货...的概率; (Ⅱ)记X 为第二天开始营业时该商品的件数,求X 的分布列和数学期望. 【测量目标】对立事件的概率,离散型随机变量的期望. 【考查方式】运用实际生活背景考查.【难易程度】容易 【试题解析】(I )P (“当天商店不进货”)=P (“当天商品销售量为0件”)+P (“当天商品销售量1件”)=153202010+=.(步骤1) (II )由题意知,X 的可能取值为2,3.51(2)()204P X P ====“当天商品销售量为1件”; (3)()+()+(1953)++32020204P X P P P ====“当天商品销售量为0件”“当天商品销售量为2件”“当天商品销售量为3件”(步骤)故X 的分布列为X2 3 P 14 34 X 的数学期望为13112+3=444EX =⨯⨯.(步骤4)19.(本题满分12分)如图,在圆锥PO 中,已知PO O = 的直径2,,A B C A B D A C=是的中点,为的中点. (I )证明:;POD PAC ⊥平面平面 (II )求二面角B PA C --的余弦值.第18题图【测量目标】面面垂直,二面角.【考查方式】在圆锥中考查. 【难易程度】容易 【试题解析】(I )连接OC , 因为OA OC =,D 为AC 中点,所以AC OD ⊥. 又,,.PO O AC O AC PO ⊥⊂⊥ 底面底面所以因为,OD PO 是平面POD 内的两条相交直线,所以AC POD ⊥平面而AC PAC ⊂平面,所以POD PAC ⊥平面平面.(步骤1)(II )在平面POD 中,过O 作OH PD ⊥于H ,由(I )知,POD PAC ⊥平面平面,所以,OH PAC ⊥平面又,PA PAC ⊂平面所以PA OH ⊥.在平面PAO 中,过O 作OG PA G ⊥于,连接HG ,则有PA OGH ⊥平面, 从而PA HG ⊥,所以OGH ∠是二面角B PA C --的平面角.(步骤2)在Rt ,sin 452ODA OD OA ==△中在Rt ,POD OH ===△中在Rt ,POA OG ===△中在Rt ,sin OH OHG OGH OG ∠===△中所以cos 5OGH ∠=. 故二面角B PA C --的余弦值为5.(步骤3)第19题图20. 如图,长方形物体E 在雨中沿面P (面积为S )的垂直方向作匀速移动,速度为(0)v v >,雨速沿E 移动方向的分速度为()c c ∈R .E 移动时单位时间....内的淋雨量包括两部分:(1)P 或P 的平行面(只有一个面淋雨)的淋雨量,假设其值与v c -×S 成正比,比例系数为110;(2)其它面的淋雨量之和,其值为12,记y 为E 移动过程中的总淋雨量,当移动距离d =100,面积S =32时. (Ⅰ)写出y 的表达式;(Ⅱ)设0<v …10,0<c …5,试根据c 的不同取值范围,确定移动速度v ,使总淋雨量y 最少.第19题图【测量目标】分段函数模型,利用函数单调性及最值. 【考查方式】利用将立体几何与函数综合考查. 【难易程度】中等【试题解析】(I )由题意知,E 移动时单位时间内的淋雨量为31||202v c -+, 故100315(||)(3||10)202y v c v c v v=-+=-+.(步骤1) (II )由(I)知,当0v c <…时,55(310)(3310)15c y c v v v+=-+=-; 当10c v <…时,55(103)(3310)15c y v c v v-=-+=+. 故5(310)15,05(103)15,10c v c vy c c v v +⎧-<⎪⎪=⎨-⎪+<⎪⎩…….(步骤2)(1)当1003c <…时,y 是关于v 的减函数.故当10v =时,min 3202cy =-.(步骤3) (2) 当1053c <…时,在(0,]c 上,y 是关于v 的减函数;在(,10]c 上,y 是关于v 的增函数;故当v c =时,min 50y c=.(步骤4) 21.(本小题满分13分) 如图,椭圆221221(0)x y C a b a b +=>>:,x轴被曲线22:C y x b =- 截得的线段长等于1C 的长半轴长.(Ⅰ)求1C ,2C 的方程;(Ⅱ)设2C 与y 轴的交点为M ,过坐标原点O 的直线l 与2C 相交于点A,B ,直线MA ,MB 分别与1C 相交于D ,E .(i )证明:MD ME ⊥;(ii)记△MAB ,△MDE 的面积分别是12,S S .问:是否存在直线l ,使得121732S S =? 请说明理由.第21题图【测量目标】椭圆的标准方程,直线与椭圆的位置关系. 【考查方式】利用直线与椭圆相交的位置关系和条件考查. 【难易程度】较难【试题解析】(I)由题意知c e a ==2a b =,又a =,解得2,1a b ==.故1C ,2C 的方程分别为2221,14x y y x +==-. (步骤1) (II )(i )由题意知,直线l 的斜率存在,设为k , 则直线l 的方程为y kx =.由21y kx y x =⎧⎨=-⎩得210x kx --=,(步骤2) 设1122(,),(,)A x y B x y ,则12,x x 是上述方程的两个实根,于是1212,1x x k x x +==-. 又点M 的坐标为(0,1)-,所以2221212121212121211(1)(1)()1111MA MBy y kx kx k x x k x x k k k k x x x x x x +++++++-++=====--故MA MB ⊥,即MD ME ⊥.(步骤3)(ii )设直线MA 的斜率为1k ,则直线MA 的方程为11y k x =-,由1211y kx y x =-⎧⎨=-⎩解得01x y =⎧⎨=-⎩或1211x k y k =⎧⎨=-⎩,则点A 的坐标为211(,1)k k -(步骤4) 又直线MB 的斜率为11k -,同理可得点B 的坐标为21111(,1)k k --.于是211111111||||||||.22||k S MA MB k k k +==-= (步骤5)由1221440y k x x y =-⎧⎨+-=⎩得2211(14)80k x k x +-=,解得01x y =⎧⎨=-⎩或12121218144114k x k k y k ⎧=⎪+⎪⎨-⎪=⎪+⎩,则点D 的坐标为2112211841(,)1414k k k k -++;(步骤6) 又直线ME 的斜率为11k -,同理可得点E 的坐标211221184(,)44k k k k --++ 于是2112221132(1)||1||||2(14)(4)k k S MD ME k k +==++ 因此21122111(417)64S k S k =++(步骤7) 由题意知,21211117(417)6432k k ++=,解得214k = 或2114k =. 又由点,A B 的坐标可知,21211111111k k k k k k k -==-+,所以3.2k =± 故满足条件的直线l 存在,且有两条,其方程分别为32y x =和32y x =-.(步骤8) 22.(本小题满分13分)已知函数f (x ) =3x ,g (x )=x(Ⅰ)求函数h (x )=f (x )-g (x )的零点个数,并说明理由;(Ⅱ)设数列*{}()n a n ∈N 满足1(0)a a a =>,1()()n n f a g a +=,证明:存在常数M ,使得对于任意的*n ∈N ,都有n a …M . 【测量目标】利用导数求单调性,不等式恒成立问题.【考查方式】给出两个函数式,利用导数及不等式求解.【难易程度】较难【试题解析】(I)由3()h x x x =-知,[0,)x ∈+∞,而(0)0h =,且(1)10,(2)60h h =-<=,则0x =为()h x 的一个零点,且()h x 在12(,)内有零点,因此()h x 至少有两个零点(步骤1) 122()(1)h x x x x -=--,记122()1x x x ϕ-=--,则321()22x x x ϕ-'=+. 当(0,)x ∈+∞时,()0x ϕ'>,因此()x ϕ在(0,)+∞上单调递增,则()x ϕ在(0,)+∞内至多只有一个零点.因此()h x 在(0,)+∞内也至多只有一个零点,综上所述,()h x 有且只有两个零点.(步骤2) (II )记()h x 的正零点为0x,即300x x =(1)当0a x <时,由1a a =,即10a x <.而332100a a x x ==,因此20a x <,由此猜测:0n a x <.下面用数学归纳法证明: ①当1n =时,10a x <显然成立;(步骤3) ②假设当(1)n k k =…时,有0k a x <成立,则当1n k =+时,由13300k k a a x x +=+<知,10k a x +<,因此,当1n k =+时,10k a x +<成立. 故对任意的*n ∈N ,0n a x <成立.(步骤4)(2)当0a x …时,由(1)知,()h x 在0(,)x +∞上单调递增.则0()()0h a h x =…,即3a a +….从而2331a a a a ==,即2a a …,由此猜测:n a a ….下面用数学归纳法证明:①当1n =时,1a a …显然成立;(步骤5) ②假设当(1)n k k =…时,有k a a …成立,则当1n k =+时,由133k k a a a a +=+知,1k a a +…,因此,当1n k =+时,1k a a +…成立.故对任意的*n ∈N ,n a a …成立. 综上所述,存在常数0max{,}M x a =,使得对于任意的*n ∈N ,都有n a M ….(步骤6)。
湖南省历年对口升学数学试卷(2011-2023)

湖南省历年对口升学数学试卷(2011-2023)本文档收集了湖南省历年对口升学数学试卷的内容,范围为2011年至2023年。
以下是每年试卷的简要介绍:- 2011年:试卷内容包括数学基础知识、代数、几何、概率和统计等方面。
涵盖了中学数学的核心概念和考点。
- 2012年:试卷难度适中,重点考察了几何和代数的应用能力。
题目形式多样,涉及到填空、选择和解答等不同类型。
- 2013年:试卷难度相对较高,涉及到应用题的比例较多。
考察了学生对于数学概念的理解和运用能力。
- 2014年:试卷整体难度适中,注重对基本概念的考察。
试题内容丰富,包括了数列、函数、几何等多个知识点。
- 2015年:试卷难度适中偏易,注重运算和推理能力的考察。
题型形式多样,包括选择、解答和填空等。
- 2016年:试卷涵盖了数学各个领域的知识点,难度适中。
注重对学生思维方法和解题思路的考察。
- 2017年:试卷整体难度较大,涉及到一些较为复杂的数学题目。
对学生的推理能力和逻辑思维提出了较高要求。
- 2018年:试卷难度中等偏难,注重对学生综合运用数学知识解决实际问题的考察。
题目形式多样,包括了选择、解答和填空等。
- 2019年:试卷整体难度适中,注重对学生数学思维和解题能力的培养。
题型灵活多样,包括选择、填空和解答等。
- 2020年:试卷难度较大,注重对学生分析、推理和创新能力的考察。
试题形式多样,包括选择、填空和解答等。
- 2021年:试卷整体难度偏易,注重对学生数学基本知识和运算能力的考察。
题目形式多样,包括选择、填空和解答等。
- 2022年:试卷整体难度适中,覆盖了数学各个领域的知识点。
强调对学生分析和解决实际问题的能力培养。
- 2023年:试卷难度适中偏难,注重对学生运算和推理能力的考察。
试题形式多样,包括选择、填空和解答等。
以上是湖南省历年对口升学数学试卷的简要介绍,希望可以对您的学习和备考有所帮助。
2011年全国高考文科数学试题及答案-湖南

2011年普通高等学校招生全国统一考试(湖南卷)文史类本试题包括选择题、填空题和解答题三部分,共6页.、时量120分钟,满分150分.、 参考公式(1)柱体体积公式V Sh =,其中S 为底面面积,h 为高.、 (2)球的体积公式343V R π=,其中R 为球的半径.、 一、选择题:本大题共8小题,每小题5分,共40分.、在每小题给出的四个选项中,只有一项是符合题目要求的.、1.、设全集{1,2,3,4,5},{2,4},U U M N M C N === 则N =( ) A.、{1,2,3} B.、{1,3,5} C.、{1,4,5} D.、{2,3,4} 答案:B解析:画出韦恩图,可知N ={1,3,5}.2.、若,,a b R i ∈为虚数单位,且()a i i b i +=+,则A.、1,1a b == B.、1,1a b =-= C.、1,1a b ==- D.、1,1a b =-=- 答案:C解析:因()1a i i ai b i +=-+=+,根据复数相等的条件可知1,1a b ==-. 3.、"1""||1"x x >>是的A.、充分不必要条件 B.、必要不充分条件C.、充分必要条件D.、既不充分又不必要条件 答案:A解析:因"1""||1"x x >⇒>,反之"||1""11"x x x >⇒><-或,不一定有"1"x >.4.、设图1是某几何体的三视图,则该几何体的体积为 A.、942π+ B.、3618π+ C.、9122π+ D.、9182π+答案:D解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+().正视图 侧视图俯视图 图1由2222()110(40302030)7.8()()()()60506050n ad bc K K a b c d a c b d -⨯⨯-⨯==≈++++⨯⨯⨯算得,附表:参照附表,得到的正确结论是( )A . 有99%以上的把握认为“爱好该项运动与性别有关”B . 有99%以上的把握认为“爱好该项运动与性别无关”C . 在犯错误的概率不超过0.、1%的前提下,认为“爱好该项运动与性别有关”D . 在犯错误的概率不超过0.、1%的前提下,认为“爱好该项运动与性别无关” 答案:A解析:由27.8 6.635K ≈>,而2( 6.635)0.010P K ≥=,故由独立性检验的意义可知选A.6.、设双曲线2221(0)9x y a a -=>的渐近线方程为320,x y ±=则a 的值为( ) A.、4 B.、3 C.、2 D.、1答案:C解析:由双曲线方程可知渐近线方程为3y x a=±,故可知2a =. 7.、曲线sin1sin cos 2x y x x =-+在点(,0)4M π处的切线的斜率为( )A.、12-B.、12C.、-D.答案:B 解析:22cos (sin cos )sin (cos sin )1'(sin cos )(sin cos )x x x x x x y x x x x +--==++,所以2411'|2(sin cos )44x y πππ===+.8.、已知函数2()1,()43,x f x e g x x x =-=-+-若有()(),f a g b =则b 的取值范围为A.、[2B.、(2C.、[1,3]D.、(1,3) 答案:B解析:由题可知()11xf x e =->-,22()43(2)11g x x x x =-+-=--+≤,若有()(),f a g b =则()(1,1]g b ∈-,即2431b b -+->-,解得22b <<二、填空题:本大题共8小题,考生作答7小题,每小题解分,共青团员5分,把答案填在答题卡中对应题号后的横线上.、(一)选做题(请考生在第9,10两题中任选一题作答,如果全做,则按前一题记分)9.、在直角坐标系xOy 中,曲线1C的参数方程为2cos (x y ααα=⎧⎪⎨=⎪⎩为参数).、在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为(cos sin )10,ρθθ-+=则1C 与2C 的交点个数为 .、 答案:2解析:曲线221:143x y C +=,曲线2:10C x y -+=,联立方程消y 得27880x y +-=,易得0∆>,故有2个交点.10.、已知某试验范围为[10,90],若用分数法进行4次优选试验,则第二次试点可以是 .、答案:40或60(只填一个也正确) 解析:有区间长度为80,可以将其等分8段,利用分数法选取试点:1510(9010)608x =+⨯-=,210906040x =+-=,由对称性可知,第二次试点可以是40或60.(二)必做题(11-16题)11.、若执行如图2所示的框图,输入12341,2,4,8,x x x x ====则输出的数等于 .、答案:154解析:由框图功能可知,输出的数等于12341544x x x x x +++==.12.、已知()f x 为奇函数,()()9,(2)3,(2)g x f x g f =+-==则 .、答案:6解析:(2)(2)93,(2)6g f f -=-+=-=-则, 又()f x 为奇函数,所以(2)(2)6f f =--=.13.、设向量,a b满足||(2,1),a b ==且a b 与的方向相反,则a 的坐标为 .、图2答案:(4,2)--解析:由题||b == 2(4,2).a b =-=--14.、设1,m >在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数5z x y =+的最大值为4,则m 的值为 .、 答案:3解析:画出可行域,可知5z x y =+在点1(,)11m m m++取最大值为4,解得3m =. 15.、已知圆22:12,C x y +=直线:4325.l x y +=(1)圆C 的圆心到直线l 的距离为 .、(2) 圆C 上任意一点A 到直线l 的距离小于2的概率为 .、 答案:5,16解析:(1)由点到直线的距离公式可得5d ==;(2)由(1)可知圆心到直线的距离为5,要使圆上点到直线的距离小于2,即1:4315l x y +=与圆相交所得劣弧上,由半径为3可知劣弧所对圆心角为3π,故所求概率为1326P ππ==.16、给定*k N ∈,设函数**:f N N →满足:对于任意大于k 的正整数n ,()f n n k =-(1)设1k =,则其中一个函数f 在1n =处的函数值为 ;(2)设4k =,且当4n ≤时,2()3f n ≤≤,则不同的函数f 的个数为 . 答案:(1)()a a 为正整数,(2)16解析:(1)由题可知*()f n N ∈,而1k =时,1n >则*()1f n n N =-∈,故只须*(1)f N ∈,故(1)()f a a =为正整数.(2)由题可知4k =,4n >则*()4f n n N =-∈,而4n ≤时,2()3f n ≤≤即(){2,3}f n ∈,即{1,2,3,4}n ∈,(){2,3}f n ∈,由乘法原理可知,不同的函数f 的个数为4216=.三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.、 17.、(本小题满分12分) 在ABC 中,角,,A B C 所对的边分别为,,a b c 且满足sin cos .c A a C = (I )求角C 的大小; (IIcos()4A B π-+的最大值,并求取得最大值时角,A B 的大小.、解析:(I )由正弦定理得sin sin sin cos .C A A C =因为0,A π<<所以sin 0.sin cos .cos 0,tan 1,4A C C C C C π>=≠==从而又所以则(II )由(I )知3.4B A π=-于是cos()cos()4cos 2sin().63110,,,,46612623A B A A A A A A A A A ππππππππππ-+=--=+=+<<∴<+<+== 从而当即时2sin()6A π+取最大值2.、cos()4A B π-+的最大值为2,此时5,.312A B ππ==18.、(本题满分12分)某河流上的一座水力发电站,每年六月份的发电量Y (单位:万千瓦时)与该河上游在六月份的降雨量X (单位:毫米)有关.、据统计,当X=70时,Y=460;X 每增加10,Y 增加5;已知近20年X 的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.、 (I )完成如下的频率分布表:(II )假定今年六月份的降雨量与近20年六月份的降雨量的分布规律相同,并将频率视为概率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.、 解:(I )在所给数据中,降雨量为110毫米的有3个,为160毫米的有7个,为200毫米的有3个,故近20年六月份降雨量频率分布表为(II )("132320202010P ++=发电量低于490万千瓦时或超过530万千瓦时")=P(Y<490或Y>530)=P(X<130或X>210)=故今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率为310.、 19.、(本题满分12分)如图3,在圆锥PO中,已知PO O = 的直径 2,,AB C AB D AC =∠ 点在上,且CAB=30为的中点.、(I )证明:;AC POD ⊥平面(II )求直线和平面PAC 所成角的正弦值.、 解析:(I )因为,OA OC D AC =⊥是的中点,所以AC OD.又,,.PO O AC O AC OD ⊥⊂⊥ 底面底面所以PO 是平面POD 内的两条相交直线,所以;AC POD ⊥平面(II )由(I )知,,AC POD ⊥平面又,AC PAC ⊂平面所以平面,POD PAC ⊥平面在平面POD 中,过O 作OH PD ⊥于H,则,OH PAC ⊥平面连结CH ,则CH 是OC PAC 在平面上的射影,所以OCH ∠是直线OC 和平面PAC 所成的角.、在1,3Rt POD OH === 中在,sin 3OH Rt OHC OCH OC ∠== 中20.、(本题满分13分)某企业在第1年初购买一台价值为120万元的设备M ,M 的价值在使用过程中逐年减少,从第2年到第6年,每年初M 的价值比上年初减少10万元;从第7年开始,每年初M 的价值为上年初的75%.、(I )求第n 年初M 的价值n a 的表达式; (II )设12,nn a a a A n+++=若n A 大于80万元,则M 继续使用,否则须在第n 年初对M 更新,证明:须在第9年初对M 更新.、解析:(I )当6n ≤时,数列{}n a 是首项为120,公差为10-的等差数列.、 12010(1)13010;n a n n =--=- 当6n ≥时,数列{}n a 是以6a 为首项,公比为34为等比数列,又670a =,所以 6370();4n n a -=⨯因此,第n 年初,M 的价值n a 的表达式为612010(1)13010,6370(),74n n n n n n a a n ---=-≤⎧⎪=⎨=⨯≥⎪⎩ (II)设n S 表示数列{}n a 的前n 项和,由等差及等比数列的求和公式得 当16n ≤≤时,1205(1),1205(1)1255;n n S n n n A n n =--=--=- 当7n ≥时,666786333()570704[1()]780210()4443780210()4.n n n n n n S S a a a A n---=++++=+⨯⨯⨯-=-⨯-⨯= 因为{}n a 是递减数列,所以{}n A 是递减数列,又86968933780210()780210()4779448280,7680,864996A A ---⨯-⨯==>==<所以须在第9年初对M 更新.、21.、已知平面内一动点P 到点F (1,0)的距离与点P 到y 轴的距离的等等于1.、 (I )求动点P 的轨迹C 的方程;(II )过点F 作两条斜率存在且互相垂直的直线12,l l ,设1l 与轨迹C 相交于点,A B ,2l 与轨迹C 相交于点,D E ,求AD EB ∙的最小值.、解析:(I )设动点P 的坐标为(,)x y|| 1.x =化简得222||,y x x =+当20,4;0x y x x ≥=<时当时,y=0.、所以动点P 的轨迹C 的方程为2,4(0)0)y x x x =≥<和y=0(.(II )由题意知,直线1l 的斜率存在且不为0,设为k ,则1l 的方程为(1)y k x =-.、 由2(1)4y k x y x=-⎧⎨=⎩,得2222(24)0.k x k x k -++= 设1122(,),(,),A x y B x y 则12,x x 是上述方程的两个实根,于是1212242,1x x x x k+=+=.、 因为12l l ⊥,所以2l 的斜率为1k-.、设3344(,),(,),D x y B x y 则同理可得2343424,1x x k x x +=+=故12342222()()||||||||(1)(1)(1)(1)41(2)11(24)1184()AD EB AF FD EF FB AF EF AF FB FD EF FD FB AF FB FD EF x x x x k kk k ∙=++=+++=+=+++++=+++++++=++≥8416+⨯=当且仅当221k k =即1k =±时,AD EB ∙ 取最小值16.、22.、(本小题13分) 设函数1()ln ().f x x a x a R x=--∈ (I)讨论()f x 的单调性;(II )若()f x 有两个极值点12x x 和,记过点1122(,()),(,())A x f x B x f x 的直线的斜率为k ,问:是否存在a ,使得2?k a =-若存在,求出a 的值,若不存在,请说明理由.、 解析:(I )()f x 的定义域为(0,).+∞22211'()1a x ax f x x x x -+=+-=令2()1,g x x ax =-+其判别式24.a =-(1) 当||2,0,'()0,a f x ≤≤≥ 时故()(0,)f x +∞在上单调递增.、(2) 当2a <- 时,>0,g(x)=0的两根都小于0,在(0,)+∞上,'()0f x >,故()(0,)f x +∞在上单调递增.、(3) 当2a > 时,>0,g(x)=0的两根为12x x ==, 当10x x <<时, '()0f x >;当12x x x <<时, '()0f x <;当2x x >时, '()0f x >,故()f x 分别在12(0,),(,)x x +∞上单调递增,在12(,)x x 上单调递减.、 (II )由(I )知,2a >.、 因为1212121212()()()(ln ln )x x f x f x x x a x x x x --=-+--,所以 1212121212()()ln ln 11f x f x x x k a x x x x x x --==+--- 又由(I)知,121x x =.、于是1212ln ln 2x x k a x x -=--若存在a ,使得2.k a =-则1212ln ln 1x x x x -=-.、即1212ln ln x x x x -=-.、亦即222212ln 0(1)(*)x x x x --=> 再由(I )知,函数1()2ln h t t t t=--在(0,)+∞上单调递增,而21x >,所以222112ln 12ln10.1x x x -->--=这与(*)式矛盾.、故不存在a ,使得2.k a =-。
湖南省2011年对口升学高考数学试题

湖南省2011年普通高等学校对口招生考试数学一、选择题(本大题共10个小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.不等式()()012≤+-x x 的解集是A.()2,1-B.()()+∞⋃-∞-,21,C.[]2,1-D.(][)+∞⋃-∞-,21, 2.方程02=+-q px x 有解的充分必要条件是A.042>-q pB. 042<-q pC. 042=-q pD. 042≥-q p 3.下列函数中为指数函数的是A.x y 2=B.x y 2=C.2x y =D.x y 2log = 4.曲线[]π,0,212sin ∈+=x x y 与直线1=y 的交点个数为 A.0 B.1 C.2 D.3 5.设复数()i i z +=2,则下列命题正确的是A.z 的实部为2B.5=zC.i z 21-=D.i z 432--= 6.数列{}n a 的前n 项和232-=n S n ,则1a ,4a 的值依次为A.1,21B.3,46C.1,46D.3,217.已知方程14922=-+-ky k x 表示双曲线,则k 的取值范围是 A.4>k B.4<k C.9>k D.94<<k 8.设b a ,为直线,α为平面,则下列选项能判定α⊥a 的条件是A.α⊥b b a ,//B.α//,b b a ⊥C.α⊆b b a ,//D.α⊆⊥b b a ,9.已知函数()⎪⎩⎪⎨⎧≤+>=0,320,sin x x x x axx f 在点0=x 处连续,则=aA.3B.31C.1D.0 10.函数5323123-+-=x x x y 的单调递减区间是 A.()1,∞- B.()3,1 C.()+∞,3 D.()()+∞⋃∞-,31, 二、填空题(本大题共6小题,每小题5分,共30分。
把答案填在答题卡对应的横线上)11.设集合{}12==x x M ,{}1,0=N 则N M ⋂= 。
2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)
2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高(3)球的体积公式343V R π=,其中R 为求的半径一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==- 答案:D解析:因,根据复数相等的条件可知2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 答案:A解析:因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”3.设图一是某几何体的三视图,则该几何体的体积为( )A .9122π+B .9182π+C .942π+D .3618π+答案:B解析:有三视图可知该几何体是一个长方体和球构成的()1a i i ai b i +=-+=+1,1a b ==-3 32正视图侧视图俯视图 图1组合体,其体积由22()()()()()n ad bc K a bc d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:参照附表,得到的正确结论是( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关” 答案:C解析:由,而,故由独立性检验的意义可知选C.5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为( ) A .4B .3C .2D .1答案:C解析:由双曲线方程可知渐近线方程为3yx a=±,故可知2a = 6.由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为( )A .12B .1CD 答案:D解析:由定积分知识可得3333cos sin |(22S xdx x ππππ--===--=⎰ D 3439+332=18322V ππ=⨯⨯+()27.8 6.635K ≈>2( 6.635)0.010P K ≥=7. 设1m >,在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值小于2,则m 的取值范围为( )A.(1,1+ B.(1)++∞ C .(1,3) D .(3,)+∞ 答案:A解析:画出可行域,可知5z x y =+在点1(,)11mm m++取最大值,由21211m m m +<++解得11m <<8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为( ) A .1 B .12C.2 D.2答案:D解析:由题2||ln MN x x =-,(0)x >不妨令2()ln h x x x =-,则1'()2h x x x=-,令'()0h x =解得x =,因x ∈时,'()0h x <,当)x ∈+∞时,'()0h x >,所以当2x =时,||MN达到最小即2t =二填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上一、选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题记分)9.在直角坐标系xoy 中,曲线C 1的参数方程为cos ,1sin x y αα=⎧⎨=+⎩(α为参数)在极坐标系(与直角坐标系xoy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为()cos sin 10ρθθ-+=,则1C 与2C 的交点个数为 答案:2解析:曲线221:(1)1C x y +-=,2:10C x y -+=,由圆心到直线的距离|011|012d -+==<,故1C 与2C 的交点个数为2. 10.设,x y R ∈,则222211()(4)x y y x++的最小值为 答案:9解析:由柯西不等式可知2222211()(4)(12)9x y y x++≥+= 11.如图2,,A E 是半圆周上的两个三等分点,直径4BC =,AD BC ⊥,垂足为D,BE 与AD 相交与点F ,则AF 的长为答案:233解析:由题可知,60AOB EOC ∠=∠=︒,2OA OB ==,得1OD BD ==,33DF =, 又23AD BD CD =⋅=,所以233AF AD DF =-=.二、必做题(12~16题)12、设n S 是等差数列*{}()n a n N ∈的前n 项和,且141,7a a ==,则5______S =答案:25解析:由141,7a a ==可得11,2,21n a d a n ===-,所以5(19)5252S +⨯==13、若执行如图3所示的框图,输入1231,2,3,2x x x x ====,则输出的数等于 答案:23解析:由框图的算法功能可知,输出的数为三个数的方差,则222(12)(22)(32)233S -+-+-== 14、在边长为1的正三角形ABC 中,设2,3BC BD CA CE ==,则________AD BE ⋅=答案:14-解析:由题12AD CD CA CB CA =-=-,13BE CE CB CA CB =-=-, 所以111171()()232364AD BE CB CA CA CB CB CA ⋅=-⋅-=--+⋅=-15、如图4,EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则(1)=______P A ();(2)=______P A (B|) 答案:(1)2π;(2)1=4P A (B|)解析:(1)由几何概型概率计算公式可得2==S P A S π正圆(); (2)由条件概率的计算公式可得2114===24P AB P A P A ππ⨯()(B|)()16、对于*n N ∈,将n 表示为1210012122222k k k k k n a a a a a ---=⨯+⨯+⨯++⨯+⨯,当0i =时,1i a =,当1i k ≤≤时,i a 为0或1.记()I n 为上述表示中i a 为0的个数,(例如0112=⨯,2104120202=⨯+⨯+⨯:故(1)0,(4)2I I ==)则(1)(12)_____I = (2)127()12______I n n ==∑答案:(1)2;(2)1093解析:(1)因32101212+120202=⨯⨯+⨯+⨯,故(12)2I =;(2)在2进制的(2)k k ≥位数中,没有0的有1个,有1个0的有11k C -个,有2个0的有21k C -个,……有m 个0的有1m k C -个,……有1k -个0的有111k k C --=个故对所有2进制为k 位数的数n ,在所求式中的()2I n 的和为:01122111111122223k k k k k k C C C ------⋅+⋅+⋅++⋅= 又712721=-恰为2进制的最大7位数,所以1277()1122231093I n k n k -===+=∑∑三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤 17.(本小题满分12分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足sin cos c A a C =. (I )求角C 的大小;(IIcos()4A B π-+的最大值,并求取得最大值时角,A B 的大小. 解析:(I )由正弦定理得sin sin sin cos .C A A C =因为0,A π<<所以sin 0.sin cos .cos 0,tan 1,4A C C C C C π>=≠==从而又所以则(II )由(I )知3.4B A π=-于是cos()cos()4cos 2sin().63110,,,,46612623A B A A A A A A A A A ππππππππππ-+=--=+=+<<∴<+<+==从而当即时2sin()6A π+取最大值2.cos()4A B π-+的最大值为2,此时5,.312A B ππ==18. 某商店试销某种商品20天,获得如下数据:试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充..至3件,否则不进货...,将频率视为概率 (Ⅰ)求当天商品不进货...的概率; (Ⅱ)记X 为第二天开始营业时该商品的件数,求X 的分布列和数学期望 解析:(I )P (“当天商店不进货”)=P (“当天商品销售量为0件”)+P (“当天商品销售量1件”)=153202010+= (II )由题意知,X 的可能取值为2,3.51(2)("")204P x P ====当天商品销售量为1件;(3)("")+("")+("1953")++2020204P x P P P ====当天商品销售量为0件当天商品销售量为2件当天商品销售量为3件故X 的分布列为X 2 3P14 34X 的数学期望为13112+3=444EX =⨯⨯19.(本题满分12分)如图5,在圆锥PO 中,已知2,PO O =的直径2,,AB C AB D AC =是的中点,为的中点.(I )证明:;POD PAC ⊥平面平面(II )求二面角B PA C --的余弦值. 解:(I )连接OC ,因为OA OC =,D 为的AC 中点,所以AC OD ⊥. 又,,.PO O AC O AC PO ⊥⊂⊥底面底面所以因为,OD PO 是平面POD 内的两条相交直线,所以AC POD ⊥平面。
2011年湖南省高考数学文科试题及答案

2011年普通高等学校招生全国统一考试(湖南卷)数学(文史类)本试题卷包括选择题、填空题、解答题三部分,共6页,时量120分钟,满分150分参考公式:(1)()(|)()P AB P B A P A =,其中,A B 为两个基本事件,且()0P A >. (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高. (3)球的体积公式343V R π=,其中R 为球的半径. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集{1,2,3,4,5},{2,4},U U M N M C N ===U I 则N =( )A .{1,2,3}B .{1,3,5}C .{1,4,5}D . {2,3,4} 2. 若,,a b R i ∈为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B . 1,1a b =-=C . 1,1a b ==-D . 1,1a b =-=-3. “1x >”是“||1x >”的( )A .充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件 4. 设图1是某几何体的三视图,则该几何体的体积为 ( )A .942π+B .3618π+C .9122π+ D .9182π+ 5. 通过询问110名性别不同的的大学生是否爱好某项运动,得到如下的列联表.由22()()()()()n ad bc K a b c d a c b d -=++++算得,22110(40302020)7.860506050K ⨯-⨯=≈⨯⨯⨯,附表如右下,参照附表,得到的正确结论( )A .有99%以上的把握认为“爱好该项运动与性别有关”B .有99%以上的把握认为“爱好该项运动与性别无关”C .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”6. 设双曲线2221(0)9x y a a -=>的渐近线方程为320x y =±,则a 的值为( ) A .4 B .3 C .2 D .1 7. 曲线sin 1sin cos 2x y x x =-+在点(,0)4M π处的切线的斜率为( )A .-12B . 12C . -22D . 228. 已知函数2()1,()4 3.xf x eg x x x =-=-+-若有()()f a g b =,则b 的取值范围为( )A .[2-2,2+2]B .(2-2,2+2)C . [1,3]D .(1,3)二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分.把答案填在答题卡中对应题号后的横线上.(一)选做题(请考生在第9、10两题中任选一题作答,如果全做,则按前一题记分)9. 在直角坐标系xOy 中,曲线1C的参数方程为2cos (x y ααα=⎧⎪⎨=⎪⎩为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为(cos sin )10ρθθ-+=,则1C 与2C 的交点个数为 .10. 已知某试验范围为[10,90],若用分数法进行4次优选试验,则第二次试点可以是 (只写出其中一个也正确). (二)必做题(11~16题)11. 若执行如图2所示的框图,输入12341,2,4,8,x x x x ==== 则输出的数等于 .12. 已知()f x 为奇函数,()()9g x f x =+,(2)3g -=,则(2)f = .13. 设向量a ,b 满足|a|=25,b =(2,1),且a 与b 的方向相反,则a 的坐标为 .14. 设1m >,在约束条件,,1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数5z x y =+的大值为4,则m 的值为 。
2011年普通高等学校招生全国统一考试(湖南卷)数学试题 (文科)(解析版)

2011年普通高等学校招生全国统一考试(湖南卷)数学(文)试题解析本试题包括选择题、填空题和解答题三部分,共6页.时量120分钟,满分150分. 参考公式(1)柱体体积公式V Sh =,其中S 为底面面积,h 为高. (2)球的体积公式343V R π=,其中R 为球的半径. 一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{1,2,3,4,5},{2,4},U U M N M C N ===则N =( )A .{1,2,3}B .{1,3,5} C.{1,4,5} D.{2,3,4} 答案:B解析:画出韦恩图,可知N ={1,3,5}。
2.若,,a b R i ∈为虚数单位,且()a i i b i +=+,则( )A.1,1a b == B.1,1a b =-= C.1,1a b ==- D.1,1a b =-=- 答案:C解析:因()1a i i ai b i +=-+=+,根据复数相等的条件可知1,1a b ==-。
3."1""||1"x x >>是的( )A .充分不必要条件 B.必要不充分条件 C .充分必要条件 D .既不充分又不必要条件 答案:A解析:因"1""||1"x x >⇒>,反之 "||1""11"x x x >⇒><-或,不一定有"1"x >。
4.设图1是某几何体的三视图,则该几何体的体积为( )A .942π+ B.3618π+C.9122π+ D.9182π+答案:D解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+()。
由222()110(40302030)7.8()()()()60506050n ad bc K K ab c d a c b d -⨯⨯-⨯==≈++++⨯⨯⨯算得, 附表:正视图 侧视图俯视图图1参照附表,得到的正确结论是( )A. 有99%以上的把握认为“爱好该项运动与性别有关”B. 有99%以上的把握认为“爱好该项运动与性别无关”C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” 答案:A解析:由27.8 6.635K ≈>,而2( 6.635)0.010P K ≥=,故由独立性检验的意义可知选A.6.设双曲线2221(0)9x y a a -=>的渐近线方程为320,x y ±=则a 的值为( ) A .4 B .3 C .2 D .1答案:C解析:由双曲线方程可知渐近线方程为3y x a=±,故可知2a =。
