2020届中考一轮复习讲义(Word版无解析)

合集下载

第03讲情态动词(讲义)-中考英语一轮复习讲练测(全国通用)(学生版)_1

►第03讲情态动词（讲义）目录一复习目标掌握目标及备考方向二考情分析2023年中考情态动词考情分析三网络构建知识点头脑风暴四情态动词考向1.情态动词的概说和分类2.情态动词的特点3.情态动词的基本用法4.情态动词与相关易混点的辨析5.提升必考题型归纳五真题感悟中考情态动词经典考题【复习目标】1.弄清情态动词的概说和分类2.掌握情态动词的特点3.掌握情态动词的基本用法4.掌握情态动词与相关易混点的辨析【考情分析】课标要求：情态动词是中考英语动词考察的重点，课标要求：1.掌握情态动词的语法特征；2.知道情态动词的分类；3.掌握情态动词基本语境情态色彩。

重点考查：情态动词表猜测：一肯、一否、三不定must：一般用在肯定句里表示(“有根据的肯定猜测或推测”)must be肯定是，一定是can：一般用在否定句里表示(“有根据的否定猜测或推测”)can’t be不可能是用在疑问句里可以表示（“肯定的推测或猜测”）may ; might ; could：用于肯定句里表示(“毫无根据的猜测或推测”)。

并且语气依次逐渐减弱。

主要题型设置：主要考查情态动词辨析，考查角度以语境辨析为主。

考查形式主要以单项选择、完型填空、短文填空及语法填空为主。

情态动词题型命题规律【网络构建】情态动词是初中英语里的一个重要的语法项目，也是全国各省市中考试题的考查热点。

在备战2024年中考时，考生要牢记情态动词的结构和意义以及其表示推测时的用法，多做练习，在实践中加以区分。

(一)概说情态动词表示说话人的语气和观点.情态动词有一定的词义,但不能单独作谓语,它必须和表示动作或状态的不带to 的不定式(ought 除外)连用,构成复合谓语.情态动词只有情态意义,即它表示说话人对动作的观点,如需要、可能、意愿或怀疑等.情态动词主要有:can(could),may(might),must, ought to, need, dare(dared), have to(had to).此外shall, will, should, would 在一定场合下也可用作情态动词.(二)情态动词的分类：(1)只作情态动词:must;can/could;may/might;ought to(2)既可作情态动词又可作实义动词:need,dare(3)既可作情态动词又可作助动词:shall/should;will/would(4)具有情态动词某些特征:have/had to;had better考向二情态动词的特点(1)情态动词无人称和数的变化(have to 除外);(2)情态动词后接动词原形;(3)情态动词的否定式是在其后加not; have to 除外(4)具有助动词的作用，可用来构成否定句、疑问句及用于简明答语;(5)个别情态动词有现在式和过去式两种形式,过去式用来表达更加客气、委婉的语气，时态性不强，可用于过去、现在或将来。

专题16动物的主要类群(讲义)(解析版)-2024年中考生物一轮复习讲义

专题16 动物的主要类群目录考点一动物的主要类群考向01 动物的主要特征考向02 判断动物实例所属类群考向03 动物与人类的关系考点二动物与环境相适应的特征考向01 判断动物与其生活环境相适应的特征考点三动物的呼吸器官、运动器官考向01 动物的呼吸器官、运动器官考点四动物的分类考向01 无脊椎动物和脊椎动物考向02 恒温动物和变温动物考点要求新课标要求命题预测动物的主要类群➢ 能够说出动物各类群的主要特征和代表动物，以及动物与人的关系。

动物类群的主要特征、它们与人类生活的关系和生活与其生活环境相适应的特点，在考点要求中比较突出，是这动物与环境相适应的特征➢ 能够说出动物与其生存环境相适应的特征。

部分内容的重点，是常见的考查内容，形式有选择题，填空题等。

珍稀动物的保护是社会热点问题，在近几年的中考中常结合环境保护问题出现。

考查的命题点有：动物各类群的主要特征和代表动物，以及动物与人的关系，动物与其生存环境相适应的特征，动物的呼吸器官、运动器官，脊椎动物和无脊椎动物、恒温动物和变温动物。

动物的呼吸器官、运动器官➢ 能说出动物的呼吸器官、运动器官。

动物的分类➢ 能够根据一定的特征对动物进行分类，区分脊椎动物和无脊椎动物、恒温动物和变温动物。

考点一动物的主要类群主要特征常见种类与人类的关系腔肠动物身体呈辐射对称，体表有刺细胞，有口无肛门。

水母、海葵、海蜇、珊瑚虫水螅（淡水）海蜇可食用，珊瑚虫的分泌物形成珊瑚礁。

考向01 动物的主要特征【例1】（2022·山东枣庄·中考真题）生物在进化过程中逐步形成了与其生存环境相适应的形态结构特点。

下列叙述正确的是( ) A.水螅——消化腔有口有肛门 B.蚯蚓——身体分节,用鳃呼吸 C.家兔——胎生哺乳,体内有膈 D.家鸽——体表被毛,双重呼吸【答案】D【解析】水螅属于腔肠动物,体内有消化腔,有口无肛门,A 错误。

蚯蚓属于环节动物,身体由许多相似体节构成,靠湿润的体壁呼吸,B 错误。

中考数学一轮复习讲义2__整式

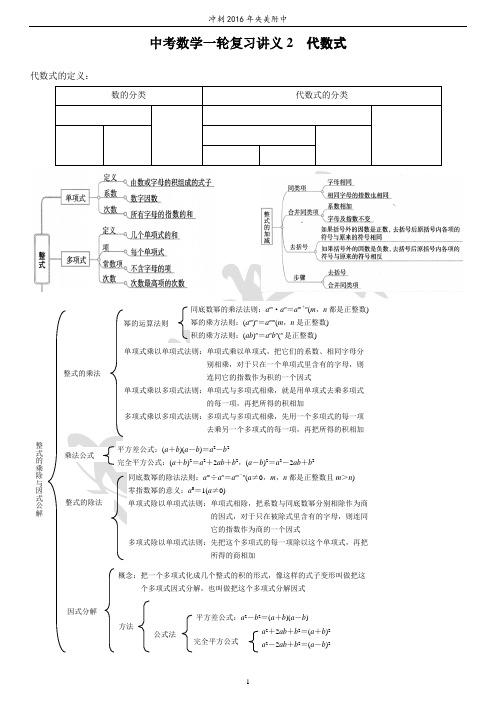
中考数学一轮复习讲义2 代数式代数式的定义：整式的乘法整式的乘除与因式公解幂的运算法则同底数幂的乘法法则：a m·a n＝a m＋n(m，n都是正整数)幂的乘方法则：(a m)n＝a mn(m，n是正整数)积的乘方法则：(ab)n＝a n b n(n是正整数)单项式乘以单项式法则：单项式乘以单项式，把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式单项式乘以多项式法则：单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加多项式乘以多项式法则：多项式与多项式相乘，先用一个多项式的每一项去乘另一个多项式的每一项，再把所得的积相加同底数幂的除法法则：a m÷a n＝a m－n(a≠0，m，n都是正整数且m＞n)零指数幂的意义：a0＝1(a≠0)单项式除以单项式法则：单项式相除，把系数与同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式多项式除以单项式法则：先把这个多项式的每一项除以这个单项式，再把所得的商相加乘法公式平方差公式：(a＋b)(a－b)＝a2－b2完全平方公式：(a＋b)2＝a2＋2ab＋b2，(a－b)2＝a2－2ab＋b2整式的除法因式分解概念：把一个多项式化成几个整式的积的形式，像这样的式子变形叫做把这个多项式因式分解，也叫做把这个多项式分解因式方法公式法平方差公式：a2－b2＝(a＋b)(a－b)完全平方公式a2＋2ab＋b2＝(a＋b)2a2－2ab＋b2＝(a－b)2题型一整式的加减运算例1 已知与是同类项，则a b 的值为. 例2 计算：（7x 2＋5x －3）－（5x 2－3x ＋2）．题型二整式的求值例3 已知（a ＋2）2＋|b ＋5|＝0，求3a 2b 一[2a 2b －（2ab －a 2b ）－4a 2]－ab 的值．例例5例例7例8例9A.解析：第二个图案中正三角形的个数为：第三个图案中正三角形的个数为：．．，；第n 个图案中正三角形的个数为：题型四：幂的运算法则及其逆运用例1 计算2x 3·(－3x )２＝．例2 计算[a 4(a 4－4a )－(－3a 5)2÷(a 2)3]÷(－2a 2)2．3313a x y --533b y x -85a +题型五：整式的混合运算与因式分解例3 计算[(a －2b )(2a －b )－(2a ＋b )2＋(a ＋b )(a －b )－(3a )2]÷(－2a )．例4 分解因式． (1)m 3－m ； (2)(x ＋2)(x ＋3)＋x 2－4．例5 分解因式a 2－2ab ＋b 2－c 2．例6 (1)已知x ＋y ＝7，xy ＝12，求(x －y )2； (2)已知a ＋b ＝8，a －b ＝2，求ab 的值．15.（2011•临沂，2，3分）下列运算中正确的是（） A 、（﹣ab ）2=2a 2b 2B 、（a+b ）2=a 2+1C 、a 6÷a 2=a 3D 、2a 3+a 3=3a 316.（2011泰安，2，3分）下列运算正确的是（） A ．3a 2＋4a 2＝7a 4B ．3a 2－4a 2＝－a 2C ．3a ×4a 2＝12a 2D ．2222434)3(a a a -=÷17.（2011四川眉山，2，3分）下列运箅正确的是（） A ．2a 2﹣a=aB ．（a+2）2=a 2+4C ．（a 2）3=a 6D ．3)3(2-=-19.（2011•南充，11，3分）计算（π﹣3）0=．20.（2011四川攀枝花，3，3分）下列运算中，正确的是（） A 、2+3=5 B 、a 2•a=a 3C 、（a 3）3=a 6D 、327=－3中考真题精选21.（2011泰安，5，3分）下列等式不成立的是（） A ．m 2－16＝（m －4）（m ＋4）B ．m 2＋4m ＝m （m ＋4）C ．m 2－8m ＋16＝（m －4）2D ．m 2＋3m ＋9＝（m ＋3）22.（2011•丹东，4，3分）将多项式x 3﹣xy 2分解因式，结果正确的是（） A 、x （x 2﹣y 2）B 、x （x ﹣y ）2C 、x （x+y ）2D 、x （x+y ）（x ﹣y ）4.（2011天水，4，4）多项式2a 2﹣4ab +2b 2分解因式的结果正确的是（） A 、2（a 2﹣2ab +b 2）B 、2a （a ﹣2b ）+2b 2C 、2（a ﹣b ）2D 、（2a ﹣2b ）25.（2011江苏无锡，3，3分）分解因式2x 2﹣4x+2的最终结果是（） A ．2x （x ﹣2）B ．2（x 2﹣2x+1） C ．2（x ﹣1）2D ．（2x ﹣2）26.（2011•台湾5，4分）下列四个多项式，哪一个是2x 2+5x ﹣3的因式（） A 、2x ﹣1B 、2x ﹣3C 、x ﹣1D 、x ﹣37.（2011台湾，24，4分）下列四个多项式，哪一个是33x ＋7的倍式（） A ．33x 2－49B ．332x 2＋49C ．33x 2＋7xD ．33x 2＋14x10.（2011梧州，6，3分）因式分解x 2y ﹣4y 的正确结果是（） A 、y （x+2）（x ﹣2）B 、y （x+4）（x ﹣4）C 、y （x 2﹣4）D 、y （x ﹣2）211.（2011河北，3，2分）下列分解因式正确的是（） A ．－a ＋a 3＝－a （1＋a 2） B ．2a －4b ＋2＝2（a －2b ）C ．a 2－4＝（a －2）2D ．a 2－2a ＋1＝（a －1）213.（2011，台湾省，25,5分）若多项式33x 2﹣17x ﹣26可因式分解成（ax+b ）（cx+d ），其中a 、b 、c 、d 均为整数，则|a+b+c+d|之值为何？（） A 、3B 、10C 、25D 、2914.（2011浙江金华，3，3分）下列各式能用完全平方式进行分解因式的是（） A ．x 2 +1 B.x 2+2x －1 C.x 2+x +1 D.x 2+4x +415.（2011浙江丽水，3，3分）下列各式能用完全平方公式进行分解因式的是（） A 、x 2+1 B 、x 2+2x ﹣1 C 、x 2+x +1D 、x 2+4x +4综合验收评估测试题1一、选择题l. 在代数式－2x 2，3xy ，，，0，mx －ny 中，整式的个数为（） A ．2 B ．3 C ．4 D. 5 2. 二下列语句正确的是（）A ．x 的次数是0B ．x 的系数是0 C. －1是一次单项式 D ．－1是单项式 3.4.5. 6. 7. 8. C ．m ≠－1，n 为大于3的整数 D ．m ≠－1，n ＝5二、填空题9. －mx n y 是关于x ，y 的一个单项式，且系数是3，次数是4，则m ＝，n ＝． 10. 多项式ab 3－3a 2b 2－a 3b －3按字母a 的降幂排列是．按字母b 的升幂排列是． 11. 当b ＝时，式子2a ＋ab －5的值与a 无关． 12. 若－7xy n ＋1 3x m y 4是同类项，则m ＋n ．13．多项式2ab －5a 2＋7b 2加上等于a 2－5ab ．b a 3xy -三、解答题14．先化简，再求值：，其中m ＝－l ，n ＝.综合验收评估测试题2一、选择题(每小题3分，共30分) 1．计算(a 3)2的结果是 ( ) A ．a 5 B ．a 6 C ．a 8 D ．a 9 2．下列运算正确的是 ( )A ．a 2·a 3＝a 4B ．(－a )4＝a 4C ．a 2＋a 3＝a 5D ．(a 2)3＝a 5 3．已知x －3y ＝－3，则5－x ＋3y 的值是 ( ) A ．0 B ．2 C ．5 D ．8 4．若m ＋n ＝3，则2m 2＋4mn ＋2n 2－6的值为 ( ) A ．12 B ．6 C ．3 D ．05．如图15－4所示，在边长为a 的正方形中挖去一个边长为b 的小正方形(a ＞b )，把余下的部分拼成一个矩形，根据两个图形中阴影部分的面积相等，可以验证 ( )A ．(a ＋b )2＝a 2＋2ab ＋b 2B ．(a －b )2＝a 2－2ab ＋b 2C ．a 2－b 2＝(a ＋b )(a －b )D ．(a ＋2b )(a －b )＝a 2＋ab －2b 2 6．下列各式中，与(a －b )2一定相等的是 ( )A ．a 2＋2ab ＋b 2B ．a 2－b 2C ．a 2＋b 2D ．a 2－2ab ＋b 0 7．已知x ＋y ＝－5，xy ＝6，则x 2＋y 2的值为 ( ) A ．1 B ．13 C ．17 D ．25 8．下列从左到右的变形是因式分解的是 ( )A ．ma ＋mb －c ＝m (a ＋b )－cB ．(a －b )(a 2＋ab ＋b 2)＝a 3－b 3C ．a 2－4ab ＋4b 2－1＝a (a －4b )＋(2b ＋1)(2b －1)D ．4x 2－25y 2＝(2x ＋5y )(2x －5y ) 9．下列各式中，能用平方差公式分解因式的是 ( ) A ．－a 2＋b 2 B ．－a 2－b 2 C ．a 2＋b 2 D ．a 3－b 3 10．如果(x －2)(x －3)＝x 2＋px ＋q ，那么p ，q 的值是 ( )A ．p ＝－5，q ＝6B ．p ＝1，q ＝－6C ．p ＝1，q ＝6D ．p ＝5，q ＝－622222212(52)3(2)2m n mn m n mn mn m n ⎛⎫+---- ⎪⎝⎭13二、填空题(每小题3分，共30分) 11．已知10m ＝2，10n ＝3，则103m＋2n＝．12．当x ＝3，y ＝1时，代数式(x ＋y )(x －y )＋y 2的值是． 13．若a －b ＝1，ab ＝－2，则(a ＋1)(b －1)＝． 14．分解因式：2m 3－8m ＝． 15．已知y ＝31x －1，那么31x 2－2xy ＋3y 2－2的值为． 16．计算：5752×12－4252×12＝．17 18192021 22(1)m 2n (m23．已知a ，b 是有理数，试说明a 2＋b 2－2a －4b ＋8的值是正数．24．先化简，再求值：(a ＋b )(a －b )＋(4ab 3－8a 2b 2)÷4ab ，其中a ＝2，b ＝1．25．(1)计算．①(a －1)(a ＋1)；②(a －1)(a 2＋a ＋1)；③(a －1)(a 3＋a 2＋a ＋1)；④(a －1)(a 4＋a 3＋a 2＋a ＋1)． (2)根据(1)中的计算，你发现了什么规律?用字母表示出来． (3)根据(2)中的结论，直接写出下题的结果． ①(a －1)(a 9＋a 8＋a 7＋a 6＋a 5＋a 4＋a 3＋a 2＋a ＋1)＝； ②若(a －1)·M ＝a 15－1，则M ＝； ③(a －b④(226(1) (2) (3) (4)(5)答案：1．D 解析：不是整式，故选D ． 2．D 解析：x 的次数是1，系数是1；－1是单项式．故选D ．3．C 解析：所含字母相同，并且相同字母的指数也相同的项叫做同类项．故选C ：4．D 解析：如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反．故选D ．5．6．B ． 7．2n ＋38．910 1112137b 2． 142×＝1．15 50πa 2＋100ab ．答：美化这块空地共需资金（50πa 2＋100ab ）元．点拨：根据题意，可以先求出建造花台及种花所需费用，再求出种草的费用，两者相加即为美化这块空地共需的资金．ba1314π4a ⨯参考答案1．B2．B[提示：选项A ：a 2·a 3＝a 5；选项C ：a 2和a 3不能合并；选项D ：(a 2)3＝a 6．] 3．D[提示：5－x ＋3y ＝5－(x －3y )＝5－(－3)＝8．]4．A ［提示：2m 2＋4mn ＋2n 2－6＝2(m ＋n )2－6＝2×32－6＝12．]5．6．7．8．9．10111213141531(x －3y )2－216] 17181920] 21＋1)(2x －1)－＝20002－(200022(x ＋y －8)2．232)2≥0，∴(a －1)＝a 2－b 2＋b 2－25n －2＋…＋a 3＋a 2＋a ＋1)＝a n ＋1－1． (3)①a 10－1 ②a 14＋a 13＋a 12＋a 11＋…＋a 3＋a 2＋a ＋1 ③a 6－b 6④32x 5－126．解：(1)各层对应的点数依次为：4，8．12，16，20，24；所有层的总点数依次为：4，12，24，40，60．84． (2)4n ． (3)2n (n ＋1)． (4)第24层． (5)有，第25层．。

2024年中考物理一轮复习讲义专题05内能、内能的利用(讲义)(解析版)

比热容及其应用
通过实验了解比热容。能运用比热容说明简单的自然现象
比热容是本单元重点内容，无论比热容的概念还是比热容的应用，都属于常考热点。对此考点的考查常见题型有选择题、填空题，有时也会出现实验探究题和简答题。无论考查题型怎样，其命题点大都是：比热容的概念、比热容的相关计算、水的比热容大的应用、探究不同物质的吸热能力等。
能量守恒定律
了解能量及其存在的不同形式。描述不同形式的能量和生产生活的联系。列举能量转化和转移具有方向性的常见实例。知道能量守恒定律。有用能量转化与守恒的观点分析问题的意识
能量守恒定律是自然界普遍遵守的规律，所以认识能量转化和转移以及在转化和转移过程中能量守恒的认识理所当然成为常考热点。命题点主要有：能量转化和转移的辨别、能量转化和转移的方向性、能量守恒定律及其应用等。
专题05 内能、内能的利用（讲义）（解析版）
一、课标考点分析
考点内容
课标要求
命题预测
分子热运动理论
知道常见的物质是由分子、原子构成的。了解分子热运动的主要特点，知道分子动理论的基本观点
分子热运动理论是常考热点，在历年中考试卷中，无论试题形式怎样，都会出现考查此考点的考题。考题形式以选择题、填空题为主，有时也会出现在综合题中。主要命题点有：对分子热运动理论的理解、物质的扩散、分子间相互作用力等。
2.分子的大小：分子的直径很小，通常以10-10m来量度，所以一个看似很小物质中都会包含大量的分子，如一个小水滴中含有约1021个水分子。
3.分子间有间隙
实验演示：取50ml的水与50ml酒精，倒入量筒中，轻轻摇晃几下，静止后观察量筒中液体体积，发现水喝酒精混合后的总体积小于100ml。
这是酒精与水的混合过程。实际上是酒精分散到了水中，从微观的角度看，酒精分子分散到了水分子中间，这一现象说明水分子和酒精分子间都有间隙。

2020届人教版中考数学一轮复习-第17讲尺规作图(有答案)

第十七节尺规作图【知识点梳理】一）尺规作图1．定义只用没有刻度的直尺和圆规作图叫做尺规作图．2．步骤①根据给出的条件和求作的图形，写出已知和求作部分；②分析作图的方法和过程；③用直尺和圆规进行作图；④写出作法步骤，即作法．二）五种基本作图1．作一条线段等于已知线段；2．作一个角等于已知角；3．作已知角的平分线；4．过一点作已知直线的垂线；5．作已知线段的垂直平分线．三）基本作图的应用1．利用基本作图作三角形(1)已知三边作三角形；(2)已知两边及其夹角作三角形；(3)已知两角及其夹边作三角形；(4)已知底边及底边上的高作等腰三角形；(5)已知一直角边和斜边作直角三角形．2．与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆)．(2)作三角形的内切圆．【课堂练习】一．选择题（共8小题）1．如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG，若AD=5，DE=6，则AG的长是（）A．6 B．8 C．10 D．12【考点】N2：作图—基本作图；L5：平行四边形的性质．【分析】连接EG，由作图可知AD=AE，根据等腰三角形的性质可知AG是DE的垂直平分线，由平行四边形的性质可得出CD∥AB，故可得出∠2=∠3，据此可知AD=DG，由等腰三角形的性质可知OA=AG，利用勾股定理求出OA的长即可．【解答】解：连接EG，∵由作图可知AD=AE，AG是∠BAD的平分线，∴∠1=∠2，∴AG⊥DE，OD=DE=3．∵四边形ABCD是平行四边形，∴CD∥AB，∴∠2=∠3，∴∠1=∠3，∴AD=DG．∵AG⊥DE，∴OA=AG．在Rt△AOD中，OA===4，∴AG=2AO=8．故选B．2．如图，在△AEF中，尺规作图如下：分别以点E，点F为圆心，大于12EF的长为半径作弧，两弧相交于G，H两点，作直线GH，交EF于点O，连接AO，则下列结论正确的是（）A．AO平分∠EAF B．AO垂直平分EF C．GH垂直平分EF D．GH平分AF 【考点】N2：作图—基本作图；KG：线段垂直平分线的性质．【分析】直接根据线段垂直平分线的作法即可得出结论．【解答】解：由题意可得，GH垂直平分线段EF．故选C．3．如图，已知线段AB，分别以A、B为圆心，大于12AB为半径作弧，连接弧的交点得到直线l，在直线l上取一点C，使得∠CAB=25°，延长AC至M，求∠BCM的度数为（）A．40°B．50°C．60°D．70°【考点】N2：作图—基本作图；KG：线段垂直平分线的性质．【分析】根据作法可知直线l是线段AB的垂直平分线，故可得出AC=BC，再由三角形外角的性质即可得出结论．【解答】解：∵由作法可知直线l是线段AB的垂直平分线，∴AC=BC，∴∠CAB=∠CBA=25°，∴∠BCM=∠CAB+∠CBA=25°+25°=50°．故选B．4．下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线，则对应选项中作法错误的是（）A．①B．②C．③D．④【考点】N2：作图—基本作图．【分析】利用作一个角等于已知角；作一个角的平分线；作一条线段的垂直平分线；过直线外一点P作已知直线的垂线的作法进而判断得出答案．【解答】解：①作一个角等于已知角的方法正确；②作一个角的平分线的作法正确；③作一条线段的垂直平分线缺少另一个交点，作法错误；④过直线外一点P作已知直线的垂线的作法正确．故选：C．5．如图，在△ABC中，∠ACB=90°，∠A=30°，BC=4，以点C为圆心，CB长为半径作弧，交AB于点D；再分别以点B和点D为圆心，大于12BD的长为半径作弧，两弧相交于点E，作射线CE交AB于点F，则AF的长为（）A．5 B．6 C．7 D．8【考点】N2：作图—基本作图；KO：含30度角的直角三角形．【分析】连接CD，根据在△ABC中，∠ACB=90°，∠A=30°，BC=4可知AB=2BC=8，再由作法可知BC=CD=4，CE 是线段BD的垂直平分线，故CD是斜边AB的中线，据此可得出BD的长，进而可得出结论．【解答】解：连接CD，∵在△ABC中，∠ACB=90°，∠A=30°，BC=4，∴AB=2BC=8．∵作法可知BC=CD=4，CE是线段BD的垂直平分线，∴CD是斜边AB的中线，∴BD=AD=4，∴BF=DF=2，∴AF=AD+DF=4+2=6．故选B．6．如图，用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，那么第二步的作图痕迹②的作法是（）A．以点F为圆心，OE长为半径画弧B．以点F为圆心，EF长为半径画弧C．以点E为圆心，OE长为半径画弧D．以点E为圆心，EF长为半径画弧【考点】N2：作图—基本作图．【分析】根据作一个角等于一直角的作法即可得出结论．【解答】解：用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，第二步的作图痕迹②的作法是以点E为圆心，EF长为半径画弧．故选D．7．如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹．步骤1：以C为圆心，CA为半径画弧①；步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；步骤3：连接AD，交BC延长线于点H．下列叙述正确的是（）A．BH垂直平分线段AD B．AC平分∠BADC．S△ABC=BC•AH D．AB=AD【考点】N2：作图—基本作图；KG：线段垂直平分线的性质．【分析】根据已知条件可知直线BC是线段AD的垂直平分线，由此一一判定即可．【解答】解：A、正确．如图连接CD、BD，∵CA=CD，BA=BD，∴点C、点B在线段AD的垂直平分线上，∴直线BC是线段AD的垂直平分线，故A正确．B、错误．CA不一定平分∠BDA．C、错误．应该是S△ABC=•BC•AH．D、错误．根据条件AB不一定等于AD．故选A．8．下列尺规作图，能判断AD是△ABC边上的高是（）A．B．C．D．【考点】N2：作图—基本作图．【分析】过点A作BC的垂线，垂足为D，则AD即为所求．【解答】解：过点A作BC的垂线，垂足为D，故选B．二．填空题（共5小题）9．如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以M，N为圆心，以大于12MN的长为半径作弧，两弧相交于点P；③作AP射线，交边CD于点Q，若DQ=2QC，BC=3，则平行四边形ABCD周长为．【考点】N2：作图—基本作图；L5：平行四边形的性质．【分析】根据角平分线的性质可知∠DAQ=∠BAQ，再由平行四边形的性质得出CD∥AB，BC=AD=3，∠BAQ=∠DQA，故可得出△AQD是等腰三角形，据此可得出DQ=AD，进而可得出结论．【解答】解：∵由题意可知，AQ是∠DAB的平分线，∴∠DAQ=∠BAQ．∵四边形ABCD是平行四边形，∴CD∥AB，BC=AD=3，∠BAQ=∠DQA，∴∠DAQ=∠DQA，∴△AQD是等腰三角形，∴DQ=AD=3．∵DQ=2QC，∴QC=DQ=，∴CD=DQ+CQ=3+=，∴平行四边形ABCD周长=2（DC+AD）=2×（+3）=15．故答案为：15．10．如图所示，已知∠AOB=40°，现按照以下步骤作图：①在OA，OB上分别截取线段OD，OE，使OD=OE；②分别以D，E为圆心，以大于12DE的长为半径画弧，在∠AOB内两弧交于点C；③作射线OC．则∠AOC的大小为．【考点】N2：作图—基本作图．【分析】直接根据角平分线的作法即可得出结论．【解答】解：∵由作法可知，OC是∠AOB的平分线，∴∠AOC=∠AOB=20°．故答案为：20°．11．如图，依据尺规作图的痕迹，计算∠α=°．【考点】N2：作图—基本作图．【分析】先根据矩形的性质得出AD∥BC，故可得出∠DAC的度数，由角平分线的定义求出∠EAF的度数，再由EF 是线段AC的垂直平分线得出∠AEF的度数，根据三角形内角和定理得出∠AFE的度数，进而可得出结论．【解答】解：∵四边形ABCD是矩形，∴AD∥BC，∴∠DAC=∠ACB=68°．∵由作法可知，AF是∠DAC的平分线，∴∠EAF=∠DAC=34°．∵由作法可知，EF是线段AC的垂直平分线，∴∠AEF=90°，∴∠AFE=90°﹣34°=56°，∴∠α=56°．故答案为：56．12．如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M，N为圆心，大于12MN的长为半径画弧，两弧在第二象限内交于点P（a，b），则a与b的数量关系是．【考点】N2：作图—基本作图；D5：坐标与图形性质；J5：点到直线的距离．【分析】根据作图方法可得点P在第二象限的角平分线上，根据角平分线的性质和第二象限内点的坐标符号，可得a与b的数量关系为互为相反数．【解答】解：根据作图方法可得，点P在第二象限角平分线上，∴点P到x轴、y轴的距离相等，即|b|=|a|，又∵点P（a，b）第二象限内，∴b=﹣a，即a+b=0，故答案为：a+b=0．13．图1是“作已知直角三角形的外接圆”的尺规作图过程已知：Rt△ABC，∠C=90°，求作Rt△ABC的外接圆．作法：如图2．（1）分别以点A和点B为圆心，大于12AB的长为半径作弧，两弧相交于P，Q两点；（2）作直线PQ，交AB于点O；（3）以O为圆心，OA为半径作⊙O．⊙O即为所求作的圆．请回答：该尺规作图的依据是．【考点】N3：作图—复杂作图；MA：三角形的外接圆与外心．【分析】由于90°的圆周角所对的弦是直径，所以Rt△ABC的外接圆的圆心为AB的中点，然后作AB的中垂线得到圆心后即可得到Rt△ABC的外接圆．【解答】解：该尺规作图的依据是到线段两端点的距离相等的点在这条线段的垂直平分线上；90°的圆周角所对的弦是直径．故答案为到线段两端点的距离相等的点在这条线段的垂直平分线上；两点确定一直线；90°的圆周角所对的弦是直径；圆的定义．三．解答题（共8小题）14．如图，△ABC中，∠ACB＞∠ABC．（1）用直尺和圆规在∠ACB的内部作射线CM，使∠ACM=∠ABC（不要求写作法，保留作图痕迹）；（2）若（1）中的射线CM交AB于点D，AB=9，AC=6，求AD的长．【考点】N2：作图—基本作图；S9：相似三角形的判定与性质．【分析】（1）根据尺规作图的方法，以AC为一边，在∠ACB的内部作∠ACM=∠ABC即可；（2）根据△ACD与△ABC相似，运用相似三角形的对应边成比例进行计算即可．【解答】解：（1）如图所示，射线CM即为所求；（2）∵∠ACD=∠ABC，∠CAD=∠BAC，∴△ACD∽△ABC，∴=，即=，∴AD=4．15．如图，在Rt△ABC中，∠B=90°，∠A=30°，AC=2．（1）利用尺规作线段AC的垂直平分线DE，垂足为E，交AB于点D，（保留作图痕迹，不写作法）（2）若△ADE的周长为a，先化简T=（a+1）2﹣a（a﹣1），再求T的值．【考点】N2：作图—基本作图；KO：含30度角的直角三角形．【分析】（1）根据作已知线段的垂直平分线的方法，即可得到线段AC的垂直平分线DE；（2）根据Rt△ADE中，∠A=30°，AE=，即可求得a的值，最后化简T=（a+1）2﹣a（a﹣1），再求T的值．【解答】解：（1）如图所示，DE即为所求；（2）由题可得，AE=AC=，∠A=30°，∴Rt△ADE中，DE=AD，设DE=x，则AD=2x，∴Rt△ADE中，x2+（）2=（2x）2，解得x=1，∴△ADE的周长a=1+2+=3+，∵T=（a+1）2﹣a（a﹣1）=3a+1，∴当a=3+时，T=3（3+）+1=10+3．16．如图，已知△ABC，请用圆规和直尺作出△ABC的一条中位线EF（不写作法，保留作图痕迹）．【考点】N3：作图—复杂作图；KX：三角形中位线定理．【分析】作线段AB的垂直平分线得到AB的中点E，作AC的垂直平分线得到线段AC的中点F．线段EF即为所求．【解答】解：如图，△ABC的一条中位线EF如图所示，方法：作线段AB的垂直平分线得到AB的中点E，作AC的垂直平分线得到线段AC的中点F．线段EF即为所求．17．如图，已知△ABC，∠B=40°．（1）在图中，用尺规作出△ABC的内切圆O，并标出⊙O与边AB，BC，AC的切点D，E，F（保留痕迹，不必写作法）；（2）连接EF，DF，求∠EFD的度数．【考点】N3：作图—复杂作图；MI：三角形的内切圆与内心．【分析】（1）直接利用基本作图即可得出结论；（2）利用四边形的性质，三角形的内切圆的性质即可得出结论．【解答】解：（1）如图1，⊙O即为所求．（2）如图2，连接OD，OE，∴OD⊥AB，OE⊥BC，∴∠ODB=∠OEB=90°，∵∠B=40°，∴∠DOE=140°，∴∠EFD=70°．18．在数学课本上，同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程：已知：直线l和l外一点P求作：直线l的垂线，使它经过点P．作法：如图：（1）在直线l上任取两点A、B；（2）分别以点A、B为圆心，AP，BP长为半径画弧，两弧相交于点Q；（3）作直线PQ．参考以上材料作图的方法，解决以下问题：（1）以上材料作图的依据是：（3）已知，直线l和l外一点P，求作：⊙P，使它与直线l相切．（尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑）【考点】N3：作图—复杂作图；MD：切线的判定．【分析】（1）根据线段垂直平分线的性质，可得答案；（2）根据线段垂直平分线的性质，切线的性质，可得答案．【解答】解：（1）以上材料作图的依据是：线段垂直平分线上的点到线段两端点的距离相等，故答案为：线段垂直平分线上的点到线段两端点的距离相等；（2）如图．19．“直角”在初中几何学习中无处不在．如图，已知∠AOB，请仿照小丽的方式，再用两种不同的方法判断∠AOB是否为直角（仅限用直尺和圆规）．【考点】N3：作图—复杂作图；KS：勾股定理的逆定理；M5：圆周角定理．【分析】（1）根据勾股定理的逆定理，可得答案；（2）根据圆周角定理，可得答案．【解答】解：（1）如图1，在OA，OB上分别，截取OC=4，OD=3，若CD的长为5，则∠AOB=90°（2）如图2，在OA，OB上分别取点C，D，以CD为直径画圆，若点O在圆上，则∠AOB=90°．20．如图，已知正七边形ABCDEFG，请仅用无刻度的直尺，分别按下列要求画图．（1）在图1中，画出一个以AB为边的平行四边形；（2）在图2中，画出一个以AF为边的菱形．【考点】N3：作图—复杂作图；L5：平行四边形的性质；L8：菱形的性质．【分析】（1）连接AF、BE、CG，CG交AF于M，交BE于N．四边形ABNM是平行四边形．（2）连接AF、DF，延长DC交AB的延长线于M，四边形AFDM是菱形．【解答】解：（1）连接AF、BE、CG，CG交AF于M，交BE于N．四边形ABNM是平行四边形．（2）连接AF、DF，∠延长DC交AB的延长线于M，四边形AFDM是菱形．21．图①、图②、图③都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点．线段AB的端点在格点上．（1）在图①、图2中，以AB为边各画一个等腰三角形，且第三个顶点在格点上；（所画图形不全等）（2）在图③中，以AB为边画一个平行四边形，且另外两个顶点在格点上．【考点】N4：作图—应用与设计作图；KI：等腰三角形的判定；KK：等边三角形的性质；L6：平行四边形的判定．【分析】（1）根据等腰三角形的定义作图可得；（2）根据平行四边形的判定作图可得．【解答】解：（1）如图①、②所示，△ABC和△ABD即为所求；（2）如图③所示，▱ABCD即为所求．。

中考物理一轮复习讲义第6章机械运动考点知识梳理+例题+满分必练

第6章机械运动考点·梳理考点1 运动的描述1、机械运动：一个物体相对于另一个物体位置的变化,叫做机械运动。

2、运动和静止的相对性：参照物：在研究一个物体是运动还是静止时,必须选择一个假定不动的物体作为标准,这个被选作标准的物体叫做参照物。

运动和静止的相对性：一个物体是运动还是静止取决于所选的参照物。

考点2 运动的快慢1、物理意义：速度是表示物体运动快慢的物理量。

2、定义：速度等于运动物体在单位时间内所通过的路程的多少。

3、公式：v ＝st ,公式中的s 表示路程,t 表示时间,v 表示速度。

4、单位：国际单位：m/s,常用单位：km/h,1 m/s ＝3.6 km/h 。

5、在匀速直线运动中,物体的速度是一个恒定不变的量,与通过的路程和所用时间无关。

6、平均速度：平均速度用来描述做变速直线运动的物体的平均运动快慢,它的大小等于运动物体通过的路程与通过该段路程所用时间之比,即v ＝st ,式中s 表示总路程,t 表示总时间。

平均速度的大小与物体通过的路程及所用的时间有关。

平均速度只是大体上反映物体在一段路程中或一段时间内的平均快慢情况。

考点3 长度和时间的测量1、长度的单位：长度的国际单位是米(m),常用单位还有千米(km)、分米(dm)、厘米(cm)、毫米(mm)、微米(μm)、纳米(nm)等,它们之间的换算关系是：1 km ＝103m 1 dm ＝10－1m 1 cm ＝10－2m 1 mm ＝10－3m 1 μm＝10－6m 1 nm ＝10－9m2、正确使用刻度尺(1)使用刻度尺前,应观察：零刻度线是否磨损；刻度尺的量程；刻度尺的分度值。

(2)正确使用刻度尺使用刻度尺测量长度时：①刻度尺必须与被测线平行,不能歪斜；②刻度尺的刻度线要紧贴被测物体；③零刻度线磨损了的刻度尺,可以从其他刻度线测起； ④读数时,视线应与尺面垂直；正确记录测量结果：测量结果包括数值和单位。

3、误差；测量值与真实值之间的差异叫误差。

2020届中考历史一轮复习讲义(九年级上册第1单元)

2020届九年级历史一轮复习讲义（九年级上册）第一单元古代亚非文明【课程标准】1.知道金字塔，初步了解古埃及文明。

（识记）2.通过《汉谟拉比法典》，初步了解古代两河流域文明。

（识记）3.通过种姓制度和佛教的创立，初步了解古代的印度社会。

（识记）【考点要求】一、知道金字塔，初步了解古埃及文明。

（识记）1.古埃及文明（1）地理位置和自然环境：古埃及位于非洲东北角，世界上最长的河流贯穿埃及南北。

古埃及文明被认为是“尼罗河的赠礼”。

（2）兴衰历程:约从公元前3500年开始出现若干个小国家；公元前3100年左右，初步实现了统一；在新王国时代法老图特摩斯三世统治时期，埃及成为强大的军事帝国；公元前525年，波斯帝国吞并古埃及；后来，亚历山大帝国和罗马帝国先后占领古埃及，古埃及近3000年的文明没有延续下去。

（3）科学文化成就：是古埃及天文学的突出成就之一。

古埃及的象形文字是世界上最早的文字之一。

2.金字塔（1）用途：国王法老的。

金字塔的修建，反映了古埃及的无限权力。

（2）地位：是古埃及文明的象征，反映了古埃及发展的较高水平，是古埃及人智慧的结晶。

（3）法老的权力：法老作为全国最高的统治者，集军、政、财、神等大权于一身。

在宗教上，法老被认为是“”，具有无上的权威。

二、通过《汉谟拉比法典》，初步了解古代两河流域文明。

（识记）1.古代两河流域文明（1）范围：“两河”指西亚的幼发拉底河和底格里斯河，两河流域又称“”。

（2）建国：约从公元前3500年起,产生了一些以城市为中心的小国。

（3）统一：约公元前24世纪,实现了初步统一。

2.古巴比伦王国（1）统一：公元前18世纪，第六代国王完成了两河流域中下游地区的统一事业,建立了统一、强大的奴隶制国家。

（2）统治：实行君主专制制度，加强中央集权，制定了一部较为系统和完整的法典。

（3）影响：汉谟拉比在位时是古巴比伦王国最强盛的时期。

3.《汉谟拉比法典》（1）地位：是迄今已知世界上第一部较为完整的法典。

2020年中考数学一轮复习讲义(上海专版) 专题29 全等三角形(解析版)

专题29 全等三角形1、全等三角形的概念能够完全重合的两个图形叫做全等形。

能够完全重合的两个三角形叫做全等三角形。

两个三角形全等时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。

夹边就是三角形中相邻两角的公共边，夹角就是三角形中有公共端点的两边所成的角。

2、全等三角形的表示和性质全等用符号“≌”表示，读作“全等于”。

如△ABC≌△DEF，读作“三角形ABC全等于三角形DEF”。

注：记两个全等三角形时，通常把表示对应顶点的字母写在对应的位置上。

3、三角形全等的判定三角形全等的判定定理：(1)边角边定理：有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”)(2)角边角定理：有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”)(3)边边边定理：有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”)。

直角三角形全等的判定：对于特殊的直角三角形，判定它们全等时，还有HL定理(斜边、直角边定理)：有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”)【例1】(2019•上海)在△ABC 和△A 1B 1C 1中，已知∠C ＝∠C 1＝90°，AC ＝A 1C 1＝3，BC ＝4，B 1C 1＝2，点D 、D 1分别在边AB 、A 1B 1上，且△ACD ≌△C 1A 1D 1，那么AD 的长是．【分析】根据勾股定理求得AB ＝5，设AD ＝x ，则BD ＝5﹣x ，根据全等三角形的性质得出C 1D 1＝AD ＝x ，∠A 1C 1D 1＝∠A ，∠A 1D 1C 1＝∠CDA ，即可求得∠C 1D 1B 1＝∠BDC ，根据等角的余角相等求得∠B 1C 1D 1＝∠B ，即可证得△C 1B 1D ∽△BCD ，根据其性质得出5−x x =2，解得求出AD 的长．【解答】解：如图，∵在△ABC 和△A 1B 1C 1中，∠C ＝∠C 1＝90°，AC ＝A 1C 1＝3，BC ＝4，B 1C 1＝2， ∴AB =√32+42=5，设AD ＝x ，则BD ＝5﹣x ，∵△ACD ≌△C 1A 1D 1，∴C 1D 1＝AD ＝x ，∠A 1C 1D 1＝∠A ，∠A 1D 1C 1＝∠CDA ，∴∠C 1D 1B 1＝∠BDC ，∵∠B ＝90°﹣∠A ，∠B 1C 1D 1＝90°﹣∠A 1C 1D 1，∴∠B 1C 1D 1＝∠B ，∴△C 1B 1D 1∽△BCD ，∴BDC 1D 1=BC C 1B 1，即5−x x =2，解得x =53，∴AD 的长为53，故答案为53．【例2】(2019春•徐汇区校级期中)如图，BF ＝EC ，∠A ＝∠D ，那么要得到△ABC ≌△DEF ，可以添加一个条件(只需填上一个正确的条件．【分析】根据全等三角形的判定方法即可解决问题．【解答】解：∵BF ＝CE ，∴BC ＝EF ，∵∠A ＝∠D ，∴当∠B ＝∠E 或∠ACB ＝∠DFE 时，△ABC ≌△DEF ，故答案为∠B ＝∠E 或∠ACB ＝∠DFE【例3】(2019秋•浦东新区期末)已知：如图，△ABC 中，∠ABC ＝45°，AD ⊥BC ，BE ⊥AC 于D ，垂足分别为点D 、E ，AD 与BE 相交于点F ．求证：DF ＝DC ．【分析】证出△ABD 是等腰直角三角形，得出BD ＝AD ，证明△BDF ≌△ADC (ASA )，即可得出结论．【解答】证明：∵∠ABC ＝45°，AD ⊥BC ，∴△ABD 是等腰直角三角形，∴BD ＝AD ，∵BE ⊥AC ，∴∠C +DBF ＝∠C +DAC ＝90°，∴∠DBF ＝∠DAC ，在△BDF 和△ADC 中，{∠BDF =∠ADC =90°BD =AD ∠DBF =∠DAC，∴△BDF ≌△ADC (ASA )，∴DF ＝DC ．1．(2019春•普陀区期末)下列判定两个等腰三角形全等的方法中，正确的是()A．一角对应相等B．两腰对应相等C．底边对应相等D．一腰和底边对应相等【分析】依据全等三角形的判定定理回答即可．【解答】解：A．有一角对应相等，没有边的参与不能证明它们全等，故本选项不符合题意；B．两腰对应相等，第三边不一定对应相等，不符合全等的条件，故不能判定两三角形全等，故本选项不符合题意；C．只有底边相等，别的边，角均不确定，不符合全等的条件，故不能判定两三角形全等，故本选项不符合题意；D．一腰和底边对应相等，相当于两腰和底边对应相等，利用SSS可以证得两个等腰三角形全等，故本选项符合题意．故选：D．2．(2019春•普陀区期末)如图，已知△ABC≌△AEF，其中AB＝AE，∠B＝∠E．在下列结论①AC＝AF，②∠BAF＝∠B，③EF＝BC，④∠BAE＝∠CAF中，正确的个数有()A．1个B．2个C．3个D．4个【分析】根据全等三角形对应边相等，全等三角形对应角相等结合图象解答即可．【解答】解：∵△ABC≌△AEF，∴AC＝AF，EF＝BC，故①③正确；∠EAF＝∠BAC，∴∠EAB＝∠F AC，故④正确；∵AF≠BF，∴∠BAF≠∠B，故②错误；综上所述，结论正确的是①③④共3个．故选：C．3．(2018秋•普陀区期中)不能使△ABC≌△DEF必定成立是()A．AB＝DE，∠A＝∠D，∠C＝∠F B．AB＝DE，BC＝EF，∠B＝∠EC．AC＝DF，BC＝EF，∠A＝∠D D．AB＝DE，BC＝EF，CA＝FD【分析】根据全等三角形的判定方法即可判断；【解答】解：A、根据AAS即可判断；本选项不符合题意；B、根据SAS即可判断；本选项不符合题意；C、错误，SSA无法判断三角形全等；本选项符合题意；D、根据SSS即可判断，本选项不符合题意；故选：C．4．(2018春•金山区期末)如图，△ABC≌△AED，点D在BC边上，BC∥AE，∠CAB＝80°，则∠BAE的度数是()A．35°B．30°C．25°D．20°【分析】根据全等三角形的性质得到∠CAB＝∠DAE，由平行可知可得∠CDA＝800°，利用等腰三角形性质可知∠C＝∠CDA＝80°，推出∠CAD＝20°即可解决问题；【解答】解：∵△ABC≌△AED，∴∠CAB＝∠DAE＝80°，∵BC∥AE，∴∠CDA＝∠DAE＝80°∵AC＝AD，∴∠C＝∠ADC＝80°，∴∠CAD＝20°，∵∠CAB＝∠DAE，∴∠CAD＝∠BAE＝20°故选：D．5．(2019秋•静安区月考)如图，已知正方形ABCD中，E是AD的中点，BF＝CD+DF，若∠ABE为α，用含α的代数式表示∠CBF的度数是．【分析】延长BC至G，使得CG＝DF，连接FG交CD于H，判定△FDH≌△GCH(AAS)，即可得出FH ＝GH，DH＝CH，再判定△ABF≌△CBH(SAS)，即可得到∠ABF＝∠CBH＝α°，进而得出∠FBC＝2∠CBH＝2α°．【解答】解：如图，延长BC至G，使得CG＝DF，连接FG交CD于H，∵BF＝CD+DF，CD＝BC，∴BF＝BG，∵∠D＝∠HCG＝90°，∠DHF＝∠CHG，DF＝CG，∴△FDH≌△GCH(AAS)，∴FH＝GH，DH＝CH，∴等腰三角形BFG中，∠FBG＝2∠HBC，∵点E是AD中点，DH＝CH，∴AE＝CH，又∵∠A＝∠BCH，AB＝CB，∴△ABF≌△CBH(SAS)，∴∠ABF＝∠CBH＝α°，∴∠FBC＝2∠CBH＝2α°．故答案为：2α．6．(2019秋•浦东新区期中)如图，已知AB＝AC，AD＝AE，∠BAC＝∠DAE，∠BAD＝22°，∠ACE＝30°，则∠ADE＝．【分析】利用全等三角形的性质得出∠ABD＝∠2＝30°，再利用三角形的外角得出得出即可．【解答】解：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠1＝∠EAC，在△ABD和△ACE中，{AB=AC∠1=∠CAE AD=AE，∴△ABD≌△ACE(SAS)；∴∠ABD＝∠2＝30°，∵∠1＝22°，∴∠3＝∠1+∠ABD＝22°+30°＝52°，故答案为：52°7．(2019春•普陀区期末)如图，△ACE≌△DBF，如果∠E＝∠F，DA＝10，CB＝2，那么线段AB的长是．【分析】直接利用全等三角形的性质得出AB＝CD，进而求出答案．【解答】解：∵△ACE≌△DBF，DA＝10，CB＝2，∴AB＝CD=AD−BC2=10−224．故答案为：4．8．(2019秋•浦东新区期中)如图，点P是△ABC三个内角的角平分线的交点，连接AP、BP、CP，∠ACB＝60°，且CA+AP＝BC，则∠CAB的度数为．【分析】由角平分线的性质可得∠ABP+∠BAP＝60°，由“SAS”可证△ACP≌△BCP，可得AP＝PE，∠CAP＝∠CEP，可得PE＝BE，由等腰三角形的性质和外角性质可得∠P AB＝2∠PBA，即可求解．【解答】解：如图，在BC上截取CE＝AC，连接PE，∵∠ACB＝60°，∴∠CAB+∠ABC＝120°∵点P是△ABC三个内角的角平分线的交点，∴∠CAP＝∠BAP=12∠CAB，∠ABP＝∠CBP=12∠ABC，∠ACP＝∠BCP，∴∠ABP+∠BAP＝60°∵CA＝CE，∠ACP＝∠BCP，CP＝CP∴△ACP≌△ECP(SAS)∴AP＝PE，∠CAP＝∠CEP∵CA+AP＝BC，且CB＝CE+BE，∴AP＝BE，∴BE＝PE，∴∠EPB＝∠EBP，∴∠PEC＝∠EBP+∠EPB＝2∠PBE＝∠CAP∴∠P AB＝2∠PBA，且∠ABP+∠BAP＝60°，∴∠P AB＝40°，∴∠CAB＝80°故答案为：80°9．(2019春•浦东新区期末)如图，△ABC≌△DCB，A、B的对应顶点分别为点D、C，如果AB＝6cm，BC＝12cm，AC＝10cm，DO＝3cm，那么OC的长是cm．【分析】根据全等三角形的性质得到DB＝AC＝10cm，∠ABC＝∠DCB，∠DBC＝∠ACB，求出OB，根据等腰三角形的性质解答．【解答】解：∵△ABC≌△DCB，∴DB＝AC＝10cm，∠ABC＝∠DCB，∠DBC＝∠ACB，∴OB＝DB﹣DO＝7cm，∠OBC＝∠OCB，∴OC＝OB＝7cm，故答案为：7．10．(2018秋•嘉定区期末)在△ABC中，AB＝5，AC＝7，AD是BC边上的中线，则AD的取值范围是．【分析】作出图形，延长中线AD到E，使DE＝AD，利用“边角边”证明△ACD和△EBD全等，根据全等三角形对应边相等可得AC＝BE，然后根据三角形任意两边之和大于第三边，两边之差小于第三边求出AE的范围，再除以2即可得解．【解答】解：如图，延长中线AD到E，使DE＝AD，∵AD是三角形的中线，∴BD＝CD，在△ACD和△EBD中，∵{BD=CD∠BDE=∠ADC DE=AD，∴△ACD≌△EBD(SAS)，∴AC＝BE，∵AB＝5，BE＝AC＝7，∴7﹣5＜2AD＜7+5，即2＜2x＜12，∴1＜AD＜6．故答案为：1＜AD＜6．11．(2019秋•虹口区校级月考)如图，CD 是经过∠BCA 顶点C 的一条直线，且直线CD 经过∠BCA 的内部，点E ，F 在射线CD 上，已知CA ＝CB 且∠BEC ＝∠CF A ＝∠α．(1)如图1，若∠BCA ＝80°，∠α＝100°，问EF ＝BE ﹣AF ，成立吗？说明理由．(2)将(1)中的已知条件改成∠BCA ＝∠β，∠α+∠β＝180°(如图2)，问EF ＝BE ﹣AF 仍成立吗？说明理由．【分析】(1)根据“AAS ”可以证明△BCE ≌△CAF ，则BE ＝CF ；(2)同理证明△BCE ≌△CAF ，则CE ＝AF ，BE ＝CF ，可得EF ＝CE ﹣CF ＝BE ﹣AF ．【解答】解：(1)EF ＝BE ﹣AF 成立，理由如下：∵∠BCA ＝80°(已知)，∴∠BCE +∠ACE ＝80°∵∠BEC ＝∠α＝100°(已知)，∴∠BEF ＝180°﹣100°＝80°(平角定义)．∴∠B +∠BCE ＝80°(三角形外角和定理)∴∠B ＝∠ACE (等量代换)．在△BCE 和△CAF 中，{∠B =∠ACF ∠BEC =∠CFA CB =AC，∴△BCE ≌△CAF (AAS )，∴BE ＝CF ，AF ＝EC (全等三角形对应边相等)．∴EF ＝CF ﹣CE ＝BE ﹣AF (等量代换)．(2)EF ＝BE ﹣AF 成立，理由如下：∵∠BCA ＝∠β，∴∠BCE +∠ACE ＝∠β∵∠BEC ＝∠α＝180°﹣∠β，∴∠BEF ＝180°﹣∠α＝∠β．∴∠B +∠BCE ＝∠β．∴∠B ＝∠ACE在△BCE 和△CAF 中，{∠B =∠ACF ∠BEC =∠CFA CB =AC，∴△BCE ≌△CAF (AAS )．∴BE ＝CF ，AF ＝EC ，∴EF ＝CF ﹣CE ＝BE ﹣AF ．12．(2019秋•浦东新区期中)已知：如图所示，AB ＝BC ，AD 为△ABC 中BC 边的中线，延长BC 至E 点，使CE ＝BC ，连接AE ．求证：∠DAC ＝∠CAE ．【分析】延长AD 到F ，使得DF ＝AD ，连接CF ．证明△ACF ≌△ACE 即可解决问题．【解答】解：延长AD 到F ，使得DF ＝AD ，连接CF ．∵AD ＝DF ，∠ADB ＝∠FDC ，D ＝DC ，∴△ADB ≌△FDC (SAS )，∴AB ＝CF ，∠B ＝∠DCF ，∵BA ＝BC ，CE ＝CB∴∠BAC ＝∠BCA ，CE ＝CF ，∵∠ACE ＝∠B +∠BAC ，∠ACF ＝∠DCF +∠ACB ，∴∠ACF ＝∠ACE ，∵AC ＝AC ，∴△ACF ≌△ACE (SAS )，∴∠CAD ＝∠CAE ．13．(2019春•长宁区期末)如图，已知AD 是△ABC 的一条中线，延长AD 至E ，使得DE ＝AD ，连接BE ．如果AB ＝5，AC ＝7，试求AD 的取值范围．【分析】根据SAS 即可证明△BED ≌△CAD ．在△ABE 利用三边关系定理即可解决．【解答】解：∵AD 是△ABC 的一条中线，∴BD ＝CD ，在△BED 和△CAD 中，{BD =CD∠BDE =∠ADC ED =AD，∴△BED ≌△CAD (SAS )，∴BE ＝AC ＝5，∵AB ＝7，∴2＜AE ＜12，∴2＜2AD ＜12，∴1＜AD ＜6．14．(2019春•长宁区期末)如图，在△ABC 中，AD ⊥BC ，垂足为D ，BE ⊥AC ，垂足为E ，AD 与BE 相交于F ，(1)∠DAC 与∠EBC 相等吗？为什么？(2)如果∠BAC ＝45°，请说明△AEF ≌△BEC 的理由；(3)如果∠BAC ＝45°，AF ＝2BD ，试说明AD 平分∠BAC 的理由．【分析】(1)由垂直的定义得到∠ADC＝90°，求得∠DAC＝90°﹣∠C，于是得到结论；(2)根据三角形的内角和得到∠ABE＝180°﹣∠BEA﹣∠BAE＝45°，求得BE＝AE，根据全等三角形的判定定理即可得到结论；(3)根据已知条件得到BC＝2BD，由D是BC的中点，得到BD＝CD，于是得到结论．【解答】解：(1)相等，理由：∵AD⊥BC，∴∠ADC＝90°，∴∠DAC+∠C＝90°，∴∠DAC＝90°﹣∠C，∴∠DAC＝∠EBC；(2)∵∠BEA＝90°，∠BAE＝45°，∴∠ABE＝180°﹣∠BEA﹣∠BAE＝45°，∴∠ABE＝∠BAE，∴BE＝AE，在△AEF与△BEC中，{∠EAF=∠EBC ∠AEF=∠BEC AE=BE，∴△AEF≌△BEC(AAS)；(3)由(2)知，AF＝BC，∵AF＝2BD，∴BC＝2BD，∴D是BC的中点，∴BD＝CD，∵AD⊥BC，∠BAD＝∠CAD=12∠BAC，∴AD平分∠BAC．。

第02讲词语理解运用(讲义)-2024年中考语文一轮复习讲练测(原卷版)

专题一积累与运用第02讲词语理解运用目录一、考情分析 (2)【课标要求】 (2)【考查重点】 (2)【主要题型】 (2)【命题趋势】 (2)【备考策略】 (3)二、知识建构 (3)考向1：成语使用的辨析 (4)考向2：辨析和选用近义词 (5)考向3：正确使用关联词语 (6)考向4：熟语、歇后语的使用 (7)三、方法总结 (7)如何正确辨析和选用近义词 (7)如何判断成语是否误用 (8)四、考场练兵 (9)【课标要求】1.在社会生活中能根据字音、字形、字义三者的关系准确认读、正确理解遇到的生字新词。

2.发现并积累不同语境下具有个性化特征的词句和段落，能根据自己的表达需要和习惯选择使用。

3.按照一定的标准分类整理学过的字词句篇等语言材料，梳理、反思自己语文学习的经验，努力提高语言文字运用能力，增强表达效果。

4.随文学习基本的词汇、语法知识，用以帮助理解课文中的语言难点5.在通读课文的基础上，理清思路，理解、分析主要内容，体味和推敲重要词句在语言环境中的意义和作用。

【考查重点】1.词语（成语）在具体语境中的理解与运用；2.辨析近义词语（成语）；3.词语（成语）感情色彩或语体色彩的恰当运用；4.了解、掌握成语典故、熟语；5.关联词语的正确运用。

【主要题型】1.客观选择题2.语段综合填空3.语段综合选择【命题趋势】词语、成语题主要考查考生理解词语、成语的含义，在具体的语言环境中正确选择词语、成语的能力以及运用词语、成语写话的能力。

考查所选用的语料涉及最新热点话题、新闻时事、富含哲理的片段、优美的散文等。

成语考查一般以选择题的形式出现，所考成语一般都是初中阶段语文课文中出现过的、应知应会的成语；词语的考查一般以选词填空的形式出现，备选的词语一般是近义词或者感情色彩不同的词语。

根据对近几年试题的分析，试卷中考查运用词语（成语）的题型大部分以选择题的形式考查，较少部分以主观题的考查形式。

实际上，在众多中考试卷中，许多考查点并不是孤立的，有时候会综合考查多个考点，需要我们答题时注意。

中考化学一轮复习酸和碱的中和反应(讲义及答案)及答案

中考化学一轮复习酸和碱的中和反应(讲义及答案)及答案一、选择题1．“盐酸化性乌龟壳，一头一尾四只脚”——如图是小王归纳的稀盐酸的化学性质，X 的物质类别与图中其他物质不同，则物质X 是下列物质中的（）A ．硝酸钾B ．氧化铜C ．碳酸钙D ．氢氧化钾解析：C【解析】根据题意，X 的物质类别与图中其他物质不同；A ．硝酸钾不与稀盐酸反应，故A 错误；B ．氧化铜能与稀盐酸反应，与氧化铁均属于金属氧化物，故B 错误；C ．碳酸钙能与盐酸反应生成氯化钙、水和二氧化碳，且碳酸钙属于盐，故C 正确；D ．氢氧化钾能与稀盐酸反应，属于碱，与氢氧化钠类别相同，故D 错误；故选C 。

2．下列化学反应属于复分解反应是（） A ．CH 4+2O 2点燃CO 2+2H 2O B ．3Fe+2O 2点燃Fe 3O 4C ．NaOH+HCl ═NaCl+H 2OD ．H 2CO 3═CO 2↑+H 2O解析：C 【解析】【详解】A 、CH 4+2O 2===点燃CO 2+2H 2O ，该反应的反应物中氧气是单质，不是两种化合物相互交换成分生成两种新的化合物的反应，不属于复分解反应，故不符合题意；B 、3Fe+2CO 2===点燃Fe 3O 4，该反应符合“多变一”的特征，属于化合反应，故不符合题意； C 、NaOH+HCl ═NaCl+H 2O ，该反应是两种化合物相互交换成分生成两种新的化合物的反应，属于复分解反应，故符合题意；D 、H 2CO 3═CO 2↑+H 2O ，该反应符合“一变多”的特征，属于分解反应，故不符合题意；故选C 【点睛】掌握复分解反应的特征（换成分，价不变）是正确解析本题的关键。

3．下列应用与中和反应原理无关的是 A ．用浓硫酸干燥湿润的氧气 B ．用熟石灰改良酸性土壤C ．服用含氢氧化铝的药物治疗胃酸过多D．用氢氧化钠溶液洗涤石油产品中的残留硫酸解析：A【解析】【分析】【详解】A、浓硫酸具有吸水性，且不与氧气反应，用浓硫酸干燥湿润的氧气，是利用的浓硫酸具有吸水性，属于物理变化，不属于中和反应，故选项正确．B、熟石灰是氢氧化钙的俗称，与酸性土壤中的酸反应生成盐和水，属于中和反应，故选项错误．C、Al（OH）3与胃液中的盐酸反应生成氯化铝和水，该反应是酸与碱反应生成盐和水的反应，属于中和反应，故选项错误．D、NaOH溶液与硫酸反应生成硫酸钠和水，该反应是酸与碱反应生成盐和水的反应，属于中和反应，故选项错误．故选A．4．下列各组物质，在pH=1的溶液中能大量共存，且形成无色溶液的是( )A．NaNO3 HCl Na2SO4B．NaNO3 NaCl CuSO4C．CaCl2 Na2SO4 Na2CO3D．NaOH BaCl2 NaSO4解析：A【解析】pH为1的水溶液显酸性，水溶液中含有大量的H+；A、三者之间不反应，能在酸性溶液中共存，且不存在有色离子，故选项正确；B、三者之间不反应，且能在酸性溶液中共存，但CuSO4溶于水呈黄色，故选项错误；C、Na2CO3中的碳酸根离子和H+在溶液中能结合生成水和二氧化碳，不能大量共存，故选项错误；D、BaCl2、Na2SO4在溶液中相互交换成分生成不溶于酸的硫酸钡沉淀，NaOH中的氢氧根离子和H+在溶液中能结合生成水，不能大量共存，故选项错误。

2023年中考苏科版数学一轮复习专题讲义与练习-图形的相似

2023年中考数学一轮复习专题讲义与练习图形的相似［课标要求］1.了解线段的比，成比例线段，了解比例的基本性质.2.了解黄金分割.3.了解相似三角形、相似多边形及相似比的概念.4.熟练掌握相似三角形的判定和性质.5.了解平行投影，理解在平行光线的照射下物高与影长的关系.6.了解中心投影，理解在点光源的照射下，物高与影长的关系7.了解位似图形及其有关概念，了解位似与相似的联系和区别，掌握位似图形的性质.画法，能够利用作位似图形的方法将一个图形放大或缩小．［要点梳理］1.比例线段：在四条线段a.b.c.d 中，如果其中两条线段的比等于另外两条线段的比即dc b a =（或a ：b ＝c ：d ）,那么这四条线段a.b.c.d 叫做成比例线段,简称比例线段. 在比例式dc b a =（或a ：b ＝b ：c ）中，a.b.c.d 称为比例的＿＿＿＿＿，a.d 为比例＿＿＿＿＿，b.c 称为比例＿＿＿＿＿，在比例式dc b a =（或a ：b ＝c ：d ）当b ＝c 时，b 叫做a 和d 的比例＿＿＿＿2.黄金分割：点C 把线段AB 分成两条线段AC 和BC （AC ＞BC ）且使AC 是AB 和BC 的比例中项，叫做把线段AB 黄金分割（点C 叫做线段的黄金分割点，AC ＝215-AB≈0.618AB ）（口诀：两式两点三个数，两种判法会画图） 3.＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿是相似图形.4.＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿叫做相似三角形.5.＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿叫做相似比.6.相似三角形的判定方法：（1）若DE ∥BC （A 型和X 型）则△ADE ∽△ABC（2）射影定理：若CD 为Rt △ABC 斜边上的高（双垂直三角形）则Rt △ABC ∽Rt △ACD ∽Rt △CBD 且AC 2=________，CD 2=_______，BC 2=__ ___；（3）两个角对应相等的两个三角形__________；（4）两边对应成_________且夹角相等的两个三角形相似；（5）三边对应成比例的两个三角形___________．7.相似三角形的性质：（1）相似三角形的对应边_________，对应角________．（2）相似三角形的对应角平分线，对应边的________线，对应边上的_______•线的比等于_______比，周长之比也等于________比.（3）相似三角形的面积比等于_________的平方．8.平行投影：在平行光的照射下，物体所产生的影.9.中心投影：在点光源的照射下，物体所产生的影.10.视点：眼睛的位置；视线：由视点发出的线；盲区：由于遮挡眼睛看不到的地方.11.在平行光照射下，在同一时刻不同物体的物高与影长成比例.12.（1）位似多边形：两个多边形的顶点A 与A’.B 与B’.C 与C’所在的直线都经过同一点O ，并且...'''OCOC OB OB OA OA ==，像这样的两个多边形叫做位似多边形，这个点O 叫做位似中心，这时的相似比又称为位似比．（2）掌握位似多边形概念，需注意：①两个图形是位似图形，根据定义可以证明它们也是相似图形，而相似图形不一定是位似图形；②两个位似图形的位似中心只有一个；③两个位似图形可能位于位似中心的两侧，也可能位于位似中心的一侧；④位似比就是相似比．利用位似图形的定义可判断两个图形是否位似．（3）位似多边形首先是相似图形，所以它具有相似图形的一切性质．位似图形是一种特殊的相似图形，它又具有特殊的性质，位似图形上任意一对对应点到位似中心的距离的比等于位似比（相似比）．（4）两个位似多边形的主要特征是：①对应顶点的连线都经过位似中心；②对应边互相平行（或在同一条直线上）．（5）利用位似，可以将一个图形放大或缩小，作图时要注意:①首先确定位似中心，若要自己确定，位似中心的位置可随意选择；②确定原图形的关键点，如四边形有四个关键点，即它的四个顶点；③确定位似比，根据位似比的取值，可以判断是将一个图形放大还是缩小；④符合要求的图形不惟一，因为所作的图形与所确定的位似中心的位置有关，并且同一个位似中心的两侧各有一个符合要求的图形．［强化训练］一、选择题1.若两个图形中，对应点到位似中心的线段比为2：3，则这两个图形的位似比为（）A ．2：3B ．4：9C ．：D ．1：2 2.△ABC 的三边长分别为2.6.2，△A'B'C'的两边长分别为1和3，如果△ABC ∽△A'B'C'，那么△A'B'C'的第三边长应为（）3.如图，在△ABC 中，点D.E 分别在AB.AC 边上，DE ∥BC ，若AD ：AB ＝3：4，AE ＝6，则AC 等于（）A ．3B ．4C ．6D ．8第3题图第4题图4.如图,AB 是斜靠在墙上的长梯,梯脚B 距墙脚1.6m,梯上点D 距墙1.4m,BD 长0.55m,则梯子的长为（）A.3.85mB.4.00mC.4.40mD.4.50m5.如图，在△ABC 中，点D.E.F 分别是边AB.AC.BC 上的点，DE ∥BC ，EF ∥AB ，且AD ∶DB = 3∶5，那么CF ∶CB 等于（）A ．5∶8B ．3∶8C ．3∶5D ．2∶56.如图，点D 在△ABC 的边AC 上，要判断△ADB 与△ABC 相似，添加一个条件，不正确的是（）A ．∠ABD ＝∠CB ．∠ADB ＝∠ABC C ．CD CB BD AB = D ．ACAB AB AD = F E AB C D 第5题第6题第7题7.如图，DE 是△ABC 的中位线，F 是DE 的中点，CF 的延长线交AB 于点G ，则AG ：GD 等于（）A ．2：1B ．3：1C ．3：2D ．4：3二、填空题8.若0234x y z ==≠，则23x y z+= ． 9.已知线段AB ＝20cm ，C 是线段AB 的黄金分割点且AC ＞BC ，则AC ＝＿＿＿cm10.如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3.4及x ，那么x 的值为＿＿＿＿＿.11.在△ABC 中，若∠AED ＝∠B ，DE ＝6，AB ＝10，AE ＝8，则BC 长为。

中考数学一轮综合复习同步讲义(第11课勾股定理)

第11课勾股定理⎪⎪⎩⎪⎪⎨⎧勾股定理逆定理：，，，，，勾股组数：勾股定理：勾股定理中考真题练习 1.如图,在边长为1个单位长度的小正方形组成的网格中,点A 、B 都是格点,则线段AB 长度为（）A.5B.6C.7D.25第1题图第2题图第3题图2.如图,在Rt ΔABC 中,∠ACB=900,BC=3,AC=4,AB 的垂直平分线DE 交BC 延长线于E,则CE 长为（）A.32B.76C.256D.23.如图,在正三角形ABC 中,D,E,F 分别是BC,AC,AB 上的点,DE ⊥AC,EF ⊥AB,FD ⊥BC,则ΔDEF 的面积与ΔABC 的面积之比等于（）A.1:3B.2:3C.3:2D.3:34.下列各三角形中，面积为无理数的是（）5.如图,△ABC 的顶点A 、B 、C 在边长为1的正方形网格的格点上，BD ⊥AC 于点D.则BD 的长为（）A.532B.543C.554D.553 第5题图第6题图第7题图6.如图,在Rt △ABC 中,∠ACB=900，D 是AB 中点,且CD=25,若Rt △ABC 面积为1,则它的周长为（） A.215+ B.15+ C.25+ D.35+ 7.如图,O ⊙的直径AB 垂直弦CD 于P,且P 是半径OB 的中点,CD=6cm,则直径AB 的长是（）A.3cmB.32cmC.42cmD.43cmADB E C8.如图,已知△ABC 中,AB=17,AC=10,BC 边上的高AD=8,则边BC 的长为（）A.21B.15C.6D.以上答案都不对第8题图第9题图第10题图9.如图,点A 的坐标是(2,2),若点P 在x 轴上,且△APO 是等腰三角形,则点P 的坐标不可能．．．是（） A.(4，0) B.(1,0） C.)0,22(- D.(2,0）10.如图,已知△ABC 中,∠ABC=900,AB=BC,三角形的顶点在相互平行的三条直线l 1，l 2，l 3上,且l 1，l 2之间的距离为2,l 2，l 3之间的距离为3,则AC 的长是（）A.172B.52C.24D.711.在△ABC 中,若AB=AC=15,BC=24,若P 是△ABC 所在平面内的点,且PB=PC=20，则AP 长为（）A.7B.5C.7或25D.5或14 12.我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示），如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a 和b,那么2)(b a +的值为（）A.49B.25C.13D.1第12题图第13题图第14题图13.将一个有450角的三角板的直角顶点放在一张宽为3cm 的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成300角,如图,则三角板的最大边的长为（）A.3cmB.6cmC.23cmD.26cm14.一渔船在海岛A 南偏东200方向的B 处遇险,测得海岛A 与B 的距离为20海里,渔船将险情报告给位于A 处的救援船后，沿北偏西800方向向海岛C 靠近.同时,从A 处出发的救援船沿南偏西100方向匀速航行.20分钟后,救援船在海岛C 处恰好追上渔船,那么救援船航行的速度为（）A.310海里/小时B.30海里/小时C.320海里/小时D.330海里/小时15.如图,Rt △ABC 中,∠ACB=900，∠ABC=600，BC=2cm,D 为BC 的中点,若动点E 以1cm/s 的速度从A 点出发,沿着A →B →A 的方向运动,设E 点的运动时间为t 秒（0≤t ＜6），连接DE ，当△BDE 是直角三角形时，t 的值为（）A.2B.2.5或3.5C.3.5或4.5D.2或3.5或4.5第15题图第16题图16.如图,在等腰直角△ABC 中,∠ACB=900,O 是斜边AB 的中点,点D 、E 分别在直角边AC 、BC 上,且∠DOE=900，DE 交OC 于点P.则下列结论：（1）图形中全等的三角形只有两对；（2）△ABC 的面积等于四边形CDOE 面积的2倍；（3）2CD CE OA +=；（4）222AD BE OP OC +=⋅．其中正确的结论有（）A.1个B.2个C.3个D.4个17.已知直角三角形的两边的长分别是3和4，则第三边长为18.若直角三角形两直角边长为a 、b,且满足04962=-++-b a a ,则该直角三角形斜边长为．19.如图,△ABC 中,CD ⊥AB 于D,E 是AC 的中点.若AD=6,DE=5,则CD 的长等于．第19题图第20题图第21题图20.如图,D 是△ABC 内一点,BD ⊥CD,AD=6,BD=4,CD=3,E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点,则四边形EFGH 的周长是．21.如图,在边长为1的等边△ABC 中,中线AD 与中线BE 相交于点O ，则OA 长度为．22.等腰三角形一腰上的高与另一腰的夹角为300，腰长为4cm,则其腰上的高为 cm ．23.等腰△ABC 中,AB=AC=10cm,BC=12cm,则BC 边上的高是 cm ．24.在△ABC 中，AB=AC=12cm ，BC=6cm,D 为BC 的中点，动点P 从B 点出发，以每秒1cm 的速度沿B A C →→的方向运动.设运动时间为t ，那么当t= 秒时，过D 、P 两点的直线将△ABC 的周长分成两个部分，使其中一部分是另一部分的2倍．25.如图，四边形ABCD中，AB∥DC，∠B=900，连接AC，∠DAC=∠BAC．若BC=4cm，AD=5cm，则AB= cm．第25题图第26题图第27题图26.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点 F.若BC=2,则DE+DF=_____________．27.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大正方形M的边长是3，则正方形A、B、C、D、E、F的面积之和是．28.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=900，AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为29.种盛饮料的圆柱形杯（如图），测得内部底面半径为2.5cm，高为12cm，吸管放进杯里，杯口外面至少要露出4.6cm，问吸管要做 cm.第29题图第30题图第31题图第32题图30.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处.另一只爬到树顶D 后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高_________米.31.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=5,则CE2+CF2=＿＿＿32.如图,AB=5,AC=3,BC边上的中线AD=2,则△ABC的面积为______33.在平面直角坐标系中，已知点)0,5( A ，)0,5(A ，点C 在坐标轴上,且AC+BC=6,写出满足条件的所有点C 的坐标．34.如图,水池中离岸边D 点1.5米的C 处,直立长着一根芦苇,出水部分BC 的长是0.5米,把芦苇拉到岸边,它的顶端B 恰好落到D 点,并求水池的深度AC.35.如图,△ABC 中,AB=AC=20,BC=32,D 是BC 上一点,且AD ⊥AC,求BD 的长．36.如图,△ABC 的三边分别为AC=5,BC=12,AB=13,将△ABC 沿AD 折叠，使AC 落在AB 上，求折痕AD 的长．37.如图,已知四边形ABCD 中,AB ⊥BC,AB=1,BC=2,CD=2,AD=3.求四边形ABCD 的面积．38.如图,△ABC 中,∠B=450,∠C=300,AB=2.求AC 的长．39.在450的Rt △ABC 中,∠A=900，DE ⊥BC,BD 是∠ABC 的平分线,且BD=13,AB=12.求△DEC 的周长.40.如图,Rt △ABC 中,∠ACB=900．在AB 的同侧分别以AB 、BC 、AC 为直径作三个半圆.图中阴影部分的面积分别记作为S 1和S 2．（1）求证：S 1+S 2=S △ABC ；（2）若Rt △ABC 的周长是62 ，斜边长为2,求图中阴影部分面积的和．41.已知a,b,c 为△ABC 三边,且满足a 2+b 2+c 2+338=10a+24b+26c.试判断△ABC 的形状．42.在某段限速公路BC 上(公路视为直线)，交通管理部门规定汽车的最高行驶速度不能超过60千米/时 (即350米/秒)，并在离该公路100米处设置了一个监测点 A.在如图所示的直角坐标系中,点A 位于y 轴上,测速路段BC 在x 轴上,点B 在A 的北偏西600方向上,点C 在A 的北偏东450方向上,另外一条高等级公路在y 轴上,AO 为其中的一段． (1)求点B 和点C 的坐标；(2)一辆汽车从点B 匀速行驶到点C 所用的时间是15秒,通过计算,判断该汽车在这段限速路上是否超速?(3)若一辆大货车在限速路上由C 处向西行驶，一辆小汽车在高等级公路上由A 处向北行驶，设两车同时开出且小汽车的速度是大货车速度的2倍，求两车在匀速行驶过程中的最近距离是多少?第11课勾股定理测试题日期：月日满分：100分时间：20分钟姓名：得分：1.下列四组线段中，可以构成直角三角形的是（）A．4，5，6 B． 1.5，2，2.5 C．2，3，4 D．1，2，32.一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（）A.165°B.120°C.150°D.135°第2题图第3题图第4题图3.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行（）A.8米B.10米C.12米D.14米4.如图,在Rt△ABC中,∠ACB=900，BD平分∠ABC.若CD=3,BC+AB=16,则△ABC的面积为（）A.16B.18C.24D.325.如图,AC=AD,BC=BD,则有（）A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB第5题图第6题图第7题图第8题图6.如图,⊙O的弦AB=6,M是AB上任意一点,且OM最小值为4,则⊙O的半径为（）A.5B.4C.3D.27.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的两条直角边的长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上）,则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是( )A.12B.14C.15D.1108.如图,△ABC中,AB=AC=6,BC=8,AE平分么BAC交BC于点E,点D为AB的中点,连结DE,则△BDE的周长是( )A.7+5B.10C.4+25D.129.如图,等腰△ABC 中,AB=AC,AD 是底边上的高,若AB=5,BC=6,则AD= cm ．第9题图第10题图第11题图第12题图10.如图,在平面直角坐标系中,点A,B 的坐标分别为（-6,0）、（0,8）.以点A 为圆心,以AB 长为半径画弧,交x 正半轴于点C,则点C 的坐标为 .11.长为4m 的梯子搭在墙上与地面成450角,作业时调整为600角（如图所示），则梯子的顶端沿墙面升高了 m ．12.如图,直线l 上有三个正方形a,b,c,若a,c 的面积分别为5和11,则b 的面积为．13.如图,OP=1,过P 作PP 1⊥OP,得OP 1=2;再过P 1作P 1P 2⊥OP 1且P 1P 2=1,得OP 2=3;又过P 2作P 2P 3⊥OP 2且P 2P 3=1,得OP 3=2；…依此法继续作下去,得OP 2015= ．14.如图，Rt △ABC 中,∠C=900，AD 平分∠CAB,DE ⊥AB 于E,若AC=6,BC=8,CD=3．（1）求DE 的长；（2）求△ADB 的面积．15.如图,AB 为一棵大树,在树上距地面10m 的D 处有两只猴子,它们同时发现地面上的C 处有一筐水果,一只猴子从D 处上爬到树顶A 处,利用拉在A 处的滑绳AC,滑到C 处,另一只猴子从D 处滑到地面B,再由B 跑到C,已知两猴子所经路程都是15m,求树高AB.16.如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB=∠ECD=900,D 为AB 边上一点.求证：（1）ACE BCD △≌△；（2）222AD DB DE +=．。

2024年中考化学一轮复习讲义专题08盐、化肥(解析版)

专题08 盐化肥目录1考点一常见的盐 4【夯基·必备基础知识梳理】 4一、盐的概念和分类 4二、盐的溶解性 4三、氯化钠 4四、粗盐的提纯 5五、碳酸盐 7【提升·必考题型归纳】 8考向01盐的俗称、性质和用途 8考向02碳酸钠、碳酸氢钠和碳酸钙 9考向03 粗盐的提纯 12考点二盐的化学性质 15【夯基·必备基础知识梳理】 15一、盐跟某些金属的反应： 15二、盐跟酸的反应： 15三、盐跟碱的反应： 16四、盐跟另一种盐的反应： 16五、盐的特性 16【提升·必考题型归纳】 16考向01 盐的化学性质 16考向02 联合制碱法(侯氏制碱法) 18考向03 离子的检验 22考向04 酸碱盐的综合探究 24考点三复分解反应 28【夯基·必备基础知识梳理】 28一、概念 28二、通式 28三、复分解反应的判断 28四、常见复分解反应类型 28五、复分解反应发生的条件 28【提升·必考题型归纳】 29考向01 复分解反应及其应用 29考向02 物质的转化 31考点四化学肥料 33【夯基·必备基础知识梳理】 33一、化学肥料概念 33二、常见的化学肥料 34三、化肥的鉴别 35四、化肥的鉴别 36【提升·必考题型归纳】 37考向01 化学肥料及作用 37考向02 化肥的鉴别 37考点五离子共存 42【夯基·必备基础知识梳理】 42一、离子共存 42二、不能共存的离子对 42【提升·必考题型归纳】 43考向01 离子共存 43考向02 酸碱盐反应的实质 45考点要求课标要求命题预测常见的盐➢掌握盐的概念和分类方法。

➢了解食盐、纯碱、小苏打、碳酸钙等盐的组成及在日常生活中的应用。

➢掌握粗盐提纯的原理、方法和操作步骤。

盐的概念和分类、常见的盐的用途、复分解反应的判断、离子共存的判断、粗盐的提纯实验细节、化肥种类及作用等考点常以选择题的形式进行考查，考查的命题点有：常见的盐的种类判断、酸碱盐之间反应的现象、反应类型的判断、离子能否共存的判断等。

河北省2020届中考数学一轮复习讲义1.第一节多边形

第五章四边形第一节多边形基础过关1.（2019河北省二模）下列图形中，内角和与外角和相等的多边形是（）2.（2019甘肃省卷）如图，足球图片正中的黑色正五边形的内角和是（）A. 180°B. 360°C. 540°D. 720°第2题图3.（2019福建）已知正多边形的一个外角等于36°，则该正多边形的边数为（）A. 12B. 10C. 8D. 64.（2019河池）如图，在正六边形ABCDEF中，AC＝23，则它的边长是（）A. 1B. 2C. 3D. 2第4题图5.如图，在五边形ABCDE中，∠A＋∠B＋∠E＝300°，DP、CP分别平分∠EDC，∠BCD，则∠P的度数是（）A. 60°B. 65°C. 55°D. 50°第5题图6.（2019石家庄新华区质量检测）如图，将正五边形ABCDE沿逆时针方向绕其顶点A旋转，若使点B 落在AE边所在的直线上，则旋转的角度可以是（）A. 72°B. 54°C. 45°D. 36°第6题图7.（2019保定高阳县演练）两个完全相同的正五边形都有一边在直线l上，且有一个公共顶点O，其摆放方式如图所示，则∠AOB＝（）A. 36°B. 72°C. 108°D. 144°第7题图8. 正方形ABCD与正五边形EFGHM的边长相等，初始位置如图所示．将正方形绕点F顺时针旋转使得BC与FG重合，再将正方形绕点G顺时针旋转使得CD与GH重合，…，按这样的方式将正方形依次绕点H，M，E旋转后，正方形中与EF重合的边是（）A. ABB. BCC. CDD. DA第8题图9.（2019廊坊安次区二模）把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合，按照如图所示的方式叠放在一起，延长LG交AF于点P，则∠APG＝（）A. 141°B. 144°C. 147°D. 150°第9题图10.（2018廊坊三中一模）一个多边形截去一个角后，形成另一个多边形的内角和为2520°，则原多边形的边数是（）A. 17B. 16C. 15D. 15或16或1711. 如图，线段AB是正八边形的一边，在正八边形的外部以AB为边作正六边形，点C、D分别为正八边形与正六边形的中心，则∠CAD的度数为（）A. 120°B. 125°C. 127.5°D. 130°第11题图12.（2019河北中考说明）在地面上，某一点周围有a个正三角形、b个正十二边形（a，b均不为0）恰能铺满地面，则a＋b＝______．13.（2019宜宾）如图，六边形ABCDEF的内角都相等，AD∠BC，则∠DAB＝________°.第13题图14.（2019株洲）如图所示，过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的角平分线相交于点P，且∠ABP＝60°，则∠APB＝______度．第14题图15.（2019石家庄十八县联考二）如图，含30°角的直角三角板的直角边AC，BC分别经过正八边形的两个顶点，则图中∠1＋∠2＝________.第15题图16.（人教九上P108习题24.3T5改编）如图，要拧开一个边长a＝12 mm的六角形螺帽，扳手张开的开口b至少为________ mm.第16题图17.（2019徐州）如图，A、B、C、D为一个外角为40°的正多边形的顶点，若O为正多边形的中心，则∠OAD＝________°.第17题图18. 如图，正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′，旋转角为α（0°≤α≤90°），若DE∠B′C′，则α＝________°.第18题图能力提升1.（2019邢台二模）如图，点P、M、N分别是边长为2的正六边形中不相邻三条边的中点，则∠PMN 的周长为（）A. 6B. 6 2C. 6 3D. 9第1题图2. 如图，正六边形ABCDEF的边长为3，点P是边BC上任意一点，过点P作PM∠AB交AF于点M，作PN∠CD交DE于点N，则PM＋PN＝（）A. 6B. 9C. 12D. 无法确定第2题图满分冲关1.（2019河北中考说明）如图，点M，N分别是正八边形相邻的边AB，BC上的点，且AM＝BN，点O 是正八边形的中心，则∠MON＝________°.第1题图2.（2019石家庄长安区质量检测）如图，将边长为2的正五边形ABCDE沿对角线BE折叠，使点A落在正五边形内部的点A′处，则B，A′和D三点______同一条直线上（填“在”或者“不在”）；点A′和D之间的距离是________．第2题图3.（2019河北省二模）已知正多边形每个内角比相邻外角大60°.（1）求这个正多边形的边数；（2）求这个正多边形的内切圆与外接圆的半径之比；（3）将这个正多边形对折，并完全重合，求所得图形的内角和（按一层计算）．参考答案第一节多边形基础过关1. B 【解析】设多边形的边数是n ，则(n －2)·180°＝360°，解得n ＝4，故选B .2. C 【解析】根据多边形的内角和公式，正五边形的内角和为180°×(5－2)＝540°，故选C .3. B 【解析】n ＝360°36°＝10，故选B .4. D 【解析】如解图，过点B 作BH ⊥AC ，交AC 于点H ，∵多边形ABCDEF 为正六边形，∴AB ＝BC ，∠ABC ＝120°，∴∠ABH ＝60°，AH ＝CH ＝12AC ＝ 3.在Rt △ABH 中，AB ＝AH sin60°＝332＝2.第4题解图5. A 【解析】由多边形内角和公式(n －2)×180°可得五边形的内角和为(5－2)×180°＝540°，∵∠A ＋∠B ＋∠E ＝300°， ∴∠EDC ＋∠BCD ＝240°，∵DP 、CP 分别平分∠EDC 、∠BCD ，∴∠PDC ＋∠PCD ＝12(∠EDC ＋∠BCD )＝120°，∴∠P ＝60°.6. A 【解析】如解图所示，易得正五边形的内角和为540°.在正五边形ABCDE 中，∠BAE ＝540°5＝108°，∴∠BAF ＝180°－108°＝72°，即若使点B 落在AE 边所在的直线上，则旋转的角度可以是72°.第6题解图7. C 【解析】如解图，∵正五边形的每个外角是360°÷5＝72°，∴∠OCD ＝∠ODC ＝72°，∴∠COD ＝36°，又∵正五边形每个内角是108°，∴∠AOB ＝360°－108°－108°－36°＝108°.第7题解图8. B 【解析】∵正方形ABCD 与正五边形EFGHM 的边长相等，∴从BC 与FG 重合开始，正方形ABCD 的各边依次与正五边形EFGHM 的各边重合，而与EF 重合是正方形的边与正五边形的边第五次重合，∴正方形中与EF 重合的边是BC .9. B 【解析】如解图，过点G 作直线MN ⊥CD 于点N ，由正多边形的轴对称性可知∠LGN ＝12∠HGL＝108°÷2＝54°，∴∠PGM ＝∠NGL ＝54°，∵由正六边形的性质知AF ∥CD ，MN ⊥CD ，∴MN ⊥AF ，即∠PMG ＝90°，∴∠APG ＝90°＋54°＝144°.第9题解图10. D 【解析】多边形的内角和可以表示成(n －2)·180°(n ≥3且n 是整数)，一个多边形截去一个角后，多边形的边数可能增加了一条，也可能不变或减少了一条，根据(n －2)·180°＝2520°，解得n ＝16，则原多边形的边数是15或16或17.11. C 【解析】∵∠CAB ＝12×（8－2）×180°8＝67.5°，∠DAB ＝12×（6－2）×180°6＝60°，∴∠CAD ＝∠CAB ＋∠DAB ＝67.5°＋60°＝127.5°. 12. 313. 60 【解析】六边形的内角和为180°×(6－2)＝720°，∴∠B ＝720°6＝120°.∵AD ∥BC ，∴∠DAB＝180°－∠B ＝180°－120°＝60°.14. 66 【解析】∵五边形ABCDE 是正五边形，∴∠EAB ＝(5－2)×180°÷5＝108°.∵AP 是∠EAB 的平分线，∴∠P AB ＝12∠EAB ＝54°.∵∠ABP ＝60°，∴∠APB ＝180°－∠P AB －∠ABP＝66°.15. 180° 【解析】∵正八边形的每个内角为（8－2）×180°8＝135°，三角形为直角三角形，∴∠1＋∠2＝2×135°－90°＝180°.16. 123 【解析】如解图，设正六边形的中心是O ，其一边是AB ，∴∠AOB ＝∠BOC ＝60°，∴OA ＝OB ＝AB ＝OC ＝BC ，∴四边形ABCO 是菱形，∵AB ＝12 mm ，∠AOB ＝60°，且cos ∠BAC ＝AMAB ，∴AM＝12×32＝63mm ，∵OA ＝OC ，且∠AOB ＝∠BOC ，∴AM ＝MC ＝12AC ，∴AC ＝2AM ＝12 3 mm.第16题解图17. 30 【解析】如解图，连接OB ，OC ，∵在正多边形中，中心角与多边形的外角相等，∴∠AOB ＝∠BOC ＝∠COD ＝40°.∴∠AOD ＝120°.又∵OA ＝OD ，∴在△AOD 中，∠OAD ＝∠ODA ＝(180°－120°)÷2＝30°.第17题解图18. 54 【解析】如解图，设DE 与B ′C ′相交于O 点，∵五边形ABCDE 为正五边形，∴∠B ＝∠BAE ＝∠E ＝（5－2）×180°5＝108°，∵正五边形ABCDE 绕点A 顺时针旋转后得到正五边形AB ′C ′D ′E ′，旋转角为α(0°≤α≤90°)，∴∠BAB ′＝α，∠B ′＝∠B ＝108°，∵DE ⊥B ′C ′，∴∠B ′OE ＝90°，∴∠B ′AE ＝360°－∠B ′－∠E －∠B ′OE ＝360°－108°－108°－90°＝54°，∴∠BAB ′＝∠BAE －∠B ′AE ＝108°－54°＝54°，∴α＝54°.第18题解图能力提升1. D 【解析】如解图所示，延长F A 、CB 交于点K .在正六边形ABCDEF 中，∠F AB ＝∠CBA ＝120°.∴∠KAB ＝∠KBA ＝60°.∴△KAB 是等边三角形．∴∠K ＝60°.∵M 、N 分别为F A 、BC 的中点，∴AM ＝BN ＝1.又∵AK ＝BK ，∴MK ＝NK .又∵∠K ＝60°，∴△KM N 是等边三角形，∴∠AMN ＝60°.过点A 作AG ⊥MN ，过点B 作BH ⊥MN ，垂足分别为G 、H .∴∠MAG ＝30°.∴MG ＝12AM ＝12.同理得HN ＝12.∵∠MAB＝120°，∠MAG ＝30°，∴∠GAB ＝∠AGH ＝∠BHG ＝90°.∴四边形ABHG 是矩形．∴GH ＝AB ＝2.∴MN ＝MG ＋GH ＋HN ＝12＋2＋12＝3.∴△PMN 的周长为3MN ＝9.第1题解图2．B 【解析】如解图，连接AD 交PM 于点G ，交PN 于点H ，∵六边形ABCDEF 是正六边形，∴∠F AB ＝∠ABP ＝∠BCD ＝∠CDE ＝120°，AB ＝BC ＝CD .∴∠BAD ＝∠F AD ＝∠CDA ＝∠EDA ＝60°.∴∠BAD ＋∠ABC ＝180°.∴AD ∥BC .∵PM ∥AB ，∴四边形ABPG 是平行四边形．∴AG ＝BP ，PG ＝AB ，∠MGA ＝∠GPB ＝∠BAG ＝60°.∴△MAG 是等边三角形，∴MG ＝AG .同理得四边形PCDH 是平行四边形，PH ＝CD ，PC ＝HD ，△HND 是等边三角形，NH ＝HD .∴MG ＋HN ＝BP ＋PC ＝BC ＝AB ，∴PM ＋PN ＝PG ＋PH ＋MG ＋HN ＝3AB ＝9.第2题解图满分冲关1. 45 【解析】如解图，连接OA 、OB 、OC ，∵正八边形是中心对称图形，∴中心角为360°÷8＝45°.∴∠OAM ＝∠OBN ＝180°－45°2＝67.5°.在△OAM 和△OBN 中，⎩⎪⎨⎪⎧OA ＝OB ，∠OAM ＝∠OBN ，AM ＝BN ，∴△OAM ≌△OBN (SAS)．∴∠AOM ＝∠BON .∴∠MOB ＝∠NOC .∵∠AOC ＝∠AOM ＋∠MOB ＋∠BON ＋∠NOC ＝90°，∴∠MON ＝∠MOB ＋∠NOB ＝12(∠AOM ＋∠MOB ＋∠NOB ＋∠NOC )＝12∠AOC ＝45°.第1题解图2. 在；5－1 【解析】∵在△AEB 中，AE ＝AB ，∠EAB ＝（5－2）×180°5＝108°，∴∠AEB ＝∠ABE＝36°.由折叠的性质可知∠BEA ′＝∠EBA ′＝36°.∴∠DEA ′＝108°－∠AEB －∠A ′EB ＝36°.∵∠EA ′B ＝∠A ＝108°，AE ＝A ′E ＝DE ，∴∠EA ′D ＝180°－36°2＝72°，∵∠EA ′D ＋∠EA ′B ＝72°＋108°＝180°，∴B 、A ′、D 三点共线．设A ′D ＝x ，∵∠EDA ′＝∠BDE ，∠DEA ′＝∠DBE ＝36°，∴△DEA ′∽△DBE .∴DE DB ＝DA ′DE .即22＋x ＝x2，解得x ＝5－1(负值舍去)．∴点A ′和D 之间的距离是5－1.3. 解：(1)设这个正多边形的每个外角的度数为x ，则每个内角为x ＋60°， ∴x ＋x ＋60°＝180°. ∴x ＝60°.∴这个正多边形的边数＝360°÷60°＝6. 故这个正多边形的边数是6；(2)如解图①，r 为内切圆半径，正多边形的边长为a ，∴外接圆的半径为a . ∴r ＝a 2－（a 2）2＝3a 2.∴r a ＝32. ∴这个正多边形的内切圆和外接圆的半径之比为 3 ∶2；第3题解图①(3)如解图②，当沿过两个端点的对称轴所在的直线折叠时，得到的图形是四边形，内角和是(4－2)×180°＝360°；如解图③，当沿对边中点所在的直线折叠时，得到的图形是五边形，内角和是(5－2)×180°＝540°.第3题解图。

2020届中考物理一轮复习考点：杠杆最小动力问题

杠杆最小动力问题考点一：最小动力作图1.如图所示，是一个电热水壶的简易图，在图中画出它所受重力的示意图（B为重心）；用力作用在壶盖上A点时，可将壶盖打开，请在A点画出所需最小动力F的示意图（O为支点）．2.如图是我们经常使用的起子。

请在图中画出作用在A点最小的力F及其力臂l。

3.如图甲是环保垃圾桶，环卫工人在B点用力使其静止，图乙为其简化示意图。

若将垃圾桶看成一个杠杆，A为支点，O点为垃圾桶重心。

请在图乙中画出：（1）作用在B点的最小动力F1的示意图及F1的力臂L1。

（2）垃圾桶所受重力的示意图。

4.地面上有一个大木箱，小明想把它向右推到，画出最省力的推力方向，并画出力臂。

5.列车上有出售食品的手推车，如图所示。

若货物均匀摆在车内，当后轮遇到障碍物A时，售货员要想办法越过它，请在图中画出此时售货员使用的最小力的示意图。

6.用独轮车搬运砖头（如图），把砖头放在车箱A区域，抬起车把时更省力．请在图中作出抬起车把时最小力的示意图．考点二：杠杆最小动力方向的判定1.O为杠杆的支点，A点挂一重物，为使杠杆在水平位置平衡，若在B点施加一个力并使该力最小，该力应沿（）A.BM方向B．BN方向C．BP方向D．BQ方向2.在电视剧《三国》中，有这样一个情景：一群士兵用力拉动一个杠杆，会将石块抛向敌方阵营。

它是一个________杠杆。

要把石块抛出去，图中作用在A点的力沿 ______方向最小（填a、b或c）。

3.在抢险救灾工作中。

救援人员使用橇棒把滚落在公路上的石块1橇离开公路，如图所示若救援人员要选择一种最省力的撬石头方法，则在橇棒应该选择______选填“A”，“B”或“C”）为支点；救援人员在撬棒D点沿_______方向（选填“DN”或“DM”）来撬起石块1。

4.如图是一种切甘蔗用的铡刀示意图。

铡刀刃很薄可以增大________。

切甘蔗时，甘蔗放在______(选填"a”成“b")点更易被切断，手沿_______(选填“F1”或“F2”)方向用力可以更省力。

2020年中考数学总复习初中数学全套基础知识复习讲义(精心整理)

2020年中考数学总复习初中数学全套基础知识复习讲义（精心整理）第1课时实数的有关概念【知识梳理】1.实数的分类：整数(包括:正整数、0、负整数)和分数(包括:有限小数和无限环循小数)都是有理数. 有理数和无理数统称为实数.2.数轴：规定了原点、正方向和单位长度的直线叫数轴．实数和数轴上的点一一对应.3.绝对值：在数轴上表示数a的点到原点的距离叫数a的绝对值，记作∣a∣，正数的绝对值是它本身；负数的绝对值是它的相反数；0的绝对值是0.4.相反数：符号不同、绝对值相等的两个数，叫做互为相反数．a的相反数是-a，0的相反数是0.5.有效数字：一个近似数,从左边笫一个不是0的数字起,到最末一个数字止,所有的数字,都叫做这个近似数的有效数字.6.科学记数法：把一个数写成a×10n的形式(其中1≤a<10,n是整数),这种记数法叫做科学记数法. 如:407000=4.07×105,0.000043=4.3×10－5.7.大小比较：正数大于0，负数小于0，两个负数，绝对值大的反而小.8.数的乘方：求相同因数的积的运算叫乘方，乘方运算的结果叫幂.9.平方根：一般地，如果一个数x的平方等于a,即x2=a那么这个数x就叫做a的平方根（也叫做二次方根）．一个正数有两个平方根，它们互为相反数；0只有一个平方根，它是0本身；负数没有平方根．10. 开平方：求一个数a 的平方根的运算，叫做开平方．11. 算术平方根：一般地，如果一个正数x 的平方等于a,即x 2=a ，那么这个正数x 就叫做a 的算术平方根，0的算术平方根是0．12. 立方根：一般地，如果一个数x 的立方等于a,即x 3=a ，那么这个数x就叫做a 的立方根（也叫做三次方根）,正数的立方根是正数;负数的立方根是负数；0的立方根是0．13. 开立方：求一个数a 的立方根的运算叫做开立方．【思想方法】数形结合，分类讨论【例题精讲】例1.下列运算正确的是（）A ．33--=B ．3)31(1-=-C 3=±D 3=-例）A ．BC ．2-D ．2例3.2的平方根是（）A ．4BC ．D ．例4.《广东省2009年重点建设项目计划（草案）》显示，港珠澳大桥工程估算总投资726亿元，用科学记数法表示正确的是（）A ．107.2610⨯ 元B ．972.610⨯ 元C ．110.72610⨯ 元D ．117.2610⨯元例5.实数a b ，在数轴上对应点的位置如图所示，则必有（）A ．0a b +>B ．0a b -<C ．0ab >D ．0a b< 例6.（改编题）有一个运算程序，可以使：a ⊕b = n (n 为常数)时，得（a +1）⊕b = n +2， a ⊕（b +1）= n -3 现在已知1⊕1 = 4，那么2009⊕2009 = ．【当堂检测】1.计算312⎛⎫- ⎪⎝⎭的结果是（）A ．16B ．16-C ．18D ．18-2.2-的倒数是（） A ．12-B ．12C ．2D ．2-3.下列各式中，正确的是（）A ．3152<<B ．4153<<C ．5154<<D ．161514<< 4.已知实数a在数轴上的位置如图所示，则化简|1|a -的结果为（） A ．1 B ．1- C ．12a - D ．21a -5.2-的相反数是（） A ．2B ．2-C ．12D ．12-第4题图0 例5图6.-5的相反数是____,-12的绝对值是=_____.7.写出一个有理数和一个无理数，使它们都是小于－1的数.8.如果2()13⨯-=，则“”内应填的实数是（）A．32B．23C．23-D．32-第2课时实数的运算【知识梳理】1．有理数加法法则：同号两数相加，取相同的符号，并把绝对值相加；异号两数相加，绝对值相等时和为0；绝对值不等时，取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值；一个数同0相加，仍得这个数．2．有理数减法法则：减去一个数，等于加上这个数的相反数．3．有理数乘法法则：两个有理数相乘，同号得正，异号得负，再把绝对值相乘；任何数与0相乘，积仍为0．4．有理数除法法则：两个有理数相除，同号得正，异号得负，并把绝对值相除；0除以任何非0的数都得0；除以一个数等于乘以这个数的倒数．5．有理数的混合运算法则：先算乘方，再算乘除，最后算加减；如果有括号，先算括号里面的．6．有理数的运算律：加法交换律：a+b=b+a(a b、为任意有理数)加法结合律：(a+b)+c=a+(b+c)(a, b,c为任意有理数)【思想方法】数形结合，分类讨论【例题精讲】例 1.某校认真落实苏州市教育局出台的“三项规定”，校园生活丰富多彩．星期二下午4 点至5点，初二年级240名同学分别参加了美术、音乐和体育活动，其中参加体育活动人数是参加美术活动人数的3倍，参加音乐活动人数是参加美术活动人数的2倍，那么参加美术活动的同学其有____________名.例2.下表是5个城市的国际标准时间（单位：时）那么北京时间2006年6月17日上午9时应是( )A ．伦敦时间2006年6月17日凌晨1时.B ．纽约时间2006年6月17日晚上22时.C ．多伦多时间2006年6月16日晚上20时 .D ．汉城时间2006年6月17日上午8时.例3.如图，由等圆组成的一组图中，第1个图由1个圆组成，第2个图由7个圆组成，第3个图由19个圆组成，……，按照这样的规律排列下去，则第9个图形由__________个圆组成.9 0-4国际标准时间（时）-5 例2图……例4.下列运算正确的是（）A ．523=+B ．623=⨯C ．13)13(2-=-D ．353522-=- 例5.计算：(1)911)1(8302+-+--+-π (2)0(tan 45π--+º(3)102)21()13(2-+--； (4)2008011(1)()3π--+-.【当堂检测】1.下列运算正确的是（）A ．a 4×a 2=a 6B ．22532a b a b -=C ．325()a a -=D ．2336(3)9ab a b =2.某市2008年第一季度财政收入为76.41亿元，用科学记数法（结果保留两个有效数字）表示为( )A ．81041⨯元B ．9101.4⨯元C ．9102.4⨯元D ．8107.41⨯元 3.估计68的立方根的大小在( )A.2与3之间B.3与4之间C.4与5之间D.5与6之间 4.如图，数轴上点P 表示的数可能是（） AB．C ． 3.2- D．5.计算：(1)02200960cos 16)21()1(-+--- （2）)1112-⎛⎫--+ ⎪⎝⎭第3课时整式与分解因式【知识梳理】1.幂的运算性质：①同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加，即n m n m a a a +=⋅（m 、n 为正整数）；②同底数幂的除法法则：同底数幂相除，底数不变，指数相减，即n m n m a a a -=÷（a≠0，m 、n 为正整数，m>n ）；③幂的乘方法则：幂的乘方，底数不变，指数相乘，即n n n b a ab =)(（n 为正整数）；④零指数：10=a （a≠0）；⑤负整数指数：nn a a 1=-（a≠0，n 为正整数）； 2.整式的乘除法:(1)几个单项式相乘除,系数与系数相乘除,同底数的幂结合起来相乘除. (2)单项式乘以多项式,用单项式乘以多项式的每一个项.(3)多项式乘以多项式,用一个多_项式的每一项分别乘以另一个多项式的每一项.(4)多项式除以单项式,将多项式的每一项分别除以这个单项式.(5)平方差公式：两个数的和与这两个数的差的积等于这两个数的平方，即22))((b a b a b a -=-+；(6)完全平方公式：两数和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍，即2222)(b ab a b a +±=± 3.分解因式：把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式． 4.分解因式的方法：第4题图⑴提公团式法：如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法．⑵运用公式法：公式22()()a ab b a b±+=±-=+-；2222()a b a b a b5．分解因式的步骤：分解因式时，首先考虑是否有公因式，如果有公因式，一定先提取公团式，然后再考虑是否能用公式法分解．6．分解因式时常见的思维误区：⑴提公因式时，其公团式应找字母指数最低的，而不是以首项为准．⑵提取公因式时，若有一项被全部提出，括号内的项“ 1”易漏掉．(3) 分解不彻底，如保留中括号形式，还能继续分解等【例题精讲】【例1】下列计算正确的是（）A. a＋2a=3a2B. 3a－2a=aC. a2•a3=a6D.6a2÷2a2=3a2【例2】（2008年茂名）任意给定一个非零数，按下列程序计算，最后输出的结果是（）+2 结果A．m B．m2C．m+1 D．m-1 【例3】若2+-=．a a526a a--=，则2320【例4】下列因式分解错误的是( )A．22()()x x x++=+-=+-B．22x y x y x y69(3)C．2()x y x y+=++=+D．222()x xy x x y【例5】如图7-①，图7-②，图7-③，图7-④，…，是用围棋棋子按照某种规律摆成的一行“广”字，按照这种规律，第5个“广”字中的棋子个数是________，第n 个“广”字中的棋子个数是________【例6】给出三个多项式：21212x x +-，21412x x ++，2122x x -．请选择你最喜欢的两个多项式进行加法运算，并把结果因式分解．【当堂检测】1.分解因式：39a a -= ， _____________223=---x x x2.对于任意两个实数对（a ，b ）和（c ，d ），规定：当且仅当a ＝c 且b ＝d 时，（a ，b ）=（c ，d ）．定义运算“⊗”：（a ，b ）⊗（c ，d ）=（ac －bd ，ad ＋bc ）．若（1，2）⊗（p ，q ）=（5，0），则p ＝，q ＝． 3. 已知a=1.6⨯109，b=4⨯103，则a 2÷2b=( )A. 2⨯107B. 4⨯1014C.3.2⨯105D. 3.2⨯1014 ． 4.先化简，再求值：22()()(2)3a b a b a b a ++-+-，其中2332a b =-=，．5．先化简，再求值：22()()()2a b a b a b a +-++-，其中133a b ==-，．第4课时分式与分式方程【知识梳理】1. 分式概念：若A 、B 表示两个整式，且B 中含有字母，则代数式BA 叫做分式．2.分式的基本性质：（1）基本性质：（2）约分：（3）通分： 3．分式运算4.分式方程的意义，会把分式方程转化为一元一次方程．5.了解分式方程产生增根的原因，会判断所求得的根是否是分式方程的增根．【思想方法】1.类比（分式类比分数）、转化（分式化为整式）2.检验【例题精讲】1．化简：2222111x x x x x x-+-÷-+2．先化简，再求值： 22224242x x x x x x --⎛⎫÷-- ⎪-+⎝⎭，其中22x =+．3．先化简11112-÷-+x xx ）（，然后请你给x 选取一个合适值,再求此时原式的值．4．解下列方程（1）013522=--+x x x x （2）41622222-=-+-+-xx x x x5．一列列车自2004年全国铁路第5次大提速后，速度提高了26千米/时，现在该列车从甲站到乙站所用的时间比原来减少了1小时，已知甲、乙两站的路程是312千米，若设列车提速前的速度是x 千米，则根据题意所列方程正确的是( )A. B.C. D.【当堂检测】1．当99a =时，分式211a a --的值是．2．当x 时，分式112--x x有意义；当x 时，该式的值为0．3．计算22()ab ab的结果为．4. ．若分式方程xxk x --=+-2321有增根，则k 为（） A. 2 B.1 C. 3 D.-25．若分式32-x 有意义，则x 满足的条件是：（） A ．0≠x B ．3≥x C ．3≠x D ．3≤x6．已知x ＝2008，y ＝2009，求x yx 4y 5x y x 4xy5x y 2xy x 2222-+-+÷-++的值7．先化简，再求值：4xx 16x )44x x 1x 2x x 2x (2222+-÷+----+，其中22+=x8.解分式方程． (1)22011xx x -=+- (2)x2)3(x 22x x -=--；(3) 11322xx x -=--- (4)11-x 1x 1x 22=+--第5课时二次根式【知识梳理】1.二次根式：(1)定义:____________________________________叫做二次根式. 2．二次根式的化简：3．最简二次根式应满足的条件：（1）被开方数中不含有能开得尽的因数或因式．（2）根号内不含分母（3）分母上没有根号4．同类二次根式：几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式就叫做同类二次根式． 5．二次根式的乘法、除法公式：（1a b=ab a 0b 0≥≥（，）（2a a=a 0b 0b b≥（，）6．.二次根式运算注意事项：（1）二次根式相加减，先把各根式化为最简二次根式，再合并同类二次根式，防止：①该化简的没化简；②不该合并的合并；③化简不正确；④合并出错．（2）二次根式的乘法除法常用乘法公式或除法公式来简化计算，运算结果一定写成最简二次根式或整式．【思想方法】非负性的应用【例题精讲】【例1】要使式子1x x+有意义，x 的取值范围是（） A ．1x ≠B ．0x ≠C ．10x x >-≠且D ．10x x ≠≥-且【例2132202）． A ．6到7之间 B ．7到8之间 C ．8到9之间 D ．9到10之间【例3】若实数x y ，满足22(3)0x y ++-=，则xy 的值是．【例4】如图，A ，B ，C ，D 四张卡片上分别写有523π7-，，，四个实数，从中任取两张卡片．A B C D（1）请列举出所有可能的结果（用字母A ，B ，C ，D 表示）；（2）求取到的两个数都是无理数的概率．【例5】计算：（1）103130tan 3)14.3(27-+︒---）（π（2）11(1)527232-⎛⎫π-+-+-- ⎪⎝⎭．【例6】先化简，再求值：)1()1112(2-⨯+--a a a ，其中33-=a ．【当堂检测】 1.计算：（1）01232tan 60(12)+--+-+．（2）cos45°·(－21)－2－(22－3)0＋｜－32｜＋121-（3）026312()cos 304sin 6022-++-+．2.如图，实数a 、b 在数轴上的位置，化简 222()a b a b -第6课时一元一次方程及二元一次方程（组）【知识梳理】1．方程、一元一次方程、二元一次方程（组）和方程（组）的解、解方程（组）的概念及解法，利用方程解决生活中的实际问题． 2．等式的基本性质及用等式的性质解方程：等式的基本性质是解方程的依据，在使用时要注意使性质成立的条件．3．灵活运用代入法、加减法解二元一次方程组．4．用方程解决实际问题：关键是找到“等量关系”，在寻找等量关系时有时可以借助图表等，在得到方程的解后，要检验它是否符合实际意义．【思想方法】方程思想和转化思想【例题精讲】例1．（1）解方程.x x +--=21152156 （2）解二元一次方程组 ⎩⎨⎧=+=+27271523y x y x 解：例2．已知x =-2是关于x 的方程()x m x m -=-284的解，求m 的值．方法1 方法2例3．下列方程组中，是二元一次方程组的是（）A. B. C. D. 例4．在中，用x 的代数式表示y ，则y=______________．例5．已知a 、b 、c 满足⎩⎨⎧=+-=-+02052c b a c b a ，则a ：b ：c= ．例6 ．某电厂规定该厂家属区的每户居民如果一个月的用电量不超过 A 度，那么这个月这户只需交 10如果超过 A 度，则这个月除了仍要交 10 元用电费外，超过部分还要按每度 0.5 元交费．①该厂某户居民 2 月份用电 90 度，超过了规定的 A 度，则超过部分应该交电费多少元（用 A 表示）？．②右表是这户居民 3 月、4 月的用电情况和交费情况：根据右表数据，求电厂规定A 度为．【当堂检测】 1．方程x -=52的解是______．2．一种书包经两次降价10%，现在售价a 元，则原售价为_______元． 3.若关于x 的方程x k =-153的解是x =-3，则k =_________．4．若⎩⎨⎧-==11y x ，⎩⎨⎧==22y x ，⎩⎨⎧==c y x 3都是方程ax+by+2＝0的解，则c=____． 5．解下列方程（组）：⎪⎩⎪⎨⎧=+=+65115y x y x ⎩⎨⎧-=+=+2102y x y x ⎩⎨⎧==+158xy y x ⎩⎨⎧=+=31y x x 032=-+y x（1）()x x -=--3252；（2）....x x +=-0713715023；（3）⎩⎨⎧=+=+832152y x y x ；（4）x x -+=-2114135；6．当x =-2时，代数式x bx +-22的值是12，求当x =2时，这个代数式的值．7．应用方程解下列问题：初一（4）班课外乒乓球组买了两副乒乓球板，若每人付9元，则多了5元，后来组长收了每人8元，自己多付了2元，问两副乒乓球板价值多少？8．甲、乙两人同时解方程组8(1)5 (2)mx ny mx ny +=-⎧⎨-=⎩由于甲看错了方程①中的m ，得到的解是42x y =⎧⎨=⎩，乙看错了方程中②的n ，得到的解是25x y =⎧⎨=⎩，试求正确,m n 的值．第7课时一元二次方程【知识梳理】1. 一元二次方程的概念及一般形式：ax 2+bx +c =0 (a ≠0)2. 一元二次方程的解法：①直接开平方法②配方法③公式法④因式分解法3．求根公式：当b 2-4ac≥0时，一元二次方程ax 2+bx +c =0 (a ≠0)的两根aacb b x 242-±-=4．根的判别式：当b 2-4ac ＞0时，方程有实数根．当b 2-4ac=0时，方程有实数根．当b 2-4ac ＜0时，方程实数根．【思想方法】1. 常用解题方法——换元法2. 常用思想方法——转化思想，从特殊到一般的思想，分类讨论的思想【例题精讲】例1．选用合适的方法解下列方程：(1) (x-15)2-225=0； (2) 3x 2－4x －1＝0（用公式法）；(3) 4x 2－8x ＋1＝0（用配方法）；（4）x 2+22x=0例2 ．已知一元二次方程0437122=-+++-m m mx x m ）（有一个根为零，求m 的值．例3．用22cm 长的铁丝，折成一个面积是30㎝2的矩形，求这个矩形的长和宽.又问：能否折成面积是32㎝2的矩形呢？为什么？例4．已知关于x 的方程x 2―(2k+1)x+4(k -0.5)=0 (1) 求证：不论k 取什么实数值，这个方程总有实数根；(2) 若等腰三角形ABC 的一边长为a=4，另两边的长b ．c 恰好是这个方程的两个根，求△ABC 的周长．【当堂检测】一、填空1．下列是关于x 的一元二次方程的有_______ ①02x 3x 12=-+ ②01x 2=+ ③)3x 4)(1x ()1x 2(2--=- ④06x 5x k 22=++ ⑤021x x 2432=--⑥0x 22x 32=-+2．一元二次方程3x 2=2x 的解是．3．一元二次方程(m-2)x 2+3x+m 2-4=0有一解为0，则m 的值是．4．已知m 是方程x 2-x-2=0的一个根，那么代数式m 2-m = ． 5．一元二次方程ax 2+bx+c=0有一根-2,则bc a 4+的值为． 6．关于x 的一元二次方程kx 2+2x －1=0有两个不相等的实数根, 则k 的取值范围是__________．7．如果关于的一元二次方程的两根分别为3和4，那么这个一元二次方程可以是．二、选择题：8．对于任意的实数x,代数式x 2－5x ＋10的值是一个( ) A.非负数 B.正数 C.整数 D.不能确定的数 9．已知(1-m 2-n 2)(m 2+n 2)=-6,则m 2+n 2的值是（） A.3 B.3或-2 C.2或-3 D. 210．下列关于x 的一元二次方程中，有两个不相等的实数根的方程是（）（A ）x 2＋4＝0 （B ）4x 2－4x ＋1＝0（C ）x 2＋x ＋3＝0（D ）x 2＋2x －1＝011．下面是李刚同学在测验中解答的填空题，其中答对的是（） A ．若x 2=4，则x=2 B ．方程x(2x-1)=2x-1的解为x=1 C ．方程x 2+2x+2=0实数根为0个 D ．方程x 2-2x-1=0有两个相等的实数根12．若等腰三角形底边长为8,腰长是方程x 2-9x+20=0的一个根,则这个三角形的周长是（） A.16 B.18 C.16或18 D.21三、解下方程：(1)(x+5)(x-5)=7 (2)x(x-1)=3-3x (3)x 2-4x-4=0(4)x 2+x-1=0 (6)（2y-1）2 -2（2y-1）-3=0第8课时方程的应用（一）【知识梳理】1. 方程（组）的应用；2. 列方程（组）解应用题的一般步骤；3. 实际问题中对根的检验非常重要．【注意点】分式方程的检验，实际意义的检验．【例题精讲】例1. 足球比赛的计分规则为：胜一场得3分，平一场得1分，负一场得0分．某队打了14场，负5场，共得19分，那么这个队胜了（） A ．4场 B ．5场 C ．6场 D ．13场例2. 某班共有学生49人.一天，该班某男生因事请假，当天的男生人数恰为女生人数的一半.若设该班男生人数为x ，女生人数为y ，则下列方程组中，能正确计算出x 、y 的是（）A ．⎩⎪⎨⎪⎧x –y= 49y=2(x+1)B ．⎩⎪⎨⎪⎧x+y= 49y=2(x+1)C ．⎩⎪⎨⎪⎧x –y= 49y=2(x –1)D ．⎩⎪⎨⎪⎧x+y= 49y=2(x –1) 例3. 张老师和李老师同时从学校出发，步行15千米去县城购买书籍，张老师比李老师每小时多走1千米，结果比李老师早到半小时，两位老师每小时各走多少千米？设李老师每小时走x 千米，依题意得到的方程是（）1515115151..12121515115151..1212A B x x x x C D x x x x -=-=++-=-=--例 4.学校总务处和教务处各领了同样数量的信封和信笺，总务处每发一封信都只用一张信笺，教务处每发出一封信都用3张信笺，结果，总务处用掉了所有的信封，•但余下50张信笺，而教务处用掉所有的信笺但余下50个信封，则两处各领的信笺数为x 张，•信封个数分别为y 个，则可列方程组．例5. 团体购买公园门票票价如下：100人．若分别购票，两团共计应付门票费1392元，若合在一起作为一个团体购票，总计应付门票费1080元．(1)请你判断乙团的人数是否也少于50人． (2)求甲、乙两旅行团各有多少人？【当堂检测】1. 某市处理污水，需要铺设一条长为1000m 的管道，为了尽量减少施工对交通所造成的影响，实际施工时，每天比原计划多铺设10米，结果提前5天完成任务．设原计划每天铺设管道xm ，则可得方程．2. “鸡兔同笼”是我国民间流传的诗歌形式的数学题， “鸡兔同笼不知数，三十六头笼中露，看来脚有100只，几多鸡儿几多兔？”解决此问题，设鸡为x 只，兔为y 只，所列方程组正确的是（）⎩⎨⎧=+=+100236.y x y x A 3636..2410022100x y x y B C x y x y +=+=⎧⎧⎨⎨+=+=⎩⎩⎩⎨⎧=+=+1002436..y x y x D 3.为满足用水量不断增长的需求，某市最近新建甲、乙、•丙三个水厂，这三个水厂的日供水量共计11.8万m 3，•其中乙水厂的日供水量是甲水厂日供水量的3倍，丙水厂的日供水量比甲水厂日供水量的一半还多1万m 3．（1）求这三个水厂的日供水量各是多少万立方米？（2）在修建甲水厂的输水管道的工程中要运走600t 土石，运输公司派出A 型，B•型两种载重汽车，A 型汽车6辆，B 型汽车4辆，分别运5次，可把土石运完；或者A 型汽车3辆，B 型汽车6辆，分别运5次，也可把土石运完，那么每辆A 型汽车，每辆B 型汽车每次运土石各多少吨？（每辆汽车运土石都以准载重量满载）4. 2009年初我国南方发生雪灾，某地电线被雪压断，供电局的维修队要到30km 远的郊区进行抢修．维修工骑摩托车先走，15min 后，抢修车装载所需材料出发，结果两车同时到达抢修点．已知抢修车的速度是摩托车速度的1.5倍，求这两种车的速度．5. 某体育彩票经售商计划用45000•元从省体彩中心购进彩票20扎，每扎1000张，已知体彩中心有A 、B 、C 三种不同价格的彩费，进价分别是A•种彩票每张1.5元，B 种彩票每张2元，C 种彩票每张2.5元．（1）若经销商同时购进两种不同型号的彩票20扎，用去45000元，请你设计进票方案；（2）若销售A 型彩票一张获手续费0.2元，B 型彩票一张获手续费0.3元，C 型彩票一张获手续费0.5元．在购进两种彩票的方案中，为使销售完时获得手续费最多，你选择哪种进票方案？（3）若经销商准备用45000元同时购进A 、B 、C 三种彩票20扎，请你设计进票方案．第9课时方程的应用（二）【知识梳理】1.一元二次方程的应用；2. 列方程解应用题的一般步骤；3. 问题中方程的解要符合实际情况．【例题精讲】例1. 一个两位数的十位数字与个位数字和是7，把这个两位数加上45后，•结果恰好成为数字对调后组成的两位数，则这个两位数是（） A ．16 B ．25 C ．34 D ．61 例2. 如图，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要551米2，则修建的路宽应为（） A ．1米B ．1.5米C ．2米D ．2.5米例3. 为执行“两免一补”政策，某地区2006年投入教育经费2500万元，预计2008年投入3600万元．设这两年投入教育经费的年平均增长百分率为x ，则下列方程正确的是（）Ａ．225003600x = Ｂ．22500(1)3600x +=Ｃ．22500(1%)3600x +=Ｄ．22500(1)2500(1)3600x x +++=例4. 某地出租车的收费标准是：起步价为7元，超过3千米以后，每增加1千米，•加收2.4元．某人乘这种出租车从甲地到乙地共付车费19元，•设此人从甲地到乙地经过的路程为x 千米，那么x 的最大值是（） A ．11 B ．8 C ．7 D ．5例5. 已知某工厂计划经过两年的时间，•把某种产品从现在的年产量100万台提高到121万台，那么每年平均增长的百分数约是________．按此年平均增长率，预计第4年该工厂的年产量应为_____万台．例6. 某商场将进货价为30元的台灯以40元售出，平均每月能售出600个．调查表明：这种台灯的售价每上涨1元，其销售量就将减少10个．为了实现平均每月10000•元的销售利润，这种台灯的售价应定为多少？这时应进台灯多少个？例7. 幼儿园有玩具若干份分给小朋友，如果每人分3件，那么还余59件．•如果每人分5件，那么最后一个人不少于3件但不足5件，试求这个幼儿园有多少件玩具，有多少个小朋友．【当堂检测】1. 某印刷厂1•月份印刷了书籍60•万册，•第一季度共印刷了200万册，问2、3月份平均每月的增长率是多少？2. 为了营造人与自然和谐共处的生态环境，某市近年加快实施城乡绿化一体化工程，创建国家城市绿化一体化城市．某校甲，乙两班师生前往郊区参加植树活动．已知甲班每天比乙班少种10棵树，甲班种150棵树所用的天数比乙班种120棵树所用的天数多2天，求甲，乙两班每天各植树多少棵？3. A、B、C、D为矩形的四个顶点，AB=16cm，AD=6cm，动点P、Q分别从点A、C同时出发，点P以3 cm/s的速度向点B移动，一直到达B 为止，点Q以2 cm/s的速度向D移动.⑴ P、Q两点从出发开始到几秒时四边形PBCQ的面积为33 cm2？⑵ P、Q两点从出发开始到几秒时，点P和点Q的距离是10 cm？4. 甲、乙两班学生到集市上购买苹果，苹果的价格如下表所示．甲班分两次共购买苹果70kg（第二次多于第一次），共付出189元，而乙班则一次购买苹果70kg．（1）乙班比甲班少付出多少元？（2）甲班第一次，第二次分别购买苹果多少千克？第10课时一元一次不等式（组）【知识梳理】1.一元一次不等式（组）的概念；2.不等式的基本性质；3.不等式（组）的解集和解法．【思想方法】1.不等式的解和解集是两个不同的概念；2.解集在数轴上的表示方法．【例题精讲】例1.如图所示，O 是原点，实数a 、b 、c 在数轴上对应的点分别为A 、B 、C ，则下列结论错误的是（）A. 0b a >-B. 0ab <C. 0b a <+D. 例2. 不等式112x ->的解集是（）Ａ．12x >- Ｂ．2x >- Ｃ．2x <-Ｄ．12x <-例3. 把不等式组21123x x +>-⎧⎨+⎩≤的解集表示在数轴上，下列选项正确的是（）A ．B ．C ．D ．例4. 不等式组221x x -⎧⎨-<⎩≤的整数解共有（）A ．3个B ．4个C ．5个D ．6个例5. 小明和爸爸妈妈三人玩跷跷板，三人的体重一共为150kg ，爸爸坐在跷跷板的一端，小明体重只有妈妈一半，小明和妈妈一同坐在跷跷板的另一端，这时爸爸那端仍然着地，那么小明的体重应小于（） A. 49kg B. 50kg C. 24kg D. 25kg例6.若关于x 的不等式x －m ≥－1的解集如图所示，则m 等于（）A ．0B ．1C ．2D ．34321B A O C)c a (b >-11- 11- 10 1- 10 1-例7.解不等式组：（1）21113x xx +<⎧⎪⎨-≥⎪⎩ （2）⎪⎩⎪⎨⎧+<+->+)6(3)4(4,5351x x x x【当堂检测】1.苹果的进价是每千克3.8元，销售中估计有5%的苹果正常损耗．为避免亏本，商家把售价应该至少定为每千克元．2. 解不等式723<-x ，将解集在数轴上表示出来，并写出它的正整数解．3. 解不等式组⎪⎩⎪⎨⎧-<+--+≥+224313322x x x x ，并把它的解集在数轴上表示出来．4. 我市某镇组织20辆汽车装运完A 、B 、C 三种脐橙共100吨到外地销售．按计划，20辆汽车都要装运，每辆汽车只能装运同一种脐橙，且必须装满．根据下表提供的信息，解答以下问题：（1）设装运A 种脐橙的车辆数为x ，装运B 种脐橙的车辆数为y ，求y 与x 之间的函数关系式；（2）如果装运每种脐橙的车辆数都不少于4辆，那么车辆的安排方案有几种？并写出每种安排方案；（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值．第11课时平面直角坐标系、函数及其图像【知识梳理】一、平面直角坐标系1. 坐标平面上的点与有序实数对构成一一对应；2. 各象限点的坐标的符号；3. 坐标轴上的点的坐标特征．4. 点P （a ，b ）关于⎪⎩⎪⎨⎧原点轴轴y x 对称点的坐标⎪⎩⎪⎨⎧----),(),(),(b a b a b a5.两点之间的距离6.线段AB 的中点C ，若),(),,(),,(002211y x C y x B y x A 则2,2210210y y y x x x +=+=二、函数的概念1.概念：在一个变化过程中有两个变量x 与y ，如果对于x 的每一个值，y 都有唯一的值与它对应，那么就说x 是自变量，y 是x 的函数.2.自变量的取值范围：（1）使解析式有意义（2）实际问题具有实际意义3.函数的表示方法；（1）解析法（2）列表法（3）图象法21212211P P )0()0()2(y y y P y P-＝，　，，，21212211P P )0()0()1(x x x P x P -＝，　，　，，　【思想方法】数形结合【例题精讲】例1.函数22y x =-中自变量x 的取值范围是 ;函数y =中自变量x 的取值范围是．例2.已知点(13)A m -，与点(21)B n +，关于x 轴对称，则m = ，n = ．例3.如图，在平面直角坐标系中，点A 的坐标是（10，0），点B 的坐标为（8，0）,点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形．求点C 的坐标．例4.阅读以下材料：对于三个数a,b,c 用M{a,b,c}表示这三个数的平均数，用min{a,b,c}表示这三个数中最小的数．例如：{}123412333M -++-==，，； min{-1,2,3}=-1；{}(1)min 121(1).a a a a -⎧-=⎨->-⎩≤；，，解决下列问题：（1）填空：min{sin30o ,sin45o ,tan30o }= ；（2）①如果M{2,x+1,2x}=min{2,x+1,2x}，求x ；②根据①，你发现了结论“如果M{a,b,c}= min{a,b,c}，那么（填a,b,c 的大小关系）”． ③运用②的结论，填空：M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y}若，则x + y= ．（3）在同一直角坐标系中作出函数y=x+1，y=(x-1)2，y=2-x 的图象（不例3图需列表描点）min{x+1, (x-1)2,2-x}x【当堂检测】1.点P在第二象限内，P到x轴的距离是4，到y轴的距离是3，那么点P的坐标为（）A．(-4,3) B．(-3,-4) C．(-3,4) D．(3,-4)2.已知点P(x,y)位于第二象限，并且y≤x+4 , x,y为整数，写出一个．．符合上述条件的点P的坐标：．3.点P(2m-1,3)在第二象限，则m的取值范围是（）A．m>0.5 B．m≥0.5C．m<0.5 D．m≤0.54.如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．⑴由图观察易知A（0，2）关于直线l的对称点A'的坐标为（2，0），请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点B'、C'的位置，并写出他们的坐标: B'、C'；⑵结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P'的坐标为（不必证明）；。

中考化学一轮复习讲义空气氧气(讲义)(解析版)

【解析】A、21%和78%指气体的体积分数，故A正确；
B、人造空气”中氧气占21%，与空气中含量一样，所以燃着的木条放在“人造空气”中不会立即熄灭，故B正确；
C、木炭燃烧生成二氧化碳气体，不能用木炭燃烧法测定“人造空气”中的氧气含量，故C错误；
D、人造空气”中21%的氧气，78%的氮气，控制二氧化碳的含量低于0.7%，空气中二氧化碳的含量低于0.03%，所以与空气中成分不完全相同，故D错误。
故选A。
【变式4-1】（2023年湖南省衡阳市中考）拉瓦锡用定量的方法研究了空气的成分。某兴趣小组利用氧气传感器来检测足量红磷燃烧过程中氧气的含量，如图所示，下列判断正确的是（）
A．a点时容器内氮气体积分数为85%
D、空气质量日报中，空气质量级别越大，空气质量状况越差，符合题意。
故选D。
考向
【例3】（2023年湖北省荆州市中考）空气是人类生产活动的重要资源。下列有关空气成分的说法错误的是（）
A.氧气可以支持可燃物燃烧
B.氮气不与任何物质发生化学反应
C.二氧化碳在蔬菜大棚中作气体肥料
D.稀有气体可制成多种用途的电光源
三、空气的污染与防治
（1）空气污染物
空气的主要污染物有有害气体和粉尘。目前计入空气污染指数的项目暂定为：二氧化硫、一氧化碳、二氧化氮、可吸入颗粒物(粒径在10微米以下的颗粒物，称PM10，又称飘尘)和臭氧等。
【特别提醒】二氧化碳属于空气的组成成分，不是空气污染物。但二氧化碳的含量过高，会加剧温室效应。
B.二氧化碳无毒，不会造成空气污染物，故B错误；
C.空气中的稀有气体化学性质虽不活泼，但不是没有任何用处，比如稀有气体可以作保护气，故C错误；
D.空气质量日报中，空气质量级别越大，说明含有的污染物越多，所以空气质量状况越差，故D正确；

中考数学总复习讲义01：数与代数

中考数学第一轮总复习讲义考点1：有理数的意义、数轴、相反数、绝对值的概念（B ） 1.有理数：(1)凡能写成)0p q ,p (p q ≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2．数轴：数轴是规定了原点、正方向、单位长度的一条直线.3．相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0；(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ；绝对值的问题经常分类讨论；注：2x =的解为2±=x ；而22=-，但少部分同学写成 22±=-．5.倒数：乘积为1的两个数互为倒数；注意：0没有倒数；若 a ≠0，那么a 的倒数是a1； a1也可表示为a -1,若ab=1⇔ a 、b 互为倒数；若ab ＝－1⇔ a 、b 互为负倒数. 6．非负数：零和正数统称非负数。

①常见的非负数的形式：|a| 、2a 、)0(≥a a ；②非负数的常用应用类型：几个非负数之和为0，则每一个非负数都为0；中考真题1. （2010安徽）在﹣1，0，1，2这四个数中，既不是正数也不是负数的是（）A 、﹣1B 、0C 、1D 、22. （2008安徽）－3的绝对值是（） A.3 B.－3 C.13 D. 13- 3．（2007安徽）34相反数是（） A.43 B.43 C.34 D. 344. （2005安徽）计算12--||结果正确的是（） A. 3 B. 1 C. -1 D. -35.（2011•安顺）﹣4的倒数的相反数是（）A 、﹣4 B 、4 C 、﹣ D 、6. 2011河北）若|x －3|＋|y ＋2|＝0，则x ＋y 的值为．考点2：有理数大小的比较（B ）实数比较大小：（1）利用数轴：数轴上的两个数，右边的数总比左边的数大；（2）利用绝对值：正数＞0＞负数，正数＞负数，两个负数，绝对值大的反而小；0,0,0a b a b a b a b a b a b a b->⇔>-=⇔=-<⇔<(3)作差比较法：设、是两个任意实数，则除此之外，还有平方法、倒数法等方法。

2020年中考英语一轮复习T开头词汇(一)讲义

2020中考一轮复习T 开头词汇（一）（讲义）❤❤以字母 T 开头的单词thing /θɪŋ/ n. 物，东西；事情；（复）用品，用具All their things were destroyed in the fire.他们所有的东西都被大火烧掉了。

Bring your swimming things if the weather’s nice.如果天气好，带上你的游泳用品。

table /'teɪb(ə)l/ n. 桌子，表格tennis /'tenɪs/ n. 网球table tennis = ping pong n. 乒乓球team /tiːm/ n. 队，组teammate /'tiːmmeɪt/ n. 同队队员；队友technology /tek'nɒlədʒɪ/n. 技术；科技；工艺telephone /'telɪfəʊn/v. 打电话n. 电话temperature /'temp(ə)rətʃə/ n. 温度；气温；体温take one’s temperature 量体温tent /tent/ n. 帐篷tiger /'taɪgə/ n. 老虎tail /teɪl/ n. 尾巴，尾部Dogs wag their tails when they are pleased.tale /teɪl/ n. 故事；传说Chinese fairy taleHe told some fascinating tales about his life in India.他讲了他在印度生活的一些奇闻轶事。

tape /teɪp/ n. 磁带；录音带a tape player 录音机、收音机tree /triː/ n. 树tea /tiː/ n. 茶；茶叶 [U]tea art 茶艺tea sets 茶具drink tea 喝茶time /taɪm/ n. 时间；时期；时刻；次，回Do you have the time? 你知道几点了吗？It’s time for… = It’s time to do…该干……的时间到了on time 准时in time 及时from time to time 偶尔；有时（at times/sometimes/now and then）bythe time 到……时；在……以前all the time 始终；一直at the time / at that timeat the time 通常用于过去时句子中，指某件事情发生的“当时”、“那时”。