电路理论基础课后答案解析(哈工大陈希有)第11章
电路理论基础(陈希有)习题解答10-14

uC (0 ) uC (0 ) 24V iL (0 ) iL (0 ) 2A
由 KVL 得开关电压:
6
6 3
Ri
u(0 ) uC (0 ) 8 iL (0 ) (24 8 2)V 8V
(b)
答案 10.3 解: t 0 时电容处于开路, i 0 ,受控源源电压 4i 0 ,所以 等 效 电 阻
由换路定律得:
t0
4 4
时 电 感 处 于 短 路 , 故
Ri
(b)
8
3 i L (0 ) 9A 3A ,由换路定律得: 63 iL (0 ) iL (0 ) 3A
求等效电阻的电路如图(b)所示。 ,
等效电阻
Ri (4 // 4) // 8 1.6
时间常数
求稳态值的电路如图(b)所示。 i ( ) 2 2 10V 3 3 4 Ri iL ( ) 4 2 2
(b) (c)
(b)
Ri (
时间常数
6 3 3 1.5 )k 3k 6 3 3 1.5
3 6 3
答案 10.13
解:当 t 0 , r 列 KVL 方程得:
-1-
答案 10.1
解: t
0 时,电容处于开路,故 uC (0 ) 10mA 2k 20V
t 0 时,求等效电阻的电路如图(b)所示。
i 6 3 4i
iL (t ) iL (0 )e t / 3e 2t A (t 0)
电感电压
由换路定律得:
u1 (t ) L
由换路定律得
L / Ri 0.5s
由三要素公式得: 解 得 A 答案 10.9 解:当 t 原始值
(整理)电路理论基础(梁贵书)第11章答案

第十一章习题解答11-1周期性矩形脉冲如图所示,试求其傅立叶级数展开形式。
t解:02212w T πππ=== 00011()22T m m U a f t dt U dt T πππ===⎰⎰ 00002211()cos 2cos sin 0Tm k m U a f t kw tdt U ktdt ktT kππππ=⋅===⎰⎰0002()sin 12sin 2211()cos ()(cos 1)21cos 41,3,5,00,2,4,Tk m mm m mb f t kw tdtT U ktdt U U kt k k k U k k U k k k πππππππππ=⋅===⋅⋅----=⎧=⎪=⎨⎪=⎩⎰⎰ ∴14mU b π=,343m U b π=,54,5mU b π=0135()sin sin 3sin 5444sin sin 3sin 5354111(sin sin 3sin 5sin 7)357mmm m m m f t a b t b t b t U U U Ut t t U U t t t t ππππππ=++++=++++=+++++11-3在图示电路中,无源一端口网络N 的 端口电压和端口电流分别为()100cos31450cos(94230)V u t t t ︒=+- 3()10cos314 1.75cos(942)A i t t t θ=++若把N 看作为RLC 串连电路,试求:(1)R,L,C 之值;(2)3θ之值;(3)电路消耗的功率。
解:(1)13()100cos31450cos(94230)()()u t t t u t u t ︒=+-=+313()10cos314 1.75cos(942)()()i t t t i t i t θ=++=+∵1()100cos314u t t =,∴.10V U ︒=∵1()10cos314i t t =,∴.10A I ︒=∵.1U 与.1I 同相,∴LC 串连分支对基波而言发生 串连谐振,∴.1.1100U R I ︒===Ω21314314C L =⇒= ∵3()50cos(94230)V u t t ︒=-,∴.330U ︒=-,3U = 33() 1.75cos(942)i t t θ=+,∴.33A I θ=∴333501.75U Z I ==== ∴22110(942)816.33942L C+-= 21(942)716.33942L C -= 194226.76942L C -=(∵w 时谐振,∴3w 时呈感性)∵21314C L =∴2194226.761942314L L -= 31494226.763LL -=∴31.9mH L =231317.94F 31431.910C μ-==⨯⨯(2)∵.330V U ︒=-,.33I θ= 33611(942)10(94231.910)942942317.941010(30 3.34)28.4769.44Z R j L j C j --︒=+-=+⨯⨯-⨯⨯=+-=∠Ω .3333.333028.4769.44U U Z I I θ︒︒==∠--≈∠ ∴33069.44θ︒︒--=∴33069.4499.44θ︒︒︒=--=-(3)1︒1()100cos314V u t t =单独作用时,1()10cos314A i t t =∴221110500W P I R =⨯=⨯= 2︒ 3()50cos(94230)V u t t ︒=-单独作用时,3() 1.75cos(94299.44)A i t t ︒=-2233101015.31W P I =⨯=⨯=1350015.31515.31W P P P =+=+=11-10图示电路为滤波电路,要求14w 的谐波电流传至负载,而使基波电流无法达到负载。
电路分析第十一章习题参考答案
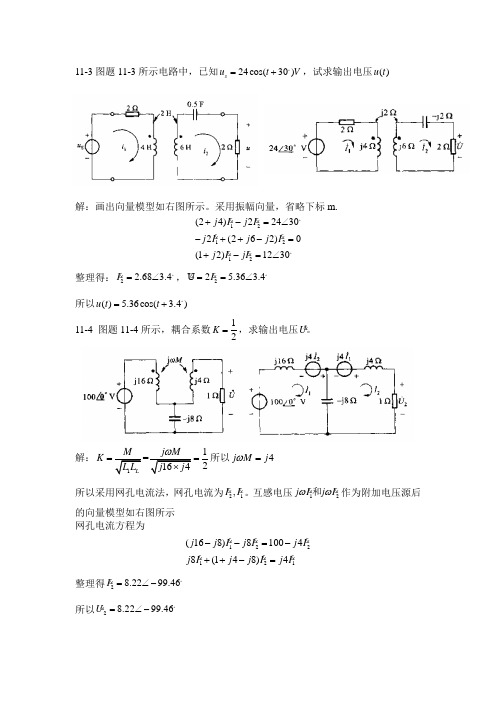
11-3图题11-3所示电路中,已知24cos(30)s u t V =+。
,试求输出电压()u t解:画出向量模型如右图所示。
采用振幅向量,省略下标m.121212(24)224302(262)0(12)1230j I j I j I j j I j I jI +-=∠-++-=+-=∠ 。
整理得:2 2.68 3.4I =∠ 。
,2U 2 5.36 3.4I ==∠ 。
所以() 5.36cos( 3.4)u t t =+。
11-4 图题11-4所示,耦合系数12K =,求输出电压U 。
解:12K ==所以4j M j ω= 所以采用网孔电流法,网孔电流为21,I I 。
互感电压12j I j I ωω 和作为附加电压源后的向量模型如右图所示网孔电流方程为122121(168)810048(148)4j j I j I j I j I j j I j I --=-++-= 整理得28.2299.46I =∠- 。
所以28.2299.46U =∠- 。
11-8电路图题11-8所示,试求对电源端的输入阻抗、电流12I I 和。
解:列网孔方程1212(24)21202(22)0j I j I j I j I +-=∠-++= 。
整理得12(22),2I j A I A =-= 所以12Z (33)22i j j =Ω=+Ω- 11-9 已知空心变压器的参数:1122L =9H,R =200,L =4H,R =1000.5.k ΩΩ=及所接负载为800Ω电阻和1F μ电容串联,所接正弦电压源频率为400rad/s, 电压有效值为300V ,内阻为500,Ω内电感为0.25H .试求传送给负载的功率P 和空心变压器的功率传输效率。
解:(1)可以画出电路如上图所示。
M=3H =做出向量模型后可以列出网孔方程为1212(500200100300)12003001200(10080016002500)0j j I j I j I j j I +++-=-+++-=整理得1271.56A 0.0596116.6A 50I I -==∠- 。
电子技术第十一章习题及答案(精华).docx

第十一章组合逻辑电路姓名______________ 班级__________一、填空题1、数字电路中的逻辑电路按功能可分为_________ 电路和________ 电路两种类型。
2、组合电路的特点:输出状态仅仅取决于_______ 输入值的组合,而与_________________无关。
3、电路结构看,组合电路具有两个特点:(1)电路由________ 电路组成,不包含任何_______ 元件,(2)电路中不存在任何_________ 回路。
4、电路的分析,是根据给定的______ 电路,写出 _______ 表达式,并以此来描述它的,确定______ 对于_______ 的关系O5、不考虑进位输入,只将本位两数相加,称为________________ o6、组合逻辑电路的分析,一般按以下步骤进行:笫一步:根据给定的逻辑电路,写出______________ 0第二步:化简逻辑电路的_______________________ O第三步:根据化简后的逻辑函数表达式列_________ O第四步:描述_________________________________ O7、当两个木位数相加,再考虑_____________ 进位数时,叫 __________ 。
8、全加器有 ___ 个输入, ____ 个输出。
9、全加器一个输出为___________ ,另一个输出为_____________ o10、___________________________________________ 全加器的本位和输岀表达式Sn=________ ,进位输出表达式O_____________________________________ O11、_____________________________________________ 一个输出N位代码的二进制编码器,可以表示种输入信号。
12、______________________________________ 二进制编码器是将输入信号编成的电路。
哈工大电路原理基础课后习题集

第一章习题1.1 图示元件当时间t<2s时电流为2A,从a流向b;当t>2s时为3A,从b流向a。
根据图示参考方向,写出电流的数学表达式。
1.2图示元件电压u=(5-9e-t/τ)V,τ>0。
分别求出t=0 和t→∞时电压u的代数值及其真实方向。
图题1.1 图题1.21.3 图示电路。
设元件A消耗功率为10W,求;设元件B消耗功率为-10W,求;设元件C发出功率为-10W,求。
图题1.31.4求图示电路电流。
若只求,能否一步求得?1.5 图示电路,已知部分电流值和部分电压值。
(1) 试求其余未知电流。
若少已知一个电流,能否求出全部未知电流?(2) 试求其余未知电压u14、u15、u52、u53。
若少已知一个电压,能否求出全部未知电压?1.6 图示电路,已知,,,。
求各元件消耗的功率。
1.7 图示电路,已知,。
求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。
1.8 求图示电路电压。
1.9 求图示电路两个独立电源各自发出的功率。
1.10 求网络N吸收的功率和电流源发出的功率。
1.11 求图示电路两个独立电源各自发出的功率。
1.12 求图示电路两个受控源各自发出的功率。
1.13 图示电路,已知电流源发出的功率是12W,求r的值。
1.14 求图示电路受控源和独立源各自发出的功率。
1.15图示电路为独立源、受控源和电阻组成的一端口。
试求出其端口特性,即关系。
1.16 讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响,加深对独立源特性的理解。
第二章习题2.1 图(a)电路,若使电流A,,求电阻;图(b)电路,若使电压U=(2/3)V,求电阻R。
2.2 求图示电路的电压及电流。
2.3 图示电路中要求,等效电阻。
求和的值。
2.4求图示电路的电流I。
2.5 求图示电路的电压U。
2.6 求图示电路的等效电阻。
2.7 求图示电路的最简等效电源。
图题2.72.8 利用等效变换求图示电路的电流I。
电路理论基础课后习题答案 陈希有主编 第十到十四章

答案10.1解:0<t时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A3)363685(V45)0(=Ω+⨯++=-i,A 2)0(366)0(=⨯+=--i i LV 24)0(8)0(=⨯=--i u C由换路定律得:V24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i由KVL 得开关电压:V8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R 时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4 解:<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t Lti Lt u --==)0(>t Ω3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
电路理论习题答案第11章

第十一章习题解答11-1周期性矩形脉冲如图所示,试求其傅立叶级数展开形式。
t解:02212w T πππ=== 00011()22T m mU a f t dt U dt T πππ===⎰⎰ 00002211()cos 2cos sin 0T m k m U a f t kw tdt U ktdt ktT kππππ=⋅===⎰⎰0002()sin 12sin 2211()cos ()(cos 1)21cos 41,3,5,00,2,4,Tk m mm m mb f t kw tdtT U ktdtU U kt k k k U k k U k k k πππππππππ=⋅===⋅⋅----=⎧=⎪=⎨⎪=⎩⎰⎰ ∴14mU b π=,343mU b π=,54,5mU b π=0135()sin sin 3sin 5444sin sin 3sin 5354111(sin sin 3sin 5sin 7)357mmm m m m f t a b t b t b t U U U Ut t t U U t t t t ππππππ=++++=++++=+++++11-3在图示电路中,无源一端口网络N 的 端口电压和端口电流分别为()100cos31450cos(94230)V u t t t ︒=+-3()10cos314 1.75cos(942)A i t t t θ=++若把N 看作为RLC 串连电路,试求:(1)R,L,C 之值;(2)3θ之值;(3)电路消耗的功率。
解:(1)13()100cos31450cos(94230)()()u t t t u t u t ︒=+-=+313()10cos314 1.75cos(942)()()i t t t i t i t θ=++=+∵1()100cos314u t t =,∴.10V U ︒=∵1()10cos314i t t =,∴.10A I ︒=∵.1U 与.1I 同相,∴LC 串连分支对基波而言发生 串连谐振,∴.1.1100U R I ︒===Ω21314314C L =⇒= ∵3()50cos(94230)V u t t ︒=-,∴.330U ︒=-,3U = 33() 1.75cos(942)i t t θ=+,∴.33A I θ=∴333501.75U Z I ====∴22110(942)816.33942L C+-=21(942)716.33942L C -=194226.76942L C -=(∵w 时谐振,∴3w 时呈感性)∵21314C L =∴2194226.761942314L L -= 31494226.763LL -=∴31.9mH L =231317.94F 31431.910C μ-==⨯⨯(2)∵.330V U ︒=-,.33I θ=33611(942)10(94231.910)942942317.941010(30 3.34)28.4769.44Z R j L j C j --︒=+-=+⨯⨯-⨯⨯=+-=∠Ω .3333.333028.4769.44U U Z I I θ︒︒==∠--≈∠ ∴33069.44θ︒︒--=∴33069.4499.44θ︒︒︒=--=-(3)1︒1()100cos314V u t t =单独作用时,1()10cos314A i t t =∴221110500W P I R =⨯=⨯=3()50cos(94230)V u t t ︒=-单独作用时,3() 1.75cos(94299.44)A i t t ︒=-2233101015.31W P I =⨯=⨯=1350015.31515.31W P P P =+=+=11-10图示电路为滤波电路,要求14w 的谐波电流传至负载,而使基波电流无法达到负载。
电路分析第十一章习题解答
∴ 电压源电流 = 9.5cos(t − 90o )A
11-9.同轴电缆的外导体与内导体之间总存在一些互感,如图 11-34 所示电缆用来传送 1MHz 信号到负载 RL,试计算耦合系数 k 为 0.75 和 1 时传送给负载的功率。
& = − jω MI & + j 0.1I & = [− j 0.05(− j10.5) + j 0.1⋅ (− j )]V QU ab 2 1
= (−0.525 + 0.1)V = −0.425V ∴ uab = −0.425cos tV
(6)左侧电感电流即 is = sin tA
& +U & = (−0.425 + 1)V = 0.575V (7)Q 电流源电压相量 = U ab s ∴ 电流源电压 = 0.575cos tV & −I & = [− j10.5 − (− j )] = − j 9.5 = 9.5∠ − 90 A (8)Q 电压源电流相量 = I 2 1
& I 1 & U 1
& I 2
jωL1
jωL2
& U 2
图 11-20
& = jω L I & & QU 2 2 2 + jωMI 1 = j ⋅6⋅3⋅ 3 2 ∠0 o + j ⋅ 6 ⋅ 2 ⋅
o
5 2
∠0 o
= j ⋅ 57 2 = 57 2∠90 ∴ u 2 = 114 cos(6t + 90 o )
+
& I
R1
L1
R2 M
L2
& U
图 11-23 解:由于两个线圈是反串,故等效电感为
电路理论基础习题答案

电路理论基础习题答案电路理论基础习题答案电路理论是电子工程的基础学科,它研究电流、电压和电阻等基本电学量之间的关系。
通过解答习题,可以帮助我们深入理解电路理论的基本概念和原理。
本文将给出一些电路理论基础习题的答案,希望对读者的学习有所帮助。
1. 电阻器串联和并联的计算(1) 串联电阻器的计算方法是将各个电阻器的阻值相加,得到总电阻。
例如,如果有三个电阻器,阻值分别为R1、R2和R3,则它们的串联总电阻为Rt = R1 + R2 + R3。
(2) 并联电阻器的计算方法是将各个电阻器的倒数相加,再取倒数。
例如,如果有三个电阻器,阻值分别为R1、R2和R3,则它们的并联总电阻为Rt = 1 /(1/R1 + 1/R2 + 1/R3)。
2. 电压和电流的计算(1) 根据欧姆定律,电压(V)等于电流(I)乘以电阻(R)。
即V = I * R。
因此,如果已知电流和电阻,可以计算电压;如果已知电压和电阻,可以计算电流;如果已知电压和电流,可以计算电阻。
(2) 电路中的电流可以通过欧姆定律和基尔霍夫定律来计算。
欧姆定律是指电流等于电压除以电阻,即I = V / R。
基尔霍夫定律则是指电流在一个节点(连接点)的总和等于从该节点流出的电流的总和。
利用这些定律,可以解决复杂的电路问题。
3. 电路功率的计算(1) 电路功率可以通过电流和电压的乘积来计算,即P = V * I。
功率的单位是瓦特(W)。
(2) 对于直流电路,功率的计算比较简单。
但对于交流电路,由于电流和电压是随时间变化的,功率的计算需要考虑相位差。
在交流电路中,有一个重要的概念叫做功率因数,它等于有功功率与视在功率之比。
有功功率是指实际产生功率的部分,视在功率是指电流和电压的乘积。
4. 电路中的电感和电容(1) 电感是指电流变化时,由于电磁感应产生的电压。
它的单位是亨利(H)。
电感的计算需要考虑电感的自感和互感。
自感是指电感对自身电流变化产生的电压,互感是指电感对其他电感或电阻的电流变化产生的电压。
电路理论基础第四版孙立山陈希有主编答案

电路理论基础第四版孙立山陈希有主编答案1. 引言《电路理论基础(第四版)》是一本系统介绍电路基本理论和基本分析方法的教材。
本文档是《电路理论基础(第四版)》的答案,提供了教材中习题的解答。
通过这些答案,学生可以检验自己对电路理论的理解,巩固知识点,提高解题能力。
2. 电路理论基础答案2.1 第一章网孔法和节点法的基本概念2.1.1 习题1-1a)略b)略c)略…2.2 第二章电阻网络的基本性质2.2.1 习题2-1a)略b)略c)略…2.3 第三章基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)2.3.1 习题3-1a)略b)略c)略…2.4 第四章电流和电压的计算2.4.1 习题4-1a)略b)略c)略…2.5 第五章电阻串联与并联的简化2.5.1 习题5-1a)略b)略c)略…2.6 第六章电流分压和电压分流2.6.1 习题6-1a)略b)略c)略…2.7 第七章网格分析法2.7.1 习题7-1a)略b)略c)略…2.8 第八章直流电路的戴维南定理2.8.1 习题8-1a)略b)略c)略…2.9 第九章交流电路频率特性2.9.1 习题9-1a)略b)略c)略…2.10 第十章交流电阻、电感和电容的阻抗2.10.1 习题10-1a)略b)略c)略…2.11 第十一章交流电路的功率2.11.1 习题11-1a)略b)略c)略…2.12 第十二章交流电路分析方法2.12.1 习题12-1a)略b)略c)略…3. 结语本文档提供了《电路理论基础(第四版)》的答案,涵盖教材中的习题。
通过阅读答案,学生可以巩固和检验自己的理论知识和解题能力。
希望本答案对学生学习电路理论有所帮助。
电路理论基础(陈希有)课后题答案

答案13.1解: (1)、(4)是割集,符合割集定义。
(2)、(3)不是割集,去掉该支路集合,将电路分成了孤立的三部分。
(5)不是割集,去掉该支路集合,所剩线图仍连通。
(6)不是割集,不是将图分割成两孤立部分的最少支路集合。
因为加上支路7,该图仍为孤立的两部分。
答案13.2解:选1、2、3为树支,基本回路的支路集合为 {1,3,4},{2,3,5},{1,2,6}; 基本割集的支路集合为 {1,4,6},{2,5,6},{3,4,5}。
答案13.3 解:(1) 由公式l t I B I T t =,已知连支电流,可求得树支电流A 1595111011010654321⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡i i i i i i (2) 由公式t t U B U -=l ,已知树支电压,可求得连支电压V 321321100111110654⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡u u u (3) 由矩阵B 画出各基本回路,如图(a)~(c)所示。
将各基本回路综合在一起得题中所求线图,如图13.3(d)所示。
(a)(b)(c)(d)答案13.4解:连支电流是一组独立变量,若已知连支电流,便可求出全部支路电流。
因此除将图中已知电流支路作为连支外,还需将支路3或4作为连支。
即补充支路3或4的电流。
若补充3i ,则得A 11=i ,A 22-=i ,34A 3-i i -=;若补充4i ,则得A 11=i ,A 22-=i ,43A 3-i i -=答案13.5解:树支电压是一组独立变量,若已知树支电压,便可求出全部支路电压。
除将图中已知支路电压作为树支外,还需在支路1、2、3、4、5中任选一条支路作为树支。
即在1u 、2u 、3u 、4u 、5u 中任意给定一个电压便可求出全部未知支路电压。
电路理论教程答案陈希有

电路理论教程答案陈希有【篇一:《电路理论基础》(第三版陈希有)习题答案第一章】电路电流的参考方向是从a指向b。
当时间t2s时电流从a流向b,与参考方向相同,电流为正值;当t2s时电流从b流向a,与参考方向相反,电流为负值。
所以电流i的数学表达式为2a t?2s? i??-3at?2s ?答案1.2解:当t?0时u(0)?(5?9e0)v??4v0其真实极性与参考方向相反,即b为高电位端,a为低电位端;当t??时u(?)?(5?9e??)v?5v0其真实极性与参考方向相同,即a为高电位端,b为低电位端。
答案1.3解:(a)元件a电压和电流为关联参考方向。
元件a消耗的功率为pa?uaia则ua?pa10w??5v ia2a真实方向与参考方向相同。
(b) 元件b电压和电流为关联参考方向。
元件b消耗的功率为pb?ubib则ib?pb?10w1a ub10v真实方向与参考方向相反。
(c) 元件c电压和电流为非关联参考方向。
元件c发出的功率为pc?ucic则uc?pc?10w10v ic1a真实方向与参考方向相反。
答案1.4解:对节点列kcl方程节点③: i4?2a?3a?0,得i4?2a?3a=5a节点④: ?i3?i4?8a?0,得i3??i4?8a?3a节点①: ?i2?i3?1a?0,得i2?i3?1a?4a节点⑤: ?i1?i2?3a?8a?0,得i1?i2?3a?8a??1a若只求i2,可做闭合面如图(b)所示,对其列kcl方程,得 i28a-3a+1a-2a0解得i2?8a?3a?1a?2a?4a答案1.5解:如下图所示(1)由kcl方程得节点①:i1??2a?1a??3a节点②:i4?i1?1a??2a节点③:i3?i4?1a??1a节点④:i2??1a?i3?0若已知电流减少一个,不能求出全部未知电流。
(2)由kvl方程得回路l1:u14?u12?u23?u34?19v回路l2:u15?u14?u45?19v-7v=12v回路l3:u52?u51?u12??12v+5v=-7v回路l4:u53?u54?u43?7v?8v??1v若已知支路电压减少一个,不能求出全部未知电压。
电路理论基础课后答案(哈工大陈希有)第11章

电路理论基础课后答案(哈工大陈希有)第11章题11.1 根据定义求和的象函数。
解: (1)(2)题11.2设求的象函数。
解:由拉氏变换的微分、线性和积分性质得:题11.3设(t 为纯数)。
分别求对应象函数、、,验证卷积定理。
解:设 , 则与的卷积为)()(t t t f ε=)(e )(t t t f atε-=2020001e 1e 1e e )()(-ss dt s s t dt t t s F stst st st=-=+-==∞-∞-∞-∞----⎰⎰ε20)(20)(00)(1e )(1e 1e e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s dt s s t dt t t s F t s t s st st t ξξετd f c t bf tt f a t f f t A t f t t )()(d )(d )(,0)0(),()e 1()(011121/1⎰-++==-=--)(2t f )(2s F )/1(//1)(1τττ+=+-=s s A s A s A s F )/1(/)()()/(]/)([)()]0()([)(22111112ττ+++=++=++-=-s s A c bs as s F s c b as s s F c s bF f s sF a s F )()()(,e 2)(,e 5)(215221t f t f t f t f t f tt *===--)(1s F )(2s F )(s F 25)}({)(11+==s t f s F L 52)}({)(22+==s t f L s F )5)(2(10)()(21++=s s s F s F )(1t f )(2t f对上式取拉氏变换得:由此验证。
题11.4求下列函数的原函数。
(a) (b)(c)解:(a), 所以(b)所以)e e (310]e 31[e 10e e 10e 2e 5)(*)(520350350)(5221tt t tt ttt d d t f t f --------=⨯==⨯=⎰⎰ξξξξξξ)5)(2(10)5121(310)}(*)({21++=+-+=s s s s t f t f L )()()}(*)({2121s F s F t f t f =L 6512)(2+++=s s s s F)2)(1(795)(23+++++=s s s s s s F 623)(2++=s s s F 6512)(2+++=s s s s F 3221+++=s A s A 3|31221-=++=-=s s s A 3|31221-=++=-=s s s A tt s s t f 321e 5e 3}3523{)(---+-=+++-=L )2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A tt t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ(c)查表得题11.5分别求图示(a)、(b)电路的等效运算阻抗或等效运算导纳。
电路理论基础(陈希有)课后题答案

答案12.1解:分别对节点①和右边回路列KCL 与KVL 方程:Cq u u i i qi C L L R C C /===--==ψ将各元件方程代入上式得非线性状态方程:C q C q f f q/)/()(21=--=ψψ方程中不明显含有时间变量t ,因此是自治的。
答案12.2解:分别对节点①、②列KCL 方程: 节点①:=1i 321S 1/)(R u u i q--= 节点②:=2i 423212//)(R u R u u q--= 将)(),(222111q f u q f u == 代入上述方程,整理得状态方程:⎩⎨⎧+-=++-=)/())((/)(/)(/)(4343223112S 3223111R R R R q f R q f q i R q f R q f q答案12.3解:分别对节点①列KCL 方程和图示回路列KVL 方程得:⎩⎨⎧-=-=(2)(1) /323321u u R u i qS ψ 3u 为非状态变量,须消去。
由节点①的KCL 方程得:0413332432=-++-=++-R u u R u i i i i 解得)/()]()([)/()(433224114332413R R R f R q f R R R i R u u ++=++=ψ 将)(111q f u =、)(222ψf i = 及3u 代入式(1)、(2)整理得:⎩⎨⎧++-+-=+++-=Su R R R R f R R R q f R R R f R R q f q)/()()/()()/()()/()(4343224331124332243111ψψψ 答案12.4解:由KVL 列出电路的微分方程:=L u )(sin )(d d 3t R u Ri tS ωβψαψ+-=+-= 前向欧拉法迭代公式:)](sin )([31k k k k t R h ωβψαψψ+-+=+后向欧拉法迭代公式:)](sin )([1311++++-+=k k k k t R h ωβψαψψ梯形法迭代公式:)](sin )()(sin )([5.013131++++-+-+=k k k k k k t R t R h ωβψαωβψαψψ答案12.5解:由图(a)得:tu C u U t C t u Ci R R C R d d )(d dd d S -=-== (1) 由式(1)可知,当0>R i 时,0d d <t u R ,R u 单调减小;当0<R i 时,0d d >tuR ,R u 单调增加。
电工学 第11章 课后习题答案 课件

第 11 章 组合逻辑电路
与非门原理电路: 与非门 与非门原理电路:TTL 与非门 门原理电路 A = 0, B = 0, F = 1 A = 0, B = 1, F = 1 A = 1, B = 0, F = 1
T1 处于饱和状态 T3 导通 T2 和 T4 处于截止
A B
RC1
B1
+5V RC2 RC3
下一节 上一页 下一页
第 11 章 组合逻辑电路
(二) 与非门电路 二 与非门电路
逻辑表达式: 逻辑表达式: 逻辑符号: 逻辑符号:
F = A⋅ B
A B
&
图 11.2.3 与非门
F
真值表
A 0 0
1
B 0 1
0
F
1 1 1
规律: 规律: 任0则1 全1则0
1
返 回
1
0
上一节 下一节 上一页 下一页
返 回
门打开 门关闭
下一节 上一页 下一页
第 11 章 组合逻辑电路
(三) 非门电路 三
非逻辑 非逻辑符号: 非逻辑符号:
1
图 11.1.4 非逻辑
A
真值表
F
波形: 波形:
A
F
0
1
A
0 1
F
1
1
0
0
非逻辑表达式: 非逻辑表达式:
F=A
返 回 返 回
逻辑非的运算规律: 逻辑非的运算规律: A+ A = 1 A⋅ A = 0 A=A
上一页 下一页
第 11 章 组合逻辑电路
逻辑乘的运算规律: 逻辑乘的运算规律:
A⋅0 = 0 A ⋅1 = A A⋅ A = A
电路理论基础(陈希有)课后题答案

答案15.1解: 波阻抗Ω500400102003c =⨯==++i u Z终端反射系数133c 2c 22=+-=Z R Z R N故负载承受的电压V k 15.24610200)1331(32222=⨯⨯+=+=++u N u u 答案15.2解:终端反射系数31c c 2=+-=Z Z Z Z N L L始端反射系数1cS cS 1-=+-=Z Z Z Z N这是一个多次反射过程,反射过程如图题15.2所示。
其中v l t d /= 当vlt 20<<时,反射波未达到始端,只有入射波。
mA 30500V 15c 11=Ω===+Z u i i 当vlt v l 42<<时,反射波到达始端, mA 101010302121=--=+-=+++i N N i N i i 当vlt v l 64<<时 ,始端电流为: mA 67.1631031010103022212212121=++--=+-+-=+++++i N N i N N i N N i N i i 达到稳态时mA 15)(211==∞R u i 所以⎪⎩⎪⎨⎧<<<<<<=v l t l/v v l t l/v v l t t i /64 16.67mA /42 10mA /20 mA30)(1 mA 15)(211==∞R u i图题15.2答案15.3解:波从始端传到中点所用的时间为:μs 10s 1010310325831==⨯⨯==-v l t (1)当μs 100<<t 时,入射波从始端发出,尚未到达中点所以 0)(=t i 。
(2)μs 30μs 10<<t 时,入射波已经过中点,但在终端所产生的反射波还没有到达中点。
A 2.0600600240)(c S S 1=+=+==+Z R U i t i(3) μs 60μs 30<<t 时,在终端所产生的反射波已经过中点,并于μs 40=t 时 刻到达始端。
哈工大电路理论基础课后习题答案(PDF精品)

答案2.1解:本题练习分流、分压公式。
设电压、电流参考方向如图所示。
(a) 由分流公式得:23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得:3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解:电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得:220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯= 再对图(a)使用分压公式得:13==30V 1+3U U ⨯答案2.3解:设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1) 由已知条件得如下联立方程:32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω 再将3R 代入(1)式得210k 3R =Ω答案2.4解:由并联电路分流公式,得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解:首先将电路化简成图(b)。
图 题2.5120Ω(a)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-= 再由图(a)得321201A 360120I I =⨯=+由KVL 得,3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解:(a )设R 和r 为1级,则图题2.6(a)为2级再加x R 。
电工学第11章习题的答案-文档资料

第 11 章 组合逻辑电路
( 2 ) A B BC C A AB(C C ) BC ( A A) C A( B B ) ABC ABC BC A BC A C AB C AB ( ABC ABC ) ( ABC ABC ) ( ABC ABC ) AC ( B B ) AB(C C ) BC ( A A) AC AB BC AB BC C A
逻辑电路见图,真值表见表。
1 1
A 0 0
B F ;
F
返回练习题题集
上一页
上一题
下一题
第 11 章 组合逻辑电路
11.3.7 求如图所示电路中 F 的逻辑表达式,化简成最简 与或式,列出真值表,分析其逻辑功能,设计出全部改用与 非门实现这一逻辑功能的电路。 & AC
因此全部改用与非门实现这一功能的电路如图所示。
A B C F 0 0 00 0 0 10 B 0 1 00 0 1 11 1 0 00 1 0 11 C 1 1 01 1 1 11
第 11 章 组合逻辑电路
11.3.5 将下列各式化简后,根据所得结果画出逻辑电 路 (门电路的类型不限),列出真值表。
( 1 ) F AB ABC AB ( D E ) ( 2 ) F A ( A B C ) B ( A B C ) C ( A B C )
≥1
AC B
A
B
C
≥1
1
B
=1
AC
&
F ( AC B )( A C ) B ( AC B )( A C ) B
( A C )B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题11.1 根据定义求和的象函数。
解: (1)(2)题11.2设求的象函数。
解:由拉氏变换的微分、线性和积分性质得:题11.3设(t 为纯数)。
分别求对应象函数、、,验证卷积定理。
解:设 , 则与的卷积为)()(t t t f ε=)(e )(t t t f atε-=2020001e 1e 1e e )()(-ss dt s s t dt t t s F stst st st=-=+-==∞-∞-∞-∞----⎰⎰ε20)(20)(00)(1e )(1e 1e e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s dt s s t dt t t s F t s t s st st t ξξετd f c t bf tt f a t f f t A t f t t )()(d )(d )(,0)0(),()e 1()(011121/1⎰-++==-=--)(2t f )(2s F )/1(//1)(1τττ+=+-=s s A s A s A s F )/1(/)()()/(]/)([)()]0()([)(22111112ττ+++=++=++-=-s s A c bs as s F s c b as s s F c s bF f s sF a s F )()()(,e 2)(,e 5)(215221t f t f t f t f t f tt *===--)(1s F )(2s F )(s F 25)}({)(11+==s t f s F L 52)}({)(22+==s t f L s F )5)(2(10)()(21++=s s s F s F )(1t f )(2t f对上式取拉氏变换得:由此验证。
题11.4求下列函数的原函数。
(a) (b)(c) 解:(a), 所以(b)所以)e e (310]e 31[e 10e e 10e 2e 5)(*)(520350350)(5221tt t tt ttt d d t f t f --------=⨯==⨯=⎰⎰ξξξξξξ)5)(2(10)5121(310)}(*)({21++=+-+=s s s s t f t f L )()()}(*)({2121s F s F t f t f =L 6512)(2+++=s s s s F)2)(1(795)(23+++++=s s s s s s F 623)(2++=s s s F6512)(2+++=s s s s F 3221+++=s A s A 3|31221-=++=-=s s s A 3|31221-=++=-=s s s A tt s s t f 321e 5e 3}3523{)(---+-=+++-=L )2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A tt t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ(c)查表得题11.5分别求图示(a)、(b)电路的等效运算阻抗或等效运算导纳。
图题11.5解:(a) 由运算电路(略)求得端口等效运算阻抗为:, (b) 画出运算电路如图11.5(c)所示在端口加电流,列写节点电压方程如下由式(2)解得代入式(1)得所以623)(2++=s s s F 22)5()1(5)5/3(++⨯=s )5sin(e 53)(t t f t -=H5.011262241)3/(142)]3/(14[21)(22i ++++=++++=s s ss s s s s s Z 112611430)(22++++=s s s s s Z i U )(2s __⎩⎨⎧-==++-=-+)2()]()([3)(3)()]5.0/(11[)()1()()()()1(2122s U s U s U s U s s U s I s U s U s )(144)(2s U s s s U ⨯+=)()()1221(s I s U s ss =+-+1212)(2i+++=s s s s Y题11.6图(a)所示电路,设电感电压零状态响应象函数为,求电源电压[用表示]。
图题11.6解:运算电路如图11.6(b)所示。
化简得题11.7图示电路,已知V ,求零状态响应。
解:)(s U L )(S s U )(s U LL u)(s U L (S s U bss U s I L L 3)()(=)()/21()()(6)(1s U s s U s I s U L L L +=+=)(/5.04/21)2/(14)()(12s U ss s s U s I L++=+=)(]/5.04/212132[)()]()([2)(12S s U sss s s U s I s I s U LL +++++=++=)()18(389136)(2S s U s s s s s U L+++=)(e 2S t u tε-=u u -+u 图题11.7由运算电路 (略)并利用分压公式求得电容电压象函数为:式中, 所以V题11.8图(a)所示电路,已知,求零状态响应。
图题11.8解:电容和电感的初始储能均为零,,画出运算电路如图11.8 (b) 所示。
由分流公式求得电容电压象函数为:式中21)](e [)(2+==-s t s U tSεL 23/1)2)(3/1()3/2()(222212222)(21+++=++=⨯+⨯++⨯=s A s A s s s s U ss s ss U SVs 152|2)3/2(3/11-=+=-=s s s A Vs 8.0|3/1)3/2(22=+=-=s s sA ]e )15/2(e 8.0[)(3/2t t t u ---=A )(S t i ε=C u.0s s I /1)(S=(b )(sU C )(s 233)()5.0/(133)(2S ++=⨯++=s s s I s s s I C )2)(1(65.01)()(++=⨯=s s s s s I s U CC 21321++++=s A s A s A Vs 3|)2)(1(61=++==s s s A所以V 题11.9图(a)所示电路,开关接通前处于稳态。
已知, 。
求开关接通后电容电压u 。
图题11.9解:由图(a)得:, 运算电路如图11.9(b)所示。
列写节点电压方程如下:解得:各待定系数为Vs 6|)2(612-=+=-=s s s A Vs 3|)1(623=+=-=s s s A )()e 3e 63()}({)(21t s U t u tt CC ε---+-==L ,2,V 2,V 1121Ω===R U U Ω==432R R F 2.0,H )6/5(==C L1U 2V 1)0(1==-U u A 25.0/)0(21==-R U iL s/(b)6/524/5/5/14/21)6/5121()()6/512.0414121(s s s s s s s U s s ++=⨯+-++++32)65(625.6)(32122++++=++++=s A s A s A s s s s s s U Vs 1|)3)(2(625.6021=++++==s s s s s A所以V题11.10图示电路在零状态下,外加电流源,已知G =2S ,L =1H ,C =1F 。
试求电压。
解:由运算电路(略)求得并联电路运算导纳电流源象函数电压象函数反变换得题11.11图(a)所示电路中外加阶跃电压,已知C 1=0.3F ,C 2=0.7F ,R =10Ω。
求零状态响应电压及电流。
Vs 25.1|)3(625.6222=+++=-=s s s s s A Vs 1|)3)(2(625.6021=++++==s s s s s A )e 25.1e 25.11()}({)(321tt s U t u ----+==L A )(e )(3St t i tε-=)(t u )图题11.10ss s s s sC sL G s Y 12121)(2++=++=++=31)}(e {)(3S+==-s t s I tεL 3Vs 75.01Vs 75.0)1(Vs 5.0)3)(12()()()(22S+-++++-=+++==s ss s s s s s Y s I s U V )()]e e (75.0e 5.0[)}({3-1t t s U u tt t ε----+-==L V )(9)(St t u ε=)(2t u )(2t i图题11.11解:运算电路如图(b)所示图中由节点电压法得解得反变换得题11.12图(a)所示电路开关断开前处于稳态。
求开关断开后电路中、及的变化规律。
)(t )(2s (S s U ss U 9)(S =)()()1(S 1221s U sC s U sC sC R=++1.07.2)(2+=s s U 1.0189.089.11.089.1)()(222+-=+==s s s s U sC s I V )(εe 7.2)}({)(1.0212t s U t u t--==L A )](e 189.0)(δ89.1[)}({)(1.0212t t s I t i tε---==L 1i 1u 2u (a)图题11.12解:时电路处于直流稳态,由图(a)求得:, t >0时的运算电路如图(b)所示。
对回路列KVL 方程得解得所以反变换得(t >0)题11.13图(a)所示电路A ,,V , A 求的变化规律。
0<t A 210V 20)0(1=Ω=-i A 110V10)0(2=Ω=-i (b)ss s I s s 103420)()103210(1--+=+++43.05.0)4(2.02)(1+-=++=s s s s s s I 44.26.34)(2)(11++-=-=s s sI s U 46.36.33)(3)(12++=+=s s sI s U A )e 3.05.0()}({)(4111ts I t i ---==L V )(e 4.2)(δWb 6.3)}({)(41-11t t s U t u t ε-+⨯-==L V)(e 6.3)(δWb 6.3)}({)(4212t t s U t u tε--+⨯==L )(3S t i ε=)(Wb 2S t u δ⨯=1)0(=-C u 2)0(=-L i C u图 题11.13解:画出运算电路如图(b)所示,列写节点电压方程如下:解得:式中, 反变换得题11.14图(a)所示电路开关接通前处于稳态,已知,,,。
