中国科学院数学与系统科学研究院2005数分
数学分析与高等代数考研真题详解--中科院卷
校教师，硕博研究生报名参与本丛书的编写工作，他们在工作学习的过程中挤时间，编写审
稿严肃认真，不辞辛苦，这使我们看到了中国数学的推广和科研的进步，离不开这些默默无
闻的广大数学工作者，我们向他们表示最崇高的敬意！
国际数学大师陈省身先生提出：“要把中国建成 21 世纪的数学大国。”每年有上万名数
学专业的学生为了更好的深造而努力考研，但是过程是艰难的。我们为了给广大师生提供更
∫∫∫ 算积分 I = ex+y+zdxdydz ． D
4．(15
⎛ 分)定义向量场 F (x, y) = ⎜⎜⎝
xe x2 + y2 ,
x2 + y2
ye
x2 + y2
⎞ ⎟, x2 + y2 > 0
x2 + y2 ⎟⎠
证明 F (x, y) 是有势
场, 并求出 F (x, y) 的一个势函数．
∑ 5．(25
没有编配解答，很多同学感到复习时没有参照标准，所以本丛书挑选了重点名校数学专业的
试题，由众多编委共同编辑整理成书。在此感谢每一位提供试题的老师，同时感谢各个院校
的教师参与解答。以后我们会继续更新丛书，编入更新的试题及解答，希望您继续关注我们
的丛书系列。也欢迎您到博士家园数学专业网站参加学术讨论，了解考研考博，下载最新试
博士家园考研丛书 （2010 版）
全国重点名校数学专业考研真题及解答
数学分析与高等代数 考研真题详解
中国科学院数学专卷 博士家园 编著
博士家园系列内部资料
《 博士家园数学专业考研丛书》
编委会
这是一本很多数学考研人期待已久的参考书，对于任何一个想通过考取重点院校的研究
2005年考研数学二真题及答案解析
d cos t
arctan(cos 1 cos2 t
04
【评注】 本题为广义积分，但仍可以与普通积分一样对待作变量代换等.
4...【分析】直接套用一阶线性微分方程 y P(x) y Q(x) 的通解公式：
y e P(x)dx [ Q(x)e P(x)dx dx C] ，
（15）（本题满分11分）
x
设函数f(x)连续，且 f (0) 0 ，求极限 lim 0 (x t) f (t)dt .
x0
x
x
f (x t)dt
0
（16）（本题满分11分）
如图， C1 和 C2
分别是
y
1 2
(1
ex)
和
y
ex
的图象，过点(0,1)的曲线 C3 是一
单调增函数的图象. 过 C2 上任一点M(x,y)分别作垂直于x轴和y轴的直线 lx 和 l y .
则有
m a m1 1 am2 2 amn n ，
a11 a21 am1
1
2
m
1
,
2
,,
n
a12
a22
am
2
（13）设 1, 2 是矩阵A的两个不同的特征值，对应的特征向量分别为1, 2 ，
则1 ， A(1 2 ) 线性无关的充分必要条件是
(A) 1 0 . (B) 2 0 . (C) 1 0 . (D) 2 0 .
[]
（14）设A为n（ n 2 ）阶可逆矩阵，交换A的第1行与第2行得矩阵B,
后转化为隐函数求导.
【详解】 方法一： y (1 sin x) x = e x ln(1sin x) ，于是 y e x ln(1sin x) [ln(1 sin x) x cos x ] ， 1 sin x
2005年硕士研究生入学考试及答案
目录1.05年北师大物理类各方向2.05年长光所3.05年东南大学4.05年中科大5.05年南京大学6.05年华中科大7.05年吉林大学（原子所）8.05年四川大学（原子与分子）9.05年北京理工10.05年河北理工11.05年长春理工北京师范大学2005年招收硕士研究生入学考试试题专业:物理类各专业科目代号:459研究方向:各方向考试科目:量子力学[注意]答案写在答题纸上，写在试题上无效。
1.(20分)一个电子被限制在一维谐振子势场中，活动范围求激发电子到第一激发态所需要的能量（用ev表示）（，，）提示：谐振子能量本征函数可以写成2.（30分）一个电子被限制在二维各向同性谐振子势场中（特征频率为）。
（1）写出其哈密顿量，利用一维谐振子能级公式找到此电子的能级公式和简并度。
（2）请推导电子的径向运动方程。
并讨论其在时的渐近解。
提示：极坐标下3．（50分）两个质量为的粒子，被禁闭在特征频率为的一维谐振子势场中，彼此无相互作用（此题中波函数无须写出具体形式）：（1）如果两个粒子无自旋可分辨，写出系统的基态（两个都在自己的基态）和第一激发能级（即一个在基态，另一个在第一激发态）的波函数和能量（注意简并情形）。
（10分）（2）如果两个粒子是不可分辨的无自旋波色子，写出系统的基态和第一激发态的能量和波函数。
如果粒子间互作用势为，计算基态能级到一级微扰项。
（15分）（3分）如果两个粒子是不可分辨的自旋1/2粒子，写出基态能级和波函数（考虑自旋）。
如果粒子间互作用能为，计算基态能量。
（15分）（4）同（3），解除势阱，两个粒子以左一右飞出。
有两个探测器分别（同时）测量它们的y方向自旋角动量。
请问测量结果为两电子自旋反向的几率是多少？（10分）4．（30分）中心力场中电子自旋与轨道角动量存在耦合能。
总角动量，是的共同本征态。
现有一电子处于态，且。
（1）在一基近似下，可用代替，请问电子的能量与态差多少？（2）请计算该电子产生的平均磁矩，并由此计算在z方向均匀磁场B中电子的能量改变多少？（），当，，当，5．（20分）一个定域（空间位置不动）的电子（自旋1/2）处于z方向强磁场中。
2005考研数一真题及解析
2005年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共6小题，每小题4分，满分24分.把答案填在题中横线上）（1）曲线122+=x x y 的斜渐近线方程为 _____________.(2)微分方程x x y y x ln 2=+'满足91)1(-=y 的解为____________。
(3)设函数181261),,(222z y x z y x u +++=，单位向量}1,1,1{31=n ,则)3,2,1(nu∂∂=.________。
（4）设Ω是由锥面22y x z +=与半球面222y x R z --=围成的空间区域，∑是Ω的整个边界的外侧，则⎰⎰∑=++zdxdy ydzdx xdydz ____________。
（5）设123,,ααα均为3维列向量,记矩阵123(,,)=A ααα，123123123(,24,39)=++++++B ααααααααα,如果1=A ,那么=B 。
（6）从数1，2,3，4中任取一个数,记为X ， 再从X ,,2,1 中任取一个数，记为Y ， 则}2{=Y P =____________。
二、选择题（本题共8小题，每小题4分，满分32分。
每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内）（7）设函数n n n x x f 31lim )(+=∞→，则()f x 在),(+∞-∞内（A)处处可导 (B ）恰有一个不可导点（C ）恰有两个不可导点 （D)至少有三个不可导点（8）设()F x 是连续函数()f x 的一个原函数，""N M ⇔表示"M 的充分必要条件是",N 则必有（A ）()F x 是偶函数()f x ⇔是奇函数 （B ）()F x 是奇函数()f x ⇔是偶函数（C ）()F x 是周期函数()f x ⇔是周期函数 （D ）()F x 是单调函数()f x ⇔是单调函数（9）设函数⎰+-+-++=yx y x dt t y x y x y x u )()()(),(ψϕϕ, 其中函数ϕ具有二阶导数，ψ 具有一阶导数，则必有(A)2222y ux u ∂∂-=∂∂（B ）2222yux u ∂∂=∂∂（C)222yu y x u ∂∂=∂∂∂(D ）222x uy x u ∂∂=∂∂∂ （10)设有三元方程ln e 1xz xy z y -+=，根据隐函数存在定理，存在点(0,1,1)的一个邻域，在此邻域内该方程(A)只能确定一个具有连续偏导数的隐函数(,)z z x y =（B ）可确定两个具有连续偏导数的隐函数(,)x x y z =和(,)z z x y = （C ）可确定两个具有连续偏导数的隐函数(,)y y x z =和(,)z z x y = （D ）可确定两个具有连续偏导数的隐函数(,)x x y z =和(,)y y x z =（11）设21,λλ是矩阵A 的两个不同的特征值，对应的特征向量分别为12,αα，则1α，12()+A αα线性无关的充分必要条件是(A ）01≠λ (B ）02≠λ (C)01=λ （D)02=λ（12)设A 为(2)n n ≥阶可逆矩阵，交换A 的第1行与第2行得矩阵**.,B A B 分别为,A B 的伴随矩阵，则（A)交换*A 的第1列与第2列得*B (B)交换*A 的第1行与第2行得*B(C ）交换*A 的第1列与第2列得*-B （D)交换*A 的第1行与第2行得*-B（13）设二维随机变量(,)X Y 的概率分布为已知随机事件}0{=X 与}1{=+Y X 相互独立，则（A ）0.2,0.3a b == （B ）0.4,0.1a b == (C)0.3,0.2a b == （D)0.1,0.4a b == (14）设)2(,,,21≥n X X X n 为来自总体(0,1)N 的简单随机样本，X 为样本均值，2S 为样本方差，则(A))1,0(~N X n （B ）22~()nS n χ(C ）)1(~)1(--n t SXn （D ）2122(1)~(1,1)nii n X F n X=--∑三 、解答题（本题共9小题,满分94分。
2005年考研数学试题详解及评分参考介绍
3n
= x lim(
n ®¥
3
1 x
3n
+ 1) = x ，故 f (x) = lim n 1 + x
n ®¥
1 n
ì ï 1, =í 3 ï îx ,
x £1 x >1
.
于是有 f -¢( -1) = lim -
- x3 - 1 = -3, x ®1 x +1 1 -1 f -¢(1) = lim = 0, x ®1- x - 1
2005 年 • 第 3 页
郝海龙：考研数学复习大全·配套光盘·2005 年数学试题详解及评分参考
z ， Fz¢ = - ln y + e xz x ，于是有 y Fx¢(0,1,1) = 2 ¹ 0 ， Fy¢(0,1,1) = -1 ¹ 0 ， Fz¢(0,1,1) = 0 . 因此根据隐函数存在定理，由此 可确定相应的隐函数 x = x( y, z ) 和 y = y ( x, z ) . 故选 (D) . Fx¢ = y + e xz z ， Fy¢ = x (11) 设 l1 , l 2 是 矩阵 A 的 两 个 不同 的 特征值 ， 对 应的 特征 向量分 别 为 a 1 , a 2 ，则 a 1 ，
2005 年 • 第 1 页
(4) 设 W 是由锥面 z =
郝海龙：考研数学复习大全·配套光盘·2005 年数学试题详解及评分参考
整个边界的外侧，则
òò xdydz + ydzdx + zdxdy =
S
.
【答】 应填 (2 - 2)p R 3 . 【解】 由高斯公式，得
2 3 òò xdydz + ydzdx + zdxdy = 3òòò dV =3ò dq ò 4 sin j dj ò r dr = (2 - 2)p R . S W 0 0 0 2p
中国科学院数学研究院数学分析试题及答案
中国科学院数学与系统科学研究院20XX 年硕士研究生招生初试试题参考解答数学分析1、求a,b 使下列函数在x=0处可导:2,1,ax b y x +≥⎧=⎨+⎩当x 0;当x<0.解：由于函数在x=0处可导，从而连续，由(00),(00)1f b f +=-=，得到b=1;又由(0),(0)0f a f +-==，得到a=0.即得。
2、 1110,,.1n n n a ∞∞==>+∑∑n n 1已知级数发散求证级数也发散a a 证明: 用反证法。
由0n a >知，1n ∞=∑n 1级数a ，111n ∞=+∑na 均为正项级数。
假设级数111n ∞=+∑n a 收敛，则1lim 01n →∞=+n a ，于是有11lim lim lim 1111111n n n n n n a a a →∞→∞→∞===-+++n n 1a a ， 从而由正项级数的比较判别法知级数1n ∞=∑n1a 收敛，矛盾，从而得证。
3、 1(1).nx dx ≥-⎰m设m,n 0为整数,求积分x 的值解：1(1),nx dx -⎰m 设I(m,n)=x 则由分部积分法有11111n101I(m,n)=(1-x)(1)|(1)(1)0111m m m n n x x x d x n x dx m m m +++-=----+++⎰⎰(1,1)1nI m n m =+-+， 从而1(,)(1,1)(2,2)112n n n I m n I m n I m n m m m -=+-=+-+++11(,0)12n n I m n m m m n -==++++!1!!()!1(1)!!n m n m n m n m n m ==+++++，即得解。
4 、0().a aa dx f x dx -=⎰⎰xf(x)设a>0,f(x)是定义在[-a,a]上的连续的偶函数,则1+e 证明：由f(x)是定义在[-a,a]上的连续的偶函数知()()f x f x -=,从而令x t =-有 ()()()11a aat t t aa af t e f t dx dt dt e e -----=-=++⎰⎰⎰xf(x)1+e 从而1()1()()212aaaat t a a aae f t dx dx dt f x dx e ----=+=+⎰⎰⎰⎰x x f(x)f(x)1+e 1+e 0000011[()()][()()]()22aaaaa f x dx f x dx f x dx f x dx f x dx -=+=+=⎰⎰⎰⎰⎰， 得证。
中科院信号与系统课程硕士研究生入学考试试题与答案
中科院2005年招收攻读硕士学位研究生入学考试试题试题名称：信号与系统 一、已知当输入信号为)(t x 时，某连续时间LTI 因果系统的输出信号为)(t y ，)(t x 和)(t y 的波形如图A-1所示。
试用时域方法求：（共26分）1. 该系统的单位阶跃响应)(t s ，并概画出)(t s 的波形；（12分）2. 在系统输入为图A-2所示的)(1t x 时的输出信号)(1t y ，并概画出)(1t y 的波形。
（14分）1t1)(1t x图A-1 图A-2二、由差分方程∑=----=--4])1[2][(]1[5.0][k k n x k n x n y n y 和非零起始条件1]1[=-y 表示的离散时间因果系统，当系统输入][][n n x δ=时，试用递推算法求：（共16分）1. 该系统的零状态响应][n y ZS （至少计算出前6个序列值）；（10分）2. 该系统的零输入响应][n y Zi （至少计算出前4个序列值）；（6分）三、已知连续时间信号)102cos()10(2)]110(2sin[)(633t t t t x ⨯--=-πππ毫安，若它是能量信号，试求其能谱密度和它在单位电阻上消耗的能量；若它是功率信号，则求其功率谱密度函数和它在单位电阻上消耗的平均功率。
（共14分）四、已知][~n x 是周期为4的周期序列，且已知8点序列][~][n x n x =，70≤≤n ，的8点DFT 系数为： ,0)(,1)6()4()2()0(=====k X X X X X 其他k 。
试求：（共24分） 1. 周期序列][~n x ，并概画出它的序列图形；（12分）2. 该周期序列][~n x 通过单位冲激响应为2222)2/(sin )1(][n n n h ππ-=的数字滤波器后的输出][n y ，并概画出它的序列图形；（12分）五、已知)(t x 是最高频率为4KHz 的连续时间带限信号，（共24分） 1. 若对)(t x 进行平顶抽样获得的已抽样信号)(t x p 如图A-3所示，试由)(t x p 恢复出)(t x 的重构滤波器的频率响应)(ωL H ，并概画出其幅频响应和相频响应；（16分）图A-32. 你在1小题求得的重构滤波器为什么不可实现？为实现无失真恢复原信号，需对抽样频率和重构滤波器频率响应)(ωL H 作怎样的修改？（8分） 六、如图A-4的信号流图所示的数字滤波器，试求：（共22分）1. 它的系统函数)(z H 及其收敛域，并画出它用一个一阶全通滤波器和一个4阶FIR 滤波器的级联实现的方框图或信号流图；（12分）2. 概画出该数字滤波器的幅频响应)(~ΩH （或)(Ωj e H ）。
2005-2010中国科学技术大学考研复试分数线
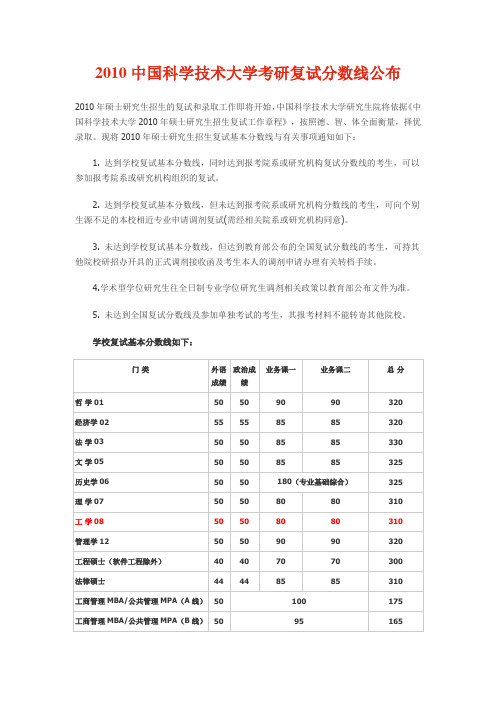
2010中国科学技术大学考研复试分数线公布2010年硕士研究生招生的复试和录取工作即将开始，中国科学技术大学研究生院将依据《中国科学技术大学2010年硕士研究生招生复试工作章程》，按照德、智、体全面衡量，择优录取。
现将2010年硕士研究生招生复试基本分数线与有关事项通知如下：1. 达到学校复试基本分数线，同时达到报考院系或研究机构复试分数线的考生，可以参加报考院系或研究机构组织的复试。
2. 达到学校复试基本分数线，但未达到报考院系或研究机构分数线的考生，可向个别生源不足的本校相近专业申请调剂复试(需经相关院系或研究机构同意)。
3. 未达到学校复试基本分数线，但达到教育部公布的全国复试分数线的考生，可持其他院校研招办开具的正式调剂接收函及考生本人的调剂申请办理有关转档手续。
4.学术型学位研究生往全日制专业学位研究生调剂相关政策以教育部公布文件为准。
5. 未达到全国复试分数线及参加单独考试的考生，其报考材料不能转寄其他院校。
学校复试基本分数线如下：补充说明：1、强军计划、单考复试分数线由相关院系、学科另行确定。
2、国家示范性软件学院软件工程专业参照(不低于)国家B类地区工程硕士分数线。
3、各院系的复试分数线以及复试内容、形式和日程安排，请访问各院系网页或与各院系教学办公室联系。
4、工商管理(MBA)/公共管理(MPA)B线申请条件请查看MBA中心主页(/)中国科学技术大学2009年硕士研究生入学考试复试基本分数线编辑提示：（箭头表示与08年该校分数线对比变化↑表示上升↓表示下降）中国科学技术大学各专业2008研究生入学考试复试分数线中国科学技术大学2007年硕士研究生入学考试复试基本分数线中国科学技术大学2006年考研复试分数线公布。
>>点击查看学校网站原文中国科学技术大学2005年考研复试基本分数线各院系联系电话、电子邮箱一览表。
中科大、中科院试卷清单总汇
中科大、中科院试卷清单总汇许多试卷属中科院系统通用试卷，适用于中科院很多单位高等数学（甲）（中国科学院研究生院命题试卷）2006——2007高等数学（乙）（中国科学院研究生院命题试卷）2005（第1种），2005（第2种），2007高等数学（A）（中国科学院-中国科学技术大学联合命题试卷）2003——2008（2003——2008有答案）高等数学（B）（中国科学院-中国科学技术大学联合命题试卷）1993——2005（1993——2004有答案）高等数学（甲）（中国科学院-中国科学技术大学联合命题试卷）2001高等数学（丙）（中国科学院-中国科学技术大学联合命题试卷）2000——2002 高等数学（乙）（中国科学院-中国科学技术大学联合命题试卷）2000——2002（2000——2002有答案）普通物理（甲）（中国科学院研究生院命题试卷）2006——2007普通物理（乙）（中国科学院研究生院命题试卷）2007普通物理（A）（中国科学院-中国科学技术大学联合命题试卷）2003——2008（2003——2008有答案）普通物理（甲）（中国科学院-中国科学技术大学联合命题试卷）1997——1998，2000普通物理（B）（中国科学院-中国科学技术大学联合命题试卷）2003——2008（2004——2008有答案）普通物理（乙型）（中国科学院-中国科学技术大学联合命题试卷）1997——2002（1998，2000——2002有答案）量子力学（中国科学院研究生院命题试卷）2006——2007量子力学（中国科学院-中国科学技术大学联合命题试卷）2003——2008（2003——2008有答案）量子力学（实验型）（中国科学技术大学命题试卷）1990——1998（1997有答案）量子力学（实验型）（中国科学院命题试卷）1998——1999量子力学（实验型）（中国科学院-中国科学技术大学联合命题试卷）（2000——2002有答案）量子力学（理论型）（中国科学院-中国科学技术大学联合命题试卷）1990——2002 固体物理（中国科学院研究生院命题试卷）2007固体物理（B）（中国科学院研究生院命题试卷）2006——2007（2006——2007有答案）固体物理（中国科学技术大学命题试卷）1997——1999（1997有答案）固体物理（中国科学院命题试卷）1998，1999固体物理（中国科学院-中国科学技术大学联合命题试卷）2000——2008（2000——2008答案）电动力学（中国科学院研究生院命题试卷）2007电动力学（中国科学院命题试卷）1998电动力学（中国科学技术大学命题试卷）1999电动力学（中国科学院-中国科学技术大学联合命题试卷）2000——2002——2008有答案）电动力学（B）（中国科学院-中国科学技术大学联合命题试卷）2003——2005分析化学（中国科学院研究生院命题试卷）2007分析化学（中国科学院-中国科学技术大学联合命题试卷）1997，1997答案，1998，1998答案，1999，1999答案，2000A卷（第1种），2000A卷（第1种）答案，2000A卷（第2种），2000B卷，2000B卷答案，2001B卷（第1种），2001B卷（第1种）答案，2001B卷（第2种），2001B卷（第2种）答案，2002A卷，2002A卷答案，2002B卷（第1种），2002B卷（第2种），2002B卷（第2种）答案，2003A卷，2003A卷答案，2003B卷，2004，2004答案，2005B卷，2005B 卷答案，2006，2006答案，2007，2007答案，2008，2008答案物理化学（甲）（中国科学院研究生院命题试卷）2006——2008物理化学（乙）（中国科学院研究生院命题试卷）2007物理化学（中国科学院-中国科学技术大学联合命题试卷）1987，1995——2008（1995——2008有答案）物理化学（B）（中国科学院-中国科学技术大学联合命题试卷）2003——2008（2003——2008有答案）物理化学（C）（中国科学院-中国科学技术大学联合命题试卷）2004物理化学（合肥智能机械研究所命题试卷）2001——2004有机化学（中国科学院研究生院命题试卷）2006——2008有机化学（中国科学院命题试卷）1986——1990，1992——1998（1986，1988，1995——1998有答案）有机化学（中国科学技术大学命题试卷）1993，1998（1998有答案）有机化学（中国科学院-中国科学技术大学联合命题试卷）1999——2008（1999——2004，2006——2008有答案）无机化学（中国科学院研究生院命题试卷）2006——2007无机化学（中国科学院-中国科学技术大学联合命题试卷）1999——2008（2001，2003——2008有答案）高分子化学（中国科学院-中国科学技术大学联合命题试卷）1989，1991，1993——1998，2003——2005高分子化学与物理（中国科学院研究生院命题试卷）2007高分子化学与物理（中国科学院-中国科学技术大学联合命题试卷）1999——2002，2004（2001——2002有答案）高分子物理（中国科学院-中国科学技术大学联合命题试卷）1994高分子物理部分（中国科学院-中国科学技术大学联合命题试卷）2003（占总分值50%）高聚物的结构与性能（中国科学院-中国科学技术大学联合命题试卷）1996——1997，2001——2002普通化学（甲）（中国科学院研究生院命题试卷）2007普通化学（乙）（中国科学院研究生院命题试卷）2007普通化学（中国科学院-中国科学技术大学联合命题试卷）2001，2004——2008（2004，2006——2008有答案）综合化学（中国科学院命题试卷）1996综合化学（中国科学技术大学命题试卷）1999——2004有答案）基础化学（中国科学院-中国科学技术大学联合命题试卷）2008（2008有答案）化工原理（中国科学院研究生院命题试卷）2005，2007化学工程学（中国科学院-中国科学技术大学联合命题试卷）2003——2004（2004有答案）半导体物理（甲）（中国科学院研究生院命题试卷）2007半导体物理（乙）（中国科学院研究生院命题试卷）2007半导体物理（中国科学院、半导体研究所、中国科学技术大学联合命题试卷）1997——2002，2004（1997——2002有答案）半导体物理（中国科学院微电子中心命题试卷）2004半导体材料（半导体研究所命题试卷）1996，1998，2000——2001（1996，2000有答案）半导体材料物理（半导体研究所命题试卷）2002——2003半导体集成电路（中国科学院-中国科学技术大学联合命题试卷）2001——2002，2004（2002有答案）半导体模拟集成电路（中国科学技术大学、半导体研究所联合命题试卷）1995——1996，1998（1996，1998，1999有答案）模拟集成电路（中国科学技术大学、半导体研究所联合命题试卷）1997（1997有答案）材料力学（中国科学院研究生院命题试卷）2007——2008材料力学（中国科学院-中国科学技术大学联合命题试卷）2001，2003——2008（2001，2003——2007有答案）材料力学（等离子体物理研究所试卷）2004（2004有答案）大气科学导论（中国科学院-中国科学技术大学联合命题试卷）2005——2008（2005——2008有答案）地球化学（中国科学院研究生院命题试卷）2007地球化学（中国科学院-中国科学技术大学联合命题试卷）2000——2002，2004——2005地球物理学（中国科学院研究生院命题试卷）2007第四纪地质学（中国科学院研究生院命题试卷）2007电磁场理论（中国科学院-中国科学技术大学联合命题试卷）2003电路（中国科学院研究生院命题试卷）2007电子技术（中国科学院研究生院命题试卷）2007电子线路（中国科学院研究生院命题试卷）2007电子线路（中国科学院-中国科学技术大学联合命题试卷）1996——2008（1996——2001，2003——2008有答案）（注：2002年的试卷共12页，缺P2—P5）电子线路（电子所命题试卷）2002——2005（2002——2004有答案）电子线路（半导体研究所命题试卷）2002——2004信号与系统（中国科学院研究生院命题试卷）2006——2007信号与系统（中国科学技术大学命题试卷）1990——1999（1996——1999有答案）（另：有《信号与系统》期末考试试题11份，每份3元。
中科院2005年研究生入学数学分析试题及解答
中科院2005年研究生入学数学分析试题及解答中国科学院硕士研究生2005年入学考试《数学分析》试题1. (15分)计算:0x →2. (15分)设,0,a b a b >≠,证明2ln ln a b a b a b -<<+-.3. (10分)求111lim 12n n n n →∞⎛⎫+++⎪+⎝⎭.4. (10分)判断级数1(1)nn n∞=-∑的敛散性.5. (15分)设函数(,)f x y 在点(0,0)的某个邻域中连续,222()(,)x y tF t f x y dxdy+≤=⎰⎰,求0()lim t F t t +→'.6. (15分)求球面2222xy z a++=包含在柱面22221x y a b+=(b a ≤)内的那部分面积.7. (15分)设函数(,)()f x y xy ϕ=,其中(0)0ϕ=,且()u ϕ在0u =的某个邻域中满足()u k u αϕ≤，其中常数12α>，0k >。
证明(,)f x y 在点(0,0)处可微,但函数(,)g x y =在点(0,0)处不可微. 8. (15分) 设()x ϕ在区间[0,)+∞上有连续的导数,并且(0)1ϕ=.令2222222()()x y z r f r x y z dxdydz ϕ++≤=++⎰⎰⎰(0r ≥).证明()f r 在0r =处三次可微,并求(0)f '''(右导数). 9. (20分)设函数()f x 在有限区间[,]a b 上可微,且满足()()0f a f b ''<(此处()f a '和()f b '分别表示f 在a 和b 处的右导数和左导数).则(,)c a b ∃∈,使得()0f c '=.10. (20分)设xe nn n e a x ∞==∑,求0123,,,a a a a ,并证明(ln )nn a e n γ-≥(2n ≥),其中γ是某个大于e 的常数.2005年中国科学院数学分析试题解答1. 解：利用()()11y y o y αα+=++，()0y →，()441135x o x =+⋅+，()()1122x o x =+-+，()113x o x =++，()112x o x =++， 所以，原式()()()()()44011315lim 111132x x o x x o x x o x x o x →⎛⎫+⋅+--+ ⎪⎝⎭=⎛⎫⎛⎫++-++ ⎪ ⎪⎝⎭⎝⎭()()0lim616x x o x x o x →+==--+. 2. 证明：不妨设0a b >>，欲证的不等式等价于ln211ab a a b b<<+-，令a x b=，不等式等价于2ln 11x x x <<+-，()1x >.令()ln f x x =-，()10f =， 因为()122f x x x x x '=+- 21022x x x x x x-==>，()1x >，所以()()10f x f >=，ln 0x ->，ln x x>，ln 1xx x<-，()1x >.令()()21ln 1x h x x x -=-+，()10h =，因为()()()()222114011x h x x x x x -'=-=>++， 所以()()1h x h >，即得()21ln 01x x x -->+，2ln 11xx x <+-，()1x >，故成立2ln 11x x x <<+-，()1x >，取a x b=，代入上式，不等式得证.3. 解：解法一 利用111ln 2n n c nε+++=++，其中lim 0n n ε→∞=， 211111ln 2212n n c n n nε++++++=+++， 111lim 12n n n n →∞⎛⎫+++ ⎪+⎝⎭11lim 12n n n →∞⎛⎫=++⎪+⎝⎭()()2lim ln 2ln n n n n c n c εε→∞⎡⎤=++-++⎣⎦ ()2lim ln 2n n n εε→∞⎡⎤=+-⎣⎦ln2=.解法二 111lim 12n nn n →∞⎛⎫+++⎪+⎝⎭111lim 1n n k kn n →∞=⎛⎫⎪= ⎪ ⎪+⎝⎭∑ ()11001ln 1ln 21dx x x ==+=+⎰. 4. 解：设n a n=，显然lim0n n a →∞=，{}n a 单调递减； 由莱布尼茨判别法知()11nn n ∞=-∑收敛，由()1n-≥，()3n ≥，得()11n n ∞=-∑发散，故()11nn ∞=-∑. 5. 解：()()200cos ,sin tF t dr f r r rd πθθθ=⎰⎰，()()20cos ,sin F t f t t td πθθθ'=⎰，由题设条件，可知()()0lim cos ,sin 0,0t f t t f θθ+→=，且关于[]0,2θπ∈是一致收敛； 于是()()2000lim lim cos ,sin t t F t f t t d tπθθθ++→→'=⎰ ()200lim cos ,sin t f t t d πθθθ+→=⎰ ()()200lim 0,00,02t f d f πθπ+→==⎰.6、计算下列曲面的面积：（1）圆柱面222a y x =+ 介乎平面0=+z x 和0=-z x 之间的部分； （2）球面2222az y x=++被椭圆柱面)0(12222a b b y a x ≤<=+所截下的部分。
中科院数学与系统科学研究院
年月日
初试成绩
总分
报考专业代码
政治理论
业务课一
外国的接收函一并寄到中科院数学与系统科学研究院研究生部，地址：中关村东路55号，100190。也可传真至62561939。收到调剂申请和接收函后，经审查通过，研究生部将考生试卷等相关材料机要寄送至接收单位。
中科院数学与系统科学研究院
报考硕士研究生考生调出申请表
中科院数学与系统科学研究院研究生部：
本人报考数学与系统科学研究院专业2013年硕士研究生，考生编号为：，联系电话为：。初试成绩（见下表）符合《2013年全国硕士研究生入学考试初试合格资格线》（A、B或C）类考生线。现本人自愿申请调剂到学校
专业，该校现已同意接收并发出接收调档函。希望学校批准，并办理相关调剂手续。
中国科学院2005年硕士研究生入学试题参考答案
2005年招收攻读硕士学位研究生入学考试试题试题名称： 固体物理一 回答下列问题1 简要阐述固体物理中的Born-Oppenheimer 近似（或绝热近似）。
并定性说明这种近似的物理依据。
答：原子核质量比电子大上千倍，电子的运动比核快得多，因而可以认为电子是在准静态的核构型的势场中运动。
从而可以被把电子与核的运动分开来讨论，即固体的运动简化成相对较简单的电子运动和核的运动。
2 固体中原子实运动的有效势场包括两大部分，分别说明其来源。
答：一部分是原子实间的静电相互作用，另一部分是电子态的能量对核构型的依赖关系 3 试用能带论简述导体、半导体、绝缘体中电子在能带中填充的特点。
答：金属或导体中价电子没有把价带填满，此为导带。
绝缘体中的价电子正好把价带填满，且更高的许可带与价带间的间隔较宽的禁带。
半导体与绝缘体相似，但禁带较窄。
二 简要回答下列问题1 写出晶体可能有的独立的点对称元素。
答：1、2、3、4、6、i 、m 、42 按对称类型分类，布拉菲（Bravas ）格子的点群类型有几种？空间群类型有几种？晶体结构的点群类型有几种?空间群类型有几种？答：7、14、32、2303 某种晶体的倒格子为体心立方结构，该晶体的正格子是什么结构？答：面心立方4 晶体中包含有N 个原胞，每个原胞有n 个原子，该晶体晶格振动的格波简正模式总数是多少？其中声学波和光学波各有多少？答：3nN 、其中声学波3N 、光学波（3n-3）N三 对面心立方布拉菲格子1 求格点密度最大的三个格点平面（晶面系）的面指数。
答：倒格子为体心立方，与三个最短的倒格矢相应，依次为{111}、{100}、{110} 2 画出这种格点平面上格点的排布。
答：六角、正方、正方（“面心”正方）3 设晶胞参数为a ，分别求出这三个晶面系相邻晶面的间距。
答：依次为a a a 42,21,23四 证明：如果一个布拉菲格子（或点阵）有一个对称平面，则存在平行该对称面的点阵平面系。
第二单元参考书目-中国科学院数学与系统科学研究院
及其应用》
用计算数学试题
同管理科学与工程
概率论基本概念：概率空间，随机变量，分布函数，概率测度及性质，数学期望与
方差，条件期望，几种收敛性及定义。 独立变量: 独立性概念，特征函数，中心极限定理，独立变量和，强大数法则，重对 数律。
鞅及鞅差序列（离散时间）: 停时，鞅收敛定理。 参考书：任何含有以上内容的教材书均可，如
张晓
杨乐、王跃飞、崔贵珍
周向宇
贺正需 张平
葛力明
命题组组长
考试覆盖内容及参考书
Eduardo D. Sontag ：Mathematical Control Theory。 <<Spin Geometry>>( wson ,M-l. Michelsohn, Princeton University Press, 1989), Chapters I & II; <<The Geometry of Physics, An Introduction>> (T. Frankel, 2nd ed, 天元基金影印系列丛书, 清华大学出版社, 2005), Chapters 11 & 19
《计算机代数基础》，张树功等著，吉林大学出版社。
现代微分几何 纠错码理论
关于编制2005年硕士入学考试
中国科学院大学硕士研究生入学考试《信号与系统》考试大纲一、考试科目基本要求及适用范围本《信号与系统》考试大纲适用于中国科学院大学通信与信息系统、信号与信息处理以及相关专业的硕士研究生入学考试。
信号与系统是电子、通信、控制科学与工程等许多学科专业的基础理论课程，它主要研究信号与系统理论的基本概念和基本分析方法，认识如何建立信号与系统的数学模型，通过时间域与变换域的数学分析对系统本身性能和系统输出信号进行求解与分析，并对所得结果赋予物理解释、物理意义。
要求考生熟练掌握以上基本概念与基本运算，并能加以灵活运用。
二、考试形式和试卷结构考试采取闭卷笔试形式，考试时间180分钟，总分150分。
试题采用填空、选择、判断对错及计算等形式。
三、考试内容（一）概论1.信号的描述、分类及典型示例；2.信号的运算；3.系统的模型与分类；4.系统分析方法。
（二）连续时间系统的时域分析1.微分方程的建立与求解；2.零输入响应与零状态响应的定义和求解；3.冲激响应与阶跃响应；4.卷积的定义、性质、计算等。
（三）傅里叶变换1.周期信号的傅里叶级数和典型周期信号频谱；2.傅里叶变换及典型非周期信号的频谱密度函数；3.傅里叶变换的性质与运算；4.周期信号的傅里叶变换；5.抽样定理、抽样信号的傅里叶变换；6.连续时间系统的傅里叶分析应用。
（四）拉普拉斯变换1.拉普拉斯变换及逆变换；2.拉普拉斯变换的性质与运算；3.线性系统拉普拉斯变换求解；4.系统函数与冲激响应；5.周期信号与抽样信号的拉普拉斯变换；6.S域分析、系统的零极点分析、系统性能判断；7.双边拉氏变换；8.拉氏变换与傅氏变换的关系。
（五）信号的矢量空间分析1.信号的正交分解；2.帕斯瓦尔定理、能量信号与功率信号、能量谱与功率谱；3.相关系数与相关函数、相关与卷积比较、相关定理；4.匹配滤波器。
（六）离散时间系统的时域分析1.离散时间信号的分类与运算；2.离散时间系统的数学模型及求解；3.单位样值响应；4.离散卷积和的定义、性质与运算等。
2005专业选择
物理学科
物理学
应用物理学
光信息科学与技术
天文学
50
符合学校要求的基本条件，一年级无不及格科目。
1、参考GPA排名，数学、物理、英语等成绩及高考成绩
2、面试，择优录取。
网上另行通知
商
学
院
信息管理与决策科学系
信息管理与信息系统
10
1、GPA>=2.6，无不及格课程
2、具较好的沟通能力与信息技术应用基础，对信息管理领域感兴趣
面试，管理沟通能力特别强的学生可适当放宽GPA要求。
另行通知
管理科学系
管理科学
15
1、GPA>=2.6，无不及格课程
2、较好的沟通、组织与协调能力，对管理科学理论与应用方法感兴趣
面试，管理沟通、对于协调能力特别强的学生，可适当放宽GPA要求
另行通知
统计与金融系
金融学
5
（非商院）
第一学期课程GPA>=2.5
面试
6月17日下午2：30西区电4楼410会议室
人文与社会科学学院
外语系
英语
5
第一学年无不及格课程，GPA＞3.0，对学习外语有浓厚的兴趣；具有较强的英语基础和较好的文学修养,口齿清晰；
面试
另行通知
信息传播与科技政策系
传播学
5-10
GPA>=2.5有特长的学生可适当放宽；
1、参考一年级成绩
2、面试,择优录取
机械设计制造及其自动化
测控技术与仪器
15
GPA＞＝3.0
面试
另行通知
热科学和能源工程系
热能与动力工程
20
成绩良好，热爱本专业
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中国科学院数学与系统科学研究院2005年硕士研究生招生初试试题及其解答 ----博士家园 计算xx xx x +-+--+>-1121313340lim解：L ’Hospital 法则得原式=.621311)1(21)1(31)21(12)31(3121322133240lim-=-=+-+-+⋅+----→x x x x x x 1、 设,,0,b a b a ≠>证明.1ln ln 2abb a b a b a <--<+ 证：令 bax =(不妨设 b a >)，则所证明的不等式可写成)1(1ln 1)1(2>-<<+-x xx x x x设 ,1)1(2ln )(+--=x x x x f 则有 )1(0)1()1()('22>>+-=x x x x x f因此)(x f 在1≥x 上严格递增,从而对任意1>x ,有0)1()(=>f x f ,即1)1(2ln +->x x x 设,ln 1)(x xx x g --=则 )1(,02)1()('2>>-=x xx x x g 因此对任意,1>x 有0)1()(=>g x g 即 )1(ln 1>>-x x xx .2、 求)21111(limnn n x ++++→ 解：)11211111(1212111nn n n n n n n ++++++=+++++ ,考虑函数x x f +=11)(,它在[0,1]上连续，把[0,1]分成n 等份，分点为),,2,1(n i ni=,在每一小区间],1[nin i -中取nii =ζ,则有ni f i +=11)(ζ.于是,原式 =n nn n n n n 1)11111(1lim lim∞→∞→+++++ =)11111(1limnn n n n ++++∞→=2ln 1110=+⎰dx x4、判断级数∑∞=-1ln )1(n n n n 的收敛性.解：令nv nn u n n 1,ln ==,+∞==∞→∞→n v u n n nn ln lim lim而∑n v 发散,因而∑nn ln 发散。
又当3≥n 时, 数列}{n u 单调递减,且趋于0.因此由Leibniz 判别法知nn nln )1(∑-收敛.所以该级数条件收敛.5.设),(y x f 在点)0,0(的某个邻域中连续,⎰⎰≤+=222),()(t y x dxdy y x f t F ,求tt F t )('0lim+→. 解:利用极坐标变换可得⎰⎰⎰⎰==≤+πϕϕϕ20)sin ,cos (),()(222tt y x rdr r r f d dxdy y x f t F由于),(y x f 在点)0,0(邻域连续，所以dtdt F =)('⎰⎰πϕϕϕ20)sin ,cos (trdr r r f d =⎰⎰πϕϕϕ20)sin ,cos (trdr r r f dt dd=⎰πϕϕϕ20)sin ,cos (d t t f则lim lim'0)(→→=+t t t t F ⎰πϕϕϕ20)sin ,cos (d t t f =⎰→πϕϕϕ20)sin ,cos (limd t t f t=).0,0(2f π6.求2222a z y x =++球面包含在柱面)(,12222a b by a x ≤=+内的那部分面积。
解:在球面坐标ϕθϕθϕcos ,sin sin ,cos sin r z r y r x ===下,所给的球面方程22a r =，于是球面的参数方程为ϕθϕθϕcos ,sin sin ,cos sin a z a y a x ===其中20,20πϕπθ≤≤≤≤.那么,cos sin ),(),(22θϕθϕa z y =∂∂ ,s i n s i n ),(),(22θϕθϕa x z =∂∂ ,c o s s i n ),(),(2ϕϕθϕa y x =∂∂所以 ϕ242sin a F EG =- 又球面的面积为它在第一卦限部分面积的4倍，所以⎰⎰⎰⎰===≤≤≤≤πππϕπθπϕϕθθϕϕ202022202028sin 4sin 4a d d ad d a S .7. 设|)(|),(xy y x f ϕ=,其中0)0(=ϕ,且)(u ϕ在0=u 的某个邻域中满足)21(|||)(|>≤αϕαu u .证明),(y x f 在)0,0(处可微,但函数||),(xy y x g =在(0,0)处不可微.(),(y x f 在)0,0(处可微性未证明) 证：0)0,()0,0(==x g dx d g x , 0)0,()0,0(==y g dyd g y 考察极限ρρyg x g g y x g y x )0,0()0,0()0,0(),(lim 0---+→ =22||lim yx xy ++→ρ当动点(x,y)沿直线kx y =趣于)0,0(时，显然对不同的k 有不同的极限值22||yx xy + 。
因此上述极限不存在，即在点)0,0(,),(y x g 不能表成)(),()0,0()0,0()0,0(22y x o y g x g g y x +=+++ρρ故||),(xy y x g =在点)0,0(不可微分。
8.设)(x ϕ在),0[∞上有连续导数，并且1)0(=ϕ,令⎰⎰⎰≤++≥++=2222)0()()(222r z y x r dxdydz z y x r f ϕ证明)(r f 在0=r 处三次可微，并求 )0('''f （右导数）证：利用球面坐标变换得⎰⎰⎰≤++++=2222)()(222r z y x dxdydz z y x r f ϕ=⎰⎰⎰ππϕααθ002220)(sin r dt t t d d =⎰rdt t t 022)(4ϕπ又)(x ϕ在),0[∞上有连续导数,则 )(x ϕ也连续，因此有22')(4)(r r r f πϕ=, )]()([8)(232'''r r r r r f ϕϕπ+=且在),0[∞上连续,则有0)(lim )0(''0''==→r f f r 。
那么由导数定义知)(r f 在0=r 处三阶可导，且rr r r r r f r f f r r 0)]()([8lim )0()(lim )0(22'30''''0'''-+=-=++→→+ϕϕπ=ππκϕϕπ8)0(8)]()([8lim 22'20==++→r r r r . 9.设)(x f 在有限区间],[b a 上可微，且满足0)()(''<b f a f （此处)('a f 和)('b f 分别表示)(x f 在a 和b 处的右导数和左导数）,则存在 0)(),,('=∍∈c f b a c 。
证:设C x f x F -=)()(则)(x F 在],[b a 上可微,且0)()()()(''''<=-+-+b f a f b F a F不妨设0)(,0)(''<>-+b F a F ,则存在),(01a U x +∈),(02b U x -∈且∍<,21x x)1()()(),()(21b F x F a F x F >>因)(x F 在],[b a 上可导,所以连续.由最值定理知,存在一点)(],,[ξξF b a ∍∈最大. 由(1)式可知b a ,≠ξ 则ξ是F 的极大值点,所以有0)('=ξF 即 ),(0)('b a f ∈=ξξ.10. 设∑∞==n nn e xa e x,求,,,,3210a a a a ,并证明)2()ln (≥≥-n n r e a nn 其中r 是某个大于e 的常数. (未给出证明) 解:令0=x 有e a =0.在0=x 处分别对等式两边求一,二,三阶导数可得1'0|)(a e e x e x===e a a e e e e e x x x e x e xx=⇒==+===2202''022|)(|)(e a a e e e ee e x x x xe x e xx6565|)3(|)(33023'''0=⇒==++===。