数字信号系统课后上机题答案
数字信号处理上机实验答案(全)1

第十章上机实验数字信号处理是一门理论和实际密切结合的课程,为深入掌握课程内容,最好在学习理论的同时,做习题和上机实验。
上机实验不仅可以帮助读者深入的理解和消化基本理论,而且能锻炼初学者的独立解决问题的能力。
本章在第二版的基础上编写了六个实验,前五个实验属基础理论实验,第六个属应用综合实验。
实验一 系统响应及系统稳定性。
实验二 时域采样与频域采样。
实验三 用FFT 对信号作频谱分析。
实验四 IIR 数字滤波器设计及软件实现。
实验五 FIR 数字滤波器设计与软件实现实验六 应用实验——数字信号处理在双音多频拨号系统中的应用任课教师根据教学进度,安排学生上机进行实验。
建议自学的读者在学习完第一章后作实验一;在学习完第三、四章后作实验二和实验三;实验四IIR 数字滤波器设计及软件实现在。
学习完第六章进行;实验五在学习完第七章后进行。
实验六综合实验在学习完第七章或者再后些进行;实验六为综合实验,在学习完本课程后再进行。
10.1 实验一: 系统响应及系统稳定性1.实验目的(1)掌握 求系统响应的方法。
(2)掌握时域离散系统的时域特性。
(3)分析、观察及检验系统的稳定性。
2.实验原理与方法在时域中,描写系统特性的方法是差分方程和单位脉冲响应,在频域可以用系统函数描述系统特性。
已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应,本实验仅在时域求解。
在计算机上适合用递推法求差分方程的解,最简单的方法是采用MA TLAB 语言的工具箱函数filter 函数。
也可以用MATLAB 语言的工具箱函数conv 函数计算输入信号和系统的单位脉冲响应的线性卷积,求出系统的响应。
系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。
重点分析实验系统的稳定性,包括观察系统的暂态响应和稳定响应。
系统的稳定性是指对任意有界的输入信号,系统都能得到有界的系统响应。
或者系统的单位脉冲响应满足绝对可和的条件。
数字信号处理,第5章课后习题答案

第五章习题与上机题5.1 已知序列12()(),0 1 , ()()()nx n a u n a x n u n u n N =<<=--,分别求它们的自相关函数,并证明二者都是偶对称的实序列。
解:111()()()()()nn mx n n r m x n x n m a u n au n m ∞∞-=-∞=-∞=-=-∑∑当0m ≥时,122()1mmnx n ma r m aaa∞-===-∑ 当0m <时,122()1m mnx n a r m aaa -∞-===-∑ 所以,12()1mx ar m a =-2 ()()()()N x n u n u n N R n =--=22210121()()()()()1,0 =1,00, =()(1)x NN n n N mn N n m N r m x n x n m Rn R n m N m N m N m m Nm N m R m N ∞∞=-∞=-∞--=-=-=-=-⎧=--<<⎪⎪⎪⎪=-≤<⎨⎪⎪⎪⎪⎩-+-∑∑∑∑其他从1()x r m 和2()x r m 的表达式可以看出二者都是偶对称的实序列。
5.2 设()e()nTx n u n -=,T 为采样间隔。
求()x n 的自相关函数()x r m 。
解:解:()()()()e()e ()nTn m T x n n r m x n x n m u n u n m ∞∞---=-∞=-∞=-=-∑∑用5.1题计算1()x r m 的相同方法可得2e()1e m Tx Tr m --=-5.3 已知12()sin(2)sin(2)s s x n A f nT B f nT ππ=+,其中12,,,A B f f 均为常数。
求()x n 的自相关函数()x r m 。
解:解:()x n 可表为)()()(n v n u n x +=的形式,其中)2sin()(11s nT f A n u π=,=)(n v 22sin(2)s A f nT π,)(),(n v n u 的周期分别为 s T f N 111=,sT f N 221=,()x n 的周期N 则是21,N N 的最小公倍数。
数字信号处理课后答案 第7章高西全

h(n)=hd(n)RN(n)= δ(n − α ) −
sin[ωc (n − α )] R N ( n) π(n − α )
为了满足线性相位条件: h(n)=h(N-1-n) 要求满足
N −1 α= 2
(3) N必须取奇数。 因为N为偶数时(情况2), H(ejπ)=0, 不能实现高通。 根据题中对过渡带宽度的要求, 4π π N应满足: , 即N≥40。 取N=41。 ≤ N 10 6. 理想带通特性为
解: (1) 由所给h(n)的取值可知,h(n)满足h(n)=h(N-1 -n), 所以FIR滤波器具有A类线性相位特性:
N −1 θ (ω ) = −ω = −2.5ω 2
由于N=6为偶数(情况2), 所以幅度特性关于ω=π点奇对称。 (2) 由题中h(n)值可知, h(n)满足h(n)=-h(N-1-n), 所以FIR滤波器具有B类线性相位特性: π N −1 π θ (ω ) = − − ω = − − 3ω 2 2 2 由于7为奇数(情况3), 所以幅度特性关于ω=0, π, 2π三点奇对 称。
e − jωa jω H d (e ) = 0
ωc ≤ | ω | ≤ π
其它
(1) 求出该理想高通的单位脉冲响应hd(n); (2) 求出加矩形窗设计的高通FIR滤波器的单位脉冲响 应h(n)表达式, 确定α与N的关系; (3) N的取值有什么限制?为什么? 解: (1) 直接用IFT[Hd(ejω)]计算:
N −1 (2) 为了满足线性相位条件, 要求 a = , N为 2 π 矩形窗函数长度。 因为要求过渡带宽度∆β≤ rad, 所以要 8 4π π 求 , 求解得到N≥32。 加矩形窗函数, 得到h(n): ≤ N 8 sin[ωc (n − a )] h(n) = hd (n) ⋅ RN (n) = R N ( n) π (n − a )
数字信号处理课后答案+第4章(高西全丁美玉第三版)

6*. 按照下面的IDFT算法编写MATLAB语言 IFFT程 序, 其中的FFT部分不用写出清单, 可调用fft函数。 并分 别对单位脉冲序列、 矩形序列、 三角序列和正弦序列进行 FFT和IFFT变换, 验证所编程序。
解: 为了使用灵活方便, 将本题所给算法公式作为函 数编写ifft46.m如下: %函数ifft46.m %按照所给算法公式计算IFET function xn=ifft46(Xk, N) Xk=conj(Xk); %对Xk取复共轭 xn=conj(fft(Xk, N))/N; %按照所给算法公式计算IFFT 分别对单位脉冲序列、 长度为8的矩形序列和三角序列 进行FFT, 并调用函数ifft46计算IFFT变换, 验证函数 ifft46的程序ex406.m如下:
快速卷积时, 需要计算一次N点FFT(考虑到H(k)= DFT[h(n)]已计算好存入内存)、 N次频域复数乘法和 一次N点IFFT。 所以, 计算1024点快速卷积的计算时间Tc 约为
Fs <
1024 = 15 625 次 /秒 65536 × 10−6
Fs 15625 = = 7.8125 kHz 2 2
1 x ( n) = IDFT[ X ( k )] = [DFT[ X * ( k )]]* N
%程序ex406.m %调用fft函数计算IDFT x1n=1; %输入单位脉冲序列x1n x2n=[1 1 1 1 1 1 1 1]; %输入矩形序列向量x2n x3n=[1 2 3 4 4 3 2 1]; %输入三角序列序列向量x3n N=8; X1k=fft(x1n, N); X2k=fft(x2n, N); X3k=fft(x3n, N); %计算x1n的N点DFT %计算x2n的N点DFT %计算x3n的N点DFT
数字信号原理课后习题答案

y(n-n0)= x(m)≠y′(n)
故系统是时变系统。 由于
T[ax1(n)+bx2(n)]=
[ax1(m)+bx2(m)]
=aT[x1(n)]+bT[x2(n)]
故系统是线性系统。
n
m0
nn0
m 0
n
m0
幻灯片 24 (8) y(n)=x(n) sin(ωn) 令输入为 x(n-n0) 输出为 y′(n)=x(n-n0) sin(ωn) y(n-n0)=x(n-n0) sin[ω(n-n0)]≠y′(n)
x(n-n0) 输出为
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2)
y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2) =y′(n)
n
x(m)
m0 幻灯片 17 故该系统是非时变系统。 因为
y(n)=T[ax1(n)+bx2(n)] =ax1(n)+bx2(n)+2[ax1(n-1)+bx2(n-1)] +3[ax1(n-2)+bx2(n-2)] T[ax1(n)]=ax1(n)+2ax1(n-1)+3ax1(n-2) T[bx2(n)]=bx2(n)+2bx2(n-1)+3bx2(n-2)
(1) 画出 x(-n)的波形;
(2) 计算 xe(n)= [x(n)+x(-n)], 并画出 xe(n)波形;
(3) 计算 xo(n)=
[x(n)-x(-n)], 并画出 xo(n)波形;
x1(n)=xe(n)+xo(n), 将 x1(n)与 x(n)进行比较, 你能得到什么结论?
数字信号处理课后习题答案完整版

数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理(姚天任江太辉)第三版课后习题答案第二章判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n )(2)x(n)=)8(π-ne j(3)x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =在图中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。
《数字信号的处理》课后上机的题目

0.1702
B =
0.0028 0.0111 0.0166 0.0111 0.0028
A =
1.0000 -2.6103 2.7188 -1.3066 0.2425
实验报告
第一章:时域离散信号和时域离散系统
*16.已知两个系统的差分方程分别为
(1) y(n)=0.6y(n-1)-0.08y(n-2)+x(n)
(2) y(n)=0.7y(n-1)-0.1y(n-2)+2x(n)-x(n-2)
分别求出所描述的系统的单位脉冲响应和单位阶跃响应.
解:(可附程序)
(1)系统差分方程的系数向量为
yn=conv(x1n,x2n)
%用DFT计算卷积ycn:
M1=length(x1n);
M2=length(x2n);
N=M1+M2-1;
X1k=fft(x1n,N); %计算x1n的N点DFT
X2k=fft(x2n,N); %计算x2n的N点DFT
Yck=X1k.*X2k;
ycn=ifft(Yck,N)
subplot(2,2,1);stem(n,hn1,'.')
title('(a)系统1的系统单位脉冲响应');
xlabel('n');ylabel('h(n)')
xn=ones(1,30);
%xn=单位阶跃序列,长度N=31
sn1=filter(B1,A1,xn,xi);
%调用filter解差分方程,求系统输出信号sn1
解:(可附程序)
hn=[5,5,5,3,3,3];
r=0.95;
Hk=fft(hn,6);
数字信号处理课后答案+第3章(高西全丁美玉第三版)

所以
kn DFT[ X (n)] = ∑ X (n)W N n =0 N −1
N −1 mn kn = ∑ ∑ x(m)W N W N n =0 m =0
N −1
n = ∑ x ( m)∑ W N ( m + k ) m =0 n =0
X (k ) − W X (k ) = ∑ WNkm − ( N − 1)
k N m =1
kn = ∑ W N − 1 − ( N − 1) = − N n =0 N −1
N −1
所以,
X (k ) =
−N , k ≠ 0 ,即 k 1 − WN N ( N − 1) k =0 2 X (k ) = −N k = 1, 2, ⋯, N − 1 k 1 − WN
=
1− e
−j
2π (m−k ) N N 2π (m−k ) N
1− e
−j
N = 0
k =m k≠m
0≤k≤N-1
(6) X (k ) = ∑ cos
n =0
N −1
1 2π kn mn ⋅ WN = (e 2 N n =0
∑
N −1
j
2π mn N
+e
-j
2π 2π mn - j kn N )e N
j
2π mn N ,
0<m< N
2π x(n) = cos mn , 0 < m < N N
(7) (8) (9)
x(n)=ejω0nRN(n) x(n)=sin(ω0n)RN(n) x(n)=cos(ω0n)RN(N)
现代数字信号处理课后习题解答

习题二1、求证:,()(,)x i j x i j xi xj R t t C t t m m =+。
证明:(,)(,)(,,,)x i j i j iji j i j i j R t t E x x x xp x x t t dx dx ==⎰⎰(,)[(),()](),()(,,,)()(,,,)(,)(,)i j i j j i i j i j j i i j i jx i j i x j x i x j x i j i j i ji j i x j x x x i j i j i j x i j x x x x x x x i j x x C t t E x m x m x m x m p x x t t dx dx x x x m x m m m p x x t t dx dx R t t m m m m m m R t t m m =--=--=--+=--+=-⎰⎰⎰⎰ 2、令()x n 和()y n 不是相关的随机信号,试证:若()()()w n x n y n =+,则w x y m m m=+和222w x y σσσ=+。
证明:(1)[()][()()][()][()]x ym E n E x n y n E x n E y n m m ωω==+=+=+ (2)2222222222[(())]{[()()()]}[(())(())][(())][(())]2[(())(())]2[]x y x y x y x y x y x y x y x y x y x yE n m E x n y n m m E x n m y n m E x n m E y n m E x n m y n m m m m m m m m m ωωσωσσσσ=-=+-+=-+-=-+-+--=++--+=+即222x y ωσσσ=+3、试证明平稳随机信号自相关函数的极限性质,即证明: ①当0τ=时,2(0),(0)x x x x R D C σ==; ②当τ=∞时,2(),()0x x x R m C ∞=∞=。
数字信号处理课后习题答案
(修正:此题有错,
(3)系统的单位脉冲响应 而改变,是两个复序列信号之和)
(4)
(修正: 随上小题答案
(修正:此图错误,乘系数应该为 0.5,输出端 y(n)应该在两个延迟器 D 之间)
1-25 线性移不变离散时间系统的差分方程为
(1)求系统函数 ; (2)画出系统的一种模拟框图; (3)求使系统稳定的 A 的取值范围。 解:(1)
(2)
(3)
解:(1)
(2)
(3)
1-7 若采样信号 m(t)的采样频率 fs=1500Hz,下列信号经 m(t)采样后哪些信号不 失真? (1) (2) (3) 解:
(1)
采样不失真
(2)
采样不失真
(3)
,
采样失真
1-8 已知
,采样信号 的采样周期为 。
(1) 的截止模拟角频率 是多少?
(2)将 进行 A/D 采样后, 如何?
(3)最小阻带衰减 5-4
由分式(5.39)根据 A 计算 ,如下: 由表 5.1 根据过度带宽度 计算窗口:
单位脉冲响应如下:
单位脉冲响应如下:
其中 为凯泽窗。 5-5 答:减小窗口的长度 N,则滤波器的过度带增加,但最小阻带衰减保持不变。 5-6:图 5.30 中的滤波器包括了三类理想滤波器,包括了低通,带通和高通,其响应的单位
(1)
,
(2)
1-18 若当 时
;时
(1)
,其中
(2) 证明:
,收敛域
,其中 N 为整数。试证明: ,
(1) 令 其中
,则 ,
(2)
,
1-19 一系统的系统方程及初时条件分别如下: ,
(1)试求零输入响应 ,零状态响应 ,全响应 ; (2)画出系统的模拟框图 解: (1)零输入响应
数字信号处理教程课后习题及答案

解:(1 )
n
y(n) = ∑ x(m ) m = −∞
n
y1 (n ) = T [x1 (n )] = ∑ x1 (m ) m = −∞
y2 (n ) = T [x2 (n )] =
n
∑ x2 (m )
m = −∞
n
ay1(n)+ by2 (n) = ∑[ax1(m) + bx2 (n)] m = −∞
β α
n +1
β α β =
n +1− N −n0
N−
N
α −β
y(n) = Nα n−n0 ,
(α = β )
, (α ≠ β )
如此题所示,因而要分段求解。
2 .已知线性移不变系统的输入为 x( n ) ,系统的单位抽样响应
为 h( n ) ,试求系统的输出 y( n ) ,并画图。
(1)x(n) = δ (n)
=
x(n)sin⎜⎝⎛
2π 9
+
π 7
⎟⎠⎞
ay1(n)+ by2 (n)
=
ax1(n
)
sin(
2π 9
+
π 7
)
+
bx2
(n)
sin(
2π 9
+
π 7
)
7. 试判断以下每一系统是否是(1)线性,(2)移不变的?
( ) T[x(n
−
m )] =
x(n
−
m)sin
2π 9
+
π 7
( ) y(n
− m)=
4
第一章 离散时间信号与系统
1 .直接计算下面两个序列的卷积和 y( n ) = x( n )* h( n )
数字信号处理第四版高西全课后答案

第 1 章 时域离散信号和时域离散系统
(6) y(n)=x(n2)
令输入为
输出为
x(n-n0)
y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)]
5. 设系统分别用下面的差分方程描述, x(n)与y(n)分别表示系统输入和输 出, 判断系统是否是线性非时变的。
(1)y(n)=x(n)+2x(n-1)+3x(n-2) (2)y(n)=2x(n)+3 (3)y(n)=x(n-n0) n0 (4)y(n)=x(-n)
第 1 章 时域离散信号和时域离散系统
, 这是2π有理1数4, 因此是周期序
3
(2) 因为ω=
,
所以
1
8
=16π, 这是无理数, 因此是非周期序列。
2π
第 1 章 时域离散信号和时域离散系统
4. 对题1图给出的x(n)要求:
(1) 画出x(-n)的波形;
(2) 计算xe(n)= (3) 计算xo(n)=
1 2 [x(n)+x(-n)], 并画出xe(n)波形; 1 [x(n)-x(-n)], 并画出xo(n)波形; 2
(5) 系统是因果系统, 因为系统的输出不取决于x(n)的未来值。 如果
|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM,
7. 设线性时不变系统的单位脉冲响应h(n)和输入序列x(n)如题7图所示,
要求画出y(n)输出的波形。
解: 解法(一)采用列表法。
数字信号处理第三版西科大课后答案第2章

第2章时域离散信号和系统的频域分析2.1学习要点与重要公式2.2FT和ZT的逆变换2.3分析信号和系统的频率特性 2.4例题2.5习题与上机题解答2.1学习要点与重要公式数字信号处理中有三个重要的数学变换工具,即傅里叶变换(FT)、Z变换(ZT)和离散傅里叶变换(DFT)。
利用它们可以将信号和系统在时域空间和频域空间相互转换,这方便了对信号和系统的分析和处理。
三种变换互有联系,但又不同。
表征一个信号和系统的频域特性是用傅里叶变换。
Z 变换是傅里叶变换的一种推广,单位圆上的Z变换就是傅里叶变换。
在z域进行分析问题会感到既灵活又方便。
离散傅里叶变换是离散化的傅里叶变换,因此用计算机分析和处理信号时,全用离散傅里叶变换进行。
离散傅里叶变换具有快速算法FFT,使离散傅里叶变换在应用中更加方便与广泛。
但是离散傅里叶变换不同于傅里叶变换和Z变换,它将信号的时域和频域,都进行了离散化,这是它的优点。
但更有它自己的特点,只有掌握了这些特点,才能合理正确地使用DFT。
本章只学习前两种变换,离散傅里叶变换及其FFT将在下一章学习。
2.1.1学习要点(1)傅里叶变换的正变换和逆变换定义,以及存在条件。
(2)傅里叶变换的性质和定理:傅里叶变换的周期性、移位与频移性质、时域卷积定理、巴塞伐尔定理、频域卷积定理、频域微分性质、实序列和一般序列的傅里叶变换的共轭对称性。
(3)周期序列的离散傅里叶级数及周期序列的傅里叶变换表示式。
(4)Z变换的正变换和逆变换定义,以及收敛域与序列特性之间的关系。
(5)Z变换的定理和性质:移位、反转、z域微分、共轭序列的Z变换、时域卷积定理、初值定理、终值定理、巴塞伐尔定理。
(6)系统的传输函数和系统函数的求解。
(7)用极点分布判断系统的因果性和稳定性。
(8)零状态响应、零输入响应和稳态响应的求解。
(9)用零极点分布定性分析并画出系统的幅频特性。
2.1.2重要公式(1)这两式分别是傅里叶变换的正变换和逆变换的公式。
数字信号处理》第三版课后习题答案

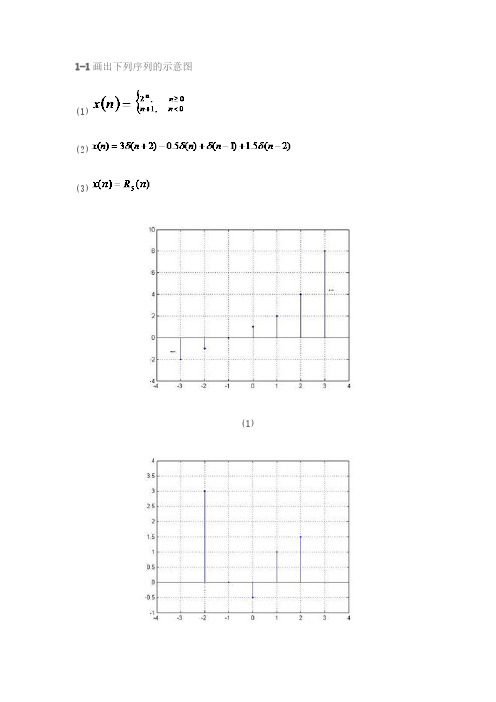
数字信号处理课后答案教材第一章习题解答1.用单位脉冲序列()nδ及其加权和表示题1图所示的序列。
解:2.给定信号:25,41 ()6,040,n nx n n+-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n序列;(3)令1()2(2)x n x n=-,试画出1()x n波形;(4)令2()2(2)x n x n=+,试画出2()x n波形;(5)令3()2(2)x n x n=-,试画出3()x n波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)(3)1()x n的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n时,先画x(-n)的波形,然后再右移2位,3()x n波形如题2解图(四)所示。
3.判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5.设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n =+-+-; (3)0()()y n x n n =-,0n 为整常数; (5)2()()y n x n =; (7)0()()nm y n x m ==∑。
解:(1)令:输入为0()x n n -,输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。
数字信号处理课后习题答案

数字信号处理(姚天任江太辉)第三版课后习题答案第二章2.1 判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n ) (2)x(n)=)8(π-nej(3)x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λnu(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)2.4 图P2.4所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a nu(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n)=∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n)=∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥32.5 已知一个线性非移变系统的单位取样响应为h(n)=a n-u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。
数字信号处理课后答案 第2章高西全

( −1) n x( n) = 2
n = −3
(4) 因为傅里叶变换的实部对应序列的共轭对称部分, 即
Re [ X (e jω )] =
n = −∞
∑
∞
x e ( n ) e − j ωn
1 xe (n) = ( x(n) + x(− n)) 2
按照上式画出xe(n)的波形如题5解图所示。
题5解图
2. 已知
jω
n = −∞
∑
∞
x( n′)e − j2ωn′ = X (e j2ω )
| ω |< ω0
1, X (e ) = 0,
ω0 <| ω | ≤ π
求X(ejω)的傅里叶反变换x(n)。
解:
1 x ( n) = 2π
∫ωe
−
0
ω0
jωn
sin ω0 n dω = πn
3. 线性时不变系统的频率响应(频率响应函数) H(ejω)=|H(ejω)|ejθ(ω), 如果单位脉冲响应h(n)为实序列, 试 证明输入x(n)=A cos(ω0n+ϕ)的稳态响应为
∑
∗
∞
x(n′)e − jω ( n + n0 ) = e − jωn0 X (e jω )
′
n = −∞
∑ x ( n )e
数字信号处理第三版西科大课后答案第2章

第2章时域离散信号和系统的频域分析2.1学习要点与重要公式2.2FT和ZT的逆变换2.3分析信号和系统的频率特性 2.4例题2.5习题与上机题解答2.1学习要点与重要公式数字信号处理中有三个重要的数学变换工具,即傅里叶变换(FT)、Z变换(ZT)和离散傅里叶变换(DFT)。
利用它们可以将信号和系统在时域空间和频域空间相互转换,这方便了对信号和系统的分析和处理。
三种变换互有联系,但又不同。
表征一个信号和系统的频域特性是用傅里叶变换。
Z 变换是傅里叶变换的一种推广,单位圆上的Z变换就是傅里叶变换。
在z域进行分析问题会感到既灵活又方便。
离散傅里叶变换是离散化的傅里叶变换,因此用计算机分析和处理信号时,全用离散傅里叶变换进行。
离散傅里叶变换具有快速算法FFT,使离散傅里叶变换在应用中更加方便与广泛。
但是离散傅里叶变换不同于傅里叶变换和Z变换,它将信号的时域和频域,都进行了离散化,这是它的优点。
但更有它自己的特点,只有掌握了这些特点,才能合理正确地使用DFT。
本章只学习前两种变换,离散傅里叶变换及其FFT将在下一章学习。
2.1.1学习要点(1)傅里叶变换的正变换和逆变换定义,以及存在条件。
(2)傅里叶变换的性质和定理:傅里叶变换的周期性、移位与频移性质、时域卷积定理、巴塞伐尔定理、频域卷积定理、频域微分性质、实序列和一般序列的傅里叶变换的共轭对称性。
(3)周期序列的离散傅里叶级数及周期序列的傅里叶变换表示式。
(4)Z变换的正变换和逆变换定义,以及收敛域与序列特性之间的关系。
(5)Z变换的定理和性质:移位、反转、z域微分、共轭序列的Z变换、时域卷积定理、初值定理、终值定理、巴塞伐尔定理。
(6)系统的传输函数和系统函数的求解。
(7)用极点分布判断系统的因果性和稳定性。
(8)零状态响应、零输入响应和稳态响应的求解。
(9)用零极点分布定性分析并画出系统的幅频特性。
2.1.2重要公式(1)这两式分别是傅里叶变换的正变换和逆变换的公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课后习题第一章
17*. 已知系统的差分方程为
y (n )=-a 1y (n -1)-a 2y (n -2)+bx (n )
其中, a 1=-0.8, a 2=0.64, b =0.866。
(1) 编写求解系统单位脉冲响应h (n )(0≤n ≤49)的程序, 并画出h (n )(0≤n ≤49);
(2) 编写求解系统零状态单位阶跃响应s (n )(0≤n ≤100)的程序, 并画出s (n )(0≤n ≤100)。
%调用filter 解差分方程,求系统单位脉冲响应和单位阶跃响
B=0.866;A=[1,-0.8,0.64];%查分方程向量
%(1)求解系统单位脉冲响应,并画出h(n)
xn=[1,zeros(1,48)]; %xn=单位脉冲序列,长度N=31
hn=filter(B,A,xn);%调用filter 解差分方程,求系统输出信号hn
n=0:length(hn)-1;
subplot(3,2,1);stem(n,hn,'.')
title(' (a)系统的单位脉冲响应');xlabel('n');ylabel('h(n)')
%(2)求解系统单位阶跃响应,并画出h(n)
xn=ones(1,100);%xn=单位阶跃序列,长度N=100
sn=filter(B,A,xn);%调用filter 解差分方程,求系统单位阶跃响应sn
n=0:length(sn)-1;
subplot(3,2,2);stem(n,sn, '.');axis([0,30,0,2])
title(' (b)系统的单位阶跃响应');xlabel('b');ylabel('s(n)')
第二章
31*. 假设系统函数如下式:
(1) 画出极、零点分布图, 并判断系统是否稳定;
(2) 用输入单位阶跃序列u (n )检查系统是否稳定。
解:(1)%程序ex231.m
%判断系统的稳定性
A=[2,-2.98,0.17,2.3418,-1.5147]; %H(z)的分母多项式系数
B=[0,0,1,5,-50]; %H(z)的分子多项式系数用极点分布判断系统是否稳定
subplot(2,1,1);
zplane(B,A); %绘制H(z)的零极点图
5147.13418.217.098.22505)(2342-++--+=z z z z z z z H
p=roots(A); %求H(z)的极点
pm=abs(p); %求H(z)的极点的模
if max(pm)<1 disp('系统因果稳定'),else
disp('系统不因果稳定'); end %画出u(n)的系统输出波形进行判断
un=ones(1,700);
sn=filter(B,A,un);
n=0:length(sn)-1;
subplot(2,1,2); plot(n,sn)
xlabel('n');ylabel('s(n)')
系统因果稳定
第三章
25*.已知序列h(n)=R6(n),x(n)=nR8(n ).
(1)计算)()(n h n y c =⑧x(n);
(2)计算)()(n h n y c = ○
16x(n)和y(n)=h(n)*x(n); (3)画出h(n)、x(n)、)(n y c 和y(n)的波形图,观察总结循环卷积与线性卷积的关系。
解:%程序ex325.m
hn=[1 1 1 1];xn=[0 1 2 3];
%用DFT 计算4点循环卷积yc4n:
H4k=fft(hn,4); %计算h(n)的4点DFT
X4k=fft(xn,4); %计算x(n)的4点DFT
Yc4k=H4k.*X4k; yc4n=ifft(Yc4k,4);
%用DFT 计算8点循环卷积yc8n:
H8k=fft(hn,8); %计算h(n)的8点DFT
X8k=fft(xn,8); %计算x(n)的8点DFT
Yc8k=H8k.*X8k; yc8n=ifft(Yc8k,8);
yn=conv(hn,xn); %时域计算线性卷积yn
第四章
19*.假设滤波器的系统函数为1
6
31325)(------=z z z z H 在单位圆上采样六点,选择r=0.95,试画出它的频率采样结构,并在计算机上用DFT 求出频率采样结构中的有关系数。
解:1631325)(------=z z z z H =1331)35)(1(----+-z
z z =1
32111)35)(1)(1(------++--z z z z z 式中,分母分子多项式各有一个零点z=1,相互抵消,因此系统仍然稳定,属于FIR 系统。
由系统函数得到单位脉冲响应为
h(n)=5δ(n)+5δ(n-1)+5δ(n-2)+3δ(n-3)+3δ(n-4)+3δ(n-5)
H(k)=DFT[h(n)] k=0,1,2,3, …,5 H(z)=(1-])3cos(211)3(1)0([1)212
211101166∑=------+-++++-k k k z r z k z a a rz H rz H N z r π
%程序ex519.m
hn=[5,5,5,3,3,3];r=0.95;
Hk=fft(hn,6);
for k=1:3,
hk(k)=Hk(k);Wk(k)=exp(-j*2*pi*(k-1)/6);
end
H0=Hk(1)
H3=Hk(4)
r0k=2*real(hk)
rlk=-2*real(r*hk.*Wk)
运行结果:
H0 =24
H3 = 2
r0k =48 4 0
rlk =-45.6000 3.8000 0
第五章
第六章
23*调用MATLAB工具箱函数remezord和remez设计线性相位高通FIR滤波器,实现对模拟信号的采样序列x(n)的数字高通滤波处理。
指标要求:采样频率为16kHz;通带截止
频率为5.5kHz,通带最小衰减为1db;过渡带宽度小于等于3.5kHz,阻带最小衰减为75db。
列出h(n)的序列数据,并画出损耗函数曲线。
解:滤波器的阻带截止频率fs=5500-3500=2000Hz。
%ex723.m:调用remezord和remez设计线性相位高通FIR滤波器
Fs=16000;f=[2000,5500];%采样频率,边界频率为模拟频率(Hz)
m=[0,1];
rp=1;rs=75;dat1=(10^(rp/20)-1)/(10^(rp/20)+1);dat2=10^(-rs/20);
rip=[dat2,dat1]
[M,fo,mo,w]=remezord(f,m,rip,Fs)
hn=remez(M,fo,mo,w)
运行结果:
hn =
0.0073 -0.0409 0.0634 0.0490 -0.3007 0.4436 -0.3007 0.0490 0.0634 -0.0409 0.0073。
