信号与线性系统五六章自测题(标准答案)
《信号与系统》自测题1(含参考答案

电子科技大学网络教育考卷(A1卷)一、单项选择(每题2分,共10分)1. 连续时间信号()x t 如图1所示,()x t '可以表示为( )。
(a )(1)2(1)(2)u t u t u t +--+-(b )(1)2(1)(2)(2)u t u t u t t δ+--+--- (c )(1)(1)(2)(2)u t u t u t t δ+--+--- (d )(1)2(1)(2)(2)u t u t u t t δ+------ 2. ()()241tt dt δ+∞-∞+-=⎰( )。
(a )3 (b )-3 (c )-5 (d )53. 已知离散时间系统的输入信号为()x n ,输出信号为()y n ,且()()(1)y n x n x n =+,这个系统是( )。
(a )非线性,时变,非因果,稳定 (b )线性,时变,非因果,不稳定 (c )非线性,时不变,非因果,稳定 (d )线性,时变,因果,不稳定4. 已知LTI 系统的输入信号()2(1)()(2)x n n n n δδδ=+-+-,单位冲激响应()3()(1)2(2)h n n n n δδδ=+-+-。
系统的输出信号()()()y n x n h n =*等于( )。
(a )(){6,1,3,1,1,2},1,0,1,2,3,4y n n =-=- (b )(){6,1,5,1,1,2},1,0,1,2,3,4y n n =-=- (c )(){6,1,3,1,3,2},1,0,1,2,3,4y n n =-=- (d )(){6,1,3,1,1,2},0,1,2,3,4,5y n n =-=5. 已知LTI 系统的单位冲激响应()h t 如图2所示,如果输入()()x t t δ'=,输出3/2()|t y t ==( )。
(a )1 (b )-1 (c )-3/2 (d )0二、计算题1. (10分)已知LTI 系统的对激励信号1()e t 产生 的响应为1()r t ,求系统对激励信号2()e t 所产生的 响应信号,并画出信号波形。
信号与线性系统分析试题及答案(10套)

信号与线性系统分析试题及答案(10套)标准答案(⼀)⼀、填空题(每空1分,共30分)1、⽆线电通信中,信号是以电磁波形式发射出去的。
它的调制⽅式有调幅、调频、调相。
2、针对不同的调制⽅式有三种解调⽅式,分别是检波、鉴频、和鉴相。
3、在单调谐放⼤器中,矩形系数越接近于1、其选择性越好;在单调谐的多级放⼤器中,级数越多,通频带越窄、(宽或窄),其矩形系数越(⼤或⼩)⼩。
4、调幅波的表达式为:uAM(t)= 20(1 +0.2COS100πt)COS107πt(V);调幅波的振幅最⼤值为24V,调幅度Ma为20℅,带宽fBW为100Hz,载波fc为5*106Hz。
5、在⽆线电技术中,⼀个信号的表⽰⽅法有三种,分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种⽅式。
7、检波有同步、和⾮同步检波两种形式。
8、反馈式正弦波振荡器按照选频⽹络的不同,可分为LC、RC、⽯英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、⽤模拟乘法器⾮线性器件实现调幅最为理想。
⼆、选择题(每⼩题2分、共20分)将⼀个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息(C )A、载波信号B、本振信号C、已调波信号2、⼩信号谐振放⼤器的主要技术指标不包含(B )A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于( A )分量A、基波B、⼆次谐波C、其它⾼次谐波D、直流分量4、并联型⽯英晶振中,⽯英谐振器相当于(C )元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为( B )A、|AF|=1,φA+φF= 2nπB、|AF| >1,φA+φF = 2nπC、|AF|>1,φA+φF ≠2nπD、|AF| =1,φA+φF ≠2nπ6、要实现集电极调制特性应使功放⼯作在(B )状态A、⽋压状态B、过压状态C、临界状态D、任意状态7、⾃动增益控制可简称为( B )A、MGCB、AGCC、AFCD、PLL8、利⽤⾮线性器件相乘作⽤来实现频率变换其有⽤项为( B )A、⼀次⽅项B、⼆次⽅项C、⾼次⽅项D、全部项9、如右图所⽰的电路是(D )A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在⼤信号包络检波器中,由于检波电容放电时间过长⽽引起的失真是(B)A、频率失真B、惰性失真C、负峰切割失真D、截⽌失真三、判断题,对的打“√”,错的打“×”(每空1分,共10分)1、谐振放⼤器是采⽤谐振回路作负载的放⼤器。
信号与系统自测题(第1章 参考答案)

8
−∞
B B 1
) 。
C δ (t )
、
、
D sin t
、
∫
9
∞
−∞
、∫
sin(π t ) sin(π t ) δ (t )dt = t t
∞
t =0
=π
−∞
(t + sin t )δ ′(t − )dt = 6
π
(
B
cos(π t ) 1
B
t =0
=π
) 。
C 1+
、π + 6 注:
A
2 3
、 −1 −
3 2
、
3 2
D
、
3
∫
∞
−∞
(t + sin t )δ ′(t − )dt = −(t + sin t )′ 6
∞ −∞
π
t=
π
6
= −(1 + cos t )
t=
π
6
π 3 = −(1 + cos ) = −(1 + ) 6 2
、 ∫ f (t )δ (t )dt = ( A ) 。 A、f (0) B、f (t )
A
f (t )
1
−1
0
1
2 t
f (5 − 2t )
1
f (5 − 2t )
1 1
f (5 − 2t )
f (5 − 2t )
1
−0.5 0 A
0.5
1 t
−1 −0.5
0 0.5
t
B
0 C
11.5 2
3t
−2 −1
0 1 t D
信号与线性系统三四章自测题(标准答案)

第三、四章自测题解答一、填空题:1、(1))(1t f 的参数为V A s T s 1,1,5.0===μμτ,则谱线间隔为__1000__kHz, 带宽为___2000__kHz 。
(2))(2t f 的参数为V A s T s 3,3,5.1===μμτ,则谱线间隔为___333__kHz, 带宽为_666__kHz 。
(3))(1t f 与)(2t f 的基波幅度之比为___1:3____。
(4))(1t f 的基波幅度与)(2t f 的三次谐波幅度之比为__1:1___。
2、由于周期锯齿脉冲信号的傅里叶技术的系数具有收敛性,因此,当k →∞时,k a =0。
3、根据尺度变化性质,可得x(2t)的频带宽度为2B ,可得x(t/2)的带宽为B/2。
4、根据帕斯瓦尔定理,可得该答案为:总和。
5、根据吉布斯现象,可得该题答案为:吉布斯现象。
6、设f (t)的傅里叶变换为)(ωj F ,则)(jt F 的傅里叶变换为2f ()πω-。
7、单个矩形脉冲的频谱宽度一般与其脉宽τ有关,τ越大,则频谱宽度 越窄 。
8、矩形脉冲通过RC 低通网络时,波形的前沿和后沿都将产生失真,这种失真的一个主要的原因是RC 低通网络不是理想低通滤波器,脉冲中的高频成分被削弱 。
9、(1)0j t Ke ω-(K 为常数),(2)0K (t-t )δ(0t 为常数) 10、系统对输入信号tj t j e a e a E t x 0011)(ωω--++=的响应为)()()0()(010100ωωωωj H e a j H e a j EH t y t j t j -++=--。
二、判断题 1、错 2、对三、选择题1、( A );2、( A );3、( B );4、( E );5、( C );6、( A );7、(B 、C ); 四、解:(a) 基频 Ω=1600πrad/s ; 21 1.25800T ms π===Ω (b) 傅里叶级数的系数 00F =26/6sin {20n n n n a n n π⎛⎫== ⎪⎝⎭为奇数为偶数 0n b = n n A a =,0n ϕ=,0.5n na F∙=;0000F A a ===(c ) ()f t 对称性:偶函数和奇谐函数(偶对称和半波对成)。
信号与线性系统课后习题答案5

(15) te−(t ε −3) (t −1)
解:(2)
Q
LT [ε
(t)]
=
1 s
,∴
LT [ε
(t
−
2)]
=
1 s
e−2s
∴ LT{e−t[ε (t) − ε (t − 2)]} = 1 (1− e−2(s+1) ) s +1
(7)
(16) te−αt cos(βt)ε (t)
Q sin(2t − π / 4)ε (t) = 1 [sin(2t) − cos(2t)]ε (t) 2
(1) 1− e−Ts s +1
(3) e−2(s+3) s+3
(5)
π (1 s2
+ +
e−s π2
)
解:(1)
Q
LT[e−tε (t)]
=
1 s +1
,
∴ f (t) = LT −1[1 − e−Ts ] = e−tε (t) − e−(t−T )ε (t − T )] ,画出波形图如下图(1) s +1
(1) y′′(t) + 4 y′(t) + 3y(t) = f ′(t) − 3 f (t) 解:(1)
对原微分方程等式两边同时求初始状态为零的单边拉普拉斯变换,令 Yf (s) = LT[ y f (t)] , F (s) = LT[ f (t)],
6
H (s) = Yf (s) = s − 3 , F(s) s2 + 4s + 3
=
s2
s+4 × + 3s + 2
s
1 +2
=
信号与线性系统分析习题答案

1 / 257信号与线性系统课后答案第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fε=t(t(sin)(5))tf=(sinr(t)2 / 257(7))tf kε(k=(2)(10))f kεk-=(k+]()1()1[3 / 2574 / 2571-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε5 / 2576 / 257(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε7 / 2571-3 写出图1-3所示各波形的表达式。
8 / 2571-4 写出图1-4所示各序列的闭合形式表达式。
信号与系统 测试题(附答案)

《信号与系统》测试题2一、选择题(共10题,每题3分 ,共30分,每题给出四个答案,其中只有一个正确的)1、 卷积f 1(k+5)*f 2(k-3) 等于 。
(A )f 1(k)*f 2(k) (B )f 1(k)*f 2(k-8)(C )f 1(k)*f 2(k+8)(D )f 1(k+3)*f 2(k-3)2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。
(A )1.25(B )2.5(C )3(D )5 3、 序列f(k)=-u(-k)的z 变换等于 。
(A )1-z z (B )-1-z z(C )11-z (D )11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。
(A ))2(41t y (B ))2(21t y (C ))4(41t y (D ))4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —tu(t)时,系统的零状态响应y f (t)等于(A )(-9e -t +12e -2t )u(t) (B )(3-9e -t +12e -2t )u(t)(C ))(t δ+(-6e -t +8e -2t )u(t) (D )3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有(A ) 连续性、周期性 (B )连续性、收敛性(C )离散性、周期性 (D )离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于(A ) 1(B )2(C )3(D )4 8、序列和()∑∞-∞=-k k 1δ等于(A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku 9、单边拉普拉斯变换()se ss s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D10、信号()()23-=-t u te t f t 的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s ()()()2323++-s se C s ()()332++-s s e D s二、填空题(共9小题,每空3分,共30分)1、 卷积和[(0.5)k+1u(k+1)]*)1(k -δ=________________________2、 单边z 变换F(z)=12-z z的原序列f(k)=______________________3、 已知函数f(t)的单边拉普拉斯变换F(s)=1+s s,则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________ 4、 频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、 单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、 已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ,则系统的单位序列响应h(k)=_______________________7、 已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=20)()(t dxx f t y 的单边拉氏变换Y(s)=______________________________ 8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ,=k t 22三、(8分)已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换。
大学科目《信号与系统》各章节习题答案
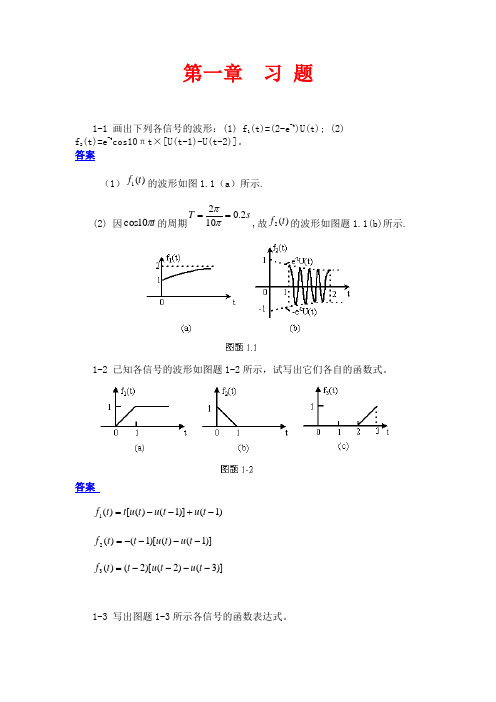
第一章 习 题1-1 画出下列各信号的波形:(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。
答案(1))(1t f 的波形如图1.1(a )所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示,试写出它们各自的函数式。
答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。
答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形:(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。
答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号,若是周期信号,求其周期T 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
第五、六章自测题标准答案
1. 判断题
(1) 当且仅当一个连续时间线性时不变系统的阶跃响应是绝对可积的,则该系统是稳定的。
( × )
(2) 若h(t)是一个线性时不变系统的单位冲激响应,并且h(t)是周期的且非零,则系统是非
稳定的。 ( √ )
(3) 对于一个因果稳定的系统,可以利用jssHjH|)()( 求系统的频率响应。
( √ )
(4) 一个稳定的连续时间系统,其系统函数的零极点都必定在s平面的左半平面。
( × )
2.填空题
(1)某二阶系统起始状态为2_)0(',1_)0(rr;初始条件为,1)0(',3)0(rr则
确定零输入响应待定系数的初始条件为)0(zir= -1 ,)0('zir= 2 ;而确
定零状态响应待定系数的初始条件为 )0(zsr= 4 ,)0('zsr= -1 。
(2)23)(2ssesFs的逆变换为 )(][ )1(2)1(teett。
(3))()sin()(tttf的拉普拉斯变换为2222sincos)(ssssF。
3.求图5-1中所示单边周期信号的拉氏变换。
图5-1
解:)23()()2()()(TtTtTtttf
4.一个单位冲激响应为h(t)的因果LTI系统有下列性质:
(1)当系统的输入为tetx2)(时,对所有t值,输出tety261)(。
(2)单位冲激响应h(t)满足微分方程)()()(2)(4tbtethdttdht。这里b为一个未知
常数。
确定该系统的系统函数。
解:本题中用到了特征函数的概念。一个信号,若系统对该信号的响应仅是一个常数(可
能是复数)乘以输入,则该信号为系统的特征函数。(请注意:上面所指的系统必须是线性
时不变系统。)
因为tetx2)(是因果LTI系统的特征函数,所以ttseesHty22261|)()(。即
2
对所给的微分方程两边取拉普拉斯变换,得
将s=2代入上式,得
6426261)2(
b
H
, b=1
所以
5.已知系统微分方程为)()('2)(2)('3)(''tftftytyty,输入为
)(2)(3tetft
,系统的起始条件为1)0(',1)0(yy,(1)求系统的系统函数和单
位冲激响应;(2)求系统的零输入响应,零状态响应,完全响应,自由响应和强迫响应。
解:(1)11232312)(2ssssssH
冲激响应)()3()(2teethtt
(2)零输入响应
所以 )()32()(2teetrttzi
(3) 零状态响应
所以 )()56()(32teeetrtttzs
完全响应 )()524()()()(32teeetrtrtrtttzszi
自由响应:)()24(2teett
强迫响应:)(53tet
6.某反馈系统如图5-2所示,已知子系统的系统函数为65)(2ssssG。试确定
(1)为使系统稳定,实系数k应满足什么条件;
(2)若系统为临界稳定,求k及单位冲激响应h(t)。
解:65)(1)()()()(2kssssskGsGsEsRsH
为使系统稳定,k<5
k=5时,系统临界稳定,此时
7. 系统如图5-3所示,激励为i1(t),
响应为i2(t).
(1) 求系统函数H(s);
(2) 若i1(t)=2A,求i2(t)。
已知R1=R2=1Ω,C=1F,L=1H .
R(s)
E(s)
图5-2
G(s)
Σ
k
+
+
i2(t)
R
2
_
R
1
C
L
图5-3
3
解:(1)sLRsCRsCRsIsIsH2111211)()()(
(2)sssIsHsI211)()()(12
8.已知一线性时不变系统激励为),()()(3teetftt
系统响应为)()22()(4teetytt,求:
(1)系统的单位冲激响应h(t);
(2)系统激励-响应微分方程。
解答:(1))4)(2(9331114212)()()(ssssssssFsYsH
(2)系统的激励-响应微分方程
9.已知一LTI系统函数H(s)的零点z=1,极点p=-1,且冲激响应初值2)0(h,试求:
(1)系统函数H(s);
(2)系统的幅频特性H(ω),相频特性φ(ω);
(3)若激励)(3sin3)(ttte,求系统稳态响应。
解:(1)2)(lim)0(0ssHhs
(2)2)1()1(2)(jjjH
(3)将3代入)(jH和),(
求得系统的稳态响应为ttys3sin3)(
