函数的极值与导数(人教A版)

合集下载

高中数学人教A版选修1-1习题：第三章3.3-3.3.2函数的极值与导数 Word版含答案

第三章导数及其应用3.3 导数在研究函数中的应用3.3.2 函数的极值与导数A级基础巩固一、选择题1．可导“函数y＝f(x)在一点的导数值为0”是“函数y＝f(x)在这点取得极值”的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：对于f(x)＝x3，f′(x)＝3x2，f′(0)＝0，不能推出f(x)在x＝0处取极值，反之成立．答案：B2．已知可导函数f(x)，x∈R，且仅在x＝1处，f(x)存在极小值，则( )A．当x∈(－∞，1)时，f′(x)＞0；当x∈(1，＋∞)时，f′(x)＜0B．当x∈(－∞，1)时，f′(x)＞0；当x∈(1，＋∞)时，f′(x)＞0C．当x∈(－∞，1)时，f′(x)＜0；当x∈(1，＋∞)时，f′(x)＞0D．当x∈(－∞，1)时，f′(x)＜0；当x∈(1，＋∞)时，f′(x)＜0解析：因为f(x)在x＝1处存在极小值，所以x＜1时，f′(x)＜0，x＞1时，f′(x)＞0.答案：C3．函数y＝x3－3x2－9x(－2＜x＜2)有( )A．极大值5，极小值－27B．极大值5，极小值－11C．极大值5，无极小值D．极小值－27，无极大值解析：由y′＝3x2－6x－9＝0，得x＝－1或x＝3，当x＜－1或x＞3时，y′＞0；当－1＜x＜3时，y′＜0.故当x＝－1时，函数有极大值5；x取不到3，故无极小值．答案：C4．已知f(x)＝x3＋ax2＋(a＋6)x＋1有极大值和极小值，则a的取值范围为( ) A．－1＜a＜2 B．－3＜a＜6C．a＜－1或a＞2 D．a＜－3或a＞6解析：f′(x)＝3x2＋2ax＋(a＋6)，因为f(x)既有极大值又有极小值，那么Δ＝(2a)2－4×3×(a＋6)＞0，解得a＞6或a＜－3.答案：D5．设a∈R，若函数y＝e x＋ax，x∈R有大于零的极值点，则( )A．a＜－1 B．a＞－1C．a＞－1eD．a＜－1e解析：y′＝e x＋a＝0，e x＝－a，因为x＞0，所以 e x＞1，即－a＞1，所以a＜－1.答案：A二、填空题6．函数f(x)＝x3－6x＋a的极大值为________，极小值为________．解析：f′(x)＝x2－6令f′(x)＝0，得x＝－2或x＝2，所以f(x)极大值＝f(－2)＝a＋42，f(x)极小值＝f(2)＝a－4 2.答案：a＋42，a－4 2.7．已知函数y＝x3＋ax2＋bx＋27在x＝－1处取极大值，在x＝3处取极小值，则a＝________，b＝________．解析：y′＝3x2＋2ax＋b，根据题意知，－1和3是方程3x2＋2ax＋b＝0的两根，由根与系数的关系可求得a＝－3，b＝－9.经检验，符合题意．答案：－3 －98．已知函数f(x)＝ax3＋bx2＋cx，其导函数y＝f′(x)的图象经过点(1，0)，(2，0)，如图所示．则下列说法中不正确的是________．①当x ＝32时，函数取得极小值；②f (x )有两个极值点；③当x ＝2时，函数取得极小值； ④当x ＝1时，函数取得极大值．解析：由图象可知当x ∈(－∞，1)时，f ′(x )>0；当x ∈(1，2)时，f ′(x )<0；当x ∈(2，＋∞)时，f ′(x )>0，所以f (x )有两个极值点1和2，且当x ＝2时，函数取得极小值，当x ＝1时，函数取得极大值．故只有①不正确．答案：① 三、解答题9．已知f (x )＝13x 3－12x 2－2x ，求f (x )的极大值与极小值．解：由已知得f (x )的定义域为R.f ′(x )＝x 2－x －2＝(x ＋1)(x －2)．令f ′(x )＝0，得x ＝－1或x ＝2.当x 变化时，f ′(x )与f (x )的变化情况如下表：↗↘↗因此，当x ＝－1时，f (x )取得极大值，且极大值为f (－1)＝3×(－1)3－2×(－1)2－2×(－1)＝76；当x ＝2时，f (x )取得极小值，且极小值为f (2)＝13×23－12×22－2×2＝－103.从而f (x )的极大值为76，极小值为－103.10．已知函数f (x )＝x 3＋ax 2＋bx ＋a 2在x ＝1处取极值10，求f (2)的值．解：f ′(x )＝3x 2＋2ax ＋b .由题意得⎩⎪⎨⎪⎧f （1）＝10，f ′（1）＝0，即⎩⎪⎨⎪⎧a 2＋a ＋b ＋1＝10，2a ＋b ＋3＝0，解得⎩⎪⎨⎪⎧a ＝4，b ＝－11或⎩⎪⎨⎪⎧a ＝－3，b ＝3. 当a ＝4，b ＝－11时，令f ′(x )＝0，得x 1＝1，x 2＝－113.当x 变化时，f ′(x )，f (x )的变化情况如下表：↗↘↗当a ＝－3，b ＝3时，f ′(x )＝3x 2－6x ＋3＝3(x －1)2≥0，所以 f (x )在x ＝1处没有极值，不合题意．综上可知f (2)＝18.B 级能力提升1．等差数列{a n }中的a 1，a 4 031是函数f (x )＝13x 3－4x 2＋6x －1的极值点，则log 2a 2 016的值为( )A ．2B ．3C ．4D ．5解析：因为f ′(x )＝x 2－8x ＋6，且a 1，a 4 031是函数f (x )＝13x 3－4x 2＋6x －1的极值点，所以a 1，a 4 031是方程x 2－8x ＋6＝0的两个实数根，则a 1＋a 4 031＝8.而{a n }为等差数列，所以a 1＋a 4 031＝2a 2 016，即a 2 016＝4，从而log 2a 2 016＝log 24＝2.故选A.答案：A2．若函数f (x )＝x 3＋3ax 2＋3(a ＋2)x ＋1有极大值和极小值，则实数a 的取值范围是________．解析：函数f (x )为三次函数，其导函数f ′(x )＝3x 2＋6ax ＋3(a ＋2)为二次函数，要使函数f (x )既有极大值又有极小值，需f ′(x )＝0有两个不等的实数根，所以Δ＝(6a )2－4×3×3(a ＋2)>0，解得a <－1或a >2.答案：(－∞，－1)∪(2，＋∞)3．设a 为实数，函数f (x )＝x 3－x 2－x ＋a . (1)求f (x )的极值；(2)当a 在什么范围内取值时，曲线y ＝f (x )与x 轴仅有一个交点？解：(1)f ′(x )＝3x 2－2x －1. 令f ′(x )＝0，则x ＝－13或x ＝1.当x 变化时，f ′(x )，f (x )的变化情况如下表：↗↘↗所以f (x )的极大值是f ⎝ ⎛⎭⎪⎫－3＝27＋a ，极小值是f (1)＝a －1.(2)函数f (x )＝x 3－x 2－x ＋a ＝(x －1)2(x ＋1)＋a －1，由此可知，x 取足够大的正数时，有f (x )＞0，x 取足够小的负数时，有f (x )＜0，所以曲线y ＝f (x )与x 轴至少有一个定点．由(1)知f (x )最大值＝f ⎝ ⎛⎭⎪⎫－13＝527＋a ，f (x )极小值＝f (1)＝a －1.因为曲线y ＝f (x )与x 轴仅有一个交点，所以f (x )极大值＜0或f (x )极小值＞0，即527＋a ＜0或a －1＞0，所以a ＜－527或a ＞1，所以当a ∈⎝ ⎛⎭⎪⎫－∞，－527∪(1，＋∞)时，曲线y ＝f (x )与x 轴仅有一个交点．。

人教a版数学【选修2-2】练习：1.3.2函数的极值与导数(含答案)

选修2-2 第一章 1.3 1.3.2一、选择题1．已知函数f (x )在点x 0处连续，下列命题中，正确的是( ) A ．导数为零的点一定是极值点B ．如果在点x 0附近的左侧f ′(x )>0，右侧f ′(x )<0，那么f (x 0)是极小值C ．如果在点x 0附近的左侧f ′(x )>0，右侧f ′(x )<0，那么f (x 0)是极大值D ．如果在点x 0附近的左侧f ′(x )<0，右侧f ′(x )>0，那么f (x 0)是极大值 [答案] C[解析] 导数为0的点不一定是极值点，例如f (x )＝x 3，f ′(x )＝3x 2，f ′(0)＝0，但x ＝0不是f (x )的极值点，故A 错；由极值的定义可知C 正确，故应选C.2．(2013·北师大附中高二期中)函数y ＝14x 4－13x 3的极值点的个数为( )A ．0B ．1C ．2D ．3[答案] B[解析] y ′＝x 3－x 2＝x 2(x －1)，由y ′＝0得x 1＝0，x 2＝1. 当x 变化时，y ′、y 的变化情况如下表3．函数y ＝ax 3＋bx 2取得极大值和极小值时的x 的值分别为0和13，则( )A ．a －2b ＝0B ．2a －b ＝0C ．2a ＋b ＝0D ．a ＋2b ＝0[答案] D[解析] y ′＝3ax 2＋2bx 由题设0和13是方程3ax 2＋2bx ＝0的两根，∴a ＋2b ＝0.4．若a >0，b >0，且函数f (x )＝4x 3－ax 2－2bx ＋2在x ＝1处有极值，则ab 的最大值等于( )A ．2B ．3C ．6D ．9[答案] D[解析] f ′(x )＝12x 2－2ax －2b ＝0的一根为x ＝1，即12－2a －2b ＝0. ∴a ＋b ＝6，∴ab ≤(a ＋b 2)2＝9，当且仅当a ＝b ＝3时“＝”号成立．5．已知实数a 、b 、c 、d 成等比数列，且曲线y ＝3x －x 3的极大值点坐标为(b ，c )，则ad 等于( )A ．2B ．1C ．－1D ．－2[答案] A[解析] ∵a 、b 、c 、d 成等比数列，∴ad ＝bc ，又(b ，c )为函数y ＝3x －x 3的极大值点， ∴c ＝3b －b 3，且0＝3－3b 2，∴⎩⎪⎨⎪⎧ b ＝1，c ＝2，或⎩⎪⎨⎪⎧b ＝－1，c ＝－2.∴ad ＝2. 6．(2013·辽宁实验中学期中)函数f (x )＝－x e x (a <b <1)，则( )A ．f (a )＝f (b )B ．f (a )<f (b )C ．f (a )>f (b )D ．f (a )，f (b )的大小关系不能确定[答案] C[解析] f ′(x )＝(－x e x )′＝(－x )′·e x －(－x )·(e x )′(e x )2＝x －1e x. 当x <1时，f ′(x )<0，∴f (x )为减函数， ∵a <b <1，∴f (a )>f (b )．二、填空题7．(2014·福建安溪一中、养正中学联考)曲线y ＝x (3ln x ＋1)在点(1,1)处的切线方程为________．[答案] 4x －y －3＝0[解析] y ′|x ＝1＝(3ln x ＋4)|x ＝1＝4，∴切线方程为y －1＝4(x －1)，即4x －y －3＝0. 8．(2014·河北冀州中学期中)若函数f (x )＝x ＋a sin x 在R 上递增，则实数a 的取值范围为________．[答案] [－1,1][解析] f ′(x )＝1＋a cos x ，由条件知f ′(x )≥0在R 上恒成立，∴1＋a cos x ≥0，a ＝0时显然成立；a >0时，∵－1a ≤cos x 恒成立，∴－1a ≤－1，∴a ≤1，∴0<a ≤1；a <0时，∵－1a≥cos x 恒成立，∴－1a≥1，∴a ≥－1，即－1≤a <0，综上知－1≤a ≤1.9．设x ＝1与x ＝2是函数f (x )＝a ln x ＋bx 2＋x 的两个极值点，则常数a ＝________. [答案] －23[解析] f ′(x )＝ax ＋2bx ＋1，由题意得⎩⎪⎨⎪⎧a ＋2b ＋1＝0，a 2＋4b ＋1＝0.∴a ＝－23.三、解答题10．已知f (x )＝ax 3＋bx 2＋cx (a ≠0)在x ＝±1时取得极值，且f (1)＝－1. (1)试求常数a 、b 、c 的值；(2)试判断x ＝±1时函数取得极小值还是极大值，并说明理由． [解析] (1)由f ′(－1)＝f ′(1)＝0，得3a ＋2b ＋c ＝0,3a －2b ＋c ＝0. 又f (1)＝－1，∴a ＋b ＋c ＝－1. ∴a ＝12，b ＝0，c ＝－32.(2)f (x )＝12x 3－32x ，∴f ′(x )＝32x 2－32＝32(x －1)(x ＋1)．当x <－1或x >1时，f ′(x )>0；当－1<x <1时，f ′(x )<0，∴函数f (x )在(－∞，－1)和(1，＋∞)上是增函数，在(－1,1)上为减函数．∴当x ＝－1时，函数取得极大值f (－1)＝1；当x ＝1时，函数取得极小值f (1)＝－1. [点评] 若函数f (x )在x 0处取得极值，则一定有f ′(x 0)＝0，因此我们可根据极值得到两个方程，再由f (1)＝－1得到一个方程，解上述方程组成的方程组可求出参数．一、选择题11．(2014·山东省德州市期中)已知函数f (x )＝e x (sin x －cos x )，x ∈(0,2013π)，则函数f (x )的极大值之和为( )A ．e 2π(1－e 2012π)e 2π－1B ．e π(1－e 2012π)1－e 2πC ．e π(1－e 1006π)1－e 2πD ．e π(1－e 1006π)1－e π[答案] B[解析] f ′(x )＝2e x sin x ，令f ′(x )＝0得sin x ＝0，∴x ＝k π，k ∈Z ，当2k π<x <2k π＋π时，f ′(x )>0，f (x )单调递增，当(2k －1)π<x <2k π时，f ′(x )<0，f (x )单调递减，∴当x ＝(2k ＋1)π时，f (x )取到极大值，∵x ∈(0,2013π)，∴0<(2k ＋1)π<2013π，∴0≤k <1006，k ∈Z .∴f (x )的极大值之和为S ＝f (π)＋f (3π)＋f (5π)＋…＋f (2011π)＝e π＋e 3π＋e 5π＋…＋e 2011π＝e π[1－(e 2π)1006]1－e 2π＝e π(1－e 2012π)1－e 2π，故选B.12．已知函数f (x )＝x 3－px 2－qx 的图象与x 轴切于(1,0)点，则f (x )的极大值、极小值分别为( )A ．427，0B ．0，427C ．－427，0D ．0，－427[答案] A[解析] f ′(x )＝3x 2－2px －q ，由f ′(1)＝0，f (1)＝0得，⎩⎪⎨⎪⎧ 3－2p －q ＝0，1－p －q ＝0，解得⎩⎪⎨⎪⎧p ＝2，q ＝－1，∴f (x )＝x 3－2x 2＋x . 由f ′(x )＝3x 2－4x ＋1＝0得x ＝13或x ＝1，易得当x ＝13时f (x )取极大值427.当x ＝1时f (x )取极小值0.13．(2014·西川中学高二期中)已知f (x )＝x 3＋ax 2＋(a ＋6)x ＋1有极大值和极小值，则a 的取值范围是( )A ．－1<a <2B ．－3<a <6C ．a <－3或a >6D ．a <－1或a >2[答案] C[解析] f ′(x )＝3x 2＋2ax ＋a ＋6， ∵f (x )有极大值与极小值， ∴f ′(x )＝0有两不等实根，∴Δ＝4a 2－12(a ＋6)>0，∴a <－3或a >6. 二、填空题14．已知函数y ＝x 3＋ax 2＋bx ＋27在x ＝－1处有极大值，在x ＝3处有极小值，则a ＝________________，b ＝________.[答案] －3 －9[解析] y ′＝3x 2＋2ax ＋b ，方程y ′＝0有根－1及3，由韦达定理应有⎩⎨⎧－1＋3＝－2a3，－3＝b 3.∴⎩⎪⎨⎪⎧a ＝－3，b ＝－9.经检验a ＝－3，b ＝－9符合题意．三、解答题15．(2013·新课标Ⅰ文，20)已知函数f (x )＝e x (ax ＋b )－x 2－4x ，曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝4x ＋4.(1)求a ，b 的值；(2)讨论f (x )的单调性，并求f (x )的极大值． [解析] (1)f ′(x )＝e x (ax ＋a ＋b )－2x －4. 由已知得f (0)＝4，f ′(0)＝4，故b ＝4，a ＋b ＝8. 从而a ＝4，b ＝4.(2)由(1)知，f (x )＝4e x (x ＋1)－x 2－4x ， f ′(x )＝4e x (x ＋2)－2x －4＝4(x ＋2)(e x －12)．令f ′(x )＝0得，x ＝－ln2或x ＝－2.从而当x ∈(－∞，－2)∪(－ln2，＋∞)时，f ′(x )>0；当x ∈(－2，－ln2)时，f ′(x )<0. 故f (x )在(－∞，－2)，(－ln2，＋∞)上单调递增，在(－2，－ln2)上单调递减．当x ＝－2时，函数f (x )取得极大值，极大值为f (－2)＝4(1－e －2)．16．(2014·三峡名校联盟联考)已知函数f (x )＝ln x ＋x 2＋ax . (1)当a ＝－3时，求函数y ＝f (x )的极值点；(2)当a ＝－4时，求方程f (x )＋x 2＝0在(1，＋∞)上的根的个数． [解析] (1)f (x )＝ln x ＋x 2－3x ，f ′(x )＝1x ＋2x －3，令f ′(x )＝0，则x ＝1或x ＝12，由f ′(x )>0得0<x <12，或x >1，∴f (x )在(0，12)和(1，＋∞)上单调递增，在(12，1)上单调递减，∴f (x )的极大值点x ＝12，极小值点x ＝1.(2)当a ＝－4时，f (x )＋x 2＝0，即ln x ＋2x 2－4x ＝0，设g (x )＝ln x ＋2x 2－4x ，则g ′(x )＝1x ＋4x －4＝4x 2－4x ＋1x ≥0，则g (x )在(0，＋∞)上单调递增，又g (1)＝－2<0，g (2)＝ln2>0，所以g (x )在(1，＋∞)上有唯一实数根．17．(2014·温州八校联考)已知函数f (x )＝－x 3＋ax 2＋b (a 、b ∈R )． (1)求函数f (x )的单调递增区间；(2)若对任意a ∈[3,4]，函数f (x )在R 上都有三个零点，求实数b 的取值范围． [解析] (1)∵f (x )＝－x 3＋ax 2＋b ， ∴f ′(x )＝－3x 2＋2ax ＝－3x (x －2a 3)．当a ＝0时，f ′(x )≤0函数f (x )没有单调递增区间；当a >0时，令f ′(x )>0，得0<x <2a3，函数f (x )的单调递增区间为(0，23a )；当a <0时，令f ′(x )>0，得2a3<x <0，函数f (x )的单调递增区间为(23a,0)．(2)由(1)知，a ∈[3,4]时，x 、f ′(x )、f (x )的取值变化情况如下：∴f (x )极小值＝f (0)＝b ，f (x )极大值＝f (2a 3)＝4a 327＋b ，∵对任意a ∈[3,4]，f (x )在R 上都有三个零点， ∴⎩⎪⎨⎪⎧ f (0)<0，f (2a 3)>0，即⎩⎪⎨⎪⎧b <0，4a 327＋b >0.得－4a 327<b <0.∵对任意a ∈[3,4]，b >－4a 327恒成立，∴b >(－4a 327)max ＝－4×3327＝－4.∴实数b 的取值范围是(－4,0)．。

函数的极值课件-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册

解：因为 = − − + , 所以′ = − −
令��′() = ，解得 = − ，或 = .
当变化时，′() ，的变化情况如下表所示 .
x
(−∞, −)
′
+
y
单调递增
-1
(-1,3)
3
(, +∞)
0
-
0
+
单调递减
极小值
y
且 0 = 0 ，可知 d=0 .
∴ f′(x)先为负，再变为正，再变为负.
O
x
又 ′ = 3 2 + 2 +
∴ a<0
且 = 0 是在增区间内，即f ′ 0 > 0,
则c>0,对称轴 −
b
2a
> 0,可知b>0
综上， a<0，b>0，c>0，d=0 .
总结
函数的极值
函数f(x)，f′(a)＝0，而且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则点a叫做
（2）如果在附近的左侧 ′ < ，右侧 ′ > ，那么( )是极小值.
课堂检测
判断正误
(1) 函数的极大值一定比极小值大．(
×)
(2) 对可导函数f(x)，f′(x0)＝0 是x0为极值点的充要条件．(
×
)
(3) 函数的最大值不一定是极大值，函数的最小值也不一定是极小值．(
′ = ；而且在点 x=a 附近的左侧′ < ，右侧′ > .
把 a 叫做函数 y=f(x)的极小值点， f(a)叫做函数 y=f(x)的极小值；
y
a
O

人教新课标A版高二数学《选修1-1》3.3.2 函数的极值与导数

令f′(x)=0,即4x3-3x2=0,得x2(4x-3)=0. ∴x=0或x=
3 4
.
当x变化时，f(x),f′(x)的变化情况如下表：
x
(-∞,0)
0 0 不是极值
3;∞) 4
f′(x)
f (x )
↘
↘

0
27 256
+ ↗
3 ) 4
由上表可知,函数f(x)在区间(-∞,0)上是减函数,在区间(0,
第三章导数及其应用
§3.3 导数在研究函数中的应用
3.3.2 函数的极值与导数
1.了解函数极值的概念，会从几何的角度直观理解函数的极值与导数的关系，并会灵活应用. 2.结合函数的图象，了解函数在某点处取得极值的必要条件和充分条件.
3.会用导数求最高次幂不超过三次的多项式函数
的极大值、极小值.
题目类型一、求已知函数的极值【技法点拨】求函数极值的步骤求定义域确定函数f(x)的定义域求导函数f′(x)
求导数
求方程的根列表
求f′(x)在定义域内的所有根用f′(x)=0的根将定义域分成若干区间，列表由各个区间内f′(x)的符号，判断极值情况
求极值
【典例训练】(建议教师以第2题为例题重点讲解)
极值点时,函数f(x)在该区间内的极大值点与极小
值点是交替出现的.
2.极值点与导数为零的点的辨析
(1)可导函数的极值点是导数为零的点，但是导数
为零的点不一定是极值点，即“点x0是可导函数
f(x)的极值点”是“f′(x0)=0”的充分不必要条件； (2)可导函数f(x)在点x0处取得极值的充要条件是 f′(x0)=0，且在x0左侧和右侧f′(x)的符号不同. (3)如果在x0的两侧f′(x)的符号相同，则x0不是f(x) 的极值点.

高中数学第一章导数及其应用 1.3.2 函数的极值与导数课件新人教A版选修2-2

复习课件
高中数学第一章导数及其应用 1.3.2 函数的极值与导数课件新人教A版选修2-2
1.3.2 函数的极值与导数
目标定位
重点难点
1.了解函数在某点取得极值的必要条重点：求函数极值的
件和充分条件方法和步骤
2.理解极大值和极小值的概念难点：函数极值的概
3.掌握求可导函数极大值和极小值的念的理解
设f(x)在x0处连续且f′(x0)＝0，判别f(x0)是极大(小)值的方法：
(1)若在x0两侧f′(x)符号相同，则x0不是f(x)的极值点； (2)若在x0附近的左侧f′(x)＞0，右侧f′(x)＜0，则f(x0)是极大值；
(3)若在x0附近的左侧f′(x)＜0，右侧f′(x)＞0，则f(x0)是极小值．
解得ab＝＝4－，11 或ab＝＝3－. 3，故a＋b＝－7或a＋b＝0.
【错因分析】可导函数在一点的导数值为0是函数在这一点取得极值的必要条件，而非充分条件，本题忽略了对所得两组解进行检验，从而出现了错误．
【正解】(接错解)当a＝4，b＝－11时， f(x)＝x3＋4x2－11x＋16，得f′(x)＝3x2＋8x－11＝(3x＋11)(x－1)．当x∈－131，1时，f′(x)＜0；当x∈(1，＋∞)时，f′(x)＞0.
(3) 如果 f′(x) 在点 x0 的左右两侧符号不变，则 f(x0) _不__是__极__值___．
1．函数f(x)＝x3－3bx＋3b在(0,1)内有极小值，则( )
A．0<b<1
B．b<0
C．b>0 【答案】A
D．b<12
2．已知函数y＝x3－3x＋2，则( ) A．y无极小值，也无极大值 B．y有极小值0，但无极大值 C．y有极小值0，极大值4 D．y有极大值4，但无极小值【答案】C

函数的极值(第一课时)高二数学课件(人教A版2019选择性必修第二册)

在 = 1处取得极小值，故D正确.
练习
题型二：运用导数解决函数的极值问题
例2.求函数() = 2 − 的极值.
解：函数的定义域为，
’ () = 2 − + 2 − ∙ (−1) = 2 − − 2 − = (2 − ) − .
令 ’ () = 0，得(2 − ) − = 0，解得 = 0或 = 2.
(3)解方程 ’ () = 0得方程的根；
(4)利用方程 ’ () = 0的根将定义域分成若干个小开区间，列表，判定导函数在各
个小开区间的符号；
(5)确定函数的极值，如果 ’ ()的符号在0 处由正(负)变负(正)，则()在0 处取
得极大(小)值.
练习
方法技巧：
2.已知函数极值求参数时的注意点：
答案：√，√，×.
辨析2.函数() = + 2
A.0

6
B.
答案：B.
C.

3

2
D.

在[0， ]上的极大值点为(
2
).
例析
1
l l 3
1
= 3
3
例5.求函数() = 3 − 4 + 4的极值.
解：因为()
− 4 + 4，所以
’ () = 2 − 4 = ( − 2)( + 2).
练习
变1.(多选)已知函数 = ’ ()的图象如图所示，则下列说
法正确的是(
).
A.函数()在区间(1， + ∞)上是增函数
B.函数()在区间(−1，1)上无单调性
C.函数()在 =
1
− 处取得极大值
2
D.函数()在 = 1处取极小值

高中数学 1.3.2 函数的极值与导数课件新人教A版选修2

对于可导函数，极值点的导数必为0.
因此对于可导函数，导数为0是点为极值点的必要而不充分条件．
(2)函数的导数不存在的点也可能是极值点．如函数f(x)＝|x|，在x＝0处，左侧(x＜0时)f′(x)＝－1＜0，右侧(x＞0时)f′(x)＝1＞0，当x＝0时f(x) ＝0是f(x)的极小值点，但f′(0)不存在．
．
• 极小值点、极大值点统称为极值点，> 极大值和极小值统
称为极值．极值反映了函数在某一点附近的大小情况，
刻画的是函数的局部性质．
<
减
• 2．求可导函数y＝f(x)的极值的方法是：
• 解方程f′(x)＝0.当f′(x0)＝0时： • (1)如果在x0附近的左侧
，那么f(x0)是极大值； • (2)f′如(x)果＜在0 x0附近的左侧
，那么f(x0)是极小值．
，右侧 f′(x)＞0
，右侧 f′(x)＜0
f′(x)＞0
• [例1] 判断函数y＝x3在x＝0处能否取得极值． • [分析] 可由极值的定义来判断，也可由导数来判断． • [解析] 解法1：当x＝0时，f(x)＝0，在x＝0的附近区域
内，f(x)有正有负，不存在f(0)>f(x)(或f(0)<f(x))，因此y＝ x3在x＝0处取不到极值． • 解法2：y′＝3x2，当x≠0时，y′>0， • 当y＝0时，f(x)＝0，因此y＝x3在(－∞，＋∞)上是增函数，因为单调函数没有极值，所以y＝x3在x＝0处取不到极值．
• 设函数y＝f(x)在点x0及其附近可导，且f′(x0)＝0. • (1)如果f′(x)的符号在点x0的左右由正变负，则f(x0)
为函数f(x)的极大值．
• (2)如果f′(x)的符号在点x0的左右由负变正，则f(x0) 为函数f(x)的极小值．

(新课标)高中数学《3.3.2-函数的极值与导数》课件-新人教A版选修1-1

第17页，共29页。
规律方法已知函数极值情况，逆向应用确定函数的解析式，进而研究函数性质时注意两点： (1)常根据极值点处导数为 0 和极值两个条件列方程组，利用待定系数法求解． (2)因为导数值等于零不是此点为极值点的充要条件，所以利用待定系数法求解后必须验证根的合理性．
第18页，共29页。
第22页，共29页。
如图(1)，此时曲线 f(x)与 x 轴恰有两个交点，即方程 f(x)＝0 恰好有两个实数根，所以 a＋2＝0，a＝－2.(10 分) 如图(2)，当极小值等于 0 时，有极大值大于 0，此时曲线 f(x) 与 x 轴恰有两个交点，即方程 f(x)＝0 恰好有两个实数根，所以 a－2＝0，a＝2.综上，当 a＝2，或 a＝－2 时方程恰有两个实数根．(12 分)
第8页，共29页。
2．极值点与导数的关系 (1)可导函数的极值点一定是导数为 0 的点，但导数为 0 的点不一定是函数的极值点． (2)导数为 0 的点可能是函数的极值点，如 y＝x2，y′(0)＝0，x ＝0 是极小值．导数为 0 的点也可能不是函数的极值点，如 y ＝x3，y′(0)＝0，x＝0 不是极值点．
第23页，共29页。
【题后反思】用求导的方法确定方程根的个数是一种很有效的方法，它是通过函数的变化情况，运用数形结合的思想来确定函数的图象与 x 轴的交点个数．
第24页，共29页。
【变式 3】设函数 f(x)＝x3－6x＋5，x∈R. (1)求函数 f(x)的单调区间和极值； (2)若关于 x 的方程 f(x)＝a 有三个不同的实数根，求实数 a 的取值范围．解 (1)f′(x)＝3x2－6，令 f′(x)＝0，解得 x＝－ 2或 x＝ 2. 因为当 x＞ 2或 x＜－ 2时，f′(x)＞0；当－ 2＜x＜ 2时，f′(x)＜0，所以 f(x)的单调递增区间为(－∞，－ 2)，( 2，＋∞)；单调递减区间为(－ 2， 2)．

人教A版选择性必修第二册5-3-2-1函数的极值课件(47张)

3．已知函数 f(x)的导数为 f′(x)＝4x3－4x，且 f(x)的图象过点(1，－6)，当函数 f(x)取得
极大值－5 时，x 的值应为( D )
A．1
B．0
C．－5
D．5
解析：设 f(x)＝x4－2x2＋c，又 f(x)的图象过点(1，－6)，所以 c＝－5.故 f(x)＝x4－2x2－5. 又当 f′(x)＝0 时，x＝0 或 1 或－1，所以当函数 f(x)取得极大值－5，即 f(x)＝－5 时，x＝0.
2．极大值点与极大值函数 y＝f(x)在点 x＝b 的函数值 f(b)比它在点 x＝b 附近其他点的函数值都大，f′(b)＝ ____0____，而且在点 x＝b 附近的左侧__f′_(x_)_>_0__，右侧__f_′(_x_)<_0__，就把____b____叫做函数 y ＝f(x)的极大值点，___f_(b_)___叫做函数 y＝f(x)的极大值． 3．极小值点、极大值点统称为_极__值__点___；极小值、极大值统称为___极__ f′(x0)＝0 的关系一般来说，“f′(x0)＝0”是“函数 y＝f(x)在点 x0 处取得极值”的必要不充分条件．若可导函数 y＝f(x)在点 x0 处可导，且在点 x0 处取得极值，那么 f′(x0)＝0；反之，若 f′(x0)＝0，则点 x0 不一定是函数 y＝f(x)的极值点．
强研习·重点难点要突破
研习 1 求函数的极值(点) [典例 1] (1)(多选)已知函数 y＝f(x)，其导函数 y＝f′(x)的图象如图所示，则 y＝
f(x)( BCD )
A．在(－∞，0)上单调递减 C．在(4，＋∞)上单调递减 (2)求函数 f(x)＝x2e－x 的极值．
B．在 x＝0 处取极大值 D．在 x＝2 处取极小值

人教a版数学【选修2-2】1.3.2《函数的极值与导数》ppt课件

成才之路 · 数学
人教A版 · 选修2-2
路漫漫其修远兮吾将上下而求索
第一章
导数及其应用
第一章
1.3 导数在研究函数中的应用
1.3.2 函数的极值与导数
1
自主预习学案
2
Hale Waihona Puke 典例探究学案3巩固提高学案
4
备选练习
自主预习学案
1.掌握极值的概念，了解函数在某点取得极值的必要条件和充分条件． 2．会用导数求不超过三次的多项式函数的极大值、极小值，及其他简单函数的极值．
2．一般地，已知函数y＝f(x)及其定义域内一点x0，对于包含 x0在内的开区间内的所有点x，如果都有__________，则称函 f(x)<f(xf0()x)的一个数f(x)在点x0处取得__________，并把x0称为函数 __________；如果都有 __________，则称函数f(x)在点x0处取极大值得________，并把x0称为函数f(x)的一个__________．极大值 f(，极大值点与极小值点统称为 x)>f(x0) 极大值点与极小值统称为______ 极小值极小值点 ________．极值极值点
重点：函数极值的概念与求法．难点：函数的单调性与极值的综合应用．
函数的极值与导数的关系思维导航在函数的图象上，有的点左、右两侧函数的单调性相同，有的点左、右两侧的单调性相反，有些情形下左增右减，在些情况下左减右增，这些点对研究函数有何特殊意义？
新知导学
1．如图是函数y＝f(x)的图象，在x＝a邻近的左侧f(x)单调．．
极大值极小值－ 0 4e 2 由上表可以看出，当x＝0时，函数有极小值，且f(0)＝0. 4 当x＝2时，函数有极大值，且f(2)＝e2.

高二数学(人教A版)《3.3.2函数的极值与导数》导学案

3.3.2函数的极值与导数[自学目标]:1.理解函数的极大值、极小值、极值点的意义；2.掌握函数极值的判别方法.进一步体验导数的作用.[重点]: 极大、极小值的概念和判别方法。

[难点]: 严格套用求极值的步骤[教材助读]一般地，设函数f (x )在点x 0附近有定义，如果对x 0附近的所有的点，都有________我们就说f (x 0)是函数f (x )的一个极大值，记作y 极大值＝f (x 0)；如果对x 0附近的所有的点，都有________，我们就说f (x 0)是函数f (x )的一个极小值，记作y 极小值＝f (x 0)．利用导数判别函数的极大（小）值：一般地，当函数f (x )在点x 0处连续时，判别f (x 0)是极大（小）值的方法是：⑴如果在x 0附近的左侧f '(x )＞0，右侧f '(x )＜0，那么，f (x 0)是________⑵如果在x 0附近的左侧f '(x )＜0，右侧f '(x )＞0，那么，f (x 0)是________注意：导数为0的点不一定是极值点．[预习自测]1．函数y =f (x )的导数y /与函数值和极值之间的关系为( )A 、导数y /由负变正,则函数y 由减变为增,且有极大值B 、导数y /由负变正,则函数y 由增变为减,且有极大值C 、导数y /由正变负,则函数y 由增变为减,且有极小值D 、导数y /由正变负,则函数y 由增变为减,且有极大值2．求函数x e x y -=2的极值。

上与老师和同学探究解决。

[合作探究展示点评]探究一：极值点两侧导数正负符号有何规律?1．求()31443f x x x =-+的极值填写下表并求极值探究二：极值点处导数值(即切线斜率）有何特点？2．求y =(x 2－1)3+1的极值[当堂检测]1．求下列函数的极值:（1）2()62f x x x =-- （2）3()27f x x x =-（3）3()612f x x x =+- （4）3()3f x x x =-2．已知32()(0)f x ax bx cx a =++≠在x ＝±1时取得极值，且f (1)＝－1，(1)试求常数a 、b 、c 的值；(2)试判断x ＝±1时函数取得极小值还是极大值，并说明理由．[拓展提升]1．函数2()ln 3f x a x bx x =++的极值点为11x =，22x =，则a = ，b = ．★2．已知函数32()32f x x ax bx =-+在1x =处有极小值1-，试求,a b 的值，并求出()f x 的单调区间．★★3.已知某工厂生产x 件产品的成本为212500020040C x x =++（元），问：（1）要使平均成本最低，应生产多少件产品？（2）若产品以每件500元售出，要使利润最大，应生产多少件产品？。

最新2019版高中数学第一章 1.3.2 函数的极值与导数(一)教案新人教A版选修2-2

1．3.2 函数的极值与导数(一)学习目标 1.了解函数极值的概念，会从几何方面直观理解函数的极值与导数的关系.2.掌握函数极值的判定及求法.3.掌握函数在某一点取得极值的条件．知识点一函数的极值点和极值思考观察函数y＝f(x)的图象，指出其极大值点和极小值点及极值．答案极大值点为e，g，i，极大值为f(e)，f(g)，f(i)；极小值点为d，f，h，极小值为f(d)，f(f)，f(h)．梳理(1)极小值点与极小值若函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0，而且在点x＝a附近的左侧f′(x)<0，右侧f′(x)>0，就把点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．(2)极大值点与极大值若函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0，而且在点x＝b附近的左侧f′(x)>0，右侧f′(x)<0，就把点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．(3)极大值点、极小值点统称为极值点；极大值、极小值统称为极值．知识点二函数极值的求法与步骤(1)求函数y＝f(x)的极值的方法解方程f′(x)＝0，当f′(x0)＝0时，①如果在x0附近的左侧函数单调递增，即f′(x)>0，在x0的右侧函数单调递减，即f′(x)<0，那么f(x0)是极大值；②如果在x0附近的左侧函数单调递减，即f′(x)<0，在x0的右侧函数单调递增，即f′(x)>0，那么f(x0)是极小值．(2)求可导函数f(x)的极值的步骤①确定函数的定义区间，求导数f′(x)；②求方程f′(x)＝0的根；③列表；④利用f ′(x )与f (x )随x 的变化情况表，根据极值点左右两侧单调性的变化情况求极值．1．导数为0的点一定是极值点．( × ) 2．函数的极大值一定大于极小值．( × ) 3．函数y ＝f (x )一定有极大值和极小值．( × ) 4．极值点处的导数一定为0.( × )类型一求函数的极值点和极值命题角度1 不含参数的函数求极值例1 求下列函数的极值． (1)f (x )＝2x x 2＋1－2；(2)f (x )＝ln xx. 考点函数在某点处取得极值的条件题点不含参数的函数求极值问题解 (1)函数f (x )的定义域为R . f ′(x )＝2(x 2＋1)－4x 2(x 2＋1)2＝－2(x －1)(x ＋1)(x 2＋1)2. 令f ′(x )＝0，得x ＝－1或x ＝1.当x 变化时，f ′(x )，f (x )的变化情况如下表：由上表可以看出，当x ＝－1时，函数有极小值，且极小值为f (－1)＝－3；当x ＝1时，函数有极大值，且极大值为f (1)＝－1. (2)函数f (x )＝ln xx的定义域为(0，＋∞)，且f ′(x )＝1－ln x x2. 令f ′(x )＝0，解得x ＝e.当x 变化时，f ′(x )与f (x )的变化情况如下表：↗因此，x ＝e 是函数的极大值点，极大值为f (e)＝1e ，没有极小值．反思与感悟函数极值和极值点的求解步骤 (1)确定函数的定义域． (2)求方程f ′(x )＝0的根．(3)用方程f ′(x )＝0的根顺次将函数的定义域分成若干个小开区间，并列成表格． (4)由f ′(x )在方程f ′(x )＝0的根左右的符号，来判断f (x )在这个根处取极值的情况．特别提醒：当实数根较多时，要充分利用表格，使极值点的确定一目了然．跟踪训练1 求下列函数的极值点和极值． (1)f (x )＝13x 3－x 2－3x ＋3；(2)f (x )＝x 2e －x.考点函数在某点处取得极值的条件题点不含参数的函数求极值问题解 (1)f ′(x )＝x 2－2x －3. 令f ′(x )＝0，得x 1＝－1，x 2＝3，当x 变化时，f ′(x )，f (x )的变化情况如下表：↘由上表可以看出，当x ＝－1时，函数有极大值，且极大值f (－1)＝143，当x ＝3时，函数有极小值，且极小值f (3)＝－6. (2)函数f (x )的定义域为R .f ′(x )＝2x e －x －x 2e －x ＝x (2－x )e －x .令f ′(x )＝0，得x ＝0或x ＝2.当x 变化时，f ′(x )，f (x )的变化情况如下表：当x ＝2时，函数有极大值，且极大值为f (2)＝4e －2. 命题角度2 含参数的函数求极值例2 已知函数f (x )＝(x 2＋ax －2a 2＋3a )e x(x ∈R )，当实数a ≠23时，求函数f (x )的单调区间与极值．考点函数在某点处取得极值的条件题点含参数求极值问题解 f ′(x )＝[x 2＋(a ＋2)x －2a 2＋4a ]e x. 令f ′(x )＝0，解得x ＝－2a 或x ＝a －2，由a ≠23知－2a ≠a －2.分以下两种情况讨论： ①若a >23，则－2a <a －2.当x 变化时，f ′(x )，f (x )的变化情况如下表：所以f (x )在(－∞，－2a )，(a －2，＋∞)上是增函数，在(－2a ，a －2)上是减函数，函数f (x )在x ＝－2a 处取得极大值f (－2a )，且f (－2a )＝3a e－2a，函数f (x )在x ＝a －2处取得极小值f (a －2)，且f (a －2)＝(4－3a )e a －2.②若a <23，则－2a >a －2.当x 变化时，f ′(x )，f (x )的变化情况如下表：所以f (x )在(－∞，a －2)，(－2a ，＋∞)上是增函数，在(a －2，－2a )上是减函数，函数f (x )在x ＝a －2处取得极大值f (a －2)，且f (a －2)＝(4－3a )e a －2，函数f (x )在x ＝－2a 处取得极小值f (－2a )，且f (－2a )＝3a e－2a.反思与感悟讨论参数应从f ′(x )＝0的两根x 1，x 2相等与否入手进行．跟踪训练2 已知函数f (x )＝x －a ln x (a ∈R )．(1)当a ＝2时，求曲线y ＝f (x )在点A (1，f (1))处的切线方程； (2)求函数f (x )的极值．考点函数在某点处取得极值的条件题点含参数求极值问题解函数f (x )的定义域为(0，＋∞)，f ′(x )＝1－a x. (1)当a ＝2时，f (x )＝x －2ln x ，f ′(x )＝1－2x(x >0)，因而f (1)＝1，f ′(1)＝－1.所以曲线y ＝f (x )在点A (1，f (1))处的切线方程为y －1＝－(x －1)，即x ＋y －2＝0.(2)由f ′(x )＝1－a x ＝x －ax，x >0，知①当a ≤0时，f ′(x )>0，函数f (x )为(0，＋∞)上的增函数，函数f (x )无极值； ②当a >0时，由f ′(x )＝0，解得x ＝a . 又当x ∈(0，a )时，f ′(x )<0，当x ∈(a ，＋∞)时，f ′(x )>0，从而函数f (x )在x ＝a 处取得极小值，且极小值为f (a )＝a －a ln a ，无极大值．综上，当a ≤0时，函数f (x )无极值；当a >0时，函数f (x )在x ＝a 处取得极小值a －a ln a ，无极大值．类型二利用函数的极值求参数例3 (1)已知函数f (x )的导数f ′(x )＝a (x ＋1)(x －a )，若f (x )在x ＝a 处取到极大值，则a 的取值范围是( )A ．(－∞，－1)B ．(0，＋∞)C ．(0,1)D ．(－1,0)(2)已知函数f (x )＝x 3＋3ax 2＋bx ＋a 2在x ＝－1时有极值0，则a ＝________，b ＝________. 考点利用导数研究函数的极值题点已知极值点求参数答案 (1)D (2)2 9解析 (1)若a <－1，因为f ′(x )＝a (x ＋1)(x －a )，所以f (x )在(－∞，a )上单调递减，在(a ，－1)上单调递增，所以f (x )在x ＝a 处取得极小值，与题意不符；若－1<a <0，则f (x )在(－1，a )上单调递增，在(a ，＋∞)上单调递减，从而在x ＝a 处取得极大值．若a >0，则f (x )在(－1，a )上单调递减，在(a ，＋∞)上单调递增，与题意不符，故选D. (2)因为f (x )在x ＝－1时有极值0，且f ′(x )＝3x 2＋6ax ＋b ，所以⎩⎪⎨⎪⎧f ′(－1)＝0，f (－1)＝0，即⎩⎪⎨⎪⎧3－6a ＋b ＝0，－1＋3a －b ＋a 2＝0，解得⎩⎪⎨⎪⎧a ＝1，b ＝3或⎩⎪⎨⎪⎧a ＝2，b ＝9.当a ＝1，b ＝3时，f ′(x )＝3x 2＋6x ＋3＝3(x ＋1)2≥0，所以f (x )在R 上为增函数，无极值，故舍去．当a ＝2，b ＝9时，f ′(x )＝3x 2＋12x ＋9＝3(x ＋1)(x ＋3)．当x ∈(－3，－1)时，f (x )为减函数，当x ∈(－1，＋∞)时，f (x )为增函数，所以f (x )在x ＝－1处取得极小值，因此a ＝2，b ＝9. 反思与感悟已知函数的极值求参数时应注意两点(1)待定系数法：常根据极值点处导数为0和极值两个条件列出方程组，用待定系数法求解． (2)验证：因为导数值为0不一定此点就是极值点，故利用上述方程组解出的解必须验证．跟踪训练3 设x ＝1与x ＝2是函数f (x )＝a ln x ＋bx 2＋x 的两个极值点． (1)试确定常数a 和b 的值；(2)判断x ＝1，x ＝2是函数f (x )的极大值点还是极小值点，并说明理由．考点利用导数研究函数的极值题点已知极值点求参数解 (1)∵f (x )＝a ln x ＋bx 2＋x ， ∴f ′(x )＝ax＋2bx ＋1，∴f ′(1)＝f ′(2)＝0，∴a ＋2b ＋1＝0且a2＋4b ＋1＝0，解得a ＝－23，b ＝－16.(2)由(1)可知f (x )＝－23ln x －16x 2＋x ，且定义域是(0，＋∞)，f ′(x )＝－23x －1－13x ＋1＝－(x －1)(x －2)3x.当x ∈(0,1)时，f ′(x )<0；当x ∈(1,2)时，f ′(x )>0；当x ∈(2，＋∞)时，f ′(x )<0.故x ＝1是函数f (x )的极小值点，x ＝2是函数f (x )的极大值点.1.函数f (x )的定义域为R ，它的导函数y ＝f ′(x )的部分图象如图所示，则下面结论错误的是( )A ．在(1,2)上函数f (x )为增函数B ．在(3,4)上函数f (x )为减函数C ．在(1,3)上函数f (x )有极大值D ．x ＝3是函数f (x )在区间[1,5]上的极小值点考点函数极值的综合应用题点函数极值在函数图象上的应用答案 D解析根据导函数图象知，x ∈(1,2)时，f ′(x )>0，x ∈(2,4)时，f ′(x )<0，x ∈(4,5)时，f ′(x )>0.∴f (x )在(1,2)，(4,5)上为增函数，在(2,4)上为减函数，x ＝2是f (x )在[1,5]上的极大值点，x ＝4是极小值点．故选D. 2．设函数f (x )＝2x＋ln x ，则( )A ．x ＝12为f (x )的极大值点B ．x ＝12为f (x )的极小值点C ．x ＝2为f (x )的极大值点D ．x ＝2为f (x )的极小值点考点函数在某点处取得极值的条件题点不含参数的函数求极值问题答案 D解析函数f (x )＝2x＋ln x 的定义域为(0，＋∞)．f ′(x )＝1x －2x2，令f ′(x )＝0，即1x －2x2＝0得，x ＝2，当x ∈(0,2)时，f ′(x )<0，当x ∈(2，＋∞)时，f ′(x )>0. 因为x ＝2为f (x )的极小值点，故选D.3．函数f (x )＝ax －1－ln x (a ≤0)在定义域内的极值点的个数为________．考点函数在某点处取得极值的条件题点判断极值点的个数答案 0解析因为x >0，f ′(x )＝a －1x ＝ax －1x，所以当a ≤0时，f ′(x )<0在(0，＋∞)上恒成立，所以函数f (x )在(0，＋∞)上单调递减，所以f (x )在(0，＋∞)上没有极值点．4．已知曲线f (x )＝x 3＋ax 2＋bx ＋1在点(1，f (1))处的切线斜率为3，且x ＝23是y ＝f (x )的极值点，则a ＋b ＝________. 考点利用导数研究函数的极值题点已知极值(点)求参数答案－2解析 f ′(x )＝3x 2＋2ax ＋b ，由题意知⎩⎪⎨⎪⎧f ′(1)＝3，f ′⎝ ⎛⎭⎪⎫23＝0，即⎩⎪⎨⎪⎧3＋2a ＋b ＝3，43＋43a ＋b ＝0，解得⎩⎪⎨⎪⎧a ＝2，b ＝－4，则a ＋b ＝－2.5．已知函数f (x )＝ax 2＋b ln x 在x ＝1处有极值12.(1)求a ，b 的值；(2)判断f (x )的单调区间，并求极值．考点利用导数研究函数的极值题点已知极值(点)求参数解 (1)f ′(x )＝2ax ＋b x，由题意得⎩⎪⎨⎪⎧f ′(1)＝0，f (1)＝12，即⎩⎪⎨⎪⎧2a ＋b ＝0，a ＝12，∴a ＝12，b ＝－1.(2)由(1)得，f ′(x )＝x －1x ＝x 2－1x ＝(x ＋1)(x －1)x.又f (x )的定义域为(0，＋∞)，令f ′(x )＝0，解得x ＝1.当x 变化时，f ′(x )，f (x )的变化情况如下表：∴f (x )的单调递减区间为(0,1)，单调递增区间为(1，＋∞)．f (x )极小值＝f (1)＝12.1．求函数极值的步骤 (1)确定函数的定义域； (2)求导数f ′(x )；(3)解方程f ′(x )＝0得方程的根；(4)利用方程f ′(x )＝0的根将定义域分成若干个小开区间，列表，判定导函数在各个小开区间的符号；(5)确定函数的极值，如果f ′(x )的符号在x 0处由正(负)变负(正)，则f (x )在x 0处取得极大(小)值．2．已知函数极值，确定函数解析式中的参数时，注意两点(1)根据极值点的导数为0和极值这两个条件列方程组，利用待定系数法求解；(2)因为导数值等于零不是此点为极值点的充要条件，所以利用待定系数法求解后必须验证充分性．一、选择题1．下列函数中存在极值的是( ) A ．y ＝1xB ．y ＝x －e xC ．y ＝2D ．y ＝x 3考点利用导数研究函数的极值题点极值存在性问题答案 B解析对于y ＝x －e x ，y ′＝1－e x，令y ′＝0，得x ＝0. 在区间(－∞，0)上，y ′>0；在区间(0，＋∞)上，y ′<0.故x ＝0为函数y ＝x －e x的极大值点．2．函数f (x )＝ln x －x 在区间(0，e)上的极大值为( ) A ．－e B ．1－e C ．－1D ．0考点函数在某点处取得极值的条件题点不含参数的函数求极值问题答案 C解析 f (x )的定义域为(0，＋∞)，f ′(x )＝1x－1.令f ′(x )＝0，得x ＝1.当x ∈(0,1)时，f ′(x )>0，当x ∈(1，e)时，f ′(x )<0，故f (x )在x ＝1处取得极大值f (1)＝ln 1－1＝0－1＝－1.3．已知函数f (x )＝2x 3＋ax 2＋36x －24在x ＝2处有极值，则该函数的一个递增区间是( ) A ．(2,3) B ．(3，＋∞) C ．(2，＋∞)D ．(－∞，3)考点利用导数研究函数的极值题点已知极值(点)求参数答案 B解析因为f ′(x )＝6x 2＋2ax ＋36，且在x ＝2处有极值，所以f ′(2)＝0，即24＋4a ＋36＝0，解得a ＝－15，所以f ′(x )＝6x 2－30x ＋36 ＝6(x －2)(x －3)，由f ′(x )>0，得x <2或x >3.4．设三次函数f (x )的导函数为f ′(x )，函数y ＝xf ′(x )的图象的一部分如图所示，则( )A ．f (x )极大值为f (3)，极小值为f (－3)B ．f (x )极大值为f (－3)，极小值为f (3)C ．f (x )极大值为f (－3)，极小值为f (3)D ．f (x )极大值为f (3)，极小值为f (－3) 考点函数极值的综合应用题点函数极值在函数图象上的应用答案 D解析当x <－3时，y ＝xf ′(x )>0，即f ′(x )<0；当－3<x <3时，f ′(x )≥0；当x >3时，f ′(x )<0. ∴f (x )的极大值是f (3)，f (x )的极小值是f (－3)．5．已知函数f (x )＝x 3－px 2－qx 的图象与x 轴切于点(1,0)，则f (x )的( ) A ．极大值为427，极小值为0B ．极大值为0，极小值为427C ．极小值为－427，极大值为0D ．极大值为－427，极小值为0考点函数某点处取得极值的条件题点不含参数的函数求极值问题答案 A解析 f ′(x )＝3x 2－2px －q .由函数f (x )的图象与x 轴切于点(1,0)，得p ＋q ＝1， ∴q ＝1－p ，① 3－2p －q ＝0，②联立①②，解得p ＝2，q ＝－1， ∴函数f (x )＝x 3－2x 2＋x ，则f ′(x )＝3x 2－4x ＋1，令f ′(x )＝0得x ＝1或x ＝13.当x ≤13时，f ′(x )≥0，f (x )单调递增，当13<x <1时，f ′(x )<0，f (x )单调递减，当x ≥1时，f ′(x )≥0，f (x )单调递增，∴f (x )极大值＝f ⎝ ⎛⎭⎪⎫13＝427，f (x )极小值＝f (1)＝0.故选A.6．设a <b ，函数y ＝(x －a )2(x －b )的图象可能是( )考点函数极值的综合应用题点函数极值在函数图象上的应用答案 C解析 y ′＝(x －a )(3x －a －2b )，由y ′＝0得x 1＝a ，x 2＝a ＋2b3.当x ＝a 时，y 取得极大值0，当x ＝a ＋2b3时，y 取得极小值且极小值为负，故选C.7．已知函数f (x )＝e x(sin x －cos x )，x ∈(0,2 017π)，则函数f (x )的极大值之和为( ) A.e 2π(1－e 2 018π)e 2π－1B.e π(1－e 2 016π)1－e 2πC.e π(1－e 1 008π)1－e2πD.e π(1－e 1 008π)1－eπ考点函数某点处取得极值的条件题点不含参数的函数求极值问题答案 B解析 f ′(x )＝2e xsin x ，令f ′(x )＝0得sin x ＝0， ∴x ＝k π，k ∈Z ，当2k π<x <2k π＋π时，f ′(x )>0，f (x )单调递增，当(2k －1)π<x <2k π时，f ′(x )<0，f (x )单调递减， ∴当x ＝(2k ＋1)π时，f (x )取到极大值， ∵x ∈(0,2 017π)，∴0<(2k ＋1)π<2 017π， ∴0≤k <1 008，k ∈Z . ∴f (x )的极大值之和为S ＝f (π)＋f (3π)＋f (5π)＋…＋f (2 015π)＝e π＋e 3π＋e 5π＋…＋e 2 015π＝e π[1－(e 2π)1 008]1－e 2π＝e π(1－e 2 016π)1－e2π，故选B.二、填空题8．函数y ＝x e x在其极值点处的切线方程为________．考点函数某点处取得极值的条件题点不含参数的函数求极值问题答案 y ＝－1e解析令y ′＝e x ＋x e x ＝(1＋x )e x＝0，得x ＝－1，∴y ＝－1e，∴在极值点处的切线方程为y ＝－1e.9．若函数f (x )＝(x －2)(x 2＋c )在x ＝2处有极值，则函数f (x )的图象在x ＝1处的切线的斜率为________．考点利用导数研究函数的极值题点已知极值(点)求参数答案－5解析 ∵函数f (x )＝(x －2)(x 2＋c )在x ＝2处有极值， ∴f ′(x )＝(x 2＋c )＋(x －2)×2x ，令f ′(2)＝0，∴(c ＋4)＋(2－2)×2×2＝0，∴c ＝－4， ∴f ′(x )＝(x 2－4)＋(x －2)×2x .∴函数f (x )的图象在x ＝1处的切线的斜率为f ′(1)＝(1－4)＋(1－2)×2＝－5.10．若x ＝－2是函数f (x )＝(x 2＋ax －1)e x －1的极值点，则f (x )的极小值为________．考点利用导数研究函数的极值题点已知极值(点)求参数答案－1解析函数f (x )＝(x 2＋ax －1)e x －1，则f ′(x )＝(2x ＋a )e x －1＋(x 2＋ax －1)·ex －1＝ex －1·[x 2＋(a ＋2)x ＋a －1]．由x ＝－2是函数f (x )的极值点，得f ′(－2)＝e －3·(4－2a －4＋a －1)＝(－a －1)e －3＝0，所以a ＝－1.所以f (x )＝(x 2－x －1)ex －1，f ′(x )＝e x －1·(x 2＋x －2)．由ex －1>0恒成立，得当x ＝－2或x ＝1时，f ′(x )＝0，且x <－2时，f ′(x )>0；当－2<x <1时，f ′(x )<0；当x >1时，f ′(x )>0.所以x ＝1是函数f (x )的极小值点．所以函数f (x )的极小值为f (1)＝－1.11．已知函数f (x )＝x 3＋ax 2＋bx ＋a 2在x ＝1处取得极值10，则f (－1)＝________. 考点利用导数研究函数的极值题点已知极值(点)求参数答案 30解析由题意知⎩⎪⎨⎪⎧f ′(1)＝0，f (1)＝10，即⎩⎪⎨⎪⎧3＋2a ＋b ＝0，1＋a ＋b ＋a 2＝10，解得⎩⎪⎨⎪⎧a ＝4，b ＝－11或⎩⎪⎨⎪⎧a ＝－3，b ＝3.经检验知，当⎩⎪⎨⎪⎧a ＝－3，b ＝3时，f ′(x )≥0，不合题意．∴f (x )＝x 3＋4x 2－11x ＋16，则f (－1)＝30. 三、解答题12．设函数f (x )＝a ln x ＋12x ＋32x ＋1，其中a ∈R ，曲线y ＝f (x )在点(1，f (1))处的切线垂直于y 轴．(1)求a 的值；(2)求函数f (x )的极值．考点函数在某点处取得极值的条件题点不含参数函数求极值解 (1)f ′(x )＝a x －12x 2＋32. 由题意知，曲线在x ＝1处的切线斜率为0，即f ′(1)＝0，从而a －12＋32＝0，解得a ＝－1.(2)由(1)知f (x )＝－ln x ＋12x ＋32x ＋1(x >0)，f ′(x )＝－1x －12x 2＋32＝3x 2－2x －12x 2＝(3x ＋1)(x －1)2x2. 令f ′(x )＝0，解得x 1＝1，x 2＝－13(舍去)．当x ∈(0,1)时，f ′(x )<0，故f (x )在(0,1)上为单调递减函数；当x ∈(1，＋∞)时，f ′(x )>0，故f (x )在(1，＋∞)上为单调递增函数．故f (x )在x ＝1处取得极小值，极小值为f (1)＝3.13．已知函数f (x )＝x 3＋12mx 2－2m 2x －4(m 为常数，且m >0)有极大值－52，求m 的值．考点利用导数研究函数的极值题点已知极值(点)求参数解 ∵f ′(x )＝3x 2＋mx －2m 2＝(x ＋m )(3x －2m )，令f ′(x )＝0，得x ＝－m 或x ＝23m .当x 变化时，f ′(x )，f (x )的变化情况如下表：∴f (x )有极大值f (－m )＝－m 3＋12m 3＋2m 3－4＝－52，∴m ＝1. 四、探究与拓展14．设函数f (x )在R 上可导，其导函数为f ′(x )，且函数f (x )在x ＝－2处取得极小值，则函数y ＝xf ′(x )的图象可能是( )考点函数极值的综合应用题点函数极值在函数图象上的应用答案 C解析由题意可得f′(－2)＝0，而且当x∈(－∞，－2)时，f′(x)<0，此时xf′(x)>0；排除B，D，当x∈(－2，＋∞)时，f′(x)>0，此时若x∈(－2,0)，xf′(x)<0，若x∈(0，＋∞)，xf′(x)>0，所以函数y＝xf′(x)的图象可能是C.15．已知函数f(x)＝(x2＋ax＋a)e x(a≤2，x∈R)．(1)当a＝1时，求f(x)的单调区间；(2)是否存在实数a，使f(x)的极大值为3？若存在，求出a的值，若不存在，请说明理由．考点利用导数研究函数的极值题点已知极值(点)求参数解(1)f(x)＝(x2＋x＋1)e x，f′(x)＝(2x＋1)e x＋(x2＋x＋1)e x＝(x2＋3x＋2)e x.当f′(x)>0时，解得x<－2或x>－1，当f′(x)<0时，解得－2<x<－1，所以函数的单调递增区间为(－∞，－2)，(－1，＋∞)；单调递减区间为(－2，－1)．(2)令f′(x)＝(2x＋a)e x＋(x2＋ax＋a)e x＝[x2＋(2＋a)x＋2a]e x＝(x＋a)(x＋2)e x＝0，得x＝－a或x＝－2.当a＝2时，f′(x)≥0恒成立，函数无极值，故舍去；当a<2时，－a>－2.当x变化时，f′(x)，f(x)的变化情况如下表：由表可知，f(x)极大值＝f(－2)＝(4－2a＋a)e－2＝3，解得a＝4－3e2<2，所以存在实数a<2，使f(x)的极大值为3，此时a＝4－3e2.。

高二数学人教A版选修1-1第三章3.3.2函数的极值与导数导学案(含答案)

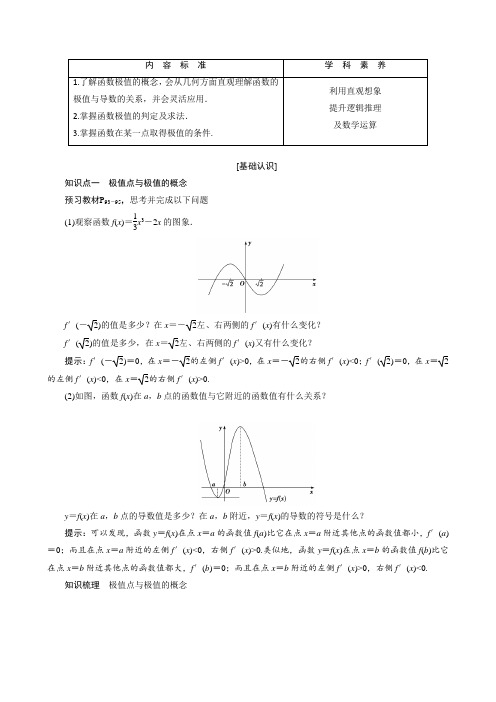
内容标准学科素养 1.了解函数极值的概念，会从几何方面直观理解函数的极值与导数的关系，并会灵活应用． 2.掌握函数极值的判定及求法． 3.掌握函数在某一点取得极值的条件.利用直观想象提升逻辑推理及数学运算[基础认识]知识点一极值点与极值的概念预习教材P 93－95，思考并完成以下问题 (1)观察函数f (x )＝13x 3－2x 的图象．f ′(－2)的值是多少？在x ＝－2左、右两侧的f ′(x )有什么变化？ f ′(2)的值是多少，在x ＝2左、右两侧的f ′(x )又有什么变化？提示：f ′(－2)＝0，在x ＝－2的左侧f ′(x )>0，在x ＝－2的右侧f ′(x )<0；f ′(2)＝0，在x ＝2的左侧f ′(x )<0，在x ＝2的右侧f ′(x )>0.(2)如图，函数f (x )在a ，b 点的函数值与它附近的函数值有什么关系？y ＝f (x )在a ，b 点的导数值是多少？在a ，b 附近，y ＝f (x )的导数的符号是什么？提示：可以发现，函数y ＝f (x )在点x ＝a 的函数值f (a )比它在点x ＝a 附近其他点的函数值都小，f ′(a )＝0；而且在点x ＝a 附近的左侧f ′(x )<0，右侧f ′(x )>0.类似地，函数y ＝f (x )在点x ＝b 的函数值f (b )比它在点x ＝b 附近其他点的函数值都大，f ′(b )＝0；而且在点x ＝b 附近的左侧f ′(x )>0，右侧f ′(x )<0.知识梳理极值点与极值的概念(1)极小值点与极小值如图，函数y ＝f (x )在点x ＝a 的函数值f (a )比它在点x ＝a 附近其他点的函数值都小，f ′(a )＝0；而且在点x ＝a 附近的左侧f ′(x )<0，右侧f ′(x )>0，则把点a 叫做函数y ＝f (x )的极小值点，f (a )叫做函数y ＝f (x )的极小值．(2)极大值点与极大值如(1)中图，函数y ＝f (x )在点x ＝b 的函数值f (b )比它在点x ＝b 附近其他点的函数值都大，f ′(b )＝0；而且在点x ＝b 的左侧f ′(x )>0，右侧f ′(x )<0，则把点b 叫做函数y ＝f (x )的极大值点，f (b )叫做函数y ＝f (x )的极大值．极大值点、极小值点统称为极值点，极大值和极小值统称为极值．知识点二求函数y ＝f (x )的极值的方法知识梳理解方程f ′(x )＝0，当f ′(x 0)＝0时：(1)如果在x 0附近的左侧f ′(x )>0，右侧f ′(x )<0，那么f (x 0)是________． (2)如果在x 0附近的左侧f ′(x )<0，右侧f ′(x )>0，那么f (x 0)是________．提示：(1)极大值 (2)极小值[自我检测]1.函数f (x )的定义域为R ，导函数f ′(x )的图象如图所示，则函数f (x )( )A ．无极大值点，有四个极小值点B ．有三个极大值点，两个极小值点C ．有两个极大值点，两个极小值点D ．有四个极大值点，无极小值点答案：C2．已知函数f (x )＝x ＋1x ，则f (x )( )A ．有极大值2，极小值－2B ．有极大值－2，极小值2C ．无极大值，但有极小值－2D ．有极大值2，无极小值答案：B探究一极值与极值点的判断与求解[教材P98习题3.3A组4题]如图是导函数y＝f′(x)的图象，在标记的点中，在哪一点处：(1)导函数y＝f′(x)有极大值？(2)导函数y＝f′(x)有极小值？(3)函数y＝f(x)有极大值？(4)函数y＝f(x)有极小值？解析：(1)点x2处f′(x)有极大值．(2)点x1、x4处f′(x)有极小值．(3)点x3处f(x)有极大值．(4)点x5处f(x)有极小值．[例1](1)已知函数y＝f(x)，其导函数y＝f′(x)的图象如图所示，则y＝f(x)()A．在(－∞，0)上为减函数B．在x＝0处取极小值C．在(4，＋∞)上为减函数D．在x＝2处取极大值[解析]由导函数的图象可知：当x∈(－∞，0)∪(2,4)时，f′(x)>0，当x∈(0,2)∪(4，＋∞)时，f′(x)<0，因此f(x)在(－∞，0)，(2,4)上为增函数，在(0,2)，(4，＋∞)上为减函数，所以在x＝0处取得极大值，在x ＝2处取得极小值，在x＝4处取得极大值，故选C.[答案] C(2)求下列函数的极值：①f(x)＝2x3＋3x2－12x＋1；②f(x)＝x2－2ln x.[解析]①函数f(x)＝2x3＋3x2－12x＋1的定义域为R，f′(x)＝6x2＋6x－12＝6(x＋2)(x－1)，解方程6(x＋2)(x－1)＝0，得x1＝－2，x2＝1.当x变化时，f′(x)与f(x)的变化情况如下表：x (－∞，－2)－2 (－2,1) 1 (1，＋∞)f ′(x ) ＋0 － 0 ＋ f (x )极大值21极小值－6所以当x 当x ＝1时，f (x )取极小值－6.②函数f (x )＝x 2－2ln x 的定义域为(0，＋∞)， f ′(x )＝2x －2x ＝2(x ＋1)(x －1)x ，解方程2(x ＋1)(x －1)x ＝0，得x 1＝1，x 2＝－1(舍去)．当x 变化时，f ′(x )与f (x )的变化情况如下表：x (0,1) 1 (1，＋∞)f ′(x ) －0 ＋ f (x )极小值1因此当x ＝1时，f (方法技巧 1.通过导函数值的正负确定函数单调性，然后进一步明确导函数图象与x 轴交点的横坐标是极大值点还是极小值点．2．求可导函数f (x )的极值的步骤 (1)确定函数的定义域，求导数f ′(x )． (2)求f (x )的拐点，即求方程f ′(x )＝0的根．(3)利用f ′(x )与f (x )随x 的变化情况表，根据极值点左右两侧单调性的变化情况求极值．特别提醒：在判断f ′(x )的符号时，借助图象也可判断f ′(x )各因式的符号，还可用特殊值法判断．跟踪探究 1．如图为y ＝f (x )的导函数的图象，则下列判断正确的是( )①f (x )在(－3，－1)上为增函数；②x ＝－1是f (x )的极小值点；③f (x )在(2,4)上为减函数，在(－1,2)上为增函数；④x ＝2是f (x )的极小值点．A ．①②③B ．②③C ．③④D ．①③④解析：由f ′(x )的图象知，－3<x <－1时，f ′(x )<0；f ′(－1)＝0；－1<x <2时，f ′(x )>0；f ′(2)＝0；2<x <4时，f ′(x )<0故f (x )在(－3，－1)和(2,4)上是减函数，在(－1,2)上是增函数，f (－1)是极小值，f (2)是极大值，所以②③正确，故选B.答案：B2．判断下列函数有无极值，如果有极值，请求出极值；如果没有极值，请说明理由． (1)y ＝13x 3＋4；(2)y ＝e xx (x >0)．解析：(1)f ′(x )＝x 2. 令f ′(x )＝0，解得x ＝0.当x 变化时，f ′(x )，f (x )的变化情况如下表：x (－∞，0)0 (0，＋∞)f ′(x ) ＋ 0 ＋ f (x )单调递增无极值单调递增(2)y ′＝e x ·x －e x x 2＝e x (x －1)x 2，令y ′＝0，得x ＝1.当x 变化时，f ′(x )，f (x )的变化情况如下表：x (0,1) 1 (1，＋∞)f ′(x ) － 0 ＋ f (x )单调递减极小值单调递增探究二利用函数极值确定参数的值[教材P 110复习参考题A 组7题]已知函数f (x )＝x (x －c )2在x ＝2处有极大值，求c 的值．解析：∵f (x )＝x 3－2cx 2＋c 2x ， ∴f ′(x )＝3x 2－4cx ＋c 2.∴f ′(2)＝0，即3×4－8c ＋c 2＝0，得c ＝2，或c ＝6. 但c ＝2时，f (2)是极小值，不合题意，舍去，所以c ＝6.[例2] (1)已知函数f (x )＝x 3＋3ax 2＋bx ＋a 2在x ＝－1处有极值0，则a ＝________，b ＝________. (2)若函数f (x )＝13x 3－x 2＋ax －1有极值点，则a 的取值范围为________．[解析] (1)∵f ′(x )＝3x 2＋6ax ＋b ，且函数f (x )在x ＝－1处有极值0，∴⎩⎪⎨⎪⎧f ′(－1)＝0，f (－1)＝0，即⎩⎪⎨⎪⎧3－6a ＋b ＝0，－1＋3a －b ＋a 2＝0，解得⎩⎪⎨⎪⎧ a ＝1，b ＝3或⎩⎪⎨⎪⎧a ＝2，b ＝9.当a ＝1，b ＝3时，f ′(x )＝3x 2＋6x ＋3＝3(x ＋1)2≥0，此时函数f (x )在R 上为增函数，无极值，故舍去．当a ＝2，b ＝9时，f ′(x )＝3x 2＋12x ＋9＝3(x ＋1)(x ＋3)．当x ∈(－∞，－3)时，f ′(x )>0，此时f (x )为增函数；当x ∈(－3，－1)时，f ′(x )<0，此时f (x )为减函数；当x ∈(－1，＋∞)时，f ′(x )>0，此时f (x )为增函数．故f (x )在x ＝－1处取得极小值， ∴a ＝2，b ＝9.(2)∵f ′(x )＝x 2－2x ＋a ，由题意得方程x 2－2x ＋a ＝0有两个不同的实数根， ∴Δ＝4－4a >0，解得a <1. [答案] (1)2 9 (2)(－∞，1)方法技巧已知函数极值的情况，逆向应用确定函数的解析式时，应注意以下两点： (1)根据极值点处导数为0和极值两个条件列方程组，利用待定系数法求解．(2)因为导数值等于零不是此点为极值点的充要条件，所以利用待定系数法求解后必须验证根的合理性．跟踪探究 3.已知函数f (x )＝ax 3＋bx 2＋cx (a ≠0)在x ＝±1处取得极值，且f (1)＝－1. (1)求常数a ，b ，c 的值；(2)判断x ＝±1是函数的极大值点还是极小值点，试说明理由，并求出极值．解析：(1)f ′(x )＝3ax 2＋2bx ＋c ， ∵x ＝±1是函数f (x )的极值点，∴x ＝±1是方程f ′(x )＝3ax 2＋2bx ＋c ＝0的两根，由根与系数的关系，得⎩⎨⎧－2b3a＝0， ①c3a ＝－1， ②又f (1)＝－1，∴a ＋b ＋c ＝－1.③ 由①②③解得a ＝12，b ＝0，c ＝－32.(2)由(1)知f (x )＝12x 3－32x ，∴f ′(x )＝32x 2－32＝32(x －1)(x ＋1)，当x <－1或x >1时，f ′(x )>0，当－1<x <1时，f ′(x )<0，∴函数f (x )在(－∞，－1)和(1，＋∞)上是增函数，在(－1,1)上是减函数，∴当x ＝－1时，函数取得极大值f (－1)＝1，当x ＝1时，函数取得极小值f (1)＝－1. 探究三函数极值的综合应用[例3] 已知函数f (x )＝x 3－3ax －1(a ≠0)．若函数f (x )在x ＝－1处取得极值，直线y ＝m 与y ＝f (x )的图象有三个不同的交点，求m 的取值范围．[解析] 因为f (x )在x ＝－1处取得极值且f ′(x )＝3x 2－3a ，所以f ′(－1)＝3×(－1)2－3a ＝0，所以a ＝1，所以f (x )＝x 3－3x －1，f ′(x )＝3x 2－3，由f ′(x )＝0，解得x 1＝－1，x 2＝1. 当x <－1时，f ′(x )>0；当－1<x <1时，f ′(x )<0；当x >1时，f ′(x )>0.所以f (x )的单调增区间为(－∞，－1)，(1，＋∞)；单调减区间为(－1,1)， f (x )在x ＝－1处取得极大值f (－1)＝1，在x ＝1处取得极小值f (1)＝－3. 作出f (x )的大致图象如图所示．因为直线y ＝m 与函数y ＝f (x )的图象有三个不同的交点，结合f (x )的图象可知，m 的取值范围是(－3,1)．方法技巧利用导数可以判断函数的单调性，研究函数的极值情况，并能在此基础上画出函数的大致图象，从直观上判断函数图象与x 轴的交点或两个函数图象的交点的个数，从而为研究方程根的个数问题提供了方便．延伸探究若本例“三个不同的交点”改为“两个不同的交点”，结果如何？改为“一个交点”呢？解析：由本例解析可知当m ＝－3或m ＝1时，直线y ＝m 与y ＝f (x )的图象有两个不同的交点；当m <－3或m >1时，直线y ＝m 与y ＝f (x )的图象只有一个交点．跟踪探究 4.已知函数f (x )＝x 3－6x 2＋9x ＋3，若函数y ＝f (x )的图象与y ＝13f ′(x )＋5x ＋m 的图象有三个不同的交点，求实数m 的取值范围．解析：由f (x )＝x 3－6x 2＋9x ＋3，可得f ′(x )＝3x 2－12x ＋9，∴13f ′(x )＋5x ＋m ＝13(3x 2－12x ＋9)＋5x ＋m ＝x 2＋x ＋3＋m ，则由题意可得x 3－6x 2＋9x ＋3＝x 2＋x ＋3＋m 有三个不相等的实根，即g (x )＝x 3－7x 2＋8x －m 的图象与x 轴有三个不同的交点．∵g ′(x )＝3x 2－14x ＋8 ＝(3x －2)(x －4)，∴令g ′(x )＝0，得x ＝23或x ＝4.当x 变化时，g (x )，g ′(x )的变化情况如下表：则函数g (x )的极大值为g ⎝⎛⎭⎫23＝6827－m ，极小值为g (4)＝－16－m . ∵由y ＝f (x )的图象与y ＝13f ′(x )＋5x ＋m 的图象有三个不同交点，得⎩⎪⎨⎪⎧g ⎝⎛⎭⎫23＝6827－m >0，g (4)＝－16－m <0，解得－16<m <6827.即m 的取值范围为⎝⎛⎭⎫－16，6827.[课后小结](1)在极值的定义中，取得极值的点称为极值点，极值点指的是自变量的值，极值指的是函数值． (2)函数的极值是函数的局部性质．可导函数f (x )在点x ＝x 0处取得极值的充要条件是f ′(x 0)＝0且在x ＝x 0两侧f ′(x )符号相反．(3)利用函数的极值可以确定参数的值，解决一些方程的解和图象的交点问题．[素养培优]1．误把导函数的零点当作函数的极值点求函数f (x )＝x 4－x 3的极值，并说明是极小值还是极大值．易错分析本题易错将导数为零的点都认为是极值点，其实不然，导数为零仅是零点是极值点的必要不充分条件，错解中还有一个误区就是认为极大值一定大于极小值．事实上，极值仅描述函数在该点附近的局部特征，极大值未必一定大于极小值．考查逻辑推理及数学运算．自我纠正 f ′(x )＝4x 3－3x 2，令f ′(x )＝0, 即4x 3－3x 2＝0时，得x 1＝0，x 2＝34.当x 变化时，f (x )，f ′(x )的变化情况如下表：由上表可知函数f (x )在区间(－∞，0)上是减函数，在区间⎝⎛⎭⎫0，34上还是减函数，所以x ＝0不是函数的极值点，而函数f (x )在区间⎝⎛⎭⎫0，34上是减函数，在区间⎝⎛⎭⎫34，＋∞上是增函数，所以函数f (x )在x ＝34处取得极小值，极小值为－27256.2．误把切点当作函数的极值点已知函数f (x )＝ax 4＋bx 2＋c 的图象经过点(0,1)，且在x ＝1处的切线方程是y ＝x －2，求f (x )的解析式．易错分析本题错在将切点当做极值点，得到f ′(1)＝0的错误结论．其实，虽然切点和极值点都与导数有关，但它们却是两个完全不同的概念，不能混为一谈．考查逻辑推理及数学运算的学科素养．自我纠正 f ′(1)表示函数f (x )的图象在点(1，－1)处的切线斜率，应有f ′(1)＝1，再联立f (0)＝1，f (1)＝－1便可得到正确答案：a ＝52，b ＝－92，c ＝1，因此f (x )＝52x 4－92x 2＋1.。

【课件】函数的极值课件-高二下学期数学人教A版(2019)选择性必修第二册

处函数有什么性质呢？
情境
苏轼在《题西林壁》中这
样写道：“横看成岭侧成
峰，远近高低各不同”，
描述的就是庐山的高低起
伏，错落有致。各个山峰
的顶端，虽然不是群山的
最高处，但它却是其附近
的最高点。
那么，在数学上，这种
现象如何来刻画呢？
探究
• 思考1：从单调性的变化来看，
图中哪些点比较特殊？
极值
• 思考2：这些点处的函数值有
-
f(x)
单调递减
极小值0
单调递增
极大值4e-2
单调递减
因此,当x=0时,f(x)有极小值,并且极小值为f(0)=0;当x=2时,f(x)有极大值,并
4
且极大值为f(2)= e2
.
（2） (－∞，－1)∪(2，＋∞) [f ′(x)＝3x2＋6ax＋3(a＋2)，∵函数f (x)既有
极大值又有极小值，∴方程f ′(x)＝0有两个不相等的实根，∴Δ＝36a2－36(a
f '( x)
+
0
+
f ( x) 单调递增
y f ( x )
y
单调递增
f ( x6 )既不是极大值也不是极小值.
a x1 O
x2
x3
x4 x5
x6
b
x
问题4 导数值为0的点一定是函数的极值点吗？
那么，极值存在的条件是什么？
若函数有极值点，则在极值点处导数为0,但导数为0的
点可能不是函数的极值点.也就是说,“f'(c)=0”是“f (x)在
=3
当
= 2,
时,f'(x)=3x2+12x+9=3(x+3)(x+1),令 f'(x)>0 得 x<-3 或 x>-1;

高中数学人教A版选择性必修第二册函数的极值与导数课件

f (x)在x 2, x 1取得极值
f (2) 0且f (1) 0
a 1 ,b 1，经检验符合题意 32
f (x) 1 x3 1 x2 2x 32
你能画出它的大致图像吗？
你学会了什么？
看我来记忆
结论：根据导数定函数，两侧互异有极值，先正后负为极大，先负后正为极小。
“不识庐山真面目，只缘身在此山中”讲的是为什么不能辨别庐山的真面目呢？它其实就是我
对于不导函数f(x)有可能存在极值点，例如 f (x) x
例1 求函数 f (x) 1 x3 4x 4 的极值.
3
定义域求导函数f '(x) 求f '(x)的零点
列表断号下结论
例2 求函数 f (x) ln x 1 x2 的极值.
2
解：定义域0，
你考虑定义域了吗？
f (x) 1 x 1 x2 (1 x)(1 x)
x
x
x
f (x) 0, x 1, x 1(舍)
(0, 1) ＋
1 (1, ＋∞)
0
－
单调递增
单调递减
极大值f (x) 1 ，无极小值 2
你写了无极小值吗？
思考：已知函数 f x ax3 bx2 2x 在 x 2, x 1 处取得极值。
Hale Waihona Puke 求函数 f x 的解析式。解： f (x) 3ax2 2bx 2
的函数值f(b)比它在x＝b附近其他的函数值_都__大_，且_f′__(b_)_＝__0；而且在x＝b
的左侧__f′__(_x_)_>_0，右侧_f_′__(_x_)<_0_，则把b叫做函数y＝f(x)的极大值点，f(b) 叫做函数y＝f(x)的极大值．

人教A版高考总复习数学精品课件第四章一元函数的导数及其应用第三节利用导数研究函数的极值、最值

强基础固本增分
1.函数的极值
函数极值反映的是函数局部的性质
取得极值的条件
极值
函数y=f(x)在点x=a的函数值f(a)比它在点x=a
f(a)叫做
附近其他点的函数值都小
f'(a)=0
函数
y=f(x)的
在点x=a附近的左侧 f'(x)<0 ,右侧 f'(x)>0 极小值
函数y=f(x)在点x=b的函数值f(b)比它在点x=b
提示必要不充分条件.当f'(x0)=0时,f(x)不一定在x=x0处取得极值,例如函数
f(x)=x3;但当f(x)在x=x0处取得极值时,由极值定义可知必有f'(x0)=0.
2.函数的最值
反映的是函数整体的性质
(1)一般地,如果在区间[a,b]上函数y=f(x)的图象是一条
连续不断
的曲
线,那么它必有最大值和最小值.
故
1+
g(t)min=g(2)= 2 =1,解得
a=1;
当√1 + >2,即 a>3 时,当 2≤x<√1 + 时,g'(x)<0,g(x)单调递减,
当 x>√1 + 时,g'(x)>0,g(x)单调递增,
故 g(x)min=g(√1 + )=2√1 + -2=1,解得
上,a=1.
5
a=4,不符合
x> ,所以函数 f(x)
, + ∞ 上单调递增,f(x)在区间(0,+∞)上不
存在最大值,不符合题意.当 a<0 时,若 b≥0,则 x>0 时,f'(x)<0,f(x)在区间(0,+∞)