江苏省苏、锡、常、镇四市2014届高三教学情况调查(一)文科数学试卷(带解析)
苏锡常镇四市2014届高三教学情况调研一

苏锡常镇四市2014届高三教学情况调研 (一)政 治 2014.3第Ⅰ卷(选择题 共66分)一、单项选择题:本大题共33小题,每小题2分,共66分。
在每题给出的四个选项中,只有一个选项是最符合题意的。
1.2014年2月,中国人民银行表示,将保持适度流动性,实现货币信贷及社会融资规模合理增长。
这意味着今后央行货币供应既不会大开闸门放水,也不会紧缩以致闹“钱荒”。
保持适度流动性A.可以避免通货膨胀的出现B.是纸币流通规律的客观要求C.会直接影响商业银行利润D.是国家运用财政政策的表现2.在不考虑其它因素的情况下,下列选项中与图1需求曲线变化 相吻合的是A.汽油价格上调后,新能源汽车需求量的变化B.政府取消汽车购置税优惠后,汽车需求量的变化C.人民币汇率下降后,进口汽车需求量的变化D.政府优先发展公共交通后,汽车需求量的变化图13. 随着消费者对移动网络宽带化需求的日益迫切,第四代移动通信技术(4G)应运而生。
4G能够快速传输高质量视频图像,更好地满足用户对于无线服务的要求。
这表明①消费对生产的调整和升级起导向作用 ②消费是经济增长的根本动力③企业要坚持“高精尖”的战略定位 ④生产决定消费的质量和水平A.①②B.①④C.②③D.③④4.《中国劳动力动态调研:2013年报告》显示,有38.42%的职工在调查的上个月加过班,但其中只有45.57%拿到了加班工资。
劳动者因担心“不加班、或者要加班工资可能丢饭碗”而选择忍气吞声。
解决这一问题需要A.完善市场机制,改善就业结构B.加强劳动保护,改善劳动条件C.规范劳动制度,加强监管力度D.健全社会保障,依法维护权利5. 赵某花5万元在银行购买了一款理财产品,工作人员称收益率在5.5%,而且无风险。
产品到期后,赵某只获得300多元收益。
银行解释说,这款理财产品收益率是0.36%—5.5%。
经消协调解,银行以高于当前的银行定期利率补偿了赵某损失。
这说明①存款业务是商业银行的基础业务 ②诚实守信是规范市场秩序的治本之策③市场调节存在自发性的固有缺陷 ④银行理财产品的收益与风险是并存的A.①②B. ②③C. ②④D.③④2014年中央一号文件——《关于全面深化农村改革加快推进农业现代化的若干意见》全面定调2014年及今后一个时期农业农村工作。
2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)

一、填空题(题型注释)1、已知集合,,,则 .来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)2、函数的最小正周期是.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)3、= .来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)4、在等差数列中,若,则.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)5、若正实数满足,则的最小值是 ______.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)6、若方程的解所在区间为,则 .来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)7、设,函数有意义, 实数取值范围 .来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)8、已知都是单位向量,且,则的值为.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)9、已知函数的图象关于直线对称,则的单调递增区间为.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)10、椭圆中有如下结论:椭圆上斜率为1的弦的中点在直线上,类比上述结论得到正确的结论为:双曲线上斜率为1的弦的中点在直线上.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)11、设,则的值为.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)12、函数在区间上的最小值为_________.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)13、已知是边长为4的正三角形,是内部两点,且满足,,则的面积为.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)14、已知函数,若,且,则的最小值是 .来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)二、解答题(题型注释)15、如图,正三棱柱中,点是的中点.(Ⅰ)求证: 平面;(Ⅱ)求证:平面.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)16、已知,.(1)若,求的值;(2)若,求的值.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)17、如图,在中,边上的中线长为3,且,.(Ⅰ)求的值;(Ⅱ)求边的长.来源:2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)18、如图所示,将一矩形花坛扩建成一个更大的矩形花坛,要求在的延长线上,在的延长线上,且对角线过点.已知米,米。
苏锡常镇高三数学一模试卷及参考答案纯word版
▲.
,若函数
C1
B1
A
O
(第 12 题)
C (第 16 题)
B
G D
D
A1
C
A
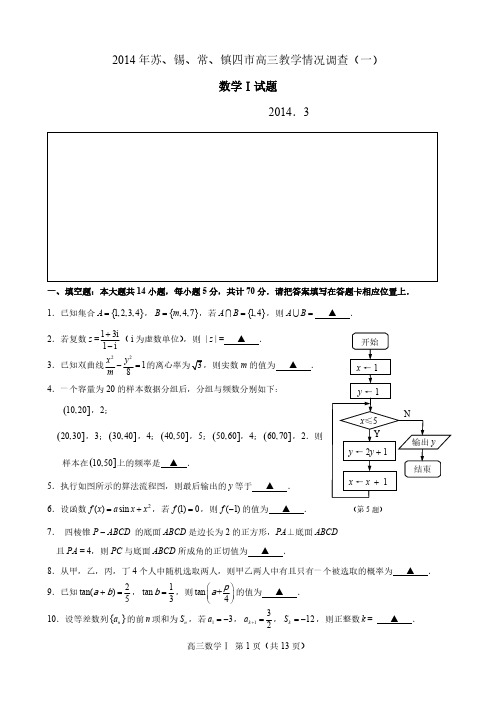
17.(本小题满分 14 分) 一个圆柱形圆木的底面半径为 1m,长为 10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中 一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形 ABCD (如图所示,其中 O 为圆心, C, D 在半圆上),设 BOC q ,木梁的体积为 V(单位:m3),表面积为 S(单位:m2). (1)求 V 关于 θ 的函数表达式; (2)求 q 的值,使体积 V 最大; (3)问当木梁的体积 V 最大时,其表面积 S 是否也最大?请说明理由.
且 PA = 4,则 PC 与底面 ABCD 所成角的正切值为 ▲ .
8.从甲,乙,丙,丁 4 个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 ▲ .
9.已知
tan(a
b)
10.设等差数列an的前 n 项和为 Sn
2 5
,
tan
b
1 3
,则
tan
,若 a1
a
+
p 4
AG
13.已知函数
,若
AD
f
(
x)
1
5
AB
(2x x 2
AC
(
x2 )ex , x ≤ 4x 3, x
g(x) 恰有两个不同的零点,则实数 k 的取值范围为 ▲ .
14.在平面直角坐标系 xOy 中,已知点 P(3, 0) 在圆
江苏省苏、锡、常、镇四市2014届高三下学期教学情况调查数学(文)试题Word版含解析

2014年苏、锡、常、镇四市高三教学情况调查(一)文科数学一、填空题:1.已知集合{}1,2,3,4A =,{},4,7B m =,若{}1,4AB =,则AB = ▲ .2.若复数z =13i1i+-(i 为虚数单位),则 | z | = ▲ .【解析】 试题分析:因为13i 1i +-,21242i i+-=+-=所以.5||=z 也可利用复数模的性质求解,即.5210|1||31|||==-+=i i z考点:复数的模3.已知双曲线2218x y m -=m 的值为 ▲ .4.一个容量为20的样本数据分组后,分组与频数分别如下:(]10,20,2;(]20,30,3;(]30,40,4;(]40,50,5;(]50,60,4;(]60,70,2.则样本在(]10,50上的频率是 ▲ . 【答案】710【解析】试题分析:因为样本在(]10,50上的频数共有 145432=+++,所以样本在(]10,50上的频率是1072014=.也可从反面求解,即样本不在(]10,50上的频数共有 624=+,所以样本在(]10,50上的频率是107206-1=. 考点:样本频率5.执行如图所示的算法流程图,则最后输出的y 等于 ▲ .6.设函数2()sin f x a x x =+,若(1)0f =,则(1)f -的值为 ▲ . 【答案】2 【解析】试题分析:因为(1)0f =,所以1sin 1-=a .因此(1)f -.211sin =+-=a 本题也可应用函数性质求解,因为2)()(=-+x f x f ,所以,2)1()1(=-+f f .2)1(=-f 考点:函数性质7.四棱锥P - ABCD 的底面ABCD 是边长为2的正方形,PA ⊥底面ABCD 且PA = 4,则PC 与底面ABCD 所成角的正切值为 ▲ .8.从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 ▲ .9.已知2tan()5a b +=,1tan 3b =,则tan +4p a ⎛⎫ ⎪⎝⎭的值为 ▲ .【答案】98【解析】试题分析:因为171315213152tan )tan(1tan )tan()tan(tan =⋅+-=++-+=-+=bb a b b a b b a a ,所以8917111711tan 1tan 1)4tan(=-+=-+=+a a a π. 考点:两角和与差正切10.设等差数列{}n a 的前n 项和为n S ,若13a =-,132k a +=,12k S =-,则正整数k = ▲ .11.已知正数,x y满足22x y+=,则8x yxy+的最小值为▲.12.如图,在△ABC中,BO为边AC上的中线,2BG GO=,设CD∥AG,若15AD AB AC=+λ()∈Rλ,则λ的值为▲.【答案】6 513.已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+,若函数()g x 恰有两个不同的零点,则实数k 的取值范围为 ▲ .考点:利用导数研究函数图像14.在平面直角坐标系xOy 中,已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内,动直线AB 过点P 且交圆C 于,A B 两点,若△ABC 的面积的最大值为16,则实数m 的取值范围为 ▲ .二、解答题15.(本小题满分14分)设函数2()6cos cos f x x x x =-. (1)求()f x 的最小正周期和值域;(2)在锐角△ABC 中,角,,A B C 的对边分别为,,a b c ,若()0f B =且2b =,4cos 5A =,求a 和sin C .16.(本小题满分14分)如图,在三棱柱111ABC A B C -中,侧面11AA B B 为菱形, 且160A AB ∠=︒,AC BC =,D 是AB 的中点. (1)求证:平面1A DC ⊥平面ABC ; (2)求证:1BC ∥平面1A DC .【答案】(1)详见解析,(2)详见解析. 【解析】试题分析:(1)证明面面垂直,关键找出线面垂直.因为侧面11AA B B 为菱形, 且160A AB ∠=︒,所以△17.(本小题满分14分)一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,,C D在半圆上),设BOC q∠=,木梁的体积为V(单位:m3),表面积为S(单位:m2).(1)求V关于θ的函数表达式;(2)求q的值,使体积V最大;(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.【答案】(1)()10(sin cos sin ),(0,)2V p q q q q q =+∈,(2)3pq =,(3)当木梁的体积V 最大时,其表面积S也最大.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,已知A ,B ,C 是椭圆22221(0)x y a b a b+=>>上不同的三点,A ,(3,3)B --,C 在第三象限,线段BC 的中点在直线OA 上.(1)求椭圆的标准方程; (2)求点C 的坐标;(3)设动点P 在椭圆上(异于点A ,B ,C )且直线PB ,PC 分别交直线OA 于M ,N 两点,证明OM ON ⋅为定值并求出该定值.【答案】(1)求椭圆方程一般用待定系数法.本题已知椭圆过两点,列两个方程222291821,991,a b ab ⎧⎪+=⎪⎨⎪+=⎪⎩,解出b a ,的值,(2)求点(,)C m n 的坐标,需列出两个方程.一是点C 在椭圆上,即22227m n +=,二是BC 的中点在直线OA 上,即23m n =-.注意到C 在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点N M ,的坐标,算出ON OM ⋅为定值.难点是如何消去参数.因为点N M ,在直线OA : 20x y -=上,所以可设11(2,)M y y ,22(2,)N y y .选择00(,)P x y 作为参数,即用00(,)P x y 表示点N M ,的坐标.由,,P B M 三点共线,解得001003()23y x y x y -=--,同理解得00200523y x y x y -=-+.从而有22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+,这里主要用到2200227x y +=代入化简.本题也可利用椭圆参数方程或三角表示揭示21y y 为定值.∵,,P C N 三点共线,∴022011255y y y x ++=++,整理,得00200523y x y x y -=-+.…………………10分∵点C 在椭圆上,∴2200227x y +=,2200272x y =-.从而22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+. …………………14分 所以124552OM ON y y ⋅==. …………………15分 ∴OM ON ⋅为定值,定值为452. …………………16分考点:椭圆标准方程,直线与椭圆位置关系19.(本小题满分16分)设各项均为正数的数列{}n a 的前n 项和为S n ,已知11a =,且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立. (1)若λ = 1,求数列{}n a 的通项公式; (2)求λ的值,使数列{}n a 是等差数列.∴当2n ≥时,12n n S a +=.② ② - ①,得12n n a a +=, ∴12n na a +=(2n ≥). ………………… 6分 ∵当n = 1时, 22a =,∴n = 1时上式也成立,∴数列{an}是首项为1,公比为2的等比数列, an = 2n -1(*n ∈N ). …………………8分20.(本小题满分16分)已知函数e ()ln ,()e xxf x mx a x mg x =--=,其中m ,a 均为实数. (1)求()g x 的极值;(2)设1,0m a =<,若对任意的12,[3,4]x x ∈12()x x ≠,212111()()()()f x f xg x g x -<-恒成立,求a 的最小值;(3)设2a =,若对任意给定的0(0,e]x ∈,在区间(0,e]上总存在1212,()t t t t ≠,使得120()()()f t f t g x == 成立,求m 的取值范围.【答案】(1)极大值为1,无极小值.(2)3 -22e 3.(3)3[,)e 1+∞-. 【解析】试题解析:(1)e(1)()e xx g x -'=,令()0g x '=,得x = 1. ………………… 1分 列表如下:∵g(1) = 1,∴y =()g x 的极大值为1,无极小值. …………………3分 (2)当1,0m a =<时,()ln 1f x x a x =--,(0,)x ∈+∞.∵()0x af x x -'=>在[3,4]恒成立,∴()f x 在[3,4]上为增函数. …………………4分 设1e ()()e x h x g x x ==,∵12e (1)()x x h x x --'=> 0在[3,4]恒成立, ∴()h x 在[3,4]上为增函数. …………………5分 设21x x >,则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-, 即2211()()()()f x h x f x h x -<-.设1e ()()()ln 1e xu x f x h x x a x x=-=---⋅,则u(x)在[3,4]为减函数.∴21e (1)()10e x a x u x x x -'=--⋅≤在(3,4)上恒成立. …………………6分 ∴11e ex x a x x---+≥恒成立. 设11e ()e x x v x x x --=-+,∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+,x ∈[3,4], ∴1221133e [()]e 1244x x --+>>,∴()v x '< 0,()v x 为减函数.∴()v x 在 [3,4]上的最大值为v(3) = 3 -22e 3. ………………… 8分∴a ≥3 -22e 3,∴a 的最小值为3 -22e 3. …………………9分∵e e 3()1e 1m mf m m m --+=>>-≥,∴3e 1m -≥时,命题成立. 综上所述,m 的取值范围为3[,)e 1+∞-. …………………16分 考点:函数极值,不等式恒成立。
2014全国统一高考数学真题及逐题详细解析(文科)—江苏卷

2014年普通高等学校招生全国统一考试(江苏卷)解析版数学Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1. 已知集合A ={4,3,1,2--},}3,2,1{-=B ,则=B A I . 2. 已知复数2)i 25(+=z (i 为虚数单位),则z 的实部为 . 3. 右图是一个算法流程图,则输出的n 的值是 .4. 从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是 .5. 已知函数x y cos =与)2sin(ϕ+=x y (0≤πϕ<),它们的图象有一个横坐标为3π的交点,则ϕ的值是 .6. 设抽测的树木的底部周长均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有 株树木的底部周长小于100cm.7. 在各项均为正数的等比数列}{n a 中,,12=a 4682a a a +=,则6a 的值是 . 8. 设甲、乙两个圆柱的底面分别为1S ,2S ,体积分别为1V ,2V ,若它们的侧面积相等,且4921=S S ,则21V V 的值是 .100 80 90 110 120 130 底部周长/cm(第6题)(第3题)9. 在平面直角坐标系xOy 中,直线032=-+y x 被圆4)1()2(22=++-y x 截得的弦长 为 .10. 已知函数2()1f x x mx =+-,若对于任意]1,[+∈m m x ,都有0)(<x f 成立,则实数m 的取值范围是 .11. 在平面直角坐标系xOy 中,若曲线xbax y +=2(a ,b 为常数)过点)5,2(-P ,且该曲线在点P 处的切线与直线0327=++y x 平行,则b a +的值是 .12. 如图,在平行四边形ABCD 中,已知8AB =,5AD =,3CP PD =u u u r u u u r ,2AP BP ⋅=u u u r u u u r ,则AB AD ⋅u u u r u u u r的值是 .13. 已知)(x f 是定义在R 上且周期为3的函数,当)3,0[∈x 时,21()22f x x x =-+. 若函数a x f y -=)(在区间]4,3[-上有10个零点(互不相同),则实数a 的取值范围是 .14. 若△ABC 的内角满足C B A sin 2sin 2sin =+,则C cos 的最小值是 .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15. (本小题满分14分)已知),2(ππα∈,55sin =α.(1)求)4sin(απ+的值; (2)求)265cos(απ-的值.16. (本小题满分14分)如图,在三棱锥ABC P -中,D ,E ,F 分别为棱AB AC PC ,,的中点.已知AC PA ⊥,6PA =,8BC =,5DF =.求证:(1) 直线//PA 平面DEF ;(2) 平面⊥BDE 平面ABC .(第16题)PDCEFBA(第12题)如图,在平面直角坐标系xOy 中,21,F F 分别是椭圆22221(0)x y a b a b +=>>的左、右焦点,顶点B的坐标为),0(b ,连结2BF 并延长交椭圆于点A ,过点A 作x 轴的垂线交椭圆于另一点C ,连结C F 1.(1) 若点C 的坐标为)31,34(,且22=BF ,求椭圆的方程;(2) 若1F C AB ⊥,求椭圆离心率e 的值.18. (本小题满分16分)如图,为了保护河上古桥OA ,规划建一座新桥BC ,同时设立一个圆形保护区. 规划要求:新桥BC 与河岸AB 垂直;保护区的边界为圆心M 在线段OA 上并与BC 相切的圆. 且古桥两端O 和A 到该圆上任意一点的距离均不少于80m. 经测量,点A 位于点O 正北方向60m 处,点C 位于点O 正东方向170m 处(OC 为河岸),34tan =∠BCO . (1) 求新桥BC 的长;(2) 当OM 多长时,圆形保护区的面积最大?19. (本小题满分16分)已知函数x x x f -+=e e )(,其中e 是自然对数的底数. (1) 证明:)(x f 是R 上的偶函数;(2) 若关于x 的不等式)(x mf ≤1e -+-m x 在),0(+∞上恒成立,求实数m 的取值范围;(3) 已知正数a 满足:存在),1[0+∞∈x ,使得)3()(030x x a x f +-<成立. 试比较1e -a 与1e -a 的大小,并证明你的结论.设数列}{n a 的前n 项和为n S .若对任意正整数n ,总存在正整数m ,使得m n a S =,则称}{n a 是“H 数列”.(1) 若数列}{n a 的前n 项和n n S 2=(∈n N *),证明:}{n a 是“H 数列”;(2) 设}{n a 是等差数列,其首项11=a ,公差0<d . 若}{n a 是“H 数列”,求d 的值; (3) 证明:对任意的等差数列}{n a ,总存在两个“H 数列”}{n b 和}{n c ,使得n n n c b a += (∈n N *)成立.数学Ⅱ(附加题)21.[选修4—1:几何证明选讲](本小题满分10分)如图,AB 是圆O 的直径,C 、D 是圆O 上位于AB 异侧的两点. 证明:∠ OCB =∠ D .22.[选修4—2:矩阵与变换](本小题满分10分)已知矩阵A 121x -⎡⎤=⎢⎥⎣⎦,B 1121⎡⎤=⎢⎥-⎣⎦,向量2y ⎡⎤=⎢⎥⎣⎦α,x ,y 为实数.若=A αB α,求x +y 的值. 23.[选修4—4:坐标系与参数方程](本小题满分10分) 在平面直角坐标系xOy 中,已知直线l 的参数方程21,2)(2;xt t y t ⎧=-⎪⎪⎨⎪=+⎪⎩为参数,直线l 与抛物线24y x =相交于A 、B 两点,求线段AB 的长.24.[选修4—4:不等式证明选讲](本小题满分10分) 已知x >0,y >0,证明:22(1)(1)9x y x y xy ++++≥. 25. (本小题满分10分)盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同. (1) 从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P ;(2) 从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为x 1、x 2、x 3, 随机变量X 表示x 1、x 2、x 3中的最大数,求X 的概率分布和数学期望E (X ). 26. (本小题满分10分)已知函数sin ()(0)xf x x x=>,设()n f x 是1()n f x -的导数,n ∈*N . (1) 求12πππ2()()222f f +的值;(2) 证明:对于任意n ∈*N ,等式1πππ2()()444n n nf f -+=都成立.(第21—A 题)参考答案一、选择题 1.【答案】{1,3}-解析:由题意得{1,3}A B =-I 【考点】交集、并集、补集 (B). 【答案】}3,1{-【解析】根据集合的交集运算,两个集合的交集就是所有既属于集合A 又属于集合B 的元素组成的集合,从所给的两个集合的元素可知,公共的元素为-1和3,所以答案为}3,1{-【点评】本题重点考查的是集合的运算,容易出错的地方是审错题目,把交集运算看成并集运算。
江苏省苏、锡、常、镇四市2014届高三教学情况调查(一)数学试题(解读) 含解析

【名师综述】1.本试卷难度适中,知识点单一的小题较多,如前十题,也有拉开档次的题目(如,13,14,19,20),考查知识点和能力点基本到位。
其中,第14题将圆中弦长问题和最值问题交汇在一起,试题的选拔性和交汇性极高。
挖掘“圆心到直线距离不大于CP ”这一隐含条件是确保解题正确关键.第13题,容易在研究“-∞→x 时,函数)(x f 恒小于零”上出错。
运用数学结合解题应严格分析图形在各单调区间趋势范围。
第18题求椭圆定值问题,有一定运算量.学生失分原因:除去畏难心理外,还有忽略整体感知,导致方向性错误的因素。
建议考生:多练、多思。
2.本套试题题型稳中有变,内容鲜活,富有时代气息.第19题数列题,一改其常规面目,以“类等比”给出n S 与na 关系式,将“叠乘法” 化简数列 “隐身”其中,试题的交汇天衣无缝!第20题是导数题,是对恒成立的考查,以两种不同说法的形式,给出了问题,动中有静,静中有动,动静结合,命题者独具匠心!恒成立问题关键在于等价转化不等式。
第20题第(2)小题设计两道坎,一是绝对值,二是两个变量依存关系。
第20题第(3)小题,难度上升一个层次,设计三个参量,重点考查学生思维能力。
【易错题解读】1.【理科试卷第13题】已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+,若函数()g x 恰有两个不同的零点,则实数k 的取值范围为 .【原创题解读】1。
【理科试卷第14 题】在平面直角坐标系xOy中,已知点(3,0)P在圆222+--+-=内,动直线AB过点P且交圆C于,A B两点,若△ABC :24280C x y mx y m的面积的最大值为16,则实数m的取值范围为.【举一反三】在平面直角坐标系xOy中,过点O作直线l与圆。
江苏省苏、锡、常、镇四市2014届高三教学情况调查(一)理科数学试卷(带解析)

江苏省苏、锡、常、镇四市2014届高三教学情况调查(一)理科数学试卷(带解析)1.已知集合{}1,2,3,4A =,{},4,7B m =,若{}1,4A B =,则AB = .【答案】{}1,2,3,4,7 【解析】 试题分析:因为{}1,4AB =,所以B ∈1,.1=m 因此AB ={}1,2,3,4,7.考点:集合运算 2.若复数z =13i1i+-(i 为虚数单位),则|z |= .【解析】试题分析:因为13i 1i +-,21242i i +-=+-=所以.5||=z 也可利用复数模的性质求解,即.5210|1||31|||==-+=i i z考点:复数的模3.已知双曲线2218x y m -=m 的值为 .【答案】4 【解析】试题分析:由题意得:,38=+mm 解得.4=m 解答此类问题,要明确对应关系,一是,8,22==b m a 二是双曲线中.222b a c +=考点:双曲线离心率4.一个容量为20的样本数据分组后,分组与频数分别如下:(]10,20,2;(]20,30,3;(]30,40,4;(]40,50,5;(]50,60,4;(]60,70,2.则样本在(]10,50上的频率是 . 【答案】710【解析】试题分析:因为样本在(]10,50上的频数共有 145432=+++,所以样本在(]10,50上的频率是1072014=.也可从反面求解,即样本不在(]10,50上的频数共有 624=+,所以样本在(]10,50上的频率是107206-1=.考点:样本频率5.执行如图所示的算法流程图,则最后输出的y 等于 .【答案】63 【解析】试题分析:第一次循环,,2,3==x y 第二次循环,,3,7==x y 第三次循环,,4,15==x y 第四次循环,,5,31==x y 第六次循环,,56,63>==x y 终止循环,输出63=y . 考点:流程图6.设函数2()sin f x a x x =+,若(1)0f =,则(1)f -的值为 . 【答案】2 【解析】试题分析:因为(1)0f =,所以1sin 1-=a .因此(1)f -.211sin =+-=a 本题也可应用函数性质求解,因为2)()(=-+x f x f ,所以,2)1()1(=-+f f .2)1(=-f考点:函数性质 7.四棱锥P - ABCD 的底面ABCD 是边长为2的正方形,PA ⊥底面ABCD 且PA =4,则PC 与底面ABCD 所成角的正切值为 .【解析】试题分析:因为PA ⊥底面ABCD ,所以PC 与底面ABCD 所成角的为.PCA ∠,因此.2224tan ===∠AC PA PCA考点:直线与平面所成角8.从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 . 【答案】23【解析】试题分析:从甲,乙,丙,丁4个人中随机选取两人共有624=C 种基本事件,而甲乙两人中有且只有一个被选取包含41212=C C 种基本事件,所以所求概率为3264=.考点:古典概型概率9.已知2tan()5a b +=,1tan 3b =,则tan +4p a ⎛⎫ ⎪⎝⎭的值为 .【答案】98【解析】试题分析:因为171315213152tan )tan(1tan )tan()tan(tan =⋅+-=++-+=-+=bb a b b a b b a a ,所以8917111711tan 1tan 1)4tan(=-+=-+=+aa a π. 考点:两角和与差正切10.设等差数列{}n a 的前n 项和为n S ,若13a =-,132k a +=,12k S =-,则正整数k = . 【答案】13 【解析】试题分析:设等差数列{}n a 公差为d ,则12)1(213,233-=-+-=+-d k k k kd ,消去d得:.13=k考点:等差数列通项公式及前n 项和公式11.已知正数,x y 满足22x y +=,则8x yxy +的最小值为 .【答案】9 【解析】 试题分析:因为9)16210(21)1610(21)22)(81(818=+≥++=++=+=+x y y x y x x y x y xy y x ,当且仅当22,16=+=y x x y y x 即31,34==y x 时取等号,所以8x y xy +的最小值为9. 考点:基本不等式求最值12.如图,在△ABC 中,BO 为边AC 上的中线,2BG GO =,设CD ∥AG ,若15A D AB A C=+λ()∈R λ,则λ的值为 .【答案】65【解析】试题分析:因为,2=所以31313231+=+=.又CD ∥AG ,可设,AG m CD =从而mm m m 3)31(33++=++=+=.因为15A D A B A C =+λ,所以5631,513=+==m m λ. 考点:向量共线表示13.已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+,若函数()g x 恰有两个不同的零点,则实数k 的取值范围为 . 【答案】27321,{0,22e +⎛⎫-- ⎪⎝⎭ 【解析】试题分析:由2(2)(0)x y x x e x =-≤求导得2(2)x y x e '=-,故2(2)(0)xy x x e x =-≤在(上单调增,在(,-∞上单调减,且当0x <时,恒有2(2)0xy x x e =-<.又243(0)y x x x =-++>在(0,2)上单调增,在(2,)+∞上单调减,所以可作出函数()y f x =的图像,如图.由图可知,要使函数()g x 恰有两个不同的零点,需20k -=或2k -=327k <-<,即实数k 的取值范围为27321,{0,22e +⎛⎫-- ⎪⎝⎭.考点:利用导数研究函数图像14.在平面直角坐标系xOy 中,已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内,动直线AB 过点P 且交圆C 于,A B 两点,若△ABC 的面积的最大值为16,则实数m 的取值范围为 .【答案】[3(327,3++-- 【解析】试题分析:由题意得圆心(,2),C m 半径.r =因为点(3,0)P 在圆222:24280C x y m x y m +--+-=内,所以223060280m m +--+-<,解得3727.m-<<设C 到直线距离为d,则.d CP ≤又222211162222ABCd r d r S d AB d ∆+-=⋅=⋅==,当且仅当222d r d =-,即216,4d d ==时取等号,因此4CP ≥≥,即3m ≥+3m ≤-综上实数m 的取值范围为[3(327,3++--. 考点:直线与圆位置关系15.设函数2()6cos cos f x x x x =-.(1)求()f x 的最小正周期和值域;(2)在锐角△ABC 中,角,,A B C 的对边分别为,,a b c ,若()0f B =且2b =,4cos 5A =,求a 和sin C .【答案】(1) π,[3-+,(2)534,10343+.【解析】试题分析:(1)要研究三角函数的性质,首先先将三角函数化为B x A y ++=)sin(ϕω型.利用降幂公式22cos 1cos 2x x +=及倍角公式xx x 2sin 21cos sin =可将函数次数化为一次,再利用配角公式)sin(cos sin 22ϕ++=+x b a x b x a 化为3)62s i n (32++=πx y ,然后利用基本三角函数图像求其最小正周期和值域,(2)解三角形问题,一般利用正余弦定理解决.本题为已知两角及一对边,选用正弦定理.由于是锐角△ABC ,开方时取正.试题解析:(1)1+cos2()622xf x x =⨯=3cos223x x +=)36x p++. 3分 所以()f x 的最小正周期为22T pp ==, 4分值域为[3-+. 6分(2)由()0f B =,得πcos(2)6B +=. B 为锐角,∴ππ7π2666B <+<,π5π266B +=,∴π3B =. 9分 ∵4cos 5A =,(0,)A p ∈,∴3sin 5A ==. 10分 在△ABC中,由正弦定理得32sin sin b A a B⨯===. 12分∴21sin sin()=sin()sin 32C A B A A A p p =---=+= 14分考点:倍角公式,正余弦定理16.如图,在三棱柱111ABC A B C -中,侧面11AA B B 为菱形, 且160A AB ∠=︒,AC BC =,D 是AB 的中点.(1)求证:平面1A DC ⊥平面ABC ; (2)求证:1BC ∥平面1A DC . 【答案】(1)详见解析,(2)详见解析. 【解析】试题分析:(1)证明面面垂直,关键找出线面垂直.因为侧面11AA B B 为菱形, 且160A AB ∠=︒,所以△1A AB 为正三角形,因而有1AB A D ⊥.又AC BC =,D 是AB 的中点,所以有A B C D ⊥,这样就可得到AB ⊥平面1A DC ,进而可证平面1A DC ⊥平面ABC .(2)证明线面平行,关键找出线线平行. 条件“D 是AB 的中点”,提示找中位线.取1AC 中点E ,就可得DE ∥1BC ,利用线面平行判断定理即可.解决此类问题,需注意写全定理成立的所有条件,不可省略.试题解析:(1)证明:∵ 11ABB A 为菱形,且160A AB ∠=︒, ∴△1A AB 为正三角形. 2分D 是AB 的中点,∴1AB A D ⊥.∵AC BC =,D 是AB 的中点,∴ AB CD ⊥. 4分 1A DCD D =,∴AB ⊥平面1A DC . 6分∵AB ⊂平面ABC ,∴平面1A DC ⊥平面ABC . 8分 (2)证明:连结1C A ,设11AC AC E =,连结DE .∵三棱柱的侧面11AA C C 是平行四边形,∴E 为1AC 中点. 10分 在△1ABC 中,又∵D 是AB 的中点,∴DE ∥1BC .12分∵DE ⊂平面1A DC ,1BC ⊄平面1A DC ,∴ 1BC ∥平面1A DC . 14分考点:面面垂直判定定理,线面平行判定定理 17.一个圆柱形圆木的底面半径为1m ,长为10m ,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD (如图所示,其中O 为圆心,,C D 在半圆上),设BOC q ∠=,木梁的体积为V (单位:m 3),表面积为S (单位:m 2).(1)求V 关于θ的函数表达式; (2)求q 的值,使体积V 最大;(3)问当木梁的体积V 最大时,其表面积S 是否也最大?请说明理由.【答案】(1)()10(sin cos sin ),(0,)2V p q q q q q =+∈,(2)3pq =,(3)当木梁的体积V 最大时,其表面积S 也最大.【解析】 试题分析:(1)解答实际问题关键读懂题意.本题所求体积为直四棱柱体积,体积为高与底面积的乘积.高为圆木的长,底面积为梯形ABCD 的面积.利用角BOC q ∠=表示出梯形上下底及高,就可得到所求关系式. (2)先求出函数的导数2()10(2cos cos 1)10(2cos 1)(cos 1)V q q q q q '=+-=-+,再根据导数为零时,定义区间导数值的正负讨论其单调性,研究其图像变化规律,确定其极值、最值.本题函数先增后减,在3pq =时,取极大值,也是最大值.(3)本题实质是求表面积的最大值,并判断取最大值时3p q =是否成立.首先先建立表面积的函数关系式.表面积由两部分组成,一是底面积,二是侧面积. 底面积为梯形ABCD 的面积,有两个. 侧面积为梯形ABCD 周长与圆木的长的乘积.再利用导数求出其最大值及取最大值时角的取值. 试题解析:(1)梯形ABCD 的面积 2cos 2sin 2ABCD S q q +=⋅=sin cos sin q q q +,(0,)2pq ∈. 2分 体积()10(sin cos sin ),(0,)2V pq q q q q =+∈. 3分 (2)2()10(2cos cos 1)10(2cos 1)(cos 1)V q q q q q '=+-=-+.令()0V q '=,得1cos 2q =,或cos 1q =-(舍).∵(0,)2p q ∈,∴3pq =. 5分 当(0,)3p q ∈时,1cos 12q <<,()0,()V V q q '>为增函数;当(,)32p p q ∈时,10cos 2q <<,()0,()V V q q '<为减函数. 7分 ∴当3pq =时,体积V 最大. 8分(3)木梁的侧面积210S AB BC CD =++⋅侧()=20(cos 2sin 1)2q q ++,(0,)2pq ∈.2ABCD S S S =+侧=2(sin cos sin )20(cos 2sin 1)2q q q q q ++++,(0,)2pq ∈. 10分 设()cos 2sin 12g q q q =++,(0,)2p q ∈.∵2()2sin 2sin 222g q qq =-++,∴当1sin22q =,即3pq =时,()g q 最大. 12分又由(2)知3pq =时,sin cos sin q q q +取得最大值,所以3p q =时,木梁的表面积S 最大. 13分 综上,当木梁的体积V 最大时,其表面积S 也最大. 14分 考点:利用导数求函数最值18.如图,在平面直角坐标系xOy 中,已知A ,B ,C 是椭圆22221(0)x y a b a b+=>>上不同的三点,A ,(3,3)B --,C 在第三象限,线段BC 的中点在直线OA 上.(1)求椭圆的标准方程; (2)求点C 的坐标;(3)设动点P 在椭圆上(异于点A ,B ,C )且直线PB ,PC 分别交直线OA 于M ,N 两点,证明OM ON ⋅为定值并求出该定值.【答案】(1)求椭圆方程一般用待定系数法.本题已知椭圆过两点,列两个方程222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩,解出b a ,的值,(2)求点(,)C m n 的坐标,需列出两个方程.一是点C 在椭圆上,即22227m n +=,二是BC 的中点在直线OA 上,即23m n =-.注意到C 在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点N M ,的坐标,算出OM 为定值.难点是如何消去参数.因为点N M ,在直线OA : 20x y -=上,所以可设11(2,)M y y ,22(2,)N y y .选择00(,)P x y 作为参数,即用00(,)P x y 表示点N M ,的坐标.由,,P B M 三点共线,解得001003()23y x y x y -=--,同理解得00200523y x y x y -=-+.从而有2220000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+,这里主要用到2200227x y +=代入化简.本题也可利用椭圆参数方程或三角表示揭示21y y 为定值. 【解析】试题分析:(1)22127272x y +=,(2)(5,1)--,(3)452.试题解析:(1)由已知,得222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩ 解得2227,27.2a b ⎧=⎪⎨=⎪⎩2分 所以椭圆的标准方程为22127272x y +=. 3分(2)设点(,)C m n (0,0)m n <<,则BC 中点为33(,)22m n --.由已知,求得直线OA 的方程为20x y -=,从而23m n =-.①又∵点C 在椭圆上,∴22227m n +=.②由①②,解得3n =(舍),1n =-,从而5m =-. 5分 所以点C 的坐标为(5,1)--. 6分(3)设00(,)P x y ,11(2,)M y y ,22(2,)N y y .∵,,P B M 三点共线,∴11033233y y y x ++=++,整理,得001003()23y x y x y -=--. 8分∵,,P C N 三点共线,∴22011255y y y x ++=++,整理,得00200523y x y x y -=-+. 10分∵点C 在椭圆上,∴2200227x y +=,2200272x y =-.从而22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+. 14分所以124552OM ON y y ⋅==15分∴OM ON ⋅为定值,定值为452. 16分考点:椭圆标准方程,直线与椭圆位置关系19.设各项均为正数的数列{}n a 的前n 项和为S n ,已知11a =,且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立.(1)若λ=1,求数列{}n a 的通项公式; (2)求λ的值,使数列{}n a 是等差数列. 【答案】(1)an = 2n -1(2)λ = 0. 【解析】试题分析:(1)本题属于“已知n S 求n a ”,利用)2(1≥-=-n S S a n n n 化简关系式. 因为11(1)(1)n n n n S a S a +++=+,所以先分离n S 与n a ,即1111n n n nS a S a +++=+,这是类等比,利用叠乘法得到1112n n S a +++=,再利用)2(1≥-=-n S S a n n n ,消去n S 得12n n a a +=.求数列{an}通项公式时,需讨论当n = 1时是否满足2n ≥的情形.(2)解答本题需注意逻辑关系,由数列{}n a 是等差数列得λ= 0,这是一个必要条件,还需验证其充分性,即λ = 0时,数列{}n a 是等差数列.这可类似(1)的解答过程.试题解析:解:(1)若λ = 1,则11(1)(1)n n n n S a S a +++=+,111a S ==.又∵00n n a S >>,, ∴1111n n n nS a S a +++=+, 2分 ∴3131221212111111n n n nS S a a S a S S S a a a +++++⋅⋅⋅=⋅⋅⋅+++,化简,得1112n n S a +++=.①4分∴当2n ≥时,12n n S a +=.②② - ①,得12n n a a +=,∴12n na a +=(2n ≥).6分∵当n = 1时, 22a =,∴n = 1时上式也成立,∴数列{an}是首项为1,公比为2的等比数列, an = 2n -1(*n ∈N ).8分(2)令n = 1,得21a λ=+.令n = 2,得23(1)a λ=+. 10分要使数列{}n a是等差数列,必须有2132a a a =+,解得λ = 0. 11分当λ = 0时,11(1)n n n n S a S a ++=+,且211a a ==. 当n ≥2时,111()(1)()n n n n n n S S S S S S +-+-=+-,整理,得2111n n n n n S S S S S +-++=+,1111n n n nS S S S +-+=+, 13分从而3312412123111111n n n nS S S S S S S S S S S S +-+++⋅⋅⋅=⋅⋅⋅+++,化简,得11n n S S ++=,所以11n a +=. 15分 综上所述,1n a =(*n ∈N ), 所以λ = 0时,数列{}n a 是等差数列. 16分考点:已知n S 求n a20.已知函数e ()ln ,()e xxf x mx a x mg x =--=,其中m ,a 均为实数. (1)求()g x 的极值;(2)设1,0m a =<,若对任意的12,[3,4]x x ∈12()x x ≠,212111()()()()f x f xg x g x -<-恒成立,求a 的最小值;(3)设2a =,若对任意给定的0(0,e ]x ∈,在区间(0,e ]上总存在1212,()t t t t ≠,使得120()()()f t f t g x == 成立,求m 的取值范围.【答案】(1)极大值为1,无极小值.(2)3 -22e 3.(3)3[,)e 1+∞-.【解析】试题分析:(1)求函数极值,先明确定义域为,R 再求其导数为e(1)()e x x g x -'=.由()0g x '=,得x = 1.分析导数在定义区间符号正负,确定函数先增后减,所以y =()g x 有极大值为1,无极小值.(2)不等式恒成立问题,先化简不等式212111()()()()f x f xg x g x -<-.化简不等式的难点有两个,一是绝对值,二是两个参量12,.x x 可从函数单调性去绝对值,分析两个函数,一是()y f x =,二是1()y g x =.利用导数可知两者都是增函数,故原不等式等价于21212111()(),()()()f x f x x xg x g x -<->,变量分离调整为21212111()(),()()()f x f x x x g x g x -<->,这又等价转化为函数1()()()u x f x g x =-在区间[3,4]上为减函数,即21e (1)()10e x a x u x x x -'=--⋅≤在[3,4]上恒成立.继续变量分离得11e ex x a x x ---+≥恒成立,即11m a xe (e )x x a x x---+≥.最后只需求函数11e ex x y x x --=-+在[3,4]上最大值,就为a 的最小值.(3)本题含义为:对于函数()y g x =在(0,e]上值域中每一个值,函数()y f x =在(0,e]上总有两个不同自变量与之对应相等.首先求出函数()y g x =在(0,e]上值域(0,1],然后根据函数()y f x =在(0,e]上必须不为单调函数且每段单调区间对应的值域都需包含(0,1].由()f x 在(0,e]不单调得2e m >,由每段单调区间对应的值域都需包含(0,1]得(e)1f ≥,3e 1m -≥. 试题解析:(1)e(1)()e x x g x -'=,令()0g x '=,得x = 1. 1分列表如下:∵g(1) = 1,∴y =()g x 的极大值为1,无极小值. 3分 (2)当1,0m a =<时,()ln 1f x x a x =--,(0,)x ∈+∞. ∵()0x af x x -'=>在[3,4]恒成立,∴()f x 在[3,4]上为增函数. 4分设1e ()()e x h x g x x ==,∵12e (1)()x x h x x --'=> 0在[3,4]恒成立,∴()h x 在[3,4]上为增函数. 5分设21x x >,则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-,即2211()()()()f x h x f x h x -<-.设1e ()()()ln 1e xu x f x h x x a x x =-=---⋅,则u(x)在[3,4]为减函数. ∴21e (1)()10e x a x u x x x -'=--⋅≤在(3,4)上恒成立. 6分∴11e ex x a x x---+≥恒成立.设11e ()ex x v x x x--=-+,∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+,x ∈[3,4], ∴1221133e [()]e 1244x x --+>>,∴()v x '< 0,()v x 为减函数.∴()v x 在[3,4]上的最大值为v(3) = 3 -22e3. 8分∴a ≥3 -22e 3,∴a 的最小值为3 -22e3. 9分(3)由(1)知()g x 在(0,e]上的值域为(0,1]. 10分 ∵()2ln f x mx x m =--,(0,)x ∈+∞,当0m =时,()2ln f x x =-在(0,e]为减函数,不合题意. 11分当0m ≠时,2()()m x mf x x-'=,由题意知()f x 在(0,e]不单调,所以20e m <<,即2e m >.①12分 此时()f x 在2(0,)m 上递减,在2(,e)m 上递增,∴(e)1f ≥,即(e)e 21f m m =--≥,解得3e 1m -≥.②由①②,得3e 1m -≥. 13分 ∵1(0,e]∈,∴2()(1)0f f m =≤成立. 14分下证存在2(0,]t m ∈,使得()f t ≥1. 取emt -=,先证e 2m m -<,即证2e 0mm ->.③设()2e xw x x =-,则()2e 10xw x '=->在3[,)e 1+∞-时恒成立.∴()w x 在3[,)e 1+∞-时为增函数.∴3e ))01((w x w ->≥,∴③成立.再证()e mf -≥1.∵e e 3()1e 1m mf m m m --+=>>-≥,∴3e 1m -≥时,命题成立. 综上所述,m 的取值范围为3[,)e 1+∞-. 16分考点:函数极值,不等式恒成立21.如图,⊙O 为四边形ABCD 的外接圆,且AB AD =,E 是CB 延长线上一点,直线EA 与圆O 相切.求证:CD ABAB BE=. 【答案】详见解析 【解析】试题分析:要证明CD ABAB BE =,主要利用相似三角形.难点在找出对应的两个三角形.由AB AD =,可证CDA ∆与ABE ∆相似.利用圆内接四边形性质得D ABE ∠=∠,再由等弦对等角得EAB ACB ∠=∠,ACD ACB ∠=∠,从而ACD EAB ∠=∠.试题解析:证明:连结AC .EA 是圆O 的切线,∴EAB ACB ∠=∠. 2分AB AD =,∴ACD ACB ∠=∠. ∴ACD EAB ∠=∠ 4分圆O 是四边形ABCD 的外接圆,∴D ABE ∠=∠. 6分 ∴CDA ∆∽ABE ∆. 8分 ∴CD DAAB BE =,AB AD =,∴CD ABAB BE =. 10分考点:圆内接四边形性质22.已知矩阵1221⎡⎤=⎢⎥⎣⎦M ,17⎡⎤=⎢⎥⎣⎦β,计算6M β. 【答案】29132919⎡⎤⎢⎥⎣⎦【解析】试题分析:利用矩阵特征值λ及其对应特征向量α性质:n nM αλα=进行化简.先根据矩阵M 的特征多项式求出其特征值123,1λλ==-,进而求出对应的特征向量111⎡⎤=⎢⎥⎣⎦α,211⎡⎤=⎢⎥-⎣⎦α.再将17⎡⎤=⎢⎥⎣⎦β分解成特征向量,即1243=-βαα,最后利用性质求结果,即6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α试题解析:解:矩阵M 的特征多项式为212()2321f λλλλλ--==----.令12()031f λλλ===-,解得,,对应的一个特征向量分别为111⎡⎤=⎢⎥⎣⎦α,211⎡⎤=⎢⎥-⎣⎦α. 5分 令12m n =+βαα,得4,3m n ==-.6666661212112913(43)4()3()433(1)112919⎡⎤⎡⎤⎡⎤=-=-=⨯--=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦M βM ααM αM α. 10分考点::矩阵特征值、特征向量及其应用23.在平面直角坐标系xOy 中,圆的参数方程为22cos ,()2sin x y a a a =+⎧⎨=⎩为参数,以坐标原点O为极点,x 轴的正半轴为极轴建立极坐标系.求:(1)圆的直角坐标方程; (2)圆的极坐标方程.【答案】(1)22(2)4x y -+=.(2)4cos ρθ=.【解析】试题分析:(1)根据22sin cos 1αα+=消去参数α得圆的直角坐标方程:22(2)4x y -+=.(2)利用cos ,sin ,x y ρθρθ=⎧⎨=⎩代入22(2)4x y -+=,可得圆的极坐标方程为4cos ρθ=.试题解析:解:(1)圆的直角坐标方程为22(2)4x y -+=. 5分 (2)把cos ,sin ,x y ρθρθ=⎧⎨=⎩代入上述方程,得圆的极坐标方程为4cos ρθ=. 10分考点:参数方程、极坐标方程、直角坐标方程之间互化24.已知函数2()122f x x x a a =++---,若函数()f x 的图象恒在x 轴上方,求实数a 的取值范围. 【答案】(1,3)- 【解析】 试题分析:因为12|(1)(2)|3x x x x ++-≥+--=,所以()f x 的最小值为232a a --.因为函数()f x 的图象恒在x 轴上方,所以min ()0.f x ≥因此有223a a -<,解得(1,3)a ∈-.试题解析:解:()f x 的最小值为232a a --, 5分由题设,得223a a -<,解得(1,3)a ∈-. 10分考点:绝对值不等式的应用25.甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为23,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(1)求甲同学至少有4次投中的概率;(2)求乙同学投篮次数x 的分布列和数学期望. 【答案】(1)112,(2)12181E =x,.【解析】 试题分析:(1)求概率问题关键在于明确题意,即事件是什么. 甲同学至少有4次投中,指甲同学在5次投篮中“恰投中4次”及“恰投中5次”这两个互斥事件.其概率为441550552222()(1)()(1)3333C C -+-=112243.(2)求概率分布,首先正确确定随机变量取值情况,本题1,2,3,4,5=x ,其次要正确确定随机变量对应各个概率,本题中5=x 的概率,直接求时要注意,第5次乙同学不论是否投中都停止,即第5次不考虑乙同学是否投中.也可间接求,利用各概率和为1,即(5)1(1)(2)(3)(4)P PP P P ==-=-=-=-=x x x x x ,这也是一种验证方法.试题解析:解:(1)设甲同学在5次投篮中,有x 次投中,“至少有4次投中”的概率为P ,则(4)(5)P P x P x ==+= 2分=441550552222()(1)()(1)3333C C -+-=112243 4分 (2)由题意1,2,3,4,5=x .2(1)3P ==x ,122(2)339P ==⨯=x ,1122(3)33327P ==⨯⨯=x ,3122(4)3381P x ⎛⎫==⨯= ⎪⎝⎭, 411(5)381P x ⎛⎫===⎪⎝⎭. x 的分布表为8分x 的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=x . 10分 考点:概率分布,数学期望值26.设01212(1)m m n n n n n m S C C C C ---=-+-+-,*,m n ∈N 且m n <,其中当n 为偶数时,2nm =;当n 为奇数时,12n m -=. (1)证明:当*n ∈N ,2n ≥时,11n n n S S S +-=-;(2)记01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-,求S 的值. 【答案】(1)详见解析,(2)12014S =-. 【解析】试题分析:(1)利用组合数性质111r r r n n n C C C +++=+进行化简.根据奇偶性,对n 进行分类讨论,这不增加难度,仅是便于表示.00112211112()()()n n n n n n n n S S C C C C C C ++----=---+-=01120n n C C ---+-,规律清晰,易于归纳(2)利用组合数性质11k k n n kC nC --=进行化简.123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+-0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C =-+++-++-+010213210071006201420132012201220112011201010071006()()()()C C C C C C C C C =-+++-++-+=20142012S S -.再根据11n n n S S S +-=-得周期6T =,从而20142012421S S S S -=-=-,12014S =-.试题解析:解:(1)当n 为奇数时,1n +为偶数,1n -为偶数, ∵1101221112(1)n n n n nn S CC C+++++=-++-,110122112(1)n n n n n n S C C C---+=-++-,11012211212(1)n n n n n n S CCC------=-++-,∴1111110011222221111111222()()(1)()(1)n n n n n n n n n n n n n n S S C C C C CCC-+-++-++-++++-=---++--+-=11012212112((1))n n n n n n CCCS --------++-=-.∴当n 为奇数时,11n n n S S S +-=-成立 5分同理可证,当n 为偶数时, 11n n n S S S +-=-也成立. 6分(2)由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-,得123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+- =0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -. 9分又由11n n n S S S +-=-,得6n n S S +=, 所以20142012421S S S S -=-=-,12014S =-. 10分考点:组合数性质。
2014度苏锡常镇四市高三数学调研二模试卷及答案word版

2014-2015学年度苏锡常镇四市高三数学调研(二模)试卷2015/05/04一.填空题(5×14=70分)1.已知集合{}{}{}1,1,3,2,21,1a A B A B =-=-=,则实数a 的值为 ▲2.设12a b +i=2i(+i)(i 为虚数单位,,a b ∈R ),则a b +的值为 ▲3.某工厂生产某种产品5000件,它们来自甲、乙、丙3条不同的生产线.为检查这批产品的质量,决定采用分层抽样的方法进行抽样.若从甲、乙、丙3条生产线抽取的件数之比为::122,则乙生产线生产了 ▲ 件产品4.根据如图所示的伪代码,若输入的x 值为1-,则输出的y 值为 ▲5.从3名男生和1名女生中随机选取两人,则两人恰好是一名男生和一名女生的概率为 ▲6.已知双曲线22221(,0)x y a b a b-=>的离心率等于2,它的焦点 到渐近线的距离等于1,则该双曲线的方程为 ▲7.已知向量()()()1,2,0,1,,2a b c k ==-=-,若()2c a b -⊥,则实数k = ▲8.已知常数0a >,函数()(1)1a f x x x x =+>-的最小值为3,则a 的值为 ▲ 9.函数3sin(2)4y x π=+的图象向左平移(0)2πϕϕ<<个单位后,所得函数图象关于原点成中心对称,则ϕ= ▲ 10.已知等差数列{}n a 满足:128,6a a =-=-.若将145,,a a a 都加上同一个数m ,所得的三个数依次成等比数列,则m 的值为 ▲11.已知圆锥的底面半径和高相等,侧面积为,过圆锥的两条母线作截面,截面为等边三角形,则圆锥底面中心到截面的距离为 ▲12.已知A 为椭圆22195x y +=上的动点,MN 为圆22(1)1x y -+=的一条直径,则AM AN ⋅的最大值为 ▲13.已知函数()342f x x x ax =-+-恰有2个零点,则实数a 的取值范围为 ▲ 14.已知,,0a b a ∈≠R ,曲线2,21a y y ax b x +==++,若两条曲线在区间[3,4]上至少有一个公共点,则22a b +的最小值为 ▲二.解答题(本大题共6小题,共计90分)15.(本小题满分14分)已知函数()sin()cos 6f x x x π=++(1)求函数()f x 的最大值,并写出当()f x 取得最大值时x 的取值集合;(2)若(0,),()265f ππαα∈+=,求()2f α的值16.(本小题满分14分)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,2,AB AD ==,PD ⊥平面ABCD ,,E F 分别为,CD PB 的中点求证:(1)//CF 平面PAE ;(2)AE ⊥平面PBD17.(本小题满分14分)如图,甲船从A 处以每小时30海里的速度沿正北方向航行,乙船在B 处沿固定方向匀速航行,B 在A 北偏西0105方向且与A 相距20分钟到达C 处时,乙船航行到甲船的北偏西0120方向的D 处,此时两船相距10海里(1)求乙船每小时航行多少海里?(2)在C 处的北偏西030方向且与C E ,暗礁E 海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?如果有危险,从有危险开始多少小时后能脱离危险?如无危险,请说明理由18.(本小题满分16分)如图,在平面直角坐标系xOy 中,四边形ABCD 的顶点都在椭圆22221(0)x y a b a b+=>> 上,对角线AC 与BD 分别过椭圆的左焦点1(1,0)F -和右焦点2(1,0)F ,且AC BD ⊥,椭圆的一条准线方程为4x =(1)求椭圆方程;(2)求四边形ABCD 面积的取值范围19.(本小题满分16分)已知函数()x ex f x e=,其导数记为()f x '(e 为自然对数的底数) (1)求函数()f x 的极大值;(2)解方程()()f f x x =;(3)若存在实数1212,()x x x x ≠使得12()()f x f x =,求证:1202x x f +⎛⎫'<⎪⎝⎭20.(本小题满分16分)已知,λμ为常数,且为正整数,1λ≠,无穷数列{}n a 的各项均为正整数,其前n 项和为n S ,对任意正整数n ,n n S a λμ=-.数列{}n a 中任意不同两项的和构成集合A(1)证明无穷数列{}n a 为等比数列,并求λ;(2)如果2015A ∈,求μ;(3)当1n ≥时,设集合{}13232,n n n B x x x A μμ-=⋅<<⋅∈,n B 中元素的个数记为n b 求数列{}n b 的通项公式.。
2014年苏锡常镇四市高三教学情况调研(一)

2013—2014学年度苏锡常镇四市高三教学情况调研(一)历史参考答案及评分标准一、选择题:本大题共20题,每题3分,共计60分。
在每题列出的四个选项中,只有一项最符合题目要求。
1.《周礼.地官.司市》记载:“人市,日昃(太|5H偏西)而市,百族为主:朝市,朝时而市,商贾为主;夕市,夕时而市,贩夫贩妇为主”。
材料说明先秦时期A.按时段分类交易 B.已经出现了夜市C.交易场所已趋I制定 D.市场初显专业化2.班固曰:“自武帝初立,魏其、武安侯为相而隆儒矣。
及仲舒对策,推明孔氏,抑黜百家,立学校之官,州郡举茂才、孝廉,皆自仲舒发之。
”材料表明A.在起用董仲舒之前,儒学的正统地位已确立B.举孝廉、兴太学的做法是为了提高儒学地位C.武帝拜董仲舒为相后,实行了一些尊儒措施D.罢黜百家、独尊儒术有利于教育事业的发展3.唐太宗曾对王珪说:“国家本置中书、门下以相检察,中书诏敕或有差失,则门下当行驳正。
人心所见,互有不同……比来(近来)护己之短,遂成冤隙。
或苟避私冤,知非不正,顺一人之颜情,为兆民之深患。
”对唐太宗的话理解正确的是A.中书、门下之间在运作时存在不尽如人意之处B.中书与门下分工明确,有利于提高决策效率C.中书与门下相互制约,可抑制宰相权力的膨胀p,中书、门下之间易相互扯皮,降低行政效率4.下列有关右侧《木棉拨车图》的叙述正确的是①图中工具反映出农业技术的进步②图中工具主要用于棉纱加工③拨车产品主要供家庭消费④该图经机器印刷而成A.①②B.②③C.①④D.③④5.顾炎武曾说:“昔之清谈谈老庄,今之清淡谈孔孟。
未得其精而己遗尺粗,未究其本而先辞其末,不习六艺之文,不考百王之典,不综当代之务,举夫子论学论政之大端一切不问,而曰一贯,曰无言。
”由此可见顾炎武A.批判理学家空谈义理,脱离现实 B.指责理学家抛弃先秦时期孔孟之说C.深刻地揭示出了明朝灭亡的根源 D.认识到明清儒学已不适应时代需要6.孙中山在《中国问题的真解决》中指山:“在中国人民中有许多极有教养的能干人物,他们能够担当起组织新政府的任务;把过时的满清君主政体改变为“中华民国”的计划,经慎重考虑之后,早就制订出米了。
2014年高考文科数学江苏卷及答案解析

绝密★启用前2014年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:圆柱的侧面积公式:=S cl 侧面积,其中c 是圆柱底面的周长,l 为母线长 圆柱的体积公式:V Sh =圆柱,其中S 是圆柱的底面积,h 为高一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应.....位置上.... 1.已知集合={2,1,3,4}A --,={1,2,3}B -,则AB = .2.已知复数2(52i)z =+(i 为虚数单位),则z 的实部为 .3.右图是一个算法流程图,则输出的n 的值是 .4.从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是 .5.已知函数cos y x =与sin(2)(0π)y x ϕϕ=+≤<,它们的图象有一个横坐标为π3的交点,则ϕ的值是 .6.为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm ),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有 株树木的底部周长小于100cm . 7.在各项均为正数的等比数列{}n a 中,若21a =,8642a a a =+,则6a 的值是 .8.设甲、乙两个圆柱的底面积分别为1S ,2S ,体积分别为1V ,2V .若它们的侧面积相等,且1294S S =,则12VV 的值是 . 9.在平面直角坐标系xOy 中,直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为 .10.已知函数2()1f x x mx =+-,若对于任意[,1]x m m ∈+,都有()0f x <成立,则实数m 的取值范围是 .11.在平面直角坐标系xOy 中,若曲线2by ax x=+(a ,b 为常数)过点(2,5)P -,且该曲线在点P 处的切线与直线7230x y ++=平行,则a b +的值是 .12.如图,在平行四边形ABCD 中,已知8AB =,5AD =,3CP PD =,2AP BP =,则AB AD 的值是 .13.已知()f x 是定义在R 上且周期为3的函数,当[0,3)x ∈时,21()22f x x x =-+.若函数()y f x a =-在区间[3,4]-上有10个零点(互不相同),则实数a 的取值范围是 .14.若ABC △的内角满足sin 2sin A B C =,则cos C 的最小值是 .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)已知π(,π)2α∈,sin α=(Ⅰ)求πsin()4α+的值; (Ⅱ)求5πcos(2)6α-的值.16.(本小题满分14分)如图,在三棱锥P ABC -中,D ,E ,F 分别为棱PC ,AC ,AB 的中点.已知PA AC ⊥,6PA =,8BC =,5DF =.求证:(Ⅰ)直线PA ∥平面DEF ; (Ⅱ)平面BDE ⊥平面ABC .17.(本小题满分14分)如图,在平面直角坐标系xOy 中,1F ,2F 分别是椭圆22221(0)x y a b a b+=>>的左、右焦点,顶点B 的坐标为(0,)b ,连接2BF 并延长交椭圆于点A ,过点A 作x 轴的垂线交椭圆于另一点C ,连接1F C .(Ⅰ)若点C 的坐标为41(,)33,且2BF =求椭圆的方程;(Ⅱ)若1F C AB ⊥,求椭圆离心率e 的值.姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无------------------------------------18.(本小题满分16分)如图,为保护河上古桥OA ,规划建一座新桥BC ,同时设立一个圆形保护区.规划要求:新桥BC 与河岸AB 垂直;保护区的边界为圆心M 在线段OA 上并与BC 相切的圆,且古桥两端O 和A 到该圆上任意一点的距离均不少于80m .经测量,点A 位于点O 正北方向60m 处,点C 位于点O 正东方向170m 处(OC 为河岸),4tan 3BCO ∠=.(Ⅰ)求新桥BC 的长;(Ⅱ)当OM 多长时,圆形保护区的面积最大?19.(本小题满分16分)已知函数()e e x xf x -=+,其中e 是自然对数的底数.(Ⅰ)证明:()f x 是R 上的偶函数; (Ⅱ)若关于x 的不等式()e1xmf x m -+-≤在(0,)+∞上恒成立,求实数m 的取值范围;(Ⅲ)已知正数a 满足:存在0[1,)x ∈+∞,使得3000()(3)f x a x x -+<成立.试比较1e a -与e 1a -的大小,并证明你的结论.20.(本小题满分16分)设数列{}n a 的前n 项和为n S .若对任意的正整数n ,总存在正整数m ,使得n m S a =,则称{}n a 是“H 数列”.(Ⅰ)若数列{}n a 的前n 项和*2()n n S n =∈N ,证明:{}n a 是“H 数列”;(Ⅱ)设{}n a 是等差数列,其首项11a =,公差0d <.若{}n a 是“H 数列”,求d 的值;(Ⅲ)证明:对任意的等差数列{}n a ,总存在两个“H 数列”{}n b 和{}n c ,使得+n n na b c =*()n ∈N 成立.数学Ⅱ(附加题)21.【选做题】在A ,B ,C ,D 四小题中只能选做两题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.A .(本小题满分10分)选修4—1:几何证明选讲如图,AB 是圆O 的直径,C ,D 是圆O 上位于AB 异侧的两点.证明:OCB D ∠=∠.B .(本小题满分10分)选修4—2:矩阵与变换已知矩阵121x -⎡⎤=⎢⎥⎣⎦A ,1121⎡⎤=⎢⎥-⎣⎦B ,向量2y ⎡⎤=⎢⎥⎣⎦α,x ,y 为实数,若=A αB α,求x y +的值.C .(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知直线l的参数方程为1,2,2x y ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),直线l与抛物线24y x =相交于A ,B 两点,求线段AB 的长.D .(本小题满分10分)选修4—5:不等式选讲已知0x >,0y >,证明:22(1)(1)9x y x y xy ++++≥.【必做题】第22,23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.22.(本小题满分10分)盒中共有9个球,其中有4个红球、3个黄球和2个绿球,这些球除颜色外完全相同. (Ⅰ)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P ;(Ⅱ)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为1x ,2x ,3x ,随机变量X 表示1x ,2x ,3x 中的最大数,求X 的概率分布和数学期望()E X .23.(本小题满分10分)已知函数0sin ()(0)xf x x x =>,设()n f x 为1()n f x -的导数,*n ∈N . (Ⅰ)求12πππ2()()222f f +的值;(Ⅱ)证明:对任意的*n ∈N ,等式1πππ()()444n n nf f -+.【答案】22以AB ,AD 为基底,因为3CP PD =,2AP BP =,1AP AD DP AD AB =+=+, 34BP BC CP AD AB =+=-则13244AP BP AD AB AD AB ⎛⎫⎛⎫==+- ⎪ ⎪⎝⎭⎝⎭2213216AD AD AB AB =-- 因为8AB =,5AD =则3122564162AB AD =--,故22AB AD = 由3CP PD =,可得14AP AD AB =+,34BP AD AB =-,进而由3CP PD =,2AP BP =,构造方程,进而可得答案【考点】向量在几何中的应用,平面向量数量积的运算【答案】10,⎛⎫⎪AC EF E =,3233b b c a c c =+21.【选做题】,向量2α⎡⎤=⎢⎥,A Bαα=,A B αα=,可得方程组,31315364C C C + 2k x π⎫⎛⎫+⎪ ⎪⎭⎝⎭π2k x ⎫⎛⎫+⎪⎪⎭⎝⎭,1(n k k =+⎡。
2014年高考文科数学江苏卷-答案

3PD
,
AP BP 2 ,构造方程,进而可得答案
【考点】向量在几何中的应用,平面向量数量积的运算
13.【答案】
0,
1 2
3 / 11
【解析】根据题目条件,零点问题即转化为数形结合,通过找 y f (x) 与 y a 的图象交点去推出零点,先 画出 (0,3) 上 y x2 2x 1 的图象,再将 x 轴下方的图象对称到上方,利用周期为 3,将图象平移至 (3, 4) ,
示 c ,并结合基本不等式去解决,化简 a2 b2 为 ab ,消去 ab 就得出答案.
cos C
a2
b2
c2
a2
b2
a
2
2b 2
3 a2 4
1 b2 2
2 ab 3 a2 1 b2 2 4 2
2
2ab
2ab
2ab
2ab
4
2
3 a2 1 b2 42
【考点】平面与平面垂直的判定,直线与平面垂直的判定 17.【答案】(Ⅰ) x2 y2 1
2 (Ⅱ) 5
5
【解析】(Ⅰ)∵ BF2 = b2 c2
2
,将点
C
4 3
,
1 3
代入椭圆
x2 a2
y2 b2
1(a
b 0) ,
∴
16 9a2
1 9b2
1(a
b
49 2 55
5
【提示】求出已知圆的圆心为 C(2, 1) ,半径 r 2 利用点到直线的距离公式,算出点 C 到直线 l 的距离 d,
江苏省苏州市2014届高三第一次调研数学试卷Word版含答案

苏州市2014届高三调研测试数学Ⅰ试题 2014.1一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请把答案直接填在答题卡相应位置上......... 1. 已知集合A = { x | x < 2 },B = { -1,0,2,3 },则A ∩B = ▲ .2. 已知i 为虚数单位,计算2(12i)(1i)+-= ▲ .3. 若函数()sin()f x x θ=+(π02θ<<)的图象关于直线π6x =对称,则θ = ▲ .4. 设S n 为等差数列{a n }的前n 项和,已知S 5 = 5,S 9 = 27,则S 7 = ▲ . 5. 若圆锥底面半径为1,高为2,则圆锥的侧面积为 ▲ . 6. 运行右图所示程序框图,若输入值x ∈[-2,2],则输出值y 的取值范围是 ▲ . (第6题)注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷共4页,包含填空题(第1题 - 第14题)、解答题(第15题 - 第20题).本卷满分160分,考试时间为120分钟.考试结束后,请将答题卡交回.2. 答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3. 请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚.4. 如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.5. 请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔.7. 已知π3sin()45x +=,π4sin()45x -=,则tan x = ▲ . 8. 函数e ln y x x =-的值域为 ▲ .9. 已知两个单位向量a ,b 的夹角为60°,c = t a +(1 - t )b .若b ·c = 0,则实数t 的值为 ▲ .10. 已知m ∈{-1,0,1},n ∈{-1,1},若随机选取m ,n ,则直线10mx ny ++=恰好不经过第二象限的概率是 ▲ .11. 已知22(0),()(0)x x x f x x x x ⎧+⎪=⎨-+<⎪⎩≥,则不等式2(1)12f x x -+<的解集是 ▲ . 12. 在直角坐标系xOy 中,已知A (-1,0),B (0,1),则满足224PA PB -=且在圆224x y +=上的点P 的个数为 ▲ .13. 已知正实数x ,y 满足24xy x y ++=,则x + y 的最小值为 ▲ .14. 若2101m x mx -<+(m ≠ 0)对一切x ≥4恒成立,则实数m 的取值范围是 ▲ .二、解答题:本大题共六小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15. (本小题满分14分)在△ABC 中,设角A ,B ,C 的对边分别为a ,b ,c ,且1cos 2a C cb +=.(1)求角A 的大小; (2)若a =4b =,求边c 的大小.16. (本小题满分14分)如图,在四棱锥P - ABCD 中,四边形ABCD 是矩形,平面PCD ⊥平面ABCD ,M 为PC 中点.求证:(1)P A ∥平面MDB ; (2)PD ⊥BC .PMD C(第16题)甲、乙两地相距1000km ,货车从甲地匀速行驶到乙地,速度不得超过80km/h ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的14倍,固定成本为a 元.(1)将全程运输成本y (元)表示为速度v (km/h )的函数,并指出这个函数的定义域;(2)为了使全程运输成本最小,货车应以多大的速度行驶?18. (本小题满分16分)如图,已知椭圆22221(0)x y a b a b+=>>的右顶点为A (2,0),点P (2e ,12)在椭圆上(e 为椭圆的离心率).(1)求椭圆的方程;(2)若点B ,C (C 在第一象限)都在椭圆上,满足OC BA λ=,且0OC OB ⋅=,求实数λ的值.(第18题)设数列{a n }满足a n +1 = 2a n + n 2 - 4n + 1.(1)若a 1 = 3,求证:存在2()f n an bn c =++(a ,b ,c 为常数),使数列{ a n + f (n ) }是等比数列,并求出数列{a n }的通项公式;(2)若a n 是一个等差数列{b n }的前n 项和,求首项a 1的值与数列{b n }的通项公式.20. (本小题满分16分)已知a ,b 为常数,a ≠ 0,函数()()e x b f x a x=+. (1)若a = 2,b = 1,求()f x 在(0,+∞)内的极值;(2)① 若a > 0,b > 0,求证:()f x 在区间[1,2]上是增函数;② 若(2)0f <,2(2)e f --<,且()f x 在区间[1,2]上是增函数,求由所有点(,)a b 形成的平面区域的面积.苏州市2014届高三调研测试数学Ⅱ(附加题) 2014.121.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题......,并在相...应的..答题区域....内.作答..,若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .选修4 1:几何证明选讲(本小题满分10分)如图,MN 为两圆的公共弦,一条直线与两圆及公共弦依次交于A ,B ,C ,D ,E , 求证:AB ·CD = BC ·DE .注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷只有解答题,供理工方向考生使用.本试卷第21题有A 、B 、C 、D 4个小题供选做,每位考生在4个选做题中选答2题.若考生选做了3题或4题,则按选做题中的前2题计分.第22、23题为必答题.每小题10分,共40分.考试时间30分钟.考试结束后,请将答题卡交回.2. 答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3. 请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚.4. 如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.5. 请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔. NME D C B AB.选修4 - 2:矩阵与变换(本小题满分10分)已知a,b∈R,若M=13ab-⎡⎤⎢⎥⎣⎦所对应的变换T M 把直线2x-y = 3变换成自身,试求实数a,b.(第21-A题)C .选修4 - 4:坐标系与参数方程(本小题满分10分)在极坐标系中,求点M π(2,)6关于直线π4θ=的对称点N 的极坐标,并求MN 的长.D .选修4 - 5:不等式选讲(本小题满分10分)已知x ,y ,z 均为正数.求证:111x y z yz zx xy x y z++++≥.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)如图,在空间直角坐标系O - xyz 中,正四棱锥 P - ABCD的侧棱长与底边长都为,点M ,N 分别在P A ,BD 上,且13PM BN PA BD ==. (1)求证:MN ⊥AD ; (2)求MN 与平面P AD 所成角的正弦值.23.(本小题满分10分)设ξ为随机变量,从棱长为1的正方体ABCD - A 1B 1C 1D 1的八个顶点中任取四个点,当四点共面时,ξ= 0,当四点不共面时,ξ的值为四点组成的四面体的体积.(1)求概率P (ξ= 0);(2)求ξ的分布列,并求其数学期望E (ξ).(第22题)。
2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)

绝密★启用前2014届江苏省无锡市市北高中高三期初考试文科数学试卷(带解析)试卷副标题考试范围:xxx ;考试时间:122分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)第II卷(非选择题)一、填空题(题型注释)1、已知函数,若,且,则的最小值是 .2、函数在区间上的最小值为_________.3、设,则的值为.4、已知函数的图象关于直线对称,则的单调递增区间为.5、已知都是单位向量,且,则的值为.6、设,函数有意义, 实数取值范围 .7、若方程的解所在区间为,则 .8、若正实数满足,则的最小值是______.9、在等差数列中,若,则.10、= .11、函数的最小正周期是.13、椭圆中有如下结论:椭圆上斜率为1的弦的中点在直线上,类比上述结论得到正确的结论为:双曲线上斜率为1的弦的中点在直线 上.14、已知是边长为4的正三角形,是内部两点,且满足,,则的面积为 .二、解答题(题型注释)15、已知数列中,,前和(Ⅰ)求证:数列是等差数列; (Ⅱ)求数列的通项公式;(Ⅲ)设数列的前项和为,是否存在实数,使得对一切正整数都成立?若存在,求的最小值,若不存在,试说明理由.16、设二次函数在区间上的最大值、最小值分别是,集合. (Ⅰ)若,且,求的值; (Ⅱ)若,且,记,求的最小值.17、如图,在中,边上的中线长为3,且,.(Ⅰ)求的值;(Ⅱ)求边的长.18、已知,.(1)若,求的值;(2)若,求的值.19、如图,正三棱柱中,点是的中点.(Ⅰ)求证: 平面;(Ⅱ)求证:平面.20、如图所示,将一矩形花坛扩建成一个更大的矩形花坛,要求在的延长线上,在的延长线上,且对角线过点.已知米,米。
(1)设(单位:米),要使花坛的面积大于32平方米,求的取值范围;(2)若(单位:米),则当,的长度分别是多少时,花坛的面积最大?并求出最大面积.参考答案1、2、03、284、5、6、7、18、189、410、11、112、13、14、15、(Ⅰ)详见解析;(Ⅱ);(Ⅲ)存在,.16、(Ⅰ),;(Ⅱ).17、(Ⅰ);(Ⅱ)4;18、(Ⅰ);(Ⅱ)或7.19、(Ⅰ)详见解析;(Ⅱ)详见解析.20、(Ⅰ);(Ⅱ)花坛的面积最大27平方米,此时米,米 .【解析】1、试题分析:画出函数图象,从图象上可知,所以由可得,所以,设,当时,,当时,,所以函数在上的最小值为.考点:二次函数、导数的应用.2、试题分析:求导得,当,,所以在区间是增函数,所以它的最小值为.考点:函数的导数及其应用.3、试题分析:是由反比例函数先向右平移17个单位,再向上平移1个单位得到的,所以它关于点对称,所以当时,所以.考点:函数的中心对称,数列的求和.4、试题分析:因为函数图象的对称轴为,所以也就是函数的最值,,解得,所以,由不等式得,所以函数的递增区间为.考点:三角函数的图象与性质.5、试题分析:由得,两边平方得,又都是单位向量,所以有,所以.考点:向量的数量积.6、试题分析:由题意得,对都成立,当时,显然成立,或当即时不等式也成立,所以实数取值范围.考点:对数函数的定义域、一元二次不等式.7、试题分析:设,则函数是增函数,又,,所以函数在区间有唯一零点,所以方程的唯一解所在区间为,所以.考点:函数的零点、根的存在性的判定.8、试题分析:因为是正实数,所民由基本不等式得,,设,则,即,所以,所以,所以的最小值是18.考点:基本不等式、一元二次不等式.9、试题分析:设的公差为,,所以.考点:等差数列的通项公式和性质.10、试题分析:.考点:复数的四则运算.11、试题分析:,所以函数的最小正周期.考点:二倍角公式、三角函数的周期.12、试题分析:根据并集的定义有,再由补集的定义有.考点:集合的运算.13、试题分析:根据结构上的类似容易类比得到结论,下面给出证明:设双曲线上斜率为1的弦的两端点,则,且,,两式相减得,由得,也即,所以弦的中点在直线上.考点:合情推理和演绎推理.14、试题分析:以为原点,以的垂直平分线为轴建立如图所示坐标系,由三角形边长为4得,,得,故,又由,由图可知的面积.考点:向量的运算,数形结合的思想.15、试题分析:(Ⅰ)对条件式进行变形,得到递推关系得证;(Ⅱ)由条件求出首项和公差即得;(Ⅲ)利用裂项相消法求出,再考察的上确界,可得的最小值.试题解析:(Ⅰ)因为,所以,整理,得,所以,所以,所以,所以,所以,数列为等差数列。
2014年高考文科数学江苏卷及答案

绝密★启用前2014年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:圆柱的侧面积公式:=S cl 侧面积,其中c 是圆柱底面的周长,l 为母线长 圆柱的体积公式:V Sh =圆柱,其中S 是圆柱的底面积,h 为高一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应.....位置上.... 1.已知集合={2,1,3,4}A --,={1,2,3}B -,则AB = .2.已知复数2(52i)z =+(i 为虚数单位),则z 的实部为 . 3.右图是一个算法流程图,则输出的n 的值是 .4.从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是 .5.已知函数cos y x =与sin(2)(0π)y x ϕϕ=+≤<,它们的图象有一个横坐标为π3的交点,则ϕ的值是 .6.为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm ),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有 株树木的底部周长小于100cm . 7.在各项均为正数的等比数列{}n a 中,若21a =,8642a a a =+,则6a 的值是 .8.设甲、乙两个圆柱的底面积分别为1S ,2S ,体积分别为1V ,2V .若它们的侧面积相等,且1294S S =,则12VV 的值是 . 9.在平面直角坐标系xOy 中,直线230x y +-=被圆22(2)(1)4x y -++=截得的弦长为 .10.已知函数2()1f x x mx =+-,若对于任意[,1]x m m ∈+,都有()0f x <成立,则实数m 的取值范围是 .11.在平面直角坐标系xOy 中,若曲线2by ax x=+(a ,b 为常数)过点(2,5)P -,且该曲线在点P 处的切线与直线7230x y ++=平行,则a b +的值是 .12.如图,在平行四边形ABCD 中,已知8AB =,5AD =,3CP PD =,2AP BP =,则AB AD 的值是 .13.已知()f x 是定义在R 上且周期为3的函数,当[0,3)x ∈时,21()22f x x x =-+.若函数()y f x a =-在区间[3,4]-上有10个零点(互不相同),则实数a 的取值范围是 .14.若ABC △的内角满足sin 2sin A B C =,则cos C 的最小值是 .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)已知π(,π)2α∈,sin α=(Ⅰ)求πsin()4α+的值; (Ⅱ)求5πcos(2)6α-的值.16.(本小题满分14分)如图,在三棱锥P ABC -中,D ,E ,F 分别为棱PC ,AC ,AB 的中点.已知PA AC ⊥,6PA =,8BC =,5DF =.求证:(Ⅰ)直线PA ∥平面DEF ; (Ⅱ)平面BDE ⊥平面ABC .17.(本小题满分14分)如图,在平面直角坐标系xOy 中,1F ,2F 分别是椭圆22221(0)x y a b a b+=>>的左、右焦点,顶点B 的坐标为(0,)b ,连接2BF 并延长交椭圆于点A ,过点A 作x 轴的垂线交椭圆于另一点C ,连接1F C .(Ⅰ)若点C 的坐标为41(,)33,且2BF =求椭圆的方程;(Ⅱ)若1F C AB ⊥,求椭圆离心率e 的值.姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无------------------------------------18.(本小题满分16分)如图,为保护河上古桥OA ,规划建一座新桥BC ,同时设立一个圆形保护区.规划要求:新桥BC 与河岸AB 垂直;保护区的边界为圆心M 在线段OA 上并与BC 相切的圆,且古桥两端O 和A 到该圆上任意一点的距离均不少于80m .经测量,点A 位于点O 正北方向60m 处,点C 位于点O 正东方向170m 处(OC 为河岸),4tan 3BCO ∠=.(Ⅰ)求新桥BC 的长;(Ⅱ)当OM 多长时,圆形保护区的面积最大?19.(本小题满分16分)已知函数()e e x xf x -=+,其中e 是自然对数的底数.(Ⅰ)证明:()f x 是R 上的偶函数; (Ⅱ)若关于x 的不等式()e1xmf x m -+-≤在(0,)+∞上恒成立,求实数m 的取值范围;(Ⅲ)已知正数a 满足:存在0[1,)x ∈+∞,使得3000()(3)f x a x x -+<成立.试比较1e a -与e 1a -的大小,并证明你的结论.20.(本小题满分16分)设数列{}n a 的前n 项和为n S .若对任意的正整数n ,总存在正整数m ,使得n m S a =,则称{}n a 是“H 数列”.(Ⅰ)若数列{}n a 的前n 项和*2()n n S n =∈N ,证明:{}n a 是“H 数列”;(Ⅱ)设{}n a 是等差数列,其首项11a =,公差0d <.若{}n a 是“H 数列”,求d 的值;(Ⅲ)证明:对任意的等差数列{}n a ,总存在两个“H 数列”{}n b 和{}n c ,使得+n n na b c =*()n ∈N 成立.数学Ⅱ(附加题)21.【选做题】在A ,B ,C ,D 四小题中只能选做两题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.A .(本小题满分10分)选修4—1:几何证明选讲如图,AB 是圆O 的直径,C ,D 是圆O 上位于AB 异侧的两点.证明:OCB D ∠=∠.B .(本小题满分10分)选修4—2:矩阵与变换已知矩阵121x -⎡⎤=⎢⎥⎣⎦A ,1121⎡⎤=⎢⎥-⎣⎦B ,向量2y ⎡⎤=⎢⎥⎣⎦α,x ,y 为实数,若=A αB α,求x y +的值.C .(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知直线l的参数方程为1,2,2x y ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),直线l与抛物线24y x =相交于A ,B 两点,求线段AB 的长.D .(本小题满分10分)选修4—5:不等式选讲已知0x >,0y >,证明:22(1)(1)9x y x y xy ++++≥.【必做题】第22,23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.22.(本小题满分10分)盒中共有9个球,其中有4个红球、3个黄球和2个绿球,这些球除颜色外完全相同. (Ⅰ)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P ;(Ⅱ)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为1x ,2x ,3x ,随机变量X 表示1x ,2x ,3x 中的最大数,求X 的概率分布和数学期望()E X .23.(本小题满分10分)已知函数0sin ()(0)xf x x x =>,设()n f x 为1()n f x -的导数,*n ∈N . (Ⅰ)求12πππ2()()222f f +的值;(Ⅱ)证明:对任意的*n ∈N ,等式1πππ()()444n n nf f -+.2014普通高等学校招生全国统一考试(江苏卷)数学答案解析。
江苏省苏、锡、常、镇四市2014届高三数学教学情况调查(一)试题(含解析)新人教A版

2014年苏、锡、常、镇四市高三教学情况调查(一)一、填空题:1.【题文】已知集合{}1,2,3,4A=,{},4,7B m=,若{}1,4A B=,则A B=.【结束】2.【题文】若复数z =13i1i+-(i为虚数单位),则 | z | = .3.【题文】已知双曲线2218x ym-=的离心率为3,则实数m的值为.4.【题文】一个容量为20的样本数据分组后,分组与频数分别如下:(]10,20,2;(]20,30,3;(]30,40,4;(]40,50,5;(]50,60,4;(]60,70,2.则样本在(]10,50上的频率是.5.【题文】执行如图所示的算法流程图,则最后输出的y 等于 .【结束】6.【题文】设函数2()sin f x a x x =+,若(1)0f =,则(1)f -的值为 . 【答案】2 【解析】结束开始 x ← 1 y ← 1 y ← 2y + 1 输出y N Y(第5题)x ≤5x ← x + 1Y【结束】7.【题文】四棱锥P - ABCD 的底面ABCD 是边长为2的正方形,PA ⊥底面ABCD 且PA = 4,则PC 与底面ABCD 所成角的正切值为 .【结束】8.【题文】从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 .【结束】9.【题文】已知2tan()5+=,1tan 3=,则tan +4⎛⎫⎪⎝⎭的值为 .【答案】98【解析】试题分析:因为171315213152tan )tan(1tan )tan()tan(tan =⋅+-=++-+=-+=bb a b b a b b a a ,所以8917111711tan 1tan 1)4tan(=-+=-+=+a a a π.考点:两角和与差正切 【结束】10.【题文】设等差数列{}n a 的前n 项和为n S ,若13a =-,132k a +=,12k S =-,则正整数k = .【结束】11.【题文】已知正数,x y 满足22x y +=,则8x yxy+的最小值为 . 【结束】12.【题文】如图,在△ABC 中,BO 为边AC 上的中线,2BG GO =,设CD ∥AG ,若15AD AB AC =+λ()∈R λ,则λ的值为 .(第12题)ABCDOG【结束】13.【题文】已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+,若函数()g x 恰有两个不同的零点,则实数k 的取值范围为 .【结束】14.【题文】在平面直角坐标系xOy 中,已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内,动直线AB过点P且交圆C于,A B两点,若△ABC的面积的最大值为16,则实数m的取值范围为.【结束】二、解答题15.【题文】(本小题满分14分)设函数2()6cos23sin cosf x x x x=-.(1)求()f x的最小正周期和值域;(2)在锐角△ABC中,角,,A B C的对边分别为,,a b c,若()0f B=且2b=,4cos5A=,求a和sin C.【结束】16.【题文】(本小题满分14分)如图,在三棱柱111ABC A B C -中,侧面11AA B B 为菱形, 且160A AB ∠=︒,AC BC =,D 是AB 的中点. (1)求证:平面1A DC ⊥平面ABC ; (2)求证:1BC ∥平面1A DC .111DC B CBA (第16题)【结束】17.【题文】(本小题满分14分)一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,,C D在半圆上),设BOC∠=,木梁的体积为V(单位:m3),表面积为S(单位:m2).(1)求V关于θ的函数表达式;(2)求的值,使体积V最大;(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.(2)2()10(2cos cos 1)10(2cos 1)(cos 1)V '=+-=-+. 令()0V '=,得1cos 2=,或cos 1=-(舍). ∵(0,)2∈,∴3=. …………………5分当(0,)3∈时,1cos 12<<,()0,()V V '>为增函数;当(,)32∈时,10cos 2<<,()0,()V V '<为减函数. …………………7分θD CBAO(第17题)【结束】18.【题文】(本小题满分16分)如图,在平面直角坐标系xOy中,已知A,B,C是椭圆22221(0)x ya ba b+=>>上不同的三点,32(32,)A,(3,3)B--,C在第三象限,线段BC的中点在直线OA上.(1)求椭圆的标准方程;(2)求点C的坐标;(3)设动点P在椭圆上(异于点A,B,C)且直线PB,PC分别交直线OA于M,N两点,证明OM ON⋅为定值并求出该定值.NMPCBAyxO(第18题)【解析】试题分析:(1)22127272x y +=,(2)(5,1)--,(3)452.试题解析:(1)由已知,得222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩ 解得2227,27.2a b ⎧=⎪⎨=⎪⎩ …………………2分所以椭圆的标准方程为22127272x y +=. …………………3分(2)设点(,)C m n (0,0)m n <<,则BC 中点为33(,)22m n --. 由已知,求得直线OA 的方程为20x y -=,从而23m n =-.① 又∵点C 在椭圆上,∴22227m n +=.②由①②,解得3n =(舍),1n =-,从而5m =-. …………………5分 所以点C 的坐标为(5,1)--. …………………6分 (3)设00(,)P x y ,11(2,)M y y ,22(2,)N y y . ∵,,P B M 三点共线,∴011033233y y y x ++=++,整理,得001003()23y x y x y -=--.…………………8分【结束】19.【题文】(本小题满分16分)设各项均为正数的数列{}n a 的前n 项和为S n ,已知11a =,且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立. (1)若λ = 1,求数列{}n a 的通项公式; (2)求λ的值,使数列{}n a 是等差数列.∴当2n ≥时,12n n S a +=.②【结束】20.【题文】(本小题满分16分) 已知函数e ()ln ,()e xxf x mx a x mg x =--=,其中m ,a 均为实数. (1)求()g x 的极值;(2)设1,0m a =<,若对任意的12,[3,4]x x ∈12()x x ≠,212111()()()()f x f xg x g x -<-恒成立,求a 的最小值;(3)设2a =,若对任意给定的0(0,e]x ∈,在区间(0,e]上总存在1212,()t t t t ≠,使得120()()()f t f t g x == 成立,求m 的取值范围.【答案】(1)极大值为1,无极小值.(2)3 -22e 3.(3)3[,)e 1+∞-. 【解析】列表如下:∵g(1) = 1,∴y =()g x 的极大值为1,无极小值. …………………3分 (2)当1,0m a =<时,()ln 1f x x a x =--,(0,)x ∈+∞.∵()0x af x x -'=>在[3,4]恒成立,∴()f x 在[3,4]上为增函数. …………………4分 设1e ()()e x h x g x x ==,∵12e (1)()x x h x x --'=> 0在[3,4]恒成立, ∴()h x 在[3,4]上为增函数. …………………5分 设21x x >,则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-, x (-∞,1) 1 (1,+∞) ()g x '+ 0 - g(x)↗极大值↘由①②,得3e 1m -≥. …………………13分 ∵1(0,e]∈,∴2()(1)0f f m =≤成立. …………………14分下证存在2(0,]t m ∈,使得()f t ≥1.取e m t -=,先证e2mm-<,即证2e 0m m ->.③ 设()2e x w x x =-,则()2e 10x w x '=->在3[,)e 1+∞-时恒成立. ∴()w x 在3[,)e 1+∞-时为增函数.∴3e ))01((w x w ->≥,∴③成立. 再证()e m f -≥1.∵e e 3()1e 1m mf m m m --+=>>-≥,∴3e 1m -≥时,命题成立.综上所述,m 的取值范围为3[,)e 1+∞-. …………………16分 考点:函数极值,不等式恒成立 【结束】附加题21.【选做题】在A 、B 、C 、D 四小题中只能选做两题......,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 21.【题文】A .选修4—1:几何证明选讲如图,⊙O 为四边形ABCD 的外接圆,且AB AD =,E 是CB 延长线上一点,直线EA 与圆O 相切. 求证:CD ABAB BE=.考点:圆内接四边形性质 【结束】21.【题文】B .选修4—2:矩阵与变换ODCB A(第21-A 题)已知矩阵1221⎡⎤=⎢⎥⎣⎦M ,17⎡⎤=⎢⎥⎣⎦β,计算6M β. 【结束】21.【题文】C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,圆的参数方程为22cos ,()2sin x y =+⎧⎨=⎩为参数,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.求: (1)圆的直角坐标方程; (2)圆的极坐标方程.【答案】(1)22(2)4x y -+=.(2)4cos ρθ=.【结束】21.【题文】D .选修4—5:不等式选讲已知函数2()122f x x x a a =++---,若函数()f x 的图象恒在x 轴上方,求实数a 的取值范围.【结束】22.【题文】(本小题满分10分)甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为23,且各次投篮的结果互不影响.甲 同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次. (1)求甲同学至少有4次投中的概率; (2)求乙同学投篮次数的分布列和数学期望. 【答案】(1)112,(2) ,12181E =. 12345P 23 29 227 281 181的分布表为12345P 23 29 227 281 181…………………8分的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=. …………………10分考点:概率分布,数学期望值 【结束】23.【题文】(本小题满分10分)设01212(1)m m n n n n n m S C C C C ---=-+-+-,*,m n ∈N 且m n <,其中当n 为偶数时,2nm =;当n 为奇数时,12n m -=. (1)证明:当*n ∈N ,2n ≥时,11n n n S S S +-=-; (2)记01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-,求S 的值.∴当n 为奇数时,11n n n S S S +-=-成立. …………………5分 同理可证,当n 为偶数时, 11n n n S S S +-=-也成立. …………………6分 (2)由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-,得 0123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+-=0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -. …………………9分 又由11n n n S S S +-=-,得6n n S S +=,所以20142012421S S S S -=-=-,12014S =-. …………………10分 考点:组合数性质 【结束】2014年苏、锡、常、镇四市高三教学情况调查(一)数学Ⅱ(附加题) 参考答案21、【选做题】在A 、B 、C 、D 四小题中只能选做两题......,每小题10分,共计20分. 解:(1)圆的直角坐标方程为22(2)4x y -+=. …………………5分 (2)把cos ,sin ,x y ρθρθ=⎧⎨=⎩代入上述方程,得圆的极坐标方程为4cos ρθ=.…………………10分D .选修4—5:不等式选讲解:()f x 的最小值为232a a --, …………………5分由题设,得223a a -<,解得(1,3)a ∈-. …………………10分【必做题】第22题、第23题,每题10分,共计20分.的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=. …………………10分23.解:(1)当n 为奇数时,1n +为偶数,1n -为偶数, ∵1101221112(1)n n n n nn S CC C+++++=-++-,110122112(1)n n n n n n S C C C---+=-++-,11012211212(1)n n n n n n S C CC------=-++-,∴1111110011222221111111222()()(1)()(1)n n n n n n n n n n n n n n S S C C C C CCC-+-++-++-++++-=---++--+-=11012212112((1))n n n n n n CCCS --------++-=-.∴当n 为奇数时,11n n n S S S +-=-成立. …………………5分 同理可证,当n 为偶数时, 11n n n S S S +-=-也成立. …………………6分 (2)由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-,得123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+-=0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -. …………………9分 又由11n n n S S S +-=-,得6n n S S +=, 所以20142012421S S S S -=-=-,12014S =-. …………………10分。
江苏省苏、锡、常、镇四市高三数学教学情况调查(一)试题(含解析)新人教A版

2014年苏、锡、常、镇四市高三教学情况调查(一)一、填空题:1.【题文】已知集合{}1,2,3,4A =,{},4,7B m =,若{}1,4AB =,则AB = .【结束】2.【题文】若复数z =13i1i+-(i 为虚数单位),则 | z | = .3.【题文】已知双曲线2218x y m -=m 的值为 .4.【题文】一个容量为20的样本数据分组后,分组与频数分别如下:(]10,20,2;(]20,30,3;(]30,40,4;(]40,50,5;(]50,60,4;(]60,70,2.则样本在(]10,50上的频率是 .5.【题文】执行如图所示的算法流程图,则最后输出的y 等于 .【结束】6.【题文】设函数2()sin f x a x x =+,若(1)0f =,则(1)f -的值为 . 【答案】2 【解析】(第5题)【结束】7.【题文】四棱锥P - ABCD 的底面ABCD 是边长为2的正方形,PA ⊥底面ABCD 且PA = 4,则PC 与底面ABCD 所成角的正切值为 .【结束】8.【题文】从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 .【结束】9.【题文】已知2tan()5a b +=,1tan 3b =,则tan +4p a ⎛⎫ ⎪⎝⎭的值为 .【答案】98【解析】试题分析:因为171315213152tan )tan(1tan )tan()tan(tan =⋅+-=++-+=-+=bb a b b a b b a a ,所以8917111711tan 1tan 1)4tan(=-+=-+=+aa a π.考点:两角和与差正切 【结束】10.【题文】设等差数列{}n a 的前n 项和为n S ,若13a =-,132k a +=,12k S =-,则正整数k = .【结束】11.【题文】已知正数,x y 满足22x y +=,则8x yxy+的最小值为 .【结束】12.【题文】如图,在△ABC 中,BO 为边AC 上的中线,2BG GO =,设CD ∥AG ,若15A D A BA C =+λ()∈R λ,则λ的值为 .(第12题)ABCDOG【结束】13.【题文】已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+,若函数()g x 恰有两个不同的零点,则实数k 的取值范围为 .【结束】14.【题文】在平面直角坐标系xOy 中,已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内,动直线AB过点P 且交圆C 于,A B 两点,若△ABC 的面积的最大值为16,则实数m 的取值范围为 .【结束】 二、解答题15.【题文】(本小题满分14分)设函数2()6cos cos f x x x x =-. (1)求()f x 的最小正周期和值域;(2)在锐角△ABC 中,角,,A B C 的对边分别为,,a b c ,若()0f B =且2b =,4cos 5A =,求a 和sin C .【结束】16.【题文】(本小题满分14分)如图,在三棱柱111ABC A B C -中,侧面11AA B B 为菱形, 且160A AB ∠=︒,AC BC =,D 是AB 的中点. (1)求证:平面1A DC ⊥平面ABC ; (2)求证:1BC ∥平面1A DC .111DC B CBA (第16题)【结束】17.【题文】(本小题满分14分)一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,,C D在半圆上),设BOC q∠=,木梁的体积为V(单位:m3),表面积为S(单位:m2).(1)求V关于θ的函数表达式;(2)求q的值,使体积V最大;(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.(2)2()10(2cos cos 1)10(2cos 1)(cos 1)V q q q q q '=+-=-+. 令()0V q '=,得1cos 2q =,或cos 1q =-(舍). ∵(0,)2p q ∈,∴3pq =. …………………5分当(0,)3p q ∈时,1cos 12q <<,()0,()V V q q '>为增函数;当(,)32p p q ∈时,10cos 2q <<,()0,()V V q q '<为减函数. …………………7分θD CBAO(第17题)【结束】18.【题文】(本小题满分16分)如图,在平面直角坐标系xOy中,已知A,B,C是椭圆22221(0)x ya ba b+=>>上不同的三点,A,(3,3)B--,C在第三象限,线段BC的中点在直线OA上.(1)求椭圆的标准方程;(2)求点C的坐标;(3)设动点P在椭圆上(异于点A,B,C)且直线PB,PC分别交直线OA于M,N两点,证明OM ON⋅为定值并求出该定值.(第18题)【解析】试题分析:(1)22127272x y +=,(2)(5,1)--,(3)452.试题解析:(1)由已知,得222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩ 解得2227,27.2a b ⎧=⎪⎨=⎪⎩ …………………2分所以椭圆的标准方程为221272x y +=. …………………3分(2)设点(,)C m n (0,0)m n <<,则BC 中点为33(,)22m n --. 由已知,求得直线OA 的方程为20x y -=,从而23m n =-.① 又∵点C 在椭圆上,∴22227m n +=.②由①②,解得3n =(舍),1n =-,从而5m =-. …………………5分 所以点C 的坐标为(5,1)--. …………………6分 (3)设00(,)P x y ,11(2,)M y y ,22(2,)N y y . ∵,,P B M 三点共线,∴011033233y y y x ++=++,整理,得001003()23y x y x y -=--.…………………8分【结束】19.【题文】(本小题满分16分)设各项均为正数的数列{}n a 的前n 项和为S n ,已知11a =,且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立. (1)若λ = 1,求数列{}n a 的通项公式; (2)求λ的值,使数列{}n a 是等差数列.∴当2n ≥时,12n n S a +=.②【结束】20.【题文】(本小题满分16分) 已知函数e ()ln ,()e xxf x mx a x mg x =--=,其中m ,a 均为实数. (1)求()g x 的极值;(2)设1,0m a =<,若对任意的12,[3,4]x x ∈12()x x ≠,212111()()()()f x f xg x g x -<-恒成立,求a 的最小值;(3)设2a =,若对任意给定的0(0,e]x ∈,在区间(0,e]上总存在1212,()t t t t ≠,使得120()()()f t f t g x == 成立,求m 的取值范围.【答案】(1)极大值为1,无极小值.(2)3 -22e 3.(3)3[,)e 1+∞-. 【解析】列表如下:∵g(1) = 1,∴y =()g x 的极大值为1,无极小值. …………………3分 (2)当1,0m a =<时,()ln 1f x x a x =--,(0,)x ∈+∞.∵()0x af x x-'=>在[3,4]恒成立,∴()f x 在[3,4]上为增函数. …………………4分 设1e ()()e x h x g x x ==,∵12e (1)()x x h x x --'=> 0在[3,4]恒成立, ∴()h x 在[3,4]上为增函数. …………………5分 设21x x >,则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-,由①②,得3e 1m -≥. …………………13分 ∵1(0,e]∈,∴2()(1)0f f m =≤成立. …………………14分下证存在2(0,]t m ∈,使得()f t ≥1.取e m t -=,先证e2mm-<,即证2e 0m m ->.③ 设()2e x w x x =-,则()2e 10x w x '=->在3[,)e 1+∞-时恒成立. ∴()w x 在3[,)e 1+∞-时为增函数.∴3e ))01((w x w ->≥,∴③成立. 再证()e m f -≥1.∵e e 3()1e 1m mf m m m --+=>>-≥,∴3e 1m -≥时,命题成立.综上所述,m 的取值范围为3[,)e 1+∞-. …………………16分 考点:函数极值,不等式恒成立 【结束】附加题21.【选做题】在A 、B 、C 、D 四小题中只能选做两题......,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 21.【题文】A .选修4—1:几何证明选讲如图,⊙O 为四边形ABCD 的外接圆,且AB AD =,E 是CB 延长线上一点,直线EA 与圆O 相切. 求证:CD ABAB BE=.考点:圆内接四边形性质 【结束】21.【题文】B .选修4—2:矩阵与变换(第21-A 题)已知矩阵1221⎡⎤=⎢⎥⎣⎦M ,17⎡⎤=⎢⎥⎣⎦β,计算6M β.【结束】21.【题文】C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,圆的参数方程为22cos ,()2sin x y a a a=+⎧⎨=⎩为参数,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.求: (1)圆的直角坐标方程; (2)圆的极坐标方程.【答案】(1)22(2)4x y -+=.(2)4cos ρθ=.【结束】21.【题文】D .选修4—5:不等式选讲已知函数2()122f x x x a a =++---,若函数()f x 的图象恒在x 轴上方,求实数a 的取值范围.【结束】22.【题文】(本小题满分10分)甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为23,且各次投篮的结果互不影响.甲 同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次. (1)求甲同学至少有4次投中的概率; (2)求乙同学投篮次数x 的分布列和数学期望. 【答案】(1)112,(2) ,12181E =x .x 的分布表为…………………8分x 的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=x . …………………10分考点:概率分布,数学期望值 【结束】23.【题文】(本小题满分10分)设01212(1)m mn n n n n m S C C C C ---=-+-+-,*,m n ∈N 且m n <,其中当n 为偶数时,2nm =;当n 为奇数时,12n m -=. (1)证明:当*n ∈N ,2n ≥时,11n n n S S S +-=-; (2)记01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-,求S 的值.∴当n 为奇数时,11n n n S S S +-=-成立. …………………5分 同理可证,当n 为偶数时, 11n n n S S S +-=-也成立. …………………6分 (2)由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-,得 0123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+-=0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -. …………………9分 又由11n n n S S S +-=-,得6n n S S +=,所以20142012421S S S S-=-=-,12014S=-.…………………10分考点:组合数性质【结束】2014年苏、锡、常、镇四市高三教学情况调查(一)数学Ⅱ(附加题)参考答案21、【选做题】在A、B、C、D 四小题中只能选做两题......,每小题10分,共计20分.解:(1)圆的直角坐标方程为22(2)4x y-+=.…………………5分(2)把cos,sin,xyρθρθ=⎧⎨=⎩代入上述方程,得圆的极坐标方程为4cosρθ=.…………………10分D.选修4—5:不等式选讲解:()f x 的最小值为232a a --, …………………5分由题设,得223a a -<,解得(1,3)a ∈-. …………………10分【必做题】第22题、第23题,每题10分,共计20分.x 的数学期望22221121123453927818181E =⨯+⨯+⨯+⨯+⨯=x . …………………10分 23.解:(1)当n 为奇数时,1n +为偶数,1n -为偶数, ∵1101221112(1)n n n n nn S CC C+++++=-++-,110122112(1)n n n n n n S C C C---+=-++-,11012211212(1)n n n n n n S C CC------=-++-,∴1111110011222221111111222()()(1)()(1)n n n n n n n n n n n n n n S S C C C C CCC-+-++-++-++++-=---++--+-=11012212112((1))n n n n n n CCCS --------++-=-.∴当n 为奇数时,11n n n S S S +-=-成立. …………………5分 同理可证,当n 为偶数时, 11n n n S S S +-=-也成立. …………………6分 (2)由01231007201420132012201110071111120142013201220111007S C C C C C =-+-+-,得123100720142013201220111007201420142014201420142013201220111007S C C C C C =-+-+-=0112233100710072014201320132012201220112011100710071231007()()()()2013201220111007C C C C C C C C C -+++-++-+=0121007012100620142013201210072012201120101006()()C C C C C C C C -+----+-+=20142012S S -. …………………9分 又由11n n n S S S +-=-,得6n n S S +=, 所以20142012421S S S S -=-=-,12014S =-. …………………10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省苏、锡、常、镇四市2014届高三教学情况调查(一)文科数学试卷(带解析)1.已知集合{}1,2,3,4A =,{},4,7B m =,若{}1,4A B =,则AB = .【答案】{}1,2,3,4,7 【解析】 试题分析:因为{}1,4AB =,所以B ∈1,.1=m 因此AB ={}1,2,3,4,7.考点:集合运算 2.若复数z =13i1i+-(i 为虚数单位),则|z |= .【解析】试题分析:因为13i 1i +-,21242i i +-=+-=所以.5||=z 也可利用复数模的性质求解,即.5210|1||31|||==-+=i i z考点:复数的模3.已知双曲线2218x y m -=m 的值为 .【答案】4 【解析】试题分析:由题意得:,38=+mm 解得.4=m 解答此类问题,要明确对应关系,一是,8,22==b m a 二是双曲线中.222b a c +=考点:双曲线离心率4.一个容量为20的样本数据分组后,分组与频数分别如下:(]10,20,2;(]20,30,3;(]30,40,4;(]40,50,5;(]50,60,4;(]60,70,2.则样本在(]10,50上的频率是 .【答案】710【解析】 试题分析:因为样本在(]10,50上的频数共有 145432=+++,所以样本在(]10,50上的频率是1072014=.也可从反面求解,即样本不在(]10,50上的频数共有 624=+,所以样本在(]10,50上的频率是107206-1=.考点:样本频率5.执行如图所示的算法流程图,则最后输出的y 等于 .【答案】63 【解析】试题分析:第一次循环,,2,3==x y 第二次循环,,3,7==x y 第三次循环,,4,15==x y 第四次循环,,5,31==x y 第六次循环,,56,63>==x y 终止循环,输出63=y . 考点:流程图6.设函数2()sin f x a x x =+,若(1)0f =,则(1)f -的值为 . 【答案】2 【解析】试题分析:因为(1)0f =,所以1sin 1-=a .因此(1)f -.211sin =+-=a 本题也可应用函数性质求解,因为2)()(=-+x f x f ,所以,2)1()1(=-+f f .2)1(=-f考点:函数性质7.四棱锥P - ABCD 的底面ABCD 是边长为2的正方形,PA ⊥底面ABCD 且PA =4,则PC 与底面ABCD 所成角的正切值为 .【解析】试题分析:因为PA ⊥底面ABCD ,所以PC 与底面ABCD 所成角的为.PCA ∠,因此.2224t an ===∠AC PA PCA考点:直线与平面所成角8.从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 . 【答案】23【解析】试题分析:从甲,乙,丙,丁4个人中随机选取两人共有624=C 种基本事件,而甲乙两人中有且只有一个被选取包含41212=C C 种基本事件,所以所求概率为3264=. 考点:古典概型概率9.已知2tan()5a b +=,1tan 3b =,则tan +4p a ⎛⎫ ⎪⎝⎭的值为 .【答案】98【解析】试题分析:因为1713513152tan )tan(1tan )tan()tan(tan =⋅+-=++-+=-+=bb a b b a b b a a ,所以8917111711tan 1tan 1)4tan(=-+=-+=+aa a π. 考点:两角和与差正切10.设等差数列{}n a 的前n 项和为n S ,若13a =-,132k a +=,12k S =-,则正整数k = . 【答案】13 【解析】试题分析:设等差数列{}n a公差为d ,则12)1(213,233-=-+-=+-d k k k kd ,消去d 得:.13=k考点:等差数列通项公式及前n 项和公式11.已知正数,x y 满足22x y +=,则8x yxy +的最小值为 .【答案】9 【解析】 试题分析:因为9)16210(21)1610(21)22)(81(818=+≥++=++=+=+x y y x y x x y x y xy y x ,当且仅当22,16=+=y x x y y x 即31,34==y x 时取等号,所以8x y xy +的最小值为9. 考点:基本不等式求最值12.如图,在△ABC 中,BO 为边AC 上的中线,2BG GO =,设CD ∥AG ,若15A D AB A C=+λ()∈R λ,则λ的值为 .【答案】65【解析】 试题分析:因为,2=所以31313231+=+=.又CD ∥AG ,可设,m =从而mm m m 3)31(33++=++=+=.因为15A D A B A C =+λ,所以5631,513=+==m m λ. 考点:向量共线表示13.已知函数22(2)e ,0,()43,0,x x x x f x x x x ⎧-=⎨-++>⎩≤()()2g x f x k =+,若函数()g x 恰有两个不同的零点,则实数k 的取值范围为 . 【答案】27321,{0,22e +⎛⎫-- ⎪⎝⎭ 【解析】试题分析:由2(2)(0)x y x x e x =-≤求导得2(2)x y x e '=-,故2(2)(0)xy x x e x =-≤在(上单调增,在(,)-∞上单调减,且当0x <时,恒有2(2)0x y x x e =-<.又243(0)y x x x =-++>在(0,2)上单调增,在(2,)+∞上单调减,所以可作出函数()y f x =的图像,如图.由图可知,要使函数()g x 恰有两个不同的零点,需20k -=或2k -=327k <-<,即实数k 的取值范围为27321,{0,22e +⎛⎫-- ⎪⎝⎭.考点:利用导数研究函数图像14.在平面直角坐标系xOy 中,已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内,动直线AB 过点P 且交圆C 于,A B 两点,若△ABC 的面积的最大值为16,则实数m 的取值范围为 .【答案】[3(327,3++-- 【解析】试题分析:由题意得圆心(,2),C m 半径.r =因为点(3,0)P 在圆222:24280C x y m x y m +--+-=内,所以223060280m m +--+-<,解得3727.m-<<设C 到直线距离为d,则.d CP ≤又222211162222ABCd r d r S d AB d ∆+-=⋅=⋅==,当且仅当222d r d =-,即216,4d d ==时取等号,因此4CP ≥,即3m ≥+3m ≤-综上实数m 的取值范围为[3(327,3++--. 考点:直线与圆位置关系15.设函数2()6cos cos f x x x x =-. (1)求()f x 的最小正周期和值域;(2)在锐角△ABC 中,角,,A B C 的对边分别为,,a b c ,若()0f B =且2b =,4cos 5A =,求a 和sin C .【答案】(1) π,[3-+,(2)534,10343+.【解析】试题分析:(1)要研究三角函数的性质,首先先将三角函数化为B x A y ++=)sin(ϕω型.利用降幂公式22cos 1cos 2x x +=及倍角公式xx x 2sin 21cos sin =可将函数次数化为一次,再利用配角公式)sin(cos sin 22ϕ++=+x b a x b x a 化为3)62s i n (32++=πx y ,然后利用基本三角函数图像求其最小正周期和值域,(2)解三角形问题,一般利用正余弦定理解决.本题为已知两角及一对边,选用正弦定理.由于是锐角△ABC ,开方时取正.试题解析:(1)1+cos2()622xf x x =⨯=3cos223x x +=)36x p++. 3分 所以()f x 的最小正周期为22T pp ==, 4分值域为[3-+. 6分(2)由()0f B =,得πcos(2)6B +=. B 为锐角,∴ππ7π2666B <+<,π5π266B +=,∴π3B =. 9分 ∵4cos 5A =,(0,)A p ∈,∴3sin 5A =. 10分 在△ABC中,由正弦定理得32sin sin b A a B⨯===. 12分∴21sin sin()=sin()sin 32C A B A A A p p =---=+=. 14分考点:倍角公式,正余弦定理16.如图,在三棱柱111ABC A B C -中,侧面11AA B B 为菱形, 且160A AB ∠=︒,AC BC =,D 是AB 的中点.(1)求证:平面1A DC ⊥平面ABC ; (2)求证:1BC ∥平面1A DC . 【答案】(1)详见解析,(2)详见解析. 【解析】试题分析:(1)证明面面垂直,关键找出线面垂直.因为侧面11AA B B 为菱形, 且160A AB ∠=︒,所以△1A AB 为正三角形,因而有1AB AD ⊥.又AC BC =,D 是AB 的中点,所以有AB CD ⊥,这样就可得到AB ⊥平面1A DC ,进而可证平面1A DC ⊥平面ABC .(2)证明线面平行,关键找出线线平行. 条件“D 是AB 的中点”,提示找中位线.取1AC 中点E ,就可得DE ∥1BC ,利用线面平行判断定理即可.解决此类问题,需注意写全定理成立的所有条件,不可省略.试题解析:(1)证明:∵ 11ABB A 为菱形,且160A AB ∠=︒, ∴△1A AB 为正三角形. 2分D 是AB 的中点,∴1AB A D ⊥.∵AC BC =,D 是AB 的中点,∴ AB CD ⊥. 4分 1A D CD D =,∴AB ⊥平面1A DC . 6分∵AB ⊂平面ABC ,∴平面1A DC ⊥平面ABC . 8分 (2)证明:连结1C A ,设11AC AC E =,连结DE . ∵三棱柱的侧面11AA C C 是平行四边形,∴E 为1AC 中点. 10分 在△1ABC 中,又∵D 是AB 的中点,∴DE ∥1BC . 12分∵DE ⊂平面1A DC ,1BC ⊄平面1A DC ,∴ 1BC ∥平面1A DC . 14分考点:面面垂直判定定理,线面平行判定定理 17.一个圆柱形圆木的底面半径为1m ,长为10m ,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD (如图所示,其中O 为圆心,,C D 在半圆上),设BOC q ∠=,木梁的体积为V (单位:m 3),表面积为S (单位:m 2).(1)求V 关于θ的函数表达式; (2)求q 的值,使体积V 最大;(3)问当木梁的体积V 最大时,其表面积S 是否也最大?请说明理由.【答案】(1)()10(sin cos sin ),(0,)2V p q q q q q =+∈,(2)3pq =,(3)当木梁的体积V 最大时,其表面积S 也最大.【解析】 试题分析:(1)解答实际问题关键读懂题意.本题所求体积为直四棱柱体积,体积为高与底面积的乘积.高为圆木的长,底面积为梯形ABCD 的面积.利用角BOC q ∠=表示出梯形上下底及高,就可得到所求关系式. (2)先求出函数的导数2()10(2cos cos 1)10(2cos 1)(cos 1)V q q q q q '=+-=-+,再根据导数为零时,定义区间导数值的正负讨论其单调性,研究其图像变化规律,确定其极值、最值.本题函数先增后减,在3pq =时,取极大值,也是最大值.(3)本题实质是求表面积的最大值,并判断取最大值时3p q =是否成立.首先先建立表面积的函数关系式.表面积由两部分组成,一是底面积,二是侧面积. 底面积为梯形ABCD 的面积,有两个. 侧面积为梯形ABCD 周长与圆木的长的乘积.再利用导数求出其最大值及取最大值时角的取值. 试题解析:(1)梯形ABCD 的面积2cos 2sin 2ABCD S q q +=⋅=sin cos sin q q q +,(0,)2pq ∈. 2分 体积()10(sin cos sin ),(0,)2V pq q q q q =+∈. 3分 (2)2()10(2cos cos 1)10(2cos 1)(cos 1)V q q q q q '=+-=-+. 令()0V q '=,得1cos 2q =,或cos 1q =-(舍).∵(0,)2p q ∈,∴3p q =. 5分 当(0,)3p q ∈时,1cos 12q <<,()0,()V V q q '>为增函数; 当(,)32p p q ∈时,10cos 2q <<,()0,()V V q q '<为减函数. 7分 ∴当3pq =时,体积V 最大. 8分(3)木梁的侧面积210S AB BC CD =++⋅侧()=20(cos 2sin 1)2q q ++,(0,)2pq ∈.2ABCD S S S =+侧=2(sin cos sin )20(cos 2sin 1)2q q q q q ++++,(0,)2pq ∈. 10分 设()cos 2sin 12g q q q =++,(0,)2p q ∈.∵2()2sin 2sin 222g q qq =-++, ∴当1sin22q =,即3pq =时,()g q 最大. 12分又由(2)知3pq =时,sin cos sin q q q +取得最大值,所以3p q =时,木梁的表面积S 最大. 13分 综上,当木梁的体积V 最大时,其表面积S 也最大. 14分 考点:利用导数求函数最值18.如图,在平面直角坐标系xOy 中,已知A ,B ,C 是椭圆22221(0)x y a b a b+=>>上不同的三点,A ,(3,3)B --,C 在第三象限,线段BC 的中点在直线OA 上.(1)求椭圆的标准方程; (2)求点C 的坐标;(3)设动点P 在椭圆上(异于点A ,B ,C )且直线PB ,PC 分别交直线OA 于M ,N 两点,证明OM ON ⋅为定值并求出该定值.【答案】(1)求椭圆方程一般用待定系数法.本题已知椭圆过两点,列两个方程222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩,解出b a ,的值,(2)求点(,)C m n 的坐标,需列出两个方程.一是点C 在椭圆上,即22227m n +=,二是BC 的中点在直线OA 上,即23m n =-.注意到C 在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点N M ,的坐标,算出OM 为定值.难点是如何消去参数.因为点N M ,在直线OA : 20x y -=上,所以可设11(2,)M y y ,22(2,)N y y .选择00(,)P x y 作为参数,即用00(,)P x y 表示点N M ,的坐标.由,,P B M 三点共线,解得001003()23y x y x y -=--,同理解得00200523y x y x y -=-+.从而有22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+,这里主要用到2200227x y +=代入化简.本题也可利用椭圆参数方程或三角表示揭示21y y 为定值. 【解析】试题分析:(1)221272x y +=,(2)(5,1)--,(3)452.试题解析:(1)由已知,得222291821,991,a b a b ⎧⎪+=⎪⎨⎪+=⎪⎩ 解得2227,27.2a b ⎧=⎪⎨=⎪⎩ 2分 所以椭圆的标准方程为22127272x y +=. 3分(2)设点(,)C m n (0,0)m n <<,则BC 中点为33(,)22m n --.由已知,求得直线OA 的方程为20x y -=,从而23m n =-.①又∵点C 在椭圆上,∴22227m n +=.②由①②,解得3n =(舍),1n =-,从而5m =-. 5分 所以点C 的坐标为(5,1)--. 6分(3)设00(,)P x y ,11(2,)M y y ,22(2,)N y y .∵,,P B M 三点共线,∴11033233y y y x ++=++,整理,得001003()23y x y x y -=--. 8分∵,,P C N 三点共线,∴22011255y y y x ++=++,整理,得00200523y x y x y -=-+. 10分∵点C 在椭圆上,∴2200227x y +=,2200272x y =-.从而22200000001222200000003(56)3(3627)393449241822x y x y y x y y y x y x y y x y +--+===⨯=+---+. 14分所以124552OM ON y y ⋅==. 15分∴OM ON ⋅为定值,定值为452. 16分 考点:椭圆标准方程,直线与椭圆位置关系19.设各项均为正数的数列{}n a 的前n 项和为S n ,已知11a =,且11()(1)n n n n S a S a λ+++=+对一切*n ∈N 都成立.(1)若λ = 1,求数列{}n a 的通项公式; (2)求λ的值,使数列{}n a 是等差数列. 【答案】(1)an=2n -1(2)λ=0. 【解析】试题分析:(1)本题属于“已知n S 求n a ”,利用)2(1≥-=-n S S a n n n 化简关系式. 因为11(1)(1)n n n n S a S a +++=+,所以先分离n S 与n a ,即1111n n n nS a S a +++=+,这是类等比,利用叠乘法得到1112n n S a +++=,再利用)2(1≥-=-n S S a n n n ,消去n S 得12n n a a +=.求数列{an}通项公式时,需讨论当n = 1时是否满足2n ≥的情形.(2)解答本题需注意逻辑关系,由数列{}n a 是等差数列得λ= 0,这是一个必要条件,还需验证其充分性,即λ = 0时,数列{}n a 是等差数列.这可类似(1)的解答过程.试题解析:解:(1)若λ = 1,则11(1)(1)n n n n S a S a +++=+,111a S ==.又∵00n n a S >>,, ∴1111n n n nS a S a +++=+, 2分∴3131221212111111n n n nS S a a S a S S S a a a +++++⋅⋅⋅=⋅⋅⋅+++,化简,得1112n n S a +++=.① 4分 ∴当2n ≥时,12n n S a +=.②② - ①,得12n n a a +=,∴12n na a +=(2n ≥). 6分∵当n = 1时, 22a =,∴n = 1时上式也成立,∴数列{an}是首项为1,公比为2的等比数列, an = 2n -1(*n ∈N ). 8分(2)令n = 1,得21a λ=+.令n = 2,得23(1)a λ=+. 10分要使数列{}n a是等差数列,必须有2132a a a =+,解得λ = 0. 11分当λ = 0时,11(1)n n n n S a S a ++=+,且211a a ==. 当n ≥2时,111()(1)()n n n n n n S S S S S S +-+-=+-,整理,得2111n n n n n S S S S S +-++=+,1111n n n nS S S S +-+=+, 13分从而3312412123111111n n n nS S S S S S S S S S S S +-+++⋅⋅⋅=⋅⋅⋅+++,化简,得11n n S S ++=,所以11n a += 15分 综上所述,1n a =(*n ∈N ),所以λ = 0时,数列{}n a是等差数列. 16分考点:已知n S 求n a20.已知函数e ()ln ,()e xxf x mx a x mg x =--=,其中m ,a 均为实数. (1)求()g x 的极值;(2)设1,0m a =<,若对任意的12,[3,4]x x ∈12()x x ≠,212111()()()()f x f xg x g x -<-恒成立,求a 的最小值;(3)设2a =,若对任意给定的0(0,e]x ∈,在区间(0,e ]上总存在1212,()t t t t ≠,使得120()()()f t f t g x == 成立,求m 的取值范围.【答案】(1)极大值为1,无极小值.(2)3 -22e 3.(3)3[,)e 1+∞-.【解析】试题分析:(1)求函数极值,先明确定义域为,R 再求其导数为e(1)()e x x g x -'=.由()0g x '=,得x = 1.分析导数在定义区间符号正负,确定函数先增后减,所以y =()g x 有极大值为1,无极小值.(2)不等式恒成立问题,先化简不等式212111()()()()f x f xg x g x -<-.化简不等式的难点有两个,一是绝对值,二是两个参量12,.x x 可从函数单调性去绝对值,分析两个函数,一是()y f x =,二是1()y g x =.利用导数可知两者都是增函数,故原不等式等价于21212111()(),()()()f x f x x xg x g x -<->,变量分离调整为21212111()(),()()()f x f x x x g x g x -<->,这又等价转化为函数1()()()u x f x g x =-在区间[3,4]上为减函数,即21e (1)()10e x a x u x x x -'=--⋅≤在[3,4]上恒成立.继续变量分离得11e ex x a x x ---+≥恒成立,即11m a xe (e )x x a x x---+≥.最后只需求函数11e ex x y x x --=-+在[3,4]上最大值,就为a 的最小值.(3)本题含义为:对于函数()y g x =在(0,e]上值域中每一个值,函数()y f x =在(0,e]上总有两个不同自变量与之对应相等.首先求出函数()y g x =在(0,e]上值域(0,1],然后根据函数()y f x =在(0,e]上必须不为单调函数且每段单调区间对应的值域都需包含(0,1].由()f x 在(0,e]不单调得2e m >,由每段单调区间对应的值域都需包含(0,1]得(e)1f ≥,3e 1m -≥. 试题解析:(1)e(1)()e x x g x -'=,令()0g x '=,得x = 1. 1分列表如下:∵g(1) = 1,∴y =()g x 的极大值为1,无极小值. 3分 (2)当1,0m a =<时,()ln 1f x x a x =--,(0,)x ∈+∞.∵()0x af x x -'=>在[3,4]恒成立,∴()f x 在[3,4]上为增函数. 4分设1e ()()e x h x g x x ==,∵12e (1)()x x h x x --'=> 0在[3,4]恒成立,∴()h x 在[3,4]上为增函数. 5分设21x x >,则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-,即2211()()()()f x h x f x h x -<-.设1e ()()()ln 1e xu x f x h x x a x x =-=---⋅,则u(x)在[3,4]为减函数. ∴21e (1)()10e x a x u x x x -'=--⋅≤在(3,4)上恒成立 6分 ∴11e ex x a x x ---+≥恒成立.设11e ()ex x v x x x --=-+,∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+,x ∈[3,4], ∴1221133e [()]e 1244x x --+>>,∴()v x '< 0,()v x 为减函数.∴()v x 在[3,4]上的最大值为v(3) = 3 -22e3. 8分∴a ≥3 -22e 3,∴a 的最小值为3 -22e3. 9分 (3)由(1)知()g x 在(0,e]上的值域为(0,1]. 10分 ∵()2ln f x mx x m =--,(0,)x ∈+∞,当0m =时,()2ln f x x =-在(0,e]为减函数,不合题意. 11分当0m ≠时,2()()m x mf x x-'=,由题意知()f x 在(0,e]不单调,所以20e m <<,即2e m >.① 12分 此时()f x 在2(0,)m 上递减,在2(,e)m 上递增,∴(e)1f ≥,即(e)e 21f m m =--≥,解得3e 1m -≥.②由①②,得3e 1m -≥. 13分 ∵1(0,e]∈,∴2()(1)0f f m =≤成立. 14分下证存在2(0,]t m ∈,使得()f t ≥1. 取emt -=,先证e 2m m -<,即证2e 0mm ->.③设()2e xw x x =-,则()2e 10xw x '=->在3[,)e 1+∞-时恒成立.∴()w x 在3[,)e 1+∞-时为增函数.∴3e ))01((w x w ->≥,∴③成立.再证()e mf -≥1. ∵e e 3()1e 1m mf m m m --+=>>-≥,∴3e 1m -≥时,命题成立. 综上所述,m 的取值范围为3[,)e 1+∞-. 16分考点:函数极值,不等式恒成立。
