高三数学(文)集合人教版知识精讲
第一章 集合与常用逻辑用语 章末重难点归纳总结(原卷版)--人教版高中数学精讲精练必修一
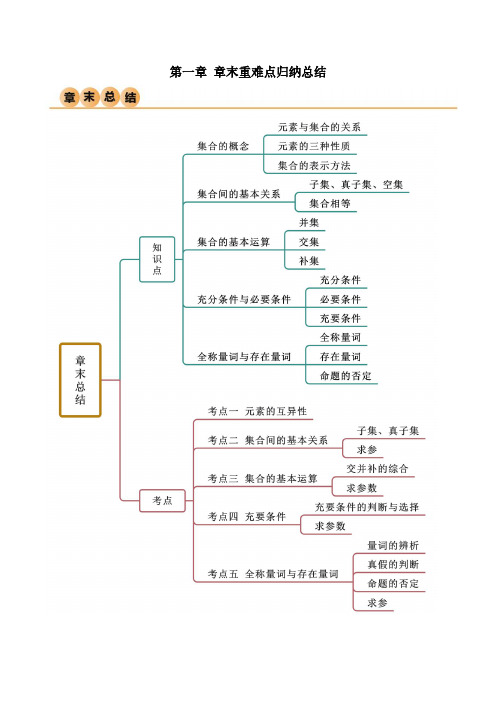
条件,那么丙是甲的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4.(2022 秋·江西景德镇·高一统考期中)(多选)已知命题 p :关于 x 的不等式 x 21≥0 ,命题 q:a x a 1, 若 p 是 q的必要非充分条件,则实数 a 的取值可以为( )
A. a 0
4(2022 秋·广东汕尾·高一华中师范大学海丰附属学校校考阶段练习)已知集合 A x x 2 3x 2 0 , B x x2 ax a 1 0 , C x x2 mx 2 0 .
(1)命题 p :“ x B ,都有 x A ”,若命题 p 为真命题,求实数 a 的值; (2)若 A C C ,求实数 m 的取值范围.
(2)“命题 q: x A , x B ”是假命题,求 m 的取值范围.
3.(2023·江苏南京)已知命题 p:“ x R ,使不等式 mx2 mx 1 0 成立”. (1)若命题 p 是假命题,求实数 m 的取值集合 A; (2)若 q : 4 m a 4 是 p 的必要不充分条件,求实数 a 的取值范围.
A. 1, 3, 5
B. 1, 3
C.1, 2, 4
D.1, 2, 4,5
【例 3-2】(2023·广东·校联考模拟预测)已知全集U R ,集合 A {x x 4 或 x 0} ,B {x x 4 或 x £ -2}, 则图中阴影部分表示的集合为( )
A. 2,0
C.2, 0 4
B. 2, 0
2.(2023·浙江金华)已知集合 A {x∣3 x 7}, B {x∣2 x 10} ,则 ðR A B ( )
A. , 210, B.3, 7
C. 2,3 7,10 D. R
《新课标》 第01讲 集合

《新课标》高三数学(人教版)第一轮复习单元讲座第一讲集合一.课标要求:1.集合的含义与表示(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系;(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用;2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集;(2)在具体情境中,了解全集与空集的含义;3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;(3)能使用V enn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用。
二.命题走向有关集合的高考试题,考查重点是集合与集合之间的关系,近年试题加强了对集合的计算化简的考查,并向无限集发展,考查抽象思维能力,在解决这些问题时,要注意利用几何的直观性,注意运用Venn图解题方法的训练,注意利用特殊值法解题,加强集合表示方法的转换和化简的训练。
考试形式多以一道选择题为主,分值5分。
预测2007年高考将继续体现本章知识的工具作用,多以小题形式出现,也会渗透在解答题的表达之中,相对独立。
具体题型估计为:(1)题型是1个选择题或1个填空题;(2)热点是集合的基本概念、运算和工具作用。
三.要点精讲1.集合:某些指定的对象集在一起成为集合。
a∈;若b不是集合A的元(1)集合中的对象称元素,若a是集合A的元素,记作Ab∉;素,记作A(2)集合中的元素必须满足:确定性、互异性与无序性;确定性:设A是一个给定的集合,x是某一个具体对象,则或者是A的元素,或者不是A的元素,两种情况必有一种且只有一种成立;互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素;无序性:集合中不同的元素之间没有地位差异,集合不同于元素的排列顺序无关;(3)表示一个集合可用列举法、描述法或图示法;列举法:把集合中的元素一一列举出来,写在大括号内;描述法:把集合中的元素的公共属性描述出来,写在大括号{}内。
人教版高中数学必修一知识点总结(完整版)

第一章集合与函数概念课时一:集合有关概念1.集合的含义:集合为一些确定的、不同的东西的全体,人们能意识到这些东西,并且能判断一个给定的东西是否属于这个整体。
2.一般的研究对象统称为元素,一些元素组成的总体叫集合,简称为集。
3.集合的中元素的三个特性:(1)元素的确定性:集合确定,则一元素是否属于这个集合是确定的:属于或不属于。
例:世界上最高的山、中国古代四大美女、教室里面所有的人……(2)元素的互异性:一个给定集合中的元素是唯一的,不可重复的。
例:由HAPPY的字母组成的集合{H,A,P,Y}(3)元素的无序性:集合中元素的位置是可以改变的,并且改变位置不影响集合例:{a,b,c}和{a,c,b}是表示同一个集合3.集合的表示:{…} 如:{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋}(1)用大写字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}(2)集合的表示方法:列举法与描述法。
1)列举法:将集合中的元素一一列举出来 {a,b,c……}2)描述法:将集合中元素的公共属性描述出来,写在大括号内表示集合。
{x∈R| x-3>2} ,{x| x-3>2}①语言描述法:例:{不是直角三角形的三角形}②Venn图:画出一条封闭的曲线,曲线里面表示集合。
4、集合的分类:(1)有限集:含有有限个元素的集合(2)无限集:含有无限个元素的集合(3)空集:不含任何元素的集合例:{x|x2=-5}5、元素与集合的关系:(1)元素在集合里,则元素属于集合,即:a∈A(2)元素不在集合里,则元素不属于集合,即:a A注意:常用数集及其记法:非负整数集(即自然数集)记作:N正整数集 N*或 N+整数集Z有理数集Q实数集R课时二、集合间的基本关系1.“包含”关系—子集(1)定义:如果集合A 的任何一个元素都是集合B 的元素,我们说这两个集合有包含关系,称集合A 是集合B 的子集。
记作:B A ⊆(或B ⊇A)注意:B A ⊆有两种可能(1)A 是B 的一部分,;(2)A 与B 是同一集合。
高中数学人教版集合教案

高中数学人教版集合教案
教学目标:
1. 熟练掌握集合的概念和表示方法;
2. 能够进行集合的基本运算;
3. 能够解决与集合相关的问题。
教学重点和难点:
重点:集合的定义和表示方法,集合的基本运算
难点:集合的应用题目解答
教学准备:教材《人教版高中数学》,课件,黑板,彩色粉笔
教学过程:
一、导入(5分钟)
通过举例的方式引出问题:在日常生活中,我们经常听到“集合”的说法,你们知道集合是什么吗?集合有哪些表示方法?
二、讲解与示范(15分钟)
1. 集合的概念:集合是由一些对象组成的总体,这些对象称为集合的元素,用大括号{}表示。
2. 集合的表示方法:列举几个例子,让学生理解集合的表示方法。
3. 集合的基本运算:并集、交集、差集的概念及表示方法。
三、练习与讨论(20分钟)
1. 让学生做一些与集合相关的练习题,巩固集合的概念和基本运算。
2. 引导学生讨论集合的应用题目,如排列组合等。
四、小结与展示(10分钟)
总结本节课的学习内容,强调集合的重要性和应用价值。
五、作业布置(5分钟)
布置相关的练习题,巩固学生的学习成果。
教学反思:
本节课主要是介绍集合的概念和表示方法,以及集合的基本运算。
通过示范和练习,学生能够更好地理解集合的相关知识,并能够在实际问题中灵活运用。
在教学过程中,可以引导学生进行讨论和合作,提高他们的思维能力和解决问题的能力。
高三数学 集合、映射与函数、函数的解析式与定义域、函数的值域 知识精讲

高三数学集合、映射与函数、函数的解析式与定义域、函数的值域知识精讲(一)集合1. 集合的概念及集合中元素的三个特征:一组对象的全体形成一个集合,集合里的各个对象叫做集合的元素,集合的元素具有三个特征:(1)确定性:对于一个给定的集合,任何一个对象或者是这个集合中的元素,或者不是它的元素,这是集合的最基本特征。
(2)互异性:集合中的任何两个元素都是能区分的(即互不相同的)相同的对象归入任何一个集合时,只能算作这个集合中的一个元素。
(3)无序性:在一个集合中通常不考虑它的元素之间的顺序,也就是说,由a 、b 两个元素组成的集合与由{}b a ,两个元素组成的集合是相同的。
元素与集合,集合与集合的关系:元素与集合的关系是从属关系,用符号“∈”与“∉”表示,集合与集合的关系是包含关系,用符号“⊆”、“⊂”或“/⊆”、“⊄”表示。
2. 集合的运算:(1)并集:{}A B x x A x B =∈∈|或性质:A A A A B B A A A A A B B A B ==∅=⊆⊆,,,,(2)交集:{}A B x x A x B =∈∈|,且性质:A B B A A A A A A B A A B B ==∅=∅⊆⊆,,,,(3)全集与补集:全集用字母I 表示,补集:{}A x x I x A =∈∉|且 性质:A I I I =∅==∅,,3. 几个重要结论:(1)A B A B A B A B ==,(2)A B A B A A B B ⊆⇔=⇔=A B A B A B ⊆⊆()或(3)由n 个元素组成的集合,其子集个数为2n ,即是C C C C n n n n n n 0122++++=…。
(4)空集∅是一个特殊的集合,是任何集合的子集,在解题中要注意对空集的讨论。
(5)进行集合运算时,要注意发挥数轴、韦恩图的作用,通过数形结合直观地解决问题。
(二)映射与函数1. 映射:一般地,设A 、B 是两个集合,如果按照某种对应法则f 对于集合A 中的任何一个元素,在集合B 中都有唯一的元素和它对应,这样的对应叫做从集合A 到集合B 的映射,记作f A B :→。
人教版高中数学知识点汇总(全册版)

① f (x) 是整式时,定义域是全体实数. ② f ( x) 是分式函数时,定义域是使分母不为零的一切实数. ③ f ( x) 是偶次根式时,定义域是使被开方式为非负值时的实数的集合.
④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于 1.
⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论. ⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义. (4)求函数的值域或最值 求函数最值的常用方法和求函数值域的方法基本上是相同的.事实上,如果在函数的值域中存在一个 最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,只是
提问的角度不同.求函数值域与最值的常用方法: ①观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值.
②配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数 的值域或最值.
对象 a 与集合 M 的关系是 a M ,或者 a M ,两者必居其一.
(4)集合的表示法 ①自然语言法:用文字叙述的形式来描述集合. ②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.
③描述法:{ x | x 具有的性质},其中 x 为集合的代表元素.
④图示法:用数轴或韦恩图来表示集合. (5)集合的分类
人教版高中数学知识点(必修+选修)
高中数学 必修 1 知识点
第一章 集合与函数概念 【1.1.1】集合的含义与表示
(1)集合的概念 集合中的元素具有确定性、互异性和无序性.
(2)常用数集及其记法
N 表示自然数集, N 或 N 表示正整数集, Z 表示整数集, Q 表示有理数集, R 表示实数集.
人教版高中数学精讲精练选择性必修三6.3 二项式定理(解析版)
6.3二项式定理考法一二项式的展开式【例1-1】(2023上·高二课时练习)求411x ⎛⎫⎪⎝⎭+的展开式.【答案】答案见解析【解析】4123404132231404444411111C 1C 1C C 1C 1111x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯+⨯+⨯ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭+⎭⎝⎝⎭⎝⎭23446411x x x x =++++.【例1-2】(2023·黑龙江)()12312C 4C 8C 2C nnn n n n -+-++-= ().A .1B .-1C .(-1)nD .3n【答案】C【解析】原式=()()()()()()0120122222121n n nn n n n n -+-+-++-=-=-C C C C L .故选:C.【一隅三反】1.(2023·甘肃)若对x ∀∈R ,()()()()()()55432252102102521ax b x x x x x +=+-+++-+++-恒成立,其中,a b ∈R ,则a b +=()A .1-B .0C .2D .3【答案】C【解析】由()()()()()()()543255252102102521211x x x x x x x +-+++-+++-=+-=+,得()()551ax b x +=+,所以1a b ==,2a b +=.故选:C.2.(2023·安徽安庆)如果12212C 2C 2C 2187n n n n n ++++= ,则22223C C C n +++=.【答案】56【解析】依题意,1220012212C 2C 2C 2C 2C 2C 2C n n n n n n n n n n n+++++++=+ ()1232187nn =+==,解得7n =,222322237337C C C C C C =++++++ 32232224475567C C C C C C C =+++=+++ 322323667778C C C C C C 87656321⨯⨯=====⨯⨯+++.故答案为:563.(2023·高二课时练习)(1)求4⎛⎫ ⎪⎝⎭的展开式(2)求()()55211x x x -++的展开式;(3)化简()()()()()5432151********x x x x x -+-+-+-+-.【答案】(1)221218110854x x x x-+-+(2)答案见解析;(3)51x -【解析】(1)()4442131x x ⎛⎫⎫==- ⎪⎪⎝⎭⎭()()()()()()()()432234012344444421C 3C 31C 31C 31C 1x x x x x⎡⎤=+⋅-+⋅-+⋅-+-⎣⎦()432218110854121x x x x x=-+-+221218110854x x x x =-+-+.(2)()()()5555223(1)1(1)11x x x x x x x -++-++⎦=⎣-⎡⎤=()()()()()123405314323332341355555C 1C 1C 1C 1C 1x x x x x =⨯⨯⨯+⨯+⨯-+-+---()55035C 1x+⨯-3691215151010 5x x x x x =-+-+-.(3)原式0514********555555C (1)C (1)C (1)C (1)C (1)C (1)1x x x x x x =-+-+-+-+-+--55[(1)1]11x x =-+-=-.考法二二项式指定项的系数【例2-1】(2024·四川绵阳)51x ⎫-⎪⎭的展开式中,x 的系数为()A .5-B .10-C .5D .10【答案】A【解析】51x ⎫⎪⎭的展开式的通项为53521551C (1)C rr r r r rr T x x --+⎛⎫=⋅⎭⋅-=-⋅⋅ ⎪⎝.令5312r-=,得1r =.x ∴的系数为15C 5-=-.故选:A .【例2-2】.(2024·湖南)二项式741x ⎫-⎪⎭的展开式中常数项为()A .7-B .21-C .7D .21【答案】A【解析】二项式741x ⎫⎪⎭的通项公式为()14147317741C C 1rrrr r rr T x x --+⎛⎫=⋅⋅-=⋅-⋅ ⎪⎝⎭,令1414013r r -=⇒=,所以常数项为()17C 17⋅-=-,故选:A 【例2-3】(2024·云南)写出623x⎛⎝展开式中的一个有理项为.【答案】12729x (答案不唯一)【解析】623x⎛⎝展开式的通项公式为所以展开式中的有理项分别为:0r =时,6121213729T x x ==;2r =时,4277363C 1215T x x ==;4r =时,2422563C 135T x x ==;6r =时,37-=T x .故答案为:12729x (四个有理项任写其一均可).【一隅三反】1.(2024·河南)29(2x x-展开式中的常数项为()A .672B .672-C .5376-D .5376【答案】D【解析】二项式29(2)x x -的展开式的通项218319992C )()(N 2)C (,9,r r r r r rr T r x xr x--+=-=-≤∈,令1830r -=,得6r =,所以二项展开式中的常数项为669C 2)7(536-=.故选:D2.(2024安徽)9a x x ⎛⎫+ ⎪⎝⎭展开式中含3x 项的系数为84-,则实数a 的值为()A .1-B .2-C .3-D .4-【答案】A 【解析】()992199C C 0,1,2,,9rr rr r r r a T xa x r x --+⎛⎫=⋅==⋅⋅⋅ ⎪⎝⎭,令923r -=,得3r =.∴3333349C 84T a x a x ==,依题意38484a =-,∴1a =-.故选:A.3.(2023·全国·模拟预测)5的展开式中,有理项是第项.【答案】3【解析】5的展开式的通项511051362155C 3C 3kkkk k k k T x x x ---+⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭⋅,其中0,1,2,3,4,5k =,当1k T +为有理项时,1056k-为整数,结合0,1,2,3,4,5k =,所以2k =,即有理项是展开式中的第3项,故答案为:3考法三两个二项式乘积的系数【例3-1】(2024·广东广州)在()()511x x +-展开式中3x 的系数为()A .1-B .0C .1D .2【答案】B【解析】显然()()()()5551111x x x x x +-=-+-,则()51x -展开式第1r +项55155,N,5C (1)C (1)r rr rr r r T xr x r --+-∈=-≤=,当3r =时,33235C (1)10x x x ⋅-=-,当2r =时,22335C (1)10x x -=,所以展开式中含3x 的项为3310100x x -+=,即展开式中3x 的系数为0.故选:B【例3-2】(2023·全国·模拟预测)()7y m x y x ⎛⎫+- ⎪⎝⎭的展开式中34x y 的系数为105-,则实数m =()A .2B .1C .1-D .2-【答案】D【解析】()7x y -的展开式的通项公式为()7171C r r r rr T x y -+=-,所以()61171C r r r r r y T x y x-++=-.令6314r r -=⎧⎨+=⎩,解得3r =,()7171C r r r rr mT m x y -+=⋅-.令734r r -=⎧⎨=⎩,解得4r =.由题意,可知()()()3434343777771C 1C C C 1C 105m m m -+⋅-=-+=-=-,所以2m =-.故选:D .【一隅三反】1.(2023·湖北)若()()542x m x --的展开式中的3x 的系数为600-,则实数m =()A .8B .7C .9D .10【答案】B【解析】由题意知,()52x -展开式的通项公式为()55C 2rr rx --,故3x 的系数为()()3232554C 2C 232040600m m ⨯---=--=-,解得7m =.故选:B .2.(2024·广东·)()()42112x x +⋅-的展开式中3x 的系数为.【答案】40-【解析】()()42112x x +⋅-的展开式中3x 的项为:()()313213441C 2C 240x x x x ⨯-+⨯-=-,所以展开式中3x 的系数为40-.故答案为:40-3.(2024·山东滨州)()622x x y y ⎛⎫+- ⎪⎝⎭的展开式中42x y 的系数为.(用数字作答)【答案】40-【解析】()62x y -的通项公式为()()66166C 2C 2rrr r rr r r T x y x y --+=-=-,令2r =得,()22424236C 260T x y x y =-=,此时4242602120x y x y ⋅=,令3r =得,()33333346C 2160T x y x y =-=-,此时3342160160xx y x y y-⋅=-,故42x y 的系数为12016040-=-故答案为:40-考法四三项式指定项的系数【例4-1】(2023·全国·校联考模拟预测)在6221x x ⎛⎫+- ⎪⎝⎭的展开式中常数项为()A .721B .-61C .181D .-59【答案】D【解析】6221x x ⎛⎫+- ⎪⎝⎭ =()6221x x ⎡⎤+-⎢⎥⎣⎦的展开式的通项公式为1r T +=()6622C 1rrrx x -⎛⎫+- ⎪⎝⎭=()()626C 21r r rr x x ---+,其中()66rx -+的展开式的通项公式为1k T +=66C kr kr x---,当0r =时,60r k --=,6k ∴=,常数项为()00666C C 2-;当1r =时,62r k --=,3k ∴=,常数项为()1365C C 2-;当2r =时,64r k --=,0k ∴=,常数项为()22064C C 2-;故常数项为()00666C C 2-+()1365C C 2-+()22064C C 259-=-.故选:D【例4-2】(2023·广东广州)()522x x y +-的展开式中52x y 的系数为(用数字作答).【答案】120【解析】由于()22522x y x y x =⋅⋅,所以()522x x y +-的展开式中含52x y 的项为()()222211252532C 2C C 120x x y x y ⨯⨯-=,所以()522x x y +-的展开式中52x y 的系数为120.故答案为:120【一隅三反】1(2023上·高二课时练习)()52123x x +-的展开式中5x 的系数为.【答案】92【解析】()()()5552123113x x x x +-=-+,又()51x -展开式的通项()()5155C 1C 1,0,1,2,3,4,5rrr r r r r T x x r -+=-=-=,()513x +展开式的通项()5155C 13C 3,0,1,2,3,4,5kk k k k k k S x x k -+===,所以含5x 的项为162534435261T S T S T S T S T S T S ++⋅+⋅++则含5x 的系数()()()()()()012345055144233322411500555555555555C 1C 3C 1C 3C 1C 3C 1C 3C 1C 3C 1C 392-+-+-+-+-+-=.故答案为:92.2.(2024·福建)412x x ⎛⎫+- ⎪⎝⎭的展开式中,常数项为()A .72-B .70-C .70D .72【答案】C【解析】方法一:8412xx ⎛⎫+-= ⎪⎝⎭展开式中,第()1r +项()84188C 1C rrrrrr r T x--+⎛==- ⎝,所以常数项为()44581C 70T =-=,方法二:441122x x x x ⎡⎤⎛⎫=- ⎪⎛⎫+-+ ⎢⎭⎝⎣⎪⎭⎥⎝⎦展开式中,第()1r +项()4141C 2rrrr T x x -+⎛⎫=-+ ⎪⎝⎭,当0r =时,()4041C 2x x ⎛⎫-+ ⎪⎝⎭展开式中常数项为24C 6=;当2r =时,()22241C 2x x ⎛⎫-+ ⎪⎝⎭展开式中常数项为21424C C 48⨯=;当4r =时,()04441C 216x x ⎛⎫-+= ⎪⎝⎭,所以412x x ⎛⎫+- ⎪⎝⎭的展开式中,常数项为70,故选:C .3.(2023上·河北唐山)()423a b c --的展开式中2abc 的系数为()A .208B .216-C .217D .218-【答案】B【解析】根据二项式定理可得,()423a b c --的展开式中,含2abc 的项为()()211122432C C 2C 3216a b c abc ⋅⋅⋅-⋅⋅-=-.所以,()423a b c --的展开式中2abc 的系数为216-.故选:B.考法五(二项式)系数的最值【例5-1】(2023上·辽宁朝阳·高三建平县实验中学校联考阶段练习)在二项式612x ⎫⎪⎭的展开式中,二项式系数最大的是()A .第3项B .第4项C .第5项D .第3项和第4项【答案】B【解析】二项式612x ⎫⎪⎭的展开式共有7项,则二项式系数最大的是第4项.故选:B.【例5-2】(2023·四川雅安)10(1)x -的展开式中,系数最小的项是()A .第4项B .第5项C .第6项D .第7项【答案】C【解析】依题意,10(1)x -的展开通项公式为()11010C ()(1)N C 010,r r r r r r T x x r r +≤≤=-=∈-,其系数为10(1)C r r-,当r 为奇数时,10(1)C r r-才能取得最小值,又由二项式系数的性质可知,510C 是{}10C r 的最大项,所以当=5r 时,10(1)C r r-取得最小值,即第6项的系数最小.故选:C .【一隅三反】1.(2022·重庆)(多选)若1nx x ⎛⎫+ ⎪⎝⎭的展开式中第3项与第8项的系数相等,则展开式中二项式系数最大的项为()A .第4项B .第5项C .第6项D .第7项【答案】BC【解析】 1n x x ⎛⎫+ ⎪⎝⎭的展开式的通项为211rr n r r n rr n n T C x C x x --+⎛⎫== ⎪⎝⎭,因为展开式中第3项与第8项的系数相等,∴27nnC C =,所以9n =,则91x x ⎛⎫+ ⎪⎝⎭展开式中二项式系数最大的项为第5项和第6项;故选:BC .2.(2024·海南)在()1nx +的二项展开式中,系数最大的项为3x 和4x ,则展开式中含x 项的系数为.【答案】7【解析】()1C 0,1,,kn kk n T xk n -+==⋅⋅⋅,因为系数最大的项为3x和4x ,所以n 为奇数,1142n n +⎛⎫--= ⎪⎝⎭,且132n n +-=,解得7n =.所以含x 项的系数为67C 7=.故答案为:73.(2023·上海嘉定)已知6(12)x +的二项展开式中系数最大的项为.【答案】4240x 【解析】设系数最大的项为()61C 2kkk T x +=,则11661166C 2C 2C 2C 2k k k k k k k k ++--⎧⋅≥⋅⎨⋅≥⋅⎩,解得111433k ≤≤,因为06k ≤≤且k 为整数,所以4k =,此时最大的项为()44456C 2240T x x ==.故答案为:4240x 4.(2023·上海)二项式()71x -的展开式中,系数最大的项为.【答案】335x 【解析】()71x -展开式通项公式为()717C 1rr rr T x -+=-,07r ≤≤且r 为整数.要想系数最大,则r 为偶数,其中()007717C 1T x x =-=,()225537C 121T x x =-=,()44357C 135T x x 3=-=,()6677C 17T x x =-=,显然系数最大项为3535T x =.故答案为:335x 考法六(二项式)系数和--赋值法【例6-1】(2023·广东佛山)(多选)已知()()()()102108012102111x x a a x a x a x ++=+++++++ ,则下列结论正确的是()A .02a =B .217a =C .13579384a a a a a ++++=D .0121023116144a a a a ++++= 【答案】ACD【解析】对于A ,令=1x -,则1080(12)(1)112a =-++-=+=,故A 正确;对于B ,因为108108(2)[(1)1][(1)1]x x x x ++=++++-,所以8662108C C (1)73a =+⋅-=,B 错误;对于C ,令0x =,则10011021024a a a +++== ,令2x =-,则8012102256a a a a -+-+== ,所以1357910242563842a a a a a -++++==,故C 正确;对于D ,由选项B 可知,977564110831084108C C (1)2,C C 64,C C 280a a a =+-==+⨯=-==,5342312510861087108810C C 196,C C 238,C C 112,C 146,a a a a =-==+==-==+=109101010C 10,C 1a a ====,所以01210231122237346452806196a a a a +++⋯+=+⨯+⨯+⨯+⨯+⨯7238811294610101116144+⨯+⨯+⨯+⨯+⨯=,故D 正确.故选:ACD.【例6-2】(2023·广东佛山)(多选)若5250125(1)(1)(1)x a a x a x a x =+-+-++- ,其中(0,1,,5)i a i = 为实数,则()A .01a =B .310a =C .13516a a a ++=-D .1251a a a +++= 【答案】AC【解析】令1x =可得01a =,A 正确.()5511x x =-+,其展开式的第三项是()()33235C 1101T x x =-=--,所以310a =-,B 不正确.令0x =可得01250a a a a ++++= ,所以1251a a a +++=- ,D 不正确.令2x =可得012532a a a a -++-= ,与01250a a a a ++++= 相减可得13516a a a ++=-,C 正确.故选:AC【一隅三反】1.(2023·河北)(多选)若()()20232320230123202332R x a a x a x a x a x x -=+++++∈ ,则()A .202302a =B .20230242022152a a a a -++++=C .20231352023512a a a a --++++=D .20233202312232023213333a a a a ++++=- 【答案】BD【解析】对于A ,当0x =时,()20232023022a =-=-,A 错误;对于B ,C ,当1x =时,20230123202311a a a a a +++++== ,当=1x -时,20230123202220235a a a a a a -+-++-=- ,所以20230242022152a a a a -++++= ,13a a+202352023512a a ++++= ,所以B 正确,C 错误;对于D ,当13x =时,20232023120220231323333a a a a ⎛⎫⨯-=++++ ⎪⎝⎭,所以()20232023123202302320231213333a a a a a ++++=--=- ,D 正确.故选:BD .2.(2023·江苏扬州·高二统考期中)(多选)()201212nn n x a a x a x a x -=++++ 的展开式中第3项和第11项的二项式系数相等,则以下判断正确的是()A .第7项的二项式系数最大B .所有奇数项二项式系数的和为132C .21212121222a a a+++=- D .12312231212a a a a ++++=- 【答案】AC【解析】由题意,可得210C C n n =,所以12n =,对于A 中,根据二项式定理的性质,可得中间项第7项的二项式系数最大,所以A 正确;对于B 中,根据二项式系数的性质,可得所有奇数项二项式系数的和为112,所以B 错误;对于C 中,对于C 中,令12x =,可得1212122102(11)0222a a a a ++++=-= ,令0x =,可得01a =,所以21212121222a a a +++=- ,所以C 正确;对于D 中,由()122120121212x a a x a x a x -=++++ ,可得()122120121212()x a a x a x a x '⎡⎤-=++++⎣⎦' ,即2111231211224(12)312a a x a x x a x -=+++-+ ,令1x =,可得1231112231224(12)24a a a a =+--+⨯+=+ ,所以D 错误.故选:AC.3.(2024·黑龙江·高二校联考期末)(多选)若()82801281(1)(1)x a a x a x a x =+-+-++- ,其中0128,,,,a a a a 为实数,则()A .01a =B .656a =C .1357128a a a a +++=D .2468128a a a a +++=【答案】AC【解析】令1t x =-,则原式转化为8280128(1)t a a t a t a t +=++++ ,对A ,令0=t ,得01a =,故A 正确;对B ,由二项式定理得6a =28C 28=,故B 错误;对CD ,令1t =,得801282a a a a ++++= ,令1t =-,得01280a a a a -+-+= ,所以71357024682128a a a a a a a a a +++=++++==,所以2468127a a a a +++=,故C 正确,D 错误.故选:AC考法七余数与小数【例7-1】(2023下·河南郑州·高二校联考期中)108除以49所得的余数是.【答案】22【解析】法一:由10010198291010101010(71)C 7C 7...C 7C 718=+=+++++,前9项可以被49整除,而910C 71714922+==+,故余数为22.法二:由510564(58491)==+5423324549515491015491015495154915=+⨯⨯+⨯⨯+⨯⨯+⨯⨯+,而515759375491549722==⨯+,故余数为22.故答案为:22【例7-2】.(2023·高二课时练习)将50.991精确到0.01的近似值是.【答案】0.96【解析】因为()55011225550.99110.009C 1C 0.009C 0.00910.0450.000810.95581=-=⨯-⨯+⨯-≈-+= ,且将50.991精确到0.01,故近似值为0.96故答案为:0.96【一隅三反】1.(2023安徽)1.028的近似值是.(精确到小数点后三位)【答案】1.172【解析】由题意得:8801223388881.02(10.02)0.020.020.02 1.172C C C C =+≈+⋅+⋅+⋅≈.故答案为:1.1722.(2023上·河北)1098除以1000的余数是.【答案】24【解析】因为10101922899101010101010109(1002)100+C (2)100+C (2)10C 80(2)100+C (2)=-=⨯-⨯⨯-⨯++⨯-⨯⨯-L 101922891010=[100+C (2)100+C (2)100(2)1000]+1024⨯-⨯⨯-⨯++-⨯L 101922891010=[100+C (2)100+C (2)100(2)1000+1000]24⨯-⨯⨯-⨯++-⨯+L ,所以1098除以1000的余数是:24.故答案为:243.(2023下·江苏淮安·高二江苏省郑梁梅高级中学校考阶段练习)今天是星期日,经过7天后还是星期日,那么经过202315天后是()A .星期日B .星期一C .星期三D .星期四【答案】B【解析】()202320232023120222022202320231514114C 14C 141=+=+++⨯+ ,因为20231202220222023202314C 14C 14+++⨯ 能被7整除,所以202315除以7余1,所以经过202315天后是星期一.故选:B.4.(2024·甘肃武威)干支纪年是中国古代的一种纪年法.分别排出十天干与十二地支如下:天干:甲乙丙丁戊己庚辛壬癸地支:子丑寅卯辰巳午未申酉戌亥把天干与地支按以下方法依次配对:把第一个天干“甲”与第一个地支“子”配出“甲子”,把第二个天干“乙”与第二个地支“丑”配出“乙丑”,L ,若天干用完,则再从第一个天干开始循环使用.已知2023年是癸卯年,则8132+年以后是年.【答案】丙午【解析】因为88817788132(121)212C 12C 123+=++=+⨯++⨯+ ,所以8132+年以后地支为“午”.因为8881777888132(103)210C 103C 10332+=++=+⨯⨯++⨯⨯++ ,又因为88326563,32+=+除以10余数为3,所以8132+年以后天干为“丙”,故8132+年以后是丙午年.故答案为:丙午考法八杨辉三角的应用【例8】(2023·广东广州)(多选)我国南宋数学家杨辉在1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.该表蕴含着许多的数学规律,下列结论正确的是()第0行1第1行11第2行121第3行1331第4行14641第5行15101051第6行1615201561…………A .3333434520232024C C C C C ++++= B .11111=,211121=,L ,51115101051=C .从左往右逐行数,第2023项在第63行第7个D .第5行到第10行的所有数字之和为2024【答案】AC【解析】对于A 选项,由组合数的计算性质()1*1C C C ,,m m m n n n m n m n -++=∈<N ,所以,3333433334520234452023C C C C C C C C ++++=++++ 433434552023202320232024C C C C C C =+++==+= ,A 对;对于B 选项,()555122334455555111101C 10C 10C 10C 1010=+=+⋅+⋅+⋅+⋅+15010001000050000100000161051=+++++=,B 错;对于C 选项,第()n n ∈N 行共有1n +项,从左往右逐行数,第n 行最后一项对应的项数为()()()1212312n n n n ++++++++= ,因为()()62162220162++=,且202320167=+,所以,从左往右逐行数,第2023项在第63行第7个,C 对;对于D 选项,第()*n n ∈N 行所有项之和为01C C C 2n n n n n ++=+ ,所以,第5行到第10行的所有数字之和为()565610212222201612-+++==- ,D 错.故选:AC.【一隅三反】1.(2023·山东青岛·高二校联考期中)(多选)我国南宋数学家杨辉1261年所著的《详解九章算法》一书中展示了二项式系数表,数学爱好者对杨辉三角做了广泛的研究.则下列结论正确的是()A .123367891C C C C +++=B .第2023行的第1012个和第1013个数最大C .第6行、第7行、第8行的第7个数之和为第9行的第7个数D .第34行中从左到右第14个数与第15个数之比为2:3【答案】ABD【解析】A 选项,123678768761C C C 168421321⨯⨯⨯+++=+++=⨯⨯⨯,39987C 84321⨯⨯==⨯⨯,故A 正确;B 选项,由图可知:第n 行有1n +个数字,如果n 是奇数,则第12n +和第112n ++个数字最大,且这两个数字一样大;如果n 是偶数,则第12n+个数字最大,故第2023行的第1012个和第1013个数最大,故B 正确;C 选项,第6行,第7行,第8行的第7个数字分别为:1,7,28,其和为36;第9行第7个数字是84,故C 错误;D 选项,依题意:第34行第14个数字是133434!C 13!21!=⨯,第34行第15个数字是143434!C 14!20!=⨯,所以133443434!C213!21!2:334!C314!20!⨯===⨯,故D 正确.故选:ABD.2.(2024上·江西·高二校联考期末)杨辉三角(如下图所示)是数学史上的一个伟大成就,杨辉三角中从第2行到第2023行,每行的第3个数字之和为()A .32023C B .32024C C .32023C 1-D .32024C 1-【答案】B【解析】()()()()()()()1!C !1!!!+!!1!1!C 1!r r n n n r n n r n n r n r r n r r n r +⋅++⋅-=+=-+--+-()()()()()()11!11!1!!1!C !r n n n n r n r r n r ++⋅++===+-+-,由题意可得,第2行到第2023行,每行的第3个数字之和为2222322232223420233342023442023C C C C C C C C C C C ++++=++++=+++ 323202320232024C C C ==+= ,故选:B .3.(2023上·湖北)如图,“杨辉三角”是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现,比欧洲发现早500年左右.现从杨辉三角第20行随机取一个数,该数大于2023的概率为()A .1321B .1320C .57D .34【答案】A【解析】由杨辉三角的性质知第20行的数为()20C 020,N ii i ≤≤∈,一共有21个数,其中012342020202020C 1,C 20,C 190,C 1140,C 48452023=====>,由杨辉三角的对称性可知,第20行中大于2023的数的个数为214231-⨯=,故所求概率为1321.故选:A.一.单选题1.(2023·四川南充)二项式62x ⎫-⎪⎭的展开式中常数项为()A .60-B .60C .210D .210-【答案】B【解析】展开式的通项为()611216=C 2kkk k T x x --+骣琪-琪桫,所以()()161022k k k -+-´=Þ=,常数项为()2665C 24602k´-=´=,故选:B.2.(2023·河北)若()()()2202020202019201801220201111a x a x x a x x a x +-+-++-= ,则012020a a a +++= ()A.1B.0C.20202D.20212【答案】C【解析】()2020201920182202001220202020(1)(1(1)11)x x a x a x x a x x a x +-+-++-=⎡⎤⎣⎦+-=L Q ,当02020k ≤≤且k ∈N 时,2020kk a C =,因此,01220202020202020202020012202020202a a a C C a C C =++++=+++⋅⋅⋅+L .故选:C.3.(2024上海)二项式30的展开式中,其中是有理项的项数共有()A.4项B.7项C.5项D.6项【答案】D【解析】二项式30的展开式中,通项公式为5153063030rr r r rC C x --⋅⋅=⋅,030r ≤≤,0,6,12,18,24,30r ∴=时满足题意,共6项.故选:D.4.(2023安徽省)在12nx ⎫-⎪⎭的展开式中,只有第5项的二项式系数最大,则展开式中5x 的系数为()A.7-B.358-C.358D.7【答案】D【解析】因为在12n x ⎫-⎪⎭的展开式中,只有第5项的二项式系数最大所以8n =所以812x ⎫-⎪⎭的展开式的通项88218811,0,1,2,,822rrrr r r r T C x C x r +-+⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭令852r +=,得2r =所以展开式中5x 的系数为228172C ⎛⎫-= ⎪⎝⎭故选:D 5.(2023安徽)()6111x x ⎛⎫++ ⎪⎝⎭展开式中2x 的系数为()A.15B.20C.30D.35【答案】D【解析】因为()61x +展开式的通项为6C r r x ,所以()6111x x ⎛⎫++ ⎪⎝⎭展开式中含2x 的项为2261C x ⋅和3631x C x ⋅.因为2366152035C C +=+=,所以()6111x x ⎛⎫++ ⎪⎝⎭展开式中2x 的系数为35.故选:D6.(2023下·四川达州·高二统考期末)()3212x x -+的展开式中,3x 的系数为()A .20B .20-C .15-D .15【答案】B 【解析】()()632112x x x --+=,其展开式的通项为:()616C 1rrr r T x -+=⋅⋅-,取3r =得到3x 的系数为()336C 120⋅-=-.故选:B .7.(2023云南)在71x x ⎛⎫- ⎪⎝⎭的二项展开式中,系数最大的是第()项A.3B.4C.5D.6【答案】C【解析】在二项式71x x ⎛⎫- ⎪⎝⎭的展开式中,通项公式为772+177()()r r r r r r rr T C x x C x ---=⋅⋅-=-,故第r +1项的系数为7(1)r rC -,当0,2,4,6r =时,系数为正,因为0162477777C C C C C <=<<,所以当r =4时,系数最大的项是第5项.故选:C8.(2023·江西赣州·)在52x x ⎛⎫- ⎪⎝⎭的展开式中,下列说法不正确的是()A .不存在常数项B .所有二项式系数的和为32C .第3项和第4项二项式系数最大D .所有项的系数和为1【答案】D【分析】根据给定的二项式,写出展开式判断A ;利用二项式性质判断BC ;利用赋值法计算判断D 作答.【详解】523450514233245555555222222C C C C C C x x x x x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=+⋅-+⋅-+⋅-+⋅-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭53358080321040x x x x x x =-+-+-,因此在52(x x-的展开式中没有常数项,A 正确;52(x x-的展开式的所有二项式系数的和为5232=,B 正确;52(x x -的展开式的第3项和第4项二项式系数相等,并且最大,C 正确;当1x =时,52(x x-的展开式的所有项的系数和为5(1)1-=-,D 错误.故选:D二.多选题9.(2024·辽宁辽阳)若2nx⎛⎝展开式的二项式系数之和为64,则下列结论正确的是()A .该展开式中共有6项B .各项系数之和为1C .常数项为60-D .只有第4项的二项式系数最大【答案】BD【解析】因为二项式系数之和为64,即有264n =,所以6n =,则该展开式中共有7项,A 错误;令1x =,得该展开式的各项系数之和为1,B 正确;通项()()36662166C 21C 2rr rr r r rr T x x---+⎛=⋅⋅=-⋅⋅⋅ ⎝,令3602r -=,得4r =,()442561C 260T =-⨯⨯=,C 错误;二项式系数最大的是36C ,它是第4项的二项式系数,D 正确.故选:BD.10.(2023·辽宁朝阳)已知2,n ,8成等差数列,则在12nx x ⎛⎫- ⎪⎝⎭的展开式中,下列说法正确的是()A .二项式系数之和为32B .各项系数之和为1C .常数项为40D .展开式中系数最大的项为80x【答案】ABD【解析】由题意可得:22810n =+=,则5n =,对于选项A :二项式系数之和为5232=,故A 正确;对于选项B :令1x =,可得各项系数之和为()5211-=,故B 正确;对于选项C 、D :因为512x x ⎛⎫- ⎪⎝⎭的展开式的通项公式为:()()55521551C 21C 2,0,1,2,3,4,5rrr r r r rr T x x r x ---+⎛⎫=-=-⋅⋅= ⎪⎝⎭,所以553135123280804010x x x x x x x x ---⎛⎫-=-+-+- ⎪⎝⎭,展开式中没有常数项,故C 错误;展开式中系数最大的项为80x ,故D 正确;故选:ABD.11.(2022上·辽宁本溪·高二校考期末)若202123202101232021(12)(R)x a a x a x a x a x x -=+++++∈ ,则()A .01220211a a a a ++++=-LB .20211352021312a a a a +++++=C .20210242020132a a a a -++++=D .123202123202112222a a a a++++=- 【答案】AD【解析】由题意,当0x =,2021011a ==,当1x =时,202101232021(1)1a a a a a +++++=-=- ,A 正确;当=1x -时,2021012320213a a a a a -+-+-= ,所以20211352021312a a a a +++++=- ,20210242020312a a a a -++++= ,B ,C 错误;2202120211212202122021111222222a a a a a a ⎛⎫⎛⎫+++=⨯+⨯++⨯ ⎪ ⎪⎝⎭⎝⎭,当12x =时,2202101220211110222a a a a ⎛⎫⎛⎫=+⨯+⨯++⨯ ⎪ ⎪⎝⎭⎝⎭,所以2202112202101111222a a a a ⎛⎫⎛⎫⨯+⨯++⨯=-=- ⎪ ⎪⎝⎭⎝⎭,D 正确.故选:AD .12.(2023下·河北沧州·高二统考期中)已知()112110121123x a a x a x a x -=++++ ,则()A .111231112a a a a ++++=-- B .11135791115a a a a a a +++++=-C .11111231152a a a a ++++=- D .12311231133a a a a ++++=- 【答案】ACD【解析】因为()112110121123x a a x a x a x -=++++ ,令0x =可得1102a =,令1x =可得()11012112311a a a a ++++=-⨯=- ①,所以111231112a a a a ++++=-- ,故A 正确;令=1x -可得()1111012310112315a a a a a a -+-++-=+⨯= ②,①-②得111357911152a a a a a a --+++++=,故B 错误;①+②得110246810152a a a a a a -++++++=,又()1123x -展开式的通项为()11111C 23rrr r T x -+=⋅⋅-(011r ≤≤且N r ∈),所以当r 为奇数时展开式系数为负数,当r 为偶数时展开式系数为正数,即0246810,,,,,0a a a a a a >,1357911,,,,,0a a a a a a <,所以12311a a a a ++++ 1111123101152a a a a a =-+-++-=- ,故C 正确;将()112110121123x a a x a x a x -=++++ 两边对x 求导可得:()102101231133232311x a a x a x a x --=++++ ,再令1x =可得()101231123113323133a a a a ++++=--⨯=- ,故D 正确;故选:ACD 三.填空题13.(2023下·安徽合肥·高二统考期末)已知012233C 4C 4C 4C (1)4C 729n n nn n n n n -+-++-= ,则n 的值为.【答案】6【解析】由012233C 4C 4C 4C (1)4C 729n n nn n n n n -+-++-= ,可得001112220C 1(4)C 1(4)C 1(4)C 1(4)729n n n n nn n n n--⋅⋅-+⋅⋅-+⋅⋅-++⋅⋅-= 则(14)729n -=,即6(3)729(3)n -==-,解得6n =.故答案为:6.14.(2023下·山西吕梁·高二统考阶段练习)20242023被4除的余数为.【答案】1【解析】因为20242024020241202322022202320242024202420242023(20241)C 2024C 2024C 2024C 20241=-=-+--+ ,且2024可以被4整除,所以余数为1.故答案为:1.15.(2023·北京)()82212x x x ⎛⎫-+ ⎪⎝⎭的展开式中常数项为.(用数字作答)【答案】2464-【解析】82x x ⎛⎫+ ⎪⎝⎭的展开式的通项8821882C C 2rr r r r rr T x x x --+⎛⎫=⋅= ⎪⎝⎭(0r =,1,2, (8).当4r =时,其展开式的常数项为448C 21120=;当=5r 时,其展开式中21x的系数为558C 21792=,则()82212x x x ⎛⎫-⋅+ ⎪⎝⎭的展开式中常数项为1120217922464-⨯=-.故答案为:2464-16.(2023上·山东·高二校联考阶段练习)()21nx x ++展开式中各项的系数可以仿照杨辉三角构造如图所示的广义杨辉三角,其性质是以下各行每个数是它正上方和左、右两边三个数的和(不足3个数时,用0补上),则()52(3)1x x x -++的展开式中,7x 项的系数为.【答案】45-【解析】根据题意,可得广义杨辉三角如图所示,可知()521x x ++的展开式中,6x 项的系数为745,x 项的系数为30,所以()()5231x x x -++的展开式中,7x 项的系数为14533045⨯-⨯=-.故答案为:45-四.解答题17.(2023·广东梅州)在二项式()92x y -的展开式中,求:(1)二项式系数之和;(2)各项系数之和;(3)所有偶数项系数之和;(4)系数绝对值之和.【答案】(1)512(2)1(3)9841-(4)19683【解析】(1)设()99872901292.x y a x a x y a x y a y -=++++ 二项式系数之和为012999999C C C C 2512++++== (2)设9987290129()2x y a x a x y a x y a y -=++++ ,则各项系数之和为0129a a a a ++++ ,令1,1,x y ==得()9012921 1.a a a a ++++=-= (3)由(2)知01291,a a a a ++++= 令1,1x y ==-可得:901293,a a a a -+--= 将两式相减,可得:9135791398412a a a a a -++++==-,故所有偶数项系数之和为9841-.(4)方法一:012901239,a a a a a a a a a ++++=-+-+- 令1,1,x y ==-则9012901239319683a a a a a a a a a ++++=-+-+-== 方法二:0129a a a a ++++ 即为()92x y +展开式中各项系数和,令1,1x y ==得90129319683a a a a ++++== 故系数绝对值之和为19683.18.(2023·全国·高二随堂练习)(1)求92x⎛⎝的展开式中的常数项;(2)若621x ax ⎛⎫+ ⎪⎝⎭的展开式中3x 的系数为52,求a 的值;(3)求(10611⎛⎝的展开式中的常数项;(4)若3nx ⎛⎫⎝的展开式中各项系数之和为128,求展开式中31x 的系数.【答案】答案见详解【解析】(1)设92x⎛⎝的展开式通项为:1r T +,则()()1199922199C 2C 21r r rr rr rr T x x r x -----+⎛⎫=⋅⋅-=⋅⋅-⋅ ⎪⎝⎭,当6r =时,6379C 2672T =⨯=;故92x⎛⎝的展开式中的常数项为672;(2)设621x ax ⎛⎫+ ⎪⎝⎭的展开式通项为:1r T +,则()62112316611C C r rrrr r r T xx x a a ---+⎛⎫⎛⎫=⋅⋅=⋅⋅ ⎪ ⎪⎝⎭⎝⎭,当3r =时,结合题意知此时3333334661515C C 222T x x a a a ⎛⎫⎛⎫=⋅⋅=⇒⋅=⇒= ⎪ ⎪⎝⎭⎝⎭;故a 的值为2;(3)设(10611⎛⎫ ⎪⎝⎭、的展开式通项分别为:11r m T H ++、,则3416110C C r m rm r m Tx H x -++==、,当0r m ==时,111T H ⨯=,当3,4r m ==时,454200T H ⨯=,当6,8r m ==时,7945T H ⨯=故(10611⎛⎝的展开式中的常数项为14200454246++=;(4)令1x =,则由题意可知21287n n =⇒=,设3nx ⎛⎫ ⎝的展开式通项为1r T +,则()()2577733177C 3C 31rrr r r r r r T x x x ----+⎛⎫=-=- ⎪⎝⎭,当6r =时,63377C 321T x x --=⨯=,故展开式中31x 的系数为21.19.(2023上·四川攀枝花·高二统考期末)从①第4项的系数与第2项的系数之比是74;②第3项与倒数第2项的二项式系数之和为36;这两个条件中任选一个,再解决补充完整的题目.已知()201221nn n x a a x a x a x -=+++⋅⋅⋅+(*N n ∈),且()21nx -的二项展开式中,____.(1)求n 的值;(2)①求二项展开式的中间项;②求123n a a a a +++⋅⋅⋅+的值.【答案】(1)条件选择见解析,8n =(2)①451120T x =;②831-.【解析】(1)若选择①第4项的系数与第2项的系数之比是74,则有()()()()()()33113112C 211273214244C 21 nn n n n n n n n n ----⋅⋅---⨯⨯=⋅⋅-==,化简可得24400n n --=,求得8n =或7n =-(舍去).若选择②第3项与倒数第2项的二项式系数之和为36,则有()221211C CC C 3622n nnnnn n n nn --+++=+===,化简可得2720n n +-=,求得8n =或9n =-(舍去).(2)由(1)可得8n =,①()821x -的二项展开式的中间项为()()454458C 211120T x x =⋅⋅-=.②二项式()821x -展开式的通项公式为()()()88888C 2112C rrrrr rr x x ---⋅⋅-=-⋅⋅⋅,所以0a 、2a 、4a 、6a 、8a 为正数,1a 、3a 、5a 、7a 为负数.在()828012821x a a x a x a x -=+++⋅⋅⋅+中,令00,1x a ==.再令1x =-,可得801238123831a a a a a a a a a =-+-+⋅⋅⋅+=++++⋅⋅⋅+,∴1238831a a a a +++⋅⋅⋅+=-.20.(2023下·江苏宿迁·高二统考期中)在()2021212222121D D D D D nn n n n nn n n n n x x x x x x ---++=+++++L 的展开式中,把0122,,,D D D D ,nn n n n 叫做三项式的n 次系数列.(1)求02463333D D D D +++的值;(2)根据二项式定理,将等式2(1)(1)(1)n n n x x x +=++的两边分别展开,可得左右两边的系数对应相等,如()()()()2222122C C C C C n n n nnnn=++++ ,利用上述思想方法,求001122202120212022202220232023202320232023202320232023202320232023202320232023D C D C D C D C D C D C -+--+- 的值.【答案】(1)14(2)0【解析】(1)230615563333(1)D D D D x x x x x ++=++++ 令1x =得:3015633333D D D D =++++ ①令=1x -得:015633331D D D D =-+-+ ②①+②得:02463333282(D D D D )=+++,所以02463333D D D D 14+++=.(2)因为321(1)(1)x x x x -=-++所以()202332023220231(1)(1)x x x x -=-++,右边展开式中含4046x 项的系数为001122202120212022202220232023202320232023202320232023202320232023202320232023D C D C D C D C D C D C -+--+- ,而展开式中左边含4046x 项的系数为0,所以001122202120212022202220232023202320232023202320232023202320232023202320232023D C D C D C D C D C D C 0-+--+-= .21.(2023北京)在()20122112121221D D D D D D D nr r r r n n n nn n n n n n n x x x x x x x x ++--++=+++⋅⋅⋅+++⋅⋅⋅++中,把0122D ,D ,D ,,D nn n n n ⋅⋅⋅叫做三项式系数.(1)当2n =时,写出三项式系数0123422222D ,D ,D ,D ,D 的值;(2)()()*na b n N +∈的展开式中,二项式系数可用杨辉三角表示,如图:第1行11第2行121第3行1331第4行14641第5行15101051…………当04n <≤,*n ∈N 时,类比杨辉三角,请列出三项式系数表;(3)求011223398989999999999999999999999999999D C D C D C D C D C D C -+-+⋅⋅⋅+-的值(可用组合数作答).【答案】(1)02D 1=,12D 2=,22D 3=,32D 2=,42D 1=;(2)系数表见解析;(3)3399C .【解析】(1)因为()2223411232x x x x x x ++=++++,所以02D 1=,12D 2=,22D 3=,32D 2=,42D 1=.(2)当04n <≤,*n ∈N 时,三项式系数表如下:第1行111第2行12321第3行1367631第4行14101619161041(3)()()()9999201223319719719819899999999999911D D D D D D x x x x x x x x++⋅-=++++⋅⋅⋅++()09919829798999999999999C C C C C x x x x ⋅-+-⋅⋅⋅++,其中含99x 项的系数为0011229898999999999999999999999999D C D C D C D C D C -+-⋅⋅⋅+-,又()()()99999923111x x x x ++⋅-=-,()9931x -的展开式中的第1r +项为()()9931991C rrrr T x -+=-,令()39999r -=,解得66r =,所以含99x 项的系数为66339999C C =;所以001122339898999966339999999999999999999999999999D C D C D C D C D C D C C C -+-+⋅⋅⋅+-==.22.(2023上·上海松江·高二上海市松江二中校考阶段练习)已知函数()y f x =,*x ∈N ,满足:①对任意*,a b ∈N ,都有()()()()af a bf b af b bf a +>+;②对任意*n ∈N 都有()3f f n n ⎡⎤=⎣⎦.(1)试证明:()f x 为*N 上的严格增函数;(2)求()()()1628f f f ++;(3)令()3nn a f =,*n ∈N ,试证明:121111424n n n a a a ≤+++<+ .【答案】(1)证明见解析(2)66。
人教版(新教材)高中数学第一册(必修1)精品课件:第一章集合与常用逻辑用语章末复习课

【例1】 (1)设集合A={1,2,4},集合B={x|x=a+b,a∈A,b∈A},则集合B中元
素的个数是( )
A.4
B.5
C.6
D.7
(2)已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是( )
A.1
B.3
ቤተ መጻሕፍቲ ባይዱ
C.5
D.9
解析 (1)∵a∈A,b∈A,x=a+b,所以x=2,3,4,5,6,8,∴B中有6个元素, 故选C. (2)当x=0,y=0时,x-y=0;当x=0,y=1时,x-y=-1;当x=0,y=2时,x-y =-2;当x=1,y=0时,x-y=1;当x=1,y=1时,x-y=0;当x=1,y=2时,x -y=-1;当x=2,y=0时,x-y=2;当x=2,y=1时,x-y=1;当x=2,y=2时, x-y=0.根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个. 答案 (1)C (2)C
【训练4】 (1)若p:x2+x-6=0是q:ax+1=0的必要不充分条件,则实数a的值为 ________. (2) 若 - a<x< - 1 成 立 的 一 个 充 分 不 必 要 条 件 是 - 2<x< - 1 , 则 a 的 取 值 范 围 是 ________.
解析 (1)p:x2+x-6=0,即x=2或x=-3. q:ax+1=0,当 a=0 时,方程无解;当 a≠0 时,x=-1a. 由题意知p q,q p,故a=0舍去;
当 a≠0 时,应有-1a=2 或-1a=-3,解得 a=-12或 a=13. 综上可知,a=-12或 a=13. (2)根据充分条件、必要条件与集合间的包含关系,应有{x|-2<x<-1} {x|-a<x< -1},故有a>2. 答案 (1)-12或13 (2)a>2
高三数学集合的概念及运算知识精讲

高三数学集合的概念及运算【本讲主要内容】集合的概念及运算【知识掌握】 【知识点精析】集合的基本概念及其表示法掌握之后,研究集合的关系,运算是后续基础知识,与第一讲的知识点构成集合的整体;为以后运用集合工具形成集合思想打基础。
1. 集合间的关系是包含与不包含,相等与不相等的关系,集合A 与集合B 之间的关系很直观地用文代图示于:A 是B 的子集⇔A 包含于B (B 包含A )A 不是B 的子集⇔A 不包含于B (B 不包含A )A 是B 的子集且B 是A 的子集⇔A 、B 相等客观存在很多如上关系,如数集之间的关系2. 集合的运算,由已知集合中的元素构造出与之相关的新集合,可以写作是已知集合的运算结果,定义运算是人为的,常用的集合运算有:(以两个集合为例)① 交集——由两个集合中的公共元素构成的集合。
② 并集——由两个集合中的所有元素构成的集合。
③ 补集——存在于全集中的某个集合的补集是由非本集合中的全集中其它元素构成的集合。
三. 要认识到以下几点:第一,从运算的角度认识“交集”、“并集”、“补集”运算的对象与结果都是集合。
第二,从相互间的联系认识运算的结果,结果又是集合家族的繁衍。
第三,运用变化的联系的观点认识不同关系下各种运算的结果,有怎样的联系。
第四,定义从两个集合的运算为基础,可扩展到多个集合间的运算。
四. 知识讲解程序: (一)集合间的关系1. 子集:设A 、B 是两个集合,如果集合A 中的任意一个元素都是集合B 中的元素,则称这两个集合有包含关系,且称A 是B 的子集,记作B A ⊆(或A B ⊇)(读作A 包含于B 或B 包含A )说明:① 两个集合具有包含关系亦即一个集合是另一个集合的子集。
② 符号语言:A 是B 的子集⇔B A ⊆(读作A 包含于B )⇔A B ⊇(B 包含A )⇔A x ∈∀,都有B x ∈。
③ 图形语言(Venn 图示)思考:两图是否符合子集定义?2. 相等:如果A 是B 的子集,且B 是A 的子集,则称两个集合相等,记作A=B 。
高三数学(文)函数y=f(x)对称性与周期性关系人教版知识精讲

高三数学(文)函数y=f(x)对称性与周期性关系人教版【本讲教育信息】教学内容:函数y f (x)对称性与周期性关系【典型例题】1.定义在R上的函数f (x),若总有f (a x) f (a x)成立,贝U函数f(x)的图象是关于直线x a成轴对称图形。
反之,若函数 f (x)的图象关于直线x a成轴对称图形,则必有f (a x) f (a x)推论,对于定义在R上的函数,若有f (a x) f (b x),则f (x)图象关于直线x旦b成轴对称图形,反之亦真。
2证明:若对x R,总有f (a x) f (a x),设点(x°, f(x。
)),在y f (x)的图象上,点(x o,f (x o))关于x a 的对称点(2a x°, f(x°)),由f(x°) f[a (a x。
)]f[a (a X o)] f (2a x°),则点(2a X o,f(x。
))在函数y f (x)的图象上,由x°的任意性知f (x)的图象关于直线x a对称,反之证明略。
◎ x t2 a b a b推论,由f (a x) f (b x) f (- - t) f (— - t)显然2 2[例1]已知f(x) x2 bx c,满足f( 1 x) f( 1 x)且f(0) 3,当x 0 时,比较f (b x)与f (c x)的大小。
解:由f( 1 x) f( 1 x)知f(x)关于x 1对称,故b 2,又由f(0) 3知c 3,贝U f (x)在(,1]递减,在[1,)上递增。
当x 0 时,3x 2x 1 ••• f (3x) f(2x)即f(b x) f (c x)当x 0 时,0 3x 2x 1 •••f(3x) f(2x),即f(b x) f (c x)1[例4]设f(x)对任意x R ,满足f(3 x) f (3 x)且方程f(x) 0恰有6个不同的 实根,则此六个实根之和为 ________ 。
(完整版)人教版高中数学必修一第一章知识点
第一章 集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示(1)集合的概念集合中的元素具有确定性、互异性和无序性. (2)常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.(3)集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. (4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. (5)集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系(6)子集、真子集、集合相等(7)已知集合A 有(1)n n ≥个元素,则它有2n 个子集,它有21n -个真子集,它有21n -个非空子集,它有22n-非空真子集.(8)交集、并集、补集【1.1.3】集合的基本运算名称记号意义性质示意图交集A B{|,x x A∈且}x B∈(1)A A A=(2)A∅=∅(3)A B A⊆A B B⊆BA并集A B{|,x x A∈或}x B∈(1)A A A=(2)A A∅=(3)A B A⊇A B B⊇BA补集U A {|,}x x U x A∈∉且1()UA A=∅2()UA A U=【补充知识】含绝对值的不等式与一元二次不等式的解法(1)含绝对值的不等式的解法不等式解集||(0)x a a<>{|}x a x a-<<||(0)x a a>>|x x a<-或}x a>||,||(0) ax b c ax b c c+<+>>把ax b+看成一个整体,化成||x a<,||(0)x a a>>型不等式来求解(2)一元二次不等式的解法判别式24b ac ∆=-∆>0∆=0∆<二次函数2(0)y ax bx c a=++>的图象O一元二次方程20(0) ax bx c a++=>的根21,242b b acxa-±-=(其中12)x x<122bx xa==-无实根20(0) ax bx c a++>>的解集1{|x x x<或2}x x>{|x}2bxa≠-R ()()()U U UA B A B=()()()U U UA B A B=〖1.2〗函数及其表示 【1.2.1】函数的概念(1)函数的概念①设A 、B 是两个非空的数集,如果按照某种对应法则f,对于集合A 中任何一个数x ,在集合B中都有唯一确定的数()f x 和它对应,那么这样的对应(包括集合A ,B 以及A 到B 的对应法则f )叫做集合A 到B 的一个函数,记作:f A B →.②函数的三要素:定义域、值域和对应法则.③只有定义域相同,且对应法则也相同的两个函数才是同一函数. (2)区间的概念及表示法①设,a b 是两个实数,且a b <,满足a x b ≤≤的实数x 的集合叫做闭区间,记做[,]a b ;满足a xb <<的实数x 的集合叫做开区间,记做(,)a b ;满足a x b ≤<,或a x b <≤的实数x 的集合叫做半开半闭区间,分别记做[,)a b ,(,]a b ;满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞. 注意:对于集合{|}x a x b <<与区间(,)a b ,前者a 可以大于或等于b ,而后者必须a b <.(3)求函数的定义域时,一般遵循以下原则:①()f x 是整式时,定义域是全体实数.②()f x 是分式函数时,定义域是使分母不为零的一切实数.③()f x 是偶次根式时,定义域是使被开方式为非负值时的实数的集合.④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1. ⑤tan y x =中,()2x k k Z ππ≠+∈.⑥零(负)指数幂的底数不能为零. ⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集.⑧对于求复合函数定义域问题,一般步骤是:若已知()f x 的定义域为[,]a b ,其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出.⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论. ⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义. (4)求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,只是提问的角度不同.求函数值域与最值的常用方法:①观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值.②配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的值域或最值. ③判别式法:若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=,则在()0a y ≠时,由于,x y 为实数,故必须有2()4()()0b y a y c y ∆=-⋅≥,从而确定函数的值域或最值.④不等式法:利用基本不等式确定函数的值域或最值.⑤换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题.⑥反函数法:利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值. ⑦数形结合法:利用函数图象或几何方法确定函数的值域或最值. ⑧函数的单调性法.【1.2.2】函数的表示法(5)函数的表示方法表示函数的方法,常用的有解析法、列表法、图象法三种.解析法:就是用数学表达式表示两个变量之间的对应关系.列表法:就是列出表格来表示两个变量之间的对应关系.图象法:就是用图象表示两个变量之间的对应关系. (6)映射的概念①设A 、B 是两个集合,如果按照某种对应法则f,对于集合A 中任何一个元素,在集合B 中都有唯一的元素和它对应,那么这样的对应(包括集合A ,B 以及A 到B 的对应法则f )叫做集合A 到B 的映射,记作:f A B →.②给定一个集合A 到集合B 的映射,且,a A b B ∈∈.如果元素a 和元素b 对应,那么我们把元素b 叫做元素a 的象,元素a 叫做元素b 的原象.yxo〖1.3〗函数的基本性质 【1.3.1】单调性与最大(小)值(1)函数的单调性①定义及判定方法 函数的 性 质定义图象判定方法 函数的 单调性如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x .1.< x ..2.时,都有f(x ...1.)<f(x .....2.).,那么就说f(x)在这个区间上是增函数.... x 1x 2y=f(X)xy f(x )1f(x )2o(1)利用定义(2)利用已知函数的单调性(3)利用函数图象(在某个区间图象上升为增) (4)利用复合函数 如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x .1.< x ..2.时,都有f(x ...1.)>f(x .....2.).,那么就说f(x)在这个区间上是减函数.... y=f(X)yxox x 2f(x )f(x )211(1)利用定义(2)利用已知函数的单调性(3)利用函数图象(在某个区间图象下降为减) (4)利用复合函数②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数. ③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为减,()u g x =为减,则[()]y f g x =为增;若()y f u =为增,()ug x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则[()]y f g x =为减.(2)打“√”函数()(0)af x x a x=+>的图象与性质()f x 分别在(,]a -∞-、,)a +∞上为增函数,分别在[,0)a 、]a 上为减函数.(3)最大(小)值定义 ①一般地,设函数()y f x =的定义域为I,如果存在实数M 满足:(1)对于任意的x I ∈,都有()f x M≤;(2)存在0x I ∈,使得0()f x M=.那么,我们称M 是函数()f x 的最大值,记作max ()f x M=.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法 函数的 性 质定义图象判定方法 函数的 奇偶性如果对于函数f(x)定义域内任意一个x ,都有f(..-.x)=...-.f(x)....,那么函数f(x)叫做奇函..数..(1)利用定义(要先判断定义域是否关于原点对称)(2)利用图象(图象关于原点对称)如果对于函数f(x)定义域内任意一个x ,都有f(..-.x)=...f(x)....,那么函数f(x)叫做偶函数....(1)利用定义(要先判断定义域是否关于原点对称)(2)利用图象(图象关于y 轴对称) ②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y 轴两侧相对称的区间增减性相同,偶函数在y 轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.〖补充知识〗函数的图象(1)作图利用描点法作图:①确定函数的定义域; ②化解函数解析式; ③讨论函数的性质(奇偶性、单调性); ④画出函数的图象. 利用基本函数图象的变换作图:要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象. ①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴 ()()y f x y f x =−−−→=--原点1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象,并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去(2)识图对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系. (3)用图函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具.要重视数形结合解题的思想方法.。
高三数学文函数的奇偶性 知识精讲 试题

高三数学〔文〕函数的奇偶性人教版本卷贰O 贰贰年贰月捌日编写; 出题人:令狐学复;欧阳化语;令狐理总。
【本讲教育信息】一. 教学内容:函数的奇偶性 1. 概念一般地,对于函数)(x f y =〔1〕假如对于函数定义域内任意一个x ,都有)()(x f x f -=-,那么函数)(x f y =就叫奇函数。
〔2〕假如对于函数定义域内任意一个x ,都有)()(x f x f =-,那么函数)(x f 就叫做偶函数。
注:① 函数为奇函数或者偶函数的一个必要条件是函数的定义域关于原点对称 ② 对于)()(x f x f -=-与)()(x f x f =-应从数形两方面理解 ⎭⎬⎫值域的对称性定义域的对称性点),(y x 的对称性,即函数图象的对称性⎪⎪⎭⎪⎪⎬⎫-==-'⇔=--=-=--'⇔-=-)(),(),(),,()()()(),(),(),,()()(a f b a f b b a P b a P x f x f a f b a f b b a P b a P x f x f P 与P '均在)(x f y =图象上③ 刻画的为函数的整体性质 2. 奇偶性的性质〔1〕奇函数的图象关于原点成中心对称图形,反过来,假如一个函数的图象关于原点成中心对称图形,那么此函数是奇函数。
证〔⇒〕设函数)(x f 是奇函数,那么)()(x f x f -=-,在函数)(x f y =图象上任取一点P 〔)(,a f a 〕,那么))(,(a f a P --'即))(,(a f a P --'也是图象上一点,而P '是P 关于原点O 的对称点,所以函数y )(x f =图象上任意一点关于原点的对称点都在)(x f y =图象上,即)(x f y =的图象关于原点成中心对称〔⇐〕设)(x f y =图象成中心对称,在)(x f y =图象上任取一点P 〔)(,a f a 〕,那么P 关于原点的对称点P '〔)(,a f a --〕也在)(x f y =上∵ a x -=时,)()(a f x f -=而函数值是唯一的,∴ )()(a f a f -=- 由x 的任意性知,在)(x f 的定义域内有)()(x f x f -=-,故)(x f 为奇函数〔2〕偶函数的图象关于y 轴成轴对称图形,反过来,假设一个函数的图象关于y 轴成轴对称图形,那么此函数是偶函数。
高三数学(文)抛物线复习(一)知识精讲 人教版

高三数学(文)抛物线复习(一)知识精讲 人教版一. 本周教学内容:抛物线复习(一) (一)抛物线基础知识 1. 定义:平面内到定点和定直线(定点不在定直线上)距离相等的点的轨迹,若定点在定直线上,则轨迹为一条直线即过定点且与定直线垂直的直线。
2. 性质:图形标准方程 px y 22= (0>p )px y 22-= (0>p )py x 22= (0>p )py x 22-= (0>p )焦点坐标 (0,2p) (0,2p-)(2,0p )(2,0p -)准线方程2p x -=2p x =2p y -=2p y =3. 直线与抛物线位置关系把直线方程与抛物线方程联立得关于x 或y 的一元二次方程,利用∆判别式判定它们的位置关系。
【典型例题】[例1] 已知抛物线px y 22=(0>p )上的一点,M 到定点A (4,27)和焦点F 的距离之和的最小值等于5,求抛物线的方程。
解:(1)当点A 在抛物线内部时,27242⋅<p 即716>p 时,MA A M MA MF +'=+ 当A 、M 、A '共线时5)(min =+MA MF故3232752=⇒=-=p p ,满足7163> 所以抛物线方程为x y 62=(2)当点A 在抛物线外部或在抛物线上时27242⋅≥p 即7160≤<p 时,连AM 交抛物线于M ,此时最小)(MF MA + 即5min =AF ,254)227(22=+-p 3227±=-p 1=⇒p 或13=p (舍)抛物线方程x y 22=综上抛物线方程为x y 62=或x y 22=[例2] 在抛物线x y 22=上求一点P ,使点P 到直线03=+-y x 的距离最短。
解法1:设P (00,y x )为抛物线上任意一点,则P 到l 距离2200113++-=y x d5)1(22162221322120020020+-=+-=+-⋅=y y y y y由R y ∈0,则10=y 时,245225min ==d 解法2:设与03=+-y x 平行的直线l 的方程为:0=+-c y x (3≠c ) 当l 与抛物线相切时,切点到03=+-y x 的距离最短将22y x =代入0=+-c y x 中得022=+-c y y ,2102141=⇒=⨯-=∆c c 2452213=-=d[例3] 抛物线x y 42=,过其焦点作一弦AB ,如果弦长不超过8,且弦所在的直线与椭圆22322=+y x 相交,试确定弦AB 所在直线倾斜角α的X 围。
高三数学第一轮复习:角函数总结及统练人教版(文)知识精讲

高三数学第一轮复习:角函数总结及统练人教版(文)【本讲教育信息】一. 本周教学内容:三角函数总结及统练(一)基础知识1. 与角α终边相同的角的集合},2{Z k k S ∈+==απβ2. 三角函数的定义(六种)——三角函数是x 、y 、r 三个量的比值3. 三角函数的符号——口诀:一正二弦,三切四余弦。
4. 三角函数线正弦线MP=αsin 余弦线OM=αcos 正切线AT=αtan5. 同角三角函数的关系 平方关系:商数关系:倒数关系:1cot tan =⋅αα1csc sin =⋅αα1sec cos =⋅αα 口诀:凑一拆一;切割化弦;化异为同。
ααπ+k 2 α- απ- απ+απ-2 απ-2απ+2正弦 αsin αsin - αsin αsin - αsin - αcos αcos 余弦 αcos αcos αcos - αcos - αcos αsin αsin - 正切 αtan αtan - αtan - αtan αtan - αcot αcot - 余切αcotαcot -αcot -αcotαcot -αtanαtan -⎪⎪⎩⎪⎪⎨⎧⋅+-=-⋅-+=+⇒⎪⎪⎩⎪⎪⎨⎧⋅+⋅=-⋅-⋅=+⋅-⋅=-⋅+⋅=+βαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαtan tan 1tan tan )tan(tan tan 1tan tan )tan(sin sin cos cos )cos(sin sin cos cos )cos(sin cos cos sin )sin(sin cos cos sin )sin( 8. 二倍角公式——代换:令αβ=⎪⎪⎩⎪⎪⎨⎧-=-=-=-=⋅=ααααααααααα22222tan 1tan 22tan sin cos sin 211cos 22cos cos sin 22sin 降幂公式⎪⎪⎩⎪⎪⎨⎧+=-=22cos 1cos 22cos 1sin 22αααα半角公式:2cos 12sinαα-±=;2cos 12cos αα+±=;αααcos 1cos 12tan +-±=αααααcos 1sin sin cos 12tan+=-=9. 三角函数的图象和性质函数x y sin =x y cos = x y tan =图象定义域RR⎭⎬⎫⎩⎨⎧∈+≠∈Z k k x R x x ,2|ππ且10. 函数)sin(ϕω+=x A y 的图象变换 0,0>>ωA函数)sin(ϕω+=x A y 的图象可以通过下列两种方式得到:(1)−−−−−−−−−→−+=−−−−→−=倍横坐标缩短到原来的图象左移ωϕϕ1)sin(sin x y x y )sin(ϕω+=x y )sin(ϕω+=−−−−−−−−−→−x A y A 倍纵坐标伸长为原来的(2)−−−−→−=−−−−−−−−−→−=ωϕωω图象左移倍横坐标缩短到原来的)sin(sin 1x y x y )sin(ϕω+=x y )sin(ϕω+=−−−−−−−−−→−x A y A 倍纵坐标伸长为原来的(二)数学思想与基本解题方法1. 式子变形原则:凑一拆一;切割化弦;化异为同。
高三数学(文)抛物线部分 知识精讲 人教版

高三数学(文)抛物线部分 知识精讲 人教版【本讲教育信息】一. 教学内容:抛物线部分【典型例题】[例1] 如图所示,F 为抛物线)0(22>=p px y 的焦点,A (4,2)为抛物线内一定点,P 为抛物线上一动点,PF PA +的最小值为8。
(1)求抛物线的方程;(2)若 O 为坐标原点,问是否存在点M ,使过点M 的动直线与抛物线交于B 、C 两点。
且︒=∠90BOC ,证明你的结论。
解:(1)由抛物线性质可知min )(PF PA +84282=⇒+=⇒+=p px p A 故抛物线方程为x y 162=(2)若斜率存在,设过M 的直线方程为b kx y +=,显然0≠k ,0≠b ,直线交抛物线于B 、C由0190=⋅+⋅⇒-=⋅⇒︒=∠C B C B CO BO y y x x k k BOC由k by y b y ky xy b kx y C B 16016161622=⋅⇒=+-⇒⎩⎨⎧=+=2222216k b y y x x C B C B =⋅=⋅⇒故01622=+k bkb k b 16-=⇒动直线方程为k kx y 16-=即)16(-=x k y[例2] 已知抛物线x y 42=的准线与x 轴交于M 点,过M 作直线与抛物线交于A 、B 两点,若AB 的垂直平分线与x 轴交于E (0,0x )。
(1)求0x 的取值X 围;(2)ABE ∆能否是正三角形?若能,求0x 的值;若不能,请说明理由。
解:(1)由题意得直线l :)1(+=x k y ,代入x y 42=,得0)2(22222=+-+k x k x k由04)2(4422>--=∆k k ,则11<<-k ,且0≠k设方程两根21,x x 分别为A 、B 两点的横坐标,则其中点坐标为)2,2(22k kk - 则AB 的垂直平分线方程为)2(1222k k x k k y ---=- 令0=y ,得3312020>⇒>+=x kx(2)若ABE ∆为正三角形,则点E 到AB 的距离d 为AB 的23倍由k k d 212+=(221122sin kk BME ME HE ++=∠⋅=)2414k k AB -=,得23341214232224±=⇒=⇒+=-⋅k k k k k k3111220=+=kx[例3] 已知抛物线C :y x 22=,点A (a ,0),如果抛物线C 上到点A 距离最近的是抛物线C 的顶点,那么a 的取值X 围是()A. 1=aB. 10≤≤aC. 1≤aD. 0≤a 解法一:从方程角度看命题的等价转化方程组⎪⎩⎪⎨⎧=-+=)2()()1(22222a a y x y x 只有一解⇔方程0)22(2=-+y a y (3)在),0[+∞上只有一个解0=y由(3)有两个解22,021-==a y y ,故022≤-a解法二:从函数角度看命题的等价转化 函数22)(a y x d -+=(当0==y x 时,有最小值a )⇔函数22)22(a y a y +-+(在定义域),0[+∞的左端点取最小值)这样只须令二次函数22)22(a y a y +-+的对称轴位于原点的左侧,即0222≤-a 解法三:从不等式角度看命题的转化关于x 、y 的不等式222)(a a y x ≥-+(4)(对一切满足y x 22=的实数成立,且0==y x 时,等号成立)⇔关于y 的不等式0)22(2≥-+y a y (5)(在),0[+∞上成立,且0=y 时等号成立)由于(5)的解集是“两根之外”,因此),0[+∞应在大根之外,故另一根022≤-a[例4] 已知抛物线)0(22>=p px y 过动点M (0,a )且斜率为1的直线l 与抛物线交于不同的两点A 、B ,p AB 2≤。
高三数学(文)函数的周期性人教版知识精讲

高三数学(文)函数的周期性人教版【本讲教育信息】一. 教学内容:函数的周期性(一)概念对于函数)(x f y =,如果存在一个不为零的常数T ,使得当x 取定义域内的每一个值时,)()(x f T x f =+都成立,则把函数)(x f y =叫做周期函数,不为零的常数T 叫做这个函数的周期,如果在所有的周期中存在着一个最小的正数,这个最小的正数叫最小正周期。
注:(1)周期函数的周期T 未必是正数未必有正周期如:]0,(,sin -∞∈=x x y ,显然π2-=T 是函数的一个周期,故x y sin =,]0,(-∞∈x 是周期函数,假设)(x f 有一个正周期T ',当)0,(T x '-∈时,]0,(-∞∉'+T x ,故)(T x f '+无意义,所以]0,(,sin -∞∈=x x y 不存在正周期。
(2)若T 是周期函数的周期,T -未必是函数的一个周期,但若)(x f 是定义在R 上的周期函数,则成立。
如]0,(,sin -∞∈=x x y ,π2-是函数的一个周期,而π2不是周期。
(3)有正周期的周期函数,未必有最小正周期如⎩⎨⎧=为无理数为有理数x x x D ,0,1)(任一有理数是)(x f 的一个周期,因有理数不存在最小正数,故所给函数不存在最小正周期。
(4)周期函数的周期不止一个事实上,如果T 是周期函数)(x f 的周期,用数学归纳法易证nT (*N n ∈)也是)(x f 的周期,换言之,一个周期函数必有其周期集合,且此集合是一个至少一方无界的无穷点集。
(5)周期函数的定义域至少是一方无界因函数的周期集合是定义域的子集,由(4)知周期集合至少一方无界,故定义域至少一方无界。
(6)周期函数的定义域内的点不一定是连续的,可能是有间断的,如函数),(1Z n n x y ∈==是周期函数,定义域是整数集。
(7)两个周期函数的和未必是周期函数 如x x x f 2sin cos )(+=,假设)(x f 是以T 为周期的周期函数 则x x T x T x 2sin cos )(2sin )cos(+=+++,对任R x ∈恒成立令T x x -==,0代入上式,有⎪⎩⎪⎨⎧=-=+⇒⎪⎩⎪⎨⎧-+-=++=+12sin cos 12sin cos )(2sin )cos(0sin 0cos 0sin 0cos 2sin cos T T T T T T T T )(22)(202sin 1cos Z n n T Z m m T T T ∈=∈=⇒⎩⎨⎧==⇒ππ ∵0≠T ∴0≠⋅n m 于是nm 42=矛盾,故)(x f 非周期函数(二)性质1. 设)(x f 是以T 为周期的函数,证明(1)对任意正整数n ,nT 也是)(x f 的周期(2))(x f 有最小正周期T ,则)(x f 的所有周期都是T 的整数倍注:若)(x f 是定义在R 上的周期函数,则(1)中Z n ∈证:(1))(])1([])1([)(x f T n x f T T n x f nT x f ==-+=+-+=+(2)设t 是)(x f 的任意一个周期,且T t ≠,则存在N n ∈,使r nT t +=(T r <≤0)若0>r ,则 )()()()(r x f r nT x f t x f x f +=++=+=,即r 也是)(x f 正周期,而T r <与T 的最小性矛盾,故nT t r ==,02.(1)若)(x f 是数集A 上的周期函数,则)(1x f 是数集},0)(|{A x x f x ∈≠上的周期函数 (2)若)(x f 有最小正周期T ,则T 也是函数)(1x f 的最小正周期 证: (1)设T 为)(x f 周期,则任A x ∈,A T x ∈+,且0)(≠x f 有)()(x f T x f =+从而)(1)(1x f T x f =+,即T 是)(1x f 的周期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学(文)集合人教版
【同步教育信息】
一. 本周教学内容:
集合
二. 复习目标:
理解集合、子集、交集、并集、补集的概念,了解空集和全集的意义,了解属于、包含、相等关系的意义,能够掌握有关术语和符号、能正确地表示一些简单的集合。
【典型例题】
[例1] 设集合}01|{<<-=m m P ,044|{2<-+∈=mx mx R m Q 对任意实数x 恒成立},则下列关系中成立的是( )
A. Q P ≠⊂
B. P Q ≠⊂
C. Q P =
D. Q Q P =⋂
解:对集合Q :0442<-+m mx 对R x ∈恒成立
(1)当0=m 时,04<-适合
(2)当0<m 时,由0)4(4)4(2
<--=∆m m 解得010100
2<<-⇔⎩⎨⎧<<-<⇔⎩⎨
⎧<+<m m m m m m 则}01|{≤<-=m m Q 故Q P ≠⊂ 答案:A
小结:本题主要考察集合的关系,集合的表示法,要注意描述法中代表元素m 的含义。
[例2](1)已知},1|),{(2R x x y y x A ∈-==,},7|),{(2R x x y y x B ∈-==,
则B A ⋂= 。
(2)已知},1|{2R x x y y A ∈-==,},7|{2R x x y y B ∈-==,则=⋂B A 。
解:
(1)由⎪⎩⎪⎨⎧-=-=2271x
y x y 解得⎩⎨⎧=-=32y x 或⎩⎨⎧==32y x 即曲线12-=x y 和27x y -=的两个交点分别为(2-,3)和(2,3),故)}3,2(),3,2{(-=⋂B A
(2)集合P 和Q 分别表示一元二次函数12-=x y 和27x y -=的值域,则 }1|{-≥=y y A ,}7|{≤=y y B
故}71|{≤≤-=⋂y y B A
[例3] 设集合}08147|{23=-+-=x x x x A ,}0,022|{2223≥=--+=c c x c x x x B
(1)求A 、B
(2)取集合B A ⋃中的元素作一元二次方程:02
=++q px x 的两个根,试在函数)(x f q px x ++=2的最小值中,求出最小的值。
解:
(1)由)4)(2)(1(81472
3---=-+-x x x x x x ,则=A {1,2,4}
由))()(2(222223c x c x x c x c x x -++=--+则
① 当0=c 时,B={2-,0}
② 当2=c 时,}2,2{-=B
③ 当0≠c ,2≠c 时,},,2{c c B --=
(2)设方程02=++q px x 的根为b a , 由)4(4
1)4(41)(22min q p p q x f --=-=根据韦达定理有p b a -=+,q ab = 则22min )(4
1]4)[(41)(b a ab b a x f --=-+-= 因此,当||b a -取最大值时,)(min x f 有最小值2)(4
1b a -- ① 当≥c 4时,||b a -最大值为c c c 2)(=--
故)(min x f 有最小值22)2(4
1c c -=⋅- ② 当42<≤c 时,||b a -最大值为c c +=--4)(4
故)(min x f 有最小值2)4(4
1c +- ③ 当20<≤c 时,||b a -最大值为6)2(4=--
故)(min x f 有最小值964
12-=⋅- 小结:注意(1)中要讨论0=c 和2=c 情况不能只写成},,2{c c B --=,因为根据集合元素的互异性,这种写法表示B 中有且只有三个元素。
[例4] 已知集合},12|{Z n n x x N ∈+==,},14|{Z ∈±==m m x x M ,则下列正确的是( )
A. M N ⊆
B. M N ⊇
C. M N =
D. M N ≠
解:},1)12(21)2(2|{Z ∈+-=+==m m x m x x N 或
},1414|{Z ∈-=+==m m x m x x 或
},14|{Z ∈±==m m x x
M =
答案:C
小结:判断集合相等时,可以变形集合中属性的形式,也可以利用集合之间的相互包含的关系,如例5。
[例5] 已知},,|{221Z ∈Z ∈-==y x y x m m M ,∈=+==k k m k m m M ,412|{2或
Z},求证21M M =。
证:设1M m ∈,则存在x 、y Z ∈,使))((22y x y x y x m -+=-=
(1)若x ,y 一奇一偶,则y x ±均为奇数,则m 也为奇数,即12+=k m ,Z ∈k ,2M m ∈
(2)若x 、y 同奇同偶,则y x ±均为偶数,故m 为4的倍数,即k m 4=,Z ∈k ,2M m ∈,综上,有21M M ⊆
设2M m ∈,则12+=k m 或k m 4=,Z ∈k
① 若12+=k m ,则22)1(k k m -+=,则1M m ∈
② 若k m 4=,则22)1()1(--+=k k m ,则1M m ∈
综上12M M ⊆,所以21M M =
[例6] 设I 为全集,1S 、2S 、3S 是I 的三个非空子集,且I S S S =⋃⋃321,则下列论断正确的是( )
A. φ=⋃⋂)(311S S S C I
B. 321S C S C S I I ⋂⊆
C. φ=⋂⋂321S C S C S C I I I
D. 321S C S C S I I ⋃⊆ 解:利用摩根律,有)(321321S S S C S C S C S C I I I I ⋃⋃=⋂⋂
又 I S S S =⋃⋃321,则φ=⋂⋂321S C S C S C I I I
[例7] 设12)(+=n n f ,N n ∈,=P {1,2,3,4,5},Q={3,4,5,6},记)(|{n f N n P ∈=∧
}P ∈,})(|{Q n f N n Q ∈∈=∧,则)()(∧∧∧∧⋂⋃⋂P C Q Q C P N N =( )
A. {0,3}
B. {1,2}
C. {3,4,5}
D. {1,2,6,7}
解:由已知}2,1,0{=∧P ,}3,2,1{=∧Q ,}0{=⋂∧∧Q C P N ,}3{=⋂∧
∧P C Q N
则}3,0{)()(=⋂⋃⋂∧∧∧∧P C Q Q C P N N
小结:此题为2005年浙江省高考题,主要考查集合的并、交、补集的运算。
[例8] 设R U =,}1|{>=x x A ,}034|{2<++=x x x B 求集合C ,使其同时满足下列条件:
(1)Z ⋂⋃⊆)(B A C C U
(2)φ≠⋂B C
(3)C 中有2个元素
解:}11|{-<>=x x x A 或,}13|{-<<-=x x B
则}13|{}11|{-<<-⋃≤≤-=⋃x x x x B A C U }13|{≤<-=x x
故}1,0,1,2{)(--=Z ⋂⋃B A C U
要满足条件(2),则由C ∈-2,则C 中必含有2-又由条件(3),则
}1,2{--=C 或}0,2{-=C 或}1,2{-=C
【模拟试题】(答题时间:30分钟)
一. 选择题:
1. 集合*
N S ⊆,φ≠S 且当S x ∈时,有S x ∈-8,这样的集合S 的个数是( )
A. 1个
B. 4个
C. 16个
D. 15个
2. 集合}}{,{φφ的子集合个数为( )
A. 1
B. 2
C. 3
D. 4
3. 对非空集合M 、N ,规定N C M N M I ⋂=\,其中I 为全集,则)\(\N M M 等于( )
A. N
B. M
C. N M ⋂
D. N M ⋃
4. 设},2|{Z ∈==k k x x M ,},3|{Z ∈==k k x x N ,则=N M \( )
A. },13|{Z ∈±=k k x x
B. },24|{Z ∈+=k k x x
C. },26|{Z ∈±=k k x x
D. },244|{Z ∈+==k k x k x x 或 5. 设}3,1,23{x A -=,},1{2x B =,若A B A =⋃,则实数x 的个数是( )
A. 4
B. 3
C. 2
D. 1
6. }2|),{(x y y x A >=,}2
1|),{(2x y y x B <=,},|),{(Z ∈=y x y x C ,则集合)]([C C B A C O O ⋃⋃(O 为坐标平面上所有点的集合)含元素个数( )
A. 10
B. 9
C. 3
D. 无穷多个
7. 设n m >,},,2,1{m A =,},,2,1{n B =,满足φ≠⋂B C 且C A C =⋂的集合C 的个数是( )
A. 12
2---n m m B. n m m --22 C. 122+--n m m D. 以上均错
[参考答案]
1. D 2. D 3. C 4. C 5. B 6. B 7. B。
