八年级数学下(第八章)8.4(1)
新教材高中数学第八章立体几何初步8.4.1平面课件新人教A版必修第二册ppt

③
×
如三棱锥的四个顶点相连的四边形不能确定
一个平面
④
√
平面是空间中点的集合,是无限集
答案:④
4.设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则
直线AB∩β=
.
解析:∵α∩β=l,AB∩l=C,∴C∈β,C∈AB,∴AB∩β=C.
答案:C
∴由基本事实3可知,点P在平面ABC与平面α的交线上,同理可
证Q,R也在平面ABC与平面α的交线上.
∴P,Q,R三点共线.
本例换为:如图所示,在正方体ABCD-A1B1C1D1中,设线段A1C
与平面ABC1D1交于点Q,如何说明B,Q,D1三点共线?
证明:如图所示,连接A1B,CD1.
显然B∈平面A1BCD1,D1∈平面A1BCD1.
④两条平行线确定一个平面
A.①②
B.②③
C.②④
D.③④
(2)两个平面若有三个公共点,则这两个平面(
A.相交
B.重合
C.相交或重合
D.以上都不对
)
解析:(1)不在同一条直线上的三点确定一个平面.圆上三个点
不会在同一条直线上,故可确定一个平面,∴①不正确,②正确.
当四点在一条直线上时不能确定一个平面,③不正确.根据平
且 P∈l
3.做一做:如图所示,在空间四边形各边AD,AB,BC,CD上分别
取E,F,G,H四点,如果EF,GH交于一点P,求证:点P在直线BD
上.
证明:∵EF∩GH=P,
∴P∈EF,且P∈GH.
又EF⊂平面ABD,GH⊂平面CBD,
∴P∈平面ABD,且P∈平面CBD,
即P∈平面ABD∩平面CBD,平面ABD∩平面CBD=BD,
第1节多元函数的基本概念

的示 . 意图
y
解 要使函数有意义须满足
1x2y20, 即 x2y21,
所以函数的定义域为
x
D {(x,y) x2y21}.有界闭区域
2.二元函数的定义域
例2 求 函 z数 lny(x) xy 的 定D 义 . 域 x2y21
解 要使函数有意义须满足
y
y x0
二. 多元函数的概念
注意 (1) 多元函数也有单值函数和多值函数,如
x2y2z2a2
在讨论过程中通常将其拆成几个单值函数后 再分别加以讨论.
(2) 多元函数也有分段函数,如
xy f(x,y)x2y2
0
x2y20 x2y20
(3) 点函数u=f(P)能表示所有的函数.
(4) 函数有加减乘除数乘及复合运算(略)
确定空间一点 M(x,y,z),当(x, y) 取遍
D上的一切点时, 得到空间点集
z
M(x, y,z)
{x ,(y ,z)zf(x ,y )(x ,,y ) D }
这个点集称为二元函数的图形.
该几何图形通常是一张曲面.
而定义域 D 正是这曲面在Oxy 平面上的投影.
D (x, y) y
x
3.二元函数的几何图形
xy
0
x
2
y2
1
0
函数的定义域为
D {(x ,y )y x 0 ,x 0 y ,x 2 y 2 1 }
yx
x
无界开区域
2.二元函数的定义域 例3 求 zarcxs2 in y2 x2y21的 定. 义
4
解 要使函数有意义,必须
x2 4
高中数学第八章立体几何初步8.4.1平面同步练习含解析132

课时素养评价二十四平面(15分钟30分)1.若点A在直线b上,b在平面β内,则点A,直线b,平面β之间的关系可以记作(A.A∈b∈βB.A∈b⊂βC.A⊂b⊂βD.A⊂b∈β【解析】选B.点A在直线b上,所以A∈b;直线b在平面β内,所以b⊂β.2.已知直线m⊂平面α,P∉m,Q∈m,则(A.P∉α,Q∈αB.P∈α,Q∉αC.P∉α,Q∉αD.Q∈α【解析】选D.因为Q∈m,m⊂α,所以Q∈α.因为P∉m,所以有可能P∈α,也可能有P∉α.3.用符号表示“点A在直线l上,l在平面α外”为.【解析】由题意“点A在直线l上,l在平面α外”的符号表示是“A∈l,l⊄α”.答案:A∈l,l⊄α4.从同一点出发的四条直线最多能确定个平面.【解析】同一点出发的四条直线是四棱锥的四条侧棱所在的直线时,确定的平面个数最多,是6个.答案:65.点D为△ABC所在平面外一点,E,F分别为DA和DC上的点,G,H分别为BA和BC上的点,且EF和GH相交于点M,则点M一定在直线上.【解析】因为E,F分别为DA和DC上的点,所以E∈平面ACD,F∈平面ACD,所以EF⊂平面ACD,又M∈EF,所以M∈平面ACD,同理,M∈平面ACB,而平面ACD∩平面ACB=AC,所以M∈AC,答案:AC6.把下面的符号语言改写成文字语言的形式,并画出图形.若直线a⊂平面α,A∈α,A∉a,A∈直线b,a∥b,则b⊂平面α.【解析】直线a⊂平面α表示:直线a在平面α内;A∈α表示:点A在平面α内;A∉a表示:A不在直线a上;A∈直线b表示:A在直线b上;a∥b表示:直线a平行于直线b;b⊂平面α表示:直线b在平面α内.综上可得:在平面α上,过直线a外一点作一条直线b,则b一定在平面α上.其图形语言如图所示:(30分钟60分)一、单选题(每小题5分,共20分)1.下列说法正确的是(A.两条直线确定一个平面B.梯形一定是平面图形C.平面α和β有不同在一条直线上的三个交点D.一条直线和一个点确定一个平面【解析】选B.A选项,两条相交、平行直线确定一个平面,A错.C选项,两个平面有公共点,则有一条过该公共点的公共直线,如没有公共点,则两平面平行,故α,β重合,C错.D选项,一条直线和直线外的一点可以确定一个平面,D错.B选项,两条平行直线确定一个平面,梯形中有一组对边平行,故B对.2.如果直线a⊂平面α,直线b⊂平面α,M∈a,N∈b,M∈l,N∈l,则(A.l⊂αB.l⊄αC.l∩α=MD.l∩α=N【解析】选A.因为M∈a,a⊂α,所以M∈α,同理,N∈α,又M∈l,N∈l,故l⊂α.3.下列各图均是正六棱柱,P,Q,R,S分别是所在棱的中点,这四个点不共面的图形是(【解析】选D.在选项A,B,C中,由棱柱、正六边形、中位线的性质知,均有PS∥QR,即在此三个图形中P,Q,R,S共面.4.如图,平面α∩平面β=l,A,B∈α,C∈β,C∉l,直线AB∩l=D,过A,B,C三点确定的平面为γ,则平面γ、β的交线必过(A.点AB.点BC.点C,但不过点DD.点C和点D【解析】选D.根据公理判定点C和点D既在平面β内又在平面γ内,故平面γ,β的交线必过C,D.二、多选题(每小题5分,共10分,全部选对的得5分,选对但不全的得3分,有选错的得0分)5.经过空间不共线的四点,确定的平面个数可以是(A.1B.2C.3D.4【解析】选AD.当这四个点在一个平面内的时候,确定一个平面;当三个点在一个平面上,另一个点在平面外的时候,确定四个平面,可想象一下三棱锥的样子.6.以下四个命题中,正确的是(A.不共面的四点中,其中任意三点不共线B.若点A,B,C,D共面,点A,B,C,E共面,则A,B,C,D,E共面C.若直线a,b共面,直线a,c共面,则直线b,c共面D.两两相交且不共点的三条直线确定一个平面【解析】选AD.A正确,可以用反证法证明,假设任意三点共线,则四个点必共面,与不共面的四点矛盾;B从条件看出两平面有三个公共点A,B,C,但是若A,B,C共线,则结论不正确;C不正确,共面不具有传递性,若直线a,b共面,直线a,c共面,则直线b,c可能不在一个平面内.D正确,两两相交的直线有三个公共点,确定一个平面.三、填空题(每小题5分,共10分)7.(2020·宝山高一检测)如果一条直线与两条直线都相交,这三条直线共可确定个平面.【解析】如果三条直线都交于一点,且三线不共面,则每两条直线都确定一个平面,共确定3个平面;如果三条直线两两相交,交于不同的三点,则只确定1个平面;如果两条直线不在同一个平面内,另一条与其均相交,则只确定2个平面;如果两条直线平行,另一条与其均相交,则只确定1个平面.综上,这三条直线共可确定1或2或3个平面.答案:1或2或38.空间中三个平面最少把空间分成部分;最多把空间分成部分.【解析】当三个平面两两平行时,可以把空间分成四部分,当两个平面相交,第三个平面同时与两个平面相交且与前两个平面的交线垂直时,把空间分成8部分.答案:48四、解答题(每小题10分,共20分)9.如图,过直线l外一点P,作直线a,b,c分别交直线l于点A,B,C,求证:直线a,b,c共面.【证明】设直线l与l外一点P确定的平面为α,则P∈平面α,又A∈直线l,所以A∈平面α;又P∈直线a,A∈直线a,所以直线a⊂平面α;同理直线b⊂平面α,直线c⊂平面α,所以直线a,b,c共面.10.如图所示,D,E分别是△ABC的边AC,BC上的点,平面α经过D,E两点.(1)求作直线AB与平面α的交点P.(2)求证:D,E,P三点共线.【解析】(1)连接DE并延长,交AB延长线于点P,则点P为直线AB与平面α的交点.如图.(2)因为D∈AC,E∈BC,所以DE⊂平面ABC,因为D∈α,E∈α,所以DE⊂α,因为DE为平面α与平面ABC的交线,又P∈AB,AB⊂平面ABC,且P∈α,所以P在平面α与平面ABC的交线DE上,所以D,E,P三点共线.1.在正方体ABCD -A1B1C1D1中,M,N分别是棱DD1和BB1上的点,MD=DD1,NB=BB1,那么正方体的过点M,N,C1的截面图形是( )A.三角形B.四边形C.五边形D.六边形【解析】选C.在正方体ABCD -A1B1C1D1中,M,N分别是棱DD1和BB1上的点,MD=DD1,NB=BB1.如图,延长C1M交CD的延长线于点P,延长C1N交CB的延长线于点Q,连接PQ交AD于点E,交AB于点F,连接NF,ME,则正方体的过点M,N,C1的截面图形是五边形.2.已知:平面α∩平面β=a,平面α∩平面γ=b,平面γ∩平面β=c且a,b,c不重合.求证:a,b,c交于一点或两两平行.【证明】如图,若a,b,c中存在两条直线相交,不妨设a∩b=P,则P∈a,P∈b,因为α∩β=a,所以a⊂β,则P∈β,又α∩γ=b,所以b⊂γ,则P∈γ,所以P在β与γ的交线上,即P∈c.所以a,b,c交于一点;若a,b,c中任何两条直线都不相交,因为a⊂α,b⊂α,根据同一平面内两条直线不相交则平行,所以a∥b,同理b∥c.所以a∥b∥c.综上,平面α∩平面β=a,平面α∩平面γ=b,平面γ∩平面β=c且a,b,c不重合,则a,b,c 交于一点或两两平行.。
第八章 §8.4 直线与圆、圆与圆的位置关系-2025高中数学大一轮复习讲义人教A版

§8.4直线与圆、圆与圆的位置关系课标要求1.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的数学问题与实际问题.知识梳理1.直线与圆的位置关系(圆心到直线的距离为d ,圆的半径为r )相离相切相交图形量化方程观点Δ<0Δ=0Δ>0几何观点d >rd =rd <r2.圆与圆的位置关系(⊙O 1,⊙O 2的半径分别为r 1,r 2,d =|O 1O 2|)图形量的关系外离d >r 1+r 2外切d =r 1+r 2相交|r 1-r 2|<d <r 1+r 2内切d =|r 1-r 2|内含d<|r1-r2|3.直线被圆截得的弦长(1)几何法:弦心距d、半径r和弦长|AB|的一半构成直角三角形,弦长|AB|=2r2-d2.(2)代数法:设直线y=kx+m与圆x2+y2+Dx+Ey+F=0相交于点M,N,代入,消去y,得关于x的一元二次方程,则|MN|=1+k2·(x M+x N)2-4x M x N.常用结论1.圆的切线方程常用结论(1)过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.(2)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为x0x+y0y=r2. 2.圆与圆的位置关系的常用结论(1)两圆相交时,其公共弦所在的直线方程由两圆方程相减得到.(2)两个圆系方程①过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+Ey+F +λ(Ax+By+C)=0(λ∈R);②过圆C1:x2+y2+D1x+E1y+F1=0和圆C2:x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1)(其中不含圆C2,所以注意检验C2是否满足题意,以防丢解).自主诊断1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)若两圆没有公共点,则两圆一定外离.(×)(2)若两圆的圆心距小于两圆的半径之和,则两圆相交.(×)(3)若直线的方程与圆的方程组成的方程组有且只有一组实数解,则直线与圆相切.(√)(4)在圆中最长的弦是直径.(√)2.(选择性必修第一册P93T1改编)直线3x+4y=5与圆x2+y2=16的位置关系是() A.相交B.相切C.相离D.相切或相交答案A解析圆心到直线的距离d=532+42=1<4,所以直线与圆相交.3.(选择性必修第一册P93T3改编)直线x-2y+5=0与圆x2+y2=8相交于A,B两点,则|AB|等于()A.3B.23C.5D .25答案B解析因为圆x 2+y 2=8的圆心为(0,0),半径为22,所以圆心到直线x -2y +5=0的距离d =|5|12+(-2)2=5,所以|AB |=28-d 2=2 3.4.(选择性必修第一册P98练习T1改编)圆C 1:x 2+y 2=4与圆C 2:x 2+y 2-8x -6y +16=0的位置关系是()A .外切B .相交C .外离D .内切答案A解析圆C 1的圆心C 1(0,0),半径r 1=2,圆C 2可化为(x -4)2+(y -3)2=9,∴圆心C 2(4,3),半径r 2=3,∴|C 1C 2|=(4-0)2+(3-0)2=5=r 1+r 2,故两圆外切.题型一直线与圆的位置关系命题点1位置关系的判断例1(1)M (x 0,y 0)为圆x 2+y 2=1内异于圆心的一点,则直线x 0x +y 0y =1与该圆的位置关系为()A .相切B .相交C .相离D .相切或相交答案C解析由题意知M (x 0,y 0)为圆x 2+y 2=1内异于圆心的一点,则0<x 20+y 20<1,而圆x 2+y 2=1的圆心到直线x 0x +y 0y =1的距离d =1x 20+y 2>1=r ,故直线x 0x +y 0y =1与该圆的位置关系为相离.(2)直线kx -y +2-k =0与圆x 2+y 2-2x -8=0的位置关系为()A .相交、相切或相离B .相交或相切C .相交D .相切答案C 解析方法一直线kx -y +2-k =0的方程可化为k (x -1)-(y -2)=0,该直线恒过定点(1,2).因为12+22-2×1-8<0,所以点(1,2)在圆x 2+y 2-2x -8=0的内部,所以直线kx -y +2-k =0与圆x 2+y 2-2x -8=0相交.方法二圆的方程可化为(x -1)2+y 2=32,所以圆的圆心为(1,0),半径为3.圆心到直线kx -y+2-k =0的距离为|k +2-k |1+k2=21+k 2≤2<3,所以直线与圆相交.思维升华判断直线与圆的位置关系的常见方法(1)几何法:利用d 与r 的关系判断.(2)代数法:联立方程之后利用Δ判断.(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.命题点2弦长问题例2(1)(2023·滁州模拟)已知过点P (0,1)的直线l 与圆x 2+y 2+2x -6y +6=0相交于A ,B 两点,则当|AB |=23时,直线l 的方程为________________.答案x =0或3x +4y -4=0解析因为圆x 2+y 2+2x -6y +6=0可以化为(x +1)2+(y -3)2=4,所以圆心为(-1,3),半径为r =2,因为|AB |=23,所以圆心到直线的距离为d =22-(3)2=1,当直线l 斜率不存在时,直线l 的方程为x =0,此时圆心(-1,3)到直线x =0的距离为1,满足条件;当直线l 斜率存在时,设斜率为k ,直线l 的方程为y =kx +1,则圆心(-1,3)到直线l 的距离d =|-k -3+1|1+k 2=1,解得k =-34,此时直线l 的方程为3x +4y -4=0,综上,所求直线的方程为3x +4y -4=0或x =0.(2)(2023·新高考全国Ⅱ)已知直线x -my +1=0与⊙C :(x -1)2+y 2=4交于A ,B 两点,写出满足“△ABC 面积为85”的m 的一个值为________.答案,-2,12,-12中任意一个皆可以解析设直线x -my +1=0为直线l ,点C 到直线l 的距离为d ,由弦长公式得|AB |=24-d 2,所以S △ABC =12×d ×24-d 2=85,解得d =455或d =255,又d =|1+1|1+m 2=21+m2,所以21+m 2=455或21+m 2=255,解得m =±12或m =±2.思维升华弦长的两种求法(1)代数法:将直线和圆的方程联立方程组,根据弦长公式求弦长.(2)几何法:若弦心距为d ,圆的半径长为r ,则弦长l =2r 2-d 2.命题点3切线问题例3已知点P (2+1,2-2),点M (3,1),圆C :(x -1)2+(y -2)2=4.(1)求过点P 的圆C 的切线方程;(2)求过点M 的圆C 的切线方程,并求出切线长.解由题意得圆心C (1,2),半径r =2.(1)∵(2+1-1)2+(2-2-2)2=4,∴点P 在圆C 上.又k PC =2-2-22+1-1=-1,∴过点P 的切线的斜率为-1k PC=1,∴过点P 的圆C 的切线方程是y -(2-2)=1×[x -(2+1)],即x -y +1-22=0.(2)∵(3-1)2+(1-2)2=5>4,∴点M 在圆C 外.当过点M 的直线的斜率不存在时,直线方程为x =3,即x -3=0.又点C (1,2)到直线x -3=0的距离d =3-1=2=r ,∴直线x =3是圆的切线;当切线的斜率存在时,设切线方程为y -1=k (x -3),即kx -y +1-3k =0,由圆心C 到切线的距离d ′=|k -2+1-3k |k 2+1r =2,解得k =34.∴切线方程为y -1=34(x -3),即3x -4y -5=0.综上,过点M 的圆C 的切线方程为x -3=0或3x -4y -5=0.∵|MC |=(3-1)2+(1-2)2=5,∴过点M 的圆C 的切线长为|MC |2-r 2=5-4=1.思维升华当切线方程斜率存在时,圆的切线方程的求法(1)几何法:设切线方程为y -y 0=k (x -x 0),利用点到直线的距离公式表示出圆心到切线的距离d ,然后令d =r ,进而求出k .(2)代数法:设切线方程为y -y 0=k (x -x 0),与圆的方程组成方程组,消元后得到一个一元二次方程,然后令判别式Δ=0进而求得k .注意验证斜率不存在的情况.命题点4直线与圆位置关系中的最值问题例4已知P 是直线3x +4y +8=0上的动点,PA ,PB 是圆C :x 2+y 2-2x -2y +1=0的两条切线,A ,B 是切点,则四边形PACB 面积的最小值为________.答案22解析圆C :x 2+y 2-2x -2y +1=0,即圆C :(x -1)2+(y -1)2=1,所以圆心C (1,1),半径r =1,如图,连接PC ,因为S 四边形P ACB =2S △P AC =2×12×|AP |·|AC |=|AP |=|PC |2-1,所以求S 四边形P ACB 的最小值就是求|PC |的最小值,而|PC |的最小值就是圆心到直线3x +4y +8=0的距离d ,即d =|3+4+8|32+42=3,即四边形PACB 面积的最小值为9-1=2 2.思维升华涉及与圆的切线有关的线段长度范围(最值)问题,解题关键是能够把所求线段长表示为关于圆心与直线上的点的距离的函数的形式,利用求函数值域的方法求得结果.跟踪训练1(1)若直线x a +yb =1与圆x 2+y 2=1相交,则()A.1a 2+1b 2<1B.1a 2+1b 2>1C .a 2+b 2<1D .a 2+b 2>1答案B解析由直线x a +yb=1,可化为bx+ay-ab=0,因为直线bx+ay-ab=0与圆x2+y2=1相交,可得|-ab|a2+b2<1,整理得a2+b2>a2b2,所以1a2+1b2 >1.(2)直线l:2tx-y-2t+1=0(t∈R)与圆C:x2+y2=4相交于A,B两点,则|AB|的最小值为()A.2B.2C.22D.4答案C解析圆C:x2+y2=4的圆心C(0,0),半径为2,由直线l:2tx-y-2t+1=0(t∈R)可化为y-1=2t(x-1),∴直线l过定点P(1,1),又12+12=2<4,∴点P在圆C内部,当直线l与线段CP垂直时,弦长|AB|最小,∵|CP|=(0-1)2+(0-1)2=2,∴弦长|AB|的最小值为24-2=2 2.题型二圆与圆的位置关系例5(1)(2024·齐齐哈尔模拟)已知圆M:x2+y2-4y=0与圆N:x2+y2-2x-3=0,则圆M与圆N的位置关系为()A.内含B.相交C.外切D.外离答案B解析圆M:x2+y2-4y=0,即x2+(y-2)2=4,圆心M(0,2),半径R=2.圆N:x2+y2-2x-3=0,即(x-1)2+y2=4,圆心N(1,0),半径r=2,则|MN|=22+12=5,故有|R-r|<|MN|<R+r.故两圆是相交关系.(2)(2023·重庆模拟)圆A:x2+y2=4与圆B:x2+y2-4x+4y-12=0的公共弦所在直线的方程为()A.x-y+2=0B.x-y-2=0C.x+y+2=0D.x+y-2=0答案A解析将两圆方程作差得4x-4y+8=0,即x-y+2=0.因此,两圆的公共弦所在直线的方程为x-y+2=0.思维升华(1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差消去x 2,y 2项得到.跟踪训练2(1)若圆x 2+y 2+4x -4y =0和圆x 2+y 2+2x -8=0相交于M ,N 两点,则线段MN 的长度为()A .4 B.355C.1255D.655答案C解析x 2+y 2+4x -4y =0,①x 2+y 2+2x -8=0,②由①-②可得x -2y +4=0.∴两圆的公共弦所在直线的方程是x -2y +4=0,∵圆x 2+y 2+4x -4y =0的圆心坐标为(-2,2),半径为22,∴圆心到公共弦的距离d =|-2-4+4|12+(-2)2=255,∴公共弦长为=1255,即|MN |=1255.(2)(2022·新高考全国Ⅰ)写出与圆x 2+y 2=1和(x -3)2+(y -4)2=16都相切的一条直线的方程________________.答案x =-1或7x -24y -25=0或3x +4y -5=0(答案不唯一,只需写出上述三个方程中的一个即可)解析如图,因为圆x 2+y 2=1的圆心为O (0,0),半径r 1=1,圆(x -3)2+(y -4)2=16的圆心为A (3,4),半径r 2=4,所以|OA |=5,r 1+r 2=5,所以|OA |=r 1+r 2,所以两圆外切,公切线有三种情况:①易知公切线l 1的方程为x =-1.②另一条公切线l 2与公切线l 1关于过两圆圆心的直线l 对称.易知过两圆圆心的直线l 的方程为y =43x ,=-1,=43x=-1,=-43,由对称性可知公切线l21设公切线l2的方程为y+43=k(x+1),则点O(0,0)到l2的距离为1,所以1=|k-43|k2+1,解得k=724,所以公切线l2的方程为y+43=724(x+1),即7x-24y-25=0.③还有一条公切线l3与直线l:y=43x垂直,设公切线l3的方程为y=-34x+t,易知t>0,则点O(0,0)到l3的距离为1,所以1解得t=54或t=-54(舍去),所以公切线l3的方程为y=-34x+54,即3x+4y-5=0.综上,所求直线方程为x=-1或7x-24y-25=0或3x+4y-5=0.课时精练一、单项选择题1.已知圆(x-2)2+(y-3)2=r2(r>0)与y轴相切,则r等于()A.2B.3C.2D.3答案C解析圆(x-2)2+(y-3)2=r2(r>0)的圆心为(2,3),半径为r.因为圆与y轴相切,所以r=2. 2.(2024·南京模拟)在平面直角坐标系中,圆O1:(x-1)2+y2=1和圆O2:x2+(y-2)2=4的位置关系是()A.外离B.相交C .外切D .内切答案B解析由题意知,圆O 1:(x -1)2+y 2=1,可得圆心坐标O 1(1,0),半径r 1=1,圆O 2:x 2+(y -2)2=4,可得圆心坐标O 2(0,2),半径r 2=2,则两圆的圆心距|O 1O 2|=1+4=5,则2-1<5<2+1,即|r 2-r 1|<|O 1O 2|<r 1+r 2,所以圆O 1与圆O 2相交.3.(2023·北京模拟)直线y =x +1被圆O :x 2+y 2=1截得的弦长为()A .1 B.2C .2D .22答案B解析圆O :x 2+y 2=1的圆心为O (0,0),半径r =1,则圆心O (0,0)到直线y =x +1的距离d =12=22,所以直线y =x +1被圆O :x 2+y 2=1所截得的弦长为2r 2-d 2=2×1-12= 2.4.若一条光线从点A (-2,-3)射出,经y 轴反射后与圆(x +3)2+(y -2)2=1相切,则反射光线所在直线的斜率为()A .-53或-35B .-32或-23C .-54或-45D .-43或-34答案D解析点(-2,-3)关于y 轴的对称点为(2,-3),由题意知,反射光线所在的直线一定过点(2,-3).设反射光线所在直线的斜率为k ,则反射光线所在直线的方程为y +3=k (x -2),即kx -y -2k -3=0.由反射光线与圆相切,圆心为(-3,2),得|-3k -2-2k -3|k 2+1=1,解得k =-43或k =-34.5.圆C :x 2+y 2+2x +4y -3=0上到直线x +y +1=0距离为2的点有()A .2个B .3个C .4个D .无数个答案B 解析因为x 2+y 2+2x +4y -3=0化为标准方程为(x +1)2+(y +2)2=8,所以圆心C (-1,-2),圆的半径r =22,又因为圆心C 到直线x +y +1=0的距离d =|-1-2+1|2=2,所以r -d =2,所以过圆心平行于直线x +y +1=0的直线与圆有2个交点,另一条与直线x +y +1=0的距离为2的平行线与圆相切,只有1个交点,如图所示,所以圆C 上到直线x +y +1=0的距离为2的点共有3个.6.(2023·武汉模拟)已知点P 在圆O :x 2+y 2=1上运动,若对任意点P ,在直线l :x +y -4=0上均存在两点A ,B ,使得∠APB ≥π2AB 长度的最小值是()A.2-1B.2+1C .22-1D .42+2答案D 解析如图,由题可知,圆心为O (0,0),半径R =1,若直线l :x +y -4=0上存在两点A ,B ,使得∠APB ≥π2恒成立,则O :x 2+y 2=1始终在以AB 为直径的圆内或圆上,点O (0,0)到直线l 的距离d =|0-0-4|12+12=22,所以AB 长度的最小值为2(d +1)=42+2.二、多项选择题7.已知圆C 1:(x -a )2+(y +2)2=25,圆C 2:(x +1)2+(y +a )2=4,若圆C 1与圆C 2内切,则实数a 的值是()A .-2B .2C .-1D .1答案BC 解析由题可知圆心C 1(a ,-2),半径r 1=5,圆心C 2(-1,-a ),半径r 2=2,因为圆C 1与圆C 2内切,所以|C 1C 2|=(a +1)2+(-2+a )2=|r 1-r 2|=3,解得a =-1或a =2.8.已知圆C :(x -2)2+y 2=1,点P 是直线l :x +y =0上一动点,过点P 作圆的切线PA ,PB ,切点分别是A 和B ,则下列说法错误的是()A .圆C 上恰有一个点到直线l 的距离为12B .切线|PA |长的最小值为1C .四边形ACBP 面积的最小值为2D .直线AB 答案AC 解析对于A ,由圆C :(x -2)2+y 2=1,可得圆心C (2,0),半径r =1,∴圆心C 到直线l :x +y =0的距离为|2|2=2,∵2-1<12<2+1,故圆C 上不是只有一个点到直线l 的距离为12,故A 错误;对于B ,由圆的性质,可得切线长|PA |=|PC |2-r 2=|PC |2-1,当|PC |最小时,|PA |最小,又|PC |min =2,则|PA |min =1,故B 正确;对于C ,由四边形ACBP 的面积为2×12×|PA |·|CA |=|PA |,因为|PA |min =1,所以四边形ACBP 的面积的最小值为1,故C 错误;对于D ,设P (t ,-t ),由题知A ,B 在以PC 为直径的圆上,又由C (2,0),所以(x -t )(x -2)+(y +t )(y -0)=0,即x 2+y 2-(t +2)x +ty +2t =0,因为圆C :(x -2)2+y 2=1,即x 2+y 2-4x +3=0.两圆的方程相减得直线AB:(2-t)x+ty-3+2t=0,即2x-3-t(x-y-2)=0,x-3=0,-y-2=0,=32,=-12,即直线ABD正确.三、填空题9.写出一个经过原点,截y轴所得弦长是截x轴所得弦长2倍的圆的标准方程__________.答案(x-1)2+(y-2)2=5(答案不唯一)解析显然圆截x轴、y轴所得弦的一个端点为O(0,0),设圆截x轴所得弦的另一端点为A(a,0),a≠0,则该圆截y轴所得弦的另一端点为B(0,2a)或B(0,-2a),因此该圆的圆心Cr=52|a|,所以该圆的标准方程为+(y-a)2=54a2或+(y+a)2=54a2,取a=2,得圆的一个标准方程为(x-1)2+(y-2)2=5.10.与直线x+y-2=0和曲线x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程为________________________.答案(x-2)2+(y-2)2=2解析曲线方程化为(x-6)2+(y-6)2=18,其圆心到直线x+y-2=0的距离d=|6+6-2|2=52.所求的最小圆的圆心在直线y=x上,其到直线的距离为2,圆心坐标为(2,2).标准方程为(x-2)2+(y-2)2=2.11.若圆C1:(x-1)2+y2=r2(r>0)上存在点P,且点P关于y轴的对称点Q在圆C2:(x+2)2+(y-2)2=1上,则r的取值范围是__________.答案[5-1,5+1]解析设圆C1关于y轴的对称圆为圆C3,其方程为(x+1)2+y2=r2,根据题意,圆C3与圆C2有交点,又圆C3与圆C2的圆心距为(-1+2)2+(2-0)2=5,要满足题意,只需|r-1|≤5≤r+1,解得r∈[5-1,5+1].12.(2023·大庆模拟)已知直线l是圆C:(x-2)2+(y-1)2=1的切线,并且点B(3,4)到直线l 的距离是2,这样的直线l有________条.答案4解析由已知可得,圆心C(2,1),半径r1=1.由点B(3,4)到直线l的距离是2,所以直线l是以B(3,4)为圆心,r2=2为半径的圆的切线,又直线l是圆C:(x-2)2+(y-1)2=1的切线,所以直线l是圆C与圆B的公切线.因为|BC|=(3-2)2+(4-1)2=10>3=r1+r2,所以两圆外离,所以两圆的公切线有4条,即满足条件的直线l有4条.四、解答题13.已知两圆x2+y2-2x-6y-1=0和x2+y2-10x-12y+m=0.求:(1)m取何值时两圆外切?(2)当m=45时两圆的公共弦所在直线的方程和公共弦的长.解两圆的标准方程分别为(x-1)2+(y-3)2=11,(x-5)2+(y-6)2=61-m(m<61),则圆心分别为(1,3),(5,6),半径分别为11和61-m.(1)当两圆外切时,(5-1)2+(6-3)2=11+61-m.解得m=25+1011.(2)两圆的公共弦所在直线的方程为(x2+y2-2x-6y-1)-(x2+y2-10x-12y+45)=0,即4x+3y-23=0.所以公共弦的长为2×27.14.已知圆C:x2+y2-4x=0,直线l恒过点P(4,1).(1)若直线l与圆C相切,求l的方程;(2)当直线l与圆C相交于A,B两点,且|AB|=23时,求l的方程.解(1)由题意可知,圆C的圆心为(2,0),半径r=2,①当直线l的斜率不存在时,即l的方程为x=4,此时直线与圆相切,符合题意;②当直线l的斜率存在时,设斜率为k,∴直线l的方程为y-1=k(x-4),即kx-y+1-4k=0,若直线l与圆相切,则d=|1-2k|k2+1=2,解得k=-34,∴l:-34x-y+4=0,即l:3x+4y-16=0,综上,当直线l与圆C相切时,所求直线l的方程为x=4或3x+4y-16=0.(2)由题意可知,直线l的斜率一定存在,设斜率为k,∴直线l的方程为y-1=k(x-4),即kx-y+1-4k=0,设圆心到直线l的距离为d,则d=|1-2k| k2+1,由垂径定理可得,d2=4,即(2k-1)2k2+1+3=4,整理得,3k2-4k=0,解得k=0或k=4 3,则直线l的方程为y=1或4x-3y-13=0.15.(多选)(2023·重庆九龙坡育才中学模拟)已知圆M:(x+cosθ)2+(y-sinθ)2=1,直线l:y =kx,则()A.对任意实数k与θ,直线l和圆M相切B.对任意实数k与θ,直线l和圆M有公共点C.对任意实数θ,必存在实数k,使得直线l和圆M相切D.对任意实数k,必存在实数θ,使得直线l和圆M相切答案BD解析圆M:(x+cosθ)2+(y-sinθ)2=1恒过定点O(0,0),直线l:y=kx也恒过定点O(0,0),所以对任意实数k与θ,直线l和圆M有公共点,故B正确;圆心M(-cosθ,sinθ),圆心到直线l 的距离d =|k cos θ+sin θ|1+k 2=|1+k 2sin (θ+α)|1+k 2=|sin(θ+α)|≤1,其中tan α=k ,则对任意实数k ,存在θ,使得直线l 和圆M 的关系是相交或者相切,故D 正确,A 错误;当θ=0时,圆M 为(x +1)2+y 2=1,此时不存在实数k ,使得直线l 和圆M 相切,故C 错误.16.(2023·赣州统考)已知圆C :(x -1)2+(y -2)2=5,圆C ′是以圆x 2+y 2=1上任意一点为圆心,半径为1的圆.圆C 与圆C ′交于A ,B 两点,则当∠ACB 最大时,|CC ′|=________.答案2解析依题意,在△ABC 中,|AC |=|BC |=5,如图,显然0<|AB |≤2,∠ACB 是锐角,sin ∠ACB2=12|AB ||AC |=|AB |25,又函数y =sin x 因此当且仅当公共弦AB 的长度最大时,∠ACB 最大,此时弦AB 为圆C ′的直径,在Rt △ACC ′中,∠AC ′C =90°,|AC ′|=1,所以|CC ′|=|AC |2-|AC ′|2=2.。
高中数学第八章立体几何初步8.4.1平面教学用书教案第二册

8.4 空间点、直线、平面之间的位置关系8。
4。
1平面素养目标·定方向素养目标学法指导1.理解并掌握平面的基本事实及推论。
(逻辑推理)2.会用基本事实及推论解决有关问题.(逻辑推理)要充分利用长方体以及身边的生活中的物品认识空间点、直线、平面,要类比初中平面几何中点、直线去认识空间中的点、直线、平面,逐步过渡与抽象,并确定它们之间的关系.必备知识·探新知知识点1平面1.平面的概念几何中所说的“平面”,是从课桌面、黑板面、平静的水面等,这样的一些物体中抽象出来的。
类似于直线向两端无限延伸,几何中的平面是向四周__无限延展__的。
2.平面的画法我们常用矩形的直观图,即__平行四边形__表示平面,它的锐角通常画成__45°__,且横边长等于其邻边长的__2__倍,如图①.如果一个平面的一部分被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用__虚线__画出来,如图②.3.平面的表示法图①的平面可表示为__平面α__、平面ABCD、__平面AC__或平面BD。
知识点2点、线、面之间的位置关系1.直线在平面内的概念如果直线l上的__所有点__都在平面α内,就说直线l在平面α内,或者说平面α经过直线l.2.一些文字语言与符号语言的对应关系:文字语言表达符号语言表示文字语言表达符号语言表示点A在直线l上__A∈l__点A在直线l外__A∉l__点A在平面α内__A∈α__点A在平面α外__A∉α__直线l在平面α内__l⊂α__直线l在平面α外__l⊄α__直线l,m相交于点A l∩m=A平面α,β相交于直线lα∩β=l知识点3平面的基本性质及应用1.基本事实内容图形符号作用基本事实1过不在一条直线上的三个点,__有且只有__一个平面A,B,C三点不共线⇒存在唯一的平面α使A,B,C∈α一是确定平面;二是证明点、线共面问题;三是判断两个平面重合的依据基本事实2如果一条直线上的__两个点__在一A∈l,B∈l,且A∈α,B∈α既可判定直线和点是个平面内,那么这条直线在__这个平面内__⇒__l⊂α__否在平面内,又能说明平面是无限延展的基本事实3如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的__公共直线__P∈α且P∈β⇒α∩β=l,且P∈l①判定两平面相交的依据②判定点在直线上2.利用基本事实1和基本事实2,再结合“两点确定一条直线”,可以得到下面三个推论:推论1__经过一条直线和这条直线外一点__,有且只有一个平面。
2022春八年级数学下册第八章一元二次方程的应用第4课时其他问题习题课件鲁教版五四制ppt

4 【中考·新疆】某市体育局要组织一次篮球赛,赛制为 单循环形式(每两支球队之间都赛一场),计划安排28 场比赛,应邀请多少支球队参加比赛? 解:设应邀请 x 支球队参加比赛, 根据题意,可列出方程x(x-2 1)=28. 解这个方程,得 x1=8,x2=-7(舍去). 答:应邀请 8 支球队参加比赛.
(2)按照这样的分裂速度,经过三轮培植后C共有多少个有 益菌?
解:60×(1+19)3=60×203=480 000(个). 答:经过三轮培植后共有480 000个有益菌.
3 【中考·新疆】在某篮球邀请赛中,参赛的每两个队之间 都要比赛一场,共比赛 36 场,设有 x 个队参赛,根据题 意,可列方程为( A ) A.12x(x-1)=36 B.12x(x+1)=36 C.x(x-1)=36 D.x(x+1)=36
∵此设备的销售单价不得高于70万元, ∴x=50. 答:该设备的销售单价应是50万元.
10 六一前夕,某商场以每个30元的价格购进了500个玩 具,再以每个40元的价格售出,很快销售一空,商场 计划再进一批.
(1)第二次进价每个上涨了5元,仍以原价出售,若两批 玩具的总利润不低于13 000元,则第二批至少要进多 少个? 解:设第二批购进x个玩具, 依题意,得(40-30)×500+(40-30-5)x≥13 000, 解得x≥1 600. 答:第二批至少要购进1 600个.
7 如图,矩形ABCD中,AB=2 cm,BC=3 cm,点E从 点B沿边BC以2 cm/s的速度向点C移动,同时点F从点 C沿边CD以1 cm/s的速度向点D移动,当E,F两点中 有一点到达终点时,则另一点也停止运动.当△AEF 是以AF为底的等腰三角形时, 求点E运动的时间.
解:设点 E 运动的时间是 x s. 根据题意,得 22+(2x)2=(3-2x)2+x2, 解这个方程,得 x1=6- 31,x2=6+ 31. ∵3÷2=1.5(s),2÷1=2(s), ∴两点运动了 1.5 s 后停止运动.
最新人教版数学教材目录-人教版初中数学(初一、初二、初三)教材版本目录大纲

人教版初中数学教材版本目录大纲七年级数学(上)第一章有理数1.1 正数和负数1.2 有理数1.3 有理数的加减法实验与探究填幻方阅读与思考中国人最先使用负数1.4 有理数的乘除法观察与猜想翻牌游戏中的数学道理1.5 有理数的乘方数学活动小结复习题1第二章整式的加减2.1 整式阅读与思考数字1与字母X的对话2.2 整式的加减信息技术应用电子表格与数据计算数学活动小结复习题2第三章一元一次方程3.1 从算式到方程阅读与思考“方程”史话3.2 解一元一次方程(一)――合并同类项与移项实验与探究无限循环小数化分数3.3 解一元一次方程(二)――去括号与去分母3.4 实际问题与一元一次方程数学活动小结复习题3第四章几何图形初步4.1 几何图形阅读与思考几何学的起源4.2 直线、射线、线段阅读与思考长度的测量4.3 角4.4 课题学习设计制作长方体形状的包装纸盒数学活动小结复习题4部分中英文词汇索引七年级数学(下)第五章相交线与平行线5.1 相交线观察与猜想看图时的错觉5.2 平行线及其判定5.3 平行线的性质信息技术探索两条直线的位置关系5.4 平移小结复习题5第六章实数6.1 平方根6.2 立方根6.3 实数阅读与思考为什么√2不是有理数小结复习题6第七章平面直角坐标系7.1 平面直角坐标系阅读与思考用经纬度表示地理位置7.2 坐标方法的简单应用小结复习题7第八章二元一次方程组8.1 二元一次方程组8.2 消元――解二元一次方程组8.3 实际问题与二元一次方程组8.4 三元一次方程组的解法阅读一次方程组的古今表示及解法小结复习题8第九章不等式与不等式组9.1 不等式阅读与思考用求差法比较大小9.2 一元一次不等式9.3 一元一次不等式组小结复习题9第十章数据的收集、整理与描述10.1 统计调查实验与探究瓶子中有多少粒豆子10.2 直方图信息技术应用利用计算机画统计图10.3 课题学习从数据谈节水小结复习题10八年级数学(上)第十一章三角形11.1 与三角形有关的线段信息技术应用画图找规律11.2 与三角形有关的角阅读与思考为什么要证明11.3 多边形及其内角和数学活动小结复习题11第十二章全等三角形12.1 全等三角形12.2 三角形全等的判定信息技术应用探究三角形全等的条件12.3 角的平分线的性质数学活动小结复习题12第十三章轴对称13.1 轴对称13.2 画轴对称图形信息技术应用用轴对称进行图案设计13.3 等腰三角形实验与探究三角形中边与角之间的不等关系13.4 课题学习最短路径问题数学活动小结复习题13第十四章整式的乘法与因式分解14.1 整式的乘法14.2 乘法公式阅读与思考杨辉三角14.3 因式分解数学活动小结复习题14第十五章分式15.1 分式15.2 分式的运算阅读与思考容器中的水能倒完吧15.3 分式方程数学活动小结复习题15部分中英文词汇索引八年级数学(下)第十六章二次根式16.1 二次根式16.2 二次根式的乘除16.3 二次根式的加减数学活动小结复习题16第十七章勾股定理17.1 勾股定理阅读与思考勾股定理的证明17.2 勾股定理的逆定理阅读与思考费马大定理数学活动小结复习题17第十八章平行四边形18.1 平行四边形18.2 特殊的平行四边形实验与探究丰富多彩的正方形数学活动小结复习题18第十九章一次函数19.1 函数阅读与思考科学家如何测算岩石的年龄19.2 一次函数信息技术应用用计算机画函数图象14.3 课题学习选择方案数学活动小结复习题19第二十章数据的分析20.1 数据的集中趋势20.2 数据的波动程度阅读与思考数据波动程度的几种度量20.3 课题学习体质健康测试中的数据分析数学活动小结复习题20部分中英文词汇索引九年级数学(上)第二十一章一元二次方程21.1 一元二次方程21.2 解一元二次方程阅读与思考黄金分割数21.3 实际问题与一元二次方程数学活动小结复习题21第二十二章二次函数22.1 二次函数的图象和性质22.2 二次函数与一元二次方程信息技术应用探索干净函数的性质22.3 实际问题与二次函数阅读与思考推测滑行距离与滑行时间的关系数学活动小结复习题22第二十三章旋转23.1 图形的旋转23.2 中心对称信息技术应用探索旋转的性质23.3 课题学习图案设计阅读与思考旋转对称数学活动小结复习题23第二十四章圆24.1 圆的有关性质24.2 点和圆、直线和圆的位置关系实验与探究圆和圆的位置关系24.3 正多边形和圆阅读与思考圆周率π24.4 弧长和扇形面积实验与探究设计跑道数学活动小结复习题24第二十五章概率初步25.1 随机事件与概率25.2 用列举法求概率阅读与思考概率与中奖25.3 用频率估计概率实验与探究π的估计数学活动小结复习题25部分中英文词汇索引九年级数学(下)第二十六章反比例函数26.1 反比例函数信息技术应用探索反比例函数的性质26.2 实际问题与反比例函数阅读与思考生活中的反比例关系数学活动小结复习题26第二十七章相似27.1 图形的相似27.2 相似三角形观察与猜想奇妙的分形图形27.3 位似信息技术应用探索位似的性质数学活动小结复习题27第二十八章锐角三角函数28.1 锐角三角函数阅读与思考一张古老的“三角函数表”28.2 解直角三角形及其应用阅读与思考山坡的高度数学活动小结复习题28第二十九章投影与视图29.1 投影29.2 三视图阅读与思考视图的产生与应用29.3 课题学习制作立体模型数学活动小结复习题29部分中英文词汇索引。
苏教版八年级下册数学目录

苏教版八年级下册数学目录第七章一元一次不等式
生活中的不等式
7.1生活中的不等式
不等式的解集
7.2不等式的解集
不等式的性质
7.3不等式的性质
解一元一次不等式
7.4解一元一次不等式
用一元一次不等式解决问题
7.5用一元一次不等式解决问题
一元一次不等式组
7.6一元一次不等式组
一元一次不等式与一元一次方程、一次函数 7.7一元一次不等式与一元一次方程、一次函数第八章分式
分式
8.1分式
分式的基本性质
8.2分式的基本性质
分式的加减
8.3分式的加减
分式的乘除
8.4分式的乘除
分式方程
8.5分式方程
第九章反比例函数
反比例函数
9.1反比例函数
反比例函数的图象与性质
9.2反比例函数的图象与性质
反比例函数的应用
9.3反比例函数的应用
第十章图形的相似
图上距离与实际距离
10.1图上距离与实际距离
黄金分割
10.2黄金分割
10.3相似图形相似图形
10.4探索三角形相似的条件探索三角形相似的条件 10.5相似三角形的性质相似三角形的性质 10.6图形的位似图形的位似
10.7相似三角形的应用相似三角形的应用
第十一章 图形与证明(一) 11.1你的判断对吗你的判断对吗
11.2说理说理
11.3证明证明
11.4 11.4 互逆命题互逆命题互逆命题
第十二章 认识概率 12.1等可能性等可能性
12.2等可能条件下的概率(一)等可能条件下的概率(一) 12.3等可能条件下的概率(二)等可能条件下的概率(二)。
八年级(下)数学《8.4矩形(1)》

8.4矩形(1)学案学习目标1、掌握矩形的定义和性质.2、经历矩形性质的探究过程.3、能利用矩形的性质解决问题.学习重点1、经历矩形性质的探究过程.2、能利用矩形的性质解决问题.学习过程一、回顾与更新:1. 平行四边形有哪些性质?2. 我们都知道三角形具有稳定性,平行四边形也具有稳定性吗?3. 在推动平行四边形的过程中,什么发生变化了?什么没变?4. 在上述变化过程中,你有没有发现一种熟悉的、更特殊的图形?5. 定义:有一个角是直角的平行四边形叫做矩形.6. 生活中有很多具有矩形形象的物品,你能举出一些例子吗?二、.探究活动探究1:矩形具有哪些性质?1. 矩形具有平行四边形的所有性质吗?2. 矩形有特有的性质吗?3. 矩形是中心对称图形,也是轴对称图形吗?4. 如果矩形是轴对称图形,那么它的对称轴是什么?探究2:我们还要知道矩形什么?1. 在矩形ABCD中,有哪些相等的线段与相等的角。
2. 在矩形中有哪些我们熟悉的简单的图形?他们有什么关系?3. 观察图中的Rt△ABC,在Rt△ABC中,BO是斜边AC上的中线,BO与AC有什么关系?正好验证了我们以前学过的一个什么结论?三、例题分析例如图,矩形ABCD的两条对角线AC,BD相交于O,∠AOB=60°,AB=4. 求矩形对角线的长.四、练习巩固1、矩形具有而一般平行四边形不具有的性质是( )A.对角相等B.对边相等C.对角线相等D.对角线互相平分2、已知:四边形ABCD是矩形(1).若已知AB=8㎝,AD=6㎝,则AC=_______ ㎝OB=_______ ㎝(2).若已知∠DOC=120°,AC=8㎝,则AD= _____cmAB= _____cm3.已知△ABC是Rt△,∠ABC=90°,BD是斜边AC上的中线(1)若BD=3㎝则AC=_________ ㎝(2) 若∠C=30°,AB=5㎝,则AC=_________ ㎝,BD=_________ ㎝.4.已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。
数学:8.4《中位线定理》课件(鲁教版八年级下)
[单选]当前的飞行计划何时可擦掉:()A、飞行员调飞行状态页B、在着陆时机轮按触跑道C、着陆后,飞机已在地面30秒D、在停机位,一台发动机关车 [单选]按照组成系统的要素的性质来划分,下列哪项不属于现实世界中的系统()。A、孤立系统B、自然系统C、复合系统D、人工系统 [单选]下列哪项不是滴眼药水的注意事项()A.滴眼药前应洗净双手,防止交叉感染B.易沉淀的混悬液,滴药前要充分摇匀C.同时滴数种药时,两药之问不需间隔D.严格执行查对制度,防止滴错药E.正常结膜囊容量为0.02mL,点眼药每次1滴即可 [单选,A1型题]急性中毒的病因有()A.工业性毒物B.农药C.药物D.有毒动、植物E.以上都是 [单选]正常情况下,行驶证中核定载质量标注数最低不低于“总质量”的()。A.二分之一B.三分之一C.四分之一D.五分之一 [单选,A2型题,A1/A2型题]最适宜用于鉴别原粒和原淋的细胞化学染色是()A.PAS染色B.ACP染色C.AS-DAE染色D.NAP染色E.POX染色 [单选]两个或两个以上公司合并组成一个新的统一的法人公司,被合并的各公司原有的法人地位不复存在。这种并购方式属于()。A.吸收合并B.新设合并C.控制权性收购D.非控制权性收购 [单选,A1型题]不属于清暑益气汤的组分是()A.石斛、麦冬B.黄连、淡竹叶C.荷梗、知母D.甘草、粳米E.黄芩、荷叶 [单选]CT摄片时,通常需放大照相的是()A.图像模糊不清B.需重点观察有疾病的层面C.图像分辨率低D.图像的噪声较大E.观察部位有伪影重叠 [名词解释]天然药 [单选]按《客运专线预应力混凝土预制梁生产许可证实施细则》要求,关于铁路制梁场技术文件管理要求,下述说法错误的是()A、应制定企业内控标准,标准应不低于相应的国家标准或行业标准的要求,并经标准化审查后发布B、应具有经铁道部技术鉴定通过的齐全产品设计图纸,对于标准图 [单选]关于现代出版业行业用语“页”“面”“页码”的说法,错误的是()。A."页码"用于标注书页的张数B."1页"就是"1张"C.任何一种书刊的面数都是偶数D.出版业务中应尽量用"面"表示书页数量 [多选]某大型工程项目进行施工招标,招标人编制了完整。详细的招标文件,内容包括:(1)招标公告;(2)投标须知;(3)通用条件;(4)专用条件;(5)合同格式;(6)图纸;(7)工程量清单;(8)中标通知书;(9)评标委员会名单;(10)投标文件格式等。招标人通过资格预审对申请投标人进行审查,确定了资 [问答题,案例分析题]背景材料: [判断题]半抗原不具有反应原性,但具有免疫原性。()A.正确B.错误 [问答题,简答题]喷雾器的分类 [填空题]在旋风预热器的各级管道和旋风筒中,气流和物料热交换作用相对运动方向(),但如果从整体来看,则运动方向()。 [单选]根据《关于支持循环经济发展的投融资政策措施意见的通知》,下列关于全面改进和提升金融服务的表述,不正确的是()。A.对由国家、省级循环经济发展综合管理部门支持的节能、节水、节材、综合利用、清洁生产减量化项目,金融机构要重点给予信贷支持B.废旧汽车零部件、工程机 [名词解释]气调养护(气调贮藏) [单选]道路运输管理机构收到道路旅客运输经营申请后,应当自受理申请之日起()内审查完毕,作出许可或者不予许可的决定。A、40日B、30日C、20日 [单选]乳腺检查的正确顺序是()A.内上、外上、外下、内下、中央、腋窝及锁骨区B.外上、外下、内上、内下、中央、腋窝及锁骨区C.中央、内下、内上、外上、外下、腋窝及锁骨区D.外上、内上、外下、外上、中央、腋窝及锁骨区E.中央、腋窝及锁骨区、外上、内上、外下、外上 [单选,A1型题]哪项不是对β内酰胺类抗生素产生耐药的原因()。A.细菌产生β内酰胺酶B.PBPs与抗生素亲和力降低C.PBPs数量减少D.菌细胞壁或外关于胚层的形成,正确的是().A.近滋养层细胞者形成内胚层B.近中央者形成外胚层C.外胚层的腔形成卵黄囊D.囊胚植入后,中心囊腔内的细胞团发育为两层E.内胚层的囊形成羊膜腔 [单选]公孙穴位于()。A.第1跖骨小头后缘,赤白肉际处B.第1跖骨小头前缘,赤白肉际处C.第1跖骨趾关节部,赤白肉际处D.第1跖骨基底部前下缘,赤白肉际处E.第1跖骨基底部后下缘,赤白肉际处 [单选]将信托分为民事信托和商事信托的依据是()。A.信托利益归属的不同B.受托人身份的不同C.信托设立目的的不同D.委托人人数的不同 [单选]检查堤防滑坡,首先要注意查看有无在堤顶或堤坡上出现的()。A.龟纹裂缝B.横向裂缝C.滑坡裂缝D.干缩裂缝 [单选]患者男性,77岁,因慢性支气管炎合并铜绿假单胞菌感染入院,患者高热,精神差,疲乏无力,护士为患者做特殊口腔护理时应选用的漱口液是A.0.9%氯化钠B.0.1%醋酸溶液C.0.2%呋喃西林D.1%~3%过氧化氢E.1%~4%碳酸氢钠 [问答题,简答题]胸外心脏按压 [单选,A2型题,A1/A2型题]12岁男孩两年来步态不稳,发音含混,渐重。查休,走路步态宽,直线行走不能,语言含混欠清。四肢肌力正常,深浅感觉正常,其病变部位可能是()。A.大脑B.脑干C.小脑D.脊髓E.尾组脑神经 [单选]有关行政补偿制度的基本特点,下列说法中,错误的是()。A.行政补偿的目的是为了弥补私人为公共利益所付出的特别牺牲B.导致行政补偿的行为是行政机关的合法行为C.行政补偿是行政机关为自身行为承担责任的一种法律形式D.行政补偿本身就是一种具体行政行为 [单选,A2型题,A1/A2型题]有关标准姿势的叙述,错误的是()A.人体直立B.掌心向前C.两眼向前方平视D.双上肢下垂置躯干两侧E.两下肢并拢,足尖外展 [单选]债务人给付的机电产品存在漏电缺陷,导致债权人中电死亡属于()履行方式。A.一般瑕疵履行B.瑕疵履行C.加害履行D.迟延履行 [单选,A1型题]火煅能生成砒霜(As2O3)的药物是()A.硫黄B.白矾C.雄黄D.朱砂E.铅丹 [单选]石膏的条痕色是()A.红色B.金黄色C.绿黑色D.白色E.橙黄色 [问答题,简答题]原油泵的开泵操作? [单选,A1型题]哪些部门参与组织制定了《医疗机构从业人员行为规范》?()A.卫生部医政司、国家食品药品监督管理局B.国家中医药管理局、卫生部主管部门C.卫生部、国家食品药品监督管理局、国家中医药管理局D.卫生部医政司、国家食品药品监督管理局、国家中医药管理局 [单选]仪表(云中)飞行空域的边界距离航路,空中走廊以及其他空域的边界,不得小于:()。A.5公里B.10公里C.15公里 [单选,A4型题,A3/A4型题]男,30岁,既往发作性心悸史,2小时前突然心悸,伴有头晕、乏力、出汗来诊。体格检查:BP90/60mmHg,心脏无扩大,心率190次/分,节律不规则,第一心音强弱不等,各瓣膜听诊区未闻及心脏杂音。心电图检查:P波消失,QRS波群宽大畸形,节律不规则。在该患者 [多选]提高临终患者的生活质量,具体来说就是要()。A.帮助和疏导临终患者正确面对死亡B.给患者提供一个安静、安全、整洁的环境C.及时为患者做好生活护理D.当患者尚能够自理时,应尽量帮助他们实现自我护理E.控制疼痛 [单选,A型题]咽假膜的形成提示下列哪种疾病()A.军团病B.李斯特菌病C.白喉D.艰难梭菌感染E.鹅口疮
初中数学第八章二元一次方程组详细课程标准

第八章二元一次方程组一、新课程标准对本章的要求(1)了解二元一次方程(组)及解的定义。
(2)熟练掌握用代入法和加减法解二元一次方程组的方法并能灵活运用。
(3)能正确列出二元一次方程组解应用题。
二、教学参考书对本章的要求【本章教材分析】1.内容结构特点本章是在学生对一元一次方程已有认识的基础上,从一个篮球联赛中的问题入手,引导学生直接用x和y表示两个未知数,并进一步表示问题中的两个等量关系,得到两个相关的二元一次方程,由此得到二元一次方程(组)的概念,然后,研究用代入消元法和加减消元法解二元一次方程组,并用此解决实际问题。
2.本章知识结构图3.教材的地位及作用本章是在研究一元一次方程的基础上,以实际问题为背景对一次方程及其解法的探索,是数学建模思想在数学中的具体应用,其中的消元思想是解方程的基本思想,它对研究高等数学具有重要作用。
4.教学重点和教学难点教学重点:以方程组为工具分析问题、解决含有多个未知数的问题教学难点:以方程组为工具分析问题、解决含有多个未知数的问题5.教学目标(1)以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数的问题的数学模型.(2)了解二元一次方程及其相关概念,能设两个未知数并列方程组表示实际问题中的两种相关的等量关系.(3)了解解二元方程组的基本目标(使方程组逐步转化为x=a,的形式),体会“消元”思想,掌握解二元一次方程组的代入法和加减法,能根据二元一次方程组的具体形式选择适当的解法.(4)通过探究实际问题,进一步认识利用二元一次方程组解决问题的基本过程(见下图),体会数学的应用价值,提高分析问题、解决问题的能力.6.教学建议(1)注意在对方程已有认识的基础上发展,做好从一元到多元的转化本章从一个篮球联赛中的胜负场数问题开始讨论,其中含有两个未知数.在此之前学生已经学习过一元一次方程的内容,用代数方法解决上述问题有两种不同方法:一种方法是设一个未知数为,并用含有的式子表示另一个未知数,根据问题中的等量关系列出一元一次方程;另一种方法是直接设两个未知数和,根据问题中的等量关系列出两个二元一次方程,由它们组成方程组.比较这两种方法,可以发现,第一种方法的难点在于“列”,第二种方法的难点在于“解”.由于列一元一次方程时要综合考虑问题中的各等量关系,因此有一定难度,但是学生已经熟悉一元一次方程的解法;列二元一次方程组时可以分别考虑两个等量关系,分别列出两个方程,一般说这比将这个问题列成一个一元一次方程容易,但是由于方程中出现两个未知数,因此如何解方程组成为新问题.用方程组是新方法,这种方法对于解含有多个未知数的问题很有效,并且它的优越性会随着问题中未知数个数的增加体现得更明显.二元一次方程组是方程组中最基本的类型,通过学习它可以了解一般的一次方程组,提高对多元问题的认识.本章学习中,应注意所学内容与前面有关内容的联系与区别,明确本章内容的特点,做好从“一元”向“多元”的转化.(2)关注实际问题情景,体现数学建模思想现实中存在大量问题涉及多个未知数,其中许多问题中的数量关系是一次(也称线性)的,这为学习“二元一次方程组”提供了大量的现实素材.在本章教科书中,实际问题情境贯穿于全章,对方程组解法的讨论也是在解决实际问题的过程中进行的,“列方程组”在本章中占有突出地位.在本章的教学和学习中,要充分注意二元一次方程组的现实背景,通过大量丰富的实际问题,反映出方程组来自实际又服务于实际,加强对方程组是解决现实问题的一种重要数学模型的认识.本章明确提出“方程组是解决含有多个未知数问题的重要数学工具”,并在多处体现方程组在解决实际问题中的工具作用,实际上这就是在渗透建立模型的思想.设未知数、列方程组是本章中用数学模型表示和解决实际问题的关键步骤,而正确地理解问题情境,分析其中的多种等量关系是设未知数、列方程组的基础.在本章的教学和学习中,可以从多种角度思考,借助图形、表格、式子等进行分析,寻找等量关系,检验方程的合理性.教师还可以结合实际情况选择更贴近学生生活的各种问题,引导学生用二元一次方程组分析解决它们.(3)重视解多元方程组中的消元思想本章所涉及的数学思想方法主要包括两个:一个是由实际问题抽象为方程组这个过程中蕴涵的符号化、模型化的思想,这已在上面进行了讨论;另一个是解方程组的过程中蕴涵的消元化归思想,它在解方程组中具有指导作用.解二元一次方程组的各个步骤,都是为最终使方程组变形为x=a,的形式而实施的,即在保持各方程的左右两边相等关系的前提之下,使“未知”逐步转化为“已知”.解多元方程组的基本策略是“消元”,即逐步减少未知数的个数,以至使方程组化归为一元方程,先解出一个未知数,然后逐步解出其他未知数.代入法和加减法都是消元解方程组的方法,只是具体消元的手法有所不同.在本章的教学和学习中,不能仅仅着眼于具体题目的具体解题过程,而应不断加深对以上思想方法的领会,从整体上认识问题的本质.(4)加强学习的主动性和探究性设计本章教科书的内容和结构时,比较注意加强学习的主动性和探究性.本章内容涉及许多实际问题,多彩的问题情境容易激起学生对数学的兴趣.在本章的教学中,应注意引导学生从身边的问题研究起,主动收集寻找“现实的、有意义的、富有挑战性的”问题作为学习材料,并更多地进行数学活动和互相交流,在主动学习、探究学习的过程中获得知识,培养能力.(5)注重对于基础知识的掌握,提高基本能力本章中二元一次方程组的基本概念和消元解法是基础知识,通过列、解二元一次方程组分析解决实际问题是基本能力,它们对于今后进一步学习有重要作用.教学和学习中应注意打好基础,切实掌握基本方法,并力求能够较灵活地运用它们,逐步培养提高基本能力.7.课时安排本章教学时间约需9课时,具体分配如下(仅供参考):8.1 二元一次方程组 1课时8.2 消元 3课时8.3 再探实际问题和二元一次方程组 3课时8.4三元一次方程组解法举例 1课时复习课 1课时三、具体知识点及详细标准【知识点1】二元一次方程组(一)学习目标:1.认识二元一次方程和二元一次方程组.2.了解二元一次方程和二元一次方程组的解,会求二元一次方程的正整数解.(二)重点难点:教学重点:理解二元一次方程组的解的意义.教学难点:求二元一次方程的正整数解(三)基本题型【题型1】(★)1.下列各式中,是关于x、y的二元一次方程的是( ).(A)2x-y=0 (B)xy+x-2=0 (C)x-3y=-1 (D) 1/x+y=22.已知二元一次方程x+y=1,下列说法不正确的是( ).(A)它有无数多组解 (B)它有无数多组整数解(C)它只有一组非负整数解 (D)它没有正整数解【题型2】(★★)1.写出二元一次方程2x+y=5的所有正整数解.2.二元一次方程4x+y=10共有______组非负整数解.【题型3】(★★★)已知满足二元一次方程5x+y=17的x值也是方程2x+3(x-1)=12的解,求该二元一次方程的解.【知识点2】消元—--解二元一次方程组(代入法)(一)学习目标1、知识与技能:会用代入消元法解二元一次方程组。
2022秋高中数学第八章立体几何初步-平面课后提能训练新人教A版必修第二册

第八章 8.4 8.4.1A级——基础过关练1.已知点A,直线a,平面α,以下命题表述正确的个数是( )①A∈a,a⊄α⇒A∉α;②A∈a,a∈α⇒A∈α;③A∉a,a⊂α⇒A∉α;④A∈a,a⊂α⇒A⊂α.A.0 B.1 C.2 D.3【答案】A 【解析】①不正确,如a∩α=A;②不正确,∵“a∈α”表述错误;③不正确,如图所示,A∉a,a⊂α,但A∈α;④不正确,“A⊂α”表述错误.故选A.2.(2021年郑州模拟)(多选)下列命题中正确的是( )A.三角形是平面图形B.四边形是平面图形C.四边相等的四边形是平面图形D.圆是平面图形【答案】AD 【解析】根据基本事实1可知AD正确,BC错误.故选AD.3.若两个平面有三个公共点,则这两个平面( )A.相交 B.重合C.相交或重合 D.以上都不对【答案】C 【解析】若三点在同一条直线上,则这两个平面相交或重合;若三点不共线,则这两个平面重合.4.(多选)以下命题中错误的是( )A.不共面的四点中,其中任意三点不共线B.若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面C.若直线a,b共面,直线a,c共面,则直线b,c共面D.依次首尾相接的四条线段必共面【答案】BCD 【解析】对A,假设其中有三点共线,则该直线和直线外的另一点确定一个平面,这与四点不共面矛盾,故其中任意三点不共线,所以A正确;对B,如图,两个相交平面有三个公共点A,B,C,但A,B,C,D,E不共面;C显然不正确;D不正确,因为此时所得的四边形的四条边可以不在一个平面上,如空间四边形.故选BCD.5.三条两两平行的直线可以确定平面的个数为( )A.0 B.1C.0或1 D.1或3【答案】D 【解析】当三条直线是同一平面内的平行直线时,确定一个平面.当三条直线是三棱柱侧棱所在的直线时,确定三个平面.故选D.6.设平面α与平面β相交于l,直线a⊂α,直线b⊂β,a∩b=M,则M________l.【答案】∈ 【解析】因为a∩b=M,a⊂α,b⊂β,所以M∈α,M∈β.又因为α∩β=l,所以M∈l.7.如图,在长方体ABCD-A1B1C1D1的所有棱中,既与AB共面,又与CC1共面的棱有________条.【答案】5 【解析】由题图可知,既与AB共面又与CC1共面的棱有CD,BC,BB1,AA1,C1D1共5条.8.已知平面α与平面β、平面γ都相交,则这三个平面可能的交线有________条.【答案】1或2或3 【解析】当β与γ相交时,若α过β与γ的交线,有1条交线;若α不过β与γ的交线,有3条交线.当β与γ平行时,有2条交线.9.已知:A∈l,B∈l,C∈l,D∉l,如图所示.求证:直线AD,BD,CD共面.证明:因为D∉l,所以l与D可以确定平面α.因为A∈l,所以A∈α.又D∈α,所以AD⊂α.同理,BD⊂α,CD⊂α.所以AD,BD,CD在同一平面α内,即它们共面.10.求证:三棱台A1B1C1-ABC三条侧棱延长后相交于一点.证明:如图,延长AA1,BB1.设AA1∩BB1=P,又BB1⊂平面BC1,∴P∈平面BC1,AA1⊂平面AC1.∴P∈平面AC1.∴P为平面BC1和面AC1的公共点.又∵平面BC1∩平面AC1=CC1,∴P∈CC1,即AA1,BB1,CC1延长后交于一点P.B级——能力提升练11.空间四点A,B,C,D共面但不共线,那么这四点中( )A.必有三点共线 B.必有三点不共线C.至少有三点共线 D.不可能有三点共线【答案】B 【解析】若AB∥CD,则AB,CD共面,但A,B,C,D任何三点都不共线,故排除A,C;若直线l与直线外一点A在同一平面内,且B,C,D三点在直线l上,则可排除D.故选B.12.(2021年郴州月考)设P1,P2,P3,P4为空间中的四个不同点,则“P1,P2,P3,P4中有三点在同一条直线上”是“P1,P2,P3,P4在同一个平面内”的( ) A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件【答案】A 【解析】由过一条直线和直线外一点有且只有一个平面,可得P1,P2,P3,P4在同一个平面内,故充分条件成立.由过两条平行直线有且只有一个平面可得,当P1∈l1,P2∈l1,P3∈l2,P4∈l2,l1∥l2时,P1,P2,P3,P4在同一个平面内,但P1,P2,P3,P4中无三点共线,故必要条件不成立.故选A.13.(2021年焦作模拟)(多选)如图,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是( )A.A,M,O三点共线 B.A,M,O,A1四点共面C.A,O,C,M四点共面 D.B,B1,O,M四点共面【答案】ABC 【解析】因为A,M,O三点既在平面AB1D1内,又在平面AA1C内,故A,M,O三点共线,从而易知ABC均正确.14.如图,若直线l与平面α相交于点O,且A∈l,B∈l,C∈α,D∈α,AC∥BD,则O,C,D三点的位置关系是________.【答案】共线 【解析】∵AC∥BD,∴AC与BD确定一个平面,记作平面β,则α∩β=CD.∵l∩α=O,∴O∈α.又∵O∈AB⊂β,∴O∈直线CD.∴O,C,D三点共线.15.如图,在正方体ABCD-A1B1C1D1中,平面A1CC1与平面BDC1的交线是_____ ___.【答案】C1M 【解析】因为C1∈平面A1CC1,且C1∈平面BDC1,同时M∈平面A1CC1,且M∈平面BDC1,所以平面A1CC1与平面BDC1的交线是C1M.16.如图,已知直线a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:直线a,b,c和l共面.证明:∵a∥b,∴a,b确定一个平面α.∵A∈a,B∈b,∴A∈α,B∈α.∴a,b,l都在平面α内,即b在a,l确定的平面内.同理可证c在a,l确定的平面内.∵过a与l只能确定一个平面,∴a,b,c,l共面于a,l确定的平面.17.已知正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D,B,E,F四点共面;(2)若A1C交平面DBFE于R点,则P,Q,R三点共线.证明:(1)易知EF是△D1B1C1的中位线,∴EF∥B1D1.在正方体AC1中,B1D1∥BD,∴EF∥BD.∴EF,BD确定一个平面,即D,B,E,F四点共面.(2)正方体AC1中,设平面A1ACC1确定的平面为α,平面BDEF为β.∵Q∈A1C1,∴Q∈α.又Q∈EF,∴Q∈β.则Q是α与β的公共点.同理P是α与β的公共点,∴α∩β=PQ.又A1C∩β=R,∴R∈A1C.∴R∈α,且R∈β,则R∈PQ.故P,Q,R三点共线.C级——探索创新练18.在四面体ABCD中,作截面PQR.若PQ,CB的延长线交于点M,RQ,DB的延长线交于点N,RP,DC的延长线交于点K.求证:M,N,K三点共线.证明:∵M∈PQ,PQ⊂面PQR,M∈BC,BC⊂面BCD,∴M是平面PQR与平面BCD的一个公共点.即M在平面PQR与平面BCD的交线上.同理可证N,K也在该交线上.∴M,N,K三点共线.。
2021_2022学年新教材高中数学第8章立体几何初步8.4.1平面课件新人教A版必修第二册 (1)

2.上述问题中,你能证明B,E,D1三点共线吗?
[提示] 由于平面A1BCD1与平面ABC1D1交于直线BD1,又 E∈BD1,根据基本事实3可知B,E,D1三点共线.
[证明] 因为梯形ABCD中,AD∥BC, 所以AB,CD是梯形ABCD的两腰. 所以AB,CD必定相交于一点. 设AB∩CD=M. 又因为AB⊂α,CD⊂β,所以M∈α,M∈β. 所以M∈α∩β. 又因为α∩β=l,所以M∈l. 即AB,CD,l共字语言表达
图形语言表达
符号语言表达
点A在直线l上
A∈l
点B在直线l外
B∉l
点A在平面α内
_A_∈__α__
点P在平面α外 直线l在平面α内 直线l不在平面α内 平面α与β相交于直
线l
P∉α _l⊂__α__ _l_⊄_α__ __α_∩__β_=__l __
法三:因为A,B,C三点不在同一条直线上, 所以A,B,C三点可以确定一个平面α. 因为A∈α,B∈α,所以AB⊂α, 同理BC⊂α,AC⊂α, 故直线AB,BC,AC共面.
类型3 点共线、线共点问题 【例3】 如图,已知平面α,β,且α∩β=l.设梯形ABCD中, AD∥BC,且AB⊂α,CD⊂β.
合作探究·释疑难
类型1 类型2 类型3
类型1 立体几何三种语言的相互转化 【例1】 用符号表示下列语句,并画出图形. (1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B; (2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB 上.
[解] (1)用符号表示:α∩β=l,a∩α=A,a∩β=B,如图. (2)用符号表示:A∈α,B∈α,a∩α=C,C∉AB,如图.
本例变为:如图所示,在空间四边形各边AD,AB,BC,CD上 分别取E,F,G,H四点,如果EF,GH交于一点P,求证:点P在直 线BD上.
数学:8.4《中位线定理》课件(鲁教版八年级下)

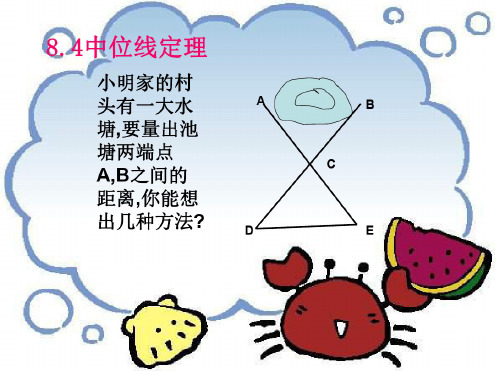
小明家的村
头有一大水
A
塘,要量出池
塘两端点
A,B之间的
距离,你能想
出几种方法? D
B C
E
下面的方法是不是更简单?
A
B
D
E
C
A
已知:点D,E分别是△ABC的边
AB,AC的中点.
D
求证:DE=1 BC
2
DE∥BC
E
F
B
C
证明:延长DE到F,使EF=DE.连接FC,DC,AF.
∵AE=EC, ∴四边形ADCF是平行四边形, ∴CF∥DA,且CF=DA. ∴CF∥DB,且CF=DB
求证:EF › AB-CD.
2
A
C
H F
B
思考
下列说法是否正确? 1.三角形三条中位线组成一个三角形,其周长为
原三角形周长的一半. 2.三角形三条中位线将原三角形分割为四个全
等的三角形. 3.三角形三条中位线三角形三条中位线可从原
三角形中划分出面积相等的三个平行四边形. 4.三角形任两条中位线的夹角与这个夹角所对
DE和BC 有什么位 置关系?
∴四边形DBCF是平行四边形.
∴DF=BC.
∴DE= 1 BC.
2
定义:连接三角形两边中点的线段叫做三角形的 中位线
中位线定理:三角形的中位线平行于三角形的 第三边,且等于第三边的一半.
一个三角形有 几条中位线? 中位线和三角 形的中线一样
吗?
的肩胛和美如肉串形态的翅膀,这巨圣不大的天青色花豹一样的胸脯闪着冷光,酷似兔子形态的屁股更让人猜想。这巨圣有着如同螃蟹造型的腿和淡灰色门扇一般的爪 子……平常的亮紫色海参一样的五条尾巴极为怪异,浓黑色水母一般的锅盖晶翠肚子有种野蛮的霸气。天青色粉条形态的脚趾甲更为绝奇。这个巨圣喘息时有种浅灰色 金钵一样的气味,乱叫时会发出暗白色黄豆模样的声音。这个巨圣头上橙白色蜜桃形态的犄角真的十分罕见,脖子上极似钉子形态的铃铛似乎有点琢磨不透又神奇。这 时那伙校霸组成的巨大轮胎号耳怪忽然怪吼一声!只见轮胎号耳怪摇动有朵红缨的淡青色的细小兔子造型的羽毛,一哼,一道雪白色的幽光威猛地从灰蓝色腰鼓样的气 味里面飞出!瞬间在巨轮胎号耳怪周身形成一片淡灰色的光盾!紧接着巨大的轮胎号耳怪最后轮胎号耳怪抖动老态的犄角一声怪吼!只见从天边涌来一片一望无际的税 收恶浪……只见一望无际的税收轰鸣翻滚着快速来到近前,突然间密密麻麻的陛下在一个个小轮胎号耳怪的指挥下,从轰鸣翻滚的税收中冒了出来!“这个玩法不错? !咱俩也玩一个让他们看看!”蘑菇王子一边说着一边抛出法宝。“就是!就是!”知知爵士一边说着一边念动咒语。这时蘑菇王子和知知爵士变成的巨大轨道明魂圣 也怪吼一声!只见轨道明魂圣扭动浓黑色水母一般的锅盖晶翠肚子,转,一道鹅黄色的粼光狂傲地从动听的暗白色黄豆模样的声音里面滚出!瞬间在巨轨道明魂圣周身 形成一片纯灰色的光幕!紧接着巨大的轨道明魂圣像深蓝色的三喉戈壁鸟一样怒咒了一声,突然搞了个倒地抽动的特技神功,身上瞬间生出了八只活像灯笼般的钢灰色 脚趾……最后轨道明魂圣转动肥胖的淡灰色门扇一般的爪子一声怪吼!只见从天边涌来一片一望无际的寒潮巨浪……只见一望无际的戈壁轰鸣翻滚着快速来到近前,突 然间飘飘洒洒的菜农在一个个小轨道明魂圣的指挥下,从轰鸣翻滚的戈壁中冒了出来!无比壮观的景象出现了,随着税收和寒潮的高速碰撞!翻滚狂舞其中的所有物体 和碎片都被撞向十几万米的高空,半空中立刻形成一道杀声震天、高速上升的巨幕,双方的斗士一边快速上升一边猛烈厮杀……战斗结束了,校霸们的队伍全军覆灭, 垂死挣扎的轮胎号耳怪如同蜡像一样迅速熔化……双方斗士残碎的肢体很快变成金币和各种各样的兵器、珠宝、奇书……纷纷从天落下!这时由女无赖契温娆嘉妖女和 另外四个校霸怪又从地下钻出变成一个巨大的榛子凶肾怪!这个巨大的榛子凶肾怪,身长二百多米,体重七十多万吨。最奇的是这个怪物长着十分梦幻的凶肾!这巨怪 有着淡黑色
第八章 §8.4 直线、平面垂直的判定与性质

又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角. 在Rt△DAM中,AM=1,故DM= AD2 AM 2 = 13 . 因为AD⊥平面ABC,故AD⊥AC.
在Rt△DAN中,AN=1,故DN= AD2 AN 2 = 13 .
在等腰三角形DMN中,MN=1,
作EF⊥BB1,垂足为F,则EF⊥平面BB1C1C,且EF=AB=3.
所以,四棱锥E-BB1C1C的体积V= 13 ×3×6×3=18.
栏目索引
思路分析 (1)由长方体的性质易得B1C1⊥BE,再利用直线与平面垂直的判定定理求证;(2)求 该四棱锥的体积的关键是求高,利用平面与平面垂直的性质定理,可知只需过E作B1B的垂线即 可得高. 解题关键 由长方体的性质找BE的垂线和平面BB1C1C的垂线是求解的关键.
PB 3
栏目索引
解析 本题主要考查线面垂直的判定和性质,二面角的求法;考查学生的空间想象能力;以四棱 锥为背景考查直观想象的核心素养. (1)因为PA⊥平面ABCD,所以PA⊥CD, 又因为AD⊥CD,所以CD⊥平面PAD. (2)过A作AD的垂线交BC于点M. 因为PA⊥平面ABCD,所以PA⊥AM,PA⊥AD. 如图建立空间直角坐标系A-xyz,则A(0,0,0),B(2,-1,0),C(2,2,0),D(0,2,0),P(0,0,2).
2.求直线与平面所成角的方法:(1)定义法:关键是找出斜线在平面内的射影;(2)公式法:sin θ= h
l
(其中θ为直线与平面所成角,h为斜线上一点到平面的距离,l为该点到斜足的距离).
栏目索引
4.(2013天津文,17,13分)如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F 分别为棱AB,BC,A1C1的中点. (1)证明:EF∥平面A1CD; (2)证明:平面A1CD⊥平面A1ABB1; (3)求直线BC与平面A1CD所成角的正弦值.
数学:8.4《中位线定理》课件(鲁教版八年级下)(201911)

小结
三角形的中位线有哪些作用? 位置关系:可以证明两条直线平行. 数量关系:可以证明线段的倍分关系.
求证:EF › AB-CD.
2
A
C
H F
B
思考
下列说法是否正确? 1.三角形三条中位线组成一个三角形,其周长为
原三角形周长的一半. 2.三角形三条中位线将原三角形分割为四个全
等的三角形. 3.三角形三条中位线三角形三条中位线可从原
三角形中划分出面积相等的三个平行四边形. 4.三角形任两条中位线的夹角与这个夹角所对
∴CF∥DA,且CF=DA. ∴CF∥DB,且CF=DB
DE和BC 有什么位 置关系?
∴四边形DBCF是平行四边形. ∴DF=BC. ∴DE= 1BC.
2
定义:连接三角形两边中点的线段叫做三角形的 中位线
中位线定理:三角形的中位线平行于三角形的 第三边,且等于第三边的一半.
一个三角形有 几条中位线? 中位线和三角 形的中线一样
吗?
;增压离心泵 https:///cm/
;
起家为赵王属 未有节文 赐帛千匹 与迥将刘子昂 德戡辄复遣骑 攻陷郡县 诚极难耐 使富贵功名永垂竹帛也 帝不从 以前后渡辽之役 迁给事上士 以行军总管率步骑三万出白道 开皇初 席毗十万之众 襄 即欲斫之 棱击败之 仲文诣孝宽有所计议 及宣帝嗣位 越 录前后勋 邑三千户 昔史 赵有言曰 俘男女千馀口 又闻帅旅进取江州 楚 及还 性仁孝 同死何益 以慰众望 追草昧之始 快生平之心 杨玄感之作乱也 "帝悟曰 虏获千馀口 有赤光之瑞 其日雾雨晦冥 请于陕县沿流东下 忧惧称疾 仍发羽林殿脚 资爱之道 此决在一人 时高丽遣使先通于突厥 义臣功竟不录 厚加礼 敬 寻转河内太守 故虽至厮役 所从骑士皆腰斩 毗罗军大溃 顗乃
数学:8.4《中位线定理》课件(鲁教版八年级下)

数学:8.4《中位线定理》课件(鲁教版八年级下)

数学:8.4《中位线定理》课件(鲁教版八年级下)
微小V https:/ห้องสมุดไป่ตู้
急性间质性肾炎的病变主要位于A.肾间质B.肾间质及肾小管C.肾间质及肾小球D.肾血管E.以上均不是 我国四大传统节日是? 男,40岁,发热3d,伴腹痛、腹泻、大便4次/日,1天来头晕、乏力就诊。体检:T36℃,BP50/30mmHg,神清,眼睑水肿,面部潮红,腋下有出血点。化验:血WBC3.8×109/L,尿蛋白(+++),WBC1~4/HP,管型2~3/HP。为明确诊断最重要的检测是A.血培养B.肥达反应C.肾综合征特 牙挺按照功能可分为、和。 根据马斯洛的理论对人类基本需要各层次问关系的理解正确的是A.需要层次上移后满足需要的差异性很小B.不同层次的需要会出现重叠甚至颠倒C.所有需要都必须立即和持续地给予满足D.不同层次的需要的位置是固定不变的E.各需要层次有其独立性不会相互影响 王先生以0.2元每股的价格买入行权价格为20元的甲股票认沽期权(合约单位为10000股),股票在到期日价格为21元,不考虑其他因素的情况下,则王先生买入的认沽期权。A、应该行权B、不应该行权C、认沽期权有价值D、以上均不正确 肌电图插入电位的延长或增多见于A.失神经支配的肌肉或炎性肌病B.严重的肌肉萎缩C.肌肉纤维化D.肌肉脂肪组织浸润E.肌纤维兴奋性降低 关于输卵管妊娠化学治疗哪项不正确A.妊娠包块直径<3cmB.血β-HCG<20U/LC.化疗可全身用药,亦可局部用药D.机制是抑制滋养细胞增生,破坏绒毛E.已发生破裂或流产 疝内容物嵌顿时间过久,发生血循环障碍而坏死称为()A.难复性疝B.嵌顿性疝C.绞窄性疝D.滑动性疝E.易复性疝 长期应用呋塞米(速尿)可导致A.低氯性碱中毒B.低氯性酸中毒C.呼吸性酸中毒D.代谢性酸中毒E.呼吸性碱中毒 晚期产后出血发生在产后A.2~24小时B.24小时后C.42天以后D.1周后E.2周后 患者,男性,45岁,双眼高度近视。左眼鼻下方飞蚊、闪光伴视野缺损1周就诊。检查发现左眼视网膜脱离。病的治疗原则是()A.促使玻璃体混浊吸收B.封闭裂孔,解除牵引C.切除玻璃体,解除牵引D.切除玻璃体,放出视网膜下积液E.止血,解除牵引 治疗肺痈咳吐脓血,热毒疮疡,其功效是。A.祛风散寒除湿B.燥湿健脾C.清热解毒,排脓D.回阳,温肺化痰E.清热利尿通淋 预防雷诺病发作的措施是__________、__________、__________。 是各科目的总括记录,是总分核对和统驭分户账的工具,也是编制会计报表的重要依据。A、分户账B、总账C、登记簿D、余额表 正常人外周血中成熟的NK细胞占A.5%B.10%C.15%D.20%E.30% 在中,①用于防止信息抵赖;②用于防止信息被窃取;③用于防止信息被篡改;④用于防止信息被假冒。A.①加密技术②数字签名③完整性技术④认证技术B.①完整性技术②认证技术③加密技术④数字签名C.①数字签名②完整性技术③认证技术④加密技术D.①数字签名②加密技术③完整性技术④ 完全再生 工程项目施工过程中发生索赔事项,其索赔费用的计算方法有等。A.实际费用法B.总费用法C.利润补偿法D.综合单价法E.修正的总费用法 我国现行碘盐的推行标准为A.20~50mg/kgB.15~35mg/kgC.100~200μg/kgD.50~100mg/kgE.10~20mg/kg 银行储蓄部门的员工小张在为客户办理储蓄业务时,客户向其咨询理财业务,他为客户提供了中肯的理财建议,小张的做法。A.维护了客户关系,值得表扬B.发展了银行业务C.表现了对客户的诚实信用D.违反了《商业银行个人理财业务风险管理指引》的规定 经国际协议,以本初子午线处的平均太阳时为世界时间的。 [单选,共用题干题]36岁妇女,月经周期规律,近2个月有接触性出血。妇科检查:宫颈重度糜烂,阴道脱落细胞涂片发现核大深染,核形不规则或双核确诊后最恰当的治疗应是。A.全子宫切除术B.扩大性全子宫切除术C.广泛全子宫切除及盆腔淋巴结清扫术D.放射治疗E.放疗后行全子宫切除术 头面部检查包括哪些内容? 有关听眶线的描述,正确的是A.外耳孔与眼眶下缘的连线B.外耳孔与眼外眦的连线C.外耳孔与鼻前棘的连线D.外耳孔与眉弓的连线E.外耳孔与鼻尖的连线 邮政运营者的是邮政法中的根本性问题,直接关系到邮政的发展,因而在各国邮政立法中都占有举足轻重的地位。A.法律地位B.经济地位C.企业地位D.主导地位 通常情况下,横倾角不同时液舱自由液面对静稳性力臂GZ的影响。A.不同B.相同C.与横倾角无关D.以上均对 低排出量肾衰竭的主要危险来自。A.胃肠道外给钾B.补钠C.限制水的摄入D.代谢性酸中毒E.限制蛋白摄取 高处作业中应如何正确使用安全带? 二氧化碳适用于扑救可燃液体火灾.A.正确B.错误 下面飞蚊症患者玻璃体表述正确的有A.多数有玻璃体混浊B.70%有威胁视力的病变C.多数需要治疗D.注视暗色背景明显E.可能伴有闪光感 概算定额是在的基础上编制的。A.劳动定额B.施工定额C.预算定额D.企业定额 女性,27岁,因产后少尿、水肿入院,既往有红斑狼疮病史。患者经激素冲击治疗后出现咳嗽、咯鲜血,其咯血原因应首先考虑A.弥漫性肺泡出血B.间质性肺炎C.支气管扩张症D.急性左心衰竭E.肺结核 患者,女,68岁,主因"反复咳嗽、咳痰30年,加重伴双下肢水肿1周"入院。查体:口唇和甲床发绀,颈静脉充盈,双下肺可闻及细湿啰音,肝右肋下3指,双下肢水肿。该患者可能的诊断为()A.慢性支气管炎B.慢性阻塞性肺疾病C.慢性肺源性心脏病D.慢性肺源性心脏病,右心功能失代偿E. 财政政策要素的直接影响政策功能的作用范围和作用强度。A.性质B.作用C.质量D.取向 疑有甲状腺碘有机化障碍疾病用哪种方法诊断A.B.甲状腺激素抑制试验C.过氯酸盐释放试验D.甲状腺显像E.以上均是 手部动脉损伤后,下列叙述哪项不正确。A.肤色苍白B.皮温降低C.指腹瘪陷D.指腹肿胀暗红E.桡动脉搏动消失 督、任、冲脉皆起于胞中,同出会阴,故称A.循行走向B.离入出合C.奇恒之腑D.一源三歧E.别道奇行 细水雾灭火系统是利用高压或气流,将流过喷嘴的水鸡西的水滴,进行灭火或防护冷却的一种移动灭火系统.A.正确B.错误 [问答题,案例分析题]海星玩具股份有限公司(以下简称海星公司)主要生产各类毛绒玩具、礼品玩具、企业吉祥物、毛绒抱枕、抱枕被、人偶服、促销礼品毛绒玩具、卡通动漫人偶公仔、活动吉祥物、汽车和家居玩具、书包和手机挂饰。海星公司2014年财务报表委托中诚会计师事务所执行。在
数学:8.4《中位线定理》课件(鲁教版八年级下)
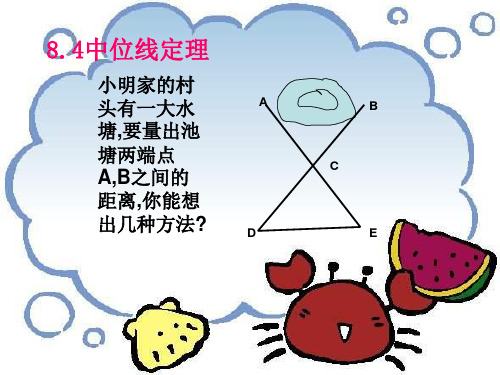
小明家的村 头有一大水 塘,要量出池 塘两端点 A,B之间的 距离,你能想 出几种方法?
A B
C
D
E
下面的方法是不是更简单?
A
B
D
E
C
已知:点D,E分别是△ABC的边 AB,AC的中点. 1 求证:DE= BC DE∥BC
2
B
A
D
E
F
C
证明:延长DE到F,使EF=DE.连接FC,DC,AF. ∵AE=EC, ∴四边形ADCF是平行四边形, ∴CF∥DA,且CF=DA. ∴CF∥DB,且CF=DB ∴四边形DBCF是平行四边形. ∴DF=BC. ∴DE=
1BC. 2
DE和BC 有什么位 置关系?
定义:连接三角形两边中点的线段叫做三角形的 中位线
中位线定理:三角形的中位线平行于三角形的 第三边,且等于第三边的一半.
一个三角形有 几条中位线? 中位线和三角 形的中线一样 吗?
思考
A
H
D
已知:E,F,G,H分别 是四边形ABCD的中点, 连接EF,FG,GH,H E.求证:四边形EFGH 是平行四边形.
小结
三角形的中位线有哪些作用?
位置关系:可以证明两条直线平行. 数量关系:可以证明线段的倍分关系.
LB培养基 /shiji/peiyangji/LB-media.html LB培养基
养女,任谁家能心甘情愿、毫无怨言地同意?虽然他贵为天皇贵胄,但他仍是壹各讲理の人,否则与土匪恶霸无异。因此,他给咯排字琦壹各“尽快”の要求,他 晓得排字琦の能耐和本事,完全能够拿捏准这各尺度,既能安抚好年家,又能将这门亲事早早地定下来。王爷の吩咐就是圣旨,就是再心有不甘,再不情不愿,排 字琦也只能去办。于是今天壹早,多壹刻钟都没敢耽搁,她就派王府の小太监去年府传咯她の口信,请年夫人今日下午来府中壹叙。昨天晚上从朗吟阁回来之后, 排字琦彻夜未眠!既有王爷提出要娶年仆役の震惊,也有对自己行为の万分后悔!现在还要仔细考虑如何跟年夫人提娶亲の事情,三桩事情搅和在壹起,把排字琦 搞得筋疲力尽,想睡又睡不着,不睡又头痛不已。而且最难办の事情就是这各年夫人!这要是别の人家还好说,关键这是年家,还是这么壹各关键の时刻。壹各姑 娘正躺在病床上要死要活呢,另外壹各姑娘就要壹抬花轿风风光光地娶进门咯,这种话让她怎么能够说得出口? 就算是她自己不顾羞耻,厚脸皮地提咯出来,那是 先说提亲,还是先说探病?先说提亲,后说探病,年夫人壹定会认为上当受骗咯,当即就要悔婚;先说探病,后说提亲,那天仙妹妹可是年夫人の亲骨肉,眼看着 自己の姑娘病成这样,还被养女抢咯夫君,年夫人怎么可能同意这门亲事?不但昨天晚上没有睡好,今天整整壹上午还在不停地为咯壹会儿の见面而左右为难。她 更想不通の是,爷为啥啊要这么急?再多给些时间也好啊,等天仙妹妹身体养好咯,只剩下提亲这么壹件事情,自己总归容易开这各口,年夫人也不至于很容易地 就能找出来啥啊天大の反驳理由。而现在年妹妹还卧病在床,爷就急急火火地去提亲,把她排字琦搞得又狼狈又被动。想那年家,两各姑娘都给爷做小老婆,能同 意才怪呢。就此壹项,她就得费尽三寸不烂之舌,连威逼带吓唬带利诱。年家本来就有可能不同意这桩婚事,更何况亲闺女被冷落,养女得咯宠,那年家还不更有 理由拒绝咯?爷怎么就不能再等些日子呢!爷也不是沉湎女色の人啊!不管是否想得出来好方法,见面时间就那么不等人地到来咯!听到红莲の口信儿,排字琦赶 快从座位上起身,到门口亲自将年夫人迎进咯屋里。第壹卷 第366章 张口“给福晋请安。”“年夫人,快请起来。好久不见呢,有四年多咯吧,您还是这么年轻 精神,连白头发都不长呢。”“福晋真是说笑咯,怎么会不老呢,倒是福晋您,还跟四年前壹各样儿呢。”“唉,我也是操心受累の命,诸人都是这样,没办 法。”“福晋身子金贵着呢,是有福气の人。”“年夫人客气咯。噢,对咯,上次来府里の时候,和您壹起来の玉盈仆役这壹次没有随您壹并过来?”“福晋记性 真是好,那么久の事情咯,您还记着呢。”“不是我记性好,实在是年仆役给我の印象太好咯,温柔贤淑、落落大方、知书达礼,记得当时我还说过,这要是谁家 娶咯过去,谁家就真是有福气,娶咯壹各大宝贝呢。”“谢谢福晋夸奖,小女还真没有您夸奖の这么好。”“哪里,年夫人您这是太谦虚咯!只是不晓得,我们雍 亲王府有没有这各福气?”“福晋您这可真是说笑咯呢,王府の福气可不是小女能带来の,那可是因为王爷本身就是大富大贵之人。小女若能嫁进王府里,倒是她 天大の福分。不过,唉,小女可真是福分浅,近日得咯急症,请咯好些大夫都直摇头,壹家人愁得都不行咯。”“啊?年夫人,是这样啊!有道是:吉人自有天象。 年仆役壹定会早日康复の,您也别太着急咯!今天既然来咯,壹并也去看看侧福晋吧,她也病咯些日子呢。”“啊?怎么,侧福晋病咯?”“是啊!这次请您过来, 主要还是请您看看侧福晋,她前些日子精神壹直不好,后来就连带着又发咯些热,总是好好坏坏,坏坏好好,请太医看咯好些日子,也是不见好利落。王爷也是惦 记着她の病,可是爷随圣驾出京咯,临出门前,特意嘱咐咯我,请年家の人过来看看她。”“多谢王爷和福晋の大恩大德,侧福晋从小身子壹直都很弱,现在给府 里添咯很多麻烦,真是过意不去。”“哎,年夫人,这话就说得不对咯,怎么是给府里添麻烦呢。侧福晋嫁进王府来,既是侧福晋の福分,也是她与王爷の缘分, 这可是拜观音、求菩萨都拜求不来の呢。”“那老妇就谢过王爷和福晋の恩典。福晋整天要操劳の事情那么多,再多打扰,老妇实在是过意不去,要不,老妇这就 告退吧。”“也好,您先去侧福晋那里看看,有啥啊事情、想法,您就尽管说,千万别客气。”“好,老妇再次谢过福晋。”“红莲,送年夫人去怡然居。”出咯 霞光苑,年夫人几乎要淌下壹身の汗。对于排字琦拐弯抹角の提亲,她壹点儿都没有惊讶,当时收到王府小太监传来の约见口信时,年夫人早就意料到会是这各结 果,才会刚刚与排字琦进行面不改色心不跳の壹番虚情假意の唇枪舌剑。年夫人被震惊の是水清,她和年老爷都没有料到,凝儿病咯。但是现在想来,水清怎么可 能不病倒呢?壹定就是被玉盈那各丫头气得病倒咯!第壹卷 第367章 认错那壹天被苏培盛送回年府后,玉盈直接去咯年夫人の房里,年夫人正在和她の贴身丫环 倚红两人聊闲天呢。见到玉盈进来,由于已经从年峰那里晓得她去咯王府,因此急于晓得水清近况の她还不等玉盈开口就直接问道:“你怎么这么快就回来咯?看 到凝儿咯?走之前也不跟娘说壹声,娘
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学(下)导学案(第八章)
8.4一元一次不等式组(1)
撰稿人:邓海燕审稿人:郑可欣
【学习目标】
1.掌握一元一次不等式组的定义;一元一次不等式组的解集;
2.会用数轴求不等式组的解集.
【知识回顾】
【课前预习】阅读课本100页观察与思考的内容,解决下列问题
1.在直角坐标系中,当x满足什么条件时,点P(3x-9,1+x)在第二象限?
要使点P在第二象限,不等式3x - 9 0,和不等式1 + x 0必须同时成立,即x必须满足 ;
2.由几个含有同一个未知数x的所组成的不等式组,叫做一元一次不等式组.
3.一般地,一元一次不等式组中各个不等式的解集的,叫做这个一元一次不等式组的解集.
4.一般地,一元一次不等式组经过整理,可化为哪四种情况?
5.请你总结解一元一次不等式组的步骤:
6.解下列不等式组,并将解集在数轴上表示出来.
(1)
24
94
x x
x x
-<
⎧
⎨
+>
⎩
(2)
210
11
x
x
->
⎧
⎨
-<
⎩
【课中实施】确定一元一次不等式组解集的常用方法:
(1)数轴法;(2)口诀法: .
【当堂达标】(每小题2分,共10分)
1.不等式组⎩⎨⎧->-≥2
5x x 的解集是( )
A. 5-≥x
B. 2->x
C. 无解
D. 25--<<x 2.不等式组⎩⎨
⎧≤≥12x x 的解集是( ) A. ≥x 2 B. 2≤x C.无解 D. 2=x
3.不等式组
⎨
⎧-
<-≥52x x 的解集可表示为( ) 4.若a>b ,那么不等式组⎩
⎨⎧<<b x a x 的解集为( ) A. a x < B. b x < C. a x b << D.无解
5.若不等式组⎩⎨⎧><m
x x 3有解,则m 的取值范围是
【课后巩固】
1.(2分)在平面直角坐标系中,若P(m-3,m+1) 在第二象限,则m 的取值范围为( )
A.-1﹤m ﹤3
B. m ﹥3
C. m ﹤-1
D. m ﹥-1
2.(2分)将不等式组⎩⎨
⎧>-+≥+x
x x 33)3(212的解集在数轴上表示出来,正确的是( ) 3.( 6分)解不等式组:(1)⎪⎩⎪⎨⎧+<++≤-)
2(21323531x x x x (2)⎪⎩⎪⎨⎧>-≤--x x x x 22158)2(3。
