Eviews面板大数据之固定效应模型
Eviews面板数据之固定效应模型

Eviews 面板数据之固定效应模型在面板数据线性回归模型中,如果对于不同的截面或不同的时间序列,只是模型的截距项是不同的,而模型的斜率系数是相同的,则称此模型为固定效应模型。
固定效应模型分为三类:1.个体固定效应模型个体固定效应模型是对于不同的纵剖面时间序列(个体)只有截距项不同的模型:2Kit i k kit it k y x u λβ==++∑ (1)从时间和个体上看,面板数据回归模型的解释变量对被解释变量的边际影响均是相同的,而且除模型的解释变量之外,影响被解释变量的其他所有(未包括在回归模型或不可观测的)确定性变量的效应只是随个体变化而不随时间变化时。
检验:采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量,以检验设定个体固定效应模型的合理性。
F 模型的零假设:01231:0N H λλλλ-===⋅⋅⋅==()1(1,(1)1)(1)RRSS URSS N F F N N T K URSSNT N K --=---+--+RRSS 是有约束模型(即混合数据回归模型)的残差平方和,URSS 是无约束模型ANCOVA 估计的残差平方和或者LSDV 估计的残差平方和。
实践:一、数据:已知1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(cp ,不变价格)和人均收入(ip ,不变价格)居民,利用数据(1)建立面板数据(panel data)工作文件;(2)定义序列名并输入数据;(3)估计选择面板模型;(4)面板单位根检验。
年人均消费(consume)和人均收入(income)数据以及消费者价格指数(p)分别见表1,2和3。
表1 1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(元)数据表2 1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均收入(元)数据表3 1996—2002年中国东北、华北、华东15个省级地区的消费者物价指数物价指数1996 1997 1998 1999 2000 2001 2002 PAH 109.9 101.3 100 97.8 100.7 100.5 99 PBJ 111.6 105.3 102.4 100.6 103.5 103.1 98.2 PFJ 105.9 101.7 99.7 99.1 102.1 98.7 99.5 PHB 107.1 103.5 98.4 98.1 99.7 100.5 99 PHLJ 107.1 104.4 100.4 96.8 98.3 100.8 99.3 PJL 107.2 103.7 99.2 98 98.6 101.3 99.5 PJS 109.3 101.7 99.4 98.7 100.1 100.8 99.2 PJX 108.4 102 101 98.6 100.3 99.5 100.1 PLN 107.9 103.1 99.3 98.6 99.9 100 98.9 PNMG 107.6 104.5 99.3 99.8 101.3 100.6 100.2 PSD 109.6 102.8 99.4 99.3 100.2 101.8 99.3 PSH 109.2 102.8 100 101.5 102.5 100 100.5 PSX 107.9 103.1 98.6 99.6 103.9 99.8 98.4 PTJ 109 103.1 99.5 98.9 99.6 101.2 99.6 PZJ 107.9 102.8 99.7 98.8 101 99.8 99.1二、1.输入操作:步骤:(1)File——New——Workfile步骤:(2)Start date——End date——OK步骤:(3)Object——New Object步骤:(4)Type of object——Pool步骤:(5)输入所有序列名称步骤:(6)定义各变量点击sheet—输入consume?income?p?步骤:(7)将表1、2、3中的数据复制到Eviews中2.估计操作:步骤:(1)点击poolmodel——Estimate对话框说明Dependent variable:被解释变量;Common:系数相同部分Cross-section specific:截面系数不同部分步骤:(2)将截距项选择区选Fixed effects(固定效应)Cross-section:Fixed得到如下输出结果:接下来用F 统计量检验是应该建立混合回归模型,还是个体固定效应回归模型。
EVIEWS面板数据分析操作教程及实例解析

模型选择对分析结果影响
模型适用性
根据研究目的和数据特征选择合 适的面板数据模型,如固定效应 模型、随机效应模型等。
模型假设
确保所选模型满足基本假设,如 线性关系、误差项独立同分布等 ,否则可能导致结果不准确。
模型比较与选择
通过比较不同模型的拟合优度、 参数显著性等指标,选择最优模 型进行分析。
操作规范性与结果可靠性保障措施
操作步骤规范
结果验证与解读
对分析结果进行验证,确保结果的合理性和准确性 ;同时,正确解读分析结果,避免误导读者。
严格按照EVIEWS软件的操作步骤进行分析 ,避免操作失误或遗漏关键步骤。
数据分析报告
编写详细的数据分析报告,包括数据来源、 处理方法、模型选择、分析结果及解读等, 以便读者全面了解分析过程。
方和来估计模型参数。
广义最小二乘法(GLS)
02
当存在异方差性或自相关性时,采用广义最小二乘法进行参数
估计,以提高估计效率。
最大似然法(ML)
03
适用于随机效应模型等复杂面板数据模型,通过最大化似然函
数来估计模型参数。
模型诊断与检验
残差分析
检查残差是否满足独立同分布等假设条件, 以评估模型的拟合效果。
07 EVIEWS面板数 据分析操作注意 事项
数据质量对分析结果影响
数据来源
确保数据来自可靠、权威的来源,避免使用不准确或存在偏见的数 据。
数据完整性
检查数据是否存在缺失值、异常值或重复值,这些问题可能导致分 析结果失真。
数据处理
对数据进行适当的预处理,如清洗、转换和标准化,以提高数据质量 和一致性。
增强了解决实际问题的能力
通过实例解析和操作演示,学员们学会了如何运用所学知识解决实际问题,提高了分析 问题和解决问题的能力。
使用Eviews进行面板数据操作(有详图,包括Hausman检验,单位根检验)

每个个体有共
同的参数 bi
bi 随个体不
同而发生
变
变化
参
数
bi 随个体不 同而发生
模 型
变化
下面为个体固定效应的结果。 点击view——representation可以显示具体的回归方程式。
2. 面板数据的检验
① Hausman检验(要在随机效应结果窗口中进行) 对数据进行随机效应模型估计,在估计结果窗口点击view——Fixed/Random Effects testing——Correlated Random Effect-Hausman Test(6.0以上的 版本才可以)
⑤ 在打开的数据组中点击view——graph——scatter——simple scatter, 便可得到不同时间的散点图。
⑥ 同理,按ctrl键,分别选择ip_i, ip_ah,I p_bj, ip_hb…便可得到不同个体 的散点图。
由于是用同一组数据画出的图形,所以虽然采用的 是不同的方法,但是绘出的两个图形一样。
在估计结果中点击proc——Make Model可以出现估计结果的联立方 程形式,进一步点击Solve键可以 在弹出的对话框中进行动态和静态 预测。
在估计结果或原始的面包数据窗口中点击view——unit root test
这里默认为 Schwarz检 验,因为在 小样本情况 下Schwarz 检验效果最 好。
注意:只有在随机效应估计窗口中才能 进行Hausman检验,只有在固定效应估 计窗口中才能进行似然比检验
Hausman检验的原假设是个体效 应与回归变量无关,应建立随机效 应模型,因此当Hausman值较大, 其对应的P值远小于0.05时,拒绝
Eviews数据统计与分析教程12章-面板数据(Panel-Data)模型

EViews统计分析基础教程
二、Pool对象的基本操作
2.Pool对象数据的输入 (2)非堆积数据
在非堆积数据中,给定的截面数据和变量是放在一起的,但 同其他的截面成员和变量的数据是分开的。每一个截面成员 的观测值被放在一纵列中,每一列是截面成员不同时期的样 本观测值。 非堆积数据形式的导入方法与第三章所介绍的数据导入方法 相同。
EViews统计分析基础教程
二、Pool对象的基本操作
1.Pool对象的建立
在Pool对象的编辑窗口中输入截面成员的标识名称,例如做 中国省际面板数据分析时,选取中部五省份为截面成员,即 湖南、湖北、河南、江西和安徽,分布用字母HN,HB,HE, JX,AH表示。这些截面成员各名称之间可用空格隔开,也 可以通过回车键进行换行,即每一个名称占一行。需注意的 是,截面成员的标识名称的设定需简单,便于操作。通常可 以在截面成员标识名称前加下划线“_”。如下图所示。
EViews统计分析基础教程
三、Pool对象模型估计
通过Pool对象可以对固定影响、随机影响变截距模型和固定 影响变系数模型进行估计。常用的方法有最小二乘估计法、 加权最小二乘法等。
EViews统计分析基础教程
三、Pool对象模型估计
在EViews操作中,单击Pool对象工具栏中的“Estimate”或者 选择“Proc”|“Estimate”选项,将弹出下图所示的对话框。
EViews统计分析基础教程
第12章 面板数据(Panel Data)模型
重点内容: • Pool对象的建立 • Pool对象数据分析 • Pool对象模型估计
EViews统计分析基础教程
一、Panel Data模型原理
面板数据模型的基本形式是
面板固定效应模型的解释

面板固定效应模型的解释面板固定效应模型是一种用于分析面板数据的统计模型,其主要目的是通过控制个体固定效应和时间固定效应,去除个体和时间上的不可观测因素对变量之间关系的干扰,从而得到更加准确和稳健的估计结果。
在面板数据分析中,个体固定效应指的是不同个体之间的固定因素对变量之间关系的影响,而时间固定效应则是在不同时间点上固定的因素对变量之间关系的影响。
通过引入这些固定效应,面板固定效应模型能够更好地解释面板数据的动态变化和个体差异,从而提高了分析的有效性和可靠性。
面板数据是指在一段时间内对多个个体(例如个人、家庭、公司等)的多次观测数据的集合。
对于这种数据,传统的截面数据分析方法往往无法准确反映出个体和时间的固定特征对变量之间关系的影响,因此需要引入面板数据分析方法来解决这一问题。
面板固定效应模型正是针对面板数据而提出的一种分析方法,其基本思想是通过引入个体固定效应和时间固定效应来消除个体和时间上的不可观测因素对分析结果的影响,从而更好地研究变量之间的关系。
面板固定效应模型的基本形式可以表示为:\[ Y_{it} = \alpha + \beta X_{it} + \theta_i + \lambda_t + \varepsilon_{it} \]其中,\(Y_{it}\)表示面板数据中第i个个体在第t个时间点上的表现变量,\(X_{it}\)表示解释变量,\(\alpha\)为截距项,\(\beta\)为解释变量的系数,\(\theta_i\)为个体固定效应,\(\lambda_t\)为时间固定效应,\(\varepsilon_{it}\)为误差项。
个体固定效应\(\theta_i\)表示个体特定的不可观测因素对\(Y_{it}\)的影响,时间固定效应\(\lambda_t\)表示时间特定的不可观测因素对\(Y_{it}\)的影响。
通过控制这些固定效应,可以减少由个体和时间差异引起的干扰,得到更加稳健和准确的系数估计结果。
固定效应模型结果解读

固定效应模型结果解读固定效应模型(FixedEffectsModel)是一种常见的面板数据分析方法,它可以用于探究个体间的异质性和时间趋势对数据的影响。
本文将从固定效应模型的基本原理、模型结果解读以及应用案例三个方面进行阐述。
一、固定效应模型的基本原理固定效应模型是一种面板数据模型,其基本假设是个体效应与时间无关,且个体效应与解释变量之间不存在相关性。
换句话说,固定效应模型假设个体间的差异是固定的,不随时间变化,只有时间上的变异才会影响因变量。
因此,固定效应模型的核心是控制个体间的异质性,以便更准确地估计时间变化对因变量的影响。
固定效应模型的基本形式为:Yit = αi + β1 X1it + β2 X2it + … + βk Xkit + uit 其中,Yit表示第i个个体在第t个时间点的因变量值,αi表示第i个个体的固定效应,也就是不变的个体差异,X1it ~ Xkit为解释变量,β1 ~ βk为各解释变量的系数,uit为误差项。
为了控制个体间的异质性,固定效应模型通常采用差分(demean)方法,即对每个个体的变量值减去该个体的平均值,以消除个体间的固定效应。
因此,固定效应模型的估计方法是OLS(最小二乘法),但需要考虑个体间的聚类效应,因此需要进行异方差-稳健标准误(heteroskedasticity-robust standard errors)估计。
二、固定效应模型结果解读固定效应模型的核心是控制个体间的异质性,因此其系数解释应该是“时间变化对因变量的影响”,而不是“个体间差异对因变量的影响”。
因此,在解读固定效应模型结果时,需要关注系数的符号、大小和显著性,以及控制变量的影响。
1. 系数符号系数符号表示自变量的变化方向与因变量的变化方向是否一致。
如果系数为正,表示自变量的增加带来因变量的增加;如果系数为负,表示自变量的增加带来因变量的减少。
在探究时间变化对因变量的影响时,系数的符号应该与预期一致,即随着时间的增加,因变量的变化方向应该与系数符号一致。
面板数据eviews应用

高效稳定
03
Eviews在处理大规模数据集时表现出高效稳定的性能,能够快
速得出分析结果。
Eviews软件应用领域
经济学
Eviews在经济学领域的应用非常 广泛,主要用于实证研究和政策 分析,如劳动经济学、发展经济 学等。
金融学
Eviews在金融学领域的应用主要 涉及时间序列分析和回归分析, 如股票价格分析、风险管理等。
感谢您的观看
THANKS
社会学
Eviews在社会学领域的应用主要 涉及面板数据分析,如人口统计 学、社会调查等。
02 面板数据基础知识
面板数据定义
面板数据
面板数据也称为时间序列数据,它同时包含了横截面和时间序列两个维度的信息,能够更全面地反映经济现象的 变化规律。
面板数据的特点
面板数据能够提供更丰富的信息,可以控制不可观测的异质性,并且能够更好地揭示经济现象的动态变化。
根据诊断结果对模型进行调整或优化,如添加或删除变 量、调整模型形式等。
对模型的残差进行自相关检验和异方差检验,以判断模 型的残差是否存在自相关或异方差问题。
对优化后的模型进行重新估计和检验,确保模型的质量 和稳定性。
04 面板数据Eviews应用实例
实例一:混合效应模型分析
总结词
混合效应模型是一种同时考虑固定效应和随机效应的模型,适用于面板数据。
面板数据类型
长面板
长面板是指样本数量相对较小,但每个样本的观测期较长。
短面板
短面板是指样本数量相对较大,但每个样本的观测期较短。
超长面板
超长面板是指样本数量和观测期都较长,通常用于研究长期经济 现象。
面板数据估计方法
固定效应模型
固定效应模型是一种常用的面板数据估计 方法,它通过控制不可观测的异质性来估
Eviews面板数据之固定效应模型

Eviews 面板数据之固定效应模型在面板数据线性回归模型中,如果对于不同的截面或不同的时间序列,只是模型的截距项是不同的,而模型的斜率系数是相同的,则称此模型为固定效应模型。
固定效应模型分为三类:1.个体固定效应模型个体固定效应模型是对于不同的纵剖面时间序列(个体)只有截距项不同的模型:2Kit i k kit it k y x u λβ==++∑ (1)从时间和个体上看,面板数据回归模型的解释变量对被解释变量的边际影响均是相同的,而且除模型的解释变量之外,影响被解释变量的其他所有(未包括在回归模型或不可观测的)确定性变量的效应只是随个体变化而不随时间变化时。
检验:采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量,以检验设定个体固定效应模型的合理性。
F 模型的零假设:01231:0N H λλλλ-===⋅⋅⋅==()1(1,(1)1)(1)RRSS URSS N F F N N T K URSSNT N K --=---+--+RRSS 是有约束模型(即混合数据回归模型)的残差平方和,URSS 是无约束模型ANCOV A 估计的残差平方和或者LSDV 估计的残差平方和。
实践:一、数据:已知1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(cp ,不变价格)和人均收入(ip ,不变价格)居民,利用数据(1)建立面板数据(panel data )工作文件;(2)定义序列名并输入数据;(3)估计选择面板模型;(4)面板单位根检验。
年人均消费(consume )和人均收入(income )数据以及消费者价格指数(p )分别见表1,2和3。
表1 1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(元)数据表2 1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均收入(元)数据二、1.输入操作:步骤:(1)File——New——Workfile步骤:(2)Start date——End date——OK 步骤:(3)Object——New Object步骤:(4)Type of object——Pool步骤:(5)输入所有序列名称步骤:(6)定义各变量点击sheet—输入consume?income?p?步骤:(7)将表1、2、3中的数据复制到Eviews中2.估计操作:步骤:(1)点击poolmodel——Estimate对话框说明Dependent variable:被解释变量;Common:系数相同部分Cross-section specific:截面系数不同部分步骤:(2)将截距项选择区选Fixed effects(固定效应)Cross-section:Fixed得到如下输出结果:接下来用F 统计量检验是应该建立混合回归模型,还是个体固定效应回归模型。
Eviews面板数据之固定效应模型

Eviews 面板数据之固定效应模型在面板数据线性回归模型中,如果对于不同的截面或不同的时间序列,只是模型的截距项是不同的,而模型的斜率系数是相同的,则称此模型为固定效应模型。
固定效应模型分为三类:1.个体固定效应模型个体固定效应模型是对于不同的纵剖面时间序列(个体)只有截距项不同的模型:2Kit i k kit it k y x u λβ==++∑ (1)从时间和个体上看,面板数据回归模型的解释变量对被解释变量的边际影响均是相同的,而且除模型的解释变量之外,影响被解释变量的其他所有(未包括在回归模型或不可观测的)确定性变量的效应只是随个体变化而不随时间变化时。
检验:采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量,以检验设定个体固定效应模型的合理性。
F 模型的零假设:RRSS 是有约束模型(即混合数据回归模型)的残差平方和,URSS 是无约束模型ANCOV A 估计的残差平方和或者LSDV 估计的残差平方和。
实践:一、数据:已知1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(cp ,不变价格)和人均收入(ip ,不变价格)居民,利用数据(1)建立面板数据(panel data )工作文件;(2)定义序列名并输入数据;(3)估计选择面板模型;(4)面板单位根检验。
年人均消费(consume )和人均收入(income )数据以及消费者价格指数(p )分别见表1,2和3。
表3 1996—2002年中国东北、华北、华东15个省级地区的消费者物价指数步骤:(1)File——New——Workfile步骤:(2)Start date——End date——OK步骤:(3)Object——New Object步骤:(4)Type of object——Pool步骤:(5)输入所有序列名称步骤:(6)定义各变量点击sheet—输入consume?income?p?步骤:(7)将表1、2、3中的数据复制到Eviews中2.估计操作:步骤:(1)点击poolmodel——Estimate对话框说明Dependent variable:被解释变量;Common :系数相同部分 Cross-section specific:截面系数不同部分步骤:(2)将截距项选择区选Fixed effects (固定效应) Cross-section :Fixed 得到如下输出结果:接下来用F 统计量检验是应该建立混合回归模型,还是个体固定效应回归模型。
面板数据分析与固定效应模型的应用

面板数据分析与固定效应模型的应用面板数据分析是一种统计方法,用于处理涉及多个个体(面板)和多个时间点的数据。
它可以帮助研究人员分析个体间的异质性以及时间的变动对变量的影响。
其中一种常用的面板数据模型是固定效应模型,它允许个体间存在固定的个体特征,从而控制这些个体特征对变量的影响。
本文将介绍面板数据分析的基本概念,以及固定效应模型的应用。
一、面板数据分析简介面板数据是在多个时间点上对多个个体进行观察的数据。
它常用于经济学、社会学、管理学等领域的研究中。
与传统的截面数据(只包含一个时间点)或者时间序列数据(只包含一个个体)相比,面板数据可以提供更多的信息,因为它包含了个体间和时间间的变动。
面板数据可以分为平衡面板和非平衡面板。
平衡面板意味着每个个体在每个时间点上都有观测值,而非平衡面板则意味着某些个体在某些时间点上没有观测值。
根据面板数据的特点,我们可以利用面板数据分析方法来揭示个体间的异质性以及时间的变动对变量的影响。
二、固定效应模型的基本原理固定效应模型是一种用于处理面板数据的回归模型。
它允许个体间存在固定的个体特征,并通过控制这些个体特征来分析时间的变动对变量的影响。
在固定效应模型中,我们假设个体间的异质性是固定不变的,只有时间变动会对变量产生影响。
固定效应模型的基本方程可以表示为:Y_it = α_i + β*X_it + u_it其中,Y_it是个体i在时间t上的观测值,α_i是个体i的固定效应,表示个体特征对Y的影响,β是自变量X对因变量Y的影响的系数,u_it是误差项。
为了估计固定效应模型,我们常常使用最小二乘法(OLS)。
由于固定效应模型控制了个体特征的影响,OLS估计结果可以更准确地检验时间变动对变量的影响。
此外,为了控制个体特征的影响,还可以使用虚拟变量回归或者差分法进行估计。
三、固定效应模型的应用案例固定效应模型在社会科学和经济学研究中有着广泛的应用。
以下是一些常见的应用案例:1. 企业绩效研究:研究人员可以使用固定效应模型来分析企业绩效与时间的关系。
关于面板数据的计量方法选择

关于面板数据的计量方法选择在硕士论文中我主要是面板数据分析,并在面板数据分析中使用了子集回归法,下面我将简单介绍面板数据分析的思路和Eviews操作。
面板数据一般有三种:混合估计模型;随机效应模型和固定效应模型。
首先,第一步是作固定效应和随机效应模型的选择,一般是用Hausman检验。
如果你选用的是所有的企业,反映的是总体的效应,则选择固定效应模型,如果你选用的是抽样估计,则要作Hausman检验。
这个可以在Eviews 5.1里头做。
H0:应该建立随机效应模型。
H1:应该建立固定效应模型。
先使用随机效应回归,然后做Hausman检验,如果是小概率事件,拒绝原假设则应建立固定效应模型,反之,则应该采用随机效应模型进行估计。
第二步,固定效应模型分为三种:个体固定效应模型、时刻固定效应模型和个体时刻固定效应模型(这三个模型的含义我就不讲了,大家可以参考我列的参考书)。
如果我们是对个体固定,则应选择个体固定效用模型。
但是,我们还需作个体固定效应模型和混合估计模型的选择。
所以,就要作F值检验。
相对于混合估计模型来说,是否有必要建立个体固定效应模型可以通过F检验来完成。
H0:对于不同横截面模型截距项相同(建立混合估计模型)。
SSErH1:对于不同横截面模型的截距项不同(建立时刻固定效应模型)。
SSEuF统计量定义为:F=[( SSEr - SSEu)/(T+k-2)]/[ SSEu/(NT-T-k)]其中,SSEr,SSEu分别表示约束模型(混合估计模型的)和非约束模型(个体固定效应模型的)的残差平方和(Sum squared resid)。
非约束模型比约束模型多了T–1个被估参数。
需要指出的是:当模型中含有k个解释变量时,F统计量的分母自由度是NT-T- k。
通过对F统计量我们将可选择准确、最佳的估计模型。
在作回归是也是四步:第一步,先作混合效应模型:在cross-section 一栏选择None ,Period也是None;Weights是cross-section Weights,然后把回归结果的Sum squared re sid值复制出来,就是SSEr第二步:作个体固定效用模型:在cross-section 一栏选择Fixed ,Period也是None;Weights是cross-section Weights,然后把回归结果的Sum squared resid值复制出来,就是SSEu第三步:根据公式F=[( SSEr - SSEu)/(T+k-2)]/[ SSEu/(NT-T-k)]。
面板数据分析与固定效应模型

面板数据分析与固定效应模型面板数据是一种特殊的数据结构,包含了多个单位(如个人、企业、国家等)在多个时间点上的观测值。
面板数据分析是通过对这些数据进行统计分析,揭示变量之间的关系,以及对单位和时间的固定效应进行建模和估计。
在本文中,我们将介绍面板数据分析的基本概念和方法,并重点讨论固定效应模型的应用。
第一部分:面板数据分析概述面板数据的特点和分类:面板数据可以分为平衡面板和非平衡面板,平衡面板是指每个单位在每个时间点上都有观测值,而非平衡面板则相反。
面板数据可以用来分析变量随时间的变化以及单位之间的差异。
面板数据的优势:与横截面数据和时间序列数据相比,面板数据具有更多的信息,可以提高估计的效率和精确性。
另外,面板数据还可以解决时间固定效应和单位固定效应的问题,减少了估计的偏误。
第二部分:固定效应模型固定效应模型的基本概念:固定效应模型是面板数据分析中常用的一种模型,用于解决单位固定效应的问题。
它假设每个单位都有一个与单位相关的不变的效应,该效应对观测值产生影响。
固定效应模型可以通过不同的方法进行估计,如最小二乘法、差分法等。
固定效应模型的优点:固定效应模型可以消除单位固定效应的偏误,提高估计的准确性。
同时,固定效应模型还可以控制单位间的异质性,揭示出不同单位之间的差异。
固定效应模型的推断:在进行固定效应模型的推断时,需要考虑面板数据的特殊性质,如时间相关性和异方差性。
一般来说,可以利用异方差稳健标准误差或者聚类标准误差来进行推断。
第三部分:固定效应模型的应用固定效应模型在经济学和社会科学研究中有广泛的应用。
例如,在劳动经济学领域,固定效应模型可以用来研究不同单位间的工资差异和收入分配问题。
在发展经济学领域,固定效应模型可以用来研究不同国家间的经济增长和发展差异。
此外,固定效应模型还可以用于政策评估和政策效果分析。
通过比较政策实施前后的面板数据,可以估计政策对观测变量的影响,评估政策的效果。
结论面板数据分析与固定效应模型是一种强大的统计工具,可以帮助我们揭示变量之间的关系,并进行推断和预测。
面板固定效应模型的解释

面板固定效应模型的解释
固定效应模型(fixed effects model),即固定效应回归模型,简称FEM,是一种面板数据分析方法。
它是指实验结果只想比较每一自变项之特定类目或类别间的差异及其与其他自变项之特定类目或类别间交互作用效果,而不想依此推论到同一自变项未包含在内的其他类目或类别的实验设计。
固定效应回归是一种空间面板数据中随个体变化但不随时间变化的一类变量方法。
固定效应模型有n个不同的截距,其中一个截距对应一个个体。
可以用一系列二值变量来表示这些截距。
在面板数据线性回归模型中,如果对于不同的截面或不同的时间序列,只是模型的截距项是不同的,而模型的斜率系数是相同的,则称此模型为固定效应模型。
除了固定效应模型,典型的面板数据分析方法还有随机效应模型和混合效应模型。
固定效应模型(FEM)假设所有的纳入研究拥有共同的真实效应量,而随机效应模型(REM)中的真实效应随研究的不同而改变。
基于不同模型的运算,所得到的合并后的效应量均数值也不相同。
早在1976年,第一篇Meta分析就使用FEM进
行了数据合并,基于其统计简洁性及异质性认知,致使FEM广泛使用,直到2006年仍然有四分之三的Meta分析的文章在使用。
然而,随着方法学不断更新及异质性理解,方法学家们对于证据合并内在结构理解与剖析,已开始逐渐对“理想”状态的FEM产生疑问。
随后,REM逐渐被使用,并替代部分FEM。
固定效应变截距模型eviews

《固定效应变截距模型eviews》在统计学中,固定效应变截距模型是一种多元回归分析方法,通常用于研究面板数据中的固定效应和变截距。
而EViews作为一款强大的计量经济学软件,可以帮助研究者进行各种计量分析,包括固定效应变截距模型的估计和推断。
在本文中,我们将深入探讨固定效应变截距模型在EViews中的应用,以及个人对这一主题的理解和观点。
一、固定效应变截距模型的基本概念1.1 什么是固定效应变截距模型固定效应变截距模型是一种用于分析面板数据的统计模型,它包括了固定效应和变截距。
固定效应指的是个体特定的不变因素,而变截距则是个体特定的斜率。
这种模型能够更准确地捕捉面板数据中个体间的差异,因此在实证研究中得到了广泛的应用。
1.2 模型的基本假设在使用固定效应变截距模型进行分析时,需要满足一些基本假设,比如个体效应与解释变量之间不能存在内生性,个体效应是固定的等等。
只有在这些基本假设成立的情况下,才能够对模型进行有效的估计和推断。
二、EViews中固定效应变截距模型的应用2.1 数据准备在EViews中进行固定效应变截距模型分析之前,首先需要对面板数据进行准备。
这包括导入数据、设定面板数据格式、检查面板数据的平稳性和异方差性等步骤。
2.2 模型估计通过EViews的面板数据估计功能,可以轻松地对固定效应变截距模型进行估计。
在进行模型估计时,需要设定固定效应和变截距,并进行相应的推断。
2.3 结果解读EViews将模型估计的结果以表格和图形的形式呈现出来,研究者可以通过这些结果来判断模型的拟合程度和各个变量的显著性。
EViews还提供了对估计结果进行进一步分析的功能,比如残差分析、模型诊断等。
三、个人观点和理解作为一名计量经济学研究者,我深刻理解固定效应变截距模型在面板数据分析中的重要性。
这种模型能够更好地控制面板数据中的个体特异性,提高了分析的准确性和可信度。
而EViews作为一款优秀的计量经济学软件,为研究者提供了便捷、高效的分析工具,使得固定效应变截距模型的应用变得更加简单和灵活。
eviews面板模型与选择
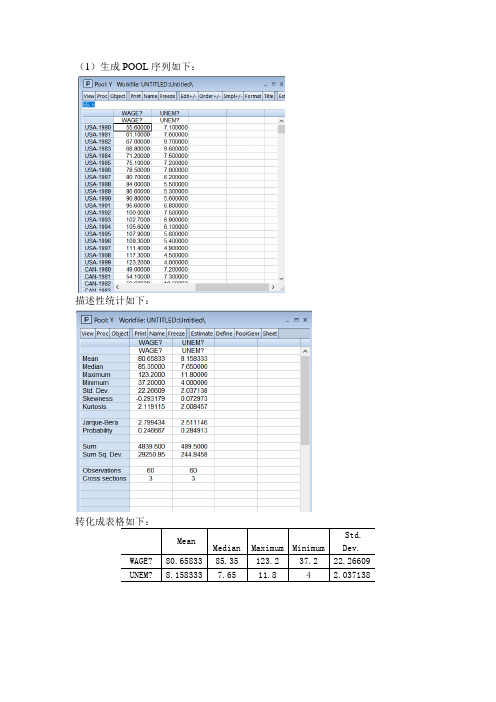
(1)生成POOL序列如下:描述性统计如下:
转化成表格如下:
Mean
Median Maximum Minimum Std. Dev.
WAGE? 80.65833 85.35 123.2 37.2 22.26609 UNEM? 8.158333 7.65 11.8 4 2.037138
从回归结果来看,小时工资的系数为负,且其t统计量对应的p值小于5%,因此在5%的显著性水平,其对失业率有显著的负向影响。
这点可能是随着小时工资的提高,个人倾向于寻求就业,从而使失业率降低,具体而言,小时工资每提高1美元,失业率平均下降0.03707%。
而由不同国家的截距差异可以看出,在小时工资不变的情况下,美国的失业率最低,加拿大次之,英国最高,同时也注意到不同年份也存在一定的差异,这可能是由于经济发展正常的波动。
个体时间双随机变截距情况下,小时工资的系数为负且通过1%的显著性检验,即小时工资的提高可以显著降低失业率,这可能是随着小时工资的提高,劳动者更倾向于参与劳动,从而对失业率有显著的削弱作用,具体而言,小时工资每增加1美元,失业率平均下降0.04586%。
此外,不同国家的失业率在小时工资不变的情况下,也有所差异,美国最低,加拿大次之,最高的是英国,同时年份的不同也是失业率差异的因素,这可能与经济周期发展有关。
(4)在随机效应的基础上进行Hausman检验,结果如下:
从Hausman检验的结果来看,针对个体随机变截距效应的原假设,p值大于5%,因此不拒绝原假设,即个体随机效应是存在的,而针对时间随机效应变截距的原假设,p值大于5%,因此也不拒绝原假设,时间随机效应也是存在的,针对同时存在个体时间双随机变截距的原假设,p值也是大于5%,因此,模型在设定上应该为个体时点双随机模型。
eviews关于面板数据模型截距,系数,固定效应还是随机效应的选取得检验方法及具体事例

面板数据模型1.面板数据定义。
时间序列数据或截面数据都是一维数据。
例如时间序列数据是变量按时间得到的数据;截面数据是变量在截面空间上的数据。
面板数据(panel data)也称时间序列截面数据(time series and cross section data)或混合数据(pool data)。
面板数据是同时在时间和截面空间上取得的二维数据。
面板数据示意图见图1。
面板数据从横截面(cross section)上看,是由若干个体(entity, unit, individual)在某一时刻构成的截面观测值,从纵剖面(longitudinal section)上看是一个时间序列。
面板数据用双下标变量表示。
例如y i t, i = 1, 2, …, N; t = 1, 2, …, TN表示面板数据中含有N个个体。
T表示时间序列的最大长度。
若固定t不变,y i ., ( i = 1, 2, …, N)是横截面上的N个随机变量;若固定i不变,y. t, (t = 1, 2, …, T)是纵剖面上的一个时间序列(个体)。
图1 N=7,T=50的面板数据示意图例如1990-2000年30个省份的农业总产值数据。
固定在某一年份上,它是由30个农业总产总值数字组成的截面数据;固定在某一省份上,它是由11年农业总产值数据组成的一个时间序列。
面板数据由30个个体组成。
共有330个观测值。
对于面板数据y i t, i = 1, 2, …, N; t = 1, 2, …, T来说,如果从横截面上看,每个变量都有观测值,从纵剖面上看,每一期都有观测值,则称此面板数据为平衡面板数据(balanced panel data)。
若在面板数据中丢失若干个观测值,则称此面板数据为非平衡面板数据(unbalanced panel data)。
注意:EViwes 3.1、4.1、5.0既允许用平衡面板数据也允许用非平衡面板数据估计模型。
Eviews面板大数据之固定效应模型

Eviews 面板数据之固定效应模型在面板数据线性回归模型中,如果对于不同的截面或不同的时间序列,只是模型的截距项是不同的,而模型的斜率系数是相同的,则称此模型为固定效应模型。
固定效应模型分为三类:1.个体固定效应模型个体固定效应模型是对于不同的纵剖面时间序列(个体)只有截距项不同的模型:2Kit i k kit it k y x u λβ==++∑ (1)从时间和个体上看,面板数据回归模型的解释变量对被解释变量的边际影响均是相同的,而且除模型的解释变量之外,影响被解释变量的其他所有(未包括在回归模型或不可观测的)确定性变量的效应只是随个体变化而不随时间变化时。
检验:采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量,以检验设定个体固定效应模型的合理性。
F 模型的零假设:01231:0N H λλλλ-===⋅⋅⋅==()1(1,(1)1)(1)RRSS URSS N F F N N T K URSSNT N K --=---+--+RRSS 是有约束模型(即混合数据回归模型)的残差平方和,URSS 是无约束模型ANCOVA 估计的残差平方和或者LSDV 估计的残差平方和。
实践:一、数据:已知1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(cp ,不变价格)和人均收入(ip ,不变价格)居民,利用数据(1)建立面板数据(panel data )工作文件;(2)定义序列名并输入数据;(3)估计选择面板模型;(4)面板单位根检验。
年人均消费(consume )和人均收入(income )数据以及消费者价格指数(p )分别见表1,2和3。
表1 1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(元)数据表2 1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均收入(元)数据二、1.输入操作:步骤:(1)File——New——Workfile步骤:(2)Start date——End date——OK 步骤:(3)Object——New Object步骤:(4)Type of object——Pool步骤:(5)输入所有序列名称步骤:(6)定义各变量点击sheet—输入consume?income?p?步骤:(7)将表1、2、3中的数据复制到Eviews中2.估计操作:步骤:(1)点击poolmodel——Estimate对话框说明Dependent variable:被解释变量;Common coefficients:系数相同部分Cross-section specific:截面系数不同部分步骤:(2)将截距项选择区选Fixed effects(固定效应)Cross-section:Fixed得到如下输出结果:接下来用F 统计量检验是应该建立混合回归模型,还是个体固定效应回归模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Eviews 面板数据之固定效应模型在面板数据线性回归模型中,如果对于不同的截面或不同的时间序列,只是模型的截距项是不同的,而模型的斜率系数是相同的,则称此模型为固定效应模型。
固定效应模型分为三类:1.个体固定效应模型个体固定效应模型是对于不同的纵剖面时间序列(个体)只有截距项不同的模型:2Kit i k kit it k y x u λβ==++∑ (1)从时间和个体上看,面板数据回归模型的解释变量对被解释变量的边际影响均是相同的,而且除模型的解释变量之外,影响被解释变量的其他所有(未包括在回归模型或不可观测的)确定性变量的效应只是随个体变化而不随时间变化时。
检验:采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量,以检验设定个体固定效应模型的合理性。
F 模型的零假设:01231:0N H λλλλ-===⋅⋅⋅==()1(1,(1)1)(1)RRSS URSS N F F N N T K URSSNT N K --=---+--+:RRSS 是有约束模型(即混合数据回归模型)的残差平方和,URSS 是无约束模型ANCOVA 估计的残差平方和或者LSDV 估计的残差平方和。
实践:一、数据:已知1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(cp ,不变价格)和人均收入(ip ,不变价格)居民,利用数据(1)建立面板数据(panel data)工作文件;(2)定义序列名并输入数据;(3)估计选择面板模型;(4)面板单位根检验。
年人均消费(consume)和人均收入(income)数据以及消费者价格指数(p)分别见表1,2和3。
表1 1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费(元)数据表2 1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均收入(元)数据INCOMESD 4890.28 5190.79 5380.08 5808.96 6489.97 7101.08 7614.36 INCOMESH 8178.48 8438.89 8773.1 10931.64 11718.01 12883.46 13249.8 INCOMESX 3702.69 3989.92 4098.73 4342.61 4724.11 5391.05 6234.36 INCOMETJ 5967.71 6608.39 7110.54 7649.83 8140.5 8958.7 9337.56 INCOMEZJ 6955.79 7358.72 7836.76 8427.95 9279.16 10464.67 11715.6表3 1996—2002年中国东北、华北、华东15个省级地区的消费者物价指数物价指数1996 1997 1998 1999 2000 2001 2002 PAH 109.9 101.3 100 97.8 100.7 100.5 99PBJ 111.6 105.3 102.4 100.6 103.5 103.1 98.2PFJ 105.9 101.7 99.7 99.1 102.1 98.7 99.5 PHB 107.1 103.5 98.4 98.1 99.7 100.5 99PHLJ 107.1 104.4 100.4 96.8 98.3 100.8 99.3PJL 107.2 103.7 99.2 98 98.6 101.3 99.5PJS 109.3 101.7 99.4 98.7 100.1 100.8 99.2PJX 108.4 102 101 98.6 100.3 99.5 100.1 PLN 107.9 103.1 99.3 98.6 99.9 100 98.9 PNMG 107.6 104.5 99.3 99.8 101.3 100.6 100.2 PSD 109.6 102.8 99.4 99.3 100.2 101.8 99.3 PSH 109.2 102.8 100 101.5 102.5 100 100.5 PSX 107.9 103.1 98.6 99.6 103.9 99.8 98.4PTJ 109 103.1 99.5 98.9 99.6 101.2 99.6PZJ 107.9 102.8 99.7 98.8 101 99.8 99.1二、1.输入操作:步骤:(1)File——New——Workfile步骤:(2)Start date——End date——OK步骤:(3)Object——New Object步骤:(4)Type of object——Pool步骤:(5)输入所有序列名称步骤:(6)定义各变量点击sheet—输入consume?income?p?步骤:(7)将表1、2、3中的数据复制到Eviews中2.估计操作:步骤:(1)点击poolmodel——Estimate对话框说明Dependent variable:被解释变量;Common coefficients:系数相同部分Cross-section specific:截面系数不同部分步骤:(2)将截距项选择区选Fixed effects(固定效应)Cross-section:Fixed得到如下输出结果:接下来用F 统计量检验是应该建立混合回归模型,还是个体固定效应回归模型。
0H :i αα=。
模型中不同个体的截距相同(真实模型为混合回归模型)。
1H :模型中不同个体的截距项i α不同(真实模型为个体固定效应回归模型)。
对模型进行检验:0.05()115-1==7.69=.90(1)RRSS URSS N F F URSS NT N K --=>--+(4965275-2259743)(14,90)180232259743所以推翻原假设,建立个体固定效应回归模型更合理。
RRSS 求法请参见Eview 面板数据之混合回归模型 相应的表达式为:1215596.500.6953.23592.44...230.16it it Consume Income D D D =+-+++(6.64) (49.55) 20.99,2259743r R SSE ==其中虚拟变量1215,,...,D D D 的定义是:1,1,2,...,150,i i i D =⎧=⎨⎩如果属于第个个体,其他 15个省级地区的城镇人均指出平均占收入68.62%。
从上面的结果可以看出北京市居民的自发性消费明显高于其他地区。
2.时点固定效应模型时点固定效应模型就是对于不同的截面(时点)有不同截距的模型。
如果确知对于不同的截面,模型的截距显著不同,但是对于不同的时间序列(个体)截距是相同的,那么应该建立时点固定效应模型:2Kit t k kit it k y x u γβ==++∑ (2)时点固定效应模型与个体固定效应模型的操作区别在于步骤(2),将时间项选择区选 Period :Fixed (时间固定效应)得到如下结果:接下来用F 统计量检验是应该建立混合回归模型,还是个体固定效应回归模型。
0H :i αα=。
模型中不同个体的截距相同(真实模型为混合回归模型)。
1H :模型中不同个体的截距项t α不同(真实模型为时间固定效应回归模型)。
对模型进行检验:0.05()7-11==3.54=.98(1)RRSS URSS T F F URSS NT T K --=>--+(4965275-4080749)(6,98)2194080749所以推翻原假设,可以建立时点固定效应回归模型 RRSS 求法请参见Eview 面板数据之混合回归模型 相应的表达式为:1272.60.78114137.5...97.7it it Consume IP D D D =-++++-(76.0) 20.986,4080749R SSE ==其中虚拟变量127,,...,D D D 的定义是:1,0,t D ⎧=⎨⎩如果属于第t 个截面,t=1996,...,2002其他3.时点个体固定效应模型时点个体固定效应模型就是对于不同的截面(时点)、不同的时间序列(个体)都有不同截距模型。
如果确知对于不同的截面、不同的时间序列(个体)模型的截距都显著地不相同,那么应该建立时点个体固定效应模型:2Kit t t k kit it k y x u λγβ==+++∑ (3)时点固定效应模型与个体固定效应模型的操作区别在于步骤(2),将截距项选择区域:Cross-section :fixed (个体固定效应),时间项选择区选 Period :Fixed (时间固定效应)得到结果如下:Dependent Variable: CONSUME?Method: Pooled Least SquaresDate: 07/21/14 Time: 15:44Sample: 1996 2002Included observations: 7Cross-sections included: 15Total pool (balanced) observations: 105Variable Coefficient Std. Error t-Statistic Prob.C 806.6751 221.2143 3.646578 0.0005INCOME? 0.653338 0.034541 18.91504 0.0000 Fixed Effects (Cross)AH--C -94.50854BJ--C 698.0132FJ--C -18.86465HB--C -200.3997HLJ--C -246.3712JL--C -54.16421JS--C -31.26919JX--C -392.9844LN--C 47.39508NMG--C -284.2660SD--C -150.8912SH--C 465.4906SX--C -152.6560TJ--C 103.9569ZJ--C 311.5193Fixed Effects (Period)1996--C -59.123731997--C 17.954691998--C -31.455641999--C -57.240422000--C 36.243822001--C -29.264152002--C 122.8854Effects SpecificationCross-section fixed (dummy variables)Period fixed (dummy variables)R-squared 0.993278 Mean dependent var 4981.017 Adjusted R-squared 0.991577 S.D. dependent var 1700.985 S.E. of regression 156.1067 Akaike info criterion 13.12288 Sum squared resid 2022652. Schwarz criterion 13.67895 Log likelihood -666.9514 Hannan-Quinn criter. 13.34821F-statistic 584.0406 Durbin-Watson stat 1.455623Prob(F-statistic)0.000000 接下来用F 统计量检验是应该建立混合回归模型,还是个体固定效应回归模型。
