高中数学第1章推理与证明1.2.2分析法学案北师大版选修2_2
陕西省高中数学 第一章 推理与证明 归纳推理教案2 北师大版选修2-2
1.1 归纳推理教学过程: 1.创设情景:1.情景㈠:苹果落地的故事,正是基于这个发现,牛顿大胆地猜想,然后小心求证,终于发现了伟大的“万有引力定理” 思考:整个过程对你有什么启发?教师:“科学离不开生活,离不开观察,也离不开猜想和证明”。
2.情景㈡:陈景润和他在“歌德巴赫猜想”证明中的伟大成就:任何一个大于4的偶数都可以写成两个奇素数之和。
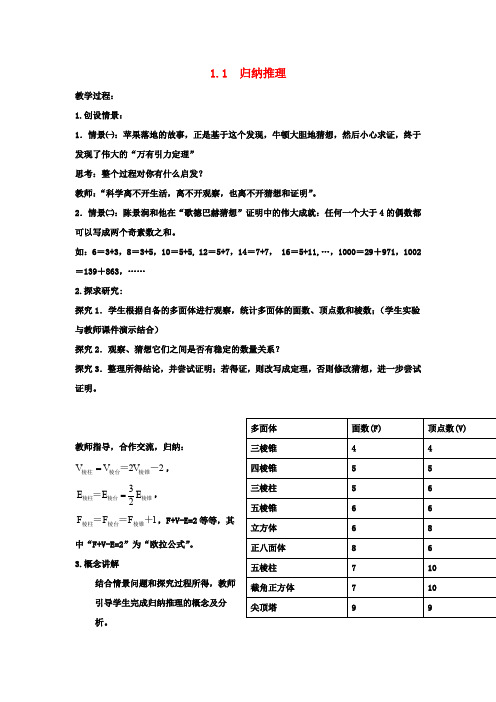
如:6=3+3,8=3+5,10=5+5, 12=5+7,14=7+7, 16=5+11,…,1000=29+971,1002=139+863,…… 2.探求研究:探究1.学生根据自备的多面体进行观察,统计多面体的面数、顶点数和棱数;(学生实验与教师课件演示结合)探究2.观察、猜想它们之间是否有稳定的数量关系?探究3.整理所得结论,并尝试证明;若得证,则改写成定理,否则修改猜想,进一步尝试证明。
教师指导,合作交流,归纳:22V V V =棱柱棱台棱锥=-,32E E E =棱柱棱台棱锥=,1F F F 棱柱棱台棱锥==+,F+V-E=2等等,其中“F+V-E=2”为“欧拉公式”。
3.概念讲解结合情景问题和探究过程所得,教师引导学生完成归纳推理的概念及分析。
定义:根据一类事物的部分事物具有某种属性,推断该类事物的每一个都具有这种属性的推理,或者由个别事实概括出一般结论的推理,称为归纳推理(简称归纳).说明:⑴归纳推理的作用:发现新事实,获得新结论;(2)归纳推理的一般步骤:试验、观察→概括、推广→猜测一般性结论→证明;⑶归纳推理的结论不一定成立。
4.例题解析例1:在数列{}n a 中,()*1121,,2nn n a a a n N a +==∈+猜想这个数列的通项公式? 解析:先由学生计算:234521222,,,32456a a a a ===== 归纳:*2()1n a n N n =∈+ 说明(学生完成):⑴有整数和分数时,往往将整数化为分数;⑵当分子分母都在变化时,往往统一分子(或分母),再寻找另一部分的变化规律.例2:(拓展)问:如果面积是一定的,什么样的平面图形周长最小?试猜测结论。
高中数学第一章推理与证明全套教案北师大版选修2-2

观察、比较
联想、类推
猜想新结论
例 3. 在平面上 , 设 ha,h b,h c 是三角形 ABC三条边上的高 .P 为三角形内任一点 ,P 到相应三边的距离分别为
pa ,p b,p c, 我们可以得到结论 : 试通过类比 , 写出在空间中的类似结论 .
pa pb pc 1 ha hb hc
巩固提高
用心 爱心 专心
-------------------------------------------------------------------------------------------
------------------------
2.类比平面内直角三角形的勾股定理 , 试给出空间中四面体性质的猜想.
类比推理是从特殊到特殊的推理,是寻找事物之间的共同或相似性质,类比的性质相似性越多,相似 的性质与推测的性质之间的关系就越相关,从而类比得出的结论就越可靠。 (三)情感态度与价值观: 1.正确认识合情推理在数学中的重要作用,养成从小开始认真观察事物、分析问题、发现事物之间的质 的联系的良好个性品质,善于发现问题,探求新知识。 2.认识数学在日常生产生活中的重要作用,培养学生学数学,用数学,完善数学的正确数学意识。 ●教学重点: 了解合情推理的含义,能利用类比进行简单的推理。 ●教学难点: 用类比进行推理,做出猜想。 ●教具准备: 与教材内容相关的资料。 ●课时安排: 1 课时 ● 教学过程:
第一章 推理与证明
合情推理(一)——归纳推理
课时安排 :一课时
课型 :新授课
教学目标 :
1、通过对已学知识的回顾,进一步体会合情推理这种基本的分析问题法,认识归纳推理的基本方法与步
骤,并把它们用于对问题的发现与解决中去。
高中数学 第一章 推理与证明 1.2.2 分析法学案(含解析)北师大版选修2-2-北师大版高二选修2

1.2.2 分析法1.了解分析法的思维过程、特点.(重点)2.会用分析法证明数学问题.(难点)[基础·初探]教材整理分析法阅读教材P9~P11,完成下列问题.1.分析法的定义从求证的结论出发,一步一步地探索保证前一个结论成立的充分条件,直到归结为这个命题的条件,或者归结为定义、公理、定理等,这种思维方法称为分析法.2.分析法证明的思维过程用Q表示要证明的结论,则分析法的思维过程可用框图表示为:Q⇐P1→P1⇐P2→P2⇐P3→…→得到一个明显成立的条件3.综合法和分析法的综合应用在解决问题时,我们经常把综合法和分析法结合起来使用:根据条件的结构特点去转化结论,得到中间结论Q′;根据结论的结构特点去转化条件,得到中间结论P′.若由P′可以推出Q′成立,即可证明结论成立.判断(正确的打“√”,错误的打“×”)(1)分析法就是从结论推向已知.( )(2)分析法的推理过程要比综合法优越.( )(3)并不是所有证明的题目都可使用分析法证明.( )【解析】(1)错误.分析法又叫逆推证法,但不是从结论推向已知,而是寻找使结论成立的充分条件的过程.(2)错误.分析法和综合法各有优缺点.(3)正确.一般用综合法证明的题目均可用分析法证明,但并不是所有的证明题都可使用分析法证明.【答案】 (1)× (2)× (3)√[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问1: 解惑: 疑问2: 解惑: 疑问3: 解惑:[小组合作型]应用分析法证明不等式已知a >b >0,求证:(a -b )28a <a +b 2-ab <(a -b )28b.【精彩点拨】 本题用综合法不易解决,由于变形后均为平方式,因此要先将式子两边同时开方,再找出使式子成立的充分条件.【自主解答】 要证(a -b )28a <a +b 2-ab <(a -b )28b ,只需证(a -b )28a <(a -b )22<(a -b )28b .∵a >b >0,∴同时除以(a -b )22,得(a +b )24a <1<(a +b )24b ,同时开方,得a +b 2a <1<a +b2b, 只需证a +b <2a ,且a +b >2b , 即证b <a ,即证b <a . ∵a >b >0,∴原不等式成立, 即(a -b )28a <a +b 2-ab <(a -b )28b.1.分析法证明不等式的思维是从要证的不等式出发,逐步寻求使它成立的充分条件,最后得到的充分条件为已知(或已证)的不等式.2.分析法证明数学命题的过程是逆向思维,即结论⇐…⇐…⇐…已知,因此,在叙述过程中,“要证”“只需证”“即证”等词语必不可少,否则会出现错误.[再练一题]1.(2016·合肥高二检测)已知a >0,求证:a 2+1a 2-2≥a +1a-2.【证明】 要证a 2+1a 2-2≥a +1a-2,只需证a 2+1a 2+2≥a +1a+2,即证⎝⎛⎭⎪⎫a 2+1a 2+22≥⎝⎛⎭⎪⎫a +1a +22,即a 2+1a2+4 a 2+1a 2+4≥a 2+1a 2+2 2⎝ ⎛⎭⎪⎫a +1a +4,只需证2a 2+1a 2≥ 2⎝ ⎛⎭⎪⎫a +1a .只需证4⎝ ⎛⎭⎪⎫a 2+1a 2≥2⎝ ⎛⎭⎪⎫a 2+2+1a 2,即a 2+1a2≥2.上述不等式显然成立,故原不等式成立.用分析法证明其他问题(2016·合肥高二检测)求证:以过抛物线y 2=2px (p >0)焦点的弦为直径的圆必与直线x =-p2相切.【精彩点拨】【自主解答】 如图所示,过点A ,B 分别作AA ′,BB ′垂直准线于点A ′,B ′,取AB 的中点M ,作MM ′垂直准线于点M ′.要证明以AB 为直径的圆与准线相切,只需证|MM ′|=12|AB |.由抛物线的定义有|AA ′|=|AF |,|BB ′|=|BF |,所以|AB |=|AA ′|+|BB ′|,因此只需证|MM ′|=12(|AA ′|+|BB ′|).根据梯形的中位线原理可知上式是成立的,所以以过抛物线y 2=2px 焦点的弦为直径的圆必与直线x =-p2相切.1.分析法是逆向思维,当已知条件与结论之间的联系不够明显、直接或证明过程中所需要用的知识不太明确、具体时,往往采用分析法.2.分析法的思路与综合法正好相反,它是从要求证的结论出发,倒着分析,由未知想需知,由需知逐渐地靠近已知,即已知条件、已经学过的定义、定理、公理、公式、法则等.[再练一题]2.已知1-tan α2+tan α=1,求证:cos α-sin α=3(cos α+sin α).【证明】 要证cos α-sin α=3(cos α+sin α), 只需证cos α-sin αcos α+sin α=3,只需证1-tan α1+tan α=3,只需证1-tan α=3(1+tan α),只需证tan α=-12.∵1-tan α2+tan α=1,∴1-tan α=2+tan α,即2tan α=-1.∴tan α=-12显然成立,∴结论得证.[探究共研型]综合法与分析法的综合应用探究【提示】 综合法与分析法的推理过程是演绎推理,它们的每一步推理都是严密的逻辑推理,从而得到的每一个结论都是正确的,不同于合情推理中的“猜想”.探究2 综合法与分析法有什么区别?【提示】 综合法是从已知条件出发,逐步寻找的是必要条件,即由因导果;分析法是从待求结论出发,逐步寻找的是充分条件,即执果索因.在某两个正数x ,y 之间,若插入一个数a ,则能使x ,a ,y 成等差数列;若插入两个数b ,c ,则能使x ,b ,c ,y 成等比数列,求证:(a +1)2≥(b +1)(c +1).【精彩点拨】 可用分析法找途径,用综合法由条件顺次推理,易于使条件与结论联系起来.【自主解答】 由已知条件得⎩⎪⎨⎪⎧2a =x +y ,b 2=cx ,c 2=by ,消去x ,y 得2a =b 2c +c 2b,且a >0,b >0,c >0.要证(a +1)2≥(b +1)(c +1),只需证a +1≥(b +1)(c +1),因(b +1)(c +1)≤(b +1)+(c +1)2,只需证a +1≥b +1+c +12,即证2a ≥b +c .由于2a =b 2c +c 2b ,故只需证b 2c +c 2b≥b +c ,只需证b 3+c 3=(b +c )(b 2+c 2-bc )≥(b +c )bc , 即证b 2+c 2-bc ≥bc ,即证(b -c )2≥0.因为上式显然成立,所以(a +1)2≥(b +1)(c +1).综合法推理清晰,易于书写,分析法从结论入手,易于寻找解题思路,在实际证明命题时,常把分析法与综合法结合起来使用,称为分析综合法,其结构特点是根据条件的结构特点去转化结论,得到中间结论Q ;根据结论的结构特点去转化条件,得到中间结论P ;若由P 可推出Q ,即可得证.[再练一题]3.已知△ABC 的三个内角A ,B ,C 成等差数列,求证:1a +b +1b +c =3a +b +c. 【证明】 要证1a +b +1b +c =3a +b +c, 即证a +b +c a +b +a +b +cb +c =3, 即证c a +b +ab +c=1,只需证c (b +c )+a (a +b )=(a +b )(b +c ), 只需证c 2+a 2=ac +b 2.∵A ,B ,C 成等差数列, ∴2B =A +C ,又A +B +C =180°,∴B =60°. ∵c 2+a 2-b 2=2ac cos B , ∴c 2+a 2-b 2=ac , ∴c 2+a 2=ac +b 2, ∴1a +b +1b +c =3a +b +c成立. [构建·体系]1.要证明2+7>23,可选择的方法有以下几种,其中最合理的是( ) A.综合法 B.分析法 C.比较法D.归纳法【解析】 由分析法和综合法定义可知选B. 【答案】 B2.已知a ≥0,b ≥0,且a +b =2,则( ) A.a ≤12B.ab ≥12C.a 2+b 2≥2D.a 2+b 2≤3【解析】 ∵a +b =2≥2ab ,∴ab ≤1. ∵a 2+b 2=4-2ab ,∴a 2+b 2≥2. 【答案】 C3.3a -3b <3a -b 成立的充要条件是( ) A.ab (b -a )>0 B.ab >0且a >b C.ab <0且a <b D.ab (b -a )<0【解析】3a -3b <3a -b ⇔(3a -3b )3<(3a -b )3⇔a -b -33a 2b +33ab 2<a -b ⇔3ab 2<3a 2b⇔ab 2<a 2b ⇔ab (b -a )<0.【答案】 D4.设a >0,b >0,c >0,若a +b +c =1,则1a +1b +1c的最小值为________.【解析】 因为a +b +c =1,且a >0,b >0,c >0, 所以1a +1b +1c =a +b +c a +a +b +c b +a +b +c c=3+b a +a b +c b +b c +a c +ca≥3+2b a ·a b+2c a ·a c +2c b ·b c=3+6=9.当且仅当a =b =c 时等号成立. 【答案】 95.已知a ,b ,c ∈R 且不全相等,求证:a 2+b 2+c 2>ab +bc +ca . 【证明】 法一:(分析法) 要证a 2+b 2+c 2>ab +bc +ca , 只需证2(a 2+b 2+c 2)>2(ab +bc +ca ),只需证(a 2+b 2-2ab )+(b 2+c 2-2bc )+(c 2+a 2-2ca )>0, 只需证(a -b )2+(b -c )2+(c -a )2>0, 因为a ,b ,c ∈R ,所以(a -b )2≥0,(b -c )2≥0,(c -a )2≥0. 又因为a ,b ,c 不全相等,所以(a -b )2+(b -c )2+(c -a )2>0成立. 所以原不等式a 2+b 2+c 2>ab +bc +ca 成立. 法二:(综合法) 因为a ,b ,c ∈R ,所以(a -b )2≥0,(b -c )2≥0,(c -a )2≥0. 又因为a ,b ,c 不全相等, 所以(a -b )2+(b -c )2+(c -a )2>0,所以(a 2+b 2-2ab )+(b 2+c 2-2bc )+(c 2+a 2-2ca )>0, 所以2(a 2+b 2+c 2)>2(ab +bc +ca ), 所以a 2+b 2+c 2>ab +bc +ca .我还有这些不足:(1)(2)我的课下提升方案:(1)(2)。
高中数学第一章推理与证明2综合法与分析法教学案北师大版选修2_2

高中数学第一章推理与证明2综合法与分析法教学案北师大版选修2_2例:若实数a,b满足a+b=2,证明:2a+2b≥4.证明:因为a+b=2,所以2a+2b≥2=2=2=4,故2a+2b≥4成立.问题1:本题利用什么公式?提示:基本不等式.问题2:本题证明顺序是什么?提示:从已知到结论.综合法(1)含义:从命题的条件出发,利用定义、公理、定理及运算法则,通过演绎推理,一步一步地接近要证明的结论,直到完成命题的证明的思维方法,称为综合法.(2)思路:综合法的基本思路是“由因导果”.(3)模式:综合法可以用以下的框图表示:P⇒Q1→→→…→Qn⇒Q其中P为条件,Q为结论.案中的推理,给人印象太深刻了.有时,他先假定一个结论成立,然后逐步寻找这个结论成立的一个充分条件,直到找到一个明显的证据.问题1:他的推理如何入手?提示:从结论成立入手.问题2:他又是如何分析的?提示:逐步探寻每一结论成立的充分条件.问题3:这种分析问题方法在数学问题证明中可以借鉴吗?提示:可以.分析法(1)含义:从求证的结论出发,一步一步地探索保证前一个结论成立的充分条件,直到归结为这个命题的条件,或者归结为定义、公理、定理等.这种证明问题的思维方法称为分析法.(2)思路:分析法的基本思路是“执果索因”.(3)模式:若用Q表示要证明的结论,则分析法可以用如下的框图来表示:Q⇐P1→→→…→得到一个明显成立的条件1.综合法是从“已知”看“可知”逐步推向未知,由因导果通过逐步推理寻找问题成立的必要条件.它的证明格式为:因为×××,所以×××,所以×××……所以×××成立.2.分析法证明问题时,是从“未知”看“需知”,执果索因逐步靠拢“已知”,通过逐步探索,寻找问题成立的充分条件.它的证明格式:要证×××,只需证×××,只需证×××……因为×××成立,所以×××成立.。
高中数学第一章推理与证明2综合法与分析法教学案北师大版选修2-2(2021学年)

2017-2018学年高中数学第一章推理与证明2 综合法与分析法教学案北师大版选修2-2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中数学第一章推理与证明2综合法与分析法教学案北师大版选修2-2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中数学第一章推理与证明2综合法与分析法教学案北师大版选修2-2的全部内容。
§2综合法与分析法错误!综合法阅读下面的例题.例:若实数a,b满足a+b=2,证明:2a+2b≥4。
证明:因为a+b=2,所以2a+2b≥2错误!=2错误!=2错误!=4,故2a+2b≥4成立.问题1:本题利用什么公式?提示:基本不等式.问题2:本题证明顺序是什么?提示:从已知到结论.综合法(1)含义:从命题的条件出发,利用定义、公理、定理及运算法则,通过演绎推理,一步一步地接近要证明的结论,直到完成命题的证明的思维方法,称为综合法.(2)思路:综合法的基本思路是“由因导果”.(3)模式:综合法可以用以下的框图表示:\x(P⇒Q1)→\x(Q1⇒Q2)→\x(Q2⇒Q3)→…→\x(Q n⇒Q)其中P为条件,Q为结论。
分析法你们看过侦探小说《福尔摩斯探案集》吗?尤其是福尔摩斯在探案中的推理,给人印象太深刻了.有时,他先假定一个结论成立,然后逐步寻找这个结论成立的一个充分条件,直到找到一个明显的证据.问题1:他的推理如何入手?提示:从结论成立入手.问题2:他又是如何分析的?提示:逐步探寻每一结论成立的充分条件.问题3:这种分析问题方法在数学问题证明中可以借鉴吗?提示:可以.分析法(1)含义:从求证的结论出发,一步一步地探索保证前一个结论成立的充分条件,直到归结为这个命题的条件,或者归结为定义、公理、定理等.这种证明问题的思维方法称为分析法.(2)思路:分析法的基本思路是“执果索因”.(3)模式:若用Q表示要证明的结论,则分析法可以用如下的框图来表示:Q⇐P→\x(P1⇐P2)→错误!→…→得到一个明显成立的条件11.综合法是从“已知"看“可知”逐步推向未知,由因导果通过逐步推理寻找问题成立的必要条件.它的证明格式为:因为×××,所以×××,所以×××……所以×××成立.2.分析法证明问题时,是从“未知”看“需知”,执果索因逐步靠拢“已知”,通过逐步探索,寻找问题成立的充分条件.它的证明格式:要证×××,只需证×××,只需证×××……因为×××成立,所以×××成立.错误!综合法的应用[例1] 已知a,b是正数,且a+b=1,求证:错误!+错误!≥4.[思路点拨] 由已知条件出发,结合基本不等式,即可得出结论.[精解详析]法一:∵a,b为正数,且a+b=1,∴a+b≥2ab,∴错误!≤错误!,∴1a+\f(1,b)=\f(a+b,ab)=错误!≥4。
高中数学 第一章 推理与证明 1.2.2 分析法课件 北师大版选修2-2

2.分析法证明的思维过程 用Q表示要证明的结论,则分析法的思维过程可用框图 表示为:
66
【思考】 分析法的推理过程是归纳推理或类比推理吗? 提示:不是归纳推理或类比推理,是演绎推理.
77
3.分析法和综合法的对比
分析法 综合法 联系
优点
缺点
思考起来比较自然,容易寻找 思路逆行,叙
到解题的思路和方法
4455
(2)要证a2+b2+c2<2S,即证a2+b2+c2-2ab-2bc2ac<0,即证(a2-ab-ac)+(b2-ab-bc)+(c2-acbc)<0,即证a[a-(b+c)]+b[b-(a+c)]+c[c(a+b)]<0. 因为a,b,c为任意三角形的三边长,所以a>0, b>0,c>0,且a+b>c,a+c>b,b+c>a,
法是执果索因法;④分析法是间接证明法;⑤分析法
是逆推法.
其中正确的表述有 ( )
A.2个
B.3个
C.4个
D.5个
1122
【解析】选C.结合综合法和分析法的定义可知①②③ ⑤均正确,分析法和综合法均为直接证明法,故④不 正确.
1133
3.下列条件①ab>0,②ab<0,③a>0,b>0,④a<0,
2299
【思维·引】 可用分析法找途径,用综合法由条件顺次推理,易于 使条件与结论联系起来.
3300
2a= x y,
【证明】由已知条件得
b
2=
cx,
c
2=
by.
高级中学高中数学(北师大版)选修2-2导学案:第一章 推理与证明(第8讲)

1.设 ()11x
f x x
+=
-,又记()()()()()11,,1,2,...,k k f x f x f x f f x k +=== 则()2017f x =( )
A .
11x x +-; B .11x x -+; C .x ; D .1
x
-; 2.在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝, 第
二件首饰是由6颗珠宝构成如图1所示的正六边形, 第三件首饰是由15颗珠宝构成如图2所示的正六边形, 第四件首饰是由28颗珠宝构成如图3所示的正六边形, 第五件首饰是由45颗珠宝构成如图4所示的正六边形, 以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断第7件首饰上的颗珠宝数是:
图1
图2
图3
A.97
B.103
C.88
D.91
3.用数学归纳法证明(1)(2)()2n n n n n +++=L 13...(21)()n n N *⋅⋅⋅+∈,从“k 到k+1”左端需乘的代数式是( )
A.2k+1
B.)12(2+k
C.
112++k k D.1
3
2++k k 4. 已知0>>b a ,用分析法证明b a b a -<-
5.已知:,,(0,)a b c ∈+∞,求证:222
b c a a b c a b c
++≥++。
高中数学第一章推理与证明1.2综合法与分析法1.2.2分析法课件北师大版选修2_2

2 2
(������
+
������)
2
,
即证明 a2+b2≥12 (������2 + ������2 + 2������������), 即证明a2+b2≥2ab.
∵a2+b2≥2ab 对一切实数恒成立,∴
������2 + ������2 ≥
2 2
(������
+
������)成立.
综上所述,不等式得证.
+
������ 2������+������
恒成立.
M 目标导航 UBIAODAOHANG
题型一 题型二 题型三 题型四
Z 知识梳理 HISHI SHULI
D 典例透析 IANLI TOUXI
S 随堂演练 UITANGYANLIAN
题型三 综合法与分析法的综合应用
【例 3】 已知 f(x)=ax2+bx+c(a≠0),若函数 f(x+1)与 f(x)的图像
题型一 题型二 题型三 题型四
Z 知识梳理 HISHI SHULI
D 典例透析 IANLI TOUXI
S 随堂演练 UITANGYANLIAN
∵ ������ ≥ ������ > 0, ∴ 只需 ������������ − 1≥0,即 cμ≥1.
∴μ≥1������ , 也就是x2+c≥1������,
(������-������)2
∴ 8������ < 2 − ������������ < 8������ .
M 目标导航 UBIAODAOHANG
题型一 题型二 题型三 题型四
Z 知识梳理 HISHI SHULI
高中数学第一章推理与证明1.2综合法与分析法分析法2教案北师大版选修2_2

分析法一、教学目标:结合已经学过的数学实例,了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点。
二、教学重点:了解分析法和综合法的思考过程、特点。
难点:分析法的思考过程、特点三、教学方法:探析归纳,讲练结合四、教学过程(一)、复习:直接证明的方法:综合法、分析法。
(二)、引入新课分析法和综合法是思维方向相反的两种思考方法。
在数学解题中,分析法是从数学题的待证结论或需求问题出发,一步一步地探索下去,最后达到题设的已知条件。
综合法则是从数学题的已知条件出发,经过逐步的逻辑推理,最后达到待证结论或需求问题。
对于解答证明来说,分析法表现为执果索因,综合法表现为由果导因,它们是寻求解题思路的两种基本思考方法,应用十分广泛。
在很多数学命题的证明中,往往需要综合地运用这两种思维方法。
(三)、例题讲解:例1:如图、已知BE ,CF 分别为△ABC 的边AC ,AB 上的高,G 为EF 的中点,H 为BC 的中点.求证:HG ⊥EF .证明:考虑待证的结论“HG ⊥EF ” .根据命题的条件:G 为EF 的中点,连接EH ,HF ,只要证明△EHF 为等腰三角形,即EH =HF .根据条件CF ⊥AB ,且H 为BC 的中点,可知FH 是Rt △BCF 斜边上的中线.所以 BC FH 21=. 同理 BC HE 21=. 这样就证明了△EHF 为等腰三角形.所以 HG ⊥EF .例2:已知:a ,b ,c 都是正实数,且ab +bc +ca =1.求证:a +b +c 3≥. 证明:考虑待证的结论“a +b +c 3≥” ,因为a +b +c >0,只需证明3)(2≥++c b a ,即 3)(2222≥+++++ac bc ab c b a .又 ab +bc +ca =1,所以,只需证明1222≥++c b a ,即 01222≥-++c b a .因为 ab +bc +ca =1,所以,只需证明 0)(222≥++-++ac bc ab c b a ,只需证明 0)(2222222≥++-++ac bc ab c b a ,即0)()()(222≥-+-+-a c c b b a .由于任意实数的平方都非负,故上式成立.所以 a +b +c 3≥.例3.如图,SA ⊥平面ABC,AB ⊥BC,过A 作SB 的垂线,垂足为E,过E 作SC 的垂线,垂足为F,求证 AF ⊥SC证明:要证AF ⊥SC ,只需证:SC ⊥平面AEF ,只需证:AE ⊥SC ,只需证:AE ⊥平面SBC 只需证:AE ⊥BC ,只需证:BC ⊥平面SAB ,只需证:BC ⊥SA ,只需证:SA ⊥平面ABC因为:SA ⊥平面ABC 成立。
「精品」高中数学第一章推理与证明1.2综合法与分析法分析法1教案北师大版选修22

分析法一、教学目标:1、结合已经学过的数学实例,了解直接证明的基本方法之一:分析法;2、了解分析法的思考过程、特点。
二、教学重点:了解分析法的思考过程、特点;难点:分析法的思考过程、特点。
三、教学方法:探析归纳,讲练结合四、教学过程(一)、复习:综合法的思考过程、特点(二)、引入新课在数学证明中,分析法是从数学题的待证结论或需求问题出发,一步一步地探索下去,最后达到题设的已知条件。
对于解答证明来说,分析法表现为执果索因,它是寻求解题思路的一种基本思考方法,应用十分广泛。
从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件为止,这种证明的方法叫做分析法.这个明显成立的条件可以是:已知条件、定理、定义、公理等。
特点:执果索因。
即:要证结果Q ,只需证条件P(三)、例题探析例1、已知:a ,b 是不相等的正数。
求证:2233ab b a b a +>+。
证明:要证明2233ab b a b a +>+只需证明 )())((22b a ab b ab a b a +>+-+,只需证明 0)())((22>+-+-+b a ab b ab a b a ,只需证明 0)2)((22>+-+b ab a b a ,只需证明 0))((2>-+b a b a ,只需证明 0)(0)(2>->+b a b a 且。
由于命题的条件“a ,b 是不相等的正数”,它保证上式成立。
这样就证明了命题的结论。
例2、求证:10578+>+。
证明:要证明 10578+>+,只需证明 22)105()78(+>+,即 50210556278++>++,只需证明 5056>,即 56>50,这显然成立。
这样就证明了10578+>+ 例3、求证:函数16122)(2+-=x x x f 在区间(3,+∞)上是增加的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2 分析法1.了解分析法的思维过程、特点.(重点)2.会用分析法证明数学问题.(难点)[基础·初探]教材整理分析法阅读教材P9~P11,完成下列问题.1.分析法的定义从求证的结论出发,一步一步地探索保证前一个结论成立的充分条件,直到归结为这个命题的条件,或者归结为定义、公理、定理等,这种思维方法称为分析法.2.分析法证明的思维过程用Q表示要证明的结论,则分析法的思维过程可用框图表示为:Q⇐P1→P1⇐P2→P2⇐P3→…→得到一个明显成立的条件3.综合法和分析法的综合应用在解决问题时,我们经常把综合法和分析法结合起来使用:根据条件的结构特点去转化结论,得到中间结论Q′;根据结论的结构特点去转化条件,得到中间结论P′.若由P′可以推出Q′成立,即可证明结论成立.判断(正确的打“√”,错误的打“×”)(1)分析法就是从结论推向已知.( )(2)分析法的推理过程要比综合法优越.( )(3)并不是所有证明的题目都可使用分析法证明.( )【解析】(1)错误.分析法又叫逆推证法,但不是从结论推向已知,而是寻找使结论成立的充分条件的过程.(2)错误.分析法和综合法各有优缺点.(3)正确.一般用综合法证明的题目均可用分析法证明,但并不是所有的证明题都可使用分析法证明.【答案】 (1)× (2)× (3)√[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问1: 解惑: 疑问2: 解惑: 疑问3: 解惑:[小组合作型]已知a >b >0,求证:8a <2-ab <8b.【精彩点拨】 本题用综合法不易解决,由于变形后均为平方式,因此要先将式子两边同时开方,再找出使式子成立的充分条件.【自主解答】 要证(a -b )28a <a +b 2-ab <(a -b )28b ,只需证(a -b )28a <(a -b )22<(a -b )28b .∵a >b >0,∴同时除以(a -b )22,得(a +b )24a <1<(a +b )24b ,同时开方,得a +b 2a <1<a +b2b, 只需证a +b <2a ,且a +b >2b , 即证b <a ,即证b <a . ∵a >b >0,∴原不等式成立, 即(a -b )28a <a +b 2-ab <(a -b )28b.1.分析法证明不等式的思维是从要证的不等式出发,逐步寻求使它成立的充分条件,最后得到的充分条件为已知(或已证)的不等式.2.分析法证明数学命题的过程是逆向思维,即结论⇐…⇐…⇐…已知,因此,在叙述过程中,“要证”“只需证”“即证”等词语必不可少,否则会出现错误.[再练一题]1.(2016·合肥高二检测)已知a >0,求证:a 2+1a 2-2≥a +1a-2.【导学号:94210013】【证明】 要证a 2+1a 2-2≥a +1a-2,只需证a 2+1a 2+2≥a +1a+2,即证⎝⎛⎭⎪⎫a 2+1a 2+22≥⎝⎛⎭⎪⎫a +1a +22,即a 2+1a2+4 a 2+1a 2+4≥a 2+1a 2+2 2⎝ ⎛⎭⎪⎫a +1a +4,只需证2a 2+1a 2≥ 2⎝ ⎛⎭⎪⎫a +1a .只需证4⎝ ⎛⎭⎪⎫a 2+1a 2≥2⎝ ⎛⎭⎪⎫a 2+2+1a 2,即a 2+1a2≥2.上述不等式显然成立,故原不等式成立.与直线x =-p2相切.【精彩点拨】【自主解答】 如图所示,过点A ,B 分别作AA ′,BB ′垂直准线于点A ′,B ′,取AB 的中点M ,作MM ′垂直准线于点M ′.要证明以AB 为直径的圆与准线相切,只需证|MM ′|=12|AB |.由抛物线的定义有|AA ′|=|AF |,|BB ′|=|BF |,所以|AB |=|AA ′|+|BB ′|,因此只需证|MM ′|=12(|AA ′|+|BB ′|).根据梯形的中位线原理可知上式是成立的,所以以过抛物线y 2=2px 焦点的弦为直径的圆必与直线x =-p2相切.1.分析法是逆向思维,当已知条件与结论之间的联系不够明显、直接或证明过程中所需要用的知识不太明确、具体时,往往采用分析法.2.分析法的思路与综合法正好相反,它是从要求证的结论出发,倒着分析,由未知想需知,由需知逐渐地靠近已知,即已知条件、已经学过的定义、定理、公理、公式、法则等.[再练一题]2.已知1-tan α2+tan α=1,求证:cos α-sin α=3(cos α+sin α).【导学号:94210014】【证明】 要证cos α-sin α=3(cos α+sin α), 只需证cos α-sin αcos α+sin α=3,只需证1-tan α1+tan α=3,只需证1-tan α=3(1+tan α),只需证tan α=-12.∵1-tan α2+tan α=1,∴1-tan α=2+tan α,即2tan α=-1.∴tan α=-12显然成立,∴结论得证.[探究共研型]探究【提示】 综合法与分析法的推理过程是演绎推理,它们的每一步推理都是严密的逻辑推理,从而得到的每一个结论都是正确的,不同于合情推理中的“猜想”.探究2 综合法与分析法有什么区别?【提示】 综合法是从已知条件出发,逐步寻找的是必要条件,即由因导果;分析法是从待求结论出发,逐步寻找的是充分条件,即执果索因.在某两个正数x ,y 之间,若插入一个数a ,则能使x ,a ,y 成等差数列;若插入两个数b ,c ,则能使x ,b ,c ,y 成等比数列,求证:(a +1)2≥(b +1)(c +1).【精彩点拨】 可用分析法找途径,用综合法由条件顺次推理,易于使条件与结论联系起来.【自主解答】 由已知条件得⎩⎪⎨⎪⎧2a =x +y ,b 2=cx ,c 2=by ,消去x ,y 得2a =b 2c +c 2b,且a >0,b >0,c >0.要证(a +1)2≥(b +1)(c +1),只需证a +1≥(b +1)(c +1),因(b +1)(c +1)≤(b +1)+(c +1)2,只需证a +1≥b +1+c +12,即证2a ≥b +c .由于2a =b 2c +c 2b ,故只需证b 2c +c 2b≥b +c ,只需证b 3+c 3=(b +c )(b 2+c 2-bc )≥(b +c )bc , 即证b 2+c 2-bc ≥bc ,即证(b -c )2≥0.因为上式显然成立,所以(a +1)2≥(b +1)(c +1).综合法推理清晰,易于书写,分析法从结论入手,易于寻找解题思路,在实际证明命题时,常把分析法与综合法结合起来使用,称为分析综合法,其结构特点是根据条件的结构特点去转化结论,得到中间结论Q ;根据结论的结构特点去转化条件,得到中间结论P ;若由P 可推出Q ,即可得证.[再练一题]3.已知△ABC 的三个内角A ,B ,C 成等差数列,求证:1a +b +1b +c =3a +b +c. 【证明】 要证1a +b +1b +c =3a +b +c, 即证a +b +c a +b +a +b +cb +c =3, 即证c a +b +ab +c=1,只需证c (b +c )+a (a +b )=(a +b )(b +c ),只需证c 2+a 2=ac +b 2. ∵A ,B ,C 成等差数列, ∴2B =A +C ,又A +B +C =180°,∴B =60°. ∵c 2+a 2-b 2=2ac cos B , ∴c 2+a 2-b 2=ac , ∴c 2+a 2=ac +b 2, ∴1a +b +1b +c =3a +b +c成立. [构建·体系]1.要证明2+7>23,可选择的方法有以下几种,其中最合理的是( ) A.综合法 B.分析法 C.比较法D.归纳法【解析】 由分析法和综合法定义可知选B. 【答案】 B2.已知a ≥0,b ≥0,且a +b =2,则( ) A.a ≤12B.ab ≥12C.a 2+b 2≥2D.a 2+b 2≤3【解析】 ∵a +b =2≥2ab ,∴ab ≤1. ∵a 2+b 2=4-2ab ,∴a 2+b 2≥2. 【答案】 C3.3a -3b <3a -b 成立的充要条件是( ) A.ab (b -a )>0 B.ab >0且a >b C.ab <0且a <bD.ab (b -a )<0【解析】 3a -3b <3a -b ⇔(3a -3b )3<(3a -b )3⇔a -b -33a 2b +33ab 2<a -b ⇔3ab 2<3a 2b⇔ab 2<a 2b ⇔ab (b -a )<0.【答案】 D4.设a >0,b >0,c >0,若a +b +c =1,则1a +1b +1c的最小值为________.【导学号:94210015】【解析】 因为a +b +c =1,且a >0,b >0,c >0, 所以1a +1b +1c =a +b +c a +a +b +c b +a +b +c c=3+b a +a b +c b +b c +a c +ca≥3+2b a ·a b+2c a ·a c +2c b ·b c=3+6=9.当且仅当a =b =c 时等号成立. 【答案】 95.已知a ,b ,c ∈R 且不全相等,求证:a 2+b 2+c 2>ab +bc +ca . 【证明】 法一:(分析法) 要证a 2+b 2+c 2>ab +bc +ca , 只需证2(a 2+b 2+c 2)>2(ab +bc +ca ),只需证(a 2+b 2-2ab )+(b 2+c 2-2bc )+(c 2+a 2-2ca )>0, 只需证(a -b )2+(b -c )2+(c -a )2>0, 因为a ,b ,c ∈R ,所以(a -b )2≥0,(b -c )2≥0,(c -a )2≥0. 又因为a ,b ,c 不全相等,所以(a -b )2+(b -c )2+(c -a )2>0成立. 所以原不等式a 2+b 2+c 2>ab +bc +ca 成立. 法二:(综合法) 因为a ,b ,c ∈R ,所以(a -b )2≥0,(b -c )2≥0,(c -a )2≥0. 又因为a ,b ,c 不全相等, 所以(a -b )2+(b -c )2+(c -a )2>0,所以(a 2+b 2-2ab )+(b 2+c 2-2bc )+(c 2+a 2-2ca )>0,所以2(a2+b2+c2)>2(ab+bc+ca),所以a2+b2+c2>ab+bc+ca.我还有这些不足:(1)(2)我的课下提升方案:(1)(2)学业分层测评(四)(建议用时:45分钟)[学业达标] 一、选择题1.若a,b∈R,则1a3>1b3成立的一个充分不必要条件是( )A.ab>0B.b>aC.a<b<0D.ab(a-b)<0【解析】由a<b<0⇒a3<b3<0⇒1a3>1b3,但1a3>1b3不能推出a<b<0,∴a<b<0是1a3>1b3的一个充分不必要条件.【答案】 C2.求证:7-1>11- 5.证明:要证7-1>11-5,只需证7+5>11+1,即证7+27×5+5>11+211+1,即证35>11,∵35>11,∴原不等式成立.以上证明应用了( )A.分析法B.综合法C.分析法与综合法配合使用D.间接证法【解析】 该证明方法符合分析法的定义,故选A. 【答案】 A3.(2016·汕头高二检测)要证a 2+b 2-1-a 2b 2≤0,只要证明( ) A.2ab -1-a 2b 2≤0 B.a 2+b 2-1-a 4+b 42≤0C.(a +b )22-1-a 2b 2≤0D.(a 2-1)(b 2-1)≥0【解析】 要证a 2+b 2-1-a 2b 2≤0,只要证明(a 2-1)+b 2(1-a 2)≤0,只要证明(a 2-1)(1-b 2)≤0,即证(a 2-1)(b 2-1)≥0.【答案】 D4.在不等边三角形中,a 为最大边,要想得到∠A 为钝角的结论,三边a ,b ,c 应满足什么条件( )A.a 2<b 2+c 2B.a 2=b 2+c 2C.a 2>b 2+c 2D.a 2≤b 2+c 2【解析】 由余弦定理得cos A =b 2+c 2-a 22bc<0,∴b 2+c 2-a 2<0, 即b 2+c 2<a 2. 【答案】 C5.分析法又称执果索因法,若用分析法证明“设a >b >c ,且a +b +c =0,求证:b 2-ac <3a ”,索的因应是( )A.a -b >0B.a -c >0C.(a -b )(a -c )>0D.(a -b )(a -c )<0【解析】 由题意知b 2-ac <3a ⇐b 2-ac <3a 2⇐b 2+a (a +b )<3a 2⇐b 2+a 2+ab <3a 2⇐b 2+ab <2a 2⇐2a 2-ab -b 2>0⇐a 2-ab +a 2-b 2>0⇐a (a -b )+(a +b )(a -b )>0 ⇐a (a -b )-c (a -b )>0⇐(a -b )(a -c )>0,故选C. 【答案】 C 二、填空题6.(2016·烟台高二检测)设A =12a +12b ,B =2a +b(a >0,b >0),则A ,B 的大小关系为________.【解析】 ∵A -B =a +b 2ab -2a +b =(a +b )2-4ab 2ab (a +b )=(a -b )22ab (a +b )≥0,∴A ≥B .【答案】 A ≥B7.(2016·西安高二检测)如果a a >b b ,则实数a ,b 应满足的条件是________.【导学号:94210016】【解析】 要使a a >b b 成立,只需(a a )2>(b b )2,只需a 3>b 3>0,即a ,b 应满足a >b >0. 【答案】 a >b >08.如图125,四棱柱ABCD A 1B 1C 1D 1的侧棱垂直于底面,满足________时,BD ⊥A 1C (写出一个条件即可).图125【解析】 要证BD ⊥A 1C ,只需证BD ⊥平面AA 1C .因为AA 1⊥BD ,只要再添加条件AC ⊥BD ,即可证明BD ⊥平面AA 1C ,从而有BD ⊥A 1C .【答案】 AC ⊥BD (或底面为菱形) 三、解答题9.设a ,b >0,且a ≠b ,求证:a 3+b 3>a 2b +ab 2. 【证明】 法一:分析法 要证a 3+b 3>a 2b +ab 2成立,只需证(a +b )(a 2-ab +b 2)>ab (a +b )成立, 又因a +b >0,只需证a 2-ab +b 2>ab 成立, 只需证a 2-2ab +b 2>0成立, 即需证(a -b )2>0成立.而依题设a ≠b ,则(a -b )2>0显然成立, 由此命题得证. 法二:综合法a ≠b ⇒a -b ≠0⇒(a -b )2>0⇒a 2-2ab +b 2>0⇒a 2-ab +b 2>ab .注意到a ,b >0,a +b >0,由上式即得 (a +b )(a 2-ab +b 2)>ab (a +b ), ∴a 3+b 3>a 2b +ab 2.10.(2016·深圳高二检测)已知三角形的三边长为a ,b ,c ,其面积为S ,求证:a 2+b 2+c 2≥43S .【证明】 要证a 2+b 2+c 2≥43S ,只要证a 2+b 2+(a 2+b 2-2ab cos C )≥23ab sin C , 即证a 2+b 2≥2ab sin(C +30°),因为2ab sin(C +30°)≤2ab ,只需证a 2+b 2≥2ab ,显然上式成立,所以a 2+b 2+c 2≥43S .[能力提升]1.已知a ,b ,c ,d 为正实数,且a b <c d ,则( )A.a b <a +cb +d <c dB.a +cb +d <a b <c dC.a b <c d <a +cb +dD.以上均可能【解析】 先取特殊值检验,∵a b <c d ,可取a =1,b =3,c =1,d =2,则a +c b +d =25,满足a b <a +cb +d <cd .∴B ,C 不正确.要证a b <a +cb +d ,∵a ,b ,c ,d 为正实数,∴只需证a (b +d )<b (a +c ),即证ad <bc .只需证a b <c d ,而a b <c d 成立,∴a b <a +cb +d .同理可证a +cb +d <cd .故A 正确,D 不正确.【答案】 A2.(2016·黄冈高二检测)下列不等式不成立的是()A.a 2+b 2+c 2≥ab +bc +caB.a +b >a +b (a >0,b >0)C.a -a -1<a -2-a -3(a ≥3)D.2+10>2 6【解析】 对于A ,∵a 2+b 2≥2ab ,b 2+c 2≥2bc ,a 2+c 2≥2ac ,∴a 2+b 2+c 2≥ab +bc +ca ;对于B ,∵(a +b )2=a +b +2ab ,(a +b )2=a +b ,∴a +b >a +b ;对于C ,要证a -a -1<a -2-a -3(a ≥3)成立,只需证明a +a -3<a -2+a -1,两边平方得2a -3+2a (a -3)<2a -3+2(a -2)(a -1),即a (a -3)<(a -2)(a -1),两边平方得a 2-3a <a 2-3a +2,即0<2.因为0<2显然成立,所以原不等式成立;对于D ,(2+10)2-(26)2=12+45-24=4(5-3)<0,∴2+10<26,故D 错误.【答案】 D3.使不等式3+22>1+p 成立的正整数p 的最大值是________.【导学号:94210017】【解析】 由3+22>1+p ,得p <3+22-1,即p <(3+22-1)2,所以p <12+46-42-23,由于12+46-42-23≈12.7,因此使不等式成立的正整数p 的最大值是12.【答案】 124.(2016·唐山高二检测)已知a ,b ,c 是不全相等的正数,且0<x <1,求证:log x a +b 2+log x b +c 2+log x a +c 2<log x a +log x b +log x c .【证明】 要证明log xa +b 2+log x b +c 2+log x a +c 2<log x a +log x b +log x c , 只需要证明log x ⎝ ⎛⎭⎪⎫a +b 2·b +c 2·a +c 2<log x (abc ), 而已知0<x <1,故只需证明a +b 2·b +c 2·a +c 2>abc . ∵a ,b ,c 是不全相等的正数,∴a +b 2≥ab >0,b +c 2≥bc >0,a +c 2≥ac >0, ∴a +b 2·b +c 2·a +c 2>a 2b 2c 2=abc , 即a +b 2·b +c 2·a +c 2>abc 成立,∴log x a +b 2+log x b +c 2+log x a +c 2<log x a +log x b +log x c 成立.。
