2006年河南科技大学硕士研究生入学考试理论力学真题
2007年2

哈工大2006年秋季理论力学试题一、填空题1.已知图示正方体边长为a , 在右侧面作用已知力F ,在顶面作用矩为M 的已知力偶矩,如图所示。
求力系对x ,y ,z 轴的力矩。
(6分)x M∑=( ),y M ∑=( ) zM ∑=( )2. 已知:图示机构位于铅垂面内,匀质杆OA 质量为m ,长为l ,且l =4R ,匀质圆盘质量为m ,半径为R ,与杆在A 端固接。
图示瞬时,杆的角速度ω=0,角加速度为α。
求惯性力系向O 点简化结果。
(6分)主失大小=( ),主矩大小=( ) 方向在图中标出。
二.在图示机构中,已知:OB=OD=DA=20cm ,AC =40cm ,AB ⊥AC ,角θ=30,1F =150N,弹簧的刚度系数k =150N/cm,在图示位置已有压缩变形δ=2cm,不计各构件重量,用虚位移原理求构件在图示位置平衡时,力2F 的大小。
(用其他方法做不给分)(8分)三.已知:图示平面结构,各杆自重不计。
M =10kN ⋅m ,F =20kN ,max q =8kN/m ,2l m =,A ,B ,D 处为铰链连接,E 处为固定端。
求:A,E处的约束力。
(20分)四.已知:平面机构如图:圆轮A沿水平面纯滚动,滑块B上铰链两直杆AB,BD,BD穿过做定轴转动的套筒C,15,45/,0A A R cm v cm s a ===,图示瞬时,45,30,30l cm θϕ=== 。
求:图示瞬时,AB,BD杆的角速度,AB BD ωω;点B的加速度B a ;BD杆的角加速度BD α。
(20)五.已知:图示系统中,物块A质量为3m ,均质圆盘B与均质圆柱C质量均为m ,半径均为R,弹簧刚度系数为k ,初始时系统静止,弹簧为原长。
系统由静止释放后,圆柱C做纯滚动。
斜面倾角为30 ,弹簧与绳的倾斜段与斜面平行。
求:当物块A下降距离为s (未达最低位置)时的速度与加速度,两段绳中的拉力。
(20分)。
理论力学试卷2006,2
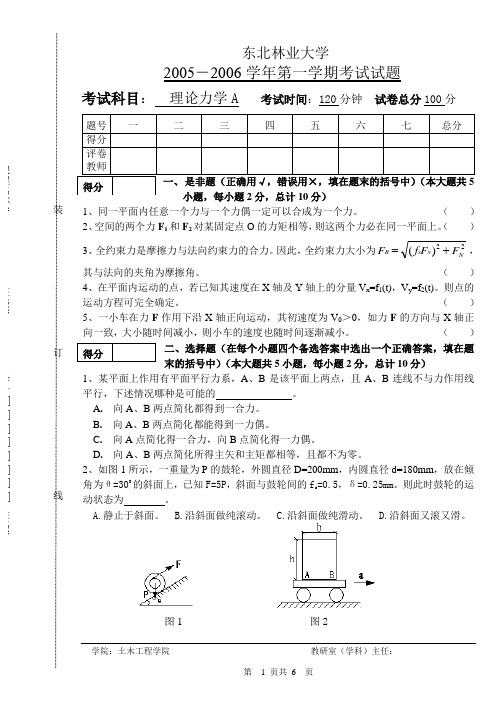
东北林业大学2005-2006学年第一学期考试试题考试科目:理论力学A 考试时间:120分钟试卷总分100分1、同一平面内任意一个力与一个力偶一定可以合成为一个力。
()2、空间的两个力F1和F2对某固定点O的力矩相等,则这两个力必在同一平面上。
()3、全约束力是摩擦力与法向约束力的合力。
因此,全约束力大小为22)(NR FFfF NS+=,其与法向的夹角为摩擦角。
()4、在平面内运动的点,若已知其速度在X轴及Y轴上的分量V x=f1(t),V y=f2(t)。
则点的运动方程可完全确定。
()5、一小车在力F作用下沿X轴正向运动,其初速度为V0>0,如力F的方向与X轴正向一致,大小随时间减小,则小车的速度也随时间逐渐减小。
()二、选择题(在每个小题四个备选答案中选出一个正确答案,填在题末的括号中)(本大题共5小题,每小题2分,总计10分)1、某平面上作用有平面平行力系,A、B是该平面上两点,且A、B连线不与力作用线平行,下述情况哪种是可能的。
A. 向A、B两点简化都得到一合力。
B.向A、B两点简化都能得到一力偶。
C.向A点简化得一合力,向B点简化得一力偶。
D. 向A、B两点简化所得主矢和主矩都相等,且都不为零。
2、如图1所示,一重量为P的鼓轮,外圆直径D=200mm,内圆直径d=180mm,放在倾角为θ=300的斜面上,已知F=5P,斜面与鼓轮间的f s=0.5,δ=0.25mm。
则此时鼓轮的运动状态为。
A.静止于斜面。
B.沿斜面做纯滚动。
C.沿斜面做纯滑动。
D.沿斜面又滚又滑。
图1 图23、点作直线运动,已知某瞬时加速度为a=-4m/s 2,t=1s 时速度为V 1= 4m/s ,则t=2s 时,该点的速度的大小为 。
A . 0;B . – 4m/s ;C . 8m/s ;D . 无法确定。
4、某一瞬时,作平面运动的平面图形内任意两点的加速度在此两点连线上投影相等,则可以断定该瞬时平面图形的 。
A . 角速度ω=0;B . 角加速度α=0;C . ω、α同时为零; D. ω、α均不为零。
2006-数一真题大全及答案

2006年全国硕士研究生入学考试数学一真题一、填空题(1)0ln(1)lim1cos x x x x→+=−. (2)微分方程(1)y x y x−'=的通解是 .(3)设∑是锥面z =(01z ≤≤)的下侧,则23(1)xdydz ydzdx z dxdy ∑++−=⎰⎰.(4)点(2,1,0)到平面3450x y z ++=的距离z = .(5)设矩阵2112A ⎛⎫= ⎪−⎝⎭,E 为2阶单位矩阵,矩阵B 满足2BA B E =+,则B =.(6)设随机变量X 与Y 相互独立,且均服从区间[0, 3]上的均匀分布,则{}max{,}1P X Y ≤= . 二、选择题(7)设函数()y f x =具有二阶导数,且()0,()0f x f x '''>>,x ∆为自变量x 在0x 处的增量,y ∆与dy分别为()f x 在点0x 处对应的增量与微分,若0x ∆>,则(A )0.dx y <<∆ (B )0.y dy <∆<(C )0.y dy ∆<<(D )0.dy y <∆<【 】(8)设(,)f x y 为连续函数,则14(cos ,sin )d f r r rdr πθθθ⎰⎰等于(A)(,).xf x y dy ⎰⎰(B)(,).f x y dy ⎰⎰(C)(,).yf x y dx ⎰⎰(C)(,).f x y dx ⎰⎰【 】(9)若级数1nn a∞=∑收敛,则级数(A )1nn a∞=∑收敛. (B )1(1)nn n a ∞=−∑收敛.(C )11n n n a a ∞+=∑收敛.(D )112n n n a a ∞+=+∑收敛. 【 】(10)设(,)f x y 与(,)x y ϕ均为可微函数,且1(,)0y x y ϕ≠. 已知00(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点,下列选项正确的是(A )若00(,)0x f x y '=,则00(,)0y f x y '=. (B )若00(,)0x f x y '=,则00(,)0y f x y '≠. (C )若00(,)0x f x y '≠,则00(,)0y f x y '=. (D )若00(,)0x f x y '≠,则00(,)0y f x y '≠.【 】(11)设12,,,,a a a 均为n 维列向量,A 是m n ⨯矩阵,下列选项正确的是(A )若12,,,,a a a 线性相关,则12,,,,Aa Aa Aa 线性相关. (B )若12,,,,a a a 线性相关,则12,,,,Aa Aa Aa 线性无关.(C )若12,,,,a a a 线性无关,则12,,,,Aa Aa Aa 线性相关.(D )若12,,,,a a a 线性无关,则12,,,,Aa Aa Aa 线性无关. 【 】(12)设A 为3阶矩阵,将A 的第2行加到第1行得B ,再将B 的第1列的-1倍加到第2列得C ,记110010001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则(A )1.C P AP −= (B )1.C PAP −=(C ).T C P AP =(D ).TC PAP = 【 】(13)设,A B 为随机事件,且()0,(|)1P B P A B >=,则必有 (A )()().P A B P A ⋃> (B )()().P A B P B ⋃>(C )()().P A B P A ⋃=(D )()().P A B P B ⋃= 【 】(14)设随机变量X 服从正态分布211(,)N μσ,Y 服从正态分布222(,)N μσ,且12{||1}{||1},P X P Y μμ−<>−<(A )1 2.σσ< (B )1 2.σσ>(C )1 2.μμ<(D )1 2.μμ> 【 】三 解答题 15 设区域D=(){}22,1,0x y x y x +≤≥,计算二重积分2211DxyI dxdy x y +=++⎰⎰.16 设数列{}n x 满足()110,sin 1,2,...n x x x n ππ+<<== . 求: (Ⅰ)证明lim n x x →∞存在,并求之 .(Ⅱ)计算211lim n x n x n x x +→∞⎛⎫ ⎪⎝⎭. 17 将函数()22xf x x x=+−展开成x 的幂级数. 18 设函数()()0,,f u +∞在内具有二阶导数且z f=满足等式22220z zx y∂∂+=∂∂.(Ⅰ)验证()()0f u f u u'''+=. (Ⅱ)若()()()10,11,f f f u '==求函数的表达式. 19 设在上半平面D=(){},0x y y >内,数(),f x y 是有连续偏导数,且对任意的t>0都有()()2,,f tx ty t f x y =.证明: 对L 内的任意分段光滑的有向简单闭曲线L,都有0),(),(=−⎰dy y x xf dx y x yf L.20 已知非齐次线性方程组12341234123414351331x x x x x x x x ax x x bx +++=−⎧⎪++−=−⎨⎪++−=⎩有个线性无关的解 Ⅰ证明方程组系数矩阵A 的秩()2r A = Ⅱ求,a b 的值及方程组的通解21 设3阶实对称矩阵A 的各行元素之和均为3,向量()()121,2,1,0,1,1TTαα=−−=−是线性方程组A x =0的两个解, (Ⅰ)求A 的特征值与特征向量 (Ⅱ)求正交矩阵Q 和对角矩阵A,使得TQ AQ A =.22 随机变量x 的概率密度为()()21,1021,02,,40,x x f x x y x F x y ⎧−<<⎪⎪⎪=≤<=⎨⎪⎪⎪⎩令其他为二维随机变量(X,Y)的分布函数.(Ⅰ)求Y 的概率密度()Y f y (Ⅱ)1,42F ⎛⎫−⎪⎝⎭23 设总体X 的概率密度为()()01,0112010x F X x θθθθ<<⎧⎪=−≤<<<⎨⎪⎩其中是未知参数其它,12n ,...,X X X 为来自总体X 的简单随机样本,记N 为样本值12,...,1n x x x 中小于的个数,求θ的最大似然估计.2006年全国硕士研究生入学考试数学一真题解析一、填空题(1)0ln(1)lim1cos x x x x→+−= 2 .221cos 1,)1ln(x x x x −+ (0x →当时)(2)微分方程(1)y x y x−'=的通解是(0)xy cxe x −=≠,这是变量可分离方程.(3)设∑是锥面1)Z ≤≤的下侧,则23(1)2xdydz ydzdx z dxdy π∑++−=⎰⎰补一个曲面221:1x y z ⎧+≤∑⎨=⎩1上侧,2,3(1)P x Q y R z ===−1236P Q R x y z∂∂∂++=++=∂∂∂ ∴16dxdydz ∑∑Ω+=⎰⎰⎰⎰⎰⎰⎰(Ω为锥面∑和平面1∑所围区域)6V =(V 为上述圆锥体体积)623ππ=⨯= 而123(1)0dydz ydzdx z dxdy ∑⨯++−=⎰⎰(∵在1∑上:1,0z dz ==)(4),1,0,450x y z d ++==点(2)到平面3的距离d ====(5)设A = 2 1 ,2阶矩阵B 满足BA =B +2E ,则|B |= .-1 2解:由BA =B +2E 化得B (A -E )=2E ,两边取行列式,得|B ||A -E |=|2E |=4,计算出|A -E |=2,因此|B |=2. (6)91 二、选择题(7)设函数()y f x =具有二阶导数,且()0f x '>,()0f x ''>,x ∆为自变量x 在0x 处的增量,y ∆与dy 分别为()f x 在点0x 处对应的增量与微分.若0>∆x ,则[A]0)(0)(0)(0)(<∆<<<∆<∆<∆<<y dy D dy y C dy y B y dy A()0,()f x f x '>因为则严格单调增加 ()0,()f x f x ''>则是凹的 y dy x ∆<<>∆0,0故又1(8)(,)(cos ,sin )[C](A)(,)(B)(,)xf x y d f r r rdr f x y dy f x y dy πθθθ⎰⎰⎰⎰⎰⎰40设为连续函数,则等于(C)(,)(D)(,)ydy f x y dxf x y dx ⎰⎰⎰111111111(9)[D]()()(1)()()()2n n n n n n n n n n n n n n n a A a B a a aC a aD a∞=∞∞==∞∞∞+++===−+∑∑∑∑∑∑若级数收敛,则级数收敛收敛收敛收敛也收敛00000000000000000(10)(,)(,)(,)0,(,)(,)0y x y x y x y x y f x y x y x y x y f x y x y f x y f x y f x y f x y f x y f x y f x y f x ϕϕϕ'≠=''''≠''''≠≠设与均为可微函数,且已知(,)是在约束条件下的一个极值点,下列选项正确的是[D](A)若(,)=0,则(,)=0(B)若(,)=0,则(,)0(C)若(,)0,则(,)=0(D)若(,)0,则(,00000000000000000(,)(,)(,)(,)0(1)(,)(,)0(2)(,)0(,)(,)(,)(,)0,(,)(,)(,)(,)0x x x y y y y y x y x y y x y f x y x y f x y x y f x y x y x y f x y f x y x y x y f x y x y x y f x y λλϕλϕλϕϕϕϕλϕϕ≠+'''⎧+=⎪'''+=⎨⎪'=⎩'''''≠∴=−='''≠)0构造格朗日乘子法函数F=F =F =F =今代入(1)得今00,(,)0[]y f x y D '≠则故选(11)设α1,α2,…,αs 都是n 维向量,A 是m ⨯n 矩阵,则( )成立.(A) 若α1,α2,…,αs 线性相关,则A α1,A α2,…,A αs 线性相关. (B) 若α1,α2,…,αs 线性相关,则A α1,A α2,…,A αs 线性无关. (C) 若α1,α2,…,αs 线性无关,则A α1,A α2,…,A αs 线性相关. (D) 若α1,α2,…,αs 线性无关,则A α1,A α2,…,A αs 线性无关. 解: (A)本题考的是线性相关性的判断问题,可以用定义解.若α1,α2,…,αs 线性相关,则存在不全为0的数c 1,c 2,…,c s 使得c 1α1+c 2α2+…+c s αs =0,用A 左乘等式两边,得c 1A α1+c 2A α2+…+c s A αs =0,于是A α1,A α2,…,A αs 线性相关.如果用秩来解,则更加简单明了.只要熟悉两个基本性质,它们是: 1. α1,α2,…,αs 线性无关⇔ r(α1,α2,…,αs )=s. 2. r(AB )≤ r(B ).矩阵(A α1,A α2,…,A αs )=A ( α1, α2,…,αs ),因此r(A α1,A α2,…,A αs )≤ r(α1, α2,…,αs ).由此马上可判断答案应该为(A).(12)设A 是3阶矩阵,将A 的第2列加到第1列上得B ,将B 的第1列的-1倍加到第2列上得C .记 1 1 0P = 0 1 0 ,则 0 0 1(A) C =P -1AP . (B) C =PAP -1.(C) C =P T AP . (D) C =PAP T.解: (B)用初等矩阵在乘法中的作用得出B =PA ,1 -1 0C =B 0 1 0 =BP -1= PAP -1. 0 0 1(13)根据乘法公式与加法公式有: P(AB)=P(B)P(A/B)=P(B)P(A ⋃B)=P(A)+P(B)-P(AB)=P(A) 应选C (14)依题:).1,0(~),10(~2211N Y N x σμσμ−−,,1}1{1111⎭⎬⎫<⎩⎨⎧−=<−σσμμX P X P.1}1{2222⎭⎬⎫⎩⎨⎧<−=<−σσμμY P Y P 因 },1{}1{21<−><−μμY P X P 即 .11222111⎭⎬⎫⎩⎨⎧<−>⎭⎬⎫⎩⎨⎧<−σσμσσμY P X p 所以.,112121σσσσ<>应选A三、解答题{}22222212120222021(15)(,)1,0,1:011ln(1)ln 21122DD DxyD x y x y x I dxdyx y xydxdy x y r I dxdy d dr r x yr ππππθ−+=+≤≥=++=++===+=+++⎰⎰⎰⎰⎰⎰⎰⎰设区域计算二重积分解{}{}{}211112121(16)0,sin (1,2,)(1)lim (2)lim():(1)sin ,01,2sin ,0,lim ,n n n n n n x n n nn n n n n n n n x x x x n x x x x x x n x x x x x x x A π+→∞+→∞+→∞<<===∴<≤≥=≤≥∴=设数列满足求证明存在,并求之计算解因此当时单调减少又有下界,根据准则1,存在递推公式两边取极限得sin ,0A A A =∴=21sin (2)lim(),n x n n n x x ∞→∞原式=为"1"型离散型不能直接用洛必达法则22011sin lim ln()0sin lim()t ttt tt t e t→→=先考虑2323203311(cos sin )1110()0()lim26cos sin sin 1262limlim2262t t t t t t t t t t t t t t tt t t ttteeeee →→→⎡⎤⎡⎤−−+−−+⎢⎥⎢⎥−⎢⎥⎢⎥−⎣⎦⎣⎦−=====2(17)()2xf x x x x =+−将函数展开成的幂极数 ()(2)(1)21x A Bf x x x x x ==+−+−+解: 2(1)(2)2,32,3A xB x xx A A ++−====令 11,31,3x B B =−=−=−令)](1[131)21(131)1(131)2(132)(x x x x x f −−⨯−−⨯=+⨯−−⨯= 10001111()(1)(1),132332n n n n n n n n n x x x x ∞∞∞+===⎡⎤=−−=+−<⎢⎥⎣⎦∑∑∑(18)设函数()(0,)f u +∞在内具有二阶导数,且Z f=满足等式22220z zx y∂∂+=∂∂ (I )验证()()0f u f u u'''+= (II )若(1)0,(1)1f f '== 求函数()f u 的表达式 证:(I)zzf f xy∂∂''==∂∂()22222zxf f xx y ∂'''=+∂+()()22322222x y f f x y x y '''=+++()()2223222222zy x f f yx y x y ∂'''=+∂++同理22220()()0z z f x y f u f u u∂∂''+=+=∂∂'''∴+=代入得成立(II )令(),;dp p dp du f u p c du u p u'==−=−+⎰⎰则ln ln ,()cp u c f u p u'=−+∴==22(1)1,1,()ln ||,(1)0,0()ln ||f c f u u c f c f u u '===+===由得于是(19)设在上半平面{}(,)|0D x y y =>内,函数(,)f x y 具有连续偏导数,且对任意0t >都有2(,)(,)f tx ty t f x y −=证明:对D 内任意分段光滑的有向简单闭曲线L ,都有0),(),(=−⎰dy y x xf dx y x yf L.证:把2(,)(,)f tx ty t f x y t −=两边对求导得:(,)(,)2(,)x y xf tx ty yf tx ty tf x y ''+=− 令 1t =,则(,)(,)2(,)x y xf x y yf x y f x y ''+=− 再令 (,),(,)P yf x y Q xf x y ==−所给曲线积分等于0的充分必要条件为Q Px y∂∂=∂∂ 今(,)(,)x Qf x y xf x y x∂'=−−∂(,)(,)y Pf x y yf x y y∂'=+∂ 要求Q Px y∂∂=∂∂成立,只要(,)(,)2(,)x y xf x y yf x y f x y ''+=− 我们已经证明,Q Px y∂∂∴=∂∂,于是结论成立. (20)已知非齐次线性方程组 x 1+x 2+x 3+x 4=-1, 4x 1+3x 2+5x 3-x 4=-1,a x 1+x 2+3x 3+bx 4=1 有3个线性无关的解.① 证明此方程组的系数矩阵A 的秩为2. ② 求a,b 的值和方程组的通解.解:① 设α1,α2,α3是方程组的3个线性无关的解,则α2-α1,α3-α1是AX =0的两个线性无关的解.于是AX =0的基础解系中解的个数不少于2,即4-r(A )≥2,从而r(A )≤2.又因为A 的行向量是两两线性无关的,所以r(A )≥2.两个不等式说明r(A )=2.② 对方程组的增广矩阵作初等行变换: 1 1 1 1 -1 1 1 1 1 -1 (A |β)= 4 3 5 -1 -1 → 0 –1 1 –5 3 ,a 1 3b 1 0 0 4-2a 4a+b-5 4-2a由r(A )=2,得出a=2,b=-3.代入后继续作初等行变换:1 02 -4 2→ 0 1 -1 5 -3 .0 0 0 0 0得同解方程组x 1=2-2x 3+4x 4,x 2=-3+x 3-5x 4,求出一个特解(2,-3,0,0)T 和AX =0的基础解系(-2,1,1,0)T ,(4,-5,0,1) T .得到方程组的通解:(2,-3,0,0)T +c 1(-2,1,1,0)T +c 2(4,-5,0,1)T , c 1,c 2任意.(21) 设3阶实对称矩阵A 的各行元素之和都为3,向量α1=(-1,2,-1)T , α2=(0,-1,1)T 都是齐次线性方程组AX =0的解.① 求A 的特征值和特征向量.② 求作正交矩阵Q 和对角矩阵Λ,使得Q T AQ =Λ.解:① 条件说明A (1,1,1)T =(3,3,3)T ,即 α0=(1,1,1)T 是A 的特征向量,特征值为3.又α1,α2都是AX =0的解说明它们也都是A 的特征向量,特征值为0.由于α1,α2线性无关, 特征值0的重数大于1.于是A 的特征值为3,0,0.属于3的特征向量:c α0, c ≠0.属于0的特征向量:c 1α1+c 2α2, c 1,c 2不都为0.② 将α0单位化,得η0=(33,33,33)T . 对α1,α2作施密特正交化,的η1=(0,-22,22)T , η2=(-36,66,66)T . 作Q =(η0,η1,η2),则Q 是正交矩阵,并且3 0 0Q T AQ =Q -1AQ = 0 0 0 .0 0 0(22)随机变量X 的概率密度为⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<−=其他,020,4101,21)(x x x f X ,令2X Y =,),(y x F 为二维随机变量)(Y X ,的分布函数.(Ⅰ)求Y 的概率密度;(Ⅱ))4,21(−F 解: (Ⅰ)⎪⎪⎩⎪⎪⎨⎧≤<≤<≤<=≤=≤=yy y y y X P y Y P y F Y 4,141,)2(10,)1(0,0)()()(2式式 ⎰⎰=+=≤≤−=−yy y dx dx y X y P 00434121)()1(式; ⎰⎰+=+=≤≤−=−y y dx dx y X y P 00141214121)()2(式. 所以:⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<==其他,041,8110,83)()('y yy y y F y f Y Y这个解法是从分布函数的最基本的概率定义入手,对y 进行适当的讨论即可,在新东方的辅导班里我也经常讲到,是基本题型.(Ⅱ))4,21(−F )212()22,21()4,21()4,21(2−≤≤−=≤≤−−≤=≤−≤=≤−≤=X P X X P X X P Y X P 4121211==⎰−−dx . (23)设总体X 的概率密度为⎪⎩⎪⎨⎧≤≤−<<=其他,021,110,),(x x x f θθθ,其中θ是未知参数(0<θ<1).n X X X ,,21为来自总体的简单随机样本,记N 为样本值n x x x ,,21中小于1的个数.求θ的最大似然估计.解:对样本n x x x ,,21按照<1或者≥1进行分类:pN p p x x x ,,21<1,pn pN pN x x x ,,21++≥1.似然函数⎩⎨⎧≥<−=++−其他,,01,,,1,,)1()(2121pn pN pN pN p p N n N x x x x x x L θθθ, 在pN p p x x x ,,21<1,pn pN pN x x x ,,21++≥1时, )1ln()(ln )(ln θθθ−−+=N n N L ,01)(ln =−−−=θθθθN n N d L d ,所以nN =最大θ.。
考卷二河南工业大学理论力学习题答案级考试试卷

试卷2一、填空题(每空3分,共21分)分)1(3分)、质点在柱坐标系中速度和加速度分别为 , 。
2(3分)、质点在自然坐标系中速度和加速度分别为3(3分)、质点力矩的分量表达式为、质点力矩的分量表达式为4(3分)、质点动量矩的分量表达式为、质点动量矩的分量表达式为5(3分)、对于定轴转动,如取基点在转轴上,则刚体内任意点的速度和加速度分别为6(3分)、瞬心的确定有两种方法,分别为:、瞬心的确定有两种方法,分别为: 和 。
7(3分)、物理摆的振动周期为、物理摆的振动周期为 ,其中,其中 为等值摆长。
二、简答题(共24分)分)1(5分)、质点在有心力场中运动可以用哪两个方程组来解决?2(5分)、检验下列的力是否为保守力,如是,则求出其势能(a )F x =6abz 3y-20bx 3y 2, F y =6abxz 3-10bx 4y , F z =18abxyz 2 (b)F =F x (x)i +F y (y)j +F z (z)k3(5分)、保守力的基本特性为:、保守力的基本特性为:4(2分)、画出下列图的瞬心、画出下列图的瞬心5(2分)、画出下列图的虚位移、画出下列图的虚位移得分得分 评卷人评卷人 得分得分 评卷人评卷人6(5分)、怎样求质心的位置?内力是否能改变质心的运动状态?三、计算题1(10分).质量为m 的小球以初速v 0竖直上抛,空气的阻力R=kmv 2 求:(1)上升的最大高度;)上升的最大高度;2)返回到地面时小球的速度。
)返回到地面时小球的速度。
2(15).如图所示,无重杆OA 和AB 以光滑铰链相连,O 端为固定铰链,杆长OA = a , A B AB =b 今在A 点作用一铅垂向下的力P ,在自由端作用一水平力F , 在AB 杆上作用一矩为作用一矩为 M 的力偶.当系统在铅垂平面内处于平衡时当系统在铅垂平面内处于平衡时 , 求对应于广义坐标的广义力. 得分得分 评卷人评卷人得分得分 评卷人评卷人3(15).椭圆规尺AB 的两端点分别沿相互垂直的直线槽Ox 及Oy 滑动,已知B 端以匀速u 运动。
河南科技大学各专业历年考研试题

河南科技大学2012年硕士研究生入学考试试题考试科目代码:805考试科目名称:机械制造技术基础(如无特殊注明,所有答案必须写在答题纸上,否则以“0”分计算)一.单项选择题(在每小题的四个备选答案中选出一个正确的答案,并将其代码写在答题纸上,错选或未选均无分。
每小题1分,共15分)1.在加工表面、切削刀具以及切削速度和进给量都不变的情况下所连续完成的那部分工艺过程,称为()。
A、工位B、工序C、工步D、走刀2.在正交平面内测量的角度是()。
A、主偏角B、刃倾角C、前角D、副偏角3.适宜于粗加工碳钢及合金钢的刀具材料是()。
A、YT5B、YG6C、金刚石D、YG84.在下列要素中,对切削温度影响最大的是()。
A、切削速度B、进给量C、切削深度D、切削层厚度5.中小批生产中加工7级中小孔径常用的方法是()。
A、钻-扩B、钻-扩-铰C、钻-精镗D、钻-拉削6.加工9级齿轮的方法一般选用()。
A、铣齿B、插齿C、剃齿D、磨齿7.在车床上车削长轴时使用反三爪和右顶尖组合定位,相当于()支承点。
A、6个B、5个C、4个D、3个8.各种零件在全部加工完毕后,应安排()工序。
A、抛光B、磁力探伤C、密封性试验D、检验9.在零件的粗加工阶段和半精加工阶段之间安排的热处理工序是()。
A、淬火B、回火C、调质D、渗碳10.适合于大批生产时用钻头钻孔的钻套是()A、固定钻套B、可换钻套C、快换钻套D、特殊钻套11.大批生产中,对于组成环数多而装配精度要求高的产品,应采用()A、互换法B、选配法C、修配法D、调整法12.当某些加工表面的位置精度要求很高时,选择精基准时应遵循()原则。
A、基准重合B、基准统一C、互为基准D、自为基准13.车削时刀具上与工件加工表面相对的表面是指车刀的( )。
A、前刀面B、主后刀面C、副后刀面D、基面14.毛坯制造误差属于()。
A、常值系统误差B、变值系统误差C、系统动误差D、随机误差15.下述支承中不起定位作用的支承是()A、固定支承B、可调支承C、辅助支承D、浮动支承二、判断题(对下述说法中正确的,请在答题纸上对应的题号后划“√”,错误的划“×”,每小题1分,共10分)1.在机床上加工零件时,主运动都是回转运动。
2011年硕士生入学考试试题(理论力学)

一、问答题(共60分)1.“悬挂的小球能够静止不动是因为小球对绳向下的拉力和绳对小球向上的拉力互相抵消的缘故”。
这种说法对不对?为什么?(10分)2. 平面任意力系简化的最终结果有几种可能?每种可能结果对原力系说明了什么?(10分)3.确定动点相对于参考体位置的常用方法有哪几种?(列出三种以上方法)(10分)4.在运用点的速度合成定理及动系作平动时点的加速度合成定理解题时,用几何法与解析法那一种较为简捷?(10分)5.如图所示的平面机构中,AC//BD,且a=,均质杆ABBDAC=质量为m,长为l。
问杆AB作何种运动?其惯性力系的简化结果是什么?若杆AB是非均质杆又其惯性力系的简化结果如何?(10分)6.在光滑水平面上放置一静止均质圆盘,当它受到一个力偶作用时,盘心将如何运动?盘心的运动与力偶的作用位置有关吗?如果圆盘面内受一个大小和方向都不变的力的作用,盘心将如何运动?盘心的运动情况与力的作用点位置有关吗?(10分)二、计算题(15分)如图所示的水平简支横梁AB ,A 端为固定铰链支座,B 端为滚动支座。
梁的长为a 4,梁重P ,作用在梁的中点C 。
在梁的AC 段上受均布载荷q 作用,在梁的BC 段上受力偶作用,力偶矩Pa M =。
试求A 和B 处的支座约束力。
三、计算题(15分)在平面机构中,各杆重力不计,物块B 重力的大小N P 100=,与铅垂面间的静摩擦因数1.0=s f ,mm OA 200=,杆OA 受力偶作用,B A O 、、处为光滑铰链。
杆AB 处于水平位置时系统平衡。
试求力偶矩M 的最小值。
2a4a四、计算题(10分)曲柄OA 在图示瞬时以0ω绕轴O 转动,并带动直角曲杆BC O 1在图示平面内运动。
l 已知、︒=45θ,且BC 恰好处于水平位置,试求曲杆BC O 1的角速度。
五.计算题(20分)平面机构如图所示。
已知:cm AB OA 20==,半径cm r 5=的圆轮可沿铅垂面作纯滚动。
理论力学期末考试试卷(含答案)B
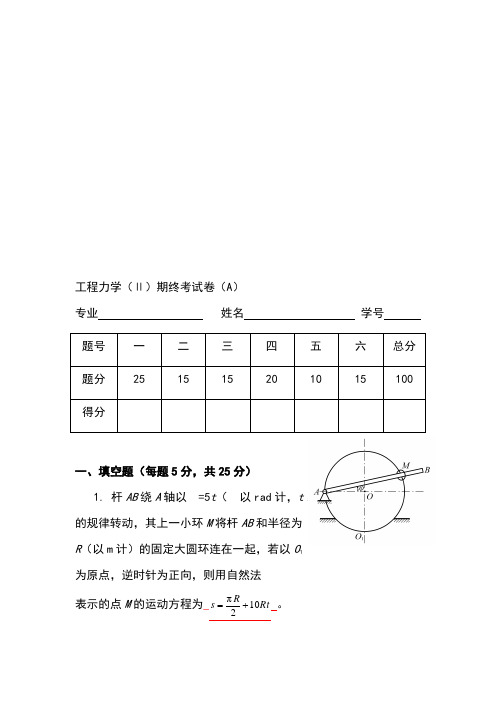
工程力学(Ⅱ)期终考试卷(A )专业 姓名 学号 题号 一 二 三 四 五 六 总分 题分 25 15 15 20 10 15 100 得分一、填空题(每题5分,共25分)1. 杆AB 绕A 轴以=5t (以rad 计,t 以s 计)的规律转动,其上一小环M 将杆AB 和半径为R (以m 计)的固定大圆环连在一起,若以O 1为原点,逆时针为正向,则用自然法 表示的点M 的运动方程为_Rt Rs 102π+=。
2. 平面机构如图所示。
已知AB //O 1O 2,且AB =O 1O 2=L ,AO 1=BO 2=r ,ABCD 是矩形板, AD =BC =b ,AO 1杆以匀角速度绕O 1轴转动,则矩形板重心C '点的速度和加速度的大小分别 为v =_ r_,a =_ r。
并在图上标出它们的方向。
3. 两全同的三棱柱,倾角为,静止地置于 光滑的水平地面上,将质量相等的圆盘与滑块分 别置于两三棱柱斜面上的A 处,皆从静止释放, 且圆盘为纯滚动,都由三棱柱的A 处运动到B 处, 则此两种情况下两个三棱柱的水平位移 ___相等;_____(填写相等或不相等), 因为_两个系统在水平方向质心位置守恒 。
4. 已知偏心轮为均质圆盘,质心在C 点,质量 为m ,半径为R ,偏心距2ROC =。
转动的角速度为,角加速度为,若将惯性力系向O 点简化,则惯性力系的主矢为_____ me ,me2;____;惯性力系的主矩为__2)2(22αe R m +__。
各矢量应在图中标出。
5.质量为m 的物块,用二根刚性系数分别为k 1和k 2 的弹簧连接,不计阻尼,则系统的固有频率为_______________,若物体受到干扰力F =H sin (ωt ) 的作用,则系统受迫振动的频率为______________ 在____________条件下,系统将发生共振。
二、计算题(本题15分)图示平面机构中,杆O 1A 绕O 1轴转动,设O 2B = L ,在图示= 30°位置时,杆O 1A 的角速度为,角加速度为零。
河南科技大学考研真题答案
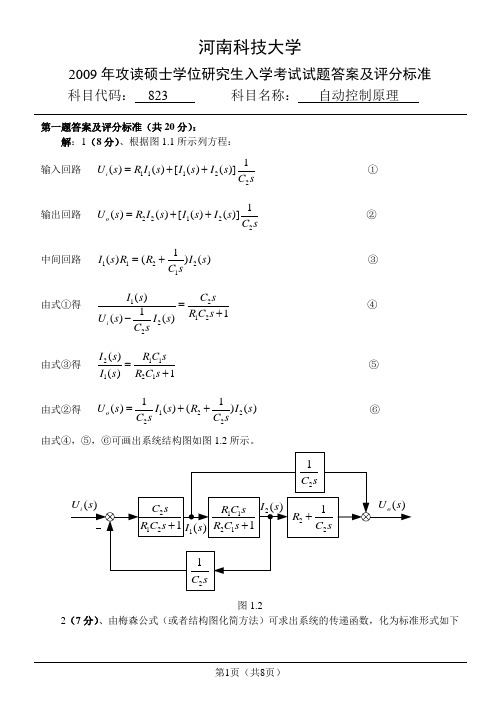
河南科技大学2009年攻读硕士学位研究生入学考试试题答案及评分标准 科目代码: 823 科目名称: 自动控制原理第一题答案及评分标准(共20分):解:1(8分)、根据图1.1所示列方程: 输入回路 111221()()[()()]i U s R I s I s I s C s=++ ① 输出回路 221221()()[()()]o U s R I s I s I s C s=++ ② 中间回路 112211()(()I s R R I s C s=+③ 由式①得121222()11()()i I s C sR C s U s I s C s =+- ④由式③得211121()()1I s R C sI s R C s =+ ⑤ 由式②得 1222211()()(()o U s I s R I s C s C s=++ ⑥ 由式④,⑤,⑥可画出系统结构图如图1.2所示。
图1.22(7分)、由梅森公式(或者结构图化简方法)可求出系统的传递函数,化为标准形式如下2121212121212112112()()1()()1o i U s R R C C s R R C s U s R R C C s R C R C R C s +++=++++ 3(5分)、讨论:从系统的传递函数可以看出,元件1R 、2R 、1C 、2C 参数均为大于零的常数,系统特征多项式是二阶的,并且系统特征多项式系数总大于零,因此,无论1R 、2R 、1C 、2C 怎样取值,均不影响RC 网络的稳定性。
第二题答案及评分标准(共20分):解:由题意,系统的开环传递函数为(2)()()()(2)1(2)KK s s G s H s G s K s s aK as s s +===+++⨯+系统的闭环传递函数为2()()1()(2)G s Ks G s s aK s KΦ==++++。
1(5分)、当0a =,8K =时,代入可得28()28s s s Φ=++,可得:2n 8ω=,n 2.828rad/s ω=≈,n 22ςω=,0.3536ς=≈,0lim ()()4v s K sG s H s →==,()r t t=作用下系统的稳态误差10.25ss ve K ==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、(20分)图示平面机构,直角三角板ABC与曲柄OA和O1B铰接,OA=O1B= r =15cm,O1O=AB=30cm,AC=10cm。当曲柄OA转动时,通过三角板带动顶杆DE沿导轨作铅垂运动,在图示瞬时OA杆铅直,AB水平,曲柄OA的角速度ω=2rad/s,角加速度α=3rad/s2,均为逆时针转向,试求该瞬时顶杆DE的速度和加速度。
四、(40分) 1.平面机构如图所示。等边三角形ABE分别以铰链与滑块A及两杆连接。已知:三角板边长为l,O1B=O2E=l。在图示位置时,θ=60º。OA=AD=l,且A、E、O2三点恰处水平。O1B杆处于铅直,角速度为ω1,OD杆的质量为m。试求该瞬时:⑴OD杆的动量;⑵OD杆对O轴的动量矩。
2.如图所示的均质杆AB质量为m,长为l,在A端铰接质量也为m的滑块,今均质杆AB静止在铅直上方,受微小干扰后,无初速地自由倒下,不计滑块与滑槽的摩擦,求AB达到水平位置时,滑块A移动的距离,并画在图上。
五、(20分)图示均质圆盘和滑块质量均为m,圆盘的半径为r。杆AB平行于斜面,质量不计。斜面的倾斜角为θ,滑块与斜面间的动摩擦系数为f,设圆盘和滑块自静止开始运动,圆盘在斜面上只滚动不滑动。求系统由静止开始沿斜面运动s距离时滑块的速度和加速度。
六、(20分)图示摆由半径为r、质量为m的均质圆盘和质量也为m,长为L=2r的均质杆焊接而成,O处为光滑铰Байду номын сангаас支座,B处用绳索将摆悬挂于水平位置,摆处于静止;试用动静法求突然剪断绳索BD的瞬时:⑴摆的角加速度;⑵O处的动反力。
三、(25分)图示平面机构中,半径为R的圆轮在水平直线轨道上作纯滚动。AB杆的A端与圆轮边缘铰接,B端与OB杆铰接。图示瞬时OB杆铅直,AB杆与水平线间夹角θ=45º,轮心C的速度为VC,加速度为aC,方向如图所示。已知:R=0.1m,VC=1m/s,aC=2m/s2;试求该瞬时OB杆的角速度和角加速度。
