2019中考数学复习课件第二章第四节一元一次不等式(组)(33张)
云南省2019年中考数学总复习第二章方程组与不等式组第四节一元一次不等式组课件

h
7
命题角度❷ 求不等式组的特殊解
例3(2018·天津改编)解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得
;
(2)解不等式②,得
;
h
8
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为
.
(5)该不等式组的非负整数解是
.
h
9
【自主解答】 解:(1)x≥-2; (2)x≤1; (3)
解集的口诀:同大取大,同小取小;大小小大中间找,大大
小小找不到,确定解集,在数轴上表示解集时,要注意数轴
空心圆圈与实心圆点的区别以及开口的方向.
h
5
1.解不等式组: 出来.
并把解集在数轴上表示
h
6
解:解不等式-2x<6得x>-3; 解不等式3(x-2)≤x-4得x≤1; ∴不等式组的解集为-3<x≤1. 解集在数轴上表示如解图所示.
当m=9时,总费用为9×130+1×100=1 270(元);
当m=10时,总费用为10×130=1 300(元).
∴当安排大货车8辆,小货车2辆时费用最省,最小费用为
1 240元.
h
26
提醒:
列不等式解应用题的“三点注意”
(1)在设未知数和写答案时,一定要写清单位,列不等式
时两边所表示的量应相同,并且单位要统一.
(4)-2≤x≤1. (5)0,1.
h
10
总结:
确定不等式组整数解的要点
确定不等式组的整数解,可先解不等式组求出解集,再
确定解集中整数的个数,注意解集两端是否包含,两端均为
整数时,若为“>或<”,则不包含;若为“≥或≤”,则
中考数学总复习课件:一元一次不等式(组)(共26张PPT)

★知识点2 ★考点2
★知识点3 ★考点3
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3★知识要点导航 ★热点分类析★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/72021/9/72021/9/72021/9/79/7/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月7日星期二2021/9/72021/9/72021/9/7 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/72021/9/72021/9/79/7/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/72021/9/7September 7, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/72021/9/72021/9/72021/9/7
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
人教版中考数学考点系统复习 第二章 方程(组)与不等式(组) 第四节 一元一次不等式(组)及其应用

有 3 个整数解,则 a 的取值范围为
( A)
A.1<a≤2
B.1<a<2
C.1≤a<2
D.1≤a≤2
6 . (2019 · 鄂 州 第 12 题 3 分 ) 若 关 于 x , y 的 二 元 一 次 方 程 组
x-3y=4m+3,
x+5y=5
的解满足 x+y≤0,则 m
的取值范围是__mm≤≤--22__.
③学校购买篮球和足球共 40 个.
(1)
若④购买篮球的个数不少于足球个数的23,则最少可购买篮球
116 6
个;
【分层分析】(1)设购买篮球 x 个,则由题干③可得购买足球((440 0--x)
个,由题干④可列不等式为
2 xx≥≥3((4400--xx)),解此不等式得
x) xx≥≥1166.
(2)若⑤购买篮球的费用不超过购买足球的费用,则最多可购买篮球115
(2)若此不等式组的解集为-4≤x<1,则 a 的值为--22; 【分层分析】(2)由题意得1a.-25168=0--m4 m,即 a=--22;
重难点 2:一元一次不等式的应用
(一题多设问)某校为举行体育比赛活动,准备购买若干个足球和篮
球作为奖品,已知①篮球的单价为 100 元/个,②足球的单价为 60 元/个,
第四节 一元一次不等式 (组)及其应用
【考情分析】湖北近 3 年主要考查:1.一元一次不等式(组)的解法及解集 表示,考查形式有:①求不等式(组)的解集;②求不等式(组)的解集并在 数轴上表示;③求不等式组的整数解;④确定不等式组中字母参数的取 值范围.2.一元一次不等式的应用,考查形式有:①利用不等式判断哪种 方案合算;②与方程(组)、函数结合确定方案问题,设题背景有购买问题、 销售费用问题,以解答题为主
2019年中考数学全国通用复习讲义§2.4 一元一次不等式(组)(讲解部分)

(5 分)
(4 分)
(Hale Waihona Puke 分)㊀ ㊀ 用转化思想将实际问题中的不等关系抽象出来, 用不等式 ( 组) 的知识解答应用题和方案设计型问题. 例 2㊀ ( 2017 四川绵阳,21,11 分) 江南农场收割小麦, 已知
方法二㊀ 一元一次不等式( 组) 的应用
(4)1ɤxɤ3.
1 台大型收割机和 3 台小型收割机 1 小时可以收割小麦 1. 4 公
是大于等于或小于等于,那么这个点一定是实心点; 如果是大于 ㊀ ㊀ 变式训练 1㊀ 3x -5<-2x,① 组: 3x +2 ȡ1. ㊀ ② 2 由②得 xȡ0, 或小于,那么这个点应用空心圈表示. ( 2017 湖 北 黄 冈, 15, 5 分 ) 解 不 等 式
易错警示㊀ 在数轴上表示不等式的解集时, 要注意如果
考点三㊀ 一元一次不等式( 组) 的应用
的两边乘( 或除以) 同一个负数时,不等号的方向改变.
(1) 审:认真审题,分清已知量, 未知量及其关系, 找出题中 小于
不大
㊀ ㊀ 1. 定义:类似于方程组,把几个含有相同未知数的 ⑨㊀ 一元一 次不等式㊀ 合起来,就组成了一个一元一次不等式组. 这几个不等式所组成的不等式组的解集.
11 ㊀
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
4. 由两个一元一次不等式组成的不等式组的解集的四种情
中考数学一轮复习 第二章 方程与不等式 第四节 一元一次不等式(组)课件

No 出规范结果,并。表示在数轴上如D选项所示.故选D.。求不等式组的解集,应遵循以下原则:同大取较大,
同小。取较小,小大大小中间找,大大小小(dà dà xiǎo xiǎo)解不了.。一商场抓住商机,从厂家购进了A, B两种型号家用净水器。运用不等式解决实际问题时,关键是分析问题中的数量关。答:最多购买B型学习 用品800件.
2.一元一次不等式组的解法
(1)解一元一次不等式组的一般步骤(bùzhòu):先求出这个不等式组
中每个一元一次不等式的解集,然后求出不等式解集的公共 部分,得出不等式组的解集.
2021/12/8
第七页,共二十九页。
(2)常见(chánɡ jiàn)的几种不等式组解集的表示(其中a>b):
2021/12/8
2021/12/8
第二十二页,共二十九页。
(2)设每台A型号家用净水器的毛利润是a元,则每台B型号
家用净水器的毛利润是2a元, 由题意(tíyì)得100a+60×2a≥11 000,解得a≥50, 150+50=200(元).
答:每台A型号家用净水器的售价至少是200元.
2021/12/8
第二十三页,共二十九页。
2021/12/8
第二十七页,共二十九页。
(2)设可以购买(gòumǎi)B型学习用品a件,则A型学习用品
(1 000-a)件, 由题意得20(1 000-a)+30a≤28 000,
解得a≤800.
答:最多购买B型学习用品800件.
2021/12/8
第二十八页,共二十九页。
内容(nèiróng)总结
2019年中考数学一轮复习讲义第二章第四节 一元一次不等式(组)
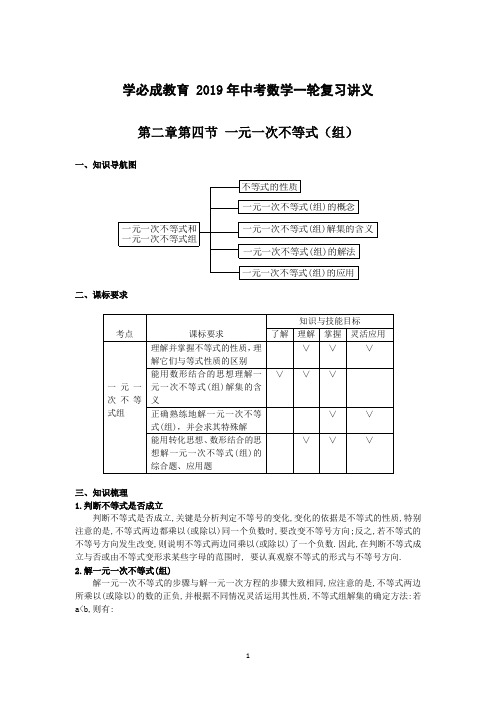
学必成教育 2019年中考数学一轮复习讲义 第二章第四节 一元一次不等式(组)一、知识导航图一元一次不等式(组)的应用一元一次不等式(组)的解法一元一次不等式(组)解集的含义一元一次不等式(组)的概念不等式的性质一元一次不等式和一元一次不等式组二、课标要求三、知识梳理1.判断不等式是否成立判断不等式是否成立,关键是分析判定不等号的变化,变化的依据是不等式的性质,特别注意的是,不等式两边都乘以(或除以)同一个负数时,要改变不等号方向;反之,若不等式的不等号方向发生改变,则说明不等式两边同乘以(或除以)了一个负数.因此,在判断不等式成立与否或由不等式变形求某些字母的范围时, 要认真观察不等式的形式与不等号方向. 2.解一元一次不等式(组)解一元一次不等式的步骤与解一元一次方程的步骤大致相同,应注意的是,不等式两边所乘以(或除以)的数的正负,并根据不同情况灵活运用其性质,不等式组解集的确定方法:若a<b,则有:(1)0a b <⎧⎨<⎩ 的解集是x<a,即“小小取小”.(2)00a b >⎧⎨>⎩的解集是x>b,即“大大取大”. (3) 00a b >⎧⎨<⎩的解集是a<x<b,即“大小小大取中间”.(4)0a b <⎧⎨>⎩ 的解集是空集,即“大大小小取不了”.一元一次不等式(组)常与分式、根式、一元二次方程、函数等知识相联系,解决综合性问题。
3.求不等式(组)的特殊解不等式(组)的解往往是有无数多个,但其特殊解在某些范围内是有限的,如整数解、非负整数解,要求这些特殊解,首先是确定不等式(组)的解集, 然后再找到相应的答案.注意应用数形结合思想.4.列不等式(组)解应用题注意分析题目中的不等量关系,考查的热点是与实际生活密切相联的不等式(组)应用题.四、题型例析1.判断不等式是否成立例12.在数轴上表示不等式的解集例2 3.求字母的取值范围例3 4.解不等式组例45.列不等式(组)解应用题例5一元一次不等式(组)【课前热身】 【知识点链接】1.不等式的有关概念:用 连接起来的式子叫不等式;使不等式成立的 的值叫做不等式的解;一个含有 的不等式的解的 叫做不等式的解集.求一个不等式的 的过程或证明不等式无解的过程叫做解不等式. 2.不等式的基本性质:(1)若a <b ,则a +c c b +;(2)若a >b ,c >0则ac bc (或c a c b ); (3)若a >b ,c <0则ac bc (或c a cb).3.一元一次不等式:只含有 未知数,且未知数的次数是 且系数 的不等式,称为一元一次不等式;一元一次不等式的一般形式为 或ax b <;解一元一次不等式的一般步骤:去分母、 、移项、 、系数化为1. 4.一元一次不等式组:几个 合在一起就组成一个一元一次不等式组. 一般地,几个不等式的解集的 ,叫做由它们组成的不等式组的解集. 5.由两个一元一次不等式组成的不等式组的解集有四种情况:(已知a b <)x a x b <⎧⎨<⎩的解集是x a <,即“小小取小”;x ax b>⎧⎨>⎩的解集是x b >,即“大大取大”;x ax b >⎧⎨<⎩的解集是a x b <<,即“大小小大中间找”;x ax b<⎧⎨>⎩的解集是空集,即“大大小小取不了”. 6.易错知识辨析:(1)不等式的解集用数轴来表示时,注意“空心圆圈”和“实心点”的不同含义. (2)解字母系数的不等式时要讨论字母系数的正、负情况. 如不等式ax b >(或ax b <)(0a ≠)的形式的解集: 当0a >时,b x a >(或bx a <) 当0a <时,b x a <(或bx a >)当0a <时,b x a <(或bx a>)一元一次不等式(组)及其应用【知识点链接】1.求不等式(组)的特殊解:不等式(组)的解往往有无数多个,但其特殊解在某些范围内是有限的,如整数解,非负整数解,求这些特殊解应先确定不等式(组)的解集,然后再找到相应答案. 2.列不等式(组)解应用题的一般步骤:①审:审题,分析题中已知什么、求什么,明确各数量之间的关系;②找:找出能够表示应用题全部含义的一个不等关系;③设:设未知数(一般求什么,就设什么为x ;④列:根据这个不等关系列出需要的代数式,从而列出不等式(组);⑤解:解所列出的不等式(组),写出未知数的值或范围;⑥答:检验所求解是否符合题意,写出答案(包括单位).3.易错知识辨析:判断不等式是否成立,关键是分析不等号的变化,其根据是不等式的性质. 类型一:不等式性质1(2009柳州)3.若b a <,则下列各式中一定成立的是( )A .11-<-b aB .33b a >C . b a -<-D . bc ac < 2(2009宜昌)如果ab <0,那么下列判断正确的是( ).A .a <0,b <0B . a >0,b >0C . a ≥0,b ≤0 D. a <0,b >0或a >0,b <0 3(2008肇庆)下列式子正确的是( )A .>0 B .≥0 C .a+1>1 D .a ―1>14(2008黄石)若,则的大小关系为( ) A . B . C . D .不能确定 5 (2008恩施)如果a<b<0,下列不等式中错误..的是( ) A. ab >0 B. a+b<0 C.<1 D. a-b<06(2009临沂)若x y >,则下列式子错误的是( ) A .33x y ->- B .33x y ->- C .32x y +>+D .33x y> 类型二:比较大小1(2009牡丹江)若01x <<,则21x x x,,的大小关系是( )A .21x x x << B .21x x x << C .21x x x << D .21x x x<< 2(2008盐城)实数在数轴上对应的点如图所示,则,,的大小关系正确的是( )A .B .C .D .3(2008永州) 如图,a 、b 、c 分别表示苹果、梨、桃子的质量.同类水果质量相等,则下列关系正确的是( )A .a >c >bB .b >a >cC .a >b >cD .c >a >b类型四:解一元一次不等式 1(2008沈阳)不等式的解集为 . 2(2008宜昌)解不等式:2(x +)-1≤-x +9类型1:不等式中字母的取值范围1(2009泸州)关于x 的方程x kx 21=-的解为正实数,则k 的取值范围是 2(2009厦门)已知2ab =.(1)若3-≤b ≤1-,则a 的取值范围是____________.(2)若0b >,且225a b +=,则a b +=____________.A 、0B 、2C 、-2D 、-44(2007天门)关于x 的不等式2x -a ≤-1的解集如图2所示, 则a 的取值是( )。
第二章 一元一次不等式与一元一次不等式组复习 课件(共23张PPT)

不等式的两边都乘(或都除以)同一个正数,所得的
不等式仍成立;
a>b,且c>0 => ac>bc, a b
cc
不等式的两边都乘(或都除以)同一个负数,必须
改变不等号的方向,所得的不等式成立;
a>b,且c>0 => ac<bc, a < b
cc
【练习】
• -5 -4 -3 -2 -1 0 1 2 3 4 5 • -5 -4 -3 -2 -1 0 1 2 3 4 5
x<-2 x≥0 -3<x≤2
a≤x<b
不等式的传递性.
a b,b c a c 推出
不等式的两边都加上(或减去)同一个数,所得到 的不等式仍成立.
a>b => a+c>b+c , a-c>b-c;
-2 -1 0 1 2
× x 1
x 1 1<x< -1
-2 -1 0 1 2
无解
大大取大 小小取小
一大一小夹中间
1.若不等式组
x 2 x a
的解为
x<-2 ,则下列各式正确的是 ( D )
(A) a = -2
(B) a<-2
(C) a ≤ -2
(D) a≥-2
2. 若a x 3有解,则a的范围是 _a_<__3 3. 若a x 3无解,则a的范围是 _a_≥__3
解:设导火索长度为x米,则
3 x 100 0.015
解得 x≥0.5 答:导火索的长度至少取0.5米。
本利和=本金+利息 =本金+本金×利率×期数
某企业向银行贷款1000万元,一年后归还银行贷款的 本利和超过1040万元,问年利率在怎样的一个范围 内?
中考第一轮复习第四讲一元一次不等式PPT共33页

6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
END
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B.在不等式a+c>b+c的两边同时减去c,不等式仍成立,
即a>b,不符合题意;
C.当c=0时,若a>b,则不等式ac2>bc2不成立,符合题 意; D.在不等式ac2>bc2的两边同时除以不为0的c2,该不等式
仍成立,即a>b,不符合题意.
故选C.
在应用不等式的性质时,要注意何时“变号”,何时“不变 号”.同时,注意“特殊值法”的应用,往往会起到事半功
A.4<a<6 C.4<a≤6 B.4≤a<6 D.2<a≤4 C
)
8.(2017·泰安中考)不等式组 x<2,则k的取值范围为( ) C B.k<1 D.k≤1
的解集为
A.k>1
C.k≥1
考点四 一元一次不等式(组)的应用
(5年4考)
例5 (2015·潍坊中考)为提高饮水质量,越来越多的居民选 购家用净水器.一商场抓住商机,从厂家购进了A,B两种型
号的家用净水器共160台,A型号家用净水器进价是150元/台,
B型号家用净水器进价是350元/台,购进两种型号的家用净水 器共用去36000元.
(1)求A,B两种型号家用净水器各购进了多少台; (2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保 证售完这160台家用净水器的毛利润不低于11000元,求每
(2)设每台A型号家用净水器的毛利润是a元,则每台B型号家 用净水器的毛利润是2a元. 由题意得100a+60×2a≥11 000,
解得a≥50,
150+50=200(元). 答:每台A型号家用净水器的售价至少是200元.
运用不等式解决实际问题时,关键是分析问题中的数量关系, 要注意抓住问题中的关键字,如“至少”“不低于”“不超
第四节 一元一次不等式(组)
考点一 不等式的性质
(5年0考) ) B.若a+c>b+c,则a>b
例1 下列说法不一定成立的是( A.若a>b,则a+c>b+c
C.若a>b,则ac2>bc2
D.若ac2>bc2,则a>b
【分析】 根据不等式的性质进行判断. 【自主解答】 A.在不等式a>b的两边同时加上c,不等式 仍成立,即a+c>b+c,不符合题意;
并写出正确的解答过程即可.
【自主解答】 错误的是①②⑤,正确解答过程如下:
去分母得3(1+x)-2(2x+1)≤6,
去括号得3+3x-4x-2≤6, 移项得3x-4x≤6-3+2, 合并同类项得-x≤5,
两边都除以-1得x≥-5.
解一元一次不等式的易错点 解一元一次不等式并用数轴表示解集时,最易出错的有以下 三点:
10.(2018·寿光模拟)冬天来临,某商场计划购进甲、乙两 种手套,已知一件甲种手套的进价与一件乙种手套的进价的 和为40元,用90元购进甲种手套的件数与用150元购进乙种
手套的件数相同.
(1)求每件甲种、乙种手套的进价分别是多少元?
(2)商场计划购进甲、乙两种手套共48件,其中甲种手套的 件数少于乙种手套的件数,商场决定此次进货的总资金不超 过1000元,求商场共有几种进货方案?
(1)去分母时常数项漏乘;
(2)两边同乘负数时,不等号方向忘记改变; (3)用数轴表示解集时,忽略“实心圆点”与“空心圆圈” 的区别.
3.(2018·衢州中考)不等式3x+2≥5的解集是( A ) A.x≥1 B.x≥ 7 C.x≤1 D.x≤-1 4.(2018·南充中考 3 )不等式x+1≥2x-1的解集在数轴上表
∵y是整数,∴y取20,21,22,23,
答:商场共有4种进货方案.
1392578086@ https:/// /
倍的作用.
1.(2018·广西中考)若m>n,则下列不等式正确的是( A.m-2<n-2 C.6m<6n B. D.-8m>-8n
B
)
2.(2018·宿迁中考)若a<b,则下列结论不一定成立的是
( ) B.2a<2b C. D.a2 <b2
A.a-1<b-1 D
考点二 一元一次不等式的解法
(5年0考)
解:(1)设甲种手套进价x元/件,则乙种手套进价为(40-x) 元/件. 由题意得=
解得x=15.
经检验,x=15是原方程的解,且符合题意, ∴40-x=25. 答:甲、乙两种手套的进价分别是15元/件、25元/件.
(2)设购进甲种手套y件,则购进乙种手套(48-y)件. 由题意得 解得20≤y<24.
例2 (2017·嘉兴中考)小明解不等式-≤1的过程如图.请指 出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母得3(1+x)-2(2x+1)≤1,①
去括号得3+3x-4x+1≤1,② 移项得3x-4x≤1-3-1,③
合并同类项得-x≤-3,④ 两边都除以-1得x≤3,⑤ 【分析】 根据一元一次不等式的解法,找出错误的步骤,
台A型号家用净水器的售价至少是多少元.(注:毛利润=售
价-进价)
【分析】 (1)设A种型号家用净水器购进了x台,B种型号家用 净水器购进了y台,根据“购进了A,B两种型号家用净水器共 160台”“购进两种型号的家用净水器共用去 36000元”列
出方程组解答即可;(2)设每台A型号家用净水器的毛利润是a
元,则每台B型号家用净水器的毛利润是2a元,根据保证售完 这160台家用净水器的毛利润不低于11000元,列出不等式解 答即可.
【自主解答】 (1)设A种型号家用净水器购进了x台,B种型 号家用净水器购进了y台. 由题意得 解得 答:A种型号家用净水器购进了100台,B种型号家用净水器
购进了60台.
解不等式-3x+9≥0得x≤3,
∴不等式组的解集为- <x≤3,
1 2
;
∴不等式组的整数解为0,1,2,3,∴0+1+2+3=6.故选 D.
1 2
5.(2018·滨州中考)把不等式组 式的解集在同一条数轴上表示出来,正确的为(
中每个不等 ) B
6.(2018·青岛中考)解不等式组: 解:解不等式<1得x<5, 解不等式2x+16>14得x>-1,
示为(
B
)
考点三 一元一次不等式组的解法 命题角度❶ 解一元一次不等式组
(5年3考)
例3 (2015·潍坊中考)不等式组的所有整数解的和是( A.2 B .3 C.5 D .6
)
【分析】 先求出不等式组的解集,再求出不等式组的整数 解,最后求出答案即可. 【自主解答】 解不等式2x>-1得x>-
解1-2x>x-2得x<1.
∵不等式组无解,∴-a≥1,解得a≤-1.故选D.
若不等式(组)中含有待定字母,则可根据不等式(组)的解集
ቤተ መጻሕፍቲ ባይዱ
情况或整数解的个数确定待定字母的取值.解决此问题时,
应把待定字母看作已知数,并结合数轴.
7.(2018·高密二模)关于x的不等式组
的整
数解有4个,那么a的取值范围是(
过”“不少于”等,找出不等关系,从而列出不等式求解.
9.(2018·山西中考)2018年国内航空公司规定:旅客乘机 时,免费携带行李箱的长、宽、高三者之和不超过115 cm. 某厂家生产符合该规定的行李箱.已知行李箱的宽为 20 cm,
长与高的比为8∶11,则符合此规定的行李箱的高的最大值为
_____cm. 55
则不等式组的解集为-1<x<5.
命题角度❷
由解集求字母系数的值或范围 无解,则
例4 (2014·潍坊中考)若不等式组 实数a的取值范围是( A.a≥-1 C.a≤1 ) B.a<-1 D.a≤-1
【分析】 分别求出各不等式的解集,再与已知不等式组无 解相比较即可得出a的取值范围. 【自主解答】 解x+a≥0得x≥-a;
